Содержание
Как решать уравнения с дробями. Показательное решение уравнений с дробями.
Решение уравнений с дробями рассмотрим на примерах. Примеры простые и показательные. С их помощью вы наиболее понятным образом сможете усвоить, как решать уравнения с дробями.
Например, требуется решить простое уравнение x/b + c = d.
Уравнения такого типа называется линейным, т.к. в знаменателе находятся только числа.
Решение выполняется путем умножения обоих частей уравнения на b, тогда уравнение принимает вид x = b*(d – c), т.е. знаменатель дроби в левой части сокращается.
Например, как решить дробное уравнение:
x/5+4=9
Умножаем обе части на 5. Получаем:
х+20=45
x=45-20=25
Другой пример, когда неизвестное находится в знаменателе:
b/x + c = d
Уравнения такого типа называются дробно-рациональными или просто дробными.
Решать дробное уравнение бы будем путем избавления от дробей, после чего это уравнение, чаще всего, превращается в линейное или квадратное, которое решается обычным способом. Следует только учесть следующие моменты:
Следует только учесть следующие моменты:
- значение переменной, обращающее в 0 знаменатель, корнем быть не может;
- нельзя делить или умножать уравнение на выражение =0.
Здесь вступает в силу такое понятие, как область допустимых значений (ОДЗ) – это такие значения корней уравнения, при которых уравнение имеет смысл.
Таким образом решая уравнение, необходимо найти корни, после чего проверить их на соответствие ОДЗ. Те корни, которые не соответствуют нашей ОДЗ, из ответа исключаются.
Например, требуется решить дробное уравнение:
1/x + 2 = 5
Исходя из вышеуказанного правила х не может быть = 0, т.е. ОДЗ в данном случае: х – любое значение, отличное от нуля.
Избавляемся от знаменателя путем умножения всех членов уравнения на х
1 + 2x = 5х
И решаем обычное уравнение
5x – 2х = 1
3x = 1
х = 1/3
Ответ: х = 1/3
Решим уравнение посложнее:
Здесь также присутствует ОДЗ: х -2.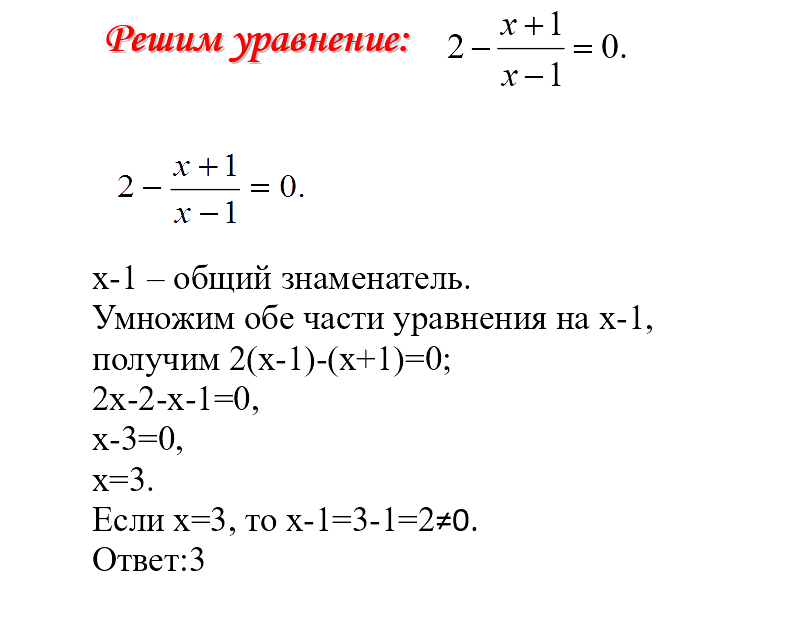
Решая это уравнение, мы не станем переносить все в одну сторону и приводить дроби к общему знаменателю. Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.
Для сокращения знаменателей требуется левую часть умножить на х+2, а правую — на 2. Значит, обе части уравнения надо умножать на 2(х+2):
Это самое обычное умножение дробей, которое мы уже рассмотрели выше
Запишем это же уравнение, но несколько по-другому
Левая часть сокращается на (х+2), а правая на 2. После сокращения получаем обычное линейное уравнение:
4 = х + 2
х = 4 – 2 = 2, что соответствует нашей ОДЗ
Ответ: х = 2.
Для закрепления материала рекомендуем еще посмотреть видео.
Решение уравнений с дробями не так сложно, как может показаться. В этой статье мы на примерах это показали. Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в комментариях.
Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в комментариях.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Линейные уравнения с дробями | Алгебра
Линейные уравнения с дробями не содержат переменной в знаменателе. Чтобы решить линейное уравнение с дробями, удобно избавиться от знаменателей.
Для этого нужно найти наименьший общий знаменатель всех входящих в уравнение дробей и обе части уравнения умножить на это число.
Наименьший общий знаменатель данных дробей равен 6. Дополнительный множитель к первой дроби равен 2, ко второй — 3, к 5 — 6. Умножаем обе части уравнения на наименьший общий знаменатель:
В результате наименьший общий знаменатель и знаменатель каждой дроби сокращаются, и получаем линейное уравнение, не содержащее дробей.
Раскроем скобки и приведём подобные слагаемые:
Обе части уравнения делим на число, стоящее перед иксом:
Из полученной неправильной дроби выделяем целую часть
Ответ: -4 6/7.
Наименьший общий знаменатель данных дробей равен 20. Найдем дополнительный множитель к каждой дроби и умножим обе части уравнения на 20:
Можно, конечно, сразу же умножить дополнительный множитель на числитель каждой дроби. Но, к сожалению, наибольшее количество ошибок при решении линейных уравнений с дробями допускается именно на этом шаге. Скобки — друзья ученика :). Поэтому лучше воспользоваться их помощью:
Особенно полезны скобки в случае, когда перед дробью стоит знак «минус».
После раскрытия скобок можно сразу же перенести неизвестные в одну сторону уравнения, известные — в другую (не забыв при переносе изменить их знаки), а можно сначала упростить каждую часть, приведя подобные слагаемые, а потом уже переносить.
Ответ: -34.
Здесь наименьший общий знаменатель дробей равен 12. Находим дополнительный множитель к каждой дроби и умножаем обе части уравнения на 12:
Раскрываем скобки и упрощаем
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: -5.
Уравнения такого вида можно решить, использовать основное свойство пропорции (в верной пропорции произведение крайних членов равно произведению средних членов):
при делении двух отрицательных чисел получается положительное число, поэтому минусы можно сразу же не писать.
Если это возможно, лучше ответ записать в виде десятичной дроби:
Ответ: 0,1875.
Решение уравнений с переменной в знаменателе дроби
$\frac{2x+3}{2x-1}=\frac{x-5}{x+3}$
Решение:
1.Перенесем дробь из правой части уравнения в левую
\[\frac{2x+3}{2x-1}-\frac{x-5}{x+3}=0\]
Для того чтобы правильно это сделать, вспомним, что при перенесении элементов в другую часть уравнения меняется знак перед выражениями на противоположный. Значит, если в правой части перед дробью был знак «+», то в левой перед ней будет знак «-».Тогда в левой части получим разность дробей. 2+11х-5=20х+4$
2+11х-5=20х+4$
Тогда дробь примет вид
\[\frac{{\rm 20х+4}}{(2x-1)(х+3)}=0\]
3.Дробь равна $0$, если ее числитель равен 0. Поэтому мы приравниваем числитель дроби к $0$.
\[{\rm 20х+4=0}\]
Решим линейное уравнение:
$20x=-4$
$X=-0,2$
4.Проведем выборку корней. Это значит, что необходимо проверить, не обращаются ли знаменатели исходных дробей в $0$ при найденных корнях.
Поставим условие, что знаменатели не равны $0$
\[2x-1\ne 0 x+3\ne 0\]
х$\ne 0,5$ х$\ne -3$
Значит допустимы все значения переменных, кроме $-3$ и $0,5$.
Найденный нами корень является допустимым значением, значит его смело можно считать корнем уравнения. Если бы найденный корень был бы не допустимым значением, то такой корень был бы посторонним и ,конечно, не был бы включен в ответ.
Ответ:$-0,2.$
Решение задач с помощью дробных рациональных уравнений 8 класс онлайн-подготовка на Ростелеком Лицей
Решение задач с помощью дробных рациональных уравнений.
Напомним, что рациональные уравнения – это уравнения, у которых левая и правая части являются рациональными выражениями. Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называют дробным.
Очень часто решение задач сводится к решению дробных рациональных уравнений. Решим несколько задач, которые сводятся к решению таких уравнений.
Задача 1. Числитель дроби на 3 меньше её знаменателя. Сумма дроби и обратной ей дроби в 7,25 раза больше исходной дроби. Найти исходную дробь.
Решение: обозначим за хзнаменатель дроби. Тогда (х-3) – числитель этой дроби. Значит, исходная дробь имеет вид х-3х. Так как по условию задачи сумма дробих-3хи обратной ей дробихх-3 в 7,25 раза больше исходной дроби, то можем составить уравнение:
x-3x+xx-3=7,25x-3x
Представим 7,25 в виде неправильной дроби:
x-3x+xx-3=29(x-3)4x
Умножим обе части уравнения на 4x(x-3) при x≠0, x≠3, чтобы избавиться от знаменателей:
4x-3x-3+4×2=29(x-3)(x-3)
4×2-24x+36+4×2=29×2-174x+261
21×2-150x+225=0
D=(-150)2-4∙21∙225=3600
D=60
x1=—150-602∙21=9042=157 не соответствует условию задачи.
x2=—150+602∙21=21042=5
Значит, 5 – знаменатель, 5-3 = 2 – числитель.
Ответ: 25 – исходная дробь.
Задача 2. Велосипедисту надо проехать 30 км. Он выехал на полчаса позже намеченного срока и, чтобы приехать вовремя, увеличил скорость на 2 км/ч. С какой скоростью ехал велосипедист?
Пусть х (км/ч) – скорость велосипедиста. Тогда расстояние в 30 км велосипедист проедет за 30х часов. Если бы велосипедист выехал вовремя, то его скорость была бы равна (х-2) км/ч. И тогда расстояние в 30 км он проехал бы за 30х-2 часов. По условию задачи, велосипедист выехал на 30 минут позже намеченного срока, или, что тоже самое, на 3060=12 часа позже. Составим уравнение:
30x-2-30x=12
Умножим обе части уравнения на 2x(x-2) при x≠0, x≠2, чтобы избавиться от знаменателей:
30∙2x-30∙2x-2=x(x-2)
60x-60x+120=x2-2x
x2-2x-120=0
D=(-2)2-4∙1∙-120=4+480=484
D=484=22
x1=—2-222=-10 не соответствует условию задачи.
x2=—2+222=12
Ответ: 12 км/ч.
Задача 3. Лодка прошла вниз по реке 42 км, а затем 27 км против течения, затратив на весь путь 15 часов. Найти скорость течения реки, если скорость моторной лодки в стоячей воде равна 5 км/ч.
Пусть х (км/ч) – скорость течения реки. Тогда (5+х) км/ч скорость моторной лодки по течению реки и (5-х) км/ч скорость моторной лодки против течения. Известно, что моторная лодка прошла по течению реки 42 км, а значит, затратила на это расстояние 425+х часов. Затем против течения лодка прошла 27 км, затратив на это расстояние 275-х часов. По условию известно, что на весь путь моторная лодка затратила 15 часов. Составим уравнение:
425+x+275-x=15
Умножим обе части уравнения на (5+x)(5-x) при x≠-5, x≠5, чтобы избавиться от знаменателей:
425-x+275+x=15(5+x)(5-x)
210-42x+135+27x=375-15×2
5×2-5x-10=0
x2-x-2=0
По теореме Виета
x1+x2=1×1∙x2=-2
Следовательно, x1=-1; x2=2.
Ответ: 2 км/ч
Решение уравнений с дробями 5 класс
Обыкновенные дроби
часть 3
5 класс
— Сложение дробей с одинаковыми знаменателями.
— Вычитание дробей с одинаковыми знаменателями.
— Решение уравнений.
— Решение задач.
Сложение дробей с одинаковыми знаменателями.
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить прежним.
3
3+1
1
4
=
+
=
8
8
8
8
1
8
3
3+5
5
=
=
+
=
8
8
8
8
Вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
3
3-1
1
2
=
—
=
8
8
8
8
0
3
3
—
=
8
8
Решение уравнений.
При решении уравнений необходимо пользоваться правилами решения уравнений, свойствами сложения и вычитания.
Решение уравнений с применением свойств.
Решение уравнений с использованием правил.
Решите уравнение.
Подсказка 1
Выражение в левой части уравнения является суммой.
51
32
=
;
х
+
85
85
32
51
Подсказка 2
слагаемое + слагаемое = сумма.
х
=
—
;
85
85
19
х
=
.
85
Подсказка 3
Чтобы найди неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
19
Ответ:
85
Решите уравнение.
Выражение в левой части уравнения является разностью.
Подсказка 1
12
78
=
;
у
—
90
90
12
78
Подсказка 2
уменьшаемое – вычитаемое = разность
у
=
—
;
90
90
66
у
=
.
90
Чтобы найди неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Подсказка 3
66
Ответ:
90
Решите уравнение.
Выражение в левой части уравнения является разностью.
Подсказка 1
8
11
а
=
—
;
25
25
8
11
Подсказка 2
уменьшаемое – вычитаемое = разность
а
=
+
;
25
25
19
а
=
.
Чтобы найди неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Подсказка 3
25
19
Ответ:
25
Решите уравнение.
(
7
3
18
ИСПОЛЬЗОВАНИЕ ПРАВИЛ РЕШЕНИЯ УРАВНЕНИЙ.
+
х
+
=
(
;
19
19
19
В левой части уравнения выражение является суммой.
Подсказка 1
3
18
7
+
=
х
;
—
19
19
19
3
11
=
х
+
Подсказка 2
;
Неизвестное содержится в слагаемом.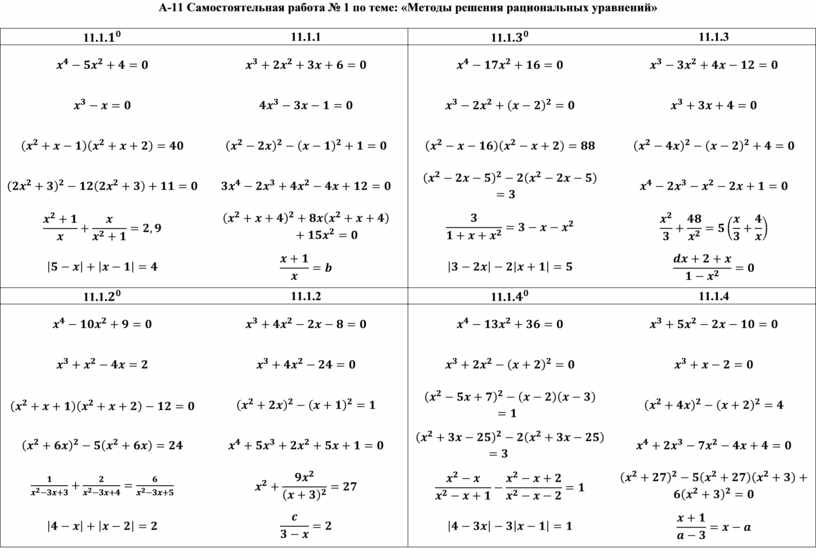
19
19
11
3
х
=
;
—
19
19
8
8
х
.
=
Ответ:
19
19
Решите уравнение.
(
5
37
17
ИСПОЛЬЗОВАНИЕ ПРАВИЛ РЕШЕНИЯ УРАВНЕНИЙ.
—
у
=
(
+
;
44
44
44
В левой части уравнения выражение является разностью.
Подсказка 1
5
37
17
=
у
+
;
—
44
44
44
5
20
=
у
+
Подсказка 2
;
Неизвестное содержится в вычитаемом.
44
44
20
5
у
=
;
—
44
44
15
15
у
.
=
Ответ:
44
44
Решите уравнение.
18
8
21
ИСПОЛЬЗОВАНИЕ ПРАВИЛ РЕШЕНИЯ УРАВНЕНИЙ.
b
+
=
—
;
73
73
73
Подсказка 1
В левой части уравнения выражение является разностью.
18
8
21
b
+
;
=
+
73
73
73
29
18
=
+
Подсказка 2
Неизвестное содержится в уменьшаемом.
b
;
73
73
29
18
=
b
;
—
73
73
11
11
b
Ответ:
.
=
73
73
Решите уравнение.
(
7
3
18
ПРИМЕНЕНИЕ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
+
х
+
=
(
;
19
19
19
В левой части уравнения можно применить сочетательное свойство сложения .
Подсказка 1
7
3
18
+
;
+
=
х
19
19
19
10
18
=
х
+
Подсказка 2
;
Чтобы к числу прибавить сумму , можно к этому числу прибавить сначала одно слагаемое, а потом другое.
19
19
18
10
х
=
;
—
19
19
8
8
х
.
=
Ответ:
19
19
Решите уравнение.
(
5
37
17
ПРИМЕНЕНИЕ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
—
у
=
(
+
;
44
44
44
В левой части уравнения можно применить свойство вычитания суммы из числа. .
Подсказка 1
37
5
17
—
;
—
=
у
44
44
44
32
17
=
у
—
Подсказка 2
;
Чтобы из числа вычесть сумму, можно вычесть сначала одно слагаемое, а потом другое.
44
44
32
17
у
=
;
—
44
44
15
15
у
.
=
Ответ:
44
44
Решите уравнение.
8
18
21
ПРИМЕНЕНИЕ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
+
b
=
—
;
73
73
73
Подсказка 1
В левой части уравнения можно применить свойство вычитания числа из суммы.
18
21
8
—
;
+
=
b
73
73
73
10
21
=
b
+
Подсказка 2
Чтобы вычесть число из суммы, можно сначала вычесть это число из одного слагаемого, а потом прибавить другое.
;
73
73
21
10
=
b
;
—
73
73
11
11
b
.
=
Ответ:
73
73
Решение задач.
2
В первый день Саша прочитал книги, а во второй день — книги. Сколько страниц прочитал Саша за два дня, если в книге 144 страницы?
9
4
9
144 стр.
4
2
9
9
2
4
6
1) + = (книги) – прочитал Саша за 2 дня.
9
9
9
2) 144 : 9 ∙ 6 = 96 (стр.)
Ответ: За 2 дня Саша прочитал 96 страниц.
Решение задач.
5
В первый день Маша прочитала книги, а во второй день — книги. 2=6\)
2=6\)
Как решаются дробно-рациональные уравнения?
Главное, что надо запомнить про дробно-рациональные уравнения – в них надо писать ОДЗ. И после нахождения корней – обязательно проверять их на допустимость. Иначе могут появиться посторонние корни, и все решение будет считаться неверным.
Алгоритм решения дробно-рационального уравнения:
-
Выпишите и «решите» ОДЗ. -
Найдите общий знаменатель дробей. -
Умножьте каждый член уравнения на общий знаменатель и сократите полученные дроби. Знаменатели при этом пропадут. -
Запишите уравнение, не раскрывая скобок. -
Раскройте скобки и приведите подобные слагаемые. -
Решите полученное уравнение. 2+9x-5=0\)
2+9x-5=0\)
Находим корни уравнения
\(x_1=-5;\) \(x_2=\frac{1}{2}.\)
Один из корней не подходи под ОДЗ, поэтому в ответ записываем только второй корень.
Ответ: \(\frac{1}{2}\).
Смотрите также:
Дробно-рациональные неравенстваСкачать статью
Страница не найдена — Гимназия №8 г. Дубны
Приказ «О внесении изменений в годовой календарный учебный график на 2020-2021 учебный год». Подробнее …
В раздел ОГЭ-2021 добавлена информация и проведении итоговых контрольных работ для учащихся 9-х классов, подробнее…
В разделе «Сведения об ОО. Образование. Итоговая аттестация. Итоговое собеседование» размещена информация об итоговом собеседовании в 2021 году, подробнее…
Внимание учащихся 7-8 классов!
Это ваш шанс поучаствовать в олимпиадном движении, если вы что-то пропустили на школьном или муниципальном этапе! Результаты Подмосковной олимпиады будут учитываться при рассмотрении заявок на образовательные смены в РЦОД Взлет.
 Не упустите свой шанс. Старт уже 1 декабря. Ознакомьтесь с правилами регистрации по ссылкам в посте и действуйте! Выход на Подмосковную Олимп аду через ваш личный кабинет в Школьном портале.
Не упустите свой шанс. Старт уже 1 декабря. Ознакомьтесь с правилами регистрации по ссылкам в посте и действуйте! Выход на Подмосковную Олимп аду через ваш личный кабинет в Школьном портале.
Расписание олимпиады — http://student-mo.olymponline.ru/article/24160
Инструкция для участников — http://student-mo.olymponline.ru/article/24159«Государственный гуманитарно- технологический университет» 20.11.2020 в 15:00 по МСК проводит День открытых дверей онлайн, подробнее …
Уважаемые родители!
Информируем вас о том, что записаться на «Родительский контроль» — проект по оценке качества питания в школах — в Подмосковье теперь можно в режиме онлайн. Сделать это можно на Школьном портале региона. Регистрация проходит быстро — вся процедура займет не более трех минут.
— Нужно перейти во вкладку «Родительская»;
— Перейти в раздел «Школьное питание»;
— Выбрать желаемую дату и время;
— Нажать кнопку «Записаться».
Школа автоматически получит заявку и в назначенное время родителя будет ожидать классный руководитель или ответственный за питание.
Независимая оценка качества образования
Уважаемые родители и учащиеся! По ссылке — https://анкета.независимаяоценкакачества.рф/hello/
Вы можете пройти анкетирование по независимой оценке качества образования. Просим Вас принять активное участие! С уважением, администрация гимназииДень Здоровья
11 сентября в гимназии в рамках месячника безопасности и акции «Здоровье — твое богатство» проводится общешкольный День Здоровья (по классам). Более подробно с приказом о проведении Дня Здоровья можно ознакомиться по ссылке …
Внимание
Уважаемые родители!
С 11.09.2020 года в гимназии начинается вакцинация учащихся против гриппа. Вакцинация будет производиться препаратом «Совигрипп»
НАЧАЛАСЬ РЕГИСТРАЦИЯ НА ШКОЛЬНЫЙ ЭТАП ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ШКОЛЬНИКОВ
Сегодня на платформе mo.olymponline.ru стартовала регистрация на Школьный этап Всероссийской олимпиады школьников.
Впервые Школьный этап пройдёт в дистанционном формате.
 Потренироваться в решении заданий можно уже сейчас: на платформе доступен пробный тест.
Потренироваться в решении заданий можно уже сейчас: на платформе доступен пробный тест.Переход на платформу осуществляется через Школьный портал.
Инструкция student-mo.olymponline.ru/article/22352
Чат технической поддержки работает с 10:00 до 20:00
Всероссийская олимпиада школьников 2020-2021
В разделе «Сведения об ОО. Образование. Работа с одаренными детьми» размещен график проведения школьного этапа ВСОШ и этапы проведения олимпиады
С 25 по 27 августа дистанционно пройдёт Подмосковная комплексная олимпиада школьников по истории, обществознанию и праву. К участию приглашаются ученики 8–11 классов. Олимпиада пройдет на специализированной платформе, вход в которую возможен через авторизацию на Школьном портале. Для участия воспользуйтесь инструкцией.
Инструкция: http://student_olymponline.usedocs.com/article/22125
Подробнее об Олимпиаде: https://olympmo.ru/mosreg-olymp.html
Внимание!
Уважаемые родители будущих первоклассников! Пройдя по ссылке Вы сможете ознакомиться с примерным перечнем школьных принадлежностей при поступлении в школу, а также с требованиями к внешнему виду обучающихся подробнее…
Внимание
В раздел «Сведения об ОО.
 Образование. Государственная итоговая аттестация. ЕГЭ» добавлены нормативные акты по ГИА-11 подробнее…
Образование. Государственная итоговая аттестация. ЕГЭ» добавлены нормативные акты по ГИА-11 подробнее…Внимание!
«Уважаемые выпускники 11-го класса! В разделе «Единый государственный экзамен» размещены методические рекомендации по подготовке обучающихся к сдаче ЕГЭ по математике в режиме консультаций, а также график консультаций с учителями гимназии по подготовке к ЕГЭ — 2020. Все материалы Вы можете посмотреть, пройдя по ссылке —
Северное инспекторское отделение Центра ГИМС ГУ МЧС России по
Московской области информирует.
Сейчас на территории Подмосковья действует режим самоизоляции и
покидать дома без острой необходимости запрещается, а прогулки у воды без
присмотра взрослых могут стоить жизни. К сожалению, не все родители
объясняют своим детям, что же означает этот режим, и к каким последствиям
могут привести прогулки.
Самоизоляция – это комплекс ограничительных мер для населения,
которые вводит правительство на определенный срок для борьбы с
распространением опасного заболевания. Граждан просят соблюдать режим: не
Граждан просят соблюдать режим: не
выходить на улицу без острой необходимости, ограничить контакты с другими
людьми и соблюдать все рекомендации по профилактике вирусных заболеваний,
предложенные медицинским сообществом.
Уважаемые родители и учащиеся! Просим Вас не пользоваться береговой зоной
водоемов и не нарушать режим самоизоляции.
Берегите себя и своих близких!!!Уважаемые родители!
Учебный год в нашей школе для учащихся 1-8-х и 10-х классов закончится по графику 28 мая.
Для учащихся 9-х и 11-х классов даты окончания учебного года будут объявлены дополнительно. Мы обязательно сообщим всем родителям, когда даты будут определены.
Берегите себя и будьте здоровы!Федеральная служба по надзору в сфере образования и науки и Министерство просвещения Российской Федерации подготовили проект нового расписания государственной итоговой аттестации для выпускников 9 классов (ГИА-9).
В соответствии с ним, основной период основного государственного экзамена (ОГЭ) и государственного выпускного экзамена (ГВЭ) для выпускников 9 классов в 2020 году пройдут в сроки с 8 июня по 31 июля.
 Региональные органы исполнительной власти, а также учредители заграншкол могут сами определить основные и резервные сроки проведения экзаменов по русскому языку и математике в рамках этого периода. ОГЭ по предметам по выбору в 2020 году проводиться не будет.
Региональные органы исполнительной власти, а также учредители заграншкол могут сами определить основные и резервные сроки проведения экзаменов по русскому языку и математике в рамках этого периода. ОГЭ по предметам по выбору в 2020 году проводиться не будет.Участники экзаменов, не прошедшие ОГЭ и ГВЭ или получившие неудовлетворительные результаты по одному или обоим обязательным предметам в резервные сроки, смогут пересдать их в дополнительный период в сентябре. 4 сентября в дополнительный период планируется провести экзамен по русскому языку, 7 сентября – по математике. Резервные дни для проведения экзаменов в дополнительный период: 14 сентября – русский язык, 15 сентября – математика, 18 сентября – русский язык и математика.
Внимание!
Информация «Об основных принципах карантина в домашних условиях» подробнее…
В разделе «Родителям. Зачисление в первый класс» размещена информация о закреплении муниципальных общеобразовательных учреждений за территориями (микрорайонами) городского округа Дубна.
 Подробнее…
Подробнее…Адаптированные электронные ресурсы для обучающихся с инвалидностью и обучающихся с ограниченными возможностями здоровья на портале «Российская электронная школа» https://resh.edu.ru/search
Государственный университет «Дубна» приглашает школьников 9-11 классов к участию в III Зимней школе «Информационная безопасность», которая пройдет с 25 по 31 января 2020 года:
- 25 и 26 января* — очный этап: Программа
- 27-31 января — заочный этап: Олимпиада
Регистрация обязательна: https://forms.gle/TeK7qsMDZ7KhWDnr5
В программе очного этапа:- Анализ и защита компьютерных сетей;
- Мастер-класс по интеллектуальным системам;
- Методы обнаружения закладных устройств снятия и передачи акустической информации;
- Безопасность Wi-Fi;
- Введение в Python ;
- Криптография, стеганография.
По итогам школы будет проведена олимпиада по информатике. Победители и призеры (11 класс) получат дополнительные баллы к ЕГЭ при поступлении в университет «Дубна» в 2020 году:
Диплом победителя (1 место) – 10 баллов,
Диплом призера (2 и 3 места) – 8 баллов.
Спешите, количество мест ограничено!
* проживание для иногородних участников университетом не предоставляется.
График проведения муниципального этапа всероссийской олимпиады школьников в г.о. Дубна в 2019-2020 учебном году подробнее…
Федеральная служба по надзору в сфере образования и науки подготовила новые анимированные видеоролики и плакаты, рассказывающие о государственной итоговой аттестации. Подробнее…
Всероссийское соревнование по компьютерному спорту среди команд общеобразовательных организаций «Всероссийская интеллектуально-киберспортивная лига», организованные в целях развития компьютерного спорта на территории Российской Федерации.
К соревнованиям допускаются сборные команды общеобразовательных организаций, укомплектованные обучающимися, достигшими 14 лет на дату 21 октября 2019 года и не имеющие действующих профессиональных контрактов в сфере спорта.
Сроки проведения:- I этап (региональный) — с 21 октября по 3 ноября 2019 года
- II этап (зональный) — с 4 по 11 ноября 2019 года
- III этап (финальный) — с 22 по 24 ноября 2019 года
Положение о соревнованиях
Подробности и регистрация…10.
 09.2019
09.201920 сентября начинается школьный этап Всероссийской олимпиады школьников в Дубне подробнее…
11 сентября, в 12:30 в Москве состоится презентация проекта для слепых и слабовидящих детей «Белая Книга» при участии Дианы Гурцкой, Антона Кульбачевского, Нины Шацкой подробнее…
Всероссийский конкурс школьных генеалогических исследований «Моя родословная» — «Страна сильна семьями» подробнее…
24.07.2019
Всероссийский конкурс «Добро не уходит на каникулы» подробнее…
Расписание консультаций ГИА 9-х и 11 классов размещено в разделе «Сведения об ОО, Образование, Государственная итоговая аттестация, ЕГЭ/ОГЭ».
С 14 по 24 мая в школах пройдет всероссийская акция «Урок Цифры» подробнее…
Генеральная прокуратура Российской Федерации выступает организатором Международного молодежного конкурса социальной антикоррупционной рекламы «Вместе против коррупции». Правила проведения конкурса доступны на официальном сайте конкурс http://www.
 anticorruption.life/
anticorruption.life/Всероссийский онлайн — зачет по финансовой грамотности подробнее…
С 1 апреля Молодежная палата Центрального федерального округа проводит конкурс: «А что ты знаешь о защите персональных данных в сети Интернет?» В конкурсе принимают участие дети и молодежь от 7 до 25 лет. Конкурс проходит в 3 номинациях: «Рисунок», «Логотип Молодежной палаты» и «Видеоролик» на тему защиты персональных данных. Подробнее…
Всероссийская добровольная интернет-акция «Противопожарная безопасность» подробнее…
Общероссийское общественное движение «БЕССМЕРТНЫИ ПОЛК РОССИИ» с 11 по 31 марта проводит Всероссийский конкурс исследовательских работ «Мой прадед» подробнее…
С 1 февраля по 30 июня 2019 года проходит Всероссийская акция «Сделаем вместе!» подробнее…
21.02.19
Всероссийский патриотический конкурс «Сыны и Дочери Отечества» подробнее…
Уважаемые юнармейцы!
В период с 25 апреля по 16 мая 2019 года проводится конкурсный отбор участников Пятой Военно-спортивной смены «Юнармеец», реализуемой на базе детского лагеря «Штормовой» Всероссийского детского центра «Орленок» (Краснодарский край).
 Отбор участников Программы производится на основании Положения, утвержденного Главным штабом движения «Юнармия».
Отбор участников Программы производится на основании Положения, утвержденного Главным штабом движения «Юнармия».К участию в конкурсе приглашаются юнармейцы в возрасте от 12 до 16 лет, победители и призеры спортивных и военно-патриотических игр, мероприятий патриотической направленности. С Положением о конкурсе на участие по Программе можно ознакомиться на официальном сайте движения «Юнармия» в разделе «Документы», вкладка «Юнармейское лето».
Методические рекомендации по выявлению в сети интернет экстремистских материалов. Подробнее…
Учитель шахмат
Департамент государственной политики в сфере общего образования Минпросвещения России информирует о проведении конкурса «Учитель шахмат», организатором которого является Общероссийская общественная организация «Федерация шахмат России». Заявки на участие в конкурсе принимаются до 15 апреля 2019 года. Форму заявки можно скачать ТУТ
Конкурсные материалы принимаются с 16 апреля до 30 июня 2019 года.
 Форма для прикрепления конкурсных материалов доступна по ССЫЛКЕ
Форма для прикрепления конкурсных материалов доступна по ССЫЛКЕКонтактное лицо: руководитель проекта «Шахматный всеобуч России» Костьев Александр Николаевич, тел. 8(968)732-00-74, адрес электронной почты: [email protected].
Урок мужества
Минпросвещения России совместно с Фондом социально-культурных инициатив рекомендуют провести в общеобразовательных организациях Урок мужества, посвященный Всероссийской общественно-государственной инициативе «Горячее сердце», в день Торжественной церемонии награждения лауреатов 1 марта 2019 года. Методические рекомендации по проведению в общеобразовательных организациях Урока мужества прилагаются.
Методические рекомендации…
22.11.2018
В период с 03.12.2018 по 09.12.2018 в гимназии будет проведен тематический урок информатики в рамках всероссийского мероприятия «Урок Цифры»
22.11.2018
Акция «Тест по истории отечества»
Молодежный парламент при Государственной Думе Федерального Собрания Российской Федерации проводит Международную акцию «Тест по истории Отечества», которая состоится 30.
 11.2018 в 11.00
11.2018 в 11.00Внимание!
Министерство образования Московской области информирует: с 29 октября по 23 ноября 2018 года Ресурсный центр русского языка (МГОУ) организует работу областной школы юного филолога. Для участия приглашаются ученики 5-11 классов. Прием заявок осуществляется на сайте МГОУ https://mgou.ru
(Обучение/ Дополнительное образование/ Ресурсный центр русского языка/ Подать заявку) до 26 октября.14.09.18
В разделе «Родителям» размещена информация по вопросу проведения мероприятий (акций), направленных на блокировку опасного контента
(информации, причиняющей вред здоровью и развитию детей)ВНИМАНИЕ
21 августа 2018 года с 10:00 в Приёмной Правительства Московской области, Министерстве образования Московской области, администрациях муниципальных образований, общественных приёмных исполнительных органов государственной власти Московской области состоится тематический приём граждан ко Дню знаний, по вопросам подготовки к новому учебному году.

23.07.2018
Министерство образования Московской области информирует о проведении III-го Общероссийского синхронного фестиваля интеллектуальных игр «Проксима Центавра 2018/19», который пройдет в период с 15 сентября по 30 ноября 2018 года. Организаторами Фестиваля выступает российская ассоциация интеллектуальных клубов при поддержке Московского Центра интеллектуальных игр «Сириус» и Московского Университета Синергия.
Подробная информация о Фестивале размещена на официальном сайте moskvasirius.ru.Список литературы
В разделе «Учащимся» размещен список обязательной литературы для чтения летом будущим учащимся 10-го класса
Решение уравнений — оценка 9
Приведены примеры для 9 классов с подробным пошаговым подходом к решению простых уравнений и уравнений с использованием скобок и дробей. Также обсуждается проверка решений уравнения.
 Также включены другие вопросы и их решения с подробными объяснениями.
Также включены другие вопросы и их решения с подробными объяснениями.Что такое уравнение и его решение?
Сначала мы рассмотрим понятие уравнений и решение уравнения.
Уравнение — это утверждение, которое выражает равенство двух математических выражений.Уравнение имеет знак равенства, выражение с правой и с левой стороны.Пример 1
Это примеры уравнений с неизвестным \ (x \)
\ (\ quad 2 x = — 6 \), \ (\ quad x + 3 = 7 \), \ (\ quad 2 (x + 3) = — (2x + 4) \)У каждого уравнения есть знак равенства, который разделяет левую и правую части уравнения.
Левая часть уравнения \ (\ quad \ color {red} {2 x — 6} = x + 5 \) равна \ (\ quad \ color {red} {2 x — 6} \).
Правая часть уравнения \ (\ quad 2 x — 6 = \ color {red} {x + 5} \) равна \ (\ quad \ color {red} {x + 5} \).Решение уравнения с неизвестным \ (x \) — это набор всех значений \ (x \), которые делают уравнение истинным.
Пример 2
Какое из следующих значений \ (x \): \ (- 4, 2 \) является / являются решением (ями) уравнения \ (2 x + 2 = x + 4 \)?Решение примера 2
Заменить \ (x \) его числовым значением в левой и правой частях уравнения.а) Проверить \ (\ color {red} {x = — 4} \)
Вычислить левую часть: \ (2 \ color {red} x + 2 = 2 \ color {red} {(- 4)} + 2 = — 8 + 2 = — 6 \),
Оцените правую сторону: \ (\ color {red} x + 4 = \ color {red} {(- 4)} + 4 = 0 \)
Числовые значения левой и правой частей не равны, поэтому \ (x = — 4 \) не является решением уравнения \ (2 x + 2 = x + 4 \).
а) Проверить \ (\ color {red} {x = 2} \)
Вычислить левую часть: \ (2 x + 2 = 2 \ color {red} {(2)} + 2 = 4 + 2 = 6 \),
Оцените правую сторону: \ (\ color {red} x + 4 = \ color {red} {(2)} + 4 = 6 \)
Числовые значения левой и правой частей равны, поэтому \ (x = 2 \) — это решение уравнения \ (2 x + 2 = x + 4 \).Важные свойства для решения уравнений
Чтобы решить уравнение, нам нужны математические шаги, которые помогут получить все члены с неизвестным с одной стороны и постоянными с другой стороны.
Некоторые из наиболее важных свойств, используемых для решения уравнений, перечислены ниже.
1) Если мы прибавим или вычтем одну и ту же величину к обеим сторонам уравнения, мы получим уравнение, имеющее то же решение, что и исходное.
1) Если мы умножим или разделим обе части уравнения на одну и ту же величину, НЕ равную нулю, мы получим уравнение, имеющее то же решение, что и исходное.Решение простых уравнений
Пример 3
Решите уравнение \ (2x + 1 = — 5 \) и проверьте полученное решение.Решение примера 3
Основная идея состоит в том, чтобы иметь все члены с неизвестным \ (x \) на одной стороне и все постоянные члены на другой стороне уравненияДавайте оставим члены \ (2x \) слева и постоянные члены справа.
 Это можно сделать, вычтя \ (1 \) из обеих частей уравнения
Это можно сделать, вычтя \ (1 \) из обеих частей уравнения
\ (\ quad \ quad 2x + 1 \ color {red} {- 1} = — 5 \ color {red} {- 1} \)Упростите, чтобы получить
\ (\ квад \ квад 2x = — 6 \)Чтобы получить \ (x \) из \ (2x \), разделим обе части приведенного выше уравнения на 2.
\ (\ quad \ quad \ dfrac {2 x} {\ color {red} 2} = \ dfrac {-6} {\ color {red} 2} \)Упростить
\ (\ quad \ quad x = -3 \)Проверить решение, полученное в исходном (заданном) уравнении
Вычислите левую часть уравнения для \ (x = — 3 \): \ (\ quad 2x + 1 = 2 (-3) + 1 = — 5 \)
Вычислите левую часть уравнения для \ (x = — 3 \): \ (\ quad — 5 \)
Левая и правая стороны равны \ (- 5 \) для \ (x = — 3 \), поэтому \ (x = — 3 \) является решением данного уравнения.Пример 4
Решите уравнение \ (x — 2 — 3x = — 7 — x \) и проверьте полученное решение.Решение примера 4
Сгруппируйте одинаковые члены в двух частях уравнения. \ (x \) и \ (- 3x \) похожи на член слева и могут быть сгруппированы, чтобы получить
\ (x \) и \ (- 3x \) похожи на член слева и могут быть сгруппированы, чтобы получить
\ (\ quad \ quad — 2x — 2 = — 7 — x \)Добавьте \ (2 \) к обеим сторонам уравнения, чтобы исключить постоянные члены из левой части.
\ (\ quad \ quad — 2x — 2 \ color {red} {+ 2} = — 7 — x \ color {red} {+ 2} \)Упростить
\ (\ quad \ quad — 2x = — x — 5 \)Добавьте \ (x \) к обеим сторонам уравнения, чтобы исключить члены с \ (x \) из правой части.
\ (\ quad \ quad — 2x \ color {красный} {+ x} = — x — 5 \ color {red} {+ x} \)Упростите, чтобы получить
\ (\ квад \ квад — х = — 5 \)Если мы знаем \ (- x \) и нам нужно \ (x \), мы умножаем обе части уравнения на \ (- 1 \)
\ (\ quad \ quad \ color {red} {(- 1)} (- x) = \ color {red} {(- 1)} (- 5) \)Упростить
\ (\ quad \ quad x = 5 \)Проверить решение, полученное в исходном (заданном) уравнении
Левая часть уравнения для \ (x = 5 \): \ (\ quad x — 2 — 3x = 5-2-3 (5) = — 12 \)
Правая часть уравнения для \ (x = 5 \): \ (\ quad — 7 — x = — 7 — (5) = — 12 \)
Левая и правая стороны равны \ (- 12 \) для \ (x = 5 \), поэтому \ (x = — 3 \) является решением данного уравнения.
Решите уравнения в скобках
Пример 5
Решите уравнение \ (- 2 (x — 2) + 3 = 3 (-x + 4) — 3 \) и проверьте полученное решение.Решение примера 5
Данное уравнение
\ (\ quad \ quad \ color {red} {- 2} (x — 2) + 3 = \ color {red} 3 (-x + 4) — 3 \)
Используйте закон распределения: \ (\ quad a (b + c) = ab + ac \ quad \), который является одним из основных правил алгебры, чтобы убрать скобки.
Распределите \ (\ color {red} {- 2} \) и \ (\ color {red} 3 \).
\ (\ quad \ quad \ color {red} {- 2} (x) \ color {red} {- 2} (- 2) + 3 = \ color {red} 3 (-x) + \ color {красный } 3 (4) — 3 \)
Упростить
\ (\ квад \ квад — 2 х + 4 + 3 = — 3 х + 12 — 3 \)Сгруппируйте одинаковые члены в обеих частях уравнения.

\ (\ квад \ квад — 2 х + 7 = — 3 х + 9 \)Вычтем \ (7 \) к обеим частям уравнения, чтобы исключить постоянные члены из левой части уравнения.
\ (\ квад \ квад — 2 х + 7-7 = — 3 х + 9-7 \)Группировать похожие термины
\ (\ квад \ квад — 2x = — 3x + 2 \)Добавьте \ (3x \) к обеим сторонам уравнения, чтобы исключить члены в \ (x \) из левой правой части уравнения.
\ (\ квад \ квад — 2x + 3 x = — 3x + 2 + 3x \)Объединяйте термины в группу и упрощайте
\ (\ quad \ quad x = 2 \)Проверить решение, полученное в исходном (заданном) уравнении
Вычислите левую часть уравнения для \ (x = 2 \): \ (\ quad — 2 (x — 2) + 3 = — 2 ((2) — 2) + 3 = 3 \)
Вычислите правую часть уравнения для \ (x = 2 \): \ (\ quad 3 (-x + 4) — 3 = 3 (- (2) + 4) — 3 = 3 \)
Левая и правая стороны равны 3 для \ (x = 2 \), поэтому \ (x = 2 \) является решением данного уравнения.Решите уравнения с дробями
Используемый здесь метод решения уравнений с дробями — это метод, при котором мы сначала избавляемся от дробей (чтобы не иметь дела с дробями) путем умножения, а затем решаем уравнение.

Пример 6
Решите уравнение \ (\ quad \ dfrac {x} {2} = — 3 \) и проверьте полученное решение.Решение примера 6
Чтобы исключить знаменатель \ (2 \) в \ (\ dfrac {x} {2} \), мы умножаем две части уравнения на знаменатель \ (2 \)\ (\ quad \ color {red} 2 \ left (\ dfrac {x} {2} \ right) = \ color {red} 2 (- 3) \)
Упростить
\ (\ quad x = — 6 \)Проверить решение, полученное в исходном (заданном) уравнении
Левая часть уравнения для \ (x = -6 \): \ (\ quad \ dfrac {x} {2} = \ dfrac {-6} {2} = — 3 \)
Левая и правая стороны равны \ (- 3 \) для \ (x = — 6 \), поэтому \ (x = — 6 \) является решением данного уравнения.Пример 7
Решите уравнение \ (\ quad \ dfrac {x} {3} — \ dfrac {1} {2} = \ dfrac {1} {3} \) и проверьте полученное решение.
Решение примера 7
Теперь у нас есть две дроби со знаминателями \ (2 \) и \ (3 \) в данном уравнении. Чтобы избавиться от дробей, нам нужно умножить обе части уравнения на НОК (наименьшее общее кратное) двух разных знаменателей \ (2 \) и \ (3 \).
Найдите НОК \ (2 \) и \ (3 \), которое равно \ (6 \).
Умножьте обе части уравнения на НОК, равное \ (6 \).
\ (\ quad \ quad \ color {red} 6 \ left (\ dfrac {x} {3} — \ dfrac {1} {2} \ right) = \ color {red} 6 \ left (\ dfrac {1 } {3} \ right) \)Распределите коэффициент \ (6 \)
\ (\ quad \ quad 6 \ left (\ dfrac {x} {3} \ right) — 6 \ left (\ dfrac {1} {2} \ right) = 6 \ left (\ dfrac {1} {3 } \верно) \)Переставить как
\ (\ quad \ quad \ left (\ dfrac {6} {3} \ right) x — \ left (\ dfrac {6} {2} \ right) = \ left (\ dfrac {6} {3} \ верно) \)Упростить
\ (\ квад \ квад 2x — 3 = 2 \)ПРИМЕЧАНИЕ.
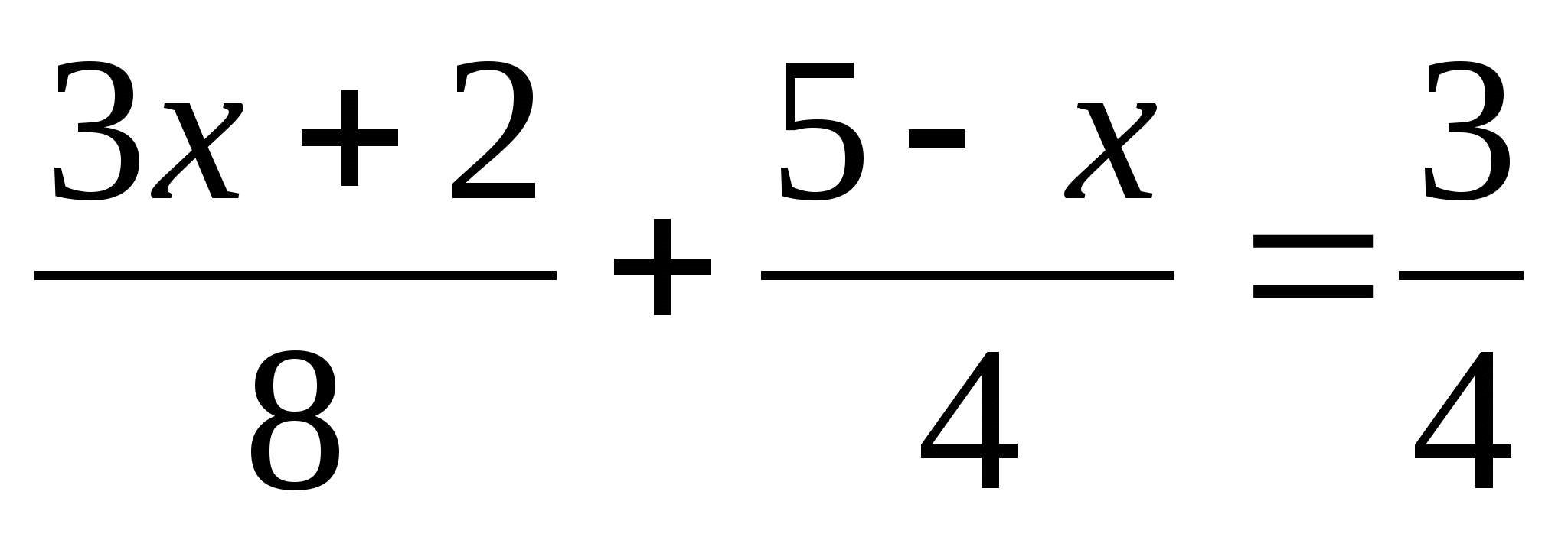 Один шаг, который представляет собой умножение обеих частей уравнения на НОК знаменателей, необходим, чтобы избавиться от дробей, поскольку НОК является кратным каждому знаменателю.
Один шаг, который представляет собой умножение обеих частей уравнения на НОК знаменателей, необходим, чтобы избавиться от дробей, поскольку НОК является кратным каждому знаменателю.Решите указанное выше уравнение, добавив \ (3 \) к обеим сторонам и упростив, чтобы получить
\ (\ quad \ quad 2 x = 5 \)Разделите обе стороны на \ (2 \)
\ (\ quad \ quad x = \ dfrac {5} {2} \)Проверить решение, полученное в исходном (заданном) уравнении
Левая часть уравнения для \ (x = \ dfrac {5} {2} \): \ (\ quad \ dfrac {x} {3} — \ dfrac {1} {2} = \ dfrac {1} {3 } x — \ dfrac {1} {2} = \ dfrac {1} {3} \ left (\ dfrac {5} {2} \ right) — \ dfrac {1} {2} = \ dfrac {1} { 3} \)Левая и правая стороны равны \ (\ dfrac {1} {3} \) для \ (x = \ dfrac {5} {2} \), поэтому \ (x = \ dfrac {5} {2 } \) является решением данного уравнения.
Пример 8
Решите уравнение \ (\ quad \ dfrac {2x + 1} {5} + 2 = — \ dfrac {x} {3} \) и проверьте полученное решение.
Решение примера 8
Теперь у нас есть дроби со знаменателями \ (5 \) и \ (3 \) в данном уравнении. Нам нужно умножить обе части уравнения на НОК (наименьшее общее кратное) двух разных знаменателей \ (5 \) и \ (3 \).
Найдите НОК \ (5 \) и \ (3 \), который равен \ (15 \).
ПРИМЕЧАНИЕ. Один шаг, который представляет собой умножение обеих частей уравнения на НОК знаменателей, необходим, чтобы избавиться от дробей, поскольку НОК является кратным каждому знаменателю.Умножаем обе части уравнения на НОК \ (15 \)
\ (\ quad \ quad \ color {red} {15} \ left (\ dfrac {2x + 1} {5} + 2 \ right) = \ color {red} {15} \ left (\ — \ dfrac { x} {3} \ right) \)Распределите коэффициент \ (15 \)
\ (\ quad \ quad 15 \ left (\ dfrac {2x + 1} {5} \ right) + 15 (2) = 15 \ left (- \ dfrac {x} {3} \ right) \)Переставить как
\ (\ quad \ quad \ dfrac {15} {5} (2x + 1) + 15 (2) = \ dfrac {15} {3} (- x) \)Упростить
\ (\ квад \ квад 3 (2x + 1) + 30 = — 5x \)Распределите коэффициент \ (3 \) в левой части и сгруппируйте похожие термины
\ (\ quad \ quad 6 x + 3 + 30 = — 5x \)
\ (\ quad \ quad 6x + 33 = — 5 x \)Вычтите \ (33 \) с обеих сторон и прибавьте \ (5x \) к обеим сторонам.
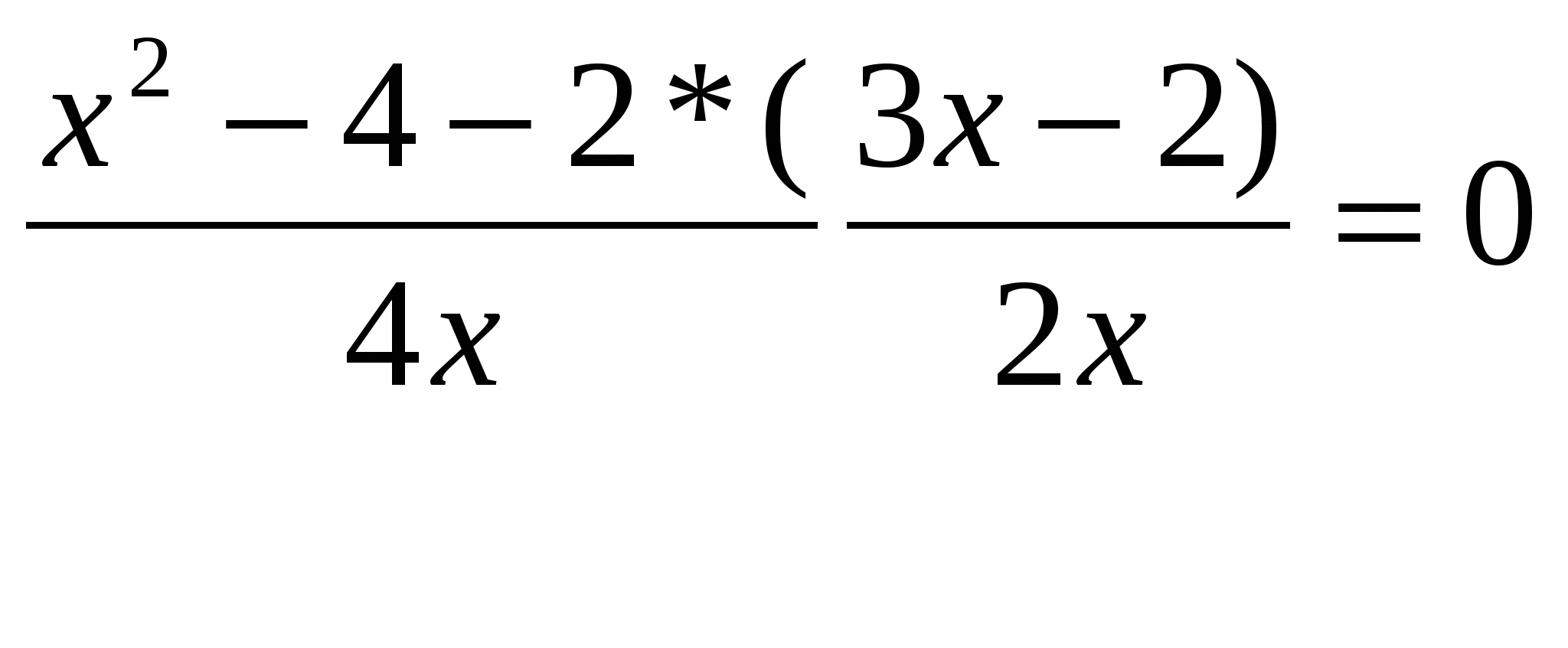 (ПРИМЕЧАНИЕ: мы выполнили две операции за один шаг.)
(ПРИМЕЧАНИЕ: мы выполнили две операции за один шаг.)\ (\ quad \ quad 6x + 33 \ color {red} {- 33 + 5x} = — 5 x \ color {red} {- 33 + 5x} \)
Группировать похожие термины
\ (\ quad \ quad 11 x = — 33 \)Разделите обе стороны на \ (11 \)
\ (\ quad \ quad \ dfrac {11 x} {11} = \ dfrac {-33} {11} \)
Упростить
\ (\ quad \ quad x = — 3 \)Проверьте решение, полученное в исходном (заданном) уравнении
Левая часть уравнения для \ (x = — 3 \): \ (\ quad \ dfrac {2x + 1} {5} + 2 = \ dfrac {2 (- 3) + 1} {5} + 2 = 1 \)Правая часть уравнения для \ (x = -3 \): \ (\ quad — \ dfrac {x} {3} = — \ dfrac {-3} {3} = 1 \)
Левая и правая стороны равны \ (1 \) для \ (x = -3 \), поэтому \ (x = — 3 \) является решением данного уравнения.Вопросы
- Решите следующие уравнения и проверьте найденное решение.

- ) \ (2x + 2 = 6 \)
- ) \ (5y — 2 = 7y — 8 \)
- ) \ (-2x + 4 + 5x = 7 + 4x — 3 \)
- ) \ (0,2 d + 4 = — 0,1 d — 2 \)
- ) \ (-2 (2x- 6) = — (x — 4) \)
- ) \ (- (х + 2) +4 = 2 (х + 3) + х \)
- ) \ (\ dfrac {x} {5} = — 6 \)
- ) \ (- \ dfrac {x} {3} = \ dfrac {1} {2} \)
- ) \ (- \ dfrac {x} {4} = \ dfrac {1} {2} — x \)
- ) \ (- \ dfrac {x-3} {7} = \ dfrac {1} {2} (- 2x + 6) \)
- ) \ (- \ dfrac {1} {2} — x + 5 = \ dfrac {1} {5} + 2 (x-2) \)
Включены ответы на вышеуказанные вопросы.
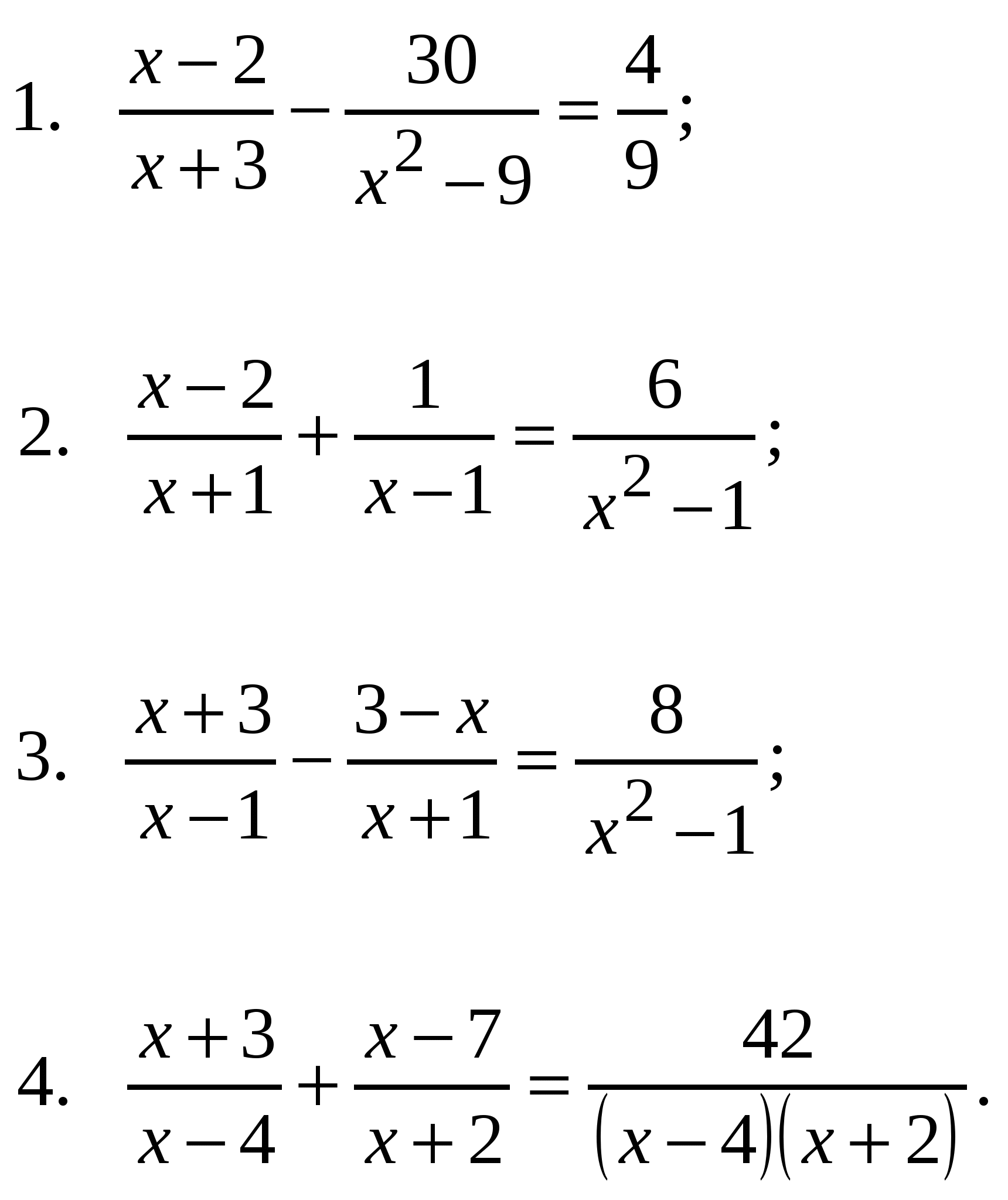
Дополнительные ссылки и ссылки
Решите уравнения, системы уравнений и неравенства
Найдите наименьшее общее кратное
Математика для средней школы (6, 7, 8, 9 классы) — бесплатные вопросы и проблемы с ответами
Математика в средней школе (10, 11 и 12) — Бесплатные вопросы и задачи с ответами
Начальная математика (4 и 5 классы) с бесплатными вопросами и задачи с ответамиРешение линейных уравнений с дробями
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.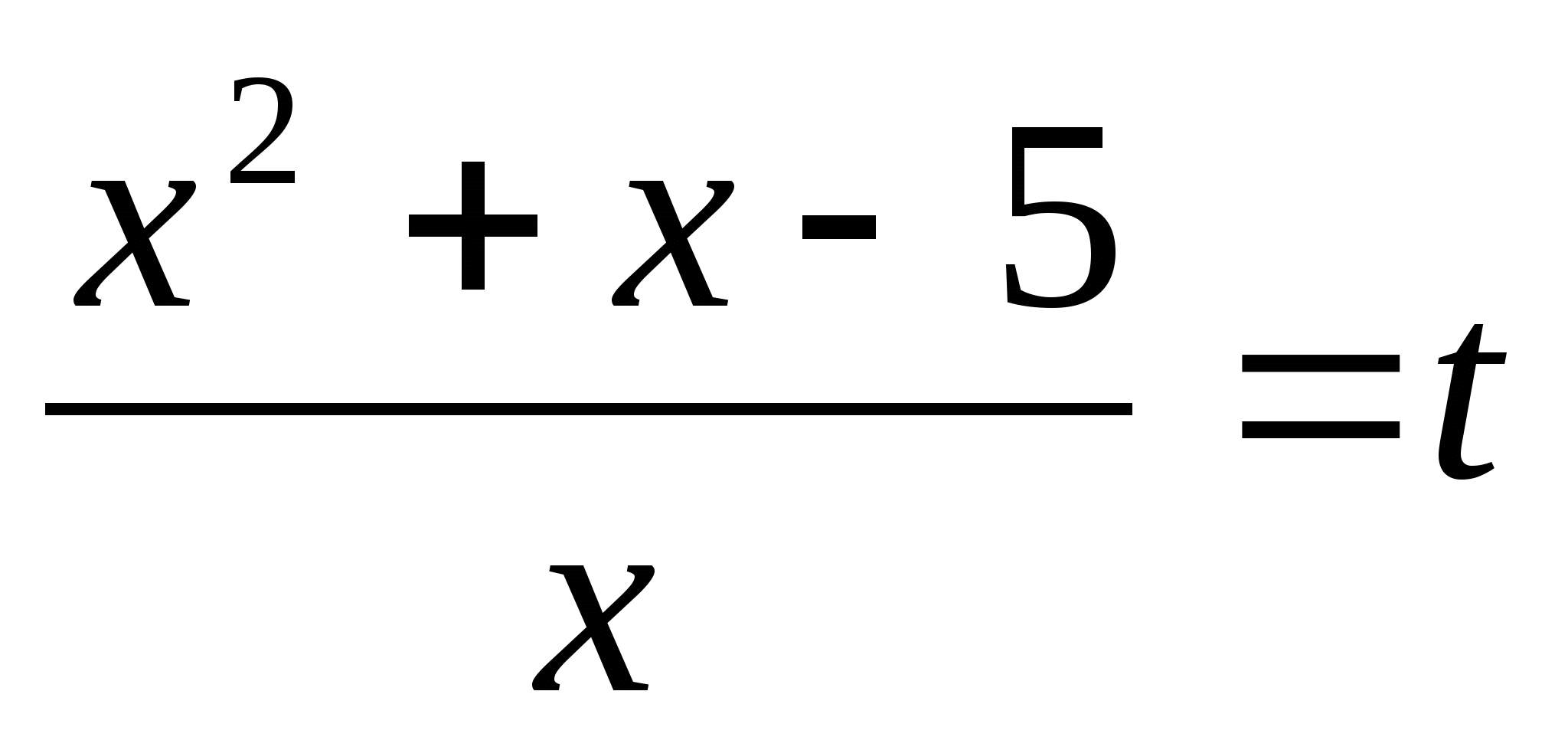 д. — относится ваша жалоба;
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
Решайте уравнения с дробями или десятичными знаками — элементарная алгебра
Решение линейных уравнений и неравенств
Цели обучения
К концу этого раздела вы сможете:
- Решите уравнения с дробными коэффициентами
- Решите уравнения с десятичными коэффициентами
Прежде чем вы начнете, пройдите тест на готовность.

- Умножить:
Если вы пропустили эту проблему, просмотрите (рисунок). - Найдите ЖК-дисплей и.
Если вы пропустили эту проблему, просмотрите (рисунок). - Умножьте 4,78 на 100.
Если вы пропустили эту проблему, просмотрите (рисунок).
Решите уравнения с дробными коэффициентами
Давайте воспользуемся общей стратегией решения линейных уравнений, введенной ранее для решения уравнения,.
Этот метод работал нормально, но многие студенты не чувствуют себя уверенно, когда видят все эти дроби.Итак, мы собираемся показать альтернативный метод решения уравнений с дробями. Этот альтернативный метод исключает дроби.
Мы применим свойство равенства умножения и умножим обе части уравнения на наименьший общий знаменатель всех дробей в уравнении. Результатом этой операции будет новое уравнение, эквивалентное первому, но без дробей. Этот процесс называется «очисткой» уравнения дробей.
Давайте решим аналогичное уравнение, но на этот раз воспользуемся методом исключения дробей.
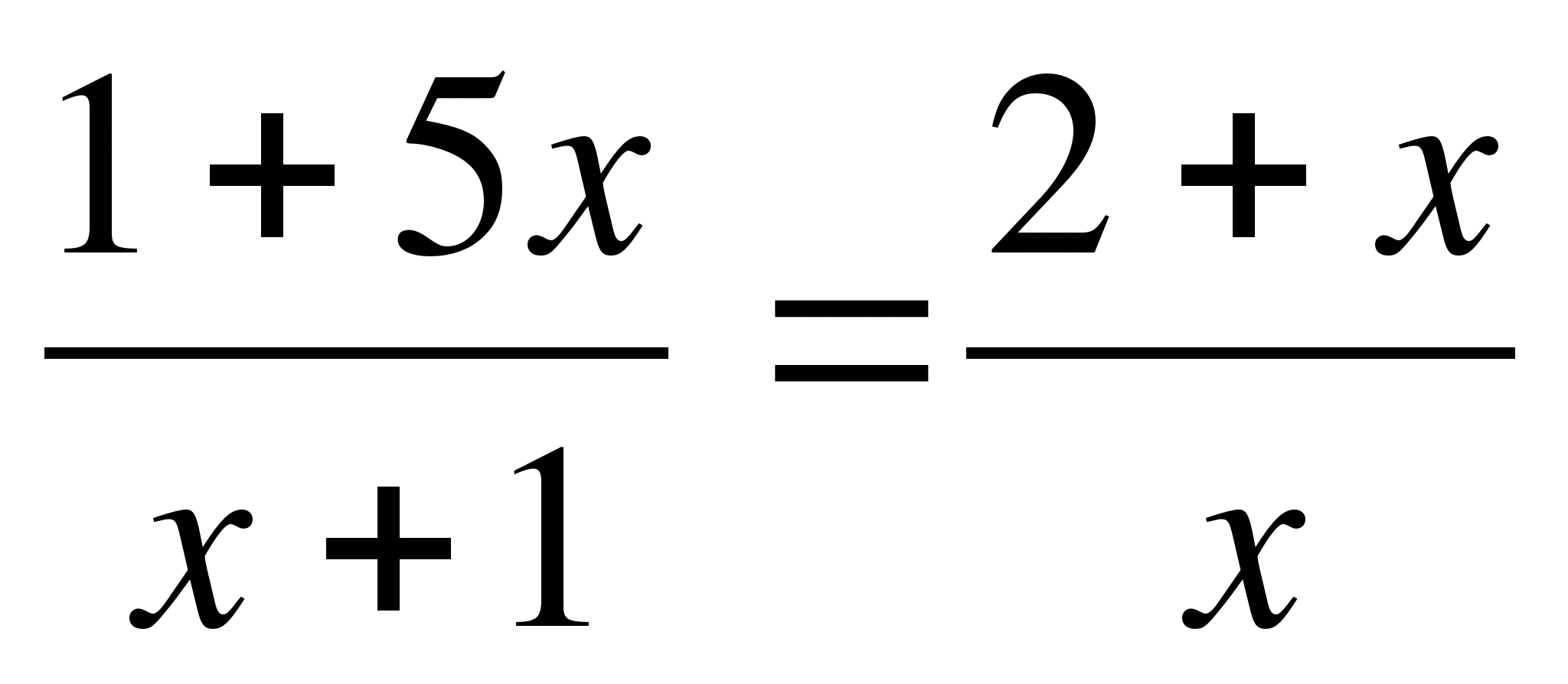
Как решать уравнения с дробными коэффициентами
Решить:.
Решить:.
Решить:.
Обратите внимание на (рисунок), когда мы очистили уравнение дробей, уравнение было похоже на те, которые мы решали ранее в этой главе. Мы изменили проблему на ту, которую уже знали, как решить! Затем мы использовали общую стратегию решения линейных уравнений.
Стратегия решения уравнений с дробными коэффициентами.
- Найдите наименьший общий знаменатель всех дробей в уравнении.
- Умножьте обе части уравнения на этот ЖК-дисплей. Это очищает фракции.
- Решите, используя общую стратегию решения линейных уравнений.
Решить:.
Решение
Мы хотим очистить дроби, умножив обе части уравнения на ЖК-дисплей всех дробей в уравнении.
Решить:.
Решить:.
В следующем примере у нас снова есть переменные по обе стороны уравнения.

Решить:.
Решить:.
Решить:.
В следующем примере мы начнем с использования свойства распределения. Этот шаг сразу очищает дроби.
Решить:.
Решить:.
Решить:.
В следующем примере, даже после распределения, у нас все еще есть дроби, которые нужно очистить.
Решить:.
Решить:.
Решить:.
Решить:.
Решить:.
Решить:.
Решить:.
Решить:.
Решить:.
Решить:.
Решить:.
Решить:.
Решите уравнения с десятичными коэффициентами
В некоторых уравнениях есть десятичные дроби.Такое уравнение возникает, когда мы решаем проблемы, связанные с деньгами или процентами.
 Но десятичные дроби также можно выразить дробями. Например, и. Итак, с уравнением с десятичными знаками мы можем использовать тот же метод, который мы использовали для очистки дробей, — умножить обе части уравнения на наименьший общий знаменатель.
Но десятичные дроби также можно выразить дробями. Например, и. Итак, с уравнением с десятичными знаками мы можем использовать тот же метод, который мы использовали для очистки дробей, — умножить обе части уравнения на наименьший общий знаменатель.Решить:.
Решение
Посмотрите на десятичные дроби и подумайте об эквивалентных дробях.
Обратите внимание, ЖК-дисплей — 100.
Умножая на ЖК-дисплей, мы удалим десятичные дроби из уравнения.
Решить:.
Решить:.
В следующем примере используется уравнение, которое типично для денежных приложений из следующей главы. Обратите внимание, что мы распределяем десятичную дробь до того, как очистим все десятичные дроби.
Решить:.
Решить:.
Решить:.
Ключевые понятия
- Стратегия решения уравнения с дробными коэффициентами
- Найдите наименьший общий знаменатель всех дробей в уравнении.
- Умножьте обе части уравнения на этот ЖК-дисплей. Это очищает фракции.
- Решите, используя общую стратегию решения линейных уравнений.
Практика ведет к совершенству
Решите уравнения с дробными коэффициентами
В следующих упражнениях решите каждое уравнение с дробными коэффициентами.
Решите уравнения с десятичными коэффициентами
В следующих упражнениях решите каждое уравнение с десятичными коэффициентами.
Повседневная математика
Монеты У Тейлора? 2.00 в десять центов и пенни. Количество пенни на 2 больше, чем количество монет. Решите уравнение для количества десятицентовиков.
Марки Паула купила марки стоимостью 49 центов и марки 21 цент на сумму 22,82 фунта стерлингов. Марок номиналом 21 цент было на 8 меньше, чем марок стоимостью 49 центов. Решите уравнение для s , чтобы найти количество 49-центовых марок, купленных Паулой.
Письменные упражнения
Объясните, как найти наименьший общий знаменатель для, и.
Если уравнение состоит из нескольких дробей, как умножение обеих частей на ЖК-дисплей упрощает решение?
Если в уравнении дроби только с одной стороны, зачем нужно умножать обе части уравнения на ЖК-дисплей?
Что такое ЖК-дисплей в уравнении? Откуда вы знаете?
100. Обоснования могут быть разными.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ В целом, после просмотра контрольного списка, думаете ли вы, что хорошо подготовились к следующему разделу? Почему или почему нет?
% PDF-1.4
%
221 0 объект>
эндобджxref
221 108
0000000016 00000 н.
0000004576 00000 н.
0000004713 00000 н.
0000004930 00000 н.
0000004973 00000 н.
0000005177 00000 н.
0000005408 00000 н.
0000005497 00000 н.
0000009994 00000 н.
0000014647 00000 п.
0000019217 00000 п.
0000023874 00000 п.
0000028451 00000 п.
0000033053 00000 п.
0000033811 00000 п.
0000034565 00000 п.
0000035383 00000 п.
0000035787 00000 п.
0000036168 00000 п.
0000036523 00000 п.
0000036697 00000 п.
0000036784 00000 п.
0000037246 00000 п.
0000037463 00000 п.
0000037760 00000 п.
0000037829 00000 п.
0000042458 00000 п.
0000046595 00000 п.
0000050573 00000 п.
0000053586 00000 п.
0000057011 00000 п.
0000057178 00000 п.
0000057784 00000 п.
0000058390 00000 н.
0000058513 00000 п.
0000058621 00000 п.
0000059089 00000 н.
0000059556 00000 п.
0000059699 00000 н.
0000059807 00000 п.
0000059974 00000 н.
0000060443 00000 п.
0000060911 00000 п.
0000061034 00000 п.
0000061142 00000 п.
0000061628 00000 п.
0000062122 00000 п.
0000062245 00000 п.
0000062353 00000 п.
0000062988 00000 п.
0000063111 00000 п.
0000063219 00000 п.
0000063319 00000 п.
0000063390 00000 п.
0000063487 00000 п.
0000063559 00000 п.
0000063615 00000 п.
0000063718 00000 п.
0000063774 00000 п.
0000063877 00000 п.
0000063933 00000 п.
0000064098 00000 п.
0000064154 00000 п.
0000064278 00000 н.
0000064334 00000 п.
0000064452 00000 п.
0000064508 00000 п.
0000064628 00000 п.
0000064684 00000 п.
0000064822 00000 н.
0000064878 00000 п.
0000065008 00000 п.
0000065064 00000 п.
0000065189 00000 п.
0000065245 00000 п.
0000065372 00000 п.
0000065428 00000 п.
0000065539 00000 п.
0000065595 00000 п.
0000065723 00000 п.
0000065779 00000 п.
0000065926 00000 п.
0000065982 00000 п.
0000066112 00000 п.
0000066168 00000 п.
0000066284 00000 п.
0000066340 00000 п.
0000066444 00000 п.
0000066500 00000 п.
0000066552 00000 п.
0000066604 00000 п.
0000066657 00000 п.
0000066711 00000 п.
0000066763 00000 п.
0000066815 00000 п.
0000066867 00000 п.
0000066919 00000 п.
0000066971 00000 п.
0000067023 00000 п.
0000067075 00000 п.
0000067127 00000 п.
0000067179 00000 п.
0000067231 00000 п.
0000067283 00000 п.
0000067335 00000 п.
0000067383 00000 п.
0000067431 00000 п.
0000002456 00000 н.
трейлер
] >>
startxref
0
%% EOF
328 0 obj> поток
# | LmhyOec> & ȡE6> T6h4n {F
FN {30G ڭ N3h3 ؐ X a [j̷ ‘]% _f * q
msldw’Z6.вуЛ! rwg̟RkuT @ CotO (u «# cB_D # fu- @ eHQ?, EmF] b \ o.% WHrlV]} EKАлгебра 2 (Решение уравнений, глава 4) (Математические классы миссис Бенке)
Глава 3: Алгебра 2 ( Решение уравнений, глава 4) (Уроки математики миссис Бенке)
БЛОК 3 АННОТАЦИЯ:
U3D0 — Схема решения уравнений Это версия для печати схемы установки
MPM 1DI БЛОК 3 — РЕШЕНИЕ УРАВНЕНИЙ Учебная цель (Я буду):
В этом модуле мы будем решать уравнения первой степени, а задачи со словами можно смоделировать с помощью уравнений первой степени.
Критерии успеха (я могу…):
- Решите простые уравнения
- Решите многоступенчатые уравнения
- Решите уравнения с дробями
- Переставить формулы с переменными первой степени
- Решите задачи со словами, которые можно смоделировать с помощью уравнения с одной переменной
- Решить проблемы с применением процента, отношения, ставки и пропорции
День
Урок
Текст
Арт.
Назначить. / Домашнее задание
1 Диагностическая викторина
U3D1 Решение простых уравнений
U3D1_T_ Решение простых уравнений
4,1
стр. 193-195 № 3, 5, 6, 8-13, 16, 18, 20
2 U3D2_S_ Решение многоступенчатых уравнений
U3D2_T_ Решение многоступенчатых уравнений
4.2
стр. 200-202 # 2, 4 («корень» просто означает «решение»), 5a, 6a, 8, 9, 10, 13
Вызов Страница 203 # 18-21
Дополнительная практика-решение-уравнения-рабочий лист
Тест №1 ПРАКТИКА
Практика для решения викторины №1
3 ВИКТОРИНА № 1
U3D3_S — Решение уравнений с дробями, часть 1
U3D3_T — Решение уравнений с дробями I
(перекрестное умножение)
4.3 стр. 208-209 # 1, 3ac, 4ac, 5-8
4 U3D4_S — Решение уравнений с дробями, часть 2
U3D4_T — Решение уравнений с дробями II
4,3
стр. 208-210 # 3bd, 4bd, 11, 12,
Рабочий лист 3.3 Решение уравнений с дробями
Рабочий лист 3.3 Решения
Страница задания 210 # 13
U3D4 Тест №2 ПРАКТИКА
U3D4_Quiz # 2 ПРАКТИКА Решения
5 ВИКТОРИНА № 2
U3D5_S — Моделирование с помощью формул
(Перестановка уравнений)
U3D5_T — Моделирование с помощью формул
4.4
стр. 215-219 № 1-3, 6-8, 10-12, 15, 16а
Вызов Страница 219 # 18, 19
U3D5_W — Рабочий лист — Дополнительная практика с уравнениями
6 U3D6_S Номер История Вопросы
U3D6_T Номер История Вопросы
4,5 стр. 226-227 № 1-11
Дополнительная практика:
Рабочий лист 3.4 Номер Рассказ Вопросы Дополнительная практика
Рабочий лист 3.4 Решения
7 U3D7_S Расценки на единицу продукции Вопросы
U3D7_T Расценки на единицу продукции Вопросы
4,5
Рабочий лист 3.5 Вопросы для рассказа о расценках
Рабочий лист 3.5 Решения
8 Блок 3 Обзор
U3D8_S Информация о обзоре
См. Старый тест в Google Classroom, чтобы понять, чего ожидать.
Pg 230-231 # 2, 5, 7, 8, 9, 11, 12-16,
Finish U3D5_W — Рабочий лист — Дополнительная практика с уравнениями для большей практики
Дополнительная практика: Стр. 232-233 № 1-10
U3D8_W_Extra Review Story Вопросы
U3D8_W_Extra Review РЕШЕНИЯ История вопросов
9 ТЕСТ Срок действия этой информации истекает после печати.Пожалуйста, всегда обращайтесь к онлайн-версии для получения самой последней информации.
8.6: Решение уравнений с дробными или десятичными коэффициентами
Решение уравнений с дробными коэффициентами
Давайте воспользуемся общей стратегией решения линейных уравнений, представленной ранее, для решения уравнения \ (\ dfrac {1} {8} x + \ dfrac {1} {2} = \ dfrac {1} {4} \).
Чтобы изолировать член x, вычтите \ (\ dfrac {1} {2} \) с обеих сторон. $$ \ dfrac {1} {8} x + \ dfrac {1} {2} \ textcolor {red} {- \ dfrac {1} {2}} = \ dfrac {1} {4} \ textcolor {красный } {- \ dfrac {1} {2}} $$ Упростите левую часть. $$ \ dfrac {1} {8} x = \ dfrac {1} {4} — \ dfrac {1} {2} $$ Измените константы на эквивалентные дроби с помощью ЖК-дисплея. $$ \ dfrac {1} {8} x = \ dfrac {1} {4} — \ dfrac {2} {4} $$ Вычесть. $$ \ dfrac {1} {8} x = — \ dfrac {1} {4} $$ Умножьте обе части на обратную величину \ (\ dfrac {1} {8} \). $$ \ textcolor {red} {\ dfrac {8} {1}} \ cdot \ dfrac {1} {8} x = \ textcolor {red} {\ dfrac {8} {1}} \ left (- \ dfrac {1} {4} \ right) $$ Упростить. $$ x = -2 $$ Этот метод работал нормально, но многие студенты не чувствуют себя уверенно, когда видят все эти дроби. Итак, мы собираемся показать альтернативный метод решения уравнений с дробями. Этот альтернативный метод исключает дроби.
Мы применим свойство равенства умножения и умножим обе части уравнения на наименьший общий знаменатель всех дробей в уравнении.Результатом этой операции будет новое уравнение, эквивалентное первому, но без дробей. Этот процесс называется , очищая уравнение дробей . Давайте снова решим то же уравнение, но на этот раз воспользуемся методом очистки дробей.
Пример \ (\ PageIndex {1} \):
Решение: \ (\ dfrac {1} {8} x + \ dfrac {1} {2} = \ dfrac {1} {4} \).
Решение
Найдите наименьший общий знаменатель всех дробей в уравнении. $$ \ dfrac {1} {8} x + \ dfrac {1} {2} = \ dfrac {1} {4} \ quad LCD = 8 $$ Умножьте обе части уравнения на этот ЖК-дисплей, 8. Это очистит дроби. $$ \ textcolor {красный} {8} \ left (\ dfrac {1} {8} x + \ dfrac {1} {2} \ right) = \ textcolor {red} {8} \ left (\ dfrac { 1} {4} \ right) $$ Используйте свойство распределения. $$ 8 \ cdot \ dfrac {1} {8} x + 8 \ cdot \ dfrac {1} {2} = 8 \ cdot \ dfrac {1} {4} $$ Упростите — и заметьте, никаких дробей! $$ x + 4 = 2 $$ Решите, используя общую стратегию решения линейных уравнений. $$ x + 4 \ textcolor {красный} {- 4} = 2 \ textcolor {красный} {- 4} $$ Упростить. $$ x = -2 $$ Проверка: пусть x = −2. $$ \ begin {split} \ dfrac {1} {8} x + \ dfrac {1} {2} & = \ dfrac {1} {4} \\ \ dfrac {1} {8} (\ textcolor { красный} {- 2}) + \ dfrac {1} {2} & \ stackrel {?} {=} \ dfrac {1} {4} \\ — \ dfrac {2} {8} + \ dfrac {1} {2} & \ stackrel {?} {=} \ Dfrac {1} {4} \\ — \ dfrac {2} {8} + \ dfrac {4} {8} & \ stackrel {?} {=} \ dfrac {1} {4} \\ \ dfrac {2} {4} & \ stackrel {?} {=} \ dfrac {1} {4} \\ \ dfrac {1} {4} & = \ dfrac {1 } {4} \; \ checkmark \ end {split} $$ Упражнение \ (\ PageIndex {1} \):
Решение: \ (\ dfrac {1} {4} x + \ dfrac {1} {2} = \ dfrac {5} {8} \).
- Ответ
\ (x = \ frac {1} {2} \)
Упражнение \ (\ PageIndex {2} \):
Решение: \ (\ dfrac {1} {6} y — \ dfrac {1} {3} = \ dfrac {1} {6} \).
- Ответ
г = 3
Обратите внимание, что в примере 8.37, когда мы очистили уравнение дробей, оно было похоже на те, которые мы решали ранее в этой главе. Мы изменили проблему на ту, которую уже знали, как решить! Затем мы использовали общую стратегию решения линейных уравнений.
КАК: РЕШИТЬ УРАВНЕНИЯ С КОЭФФИЦИЕНТАМИ ФРАКЦИЙ, ОЧИСТЯ ДРОБИ
Шаг 1. Найдите наименьший общий знаменатель всех дробей в уравнении.
Шаг 2. Умножьте обе части уравнения на этот ЖК-дисплей. Это очищает фракции.
Шаг 3. Решите, используя общую стратегию решения линейных уравнений.
Пример \ (\ PageIndex {2} \):
Решение: 7 = \ (\ dfrac {1} {2} x + \ dfrac {3} {4} x — \ dfrac {2} {3} x \).
Решение
Мы хотим очистить дроби, умножив обе части уравнения на ЖК-дисплей всех дробей в уравнении.
Найдите наименьший общий знаменатель всех дробей в уравнении. $$ 7 = \ dfrac {1} {2} x + \ dfrac {3} {4} x — \ dfrac {2} {3} x \ quad LCD = 12 $$ Умножьте обе части уравнения на 12. $$ \ textcolor {red} {12} (7) = \ textcolor {red} {12} \ cdot \ dfrac {1} {2} x + \ dfrac {3} {4} x — \ dfrac {2} {3} х $
Распространить. $$ 12 (7) = 12 \ cdot \ dfrac {1} {2} x + 12 \ cdot \ dfrac {3} {4} x — 12 \ cdot \ dfrac {2} {3} x $$ Упростите — и заметьте, никаких дробей! $$ 84 = 6x + 9x — 8x $$ Объедините похожие термины. $$ 84 = 7x $$ Разделить на 7. $$ \ dfrac {84} {\ textcolor {red} {7}} = \ dfrac {7x} {\ textcolor {red} {7}} $$ Упростить. $$ 12 = x $$ Проверка: пусть x = 12. $$ \ begin {split} 7 & = \ dfrac {1} {2} x + \ dfrac {3} {4} x — \ dfrac {2} {3} x \\ 7 & \ stackrel {?} { =} \ dfrac {1} {2} (\ textcolor {red} {12}) + \ dfrac {3} {4} (\ textcolor {red} {12}) — \ dfrac {2} {3} (\ textcolor {красный} {12}) \\ 7 & \ stackrel {?} {=} 6 + 9 — 8 \\ 7 & = 7 \; \ checkmark \ end {split} $$ Упражнение \ (\ PageIndex {3} \):
Решение: 6 = \ (\ dfrac {1} {2} v + \ dfrac {2} {5} v — \ dfrac {3} {4} v \).
- Ответ
v = 40
Упражнение \ (\ PageIndex {4} \):
Решить: -1 = \ (\ dfrac {1} {2} u + \ dfrac {1} {4} u — \ dfrac {2} {3} u \).
- Ответ
u = -12
В следующем примере у нас будут переменные и дроби с обеих сторон уравнения.
Пример \ (\ PageIndex {3} \):
Решение: \ (x + \ dfrac {1} {3} = \ dfrac {1} {6} x — \ dfrac {1} {2} \).
Решение
Найдите на ЖК-дисплее все дроби в уравнении. $$ x + \ dfrac {1} {3} = \ dfrac {1} {6} x — \ dfrac {1} {2} \ quad LCD = 6 $$ Умножьте обе стороны на ЖК-дисплей. $$ \ textcolor {красный} {6} \ left (x + \ dfrac {1} {3} \ right) = \ textcolor {red} {6} \ left (\ dfrac {1} {6} x — \ dfrac {1} {2} \ right) $$ Распространить. $$ 6 \ cdot x + 6 \ cdot \ dfrac {1} {3} = 6 \ cdot \ dfrac {1} {6} x — 6 \ cdot \ dfrac {1} {2} $$ Упростите — больше никаких дробей! $$ 6x + 2 = x — 3 $$ Вычтите x с обеих сторон. $$ 6x \ textcolor {красный} {- x} + 2 = x \ textcolor {красный} {- x} — 3 $$ Упростить. $$ 5x + 2 = -3 $$ Вычтите 2 с обеих сторон. $$ 5x + 2 \ textcolor {красный} {- 2} = -3 \ textcolor {красный} {- 2} $$ Упростить. $$ 5x = -5 $$ Разделить на 5. $$ \ dfrac {5x} {\ textcolor {red} {5}} = \ dfrac {-5} {\ textcolor {red} {5}} $$ Упростить. $$ x = -1 $$ Проверить: подставить x = −1. $$ \ begin {split} x + \ dfrac {1} {3} & = \ dfrac {1} {6} x — \ dfrac {1} {2} \\ (\ textcolor {red} {- 1} ) + \ dfrac {1} {3} & \ stackrel {?} {=} \ dfrac {1} {6} (\ textcolor {red} {- 1}) — \ dfrac {1} {2} \\ ( -1) + \ dfrac {1} {3} & \ stackrel {?} {=} — \ dfrac {1} {6} — \ dfrac {1} {2} \\ — \ dfrac {3} {3} + \ dfrac {1} {3} & \ stackrel {?} {=} — \ dfrac {1} {6} — \ dfrac {3} {6} \\ — \ dfrac {2} {3} & \ stackrel {?} {=} — \ dfrac {4} {6} \\ — \ dfrac {2} {3} & = — \ dfrac {2} {3} \; \ checkmark \ end {split} $$ Упражнение \ (\ PageIndex {5} \):
Решение: \ (a + \ dfrac {3} {4} = \ dfrac {3} {8} a — \ dfrac {1} {2} \).
- Ответ
а = -2
Упражнение \ (\ PageIndex {6} \):
Решение: \ (c + \ dfrac {3} {4} = \ dfrac {1} {2} c — \ dfrac {1} {4} \).
- Ответ
с = -2
В примере 8.40 мы начнем с использования свойства распределения. Этот шаг сразу очистит дроби!
Пример \ (\ PageIndex {4} \):
Решение: 1 = \ (\ dfrac {1} {2} \) (4x + 2).
Решение
Распространить. $$ 1 = \ dfrac {1} {2} \ cdot 4x + \ dfrac {1} {2} \ cdot 2 $$ Упростить. Теперь дробей нет! $$ 1 = 2x + 1 $$ Вычтите 1 с обеих сторон. $$ 1 \ textcolor {красный} {- 1} = 2x + 1 \ textcolor {красный} {- 1} $$ Упростить. $$ 0 = 2x $$ Разделить на 2. $$ \ dfrac {0} {\ textcolor {red} {2}} = \ dfrac {2x} {\ textcolor {red} {2}} $$ Упростить. $$ 0 = x $$ Проверка: пусть x = 0. $$ \ begin {split} 1 & = \ dfrac {1} {2} (4x + 2) \\ 1 & \ stackrel {?} {=} \ Dfrac {1} {2} [4 (\ textcolor { красный} {0}) + 2] \\ 1 & \ stackrel {?} {=} \ dfrac {1} {2} (2) \\ 1 & \ stackrel {?} {=} \ dfrac {2} { 2} \\ 1 & = 1 \; \ checkmark \ end {split} $$ Упражнение \ (\ PageIndex {7} \):
Решить: −11 = \ (\ dfrac {1} {2} \) (6p + 2).
- Ответ
п = -4
Упражнение \ (\ PageIndex {8} \):
Решение: 8 = \ (\ dfrac {1} {3} \) (9q + 6).
- Ответ
q = 2
Часто дроби остаются даже после распределения.
Пример \ (\ PageIndex {5} \):
Решение: \ (\ dfrac {1} {2} \) (y — 5) = \ (\ dfrac {1} {4} \) (y — 1).
Решение
Распространить. $$ \ dfrac {1} {2} \ cdot y — \ dfrac {1} {2} \ cdot 5 = \ dfrac {1} {4} \ cdot y — \ dfrac {1} {4} \ cdot 1 $ Упростить. $$ \ dfrac {1} {2} y — \ dfrac {5} {2} = \ dfrac {1} {4} y — \ dfrac {1} {4} $$ Умножить на ЖК-дисплей, 4. $$ \ textcolor {красный} {4} \ left (\ dfrac {1} {2} y — \ dfrac {5} {2} \ right) = \ textcolor {red} {4} \ left (\ dfrac { 1} {4} y — \ dfrac {1} {4} \ right) $$ Распространить. $$ 4 \ cdot \ dfrac {1} {2} y — 4 \ cdot \ dfrac {5} {2} = 4 \ cdot \ dfrac {1} {4} y — 4 \ cdot \ dfrac {1} {4 } $$ Упростить. $$ 2y — 10 = y — 1 $$ Соберите элементы y слева. $$ 2y — 10 \ textcolor {красный} {- y} = y — 1 \ textcolor {красный} {- y} $$ Упростить. $$ y — 10 = -1 $$ Соберите константы справа. $$ y — 10 \ textcolor {красный} {+ 10} = -1 \ textcolor {красный} {+ 10} $$ Упростить. $$ y = 9 $$ Проверка: замените 9 на y. $$ \ begin {split} \ dfrac {1} {2} (y — 5) & = \ dfrac {1} {4} (y — 1) \\ \ dfrac {1} {2} (\ textcolor { красный} {9} — 5) & \ stackrel {?} {=} \ dfrac {1} {4} (\ textcolor {red} {9} — 1) \\ \ dfrac {1} {2} (4) & \ stackrel {?} {=} \ dfrac {1} {4} (8) \\ 2 & = 2 \; \ checkmark \ end {split} $$ Упражнение \ (\ PageIndex {9} \):
Решение: \ (\ dfrac {1} {5} \) (n + 3) = \ (\ dfrac {1} {4} \) (n + 2).
- Ответ
п = 2
Упражнение \ (\ PageIndex {10} \):
Решение: \ (\ dfrac {1} {2} \) (m — 3) = \ (\ dfrac {1} {4} \) (m — 7).
- Ответ
м = -1
Решите уравнения с десятичными коэффициентами
В некоторых уравнениях есть десятичные дроби. Такое уравнение возникает, когда мы решаем проблемы, связанные с деньгами и процентами. Но десятичные дроби — это еще один способ представления дробей.Например, 0,3 = \ (\ dfrac {3} {10} \) и 0,17 = \ (\ dfrac {17} {100} \). Итак, когда у нас есть уравнение с десятичными знаками, мы можем использовать тот же процесс, который мы использовали для очистки дробей, — умножить обе части уравнения на наименьший общий знаменатель.
Пример \ (\ PageIndex {6} \):
Решить: 0,8x — 5 = 7.
Решение
Единственная десятичная дробь в уравнении — 0,8. Так как 0.8 = \ (\ dfrac {8} {10} \), на ЖК-дисплее будет 10. Мы можем умножить обе стороны на 10, чтобы очистить десятичную дробь.
Умножьте обе стороны на ЖК-дисплей. $$ \ textcolor {красный} {10} (0,8x — 5) = \ textcolor {красный} {10} (7) $$ Распространить. $$ 10 (0,8x) — 10 (5) = 10 (7) $$ Умножьте и обратите внимание, больше никаких десятичных знаков! $$ 8x — 50 = 70 $$ Добавьте 50, чтобы сдвинуть все константы вправо. $$ 8x — 50 \ textcolor {красный} {+ 50} = 70 \ textcolor {красный} {+ 50} $$ Упростить. $$ 8x = 120 $$ Разделите обе стороны на 8. $$ \ dfrac {8x} {\ textcolor {red} {8}} = \ dfrac {120} {\ textcolor {red} {8}} $$ Упростить. $$ x = 15 $$ Проверка: пусть x = 15. $$ \ begin {split} 0.8 (\ textcolor {red} {15}) — 5 & \ stackrel {?} {=} 7 \\ 12 — 5 & \ stackrel {?} {=} 7 \\ 7 & = 7 \; \ checkmark \ end {split} $$ Упражнение \ (\ PageIndex {11} \):
Решить: 0.6x — 1 = 11.
- Ответ
х = 20
Упражнение \ (\ PageIndex {12} \):
Решить: 1,2x — 3 = 9.
- Ответ
х = 10
Пример \ (\ PageIndex {7} \):
Решить: 0,06x + 0,02 = 0,25x — 1,5.
Решение
Посмотрите на десятичные дроби и подумайте об эквивалентных дробях.
\ [0.06 = \ dfrac {6} {100}, \ qquad 0.02 = \ dfrac {2} {100}, \ qquad 0.25 = \ dfrac {25} {100}, \ qquad 1.5 = 1 \ dfrac {5} {10} \]
Обратите внимание, на ЖК-дисплее 100. Умножая на ЖК-дисплей, мы очищаем десятичные дроби.
Умножьте обе стороны на 100. $$ \ textcolor {красный} {100} (0,06x + 0,02) = \ textcolor {красный} {100} (0,25x — 1,5) $$ Распространить. $$ 100 (0,06x) + 100 (0,02) = 100 (0,25x) — 100 (1,5) $$ Умножьте, и больше никаких десятичных знаков. $$ 6x + 2 = 25x — 150 $$ Соберите переменные справа. $$ 6x \ textcolor {красный} {- 6x} + 2 = 25x \ textcolor {красный} {- 6x} — 150 $$ Упростить. $$ 2 = 19x — 150 $$ Соберите константы слева. $$ 2 \ textcolor {красный} {+ 150} = 19x — 150 \ textcolor {красный} {+ 150} $$ Упростить. $$ 152 = 19x $$ Разделить на 19. $$ \ dfrac {152} {\ textcolor {red} {19}} = \ dfrac {19x} {\ textcolor {red} {19}} $$ Упростить. $$ 8 = x $$ Проверка: пусть x = 8. $$ \ begin {split} 0,06 (\ textcolor {red} {8}) + 0,02 & = 0,25 (\ textcolor {red} {8}) — 1,5 \\ 0,48 + 0,02 & = 2,00 — 1,5 \\ 0,50 & = 0,50 \; \ checkmark \ end {split} $$ Упражнение \ (\ PageIndex {13} \):
Решить: 0.14ч + 0,12 = 0,35ч — 2,4.
- Ответ
ч = 12
Упражнение \ (\ PageIndex {14} \):
Решить: 0,65k — 0,1 = 0,4k — 0,35.
- Ответ
к = -1
В следующем примере используется уравнение, типичное для тех, которые мы увидим в денежных приложениях в следующей главе. Обратите внимание, что мы сначала распределим десятичные дроби, прежде чем очистим все десятичные числа в уравнении.
Пример \ (\ PageIndex {8} \):
Решить: 0,25x + 0,05 (x + 3) = 2,85.
Решение
Раздать первым. $$ 0,25x + 0,05x + 0,15 = 2,85 $$ Объедините похожие термины. $$ 0,30x + 0,15 = 2,85 $$ Чтобы очистить десятичные дроби, умножьте на 100. $$ \ textcolor {красный} {100} (0,30x + 0,15) = \ textcolor {красный} {100} (2.85) $$ Распространить. $$ 30x + 15 = 285 $$ Вычтите 15 с обеих сторон. $$ 30x + 15 \ textcolor {красный} {- 15} = 285 \ textcolor {красный} {- 15} $$ Упростить. $$ 30x = 270 $$ Разделить на 30. $$ \ dfrac {30x} {\ textcolor {red} {30}} = \ dfrac {270} {\ textcolor {red} {30}} $$ Упростить. $$ x = 9 $$ Проверка: пусть x = 9. $$ \ begin {split} 0,25x + 0,05 (x + 3) & = 2,85 \\ 0,25 (\ textcolor {red} {9}) + 0,05 (\ textcolor {red} {9} + 3) & \ stackrel {?} {=} 2,85 \\ 2,25 + 0,05 (12) & \ stackrel {?} {=} 2,85 \\ 2,25 + 0,60 & \ stackrel {?} {=} 2,85 \\ 2,85 & = 2,85 \; \ checkmark \ end {split} $$ Упражнение \ (\ PageIndex {15} \):
Решить: 0,25n + 0,05 (n + 5) = 2.95.
- Ответ
п = 9
Упражнение \ (\ PageIndex {16} \):
Решить: 0,10d + 0,05 (d — 5) = 2,15.
- Ответ
г = 16
Дробей по алгебре
Мы можем складывать, вычитать, умножать и делить дроби в алгебре так же, как и в простой арифметике.
Сложение дробей
Для сложения дробей существует простое правило:
(Узнайте, почему это работает, на странице общего знаменателя).
Пример:
х
2
+
y
5
знак равно
(х) (5) + (2) (у)
(2) (5)=
5x + 2y
10Пример:
х + 4
3
+
х — 3
4
знак равно
(х + 4) (4) + (3) (х − 3)
(3) (4)=
4х + 16 + 3х − 9
12=
7x + 7
12Вычитание дробей
Вычитание дробей очень похоже, за исключением того, что + теперь —
Пример:
х + 2
х
—
х
х — 2
знак равно
(х + 2) (х − 2) — (х) (х)
х (х − 2)=
(x 2 — 2 2 ) — x 2
x 2 — 2x=
−4
x 2 — 2xУмножение дробей
Умножение дробей — самый простой из всех, просто перемножьте верхнюю часть вместе и нижнюю часть:
Пример:
3x
х − 2
×
х
3
знак равно
(3x) (х)
3 (х − 2)=
3x 2
3 (х − 2)=
х 2
х − 2На дроби
Чтобы разделить дроби, сначала «переверните» дробь, на которую мы хотим разделить, затем используйте тот же метод, что и для умножения:
Пример:
3 года 2
х + 1
÷
y
2
знак равно
3 года 2
х + 1
×
2
y=
(3 года 2 ) (2)
(х + 1) (у)=
6лет 2
(х + 1) (у)=
6лет
х + 1
Жесткий:.
