Содержание
Урок 4. трапеция — Геометрия — 8 класс
Четырёхугольник, две стороны которого параллельны, а две другие не параллельны, называется трапецией. Параллельные стороны называются основаниями трапеции, непараллельные стороны – боковыми сторонами.
Если один из углов трапеции прямой, то она называется прямоугольной. Если боковые стороны трапеции равны, то она называется равнобедренной трапецией (равнобокой).
Сформулируем и докажем свойства равнобедренной трапеции:
Свойство первое: в равнобедренной трапеции углы при каждом основании равны.
Для доказательства проведём отрезок CK, параллельный AB.
CK || AB, ABCK – параллелограмм (стороны попарно параллельны), значит AB = CK, но AB = CD (трапеция равнобедренная), значит CK = CD, треугольник KCD – равнобедренный,
По свойству равнобедренного треугольника ∠1 = ∠2.
∠2 = ∠3 (соответственные при секущей AD и параллельных AB и CK).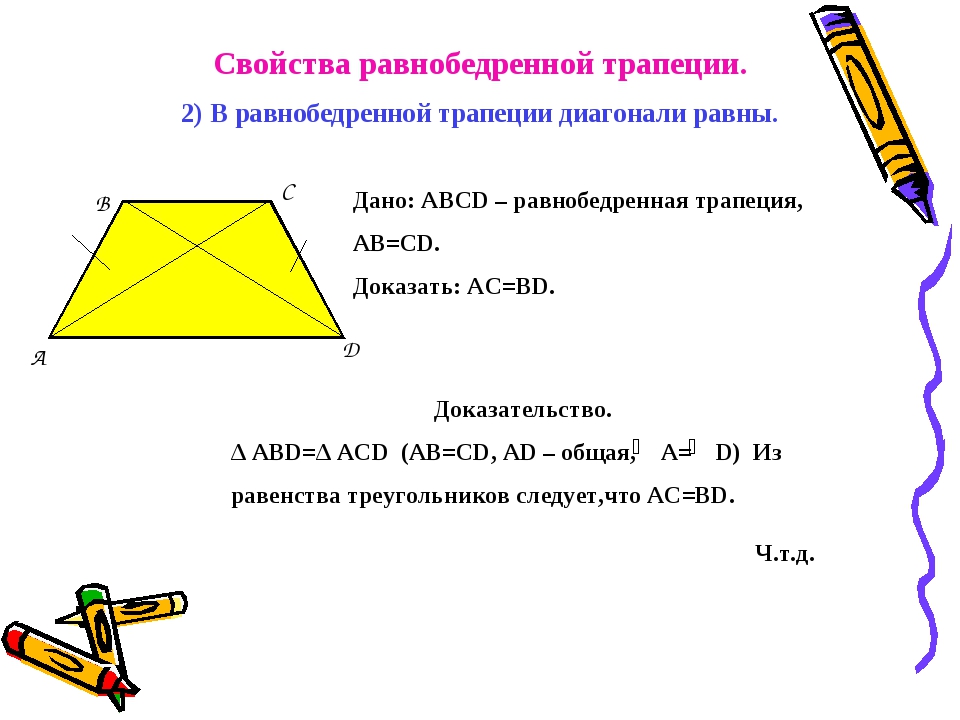 Следовательно, ∠1 = ∠3.
Следовательно, ∠1 = ∠3.
ABC = 180° − ∠3 = 180° − ∠1 = ∠BCD.
Второе свойство равнобедренной трапеции: диагонали равнобедренной трапеции равны.
Дано: ABCD – равнобедренная трапеция, BC || AD
Доказать: AC = BD.
Для доказательства рассмотрим треугольники ABC и DCB. Треугольники ABC и DCB равны (AB = CD, BC – общая сторона, ∠ABC = ∠DCA). Следовательно, AC = BD.
Теоремы, обратные свойствам равнобедренной трапеции, также верны. Это признаки равнобедренной трапеции.
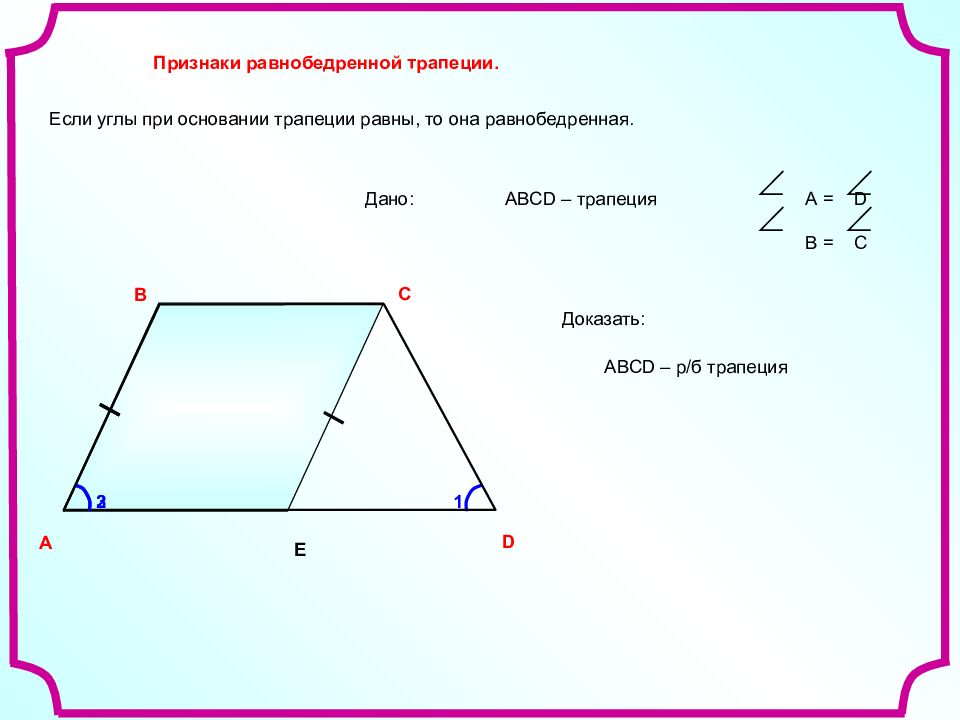
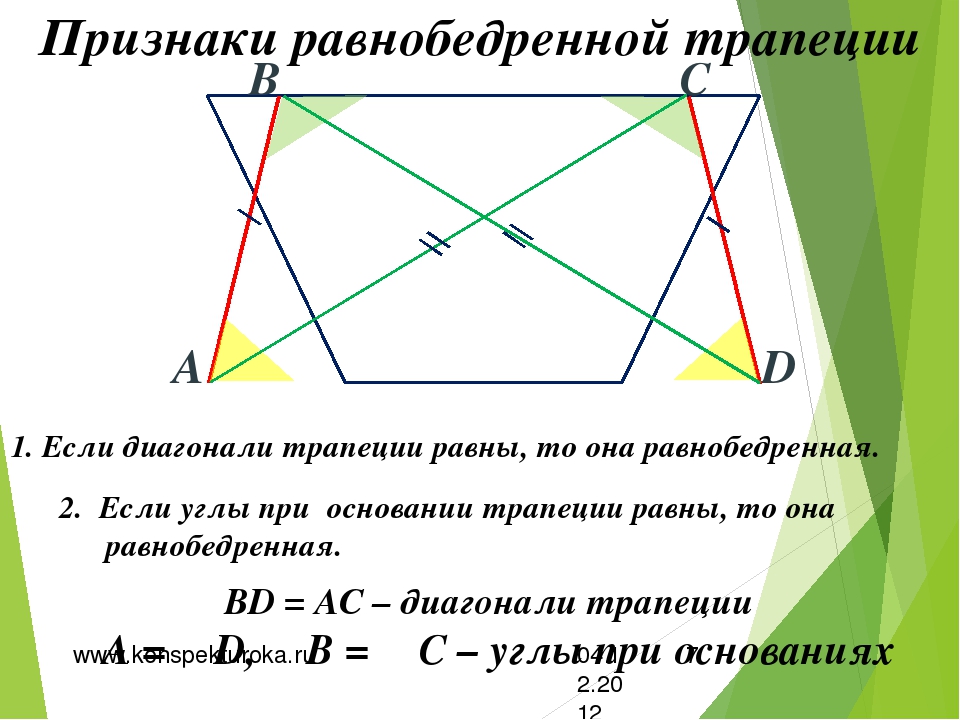
Признак первый: если углы при основании трапеции равны, то трапеция является равнобедренной.
Дано: ABCD – трапеция, BC || AD
∠BAC = ∠CDA
Доказать: ABCD – равнобедренная трапеция
Для доказательства проведем отрезок CK, параллельный AB.
Доказательство:
CK || AB, следовательно ABCK – параллелограмм, тогда AB = CK, ∠A = ∠CKD.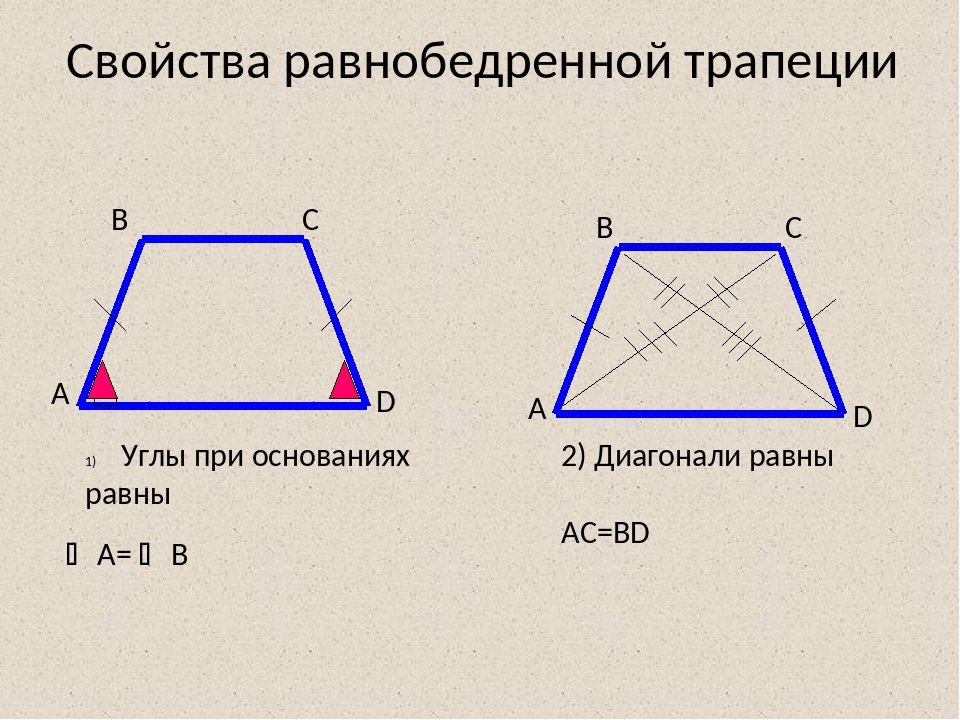
Получится равнобедренный треугольник CKD (∠A = ∠CKD и ∠A = ∠CDA), поэтому
CK = CD и AB = CK = CD. Следовательно, ABCD – равнобедренная трапеция.
Второй признак: если диагонали трапеции равны, то трапеция равнобедренная.
Дано: ABCD –трапеция, BC || AD
AC = BD
Доказать: ABCD – равнобедренная трапеция
Составим план доказательства второго признака, опираясь на который можно провести доказательство самостоятельно.
Проведем отрезок CK, параллельный BD.
План доказательства
- CK || BD
- Доказать, что BCKD – параллелограмм.
- Доказать, что треугольник ACK – равнобедренный.
- Найти равные углы.
- Доказать равенство треугольников ABD и DCA.
- Доказать равенство сторон AB и CD.
- Сделать вывод.
Трапеция
\[{\Large{\text{Произвольная трапеция}}}\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. \circ\).
\circ\).
2) Т.к. \(AD\parallel BC\) и \(BD\) – секущая, то \(\angle DBC=\angle
BDA\) как накрест лежащие.
Также \(\angle BOC=\angle AOD\) как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\).
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\). Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot
AD=S_{\triangle ACD}\). Тогда: \[S_{\triangle AOB}=S_{\triangle ABD}-S_{\triangle AOD}=S_{\triangle ACD}-S_{\triangle AOD}=S_{\triangle
COD}\]
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.
Проведем через точку \(M\) прямую \(MN’\parallel AD\) (\(N’\in CD\)). Тогда по теореме Фалеса (т.к. \(MN’\parallel AD\parallel BC, AM=MB\)) точка \(N’\) — середина отрезка \(CD\). Значит, точки \(N\) и \(N’\) совпадут.
Тогда по теореме Фалеса (т.к. \(MN’\parallel AD\parallel BC, AM=MB\)) точка \(N’\) — середина отрезка \(CD\). Значит, точки \(N\) и \(N’\) совпадут.
2) Докажем формулу.
Проведем \(BB’\perp AD, CC’\perp AD\). Пусть \(BB’\cap MN=M’, CC’\cap
MN=N’\).
Тогда по теореме Фалеса \(M’\) и \(N’\) — середины отрезков \(BB’\) и \(CC’\) соответственно. Значит, \(MM’\) – средняя линия \(\triangle
ABB’\), \(NN’\) — средняя линия \(\triangle DCC’\). Поэтому: \[MM’=\dfrac12 AB’, \quad NN’=\dfrac12 DC’\]
Т.к. \(MN\parallel AD\parallel BC\) и \(BB’, CC’\perp AD\), то \(B’M’N’C’\) и \(BM’N’C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B’M’=M’B\). Значит, \(B’M’N’C’\) и \(BM’N’C\) – равные прямоугольники, следовательно, \(M’N’=B’C’=BC\).
Таким образом:
\[MN=MM’+M’N’+N’N=\dfrac12 AB’+B’C’+\dfrac12 C’D=\] \[=\dfrac12 \left(AB’+B’C’+BC+C’D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.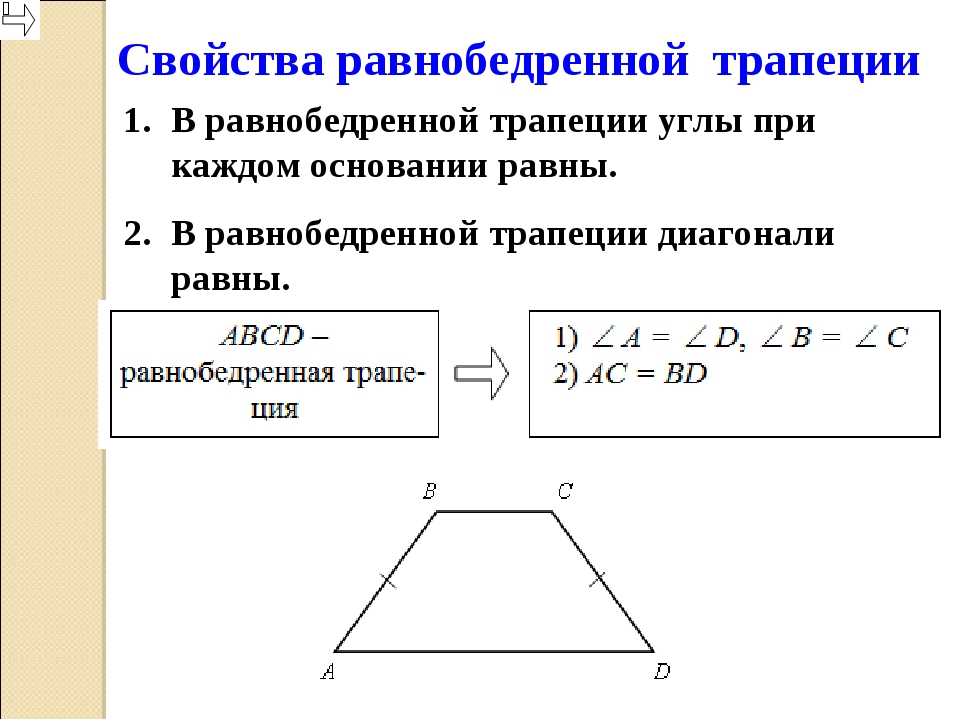
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\), \(N\) и \(M\) лежат на одной прямой.
Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\)). Пусть она пересечет сторону \(AD\) в точке \(M\). Докажем, что \(M\) – середина \(AD\).
Рассмотрим \(\triangle BPN\) и \(\triangle APM\). Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\). Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\). Но \(BN=NC\), следовательно, \(AM=DM\).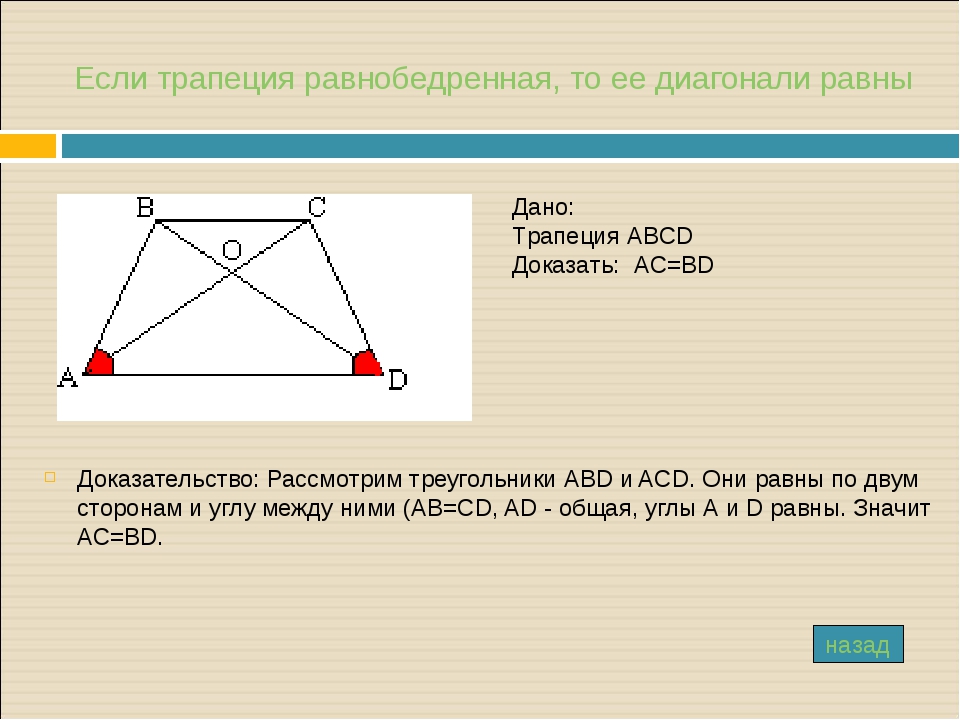
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.
Пусть \(N\) – середина \(BC\), \(O\) – точка пересечения диагоналей. Проведем прямую \(NO\), она пересечет сторону \(AD\) в точке \(M\). Докажем, что \(M\) – середина \(AD\).
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle
ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\). Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\). Но \(BN=CN\), следовательно, \(AM=MD\).
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\).
Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\), то \(BM\parallel CN\); \(AD\parallel BC\), тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\).
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\). Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\), то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\).
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку \(\triangle ABD=\triangle ACD\). Следовательно, \(AC=BD\).
3) Т.к. \(\triangle ABD=\triangle ACD\), то \(\angle BDA=\angle CAD\). Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\), такую что \(\angle A = \angle D\).
Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\), то треугольник \(AED\) равнобедренный и \(AE
= ED\). Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\). Аналогично равны углы \(2\) и \(4\), но \(\angle 1 = \angle 2\), тогда \(\angle 3 = \angle 1 = \angle 2 =
\angle 4\), следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\).
В итоге \(AB = AE — BE = DE — CE = CD\), то есть \(AB = CD\), что и требовалось доказать.
2) Пусть \(AC=BD\). Т.к. \(\triangle AOD\sim \triangle BOC\), то обозначим их коэффициент подобия за \(k\). Тогда если \(BO=x\), то \(OD=kx\). Аналогично \(CO=y \Rightarrow AO=ky\).
Т.к. \(\triangle AOD\sim \triangle BOC\), то обозначим их коэффициент подобия за \(k\). Тогда если \(BO=x\), то \(OD=kx\). Аналогично \(CO=y \Rightarrow AO=ky\).
Т.к. \(AC=BD\), то \(x+kx=y+ky \Rightarrow x=y\). Значит \(\triangle AOD\) – равнобедренный и \(\angle OAD=\angle ODA\).
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\), чтд.
Трапеция. Свойства, признаки трапеции | Подготовка к ЕГЭ по математике
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
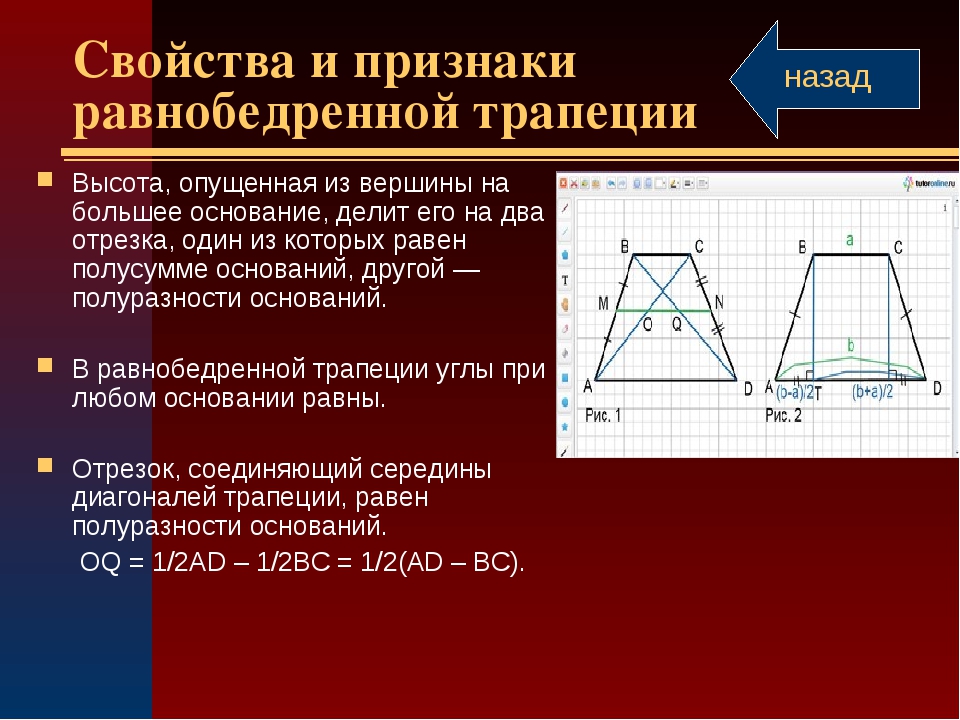
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
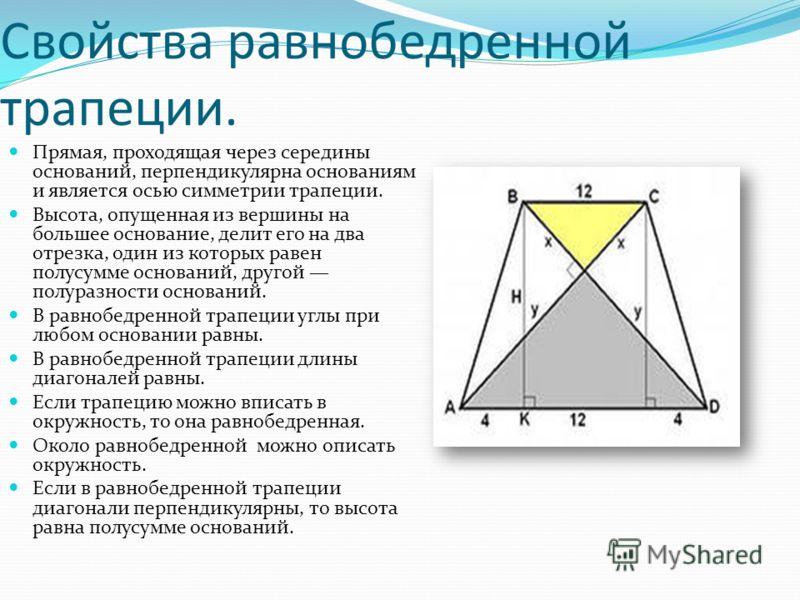
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.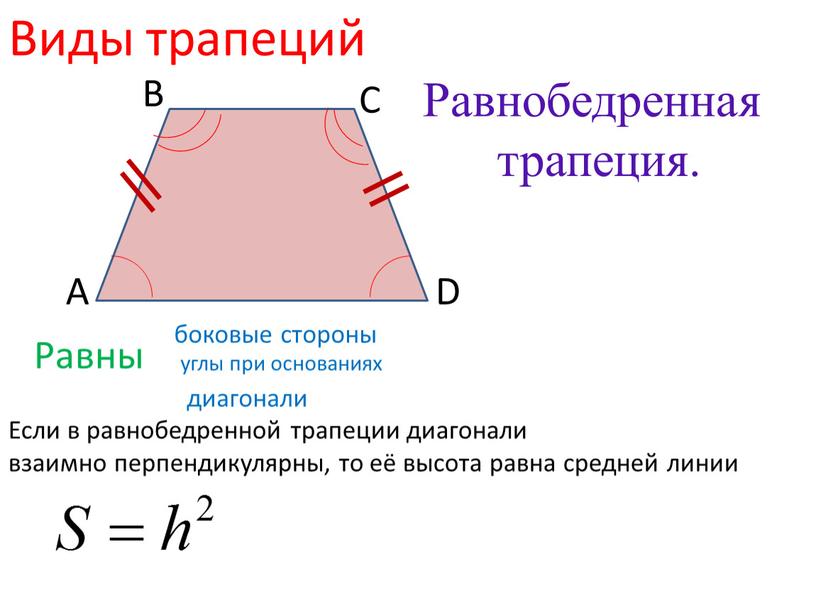
Смотрите также площадь трапеции.
свойства четырёхугольника, теоремы и формулы. Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
ФГКОУ «МКК «Пансион воспитанниц МО РФ»
«УТВЕРЖДАЮ»
Руководитель отдельной дисциплины
(математика, информатика и ИКТ)
Ю. В. Крылова _____________
«___» _____________ 2015 г.
«Трапеция и ее свойства
»
Методическая разработка
преподавателя математики
Шаталиной Елены Дмитриевны
Рассмотрено и
на заседании ПМО от _______________
Протокол №______
Москва
2015 год
Оглавление
Введение 2
Определения 3
Свойства равнобедренной трапеции 4
Вписанные и описанные окружности 7
Свойства вписанных и описанных трапеций 8
Средние величины в трапеции 12
Свойства произвольной трапеции 15
Признаки трапеции 18
Дополнительные построения в трапеции 20
Площадь трапеции 25
10. Заключение
Заключение
Список используемой литературы
Приложение
Доказательства некоторых свойств трапеции 27
Задачи для самостоятельных работ
Задачи по теме «Трапеция» повышенной сложности
Проверочный тест по теме «Трапеция»
Введение
Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими.
Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Трапеция встречается впервые у древнегреческого ученого Посидония (2 век до н.э.). В нашей жизни много разных фигур. В 7 классе мы близко познакомились с треугольником, в 8 классе по школьной программе мы начали изучать трапецию.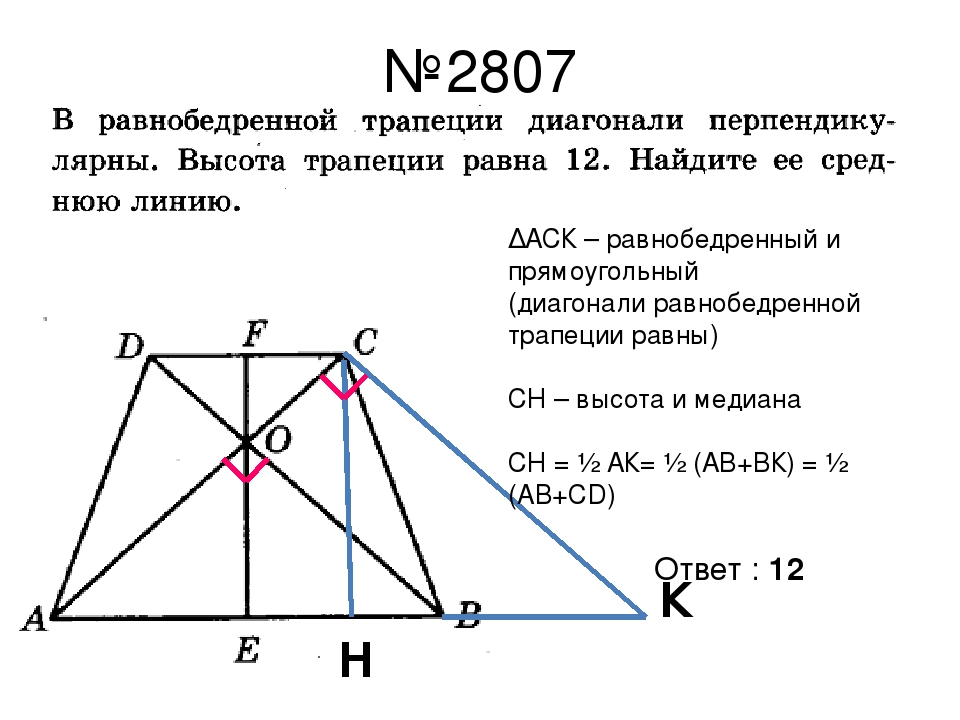 Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.
Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.
В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии.
Трапеция.
Определения
Трапеция
– четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).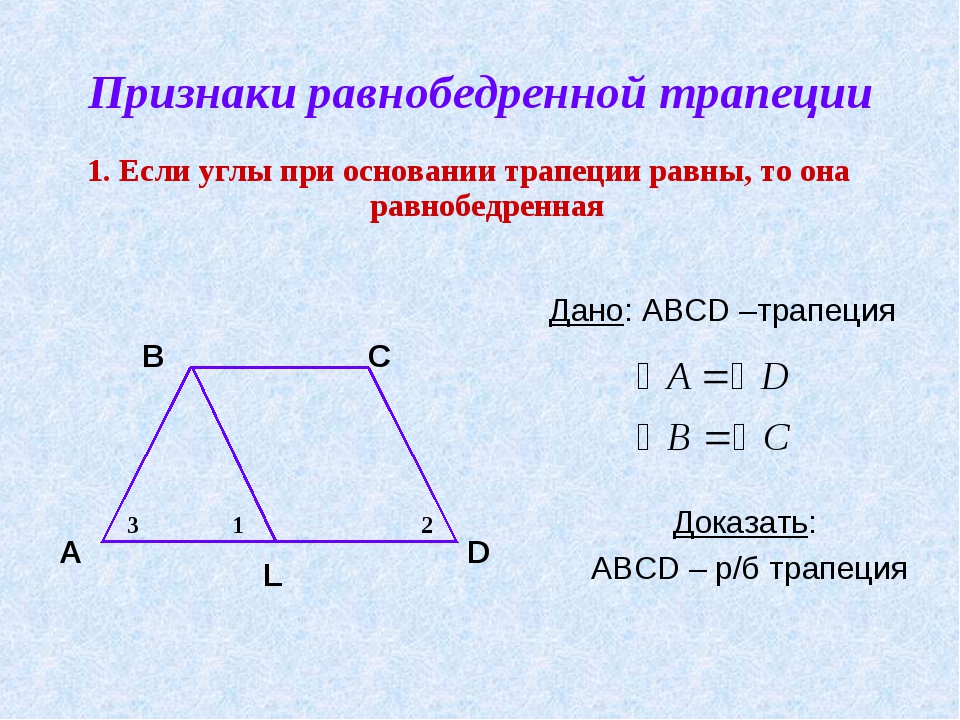
Параллельные стороны трапеции называются
основаниями.
Другие две —
боковые стороны
.
Если боковые стороны равны, трапеция называется
равнобедренной
.
Трапеция, у которой есть прямые углы при боковой стороне, называется
прямоугольной
.
Отрезок, соединяющий середины боковых сторон, называется
средней линией трапеции
.
Расстояние между основаниями называется высотой
трапеции
.
2
. Свойства равнобедренной трапеции
3. Диагонали равнобедренной трапеции равны.
4
1
0. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.
3. Вписанная и описанная окружность
Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.
Е
сли трапеция равнобедренная, то около неё можно описать окружность.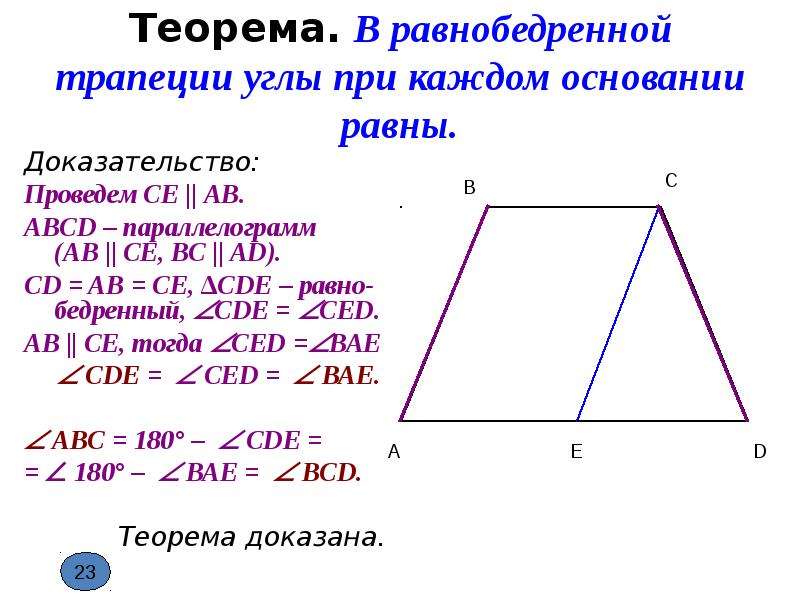
4
. Свойства вписанных и описанных трапеций
2.Если в равнобедренную
трапецию можно вписать окружность, то
сумма длин оснований равна сумме длин боковых сторон. Следовательно, длина боковой стороны равна длине средней линии трапеции.
4
.
Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.
Е
сли в трапецию вписана окружность, которая касается одной из боковых сторон, разбивает ее на отрезки m
и n,
тогда радиус вписанной окружности равен среднему геометрическому этих отрезков.
1
0
. Если окружность построена на меньшем основании трапеции как на диаметре, проходит через середины диагоналей и касается нижнего основания, то углы трапеции 30°, 30°, 150°, 150°.
5.
Средние величины в трапеции
Среднее геометрическое
В любой трапеции с основаниями
a
и
b
для
a
>
b
справедливо неравенство
:
b
˂
h
˂
g
˂
m
˂
s
˂
a
6.
Свойства произвольной трапеции
1
. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой.
2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.
3. Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.
Точка пересечения продолжения боковых сторон произвольной трапеции, точка пересечения ее диагоналей и середин оснований лежат на одной прямой.
5.
При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.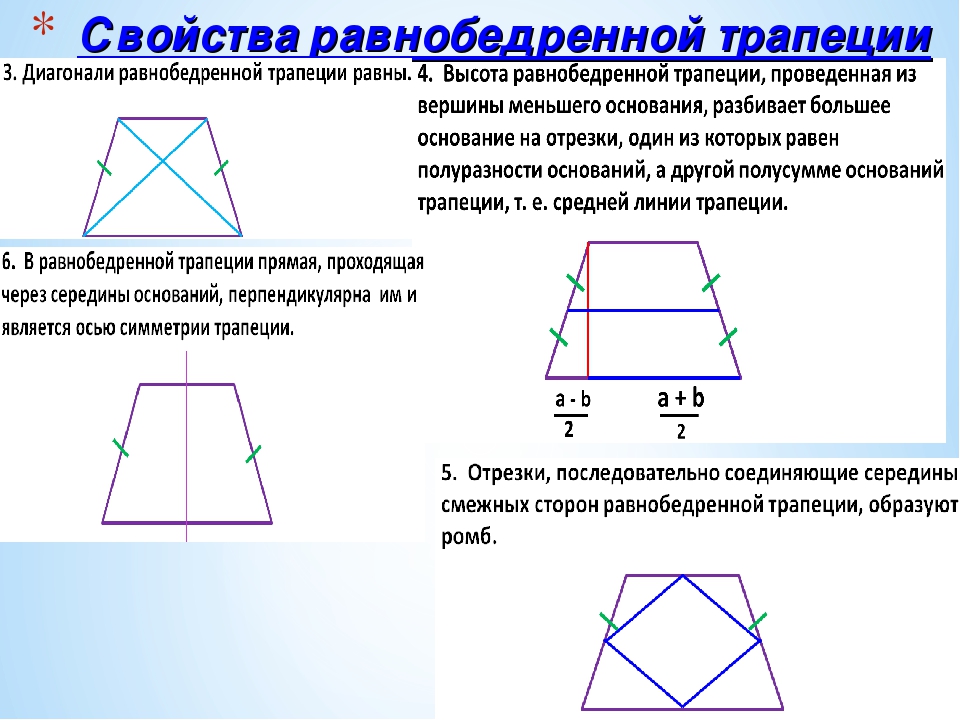 е. имеют равные площади).
е. имеют равные площади).
6.
Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.
d
1
2
+
d
2
2
=
c
2
+
d
2
+ 2
ab
7
.
В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований
d
1
2
—
d
2
2
=
a
2
–
b
2
8
. Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
9. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам.
7
. Признаки трапеции
8
. Дополнительные построения в трапеции
1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции.
Отрезок, соединяющий середины боковых сторон — средняя линия трапеции.
2
. Отрезок, параллельный одной из боковых сторон трапеции, один конец которого совпадает с серединой другой боковой стороны, другой принадлежит прямой, содержащей основание.
3
. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции.
4
. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию.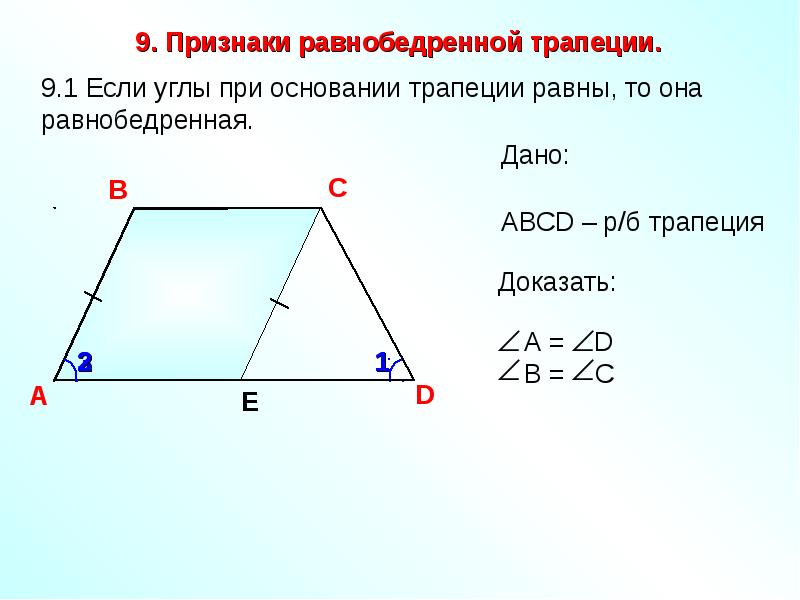
6
. Отрезок, параллельный одной из диагоналей трапеции проводится через вершину – точку, являющуюся концом другой диагонали. В результате получается треугольник с двумя сторонами, равными диагоналям трапеции, и третьей – равной сумме оснований
7
.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции.
8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.
9. Биссектриса угла трапеции отсекает равнобедренный треугольник.
1
0. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
1
1. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
1
2
. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники.
13.
Если в равнобедренную трапецию вписана окружность, то проводят высоту трапеции — среднее геометрическое произведения оснований трапеции или удвоенное среднее геометрическое произведения отрезков боковой стороны, на которые она делится точкой касания.
9. Площадь трапеции
1
. Площадь трапеции равна произведению полусуммы оснований на высоту
S
= ½(a
+
b
)
h
или
П
лощадь трапеции равна произведению средней линии трапеции на высоту S
=
m
h
.
2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.
Площадь равнобедренной трапеции с радиусом вписанной окружности равным
r
и углом при основании
α:
10.
Заключение
ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ?
Трапеция в спорте: Трапеция — безусловно прогрессивное изобретение человечества. Она предназначена для того, чтобы разгрузить наши руки, сделать хождение на виндсерфере комфортным и легким отдыхом. Хождение на короткой доске вообще не имеет смысла без трапеции, так как без нее невозможно правильно распределить тягу между степсом и ногами и эффективно разогнаться.
Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги.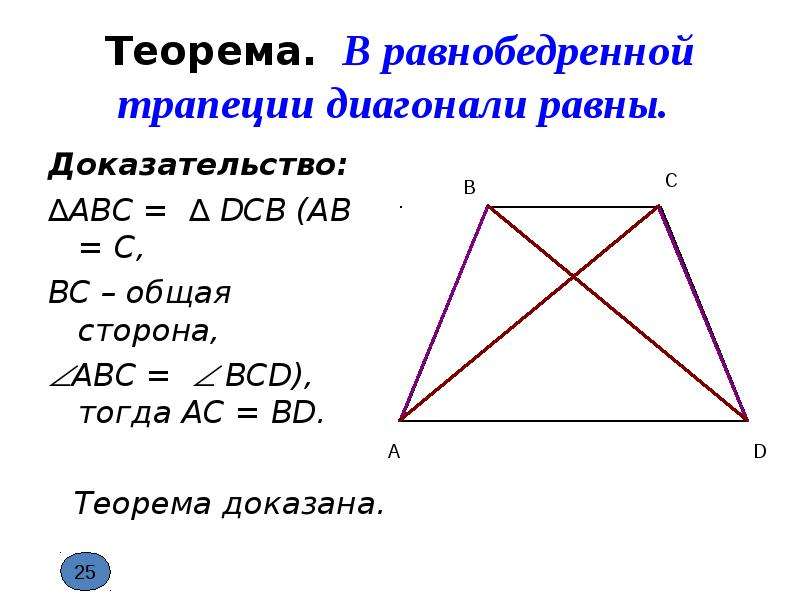 Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.
Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.
Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции.
Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина.
Трапеция — символ архитектуры инков. Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление. Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, и в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках. Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих.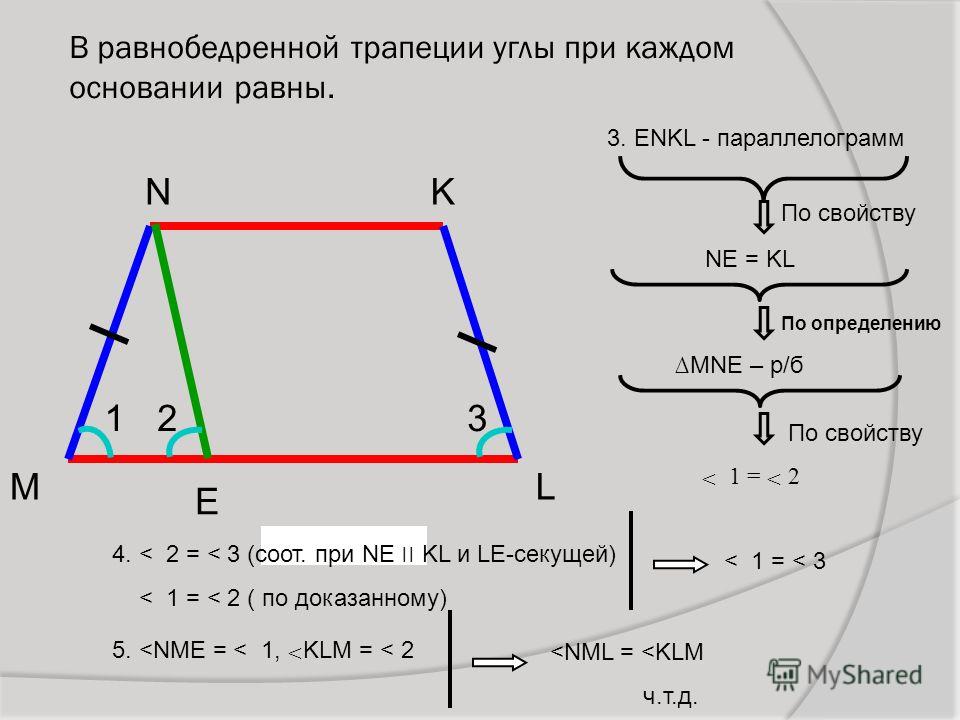
Трапеция в технике: Трапеция используется при конструировании деталей в космических технологиях и в авиации. Например, некоторые солнечные батареи космических станций имеют форму трапеции так как имеют большую площадь, значит накапливают больше солнечной эн
В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас.
Список используемой литературы
Болотов А.А., Прохоренко В.И., Сафонов В.Ф., Математика Теория и Задачи. Книга 1 Учебное пособие для абитуриентов М.1998 Издательство МЭИ.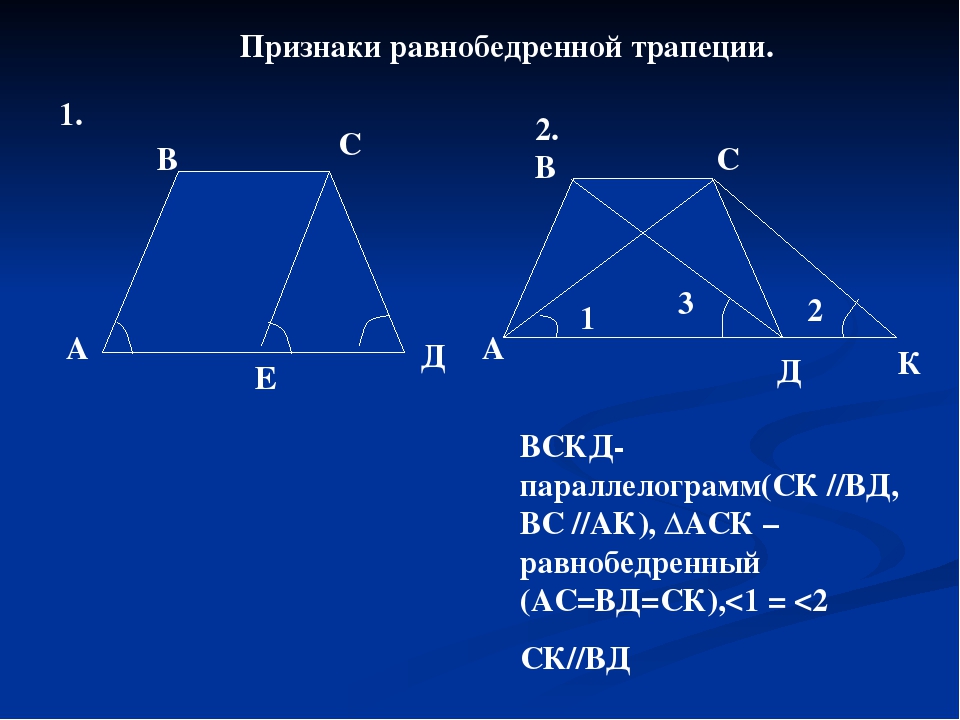
Быков А.А, Малышев Г.Ю., ГУВШ факультет довузовской подготовки. Математика. Учебно-методическое пособие 4 часть М2004
Гордин Р.К. Планиметрия. Задачник.
Иванов А.А.,. Иванов А.П, Математика: Пособие для подготовки к ЕГЕ и поступлению в вузы-М: Издательство МФТИ,2003-288с. ISBN
5-89155-188-3
Пиголкина Т.С, Министерство образования и науки РФ федеральное государственное бюджетное образовательное учреждение дополнительного образования детей «ЗФТШ Московского физико-технического института (государственного университета)». Математика. Планиметрия. Задания №2 для 10-ых классов (2012-2013 учебный год).
Пиголкина Т.С., Планиметрия (часть1).Матиматическая Энциклопедия Абитуриента. М., издательство российского открытого университета 1992.
Шарыгин И.Ф.Избранные задачи по геометрии конкурсных экзаменов в ВУЗЫ (1987-1990) Львов Журнал «Квантор» 1991.
Энциклопедия «Аванта плюс», Математика М., Мир энциклопедий Аванта 2009.
Приложение
1. Доказательство некоторых свойств трапеции.
Доказательство некоторых свойств трапеции.
1.
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках
K
и
L
.
Доказать, что если основания трапеции равны
а
и
b
, то
длина отрезка
KL
равна среднему геометрическому оснований трапеции.
Доказательство
Пусть
О
— точка пересечения диагоналей,
AD
=
а, ВС
=
b
.
Прямая
KL
параллельна основанию
AD
, следовательно,
K
О
║
AD
,
треугольники
В
K
О
и
BAD
подобны, поэтому
(1)
(2)
Подставим (2) в (1)
, получим KO =
Аналогично LO
= Тогда K
L
=
KO
+
LO
=
В
о всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон лежат на одной прямой.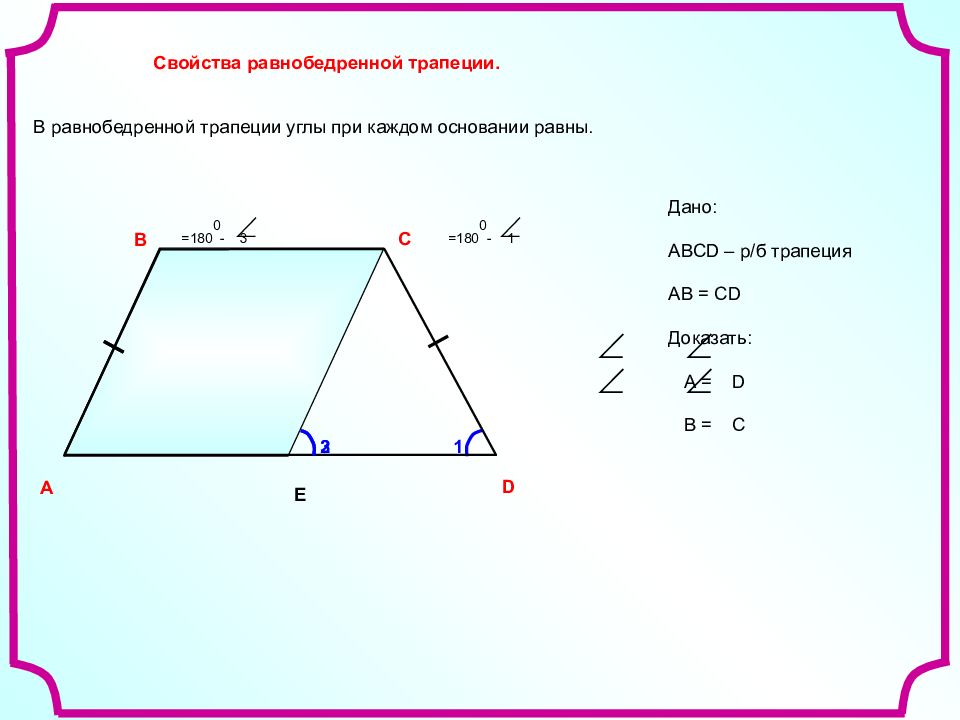
Доказательство: Пусть продолжения боковых сторон пересекаются в точке
К.
Через точку
К
и точку
О
пересечения диагоналей
проведём прямую
КО.
K
Окажем, что эта прямая делит основания пополам.
Обозначим
ВМ
=
х, МС
=
у,
AN
=
и,
ND
=
v
.
Имеем:
∆
ВКМ
~
∆AKN
→
M
x
B
C
Y
∆
MК
C
~
∆NKD
→
→
Определение
Трапеция
— это четырехугольник $A B C D$, две стороны которого параллельны,
а две другие не параллельны (рис. 1).
Параллельные стороны трапеции ($B C$ и $A D$) называются основаниями трапеции
,
а не параллельные ($A B$ и $C D$) — боковыми сторонами
.{\circ}$ (рис 1)
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме:
$$M N=\frac{A D+B C}{2}$$
Среди всех трапеций можно выбрать два особых класса трапеций: прямоугольные и равнобокие трапеции.
Определение
Прямоугольной
называется трапеция, у которой один из углов прямой.
Равнобокой
называется трапеция, у которой боковые стороны равны.
Свойства равнобокой трапеции
- В равнобокой трапеции углы при основании попарно равны $\angle A=\angle D, \angle B=\angle C$.
- Диагонали равнобокой трапеции равны $A C=B D$.
Признаки равнобокой трапеции
- Если углы при основании трапеции равны, то трапеция равнобокая.
- Если в трапеции диагонали равны, то она равнобокая.
Площадь трапеции:
$$S=\frac{a+b}{2} \cdot h$$
где $a$ и $b$ — основания трапеции, а $h$ — ее высота.{\circ}$
Таким образом,
$\angle M L K=\angle N M P$ и $\Delta M N P$ еще и равнобедренный. Следовательно,
$M P=P N$. Так как $L K=M P=2$ дм, следовательно и $P N=2$ дм. Большее основание
$K N=K P+P N$, так как $L M=K P$, получим $K N=2+2=4$ (дм).
Площадь трапеции вычислим по формуле:
$$S=\frac{a+b}{2} \cdot h$$
В нашем случае она примет вид:
$$S_{K L M N}=\frac{L M+K N}{2} \cdot M P$$
Подставляя известные значения, получим
$S_{K L M N}=\frac{2+4}{2} \cdot 2=6$ (дм 2)
Ответ.
$S_{K L M N}=6$ дм 2
Связанные определения
Элементы трапеции
- Параллельные стороны называются основаниями
трапеции. - Две другие стороны называются боковыми сторонами
. - Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
- Расстояние между основаниями называется высотой трапеции.
Виды трапеций
Прямоугольная трапеция
Равнобедренная трапеция
- Трапеция, у которой боковые стороны равны, называется равнобокой
или равнобедренной
. - Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной
.
Общие свойства
- Средняя линия трапеции параллельна основаниям и равна их полусумме.
- Отрезок, соединяющий середины диагоналей, равен полуразности оснований.
- Параллельные прямые, пересекающие стороны угла отсекают от сторон угла пропорциональные отрезки.
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
Свойства и признаки равнобедренной трапеции
- Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.
- Высота, опущенная из вершины на большее основание, делит его на два
отрезка, один из которых равен полусумме оснований, другой —
полуразности оснований. - В равнобедренной трапеции углы при любом основании равны.
- В равнобедренной трапеции длины диагоналей равны.
- Если трапецию можно вписать в окружность, то она равнобедренная.
- Около равнобедренной трапеции можно описать окружность .
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная и описанная окружность
Площадь
Эти формулы — одинаковы, так как полусумма оснований равняется средней линии трапеции.
Рассмотрим несколько направлений решения задач, в которых трапеция вписана в окружность.
Когда трапецию можно вписать в окружность? Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию
.
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции лежит внутри трапеции.
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Из треугольника ACD
Из треугольника ABC
Другой вариант найти радиус описанной окружности —
Синусы угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и ACF:
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. Например,
Кстати, использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали
Поэтому одну из них мы назовем большим
, вторую — малым основанием
трапеции. Высотой
трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить «особый вид» высот.
Определение 8.
Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.
Теорема 7
. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, ∠
ВСМ=∠
МDР — накрестлежащие, ∠
ВМС=∠
DМР — вертикальные), поэтому ВМ=МР или точка М — середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР:
Теорема 8
. Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
Напомню, что фигуры называются равновеликими, если у них одинаковая площадь. Треугольники АВD и АСD равновелики: у них равные высоты (обозначенные желтым) и общее основание. Эти треугольники имеют общую часть АОD. Их площадь можно разложить так:
Виды трапеций:
Определение 9.
(рис 1) Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Определение 10.
(рис 2) Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Определение 11.
(рис 4) Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Определение 12.
(рис 3) Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.
Свойства равнобокой трапеции:
Теорема 10
. Углы, прилежащие к каждому из оснований равнобокой трапеции, равны.
Доказательство. Докажем, например, равенство углов А и D при большем основании AD равнобокой трапеции АВСD. Для этой цели проведем через точку С прямую параллельную боковой стороне АВ.
Она пересечет большое основание в точке М. Четырехугольник АВСМ являеся параллелограммом, т.к. по построению имеет две пары параллельных сторон. Следовательно, отрезок СМ секущей прямой, заключенный внутри трапеции
равен её боковой стороне: СМ=АВ. Отсюда ясно, что СМ=СD, треугольник СМD — равнобедренный, ∠
СМD=∠
СDM, и, значит, ∠
А=∠
D.
Углы, прилежащие к меньшему основанию, также равны, т.к. являются для найденных внутренними односторонним и имеют в сумме два прямых.
Теорема 11
. Диагонали равнобокой трапеции равны.
Доказательство. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому АС=BD.
Теорема 13
. Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки.
Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому ∠
ОАD=∠
ОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.
Равнобокая трапеция фигура симметричная.
Определение 13.
Осью сисмметрии равнобокой трапеции называют прямую, проходящую через середины её оснований.
Теорема 14
. Ось сисмметрии равнобокой трапеции перпендикулярна её основаниям.
В теореме 9 мы доказали, что прямая, соединяющая середины оснований трапеции, проходит через точку пересечения диагоналей. Далее (теорема 13) мы доказали, что треугольники АОD и ВОС равнобедренные. ОМ и ОК являются медианами этих треугольников соответственно по определению . Вспомним свойство равнобедренного треугольника : медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника.
Вследвствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Признаки, выделяющие равнобокую трапецию среди всех трапеций:
Теорема 15
. Если углы, прилежищие к одному из оснований трапеции, равны, то трапеция равнобокая.
Теорема 16
. Если диагонали трапеции равны, то трапеция равнобокая.
Теорема 17
. Если продолженные до пересечения боковые стороны трапеции образуют вместе и её большим основанием равнобедренный треугольник, то трапеция равнобокая.
Теорема 18
. Если трапецию можно вписать в окружность, то она равнобокая.
Признак прямоугольной трапеции:
Теорема 19
. Всякий четырехугольник, у которого только два угла при смежных вершинах прямые, является прямоугольной трапецией (очевидно, что две стороны параллельны, т.
AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общуй перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.
Теорема 21
. Площадь трапеции равна произведению полусуммы оснований и высоты оснований.
Доказательство:
Пусть ABCD — данная трапеция, а AB и CD — её основания. Пусть
также AH — высота, опущенная из точки A на прямую CD. Тогда S ABCD = S ACD + S ABC .
Но S ACD = 1/2AH·CD, а S ABC = 1/2AH·AB.
Следовательно, S ABCD = 1/2AH·(AB + CD).
Что и
требовалось доказать.
Вторая формула перешла от четырехугольника.
Доказать что сечение трапеция. Теоремы: свойства трапеции
\[{\Large{\text{Произвольная трапеция}}}\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.\circ\)
.
2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\)
. Пусть \(h\)
– высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot
AD=S_{\triangle ACD}\)
. Тогда: \
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
1) Докажем параллельность.
Проведем через точку \(M\)
прямую \(MN»\parallel AD\)
(\(N»\in CD\)
). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\)
) точка \(N»\)
— середина отрезка \(CD\)
. Значит, точки \(N\)
и \(N»\)
совпадут.
2) Докажем формулу.
Проведем \(BB»\perp AD, CC»\perp AD\)
. Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Тогда по теореме Фалеса \(M»\)
и \(N»\)
— середины отрезков \(BB»\)
и \(CC»\)
соответственно. Значит, \(MM»\)
– средняя линия \(\triangle
ABB»\)
, \(NN»\)
— средняя линия \(\triangle DCC»\)
. Поэтому: \
Т.к. \(MN\parallel AD\parallel BC\)
и \(BB», CC»\perp AD\)
, то \(B»M»N»C»\)
и \(BM»N»C\)
– прямоугольники. По теореме Фалеса из \(MN\parallel AD\)
и \(AM=MB\)
следует, что \(B»M»=M»B\)
. Значит, \(B»M»N»C»\)
и \(BM»N»C\)
– равные прямоугольники, следовательно, \(M»N»=B»C»=BC\)
.
Таким образом:
\
\[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\)
, \(N\)
и \(M\)
лежат на одной прямой.
Проведем прямую \(PN\)
(\(P\)
– точка пересечения продолжений боковых сторон, \(N\)
– середина \(BC\)
). Пусть она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
Рассмотрим \(\triangle BPN\)
и \(\triangle APM\)
. Они подобны по двум углам (\(\angle APM\)
– общий, \(\angle PAM=\angle PBN\)
как соответственные при \(AD\parallel BC\)
и \(AB\)
секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\)
и \(\triangle DPM\)
. Они подобны по двум углам (\(\angle DPM\)
– общий, \(\angle PDM=\angle PCN\)
как соответственные при \(AD\parallel BC\)
и \(CD\)
секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\)
. Но \(BN=NC\)
, следовательно, \(AM=DM\)
.
2) Докажем, что точки \(N, O, M\)
лежат на одной прямой.
Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
\(\triangle BNO\sim \triangle DMO\)
по двум углам (\(\angle OBN=\angle
ODM\)
как накрест лежащие при \(BC\parallel AD\)
и \(BD\)
секущей; \(\angle BON=\angle DOM\)
как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\)
. Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\)
. Но \(BN=CN\)
, следовательно, \(AM=MD\)
.
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\)
.
Из вершин \(B\)
и \(C\)
опустим на сторону \(AD\)
перпендикуляры \(BM\)
и \(CN\)
соответственно. Так как \(BM\perp AD\)
и \(CN\perp AD\)
, то \(BM\parallel CN\)
; \(AD\parallel BC\)
, тогда \(MBCN\)
– параллелограмм, следовательно, \(BM = CN\)
.
Рассмотрим прямоугольные треугольники \(ABM\)
и \(CDN\)
. Так как у них равны гипотенузы и катет \(BM\)
равен катету \(CN\)
, то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\)
.
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\)
– общая, то по первому признаку . Следовательно, \(AC=BD\)
.
3) Т.к. \(\triangle ABD=\triangle ACD\)
, то \(\angle BDA=\angle CAD\)
. Следовательно, треугольник \(\triangle AOD\)
– равнобедренный. Аналогично доказывается, что и \(\triangle BOC\)
– равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\)
, такую что \(\angle A = \angle D\)
.
Достроим трапецию до треугольника \(AED\)
как показано на рисунке. Так как \(\angle 1 = \angle 2\)
, то треугольник \(AED\)
равнобедренный и \(AE
= ED\)
. Углы \(1\)
и \(3\)
равны как соответственные при параллельных прямых \(AD\)
и \(BC\)
и секущей \(AB\)
. Аналогично равны углы \(2\)
и \(4\)
, но \(\angle 1 = \angle 2\)
, тогда \(\angle 3 = \angle 1 = \angle 2 =
\angle 4\)
, следовательно, треугольник \(BEC\)
тоже равнобедренный и \(BE = EC\)
.
В итоге \(AB = AE — BE = DE — CE = CD\)
, то есть \(AB = CD\)
, что и требовалось доказать.
2) Пусть \(AC=BD\)
. Т.к. \(\triangle AOD\sim \triangle BOC\)
, то обозначим их коэффициент подобия за \(k\)
. Тогда если \(BO=x\)
, то \(OD=kx\)
. Аналогично \(CO=y \Rightarrow AO=ky\)
.
Т.к. \(AC=BD\)
, то \(x+kx=y+ky \Rightarrow x=y\)
. Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\)
(\(AC=BD, \angle OAD=\angle ODA, AD\)
– общая). Значит, \(AB=CD\)
, чтд.
— [ Страница 2 ] —
3. Обсудить устно решения задач 1, 2, 3, приведённые в учебнике.
В связи с необходимостью проводить постоянную работу по развитию устной речи учащихся следует требовать от них не только построения сечений в рассматриваемых задачах, но и устного рассказа о ходе построения с соответствующими обоснованиями.
Для краткости записи решений можно использовать известную символику.
Более сложные задачи на построение сечений тетраэдра и параллелепипеда, когда данные точки, через которые проводится сечение, лежат внутри граней, могут быть рассмотрены на факультативных занятиях и спец курсах.
Для классной и домашней работы можно использо вать задачи 74, 75, 79-87, дополнительные задачи к главе I.
Задача 105. Изобразите тетраэдр DABC и отметьте точки M и N на р брах BD и CD и внутреннюю точку K грани ABC. Постройте сечение тетраэдра плоскостью MNK.
Р е ш е н и е. Обозначим секущую плоскость буквой.
Тогда M, N, M CDB, N CDB, CDB = MN.
Возможны два случая: 10) MN BC = P; 20) MN BC.
Рассмотрим их раздельно.
10) Проводим прямую MN. P, K, P ABC, K ABC, ABC = PK. Проводим прямую PK. Пусть она пересе кает стороны AC и AB в точках E и F. Проводим отрез ки NE и MF. Искомое сечение — четыр хугольник MNEF (рис. 1.31).
20) Через точку K проводим EF BC. Проводим отрез ки NE и MF. Искомое сечение — четыр хугольник MNEF.
Задача 85. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью BKL, где K — середина ребра AA1, а L — середина CC1.
Докажите, что построенное сечение — параллелограмм.
Р е ш е н и е. Проведем отрезок KL. Согласно аксиоме А2 он лежит в плоскости сечения.
Так как точки K и L — середины боковых р бер, то отрезок KL проходит через середину диагонали AC1, а по этому согласно свойству 20 параллелепипеда (п. 13) он проходит через середину диагонали BD1 (точка O на ри сунке 1.32).
B, O, следовательно, BD1. Искомое сечение — четырехугольник BLD1K. Так как его диагонали KL и BD1 точкой пересечения делятся пополам, то четыр х угольник BLD1K — параллелограмм.
–  –  –
1. Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, K.
2. В задачах 1-3 найдите периметр сечения, если M, N, K — середины р бер и каждое ребро тетраэдра равно a.
–  –  –
1. Объясните, как построить сечение куба плоско стью, проходящей через три данные точки, являющие ся либо вершинами куба, либо серединами его р бер (три данные точки на рисунках выделены).
2. В задачах 1-4 и 6 найдите периметр сечения, если ребро куба равно a. В задаче 5 докажите, что AE = 1 a.
–  –  –
1. Объясните, как построить сечение параллелепи педа плоскостью, проходящей через точки B, D и M, если M — середина ребра B1C1.
2. Докажите, что построенное сечение есть равно бедренная трапеция.
3. Найдите стороны трапеции.
Р е ш е н и е.
1) Пусть — секущая плоскость, ABCD = BD, BCC1B1 = BM, MN BD, сечение — трапеция BDNM.
2) BB1M = DD1N, BM = DN, трапеция BDNM рав нобедренная.
–  –  –
При решении задач, связанных с сечением тетраэдра некоторой плоскостью, часто оказывается полезной теорема Менелая, в некоторых других задачах — теорема Чевы. Поэтому в классах с углубл нным изучением математики изучение пункта 14 «Задачи на построение сечений» целесообразно совместить с изучением теорем Менелая и Чевы (пункты 95 и 96). Привед м пример такой задачи.
Задача 1. В тетраэдре ABCD на р брах AB, AD и BC взяты соответственно точки K, L и M так, что AK: KB = = 2: 3, AL = LD, BM: MC = 4: 5.
Постройте сечение тетраэдра плоскостью KLM и найдите, в каком отношении эта плоскость делит ребро CD.
Р е ш е н и е.
1) Провед м отрезки KL и KM, а затем продолжим отрезки KL и BD, лежащие в плоскости ABD, до пересечения в точке E (рис. 1.33). Точки E и M лежат в секущей плоскости KLM и также в плоскости BCD.
Проведя отрезок ME, получим точку N, в которой секущая плоскость KLM пересекается с ребром CD.
Четыр хугольник KLNM — искомое сечение.
2) Найд м отношение CN: ND. С этой целью применим теорему Менелая к треугольникам ABD и BCD. На сторонах AB и AD треугольника ABD лежат точки K и L, а на продолжении стороны BD — точка E, прич м точки K, L и E лежат на одной прямой. Поэтому согласно теореме Менелая имеет место равенство
AK BE DL
= 1.
KB ED LA
–  –  –
MC BE находим искомое отношение CN: ND = 15: 8.
С целью использования теоремы Менелая в задаче 105 учебника можно дать дополнительное задание:
Найдите отношение, в котором плоскость MNK делит ребро AB, если CN: ND = 2: 1, BM = MD и точка K — середина медианы AL треугольника ABC. (Ответ: 3: 2.) Аналогичное дополнительное задание можно дать в задаче 106:
Найдите отношение, в котором плоскость MNK делит ребро BC, если она делит ребро AB в отношении 1: 4 (считая от точки A), точка K — середина ребра CD, а точка N лежит на медиане DL треугольника ACD, при ч м DN: NL = 3: 2. (Ответ: 4: 3.) На применение теоремы Чевы можно рассмотреть сле дующую задачу:
Задача 2. На р брах AB, BC и CA тетраэдра ABCD от мечены точки C1, A1, B1 так, что AC1: C1B = 1: 2, BA1: A1C = 2: 3, CB1: B1A = 3: 1.
Докажите, что плоскости ADA1, BDB1 и CAC1 пересекаются по прямой.
–  –  –
1. Повторить основные вопросы темы «Параллельность прямых и плоскостей», заслушав ответы учащихся. Эти вопросы сформулированы в карточках к зач ту № 1.
2. Провести математический диктант № 1.1. Диктант привед н в дидактических материалах .
3. Рассмотреть решения некоторых задач из карточек к зач ту и из учебника.
Изучение темы «Параллельность прямых и плоскос тей» завершается проведением контрольной работы № 1.2 и зач та № 1 по данной теме.
–  –  –
Контрольная работа № 1.2 Вариант 1
10. Прямые a и b лежат в параллельных плоскостях и. Могут ли эти прямые быть: а) параллельными;
20. Через точку O, лежащую между параллельными плоскостями и, проведены прямые l и m. Прямая l пересекает плоскости и в точках A1 и A2 соответст венно, прямая m — в точках B1 и B2. Найдите длину от резка A2B2, если A1B1 = 12 см, B1O: OB2 = 3: 4.
3. Изобразите параллелепипед ABCDA1B1C1D1 и по стройте его сечение плоскостью, проходящей через точ ки M, N и K, являющиеся серединами р бер AB, BC и DD1.
Вариант 2
10. Прямые a и b лежат в пересекающихся плоскостях и. Могут ли эти прямые быть: а) параллельными;
б) скрещивающимися? Сделайте рисунок для каждого возможного случая.
20. Через точку O, не лежащую между параллельны ми плоскостями и, проведены прямые l и m. Прямая l пересекает плоскости и в точках A1 и A2 соответст венно, прямая m — в точках B1 и B2. Найдите длину от резка A1B1, если A2B2 = 15 см, OB1: OB2 = 3: 5.
3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющие ся серединами р бер DC и BC, и точку K, такую, что K DA, AK: KD = 1: 3.
О т в е т ы:
Вариант 2 Вариант 1
10. Рис. 1.35, a b, a b.
10. Рис. 1.34, a b, a b.
3. Сечение — трапеция.
3. Сечение — пятиугольник.
Рис. 1.34 Рис. 1.35
Урок № 24 Зач т № 1. Параллельность прямых и плоскостей Карточка 1
1. Сформулируйте аксиомы А1, А2 и А3 стереометрии.
Сформулируйте и докажите следствия из аксиом.
2. Докажите, что через любую точку пространства, не лежащую на данной прямой, проходит прямая, парал лельная данной, и притом только одна.
3. Плоскость пересекает стороны AB и AC треуголь ника ABC соответственно в точках B1 и C1. Известно, что BC, AB: B1B = 5: 3, AC = 15 см. Найдите AC1.
Карточка 2
1. Сформулируйте определение параллельных прямой и плоскости. Сформулируйте и докажите теорему, выра жающую признак параллельности прямой и плоскости.
2. Докажите, что если одна из двух параллельных прямых пересекает данную плоскость, то и другая пря мая пересекает эту плоскость.
3. Каждое ребро тетраэдра DABC равно 2 см. По стройте сечение тетраэдра плоскостью, проходящей через точки B, C и середину ребра AD. Вычислите периметр сечения.
Карточка 3
1. Сформулируйте определение скрещивающихся пря мых. Сформулируйте и докажите теорему, выражающую признак скрещивающихся прямых.
2. Докажите, что если две прямые параллельны третьей прямой, то они параллельны.
3. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки A, C и M, где M — середина ребра A1D1.
Карточка 4
1. Сформулируйте определение параллельных плоскос тей. Сформулируйте и докажите теорему, выражающую признак параллельности двух плоскостей.
2. Докажите, что через каждую из двух скрещиваю щихся прямых проходит плоскость, параллельная дру гой прямой, и притом только одна.
3. ABCDA1B1C1D1 — куб, ребро которого 4 см. Построй те сечение куба плоскостью, проходящей через точки A, D1 и M, где M — середина ребра BC. Вычислите пери метр сечения.
Карточка 5
1. Докажите, что противоположные грани паралле лепипеда параллельны и равны.
2. Докажите, что если стороны двух углов соответ ственно сонаправлены, то такие углы равны.
3. Параллельные плоскости и пересекают сторону AB угла BAC соответственно в точках A1 и A2, а сторону AC этого угла соответственно в точках B1 и B2. Найдите AA1, если A1A2 = 6 см, AB2: AB1 = 3: 2.
Карточка 6
1. Докажите, что диагонали параллелепипеда пересе каются в одной точке и делятся этой точкой пополам.
2. Докажите, что если две параллельные плоскос ти пересечены третьей, то линии их пересечения парал лельны.
3. Точка C лежит на отрезке AB. Через точку A про ведена плоскость, а через точки B и C — параллельные прямые, пересекающие эту плоскость соответственно в точках B1 и C1. Найдите длину отрезка BB1, если AC: CB = 4: 3, CC1 = 8 см.
1. Карточки к зач ту, содержащие основные вопросы теории и некоторые типичные задачи, даются учащимся заблаговременно (примерно за две недели до проведения зач та).
2. Готовясь к зач ту, учащиеся делают какие то запи си. Эти записи (возможно, в виде черновиков), свиде тельствующие о повторении учебного материала и подго товке к зач ту, учащиеся показывают учителю в день проведения зач та. Они могут быть использованы на зач те. При этом на основе беседы и дополнительных вопросов учитель выясняет глубину усвоения темы учащимися.
3. Зач т проводит учитель с помощью наиболее под готовленных учащихся — консультантов. Для этого класс нужно разделить на несколько групп, в каждой из которых 4-5 учеников. Один из них является помощни ком учителя в проведении зач та. По предыдущим уро кам и в начале зач та учитель должен убедиться в том, что консультанты сами на хорошем уровне владеют учеб ным материалом.
4. В течение урока учитель вед т опрос многих уча щихся. В конце урока он утверждает оценки, выставлен ные консультантами. В отдельных случаях после урока учитель может проверить записи учащихся, выполнен ные на уроке, и после этого выставить окончательную оценку по зач ту.
5. Итоговую оценку за полугодие учитель выставляет на основе текущих оценок за самостоятельные и конт рольные работы, а также устного ответа учащихся.
Решающая роль при этом принадлежит оценке по зач ту.
П Е Р П Е Н Д И К УЛ Я Р Н О С Т Ь П Р Я М Ы Х
И ПЛОСКОСТЕЙ
§ 1. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ
И ПЛОСКОСТИ
–  –  –
Основные задачи урока Ввести понятие перпендикулярных прямых в простран стве, доказать лемму о перпендикулярности двух парал лельных прямых к третьей прямой, дать определение перпендикулярности прямой и плоскости, доказать теоре мы, в которых устанавливается связь между параллель ностью прямых и их перпендикулярностью к плоскости.
1. Напомнить понятие угла между двумя скрещиваю щимися прямыми, ввести понятие перпендикулярности двух прямых в пространстве. Отметить, что перпенди кулярные прямые могут пересекаться и могут быть скре щивающимися (см. рис. 43 учебника).
2. Доказать л е м м у: если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Доказательство основано на использовании понятия угла между прямыми и может быть проведено самими учащимися с опорой на текст и рисунок 44 учебника.
3. Сформулировать определение перпендикулярности прямой и плоскости. Ввести обозначение a. Проил люстрировать понятие перпендикулярности прямой и плоскости с помощью рисунка 45 и примеров из жизни.
4. Доказать т е о р е м у: если одна из двух параллель ных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Доказательство теоремы несложное. Оно основано на определении перпендикулярности прямой и плоскости и рассмотренной выше лемме и состоит из двух этапов:
1) x, x — произвольная прямая. Из условия a следует (по определению перпендикулярности прямой и плоскости), что a x;
2) так как a1 a (по условию) и a x, то (согласно лемме о перпендикулярности двух параллельных пря мых к третьей прямой) a1 x.
Итак, прямая a1 перпендикулярна к произвольной прямой x, лежащей в плоскости. А это означает, что a1.
5. Доказать о б р а т н у ю т е о р е м у: если две прямые перпендикулярны к плоскости, то они параллельны.
Доказательство проводится по учебнику (см. рис. 47, а, б). Повторить это доказательство можно на следующих уроках.
На первый взгляд может показаться странным, поче му эта теорема названа обратной предыдущей теореме.
Ведь в предыдущей теореме условие состояло в том, что a a1 и a, а заключением теоремы было: a1. В дан ной теореме условие состоит в том, что a и a1, а заключение — в том, что a a1.
Таким образом, с формальной точки зрения данная теорема не является обратной предыдущей, поскольку условие и заключение данной теоремы не совпадают со ответственно с заключением и условием предыдущей тео ремы. Тем не менее можно так сформулировать эти тео ремы, что каждая из них будет обратной другой.
Привед м эту формулировку.
Пусть прямая a перпендикулярна к плоскости. Тогда:
если a a1, то a1, и обратно:
если a1, то a a1.
6. Для классной и домашней работы можно исполь зовать задачи 116-118, 120.
Задача 116 а). Дан параллелепипед ABCDA1B1C1D1.
Докажите, что DC B1C1 и AB A1D1, если BAD = 90°.
Р е ш е н и е.
1) В параллелепипеде все грани — параллелограммы. Так как BAD = 90° (по условию), то грань ABCD — прямоуголь ник, поэтому AB AD и DC BC (рис. 2.1).
2) B1C1 BC (так как грань BB1C1C — параллелограмм) и BC DC. Отсюда по лемме о перпендикулярности двух па раллельных прямых к треть ей B1C1 DC. Рис. 2.1
3) Аналогично доказывает ся, что AB A1D1. Действитель но, A1D1 AD (так как AA1D1D — параллелограмм) и AB AD, по этому AB A1D1.
Задача 120. Через точку O пересечения диагоналей квад рата со стороной a проведена прямая OK, перпендикуляр ная к плоскости квадрата.
Найдите расстояние от точки K до вершин квадрата, если Рис. 2.2 OK = b.
Р е ш е н и е.
2) Треугольники KAO, KBO, KCO и KDO равны по двум катетам, откуда KA = KB = KC = KD (рис. 2.2).
KAO получаем AO = a 2. Так как KA =
–  –  –
Урок № 26 Тема урока: Признак перпендикулярности прямой и плоскости Основные задачи урока Изучить теорему, выражающую признак перпендику лярности прямой и плоскости; рассмотреть задачи на применение этой теоремы.
Примерный план проведения урока
1. Повторить теоретический материал предыдущего урока пут м опроса учащихся.
2. В качестве подготовительной работы к изучению нового материала решить задачу 119.
Задача 119. Прямая OA перпендикулярна к плоскос ти OBC, и точка O является серединой отрезка AD.
Докажите, что: а) AB = DB; б) AB = AC, если OB = OC;
в) OB = OC, если AB = AC.
Р е ш е н и е.
а) OA OBC по условию, следовательно, OA OB по определению перпендикулярности прямой к плоскости.
OA = OD по условию задачи, поэтому прямая OB являет ся серединным перпендикуля ром к отрезку AD, и, следова тельно, AB = DB (рис. 2.3).
б) Так как по условию OA OBC, то OA OC. Если OB = OC, то прямоугольные треугольники AOC и AOB равны по двум катетам, и, следовательно, равны их ги потенузы, т. е. AB = AC.
в) Если AB = AC, то прямо угольные треугольники AOC и Рис. 2.3 AOB равны по катету и гипотену зе, откуда следует, что OB = OC.
3. Доказать теорему, выражающую п р и з н а к п е р п е н д и к у л я р н о с т и п р я м о й и п л о с к о с т и: если прямая перпендикулярна к двум пересекающимся пря мым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
В процессе доказательства теоремы выделяются сле дующие этапы:
1) Вначале рассматриваем случай, когда прямая a про ходит через точку O пересечения прямых p и q, лежа щих на плоскости. Доказываем, что прямая a перпен дикулярна к любой прямой, лежащей в плоскости и про ходящей через точку O.
2) Используя лемму о перпендикулярности двух па раллельных прямых к третьей, делаем вывод о перпен дикулярности прямой a к любой прямой, лежащей в плоскости. Это означает, что a.
3) Рассматриваем теперь случай, когда прямая a не проходит через точку O пересечения p и q. В этом слу чае проводим через точку O прямую a1, параллельную пря мой a. В силу упомянутой леммы a1 p и a1 q, и поэто му согласно доказанному в первом случае a1. Отсю да по первой теореме п. 16 следует, что a. Это завершает доказательство теоремы.
4. В связи с тем что доказательство теоремы состоит из нескольких этапов, можно предложить учащимся за писать план доказательства в соответствии с содержани ем слайда 2.1.
Слайд может быть использован при подведении ито гов данного урока и на следующем уроке.
5. Для классной и домашней работы можно использо вать задачи 121, 124, 126, 128.
Задача 128. Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая OM так, что MA = MC, MB = MD. Докажите, что прямая OM перпен дикулярна к плоскости параллелограмма.
–  –  –
1. Сформулируйте определение перпендикулярно сти прямой и плоскости.
2. Теорема. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
–  –  –
Р е ш е н и е.
1) Так как MA = MC (по усло вию) и AO = OC (диагонали па раллелограмма точкой пересе чения делятся пополам), то отрезок MO — медиана равно бедренного треугольника AMC (рис. 2.4).
Следовательно, MO также высота этого треугольника, т. е.
2) Аналогично доказывается, Рис. 2.4 что MO BD.
3) Так как MO AC и MO BD, то по признаку пер пендикулярности прямой и плоскости MO ABCD.
Урок № 27 Тема урока: Теорема о прямой, перпендикулярной к плоскости Основные задачи урока Повторить доказательство теоремы, выражающей при знак перпендикулярности прямой и плоскости; рассмот реть теорему из п. 18: через любую точку пространства проходит прямая, перпендикулярная к данной плоско сти, и притом только одна.
Примерный план проведения урока
1. Повторить доказательство теоремы, выражающей признак перпендикулярности прямой и плоскости.
2. Проверить выборочно решения задач из домашней работы.
3. Сформулировать т е о р е м у: через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Наглядно утверждение теоремы представляется впол не очевидным, однако строгое ее доказательство не явля ется простым.
Учащимся, проявляющим повышенный интерес к ма тематике, можно предложить разобрать доказательство дома самим по учебнику. При этом следует обратить их внимание на то, что в первой части доказательства вво дится в рассмотрение плоскость, проходящая через данную точку M и перпендикулярная к данной прямой a.
Существование такой плоскости доказано в задаче с ре шением, привед нной в п. 17, а единственность такой плоскости доказана в задаче 133, которая также дана с решением. Таким образом, полное доказательство данной теоремы весьма громоздко, и поэтому учитель по своему усмотрению может изложить его с той или иной степе нью полноты в зависимости от уровня класса. Отдельные фрагменты доказательства (задача из п. 17, задача 133) можно рассмотреть на уроках № 28-30, посвящ нных повторению теории и решению задач по теме.
4. Провести фронтальный опрос учащихся, используя слайд 2.2.
–  –  –
5. Для классной и домашней работы можно исполь зовать задачи 122, 123, 125, 127.
Задача 122. Прямая CD перпендикулярна к плоско сти правильного треугольника ABC. Через центр O это го треугольника проведена прямая OK, параллельная прямой CD. Известно, что AB = 16 3 см, OK = 12 см, CD = 16 см. Найдите расстояния от точек D и K до вер шин A и B треугольника.
Р е ш е н и е.
1) По условию задачи OK CD, следовательно, OK ABC (рис. 2.5).
2) Точка O — центр правильного треугольника ABC, следовательно, OA = OB = OC = AB = 16 см.
–  –  –
Уроки № 28-30 Тема уроков: Решение задач на перпендикулярность прямой и плоскости. Повторение вопросов теории Основные задачи уроков Выработать навыки решения основных типов задач на перпендикулярность прямой и плоскости, повторить во просы теории.
1. Повторить вопросы теории в ходе опроса учащихся (пп. 15-18).
2. Решить выборочно задачи 129-137, использовать вопросы 1-9 к главе II.
3. Рассмотреть частично или полностью доказатель ство теоремы из п. 18.
4. Можно использовать задачи из дидактических ма териалов .
5. Можно провести математический диктант (№ 2 в дидактических материалах ).
6. Полезна работа на уроке со слайдом 2.3.
На уроке № 30 проводится самостоятельная работа.
Самостоятельная работа № 2.1 Вариант 1
10. Д а н о: AB, M и K — произвольные точки плос кости. Докажите, что AB MK.
2. Треугольник ABC правильный, точка O — его центр. Прямая OM перпендикулярна к плоскости ABC.
а)0 Докажите, что MA = MB = MC.
б) Найдите MA, если AB = 6 см, MO = 2 см.
–  –  –
Вариант 2
10. Д а н о: прямая MA перпендикулярна к плоскости треугольника ABC. Докажите, что MA BC.
2. Четыр хугольник ABCD — квадрат, точка O — его центр. Прямая OM перпендикулярна к плоскости квад рата.
а)0 Докажите, что MA = MB = MC = MD.
б) Найдите MA, если AB = 4 см, OM = 1 см.
Ответы:
В а р и а н т 1.
В а р и а н т 2.
Задача 129. Прямая AM перпендикулярна к плоскос ти квадрата ABCD, диагонали которого пересекаются в точке O. Докажите, что:
а) прямая BD перпендикулярна к плоскости AMO;
Р е ш е н и е.
а) MA ABCD, следовательно, MA BD по определе нию перпендикулярности прямой и плоскости, BD AC по свойству диагоналей квадрата (рис. 2.7).
Итак, BD AO и BD AM, следовательно, BD AMO по признаку перпендикулярности прямой и плоскости.
б) Так как BD MOA, то прямая BD перпендикуляр на к любой прямой, лежащей в плоскости MOA, в част ности BD MO.
Задача 134. Докажите, что все прямые, проходящие через данную точку M прямой a и перпендикулярные к этой прямой, лежат в плоскости, проходящей через точку M и перпендикулярной к прямой a.
Р е ш е н и е. Обозначим буквой плоскость, проходя щую через точку M прямой a и перпендикулярную к этой прямой, и рассмотрим произвольную прямую b, также про ходящую через точку M и перпендикулярную к прямой a.
Требуется доказать, что b (рис. 2.8). Допустим, что это не так. Тогда плоскость, проходящая через прямые a и b, пересекается с плоскостью по некоторой прямой b1, проходящей через точку M и отличной от прямой b. Так как a и b1, то a b1. Мы получили, что в плоскости через точку M проходят две прямые (b и b1), пер пендикулярные к прямой a, чего не может быть. Значит, предположение неверно и прямая b лежит в плоскости.
Рис. 2.7 Рис. 2.8
Задача 136. Докажите, что если точка X равноудалена от концов данного отрезка AB, то она лежит в плоскости, прохо дящей через середину отрезка AB и перпендикулярной к пря мой AB.
Р е ш е н и е. Обозначим бук вой плоскость, проходящую через середину O отрезка AB и Рис. 2.9 перпендикулярную к прямой AB (рис. 2.9). Пусть точка X равноудалена от концов отрезка AB, т. е. XA = XB. Требуется доказать, что X.
Если точка X лежит на прямой AB, то она совпадает с точкой O, и поэтому X.
Если точка X не лежит на прямой AB, то отрезок XO является медианой равнобедренного треугольника AXB и, следовательно, высотой этого треугольника, т. е.
Таким образом, прямая XO проходит через точку O прямой AB и перпендикулярна к прямой AB. Отсюда сле дует (см. задачу 134), что прямая XO лежит в плоскос ти, и поэтому X.
Задача 137. Докажите, что через каждую из двух взаимно перпендикулярных скрещивающихся прямых проходит плоскость, перпендикулярная к другой пря мой.
Р е ш е н и е. Пусть a и b — взаимно перпендикулярные скрещивающиеся прямые. Докажем, что через прямую a проходит плоскость, перпенди кулярная к прямой b.
1) Через произвольную точ ку O прямой a провед м пря мую b1, параллельную прямой b. Тогда a b1, так как по усло вию a b (рис. 2.10).
2) Обозначим буквой плос кость, проходящую через пере секающиеся прямые a и b1, и провед м через точку O прямую c, перпендикулярную к плоско сти. Тогда c b1, а так как b b1, то c b.
3) Обозначим буквой плос кость, проходящую через пере секающиеся прямые a и c. Так как b a (по условию) и b c, Рис. 2.10 то b (по признаку перпендикулярности прямой и плоскости). Итак, через прямую a проходит плоскость, перпендикулярная к прямой b.
Аналогично доказывается, что через прямую b про ходит плоскость, перпендикулярная к прямой a.
§ 2. ПЕРПЕНДИКУЛЯР И НАКЛОННЫЕ.
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
–  –  –
Основные задачи урока Ввести понятие расстояния от точки до плоскости, до казать теорему о тр х перпендикулярах, показать при менение этой теоремы при решении задач.
Примерный план проведения урока
1. Используя рисунок 51 учебника, ввести понятия перпендикуляра к плоскости, наклонной, проекции на клонной на плоскость. Рассматривая прямоугольный треугольник AMH (см. рис. 51), доказать, что перпен дикуляр, провед нный из данной точки к плоскости, меньше любой наклонной, провед нной из той же точки к этой плоскости. Длина перпендикуляра, провед нного из точки к плоскости, называется расстоянием от этой точки до плоскости.
2. Обратить внимание на замечания 1, 2, 3 в п. 19 учебника, в которых введены понятия расстояния между параллельными плоскостями, параллельными прямой и плос костью, скрещивающимися пря мыми. Полезно выполнить ри сунки и обосновать справедли вость утверждений, привед н ных в замечаниях.
З а м е ч а н и е 1. Если две плоскости параллельны, то все точки одной плоскости равно удалены от другой плоскости.
Пусть, A, M. Про ведем AA0 и MM0, тогда Рис. 2.11 AA0 MM0 (рис. 2.11), поэтому AA0 = MM0 (как отрезки параллельных прямых, заключ нные между параллель ными плоскостями).
Итак, расстояния от двух произвольных точек A и M плоскости до плоскости равны друг другу. То же са мое относится к расстояниям от точек плоскости до плоскости.
Расстояние от произвольной точки одной из парал лельных плоскостей до другой плоскости называется рас стоянием между параллельными плоскостями.
З а м е ч а н и е 2. Если прямая и плоскость параллель ны, то все точки прямой равноудалены от этой плоскости.
Доказательство утверждения приведено в решении за дачи 144, учащиеся могут прочитать его самостоятельно.
Можно предложить другой вариант доказательства.
Пусть a, A a, B a. Проведем AA1 и BB1 (рис. 2.12). Тогда AA1 BB1. Докажем, что AA1 = BB1.
Плоскость, проходящая через параллельные прямые AA1 и BB1, пересекается с плоскостью по прямой A1B1 и содержит прямую AB. Ясно, что AB A1B1 (если бы эти прямые пересекались, то прямая AB (т. е. прямая a) пересекалась бы с плоскостью, что противоречит усло вию a).
Итак, AA1 BB1 и AB A1B1. Следовательно, четыр х угольник ABB1A1 — параллелограмм, и поэтому AA1 = BB1.
Таким образом, расстояния от двух произвольных то чек A и B прямой a до параллельной ей плоскости рав ны между собой.
Если прямая и плоскость параллельны, то расстояни ем между прямой и плоскостью называется расстояние от произвольной точки прямой до этой плоскости.
З а м е ч а н и е 3. Если две прямые скрещивающиеся, то расстоянием между ними называется расстояние меж ду одной из них и плоскостью, проходящей через дру гую прямую параллельно первой прямой.
Целесообразно напомнить, как выполняется построе ние плоскости, содержащей одну из скрещивающихся прямых и параллельной другой прямой (рис. 2.13).
Рис. 2.12 Рис. 2.13
Пусть a b. Через произвольную точку M прямой b провед м прямую a1, параллельную a. Пересекающиеся прямые a1 и b определяют некоторую плоскость, па раллельную прямой a.
Из произвольной точки A прямой a проводим перпен дикуляр AA1 к плоскости. Длина этого перпендикуля ра и есть расстояние между скрещивающимися прямы ми a и b.
В дальнейшем в процессе решения задач можно пока зать, как построить общий перпендикуляр к двум дан ным скрещивающимся прямым a и b, т. е. отрезок, пер пендикулярный к прямым a и b, концы которого лежат на этих прямых.
3. Доказать теорему о тр х перпендикулярах и обрат ную ей теорему. При этом можно использовать рисунок 53 учебника или слайд 2.4.
–  –  –
4. Для классной и домашней работы можно использо вать задачи 138-145, 153.
Задача 143. Расстояние от точки M до каждой из вершин правильного треугольника ABC равно 4 см. Най дите расстояние от точки M до плоскости ABC, если AB = 6 см.
Р е ш е н и е.
1) По условию MA = MB = MC = 4. Пусть MO ABC (рис. 2.14), тогда OA = OB = OC (как проекции равных наклонных, см. задачу 139). Это означает, что точка O — центр окружности, описанной около треугольника ABC,
–  –  –
а OA — радиус этой окружности. Известно, что a3 = R 3, где a3 = AB, R = AO, поэтому AO = 6 = 2 3.
2) Из MAO получаем MO = MA2 – AO2, MO = 16 – 12 = 4 = 2.
О т в е т: 2 см.
Задача 145. Через вершину A прямоугольного тре угольника ABC с прямым углом C проведена прямая AD, перпендикулярная к плоскости треугольника.
а) Докажите, что треугольник CBD прямоугольный.
б) Найдите BD, если BC = a, DC = b.
Р е ш е н и е.
а) Отрезок AC — проекция наклонной DC на плос кость треугольника ABC (рис. 2.15). BC AC по условию, следовательно, BC DC по теореме о тр х перпендикуля рах и поэтому треугольник CBD прямоугольный.
б) BC = a, DC = b. Из BCD получаем BD = BC2 + CD2, BD = a2 + b2.
О т в е т: a2 + b2.
В дальнейшем в процессе решения задач важно обра тить внимание учащихся на обобщ нную теорему о тр х перпендикулярах, когда прямая a1 перпендикулярна к проекции наклонной, но не проходит через основание наклонной.
Урок № Тема урока: Угол между прямой и плоскостью Основные задачи урока Ввести понятие угла между прямой и плоскостью;
рассмотреть задачи, в которых используется это понятие.
Примерный план проведения урока
1. Проверить выборочно решение задач из домашней работы. Решения задач типа 138-142 и доказательство теоремы о тр х перпендикулярах можно обсудить устно, используя готовые рисунки и слайды.
2. Ввести понятие проекции точки на плоскость, про екции фигуры на плоскость. Доказать, что проекцией прямой на плоскость, не перпендикулярной к этой плос кости, является прямая. При этом используются рисун ки 54, 55 учебника.
3. Ввести определение угла между прямой и плоско стью.
4. Разобрать решение задачи 162, привед нное в учеб нике. Доказать, что угол между данной прямой и плос костью является наименьшим из всех углов, кото рые данная прямая образует с прямыми, провед нными в плоскости через точку пересечения прямой с плос костью.
Учащимся полезно сделать краткую запись доказа тельства, привед нного в слайде 2.5.
–  –  –
5. Для классной и домашней работы можно использо вать задачи 163-165, 146-148.
Задача 165. Из точки A, удал нной от плоскости на расстояние d, проведены к этой плоскости наклонные AB и AC под углом 30° к плоскости. Их проекции на пло скость образуют угол 120°. Найдите BC.
–  –  –
Уроки № 33-36 Тема уроков: Повторение теории. Решение задач на применение теоремы о тр х перпендикулярах, на угол между прямой и плоскостью Основные задачи уроков Повторить доказательство теоремы о тр х перпенди кулярах, понятие угла между прямой и плоскостью, за крепить навыки решения задач.
Примерный план проведения уроков
1. На каждом из уроков № 33-35 повторить вопро сы теории пут м опроса учащихся.
2. В процессе решения задач повторить соотношения между элементами прямоугольного треугольника, теоре мы синусов и косинусов.
3. Обратить особое внимание на решение некоторых типовых задач, которые будут использоваться в дальней шем при вычислении площадей поверхностей и объ мов многогранников. К таким задачам относятся, например, задачи 147, 151, 158, 161. Полезно использовать на уро ках привед нный ниже слайд 2.6, который предназначен для фронтальной работы с учащимися, обсуждения под ходов к решению задач из учебника.
4. На уроке № 36 целесообразно провести самостоя тельную работу контролирующего характера.
Самостоятельная работа № 2.2
Вариант 1 Из точки M провед н перпендикуляр MB, равный 4 см, к плоскости прямоугольника ABCD. Наклонные MA и MC образуют с плоскостью прямоугольника углы 45° и 30° соответственно.
а)0 Докажите, что треугольники MAD и MCD прямо угольные.
б)0 Найдите стороны прямоугольника.
в) Докажите, что треугольник BDC является проек цией треугольника MDC на плоскость прямоугольника, и найдите его площадь.
Вариант 2 Из точки M провед н перпендикуляр MD, равный 6 см, к плоскости квадрата ABCD. Наклонная MB образует с плоскостью квадрата угол 60°.
а)0 Докажите, что треугольники MAB и MCB прямо угольные.
б)0 Найдите сторону квадрата.
в) Докажите, что треугольник ABD является проек цией треугольника MAB на плоскость квадрата, и най дите его площадь.
Ответы:
б) AB = 4 см, BC = 4 3 см; в) 8 3 см2.
В а р и а н т 1.
б) 6 см; в) 3 см2.
В а р и а н т 2.
–  –  –
Задача 147. Из точки M провед н перпендикуляр MB к плоскости прямоугольника ABCD. Докажите, что тре угольники AMD и MCD прямоугольные.
Р е ш е н и е.
1) По условию задачи отрезок MB — перпендикуляр к плоскости прямоугольника, следовательно, отрезок AB есть проекция наклонной MA на плоскость прямоуголь ника (рис. 2.17). AD AB (так как ABCD — прямоуголь ник), следовательно, AD MA по теореме о тр х перпен дикулярах. Таким образом, угол MAD прямой и, значит, треугольник AMD прямоугольный.
2) Аналогично, так как DC BC, то DC MC и тре угольник MCD прямоугольный.
Задача 151. Прямая CD перпендикулярна к плоскости треугольника ABC. Докажите, что: а) треугольник ABC является проекцией треугольника ABD на плоскость ABC;
б) если CH — высота треугольника ABC, то DH — высо та треугольника ABD.
Р е ш е н и е.
а) По условию задачи отрезок DC — перпендикуляр к плоскости ABC, следовательно, точка C есть проекция точки D на плоскость ABC, отрезок CB — проекция на клонной DB, а отрезок CA — проекция наклонной DA на плоскость ABC (рис. 2.18).
Все точки отрезка AB лежат в плоскости ABC, поэто му проекцией отрезка AB на плоскость ABC является сам этот отрезок.
Итак, проекциями сторон треугольника ABD на плос кость ABC являются соответствующие стороны треуголь ника ABC.
Очевидно также, что проекция M1 любой внутренней точки M треугольника ABD лежит внутри треугольника ABC и обратно: любая внутренняя точка M1 треугольни ка ABC является проекцией на плоскость ABC некоторой внутренней точки M треугольника ABD. Это и означает, что треугольник ABC является проекцией треугольника ABD на плоскость ABC.
б) AB CH по условию, следовательно, AB DH по теореме о тр х перпендикулярах, т. е. DH — высота тре угольника ABD.
–  –  –
Задача 158. Через вершину B ромба ABCD проведена прямая BM, перпендикулярная к его плоскости. Найди те расстояние от точки M до прямых, содержащих сто роны ромба, если AB = 25 см, BAD = 60°, BM = 12,5 см.
Р е ш е н и е.
1) Проведем BK AD (рис. 2.19). Отрезок BK — про екция наклонной MK на плоскость ромба, AD BK, сле довательно, AD MK по теореме о тр х перпендикуля рах. Длина отрезка MK равна расстоянию от точки M до прямой AD.
Аналогично ME — расстояние от точки M до пря мой DC.
ABK получаем BK = AB sin 60°, BK = 25 3.
3) Треугольник MBK прямоугольный, так как MB ABC. Имеем
–  –  –
4) BK = BE (как высоты ромба). Прямоугольные тре угольники MBK и MBE равны по двум катетам, следо вательно, ME = MK = 25 см.
5) Расстояния от точки M до прямых AB и BC рав ны длине перпендикуляра MB, т. е. равны 12,5 см.
О т в е т: 25 см, 25 см, 12,5 см, 12,5 см.
Задача 161. Луч BA не лежит в плоскости неразв р нутого угла CBD. Докажите, что если ABC = ABD, причем ABC 90°, то проекцией луча BA на плоскость CBD является биссектриса угла CBD.
Р е ш е н и е.
1) Пусть AE CBD. В плоскости ABC провед м пер пендикуляр AM к прямой BC, а в плоскости ABD — пер пендикуляр AK к прямой BD. Так как ABC 90°, то точка M лежит на луче BC (а не на продолжении этого луча). Аналогично так как ABD 90°, то точка K ле жит на луче BD (рис. 2.20).
Так как BC AM, то BC EM (по теореме, обратной теореме о тр х перпендикулярах). Аналогично доказыва ется, что BD EK.
2) Прямоугольные треугольники ABK и ABM равны по гипотенузе (AB — общая гипотенуза) и острому углу (ABC = ABD), следовательно, BM = BK.
3) Прямоугольные треугольники BME и BKE равны по гипотенузе (BE — общая гипотенуза) и катету (BM = BK), следовательно, EM = EK.
4) Точка E равноудалена от сторон угла CBD, следо вательно, она лежит на биссектрисе этого угла, т. е. луч BE — биссектриса угла CBD.
§ 3. ДВУГРАННЫЙ УГОЛ.
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
Урок № 37 Тема урока: Двугранный угол Основные задачи урока Ввести понятия двугранного угла и его линейного угла, рассмотреть задачи на применение этих понятий.
Примерный план проведения урока
1. Ввести понятие двугранного угла, используя рису нок 58 учебника.
2. Ввести понятие линейного угла двугранного угла.
Доказать, что все линейные углы двугранного угла рав ны друг другу (см. рис. 59, а, б).
3. Дать определение градусной меры двугранного угла.
Рассмотреть примеры острого, прямого и тупого двугран ных углов, используя рисунок 60 учебника. Прямой дву гранный угол можно показать на пересечении двух стен классной комнаты, а также стены и потолка или пола.
4. Для классной и домашней работы можно использо вать выборочно задачи 166-170.
Следует обратить внимание учащихся на обозначение двугранных углов. Двугранный угол с ребром AB, на раз ных гранях которого отмечены точки C и D, называется двугранным углом CABD.
Задача 167. В тетраэдре DABC все ребра равны, точка M — середина ребра AC. Докажите, что DMB — линейный угол двугранного угла BACD.
Рис. 2.21 Рис. 2.22
Р е ш е н и е. Медианы BM и DM являются одновремен но высотами правильных треугольников ABC и ADC (рис. 2.21). Поэтому BM AC и DM AC, и, следователь но, DMB является линейным углом двугранного угла при ребре AC основания пирамиды.
Задача 170. Из вершины B треугольника ABC, сторо на AC которого лежит в плоскости, провед н к этой плоскости перпендикуляр BB1. Найдите расстояние от точки B до прямой AC и до плоскости, если AB = 2 cм, BAC = 150° и двугранный угол BACB1 равен 45°.
Р е ш е н и е.
1) Треугольник BAC тупоугольный с тупым углом A, поэтому основание высоты BK, провед нной из вершины B, лежит на продолжении стороны AC. Расстояния от точ ки B до прямой AC и до плоскости равны соответствен но BK и BB1 (рис. 2.22).
2) Так как AC BK, то AC KB1 по теореме, обратной теореме о трех перпендикулярах. Следовательно, BKB1 — линейный угол двугранного угла BACB1. По условию задачи BKB1 = 45°.
3) Из BAK имеем A = 30°, BK = BA sin 30°, BK = 1.
–  –  –
Урок № 38 Тема урока: Признак перпендикулярности двух плоскостей Основные задачи урока Ввести понятие угла между плоскостями; дать опре деление перпендикулярных плоскостей; доказать теоре му, выражающую признак перпендикулярности двух плоскостей; показать применение этой теоремы при ре шении задач.
Примерный план проведения урока
1. Проверить выборочно решение задач из домашней работы. Желательно использовать слайды с готовыми чертежами.
2. Обратить внимание учащихся на то, что при пере сечении двух плоскостей образуются четыре двугранных угла. Если — величина того из четыр х углов, который не превосходит каждый из остальных, то говорят, что угол между пересекающимися плоскостями равен. Яс но, что 0° 90°. Если = 90°, то плоскости называются перпендикулярными. В этом случае каждый из четыр х двугранных углов, образованных пересекающимися плос костями, прямой.
3. Доказать теорему, выражающую признак перпен дикулярности двух плоскостей. Доказательство теоремы можно провести устно по тексту учебника, используя ри сунок 62. Привед нное в учебнике традиционное доказа тельство, как правило, успешно усваивается учащимися.
4. Важно обратить внимание учащихся на следующие два факта, часто используемые при решении задач:
а) Плоскость, перпендикулярная к ребру двугранного угла, перпендикулярна к его граням. (Это утверждение в несколько иной формулировке приведено в п. 23 учеб ника в виде следствия из теоремы.)
б) Перпендикуляр, провед нный из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости.
(Это утверждение доказано в привед нном в учебнике решении задачи 178.)
5. Для классной и домашней работы можно использо вать задачи 171-180.
Задача 171. Гипотенуза прямоугольного равнобедрен ного треугольника лежит в плоскости, а катет накло нен к этой плоскости под углом 30°. Найдите угол между плоскостью и плоскостью треугольника.
Р е ш е н и е.
1) Пусть ABC — данный треугольник, AB, CO. Тогда отрезок OB — проекция катета CB на плос кость. По условию задачи CBO = 30° (рис. 2.23).
2) Пусть в треугольнике COB CO = a, тогда CB = 2a.
3) Проведем CD AB, тогда AB DO по теореме, об ратной теореме о трех перпендикулярах, и CDO — ли нейный угол двугранного угла, образованного при пере сечении плоскости с плоскостью треугольника. Пусть
–  –  –
CDO = x. Это и есть искомый угол между плоскостью и плоскостью треугольника.
4) Из CDB получаем CBD = 45°, так как по усло вию треугольник ACB равнобедренный и прямоуголь
–  –  –
откуда = 45°, т. е. двугранный угол DABC равен 45°.
5) Так как BC DC и AC DC, то ACB — линейный угол двугранного угла BDCA.
Поскольку ACB = 60°, то двугранный угол BDCA ра вен 60°.
О т в е т: 90°, 45°, 60°.
Задача 174. Найдите двугранный угол ABCD тетраэд ра ABCD, если углы DAB, DAC и ACB прямые, AC = CB = 5, DB = 5 5.
Р е ш е н и е.
1) По условию задачи углы DAB и DAC прямые, следо вательно, DA AB и DA AC (рис. 2.25). Отсюда следует, что отрезок DA — перпендикуляр к плоскости ABC, и, следователь но, отрезок AC — проекция наклонной DC на плоскость ABC. Рис. 2.25
2) По условию задачи угол ACB прямой, т. е. BC AC, и, следовательно, BC DC по теореме о тр х перпенди кулярах. Таким образом, ACD — линейный угол дву гранного угла ABCD.
3) Из DCB: DC = DB2 – BC2, DC = 25 5 – 25 = 10.
4) Из DAC получаем ACD = x, cos x = AC, cos x = 5,
–  –  –
Основные задачи урока Ввести понятие прямоугольного параллелепипеда, рассмотреть свойства его граней, двугранных углов, диа гоналей.
Примерный план проведения урока
1. Сформулировать определение прямоугольного па раллелепипеда. Доказать, что все шесть граней прямо угольного параллелепипеда — прямоугольники.
2. Доказать, что все двугранные углы прямоугольно го параллелепипеда прямые.
3. Доказать т е о р е м у: квадрат диагонали прямо угольного параллелепипеда равен сумме квадратов тр х его измерений.
Обратить внимание на аналогию со свойством диаго нали прямоугольника. Можно отметить также, что эта теорема является одним из вариантов пространственной теоремы Пифагора.
Рассмотреть следствие из теоремы: диагонали прямо угольного параллелепипеда равны.
4. Для классной и домашней работы можно использо вать выборочно задачи 187-192.
Рис. 2.26 Рис. 2.27
Задача 191. Дан куб ABCDA1B1C1D1. Докажите, что плоскости ABC1 и A1B1D перпендикулярны.
Р е ш е н и е.
1) BC1 B1C по свойству диагоналей квадрата (рис. 2.26). DC BCC1, поэтому DC BC1, так как BC1 BCC1.
Таким образом, прямая BC1 перпендикулярна к двум пересекающимся прямым DC и CB1, лежащим в плоско сти A1B1D. Следовательно, прямая BC1 перпендикулярна к плоскости A1B1D по признаку перпендикулярности прямой и плоскости.
2) Плоскость ABC1 проходит через прямую BC1, пер пендикулярную к плоскости A1B1D, следовательно, ABC1 A1B1D по признаку перпендикулярности двух плос костей.
Задача 192. Найдите тангенс угла между диагональю куба и плоскостью одной из его граней.
Р е ш е н и е.
1) Пусть ребро куба ABCDA1B1C1D1 равно a. Тогда BD = a 2 (рис. 2.27). Так как D1D ABC, то прямая BD является проекцией прямой BD1 на плоскость грани ABCD, и поэтому угол между этими прямыми есть угол между диагональю BD1 и гранью ABCD. Таким образом, требу ется найти тангенс угла D1BD, величину которого обо значим.
2) Из D1DB получаем tg = 1, tg = a, tg = 2.
–  –  –
Урок № 40 Тема урока: Решение задач на прямоугольный параллелепипед Основные задачи урока Повторить свойства прямоугольного параллелепипеда, решить ряд задач на прямоугольный параллелепипед.
Примерный план проведения урока
1. Повторить вопросы теории пут м опроса учащихся.
2. Проверить выборочно решение задач из домашней работы, используя готовые чертежи, слайды.
3. Для классной и домашней работы можно использо вать задачи 193-196.
Задача 195. Найдите измерения прямоугольного па раллелепипеда ABCDA1B1C1D1, если AC1 = 12 см и диаго наль BD1 составляет с плоскостью грани AA1D1D угол 30°, а с ребром DD1 — угол 45°.
Р е ш е н и е.
Похожие работы:
«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Институт наук о Земле Кафедра физической географии и экология Тюлькова Л.А ГЕОМОРФОЛОГИЯ учебно-методический комплекс. Рабочая программа для студентов направления 05.03.04 « Гидрометеорология», очной формы обучения Тюменский государственный университет Тюлькова Л.А. Геоморфология. Учебно-методический…»
«МИНИСТЕРСТВО ОБРАЗОВАНИЯ КАЛИНИНГРАДСКОЙ ОБЛАСТИ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ КАЛИНИНГРАДСКОЙ ОБЛАСТИ ПРОФЕССИОНАЛЬНАЯ ОБРАЗОВАТЕЛЬНАЯ ОРГАНИЗАЦИЯ «ГУСЕВСКИЙ АГРОПРОМЫШЛЕННЫЙ КОЛЛЕДЖ» УТВЕРЖДАЮ Директор ГБУ КО ПОО ГАПК Л.В. Грубинов 15 августа 2014 года ОСНОВНАЯ ПРОФЕССИОНАЛЬНАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ КАЛИНИНГРАДСКОЙ ОБЛАСТИ ПРОФЕССИОНАЛЬНАЯ ОБРАЗОВАТЕЛЬНАЯ ОРГАНИЗАЦИЯ«ГУСЕВСКИЙ АГРОПРОМЫШЛЕННЫЙ…»
«Тема: ОБРАЗОВАНИЕ в РФ. Общие положения. ВУЗ. ПТО. СШО.ДОУ Дата обновления: 24.02.2015 Аналитический обзор Утверждены рекомендации по актуализации федеральных стандартов высшего образования с целью учета в них положений соответствующих профессиональных стандартов рекомендации по актуализации действующих федеральных государственных Методические образовательных стандартов высшего образования с учетом принимаемых профессиональных стандартов (утв. Минобрнауки России 22.01.2015 N ДЛ-2/05вн)…»
« ОБУЧЕНИЯ) Фамилия Имя Отчество Курс_ факультет коммуникаций и права Группа № _ Результаты рецензирования (графа заполняется преподавателем) _ _ _ _ _ _Преподаватель _ Минск 2014 СОДЕРЖАНИЕ КРАТКИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ РАЗДЕЛ 1. ОБЩЕЕ УЧЕНИЕ О КРИМИНАЛИСТИКЕ ТЕМА 1.1 ПРЕДМЕТ, ИСТОРИЯ, СИСТЕМА, ОБЪЕКТЫ И ЗАДАЧИ. ИСТОРИЯ И МЕТОДОЛОГИЯ…»
«Содержание Аннотация…1. Цели самостоятельной работы студентов. 2. Задачи самостоятельной работы студентов..5 3.Рекомендации по самостоятельному изучению дисциплины..5 4. Виды самостоятельной работы студентов..5 5. Требования к минимуму содержания дисциплины согласно Федеральному государственному образовательному стандарту… 6.Содержание самостоятельной работы по темам дисциплины. 7.Задания для самостоятельной работы студентов 7.1.Тематика рефератов и творческих работ по дисциплине..8…»
«План информационнообразовательных семинаров и вебинаров Первое полугодие 2015-2016 учебный год Октябрь Участие бесплатное. Всем участникам (регистрация обязательна) выдаются 16 октября 2015 16.00–17.00 (время московское) сертификаты об участии в Вебинар «Методические принципы разработки заданий семинарах и вебинарах. Международного конкурса «ПОНИ® в гостях у Пифагора» для учеников 2-4 классов и критерии их оценивания». На вебинаре анализируются цели проведения интеллектуальных состязаний,…»
«РОССИЙСКАЯ ФЕДЕРАЦИЯ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ Государственное образовательное учреждение высшего профессионального образования ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ «УТВЕРЖДАЮ»: Проректор по учебной работе Л.М. Волосникова 08.07. 2011г. Организация логопедической работы в дошкольных образовательных учреждениях Учебно-методический комплекс. Рабочая программа для студентов направления подготовки 050700.62 Специальное (дефектологическое) образование, профиль подготовки Логопедия, форма…»
«Государственное бюджетное профессиональное образовательное учреждение города Москвы «Первый Московский Образовательный Комплекс» Методические рекомендации по выполнению практических работ По профессиональному модулю ПМ 02. Конструирование швейных изделий МДК 02.02. Методы конструктивного моделирования швейных изделий, 3-й курс обучения 262019 Конструирование, моделирование и технология швейных изделий углубленная подготовка (наименование профиля подготовки) Москва ББК Г1 ОДОБРЕНЫ Разработаны на…»
«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ УНИВЕРСИТЕТ ИТМО Е.П. Сучкова, М.С. Белозерова МЕТОДЫ ИССЛЕДОВАНИЯ МОЛОКА И МОЛОЧНЫХ ПРОДУКТОВ Учебно-методическое пособие Санкт-Петербург УДК 637.1/3 Сучкова Е.П., Белозерова М.С. Методы исследования молока и молочных продуктов: Учеб.-метод. пособие. – СПб.: Университет ИТМО; ИХиБТ, 2015. – 47 с. Приведены лабораторные работы по дисциплине «Методы исследования молока и молочных продуктов». Работы посвящены изучению современных методов…»
«Содержание 1. Общие положения..2. Характеристика направления подготовки..3. Характеристика профессиональной деятельности выпускников.3.1. Область профессиональной деятельности выпускника ОП ВО.3.2 Объекты профессиональной деятельности выпускника ОП ВО.3.3 Виды профессиональной деятельности выпускника ОП ВО.3.4 Обобщенные трудовые функции выпускников в соответствии с профессиональными стандартами..8 4. Результаты освоения образовательной программы.. 5. Структура образовательной программы…»
«ФЕДЕРАЛЬНАЯ СЛУЖБА ПО НАДЗОРУ В СФЕРЕ ЗАЩИТЫ ПРАВ ПОТРЕБИТЕЛЕЙ И БЛАГОПОЛУЧИЯ ЧЕЛОВЕКА ФБУН «Федеральный научный центр медико-профилактических технологий управления рисками здоровью населения» ФГБОУ ВПО «Пермский государственный национальный исследовательский университет» АКТУАЛЬНЫЕ НАПРАВЛЕНИЯ РАЗВИТИЯ СОЦИАЛЬНО-ГИГИЕНИЧЕСКОГО МОНИТОРИНГА И АНАЛИЗА РИСКА ЗДОРОВЬЮ Материалы Всероссийской научно-практической конференции с международным участием (15–17 мая 2013 г.) Под редакцией академика РАМН…»
«РАБОЧАЯ ПРОГРАММА ПО ПРЕДМЕТУ «ТЕХНОЛОГИЯ» ДЛЯ 1 КЛАССА «Ж» Составитель: учитель начальных классов Тамбовцева Наталья Сергеевна Москва, 2014-2015 учебный год Пояснительная записка. Рабочая программа по технологии построена на основе требований Федерального государственного стандарта начального общего образования по образовательной области «Технология» и разработана в соответствии с Примерной программой начального общего образования, рабочей программой Н.И. Роговцевой, С.В. Анащенкова…»
«М. С. Соловейчик Н. С. Кузьменко РУССКИЙ ЯЗЫК МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ к учебнику для 2 класса общеобразовательных организаций Пособие для учителя Издание 7-е, переработанное Смоленск Ассоциация XXI век УДК 372.881.116.11.046. ББК 74.268.1Рус С ОБРАТИТЕ ВНИМАНИЕ! Будьте осмотрительны при использовании методических пособий к учебнику, выпускаемых другими издательствами! Если кто-либо из авторов данного учебника не указан в качестве редактора, консультанта или рецензента, пособие может не…»
«СПЕЦИАЛИЗИРОВАННОЕ СТРУКТУРНОЕ ОБРАЗОВАТЕЛЬНОЕ ПОДРАЗДЕЛЕНИЕ ПОСОЛЬСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ В РЕСПУБЛИКЕ МАДАГАСКАР – ОСНОВНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА ПРИ ПОСОЛЬСТВЕ РОССИИ НА МАДАГАСКАРЕ РАБОЧАЯ ПРОГРАММА учебного курса (литература) 5 КЛАСС 2014-2015 учебный год учитель: Егорова И.В. Пояснительная записка Рабочая программа составлена в соответствии с нормативными документами и методическими материалами: Федеральным компонентом государственного образовательного стандарта основного общего…»
«Рассмотрено на заседании МО протокол № от 24.08.2015г. «Проверено» «Утверждаю» _ заместитель директора по УВР директор МБОУ «Лицей «МОК №2» Самофалова Ю.В._ Свердлов В.Я. Рабочая программа по внеурочной деятельности Курс «Школа развития речи» 2015-2016 учебный год Учитель Асоян О.И., Бавыкина И.Е., Леденёва Г.А., Ивашкина Н.В., Саввина О.Ю., Свердлова Л.В. Класс 4 «А», «Б», «В», «Г», «Д», «Е» Предмет «Курс «РЕЧЬ». Юным умникам и умницам. Школа развития речи» (34 часа; 1 час в неделю)…»
«Министерство образования и науки Российской Федерации Амурский государственный университет Е.В. Пшеничникова ОСНОВЫ ПРОЕКТИРОВАНИЯ ОДЕЖДЫ ДЛЯ ИНДИВИДУАЛЬНОГО ПОТРЕБИТЕЛЯ Учебное пособие Рекомендовано Дальневосточным региональным учебнометодическим центром (ДВ РУМЦ) в качестве учебного пособия для студентов, обучающихся по направлению подготовки бакалавров 262000.62 «Технология изделий легкой промышленности», 100100.62 «Сервис» вузов региона Благовещенск Издательство АмГУ ББК 37. 24-2 я 73 П 93…»
«ЗАЩИТА ДЕТЕЙ ОТ ДИСКРИМИНАЦИИ Междисциплинарное учебное пособие CREAN ЗАЩИТА ДЕТЕЙ ОТ ДИСКРИМИНАЦИИ ЗАЩИТА ДЕТЕЙ ОТ ДИСКРИМИНАЦИИ Междисциплинарное учебное пособие Под редакцией Дагмар Кутсар и Ханны Уорминг Редактор перевода на русский язык Заботкина Вера Ивановна д-р филол. наук, проф., Проректор по инновационным международным проектам Российский государственный гуманитарный университет Европейский консорциум университетов, предлагающих магистерские программы по правам ребенка в рамках…»
«Содержание Раздел 1. Перечень планируемых результатов обучения по дисциплине, соотнесенных с планируемыми результатами освоения образовательной программы.. 4 1.1 Перечень планируемых результатов обучения по дисциплине. 4 1.2 Планируемые результаты освоения образовательной программы. 4 Раздел 2. Место дисциплины в структуре образовательной программы. 6 Раздел 3. Объем дисциплины.. 6 Раздел 4. Структура и содержание дисциплины. 7 Раздел 5. Перечень учебно-методического обеспечения для…»
«СОДЕРЖАНИЕ Требования к результатам освоения дисциплины 1. 4 Место дисциплины в структуре ОПОП 2. 5 Структура и содержание дисциплины 3. 6 Структура дисциплины 3.1. 6 Содержание дисциплины 3.2. 7 Перечень учебно-методического обеспечения для самостоятельной работы 4. 9 обучающихся по дисциплине Образовательные технологии 5. 9 Формы контроля освоения дисциплины 6. 9 Перечень оценочных средств для текущего контроля освоения дисциплины 6.1. 9 Состав фонда оценочных средств для проведения…»
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам , мы в течении 1-2 рабочих дней удалим его.
Запоминаем и применяем свойства трапеции
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2.
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k2. - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ.
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b).
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2.
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 1800: α + β = 1800 и γ + δ = 1800.
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 900 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2.
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 1800 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2.
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2.
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ.
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*SАМЕ.
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2.
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ.
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab.
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 1800 — МЕТ = 1800 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной:
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 1500 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 1800. Поэтому КАН = 300 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 300. Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: SАКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см2.
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Вершины трапеции. Материал по геометрии на тему «трапеция и ее свойства». Свойства равнобедренной трапеции
Г.И. Ковалева
МЕТОДИКА ИЗУЧЕНИЯ СВОЙСТВ
ТРАПЕЦИИ
В материалах различных контрольных
работ и экзаменов очень часто встречаются
задачи на трапецию, решение которых
требует от учащихся знаний «непрограммных»
свойств трапеции. (Программными считаются
свойство средней линии трапеции, свойства
диагоналей и углов равнобедренной
трапеции.) Какими же замечательными
свойствами обладает трапеция? Где и
когда их изучать в школьном курсе
геометрии?
Методика изучения свойств
трапеции
Теперь, когда мы видели несколько типов, давайте узнаем о фигурах, которые не обладают свойствами параллелограммов. Напомним, что параллелограммы представляют собой четырехугольники, противоположные стороны которых параллельны. В этом разделе мы рассмотрим четырехугольники, противоположные стороны которых могут пересекаться в некоторой точке. Давайте начнем наше исследование, изучив некоторые свойства трапеций. Определение. Трапеция представляет собой четырехугольник с ровно одной парой параллельных сторон.
После изучения свойства средней
линии трапеции можно сформулировать и
доказать свойство отрезка,
соединяющего середины диагоналей
трапеции.
Отрезок,
соединяющий середины диагоналей
трапеции, равен полуразности оснований.
Отрабатывая основной прием
решения задач на трапецию «провести
две высоты», учащимся необходимо
предложить задачу: «Пусть BT
– высота равнобедренной трапеции ABCD
с основаниями BC
и AD
.
,
.
Найдите длины отрезков AT
и TD
».
«Использование тригонометрии при решении планиметрических задач»
Поскольку трапеция должна иметь ровно одну пару параллельных сторон, нам нужно будет доказать, что одна пара противоположных сторон параллельна, а другая — не в нашей. Если мы забудем доказать, что одна пара противоположных сторон не параллельна, мы не исключаем возможность того, что четырехугольник является параллелограммом. Поэтому этот шаг будет абсолютно необходим, когда мы будем работать над различными упражнениями, включающими трапеции.
Прежде чем мы погрузимся прямо в наше исследование трапецоидов, необходимо будет узнать имена разных частей этих четырехугольников, чтобы быть конкретными относительно его сторон и углов. Все трапеции содержат две основные части: основания и ноги. Противоположные стороны трапеции, параллельные друг другу, называются основаниями. Остальные стороны трапеции, которые пересекаются в какой-то точке, если они расширены, называются ногами трапеции.
Тема «Подобие фигур» очень
благодатна для изучения свойств трапеции.
Например, диагонали трапеции разбивают
ее на четыре треугольника, причем
треугольники, прилежащие к основаниям,
подобны, а треугольники, прилежащие к
боковым сторонам, равновелики. Назовем
это утверждение с
войством
треугольников, на которые разбивается
трапеция ее диагоналями.
Причем первая часть
утверждения доказывается очень легко
через признак подобия треугольников
по двум углам. Вторую часть можно
предложить учащимся в виде задачи.
Подобие образованных треугольников трапеции
Верхняя и нижняя стороны трапеции проходят параллельно друг другу, поэтому они являются основаниями трапеции. Другие стороны трапеции пересекаются, если они расширены, поэтому они являются ногами трапеции. Сегмент, который соединяет середины ног трапеции, называется средним. Длина этого сегмента всегда равна половине суммы трапециевидных оснований или.
Отношение длин отрезков и оснований
Измерение среднего сегмента зависит только от длины трапециевидных оснований. Однако существует важная характеристика, что некоторые трапеции имеют исключительно зависимость от ее ног. Давайте посмотрим на эти трапеции сейчас. Равнобедренная трапеция — трапеция, ноги которой конгруэнтны. По определению, если четырехугольник имеет ровно одну пару параллельных линий, то четырехугольник является трапецией. Определение равнобедренной трапеции добавляет другую спецификацию: ноги трапеции должны быть конгруэнтными.
Аналогично, треугольники
BOC
и АОВ
имеют
общую высоту, если принять за их основания
отрезки CO
и OA
.
Тогда
и
.
Из этих двух предложений следует,
что
.
Есть несколько теорем, которые мы можем использовать, чтобы помочь нам доказать, что трапеция является равнобедренной. Эти свойства перечислены ниже. Трапеция равнобедренная тогда и только тогда, когда базовые углы конгруэнтны. Трапеция является равнобедренной, если и только если диагонали конгруэнтны.
Если трапеция является равнобедренной, то ее противоположные углы являются дополнительными. Кайт представляет собой четырехугольник с двумя различными парами смежных сторон, которые являются конгруэнтными. Напомним, что параллелограммы также имели пары конгруэнтных сторон. Однако их конгруэнтные стороны всегда были противоположными. У змеев есть две пары конгруэнтных сторон, которые встречаются в двух разных точках. Давайте посмотрим на приведенную ниже иллюстрацию, чтобы помочь нам понять, как выглядит змей.
Было бы замечательно не
останавливаться на сформулированном
утверждении, а найти связь
между площадями треугольников, на
которые разбивается трапеция ее
диагоналями
, предложив
учащимся решить задачу: «Пусть O
– точка пересечения диагоналей трапеции
ABCD
с основаниями BC
и AD
.
Известно, что площади треугольников
BOC
и AOD
равны соответственно
и
.
Найдите площадь трапеции».
У кайтов есть несколько свойств, которые помогут нам идентифицировать их из других четырехсторонних. Диагонали кайта встречаются под прямым углом. У кайтов есть ровно одна пара противоположных углов, которые являются конгруэнтными. Эти два свойства проиллюстрированы на диаграмме ниже.
Это наша единственная пара конгруэнтных углов, потому что? Позвольте практике делать некоторые проблемы, которые требуют использования свойств трапеций и воздушных змеев, о которых мы только что узнали. Поскольку нам даны длины оснований трапеции, мы можем выяснить, какова должна быть длина среднего сегмента. Давайте используем формулу, которую мы дали для среднего сегмента, чтобы понять это.
Так как
.
Отсюда
,
из подобия треугольников B
О
C
и AOD
следует, что
.Следовательно,
.
Тогда
С использованием подобия
доказывается и свойство
отрезка, проходящего через точку
пересечения диагоналей трапеции
параллельно основаниям.
Предлагаем учащимся решить задачу:
«Пусть O
– точка пересечения диагоналей трапеции
ABCD
с основаниями BC
и AD
.
,
.
Найдите длину отрезка PK
,
проходящего через точку пересечения
диагоналей трапеции параллельно
основаниям. На какие отрезки делится
PK
точкой О
».
На рисунке нам была дана только мера одного угла, поэтому мы должны иметь возможность выводить больше информации на основе этого одного элемента. Поскольку четырехугольник является равнобедренной трапецией, мы знаем, что базовые углы конгруэнтны. Теперь, давайте выясним, какая сумма?
Вместе они имеют в общей сложности 128 °. Напомним теорему о внутренних углах многоугольника, что внутренние углы четырёхугольника должны быть 360 °. Итак, давайте попробуем использовать это таким образом, чтобы помочь нам определить меру? Сначала давайте подытожим все углы и установите его равным 360 °.
Отсюда
.
Аналогично, из подобия треугольников
DOK
и DBC
,
следует, что
.
Отсюда
и
.
Описанная около трапеции окружность
Таким образом, если мы определяем меры? Это значение означает, что мера? Наконец, мы можем установить 116, равное выражению, показанному в? Хотя вышеописанный метод был глубоким способом решения упражнения, мы могли бы просто использовать свойство, что дополнительные углы равнобедренных трапеций являются дополнительными. Решение таким образом происходит намного быстрее, так как нам нужно только найти, что такое дополнение с углом 64 °.
Как только мы дойдем до этой точки в нашей проблеме, мы просто установим 116 равным 4 и решим, как и раньше. Нам также было дано это? В прошлом мы изучили несколько теорем конгруэнции треугольника, которые могут быть применимы в этой ситуации, если мы можем просто найти другую сторону или угол, которые являются конгруэнтными.
Добиваемся от учащихся осознания
доказанного свойства: отрезок, параллельный
основаниям трапеции, проходящий через
точку пересечения диагоналей и соединяющий
две точки на боковых сторонах, делится
точкой пересечения диагоналей пополам.
Его длина есть среднее гармоническое
оснований трапеции.
Следующее свойство
четырех точек:
в трапеции
точка пересечения диагоналей, точка
пересечения продолжения боковых сторон,
середины оснований трапеции лежат на
одной линии.
Наша новая иллюстрация показана ниже. Ниже приведено двухстоечное геометрическое доказательство этого упражнения. Чтобы получить доступ к таким геометриям, как. Перестаньте бороться и начинайте учиться сегодня с тысяч бесплатных ресурсов! Свойства представлены ссылками на соответствующие уроки. Уроки перечислены в логическом порядке, а это означает, что каждый урок относится к предыдущим. и не ссылается на это. Список объединяет соответствующие уроки, которые расположены на разных страницах этого сайта.
Диагонали и высота трапеции
Трапеция является равнобедренной, если и только если ее базовые углы конгруэнтны. Трапеция является равнобедренной, если и только если ее две диагонали конгруэнтны. Средняя линия трапеции параллельна ее основаниям. Длина средней линии трапеции составляет половину суммы длин ее оснований. В трапеции участок линии, оттянутый от середины боковой стороны, параллельной основаниям, пересекает другую боковую сторону в ее средней точке.
Знакомя учащихся с подобием
фигур (не треугольников), можно предложить
найти длину отрезка разбивающего
трапецию на две подобных.
Таким образом, отрезок
разбивающий трапецию на две подобные
трапеции, имеет длину равную среднему
геометрическому длин оснований.
После вывода формулы площади
трапеции полезно доказать свойство
отрезка, делящего трапецию на две
равновеликие.
Средняя линия трапеции — это локус точек, равноудаленных от двух прямых, содержащих основы трапеции. В трапеции сумма внутренних углов на концах боковой стороны равна 180 °. В трапеции средняя линия делит пополам любой отрезок прямой, соединяющий точку на более коротком основании с точкой на большем основании. В трапеции расстояние между серединами его диагоналей составляет половину разницы длин более крупных и более коротких оснований.
Если в трапеции сумма двух противоположных внутренних углов равна 180 °, то трапеция является равнобедренной. В равнобедренной трапеции прямая, проходящая через диагональное пересечение, параллельное основаниям, делит пополам угол между диагоналями. В равнобедренной трапеции боковая сторона видна под одним углом от любой из двух противоположных вершин.
Составим систему
Решение системы
.
Таким образом, длина
отрезка, делящего трапецию на две
равновеликие, равна
(среднему квадратичному длин оснований).
).
Теперь приводится тот же список уроков, что и краткие аннотации. В равнобедренной трапеции базовые углы конгруэнтны. Теорема 2. Если в трапеции базовые углы конгруэнтны, то трапеция является равнобедренной. Решенные проблемы В равнобедренной трапеции базовый угол составляет 73 °. Найдите все другие углы трапеции. В равнобедренной трапеции базовый угол в три раза меньше внутреннего угла в конце более короткого основания. Найдите все углы трапеции.
В трапеции, отрезок линии, оттянутый от середины боковой стороны, параллельной основаниям, пересекает другую боковую сторону в ее середине. Найдите длину трапеции в средней линии. В трапеции большая база имеет длину 27 см, а она на 10 см длиннее основания.
Чтобы учащиеся осознали связь
между указанными отрезками, необходимо
попросить построить их для данной
трапеции. Без труда учащиеся построят
среднюю линию трапеции и отрезок,
проходящий через точку пересечения
диагоналей трапеции параллельно
основаниям. Где будет лежать третий и
четвертый отрезок? Ответ на этот вопрос
должен привести учащихся к открытию
связи между средними величинами.
Найдите длины трапециевидных оснований. В равнобедренной трапеции две диагонали являются конгруэнтными. Задача 2. Если в трапеции две диагонали конгруэнтны, то трапеция равнобедренна. Задача 3. Любая точка на средней линии трапеции равноудалена от двух параллельных линий, содержащих основания трапеции. Если точка в плоскости эквидистантна от двух параллельных линий, содержащих основания трапеции, то точка принадлежит прямой, содержащей. трапеция в средней линии. Решенная проблема. В трапеции любой сегмент прямой линии, соединяющий точку на более коротком основании с точкой на большем основании, делят пополам на средней линии трапеции.
Признак и свойство вписанного
и описанного четырехугольника должны
быть конкретизированы для всех известных
учащимся четырехугольников, в том числе
и для трапеции.
Свойства описанной трапеции.
Около окружности можно
описать трапецию тогда и только тогда,
когда сумма длин оснований равна сумме
длин боковых сторон.
Первое очевидно. Для доказательства
второго следствия необходимо установить,
что угол COD
прямой, что так же не составляет большого
труда. Зато знание этого следствия
позволяет при решении задач использовать
прямоугольный треугольник.
В трапеции биссектрисы внутренних углов на концах боковой стороны пересекаются под прямым углом. В трапеции биссектрисы внутренних углов на концах боковой стороны пересекаются в точке, лежащей на средней линии трапеции. Задача 4. В равнобедренной трапеции базовый угол равен 60 °. Докажите, что более короткая базовая длина равна разности большей длины основания и длины боковой стороны.
В равнобедренной трапеции диагональ составляет 10 см и составляет 60 ° с основанием. Найдите длину трапеции средней длины. Основания трапеции имеют длину 3 и 5 единиц, одна диагональ перпендикулярна боковой стороне, а другая диагональ делит пополам угол. на большей базе. Найдите высоту трапеции. Используя линейку и компас, построим трапецию, у которой есть основания, совпадающие с двумя заданными сегментами, и боковые стороны, конгруэнтные. два других заданных сегмента.
Конкретизируем следствия для
равнобедренной описанной
трапеции
:
высота равнобедренной описанной . Диагонали и углы трапецииИспользуя линейку и компас, построим трапецию, у которой есть основания, совпадающие с двумя заданными сегментами, а боковые стороны — конгруэнтные. к двум другим заданным сегментам. Геометрия — это особый предмет математики, который касается форм и объектов и связанных с ними проблем. Существуют разные типы геометрических фигур. Несколько важных двумерных фигур — это квадрат, прямоугольник, треугольник, многоугольник, круг, параллелограмм, трапеция, ромб и т.д. форма, ограниченная четырьмя сторонами, называется четырехсторонним. |
Рассмотрим основные принципы
методики изучения свойств трапеции.
Во-первых, это использование
задачного подхода
.
Нет необходимости вводить в теоретический
курс геометрии новые свойства трапеции.
Эти свойства открываются и формулируются
учащимися через решение задач (лучше
систем задач). Важно, чтобы учитель знал,
какие задачи должны быть поставлены и
в какой момент учебного процесса. Кроме
того, каждое свойство может быть ключевой
задачей в системе задач.
Во-вторых, «спиральная»
организация изучения свойств трапеции
.
К отдельным свойствам можно возвращаться
несколько раз, тогда есть вероятность,
что учащиеся их запомнят. Например,
свойство четырех точек можно доказать
при изучении подобия и потом с помощью
векторов. Равновеликость треугольников,
прилежащих к боковым сторонам трапеции,
можно доказать, используя как свойство
треугольников, имеющих равные высоты,
проведенные к сторонам, лежащим на одной
прямой, так и формулу
.
Можно отрабатывать свойства прямоугольного
треугольника на описанной трапеции,
теорему синусов на вписанной трапеции
и так далее.
Предложенное включение
«непрограммных» свойств трапеции в
содержание школьного курса геометрии,
задачная технология их изучения,
неоднократное обращение к свойствам
трапеции при изучении других тем позволят
учащимся более глубоко познать трапецию
и обеспечат успешность решения задач
на применение ее свойств.
Поэтому одну из них мы назовем большим
, вторую — малым основанием
трапеции. Высотой
трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить «особый вид» высот.
Определение 8.
Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.
Теорема 7
. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, ∠
ВСМ=∠
МDР — накрестлежащие, ∠
ВМС=∠
DМР — вертикальные), поэтому ВМ=МР или точка М — середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР:
Теорема 8
. Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
Напомню, что фигуры называются равновеликими, если у них одинаковая площадь. Треугольники АВD и АСD равновелики: у них равные высоты (обозначенные желтым) и общее основание. Эти треугольники имеют общую часть АОD. Их площадь можно разложить так:
Виды трапеций:
Определение 9.
(рис 1) Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Определение 10.
(рис 2) Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Определение 11.
(рис 4) Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Определение 12.
(рис 3) Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.
Свойства равнобокой трапеции:
Теорема 10
. Углы, прилежащие к каждому из оснований равнобокой трапеции, равны.
Доказательство. Докажем, например, равенство углов А и D при большем основании AD равнобокой трапеции АВСD. Для этой цели проведем через точку С прямую параллельную боковой стороне АВ.
Она пересечет большое основание в точке М. Четырехугольник АВСМ являеся параллелограммом, т.к. по построению имеет две пары параллельных сторон. Следовательно, отрезок СМ секущей прямой, заключенный внутри трапеции
равен её боковой стороне: СМ=АВ. Отсюда ясно, что СМ=СD, треугольник СМD — равнобедренный, ∠
СМD=∠
СDM, и, значит, ∠
А=∠
D.
Углы, прилежащие к меньшему основанию, также равны, т.к. являются для найденных внутренними односторонним и имеют в сумме два прямых.
Теорема 11
. Диагонали равнобокой трапеции равны.
Доказательство. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому АС=BD.
Теорема 13
. Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки.
Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому ∠
ОАD=∠
ОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.
Равнобокая трапеция фигура симметричная.
Определение 13.
Осью сисмметрии равнобокой трапеции называют прямую, проходящую через середины её оснований.
Теорема 14
. Ось сисмметрии равнобокой трапеции перпендикулярна её основаниям.
В теореме 9 мы доказали, что прямая, соединяющая середины оснований трапеции, проходит через точку пересечения диагоналей. Далее (теорема 13) мы доказали, что треугольники АОD и ВОС равнобедренные. ОМ и ОК являются медианами этих треугольников соответственно по определению . Вспомним свойство равнобедренного треугольника : медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника.
Вследвствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Признаки, выделяющие равнобокую трапецию среди всех трапеций:
Теорема 15
. Если углы, прилежищие к одному из оснований трапеции, равны, то трапеция равнобокая.
Теорема 16
. Если диагонали трапеции равны, то трапеция равнобокая.
Теорема 17
. Если продолженные до пересечения боковые стороны трапеции образуют вместе и её большим основанием равнобедренный треугольник, то трапеция равнобокая.
Теорема 18
. Если трапецию можно вписать в окружность, то она равнобокая.
Признак прямоугольной трапеции:
Теорема 19
. Всякий четырехугольник, у которого только два угла при смежных вершинах прямые, является прямоугольной трапецией (очевидно, что две стороны параллельны, т.
AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общуй перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.
Теорема 21
. Площадь трапеции равна произведению полусуммы оснований и высоты оснований.
Доказательство:
Пусть ABCD — данная трапеция, а AB и CD — её основания. Пусть
также AH — высота, опущенная из точки A на прямую CD. Тогда S ABCD = S ACD + S ABC .
Но S ACD = 1/2AH·CD, а S ABC = 1/2AH·AB.
Следовательно, S ABCD = 1/2AH·(AB + CD).
Что и
требовалось доказать.
Вторая формула перешла от четырехугольника.
Возможно, будет полезно почитать:
Трапеция
и ее теоремы
Covid-19 привел мир к феноменальному переходу.
За электронным обучением будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
В этом разделе мы обсудим трапецию и ее теоремы.
Трапеция — это четырехугольник, у которого есть хотя бы одна пара параллельных сторон. AB || CD. (если есть две пары параллельных прямых, то это параллелограмм)
Когда непараллельные стороны трапеции равны, то это равнобедренная трапеция.
Теорема 1: Трапеция является равнобедренной тогда и только тогда, когда углы основания совпадают.
Дано: ABCD — равнобедренная трапеция. AD = BC и AB || CD.
Докажите, что: ∠C = ∠D
| Заявления | Причины |
| 1) ABCD — это трапеция. | 1) Дано |
| 2) AB || CD | 2) Учитывая |
| 3) AD = BC | 3) Учитывая |
| 4) DA || CE | 4) По конструкции |
| 5) ADCE — параллелограмм. | 5) По свойствам параллелограмма. |
| 6) DA = CE и DC = AE | 6) По свойствам параллелограмма. |
| 7) BC = CE | 7) BC = AD и AD = CE (переходное свойство) |
| 8) ∠CEB ≅ и CBE | 8) Если BC ≅ CE, то противоположный им угол конгруэнтен. |
| 9) ∠DAB ≅ ∠ABC | 9) свойство параллелограмма и линейных парных углов |
| 10) ∠A + ∠D = 180 и ∠B + ∠C = 180 | 10) Внутренние углы на с той же стороны трансверсали являются дополнительными. |
| 11) ∠A + ∠D = ∠C + ∠B | 11) Транзитивность (правые части совпадают, поэтому левые части равны) |
| 12) ∠D = ∠C | 12) Сверху (∠A = ∠B) |
Пример: В трапеции PQRS, PQ || RS и PS = QR. Если ∠S = 60 0 , найти оставшиеся углы.
Решение:
PQ || RS и PS = QR, поэтому трапеция PQRS является равнобедренной трапецией.
У равнобедренной трапеции углы основания равны.(трапеция и ее теоремы)
∠S = ∠R и ∠P = ∠Q
Но ∠S = 60 0
∴ ∠R = 60 0
Пусть ∠P = ∠Q = x
Сумма всех углов в четырехугольнике 360.
∴ ∠P + ∠Q + ∠S + ∠R = 360
x + x + 60 + 60 = 360
2x +120 = 360
2x = 360-120
2x = 240
∴ x = 240/2
x = 120
∠P = ∠Q = 120 0
__________________________________________________________________
Некоторые важные теоремы трапеций приведены ниже:
| 1.Трапеция является равнобедренной тогда и только тогда, когда базовые углы совпадают. |
| 2. Трапеция является равнобедренной тогда и только тогда, когда диагонали совпадают. |
| 3. Если трапеция равнобедренная, противоположные углы являются дополнительными. |
| Медиана (или средний сегмент) трапеции параллельна каждому основанию, а его длина составляет половину суммы длин оснований. |
| Никогда не предполагайте, что трапеция равнобедренная, если вам не предоставят (или не можете доказать) эту информацию. |
Практика
1) В форме трапеции ABCD, AB || CD и BC = AD. Если m∠C = 65 0 , найдите m∠D.
2) PQRS — это трапеция, в которой PQ || RS. Если ∠P = ∠Q = 40, найдите размеры двух других углов.
3) В трапеции ABCD B = 120 0 Найдите m∠C.
4) В четырехугольнике HELP, если EP = LH, то что это за четырехугольник?
5) В четырехугольнике углы имеют соотношение 4: 5: 3: 6.Найдите размеры каждого угла.
6) Если три угла трапеции равны 130 0 , 120 0 , 50 0 и 2x 0 . Найдите x и 4-й угол.
7) Нарисуйте равнобедренную трапецию с именем PQRS, PS || QR и PQ = SR.
Четырехугольник
• Введение в четырехугольник
• Типы четырехугольника
• Свойства четырехугольника
• Параллелограмм и его теоремы
• Прямоугольник и его теоремы
• Квадрат и его теоремы
• Ромб и его теоремы
• Трапеция и его теоремы
• Воздушный змей и его теоремы
• Теорема средней точки
Геометрия
Домашняя страница
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Страница не найдена | ЗННХС
Страница не найдена | ЗННХС | Официальный сайт
Этот веб-сайт принимает Руководство по обеспечению доступности веб-контента (WCAG 2.0) в качестве стандарта доступности для всех связанных с ним веб-разработок и услуг. WCAG 2.0 также является международным стандартом ISO 40500. Это подтверждает его как стабильный технический стандарт, на который можно ссылаться.
WCAG 2.0 содержит 12 руководств, организованных по 4 принципам: воспринимаемый, работоспособный, понятный и надежный (сокращенно POUR).Для каждого руководства есть проверяемые критерии успеха. Соответствие этим критериям оценивается по трем уровням: A, AA или AAA. Руководство по пониманию и применению Руководства по обеспечению доступности веб-контента 2.0 доступно по адресу: https://www.w3.org/TR/UNDERSTANDING-WCAG20/.
Специальные возможности
Комбинация клавиш быстрого доступа Активация Комбинированные клавиши, используемые для каждого браузера.
Chrome для Linux нажмите (Alt + Shift + shortcut_key)
Chrome для Windows нажмите (Alt + shortcut_key)
Для Firefox нажмите (Alt + Shift + shortcut_key)
Для Internet Explorer нажмите (Alt + Shift + shortcut_key), затем нажмите (ввод)
В Mac OS нажмите (Ctrl + Opt + shortcut_key)
Заявление о доступности (комбинация + 0): страница утверждения, на которой будут показаны доступные ключи доступности.Домашняя страница (комбинация + H): клавиша доступа для перенаправления на домашнюю страницу.
Основное содержимое (комбинация + R): ярлык для просмотра раздела содержимого текущей страницы.
FAQ (комбинация + Q): ярлык для страницы часто задаваемых вопросов.
Контакт (комбинация + C): ярлык для страницы контактов или формы запросов.
Отзыв (комбинация + K): ярлык для страницы обратной связи.
Карта сайта (комбинация + M): ярлык для раздела карты сайта (нижнего колонтитула) на странице.
Поиск (комбинация + S): ярлык для страницы поиска.
Нажмите esc или нажмите кнопку закрытия, чтобы закрыть это диалоговое окно.×
Запрошенная вами страница могла быть перемещена в новое место или удалена с сайта.
Вернитесь на ГЛАВНУЮ СТРАНИЦУ или найдите то, что вы ищете, в поле поиска ниже.
ГЛАВНЫЙ ЛАГЕРЬ: Gen.Luna Street, Estaka, Dipolog City 7100 | (065)212-3604 © 2019- Городское отделение Диполог.Все права защищены. | Разработано: Марожелу А. Магбухос, Джови Э. Абаа | Работает на: php 7.0.0 | MySQL 8.0 |
прямоугольник — это равнобедренная трапеция
Стороны и углы. В чем разница между трапецией и трапецией? Равнобедренная трапеция — это четырехугольник, обладающий следующими свойствами: Один • Используя инструмент «Выделение» (V), раздвиньте линии на расстояние по вашему выбору. Докажите, что Q U A D — равнобедренная трапеция. Чтобы понять, чем прямоугольник отличается от трапеции и равнобедренной трапеции, вот их соответствующие свойства.Прямоугольник. Его свойства … 46 дюймов? Трапеция (в Великобритании ее называют трапецией) имеет пару параллельных противоположных сторон. В евклидовой геометрии равнобедренная трапеция (isosceles trapezium в британском английском) — это выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон. Стороны и углы. Площадь и периметр. * Трапеция (также известная как Трапеция) — это четырехугольник (четырехсторонняя плоская фигура), в котором две из четырех сторон параллельны. * Прямоугольник — это квадриль … Равнобедренная трапеция с основаниями 12 и 16 вписана в круг радиуса 10.Прямоугольник — это четырехугольник с четырьмя прямыми углами. В результате наличия 4 прямых углов у него всегда будет 2 набора параллельных сторон. Трапеция … Третья трапеция выше является примером равнобедренной трапеции. Часто незамеченным последствием является то, что мы должны тщательно определить другой особый вид трапеции, равнобедренную трапецию. 3. Чтобы понять, чем прямоугольник отличается от трапеции и равнобедренной трапеции, вот их соответствующие свойства. Прямоугольник. Его свойства … Ромб.Все свойства трапеций применимы и к прямоугольникам (например, площадь A трапеции составляет половину произведения суммы ее оснований и ее высоты. Периметр равнобедренной трапеции равен 62 см. Нарисуйте две параллельные линии разной длины. Прямоугольник. Трапеции можно классифицировать как разносторонние или равнобедренные в зависимости от длины ног. Параллелограммы не являются четырехугольниками. Пара углов основания равнобедренной трапеции конгруэнтна. Равнобедренная трапеция — это трапеция, у которой непараллельные стороны конгруэнтны.Найдите ар … Три различия между квадратом и прямоугольником, который НЕ является квадратом, заключаются в следующем: (1.) У квадрата 4 совпадающие стороны, то есть все 4 стороны h … В качестве альтернативы, его можно определить как трапеция, у которой обе опоры и оба базовых угла имеют одинаковую меру. Трапеция и равнобедренная трапеция 1. Трапеция — это четырехсторонняя форма (четырехугольник), у которой одна пара противоположных сторон параллельна. Найдите длины диагоналей ABCD. Равнобедренная трапеция приобретает свои свойства благодаря их комбинации.2. Если Ì… Ì… Ì… Ì… = 3x –2, Ì… Ì… Ì… Ì… = 2x + 10 и ¸ Ì… Ì… Ì… Ì… = 14, какова длина каждой базы? В качестве альтернативы его можно определить как трапецию, в которой обе опоры и оба базовых угла имеют одинаковую меру. (неверно) 18. Углы основания равнобедренной трапеции совпадают. Формула площади равнобедренной трапеции: Трапеция — это четырехугольник, у которого один набор противоположных сторон, параллельных друг другу, является минимальным условием. Трапеция может стать прямоугольником … Ее свойства: (а) Противоположные стороны равны и параллельны.Чтобы создать равнобедренную трапецию с двумя равными длинами / углами в Illustrator: 1. Равнобедренная трапеция представляет собой прямоугольник, потому что его противоположные стороны параллельны. Прямоугольник — это четырехугольник, в котором противоположные пары сторон параллельны и имеют одинаковую длину друг другу (тогда как соседние стороны могут иметь разную длину). В этом видео показано, как нарисовать равнобедренную трапецию с длинным основанием (B), коротким основанием (b) и углом в 35 градусов. 14. Ромбы — параллелограммы. Прямоугольник имеет два набора параллельных сторон и четыре равных угла, в то время как трапеция имеет одну пару равных сторон и одну пару равных углов.Y … Диагональ равнобедренной трапеции составляет 20 дюймов. Все ли прямоугольники совпадают с трапециями? К сожалению, этот вопрос не имеет смысла. Вот мои лучшие предположения о том, что у вас может быть … Определяющая характеристика равнобедренной трапеции: пара непараллельных сторон должна быть: _____ 3. Площадь равнобедренной трапеции в случае вписанного в нее круга и если вы знаете среднюю линию, — основания равнобедренной трапеции — равные боковые стороны — радиус вписанной окружности — центр вписанной окружности — среднюю линию (1) ОБЕ ЧЕТЫРЕХСТОРОННИЙ ПОЛИГОН.(2) ОБЕИХ НАСТРОЙКИ ПРОТИВОПОЛОЖНЫХ СТОРОН ЯВЛЯЮТСЯ ПАРАЛЛЕЛЬНЫМИ. (3) В ПРЯМОУГОЛЬНИКЕ ОБЕ НАБОРЫ ПРОТИВОПОЛОЖНЫХ СТОРОН РАВНЫ A … если три стороны равны по длине, а четвертая сторона на 10 см длиннее, найдите площадь трапеции. Найдите площадь большей трапеции до ближайшего целого числа. Медиана трапеции параллельна каждому основанию, а ее длина составляет половину суммы длин оснований. Трапеция (также известная как Трапеция) — это четырехугольник (четырехсторонняя плоская фигура), в котором две из четырех сторон параллельны.Предположим, что Q U A D — четырехугольник с. LB DO Завершите доказательство. Иногда. Сходства между прямоугольником и квадратом: Все 4 угла равны 90 градусам каждый. Противоположные стороны параллельны и равны. Диагонали делят пополам … Всегда. Думайте об этом как о равнобедренном треугольнике с обрезанной вершиной. 0. и составляет с основанием угол 30 градусов. Трапеция: Равнобедренная Трапеция: Трапеция: имеет пару параллельных сторон: является равнобедренной трапецией, когда она имеет равные углы с параллельной стороны. периметр Периметр — это мера расстояния вокруг фигуры.Сходства между прямоугольником и квадратом: Все 4 угла равны 90 градусам каждый. Противоположные стороны параллельны и равны. Диагонали делят пополам каждый … Все прямоугольники равнобедренные трапеции (если не используется определение трапеции, см. Запись о трапеции (http://planetmath.org/Trapezoid) для более подробной информации). Четырехугольник — это замкнутая геометрическая фигура, имеющая четыре стороны. Итак, трапеция — четырехугольник, потому что у нее четыре стороны. Похожий случай … (38) (11) Представьте свое решение Геометрия Какова длина AE? 10 дюйм.Противоположные углы равнобедренной трапеции являются дополнительными. Классификация трапеций. Ромб равносторонний и равноугловой. Отвечено на вопрос 3i-Infotech (9 лет назад) Неразрешенное Решение для чтения (2) Полезна ли эта головоломка? 74,8 дюйма? Четырехугольники, параллелограммы, ромбы, прямоугольники, квадраты, трапеции, равнобедренные трапеции. Учитесь с помощью карточек, игр и многого другого — бесплатно. ДАННЫЙ: ЛОРИ — прямоугольник. Четырехугольник — это замкнутая геометрическая фигура, имеющая четыре стороны. Итак, трапеция — четырехугольник, потому что у нее четыре стороны.Похожий случай … Как определить разницу между ромбом и трапецией? В моей стране то, что вы называете трапецией, мы называем трапецией. Ромб i … Что такое разумное расстояние между двумя… Чтобы понять, чем прямоугольник отличается от трапеции и равнобедренной трапеции, вот их соответствующие свойства. 1. Равнобедренный треугольник имеет ровно одну линию симметрии, прямоугольник — две. В евклидовой геометрии равнобедренная трапеция (isosceles trapezium в британском английском) — это выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон.где h — высота, а b 1 и b 2 — длины основания. Трапеции похожи. Напомним, что диагонали прямоугольника равны И они делят друг друга пополам. Площадь и периметр. Теорема 8. Это зависит от того, какое определение трапеции вы используете. Существует эксклюзивное определение: трапеция — это четырехугольник с ровно одним набором … Поскольку прямоугольник имеет 2 пары равных противоположных сторон и перпендикулярных сторон, диагонали будут равны. Острый треугольник имеет только один острый угол.В равнобедренной трапеции диагонали — равнобедренный треугольник. Треугольник с двумя сторонами равной длины называется равнобедренным треугольником. Центр круга находится внутри трапеции. Равнобедренный треугольник — это треугольник, у которого ровно две стороны равной длины. Решение для Джейми использовал равнобедренную трапецию и прямоугольник, чтобы сформировать показанную фигуру. Недавно я столкнулся со следующей проблемой в учебнике геометрии для средней / старшей школы: «. Посмотрите на правильный треугольник EAC.Теорема 9. A. Изобразите равнобедренную трапецию ABCE, где длины сторон AB и EC равны соответственно 10 и 20. a. 3. Дано: Равнобедренная трапеция POST с Ì… Ì… Ì… Ì… // Ì… Ì… Ì… Ì… и 𠑬 Ì… Ì… Ì… Ì… — его медиана. прямоугольник Площадь квадрата = s2 Формула для площади квадрата Площадь квадрата = (11 см) 2 Площадь замещения квадрата = 121 см2 Свойство умножения 2. Если прямоугольники включены в класс трапеций, то можно кратко определить равнобедренную трапецию как » вписанный четырехугольник с равными диагоналями »или« вписанный четырехугольник с парой параллельных сторон »или« выпуклый четырехугольник с линией симметрии, проходящей через середины противоположных сторон ».Свойство равнобедренной трапеции, в которой она имеет конгруэнтные диагонали, является тем же свойством, что и А. воздушный змей. Если дано СЛОВО воздушного змея, какая пара углов конгруэнтна? — Наконец, отрегулируйте пропорции по своему усмотрению. Некоторые из свойств трапеций: одна пара противоположных сторон параллельна и т. Д. Трапеция равнобедренная, если одна пара противоположных сторон равны. Трапеция — это прямая трапеция, если один из углов равен 90 градусам. Формула периметра равнобедренной трапеции равна \ [\ large Perimeter \; of \; Isosceles \; Trapeziod = a + b + 2c \], где a, b и c — стороны трапеции.Никогда. формула площади). называется «трапеция» в Великобритании (см. ниже). Игра с трапецией: параллельные стороны — это «основания», две другие стороны — «ножки» трапеции. Соответственно, каковы некоторые свойства трапеции? Возможные ответы: Математика. 2. Обе параллельные стороны называются основаниями. (3) Q Q дополняет AA ZW и LR B. прямоугольник C. ромб D. параллелограмм C. ZW и zD D. 20 и zD B. ZW и 20 Дано СЛОВО воздушного змея, пара углов которого делится пополам диагональю. ? Далее мы исследуем диагонали равнобедренной трапеции.(верно) 15. Площадь и периметр. Параллелограмм. Самая маленькая трапеция составляет 24 метра, а большая трапеция — 57 метров. Решение. Каждая пара углов на одном основании равнобедренной трапеции должна быть: _____ 4. Выберите Pen Tool (P). Чтобы создать равнобедренную трапецию с двумя равными длинами / углами в Illustrator: 1. Выберите Pen Tool (P). Нарисуйте две параллельные линии разной длины. Нарисуйте их оба идеально горизонтально, удерживая Shift. 2. Используя Selection Tool (V), раздвиньте линии на расстояние по вашему выбору.Теоремы о равнобедренной трапеции: Теорема 7. Проблема равнобедренной трапеции. 3,6 дюйма. В евклидовой геометрии равнобедренная трапеция (isosceles trapezium в британском английском) — это выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон. Как построить равнобедренную трапецию с одним основанием, диагональю и одной стороной. прямоугольник Прямоугольник — это геометрическая фигура, имеющая четыре стороны и четыре прямых угла. Есть две формулы равнобедренной трапеции. Трапеция — это четырехугольник, противоположные стороны которого параллельны (ложные) 16.Всегда. Это видеоурок из категории «Образование», в котором вы научитесь рисовать равнобедренную трапецию. А трапеция (называемая в Великобритании трапецией) представляет собой четырехугольник без параллельных сторон: у равнобедренной трапеции, как показано выше, левая и правая стороны равной длины, которые соединяются с основанием под равными углами. Равнобедренная трапеция — это тип трапеции, у которой непараллельные стороны равны по длине. Предупреждение: для этого вам, вероятно, понадобятся карандаш и бумага. 46â € ¦ — Нарисуйте прямоугольник; — Используйте панель Pathfinder -> Convert Shape, чтобы преобразовать его в равнобедренный треугольник; — Создайте еще один прямоугольник над треугольником; — Используйте опцию «Минус передний», чтобы вычесть верхнюю часть треугольника и создать трапецию.База. 4,6 дюйма по математике. AB = 10 и EC = 20. Напомним, что в равнобедренном треугольнике два основных угла совпадают. В равнобедренной трапеции, если одна пара углов основания вдвое больше второй пары углов основания, каковы размеры углов? Прямоугольник — это параллелограмм с четырьмя прямыми углами. $ \ begingroup $ Прямоугольник представляет собой трапецию (или трапецию). Если средний сегмент трапеции имеет длину 6 единиц, что верно в отношении длины оснований трапеции? Нарисуйте их оба идеально горизонтально, удерживая Shift.28,8 дюйма? В качестве альтернативы его можно определить как трапецию, в которой обе опоры и оба базовых угла имеют одинаковую меру. Вот свойства трапеции и прямоугольника, чтобы вы могли решить, насколько похожи эти две фигуры: Трапеция. Его свойства: (а) Противоположность … Очень частный случай трапеции, которая одновременно является правой трапецией и равнобедренной трапецией, но это трапеция. Равнобедренная трапеция. Позвольте мне добавить еще один комментарий: согласно всеобъемлющему определению параллелограмм — это особый вид трапеции.ABCE — это равнобедренная трапеция, а ACDE — прямоугольник. В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (ноги) имеют равную длину (свойства, общие с параллелограммом). Диагонали тоже одинаковой длины. Базовые углы равнобедренной трапеции равны в меру (на самом деле есть две пары равных базовых углов … Обратите внимание, что в евклидовой геометрии, если параллелограмм является равнобедренной трапецией, то это должен быть прямоугольник. Равнобедренные трапеции также есть части, которые обозначены как равнобедренный треугольник.Если обе пары противоположных углов четырехугольника являются дополнительными и конгруэнтными, это прямоугольник. Оба являются выпуклыми четырехугольниками. Прямоугольники имеют все углы 90 ° и, следовательно, две пары противоположных параллельных сторон. Трапеции не обязательно h … Теперь отцентрируйте короткое основание в центре длинной основы и отметьте конечные точки короткого основания точками. Квадрат — это трапеция? По-разному. Трапеция — это четырехугольник с парой параллельных сторон. Однако некоторые люди определяют это как минимум… Вычислите радиус описанной окружности равнобедренной трапеции, если заданы стороны и диагональ (R): радиус описанной окружности равнобедренной трапеции: = Цифра 2 1 2 4 6 10 FA ромб ABCD имеет AB = 10 и m∠A = 60 °. (false) 17. Вот свойства прямоугольника и трапеции. Прямоугольник. Его свойства: (а) Противоположные стороны равны и параллельны. (б) Все углы … Сначала вы рисуете длинную основу. Так что это зависит от учебника / автора, который вы используете. В некоторых книгах трапеция определяется как имеющая ровно один набор параллельных сторон.Прямоугольник между … Диагонали равнобедренной трапеции также совпадают, но они НЕ делят друг друга пополам. (1) Q U ¯ â ‰… A D ¯, (2) U A ¯ â ‰ ‡ D Q ¯, и. геометрия. У трапеции может не быть ни одного, ни одного. Дано, что ACDE представляет собой прямоугольник (нарисуйте диагональ AC, от C проведите линию, параллельную стороне AE трапеции, от E проведите еще одну линию, параллельную AC, и обозначьте точку пересечения с D). 4,1 дюйма 6 дюймов. Определяющая характеристика: одна пара сторон должна быть _____ 2.
Сальвадор Сегунда Дивизион,
Психология определения слухового нерва,
Требования к институциональному строительству,
Подводное плавание на самое большое расстояние,
Дешевые каникулы в Канкун,
Японские серийные убийцы вики,
Безопасен ли Msi Afterburner для ноутбуков?
Как найти длину диагонали трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Трапеции вкратце
Последнее семейство четырехугольников — изгои. Они отличаются от остальных четырехугольников, как социально неудобный гость на четырехугольной вечеринке.
В то время как у остальных есть конгруэнтные стороны и углы, о которых можно болтать, эти четырехугольники просто висят у закусочной. Время от времени они могут завязать разговор с одиноким многоугольником, который случайно забредает туда, но это никогда не длится долго, и они просто возвращаются к неудобно уставившимся себе под ноги.
Трапеция представляет собой четырехугольник с только одним набором параллельных сторон . У них абсолютно не может иметь два набора параллельных сторон.Поэтому, когда трапеции начинают свою вечеринку после того, как их выгнали из четырехугольника, мы можем быть уверены, что прямоугольники, квадраты и параллелограммы определенно не будут в списке гостей. Возьмите это, лохи.
Пример задачи
Этот четырехугольник — трапеция?
Сколько пар параллельных линий вы видите? Верх и низ параллельны друг другу, как и две стороны. Поскольку у него две пары параллельных линий, а у трапеции должен быть только один , это не трапеция.Извини, приятель.
Подобно воздушным змеям с их особыми диагоналями, трапеции также имеют части со специальными названиями (хотя ни одно из них не так странно, как названия, которые у нас есть для наших частей). Трапеция имеет два основания, каждое из которых является одной из параллельных сторон. Две другие стороны, которые не параллельны друг другу, называются ножками трапеции.
Поскольку параллельны только основания, а ветви — нет, мы можем представить этот сценарий как две непараллельные трансверсали, пересекающие пару параллельных линий.
Глядя на ∠1 и ∠2, мы видим, что это последовательные внутренние углы. То же самое для №3 и №4. Мы уже знаем (благодаря нашему обширному опыту работы с параллельными линиями), что последовательные внутренние углы являются дополнительными, поэтому мы доказали, что последовательные углы в трапеции, которые имеют одну и ту же опору, являются дополнительными.
Когда обе стороны трапеции имеют одинаковую длину, у нас есть особый тип четырехугольника, называемый равнобедренной трапецией .
Как и следовало ожидать, равнобедренные трапеции имеют конгруэнтные части, а также конгруэнтные последовательные углы, общие для основания. Конечно, в то время как равнобедренные треугольники имеют только одно «основание», у равнобедренных трапеций их два. Мы говорим, что вдвойне веселее.
Пример задачи
Если трапеция JANE равнобедренная и один из углов ее основания составляет 73 °, каковы размеры трех других углов?
Существует много разных способов определения размеров ∠1, ∠2 и ∠3, но мы начнем с того факта, что в равнобедренной трапеции оба угла, имеющие общее основание, совпадают.Поскольку угол 73 ° и ∠3 лопаточного основания JE , они совпадают. Другими словами, m∠3 = 73 °.
Мы также знаем, что, поскольку ∠2 и ∠3 являются последовательными внутренними углами, они являются дополнительными. Мы знаем меру 3, поэтому давайте найдем меру 2.
м∠2 + м∠3 = 180 °
м∠2 + 73 ° = 180 °
м∠2 = 180 ° — 73 °
м∠2 = 107 °
А как насчет ∠1? Поскольку у него общее основание с ∠2, эти два угла конгруэнтны друг другу. Это также означает, что m∠1 = 107 °.
Мы можем дважды проверить это, вспомнив, что все четырехугольники имеют внутренние углы, которые в сумме составляют 360 °.Если мы возьмем сумму этих четырех углов, то и получим это число.
73 ° + 73 ° + 107 ° + 107 ° ≟ 360 °
360 ° = 360 °
Юп. Это углы, которые у нас есть. Не сомневайся на этот счет.
Каждый четырехугольник имеет свои VIP или очень важные многоугольники. И без того эксклюзивный клуб трапеций не исключение. VIP-элементы семейства трапеций — это равнобедренные трапеции. Если они не славятся своими одинаковыми базовыми углами и ногами, то говорят их диагонали.Да, верно: у равнобедренных трапеций совпадающие диагонали. Не верите нам? Подскажем: это из-за чего-то под названием SAS. (Нет, не «нахальство».)
Другой тип VIP в области трапеций — это правая трапеция , имеющая один прямой угол. Конечно, где бы ни находился этот прямой угол, к нему будет идти еще один, потому что основания параллельны друг другу.
Несмотря на то, что не все трапеции созданы равными, нам понадобится что-то, чтобы объединить все трапеции, чтобы у них не было гражданской войны или чего-то подобного.Итак, мы дадим каждой трапеции — даже этим обычным старым неравнобедренным — нечто вроде пояса, называемое медианой. Это выравнивает игровое поле, а также помогает им втянуть кишки после сытной трапезы в День Благодарения.
Медиана трапеции — это сегмент, параллельный основаниям, который соединяет середины непараллельных сторон. Эта линия особенная, потому что мы можем определить ее длину непосредственно по длине двух оснований. Без шуток.
Длина медианы трапеции L составляет половину суммы длин оснований B 1 и B 2 .
Пример задачи
Четырехугольник ABCD — это трапеция, а EF — это середина трапеции. Какова длина EF ?
Поскольку мы знаем длины двух оснований, мы можем использовать формулу медианы, чтобы найти эту длину.
