Числа: натуральные, целые, рациональные, иррациональные, действительные, комплексные

Тестирование онлайн

• Округление чисел

Натуральные числа

Это числа, которые используются при счете: 1, 2, 3… и т.д.

Ноль не является натуральным.

Натуральные числа принято обозначать символом N.

Целые числа. Положительные и отрицательные числа

Два числа отличающиеся друг от друга только знаком, называются противоположными, например, +1 и -1, +5 и -5. Знак «+» обычно не пишут, но предполагают, что перед числом стоит «+». Такие числа называются положительными. Числа, перед которыми стоит знак «-«, называются отрицательными.

Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.

Рациональные числа

Это конечные дроби и бесконечные периодические дроби . Например,

Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.

Иррациональные числа

Бесконечная непериодическая дробь называется иррациональным числом. Например:

Множество иррациональных чисел обозначается J.

Действительные числа

Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.

Действительные числа обозначаются символом R.

Округление чисел

Рассмотрим число 8,759123… . Округлить до целой части означает записать лишь ту часть числа, которая находится до запятой. Округлить до десятых означает записать целую часть и после запятой одну цифру; округлить до сотых — после запятой две цифры; до тысячных — три цифры и т.д.

Округлить 8,759123… с точностью до целой части.

Округлить 8,759123… с точностью до десятой части.

Округлить 8,759123… с точностью до сотой части.

Округлить 8,759123… с точностью до тысячной части.

Математика для блондинок: Натуральные числа

Определения натуральных чисел, которые приводятся в Википедии и математической литературе, возможно, кому-то не совсем понятны. Наверное, многие задают вопрос: «Натуральные числа — это какие?».

Для того, чтобы понимать, какие числа в математике называются натуральными, могу предложить такой вариант распознания натуральных чисел: единица и все числа, которые можно получить в результате сложения единиц, будут натуральными числами.

Если кто-то считает, что нуль принадлежит к натуральным числам, ничего страшного. Просто выучите наизусть, что ноль является натуральным числом и всё. В разных странах этот вопрос решается по-разному. Например, в англоязычной математике ноль считается натуральным числом. Спросите у любого шпиона))) Кстати, разведчики точно также могут проколоться на этом вопросе)))

Что мы сделали? Мы счетные палочки в руке заменили единичками в математике. Теперь проверим на практике, как это работает. Рассмотрим число 2 (два):

1 + 1 = 2

Число 2 является натуральным числом, так как может быть представлено в виде суммы двух единиц, что соответствует двум счетным палочкам или двум другим предметам «для счета естественным образом» (цитата из классического определения натуральных чисел).

Возьмем пример по сложнее. Если дробное число 7,5 разделить на другое дробное число 2,5, будет ли результат натуральным числом?

7,5 : 2,5 = 3

Да, в результате деления двух дробных чисел мы получили натуральное число 3, поскольку оно может быть получено в результате сложения трех единиц.

1 + 1 + 1 = 3

Если число рассыпается на единички без шума и пыли, такое число является натуральным. Например, число 2,5 (два с половиной) не является натуральным, так как кроме двух единичек со страшным грохотом отваливается дробная часть числа 0,5:

1 + 1 + 0,5 = 2,5

Еще один пример. Число -4 (минус четыре) не является натуральным, поскольку при разложении на единички отпадает знак минус и поднимает целую кучу пыли. Отрицательные числа невозможно получить сложением положительных единиц. Кстати, в пыли отрицательных чисел математики блуждали, как ежики в тумане. Вместо того, чтобы разобраться в причинах пылевой бури, они придумали модуль числа, чем еще больше всех запутали.

Надеюсь, мое пояснение поможет вам лучше ориентироваться в таких разных названиях таких одинаковых чисел.

Может ли дробное число быть натуральным? — нет, дробные числа не относятся к натуральным числам.

Что такое рациональное число? Ответ на webmath.ru

Содержание:

Рациональные числа появились как форма записи чисел, более «мелких», нежели
натуральных.

Определение рационального числа

Определение

Рациональное число (лат. ratio — отношение, деление, дробь) —
это число которое может быть представлено в виде дроби  $\frac{m}{n}$  , где
числитель$m$ — целое число, а
знаменатель
$n$ — натуральное. Множество рациональных чисел $Q$ обозначается (от англ. quotient «частное») и
может быть записано в виде: $Q=\left\{\frac{m}{n} : m \in Z, n \in N\right\}$ . Числа вида
 $\frac{m}{n}$  — называют еще
обыкновенными дробями. Если
$m \lt n$, то дробь $\frac{m}{n}$  называется правильной, если $m \geq n$, то — неправильной.

Пример

Задание. Указать какие из записанных чисел являются рациональными:

$$-49 ; 17 ; \frac{14}{3} ; \frac{3}{4} ; 3,2 ; \sqrt[3]{11} ; \sqrt{7}$$

Решение. Рациональными будут числа:
 $\frac{14}{3} ; \frac{3}{4}$  а так же
 $-49 ; 17 ; 3,2$  так как их можно представить в виде рациональных дробей —
 $\frac{-49}{1} ; \frac{17}{1} ; \frac{32}{10}$  соответственно.

Ответ. $-49 ; 17 ; \frac{14}{3} ; \frac{3}{4} ; 3,2$

Если $m$ — нацело делится на $n$ или $n=1$, то рациональное число $\frac{m}{n}$  также будет
целым числом; если при этом
$m$ будет натуральным, то в таком случае дробь $\frac{m}{n}$  будет еще и натуральным числом. Поэтому для этих чисел имеет место такая цепочка вложений:
$N \subset Z \subset Q$ .

Операции над рациональными числами

На множестве рациональных можно ввести четыре арифметические операции:
сложение,
вычитание,
умножение и
деление; которые вычисляются по следующим правилам.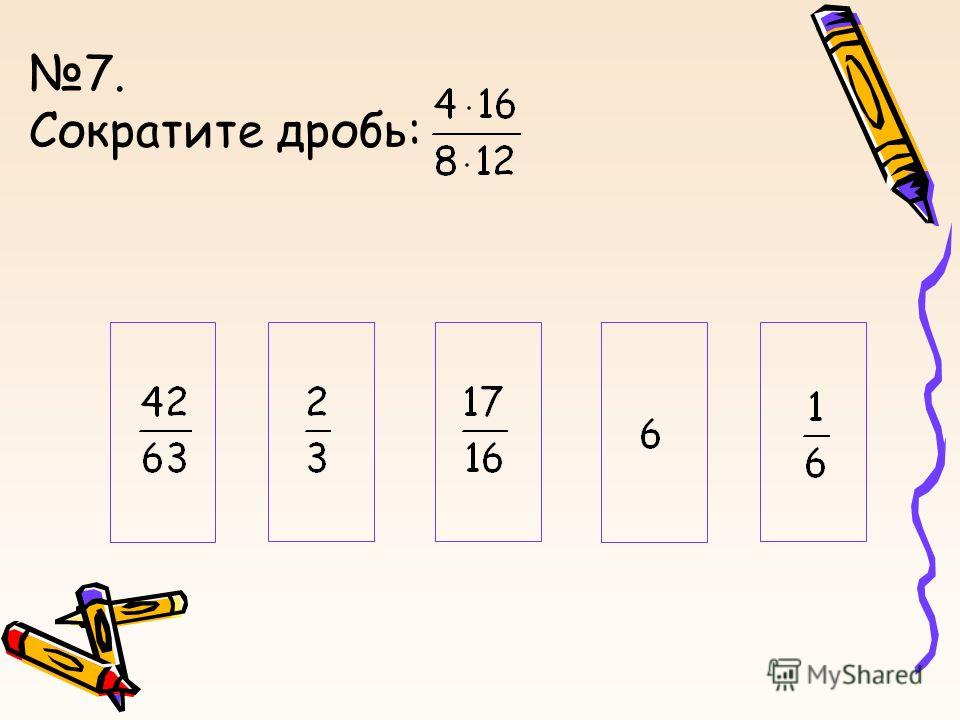

Правило вычисления суммы двух рациональных чисел:

$$\frac{m}{n}+\frac{p}{q}=\frac{m \cdot q+n \cdot p}{n \cdot q}$$

Правило вычисления разности двух рациональных чисел:

$$\frac{m}{n}-\frac{p}{q}=\frac{m \cdot q-n \cdot p}{n \cdot q}$$

Правило вычисления произведения двух рациональных чисел:

$$\frac{m}{n} \cdot \frac{p}{q}=\frac{m \cdot p}{n \cdot q}$$

Правило вычисления частного двух рациональных чисел:

$$\frac{m}{n} : \frac{p}{q}=\frac{m \cdot q}{n \cdot p}$$

Слишком сложно?

Что такое рациональное число не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Найти сумму, разность, произведение и частное чисел
 $\frac{5}{7}$  и $\frac{2}{3}$ 

Решение. По правилу вычисления суммы двух рациональных чисел:

$$\frac{5}{7}+\frac{2}{3}=\frac{5 \cdot 3+7 \cdot 2}{7 \cdot 3}=\frac{15+14}{21}=\frac{29}{21}$$

По правилу вычисления разности двух рациональных чисел:

$$\frac{5}{7}-\frac{2}{3}=\frac{5 \cdot 3-7 \cdot 2}{7 \cdot 3}=\frac{15-14}{21}=\frac{1}{21}$$

По правилу вычисления произведения двух рациональных чисел:

$$\frac{5}{7} \cdot \frac{2}{3}=\frac{5 \cdot 2}{7 \cdot 3}=\frac{10}{21}$$

По правилу вычисления частного двух рациональных чисел:

$$\frac{5}{7} : \frac{2}{3}=\frac{5 \cdot 3}{7 \cdot 2}=\frac{15}{14}$$

Ответ.  

$$\frac{5}{7}+\frac{2}{3}=\frac{29}{21} ; \frac{5}{7}-\frac{2}{3}=\frac{1}{21}$$

$$\frac{5}{7} \cdot \frac{2}{3}=\frac{10}{21} ; \frac{5}{7} : \frac{2}{3}=\frac{15}{14}$$

Больше примеров решений
Операции с дробями онлайн

Читать дальше: что такое сумма чисел.

Рациональные числа: определения, примеры

Данная статья посвящена изучению темы «Рациональные числа». Ниже приведены определения рациональных чисел, даны примеры, рассказано о том, как определить, является ли число рациональным, или нет. 

Рациональные числа. Определения

Прежде чем дать дефиницию рациональных чисел вспомним, какие еще есть множества чисел, и как они связаны между собой. 

Натуральные числа, в совокупности с противоположными им и числом ноль образуют множество целых чисел. В свою очередь, совокупность целых дробных чисел образует множество рациональных чисел.

Определение 1. Рациональные числа

Рациональные числа — числа, которые можно представить в виде положительной обыкновенной дроби ab, отрицательной обыкновенной дроби -ab или числа ноль. 

Таким образом, можно оставить ряд свойств рациональных чисел:

1. Любое натуральное число является рациональным числом. Очевидно, каждое натуральное число n можно представить в виде дроби 1n.
2. Любое целое число, включая число 0, является рациональным числом. Действительно, любое целое положительное и целое отрицательное число легко представляется в виде соответственно положительной или отрицательной обыкновенной дроби. Например, 15=151, -352=-3521.
3. Любая положительная или отрицательная обыкновенная дробь ab является рациональным числом. Это следует напрямую из данного выше определения.
4. Любое смешанное число является рациональным. Действительно, ведь смешанное число можно представить в виде обыкновенной неправильной дроби.
5. Любую конечную или периодическую десятичную дробь можно представить в виде обыкновенной дроби. Поэтому, каждая периодическая или конечная десятичная дробь является рациональным числом. 
6. Бесконечные и непериодическое десятичные дроби не являются рациональными числами. Их невозможно представить в форме обыкновенных дробей.

Приведем примеры рациональных чисел. Числа 5, 105, 358, 1100055 являются натуральными, положительными и целыми. Сдедовательно, это рациональные числа. Числа -2, -358, -936 представляют собой целые отрицательные числа, и они также рациональны в соответствии с определением. Обыкновенные дроби 35, 87, -358 также являются примерами рациональных чисел.  

Приведенное выше определение рациональных чисел можно сформулировать более кратко. Еще раз ответим на вопрос, что такое рациональное число.

Определение 2. Рациональные числа

Рациональные числа — это такие числа, которые можно представить в виде дроби ±zn, где z — целое число, n — натуральное число.

Можно показать, что данное определение равносильно предыдущему определению рациональных чисел. Чтобы сделать это, вспомним, что черта дроби равносильна знаку деления. С учетом правил и свойств деления целых чисел, можно записать следующие справедливые неравенства:

0n=0÷n=0; -mn=(-m)÷n=-mn.

Таким образом, можно записать:

zn=zn, при z>00, при z=0-zn, при z<0

Собственно, данная запись и является доказательством. Приведем примеры рациональных чисел, основываясь на втором определении. Рассмотрим числа -3, 0, 5, -755, 0,0125 и -135. Все эти числа являются рациональными, так как  их можно записать в виде дроби с целым числителем и натуральным знаменателем: -31, 01,-755, 12510000, 85.

Приведем еще одну эквивалентную форму определения рациональных чисел.

Определение 3. Рациональные числа

Рациональное число — это такое число, которое можно записать в виде конечной или бесконечной периодической десятичной дроби.

Данное определение напрямую следует из самого первого определения этого пункта. 

Подведем итог и сформулируем резюме по данному пункту:

1. Положительные и отрицательные дробные и целые числа составляют множество рациональных чисел.
2. Каждое рациональное число можно представить в виде обыкновенной дроби, числитель которой является целым числом, а знаменатель — натуральным числом.
3. Каждое рациональное число можно также представить в виде десятичной дроби: конечной или бесконечной периодической.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Какое из чисел является рациональным?

Как мы уже выяснили, любое натуральное число, целое число, правильная и неправильная обыкновенная дробь, периодическая и конечная десятичная дробь являются рациональными числами. Вооружившись этими знаниями можно без труда определить, является ли какое-то число рациональным.

Однако на практике часто приходится иметь дело не с числами, а с числовыми выражениями, которые содержат корни, степени и логарифмы. В некоторых случаях ответ на вопрос «рационально ли число?» является далеко не очевидным. Рассмотрим методы ответа на этот вопрос.

Если число задано в виде выражения, содержащего только рациональные числа и арифметические действия между ними, то результат выражения — рациональное число.

Например, значение выражения 2·318-0,250,(3) является рациональным числом и равно 18. 

Таким образом, упрощение сложного числового выражения позволяет определить, рационально ли заданное им число.

Теперь разберемся со знаком корня.

Оказывается, что число mn, заданное в видя корня степени n от числа m рационально лишь тогда, когда m является n-ой степенью какого-то натурального числа.

Обратимся к примеру. Число 2 не является рациональным. Тогда как 9, 81 — рациональные числа. 9 и 81 — полные квадраты чисел 3 и 9 соответственно. Числа 199, 28, 151 не являются рациональными числами, так как числа под знаком корня не являются полными квадратами каких-либо натуральных чисел. 

Теперь возьмем более сложный случай. Является ли рациональным число 2435? Если возвести 3 в пятую степень, получается 243, поэтому исходное выражение можно переписать так: 2435=355=3. Следовательно, данное число рационально. Теперь возьмем число 1215. Это число нерационально, так как не существует натурального числа, возведение которого в пятую степень даст 121.

Для того, чтобы узнать, является ли логарифм какого-то числа a по основанию b рациональным числом необходимо применить метод от противного. К примеру, узнаем, рационально ли число log25. Предположим, что данное число рационально. Если это так, то его можно записать в виде обыкновенной дроби log25=mn.По свойствам логарифма и свойствам степени справедливы следующие равенства:

5=2log25=2mn5n=2m

Очевидно, последнее равенство невозможно так как в левой и правой частях находятся соответственно нечетное и четное числа. Следовательно, сделанное предположение неверно, и число log25 не является рациональным числом.

Стоит отметить, что при определении рациональности и иррациональности чисел не стоит принимать скоропостижных решений. Например, результат произведения иррациональных чисел не всегда является иррациональным числом.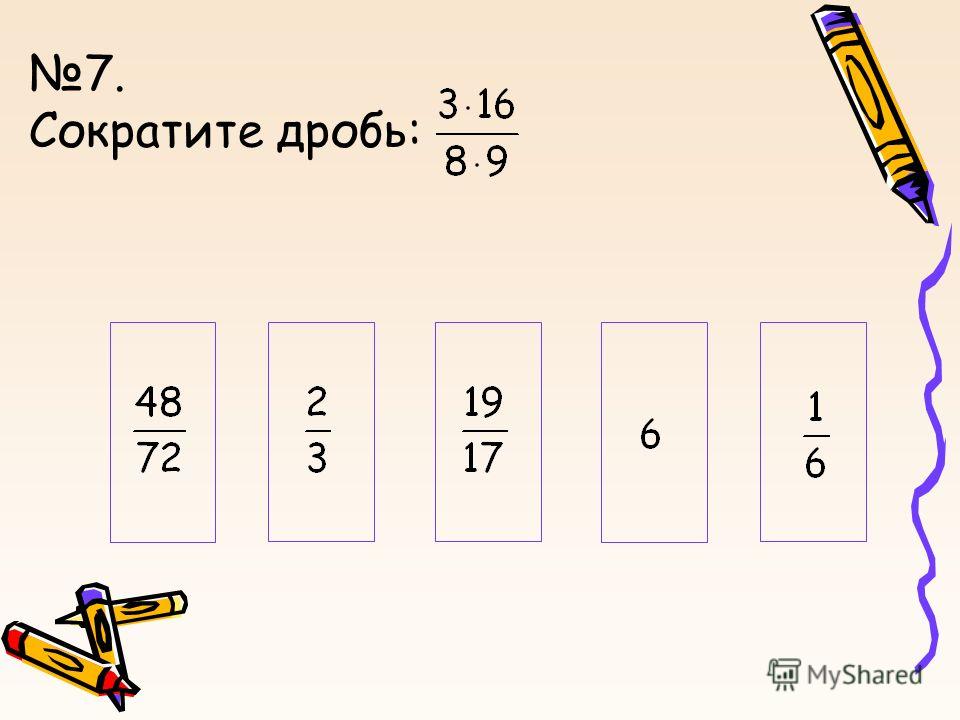 Наглядный пример: 2·2=2.

Также существуют иррациональные числа, возведение которых в иррациональную степень дает рациональное число. В степени вида 2log23 основание и показатель степени являются иррациональными числами. Однако само число является рациональным: 2log23=3.

ЧИСЛО ПИ — это… Что такое ЧИСЛО ПИ?

Рациональные (обыкновенные) дроби и действия с ними. Простые числа

Факт 1.
\(\bullet\) Множество натуральных чисел \(\mathbb{N}\) – это числа \(1,
\ 2, \ 3, \ 4 \ \) и т. д.
\(\bullet\) Множество целых чисел \(\mathbb{Z}\) состоит из натуральных чисел, противоположных им (\(-1, \ -2, \ -3 \) и т.д.) и нуля \(0\).
\(\bullet\) Рациональные числа \(\mathbb{Q}\) – числа вида \(\dfrac ab\), где \(a\in \mathbb{Z}\), \(b\in \mathbb{N}\) (обыкновенные дроби).
 
Таким образом, существует включение: \(\mathbb{N}\) содержится в \(\mathbb{Z}\), а \(\mathbb{Z}\) содержится в \(\mathbb{Q}\).
Это просто термины, которые стоит запомнить, чтобы правильно понимать условия задач.
 

Факт 2.
Таблица умножения:
Заметим, что любое целое число можно представить в виде дроби. Например, \(3=\dfrac31\).
Также напоминаем, что при умножении на любое число (не равное нулю) числителя и знаменателя дроби значение этой дроби не меняется. Например, \(\dfrac31=\dfrac62=\dfrac93\) и т.п.
 

Факт 3.
\(\bullet\) Простое число – это натуральное число, имеющее ровно два делителя: \(1\) и само это число.
Пример: \(2, 3, 5, 7, 11, 13, 17\) и т. д.
Заметим, что число \(1\) не является простым, так как делится только на \(1\), то есть имеет ровно один делитель.
\(\bullet\) Признак делимости на \(2\): число \(a\) делится на \(2\), если оно заканчивается на \(0,2,4,6\) и \(8\). Например, числа \(56\) и \( 900\) делятся на \(2\), а числа \(71\) и \( 1973\) не делятся на \(2\). Числа, делящиеся на \(2\), называются четными; числа, не делящиеся на \(2\), называют нечетными.
Признак делимости на \(3\): число \(a\) делится на \(3\), если его сумма цифр делится на \(3\). Например, числа \(198\) и \( 105\) делятся на \(3\), а числа \(179\) и \( 5869\) не делятся на \(3\).
Признак делимости на \(5\): число \(a\) делится на \(5\), если оно заканчивается на \(5\) или на \(0\). Например, числа \(505\) и \( 160\) делятся на \(5\), а число \(367\) не делится на \(5\).
Признак делимости на \(9\): число \(a\) делится на \(9\), если его сумма цифр делится на \(9\). Например, числа \(198\) и \( 108\) делятся на \(9\), а числа \(149\) и \( 5109\) не делятся на \(9\). 2\cdot 3\cdot 7\] Разложение на простые множители используется при сокращении дробей.
 
\(\bullet\) Сокращение дробей – деление числителя и знаменателя на одно и то же число, отличное от нуля.
Пример:
 
\(\begin{aligned} &\dfrac{98}6=\dfrac{49\cdot
2\llap{/}}{3\cdot
2\llap{/}}=\dfrac{49}3\\[2ex]
&\dfrac{4\cdot 14}{7\cdot 5}=\dfrac{4\cdot 2\cdot
7\llap{/}}{7\llap{/}\cdot
5}=\dfrac 85\\[2ex]
&\dfrac{4\cdot 7}{5\cdot 6}=\dfrac {2\llap{/}\cdot 2\cdot 7}{5\cdot
3\cdot
2\llap{/}}=\dfrac{14}{15}\end{aligned}\)
 
Заметим, что если ответом к задаче является дробь, то она должна быть несократимой, то есть ее числитель и знаменатель не должны иметь общих делителей. Например, будет неправильным записать ответ к задаче как \(\dfrac{13}{65}\). Нужно заметить, что \(65=13\cdot
5\), следовательно, \[\dfrac{13}{65}=\dfrac{13\llap{/}}{5\cdot 13\llap{/}}=\dfrac15\] То есть правильным ответом будет \(\dfrac15\).
 

Факт 4.
\(\bullet\) Правила сложения дробей: Значит, когда мы складываем две дроби с одинаковыми знаменателями, мы получаем дробь, у которой :
– знаменатель остается таким же;
– числитель равен сумме числителей этих двух дробей.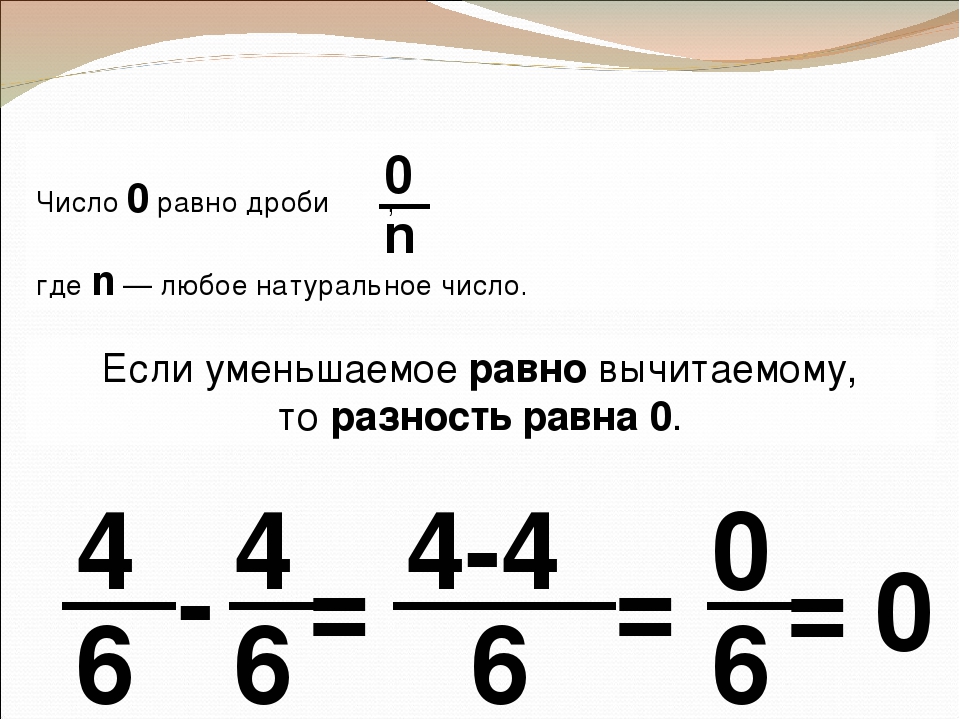
Точно так же мы поступаем и с разностью двух дробей. Значит, когда мы складываем две дроби с разными знаменателями, мы:
– приводим их к одинаковому знаменателю, домножив первую дробь на знаменатель второй, а вторую – на знаменатель первой;
– таким образом мы получаем две дроби с одинаковыми знаменателями и их можно сложить как дроби с одинаковыми знаменателями (то есть пользуясь первой формулой).
Это первый, более сложный способ сложения двух дробей с разными знаменателями. Второй способ, который упрощает вычисления и тем самым уменьшает вероятность допустить вычислительную ошибку, будет показан чуть позже
Примеры:
 
1) \(\dfrac {31}6+\dfrac {67}6=\dfrac{31+67}6=\dfrac{98}6\)
 
2) \(\dfrac{17}2-\dfrac{11}2=\dfrac{17-11}2=\dfrac62\)
 
3) \(\dfrac12+\dfrac{11}3=\dfrac{1\cdot 3+11\cdot 2}{2\cdot
3}=\dfrac{25}{6}\)
 
\(\bullet\) Правила умножения дробей: Если мы умножаем две дроби, то мы получаем дробь, у которой:
– числитель равен произведению числителей двух дробей;
– знаменатель равен произведению знаменателей двух дробей.
 
Пример: \(\dfrac 47\cdot \dfrac{14}5=\dfrac{4\cdot 14}{7\cdot 5}\)
 
\(\bullet\) Правила деления дробей: Данное правило часто называют так: <<чтобы разделить одну дробь на вторую, нужно первую дробь умножить на “перевернутую” вторую>>.
 
Пример:
 
1) \(\dfrac 45 :\dfrac 67=\dfrac 45\cdot \dfrac 76\);
 
2) \(\dfrac 12:3=\dfrac12:\dfrac31=\dfrac12\cdot \dfrac13=\dfrac16\)
 
\(\bullet\) Для того, чтобы перевести дробь смешанную дробь, например, \(4\dfrac{5}{11}\), в неправильную, нужно проделать следующие действия: \[4+\dfrac5{11}=\dfrac41+\dfrac5{11}=\dfrac{4\cdot
11+5}{11}=\dfrac{49}{11}\]
\(\bullet\) Разложение чисел на простые множители, помимо сокращения дробей, необходимо для того, чтобы наиболее оптимально приводить дроби к общему знаменателю (общий знаменатель – число, которое делится на знаменатель каждой дроби).
Пусть нам нужно привести две дроби \(\dfrac1{21}\) и \(\dfrac1{15}\) к общему знаменателю. По правилу из Факта 3 можно просто перемножить их знаменатели и получить дроби \(\dfrac{15}{21\cdot 15}\) и \(\dfrac{21}{15\cdot 21}\).
 
Но тогда общий знаменатель этих дробей получается достаточно большим: \(15\cdot 21=315\).
 
Покажем другой оптимальный способ приведения дробей к общему знаменателю. Так как \(21=7\cdot 3\) и \(15=3\cdot 5\), то наименьшее число, которое делится и на \(21\), и на \(15\) – это \(7\cdot 3\cdot
5=105\). Следовательно, это и есть их наименьший общий знаменатель. Для того, чтобы дробь \(\dfrac1{21}\) имела знаменатель \(105\), нужно умножить ее числитель и знаменатель на \(5\); для того, чтобы дробь \(\dfrac1{15}\) имела знаменатель \(105\), нужно умножить ее числитель и знаменатель на \(7\). Таким образом, получаем: \(\dfrac1{21}=\dfrac5{105}\) и \(\dfrac1{15}=\dfrac7{105}\).
 
Покажем еще один пример, демонстрирующий, что не всегда удобно и нужно раскладывать знаменатели прямо до простых множителей. Пусть нам нужно сложить дроби \(\dfrac1{49}\) и \(\dfrac1{98}\). Замечаем,что \(98=2\cdot 49\) (для того, чтобы это заметить, нужно хорошо выучить таблицу умножения и потренировать устный счет ). Тогда можно записать \(\dfrac1{49}\) и \(\dfrac1{2\cdot 49}\). Следовательно, для того, чтобы у дробей стали одинаковые знаменатели, нужно всего лишь домножить первую дробь на \(2\): \(\dfrac2{2\cdot 49}\) и \(\dfrac1{2\cdot 49}\).
 
А теперь представьте, что вы пользуетесь первым способом. Тогда ваш общий знаменатель будет равен \(49\cdot 98=4802\)! Неудобно, верно?
 

Калькулятор онлайн — Сокращение дробей

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.

Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Обыкновенные дроби. Деление с остатком

Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:

497 : 4 = 124 (1 остаток).

Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель.
Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний
компонент, которого нет в обычном делении, — остаток.
В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при
таком делении остаток равен нулю. В нашем случае остаток равен 1.

Остаток всегда меньше делителя.

Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать
так: 64 = 32 * 2.

Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,

где а — делимое, b — делитель, n — неполное частное, r — остаток.

Частное от деления натуральных чисел можно записать в виде дроби.

Числитель дроби — это делимое, а знаменатель — делитель.

Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление.
Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».

Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:

\( m:n = \frac{m}{n} \)

Верны следующие правила:

Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.

Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n.

Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель
дроби, которая выражает эту часть.

Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на
знаменатель дроби, которая выражает эту часть.

Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:

\( \large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)

Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:

\( \large \frac{a}{b} = \frac{a : m}{b : m} \)

Это свойство называют основным свойством дроби.

Два последних преобразования называют сокращением дроби.

Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к
общему знаменателю.

Правильные и неправильные дроби. Смешанные числа

Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например,
дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались
для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими
дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби,
у которых числитель больше знаменателя или равен ему, называют неправильными дробями. Остальные дроби, т. е. дроби, у которых
числитель меньше знаменателя, называют правильными дробями.

Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на
знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали
неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.

Если число состоит из целой части и дроби, то такие дроби называются смешанными.

Например:

\( 5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \( \frac{2}{3} \) — дробная часть.

Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:

\( \large \frac{a}{b} : n = \frac{a:n}{b} \)

Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:

\( \large \frac{a}{b} : n = \frac{a}{bn} \)

Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.

Действия с дробями. Сложение дробей.

С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей.
Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \).
Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.

Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:

\( \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)

Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:

\( \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.

Сложение смешанных дробей

Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями. При этом число 2 называют целой частью смешанной
дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».

При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное
число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)

Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят,
что из неправильной дроби выделили целую часть.

Вычитание дробей (дробных чисел)

Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:

\( \frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \( \frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)

Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.

С помощью букв это правило записывается так:

\( \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)

Умножение дробей

Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а
второе — знаменателем.

С помощью букв правило умножения дробей можно записать так:

\( \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)

Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать
смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.

Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное
свойство умножения относительно сложения.

Деление дробей

Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \).
Эту дробь называют обратной дроби \( \frac{2}{3} \).

Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как
\( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.

Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).

С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)

Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)

Используя взаимно обратные дроби, можно деление дробей свести к умножению.

Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.

Используя буквы, правило деления дробей можно записать так:

\( \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)

Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления
дробей, его надо предварительно представить в виде неправильной дроби.

Классификация чисел [Видео и практические вопросы]

Классификация чисел

Почему мы классифицируем числа? Почему мы даем им имена, например, целые, иррациональные или отрицательные числа? По той же причине, по которой мы все классифицируем, мы хотим убедиться, что каждый понимает, какие конкретные числа называются и что они означают. В конце концов, есть разница между 25, -32 и 4⁶.

В этом видео о Mometrix мы предлагаем обзор чисел и их классификацию.

Номера — наш способ навести порядок. Считаем, сколько денег у нас есть. Измеряем расстояние. Мы используем процентов для обозначения продажи. Числа являются неотъемлемой частью нашей повседневной жизни, будь то целые числа, рациональных чисел или первый тип чисел, на которые мы собираемся взглянуть, действительные числа.

Действительные числа

Действительное число — это любое значение непрерывной величины, которое может представлять расстояние на числовой прямой. По сути, это любое число, которое вы можете придумать.Пятьдесят (50) — действительное число. Один миллиард (1 000 000 000) — очень большое действительное число. Действительные числа включают три классификации чисел, о которых мы поговорим чуть позже. Целые числа, рациональные числа и иррациональные числа — все это действительные числа.

Мнимые числа

Мнимые числа не являются действительными числами. Это комплексные числа, которые записываются как действительное число, умноженное на мнимую единицу (\ (i \)). Например, \ (\ sqrt {-1} \) вычисляется как мнимое число «\ (i \)» и \ (\ sqrt {-25} = 5i \).Хотя мнимые числа не являются «действительными числами», они имеют ценность. Электрики используют мнимые числа при работе с токами и напряжением. Мнимые числа также используются в сложных вычислительных вычислениях. Поэтому то, что эти числа называются «воображаемыми», не означает, что они бесполезны.

Целые числа

Целые числа — это числа, которыми мы считаем. 1, 2, 3, 4 и 5 — все целые числа. Таковы -17 и 0. Целые числа не имеют дробей и десятичных знаков.

Все целые числа называются целыми числами .Целые числа могут быть положительными или отрицательными целыми числами.

Рациональные и иррациональные числа

Все целые и целые числа являются частью большой группы, называемой рациональными числами . В эту группу также входят дроби и десятичные знаки. Это означает, что \ (\ frac {3} {5} \) и 7.25 — рациональные числа. Рациональные числа также могут быть положительными или отрицательными.

Рациональные числа имеют противоположности, которые называются иррациональными числами . Эти числа нельзя записать в виде простой дроби.Пи (\ (\ pi \)) — самое известное иррациональное число. У нас есть близкое приближение к тому, как вычислить Пи, но это всего лишь близкое приближение. Пи известен тем, что продолжается вечно. Вот почему это иррациональное число. Вы не можете легко записать это дробью.

Натуральные и отрицательные числа

Натуральные числа — это те, которые являются положительными целыми числами, хотя есть некоторые споры относительно того, начинаются ли натуральные числа с 0 или 1. Отрицательные числа — это именно то, что вам нужно.Это числа ниже 0.

Четные и нечетные числа

Есть также несколько других классификаций чисел. Номера делятся на четные и нечетные. Если вы можете разделить число на 2, это число будет четным. Итак, 24, 36 и 74 — все четные числа, потому что если вы разделите их на 2, вы получите 12, 18 и 37. Четные числа всегда заканчиваются на 0, 2, 4, 6 или 8.

Нечетные числа могут не делить на 2 и оставлять целое число. Любое нечетное число, разделенное на 2, даст дробь.Итак, 17 ÷ 2 = 8,5, а 23 ÷ 2 = 11,5. Все нечетные числа оканчиваются на 1, 3, 5, 7 или 9.

Дроби

Числители и знаменатели образуют дроби, состоящие из двух целых чисел. Число вверху — числитель; число внизу — знаменатель. Числитель , верхнее число, показывает, сколько деталей у нас есть. Знаменатель , нижнее число, показывает, сколько частей составляет целое.

Допустим, у вас есть 6 яблок, и 3 из них съедены.Количество оставшихся у вас яблок будет отображаться как \ (\ frac {3} {6} \).

Затем вы разделите 3, верхнее число, на 6, нижнее число, чтобы определить процент оставшихся яблок. В этом случае цифра составляет 50%.

Итак, вот наш взгляд на числа и их классификацию. От целых чисел до иррациональных чисел нам нужно знать, как называть числа, чтобы знать, что они означают.

Надеюсь, этот обзор был вам полезен!

2.1 — Типы чисел

2.1 — Типы чисел

2.1 — Типы чисел

Рассмотрим типы чисел. Посмотрим на натуральные и целые числа,
целые числа, рациональные числа,
иррациональные числа, действительные числа,
мнимые числа и комплексные числа.

Натуральные и целые числа

Начнем с натуральных чисел . Это числа
1, 2, 3,… (Символ… означает, что последовательность продолжается бесконечно.)
Они используются для подсчета. Если мы включим ноль, то получим
целые числа , 0, 1, 2, 3,….

Натуральные и целые числа обычно считаются точными.
(например, у машины 4 колеса, у паука 8 ног). Но иногда они приблизительны
(например, в толпе было 1000 человек).

Вот целые числа, отображаемые в строке номера :

Целые числа

Теперь для каждого из чисел 1, 2, 3,… давайте создадим его , противоположное или отрицательное , и поместим его напротив
сторону числовой прямой, например:

Мы говорим, что 1 и −1 — противоположности, 2 и −2 — противоположности и т. д.и мы также говорим, что
−1 — противоположность 1, а 1 — противоположность −1.

Отрицательные числа используются для описания долгов, а не активов,
температуры ниже нуля в отличие от температур выше нуля,
высоты ниже уровня моря, а не высоты над уровнем моря и т. д.

Набор чисел…, −3, −2, −1, 0, 1, 2, 3,…
(целые числа и их противоположности) называется целыми числами .

Рациональные числа

Далее идут рациональные числа.Они являются обобщением
общие дроби, поэтому давайте сначала рассмотрим их.
Помните, что дробное обозначение a / b означает, что мы разбиваем что-то на b равных частей, и у нас есть a этих частей.
Например, если мы разбиваем пирог на 4 части, и у нас есть 1 кусок, то у нас есть 1/4 части пирога:

Рациональное число определяется как любое число, которое может быть выражено как частное или отношение
из два целых числа .Мы используем то же обозначение дробей
для выражения рациональных чисел:

Целое число a называется числителем, а целое число b называется знаменателем. Знаменатель не может быть равен нулю.

Обратите внимание, что если a и b являются натуральными числами (1, 2, 3 и т. Д.), То мы получаем обычную дробь. Таким образом, рациональные числа включают обыкновенные дроби.

Обратите внимание, что 3/1 = 3 и −5/1 = −5, поэтому рациональные числа включают все целые числа.

Рациональные числа также можно записывать в десятичной системе счисления вместо дробной. Например:

1/4 = 0,25

Десятичная запись 0,25 означает буквально «25/100», а 25/100 и 1/4 — эквивалентные дроби.

Обратите внимание, что некоторые рациональные числа не имеют точного десятичного эквивалента. Например 1/3
примерно равно 33/100, но не совсем:

1/3 ≈ 0,33

(Символ ≈ означает « примерно равно ».)
Рациональными числами обычно считаются , точные . По этой причине
программа Algebra Coach не преобразует дроби в десятичные, когда работает в точном режиме.

Иррациональные числа

Иррациональные числа — это числа, которые нельзя выразить как отношение двух целых чисел.
Примерами являются, а также квадратные корни из многих других чисел,
и специальные числа, такие как e и π. Получается, что иррациональных чисел столько же
как рационально.У иррациональных чисел нет точных десятичных эквивалентов. Чтобы написать любое иррациональное число
в десятичной системе счисления потребовалось бы бесконечное количество десятичных цифр.
Таким образом, это только приблизительные значения:

≈ 1,732, e ≈ 2,718 и π ≈ 3,14,

По этой причине программа Algebra Coach не преобразует иррациональные числа в десятичные.
когда он работает в точном режиме.

Реальные числа

Рациональные числа и иррациональные числа вместе составляют действительных чисел .Реальные числа
Говорят, что это плотный . Они включают в себя все числа в числовой строке.

Числовая строка полезна для понимания порядка чисел . Меньшие числа левее
а большие числа — правее.

Мы используем символ <для обозначения « меньше » и
символ> означает « больше ». Вот несколько примеров использования этих символов:

• 5 <8, потому что 5 находится слева от 8.
• −5 <2, потому что −5 находится слева от 2. Фактически любое отрицательное число меньше любого положительного числа.
• 5 <8 и 8> 5 — два способа констатировать один и тот же факт.
• 3,14 <π <3,15 Я называю это «меньше, чем бутерброд». Это означает, что 3.14 <π, а также π <3.15. Другими словами, число π находится где-то между 3,14 и 3,15.

Реальные числа часто получаются в результате измерений, а измерения всегда являются приблизительными.Например, с одним устройством длина объекта может составлять 5,28
(в некоторых единицах). Это не значит, что длина точно 5,28. Это просто означает, что это
ближе к 5,28, чем к 5,27 или 5,29.
При более точном (и обычно гораздо более дорогом оборудовании) длина
может быть измерено как 5,283, что просто означает, что оно ближе к 5,283, чем к
5.282 или 5.284 и так далее. Если выражение содержит приблизительное число, то это
все выражение также является приблизительным.

Щелкните здесь, чтобы получить дополнительную информацию о точности и значащих числах.

Мнимые числа и комплексные числа

Если действительные числа включают каждое число в числовой строке, то какие еще могут быть числа?
Чтобы ответить на этот вопрос, подумайте, как мы до сих пор строили систему счисления:

• Мы начали с целых чисел (например, 3)
• Нам нужны были противоположности для этих чисел, поэтому мы создали целые числа (числа вроде −3)
• Мы хотели разделить эти числа, но нуждались в рациональных числах для описания
  некоторые результаты (числа вроде 3/4)
• Мы хотели извлечь квадратный корень из этих чисел, но нам потребовались иррациональные числа для описания
  некоторые результаты (например,грамм. )

Теперь мы хотим извлечь квадратный корень из отрицательных чисел, но нам понадобится новый тип числа.
описать результат. Определим квадратный корень отрицательного числа
быть мнимым числом . Насколько дальше может этот процесс
создание новых типов номеров идет? Ответ — еще один шаг.
Мы можем добавить действительное число к мнимому. Результат называется комплексным числом .
Это конец строки, потому что оказывается, что каждая возможная операция со всевозможным комплексным числом
приводит только к другим комплексным числам.Мы говорим, что комплексные числа делают числа полными.

Где на числовой прямой идут мнимые и комплексные числа? Ответ — нет.
На этом рисунке показана комплексная плоскость . Он содержит числовую строку
(которая теперь называется реальной осью ) и новой осью, называемой
мнимая ось , перпендикулярная ей. Реальные числа лежат на действительной оси, мнимые числа
лежат на мнимой оси, а комплексные числа обычно лежат вне действительной оси,
либо над ним, либо под ним.

Программа Algebra Coach может работать в реальном или сложном режиме. В реальном режиме не будет
выполнить любую операцию, которая приводит к не действительному числу (например, извлечение квадратного корня
отрицательного числа).

Щелкните здесь, чтобы получить дополнительную информацию о комплексных числах.

Если вы нашли эту страницу в поиске в Интернете, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.

натуральных чисел | Encyclopedia.com

Натуральные числа — это обычные числа 1, 2, 3 ,. . . с которым люди рассчитывают. Иногда их называют счетными числами. Натуральные числа были названы естественными, потому что большая часть человеческого опыта с младенчества имеет дело с дискретными объектами, такими как пальцы, шарики, арахис и т. Д. Люди быстро, если не естественно, учатся их считать. Сообщается, что немецкий математик и логик Леопольд Кронекер (1823–1891) сказал: «Бог создал натуральные числа; все остальное — дело рук человека.«Число ноль иногда считают натуральным числом, но включение нуля приводит к осложнениям, которых обычно хочется избежать. Например, подсчет группы объектов — это процесс их взаимно однозначного соответствия с натуральными числами. Никто не считает, начиная с нуля, «0, 1, 2, 3». потому что тогда последнее использованное число больше не является количеством объектов в группе, и ответ будет неправильным.

Предполагается, что натуральные числа возникли до того, как люди начали считать вещи.Вавилоняне разработали систему счисления знаков, основанную на числовых значениях 1 (один) и 10 (десять). Древние египтяне добавили к этой системе все степени от 10 до миллиона. Натуральные числа впервые были серьезно изучены такими греческими философами и математиками, как Пифагор (582–500 до н. Э.) И Архимед (287–212 до н. Э.).

Из-за некоторой неоднозначности значения натурального числа вместо него часто используются термины положительные целые числа (которые не включают ноль) и неотрицательные целые числа (которые включают).Однако специалисты по основам математики утверждают, что натуральные числа отличаются от положительных целых чисел, хотя разница только в том, как числа определены. Для практических целей они одинаковы.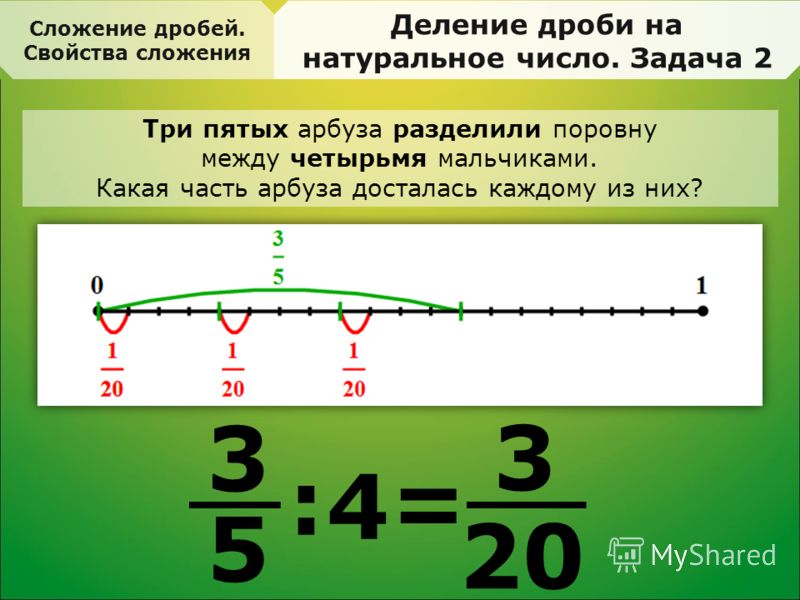

В конечном итоге вся арифметика основана на натуральных числах. Если, например, 1,72 умножить на 0,047, умножение будет выполнено на натуральные числа 172 и 47; затем результат преобразуется в десятичную дробь путем вставки десятичной точки в нужное место — процесс, который также выполняется путем подсчета.Если сложить дроби 1/3 и 2/7, сложение не выполняется напрямую, а только после преобразования дробей в 7/21 и 6/21. Затем числители складываются, используя арифметику с натуральными числами, и знаменатели копируются. Даже компьютеры и калькуляторы сводят свои сложные и молниеносные вычисления к простым шагам, включающим только натуральные числа.

Измерения также основаны на натуральных числах. Если кто-то измеряет объект сантиметровой линейкой, он или она полагается на числа, напечатанные рядом с сантиметровыми отметками, чтобы считать сантиметры, а глаз — на миллиметры.Независимо от того, подсчитываются ли единицы механическим, электронным или физическим способом, счет продолжается, и счет выполняется с использованием натуральных чисел.

Натуральные числа можно определить формально, связав их с наборами. Тогда ноль — это количество элементов в пустом наборе; 1 — количество элементов в наборе, содержащем одно натуральное число; и так далее. Другой метод — основывать их на постулатах Пеано. Здесь 2 определяется как преемник 1; 3 наследник 2; и так далее. Затем в постулатах указывается, какими свойствами будут обладать 1 и его последователи.

Есть один раздел математики, который занимается исключительно свойствами натуральных чисел (включая модульную арифметику, основанную на натуральных числах). Это раздел, известный как теория чисел. Со времен древних греков математики, как любители, так и профессионалы, исследовали эти свойства ради самих себя и для предполагаемой связи со сверхъестественным. Кроме того, в последнее время натуральные числа и их особые свойства были найдены во многих практических целях, помимо счета и вычислений.К ним относятся системы контрольных цифр, секретные коды и другие способы использования.

Натуральные числа (определение и примеры)

Если есть на что вы можете рассчитывать, так это на пальцы ног. На самом деле, пальцы рук и ног — это, естественно, одни из первых объектов, которые люди считают. Вы научились считать пальцы рук и ног и игрушки, когда были совсем маленькими. Вы считали натуральными числами.

Натуральные числа — основы математики.

Содержание

1. Что такое натуральные числа?
2. 0 — натуральное число?
3. Объединение натуральных чисел
4. Примеры натуральных чисел

Что такое натуральные числа?

В алгебре Натуральные числа определяются как счетные числа; положительные целые числа, начинающиеся с 1 и постоянно увеличивающиеся на 1.Ноль не является натуральным числом.

Другое определение натуральных чисел — целые положительные числа. Натуральные числа никогда не являются отрицательными числами или дробями, поэтому не все рациональные числа являются натуральными числами.

В математике символ для набора натуральных чисел — это N.

Набор натуральных чисел

Когда математики описывают группу или набор целых чисел, они используют скобки и эллипсы, например: ….

Многоточие означает, что набор продолжается в одном или двух направлениях, уменьшаясь или увеличиваясь предсказуемым образом.

Набор натуральных чисел выглядит так:

{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 …}

Первые пять натуральных чисел — это 1, 2, 3, 4, 5. Обратите внимание, что набор начинается с 1, а не с 0.

Набор натуральных чисел всегда будет набором положительных целых чисел.

Посмотрите на свои пальцы. Вы можете мысленно сосчитать, используя натуральные числа, и обнаружить, что у вас (в большинстве случаев) восемь пальцев и два больших пальца.

футов? Две ноги; десять пальцев.Волосы на голове? Что ж, это может занять больше времени, но в среднем у вас будет 100000 таких чисел из этой части набора целых чисел:

. .. 99 996; 99,997; 99,998; 99,999; 100 000 … 9 000 5

Когда вам нужны запятые для разделения точек в числах, вы заменяете запятую между числами в наборе точкой с запятой.

Натуральные числа называются «натуральными», потому что они являются естественным способом подсчета объектов с использованием взаимно однозначного соответствия . У нас есть одно число для каждого объекта, независимо от того, что мы считаем, реальное или воображаемое.

Вот ровно девять счетных примеров:

1. Кексы для обмена
2. Книги на полке
3. Идеи, о которых вы думали между 9:17 и 9:41
4. Атомы в вашем теле
5. Песчинки на пляже
6. Количество элементов в таблице Менделеева
7. звезд в нашей солнечной системе
8. Галактики во Вселенной
9. Атомы во всех звездах всех галактик Вселенной

Кардинальные числа — это натуральные числа, используемые для счета.Порядковые числа — это натуральные числа, используемые для упорядочивания.

Ни в коем случае процесс подсчета этих предметов не начинается с 0, что является проблемой.

0 — натуральное число?

Большинство математиков, учителей и профессоров считают 0 целым числом, но не натуральным числом. Некоторые, однако, действительно считают 0 натуральным числом:

{0, 1, 2, 3, 4, 5…}

Его использование в физике, например, допускает нулевой закон термодинамики.

Если вы не уверены, как в вашем учебнике, учителе или профессоре используется 0 (целое число, натуральное число или что-то еще?), Спросите.

Для этого класса, курса или учебника следуйте тому, что вам говорят, но имейте в виду, что математика часто является таким же мнением, как и точность, поэтому другой курс, учебник или класс могут рассматривать 0 по-другому.

Объединение натуральных чисел

Натуральные числа можно комбинировать с помощью операций:

• Сложение — сложение натуральных чисел всегда дает еще одно натуральное число
• Вычитание — Вычитание натуральных чисел может привести к отрицательному целому числу
• Умножение — Умножение натуральных чисел всегда дает другое натуральное число
• Раздел — При делении натуральных чисел можно получить десятичные, дробные или смешанные числа

Вот четыре примера, демонстрирующих эти качества:

1. 2 + 7 = 9
2. 7-2 = 5, но 2-7 = -5
3. 2 × 7 = 14
4. 72 = 3. 5 или 3 12

Примеры натуральных чисел

Вот ровно восемь задач, чтобы узнать, знаете ли вы свои натуральные числа:

1. Напишите натуральные числа, заканчивающиеся на 11.
2. 100 — натуральное число?
3. Если вы пересчитаете все книги по математике на полках, вы получите натуральное число или что-то еще?
4. Какое из этих натуральных чисел? -1, 0, 365
5. Какое натуральное число находится между 5,5 и 7,1?
6. Какие натуральные числа больше 23 12, но меньше 31 13?
7. Является ли ответ 4 × 9 натуральным числом?
8. Является ли ответ на 5-5 натуральным числом?

Мы знаем, что вы, естественно, хотите подглядывать, но не делайте этого! Сначала проработайте их, а затем посмотрите ответы ниже.

1. Натуральные числа, оканчивающиеся на 11: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}. Обратите внимание, что эллипса нет, поскольку это конечный набор действительных чисел.
2. Число 100 — натуральное число.
3. Количество книг по математике на ваших книжных полках будет натуральным числом.
4. Только 365 — натуральное число, потому что -1 — отрицательное целое число, а 0 — целое число, но не натуральное число (в большинстве случаев).
5. Натуральное число между 5.5 и 7,1 равно 6.
6. Натуральные числа больше 23 12, но меньше 31 13 равны {24, 25, 26, 27, 28, 29, 30}.
7. Ответ на 4 × 9, 36 — натуральное число.
8. Ответ на 5 — 5, 0 обычно не считается натуральным числом.

Если мы спросим вас, сколько натуральных чисел находится между 1 и 2, в качестве ответа вы могли бы получить пустой набор , {}. Пустой набор — это набор, не имеющий элементов; его мощность равна нулю.

Следующий урок:

Система аксиоматики

целых чисел | Математика ∞ Блог

Что такое целые числа?

Целые числа — это набор чисел, который включает в себя ноль и все положительные числа, которые мы используем для подсчета, например 0, 1, 2, 3, 4, 5 и т. Д.В этот набор не входят отрицательные числа и числа, выраженные в виде дробей или десятичных знаков. Другими словами, целые числа включают ноль и все положительные целые числа. Набор целых чисел продолжается вечно.

Еще немного о терминологии

Термин «целое число» иногда используется как синоним «натурального числа», хотя набор натуральных чисел (или счетных чисел) не включает ноль. Есть некоторые споры о том, является ли ноль целым числом, но для целей этого урока мы будем считать его одним.

Различение целых, целых, дробных и десятичных чисел

Задание: посмотрите на следующие числа и решите, какие из них являются целыми числами.

-3, -1, 0, 1, 3, 1/3, 0,333

Ответ:

-3 и -1 — отрицательные числа, поэтому они не являются целыми числами.

0, 1 и 3 — целые числа.

1/3 — это не целое число, потому что это дробь.

0,333 — это не целое число, потому что это десятичное число.

Четные и нечетные числа

Все целые числа, кроме нуля, могут быть описаны как четные или нечетные.Число называется «четным», если его можно разделить на 2 без остатка. Поскольку 4 ÷ 2 = 2, число 4 четное. Фактически, все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными числами.

Нечетные числа, с другой стороны, не делятся на 2. Если мы попытаемся разделить 5 на 2, например, мы получим частное 2 с остатком 1. Все числа, оканчивающиеся на нечетные числа (1, 3 , 5, 7 и 9) — нечетные числа.

Задание: посмотрите на следующие числа и решите, какие из них нечетные, а какие четные.

12, 24, 33, 49, 50, 62, 75, 88, 91, 100

Ответ: Посмотрев на последнюю цифру каждого числа, мы можем определить, что 12, 24, 50, 62, 88 и 100 — четные, а 33, 49, 75 и 91 — нечетные.

Основные операции с четными и нечетными целыми числами

Полезно запомнить несколько правил взаимодействия нечетных и четных чисел в уравнениях.

Правило сложения 1: Четный + Четный = Четный (Пример: 2 + 6 = 8)

Правило сложения 2: Четный + Нечетный = Нечетный (Пример: 2 + 5 = 7)

Правило сложения 3: Нечетный + Нечетный = Четный (Пример: 3 + 5 = 8)

Правила вычитания отражают правила сложения.

Правило вычитания 1: Четное — Четное = Четное (Пример: 8-6 = 2)

Правило вычитания 2: Четное — Нечетное = Нечетное (Пример: 8-5 = 3)

Правило вычитания 3: Нечетный — Нечетный = Четный (Пример: 7-5 = 2)

Правила умножения немного отличаются.

(Обратите внимание, что нет правил деления нечетных и четных чисел.)

Правило умножения 1: Четный x Четный = Четный (Пример: 2 x 4 = 8)

Правило умножения 2: Четный x Нечетный = Четный (Пример: 2 x 3 = 6)

Правило умножения 3: Нечетный x Нечетный = Нечетный (Пример: 3 x 5 = 15)

Является ли каждое рациональное число дробью? — Верно или неверно и причины

Каждая дробь является рациональным числом, однако рациональное число не обязательно должно быть дробью.Просмотрите всю статью, чтобы узнать, являются ли все рациональные числа дробными.

Рассмотрим a / b как дробь, где a, b — натуральные числа. Мы знаем, что каждое натуральное число является целым числом, поэтому a, b тоже целые числа. Следовательно, дробь a / b представляет собой частное двух целых чисел при условии, что b 0.

Таким образом, a / b — рациональное число. У нас есть случаи, когда a / b — рациональное число, а не дробь. Чтобы помочь вам, мы привели пример.

4 / -3 — это рациональное число, но не дробная часть, поскольку знаменатель не является натуральным числом.

Смешанная дробь, состоящая как из целой части, так и из дробной части, может быть выражена как неправильная дробь, которая является частным от двух целых чисел. Следовательно, мы можем сказать, что каждая смешанная дробь является рациональным числом. Таким образом, каждая дробь — это рациональное число.

Определите, являются ли следующие рациональные числа дробными числами

(i) 2/3

2/3 — это дробь, так как числитель 2 и знаменатель 3 являются натуральными числами.

(ii) 3/4

3/4 — это дробь, так как числитель 3 и знаменатель 4 являются натуральными числами.

(iii) -6 / -2

-6 / -2 не является дробью, так как числитель -6 и знаменатель -2 не являются натуральными числами.

(iv) -15/9

-15/9 не является дробью, поскольку числитель -15 не является натуральным числом.

(в) 36 / -4

36 / -4 не является дробью, поскольку числитель -36 не является натуральным числом.

(vi) 45/1

45/1 — дробь, поскольку числитель 45 и знаменатель 1 являются натуральными числами.

(vii) 0/5

0/5 не является реакцией, поскольку числитель 0 не является натуральным числом.

(viii) 2/10

2/10 — это дробь, так как числитель 2 и знаменатель 10 являются натуральными числами.

Ссылаясь на приведенные выше примеры, мы можем сделать вывод, что не каждое рациональное число является дробью.

В чем разница между целыми и действительными числами?

Определение действительного числа настолько широко, что охватывает почти все числа в математической вселенной. Целые числа и целые числа являются подмножеством действительных чисел, равно как и рациональные, и иррациональные числа.Множество действительных чисел обозначается символом ℝ.

Целые числа и целые числа

Числа, которые мы обычно используем для подсчета, известны как натуральные числа (1, 2, 3 …). Когда вы включаете ноль, у вас есть группа, известная как целые числа (0, 1, 2, 3 …). Целые числа — это набор чисел, который включает все целые числа вместе с отрицательными версиями натуральных чисел. Набор целых чисел представлен символом.

Рациональные числа

Числа, которые мы обычно воспринимаем как дроби, составляют набор рациональных чисел.Дробь — это число, представленное как отношение между двумя целыми числами, a и b , в форме a / b , где b не равно нулю. Дробь с нулем в правой части отношения не определена или неопределена. Рациональное число также может быть представлено в десятичной форме. Десятичное расширение рационального числа всегда будет либо завершено, либо иметь шаблон чисел, который повторяется справа от десятичной точки.Все целые числа являются рациональными числами, поскольку любое целое число может быть представлено соотношением a / 1 . Множество рациональных чисел представлено символом.

Иррациональные числа

Набор чисел, который не может быть представлен как отношение между целыми числами, называется иррациональным числом. Представленное в десятичной форме иррациональное число не является завершающим и имеет неповторяющийся образец чисел справа от десятичной точки. Стандартного символа для множества иррациональных чисел не существует.Набор рациональных и иррациональных чисел является взаимоисключающим, что означает, что все действительные числа либо рациональны, либо иррациональны, но не оба одновременно.

Действительные числа и числовая линия

Действительный числовой набор представляет собой упорядоченный набор значений, который может быть представлен на числовой прямой, проведенной горизонтально, с увеличивающимися значениями вправо и уменьшающимися значениями влево.