Содержание
Уравнения с дробями 7 класса онлайн
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только
возрастает. Линейные уравнения с дробями 7 класс решаются по стандартной схеме, когда производят перенос
членов уравнения с неизвестной в одну сторону, а с известной — в другую, учитывая правила переноса. Если
схема не подходит для вашего случая, тогда можно попробовать упростить уравнение, преобразовав его с
линейного с дробями в линейное с целыми значениями.
Так же читайте нашу статью «Решить уравнения с дробями 8
класса онлайн решателем»
Допустим, дано следующее уравнение:
\[\frac {3}{8}x-\frac{5}{6}=\frac {7}{12}x-\frac {2}{3}\]
Решим его по стандартной схеме и выполним перенос членов уравнения:
\[\frac {3}{8}x-\frac{7}{12}x=-\frac{2}{3}+\frac{5}{6}\]
Далее выполним приведение каждой части уравнения к общему знаменателю:
\[\frac{9-14}{24}x=\frac{4-+5}{6}\]
\[-\frac{5}{25}x=\frac{1}{6}\]
Делим левую и правую часть на число правой части:
\[x=\frac{1}{6}:(-\frac{5}{24})\]
Выполняем деление:
\[x=-\frac {1 \cdot 24}{6 \cdot 5}\]
Есть возможность сократить:
\[x=-\frac{4}{5}\]
Чтобы наглядно увидеть другой способ решения, решим такое уравнение:
\[\frac{3}{8}x — \frac{5}{6}=\frac{7}{12}x-\frac{2}{3}\]
Произведем умножение и приведем к 24 (наименьший общий знаменатель) каждый знаменатель:
\[\frac{3}{8}x-\frac{5}{6}=\frac{7}{12}x — \frac{2}{3}\]
В знаменателе остается 1, который мы не пишем:
\[9x-20=14x-16\]
Осталось решить простое линейное уравнения:
\[9x-14x=-16+20\]
\[-5x=4\]
Делим левую и правую часть на \[-5:\]
\[x=-\frac{4}{5}\]
Где можно решить уравнение онлайн решателем?
Решить уравнение вы можете на нашем сайте https://pocketteacher. ru. Бесплатный онлайн решатель
ru. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Тренажер по математике на тему «Решение уравнений, сводящихся к линейным» (7 класс)
Государственное бюджетное общеобразовательное учреждение школа №60
Выборгского района Санкт-Петербурга
Учитель: Воронова Лариса Валентиновна
Методическая разработка тренажера по математике
для 6 — 7 класса по теме:
«Решение уравнений, сводящихся к линейным»
Аннотация.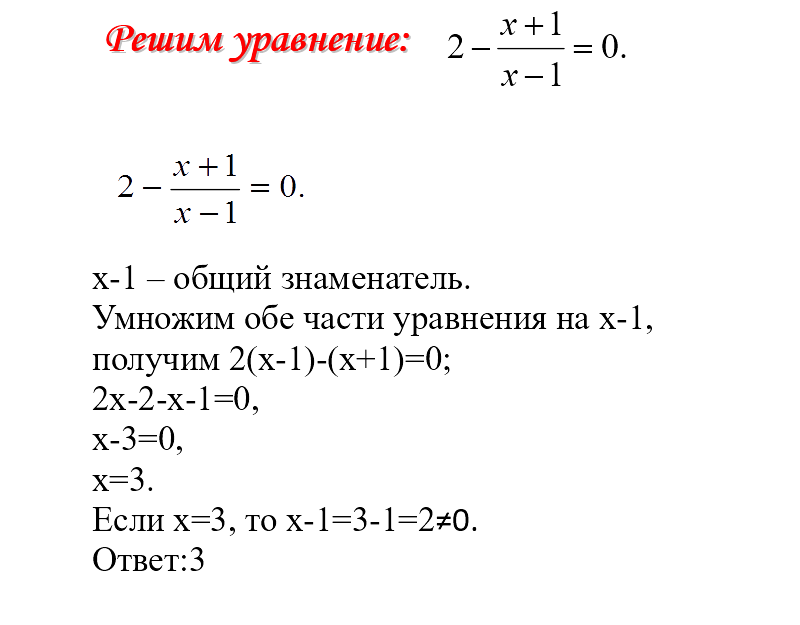
Тренажер предназначен для учащихся 6–7 классов с целью отработки и совершенствования навыков решения уравнений первой степени, содержащих дробную часть.
Тренажер содержит:
— пошаговую инструкцию преобразования заданного уравнения к более простому виду, что в итоге приводит к линейному уравнению вида ax=b;
— задания в двух уровнях: уровень А (базовый) и уровень В (повышенный).
— ответы к заданиям;
— примеры решения уравнений.
Тренажер может быть использован для самостоятельной работы учащихся в классе и дома, на дополнительных индивидуальных занятиях, а также при подготовке к итоговой аттестации.
Материал тренажера можно использовать для составления раздаточного материала.
Тренажер по теме:
«Решение уравнений, сводящихся к линейным»
(уровень А)
Алгоритм решения.
Найти общий знаменатель всех дробей, входящих в уравнение (наименьшее общее кратное всех знаменателей).
Умножить каждый член в левой и правой частях уравнения на общий знаменатель.
Сократить получившиеся дроби.
Упростить левую и правую части уравнения (раскрыть скобки).
Перенести неизвестные члены уравнения в левую часть, а известные – в правую, изменив при этом их знак на противоположный.
Привести подобные слагаемые в левой части и найти значение правой части.
Получится линейное уравнение вида ax = b.
Найти значение x, разделив обе части уравнения на коэффициент при неизвестном a.
Решить уравнения
У р о в е н ь А
№п/п
Вариант 1
Вариант 2
Тренажер по теме:
Решение уравнений, сводящихся к линейным
(уровень В)
Алгоритм решения.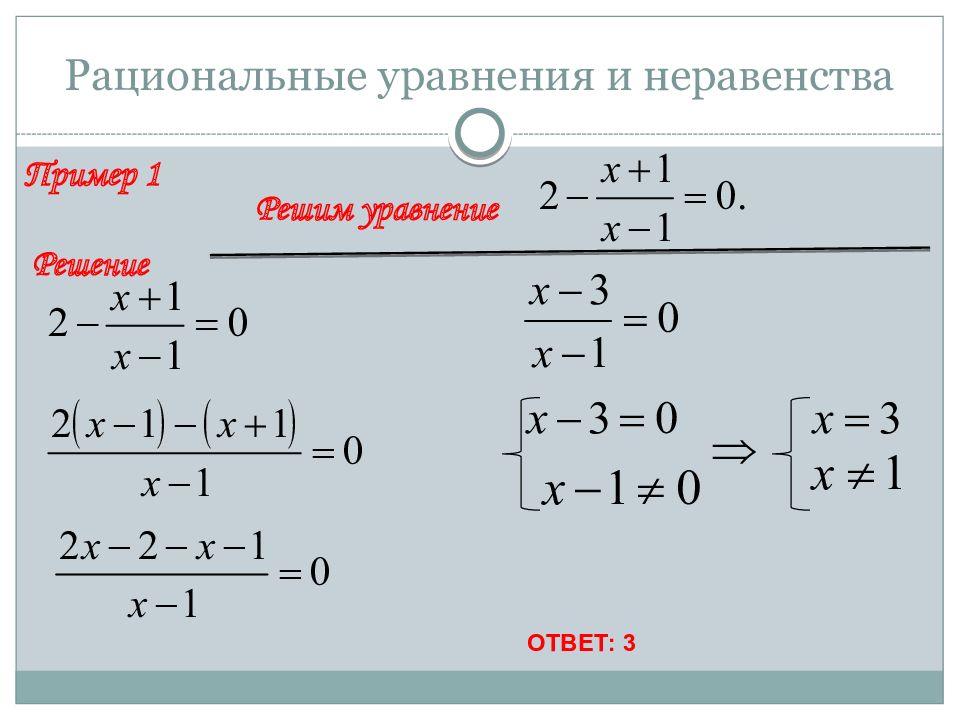
1. Найти общий знаменатель всех дробей, входящих в уравнение (наименьшее общее кратное всех знаменателей).
2. Умножить каждый член в левой и правой частях уравнения на общий знаменатель.
3. Сократить получившиеся дроби.
4. Упростить левую и правую части уравнения (раскрыть скобки).
5. Перенести неизвестные члены уравнения в левую часть, а известные – в правую, изменив при этом их знак на противоположный.
6. Привести подобные слагаемые в левой части и найти значение правой части.
Получится линейное уравнение вида ax = b.
7. Найти значение x, разделив обе части уравнения на коэффициент при неизвестном a.
Решить уравнения
У р о в е н ь В
№п/п
Вариант 1
Вариант 2
9 —
2x —
6 —
Ответы к тренажеру
«Решение уравнений, сводящихся к линейным»
Уровень А
Уровень В
Вариант 1
Вариант 2
1
17
13
2
11
-4
3
-3
11
4
17
17
5
13
2
6
-7
-7
7
2
8
1
9
2,5
10
-1
Вариант 1
Вариант 2
1
2
3
-2,5
4
45
170
5
4
—
6
12
2
7
2
2
8
49
7
9
11
-8
10
5
7
Примеры решения уравнений
I способ II способ
1) или
— пропорция
1 / 3/
|•6
x — 7 = 3(x+1)
x – 7 = 3x + 3
x — 3x = 3+7
-2x = 10
x = 10: (–2)
x = –5
Основное свойство пропорции: произведение крайних членов пропорции
равно произведению ее средних членов.
(x – 7)·2 = 6·(x+1)
2 x – 14 = 6x + 6
2 x –6 x = 6 + 14
-4x = 20
x = 20: (-4)
x = –5
2)
3)
8/ 7/ 56/
= 5 |·56
8(5y + 8) – 7(3y — 1) = 56·5
40y + 64 – 21y +7 = 280
19y = 280 – 64 – 7
19y = 209
y = 209 : 19
y = 11
3/ 5/ 15/
— 7|·15
3(х — 5) = 5(2х + 1) — 15·7
3х – 15 = 10х +5 – 105
3х – 10х = -100 + 15
-7х = -85
х = -85: (-7)
х = = 12
4)
5)
3/ 2/ 42/
– + = 0 |·42
–3(1 – 5m) + 2(1 +3m) = 0
–3 + 15m + 2 + 6m = 0
21m = 0 + 3 – 2
21m = 1
m = 1 : 21
m =
6/ 2/ 3/ 6/
2x — = + 6 |·6
6·2x – 2(16 – x) = 3(x +3) +6·6
12x – 32 + 2x = 3x + 9 + 36
14x – 3x = 45 + 32
11x = 77
x= 77 : 11
x = 7
Ответ: 1) —5; 2) 11; 3) 12; 4) ; 5) 7.
Алгебра 7-9 классы. 14. Решение типовых заданий по теме: «Дробные рациональные выражения»
Алгебра 7-9 классы. 14. Решение типовых заданий по теме: «Дробные рациональные выражения»
- Подробности
- Категория: Алгебра 7-9 классы
Сумма и разность дробей
Сложение и вычитание дробей с одинаковыми знаменателями
При сложении обыкновенных дробей с одинаковыми знаменателями складывают их числители, а знаменатель оставляют прежним. Например:
Таким же образом складывают любые рациональные дроби с одинаковыми знаменателями:
где а, b и с — многочлены, причем с — ненулевой многочлен.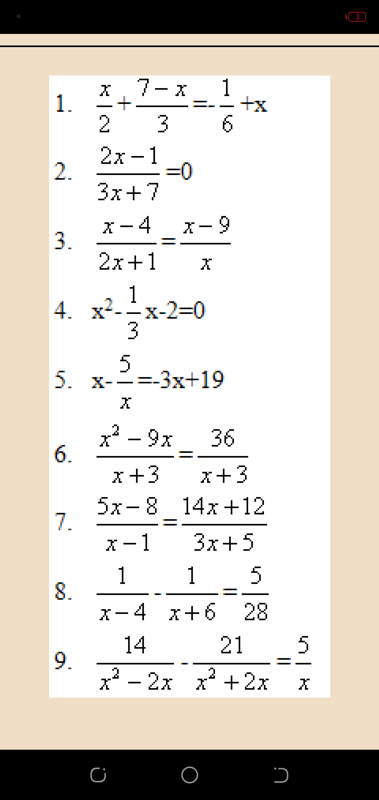
Это равенство выражает правило сложения рациональных дробей с одинаковыми знаменателями:
чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же
Вычитание рациональных дробей выполняется аналогично сложению:
Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.
Пример 1. Сложим дроби
Пример 2. Вычтем дроби
Пример 3. Упростим выражение
Здесь удобно сложение и вычитание дробей выполнять не последовательно, а совместно:
Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание рациональных дробей с разными знаменателями сводится к сложению и вычитанию рациональных дробей с одинаковыми знаменателями. Для этого данные дроби приводят к общему знаменателю.
Для этого данные дроби приводят к общему знаменателю.
Пример 1. Сложим дроби
Знаменатели дробей представляют собой одночлены. Наиболее простым общим знаменателем является одночлен . Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей дробей, а каждая переменная взята с наибольшим показателем, с которым она входит в знаменатели дробей. Дополнительные множители к числителям и знаменателям этих дробей соответственно равны .
Имеем
Пример 2. Преобразуем разность
Чтобы найти общий знаменатель, разложим знаменатель каждой дроби на множители:
Простейшим общим знаменателем служит выражение Дополнительные множители к числителям и знаменателям этих дробей соответственно равны b и а.
Имеем
Преобразование рационального выражения, которое является суммой или разностью целого выражения и дроби, сводится к преобразованию суммы или разности дробей.
Пример 3. Упростим выражение
Представим выражение а — 1 в виде дроби со знаменателем 1 и выполним вычитание дробей:
Произведение и частное дробей
Умножение дробей. Возведение дроби в степень
При умножении обыкновенных дробей перемножают отдельно их числители и их знаменатели и первое произведение записывают в числителе, а второе — в знаменателе дроби. Например:
Таким же образом перемножают любые рациональные дроби:
где а, b, с и d — некоторые многочлены, причем b и d — ненулевые многочлены. Это равенство выражает правило умножения рациональных дробей:
чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе — знаменателем дроби.
Пример 1. Умножим дробь на дробь
Воспользуемся правилом умножения дробей:
Пример 2. Умножим дробь на дробь
Имеем
Пример 3. Представим произведение в виде рациональной дроби.
Имеем
Пример 4. Умножим дробь на многочлен
При умножении дроби на многочлен этот многочлен записывают в виде дроби и затем применяют правило умножения дробей:
Правило умножения дробей распространяется на произведение трех и более рациональных дробей. Например:
Выясним теперь, как выполняется возведение рациональной дроби в степень.
Рассмотрим выражение , являющейся n-й степенью рациональной дроби и докажем, что
По определению степени имеем
Применяя правило умножения рациональных дробей и определение степени, получим
Следовательно ,
Из доказанного тождества следует правило возведения рациональной дроби в степень:
чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй — в знаменателе дроби.
Пример 5. Возведем дробь в третью степень.
Воспользуемся правилом возведения в степень:
Деление дробей
При делении обыкновенных дробей первую дробь умножают на дробь, обратную второй. Например:
Так же поступают при делении любых рациональных дробей:
где а, b, с и d — некоторые многочлены, причем b, c и d — ненулевые многочлены.
Это равенство выражает правило деления рациональных :
чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
Пример 1. Разделим дробь на дробь .
Воспользуемся правилом деления дробей:
Пример 2. Разделим дробь на дробь
Имеем
Пример 3. Разделим дробь на многочлен a + 3.
Разделим дробь на многочлен a + 3.
При делении дроби на многочлен этот многочлен записывают в виде дроби и затем применяют правило деления дробей:
Преобразование рациональных выражений
Рациональное выражение представляет собой частное от деления суммы рациональных дробей многочлен. Деление на можно заменить умножением на дробь Поэтому преобразование данного выражения сводится к сложению дробей и умножению результата на дробь Вообще преобразование любого рационального выражения можно свести к сложению, вычитанию, умножению или делению рациональных дробей.
Из правил действий с дробями следует, что сумму, разнос произведение и частное рациональных дробей всегда можно предс вить в виде рациональной дроби. Значит, и всякое рациональное выражение можно представить в виде рациональной дроби.
Пример 1. Преобразуем в рациональную дробь выражение
Сначала выполним умножение дробей, затем полученный результат вычтем из многочлена x + 1:
Запись можно вести иначе:
Пример 2. Представим выражение
Представим выражение
в виде рациональной дроби.
Сначала сложим дроби, заключенные в скобки, затем найденный результат умножим на дробь и, наконец, к полученному произведению прибавим 1:
Калькулятор уравнений, интегралов, производных, пределов и пр.
Онлайн-калькулятор позволяет решать математические выражения любой сложности с выводом подробного результата решения по шагам. Также универсальный калькулятор умеет решать уравнения, неравенства, системы уравнений/неравенств и выражения с логарифмами, вычислять пределы функций, определенные/неопределенные интегралы и производные любого порядка (дифференцирование), производить действия с комплексными числами, калькулятор дробей и пр.
Пояснения к калькулятору
- Для решения математического выражения необходимо набрать его в поле ввода с помощью предложенной виртуальной клавиатуры и нажать кнопку ↵.

- Управлять курсором можно кликами в нужное местоположение в поле ввода или с помощью клавиш со стрелками ← и →.
- ⌫ — удалить в поле ввода символ слева от курсора.
- C — очистить поле ввода.
- При использовании скобок ( ) в выражении в целях упрощения может производится автоматическое закрытие, ранее открытых скобок.
- Для того чтобы ввести смешанное число или дробь необходимо нажать кнопку ½, ввести сначала значение числителя, затем нажать кнопку со стрелкой вправо → и внести значение знаменателя дроби. Для ввода целой части смешанного числа необходимо установить курсор перед дробью с помощью клавиши ← и ввести число.
- Ввод числа в n-ой степени и квадратного корня прозводится кнопками ab и √ соответственно. Завершить ввод значения в степени или в корне можно клавишей →.
Упрощение выражений, раскрытие скобок, разложение многочленов на множители
Калькулятор позволяет произвести некоторые алгебраические преобразования с выражениями. 2}(решить неравенство)
2}(решить неравенство)
Решение систем уравнений и неравенств
Системы уравнений и неравенств также решаются с помощью онлайн калькулятора. Чтобы задать систему необходимо ввести уравнения/неравенства, разделяя их точкой с запятой с помощью кнопки ;.
Вычисление выражений с логарифмами
В калькуляторе кнопкой loge(x) возможно задать натуральный логарифм, т.е логарифм с основанием «e»: loge(x) — это ln(x). Для того чтобы ввести логарифм с другим основанием нужно преобразовать логарифм по следующей формуле: $$\log_a \left(b\right) = \frac{\log \left(b\right)}{\log \left(a\right)}$$ Например, $$\log_{3} \left(5x-1\right) = \frac{\log \left(5x-1\right)}{\log \left(3\right)}$$
$$\log _2\left(x\right)=2\log _x\left(2\right)-1$$ преобразуем в $$\frac{\log \left(x\right)}{\log \left(2\right)}=2\cdot \frac{\log \left(2\right)}{\log \left(x\right)}-1$$ (найти x в уравнении)
Вычисление пределов функций
Предел функции задается последовательным нажатием групповой кнопки f(x) и функциональной кнопки lim.
Решение интегралов
Онлайн калькулятор предоставляет инструменты для интегрирования функций. Вычисления производятся как с неопределенными, так и с определенными интегралами. Ввод интегралов в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:
∫ f(x) — для неопределенного интеграла;
ba∫ f(x) — для определенного интеграла.
В определенном интеграле кроме самой функции необходимо задать нижний и верхний пределы.
Вычисление производных
Математический калькулятор может дифференцировать функции (нахождение производной) произвольного порядка в точке «x». Ввод производной в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:
f'(x) — производная первого порядка;
f»(x) — производная второго порядка;
f»'(x) — производная третьего порядка.
fn(x) — производная любого n-о порядка.
Действия над комплексными числами
Онлайн калькулятор имеет функционал для работы с комплексными числами (операции сложения, вычитания, умножения, деления, возведения в степень и пр. ). Комплексное число обзначается символом «i» и вводится с помощью групповой кнопки xyz и кнопки i
). Комплексное число обзначается символом «i» и вводится с помощью групповой кнопки xyz и кнопки i
.
| Класс | Название урока | Ссылка на учебные материалы | |
| 7 | Числовые выражения | https://resh.edu.ru/subject/lesson/7261/main/248922/ | |
| 7 | Буквенные выражения | https://resh.edu.ru/subject/lesson/7258/main/248957/ | |
| 7 | Сравнение значений выражений | https://onliskill.ru/video/1844-algebra-7-klass-sravnenie-znachenii-vyrazhenii.html | |
| 7 | Основные свойства действительных чисел | https://resh.edu.ru/subject/lesson/7230/main/248010/ | |
| 7 | Тождество. Тождественные преобразования выражений | https://resh. edu.ru/subject/lesson/1166/ edu.ru/subject/lesson/1166/ | |
| 7 | Уравнения первой степени с одним неизвестным. Линейные уравнения с одним неизвестным | https://resh.edu.ru/subject/lesson/7277/main/248200/ | |
| 7 | Решение линейных уравнений с одним неизвестным | https://resh.edu.ru/subject/lesson/7278/main/248165/ | |
| 7 | Решение задач с помощью линейных уравнений | https://resh.edu.ru/subject/lesson/7274/main/248060/ | |
| 7 | Обобщение и систематизация знаний по теме «Линейные уравнения» | https://resh.edu.ru/subject/lesson/7280/main/247870/ | |
| 7 | Понятие функции и графика функции | https://resh.edu.ru/subject/lesson/3139/main/ | |
| 7 | Функция y = x и её график | https://resh.edu.ru/subject/lesson/2910/main/ | |
| 7 | График функции y = kx | https://resh. 2 и её график 2 и её график | https://resh.edu.ru/subject/lesson/2908/main/ |
| 7 | Понятие многочлена. Свойства многочленов | https://resh.edu.ru/subject/lesson/7256/main/247975/ | |
| 7 | Сумма и разность многочленов | https://resh.edu.ru/subject/lesson/7254/main/247920/ | |
| 7 | Произведение одночлена и многочлена | https://resh.edu.ru/subject/lesson/7253/main/248795/ | |
| 7 | Произведение многочленов | https://resh.edu.ru/subject/lesson/7262/main/248762/ | |
| 7 | Способ группировки | https://resh.edu.ru/subject/lesson/1069/ | |
| 7 | Обобщение и систематизация знаний по теме «Одночлены, многочлены» | https://resh.edu.ru/subject/lesson/7251/main/248430/ | |
| 7 | Квадрат суммы | https://resh.edu.ru/subject/lesson/7250/main/269675/ | |
| 7 | Квадрат разности | https://resh. edu.ru/subject/lesson/7264/main/269690/ edu.ru/subject/lesson/7264/main/269690/ | |
| 7 | Выделение полного квадрата | https://resh.edu.ru/subject/lesson/7249/main/248585/ | |
| 7 | Разность квадратов | https://resh.edu.ru/subject/lesson/7265/main/248445/ | |
| 7 | Сумма кубов. Разность кубов | https://resh.edu.ru/subject/lesson/7248/main/269620/ | |
| 7 | Куб суммы. Куб разности | https://resh.edu.ru/subject/lesson/7247/main/247675/ | |
| 7 | Целое выражение | https://resh.edu.ru/subject/lesson/7263/main/248688/ | |
| 7 | Числовое значение целого выражения. Тождественное равенство целых выражений | https://resh.edu.ru/subject/lesson/7252/main/248725/ | |
| 7 | Применение формул сокращённого умножения. Разложение многочленов на множители | https://resh. edu.ru/subject/lesson/7266/main/247640/ edu.ru/subject/lesson/7266/main/247640/ | |
| 7 | Обобщение и систематизация знаний по теме «Формулы сокращённого умножения» | https://resh.edu.ru/subject/lesson/7246/main/248360/ | |
| 7 | Уравнения первой степени с двумя неизвестными | https://resh.edu.ru/subject/lesson/7273/main/248025/ | |
| 7 | Линейная функция и её график | https://resh.edu.ru/subject/lesson/1340/ | |
| 7 | Графический способ решения линейных уравнений | https://resh.edu.ru/subject/lesson/1212/ | |
| 7 | Система уравнений первой степени с двумя неизвестными | https://resh.edu.ru/subject/lesson/7279/main/247780/ | |
| 7 | Решение задач при помощи уравнений первой степени | https://resh.edu.ru/subject/lesson/7271/main/249248/ | |
| 7 | Обобщение и систематизация знаний по теме «Линейные уравнения» | https://resh. edu.ru/subject/lesson/7280/main/247870/ edu.ru/subject/lesson/7280/main/247870/ | |
| 7 | Сбор и группировка статистических данных | https://resh.edu.ru/subject/lesson/1556/main/ | |
| 7 | Наглядное представление статистической информации | https://resh.edu.ru/subject/lesson/1988/main/ | |
| 7 | Случайная изменчивость. Примеры случайной изменчивости | https://resh.edu.ru/subject/lesson/1556/main/ | |
| 7 | Дисперсия и среднее квадратичное отклонение | https://resh.edu.ru/subject/lesson/3409/main/ | |
| 8 | Рациональные выражения | https://resh.edu.ru/subject/lesson/2907/main/ | |
| 8 | Преобразование рациональных выражений. Построение графика функции y = k/x | https://infourok.ru/videouroki/3050 | |
| 8 | Основное свойство дроби. Сокращение дробей | https://resh. edu.ru/subject/lesson/1549/main/ edu.ru/subject/lesson/1549/main/ | |
| 8 | Сложение и вычитание дробей с одинаковыми знаменателями | https://resh.edu.ru/subject/lesson/1550/main/ | |
| 8 | Сложение и вычитание дробей с разными знаменателями | https://resh.edu.ru/subject/lesson/1967/main/ | |
| 8 | Умножение дробей. Возведение в степень | https://resh.edu.ru/subject/lesson/1968/main/ | |
| 8 | Деление дробей | https://resh.edu.ru/subject/lesson/1969/main/ | |
| 8 | Преобразование рациональных выражений | https://resh.edu.ru/subject/lesson/1970/main/ | |
| 8 | Функция y = 1/x и её график | https://resh.edu.ru/subject/lesson/2909/main/ | |
| 8 | Функция y = k/x и её график | https://resh.edu.ru/subject/lesson/2501/main/ | |
| 8 | Решение уравнений графическим способом | https://resh. 2 = а 2 = а | https://resh.edu.ru/subject/lesson/1973/main/ |
| 8 | Нахождение приближенных значений квадратного корня | https://resh.edu.ru/subject/lesson/2916/main/ | |
| 8 | Функция у = √х и её график | https://resh.edu.ru/subject/lesson/2917/main/ | |
| 8 | Квадратный корень из произведения и дроби | https://resh.edu.ru/subject/lesson/2915/main/ | |
| 8 | Квадратный корень из степени | https://resh.edu.ru/subject/lesson/1974/main/ | |
| 8 | Вынесение множителя за знак корня. Внесение множителя под знак корня | https://resh.edu.ru/subject/lesson/2913/main/ | |
| 8 | Преобразование выражений, содержащих квадратные корни | https://resh.edu.ru/subject/lesson/1975/main/ | |
| 8 | Квадратные уравнения. Неполные квадратные уравнения | https://resh. edu.ru/subject/lesson/1976/main/ edu.ru/subject/lesson/1976/main/ | |
| 8 | Решение квадратных уравнений вида ax2+bx+c = 0. Формула корней квадратного уравнения | https://resh.edu.ru/subject/lesson/3137/main/ | |
| 8 | Решение приведённых квадратных уравнений. Теорема Виета | https://resh.edu.ru/subject/lesson/1552/main/ | |
| 8 | Решение задач с помощью квадратных уравнений | https://resh.edu.ru/subject/lesson/1977/main/ | |
| 8 | Решение дробных рациональных уравнений | https://resh.edu.ru/subject/lesson/1978/main/ | |
| 8 | Решение задач с помощью рациональных уравнений | https://resh.edu.ru/subject/lesson/1979/main/ | |
| 8 | Уравнения с параметром. Контрольный урок | https://resh.edu.ru/subject/lesson/1980/main/ | |
| 8 | Числовые неравенства. Свойства числовых неравенств | https://resh. edu.ru/subject/lesson/1983/main/ edu.ru/subject/lesson/1983/main/ | |
| 8 | Сложение и умножение числовых неравенств | https://resh.edu.ru/subject/lesson/1984/main/ | |
| 8 | Погрешность и точность приближения | https://resh.edu.ru/subject/lesson/1985/main/ | |
| 8 | Множества чисел | https://resh.edu.ru/subject/lesson/1553/main/ | |
| 8 | Пересечение и объединение множеств | https://resh.edu.ru/subject/lesson/1986/main/ | |
| 8 | Числовые промежутки | https://resh.edu.ru/subject/lesson/3407/main/ | |
| 8 | Решение неравенств с одной переменной | https://resh.edu.ru/subject/lesson/2578/main/ | |
| 8 | Решение систем неравенств с одной переменной | https://resh.edu.ru/subject/lesson/1987/main/ | |
| 8 | Доказательство неравенств | https://resh. edu.ru/subject/lesson/3408/main/ edu.ru/subject/lesson/3408/main/ | |
| 8 | Определение степени с целым показателем. Свойства степени с целым показателем | https://resh.edu.ru/subject/lesson/7242/main/248570/ | |
| 8 | Стандартный вид числа | https://resh.edu.ru/subject/lesson/7269/main/248095/ | |
| 8 | Сбор и группировка статистических данных | https://resh.edu.ru/subject/lesson/1556/main/ | |
| 8 | Наглядное представление статистической информации | https://resh.edu.ru/subject/lesson/1988/main/ | |
| 8 | Дисперсия и среднее квадратичное отклонение | https://resh.edu.ru/subject/lesson/3409/main/ | |
| 8 | Вероятности событий | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/3883737 | |
| 8 | Случайные опыты и случайные события | https://uchebnik.mos.ru/my_materials/material_view/atomic_objects/5795185 | |
| 8 | Элементарные события. Равновозможные элементарные события | https://uchebnik.mos.ru/my_materials/material_view/atomic_objects/5795141 | |
| 8 | Благоприятствующие элементарные события | https://uchebnik.mos.ru/my_materials/material_view/atomic_objects/5795141 | |
| 8 | Опыты с равновозможными элементарными событиями | https://uchebnik.mos.ru/my_materials/material_view/atomic_objects/5795141 | |
| 8 | Противоположное событие. Диаграммы Эйлера | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/1238874 | |
| 8 | Объединение и пересечение событий | https://uchebnik.mos.ru/my_materials/material_view/atomic_objects/5795009 | |
| 8 | Несовместные события. Правило сложения вероятностей | https://uchebnik.n | https://resh.edu.ru/subject/lesson/3182/main/ |
| 9 | Корень n-ой степени | https://resh.edu.ru/subject/lesson/1558/main/ | |
| 9 | Повторительно-обобщающий урок «Функции и их свойства, квадратный трехчлен» | https://resh.edu.ru/subject/lesson/1992/main/ | |
| 9 | Дробно-линейная функция и её график | https://resh.edu.ru/subject/lesson/2912/main/ | |
| 9 | Степень с рациональным показателем | https://resh.edu.ru/subject/lesson/2911/main/ | |
| 9 | Квадратный трёхчлен и его корни | https://resh.edu.ru/subject/lesson/1557/main/ | |
| 9 | Разложение квадратного трёхчлена на множители | https://resh.edu.ru/subject/lesson/1991/main/ | |
| 9 | Повторительно-обобщающий урок «Функции и их свойства, квадратный трёхчлен» | https://resh.edu.ru/subject/lesson/1992/main/ | |
| 9 | Некоторые приёмы решения целых уравнений | https://resh.edu.ru/subject/lesson/1997/main/ | |
| 9 | Дробные рациональные уравнения | https://resh.edu.ru/subject/lesson/2741/main/ | |
| 9 | Повторительно-обобщающий урок по теме «Уравнения с одной переменной» | https://resh.edu.ru/subject/lesson/2575/main/ | |
| 9 | Решение уравнений графическим способом (8 класс) | https://resh.edu.ru/subject/lesson/1548/main/ | |
| 9 | Решение задач с помощью рациональных уравнений (8 класс) | https://resh.edu.ru/subject/lesson/1979/main/ | |
| 9 | Решение неравенств второй степени с одной переменной | https://resh.edu.ru/subject/lesson/3118/main/ | |
| 9 | Решение неравенств методом интервалов | https://resh.edu.ru/subject/lesson/1996/main/ | |
| 9 | Некоторые приёмы решения целых уравнений | https://resh.edu.ru/subject/lesson/1997/main/ | |
| 9 | Неравенства с двумя переменными | https://resh.edu.ru/subject/lesson/2574/main/ | |
| 9 | Системы неравенств с двумя переменными | https://resh.edu.ru/subject/lesson/2001/main/ | |
| 9 | Уравнение с двумя переменными и его график | https://resh.edu.ru/subject/lesson/2740/main/ | |
| 9 | Решение систем уравнений второй степени | https://resh.edu.ru/subject/lesson/1999/main/ | |
| 9 | Решение задач с помощью систем уравнений второй степени | https://resh.edu.ru/subject/lesson/2000/main/ | |
| 9 | Повторительно-обобщающий урок по теме «Уравнения и неравенства с двумя переменными» | https://resh.edu.ru/subject/lesson/2739/main/ | |
| 9 | Последовательности | https://resh.edu.ru/subject/lesson/2003/main/ | |
| 9 | Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии | https://resh.edu.ru/subject/lesson/2004/main/ | |
| 9 | Характеристическое свойство арифметической прогрессии | https://resh.edu.ru/subject/lesson/1561/main/ | |
| 9 | Формула суммы первых n членов арифметической прогрессии | https://resh.edu.ru/subject/lesson/2005/main/ | |
| 9 | Повторительно-обобщающий урок по теме «Арифметическая прогрессия» | https://resh.edu.ru/subject/lesson/2006/main/ | |
| 9 | Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии | https://resh.edu.ru/subject/lesson/2007/main/ | |
| 9 | Свойство геометрической прогрессии | https://resh.edu.ru/subject/lesson/2008/main/ | |
| 9 | Формула суммы n первых членов геометрической прогрессии | https://resh.edu.ru/subject/lesson/1562/main/ | |
| 9 | Метод математической индукции | https://resh.edu.ru/subject/lesson/2122/main/ | |
| 9 | Повторительно-обобщающий урок по теме «Геометрическая прогрессия» | https://resh.edu.ru/subject/lesson/2121/main/ | |
| 9 | Целое уравнение и его корни | https://resh.edu.ru/subject/lesson/2573/main/ | |
| 9 | Некоторые приёмы решения систем уравнений второй степени с двумя переменными | https://resh.edu.ru/subject/lesson/2002/main/ | |
| 9 | Повторительно-обобщающий урок по теме «Неравенства с одной переменной» | https://resh.edu.ru/subject/lesson/1998/start/ | |
| 9 | Решение сложных задач на движение | https://resh.edu.ru/subject/lesson/1377/ | |
| 9 | Решение сложных текстовых задач на работу | https://resh.edu.ru/subject/lesson/1376/ | |
| 9 | Решение сложных текстовых задач на проценты | https://resh.edu.ru/subject/lesson/1344/ | |
| 9 | Графический способ решения систем уравнений | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/3976540 | |
| 9 | Правило умножения. Примеры комбинаторных задач | https://infourok.ru/videouroki/1400 | |
| 9 | Перестановки. Факториал числа | https://infourok.ru/videouroki/1401 | |
| 9 | Правило умножения и перестановки в задачах на вычисление вероятностей | https://infourok.ru/videouroki/1406 | |
| 9 | Сочетания | https://infourok.ru/videouroki/1403 | |
| 9 | Испытания Бернулли. Вероятность событий в испытаниях Бернулли | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/2091951 | |
| 9 | Треугольник Паскаля | https://oblako-media.ru/behold/0bhpfZgZIAk/treugolynik-paskalya-1-postroenie-sverhu-vniz/ | |
| 9 | Примеры случайных величин. Распределение вероятностей случайной величины | http://specclass.ru/v0179_tv05_sluchaynaya_velichina_zakon_raspredeleniya/#comments | |
| 9 | Математическое ожидание случайной величины | http://specclass.ru/v0065_teorver_task_mat_ojidanie_dispersiya/ | |
| 9 | Понятие о законе больших чисел | https://clck.ru/MWUec |
Дробно-рациональные уравнения. Алгоритм решения
Проще говоря, это уравнения, в которых есть хотя бы одна дробь с переменной в знаменателе.2=6\)
Как решаются дробно-рациональные уравнения?
Главное, что надо запомнить про дробно-рациональные уравнения – в них надо писать ОДЗ. И после нахождения корней – обязательно проверять их на допустимость. Иначе могут появиться посторонние корни, и все решение будет считаться неверным.
Алгоритм решения дробно-рационального уравнения:
-
Выпишите и «решите» ОДЗ. -
Найдите общий знаменатель дробей. -
Умножьте каждый член уравнения на общий знаменатель и сократите полученные дроби. Знаменатели при этом пропадут. -
Запишите уравнение, не раскрывая скобок. -
Раскройте скобки и приведите подобные слагаемые. -
Решите полученное уравнение.2+9x-5=0\)
Находим корни уравнения
\(x_1=-5;\) \(x_2=\frac{1}{2}.\)
Один из корней не подходи под ОДЗ, поэтому в ответ записываем только второй корень.
Ответ: \(\frac{1}{2}\).
Смотрите также:
Дробно-рациональные неравенстваСкачать статью
Внеклассный урок — Система уравнений с двумя переменными. Системы уравнений с двумя переменными. Способы решения.
Система уравнений с двумя переменными. Уравнения первой степени. Способы решения
Уравнение может содержать не одну, а две переменных. Понятно, что такие уравнения называются уравнениями с двумя переменными.
Система уравнений – это два и более уравнений, которыми можно манипулировать для нахождения общих решений. Система из двух уравнений вкючает в себя две переменных, значения которых являются общими для обоих уравнений. С помощью одного уравнения системы решается другое, а в итоге решаются оба уравнения системы.
Способы решения системы уравнений первой степени.
1. Решение методом подстановки.
Суть в том, что в системе уравнений выбираете наиболее простое, в котором одну переменную выражаете через другую. Результат подставляете во второе уравнение, благодаря чему преобразуете его в более простое уравнение с одной переменной. Вычисляете это уравнение и получаете значение одной из переменных. Подставляется его в первое уравнение и получаете значение второй переменной. Так вы решаете всю систему уравнений.
Пример: Решим систему уравнений
│x + y = 1
│2x – y = 2Решение:
Первое уравнение системы проще второго – его и используем.
Выразим в нем x через у:x = 1 – y
Подставляем это значение x в наше второе уравнение и находим значение y:
2(1 – y) – y = 2
2 – 2y – y = 2
2 – 3y = 2
3y = 2 – 2
3y = 0
y = 0.
Мы получили значение y. Подставляем его в наше первое уравнение и находим теперь уже значение x:
x + 0 = 1
x = 1
Мы нашли значения обеих переменных.
Ответ:
│x = 1
│y = 02. Решение методом сложения.
Этот метод целесообразно применять, если при сложении одно из неизвестных пропадает.
Пример 1: Решим систему уравнений
│x + y = 5
│x – y = 1Решение.
Сложим (вычтем) почленно оба уравнения системы:
│(x + y) + (x – y) = 5 + 1
│(x + y) – (x – y) = 5 – 1Раскрываем скобки в обоих уравнениях и сводим подобные члены. В результате в первом уравнении пропадает у, во втором х. Мы получаем уравнения с одной переменной, которые проще решать:
│ x + y + x – y = 6
│ x + y – x + y = 4↓
│2x = 6
│2y = 4↓
│x = 6 : 2
│y = 4 : 2↓
│x = 3
│y = 2Пример решен.
Необязательно производить взаимное сложение и вычитание двух уравнений системы. Часто достаточно бывает произвести одно из двух действий, чтобы вычислить значение одной из двух переменных. А зная одну переменную, мы уже легко сможем найти и вторую.
Пример 2. Решить систему уравнений
│2х + 4у = 26
│8х + 4у = 44В обоих уравнениях есть число 4у. Значит, можем применить метод сложения. При этом произвести не взаимное сложение, а совершить лишь одно действие: вычесть из первого уравнения второе, чтобы 4у исчезло и чтобы в результате мы получили уравнение с одной переменной:
2х + 4у – 8х – 4у = 26 – 44.
-6х = -18
х = -18 : (-6)
х = 3
Теперь можем найти и значение у, подставив значение х в любое из двух уравнений системы:
2 · 3 + 4у = 26
6 + 4у = 26
4у = 20
у = 20 : 4
у = 5
Ответ: х = 3, у = 5.
Однако рассмотрим еще один пример.
Пример 3: Решим систему уравнений
│3х + 5у = 21
│8х – 3у = 7Здесь нет переменных с одинаковыми коэффициентами, чтобы при вычитании они исчезли. Что делать в этом случае? Для таких случаев придумано оригинальное решение: умножим почленно первое уравнение на 3, а второе на 5. От этого истина не пострадает, потому что мы просто получим равносильные уравнения. Зато благодаря этому приему у нас появятся одинаковые переменные 15у:
│(3х + 5у = 21) · 3
│(8х – 3у = 7) · 5↓
│3 · 3х + 3 · 5у = 3 · 21
│5 · 8х – 5 · 3у = 5 · 7↓
│9х + 15у = 63
│40х – 15у = 35Итак, у нас появились одинаковые переменные и мы можем сложить два уравнения, чтобы прийти к уравнению с одной переменной:
9х + 15у + 40х – 15у = 63 + 35
49х = 98
х = 2
Осталось найти значение второй переменной, подставив значение х, например, в первое уравнение системы:
3 · 2 + 5у = 21
6 + 5у = 21
5у = 21 – 6
5у = 15
у = 3.
Ответ: х = 2; у = 3.
Опять же не всегда нужно преобразовывать оба уравнения системы так, как было в предыдущем примере. Бывает и так, что достаточно изменить лишь одно из уравнений.
Пример 4. Решим систему уравнений:
│3х – 4у = 7
│х + 3у = 11Здесь достаточно второе уравнение умножить на –3. Тогда мы получим число –3х, а при сложении двух уравнений придем к уравнению с одной переменной.
Итак, умножаем второе уравнение на –3:(х + 3у = 11) · (–3)
–3х – 9у = –33
Теперь складываем два уравнения, приходим к уравнению с одной переменной у и решаем его:
3х – 4у –3х – 9у = 7 – 33
–13у = –26
у = 2.
И находим значение х. Это проще сделать во втором уравнении:
х + 3 · 2 = 11
х + 6 = 11
х = 5.
Ответ: х = 5; у = 2.
3. Решение методом введения новой переменной.
Пример. Решить систему уравнений
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 8 9
│———— – ———— = 1
│ х – 3у 2х + уПеред нами система сложных уравнений, осложненных дробными числами. Наша задача – упростить их, чтобы потом решить. Если применить какой-нибудь из первых двух методов, получатся еще более сложные уравнения. Зато хорошо подходит метод введения новой переменной, благодаря которому мы целую дробь можем заменить одной переменной. Как это сделать?
Обратите внимание: у первых чисел обоих уравнений одинаковые знаменатели х – 3у, при этом их числители делятся на 2. У вторых чисел тоже одинаковые знаменатели 2х + у, а их числители делятся на 3. Этим и воспользуемся.
1) Выпишем снова нашу систему уравнений, разложив на множители числители второго уравнения и вынеся их за дробь:
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 2 3
│4 · ———— – 3 · ———— = 1
│ х – 3у 2х + уТеперь в обоих уравнениях у нас абсолютно одинаковые первые дроби и абсолютно одинаковые вторые дроби.
2) Заменим эти дроби новыми переменными a и b следующим образом:
2 3
———— = а, ———— = b.
х – 3у 2х + уТак мы существенно упрощаем уравнения, которые обретают совсем иной вид:
│ а + b = 2
│4а – 3b = 13) Применяем уже известный нам метод подстановки.
Первое уравнение проще, поэтому сначала выражаем в нем а через b:
а = 2 – b.
Подставляем полученное значение а во второе уравнение, раскрываем скобки, приводим подобные члены и вычисляем численное значение b:
4 · (2 – b) – 3b = 1
8 – 4b – 3b = 1
8 – 7b = 1
7b = 8 – 1
7b = 7
b = 1
Раз нам известно численное значение b, то мы легко можем найти и численное значение а. Это проще сделать с помощью первого уравнения:
а + b = 2
а + 1 = 2
а = 2 – 1
а = 1.
Итак:
а = 1, b = 1.
Вписываем в дроби эти значения а и b:
│ 2
│———— = 1
│ х – 3у
│
│ 3
│———— = 1
│ 2х + у4) Преобразуем эти уравнения по известному вам правилу: неизвестные влево, известные вправо:
│ х – 3у = 2 : 1
│2х + у = 3 : 1↓
│ х – 3у = 2
│2х + у = 35) Решаем эту систему уравнений снова с помощью метода подстановки. Для этого в первом уравнении х выражаем через у:
х = 2 + 3у.
Подставляем во второе уравнение и находим у:
2 · (2 + 3у) + у = 3
4 + 6у + у = 3
7у = 3 – 4
7у = –1
у = –1/7
И с помощью первого уравнения находим х:
х – 3у = 2
х – 3 · (–1/7) = 2
х + 3/17 = 2
х = 2 – 3/7
х = 11/7.
Мы нашли значения х и у в нашей исходной системе уравнений – а значит, решили ее.
Ответ: х = 11/7, у = –1/7
ПРИМЕЧАНИЕ.
Как видно из этого примера, нередки случаи, когда при решении системы уравнений надо последовательно применить сразу несколько методов.
Урок седьмого класса Решение уравнений с дробями
Учащимся предлагается скопировать цель, написанную на доске перед классом (KWBAT решает двухшаговые уравнения с дробными коэффициентами, константами и / или дробными решениями), как а также определение уравнения, написанное на доске. Студентам важно понимать, что уравнение состоит из двух выражений, разделенных знаком равенства. Многие студенты изо всех сил пытаются понять эту концепцию, которая влияет на их способность правильно выделять переменные термины, а также на их способность правильно выполнять шаги проверки.
Например, в таком уравнении, как 3x + 3/2 = 9, студенты часто делят член переменной на 3, чтобы изолировать переменную, и делят константу в правой части уравнения на три. Если учащийся также не разделит неправильную дробь 3/2 на 3, он делает математическую ошибку при решении уравнения. Понимание того, что обе стороны уравнения являются эквивалентными величинами, позволяет мне объяснять эти типы ошибок студентам. Я приложил образец работы, использованной для иллюстрации этой ошибки.
Я использую примеры из заметок для класса, чтобы показать студентам, как использовать свои учебные пособия для решения уравнений. Например, 5/6 — m = –11/12, я прошу студента определить переменные термины. Это термин, который мы хотим выделить в первую очередь. Поскольку положительное значение 5/6 составляет выражение, мы должны сначала сократить +5/6 с –5/6 с обеих сторон. Это приводит к выражению
–11/12 — 5/6
на противоположной стороне. Мы будем следовать правилу «при вычитании из отрицательного ответ останется отрицательным, и вы должны добавить абсолютные значения».Чтобы сложить 11/12 и 5/6, мы должны написать эквивалентную дробь для 5/6 с общим знаменателем 12:
.
— m = –11/12 — 5/6
— m = –11/12 — 10/12
— m = — [11/12 + 10/12]
— m = — [21/12]
— m = — 1 9/12 = — 1 ¾
Последний шаг — выделить переменную:
— м = — 1 ¾
(разделить на –1 с обеих сторон)
m = 1 ¾
Решение многоступенчатых линейных уравнений с дробями
Нам нужно более двух операций, чтобы решить
линейное уравнение
.Использовать
обратные операции
для отмены каждой операции в обратном порядке.
Если уравнение содержит дроби, умножьте обе части уравнения на
наименьший общий знаменатель
(ЖК-дисплей) для очистки дробей.
Шаги для решения многоступенчатого уравнения:
Шаг 1
Очистите уравнение дробей.
Шаг 2
ИспользоватьРаспределительное свойство
чтобы убрать скобки с каждой стороны.
Шаг 3
Объединение похожих терминов
с каждой стороны.
Шаг 4
Отменить сложение или вычитание.
Шаг 5
Отменить умножение или деление.
Пример:
Решать
2
у
3
+
у
2
знак равно
7
.
Решение
Наименьший общий знаменатель (ЖКД) в этом случае —
6
.Итак, умножьте обе части уравнения на
6
.
6
(
2
у
3
+
у
2
)
знак равно
6
(
7
)
Использовать
распределительный закон
в левой части уравнения.
6
(
2
у
3
)
+
6
(
у
2
)
знак равно
6
(
7
)
Умножить.
4
у
+
3
у
знак равно
42
Объедините похожие термины.
7
у
знак равно
42
Отменить умножение. Разделите каждую сторону на
7
.
7
у
7
знак равно
42
7
Упрощать.
у
знак равно
6
Дроби и смешанные числа — 7 класс Вопросы по математике и задачи с решениями и пояснениями
Заметки:
1 — На этой странице дроби написаны диагональными полосами.Например, 5/8 — это дробь, числитель которой равен 5, а знаменатель — 8.
11 1/4 — смешанное число, означающее 11 + 1/4.
2 — Не используйте калькулятор для решения приведенных ниже вопросов.-
Найдите дробь F со знаминателем меньше 8 такую, что 2/8 + F = 1
Раствор
Решить относительно F
F = 1-2 / 8
= 8/8 — 2/8, общий знаменатель
= 6/8, вычесть числитель
= 3/4, уменьшить дробь -
Найдите две дроби F1 и F2 с одинаковым знаменателем, равным 6, такие, что F1 + F2 = 1 и F1 — F2 = 2/3
Раствор
Запишем F1 + F2 и F1 — F2 следующим образом
F1 + F2 = 1 = 6/6
F1 — F2 = 2/3 = 4/6
F1 и F2 — дроби со знаминателем 6.Их числитель должен составлять 6, а их разница равна 4. Следовательно, F1 и F2 равны
F1 = 5/6 и F2 = 1/6 - Раствор
16% записывается дробью и сокращается
16% = 16/100 = 4/25 -
Какая дробь эквивалентна 300/1000- 3/100
- 3/1000
- 3/10
- 300/10
Раствор
Уменьшить данную фракцию
300/1000 = 3/10, разделите числитель и знаменатель на 100.
300/1000 эквивалентно 3/10 -
1/2 + 1/5 + 1/6 =
Раствор
Сначала вычисляется НОК 2, 5 и 6.
2 = 2
5 = 5
6 = 2 3
НОК = 2 5 3 = 30
Мы используем НОК как наименьший общий знаменатель для всех трех дробей.
1/2 + 1/5 + 1/6 = (115) / (215) + (16) / (56) + (15) / (65)
Упростить
= 15/30 + 6/30 + 5/30
Добавить и уменьшить
= 26/30 = 13/15 -
3 3/5 + 5 1/2 =
Раствор
Сложить целые части вместе и дробные части вместе
3 3/5 + 5 1/2 = (3 + 5) + (3/5 + 1/2)
Общий знаменатель дробей 3/5 и 1/2
= 8 + (6/10 + 5/10) = 8 + 11/10
Заменить неправильную дробь 11/10 на смешанное число и сложить
= 8 + 10/10 + 1/10 = 8 + 1 + 1/10 = 9 1/10 -
1/7 2 2/5 =
Раствор
Преобразуйте смешанное число 2 2/5 на дробь и умножьте
1/7 2 2/5 = 1/7 12/5 = 12/35 -
1/12 0.2 =
Раствор
Заменить десятичное число 0,2 на дробное
0,2 = 2/10 = 1/5
Умножение двух дробей
1/12 0,2 = 1/12 1/5 = 1/60 -
2/5 6 =
.
Раствор
Использовать правило деления
2/5 6 = 2/5 6/1 = 2/5 1/6 = 2/30
Уменьшить фракцию
= 1/15 -
9/7 + 2 =
.
Раствор
Замените 2 на дробь 2/1 и установите общий знаменатель.
9/7 + 2 = 9/7 + 2/1 = 9/7 + 14/7 = 23/7 = 3 2/7 -
2 1/3 + 4/2 =
.
Раствор
Упростите 4/2 и добавьте.
2 1/3 + 4/2 = 2 1/3 + 2 = 4 1/3 -
3 1/5 5 =
Раствор
Замените смешанное число 3 1/5 на frcation и перепишите 5 как дробь 5/1.
3 1/5 5 = 16/5 5/1 =
Примените правило деления дробей и упростите.
= 16/5 1/5 = 16/25 -
1/2 + 4 1/3 — 3 2/5 =
Раствор
Сложить / вычесть целые части и дробные части отдельно.
1/2 + 4 1/3 — 3 2/5 = 4 — 3 + 1/2 + 1/3 — 2/5
Найдите НОК 2, 3 и 5.
2 = 2
3 = 3
5 = 5
НОК (2,3,5) = 235 = 30
Используйте НОК в качестве общего знаменателя.
= 1 + (15/30 + 10/30 — 12/30) = 1 + 13/30 = 1 13/30 -
5/2 7/2 — 1/5 =
Раствор
Порядок работы первого подразделения
5/2 7/2 — 1/5 = 5/2 2/7 — 1/5
Упростить
= 5/7 — 1/5
Общий знаменатель и вычесть
= 25/35 — 7/35 = 18/35 -
(0.2 + 1/5) 2/7 = 90 · 107
Раствор
Заменить десятичное число 0,2 на дробь 1/5
(0,2 + 1/5) 2/7 = (1/5 + 1/5) 2/7
Использовать порядок действий
= 2/5 2/7
= 4/35 -
(3 1/2 + 3/5) 1/7 =
Раствор
Преобразовать смешанное число 3 1/2 на дробное
(3 1/2 + 3/5) 1/7 = (7/2 + 3/5) 1/7
Найдите общий знаменатель для 7/2 и 3/5 и сложите
= (35/10 + 6/10) 1/7 = 41/10 1/7
Умножение дробей
= 41/70 -
40/4000 =- 1%
- 40%
- 4%
- 10%
Раствор
Уменьшить дробь так, чтобы ее знаменатель был равен 100
40/4000 = 1/100 = 1% -
(1/2 + 2/3) 0.2 =
Раствор
Сложите дроби в скобках и запишите 0,2 как дробь 1/5
(1/2 + 2/3) 0,2 = (3/6 + 4/6) 1/5 = 7/6 1/5
Используйте правило деления дробей
= 7/6 5/1 = 35/6 = 5 5/6 -
Порядок от наименьшего к наибольшему: 3 4/7, 3 3/5, 3 1/2, 3 11/20 .
Раствор
Все данные смешанные числа имеют одинаковые целые части, но разные дроби.
Дроби легче сравнивать, если у них общий знаменатель.Общим знаменателем дробных частей является НОК 7,5,2 и 20.
7 = 7
5 = 5
2 = 2
20 = 2 2 5
НОК (7,5,2,20) = 7 5 2 2 = 140
Теперь перепишем все смешанное с дробными частями с тем же знаменателем.
3 4/7 = 3 80/140
3 3/5 = 3 84/140
3 1/2 = 3 70/140
3 11/20 = 3 77/140
Теперь мы упорядочиваем смешанные числа от наименьшего к наибольшему
3 1/2, 3 11/20, 3 4/7, 3 3/5 -
Порядок от наименьшего к наибольшему: 2 7/8, 2.66, 262%, 25/8 .
Раствор
Нам нужно переписать данные числа в единую форму. Запишем их в десятичной форме
2 7/8 = 2 + 7/8 = 2 + 0,875 = 2,875
2,66 = 2,66
262% = 262/100 = 2,62
25/8 = 24/8 + 1/8 = 3 + 0,125 = 3,125
Теперь мы используем десятичную форму заданных чисел, чтобы отсортировать их от наименьшего к наибольшему.
262%, 2,66, 2 7/8, 25/8
Решение рациональных уравнений: Введение | Purplemath
Purplemath
Хотя добавление и вычитание рациональных выражений может быть настоящей головной болью, решение рациональных уравнений, как правило, проще, даже если рациональные выражения добавляются в эти уравнения.(Обратите внимание: я не говорю, что решение рациональных уравнений «просто»; я просто говорю, что это просто или .) Это потому, что, как только вы перейдете от рационального выражения (то есть чего-то без «равно») в рациональное уравнение (то есть что-то со знаком «равно» посередине), вы получаете совершенно другой набор инструментов для работы. В частности, если у вас есть знак «равно» в середине, у вас есть две стороны, что означает, что вы можете умножать обе эти части уравнения, и это позволяет вам избавиться от знаменателей.
MathHelp.com
Решите следующее уравнение:
Это уравнение настолько простое, что я могу решить его, просто взглянув на него! Как?
У меня две дроби.У этих дробей один и тот же знаменатель. Эти дроби будут равны, если их числители также совпадают, и только тогда. Итак, я могу приравнять числители и получить ответ. Поскольку числители такие простые, я сразу прихожу к своему ответу:
Решите следующее уравнение:
( x — 3) / 7 = (4 x + 12) / 7
В этом уравнении дроби по обе стороны от знака «равно».У двух дробей одинаковый знаменатель. Две дроби будут равны, если их числители равны, поэтому я могу «приравнять» числители (то есть я могу сделать их равными) и решить полученное уравнение:
x — 3 = 4 x + 12
–3 — 12 = 4 x — x
–15 = 3 x
–5 = x
Решите следующее уравнение:
Это уравнение состоит из двух равных друг другу дробей (которые можно рассматривать как пропорцию).Я могу решить эту проблему тремя способами. Я покажу каждую, и вы сможете выбрать то, что вам больше нравится.
Метод 1: преобразование к общему знаменателю:
Я могу преобразовать в общий знаменатель 15:
Теперь, когда у меня есть «(одна дробь) равна (другая дробь)», я могу приравнять числители:
Метод 2: Умножение на общий знаменатель:
Наименьший общий знаменатель равен 15.Вместо того, чтобы преобразовывать дроби в этот знаменатель (что-то, что было бы , требовало , если бы я складывал или вычитал эти рациональные дроби), я могу вместо этого умножить (то есть умножить обе части уравнения) на 15. Это дает мне:
x — 1 = 2 (3)
x — 1 = 6
x = 7
Метод 3: Перекрестное умножение:
Термин «кросс-умножение» не является техническим, и некоторые инструкторы его абсолютно ненавидят.Но это термин, который вы услышите, и он обозначает метод, который может оказаться полезным.
Так как это уравнение, я могу умножить на все, что захочу. В частности, чтобы избавиться от знаменателей, я могу умножить их на эти знаменатели. В этом случае я бы умножил 15 из знаменателя левой части на 2 в числителе правой части; и я бы умножил 5 из знаменателя правой части на x — 1 в числителе левой части.Другими словами, я бы сделал это:
Этот процесс «пересечения» знака «равно» с каждым знаменателем и умножения каждого на противоположный числитель — это то, что подразумевается под «перекрестным умножением». Это сокращение от «умножения на общие знаменатели, когда есть только две дроби, равные самим себе, а затем упрощение того, что осталось», и может быть хорошим сокращением.
Перекрестное умножение дает мне следующее новое (и линейное) уравнение:
5 ( x — 1) = 15 (2)
5 x — 5 = 30
5 x = 35
x = 7
Итак, по каждому из методов мой ответ:
Примечание. Перекрестное умножение (то есть способ 3 выше) работает только , если уравнение имеет ровно одну дробь с одной стороны от знака «равно», равное ровно одной дроби с другой стороны от знака «равно». .Если в любой из сторон уравнения добавлены (или вычтены) дроби, должны, использовать метод 1 или метод 2.
Решите следующее уравнение:
В этом уравнении в левой части были вычтены дроби, поэтому я не могу выполнить перекрестное умножение. Кроме того, в знаменателе появилась новая складка переменных.Это означает, что мне нужно отслеживать значения x , которые вызовут деление на ноль. Эти ценности не могут быть частью моего окончательного ответа. В этом случае знаменатели говорят мне, что мой ответ будет иметь следующее ограничение:
Метод 1. Чтобы решить это уравнение, я могу преобразовать все в общий знаменатель 5 x ( x + 2), а затем сравнить числители:
Здесь знаменатели те же.Так действительно ли они имеют значение? Не совсем — кроме как сказать, какими значениями x быть не может из-за проблем с делением на ноль. На этом этапе две стороны уравнения будут равны, пока числители равны. То есть все, что мне действительно нужно сейчас сделать, это решить числители:
15 x — (5 x + 10) = x + 2
10 x — 10 = x + 2
9 x = 12
x = 12 / 9 = 4 / 3
Поскольку x = 4 / 3 не вызовет каких-либо проблем с делением на ноль в дробях в исходном уравнении, то это решение действительно.
Метод 2: Другой метод — найти общий знаменатель, но вместо того, чтобы преобразовывать все в этот знаменатель, я воспользуюсь тем фактом, что здесь у меня есть уравнение. То есть я умножу обе части на общий знаменатель. Это избавит от знаменателей. Я использовал цвета ниже, чтобы выделить части, которые отменяются:
В любом случае мой ответ один и тот же:
Я считаю, что метод 2 быстрее и проще, но это только мои личные предпочтения.По моему опыту в классе, студенты обычно довольно равномерно разделяют свои предпочтения в отношении методов 1 и 2. Вам следует использовать тот метод, который лучше всего подходит для вас.
URL: https://www.purplemath.com/modules/solvrtnl.htm
вопросов по алгебре с ответами и решениями для 8 класса
-
-
A) -2x + 5 + 10x — 9: дано
= (10x — 2x) + (5-9): сложите одинаковые термины вместе
= 8x — 4: группаB) 3 (x + 7) + 2 (-x + 4) + 5x: дано
= 3x + 21 — 2x + 8 + 5x: развернуть
= (3x — 2x + 5x) + (21 + 8): сложите одинаковые термины вместе
= 6x + 29: группа -
A) (2x — 6) / 2: дано
= 2 (x — 3) / 2: множитель 2 в числителе
= x — 3: разделите числитель и знаменатель на 2 для упрощенияB) (-x — 2) / (x + 2): задано
= -1 (x + 2) / (x + 2): множитель -1 в числителе
= -1: разделите числитель и знаменатель на x + 2, чтобы упроститьC) (5x — 5) / 10: дано
= 5 (x — 1) / 10: множитель 5 в числителе
= (x — 1) / 2: разделите числитель и знаменатель на 5 для упрощения -
A) -x = 6: дано
x = -6: умножьте обе части уравнения на -1B) 2x — 8 = -x + 4: задано
2x — 8 + 8 = -x + 4 + 8: прибавить +8 к обеим сторонам уравнения
2x = -x + 12: группировать похожие термины
2x + x = -x + 12 + x: добавить + x к обеим сторонам
3x = 12: группировать похожие термины
x = 4: взаимно обе стороны на 1/3C) 2x + 1/2 = 2/3: дано
2x + 1/2 — 1/2 = 2/3 — 1/2: вычесть 1/2 с обеих сторон
2x = 1/6: группировать похожие термины
x = 1/12: умножить обе стороны на 1/2D) x / 3 + 2 = 5: дано
x / 3 + 2-2 = 5-2: вычесть 2 с обеих сторон
x / 3 = 3: группировать похожие термины
x = 9: умножить обе стороны на 1/2E) -5 / x = 2: задано
-5 = 2x: умножить обе стороны на x и упростить
-5/2 = x:: умножить обе стороны на 1/2 -
A) x 2 — y 2 , x = 4, y = 5: задано
4 2 -5 2 : замените x и y заданными значениями
= 16-25 = -9B) | 4x — 2y | , x = -2, y = 3: задано
| 4 (-2) — 2 (3) | : заменить x и y заданными значениями
= | -14 | = 14: оценитьC) 3x 3 — 4y 4 , x = -1, y = -2: задано
3 (-1) 3 — 4 (-2) 4 : заменить x и y заданными значениями
= -3 — 64 = -67: оценить -
A) x + 6 <0: задано
x + 6-6 <-6: вычесть 6 с обеих сторон
x <-6: группировать похожие терминыB) x + 1> 5: дано
x + 1-1> 5-1: вычесть 1 с обеих сторон
x> 4: группировать похожие терминыC) 2 (x — 2) <12: задано
x — 2 <6: одновременно обе стороны на 1/2
x — 2 + 2 <6 + 2: прибавить 2 к обеим сторонам
x <8: сгруппировать термины -
A) (-1) a = 1: определение: a — величина, обратная -1
a = 1 / -1 = -1: решить относительно a; -1 является обратной величиной -1B) (0) b = 1: определение: b является обратной величиной 0
b = undefined: ни одно значение b не удовлетворяет приведенному выше уравнениюC) (3/4) c = 1: определение: c является обратной величиной 3/4
c = 4/3: решить относительно c; c = 4/3 — величина, обратная 3/4D) (2 5/7) d = 1: определение: d — величина, обратная 2 5/7.
(19/7) d = 1: преобразовать смешанное число 2 5/7 в дробь.
d = 7/19:: решить относительно d; d = 7/19 является обратной величиной 2 (5/7)E) 0,02 d = 1: определение: d — величина, обратная 0,02.
d = 1 / 0,02: решить относительно d; d = 50 — величина, обратная 0,02 -
A) 3 3/4 + 6 1/7: дано
= (3 + 6) + (3/4 + 1/7): сложите целые части вместе, а дробные части.
= 9 + (21/28 + 4/28): прибавить.
= 9 25/28B) (1 3/5) (3 1/3) — 2 1/2: дано
= (8/5) (10/3) — 2 1/2: преобразовать смешанные числа в дробные числа.
= 80/15 — 2 1/2 = 5 1/3 — 2 1/2 = 4 4/3 — 2 1/2: кратко и напишите смешанное число, если это возможно
= (4-2) + (4/3 — 1/2): вычесть
= 2 5/6C) (5 2/3) (4 1/5): дано
= (17/3) (21/5): преобразование смешанных чисел в дроби.
= 85/63: делить дроби
= 1 22/63: записать как смешанное числоD) (3 4/7 — 1 1/2) (2 3/8 + 2 1/4): дано
= [(3 — 1) + (4/7 — 1/2)] [(2 + 2) + (3/8 + 1/4)]: вычислить числитель и знаменатель как дроби.
= (2 1/14) (4 5/8)
= (29/14) (37/8)
= 116/259 -
A) — 4 2 = — (4 4) = -16: развернуть и вычислитьB) (-2) 3 = (-2) (- 2) (- 2) = -8: развернуть и вычислить
C) 1000 0 = 1: определение: любое ненулевое число в нулевой степени дает 1
D) 566 1 = 566
-
А) 0,02 = 1/50
В) 12% = 3/25
C) 0,5% = 1/200
D) 1,12 = 28/25 -
А) 1/5 = 0.2
В) 120% = 1,2
C) 0,2% = 0,002
D) 4 8/5 = 5,6 -
А) 3/10 = 30%
B) 1,4 = 140%
С) 123,45 = 12345%
D) 2 4/5 = 280% -
A) 156312, делится на 3
B) 176314, не делится на 3 -
A) 3432, делится на 4
B) 1257, не делится на 4 -
A) 1233, не делится на 6
B) 3432, делится на 6 -
A) 2538, делится на 9
B) 1451, не делится на 9 -
Вычислите 8x + 7, учитывая, что x — 3 = 10.
x — 3 = 10: данное уравнение
x = 10 + 3 = 13: решить данное уравнение.
8 (13) + 7 = 111 замените x на 3 в данном выражении и оцените. - Понять Спросите: «Если бы я продолжал рисовать стрелки, как долго была бы стрелка для цифры« 3 »в тысячных долях? Как бы это было по сравнению со стрелкой «3» в разряде десятков? » Было бы слишком мало, чтобы увидеть. Потребовалось бы 10 000 из них, чтобы они равнялись длине стрелки для цифры «3» в разряде десятков.
- Оценить На доске напишите 1234 и 0,1234 . Спросите: «Как совмещенное значение последних трех цифр в каждом числе соотносится со значением первой цифры?» В обоих случаях суммарное значение цифр 2, 3 и 4 меньше, чем 1 ⁄ 4 значения первой цифры.
Задания и игры по математике для 7-х классов
Физические и визуальные модели десятичных знаков трудно распространить более чем на несколько мест, потому что размер модели сильно меняется при переходе с места на место. Просмотр десятичных дробей как суммы дробей дает учащимся другой способ думать о десятичных дробях.
Напишите на доске 237,9036 в стандартной десятичной форме и как сумму произведений.
Затем нарисуйте числовую линию, как показано ниже. Используйте стрелку, чтобы обозначить каждую цифру числа, написанного на доске. По мере того, как вы «наращиваете» число, учащиеся могут видеть, как относительно мало цифра в каждом дополнительном десятичном разряде влияет на размер десятичной дроби.
Начинается с первых двух цифр: 2 3 _._ _ _ _
Обратите внимание, что даже если бы цифра десятков была 9 (максимально возможная), число не достигло бы 300. Напишите следующую цифру и нарисуйте ее стрелку: 2 3 7 . _ _ _ _
Обратите внимание, что даже если бы количество единиц было 9 (максимально возможное), число не достигло бы 240. Продолжайте со следующей цифры: 2 3 7. 9 _ _ _
Обратите внимание, что даже несмотря на то, что десятые доли равны 9 (максимально возможное), число не достигает 238.
Обсудите тот факт, что независимо от размера каждой последующей цифры, ее стрелка не может быть длиннее, чем стрелка перед ней.
Стратегии запросов
MVM Team Green — Math Grade 7 Period A
Blizzard Bag — перейдите по этой ссылке
https: // drive.google.com/drive/folders/1PRHXPODqeeqxOOmuVvzkKFtXKDwjBeHY
Неделя с 4 марта по 8 марта
Понедельник. Продолжайте практиковаться в классе с масштабными коэффициентами для длин и областей, которые увеличиваются, уменьшаются или остаются такими же. Стр. 51-52. Домашнее задание — сдать завтра — стр. 45-46, масштабирование
, вторник — обзор масштабных коэффициентов (соотношения, пропорции, масштабные коэффициенты, увеличение фигур, уменьшение фигур, длины и площади).
Среда — Викторина по масштабным факторам. Если время начать масштабирование проекта)
Четверг — масштабирование проекта — будет считаться тестом.Мы будем работать над этим на следующей неделе в классе.
Пятница — Никаких занятий из-за полного рабочего дня.
Неделя с 25 февраля по 1 марта
Понедельник — Начало Глава № 5 — Масштабирование модели вашего стола с 3 объектами на нем — используйте миллиметровую бумагу
Вторник — Просмотрите измерения углов с помощью транспортира. Классифицируйте углы
Среда — Модель в масштабе Практика — Треугольники — Страница 39-40
Четверг — Модели в масштабе и пропорции — Страницы 41-43. При необходимости закончите домашнее задание.
Пятница — Sec 5.2c Страницы 47-48
Неделя с 11 февраля по 15 февраля
Понедельник — Pg 181 # 1 в классе и # 2 для домашнего задания
Вторник — Обзор главы # 4
Среда — Карибу Математический конкурс
Четверг — Глава 4 Тест на пропорции
Пятница — Задачи TeamGO в помещении и на улице
Неделя с 4 по 8 февраля
Понедельник — Коэффициенты вероятности.
Вторник — Вероятность процентов. HW — ожидается завтра — Спиральный обзор
Среда — Пропорции вероятности или проценты.HW — ожидается завтра — страница обзора спирали 160 и 166
Четверг — Mark Up & Mark Downs — В классе я буду моделировать страницу 177. HW — ожидается завтра — 4.3e Pg 178
Пятница — Вероятностные игры — СНИМИТЕ! & SKUNK
Неделя с 28 января по 1 февраля
Понедельник — IXL Grade 7 DD.1, DD.4, DD.5 & Freckle
Вторник — Вероятность — Подбрасывание монеты — Экспериментальный VS Теоретический. Какова вероятность того, что событие произойдет?
Среда — Вероятность продолжения.
Четверг — ВЫБИРАЙТЕ Вероятностная игра — вам нужен партнер.
Пятница — Вероятность и проценты
Они должны быть в вашей папке
Приветственное письмо
Письмо об ожидании
4 разделителя с этикетками
Папка с домашним заданием
Без вкладышей
Без бумаг в боковых карманах 2 Warmps
9000 Раздел
Примечания в Примечаниях Раздел
Классная работа / Домашнее задание
Викторины и тесты
Неделя с 21 января по 25 января
Вторник — Подготовьте папки для проверки папки в пятницу.Работа над пропорциями бумаги 4.2f. Домашнее задание — сдать завтра — Spiral Review Pg 76
Среда — Закончите документ 4.2f и сдайте. Найдите и исправьте ошибку.
Четверг — Обзор: Представления о пропорциях. Пропорция VS. Непропорции.
Пятница — Проверка на переплет и викторина по изображениям пропорций и пропорций VS. Непропорции.
Неделя с 14 января по 18 января
Понедельник — Пропорции — Расход топлива Романа
Вторник — Пропорции — Cookies & Snowfall Rates
Среда — Пропорции VS Non Proportions
Четверг — Математический конкурс Карибу
Пятница — Модели для пропорций — Барные модели, уравнения, таблицы, графики
Неделя с 7 января по 11 января
Понедельник — Эквивалентные соотношения и удельные цены — Сравните рецепты лимонада.Стр. 6. Это включает в себя создание таблицы и графическое отображение рецептов соотношений. Домашнее задание — Спиральный обзор стр. 21 — должен завтра
Вторник — Обзор эквивалентных соотношений с 6 класса. Это включает создание удельных расценок. Примечания к страницам 14-15. В классе, если нужно, закончите домашнее задание, стр. 16–18.
Среда — Таблица и график эквивалентных соотношений черная кошка и полосатая кошка для вашего класса на стр. 17 # 2b. Что такое удельная ставка?
Четверг — приглашенный докладчик по информатике. Мы присоединимся к классу мистера Эриксона в комнате 205.
Пятница — Стр. 20-21 Расход топлива Романа. Составьте таблицу и график данных (эквивалентные соотношения для расхода бензина Романа). Что такое удельная ставка?
Неделя с 31 декабря по 4 января С Новым годом!
Среда — просмотрите главу 3 «Модульное тестирование». При необходимости закончите домашнее задание. Учебное пособие — математические свойства, упрощение числовых выражений, решение алгебраических уравнений, написание эквивалентных выражений для словесной задачи.
Четверг — Продолжение обзора модульного теста главы 3.IXL класс 7 R.12 (упрощение выражений с помощью математических свойств) и S.6 (решение алгебраических уравнений).
Пятница — Глава 3 Модульный тест — Выражения и уравнения.
Неделя с 17 декабря по 21 декабря
Понедельник — Решение текстовых задач Pg 119-120
Вторник — Решите процентные задачи с помощью модели и уравнения. Стр. 122-123 — при необходимости закончить работу по дому.
Среда — Продолжение практики решения процентных задач с использованием моделей и уравнений. Стр. 128–129, при необходимости закончите домашнее задание.
Четверг — проблема с картинками в шкафчике.
Пятница — Зеленые мероприятия команды — Принесите подарок, если хотите участвовать в обмене подарками. Сделайте или купите подарок, подходящий для мальчика или девочки, стоимостью не более 10 долларов.
Глава 3 «Обзор и проверка» будет после перерыва в отпуске.
Неделя с 10 декабря по 14 декабря
Понедельник — IXL Решение алгебраических уравнений 8 степени W8 и W12
Вторник — Решение и проверка многоступенчатых уравнений — Стр. 102
Среда — Викторина — Решить и проверить многошаговый Уравнения.После викторины Стр. 104. Уравнения с рациональными числами. (дроби, десятичные дроби)
Четверг — Дополнительная практика и обзор решения уравнений. Pg 109 или Pg 111-112
Friday — Real World Application Problems Pg 119-120. Головоломки со словами
Неделя с 3 декабря по 7 декабря
Понедельник — Распределительное свойство в алгебраических выражениях и уравнениях. Pg 52
Вторник — Факторинг (противоположность распределению!) Стр. 56-57. Завтра сдать домашнее задание стр. 58.
Среда — объедините похожие термины, включая некоторые выражения, имеющие свойство распределения.Pg 64-65
Четверг: решайте алгебраические уравнения. Проверьте свое решение. Стр. 79. Домашнее задание — стр. 83 — сдать завтра.
Пятница — Найдите ошибки, когда кто-то решил алгебраическое уравнение. Заметки. Pg 90
В следующую среду будет викторина по решению и проверке алгебраических уравнений.
Неделя с 26 ноября по 30 ноября
Понедельник — задачи со словами и числовые выражения Стр. 19-20. Завтра должен быть сдан обзор спирали домашнего задания, стр. 24.
Вторник — Алгебраические выражения Стр. 25-26
Среда — Упростите алгебраические выражения.(Термины, коэффициенты, константы, подобные термины). Стр. 36 и стр. 38. Домашнее задание — сдать завтра — стр. 46
Четверг — Распределительная собственность. Pg 52 и Pre-Alg
Friday — Quiz — Преобразование задач в числовые или алгебраические выражения, математические свойства, упрощение числовых или алгебраических выражений.
Неделя с 19 ноября по 23 ноября
Понедельник — конец страницы 17 с пятницы. Страница 18 в классе и заполнена для домашнего задания, если необходимо. До завтра.
Вторник — Math Jeopardy — играли в командах
Неделя с 12 ноября по 16 ноября
Понедельник — Без школы — День ветеранов
Вторник — Math Properties.Домашнее задание — сдать завтра — Page 13 привести примеры данного математического свойства.
Среда — стр. 14 назовите математическое свойство для данного выражения, за которым следуют числовые выражения для задач со словами, стр. 16.
Четверг — Конкурс математики Карибу. IXL Grade 7 N1, F5 или R9 или задания, перечисленные в математике Веснушек, если время после конкурса Карибу.
Пятница — стр. 17-18. Продолжена работа по преобразованию текстовых задач в эквивалентные числовые выражения.
Неделя с 5 ноября по 9 ноября
Понедельник — Подготовьтесь к проверке папки в этот четверг.Имейте свои приветственные письма и письма с ожиданием, 4 разделителя, папку с домашними заданиями, заметки, навыки / разминки, классные / домашние задания, графики кружки, викторины и не кладите в карманы отдельные листы или бумаги. Мы также закроем страницы 83 и 84 с пятницы, если потребуется.
Вторник — Без школы — Полный рабочий день.
Среда — повторение теста по главе № 2 в пятницу. Тест будет включать в себя все операции для целых и рациональных чисел, GEMDAS, построение графиков на координатном плане, который включает в себя то, что произойдет, если мы умножим или разделим координаты на целое число, а также проблемы со словами приложения.В классе страницы 86 и 87.
Четверг — переплет. Завершить тестовый обзор целых и рациональных чисел. Стр. 90 и стр. 82.
Пятница — Глава 2 Тест на целые и рациональные числа. Тест будет включать в себя все операции для целых и рациональных чисел, GEMDAS, построение графиков на координатном плане, который включает в себя то, что произойдет, если мы умножим или разделим координаты на целое число, а также проблемы со словами приложения.
Неделя с 29 октября по 2 ноября
Понедельник — сложение и вычитание рациональных чисел.Примечание. В классе стр. 72. Домашнее задание — сдать завтра — стр. 73 Обзор спирали
Вторник — IXL класс 7 E1, E2, G1, G2. Математика веснушек — см. Задания. Получите код доступа с доски.
Среда — умножайте и делите рациональные числа. Примечание. В классе стр. 78
Четверг — IXL класс 7 E3, E5, G9, G10, G12, G13. Математика с веснушками — см. Задания. получите код доступа с доски.
Пятница — приложения рациональных чисел — словесные задачи.
Неделя с 15 октября по 19 октября
Понедельник — завершение работы GEMDAS.Графическая кружка с изменениями.
Вторник — кружка в движении — посмотрите, что умножение координат исходной кружки на целые числа делает с кружкой !. Домашнее задание — Создайте свою КРУЖКУ. Вам понадобится миллиметровая бумага, и вам нужно будет указать свои изменения и то, как вы их получили. До завтра.
Среда — Викторина по всем операциям с целыми числами.
Четверг — Соревнование по математике Карибу
Пятница — Модель Frayer рациональных чисел. Математические операции с рациональными числами. Дроби и десятичные дроби!
Неделя с 8 по 12 октября
Вторник — стр. 45 Обзор сложения и вычитания целых чисел.Сюда входят задачи со словами и числовые линии. Домашнее задание — стр. 57 Целые числа
Среда — Тест по сложению и вычитанию целых чисел с абсолютными значениями. Сюда входят задачи со словами и моделирование числовых линий. После викторины — стр. 47 «Умножение и деление целых чисел»
Четверг — операции с смешанными целыми числами. Pg 67
Пятница. Отображение целых чисел в 4-х квадрантах. Встречайте Mug!
Неделя с 1 по 5 октября
Понедельник — Модель Фрайера на целых числах. Стр. 25-26 Сложить или вычесть целые числа.
Вторник — Продолжение целочисленной практики Стр. 30-31.
Среда — стр. 32. Домашнее задание — сдать завтра Стр. 33
Четверг — Абсолютные значения — стр. 35-36 Применение целых чисел.
Friday- Pg 40-41 & Упростите выражения, содержащие абсолютные значения.
Неделя с 24 по 28 сентября
Понедельник — стр. 56-57. Вероятность, проценты, дроби, десятичные дроби. Решайте уравнения и задачи со словами, в том числе используя модель. Измените эквивалентные значения между дробями, десятичными знаками и процентами.Поместите десятичные дроби, дроби и проценты в порядке от наименьшего к наибольшему, в том числе на горизонтальной или вертикальной числовой строке.
Вторник — обзор теста Раздела 1 Стр. 52-53. При необходимости закончите домашнее задание.
Среда — Тест Глава 1 — Вероятность, проценты, дроби, десятичные дроби. Решайте уравнения и задачи со словами, в том числе используя модель. Измените эквивалентные значения между дробями, десятичными знаками и процентами. Поместите десятичные дроби, дроби и проценты в порядке от наименьшего к наибольшему, в том числе на горизонтальной или вертикальной числовой строке.
Четверг — Целые числа Глава 2 Стр. 14 Обзор спирали
Пятница — Больше целых чисел. Игра «Сумма или произведение целых чисел».
Неделя с 17 сентября по 21 сентября
Понедельник — Задание по шаблону — Сложение дробей
Вторник — 1.
