Содержание
расчет электродвижущей силы по формуле
Электромагнитная индукция – генерирование электротоков магнитными полями, изменяющимися во времени. Открытие Фарадеем и Генри этого феномена ввело определенную симметрию в мир электромагнетизма. Максвеллу в одной теории удалось собрать знания об электричестве и магнетизме. Его исследования предсказывали существование электромагнитных волн перед экспериментальными наблюдениями. Герц доказал их существование и открыл человечеству эпоху телекоммуникаций.
Эксперименты Фарадея
Законы Фарадея и Ленца
Электрические токи создают магнитные эффекты. А возможно ли, чтобы магнитное поле порождало электрическое? Фарадей обнаружил, что искомые эффекты возникают вследствие изменения МП во времени.
Когда проводник пересекается переменным магнитным потоком, в нем индуцируется электродвижущая сила, вызывающая электроток. Системой, которая генерирует ток, может быть постоянный магнит или электромагнит.
Явление электромагнитной индукции регулируется двумя законами: Фарадея и Ленца.
Закон Ленца позволяет охарактеризовать электродвижущую силу относительно ее направленности.
Важно! Направление индуцированной ЭДС такое, что вызванный ею ток стремится противостоять создающей его причине.
Фарадей заметил, что интенсивность индуцированного тока растет, когда быстрее изменяется число силовых линий, пересекающих контур. Другими словами, ЭДС электромагнитной индукции находится в прямой зависимости от скорости движущегося магнитного потока.
ЭДС индукции
Формула ЭДС индукции определена как:
Е = — dФ/dt.
Знак «-» показывает, как полярность индуцированной ЭДС связана со знаком потока и меняющейся скоростью.
Получена общая формулировка закона электромагнитной индукции, из которой можно вывести выражения для частных случаев.
Движение провода в магнитном поле
Когда провод длиной l движется в МП, имеющем индукцию В, внутри него будет наводиться ЭДС, пропорциональная его линейной скорости v. Для расчета ЭДС применяется формула:
Для расчета ЭДС применяется формула:
- в случае движения проводника перпендикулярно направлению магнитного поля:
Е = — В x l x v;
- в случае движения под другим углом α:
Е = — В x l x v х sin α.
Индуцированная ЭДС и ток будут направлены в сторону, которую находим, пользуясь правилом правой руки: расположив руку перпендикулярно силовым линиям магнитного поля и указывая большим пальцем в сторону перемещения проводника, можно узнать направление ЭДС по оставшимся четырем распрямленным пальцам.
Перемещение провода в МП
Вращающаяся катушка
Работа генератора электроэнергии основана на вращении контура в МП, имеющего N витков.
ЭДС индуцируется в электроцепи всегда, когда магнитный поток ее пересекает, в соответствии с определением магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на поверхностную площадь, через которую проходит МП, и косинус угла, образованного вектором В и перпендикулярной линией к плоскости S).
Из формулы следует, что Ф подвержен изменениям в следующих случаях:
- меняется интенсивность МП – вектор В;
- варьируется площадь, ограниченная контуром;
- изменяется ориентация между ними, заданная углом.
В первых опытах Фарадея индуцированные токи были получены путем изменения магнитного поля В. Однако можно индуцировать ЭДС, не двигая магнит или не меняя ток, а просто вращая катушку вокруг своей оси в МП. В данном случае магнитный поток меняется из-за изменения угла α. Катушка при вращении пересекает линии МП, возникает ЭДС.
Если катушка вращается равномерно, это периодическое изменение приводит к периодическому изменению магнитного потока. Или количество силовых линий МП, пересекаемых каждую секунду, принимает равные значения с равными интервалами времени.
Вращение контура в МП
Важно! Наведенная ЭДС меняется вместе с ориентацией с течением времени от положительной до отрицательной и наоборот.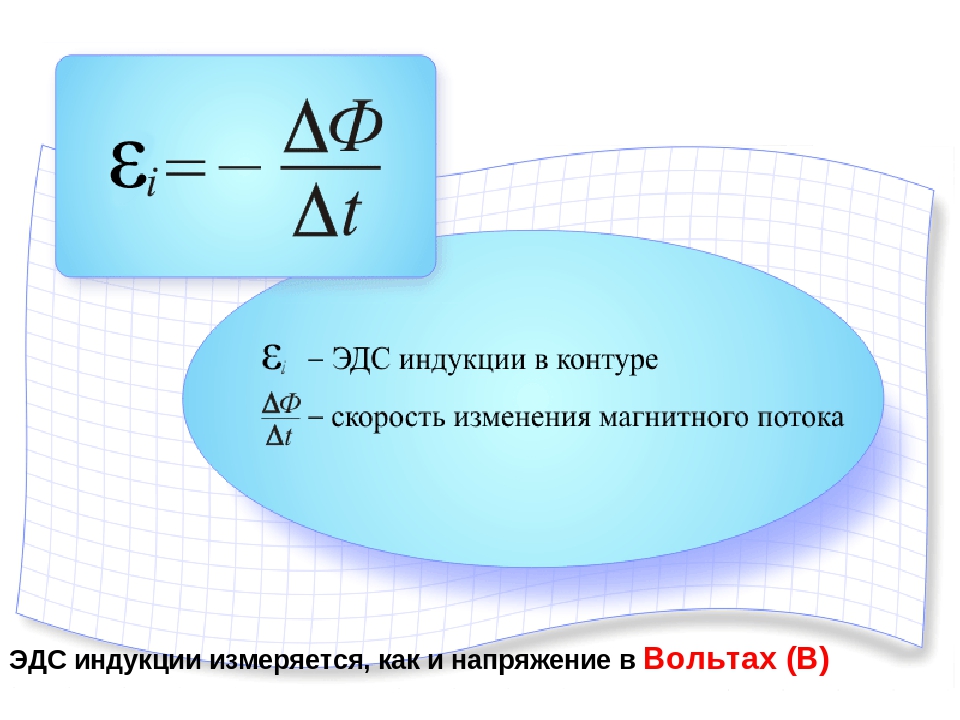 Графическое представление ЭДС представляет собой синусоидальную линию.
Графическое представление ЭДС представляет собой синусоидальную линию.
Для формулы ЭДС электромагнитной индукции применяется выражение:
Е = В х ω х S x N x sin ωt, где:
- S – площадь, ограниченная одним витком или рамкой;
- N – количество витков;
- ω – угловая скорость, с которой вращается катушка;
- В – индукция МП;
- угол α = ωt.
На практике в генераторах переменного тока часто катушка остается неподвижной (статор), а электромагнит вращается вокруг нее (ротор).
ЭДС самоиндукции
Когда через катушку проходит переменный ток, он генерирует переменное МП, обладающее изменяющимся магнитным потоком, индуцирующим ЭДС. Этот эффект называется самоиндукцией.
Поскольку МП пропорционально интенсивности тока, то:
Ф = L x I,
где L – индуктивность (Гн), определяемая геометрическими величинами: количеством витков на единицу длины и размерами их поперечного сечения.
Для ЭДС индукции формула принимает вид:
Е = — L x dI/dt.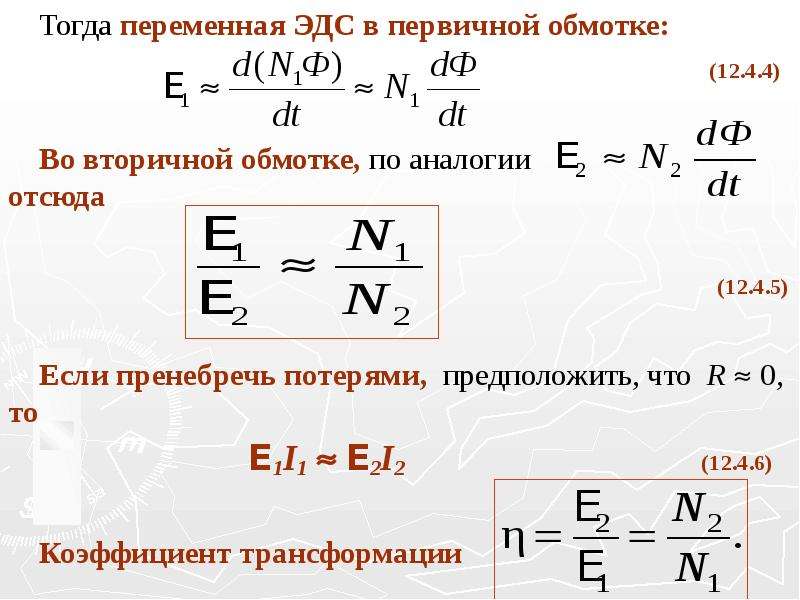
Взаимоиндукция
Если две катушки расположены рядом, то в них наводится ЭДС взаимоиндукции, зависящая от геометрии обеих схем и их ориентации относительно друг друга. Когда разделение цепей возрастает, взаимоиндуктивность снижается, так как уменьшается соединяющий их магнитный поток.
Взаимоиндукция
Пусть имеется две катушки. По проводу одной катушки, обладающей N1 витками, протекает ток I1, создающий МП, проходящее через катушку с N2 витками. Тогда:
- Взаимоиндуктивность второй катушки относительно первой:
М21 = (N2 x F21)/I1;
- Магнитный поток:
Ф21 = (М21/N2) x I1;
- Найдем индуцированную ЭДС:
Е2 = — N2 x dФ21/dt = — M21x dI1/dt;
- Идентично в первой катушке индуцируется ЭДС:
Е1 = — M12 x dI2/dt;
Важно! Электродвижущая сила, вызванная взаимоиндукцией в одной катушке, всегда пропорциональна изменению электротока в другой.
Взаимную индуктивность можно признать равной:
М12 = М21 = М.
Соответственно, E1 = — M x dI2/dt и E2 = M x dI1/dt.
М = К √ (L1 x L2),
где К – коэффициент связи между двумя индуктивностями.
Явление взаимоиндукции используется в трансформаторах – электроаппаратах, позволяющих изменить значение напряжения переменного электротока. Аппарат представляет собой две катушки, намотанные вокруг одного сердечника. Ток, присутствующий в первой, создает меняющееся МП в магнитопроводе и электроток в другой катушке. Если количество витковых оборотов первой обмотки меньше, чем другой, напряжение увеличивается, и наоборот.
Кроме генерирования, трансформации электроэнергии магнитная индукция применяется в иных устройствах. Например, в магнитных левитационных поездах, которые двигаются не в непосредственном контакте с рельсами, а на несколько сантиметров выше из-за электромагнитной силы отталкивания.
Видео
Оцените статью:
Глава 23. Закон электромагнитной индукции
Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС. Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.
Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как
Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как
(23.1) |
где — индукция поля, — площадь контура, — угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см. рисунок; перпендикуляр к плоскости контура показан пунктиром). Единицей магнитного потока в международной системе единиц измерений СИ является Вебер (Вб), который определяется как магнитный поток через контур площади 1 м2 однородного магнитного поля с индукцией 1 Тл, перпендикулярной плоскости контура.
Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока
(23.2) |
Здесь — изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле. Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.
Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле. Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.
Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило. Например, при увеличении потока внешнего магнитного поля через контур в нем возникнет индукционный ток, магнитное поле которого будет направлено противоположно внешнему магнитному полю так, чтобы уменьшить внешнее поле и сохранить, таким образом, первоначальную величину магнитного поля. При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.
При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.
Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи
(23. |
где — сила тока в цепи, — коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи. Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции
(23.4) |
Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током
(23. |
где — индуктивность контура, — сила тока в нем.
Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.
Рассмотрим теперь задачи.
Из перечисленных в задаче 23.1.1 явлений только одно есть следствие закона электромагнитной индукции — появление тока в кольце при проведении сквозь него постоянного магнита (ответ 3). Все остальное — результат магнитного взаимодействия токов.
Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23. 1.2), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2).
1.2), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2).
Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (задача 23.1.3) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом. А вот направление индукционного тока в этих случаях будет различным. Это связано с тем, что при приближении магнита к кольцу разными полюсами, поле в плоскости кольца в одном случае будет направлено противоположно полю в другом. Поэтому для компенсации этих изменений внешнего поля магнитное поле индукционного тока должно быть в этих случаях направлено по-разному. Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4).
Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в задаче 23.1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1).
А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в задаче 23.1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1).
При вращении рамки 1 (задача 23.1.5) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота — будет равен , где — индукция, — площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ 2).
В задаче 23.1.6 индукционный ток возникает только в случае 2 (ответ 2). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется. При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток
Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется. При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток
В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче — 2.
Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию задачи 23.1.8 индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ 3).
В задаче 23.1.9 ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ 4). Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.
В задаче 23.1.10 во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ 1).
При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (задача 23. 2.2 — ответ 3).
2.2 — ответ 3).
Используя формулу (23.3) находим в задаче 32.2.3 Гн (ответ 4).
Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) — ответ 3.
Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23.2.5) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2).
Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6 этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2).
Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1).
При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.
Задача 23.2.9 также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина — приближение магнита, кольцо будет отталкиваться от него (ответ 2). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.
Задача 23.2.10 — единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур . Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4).
что это такое, основные формулы, в чем измеряется, от чего зависит.
В материале разберемся в понятии ЭДС индукции в ситуациях ее возникновения. Также рассмотрим индуктивность в качестве ключевого параметра возникновения магнитного потока при появлении электрического поля в проводнике.
Электромагнитная индукция представляет собой генерирование электрического тока магнитными полями, которые изменяются во времени. Благодаря открытиям Фарадея и Ленца закономерности были сформулированы в законы, что ввело симметрию в понимание электромагнитных потоков. Теория Максвелла собрала воедино знания об электрическом токе и магнитных потоках. Благодаря открытия Герца человечество узнало о телекоммуникациях.
Магнитный поток
Вокруг проводника с электротоком появляется электромагнитное поле, однако параллельно возникает также обратное явление – электромагнитная индукция. Рассмотрим магнитный поток на примере: если рамку из проводника поместить в электрическое поле с индукцией и перемещать ее сверху вниз по магнитным силовым линиям или вправо-влево перпендикулярно им, тогда магнитный поток, проходящий через рамку, будет постоянной величиной.
При вращении рамки вокруг своей оси, тогда через некоторое время магнитный поток изменится на определенную величину. В результате в рамке возникает ЭДС индукции и появится электрический ток, который называется индукционным.
ЭДС индукции
Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.
Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.
Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.
Законы Фарадея и Ленца
Законы Фарадея и Ленца отображают закономерности возникновения электромагнитной индукции.
Фарадей выявил, что магнитные эффекты появляются в результате изменения магнитного потока во времени. В момент пересечения проводника переменным магнитным током, в нем возникает электродвижущая сила, которая приводит к возникновению электрического тока. Генерировать ток может как постоянный магнит, так и электромагнит.
Ученый определил, что интенсивность тока возрастает при быстром изменении количества силовых линий, которые пересекают контур. То есть ЭДС электромагнитной индукции пребывает в прямой зависимости от скорости магнитного потока.
Согласно закону Фарадея, формулы ЭДС индукции определяются следующим образом:
Е = — dФ/dt.
Знак «минус» указывает на взаимосвязь между полярностью индуцированной ЭДС, направлением потока и изменяющейся скоростью.
Согласно закону Ленца, можно охарактеризовать электродвижущую силу в зависимости от ее направленности. Любое изменение магнитного потока в катушке приводит к появлению ЭДС индукции, причем при быстром изменении наблюдается возрастающая ЭДС.
Если катушка, где есть ЭДС индукции, имеет замыкание на внешнюю цепь, тогда по ней течет индукционный ток, вследствие чего вокруг проводника появляется магнитное поле и катушка приобретает свойства соленоида. В результате вокруг катушки формируется свое магнитное поле.
Э.Х. Ленц установил закономерность, согласно которой определяется направление индукционного тока в катушке и ЭДС индукции. Закон гласит, что ЭДС индукции в катушке при изменении магнитного потока формирует в катушке ток направления, при котором данный магнитный поток катушки дает возможность избежать изменения постороннего магнитного потока.
Закон Ленца применяется для всех ситуаций индуктирования электротока в проводниках, вне зависимости от их конфигурации и метода изменения внешнего магнитного поля.
Движение провода в магнитном поле
Значение индуктированной ЭДС определяется в зависимости от длины проводника, пересекаемого силовыми линиями поля. При большем количестве силовых линий возрастает величина индуктируемой ЭДС. При увеличении магнитного поля и индукции, большее значение ЭДС возникает в проводнике. Таким образом, значение ЭДС индукции в движущемся в магнитном поле проводнике находится в прямой зависимости от индукции магнитного поля, длины проводника и скорости его движения.
Данная зависимость отражена в формуле Е = Blv, где Е — ЭДС индукции; В — значение магнитной индукции; I — длина проводника; v —скорость его перемещения.
Отметим, что в проводнике, который движется в магнитном поле, ЭДС индукции появляется, только когда он пересекает силовые линии магнитного поля. Если проводник движется по силовым линиям, тогда ЭДС не индуктируется. По этой причине формула применяется только в случаях, когда движением проводника направлено перпендикулярно силовым линиям.
Направление индуктированной ЭДС и электротока в проводнике определяется направлением движения самого проводника. Для выявления направления разработано правило правой руки. Если держать ладонь правой руки таким образом, чтобы в ее направлении входили силовые линии поля, а большой палец указывает направление движения проводника, тогда остальные четыре пальца показывают направление индуктированной ЭДС и направление электротока в проводнике.
Вращающаяся катушка
Функционирование генератора электротока основывается на вращении катушки в магнитном потоке, где имеется определенное количество витков. ЭДС индуцируется в электрической цепи всегда при пересечении ее магнитным потоком, на основании формулы магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на площадь поверхности, через которую проходит магнитный поток, и косинус угла, сформированный вектором направления и перпендикулярной плоскости линии).
Согласно формуле, на Ф воздействуют изменения в ситуациях:
- при изменении магнитного потока меняется вектор направления;
- изменяется площадь, заключенная в контур;
- меняется угол.
Допускается индуцирование ЭДС при неподвижном магните или неизменном токе, а просто при вращении катушки вокруг своей оси в пределах магнитного поля. В данном случае магнитный поток изменяется при смене значения угла. Катушка в процессе вращения пересекает силовые линии магнитного потока, в итоге появляется ЭДС. При равномерном вращении возникает периодическое изменение магнитного потока. Также число силовых линий, которые пересекаются ежесекундно, становится равным значениям через равные временные промежутки.
На практике в генераторах переменного электротока катушка остается в неподвижном состоянии, а электромагнит выполняет вращения вокруг нее.
ЭДС самоиндукции
При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.
В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:
Ф = L x I, где L – индуктивность, которая измеряется в Гн. Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.
Взаимоиндукция
При расположении двух катушек рядом в них наблюдается ЭДС взаимоиндукции, которая определяется конфигурацией двух схем и их взаимной ориентацией. При возрастании разделения цепей значение взаимоиндуктивности уменьшается, поскольку наблюдается уменьшение общего для двух катушек магнитного потока.
Рассмотрим детально процесс возникновения взаимоиндукции. Есть две катушки, по проводу одной с N1 витков течет ток I1, которым создается магнитный поток и идет через вторую катушку с N2 числом витков.
Значение взаимоиндуктивности второй катушки в отношении первой:
М21 = (N2 x F21)/I1.
Значение магнитного потока:
Ф21 = (М21/N2) x I1.
Индуцированная ЭДС вычисляется по формуле:
Е2 = — N2 x dФ21/dt = — M21x dI1/dt.
В первой катушке значение индуцируемой ЭДС:
Е1 = — M12 x dI2/dt.
Важно отметить, что электродвижущая сила, спровоцированная взаимоиндукцией в одной из катушек, в любом случае прямо пропорциональна изменению электрического тока в другой катушке.
Тогда взаимоиндуктивность считается равной:
М12 = М21 = М.
Вследствие этого , E1 = — M x dI2/dt и E2 = M x dI1/dt. М = К √ (L1 x L2), где К является коэффициентом связи между двумя значениями инжуктивности.
Взаимоиндукция широко используется в трансформаторах, которые дают возможность менять значения переменного электротока. Прибор представляет собой пару катушек, которые намотаны на общий сердечник. Ток в первой катушке формирует изменяющийся магнитный поток в магнитопроводе и ток во второй катушке. При меньшем числе витков в первой катушке, чем во второй, возрастает напряжение, и соответственно при большем количестве витков в первой обмотке напряжение снижается.
Помимо генерирования и трансформации электрической энергии, явление магнитной индукции используется в прочих приборах. К примеру, в магнитных левитационных поездах, движущихся без непосредственного контакта с током в рельсах, а на пару сантиметров выше по причине электромагнитного отталкивания.
Закон электромагнитной индукции. Курсы по физике
Тестирование онлайн
Электромагнитная индукция. Основные понятия
Закон электромагнитной индукции
ЭДС индукции в движущемся проводнике
Взаимосвязь электрических и магнитных явлений всегда интересовала физиков. Английский физик Майкл Фарадей был совершенно уверен в единстве электрических и магнитных явлений. Он рассуждал, что электрический ток способен намагнитить кусок железа. Не может ли магнит в свою очередь вызвать появление электрического тока? Эта задача была решена.
Если в постоянном магнитном поле перемещается проводник, то свободные электрические заряды внутри него тоже перемещаются (на них действует сила Лоренца). Положительные заряды концентрируются в одном конце проводника (провода), отрицательные — в другом. Возникает разность потенциалов — ЭДС электромагнитной индукции. Явление возникновения ЭДС индукции в проводнике, движущемся в постоянном магнитном поле, называется явлением электромагнитной индукции.
Правило определения направления индукционного тока (правило правой руки):
В проводнике, движущемся в магнитном поле, возникает ЭДС индукции, энергия тока в этом случае определяется по закону Джоуля-Ленца:
Работа внешней силы по перемещению проводника с током в магнитном поле
ЭДС индукции в контуре
Рассмотрим изменение магнитного потока через проводящий контур (катушку). Явление электромагнитной индукции было открыто опытным путем:
Закон электромагнитной индукции (закон Фарадея): ЭДС электромагнитной индукции, возникающая в контуре, прямо пропорциональна скорости изменения магнитного потока через него.
Знак «минус» является математическим выражением следующего правила. Направление индукционного тока, возникающего в контуре, определяется по правилу Ленца: возникающий в контуре индукционный ток имеет такое направление, что созданный им магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.
Формула ЭДС индукции, E
Закон Фарадея – Максвелла для электромагнитной индукции
Основной формулой, которая определяет ЭДС индукции, является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). Этот закон утверждает, что ЭДС индукции в контуре, находящемся в переменном магнитном поле, равна по величине и противоположна по знаку скорости изменения магнитного потока () через поверхность, которую ограничивает данный контур:
где – скорость изменения магнитного потока. Полная производная в законе (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) соответствует правилу Ленца. Формула (1) для ЭДС индукции записана для системы СИ.
В случае равномерного изменения магнитного потока формулу ЭДС индукции можно записать как:
Частные случаи формул ЭДС индукции
Если контур содержит N витков, которые соединяются последовательно, то ЭДС индукции вычисляют как:
где – потокосцепление.
При движении прямолинейного проводника в однородном магнитном поле в нем возникает ЭДС индукции, которая равна:
где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; .
При вращении с постоянной скоростью в однородном магнитном поле плоского контура вокруг оси, которая лежит в плоскости контура в нем возникает ЭДС индукции, равная:
где S – площадь, которую ограничивает виток; – поток самоиндукции витка; — угловая скорость; () – угол поворота контура. Следует учесть, что формула (5) справедлива, если ось вращения составляет прямой угол с направлением вектора внешнего поля .
Если во вращающейся рамке имеется N витков и самоиндукцией рассматриваемой системы можно пренебречь, то:
В стационарном проводнике, который находится в переменном магнитном поле, ЭДС индукции находят по формуле:
Примеры решения задач по теме «ЭДС индукции»
ЭДС индукции — Энциклопедия по машиностроению XXL
Закон электромагнитной индукции. Экспериментальное исследование зависимости ЭДС индукции от изменения магнитного потока привело к установлению закона электромагнитной индукции ЭДС индукции в замкнутом контуре пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром. [c.188]
В СИ единица магнитного потока выбрана такой, чтобы коэффициент пропорциональности между ЭДС индукции и изменением магнитного потока был равен единице. При этом закон электромагнитной индукции формулируется следующим образом ЭДС индукции в замкнутом контуре равна модулю скорости изменения магнитного потока через поверхность, ограниченную контуром [c.188]
Если в последовательно соединенных контурах происходят одинаковые изменения магнитного потока, то ЭДС индукции в них равна сумме ЭДС индукции в каждом из контуров. Поэтому при изменении магнитного потока в катушке, состоящей из п одинаковых витков провода, общая ЭДС индукции в п раз больше ЭДС индукции в одиночном контуре
[c.188]
Единица магнитного потока в Международной системе единиц называется вебером (Вб). Она определяется на основании использования закона электромагнитной индукции. Магнитный поток через площадь, ограниченную замкнутым контуром, равен 1 Вб, если при равномерном убывании этого потока до нуля за 1 с в контуре возникает ЭДС индукции 1 В [c.188]
ЭДС индукции в движущихся проводниках. Явление электромагнитной индукции наблюдается и в тех случаях, когда магнитное поле не изменяется во времени, но магнитный поток через контур изменяется из-за движения проводников контура в магнитном поле. В этом случае причиной возникновения ЭДС индукции является не вихревое электрическое поле, а сила Лоренца. [c.189]
Поэтому ЭДС индукции в контуре будет равна [c.189]
Совпадение выражений (54.5) и (54.7) показывает, что причиной возникновения ЭДС индукции в контуре в этом случае является действие силы Лоренца на заряды в движущемся проводнике. [c.190]
Самоиндукция. При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке. Явление возникновения ЭДС индукции в [c.190]
Мы получили, что работа внешних сил, вызывающих движение проводника в магнитном поле, равна работе ЭДС индукции в электрической цепи. [c.196]
Машнна постоянного тока как электрический генератор. Физический принцип действия машины постоянного тока как генератора основан на явлении возникновения ЭДС индукции в рамке из проводника при вращении ее в магнитном поле (рис. 203). [c.196]
При вращении якоря в магнитном поле индуктора в проводах его обмоток возникает ЭДС индукции. [c.196]
С потребителями электрической энергии через скользящие контакты коллектора и электрических щеток соединяются концы той обмотки якоря, в которой в данный момент времени ЭДС индукции имеет максимальное значение. [c.196]
Провода обмотки движутся перпендикулярно линиям индукции магнитного поля. При этом между концами проводника возникает ЭДС индукции, которая прямо пропорциональна скорости [c.196]
При равномерном увеличении магнитного потока через контур ЭДС индукции и сила тока в цепи постоянны. В этом случае электрический заряд Aq равен q = IM. Следовательно, нужно найти силу тока в цепи.
[c.210]
При зарядке и разрядке конденсатора колебательного контура изменения силы тока в катушке Lk контура вызывают изменения магнитного поля вокруг нее. При этом происходят изменения магнитного потока и возникает ЭДС индукции во второй катушке Lqb, называемой катушкой обратной связи. Один конец катушки обратной связи соединен с эмиттером транзистора, второй через конденсатор С — с его базой. Катушка обратной связи включена таким образом, что при увеличении силы тока в цепи коллектора на базу подается напряжение, отпирающее транзистор [c.235]
Изменения магнитного потока создают ЭДС индукции е в витке, согласно закону электромагнитной индукции равную производной потока магнитной индукции, взятой со знаком минус [c.237]
Следовательно, изменения ЭДС индукции со временем будут происходить по гармоническому закону [c.237]
Если с помощью контактных колец и скользящих по ним щеток соединить концы витка с электрической цепью, то под действием этой ЭДС индукции в электрической цепи возникнут вынужденные гармонические колебания силы тока — переменный ток. [c.237]
Отношение ЭДС самоиндукции l в первичной катушке к ЭДС индукции в2 во вторичной катушке равно отношению числа витков П1 в первичной катушке к числу витков Л2 во вторичной катушке [c.246]
При разомкнутой цепи вторичной катушки — режим холостого хода трансформатора — напряжение 2 на [c.246]
Вторичную катушку пронизывает тот же самый магнитный поток, который проходит через первичную катушку. При изменениях магнитного потока в каждом ее витке возникает ЭДС индукции, изменяющаяся по гармоническому закону, амплитуда изменений ЭДС индукции в одном витке имеет такое же значение, что и ЭДС самоиндукции в одном витке первичной катушки. Если число витков провода вторичной катушки /12, то мгновенное значение ЭДС в ней равно [c.246]
Виток провода площадью 2,5-10 м вращается с частотой 5 с в однородном магнитном поле с индукцией 1,1 Тл. Определите амплитуду колебаний ЭДС индукции в витке. [c.295]
С какой частотой должен вращаться виток провода в однородном магнитном поле с индукцией 1,2 Тл, чтобы амплитуда колебаний ЭДС индукции в нем была 1 В Площадь витка 2,5-10″ м . [c.295]
Ротор электрического генератора длиной Тми диаметром 1,25 м вращается с частотой 3000 оборотов в минуту. Индукция магнитного поля 2 Тл. Определите амплитуду колебаний ЭДС индукции в одном витке обмотки генератора. [c.296]
ЭДС индукции 188 Эквипотенциальная поверхность 139 Электрическая емкость 143 [c.365]
Зависимость (55), называемая законом электромагнитной индукции Фара дея, устанавливает и величину, и направление ЭДС индукции. [c.191]
Если в переменное магнитное поле помещен неподвижный проводник, то поток магнитной индукции сквозь сечение контура, охватываемого проводником, изменяется, в связи с чем в проводнике по закону Фарадея возникает ЭДС индукции [c.191]
Аналогичное соотношение можно получить и для электрического вихревого поля. Согласно (55), ЭДС индукции [c.192]
Индуктивность и взаимная индуктивность. При изменении магнитного потока, сцепленного с данным контуром, в последнем возникает электродвижущая сила (ЭДС) индукции, определяемая законом Фарадея [c.253]
Единицу индуктивности можно определить как индуктивность такого контура, который сцеплен с потоком в один максвелл, при протекании по нему тока, равного с единиц, Согласно другому определению единицей индуктивности является индуктивность такого контура, в котором возникает ЭДС индукции, равная единице, при изменении тока в контуре на единиц в секунду. В соответствии с размерностью иногда указанную единицу индуктивности называют сантиметром индуктивности. [c.255]
ИНДУКЦИОННЫЙ УСКОРИТЕЛЬ — ускоритель заряженных частиц, в к-ром прирост энергии частиц происходит за счёт эдс индукции, создаваемой перем. магн, потоком. Различают циклич. И. у. бетатрон), в к-ром частицы обращаются в магн. поле по траекториям, близким к окружности, а магн. поток пронизывает эту окружность, и линейный индукционный ускоритель, в к-ром частицы движутся почти прямолинейно, а ускоряющее электрич. поле индукции создаётся охватывающим траекторию перем. магн. потоком.
[c.144]
Появление электрического тока в замкнутом контуре при изменениях магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил неэлектростатической природы или о возникновении ЭДС индукции. Количественное описание явления электромагнитной индукции дается на основе установления связи между ЭДС индукции и физической величиной, называемой магнитным потоком. [c.187]
Основными частями машины постоянного тока являются индуктор, с помощью которого создается магнитное поле, якорь, в обмотке которого наводлтся ЭДС индукции, гсоллектор и электрические щетки. Коллектором называются изолированные друг от друга проводящие пластипы, присоединенные к катушкам. По пластинам коллектора скользят электрические щетки, соединяющие концы обмоток с внешней йлектрической цепью. [c.196]
Если внутреннее сопротивление источника тока, т. е. сопротивление проводов обмотки статора, значительно меньше сопротивления внешней электрической цепи, то напряжение и на выходе генератора можно считать равным по абсолютному значению ЭДС индукции в п последовательно включенных витках обмотки и = пе = пВЗш sin ot. (68.5) [c.238]
В системах магнитоэлектрического типа в последнем урав-пеиии вая ную роль играет ЭДС индукции. D частном случае, когда ироводппк длины I перемещается в равномерном магнитном поле перпендикулярно вектору пндукцни В, наведенная ЭДС индукции онределяется по формуле [c.284]
Отложения оксидов металлов в трубе обнаруживают при помощи индукционного датчика, представляющего собой постоянный магнит с обмоткой медного провода (оператор водит прибором по поверхности исследуемого трубопровода). При прохождении участка с металлооксидными отложениями магнитное сопротивление цепи магнит — трубопровод уменьщается, что приводит к изменению напряженности магнитного поля магнита и сопровождается возникновением в обмотке магнита ЭДС индукции, поступающей на вход двухкаскадного транзисторного усилителя постоянного тока, и усиленный импульс регистрируется микроамперметром. Отклонение стрелки прибора зависит от толщины слоя отложения и скорости движения датчика по трубопроводу. Однако из-за малой длительности импульса индуктируемой ЭДС, наличия омического сопротивления обмотки магнита и инерционности подвижной части микроамперметра [c.49]
Формулы (7.62) и (7.63) представляют собой частный случай, когда поток, изменения которого порождают ЭДС индукции, создан в тороиде или длинном соленоиде. В более общем случае контура любой формы с любым числом произвольно расположенньис витков можно, основываясь на законе Био, Савара и Лапласа, выразить потокосцепление с этим контуром в виде [c.254]
Если мы имеем два контура, более или менее близко расположенных друг относительно друга, то при протекании тока по одному из контуров часть потока или весь поток оказывается сцепленным со вторым контуром. Изменение тока в первом из контуров вызывает возникновение ЭДС индукции во втором контуре. Потокосцеп-ление в одном контуре в зависимости от тока в другом имеет вид, аналогичный (7.64) [c.255]
ЯВЛЕНИЕ (взаимной индукции заключается в наведении ЭДС индукции во всех проводниках, находящихся вблизи цепи переменного тока самоиндукции — возникновение ЭДС электромагнитной индукции в электрической цепи вследствие изменения в ней электрического тока гидратации — взаимодействие ионов растворенного вещества с молекулами растворителя осмоса — ппоникновение растворителя в раствор через пористую перегородку (мембрану), непроницаемую для растворенного вещества и отделяющую раствор от чистой жидкости сверх гекучестп гелия состоит в способности жидкого гелия-2 протекать без трения через узкие щели и капилляры при температуре Г[c.302]
Линейный индукционный ускоритель — Л. у., в к-ром для ускорения используется эдс индукции, возникающей при изменении во времени магн. потока, охватывающего нрямолинейные траектории частиц. Ускоряющее поло в индукц. Л. у. за время пролёта частиц существенно не меняется. [c.586]
Зарядовая нейтрализация пучка происходит при инжекции в достаточно плотную плаз.му за счёт вытеснения из его объёма медленных плазменных электронов с характерным временем (4яа) , где а — проводимость плазмы. Если к моменту достижения нейтрализации ток С. п. продолжает нарастать, то эдс индукции создаёт ток оставшихся плазменных электронов, направленный против тока пучка и вызывающий токовую нейтрализацию. При небольшой плотности плазмы, когда плазменная частота озр распределён по всему объёму, так что токовая нейтрализация неполна и имеет интегральный характер. При Ыр > da происходит локальная нейтрализация, за исключением поверхности С. п., где образуется двойной токовый слой толщиной — juip и сосредоточено ыагн. поле. В таких условиях частицы С. и. практически свободны, а сам он электродинамически венаблюдаем. Эффективность переноса пучком мощности и энергии через плазму на расстояния 1м близка к 100%, но на больших расстояниях уменьшается за счёт раал. неустойчивостей С. п., в первую очередь поперечной неустойчивости, выражающейся в изгибании пучка как целого и разбиения его на отд, нити. [c.503]
Если через замкнутый проводник или контур будет изменяться магнитный поток Ф, а значит магнитное поле, то в нем будет возникать ЭДС индукции и электрический ток.
Источниками переменного магнитного поля являются:
а) движущийся постоянный магнит;
б)движущийся проводник с постоянным током;
в) неподвижный проводник с переменным током.
Причем, чем быстрее изменяется магнитный поток магнитного поля через контур, тем большая ЭДС индукции, а значит и сила тока возникает в нем, таким образом, величина ЭДС индукции зависит от скорости изменения магнитного потока через контур, т.е.
– это и будет законом электромагнитной индукции, для замкнутого проводника или контура:
“ЭДС индукции ?инд, возникающая в контуре прямо пропорциональна скорости изменения магнитного потока через него”.
Электромагнитная индукция – это создание ЭДС индукции в проводнике, а если он замкнут, то и электрического тока в нем, под действием переменного магнитного поля.
Закон электромагнитной индукции для катушки:
“ЭДС индукции возникающая в катушке прямо пропорциональна числу витков катушки и скорости изменения магнитного потока через нее”.
Если прямолинейный проводник будет двигаться в однородном магнитном поле равномерно, то в нем будет возникать ЭДС индукции, величина которой будет определяться по формуле:
где l – длина проводника, – скорость его движения, – угол между направлением и .
“ЭДС индукции возникающая в прямолинейном проводнике равномерно движущимся в однородном магнитном поле с индукцией , прямо пропорциональна длине проводника, скорости его движения, синусу угла между направлениями магнитной индукции магнитного поля и скорости движения проводника в магнитном поле ”.
Знак «-» в законе электромагнитной индукции указывает на направление индукционного тока в замкнутом проводнике, определяемое по правилу Ленца: “Индукционный ток всегда имеет такое направление, что своим магнитным полем препятствует изменению магнитного поля, которое вызвало индукционный ток”.
Если магнитное поле, вызвавшее индукционный ток нарастает или увеличивается через замкнутый проводник, то магнитное поле индукционного тока направлено ему противоположно и не будет давать ему нарастать, если же магнитное поле, вызвавшее индукционный ток убывает, то магнитное поле индукционного тока направленно также, как и убывающее магнитное поле и препятствует убыванию магнитного поля вызывающего индукционный ток.
Величина индукционного поля определяется по закону Ома: “Сила индукционного тока прямо пропорциональна ЭДС индукции возникающей в замкнутом проводнике и обратно пропорциональна сопротивлению замкнутого проводника”.
Индукционным током называется ток, полученный в замкнутом проводнике под действием переменного магнитного поля, т.е. благодаря электромагнитной индукции.
Проводник с переменным током в пространстве вокруг себя образует переменное магнитное поле, в котором будет находиться сам проводник с переменным током, поэтому в нем будет возникать ЭДС индукции, которую называют ЭДС самоиндукции, а явление электромагнитной индукции в проводнике с переменным током называют самоиндукцией.
Таким образом, самоиндукция – это частный случай электромагнитной индукции, который имеет место в проводнике с переменным током. Величина ЭДС самоиндукции, возникающая в проводнике с переменным током определяется по закону самоиндукции: “ЭДС самоиндукции, возникающая в проводнике с переменным током прямо пропорциональна скорости изменения силы тока, текущего в проводнике”.
где – скорость изменения силы тока в проводнике, характеризует быстроту изменения тока в проводнике, и показывает на сколько изменяется ток за единицу времени;
L — индуктивность проводника – это характеристика проводника по которому течет переменный ток зависит от размеров и формы проводника, и не зависит от его материала.
L показывает какая ЭДС самоиндукции возникает в проводнике при скорости изменения тока в нем равной единице или какая ?сам возникает в проводнике, если ток в нем изменяется на единицу за единицу времени.
СИ: – это индуктивность такого проводника, в котором возникает ЭДС самоиндукции равная 1 В при изменении тока на 1 А за 1 секунду.
Знак «-» в законе самоиндукции указывает на направление тока самоиндукции, определяемого по правилу Ленца. Например, при замыкании цепи ток увеличивается, возникает ЭДС самоиндукции, которая препятствует нарастанию тока; если же ток уменьшается, что происходит при размыкании цепи, то ЭДС самоиндукции будет поддерживать убывающий ток, не давая ему убывать, поэтому при размыкании цепи большой индуктивности искрит рубильник из-за большого тока самоиндукции, определяемого по закону Ома для тока самоиндукции:
.
Вариант №1
1. В каком случае в катушке замкнутой на гальванометр возникает электрический ток?
2. Что определяет закон электромагнитной индукции?
3. От чего зависит ЭДС индукции, возникающая в катушке?
4. В замкнутую катушку вдвигают постоянный магнит: один раз быстро, второй медленно. В каком случае в ней возникнет больший индукционный ток?
5. Что определяют по правилу Ленца? по правилу левой руки? правого винта?
6. Из формул
а)силы Ампера выразить силу тока;
б)силы Лоренца выразить скорость движения частиц;
в) закона индукции электромагнитной индукции выразить изменение магнитного потока.
7. Что такое самоиндукция? Где она имеет место?
8. В каких единицах измеряются
а)магнитная индукция;
б)магнитный поток;
в)ЭДС индукции;
г)индуктивность проводника.
Вариант №2
1. В чем заключается явление электромагнитной индукции?
2. Какое поле создает ЭДС индукции в замкнутом проводнике? Разве может магнитное поле заставить двигаться неподвижные электрические заряды?
3. В каком случае может возникать, а в каком не возникать, ЭДС индукции в прямолинейном проводнике, движущимся в однородном магнитном поле?
4. Почему в проводнике с постоянным током не возникает ЭДС индукции, а в проводнике с переменным возникает?
5. За 3 секунды магнитный поток, пронизывающий проволочную рамку, равномерно увеличивается с 6 Вб до 9 Вб. Чему равно при этом значение ЭДС индукции в рамке?
6. Чему равна ЭДС самоиндукции в катушке индуктивностью L = 3 Гн, при равномерном уменьшении силы тока от 5 А до 1 А за 2 секунды?
Вариант №3
1. Как направлена сила Лоренца, действующая на движущуюся заряженную частицу в магнитном поле?
2. Как направлена магнитная индукция внешнего магнитного поля, в котором против часовой стрелки движется отрицательно заряженная частица?
3. Электрон влетел в магнитное поле со скоростью V перпендикулярно линиям магнитной индукции и стал двигаться по окружности радиуса R. Определите величину вектора магнитной индукции магнитного поля. (заряд электрона e, m – масса электрона)
4. Под каким углом расположен проводник с током 3 А длиной 0,1 м в однородном магнитном поле с индукцией 4 Тл, если на него действует сила Ампера равная 0,6 Н?
5. Что происходит с индукционным током в кольце, плоскость которого перпендикулярна линиям магнитной индукции, если ее величина равномерно увеличивается?
6. Чему равна индуктивность проволочной рамки, если при силе тока I = 3 А в рамке возникает магнитный поток Ф = 6 Вб?
7. Катушка сопротивлением 100 Ом, состоящая из 1000 витков площадью 5 см2, внесена в однородное магнитное поле. В течение некоторого времени индукция магнитного поля уменьшилась от 0,8 Тл до 0,3 Тл. Какой заряд будет индуцирован в проводнике за это время?
индуктивность | Физика
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными для создания желаемого напряжения и тока с очень небольшими потерями энергии в другие формы. Есть ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется , индуктивность . Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. См. Рис. 1, где простые катушки индуцируют ЭДС друг в друге.
Рис. 1. Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2.(Обратите внимание, что « E 2 индуцированная» представляет наведенную ЭДС в катушке 2.)
Во многих случаях, когда геометрия устройств является фиксированной, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС 2 в другом. Мы выражаем это в форме уравнения как
[латекс] {\ text {emf}} _ {2} = — M \ frac {\ Delta {I} _ {1}} {\ Delta t} \\ [/ latex],
, где M определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Например, катушки на Рисунке 1 имеют небольшой размер M по сравнению с катушками трансформатора на Рисунке 3 от Transformers. Единицами измерения для M являются (В с) / A = Ом ⋅ с, который назван генри (H) в честь Джозефа Генри. То есть 1 H = 1 Ω⋅s. Природа здесь симметрична. Если мы изменим ток I 2 в катушке 2, мы индуцируем ЭДС 1 в катушке 1, что равно
[латекс] {\ text {emf}} _ {1} = — M \ frac {\ Delta {I} _ {2}} {\ Delta t} \\ [/ latex],
, где M то же самое, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M . Большая взаимная индуктивность M может быть, а может и не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки против ветра, чтобы нейтрализовать создаваемое магнитное поле.(См. Рисунок 2.)
Рис. 2. Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность относительно корпуса сушилки.
Самоиндукция , действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение магнитного потока полностью связано с изменением тока Δ I через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
[латекс] \ text {emf} = — L \ frac {\ Delta I} {\ Delta t} [/ latex],
, где L — собственная индуктивность устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется катушкой индуктивности и обозначено символом на рисунке 3.
Рисунок 3.
Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера L , например, за счет встречной намотки катушек, как показано на рисунке 2.Катушка индуктивности 1 H — это большая катушка индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с L = 1,0 Гн, через которое протекает ток 10 А. Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная как ЭДС = — L (Δ I / Δ t ), будет препятствовать изменению. Таким образом, ЭДС будет индуцирована ЭДС = — L (Δ I / Δ t ) = (1,0 H) [(10 A) / (1,0 мс)] = 10 000 В. Знак плюс означает, что это большое напряжение идет в том же направлении, что и ток, противодействуя его уменьшению.Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока. Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются батарея, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт.(Вы можете услышать пронзительный вой от трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки. (См. Рисунок 4.)
Рис. 4. Благодаря быстрому переключению катушки индуктивности можно использовать батареи 1,5 В для индукции ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.
Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле.В большинстве случаев это сложно из-за сложности создаваемого поля. Таким образом, в этом тексте индуктивность L обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что наведенная ЭДС определяется законом индукции Фарадея как ЭДС = — Н (Δ Φ / Δ t ) и, по определению самоиндукции, как ЭДС = — L (Δ I / Δ т ).Приравнивая эти доходности к
[латекс] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} = — L \ frac {\ Delta I} {\ Delta t} \\ [/ latex]
Решение для л дает
[латекс] L = N \ frac {\ Delta \ Phi} {\ Delta I} \\ [/ latex]
Это уравнение для самоиндукции L устройства всегда верно. Это означает, что самоиндукция L зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем больше Δ Φ / Δ I .Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь A соленоида является фиксированной, изменение магнитного потока составляет Δ Φ = Δ ( B A ) = A Δ B . Чтобы найти Δ B , заметим, что магнитное поле соленоида определяется выражением [латекс] B = {\ mu} _ {0} {nI} = {\ mu} _ {0} \ frac {NI} { \ ell} \\ [/ latex]. (Здесь n = N / , где N — количество катушек, а ℓ — длина соленоида.{2} A} {\ ell} \ text {(соленоид)} \\ [/ latex].
Это самоиндукция соленоида с площадью поперечного сечения A и длиной . Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением.
Пример 1. Расчет самоиндукции соленоида среднего размера
Рассчитайте самоиндукцию соленоида длиной 10,0 см и диаметром 4,00 см, который имеет 200 катушек.
Стратегия
Это прямое применение [латекса] L = \ frac {{\ mu} _ {0} {N} ^ {2} A} {\ ell} \\ [/ latex], поскольку все величины в уравнении, кроме L известны. {2} \ влево (1.{2} \ right)} {0.100 \ text {m}} \\ & = & 0.632 \ text {mH} \ end {array} \\ [/ latex].
Обсуждение
Этот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.
Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающей машины. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет.Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал в катушке передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать приблизительное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, которая была обнаружена на «бомбардировщике в нижнем белье.”) См. Рисунок 5.
Рис. 5. Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Источник: Alexbuirds, Wikimedia Commons)
Физика для науки и техники II

 3)
3) 5)
5)