Сколькими способами можно разбить 14 человек на пары: Сколькими способами можно разбить 14 человек на пары — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Олимпиадные задачи по теме «Комбинаторика».

Задача 1:

В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?

Решение:

Выберем чашку. В комплект к ней можно выбрать любое из трех блюдец. Поэтому есть 3 разных комплекта, содержащих выбранную чашку. Поскольку чашек всего 5, то число различных комплектов равно 15 (15 = 5 • 3).

Задача 2:

В магазине «Все для чая» есть еще 4 чайные ложки. Сколькими способами можно купить комплект из чашки, блюдца и ложки?

Решение:

Выберем любой из 15 комплектов предыдущей задачи. Его можно дополнить ложкой четырьмя различными способами. Поэтому общее число возможных комплектов равно 60 (60 = 15 • 4 = 5 • 3 • 4).

Задача 3:

В Стране Чудес есть три города: А, Б и В. Из города А в город Б ведет 6 дорог, а из города Б в город В – 4 дороги. Сколькими способами можно проехать от А до В?

Решение:

Ответ: 24 = 6 • 4.

Задача 4:

В Стране Чудес есть четыре города: А, Б и В и Г. Из города А в город Б ведет 6 дорог, а из города Б в город В – 4 дороги, Из города А в город Г – две дороги, и из города Г в город В – тоже две дороги. Сколькими способами можно проехать от А до В?

Решение:

Выделим два случая: путь проходит через город Б или через город Г. В каждом из этих случаев легко сосчитать количество возможных маршрутов: в первом – 24, во втором – 6. Складывая, получаем общее количество маршрутов: 30.

Задача 5:

В магазине «Все для чая» по-прежнему продается 5 чашек, 3 блюдца и 4 чайные ложки. Сколькими способами можно купить два предмета с разными названиями?

Решение:

Возможны три разных случая: первый – покупаются чашка с блюдцем, второй – чашка с ложкой, третий – блюдце и ложка. В каждом из этих случаев легко сосчитать количество возможных вариантов (в первом – 15, во втором – 20, в третьем – 12). Складывая, получаем общее число возможных вариантов: 47.

Задача 6:

Назовем натуральное число «симпатичным» , если в его записи встречаются только нечетные цифры. Сколько существует 4-значных «симпатичных» чисел?

Решение:

Понятно, что однозначных «симпатичных» чисел ровно 5. К каждому однозначному «симпатичному» числу вторая нечетная цифра может быть дописана пятью различными способами. Таким образом, двузначных «симпатичных» чисел всего 5 • 5 = 25. Аналогично, трехзначных «симпатичных» чисел 5 • 5 • 5 = 125, и четырехзначных – 5 • 5 • 5 • 5 = 54 = 625.

Задача 7:

Монету бросают трижды. Сколько разных последовательностей орлов и решек можно при этом получить?

Решение:

Ответ: 2?.

Задача 8:

Каждую клетку квадратной таблицы 2 ? 2 можно покрасить в черный или белый цвет. Сколько существует различных раскрасок этой таблицы?

Решение:

Ответ: 24.

Задача 9:

Сколькими способами можно заполнить одну карточку в лотерее «Спорт-про-г-ноз»? (В этой лотерее нужно предсказать итог тринадцати спортивных матчей. Итог каждого матча – победа одной из команд либо ничья; счет роли не играет).

Решение:

Ответ: 3?3.

Задача 10:

Алфавит племени Мумбо-Юмбо состоит из трех букв А, Б и В. Словом является любая последовательность, состоящая не более, чем из 4 букв. Сколько слов в языке племени Мумбо-Юмбо? Указание. Сосчитайте отдельно количества одно-, двух-, трех- и четырехбуквенных слов.

Решение:

Ответ: 3 + 3? + 3? + 34 = 120.

Задача 11:

В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?

Решение:

Капитаном может стать любой из 11 футболистов. После выбора капитана на роль его заместителя могут претендовать 10 оставшихся человек. Таким образом, всего есть 11 • 10 = 110 разных вариантов выборов.

Задача 12:

Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины, если имеется материя шести различных цветов?

Решение:

Цвет для верхней полоски флага можно выбрать шестью разными способами. После этого для средней полоски флага остается пять возможных цветов, а затем для нижней полоски флага – четыре различных цвета. Таким образом, флаг можно сделать 6 • 5 • 4 = 120 способами.

Задача 13:

Сколькими способами можно поставить на шахматную доску белую и черную ладьи так, чтобы они не били друг друга?

Решение:

Белую ладью можно поставить на любую из 64 клеток. Независимо от своего расположения она бьет 15 полей (включая поле, на котором она стоит). Поэтому остается 49 полей, на которые можно поставить черную ладью. Таким образом, всего есть 64 • 49 = 3136 разных способов.

Задача 14:

Сколькими способами можно поставить на шахматную доску белого и черного королей так, чтобы получилась допустимая правилами игры позиция?

Решение:

Белого короля можно поставить на любое из 64 полей. Однако количество полей, которые он при этом будет бить, зависит от его расположения. Поэтому необходимо разобрать три случая:

а) если белый король стоит в углу (углов всего 4), то он бьет 4 поля (включая то, на котором стоит), и остается 60 полей, на которые можно поставить черного короля;

б) если белый король стоит на краю доски, но не в углу (таких полей – 24), то он бьет 6 полей, и для черного короля остается 58 возможных полей;

в) если же белый король стоит не на краю доски (таких полей – 36), то он бьет 9 полей, и для черного короля остается 55 возможных полей.

Таким образом, всего есть 4 • 60 + 24 • 58 + 36 • 55 = 3612 способов расстановки королей.

Задача 15:

Сколько существует трехзначных чисел, в записи которых цифры 1, 2, 3 встречаются ровно по одному разу?

Решение:

Будем рассуждать точно так же, как при решении задач предыдущего цикла. На первое место можно поставить любую из трех цифр, на второе – любую из двух оставшихся, а на третье – последнюю оставшуюся цифру. Таким образом, всего получается 3 • 2 • 1 = 3! чисел.

Задача 16:

Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?

Решение:

На первое место можно положить любой из четырех шариков, на второе – любой из трех оставшихся, на третье – любой из двух оставшихся, а на четвертое – последний оставшийся шарик. Итак, ответ: 4 • 3 • 2 • 1 = 4!.

Задача 17: Слово – любая конечная последовательность букв русского алфавита. Выясните, сколько различных слов сожно составить из слов

а) «ВЕКТОР»;

б) «ЛИНИЯ»;

в) «ПАРАБОЛА»;

г) «БИССЕКТРИСА»;

д) «МАТЕМАТИКА»;

Решение:

а) Так как все буквы слова различны, то всего можно получить 6! слов.

б) В этом слове две буквы И, а все остальные буквы разные. Временно будем считать разными и буквы И, обозначив их через И1 и И2. При этом предположении получится 5! = 120 разных слов. Однако те слова, которые получаются друг из друга только перестановкой букв И1 и И2, на самом деле одинаковы. Таким образом, полученные 120 слов разбиваются на пары одинаковых. Поэтому разных слов всего 120:2 = 60.

в) Считая три буквы А этого слова различными (А1, А2, А3), получим 8! разных слов. Однако слова, отличающиеся лишь перестановкой букв А, на самом деле одинаковы. Поскольку буквы А1, А2, А3 можно переставлять 3! способами, все 8! слов разбиваются на группы по 3! одинаковых. Поэтому разных слов всего 8!/3!.

г) В этом слове три буквы С и две буквы И. Считая все буквы различными, получаем 11! слов. Отождествляя слова, отличающиеся лишь перестановкой букв И, но не С, получаем 11!/2! различных слов. Отождествляя теперь слова, отличающиеся перестановкой букв С, получаем окончательный результат 11!/(2! • 3!).

д) Ответ: 10!/(3! • 2! • 2!).

Задача 22:

В стране 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране?

Решение:

Каждая авиалиния соединяет два города. В качестве первого города можно взять любой из 20 городов (город А), а в качестве второго – любой из 19 оставшихся (город В). Перемножив эти числа, получаем 20 • 19 = 380. Однако при этом подсчете каждая авиалиния учтена дважды (первый раз, когда в качестве первого города был выбран город А, а второго – город В, а второй раз – наоборот). Таким образом, число авиалиний равно 380:2 = 190.

Задача 23:

Сколько диагоналей в выпуклом n-угольнике?

Решение:

Ответ: n(n – 3)/2.

Задача 24:

Бусы – это кольцо, на которое нанизаны бусины. Бусы можно поворачивать, но не переворачивать. Сколько различных бус можно сделать из 13 разноцветных бусин?

Решение:

Ответ: 13!/13 = 12!.

Задача 25:

Предположим теперь, что бусы можно и переворачивать. Сколько тогда различных бус можно сделать из 13 разноцветных бусин?

Решение:

Ответ: 12!/2.

Задача 26:

Сколько существует 6-значных чисел, в записи которых есть хотя бы одна четная цифра?

Решение:

Вместо того, чтобы подсчитывать количество требуемых 6-значных чисел, определим количество 6-значных чисел, не обладающих нужным свойством. Так как это в точности те числа, в записи которых встречаются только нечетные цифры, то их количество, очевидно, равно 56 = 15625. Всего 6-значных чисел 900000. Поэтому количество 6-значных чисел, обладающих указанным свойством, равно 900000 – 15625 = 884375.

Задача 27:

В алфавите племени Бум-Бум шесть букв. Словом является любая последовательность из шести букв, в которой есть хотя бы две одинаковые буквы. Сколько слов в языке племени Бум-Бум?

Решение:

Ответ: 66 – 6!.

Задача 28:

В киоске «Союзпечать» продаются 5 видов конвертов и 4 вида марок. Сколькими способами можно купить конверт с маркой?

Решение:

Ответ: 5 • 4 = 20

Задача 29:

Сколькими способами можно выбрать гласную и согласную буквы из слова «КРУЖОК»?

Решение:

Ответ: 2 • 3 = 6

Задача 30:

На доске написаны 7 существительных, 5 глаголов и 2 прилагательных. Для предложения нужно выбрать по одному слову каждой из этих частей речи. Сколькими способами это можно сделать?

Решение:

Ответ: 7 • 5 • 2 = 70

Задача 31:

У двух начинающих коллекционеров по 20 марок и по 10 значков. Честным обменом называется обмен одной марки на одну марку или одного значка на один значок. Сколькими способами коллекционеры могут осуществить честный обмен?

Решение:

Ответ: 20 • 20 + 10 • 10 = 500

Задача 32:

Сколько существует 6-значных чисел, все цифры которых имеют одинаковую четность?

Решение:

Ответ: 56 + 4 • 55

Задача 33:

Надо послать 6 срочных писем. Сколькими способами это можно сделать, если для передачи писем можно использовать трех курьеров и каждое письмо можно дать любому из курьеров?

Решение:

Ответ: 36

Задача 34:

Сколькими способами из полной колоды (52 карты) можно выбрать 4 карты разных мастей и достоинств?

Решение:

Ответ: 13 • 12 • 11 • 10

Задача 35:

На полке стоят 5 книг. Сколькими способами можно выложить в стопку несколько из них (стопка может состоять и из одной книги)?

Решение:

Ответ: 5 + 5 • 4 + 5 • 4 • 3 + 5 • 4 • 3 • 2 + 5 • 4 • 3 • 2 • 1 = 325

Задача 36:

Сколькими способами можно поставить 8 ладей на шахматную доску так, чтобы они не били друг друга?

Решение:

Ответ: 8!

Задача 37:

На танцплощадке собрались N юношей и N девушек. Сколькими способами они могут разбиться на пары для участия в очередном танце?

Решение:

Ответ: n!

Задача 38:

Чемпионат России по шахматам проводится в один круг. Сколько играется партий, если участвуют 18 шахматистов?

Решение:

Ответ: 18 • 17/2 = 153

Задача 39:

Сколькими способами можно поставить на шахматную доску так, чтобы они не били друг друга а) две ладьи; б) двух королей; в) двух слонов; г) двух коней; д) двух ферзей?

Решение:

Ответ: a) 64 • 49/2 = 1568 б) (4 • 60 + 24 • 58 + 36 • 55)/2 = 1806 в) (28 • 56 + 20 • 54 + 12 • 52 + 4 • 50)/2 = 1736 г) (4 • 61 + 8 • 60 + 20 • 59 + 16 • 57 + 16 • 55)/2 = 1848 д) (28 • 42 + 20 • 40 + 12 • 38 + 4 • 36)/2 = 1288

Задача 40:

У мамы два яблока, три груши и четыре апельсина. Каждый день в течение девяти дней подряд она дает сыну один из оставшихся фруктов. Сколькими способами это может быть сделано?

Решение:

Ответ: 9!/2!3!4!

Задача 41:

Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную?

Решение:

Ответ: 7!/1!2!4!

Задача 42:

Сколькими способами можно расставить на первой горизонтали шахматной доски комплект белых фигур (король, ферзь, две ладьи, два слона и два коня)?

Решение:

Ответ: 8!/2!2!2!

Задача 43:

Сколько слов можно составить из пяти букв А и не более чем из трех букв Б?

Решение:

Ответ: 1 + 6!/5!1! + 7!/5!2! + 8!/5!3! = 84

Задача 44:

Сколько существует 10-значных чисел, в которых имеется хотя бы две одинакоые цифры?

Решение: 9 • 109 – 9 • 9!

Задача 45:

Каких 7-значных чисел больше: тех, в записи которых есть 1, или остальных?

Решение:

8 • 96

Задача 46:

Кубик бросают трижды.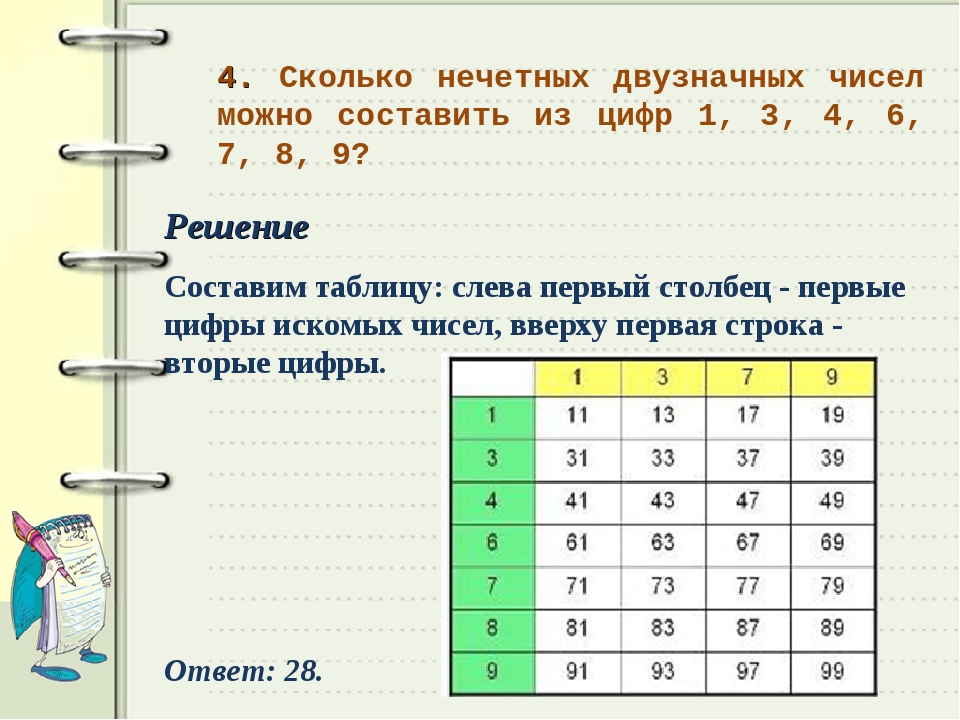 Среди всех возможных последовательностей результатов есть такие, в которых хотя бы один раз встречается шестерка. Сколько их?

Решение:

Ответ: 6? – 5?

Задача 47:

Сколькими способами можно разбить 14 человек на пары?

Решение:

Ответ: 13 • 11 • 9 • 7 • 5 • 3 • 1

Задача 48:

Сколько существует 9-значных чисел, сумма цифр которых четна?

Решение:

Ответ: 9 • 107 • 5

КОМБИНАТОРИКА

КОМБИНАТОРИКА

Задача 1:

В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца.
Сколькими способами можно купить чашку с блюдцем?

Решение:

Выберем чашку. В комплект к ней можно выбрать любое из трех блюдец.
Поэтому есть 3 разных комплекта, содержащих выбранную
чашку. Поскольку чашек всего 5, то число различных комплектов равно 15
(15 = 5 • 3).

Задача 2:

В магазине «Все для чая» есть еще 4 чайные ложки. Сколькими способами
можно купить комплект из чашки, блюдца и ложки?

Решение:

Выберем любой из 15 комплектов предыдущей задачи. Его можно дополнить
ложкой четырьмя различными способами. Поэтому общее число возможных комплектов
равно 60
(60 = 15 • 4 = 5 • 3 • 4).

Задача 3:

В Стране Чудес есть три города: А, Б и В. Из города А в город Б ведет 6
дорог, а из города Б в город В – 4 дороги. Сколькими способами можно проехать
от А до В?

Решение:

Ответ: 24 = 6 • 4.

Задача 4:

В Стране Чудес есть четыре города: А, Б и В и
Г. Из города А в город Б ведет 6 дорог, а из города Б в город В – 4 дороги, Из
города А в город Г – две дороги, и из города Г в город В – тоже две
дороги. Сколькими способами можно проехать от А до В?

Решение:

Выделим два случая: путь проходит через город Б
или через город Г. В каждом из этих случаев легко сосчитать количество возможных
маршрутов: в первом – 24, во втором – 6. Складывая, получаем общее количество
маршрутов: 30.

Задача 5:

В магазине «Все для чая» по-прежнему продается 5 чашек, 3 блюдца и 4
чайные ложки. Сколькими способами можно купить два предмета с разными названиями?

Решение:

Возможны три разных случая: первый – покупаются чашка с блюдцем, второй
– чашка с ложкой, третий – блюдце и ложка. В каждом из этих случаев легко
сосчитать количество возможных вариантов (в первом – 15, во втором – 20, в
третьем – 12). Складывая, получаем общее число возможных вариантов: 47.

Задача 6:

Назовем натуральное число «симпатичным» , если
в его записи встречаются только нечетные цифры. Сколько существует 4-значных
«симпатичных» чисел?

Решение:

Понятно, что однозначных «симпатичных» чисел ровно 5. К каждому
однозначному «симпатичному» числу вторая нечетная цифра может быть дописана
пятью различными способами. Таким образом, двузначных «симпатичных» чисел всего
5 • 5 = 25. Аналогично, трехзначных «симпатичных» чисел
5 • 5 • 5 = 125, и четырехзначных –
5 • 5 • 5 • 5 = 54 = 625.

Задача 7:

Монету бросают трижды. Сколько разных последовательностей орлов и решек можно при этом получить?

Решение:

Ответ: 2³.

Задача 8:

Каждую клетку квадратной таблицы 2 × 2 можно покрасить в
черный или белый цвет. Сколько существует различных раскрасок этой таблицы?

Решение:

Ответ: 2⁴.

Задача 9:

Сколькими способами можно заполнить одну карточку в лотерее «Спорт-про-г-ноз»? (В этой лотерее нужно
предсказать итог тринадцати спортивных матчей. Итог каждого
матча – победа одной из команд либо ничья; счет роли не играет).

Решение:

Ответ: 3¹3.

Задача 10:

Алфавит племени Мумбо-Юмбо состоит из трех
букв А, Б и В. Словом является любая
последовательность, состоящая не более, чем из 4 букв. Сколько слов в языке
племени Мумбо-Юмбо? Указание. Сосчитайте отдельно
количества одно-, двух-, трех- и четырехбуквенных слов.

Решение:

Ответ: 3 + 3² + 3³ + 3⁴ = 120.

Задача 11:

В футбольной команде (11 человек) нужно выбрать капитана и его
заместителя. Сколькими способами это можно сделать?

Решение:

Капитаном может стать любой из 11 футболистов. После выбора капитана на
роль его заместителя могут претендовать 10 оставшихся человек. Таким образом,
всего есть 11 • 10 = 110 разных вариантов выборов.

Задача 12:

Сколькими способами можно сделать трехцветный флаг с горизонтальными
полосами одинаковой ширины, если имеется материя шести различных цветов?

Решение:

Цвет для верхней полоски флага можно выбрать шестью разными способами.
После этого для средней полоски флага остается пять возможных цветов, а затем
для нижней полоски флага – четыре различных цвета. Таким образом, флаг можно
сделать 6 • 5 • 4 = 120 способами.

Задача 13:

Сколькими способами можно поставить на шахматную доску белую и черную
ладьи так, чтобы они не били друг друга?

Решение:

Белую ладью можно поставить на любую из 64 клеток. Независимо от своего
расположения она бьет 15 полей (включая поле, на котором она стоит). Поэтому
остается 49 полей, на которые можно поставить черную ладью. Таким образом,
всего есть 64 • 49 = 3136 разных способов.

Задача 14:

Сколькими способами можно поставить на шахматную доску белого и черного
королей так, чтобы получилась допустимая правилами игры позиция?

Решение:

Белого короля можно поставить на любое из 64 полей. Однако количество
полей, которые он при этом будет бить, зависит от его расположения. Поэтому
необходимо разобрать три случая:

а) если белый король стоит в углу (углов всего 4),
то он бьет 4 поля (включая то, на котором стоит), и остается 60 полей, на которые
можно поставить черного короля;

б) если белый король стоит на краю доски, но не в углу (таких полей –
24), то он бьет 6 полей, и для черного короля остается 58 возможных полей;

в) если же белый король стоит не на краю доски (таких полей – 36), то он
бьет 9 полей, и для черного короля остается 55 возможных полей.

Таким образом, всего есть
4 • 60 + 24 • 58 + 36 • 55 = 3612
способов расстановки королей.

Задача 15:

Сколько существует трехзначных чисел, в записи которых цифры 1, 2, 3
встречаются ровно по одному разу?

Решение:

Будем рассуждать точно так же, как при решении задач предыдущего цикла.
На первое место можно поставить любую из трех цифр, на второе – любую из двух
оставшихся, а на третье – последнюю оставшуюся цифру. Таким образом, всего получается
3 • 2 • 1 = 3! чисел.

Задача 16:

Сколькими способами можно выложить в ряд красный, черный, синий и
зеленый шарики?

Решение:

На первое место можно положить любой из четырех шариков, на второе –
любой из трех оставшихся, на третье – любой из двух оставшихся, а на четвертое
– последний оставшийся шарик. Итак, ответ:
4 • 3 • 2 • 1 = 4!.

Задача 17: Слово – любая конечная последовательность букв
русского алфавита. Выясните, сколько различных слов сожно
составить из слов

а) «ВЕКТОР»;

б) «ЛИНИЯ»;

в) «ПАРАБОЛА»;

г) «БИССЕКТРИСА»;

д) «МАТЕМАТИКА»;

Решение:

а) Так как все буквы слова различны, то всего можно получить 6! слов.

б) В этом слове две буквы И, а все остальные
буквы разные. Временно будем считать разными и буквы И,
обозначив их через И₁ и И₂. При этом предположении
получится 5! = 120 разных слов. Однако те слова, которые получаются
друг из друга только перестановкой букв И₁
и И₂, на самом деле одинаковы. Таким образом,
полученные 120 слов разбиваются на пары одинаковых. Поэтому разных слов
всего 120:2 = 60.

в) Считая три буквы А этого слова различными (А₁,
А₂, А₃), получим 8! разных слов. Однако слова,
отличающиеся лишь перестановкой букв А, на самом деле
одинаковы. Поскольку буквы А₁, А₂,
А₃ можно переставлять 3! способами, все 8! слов разбиваются на
группы по 3! одинаковых. Поэтому разных слов всего 8!/3!.

г) В этом слове три буквы С и две буквы И.
Считая все буквы различными, получаем 11! слов. Отождествляя слова,
отличающиеся лишь перестановкой букв И, но не С,
получаем 11!/2! различных слов. Отождествляя теперь слова, отличающиеся
перестановкой букв С, получаем окончательный результат
11!/(2! • 3!).

д) Ответ: 10!/(3! • 2! • 2!).

Задача 22:

В стране 20 городов, каждые два из которых соединены авиалинией. Сколько
авиалиний в этой стране?

Решение:

Каждая авиалиния соединяет два города. В качестве первого города можно
взять любой из 20 городов (город А), а в качестве второго – любой из 19
оставшихся (город В). Перемножив эти числа, получаем
20 • 19 = 380. Однако при этом подсчете каждая авиалиния
учтена дважды (первый раз, когда в качестве первого города был выбран город А, а второго – город В, а второй раз – наоборот). Таким
образом, число авиалиний равно 380:2 = 190.

Задача 23:

Сколько диагоналей в выпуклом n-угольнике?

Решение:

Ответ: n(n – 3)/2.

Задача 24:

Бусы – это кольцо, на которое нанизаны бусины. Бусы можно поворачивать,
но не переворачивать. Сколько различных бус можно сделать из 13 разноцветных
бусин?

Решение:

Ответ: 13!/13 = 12!.

Задача 25:

Предположим теперь, что бусы можно и переворачивать. Сколько тогда
различных бус можно сделать из 13 разноцветных бусин?

Решение:

Ответ: 12!/2.

Задача 26:

Сколько существует 6-значных чисел, в записи которых есть хотя бы одна
четная цифра?

Решение:

Вместо того, чтобы подсчитывать количество
требуемых 6-значных чисел, определим количество 6-значных чисел, не обладающих
нужным свойством. Так как это в точности те числа, в записи которых встречаются
только нечетные цифры, то их количество, очевидно, равно 5⁶ = 15625.
Всего 6-значных чисел 900000. Поэтому количество 6-значных чисел, обладающих
указанным свойством, равно 900000 – 15625 = 884375.

Задача 27:

В алфавите племени Бум-Бум шесть букв. Словом является любая
последовательность из шести букв, в которой есть хотя бы две одинаковые буквы.
Сколько слов в языке племени Бум-Бум?

Решение:

Ответ: 6⁶ – 6!.

Задача 28:

В киоске «Союзпечать» продаются 5 видов конвертов и 4 вида марок.
Сколькими способами можно купить конверт с маркой?

Решение:

Ответ: 5 • 4 = 20

Задача 29:

Сколькими способами можно выбрать гласную и согласную буквы из слова
«КРУЖОК»?

Решение:

Ответ: 2 • 3 = 6

Задача 30:

На доске написаны 7 существительных, 5 глаголов
и 2 прилагательных. Для предложения нужно выбрать по одному слову каждой из
этих частей речи. Сколькими способами это можно сделать?

Решение:

Ответ: 7 • 5 • 2 = 70

Задача 31:

У двух начинающих коллекционеров по 20 марок и по 10 значков. Честным
обменом называется обмен одной марки на одну марку или одного значка на один
значок. Сколькими способами коллекционеры могут осуществить честный обмен?

Решение:

Ответ: 20 • 20 + 10 • 10 = 500

Задача 32:

Сколько существует 6-значных чисел, все цифры которых имеют одинаковую
четность?

Решение:

Ответ: 5⁶ + 4 • 5⁵

Задача 33:

Надо послать 6 срочных писем. Сколькими способами это можно сделать,
если для передачи писем можно использовать трех курьеров и каждое письмо можно
дать любому из курьеров?

Решение:

Ответ: 3⁶

Задача 34:

Сколькими способами из полной колоды (52 карты) можно выбрать 4 карты разных
мастей и достоинств?

Решение:

Ответ: 13 • 12 • 11 • 10

Задача 35:

На полке стоят 5 книг. Сколькими способами можно выложить в стопку
несколько из них (стопка может состоять и из одной книги)?

Решение:

Ответ:
5 + 5 • 4 + 5 • 4 • 3 + 5 • 4 • 3 • 2 + 5 • 4 • 3 • 2 • 1 = 325

Задача 36:

Сколькими способами можно поставить 8 ладей на шахматную доску так,
чтобы они не били друг друга?

Решение:

Ответ: 8!

Задача 37:

На танцплощадке собрались N юношей и N девушек. Сколькими способами они
могут разбиться на пары для участия в очередном танце?

Решение:

Ответ: n!

Задача 38:

Чемпионат России по шахматам проводится в один круг. Сколько играется
партий, если участвуют 18 шахматистов?

Решение:

Ответ: 18 • 17/2 = 153

Задача 39:

Сколькими способами можно поставить на шахматную доску так, чтобы они не
били друг друга а) две ладьи; б) двух королей; в) двух слонов; г) двух коней; д) двух ферзей?

Решение:

Ответ: a) 64 • 49/2 = 1568
б)
(4 • 60 + 24 • 58 + 36 • 55)/2 = 1806
в)
(28 • 56 + 20 • 54 + 12 • 52 + 4 • 50)/2 = 1736
г)
(4 • 61 + 8 • 60 + 20 • 59 + 16 • 57 + 16 • 55)/2 = 1848
д)
(28 • 42 + 20 • 40 + 12 • 38 + 4 • 36)/2 = 1288

Задача 40:

У мамы два яблока, три груши и четыре апельсина. Каждый день в течение
девяти дней подряд она дает сыну один из оставшихся фруктов. Сколькими
способами это может быть сделано?

Решение:

Ответ: 9!/2!3!4!

Задача 41:

Сколькими способами можно поселить 7 студентов в три комнаты:
одноместную, двухместную и четырехместную?

Решение:

Ответ: 7!/1!2!4!

Задача 42:

Сколькими способами можно расставить на первой горизонтали шахматной
доски комплект белых фигур (король, ферзь, две ладьи, два слона и два коня)?

Решение:

Ответ: 8!/2!2!2!

Задача 43:

Сколько слов можно составить из пяти букв А и
не более чем из трех букв Б?

Решение:

Ответ:
1 + 6!/5!1! + 7!/5!2! + 8!/5!3! = 84

Задача 44:

Сколько существует 10-значных чисел, в которых имеется хотя бы две одинакоые цифры?

Решение: 9 • 10⁹ – 9 • 9!

Задача 45:

Каких 7-значных чисел больше: тех, в записи которых есть 1, или
остальных?

Решение:

8 • 9⁶ < 9 • 10⁶ – 8 • 9⁶,
и потому чисел с единицей больше.

Задача 46:

Кубик бросают трижды. Среди всех возможных последовательностей
результатов есть такие, в которых хотя бы один раз
встречается шестерка. Сколько их?

Решение:

Ответ: 6³ – 5³

Задача 47:

Сколькими способами можно разбить 14 человек на пары?

Решение:

Ответ:
13 • 11 • 9 • 7 • 5 • 3 • 1

Задача 48:

Сколько существует 9-значных чисел, сумма цифр которых четна?

Решение:

Ответ: 9 • 10⁷ • 5

Методические разработки: углублённое преподавание математики

Современные ученики должны иметь глубокие знания по широкому кругу вопросов и уметь результативно использовать эти знания, делать выводы и обосновывать результаты собственных исследований. Для этого прежде всего необходима глубокая математическая подготовка. Имея большой опыт преподавания в классах с углублённым изучением математики, я могу поделиться своими наработками. Данные методические разработки также можно найти в журнале «Математика в школах Украины».

Планируя изучение каждой темы я выделяю тот материал, который необходимо будет глубже рассмотреть на факультативных занятиях, и решить задачи, которые обычно встречаются на математических олимпиадах разных уровней.

Разработка урока по алгебре и началам анализа «Основные методы интегрирования» (укр.яз)

Использование наследия В.А.Сухомлинского в процессе преподавания математики (укр.яз, 11 кБ)

Первый урок «Знання – це скарб, а вміння вчитись – це ключ до нього» (укр.яз, 16 кБ) Цель урока: Воспитывать сознательное отношение к учёбе, развитие познавательной активности и культуры умственного труда.

Образцы поэлементного анализа контрольных работ по математике в 8, 9 и 10 классах. (укр.яз, 20 кБ) Анализируя контрольную работу учитель ставит перед собой задачу выяснить пробелы знаниях учащихся и работать над их ликвидацией. Поэтому после проверки каждой контрольной работы я составляю схему поэлементного анализа. Это помогает в дальнейшей работе.

Методика преподавания теоремы косинусов и её применение в решении задач в 9 классе с углублённым изучением математики. (укр.яз., 158 кБ) Одним из методов, которые я применяю при работе на уроках есть работа в группах. Такой вид работы помогает учащимся решать сложные математические задачи проблеммного, исследовательского характера, убедительно отстаивать своё решение, а также учит школьников брать участие в дискуссиях.

Методика использования элементов групповой работы при изучении алгебры и начал анализа в 11 классе. (укр.яз, 170 кБ)

Методические рекомендации по решению задач на комбинацию геометрических тел при изучении стереометрии в 11 классе (укр.яз, 340 кБ)

Площадь ортогональной проекции многоугольника (укр.яз, 670 кБ) Цель урока:: проверить и установить уровень овладения учениками основами знаний и способами познавательной деятельности; повторить, глубоко осмыслить учебный материал, скорректировать умения и навыки учеников; развивать навыки общения в группе.

Делимость натуральных чисел (укр.яз, 110 кБ) Основная цель изучения темы – завершить изучение натуральных чисел, подготовить основание для изучения действий над обычными дробями. В этой теме завершается изучение понятий делителя и общего кратного, которые используются затем при сокращении дробей и сведении дробей к общему знаменателю.

Программа курса «Енергозбереження для учнів» (укр.яз, 19 кБ) Тема сохранения энергии и открытия новых нетрадиционных источников необычно актуальна в наши дни. У нас в лицее была создана творческая группа по созданию программы, которая охватывает курсы начальной, основной и старшей школы. Деятельность учителей была направлена на приобретение и усвоение учащимися знаний об основах сохранения энергии, воспитания у них и их родителей экономного отношения в энергетическим ресурсам и небезраличного отношения к нерациональному использованию энергии.

Программа факультативного курса для учеников 11 класса (укр.яз, 17 кБ)

Программа факультативного курса по математике для 9 класса с углублённым теоретическим и практическим изучением математики (укр.яз, 10 кБ) Напечатана в сборнике «Програми для загальноосвітніх навчальних закладів. Математика.» Киев, «Навчальна книга» , 2003.

Творческая работа на областной конкурс «Система работы с одарёнными детьми» (укр.яз, 95 кБ)

Календарно-тематическое планирование по математике в 11 классе c углублённым изучением предмета, I семестр (укр.яз, 16 кБ)

Календарно-тематическое планирование по математике в 10 классе c углублённым изучением предмета, I семестр (укр.яз, 20 кБ)

Календарно-тематическое планирование по математике в 10 классе c углублённым изучением предмета, II семестр (укр.яз, 22 кБ)

Календарно-тематическое планирование по математике в 9 классе c углублённым изучением предмета, I семестр (укр.яз, 19 кБ)

Календарно-тематическое планирование по математике в 9 классе c углублённым изучением предмета, II семестр (укр.яз, 20 кБ)

Тематика заседаний методического объединения учителей математики, физики и информатики на 2007-2008 учебный год (укр.яз, 7 кБ)

Часть 1. Комбинаторика.

Пусть А – конечное множество. Через ½А½ обозначим число элементов множества А, иначе называемое мощностью множества А.

Закон аддитивности. В случае если множества А и В не имеют общих элементов, то ½АÈВ½=½А½+½В½

Задача 1. В классе 12 мальчиков и 14 девочек. Сколько всего учеников в классе?

Эта задача показывает, что закон аддитивности мы знаем давно и пользуемся этим законом с первого класса, а то и раньше.

Задача 2. Все ученики в классе обязаны посещать хотя бы один из двух кружков: по физике или по математике. Математический кружок посещают 16 человек, физический – 14. Сколько всего человек в классе?

Для решения этой задачи закон аддитивности не применим, поскольку рассматриваемые в ней множества могут иметь непустое пересечение. Стоит сказать, что для нахождения точного числа учеников в классе нужно знать, сколько человек посещают оба кружка. При отсутствии этой информации общее число учеников может меняться от 16 до 30.

Следствия из закона аддитивности.

Следствие 1. В случае если ВÌА, то ½А½=½В½+½А\В½.

Следствие 2. ½А½=½АÇВ½+½А\В½

Следствие 3. |АÈВ|=|А|+|В|–|АÇВ|.

Задача 3. Все ученики в классе обязаны посещать хотя бы один из двух кружков: по физике или по математике. Математический кружок посещают 16 человек, физический – 14. Оба кружка посещают 4 человека. Сколько всего человек в классе?

Задача 4. Докажите следствия 1–3. Укажите, где в доказательстве использован закон аддитивности.

Задача 5. Сколько существует натуральных чисел, не превосходящих 1000, которые делятся и на 3 и на 5?

Задача 6. Сколько существует натуральных чисел, не превосходящих 1000, которые делятся хотя бы на одно из чисел 3 и 5?

Задача 7. Сколько существует натуральных чисел, не превосходящих числа а = 3⁵×5³ и взаимно простых с а?

Задача 8. Сколько существует натуральных чисел, не превосходящих 1000, которые делятся на 3, но не делятся на 5?

Задача 9. Пусть уравнение f(x)=0 имеет n решений, уравнение g(x)=0 имеет m решений, а система имеет k решений. Сколько решений имеет уравнение f(x)×g(x)=0 при условии, что оба уравнения определены при всех значениях х?

Задача 10. Каждый из учеников класса ходил хотя бы в один из двух походов, причем в каждом из этих походов девочек было не больше 40% от общего числа участников. Докажите, что в классе не более девочек.

Закон аддитивности справедлив не только при подсчете количества элементов конечных множеств. Этому же закону подчиняются длины отрезков (и других множеств на прямой), площади фигур на плоскости, объёмы тел в трехмерном пространстве. Многие физические величины также подчиняются закону аддитивности.

Задача 11. На отрезке единичной длины расположено несколько непересекающихся отрезков, обладающих свойством: на этих отрезках нельзя найти двух точек, расстояние между которыми равно 0,5. Докажите, что суммарная длина данных отрезков не превосходит 0,5.

Закон мультипликативности (правило умножения).Число всевозможных пар вида (a,b), где а – элемент множества А, а b – элемент множества В, равно ½А½´½В½.

Задача 12. В классе 12 мальчиков и 15 девочек. Для участия в конкурсе нужно выбрать одного мальчика и одну девочку. Сколькими способами это можно сделать?

Задача 13. Пусть уравнение f(x)=0 имеет n решений, а уравнение g(y)=0 имеет m решений. Сколько решений имеет система ?

Задача 14. Сколько различных натуральных делителей имеет число 2ⁿ×3^m?

Задача 15. Докажите, что число обладает нечетным количеством различных натуральных делителей тогда и только тогда, когда оно является полным квадратом.

Задача 16. В условиях задачи 3 определить, сколькими способами можно выбрать для выступления в математической и физической олимпиадах по одному участнику соответствующего кружка при условии, что две эти олимпиады проходят одновременно.

Для решения этой задачи правило умножения нельзя применять непосредственно. Действительно, это правило не исключает из рассмотрения пары вида (а,а), появляющиеся в том случае, когда множества А и В имеют непустое пересечение. При этом по смыслу задачи нас не устраивают такие пары, так как один ученик не может участвовать в двух олимпиадах одновременно. То есть из общего количества пар, равного 16×14, нужно вычесть 4 пары вида (а,а).

Задача 17. Пусть |А|=n, |В|=m, |АÇВ|=k. Сколько существует пар вида (a,b), где а – элемент множества А, а b – элемент множества В, причем a¹b.

Задача 18. Пусть |А|=n. Сколько существует пар вида (a,b), где а и b – элементы множества А, причем a¹b.

Задача 19. В классе 27 человек. Сколькими способами из них можно выбрать старосту и заместителя старосты?

Эту задачу решается тем же способом, что и предыдущие две – из общего количества пар вычитаются 27 пар вида (а,а). При этом можно рассуждать по другому: старосту класса можно выбрать 27 способами, его заместителя – 26 способами; всего получается 27×26 способов.

Сформулируем правило, позволяющее решать подобные задачи.

Пускай первый элемент пары можно выбрать n способами, а второй – m способами. Тогда общее количество пар равно n´m.

Задача 20. Сколькими способами можно поставить на шахматную доску черную и белую ладьи так, чтобы они не били друг друга.

Задача 21. В классе 27 человек. Сколькими способами из них можно выбрать старосту, помощника старосты и заместителя старосты?

Задача 22. В классе 27 человек. Сколькими способами из них можно выбрать двух человек для дежурства в столовой?

Почувствуйте разницу между задачами 19 и 22. В задаче 19 из двух учеников можно образовать две пары, поскольку не все равно, кто именно будет старостой, а кто его заместителем. В задаче 22 из двух учеников можно образовать только одну пару – в связи с этим общее количество пар в этой задаче в два раза меньше.

Задача 23. В шахматном турнире, проводимом по круговой системе (каждый участник встречается с каждым по одному разу), играет 12 человек. Сколько всего партий должно быть сыграно в данном турнире.

Задача 24. На плоскости расположено 10 точек. Сколько существует отрезков с концами в этих точках?

Задача 25. Сколько диагоналей у выпуклого n-угольника?

Задача 26. В классе 8 девочек и 17 мальчиков. Сколькими способами из их числа можно выбрать двух девочек и одного мальчика?

Задача 27. В классе 27 человек. Для участия в физической, химической и математической олимпиадах крайне важно выбрать трех разных учеников. Сколькими способами это можно сделать?

Задача 28. Сколько различных натуральных делителей имеет число 2ⁿ×3^m×5^k?

Для решения трех последних задач (а также задачи 21) правило умножения нужно применить дважды. Поскольку подобная ситуация возникает довольно часто, имеет смысл сформулировать правило умножения в следующем, более общем, виде:

Пусть нам нужно составить набор из n предметов, причем первый предмет можно выбрать к₁ способами, второй предмет – к₂ способами и т.д. Тогда общее количество всевозможных наборов равно к₁×к₂×к₃×…×к_n..

Задача 29. Сколькими способами пять учеников можно построить в шеренгу?

Задача 30. Сколькими способами пять учеников можно построить в шеренгу, в случае если Вова не должен стоять первым?

Заметим, что при решении этой задачи можно рассуждать по разному. Первый способ: на первое место можно поставить одного из 4 детей (любого кроме Вовы), на второе – одного из 4 (трое оставшихся и Вова), на третье – одного из трех, на четвертое – одного из двух, на пятое место автоматически попадает оставшийся ученик; всего получается 4×4×3×2=96 вариантов. Второй способ: Вову можно поставить на одно из 4 мест, Петю – на одно из 4, Машу – на одно из трех, Марину – на одно из двух. Можно рассуждать и так: из общего количества способов (Вова стоит где угодно) вычесть количество способов, при которых Вова стоит на первом месте (таких способов 4×3×2=24).

Задача 31. Сколькими способами пять учеников можно построить в шеренгу, в случае если Вова не должен стоять с краю?

Задача 32. Сколькими способами n учеников можно построить в шеренгу?

Задача 33. Сколько анаграмм можно составить из букв слова ПТИЦА?

Задача 34. Сколько анаграмм можно составить из букв слова ПИЦЦА?

Задача 35. Сколько существует шестизначных чисел, в десятичной записи которых использованы только цифры 1, 2, 3, 4, 5?

Задача 36. Сколько существует шестизначных чисел, в десятичной записи которых использованы только цифры 0, 1, 2, 3, 4?

Задача 37. Сколько существует шестизначных чисел, в десятичной записи которых каждая цифра встречается не более одного раза?

Очень часто для решения одной задачи приходится применять как правило умножения, так и правило сложения. Обычно это происходит по следующей схеме: множество А разбивается на подмножества А_i таким образом, что число элементов каждого из них можно определить по правилу умножения.

Задача 38. Сколькими способами можно поставить на шахматную доску черного и белого королей так, чтобы они не били друг друга.

Задача 39. Сколькими способами можно построить в шеренгу пять учеников, в случае если Ваня и Маша обязательно хотят стоять рядом?

Задача 40. Сколько можно составить из букв слова ПИЦЦА таких анаграмм, в которых две буквы Ц не стоят рядом?

Задача 41. Сколько можно составить из букв слова КОМЕТА таких анаграмм, в которых гласные и согласные буквы чередуются?

Задача 42. Сколькими способами можно посадить за круглым столом 6 человек?

Мы рассмотрели ряд задач, решение которых основано на применении правил умножения и сложения. Попытаемся теперь как-то систематизировать подобные задачи. Большинство из них воспроизводит следующую ситуацию: из данных предметов крайне важно по определенному принципу выбрать несколько штук. Набор выбираемых предметов принято называть выборкой. Множество, из которого выбираются предметы – выборочным множеством. Количество выбираемых предметов – размером (или объёмом) выборки. Рассматриваются упорядоченные и неупорядоченные выборки. Неупорядоченные выборки характеризуются только своим составом, упорядоченные – составом выборки и порядком следования ее элементов (первый, второй, третий и т.д.). Вместе с тем, выборки подразделяются на две группы исходя из того, допускается ли в них выбор одного и того же предмета несколько раз (выборки с повторениями) или не допускается (выборки без повторений). Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, имеется четыре вида выборок: упорядоченные с повторениями, упорядоченные без повторений, неупорядоченные с повторениями, неупорядоченные без повторений. Упорядоченные выборки называются иначе размещениями, а неупорядоченные – сочетаниями. При этом, когда говорят просто ʼʼсочетаниеʼʼ, имеют в виду сочетание без повторений, в противном случае говорят ʼʼсочетание с повторениямиʼʼ. То же самое касается и размещений. Сочетание — ϶ᴛᴏ просто подмножество выборочного множества. Чтобы задать сочетание, нужно перечислить входящие в это подмножество элементы, записав их в фигурные скобки: . Размещение — ϶ᴛᴏ упорядоченный набор элементов выборочного множества, его принято записывать в круглых скобках. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, к примеру, две записи и означают одно и то же сочетание, а записи (x₁,x₂,x₃) и (x₂,x₃,x₁) – два разных размещения. При решении задач очень важно бывает понять, какой вид выборки рассматривается в данной задаче. Так, в случае если речь идет о трех участниках математической, физической и химической олимпиад, то мы имеем дело с упорядоченной выборкой (нам не все равно, кто в какой олимпиаде выступает). В случае если же в задаче говорится о трех участницах конкурса красоты, то выборка является неупорядоченной. В случае если три олимпиады происходят в одно время, и выступать в них должны разные ученики, то это выборка без повторений. В случае если же допускается выступление одного и того же ученика в разных олимпиадах, то выборка с повторениями.

Задача 43. Для данных ситуаций определите выборочное множество. Найдите тип и размер выборки:

а) 10 разных предметов нужно разложить по трем разным ящикам;

б) имеется 10 разных ящиков; три разных предмета нужно убрать в эти ящики, не более одного предмета в ящик;

в) учитель задал Ване 10 задачек; Ваня решил сделать 3 из них, сказав, что остальные у него не получились;

г) у Маши в холодильнике лежат яблоки, груши и апельсины; Маша решила взять в школу 10 фруктов.

Задача 44. На танцплощадке собралось 8 юношей и 8 девушек. Сколькими способами их можно разбить на пары для участия в очередном танце?

Любая выборка характеризуется не только своим типом и размером, но и мощностью выборочного множества. В этом плане принято говорить о выборке из n по k, где n – число элементов выборочного множества, а k – размер выборки. Так, говорят о сочетаниях из n по k, о размещениях из n по k, о сочетаниях с повторениями из n по k и о размещениях с повторениями из n по k. При этом число сочетаний из n по k обозначают , число размещений из n по k обозначают . Соответственно число сочетаний и размещений с повторениями обозначают и . В том случае, когда мощность выборочного множества совпадает с размером выборки (n=k), размещения называют перестановками на множестве из n элементов. Число таких перестановок обозначается P_n. Сейчас мы выведем формулы для вычисления всех этих величин.

Часть 1. Комбинаторика — Студопедия

Закон аддитивности. Если множества А и В не имеют общих элементов, то ½АÈВ½=½А½+½В½

Задача 1. В классе 12 мальчиков и 14 девочек. Сколько всего учеников в классе?

Для решения этой задачи закон аддитивности не применим, поскольку рассматриваемые в ней множества могут иметь непустое пересечение. Для нахождения точного числа учеников в классе нужно знать, сколько человек посещают оба кружка. При отсутствии этой информации общее число учеников может меняться от 16 до 30.

Следствия из закона аддитивности.

Следствие 1. Если ВÌА, то ½А½=½В½+½А\В½.

Следствие 2. ½А½=½АÇВ½+½А\В½

Следствие 3. |АÈВ|=|А|+|В|–|АÇВ|.

Задача 4. Докажите следствия 1–3. Укажите, где в доказательстве использован закон аддитивности.

Задача 5. Сколько существует натуральных чисел, не превосходящих 1000, которые делятся и на 3 и на 5?

Задача 7. Сколько существует натуральных чисел, не превосходящих числа а = 3⁵×5³ и взаимно простых с а?

Задача 8. Сколько существует натуральных чисел, не превосходящих 1000, которые делятся на 3, но не делятся на 5?

Закон аддитивности справедлив не только при подсчете количества элементов конечных множеств. Этому же закону подчиняются длины отрезков (и других множеств на прямой), площади фигур на плоскости, объемы тел в трехмерном пространстве. Многие физические величины также подчиняются закону аддитивности.

Задача 13. Пусть уравнение f(x)=0 имеет n решений, а уравнение g(y)=0 имеет m решений. Сколько решений имеет система ?

Задача 14. Сколько различных натуральных делителей имеет число 2ⁿ×3^m?

Для решения этой задачи правило умножения нельзя применять непосредственно. Действительно, это правило не исключает из рассмотрения пары вида (а,а), появляющиеся в том случае, когда множества А и В имеют непустое пересечение. Однако по смыслу задачи нас не устраивают такие пары, так как один ученик не может участвовать в двух олимпиадах одновременно. То есть из общего количества пар, равного 16×14, надо вычесть 4 пары вида (а,а).

Задача 18. Пусть |А|=n. Сколько существует пар вида (a,b), где а и b – элементы множества А, причем a¹b.

Задача 19. В классе 27 человек. Сколькими способами из них можно выбрать старосту и заместителя старосты?

Эту задачу решается тем же способом, что и предыдущие две – из общего количества пар вычитаются 27 пар вида (а,а). Однако можно рассуждать по другому: старосту класса можно выбрать 27 способами, его заместителя – 26 способами; всего получается 27×26 способов.

Сформулируем правило, позволяющее решать подобные задачи.

Задача 22. В классе 27 человек. Сколькими способами из них можно выбрать двух человек для дежурства в столовой?

Почувствуйте разницу между задачами 19 и 22. В задаче 19 из двух учеников можно образовать две пары, поскольку не все равно, кто именно будет старостой, а кто его заместителем. В задаче 22 из двух учеников можно образовать только одну пару – поэтому общее количество пар в этой задаче в два раза меньше.

Задача 24. На плоскости расположено 10 точек. Сколько существует отрезков с концами в этих точках?

Задача 25. Сколько диагоналей у выпуклого n-угольника?

Задача 27. В классе 27 человек. Для участия в физической, химической и математической олимпиадах необходимо выбрать трех разных учеников. Сколькими способами это можно сделать?

Задача 28. Сколько различных натуральных делителей имеет число 2ⁿ×3^m×5^k?

Задача 29. Сколькими способами пять учеников можно построить в шеренгу?

Задача 30. Сколькими способами пять учеников можно построить в шеренгу, если Вова не должен стоять первым?

Задача 31. Сколькими способами пять учеников можно построить в шеренгу, если Вова не должен стоять с краю?

Задача 32. Сколькими способами n учеников можно построить в шеренгу?

Задача 33. Сколько анаграмм можно составить из букв слова ПТИЦА?

Задача 34. Сколько анаграмм можно составить из букв слова ПИЦЦА?

Задача 39. Сколькими способами можно построить в шеренгу пять учеников, если Ваня и Маша обязательно хотят стоять рядом?

Задача 40. Сколько можно составить из букв слова ПИЦЦА таких анаграмм, в которых две буквы Ц не стоят рядом?

Задача 42. Сколькими способами можно посадить за круглым столом 6 человек?

Мы рассмотрели ряд задач, решение которых основано на применении правил умножения и сложения. Попытаемся теперь как-то систематизировать подобные задачи. Большинство из них воспроизводит следующую ситуацию: из данных предметов необходимо по определенному принципу выбрать несколько штук. Набор выбираемых предметов принято называть выборкой. Множество, из которого выбираются предметы – выборочным множеством. Количество выбираемых предметов – размером (или объемом) выборки. Рассматриваются упорядоченные и неупорядоченные выборки. Неупорядоченные выборки характеризуются только своим составом, упорядоченные – составом выборки и порядком следования ее элементов (первый, второй, третий и т.д.). Кроме того, выборки подразделяются на две группы в зависимости от того, допускается ли в них выбор одного и того же предмета несколько раз (выборки с повторениями) или не допускается (выборки без повторений). Таким образом, имеется четыре вида выборок: упорядоченные с повторениями, упорядоченные без повторений, неупорядоченные с повторениями, неупорядоченные без повторений. Упорядоченные выборки называются иначе размещениями, а неупорядоченные – сочетаниями. При этом, когда говорят просто «сочетание», имеют в виду сочетание без повторений, в противном случае говорят «сочетание с повторениями». То же самое касается и размещений. Сочетание – это просто подмножество выборочного множества. Чтобы задать сочетание, надо перечислить входящие в это подмножество элементы, записав их в фигурные скобки: . Размещение – это упорядоченный набор элементов выборочного множества, его принято записывать в круглых скобках. Таким образом, к примеру, две записи и означают одно и то же сочетание, а записи (x₁,x₂,x₃) и (x₂,x₃,x₁) – два разных размещения. При решении задач очень важно бывает понять, какой вид выборки рассматривается в данной задаче. Так, если речь идет о трех участниках математической, физической и химической олимпиад, то мы имеем дело с упорядоченной выборкой (нам не все равно, кто в какой олимпиаде выступает). Если же в задаче говорится о трех участницах конкурса красоты, то выборка является неупорядоченной. Если три олимпиады происходят в одно время, и выступать в них должны разные ученики, то это выборка без повторений. Если же допускается выступление одного и того же ученика в разных олимпиадах, то выборка с повторениями.

Задача 43. Для данных ситуаций определите выборочное множество. Найдите тип и размер выборки:

а) 10 разных предметов нужно разложить по трем разным ящикам;

б) имеется 10 разных ящиков; три разных предмета нужно убрать в эти ящики, не более одного предмета в ящик;

в) учитель задал Ване 10 задачек; Ваня решил сделать 3 из них, сказав, что остальные у него не получились;

г) у Маши в холодильнике лежат яблоки, груши и апельсины; Маша решила взять в школу 10 фруктов.

22. Варианты самостоятельных работ | Контрольные работы по математике

Вариант №1

1. Решить уравнение

Ответ: n=8.

2. Найти шестой член разложения .

Ответ: .

3. Сколькими способами можно составить колонну из десяти автобусов и трех легковых автомобилей, считая, что все автобусы и все автомобили одинаковых марок?

Ответ: .

4. В шахматном турнире участвуют шесть студентов и три школьника. Сколькими способами могут распределиться места, занятые в турнире школьники, если никакие два участника не набрали одинаковое число очков?

Ответ: .

5. Сколько делителей у числа 105?

Ответ: Разложим число 105 на простые множители . Тогда , или по формуле (7.3) получаем .

6. На вечере присутствуют 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары на танец?

Ответ: .

7. Сколько ожерелий можно составить из 7 бусинок различных размеров (надо использовать все бусинки)?

Ответ: Т. к. ожерелье остается неизменным при циклических перестановках бусинок и при переворачивании, то можно получить 7!/14=360 видов ожерелий.

8. В первой урне находятся 4 белых и 3 черных шара, во второй – 3 белых и 5 черных шаров. Из каждой урны случайным образом вынули по одному шару. Найти вероятность того, что все шары будут белые.

Ответ: .

9. 10 вариантов контрольной работы распределены среди 6 студентов. Найти вероятность того, что варианты с номерами 1 и 2 не будут использованы.

Ответ: .

10. Семь различных книг случайных образом расставляют на полке. Найти вероятность того, что книги трехтомника окажутся рядом в возрастающем порядке.

Ответ: .

11. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочнике соответственно равны 0,6, 0,8 и 0,9. Найти вероятность того, что формула содержится только в двух справочниках.

Ответ. 0,9×0,8×0,3+0,9×0,2×0,7+0,1×0,8×0,7=0,398.

Вариант №2

1. Решить уравнение .

Ответ: x=4.

2. В разложении вычислить член, не содержащий x.

Ответ: .

3. На плоскости проведены n прямых линий, из которых никакие две не являются параллельными и никакие три не пересекаются в одной точке. Сколько точек пересечения имеют эти прямые?

Ответ: .

4. Сколькими способами можно разложить 12 различных марок между тремя мальчиками, если один берёт 6 марок, а остальные – по 3 марки?

Ответ: .

5. Сколько делителей у числа 360?

Ответ: Поскольку , то в соответствие с формулой (7.3) получаем (3+1)(2+1)(1+1)=24 делителей.

6. В избушке на курьих ножках собрались Баба-Яга, Кощей и Леший. У Бабы-Яги есть 4 чашечки, 5 блюдец и 6 чайных ложечки (все чашки, блюдца и ложечки отличаются друг от друга). Сколькими способами она может накрыть стол для чаепития (каждый получает одну чашку, одно блюдце и одну ложечку)?

Ответ: .

7. Шесть девушек водят хоровод. Сколькими способами они могут организовать хоровод?

Ответ: Т. к. хоровод остается неизменным при циклических перестановках девушек, то можно получить 6!/6=120 способов.

8. В урне находятся 5 белых и 3 черных шаров, из которой случайно по порядку с возвращением вынимаются 4 шара. Какова вероятность того, что первые два шара будут белые, а последние два черные.

Ответ: .

9. Студент пришел на экзамен, зная лишь 24 вопроса из 32 вопросов программы. Экзаменатор задал студенту 3 вопроса. Найти вероятность того, что студент ответ на все вопросы?

Ответ: .

10. Случайным образом выписаны 3 цифры. Найти вероятность того, все цифры различные.

Ответ: .

11. При включении зажигания двигатель начинает работать с вероятностью 0,9. Найти вероятность того, что для запуска двигателя потребуется включить зажигание не более двух раз.

Ответ. 0,9+0,1×0,9=0,99.

Вариант №3

1. Решить уравнение .

Ответ: x=9, x=10.

2. Раскрыть скобки в выражении .

Ответ: .

3. Сколькими способами можно составить шестизначное число, в запись которого входят четыре двойки и две пятёрки?

Ответ: .

4. На пять сотрудников университета выделены три путёвки на один курорт. Сколькими способами их можно распределить, если: а) все путёвки в различные санатории; б) все путёвки в один санаторий.

Ответ: а) , б) .

5. Сколькими способами можно выбрать из полной колоды карт, содержащей 52 карты, по одной карте каждой масти? А ели среди вынутых карт нет ни одной пары одинаковых, т. е. двух королей, двух десяток и т. д.?

Ответ: Получаем размещения с повторениями из 13 карт по 4. Всего . Если среди карт не должно быть пар, то имеем размещения без повторений; их число .

6. Сколькими способами можно сделать трёхцветный флаг (с тремя горизонтальными полосами), если имеется материя пяти различных цветов, если цвета могут повторяться, но не рядом (полосы должны быть различными)?

Ответ: Осуществляя выбор сверху вниз, получаем способов.

7. Из 12 девушек и 10 юношей выбирают команду в составе 5 человек. Сколькими способами можно выбрать эту команду так, чтобы в неё вошло не более 3 юношей?

Ответ: .

8. Автобус должен сделать 8 остановок, в котором едут 5 пассажиров. Какова вероятность, что на каждой остановке выйдет не более одного пассажира, если предположить, что каждый пассажир имеет одинаковую вероятность выйти на любой остановке?

Ответ: .

9. На каждой из шести одинаковых карточках напечатана одна из следующих букв: а, т, м, р, с, о. Карточки тщательно перемешаны. Найти вероятность того, что на четырех, вытянутых по одной и расположенных «в одну линию» карточках, можно будет прочесть слово «трос».

Ответ: .

10. Собрание, на котором присутствуют 20 человек, в том числе 8 женщин, выбирают делегацию из 5 человек. Найти вероятность того, что в делегацию войдут 3 женщины, считая, что каждый из присутствующих может быть избран с одинаковой вероятностью.

Ответ: .

11. Вероятность для данного спортсмена улучшить свой предыдущий результат с одной попытки равна 0,6. Определить вероятность того, что на соревнованиях спортсмен улучшит свой результат, если разрешается делать две попытки.

Ответ. 1–0,42=0,84.

Вариант №4

1. Решить уравнение .

Ответ: x=11.

2. Найти член разложения , содержащий x3 .

Ответ: .

3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?

Ответ: .

4. Из семи гвоздик и пяти тюльпанов надо составить букет, состоящий из трёх гвоздик и двух тюльпанов. Сколькими способами можно это сделать?

Ответ: .

5. На призывном пункте находится 15 призывников. Сколькими способами можно поставить в колонну по три человека?

Ответ: .

6. Сколькими способами можно выбрать 12 человек из 17, если определенные два человека из этих 17 не могут быть выбраны вместе?

Ответ: .

7. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?

Ответ: .

8. 8 вариантов контрольной работы случайным образом распределены среди 6 студентов. Найти вероятность того, что варианты с номерами 7 и 8 не будут использованы?

Ответ: .

9. В первой урне находятся 5 оранжевых и 4 фиолетовых шара, во второй – 3 оранжевых и 7 фиолетовых шара. Из каждой урны случайным образом вынули по три шара. Найти вероятность того, что все шары будут одного цвета.

Ответ: .

10. В журнале из 20 страниц на каких-либо трех страницах помещают случайным образом одинаковую рекламу некоторой фирмы. Какова вероятность, что эта реклама будет размещена на страницах, идущих одна за другой?

Решение: В данной задаче порядок размещения рекламы неважен. Следовательно, в данной задаче мы имеем дело с сочетаниями. Общее число размещений рекламы в журнале . Если реклама будет размещена на страницах, идущих одна за другой, то эти страницы можно считать за одну. Тогда число страниц будет равно 18, следовательно, и число благоприятствующих исходов будет равно m=18. Таким образом, .

11. В ОТК поступают 4 детали. Вероятность того, что деталь бракованная равна 0,1. Проверка производится последовательно до обнаружения бракованной детали. Найти вероятность того, что будут проверены все 4 детали.

Ответ. 0,9×0,9×0,9=0,729.

Вариант №5

1. Уравнение .

Ответ: .

2. Найти показатель степени бинома , если его четвёртый член не зависит от a.

Ответ: .

3. На складе имеются 7 ящиков с различными фруктами и 5 ящика с различными овощами. Сколькими способами можно каждой из трёх овощных палаток выдать по одному ящику с фруктами и овощами?

Ответ: .

4. Сколькими способами 6 одинаковых монет могут распределить между собой Буратино, лиса Алиса и кот Базилио?

Ответ: .

5. В команду должны быть отобраны 4 спортсмена из имеющихся 10. Сколькими способами это можно сделать, если два определенных спортсмена должны войти в команду?

Ответ: .

6. Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях будет ровно один туз?

Ответ: .

7. Пассажирский поезд состоит из четырех багажных вагонов и десяти купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале или конце?

Ответ:

8. Собрание, на котором присутствуют 12 человек, в том числе 7 женщин, выбирают председателя, его первого и второго заместителя. Найти вероятность того, что председатель и его заместители будут женщинами, считая, что каждый из присутствующих может быть избран с одинаковой вероятностью.

Ответ: .

9. В урне находятся 5 зелёных и 3 жёлтых шара. Из урны случайным образом вынули три шара. Найти вероятность того, что все шары будут одного цвета.

Ответ: .

10. 10 вариантов контрольной работы распределяется среди случайным образом среди 10 студентов, сидящих в один ряд. Найти вероятность того, что варианты с номерами 1 и 2 достанутся рядом сидящим студентам.

Ответ: .

11. Два охотника одновременно и независимо друг от друга стреляют по зайцу. Найти вероятность того, что попадёт только один из охотников, если вероятность попадания для первого охотника равна 0,8, а для второго – 0,7.

Ответ: .

Вариант №6

1. Уравнение .

Ответ: .

2. Найти средний член разложения .

Ответ: .

3. В пространстве даны 7 точек, причем никакие четыре из них не лежат в одной плоскости. Сколько различных плоскостей можно провести через эти 7 точек?

Ответ: .

4. Эллочка Людоедка решила расставить семь различных книг на полке. Сколькими способами она может это сделать, если две наиболее красивые книги (по её мнению) в красном переплёте должны стоять по краям?

Ответ: .

5. В первенстве края по футболу участвуют 12 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 3 определенные команды?

Ответ: .

6. Сколькими способами декан может раздать 7 поручений 4 студентам?

Ответ: .

7. Сколькими способами можно выбрать на шахматной доске белое и черное поля, не лежащее на одной вертикали или горизонтали?

Ответ: .

8. Для проведения тестирования группу студентов, состоящую из 18 человек, случайным образом разбивают на две подгруппы из 12 и 6 человек. Какова вероятность, что две подружки, Оля и Тяня, окажутся в одной подгруппе?

Решение: В данной задаче порядок неважен, т. е. не принимается во внимание порядок отбора студентов в группу. Следовательно, в данной задаче мы имеем дело с сочетаниями. Для того чтобы разбить 18 студентов на две подгруппы достаточно выбрать, например, 12 студентов в одну подгруппу, тогда остальные образуют другую подгруппу. Таким образом, общее число разбиений студентов на две подгруппы будет равно . Для того, чтобы разбить команды на две подгруппы с указанными условиями, можно к Оле и Тане добавить либо 10 студентов из оставшихся 16 (это можно сделать способами ), либо добавить 4 студентов из 16 ( способов). Оставшиеся студенты будут образовывать другую подгруппу. Таким образом, число благоприятствующих исходов будет равно . В результате, получаем .

9. В газете из 16 страниц на каких-либо трех страницах помещают случайным образом разные объявления. Какова вероятность, что эти объявления будут размещены на страницах, идущих одна за другой?

Ответ: .

10. В одной урне 3 зелёных и 4 жёлтых шаров, в другой – 6 зелёных и 2 жёлтых шара. Из каждой урны взяли по два шара. Какова вероятность того, что все шары будут одного цвета?

Ответ: .

11. Студент знает 5 вопросов из 12. Какова вероятность того, что он получит зачет, если нужно ответить на все три задаваемых вопроса?

Ответ: .

Вариант №7

1. Решить уравнение .

Ответ: n=5.

2. Найти член разложения , содержащий x–1.

Ответ: .

3. Сколько диагоналей можно провести в выпуклом восьмиугольнике?

Ответ: .

4. Сколько различных «слов» можно составить, переставляя буквы слова «парабола»?

Ответ: .

5. Труппа состоит из 10 человек. Сколькими способами можно выбирать из неё в течение двух вечеров по 6 человек для участия в спектаклях так, чтобы эти составы не совпадали друг с другом?

Ответ: .

6. Сколькими способами Буратино, лиса Алиса и кот Базилио могут поделить между собой 5 одинаковых золотых монет и 2 разных брильянтовых ожерелья?

Ответ: .

7. Сколькими способами можно разложить 9 книг по 3 бандеролям по 3 книги в каждой (порядок бандеролей не принимать во внимание)?

Ответ: .

8. Для проведения тестирования группу студентов, состоящую из 18 человек, случайным образом разбивают на две подгруппы из 12 и 6 человек. Какова вероятность, что две подружки, Оля и Таня, окажутся в разных подгруппах?

Ответ: Решается аналогично задаче 8 предыдущего варианта .

9. Три охотника стреляют по 7 уткам. Каждый из охотников выбирает себе цель наудачу независимо от остальных. Найти вероятность того, что все охотники выстрелят по разным уткам.

Ответ: .

10. На каждой из шести одинаковых карточках напечатана одна из следующих букв: м, м, а, а. Карточки тщательно перемешаны. Найти вероятность того, что на четырех, вытянутых по одной и расположенных «в одну линию» карточках, можно будет прочесть слово «мама».

Ответ:

11. Вероятность боя стеклянной тары при погрузке на автомашины равна 0,03, а при транспортировке – 0,07. Какова вероятность боя стеклянной тары?

Ответ: .

< Предыдущая		Следующая >

Дидактические материалы для занятий математического кружка «Математика +» 7 класс. Занятие14-16. Введение в комбинаторику | План-конспект занятия по математике (7 класс) на тему:

Введение в комбинаторику

«Вперёд поедешь — голову сложишь,
направо поедешь — коня потеряешь,
налево поедешь — меча лишишься»

В старинных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. Добрый молодец на перепутье. Он сталкивается с проблемой выбора дальнейшего пути движения. А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Это сделать очень трудно не потому, что его нет или оно одно и поэтому его трудно найти, а приходится выбирать из множества возможных вариантов, различных способов, комбинаций. И нам всегда хочется, чтобы этот выбор был оптимальный.

Оказывается, существует целый раздел математики, именуемый комбинаторикой, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую.

Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Выбором объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например конструктору, разрабатывающему новую модель механизма, ученому-агроному, планирующему распределение с/х культур на нескольких полях, химику, изучающему строение органических молекул, имеющих данный атомный состав.

С комбинаторными задачами люди столкнулись в глубокой древности. В Древнем Китае увлекались составлением магических квадратов. В Древней Греции занимались теорией фигурных чисел.

Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. Комбинаторика становится наукой лишь в 18 в. – в период, когда возникла теория вероятности.

С комбинаторными величинами приходится иметь дело представителям многих специальностей: ученому–химику, биологу, конструктору, диспетчеру и т.п. На практике часто приходится выбирать из некоторого множества объектов подмножества элементов, обладающих теми или иными свойствами, располагать элементы одного или нескольких множеств в определенном порядке и т. д. Поскольку в таких задачах речь идет о тех или иных комбинациях объектов, их называют «комбинаторные задачи». Комбинаторная задача – задача, в которой идет речь о тех или иных комбинациях объектов.

Задачи, которые приведены в этом разделе считаются наиболее трудными, но они помогут вам творить, думать необычно, оригинально, смело, видеть то, мимо чего вы часто проходили не замечая, любить неизвестное, новое; преодолевать трудности и идти вперед.

Задача 1:

Вспомним из чего состоит флаг РФ. Из трех горизонтальных полосок разного цвета (белый, синий, красный).

Оказывается, есть государства, где флаги имеют такие же цвета.

Видим, что от перестановок цветных полосок, можно получить другой флаг. Как подсчитать, сколько таких флагов мы можем составить из трех цветных полосок?

Решение этой задачи можно записать тремя способами:

Таблица вариантов

КБС	КСБ
БСК	БКС
СБК	СКБ

Дерево вариантов

Правило умножения

1 полоса 3 способа

2 полоса 2 способа (т.к. одна полоса уже зафиксирована)

3 полоса 1 способ

Количество всех вариантов равно 3 ∙ 2 ∙ 1 = 6 Такое произведение можно записать короче 3 ∙ 2 ∙ 1= 3! (читают «три факториал»)

Ответ: 3! = 6 способов

Мы решили задачу о флагах тремя различными способами, которые используют при решении комбинаторных задач:

Дерево вариантов,
табличный,
правило умножения.

Достоинства и недостатки каждого способа приведены ниже в таблице.

Способ решения	Плюсы	Минусы
Дерево вариантов	Наглядность, возможность увидеть все варианты	Очень громоздкий и длительный, если много различных вариантов
Табличный	Наглядность, компактность, возможность увидеть все варианты	Невозможность решать задачи, в которых более двух составляющих одного события
Правило умножения	Компактность, быстрота решения	«Не видно» самих вариантов, можно только просчитать их количество.

В данной задаче мы переставляли полоски местами, т.е. занимались перестановкой элементов. Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок можно найти по формуле:

Pn = n!,

где n! = 1 ∙ 2 ∙ 3 … n.

Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.

Пример перестановок:

Задача 2:

Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?

Решение. Искомое число трехзначных чисел

P3 = 3! = 1 ∙ 2 ∙ 3 = 6.

Рассмотрим еще несколько задач с решением для лучшего усвоения материала:

Задача 3:

— Ребята, давайте вспомним басню И.А.Крылова «Квартет»:

Проказница мартышка,

Осел, Козел, Да косолапый мишка

Затеяли сыграть Квартет….

….А вы, друзья, как ни садитесь, все в музыканты не годитесь».

Сколько способами могут рассесться участники Квартета?

Решение: Квартет состоит из четырех участников. Число способов равно числу перестановок из 4 элементов. Р4=1∙2∙3∙4=24. Значит, существует 24 способа.

Задача 4: Сколькими способами могут восемь человек стать в очередь к театральной кассе?

Решение задачи:

Существует 8 мест, которые должны занять 8 человек. На первое место может стать любой из 8 человек, т.е. способов занять первое место – 8. После того, как один человек стал на первое место, осталось 7 мест и 7 человек, которые могут быть на них размещены, т.е. способов занять второе место – семь. Аналогично для третьего, четвертого и т.д. места. Используя принцип умножения, получаем произведение – . Такое произведение обозначается как 8! (читается 8 факториал) и называется перестановкой P8.

Ответ: P8 = 8! = 8∙ 7∙ 6∙ 5∙ 4∙ 3∙ 2∙ 1= 40320

Еще для успешного решения задач нам необходимо познакомиться с комбинаторными правилами:

Правило суммы.

Задача 5: Саша положил в корзину два белых гриба, а Таня – 3 подосиновика. Сколькими способами можно взять из корзины либо белый гриб, либо подосиновик?

В задаче рассматривается два множества: грибы Саши, обозначим его {а1, а2}, грибы Тани – {b1, b2, b3}. Все грибы в корзине представляют собой объединение этих двух множеств: {a1, a2, b1, b2, b3}. В полученном множестве 5 (5 = 2+3) элементов. И, значит, взять из корзины либо белый гриб, либо подосиновик можно пятью способами.

В обобщенном виде этот способ подсчета элементов в объединении пересекающихся конечных множеств называется правилом суммы и формируется следующим образом: если множество А содержит n элементов, а множество В – m элементов и множество А и В не пересекаются, то объединение множеств А и В содержит n + m элементов.

В комбинаторике, которая возникла раньше теории множеств, правило суммы формулируют иначе: если элемент a можно выбрать n способами, а элемент b – m способами, причем не один из способов выбора элемента а не совпадает со способом b, то выбор либо а, либо b можно осуществить n+m способами.

Задача 6:

«Сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7, используя в записи числа каждую из них не более одного раза?».

При решении этой задачи сначала составляется древо всех возможных вариантов.

Первая цифра	1						3						5						7
Вторая цифра	3		5		7		1		5		7		1		3		7		1		3		5
Третья цифра	5	7	3	7	3	5	5	7	1	7	1	5	3	7	1	7	1	3	3	5	1	5	1	3

Ответ на поставленный вопрос в задаче можно получить, не выписывая сами числа и не строя дерево возможных вариантов. Рассуждать будем так. Первую цифру трехзначного числа можно выбрать четырьмя способами. Так после выбора первой цифры останутся три, то вторую цифру можно выбрать из оставшихся цифр уже тремя способами. Наконец, третью цифру можно выбрать (из оставшихся двух) двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 4·3·2 = 24. Формулируем еще одно правило: «Пусть имеется n элементов и требуется выбрать один за другим некоторые k элементов. Если первый элемент можно выбрать n1 способами, после чего второй элемент можно выбрать из оставшихся n2 способами, затем третий элемент – n3 способами и т.д., то число способов, которыми могут быть выбраны все k элементов, равно произведению n1·n2·n3·…·nk».

Ответ: 24

В обобщенном виде этот способ подсчета элементов в декартовом произведении конечных множеств называется правилом произведения и формулируется следующим образом: если множество А содержит n, а множество В — m элементов, то декартово произведение этих множеств содержит n×m элементов.

Применение правила умножения рассмотрено на следующем примере:

Задача 7:

«Из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги (рис. 1). Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?

Решение. Путь из А в В туристы могут выбрать двумя способами. Далее в каждом случае они могут проехать из В в С тремя способами. Значит, имеется 2·3 вариантов маршрута из А в С. Так как из города С на пристань можно попасть двумя способами, то всего существует 2·3·2, т.е. 12 способов выбора туристами маршрута из города А к пристани.

Ответ: 12 способов.

Задача 8. Сколько двузначных чисел можно составить, используя цифры 7, 4, 5?

Прежде всего, выясняем, в чем отличие этой задачи от решенной ранее: в данной речь идет о таких двузначных числах, в записи которых цифры могут повторяться. В таком случае выбор цифры десятков и цифры единиц можно осуществить тремя способами каждый. Поэтому выбор двузначного числа можно выполнить согласно правилу произведения 3х3=9 способами.

Если эта задача решается методом перебора, то к шести числам 74, 75, 47, 45, 57, 54, в записи которых числа не повторяются, добавляются числа 77, 44, 55.

Задача 9. Сколько трехзначных чисел можно составить, используя цифры 7, 4, 5?

В этой задаче из цифр 7, 4 и 5 образуются трехзначные числа, а не двузначные, как в задаче 1.

Так как цифры в записи этих чисел могут повторяться, то цифру сотен, цифру десятков и цифру единиц можно выбрать тремя способами каждую. А поскольку запись трехзначного числа представляет собой упорядоченный набор из трех элементов, то согласно правилу произведения его выбор можно осуществить 27 способами, так как 3х3х3=27.

Задача 10. Сколько натуральных чисел, меньших 1000, можно записать, используя цифры 7. 4 и 5?

Натуральные числа, меньшие 1000, могут быть однозначными, двузначными и трехзначными. Поэтому подсчитываем, сколько чисел каждого вида можно записать, используя цифры 7, 4 и 5, а затем полученные результаты складываем.

Однозначных чисел будет 3, двузначных – 9 (см. задачу 8), трехзначных – 27 (см. задачу 9) . Всего натуральных чисел, меньших 1000, будет 3+9+27=39.

Получив этот результат, можно выяснить, изменится ли он, если в задаче будет оговорено, что цифры в записи числа не повторяются. С учетом этого условия однозначных чисел будет 3, двузначных -6, трехзначных – 6, а всего натуральных чисел, меньших 1000 и записанных с помощью цифр 7. 4 и 5 без их повторения, будет 3+6+6=15.

Кроме того, можно узнать, сколько четных натуральных чисел, меньших 1000, можно записать используя цифры 7, 4 и 5.

С помощью данных цифр можно записать такие четные числа: одно однозначное число (это 4), три двузначные (так как имеется 3 способа выбора цифры десятков и один способ выбора цифры единиц) и девять трехзначных (так как имеется 3 способа выбора цифры сотен, 3 – цифры десятков и 1 – цифры единиц).

Всего четных натуральных чисел. Меньших 1000, записанных с помощью цифр 7, 4 и 5, будет 13 (1+3+9=13).

Задача 11. Сколько всего четырехзначных чисел можно составить из цифр 0 и1?

Запись четырехзначного числа представляет собой упорядоченный набор (кортеж) из четырех цифр. Первую цифру – цифру тысяч – можно выбрать только одним способом, так как запись числа не может начинаться с нуля. Цифрой сотен может быть либо 0, либо 1, т.е. имеется два способа выбора. Сколько же способов выбора имеется для цифры десятков и цифры единиц. Тогда согласно правилу произведения с помощью цифр 0 и 1 можно записать 8 четырехзначных чисел, так как 1 х 2 х 2 х 2=8.

Можно проиллюстрировать полученный результат. Записав все эти числа, т.е. решив данную задачу методом перебора. Запишем сначала числа, в записи которых используются только цифра 1. Такое число только одно – 1111.

Затем записываем все числа, в записи которых используются три единицы и один нуль: 1110, 1101, 1011.

Далее записываем все числа, в записи которых используются две единицы и два нуля: 1100, 1010, 1001.

И, наконец, получаем число, в записи которого одна единица и три нуля 1000.

Задача 12. Сколько трехзначных чисел можно записать, используя цифры 0, 1, 3, 6, 7 и 9, если каждая из них может быть использованы в записи только один раз?

Так как запись числа не может начинаться с нуля, то цифру сотен можно выбрать пятью способами; выбор цифры десятков также можно осуществить пятью способами, поскольку цифры в записи числа не должны повторяться, а одна из шести данных цифр будет уже использована для записи сотен; после выбора двух цифр (для записи сотен и десятков) выбрать цифру единиц из данных шести можно четырьмя способами. Отсюда по правилу произведения получаем, что трехзначных чисел (из данных шести цифр) можно образовать 5х5х4=100 способами.

Заметим, что не только задачу 4, но и первые три можно решать в начальной школе методом перебора, причем в задаче 2 можно уменьшить число возможных случаев, если добавить условие, что цифры в записи числа не повторяются. При этом умение применять правило произведения для подсчета числа всевозможных комбинаторных соединений позволяет учителю контролировать правильность решения этих задач.

С помощью правила произведения легко проверяются решения комбинаторных задач, предлагаемых младшим школьникам и выполненных методом перебора. Приведем несколько примеров из статьи Р. Хазанкина «Словарь племени сю – сю», опубликованной в «Учительской газете» 21 января 1992г.

Задача 13. У марсиан 2 буквы в алфавите: А, Б. Сколько можно составить слов длины «три» из такого алфавита?

Ответ: 2 х 2 х 2=8 (слов).

Задача 14. У жителей луны в алфавите три буквы: М, Я, У. Сколько различных слов длины «три» можно составить из этих букв?

Ответ: 3х3х3=27 (слов).

Задача 15. У племени «сю – сю» в алфавите 4 буквы: М, Я, А, У. А все слова только трехбуквенные. Сколько существует различных слов у этого племени?

Ответ: 4х4х4=64 (слова).

Задачи для самостоятельного решения:

Задача 16.

Курьер должен разнести пакеты в 7 различных учреждений. Сколько маршрутов он может выбрать?

Задача 17.

Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 2, 4, 6?

Задача 18.

Сколько трехзначных чисел можно записать, используя цифры 0, 1, 3, 6, 7 и 9, если каждая из них может быть использована в записи только один раз?

Задача 19.

Имеется 6 видов конвертов без марок и 3 вида марок. Сколькими способами можно выбрать конверт и марку для посылки письма?

Задача 20.

Сколькими способами можно разместить на странице 5 различных заметок?

Задача 21.

Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?

Задача 22.

Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?

Задача 23.

Из группы теннисистов, в которую входят четыре человека – Антонов, Григорьев, Сергеев и Федоров, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?

Задача 23.

Три друга – Антон, Борис и Виктор – приобрели два билета на футбольный матч на 1-е и 2-е места первого ряда стадиона. Сколько у друзей есть вариантов занять эти два места на стадионе?

Задача 24

В турнире Архимеда участвуют команды из восьми человек. Сколькими способами можно в команде выбрать капитана и его заместителя?

Задача 25.

В математической карусели участвовали 12 команд. Сколькими способами можно распределить места между командами, если несколько команд не могут разделить одно место между собой?

Задача 26.

В школьной столовой 5 кранов для умывания. Каждый может быть закрыт или открыт. Сколькими способами может течь вода в столовой?

Задача 27.

Словом назовём произвольную последовательность букв. Сколько возможных слов можно составить, переставляя буквы в слове УЧЕНИК;

Задача 28.

Сколько разных ожерелий можно сделать из

а) 11 бусинок разных цветов;

б) 3 красных и 8 синих бусинок;

в) 3 красных и 8 синих бусинок, но красные нельзя ставить рядом?

Задача 29.

Сколькими способами можно поставить на шахматную доску белую и чёрную ладьи так, чтобы они не били друг друга?

Задача 30.

Сколькими способами можно поставить на шахматную доску белого и чёрного короля, чтобы получилась допустимая правилами игры позиция?

Задача 31.

Начальник транспортного цеха пригласил несколько человек на совещание. Каждый участник совещания, входя в кабинет, пожимал руки всем присутствующим. Сколько человек участвовали в совещании, если было всего 78 рукопожатий?

Задача 32.

Сколько существует шестизначных чисел, в записи которых есть хотя бы одна чётная цифра?

Задача 33.

Сколько семизначных чисел не содержат цифры 2?

Указание. Первую цифру можно выбрать 8 способами (потому что эта цифра — не 0 и не 2). Каждую следующую цифру можно выбрать 9 способами.

Задача 34. Чайная комбинаторика.

Задача 35 Разноцветные елки.

а) Сколькими способами можно покрасить пять елок в серебристый, зеленый и синий цвета, если количество краски неограниченно, а каждую елку красим только в один цвет?

б) Есть пять шариков: красный, зеленый, желтый, синий и золотой. Сколькими способами можно украсить ими пять елок, если на каждую требуется надеть ровно один шарик?
в) А если можно надевать несколько шариков на одну елку (и все шарики должны быть использованы)?

Задача 36. Подбираем перчатки.

Глория больше всего любит желтый и розовый цвета. В ящике для перчаток у Глории лежат шесть пар желтых и шесть пар розовых. Они перемешаны в беспорядке. Сколько перчаток Глория должна вытащить из ящика, чтобы среди них наверняка оказалась пара одного цвета? Глории все равно, какого цвета окажется эта пара — желтого или розового.

Задача 37. Выбираем варенье.

У вас в тёмном чулане стоят банки с вареньем трёх сортов: яблочное, сливовое и земляничное. Какое наименьшее количество банок вам надо взять, не глядя, чтобы среди них наверняка оказалось не менее девяти банок с вареньем одного сорта?

Задача 38. Завтрак людоеда.

У людоеда в подвале томятся 25 пленников.

а) Сколькими способами он может выбрать трех из них себе на завтрак, обед и ужин?

б) А сколько есть способов выбрать троих, чтобы отпустить на свободу?

Задача 39. Замки и ключи.

Перед нами 10 закрытых замков и 10 похожих ключей к ним. К каждому замку подходит только один ключ, но ключи смешались. Возьмем один из замков, назовем его первым и попробуем открыть его каждым из 10 ключей. В лучшем случае он откроется первым же ключом, а в худшем — только десятым.
Сколько нужно в худшем случае произвести проб, чтобы открыть все замки?

Задача 40 Сколько переводчиков?

На международную конференцию приехали 10 делегатов, не понимающих языка друг друга. Какое минимальное число переводчиков потребуется для обслуживания конференции при условии, что каждый переводчик знает только два языка?

Задача 41. Цветные шары.

В ящике лежат 70 шаров: 20 красных, 20 синих, 20 желтых, остальные черные и белые. Какое наименьшее число шаров надо взять, не видя их, чтобы среди них было не меньше 10 шаров одного цвета?

Задача 42. Две шашки.

На пустую шашечную доску надо поместить две шашки разного цвета. Сколько различных положений могут они занимать на доске?

Задача 43. С днём рождения!

Маша на свой день рождения пригласила в гости трех лучших подруг — Дашу, Глашу и Наташу. Когда все собрались, то по случаю дня рождения Маши решили обняться — каждая пара по одному разу. Сколько получилось разных пар?

Задача 44:

Задача 45:

Задача 46:

Монету бросают трижды. Сколько разных последовательностей орлов и решек можно при этом получить?

Задача 47:

Задача 48:

Задача 49:

В стране 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране?

Задача 50:

Сколькими способами из полной колоды (52 карты) можно выбрать 4 карты разных мастей и достоинств?

Задача 51:

Ответы, указания, решения:

Задача 16.

Решение:

Число маршрутов равно числу перестановок из 7 элементов.

Р7=7!= 1∙2∙3∙4∙5∙6∙7=5040

Ответ: 5040 маршрутов.

Задача 17.

Решение:

Из цифр 0, 2, 4, 6 можно получить Р4 перестановок. Из этого числа надо исключить те перестановки, которые начинаются с 0, т.к. натуральное число не может начинаться с цифры 0. число таких перестановок равно Р3. значит, искомое число четырехзначных чисел, которые можно составить из цифр 0, 2, 4, 6 равно Р4 – Р3= 4!–3!=1∙2∙3∙4 – 1∙2∙3= 24 – 6=18.

Ответ: 18 чисел.

Задача 18.

Решение:

Так как запись числа не может начинаться с нуля, то цифру сотен можно выбрать пятью способами; выбор можно также осуществить пятью способами, поскольку цифры в записи числа не должны повторяться, а одна из шести цифр будет уже использована для записи сотен; после выбора двух цифр (для записи сотен и десятков) выбрать цифру единиц из данных шести можно четырьмя способами. Отсюда, по правилу произведения, получаем, что трехзначных чисел можно образовать 5·5·4 = 100 способами.

Ответ. 100 способов

Задача 19.

Решение:

Конверт можно выбрать шестью способами, марку — тремя, с каждым из шести способов выбора конверта может совпасть любой из трех способов выбора марки. Тогда, согласно правилу умножения, имеем способов.

Ответ. 18.

Задача 20.

Решение:

т.к. имеются 5 заметок, и все они участвуют в выборе, то это перестановки. Применим формулу перестановок: Pn=n!, получаем, P5= 5! = 120.

Ответ: Существуют 120 способов разместить имеющиеся заметки.

Задача 21.

Решение:

Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12 ∙ 3 = 36 вариантов переплета.

Ответ: 36 способов.

Задача 22.

Решение:

В таких числах последняя цифра будет такая же, как и первая, а предпоследняя — как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z -любые цифры, а X — не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9∙104∙10 = 900 вариантов.

Ответ: 900 пятизначных чисел

Задача 23.

Решение:

Составим сначала все пары, в которые входит Антонов (для краткости будем писать первые буквы фамилий). Получим три пары: АГ, АС, АФ.

Выпишем теперь пары, в которые входит Григорьев, но не входит Антонов. Таких пар две: ГС, ГФ.

Далее составим пары, в которые входит Сергеев, но не входит Антонов и Григорьев. Такая пара только одна: СФ.

Других вариантов составления пар нет, так как все пары, в которые входит Федоров, уже составлены.

Итак, мы получили 6 пар: АГ, АС, АФ, ГС, ГФ, СФ. Значит, всего существует 6 вариантов выбора тренером пары теннисистов из данной группы.

Ответ: 6 вариантов выбора.

Задача 23.

Решение:

Если на матч пойдут Антон и Борис, то они могут занять места двумя способами: 1-е место – Антон, 2-е – Борис, или наоборот. Аналогично Антон и Виктор, Борис и Виктор. Таким образом, мы получили 6 вариантов: АБ, БА, АВ, ВА, БВ, ВБ.

Ответ: 6 вариантов выбора.

Задача 24

Решение.

Капитаном может быть любой из восьми человек, т.е. существует 8 способов выбрать капитана. Любой из оставшихся может стать заместителем капитана. Таким образом, для любого варианта выбора капитана (из 8 возможных) существует 7 способов выбрать его заместителя. Тогда всего 8×7=56 способов.

Ответ. 56 способами.

Задача 25.

Решение.

Первое место может занять любая из 12 команд. Второе место — любая из 11 оставшихся команд, третье — любая из 10 оставшихся, …, одиннадцатое — любая из двух ещё не выбранных команд и двенадцатое — последняя оставшаяся команда. Итого, 12·11·10·…·2·1=12! способов.

Ответ. 12!

Задача 26.

Решение.

Пронумеруем краны числами от одного до пяти. Первый кран может быть либо закрыт, либо открыт — два способа. В каждой из этих ситуаций второй кран может быть либо открыт, либо закрыт — итого имеем 2·2=4 способа. В каждой из этих четырёх ситуаций третий кран может быть либо закрыт, либо открыт, итого имеем 4·2=8 способов. И так далее. Получаем, что вода в столовой может течь 2·2·2·2·2 = 25 = 32 способами.

Ответ. 32 способами.

Задача 27.

Решение.
Всего шесть букв. Все они попарно различны. Поэтому, составляя слово из данных букв, первой мы можем поставить любую из них, второй — любую из пяти оставшихся, …, шестой — последнюю оставшуюся. Т.о. всего 6·5·4·3·2·1=6! способов.

Ответ. 6! слов

Задача 28.

а) Переформулируем условие задачи. Будем считать, что у нас есть ожерелье с одиннадцатью белыми бусинками. Нам нужно покрасить каждую бусинку в один из 11 цветов, при этом каждый цвет мы должны использовать ровно один раз.

Тогда первую бусинку мы можем покрасить в один из 11 цветов, вторую — в любой из 10 — оставшихся, …, десятую — в любой из двух оставшихся, одиннадцатую — в последний оставшийся. Т. о. всего 11! вариантов получить ожерелье. Но при этом мы не учитываем, что все варианты разбиваются на группы по 11 штук, получающихся друг из друга поворотом (а это одинаковые ожерелья). Кроме того, все ожерелья можно разбить на пары совмещающихся переворотом, причём любые два таких варианта поворотом не совмещаются, т.е. находятся в разных группах по 11 штук. Т. о. количество способов получить ожерелье равно 11!⁄(11·2).

Ответ. а) 11!/22 ожерелий; б) 10 ожерелий; в) 5 ожерелий.

Задача 29.

Решение.

Белую ладью можно поставить на любую из 64 клеток. Независимо от своего расположения она бьёт 15 полей (включая поле, на котором она стоит). Поэтому остаётся 49 полей, на которые можно поставить чёрную ладью. Таким образом, всего есть 64 · 49 = 3136 разных способов

Ответ. 3136 разных способов

Задача 30.

Решение.

Белого короля можно поставить на любое из 64 полей. Однако количество полей, которые он при этом будет бить, зависит от его расположения. Поэтому разберём три случая:

если белый король стоит в углу (углов всего 4), то он бьёт 4 поля (включая то, на котором стоит) и остаётся 60 полей, на которые можно поставить чёрного короля;

если белый король стоит на краю доски, но не в углу (таких полей 24), то он бьёт 6 полей, и для чёрного короля остаётся 58 возможных полей;

если же белый король стоит не на краю доски (таких полей 36), то он бьёт 9 полей, и для чёрного короля остаётся 55 возможных полей.

Таким образом, всего есть 4 · 60 + 24 · 58 + 36 · 55 = 3612 способов расстановки королей.

Ответ. 3612.

Задача 31. Ответ. 13.

Задача 32.

Указание.

Вместо того, чтобы подсчитывать количество требуемых шестизначных чисел, определите количество шестизначных чисел, у которых все цифры нечётны.

Решение. Количество шестизначных чисел, в записи которых встречаются только нечётные цифры, равно 56 = 15 625. Всего шестизначных чисел 900 000. Поэтому количество шестизначных чисел, в записи которых есть хотя бы одна чётная цифра, равно

900 000 – 15625 = 884 375.

Ответ. 884375.

Задача 33.

Ответ. 8 · 9 · 9 · 9 · 9 · 9 · 9 = 4 251 528.

Задача 34.

Ответ:

Задача 35

Ответ:

а) Каждую из пяти елок можно покрасить в один из трех цветов, поэтому всего различных способов существует 3*3*3*3*3 = 35 = 243.
б) На первую елку можно надеть любой из пяти шариков, на вторую елку — любой из оставшихся четырех, и так далее; всего получаем 5*4*3*2*1 = 120 способов.
в) Каждый из шариков можно надеть на любую елку, поэтому в этом случае ответ – 55 = 3125

Задача 36.

Ответ:

Может получится так, что Глория вытащит все 12 перчаток на левую руку. Но уже следующей перчатке обязательно найдется пара. Значит, для полной уверенности
нужно вытащить 13 перчаток.

Задача 37.

Ответ:

25 банок. При этом распределение по сортам будет (к примеру) таким: 8 банок — с яблочным вареньем, 8 — со сливовым и 9 — с земляничным (8+8+9=25). Двадцати четырех банок для выполнения условия уже не хватает: каждого сорта может быть только по 8 банок.

Задача 38.

Ответ:

а) На завтрак людоед может предпочесть любого из 25 человек, на обед — любого из 24 оставшихся, а на ужин — кого-то из 23 оставшихся счастливчиков. Всего получаем 25∙24∙23 = 13800 способов.

б) Заметим, что в предыдущем пункте каждую тройку пленников мы посчитали 3∙2∙1 = 6 раз. Поскольку теперь их порядок нам неважен, то ответом будет число 13800:6 = 2300.

Задача 39.

Ответ:

Для 1-го замка достаточно 9 проб (10-я не обязательна), для 2-го — 8, для 3-го — 7 и т.д., а для оставшегося 10-го не требуется ни одной.

Общее число проб составит 9+8+7+…+1+0 = 45.

Задача 40

Ответ: 9.

Задача 41.

Ответ: 38.

Задача 42.

Ответ:

Первую шашку можно поместить на любое из 64 полей доски, т.е. 64 способами. После того как первая поставлена, вторую шашку можно поместить на какое-либо из прочих 63 полей. Значит к каждому из 64 положений первой шашки можно присоединить 63 положения второй шашки. Отсюда общее число различных положений двух шашек на доске: 64 ∙ 63 = 4032.

Задача 43.

Ответ: Шесть.

Задача 44:

Решение:

Ответ: 24 = 6 • 4.

Задача 45:

Решение:

Задача 46:

Ответ: 6.

Задача 47:

Ответ: 24.

Задача 48:

Решение:

Задача 49:

Решение:

Задача 50:

Решение:

13 • 12 • 11 • 10

Задача 51:

Решение:

5 + 5 • 4 + 5 • 4 • 3 + 5 • 4 • 3 • 2 + 5 • 4 • 3 • 2 • 1 = 325

Литература и интернет — источники

Еженедельное учебно-методическое приложение “Математика” Изд. Пресса. Москва.1999 г
Л.Г. Петерсон. Математика 4 класс. Изд. Баласс. Москва.1999 г.
wiki.vladimir.i-edu.ru›images…4c
http://mmmf.msu.ru/archive/19992000/spivak67/s_combz.html

Перестановок и комбинаций — разделение на группы

Добро пожаловать на следующий урок из серии «Перестановки и комбинации». Мы прошли долгий путь, и нам еще предстоит пройти долгий путь. Надеюсь, тебе весело!

В этом уроке будет решена следующая задача.

Сколько способов можно разделить n различных объектов на r групп, размеры которых известны?

Вот несколько примеров:

Какими способами мы можем разделить 5 различных объектов на две группы размером 3 и 2?

Какими способами мы можем разделить 10 различных объектов на три группы размеров 3, 2 и 5?

Какими способами мы можем разделить 10 различных объектов на 5 пар?

Обратите внимание, что разделение на группы размера 2 и 3 эквивалентно разделению на группы размера 3 и 2.То есть имеет значение только размер, а не порядок групп. Подобным образом разделение 10 объектов на три группы размеров 3, 2 и 5 будет считаться тем же, что и их разделение на группы размеров 2, 3 и 5 или 5, 2 и 3.

Начнем с первого случая. 5 объектов, которые необходимо разделить на две группы размером 2 и 3.

Вот пять объектов:

И мы хотим это:

Или это:

Как мы можем найти количество способов сделать это?

Что ж, все, что вам нужно сделать, это выбрать 2 объекта из 5 и отложить их в сторону, образуя группу.И вам не нужно беспокоиться о второй группе, так как если отложить 2 объекта, останется 3 объекта, которые сформируют вторую группу.

И этот выбор можно сделать ⁵ C ₂ способами или \ (\ large \ frac {5!} {2! .3!} \) Способами.

Обратите внимание, что мы также могли бы сначала выбрать три объекта, оставив после себя 2. Это можно сделать способами ⁵ C ₃, что в точности совпадает с предыдущим ответом.

Возьмем теперь второй пример.Какими способами мы можем разделить 10 различных объектов на три группы размером 3, 2 и 5?

Метод будет таким же, как и ранее. Сначала мы выберем 3 объекта из 10, образуя первую группу. Это можно сделать ¹⁰ C ₃ способами.

Далее, из оставшихся 7 объектов, мы выберем 2 объекта и сформируем вторую группу ⁷ C ₂ способами. И третья группа формируется сама по себе, так как останется 3 объекта.

Количество способов выполнить обе эти задачи будет ¹⁰ C ₃.⁷ C ₂ (с использованием принципа умножения), что равно \ (\ large \ frac {10!} {3! .2! .5!} \)

А что, если бы много из 14 различных объектов имели разделить на 4 группы размеров 2,3, 4 и 5?

Вы угадали — ответ будет ¹⁴ C ₂. ¹² С ₃. ⁹ C ₄ или \ (\ large \ frac {14!} {2! .3! .4! .5!} \)

Теперь мы можем прийти к формуле для того же. Допустим, у нас есть n разных объектов, и мы должны разделить их на r групп по размерам: ₁, ₂, ₃,…, _r.Используя ту же логику, описанную выше, количество способов сделать это будет \ (\ large \ frac {n!} {A_1! .A_2! .A_3!… A_r!} \)

Небольшое примечание. На данный момент размеры групп будут считаться разными. То есть

a ₁ ≠ a ₂ ≠ a ₃ ≠… ≠ a _r

Все немного изменится, если одна или несколько групп будут иметь одинаковый размер. Я расскажу об этом на следующем уроке.

Краткое содержание урока

Количество способов разделить n различных объектов на r групп размеров a ₁ , a ₂ , a ₃ ,…, a _r равно

\ (\ frac {n!} {a_1! a_2! a_3!… a_r!} \)

Здесь a ₁ ≠ a ₂ ≠ a ₃ ≠… ≠ a _r и a ₁ + a ₂ + a ₃ +… + a _r = n.

python — Как всеми возможными способами разбить список на пары

Я сделал небольшой набор тестов для всех совместимых решений. Мне пришлось немного изменить функции, чтобы заставить их работать в Python 3. Интересно, что самая быстрая функция в PyPy в некоторых случаях является самой медленной функцией в Python 2/3.

  импорт itertools
время импорта
из коллекций импортировать OrderedDict

def tokland_org (lst, n):
    если не lst:
        урожай []
    еще:
        для группы в (((lst [0],) + xs) для xs в itertools.комбинации (lst [1:], n-1)):
            для групп в tokland_org ([x для x в lst, если x не в группе], n):
                yield [группа] + группы

tokland = лямбда x: tokland_org (x, 2)

def gatoatigrado (lst):
    N = len (lst)
    choice_indices = itertools.product (* [
        range (k) для k в обратном порядке (range (1, N, 2))])

    для выбора в choice_indices:
        # вычисляем список, соответствующий выбору
        tmp = список (lst)
        результат = []
        для индекса по выбору:
            результат.добавить ((tmp.pop (0), tmp.pop (индекс)))
        дать результат

def shang (X):
    lst = список (X)
    если len (lst) <2:
        yield lst
        возвращаться
    a = lst [0]
    для i в диапазоне (1, len (lst)):
        пара = (a, lst [i])
        для отдыха в шане (lst [1: i] + lst [i + 1:]):
            yield [пара] + остаток

def smichr (X):
    lst = список (X)
    если не lst:
        yield [кортеж ()]
    elif len (lst) == 1:
        yield [кортеж (lst)]
    elif len (lst) == 2:
        yield [кортеж (lst)]
    еще:
        если len (lst)% 2:
            для i в (None, True):
                если я не в lst:
                    lst = lst + [i]
                    PAD = i
                    перерыв
            еще:
                а chr (i) в lst:
                    я + = 1
                PAD = chr (i)
                lst = lst + [PAD]
        еще:
            PAD = False
        a = lst [0]
        для i в диапазоне (1, len (lst)):
            пара = (a, lst [i])
            для отдыха в smichr (lst [1: i] + lst [i + 1:]):
                rv = [пара] + отдых
                если PAD не False:
                    для i, t в enumerate (rv):
                        если PAD в t:
                            rv [i] = (t [0],)
                            перерыв
                yield rv

def adeel_zafar (X):
    L = список (X)
    если len (L) == 2:
        yield [(L [0], L [1])]
    еще:
        first = L.поп (0)
        для i, e в enumerate (L):
            второй = L.pop (i)
            для list_of_pairs в adeel_zafar (L):
                list_of_pairs.insert (0, (первый, второй))
                yield list_of_pairs
            L.insert (i, второй)
        L.insert (0, первый)

если __name__ == "__ main__":
    время импорта
    импортный отпечаток

    кандидаты = dict (tokland = tokland, gatoatigrado = gatoatigrado, shang = shang, smichr = smichr, adeel_zafar = adeel_zafar)

    для i в диапазоне (1,7):
        results = [frozenset ([frozenset (x) для x в кандидате (диапазон (i * 2))]) для кандидата в кандидаты.значения() ]
        assert len (frozenset (результаты)) == 1

    print («Время получения всех перестановок наборов неупорядоченных пар, состоящих из двух розыгрышей из 6-элементной колоды, пока она не станет пустой»)
    times = dict ([(k, timeit.timeit ('list ({0} (range (6)))'. format (k), setup = "from __main__ import {0}". format (k), number = 10000)) для k в кандидатах.keys ()])
    pprint.pprint ([(k, "{0: .3g}". format (v)) для k, v в OrderedDict (sorted (times.items (), key = lambda t: t [1])). items ()])

    print («Время получения первых 2000 перестановок наборов неупорядоченных пар, состоящих из двух розыгрышей из 52-элементной колоды, пока она не станет пустой»)
    раз = dict ([(k, timeit.timeit ('list (islice ({0} (range (52)), 800))'. format (k), setup = "from itertools import islice; from __main__ import {0}". format (k), number = 100)) для k в кандидатах.keys ()])
    pprint.pprint ([(k, "{0: .3g}". format (v)) для k, v в OrderedDict (sorted (times.items (), key = lambda t: t [1])). items ()])

    "" "
    print («10000-я перестановка предыдущей серии:»)
    gens = dict ([(k, v (range (52))) для k, v в кандидатах.items ()])
    десятки тысяч = dict ([(k, list (itertools.islice (permutations, 10000)) [- 1]) для k, перестановки в gens.Предметы()])
    для пары в десятках тысяч пунктов ():
        печать (пара [0])
        печать (пара [1])
    "" "

Похоже, что все они генерируют один и тот же порядок, поэтому наборы не нужны, но это гарантия будущего. Я немного поэкспериментировал с преобразованием Python 3, не всегда понятно, где строить список, но я попробовал несколько альтернатив и выбрал самый быстрый.

Вот результаты теста:

 % эхо "pypy"; pypy all_pairs.py; эхо "python2"; python all_pairs.ру; эхо "python3"; python3 all_pairs.py
pypy
Время получения всех перестановок наборов неупорядоченных пар, состоящих из двух розыгрышей, из 6-элементной колоды, пока она не станет пустой
[('gatoatigrado', '0,0626'),
 ('adeel_zafar', '0,125'),
 ('smichr', '0,149'),
 ('шанг', '0,2'),
 ('tokland', '0,27')]
Время получения первых 2000 перестановок наборов неупорядоченных пар, состоящих из двух розыгрышей из 52-элементной колоды, пока она не станет пустой
[('gatoatigrado', '0,29'),
 ('adeel_zafar', '0,411'),
 ('smichr', '0,464'),
 ('шанг', '0.493 '),
 ('tokland', '0,553')]
python2
Время получения всех перестановок наборов неупорядоченных пар, состоящих из двух розыгрышей, из 6-элементной колоды, пока она не станет пустой
[('gatoatigrado', '0,344'),
 ('adeel_zafar', '0,374'),
 ('smichr', '0,396'),
 ('шанг', '0,495'),
 ('tokland', '0,675')]
Время получения первых 2000 перестановок наборов неупорядоченных пар, состоящих из двух розыгрышей из 52-элементной колоды, пока она не станет пустой
[('adeel_zafar', '0,773'),
 ('шанг', '0,823'),
 ('smichr', '0,841'),
 ('токланд', '0.948 '),
 ('gatoatigrado', '1.38')]
python3
Время получения всех перестановок наборов неупорядоченных пар, состоящих из двух розыгрышей, из 6-элементной колоды, пока она не станет пустой
[('gatoatigrado', '0,385'),
 ('adeel_zafar', '0,419'),
 ('smichr', '0,433'),
 ('шанг', '0,562'),
 ('tokland', '0,837')]
Время получения первых 2000 перестановок наборов неупорядоченных пар, состоящих из двух розыгрышей из 52-элементной колоды, пока она не станет пустой
[('smichr', '0,783'),
 ('шанг', '0,81'),
 ('adeel_zafar', '0.835'),
 ('токланд', '0.969 '),
 ('gatoatigrado', '1.3')]
% pypy --version
Python 2.7.12 (5.6.0 + dfsg-0 ~ ppa2 ~ ubuntu16.04, 11 ноября 2016 г., 16:31:26)
[PyPy 5.6.0 с GCC 5.4.0 20160609]
% python3 --version
Python 3.5.2

Итак, я говорю, используйте решение gatoatigrado.

Разбиение n элементов на k групп

Марко Табога, доктор философии

Раздел

объекты в

группы - один из возможных способов разделения

объекты в

группы
().Правила следующие:

порядок, в котором объекты помещены в группу, не имеет значения;
каждый объект можно отнести только к одной группе.

В следующих подразделах дается чуть более формальное определение разбиения.
на группы и займемся проблемой подсчета количества возможных
разбиения на группы.

Определение разделения на группы

Позволять
,
, ...,

быть

объекты. Позволять
,
,
...,

быть

(с участием
)
группы, которым мы можем назначить

объекты.

объекты могут быть отнесены к группе
,

объекты могут быть отнесены к группе

и так далее.
,
,
...,

такие
это
раздел из
,
, ...,

групп
,
,
...,

один из возможных способов присвоения

возражает против

группы.

Подсчет количества разделов на группы

Обозначим через

количество возможных разделов на

группы (где группа

содержит

объекты).Сколько

в общем?

Номер

можно получить с помощью следующей последовательной процедуры:

Сначала мы присваиваем
объекты первой группы. Всего
объекты на выбор. Количество возможных вариантов выбора
принадлежащий
объектов равно количеству комбинаций
элементы из
.Так что есть
Затем присваиваем
объекты ко второй группе. Было
объекты, но
уже отнесены к первой группе. Итак, есть
остались объекты, которые можно отнести ко второй группе. Количество возможных
способы выбрать
из оставшихся
объектов равно количеству комбинаций
элементы из
.Так что есть
а также
Затем присваиваем
объекты к третьей группе. Было
объекты, но
уже были отнесены к первым двум группам. Итак, есть
остались объекты, которые можно отнести к третьей группе. Количество возможных
способы выбрать
из оставшихся
объектов равно количеству комбинаций
элементы из
.Так что есть
а также
И так далее, пока мы не останемся с
объекты и последняя группа. Есть только один способ сформировать последнюю группу,
что также может быть написано
as Таким образом,
там
находятся

Следовательно, согласно приведенному выше последовательному аргументу, общее количество
возможные перегородки в

группы
является

Номер

часто обозначается как
следует: и

называется полиномиальным коэффициентом .

Иногда используются следующие обозначения.
использовал:

Пример
Количество возможных разделов

объекты в

группы

объекты
является

Подробнее

В следующих разделах содержится более подробная информация о разделах.

Полиномиальные коэффициенты и
полиномиальные разложения

Полиномиальный коэффициент называется так потому, что он появляется в
полиномиальный
расширение : где

и суммирование ведется по всем
- пары

такой
что:

Решенные упражнения

Ниже вы можете найти несколько упражнений с объясненными решениями.

Упражнение 1

У Джона есть корзина с фруктами, содержащая одно яблоко, один банан, один апельсин и
один киви. Он хочет дать по одному фрукту каждой из двух своих младших сестер и двух
фрукты своему старшему брату. Сколько разных способов он может это сделать?

Решение

Джону нужно решить, как разделить 4
объекты в 3 группы, где первые две группы будут содержать один объект и
третий будет содержать два объекта.Общее количество разделов
является

Упражнение 2

Десять друзей хотят играть в баскетбол. Их нужно разделить на две команды по
пять игроков. Сколько разных способов они могут это сделать?

Решение

Им нужно решить, как разделить 10
объекты на 2 группы, каждая из которых будет содержать по 5 объектов. Общая
количество разделов
является

Как цитировать

Укажите как:

Табога, Марко (2017).«Разбиения на группы», Лекции по теории вероятностей и математической статистике, Третье издание. Kindle Direct Publishing. Онлайн-приложение. https://www.statlect.com/mat Mathematical-tools/partitions.

комбинаций и перестановок

Расследуй! 8

У вас есть набор фишек пяти разных цветов: красный, синий, зеленый, фиолетовый и желтый.

Сколько разных стеков из двух фишек вы можете собрать, если нижняя фишка должна быть красной или синей? Объясните свой ответ, используя как аддитивный, так и мультипликативный принцип.
Сколько разных стеков по три фишки вы можете собрать, если нижняя фишка должна быть красной или синей, а верхняя фишка - зеленой, фиолетовой или желтой? Как эта проблема соотносится с предыдущей?
Сколько существует различных стеков по три фишки, в которых не повторяется ни один цвет? А как насчет четырех фишек?
Предположим, вы хотите взять три фишки разного цвета и положить их в карман. Сколько у вас вариантов выбора? Что, если вам нужны четыре фишки разного цвета? Как эти проблемы соотносятся с предыдущей?

Перестановка - (возможная) перестановка объектов.Например, существует 6 перестановок букв a, b, c :

\ begin {уравнение *}
abc, ~~ acb, ~~ bac, ~~ bca, ~~ cab, ~~ cba.
\ end {уравнение *}

Мы знаем, что у нас есть все они, перечисленные выше - есть 3 варианта выбора, какую букву мы помещаем первой, затем 2 варианта выбора, для которой буква идет следующей, что оставляет только 1 выбор для последней буквы. Принцип мультипликативности гласит, что мы умножаем \ (3 \ cdot 2 \ cdot 1 \ text {.} \)

Пример1.3.1

Сколько существует перестановок букв a, b, c, d, e, f ?

Решение

Мы НЕ хотим пытаться перечислить все это.Однако, если бы мы это сделали, нам нужно было бы сначала выбрать письмо, которое нужно записать. Есть 6 вариантов для этой буквы. Для каждого выбора первой буквы есть 5 вариантов для второй буквы (мы не можем повторить первую букву; мы переставляем буквы и получаем только по одной из каждой), и для каждого из них есть 4 варианта для третьей, 3 варианты выбора для четвертой буквы, 2 варианта для пятой и, наконец, только 1 вариант для последней буквы. Итак, есть \ (6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 = 720 \) перестановки 6 букв.

Здесь может быть полезно обозначение: \ (n! \ Text {,} \) читать «\ (n \) факториал», это произведение всех положительных целых чисел, меньших или равных \ (n \) (по причинам для удобства мы также определяем 0! равным 1). Таким образом, количество перестановок из 6 букв, как показано в предыдущем примере, равно \ (6! = 6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 \ text {.} \) Это обобщает:

Перестановки элементов \ (n \)

Есть \ (n! = N \ cdot (n-1) \ cdot (n-2) \ cdot \ cdots \ cdot 2 \ cdot 1 \) перестановки \ (n \) (различных) элементов.

Пример 1.3.2 Подсчет биективных функций

Сколько функций \ (f: \ {1,2, \ ldots, 8 \} \ to \ {1,2, \ ldots, 8 \} \) являются биективными ?

Решение

Вспомните, что означает биективность функции: каждый элемент в кодомене должен быть изображением ровно одного элемента домена. Используя двухстрочную запись, мы могли бы записать одну из этих биекций как

\ begin {уравнение *}
f = \ twoline {1 \ amp 2 \ amp 3 \ amp 4 \ amp 5 \ amp 6 \ amp 7 \ amp 8} {3 \ amp 1 \ amp 5 \ amp 8 \ amp 7 \ amp 6 \ amp 2 \ amp 4}
\ end {уравнение *}

На самом деле мы просто переставляем элементы кодомена, поэтому мы создаем перестановку из 8 элементов.Фактически, «перестановка» - это еще один термин, используемый для описания биективных функций из конечного множества в себя.

Если вы верите в это, то вы видите, что ответ должен быть \ (8! = 8 \ cdot 7 \ cdot \ cdots \ cdot 1 = 40320 \ text {.} \). Вы также можете увидеть это напрямую: для каждого элемента домен, мы должны выбрать отдельный элемент кодомена для сопоставления. Есть 8 вариантов, куда отправить 1, затем 7 вариантов, куда отправить 2, и так далее. Мы умножаем по принципу мультипликативности.

Иногда мы не хотим переставлять все буквы / числа / элементы, которые нам даны.

Пример1.3.3

Сколько четырехбуквенных «слов» вы можете составить из букв с a по f без повторяющихся букв?

Решение

Это похоже на задачу перестановки 4 букв, только теперь у нас есть больше вариантов для каждой буквы. Для первой буквы есть 6 вариантов. Для каждой из них есть 5 вариантов для второй буквы. Затем есть 4 варианта для третьей буквы и 3 варианта для последней буквы. Общее количество слов равно \ (6 \ cdot 5 \ cdot 4 \ cdot 3 = 360 \ text {.} \) Это не \ (6! \), Потому что мы никогда не умножали на 2 и 1. Мы могли бы начать с \ (6! \), А затем сократить 2 и 1 и, таким образом, написать \ (\ frac {6!} {2!} \ Text {.} \)

В общем, мы можем спросить, сколько существует перестановок \ (k \) объектов, выбирающих эти объекты из большей коллекции \ (n \) объектов. (В приведенном выше примере \ (k = 4 \ text {,} \) и \ (n = 6 \ text {.} \)) Мы пишем это число \ (P (n, k) \) и иногда называем его a \ (k \) - перестановка \ (n \) элементов . Из приведенного выше примера мы видим, что для вычисления \ (P (n, k) \) мы должны применить мультипликативный принцип к числам \ (k \), начиная с \ (n \) и считая в обратном порядке.Например

\ begin {уравнение *}
P (10, 4) = 10 \ cdot 9 \ cdot 8 \ cdot 7.
\ end {уравнение *}

Еще раз обратите внимание, что \ (P (10,4) \) вначале выглядит как \ (10! \ Text {,} \), но мы останавливаемся после 7. Мы можем формально учесть эту «остановку», разделив часть факториал, который нам не нужен:

\ begin {уравнение *}
P (10,4) = \ frac {10 \ cdot 9 \ cdot 8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1} {6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1} = \ frac {10!} {6!}.
\ end {уравнение *}

Внимание! Факториал в знаменателе равен не \ (4! \), А скорее \ ((10-4)! \ Text {.} \)

\ (k \) - перестановки \ (n \) элементов

\ (P (n, k) \) - количество \ (k \) - перестановок \ (n \) элементов , количество способов расположить \ (k \) объектов, выбранных из \ ( п \) различные объекты.

\ begin {уравнение *}
P (n, k) = \ frac {n!} {(N-k)!}.
\ end {уравнение *}

Обратите внимание, что когда \ (n = k \ text {,} \) мы имеем \ (P (n, n) = \ frac {n!} {(Nn)!} = N! \) (Поскольку мы определили \ ( 0! \) Равным 1). Это имеет смысл - мы уже знаем, что \ (n! \) Дает количество перестановок всех \ (n \) объектов.

Пример 1.3.4 Подсчет инъективных функций

Сколько функций \ (f: \ {1,2,3 \} \ to \ {1,2,3,4,5,6,7,8 \} \) являются инъективными ?

Решение

Обратите внимание, что здесь нет смысла запрашивать количество биекций , так как их нет (поскольку кодомен больше домена, нет никаких сомнений). Но для того, чтобы функция была инъективной, мы просто не можем использовать элемент кодомена более одного раза.

Нам нужно выбрать элемент из кодомена, который будет изображением 1.Есть 8 вариантов. Затем нам нужно выбрать один из оставшихся 7 элементов, который будет изображением 2. Наконец, один из оставшихся 6 элементов должен быть изображением 3. Таким образом, общее количество функций равно \ (8 \ cdot 7 \ cdot 6 = П (8,3) \ text {.} \)

В целом это демонстрирует, что количество инъекций \ (f: A \ to B \ text {,} \), где \ (\ card {A} = k \) и \ (\ card {B} = n \ текст {,} \) равен \ (P (n, k) \ text {.} \)

Вот еще один способ найти количество \ (k \) - перестановок элементов \ (n \): сначала выберите, какие элементы \ (k \) будут в перестановке, затем посчитайте, сколько способов их расположить .После того, как вы выбрали \ (k \) объекты, мы знаем, что есть \ (k! \) Способов их упорядочить (переставить). Но как выбрать \ (k \) объекты из \ (n \ text {?} \). У вас есть \ (n \) объектов, и вам нужно выбрать из них \ (k \). Вы можете сделать это \ ({n \ выбрать k} \) способами. Затем для каждого выбора этих \ (k \) элементов мы можем переставить из \ (k! \) Способами. Используя мультипликативный принцип, мы получаем другую формулу для \ (P (n, k) \ text {:} \)

\ begin {уравнение *}
P (n, k) = {n \ choose k} \ cdot k !.\ end {уравнение *}

Теперь, поскольку у нас уже есть замкнутая формула для \ (P (n, k) \), мы можем заменить ее в:

\ begin {уравнение *}
\ frac {n!} {(n-k)!} = {n \ choose k} \ cdot k !.
\ end {уравнение *}

Если мы разделим обе части на \ (k! \), Мы получим замкнутую формулу для \ ({n \ choose k} \ text {.} \)

Замкнутая формула для \ ({n \ choose k} \)

\ begin {уравнение *}
{n \ choose k} = \ frac {n!} {(n-k)! k!}
\ end {уравнение *}

Мы говорим, что \ (P (n, k) \) подсчитывает перестановок , а \ ({n \ choose k} \) подсчитывает комбинаций .Формулы для каждого очень похожи, есть только лишний \ (k! \) В знаменателе \ ({n \ choose k} \ text {.} \). Этот дополнительный \ (k! \) Объясняет факт что \ ({n \ choose k} \) не делает различий между разными порядками, в которых могут появляться объекты \ (k \). Мы просто выбираем (или выбираем) объекты \ (k \), а не упорядочиваем их. Возможно, термин «комбинация» вводит в заблуждение. Мы не имеем в виду, что это кодовый замок (где порядок определенно имеет значение). Возможно, лучшая метафора - это сочетание вкусов: вам просто нужно решить, какие ароматы сочетать, а не порядок, в котором их объединять.

Чтобы проиллюстрировать связь между комбинациями и перестановками, мы закончим примером.

Пример1.3.5

Вы решили устроить званый обед. Несмотря на то, что вы невероятно популярны и имеете 14 разных друзей, у вас достаточно стульев, чтобы пригласить 6 из них.

Сколько у вас есть вариантов, для каких 6 друзей пригласить?
Что, если вам нужно решить не только, каких друзей пригласить, но и где их усадить за длинным столом? Сколько у вас тогда вариантов?

Решение

Вы должны просто выбрать 6 друзей из группы из 14 человек.Это можно сделать \ ({14 \ choose 6} \) способами. Мы можем найти это число, используя треугольник Паскаля или замкнутую формулу: \ (\ frac {14!} {8! \ Cdot 6!} = 3003 \ text {.} \)
Здесь вы должны подсчитать все способы, которыми вы можете переставить 6 друзей, выбранных из группы из 14. Итак, ответ будет \ (P (14, 6) \ text {,} \), который можно рассчитать как \ (\ frac {14 !} {8!} = 2192190 \ text {.} \)
Обратите внимание, что мы можем думать об этой проблеме подсчета как о вопросе о подсчете функций: сколько инъективных функций существует от вашего набора из 6 стульев до вашего набора из 14 друзей (функции являются инъективными, потому что у вас не может быть ни одного стула двум вашим друзьям).

Как связаны эти числа? Обратите внимание, что \ (P (14,6) \) на на больше, чем \ ({14 \ choose 6} \ text {.} \). Это имеет смысл. \ ({14 \ choose 6} \) выбирает 6 друзей, но \ (P (14,6) \) размещает 6 друзей, а также выбирает их. Фактически, мы можем точно сказать, насколько больше \ (P (14,6) \). В обеих задачах на счет мы выбираем 6 друзей из 14. Для первого мы останавливаемся на 3003 путях. Но для второй задачи подсчета каждый из этих 3003 вариантов выбора 6 друзей может быть расположен ровно \ (6! \) Способами.Итак, теперь у нас есть выбор \ (3003 \ cdot 6! \), И это точно \ (2192190 \ text {.} \)

Или взгляните на первую проблему с другой стороны. Мы хотим выбрать 6 друзей из 14, но нас не волнует порядок их выбора. Чтобы выбрать 6 друзей из 14, мы можем попробовать следующее:

\ begin {уравнение *}
14 \ cdot 13 \ cdot 12 \ cdot 11 \ cdot 10 \ cdot 9.
\ end {уравнение *}

Это разумное предположение, поскольку у нас есть 14 вариантов для первого гостя, затем 13 для второго и так далее. Но предположение неверно (на самом деле этот продукт равен \ (2192190 = P (14,6) \)).Он различает разные заказы, в которых мы могли приглашать гостей. Чтобы исправить это, мы можем разделить на количество различных расстановок 6 гостей (чтобы все они засчитывались как один результат). Существует ровно \ (6! \) Способов разместить 6 гостей, поэтому правильный ответ на первый вопрос -

.
\ begin {уравнение *}
\ frac {14 \ cdot 13 \ cdot 12 \ cdot 11 \ cdot 10 \ cdot 9} {6!}.
\ end {уравнение *}

Обратите внимание, что это можно записать по-другому:

.
\ begin {уравнение *}
\ frac {14!} {8! \ cdot 6!}.\ end {уравнение *}

- это то, что у нас было изначально.

Подраздел Упражнения

1

Пиццерия предлагает 10 начинок.

Сколько пиццы с тремя начинками они могут добавить в свое меню? Предположим, двойная начинка недопустима.
Сколько всего пицц можно приготовить с количеством начинок от нуля до десяти (но не двойных начинок)?
Пиццерия перечислит 10 начинок в двух столбцах одинакового размера в своем меню.{10} = 1024 \) пиццы. Скажите «да» или «нет» каждой начинке.
\ (P (10,5) = 30240 \) путей. Назначьте каждое из 5 мест в левом столбце уникальной начинке для пиццы.

2

Кодовый замок состоит из циферблата с 40 цифрами. Чтобы открыть замок, вы поворачиваете циферблат вправо, пока не дойдете до первого числа, затем влево, пока не дойдете до второго числа, затем снова вправо до третьего числа. Цифры должны быть разными. Сколько возможных комбинаций?

Решение

Несмотря на название, мы не ищем здесь комбинации.3 \)).

3

Используя цифры от 2 до 8, найдите количество различных 5-значных чисел, таких как:

Цифры можно использовать более одного раза.
Цифры не могут повторяться, но могут идти в любом порядке.
Цифры не могут повторяться и должны быть записаны в возрастающем порядке.
Какой из приведенных выше вопросов подсчета является комбинацией, а какой - перестановкой? Объясните, почему это имеет смысл.

4

Сколько там треугольников с вершинами из точек, показанных ниже? Обратите внимание: мы не допускаем вырожденных треугольников - треугольников, все три вершины которых лежат на одной прямой, но допускаем неправильные треугольники. Объясните, почему ваш ответ правильный.

Подсказка

Вам нужны ровно две точки на оси \ (x \) - или \ (y \) -, но не переоценивайте правые треугольники.

5

Сколько четырехугольников вы можете нарисовать, используя точки, расположенные ниже, в качестве вершин (углов)?

Решение

\ ({7 \ choose 2} {7 \ choose 2} = 441 \) четырехугольников.Мы должны выбрать две из семи точек из верхнего ряда и две из семи точек в нижнем ряду. Однако не имеет значения, какой из двух (в каждой строке) мы выберем первым, потому что после выбора этих четырех точек остается ровно один четырехугольник, который они определяют.

6

Сколько четырехугольников в предыдущей задаче может быть:

Квадраты?
Прямоугольники?
Параллелограммы?
Трапеции?
Трапеции, которые не являются параллелограммами?

Решение

5 кв.Вам нужно пропустить ровно одну точку сверху и снизу, чтобы стороны были равны. Как только вы выберете точку наверху, будут определены другие три точки.
\ ({7 \ choose 2} \) прямоугольников. Как только вы выберете две верхние точки, будут определены две нижние.
Это сложно, так как вам нужно беспокоиться о нехватке места. Один из способов посчитать: разбить дела по расположению верхнего левого угла. Вы получите \ ({7 \ choose 2} + ({7 \ choose 2} -1) + ({7 \ choose 2} - 3) + ({7 \ choose 2} - 6) + ({7 \ choose 2 } - 10) + ({7 \ choose 2} - 15) = 91 \) параллелограмм.
Всего
\ ({7 \ choose 2} {7 \ choose 2} - \ left [{7 \ choose 2} + ({7 \ choose 2} -1) + ({7 \ choose 2} - 3) + ( {7 \ choose 2} - 6) + ({7 \ choose 2} - 10) + ({7 \ choose 2} - 15) \ right] \ text {.} \) Все, кроме параллелограммов.

7

анаграмма слова - это просто перестановка его букв. Сколько существует различных анаграмм «не защищенных авторским правом»? (Это самое длинное из распространенных английских слов без повторяющихся букв.)

8

Сколько существует анаграмм слова «оценивает», начинающихся с буквы «а»?

Решение

После первой буквы (а) мы должны переставить оставшиеся 7 букв. Здесь всего две буквы (s и e), так что на самом деле это просто вопрос в виде битовой строки (подумайте о s как о 1 и e как о 0). Таким образом, существуют \ ({7 \ choose 2} = 21 \) анаграммы, начинающиеся с «a».

9

Сколько существует анаграмм у «анаграмм»?

10

В деловой поездке ваша компания из 20 бизнесменов и деловых женщин играет в гольф.

Вам нужно разделиться на четверки (группы по 4 человека): первая четверка, вторая четверка и так далее. Сколько способов это сделать?
После всей вашей тяжелой работы вы понимаете, что на самом деле вы хотите, чтобы в каждую четверку входил один из пяти членов Совета. Сколько способов это сделать?

Решение

\ ({20 \ выбрать 4} {16 \ выбрать 4} {12 \ выбрать 4} {8 \ выбрать 4} {4 \ выбрать 4} \) способов. Выберите 4 из 20 человек, которые войдут в первую четверку, затем 4 из оставшихся 16 человек для второй четверки и так далее (используйте принцип умножения для объединения).
\ (5! {15 \ choose 3} {12 \ choose 3} {9 \ choose 3} {6 \ choose 3} {3 \ choose 3} \) способов. Сначала определите время игры 5 членов совета директоров, затем выберите 3 из 15 не членов совета директоров для игры в гольф с первым членом совета директоров, затем 3 из оставшихся 12 для игры в гольф со вторым и так далее.

11

Сколько различных вариантов рассадки возможно для короля Артура и его 9 рыцарей за круглым столом?

Решение

\ (9! \) (За столом сидят 10 человек, но не имеет значения, где сидит король Артур, только тот, кто сидит слева от него, два места слева и т. Д.).{10} \) функции. Есть 17 вариантов изображения каждого элемента в домене.

\ (P (17, 10) \) инъективных функций. Есть 17 вариантов для изображения первого элемента домена, затем только 16 вариантов для второго и так далее.

13

Рассмотрим функции \ (f: \ {1,2,3,4 \} \ to \ {1,2,3,4,5,6 \} \ text {.} \)

Сколько всего функций?
Сколько функций являются инъективными?
Сколько инъективных функций увеличивают ? Быть увеличивающимся означает, что если \ (a \ lt b \), то \ (f (a) \ lt f (b) \ text {,} \) или, другими словами, выходы становятся больше по мере увеличения входов.

14

Мы видели, что формула для \ (P (n, k) \) имеет вид \ (\ dfrac {n!} {(Nk)!} \ Text {.} \) Здесь ваша задача - объяснить , почему это это правильная формула.

Предположим, у вас есть 12 фишек, каждая разного цвета. Сколько разных стопок по 5 фишек вы можете собрать? Объясните свой ответ и почему он такой же, как при использовании формулы для \ (P (12,5) \ text {.} \)
Если снова использовать сценарий с 12 фишками, что означает \ (12! \)? Что значит \ (7! \)? Объяснять.
Объясните, почему имеет смысл разделить \ (12! \) На \ (7! \) При вычислении \ (P (12,5) \) (в единицах микросхем).
Работает ли ваше объяснение для чисел, отличных от 12 и 5? Объясните формулу \ (P (n, k) = \ frac {n!} {(N-k)!} \), Используя переменные \ (n \) и \ (k \ text {.} \)

25 способов случайного распределения учащихся по парам или группам

Есть много преимуществ, когда учащиеся работают в парах и группах. Они варьируются от предоставления студентам большего количества разговорных возможностей до улучшения общей динамики класса.

Есть три основных способа группировки студентов. Мы можем позволить ученикам выбирать, с кем они хотят работать, учитель может создавать группы, или мы можем сгруппировать их случайным образом. В этом посте я покажу вам множество способов, с помощью которых вы можете случайным образом разбить учеников на пары и группы.

Предложения разделены на два набора. Первый набор предложений заставляет учеников выстроиться в линию, которую затем учитель делит на пары или группы желаемого размера. Второй набор предложений разбивает студентов прямо на пары или группы.

Оформить линию

Этот метод группировки требует, чтобы учащиеся встали и выстроились в линию в соответствии с установленным правилом. Затем учитель делит линию на пары или группы. Все, кроме одного, не требуют дополнительной подготовки перед занятием.

Когда вы в последний раз ели мороженое? - Учащиеся попадают в строку, отсортированную по времени, когда они последний раз ели мороженое (пиццу, шоколад и т. Д.). Затем учитель делит линию на пары или группы по мере необходимости.
Что-то в вашей сумке или кармане - Каждый ученик выбирает и достает личный предмет, который у него есть в сумке или кармане (поощряйте учеников выбирать более необычный предмет, а не только ручку, ключи, монету и т. Д.) . Учащиеся выстраиваются в строку в алфавитном порядке написания названия предмета, который они держат. Затем учитель делит линию на пары или группы.
Дни рождения - Учащиеся занимают строчку в порядке их дней рождения в году.Затем учитель делит линию на пары или группы.
Слова из модуля - Учитель выбирает слова из модуля учебника и записывает каждое на отдельном листе бумаги. Учитель дает каждому ученику одно слово. Учащиеся выстраиваются в строку в алфавитном порядке написания слов. Затем учитель делит линию на пары или группы.
Какая ваша любимая еда? - Студенты пишут свою любимую еду (животное, место, певец и т. Д.)) на листе бумаги. Они попадают в строку в алфавитном порядке написанного слова. Затем учитель делит линию на пары или группы.
Во сколько вы ложились спать прошлой ночью? - Студенты попадают в линию, ранжируемую по времени, когда они ложились спать прошлой ночью. Затем учитель делит линию на пары или группы.
В алфавитном порядке - Учащиеся выстраиваются в строку в алфавитном порядке написания своего имени / имени (или фамилии).Затем учитель делит линию на пары или группы. В качестве альтернативы студенты могут записывать свои имена задом наперед и располагаться в алфавитном порядке обратного написания своих имен.
Самый молодой человек, проживающий в вашем доме - Учащиеся попадают в строку, ранжируемую по возрасту самого молодого человека, живущего в их доме. Затем учитель делит линию на пары или группы.
Сколько времени вам понадобилось, чтобы добраться сюда сегодня? - Учащиеся попадают в строку, ранжируемую в порядке, сколько времени им потребовалось, чтобы добраться до школы сегодня.Затем учитель делит их на пары или группы.
Куда вы ездили в последний отпуск? - Студенты попадают в строку, отсортированную в алфавитном порядке от названия места, в котором они побывали на последних каникулах. Затем учитель делит линию на пары или группы. В качестве альтернативы, это может быть город / место, которое они больше всего хотели бы посетить.
Последние 2 цифры вашего номера телефона - Учащиеся попадают в строку, ранжируемую в порядке последних двух цифр их номера телефона.Затем учитель делит линию на пары или группы. В качестве альтернативы это можно сделать с помощью двух последних цифр личного идентификатора.
Что вы ели в последний раз? - Учащиеся пишут на листе бумаги название последней еды, которую они съели. Учащиеся выстраиваются в строку в алфавитном порядке по написанию еды, которую они последний раз ели. Затем учитель делит линию на пары или группы.
Количество букв в вашем имени - Учащиеся попадают в строку в зависимости от количества букв в их полном имени.Студенты должны решить, хотят ли они опустить какое-либо имя, которое они обычно не используют или не любят. Затем учитель делит линию на пары или группы.
Сколько времени вы вчера провели вне дома? - Студенты попадают в строку, отсортированную по количеству времени, которое они провели вдали от дома вчера. Затем учитель делит линию на пары или группы.
Последнее слово на странице - Учитель присваивает каждому студенту другой номер страницы учебника.Распределение страниц может быть выполнено несколькими способами, но самый простой, вероятно, состоит в том, чтобы ученики считали последовательно по всему классу, хотя не обязательно начиная со страницы 1 (например, 33, 34, 35 и т. Д.). Учащиеся смотрят последнее слово на назначенной им странице и располагаются в алфавитном порядке своих слов. Затем учитель делит линию на пары или группы.
Дата на монете - Каждый ученик достает монету и смотрит на год, написанный на ней. Студенты занимают строчку в порядке дат, указанных на их монетах.У некоторых студентов, вероятно, будут монеты одного года, и в этом случае они могут ранжировать себя по тому, насколько старой или новой выглядит каждая монета. Затем учитель делит линию на пары или группы.

Непосредственно на пары или группы

Большинство из этих предложений требует некоторой степени подготовки перед занятием.

Возьмите веревку - Чтобы разбить учеников на пары, у учителя есть кусочки веревочки (по одной на каждых двух учеников). Учитель держит все куски веревки в связке посередине, и каждый ученик выбирает и держит конец веревки.Затем учитель отпускает веревку, и ученики объединяются в пары с человеком, держащим другой конец веревки (Dudley, E. & E. Osváth. 2016. Mixed-Ability Teaching . OUP).
Палочки для леденцов - Учитель записывает имя каждого ученика на индивидуальной палочке для леденцов (или именной карточке). Учитель наугад выбирает палки, чтобы разделить учеников на пары или группы. Примечание. Существуют также бесплатные приложения, которые подобным образом могут случайным образом группировать учащихся.
Что за категория? - Чтобы разбить учеников на группы по 4 человека, учитель выбирает слова из 4 видов фруктов, 4 видов цветов, 4 видов животных, 4 видов мебели и т. Д. И записывает каждое слово на отдельном листе бумаги. Каждый ученик получает слово наугад. Студенты объединяются в группы с людьми, имеющими ту же категорию слов.
Длина ленты - Учитель предлагает нарезать ленту на отрезки (также можно использовать веревку или полоски повторно использованной бумаги).Например, если в классе 12 учеников, и учитель хочет создать три группы по 4 ученика, будет 4 короткие ленты, 4 ленты средней длины и 4 более длинные ленты. Учитель держит все ленты, чтобы ученики не могли видеть длину каждой ленты, и предлагает каждому ученику выбрать одну. Студенты объединяются в группы с людьми с одинаковой длиной ленты.
Части картинки - У учителя есть несколько разных картинок, каждая из которых разрезается на части (количество частей соответствует размеру требуемых групп).Каждый ученик наугад получает отрывок картинки. Студенты объединяются в группы с людьми, у которых есть другие части одной и той же картины.
Половинки предложений - Чтобы разбить учеников на пары, учитель выбирает разные предложения из раздела учебника и записывает каждое на полоске бумаги. Затем каждое предложение разрезается пополам. Каждый ученик получает половину предложения наугад. Учащиеся попадают в пары с человеком с соответствующей половиной предложения.
Letters - Учитель готовит листы бумаги с буквами A, B, C или D и т. Д.написано на каждом. Учитель дает каждому ученику по листу бумаги. Студенты объединяются в группы с людьми с одной и той же буквой. Это также можно сделать с помощью цветных жетонов или цветных бумажек.
Капитаны команд - Учитель выбирает нескольких учеников, которые должны выйти вперед и стать капитанами команд. Количество капитанов команд будет зависеть от необходимого количества групп / команд. Затем каждый капитан команды по очереди выбирает членов команды. Это может быть сделано капитанами команд, выбирающими, кем они хотят быть в своей команде, или случайным образом беря леденцы или визитки (см. 18).
Посчитайте в классе - Учитель присваивает номер каждому ученику (например, 1, 2, 3, 4, 1, 2, 3, 4, 1 и т. Д.) Вокруг класса. Когда у всех учеников есть номер, все ученики с номером 1 попадают в группу; все ученики с номером 2 попадают в группу и т. д.

Филип Хейнс переехал в Мексику из Англии в 1995 году и в настоящее время работает старшим научным консультантом Oxford University Press в Мексике. Он выступал на международном уровне на трех континентах и на национальном уровне в каждом штате Мексики.Филип является автором / соавтором нескольких серий ELT, опубликованных в Мексике.

Нравится:

Нравится Загрузка ...

Категории: Дети дошкольного возраста, Повышение квалификации, Подростки, Учащиеся | Теги: Сотрудничество, Групповая оценка, группы, партнеры, Филип Хейнс, Работа в парах | Постоянная ссылка.

Нахождение числа перестановок n различных объектов

Принцип умножения можно использовать для решения различных типов задач.Один тип проблем связан с размещением объектов по порядку. Мы расставляем буквы в слова и цифры в числа, выстраиваем в очередь фотографии, украшаем комнаты и многое другое. Порядок объектов называется перестановкой .

Нахождение числа перестановок

n различных объектов с использованием принципа умножения

Для решения задач перестановки часто бывает полезно нарисовать отрезки линии для каждого варианта. Это позволяет нам определить количество каждой опции, чтобы мы могли умножить.Например, предположим, что у нас есть четыре картины, и мы хотим найти количество способов, которыми мы можем повесить три картины по порядку на стене. Мы можем нарисовать три линии, чтобы обозначить три места на стене.

Есть четыре варианта для первого места, поэтому мы пишем 4 в первой строке.

После того, как первое место было заполнено, есть три варианта для второго места, поэтому мы пишем 3 во второй строке.

После того, как второе место было заполнено, есть два варианта для третьего места, поэтому мы пишем 2 в третьей строке.Наконец-то находим товар.

Есть 24 возможных перестановки картин.

Как сделать: учитывая различные варианты [latex] n [/ latex], определите, сколько существует перестановок.

Определите, сколько вариантов существует для первой ситуации.
Определите, сколько вариантов осталось для второй ситуации.
Продолжайте, пока все точки не будут заполнены.
Умножьте числа.

Пример 2: Нахождение числа перестановок с использованием принципа умножения

На соревнованиях по плаванию участвуют девять пловцов.

Сколько способов они могут занять первое, второе и третье места?
Сколько способов они могут занять первое, второе и третье место, если пловец по имени Ариэль занял первое место? (Предположим, есть только один участник по имени Ариэль.)
Какими способами все девять пловцов могут выстроиться в очередь, чтобы сфотографироваться?

Анализ решения

Обратите внимание, что в части c мы обнаружили 9! способы выстроиться в очередь для 9 человек. Количество перестановок различных объектов [latex] n [/ latex] всегда можно найти с помощью [latex] n! [/ Latex].

Семья из пяти человек фотографируется. Используйте принцип умножения, чтобы найти следующее.

Попробуй 3

Какими способами семья может выстроиться для портрета?

Решение

Попробовать 4

Сколько способов фотограф может выстроить в ряд из 3 членов семьи?

Решение

Попробуй 5

Сколько способов семья может выстроиться для портрета, если родители должны стоять по обе стороны?

Решение

Нахождение числа перестановок

n отдельных объектов с помощью формулы

Для некоторых задач перестановки неудобно использовать принцип умножения, потому что нужно умножить очень много чисел.К счастью, мы можем решить эти проблемы с помощью формулы. Прежде чем изучать формулу, давайте рассмотрим два распространенных обозначения перестановок. Если у нас есть набор объектов [latex] n [/ latex] и мы хотим выбрать объекты [latex] r [/ latex] из набора по порядку, мы пишем [latex] P \ left (n, r \ right) [/латекс]. Другой способ записать это - [латекс] {n} _ {} {P} _ {r} [/ latex], обозначение, обычно встречающееся на компьютерах и калькуляторах. Чтобы вычислить [латекс] P \ left (n, r \ right) [/ latex], мы начинаем с нахождения [latex] n! [/ Latex], количества способов выстроить все [латекс] n [/ latex] объекты.Затем мы делим на [latex] \ left (n-r \ right)! [/ Latex], чтобы исключить элементы [latex] \ left (n-r \ right) [/ latex], которые мы не хотим выстраивать в линию.

Давайте посмотрим, как это работает, на простом примере. Представьте себе клуб из шести человек. Им нужно избрать президента, вице-президента и казначея. Шесть человек могут быть избраны президентом, любой из пяти оставшихся человек может быть избран вице-президентом, а любой из оставшихся четырех человек может быть избран казначеем. Это можно сделать разными способами: [латекс] 6 \ умножить на 5 \ умножить на 4 = 120 [/ латекс].Используя факториалы, мы получаем тот же результат.

[латекс] \ frac {6!} {3!} = \ Frac {6 \ cdot 5 \ cdot 4 \ cdot 3!} {3!} = 6 \ cdot 5 \ cdot 4 = 120 [/ латекс]

Есть 120 способов выбрать 3 офицера по порядку из клуба с 6 членами. Мы называем это перестановкой 6, взятых по 3 за раз. Общая формула следующая.

[латекс] P \ left (n, r \ right) = \ frac {n!} {\ Left (n-r \ right)!} [/ Latex]

Обратите внимание, что формула по-прежнему работает, если мы выбираем все объекты [latex] n [/ latex] и размещаем их по порядку.В этом случае мы будем делить на [latex] \ left (nn \ right)! [/ Latex] или [latex] 0! [/ Latex], что, как мы сказали ранее, равно 1. Таким образом, количество перестановок [ latex] n [/ latex] объектов, взятых [latex] n [/ latex] за раз - это [latex] \ frac {n!} {1} [/ latex] или просто [latex] n! \ text {.} [ / латекс]

Общее примечание: формула для перестановок

n различных объектов

Для различных объектов [latex] n [/ latex] количество способов выбрать объекты [latex] r [/ latex] из набора по порядку составляет

[латекс] P \ left (n, r \ right) = \ frac {n!} {\ Left (n-r \ right)!} [/ Latex]

Практическое руководство. Учитывая проблему со словом, оцените возможные перестановки.

Определите [латекс] n [/ латекс] по данной информации.
Определите [латекс] r [/ латекс] по данной информации.
Заменить [латекс] n [/ латекс] и [латекс] r [/ латекс] в формуле заданными значениями.
Оценить.

Пример 3: Нахождение числа перестановок по формуле

Профессор создает экзамен из 9 вопросов из банка тестов из 12 вопросов. Сколько способов она может выбрать и расставить вопросы?

Решение

Заменить [латекс] n = 12 [/ latex] и [latex] r = 9 [/ latex] в формулу перестановки и упростить.

[латекс] \ begin {array} {l} \ text {} P \ left (n, r \ right) = \ frac {n!} {\ Left (nr \ right)!} \ Hfill \\ P \ left (12,9 \ right) = \ frac {12!} {\ Left (12–9 \ right)!} = \ Frac {12!} {3!} = 79 \ text {,} 833 \ text {,} 600 \ hfill \ end {array} [/ latex]

Есть 79 833 600 возможных перестановок экзаменационных вопросов!

Анализ решения

Мы также можем использовать калькулятор, чтобы найти перестановки. Для этой проблемы мы должны ввести 15, нажать функцию [latex] {} _ {n} {P} _ {r} [/ latex], ввести 12, а затем нажать знак равенства.Функция [latex] {} _ {n} {P} _ {r} [/ latex] может находиться в меню MATH с командами вероятности.

Вопросы и ответы

Можно ли было решить, используя принцип умножения?

Да. Мы могли бы умножить [латекс] 15 \ cdot 14 \ cdot 13 \ cdot 12 \ cdot 11 \ cdot 10 \ cdot 9 \ cdot 8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 [/ latex] , чтобы найти тот же ответ .

В спектакле 7 актеров готовятся к выходу на занавес. Используйте формулу перестановки, чтобы найти следующее.

Попробуй 6

Какими способами могут выстроиться 7 актеров?

Решение

Попробуй 7

Какими способами можно выбрать пятерых из семи актеров для построения линии?

Решение

идентичных объектов в разные ячейки

Предыдущие задачи и примеры касались ситуаций, в которых ячейки можно было оставить пустыми. Теперь рассмотрим, как меняется проблема, когда требуется, чтобы бункеры были непустыми. К счастью, можно использовать аналогичный подход.

Рассмотрим задачу, в которой мы пытаемся найти количество распределений 8 идентичных объектов среди 5 различных ячеек, и ячейки нельзя оставлять пустыми. Если смоделировать проблему в виде звездочек и столбиков, она будет выглядеть так:

⋆⋆⋆⋆⋆⋆⋆⋆ \ большая \ звездочка \ звездочка \ звездочка \ звездочка \ звездочка \ звездочка \ звездочка \ звезда

Как и в предыдущих примерах, количество столбцов будет на 111 меньше, чем количество ячеек. Итак, у нас есть 444 бара, которые нужно разместить. Где их разместить? Если вы помните из предыдущего примера, если столбцы помещались на концах или рядом с другими столбцами, создавались пустые группы.Таким образом, чтобы не было и пустых групп, полосы можно размещать только между звездами, и только одну полосу можно размещать между парой звезд.

⋆∣⋆∣⋆⋆∣⋆⋆∣⋆⋆ \ большая \ звездочка | \ звездочка | \ звездочка \ звездочка | \ звездочка \ звездочка | \ звездочка \ звезда

Есть ровно 777 потенциальных местоположений, которые соответствуют этим критериям. Другими словами, на 111 меньше, чем количество объектов. Из этих 777 потенциальных местоположений размещено 444 бара. Таким образом, существует (74) = 35 \ binom {7} {4} = 35 (47) = 35 возможных распределений 8 идентичных объектов в 5 различных непустых интервалов.

Предположим, есть nnn идентичных объектов, которые должны быть распределены среди rrr различных непустых интервалов, с n≥rn \ ge rn≥r. Это можно сделать точно (n − 1r − 1) \ binom {n-1} {r-1} (r − 1n − 1) способами.

Для этого типа задач n≥rn \ ge rn≥r должно быть истинным. Если n
На модели в виде звезд и столбцов нужно разместить nnn звезд и r − 1r-1r − 1 столбцов. Чтобы группы не были пустыми, полосы можно размещать только между звездами, а между парой звездочек можно размещать только одну полосу.Таким образом, существует n − 1n-1n − 1 возможных размещений стержней. Из этих n − 1n-1n − 1 возможных размещений для столбцов выбирается r − 1r-1r − 1. Следовательно, количество возможных вариантов расположения звезд и полосок равно (n − 1r − 1) \ binom {n-1} {r-1} (r − 1n − 1). Эквивалентно, существует (n − 1r − 1) \ binom {n-1} {r-1} (r − 1n − 1) распределений nnn идентичных объектов в rrr различных непустых интервалов.

У учителя есть 12 одинаковых карандашей, которые нужно распределить среди 9 разных учеников. Сколько существует способов раздать 12 карандашей так, чтобы каждый ученик получил хотя бы один карандаш?
В этом примере имеется n = 12n = 12n = 12 идентичных объектов, которые должны быть распределены по r = 9r = 9r = 9 отдельным ячейкам.Используя приведенную выше формулу, количество возможных распределений будет (118) = 165 \ binom {11} {8} = \ boxed {165} (811) = 165.

Отправьте свой ответ

Вы находитесь на вечеринке с 4 вашими друзьями (всего 5 разных людей).

Олимпиадные задачи по теме «Комбинаторика».

КОМБИНАТОРИКА

Методические разработки: углублённое преподавание математики

Часть 1. Комбинаторика.

Часть 1. Комбинаторика — Студопедия

22. Варианты самостоятельных работ | Контрольные работы по математике

Перестановок и комбинаций — разделение на группы

Краткое содержание урока

python — Как всеми возможными способами разбить список на пары

Разбиение n элементов на k групп

Определение разделения на группы

Подсчет количества разделов на группы

Подробнее

Полиномиальные коэффициенты и полиномиальные разложения

Решенные упражнения

Упражнение 1

Упражнение 2

Как цитировать

комбинаций и перестановок

Расследуй! 8

Пример1.3.1

Перестановки элементов \ (n \)

Пример 1.3.2 Подсчет биективных функций

Пример1.3.3

\ (k \) - перестановки \ (n \) элементов

Пример 1.3.4 Подсчет инъективных функций

Замкнутая формула для \ ({n \ choose k} \)

Пример1.3.5

Подраздел Упражнения

1

2

3

4

5

6

7

8

9

10

11

13

14

25 способов случайного распределения учащихся по парам или группам

Нравится:

Нахождение числа перестановок n различных объектов

Нахождение числа перестановок

Как сделать: учитывая различные варианты [latex] n [/ latex], определите, сколько существует перестановок.

Пример 2: Нахождение числа перестановок с использованием принципа умножения

Анализ решения

Попробуй 3

Попробовать 4

Попробуй 5

Нахождение числа перестановок

Общее примечание: формула для перестановок

Практическое руководство. Учитывая проблему со словом, оцените возможные перестановки.

Пример 3: Нахождение числа перестановок по формуле

Решение

Анализ решения

Вопросы и ответы

Можно ли было решить, используя принцип умножения?

Попробуй 6

Попробуй 7

идентичных объектов в разные ячейки

Добавить комментарий Отменить ответ

Полиномиальные коэффициенты и
полиномиальные разложения