Смежный угол как определить: Что такое смежные углы? Ответ на webmath.ru — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Что такое смежные углы: определение, теорема, свойства

В данной публикации мы рассмотрим, что из себя представляют смежные углы, приведем формулировку теоремы касательно них (в т.ч. следствия из нее), а также перечислим тригонометрические свойства смежных углов.

Определение смежных углов

Два прилежащих угла, внешними сторонами образующие прямую, называется смежными. На рисунке ниже это углы α и β.

Если два угла имеют одну общую вершину и сторону, они являются прилежащими. При этом внутренние области этих углов не должны пересекаться.

Принцип построения смежного угла

Одну из сторон угла протягиваем через вершину дальше, в результате чего образуется новый угол, смежный с исходным.

Теорема о смежных углах

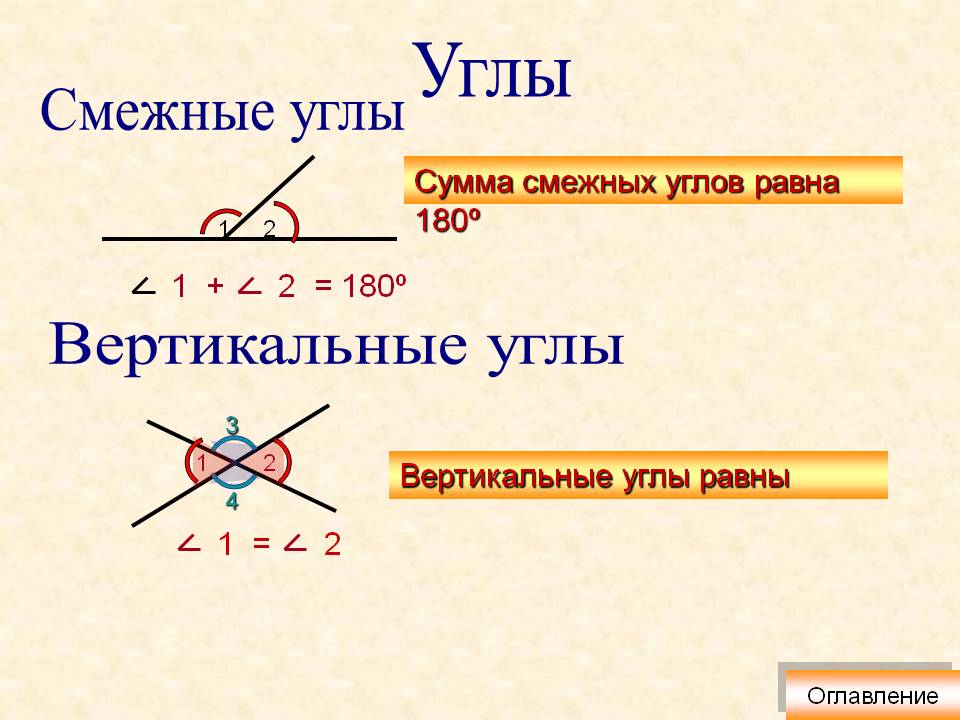
Сумма градусов смежных углов равняется 180°.

Смежн. угол 1 + Смежн. угол 2 = 180°

Пример 1
Один из смежных углов равняется 92°, чему равен второй?

Решение, согласно рассмотренной выше теореме, очевидно:
Смежн. угол 2 = 180° – Смежн. угол 1 = 180° – 92° = 88°.

Следствия из теоремы:

Смежные углы двух равных углов равны между собой.
Если угол является смежным с прямым (90°), значит он также равен 90°.
Если угол является смежным с острым, значит он больше 90°, т.е. является тупым (и наоборот).

Пример 2
Допустим, у нас есть угол, смежный с 75°. Он должен быть больше 90°. Давайте проверим это.

Воспользовавшись теоремой, находим значение второго угла:
180° – 75° = 105°.

105° > 90°, следовательно угол является тупым.

Тригонометрические свойства смежных углов

Синусы смежных уголов равны, т.е. sin α = sin β.
Величины косинусов и тангенсов смежных углов равны, но имеют противоположные знаки (кроме неопределенных значений).
- cos α = -cos β.
- tg α = -tg β.

Смежные углы | Треугольники

Что такое смежные углы? Какие у них свойства?

Определение.

Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой.

∠1 и ∠2 — смежные углы

Сколько смежных углов образуется при пересечении двух прямых?

При пересечении двух прямых образуется четыре пары смежных углов:

∠1 и ∠2, ∠3 и ∠4,

∠1 и ∠3, ∠2 и ∠4

Но, так как ∠1 =∠4, ∠2=∠3 (как вертикальные), то достаточно рассмотреть только одну из этих пар.

Свойство смежных углов.

Сумма смежных углов равна 180º.

Задачи.

1) Даны два смежных угла. Один на 42 градуса больше другого. Найти эти углы.

Дано:

∠AOC и ∠BOC — смежные,

∠AOC на 42º больше, чем ∠BOC

Найти: ∠AOC и ∠BOC.

Решение:

Пусть ∠BOC=хº, тогда ∠AOC= х+42º. Так как сумма смежных углов равна 180º, то ∠BOC+∠AOC=180º.

Имеем уравнение:

х+х+42=180

2х=180-42

2x=138

x=69

Значит, ∠BOC= 69º, ∠AOC=69+42=111º.

Ответ: 69º и 111º.

2) Найти смежные углы, если их градусные меры относятся как 4:5.

Дано:

∠1 и ∠2 — смежные,

∠1 : ∠2= 4:5

Найти:∠1 и ∠2

Решение:

Пусть k — коэффициент пропорциональности. Тогда ∠2 =4kº , ∠1=5kº. Так как сумма смежных углов равна 180º, ∠1 +∠2=180º.

Имеем уравнение:

4k+5k=180

9k=180

k=20

Значит, смежные углы равны 4∙20=80º и 5∙20=100º.

Ответ: 80º и 100º.

3) Один из углов, образованных при пересечении двух прямых, в 5 раз больше другого. Найти эти углы.

Дано: AB и CD — прямые, O — точка их пересечения,

∠AOD в 5 раз больше, чем ∠BOD

Найти: ∠AOD, ∠BOD

Решение:

При пересечении двух прямых образуются смежные и вертикальные углы.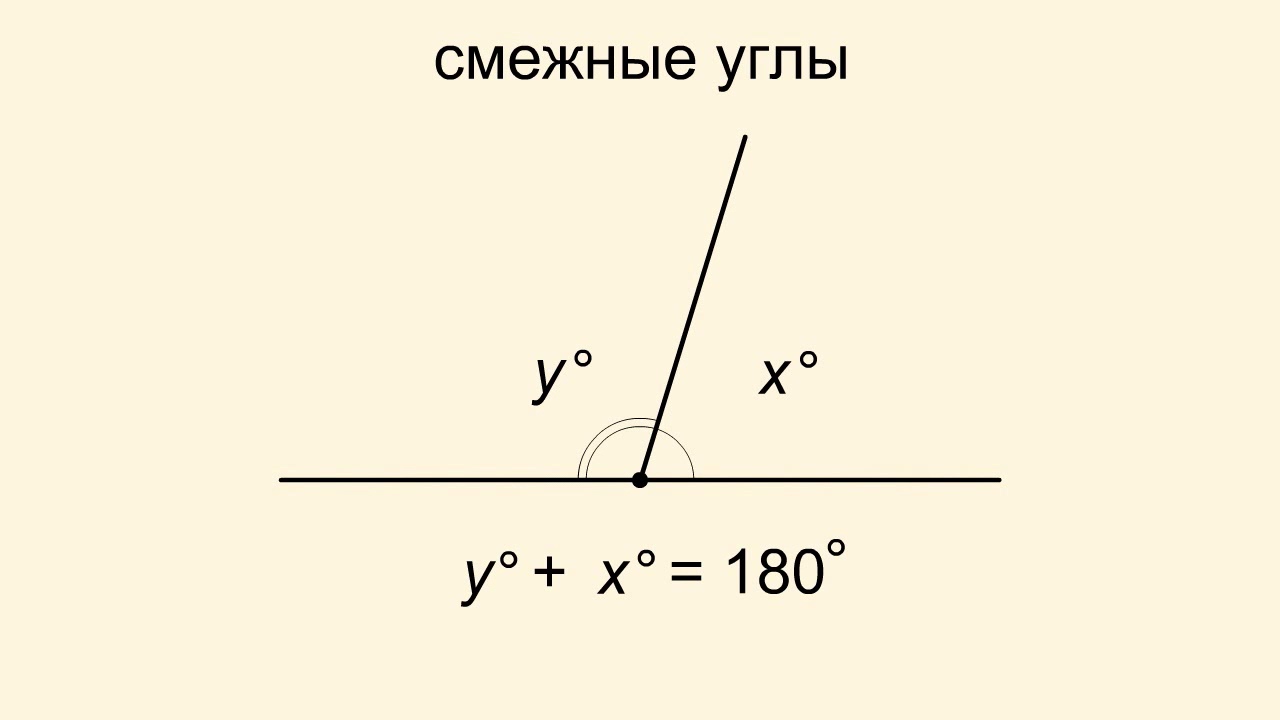 Так как вертикальные углы равны между собой, то углы∠AOD и ∠BOD — смежные. Пусть ∠BOD=xº, тогда ∠AOD=5xº. Так как сумма смежных углов равна 180º, ∠AOD +∠BOD=180º.

Имеем уравнение:

x+5x=180

6x=180

x=30

Значит, ∠BOD=30º, ∠AOD=5∙30=150º.

Ответ: 30º и 150º.

Могут ли смежные углы быть равными?

Да. Если смежные углы равны между собой, то, так как сумма смежных углов равна 180º, каждый из них равен половине суммы, то есть 90º.

Вывод:

угол, смежный с прямым, есть прямой угол.

Могут ли два смежных угла быть тупыми? Острыми?

Нет. Так как градусная мера тупого угла больше 90º, то сумма двух тупых углов больше 180º. А сумма смежных углов равна 180º.

Градусная мера острого угла меньше 90º. Значит, сумма двух острых углов меньше 180º.

Таким образом, в паре смежных углов один — тупой, другой — острый (или оба прямые).

Смежные и вертикальные углы.

\circ\).
\(\bullet\) Внешний угол \(\angle BCD\) треугольника \(ABC\) равен сумме двух углов треугольника, не смежных с ним.

Факт 4.
\(\bullet\) Биссектрисы смежных углов взаимно перпендикулярны.
\(\bullet\) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.

Факт 5.
\(\bullet\) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
\(\bullet\) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.

Факт 6.
\(\bullet\) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:

Второе свойство равнобедренного треугольника: углы при основании равны.

Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.

Факт 7.
\(\bullet\) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.

Факт 8.
\(\bullet\) Медианы в треугольнике точкой пересечения делятся в отношении \(2:1\), считая от вершины.

Факт 9.
\(\bullet\) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.

Факт 10.
\(\bullet\) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
\(\bullet\) Квадрат этой высоты равен произведению отрезков, на которые она делит гипотенузу.

Факт 11.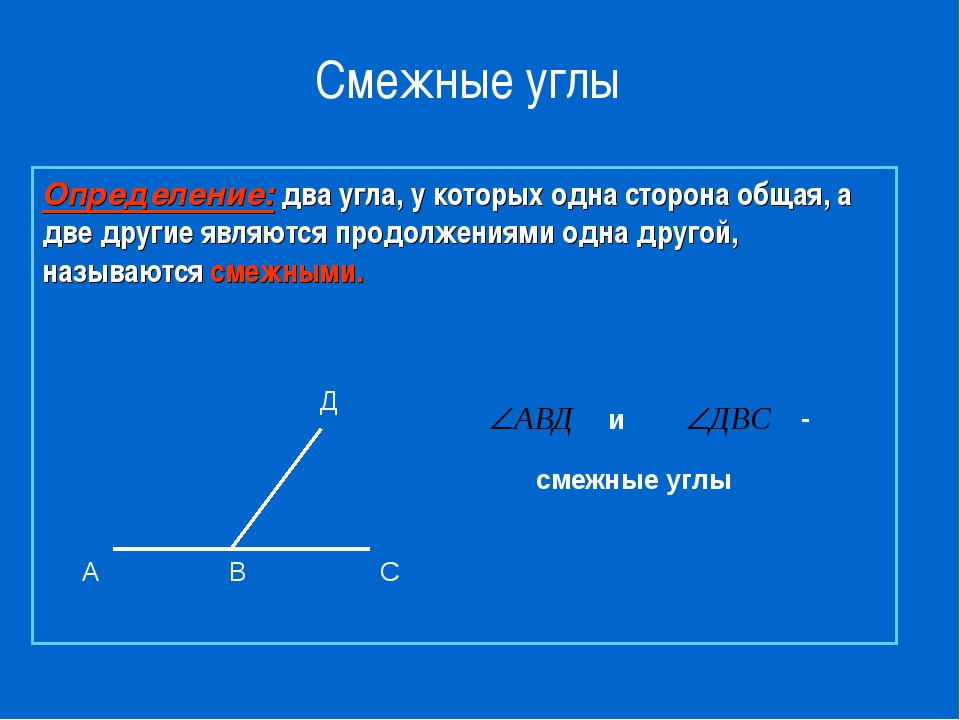
\(\bullet\) Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
\(\bullet\) 1. Средняя линия треугольника параллельна третьей стороне.
\(\bullet\) 2. Средняя линия треугольника равна половине третьей стороны.
\(\bullet\) 3. Средняя линия отсекает от треугольника подобный ему треугольник.

Что такое смежный угол

Понятие смежных углов является одним из основных в Евклидовой геометрии. Это два угла, которые вместе образуют 180 градусов. У них имеется одна общая вершина и сторона, а две остальные стороны не являются общими, но вместе они представляют собой прямую, то есть являются дополнительными лучами.Угол – это геометрическая фигура, лежащая на плоскости, которую образуют два луча, исходящие из единой точки. Величина угла измеряется по-разному: в градусной мере, в радианах, а также несколькими другими, менее распространёнными способами.

Смежные углы – это такие, которые имеют общую вершину, а также один общий луч.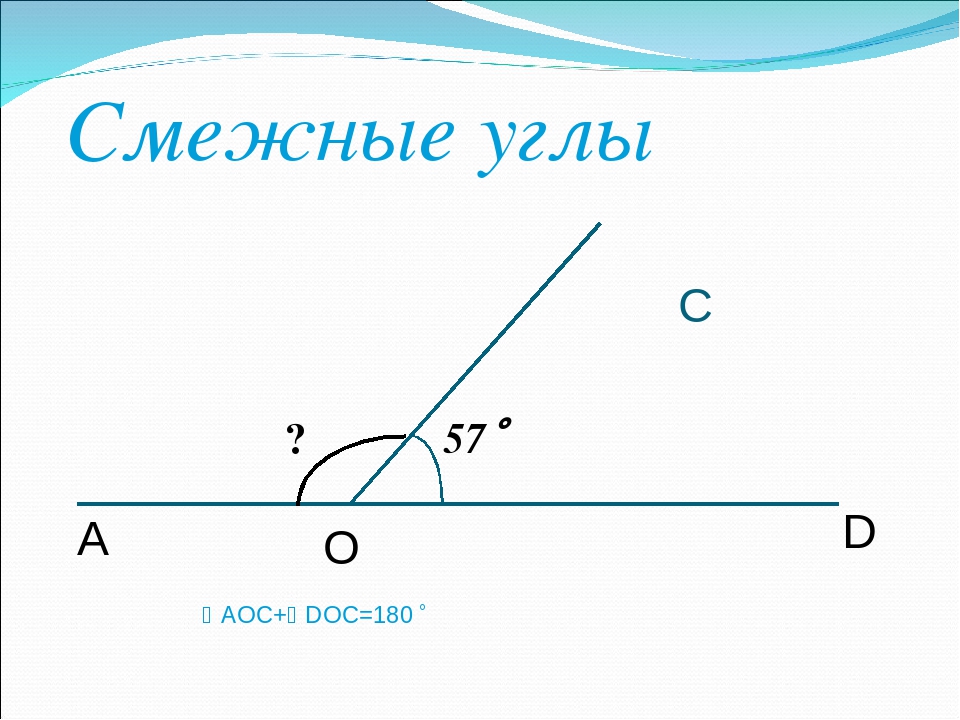 Два остальных луча смежных углов образуют развернутый угол, то есть лежат на прямой и не совпадают.

Так как сумма двух смежных углов всегда составляет 180 градусов, то можно без труда вычислить один из них, если известен второй. Например, если первый угол равен 60 градусам, то смежным к нему является угол в 120 градусов. Это одно из основных свойств смежных углов.

Существует теорема, доказывающая его. Если имеются два смежных угла, то один из лучей является общим для них, а два других, согласно определению, образуют развернутый угол. Градусная мера развернутого угла составляет 180 градусов, поэтому сумма углов, его образующих, также равна 180 градусам. Теорема доказана.

Из этого свойства имеются следствия. Если два угла одновременно являются и смежными, и равными, то они прямые. Если один из смежных углов является прямым, то есть составляет 90 градусов, то другой угол тоже прямой. Если один из смежных углов острый, то другой будет тупым. Аналогично, если один из углов тупой, то второй, соответственно, будет острым.

Острый угол – это такой, градусная мера которого меньше 90 градусов, но больше 0. Тупой угол имеет градусную меру больше 90 градусов, но меньше 180.

Другое свойство смежных углов формулируется так: если два угла равны, то углы, смежные с ними, также равны. Это значит, что если есть два угла, градусная мера для которых совпадает (например, она составляет 50 градусов) и при этом каждый из них имеет смежный угол, то значения этих смежных углов тоже совпадают (в примере их градусная мера будет равна 130 градусам).

Что такое прилегающие углы. Вертикальные углы. Что такое смежный угол

Что такое смежный угол

Угол
– это геометрическая фигура (рис.1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла).

СМЕЖНЫЕ УГЛЫ
— два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.

Смежные углы
— (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

рис. 2

На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.

рис. 3

На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.

Теорема о смежных углах

Теорема:
сумма смежных углов равна 180°

Доказательство:

Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°.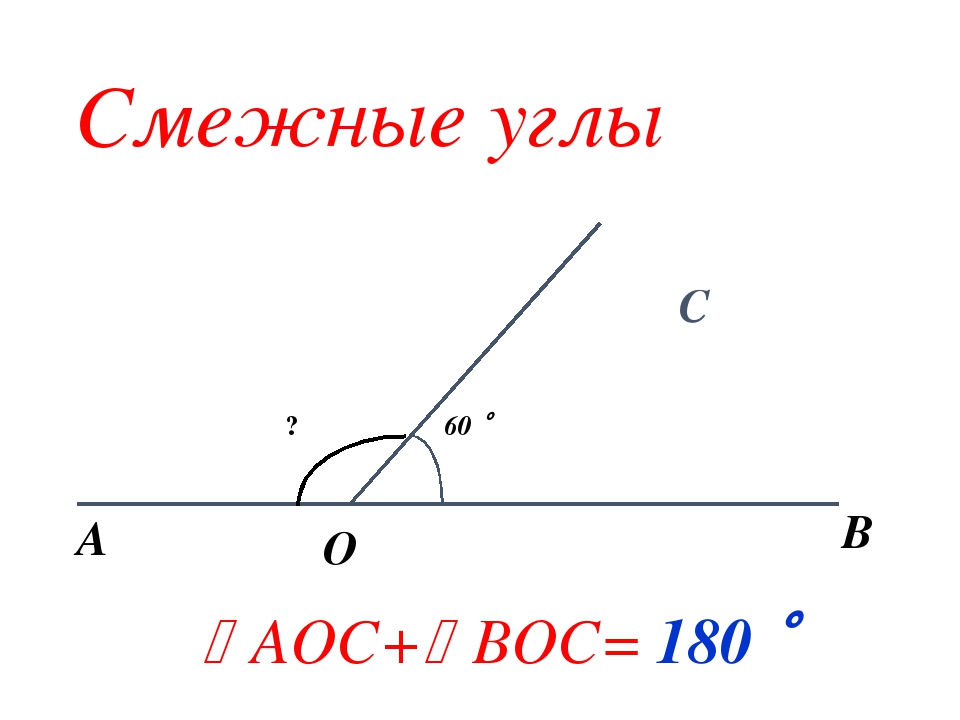 Теорема доказана.

Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.

Смежные углы
— два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.

Определение 1.
Углом называется часть плоскости, ограниченная двумя лучами с общим началом.

Определение 1.1.
Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи:

Определение 2.
Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.

Определение 3.
Прямой угол — это угол величиной в 90 градусов.

Определение 4.
Угол, меньший 90 градусов, называется острым углом.

Определение 5.
Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.

Определение 6.
Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.

Определение 7.
Углы, стороны которых продолжают друг друга, называются вертикальными углами.
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1.
Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.

рис. 4

Связь математики с музыкой

«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства. «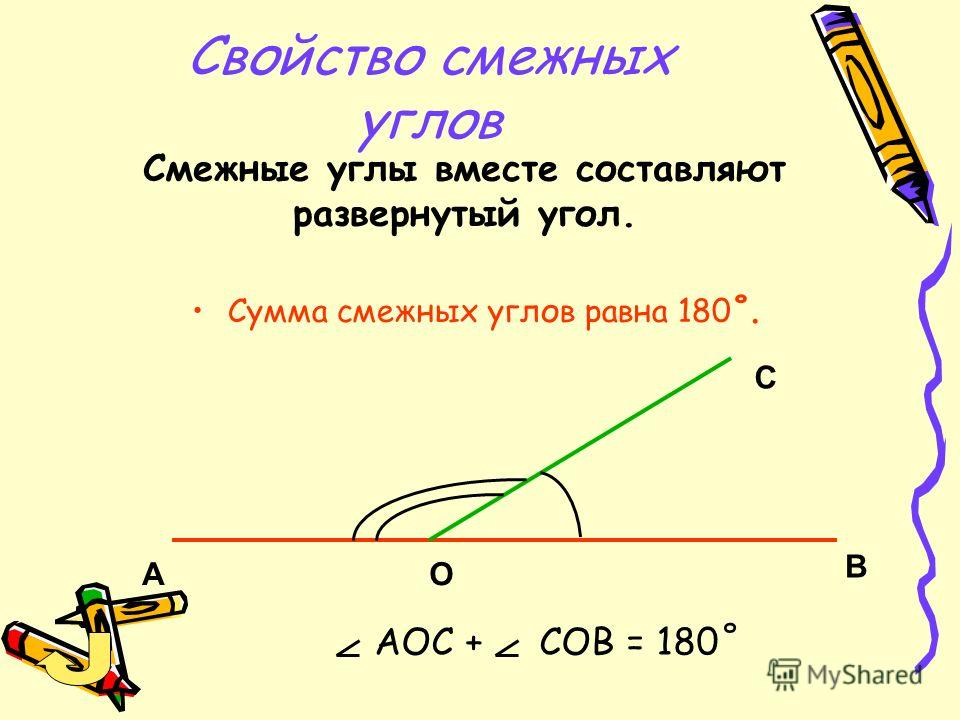
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т.е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a: l ,
где а — коэффициент, характеризующий физические свойства струны.

Так же предложу вашему внимаю забавную пародию про спор двух математиков =)

Геометрия вокруг нас

Геометрия в нашей жизни имеет немаловажное значение.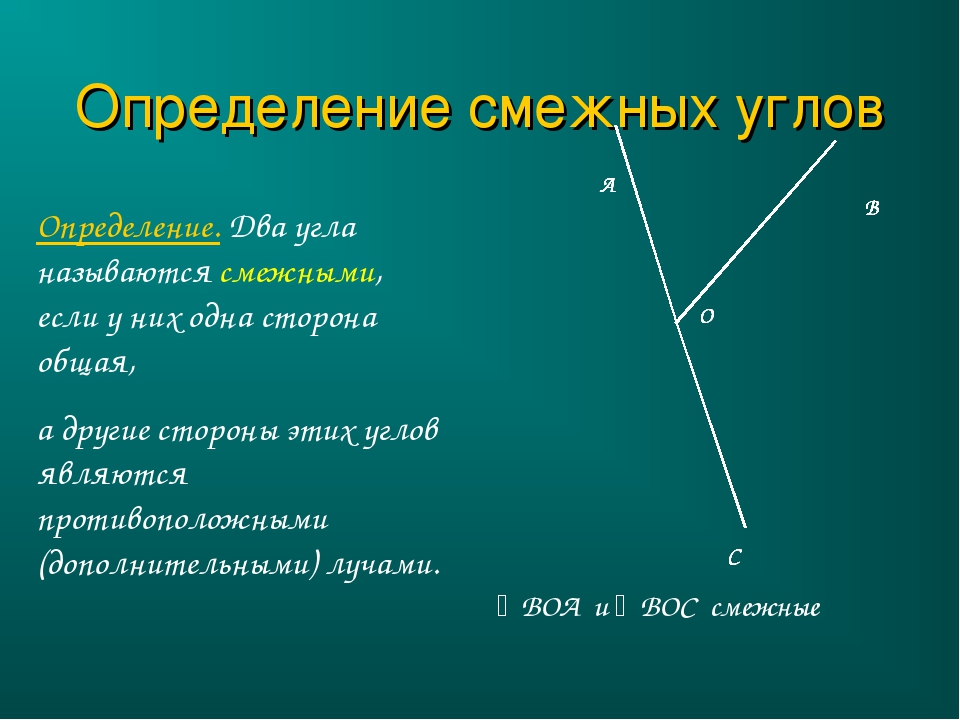 Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились.
Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов.
Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.

Задание 1.

1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?

Задание 2.

Перед вами изображена геометрическая фигура.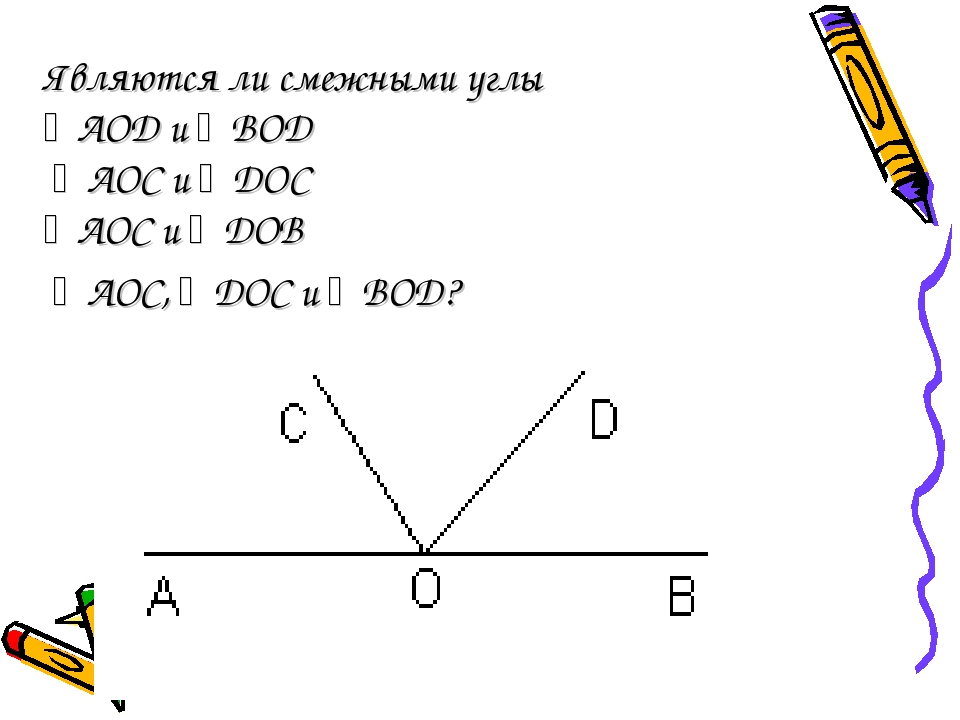 Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.

Задание 3.

Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.

Решение задач

1) Даны два угла, относящиеся друг к другу как 1: 2, а смежные с ними — как 7: 5. Нужно найти эти углы.
2) Известно, что один из смежных углов больше другого в 4 раза. Чему равны смежные углы?
3) Необходимо найти смежные углы, при условии, что один из них на 10 градусов больше от второго.

Математический диктант на повторение ранее выученного материала

1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а — через а1 и а2, а прямой b — через b1 i b2.
2) Пользуясь выполненным рисунком, впишите нужные значения и объяснения в места пропусков в тексте:
а) угол 1 и угол ….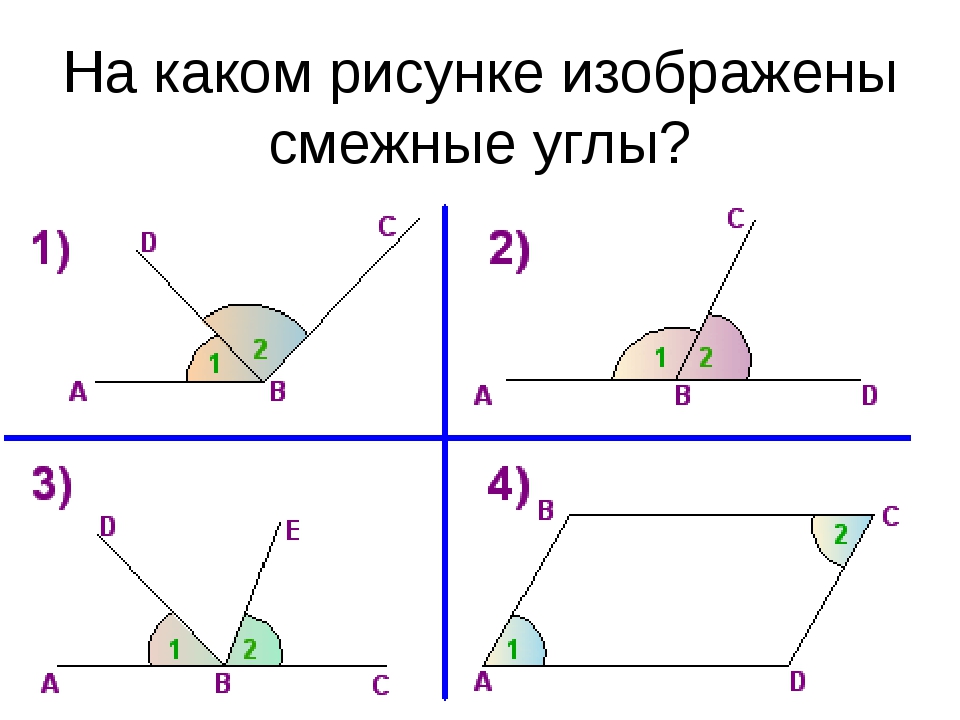 смежные, поскольку…
б) угол 1 и угол …. вертикальные, поскольку…
в) если угол 1 = 60°, то угол 2 = …, потому что…
г) если угол 1 = 60°, то угол 3 = …, потому что…

Решите задачи:

1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.

3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:

а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.

Итог урока

1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.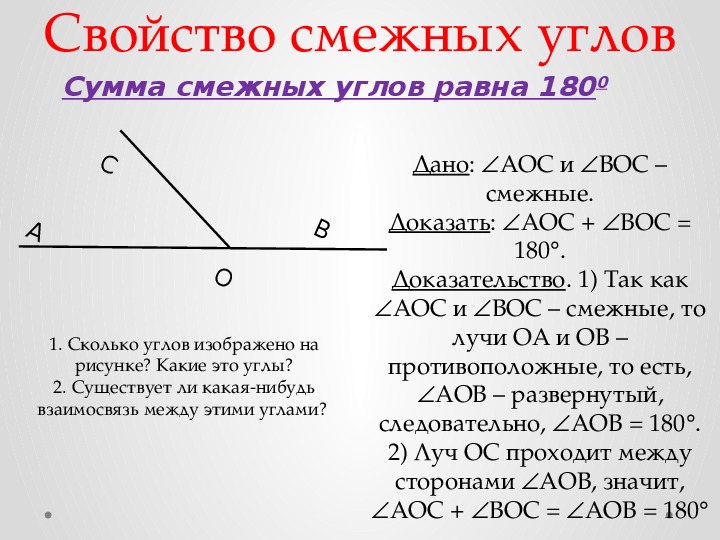

Домашнее задание:

1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1: 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.

Вопросы:

Что такое угол?
Какие бывают типы углов?
Какая особенность смежных углов?

Предмети > Математика > Математика 7 класс

Две прямые линии BA и BC (черт. 13), пересекающиеся в одной и той же точке B, образуют при точке B угол.

Определение угла
. Углом называется неопределенная часть плоскости, ограниченная двумя пересекающимися прямыми линиями. Угол есть величина, определяющая наклонение одной прямой линии к другой.

Стороны угла.
Пересекающиеся линии называются сторонами угла.

Вершина угла
. Точка пересечения двух прямых называется вершиной угла
. Величина угла не зависит от длины сторон, поэтому стороны угла можно неопределенно продолжать.

Название угла
. a) Углы называют буквой, стоящей при вершине
; так угол на черт. 13 называют углом B. b) Если при вершине несколько углов, то углы называют тремя буквами, стоящими при вершине и двух его сторонах. При этом буква при вершине произносится и пишется в середине.

На черт. 13 угол B называют угол ABC. Линии BA и BC — две стороны, а точка B — вершина угла.

Таким образом угол ABC есть угол B или

угол ABC = углу B.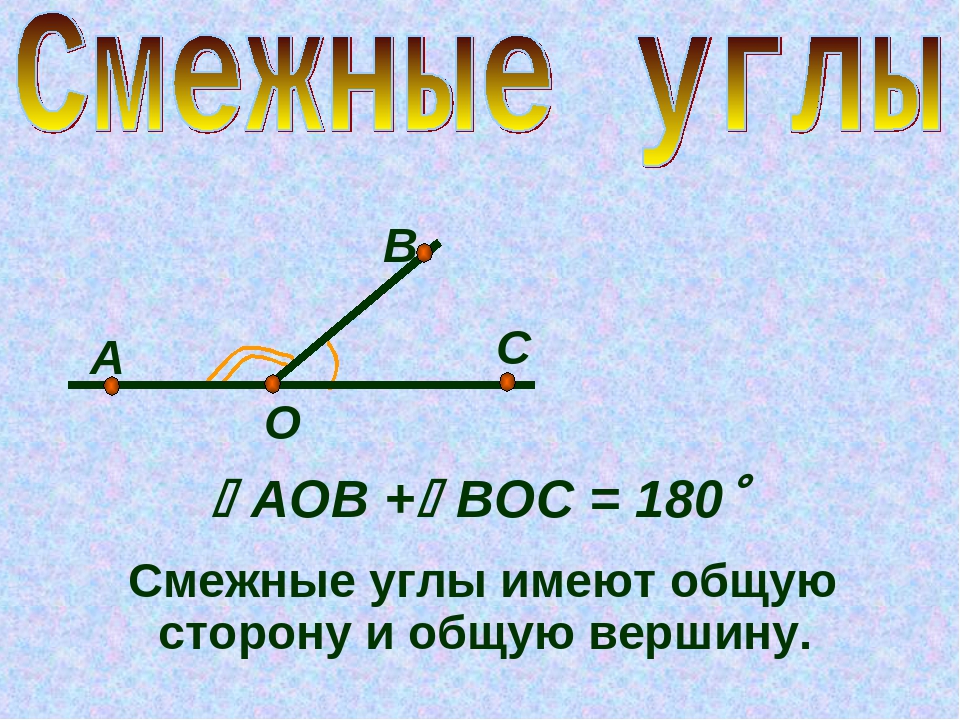

Знак угла.
Слово угол заменяют иногда знаком
∠
.

Таким образом предыдущее равенство изображают письменно:

В том случае, когда из точки выходит несколько линий, при точке B имеется несколько углов.

На черт. 14 из точки B выходят прямые линии BA, BC, BD и при вершине B имеются углы ABC, CBD, ABD.

Прилежащие углы
. Два угла называются прилежащими, когда они имеют общею вершину, по одной общей стороне, а две другие лежат по обе стороны общей стороны.

Углы ABC и CBD (черт. 14) суть прилежащие углы. Они имеют общую вершину B, общую сторону BC, а две другие стороны BA и BD лежат одна сверху, а другая снизу общей стороны BC.

Углы изменяют свою величину, если изменяется наклонение одной стороны к другой. Из двух углов, имеющих общую вершину, тот угол, внутри которого помещается другой угол, называется большим углом. На чертеже 14

уг. ABD > уг. ABC и уг. CBD

Чтобы иметь понятие о взаимной величине двух углов, имеющих разные вершины, накладывают один угол на другой.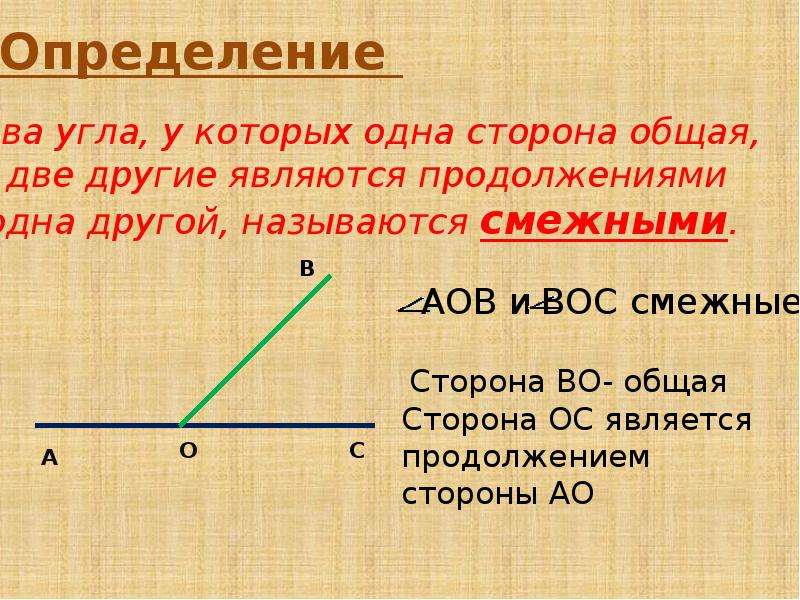 При наложении совмещают их вершины и по одной стороне, тогда направление другой стороны даст возможность сравнивать их величину. Чтобы сравнить два угла ABC и DEF (черт. 15), накладывают угол DEF на угол ABC так, чтобы сторона EF пошла по стороне BC, точка E совмещалась с точкой B; тогда сторона ED может занять три положения: она может совпасть со стороной BA, упасть внутри и вне угла ABC.

a) Если линия ED совпадет с линией BA, углы называются равными

уг. ABC = уг. DEF.

b) Если линия ED упадет внутри угла ABC и займет положение BG, угол ABC будет больше угла DEF

уг. ABC > уг. DEF.

c) Если же линия ED упадет вне угла ABC по направлению BH, угол ABC меньше угла DEF

уг. ABC

Сложение, вычитание, умножение и деление углов.
Два прилежащих угла ABC и CBD (чер. 14) образуют один угол ABC. Угол ABD называется суммой углов ABC и CBD. Это выражают письменно равенством:

∠ABD = ∠ABC + ∠CBD (a)

Из равенства (а) вытекает равенство:

∠ABC = ∠ABD — ∠CBD

∠CBD = ∠ABD — ∠ABC,

т. е. угол ABC есть разность углов ABD и CBD, и угол CBD есть разность углов ABD и ABC.

Если при точке O (черт. 16) находится несколько равных прилежащих углов, т. е. если

∠AOB = ∠BOC = ∠COD = ∠DOE,

то угол AOC, равный сумме углов AOB и BOC равен двум углам AOB,

∠AOC = ∠AOB + ∠BOC, след. ∠AOC = 2AOB.

Угол AOD равен трем углам AOB

Обратно, угол AOB составляет половину угла AOC, треть угла AOD, четверть угла AOE.

AOB = ½ AOC = 1/3 AOD = ¼ AOE.

Отсюда выводим, что углы как величины можно не только складывать и вычитать, но также умножать и делить на отвлеченное число
.

Если из двух прилежащих углов ACD и DCB (чер. 17) две стороны CA и CB лежат на одной прямой, их называют смежными.

. Смежными называются такие углы, у которых одна сторона общая, а две другие лежат на одной прямой.

Если линия CD, поворачиваясь около точки C, займет положение CE, то угол ACD уменьшаясь обратится в угол ACE, а угол BCD увеличиваясь обратится в угол BCE.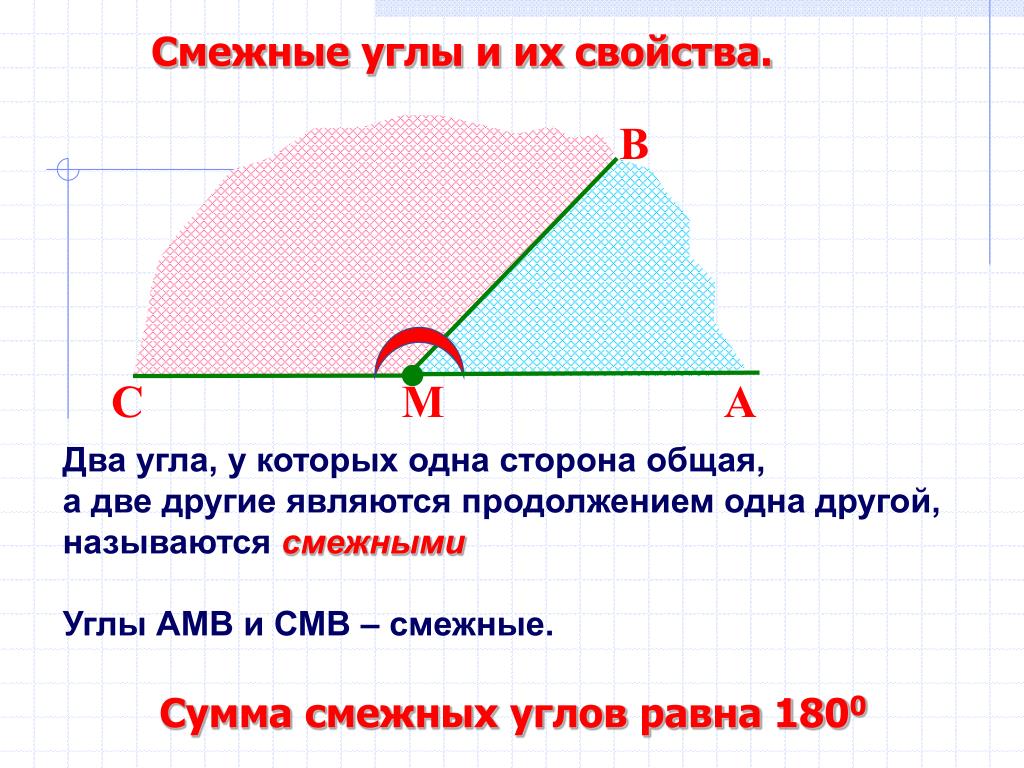 Линия CD, продолжая поворачиваться, может принять такое положение, что два смежных угла сделаются равными. Когда два смежных угла ACD и DCB равны (чер. 18), их называют прямыми углами
.

В этом случае линия CD называется перпендикулярной к линии AB или просто перпендикуляром к линии AB.

На чертеже 19 начерчен один прямой угол без другого смежного с ним.

Прямой угол есть один из равных смежных углов.

Перпендикуляр есть прямая линия, образующая с другой линией прямой угол.

На чертеже 18 углы ACD и DCB, оставаясь смежными и равными, получают название прямых углов. Линия DC будет перпендикулярной к линии AB. Такое взаимное отношение двух линий выражают иногда письменно: CD ⊥ AB.

Так как линия AB будет также перпендикулярна к линии CD, то линия AB и CD будут взаимно-перпендикулярны, т. е. если CD ⊥ AB, то и AB ⊥ CD.

Подошва перпендикуляра
. Точка взаимной встречи двух перпендикулярных линий называется подошвою перпендикуляра.

Точка C (чер. 18) есть подошва перпендикуляра CD.

В каждой точке линии AB можно провести перпендикуляр к линии AB.

Провести перпендикуляр к линии (AB) из точки, лежащей на линии, значит восставить перпендикуляр. Провести же перпендикуляр (DC) к линии (AB) из точки (D), лежащей вне прямой, значит опустить перпендикуляр
(черт. 18).

Наклонная линия

. Всякая линия неперпендикулярная к другой называется линией наклонною к ней.

На чертеже 20 линия CE будет наклона к линии AB, а линия CD перпендикулярна к линии AB.

Угол ECB меньше прямого, а угол ACE больше прямого. Угол ECB называется острым, а угол ACE тупым.

Острый угол
есть всякий угол меньше прямого
, а тупой угол
есть угол больший прямого
.

Одноименные и разноименные углы
. Два острых или два тупых угла называются одноименными, а два угла, из которых один острый, а другой тупой, называются разноименными.

Наклонная линия CE образует (черт.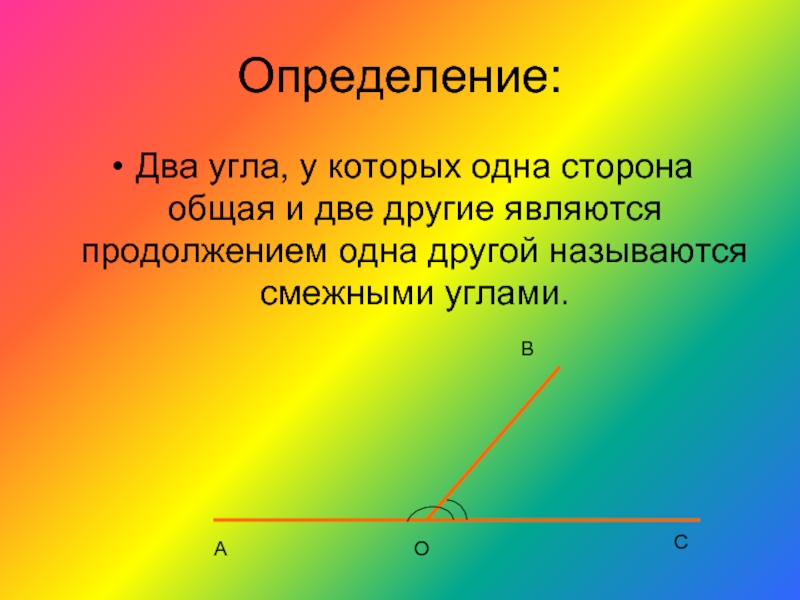 20) с прямою AB два смежных угла, из которых один меньше, а другой больше прямого, т. е. один острый, а другой тупой.

Теорема 3
. Из точки, взятой на прямой линии, можно восставить к ней только один перпендикуляр.

Дана
прямая AB и на ней точка C (черт. 20).

Требуется доказать
, что можно к ней восставить только один перпендикуляр.

Доказательство
. Положим, что можно из точки C к линии AB восставить два перпендикуляра (черт. 20) CD и CE. По свойству перпендикуляра

уг. DCB = уг. ACD (a)
уг. BCE = уг. ACE.

Если приложить к первой части последнего неравенства угол ECD, получим неравенство

уг. BCE + уг. ECD > уг. ACE, или уг. BCD > уг. ACE.

Заменяя в этом неравенстве уг. BCD равным ему углом ACD (a), получим

уг. DCA > уг. ACE,

неравенство очевидно нелепое, ибо часть не может быть более своего целого, следовательно предположение, что можно восставить два перпендикуляра, ведет к нелепости, поэтому оно ложно. Ложность предположения основана на том соображении, что из верного положения нельзя вывести неверного заключения, следовательно, наша теорема верна.

Способ доказывать справедливость данной теоремы указанием на невозможность и нелепость всякого другого предположения называется способом доказательства от противного или способом приведения к нелепости.

Теорема 4
. Все прямые углы равны.

Предположим, мы имеем две пары прямых углов: одну пару составляют углы ACD и DCB, а другую углы EGH и HGF, следовательно, CD ⊥ AB и HG ⊥ EF (черт. 21).

Требуется доказать, что прямые углы равны.

Доказательство
. Наложим линию EF на линию AB точкой G на точку C, тогда линия GH пойдет по линии CD, ибо из точки C можно восставить только один перпендикуляр, следовательно, прямой угол DCB = прямому углу HGF.

Заключение
. Прямой угол есть величина постоянная.

Мера углов
. При измерении углов прямой угол, как величину постоянную, принимают за единицу сравнения. Величину его обозначают буквою d.

В таком случае
всякий острый угол
всякий тупой угол > d.

Все углы выражаются при помощи прямого. Так, например, говорят: данный угол равен ½ d, 2/3 d и т. д.

Теорема 5
. Сумма двух смежных углов равна двум прямым.

Даны смежные углы ACD и DCB (черт. 22).

Требуется доказать, что ACD + DCB = 2d.

Доказательство
. Из точки C восставим перпендикуляр CE, тогда

ACD = ACE + ECD = d + ECD
DCB = ECB — ECD = d — ECD

Сложив эти равенства, имеем:

ACD + DCB = ACE + ECB = 2d (что и требовалось доказать).

Два смежных угла пополняют один другой до двух прямых и потому называются углами дополнительными.

Из теоремы 5 вытекает следствие
. Одна пара смежных углов равна другой паре смежных углов.

Теорема 6
(обратная теореме 5). Если сумма двух прилежащих углов равна двум прямым, то две другие стороны лежат на одной прямой.

Пусть сумма двух прилежащих углов ACD и DCB равна двум прямым (черт. 23).

Требуется доказать, что ACB прямая линия.

Доказательство
. Допустим, что ACB есть ломаная линия и что продолжение линии AC будет линия CE, тогда

Две величины равные одной и той же третьей равны (аксиома 3), следовательно

ACD + DCB = ACD + DCE

откуда выходит при сокращении

заключение нелепое (часть равна целому, см. акс. 1), следовательно линия ACB есть прямая линия (что и требовалось доказать).

Теорема 7
. Сумма углов, имеющих вершину в одной точке и расположенных по одну сторону прямой линии, равна двум прямым.

Даны углы ACD, DCE, ECF, FCG, GCB, имеющие общую вершину в точке C и расположенные по одну сторону прямой AB (черт. 24).

Требуется доказать, что

ACD + DCE + ECF + FCG + GCB = 2d.

Доказательство
. МЫ знаем, что сумма двух смежных углов ACF и FCB равна двум прямым (т. 5).

Так как ACF = ACD + DCE + ECF и FCB = FCG + GCB, то заменяя углы ACF и FCB их величинами, находим:

ACD + DCE + ECF + FCG + GCB = 2d (что и требовалось доказать).

Теорема 8
. Сумма всех углов, расположенных вокруг одной точки, равна четырем прямым.

Даны углы AOB, BOC, COD, DOE, EOA, имеющие общую вершину O и расположенные вокруг точки O (черт. 25).

Требуется доказать, что

AOB + BOC + COD + DOE + EOA = 4d.

Доказательство
. Продолжим сторону EO по направлению OG (чер. 25), тогда

Точно также

GOB + BOC + COD + DOE = 2d.

Сложив эти равенства, имеем:

EOA + AOG + GOB + BOC + COD + DOE = 4d.

Так как AOG + GOB = AOB, то

EOA + AOB + BOC + COD + DOE = 4d (ЧТД).

Угол ACB с углом DCE и угол BCD с углом ACE называются вертикальными (чер. 26).

Вертикальные углы
. Вертикальными называются такие углы, у которых стороны одного составлены из продолжения сторон другого угла.

Теорема 9
. Вертикальные углы равны между собой.

Даны вертикальные углы (чер. 26) ACB и DCE, точно также BCD и ACE.

Требуется доказать, что ACB = DCE и BCD = ACE.

Доказательство
. На основании теоремы 5 имеют место равенства:

ACB + BCD = 2d (как сумма двух смежных углов)
BCD + DCE = 2d

следовательно,

ACB + BCD = BCD + DCE

откуда, отняв по равному углу BCD, находим

Подобным же образом доказывают, что

∠BCD = ∠ACE.

Равносекущая (биссектриса

) есть линия, делящая угол пополам.

На чертеже 27 BD есть биссектриса, если ∠ABD = ∠DBC.

Теорема 10
.

Даны смежные углы ACB и BCD (чер. 28). Их биссектрисы линии CF и CE делят смежные углы BCD и BCA пополам, следовательно BCF = FCD, ACE = ECB.

Требуется доказать, что EC ⊥ CF.

Доказательство
. По условию

ECB = ½ ACB, BCF = ½ BCD

Сложив эти равенства, имеем:

ECB + BCF = ½ ACB + ½ BCD = ½ (ACB + BCD).

Так как ACB + BCD = 2d, то

ECB + BCF = ½ ·
2d = d.

Так как ECB + BCF = ECF, то

Угол ECF прямой, т. е. линии CE и CF взаимно перпендикулярны (ЧТД).

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.

Сумма смежных углов равна 180°

Теорема 1. Сумма смежных углов равна 180°.

Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180°
.

Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.

Вертикальные углы равны

Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).

Теорема 2. Вертикальные углы равны.

Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1
∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.

Отсюда заключаем, что ∠ АОВ = ∠ COD.

Следствие 1. Угол, смежный с прямым углом, есть прямой угол.

Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.

Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.

АН — перпендикуляр к прямой

Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.

Чертежный угольник

Справедлива следующая теорема.

Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).

Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.

Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».

Пример 1.
Один из смежных углов равен 44°. Чему равен другой?

Решение.

Обозначим градусную меру другого угла через x , тогда согласно теореме 1.

44° + х = 180°.

Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.

Пример 2.
Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?

Решение.

Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.

∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.

Пример 3.
Найти смежные углы, если один из них в 3 раза больше другого.

Решение.

Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.

Значит, смежные углы равны 45° и 135°.

Пример 4.
Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.

Решение.

Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1

∠ BOD = ∠ АОС = 180° — 50° = 130°.

краткое содержание других презентаций

«Определение параллельных прямых» — Самостоятельная работа. Задачи. Точка. Урок геометрии. Признаки параллельности прямых. Сумма односторонних углов. Совершенствование навыков доказательства теорем. Параллельные отрезки. Выберите рисунки с пересекающимися прямыми. Решение задач. Рисунки, на которых приведены параллельные лучи. Теорема. Углы. Секущая. Номера рисунков. Определение параллельных прямых.

«Проект «Треугольник»» — Планируемые результаты обучения. Материалы для дифференцированного обучения. Материалы на печатной основе. Программное обеспечение. Методические задачи. Зачем нужно изучать свойства треугольников. Выявление интересов и опыта самих учащихся. Сведения о проекте. Сбор и систематизация информации по теме. Краткое содержание проекта. График оценивания. Какой треугольник можно считать основным. Учебные мероприятия.

««Задачи по геометрии» 7 класс» — Углы. OE – биссектриса. Отрезок АС. AOB = 45. BOC = 23. Начальные геометрические сведения. EDK = 36. Отрезок FD. ABD = 100. Измерение углов. Отрезок AB. OC – биссектриса. Измерение отрезков. ABC = 72. Отрезок MP. Отрезок KE. OD – биссектриса. AOB = 55. Вертикальные углы. Отрезок АD. Отрезок DF. Смежные углы. Отрезок KN.

«Задачи на неравенство треугольника» — Неравенство треугольника. Диагональ. Длина любой стороны треугольника. Противоречие. Отрезок. Четырехугольник. Треугольник. Следствия из неравенства треугольника. Точки внутри четырехугольника. В четырехугольнике любая сторона меньше суммы остальных. Стороны треугольника. Целое число.

«Задачи на готовых чертежах» — Биссектриса. Условия. Угол ВАС. Доказать: FВ ll АС. Задачи на готовых чертежах. Найти: FM. Признаки параллельных прямых. Доказать: a ll b. Найти. Доказать: АB ll DF. Доказать: АК-биссектриса. Найти параллельные прямые. Доказать: АС ll ВD. Cf-биссектриса. Укажите параллельные прямые. Найти условия, при которых AB ll DC. Прямые. Секущая. Доказать:AB ll CD. Доказать: AВ ll CD. Задача. Параллельные прямые.

«Геометрия «Задачи на построение»» — Построение угла. Деление отрезка пополам. Построение угла, равного данному. Задачи на построение. Линейка и циркуль. Построение. Построение перпендикулярной прямой. Искомая прямая. Построение треугольника. Построение биссектрисы угла.

Каждый угол, в зависимости от его величины, имеет своё название:

Два угла называются смежными
, если у них одна сторона общая, а две другие стороны составляют прямую линию:

Углы MOP
и PON
смежные, так как луч OP
— общая сторона, а две другие стороны — OM
и ON
составляют прямую.

Общая сторона смежных углов называется наклонной к прямой
, на которой лежат две другие стороны, только в том случае, когда смежные углы не равны между собой. Если смежные углы равны, то их общая сторона будет перпендикуляром
.

Сумма смежных углов равна 180°.

Два угла называются вертикальными
, если стороны одного угла дополняют до прямых линий стороны другого угла:

Углы 1 и 3, а также углы 2 и 4 — вертикальные.

Вертикальные углы равны.

Докажем, что вертикальные углы равны:

Сумма ∠1 и ∠2 составляет развёрнутый угол. И сумма ∠3 и ∠2 составляет развёрнутый угол. Значит, эти две суммы равны:

∠1 + ∠2 = ∠3 + ∠2.

В этом равенстве слева и справа есть по одинаковому слагаемому — ∠2. Равенство не нарушится, если это слагаемое в левой и в правой части опустить. Тогда мы получаем.

Определение смежных. Смежные и вертикальные углы

Как найти смежный угол?

Математика — древнейшая точная наука, которую в обязательном порядке изучают в школах, колледжах, институтах и университетах. Однако, базовые знания всегда закладываются еще в школе. Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.

Рассмотрим подробнее определение и свойства смежных углов, а также как их вычислить по данным в задаче.

Определение и свойства смежных углов

Два луча, исходящие из одной точки образуют фигуру под названием «плоский угол». При этом эта точка именуется вершиной угла, а лучи являются его сторонами. Если продолжить один из лучей дальше начальной точки по прямой, то образуется еще один угол, который и называется смежным. У каждого угла в этом случае есть два смежных угла, так как стороны угла равнозначны. То есть всегда присутствует еще смежный угол в 180 градусов.

К основным свойствам смежных углов относят

Смежные углы имеют общую вершину и одну сторону;
Сумма смежных углов равна всегда 180 градусам или числу Пи, если вычисление ведется в радианах;
Синусы смежных углов всегда равны;
Косинусы и тангенсы смежных углов равны, но имеют противоположные знаки.

Как найти смежные углы

Обычно даются три вариации задач на нахождение величины смежных углов

Дана величина основного угла;
Дано соотношение основного и смежного угла;
Дана величина вертикального угла.

Каждый вариант задачи имеет свое решение. Рассмотрим их.

Дана величина основного угла

Если в задаче указана величина основного угла, то найти смежный угол очень просто. Для этого достаточно из 180 градусов вычесть величину основного угла, и вы получите величину смежного угла. Данное решение исходит из свойства смежного угла — сумма смежных углов равна всегда 180 градусам.

Если же величина основного угла дана в радианах и в задаче требуется найти смежный угол в радианах, то необходимо вычесть из числа Пи величину основного угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.

Дано соотношение основного и смежного угла

В задаче может быть дано соотношение основного и смежного угла вместо градусов и радиан величины основного угла. В этом случае решение будет выглядеть, как уравнение пропорции:

Обозначаем долю пропорции основного угла, как переменную «Y».
Долю относящуюся к смежному углу обозначаем, как переменную «Х».
Количество градусов, которые приходятся на каждую пропорцию, обозначим, например, «a».
Общая формула будет выглядеть так — a*X+a*Y=180 или a*(X+Y)=180.
Находим общий множитель уравнения «a» по формуле a=180/(X+Y).
Затем полученное значение общего множителя «а» умножаем на долю угла, который необходимо определить.

Таким образом мы можем найти величину смежного угла в градусах. Однако, если необходимо найти величину в радианах, то нужно просто перевести градусы в радианы. Для этого умножаем угол в градусах на число Пи и делим все на 180 градусов. Полученное значение будет в радианах.

Дана величина вертикального угла

Если в задаче не дана величина основного угла, но дана величина вертикального угла, то вычислить смежный угол можно по такой же формуле, что и в первом пункте, где дана величина основного угла.

Вертикальный угол — это угол, который исходит из той же точки, что и основной, но при этом он направлен в строго противоположном направлении. Тем самым получается зеркальное отражение. Это значит, что вертикальный угол по величине равен основному. В свою очередь, смежный угол вертикального угла равен смежному углу основного угла. Благодаря этому можно вычислить смежный угол основного угла. Для этого просто вычитаем из 180 градусов величину вертикального и получаем значение смежного угла основного угла в градусах.

Если же величина дана в радианах, то необходимо вычесть из числа Пи величину вертикального угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.

Также вы можете прочесть наши полезные статьи и .

Что такое смежный угол

рис. 2

На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.

рис. 3

Теорема о смежных углах

Теорема:
сумма смежных углов равна 180°

Определение 1.
Углом называется часть плоскости, ограниченная двумя лучами с общим началом.

Определение 3.
Прямой угол — это угол величиной в 90 градусов.

Определение 4.
Угол, меньший 90 градусов, называется острым углом.

рис. 4

Связь математики с музыкой

«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства.»
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т.е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a: l ,
где а — коэффициент, характеризующий физические свойства струны.

Так же предложу вашему внимаю забавную пародию про спор двух математиков =)

Геометрия вокруг нас

Задание 1.

Задание 2.

Задание 3.

Решение задач

Математический диктант на повторение ранее выученного материала

Решите задачи:

Итог урока

Домашнее задание:

Вопросы:

Что такое угол?
Какие бывают типы углов?
Какая особенность смежных углов?

Предмети > Математика > Математика 7 класс

Два угла размещнные на одной прямой и имеющие одну вершину называются смежными.

Иначе — если сумма двух углов на одной прямой равна 180 градусам и одна сторона у них общая, то это смежные углы.

1 смежный угол + 1 смежный угол = 180 градусов.

Смежные углы -это два угла, у которых одна сторона общая, а две другие стороны в целом образуют прямую линию.

Сумма двух смежных углов всегда равна 180 градусам. К примеру, если один угол 60 градусов, то второй обязательно будет равен 120 градусам (180-60).

Углы АОС и ВОС являются смежными углами, потому что соблюдается все условия характеристики смежных углов:

1.ОС -общая сторона двух углов

2.АО -сторона угла АОС, ОВ -сторона угла ВОС. Вместе эти стороны образуют прямую линию АОВ.

3.Угла два и сумма их равна 180 градусов.

Вспоминая школьный курс геометрии, про смежные углы мы можем сказать следующее:

у смежных углов — одна сторона общая, а другие две стороны принадлежат одной прямой, то есть находятся на одной прямой. Если по рисунку, то углы СОВ и ВОА — это смежные углы, сумма которых всегда равна 180 , так как они разделяют развернутый угол, а развернутый угол всегда равен 180 .

Смежные углы понятие легкое в геометрии. Смежные углы, угол плюс угол дают 180 градусов в общей сумме.

Два смежных угла — это будет один развернутый угол.

Есть еще несколько свойств. Со смежными углами задачи решать и теоремы доказывать легко.

Смежные углы образуются при проведении луча из произвольной точки прямой. Тогда эта произвольная точка оказывается вершиной угла, луч — общей стороной смежных углов, а прямая от которой проведен луч — двумя оставшимися сторонами смежных углов. Смежные углы могут быть как одинаковыми в случае перпендикуляра, так и отличатся при наклонном луче. Легко понять, что сумма смежных углов равна 180 градусов или попросту прямой линии. По другому этот угол можно объяснить простым примером — вы сперва шли в одном направлении по прямой, потом передумали, решили вернуться назад и развернувшись на 180 градусов отправились по той же прямой в обратном направлении.

Итак, что же такое смежный угол? Определение:

Смежными называются два угла с общей вершиной и одной общей стороной, причем две другие стороны этих углов лежат на одной прямой.

И небольшой видео урок, где толково показано про смежные углы, вертикальные углы, плюс про перпендикулярные прямые, которые являются частным случаем смежных и вертикальных углов

Смежные углы — это углы, у которых одна сторона общая, а вторая является одной линией.

Смежные углы — это углы, зависящие друг от друга. То есть если общую строну слегка повернуть, то один угол уменьшится на сколько-то градусов и автоматически второй угол увеличится на столько же градусов. Это свойство смежных углов позволяет в Геометрии решать различные задачи и осуществлять доказательства различных теорем.

Общая же сумма смежных углов всегда равна 180 градусов.

Из курса геометрии, (насколько я помню за 6 класс) смежными называются два угла, у которых одна сторона общая, а другие стороны являются дополнительными лучами, сумма смежных углов равна 180. Каждый из двух смежных углов, дополняет другой до развернутого угла. Пример смежных углов:

Смежные углы это два угла с общей вершиной, одна из сторон которых общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна ста восьмидесяти градусам. А вообще все это очень легко находится в гугле или учебнике геометрии.

Сумма смежных углов равна 180°

Теорема 1. Сумма смежных углов равна 180°.

Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180°
.

Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.

Вертикальные углы равны

Теорема 2. Вертикальные углы равны.

Отсюда заключаем, что ∠ АОВ = ∠ COD.

Следствие 1. Угол, смежный с прямым углом, есть прямой угол.

АН — перпендикуляр к прямой

Чертежный угольник

Справедлива следующая теорема.

Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).

Пример 1.
Один из смежных углов равен 44°. Чему равен другой?

Пример 2.
Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?

Пример 3.
Найти смежные углы, если один из них в 3 раза больше другого.

Пример 4.
Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.

Вопрос 1.
Какие углы называются смежными?
Ответ.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a 1 b) и (a 2 b) смежные. У них сторона b общая, а стороны a 1 и a 2 являются дополнительными полупрямыми.

Вопрос 2.
Докажите, что сумма смежных углов равна 180°.
Ответ.
Теорема 2.1.
Сумма смежных углов равна 180°.
Доказательство.
Пусть угол (a 1 b) и угол (a 2 b) — данные смежные углы (см. рис.31). Луч b проходит между сторонами a 1 и a 2 развёрнутого угла. Поэтому сумма углов (a 1 b) и (a 2 b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.

Вопрос 3.
Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.

Из теоремы 2.1
следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a 1 b) и (c 1 d) равны. Нам нужно доказать, что углы (a 2 b) и (c 2 d) тоже равны.
Сумма смежных углов равна 180°. Из этого следует, что a 1 b + a 2 b = 180° и c 1 d + c 2 d = 180°. Отсюда, a 2 b = 180° — a 1 b и c 2 d = 180° — c 1 d. Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° — a 1 b = c 2 d. По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.

Вопрос 4.
Какой угол называется прямым (острым, тупым)?
Ответ.
Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.

Вопрос 5.
Докажите, что угол, смежный с прямым, есть прямой угол.
Ответ.
Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол: x + 90° = 180°, x= 180° — 90°, x = 90°.

Вопрос 6.
Какие углы называются вертикальными?
Ответ.
Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.

Вопрос 7.
Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство.
Пусть (a 1 b 1) и (a 2 b 2)- данные вертикальные углы (рис. 34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т.е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.

Вопрос 8.
Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ.
Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.

Вопрос 9.
Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ.
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».

Вопрос 10.
Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3.
Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.
Доказательство.
Пусть a — данная прямая и A — данная точка на ней. Обозначим через a 1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.

Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Углы (a 1 b 1) и (a 1 c 1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a 1 . Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.

Вопрос 11.
Что такое перпендикуляр к прямой?
Ответ.
Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием
перпендикуляра.

Вопрос 12.
Объясните, в чём состоит доказательство от противного.
Ответ.
Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.

Вопрос 13.
Что называется биссектрисой угла?
Ответ.
Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Определение многоугольника

Рассмотрим n отрезков

[A₁ A₂], [A₂ A₃], … , [A_n A_{n +1}]

(1)

причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.1).

Рис. 1

Определение 1. Ломаной линией с n звеньями называют фигуру L, составленную из отрезков (1), то есть фигуру, заданную равенством

L = [A₁ A₂] U [A₂ A₃] U …
… U [A_n A_{n +1}]

В случае, когда точки A₁ и A_{n +1} совпадают, ломаную линию называют замкнутой ломаной линией (рис. 2), в противном случае её называют незамкнутой (рис.1).

Рис. 2

Определение 2. Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией без самопересечений (рис. 3). Отрезки, составляющие ломаную линию (звенья), называют сторонами многоугольника. Концы отрезков называют вершинами многоугольника.

Рис. 3

Определение 3. Многоугольник называют n – угольником, если он имеет n сторон.

Таким образом, многоугольник, имеющий 3 стороны, называют треугольником, многоугольник, имеющий 4 стороны, называют четырёхугольником и т.д.

Определение 4 . Периметром многоугольника называют сумму длин всех сторон многоугольника.

Величину, равную половине периметра, называют полупериметром.

Диагонали n — угольника

Фигура	Рисунок	Описание
Диагональ многоугольника		Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника
Диагонали n – угольника, выходящие из одной вершины		Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника
Все диагонали n – угольника		Число диагоналей n – угольника равно

Диагональ многоугольника

Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника

Диагонали n – угольника, выходящие из одной вершины

Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника

Все диагонали n – угольника

Число диагоналей n – угольника равно

Внешний угол многоугольника

Определение 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).

Рис.1

Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).

Рис.2

Замечание. Мы рассматриваем только выпуклые многоугольникивыпуклые многоугольники.

Свойства углов треугольника

Фигура

Рисунок

Формулировка теоремы

Углы треугольника

Сумма углов треугольника равна 180°

α + β + γ = 180°

Посмотреть доказательство

Внешний угол треугольника

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним

δ = α + β

Посмотреть доказательство

Свойства углов многоугольника

Свойства углов правильного n – угольника

Доказательства свойств углов многоугольника

Теорема 1. В любом треугольнике сумма углов равна 180°.

Доказательство. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).

Рис.3

Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.

Теорема 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Доказательство. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).

Рис.4

Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные. Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.

Замечание. Теорема 1 является следствием теоремы 2.

Теорема 3. Сумма углов n – угольника равна

Доказательство. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).

Рис.5

Получим n треугольников:

OA₁A₂, OA₂A₃, … OA_nA₁

Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна

что и требовалось доказать.

Теорема 4. Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°.

Доказательство. Рассмотрим рисунок 6.

Рис.6

В соответствии рисунком 6 справедливы равенства

Теорема доказана.

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Что такое смежные углы? [Примеры вопросов]

Обзор смежных углов

Определение:

В геометрии два угла смежные , если у них общая сторона и общая вершина. Другими словами, смежные углы находятся непосредственно рядом друг с другом и не перекрываются.

Примеры вопросов по соседним углам

Примеры:

В нашем первом примере ∠a находится рядом с b. У них общая вершина — угловая точка A.У них также есть общая сторона — линия AD. A и ∠b соединены линией AD, но не перекрываются.

Во втором примере мы видим ∠1, ∠2 и ∠3. Мы видим, что 1 и ∠2 смежны, поскольку имеют общую вершину и общую сторону. То же самое мы видим с ∠2 и ∠3, которые также имеют общую вершину и одну сторону. Рассмотрим ∠1 и ∠3. Хотя они имеют общую вершину, они не являются смежными, потому что у них нет общей стороны.

В нашем последнем примере мы видим два угла, ∠1 и ∠2.Оба угла имеют одну сторону, линию BC. Однако эти углы не являются смежными, потому что у них нет общей вершины.

Как определить, являются ли два угла смежными?

Основываясь на нашем определении и приведенных выше примерах, мы можем сделать вывод, что все пары смежных углов имеют два общих свойства: (1) общая вершина и (2) общая сторона. Если в них отсутствует один из этих компонентов, они не являются смежными. Мы можем классифицировать пары углов как смежные или несмежные, просматривая эти два свойства.

Между парами углов существует множество особых отношений. Определение смежных углов поможет вам распознать другие угловые отношения, такие как дополнительные и дополнительные углы.

Примеры вопросов по соседним углам

Вот несколько примеров вопросов по соседним углам.

Вопрос № 1:

Какое из следующих утверждений верно?

1 и ∠4 прилегают друг к другу

∠3 и ∠4 примыкают

∠1 и ∠2 не примыкают

82 и ∠3 прилегают

Показать ответ Вопрос № 5:

Кейша и Джеймс смотрит на карту городских улиц и замечает множество прилегающих углов.Джеймс рисует показанное изображение, чтобы проиллюстрировать найденные углы. Кейша указывает, что ∠AOE и ∠COD смежны, потому что у них общая вершина и одна сторона. Джеймс не согласен. Он говорит, что у этих углов нет общей стороны. Кто прав и почему?

Джеймс прав, потому что оба угла имеют одну и ту же вершину, но не имеют общей стороны.

Кейша верна, потому что оба угла имеют общую вершину O и линию AD.

Джеймс неверен, потому что ∠AOE и ∠COD не имеют одинаковых вершин.

Кейша неверно, потому что на карте нет ∠AOE.

Показать ответ

Вернуться к математике Примеры вопросов

Смежные углы — определение, свойства, примеры

Угол образован двумя лучами, встречающимися в общей конечной точке. Два угла называются смежными, если у них есть общее плечо (сторона) и общая вершина. Например, два кусочка пиццы рядом друг с другом в коробке для пиццы образуют пару смежных углов, когда мы отслеживаем их стороны.

Что такое смежные углы?

Два угла называются смежными углами, если они не перекрываются, у них общая вершина, у них общая сторона или луч, а другие стороны двух углов должны лежать на противоположных сторонах общей стороны.
Посмотрите на изображения ниже, чтобы получить четкое представление о прилегающих углах. Углы 1 и 2 смежны, поскольку имеют общую сторону BD и общую вершину B.

Свойства прилегающих углов

Следующие свойства, перечисленные ниже, помогают нам легко определять смежные углы.

У них общая рука.
У них общая вершина.
Они не пересекаются.
У них нет общей внутренней точки.
У них по обеим сторонам от общего плеча по одной руке.
Два смежных угла могут быть дополнительными или дополнительными в зависимости от суммы размеров отдельных углов.

Важные примечания

Ниже приведены важные примечания, касающиеся прилегающих углов.

Если два угла являются смежными, то их сумма равна углу, образованному двумя несовпадающими плечами и одним общим плечом.
Если луч стоит на прямой, то сумма углов между соседними углами равна 180 °.
Если сумма двух смежных углов равна 180 °, они называются линейной парой углов. Все линейные пары являются дополнительными, поскольку сумма дополнительных углов составляет 180 °. Однако все дополнительные углы не обязательно должны быть линейными парами. Чтобы образовать линейную пару, линии должны пересекаться друг с другом и образовывать смежные углы.
Если сумма двух смежных углов равна 180 °, то несхожие ветви образуют линию.

Статьи по смежным углам

Прочтите эти интересные статьи, чтобы узнать больше о смежных углах и связанных с ними темах.

Часто задаваемые вопросы о прилегающих углах

Могут ли 2 смежных угла быть дополнительными?

Смежные углы можно определить как два угла, которые имеют общую вершину и общую сторону. Два соседних угла могут быть дополнительными углами или дополнительными углами в зависимости от суммы измерения углов.

Могут ли быть смежными вертикальные углы?

Нет, вертикальные углы никогда не могут быть смежными. Смежные углы — это два угла, расположенные рядом друг с другом, в то время как вертикальные углы противоположны друг другу.

Что такое смежные углы в геометрии?

Смежные углы — это два угла, которые имеют общую вершину и общую сторону. Сумма двух смежных углов может быть дополняющей или дополняющей в зависимости от их размера.

Приведите несколько примеров смежных углов в повседневной жизни?

Руль машины, открытый шкаф, три стрелки часов, два кусочка пиццы рядом друг с другом в коробке для пиццы.примеры смежных углов в повседневной жизни.

Могут ли 2 смежных угла перекрываться?

Нет. Углы, расположенные рядом друг с другом на одной вершине и имеющие одну сторону, являются смежными углами. Следовательно, смежные углы не могут находиться один над другим, или, другими словами, углы не могут перекрываться.

Что такое прилегающие углы? | Определение и примеры

Содержание

Определение смежных углов
Линейные пары
Параллельные и поперечные линии
Примеры прилегающих углов

Определение соседних углов

Смежные углы — это пара углов, имеющих общую сторону и вершину.

Три особенности позволяют легко выделить смежные углы:

Соседние углы существуют в виде пар
У них общая вершина
У них общая сторона

Если два угла имеют только общую вершину, то это вертикальные углы. Вертикальные углы — это пара противоположных углов, образованных двумя пересекающимися линиями.

Что такое общая вершина?

Общая вершина — это вершина, общая для двух углов.Вершиной называется точка пересечения любых двух линейных построений.

Вы можете смешивать и сопоставлять их, чтобы создать вершин (множественное число вершин) разными способами:

Вы видите вершины в углах многоугольников, как центральные углы в кругах, и когда линейные конструкции, такие как параллельные линии и трансверсали, пересекаются.

Что такое общая сторона в геометрии?

Общая сторона — это одна линия, луч или линейный сегмент, используемые для создания двух углов, разделяющих одну и ту же вершину.Оба угла используют общую сторону и одну другую сторону.

Соседние углы всегда парные и никогда не перекрываются.

Давайте посмотрим, как одна вершина квадрата может демонстрировать смежные углы.

Здесь у нас есть простой квадрат, образованный четырьмя сторонами, образующими четыре вершины: ∠W, ∠H, ∠I и ∠Z.

Если мы соединим точку W с точкой I, мы построим диагональ WI. Это создает два дополнительных угла в точке W:

∠ZWI
∠HWI

Обратите внимание, что оба этих угла имеют общую вершину в точке W и общую сторону, отрезок WI.Углы ∠ZWI и ∠HWI — смежные углы.

Линейные пары

Когда пара смежных углов образует прямую линию или прямой угол, они образуют линейную пару. Сумма их углов составляет 180 ° или π радиан.

Углы, которые в сумме составляют 180 °, называются дополнительными углами.

Вот линейная пара. Посмотрите, сможете ли вы определить общую сторону и общую вершину:

Луч AT — это общий луч обоих углов. Вы идентифицировали ∠A как общую вершину?

Вот параллельные прямые CP и MN, пересеченные поперечной IK.Там, где поперек пересекает их, у нас есть точки H и U:

Эта конструкция не только образует восемь пар углов (смежных углов), но все эти пары также являются линейными парами! Какие углы являются смежными?

CHI и ∠PHI
CHI и ∠CHU
PHI и ∠PHU
CHU и ∠PHU
∠MUK и ∠NUK
∠MUH и ∠NUH
MUH и ∠MUK
∠NUH и ∠NUK

Это все примеры смежных углов.

Примеры прилегающих углов

12 мая — день рождения Марьям Мирзахани, известного математика, изучавшего особый вид геометрии, называемый гиперболической геометрией. Чтобы отметить ее работу, ваш математический клуб испечет именинный торт, а вам поручат разрезать его на восьмые части:

Все ли углы торта Марьям смежные?

Ну нет. ∠IMY смежна как с ∠RMI, так и с ∠YMN, но обратите внимание, что RMI не смежна с ∠YMN, даже если оба угла имеют общую вершину M.

Угловые отношения, такие как смежные углы, должны иметь как общую вершину (точка M), так и общую сторону. ∠RMI не имеет общей стороны с ∠YMN.

Сможете ли вы найти линейные пары в торте Марьям? Мы надеемся на это! На каждый диаметр торта Марьям приходится трех линейных пар !

Чтобы убедиться в этом, мы можем взять в качестве примера только один отрезок линии YA. Вы можете построить прямую YA с помощью этих трех линейных пар:

YMI и ∠IMA
∠YMR и ∠RMA
YMZ и ZMA

Смежные углы — это два угла с общей вершиной и общей стороной.Они появляются во многих местах, но выделяются параллельными линиями, пересеченными поперечными линиями.

Узнайте больше о различных типах углов, таких как внутренние углы, внешние углы и дополнительные углы.

Следующий урок:

коллинеарных точек

смежных углов

Covid-19 привел мир к феноменальному переходу.

За электронным обучением будущее уже сегодня.

Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!

Смежные углы: Два угла в плоскости называются смежными углами, если

1) они имеют общую вершину,

2) они имеют общие плечи (лучи) и

3) их другие плечи лежат на противоположных сторонах общей руки.

На приведенном выше рисунке ∠ AOC и ∠ BOC имеют общую вершину O. Также у них есть общая рука OC, а их руки — OA и OB.

Итак, ∠AOC и ∠BOC являются углами смежности.

∠AOB = ∠AOC + ∠BOC

Примеры:

1) Запишите каждую пару смежных углов из диаграммы, приведенной ниже:

Решение:
i) ∠AOB, ∠BOC ( общий луч — это OB и O — общая вершина)

ii) ∠AOC, ∠COD (общий луч — это OC, а O — общая вершина)

iii) ∠BOC, ∠COD (общий луч — это OC, а O — это общая вершина). общая вершина)

iv) ∠AOB, ∠BOD (общий луч — это OB, а O — общая вершина)

_________________________________________________________________
2) AOC и ∠BOC — смежные углы.Если m∠AOB = 75 ⁰,
∠AOC = 30 ⁰, тогда найдите m∠BOC.

Решение:
Поскольку ∠AOC и ∠BOC являются смежными углами.

∴∠AOB = ∠AOC + ∠BOC

75 ⁰ = 30 + ∠BOC

∴ BOC = 75-30

∴ ∠BOC = 45 ⁰

_________________________________________________________________
3) Сумма Два соседних угла составляют 110 ⁰. Если один угол на 30 ⁰ больше, чем другой.Найдите размеры двух углов.
Решение:
Пусть один угол равен x.
Другой угол = x + 30
Сумма двух углов = 110 ⁰
∴ x + x + 30 = 110
⇒ 2x + 30 = 110
⇒ 2x = 110-30
⇒ 2x = 80
⇒ x = 80 / 2 = 40
Один угол = 40 ⁰
Итак, другой угол = x + 30
⇒ другой угол = 40 + 30 = 70 ⁰
∴ Два угла: 40 ⁰ и 70 ⁰.
___________________________________________________________________
Базовая геометрия

• Точка
• Линии
• Углы
• Прямые и углы
• Дополнительные углы
• Дополнительные углы
• Вертикально противоположные углы
• Линейные парные углы
• Смежные углы
• Параллельные линии
• Решенные проблемы на пересекающихся линиях
• Решенные проблемы на параллельных линиях

Домашняя страница

Covid-19 повлиял на физическое взаимодействие между людьми.

Не позволяйте этому влиять на ваше обучение.

% PDF-1.4
%
470 0 объект
>
эндобдж

xref
470 349
0000000016 00000 н.
0000008680 00000 н.
0000008765 00000 н.
0000009003 00000 н.
0000010824 00000 п.
0000010871 00000 п.
0000010918 00000 п.
0000010965 00000 п.
0000011012 00000 п.
0000011058 00000 п.
0000011106 00000 п.
0000011153 00000 п.
0000011200 00000 п.
0000011247 00000 п.
0000011293 00000 п.
0000011340 00000 п.
0000011387 00000 п.
0000011434 00000 п.
0000011487 00000 п.
0000011533 00000 п.
0000011611 00000 п.
0000011687 00000 п.
0000011764 00000 п.
0000012066 00000 п.
0000012402 00000 п.
0000012728 00000 п.
0000013118 00000 п.
0000013508 00000 п.
0000013898 00000 п.
0000014323 00000 п.
0000014371 00000 п.
0000014419 00000 п.
0000014465 00000 п.
0000014511 00000 п.
0000014558 00000 п.
0000014605 00000 п.
0000014652 00000 п.
0000014698 00000 п.
0000040827 00000 н.
0000041139 00000 п.
0000041436 00000 п.
0000042089 00000 п.
0000042664 00000 п.
0000042982 00000 п.
0000043154 00000 п.
0000043799 00000 п.
0000044050 00000 п.
0000044574 00000 п.
0000044674 00000 п.
0000045109 00000 п.
0000045447 00000 п.
0000045522 00000 п.
0000045580 00000 п.
0000045640 00000 п.
0000067487 00000 п.
0000093425 00000 п.
0000094208 00000 п.
0000094314 00000 п.
0000094925 00000 п.
0000095035 00000 п.
0000095072 00000 п.
0000120845 00000 н.
0000146881 00000 н.
0000147402 00000 н.
0000173493 00000 н.
0000174114 00000 н.
0000174320 00000 н.
0000174490 00000 н.
0000174786 00000 н.
0000174845 00000 н.
0000175219 00000 н.
0000175874 00000 н.
0000177057 00000 н.
0000177404 00000 н.
0000177779 00000 н.
0000177830 00000 н.
0000178095 00000 н.
0000204175 00000 н.
0000204954 00000 н.
0000205126 00000 н.
0000205388 00000 н.
0000205649 00000 н.
0000230277 00000 н.
0000232969 00000 н.
0000233021 00000 н.
0000238969 00000 н.
0000244824 00000 н.
0000245007 00000 н.
0000245059 00000 н.
0000246014 00000 н.
0000247970 00000 п.
0000258236 00000 н.
0000259673 00000 н.
0000263520 00000 н.
0000269426 00000 н.
0000272159 00000 н.
0000276111 00000 н.
0000278576 00000 н.
0000281416 00000 н.
0000282144 00000 н.
0000282916 00000 н.
0000282987 00000 н.
0000283073 00000 н.
0000283177 00000 н.
0000283316 00000 н.
0000283393 00000 н.
0000283464 00000 н.
0000283577 00000 н.
0000283666 00000 н.
0000283755 00000 н.
0000283915 00000 н.
0000284517 00000 н.
0000284691 00000 н.
0000284801 00000 п.
0000284999 00000 н.
0000285243 00000 н.
0000285359 00000 н.
0000285436 00000 н.
0000287402 00000 н.
0000287684 00000 н.
0000287801 00000 н.
0000289013 00000 н.
0000289265 00000 н.
0000289625 00000 н.
00002

00000 н.
00002

00000 н.
0000335400 00000 н.
0000335439 00000 н.
0000376835 00000 н.
0000376874 00000 н.
0000418716 00000 н.
0000418755 00000 н.
0000418825 00000 н.
0000418914 00000 н.
0000419063 00000 н.
0000419136 00000 п.
0000419209 00000 н.
0000419318 00000 н.
0000419467 00000 н.
0000419540 00000 н.
0000419613 00000 н.
0000419722 00000 н.
0000419872 00000 н.
0000419945 00000 н.
0000420018 00000 н.
0000420127 00000 н.
0000420275 00000 н.
0000420348 00000 н.
0000420421 00000 н.
0000420530 00000 н.
0000420680 00000 н.
0000420753 00000 н.
0000420826 00000 н.
0000420935 00000 н.
0000421085 00000 н.
0000421158 00000 н.
0000421231 00000 н.
0000421340 00000 н.
0000421488 00000 н.
0000421561 00000 н.
0000421634 00000 н.
0000421743 00000 н.
0000421893 00000 н.
0000421966 00000 н.
0000422039 00000 н.
0000422148 00000 н.
0000422298 00000 н.
0000422370 00000 н.
0000422443 00000 н.
0000422552 00000 н.
0000422701 00000 н.
0000422774 00000 н.
0000422847 00000 н.
0000422956 00000 н.
0000423105 00000 п.
0000423178 00000 п.
0000423249 00000 н.
0000423358 00000 п.
0000423507 00000 н.
0000423580 00000 н.
0000423653 00000 п.
0000423762 00000 н.
0000423912 00000 н.
0000423985 00000 п.
0000424057 00000 н.
0000424166 00000 н.
0000424316 00000 н.
0000424389 00000 п.
0000424461 00000 н.
0000424570 00000 н.
0000424719 00000 н.
0000424792 00000 н.
0000424865 00000 н.
0000424974 00000 н.
0000425124 00000 н.
0000425197 00000 н.
0000425270 00000 н.
0000425379 00000 н.
0000425527 00000 н.
0000425599 00000 н.
0000425672 00000 н.
0000425781 00000 п.
0000425931 00000 н.
0000426004 00000 н.
0000426077 00000 н.
0000426186 00000 п.
0000426334 00000 н.
0000426407 00000 н.
0000426480 00000 н.
0000426589 00000 н.
0000426739 00000 н.
0000426812 00000 н.
0000426885 00000 н.
0000426994 00000 н.
0000427144 00000 н.
0000427217 00000 н.
0000427290 00000 н.
0000427399 00000 н.
0000427548 00000 н.
0000427621 00000 н.
0000427694 00000 н.
0000427803 00000 н.
0000427951 00000 н.
0000428024 00000 н.
0000428097 00000 п.
0000428206 00000 н.
0000428356 00000 п.
0000428429 00000 н.
0000428502 00000 н.
0000428611 00000 н.
0000428760 00000 н.
0000428833 00000 н.
0000428906 00000 н.
0000429015 00000 н.
0000429165 00000 н.
0000429238 00000 п.
0000429311 00000 п.
0000429420 00000 н.
0000429569 00000 н.
0000429642 00000 н.
0000429715 00000 н.
0000429824 00000 н.
0000429973 00000 н.
0000430046 00000 н.
0000430119 00000 п.
0000430228 00000 н.
0000430378 00000 п.
0000430451 00000 п.
0000430524 00000 н.
0000430633 00000 п.
0000430782 00000 н.
0000430855 00000 н.
0000430928 00000 п.
0000431037 00000 н.
0000431187 00000 н.
0000431260 00000 н.
0000431333 00000 н.
0000431442 00000 н.
0000431592 00000 н.
0000431665 00000 н.
0000431738 00000 н.
0000431847 00000 н.
0000431997 00000 н.
0000432070 00000 н.
0000432143 00000 н.
0000432252 00000 н.
0000432402 00000 н.
0000432474 00000 н.
0000432546 00000 н.
0000432655 00000 н.
0000432805 00000 н.
0000432877 00000 н.
0000432948 00000 н.
0000433057 00000 н.
0000433206 00000 н.
0000433268 00000 н.
0000433339 00000 н.
0000433448 00000 н.
0000433598 00000 н.
0000433669 00000 н.
0000433740 00000 н.
0000433811 00000 п.
0000433940 00000 н.
0000434094 00000 н.
0000434581 00000 п.
0000434730 00000 н.
0000435354 00000 п.
0000435504 00000 н.
0000435575 00000 н.
0000435645 00000 н.
0000435754 00000 п.
0000435908 00000 н.
0000435970 00000 н.
0000436079 00000 п.
0000436230 00000 н.
0000436303 00000 п.
0000436376 00000 п.
0000436485 00000 н.
0000436635 00000 н.
0000437087 00000 н.
0000437193 00000 п.
0000437266 00000 н.
0000437339 00000 п.
0000437448 00000 н.
0000437597 00000 п.
0000437670 00000 н.
0000437743 00000 н.
0000437852 00000 н.
0000438002 00000 н.
0000438073 00000 н.
0000438146 00000 п.
0000438255 00000 н.
0000438404 00000 п.
0000438477 00000 н.
0000438550 00000 н.
0000438659 00000 н.
0000438809 00000 п.
0000441502 00000 н.
0000441714 00000 н.
0000441917 00000 н.
0000442215 00000 н.
0000442477 00000 н.
0000442732 00000 н.
0000443105 00000 н.
0000444877 00000 н.
0000449820 00000 н.
0000449987 00000 н.
0000450730 00000 н.
0000450975 00000 н.
0000454801 00000 п.
0000455049 00000 н.
0000455306 00000 п.
0000456702 00000 н.
0000456884 00000 н.
0000457267 00000 н.
0000457438 00000 п.
0000458023 00000 н.
0000459387 00000 н.
0000459869 00000 н.
0000461440 00000 н.
0000462919 00000 н.
0000463128 00000 п.
0000465278 00000 н.
0000465623 00000 н.
0000465835 00000 н.
0000466091 00000 н.
0000466346 00000 н.
0000007276 00000 н.
трейлер
] / Назад 3187644 >>
startxref
0
%% EOF

818 0 объект
> поток
h ޴ UPSG =! грамм
Q (Z ~ b% H-TQ, FqE- ~ R
`qPBX * # * T ڢ uXtzwwmr6
WA

Прилегающий угол — определение, примеры и многое другое

Смежные углы — это два угла, которые имеют общую вершину и общую сторону.Вершина угла — это конечная точка лучей, образующих стороны угла. Когда мы говорим «общая вершина» и «общая сторона», мы имеем в виду, что вершина и сторона являются общими для двух углов. Мера вращения луча, когда он вращается вокруг своей конечной точки, известна как угол, образованный лучом между его начальным и конечным положением.

Иногда в геометрии используется пара углов. Существуют различные виды пар углов, такие как дополнительные углы, дополнительные углы, смежные углы, линейные пары углов, противоположные углы и т. Д.В этой статье мы собираемся подробно обсудить определение смежных углов и вертикальных углов.

Что такое соседние углы или Определение соседних углов?

Два угла называются смежными, если они имеют общую вершину и сторону. Концы луча со стороны угла называются вершиной угла. Смежные углы могут быть дополнительным углом или дополнительным углом, если они имеют общую вершину и сторону.

На рисунке выше два угла ∠BAC и ∠CAD имеют общую сторону (синий отрезок линии AC). У них также есть общая вершина (точка A). Поэтому их называют «смежными углами». Очевидно, что больший угол ∠BAD является суммой двух соседних углов.

Они не перекрывают друг друга

Два перекрывающихся угла, один внутри другого, имеющих общую сторону и вершину на рисунке справа, два угла ∠PSQ и ∠PSR перекрываются.Хотя они имеют общую сторону (PS) и общую вершину (S), они не считаются смежными углами, когда они перекрываются таким образом. Смежные углы должны располагаться рядом друг с другом, а не один над другим.

Они не перекрываются.

Другой способ их определения: «два угла, которые имеют общую сторону и вершину, но не имеют общих внутренних точек».

в полигонах

Многоугольник, показывающий его внутренние углы, и метка, указывающая на два, которые примыкают к другому использованию этого термина, относятся к внутренним углам многоугольника.

В многоугольниках

Любые два внутренних угла, которые имеют общую сторону, называются «смежными внутренними углами» многоугольника или просто «смежными углами». Здесь слово «смежные» используется в обычном английском значении «рядом друг с другом».

Прилегающие дополнительные углы

Определение: два угла, которые в сумме составляют 180 °

Два угла изменятся так, что они всегда будут складываться в 180 °

На рисунке выше два угла ∠PQR и ∠JKL являются дополнительными, потому что они всегда складываются в 180 °.

Прилегающий дополнительный угол

Два угла вместе составляют пары углов . Иногда размеры этих углов образуют особую взаимосвязь. Одно особое отношение называется дополнительными углами. Дополнительные углы — это пары углов, которые в сумме составляют ровно 90o. Другими словами, при соединении два угла образуют прямой угол.

Ниже приведены некоторые пары дополнительных углов.

Несмежный угол

У них одна и та же вершина и одна общая сторона.

На рисунке ∠1 и ∠3 — несмежные углы.

У них общая вершина, но не общая сторона.

Углы ∠1 и ∠2 — несмежные углы.

У них общая сторона, но не общая вершина.

Равен ли прилегающий угол 180?

А и Б — углы смежные. Смежные углы в сумме составляют 180 градусов. В сумме это 180 градусов (E и C также являются внутренними). Любые два угла, которые в сумме составляют 180 градусов, называются дополнительными углами.

Что такое смежные стороны и прилегающий угол?

Соседние стороны.Определение: две линии, которые пересекаются в вершине многоугольника. Обычно встречаются в треугольниках и других многоугольниках, две стороны, которые встречаются в вершине многоугольника, называются смежными сторонами.

Могут ли 2 тупых угла быть смежными?

Могут ли быть смежными два тупых угла? Да. Два тупых угла могут быть смежными. Другими словами, это между прямым и прямым углом.

Всегда ли равны прилегающие углы?

Вертикальные углы всегда совпадают, что означает, что они равны.Смежные углы — это углы, выходящие из одной вершины. Смежные углы имеют общий луч и не перекрываются.

Могут ли два соседних угла быть дополнительными?

Смежные углы — это два угла, которые имеют общую вершину, общую сторону и не имеют общих внутренних точек. Если два угла образуют линейную пару, они являются дополнительными. Линейная пара образует прямой угол, который содержит 180 градусов, поэтому у вас есть 2 угла, меры которых складываются в 180, что означает, что они являются дополнительными.

Могут ли 2 соседних угла быть дополнительными?

Два соседних угла тоже могут дополнять друг друга, если в сумме они составляют 90 °. В прямоугольном треугольнике высота от прямоугольной вершины разделит прямой угол на два смежных угла; 30 ° + 60 °, 40 ° + 50 ° и т. Д. Эти прилегающие углы дополняют друг друга. Два соседних угла тоже могут быть дополнительными, если они складываются до 180 °.

Сообщение навигации

Как распознать смежные дополнительные углы

В геометрии мы даем разные названия различным типам углов в зависимости от меры данного угла: прямые углы, смежные дополнительные углы, вертикальные углы.Но как мы узнаем, что есть что?

Начнем с основ.

Если угол составляет ровно 90 градусов, он называется прямым углом. Если угол меньше 90 градусов, это острый угол. Угол больше 90 градусов — тупой угол. Если угол равен 180 градусам, он называется прямым углом.

Также даны названия парам углов.

Вертикальные углы или противоположные углы — это два угла, прямо противоположных друг другу при пересечении двух прямых линий (Рисунок 1).

Дополнительные углы — это два угла, которые в сумме составляют 90 градусов (рисунок 2).

Дополнительные углы — это два угла, которые в сумме составляют 180 градусов (Рисунок 3).

Сравнение соседних углов и несмежных углов

Углы являются смежными, если у них общая сторона и общая вершина.

Углы 1 и 2 несмежны, а углы 3 и 4 — имеют общую сторону и вершину.

Определены смежные дополнительные углы

Теперь, когда мы понимаем определения смежных и несмежных углов, мы можем видеть, что смежные дополнительные углы — это два угла, которые имеют общую сторону, а вершины и составляют в сумме 180 градусов.

Используя это определение, посмотрите на диаграмму ниже, чтобы увидеть, какие углы являются смежными дополнительными.

Углы ABC и ABD смежны, поскольку они имеют общий сегмент AB и вершину B.

Углы EFG и HIJ не являются смежными, потому что у них нет общей стороны.

Однако угол в обеих парах дополнительных углов (ABC и ABD, EFG и HIJ) по-прежнему равен 180 градусам.

Для обзора, это означает, что EFG и HIJ являются дополнительными углами.Однако только ABC и ABD являются смежными дополнительными углами.

Распознавание смежных дополнительных углов

Напомним, что смежные дополнительные углы не только имеют общую сторону и вершину, но и составляют в сумме 180 градусов. Эти углы обычно появляются в доказательствах геометрии, поэтому, если вы не уверены, ищите прямую линию, пересекаемую другим отрезком, причем два угла имеют общую сторону и вершину.

Что такое смежные углы: определение, теорема, свойства

Определение смежных углов

Теорема о смежных углах

Тригонометрические свойства смежных углов

Смежные углы | Треугольники

Смежные и вертикальные углы.

Что такое смежный угол

Что такое прилегающие углы. Вертикальные углы. Что такое смежный угол

Что такое смежный угол

Теорема о смежных углах

Геометрия вокруг нас

Решение задач

Математический диктант на повторение ранее выученного материала

Итог урока

Определение смежных. Смежные и вертикальные углы

Определение и свойства смежных углов

Как найти смежные углы

Дана величина основного угла

Дано соотношение основного и смежного угла

Дана величина вертикального угла

Что такое смежный угол

Теорема о смежных углах

Геометрия вокруг нас

Решение задач

Математический диктант на повторение ранее выученного материала

Итог урока

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Определение многоугольника

Диагонали n — угольника

Внешний угол многоугольника

Свойства углов треугольника

Свойства углов многоугольника

Свойства углов правильного n – угольника

Доказательства свойств углов многоугольника

Что такое смежные углы? [Примеры вопросов]

Обзор смежных углов

Смежные углы — определение, свойства, примеры

Что такое смежные углы?

Свойства прилегающих углов

Статьи по смежным углам

Часто задаваемые вопросы о прилегающих углах

Могут ли 2 смежных угла быть дополнительными?

Могут ли быть смежными вертикальные углы?

Что такое смежные углы в геометрии?

Приведите несколько примеров смежных углов в повседневной жизни?

Могут ли 2 смежных угла перекрываться?

Что такое прилегающие углы? | Определение и примеры

Содержание

Определение соседних углов

Что такое общая вершина?

Что такое общая сторона в геометрии?

Линейные пары

Примеры прилегающих углов

Следующий урок:

смежных углов

Прилегающий угол — определение, примеры и многое другое

Сообщение навигации

Как распознать смежные дополнительные углы

Сравнение соседних углов и несмежных углов

Определены смежные дополнительные углы

Распознавание смежных дополнительных углов

Дополнительные домашние задания по математике

Добавить комментарий Отменить ответ