Содержание
Глава 4 Измерение Земли. Том 38. Измерение мира. Календари, меры длины и математика
Глава 4
Измерение Земли
Изучение движения небесных тел помогло определить единицы измерения времени, однако человека также интересовали очертания и размеры мира, в котором он жил, и он захотел измерить Землю. Птолемей не только внес вклад в измерение небес, но и стал непререкаемым авторитетом во всем, что касалось измерения Земли, описав в своей «Географии» весь известный мир своего времени. В XV–XVI веках, с открытием новых территорий, европейцы расширили границы привычного мира и внесли в труд Птолемея поправки. В конце XVII века были произведены более тщательные измерения размеров Земли при помощи триангуляции. Так были заложены основы геодезии. Относительно формы Земли существовало две точки зрения: согласно первой, Земля была сплюснута у полюсов, согласно второй — у экватора. Разногласия сторонников этих двух точек зрения вылились в бурную полемику, и было принято решение найти истину, измерив длину дуги меридиана величиной в один градус. Измерения должны были произвести две экспедиции в двух точках, максимально отстоящих по широте друг от друга.
Измерения должны были произвести две экспедиции в двух точках, максимально отстоящих по широте друг от друга.
Первые представления о форме и размерах Земли
В древности большинство людей верило, что обитаемая Земля плоская — по крайней мере, она выглядела именно так, если не принимать в расчет неровности рельефа. Однако древнегреческие философы начали рассматривать иные гипотезы. Анаксимандру приписывается концепция, согласно которой Земля имела цилиндрическую форму, была вытянута в длину и располагалась в центре небесной сферы. Согласно этой концепции, обитаемым был лишь верхний диск цилиндрической Земли. Считается, что Анаксимандр составил карту Земли, которую позднее исправил и усовершенствовал Гекатей Милетский (ок. 550 г. до н. э. — ок. 476 г. до н. э.). На этой карте были изображены известные на тот момент области Европы, Азии и Африки, расположенные на диске, окруженном рекой-океаном. В центральной части диска располагалась Греция.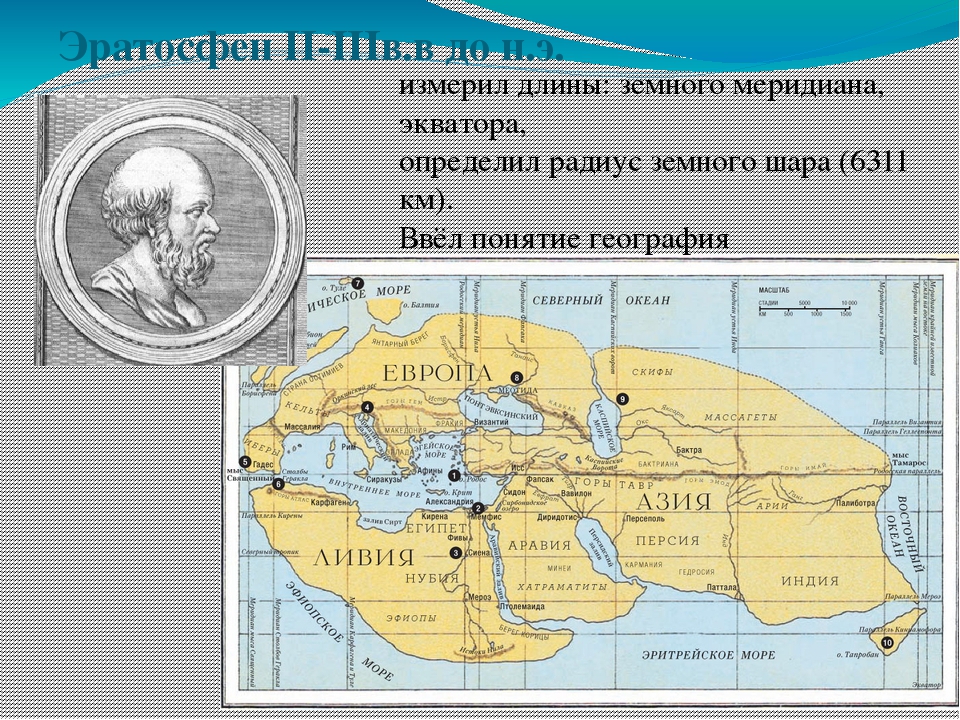
Хотя в точности оценить величину древних единиц измерения всегда непросто, считается, что диаметр диска, изображенного на карте Гекатея, составлял примерно 8000 километров.
Карта Гекатея I в. до н. э.
Если Земля была плоской, то имела ли она конец? Гекатей, по всей видимости, считал, что да. Но почему тогда океан, окружавший сушу, не переливался через края? Быть может, он упирался в некую стену, где небо соединялось с морем? Как Земля удерживалась на месте? Как видите, гипотеза о плоской форме Земли вызывала множество непростых вопросов. Древние греки предположили, что Земля имеет форму сферы, и привели убедительные доводы в поддержку этой гипотезы — об этом мы уже рассказали в главе 2. Но как греческие мыслители определили размеры Земли?
* * *
ДОВОДЫ АРИСТОТЕЛЯ В ПОЛЬЗУ СФЕРИЧЕСКОЙ ФОРМЫ ЗЕМЛИ
Аристотель привел ряд доводов против того, что Земля плоская. К примеру, он указал, что высота звезд над горизонтом меняется в зависимости отточки наблюдения. Так, путешественник, идущий на юг, видел, что созвездия поднимались все выше над горизонтом. Это означало, что горизонт на юге образовывал определенный угол с горизонтом, который видел наблюдатель на севере. Следовательно, Земля не могла быть плоской. Аналогично, тень, отбрасываемая Землей на Луну во время частичных лунных затмений, всегда имела круглую границу вне зависимости от высоты Луны над горизонтом. Какое тело, кроме сферы, могло отбрасывать круглую тень во всех направлениях?
Так, путешественник, идущий на юг, видел, что созвездия поднимались все выше над горизонтом. Это означало, что горизонт на юге образовывал определенный угол с горизонтом, который видел наблюдатель на севере. Следовательно, Земля не могла быть плоской. Аналогично, тень, отбрасываемая Землей на Луну во время частичных лунных затмений, всегда имела круглую границу вне зависимости от высоты Луны над горизонтом. Какое тело, кроме сферы, могло отбрасывать круглую тень во всех направлениях?
* * *
Измерение размеров сферической Земли. Эратосфен
В эллинистический период Александрия стала научным центром греческой цивилизации благодаря двум важнейшим учреждениям — музею и библиотеке. Именно там впервые была вычислена длина окружности Земли. Сделал это греческий мудрец, математик и географ Эратосфен Киренский (276 г. до н. э. — 194 г. до н. э.).
Будучи главой Александрийской библиотеки, он имел доступ ко множеству различных данных, записанных на папирусах.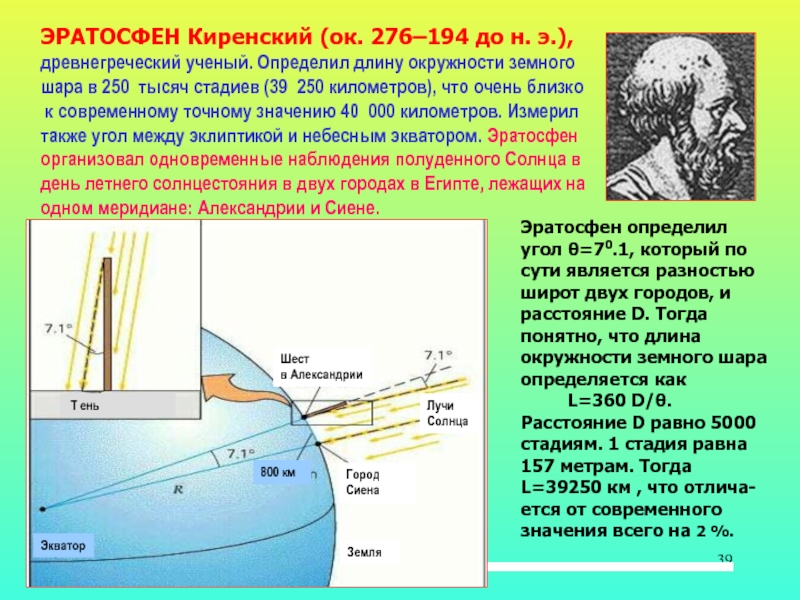 Эратосфен знал, что в городе Сиена (ныне — Асуан), расположенном к югу от Александрии, в полдень по местному времени в день летнего солнцестояния солнечные лучи достигают дна глубоких колодцев, а вертикальные шесты не отбрасывают тени. В это же время в Александрии гномон отбрасывал тень.
Эратосфен знал, что в городе Сиена (ныне — Асуан), расположенном к югу от Александрии, в полдень по местному времени в день летнего солнцестояния солнечные лучи достигают дна глубоких колодцев, а вертикальные шесты не отбрасывают тени. В это же время в Александрии гномон отбрасывал тень.
Гравюра с изображением древней Александрийской библиотеки.
Эратосфен предположил: так как Солнце находится на большом расстоянии, его лучи падают на Землю параллельно. Если Земля плоская, как в те времена по-прежнему считали многие, то одинаковые предметы в один и тот же день и час должны отбрасывать одинаковую тень вне зависимости от того, где они находятся. Но тени предметов отличались, следовательно, Земля не была плоской. В полдень в день летнего солнцестояния в Александрии Эратосфен при помощи гномона измерил угол, на который солнечные лучи отстоят от вертикали. Этот угол составил 1/50 окружности (7°12?). Предположив, что Земля имеет форму сферы (360°), а Александрия расположена к северу от Сиены на том же меридиане, путем простых рассуждений (см. рисунок) он определил, что центральный угол между двумя радиусами Земли, соответствующими Сиене и Александрии, также составляет 1/50 окружности (7°12?).
рисунок) он определил, что центральный угол между двумя радиусами Земли, соответствующими Сиене и Александрии, также составляет 1/50 окружности (7°12?).
Схема рассуждений Эратосфена.
Эратосфен знал, что расстояние между этими городами равнялось 5000 стадиев (примерно 800 километров), и определил длину окружности Земли с помощью простой пропорции. Длина окружности Земли должна была превышать расстояние между Александрией и Сиеной в 50 раз, то есть составлять 250 тысяч стадиев. Он округлил результат вычислений и принял один градус равным 70 стадиев, таким образом, общая длина земной окружности составила 252 тысячи стадиев.
К сожалению, нам неизвестно, какой была точная длина стадия, использованного Эратосфеном в расчетах. Греческий стадий примерно равен 185 м — в этом случае длина земной окружности составляет 46620 км (на 16,3 % больше, чем на самом деле). Но если предположить, что ученый использовал египетский стадий, который равнялся 157,5 м, то его результат равен 39690 км (в этом случае ошибка составляет менее 2 %).
Рассуждения Эратосфена были безошибочны, однако следует сделать небольшое замечание относительно точности проведенных им измерений: Сиена не расположена на одном меридиане с Александрией, а Солнце видится с Земли как диск, расположенный на конечном расстоянии, поэтому его нельзя считать бесконечно удаленным точечным источником света. Кроме того, в древности измерение расстояний по суше было ненадежным и становилось источником ошибок. Если учесть погрешности во всех данных, которые применил Эратосфен в вычислениях, то станет очевидно, что полученный им результат был на удивление точным.
Карты Земли: широта и долгота, географическое положение и картографические проекции
Птолемей работал в Александрии на несколько веков позже Эратосфена. В своей «Географии» он, применив строгие научные методы, описал весь известный древним грекам мир. Птолемей изложил математические методы составления точных карт при помощи различных проекций, а также указал географические координаты почти 10 тысяч точек известного в то время мира. При нанесении этих точек на карту он построил сетку параллелей и меридианов и применил такие понятия, как широта и долгота. Нулевой меридиан на карте Птолемея располагался возле Канарских островов, нулевая параллель — вблизи экватора. Северную оконечность обитаемого мира он расположил на параллели острова Туле.
При нанесении этих точек на карту он построил сетку параллелей и меридианов и применил такие понятия, как широта и долгота. Нулевой меридиан на карте Птолемея располагался возле Канарских островов, нулевая параллель — вблизи экватора. Северную оконечность обитаемого мира он расположил на параллели острова Туле.
По всей видимости, размеры Земли, использованные Птолемеем, были меньше реальных: он предполагал, что длина дуги экватора величиной в один градус составляет примерно 80 километров, таким образом, длина земной окружности была чуть меньше 30 тысяч километров. Птолемей пользовался огромным авторитетом в эпоху Возрождения, и только благодаря этому моряки осмелились пересечь океан в поисках новых земель.
Задача о представлении криволинейной поверхности на плоскости решается математическими методами. В этом смысле Птолемей также внес значимый вклад в картографию. Считается, что еще до него Гиппарх разделил земную окружность на 360° и построил сетку параллелей и меридианов. Гиппарх изучал способы изображения сферической поверхности на плоской карте и, по мнению некоторых ученых, применил для решения этой задачи стереографическую проекцию. Большое влияние на Птолемея оказал географ и картограф Марин Тирский (ок. 60 — ок. 130), который первым принял меридиан Канарских островов за нулевой, а параллель Родоса — за начало отсчета широты. По всей видимости, он же предложил использовать цилиндрическую проекцию для составления карт.
Гиппарх изучал способы изображения сферической поверхности на плоской карте и, по мнению некоторых ученых, применил для решения этой задачи стереографическую проекцию. Большое влияние на Птолемея оказал географ и картограф Марин Тирский (ок. 60 — ок. 130), который первым принял меридиан Канарских островов за нулевой, а параллель Родоса — за начало отсчета широты. По всей видимости, он же предложил использовать цилиндрическую проекцию для составления карт.
Чтобы изобразить поверхность Земли на плоскости, Птолемей разработал коническую и псевдоконическую проекции. С их помощью ему удалось изобразить на одной плоскости разные участки земной поверхности в разном масштабе. В своей конической проекции он представил параллели в виде концентрических дуг окружностей, меридианы — в виде прямых линий, сходящихся в фокусе, который совпадал с Северным полюсом. Во второй, псевдоконической проекции Птолемея меридианы также изображались кривыми линиями, сходившимися в полюсе, за счет чего ему удалось изобразить больший участок земной поверхности с меньшими искажениями.
Коническая проекция Птолемея, приведенная в его «Географии» («Geographicae enarrationis libri octo»), изданной в Лионе и Вене в 1541 году.
Коническая проекция Птолемея использовалась вплоть до XV века, пока границы известного мира существенно не расширились. С новыми открытиями для составления карт мира этой проекции оказалось недостаточно, и она стала применяться только в картах отдельных регионов.
Ни в одной картографической проекции земного шара нельзя одновременно сохранить и площади, и углы, но можно обеспечить сохранение площадей и углов с различной точностью в зависимости от типа проекции — в частности, в проекциях, предположительно созданных Гиппархом, Марином и Птолемеем.
В стереографической проекции произвольной точке сферы А, отличной от полюса Р (фокус проекции), ставится в соответствие точка плоскости, определяемая как точка пересечения прямой РА и плоскости. И напротив, каждой точке плоскости В соответствует единственная точка А, отличная от Р, которая определяется как точка пересечения сферы с прямой РВ. Птолемей объясняет эту проекцию в своей «Планисфере» и использует ее для изображения небесной сферы на плоскости. Позднее эту проекцию применили арабы при изготовлении астролябий — инструментов для определения положения звезд на небосводе.
Птолемей объясняет эту проекцию в своей «Планисфере» и использует ее для изображения небесной сферы на плоскости. Позднее эту проекцию применили арабы при изготовлении астролябий — инструментов для определения положения звезд на небосводе.
Стереографическая проекция.
В цилиндрической проекции поверхность земного шара проецируется на цилиндр, касающийся его в точке, лежащей на экваторе. Полученная карта отличается малыми искажениями возле экватора и огромными искажениями в приполярных областях. Эта проекция сохраняет углы, но не площади — они увеличиваются по мере удаления от экватора и приближения к любому из двух полюсов.
В конической проекции точки земного шара проецируются на конус, при этом в качестве фокуса выбирается один из полюсов. Приполярные области в этой проекции искажаются, но полушарие, в котором расположен полюс, выбранный в качестве фокуса, будет изображено с высокой точностью. На карте, построенной в конической проекции, искажения вдоль параллели касания невелики и возрастают по мере удаления от нее.
Арабы переняли у греков значительную часть культурного багажа, но в том, что касалось картографии и задач определения местоположения, были практичнее греков: они пересматривали и исправляли картографические данные по мере исследования новых земель. В конце XIII века крупные центры картографии находились в Средиземноморье — в Генуе, Венеции и Пальма-де-Мальорке, где изготавливались морские карты, а исследования носили ярко выраженный прикладной характер. С появлением компаса в Европе при создании морских карт стали применяться расчеты, связывавшие координаты корабля с расстояниями до различных портов.
Эти карты, в которых основное внимание уделялось морским путям, называются портуланами. В них отражены форма побережий, береговой рельеф, устья рек, направления ветров и так далее. В XIV–XV веках было изготовлено значительное количество таких карт.
Лучший из портуланов, изготовленный на Мальорке, — «Каталанский атлас» Авраама Крескеса 1375 года. На иллюстрации изображена копия этой карты, выполненная в XIX веке.
На иллюстрации изображена копия этой карты, выполненная в XIX веке.
XVI век стал вершиной мореплавания: менее чем за 100 лет было открыто столько новых земель, что площадь известного мира удвоилась. Карты Земли совершенствовались, и впервые удалось получить прямое доказательство сферической формы Земли: Фернан Магеллан (1480–1521) и Хуан Себастьян Элькано (1476–1526) совершили кругосветное путешествие. И вскоре вновь встал вопрос об измерении земного шара.
* * *
ПЕРВОЕ ПРЯМОЕ ДОКАЗАТЕЛЬСТВО СФЕРИЧЕСКОЙ ФОРМЫ ЗЕМЛИ
Первое кругосветное путешествие (1519–1522), ставшее прямым доказательством сферической формы Земли, начал Фернан Магеллан, а закончил Хуан Себастьян Элькано. Магеллан возглавил экспедицию из пяти кораблей, которые отправились в плавание из города Санлукарде-Баррамеда в испанской провинции Кадис 20 сентября 1519 года. Мореплаватель пересек Атлантику и достиг побережья Бразилии близ Рио-де-Жанейро. Затем он проследовал в направлении реки Ла-Плата и далее на юг, к Патагонии. Там Магеллан открыл пролив, который теперь носит его имя, и провел по нему свои корабли. Его команде пришлось перенести много невзгод, но экспедиция пересекла Тихий океан, открыла остров Гуам в архипелаге Марианские острова и в марте 1521 года достигла Филиппин. Там же, на Филиппинах, 27 апреля 1521 года Фернан Магеллан скончался. После его смерти экспедицию возглавил Хуан Себастьян Элькано. Отправившись в путь от Молуккских островов, он пересек Индийский океан, обогнул Африку и прибыл в Санлукар-де-Баррамеда 6 сентября 1522 года на корабле «Виктория». Так завершилось первое кругосветное путешествие.
Затем он проследовал в направлении реки Ла-Плата и далее на юг, к Патагонии. Там Магеллан открыл пролив, который теперь носит его имя, и провел по нему свои корабли. Его команде пришлось перенести много невзгод, но экспедиция пересекла Тихий океан, открыла остров Гуам в архипелаге Марианские острова и в марте 1521 года достигла Филиппин. Там же, на Филиппинах, 27 апреля 1521 года Фернан Магеллан скончался. После его смерти экспедицию возглавил Хуан Себастьян Элькано. Отправившись в путь от Молуккских островов, он пересек Индийский океан, обогнул Африку и прибыл в Санлукар-де-Баррамеда 6 сентября 1522 года на корабле «Виктория». Так завершилось первое кругосветное путешествие.
* * *
Измерение дуг меридианов посредством триангуляции
В 1669–1670 годах французский астроном аббат Жан Пикар стал первым, кому удалось вычислить размер Земли с достаточно высокой точностью. Для этого он применил принципы триангуляции и воспользовался методом лейденского астронома, математика и профессора Виллеброрда Снелла (1580–1626). Снелл спланировал и провел измерения в 1615 году, а в 1617 году описал свои методы в книге Eratosthenes Batavus («Голландский Эратосфен»), заложив тем самым основы геодезии. Его метод измерения окружности Земли заключался в определении длины дуги меридиана посредством триангуляции.
Снелл спланировал и провел измерения в 1615 году, а в 1617 году описал свои методы в книге Eratosthenes Batavus («Голландский Эратосфен»), заложив тем самым основы геодезии. Его метод измерения окружности Земли заключался в определении длины дуги меридиана посредством триангуляции.
С точки зрения геометрии триангуляция заключается в использовании треугольников и их тригонометрических свойств для вычисления неизвестных параметров (сторон и углов) на основе известных. В геодезии триангуляцией называется метод, позволяющий определить размеры Земли, покрыв ее поверхность сетью смежных треугольников. Измерения при триангуляции начинаются с грамотного выбора вершин треугольника и определения точной длины одной из сторон треугольника.
Далее из вершин этой стороны производятся измерения углов треугольника. Полученный треугольник станет первым в сети треугольников, которая в конечном итоге охватит дугу меридиана.
Гениальный писатель Жюль Верн (1828–1905) в своем романе «Приключения троих русских и троих англичан в Южной Африке» четко описывает последовательность действий при триангуляции:
«Чтобы лучше понять, что представляет собой геодезическая операция, называемая триангуляцией, позаимствуем следующие геометрические построения из учебника «Новые уроки космографии» г-на А. Гарсе, преподавателя математики лицея Генриха IV. С помощью прилагаемого здесь рисунка эта любопытная процедура будет легко понята:
Гарсе, преподавателя математики лицея Генриха IV. С помощью прилагаемого здесь рисунка эта любопытная процедура будет легко понята:
«Пусть АВ — меридиан, длину которого требуется найти. Тщательно измеряем основание (базис) АС, идущий от оконечности А меридиана до первой позиции С. Затем по обеим сторонам этого меридиана избираем дополнительные позиции D, E, F, G, Н, I и так далее, каждая из которых позволяет видеть соседнюю позицию, и измеряем с помощью теодолита углы каждого из треугольников ACD, CDE, EDF и так далее, которые они образуют между собой. Эта первая операция позволяет определить параметры различных треугольников, ибо в первом известна длина АС и углы и можно вычислить сторону CD; во втором — сторона CD и углы, и легко подсчитывается сторона DE; в третьем — известна сторона DE и углы и можно получить сторону EF и так далее. Затем определяем наклон меридиана относительно основания АС, для чего измеряем угол MAC.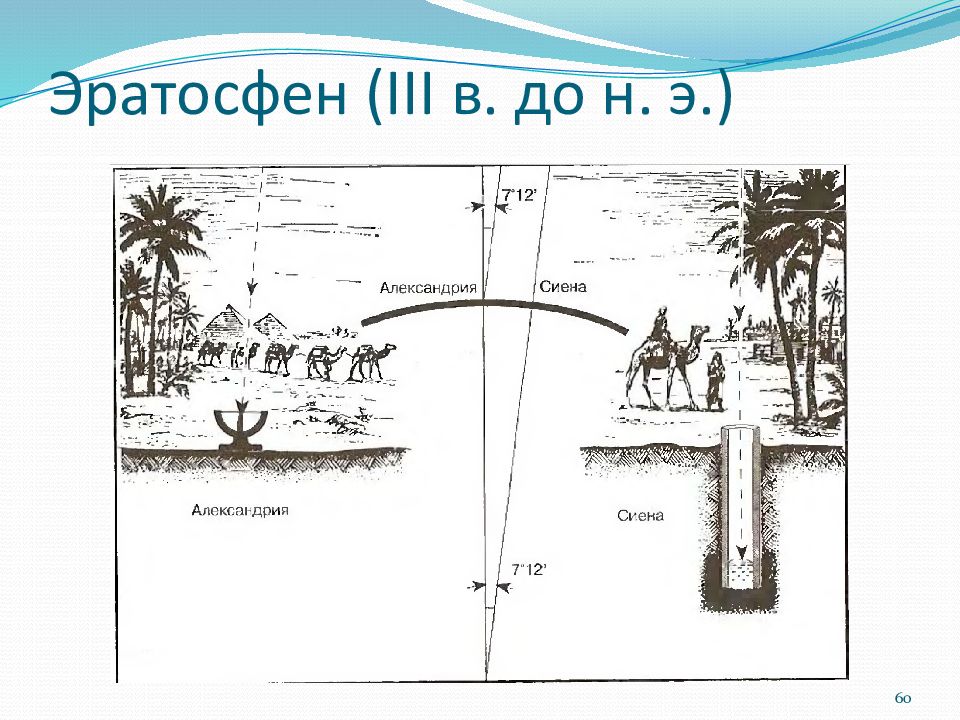 Таким образом, в треугольнике ACM известны сторона АС и прилегающие к ней углы и можно вычислить первый отрезок AM меридиана. Аналогично вычисляются угол М и сторона СМ; таким образом, в треугольнике MDN оказывается известной сторона DM = CD — СМ и прилегающие к ней углы, и можно подсчитать второй отрезок MN меридиана, угол N и сторону DN. Таким образом, в треугольнике NEP становится известна сторона EN = DE — DN и прилегающие к ней углы и можно определить третий отрезок NP меридиана, и так далее. Понятно, что таким образом получается по частям общая длина оси АВ»[3].
Таким образом, в треугольнике ACM известны сторона АС и прилегающие к ней углы и можно вычислить первый отрезок AM меридиана. Аналогично вычисляются угол М и сторона СМ; таким образом, в треугольнике MDN оказывается известной сторона DM = CD — СМ и прилегающие к ней углы, и можно подсчитать второй отрезок MN меридиана, угол N и сторону DN. Таким образом, в треугольнике NEP становится известна сторона EN = DE — DN и прилегающие к ней углы и можно определить третий отрезок NP меридиана, и так далее. Понятно, что таким образом получается по частям общая длина оси АВ»[3].
Таким образом, для проведения триангуляции необходимо как можно точнее определить длину стороны треугольника, которую мы будем называть основанием, так как от результата этого измерения (на практике оно оказывается самым сложным и трудоемким) зависят все остальные расчеты. Основание должно быть как можно длиннее, чтобы свести к минимуму возможные ошибки. Из обоих концов основания производятся измерения углов, которые основание образует с двумя другими сторонами треугольника. Эти две стороны сходятся в грамотно выбранной третьей вершине. Так определяется первый треугольник сети.
Основание должно быть как можно длиннее, чтобы свести к минимуму возможные ошибки. Из обоих концов основания производятся измерения углов, которые основание образует с двумя другими сторонами треугольника. Эти две стороны сходятся в грамотно выбранной третьей вершине. Так определяется первый треугольник сети.
Зная два угла и сторону (основание) треугольника, мы при помощи тригонометрических методов можем без труда вычислить третий угол и две оставшиеся стороны. Так мы полностью определим треугольник и сможем выбрать любую из трех его сторон в качестве основания второго, смежного треугольника. Если мы последовательно будем добавлять к сети все новые и новые смежные треугольники, то в конечном итоге сеть триангуляции охватит две крайние точки дуги меридиана, которую мы хотим измерить, и мы определим астрономическую широту и долготу этих точек.
Далее по известной длине основания необходимо найти длину его горизонтальной проекции. В общем случае вершины треугольника необязательно находятся на одной высоте, поэтому их следует спроецировать на горизонтальную плоскость или контрольную поверхность. Снелл нашел способ внести в формулы триангуляции поправки, учитывающие кривизну Земли.
Снелл нашел способ внести в формулы триангуляции поправки, учитывающие кривизну Земли.
Основой для систематического использования современных сетей триангуляции стали результаты первых измерений, выполненных Снеллом, а также рассчитанное им расстояние между городами Алкмар и Берген-оп-Зом в Нидерландах. Эти города находились приблизительно на одном меридиане и отстояли друг от друга на один градус долготы. В качестве длины основания Снелл выбрал расстояние от своего дома до башни местной церкви. Он построил сеть из 33 треугольников и измерил их углы при помощи квадранта размером 2×2 метра. Проведя измерения, он определил, что расстояние между городами составляет 117 449 ярдов (107,393 км). Фактическое расстояние между этими городами составляет примерно 111 км.
Применив методы Снелла, Пикар измерил расстояние, соответствующее одному градусу долготы парижского меридиана. Он построил сеть из тринадцати треугольников, начиная из города Мальвуазен близ Парижа до часовой башни городка Сур дон близ Амьена. Основание сети треугольников было измерено по поверхности Земли, а углы треугольников измерялись из точек, расположенных на башнях, колокольнях или иных возвышениях, откуда можно было увидеть вершины соседних треугольников.
Основание сети треугольников было измерено по поверхности Земли, а углы треугольников измерялись из точек, расположенных на башнях, колокольнях или иных возвышениях, откуда можно было увидеть вершины соседних треугольников.
Пикар впервые применил при измерениях квадрант, дополненный зрительной трубой, а также сконструировал собственные измерительные инструменты. Он использовал подвижные квадранты, дополненные зрительными трубами, а также микрометр французского астронома Адриена Озу, обеспечивший точность измерений в несколько угловых секунд. Принцип действия микрометра основан на перемещении винта, при котором небольшие расстояния, слишком малые для прямых измерений, откладываются на измерительной шкале. При триангуляции требовалось определить разницу в высоте между точками наблюдения, а также их высоту относительно плоскости отсчета. Пикару удалось произвести нивелирование с точностью порядка 1 сантиметра на километр.
* * *
ЖАН ПИКАР (1620–1682)
Французский астроном Жан Пикар, получивший образование в иезуитской школе Ла-Флеш, работал вместе с Пьером Гассенди, преподавателем математики в парижском Коллеж Рояль (ныне Коллеж де Франс).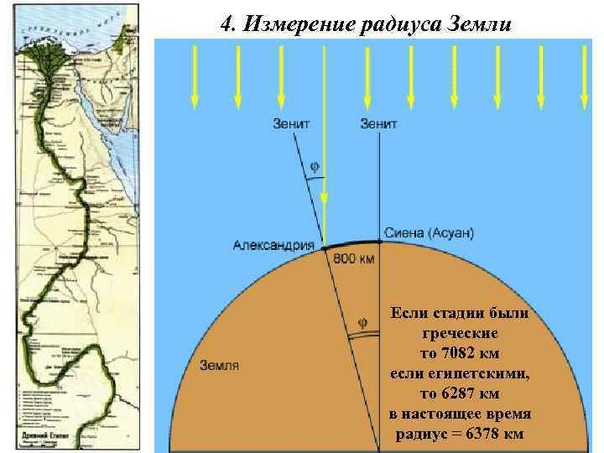 В 1655 году, после смерти Гассенди, Пикар стал преподавателем астрономии в этом учебном заведении, а в 1666 — членом недавно созданной Французской академии наук. Он сконструировал микрометр — прибор для измерения диаметров небесных тел (Солнца, Луны и планет). В 1667 году Пикар дополнил квадрант зрительной трубой, сделав его намного удобнее для наблюдений. Исследователь значительно повысил точность измерений Земли, применив метод триангуляции Снелла, а также использовал научные методы при составлении карт. В 1671 году совместно с датским астрономом Оле Рёмером в обсерватории Ураниборг он наблюдал около 140 затмений спутника Юпитера Ио. На основе полученных данных Рёмер получил первую количественную оценку скорости света.
В 1655 году, после смерти Гассенди, Пикар стал преподавателем астрономии в этом учебном заведении, а в 1666 — членом недавно созданной Французской академии наук. Он сконструировал микрометр — прибор для измерения диаметров небесных тел (Солнца, Луны и планет). В 1667 году Пикар дополнил квадрант зрительной трубой, сделав его намного удобнее для наблюдений. Исследователь значительно повысил точность измерений Земли, применив метод триангуляции Снелла, а также использовал научные методы при составлении карт. В 1671 году совместно с датским астрономом Оле Рёмером в обсерватории Ураниборг он наблюдал около 140 затмений спутника Юпитера Ио. На основе полученных данных Рёмер получил первую количественную оценку скорости света.
* * *
Целью Пикара было определить, сколько туазов (так называлась использованная им единица длины) составляла длина прямой линии между Мальвуазеном и Сурдоном, а также их разницу в широте, отсчитанную вдоль окружности меридиана. Таким образом, требовалось произвести два измерения: геодезическое (в туазах) и астрономическое (в градусах, минутах и секундах).
Он тщательно измерил длину прямой дороги между Вильжюифом и Жювизисюр-Орж (она составила 5663 туаза), а остальные результаты получил посредством триангуляции. В качестве единицы измерения он использовал туаз Шатле, или парижский туаз (позднее, в конце XVIII века, он был принят равным 1,949 м). По результатам измерений длина дуги меридиана величиной в один градус составила 57 060 туазов.
Благодаря высокой точности измерительных инструментов и усовершенствованиям, которые внес Пикар, считается, что именно он первым дал достаточно точную оценку радиуса Земли. Он получил, что один градус широты равен 110,46 км, что соответствует радиусу Земли в 6328,9 км (сегодня экваториальный радиус Земли оценивается в 6378,1 км, полярный радиус — в 6356,8 км, средний радиус — в 6371 км). Данные Пикара применил Исаак Ньютон при создании своей теории тяготения.
Пять треугольников из сети триангуляции Пикара.
После Пикара измерения длины вдоль парижского меридиана посредством триангуляции провели Джованни Доменико Кассини (1625–1712), глава Парижской обсерватории, и его сын Жак Кассини (1677–1756), сменивший отца на его посту. Жак Кассини измерил длину дуги меридиана между Дюнкерком и Перпиньяном и опубликовал результаты в 1720 году. Позднее, в 1733–1740 годах, вместе с сыном, Цезарем Франсуа Кассини, он впервые построил сеть триангуляции, которая охватила всю страну. В 1745 году благодаря его труду появилась первая точная карта Франции.
Позднее в других странах также были построены сети триангуляции. К примеру, проект триангуляции Великобритании под названием Principal Triangulation of Great Britain был начат в 1783 году, а полностью завершен лишь в середине XIX века.
Первый проект по составлению точной карты Испании предложил Хорхе Хуан в 1751 году, однако первые листы Национальной топографической карты Испании увидели свет лишь в 1875 году.
Определение местоположения и ориентирование.
Навигация и задача о долготе
Чтобы определить положение точки на плоскости, можно использовать декартову систему координат с перпендикулярными осями: осью абсцисс (х) и осью ординат (у).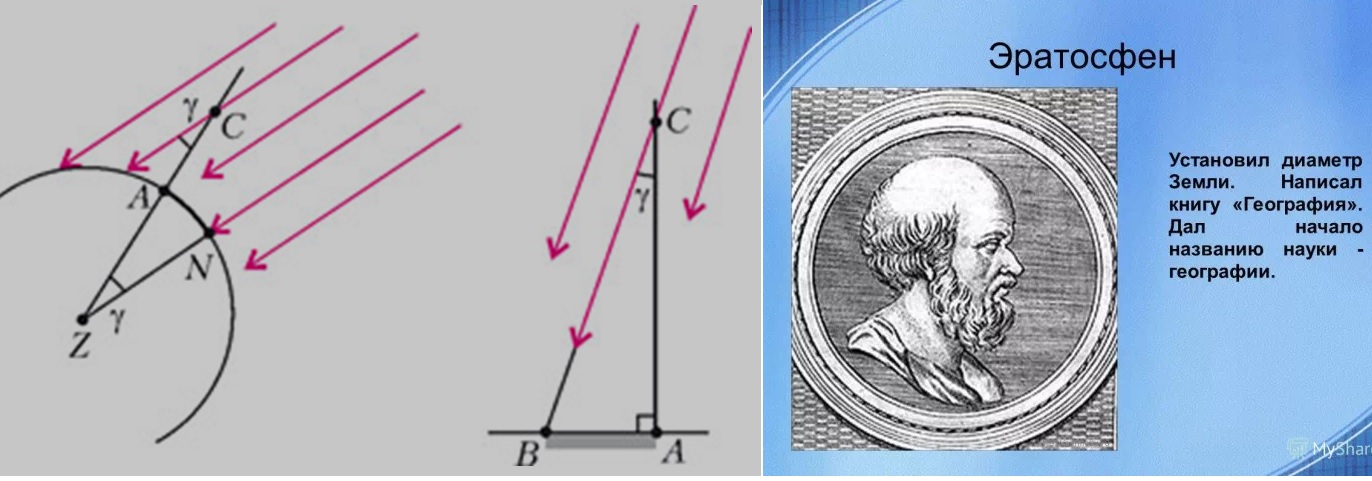 Пара значений (х, у) однозначно определяет единственную точку плоскости. Аналогично, чтобы точно определить положение любой точки на поверхности Земли (будем считать ее сферической), достаточно знать два числа — широту и долготу (географические координаты точки). В этом случае роль осей координат будут играть экватор и большой круг, проходящий через полюса, то есть меридиан, выбранный в качестве базового (меридиан 0°).
Пара значений (х, у) однозначно определяет единственную точку плоскости. Аналогично, чтобы точно определить положение любой точки на поверхности Земли (будем считать ее сферической), достаточно знать два числа — широту и долготу (географические координаты точки). В этом случае роль осей координат будут играть экватор и большой круг, проходящий через полюса, то есть меридиан, выбранный в качестве базового (меридиан 0°).
Широта точки на поверхности Земли — это угловое расстояние между экватором и этой точкой, измеренное из центра нашей планеты вдоль меридиана, проходящего через эту точку. Широта измеряется в градусах, минутах и секундах и находится на интервале от 0° до 90°. Кроме того, указывается, в каком полушарии, Северном или Южном, находится точка, к примеру 41°24?14? северной широты (с.ш.). Следовательно, все точки, расположенные на одной параллели Земли (окружности круга, параллельного экватору), имеют одинаковую широту.
Широту можно вычислить астрономическими методами. Простейший метод для Северного полушария состоял в том, чтобы найти на небе Полярную звезду (Северный полюс мира) и измерить угол между визирной линией и горизонтальной плоскостью, на которой находится наблюдатель. Полученный угол и будет искомой широтой. В Южном полушарии следует действовать аналогичным образом, выбрав для наблюдений Южный крест. Существуют и другие методы определения широты днем — к примеру, можно измерить высоту Солнца над горизонтом в полдень и применить таблицы, где указано положение Солнца относительно эклиптики в день наблюдений.
Простейший метод для Северного полушария состоял в том, чтобы найти на небе Полярную звезду (Северный полюс мира) и измерить угол между визирной линией и горизонтальной плоскостью, на которой находится наблюдатель. Полученный угол и будет искомой широтой. В Южном полушарии следует действовать аналогичным образом, выбрав для наблюдений Южный крест. Существуют и другие методы определения широты днем — к примеру, можно измерить высоту Солнца над горизонтом в полдень и применить таблицы, где указано положение Солнца относительно эклиптики в день наблюдений.
Широта и долгота точки Р на сфере.
Долгота — это значение угла между нулевым меридианом (точнее, полумеридианом), выбранным в качестве начала отсчета (0°), и меридианом, проходящим через данную точку. Этот угол измеряется из центра Земли вдоль экватора. Значения долготы лежат на интервале от 0° до 180°. Кроме того, указывается, в каком направлении от нулевого меридиана была измерена долгота — к востоку или к западу, например, 2°14?50? западной долготы (з. д.). Следовательно, все точки, расположенные на одном полумеридиане между двумя полюсами Земли, имеют одинаковую долготу.
д.). Следовательно, все точки, расположенные на одном полумеридиане между двумя полюсами Земли, имеют одинаковую долготу.
Широта и долгота отсчитываются от экватора и меридиана, выбранного в качестве начала отсчета (такой меридиан называется нулевым, его долгота равна 0°).
Сегодня нулевым меридианом обычно считается Гринвичский, но до него в качестве нулевых использовались многие другие меридианы.
Как мы уже говорили, определить широту корабля в море несложно. Также относительно просто узнать долготу корабля, если с него видна земля. Но если он находится в открытом море, то определение долготы связано с серьезными трудностями.
Эта задача обрела огромное значение после открытия Америки Христофором Колумбом. В то время долгота вычислялась приближенно, на основе расстояния, пройденного кораблем с запада на восток или наоборот. Чтобы определить скорость корабля, моряки использовали лаг, который представлял собой свободно вращающуюся катушку с намотанной на нее веревкой. На веревке через равные промежутки были завязаны узлы, а на ее конце закреплялся груз. Моряк выбрасывал лаг за корму, и когда о его руку ударялся первый узел, он давал команду, и другой моряк начинал отсчет времени при помощи песочных часов. Когда весь песок пересыпался из верхнего сосуда часов в нижний, второй моряк сообщал об этом первому, и тот указывал число ушедших за борт узлов, например, «три с половиной узла» или «шесть узлов с четвертью». Скорость судов до сих пор измеряется в узлах.
Разумеется, столь примитивный метод определения долготы сопровождался значительными ошибками, которые приводили к катастрофическим последствиям. Поэтому в XVII — начале XVIII века задача определения долготы стала стратегическим приоритетом для всех держав, имевших интересы за океаном.
Теоретически вычисление долготы можно свести к определению разницы во времени между точкой отсчета (портом отплытия или нулевым меридианом) и точкой, в которой находится корабль. Когда солнце проходит через меридиан наблюдателя (то есть меридиан корабля), то, зная точное время в точке отсчета, можно определить долготу корабля, то есть угловое расстояние до точки отсчета, а следовательно, и до нулевого меридиана. Этот метод действует благодаря тому, что разницу во времени между двумя меридианами можно пересчитать в градусы долготы. Так как Земля совершает полный оборот в 360° за 24 часа, за 1 час она поворачивается на 1/24 оборота, то есть на 13°. Если за час, то есть за 60 минут, Земля поворачивается на 13°, то разница в 4 минуты соответствует одному градусу долготы.
Следовательно, долготу можно вычислить, определив разницу во времени между двумя точками при помощи наблюдений и астрономических измерений. Была высказана идея об определении долготы по результатам наблюдений затмений, но этот метод не слишком пригоден в открытом море, да и затмения наблюдались редко.
* * *
НАБЛЮДЕНИЕ ЗАТМЕНИЙ ДЛЯ ВЫЧИСЛЕНИЯ ДОЛГОТЫ
Допустим, что нам известно, в какое время затмение будет наблюдаться в определенном месте (на суше, в обсерватории и так далее), при этом мы находимся в открытом море. Если мы определим, когда наблюдалось затмение по местному времени, то сможем вычислить долготу места, в котором находимся. Для использования этого метода нам потребуются таблицы, где указано, в какое время произойдет затмение в определенной точке (разумеется, мы не сможем обойтись без математических расчетов). В XVI веке определять долготу по наблюдениям затмений было удобно на суше, но не в открытом море — зафиксировать измерительные приборы из-за качки было очень сложно, а главное, что затмения наблюдались редко: в год происходит от двух до пяти солнечных затмений. Если же учитывать и лунные, то в год набирается не менее двух и не более семи затмений, в среднем — четыре. За весь XX век наблюдалось 375 затмений: 228 солнечных и 147 лунных. И без того редкие затмения еще и не всегда видны: наблюдениям могут помешать неблагоприятные погодные условия.
* * *
С недостаточной частотой затмений удалось справиться благодаря открытию Галилеем спутников Юпитера в 1610 году. Луны Юпитера при вращении вокруг него скрываются из вида и появляются вновь. Эти затмения наблюдаются несколько тысяч раз в год, и их время можно точно предсказать. Этот метод действительно можно было бы применять для определения долготы, но в открытом море мешала качка, а также наблюдения можно было производить только ночью, в ясную погоду и лишь в определенное время года.
Задача определения долготы в открытом море довольно долго оставалась нерешенной. Определить местное время на корабле можно было по Солнцу. Но как узнать время в точке отсчета, не располагая достаточно точными часами? Точность хода маятниковых часов снижалась, среди прочих факторов, и из-за качки корабля, кроме того, период колебаний маятника на разных широтах отличался, и в результате часы спешили или опаздывали. Корабельные часы не могли сохранять время в порту отплытия, это было причиной существенных ошибок при определении долготы.
В 1714 году Британский парламент предложил огромную премию размером в 20 тысяч фунтов стерлингов тому, кто сможет представить метод или инструмент, позволяющий определять долготу корабля в открытом море. Премия досталась английскому часовщику Джону Гаррисону (1693–1776), который после нескольких десятилетий работы смог изготовить очень точный хронометр. В 1761 году для проверки хронометр был погружен на корабль, направлявшийся на Ямайку. Хронометр проработал 147 дней, и по возвращении в Англию отклонение составило всего 1 минуту 34 секунды. Задача определения долготы была решена. Сегодня определить точное положение корабля можно благодаря системе GPS, о которой мы поговорим в главе 6.
Несферическая Земля. Научные экспедиции в вице-королевство Перу и Лапландию
При измерениях Земли, в том числе при измерениях Пикара, считалось, что она имеет форму идеальной сферы. Спустя несколько лет после опыта Пикара, в 1671–1673 годах, французский астроном Жан Рише (1630–1696), ассистент Джованни Доменико Кассини, совершил путешествие в Кайенну во Французской Гвиане, где сделал важное открытие: он обратил внимание, что в Кайенне колебания маятника были медленнее, чем в Париже, и первым понял, что сила тяготения Земли в разных ее частях отличается. Он сделал верный вывод: изменение силы тяготения объяснялось тем, что Кайенна находилась дальше от центра Земли, чем Париж. Когда новость об открытии достигла Европы, она вызвала большое оживление среди членов Французской академии наук. По возвращении на родину Рише приступил к изготовлению маятника, который отсчитывал бы секунды — иными словами, период колебаний маятника в Париже должен был составлять ровно одну секунду. Такие же маятники были изготовлены и в других частях земли, и оказалось, что длина маятника в зависимости от широты менялась. Согласно известным в то время теориям все указывало на то, что если сила, с которой Земля притягивает к себе маятник, в разных точках отличается, то Земля не может иметь форму идеальной сферы.
Ньютон принял во внимание результаты Рише в своих знаменитых «Математических началах натуральной философии», опубликованных в 1687 году, в которых излагались основы механики. Он предложил математическое описание формы Земли, связав его со своей гениальной теорией тяготения. Ньютон рассмотрел нашу планету как однородное жидкое тело вращения и сделал вывод: Земля должна быть сплюснутой у полюсов. По его мнению, Земля была сплюснутой на 1/230. Иными словами, если предположить, что поперечное сечение Земли — эллипс, то его большая ось будет длиннее малой оси на 1/230-ю.
В 1720 году во Франции был опубликован труд Жака Кассини «О размере и форме Земли», где опровергалась гипотеза Ньютона. Кассини подкрепил свою точку зрения результатами собственных астрономических наблюдений и геодезических измерений меридиана Коллиур — Париж — Дюнкерк (впрочем, некоторые члены Французской академии наук считали эти измерения не вполне точными).
Кассини назвал доводы Ньютона спекулятивными и указал, что Земля представляет собой эллипсоид, сплюснутый у экватора. На что больше похожа Земля — на арбуз или дыню? Развернулась полемика, в которую оказались вовлечены ученые из Лондонского королевского общества и Французской академии наук. В результате дискуссия стала рассматриваться как противостояние французской и английской науки.
Чтобы положить конец спорам, Французской академией наук было принято решение измерить длину дуги меридиана, соответствующей центральному углу в один градус, в максимально далеких друг от друга точках. Для этого были организованы две научные экспедиции из астрономов, математиков, натуралистов и других ученых. Первая экспедиция, возглавляемая Пьером Луи Моро де Мопертюи (1698–1739), отправилась в Лапландию. Ее членами были Пьер Шарль Ле Моннье, Алекси Клод Клеро, Шарль Этьенн Луи Камю, швед Андерс Цельсий и аббат Утье. Вторую экспедицию, которая направилась в вице-королевство Перу, на территорию современного Эквадора, возглавлял астроном Луи Годен (1704–1760).
Участниками экспедиции стали географ Шарль Мари де ла Кондамин, астроном и гидрограф Пьер Бугер, ботаник Антуан Лоран де Жюссьё и испанцы Хорхе Хуан и Антонио де Ульоа. Креольский ученый Педро Висенте Мальдонадо присоединился к экспедиции в Гуаякиле. Также в экспедицию вошли часовщик Уго, инженер и рисовальщик Моренвилль, капитан фрегата Купле, хирург и ботаник Сеньерг, мастер по изготовлению инструментов Годен де Одонне, племянник Луи Годена, картограф и военный инженер Верген.
В то время вице-королевство Перу, расположенное в экваториальных Андах, было испанской территорией, поэтому участникам экспедиции пришлось просить разрешения испанской короны. Разрешение было дано с условием, что к экспедиции присоединятся два юных одаренных офицера Кадисской академии гардемаринов — Хорхе Хуан и Антонио де Ульоа.
Участники экспедиции в Лапландию (1736–1737) благодаря способностям и проницательности математика Клеро получили нужные результаты относительно быстро.
При обустройстве наблюдательных пунктов им помогали шведские военные. Ученые проводили триангуляцию во время длинных летних дней и охватили расстояние в 100 километров между городами Киттис и Торнео. Астрономические измерения производились весной и осенью, когда ночи были уже достаточно длинными и в то же время не слишком холодными. Основание триангуляции было измерено по замерзшему руслу реки. Итоговый результат измерений, проведенных членами экспедиции Мопертюи, был таков: на средней широте 66°20? длина дуги меридиана величиной в один градус равнялась 37 438 туазам. Если сравнить этот результат с результатом измерений Пикара, проведенных близ Парижа на широте около 48° (57060 туазов), то станет очевидно, что Земля представляет собой сфероид, сплюснутый у полюсов.
Гониометрические измерения при триангуляции. Иллюстрация к роману Жюля Верна «Приключения троих русских и троих англичан в Южной Африке».
Экспедиция в Америку, в свою очередь, растянулась на десять лет и превратилась в настоящую эпопею. Участники отправились в путь из Ла-Рошели весной 1735 года и прибыли в Кито год спустя. Им пришлось столкнуться с самыми разными проблемами: помимо постоянных ученых споров, членам экспедиции мешали суровый климат, сложный рельеф, многочисленные финансовые неурядицы, а в 1741 году им и вовсе пришлось разделиться на две группы. Измерения и триангуляция были особенно сложными ввиду особенностей рельефа Анд и большой высоты, превышавшей 4 тысячи метров. Ученые решили построить масштабную триангуляцию из 43 треугольников, чтобы охватить отрезок протяженностью в 354 километра и измерить дугу меридиана величиной не в 1°, а в 3°. Бугер (1749) определил, что длина дуги меридиана величиной в один градус равна 56763 туаза, а Хуан и Ульоа (1748), равно как и ла Кондамин (1751) получили результат в 56768 туазов. Если вспомнить аналогию с арбузом или дыней, которую предложил Вольтер, то можно сказать, что Земля представляет собой скорее арбуз. Результаты измерений и математических расчетов, казалось, подтвердили правоту Ньютона.
* * *
ХОРХЕ ХУАН И КОРОЛЕВСКАЯ ОБСЕРВАТОРИЯ В САН-ФЕРНАНДО (КАДИС)
Испанский мореплаватель Хорхе Хуан и Сантасилья (1713–1773), участвовавший в экспедиции по измерению дуги меридиана на экваторе, внес весомый вклад в развитие испанской науки в XVIII веке. Следы его трудов сохранились до наших дней — он, среди прочего, основал Королевскую обсерваторию в Сан-Фернандо (Кадис) в 1757 году. Современный Королевский институт и обсерватория военно-морских сил — не только сердце астрономических и геодезических исследований, но и научно-исследовательский и культурный центр, находящийся в ведении испанской армии. Сотрудники центра занимаются вычислением эфемерид, определением точного времени, публикуют морские астрономические ежегодники и результаты метеорологических, сейсмических и магнитных наблюдений. Институт отвечает за определение официального испанского времени (всемирное координированное время, или UTC) и за хранение эталонов официальных единиц измерения Испании.
Хорхе Хуан и Сантасилья. Морской музей Мадрида.
Планета Земля. Основные параметры, происхождение.
Подробно:
© Владимир Каланов,
сайт «Знания-сила».
Земля… Такая милая, родная для всего человечества планета. Много ли мы знаем о ней? Да, много. А много ли того, чего мы не знаем о
ней? Очень много, больше того, что знаем. Тайны свои планета наша раскрывает совсем неохотно. В значительной степени это потому, что тайны планеты Земля, так
сказать, не только её личные, но это тайны и космические, тайны Вселенной.
Планета Земля
Как космическое тело Земля является планетой, вращающейся вокруг Солнца вместе с другими планетами (Меркурий, Венера, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон).
Основные параметры планеты Земля
• Среднее расстояние от Земли до Солнца — 149597870 км.
• Среднее расстояние от Земли до Луны — 384400 км.
• Время полного оборота
Земли вокруг своей оси (звёздные сутки) — 23 часа 56 мин. 4,09 сек.
• Период обращения Земли вокруг Солнца (тропический год) — 365,25 суток
• Средняя
скорость движения Земли по орбите — 29,76 км/сек.
• Масса 6 000 000 000 000 млрд. тонн.
Размеры Земного шара (эллипсоида):
• Большая полуось (экваториальный радиус), а — 6378,2 км.
• Малая полуось (полярный радиус), в — 6356,9 км.
• Сжатие с=(а-в)/а — 1 : 298,3
• Средний радиус Земли, принимаемой за шар — 6371,2 км.
• Длина меридиана — 40008,6 км.
• Длина экватора — 40075,7 км.
(диаметр экватора — 12756 км.)
• Поверхность Земли — 510 100 000 кв.км.
• Средняя высота суши над уровнем океана — 875 м.
• Средняя глубина мирового
океана — 3800 м.
• Наибольшая высота суши над уровнем океана — 8848 м. (гора Эверест)
• Наибольшая глубина мирового океана — 11022 м. (Марианская впадина)
Распределение суши и воды на земном шаре
| Поверхность земного шара | Северное полушарие | Южное полушарие | Земля в целом | |||
| млн. кв.км | % | млн. кв.км | % | млн. кв.км | % | |
| Суша | 100 | 39 | 49 | 19 | 149 | 29 |
| Вода | 155 | 61 | 206 | 81 | 361 | 71 |
| Всего | 255 | 100 | 255 | 100 | 510 | 100 |
*) Данные взяты из Малого атласа мира, издательство Москва, 1980.
Из
этих данных следует давно общепризнанный факт, что Земля незначительно сжата у полюсо́в. Однако имеются данные о том, что Земля имеет дынеобра́зную форму, т.е.
сжата по экватору так, что по вертикальной оси она на несколько десятков километров больше, чем по экваториальной оси. Но эту гипотезу учёных
Калифорнийского технологического института мы не рассматриваем и приводим здесь исключительно для све́дения любителей экзотики.
Какова́ же действительная форма Земли по современным представлениям официальной науки? Из приведенных данных (Малый а́тлас мира)
следует, что Земля — это шар с отклонениями от математически точной формы. Назвать Землю эллипсоидом рука не поднимается: слишком крохотная для размеров
Земли разница между большой и малой осями эллипсоида. Поэтому в науке форму Земли называют геоидом. Это надо понимать так, что Земля имеет форму Земли.
Правда, для людей, которые изо дня в день наблюдают окружающие их предметы и явления природы и не задумываются над их сущностью, причинами и,
тем более, происхождением, абсолютно всё равно, какую форму имеет планета Земля. Они не видят потрясающую красоту и великую мудрость окружающего мира, у них не
возникают вопросы о том, почему так всё устроено на Земле, и не возникает желания узнать что-нибудь о планете, на которой они живут. Их интересы
ограничиваются кругом повседневных житейских забот. Таких людей много, они рядом с нами. Сразу хочу заявить: наш рассказ не для них. Наш рассказ для тех
людей, которых интересует всё о Земле: её происхождение и возраст, её красота и богатство, её уникальность как космического тела и как ме́ста возникновения жизни
и пребывания нашей человеческой цивилизации. Наш рассказ для людей, которых не просто интересует, а глубоко волнует будущее Земли, её экологии, всей её
биосферы, а, значит, и будущее человечества.
В начале нашего рассказа о Земле и геосферах необходимо сказать о том, как произошла Земля. Вопрос о происхождении Земли очень сложен,
ибо речь тут может идти о происхождении всей солнечной системы и даже всей галактики, именуемой Млечным путём. На эту тему существует много научных гипотез
и просто предположений. Достаточно упомянуть о гипотезе так называемого Большого взрыва. Сразу отметим, что какой-то единой стройной теории происхождения
Вселенной и Солнечной системы до сих пор не существует. Различные гипотезы, выдвигаемые разными научными школами и отдельными учёными, часто противоречат
друг другу. Можно остановиться, например, на такой гипотезе возникновения Солнечной системы и Земли:
Образование Солнца и планет солнечной системы.
Солнце и планеты образовались около пяти миллиардов лет назад из громадного космического газопылево́го облака (1). Это облако имело приплюснутую,
чечевицеобразную форму — форму диска. Ученые полагают, что и этот диск, и Солнце образовались из одной и той же вращающейся массы межзвездного газа —
протосолнечной туманности. Наименее изучена самая ранняя стадия происхождения Солнечной системы — выделение протосолнечной туманности из гигантского
родительского молекулярного облака, принадлежащего Галактике.
Под действием гравитационных сил притяжения облако начало́ сжима́ться, и образовался вращающийся диск из веществ, основная часть которых
собралась в центре (2). Центральное ядро уменьшалось, притягивая к себе все больше материи, и в какой-то момент в его недрах под действием огромного
давления сжатия пошла ядерная реакция (3) — зажглась звезда, возникло Солнце. Остальное вещество сбивалось в меньшие образования из камней и сгустков газа —
так образовались планеты. Солнечная система приняла современный вид (4).
На начальной стадии своего формирования Солнце было очень горячим, что явилось причиной испарения в космос большой части лёгких летучих
веществ (преимущественно водорода и гелия), которые находились в области, где формировалась Земля. Другими словами, протопланетная туманность вокруг
Солнца разделилась на две различные по составу и температуре части: ближайшая к Солнцу содержала меньше легких элементов и имела достаточное насыщение тяжелыми
элементами, в отличие от более удаленной, обедненной тяжелыми элементами и состоящей преимущественно из легких газов. В более отдаленных и холодных
областях будущей Солнечной системы, легкие вещества могли конденсироваться, образуя под действием гравитации гигантские газообразные планеты — «газовые
планеты-гиганты», такие как
Юпитер и Сатурн.
Под действием гравитационных сил материя солнечной туманности аккумулировалась также и во внутренней части туманности — здесь происходило
образование Земли и других планет земной группы. Но из-за огромной температуры материя находилась в расплавленном состоянии; более плотные вещества, такие, как
железо, никель и их соединения, устремились к центру планеты, тогда как более легкие, например, силикаты разных металлов, из которых впоследствии образовались
скальные породы, остались на поверхности. Такой процесс получил название гравитационной дифференциации. По окончании этого процесса температура на Земле
постепенно понизилась настолько, что начался процесс затвердения.
Следует отметить, что этот сценарий — только один из теоретических сценариев образования Земли. Например, в 40-х годах XX века
академик О.Ю. Шмидт выдвинул ставшую общепринятой гипотезу об образовании Земли и других планет из холодных твёрдых допланетных тел — планетезималей.
Планетезима́ль (от англ. planet — планета и
infinitesimal — бесконечно малый) — тело, представляющее собой промежуточную ступень формирования планеты из протопланетного газово-пылевого
облака. Более детально основные моменты теорий образования планет мы рассмотрим в отдельной главе, посвященной происхождению Солнечной системы.
Уважаемые посетители!
У вас отключена работа JavaScript. Включите пожалуйста скрипты в браузере, и вам откроется полный функционал сайта!
Длина экватора земли составляет в км
Длина экватора — величина постоянная?
А теперь попробуем ответить на вопрос о том, в чем причина расхождения в значениях длины экватора у современных ученых и Эратосфена. Возможно, все дело не только в несовершенстве средств измерений? А если экватор просто стал длиннее? Современные ученые придерживаются теории строения Земли и дрейфа континентов на основе тектоники плит. Однако еще в 1968 году советский ученый-геолог Владимир Ларин выдвинул теорию гидридного строения ядра Земли. Он предположил, что вещество, из которого происходило формирование нашей планеты, содержало большое количество атомарного водорода. Он вступил в реакцию с железом и никелем, из которых состоит ядро Земли, в результате чего образовались гидриды этих элементов. В результате внутренних процессов в недрах планеты происходит постепенное разогревание ядра и выделение водорода. Это приводит к снижению плотности и, соответственно, к увеличению размеров Земли. Данная теория не только более полно объясняет «дрейф» материков, но и позволяет объяснить образование месторождений полезных ископаемых, в первую очередь углеводородов. Так что вполне возможно, что нефть, газ, каменный уголь имеют абиогенное происхождение, и синтез их в недрах планеты происходит и в настоящее время. Мало того, подтверждение работам советского ученого обнаружилось и в древних зороастрийских мифах, где сказано, что для увеличения поверхности Земли боги три раза на одну треть увеличили ее размеры. Данная теория, кроме всего прочего, дает возможность объяснить и массовое вымирание за короткий промежуток времени многих видов древних животных, так называемое триасовое побоище. Самое интересное, что увеличение радиуса планеты происходит и в настоящее время, примерно на два сантиметра в год. Это подтверждают регулярные измерения ученых, но ранее данные результаты не находили объяснения, если не считать таковым поглощение Землей пыли из космического пространства. Так что со временем длина экватора будет увеличиваться.
Сколько километров составляет длина экватора?
Экватор в переводе с латыни означает «уравнивать». Принято считать, что экватор — это условная окружность, делящая земной шар на северное и южное полушария, и самая длинная окружность (или параллель) Земли, перпендикулярная ее оси вращения.
Экватор является отправной точкой для определения координат любого места на планете. Без него невозможно бы было определить точное положение в пространстве любых географических объектов или это было крайне затруднительно.
Всем давно известно, что если быть академически точным, то Земля на самом деле представляет собой не сферу, а геоид. Геоид — тело, по своим пропорциям напоминающее сферу, однако ей не являющееся. И действительно, в самой высокой точке планеты высота составляет 8 848 м (гора Эверест) и в самой низкой — 10 994 м (Марианская впадина) относительно уровня моря.
То есть если учитывать все перепады высот, то любой расчет вызовет массу проблем. Поэтому в международном сообществе для простоты расчетов нашу планету принято считать сферой. В том числе экватор считается окружностью, хоть и на самом деле ею не является.
Согласно международному стандарту WGS-84 радиус Земли составляет 6 378 137 м. Согласно другому стандарту IAU-1976 и IAU-2000 радиус Земли равен 6 378 140 м. Разница в три метра связана с разницей в подходах и способах расчета. Тем не менее, длина экватора составляет 40 075 км, какой бы из стандартов мы ни взяли, поскольку после вычисления длины окружности по формуле l=2πR разница будет только во втором знаке после запятой.
История расчетов
Первые попытки подсчитать длину экватора были предприняты еще в Древней Греции Эратосфеном. Хотя, собственно, если брать известный на тот момент мир, он считал не экватор, а радиус Земли в районе Европы, который привязан к длине окружности через 2πR. В те времена еще не существовало научного понятия о Земле как планете.
Чтоб не вдаваться в подробности эксперимента, объясним его суть. Эратосфен определил, что в момент, когда в городе Сиена (ныне Асуан) Солнце находится в зените и освещает дно колодца, в этот же момент времени в Александрии оно «отстает» примерно на 7 градусов и не освещает дно колодца. Что, в свою очередь, примерно составляет 1/50 часть окружности. Теперь, зная расстояние от Сиены до Александрии (оно составляло около 5000 стадиев), можно было определить длину окружности.
Тем неожиданнее являются результаты расчетов. Эратосфен считал протяженность экватора в 252 000 стадиев. Но так как за свою жизнь он прожил и в Александрии (Египет) и в Афинах (Греция), историки и географы до сих пор не могут с уверенностью сказать, какими именно стадиями пользовался при расчетах Эратосфен. Если греческими, то по Эратосфену радиус составлял 7 082 км, если египетскими — 6 287 км. Какой бы результат вы ни взяли для своего времени, это был невероятно точный расчет радиуса.
Позже попытки рассчитать длину экватора были приняты многими европейскими учеными. Впервые о возможном усреднении радиуса для удобства вычислений при расчетах заговорил голландец Снеллиус. В XVII веке он предложил рассчитывать радиус без учета естественных преград. В XVIII веке Франция (первая из стран) перешла на метрическую систему измерения. Причем при расчете эталона длины французские ученые привязывались именно к радиусу Земли.
Расчет был привязан к длине математического маятника, полупериод колебания которого составляет одну секунду. Для своего времени идея была прорывная. Однако при путешествиях к южным широтам, французский картограф Жан Рише заметил, что период колебания увеличился. Причина была в том, что Земля представляет собой геоид и сила тяжести ближе к экватору падает.
Исследования в России
В Российской империи также проводились исследования по определению формы, длины и других параметров Земли. Пожалуй, самым крупным и важным из них был проект «Русской дуги» или «Дуги Струве» под руководством Фридриха Георга Вильгельма Струве (Василия Яковлевича Струве). Для проведения измерений было построено 265 триангуляционных пункта, представлявших собой 258 треугольников с общей стороной. Длина дуги составляла 2820 км, что является 1/14 окружности Земного шара. Дуга на тот момент проходила через территорию Норвегии, Швеции и Российской империи. Финансировалось исследование лично императором Александром I, а далее и Николаем I.
Данный проект был первым из измерений Земли, который точно определил ее форму и параметры. При измерении параметров Земли спутниковыми методами в XX веке погрешность измерений Струве составила 2 см.
В Советском Союзе геодезическая школа также предпринимала попытки расчета параметров эллипсоида Земли. В 1940 году благодаря работам А.Н. Изотова и Ф.Н. Красовского был рассчитан и принят как стандарт для геодезических работ в СССР эллипсоид Красовского, определяющий все основные параметры эллипсоида Земли. По Красовскому приняты следующие параметры:
- Малый радиус Земли (полярный радиус) составляет 6 356,863 км.
- Большой радиус (экваториальный) 6 378,245 км.
- Длина экватора составляет 40 075,696 км.
- Площадь поверхности Земли 510 083 058 км2.
Экватор Земли. Окружность земного шара
Экватор – это воображаемая круговая линия, которая опоясывает весь земной шар и проходит через центр Земли.
Линия экватора перпендикулярна оси вращения нашей планеты и находится на равном расстоянии от обоих полюсов.
Экватор: что это и зачем он нужен?
Итак, экватор – это воображаемая линия. Зачем серьезным ученым понадобилось воображать какие-то линии, очерчивающие Землю? Затем, что экватор, как и меридианы, параллели и прочие разделители планеты, которые существуют только в воображении и на бумаге, дают возможность производить подсчеты, ориентироваться в море, на суше и в воздухе, определять месторасположение различных объектов и т.д.
Экватор делит Землю на Северное и Южное полушария и служит началом отсчета географической широты: широта экватора равна 0 градусов. Он помогает ориентироваться в климатических поясах планеты. Приэкваториальная часть Земли получает самое большое количество солнечных лучей. Соответственно, чем дальше территории расположены от экваториальной линии и чем ближе они к полюсам, тем меньше солнца им достается.
Приэкваториальная область – это вечное лето, где воздух всегда горячий и очень влажный из-за постоянных испарений. На экваторе день всегда равен ночи. Солнце бывает в зените – светит вертикально вниз – только на экваторе и только дважды в год (в те дни, на которые приходятся дни равноденствий в большинстве географических поясов Земли).
Экватор проходит через 14 государств. Города, расположенные непосредственно на линии: Макапа (Бразилия), Кито (Эквадор), Накуру и Кисуму (Кения), Понтинак (остров Калиманта, Индонезия), Мбандака (Республика Конго), Кампала (столица Уганды).
Длина экватора
Экватор является самой длинной параллелью Земли. Его длина составляет 40.075 км. Первым, кто смог приблизительно вычислить протяженность экватора, был Эратосфен – древнегреческий астроном и математик. Для этого он измерял время, в течение которого солнечные лучи достигали дна глубокого колодца. Это помогло ему вычислить длину радиуса Земли и, соответственно, экватора благодаря формуле длины окружности.
Следует отметить, что Земля не является идеальной окружностью, поэтому радиус ее в разных частях немого отличается. К примеру, радиус на экваторе равен 6378,25 км, а радиус на полюсах – 6356,86 км. Поэтому для решения задач по вычислению длины экватора радиус принимают равным 6371 км.
Длина экватора является одной из ключевых метрических характеристик нашей планеты. Ее используют для вычислений не только в географии и геодезии, но в астрономии и астрологии.
ПОЧЕМУчка
- Дела домашние и школьные (55)
- Живем в доме (15)
- Наши домашние любимцы (11)
- Не забываем об осторожности (3)
- Транспорт по соседству (6)
- Удивительное в школьной жизни (20)
- Деревья, цветы и прочая зелень (62)
- Деревья (12)
- Растения – наши кормильцы (6)
- Растения в экстремальных условиях (3)
- Спорообразующие растения (7)
- Темная сторона жизни растений (7)
- Узнаем о семенах (6)
- Цветы (7)
- Что нужно знать о растениях (14)
- Животные рядом с нами (161)
- Всякая всячина (19)
- День в зоопарке (4)
- Земноводные (амфибии) (6)
- Млекопитающие (34)
- Насекомые, пауки и черви (28)
- Пресмыкающиеся (22)
- Птицы (25)
- Рыбы и другие обитатели морских глубин (19)
- Удивительные способности животных (4)
- Земля, небо и выше (109)
- Мир у нас над головой (46)
- Узнаем о планете Земля (32)
- Что важно знать о погоде (31)
- Как все это работает? (42)
- Как делают копии и получают изображения (4)
- Свет и лазеры (8)
- Средства информации и связи (9)
- Тепло и холод (7)
- Транспорт (12)
- Энергия (2)
- Моя семья и мои друзья (47)
- Всё о семье (19)
- Мы общаемся (15)
- Смерть и умирание (13)
- Новости сайта (7)
- Новый год (12)
- Путешествуем по всему миру (50)
- В деревне, на ферме (19)
- Жизнь в большом городе (13)
- Факты из географии (18)
- Разное (50)
- Разное – обо всём понемногу (15)
- О еде (7)
- Об одежде (8)
- Я и всё обо мне самом (133)
- Дела кровные (12)
- Кожа, внутри которой я нахожусь (14)
- Кости и мышцы (13)
- Мозг (3)
- Накормите меня (14)
- Откроем пошире рот (15)
- Отправляемся спать (5)
- Поговорим о туалете и ванной (9)
- Сегодня шевелюра, а завтра лысина (9)
- Слышу, вижу, различаю запахи (24)
- Что со мной, доктор? (6)
- Я появляюсь на свет (9)
Популярные темы:
параллели, меридианы и длина экватора в исследованиях ученого из Кирены
Автор Маргарита Малиновская На чтение 7 мин. Опубликовано
Современная наука базируется на знаниях, полученных древними учеными, которые посвятили свою жизнь совершению важнейших открытий. То, что открыл Эратосфен в географии и других науках, до сих пор используется в современных научных направлениях. Именно он первым употребил сам термин «география».
Краткая биография Киренского мыслителя
Пересказ того, что смог открыть, изучить и измерить Эратосфен за всю свою жизнь, огромен.
Древнегреческий математик, астроном и хранитель ныне утраченной Александрийской библиотеки Эратосфен родился в 276 году до н. э. в античном городе Кирена, который располагался на территории, занимаемой современной Ливией. В окружении Эратосфена говорили, что в нем жила настоящая, кипучая энергия, которая двигала его вперед, к знаниям. Он стремился к общению с учеными Александрии и Афин. Благодаря разностороннему образованию Эратосфен не ограничивал поле своей деятельности точными науками, а увлекался поэзией, филологией, сочинял различные философские трактаты и упражнялся в написании комедий.
По протекции своего учителя Калимаха, а также друга и наставника Аполлония Родосского, Эратосфен был приглашен в Александрийскую библиотеку, где и трудился до старости. Первые годы он выполнял обязанности рядового работника, однако уже через пять лет смог добиться поста главы библиотеки.
В то время должность хранителя Александрийской библиотеки обязывала Эратосфена быть главным учителем детей египетского царя Птолемея III Эвергета. Эратосфен запомнился современникам не только как великий ученый и отличный педагог, но и как талантливый управленец. За те годы, которые он находился во главе Александрийской библиотеки, заведение пополнилось многочисленными трудами как греческих, так и иностранных авторов.
Наиболее известными литературными произведениями и научными трактатами, созданными Эратосфеном, являются:
- художественные поэмы «Гермес», «Гесиод»;
- исторический труд «Хронография»;
- филологический трактат «О древней комедии»;
- математические сочинения «О шаре и цилиндре», «О средних величинах», «Платоник» и т. д.
Пост главы Александрийской библиотеки подарил Эратосфену возможность беспрепятственного доступа к обширному источнику знаний, но древнегреческому философу этого было недостаточно. Острая потребность в информации и желание разобраться в сути вещей толкали его на совершение никем доселе не сделанных открытий.
Однако судьба сыграла с Эратосфеном довольно злую шутку. Одной из болезней, мучивших его в старости, было сильнейшее воспаление глаз, ставшее причиной полной слепоты. Вместе с возможностью читать старец потерял и смысл жизни. Чтобы прервать свое бессмысленное существование, Эратосфен полностью отказался принимать пищу, отчего в итоге и завершил свой жизненный путь в 194 году до н. э.
Географические открытия
Эратосфен был очень увлечен географией. Следует начать с того, что сам термин «география» был создан именно Эратосфеном. С древнегреческого языка это определение можно перевести как «описание Земли». Киренский ученый настаивал, что Земля, как объект исследования, должна рассматриваться полностью, со всеми огромными пустошами, а не только те ее территориальные местности, которые уже были заселены людьми.
Одной из главных научных работ его жизни является большой трехтомный труд, имеющий название «География», посвященный детальному обзору опыта, приобретенного отважными мореплавателями и путешественникам, сумевшими побывать не только в других странах, но и на отдаленных континентах и отразивших это в своих докладах.
Также трехтомник содержит многочисленные математические расчеты, подтверждающие факт того, что Земля не стоит на трех слонах и черепахе, а является шарообразным космическим телом.
Обладая лишь скромным арсеналом античных измерительных инструментов, Эратосфен пытался вычислить расстояния от Земли до Луны и даже до Солнца.
К другим достижениям Эратосфена в сферах географии и астрономии относят:
- Разработку темы пропорций и геометрических построений, без которых невозможно представить современный географический контурный атлас.
- Написание книги «Катастеризмы», в которой он собрал все известные науке созвездия и отдельные звезды, входящие в их границы, как класс небесных светил.
- Изобретение армиллярной сферы — инструмента, использующегося для установления экваториальных координат.
- Вычисление градуса угла, образованного пересечением тропика и экватора. Он считал, что соотношение этих географических явлений составляет 11 к 83 от 180 градусов.
- Предположение о том, что фактическая длительность светового дня на разных широтах может значительно колебаться.
Поиски длины экватора
Одной из задач, которая в особенности интересовала древнегреческого мастера географии, был вопрос поиска длины окружности Земли. За основу своей теории, приведшей к удивительным для того времени результатам, исследователь взял то, что города Александрия и Сиена (ныне Асуан) расположены на одном и том же меридиане. Киренский ученый наблюдал за отношением угла падения лучей, отбрасываемых небесным светилом в день летнего солнцестояния в двух этих населенных пунктах, к поверхности земли.
В своем исследовании математик и географ пользовался гномоном — специальным устройством, изобретенным другим древнегреческим ученым Анаксимандром Милетским и позволяющим с высокой точностью определить момент астрономического полдня.
Многолетние наблюдения за светом и тенью позволили Эратосфену вычислить необходимый угол падения солнечных лучей. На основании полученных данных и произведенных с ними расчетов он высказал предположение, что фактическое расстоянием между Александрией и Сиеной равняется 785 км.
Соотнеся полученное расстояние и значение угла 1 к 50, определенное при помощи гномона, древний математик и географ смог совершить прорыв, узнав примерную длину экватора Земли, которая, согласно его подсчетам, составила около 39250 км. Согласно современным высокоточным измерениям, длина экватора равняется 40120 км.
Это великое открытие не только перевернуло античную географию, но и позволило Эратосфену прославиться за пределами своего места нахождения. Благодаря полученным данным ученый смог вычислить радиус земного шара, довольно точно определить фактическое расстояние между населенными пунктами в пределах одного материка и узнать, как далеко находятся Африка и другие континенты. Такой вклад в развитие античных представлений об окружающем мире невозможно не оценить.
Значительные успехи в картографии
Современные ученые считают, что именно Киренский географ и математик был тем самым человеком, который первым дерзнул создать максимально полную карту мира, демонстрирующую реальные расстояния между городами и странами. Античный математик и философ придерживался мнения о том, что получить довольно точное отображение трехмерного земного шара можно и в двухмерном варианте, используя выведенные им формулы математических расчетов.
С использованием методики Эратосфена картография начала уверенно развиваться. Именно благодаря ему на античных изображениях Земли стали появляться особые линии, названные параллелями и меридианами.
Не имея физической возможности отправиться в путешествие вокруг света и доказать свои предположения, поставив реальные опыты, Эратосфен все-таки выказывал различные, и весьма смелые для своего времени, предположения, основываясь лишь на своих знаниях античной географии, рассказах мореплавателей и математических расчетах.
Очевидно, что карта Эратосфена не могла в точности отображать фактическое расположение материков и океанов, но тем не менее она широко использовалась среди моряков, позволяя уточнить детали запланированного маршрута и сделать любое длительное путешествие на корабле более безопасным и кратким по сроку.
Искренняя и упорная вера в науку и пытливый ум, жаждущий открытий — качества, которые присущи настоящим ученым. Несмотря на то что древнегреческие математики, географы и астрономы были ограничены в возможности подтверждения своих самых смелых гипотез, они не боялись делать смелые, порой даже переворачивающие ви́дение мира, предположения, при этом какие-то из них всегда оказывались состоятельными.
Именно благодаря такому подходу они навечно завоевали почетное место в пантеоне древнегреческих ученых. Историю открытий Эратосфена хотя бы кратко можно найти в большинстве учебников географии, потому что оценка его достижений с поправкой на древность крайне высока. Его труды были переведены на многие языки, в том числе русский. В честь Киренского географа и математика даже назвали один из лунных кратеров. Кстати, «компанию» ему на Луне составляют и кратеры других древнегреческих светил науки — «Платон», «Аристотель», «Геродот».
основные параметры, как измерить окружность и радиус Земли
Для ученых диаметр Земли имеет практическое значение. Его рассчитывают, зная окружность планеты по экватору.
Диаметр Земли рассчитывается исходя из длины окружности экватора. Credit: s1.travelask.ru.
Основные параметры Земли
Планете Земля не менее 4,5 млрд лет. Она входит в земную группу планет наряду с Меркурием, Венерой и Марсом. В отличие от газовых гигантов (Юпитера, Сатурна, Нептуна, Урана) они состоят из горных пород, покрывающих поверхность тонким слоем. Среди планет земной группы Земля самая большая, а в Солнечной системе пятая по величине.
Главное отличие Земли — она единственная, на которой есть жизнь. Этому способствуют:
- Расстояние от Солнца, которое составляет примерно 150 млн км.
- Температура поверхности: средняя +13°С, минимальная не превышает -90°С, максимальная — +60°С.
- Вода — основа жизни — занимает 71% площади.
- Состав атмосферы: 78% азота, 21% кислорода, 1% аргона.
По физическим параметрам Земля превосходит все планеты земной группы:
- масса составляет 5,9722±0,0006×1024 кг;
- объем — 1,08321×10¹² км³;
- плотность — 5,514×10 г/см³;
- окружность по экватору — 40075,16 км, диаметр — 12756,1 км;
- между полюсами параметры меньше: окружность — 40008 км; диаметр — 12713,5 км.
Самая плотная Земля потому, что единственная с твердым внутренним ядром, занимающим около 30% объема. Оно покрыто жидкой мантией (70-80% объема) и корой (1%).
У Земли 1 спутник — Луна, среднее расстояние до которой — 384,4 тыс. км. По орбите протяженностью 939120 млн км планета оборачивается вокруг Солнца за 365,3 дней. Вокруг собственной оси — за 23,9 часа.
Форма планеты
Нашу планету называют шаром, но это неправильно с точки зрения геометрии. Дело не в океанических впадинах и горных вершинах — для глобальных масштабов разница между ними незначительная. Между наиболее низкой точкой (Марианской впадиной) и самой высокой (гора Эверест) — 19 км.
Больше влияет на форму Земли гравитация. Масса притягивается к центру (ядру), отчего небесное тело сжимается, приобретая сферическую форму. Центробежная сила, возникающая при вращении планеты, наиболее высокая на экваторе. Под ее воздействием эта область самая большая по окружности и диаметру.
Земля имеет форму неправильного шара. Credit: opiqkz.blob.core.windows.net.
Что такое экватор и зачем он нужен
Экватор — условная перпендикулярная оси вращения линия вдоль Земли на идентичном расстоянии от полюсов. Из-за сферической формы планеты эта параллель самая длинная. По отношению к плоскости орбиты расположение экватора меняется в диапазоне 22-24,5°. На наклон оси влияет притяжение планет и Солнца.
Вдоль экватора день равен ночи без малейшего отклонения. Дважды в году при равноденствии направление солнечных лучей строго вертикальное. В остальные дни оно ненамного отличается, поэтому территории экватора получают самое большое количество ультрафиолета. Здесь всегда лето, воздух горячий и влажный из-за постоянных испарений.
Чтобы проводить расчеты, требуется условное разделение планеты на параллели и меридианы. Географическая широта экватора — 0°. Это точка отсчета всех координат Земли, которая делит ее на 2 равные половины.
По параллелям и меридианам определяют положение объектов. По ним ориентируются в воздухе, на суше и воде. Кроме того, выделяют климатические зоны, часовые пояса.
Как измерить длину окружности Земли
Чтобы измерить окружность земли по экватору, существуют специальные приборы и космические спутники. Но, применяя знания по геометрии, получают данные без сложных инструментов. Впервые такую работу выполнил ученый Древней Греции Эратосфен.
Согласно преданиям, путешественники сообщили ему, что в день летнего солнцестояния они наблюдали, как освещалось дно самых глубоких колодцев, а предметы не отбрасывали тени. Солнце стояло в зените. Это происходило в 500 милях южнее Александрии, в Сиене. Астроном знал, что в родном городе предметы отбрасывают тень, а солнце не заглядывает на дно глубоких колодцев.
В полдень самого продолжительного летнего дня Эратосфен измерил длину тени городского обелиска, высоту он знал. По этим данным рассчитал протяженность условной линии, соединяющей вершины обелиска и тени. Зная эти данные, просчитал углы воображаемого треугольника — 7°. Это значило, что Сиена настолько смещена относительно Александрии.
Угол 7° — это приблизительно ⅟50 часть замкнутой окружности, которая всегда имеет 360°. Астроном продолжил вычисления дальше. Он умножил расстояние до Сиены на 50. Получилась длина окружности Земли — 25000 миль. Современные исследования показали, что ученый не сильно ошибался: экваториальная окружность планеты равна 24894 мили или 40075 км.
Погрешность Эратосфена объясняется не примитивностью расчетов, которыми он пользовался. Этот способ точный, применяется и сегодня, только с более совершенными инструментами. Ученый не знал точного расстояния между городами. Оно в те времена измерялось количеством дней, проведенных караваном в пути.
Вторая причина неточности — Александрия и Сиена расположены на разных меридианах. Сегодня рассчитывают окружность между объектами, которые находятся на одном меридиане.
Измерение окружности Земли по Эратосфену. Credit: kipmu.ru.
Вычисления радиуса и диаметра
Зная окружность, вычислить радиус и диаметр земного шара несложно. Применяют формулы: d=l/π; r=½*π. Буквами обозначены:
- d — диаметр. Соединяет противоположные стороны окружности, проходит через центр.
- l — длина окружности. Это линия на равной дистанции от центра.
- r — радиус. Так называют линию, проложенную от центра до произвольной точки на окружности.
- π — число, равное 3,14. Оно бесконечное, поэтому чем больше цифр после запятой, тем точнее расчеты.
Необязательно использовать обе формулы. Диаметр и радиус взаимосвязаны. Вычисляют один параметр, после чего узнают второй: диаметр в 2 раза больше радиуса и наоборот.
Величина окружности разная на экваторе и полюсах. Поэтому экваториальный радиус больше полярного. Первый — 6378 км, второй — 6356 км. Интересно, что диаметр Солнца больше диаметра Земли в 109 раз.
За какое время можно обойти планету пешком
Длина экваториальной окружности в километрах рассчитана. Зная эту величину и предполагаемую скорость пешехода, определяют, сколько времени понадобится, чтобы обойти Землю. Применяется формула: t=S:V. Латинские буквы обозначают:
- t — время;
- S — путь;
- V — скорость.
Чтобы пройти Землю пешком по экватору, понадобится преодолеть 40075 км. Средняя скорость пешехода — 6 км/ч. Если подставить эти значения в формулу, выйдет: 40075/6=6679 часов. После перевода в сутки получается 278.
Без остановок никто не идет. Если в день передвигаться 6 часов, понадобится времени в 4 раза больше — 1112 суток. Это составит 3 года.
Расчеты гипотетические, потому что экватор пересекает сушу только через Америку, Африку, Индонезийские острова. Остальной путь лежит через океаны: Атлантический, Индийский, Тихий.
Интересные факты об экваторе Земли
Экватор пересекает 33 острова. Credit: reader.lecta.rosuchebnik.ru.
Территория, прилегающая к экватору, отличается влажным теплым климатом. Здесь самые богатые на планете флора и фауна, густые леса, некоторые участки непроходимые. Лето длится год, средняя температура — +25…+30°С. Ночью она ненамного отличается от дневной, настолько сильно земля прогревается солнцем. Дождь идет практически каждый день.
Климат привлекает туристов, но не во всех странах созданы условия. Наибольшее количество отдыхающих ежегодно наблюдается на Мальдивских островах, привлекают туристов власти Эквадора, Бразилии, Кении.
Интересны географические достопримечательности экваториальных стран:
- Нулевая параллель пересекает 33 острова. Из них 17 — территория Индонезии. Часть островов не океанические: 2 — в озере на индонезийском острове Калимантан, 9 — в устье реки Амазонка, еще 5 — на африканском озере Виктория.
- На экваторе расположено 14 стран. В его честь назван Эквадор, которую пересекает нулевая параллель. Нет в мире путешественника, которому удалось пересечь по экватору все эти страны.
- Почти во всех экваториальных странах, кроме Габона и Сомали, установлены памятные знаки в честь нулевой параллели. Самые красивые — в Бразилии и Эквадоре.
- На архипелаге Галапагос находится действующий вулкан Вольф. Он расположен по обе стороны экватора.
- Неподалеку от г. Кито (столица Эквадора) белеет вулкан Каямбе. Его высота 4690 м, склоны покрыты вечным льдом.
- Река Конго в Африке пересекает экватор 2 раза.
Человек использует физические особенности нулевой параллели. Земля там вращается в 1,4 раза быстрее скорости звука. В этом регионе выгодно запускать космические спутники. Они сразу набирают сверхзвуковую скорость, экономится 10% топлива. На геостационарной орбите над экватором зависли спутники связи. Сигнал доходит до Земли быстрее, чем в других регионах.
Измерение Земли Эратосфеном и другие географические открытия
«Если бы не громадные размеры океана, окружающего нашу ойкумену, можно было бы, плывя на запад, достичь Индии»
Эратосфен
Чтобы совершить гениальное открытие, вовсе необязательно иметь под рукой хитроумные приборы или сверхточные снимки из космоса. Это более 2000 лет назад доказал Эратосфен. Не покидая своей библиотеки, он осуществил по тем временам невозможное — с поразительной точностью рассчитал размеры Земли.
Древнегреческий географ Эратосфен (276–194 гг. до н. э.)
Удивительная история
Древнегреческий мыслитель изучал историю, философию, литературу и множество других дисциплин. Современники посмеивались над ним и считали дилетантом, поскольку, по их мнению, он интересовался всем, но толком не знал ничего. Однако ученого это не смущало. Эратосфен работал в египетской Александрии. Однажды, возвращаясь из своего музея, он повстречал путешественников, идущих из Сиены — города, расположенного южнее Александрии, на Северном тропике (современное название — Асуан). Те поделились с ученым любопытным наблюдением: когда они находились в Сиене (а это был самый длинный день в году), ни один предмет в городе не отбрасывал тень.
Эратосфен не мог оставить сказанное без внимания, поэтому спустя год посетил Сиену и убедился, что путники его не обманули. Он заглянул в глубочайший городской колодец и увидел: солнечные лучи достигают его дна, а также подметил, что светило в данный момент располагалось ровно над головой. В это же время в Александрии оно висело гораздо ниже и абсолютно все предметы, на которые падали лучи, отбрасывали небольшую тень. Такое простое наблюдение натолкнуло Эратосфена на мысль об определении размеров Земли.
Цифры, перевернувшие сознание
В Сиене предметы не отбрасывали тени, то есть угол между ними и солнечным лучом составлял 0°. В Александрии же обелиск рядом со зданием, где трудился Эратосфен, тень давал. Измерив высоту столба и длину тени, ученый по правилу треугольника рассчитал протяженность линии, которая соединяла вершину обелиска и конец тени.
Схема расчетов Эратосфена
Затем с помощью известных тогда правил геометрии он вычислил угол отклонения обелиска от солнечного луча — получилось 7,2°. Это означало, что Александрия отстоит от Сиены по земной окружности (равной 360°) на такое же количество градусов. Угол в 7,2° — приблизительно 1/50 часть окружности. Расстояние между Александрией и Сиеной Эратосфену было хорошо известно: его неоднократно преодолевали путники на верблюдах и знали, что оно составляет около 500 стадий (стадия соответствует примерно 160 м). Умножив 500 на 50, ученый определил длину окружности Земли — около 250 тыс. стадий.
Гораздо позже с помощью точных приборов было определено, что длина окружности Земли, или экватора, составляет 40 075 км. То есть Эратосфен оказался одаренным ученым, а не дилетантом. Не пользуясь ничем, кроме смекалки и логики, он невероятно точно вычислил размеры земного шара.
Суша размером с ладонь
Эратосфен первым высказал предположение, что если плыть от берегов Иберии (современной Испании) на запад, то можно достичь Индии.
Однако позже эта мысль показалась ученому безумной: он был убежден, что никто и никогда подобного не сделает, ибо «громадные размеры океана, окружающего нашу ойкумену, не позволят», — и ошибся. Его утверждение через множество столетий заставило задуматься Христофора Колумба, который бросил все и отправился на поиски Индии западным путем.
Карта Эратосфена: желтым цветом обозначена суша, голубым ― Мировой океан
Рассуждения о том, что представляет собой Земля, населенная людьми, Эратосфен подкрепил географической картой. Мир у ученого получился крохотным. В нем не было привычных нам Америки и Австралии. Эратосфен даже не мог предположить, что эти земли откроют лишь спустя 1,5 тыс. лет! Зато он весьма точно изобразил берега Средиземного моря, Персию, Скифию, чего до него никто никогда не делал. Кроме того, Эратосфен расчертил карту чем-то похожим на параллели и меридианы, а также показал контуры материков, обозначил горные хребты, реки, города и другие объекты.
Поделиться ссылкой
Земной шар по экватору расстояние. Чему равна окружность Земли в километрах — как посчитали эту величину
Всем известно, что планета Земля обладает круглой формой. Но какие размеры имеет планета, мало кто сможет сказать. Какова длина окружности земли по экваториальной линии или по меридиану? Чему равен диаметр Земли? Постараемся ответить на эти вопросы максимально подробно.
Прежде всего рассмотрим основные понятия
, с которыми мы столкнёмся при ответе на вопрос о длине окружности Земли.
Что называют экватором? Это круговая линия, опоясывающая планету и проходящая через её центр. Экватор перпендикулярен оси земного вращения. Он удалён одинаково от одного и другого полюса. Экватор разделяет планету на два полушария, называемые Северным и Южным. Он играет большую роль в определении климатических поясов на планете. Чем ближе к экватору, тем климат жарче, ведь этим территориям достаётся больше солнечного света.
Что такое меридианы? Это такие линии, которые разделяют весь земной шар
. Всего их 360, то есть каждая доля между ними равняется одному градусу. Меридианы пролегают через полюса планеты. По меридианам считают географическую долготу. Отсчёт начинается от нулевого меридиана, который также именуют Гринвичским, поскольку он пролегает через Гринвичскую обсерваторию в Англии. Долготу называют восточной или западной — в зависимости от того, в каком направлении идёт отсчёт.
В древние времена
Впервые окружность Земли измерили ещё в Древней Греции. Это был математик Эратосфен из города Сиены. В то время уже было известно
, что планета обладает шаровидной формой. Эратосфен наблюдал за Солнцем и заметил, что светило в одно и то же время суток при наблюдении из Сиены расположено точно в зените, а в Александрии оно имеет угол отклонения.
Эти измерения производились Эратосфеном в день солнцестояния в летний период. Учёный измерил угол и обнаружил, что его величина составляет 1/50 часть от целой окружности, равняемой 360 градусам. Зная хорду угла в один градус, её нужно умножить на 360. Затем Эратосфен взял в качестве длины хорды интервал между двумя городами (Сиеной и Александрией), предположил, что они находятся на одном меридиане, произвёл расчёты и назвал цифру 252 тысячи стадий. Это число и означало окружность Земли.
Для того времени подобные измерения
считались точными, ведь никаких способов измерить величину окружности Земли более точно, не существовало. Современные учёные признаются, что величина, посчитанная Эратосфеном, получилась довольно точной, несмотря на то, что:
- эти два города — Сиена и Александрия не расположены на одном меридиане;
- древний учёный получил цифру, исходя из дней пути верблюдов, а ведь ходили они не по идеально прямой линии;
- неизвестно, какой прибор применял учёный для измерения углов;
- непонятно, чему равнялся стадий, используемый Эратосфеном.
Тем не менее, учёные до сих пор придерживаются мнения о точности и уникальности метода Эратосфена, впервые измерившего диаметр Земли.
В Средние века
В XVII веке учёный из Голландии по имени Сибелиус изобрёл метод расчёта расстояний с помощью теодолитов. Это специальные приборы для измерения углов
, используемые в геодезии. Метод Сибелиуса назвали триангуляцией, он заключался в построении треугольников и измерении их базисов.
Триангуляция практикуется и в наши дни. Учёные условно поделили всю поверхность земного шара на треугольные участки.
Российские исследования
Учёные из России в XIX веке также внесли свой вклад в вопрос измерения длины экватора. Исследования велись в Пулковской обсерватории. Руководил процессом В. Я Струве.
Если ранее Землю считали шаром идеальной формы, то позднее накопились факты, согласно которым сила земного притяжения уменьшалась от экватора к полюсам. Учёные пытались дать объяснение этому явлению
. Было несколько теорий. Самой популярной из них считалась теория о сжатии Земли со стороны того и другого полюса.
Чтобы проверить верность гипотезы, Французская академия организовала экспедиции в 1735 и 1736 годах. В результате учёные измерили длину экваториального и полярного градуса в двух точках земного шара — в Перу и Лапландии. Выяснилось, что на экваторе градус имеет меньшую длину.21 тонн. Доля воды в этой величине составляет 7%.
Видео
Посмотрите интересный эксперимент, демонстрирующий, каким способом Эратосфену удалось высчитать окружность Земли.
Не получили ответ на свой вопрос? Предложите авторам тему.
Вряд ли нужно много писать о форме Земли. Всем ясно, что Земля представляет собой шар, слегка сплюснутый у полюсов, т. е. так называемый эллипсоид. Однако правильное, современное представление о форме и размерах Земли было достигнуто далеко не сразу и достигалось порою в тяжелой борьбе науки с религией.
Греческий поэт Гомер (IX–VIII в. до н. э.) изображал Землю в виде круга, схваченного со всех сторон рекой Океаном, «которая катит свои могучие воды по ободу богатого щита»; такое изображение Земли было выгравировано, якобы, на щите мифического героя Ахиллеса. Философ Фалес (VI в. до н. э.) полагал, что Земля — шар, а его ученик Анаксимандр изображал Землю в виде цилиндра. Другие философы и ученые Древней Греции представляли Землю то в виде куба, то в виде лодки и т. д.; ученики Ксенофонта и Анаксимена считали, что Земля — очень высокая гора. Греческая мифология содержит легенду о том, как Зевс, желая определить размеры Земли, выпустил одновременно двух орлов, одного на запад, другого на восток: они встретились в городе Дельфах; это называлось «обнаружение Земли путем слета двух орлов».
На протяжении ряда веков, через дебри схоластики и религии средневековья, пробивала себе путь истина.
Еще совсем недавно, в 1862 г., немецкий ученый П. Иоселиани, определяя «глубину толстоты земного шара», получил 4536,8 км
, что в 1 1 / 2 раза меньше действительной величины. Трудно поверить, но еще в 1876 г. в Петербурге была издана брошюра под названием: «Земля неподвижна, популярная лекция, доказывающая, что земной шар не вращается ни около оси, ни около Солнца. Читана в Берлине, доктором Шепфером. Перевод с немецкого Н. Соловьева. Издание 2-е, исправленное». Мы не будем останавливаться на подобных заблуждениях, и не будем касаться истории вопроса. Рассмотрим сведения, более существенные для нас в данном случае.
В 1841 г. немецкий астроном Ф. Бессель, используя градусные измерения, вычислил радиус Земли и ее сжатие у полюсов, т. е. получил цифры, характеризующие основные элементы земного эллипсоида. Результат был настолько точным, что эти цифры использовались при различных геодезических исследованиях, в картографии и т. п. в течение 100 лет.
Однако за последние десятилетия накопился огромный материал; появилась возможность уточнить прежние данные о форме и размерах Земли. К тридцатым годам была выполнена работа по пересмотру всех новых данных, и в 1936 г. советский ученый Ф. Н. Красовский опубликовал новые цифры, характеризующие размеры земного эллипсоида еще точнее.
Эллипсоид Ф. Н. Красовского имеет следующие размеры (рис. 3): большая полуось, т. е. расстояние от центра Земли до экватора, равна 6 378 254 метрам; малая полуось, т. е расстояние от центра Земли до одного из полюсов равна 6 356 863 метрам. Таким образом полярный радиус (от центра к полюсу) короче экваториального радиуса (от центра к экватору) приблизительно на 21 км
. Отсюда следует, что Земля действительно эллипсоид вращения, т. е. шар, сплюснутый, хотя и очень незначительно, у полюсов. Величина сжатия, вызванного вращением Земли вокруг своей оси, равна 1: 298,3. На школьном глобусе разница в длине экваториального и полярного диаметров равна всего лишь 0,5 мм
, т. е. практически незаметна.
Итак, в первом, и достаточно хорошем, приближении Земля должна быть принята за эллипсоид вращения, элементы которого опубликованы в 1936 г. и которые приняты в Советском Союзе в качестве официальных, т. е. обязательных для использования во всех специальных работах.
Рис. 3. Земля — эллипсоид вращения;
а — большая полуось; с — малая полуось.
Однако геодезисты нередко нуждаются в измерениях еще большей точности, и тогда для изображения формы Земли они пользуются не эллипсоидом, а другой фигурой, так называемым геоидом. Геоид несколько ближе к истинной фигуре Земли, со всеми ее возвышенностями и впадинами, чем эллипсоид, и представляет фигуру, весьма сложную по виду. Наконец, теперь выяснено, что и экватор Земли не является окружностью; скорее это эллипс, т. е. окружность, слегка сжатая. Приходится считать также, что северное и южное полушария, как показал русский ученый А. А. Иванов, не вполне симметричны относительно плоскости экватора.
В заключение приведем некоторые цифры, характеризующие размеры земного шара:
Экваториальный диаметр = 12 756,5 километра
Полярный диаметр = 12 713,7 километра
Длина окружности меридиана = 40 008,6 километра
Длина окружности экватора = 40 075,7 километра
Поверхность Земли = 510 миллионам квадратных километров
Объем Земли = 1080 миллиардам кубических километров
Люди давным-давно догадывались, что Земля, на которой они обитают, похожа на шар. Одним из первых высказал мысль о шарообразности Земли древнегреческий математик и философ Пифагор (ок. 570—500 до н. э.). Величайший мыслитель древности Аристотель, наблюдая лунные затмения, подметил, что край земной тени, падающей на Луну, всегда имеет круглую форму. Это и позволило ему с уверенностью судить о том, что наша Земля шарообразна. Теперь же, благодаря достижениям космической техники, все мы (и не раз) имели возможность любоваться красотой земного шара по снимкам, сделанным из космоса.
Уменьшенным подобием Земли, ее миниатюрной моделью является глобус. Чтобы узнать длину окружности глобуса, достаточно обернуть его питью, а затем определить длину этой нити. По огромную Землю с мерной лептой по меридиану или экватору не обойдешь. Да и в каком бы направлении мы ни стали ее измерять, па пути обязательно появятся непреодолимые препятствия — высокие горы, непроходимые болота, глубокие моря и океаны…
А можно ли узнать размеры Земли, не измеряя всей ее окружности? Конечно, можно.
Известно, что в окружности 360 градусов. Поэтому, чтобы узнать длину окружности, в принципе достаточно измерить точно длину одного градуса и результат измерения умножить на 360.
Первое измерение Земли таким способом произвел древнегреческий ученый Эратосфен (ок. 276—194 до и. э.), живший в египетском городе Александрии, па берегу Средиземного моря.
С юга в Александрию приходили караваны верблюдов. От сопровождавших их людей Эратосфен узнал, что в городе Сиене (нынешнем Асуане) в день летнего солнцестояния Солнце в иол-день находится над головой. Предметы в это время не дают никакой тени, а солнечные лучи проникают даже в самые глубокие колодцы. Стало быть, Солнце достигает зенита.
Путем астрономических наблюдений Эратосфен установил, что в этот же самый день в Александрии Солнце отстоит от зенита на 7,2 градуса, что составляет ровно 1/50 часть окружности. (В самом деле: 360: 7,2 = 50.) Теперь, чтобы узнать, чему равна окружность Земли, оставалось измерить расстояние между городами и умножить его па 50. Но измерить это расстояние, пролегающее по пустыне, Эратосфену было не под силу. Не могли измерить его и проводники торговых караванов. Они лишь знали, сколько времени тратят их верблюды на один переход, и считали, что от Сиены до Александрии 5000 египетских стадий. Значит, вся окружность Земли: 5000 x 50 = 250 000 стадий.
К сожалению, мы не знаем точно длину египетской стадии. По некоторым данным, она равна 174,5 м, что дает для земной окружности 43 625 км. Известно, что радиус в 6,28 раза меньше длины окружности. Получалось, что радиус Земли, но Эратосфену,— 6943 км. Вот так более двадцати двух веков тому назад впервые были определены размеры земного шара.
По современным данным, средний радиус Земли составляет 6371 км. По почему средний? Ведь если Земля — шар, то идее земные радиусы должны быть одинаковыми. Об этом мы расскажем дальше.
Способ точного измерения больших расстояний впервые предложил голландский географ и математик Вилдеброрд Сиеллиус (1580-1626).
Представим себе, что необходимо измерить расстояние между точками А и Б, удаленными одна от другой на сотни километров. Решение этой задачи следует начать с построения на местности так называемой опорной геодезической сети. В простейшем варианте она создается в виде цепочки треугольников. Вершины их выбираются на возвышенных местах, где сооружаются так называемые геодезические знаки в виде специальных пирамид, и обязательно так, чтобы из каждого пункта были видны направления на все соседние пункты. А еще эти пирамиды должны быть удобны для работы: для установки угломерного инструмента — теодолита — и измерения всех углов в треугольниках этой сети. Кроме того, в одном из треугольников измеряется одна сторона, которая пролегает по ровной и открытой местности, удобной для линейных измерений. В результате получается сеть треугольников с известными углами и исходной стороной — базисом. Затем следуют вычисления.
Решение наминается с треугольника, содержащего базис. По стороне и углам вычисляются две другие стороны первого треугольника. Но одна из его сторон является одновременно стороной смежного с ним треугольника. Она служит исходной для вычисления сторон второго треугольника и так далее. В конце концов находятся стороны последнего треугольника и вычисляется искомое расстояние — дуга меридиана АБ.
Геодезическая сеть обязательно опирается на астрономические пункты А и Б. Методом астрономических наблюдений звезд определяются их географические координаты (широты и долготы) и азимуты (направления на местные предметы).
Теперь, когда известна протяженность дуги меридиана АБ, а также ее выражение в градусной мере (как разность широт астропунктов А и Б), не составит особого труда вычислить длину дуги 1 градуса меридиана путем простого деления первой величины на вторую.
Этот способ измерения больших расстояний на земной поверхности получил название триангуляции — от латинского слова «триапгулюм», что значит «треугольник». Он оказался удобным для определения размеров Земли.
Изучением размеров нашей планеты и формы се поверхности занимается наука геодезия, что в переводе с греческого означает «землеизмерение». Ее зарождение следует отнести к Эратосфсну. Но собственно научная геодезия началась с триангуляции, впервые предложенной Сиеллиусом.
Самое грандиозное градусное измерение XIX века возглавил основатель Пулковской обсерватории В. Я. Струве. Под руководством Струве русские геодезисты совместно с норвежскими измерили дугу» простиравшуюся от Дуная по западным областям России в Финляндию и Норвегию до побережья Северного Ледовитого океана. Общая протяженность этой дуги превысила 2800 км! В ней было заключено более 25 градусов, что составляет почти 1/14 часть земной окружности. В историю науки она -вошла под названием «дуги Струве». Автору этой книги в послевоенные годы довелось работать на наблюдениях (измерениях углов) на пунктах государственной триангуляции, примыкавших непосредственно к знаменитой «дуге».
Градусные измерения показали, что паша Земля не является в точности шаром, а похожа на эллипсоид, то есть она сжата у полюсов. У эллипсоида все меридианы представляют собой эллипсы, а экватор и параллели — окружности.
Чем длиннее измеряемые дуги меридианов и параллелей, тем точнее можно вычислить радиус Земли и определить ее сжатие.
Отечественные геодезисты промерили государственную триангуляционную сеть почти на половине территории СССР. Это позволило советскому ученому Ф. Н. Красовскому (1878-1948) более точно определить размеры и форму Земли. Эллипсоид Красовского: экваториальный радиус — 6378,245 км, полярный радиус — 6356,863 км. Сжатие планеты — 1/298,3, то есть на такую часть полярный радиус Земли короче экваториального (в линейной мере — 21,382 км).
Представим себе, что па глобусе с поперечником 30 см решили изобразить сжатие земного шара. Тогда полярную ось глобуса пришлось бы укоротить на 1 мм. Это так мало, что совершенно незаметно для глаза. Вот так и Земля с большого расстояния кажется совершенно круглой. Такой ее наблюдают космонавты.
Изучая форму Земли, ученые прийти к выводу, что она сжата не только вдоль оси вращения. Экваториальное сечение земного шара в проекции на плоскость дает кривую, которая тоже отличается от правильной окружности, правда совсем немного — на сотни метров. Все это свидетельствует о том, что фигура у нашей планеты более сложная, чем казалось раньше.
Теперь уже совершенно ясно, что Земля не является правильным геометрическим телом, то есть эллипсоидом. К тому же поверхность нашей планеты далеко не гладкая. На ней есть возвышенности и высокие горные хребты. Правда, суши почти в три раза меньше, чем воды. Что же в таком случае мы должны подразумевать подземной поверхностью?
Как известно, океаны и моря, сообщаясь друг с другом, образуют на Земле обширную водную гладь. Поэтому ученые условились принимать за поверхность планеты поверхность Мирового океана, находящегося в спокойном состоянии.
А как поступать в районах континентов? Что там считать поверхностью Земли? Тоже поверхность Мирового океана, мысленно продолженную под всеми материками и островами.
Вот эта фигура, ограниченная поверхностью среднего уровня Мирового океана, была названа геоидом. От поверхности геоида и ведется отсчет всех известных «высот над уровнем моря». Слово «геоид», или «землеподобный», специально придумало для названия фигуры Земли. В геометрии такой фигуры не существует. Близок по форме к геоиду геометрически правильный эллипсоид.
4 октября 1957 года с запуском в нашей стране первого искусственного спутника Земли человечество вступило в космическую эру. 11ачалось активное исследование околоземного пространства. При этом выяснилось, что спутники очень полезны и для познания самой Земли. Даже в области геодезии они сказали свое «веское слово».
Как известно, классическим методом изучения геометрических характеристик Земли является триангуляция. Но раньше геодезические сети развивали лишь в пределах материков, а между собой они не были связаны. Ведь на морях и океанах триангуляцию не построишь. Поэтому расстояния между материками были определены менее точно. За счет этого снижалась точность определения размеров самой Земли.
С запуском спутников геодезисты сразу поняли: появились «визирные цели» на большой высоте. Теперь можно будет измерить большие расстояния.
Идея метода космической триангуляции проста. Синхронные (одновременные) наблюдения спутника из нескольких отдаленных пунктов земной поверхности позволяют привести их геодезические координаты к единой системе. Так были связаны воедино триангуляции, построенные на разных материках, а заодно были уточнены размеры Земли: экваториальный радиус — 6378,160 км, полярный радиус — 6356,777 км. Величина сжатия — 1/298,25, то есть почти такая же, как у эллипсоида Красовского. Разница между экваториальным и полярным диаметрами Земли достигает 42 км 766 м.
Если бы наша планета была правильным шаром, а массы внутри нее распределены равномерно, то спутник мог бы двигаться вокруг Земли по круговой орбите. Но отклонение формы Земли от шарообразной и неоднородность ее недр приводят к тому, что над различными точками земной поверхности сила притяжения неодинаковая. Изменяется сила притяжения Земли — изменяется орбита спутника. И все, даже малейшие изменения в движении спутника с низкой орбитой — то результат гравитационного воздействия на него той или иной земной выпуклости или и падины, над которой он пролетает.
Оказалось, что наша планета имеет еще и слегка грушевидную форму. Ее Северный полюс приподнят над плоскостью экватора па 16 м, а Южный — примерно на столько же опущен (как бы вдавлен). Вот и получается, что в сечении по меридиану фигура Земли напоминает грушу. Она чуть-чуть вытянута к северу и приплюснута у Южного полюса. Налицо полярная асимметрия: Се пер нос полушарие нетождественно Южному. Так на основании спутниковых данных было получено самое точное представление об истинной форме Земли. Как видим, фигура нашей планеты заметно отклоняется от геометрически правильной формы шара, а также от фигуры эллипсоида вращения.
Каждый раз при изучении карты мира экватор видится нам настолько значимой деталью, что бывает сложно поверить в его условное существование.
Экваториальную линию можно пересечь множество раз, даже не замечая этого, однако среди моряков существует замечательная традиция устраивать настоящие празднества, когда их корабль проходит экватор по морю. Что же подразумевают под этим понятием? Какова длина экватора и зачем ученым понадобилось рисовать его на географических картах?
Что означает слово «экватор»?
Термин «экватор»
связывают с латинским словом aequator, означающим «уравнивать, уравновешивать»
. Вместе с тем, его первоначальная трактовка соотносится с более древним праиндоевропейским понятием aik, переводимым как «ровный».
В русскую речь термин попал из Германии, откуда нашими предками было заимствовано немецкое слово Äquator.
Что такое экватор?
Экватором называют воображаемую линию, которая опоясывает нашу планету и проходит через ее центр. Линия проложена перпендикулярно и отстоит на одинаковом расстоянии от Северного и Южного полюса. Поскольку по своей форме планета не является строго шарообразной, при обозначении экватора ученые приняли условную окружность, радиус которой равняется усредненному радиусу Земли.
Все линии, которые проходят к югу и северу от экватора, называются параллелями и уступают ему по протяженности. В районе экваториальной линии всегда царит жаркое лето, а день равняется ночи. Только здесь Солнце может находиться в зените, то есть светить строго вертикально по отношению к земной поверхности.
Где проходит экватор?
Экватор разделяет Землю на Южное и Северное полушарие и выступает началом отсчета географической широты. Условная линия тянется через 14 стран, в числе которых Эквадор, Бразилия, Индонезия, Кения, Конго. В некоторых местах экватор проходит таким образом, что разделяет пополам отдельные населенные пункты и географические объекты.
В частности, непосредственно на линии расположены эквадорская столица Кито, бразильский город Макапа и эквадорский вулкан Вольф. Кроме того, экватор пересекает 33 острова в Индонезии, на африканском озере Виктория на реке Амазонка.
Чему равна длина экватора?
Для этого ему пришлось измерить время, в течение которого лучи Солнца достигали колодца в его дворе, а затем вычислить длину радиуса планеты и, соответственно, экватора. Согласно его расчетам, экваториальная линия равнялась 39 690 км, что с небольшой погрешностью практически соответствует современному значению.
Впоследствии рассчитать длину экватора пытались астрономы и математики многих стран мира. В начале XVII столетия голландский ученый Снеллиус предложил определять протяженность линии без учета находящихся на ней преград (возвышенностей, горных хребтов), а в в 1941 году советский геодезист Федор Красовский сумел вычислить длину эллипса Земли, которая в настоящее время является эталоном при научных исследованиях.
Реальная длина экватора, составляющая 40 075,696 км, была принята за основу международными организациями IAU и IUGG с учетом погрешности в 3 метра, которые отражают существующую неопределенность в среднем радиусе планеты.
Зачем нужен экватор?
Экватор на географических картах помогает ученым производить расчеты, определять местоположение различных объектов, ориентироваться в климатических поясах Земли. Находясь ближе всего к Солнцу, воображаемая линия получает наибольшее количество солнечного света, соответственно, чем дальше определенные территории расположены от экватора, тем они холоднее.
Протяженность экватора выступает одним из ключевых метрических значений земного шара. Ее используют в геодезии и географии, а также применяют в таких науках, как астрология и астрономия.
Меня периодически посещает ощущение что многие простые вещи специально излагаются так, чтобы читатель ничего не понимал и тупо заучивал, либо прочувствовал свою ничтожность перед изощренностью науки. Это всецело относится к известному по школьным учебникам феерическому способу
Эратосфена
измерения
окружности земного шара. Может быть он на самом деле вычислял таким извращенским способом, но зачем этот бред тиражировать со школы?
О том, как можно запудрить мозги в простом вопросе, посмотрим на примере вычисления длины окружности Земли в морских милях, который является частным случаем измерения широты местности и длины пройденного пути по меридиану.
Если современному человеку дать задачу вычислить длину окружности Земли в морских милях, он в подавляющем большинстве случаев заглянет в интернет/справочники и решит примерно так: длину окружности Земли например по парижскому меридиану 40.000 км с помощью калькулятора разделит на современную морскую милю 1,852 км и получит 21.598,3 морских миль, что будет близко к действительности.
Теперь покажу как вычислить длину окружности Земли в уме и абсолютно точно
. Для этого надо знать только одно: «Морская миля — единица измерения расстояния, применяемая в мореплавании и авиации. Первоначально морская миля определялась как длина дуги большого круга на поверхности земного шара размером в одну угловую минуту
.» via
В одном угловом градусе 60 минут, в окружности — 360 градусов, то есть в окружности 360х60=21.600 угловых минут, что в данном случае соответствует длине окружности земного шара в
21.600
морских миль. И это — абсолютно точно, поскольку длина окружности земного шара по меридиану является эталоном, а угловая минута-миля — производная единица. Поскольку Земля — не идеальный сфероид, а слегка кривоватый, то мили на разных меридианах будут немного отличаться друг от друга, но это совершенно неважно для навигации, ибо угловая минута — она и в Африке угловая минута.
Широту местности с точностью до градусов вполне можно измерить даже примитивными приспособлениями вроде транспортира с отвесом, который не сильно отличается от реально применявшегося моряками квадранта и по существу то же самое что и астролябия:
Для более точных измерений углов впоследствии был изобретен секстант (мор. арго — секстан):
Современные люди слабо представляют себе что такое аналоговые вычислительные машины
и как ими пользоваться. Для того, чтобы вычислить расстояние между двумя точками в меридиональном направлении, надо всего лишь измерить широты точек, а разность широт выраженная в угловых минутах и будет расстоянием между ними в морских милях
. Все просто, удобно и практически применимо.
Если уж так сильно хочется выяснить сколько в морской миле стадий, саженей, аршинов или там египетских локтей, надо аккуратно на коленках промерить ими расстояние между точками с известным расстоянием в морских милях-угловых минутах. Но зачем? Как это практически применимо?
Эратосфен будто бы измерял углы с точностью до угловых секунд и разница широт Александрии составила у него 7° 6,7″, то есть 7х60=420+6,7=426,7 морских миль (угловых минут). Кажется, что еще надо? Но ему почему-то требуются дни пути верблюдов и стадии. Возникает ощущение чего-то надуманного — фейка или розыгрыша.
Метод Эратосфена согласно В. А. Бронштейн, Клавдий Птолемей, Гл.12. Работы Птолемея в области географии:
«Как известно, метод Эратосфена заключался в определении дуги меридиана между Александрией и Сиеной в день летнего солнцестояния. В этот день, по рассказам лиц, посещавших Сиену, Солнце в полдень освещало дно самых глубоких колодцев и, значит, проходило через зенит. Следовательно, широта Сиены равнялась углу наклона эклиптики к экватору, который Эратосфен определил в 23°51″20″
. В тот же день и час в Александрии
тень от вертикального столбика гномона закрывала 1/50 часть окружности, центром которой служил кончик гномона. Это значит, что Солнце отстояло в полдень от зенита на 1/50 часть окружности, или на 7° 12″. Приняв расстояние между Александрией и Сиеной равным 5000 стадиев
, Эратосфен нашел, что окружность земного шара равна 250 000 стадиев. Вопрос о точной длине стадия, принятого Эратосфеном, долгое время служил предметом дискуссий, поскольку существовали стадии длиной от 148 до 210 м . Большинство исследователей принимали длину стадия 157,5 м
(«египетский» стадий). Тогда окружность Земли равна, по Эратосфену, 250 000-0,1575 = 39 375 км
, что очень близко к действительному значению 40 008 км
. Если же Эратосфен пользовался греческим («олимпийским») стадием длиной 185,2 м
, то получалась окружность Земли уже 46 300 км.
По современным измерениям широта Музея в Александрии 31°11,7″ широта Асуана (Сиены) 24° 5,0″, разница широт 7° 6,7″
, чему соответствует расстояние между этими городами 788 км
. Деля это расстояние на 5000, получим длину стадия, использованного Эратосфеном, 157,6 м.
Значит ли это, что он использовал египетский стадий?
Этот вопрос сложнее, чем может показаться.
Уже одно то, что Эратосфен привел явно округленное число — 5000 стадиев (а, скажем, не 5150 или 4890) не внушает к нему доверия
. А если оценка Эратосфена была завышена хотя бы на 15%, получим, что он использовал египетский стадий в 185 м
. Решить этот вопрос пока нельзя.»
via
Теперь обратим внимание на следующие обстоятельства:
Асуан (Сиена) и Александрия не находятся
на одном меридиане, разница по долготе составляет 3°, то есть около 300 километров.
Эратосфен не измерил расстояние, а
принял
исходя из дней пути верблюдов, которые ходили явно не по прямой линии.
Совершенно неясно каким прибором
Эратосфен измерял углы с точностью до секунд
Непонятно какой стадий
использован Эратосфеном для измерения расстояний и т.п.
Но при этом он будто бы получил достаточно точный результат! Или историками сделана подгонка под результат?
Из Википедии: «Эратосфен говорит, что Сиена и Александрия лежат на одном меридиане. И поскольку меридианы в космосе являются большими кругами, такими же большими кругами обязательно будут и меридианы на Земле. И поскольку таков солнечный круг между Сиеной и Александрией, то и путь между ними на Земле с необходимостью идёт по большому кругу. Теперь он говорит, что Сиена лежит на круге летнего тропика. И если бы летнее солнцестояние в созвездии Рака происходило ровно в полдень, то солнечные часы в этот момент времени с необходимостью не отбрасывали бы тени, поскольку Солнце находилось бы точно в зените; дела и в самом деле обстоят таким образом в [полосе шириной] в 300 стадиев. А в Александрии в этот же час солнечные часы отбрасывают тень, поскольку этот город лежит к югу от Сиены. Эти города лежат на одном меридиане и на большом круге. На солнечных часах в Александрии проведём дугу, проходящую через конец тени гномона и основание гномона, и этот отрезок дуги произведёт большой круг на чаше, поскольку чаша солнечных часов расположена на большом круге. Далее, вообразим две прямые, опускающиеся под Землю от каждого гномона и встречающиеся в центре Земли. Солнечные часы в Сиене находятся отвесно под Солнцем, и воображаемая прямая проходит от Солнца через вершину гномона солнечных часов, производя одну прямую от Солнца до центра Земли. Вообразим ещё одну прямую, проведённую от конца тени гномона через вершину гномона к Солнцу на чаше в Александрии; и она будет параллельна уже названной прямой, поскольку уже сказано, что прямые от разных частей Солнца к разным частям Земли параллельны (а это он откуда знает?). Прямая, проведённая от центра Земли к гномону в Александрии, образует с этими параллельными равные накрестлежащие углы. Один из них — с вершиной в центре Земли, при встрече прямых, проведённых от солнечных часов к центру Земли, а другой — с вершиной на конце гномона в Александрии, при встрече с прямой, идущей от этого конца к концу его же тени от Солнца, там где эти прямые встречаются наверху. Первый угол опирается на дугу от конца тени гномона до его основания, а второй — на дугу с центром в центре Земли, проведённую от Сиены до Александрии. Эти дуги подобны между собой, поскольку на них опираются равные углы. И какое отношение имеет дуга на чаше к своему кругу, такое же отношение имеет и дуга от Сиены до Александрии [к своему кругу]. Но найдено, что на чаше она составляет пятидесятую часть своего круга. Поэтому и расстояние от Сиены до Александрии с необходимостью будет составлять пятидесятую часть большого круга Земли. Но оно равно 5 000 стадиев. Поэтому весь круг будет равен 250 000 стадиям. Таков метод Эратосфена».
Позднее полученное Эратосфеном число было увеличено до 252 000 стадиев. Определить, насколько эти оценки близки к реальности, трудно, поскольку неизвестно, каким именно стадием пользовался Эратосфен. Но если предположить что речь идёт о греческом (178 метров), то его радиус земли равнялся 7 082 км, если египетским (157,5), то 6 287 км. Современные измерения дают для усреднённого радиуса Земли величину 6 371 км, что делает вышеописанный расчёт выдающимся достижением и первым достаточно точным расчётом размеров нашей планеты.» via
Обращаю внимание на то, что в Википедии кроме подгонки результатов также сначала говорится об измерении Эратосфеном длины окружности Земли, а в итоге делается вывод о точности вычисления радиуса Земли. В общем, в огороде бузина, а в Киеве — дядька, хоть они и взаимосвязаны.
Диагноз очень простой: в учебниках по-прежнему будут тиражировать не дающий ничего для понимания сущности и практической применимости метод Эратосфена, но ни словом не будут упоминать связку «морская миля — угловая минута» как пример пропорционального мышления древних, потому что современный тренд заточен под дискретные вычислительные машины, а об аналоговых вычислительных машинах древности
приходится рассказывать заново.
Измерьте окружность Земли с помощью тени
Ключевые концепции
Математика
Геометрия
Окружность
Уголки
Экватор Земли
Введение
Если бы вы хотели измерить окружность Земли, какой длины должна быть ваша рулетка? Придется ли вам обойти весь мир, чтобы найти ответ? Как вы думаете, вы можете сделать это с помощью всего лишь измерительной линейки в одном месте? Попробуйте этот проект, чтобы узнать!
Перед тем, как вы начнете, важно отметить, что этот проект будет работать только в течение примерно двух недель после весеннего или осеннего равноденствия (обычно около 20 марта и 23 сентября соответственно).
Фон
Какова окружность Земли? В век современных технологий ученым может показаться, что на этот вопрос легко ответить с помощью таких инструментов, как спутники и GPS, и вам будет еще проще найти ответ в Интернете. Может показаться, что измерить окружность нашей планеты одним измерителем невозможно. Однако греческий математик Эратосфен смог оценить окружность Земли более 2000 лет назад без помощи каких-либо современных технологий.Как? Он использовал немного знаний о геометрии!
В то время Эратосфен находился в городе Александрия в Египте. Он читал, что в городе под названием Сиена к югу от Александрии в определенный день года в полдень на дне глубокого колодца было видно отражение солнца. Это означало, что солнце должно было находиться прямо над головой. (Еще один способ подумать об этом: идеально вертикальные объекты не отбрасывают тени.) В тот же день в Александрии вертикальный объект действительно отбрасывал тень. Используя геометрию, он вычислил длину окружности Земли на основе нескольких вещей, которые он знал (и того, что он не знал):
- Он знал, что в круге 360 градусов.
- Он мог измерить угол тени, отбрасываемой высоким объектом в Александрии.
- Он знал расстояние по суше между Александрией и Сиеной. (Два города находились достаточно близко, чтобы расстояние можно было измерить пешком.)
- Единственное, что неизвестно в уравнении — это окружность Земли!
Полученное уравнение было:
Угол тени в Александрии / 360 градусов = Расстояние между Александрией и Сиеной / Окружность Земли
В этом проекте вы сделаете этот расчет самостоятельно, измерив угол, образованный тенью измерителя в вашем местоположении.Вам нужно будет сделать тест около осеннего или весеннего равноденствия, когда солнце находится прямо над земным экватором. Затем вы можете найти расстояние между вашим городом и экватором и использовать то же уравнение, которое Эратосфен использовал для вычисления окружности Земли. Как вы думаете, насколько близок ваш результат к «реальному» значению?
Существует геометрическое правило относительно углов, образованных линией, пересекающей две параллельные прямые. Эратосфен предположил, что Солнце находится достаточно далеко от нашей планеты, чтобы его лучи были фактически параллельны, когда они достигли Земли.Это говорило ему, что угол тени, который он измерил в Александрии, был равен углу между Александрией и Сиеной, измеренному в центре Земли. Если это вас сбивает с толку, не волнуйтесь! Визуализировать с помощью картинки намного проще. См. Ссылки в разделе «Еще для изучения», где можно найти полезные диаграммы и более подробное объяснение задействованной геометрии.
Материалы
- Солнечный день в период весеннего или осеннего равноденствия или около него (примерно 20 марта или 23 сентября соответственно)
- Плоский ровный участок под прямыми солнечными лучами около полудня
- Измерительная палочка
- Вызовитесь добровольцем, чтобы помочь держать измеритель во время измерения (Или, если вы проводите тест в одиночку, вы можете использовать ведро с песком или грязью, чтобы вставить один конец измерителя, чтобы держать его в вертикальном положении.)
- Палка или камень, чтобы отметить место тени
- Калькулятор
- Транспортир
- Тросик длинный
- Дополнительно: отвес (его можно сделать, привязав небольшой груз к концу веревки) или опорный уровень, чтобы убедиться, что измерительная линейка расположена вертикально.
Подготовка
- Посмотрите свой местный прогноз погоды на несколько дней вперед и выберите день, в который, по всей видимости, будет преимущественно солнечно около полудня.(У вас есть окно в несколько недель для выполнения этого проекта, поэтому не расстраивайтесь, если он окажется облачным! Вы можете попробовать еще раз.)
- Посмотрите время восхода и захода солнца для этого дня в местной газете или на веб-сайте календаря, погоды или астрономии. Вам нужно будет вычислить «солнечный полдень» — время точно на полпути между восходом и закатом, когда солнце будет находиться прямо над головой. Вероятно, это будет не ровно 12 часов дня.
- Выйдите на улицу и подготовьте материалы за 10 минут до солнечного полудня, чтобы у вас было все готово.
Процедура
- Установите измерительную ручку вертикально на улице в солнечном месте незадолго до солнечного полудня.
- Если у вас есть доброволец, который может помочь, попросите его подержать измерительную линейку. В противном случае закопайте один конец измерительной линейки в ведро с песком или грязью, чтобы он оставался в вертикальном положении.
- Если у вас есть столбчатый уровень или отвес, используйте его, чтобы убедиться, что измерительная линейка находится в идеальном вертикальном положении. В противном случае постарайтесь не пропустить его.
- В солнечный полдень отметьте конец тени измерителя на земле палкой или камнем.
- Проведите воображаемую линию между вершиной измерительной линейки и кончиком ее тени. Ваша цель — измерить угол между этой линией и измерителем. Попросите добровольца натянуть веревку между вершиной измерительной линейки и концом ее тени.
- С помощью транспортира измерьте угол между тетивой и измерителем в градусах. Запишите этот угол.
- Посмотрите расстояние между вашим городом и экватором.
- Рассчитайте длину окружности Земли по этому уравнению:
Окружность = 360 x расстояние между вашим городом и экватором / угол тени, который вы измерили
- Какую ценность вы получаете? Насколько близок ваш ответ к истинной окружности Земли (см. Раздел «Наблюдения и результаты»)?
- Дополнительно: Попробуйте повторить тест в разные дни до, во время и после равноденствия; или в разное время до, в полдень и после него. Насколько изменится точность вашего ответа?
- Дополнительно: Попросите друга или члена семьи из другого города пройти тест в тот же день и сравнить ваши результаты. Получаете такой же ответ?
Наблюдения и результаты
В 200 г. до н. Э. Эратосфен оценил окружность Земли примерно в 46 250 километров (28 735 миль). Сегодня мы знаем, что окружность нашей планеты составляет примерно 40 000 километров (24 850 миль).Неплохо для оценки возрастом более 2000 лет, сделанной без использования современных технологий! В зависимости от погрешности ваших измерений — например, точного дня и времени, когда вы проводили тест, насколько точно вы смогли измерить угол или длину тени и насколько точно вы измерили расстояние между вашим городом и экватором, — вам следует уметь вычислить значение, довольно близкое к 40 000 километров (в пределах нескольких сотен или, может быть, нескольких тысяч). И все это не выходя из собственного двора!
Больше для изучения
Расчет окружности Земли, от друзей науки
Урок: Измерение окружности Земли, из eGFI
Углы, параллельные линии и поперечные направления, из Math Planet
Science Activities for All Ages !, from Science Buddies
Это задание предоставлено вам в сотрудничестве с Science Buddies
Представьте себе Вселенную!
Об изображении
Кредит изображения: НАСА, Аполлон 17, NSSDC
Экипаж Аполлона-17 сделал эту фотографию Земли в декабре 1972 года, когда их космический корабль путешествовал между Землей и Луной.Оранжево-красные пустыни Африки и Саудовской Аравии резко контрастируют с темно-синим цветом океанов и белизной облаков и заснеженной Антарктиды.
Информация о расстоянии
Диаметр Земли на экваторе составляет 12 756 километров (км).
Как рассчитать расстояния такой величины?
Кредит изображения: Клементина, Военно-морская исследовательская лаборатория. Это без авторских прав.
В 200 г. до н.э. размер Земли был рассчитан с точностью до 1%! Эратосфен использовал идею Аристотеля о том, что если бы Земля была круглой, далекие звезды в ночном небе появлялись бы в разных положениях для наблюдателей на разных широтах.Эратосфен знал, что в первый день лета Солнце проходит прямо над Сиеной в Египте. В полдень того же дня он измерил угловое смещение Солнца над головой в городе Александрия на расстоянии 5000 стадий от Сиены. Он обнаружил, что угловое смещение составляет 7,2 градуса — в круге 360 градусов, что составляет 7,2 градуса, эквивалентных 1/50 окружности. Геометрия говорит нам, что отношение 1/50 равно отношению расстояния между Сиеной и Александрией к общей окружности Земли.Таким образом, окружность можно оценить, умножив расстояние между двумя городами, 5000 стадий, на 50, что равно 250 000 стадий.
Как перевести в километры? Что ж, мы считаем, что блок «стадион» составлял около 0,15 км. Это означает, что Эратосфен оценил окружность Земли примерно в 40 000 км. Он также знал, что длина окружности равна 2 π (3,1415 …), умноженному на радиус круга. (C = 2πr) Используя эту информацию, Эратосфен сделал вывод, что радиус Земли составляет 6366 км.Оба эти значения очень близки к принятым современным значениям для окружности и радиуса Земли, 40 070 км и 6378 км соответственно, которые с тех пор были измерены с помощью орбитальных космических аппаратов.
Диаметр круга в два раза больше радиуса, что дает диаметр Земли 12 756 км.
Примечание: Земля почти, но не совсем идеальная сфера. Его экваториальный радиус составляет 6378 км, а полярный радиус — 6357 км — другими словами, Земля немного сплюснута. Эратосфен измерял полярный радиус и его значение (используя 0.15 км / стадион преобразования) находится между полярным и экваториальным значениями.
Почему эти расстояния важны для астрономов?
В XVIII и XIX веках астрономы использовали диаметр Земли в качестве основного критерия при определении размера Солнечной системы. Сегодняшним астрономам обычно не нужно знать размер Земли для повседневной исследовательской деятельности. Тем не менее, диаметр Земли по-прежнему является первым шагом для нас, жителей этой планеты, в нашей попытке понять масштаб космических расстояний.
Время в пути
Орбитальный аппарат космического корабля «Шаттл» со скоростью 27 880 км в час (17 322 мили в час) выходит на орбиту или выходит за пределы окружности Земли примерно за 90 минут. На высоте 322 км (200 миль) орбитальный аппарат преодолевает около 41300 км (26000 миль) за одну орбиту.
Задний
Как Эратосфен вычислил окружность Земли
В середине 20 века мы начали запускать в космос спутники, которые помогли нам определить точную окружность Земли: 40 030 км.Но более 2000 лет назад человек в Древней Греции придумал почти такую же фигуру, используя всего лишь палку и свой мозг. Ниже приводится стенограмма видео.
Как древнегреческий математик рассчитал длину окружности Земли. В середине 20 века мы начали запускать в космос спутники, которые помогли бы нам определить точную окружность Земли — 40 030 км.
Но более 2000 лет назад в Древней Греции человек получил почти такую же фигуру, воткнув палку в землю.Этим человеком был Эратосфен. Греческий математик и глава Александрийской библиотеки.
Эратосфен слышал, что в Сиене, городе к югу от Александрии, в полдень летнего солнцестояния вертикальные тени не отбрасываются. Солнце стояло прямо над головой. Он задавался вопросом, верно ли это и в Александрии.
Итак, 21 июня он воткнул палку прямо в землю и ждал, не отбросит ли тень в полдень. Оказывается, один был. И это было около 7 градусов.
Итак, если солнечные лучи входят под одним и тем же углом в одно и то же время дня, и палка в Александрии отбрасывает тень, а палка в Сиене — нет, это должно означать, что поверхность Земли изогнута.И, вероятно, Эратосфен это уже знал.
Идея сферической Земли была выдвинута Пифагором около 500 г. до н.э. и подтверждена Аристотелем пару столетий спустя. Если бы Земля действительно была сферой, Эратосфен мог бы использовать свои наблюдения, чтобы оценить окружность всей планеты.
Поскольку разница в длине тени составляет 7 градусов в Александрии и Сиене, это означает, что два города находятся на расстоянии 7 градусов друг от друга на 360-градусной поверхности Земли. Эратосфен нанял человека, чтобы измерить расстояние между двумя городами, и узнал, что они находятся на расстоянии 5000 стадий друг от друга, что составляет около 800 километров.
Затем он мог бы с помощью простых пропорций найти окружность Земли — 7,2 градуса составляют 1/50 от 360 градусов, так что 800 умножить на 50 равно 40 000 километров. И вот так 2200 лет назад человек нашел окружность всей нашей планеты с помощью всего лишь палки и своего мозга.
Это видео снял Алекс Кузоян.
Это видео было первоначально опубликовано 3 июля 2016 года.
Как человечество впервые определило размер Земли? | Ребята из науки
Как человечество впервые определило размер Земли и какие ценности известны сегодня?
июль 2001
Вопреки распространенному мнению, Колумб и наиболее образованные люди его времени знали, что Земля была сферой, а не плоской.Но его оценка размера Земли была заимствована у современных арабских астрономов, чьи оценки окружности Земли были слишком малы примерно на треть. Таким образом Колумб пытался отправиться в Восточную Азию, двигаясь на запад из Испании. И когда он высадился на Эспаньоле 2 октября 1492 года, он объявил, что достиг «Индии». Вскоре европейцы узнали, что Колумб достиг Нового Света, а не Индии и Восточной Азии.
Они могли бы избавить себя от множества неприятностей. Превосходная оценка окружности Земли была рассчитана уже за 200 лет до Рождества Христова! Еще до этого Пифагор (570-500 до н.э.) и Аристотель (384-322 до н.э.) предположили, что Земля была сферой.Аристотель заметил, что Земля отбрасывает круглые тени на Луну во время лунных затмений, но его оценка окружности Земли была занижена примерно на 60 процентов.
Эратосфен (276–194 до н.э.) работал главным библиотекарем в известной библиотеке в Александрии, Египет. Он наткнулся на интересные отчеты, в которых подробно описываются наблюдения за солнцем, сделанные путешественниками из Сиены (Асуан, Египет), которая находится к югу от Александрии. В день летнего солнцестояния (первый день лета) лучи солнечного света освещают дно глубоких колодцев в Сиене.Эратосфен понял, что в этот день Солнце должно быть прямо над Сиеной или в ее зените. Он также знал, что Солнце находится на расстоянии 7 градусов от зенита в Александрии в день солнцестояния (что составляет примерно 1/50 окружности круга). Затем, используя простую геометрию, Эратосфен показал, что это означает, что расстояние от Александрии до Сиены составляет 1/50 окружности Земли.
Используя скорость, с которой средний верблюд мог путешествовать, и количество дней, которое потребовалось верблюду, чтобы добраться из Александрии в Сиену, он оценил, что расстояние от Сиены до Александрии составляет 5000 стадий.Поскольку он рассчитал, что это расстояние также составляет 1/50 окружности Земли, то 50 умноженных на 5000 стадий дают 250 000 стадий для окружности Земли. Теперь стадион (единственное из стадионов) в древности имел разную длину. Традиционно предполагается, что в одном километре (км) есть 6 стадий, а это означает, что Эратосфен определил, что окружность Земли составляет около 42000 км (26000 миль). Используя это определение стадий, Эратосфен только на 4% выше в своем оценивать! Даже если бы он использовал более крупный олимпийский стадион в качестве базовой единицы длины, его оценка была бы лишь примерно на 14 процентов больше.Столь точный расчет, основанный на таком небольшом количестве инструментов и измерений, — потрясающее достижение.
Благодаря точным измерениям гравитационного поля Земли, а также спутниковым изображениям, мы теперь понимаем, что Земля — не идеальная сфера, а на самом деле сплюснутый сфероид. Земля немного выпирает вдоль своего экватора (в отличие от нас, ученых-парней!). Расстояние между северным и южным полюсами составляет примерно 7900 миль, а экваториальный диаметр немного больше — 7930 миль.
Окружность Земли равна ее среднему диаметру, 7915 миль, умноженному на число Пи, где Пи равно 3,14159. Это дает нам около 25 000 миль для окружности Земли. Таким образом, Эратосфен промахнулся по окружности примерно на 4 процента. Это была действительно выдающаяся точность для 2200 лет назад.
ЭРАСТОТЕНОВ — ОСНОВАТЕЛЬ МАТЕМАТИЧЕСКОЙ ГЕОГРАФИИ
Эрастосфен, сын Аглааса, родился в Кирене, но прожил
большую часть жизни работал в Александрии, где возглавлял
библиотека при знаменитом музее с 235 г. до его смерти.Эратосфен был одним из выдающихся ученых своего времени и произвел
труды по географии, математике, философии, хронологии, литературной
критика и грамматика, а также написание стихов. Его самый продолжительный
работа была в области географии, наиболее заметным из его измерений
окружность земли. Эта работа была одной из первых попыток
поставить географические исследования на доказанную математическую основу. Следовательно,
его называют основоположником математической географии.
Вычисление Эратосфеном окружности Земли
Эратосфен предположил, что город Сиена находится на тропическом берегу.
Рака, потому что в полдень в день летнего солнцестояния колодец, особенно
выкопанный по этой причине, был освещен до дна солнечными лучами.
лучи.Также предполагалось, что города Александрия и Сиена
были на одном меридиане. В следующее солнцестояние Эратосфен
измерил тень, отбрасываемую на Александрию в полдень, по вертикали
указатель (тонкий стилус) известной высоты. Вертикальный угол этого
тень оказалась 82 градуса 48 минут. Северный полюс тропик
Рака Александрия лучи солнца Экватор Сиена С угла
солнечных лучей в день летнего солнцестояния составляет 90 градусов, тогда оба
вертикальные линии, протянутые к центру земли, образуют
угол 7 градусов 12 минут (все три угла в сумме 180
градусов).Следовательно, дуговое расстояние между Сиеной и Александрией
относительно окружности Земли будет 7 градусов 12 минут / 360
градусов, или 1/50 окружности.
Эратосфен предположил, что расстояние между двумя городами составляет
5000 стадионов (575 миль). Поскольку это расстояние составляло 1/50 от
весь круг, общая окружность была определена как 250 000
стадий (5000 стадий X 50) или 28750 миль.
Метод, использованный Эратосфеном, был хорош в теории, но его
данные и предположения были неточными.Хотя цифра 1/50
круга для разницы в широте правильно, Сиена
не находится прямо на тропике Рака. Александрия не лжет
на том же меридиане (лежит примерно на 3 градуса западнее). А также
расстояние между двумя городами ближе к 4530 стадиям,
не 5000. Эратосфен знал, что расстояние между
два города было сомнительным, поэтому, чтобы компенсировать ошибку, он добавил
2,00 стадиона до окончательного результата.
Несмотря на эти неточности, все измерения были очень
ценное достижение и не было улучшено до наших дней.Окончательный расчет Эратосфена окружности Земли
была всего на 15 процентов больше современной фигуры маленького
менее 25 000 км.
Как Эратосфен так сблизился?
Сиена, недалеко от современного Асвана, Египет, находится недалеко от тропика Рака (23,5 ° с.ш.). На этой линии широты в полдень во время летнего солнцестояния (20 или 21 июня) Солнце находится прямо над головой. Стой там, и тени у тебя не будет. Александрия находится дальше на север, поэтому полуденное Солнце находится не совсем над головой в день солнцестояния.Вы или палка отбрасываете тень под углом около 7 °.
Оба города лежат около одного и того же меридиана или линии долготы, которая представляет собой большой круг с севера на юг (на самом деле, окружность) вокруг Земли. Как и все круги, меридиан имеет 360 °. Поскольку 7 ° составляет примерно 1/50 от 360 °, расстояние между двумя городами (5000 стадий) должно составлять 1/50 расстояния по меридиану. Умножив 5000 на 50, Эратосфен оценил окружность Земли в 250 000 стадий.Затем, поскольку он стремился к простому в использовании номеру, он добавил 2 000 стадий и получил 252 000. (Оно делится без остатка на 60 и 360.)
Итак, вы, возможно, уже задались вопросом, как долго был стадион (в единственном числе стадионов)? Эксперты не совсем уверены, но говорят, что это от 150 до 158 метров (от 164 до 173 ярдов). Популярный выбор Эратосфена составляет 157 метров (172 ярда), поэтому окружность Земли составляет около 39 250 километров (24 390 миль). Это удивительно близко к сегодняшним меркам окружности с севера на юг, которая составляет около 40 000 километров (24 855 миль).
Почему было так сложно?
Современные спутники могут отображать и измерять Землю с точностью до дюйма. Для Эратосфена это было не так просто. У него не было возможности хорошо измерить большие расстояния, и даже очень тщательный подсчет шагов — вещь неравномерная. Круглое число 5000 стадий указывает на то, что Эратосфен знал, что результат был приблизительным.
Кроме того, Александрия не совсем к северу от Асвана / Сиены. Это в паре градусов к западу от него. Асван / Сиена не в тропике Рака.Это немного севернее. Эратосфен не мог знать об этих слегка нестандартных позициях, которые немного скомпрометировали его результат.
Есть еще одна вещь, о которой тогда никто не знал: Земля выпуклая посередине и немного сплющенная на полюсах. Это делает меридианы (большие круги с севера на юг) немного короче экватора с запада на восток, длина которого составляет 40 075 километров (24 901 миля).
Эти крошечные причуды, вероятно, не имели бы значения для Эратосфена. Он ошибся, добавив дополнительные стадионы, чтобы упростить математику, что показывает, что он не стремился к совершенству.Он просто хотел получить точную оценку, и у него все получилось очень хорошо.
Джой Хаким, бывший учитель, репортер и редактор, пишет научную литературу для детей. Ее последний проект — серия из шести томов под названием The Story of Science , из которой эта статья взята с разрешения. © 2004 История науки , Smithsonian Books. Ее 10-томная серия, A History of US , была удостоена премии Миченера в письменной форме и была преобразована в специальный выпуск PBS под названием « Freedom». «
Статьи по теме
Фантастическое путешествие
Как ученые определили форму и размер Земли
Джой Хаким
Как Эратосфен так сблизился?
10 Шаг назад 10
История науки: причины писателя
Окружность Земли, Эратосфен, Астрономия, Солнцестояния, Равноденствия, Широта, Наука и Математика
Эратосфен
Эратосфен, греческий географ (около 276–194 гг. До н.э.), сделал удивительно точную оценку окружности Земли.
В большой библиотеке в Александрии, Египет, он прочитал, что есть глубокий вертикальный колодец недалеко от Сиены, на юге Египта, который полностью освещался солнцем до дна колодца в полдень один раз в год: летнее солнцестояние . Эратосфен понимал, что если солнце находится прямо над головой, его лучи падают прямо в колодец и освещают дно.
Солнцестояние либо два раза в году: летнее солнцестояние и зимнее солнцестояние .Солнцестояние — это когда солнце находится в самой высокой или самой низкой точке неба в полдень. Что делает самые длинные и самые короткие дни (примерно 22 июня и 20 декабря). Вызвано тем, что движение Солнца является самым длинным или кратчайшим путем по небу.
Тропик Рака находится к северу от экватора на 23,4372 ° широты. Это широта, на которой раз в год солнце находится прямо над головой во время летнего солнцестояния .
Тропик Козерога находится к югу от экватора в -23.4372 ° широты. Это широта, на которой раз в год солнце находится прямо над головой во время зимнего солнцестояния .
Равноденствие — это день (дважды в год), когда солнце пересекает небесный экватор, когда день и ночь имеют одинаковую длину (примерно 22 сентября и 20 марта) .
Эратосфен понимал движение Солнца по небу. Он знал, что в Александрии, Египет, в полдень летнего солнцестояния года солнце не стояло прямо над головой, потому что там вертикальные объекты отбрасывали тень.Он знал, что Александрия находится в 5000 стадионах почти к северу от Сиены, Египет. И он достаточно разбирался в геометрии, чтобы использовать эту информацию для вычисления окружности Земли.
Допущения :
- He предположил, что : Земля круглая (извините, Колумб).
- Солнечные лучи двигались по прямой. и
- Лучи в обоих местах были практически параллельны.
Данные :
Он установил вертикальный столб в Александрии и измерил угол его тени во время летнего солнцестояния (7.2 градуса), когда колодец в Сиене был полностью освещен солнцем, что означало, что солнце стояло над колодцем вертикально.
Рассуждения :
- Из геометрии, Эратосфен знал, что угол тени в Сиене равен углу в центре Земли между Сиеной и Александрией. Линия, пересекающая параллельные линии, будет иметь одинаковые углы.
- Следовательно, дуга угла этого размера составляла 1/50 окружности (360 ° / 7,2 ° ≈ 50). На основе предположения о круглой Земле на 360 °.
- Расстояние между Сиеной и Александрией составляло 5000 стадий.
- Итак, он умножил 5000 на 50, чтобы найти длину окружности Земли.
- Его результат, 250 000 стадий (около 46 250 км), довольно близок к современным измерениям (40 075 км на экваторе).
Источник Исследование Земли , AGI, 1970, Глава 3, с. 66.
Используемая формула Эратосфен :
(360 ° / угол тени вертикальной палки) * расстояние от Сиены до Александрии = окружность Земли
Формула, которую можно использовать для вычисления окружности Земли .
(360 ° / угол тени вертикальной палки) * расстояние от Сиены = окружность Земли
Сиена расположена на тропике Рака (23,5 ° с.ш.) или рядом с ним, где Солнце будет над головой в день летнего солнцестояния.
- Солнце находится прямо над тропиком Рака (23,5 ° с.ш.) в день летнего солнцестояния
- Над головой тропика Козерога (23,5 ° ю.ш.) в день зимнего солнцестояния
- Над экватором (0 ° с.ш.) весной, осенью и в дни равноденствия.
г.
Используйте эти идеи для определения окружности Земли.
- В день летнего солнцестояния поместите вертикальную палку в
земля. - Когда солнце достигает самой высокой вертикали
согласие на день (солнечный полдень, поэтому длина тени будет самой короткой),
Измерьте угол тени (угол тени вертикальной палки).
(360 ° / угол тени вертикальной палки) * расстояние от Тропика Рака = Окружность Земли
В день равноденствия вертикаль
лучи солнца идут прямо над экватором.Как бы вы рассчитали окружность Земли, используя тот же метод во время равноденствия?
Как насчет того, чтобы поделиться измерением угла тени с другими людьми в реальном мире?
глобус. Свяжитесь с другими, которые хотели бы собирать те же данные
и обменять его, возможно, используя следующий формат.
Дата измерения ____________
Ваше измерение угла тени ____________ градусов
Город вашего местонахождения ____________________________________
Страна вашего местонахождения _________________________________
Ваша широта _________________________________________
Ваша долгота ________________________________________
Когда у вас есть разные наборы данных, скомпилируйте их и сравните разные
локации и углы.
Оригинальная идея Джима Мейнке (сентябрь 1994 г.), Лейквуд
Средняя школа в Кливленде.
Заметки доктора Роберта Свитленда
[Домашняя страница: thehob.net]
.
