Содержание
Закон сохранения импульса — опредление, формулы, формулировка
Импульс: что это такое
Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.
Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.
Импульс тела → → p — импульс тела [кг*м/с] m — масса тела [кг] v — скорость [м/с] |
Закон сохранения импульса
В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Закон сохранения импульса Векторная сумма импульсов тел в замкнутой системе постоянна |
А выглядит — вот так:
Закон сохранения импульса → → → p — импульс тела [кг*м/с] |
Простая задачка
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Решение:
Запишем закон сохранения импульса для данного процесса.
→ → →
p0 = p1 + p2
p0 — это импульс системы мальчик + лодка до того, как мальчик спрыгнул,
p1 — это импульс мальчика после прыжка,
p2 — это импульс лодки после прыжка.
Изобразим на рисунке, что происходило до и после прыжка.
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
0 = p1 — p2
p1 = p2
Подставим формулу импульса.
mV1 = MV2
Выразим скорость лодки V2:
V2 = mV1/M
Подставим значения:
V2 = 45*3/270 = 3/6 = ½ = 0,5 м/с
Ответ: скорость лодки после прыжка равна 0,5 м/с
Задачка посложнее
Тело массы m1 = 800 г движется со скоростью v1 = 3 м/с по гладкой горизонталь- ной поверхности.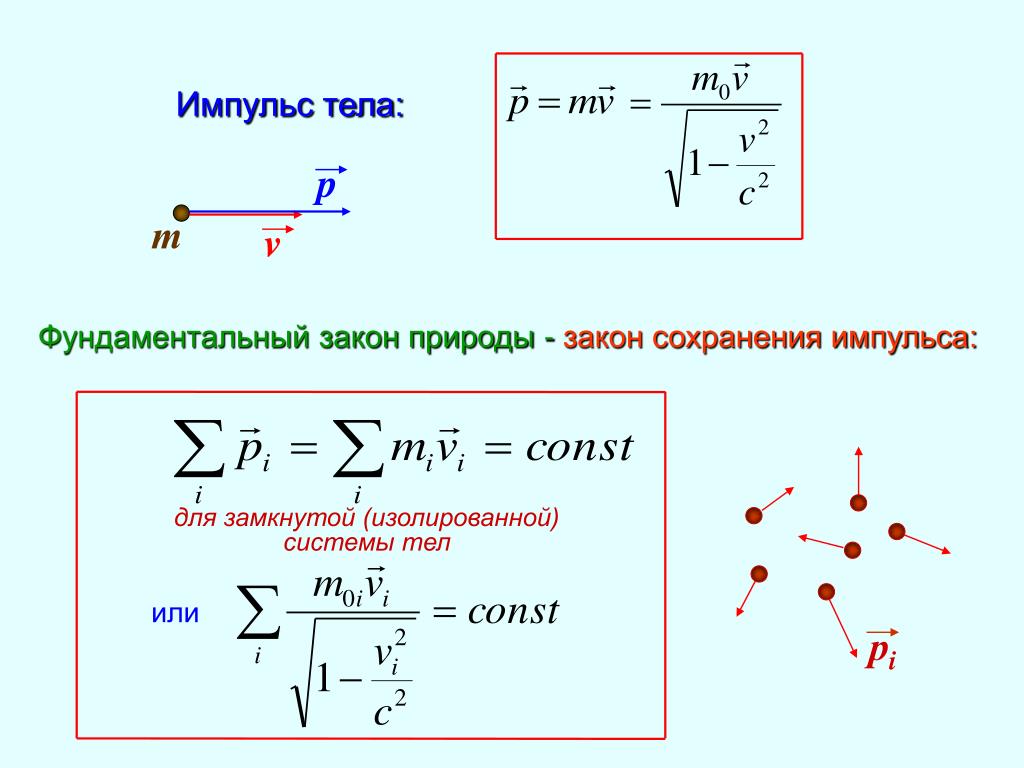 Навстречу ему движется тело массы m2 = 200 г со скоростью v2 = 13 м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.
Навстречу ему движется тело массы m2 = 200 г со скоростью v2 = 13 м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.
Решение: Для данной системы выполняется закон сохранения импульса:
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.
p1 + p2 = p.
Спроецируем импульсы на ось х:
p1 — p2 = p
После неупругого удара получилось одно тело массы m1 + m2, которое движется с искомой скоростью:
m1v1 — mv2 = (m1 + m2) v
Отсюда находим скорость тела, образовавшегося после удара:
v = (m1v1 — mv2)/(m1 + m2)
Переводим массу в килограммы и подставляем значения:
v = (0,8·3−0,2·13)/(0,8 + 0,2) = 2,4 — 2,6 = -2,6 м/с
В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на значение получившееся значение.
Ответ: скорость системы тел после соударения равна v = 0,2 м/с.
Второй закон Ньютона в импульсной форме
Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:
a = F/m
Применим выражение для ускорения
a = Δv/Δt
В этих уравнениях слева находится величина a . Так как левые части уравнений равны, можно приравнять правые их части
F/m = Δv/Δt
Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:
F⋅Δt = Δv⋅m
В правой части находится Δv =v —v0 — это разница между конечной и начальной скоростью.
Преобразуем правую часть
Δv⋅m = (v —v0)⋅m
Раскрыв скобки, получим
Δv⋅m= v ⋅m—v0⋅m
Заменим произведение массы и скорости на импульс:
v⋅m=p
v0⋅m=p0
Подставляем:
Δv⋅m=p —p0
p —p0 =Δp
Или, сокращенно:
Δv⋅m=Δp
То есть, вектор Δv⋅m – это вектор Δp.
Тогда второй закон Ньютона в импульсной форме запишем так
F⋅Δt =Δp
Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.
→
F⋅Δt =Δp⃗
Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. |
Решение:
Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).
Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.
Реактивное движение
В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.
Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.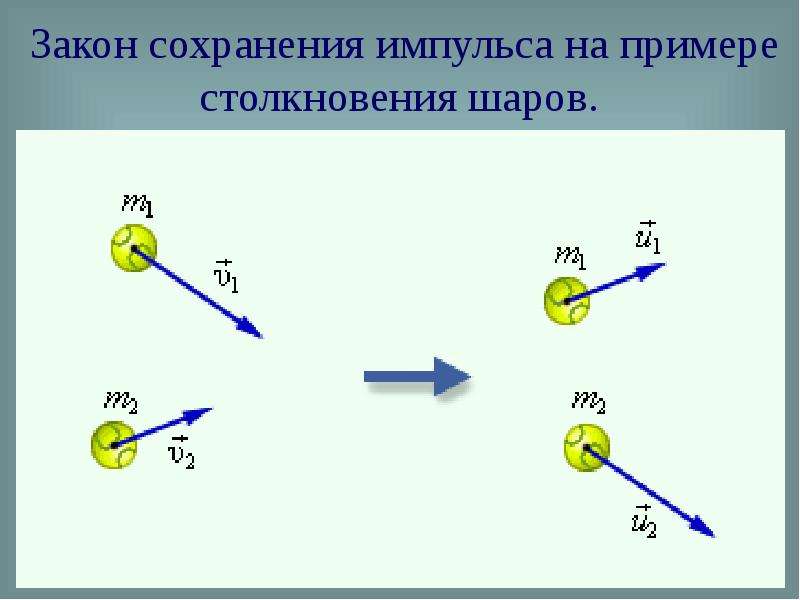
Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:
→ →
F1 = — F2
Сила F2 называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.
Закон сохранения импульса позволяет оценить скорость ракеты.
mг vг = mр vр,
где mг — это масса горючего,
vг — скорость горючего,
mр — масса ракеты,
vр — скорость ракеты.
Отсюда можно выразить скорость ракеты:
vр = mг vг / mр
Скорость ракеты при реактивном движении vр = mг vг / mр vг — скорость горючего [м/с] mр — масса ракеты [кг] v р — скорость ракеты [м/с] |
Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.
Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.
Урок 11. импульс. закон сохранения импульса — Физика — 10 класс
Физика, 10 класс
Урок 11.Импульс. Закон сохранения импульса
Перечень вопросов, рассматриваемых на уроке:
1) импульс тела, импульс силы, замкнутая система;
2) абсолютно упругий, абсолютно неупругий удар;
3) закон сохранения импульса;
4) границы применимости закона;
5) проявление закона сохранения импульса в технике и природе.
Глоссарий по теме
Импульс тела (материальной точки) — векторная величина, равная произведению массы тела на скорость тела.
Импульс силы — произведение силы на время её действия.
Импульс тела равен сумме импульсов отдельных его элементов.
Импульс системы тел равен векторной сумме импульсов каждого из тел системы.
Внутренние силы — это силы, с которыми взаимодействуют тела системы между собой.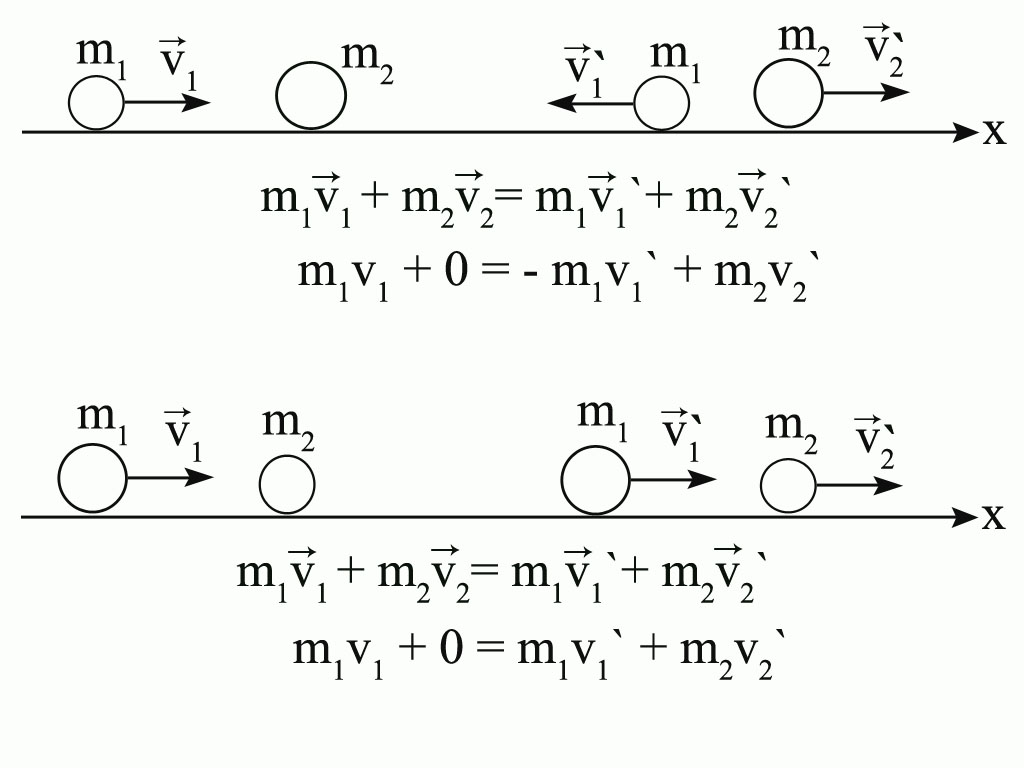
Внешние силы — это силы, создаваемые телами, которые не принадлежат к данной системе.
Замкнутая система — это система, в которой внешние силы не действуют или сумма внешних сил равна нулю.
Абсолютно неупругий удар — это столкновение двух тел, которые объединяются и движутся дальше как одно целое.
Абсолютно упругий удар — столкновение тел, при котором тела не соединяются и их внутренние энергии остаются неизменными.
Закон сохранения импульса: векторная сумма импульсов тел, образующих замкнутую систему, не меняется при любых взаимодействиях между телами системы.
Основная и дополнительная литература по теме урока:
Г.Я. Мякишев., Б.Б.Буховцев., Н.Н.Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 123 – 130.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.
Открытые электронные ресурсы:
http://kvant.mccme.ru/1979/10/zakon_sohraneniya_impulsa_reak.htm
Основное содержание урока
Импульс тела (материальной точки) представляет собой векторную величину, равную произведению массы тела на скорость тела:
Направление импульса всегда совпадает с направлением скорости, так как m > 0, то
Любое движущееся тела имеет импульс.
Единица измерения импульса:
.
Произведение силы на время её действия называется импульсом силы.
Второй закон Ньютона в импульсной форме.
Изменение импульса тела (материальной точки) равно импульсу действующей на него силы:
Импульс тела равен сумме импульсов отдельных его элементов:
Импульс системы тела равен векторной сумме импульсов каждого из тел системы:
Импульс обладает интересным свойством сохраняться, которое есть только у нескольких физических величинах.
Силы, с которыми взаимодействуют тела системы друг с другом, называются внутренними, а силы, создаваемые телами, которые не принадлежат этой системе, являются внешними силами.
Система, в которой внешние силы не действуют или сумма внешних сил равна нулю, называется замкнутой.
Полный импульс тел сохраняется, в замкнутой системе тела могут только обмениваться импульсами.
Столкновение тел представляет собой взаимодействие тел при их относительном перемещении. Абсолютно неупругий удар — это столкновение двух тел, которые объединяются и движутся дальше как одно целое.
Абсолютно неупругий удар — это столкновение двух тел, которые объединяются и движутся дальше как одно целое.
Закон сохранения импульса при неупругом ударе:
Абсолютно упругий удар — столкновение тел, при котором тела не соединяются в одно целое и их внутренние энергии остаются неизменными.
Закон сохранения импульса при упругом ударе:
Закон сохранения импульса.
Если внешние силы на систему не действуют или их сумма равна нулю, то импульс системы остается неизменным:
Закон сохранения импульса является одним из основных законов физики.
Границы применимости закона сохранения импульса: замкнутая система.
Закон сохранения импульса с честью выдержал испытание временем и до сих пор он продолжает свое триумфальное шествие.
Он дал неоценимый инструмент для исследования ученым, как один из фундаментальных законов физики, ставя запрет одним процессам и открывая дорогу другим.
Действие этого закона проявляется в науке, в технике, в природе и в повседневной жизни. Всюду этот закон работает отлично — реактивное движение, атомные и ядерные превращения, взрыв и т.д.
Всюду этот закон работает отлично — реактивное движение, атомные и ядерные превращения, взрыв и т.д.
Во многих повседневных ситуациях помогает разобраться понятие импульса.
Рене Декарт попытался использовать термин «импульс» вместо силы. Это связано с тем, что силу трудно измерить, а массу и скорость измерить несложно. Поэтому вместо импульса часто говорят количество движения (Именно Ньютон первым назвал произведение массы тела на скорость количеством движения).
Декарт понимал большое значение понятия количества движения — или импульса тела — как произведения массы тела на скорость. Но он совершил ошибку, не рассматривая количество движения как векторную величину. Ошибка эта была исправлена в начале XVIII века.
Используя закон сохранения импульса можно «найти» и невидимые объекты, например, электромагнитные волны, излучаемые открытым колебательным контуром, или антинейтрино – субатомные частицы, не оставляющие следов в детекторах.
Разбор тренировочных заданий
1. Тело свободно падает без начальной скорости. Изменение модуля импульса этого тела за промежуток времени 2 с равно 10 кг∙м/с. Чему равна масса тела?
Тело свободно падает без начальной скорости. Изменение модуля импульса этого тела за промежуток времени 2 с равно 10 кг∙м/с. Чему равна масса тела?
Дано: ∆t =𝟤 c; g ≈ 𝟣0 м∕с2; ∆р =𝟣0 кг∙м ∕с.
Найти: m.
Решение:
т.к. тело свободно падает.
Запишем второй закон Ньютона в импульсной форме:
∆р = F∆t,
F = mg – т.к. при свободном падении действует только сила тяжести,
тогда ∆р = mg∆t, откуда:
Делаем расчёт:
Ответ: m = 0,5 кг.
2. Тело массой 400 г изменяет свои координаты по закону:
Тело будет иметь импульс 8 Н·с после начала движения за промежуток времени равный __________?
Дано:
m = 400 г = 0,4 кг; p = 8 Н∙с
Найти: t.
Решение:
Записываем формулу импульса:
p = mv,
скорость равна 1-й производной от х по времени:
v = x'(t)= 4 + 4t
Из 1-й формулы скорость равна: v = p/m
4 + 4t = 8 / 0,4,
4t = 20 − 4 = 16,
t = 16 / 4,
t = 4 с.
Ответ: t = 4 с.
Закон сохранения импульса — урок. Физика, 9 класс.
Рассмотрим изменение импульсов тел при их взаимодействии друг с другом.
Если два или несколько тел взаимодействуют только между собой (то есть не подвергаются воздействию внешних сил), то эти тела образуют замкнутую систему.
Импульс, равный векторной сумме импульсов тел, входящих в замкнутую систему, называется суммарным импульсом этой системы.
Результирующая векторная величина импульса системы тел равна векторной сумме импульсов тел, её составляющих:
pсум→=p1→+p2→+…+pn→.
Закон сохранения импульса
Суммарный импульс системы тел до взаимодействия равен суммарному импульсу этой системы тел после взаимодействия.
В этом заключается закон сохранения импульса, который называют также законом сохранения количества движения.
Закон сохранения импульса впервые был сформулирован Р. Декартом. В одном из своих писем он написал:
«Я принимаю, что во Вселенной, во всей созданной материи есть известное количество движения, которое никогда не увеличивается, не уменьшается, и, таким образом, если одно тело приводит в движение другое, то теряет столько своего движения, сколько его сообщает».
Для примера возьмем систему из двух тел: шары массами m1 и m2 равномерно и прямолинейно движутся со скоростями v1 и v2, причем их скорости противоположно направлены, то есть шары движутся навстречу друг другу. Импульсы шаров записываются p1→=m1v1→ и p2→=m2v2→ соответственно.
Когда шары приблизятся друг к другу, произойдет столкновение. Удар не будет мгновенным, он займёт пусть малое, но вполне измеримое время \(t\), при этом появятся силы взаимодействия F1→ и F2→, которые будут приложены к первому и второму шарам соответственно. Как известно, под действием силы скорость тела меняется, поэтому изменятся и скорости шаров. После столкновения модули и направления скоростей могут быть совершенно иными, поэтому обозначим скорости v1′ и v2′ соответственно. Изменятся и импульсы шаров, они станут равны p1→′=m1v1→′ и p2→′=m2v2→′ соответственно.
Тогда, согласно закону сохранения импульса, имеют место равенства:
p1→+p2→=p1→′+p2→′
или
m1v1→+m2v2→=m1v1→′+m2v2→′.
Данные равенства являются математической записью закона сохранения импульса.
Закон сохранения импульса выполняется и в том случае, если на тела системы действуют внешние силы, векторная сумма которых равна нулю.
Таким образом, более точно закон сохранения импульса формулируется так:
векторная сумма импульсов всех тел замкнутой системы — величина постоянная, если внешние силы, действующие на неё, отсутствуют или же их векторная сумма равна нулю.
Импульс системы тел может измениться только в результате действия на систему внешних сил. И тогда закон сохранения импульса действовать не будет.
Пример:
при стрельбе из пушки возникает отдача: снаряд летит вперёд, а само орудие откатывается назад. Почему?
Снаряд и пушка — замкнутая система, в которой действует закон сохранения импульса. В результате выстрела из пушки импульс самой пушки и импульс снаряда изменятся. Но сумма импульсов пушки и находящегося в ней снаряда до выстрела останется равной сумме импульсов откатывающейся пушки и летящего снаряда после выстрела.
Обрати внимание!
В природе замкнутых систем не существует. Но если время действия внешних сил очень мало, например, во время взрыва, выстрела и т. п., то в этом случае воздействием внешних сил на систему пренебрегают, а саму систему рассматривают как замкнутую.
Кроме того, если на систему действуют внешние силы, но сумма их проекций на одну из координатных осей равна нулю (то есть силы уравновешены в направлении этой оси), то в этом направлении закон сохранения импульса выполняется.
Великий учёный Исаак Ньютон изобрёл наглядную демонстрацию закона сохранения импульса — маятник, или её ещё называют «колыбель». Это устройство представляет собой конструкцию из пяти одинаковых металлических шаров, каждый из которых крепится с помощью двух тросов к каркасу, а тот в свою очередь — к прочному основанию П-образной формы.
Маятник Ньютона устроен так, что начальный шар передаёт импульс второму шарику, а затем замирает. Нашему глазу на первый взгляд не заметно, как следующий шарик принимает импульс от предыдущего, мы не можем проследить его скорость. Но, если взглянуть пристальнее, можно заметить, как шарик немножко «вздрагивает». Это объясняется тем, что он совершает движения с посланной ему скоростью, но поскольку расстояние очень маленькое, ему некуда разогнаться, то он может на своём коротком пути передать импульс третьему шарику и в итоге остановиться.
Но, если взглянуть пристальнее, можно заметить, как шарик немножко «вздрагивает». Это объясняется тем, что он совершает движения с посланной ему скоростью, но поскольку расстояние очень маленькое, ему некуда разогнаться, то он может на своём коротком пути передать импульс третьему шарику и в итоге остановиться.
Такое же действие совершает и следующий шарик и т. д. Последнему шарику некуда передавать свой импульс, поэтому он свободно колеблется, поднимаясь на определённую высоту, а затем возвращается, и весь процесс передачи импульсов повторяется в обратном порядке.
Закон сохранения линейного импульса • Джеймс Трефил, энциклопедия «Двести законов мироздания»
Линейный импульс замкнутой системы сохраняется.
Начав двигаться, тело имеет тенденцию продолжать движение. Первый закон механики Ньютона гласит: если тело движется, то при отсутствии внешних воздействий оно так и будет двигаться дальше прямолинейно и равномерно до тех пор, пока оно не подвергнется воздействию внешней силы. Эту тенденцию называют линейным импульсом. С ней часто сталкиваемся в повседневной жизни. Бильярдный шар катится по столу с той скоростью, которая придана ему кием, копье летит с той скоростью, с которой его метнули.
Эту тенденцию называют линейным импульсом. С ней часто сталкиваемся в повседневной жизни. Бильярдный шар катится по столу с той скоростью, которая придана ему кием, копье летит с той скоростью, с которой его метнули.
Физики определяют линейный импульс тела p как его массу m, умноженную на его скорость v:
p = mv
Буквы p и v выделены полужирным шрифтом, чтобы показать, что эти величины характеризуются не только абсолютным значением, но и направлением. Так, применительно к скорости, мы не просто говорим, что машина движется со скоростью 40 км/ч, а что она движется со скоростью 40 км/ч, например, на север. Величина, которая кроме абсолютного значения имеет направление, называется вектором.
Понятно, что, согласно первому закону Ньютона, количество движения отдельно взятого тела в отсутствии внешних сил сохраняется. Закон же сохранения импульса гласит, что при соблюдении этого условия сохраняется векторная сумма импульсов всех тел, входящих в замкнутую механическую систему. В таком представлении система из двух бильярдных шаров массой m, пущенных друг навстречу другу с одинаковыми скоростями v, будет иметь нулевой момент импульса, хотя каждый из шаров по отдельности и обладает импульсом mv. Однако импульсы шаров взаимно погасятся вследствие их векторной природы (поскольку их скорости противоположно направлены).
В таком представлении система из двух бильярдных шаров массой m, пущенных друг навстречу другу с одинаковыми скоростями v, будет иметь нулевой момент импульса, хотя каждый из шаров по отдельности и обладает импульсом mv. Однако импульсы шаров взаимно погасятся вследствие их векторной природы (поскольку их скорости противоположно направлены).
Вообще, любая величина, характеризующая систему и не изменяющаяся в результате взаимодействия внутри нее, называется консервативной, и для нее имеется свой закон сохранения. В частности, в механических системах, помимо закона сохранения импульса действует еще и закон сохранения момента импульса или количества вращения — величины, которая описывает количество движения тел вокруг собственной оси и по изогнутым траекториям.
Что же происходит при прямолинейном соударении двух бильярдных шаров на встречных курсах? Происходит сразу несколько явлений. Во-первых, в момент столкновения шары слегка деформируются и часть их кинетической энергии переходит в тепловую. Во-вторых, мы знаем, что совокупный импульс системы из двух шаров не изменяется и остается равным нулю. Значит, видя, что один шар откатывается после лобового столкновения в обратном направлении с определенной скоростью, мы можем с уверенностью сказать, что второй шар в данный момент времени катится в обратном направлении с ровно той же скоростью.
Во-вторых, мы знаем, что совокупный импульс системы из двух шаров не изменяется и остается равным нулю. Значит, видя, что один шар откатывается после лобового столкновения в обратном направлении с определенной скоростью, мы можем с уверенностью сказать, что второй шар в данный момент времени катится в обратном направлении с ровно той же скоростью.
Второй закон механики Ньютона, кстати, можно легко интерпретировать и как формулу, согласно которой скорость изменения импульса равна силе, приложенной к замкнутой системе. Таким образом, чтобы изменить импульс системы, требуется внешняя сила. В молекулярно-кинетической теории, например, это наглядно просматривается: давление объясняется импульсами ударов молекул о стенки сосуда, содержащего газ. Поскольку молекулы газа упруго отскакивают в обратном направлении, их импульсы меняются на противоположные, а значит, стенка оказывает силовое воздействие на ударяющиеся об нее молекулы. Но это означает, что и молекулы, в силу третьего закона Ньютона, оказывают силовое воздействие на стенку, которое и воспринимается нами как давление.
Закон сохранения импульса, замкнутая система тел, вектор импульса
Тестирование онлайн
Замкнутая система тел
Это система тел, которые взаимодействуют только друг с другом. Нет внешних сил взаимодействия.
В реальном мире такой системы не может быть, нет возможности убрать всякое внешнее взаимодействие. Замкнутая система тел — это физическая модель, как и материальная точка является моделью. Это модель системы тел, которые якобы взаимодействуют только друг с другом, внешние силы не берутся во внимание, ими пренебрегают.
Закон сохранения импульса
В замкнутой системе тел векторная сумма импульсов тел не изменяется при взаимодействии тел. Если импульс одного тела увеличился, то это означает, что у какого-то другого тела (или нескольких тел) в этот момент импульс уменьшился ровно на такую же величину.
Рассмотрим такой пример. Девочка и мальчик катаются на коньках. Замкнутая система тел — девочка и мальчик (трением и другими внешними силами пренебрегаем). Девочка стоит на месте, ее импульс равен нулю, так как скорость нулевая (см. формулу импульса тела). После того как мальчик, движущийся с некоторой скоростью, столкнется с девочкой, она тоже начнет двигаться. Теперь ее тело обладает импульсом. Численное значение импульса девочки ровно такое же, на сколько уменьшился после столкновения импульс мальчика.
Девочка стоит на месте, ее импульс равен нулю, так как скорость нулевая (см. формулу импульса тела). После того как мальчик, движущийся с некоторой скоростью, столкнется с девочкой, она тоже начнет двигаться. Теперь ее тело обладает импульсом. Численное значение импульса девочки ровно такое же, на сколько уменьшился после столкновения импульс мальчика.
Одно тело массой 20кг движется со скоростью , второе тело массой 4кг движется в том же направлении со скоростью . Чему равны импульсы каждого тела. Чему равен импульс системы?
Импульс системы тел — это векторная сумма импульсов всех тел, входящих в систему. В нашем примере, это сумма двух векторов (так как рассматриваются два тела), которые направлены в одну сторону, поэтому
Сейчас вычислим импульс системы тел из предыдущего примера, если второе тело двигается в обратном направлении.
Так как тела двигаются в противоположных направлениях, получаем векторную сумму импульсов разнонаправленных. Подробнее о сумме векторов.
Главное запомнить
1) Что такое замкнутая система тел;
2) Закон сохранения импульса и его применение
Закон сохранения импульса. Реактивное движение
Закон сохранения импульса
Закон сохранения импульса можно наблюдать повсюду. Он достаточно точно выполняется в реальных условиях, если пренебречь сопротивлением воздуха, силами трения и т.д. Примеры проявления этого закона:
- стрелок ощущает отдачу при выстреле из ружья;
- рыбак переходит с кормы на нос лодки, а лодка при этом движется в противоположную сторону;
- шары сталкиваются на бильярдном столе.
Однако, прежде чем говорить о законе сохранении импульса, рассмотрим понятие замкнутой системы.
Замкнутая система — система тел, на которую со стороны других тел не действуют внешние силы.
Формулировка закона сохранения импульса (ЗСИ)
Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях этих тел между собой внутри системы.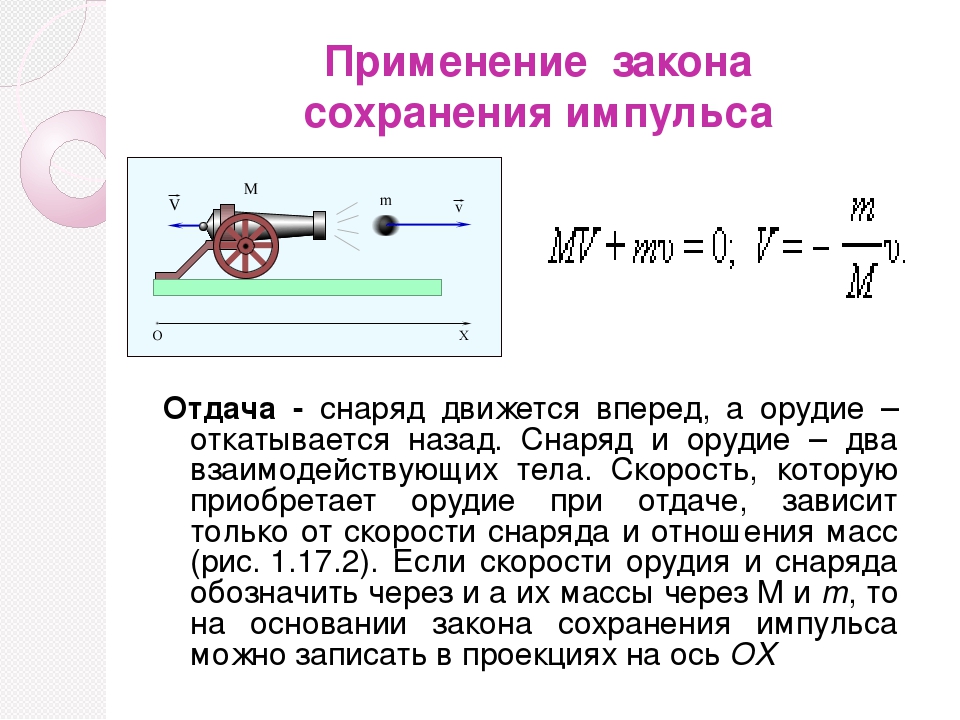
Данный закон является следствием из второго и третьего законов Ньютона. Покажем это.
Возьмем замкнутую систему из двух взаимодействующих тел. Силы F1→ и F2→ — это силы взаимодействия между телами. Третий закон Ньютона гласит, что F2→=-F1→. Пусть тела взаимодействуют во течение времени t. Тогда импульсы сил одинаковы по модулю и противоположны по направлению, как и сами силы.
F2t→=-F1→t.
По второму закону Ньютона:
F1→t=m1v1’→-m1v1→; F2→t=m1v2’→-m1v2→
Здесь v1’→ и v2’→ — скорости тел в конце взаимодействия. Соответственно, скорости без штрихов обозначают эти величины в начальный момент взаимодействия.
Из записанного выше следует соотношение:
m1v1→+m2v2→=m1v1’→+m2v2’→
Это равенство — математическая форма записи закона сохранения импульса. Оно означает, что суммарный импульс системы в результате какого-то взаимодействия не изменился.
Проиллюстрируем закон сохранения импульса на примере соударения шаров разных масс. Один из шаров до удара покоился.
Как видим, после удара векторная сумма импульсов двух шаров равна первоначальному импульсу движущегося шара.
Важно! Закон сохранения выполняется и для проекций векторов на координатные оси.
Закон сохранения импульса позволяет решать задачи и находить скорости тел не зная значений действующих сил.
Рассмотрим снаряд, вылетающий из пушки.
В данном случае взаимодействующие тела — это снаряд и пушка. Сначала тела не движутся. При выстреле снаряд приобретает скорость v→ и летит вперед, а пушка откатывается назад со скоростью V→. Откатывание пушки называется отдачей от выстрела.
По закону сохранения импульса в проекции на ось OX можно записать:
mv-MV=0
V=mvM.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Реактивное движение
Реактивное движение также основано на принципе отдачи. Нагретые газы выбрасываются из сопла реактивного двигателя со скоростью u→. Пусть масса газов равна m, а масса ракеты после истечения газов — M. Рассматривая замкнутую систему «ракета-газы» и применяя к ней закон сохранения импульса, можно вычислить скорость ракеты V после истечения газов.
V=muM
Формула для пушки и снаряда не применима к ракете, так как дает лишь приблизительное представление о движении ракеты, На самом деле вся масса газов выходит из сопла не сразу, а постепенно.
Рассмотрим этот процесс подробнее. Пусть масса ракеты в момент времени t равна M, а сама ракета движется со скоростью v→. В течение малого промежутка времени ∆t из сопла ракеты выбрасывается порция газа с относительной скоростью u→. По истечении времени ∆t ракета будет двигаться со скоростью v+∆v, а масса ракеты станет равной M-∆M.
В момент t+∆t импульс ракеты равен:
M-∆M·v→+∆v→.
Импульс реактивных газов:
∆M·v→+u→.
По закону сохранения импульса:
Mv→=M-∆M·v→+∆v→+∆M·v→+u→.
Или
M∆v→=∆M·u→-∆M·∆v→.
Величиной ∆M·∆v→ можно пренебречь, так как ∆M намного меньше M.
Разделим последнее равенство на ∆t и перейдем к пределу ∆t→0.
M∆v→∆t=∆M·u→∆t (∆t→0)
Ma→=-μu→.
Здесь μ — расход топлива в единицу времени, а -μu→ — реактивная сила тяги. Направление этой силы совпадает с направлением движения ракеты.
Формула Ma→=-μu→ выражает второй закон Ньютона для тела переменной массы. В скалярном виде ее можно переписать так:
Ma=μu.
Конечная скорость ракеты определяется по формуле:
v=ulnM0M.
Это так называемая формула Циолковского, согласно которой конечная скорость ракеты может превышать скорость истечения газов из сопла двигателя. Правда, достижение такой скорости связано с определенными сложностями. Во-первых такими, как значительный расход топлива.
Для того, чтобы развить первую космическую скорость v=v1=7,9·103 мс при скорости истечения газов u=3·103 мс стартовая масса ракеты должна быть примерно в 14 раз больше конечной массы.
Современное ракетостроение развивается в направлении экономичных многоступенчатых ракет. Сброс отсеков с отработанным топливом позволяет значительно сократить массу ракеты и оптимизировать дальнейший расход топлива для ее разгона.
Закон сохранения импульса, кинетическая и потенциальные энергии, мощность силы | ЕГЭ по физике
Импульс тела
Импульсом тела называется величина, равная произведению массы тела на его скорость.
Следует помнить, что речь идет о теле, которое можно представить как материальную точку. Импульс тела ($р$) называют также количеством движения. Понятие количества движения было введено в физику Рене Декартом (1596—1650). Термин «импульс» появился позже (impulsus в переводе с латинского означает «толчок»). Импульс является векторной величиной (как и скорость) и выражается формулой:
$p↖{→}=mυ↖{→}$
Направление вектора импульса всегда совпадает с направлением скорости.
За единицу импульса в СИ принимают импульс тела массой $1$ кг, движущегося со скоростью $1$ м/с, следовательно, единицей импульса является $1$ кг $·$ м/с.
Если на тело (материальную точку) действует постоянная сила в течение промежутка времени $∆t$, то постоянным будет и ускорение:
$a↖{→}={{υ_2}↖{→}-{υ_1}↖{→}}/{∆t}$
где, ${υ_1}↖{→}$ и ${υ_2}↖{→}$ — начальная и конечная скорости тела. Подставив это значение в выражение второго закона Ньютона, получим:
${m({υ_2}↖{→}-{υ_1}↖{→})}/{∆t}=F↖{→}$
Раскрыв скобки и воспользовавшись выражением для импульса тела, имеем:
${p_2}↖{→}-{p_1}↖{→}=F↖{→}∆t$
Здесь ${p_2}↖{→}-{p_1}↖{→}=∆p↖{→}$ — изменение импульса за время $∆t$. Тогда предыдущее уравнение примет вид:
$∆p↖{→}=F↖{→}∆t$
Выражение $∆p↖{→}=F↖{→}∆t$ представляет собой математическую запись второго закона Ньютона.
Произведение силы на время ее действия называют импульсом силы. Поэтому изменение импульса точки равно изменению импульса силы, действующей на нее.
Выражение $∆p↖{→}=F↖{→}∆t$ называется уравнением движения тела. Следует заметить, что одно и то же действие — изменение импульса точки — может быть получено малой силой за большой промежуток времени и большой силой за малый промежуток времени.
Импульс системы тел. Закон изменения импульса
Импульсом (количеством движения) механической системы называется вектор, равный сумме импульсов всех материальных точек этой системы:
${p_{сист}}↖{→}={p_1}↖{→}+{p_2}↖{→}+…$
Законы изменения и сохранения импульса являются следствием второго и третьего законов Ньютона.
Рассмотрим систему, состоящую из двух тел. Силы ($F_{12}$ и $F_{21}$ на рисунке, с которыми тела системы взаимодействуют между собой, называются внутренними.
Пусть кроме внутренних сил на систему действуют внешние силы ${F_1}↖{→}$ и ${F_2}↖{→}$. Для каждого тела можно записать уравнение $∆p↖{→}=F↖{→}∆t$. Сложив левые и правые части этих уравнений, получим:
${∆p_1}↖{→}+{∆p_2}↖{→}=({F_{12}}↖{→}+{F_{21}}↖{→}+{F_1}↖{→}+{F_2}↖{→})∆t$
Согласно третьему закону Ньютона ${F_{12}}↖{→}=-{F_{21}}↖{→}$.
Следовательно,
${∆p_1}↖{→}+{∆p_2}↖{→}=({F_1}↖{→}+{F_2}↖{→})∆t$
В левой части стоит геометрическая сумма изменений импульсов всех тел системы, равная изменению импульса самой системы — ${∆p_{сист}}↖{→}$.С учетом этого равенство ${∆p_1}↖{→}+{∆p_2}↖{→}=({F_1}↖{→}+{F_2}↖{→})∆t$ можно записать:
${∆p_{сист}}↖{→}=F↖{→}∆t$
где $F↖{→}$ — сумма всех внешних сил, действующих на тело. Полученный результат означает, что импульс системы могут изменить только внешние силы, причем изменение импульса системы направлено так же, как суммарная внешняя сила. В этом суть закона изменения импульса механической системы.
Внутренние силы изменить суммарный импульс системы не могут. Они лишь меняют импульсы отдельных тел системы.
Закон сохранения импульса
Из уравнения ${∆p_{сист}}↖{→}=F↖{→}∆t$ вытекает закон сохранения импульса. Если на систему не действуют никакие внешние силы, то правая часть уравнения ${∆p_{сист}}↖{→}=F↖{→}∆t$ обращается в ноль, что означает неизменность суммарного импульса системы:
${∆p_{сист}}↖{→}=m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=const$
Система, на которую не действуют никакие внешние силы или равнодействующая внешних сил равна нулю, называется замкнутой.
Закон сохранения импульса гласит:
Суммарный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел системы между собой.
Полученный результат справедлив для системы, содержащей произвольное число тел. Если сумма внешних сил не равна нулю, но сумма их проекций на какое-то направление равна нулю, то проекция импульса системы на это направление не меняется. Так, например, система тел на поверхности Земли не может считаться замкнутой из-за силы тяжести, действующей на все тела, однако сумма проекций импульсов на горизонтальное направление может оставаться неизменной (при отсутствии трения), т. к. в этом направлении сила тяжести не действует.
Реактивное движение
Рассмотрим примеры, подтверждающие справедливость закона сохранения импульса.
Возьмем детский резиновый шарик, надуем его и отпустим. Мы увидим, что когда воздух начнет выходить из него в одну сторону, сам шарик полетит в другую. Движение шарика является примером реактивного движения. Объясняется оно законом сохранения импульса: суммарный импульс системы «шарик плюс воздух в нем» до истечения воздуха равен нулю; он должен остаться равным нулю и во время движения; поэтому шарик движется в сторону, противоположную направлению истечения струи, и с такой скоростью, что его импульс по модулю равен импульсу воздушной струи.
Реактивным движением называют движение тела, возникающее при отделении от него с какой- либо скоростью некоторой его части. Вследствие закона сохранения импульса направление движения тела при этом противоположно направлению движения отделившейся части.
На принципе реактивного движения основаны полеты ракет. Современная космическая ракета представляет собой очень сложный летательный аппарат. Масса ракеты складывается из массы рабочего тела (т. е. раскаленных газов, образующихся в результате сгорания топлива и выбрасываемых в виде реактивной струи) и конечной, или, как говорят, «сухой» массы ракеты, остающейся после выброса из ракеты рабочего тела.
Когда реактивная газовая струя с большой скоростью выбрасывается из ракеты, сама ракета устремляется в противоположную сторону. Согласно закону сохранения импульса, импульс $m_{p}υ_p$, приобретаемый ракетой, должен быть равен импульсу $m_{газ}·υ_{газ}$ выброшенных газов:
$m_{p}υ_p=m_{газ}·υ_{газ}$
Отсюда следует, что скорость ракеты
$υ_p=({m_{газ}}/{m_p})·υ_{газ}$
Из этой формулы видно, что скорость ракеты тем больше, чем больше скорость выбрасываемых газов и отношение массы рабочего тела (т. е. массы топлива) к конечной («сухой») массе ракеты.
Формула $υ_p=({m_{газ}}/{m_p})·υ_{газ}$ является приближенной. В ней не учитывается, что по мере сгорания топлива масса летящей ракеты становится все меньше и меньше. Точная формула для скорости ракеты была получена в 1897 г. К. Э. Циолковским и носит его имя.
Формула Циолковского позволяет рассчитать запасы топлива, необходимые для сообщения ракете заданной скорости.
Работа силы
Термин «работа» был введен в физику в 1826 г. французским ученым Ж. Понселе. Если в обыденной жизни работой называют лишь труд человека, то в физике и, в частности, в механике принято считать, что работу совершает сила. Физическую величину работы обычно обозначают буквой $А$.
Работа силы — это мера действия силы, зависящая от ее модуля и направления, а также от перемещения точки приложения силы. Для постоянной силы и прямолинейного перемещения работа определяется равенством:
$A=F|∆r↖{→}|cosα$
где $F$ — сила, действующая на тело, $∆r↖{→}$ — перемещение, $α$ — угол между силой и перемещением.
Работа силы равна произведению модулей силы и перемещения и косинуса угла между ними, т. е. скалярному произведению векторов $F↖{→}$ и $∆r↖{→}$.
Работа — величина скалярная. Если $α 0$, а если $90°
При действии на тело нескольких сил полная работа (сумма работ всех сил) равна работе результирующей силы.
Единицей работы в СИ является джоуль ($1$ Дж). $1$ Дж — это работа, которую совершает сила в $1$ Н на пути в $1$ м в направлении действия этой силы. Эта единица названа в честь английского ученого Дж. Джоуля (1818-1889): $1$ Дж = $1$ Н $·$ м. Часто применяются также килоджоули и миллиджоули: $1$ кДж $= 1 000$ Дж, $1$ мДж $= 0.001$ Дж.
Работа силы тяжести
Рассмотрим тело, скользящее по наклонной плоскости с углом наклона $α$ и высотой $Н$.
Выразим $∆x$ через $H$ и $α$:
$∆x={H}/{sinα}$
Учитывая, что сила тяжести $F_т=mg$ составляет угол ($90° — α$) с направлением перемещения, используя формулу $∆x={H}/{sin}α$, получим выражение для работы силы тяжести $A_g$:
$A_g=mg·cos(90°-α)·{H}/{sinα}=mgH$
Из этой формулы видно, что работа силы тяжести зависит от высоты и не зависит от угла наклона плоскости.
Отсюда следует, что:
- работа силы тяжести не зависит от формы траектории, по которой движется тело, а лишь от начального и конечного положения тела;
- при перемещении тела по замкнутой траектории работа силы тяжести равна нулю, т. е. сила тяжести — консервативная сила (консервативными называются силы, обладающие таким свойством).
Работа сил реакции, равна нулю, поскольку сила реакции ($N$) направлена перпендикулярно перемещению $∆x$.
Работа силы трения
Сила трения направлена противоположно перемещению $∆x$ и составляет с ним угол $180°$, поэтому работа силы трения отрицательна:
$A_{тр}=F_{тр}∆x·cos180°=-F_{тр}·∆x$
Так как $F_{тр}=μN, N=mg·cosα, ∆x=l={H}/{sinα},$ то
$A_{тр}=μmgHctgα$
Работа силы упругости
Пусть на нерастянутую пружину длиной $l_0$ действует внешняя сила $F↖{→}$, растягивая ее на $∆l_0=x_0$. В положении $x=x_0F_{упр}=kx_0$. После прекращения действия силы $F↖{→}$ в точке $х_0$ пружина под действием силы $F_{упр}$ сжимается.
Определим работу силы упругости при изменении координаты правого конца пружины от $х_0$ до $х$. Поскольку сила упругости на этом участке изменяется линейно, в законе Гука можно использовать ее среднее значение на этом участке:
$F_{упр.ср.}={kx_0+kx}/{2}={k}/{2}(x_0+x)$
Тогда работа (с учетом того, что направления ${F_{упр.2}/{2}$
Можно показать, что вид последней формулы не зависит от угла между ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$. Работа сил упругости зависит лишь от деформаций пружины в начальном и конечном состояниях.
Таким образом, сила упругости, подобно силе тяжести, является консервативной силой.
Мощность силы
Мощность — физическая величина, измеряемая отношением работы к промежутку времени, в течение которого она произведена.
Другими словами, мощность показывает, какая работа совершается за единицу времени (в СИ — за $1$ с).
Мощность определяется формулой:
$N={A}/{∆t}$
где $N$ — мощность, $А$ — работа, совершенная за время $∆t$.
Подставив в формулу $N={A}/{∆t}$ вместо работы $A$ ее выражение $A=F|{∆r}↖{→}|cosα$, получим:
$N={F|{∆r}↖{→}|cosα}/{∆t}=Fυcosα$
Мощность равна произведению модулей векторов силы и скорости на косинус угла между этими векторами.
Мощность в системе СИ измеряется в ваттах (Вт). Один ватт ($1$ Вт) — это такая мощность, при которой за $1$ с совершается работа $1$ Дж: $1$ Вт $= 1$ Дж/с.
Эта единица названа в часть английского изобретателя Дж. Ватта (Уатта), построившего первую паровую машину. Сам Дж. Ватт (1736-1819) пользовался другой единицей мощности — лошадиной силой (л. с.), которую он ввел для того, чтобы можно было сравнивать работоспособности паровой машины и лошади: $1$ л.с. $= 735.5$ Вт.
В технике часто применяются более крупные единицы мощности — киловатт и мегаватт: $1$ кВт $= 1000$ Вт, $1$ МВт $= 1000000$ Вт.
Кинетическая энергия. Закон изменения кинетической энергии
Если тело или несколько взаимодействующих между собой тел (система тел) могут совершать работу, то говорят, что они обладают энергией.
Слово «энергия» (от греч. energia — действие, деятельность) нередко употребляется в быту. Так, например, людей, которые могут быстро выполнять работу, называют энергичными, обладающими большой энергией.
Энергия, которой обладает тело вследствие движения, называется кинетической энергией.
Как и в случае определения энергии вообще, о кинетической энергии можно сказать, что кинетическая энергия — это способность движущегося тела совершать работу.2$ выражается следующим образом:
$A=E_{p_1}-E_{p_2}=-(E_{p_2}-E_{p_1})=-∆E_p$
Эта формула позволяет дать общее определение потенциальной энергии.
Потенциальной энергией системы называется зависящая от положения тел величина, изменение которой при переходе системы из начального состояния в конечное равно работе внутренних консервативных сил системы, взятой с противоположным знаком.
Знак «минус» в правой части уравнения $A=E_{p_1}-E_{p_2}=-(E_{p_2}-E_{p_1})=-∆E_p$ означает, что при совершении работы внутренними силами (например, падение тела на землю под действием силы тяжести в системе «камень — Земля») энергия системы убывает. Работа и изменение потенциальной энергии в системе всегда имеют противоположные знаки.
Поскольку работа определяет лишь изменение потенциальной энергии, то физический смысл в механике имеет только изменение энергии. Поэтому выбор нулевого уровня энергии произволен и определяется исключительно соображениями удобства, например, простотой записи соответствующих уравнений.
Закон изменения и сохранения механической энергии
Полной механической энергией системы называется сумма ее кинетической и потенциальной энергий:
$E=E_k+E_p$
Она определяется положением тел (потенциальная энергия) и их скоростью (кинетическая энергия).
Согласно теореме о кинетической энергии,
$E_k-E_{k_1}=A_p+A_{пр},$
где $А_р$ — работа потенциальных сил, $А_{пр}$ — работа непотенциальных сил.
В свою очередь, работа потенциальных сил равна разности потенциальной энергии тела в начальном $Е_{р_1}$ и конечном $Е_р$ состояниях. Учитывая это, получим выражение для закона изменения механической энергии:
$(E_k+E_p)-(E_{k_1}+E_{p_1})=A_{пр}$
где левая часть равенства — изменение полной механической энергии, а правая — работа непотенциальных сил.
Итак, закон изменения механической энергии гласит:
Изменение механической энергии системы равно работе всех непотенциальных сил.
Механическая система, в которой действуют только потенциальные силы, называется консервативной.
В консервативной системе $А_{пр} = 0$. Отсюда следует закон сохранения механической энергии:
В замкнутой консервативной системе полная механическая энергия сохраняется (не изменяется со временем):
$E_k+E_p=E_{k_1}+E_{p_1}$
Закон сохранения механической энергии выводится из законов механики Ньютона, которые применимы для системы материальных точек (или макрочастиц).
Однако закон сохранения механической энергии справедлив и для системы микрочастиц, где сами законы Ньютона уже не действуют.
Закон сохранения механической энергии является следствием однородности времени.
Однородность времени состоит в том, что при одинаковых начальных условиях протекание физических процессов не зависит от того, в какой момент времени эти условия созданы.
Закон сохранения полной механической энергии означает, что при изменении кинетической энергии в консервативной системе должна меняться и ее потенциальная энергия, так что их сумма остается постоянной. Это означает возможность превращения одного вида энергии в другой.
В соответствии с различными формами движения материи рассматривают различные виды энергии: механическую, внутреннюю (равную сумме кинетической энергии хаотического движения молекул относительно центра масс тела и потенциальной энергии взаимодействия молекул друг с другом), электромагнитную, химическую (которая складывается из кинетической энергии движения электронов и электрической энергии их взаимодействия друг с другом и с атомными ядрами), ядерную и пр. Из сказанного видно, что деление энергии на разные виды достаточно условно.
Явления природы обычно сопровождаются превращением одного вида энергии в другой. Так, например, трение частей различных механизмов приводит к превращению механической энергии в тепло, т. е. во внутреннюю энергию. В тепловых двигателях, наоборот, происходит превращение внутренней энергии в механическую; в гальванических элементах химическая энергия превращается в электрическую и т. д.
В настоящее время понятие энергии является одним из основных понятий физики. Это понятие неразрывно связано с представлением о превращении одной формы движения в другую.
Вот как в современной физике формулируется понятие энергии:
Энергия — общая количественная мера движения и взаимодействия всех видов материи. Энергия не возникает из ничего и не исчезает, она может только переходить из одной формы в другую. Понятие энергии связывает воедино все явления природы.
Простые механизмы. КПД механизмов
Простыми механизмами называются приспособления, изменяющие величину или направление приложенных к телу сил.
Они применяются для перемещения или подъема больших грузов с помощью небольших усилий. К ним относятся рычаг и его разновидности — блоки (подвижный и неподвижный), ворот, наклонная плоскость и ее разновидности — клин, винт и др.
Рычаг. Правило рычага
Рычаг представляет собой твердое тело, способное вращаться вокруг неподвижной опоры.
Правило рычага гласит:
Рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам:
${F_2}/{F_1}={l_1}/{l_2}$
Из формулы ${F_2}/{F_1}={l_1}/{l_2}$, применив к ней свойство пропорции (произведение крайних членов пропорции равно произведению ее средних членов), можно получить такую формулу:
$F_1l_1=F_2l_2$
Но $F_1l_1=M_1$ — момент силы, стремящейся повернуть рычаг по часовой стрелке, а $F_2l_2=M_2$ — момент силы, стремящейся повернуть рычаг против часовой стрелки. Таким образом, $M_1=M_2$, что и требовалось доказать.
Рычаг начал применяться людьми в глубокой древности. С его помощью удавалось поднимать тяжелые каменные плиты при постройке пирамид в Древнем Египте. Без рычага это было бы невозможно. Ведь, например, для возведения пирамиды Хеопса, имеющей высоту $147$ м, было использовано более двух миллионов каменных глыб, самая меньшая из которых имела массу $2.5$ тонн!
В наше время рычаги находят широкое применение как на производстве (например, подъемные краны), так и в быту (ножницы, кусачки, весы).n}$
Винт
Винт представляет собой наклонную плоскость, навитую на ось.
Условие равновесия сил, действующих на винт, имеет вид:
$F_1={F_2h}/{2πr}=F_2tgα, F_1={F_2h}/{2πR}$
где $F_1$ — внешняя сила, приложенная к винту и действующая на расстоянии $R$ от его оси; $F_2$ — сила, действующая в направлении оси винта; $h$ — шаг винта; $r$ — средний радиус резьбы; $α$ — угол наклона резьбы. $R$ — длина рычага (гаечного ключа), вращающего винт с силой $F_1$.
Коэффициент полезного действия
Коэффициент полезного действия (КПД) — отношение полезной работы ко всей затраченной работе.
Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой $η$ («эта»):
$η={A_п}/{A_3}·100%$
где $А_п$ — полезная работа, $А_3$ — вся затраченная работа.
Полезная работа всегда составляет лишь часть полной работы, которую затрачивает человек, используя тот или иной механизм.
Часть совершенной работы тратится на преодоление сил трения. Поскольку $А_3 > А_п$, КПД всегда меньше $1$ (или $< 100%$).
Когда КПД немного меньше $1$, можно считать, что затраченная работа примерно равна полезной: $А_3 ≈ А_п$.
Поскольку каждую из работ в этом равенстве можно выразить в виде произведения соответствующей силы на пройденный путь, то его можно переписать так: $F_1s_1≈F_2s_2$.
Отсюда следует, что, выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот. Этот закон называют золотым правилом механики.
Золотое правило механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.
Так, например, благодаря этому правилу сразу можно сказать, что рабочему, изображенному на рисунке, при двукратном выигрыше в силе подъема груза на $10$ см придется опустить противоположный конец рычага на $20$ см.
Столкновение тел. Упругий и неупругий удары
Законы сохранения импульса и механической энергии применяются для решения задачи о движении тел после столкновения: по известным импульсам и энергиям до столкновения определяются значения этих величин после столкновения. Рассмотрим случаи упругого и неупругого ударов.
Абсолютно неупругим называется удар, после которого тела образуют единое тело, движущееся с определенной скоростью. Задача о скорости последнего решается с помощью закона сохранения импульса системы тел с массами $m_1$ и $m_2$ (если речь идет о двух телах) до и после удара:
$m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=(m_1+m_2)υ↖{→}$
Очевидно, что кинетическая энергия тел при неупругом ударе не сохраняется (например, при ${υ_1}↖{→}=-{υ_2}↖{→}$ и $m_1=m_2$ она становится равной нулю после удара).
Абсолютно упругим называется удар, при котором сохраняется не только сумма импульсов, но и сумма кинетических энергий ударяющихся тел.
Для абсолютно упругого удара справедливы уравнения
$m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=m_1{υ’_1}↖{→}+m_2{υ’_2}↖{→};$
${m_{1}υ_1^2}/{2}+{m_{2}υ_2^2}/{2}={m_1(υ’_1)^2}/{2}+{m_2(υ’_2)^2}/{2}$
где $m_1, m_2$ — массы шаров, $υ_1, υ_2$ —скорости шаров до удара, $υ’_1, υ’_2$ —скорости шаров после удара.
сохранение импульса | Определение, примеры и факты
Сохранение количества движения , общий закон физики, согласно которому величина, называемая импульсом, которая характеризует движение, никогда не изменяется в изолированном наборе объектов; то есть полный импульс системы остается постоянным. Импульс равен массе объекта, умноженной на его скорость, и эквивалентен силе, необходимой для остановки объекта за единицу времени. Для любого массива из нескольких объектов полный импульс — это сумма отдельных импульсов.Однако есть особенность в том, что импульс является вектором, включающим как направление, так и величину движения, так что импульсы объектов, движущихся в противоположных направлениях, могут сокращаться, давая общую сумму нулю.
Британская викторина
Викторина «Все о физике»
Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.
Перед запуском полный импульс ракеты и ее топлива равны нулю. Во время запуска нисходящий импульс расширяющихся выхлопных газов по величине равен восходящему импульсу восходящей ракеты, так что общий импульс системы остается постоянным — в данном случае нулевым значением. При столкновении двух частиц сумма двух импульсов до столкновения равна их сумме после столкновения. Какой импульс одна частица теряет, другая получает.
Закон сохранения количества движения в изобилии подтвержден экспериментом и может быть даже математически выведен на основе разумного предположения, что пространство однородно, то есть что в законах природы нет ничего, что выделяло бы одно положение в пространстве как особенное по сравнению с с любым другим.
Существует аналогичный закон сохранения для углового момента, который описывает вращательное движение практически так же, как обычный импульс описывает линейное движение. Хотя точное математическое выражение этого закона несколько сложнее, примеры его многочисленны. Например, всем вертолетам для стабилизации требуется как минимум два гребных винта (ротора). Корпус вертолета вращался бы в противоположном направлении, чтобы сохранить угловой момент, если бы наверху был только один горизонтальный пропеллер.В соответствии с принципом сохранения углового момента фигуристы вращаются быстрее, когда они тянут руки к своему телу, и медленнее, когда они их вытягивают.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Сохранение углового момента также было тщательно установлено экспериментально, и можно показать математически, что оно следует из разумного предположения, что пространство однородно относительно ориентации, то есть что в законах природы нет ничего, что выделяло бы одно направление в пространстве. пространство как особенное по сравнению с любым другим.
Принцип сохранения импульса
Один из самых сильных законов физики — закон сохранения количества движения. Закон сохранения количества движения можно сформулировать следующим образом.
Для столкновения, происходящего между объектом 1 и объектом 2 в изолированной системе, общий импульс двух объектов до столкновения равен общему импульсу двух объектов после столкновения. То есть импульс, потерянный объектом 1, равен импульсу, полученному объектом 2.
Вышеупомянутое утверждение говорит нам, что общий импульс совокупности из объектов (система ) равен сохраняемым — то есть общее количество импульса является постоянным или неизменным значением. Этот закон сохранения импульса будет в центре внимания оставшейся части Урока 2. Чтобы понять основы сохранения импульса, давайте начнем с краткого логического доказательства.
Логика сохранения импульса
Рассмотрим столкновение двух объектов — объекта 1 и объекта 2.Для такого столкновения силы, действующие между двумя объектами, равны по величине и противоположны по направлению (третий закон Ньютона). Это утверждение можно выразить в виде уравнения следующим образом.
Силы действуют между двумя объектами в течение заданного времени. В некоторых случаях время велико; в других случаях времени мало. Независимо от того, сколько времени длится, можно сказать, что время, в течение которого сила действует на объект 1, равно времени, в течение которого сила действует на объект 2.Это просто логично. Силы возникают в результате взаимодействия (или контакта) между двумя объектами. Если объект 1 контактирует с объектом 2 в течение 0,050 секунды, то объект 2 должен контактировать с объектом 1 в течение того же времени (0,050 секунды). В виде уравнения это может быть указано как
Поскольку силы между двумя объектами равны по величине и противоположны по направлению, и поскольку время, в течение которого эти силы действуют, одинаковы по величине, отсюда следует, что импульсы, испытываемые двумя объектами, также равны по величине и противоположны по направлению. .В виде уравнения это может быть указано как
Но импульс, испытываемый объектом, равен изменению количества движения этого объекта (теорема об изменении импульса-импульса). Таким образом, поскольку каждый объект испытывает равные и противоположные импульсы, логически следует, что они также должны испытывать равные и противоположные изменения импульса. В виде уравнения это может быть указано как
Закон сохранения импульса
Приведенное выше уравнение является одним из утверждений закона сохранения количества движения.При столкновении изменение количества движения объекта 1 равно и противоположно изменению количества движения объекта 2. То есть, импульс, потерянный объектом 1, равен импульсу, полученному объектом 2. В большинстве столкновений между двумя объектами один объект замедляется и теряет импульс, в то время как другой объект ускоряется и набирает скорость. Если объект 1 теряет 75 единиц импульса, то объект 2 получает 75 единиц импульса. Тем не менее, общий импульс двух объектов (объект 1 плюс объект 2) до столкновения такой же, как и после столкновения.Общий импульс системы (совокупность двух объектов) сохраняется.
Полезная аналогия для понимания сохранения импульса включает денежную транзакцию между двумя людьми. Давайте называть этих двух людей Джеком и Джилл. Предположим, что мы должны были проверить карманы Джека и Джилл до и после денежной транзакции, чтобы определить, сколько денег у каждого из них. До транзакции у Джека было 100 долларов, а у Джилл — 100 долларов.Общая сумма денег двух человек до транзакции составляет 200 долларов. Во время транзакции Джек платит Джилл 50 долларов за покупаемый предмет. Из кармана Джека в карман Джилл переводится 50 долларов. Джек потерял 50 долларов, а Джилл получила 50 долларов. Деньги, потерянные Джеком, равны деньгам, полученным Джилл. После транзакции у Джека в кармане осталось 50 долларов, а у Джилл — 150 долларов. Тем не менее, общая сумма денег двух человек после транзакции составляет 200 долларов. Общая сумма денег (деньги Джека плюс деньги Джилл) до транзакции равна общей сумме денег после транзакции.Можно сказать, что общая сумма денег в системе (сбор двух человек) сохранена. Это то же самое, что и до транзакции, и после нее.
Полезным средством изображения передачи и сохранения денег между Джеком и Джилл является таблица.
В таблице показано количество денег, которыми владели эти два человека до и после взаимодействия. Он также показывает общую сумму денег до и после взаимодействия.Обратите внимание, что общая сумма денег (200 долларов) одинакова до и после взаимодействия — она сохраняется. Наконец, таблица показывает изменение количества денег, которыми владеют два человека. Обратите внимание, что изменение денежного счета Джека (-50 долларов США) равно и противоположно изменению денежного счета Джилл (+50 долларов США).
Для любого столкновения, происходящего в изолированной системе, импульс сохраняется. Общий импульс совокупности объектов в системе до столкновения такой же, как и после столкновения.Обычная физическая лаборатория включает в себя падение кирпича на движущуюся тележку.
Выпавший кирпич находится в состоянии покоя и начинается с нулевого импульса. Загруженная тележка (тележка с кирпичом на ней) движется со значительной инерцией. Фактический импульс загруженной тележки можно определить, используя скорость (часто определяемую анализом тикерной ленты) и массу. Общий импульс — это сумма импульса брошенного кирпича (0 единиц) и импульса загруженной тележки.После столкновения импульсы двух отдельных объектов (упавшего кирпича и загруженной тележки) можно определить по их измеренной массе и их скорости (часто обнаруживаемой при анализе тикерной ленты). Если импульс сохраняется во время столкновения, то сумма импульса брошенного кирпича и загруженной тележки после столкновения должна быть такой же, как и до столкновения. Импульс, потерянный загруженной тележкой, должен равняться (или приблизительно равняться) импульсу, набранному упавшим кирпичом. Данные по моменту взаимодействия между упавшим кирпичом и загруженной тележкой можно представить в виде таблицы, аналогичной таблице денег выше.
| До Столкновение Импульс | После Столкновение Импульс | Изменение в Импульс | |
| Выпавший кирпич | 0 единиц | 14 шт. | +14 единиц |
| Тележка с грузом | 45 единиц | 31 шт. | -14 единиц |
| Итого | 45 единиц | 45 единиц |
Обратите внимание, что загруженная тележка потеряла 14 единиц импульса, а упавший кирпич получил 14 единиц импульса.Отметим также, что полный импульс системы (45 единиц) был таким же до столкновения, как и после столкновения.
Столкновения обычно происходят в контактных видах спорта (например, футбол) и в видах спорта с ракетками и летучими мышами (например, бейсбол, гольф, теннис и т. Д.). Рассмотрим столкновение в футболе между защитником и полузащитником во время стойки у линии ворот . Защитник прыгает через линию ворот и в воздухе сталкивается с полузащитником. Полузащитник и защитник держат друг друга и едут вместе после столкновения.У защитника есть импульс 100 кг * м / с, восток перед столкновением, а полузащитник имеет импульс 120 кг * м / с, запад перед столкновением. Полный импульс системы перед столкновением составляет 20 кг * м / с, запад (при необходимости просмотрите раздел о добавлении векторов). Следовательно, полный импульс системы после столкновения также должен быть 20 кг * м / с, запад. Защитник и полузащитник движутся вместе как единое целое после столкновения с общим импульсом 20 кг * м / с. Импульс сохраняется при столкновении.Векторная диаграмма может быть использована для представления этого принципа сохранения импульса; на такой диаграмме стрелка используется для обозначения величины и направления вектора импульса для отдельных объектов до столкновения и объединенного импульса после столкновения.
Теперь предположим, что набивной мяч брошен клоуну, который отдыхает на льду; клоун ловит набивной мяч и скользит вместе с мячом по льду.Импульс набивного мяча до столкновения составляет 80 кг * м / с. Импульс клоуна до столкновения равен 0 м / с. Полный импульс системы до столкновения составляет 80 кг * м / с. Следовательно, полный импульс системы после столкновения также должен составлять 80 кг * м / с. Клоун и набивной мяч движутся вместе как единое целое после столкновения с общим импульсом 80 кг * м / с. Импульс сохраняется при столкновении.
Импульс сохраняется для любого взаимодействия между двумя объектами, происходящего в изолированной системе.Это сохранение импульса можно наблюдать с помощью анализа полного импульса системы или анализа изменения импульса. Полезные средства представления такого анализа включают таблицу импульсов и векторную диаграмму. Позже в Уроке 2 мы будем использовать принцип сохранения импульса для решения задач, в которых предсказывается скорость объектов после столкновения.
Смотри!
Используя датчики движения и тележки на трассе с низким коэффициентом трения, можно собирать данные, демонстрирующие закон сохранения количества движения.Видео ниже демонстрирует процесс.
Мы хотели бы предложить …
Иногда просто прочитать об этом недостаточно. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием наших интерактивных тележек и кирпичей, интерактивных тележек взрывающихся тележек и / или наших интерактивных тележек для столкновений.Эти интерактивные элементы можно найти в разделе Physics Interactive на нашем веб-сайте, и они предоставляют интерактивный опыт анализа импульса отдельных объектов и систем объектов при столкновениях.
Проверьте свое понимание
Выразите свое понимание концепции и математики импульса, ответив на следующие вопросы. Нажмите на кнопку, чтобы просмотреть ответы.
1. При тушении пожара пожарный должен проявлять особую осторожность, держа шланг, из которого на высокой скорости выделяется большое количество воды. Почему такая задача может быть сложной?
2. Лобовое столкновение большого грузовика и Volkswagen.
а. Какой автомобиль испытывает наибольшую силу удара?
г.Какой автомобиль испытывает наибольший импульс?
г. Какой автомобиль претерпевает наибольшие изменения?
г. Какой автомобиль испытывает наибольшее ускорение?
3. Майлз Туго и Бен Травлун едут в автобусе со скоростью шоссе в хороший летний день, когда на лобовое стекло попадает несчастный жук. Майлз и Бен начинают обсуждать физику ситуации.Майлз предполагает, что изменение скорости движения жука намного больше, чем у автобуса. В конце концов, утверждает Майлз, не было заметного изменения скорости автобуса по сравнению с очевидным изменением скорости ошибки. Бен полностью не согласен, утверждая, что и жук, и автобус сталкиваются с одной и той же силой, изменением импульса и импульсом. С кем ты согласен? Поддержите свой ответ.
4.Если мяч выбрасывается вверх от земли с десятью единицами импульса, каков импульс отдачи Земли? ____________ Мы чувствуем это? Объяснять.
5. Если шар для боулинга весом 5 кг проецируется вверх со скоростью 2,0 м / с, то какова скорость отдачи Земли (масса = 6,0 x 10 24 кг).
6.Линейный игрок весом 120 кг, движущийся на запад со скоростью 2 м / с, захватывает 80-килограммового защитника, движущегося на восток со скоростью 8 м / с. После столкновения оба игрока движутся на восток со скоростью 2 м / с. Нарисуйте векторную диаграмму, на которой импульсы каждого игрока до и после столкновения представлены вектором импульса. Обозначьте величину каждого вектора импульса.
См. Ответ ниже.
7. Стремясь применить самую суровую смертную казнь к довольно непопулярному заключенному, команда казней в тюрьме Темных веков ищет пулю, которая в десять раз массивнее самой винтовки.Какой тип людей захочет стрелять из винтовки с пулей, которая в десять раз массивнее винтовки? Объяснять.
8. Бейсболист свободно держит биту и бьет по мячу. Выразите свое понимание сохранения импульса, заполнив таблицы ниже.
9.Крылатая ракета «Томагавк» запускается из ствола мобильной ракетной установки. Пренебрегайте трением. Выразите свое понимание сохранения импульса, заполнив таблицы ниже.
Вернитесь к вопросу № 6.
Сохранение импульса
Сохранение импульса — фундаментальная концепция физики.
вместе с
сохранение энергии
и
сохранение массы.Импульс определяется как масса объекта, умноженная на скорость
объекта.
Сохранение импульса утверждает, что,
в некоторой проблемной области количество импульса остается постоянным;
импульс не создается и не уничтожается, а только изменяется
через действие сил , как описано в уравнении Ньютона.
законы движения.
Работать с импульсом труднее, чем с массой и энергией, потому что
импульс — это
векторная величина
имеющий как величину, так и направление. Импульс сохраняется во всех трех
физические направления одновременно.Еще сложнее иметь дело с
газ
потому что силы в одном направлении могут влиять на импульс в другом направлении
из-за столкновений многих молекул.
На этом слайде мы представим очень и очень упрощенную задачу потока.
где свойства меняются только в одном направлении.
Проблема еще больше упрощается, если рассмотреть установившийся поток, который
не меняться со временем и ограничивая силы только теми
связанный с
давление.
Имейте в виду, что реальных проблем с потоком очень много.
более сложный
чем этот простой
пример.
Рассмотрим течение газа через область, в которой свойства течения
только изменение в одном направлении, которое мы назовем «х». Газ попадает в домен
на станции 1 с некоторой скоростью u и некоторым давлением p
и выходит на станции 2 с другим значением
скорости и давления. Для простоты будем считать, что
плотность r остается постоянной в пределах области
и что область A , через которую
расход газа также остается постоянным.Расположение станций 1 и 2 разделено.
на расстоянии del x . (Дельта — маленький треугольник на слайде
и это греческая буква «д». Математики часто используют этот символ для обозначения
изменение или изменение количества. Шрифт веб-печати не поддерживает
греческие буквы, поэтому мы будем называть его просто «дель».)
Изменение с расстоянием называется градиентом
чтобы избежать путаницы с изменением времени, которое называется коэффициентом .
Градиент скорости обозначен как del u / del x ;
изменение скорости на
изменение расстояния.Итак, на станции 2 скорость определяется скоростью
на 1 плюс градиент, умноженный на расстояние.
u2 = u1 + (del u / del x) * del x
Аналогичное выражение дает давление
на выходе:
p2 = p1 + (del p / del x) * del x
Ньютона
второй закон движения состояний
что сила F равна изменению количества движения с
уважение ко времени. Для объекта постоянной массы
м это сводится к массе, умноженной на ускорение a .Ускорение — это изменение скорости с изменением времени.
(дель у / дель т) . Потом:
F = m * a = m * (del u / del t)
Сила в этой проблеме
происходит из-за градиента давления. Поскольку давление — это сила на единицу площади,
чистая сила, действующая на нашу жидкую область, равна давлению, умноженному на площадь в
на выходе минус давление, умноженное на площадь у входа.
F = — [(p * A) 2 — (p * A) 1] = m * [(u2 — u1) / del t]
Знак минус у
начало этого выражения используется потому, что газы движутся из области
от высокого давления до области низкого давления; если давление увеличивается с
x скорость уменьшится.Подставляя наши выражения для скорости
и давление:
— [{(p + (del p / del x) * del x} * A) — (p * A)] = m * [(u + (del u / del x) * del x — u) /
дель т]
Упрощать:
— (del p / del x) * del x * A = m * (del u / del x) * del x / del t
Отметив, что (del x / del t) — это
скорость и что масса равна плотности r, умноженной на объема (площадь, умноженная на del x):
— (del p / del x) * del x * A = r * del x * A * (del u / del x) * u
Упрощать:
— (del p / del x) = r * u * (del u / del x)
del p / del x и del u / del x
представляют градиенты давления и скорости.Если мы уменьшим нашу область до различных размеров, эти градиенты станут дифференцированными:
— dp / dx = r * u * du / dx
Это одномерная устойчивая форма
Уравнение Эйлера.
Интересно отметить, что падение давления
жидкости (член слева) пропорционален как значению
скорость и градиент скорости.
Решение этого уравнения импульса дает нам вид
динамическое давление
что появляется в
Уравнение Бернулли.
Действия:
Экскурсии с гидом
Основные уравнения динамики жидкости:
Навигация..
- Руководство для начинающих Домашняя страница
9.3 Сохранение линейного импульса — University Physics Volume 1
Учебные цели
К концу этого раздела вы сможете:
- Объясните значение выражения «сохранение импульса»
- Правильно определить, закрыта ли система
- Определите систему, импульс которой сохраняется
- Математически выразить сохранение импульса для данной системы
- Вычислить неизвестную величину, используя закон сохранения количества движения
Вспомните третий закон Ньютона: когда два объекта масс m1m1 и m2m2 взаимодействуют (что означает, что они прикладывают силы друг к другу), сила, которую объект 2 применяет к объекту 1, равна по величине и противоположна по направлению силе, которую прикладывает объект 1 на объекте 2.Пусть:
- F → 21 = F → 21 = сила на m1m1 от m2m2
- F → 12 = F → 12 = сила на м2м2 от m1m1
Тогда в символах третий закон Ньютона говорит:
F → 21 = −F → 12m1a → 1 = −m2a → 2.F → 21 = −F → 12m1a → 1 = −m2a → 2.
9,10
(Напомним, что эти две силы не отменяются, потому что они применяются к разным объектам. F21F21 заставляет m1m1 ускоряться, а F12F12 заставляет m2m2 ускоряться.)
Хотя величины сил, действующих на объекты, одинаковы, ускорения нет, просто потому, что массы (в общем) разные.Следовательно, изменения скорости каждого объекта различны:
Дв → 1дт ≠ дв → 2дт. dv → 1дт ≠ дв → 2дт.
Однако произведения массы и изменения скорости равны (по величине):
m1dv → 1dt = −m2dv → 2dt.m1dv → 1dt = −m2dv → 2dt.
9,11
На этом этапе неплохо было бы убедиться, что вы ясно понимаете физический смысл производных в уравнении 9.3. Из-за взаимодействия скорость каждого объекта изменяется на величину dv .Кроме того, взаимодействие происходит в интервале времени dt , что означает, что изменение скоростей также происходит в течение dt . Этот временной интервал одинаков для каждого объекта.
Предположим на время, что массы объектов не меняются во время взаимодействия. (Мы ослабим это ограничение позже.) В этом случае мы можем перетянуть массы внутрь производных:
ddt (m1v → 1) = — ddt (m2v → 2) ddt (m1v → 1) = — ddt (m2v → 2)
9,12
и, следовательно,
dp → 1dt = −dp → 2dt.dp → 1dt = −dp → 2dt.
9,13
Это говорит о том, что скорость изменения импульса одинакова для обоих объектов. Массы разные, и изменения скорости разные, но скорость изменения произведения м и v → v → одинаковы.
Физически это означает, что во время взаимодействия двух объектов (m1andm2m1andm2) у обоих объектов изменился импульс; но эти изменения идентичны по величине, хотя и противоположны по знаку.Например, импульс объекта 1 может увеличиться, что означает, что импульс объекта 2 уменьшается точно на такую же величину.
В свете этого давайте переписываем уравнение 9.12 в более понятной форме:
dp → 1dt + dp → 2dt = 0. dp → 1dt + dp → 2dt = 0.
9,14
Это говорит о том, что во время взаимодействия, хотя импульс объекта 1 изменяется, и импульс объекта 2 также изменяется, эти два изменения компенсируют друг друга, так что общее изменение количества движения двух объектов вместе равно нулю.
Поскольку общий суммарный импульс двух объектов вместе никогда не меняется, мы могли бы написать
ddt (p → 1 + p → 2) = 0 ddt (p → 1 + p → 2) = 0
9,15
, откуда следует, что
p → 1 + p → 2 = константа. p → 1 + p → 2 = константа.
9,16
Как показано на рисунке 9.14, общий импульс системы до и после столкновения остается неизменным.
Рис. 9.14. Перед столкновением два бильярдных шара движутся с импульсами p → 1p → 1 и p → 2p → 2. Полный импульс системы равен их сумме, как показано красным вектором, помеченным слева p → totalp → total.После столкновения два биллиардных шара движутся с разными импульсами p → ′ 1p → ′ 1 и p → ′ 2p → ′ 2. Однако общий импульс не изменился, как показано красной векторной стрелкой p → ‘totalp →’ total справа.
Обобщая этот результат на N объектов, получаем
p → 1 + p → 2 + p → 3 + ⋯ + p → N = constant j = 1Np → j = constant. p → 1 + p → 2 + p → 3 + ⋯ + p → N = постоянный j = 1Np → j = постоянная.
9,17
Уравнение 9.17 — это определение полного (или чистого) импульса системы из N взаимодействующих объектов, наряду с утверждением, что общий импульс системы объектов постоянен во времени или, лучше сказать, сохраняется.
Законы о сохранении
Если значение физической величины постоянно во времени, мы говорим, что величина сохраняется.
Требования к сохранению импульса
Однако есть одна сложность. Для сохранения импульса система должна соответствовать двум требованиям:
- Масса системы должна оставаться постоянной во время взаимодействия.
Когда объекты взаимодействуют (прикладывают силы друг к другу), они могут передавать массы друг другу; но любая масса, которую приобретает один объект, уравновешивается потерей этой массы другим.Таким образом, общая масса системы объектов остается неизменной с течением времени:
[dmdt] system = 0. [dmdt] system = 0. - Чистая внешняя сила, действующая на систему, должна быть равна нулю.
Когда объекты сталкиваются, взрываются и перемещаются, они оказывают друг на друга силу. Однако все эти силы являются внутренними по отношению к системе, и, таким образом, каждая из этих внутренних сил уравновешивается другой внутренней силой, равной по величине и противоположной по знаку. В результате изменение количества движения, вызванное каждой внутренней силой, компенсируется другим изменением количества движения, равным по величине и противоположным по направлению.Следовательно, внутренние силы не могут изменить общий импульс системы, потому что сумма изменений равна нулю. Однако, если есть некоторая внешняя сила, которая действует на все объекты (гравитация, например, или трение), то эта сила изменяет импульс системы в целом; другими словами, импульс системы изменяется под действием внешней силы. Таким образом, для сохранения импульса системы мы должны иметь
F → ext = 0 → .F → ext = 0 →.
Система объектов, отвечающая этим двум требованиям, называется закрытой системой (также называемой изолированной системой).Таким образом, ниже показан более компактный способ выразить это.
Закон сохранения импульса
Общий импульс закрытой системы сохраняется:
∑j = 1Np → j = константа. J = 1Np → j = постоянная.
Это утверждение называется Законом сохранения количества движения. Наряду с сохранением энергии это одна из основ, на которой стоит вся физика. Все наши экспериментальные данные подтверждают это утверждение: от движения скоплений галактик до кварков, составляющих протон и нейтрон, и во всех промежуточных масштабах. В закрытой системе общий импульс никогда не меняется.
Обратите внимание, что абсолютно может быть внешних сил, действующих на систему; но для того, чтобы импульс системы оставался постоянным, эти внешние силы должны уравновешиваться, так что чистая внешняя сила равна нулю. Все бильярдные шары на столе имеют силу веса, действующую на них, но веса уравновешиваются (компенсируются) нормальными силами, поэтому нет чистой силы.
Значение «системы»
Система (механическая) — это совокупность объектов, движение которых (кинематика и динамика) вас интересует.Если вы анализируете отскок мяча от земли, вас, вероятно, интересует только движение мяча, а не Земли; Таким образом, мяч — это ваша система. Если вы анализируете автокатастрофу, две машины вместе составляют вашу систему (рис. 9.15).
Рис. 9.15 Две машины вместе образуют систему, которая должна быть проанализирована. Важно помнить, что содержимое (масса) системы не изменяется до, во время или после взаимодействия объектов в системе.
Стратегия решения проблем
Сохранение импульса
Использование сохранения импульса требует четырех основных шагов.Первый шаг имеет решающее значение:
- Определите замкнутую систему (общая масса постоянна, чистая внешняя сила не действует на систему).
- Запишите выражение, представляющее полный импульс системы до «события» (взрыва или столкновения).
- Запишите выражение, представляющее общий импульс системы после «события».
- Установите эти два выражения равными друг другу и решите это уравнение для получения желаемой величины.
Пример 9.6
Встречающиеся тележки
Две тележки в лаборатории физики катятся по ровной дороге с незначительным трением. На концах этих тележек есть небольшие магниты, поэтому при столкновении они слипаются (рис. 9.16). Первая тележка имеет массу 675 граммов и катится вправо со скоростью 0,75 м / с; второй имеет массу 500 граммов и движется со скоростью 1,33 м / с, также вправо. Какова скорость двух соединенных тележек после столкновения?
Рис. 9.16 Две лабораторные тележки сталкиваются и слипаются после столкновения.
Стратегия
У нас столкновение. Нам даны массы и начальные скорости; нас спрашивают окончательную скорость. Все это предполагает использование сохранения импульса в качестве метода решения. Однако мы можем использовать его только в том случае, если у нас есть закрытая система. Таким образом, мы должны быть уверены, что выбранная нами система не подвергается действию чистой внешней силы и что ее масса не изменяется в результате столкновения.
Определение системы как двух тележек отвечает требованиям для замкнутой системы: общая масса двух тележек определенно не меняется, и хотя тележки определенно действуют друг на друга, эти силы являются внутренними по отношению к системе, поэтому они не меняют импульс системы в целом..
Значение
Принципы, применимые к двум лабораторным тележкам, одинаково применимы ко всем объектам любого типа и размера. Даже для фотонов концепции импульса и сохранения импульса по-прежнему имеют решающее значение даже в этом масштабе. (Поскольку они безмассовые, импульс фотона определяется совсем иначе, чем импульс обычных объектов. Вы узнаете об этом, когда изучите квантовую физику.)
Проверьте свое понимание 9,3
Предположим, что вторая, меньшая тележка изначально двигалась влево.Каким был бы знак конечной скорости в этом случае?
Пример 9.7
Прыгающий супербол
Супербол массой 0,25 кг падает с высоты h = 1,50 мh = 1,50 м над полом. Он подпрыгивает без потери энергии и возвращается на исходную высоту (рис. 9.17).
- Каково изменение импульса супершара во время его отскока от пола?
- Каким было изменение импульса Земли из-за столкновения шара с полом?
- Как изменилась скорость Земли в результате этого столкновения?
(Этот пример показывает, что вы должны быть осторожны при определении вашей системы.)
Рис. 9.17 Супербар падает на пол (t0t0), ударяется об пол (t1t1), отскакивает (t2t2) и возвращается на исходную высоту (t3t3).
Стратегия
Поскольку нас спрашивают только об изменении количества движения мяча, мы определяем нашу систему как мяч. Но это явно не закрытая система; гравитация применяет к мячу направленную вниз силу во время его падения, а нормальная сила, исходящая от пола, создает силу во время отскока. Таким образом, мы не можем использовать сохранение импульса в качестве стратегии.Вместо этого мы просто определяем импульс мяча непосредственно перед его столкновением с полом и сразу после него и вычисляем разницу. У нас есть масса шара, поэтому нам нужны его скорости.
Решение
- Поскольку это одномерная задача, мы используем скалярную форму уравнений. Пусть:
- p0 = p0 = величина импульса мяча в момент времени t0t0, момент, когда он был выпущен; так как он был сброшен из состояния покоя, это ноль.
- p1 = p1 = величина импульса мяча в момент времени t1t1, момент непосредственно перед тем, как он упадет на пол..
У нас нет простого способа рассчитать импульс после отскока. Вместо этого мы рассуждаем, исходя из симметрии ситуации.
Перед отскоком мяч начинает с нулевой скорости и падает на 1,50 м под действием силы тяжести, достигая некоторого количества движения непосредственно перед тем, как упасть на землю. На обратном пути (после отскока) он начинается с некоторой инерцией, поднимается на те же 1,50 м, что и упал, и заканчивается с нулевой скоростью. Таким образом, движение после отскока было зеркальным отображением движения до отскока.. - Каким было изменение импульса Земли из-за столкновения шара с полом?
Ваш инстинктивный ответ вполне мог быть либо «нулевым; Земля слишком массивна, чтобы этот крошечный шарик мог повлиять на нее »или, возможно,« больше нуля, но совершенно незначительно ». Но нет — если мы переопределим нашу систему как Супершар + Земля, тогда эта система будет замкнута (без учета гравитационного притяжения Солнца, Луны и других планет в солнечной системе), и, следовательно, полное изменение импульс этой новой системы должен быть нулевым..
Это изменение скорости Земли на совершенно незначительно.
Значение
Важно понимать, что ответ на часть (c) — это не скорость; это изменение скорости, а это совсем другое дело. Тем не менее, чтобы вы почувствовали, насколько мало это изменение скорости, предположим, что вы двигались со скоростью 4,7 × 10–25 м / с4,7 × 10–25 м / с. С такой скоростью вам потребуется около 7 миллионов лет, чтобы преодолеть расстояние, равное диаметру атома водорода.
Проверьте свое понимание 9,4
Было бы изменение импульса мяча большим, меньшим или таким же, если бы он столкнулся с полом и остановился (без отскока)?
Было бы изменение импульса мяча большим, меньшим или таким же, если бы он столкнулся с полом и остановился (без отскока)?
Пример 9,8
Хоккей 1
Две хоккейные шайбы одинаковой массы находятся на плоской горизонтальной хоккейной площадке. Красная шайба неподвижна; синяя шайба перемещается на 2.На 5 м / с влево (рисунок 9.18). Он сталкивается с неподвижной красной шайбой. Масса шайб 15 г. После столкновения красная шайба движется влево со скоростью 2,5 м / с. Какова конечная скорость синей шайбы?
Рисунок 9.18 Столкновение двух одинаковых хоккейных шайб. Верхняя диаграмма показывает шайбы за момент до столкновения, а нижняя диаграмма показывает шайбы в момент после столкновения. Чистая внешняя сила равна нулю.
Стратегия
Нам говорят, что у нас есть два сталкивающихся объекта, нам сообщают массы и начальные скорости, а также одну конечную скорость; нас просят указать обе конечные скорости.Сохранение импульса кажется хорошей стратегией. Определите систему как две шайбы; нет трения, поэтому у нас замкнутая система.
Прежде чем вы посмотрите на решение, как вы думаете, какой будет ответ?
Конечная скорость синей шайбы будет:
- ноль
- 2,5 м / с влево
- 2,5 м / с вправо
- 1,25 м / с влево
- 1,25 м / с вправо
- что-то еще
Решение
Определите направление + x , чтобы оно указывало вправо.v → bf = 0.
Значение
Очевидно, две шайбы просто обменялись моментом. Синяя шайба передала весь свой импульс красной шайбе. Фактически, это то, что происходит при подобном столкновении, когда m1 = m2.m1 = m2.
Проверьте свое понимание 9,5
Даже если бы было некоторое трение о лед, все равно можно было бы использовать сохранение импульса для решения этой проблемы, но вам нужно будет наложить дополнительное условие на задачу. Что это за дополнительное условие?
Пример 9.9
Посадка
Philae
12 ноября 2014 г. Европейское космическое агентство успешно посадило зонд под названием Philae на комету 67P / Чурюмова / Герасименко (рис. 9.19). Однако во время приземления зонд на самом деле приземлился три раза, потому что он дважды отскочил. Давайте посчитаем, насколько изменилась скорость кометы в результате первого отскока.
Рис. 9.19 Художественная визуализация Philae , приземляющихся на комету. (кредит: модификация работы Немецкого аэрокосмического центра DLR / Flickr)
Определим вверх как направление + y , перпендикулярное поверхности кометы, и y = 0y = 0, чтобы быть на поверхности кометы.
Стратегия
Нас спрашивают, насколько изменилась скорость кометы, но мы мало что знаем о комете, кроме ее массы и ускорения, которое вызывает сила тяжести. Однако нам — это , согласно которым спускаемый аппарат Philae сталкивается (приземляется) с кометой и отскакивает от нее. Столкновение предлагает импульс как стратегию решения этой проблемы.
Если мы определим систему, которая состоит как из Philae , так и из кометы 67 / P, то на эту систему не действует чистая внешняя сила, и, таким образом, импульс этой системы сохраняется.(Мы пренебрегаем гравитационной силой Солнца.) Таким образом, если мы вычислим изменение количества движения посадочного модуля, мы автоматически получим изменение количества движения кометы. Кроме того, изменение скорости кометы напрямую связано с изменением ее импульса в результате «столкновения» с ней посадочного модуля.
Решение
Пусть p → 1p → 1 будет импульсом Philae в момент непосредственно перед приземлением, а p → 2p → 2 будет его импульсом сразу после первого отскока. Тогда его импульс перед приземлением был
p → 1 = Mpv → 1 = (96 кг) (- 1..
Значение
Это очень небольшое изменение скорости, примерно одна тысячная миллиардной доли метра в секунду. Однако важно то, что это , а не ноль.
Проверьте свое понимание 9.6
Изменения импульса для Philae и кометы 67 / P были равны (по величине). Были ли равны импульсы, которые испытывали Philae и комета? А как насчет сил? А как насчет изменений кинетической энергии?
Сохранение импульса — Видео по физике от Brightstorm
Закон сохранения импульса гласит, что если два объекта сталкиваются, сила, теряемая одним объектом, равна силе, полученной другим объектом.Полный импульс системы после столкновения такой же, как и до него, как показано уравнением : начальный импульс = конечный импульс (где конечный импульс — это сумма всех импульсов, присутствующих в системе). Этот принцип аналогичен закону сохранения энергии.
Сохранение импульса, сохранение импульса просто заявляет, что импульс системы остается неизменным, несмотря на любые столкновения или взаимодействия, которые происходят в этой системе, общий импульс будет продолжать оставаться прежним.Хорошо, давайте просто рассмотрим, что такое импульс, импульс снова равен массе, умноженной на скорость, хорошо, поэтому масса обычно выражается в килограммах, метрах скорости в секунду. Хорошо, вы все это заметили, если когда-либо смотрели шары на бильярдном столе. Правильно, если у меня есть мяч, и он движется с определенным импульсом и ударяется о другой мяч, этот мяч будет продолжать движение с тем же импульсом, поскольку шары имеют одинаковую массу, они также будут двигаться с той же скоростью.
Хорошо, если у меня есть мяч, движущийся с определенным импульсом в этом направлении, и он ударяет мяч, движущийся в, с противоположным импульсом вместе, эти два шара собираются столкнуться, и они будут уравновешивать друг друга, так что наши этот шар теперь движется в эту сторону, этот шар теперь движется в этом направлении, но снова импульс этого шара продолжается, это только сейчас наблюдается в этом шаре, импульс этого шара продолжается, теперь он наблюдается в этом шаре.Итак, опять же, это оба примера сохранения количества движения. Давайте рассмотрим несколько примеров, которые вас могут попросить решить, и продемонстрировать сохранение импульса. Допустим, у меня есть пушка, и я стреляю пушечным ядром со скоростью 25 метров в секунду, и мое пушечное ядро имеет массу 5 килограммов, хорошо.
Если я решу эту проблему, мне нужно выяснить, что мой начальный импульс должен равняться моему окончательному импульсу, но мой последний импульс теперь будет иметь 2 разных импульса. У него будет импульс шара, который мы назовем импульсом b, и импульс пушки, который мы назовем импульсом c.Хорошо, но мы хотим выяснить, что после того, как этот шар будет выпущен, какой будет скорость этой пушки в этом направлении? Итак, при запуске наш начальный импульс будет по существу равным 0 килограмм на квадратный метр, потому что у нас 0 скорости. Хорошо, это будет равняться импульсу мяча, который составляет 25 килограммов, умноженных на 5, умноженные на 25 килограммов. Я перепутал свои единицы в метрах в секунду.
И это опять же означает, что сохранение означает, что я также должен добавить пушку, которая умножена на 100 килограммов v, потому что мы пытаемся решить, какова скорость пушки.Хорошо, так что v — это наше неизвестное здесь, и если мы просто 5 умножим на 25, получим 125 килограмм-метров в квадрате плюс 100 килограммов, умноженных на v, хорошо, мы разделим на 100 килограммов, и когда я это сделаю, мои единицы отменяются, и я собираюсь получить v будет равняться отрицательным 125 метрам в секунду. Хорошо, потому что, если у меня здесь положительная скорость, у меня есть 7 отрицательных скоростей, чтобы равняться этому. Таким образом, в этом случае эта скорость будет отрицательной 1,25 метра в секунду. Хорошо, давайте посмотрим на второй пример, на этот раз мы рассмотрим так называемое неупругое столкновение.В этом случае у меня есть мяч на липучке весом 1 кг, он будет лететь со скоростью 4 метра в секунду и столкнется с большим мячом на липучке весом 5 кг.
Теперь, когда они сталкиваются, у меня здесь нет начальной скорости или нулевого импульса, но когда они сталкиваются, новая система будет иметь определенную скорость и упс, что это будет за новая скорость? Хорошо, давайте посмотрим на это, хорошо, так что у нас есть начальный импульс, и он должен равняться конечному импульсу. Итак, мой начальный импульс состоит из двух компонентов: шара и шара, а также импульса каждого из них.Итак, давайте посчитаем, что у меня есть 1 килограмм, умноженный на 4 метра в секунду для этого, и я собираюсь добавить это к 5 килограммам, и моя скорость здесь составляет 0 метров в секунду, хорошо, поэтому эта единица равна 0. Мы можем забыть об этом. это, так что наш начальный импульс составляет всего 4 килограмма метра в секунду, и это будет равно нашей конечной скорости, теперь эти 2 равны 1. Итак, наша единица теперь имеет массу 1 + 5, что составляет 6 килограммов, и нам нужно выяснить, что такое скорость, мы решаем для v там.
Хорошо, как мы это решим? Что ж, нам нужно разделить 4 на 6 килограммов, чтобы избавиться от нашей единицы, и когда мы это сделаем, это отменится, и мы получим, что v равно 0.66 метров в секунду нормально. Итак, в этом случае мы использовали сохранение импульса, чтобы выяснить, какова скорость нашей новой системы после того, как меньшая система с меньшим импульсом столкнулась с более крупным объектом, и мы вычислили новую скорость. Итак, это 2 типа задач, которые вам нужно будет решить, используя сохранение импульса.
Закон сохранения импульса | Утверждение и примеры
Векторная сумма импульсов (импульс равен массе объекта, умноженной на его скорость) всех объектов системы не может быть изменен взаимодействиями внутри системы.В классической механике этот закон подразумевается законами Ньютона . Этот принцип является прямым следствием третьего закона Ньютона.
Предположим, что одномерное упругое столкновение двух бильярдных шаров, шара A и шара B. Мы предполагаем, что результирующая внешняя сила, действующая на эту систему из двух шаров, равна нулю, то есть единственной значимой силе во время Столкновение — это силы, которые каждый шар оказывает на другой. Согласно третьему закону Ньютона , две силы всегда равны по величине и противоположны по направлению.Следовательно, импульсы, которые действуют на два шара, равны и противоположны, а изменения количества движения двух шаров равны и противоположны.
Эти два шара движутся со скоростью v A и v B вдоль оси x до столкновения. После столкновения их скорости равны v ’ A и v’ B . Сохранение полного импульса требует, чтобы полный импульс до столкновения был таким же, как полный импульс после столкновения.
Если чистая внешняя сила не действует на систему частиц, полный линейный импульс системы не может измениться.
Сохранение импульса и энергии при столкновениях
Использование законов сохранения импульса и энергии очень важно также при столкновениях частиц . Это очень мощное правило, потому что оно может позволить нам определить результаты столкновения, не зная подробностей столкновения. Закон сохранения импульса гласит, что при столкновении двух объектов, таких как бильярдные шары, общий импульс сохраняется .Предположение о сохранении импульса, а также о сохранении кинетической энергии делает возможным расчет конечных скоростей в столкновениях двух тел. На этом этапе мы должны различать два типа столкновений:
Упругие столкновения
Совершенно упругое столкновение определяется как столкновение, при котором не происходит чистого преобразования кинетической энергии в другие формы (например, тепло или шум). В течение короткого момента, в течение которого два объекта находятся в контакте, некоторая (или вся) энергия мгновенно сохраняется в форме упругой потенциальной энергии .Но если мы сравним полную кинетическую энергию непосредственно перед столкновением с полной кинетической энергией сразу после столкновения, и они окажутся одинаковыми, то мы скажем, что общая кинетическая энергия сохраняется .
- Некоторые крупномасштабные взаимодействия, такие как гравитационные взаимодействия типа рогатки (также известные как планетарное качание или гравитационный маневр) между спутниками и планетами совершенно эластичны .
- Столкновения между очень твердыми сферами могут быть почти упругими , поэтому полезно рассчитать предельный случай упругого столкновения.
- Столкновения в идеальных газах приближаются к идеально упругим столкновениям, как и рассеивающие взаимодействия субатомных частиц, которые отклоняются электромагнитной силой.
- Резерфордовское рассеяние — это упругое рассеяние заряженных частиц также под действием электромагнитной силы.
- Реакция рассеяния нейтрона на ядре может быть также упругой, но в этом случае нейтрон отклоняется сильной ядерной силой.
Уравнения сохранения импульса и энергии
Предположим, что одномерное упругое столкновение двух объектов, объекта A и объекта B.Эти два объекта движутся со скоростями v A и v B вдоль оси x до столкновения. После столкновения их скорости равны v ’ A и v’ B . Сохранение полного импульса требует, чтобы полный импульс до столкновения был таким же, как полный импульс после столкновения. Аналогично, сохранение общей кинетической энергии , которое требует, чтобы общая кинетическая энергия обоих объектов до столкновения была такой же, как полная кинетическая энергия после столкновения.Оба закона могут быть выражены уравнениями как:
Относительная скорость двух объектов после столкновения имеет такую же величину (но в противоположном направлении), что и до столкновения, независимо от массы .
Неупругие столкновения
Неупругое столкновение — это такое столкновение, при котором часть кинетической энергии изменяется на некоторую другую форму энергии при столкновении. Любое макроскопическое столкновение между объектами преобразует часть кинетической энергии во внутреннюю энергию и другие формы энергии, поэтому без крупномасштабных ударов является совершенно упругим .Например, при столкновении общих тел, таких как две машины, некоторая энергия всегда передается от кинетической энергии другим формам энергии, таким как тепловой энергии или энергии звука . Неупругое столкновение двух тел всегда связано с потерей кинетической энергии системы. Наибольшие потери происходят, если тела слипаются, и в этом случае столкновение называется полностью неупругим столкновением . Таким образом, кинетическая энергия системы не сохраняется , в то время как полная энергия сохраняется в соответствии с общим принципом сохранения энергии. Импульс сохраняется при неупругих столкновениях , но невозможно отследить кинетическую энергию во время столкновения, поскольку часть ее преобразуется в другие формы энергии.
В ядерной физике неупругое столкновение — это такое столкновение, при котором падающая частица вызывает возбуждение или распад ядра, в которое она ударяется. Глубоконеупругое рассеяние — это метод исследования структуры субатомных частиц во многом так же, как Резерфорд исследовал внутреннюю часть атома (см. Рассеяние Резерфорда).
В ядерных реакторах неупругие столкновения играют важную роль в процессе замедления нейтронов . Неупругое рассеяние играет важную роль в замедлении нейтронов при высоких энергиях и на тяжелых ядрах . Неупругое рассеяние происходит выше пороговой энергии . Эта пороговая энергия выше энергии первого возбужденного состояния ядра-мишени (из-за законов сохранения) и определяется следующей формулой:
E т = ((A + 1) / A) * ε 1
, где E t известна как неупругая пороговая энергия , а ε 1 — энергия первого возбужденного состояния.Поэтому данные рассеяния 238 U , который является основным компонентом ядерного топлива в промышленных энергетических реакторах, являются одними из наиболее важных данных при расчетах переноса нейтронов в активной зоне реактора.
Пример: баллистический маятник
Баллистический маятник — это своего рода «трансформатор», меняющий высокую скорость легкого объекта (пули) на низкую скорость массивного объекта.
Баллистический маятник — это устройство для измерения скорости снаряда, например пули .Баллистический маятник — это своего рода «трансформатор», меняющий высокую скорость легкого объекта (пули) на низкую скорость массивного объекта (блока). Когда пуля попадает в блок, ее импульс передается блоку. Импульс пули можно определить по амплитуде качания маятника .
Когда пуля встраивается в блок, это происходит так быстро, что блок не перемещается заметно. Поддерживающие струны остаются почти вертикальными, поэтому на систему пуля-блок действует незначительная внешняя горизонтальная сила, и горизонтальная составляющая импульса сохраняется . Механическая энергия не сохраняется. на этом этапе, однако, потому что неконсервативная сила действительно работает (сила трения между пулей и блоком).
На втором этапе пуля и блок перемещаются вместе. Единственными силами, действующими на эту систему, являются гравитация (консервативная сила) и натяжение струны (которые не работают). Таким образом, при повороте блока сохраняется механической энергии . Импульс не сохраняется на этом этапе. , однако, потому что существует чистая внешняя сила (силы тяжести и натяжения струны не отменяются при наклоне струн).
Уравнения баллистического маятника
На первом этапе сохраняется импульс и, следовательно:
, где v — начальная скорость снаряда массой м P . v ’ — это скорость блока и встроенного снаряда (оба имеют массу м P + m B ) сразу после столкновения, до того, как они существенно переместятся.
На втором этапе механическая энергия сохраняется . Мы выбираем y = 0, когда маятник висит вертикально, и затем y = h, когда блок и система снарядов достигают максимальной высоты. Система раскачивается и останавливается на мгновение на высоте y, где ее кинетическая энергия равна нулю, а потенциальная энергия равна (m P + m B ) gh . Таким образом запишем закон сохранения энергии:
— начальная скорость снаряда и наш окончательный результат.
Если использовать реалистичные числа:
- м P = 5 г
- м B = 2 кг
- h = 3 см
- v =?
тогда имеем:
Законы сохранения при ядерных реакциях
Ядерная реакция считается процессом, в котором две ядерные частицы (два ядра или ядро и нуклон) взаимодействуют с образованием двух или более ядерных частиц или-лучей (гамма-лучей).Таким образом, ядерная реакция должна вызывать превращение по крайней мере одного нуклида в другой. Иногда, если ядро взаимодействует с другим ядром или частицей без изменения природы какого-либо нуклида, этот процесс называют ядерным рассеянием , а не ядерной реакцией.
При анализе ядерных реакций мы применяем многих законов сохранения . Ядерные реакции подчиняются классическим законам сохранения заряда, импульса, углового момента и энергии (включая энергии покоя).Дополнительные законы сохранения, не предусмотренные классической физикой, — это электрического заряда , лептонного числа и барионного числа . Некоторые из этих законов соблюдаются при любых обстоятельствах, другие — нет. Мы приняли закон сохранения энергии и количества движения. Во всех приведенных примерах мы предполагаем, что количество протонов и количество нейтронов сохраняется отдельно. Мы найдем обстоятельства и условия, при которых это правило не выполняется. Когда мы рассматриваем нерелятивистские ядерные реакции, это по сути верно.Однако, когда мы рассматриваем релятивистские ядерные энергии или энергии, связанные со слабыми взаимодействиями, мы обнаружим, что эти принципы должны быть расширены.
Некоторые принципы сохранения возникли из теоретических соображений, другие — просто эмпирические отношения. Тем не менее, любая реакция, прямо не запрещенная законами сохранения, обычно происходит, хотя, возможно, и с медленной скоростью. Это ожидание основано на квантовой механике. Если барьер между начальным и конечным состояниями бесконечно высок, всегда существует ненулевой вероятности , что система совершит переход между ними.
Для целей данной статьи достаточно отметить четыре основных закона, управляющих этими реакциями.
- Сохранение нуклонов . Общее количество нуклонов до и после реакции одинаково.
- Консервация заряда . Сумма зарядов на всех частицах до и после реакции одинакова
- Сохранение импульса . Полный импульс взаимодействующих частиц до и после реакции одинаков.
- Энергосбережение . Энергия, включая энергию массы покоя, сохраняется в ядерных реакциях.
Типы ядерных реакций
Хотя количество возможных ядерных реакций огромно, ядерные реакции можно сортировать по типам. Большинство ядерных реакций сопровождаются гамма-излучением. Вот несколько примеров:
- Упругое рассеяние . Происходит, когда между ядром-мишенью и падающей частицей не передается энергия.
208Pb (n, n) 208Pb
- Неупругое рассеяние . Возникает при передаче энергии. В возбужденном нуклиде сохраняется разница кинетических энергий.
40Ca (α, α ’) 40mCa
- Реакции захвата . Как заряженные, так и нейтральные частицы могут захватываться ядрами. Это сопровождается испусканием-лучей. В результате реакции нейтронного захвата образуются радиоактивные нуклиды (индуцированная радиоактивность).
238U (n, ˠ) 239U
- Реакции переноса . Поглощение частицы, сопровождающееся испусканием одной или нескольких частиц, называется реакцией переноса.
4He (α, p) 7Li
- Реакции деления . Ядерное деление — это ядерная реакция, при которой ядро атома распадается на более мелкие части (более легкие ядра). В процессе деления часто образуются свободные нейтроны и фотоны (в форме гамма-лучей) и выделяется большое количество энергии.
235U (n, 3 n) Продукты деления
- Реакции синтеза . Возникают, когда два или более атомных ядра сталкиваются с очень высокой скоростью и соединяются, образуя новый тип атомного ядра. Реакция слияния дейтерия и трития особенно интересна из-за ее потенциала обеспечения энергии для будущего.
3Т (д, п) 4Не
- Реакции расщепления . Происходит, когда в ядро попадает частица с достаточной энергией и импульсом, чтобы выбить несколько небольших фрагментов или разбить его на множество фрагментов.
- Ядерный распад ( Радиоактивный распад ). Возникает, когда нестабильный атом теряет энергию из-за испускания ионизирующего излучения. Радиоактивный распад — это случайный процесс на уровне отдельных атомов, в котором, согласно квантовой теории, невозможно предсказать, когда конкретный атом распадется. Есть много видов радиоактивного распада:
- Альфа-радиоактивность . Альфа-частицы состоят из двух протонов и двух нейтронов, связанных вместе в частицу, идентичную ядру гелия.Из-за своей очень большой массы (более чем в 7000 раз больше массы бета-частицы) и своего заряда он сильно ионизирует материал и имеет очень короткий радиус действия.
- Бета-радиоактивность . Бета-частицы — это высокоэнергетические, высокоскоростные электроны или позитроны, испускаемые определенными типами радиоактивных ядер, такими как калий-40. Бета-частицы имеют больший диапазон проникновения, чем альфа-частицы, но все же намного меньше, чем гамма-лучи. Испускаемые бета-частицы представляют собой форму ионизирующего излучения, также известного как бета-лучи.Образование бета-частиц называется бета-распадом.
- Гамма-радиоактивность . Гамма-лучи представляют собой электромагнитное излучение очень высокой частоты и, следовательно, являются фотонами высокой энергии. Они образуются в результате распада ядер при переходе из состояния с высокой энергией в состояние более низкого уровня, известное как гамма-распад. Большинство ядерных реакций сопровождаются гамма-излучением.
- Эмиссия нейтронов. Эмиссия нейтронов — это тип радиоактивного распада ядер, содержащих избыточные нейтроны (особенно продукты деления), при котором нейтрон просто выбрасывается из ядра. Этот тип излучения играет ключевую роль в управлении ядерным реактором, потому что эти нейтроны являются запаздывающими нейтронами.
Сохранение импульса в ядерных реакциях — нейтронное замедление
См. Также: Упругое рассеяние нейтронов
См. Также: Неупругое рассеяние нейтронов
См. Также: Модераторы нейтронов
Известно, что нейтроны деления играют важную роль в любой системе цепной реакции.Все нейтроны, образующиеся при делении, рождаются как быстрых нейтронов с высокой кинетической энергией. Прежде чем такие нейтроны смогут эффективно вызвать дополнительное деление, они должны быть замедлены столкновениями с ядрами в замедлителе реактора. Вероятность деления U-235 становится очень большой при тепловых энергиях медленных нейтронов. Этот факт означает увеличение коэффициента размножения реактора (т.е. для поддержания цепной реакции требуется меньшее обогащение топлива).
Нейтроны, высвобождающиеся при делении со средней энергией 2 МэВ в реакторе в среднем претерпевают столкновений (упругих или неупругих), прежде чем они будут поглощены.Во время реакции рассеяния часть кинетической энергии нейтрона передается ядру . Используя законы сохранения импульса и энергии и аналогию столкновений бильярдных шаров для упругого рассеяния, можно вывести следующее уравнение для массы ядра мишени или замедлителя (M), энергии падающего нейтрона (E i ) и энергии рассеянного нейтрона (E s ).
где A — атомное массовое число.В случае водорода (A = 1) в качестве ядра-мишени, падающий нейтрон может быть полностью остановлен . Но это работает, когда нейтрон полностью меняет направление (то есть рассеивается на 180 °). В действительности направление рассеяния колеблется от 0 до 180 °, а передаваемая энергия также находится в диапазоне от 0% до максимума. Поэтому средняя энергия рассеянного нейтрона принимается как среднее значение энергий с углом рассеяния 0 и 180 °.
Кроме того, полезно работать с с логарифмическими величинами , и поэтому можно определить логарифмический декремент энергии на столкновение (ξ) как ключевую материальную константу, описывающую передачу энергии во время замедления нейтрона.ξ не зависит от энергии, только от A и определяется следующим образом: Для тяжелых ядер-мишеней ξ может быть аппроксимировано следующей формулой: Из этих уравнений легко определить количество столкновений, необходимых для замедления нейтрона, из , например от 2 МэВ до 1 эВ .
Пример: Определите количество столкновений, необходимых для термализации нейтрона 2 МэВ в углероде.
ξ УГЛЕРОД = 0,158
Н ( 2МэВ → 1эВ ) = ln 2⋅10 6 / ξ = 14.5 / 0,158 = 92
Таблица среднего логарифмического декремента энергии для некоторых элементов.
Для смеси изотопов:
Пример: упругое ядерное столкновение
Нейтрон (n) массы 1,01 u , движущийся со скоростью 3,60 x 10 4 м / с , взаимодействует с ядром углерода (C) ( м C = 12,00 u ) первоначально в состоянии покоя при упругом лобовом столкновении .
Каковы скорости нейтрона и ядра углерода после столкновения?
Решение:
Это упругое лобовое столкновение двух объектов с неравной массой .Мы должны использовать законы сохранения количества движения и кинетической энергии и применить их к нашей системе двух частиц.
Мы можем решить эту систему уравнений или использовать уравнение, полученное в предыдущем разделе. Это уравнение утверждает, что относительная скорость двух объектов после столкновения имеет ту же величину (но в противоположном направлении), что и до столкновения, независимо от массы.
Знак минус для v ’говорит нам, что нейтронов рассеивают назад ядра углерода, потому что ядро углерода значительно тяжелее.С другой стороны, его скорость на меньше начальной скорости. Этот процесс известен как замедление нейтронов и существенно зависит от массы ядер замедлителя.
Импульс фотона
Фотон, квант электромагнитного излучения , представляет собой элементарную частицу, которая является переносчиком электромагнитной силы. Современная концепция фотонов была разработана (1905) Альбертом Эйнштейном для объяснения фотоэлектрического эффекта, в котором он предположил существование дискретных пакетов энергии во время передачи света.
В 1916 году Эйнштейн расширил свою концепцию световых квантов (фотонов), предположив, что квант света имеет линейный импульс . Хотя фотон без массы , у него есть импульс, который зависит от его энергии E, частоты f и длины волны следующим образом:
Таким образом, когда фотон взаимодействует с другим объектом, энергия и импульс передаются , как если бы произошло столкновение между фотоном и материей в классическом смысле.
Пример: импульс и сила фотона
Предположим, что 10 19 фотонов (пусть λ = 650 нм), испускаемых в секунду из лампочки мощностью 100 Вт .Предположим, все фотоны фокусируются на листе черной бумаги и поглощаются. Предположим, что импульс фотона изменяется с p = h / λ до нуля .
Вычислите импульс одного фотона и вычислите силу , которую все эти фотоны могут приложить к бумаге.
Решение:
Используем формулу импульса одиночного фотона:
Импульс фотонно-комптоновского рассеяния
При комптоновском рассеянии падающий гамма-фотон отклоняется на угол относительно своего первоначального направления.Это отклонение приводит к уменьшению энергии (уменьшению частоты фотона) фотона и называется эффектом Комптона.
Источник: hyperphysics.phy-astr.gsu.edu
Формула Комптона была опубликована в 1923 году в Physical Review. Комптон объяснил, что сдвиг рентгеновских лучей вызван импульсом фотонов, подобным частицам. Формула комптоновского рассеяния — это математическая зависимость между сдвигом длины волны и углом рассеяния рентгеновских лучей. В случае комптоновского рассеяния фотон с частотой f сталкивается с покоящимся электроном.При столкновении фотон отскакивает от электрона, отдавая часть своей начальной энергии (заданной формулой Планка E = hf). Пока электрон набирает импульс (масса x скорость), фотон не может снизить свою скорость . В результате закона сохранения импульса фотон должен уменьшить свой импульс, определяемый выражением:
Таким образом, уменьшение импульса фотона должно быть переведено на уменьшение частоты (увеличение длины волны Δ λ = λ ’- λ ). Сдвиг длины волны увеличивается с увеличением угла рассеяния согласно формуле Комптона :
.
, где λ — начальная длина волны фотона λ ’ — длина волны после рассеяния, h — постоянная Планка = 6.626 x 10 -34 Дж, м e — масса покоя электрона (0,511 МэВ) c — скорость света Θ — угол рассеяния. Минимальное изменение длины волны ( λ ′ — λ ) для фотона происходит, когда Θ = 0 ° (cos (Θ) = 1) и составляет по крайней мере ноль. Максимальное изменение длины волны ( λ ′ — λ ) для фотона происходит при Θ = 180 ° (cos (Θ) = — 1). В этом случае фотон передает электрону как можно больше импульса.Максимальное изменение длины волны может быть получено из формулы Комптона:
Величина h / m e c известна как комптоновская длина волны электрона и равна 2,43 × 10 −12 m .
Сохранение импульса в гидродинамике
В общем, , закон сохранения импульса или принцип сохранения импульса утверждает, что импульс изолированной системы является константой .Векторная сумма импульсов (импульс равен массе объекта, умноженной на его скорость) всех объектов системы не может быть изменен взаимодействиями внутри системы. В классической механике этот закон подразумевается законами Ньютона .
В гидродинамике анализ движения выполняется так же, как в механике твердого тела — с использованием законов движения Ньютона . Как можно видеть, движущиеся жидкости проявляют силы. Подъемная сила в самолете создается воздухом, движущимся над крылом.
Струя воды из шланга воздействует на все, на что попадает. Но здесь не ясно, какую массу движущейся жидкости мы должны использовать, и поэтому необходимо использовать другую форму уравнения.
Второй закон Ньютона можно записать:
Скорость изменения количества движения тела равна равнодействующей силе, действующей на тело, и происходит в направлении силы.
Мы предполагаем, что жидкость устойчивая и несжимаемая .Чтобы определить скорость изменения количества движения жидкости, мы рассмотрим струйную трубку ( контрольный объем ), как мы это делали для уравнения Бернулли. В этом контрольном объеме любое изменение количества движения жидкости в контрольном объеме происходит из-за действия внешних сил на жидкость внутри объема.
Как видно из рисунка, метод контрольного объема может использоваться для анализа закона сохранения количества движения в жидкости. Контрольный объем — это воображаемая поверхность , охватывающая интересующий объем.Контрольный объем может быть фиксированным или подвижным, а также жестким или деформируемым. Чтобы определить все силы, действующие на поверхности контрольного объема, мы должны решить законы сохранения в этом контрольном объеме.
Первое уравнение сохранения, которое мы должны рассмотреть в контрольном объеме, — это уравнение неразрывности (закон сохранения вещества). В простейшем виде это представлено следующим уравнением:
∑ṁ из = ∑ṁ из
Сумма массовых расходов, вводимых в единицу времени = Сумма массовых расходов, уходящих в единицу времени
Второе уравнение сохранения, которое мы должны рассмотреть в контрольном объеме, — это формула импульса .
Формула импульса
В простейшей форме формула импульса может быть представлена следующим уравнением:
–
Выбор контрольного объема
Контрольный объем может быть выбран как любой произвольный объем, через который протекает жидкость. Этот объем может быть статическим, движущимся и даже деформирующимся во время потока. Чтобы решить любую задачу, мы должны решить основные законы сохранения в этом томе. Очень важно знать все относительные скорости потока к контрольной поверхности, и поэтому очень важно точно определить границы контрольного объема во время анализа.
Пример: сила, действующая на отклоняющее колено
Колено (скажем, первичного трубопровода) используется для отклонения потока воды со скоростью 17 м / с . Диаметр трубопровода 700 мм . Манометрическое давление внутри трубы составляет около 16 МПа при температуре 290 ° C. Жидкость постоянной плотности ⍴ ~ 720 кг / м 3 (при 290 ° C). Угол колена 45 ° .
Рассчитайте силу на стену колена дефлектора (т.е.е. вычислить вектор F 3 ).
Допущения:
- Течение стабильное.
- Потери на трение незначительны.
- Вес локтя незначителен.
- Вес воды в локте незначителен.
В качестве контрольного объема принимаем колено . Контрольный объем показан на рисунке. Уравнение импульса является векторным уравнением, поэтому оно состоит из трех компонентов. Мы берем координаты x и z, как показано, и решаем задачу отдельно в соответствии с этими координатами.
Сначала рассмотрим компонент в координате x . Уравнение сохранения количества движения принимает вид:
Во-вторых, давайте рассмотрим компонент в координате y . Уравнение сохранения количества движения принимает вид:
Окончательная сила, действующая на стенку колена дефлектора, составит:
Пример: струя воды, ударяющаяся о неподвижную пластину
Неподвижную пластину (e.грамм. лопасти водяной мельницы) используется для отклонения потока воды со скоростью 1 м / с и под углом 90 ° . Это происходит при атмосферном давлении и массовом расходе Q = 1 м 3 / с .
- Рассчитайте силу давления.
- Рассчитайте силу тела.
- Рассчитайте общую силу.
- Рассчитайте равнодействующую силу.
Решение
- Сила давления равна нулю, поскольку давление на входе и выходе контрольного объема атмосферное.
- Поскольку контрольный объем невелик, мы можем игнорировать силу тела из-за веса силы тяжести.
- F x = ρ.Q. (w 1x — w 2x ) = 1000. 1. (1-0) = 1000 N
F y = 0
F = (1000, 0) - Результирующая сила на плоскости имеет ту же величину, но в противоположном направлении, что и общая сила F (трением и весом пренебрегают).
Струя воды действует на пластину с силой 1000 Н в направлении оси x.
4.2: Сохранение импульса — Physics LibreTexts
В уравнении (4.1.1), какова полная сила, действующая на все частицы? Ну, это сумма всех сил, которые частицы оказывают друг на друга, плюс все внешние силы: \ (F _ {\ text {total}} = \ sum_ {i} F _ {\ text {int}, i} + \ sum_ {i} F _ {\ text {ext}, i} \). Третий закон движения Ньютона говорит нам, что внутренние силы действуют в противоположных парах, поэтому, когда мы их суммируем, все они сокращаются, и общая результирующая сила, действующая на частицы, равна сумме внешних сил, действующих на частицы.Следовательно, согласно уравнению (4.1.1), центр масс системы частиц подчиняется второму закону движения Ньютона. А как насчет количества движения центра масс? Как и сила, полный импульс системы задается векторной суммой импульсов отдельных частиц:
\ [P _ {\ text {total}} = \ sum _ {\ alpha} \ boldsymbol {p} _ {\ alpha} = \ sum _ {\ alpha} m _ {\ alpha} \ dot {r} _ {\ alpha} = \ frac {\ mathrm {d}} {\ mathrm {d} t} \ sum _ {\ alpha} m _ {\ alpha} r _ {\ alpha} = \ frac {\ mathrm {d}} {\ mathrm {d} t} M r _ {\ mathrm {cm}} \]
, поэтому полный импульс системы равен импульсу центра масс.Более того, пока масса системы сохраняется, мы можем переписать уравнение (4.1.1) как
\ [F _ {\ text {total}} = \ frac {\ mathrm {d} P _ {\ text {total}}} {\ mathrm {d} t} \ label {ftotal} \]
Не только центр масс системы частиц подчиняется второму закону движения Ньютона, но и ее полный импульс. Более того, в отличие от одночастичного случая, уравнение (\ ref {ftotal}) имеет важное следствие для случая, когда на систему не действует внешняя сила.Для одной частицы это просто означало бы, что импульс не меняется — первый закон движения Ньютона. Но для нескольких частиц уравнение (\ ref {ftotal}) говорит нам, что отсутствие внешних сил означает, что общий импульс не изменяется. Таким образом, мы пришли к нашему второму закону сохранения:
.
Теорема 4.1 (Закон сохранения количества движения). Когда никакие внешние силы не действуют на систему частиц, полный импульс системы сохраняется.
Мы вывели закон сохранения количества движения, применяя второй и третий законы движения Ньютона, поэтому, как и сохранение энергии, это не независимый результат, а следует из наших аксиом.

 Белка понимает законы Ньютона и предотвращает падение. Но как?
Белка понимает законы Ньютона и предотвращает падение. Но как?