Содержание
Урок 6. обратные тригонометрические функции — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №6. Обратные тригонометрические функции.
Перечень вопросов, рассматриваемых в теме
- Рассмотреть свойства арксинуса и арккосинуса;
- Рассмотреть свойства арктангенса и арккотангенса;
- Объяснять расположение промежутков монотонности;
- Определять наибольшее и наименьшее значение функции;
- Применять знания при решении задач.
Глоссарий по теме
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ). Он имеет область определения и множество значений .
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения и множество значений
Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения и множество значений .
Он имеет область определения и множество значений .
Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения и множество значений
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Актуализация знаний
Обратные тригонометрические функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, косинус какого угла равен ? Первое, что хочется ответить, что это угол 60° или , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.
Например, косинус какого угла равен ? Первое, что хочется ответить, что это угол 60° или , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.
Объяснение нового материала
Рассмотрим свойства функции y=arcsin x и построим ее график.
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).
Свойства | Функции y=arcsin х |
E(f) | |
D(f) | |
Чётность | Нечётная, т.к. arcsin(-x)= — arcsin x |
Промежутки монотонности | Возрастающая |
Рис.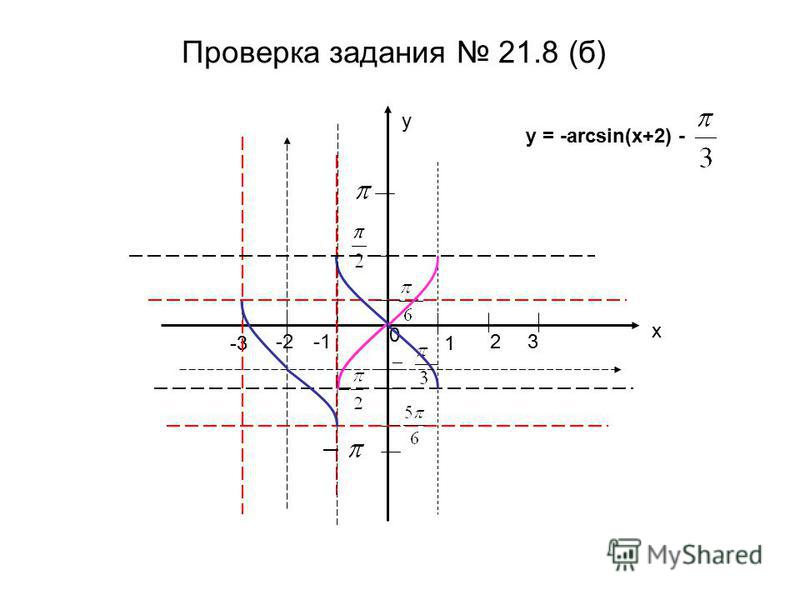 1 График функции y=arcsin х
1 График функции y=arcsin х
Рассмотрим свойства функции y=arcos x и построим ее график.
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ).
Свойства | Функции y=arccos х |
E(f) | |
D(f) |
|
Чётность | Ни чётная, ни нечётная |
Промежутки монотонности | Убывающая |
Рис.2 График функции y=arccos х
Рассмотрим свойства функции y=arctgx и y=arcctgx и построим их графики.
Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ).
Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ).
Свойства | y=arctg х | y=arcctg х |
E(f) | R | R |
D(f) | ||
Чётность | Нечётная | Нечётная |
Промежутки монотонности | Возрастающая | Убывающая |
Рис. 3 График функции y=arctgx
3 График функции y=arctgx
Рис.4 График функции y=arcсtgx
Примеры и разборы решения заданий тренировочного модуля:
Пример 1.
Найдите значение выражения
Обозначим , по определения арктангенса получаем х=60°, т.е. нам нужно найти
Ответ:
Пример 2.
Решите неравенство
;
;
;
;
Накладываем ограничения по свойствам арксинуса:
;
Ответ:
Обратные тригонометрические функции и их графики
Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.
Сначала дадим определения.
Арксинусом числа а называется число , такое, что Или, можно сказать, что это такой угол , принадлежащий отрезку , синус которого равен числу а.
Арккосинусом числа а называется число , такое, что
Арктангенсом числа а называется число , такое, что
Арккотангенсом числа а называется число , такое, что
Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.
Помните, мы уже встречались с обратными функциями.
Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.
Логарифм числа b по основанию a — такое число с, что
При этом
Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения — это и Мы не смогли бы записать их без специального символа арифметического квадратного корня.
Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: Решение этого уравнения — иррациональное число Это показатель степени, в которую надо возвести 2, чтобы получить 7.
Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение
Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна И ясно, что это не табличное значение синуса. Как же записать решения?
Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a.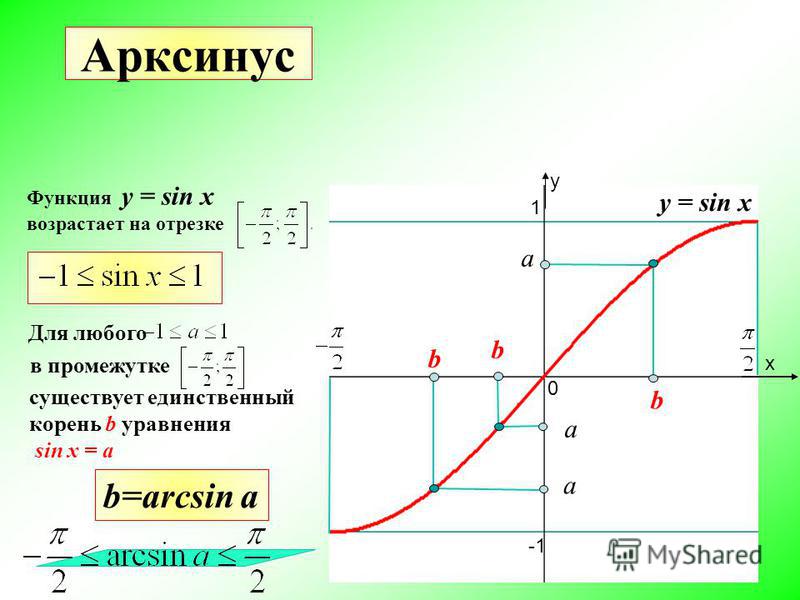 Да, все уже догадались. Это арксинус.
Да, все уже догадались. Это арксинус.
Угол, принадлежащий отрезку , синус которого равен — это арксинус одной четвертой. И значит, серия решений нашего уравнения, соответствующая правой точке на тригонометрическом круге, — это
А вторая серия решений нашего уравнения — это
Подробнее о решении тригонометрических уравнений — здесь.
Осталось выяснить — зачем в определении арксинуса указывается, что это угол, принадлежащий отрезку ?
Дело в том, что углов, синус которых равен, например, , бесконечно много. Нам нужно выбрать какой-то один из них. Мы выбираем тот, который лежит на отрезке .
Взгляните на тригонометрический круг. Вы увидите, что на отрезке каждому углу соответствует определенное значение синуса, причем только одно. И наоборот, любому значению синуса из отрезка отвечает одно-единственное значение угла на отрезке . Это значит, что на отрезке можно задать функцию принимающую значения от до
Повторим определение еще раз:
Арксинусом числа a называется число , такое, что
Обозначение: Область определения арксинуса — отрезок Область значений — отрезок .
Можно запомнить фразу «арксинусы живут справа». Не забываем только, что не просто справа, но ещё и на отрезке .
Мы готовы построить график функции
Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.
Поскольку , следовательно, х лежит в пределах от -1 до 1.
Значит, областью определения функции y = arcsin x является отрезок
Мы сказали, что у принадлежит отрезку . Это значит, что областью значений функции y = arcsin x является отрезок .
Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями и
Как всегда при построении графика незнакомой функции, начнем с таблицы.
По определению, арксинус нуля — это такое число из отрезка , синус которого равен нулю. Что это за число? — Понятно, что это ноль.
Аналогично, арксинус единицы — это такое число из отрезка , синус которого равен единице. Очевидно, это
Продолжаем: — это такое число из отрезка , синус которого равен . Да, это
Да, это
Строим график функции
Свойства функции
1. Область определения
2. Область значений
3. , то есть эта функция является нечетной. Ее график симметричен относительно начала координат.
4. Функция монотонно возрастает. Ее наименьшее значение, равное — , достигается при , а наибольшее значение, равное , при
5. Что общего у графиков функций и ? Не кажется ли вам, что они «сделаны по одному шаблону» — так же, как правая ветвь функции и график функции , или как графики показательной и логарифмической функций?
Представьте себе, что мы из обычной синусоиды вырезали небольшой фрагмент от до , а затем развернули его вертикально — и мы получим график арксинуса.
То, что для функции на этом промежутке — значения аргумента, то для арксинуса будут значения функции. Так и должно быть! Ведь синус и арксинус — взаимно-обратные функции. Другие примеры пар взаимно обратных функций — это при и , а также показательная и логарифмическая функции.
Напомним, что графики взаимно обратных функций симметричны относительно прямой
Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок
Арккосинусом числа a называется число , такое, что
Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке
Обозначение: Область определения арккосинуса — отрезок Область значений — отрезок
Очевидно, отрезок выбран потому, что на нём каждое значение косинуса принимается только один раз. Иными словами, каждому значению косинуса, от -1 до 1, соответствует одно-единственное значение угла из промежутка
Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:
Построим график функции
Нам нужен такой участок функции , на котором она монотонна, то есть принимает каждое свое значение ровно один раз.
Выберем отрезок . На этом отрезке функция монотонно убывает, то есть соответствие между множествами и взаимно однозначно. Каждому значению х соответствует свое значение у. На этом отрезке существует функция, обратная к косинусу, то есть функция у = arccosx.
Заполним таблицу, пользуясь определением арккосинуса.
Арккосинусом числа х, принадлежащего промежутку , будет такое число y, принадлежащее промежутку , что
Значит, , поскольку ;
, так как ;
, так как ,
, так как ,
Вот график арккосинуса:
Свойства функции
1. Область определения
2. Область значений
3.
Эта функция общего вида — она не является ни четной, ни нечетной.
4. Функция является строго убывающей. Наибольшее значение, равное , функция у = arccosx принимает при , а наименьшее значение, равное нулю, принимает при
5. Функции и являются взаимно обратными.
Следующие — арктангенс и арккотангенс.
Арктангенсом числа a называется число , такое, что
Обозначение: . Область определения арктангенса — промежуток Область значений — интервал .
Область определения арктангенса — промежуток Область значений — интервал .
Почему в определении арктангенса исключены концы промежутка — точки ? Конечно, потому, что тангенс в этих точках не определён. Не существует числа a, равного тангенсу какого-либо из этих углов.
Построим график арктангенса. Согласно определению, арктангенсом числа х называется число у, принадлежащее интервалу , такое, что
Как строить график — уже понятно. Поскольку арктангенс — функция обратная тангенсу, мы поступаем следующим образом:
— Выбираем такой участок графика функции , где соответствие между х и у взаимно однозначное. Это интервал Ц На этом участке функция принимает значения от до
Тогда у обратной функции, то есть у функции , область, определения будет вся числовая прямая, от до а областью значений — интервал
Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.
, значит,
, значит,
, значит,
А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?
Мы можем задать себе вопрос: для какого числа из интервала значение тангенса стремится к бесконечности? — Очевидно, это
А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте
Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте
На рисунке — график функции
Свойства функции
1. Область определения
Область определения
2. Область значений
3. Функция нечетная.
4. Функция является строго возрастающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными — конечно, когда функция рассматривается на промежутке
Аналогично, определим функцию арккотангенс и построим ее график.
Арккотангенсом числа a называется число , такое, что
График функции :
Свойства функции
1. Область определения
2. Область значений
3. Функция — общего вида, то есть ни четная, ни нечетная.
4. Функция является строго убывающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными, если рассматривать на промежутке
|
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Свойства функций
arcsin x + arccos x = /2
arctg x + arcctg x = /2
|
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Тригонометрия
Предположим, что число a удовлетворяет неравенству . Число x называют арксинусом числа a и обозначают x = arcsin a, если выполнены два условия:
Число x называют арксинусом числа a и обозначают x = arcsin a, если выполнены два условия:
Предположим, что число a удовлетворяет неравенству . Число x называют арккосинусом числа a и обозначают x = arccos a, если выполнены два условия:
Рассмотрим произвольное число a . Число x называют арктангенсом числа a и обозначают x = arctg a, если выполнены два условия:
Рассмотрим произвольное число a . Число x называют арккотангенсом числа a и обозначают x = arcctg a, если выполнены два условия:
Арксинус, арккосинус, арктангенс и арккотангенс удовлетворяют, в частности, следующим соотношениям:
| arcsin (– a) = – arcsin a , |
| arccos (– a) = = π – arccos a , |
| arctg (– a) = – arctg a , |
| arcctg (– a) = = π – arcctg a .  |
Обратными тригонометрическими функциями называют функции:
Графики этих функций изображены на рисунках 1, 2, 3, 4.
Рис. 1. График функции y = arcsin x
Таблица значений функции y = arcsin x
Рис. 2. График функции y = arccos x
Таблица значений функции y = arccos x
Рис. 3. График функции y = arctg x
Таблица значений функции y = arctg x
Рис. 4. График функции y = arcctg x
Таблица значений функции y = arcctg x
Пример. Решить уравнение
2 arcsin 2x = arccos 7x .
Решение. Возьмём косинус от обеих частей уравнения. Тогда в левой части уравнения получим:
Возьмём косинус от обеих частей уравнения. Тогда в левой части уравнения получим:
cos ( 2 arcsin 2x ) = 1 – 2sin2( arcsin 2x ) = 1 – 2 ( 2x )2 = 1 – 8x2 .
cos ( 2 arcsin 2x ) =
= 1 – 2sin2( arcsin 2x ) =
= 1 – 2 ( 2x )2 = 1 – 8x2 .
В правой части уравнения получим:
cos ( arccos 7x ) = 7x.
Следовательно, возникает квадратное уравнение:
В силу того, что область определения обратных тригонометрических функций y = arcsin x и y = arccos x имеет вид: , второй корень должен быть отброшен.
Ответ:
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
«Решение уравнений, содержащих обратные тригонометрические функции»
10 класс Хасанова З. Ф.
Ф.
Урок – лабиринт
________________________________________________________________________
Тема: «Решение уравнений, содержащих обратные тригонометрические функции».
Цели урока:
-
Образовательные – обеспечить повторение, обобщение и систематизацию мате риала темы и создать условия контроля (самоконтроля) усвоения знаний и умений; -
Развивающие – способствовать формированию умений, применять приемы сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления, внимания, памяти, т.е. активизация познавательной деятельности и формирование творческого подхода к решению задач. -
Воспитательные – содействовать воспитанию интереса к математике и ее приложениям, активности.
Тип урока: урок обобщения и систематизации знаний.
План урока.
-
Организационный момент. -
Входной контроль.
-
Блок информаций (Блок №1 — №5). -
Завершающий контроль (Блок №6). -
Подведение итогов урока.
а). Выставление оценок за урок.
б). Задание на дом.
Учитель: Сегодня у нас урок обобщения и систематизации знаний. На предыдущих уроках мы рассмотрели обратные тригонометрические функции, знаем их графики, свойства и тождества для обратных тригонометрических функций, научились решать уравнения. Урок проведем в форме лабиринта. Давайте познакомимся с его условиями.
-
Класс разбит на 4 группы и работают 2 консультанта. В лабиринте 4 маршрута. У каждой команды свой маршрут, эти листы имеются у каждой группы. -
Каждая команда должна пройти путь от края лабиринта до его центра, решая задачи на сравнение, обобщение, выделение главного, раскрытие идей решения некоторых уравнений, применяя полученные знания в нестандартных случаях и оценивая свои возможности, свои знания. -
Ворота каждого круга оцениваются определенным числом баллов. Число баллов указывает уровень сложности вопроса, чем сложнее вопрос, тем больше баллов за него начисляется.
Число баллов указывает уровень сложности вопроса, чем сложнее вопрос, тем больше баллов за него начисляется. -
Каждая команда должна пройти путь от края лабиринта до его центра, набрав 15 баллов.
-
В качестве подтверждения того, что команда прошла тот или иной круг, ей выдаются жетоны с указанием набранных баллов и в конце урока, по числу набранных баллов ставите себе оценку.
Итак, отправляемся в путешествие по лабиринту.
I – команда: 2 – 2 – 4 – 3 – 4 (=15)
II – команда: 2 – 3 – 3 – 5 – 2
III – команда: 2 – 2 – 4 – 3 – 4
IV – команда: 2 – 3 – 3 – 4 – 3
А в качестве напутствия звучит стихотворение:
Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
В лабиринт отправляемся смело –
В мир загадок и сложных задач.
Не беда, что идти далеко,
И не бойтесь, что путь будет труден.
Достижения крупные людям
Никогда не давались легко!
-
Входной контроль.
Учитель: Чтобы пройти первый круг лабиринта, надо вспомнить определение обратных тригонометрических функций. (Команды в конвертах получают задания и по очереди отвечают на вопрос, объясняя по графику).
Например: Арксинус числа а называется такое число из отрезка [-π/2; π /2], синус которого равен а. График функции y= arcsin x получается из графика функции y= sin x c помощью осевой симметрии относительно прямой y= x. Итак, функция y= arcsin x определена и монотонно возрастает на отрезке [-1;1] и областью значений arcsin a является отрезок [-π/2; π /2].
После ответов на вопросы команды считаются прошедшими I круг лабиринта.
-
Блоки информаций.
(Каждый блок содержит задания на сравнение, обобщение, выделение главного, раскрытие идей решения некоторых уравнений, предупреждение возможной ошибки, выделение общего алгоритма и другие).
Блок №2.
Каждая команда решает задания в зависимости от того, сколько баллов в воротах соответствующего круга своего маршрута.
Если нужно набрать 3 балла, то выполняют оба задания.
а). 3 равенство – неверное равенство.
б). 3 – неверно.
Блок №3.
Тождества для обратных тригонометрических функций:
Ответы: а). 3 равенство неверно, т.к. 3/2 [-1;1], равенство cos (arccos a)= a справедливо при | a | 1.
б). Равенство arccos (cos x)= x справедливо только при условии 0
Преобразуем: arccos (cos 5)= arccos (cos (-5))= arccos (cos (2 π -5)), т.к. 0 2π -5 π, то arccos (cos (2π -5))= 2π -5
в). 3 – неверно, т.к. arcsin (sin 3)= arcsin (sin (π -3))= π -3
г). 2 – неверное равенство.
arccos (cos 11π/9)= arccos (cos (11π/9 – 2π +2π))= arccos (cos (11π/9 – 2π))= arccos (cos (-7π/9))= arccos (cos 7π/9))= 7π/9.
Блок №4.
? Лишнее!
| ? Лишнее! а) 1б б) 2б б) 3б | ||
| а) | 1) arcctg x= 3π/4 | 3) arctg x= π /4 |
| 2) arccos x= π /6 | 4) arcsin x= 5 π /6 | |
| б) | 1) 3 * arccos 2x= — π /5 | 3) ½ * arcctg (5 – 8x)= 2 π /3 |
| 2) arcsin (2x – 3)= π /2 | 4) arctg (4x + 9)= — π /6 | |
| в) | 1) arctg (x – 1)= 3 π /4 | 3) arctg (x + 1)= 2 π /3 |
| 2) arcsin 2x= 5 π /6 | 4) arccos x/4= 3 π /4 | |
Ответы: а). 4 уравнение не имеет решения, остальные уравнения имеют решения, т.к. их значения принадлежат области значения этих функций.
4 уравнение не имеет решения, остальные уравнения имеют решения, т.к. их значения принадлежат области значения этих функций.
б). 3 уравнение не имеет решения, т.к. 4 π /3 (0; π).
в). 4 уравнение не имеет решения.
Задания каждого блока рассматриваются на доске. У доски объясняет задание представитель той группы, которая должна набрать самое большее количество баллов.
Блок №5.
? Особенное!
| ? Особенное! а) 2б б) 3б в) 4б | ||
| а) | 1) arccos (2x – 3)= π /2 | 3) arcsin2 x – 3 π /4 * arcsin x + π2/4= 0 |
| 2) arccos2 x – 3 π /4 * arccos x + π2/8= 0 | 4) arctg2 x – 5 π /12 * arctg x + π2/24= 0 | |
| б) | 1) arcsin (x2 – 3x + ½)= π /6 | 3) arcsin (x2 – 4x + 3)= 0 |
| 2) arccos (x2 – 4x + 3)= π /2 | 4) arcsin (x2 – 4x + 2)= — π /2 | |
| в) | 1) arcsin (x2 – 3x + ½)= π /6 | 3) arcsin (x2 – 4x + 2)= — π /2 |
| 2) arcsin2 x – π /2 * arcsin x + π2/8= 0 | 4) arccos (x2 + 4x – 1)= π /3 | |
Ответы: а). 2, 3, 4 уравнения решаются методом замены, а 1 уравнение решается по определению. Решим это уравнение.
2, 3, 4 уравнения решаются методом замены, а 1 уравнение решается по определению. Решим это уравнение.
arccos (2x – 3)= π /2
2x – 3= cos π /2
Ответ: x= 3/2
б). 1; 3; 4 уравнения даны через арксинус, а 2 уравнение через арккосинус. Решим это уравнение.
arccos (x2 – 4x + 3)= π /2
Ответ: x1= 1; x2= 3.
в). 1; 3; 4 уравнения решаются по определению, а уравнение 2 решается методом замены. Решим это уравнение.
arcsin x= y
y2 – π /2 * y + π 2/18= 0
Д= (π /6)2;
Y1= π /6; y2= π /3
arcsin x= π /6 arcsin x= π /3
Ответ: x1= 1/2 x2= /2
Учитель: Молодцы! Вы усвоили решение уравнений II-го уровня сложности. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных ситуациях.
Итак, мы дошли до центра.
Когда команды оказываются в центре лабиринта, перед ними разворачивают плакат:
Знания способны весь мир перевернуть,
Там, где есть желание, всегда найдется путь!
Учитель: Дойти до центра лабиринта – хорошо, но надо еще и выбраться из него. В этом Вам поможет кубик, каждая грань которого имеет определенное количество точек. Если кому-то выпадет грань с пятью точками – это «Счастливый случай», который дает Вам 5 баллов без вопросов и ответов.
В этом Вам поможет кубик, каждая грань которого имеет определенное количество точек. Если кому-то выпадет грань с пятью точками – это «Счастливый случай», который дает Вам 5 баллов без вопросов и ответов.
Кидают кубик поочередно.
Всего для выхода из лабиринта каждой группе надо снова набрать 15 баллов.
Если выпадет грань с тремя точками, то задания из 3-го конверта, грань с четырьмя точками – задания из конверта №4 и т.д.
Там имеются задания, которые оцениваются в 5, 10 и 15 баллов, т.е. задания II-го и III-го уровня сложности, в случае затруднений можно пользоваться подсказками, данными ниже.
| Блок №6. ? Метод решения! |
| Вариант – I 1) arcsin (x2 – 3x +1/2)= π /6 5б 2) 4 * arctg2 x + 5 π * arctg x + π2= 0 10б 3) arccos (2x3 + 3x2 + 0,1)= arccos (x + 2x2 + 0,1) 15б 4) arctg (2 * sin x)= arcctg (cos x) 15б Указание: 4) arctg f (x)= arcctg g (x) => f (x) * g (x)= 1 |
? Метод решения!
Вариант – II
1) arcsin (x2 – 4x + 2)= — π /2 5б
2) 3 * arctg2 x — 2 π * arctg x= π210б
3) arcsin (3x3 – x2 + 1)= arcsin (2x + 1) 15б
4) arcsin x * arccos x= π2 /18 15б
Указание:
2) arctg x= t, — π /2 3) arcsin f (x)= arcsin g (x)
4) arcsin x + arccos x= π /2 => arccos x= π /2 – arcsin x
arcsin x= t, — π /2
Кубик:
Вариант – I
-
arcsin (x2 – 3x + ½)= π /6
x2 – 3x + ½= sin π /6
x2 – 3x + ½= ½
x2 – 3x= 0
x (x – 3)= 0
x=0 или x – 3= 0
x= 0
Ответ: {0;3}
-
4 * arctg2 x + 5 π * arctg x + π2= 0
arctg x= t
4t2 + 5 π * t + π2 = 0
Д= 25 π2 – 4 * 4 * π2= 9 π2= (3 π)2
t1,2= (-5 π + 3 π)/8; t1= — π; t2= — π /4
Ответ: {- /2}.
-
arccos (2x3 + 3x2 + 0,1)= arccos (2x2 + x + 0,1)
x * (2x2 + x – 1)= 0
x=0 или 2x2 + x – 1= 0
Д= 12 – 4 * 2 * (-1)= 9= 32
x2= (-1 – 3)/4= -1 (постоянный корень).
x3= (-1 + 3)/4= ½ (постоянный корень).
-
arctg (2sin x)= arcctg (cos x) => f (x) * g (x)= 1.
2sin * cos x= 1 sin2x= 1 2x= π /2 + 2 π n
x= π /4 + π n, n z.
Кубик:
Вариант – II
-
arcsin (x2 – 4x + 2)= — π /2
x2 – 4x + 2= -1
x2 – 4x + 3= 0
Д= 16 – 4 * 3= 4
x1,2= (4+2)/2; x1=1; x2=3
Ответ: {1;3}.
-
3 * arctg2 x – 2 π * arctg x= 2 π2
arctg x= t
3t62 – 2 π t – π2 = 0
Д= 4 π2 – 4 * 3 * (-π2)= 16 π2 = (4 π)2
t1,2= (2 π + 4 π)/6; t1= — π /3; t2= π
arctg x= — π /3 => x= tg (-π /3)= —
arctg x= π не имеет решения.
Ответ: —
3.arcsin (3x3 – x2 + 1)= arcsin (2x + 1)
x * (3x2 – x – 2)= 0
x= 0 или 3x2– x – 2= 0
Д= 1 – 4 * 3 * (-2)= 25= 52
x1,2= (1 + 5)/6; x1= -2/3; x= 1 (постоянный корень).
Ответ:{0;-2/3}
4). arcsin x * arccos x= π2/18
arccos x= π /2 – arcsin x
arcsin x * (π /2 – arcsin x)= π 2/18
π /2 * arcsin x – arcsin2 x – π 2/18= 0
пусть arcsin x= t; | t |
18 * arcsin2 x – 9 π * arcsin x + π 2= 0 тогда
t1.2= (9 π + 3 π)/36;
t1= π /6; t= π /3.
Ответ: {1/2;/2}.
После проверки последнего задания (даются правильные ответы) по шкале оценок каждая группа ставит себе оценку в оценочный лист группы, а решение 6-го задания сдают на проверку.
В зависимости от полученного результата учащиеся получают задания на дом.
I уровень: №158 – 160 (кол.).
II уровень: №2.5.31, №2.5.32. Сборник заданий (УНГТУ), №2.5.36.
№2.5.31.
arccos (x *) + arccos x= π /2
№2.5.32.
arcsin (1 + 2 * cos x) + arccos (1 + 3 * tg x)= π /2
№ 2.5.36.
arcsin (π /6 + ctg x) + arccos (π /6 + tg x)= π /2
В конце занятия учитель награждает грамотой лучшую группу, а оценки ставятся в зависимости от числа набранных жетонов.
Оценка за весь модуль зависит от суммы баллов по всем учебным блокам.
Достарыңызбен бөлісу:
определение, формула, таблица, график, свойства
Определение
Арккосинус (arccos) – это обратная тригонометрическая функция.
Арккосинус x определяется как функция, обратная к косинусу x, при -1≤x≤1.
Если косинус угла у равен х (cos y = x), значит арккосинус x равняется y:
arccos x = cos-1 x = y
Примечание: cos-1x означает обратный косинус, а не косинус в степени -1.
Например:
arccos 1 = cos-1 1 = 0° (0 рад)
График арккосинуса
Функция арккосинуса пишется как y = arccos (x). График в общем виде выглядит следующим образом:
Свойства арккосинуса
Ниже в табличном виде представлены основные свойства арккосинуса с формулами.
Таблица арккосинусов
| x | arccos x (рад) | arccos x (°) |
| -1 | π | 180° |
| -√3/2 | 5π/6 | 150° |
| -√2/2 | 3π/4 | 135° |
| -1/2 | 2π/3 | 120° |
| 0 | π/2 | 90° |
| 1/2 | π/3 | 60° |
| √2/2 | π/4 | 45° |
| √3/2 | π/6 | 30° |
| 1 | 0 | 0° |
microexcel. ru
ru
2.4.3. Обратные тригонометрические функции
Глава 2. Алгебраические выражения
2.4.
2.4.3.
Вернемся к определению функции, данному в § 2.2.1. Отметим, что в этом определении функция f не обязана разным элементам
и
множества X ставить в соответствие разные элементы множества Y.
Если Y – множество значений функции f (x) и для любого элемента
существует единственный элемент
такой, что f (x) = y, то говорят, что функция осуществляет взаимнооднозначное соответствие между множествами X и Y. Другими словами, соответствие называется взаимнооднозначным, если каждому элементу соответствует единственный элемент
и наоборот, каждому элементу
соответствует единственный элемент Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции f существует обратная функция. Такая функция обозначается
Такая функция обозначается
и каждому элементу
ставит в соответствие такой элемент
что f (x) = y; этот факт записывают так:
Однако нам непривычна запись функции как зависимости x от y. Поэтому сделаем формальную замену переменных
что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что
− обратная функция, график которой получается из графика исходной функции y = f (x) отражением относительно биссектрисы первого и третьего координатных углов. Область определения обратной функции совпадает с областью значений самой функции:
Область значений обратной функции совпадает с множеством определения самой функции:
Рассмотрим функцию f (x) = sin x для
Тогда
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения
и областью значений
Эта обратная функция называется арксинусом. Её обозначение: y = arcsin x. График функции y = arcsin x изображён на рисунке.
|
1 |
| Рисунок 2.4.3.1. Арксинус |
|
Модель 2.11.
|
Аналогично, на промежутке D (f–1) = E (f) = [–1; 1] можно определить функцию, обратную cos x, c областью значений E (f–1) = D (f) = [0; π]
Эта обратная функция называется арккосинусом. Её обозначение: y = arccos x. График функции y = arccos x изображён на рисунке.
|
2 |
| Рисунок 2.4.3.2. Арккосинус |
|
Модель 2.12.
|
Рассмотрим функцию f (x) = tg x для
Тогда
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения
и областью значений
Эта обратная функция называется арктангенсом. Её обозначение y = arctg x. График функции y = arctg x изображён на рисунке.
|
3 |
| Рисунок 2.4.3.3. Арктангенс |
|
Модель 2.13.
|
Для построения арккотангенса выберем промежуток x (0; π). Тогда
Построим обратную функцию с областью определения
и областью значений
Эта обратная функция называется арккотангенсом. Её обозначение y = arcctg x. График функции y = arcctg x изображён на рисунке.
|
4 |
| Рисунок 2.4.3.4. Арккотангенс |
|
Модель 2.14.
|
Итак, запись b = arcsin a обозначает, что
и sin b = a. Аналогичные соотношения справедливы и для остальных обратных тригонометрических функций.
Пример 1
Докажите тождество
Пример 2
Найти соотношение между A (x) = arcsin (cos (arcsin x)) и B (x) = arccos (sin (arccos x)).
|
Обозначим через y переменную, для которой выполняется равенство:
Здесь поставлен знак «+», поскольку y − угол первой или четвёртой четверти, в которых косинус положителен. Равенство sin (arcsin x) = x справедливо по определению функции арксинус. Значит, Вычислим sin (arccos x) = sin z, где
Здесь поставлен знак плюс, поскольку z − угол первой или второй четверти, в которых синус положителен. Равенство cos (arccos x) = x справедливо по определению функции арккосинус. Отсюда Итак,
Ответ.
|
| 1 | Найдите производную — d / dx | натуральное журнал x | |
| 2 | Оцените интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную — d / dx | е ^ х | |
| 4 | Оцените интеграл | интеграл от e ^ (2x) относительно x | |
| 5 | Найдите производную — d / dx | 1 / х | |
| 6 | Найдите производную — d / dx | х ^ 2 | |
| 7 | Найдите производную — d / dx | 1 / (х ^ 2) | |
| 8 | Найдите производную — d / dx | грех (х) ^ 2 | |
| 9 | Найдите производную — d / dx | сек (x) | |
| 10 | Оцените интеграл | интеграл e ^ x относительно x | |
| 11 | Оцените интеграл | интеграл x ^ 2 относительно x | |
| 12 | Оцените интеграл | интеграл квадратного корня x относительно x | |
| 13 | Найдите производную — d / dx | соз (х) ^ 2 | |
| 14 | Оцените интеграл | интеграл от 1 / x по отношению к x | |
| 15 | Оцените интеграл | интеграл sin (x) ^ 2 относительно x | |
| 16 | Найдите производную — d / dx | х ^ 3 | |
| 17 | Найдите производную — d / dx | сек (x) ^ 2 | |
| 18 | Оцените интеграл | интеграл cos (x) ^ 2 относительно x | |
| 19 | Оцените интеграл | интеграл от sec (x) ^ 2 относительно x | |
| 20 | Найдите производную — d / dx | е ^ (х ^ 2) | |
| 21 | Оцените интеграл | интеграл от 0 до 1 кубического корня из 1 + 7x относительно x | |
| 22 | Найдите производную — d / dx | грех (2x) | |
| 23 | Найдите производную — d / dx | загар (x) ^ 2 | |
| 24 | Оцените интеграл | интеграл 1 / (x ^ 2) относительно x | |
| 25 | Найдите производную — d / dx | 2 ^ х | |
| 26 | График | натуральное бревно из | |
| 27 | Найдите производную — d / dx | cos (2x) | |
| 28 | Найдите производную — d / dx | хе ^ х | |
| 29 | Оцените интеграл | интеграл от 2x относительно x | |
| 30 | Найдите производную — d / dx | (натуральный логарифм x) ^ 2 | |
| 31 | Найдите производную — d / dx | натуральный логарифм (x) ^ 2 | |
| 32 | Найдите производную — d / dx | 3x ^ 2 | |
| 33 | Оцените интеграл | интеграл xe ^ (2x) относительно x | |
| 34 | Найдите производную — d / dx | 2e ^ x | |
| 35 | Найдите производную — d / dx | натуральное бревно 2x | |
| 36 | Найдите производную — d / dx | -sin (х) | |
| 37 | Найдите производную — d / dx | 4x ^ 2-x + 5 | |
| 38 | Найдите производную — d / dx | y = 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 39 | Найдите производную — d / dx | 2x ^ 2 | |
| 40 | Оцените интеграл | интеграл e ^ (3x) относительно x | |
| 41 | Оцените интеграл | интеграл cos (2x) относительно x | |
| 42 | Найдите производную — d / dx | 1 / (квадратный корень из x) | |
| 43 | Оцените интеграл | интеграл e ^ (x ^ 2) относительно x | |
| 44 | Оценить | e ^ бесконечность | |
| 45 | Найдите производную — d / dx | х / 2 | |
| 46 | Найдите производную — d / dx | -cos (x) | |
| 47 | Найдите производную — d / dx | грех (3x) | |
| 48 | Найдите производную — d / dx | 1 / (х ^ 3) | |
| 49 | Оцените интеграл | интеграл от tan (x) ^ 2 относительно x | |
| 50 | Оцените интеграл | интеграл 1 по x | |
| 51 | Найдите производную — d / dx | х ^ х | |
| 52 | Найдите производную — d / dx | x натуральное бревно x | |
| 53 | Найдите производную — d / dx | х ^ 4 | |
| 54 | Оценить предел | предел, когда x приближается к 3 из (3x-5) / (x-3) | |
| 55 | Оцените интеграл | интеграл x ^ 2 натуральный логарифм x относительно x | |
| 56 | Найдите производную — d / dx | f (x) = квадратный корень из x | |
| 57 | Найдите производную — d / dx | х ^ 2sin (х) | |
| 58 | Оцените интеграл | интеграл sin (2x) относительно x | |
| 59 | Найдите производную — d / dx | 3e ^ x | |
| 60 | Оцените интеграл | интеграл xe ^ x относительно x | |
| 61 | Найдите производную — d / dx | у = х ^ 2 | |
| 62 | Найдите производную — d / dx | квадратный корень из x ^ 2 + 1 | |
| 63 | Найдите производную — d / dx | грех (x ^ 2) | |
| 64 | Оцените интеграл | интеграл от e ^ (- 2x) относительно x | |
| 65 | Оцените интеграл | интеграл натурального логарифма квадратного корня x относительно x | |
| 66 | Найдите производную — d / dx | е ^ 2 | |
| 67 | Найдите производную — d / dx | х ^ 2 + 1 | |
| 68 | Оцените интеграл | интеграл sin (x) относительно x | |
| 69 | Найдите производную — d / dx | арксин (х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 of (sin (x)) / x | |
| 71 | Оцените интеграл | интеграл e ^ (- x) относительно x | |
| 72 | Найдите производную — d / dx | х ^ 5 | |
| 73 | Найдите производную — d / dx | 2 / х | |
| 74 | Найдите производную — d / dx | натуральное бревно из 3х | |
| 75 | Найдите производную — d / dx | х ^ (1/2) | |
| 76 | Найдите производную — d / d @ VAR | f (x) = квадратный корень из x | |
| 77 | Найдите производную — d / dx | соз (x ^ 2) | |
| 78 | Найдите производную — d / dx | 1 / (х ^ 5) | |
| 79 | Найдите производную — d / dx | кубический корень из x ^ 2 | |
| 80 | Оцените интеграл | интеграл cos (x) относительно x | |
| 81 | Оцените интеграл | интеграл e ^ (- x ^ 2) относительно x | |
| 82 | Найдите производную — d / d @ VAR | е (х) = х ^ 3 | |
| 83 | Оцените интеграл | интеграл от 0 до 10 из 4x ^ 2 + 7 по x | |
| 84 | Оцените интеграл | интеграл (натуральный логарифм x) ^ 2 относительно x | |
| 85 | Найдите производную — d / dx | журнал x | |
| 86 | Найдите производную — d / dx | арктан (x) | |
| 87 | Найдите производную — d / dx | натуральное бревно 5x | |
| 88 | Найдите производную — d / dx | 5e ^ x | |
| 89 | Найдите производную — d / dx | cos (3x) | |
| 90 | Оцените интеграл | интеграл x ^ 3 относительно x | |
| 91 | Оцените интеграл | интеграл x ^ 2e ^ x относительно x | |
| 92 | Найдите производную — d / dx | Корень четвертой степени из 4x ^ 4 + 4 (16) | |
| 93 | Найдите производную — d / dx | х / (е ^ х) | |
| 94 | Оценить предел | предел, когда x приближается к 3 от arctan (e ^ x) | |
| 95 | Оцените интеграл | интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x | |
| 96 | Найдите производную — d / dx | 3 ^ х | |
| 97 | Оцените интеграл | интеграл xe ^ (x ^ 2) относительно x | |
| 98 | Найдите производную — d / dx | 2sin (х) | |
| 99 | Оценить | сек (0) ^ 2 | |
| 100 | Найдите производную — d / dx | натуральный логарифм x ^ 2 |
| 1 | Найдите производную — d / dx | натуральное журнал x | |
| 2 | Оцените интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную — d / dx | е ^ х | |
| 4 | Оцените интеграл | интеграл от e ^ (2x) относительно x | |
| 5 | Найдите производную — d / dx | 1 / х | |
| 6 | Найдите производную — d / dx | х ^ 2 | |
| 7 | Найдите производную — d / dx | 1 / (х ^ 2) | |
| 8 | Найдите производную — d / dx | грех (х) ^ 2 | |
| 9 | Найдите производную — d / dx | сек (x) | |
| 10 | Оцените интеграл | интеграл e ^ x относительно x | |
| 11 | Оцените интеграл | интеграл x ^ 2 относительно x | |
| 12 | Оцените интеграл | интеграл квадратного корня x относительно x | |
| 13 | Найдите производную — d / dx | соз (х) ^ 2 | |
| 14 | Оцените интеграл | интеграл от 1 / x по отношению к x | |
| 15 | Оцените интеграл | интеграл sin (x) ^ 2 относительно x | |
| 16 | Найдите производную — d / dx | х ^ 3 | |
| 17 | Найдите производную — d / dx | сек (x) ^ 2 | |
| 18 | Оцените интеграл | интеграл cos (x) ^ 2 относительно x | |
| 19 | Оцените интеграл | интеграл от sec (x) ^ 2 относительно x | |
| 20 | Найдите производную — d / dx | е ^ (х ^ 2) | |
| 21 | Оцените интеграл | интеграл от 0 до 1 кубического корня из 1 + 7x относительно x | |
| 22 | Найдите производную — d / dx | грех (2x) | |
| 23 | Найдите производную — d / dx | загар (x) ^ 2 | |
| 24 | Оцените интеграл | интеграл 1 / (x ^ 2) относительно x | |
| 25 | Найдите производную — d / dx | 2 ^ х | |
| 26 | График | натуральное бревно из | |
| 27 | Найдите производную — d / dx | cos (2x) | |
| 28 | Найдите производную — d / dx | хе ^ х | |
| 29 | Оцените интеграл | интеграл от 2x относительно x | |
| 30 | Найдите производную — d / dx | (натуральный логарифм x) ^ 2 | |
| 31 | Найдите производную — d / dx | натуральный логарифм (x) ^ 2 | |
| 32 | Найдите производную — d / dx | 3x ^ 2 | |
| 33 | Оцените интеграл | интеграл xe ^ (2x) относительно x | |
| 34 | Найдите производную — d / dx | 2e ^ x | |
| 35 | Найдите производную — d / dx | натуральное бревно 2x | |
| 36 | Найдите производную — d / dx | -sin (х) | |
| 37 | Найдите производную — d / dx | 4x ^ 2-x + 5 | |
| 38 | Найдите производную — d / dx | y = 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 39 | Найдите производную — d / dx | 2x ^ 2 | |
| 40 | Оцените интеграл | интеграл e ^ (3x) относительно x | |
| 41 | Оцените интеграл | интеграл cos (2x) относительно x | |
| 42 | Найдите производную — d / dx | 1 / (квадратный корень из x) | |
| 43 | Оцените интеграл | интеграл e ^ (x ^ 2) относительно x | |
| 44 | Оценить | e ^ бесконечность | |
| 45 | Найдите производную — d / dx | х / 2 | |
| 46 | Найдите производную — d / dx | -cos (x) | |
| 47 | Найдите производную — d / dx | грех (3x) | |
| 48 | Найдите производную — d / dx | 1 / (х ^ 3) | |
| 49 | Оцените интеграл | интеграл tan (x) ^ 2 относительно x | |
| 50 | Оцените интеграл | интеграл 1 по x | |
| 51 | Найдите производную — d / dx | х ^ х | |
| 52 | Найдите производную — d / dx | x натуральное бревно x | |
| 53 | Найдите производную — d / dx | х ^ 4 | |
| 54 | Оценить предел | предел, когда x приближается к 3 из (3x-5) / (x-3) | |
| 55 | Оцените интеграл | интеграл x ^ 2 натуральный логарифм x относительно x | |
| 56 | Найдите производную — d / dx | f (x) = квадратный корень из x | |
| 57 | Найдите производную — d / dx | х ^ 2sin (х) | |
| 58 | Оцените интеграл | интеграл sin (2x) относительно x | |
| 59 | Найдите производную — d / dx | 3e ^ x | |
| 60 | Оцените интеграл | интеграл xe ^ x относительно x | |
| 61 | Найдите производную — d / dx | у = х ^ 2 | |
| 62 | Найдите производную — d / dx | квадратный корень из x ^ 2 + 1 | |
| 63 | Найдите производную — d / dx | грех (x ^ 2) | |
| 64 | Оцените интеграл | интеграл от e ^ (- 2x) относительно x | |
| 65 | Оцените интеграл | интеграл натурального логарифма квадратного корня x относительно x | |
| 66 | Найдите производную — d / dx | е ^ 2 | |
| 67 | Найдите производную — d / dx | х ^ 2 + 1 | |
| 68 | Оцените интеграл | интеграл sin (x) относительно x | |
| 69 | Найдите производную — d / dx | арксин (х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 of (sin (x)) / x | |
| 71 | Оцените интеграл | интеграл e ^ (- x) относительно x | |
| 72 | Найдите производную — d / dx | х ^ 5 | |
| 73 | Найдите производную — d / dx | 2 / х | |
| 74 | Найдите производную — d / dx | натуральное бревно из 3х | |
| 75 | Найдите производную — d / dx | х ^ (1/2) | |
| 76 | Найдите производную — d / d @ VAR | f (x) = квадратный корень из x | |
| 77 | Найдите производную — d / dx | соз (х ^ 2) | |
| 78 | Найдите производную — d / dx | 1 / (х ^ 5) | |
| 79 | Найдите производную — d / dx | кубический корень из x ^ 2 | |
| 80 | Оцените интеграл | интеграл cos (x) относительно x | |
| 81 | Оцените интеграл | интеграл e ^ (- x ^ 2) относительно x | |
| 82 | Найдите производную — d / d @ VAR | е (х) = х ^ 3 | |
| 83 | Оцените интеграл | интеграл от 0 до 10 из 4x ^ 2 + 7 по x | |
| 84 | Оцените интеграл | интеграл (натуральный логарифм x) ^ 2 относительно x | |
| 85 | Найдите производную — d / dx | журнал x | |
| 86 | Найдите производную — d / dx | арктан (x) | |
| 87 | Найдите производную — d / dx | натуральное бревно 5x | |
| 88 | Найдите производную — d / dx | 5e ^ x | |
| 89 | Найдите производную — d / dx | cos (3x) | |
| 90 | Оцените интеграл | интеграл x ^ 3 относительно x | |
| 91 | Оцените интеграл | интеграл от x ^ 2e ^ x относительно x | |
| 92 | Найдите производную — d / dx | 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 93 | Найдите производную — d / dx | х / (е ^ х) | |
| 94 | Оценить предел | предел, когда x приближается к 3 от arctan (e ^ x) | |
| 95 | Оцените интеграл | интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x | |
| 96 | Найдите производную — d / dx | 3 ^ х | |
| 97 | Оцените интеграл | интеграл xe ^ (x ^ 2) относительно x | |
| 98 | Найдите производную — d / dx | 2sin (х) | |
| 99 | Оценить | сек (0) ^ 2 | |
| 100 | Найдите производную — d / dx | натуральный логарифм x ^ 2 |
3.Производные обратных триггерных функций
М. Борн
Вспомните, когда мы впервые встретили обратную тригонометрию.
функции:
«sin -1 x » означает «найти угол, синус которого
равно x дюймов.
Пример 1
Если x =
sin -1 0,2588, то с помощью калькулятора x =
15 °. Мы нашли угол, синус которого равен 0,2588.
Обозначение
Мы также пишем: arcsin x , чтобы означать то же самое
вещь как грех -1 х .-1 х`. В этом разделе в основном используется нотация sin -1 x (поскольку она изначально была написана для согласования с нотацией калькулятора), однако вам рекомендуется использовать старшую нотацию, `arcsin x`.
Вы также можете вернуться к справочной информации об обратных тригонометрических уравнениях.
Производные обратных тригонометрических функций
Ниже приведены формулы для производных обратного тригонометрического
функции:
`(d (sin ^ -1u)) / (dx) = 1 / sqrt (1-u ^ 2) (du) / (dx)`
`(d (cos ^ -1u)) / (dx) = (- 1) / sqrt (1-u ^ 2) (du) / (dx)`
`(d (tan ^ -1u)) / (dx) = 1 / (1 + u ^ 2) (du) / (dx)`
Пример 2
Найти производную
из y = cos -1 5 x . 2) (du) / (dx)`
и `(du) / dx = 1 + dy / dx`.2`
Производные обратных тригонометрических функций
Введение в обратные тригонометрические функции
В предыдущем разделе мы изучили производные шести основных тригонометрических функций:
\ [{\ color {blue} {\ sin x, \;}} \ kern0pt \ color {red} {\ cos x, \;} \ kern0pt \ color {darkgreen} {\ tan x, \;} \ kern0pt \ color {magenta} {\ cot x, \;} \ kern0pt \ color {шоколад} {\ sec x, \;} \ kern0pt \ color {maroon} {\ csc x. \;} \]
В этом разделе мы рассмотрим производные обратных тригонометрических функций, которые соответственно обозначаются как
\ [{\ color {синий} {\ arcsin x, \;}} \ kern0pt \ color {red} {\ arccos x, \;} \ kern0pt \ color {darkgreen} {\ arctan x, \;} \ kern0pt \ color {magenta} {\ text {arccot} x, \;} \ kern0pt \ color {шоколад} {\ text {arcsec} x, \;} \ kern0pt \ color {maroon} {\ text {arccsc} x.\;} \]
Обратные функции существуют, когда на область определения исходных функций накладываются соответствующие ограничения.
Например, домен для \ (\ arcsin x \) находится от \ (- 1 \) до \ (1. \) Диапазон или выход для \ (\ arcsin x \) — все углы от \ (- \ большие {\ frac {\ pi} {2}} \ normalsize \) в \ (\ large {\ frac {\ pi} {2}} \ normalsize \) радианы.
Области других тригонометрических функций ограничены соответствующим образом, так что они становятся взаимно однозначными функциями и могут быть определены их обратные.2} — 1}}}.}
\]
В последней формуле абсолютное значение \ (\ left | x \ right | \) в знаменателе появляется из-за того, что произведение \ ({\ tan y \ sec y} \) всегда должно быть положительным в диапазоне допустимых значений \ (y \), где \ (y \ in \ left ({0, {\ large \ frac {\ pi} {2} \ normalsize}} \ right) \ cup \ left ({{\ large \ frac {\ pi} {2} \ normalsize}, \ pi} \ right), \) то есть производная обратной секущей всегда положительна.
Аналогичным образом можно получить выражение для производной обратной функции косеканса:
\ [
{{\ left ({\ text {arccsc} x} \ right) ^ \ prime} = {\ frac {1} {{{{\ left ({\ csc y} \ right)} ^ \ prime }}}}}
= {- \ frac {1} {{\ cot y \ csc y}}}
= {- \ frac {1} {{\ csc y \ sqrt {{{\ csc} ^ 2} y — 1}}}}
= {- \ frac {1} {{\ left | x \ right | \ sqrt {{x ^ 2} — 1}}}. 2} \]
Пример 4
\ [y = {\ frac {1} {a}} \ arctan {\ frac {x} {a}} \]
Пример 5
\ [{y = \ arctan \ frac {{x + 1}} {{x — 1}} \; \;} \ kern-0.4}}}.} \]
Производные обратных тригонометрических функций
13
Производная от y = arcsin x
Производная от y = arccos x
Производная от y = arctan x
Производная от y = arccot x
Производная от y = arcsec x
Производная от y = arccsc x
НЕ ОБЯЗАТЕЛЬНО заучивать наизусть производные этого урока.Скорее, ученик должен знать сейчас, чтобы вывести их.
В теме 19 «Тригонометрии» мы ввели обратные тригонометрические функции. По обратным отношениям:
y = arcsin x подразумевает sin y = x .
И аналогично для каждой из обратных тригонометрических функций.
Задача 1. Если y = arcsin x , покажите:
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
Начало:
| y | = | арксин x | |
| означает | |||
| 1) грех л | = | х . | |
| Следовательно, согласно пифагорейской идентичности a ‘: | |||
| cos y | = | ||
| = | |||
| согласно строке 1). | |||
Мы принимаем положительный знак, потому что cos y положителен для всех значений y в диапазоне y = arcsin x , что является 1-м и 4-м квадрантами.(Тема 19 тригонометрии.)
Задача 2. Если y = arcsec x , покажите:
Начало:
| y | = | угловых секунды x | |
| означает | |||
| сек г | = | х . | |
| Следовательно, согласно пифагорейской идентичности b : | |||
| загар г | = | ± | |
| = | ± | ||
Производная от y = arcsin x
Производная арксинуса по аргументу
равна 1 по квадратному корню
из 1 минус квадрат аргумента.
Вот доказательство:
согласно Задаче 1.
Это то, что мы хотели доказать.
Примечание: Мы могли бы напрямую использовать теорему из Урока 8:
Мы будем использовать эту теорему в следующих доказательствах.
Задача 3. Вычислить эти производные. [В частях a) и b) используйте цепное правило.]
| а) | d dx | арксин x 2 | = |
| б) | d dx | = |
| в) | d dx | x 2 arcsin x | = |
Производная от y = arccos x
Производная arccos x — это отрицательное значение производной
arcsin x .Это будет верно для инверсии каждой пары совместных функций.
Производная arccot x будет отрицательной
производной arctan x .
Производная arccsc x будет отрицательной
производной arcsec x .
For, начиная с arccos x :
Угол, косинус которого равен x , является дополнением
угла, синус которого равен x .
| arccos x | = | π 2 | — arcsin x . |
| Так как производная от | π 2 | равно 0, результат будет следующим. |
Задача 4. Вычислить эти производные.
| а) | d dx | arccos | x a | = |
| б) | d dx | x arccos 2 x | = |
Производная от y = arctan x
| d dx | арктан x | = | 1 1 + x 2 |
Первый,
y = arctan x подразумевает tan y = x .
Следовательно, согласно теореме Урока 8:
Это то, что мы хотели доказать.
Следовательно, производная от arccot x является отрицательной:
| d dx | дуга x | = — | 1 1 + x 2 |
Проблема 5.Вычислите эти производные.
| а) | d dx | арктан ( a x 2 ) | = | 2 ax 1 + a 2 x 4 |
| б) | d dx | арккот | x a | = | — a a 2 + x 2 |
| в) | d dx | арктан | 2 x | = | −2 x 2 + 4 |
| г) | d dx | дуга 2 x | = | −2 4 x 2 + 1 |
*
Остальные производные редко используются в расчетах.Тем не менее, вот доказательства.
Производная от y = arcsec x
снова,
y = arcsec x подразумевает sec y = x .
Следовательно, согласно теореме Урока 8:
Итак, согласно теореме раздела 19 тригонометрии: это произведение никогда не бывает отрицательным.Поэтому, чтобы гарантировать, что вместо того, чтобы заменять sec y на x , мы заменим его на | x |. И в задаче 2 мы возьмем только положительный корень из tan y .
Следовательно,
Это то, что мы хотели доказать.
Если бы мы приняли диапазон угловых секунд x как угол третьего квадранта между −π и −π / 2, когда x отрицательное значение, тогда нам не нужно было бы записывать абсолютное значение, и доказательство было бы простым .Мы просто заменим sec y на x и возьмем положительный корень из tan y , потому что tan y положителен в первом и третьем квадрантах. На графике y = x угловых секунд с этим диапазоном наклон для отрицательного значения x отрицательный. Недостатком использования этого диапазона является то, что, когда x является отрицательным, arcsec x не будет равняться arccos 1/ x , потому что arccos 1/ x будет углом 2-го квадранта.Но тогда в доказательстве мы должны записать абсолютное значение.
Следовательно, производная arccsc x является отрицательной:
| d dx | arccsc x | = — |
Следующий урок: Производные экспоненциальной и логарифмической функций
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Производные обратных тригонометрических функций
Теперь давайте определим производные обратных тригонометрических функций, \ (y = \ arcsin x, \) \ (y = \ arccos x, \) \ (y = \ arctan x, \ ) \ (y = \ text {arccot} \, x, \) \ (y = \ text {arcsec} \, x, \) и \ (y = \ text {arccsc} \, x.\)
Один из способов сделать это, который особенно полезен для понимания того, как получаются эти производные, — использовать комбинацию неявного дифференцирования и прямоугольных треугольников. Дополнительным преимуществом этого подхода является то, что он подготовит вас к более успешному изучению темы, называемой тригонометрической заменой.
Пример \ (\ PageIndex {1} \): поиск производной от \ (y = \ arcsin x \)
Найдите производную от \ (y = \ arcsin x \).
Решение:
Чтобы найти производную от \ (y = \ arcsin x \), мы сначала перепишем это уравнение в терминах его обратной формы.То есть \ [\ sin y = x \ label {inverseEqSine} \]
Теперь это уравнение показывает, что \ (y \) можно рассматривать как острый угол в прямоугольном треугольнике с коэффициентом синуса \ (\ dfrac {x} {1} \). Поскольку отношение синусов дает нам длину противоположной стороны по длине гипотенузы, это означает, что противоположная сторона имеет длину \ (x \), а гипотенуза имеет длину \ (1 \). См. Рисунок \ (\ PageIndex {1} \).
Рисунок \ (\ PageIndex {1} \)
Теперь давайте дифференцируем уравнение \ ref {inverseEqSine} неявно по отношению к \ (x \).2}} \]
Пример \ (\ PageIndex {2} \): поиск производной от \ (y = \ text {arcsec} \, x \)
Найдите производную от \ (y = \ text {arcsec} \, x \).
Решение:
Чтобы найти производную от \ (y = \ text {arcsec} \, x \), мы сначала перепишем это уравнение в терминах его обратной формы. То есть \ [\ sec y = x \ label {inverseEqSec} \]
Как и раньше, пусть \ (y \) считается острым углом в прямоугольном треугольнике с отношением секущих \ (\ dfrac {x} {1} \).Поскольку коэффициент секущей обратно пропорционален косинусу, он дает нам длину гипотенузы по длине прилегающей стороны, поэтому это означает, что гипотенуза имеет длину \ (x \), а прилегающая сторона имеет длину из \ (1 \). См. Рисунок \ (\ PageIndex {3} \).
Рисунок \ (\ PageIndex {3} \)
Дифференцирующее уравнение \ ref {inverseEqSec} неявно относительно \ (x \) дает нам:
\ [\ sec y \ tan y \ cdot \ frac {dy} {dx} = 1 \]
Решая это для \ (\ dfrac {dy} {dx} \), получаем:
\ [\ frac {dy} {dx} = \ frac {1} {\ sec y \ tan y} \]
Чтобы найти \ (\ tan y \) через \ (x \), нам нужно найти длину противоположной стороны, \ (a \), через \ (x \).2 — 1}}. \]
Но это не совсем правильно, по крайней мере, не для отрицательных значений \ (x \). Рассматривая график \ (y = \ text {arcsec} \, x \) на рисунке \ (\ PageIndex {5} \), мы видим, что его наклон всегда положительный. Но для отрицательных значений \ (x \) форма производной, указанная выше, будет отрицательной (и явно неверной). 2 — 1}} \]
Рассмотрим домен и диапазон исходной функции, \ (y = \ text {arcsec} \, x: \)
\ [\ text {Домен:} (- \ infty, -1] \ cup [1, \ infty) \ quad \ text {или} \ quad | x | \ geq 1 \]
\ [\ text {Диапазон:} \ big [0, \ frac {\ pi} {2} \ big) \ cup \ big (\ frac {\ pi} {2}, \ pi \ big ] \ quad \ text {или} \ quad 0 \ leq y \ leq \ pi, y \ ne \ frac {\ pi} {2} \]
Обратите внимание, что область определения производной является подмножеством области определения исходной функции, за исключением конечных точек, \ (x = -1 \) и \ (x = 1.2 года} {\ sin y} \]
Мы видим, что эта функция позволяет \ (y \) иметь все значения между \ (0 \) и \ (\ pi \), за исключением \ (y = \ frac {\ pi} {2} \), где исходное выражение \ (\ dfrac {1} {\ sec y \ tan y} \) не определено. Это подмножество диапазона исходной функции \ (y = \ text {arcsec} \, x. \). Обратите внимание, что в производной \ (y \) не может принимать значения конечных точек этого интервала, в то время как они были частью диапазона \ (y = \ text {arcsec} \, x. 2 y \ gt 0 \) для всех \ (y \ in (0, \ pi) \).2 — 1}}. \]
Обратные тригонометрические функции | Precalculus II
Понимание и использование функций обратного синуса, косинуса и тангенса
Чтобы использовать обратные тригонометрические функции, мы должны понимать, что обратная тригонометрическая функция «отменяет» то, что «делает» исходная тригонометрическая функция, как и в случае с любой другой функцией и ее обратной. Другими словами, область определения обратной функции — это диапазон исходной функции, и наоборот, как показано на рисунке 1.{−1} (б) = а [/ латекс].
Имейте в виду, что функции синуса, косинуса и тангенса не взаимно однозначны. График каждой функции не прошел бы тест горизонтальной линии. Фактически, никакая периодическая функция не может быть взаимно однозначной, потому что каждый выход в ее диапазоне соответствует по крайней мере одному входу в каждом периоде, а количество периодов бесконечно. Как и в случае с другими функциями, которые не являются взаимно однозначными, нам нужно будет ограничить область каждой функции, чтобы получить новую функцию, которая является взаимно однозначной.Мы выбираем область для каждой функции, которая включает число 0. На рисунке 2 показан график синусоидальной функции, ограниченной [latex] \ left [\ frac {- \ pi} {2} \ text {,} \ frac {\ pi } {2} \ right] [/ latex] и график функции косинуса, ограниченной [0, π].
Рис. 2. (a) Синусоидальная функция в ограниченной области [latex] \ left [- \ frac {\ pi} {2} \ text {,} \ frac {\ pi} {2} \ right] [ /латекс]; (b) Косинусная функция в ограниченной области [0, π]
На рисунке 3 показан график касательной функции, ограниченной [latex] \ left (- \ frac {\ pi} {2} \ text {,} \ frac {\ pi} {2} \ right) [/ latex].
Рисунок 3. Функция касания в ограниченной области [latex] \ left (- \ frac {\ pi} {2} \ text {,} \ frac {\ pi} {2} \ right) [/ latex]
Эти обычные варианты выбора для ограниченной области в некоторой степени произвольны, но они имеют важные полезные характеристики. Каждый домен включает начало координат и некоторые положительные значения, и, что наиболее важно, каждый результат дает взаимно однозначную функцию, которая является обратимой. Традиционный выбор для ограниченной области касательной функции также имеет то полезное свойство, что он простирается от одной вертикальной асимптоты к следующей вместо того, чтобы быть разделенным на две части асимптотой.{−1} x [/ latex] имеет домен всех действительных чисел и диапазон [latex] \ left (- \ frac {\ pi} {2} \ text {,} \ frac {\ pi} {2} \ right) [/латекс]. Чтобы найти область и диапазон обратных тригонометрических функций, переключите область и диапазон исходных функций. Каждый график обратной тригонометрической функции является отражением графика исходной функции относительно линии [латекс] y = x [/ latex].
Рисунок 4. Функция синуса и функция обратного синуса (или арксинуса)
Рисунок 5.{−1} (0,96593) \ приблизительно \ frac {5 \ pi} {12} [/ латекс]
Попробуй 1
Учитывая [латекс] \ cos (0,5) \ приблизительно 0,8776 [/ латекс], напишите соотношение, включающее обратный косинус.
Решение
Нахождение точного значения выражений, содержащих функции обратного синуса, косинуса и тангенса
Теперь, когда мы можем идентифицировать обратные функции, мы научимся их оценивать. Для большинства значений в их областях мы должны вычислять обратные тригонометрические функции с помощью калькулятора, интерполяции из таблицы или других численных методов.\ circ) [/ latex], и их отражения в другие квадранты.
Как сделать: учитывая «особое» входное значение, вычислить обратную тригонометрическую функцию.
- Найдите угол x , для которого исходная тригонометрическая функция имеет выход, равный заданному входу для обратной тригонометрической функции.
- Если x не находится в заданном диапазоне обратного преобразования, найдите другой угол y , который находится в заданном диапазоне и имеет тот же синус, косинус или тангенс, что и x , в зависимости от того, который соответствует заданному обратному. функция.{−1} (\ frac {1} {2}) [/ латекс]
Решение
Использование калькулятора для вычисления обратных тригонометрических функций
Для оценки обратных тригонометрических функций , которые не используют специальные углы, обсуждавшиеся ранее, нам понадобится калькулятор или другой тип технологии. Большинство научных калькуляторов и приложений-эмуляторов калькуляторов имеют специальные клавиши или кнопки для функций обратного синуса, косинуса и тангенса. Они могут быть помечены, например, как SIN-1, ARCSIN или ASIN.
В предыдущей главе мы работали с тригонометрией на прямоугольном треугольнике, чтобы найти стороны треугольника с учетом одной стороны и дополнительного угла. Используя обратные тригонометрические функции, мы можем найти углы прямоугольного треугольника с двумя сторонами, и мы можем использовать калькулятор, чтобы найти значения с точностью до нескольких десятичных знаков.
В этих примерах и упражнениях ответы будут интерпретироваться как углы, и мы будем использовать θ в качестве независимой переменной. Значение, отображаемое на калькуляторе, может быть в градусах или радианах, поэтому обязательно установите режим, соответствующий приложению.{\ circ} \ hfill & \ text {Оценить.} \ end {array} [/ latex]
Попробуй 4
Решите треугольник на рисунке 9 для угла θ.
Рисунок 9
Решение
Нахождение точных значений составных функций с обратными тригонометрическими функциями
Бывают случаи, когда нам нужно составить тригонометрическую функцию с обратной тригонометрической функцией. В этих случаях обычно можно найти точные значения для результирующих выражений, не прибегая к калькулятору.{−1} (\ sin x) = x \\ [/ латекс]?
Нет. Это уравнение верно, если x принадлежит ограниченной области [latex] \ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right] \\ [/ latex] , но синус определен для всех реальных входных значений, а для x вне ограниченного интервала уравнение неверно, потому что его обратное всегда возвращает значение в [latex] \ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right] \\ [\ latex] . {- 1} (\ cos \ theta) = \ frac {\ pi} {2} — \ theta \ text {if} 0 \ leq \ theta \ leq \ pi \\ [/ latex].{−1} (\ cos (\ frac {13 \ pi} {6})) \\ [/ latex]
- путем прямой оценки.
- способом, описанным ранее.
Решение
- Здесь мы можем непосредственно оценить внутреннюю часть композиции.
[латекс] \ begin {array} \ cos \ left (\ frac {13 \ pi} {6} \ right) = \ cos \ left (\ frac {\ pi} {6} +2 \ pi \ right) \ \ \ hfill = \ cos \ left (\ frac {\ pi} {6} \ right) \\ \ hfill = \ frac {\ sqrt {3}} {2} \ end {array} \\ [/ latex]
Теперь мы можем вычислить обратную функцию, как и раньше.{−1} (\ frac {4} {5}) \\ [/ latex] находится в квадранте I, [latex] \ sin {\ theta} \\ [/ latex] должно быть положительным, поэтому решением будет [latex ] \ frac {3} {5} \\ [/ latex]. См. Рисунок 11.
Рис. 11. Правый треугольник, иллюстрирующий, что если [latex] \ cos \ theta = \ frac {4} {5} [/ latex], то [latex] \ sin \ theta = \ frac {3} {5} \ \ [/ latex]
Мы знаем, что обратный косинус всегда дает угол в интервале [0, π], поэтому мы знаем, что синус этого угла должен быть положительным; поэтому [латекс] \ sin \ left (\ cos ^ {- 1} \ left (\ frac {4} {5} \ right) \ right) = \ sin \ theta = \ frac {3} {5} \\ [ /латекс].{−1} \ left (\ frac {7} {4} \ right) \ right) \\ [/ latex].
Решение
Хотя мы могли бы использовать ту же технику, что и в Примере 6, мы продемонстрируем здесь другую технику. Изнутри мы знаем, что существует такой угол, что [latex] \ tan \ theta = \ frac {7} {4} \\ [/ latex]. Мы можем представить это как противоположные и смежные стороны прямоугольного треугольника, как показано на рисунке 12.
Рис. 12. Прямоугольный треугольник с двумя известными сторонами
Используя теорему Пифагора, мы можем найти гипотенузу этого треугольника.{−1} \ left (4x \ right) \ right) \\ [/ latex] для [латекса] — \ frac {1} {4} \ leq x \ leq \ frac {1} {4} \\ [/ латекс].
Решение
Ключевые понятия
- Обратная функция — это функция, которая «отменяет» другую функцию. Область определения обратной функции — это диапазон исходной функции, а диапазон обратной функции — это область определения исходной функции.
- Поскольку тригонометрические функции не взаимно однозначны в своих естественных областях, обратные тригонометрические функции определены для ограниченных областей.{−1} \ left (\ sin x \ right) = \ frac {\ pi} {2} −x [/ latex] если [латекс] — \ frac {\ pi} {2} \ leq x \ leq \ frac {\ pi} {2} [/ латекс].
- При оценке состава тригонометрической функции с обратной тригонометрической функцией нарисуйте контрольный треугольник, чтобы помочь определить соотношение сторон, представляющее выходные данные тригонометрической функции.
- При оценке состава тригонометрической функции с обратной тригонометрической функцией вы можете использовать тригонометрические тождества для помощи в определении соотношения сторон.{−1} (2) [/ латекс]. Объясните, как это можно сделать, используя функцию косинуса или функцию обратного косинуса.
5. Почему область синусоидальной функции [latex] \ sin x [/ latex] должна быть ограничена [latex] \ left [- \ frac {\ pi} {2} \ text {,} \ frac { \ pi} {2} \ right] [/ latex] для существования функции обратного синуса?
6. Обсудите, почему это утверждение неверно: [latex] \ arccos (\ cos x) = x [/ latex] для всех x .
7. Определите, является ли следующее утверждение истинным или ложным, и объясните свой ответ: [latex] \ arccos (−x) = \ pi− \ arccos x [/ latex].{-1} х [/ латекс]? Используйте графический калькулятор, чтобы приблизиться к ответу.
53. Предположим, что к зданию прислонена 13-футовая лестница, достигающая дна окна второго этажа на высоте 12 футов над землей. Какой угол в радианах образует лестница со зданием?
54. Предположим, вы проезжаете 0,6 мили по дороге, так что вертикальное расстояние изменяется от 0 до 150 футов. Какой угол подъема дороги?
55. Равнобедренный треугольник имеет две равные стороны длиной 9 дюймов.Оставшаяся сторона имеет длину 8 дюймов. Найдите угол между стороной 9 дюймов и стороной 8 дюймов.
56. Без использования калькулятора приблизьте значение [латекс] \ arctan (10,000) [/ латекс]. Объясните, почему ваш ответ разумен.
57. Ферма крыши дома состоит из двух одинаковых прямоугольных треугольников. У каждого есть основание 12 футов и высота 4 фута. Найдите величину острого угла, примыкающего к 4-футовой стороне.
58. Линия [latex] y = \ frac {3} {5} x [/ latex] проходит через начало координат в плоскости x , y .Каков угол между линией и положительной осью x ?
59. Линия [latex] y = — \ frac {3} {7} x [/ latex] проходит через начало координат в плоскости x , y . Каков угол между линией и отрицательной осью x ?
60. Какой процентный уклон должен иметь дорога, если угол наклона дороги составляет 4 градуса? (Процентный уклон определяется как изменение высоты дороги на 100-футовом горизонтальном расстоянии.Например, уклон 5% означает, что дорога поднимается на 5 футов на каждые 100 футов горизонтального расстояния.)
61. 20-футовая лестница прислоняется к стене здания так, чтобы ее основание находилось на расстоянии 10 футов от основания здания. Если согласно спецификациям угол подъема лестницы должен составлять от 35 до 45 градусов, соответствует ли размещение этой лестницы требованиям безопасности?
62.
