Решение квадратных уравнений

6 июля 2011

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax² + bx + c = 0. Тогда дискриминант — это просто число D = b² − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D < 0, корней нет;
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x² − 8x + 12 = 0;
2. 5x² + 3x + 7 = 0;
3. x² − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)² − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3² − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)² − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.

Задача. Решить квадратные уравнения:

1. x² − 2x − 3 = 0;
2. 15 − 2x − x² = 0;
3. x² + 12x + 36 = 0.

Первое уравнение:
x² − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)² − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x² = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)² − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left( -1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left( -1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x² + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12² − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

\[x=\frac{-12+\sqrt{0}}{2\cdot 1}=-6\]

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x² + 9x = 0;
2. x² − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax² + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax² = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax² + c = 0. Немного преобразуем его:

Решение неполного квадратного уравнения

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax² + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c/a) < 0, корней нет.

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x² и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax² + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x² − 7x = 0;
2. 5x² + 30 = 0;
3. 4x² − 9 = 0.

x² − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x₁ = 0; x₂ = −(−7)/1 = 7.

5x² + 30 = 0 ⇒ 5x² = −30 ⇒ x² = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x² − 9 = 0 ⇒ 4x² = 9 ⇒ x² = 9/4 ⇒ x₁ = 3/2 = 1,5; x₂ = −1,5.

Смотрите также:

1. Теорема Виета
2. Следствия из теоремы Виета
3. Тест на тему «Значащая часть числа»
4. Правила комбинаторики в задаче B6
5. Как представить обычную дробь в виде десятичной
6. Задача B15: частный случай при работе с квадратичной функцией

Как решать квадратные уравнения? Формулы и Примеры

Понятие квадратного уравнения

Уравнения — это математическое равенство, в котором неизвестна одна или несколько величин. Значения неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать выражение 3 + x = 7, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Есть три вида квадратных уравнений:

• не имеют корней;
• имеют один корень;
• имеют два различных корня.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

• если D < 0, корней нет;
• если D = 0, есть один корень;
• если D > 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Вникать во все тонкости математической вселенной комфортнее с внимательным наставником. Наши учителя объяснят сложную тему, ответят на неловкие вопросы и вдохновят ребенка учиться. А красочная платформа с увлекательными заданиями поможет заниматься современно и в удовольствие. Запишите ребенка на бесплатный вводный урок в онлайн-школе Skysmart и попробуйте сами!

Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент может быть любым.

Давайте-ка на примерах — вот у нас есть два уравнения:

• x² — 2x + 6 = 0
• x² — x — 1/4 = 0

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x² ), а значит уравнение называется приведенным.

• 2x² − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Запоминаем!

У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.

Пример 1. Превратим неприведенное уравнение: 8x² + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x² + 2,5x — 1,125 = 0.

Полные и неполные квадратные уравнения

В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax² + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.

Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято назвать неполным.

Неполное квадратное уравнение —— это квадратное уравнение вида ax² + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.

Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Для самых любопытных объясняем откуда появились такие названия:
Если b = 0, то квадратное уравнение принимает вид ax2 + 0x+c=0 и оно равносильно ax2 + c = 0. Если c = 0, то квадратное уравнение выглядит так ax2 + bx + 0 = 0, иначе его можно написать как ax2 + bx = 0. Если b = 0 и c = 0, то квадратное уравнение выглядит так ax2 = 0. Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax² + c = 0, при b = 0;
• ax² + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax

² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x² = 0.

Как решаем:

1. Замечаем, что данному уравнению равносильно x² = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

   −6x² = 0

   x² = 0

   x = √0

   x = 0

Ответ: 0.

Как решить уравнение ax

² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

• перенесем c в правую часть: ax² = — c,
• разделим обе части на a: x² = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x² = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.

Если — c/а > 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах
Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению ax2 + c = 0, которое: не имеет корней при — c/а < 0; имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.

Пример 1. Найти решение уравнения 8x² + 5 = 0.

Как решать:

1. Перенесем свободный член в правую часть:

   8x² = — 5

2. Разделим обе части на 8:

   x² = — 5/8

3. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x² + 5 = 0 не имеет корней.

Как решить уравнение ax

² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x² + 0,125x = 0

Как решать:

1. Вынести х за скобки

   х(0,5x + 0,125) = 0

2. Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
3. Решить линейное уравнение:

   0,5x = 0,125,
   х = 0,125/0,5

4. Разделить:

   х = 0,25

5. Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Формула Виета

---

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: 

Теорема Виета Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x² + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

 

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x² + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x² + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Пифагора: x² − 6x + 8 = 0.

Как решаем:

1. Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

2. Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

   Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

   Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

3. Значит числа 4 и 2 — корни уравнения x² − 6x + 8 = 0. p>

    

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b² − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Выводим формулу корней квадратного уравнения

Продолжим изучать формулу корней квадратного уравнения.

Пусть перед нами есть задача решить квадратное уравнение ax² + bx + c = 0. Выполним ряд равносильных преобразований:

Так, мы пришли к уравнению , которое полностью равносильно исходному ax² + bx + c = 0.

Отсюда выводы про корни уравнения :

И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части. При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D.

По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько.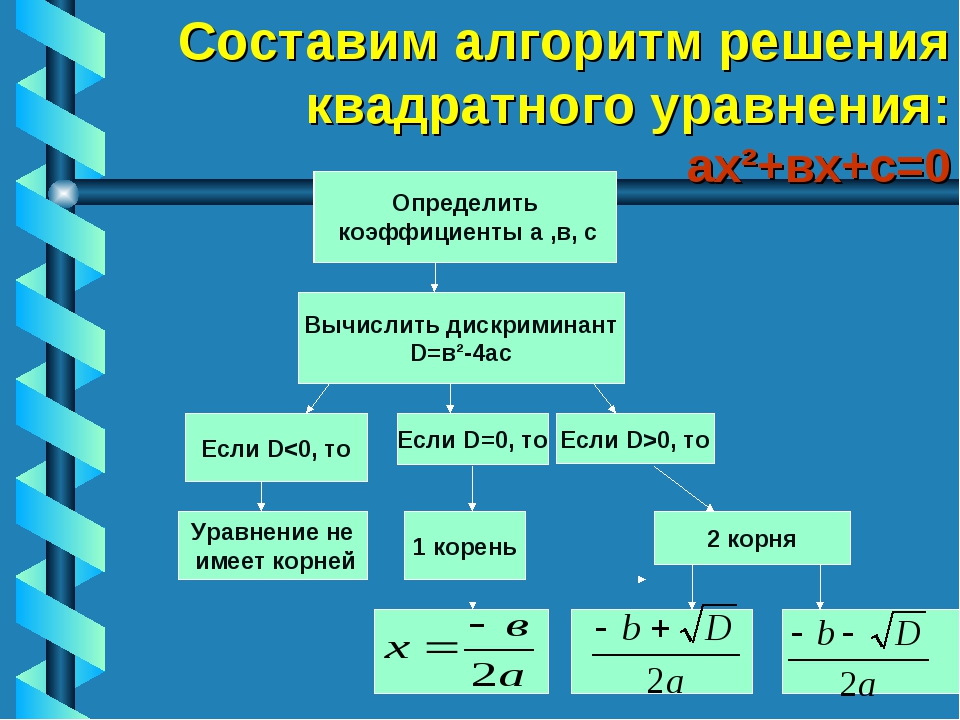

Повторим:

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax² + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b²−4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = — b²/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x² + 28x — 49 = 0.

Как решаем:

1. Найдем дискриминант: D = 28² — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

   х = — 28/2(-4)

   х = 3,5

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x² = 0.

Как решаем:

1. Произведем равносильные преобразования. Умножим обе части на −1

   54 — 6x² = 0 | *(-1)

   6x² — 54 = 0

2. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   6x² = 54

   х² = 9

   х = ±√9

   х₁ = 3, х₂ = — 3

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x²— х = 0.

Как решаем:

1. Преобразуем уравнение так, чтобы появились множители

   х(х — 1) = 0

   х₁ = 0, х₂ = 1

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x²— 10 = 39.

Как решаем:

1. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   x²— 10 = 39

   x²= 39 + 10

   x²= 49

   х = ±√49

   х₁ = 7, х₂ = −7

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x²— 4x+94 = 0.

Как решаем:

1. Найдем дискриминант по формуле

   D = (-4)² — 4 * 3 * 94 = 16 — 1128 = −1112

2. Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Приходите решать примеры на бытовых ситуациях, с красочными героями и в интерактивном формате.

Запишите вашего ребенка на бесплатный пробный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b² — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax² + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)²— 4ac = 4n² — 4ac = 4(n²— ac) и подставим в формулу корней:

Для удобства вычислений обозначим выражение n² -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n²— ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n²— ac;
• если D₁< 0, значит действительных корней нет;
• если D₁= 0, значит можно вычислить единственный корень уравнения по формуле;
• если же D₁> 0, значит можно найти два действительных корня по формуле

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x² — 4 x — 6 = 0, чем 1100x² — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x² — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x²— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x² — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x² + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x²— 3x + 7 = 0 перейти к решению 2x² + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

• x₁ + x₂ = — b/a,
• x₁* x₂ = c/a.

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x²— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

Как найти Дискриминант? 🤔 Формулы, Примеры решений.

Понятие квадратного уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 8 + 4 = 12. При вычислении левой части получается верное числовое равенство, то есть 12 = 12.

Уравнением можно назвать выражение 8 + x = 12, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени, значит, такое уравнение является квадратным.

Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Есть три вида квадратных уравнений:

• не имеют корней;
• имеют один корень;
• имеют два различных корня.

Чтобы ваш ребенок легко справиться с будущими экзаменами, запишите его на курс подготовки к ОГЭ или ЕГЭ по математике в Skysmart. На занятиях с личным преподавателем он потренируется решать пробные варианты экзамена на время, увидит свои сильные и слабые стороны, разберется в каждой сложной теме и выработает тактику поведения на экзамене, чтобы добиться отличных результатов без стресса.

Записывайтесь на бесплатный пробный урок математики: познакомим с платформой, наметим программу обучения и вдохновим ребенка.

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, которое находится под корнем в формуле нахождения корней квадратного уравнения. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Чаще всего для поиска дискриминанта используют формулу:

В этом ключе универсальная формула для поиска корней квадратного уравнения выглядит так:

Эта формула подходит даже для неполных квадратных уравнений.

Но есть и другие формулы — все зависит от вида уравнения. Чтобы в них не запутаться, сохраняйте табличку или распечатайте ее и храните в учебнике.

Как решать квадратные уравнения через дискриминант

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный. Только после этого вычисляем значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax² + bx + c = 0:

• как найти дискрининант: D = b² − 4ac;
• если дискриминант отрицательный — зафиксировать, что действительных корней нет;
• если дискриминант равен нулю — вычислить единственный корень уравнения по формуле х = — b²/2a;
• если дискриминант положительный — найти два действительных корня квадратного уравнения по формуле корней

А вот и еще одна табличка: в ней вы найдете формулы для поиска корней квадратных уравнений при помощи дискриминанта:

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, важно практиковаться. Вперед!

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x² — 4x + 2 = 0.

Как решаем:

1. Определим коэффициенты: a = 3, b = -4, c = 2.
2. Найдем дискриминант: D = b² — 4ac = (-4)² — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D < 0, корней нет.

Пример 2. Решить уравнение: x² — 6x + 9 = 0.

Как решаем:

1. Определим коэффициенты: a = 1, b = -6, c = 9.
2. Найдем дискриминант: D = b² — 4ac = (-6)² — 4 * 1 * 9 = 36 — 36 = 0.
3. D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x² — 4x — 5 = 0.

Как решаем:

1. Определим коэффициенты: a = 1, b = -4, c = -5.
2. Найдем дискриминант: D = b² — 4ac = (-4)² — 4 * 1 * (-5) = 16 + 20 = 36.
3. D > 0, значит уравнение имеет два корня:

    

x₁ = (4 + 6) : 2 = 5,

x₂ = (4 — 6) : 2 = -1.

Ответ: два корня x₁ = 5, x₂ = -1.

Не желаешь повторить формулы сокращенного умножения?

Решение (корни) квадратного уравнения

Квадратным уравнением называется уравнение вида ax² + bx + c = 0,
где x — переменная, которая в уравнении присутствует в квадрате, a, b, c — некоторые числа, причём a ≠ 0.

Например, квадратным является уравнение

2x² — 3x + 1 = 0,

в котором a = 2, b = — 3, c = 1.

В квадратном уравнении ax² + bx + c = 0
коэффициент a называют первым коэффициентом, b — вторым коэффициентом, c — свободным членом.

Уравнения вида ax² + bx = 0,

где c =0,

ax² + c = 0,

где b =0, и

ax² = 0,

где a =0 и b =0,

называются неполными квадратными уравнениями.

Найти корни квадратного уравнения значит решить квадратное уравнение.

Для вычисления корней квадратного уравния служит выражение b² — 4ac,
которое называется дискриминантом квадратного уравнения и обозначается буквой D.

Корни квадратного уравнения имеют следующие сферы применения:

— для разложении квадратного трёхлена на множители, что, в свою очередь, является
приёмом упрощения выражений (например, сокращения дробей, вынесение за скобки общего знаменателя и т.д.) в частности,
при нахождении пределов, производных и интегралов;

— для решения задач на соотношения параметров меняющегося объекта (корни квадратного уравнения,
чаще всего один, являются обычно конечным решением).

График квадратичного трёхлена ax² + bx + c —
левой части квадратного уравнения — представляет собой параболу, ось симметрии которой параллельна
оси 0y. Число точек пересечения параболы с осью
0x определяет число корней квадратного уравнения. Если точек
пересечения две, то квадратное уравнение имеет два действительных корня, если точка пересечения
одна, то квадратное уравнение имеет один действительный корень, если парабола не пересекает
ось 0x, то квадратное уравнение не имеет действительных
корней. На рисунке ниже изображены три упомянутых случая.

Как видно на рисунке, красная парабола пересекает ось 0x
в двух точках, зелёная — в одной точке, а жёлтая парабола не имеет точек пересечения с осью
0x.

1. Если дискриминант больше нуля (),
то квадратное уравнение имеет два различных действительных корня.

Они вычисляются по формулам:

и

.

Часто пишется так: .

2. Если дискриминант равен нулю (),
то квадратное уравнение имеет только один действительный корень, или, что то же самое — два равных действительных корня,
которые равны .

3. Если дискриминант меньше нуля (),
то квадратное уравнение не имеет действительных корней, а имеет комплексные корни, но нахождение комплексных корней
в этой статье рассматривать не будем. В общем случае правильным решением является констатация того,
что квадратное уравнение не имеет действительных корней.

Пример 1. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант больше нуля, следовательно, квадратное уравнение имеет два действительных корня.

Путём преобразования в квадратное уравнение следует решать и дробные
уравнения, в которых хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное, например, .
О том, как это делается — в материале Решение дробных уравнений с преобразованием в квадратное уравнение.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 2. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант равен нулю, следовательно, квадратное уравнение имеет один действительный корень.

Пример 3. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант меньше нуля, следовательно, квадратное уравнение не имеет действительных корней.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Находить корни квадратного уравнения требуется при решении многих
задач высшей математики, например, при нахождении пределов,
интегралов, исследовании
функций на возрастание и убывание и других.

Пример 4. Найти корни квадратного уравнения:

.

В примере 1 нашли дискриминант этого уравнения:

,

Решение квадратного уравнения найдём по формуле для корней:

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Корни приведённого квадратного уравнения

Формула корней приведённого уравнения имеет вид:

.

Существуют формулы, связывающие корни квадратного уравнения с его
коэффициентами. Они впервые были получены французским математиком Ф.Виетом.

Теорема Виета. Если квадратное уравнение
ax² + bx + c = 0
имеет действительные корни, то их сумма равна — b/a,
а произведение равно с/a:

Следствие. Если приведённое квадратное уравнение
x² + px + q = 0
имеет действительные корни и
, то

Пояснение формул: сумма корней приведённого квадратного уравнения равна второму
коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному
члену.

Следовательно, теорему Виета можно применять и для поиска корней
приведённого квадратного уравнения.

---

Если известны корни квадратного уравнения, то трёхчлен, представляющий собой левую часть уравнения, можно
разложить на множители по следующей формуле:

.

Этот приём часто используется для упрощения выражений, особенно сокращения дробей.

Пример 9. Упростить выражение:

.

Решение. Числитель данной дроби можем рассматривать как квадратный трёхчлен в отношении x
и разложить его на множители, предварительно найдя его корни. Найдём дискриминант квадратного уравнения:

.

Корни квадратного уравнения будут следующими:

.

Разложим квадратный многочлен на множители:

.

Упростили выражение, проще не бывает:

.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 10. Упростить выражение:

.

Решение. И числитель, и знаменатель — квадратные трёхчлены. Значит, их можно разложить
на множители, предварительно найдя корни соответствующих квадратных уравнений. Находим дискриминант первого квадратного уравнения:

.

Корни первого квадратного уравнения будут следующими:

.

Находим дискриминант второго квадратного уравнения:

.

Так как дискриминант равен нулю, второе квадратное уравнение имеет два совпадающих корня:

.

Подставим корни квадратных уравнений, разложим числитель и знаменатель на множители и получим:

.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Упрощать выражения путём решения квадратных уравнений требуется
при решении многих задач высшей математики, например, при
нахождении пределов,
интегралов,
исследовании
функций на возрастание и убывание и других.

Разумеется, квадратного трёхчлена может может и не быть в выражении в первоначальном виде,
он может быть получен в процессе предварительных преобразований выражения.

Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один
из первых дошедших до наших дней выводов этой формулы принажлежит индийскому математику
Брахмагупте (около 598 г.). Среднеазиатский учёный аль-Хорезми (IX в.) получил эту формулу
методом выделения полного квадрата с помощью геометрической иллюстрации. Суть его рассуждений
видна из рисунка ниже (он рассматривает уравнение x² + 10x = 39).

Площадь большого квадрата равна (x + 5)².
Она складывается из площади x² + 10x
заштрихованной фигуры, равной левой части рассматриваемого уравнения, и площади четырёх
квадратов со стороной 5/2, равной 25. Получается следующее уравнение и его решение:

Пример 11. Отрезок ткани стоит 180 у.ед. Если бы ткани в отрезке было на 2,5 м больше
и цена отрезка оставалась бы прежней, то цена 1 м ткани была бы на 1 у.ед. меньше. Сколько ткани в отрезке?

Решение. Примем количество ткани в отрезке за x и получим уравнение:

Приведём обе части уравнения к общему знаменателю:

Произведём дальнейшие преобразования:

Получили квадратное уравнение, которое и решим:

Ясно, что количество ткани не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь один корень — положительный.

Ответ: в отрезке 20 м ткани.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 12. Товар, количество которого 187,5 кг, взвешивают в одинаковых ящиках.
Если в каждом ящике количество товара уменьшить на 2 кг, то следовало бы использовать на 2 ящика больше и при этом
2 кг товара остались бы невзвешенными. Сколько кг товара взвешивают в каждом ящике?

Решение. Примем за x количество товара, взвешиваемого в одном ящике. Тогда получим уравнение:

Приведём обе части уравнения к общему знаменателю, произведём дальнейшие преобразования и получим квадратное уравнение.
Процесс записывается так:

Найдём дискриминант:

Найдём корни квадратного уравнения:

Количество товара не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь положительный корень.

Ответ: в одном ящике взвешивают 12,5 кг ткани.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Другие темы в блоке «Школьная математика»

Дискриминант квадратного уравнения. Формулы дискриминанта

Дискриминант квадратного уравнения — это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой  D.

Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:

Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:

1. Если дискриминант больше нуля, то уравнение имеет два корня.
2. Если дискриминант равен нулю, то уравнение имеет один корень.
3. Если дискриминант меньше нуля, то уравнение не имеет корней.

Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:

D = b² — 4ac,

так как она относится к формуле:

,

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.

Решение квадратных уравнений через дискриминант

Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.

Пример 1. Решить уравнение:

3x² — 4x + 2 = 0.

Определим, чему равны коэффициенты:

a = 3,  b = -4,  c = 2.

Найдём дискриминант:

D = b² — 4ac = (-4)² — 4 · 3 · 2 = 16 — 24 = -8,

D < 0.

Ответ: корней нет.

Пример 2.

x² — 6x + 9 = 0.

Определим, чему равны коэффициенты:

a = 1,  b = -6,  c = 9.

Найдём дискриминант:

D = b² — 4ac = (-6)² — 4 · 1 · 9 = 36 — 36 = 0,

D = 0.

Уравнение имеет всего один корень:

Ответ:  3.

Пример 3.

x² — 4x — 5 = 0.

Определим, чему равны коэффициенты:

a = 1,  b = -4,  c = -5

Найдём дискриминант:

D = b² — 4ac = (-4)² — 4 · 1 · (-5) = 16 + 20 = 36,

D > 0.

Уравнение имеет два корня:

x₁ = (4 + 6) : 2 = 5,

x₂ = (4 — 6) : 2 = -1.

Ответ:  5,  -1.

Внеклассный урок — Формулы корней квадратного уравнения. Дискриминант

 

Формулы корней квадратного уравнения. Дискриминант.

  

Формула №1:

         —b ± √D
x =  ————,  где D = b² – 4ac.
             2a

Латинской буквой D обозначают дискриминант.

Дискриминант — это выражение, от которого зависит число корней данного уравнения.

Если D < 0, то уравнение не имеет корней.

Если D = 0, то уравнение имеет один корень.

Если D > 0, то уравнение имеет два корня.

Пример. Решим уравнение 12x² + 7x + 1 = 0.

Сначала вычислим дискриминант.

Мы видим, что а = 12, b = 7, c = 1.

Итак:

D = b² – 4ac = 7² – 4 · 12 · 1 = 49 – 48 = 1.

D > 0. Значит, уравнение имеет корни (причем два корня), а значит, можно вычислять дальше.

Чтобы найти корни, применим формулу корней квадратного уравнения:

         —b ± √D      -7 ± √1         -7 ± 1
x =  ———— = ———— = ————
             2a                24                 24

Находим оба значения x:

        -7 + 1        -6      -1          1
x₁ = ——— = —— = — = – —
           24           24       4          4

 

         -7 – 1       -8       -1         1
x₂ = ——— = —— = — = – — .
           24           24       3          3

 

                        1                   1
Ответ: x₁ = – —,    x₂ = – —
                        4                   3

 

Формула №2.

Из формулы №1 можно получить другую формулу, которой удобно пользоваться в случаях, когда второй коэффициент – четное число. В этом случае раскладываем его на множители, один из которых – множитель 2. То есть второй коэффициент представляем в виде 2k, где k – это половина изначально заданного числа. Тогда удобно пользоваться формулой:

      —k ± √D₁
x = ————,   где D₁ = k² – ac
             a

Пример. Решим уравнение 5x² – 16x + 3 = 0.

Записываем -16x в виде 2 · (-8x). Тогда k = -8,  a = 5,  c = 3. Мы уже можем найти дискриминант D₁:

D₁ = k² – ac = (-8)² – 5 · 3 = 64 – 15 = 49.

Теперь находим оба значения x:

      —k ± √D₁       — (-8) ± √49      8 ± 7
x = ———— =  ————— = ———
             a                     5                  5

Отсюда:

          8 + 7       15
x₁ = ——— =  — = 3
            5            5

 

         8 – 7         1
x₂ = ——— =  — = 0,2
             5           5 

 

Ответ: x₁ = 3; x₂ = 0,2.

 

При решении квадратного уравнения по данным формулам целесообразно поступать следующим образом:

1) вычислить дискриминант и сравнить его с нулем;

2) если дискриминант положителен или равен нулю, то воспользоваться формулой корней; если дискриминант отрицателен, то записать, что корней нет.

 

Дискриминант на 4 | Алгебра

Дискриминант, делённый на 4 — D/4 — удобно использовать для упрощения вычислений при решении квадратных уравнений, если коэффициент b при x — чётное число.

Формула дискриминанта, деленного на 4 —

   

Как и для случая с обычным дискриминантом, количество корней  квадратного уравнения зависит от знака D/4.

• Если D/4>0, квадратное уравнение имеет два корня:

     

• Если D/4=0, квадратное уравнение имеет один корень

     

• Если D/4<0, квадратное уравнение не имеет действительных корней.

Рассмотрим примеры решения квадратных уравнений с помощью формулы четверти дискриминанта.

   

   

Так как b=16 — чётное число, вместо обычного дискриминанта вычислим дискриминант, делённый на 4 (иногда его еще обозначают через D1):

   

Так как D/4>0, уравнение имеет два корня:

   

   

   

Ответ: -0,2; -3.

   

   

   

   

Поскольку D/4>0, уравнение имеет два корня:

   

   

   

   

Ответ: 9; 1/3.

   

   

   

   

Так как D/4=0, данное квадратное уравнение имеет один корень

   

Ответ: -2 1/3.

   

   

   

   

Так как D/4<0, уравнение не имеет корней в действительных числах.

Ответ: нет корней.

Для решения квадратных уравнений вполне достаточно помнить обычную формулу дискриминанта и связанные с ним формулы корней. И все же, дополнительное знание формулы четверти дискриминанта не будет лишним.

Во-первых, с меньшими (по модулю) числами проще работать. Во-вторых, эта формула иногда ускоряет процесс нахождения корней уравнения.

   

   

   

   

Если находить корни через формулу обычного дискриминанта, придётся раскладывать его на множители, выносить множитель из-под корня, затем общий множитель — за скобки и сокращать дробь.

Ответ:

   

 

BioMath: квадратичные функции

В этом разделе мы узнаем, как найти корень (корень) квадратного уравнения. Корни также называются x -перехваты или нули. Квадратичная функция графически представлена ​​параболой с вершиной, расположенной в начале координат, ниже оси x или выше оси x . Следовательно, квадратичная функция может иметь один, два или нулевой корень.

Когда нас просят решить квадратное уравнение, нас действительно просят найти корни.Мы уже видели, что завершение квадрата — полезный метод решения квадратных уравнений. Этот метод можно использовать для вывода квадратной формулы, которая используется для решения квадратных уравнений. Фактически, корни функции

f ( x ) = ax ² + bx + c

даются по формуле корней квадратного уравнения. Корни функции — это перехваты x . По определению, координата y точек, лежащих на оси x , равна нулю.Следовательно, чтобы найти корни квадратичной функции, мы полагаем f ( x ) = 0 и решаем уравнение:

ax ² + bx + c = 0.

Мы можем сделать это, заполнив квадрат как,

Решая x и упрощая, получаем

Таким образом, корни квадратичной функции имеют вид,

Эта формула называется квадратной формулой , и ее вывод включен, чтобы вы могли видеть, откуда она взялась.Мы называем термин b ² −4 ac дискриминантом . Дискриминант важен, потому что он говорит вам, сколько корней имеет квадратичная функция. В частности, если

1. b 2 −4 ac <0 Настоящих корней нет. 2. b 2 −4 ac = 0 Существует один действительный корень. 3. b 2 −4 ac > 0 Есть два действительных корня.

Рассмотрим каждый случай индивидуально.

Случай 1: Нет настоящих корней

Если дискриминант квадратичной функции меньше нуля, эта функция не имеет действительных корней, а парабола, которую она представляет, не пересекает ось x . Поскольку квадратная формула требует извлечения квадратного корня из дискриминанта, отрицательный дискриминант создает проблему, потому что квадратный корень из отрицательного числа не определяется по действительной прямой.Пример квадратичной функции без действительных корней дается формулой

.

f ( x ) = x ² — 3 x + 4.

Обратите внимание, что дискриминант f ( x ) отрицательный,

b ² −4 ac = (−3) ² — 4 · 1 · 4 = 9 — 16 = −7.

Эта функция графически представлена ​​открывающейся вверх параболой, вершина которой лежит выше оси x.Таким образом, график никогда не может пересекать ось x и не имеет корней, как показано ниже,

Случай 2: Один настоящий корень

Если дискриминант квадратичной функции равен нулю, эта функция имеет ровно один действительный корень и пересекает ось x в одной точке. Чтобы увидеть это, мы установили b ² −4 ac = 0 в формулу корней квадратного уравнения, чтобы получить

Обратите внимание, что это координата x вершины параболы.Таким образом, парабола имеет ровно один действительный корень, когда вершина параболы лежит прямо на оси x . Простейший пример квадратичной функции, имеющей только один действительный корень, —

.

y = x ² ,

, где действительный корень равен x = 0.

Другой пример квадратичной функции с одним действительным корнем:

f ( x ) = −4 x ² + 12 x — 9.

Обратите внимание, что дискриминант f ( x ) равен нулю,

b ² −4 ac = (12) ² — 4 · −4 · −9 = 144 — 144 = 0.

Эта функция графически представлена ​​параболой, которая открывается вниз и имеет вершину (3/2, 0), лежащую на оси x . Таким образом, график пересекает ось x ровно в одной точке (т.е. имеет один корень), как показано ниже,

.

Случай 3: два настоящих корня

Если дискриминант квадратичной функции больше нуля, эта функция имеет два действительных корня ( x -перехвата).Извлечение квадратного корня из положительного действительного числа хорошо определено, и два корня равны,

Пример квадратичной функции с двумя действительными корнями:,

f ( x ) = 2 x ² -11 x + 5.

Обратите внимание, что дискриминант f ( x ) больше нуля,

b ² — 4 ac = (−11) ² — 4 · 2 · 5 = 121 — 40 = 81.

Эта функция графически представлена ​​открывающейся вверх параболой, вершина которой лежит ниже оси x . Таким образом, график должен пересекать ось x в двух местах (т.е. иметь два корня), как показано ниже,

*****

В следующем разделе мы будем использовать квадратную формулу для решения квадратных уравнений.

Решение квадратных уравнений

Квадратное уравнение, дискриминант, парабола

Квадратные уравнения выглядят так: ax ² + bx + c = 0
, где a, b, c — действительные числа, а a ≠ 0 (в противном случае это линейное уравнение).2 — 4ac}} {2a} $

Число D = b ² — 4ac называется «дискриминантом» . 2-32 $ $ y = 2 (x-3) (x + 5)

доллар
Y-перехват на
$ (0, -30)

$

вершина в
$ (- 1, -32) $ x-перехватывает на
$ (3, 0) $ и $ (- 5, 0) $

Парабола

График квадратного уравнения называется параболой .
Если a> 0, то его вершина указывает вниз:

Если a <0, то его вершина указывает вверх: Если a = 0, график не парабола, а прямая линия.

Вершина параболы равна $ x = — \ frac {b} {2a} $.

Формулы Виета

Если x ₁ и x ₂ являются корнями квадратного уравнения ax ² + bx + c = 0
затем:
$ x_1 + x_2 = — \ frac {b} {a} $
$ x_1x_2 = \ frac {c} {a} $
Эти формулы называются формулами Виета .
Мы можем найти корни x ₁ и x ₂ квадратного уравнения, решив совместные уравнения.

Задачи на квадратные уравнения

Задача 1. Решите уравнение:
x ² — 4 = 0
Решение: x ² — 4 = (x — 2) (x + 2)
(x — 2) (x + 2 ) = 0
x — 2 = 0 или x + 2 = 0
Корни равны x = 2 или x = -2

Решение 2:
a = 1, b = 0, c = -4
D = 0 ² — 4 ⋅ 1 ⋅ (-4) = 16
$ x_1 = \ frac {-b — \ sqrt {D}} {2a} = \ frac {- 0 — \ sqrt {16}} {2 \ cdot 1} = \ frac {-4} {2} = -2 $
$ x_2 = \ frac {-b + \ sqrt {D}} {2a } = \ frac {- 0 + \ sqrt {16}} {2 \ cdot 1} = \ frac {4} {2} = 2 $

---

Проблема 2. Решите уравнение:
3x ² + 4x + 5 = 0
Решение: дискриминант D = 4 ² — 4⋅3⋅5 = 16-60 = -44
Итак, квадратное уравнение не имеет реальных корней.

---

Задача 3. Решите уравнение:
x ² + 4x — 5 = 0; х =?
Решение: Дискриминант 4 ² — (-4⋅1⋅5) = 16 + 20 = 36> 0
Уравнение имеет 2 действительных корня: $ \ frac {-4 \ pm \ sqrt {36} } {2}
долларов США x = 1 или x = -5

---

Задача 4. Решите уравнение:
x ² + 4x + 4 = 0; х =?
Решение: Дискриминант 4 ² — (4⋅1⋅4) = 16-16 = 0
Итак, есть одно реальное решение: $ x = \ frac {-4} {2} $
x = -2

---

Задача 5. Решите уравнение:
x ² — 13x + 12 = 0
Корни: 1, 12

---

Задача 6. Решите уравнение:
8x ² — 30x + 7 = 0
Корни: 3.2 — 4ac}} {2a} $

Квадратные уравнения на математическом форуме

Задачи с квадратными уравнениями
Задачи по формулам Виета
Решение уравнений кубической и четвертой степени — 1

Форумы, посвященные квадратным уравнениям

Квадратные уравнения

Пример квадратного уравнения :

Функция создает красивые кривые, подобные этой:

Имя

Название Quadratic происходит от «quad», что означает квадрат, потому что переменная возводится в квадрат (например, x ² ).

Его также называют «уравнением степени 2» (из-за «2» на x )

Стандартная форма

Стандартная форма квадратного уравнения выглядит так:

• a , b и c — известные значения. не может быть 0.

• « x » — это переменная или неизвестно (мы еще не знаем).

Вот несколько примеров:

2x 2 + 5x + 3 = 0		В этом a = 2 , b = 5 и c = 3
x 2 — 3x = 0		Это немного сложнее: Где ? Ну a = 1 , так как мы обычно не пишем «1x 2 » b = −3 А где c ? Ну c = 0 , поэтому не показан.
5x — 3 = 0		Ой! Это , а не квадратное уравнение: оно отсутствует x 2 (другими словами a = 0 , что означает, что он не может быть квадратичным)

Поиграйте с этим

Поиграйте с «Проводником квадратного уравнения», чтобы увидеть:

• график функции и
• решений (называемых «корнями»).

Скрытые квадратные уравнения!

Как мы видели ранее, Стандартная форма квадратного уравнения — это

Но иногда квадратное уравнение так не выглядит!

Например:

Скрытый		в стандартной форме	a, b и c
x 2 = 3x — 1	Переместить все термины в левую часть	x 2 — 3x + 1 = 0	a = 1, b = −3, c = 1
2 (ширина 2 — 2w) = 5	Развернуть (снять скобки), и переместите 5 влево	2 Вт 2 — 4 Вт — 5 = 0	a = 2, b = −4, c = −5
z (z − 1) = 3	Разверните и переместите 3 влево	z 2 — z — 3 = 0	а = 1, b = −1, c = −3

Как их решить?

В « решениях » квадратного уравнения равно нулю .

Их также называют « корней », а иногда « нулей »

Обычно существует 2 решения (как показано на этом графике).

И есть несколько разных способов найти решения:

Или мы можем использовать специальную квадратичную формулу :

Просто введите значения a, b и c и выполняйте вычисления.

Сейчас мы рассмотрим этот метод более подробно.

О квадратичной формуле

Плюс / Минус

Прежде всего, что это за плюс / минус, который выглядит как ±?

± означает, что есть ДВА ответа:

x = −b + √ (b ² — 4ac) 2a

x = −b — √ (b ² — 4ac) 2a

Вот пример с двумя ответами:

Но не всегда так получается!

• Представьте, что кривая «просто касается» оси x.
• Или представьте, что кривая настолько высока , что даже не пересекает ось x!

Вот где нам помогает «Дискриминант» …

Дискриминант

Вы видите b ² — 4ac в приведенной выше формуле? Он называется дискриминантом , потому что он может «различать» возможные типы ответов:

• когда b ² — 4ac положительный, мы получаем два Реальных решения
• , когда он равен нулю, мы получаем только ОДНО реальное решение (оба ответа одинаковы)
• при отрицательном значении получаем пару Комплексных решений

Комплексные решения? Давайте поговорим о них после того, как мы увидим, как использовать формулу.

Использование квадратичной формулы

Просто введите значения a, b и c в квадратную формулу и выполните вычисления.

Пример: Решить 5x

² + 6x + 1 = 0

Коэффициенты: a = 5, b = 6, c = 1

Квадратичная формула: x =
−b ± √ (b ² — 4ac)
2a

Вставьте a, b и c: x =
−6 ± √ (6 ² — 4 × 5 × 1)
2 × 5

Решить: x =
−6 ± √ (36 ^{— 20)}
10

х =
−6 ± √ (16)
10

х =
−6 ± 4
10

х = -0.2 или -1

Ответ: x = −0,2 или x = −1

И мы их видим на этом графике.

Чек -0,2 :		5 × ( −0,2 ) 2 + 6 × ( −0,2 ) + 1 = 5 × (0,04) + 6 × (-0,2) + 1 = 0,2 — 1,2 + 1 = 0
Чек -1 :		5 × ( −1 ) 2 + 6 × ( −1 ) + 1 = 5 × (1) + 6 × (-1) + 1 = 5–6 + 1 = 0

Вспоминая формулу

Добрый читатель предложил спеть это к «Pop Goes the Weasel»:

♫	«x равно минус b		♫	«Вокруг тутового куста
	плюс или минус квадратный корень			Обезьяна погналась за лаской
	из квадрата b минус четыре a c			Обезьяна думала, что все было весело
	ВСЕ по двум a «			Поп! идет ласка »

Попробуйте спеть несколько раз, и она застрянет у вас в голове!

Или вы можете вспомнить эту историю:

х =
−b ± √ (b ² — 4ac)
2a

«Негативный мальчик думал, да или нет, о том, чтобы пойти на вечеринку,
на вечеринке он разговаривал с квадратным мальчиком, но не с четырьмя классными цыпочками.
В 2 часа ночи все было кончено. «

Комплексные решения?

Когда Дискриминант (значение b ² — 4ac ) отрицателен, мы получаем пару Комплексных решений … что это означает?

Это означает, что наш ответ будет включать мнимые числа. Ух ты!

Пример: Решить 5x

² + 2x + 1 = 0

Коэффициенты равны : a = 5, b = 2, c = 1

Обратите внимание, что дискриминант отрицательный: b ² — 4ac = 2 ² — 4 × 5 × 1
= −16

Используйте квадратичную формулу : x =
−2 ± √ (−16)
10

√ (−16)
= 4 i
(где i — мнимое число √ − 1)

Итак: x =
−2 ± 4 и
10

Ответ: x = −0.2 ± 0,4 и

График не пересекает ось абсцисс. Вот почему мы пришли к комплексным числам.

В некотором смысле это проще: нам не нужно больше вычислений, просто оставьте -0,2 ± 0,4 i .

Пример: Решить x

² — 4x + 6,25 = 0

Коэффициенты равны : a = 1, b = −4, c = 6,25

Обратите внимание, что дискриминант отрицательный: b ² — 4ac = (−4) ² — 4 × 1 × 6.25
= −9

Используйте квадратичную формулу : x = — (- 4) ± √ (−9) 2

√ (−9) = 3 i
(где i — мнимое число √ − 1)

Итак: x = 4 ± 3 i 2

Ответ: x = 2 ± 1,5 i

График не пересекает ось абсцисс.Вот почему мы пришли к комплексным числам.

НО перевернутое зеркальное отображение нашего уравнения действительно пересекает ось x в 2 ± 1,5 (примечание: отсутствует i ).

Просто интересный факт для вас!

Резюме

• Квадратное уравнение в стандартной форме: ax ² + bx + c = 0
• Квадратные уравнения могут быть разложены на множители
• Квадратичная формула: x =
  −b ± √ (b ² — 4ac)
  2a

• Когда Дискриминант ( b ² −4ac ) равен:
  • положительный, есть 2 реальных решения
  • ноль, есть одно реальное решение
  • отрицательный, есть 2 комплексных решения

Объяснение квадратичной формулы | Purplemath

Purplemath

Часто самый простой способ решить « ax ² + bx + c = 0» для значения x — это разложить на множители квадратичный коэффициент, установить каждый коэффициент равным нулю и затем решить каждый фактор.Но иногда квадратичная величина слишком беспорядочная, или она вообще не учитывается, или вам просто не хочется вводить множители. Хотя факторинг не всегда может быть успешным, квадратная формула всегда может найти решение.

Квадратичная формула использует « a », « b » и « c » из « ax ² + bx + c », где « a », » b «и» c «- это просто числа; они представляют собой «числовые коэффициенты» квадратного уравнения, которые они дали вам решить.

MathHelp.com

Квадратичная формула выводится из процесса завершения квадрата и формально обозначается как:

Квадратичная формула: для ax ² + bx + c = 0, значения x , которые являются решениями уравнения, даются как:

Чтобы квадратичная формула работала, ваше уравнение должно иметь форму «(квадратичная) = 0».Кроме того, «2 a » в знаменателе Формулы находится под всем, что указано выше, а не только под квадратным корнем. И внизу это «2 a «, а не просто «2». Убедитесь, что вы осторожны, чтобы не уронить квадратный корень или «плюс / минус» в середине ваших вычислений, иначе я могу гарантировать, что вы забудете «вставить их обратно» в свой тест, и вы запутаетесь себя вверх. Помните, что « b ² » означает «квадрат ВСЕГО из b , включая его знак», поэтому не оставляйте b ² отрицательным, даже если b отрицательно, потому что квадрат негатива — это позитив.

Другими словами, не будьте небрежны и не пытайтесь сокращать путь, потому что это только навредит вам в долгосрочной перспективе. Поверьте мне в этом!

Вот несколько примеров того, как работает квадратичная формула:

Это квадратичное значение множителя:

x ² + 3 x — 4 = ( x + 4) ( x — 1) = 0

… поэтому я уже знаю, что решения: x = –4 и x = 1. Как мое решение будет выглядеть в квадратичной формуле? Используя a = 1, b = 3 и c = –4, мое решение выглядит так:

Тогда, как и ожидалось, решение будет x = –4, x = 1.

---

Предположим, у вас есть ax ² + bx + c = y , и вам предлагается вставить ноль для y .Соответствующие значения x являются интерцепциями x на графике. Таким образом, решение ax ² + bx + c = 0 для x означает, среди прочего, что вы пытаетесь найти x -перехватывания. Поскольку было два решения для x ² + 3 x — 4 = 0, тогда на графике должно быть два интерцепта x . Построив график, мы получим кривую ниже:

Как вы можете видеть, точки пересечения x (красные точки выше) соответствуют решениям, пересекая ось x на
x = –4 и x = 1.Это показывает связь между построением графиков и решением: когда вы решаете «(квадратичный) = 0», вы обнаруживаете пересечение графика x . Это может быть полезно, если у вас есть графический калькулятор, потому что вы можете использовать квадратичную формулу (при необходимости) для решения квадратичной, а затем использовать свой графический калькулятор, чтобы убедиться, что отображаемые интервалы x имеют те же десятичные значения, что и делать решения, предоставляемые квадратной формулой.

Обратите внимание, однако, что отображение графика калькулятором, вероятно, будет иметь некоторую ошибку округления, связанную с пикселями, поэтому вы должны проверить, были ли вычисленные и нанесенные на график значения достаточно близкими; не ожидайте точного совпадения.

---

• Решите 2

  x ² — 4 x — 3 = 0. При необходимости округлите ответ до двух десятичных знаков.

Нет множителей при (2) (- 3) = –6, которые в сумме дают –4, поэтому я знаю, что эту квадратичную нельзя разложить на множители. Я буду применять квадратичную формулу. В этом случае a = 2, b = –4 и c = –3:

.

Тогда ответ будет x = –0.58, x = 2,58 с округлением до двух десятичных знаков.

Предупреждение: «Решение», «корни» или «нули» квадратичной функции обычно должны быть в «точной» форме ответа. В приведенном выше примере точная форма — это квадратный корень из десяти. Вам нужно будет получить аппроксимацию калькулятора, чтобы построить график пересечений по оси x или упростить окончательный ответ в текстовой задаче. Но если у вас нет веских оснований полагать, что ответ должен быть округленным, всегда используйте точную форму.

Сравните решения 2 x ² — 4 x — 3 = 0 с интерцепциями x на графике:

Как и в предыдущем примере, перехваты x совпадают с нулями из квадратичной формулы. Это всегда правда. «Решениями» уравнения являются также точки пересечения x соответствующего графика.

---

URL: https: // www.2} + bx + c, нам нужно, чтобы y = 0. Это означает, что у нас

ax ² + bx + c = 0

Отсюда я собираюсь применить обычные шаги, связанные с завершением квадрата, чтобы прийти к квадратной формуле.

---

Шаги по выводу квадратичной формулы

Вывести формулу корней квадратного уравнения просто! Вот так. 2} + bx + c, где a, b и c — действительные числа, но a \ ne 0.

• Шаг 2: Переместите константу \ color {red} c в правую часть уравнения, вычтя обе части на \ color {red} c.

• Шаг 3: Разделите все уравнение на коэффициент при квадрате члена, который равен \ large {a}.

• Шаг 4: Теперь определите коэффициент линейного члена \ large {x}.

• Шаг 5: Разделите его на 2 и возведите в 2-ю степень. Затем упростите его.

• Шаг 6: Добавьте результат шага 5 к обеим сторонам уравнения.

• Шаг 7: Упростите правую часть уравнения. Будьте осторожны, складывая дроби с разными знаменателями. Убедитесь, что вы нашли правильный наименьший общий знаменатель (ЖКД) при выполнении сложения.

• Шаг 8: Выразите трехчлен в левой части уравнения как квадрат бинома.

• Шаг 9: Извлеките квадратный корень из обеих частей уравнения, чтобы исключить показатель степени 2 бинома.

• Шаг 10: Упростить. Убедитесь, что вы добавили \ color {red} \ pm с правой стороны уравнения. В левой части больше нет силы 2.

• Шаг 11: Сохраните переменную x слева, вычтя обе части на \ Large {b \ over {2a}}.

• Шаг 12: Упростите, и готово!

Я надеюсь, что вы найдете пошаговое решение полезным в выяснении того, как квадратная формула выводится с использованием метода завершения квадрата.

---

Вас может заинтересовать:

Квадратичная формула

Дискриминанты и определение числа действительных корней квадратного уравнения

Что такое дискриминант?

Дискриминант — это величина, вычисляемая по квадратному уравнению. Он использует его, чтобы «различать» корни (или решения) квадратного уравнения.

Квадратное уравнение имеет вид: ax ² + bx + c

Дискриминант, D = b ² — 4ac

Примечание. Это выражение внутри квадратного корня квадратной формулы

.

Дискриминант бывает в трех случаях;

Корпус 1:

b ² — 4ac> 0

Если дискриминант больше нуля, это означает, что квадратное уравнение имеет два действительных, различных корня (разных) .

Пример

х ² — 5x + 2 = 0

а = 1, б = -5, в = 2

Дискриминант, D = b ² — 4ac

= (-5) ² — 4 * (1) * (2)

= 17

Следовательно, квадратное уравнение

имеет два действительных различных корня.

х ² — 5х + 2.

Корпус 2:

b ² — 4ac <0

Если дискриминант больше нуля, это означает, что квадратное уравнение не имеет действительных корней .

Пример

3x ² + 2x + 1 = 0

а = 3, б = 2, с = 1

Дискриминант, D = b ² — 4ac

= (2) ^{2 —} 4 * (3) * (1)

= — 8

Следовательно, у квадратного уравнения 3x ² + 2x + 1 нет действительных корней.

Корпус 3:

b ² — 4ac = 0

Если дискриминант равен нулю, это означает, что квадратное уравнение имеет два действительных идентичных корня .

Пример

х ² + 2х + 1 = 0

а = 1, б = 2, с = 1

Дискриминант, D = b ² — 4ac

= (2) ² -4 * (1) * (1)

= 0

Следовательно, есть два действительных идентичных корня квадратного уравнения x ² + 2x + 1.

Сводка

Квадратное уравнение: ax ² + bx + c

Определитель D = b ² — 4ac

D> 0 означает два реальных, различных корня.

D = 0 означает два настоящих одинаковых корня /

D <0 означает отсутствие реальных корней.

Теперь попробуйте эти (будьте осторожны со знаками минус)

Вопросы

Q1.х ² — 7x + 2 = 0

Q2. — 3x ² + 2x — 1 = 0

Q3. 9x ² — 12x + 4 = 0

Q4. — х ² + х + 1 = 0

ответы

Q1. D = 41 означает два реальных, различных корня.

Q2. D = -16 означает отсутствие настоящих корней.

Q3. D = 0 означает два настоящих одинаковых корня.

Q4. D = 5 означает два реальных, различных корня.

Как использовать квадратичную формулу для поиска корней уравнений — Видео и стенограмма урока

Квадратичная формула

Квадратичная формула — это формула, которую мы можем использовать для нахождения корней квадратного уравнения a x 2 + b x + c = 0.

Чтобы использовать квадратную формулу для нахождения корней квадратного уравнения, все, что нам нужно сделать, это получить квадратное уравнение в форме a x 2 + b x + c = 0; идентифицировать a , b и c ; а затем подключите их к формуле. Чтобы идентифицировать эти значения, мы просто помним, что a находится перед x 2, b находится перед x , а c — это само по себе число.

Например, в нашем уравнении — x 2 + 4 x + 5 = 0, число перед x 2 равно -1, поэтому a = -1. Число перед x равно 4, поэтому b = 4. Наконец, само число 5, поэтому c = 5. Мы почти у цели! Все, что нам нужно сделать, это подставить эти значения в нашу формулу корней квадратного уравнения, и тогда мы сможем найти значения x , которые делают наше уравнение истинным. Тогда мы узнаем, сколько времени нужно, чтобы мяч коснулся земли.Приступим к подключению!

Мы видим, что шар находится на высоте 0, когда x = -1 и когда x = 5. В нашем случае мы можем игнорировать x = -1. Хотя верно, что x = -1 является корнем уравнения, мы знаем, что x представляет время, и у нас не может быть -1 секунды. Единственная причина, по которой это выглядит таким образом, заключается в том, что, когда мы изначально бросали мяч на 0 секунде, мы находились на высоте 5 футов над землей.

Поскольку мы отказались от ответа x = -1, остается x = 5 как решение нашей конкретной проблемы. Это говорит нам о том, что мяч ударился о землю через 5 секунд после того, как мы его бросили, поэтому он находился в воздухе 5 секунд. Разве это не здорово, что мы могли это выяснить, используя нашу формулу корней квадратного уравнения?

Другой пример

Рассмотрим еще один пример. Допустим, мы делаем каркасную поделку. На основе имеющихся у нас материалов площадь рамы может быть представлена ​​уравнением A = x 2 + 2 x , где A — это площадь рамы, а x — это площадь рамы. ширина рамки.Мы хотим, чтобы наша область была 24 на 2, поэтому нам просто нужно найти ширину, которая делает это так.

Для этого мы подставляем 24 для A , чтобы получить

x 2 + 2 x = 24

Мы вычитаем 24 с обеих сторон, чтобы получить уравнение в правильной форме:

x 2 + 2 x — 24 = 0

Теперь мы хотим идентифицировать a , b и c на основе чисел перед x 2, x и отдельно , соответственно.Таким образом, мы имеем a = 1, b = 2 и c = -24. Все, что нам нужно сделать сейчас, это вставить их в нашу квадратную формулу:

Мы видим, что ширина равна 4 или -6.