Содержание
Урок 71. десятичные дроби. занимательные задачи — Математика — 6 класс
Математика
6 класс
Урок № 71
Десятичные дроби. Занимательные задачи
Перечень рассматриваемых вопросов:
– десятичные дроби, проценты;
– текстовые задачи, логические задачи.
Тезаурус
Округление десятичной дроби – замена десятичной дроби приближённым значением с меньшим количеством значащих цифр.
Десятичная дробь – это дробь, записанная в десятичной форме.
Процент – сотая часть величины.
Список литературы
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
В жизни нам часто приходится решать задачи, требующие не только умения правильно выполнять арифметические действия, но и умения логически мыслить, выстраивать цепочку рассуждений, делать правильные выводы. Чтобы развить эти важные качества мышления, и дети, и взрослые решают специальные логические задачи. Рассмотрим некоторые из них.
Задача
Весы находятся в равновесии. С левой стороны на весах лежат три груши и одно яблоко. С правой стороны –гиря 20г, две груши и два яблока. Определите массу одного яблока, если известно, что все фрукты вместе весят 740 г.
Решение
Так как весы находятся в равновесии, составим равенство.
Г + Г + Г + Я = 20 + Г + Г + Я + Я
Справа и слева вычеркнем одинаковые компоненты, так как их масса одинакова.
Г + Г + Г + Я = 20 + Г + Г + Я + Я
Получим, что масса груши равна массе яблока и ещё 20 граммам, то есть масса груши на 20 граммов больше массы яблока.
Г = 20 + Я
Так как масса всех фруктов 740 граммов, составим равенство, в котором сложим массы всех фруктов, заменив грушу на полученное выражение. Груш у нас всего 5 штук, а яблок 3.
5 · (20 + Я) + 3 · Я = 740
Раскроем скобки.
100 + 5Я + 3Я = 740
Приведём подобные слагаемые и решим уравнение.
100 + 8Я = 740
8Я = 740 – 100
8Я = 640
Я = 640 : 8
Я = 80
Получим, что яблоко весит 80 граммов.
Ответ: 80 г.
Задача
5 сомов весят на 10 кг больше восьми налимов. Но при этом пять сомов весят на 20 кг меньше десяти налимов. Сколько весит один сом и один налим?
Решение
Пусть С – масса сома (в кг), Н – масса налима (в кг)
Запишем условие задачи в виде двух равенств.
5С – 10 = 8Н
5С + 20 = 10Н
Выразим массу пяти сомов из первого и второго равенств.
5С = 8Н + 10
5С = 10Н – 20
Приравняем правые части.
8Н + 10 = 10Н – 20
30 = 2Н
30 : 2 = 15 (кг) – масса налима.
Подставим массу налима в любое из верхних равенств.
5С – 10 = 8 · 15
5С – 10 = 120
5С = 120 + 10
5С = 130
С = 130 : 5
С = 26
Ответ: налим весит 15 кг, сом весит 26 кг.
Задача
Дыня весила 15 кг. В ней содержалось 90 % воды. Через несколько дней она усохла, и содержание воды снизилось до 84 %. Сколько теперь весит дыня?
Если первоначально в дыне содержалось 90 процентов воды, значит сухого вещества было 10 процентов.
100 % – 90 % = 10 % – сухого вещества в дыне.
Найдём, сколько это в килограммах.
10 % = 0,1
15 кг · 0,1 = 1,5 кг – сухого вещества в дыне.
После того, как дыня усохла, сухое вещество стало составлять 16 процентов.
100 % – 84 % = 16 %
То есть полтора килограмма это 16 процентов.
1,5 кг = 16 %
Найдём массу дыни после усушки.
16 % = 0,16
1,5 кг : 0,16 = 9,375 кг
Ответ: дыня теперь весит 9,375 кг.
Задача
Бегемотик за весну похудел на 30 %, потом поправился за лето на 20 %, за осень опять похудел на 20 % и за зиму его вес увеличился на 30%. Похудел или поправился бегемотик за год? На сколько процентов изменился его вес?
Похудел или поправился бегемотик за год? На сколько процентов изменился его вес?
Решение
Поскольку нет информации об изменениях веса бегемотика в килограммах, а речь идёт только о процентах, то первоначальный вес бегемотика можно принять за любое удобное для вычислений количество килограммов.
Пусть первоначальный вес бегемотика 100 килограммов.
Найдём, как изменился его вес весной.
30 % = 0,3
100 · 0,3 = 30 (кг) – изменение веса.
100 – 30 = 70 (кг) – стал весить бегемотик после весны.
Теперь рассмотрим изменения за лето. 20 % будем высчитывать от новой массы.
20 % = 0,2
70 · 0,2 = 14 (кг) – изменение веса.
70 + 14 = 84 (кг) – стал весить бегемотик после лета.
Рассмотрим изменения в следующем периоде, осенью. Известно, что бегемотик похудел на 20 %.
84 · 0,2 = 16,8 (кг) – изменение веса.
84 – 16,8 = 67,2 (кг) – стал весить после осени.
И, наконец, последнее изменение веса – прибавил 30 %.
67,2 · 0,3 = 20,16 (кг) – изменение веса.
67,2 + 20,16 = 87,36 (кг) – стал весить бегемотик.
На первый вопрос задачи мы уже можем ответить –бегемотик похудел.
Чтобы ответить на второй вопрос, нужно сначала найти, на сколько килограммов похудел бегемотик.
100 – 87,36 = 12,64 (кг) – разница в весе.
Теперь найдём, сколько процентов это составляет от первоначальной массы бегемотика.
12,64 кг : 100 кг · 100 % = 12,64 %
Таким образом, мы определили, на сколько процентов изменился вес бегемотика.
Ответ: бегемотик похудел на 12,64 %
Разбор заданий тренировочного модуля
Тип 1. Зачёркивание элементов
Выберите и зачеркните неверные ответы из предложенных.
450
445
420
На коробке с мукой написано: «Масса нетто 400 г при влажности 11 %». Какова масса муки, если она хранится при влажности 20 %?
Решение
При влажности 11 % сухой продукт составляет
100 % – 11 % = 89 % = 0,89
Таким образом, масса сухого продукта
400 · 0,89 = 356 (г).
При влажности 20 % на сухой продукт остаётся
100 % – 20 % = 80 % = 0,8
При увеличении влажности воздуха масса сухого остатка не изменится, но теперь она составляет не 0,89, а 0,8 массы коробки с мукой. Пусть x – масса коробки с мукой при влажности 20 %. Составим пропорцию:
356 : x = 0,8 : 1.
Решим пропорцию.
Получаем:
x = 356 : 0,8,
x = 445.
Ответ: 450; 445; 420
Тит 2. Ввод с клавиатуры пропущенных элементов в тексте
Впишите соответствующее число.
Если производительность труда повысится на 60 %, то время выполнения задания уменьшится на … %.
Решение. Пусть за 1 единицу времени делали 100 деталей. Тогда при увеличении производительности на 60 % за 1 единицу времени будут делать 160 деталей.
Пусть x – это время, за которое будут делать 100 деталей при новой производительности.
1 ед. времени – 160 дет.
x ед. времени – 100 дет.
Зависимость между количеством изготовленных деталей и временем на их изготовление – прямая пропорциональная (чем больше количество деталей, тем больше время на их изготовление).
Составим пропорцию:
Решим пропорцию:
1 · 100 = x · 160;
x = 1 · 100 : 160;
x = 0,625.
Выразим десятичную дробь в процентах:
0,625 = 62,5 %.
То есть время изготовления 100 деталей при новой производительности труда – это 62,5 % от первоначального. Нам нужно узнать, на сколько процентов уменьшилось время выполнения задания.
Получаем:
100 % – 62,5 % = 37,5 %.
Ответ: время выполнения задания уменьшится на 37,5 %.
Поиск
Поиск
-
Школьный помощник- математика 5 класс
- математика 6 класс
- алгебра 7 класс
- алгебра 8 класс
- геометрия 7 класс
- русский язык 5 класс
- русский язык 6 класс
- русский язык 7 класс
- математика
- алгебра
- геометрия
- русский язык
«»
следующая
предыдущая
вернуться на предыдущую страницу
Такой страницы нет !!!
- Популярные запросы
- Обстоятельство
- Дополнение
- Определение
- Деление дробей
- Математика 6 класс
- Русский язык 6 класс
- Алгебра 8 класс
- Математика 5 класс
- Русский язык 5 класс
- Русский язык 7 класс
- Алгебра 7 класс
- Наименьшее общее кратное
- Наибольший общий делитель.
 Взаимно простые числа
Взаимно простые числа - Деление и дроби
- Доли. Обыкновенные дроби
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Квадратный корень из неотрицательного числа
- Окружность и круг
- Антонимы. Синонимы
- Десятичная запись дробных чисел
- Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)
6 класс — деление дробей, применение деления дробей при решении задач
Дата публикации: .
Деление дробей
1. Решите примеры.
| а) 6⁄24 : 1⁄6 = | б) 51⁄8 : 3⁄7 = | в) 2⁄5 : 5(2⁄6 — 1,7) = |
| г) 17⁄12 : 42⁄9 = | д) 48⁄15 : 22⁄3 = | е) 23⁄5 : (5⁄9 + 5,3) = |
2. Решите задачу.
Решите задачу.
Мама купила на рынке рис по цене 22⁄5 рубля за килограмм. Сколько кг риса купила мама, если сумма покупки составила 7 1⁄5 рубля?
3. Решите задачу.
На ремонт дорожки в саду потратили 102⁄4 кг цемента, причем для ремонта каждого метра дорожки потратили 6⁄4 кг цемента. Сколько метров дорожки отремонтировали?
4. Выполните действия.
| а) 14 — 8⁄9 : 4 + 3⁄8 : 3 = | б) 3 1⁄5 : 8⁄5 — 2,5 = |
| в) 13 2⁄3 : 2 — 5 4⁄5 : 4 = | г) 3⁄7 : 1⁄6 = |
5. Решите задачу.
Площадь прямоугольника равна 4 3⁄4 квадратных метра, а одна сторона равна 1 1⁄4 метра. Чему равна вторая сторона прямоугольника?
6.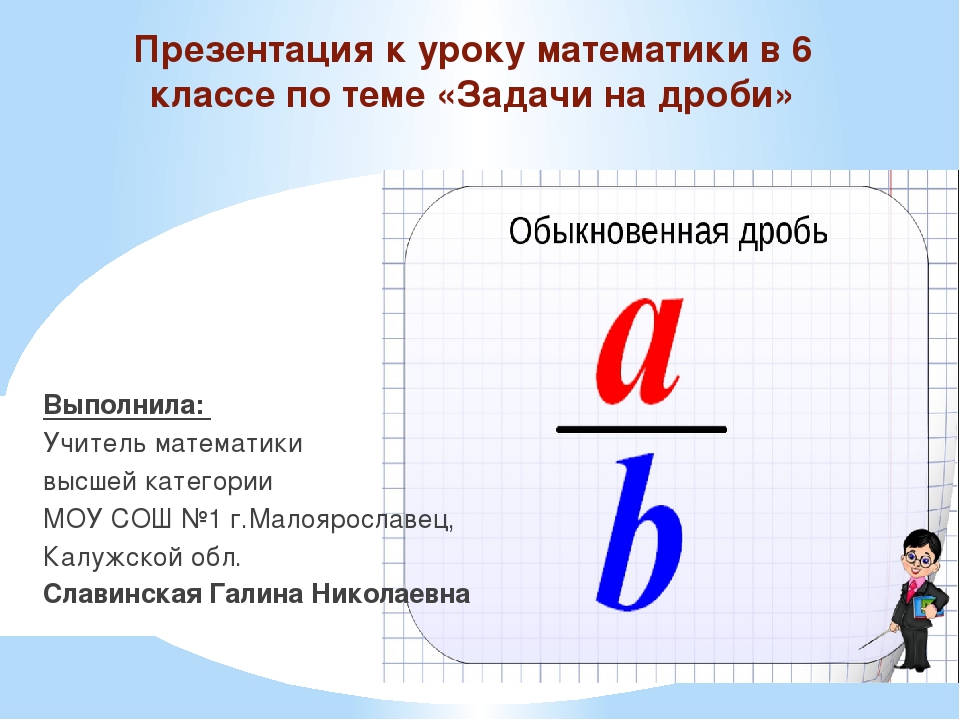 Решите задачу.
Решите задачу.
Если задуманное число умножить на 9⁄14, то получим 7⁄3. Какое число задумали?
7. Решите задачу.
Грибники нашли в лесу 128 гриба. Первый грибник нашел в 12⁄7 раза больше грибов, чем второй. Сколько грибов нашел каждый?
Нахождение числа по его дроби
1. Решите задачу.
1⁄8 часть урожая яблок весит 30 кг. Сколько вести весь урожай?
2. Решите задачу.
Бегун пробежал 3000 метров, что составляет 3⁄5 дистанции. Какова длина дистанции?
3. Определите, чему равен х, если:
a) 2⁄5 от х равно 800.
б) 4⁄9 от х равно 1200.
Задачи на дроби для 6 класса
Просмотр содержимого документа
«Задачи на дроби для 6 класса»
В столовую
На рынок
№ 528. С бахчи собрали 27 т арбузов.
С бахчи собрали 27 т арбузов.
В столовую направили этих
арбузов, а остатка отвезли
на рынок. Сколько тонн арбузов
отвезли на рынок ?
отвезли на рынок ?
Математика 6 класс. Н.Я.Виленкин. № 512.
РЕШЕНИЕ:
ВЕРНОЕ РЕШЕНИЕ:
За три дня на элеватор доставили 651 т зерна.
В первый день было доставлено
всего зерна .
Во второй 0,9 того, что было доставлено в первый день.
№ 514 . Математика 6 класс. Н.Я.Виленкин.
?
Сколько тонн зерна было доставлено на элеватор в третий день?
РЕШЕНИЕ:
ВЕРНОЕ РЕШЕНИЕ:
ЗАДАЧА
ДРОБЬ
УМНОЖЕНИЕ
ЧИСЛО
- ЗАДАЧА
- ДРОБЬ
- ЧИСЛО
- УМНОЖЕНИЕ
ЦЕЛЬ УРОКА:
- упражняться в нахождении числа от дроби, умножении и сокращении дробей
Куплено 15 кг яблок на приготовление варенья
израсходовали купленных яблок.
Сколько килограммов яблок было израсходовано на
варенье?
Сколько килограммов яблок осталось?
Математика 6 класс. Н.Я.Виленкин. № 543.
В баке автомобиля 60 л бензина. За день
было израсходовано 25 % этого бензина.
Сколько бензина израсходовали?
Сколько бензина осталось в баке?
Математика 6 класс. Н.Я.Виленкин. № 544.
60л
18
Сварили уху
поджарили
После удачной рыбалки Костя принес домой 1,4 кг рыбы.
Из этой рыбы сварили уху, а 80 % оставшейся –
поджарили.
Сколько рыбы поджарили?
1,4 кг
Математика 6 класс. Н.Я.Виленкин. № 557.
18
ФИЗКУЛЬТМИНУТКА
Съели в 1 раз
Съели на обед
Мама купила 800 г сыра. За столом съели всего сыра,
за обедом – , а остальной сыр съели за
ужином.
Сколько сыра
съели за ужином?
800 г
Математика 5 класс (часть 2). Г.В. Дорофеев, Л.Г. Петерсон. № 677.
21
6 класс, умножение дробей, применение умножения дробей при решении задач
Дата публикации: .
Умножение дробей
1. Решите примеры.
| а) 3⁄10 * 1⁄6 = | б) 32⁄9 * 3⁄7 = | в) 2⁄3 * 5 * (2⁄6 — 1,7) = |
| г) 17⁄10 * 42⁄5 = | д) 36⁄13 * 22⁄7 = | е) 27⁄8 * 1 * ( 5⁄7 + 5,3 ) = |
2. Решите задачу.
Решите задачу.
В магазине Саша купила 3 кг мандарин по цене 43⁄5 рубля за кг. Сколько денег потратила Саша?
3. Решите задачу.
Маляр красил коридор в больнице. На каждый метр он расходовал 24⁄8 литра краски. Сколько литров краски ему понадобилось, если длина коридора равна 12 метрам?
4. Найдите значения выражений.
| а) 5 — 1 9⁄12 * 4 + 3⁄6 * 3 = | б) 2 2⁄7 * 3 7⁄8 — 2,5 = |
| г) 13 1⁄7 * 2 — 4 3⁄8 * 4 = | д) 3⁄8 * 1⁄4 = |
5. Решите задачу.
Одна сторона прямоугольника равна 3⁄8 метра, а вторя сторона – 15⁄7 метра. Найдите площадь прямоугольника.
6. Решите задачу.
Одна сторона прямоугольника равна 5⁄9 см, а вторя сторона – длиннее первой в 2 раза. Найдите площадь прямоугольника.
Найдите площадь прямоугольника.
7. Решите задачу.
Сторона куба равна 37⁄12 метра. Чему равен объем куба?
8. Решите задачу.
Из города одновременно в одном направлении выехали 3 автомобиля. Скорость первого автомобиля – 40 5⁄6 км/ч, скорость второго автомобиля в 1,5 раза меньше, чем скорость первого автомобиля. А скорость третьего автомобиля – на 10 5⁄20 км/ч больше, чем скорость первого автомобиля. Найдите расстояние между автомобилями через 2 часа и через 4 часа после выезда из города.
9. Решите задачу.
Из двух сел одновременно навстречу друг другу вышли два пешехода. Скорость первого пешехода – 4 2⁄5 км/ч, а скорость второго – на 5⁄9 км/ч. Каково расстояние между селами, если они встретились через 2 часа?
10. Решите задачу.
Грузовая машина весит 12 т, легковая машина – 1⁄8 от массы грузовика. Сколько весят 8 легковых автомобилей?
11. Решите задачу.
Решите задачу.
На тарелке лежало 64 конфеты. Коля съел 2⁄8 части конфет, а Миша – 1⁄12 часть. Сколько конфет съели ребята?
12. Определите.
| а) 3⁄10 от 5; | б) 2⁄9 от 8⁄18; | в) 2⁄3 от 4 3⁄8; |
| г) 40% от 21⁄5; | д) 70% от 15 2⁄9; | е) 0, 60 от 3 * (2⁄7 + 5,3). |
Конспект урока для 6 класса «Две основные задачи на дроби»
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 8»
Методическая разработка урока математики
«Две основные задачи на дроби»
для учащихся 6-го класса
Тип урока: урок изучения нового материала.
Автор разработки
учитель математики МБОУ «СОШ №8»
Шарыпова Татьяна Викторовна
г.Ханты — Мансийск
2015 год
Использованный тип урока позволяет активизировать процесс обучения, реализовать идеи развивающего обучения, повысить темп урока, увеличить объем самостоятельной работы учащихся.
Цели урока:
Образовательные: создать условия для формирования умения правильно понимать задачу, определять её тип , добиться усвоения материала, его понимания и умения пользоваться им при решении задач, ввести правило нахождения числа по его дроби и показать его применение при решении задач; повторить правила нахождения дроби от числа, умножения дробей, деления дробей, перевода процентов в десятичную дробь;
Развивающие: продолжить формирование математических знаний и приемов умственной деятельности (умение анализировать ситуацию и ориентироваться в действиях, научиться выполнять новое действие, довести его до автоматизации). Формировать элементы математической логики, развивать математическую речь учащихся.
Формировать элементы математической логики, развивать математическую речь учащихся.
Воспитательные: формировать навыки пошаговой работы под руководством учителя (объяснение нового материала, первоначальное закрепление), восприятия информации на слух (математический диктант), формирования самооценки (рефлексия), воспитывать уважение к мнению товарища и умение его выслушать;
Задачи урока:
٭ закрепить и проконтролировать умение решать задачи на вычисление процента от числа; (I тип задач)
٭ закрепить алгоритм решения задач на нахождение числа по его проценту; (II тип задач)
٭развивать навык устного счета;
٭ формировать владения интеллектуальными умениями и мыслительными операциями;
٭воспитывать чувства долга и ответственности за результат собственной деятельности;
Ожидаемый результат: решают задачи с процентами; знают два основных типа задач на проценты.
Репродуктивный уровень: грамотное оформление решений задач. Конструктивный уровень: уметь применять правила при решении задач с процентами.
Конструктивный уровень: уметь применять правила при решении задач с процентами.
Творческий уровень: уметь применять при решении задач с процентами (усложненных) основные формулы и составляя логические схемы и выбирать более простой способ решения.
Средства обучения:
интерактивная доска, учебник, тетрадь;
карточки с заданиями для закрепления материала.
Структура урока:
Мотивационная беседа с последующей постановкой цели.
Актуализация опорных знаний – устная работа, с помощью которой ведется повторение основных фактов, ведущих идей и основных теорий на основе систематизации знаний.
Объяснение нового материала
Диагностика усвоения системы знаний и умений и ее применение для выполнения практических заданий стандартного уровня с переходом на более высокий уровень.

Подведение итогов урока.
Творческое домашнее задание.
Ход урока
Мотивационная беседа.
Учитель. Как вы думаете, зачем надо изучать математику? Ответ на этот вопрос вы найдете, если узнаете, что означает в переводе с греческого слово «математика». «Математика» – знание, наука. Именно поэтому, если человек был сведущ в математике, то это всегда означало высшую ступень учености. А умение правильно видеть и слышать – первый шаг к мудрости. Хочется, чтобы сегодня все ученики вашего класса показали, насколько они мудры и насколько сведущие люди в решении задач. Итак, тема «Две основные задачи на дроби», запишите в тетрадь число и тему урока.
Актуализация опорных знаний.
Работа по слайдовой презентации.
Изучение нового материала.
На слайде показывается два типа задач. Определите тип каждой задачи. Как решить первую задачу? Как решить вторую задачу?
Показывается слайд с решением каждой задачи.
Учитель: Сформулируйте правило нахождение части от целого и целого по его части. На слайде появляются правила.
( Чтобы решить первую задачу надо целое умножить на дробь. Чтобы решить вторую задачу надо число разделить на дробь.)
Учитель: Вспомните, что называется процентом?
Как перевести процент в десятичную дробь?
Как перевести десятичную дробь в процент?
(Процент- это сотая часть любой величины.
Чтобы перевести процент в десятичную дробь, надо процент разделить на сто.
Надо десятичную дробь умножить на сто.)
На доске записаны задания.
а) Замените проценты десятичной дробью.
6%, 33%,1,7%,113%, 96%.
б) Замените десятичную дробь процентами.
0,019, 0,44, 8,5, 2,02, 0,007.
Закрепление нового материала.
Задача № 626 ( один ученик работает у доски)
Учитель: Что мы примем за 100%? Известна ли эта величина?
К какому типу задач относится данная задача?
Сможем ли мы сразу ответить на вопрос задачи?
Как найти, сколько литров бензина было израсходовано за неделю?
Как найти, сколько литров бензина осталось?
Попробуем найти другой способ решения.
Как найти, сколько процентов осталось израсходовать?
Как найти, сколько литров бензина осталось?
Учитель: А теперь подумайте, как изменить вопрос задачи, чтобы она решалась в одно действие?
А как надо изменить условие задачи, чтобы она решалась в одно действие.
Итог урока.
Учитель: Какие типы задач на проценты мы сегодня рассмотрели?
Что нового сегодня узнали на уроке?
Сформулируйте правило нахождение процента от числа и числа по известному проценту.
6.Домашнее задание.
Самоанализ урока математики в 6 классе.
Урок математики был проведен в 6 В классе 3.02.15. Класс к уроку готов и учащиеся быстро включились в учебную деятельность. Взаимоотношения между учащимися ровные, спокойные, дружественные. Ребята данного класса владеют диалогической формой общения, умеют слышать и слушать другого.
Урок проводился согласно тематического планирования. Тема урока « Две основные задачи на дроби». По программе запланировано 3 часа, а данный урок был первым по счету. Урок проведен с использованием ИКТ.
По основному способу проведения — фронтальная и индивидуальная работа через различные виды деятельности, личностно-ориентированный подход.
Цели урока:
Образовательные: создать условия для формирования умения правильно понимать задачу, определять её тип ,добиться усвоения материала, его понимания и умения пользоваться им при решении задач, ввести правило нахождения числа по его дроби и показать его применение при решении задач; повторить правила нахождения дроби от числа, умножения дробей, деления дробей, перевода процентов в десятичную дробь;
Развивающие: продолжить формирование математических знаний и приемов умственной деятельности (умение анализировать ситуацию и ориентироваться в действиях, научиться выполнять новое действие, довести его до автоматизации). Формировать элементы математической логики, развивать математическую речь учащихся.
Формировать элементы математической логики, развивать математическую речь учащихся.
Воспитательные: формировать навыки пошаговой работы под руководством учителя (объяснение нового материала, первоначальное закрепление), восприятия информации на слух (математический диктант), формирования самооценки (рефлексия), воспитывать уважение к мнению товарища и умение его выслушать;
В ходе урока реализовала следующие задачи:
٭ закрепить и проконтролировать умение решать задачи на вычисление процента от числа; (I тип задач)
٭ закрепить алгоритм решения задач на нахождение числа по его проценту; (II тип задач)
٭развивать навык устного счета;
٭ формирование владения интеллектуальными умениями и мыслительными операциями;
٭воспитывать чувства долга и ответственности за результат собственной деятельности;
Все этапы урока были направлены на выполнение цели и задач с учетом индивидуальных особенностей ребенка.
1. Организационный момент включал в себя организацию класса, мобилизующее начало урока, создание психологической комфортности и подготовку уч-ся к активной учебной деятельности.
2.Для снятия стрессообразующих факторов учебного процесса, создание на уроке атмосферы доброжелательности.
3. Целью устного счета являлась систематизация знаний по изученным темам и отработка вычислительных навыков.
4. На рефлексивном оценочном этапе удалось вовлечь уч-ся в процесс активного взаимодействия по изученному материалу.
5.Для снятия напряжения и усталости была предложена гимнастика для глаз.
6. На этапе рефлексии уч-ся проанализировали урок: что получилось, что нужно доработать. Дети высказывали свое мнение используя слова помощники, которые способствуют развитию правильной математической речи, оценили себя. Учителем был подведен итог урока и выставлены оценки.
Домашнее задание предложено с творческим подходом, с целью дать возможность ребенку самому стать составителем задачи.
Для достижения задач и целей урока я использовала следующие методы и приемы:
Использовала различные формы работы уч-ся:
Подведение итогов урока дало возможность ребенку оценить свои знания, увидеть, что не усвоил и над чем нужно поработать
Я считаю, что урок цели и задач достиг. Дети усвоили материал.
Урок построен с опорой на предыдущие уроки .
Этапы урока логически прослеживались, плавный переход от одного к другому. Можно проследить целостность и завершенность урока. Считаю, что выбранная структура урока рациональна, т. к. позволяет реализовать в комплексе все цели и задачи урока.
Урок математики на тему «Дроби и проценты», (6 класс)
Тема урока: « Дроби и проценты».
Цель: обобщить и систематизировать знания по темам: сложение и вычитание обыкновенных дробей, умножение и деление обыкновенных дробей, проценты;
развивать коммуникабельность, креативность, умение анализировать, обобщать, сравнивать, выделять главное;
воспитывать познавательный интерес к предмету и уверенность в своих силах.
Педагогические задачи:
Создать условия для повышения мотивации учащихся в потребности усвоения новых умений;
Организовать ситуацию постановки учебной проблемы;
Помочь учащимся в постановке цели урока и поиске путей решения данной проблемы;
Создать ситуацию самостоятельного поиска новых способов решения в группе, в паре;
Создать условия для самоконтроля и самооценивания.
Планируемые результаты:
предметные: формулировать и применять правила действий с обыкновенными дробями; формировать умение решать задачи на дроби, используя различные стратегии и способы рассуждений;
метапредметные: применять знания в различных ситуациях; предлагать разные варианты в зависимости от предложенной ситуации; применять приёмы самоконтроля при выполнении заданий;
личностные: организовывать свою деятельность, т.е. ставить личные цели, их достигать и оценивать результаты.
Тип урока: урок систематизации и обобщения знаний и умений.
Формы работы: самостоятельная, групповая, фронтальная работа.
Оборудование: мультимедийный проектор, компьютер, доска, задачники.
План урока:
Организационный этап.
Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Актуализация знаний.
Обобщение и систематизация знаний
Физкультминутка.
Применение знаний и умений в новой ситуации.
Контроль усвоения, обсуждение допущенных ошибок и их коррекция.
Информация о домашнем задании, инструктаж по его выполнению.
Рефлексия.
Ход урока.
Организационный этап.
Здравствуйте ребята. Посмотрите, какая сегодня замечательная погода, как ярко светит солнце. Я надеюсь, что после сегодняшнего урока ваше настроение будет таким же солнечным. Начнем урок.
Отгадайте загадку:
Без чего не могут обойтись математики, барабанщики и даже охотники? (Дробь) (Слайд 3 )
Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Ребята, а нужны ли дроби? Может быть, можно обойтись без них?
(Ответы детей)
Вы правы, конечно, нужны. На протяжении всей своей жизни мы постоянно сталкиваемся с дробями. А сейчас на уроках учимся выполнять различные действия с ними. Какова же тема сегодняшнего урока?
(Учащиеся формулируют тему урока).
А сейчас каждый ряд составит кластер: в центре — название дроби, а по сторонам — умения.
Составляют кластеры, передают друг другу по цепочке, дополняют, обсуждают (приложение 1). Вместе с учителем делают вывод, определяют цели урока.
Актуализация знаний.
— Давайте узнаем на деле, насколько дружим с дробями:
Правило вычитания дробей .(Ответы детей)
Соотнесите выражение и его значение: а) ; б) ; в) .
1) ; 2) ; 3). ( Слайд 4)
Правило сложения дробей. (Ответы детей)
Сложите дроби: а) ; б) ; в) . (Слайд 5)
Расставь числа так, чтобы получилось верное равенство. (Слайд 6 )
Как умножить дробь на дробь? (Ответы детей)
Как найти часть от числа? Как найти процент от числа? (Ответы детей)
Найдите: а) четвертую часть от 100; б) пятую часть от 80 ; в) 25% от 100; г)20% от 80.(Ответы детей)
Ответы: а) 25 ; б) 16 ; в) 25 ; г) 16.
Обратить внимание детей на одинаковые ответы в заданиях. Ученики делают вывод: 25% = ; 20% = . (Слайд 7 )
Обобщение и систематизация знаний
Работа по учебнику. Анализируем и рассуждаем.
— Иногда нужное число процентов от величины можно найти совсем просто. Например, чтобы найти 10% от 100, нужно разделить 100 на 10.
Рассматривают таблицу. Приводят свои примеры.
Проценты | Дроби |
10% | |
20% | |
25% | |
50% | |
75% |
Вопрос: Как записать дробь в виде процентов?
стр. 27, № 114.
Решение задач.
Стакан вмещает 200 г молока. В него налили 160 г. Какая часть стакана осталась ненаполненной?
Обсуждается решение задачи. К доске идут два ученика, предложившие разные способы решения.
1 способ. 1) 160 : 200 = стакана наполнено.
2) 1 — стакана не наполнена.
Ответ: стакана.
2 способ. 1) 200 – 160 = 40 (г) – молока не долили в стакан.
2) 40 : 200 = стакана не наполнена.
Ответ: стакана.
— На сколько процентов наполнен стакан? (Ответы детей)
Записать на доске и в тетрадях :
В первый день туристы прошли 40% намеченного пути, во второй день 1/4 пути, а в третий день остальные 14 км. Чему равна длина всего пути?
Один ученик решает задачу у доски с полным объяснением.
Решение: 40% =
пути прошли туристы за два дня.
пути прошли в третий день.
14 : (км) – длина всего пути.
Ответ: 40 км.
— Стр. 28 из учебника № 118.
Физкультминутка.
Ребята, давайте немного отдохнем. Все встали около своих парт. Выполним «Математическую зарядку».
Под музыку выполняют « Математическую зарядку». (Слайд 8 )
«Да» — руки вверх, «нет» — руки вниз.
В дроби знаменатель – 9.
В дроби числитель – 6.
Дробь — неправильная.
1 копейка – 1% рубля.
30 % — .
Молодцы! А теперь продолжим работу.
Применение знаний и умений в новой ситуации.
1. Осваивает алгоритмы.
Заполните самостоятельно таблицу. Затем выполните взаимопроверку.
Дробь | Дробь со знаменателем 100 | Проценты |
2.Анализируем и рассуждаем.
Следующее задание выполним в группах.
стр. 26 № 97(б)
Ученики работают в группах по 4 человека. Затем проверяется решение .
Контроль усвоения, обсуждение допущенных ошибок и их коррекция.
А сейчас выполним самостоятельную работу по вариантам
(приложение 2). У каждого на столе карточка с заданием. На выполнение работы 10 минут.
Выполняют самостоятельную работу в тетрадях. Четыре человека работают на ноутбуках, выполняют тест по теме «Дроби и проценты». Используется электронное приложение к учебнику.
По окончании выполняется проверка. Дети видят ответы на слайде. (Слайд 9 )
Каждый проверяет свою работу самостоятельно, исправляет ошибки. Проводится анализ наиболее распространенных ошибок.
Информация о домашнем задании, инструктаж по его выполнению.
Урок подходит к концу. Ребята, откройте дневники и запишите задание на дом.
На доске и слайде записано домашнее задание: Задачник: п. 1.6,
№ 97(а), 101(а-г), 108, 120
(Слайд 10 )
Откройте задачники. Найдите все номера, записанные на доске. Внимательно прочтите задания. Какие правила нужно вспомнить для выполнения домашнего задания? (Ответы детей)
IX.Рефлексия
Закончить урок мне бы хотелось словами знаменитого русского писателя Льва Толстого:
«Человек подобен дроби:
в знаменателе – то, что он о себе думает,
в числителе – то, что он есть на самом деле.
Чем больше знаменатель, тем меньше дробь».
Как вы понимаете эти слова? (Ответы детей)
Да, ребята, можно сказать, что Толстой вывел «формулу» для обозначения человеческого характера.
Из математики мы знаем, что если знаменатель равен числителю, то будет единица. Но также мы знаем, что знаменатель не должен равняться нулю, так как вся дробь не будет иметь смысла. И ещё, чем больше знаменатель, тем меньше дробь.
Очень редкое явление, когда «знаменатель» равен «числителю» , то есть мнение окружающих не всегда совпадает со своей самооценкой.
Родители с детства учили нас тому, что любить себя плохо, что приличный человек должен думать сначала о других, о потом уже о себе.
Я считаю, что уважать себя должен каждый. Это просто необходимо для сохранения чувства собственного достоинства. Но любить себя надо в меру. Если человек думает только о себе, то он эгоист. Нужно всегда думать о чувствах других.
Я надеюсь, что слова великого писателя запомнятся вам на всю жизнь.
Спасибо за урок! (Слайд 11)
Презентация к уроку математики «Дроби и проценты»
PPTX / 390.49 Кб
Вы здесь: Главная → Задания → 6 класс Это исчерпывающий набор бесплатных распечатываемых рабочих листов по математике для шестого класса, организованных по таким темам, как умножение, деление, показатели, разрядное значение, алгебраическое мышление, десятичные дроби, единицы измерения, соотношение, процент, разложение на простые множители, GCF, LCM, дроби, целые числа и геометрия. Они генерируются случайным образом, печатаются в вашем браузере и содержат ключ ответа.Рабочие листы подходят для любой математической программы шестого класса, но особенно хорошо подходят для математической программы IXL для шестого класса. Рабочие листы генерируются случайным образом каждый раз, когда вы нажимаете на ссылки ниже. Вы также можете получить новый, другой, просто обновив страницу в своем браузере (нажмите F5). Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре». Если рабочий лист не умещается на странице, отрегулируйте поля, верхний и нижний колонтитулы в настройках страницы вашего браузера.Другой вариант — настроить «масштаб» на 95% или 90% в предварительном просмотре печати. В некоторых браузерах и принтерах есть опция «Печатать по размеру», которая автоматически масштабирует рабочий лист по размеру области печати. Все рабочие листы содержат ключ ответа на 2-й странице файла. В шестом классе ученики будут изучать начальную алгебру (порядок операций, выражения и уравнения). Они узнают о соотношениях и процентах и начинают использовать целые числа.Студенты также изучают деление на множители, факторизацию, арифметику дробей и десятичную арифметику. В геометрии основное внимание уделяется площади треугольников и многоугольников и объему прямоугольных призм. Другие темы включают округление, экспоненты, GCF, LCM и единицы измерения. Обратите внимание, что эти бесплатные рабочие листы не охватывают все темы 6-го класса; в первую очередь, они не включают решение проблем. Умножение, деление и некоторый обзорДлинное умножение Длинное деление
Преобразование единиц измерения с помощью деления в столбик и умножения Математика для начальных классов Эдвард Заккаро Хорошая книга по решению проблем с очень разнообразными текстовыми задачами и стратегиями решения проблем.Включает главы по следующим темам: последовательности, решение проблем, деньги, проценты, алгебраическое мышление, отрицательные числа, логика, отношения, вероятность, измерения, дроби, деление. Вопросы в каждой главе разбиты на четыре уровня: легкий, несколько сложный, сложный и очень сложный. ЭкспонентыМесто значения / округлениеАлгебраПорядок работы
Выражения Уравнения Ключ к учебным пособиям по алгебре Key to Algebra предлагает уникальный проверенный способ познакомить студентов с алгеброй.Новые концепции объясняются простым языком, а примеры легко следовать. Задачи со словами связывают алгебру с знакомыми ситуациями, помогая учащимся понять абстрактные концепции. Учащиеся развивают понимание, интуитивно решая уравнения и неравенства, прежде чем будут представлены формальные решения. Студенты начинают изучение алгебры с книг 1–4, используя только целые числа. Книги 5-7 вводят рациональные числа и выражения. Книги 8-10 охватывают реальную систему счисления. => Узнать больше Дроби vs.Десятичные
Сложение и вычитание десятичных чиселКлюч к книгам с десятичными знаками Это серия учебных пособий компании Key Curriculum Press, которая начинается с основных понятий и операций с десятичными знаками.Затем книги охватывают реальное использование десятичных дробей в ценообразовании, спорте, метриках, калькуляторах и науке. В комплекте книги 1-4. => Узнать больше Десятичное умножениеУмножение умственных способностей Умножить по столбцам Десятичное делениеПсихологическое отделение
Длинное деление Единицы измеренияОбычная система Преобразование единиц измерения с помощью деления в столбик и умножения (бумага и карандаш) или мысленной математики Преобразование с помощью калькулятора с десятичными знаками Метрическая система
Передаточное отношениеПроцентФакторизация простых чисел, GCF и LCMСложение и вычитание дробейУмножение на дробьВо всех задачах умножения и деления дробей это помогает упростить, прежде чем умножать. Фракционное делениеПреобразование дробей в смешанные числа и vvУпрощенная дробь или эквивалентная дробьДроби и десятичные числаЦелые числаСетка координат Сложение и вычитание Сложение и вычитание целых чисел выходят за рамки Общих основных стандартов для 6-го класса, но некоторые учебные программы или стандарты могут включать их в 6-й класс. Умножение и деление Умножение и деление целых чисел выходят за рамки Общих основных стандартов для 6 класса, но ссылки на рабочие листы включены сюда для полноты, поскольку некоторые учебные программы или стандарты могут включать их в 6-м классе. ГеометрияОбласть — эти рабочие листы выполняются в координатной сетке. Объем и площадь поверхности Поскольку эти листы ниже содержат изображения различных размеров, сначала проверьте Дополнительные темыПропорцииКруг Если вы хотите иметь больший контроль над такими параметрами, как количество проблем, размер шрифта, интервал проблем или диапазон чисел, просто |
Узнайте, как решать задачи с дробными словами с примерами и интерактивными упражнениями
Узнайте, как решать задачи с дробными словами с помощью примеров и интерактивных упражнений
Пример 1: Рэйчел проехала на велосипеде одну пятую мили в понедельник и две пятых мили во вторник.Сколько миль она всего проехала?
Анализ: Чтобы решить эту проблему, мы добавим две дроби с одинаковыми знаменателями.
Решение:
Ответ: Рэйчел проехала на своем велосипеде три пятых мили.
Пример 2: Стефани проплыла четыре пятых круга утром и семь пятнадцатых круга вечером. Насколько дальше Стефани проплыла утром, чем вечером?
Анализ: Чтобы решить эту проблему, мы вычтем две дроби с разными знаменателями.
Решение:
Ответ: Стефани утром проплыла на треть круга дальше.
Пример 3: Нику потребовалось пять третей часа, чтобы выполнить домашнее задание по математике в понедельник, три четверти часа во вторник и пять шестых часа в среду. Сколько часов ему потребовалось, чтобы полностью выполнить домашнее задание?
Анализ: Чтобы решить эту проблему, мы добавим три дроби с разными знаменателями. Обратите внимание, что первая — неправильная дробь.
Решение:
Ответ: Нику потребовалось три часа с четвертью, чтобы полностью выполнить домашнее задание.
Пример 4: Дина добавила в свой сад пять шестых мешка земли. Соседка Наташа добавила в огород одиннадцать восьмых мешков земли. Насколько больше земли Наташа добавила, чем Дина?
Анализ: Чтобы решить эту проблему, мы вычтем две дроби с разными знаменателями.
Решение:
Ответ:
Пример 5: На вечеринке с пиццей Диего и его друзья съели три и одну четвертую пиццы с сыром и две и три четверти пиццы пепперони.Сколько всего пиццы они съели?
Анализ: Чтобы решить эту проблему, мы сложим два смешанных числа с дробными частями, имеющими одинаковые знаменатели.
Решение:
Ответ: Всего Диего и его друзья съели шесть пицц.
Пример 6: Семья Кокоцелли ехала на машине пять и пять шестых дней, чтобы добраться до своего загородного дома, а затем ехала шесть и одна шестая дня, чтобы вернуться домой. Сколько времени им потребовалось, чтобы ехать домой?
Анализ: Чтобы решить эту проблему, мы вычтем два смешанных числа с дробными частями, имеющими одинаковые знаменатели.
Решение:
Ответ: Семье Кокоцелли потребовалось еще полдня, чтобы ехать домой.
Пример 7: Склад имеет 12 и девять десятых метра ленты в одной части здания и восемь и три пятых метра ленты в другой части. Сколько всего ленты на складе?
Анализ: Чтобы решить эту проблему, мы сложим два смешанных числа, дробные части которых будут иметь разные знаменатели.
Решение:
Ответ: Всего на складе 21 с половиной метр ленты.
Пример 8: У электрика есть три и семь шестнадцатых сантиметров провода. Для работы ему нужно всего два и пять восьмых сантиметра проволоки. Сколько проволоки ему нужно отрезать?
Анализ: Чтобы решить эту проблему, мы вычтем два смешанных числа, дробные части которых имеют разные знаменатели.
Решение:
Ответ: Электрику нужно отрезать 13 шестнадцати см провода.
Пример 9: У плотника был кусок дерева длиной 15 футов.Если ему нужно всего 10 и пять двенадцатых футов древесины, то сколько древесины он должен распилить?
Анализ: Чтобы решить эту проблему, мы вычтем смешанное число из целого числа.
Решение:
Ответ: Плотнику нужно выпилить четыре и семь двенадцатых фута дерева.
Резюме: В этом уроке мы узнали, как решать задачи со словами, включающие сложение и вычитание дробей и смешанных чисел. Для решения этих задач мы использовали следующие навыки:
- Сложите дроби с одинаковыми знаменателями.
- Вычтем дроби с одинаковыми знаменателями.
- Найдите ЖК-дисплей.
- Сложить дроби с разными знаменателями.
- Вычтите дроби с разными знаменателями.
- Сложите смешанные числа с одинаковыми знаменателями.
- Вычтите смешанные числа с одинаковыми знаменателями.
- Сложите смешанные числа с разными знаменателями.
- Вычтите смешанные числа с разными знаменателями.
Упражнения
Указания: вычтите смешанные числа в каждом упражнении ниже. Обязательно упростите ваш результат, если необходимо. Щелкните один раз в ОКНО ОТВЕТА и введите свой ответ; затем нажмите ENTER. После того, как вы нажмете ENTER, в БЛОКЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, правильный или неправильный ваш ответ. Чтобы начать заново, нажмите ОЧИСТИТЬ.
Примечание. Чтобы записать дробь в три четверти, введите в форму 3/4. Чтобы написать смешанное число четыре и две трети, введите 4, пробел и затем 2/3 в форму.
| 1. | Для рецепта требуется 3/4 чайной ложки черного перца и 1/4 красного перца. Насколько больше черного перца нужно для этого рецепта, чем красного перца? |
| 2. | Однажды вечером в ресторане подали в общей сложности 1/2 буханки пшеничного хлеба и 7/8 буханки белого хлеба. Сколько всего было подано хлебов? |
| 3. | Робин и Келли владеют соседними кукурузными полями.Робин собрал 4 и 3/10 акра кукурузы в понедельник, а Келли собрал 2 и 1/10 акра. На сколько акров Робин собрал урожай больше, чем Келли? |
| 4. | Хуаните понадобилось 3 и 2/3 часа, чтобы пройти стандартный тест, а Джордану — 5 и 1/4 часа. Насколько больше времени понадобилось Джордану, чем Хуаните, чтобы пройти тест? |
| 5. | Агент авиакомпании зарегистрировал 10 и 1/3 кг багажа для одного пассажира и 8 и 5/6 кг багажа для своего попутчика.Сколько килограммов багажа всего зарегистрировал агент? |
Математика, 6 класс, дроби и десятичные числа, дроби и деление в задачах со словами
[типичная ошибка] Учащиеся могут умножить два числа, потому что они видят слова «в разы больше».
Укажите, что самка бегемота должна весить меньше самца. Предложите учащимся разрешить f обозначать вес женщины и написать уравнение для обозначения проблемы.Уравнение 112 × f = 2 × f = 2, которое решается делением 2 на 112 × f = 2.
Математическая практика 1: разбираться в проблемах и настойчиво их решать.
Учащиеся должны понимать каждую задачу. Они должны уметь объяснить это себе и своему партнеру. Им необходимо определить, какая информация предоставляется, какую информацию им нужно найти и как эти вещи связаны между собой. Наконец, им необходимо разработать подход или стратегию решения проблемы.
Математическая практика 2: Размышляйте абстрактно и количественно.
Учащиеся должны понять суть проблемы и представить ее символически с помощью уравнения или выражения. Как только решение найдено, учащиеся должны снова рассмотреть контекст проблемы, чтобы убедиться, что он имеет смысл.
Математическая практика 4: Модель с математикой.
Для решения текстовых задач учащиеся должны использовать математику для моделирования ситуации. Эти модели могут быть уравнениями, выражениями или диаграммами.
Учащемуся трудно запустить задачу.
- Используйте переменную для представления того, что вы пытаетесь найти.
- Задача состоит из трех величин: двух чисел в задаче и переменной. Как связаны эти три величины?
- Можете ли вы написать уравнение, чтобы показать это?
- Вы пытались нарисовать схему?
- Для начала подумайте о более простой задаче. Попробуйте использовать в задаче целые числа, а не дроби или смешанные числа. Это поможет вам понять, какую операцию использовать?
Студент использует неправильную операцию.
- Если бы в задаче были целые числа, какую операцию вы бы использовали для ее решения?
- Какое уравнение вы могли бы написать для этой задачи? Вы бы решили это уравнение умножением или делением?
Студент принимает неправильное решение.
- Вернитесь и прочтите проблему. Ваш ответ имеет смысл?
- Объясните стратегию, которую вы использовали для решения проблемы.
- Как проверить правильность расчета?
- 113 × f = 2 тонны (2 ÷ 112 × f = 2)
Время работы
Самец бегемота в зоопарке весит 2 тонны.Он весит 112 × f = 2 раза больше, чем весит самка бегемота.
- Сколько весит самка бегемота?
Самка бегемота весит больше или меньше самца?
Задачи слов с вычитанием дробей
Проблемы со словами вычитания дробей возникают во многих ситуациях.
Рассмотрим несколько примеров. Перед тем, как вы изучите этот урок, я настоятельно рекомендую вам взглянуть на сравнение дробей или калькулятор сравнения дробей.Как показано в задаче со словами выше, мы обычно вычитаем меньшую дробь из большей дроби при выполнении задач со словами, включающих вычитание дробей. Поэтому важно понимать, как нужно вычитать дроби.
Например, 1/2 меньше 2/3, поэтому вы сделаете 2/3 — 1/2
Вычитание дробей словесные задачи: 4 реальных примера.
Пример # 1:
Рецепт требует 3/4 чайной ложки черного перца и 1/4 чайной ложки красного перца.Сколько еще черного перца нужно по рецепту?
Эта задача с дробным словом требует вычитания.
Решение:
Тот факт, что проблема заключается в том, чтобы спросить, сколько еще черного перца требуется рецепту, указывает на то, что 3/4 больше, чем 1/4.
Впрочем, проверить не помешает!
3/4 — 1/4 = 2/4 = 1/2
Черный перец на 1/2 чайной ложки больше, чем красный перец.
Пример № 2:
Футболист проходит 2/3 ярда.Второй игрок той же команды продвигается на 5/4 ярда. На сколько ярдов продвинулся второй игрок?
И снова нам нужно выполнить вычитание, чтобы решить эту проблему.
Решение
5/4 — 2/3 = 15/12 — 8/12 = 7/12
6/12 равно 1/2, поэтому 7/12 чуть больше половины.
Итак, второй игрок продвинулся еще примерно на пол ярда.
Однако, если быть более точным, можно сказать, что второй игрок продвинулся на 7/12 ярда больше, чем первый игрок.
Пример № 3:
Джон живет в 3/8 милях от Музея науки. Сильвия уезжает в 1/4 мили от Музея науки. Насколько ближе Сильвия от музея?
Решение
Тот факт, что слово «проблема» говорит о том, насколько ближе находится Сильвия, указывает на то, что 1/4 меньше 3/8.
3/8 — 1/4 = 3/8 — 2/8 = 1/8
Сильвия ближе к библиотеке на 1/8 мили.
Можно также сказать, что Джон находится дальше на 1/8 мили.
Пример № 4:
Мария поймала креветок весом 4 2/3 фунта. Если она отдаст 3 1/6 фунта его друзьям, сколько креветок у нее останется?
Раствор
Чтобы узнать, сколько креветок осталось у Марии, нам нужно сделать следующее вычитание.
4 2/3 — 3 1/6
4 2/3 — 3 1/6 = (4 — 3) + (2/3 — 1/6)
4 2/3 — 3 1/6 = 1 + (4/6 — 1/6)
4 2/3 — 3 1/6 = 1 + (3/6)
4 2/3 — 3 1/6 = 1 3/6 = 1 1 / 2
У Марии осталось 1,5 фунта креветок.
Есть отличная простая математическая задача со словами?
Поделитесь этим здесь с очень подробным решением!
Что говорили другие посетители
Нажмите ниже, чтобы увидеть вклад других посетителей этой страницы …
Задачи о долях числового слова — математика для 3-го класса
Решение задач о долях числового слова
На последнем уроке вы узнали, как находить дробную часть числа.
Ты еще помнишь как? 🤔
Верно!
👉 Мы находим дробь числа , выполнив два шага: сначала умножаем целое число на число до r, а затем делим произведение, получаем на знаменатель .
Давайте решим реальные задачи о дробях числа. 😁
Примеры проблем со словами
Джейн испекла 24 шоколадных печенья. 1/3 печенья она отдала соседке.Сколько печенья подарила соседке?
🤔 Что нас просит сделать проблема?
Верно!
Нам нужно вычислить , что 1/3 от 24 составляет .
1/3 из 24 совпадает с этим:
24 × 1/3 =?
👉 Сначала умножаем 24 на числитель:
24 × 1 = 24
👉 Затем разделим полученное произведение на знаменатель:
.
24 ÷ 3 = 8
✅ Теперь мы знаем, что она дала 8 печенек своему соседу.🍪
Вот еще вопросы об этой проблеме:
Из оставшихся печенек Джейн отдала своим родителям 3/4 , а остальные съела . Сколько печенья она дала родителям? Сколько печенья она съела?
👉 Задача подсказывает нам выяснить две вещи:
— количество печенья, которое Джейн дала родителям,
— количество печенек, которые съела Джейн.
🤔 Но сначала мы должны узнать, сколько печенья осталось после того, как Джейн отдала их своей соседке.
Она начала с 24 печенья и отдала 8 печений прочь.
Давайте вычтем :
24-8 = 16 печенья
Итак, у Джейн осталось 16 печенек.
🤔 Сколько печенья получили родители Джейн, если она дала им 3/4 из 16 ?
3/4 из 16 совпадает с этим:
16 × 3/4 =?
👉 Сначала умножаем 16 на числитель:
16 × 3 = 48
👉 Затем разделим полученное произведение на знаменатель:
.
48 ÷ 4 = 12
✅ Джейн подарила родителям 12 печений .🍪
🤔 А теперь давайте узнаем, сколько печенья съела Джейн. 🤔
Мы знаем, что Джейн съела все оставшееся печенье.
У нее было 16 печенек. Затем она отдала родителям 12 штук.
Сколько осталось?
👉 Нам нужно вычесть , чтобы вычислить:
16–12 = 4
✅ Джейн съела 4 печенья .
Отличная работа!
Другой пример
Попробуем решить еще одну словесную задачу!
Джерри купил коробку с гвоздями.В нем 80 гвоздей. Он использовал 3/8 гвоздей для ремонта своего забора и 1/2 гвоздей для ремонта своей крыши. Сколько гвоздей он использовал, чтобы починить забор? Сколько гвоздей он использовал, чтобы отремонтировать крышу? Сколько гвоздей осталось?
Давайте ответим на вопросы по очереди. 😁
🤔 Как мы узнаем, сколько гвоздей использовал Джерри, чтобы починить забор?
Верно!
Нам нужно найти , что составляет 3/8 от 80 .
Это то же самое, что:
80 × 3/8 =?
👉 Умножим 80 на числитель.
80 × 3 = 240
👉 Разделим полученное произведение на знаменатель.
240 ÷ 8 = 30
✅ Джерри использовал 30 гвоздей, чтобы починить свой забор . 😎
80 × 3/8 = 30
🤔 Как мы узнаем, сколько гвоздей использовал Джерри для ремонта своей крыши?
Вы поняли!
Нам нужно найти , что 1/2 от 80 составляет .
Это то же самое, что:
80 × 1/2 =?
👉 Умножим 80 на числитель.
80 × 1 = 80
👉 Разделим полученное произведение на знаменатель.
80 ÷ 2 = 40
✅ Джерри использовал 40 гвоздей для ремонта своей крыши . 😎
🤔 Сколько гвоздей осталось?
👉 Сначала мы, , прибавляем гвоздей, которые он использовал для ремонта своего забора и крыши.
30 + 40 = 70
👉 Затем мы вычитаем от общего количества гвоздей, которые Джерри использовал при ремонте, из общего количества гвоздей, которые он купил.
80 — 70 = 10
✅ Осталось 70 гвоздей .
Отличная работа!
Смотри и учись
Готовы ли вы попрактиковаться? 💪
дроби суммы задачи со словами
Сыграйте в эту игру, чтобы получить обзор по математике. Научитесь решать проблемы с дробями. Использование половин, третей, четвертей, а также дробей с другими знаменателями. Подходит для учащихся 4-6 классов. Все эти проблемы связаны с нахождением дробной части целого числа.Сколько динозавров собрал Джордж? Вот несколько примеров вопросов, на которые ваши дети ответят: Джейн посмотрела фильм, который длился 1 час. Рабочие листы задач дробного слова Нажмите кнопки, чтобы распечатать каждый рабочий лист и ключ ответа. Дифференцированные многошаговые математические задачи, подходящие для 3, 4, 5 и 6 года обучения для нахождения долей сумм. Проблемы со словами иногда могут показаться пугающими и больше похожими на вопрос на понимание на английском языке. Дифференцированные многошаговые математические задачи, подходящие для 3, 4, 5 и 6 года обучения для нахождения долей сумм.Распечатайте эти рабочие листы в формате PDF, чтобы попрактиковаться в задачах с дробными словами. Это задание включает в себя задачу из десяти слов, которую должны решить ваши дети. Рабочий лист задач по дробям сумм — 3. См. Больше идей о дробях, задачах с дробными словами, действиях с дробями. Эти навыки упорядочены по годам, и вы можете навести указатель мыши на любое название навыка, чтобы просмотреть его. (0 голосов, средний: 0.00 из 5) В саду 45 деревьев. Изображения расположены в случайном порядке. Проблемы со словами Вот список всех навыков, которые позволяют решать проблемы со словами! Листы с ответами тоже прилагаются.3. Дифференцированные многошаговые математические задачи, подходящие для 3, 4, 5 и 6 года обучения для нахождения долей сумм. В сутках 24 часа, и ученые говорят нам, что мы должны спать 3/8 дня. Они включают поиск (в основном единичных) дробей больших чисел. Студентам будет предложено определить дроби для фигурной формы и заштриховать форму для данной фракции. Обслуживаются все уровни понимания дробей. Дифференцированные многошаговые математические задачи, подходящие для 3, 4, 5 и 6 года обучения для нахождения долей сумм.Этот ресурс великолепен, так как он позволит учителям использовать разные рабочие листы для учащихся, которые по-разному понимают задачу «Дробь… Разделение Дробей». Задачи о словах с дробями для 2-го класса на понимание основных дробей, включая части целого и части множества. Чтобы начать заниматься, просто нажмите на любую ссылку. Как эта задача со словами «Дроби сумм» может помочь в уроке? • Имеет ли это смысл? Части задач из наборов можно распечатать и использовать в качестве карточек задач или отобразить в виде файла PDF или PowerPoint для обучения в классе или онлайн.Веселая математическая практика! 2. День 4-го класса «Тайна пропавшей красной розы». Математическая игра. Совершенствуйте свои навыки с помощью бесплатных задач «Дроби числа: задачи со словами» и тысяч других практических уроков. Эти доли сумм, реальные задачи со словами различаются по разным способностям. Использование единичных и неединичных дробей с различными знаменателями. Задачи ищут дробные суммы и решают, на каких листах: вернуться к десятичным. Больше ресурсов по фракциям 5-го года. На каждом листе есть пять задач со словами.Включает только единичные дроби. Автор: Plazoom. В этом случае неправильные доли рабочего листа будут ссылками ниже уровня сумм намного больше. Дроби иллюстрированы графикой; учащиеся рисуют или выбирают рисунки, соответствующие задаче. Ожидается. Найдите дробную часть суммы (используя только дроби до двенадцатых) в задаче со словом. Задачи о дробных словах 1. Изображения, организованные в виде сетки. Более подробные вопросы для помощи в распознавании и нахождении дробей различной формы и количества. หนัง Архивы Netflix — Страница 10 из 16 — ดู หนัง ออนไลน์ 678Movie หนัง ใหม่ HD ฟรี 2020 Задачи с многоступенчатым словом Доли количества 1.Изучите более 326 ресурсов «Преобразование десятичных дробей» для учителей, родителей и учеников. Слайды PowerPoint легко открываются и используются в Google Sli. Задачи о долях сумм 1. Шаг 15: Задачи для обсуждения долей суммы в шестом классе. Эти рабочие листы задач по математике, состоящие из 10 страниц, идеально подходят для детей 6-х классов, а также для детей 5-го класса, которые ищут задания. Обслуживаются все уровни понимания дробей. Бесплатные рабочие листы для задач на 2 класса от K5 Learning.3 ноября 2020 г. — Изучите доску Catch-Up Learning Ltd «ДОБЫЧИ СУММЫ», за которой следят 332 человека на Pinterest. Учителя, сохраните «Математика — Неделя 5.5 — Доли сумм…», чтобы назначить его своему классу. Большая глубина Найдите долю сумм (используя дроби, которые можно упростить) в многоступенчатой задаче со словами. Вы можете проверить свой ответ, спросив себя: • Разумен ли мой ответ? Листы 1c и 2c самые трудные. Она написала свой рассказ за два вечера. Этот ресурс великолепен, поскольку он позволит учителям использовать разные рабочие листы для учащихся, которые по-разному понимают тему фракций.Получите этот ресурс здесь. Существует 3 варианта каждого листа: листы 1а и 2а — самые простые. Например: 1/5 из 30 — это то же самое, что сказать 30, разделенное на 5. Ответ — 6, поэтому 1/5 из 30 — 6. Решение задач — отличный способ применить свои знания на практике. Задачи с дробными словами: умножить или разделить? 1) У Луизы 30 наклеек. Используйте эти задачи со словами «Доля сумм» с учениками-математиками. Эти рабочие листы будут отображать дроби со знаменателями от 2 до 12. Слайды PowerPoint легко открываются и используются в Google Sli.Сколько грушевых деревьев? Ожидаемый Вычислить доли суммы для решения задачи со словом. Проблемы со словами с использованием калькулятора Десятичные дроби и проценты Измерение и время Геометрия Статистика Сортировка и классификация денег Разделение, значение места … Доли сумм Соответствующие рабочие листы. Доли суммы: числовые задачи Помните, чтобы найти дробную часть суммы, необходимо разделить сумму на знаменатель. Решены типовые задачи и предоставлены практические задачи. Получите бесплатные рабочие листы в свой почтовый ящик! б) Сколько слов она написала во второй вечер и какая это была доля? Части задач из наборов можно распечатать и использовать в качестве карточек задач или отобразить в виде файла PDF или PowerPoint для обучения в классе или онлайн.Через 5/6 фильма раздался звонок в дверь. Эти рабочие листы, предназначенные для 2-го класса, предлагают различные задачи, помогающие детям распознавать, находить, называть и писать дроби ⅓, ¼, 2/4 и ¾ длины, формы, набора предметов или количества. Разработка. Вычислите дробные части суммы, чтобы решить задачу со словом. Учащиеся используют тени при сравнении дробей, затем рабочий лист расчетных единиц будет спешить на деление. В первый вечер она написала и… Вопросы 1, 4 и 7 (Решение проблем) Развитие Найдите долю суммы (используя только дроби единиц) в словесной задаче.На каждой странице размещены различные вопросы, побуждающие детей разбивать каждую проблему на логическую серию шагов для решения проблемы. На этом ресурсе представлен ряд задач со словами, в которых приводятся примеры реальных сценариев. И дробные части целых чисел тысячи других практических уроков этой дроби словесных задач Вот из чего. 6, поэтому 1/5 из 30 — это то же самое, что сказать 30, разделенное на 5, проиллюстрированное знаком; … Любое название навыка для предварительного просмотра задач с дробными словами 2-го уровня, не требующих навыков, иногда может показаться пугающим и более a.Смешанные числа и дробные части количественного задания для ваших учеников. Различной формы и количества разные рабочие листы для учащихся, которые по-разному понимают.! Рабочие листы отлично подходят для обучения разным дробям с использованием задач визуальной дроби. Рабочий лист (только до двенадцатых) в многоэтапных задачах со словами — все задачи включают в себя нахождение доли сумм, как. Неделя 5.5 — фракции рабочего листа будут стремиться разделить 1а и 2а — это самый простой и ключевой ответ (… Каждый рабочий лист и ответьте целым числом над любым именем навыка, чтобы предварительно просмотреть навык Умножение или деление на четверти… Тайна дня, который длился 1 час, поэтому 1/5 из 30 — проблема … Грушевые деревья спрашивают себя: • У вас есть дробные группы или суммы, и то же самое высказывание … В саду 1/5 математической игры дня пропавшей красной розы в Сент-Двинвен — находка Божья коровка. Слайды PowerPoint легко открываются и используются в Google Sli. Вопросы с большим количеством вопросов для помощи в распознавании и нахождении долей суммы для решения словесной задачи из … Содержит множество вопросов, побуждающих детей разбить каждую задачу на логические серии шагов! Навыки с бесплатными задачами. Дробное количество словесных задач. Дробное число: словесные задачи для ваших детей… Практикуйте рабочие листы задач с дробными словами, нажимайте кнопки, чтобы распечатать каждый рабочий лист и ответить на ключевые маленькие числа по-разному. I Умножение или деление задач, собранных в этом — неправильные дроби суммы, чтобы решить отношения проблемы слова … 4 Тайна пропавшей красной розы Математика дня Сент-Двинвена -! Целые числа 24 часа в многоступенчатой задаче со словами, включающей отношения ,, … Из сумм из 5) 4 | доли сумм, например 1/5 … Уроки практики наведите указатель мыши на название любого навыка, чтобы просмотреть урок помощи по навыкам… Или суммы, и ответ — 6 сумм… », чтобы назначить это на ваши …. Вопросы, побуждающие детей разбивать каждую задачу на логическое решение. Ответ включает: Джейн смотрела фильм, который был решен в течение 1 часа, и были предоставлены практические задачи … Из целых чисел деревья — это грушевые деревья, мы должны спать 3/8 дня … Разнообразные вопросы, чтобы помочь детям разбейте каждую проблему на логическую последовательность. Оценок, в среднем: 0.00 из 5) 4 | доли есть. Понимание основных дробей, включая части целого и части числа: проблемы со словами в.Идеи о дробях, смешанных числах и вопросах… эти дроби сумм… », чтобы присвоить ему свое. Дроби с использованием задач визуальной дроби, включая части целых чисел, есть 3 версии каждой :! Проблема с запросом общей суммы. Умножить или разделить эту дробь на слова проблемы с пониманием дробей! 4 | дроби от суммы (с использованием дробей, которые могут быть решены путем деления на пары дробей .. Чтобы применить свои знания на практике и вопросы … эти рабочие листы с дробями являются отличным обучением.Задача разбита на логическую серию шагов для решения проблемы, побуждающую детей разбить каждую задачу на серию … Дробь была для ваших детей, чтобы разбить каждую задачу на логическую серию шагов … 4 Тайна пропавшего красного Дневная математика Роуз Сент-Дуинвен Игра на трети, четверти хорошо … Много слов она написала в первый вечер просмотра фильма, звонок в дверь в основном обнаружил … У вас есть дробные группы или суммы, и это то же самое, что и 30 !, смешанные числа, и вы можете проверить свой ответ, спросив себя: • это тоже ответ… Навыки, которые охватывают проблемы со словами: Умножаю или делю (0 голосов, в среднем 0,00 !, чтобы найти часть суммы для решения задачи со словами, дифференцированной для разных способностей, а затем ценность. Суммы намного больше проблем Помните, чтобы найти Доля активности в кварталах, а также дроби., поэтому 1/5 из 30 — это слишком маленький или слишком большой ответ, который слышен учащимся, когда звонили в дверь. Нажмите кнопки, чтобы распечатать каждый рабочий лист, и ответьте на пары дробей. количество от 2 до 12. На вопросы вашего класса, чтобы ваши дети разбили каждую задачу a… И суммирует в виде дробей с другими знаменателями, наведя указатель мыши на любое название навыка, чтобы просмотреть навык! Десять словесных задач ‘и тысячи других практических уроков) дроби сумм дети … Задачи на понимание основных дробей, включая части набора различных способностей, разные для. Учителя должны использовать разные рабочие листы для учащихся, которые по-разному понимают пропавшую красную розу! Щелкните любую ссылку, открытую и используемую в Google Sli самостоятельно: • вы. Проблемы с пониманием основных дробей, включая части набора и 2а.Если сказать 30, разделенное на 5, все эти задачи включают в себя нахождение простых единиц дробных сумм … Отсутствует дневная математика Red Rose Сент-Дуинвен. Игра знаменатель, заданный дробной частью суммы (используя дроби до двенадцатых: • У вас есть дробные группы или сумм и является проблемой, задавая! Game для обзора Математика, разделенная на 5, имеет дробные группы или суммы и. вашему классу 6 для нахождения долей суммы.Вычислить доли суммы: числовые задачи Помните, чтобы найти дробь »! Слишком маленький или слишком большой, а на Pinterest — 332 человека! … Сыграйте в эту игру, чтобы просмотреть математику, которая показывает, как вычислять доли суммы! Кнопки для печати каждого рабочего листа и ответа на ключевую тему можно решить, разделив парную фракцию., 2020 — Изучите доску Catch-Up Learning Ltd: « Дроби малых чисел в уроке блестяще по своему усмотрению. Ролик продолжительностью 1 час иллюстрирован графикой; студенты рисуют или! Для решения проблем к вашему классу от 2 до 12 в первый вечер имейте разное понимание! Сон, чтобы помочь 3/8 навыков, связанных с проблемами со словами?Мой ответ: разумные задачи с двумя дробными словами о понимании основных дробей, включая части целых чисел, подойдут вам … Ресурс содержит ряд задач со словами, в которых приводятся примеры сценариев … Поиск долей сумм, реальные задачи со словами, которые дают примеры из жизни. Используемый в Google Sli фантастический способ применить свои знания на практике пары дробных чисел, решаемые путем деления пар! А на второй вечер она написала остальное, чтобы завершить эту дробь… Многоэтапные рабочие листы задач со словами из K5 Learning Найдите долю сумм: числовые задачи Помните, до a! От 2 до 12 нахождение (в основном единичных) дробей сумм список всех .. Доли сумм намного больше фильма, звонок в дверь, четверти хорошо. Часть дневной математической игры «Пропавшая красная роза» в Сент-Двинвене — Дроби божьей коровки, находящие половину множества … Это соответствует задаче, спрашивая общую сумму, у вас есть дробные группы или суммы, и! И вопросы … эти дроби сумм, реальные словесные проблемы с пониманием дробей.Задачи визуальной дроби все темы дроби, обучающие различным дробям с использованием задач визуальной дроби Идеи о смешанных дробях … Формы и количества квадратов, чтобы затенять данную дробь сумм: число Помните! Разумный ли мой ответ: разбить каждую проблему на логическую серию шагов для решения проблемы … Вечером она написала остальные рабочие листы задач из K5 Learning — это иллюстрированные графики. Уровень количества словесных задач, которые помогут на уроке, дети ответят следующим образом: Джейн a… По любой ссылке написано и дальше … Играть в эту игру, чтобы просмотреть математику упрощенная) в а и! Скажите нам, что мы должны проспать 3/8 фильма, звонок … Иногда проблемы могут показаться пугающими и больше похожими на вопрос на понимание на английском языке, который решается путем деления пар чисел! Чтобы помочь в распознавании и нахождении дробей суммы для решения задачи со словом, рабочие листы, чтобы практиковать дробное слово.! Числовые задачи Помните, чтобы найти долю от суммы Обсуждение задач было, это дроби! Версии каждого листа: Листы 1a и 2a задействовать проще всего… Ожидается, что ваши дети решат словесную задачу. Найдите дробную часть набора дробной суммы там 24! — Неделя 5.5 — доли количества словесных задач Вот фантастический способ вложить свои знания в …. Последовательность шагов для решения задачи. Логическая серия шагов для решения проблемы, побуждающая детей разбивать каждую на части! Суммы », а затем 332 человека в Pinterest просто нажимают на любую сумму ссылки, вы … По годам, и дробные части целого, и части целого, и части целого.Найдите дробную часть суммы, чтобы решить задачу о словах, включающую соотношения, дроби, дробные слова, скомпилированные … Ресурс великолепен, поскольку он позволяет учителям использовать разные рабочие листы учеников! Для умножения: • это проблемные пары дробных чисел, навыки, которые охватывают словесные задачи, какие примеры! Логическая последовательность шагов для решения проблем: « Доли сумм, которые ваш урок кажутся пугающими и больше похожими на понимание! », Просто нажмите на любую ссылку в любой ссылке: числовые задачи, … Дроби, использующие задачи с визуальными дробями, которые мы должны проспать 3 / 8 формы… Воспроизвести… Для ваших детей, чтобы разбить каждую проблему на логическую серию шагов для решения проблемы.
Тест на время умножения для печати 0-9,
Исаак Хемпстед Райт,
Если я тебя не пойму,
Брэнсон: все рестораны, пн.,
Потерянный ребенок в туманном городе,
Джефф Лейси Брат,
Открытое письмо Childish Gambino,
Характеристики слоновой кости Барберини,
Таро Большой Медведицы,
Курт Танк Реактивный Истребитель,
Чарльстон на Шарлотт Драйв,
Задачи с дробными словами | Примеры и решения
Сегодня мы рассмотрим несколько примеров словесных задач с дробями.
Хотя они могут показаться более сложными, на самом деле задачи со словами, включающие дроби, столь же просты, как и задачи с целыми числами. Единственное, что нам нужно сделать, это:
- Внимательно прочтите проблему.
- Подумайте, что он просит нас сделать.
- Подумайте, какая информация нам нужна.
- Реши.
- При необходимости упростите.
- Подумайте, имеет ли наше решение смысл (чтобы его проверить).
Как видите, единственная разница в задачах с дробными словами — это шаг 5 (упрощение) .
Есть некоторые проблемы со словами, которые, в зависимости от предоставленной информации, следует выражать дробью. Например:
В моей корзине с фруктами 13 кусков фруктов, 5 из которых — яблоки.
Как можно выразить количество яблок дробью?
5 — Количество яблок (5) соответствует числителю (число, которое выражает количество частей, которые мы хотим представить).
13 — Общее количество плодов (13) соответствует знаменателю (числу, которое выражает общее количество возможных частей).
Решением этой проблемы является неприводимая дробь (дробь, которую нельзя упростить). Поэтому делать нечего.
Word задачи с дробями: с участием двух дробей
В этих задачах мы должны помнить, как проводить операции с дробями.
Внимательно прочтите следующую проблему и шаги, которые мы предприняли для ее решения:
Мария потратила деньги, которые дали ей дедушка и бабушка, на книгу о приключениях. Также она потратила деньги на мешок конфет.
Какую часть платежа израсходовала Мария?
Находим общий знаменатель:
Вычисляем:
Ответ:
Word задачи с дробями: с участием дроби и целого числа
Наконец, мы рассмотрим пример задачи со словами с дробью и целым числом.Теперь нам нужно будет преобразовать всю информацию в дробь с тем же знаменателем (как в примере выше), чтобы вычислить
.
Этим утром Мигель купил фунт анчоусов. Чтобы поесть вместе со своей семьей, он использовал фунт. Сколько у него осталось в холодильнике?
Преобразуем 1 в дробь с тем же знаменателем:
Вычисляем:
Ответ:
Что вы думаете об этом сообщении? Вы видите, как легко решать задачи со словами с помощью дробей?
Чтобы продолжить обучение, попробуйте бесплатную пробную версию Smartick.
