Содержание
Расстояние между двумя точками на поверхности Земли | by shemanovskiy
Представим, что для чего-то понадобилось измерить расстояние между двумя точками на поверхности Земли, например, расстояние между Красной площадью и Эрмитажем. Конечно, можно попробовать решить задачу в лоб и посчитать евклидово расстояние по формуле:
но этот подход не заработает по той простой причине, что евклидова метрика предназначена для вычисления расстояния на плоскости, а поверхность Земли — это всё-таки фигура, очень близкая к сфере.
Для решения такой задачи нужно обратиться к редко используемым тригонометрическим функциям.
Одна из таких функций, называется синус-верзус, или, по-другому, версинус. Он представляет собой расстояние от центральной точки дуги, измеряемой удвоенным данным углом, до центральной точки хорды, стягивающей дугу. Вычисляется версинус по формуле:
Гаверсинус — это просто половина версинуса, и именно эта функция поможет нам в решении задачи с поиском расстояния:
Для любых двух точек на сфере гаверсинус центрального угла между ними вычисляется по формуле:
В этой формуле:
- d — это центральный угол между двумя точками, лежащими на большом круге
- r — радиус сферы
- φ₁ и φ₂ — широта первой и второй точек в радианах
- λ₁ и λ₂ — долгота первой и второй точек в радианах
Обозначим временно гаверсинус отношения длины к радиусу как переменную h:
Тогда длину d можно вынести за знак равенства:
а для того, чтобы избавиться от дроби, выразим гаверсинус через арксинус:
затем раскроем переменную h:
подставим формулу гаверсинуса и получим формулу вычисления расстояния:
Теперь вернёмся к исходной задаче поиска расстояния между Красной площадью и Эрмитажем.
Для Красной площади Гугл подсказал координаты (55.7539° N, 37.6208° E), а для Эрмитажа — (59.9398° N, 30.3146° E).
Прежде, чем подставлять координаты в формулу, их нужно перевести в радианы.
Для того, чтобы вычислить длину, нужно полученное значение арксинуса умножить на два радиуса сферы. Подсчёты усложняет тот факт, что Земля не является идеальной сферой и её радиус немного варьируется. Воспользуемся усреднённым значением радиуса, которое, в соответствии со стандартом WGS84 приблизительно равно 6371 км:
Произведя умножение, получаем искомое значение, которое приблизительно равно 634.57 км.
Кстати, из-за того, что Земля — не идеальная сфера, погрешность расчётов с использованием этой формулы, составляет около 0,5%.
Задание 13 — ГДЗ Геометрия 7-9 класс. Атанасян, Бутузов. Учебник. Вопросы для повторения к главе X. Страница 244
- Главная
- ГДЗ
-
7 класс, 8 класс, 9 класс -
Геометрия - Атанасян, Бутузов.
 Учебник
Учебник -
Вопросы для повторения к главе X - Задание 13
- ← Предыдущее
- Следующее →
Вернуться к содержанию учебника
Вопросы для повторения к главе X. Страница 244
Вопрос
Выведите формулу для вычисления расстояния между двумя точками по их координатам.
Подсказка
Вспомните:
- Координаты точки, связь между координатами вектора его начала и конца..
- Что такое вектор, его длина.
- Как найти длину вектора по его координатам, расстояние между двумя точками.

Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
- ← Предыдущее
- Следующее →
© budu5.com, 2021
Пользовательское соглашение
Copyright
Нашли ошибку?
Связаться с нами
Расстояние между точками на координатной прямой
Расстояние между двумя точками на координатной прямой равно модулю разности их координат.
Формула расстояния между точками на координатной прямой:
AB = |a — b|,
где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.
Выражение |a — b| можно заменить выражением |b — a|, так как a — b и b — a являются противоположными числами и их модули равны.
Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.
Пример 1. Найти расстояние между точками L(-3) и M(5), отмеченными на координатной прямой.
Решение. Чтобы найти расстояние между точками L и M надо из координаты точки L вычесть координату точки M или наоборот, а в качестве ответа взять модуль полученного результата:
|-3 — 5| = |-8| = 8
или
|5 — (-3)| = |5 + 3| = 8.
Ответ. Расстояние между точками L и M равно 8.
Пример 2. Найдите координаты середины отрезка AB, если A(-5) и B(5).
Решение. Обозначим середину отрезка точкой C. Так как C — середина отрезка AB, то |AC| = |CB|. Значит, чтобы найти координату точки C, надо сначала вычислить длину отрезка AB и разделить её на 2, то есть, на две равные части AC и CB:
AB = |-5 — 5| = |-10| = 10;
10 : 2 = 5, значит |AC| = |CB| = 5.
Как видно из чертежа, чтобы найти координату середины отрезка, надо половину длины отрезка либо прибавить к точке с наименьшей координатой, либо отнять от точки с наибольшей координатой:
-5 + 5 = 0
или
5 — 5 = 0.
Ответ. Координата середины отрезка C(0).
Пример 3. Найдите координату точки C, которая является серединой отрезка с концами в точках A(7) и B(25).
Решение.
AB = |7 — 25| = |-18| = 18;
AC = CB = 18 : 2 = 9;
7 + 9 = 16
или
25 — 9 = 16.
Ответ. Координата точки C — 16.
Вычисление расстояния и начального азимута между двумя точками на сфере
Измерение расстояния и начального азимута между точками без проекционных преобразований
Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения. Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.
В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.
Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут [angles-rhumb.html отличен от постоянного], следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.
большой круг
Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или pi*R, где R – радиус сферы.
Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или pi*R, где R – радиус сферы.
расстояние большого круга
На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.
Маршрут Нью-Йорк — Пекин
Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.
Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.
Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.
Существует три способа расчета сферического расстояния большого круга (подробнее).
[править] Сферическая теорема косинусов
В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением. Графическое изображение формул здесь и далее — из Википедии.
— широта и долгота двух точек в радианах
— разница координат по долготе
— угловая разница
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).
[править] Формула гаверсинусов
Используется, чтобы избежать проблем с небольшими расстояниями.
[править] Модификация для антиподов
Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.
[править] Реализация на Avenue
На языке Avenue, используя последнюю формулу для вычисления расстояния большого круга между двумя точками, можно использовать следующий код. Точки для вычисления передаются другим скриптом, либо добавляются в начало данного в виде pnt = point.make(long, lat) (скачать скрипт):
'pnt1, pnt2 - точки между которыми вычисляются расстояния 'pi - число pi, rad - радиус сферы (Земли), num - количество знаков после запятой pi = 3.14159265358979 rad = 6372795 num = 7 'получение координат точек в радианах lat1 = pnt1.getY*pi/180 lat2 = pnt2.getY*pi/180 long1 = pnt1.getX*pi/180 long2 = pnt2.getX*pi/180 'косинусы и синусы широт и разниц долгот cl1 = lat1.0.5 p4 = sl1*sl2 p5 = cl1*cl2*cdelta p6 = p4 + p5 p7 = p3/p6 anglerad = (p7.atan).SetFormatPrecision (num)
dist = anglerad*rad
'вычисление начального азимута
x = (cl1*sl2) - (sl1*cl2*cdelta)
y = sdelta*cl2
z = (-y/x).ATan.AsDegrees
if (x < 0) then z = z+180 end
z = -(z + 180 mod 360 - 180).AsRadians
anglerad2 = z - ((2*pi)*((z/(2*pi)).floor)) angledeg = (anglerad2*180)/pi'возврат значений длины большого круга и начального азимута
distlist = {dist, angledeg}
return distlist
Для вызова процедуры расчета длин приведенной выше, можно также воспользоваться следующим скриптом, результатом его работы будет расчет длин между точкой testpont до всех точек активной темы вида и запись результата в поле Newdist атрибутивной таблицы этой темы:
atheme = av.getactivedoc.getactivethemes.get(0)
aftab = atheme.getftab
f_shape = aftab.findfield("Shape")
f_dist = aftab.findfield("dist")
f_ang = aftab.findfield("ang")
'testpoint - точка отсчета
testpoint = point. make(25.85, 55.15)
aftab.seteditable(true)
'для каждой точки темы до которых считают расстояния от точки отсчета
for each rec in aftab
pnts = {}
apoint = aftab.returnvalue(f_shape, rec)
pnts.add(apoint.getx)
pnts.add(testpoint.getx)
pnts.add(apoint.gety)
pnts.add(testpoint.gety)
'Вызов процедуры расчета расстояний
'"Calc-distance" - название скрипта с процедурой в проекте
param = av.run("Calc-distance", pnts)
aftab.setvalue(f_dist, rec, param.get(0))
aftab.setvalue(f_ang, rec, param.get(1))
end
aftab.seteditable(false)
make(25.85, 55.15)
aftab.seteditable(true)
'для каждой точки темы до которых считают расстояния от точки отсчета
for each rec in aftab
pnts = {}
apoint = aftab.returnvalue(f_shape, rec)
pnts.add(apoint.getx)
pnts.add(testpoint.getx)
pnts.add(apoint.gety)
pnts.add(testpoint.gety)
'Вызов процедуры расчета расстояний
'"Calc-distance" - название скрипта с процедурой в проекте
param = av.run("Calc-distance", pnts)
aftab.setvalue(f_dist, rec, param.get(0))
aftab.setvalue(f_ang, rec, param.get(1))
end
aftab.seteditable(false)
[править] Реализация на языке Python
Реализует полный вариант расчета через atan2(), более универсальнее, чем вариант для Avenue. (скачать скрипт)
import math #pi - число pi, rad - радиус сферы (Земли) rad = 6372795 #координаты двух точек llat1 = 77.1539 llong1 = -120.398 llat2 = 77.1804 llong2 = 129.55 #в радианах lat1 = llat1*math.pi/180. lat2 = llat2*math.pi/180. long1 = llong1*math.pi/180. long2 = llong2*math.pi/180. #косинусы и синусы широт и разницы долгот cl1 = math.cos(lat1) cl2 = math.cos(lat2) sl1 = math.sin(lat1) sl2 = math.sin(lat2) delta = long2 - long1 cdelta = math.cos(delta) sdelta = math.sin(delta) #вычисления длины большого круга y = math.sqrt(math.pow(cl2*sdelta,2)+math.pow(cl1*sl2-sl1*cl2*cdelta,2)) x = sl1*sl2+cl1*cl2*cdelta ad = math.atan2(y,x) dist = ad*rad #вычисление начального азимута x = (cl1*sl2) - (sl1*cl2*cdelta) y = sdelta*cl2 z = math.degrees(math.atan(-y/x)) if (x < 0): z = z+180. z2 = (z+180.) % 360. - 180. z2 = - math.radians(z2) anglerad2 = z2 - ((2*math.pi)*math.floor((z2/(2*math.pi))) ) angledeg = (anglerad2*180.)/math.pi print 'Distance >> %.0f' % dist, ' [meters]' print 'Initial bearing >> ', angledeg, '[degrees]'
[править] Реализация в Excel
Скачать пример расчета расстояния большого круга и начального азимута в Excel. Демонстрирует расчеты через закон косинусов, гаверсинус, полное уравнение и полное уравнение через atan2(). 0.5) * 6372795
0.5) * 6372795
End With
End Function
[править] Проверочный набор данных
Если все считается правильно, должны быть получены следующие результаты (координаты точек даны как широта/долгота, расстояние в метрах, начальный угол в десятичных градусах):
| # | Точка 1 | Точка 2 | Расстояние | Угол |
| 1 | 77.1539/-139.398 | -77.1804/-139.55 | 17166029 | 180.077867811 |
| 2 | 77.1539/120.398 | 77.1804/129.55 | 225883 | 84.7925159033 |
| 3 | 77.1539/-120.398 | 77.1804/129.55 | 2332669 | 324.384112704 |
[править] Ссылки по теме
Расстояние между точками по координатам
Данный онлайн калькулятор считает расстояние между двумя точками двумерной плоскости исходя из координат этих точек. Вы можете посчитать длину отрезка между двумя точками или длину линии между двумя точками на основе координат этих точек.
Значения координат могут быть положительными и отрицательными числами или так же равными 0. Так же можно использовать десятичные значения.
Положение точек не принципиально, главное введите правильно координаты каждой из точек. Так для точки A это координаты Ax и Ay, a для точки B — координаты Bx и By. Если у вас есть координаты двух точек, можете любую из этих точек делать точкой A, вторая будет точкой B.
Укажите координаты:
Результат:
Решение:
Отправить ссылку в:
На двумерной плоскости координаты точки — это два числа, где первым числом указывается абсцисса (координата x), а вторым — ордината точки (координата y). 2}
2}
- AB — отрезок между точками A и B
- Ax — координата x в точке A
- Ay — координата y в точке A
- Bx — координата x в точке B
- By — координата y в точке B
Онлайн расчет расстояния по координатам + формула
Расчет расстояния между координатами
Данный сервис позволяет рассчитать расстояние между двумя точками с известными географическими координатами.
Как известно, кратчайшим расстоянием между двумя точками на земной поверхности является длина дуги круга, проведенного на сфере по этим двум точкам. При расчете расстояния по географическим координатам делается предположение, что Земля не плоская, а круглая (если быть точнее, имеет форму, приближенную к сфере), то есть Земля — сфероид.
Для определения расстояния между двумя точками будет применяться формула расчета длины дуги, так называемая «модифицированная формула гаверсинусов».
Поскольку в расчете участвует радиус, а у Земли, как у не совсем правильной сферы, он разный, скажем на северном полюсе — 6335.437 км, а на экваторе — 6399.592 км. В связи с этим в расчете берется среднее значение радиуса Земли равное 6372.795 км, что позволяет получать результат с точность 99,5%.
В калькуляторе ниже для примера приводится расчет расстояния между координатами г.Москва и г.Санкт-Петербург.
Формула расчета расстояния по координатам
Пусть и являются географическими широтой и долготой двух точек 1 и 2, и — их абсолютная разность. Тогда , центральный угол между ними, определяется теоремой сферических косинусов:
Формула расстояние d т.е.длины дуги, для сферы радиуса R и приведены в радианах
Больше матиматики .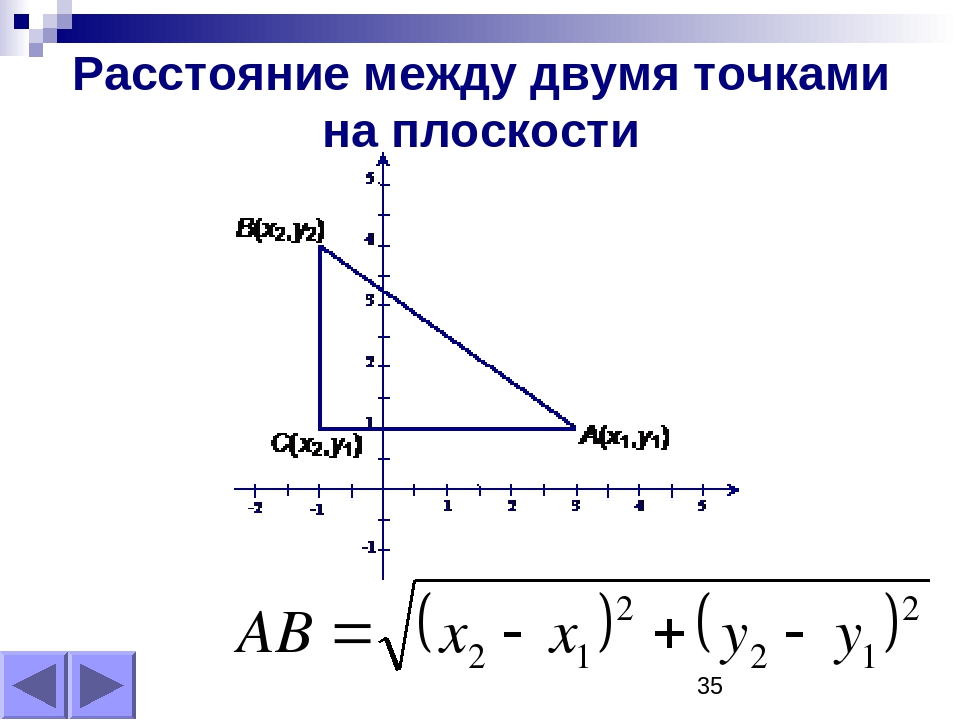 ..
..
На компьютерных системах с низкой точностью с плавающей запятой, эта формула может иметь большие ошибки округления, если расстояние не большое (если две точки находятся в 1 км друг от друга на поверхности Земли, косинус центрального угла выходит 0,99999999). Для современных 64-разрядных чисел с плавающей запятой, формула Теоремы косинусов, которая приведенна выше, не имеет серьезных ошибок округления для расстояний более нескольких метров на поверхности Земли. Эта формула лучше подходит для вычисления растояние по координатам на небольшые расстояния
Для получения более точных рузультатов на большых расстояниях стараются исполтзовать формулу посложнее, в которой сделано предположение, что сфера является эллипсоидом с одинаковыми большой и малой осями.
Более подробную информацию о выведении формулы расчета расстояния по координатам читайте здесь: http://en.wikipedia.org/wiki/Great_circle_distance
Комментарии:
Прямоугольная система координат в пространстве.
 Формула для вычисления расстояния между двумя точками. Координаты середины отрезка_геометрия 10 класс
Формула для вычисления расстояния между двумя точками. Координаты середины отрезка_геометрия 10 класс
Дата_17.02.16-19.02.16 Геометрия 10 класс
Урок 43-44
Тема урока: Прямоугольная система координат в пространстве. Формула для вычисления расстояния между двумя точками. Координаты середины отрезка.
Цели урока:
Закрепить полученные знания по теме системы координат и координаты точки в пространстве; выработать умения строить точку по заданным её координатам; находить координаты точек, изображённой в заданной системе координат;
Способствовать развитию пространственного воображения учащихся; умение развивать аналогии сравнение; способствовать выработке решения задач и развития логического мышления учащихся.
Воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Ход урока
1. Организационный момент, приветствие, пожелания плодотворной работы.
2. Мотивация урока.
Ребята, чтобы найти конкретного человека на нашей планете, что необходимо нам знать? Правильно его место нахождение, т.е. другими словами мы должны знать его координаты.
Как не потеряться в этой жизни? Я думаю нам помогут координаты!!!!
3.Актуализация знаний.
Фронтальный опрос по технологии «Микрофон».
В каком направлении можно двигаться на плоскости?
Сколькими координатами может быть задана точка в пространстве?
Чем определяются точки на координатной плоскости?
Что такое координата?
Как задать координатную плоскость?
Как называется ось 0Х, 0У, OZ?
Назовите координаты точек (по таблице)
Назовите формулу нахождения середины отрезка, длину отрезка
4.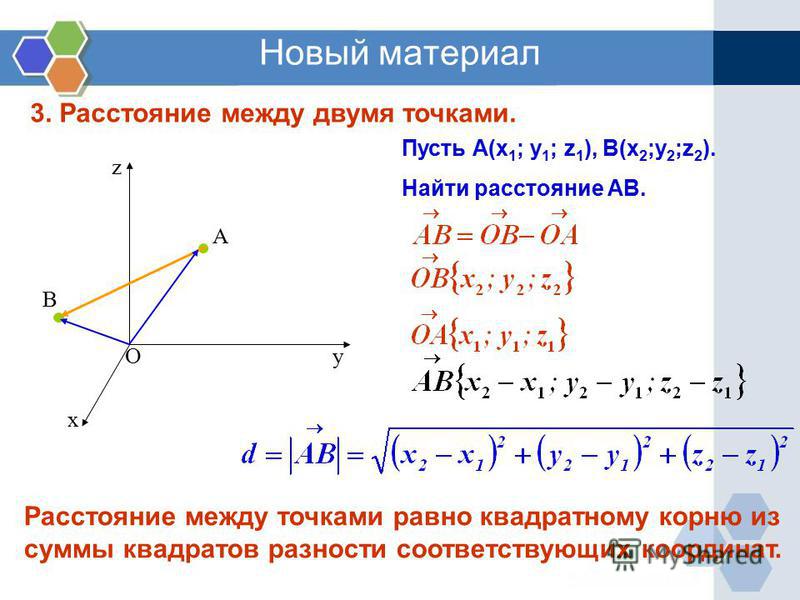 Работа с изученным материалом, Формирование первичных умений и навыков
Работа с изученным материалом, Формирование первичных умений и навыков
Вся система обозначается Охуz.
Три плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох — координатные плоскости. Их обозначают Оху, Оуz, Оzх.
В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются её координатами.
Проведем через точку М три плоскости, перепендикулярные к осям координат, и обозначим через М1, М2 и М3, точки пересечения этих плоскостей соответственно с осями абсцисс, ординат и аппликат. М1 – абсцисса, М2 – ордината, М3 – аппликата точки М. Координаты точки М записываются: М (х; у; z), х – абсцисса, у – ордината, z-аппликата.
Задание:
Назовите координаты точек, лежащих на координатных осях.
Какие из данных точек лежат на координатных осях и на какой: А(5;0;0),
В(-7;5;0), С(0;0;-9), М(0;8;0), Р(0;1;0)?
— Назовите координаты точек, лежащих в координатных плоскостях.
Какие из данных точек лежат в координатных плоскостях и в какой из плоскостей: А(3;0;5), В(-1; 4; 6), С(0;5;-9), М(5;5;0), Х(9;7;0)?
— Назовите координаты точки, совпадающей с началом координат; лежащих в пространстве.
Выбрать среди заданных точек те, которые лежат в пространстве или в начале координат: А(0;7;-2), О (0;0;0), В(2;4;-4), М(8;-5;2), Р(0;0;0).
Задача. Письменно
Дано: А (1;-1;2), В (3;1;-2)
Найдите координаты середины отрезка АВ и его длину.
Решение:
1). Пусть С – середина отрезка АВ, тогда С (; ; ), С (2;0;0)
2). АВ = = = 2.
Ответ: С (2;0;0), АВ = 2.
3) Подготовка к ЕНТ (сб. тестов НЦТ 2009 год, В 3 № 24)
Найти координаты центра тяжести треугольника с вершинами в точках
1)А(3; -4; 7), В(-5; 3; -2) и С(8; 7; -8).
2) А. (-2; -2; 1), В. (-5; 3; 9), С. (2; 2; 1),
Ответ:1) D. (2; 2; -1), 2) Е. (2; -2; -1).
Решение.
Координаты центра тяжести однородной треугольной пластинки, если не учитывать ее толщину, равны среднему арифметическому однородных координат ее вершин. Координаты центра тяжести треугольника, расположенного в пространстве будут находиться по формулам:
ZЕ =
3
Z1 + Z2 + Z3
Возвращаясь к условию задачи, получим: Е (Хц; Уц; Zц)
Хц = (3-5+8 ): 3 = 2 ; Уц = (-4+3+7) : 3 = 2 ; Zц = ( 7- 2 – 8) : 3 = -1
Е(2; 2; -1) – D.
Задача . Самостоятельно (сб. апробационных тестов НЦТ 2013 год, В 0173 № 24)
Найти координаты центра тяжести треугольника с вершинами в точках
А(7; -4), В(-1; 8) и С(-12; -1).
А. (2; 1), В. (-2; 1), С. (3; -2), D. (-1; 2), Е. (2,5; 3).
(Ответ: В(-2; 1) ).
Даны точки: А(-3; 0; 0), В(5; 0; -1), С(0; 0; 8), D (-1;5;0), Е(0; 7;4), F(-6;-1; 0), К(0;0;0), М(0;-3;5), N(2;4;-1), Р(0;-6;0). Определите точки, принадлежащие: а) осям координат х, у, z; б) координатным плоскостям ху, хz, уz.
5. Минута отдыха.
Массаж ушных раковин.
Более тысячи биологически активных точек на ухе известно в настоящее время, поэтому, массируя их, можно последовательно воздействовать на весь организм. Нужно стараться так помассировать ушные раковины, чтобы уши «горели». Упражнение можно выполнять в такой последовательности:
1) потягивание за мочки сверху вниз;
2) потягивание ушной раковины вверх;
3) потягивание ушной раковины к наружи;
4) круговые движения ушной раковины по часовой стрелке и против;
5) растирание ушей до ощущения «горения».
6. Закрепление нового материала.
7. Самостоятельная работа с последующей проверкой: тест
8. Итоги урока. Рефлексия.
9. Д/з §19, § 20, теория, составить кластер по теме (работа в группах),
№ 4, №5 стр. 66; № 8 стр. 68
На уроке закрепили знания по теме прямоугольная система координат в пространстве, научились строить точку по заданным ее координатам и находить координаты точки, изображенной в заданной системе координат.
Никитенко Ольга Александровна, учитель информатики математики
КГУ «Средняя школа№13», г. Усть-Каменогорск
Приложение
Формула расстояния
Вы знаете, что
расстояние
А
B
между двумя точками на плоскости с
Декартово
координаты
А
(
Икс
1
,
y
1
)
а также
B
(
Икс
2
,
y
2
)
дается следующей формулой:
А
B
знак равно
(
Икс
2
—
Икс
1
)
2
+
(
y
2
—
y
1
)
2
Формула расстояния на самом деле просто
Теорема Пифагора
в маскировке.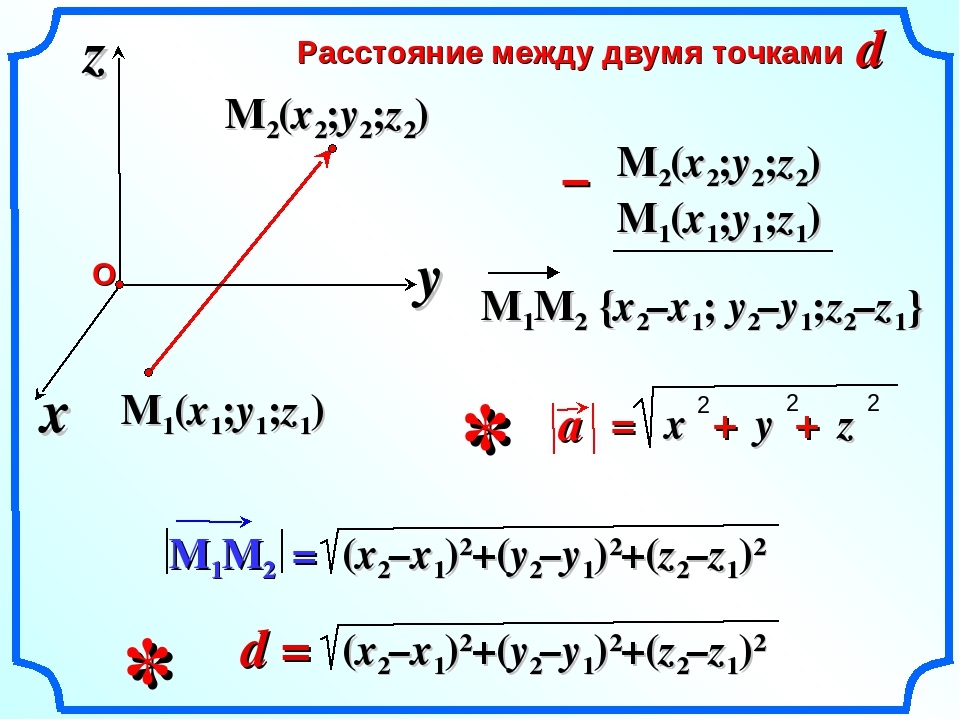
Чтобы рассчитать расстояние
А
B
между точкой
А
(
Икс
1
,
y
1
)
а также
B
(
Икс
2
,
y
2
)
сначала нарисуйте прямоугольный треугольник с отрезком
А
B
¯
как его гипотенуза.
Если длины сторон равны
а
а также
б
, то по теореме Пифагора
(
А
B
)
2
знак равно
(
А
C
)
2
+
(
B
C
)
2
Решение на расстоянии
А
B
, у нас есть:
А
B
знак равно
(
А
C
)
2
+
(
B
C
)
2
С
А
C
горизонтальное расстояние, это просто разница между
Икс
-координаты:
|
(
Икс
2
—
Икс
1
)
|
. По аналогии,
По аналогии,
B
C
это вертикальное расстояние
|
(
y
2
—
y
1
)
|
.
Поскольку мы все равно возводим эти расстояния в квадрат (а квадраты всегда неотрицательны), нам не нужно беспокоиться об этих знаках абсолютного значения.
А
B
знак равно
(
Икс
2
—
Икс
1
)
2
+
(
y
2
—
y
1
)
2
Пример:
Найдите расстояние между точками
А
а также
B
на рисунке выше.
В приведенном выше примере у нас есть:
А
(
Икс
1
,
y
1
)
знак равно
(
—
1
,
0
)
,
B
(
Икс
2
,
y
2
)
знак равно
(
2
,
7
)
так
А
B
знак равно
(
2
—
(
—
1
)
)
2
+
(
7
—
0
)
2
знак равно
3
2
+
7
2
знак равно
9
+
49
знак равно
58
или примерно
7. 6
6
единицы измерения.
Формула расстояния | Purplemath
Purplemath
Формула расстояния — это вариант теоремы Пифагора, которую вы использовали еще в геометрии. Вот как мы переходим от одного к другому:
Предположим, вам даны две точки (–2, 1) и (1, 5), и они хотят, чтобы вы выяснили, насколько они далеко друг от друга.Очки выглядят так:
MathHelp.com
Вы можете рисовать линии, образующие прямоугольный треугольник, используя эти точки в качестве двух углов:
Легко найти длины горизонтальной и вертикальной сторон прямоугольного треугольника: просто вычтите значения x и значения y :
Затем используйте теорему Пифагора, чтобы найти длину третьей стороны (которая является гипотенузой прямоугольного треугольника):
. ..so:
..so:
Этот формат верен всегда. Имея две точки, вы всегда можете построить их, нарисовать прямоугольный треугольник, а затем найти длину гипотенузы. Длина гипотенузы — это расстояние между двумя точками. Поскольку этот формат работает всегда, его можно превратить в формулу:
Формула расстояния: учитывая две точки ( x 1 , y 1 ) и ( x 2 , y 2 ), дается расстояние d между этими точками. по формуле:
Пусть вас не пугают индексы.Они только указывают на то, что есть «первая» точка и «вторая» точка; то есть у вас есть два очка. Какой из них вы назовете «первым» или «вторым» — решать вам. В любом случае расстояние будет таким же.
Какой из них вы назовете «первым» или «вторым» — решать вам. В любом случае расстояние будет таким же.
Найдите расстояние между точками (–2, –3) и (–4, 4).
Я просто подставляю координаты в формулу расстояния:
Тогда расстояние будет sqrt (53), или около 7.28 с округлением до двух десятичных знаков.
URL: https://www.purplemath.com/modules/distform.htm
Формула расстояния
| Калькулятор и пошаговые примеры // Tutors.com
Калькулятор формул расстояния
D = (x2 — x1) 2 + (y2 — y1) 2
Расстояние = (x2 − x1) 2+ (y2 − y1) 2 −−−−−−−−−−−−−−−−−− √Distance = (x2 − x1) 2+ (y2 − y1) 2
Как это работает: Введите две координаты x и две координаты y в поля ниже, и программа автоматически рассчитает расстояние между этими двумя точками и покажет вам шаг за шагом.
Ответ
(0−0) 2+ (0−0) 2 −−−−−−−−−−−−−−−− √0 – √ = 0 (0−0) 2+ (0−0) 20 = 0
Содержание
- Видео
- Калькулятор формул расстояния
- Расстояние между двумя точками
- Формула расстояния
Расстояние между двумя точками
В декартовой сетке измерить вертикальный или горизонтальный отрезок линии достаточно просто. Вы можете считать расстояние вверх и вниз по оси Y или по оси X.
А как насчет диагональных линий? Как узнать, какой длины будет отрезок линии, если он пересекает эти крошечные прямоугольники? См. Этот пример:
Вы можете использовать формулу расстояния для вычисления любого отрезка линии, если знаете координаты двух конечных точек. Вы будете мысленно строить прямоугольный треугольник, используя диагональ, как если бы это была гипотенуза.
Формула расстояния
Формула расстояния возводит в квадрат разности между двумя координатами x и двумя координатами y, затем складывает эти квадраты и, наконец, извлекает их квадратный корень, чтобы получить общее расстояние по диагональной линии:
D = (x2 — x1) 2 + (y2 — y1) 2
Выражение (x2 — x1) читается как изменение x и (y2 — y1) изменение y .
Как использовать формулу расстояния
На самом деле это вычисляет расстояние по горизонтали между значениями x, как если бы линейный сегмент составлял сторону прямоугольного треугольника, а затем проделывает это снова со значениями y, как если бы вертикальный линейный сегмент был второй стороной прямоугольный треугольник.
Остается вычислить гипотенузу, заданную вами диагональ. Формула расстояния — это специальное приложение теоремы Пифагора.
Все, что вам нужно сделать, это очень аккуратно ввести координаты.Давайте использовать конечные точки нашей строки (1, 3) и (7, 6):
D = (7-1) 2 + (6-3) 2
D = (6) 2 + (3) 2
D = 36 + 9
D = 45
D ≅ 6,7085
Примеры формул расстояния
Для использования формулы расстояния вам даже не нужно иметь координатную сетку, если у вас есть оба набора координатных точек. Итак, попробуйте эти три практических задачи!
- (-2, 4) и (10, 1)
- (5, 5) и (1, 10)
- (-11, -2) и (-21, -6)
Не оставим вас болтаться по диагонали. Вот первые шаги, которые помогут вам начать работу:
Вот первые шаги, которые помогут вам начать работу:
- D = (10 — -2) 2 + (1 — 4) 2
- D = (2-5) 2 + (10-5) 2
- D = (-21 — -11) 2 + (-6 — -2) 2
Что будет дальше?
- D = (12) 2 + (-3) 2
- D = (-3) 2 + (5) 2
- D = (-10) 2 + (-4) 2
Вы действительно должны уметь делать последние несколько шагов самостоятельно. Посмотрим, получили ли вы эти ответы:
- 153 12,369
- 34 ≅ 5,8 309
- 116 ≅ 10.7703
Пифагор
Формула расстояния получает свою точность и совершенство благодаря концепции использования углового отрезка прямой, как если бы это была гипотенуза прямоугольного треугольника, образованного на сетке. Вам не нужно строить две другие стороны для применения формулы расстояния, но вы можете видеть эти две «стороны» в разностях (расстояниях) между значениями x (горизонтальная линия) и значениями y (вертикальная линия).
Краткое содержание урока
Теперь, когда вы проработали урок и попрактиковались, вы можете применить формулу расстояния к конечным точкам любого сегмента диагональной линии, появляющегося в координатной или декартовой сетке. Вы также можете связать формулу расстояния с теоремой Пифагора.
Вы также можете связать формулу расстояния с теоремой Пифагора.
Пифагор, без сомнения, был щедрым и блестящим математиком, но он не сделал большого скачка в применении теоремы Пифагора к координатным сеткам. Чтобы вывести нас из его теоремы о соотношении сторон прямоугольных треугольников к координатным сеткам, математический мир должен был дождаться Рене Декарта. Его декартова сетка сочетает в себе геометрию и алгебру. Вы можете использовать формулы, в том числе формулу расстояния, чтобы получить точные измерения отрезков линии на сетке.
Следующий урок:
Что такое прямая линия?
Какова формула определения расстояния?
Расстояние между двумя точками
Если вы вспомните теорему Пифагора, формула расстояния на самом деле является вариацией этой теоремы.
Две точки на плоскости
Давайте углубимся в это с помощью точек на графике выше. У нас есть две точки: одна в x1, y1 и другая в x2, y2. Чтобы вычислить расстояние между ними, соедините точки вместе и сформируйте прямоугольный треугольник, который использует две точки в качестве углов.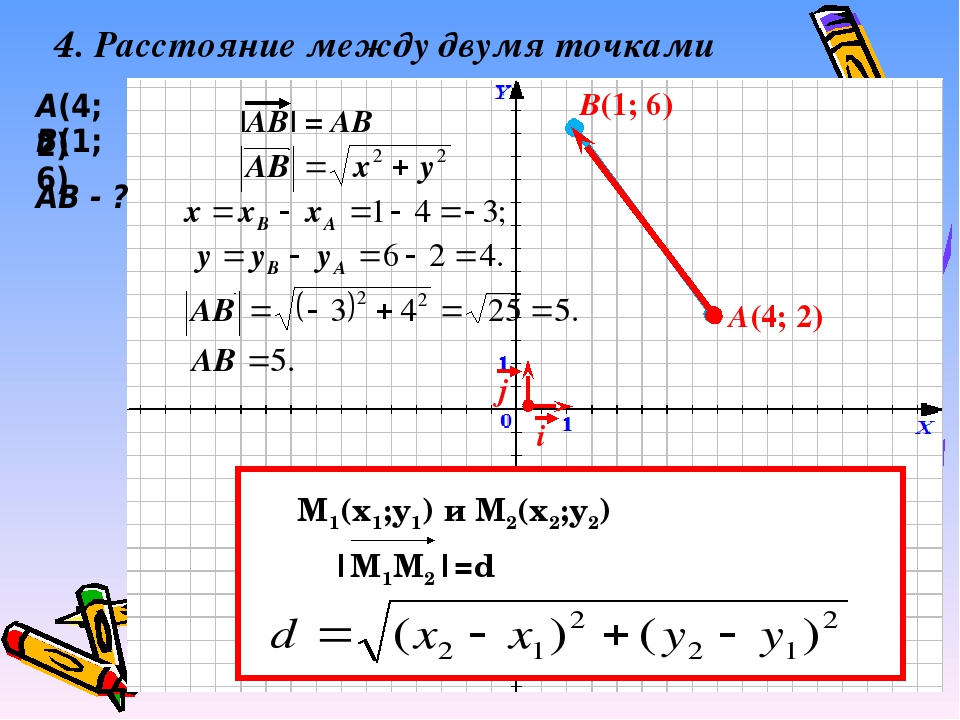 2
2
Следовательно, если бы мы подставили точки (x1, y1) и (x2, y2), а затем переместили квадрат на другую сторону уравнения, чтобы он стал квадратным корнем, мы получим формулу для
расстояние.
Какова формула расстояния?
d используется для обозначения расстояния в этом случае. Эта формула всегда верна и полезна, когда у вас есть два очка. Если вы знаете, где они находятся на графике, вы можете построить их, а затем нарисовать прямоугольный треугольник, который поможет вам найти длину его гипотенузы.Это использует теорему Пифагора, которую мы узнали еще при изучении геометрии. Гипотенуза — это расстояние, которое вы ищете между двумя точками! Теперь вы узнали, как работает формула расстояния.
При расчете расстояния необходимо помнить следующее:
1) Следите за тем, чтобы ваши значения x и y не совпадали. Убедитесь, что вы правильно сопоставили их в правильном порядке, так что если вы используете значение x в точке A, сопоставьте его со значением x в точке B при вычитании. Затем для второй части формулы убедитесь, что вы снова используете значение y из точки A, а затем вычитаете значение y из точки B.
Затем для второй части формулы убедитесь, что вы снова используете значение y из точки A, а затем вычитаете значение y из точки B.
2) Упростите то, что указано в круглых скобках, прежде чем выполнять возведение в квадрат. Это правильный порядок при решении математических задач, и он верен в формуле расстояния.
3) Не забудьте записать символ квадратного корня. Это хорошая привычка, и если вы оставите ее до конца, вы можете забыть вернуть ее и получить неправильный ответ.
Примеры определения расстояния
Давайте воспользуемся формулой для расчета расстояния с примером вопроса.
Вопрос: какое расстояние между точками A (4,2) и B (6,8)?
Мы знаем, что будем использовать как значения x, так и значения y. Просто подставьте числа в формулу расстояния. Это будет выглядеть примерно так:
Этапы использования формулы расстояния
Выше мы рассматриваем B как точку 2 и последовательно используем координаты точки 2 перед A в формуле. Не забудьте возвести в квадрат разницу между X и Y, и вы получите число под квадратным корнем. Обязательно упростите ответ, чтобы некоторые числа можно было вынести из радикального символа.
Обязательно упростите ответ, чтобы некоторые числа можно было вынести из радикального символа.
Как насчет того, чтобы делать горизонтальные или вертикальные линии? Подойдет ли формула расстояния? Короткий ответ — будет. Однако есть более простой способ сделать это. При работе с горизонтальными линиями длина линии — это просто разница между x-координатами двух точек. Аналогичным образом длину вертикальной линии можно найти, вычитая одну из координат y с другой.Вы можете свободно попробовать это самостоятельно с координатами по вертикальной или горизонтальной линии, и вы обнаружите, что получите тот же ответ, просто вычтя координаты и используя формулу расстояния.
Чтобы подытожить концепцию, вот хороший ресурс, который вы можете изучить. Если вы хотите поиграть с разными координатами и посмотреть, как работает формула расстояния, попробуйте ее на этой интерактивной диаграмме!
Определение расстояния между двумя точками
Умение находить расстояние между двумя точками — очень полезный навык «в реальной жизни». Это требуется во многих, многих профессиях и задачах. например гражданское строительство, цифровые медиа, военная промышленность, картография. Несмотря на то, что в нашем компьютеризированном мире вычисления чаще всего выполняются за нас, возможность рассчитать это расстояние вручную помогает понять и снижает вероятность ошибок.
Это требуется во многих, многих профессиях и задачах. например гражданское строительство, цифровые медиа, военная промышленность, картография. Несмотря на то, что в нашем компьютеризированном мире вычисления чаще всего выполняются за нас, возможность рассчитать это расстояние вручную помогает понять и снижает вероятность ошибок.
При необходимости вы должны просмотреть руководство по графическому изображению координат x-y и / или просмотреть теорему Пифагора, чтобы получить помощь в вычислении длин сторон прямоугольных треугольников.
При вычислении расстояния между двумя точками в системе координат мы применяем теорему Пифагора.Как показано в примере ниже, мы делаем это, соединяя две точки прямой линией, а затем рисуя прямоугольный треугольник, используя эту прямую в качестве гипотенузы, и выравнивая две другие стороны с осью x и осью y.
Мы вычисляем длину двух сторон, выровненных по осям x и y, путем нахождения разницы в значениях координат x и y. Затем, используя теорему Пифагора, мы возьмем квадрат этих сторон, сложим их, затем извлечем квадратный корень, который дает длину гипотенузы, которая является расстоянием между двумя точками.
Пример: расстояние между двумя точками
| Найдите длины коротких сторон треугольника, найдя разности координат x и y. 9-2 = 7 8-3 = 5 Квадрат, затем сложите эти 7 2 + 5 2 = 49 + 25 = 74 Извлеките квадратный корень, чтобы найти расстояние между точками . расстояние = √ 74 = 8.602 |
Формула для расстояния между двумя точками
Приведенная ниже формула выражает приведенное выше описание вычисления расстояния в алгебраических терминах.Другими словами, он говорит то же самое, используя символы и переменные.
Иногда может показаться, что формула чрезмерно усложняет то, что по сути просто нахождение разницы в координатах x и y и последующее применение теоремы Пифагора. Не имеет значения, какая координата (x 1 , y 1 ), а какая (x 2 , y 2 ), если значения координат x и y, которые вы вычитаете, взяты из одной и той же точки.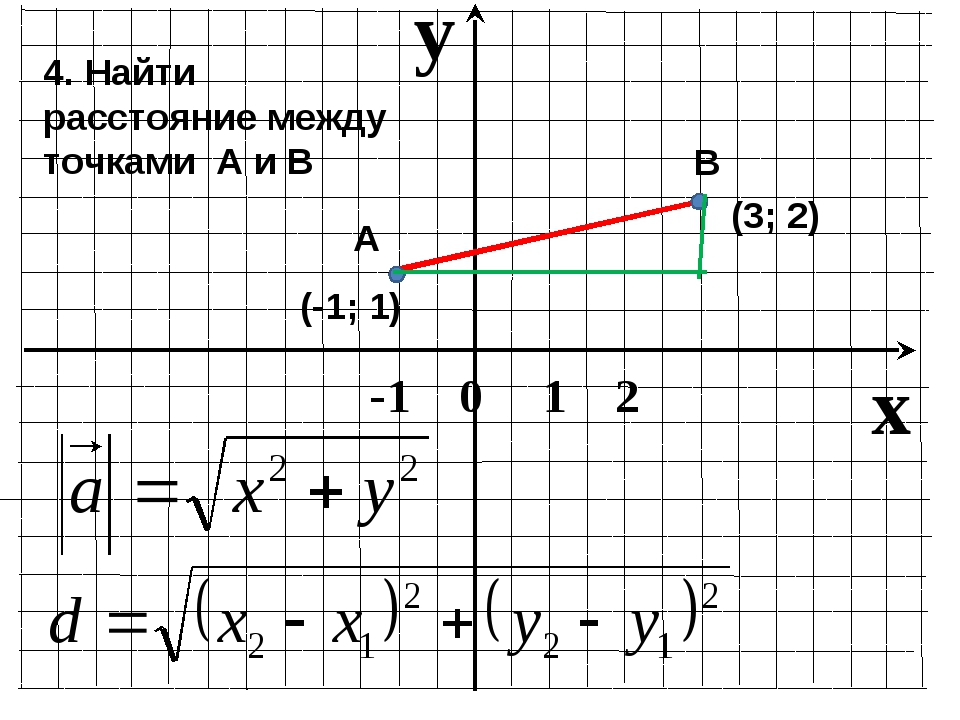 . т.е. не путайте их.
. т.е. не путайте их.
Отрицательные координаты
Найти расстояние между двумя точками может быть немного сложнее, если задействовано одно или более отрицательное значение.Однако до тех пор, пока значения координат не перепутаны и соблюдаются правила сложения и вычитания отрицательных целых чисел, можно следовать той же процедуре.
| Пример с отрицательными значениями |
| Задача: Найдите расстояние между точкой (-5,3) и точкой (4,5), показанным в таблице ниже. |
| Решение : Применение формулы расстояние = √ (x 2 — x 1 ) 2 + (y 2 — y 1 ) 2 , чтобы найти расстояние между точкой (-5,3) и точкой (4,5) получаем расстояние = √ (-5-4) 2 + (3 — (- 5)) 2 расстояние = √ (-9) 2 + (8) 2 расстояние = √ 145 расстояние = 12. 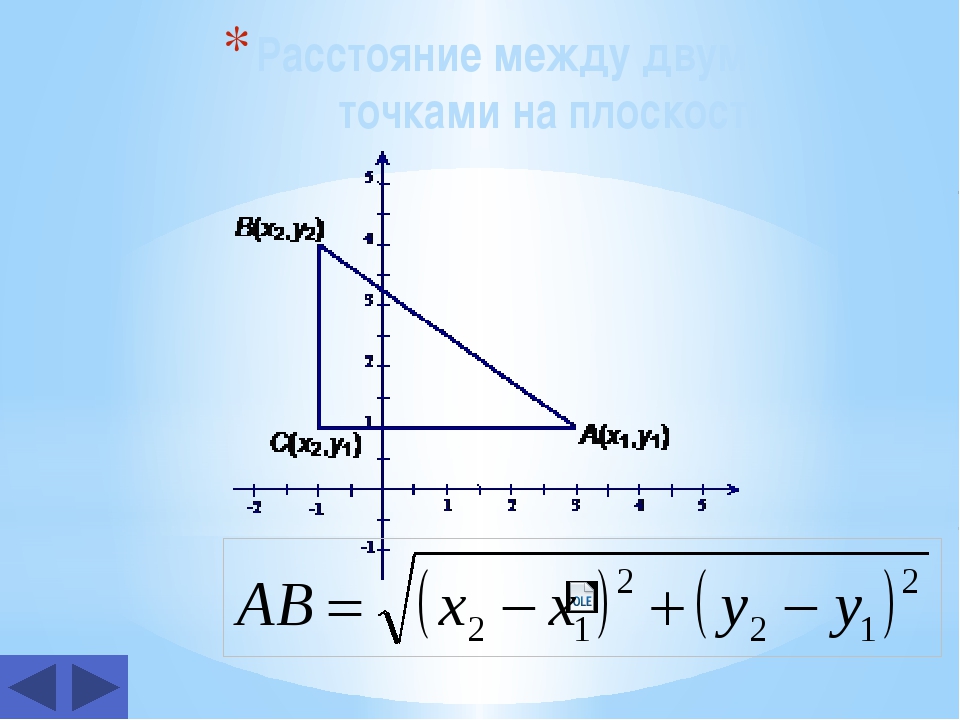 042 042 |
Набросок проблемы
Если вам представлены только два набора координат и вам нужно найти расстояние между ними, вы можете обнаружить, что вам поможет быстрый набросок двух точек на приблизительной координатной сетке. Это помогает проверить правильность расхождений, а также помогает проверить разумность ответа.
| Пример |
| Задача: Каково расстояние между точкой (-3, -6) и точкой (8, -2)? |
| Решение : Нарисовав две точки и оси, мы можем сформировать прямоугольный треугольник с двумя короткими сторонами длиной 4 и 11.Чтобы найти расстояние, мы складываем их квадраты и извлекаем квадратный корень. расстояние = √ (4) 2 + (11) 2 расстояние = 11,705 |
Рабочий лист
Попробуйте эту таблицу «Расчет расстояния между двумя точками», чтобы попрактиковаться с вопросами, аналогичными приведенным выше. 2} $$
2} $$
Разрушение
На первый взгляд, эта формула выглядит просто беспорядочно! Но просто подумайте о компонентах \ (x_ {2} -x_ {1} \) и \ (y_ {2} -y_ {1} \) как о длине в каждом направлении.Используя эти два значения, мы математически строим воображаемый треугольник с двумя катетами, длину которых мы можем вычислить. Позвольте мне показать вам, что я имею в виду визуально:
Мы просто измеряем расстояние вдоль каждой оси, а затем используем теорему Пифагора для вычисления длины гипотенузы, которая представляет собой воображаемую линию непосредственно между двумя нашими точками. Не имеет значения, какая точка равна \ ((x_ {1}, y_ {1}) \), а какая — \ ((x_ {2}, y_ {2}) \). Ключевая идея, которую следует извлечь из этого графика, заключается в том, что вас интересует только изменение на по x и изменение на по y.2} $$
Как мы пришли к этой формуле? Это просто теорема Пифагора, которая позволяет нам найти гипотенузу прямоугольного треугольника. В нашем случае гипотенуза — это расстояние между двумя точками!
В нашем случае гипотенуза — это расстояние между двумя точками!
Давайте теперь посмотрим на простой пример:
Пример:
Найдите расстояние между двумя точками (5,5) и (1,2), используя формулу расстояния.
Решение:
Вместо того, чтобы слепо подставлять числа в формулы, нарисуйте график, чтобы знать, что происходит.2} $$
$$ \ text {расстояние} = \ sqrt {16 + 9} $$
$$ \ text {расстояние} = \ sqrt {25} $$
$$ \ text {distance} = 5 $$
Как только мы узнали, что \ (x_ {2} -x_ {1} \) равно 4 и \ (y_ {2} -y_ {1} \) равно 3, мы просто вставили эти числа в формулу расстояния , чтобы решить .
Вам может быть интересно, что произойдет, если вы перевернете точки? Помните, что мы имеем дело с расстояниями, которые по своей сути положительны. Расстояние одинаково в любом направлении, от точки 1 до точки 2 или наоборот. Итак, просто используйте положительное расстояние между двумя точками.Если вы посмотрите на формулу, вы заметите, что \ (x_ {2} -x_ {1} \) и \ (y_ {2} -y_ {1} \) возведены в квадрат, что в любом случае автоматически делает их положительными. 2} $$
2} $$
$$ \ text {distance} = \ sqrt {25 + 121} $$
$$ \ text {расстояние} = \ sqrt {146} $$
$$ \ text {distance} = 12.08 $$
Формула расстояния не сложна — вам просто нужно попрактиковаться с графиком, чтобы понять, что происходит. Вы просто строите треугольник и находите длину гипотенузы. Формула расстояния — это просто теорема Пифагора!
Расширение до трех измерений
А как насчет трехмерного пространства? Как найти расстояние между точками (1,5,0) и (2,0, 8)? Конечно, построить график и измерить расстояние намного сложнее! Формула трехмерного расстояния на самом деле очень проста.2} $$
Если вы зашли так далеко, надеюсь, вы лучше понимаете формулу расстояния. Если это не так, вот еще один урок по формуле расстояния, доступный в Интернете.
Расстояние между двумя точками 2D Формула
Эта формула рассчитывает расстояние между двумя точками
| Выражение | Описание |
|---|---|
-координата первой точки. | |
| -координата первой точки. | |
| -координата второй точки. | |
| -координата второй точки. |
Для расчета расстояния между двумя точками в двух измерениях можно использовать приведенную ниже формулу.
Например, чтобы найти расстояние между точкой и точкой, подставьте их координаты в формулу следующим образом:
Рассчитайте результат.
Расстояние между двумя точками и составляет единицы.
Этот пример демонстрирует, как найти расстояние между двумя точками и.
Начните с формулы расстояния между двумя точками (2D).
Подставьте координаты точек в формулу.
Оцените выражения вычитания.
Оцените выражения абсолютного значения.
Оцените выражения экспоненты.
Оцените операцию добавления.
Извлеките квадратный корень.

Расстояние между точками и равно единицам.
Этот пример демонстрирует, как найти расстояние между двумя точками и.
Начните с формулы расстояния между двумя точками (2D).
Подставьте координаты точек в формулу.
Оцените выражения вычитания.
Оцените выражения абсолютного значения.
Оцените выражения экспоненты.
Вычислите выражение сложения.
При желании извлеките квадратный корень.
Расстояние между точками и равно единицам.
Этот пример демонстрирует, как найти расстояние между двумя точками и.
Начните с формулы расстояния между двумя точками (2D).
Подставьте координаты точек в формулу.
Оцените выражения вычитания.
Возьмите абсолютное значение двух выражений.
Вычислить выражения экспоненты.
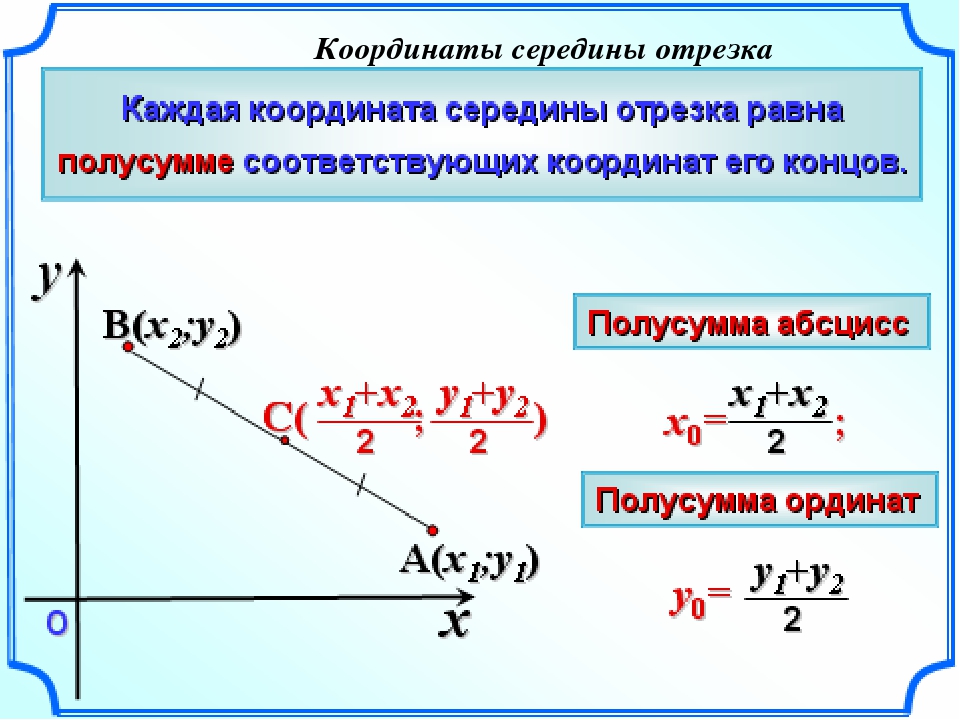
Вычислите оператор сложения.
При желании извлеките квадратный корень.
Расстояние между точками и равно единицам.
Формула для расстояния между двумя точками и может быть получена с помощью комбинации теоремы Пифагора и формулы расстояния между двумя точками (1D).
Обратите внимание, что геометрия двух точек и образует форму прямоугольного треугольника в декартовой системе координат. Гипотенуза, помеченная переменной, равна расстоянию между двумя точками. Это проиллюстрировано ниже.
Составьте уравнение теоремы Пифагора.
Переставьте уравнение и извлеките квадратный корень из обеих частей.
Найдите длины смежного и противоположного прямоугольного треугольника, применив формулу одномерного расстояния.
Подставьте эти выражения в выражение из шага три.
Наконец, измените переменную на представление расстояния, и мы вывели формулу.

