Содержание
Первообразная функции. Формула Ньютона-Лейбница — подготовка к ЕГЭ по Математике
Функция F(x), для которой f(x) является производной, называется первообразной функции y = f(x). Функции вида у = F(x) + C образуют множество первообразных функции у = f(x).
Сейчас объясним, что это значит.
Вспомним таблицу производных. В левой колонке — функции, в правой — их производные. Например, — производная от функции , — производная функции . А чем будет являться для функции ? Или — для функции ? Вы уже догадались. Первообразной.
Заметим, кстати, что — производная не только функции , но и функций , — в общем, всех функций вида Здесь C — константа, то есть постоянная величина, и ее производная равна нулю.
Аналогично, функция — производная для всех функций вида , где — константа.
Посмотрим на таблицу первообразных. Каждая функция в левом столбце таблицы является производной для функции в правом столбце.
Таблица первообразных
Первообразная суммы функций равна сумме их первообразных.
Первообразная разности функций — разности первообразных.
Первообразная от функции , где — постоянный множитель, равна произведению на первообразную функции , то есть .
Множество всех первообразных функции называется неопределенным интегралом данной функции. Записывается это так:
Нахождение первообразной называется также интегрированием функции. А нахождение производной — дифференцированием функции. Интегрирование (то есть нахождение первообразной) и дифференцирование (взятие производной) — взаимно-обратные действия.
Но интегралы — отдельная тема. В задачах ЕГЭ по математике неопределенные интегралы не встречаются, а теме «Первообразная» посвящено всего несколько задач в первой части ЕГЭ. Для их решения надо знать только таблицу первообразных и еще одну важную формулу.
Формула для вычисления площади под графиком функции (Формула Ньютона-Лейбница)
Пусть в прямоугольной системе координат задана фигура, ограниченная графиком непрерывной функции , осью и прямыми и . Пусть функция неотрицательна на отрезке [a; b].
Пусть функция неотрицательна на отрезке [a; b].
Тогда площадь этой фигуры вычисляется по формуле:
Такую фигуру называют еще криволинейной трапецией. А сама формула носит название «Формула Ньютона-Лейбница».
1. Значение первообразной функции в точке 0 равно 6. Найдите .
Найдем первообразную функции с помощью таблицы первообразных. Получим:
При получим:
Значит, и
Ответ: 40,5
2. Значение первообразной функции в точке 0 равно -13. Найдите
Найдем первообразную функции с помощью таблицы первообразных. Получим:
При x = 0 получим: Значит, и
Ответ: -14
3. На рисунке изображен график функции . Найдите значение выражения , где — одна из первообразных функции .
По формуле Ньютона-Лейбница, разность первообразных — это площадь, ограниченная графиком функции, осью X и прямыми y=a и y=b.
В этой задаче нужная фигура ограничена графиком функции, осью и прямыми и . Это квадратик, и площадь его равна 4.
Это квадратик, и площадь его равна 4.
Ответ: 4.
4. На рисунке изображён график некоторой функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
Решение. По формуле Ньютона-Лейбница, площадь под графиком функции на отрезке [a,b] равна разности значений первообразной в концах отрезка, то есть
В нашей задаче имеем:
Дальше — просто арифметика.
Ответ: 13,5.
|
Интеграл степенной функции.
|
Интеграл степенной функции.
|
|
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала.
| |
|
Интеграл экспоненциальной функции.
|
Интеграл экспоненты, где a-постоянное число.
|
|
Интеграл сложной экспоненциальной функции.
|
Интеграл экспоненциальной функции.
|
|
Интеграл, равняющийся натуральному логарифму.
|
Интеграл : «Длинный логарифм».
|
|
|
Интеграл : «Длинный логарифм».
|
|
Интеграл : «Высокий логарифм».
|
Интеграл, где х в числителе заводится под знак дифференциала
|
|
Интеграл : «Высокий логарифм».
| |
|
Интеграл косинуса.
|
Интеграл синуса.
|
|
Интеграл, равный тангенсу.
|
Интеграл, равный котангенсу.
|
|
Интеграл, равный как арксинусу, так и арккосинусу
|
Интеграл, равный как арктангенсу, так и арккотангенсу.
|
|
Интеграл, равный как арксинусу, так и арккосинусу.
|
Интеграл, равный как арктангенсу, так и арккотангенсу.
|
|
| |
|
Интеграл равный косекансу.
|
Интеграл, равный секансу.
|
|
Интеграл, равный арксекансу.
|
Интеграл, равный арккосекансу.
|
|
Интеграл, равный арксекансу.
|
Интеграл, равный арксекансу.
|
|
Интеграл, равный гиперболическому синусу.
|
Интеграл, равный гиперболическому косинусу.
|
|
Интеграл, равный гиперболическому тангенсу.
|
Интеграл, равный гиперболическому котангенсу.
|
|
Интеграл, равный гиперболическому синусу, где sinhx
|
Интеграл, равный гиперболическому косинусу, где sinhx
|
|
Интеграл, равный гиперболическому тангенсу.
|
Интеграл, равный гиперболическому котангенсу.
|
|
Интеграл, равный гиперболическому секансу.
|
Интеграл, равный гиперболическому косекансу.
|
Первообразная. Неопределённый и определённый интегралы
Первообразная
Определение. Непрерывная функция F(x) называется первообразной функции f(x), если на промежутке X, если для каждого .
Операция нахождения первообразной функции f(x), называется интегрированием.
Неопределенный интеграл
Неопределённый интеграл-это совокупность всех первообразных функции f(x). В общем случае, нахождение неопределённого интеграла выглядит следующим образом:
,
где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования. Неопределённый интеграл представляет собой, как бы, «пучок» первообразных, из-за наличия постоянной интегрирования.
Дифференциал-произвольное, бесконечно малое приращение переменной величины.
Свойства неопределённого интеграла
Таблица основных неопределённых интегралов
В виде
,
где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования.
Определённый интеграл
Определенный интеграл— Приращение одной из первообразных функции f(x) на отрезке [a;b].
Общий вид определённого интеграла:
где f(x)–подынтегральная функция, a и b-пределы интегрирования, dx-дифференциал
Свойства определённого интеграла: см. св-ва определённого интеграла.
Определённый интеграл вычисляется по формуле Ньютона –Лейбница:
Применение определённого интеграла:
1. Нахождение площади криволинейной трапеции
2. Нахождение величины скорости v по заданному закону ускорения a(t) за промежуток времени [t1;t2], т.е
Пример: Точка движется по закону ускорения a(t)=t+1. Найти величину ее скорости за промежуток времени [2;4] секунд.
Решение:
3. Нахождение пути S по закону изменения скорости v(t) за промежуток времени [t1;t2], т.е.
Нахождение пути S по закону изменения скорости v(t) за промежуток времени [t1;t2], т.е.
Пример: Найти путь, который проделала материальная точка за промежуток времени [2;4], двигаясь со скоростью, которая изменялась по закону: v(t)=2t+2.
Решение:
Стоит отметить, что, на сегодняшний день, интегральное и дифференциальное исчисление занимают лидирующие позиции в математике. Советую вам ознакомиться, более подробно, с широким применением интегралов в естествознании.
Первообразная и интеграл: формулы с примерами решения
Ранее вы ознакомились с операцией дифференцирования: нахождения производной по данной функции. Не менее важна и обратная ей операция — интегрирование: нахождение функции по её производной.
Пусть дано функцию
такую, что в каждой точке х некоторого промежутка . В этом случае функцию f(x) называют производной функции F(x), a — первообразной для f(x).
Функция F(x) называется первообразной функции
на промежутке , если для каждого значения х из этого промежутка F'(x) = f(x).
Например, на всей числовой оси (т. е. на R] функция F(x) =
является первообразной для f(x) = 2х, ибо = 2х; F(x) = sin х есть первообразной для f(x) = cos х, ибо (sin х)’ = cos х.
Функция F(x)
является первообразной для например на [1; 5]. Но не на R, поскольку F'(O) не существует, и не на , поскольку это не промежуток.
Одна ли функция
является первообразной для Нет. Ведь и и и т. д. Каким бы ни было число С (произвольная постоянная), функция — первообразная для, ибо ( )‘
Существуют ли другие функции, отличные от
, первообразные для ? Нет.
Теорема. (Основное свойство первообразных.) Каждая первообразная для функции ) имеет вид F(x) + С, где — одна из этих первообразных, а С — произвольная постоянная.
Доказательство 1. Пусть
—одна из первообразных для функции на промежутке , т. е. для каждого :.
По правилу нахождения производной суммы
Этим доказано» что какая бы ни была постоянная С, если
— первообразная для , то и — первообразная для
Пусть
и — две любые первообразные для функции
на промежутке, т. е. и для каждого . Тогда
Как видим, функция
такая, что в каждой точке её производная равна 0.
Такое свойство имеет только определённая на
функция, которая ни возрастает, ни убывает на этом промежутке. Ведь если бы на некоторой части промежутка эта функция возрастала или убывала, то там её производная была бы соответственно положительная или отрицательная. (Подробнее обоснование этого факта даётся в строгих курсах математического анализа.) Итак, , где С — постоянная, т. е. .
Ведь если бы на некоторой части промежутка эта функция возрастала или убывала, то там её производная была бы соответственно положительная или отрицательная. (Подробнее обоснование этого факта даётся в строгих курсах математического анализа.) Итак, , где С — постоянная, т. е. .
Этим доказано, что если
— одна из первообразных для функции , то каждая из функций также её первообразная и других первообразных для ) не существует. Геометрически это означает, что графики любых двух первообразных для функции такие, что их можно совместить параллельным переносом вдоль оси ординат (рис. 102).
— общий вид первообразных для функции .
Каждая первообразная рассматривается на некотором промежутке. Если же для краткости его не указывают, то имеют в виду промежуток максимально возможной длины. В частности, если функция
) определена на и промежуток не указано, то речь идет о её первообразной также на .
Операцию нахождения производной данной функции называют дифференцированием. Обратная ей операция — нахождение первообразной — называется интегрированием.
Используя формулы дифференцирования (с. 218), составим таблицу первообразных. Советуем запомнить её.
Обосновать эту таблицу можно дифференцированием функции из её второй строки. Пользуясь таблицей, можно сразу писать, что, например, для функции
первообразной есть и т.д.
Множество всех первообразных функции
часто называют неопределённым интегралом этой функции и обозначают символом (читают: интеграл эф от икс де икс).
Выражение «проинтегрировать функцию
» обозначает то же, что и «найти первообразную для функции » .
То есть, если
— первообразная для функции , а —произвольное число, то .
Слово интеграл в переводе с латинского языка означает целый. Почему его так назвали, вы поймёте, когда ознакомитесь с определённым интегралом (см. с. 241).Неопределённым его называют потому, что он при заданной функции и данном значении
с. 241).Неопределённым его называют потому, что он при заданной функции и данном значении
имеет не одно числовое значение, а бесконечно много.
Таблицу первообразных, с помощью символа неопредёлен-ного интеграла можно записать так:
Примеры с решением
Пример №1
Докажите, что функция
является первообразной для функции .
Доказательство.
.
Имеем
. Итак, по определению, функция — первообразная для функции
Пример №2
Найдите первообразную для функции : а)
; б) ;
Решение:
Воспользуемся таблицей первообразных.
а) Первообразной для функции
есть функция .
Для функции
, поэтому .
б) Первообразной для функции
есть функция
Для функции
поэтому .
Пример №3
Найдите для функции
такую первообразную, чтобы её график проходил через точку Р (2; 5).
Решение:
Пользуясь таблицей, найдём общий вид первообразных:
Поскольку график искомой первообразной проходит через точку Р (2; 5), то , отсюда С = 3.
Следовательно,
.
Ответ.
.
Пример №4
Проинтегрируйте функцию
.
Решение:
Нахождение первообразных
Выведем несколько правил, подобных правилам дифференцирования, которые облегчают нахождение первообразных.
I. Если
и — первообразные для функций ) и, то — первообразная для функции .
Действительно, если
и . то
. Если — первообразная для функции , a — произвольное число, то — первообразная для функции .
Ведь
.
Если —первообразная для функции , a ,b — произвольные числа , то — первообразная для функции .
»
Ведь
Пример №5
Найдите первообразную для функции:
а)
; б) ; в) .
Решение:
а) Для функций
и первообразными являются соответственно и .
Поэтому для суммы данных функций общий вид первообразных
б) По правилу II:
.
в) Одной из первообразных для функции
,согласно правилу III, является функция . Общий вид первообразных для данной функции
К нахождению первообразных сводятся прежде всего задачи, обратные тем, которые решаются с помощью производной. Рассмотрим пример..
Рассмотрим пример..
Если известен закон прямолинейного движения тела
,то для нахождения его скорости в момент t нужно найти производную: . Здесь дан закон движения и требуется найти его скорость. Для механики не менее важно уметь решать обратную задачу: по заданной в каждый момент скорости определять закон движения.
Задача №1.
Точка движется прямолинейно с переменной скоростью
. За перые 4 с она прошла 80 м. Найдите закон движения точки.
Решение:
Искомый закон движения выражается такой функцией
, что . Здесь s(t) — первообразная для функции . Общий вид всех таких первообразных . Поскольку за 4 с точка прошла 80м, то 80 = 5-16 + С, отсюда С = 0.
Ответ. Искомый закон движения точки
, где t — время в секундах, — расстояние в метрах.
Примеры других применений первообразной рассмотрим в следующих параграфах.
С помощью неопределённого интеграла правила интегрирования записываются так:
Пример №6
Найдите одну из первообразных для функции:
а)
; б).
Решение:
а) Для функции
одной из первообразных есть функция . Учитывая то, что первообразной для функции есть функция , запишем искомую первообразную: ;
б) преобразуем сначала формулу, задающую функцию:
Тогда
.
Пример №7
Тело движется прямолинейно с ускорением
.
Определите скорость данного движения как функцию от времени f, если в момент t = 0 она равнялась 3 м/с.
Решение:
Ускорение — производная скорости. Поэтому если
Поэтому если
— искомая скорость, то . Следовательно,) — первообразная для функции , поэтому . Поскольку , то .
Ответ.
.
Первообразная и площадь криволинейной трапеции
Пусть на координатной плоскости задан график непрерывной функции
, принимающей на промежутке [а; Ь) только неотрицательные значения. Фигуру, ограниченную таким графиком, осью абсцисс и прямыми х = а и х = Ь, называют криволинейной трапецией.
Криволинейную трапецию называют также под графиком функции
на [а; Ь].
Несколько криволинейных трапеций изображено на (рис. 105).
Каждая криволинейная трапеция имеет определённую площадь (это доказано в строгих курсах математического анализа). Эти площади можно находить с помощью первообразных.
Теорема. Площадь криволинейной трапеции, образованной графиком функции ) на промежутке [а; Ь], равна , где — первообразная для функции на [а; b].
Доказательство. Рассмотрим произвольную криволинейную трапецию, образованную графиком функции
на (риc. 106). Пусть х — произвольная точка отрезка , а S(x) — площадь криволинейной трапеции, образованной графиком функции на . Понятно, что — функция от х. Докажем, что для каждого .
Дадим переменной х приращение
, тогда функция получит приращение (pиc. 107). Это — площадь криволинейной трапеции, образованной графиком функции на промежутке , она приближённо равна площади прямоугольника с основанием , и высотой f(t), где t — некоторое число из промежутка . Поскольку функция f(x) непрерывна, такое число t обязательно найдётся.
Следовательно,
откуда .
Если
, то и , ибо функция непрерывна. Поэтому если , то , т. е. .
Поэтому если , то , т. е. .
Как видим, функция S(x) — первообразная для
на [а; Ь]. Поэтому если F(x) — какая-либо другая первообразная для ) на [a; b], то S(x) = F(x) + С, где С — постоянная. Чтобы определить С, учтём, что S(a) 0, ибо при х — а криволинейная трапеция, образованная графиком функции f(x) на [a; х], вырождается в отрезок; его площадь равна 0. Имеем: 0 = F(a) + С, отсюда С = -F(a). Следовательно,= F(х) — F(a). Если в это равенство подставим значение х = Ь, то получим площадь криволинейной трапеции, образованной графиком функции f(x) на [а; Ь]:
Значение выражения F(b) — F(a) вычисляют часто, поэтому для удобства его записывают ещё и так:.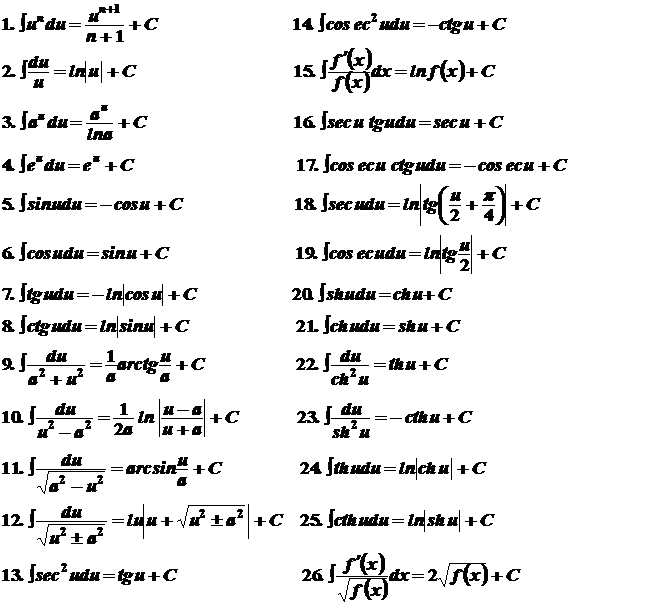
.Итак, формула (1) приобретает вид:
Задача №2.
Найдите площадь криволинейной трапеции, образованной графиком функции
на промежутке [1; 3].
Решение:
На (рис) 108 изображена фигура, площадь которой нужно найти. Для функции
первообразной есть . Следовательно, искомая площадь
Задача №3.
Найдите площадь фигуры, ограниченной одной аркой синусоиды и осью абсцисс (риc. 109).
Решение:
Надо найти площадь криволинейной трапеции, образованной графиком функции
на промежутке . Для функции первообразной есть функция . Следовательно, искомая площадь= 1 — (-1) — 2 (кв. ед.).
Пользуясь термином «криволинейная трапеция следует иметь в виду, что «криволинейная трапеция» не всегда является трапецией (риc. 109) и не всегда она криволинейная(риc. 105, б). А вообще она — не геометрическая фигура в научном понимании. Любое движение отображает каждую фигуру на равную ей фигуру такого же вида. А если «криволинейную трапецию *, например, изображенную на (рис 108), повернуть на 90°, она отображается на фигуру, которая не является криволинейной трапецией. Поэтому вместо «криволинейная трапеция» говорят и пишут «подграфик функции».
Задача №4.
Найдите площадь криволинейной трапеции, образованной графиком функции у = х на [0; 2].
Решение:
Данная криволинейная трапеция — прямоугольный треугольник с катетами 2 и 2 (риc. 110). Его площадь
(кв. ед.).
Ответ. 2кв. ед.
Задача №5.
Найдите площадь криволинейной трапеции, образованной графиком функции у -3 на [1,2].
Заданная криволинейная трапеция — прямоугольник с измерениями 1 и 3 (риc. 111). Его площадь
(кв. ед.).
Ответ. 3 кв. ед.
Задача №6.
Найдите площадь фигуры, ограниченной графиком функции
и осью абсцисс.
Решение:
Найдем абсциссы точек пересечения графика данной функции с осью Ох. В этих точках ордината функции равна нулю:
, отсюда , (риc. 112). Значит, надо найти площадь криволинейной трапеции, образованной
графиком функции
на [-2; 2].Одна из первообразных для данной функции .Поэтому искомая площадь кв,ед.
Ответ.
кв.ед.
Определённый интеграл
Рассмотрим другой подход к определению площади криволинейной трапеции.
Пусть дана криволинейная трапеция, образованная графиком функции f(x) на [a;b] (рис. 117). Разобьём отрезок [а; Ь] точками
на n равных отрезков:
Построим на первом из этих отрезков прямоугольник высотой
, на втором — прямоугольник высотой ,…, на n—м — прямоугольник высотой . В результате получим ступенчатый многоугольник, составленный из n прямоугольников. Пусть основание каждого из построенных прямоугольников равно ; тогда площадь всего ступенчатого многоугольника
Суммы такого вида называют интегральными суммами функции f(x) на [а; Ь]. Полученную интегральную сумму можно считать приближённым значением площади S криволинейной трапеции, образованной графиком функции f(x) на [а; Ь]. При этом если
то (риc. 118). Пишут: .
He только задача о нахождении площади криволинейной трапеции, но и много других важных прикладных задач приводят к вычислению пределов подобных интегральных сумм. Поэтому для такого понятия введено специальное название и обозначение.
Предел интегральной суммы функции f(x) на отрезке [а; Ь], если , называют определённым интегралом функции f(x) от а до Ь.
Его обозначают символом
(читают: интеграл от а до b эф от икс де икс). Здесь числа а и b пределы интегрирования, — знак интеграла, f(x) — подинтегральная функция, х —переменная интегрирования.
Следовательно, площадь криволинейной трапеции, образованной графиком функции f(x) на [а; Ь], равна
, т. е.. Как доказано в предыдущем пункте, эта площадь равна , где — первообразная для функции f(x). Поэтому
Это — формула Ньютона—Лейбница, основная формула математического анализа. Она даёт возможность решать много разных интересных и содержательных задач — абстрактных и прикладных, в частности — и очень важных. Решали такие задачи сотни математиков еще задолго до создания математического анализа. Но для каждой задачи раньше они находили отдельный оригинальный способ решения. Найдя и обосновав формулу Ньютона—Лейбница, учёные получили общий и очень эффективный способ решения таких задач. Не случайно открытие формулы Ньютона—Лейбница специалисты считают самым важным открытием XVII века.Рационализировать вычисления определённых интегралов часто помогает такое их с в о й с т в о:
Справедливость этой формулы вытекает из следующих преобразований:
Задача №7.
Найдите площадь фигуры, ограниченной графиками функций
и
Решение:
Построим графики данных функций (рис. 119). Надо найти площадь закрашенной фигуры. Она равна разности площадей фигур ОВАК и ОВАР. Границы интегрирования — абсциссы точек О и А, в которых пересекаются графики функций, т. е. значения х удовлетворяющие системе уравнений
и . Из системы получим уравнение корни которого и
Следовательно, искомая площадь
Ответ.
кв. ед.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Предмет высшая математика
Другие лекции по высшей математике, возможно вам пригодятся:
Интеграл степенной функции. | Интеграл степенной функции. |
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала. | |
| — | |
Интеграл экспоненциальной функции. | Интеграл экспоненты, где a-постоянное число. |
Интеграл сложной экспоненциальной функции. | Интеграл экспоненциальной функции. |
| — | |
| Интеграл, равняющийся натуральному логарифму. | Интеграл : «Длинный логарифм». |
| Интеграл : «Длинный логарифм». | |
| Интеграл : «Высокий логарифм». | Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логарифму. |
| Интеграл : «Высокий логарифм». | |
| — | |
Интеграл косинуса. | Интеграл синуса. |
Интеграл, равный тангенсу. | Интеграл, равный котангенсу. |
| — | |
Интеграл, равный как арксинусу, так и арккосинусу | Интеграл, равный как арктангенсу, так и арккотангенсу. |
Интеграл, равный как арксинусу, так и арккосинусу. | Интеграл, равный как арктангенсу, так и арккотангенсу. |
| Интеграл равный косекансу. | Интеграл, равный секансу. |
Интеграл, равный арксекансу. | Интеграл, равный арккосекансу. |
Интеграл, равный арксекансу. | Интеграл, равный арксекансу. |
| — | |
Интеграл, равный гиперболическому синусу. | Интеграл, равный гиперболическому косинусу. |
Интеграл, равный гиперболическому тангенсу. | Интеграл, равный гиперболическому котангенсу. |
Интеграл, равный гиперболическому синусу, где sinhx — гиперболический синус в ангийской версии. | Интеграл, равный гиперболическому косинусу, где sinhx — гиперболический синус в ангийской версии. |
Интеграл, равный гиперболическому тангенсу. | Интеграл, равный гиперболическому котангенсу. |
Интеграл, равный гиперболическому секансу. | Интеграл, равный гиперболическому косекансу. |
Электронный учебник по математическому анализу
7.1 Определение и основные свойства
Если мы имеем какую-то операцию, то естественно поставить и обсудить вопрос о ее обращении.
Дифференцирование функций можно рассматривать как операцию D, которая из заданной функции “изготавливает” новую функцию, ее производную:
Рассмотрим задачу обращения этой операции: для заданной функции g(x) найти такую функцию G(x), что выполняется равенство:
\begin{equation}
\frac{dG(x)}{dx}=g(x). (15)
\label{int1}
\end{equation}
Определение. Функция $G(x)$ удовлетворяющая соотношению (15), называется первообразной функции $g(x)$ (или: неопределенным интегралом от функции $g(x)$).
Обозначение. Функция $G(x)$ удовлетворяющая соотношению (15), обозначают
\[
G(x)=\int g(x)dx.
\]
Пример.
Известно, что $(\sin x)’=\cos x$. Поэтому функция $\sin x$ является первообразной функции $\cos x$.
Из свойств операции дифференцирования следует, что если $G(x)$ — первообразная функции $g(x)$, то для любой константы $C$ функция $G(x)+C$ также является первообразной функции $g(x)$. Это следует из простого вычисления: $$\frac{d}{dx}(G(x)+C)=\frac{d}{dx}G(x)+\frac{d}{dx}C=g(x)+0.$$
Вопрос: сколько первообразных может быть у функции?
Теорема.Пусть $G(x)$ — первообразная непрерывной функции $g(x)$. Тогда любая первообразная этой функции лишь на константу отличается от $G(x)$.
Доказательство.
Пусть $F(x)$ — еще одна первообразная функции $g(x)$, положим $H(x)=F(x)-G(x)$. Тогда $dH(x)/dx=0$ при всех $x$. Применим теорему Лагранжа к функции $H(x)$. Для любых точек $x_1$ и $x_2$ имеем: $H(x_1)-H(x_2)=0\cdot (x_1-x_2)=0$. Следовательно, значение $H(x)$ не зависит от $x$.
Свойства первообразной тесно связаны со свойствами, которыми обладает операция дифференцирования.
1. Первообразная от суммы функций равна сумме первообразных,
\[
\int \left(f(x)+g(x)\right )dx=\int f(x)dx+\int g(x)dx.
\]
2. Константу можно вынести за знак интеграла: если $C=const$, то
\[
\int C\cdot f(x)dx=C\cdot \int f(x)dx.
\]
3. При дифференцирование первообразной получается исходная функция,
\[
\left (\int f(x)dx\right )’=f(x).{\prime}=x+0=f(x)$
Больше примеров решений
Решение интегралов онлайн
Таким образом, если функция $y=f(x)$ имеет первообразную, то
она имеет бесконечное множество первообразных.
Теорема
(Об общем виде первообразной для функции)
Если функции $F(x)$ и
$\Phi(x)$ — две любые первообразные функции
$y=f(x)$, то их разность равна некоторой постоянной, то есть
$$\Phi(x)-F(x)=C=\text { const }$$
Последнюю теорему можно сформулировать иначе: каждая функция, которая является первообразной для функции
$f(x)$, может быть представлена в виде
$F(x)+C$.
Неопределенный интеграл
Определение
Совокупность всех первообразных функции $y=f(x)$, определенных
на заданном промежутке, называется неопределенным интегралом от функции
$y=f(x)$ и обозначается символом
$\int f(x) d x$. То есть
$\int f(x) d x=F(x)+C$
Знак $\int$ называется интегралом,
$f(x) d x$ — подынтегральным выражением,
$f(x)$ — подынтегральной функцией, а
$x$ — переменной интегрирования.
Операция нахождения первообразной или неопределенного интеграла от функции
$f(x)$ называется интегрированием функции
$f(x)$. Интегрирование представляет собой операцию,
обратную дифференцированию.
Геометрическая интерпретация неопределенного интеграла
Неопределенный интеграл представляет собой семейство параллельно расположенных кривых
$F(x)+C$, где каждому конкретному числовому значению
постоянной $C$ соответствует определенная
кривая из указанного семейства.
График каждой кривой из семейства называется интегральной кривой.
Теорема
Каждая непрерывная на промежутке $(a ; b)$ функция, имеет
на этом интервале первообразную.
Читать дальше: свойства неопределенного интеграла.
{b} f (t) dt [/ latex], мы можем найти любую первообразную F из f и оценить F ( b ) — F ( a ). Задача нахождения точного значения определенного интеграла сводится к нахождению некоторой (любой) первообразной F подынтегрального выражения и последующему вычислению F ( b ) — F ( a ). Даже найти одно первообразное может быть сложно, и мы будем придерживаться функций, у которых есть простые первообразные.
Строительные блоки
Антидифференцировка идет в обратном направлении через производный процесс.Таким образом, самые простые производные правила — это просто обратные версии самых простых производных правил. Напомним производные правила
Производные правила
Далее f и g являются дифференцируемыми функциями от x и k и n являются константами.
- Постоянное множественное правило: [latex] \ frac {d} {dx} (kf) = kf \ prime [/ latex]
- Правило суммы (или разности): [латекс] \ frac {d} {dx} (f + g) = f \ prime + g \ prime [/ latex] или [латекс] \ frac {d} { dx} (fg) = f \ prime — g \ prime [/ latex]
- Правило мощности: [латекс] \ frac {d} {dx} (x ^ n) = nx ^ {n-1} [/ latex]
Особые случаи: [латекс] \ frac {d} {dx} ( k) = 0 [/ latex] (потому что k = kx 0 ) и [latex] \ frac {d} {dx} (x) = 1 [/ latex] (потому что x = х 1 ) - Экспоненциальные функции: [латекс] \ frac {d} {dx} (e ^ x) = e ^ x [/ latex]
[латекс] \ frac {d} {dx} (a ^ x) = \ text {ln} a \ times a ^ x [/ латекс] - Натуральный логарифм: [латекс] \ frac {d} {dx} (\ text {ln} x) = \ frac {1} {x} [/ latex]
Обдумывая эти основные правила, мы пришли к первообразным 2 x и e x раньше.
Далее следуют соответствующие правила для первообразных — каждое из правил первообразных просто переписывает правило производных. Все эти первообразные можно проверить путем дифференцирования.
Есть один сюрприз — первообразное [латекса] \ frac {1} {x} [/ latex] на самом деле не просто ln ( x ), это ln | x |. Это хорошо — у первообразного есть домен, который соответствует домену [latex] \ frac {1} {x} [/ latex], который больше, чем домен ln ( x ), поэтому мы не Мне не нужно беспокоиться о том, являются ли наши x положительными или отрицательными.Но вы должны быть осторожны при включении этих абсолютных значений — иначе вы можете столкнуться с проблемами домена.
Старые правила: строительные блоки
Далее f и g являются дифференцируемыми функциями от x и k , n, и C являются константами.
- Постоянное множественное правило: [латекс] \ int kf (x) dx = k \ int f (x) dx [/ latex]
- Правило суммы (или разности): [латекс] \ int f (x) \ pm g (x) dx = \ int f (x) dx \ pm \ int f (x) dx [/ latex]
- Правило мощности: [латекс] \ int x ^ n dx = \ frac {x ^ {n + 1}} {n + 1} + C [/ latex] при условии, что n = −1
Особый случай: [латекс] \ int kdx = kx + C [/ latex] (потому что k = kx 0 ) - Экспоненциальные функции: [латекс] \ int e ^ x dx = e ^ x + C [/ latex]
[латекс] \ int a ^ x dx = \ frac {a ^ x} {\ text {ln} a } + C [/ латекс] - Натуральный логарифм: [латекс] \ int x ^ {- 1} dx = \ int \ frac {1} {x} dx = \ text {ln} | x | + C [/ латекс]
Пример
Найдите первообразную [латекса] 3x ^ 7-15 \ sqrt x + \ frac {14} {x ^ 2} [/ latex]
Решение
[латекс] \ int (3x ^ 7 — 15 \ sqrt x + \ frac {14} {x ^ 2}) dx = \ int (3x ^ 7 — 15 ^ {1/2} + 14x ^ {- 2} ) dx = 3 \ frac {x ^ 8} {8} — 15 \ frac {x ^ {3/2}} {3/2} + 14 \ frac {x ^ {- 1}} {- 1} + C [/ latex]
На это сложно смотреть, поэтому вы можете немного упростить:
[latex] \ int (3x ^ 7-15 \ sqrt x + \ frac {14} {x ^ 2}) dx = \ frac {3x ^ 8} {8} -10x ^ {3/2} — 14x ^ {- 1} + C [/ латекс]
Пример
[латекс] \ int (e ^ x + 12 — \ frac {16} {x}) dx [/ латекс]
Решение
[латекс] \ int (e ^ x + 12 — \ frac {16} {x}) dx = e ^ x + 12x — 16 \ mathrm {ln} | x | + C [/ латекс]
Пример
Найдите F ( x ) так, чтобы F ′ ( x ) = e x и F (0) = 10. 2] = \ frac {9} {2} — \ frac {1} {2} = 4 [/ latex].3) = 7 [/ латекс].
Пример
Робот был запрограммирован так, что когда он начинает двигаться, его скорость после t секунд будет 3 t 2 футов / секунду.
- Как далеко продвинется робот за первые 4 секунды движения?
- Как далеко продвинется робот за следующие 4 секунды движения?
Решение
- Расстояние в течение первых 4 секунд будет площадью под графиком (рис. 2) скорости, от t = 0 до t = 4.3 = 512 — 64 = 448 [/ латексных] футов.
Пример
Предположим, что t минут после помещения 1000 бактерий на чашку Петри скорость роста популяции составляет 6 t бактерий в минуту.
- Сколько новых бактерий добавляется к популяции за первые 7 минут?
- Какова общая численность населения через 7 минут?
Решение
- Количество новых бактерий — это площадь под графиком скорости роста (рисунок 3), а одно первообразное из 6 т составляет 3 т 2 . \ prime \ left (x \ справа) = е \ влево (х \ вправо).} \]
Дифференциальное уравнение с начальным условием \ (y \ left ({{x_0}} \ right) = {y_0} \) называется задачей начального значения.
Самая общая первообразная \ (F \ left (x \ right) + C \) функции \ (f \ left (x \ right) \) дает общее решение дифференциального уравнения \ (\ large {\ frac { {dy}} {{dx}}} \ normalsize = f \ left (x \ right). \)
Частным решением задачи начального значения является функция, которая удовлетворяет как дифференциальному уравнению, так и начальному условию.2}}}} \ normalsize,} \) \ ({x \ ne 0,} \) \ ({y \ left (1 \ right) = 5.} \)
Пример 7
Решите задачу начального значения \ (\ large {\ frac {{dy}} {{dx}}} \ normalsize = \ large {\ frac {2} {{x + 1}}} \ normalsize, \) \ (y \ left (0 \ right) = 2. \)
Пример 8
Решите задачу начального значения \ (\ large {\ frac {{dr}} {{d \ theta}}} \ normalsize = \ cos \ large {\ frac {\ theta} {2}} \ normalsize, \) \ ( r \ left ({\ large {\ frac {\ pi} {3}} \ normalsize} \ right) = 2. \)
Пример 9
Решите задачу начального значения \ (\ large {\ frac {{dz}} {{dt}}} \ normalsize = \ cos t — 2 \ sin t, \) \ (z \ left (0 \ right) = 5.\)
Пример 10
Функция \ (y \ left (x \ right) \) задается дифференциальным уравнением \ (\ large {\ frac {{dy}} {{dx}}} \ normalsize = \ large {\ frac {1} { x}} \ normalsize + 2x \) с начальным условием \ (y \ left (1 \ right) = 0. \) Найдите значение функции, когда \ (x = e. \)
Пример 11
Мяч, сброшенный с вершины высокого здания, имеет скорость \ (v \ left (t \ right) = -10t — 5 \, {\ large {\ frac {\ text {m}} {\ text {s}}} \ normalsize}. \) Найдите высоту здания, учитывая, что мяч ударяется о землю через \ (t = 4 \) секунд.2} + \ frac {1} {x} + 3.} \]
Пример 7.
Решите задачу начального значения \ (\ large {\ frac {{dy}} {{dx}}} \ normalsize = \ large {\ frac {2} {{x + 1}}} \ normalsize, \) \ (y \ left (0 \ right) = 2. \)
Решение.
Найдите общую первообразную \ (\ large {\ frac {2} {{x + 1}}} \ normalsize: \)
\ [y = 2 \ ln \ left | {x + 1} \ right | + C. \]
Используйте начальное условие \ (y \ left (0 \ right) = 2 \) для вычисления константы \ (C: \)
\ [{2 \ ln \ left | {0 + 1} \ right | + C = 2,} \; \; \ Rightarrow {2 \ cdot \ ln 1 + C = 2,} \; \; \ Rightarrow {2 \ cdot 0 + C = 2,} \; \; \ Rightarrow {C = 2.} \]
Таким образом, конкретное решение записывается как
\ [y = 2 \ ln \ left | {x + 1} \ right | + 2. \]
Пример 8.
Решите задачу начального значения \ (\ large {\ frac {{dr}} {{d \ theta}}} \ normalsize = \ cos \ large {\ frac {\ theta} {2}} \ normalsize, \) \ ( r \ left ({\ large {\ frac {\ pi} {3}} \ normalsize} \ right) = 2. \)
Решение.
Сначала запишем общую первообразную функции \ (\ cos \ large {\ frac {\ theta} {2}} \ normalsize: \)
\ [r \ left (\ theta \ right) = 2 \ sin \ frac {\ theta} {2} + C.\]
Подставьте начальное условие \ (r \ left ({\ large {\ frac {\ pi} {3}} \ normalsize} \ right) = 2 \), чтобы найти константу \ (C: \)
\ [{2 \ sin \ frac {{\ frac {\ pi} {3}}} {2} + C = 2,} \; \; \ Rightarrow {2 \ sin \ frac {\ pi} {6} + C = 2,} \; \; \ Rightarrow {2 \ cdot \ frac {1} {2} + C = 2,} \; \; \ Rightarrow {1 + C = 2,} \ Rightarrow {C = 1.} \]
Следовательно, частное решение дифференциального уравнения дается
\ [r \ left (\ theta \ right) = 2 \ sin \ frac {\ theta} {2} + 1. \]
Пример 9.
Решите задачу начального значения \ (\ large {\ frac {{dz}} {{dt}}} \ normalsize = \ cos t — 2 \ sin t, \) \ (z \ left (0 \ right) = 5. \)
Решение.
Общая первообразная функции \ (\ cos t — 2 \ sin t \) равна
\ [z \ left (t \ right) = \ sin t + 2 \ cos t + C. \]
Подставьте начальное условие \ (z \ left (0 \ right) = 5 \), чтобы вычислить константу \ (C: \)
\ [{\ sin 0 + 2 \ cos 0 + C = 5,} \; \; \ Rightarrow {0 + 2 \ cdot 1 + C = 5,} \; \; \ Rightarrow {C = 3.} \]
Итак, решение задачи начального значения дается
\ [z \ влево (t \ вправо) = \ sin t + 2 \ cos t + 3. \]
Пример 10.
Функция \ (y \ left (x \ right) \) задается дифференциальным уравнением \ (\ large {\ frac {{dy}} {{dx}}} \ normalsize = \ large {\ frac {1} { x}} \ normalsize + 2x \) с начальным условием \ (y \ left (1 \ right) = 0. 2} — 5t.2} — 5 \ cdot 4 = 0,} \; \; \ Rightarrow {H = 80 + 20 = 100 \, \ text {m}}. \]
4.10 Первообразные — Исчисление Том 1
Задачи обучения
- 4.10.1 Найти общую первообразную заданной функции.
- 4.10.2 Объясните термины и обозначения, используемые для неопределенного интеграла.
- 4.10.3 Сформулируйте правило степени для интегралов.
- 4.10.4 Использование антидифференциации для решения простых задач с начальным значением.
На этом этапе мы увидели, как вычислять производные многих функций, и познакомились с множеством их приложений.Теперь мы зададим вопрос, который меняет этот процесс: если задана функция f, f, как нам найти функцию с производной ff и почему нам может быть интересна такая функция?
Мы отвечаем на первую часть этого вопроса, определяя первообразные. Первообразной функции ff является функция с производной f.f. Почему нас интересуют первородные? Потребность в первообразных возникает во многих ситуациях, и мы смотрим на различные примеры в оставшейся части текста.Здесь мы рассмотрим один конкретный пример, который включает прямолинейное движение. В нашем исследовании в разделе «Производные прямолинейного движения» мы показали, что при заданной функции положения s (t) s (t) объекта его функция скорости v (t) v (t) является производной от s (t) s ( t), то есть v (t) = s ′ (t). v (t) = s ′ (t). Кроме того, ускорение a (t) a (t) является производной скорости v (t) v (t), то есть a (t) = v ′ (t) = s ″ (t) .a (t) ) = v ′ (t) = s ″ (t). Теперь предположим, что нам дана функция ускорения a, a, но не функция скорости vv или функция положения s.с. Поскольку a (t) = v ′ (t), a (t) = v ′ (t), определение функции скорости требует от нас найти первообразную функции ускорения. Тогда, поскольку v (t) = s ′ (t), v (t) = s ′ (t), определение функции положения требует от нас найти первообразную функции скорости. Прямолинейное движение — лишь один из случаев, когда возникает потребность в первообразных. В оставшейся части текста мы увидим еще много примеров. А пока давайте посмотрим на терминологию и обозначения первообразных и определим первообразные для нескольких типов функций.Мы исследуем различные методы поиска первообразных более сложных функций далее по тексту (Введение в методы интеграции).
Обратная дифференциация
На данный момент мы знаем, как находить производные от различных функций. Теперь зададим противоположный вопрос. Учитывая функцию f, f, как мы можем найти функцию с производной f? F? Если мы можем найти функцию FF с производной f, f, мы назовем FF первообразной f.f.
Определение
Функция FF является первообразной функции ff, если
для всех xx в области f.f.
Рассмотрим функцию f (x) = 2x.f (x) = 2x. Зная степенное правило дифференцирования, мы заключаем, что F (x) = x2F (x) = x2 является первообразной от ff, поскольку F ′ (x) = 2x.F ′ (x) = 2x. Есть ли другие первообразные f? F? Да; поскольку производная любой константы CC равна нулю, x2 + Cx2 + C также является первообразной 2x.2x. Следовательно, x2 + 5×2 + 5 и x2−2×2−2 также являются первообразными. Существуют ли другие, не имеющие вида x2 + Cx2 + C для некоторой константы C? C? Ответ — нет. Из следствия 22 теоремы о среднем значении мы знаем, что если FF и GG — такие дифференцируемые функции, что F ′ (x) = G ′ (x), F ′ (x) = G ′ (x), то F (x) −G (x) = CF (x) −G (x) = C для некоторой константы C.C. Этот факт приводит к следующей важной теореме.
Теорема 4.14
Общий вид первообразной
Пусть FF — первообразная ff на интервале I.I. Затем
- для каждой константы C, C функция F (x) + CF (x) + C также является первообразной ff по I; I;
- , если GG является первообразной ff над I, I, существует константа CC, для которой G (x) = F (x) + CG (x) = F (x) + C над I.I.
Другими словами, наиболее общая форма первообразной ff над II — это F (x) + C.F (х) + С.
Мы используем этот факт и наши знания о производных, чтобы найти все первообразные для нескольких функций.
Пример 4.50
Поиск первообразных
Найдите все первообразные для каждой из следующих функций.
- f (x) = 3x2f (x) = 3×2
- f (x) = 1xf (x) = 1x
- f (x) = cosxf (x) = cosx
- f (x) = exf (x) = ex
Решение
- Потому что
тогда F (x) = x3F (x) = x3 является первообразной 3×2.3×2. Следовательно, каждая первообразная 3x23x2 имеет вид x3 + Cx3 + C для некоторых констант C, C, и каждая функция вида x3 + Cx3 + C является первообразной 3×2,3×2.
- Пусть f (x) = ln | x | .f (x) = ln | x |. Для x> 0, f (x) = ln (x) x> 0, f (x) = ln (x) и
Для x <0, f (x) = ln (−x) x <0, f (x) = ln (−x) и
ddx (ln (−x)) = — 1 − x = 1x. ddx (ln (−x)) = — 1 − x = 1x.
Следовательно,
ddx (ln | x |) = 1x. ddx (ln | x |) = 1x.
Таким образом, F (x) = ln | x | F (x) = ln | x | является первообразной 1x.1x. Следовательно, каждая первообразная 1x1x имеет вид ln | x | + Cln | x | + C для некоторой константы CC, и каждая функция вида ln | x | + Cln | x | + C является первообразной 1x.1x. - У нас
ddx (sinx) = cosx, ddx (sinx) = cosx,
поэтому F (x) = sinxF (x) = sinx является первообразной cosx.cosx. Следовательно, каждая первообразная cosxcosx имеет форму sinx + Csinx + C для некоторой константы CC, и каждая функция формы sinx + Csinx + C является первообразной cosx.cosx. - С
тогда F (x) = exF (x) = ex является первообразной ex.ex. Следовательно, каждая первообразная exex имеет вид ex + Cex + C для некоторой константы CC, и каждая функция вида ex + Cex + C является первообразной ex.бывший.
КПП 4.49
Найдите все первообразные f (x) = sinx.f (x) = sinx.
Неопределенные интегралы
Теперь мы рассмотрим формальные обозначения, используемые для представления первообразных, и исследуем некоторые из их свойств. Эти свойства позволяют находить первообразные более сложных функций. Для функции f, f мы используем обозначение f ′ (x) f ′ (x) или dfdxdfdx для обозначения производной f.f. Здесь мы вводим обозначения для первообразных. Если FF является первообразной от f, f, мы говорим, что F (x) + CF (x) + C является самой общей первообразной от ff, и пишем
∫f (x) dx = F (x) + C.∫f (x) dx = F (x) + C.
Символ ∫∫ называется знаком интеграла , а ∫f (x) dx∫f (x) dx называется неопределенным интегралом от f.f.
Определение
Для функции f, f неопределенный интеграл от f, f, обозначенный как
— самая общая первообразная от f.f. Если FF является первообразной от f, f, то
F (x) dx = F (x) + C.∫f (x) dx = F (x) + C.
Выражение f (x) f (x) называется подынтегральным выражением , а переменная xx — это переменной интегрирования .
С учетом терминологии, введенной в этом определении, процесс поиска первообразных функции ff обычно обозначается как , интегрирующий f.f.
Для функции ff и первообразной F, F функции F (x) + C, F (x) + C, где CC — любое действительное число, часто называют семейством первообразных f.f. Например, поскольку x2x2 является первообразной 2x2x, а любая первообразная 2x2x имеет форму x2 + C, x2 + C, мы пишем
∫2xdx = x2 + C.∫2xdx = x2 + C.
Набор всех функций вида x2 + C, x2 + C, где CC — любое действительное число, известен как семейство первообразных 2x.2x. На рис. 4.85 показан график этого семейства первообразных.
Рис. 4.85. Семейство первообразных 2x2x состоит из всех функций вида x2 + C, x2 + C, где CC — любое действительное число.
Для некоторых функций вычисление неопределенных интегралов следует непосредственно из свойств производных. Например, для n −1, n ≠ −1,
∫xndx = xn + 1n + 1 + C, ∫xndx = xn + 1n + 1 + C,
, который поступает напрямую из
ddx (xn + 1n + 1) = (n + 1) xnn + 1 = xn.ddx (xn + 1n + 1) = (n + 1) xnn + 1 = xn.
Этот факт известен как правило для интегралов .
Теорема 4.15
Правило мощности для интегралов
Для n ≠ −1, n −1,
∫xndx = xn + 1n + 1 + C.∫xndx = xn + 1n + 1 + C.
Вычисление неопределенных интегралов для некоторых других функций также является несложным вычислением. В следующей таблице перечислены неопределенные интегралы для нескольких общих функций. Более полный список приведен в Приложении B.
Формула дифференциации неопределенный интеграл ddx (k) = 0ddx (k) = 0 ∫kdx = ∫kx0dx = kx + C∫kdx = ∫kx0dx = kx + C ddx (xn) = nxn − 1ddx (xn) = nxn − 1 ∫xndn = xn + 1n + 1 + C∫xndn = xn + 1n + 1 + C для n ≠ −1n ≠ −1 ddx (ln | x |) = 1xddx (ln | x |) = 1x ∫1xdx = ln | x | + C∫1xdx = ln | x | + C ddx (ex) = exddx (ex) = ex ∫exdx = ex + C∫exdx = ex + C ddx (sinx) = cosxddx (sinx) = cosx ∫cosxdx = sinx + C∫cosxdx = sinx + C ddx (cosx) = — sinxddx (cosx) = — sinx ∫sinxdx = −cosx + C∫sinxdx = −cosx + C ddx (tanx) = sec2xddx (tanx) = sec2x ∫sec2xdx = tanx + C∫sec2xdx = tanx + C ddx (cscx) = — cscxcotxddx (cscx) = — cscxcotx ∫cscxcotxdx = −cscx + C∫cscxcotxdx = −cscx + C ddx (secx) = secxtanxddx (secx) = secxtanx ∫secxtanxdx = secx + C∫secxtanxdx = secx + C ddx (cotx) = — csc2xddx (cotx) = — csc2x ∫csc2xdx = −cotx + C∫csc2xdx = −cotx + C ddx (sin − 1x) = 11 − x2ddx (sin − 1x) = 11 − x2 11 − x2 = sin − 1x + C∫11 − x2 = sin − 1x + C ddx (tan − 1x) = 11 + x2ddx (tan − 1x) = 11 + x2 ∫11 + x2dx = tan − 1x + C∫11 + x2dx = tan − 1x + C ddx (сек − 1 | x |) = 1xx2−1ddx (sec − 1 | x |) = 1xx2−1 ∫1xx2−1dx = сек − 1 | x | + C∫1xx2−1dx = сек − 1 | x | + C Таблица 4.13 формул интегрирования
Из определения неопределенного интеграла от f, f мы знаем
∫f (x) dx = F (x) + C∫f (x) dx = F (x) + C
тогда и только тогда, когда FF является первообразной f.f. Следовательно, заявляя, что
∫f (x) dx = F (x) + C∫f (x) dx = F (x) + C
важно проверить правильность этого утверждения, убедившись, что F ′ (x) = f (x) .F ′ (x) = f (x).
Пример 4.51
Проверка неопределенного интеграла
Каждое из следующих утверждений имеет вид ∫f (x) dx = F (x) + C.∫f (x) dx = F (x) + C. Убедитесь, что каждое утверждение верно, показав, что F ′ (x) = f (x) .F ′ (x) = f (x).
- ∫ (x + ex) dx = x22 + ex + C∫ (x + ex) dx = x22 + ex + C
- ∫xexdx = xex − ex + C∫xexdx = xex − ex + C
Решение
- С
ddx (x22 + ex + C) = x + ex, ddx (x22 + ex + C) = x + ex,
заявление
∫ (x + ex) dx = x22 + ex + C∫ (x + ex) dx = x22 + ex + C
верно.
Обратите внимание, что мы проверяем неопределенный интеграл для суммы. Кроме того, x22x22 и exex являются первообразными xx и ex, ex, соответственно, а сумма первообразных является первообразной суммы.Мы обсудим этот факт еще раз в этом разделе. - Используя правило произведения, мы видим, что
ddx (xex − ex + C) = ex + xex − ex = xex. ddx (xex − ex + C) = ex + xex − ex = xex.
Следовательно, выписка
∫xexdx = xex − ex + C∫xexdx = xex − ex + C
верно.
Обратите внимание, что мы проверяем неопределенный интеграл для продукта. Первообразная xex-exxex-ex не является произведением первообразных. Кроме того, произведение первообразных x2ex / 2x2ex / 2 не является первообразным xexxex с
г.
ddx (x2ex2) = xex + x2ex2 ≠ xex.ddx (x2ex2) = xex + x2ex2 ≠ xex.
В общем, продукт первообразных не является первообразным продукта.
КПП 4.50
Убедитесь, что ∫xcosxdx = xsinx + cosx + C.∫xcosxdx = xsinx + cosx + C.
В таблице 4.13 мы перечислили неопределенные интегралы для многих элементарных функций. Теперь обратимся к вычислению неопределенных интегралов для более сложных функций. Например, рассмотрим поиск первообразной суммы f + g.f + g. В примере 4.51а. мы показали, что первообразная суммы x + exx + ex задается суммой (x22) + ex (x22) + ex, то есть первообразная суммы задается суммой первообразных. Этот результат не относится к данному примеру. В общем случае, если FF и GG являются первообразными любых функций ff и g, g соответственно, то
ddx (F (x) + G (x)) = F ′ (x) + G ′ (x) = f (x) + g (x). ddx (F (x) + G (x)) = F ′ (х) + G ′ (x) = f (x) + g (x).
Следовательно, F (x) + G (x) F (x) + G (x) является первообразной от f (x) + g (x) f (x) + g (x), и мы имеем
∫ (е (х) + г (х)) dx знак равно F (х) + G (х) + С.∫ (е (х) + г (х)) dx знак равно F (х) + G (х) + С.
Аналогично
∫ (f (x) −g (x)) dx = F (x) −G (x) + C.∫ (f (x) −g (x)) dx = F (x) −G (x) + С.
Кроме того, рассмотрим задачу поиска первообразной kf (x), kf (x), где kk — любое действительное число. С
г.
ddx (kf (x)) = kddxF (x) = kf ′ (x) ddx (kf (x)) = kddxF (x) = kf ′ (x)для любого действительного числа k, k, заключаем, что
Kf (x) dx = kF (x) + C.∫kf (x) dx = kF (x) + C.
Эти свойства перечислены ниже.
Теорема 4.16
Свойства неопределенных интегралов
Пусть FF и GG — первообразные от ff и g, g, соответственно, и пусть kk — любое действительное число.
Суммы и разности
∫ (f (x) ± g (x)) dx = F (x) ± G (x) + C∫ (f (x) ± g (x)) dx = F (x) ± G (x) + C
Постоянные кратные
∫kf (x) dx = kF (x) + C∫kf (x) dx = kF (x) + C
Из этой теоремы мы можем вычислить любой интеграл, включающий сумму, разность или постоянное кратное функций с известными первообразными. Вычисление интегралов, включающих произведения, частные или композиции, является более сложным (см. Пример 4.51b. Для примера, включающего первообразную продукта). Мы рассматриваем интегралы, включающие эти более сложные функции, во Введении в интеграцию.В следующем примере мы исследуем, как использовать эту теорему для вычисления неопределенных интегралов от нескольких функций.
Пример 4.52
Вычисление неопределенных интегралов
Вычислите каждый из следующих неопределенных интегралов:
- ∫ (5×3−7×2 + 3x + 4) dx∫ (5×3−7×2 + 3x + 4) dx
- ∫x2 + 4x3xdx∫x2 + 4x3xdx
- ∫41 + x2dx∫41 + x2dx
- ∫tanxcosxdx∫tanxcosxdx
Решение
- Используя свойства неопределенных интегралов, мы можем интегрировать каждый из четырех членов подынтегрального выражения отдельно.Получаем
∫ (5×3−7×2 + 3x + 4) dx = ∫5x3dx − ∫7x2dx + ∫3xdx + ∫4dx.∫ (5×3−7×2 + 3x + 4) dx = ∫5x3dx − ∫7x2dx + ∫3xdx + ∫4dx.
Из второй части свойств неопределенных интегралов каждый коэффициент можно записать перед знаком интеграла, что дает
∫5x3dx − ∫7x2dx + ∫3xdx + ∫4dx = 5∫x3dx − 7∫x2dx + 3∫xdx + 4∫1dx.∫5x3dx − ∫7x2dx + ∫3xdx + ∫4dx = 5∫x3dx − 7∫x2dx + 3∫x 1dx.
Используя правило степеней для интегралов, заключаем, что
∫ (5×3−7×2 + 3x + 4) dx = 54×4−73×3 + 32×2 + 4x + C.∫ (5×3−7×2 + 3x + 4) dx = 54×4−73×3 + 32×2 + 4x + C. - Записываем подынтегральное выражение как
.
х2 + 4х3х = х2х + 4х3х.х2 + 4х3х = х2х + 4х3х.
Затем, чтобы вычислить интеграл, проинтегрируйте каждый из этих членов отдельно. Используя правило мощности, мы имеем
∫ (x + 4×2 / 3) dx = ∫xdx + 4∫x − 2 / 3dx = 12×2 + 41 (−23) + 1x (−2/3) + 1 + C = 12×2 + 12×1 / 3 + C.∫ (x + 4×2 / 3) dx = ∫xdx + 4∫x − 2 / 3dx = 12×2 + 41 (−23) + 1x (−2/3) + 1 + C = 12×2 + 12×1 / 3 + C. - Используя свойства неопределенных интегралов, запишите интеграл как
Затем, используя тот факт, что tan − 1 (x) tan − 1 (x) является первообразной от 1 (1 + x2) 1 (1 + x2), заключаем, что
∫41 + x2dx = 4tan − 1 (x) + C. 41 + x2dx = 4tan − 1 (x) + C. - Записываем подынтегральное выражение как
.
tanxcosx = sinxcosxcosx = sinx.tanxcosx = sinxcosxcosx = sinx.
Следовательно,
∫tanxcosx = ∫sinx = −cosx + C.∫tanxcosx = ∫sinx = −cosx + C.
КПП 4.51
Вычислить ∫ (4×3−5×2 + x − 7) dx. (4×3−5×2 + x − 7) dx.
Проблемы с начальным значением
Мы рассмотрим методы интеграции большого количества функций, включающих продукты, частные и композиции, далее по тексту. Здесь мы переходим к одному распространенному использованию первообразных, которое часто встречается во многих приложениях: решение дифференциальных уравнений.
Дифференциальное уравнение — это уравнение, которое связывает неизвестную функцию и одну или несколько ее производных. Уравнение
— простой пример дифференциального уравнения. Решение этого уравнения означает нахождение функции yy с производной f.f. Следовательно, решения уравнения 4.9 являются первообразными f.f. Если FF является одной первообразной от f, f, каждая функция вида y = F (x) + Cy = F (x) + C является решением этого дифференциального уравнения. Например, решения
дает
у = ∫6x2dx = 2×3 + C.у = ∫6x2dx = 2×3 + C.
Иногда нас интересует, проходит ли конкретная кривая решения через определенную точку (x0, y0) (x0, y0), то есть y (x0) = y0.y (x0) = y0. Задача поиска функции yy, удовлетворяющей дифференциальному уравнению
с дополнительным условием
— это пример задачи начального значения. Условие y (x0) = y0y (x0) = y0 известно как начальное условие . Например, поиск функции yy, удовлетворяющей дифференциальному уравнению
и начальное условие
— это пример задачи начального значения.Поскольку решениями дифференциального уравнения являются y = 2×3 + C, y = 2×3 + C, чтобы найти функцию yy, которая также удовлетворяет начальному условию, нам нужно найти CC такой, что y (1) = 2 (1) 3+ C = 5. y (1) = 2 (1) 3 + C = 5. Из этого уравнения мы видим, что C = 3, C = 3, и заключаем, что y = 2×3 + 3y = 2×3 + 3 является решением этой начальной задачи, как показано на следующем графике.
Рис. 4.86. Отображаются некоторые кривые решения дифференциального уравнения dydx = 6x2dydx = 6×2. Функция y = 2×3 + 3y = 2×3 + 3 удовлетворяет дифференциальному уравнению и начальному условию y (1) = 5.у (1) = 5.
Пример 4.53
Решение задачи с начальным значением
Решите задачу начального значения
dydx = sinx, y (0) = 5. dydx = sinx, y (0) = 5.
Решение
Сначала нам нужно решить дифференциальное уравнение. Если dydx = sinx, dydx = sinx, то
y = ∫sin (x) dx = −cosx + C.y = ∫sin (x) dx = −cosx + C.
Далее нам нужно найти решение yy, удовлетворяющее начальному условию. Начальное условие y (0) = 5y (0) = 5 означает, что нам нужна постоянная CC такая, что −cosx + C = 5.−cosx + C = 5. Следовательно,
C = 5 + cos (0) = 6. C = 5 + cos (0) = 6.
Решение начальной задачи: y = −cosx + 6.y = −cosx + 6.
КПП 4.52
Решите задачу начального значения dydx = 3x − 2, y (1) = 2.dydx = 3x − 2, y (1) = 2.
Проблемы с начальным значением возникают во многих приложениях. Далее мы рассмотрим задачу, в которой водитель тормозит в автомобиле. Нас интересует, сколько времени нужно, чтобы машина остановилась. Напомним, что функция скорости v (t) v (t) является производной функции положения s (t), s (t), а ускорение a (t) a (t) является производной функции скорости.В предыдущих примерах в тексте мы могли вычислить скорость по положению, а затем вычислить ускорение по скорости. В следующем примере мы работаем наоборот. Учитывая функцию ускорения, мы вычисляем функцию скорости. Затем мы используем функцию скорости для определения функции положения.
Пример 4.54
Тормозящий вагон
Автомобиль движется со скоростью 8888 фут / сек (60 (60 миль / ч) при включении тормозов. Автомобиль начинает замедляться с постоянной скоростью 1515 фут / сек. 2 .
- Сколько секунд проходит до остановки автомобиля?
- Как далеко за это время уезжает машина?
Решение
- Сначала мы вводим переменные для этой задачи. Пусть tt будет временем (в секундах) после первого нажатия на тормоза. Пусть a (t) a (t) будет ускорением автомобиля (в футах в секунду в квадрате) в момент времени t.t. Пусть v (t) v (t) — скорость автомобиля (в футах в секунду) в момент времени t.t. Пусть s (t) s (t) будет положением автомобиля (в футах) за точкой, в которой тормоза задействованы в момент времени t.т.
Автомобиль движется со скоростью 88 футов / сек. 88 футов / сек. Следовательно, начальная скорость равна v (0) = 88v (0) = 88 ft / sec. Поскольку автомобиль замедляется, ускорение составляет
a (t) = — 15 футов / с2. a (t) = — 15 футов / с2.
Ускорение — это производная скорости,
v ′ (t) = — 15. v ′ (t) = — 15.
Следовательно, нам нужно решить задачу с начальным значением:
v ′ (t) = — 15, v (0) = 88. v ′ (t) = — 15, v (0) = 88.
Интегрируя, находим, что
v (t) = — 15t + C. v (t) = — 15t + C.
Поскольку v (0) = 88, C = 88. v (0) = 88, C = 88.Таким образом, функция скорости равна
v (t) = — 15t + 88. v (t) = — 15t + 88.
Чтобы узнать, сколько времени требуется машине, чтобы остановиться, нам нужно найти время tt, при котором скорость равна нулю. Решая −15t + 88 = 0, −15t + 88 = 0, получаем t = 8815t = 8815 сек. - Чтобы узнать, как далеко машина проехала за это время, нам нужно найти позицию машины через 88158815 сек. Мы знаем, что скорость v (t) v (t) является производной от положения s (t) .s (t). Считаем, что исходное положение s (0) = 0. s (0) = 0. Следовательно, нам необходимо решить задачу начального значения
s ′ (t) = — 15t + 88, s (0) = 0.s ′ (t) = — 15t + 88, s (0) = 0.
Интегрируя, имеем
s (t) = — 152t2 + 88t + C.s (t) = — 152t2 + 88t + C.
Поскольку s (0) = 0, s (0) = 0, константа C = 0. C = 0. Следовательно, функция положения —
s (t) = — 152t2 + 88t.s (t) = — 152t2 + 88t.
После t = 8815t = 8815 с положение s (8815) ≈258,133 с (8815) ≈258,133 фута.
КПП 4.53
Предположим, автомобиль движется со скоростью 4444 фут / сек. Сколько времени нужно, чтобы машина остановилась? Как далеко поедет машина?
Раздел 4.10 Упражнения
В следующих упражнениях покажите, что F (x) F (x) являются первообразными от f (x) .f (x).
465.
F (x) = 5×3 + 2×2 + 3x + 1, f (x) = 15×2 + 4x + 3F (x) = 5×3 + 2×2 + 3x + 1, f (x) = 15×2 + 4x + 3
466.
F (x) = x2 + 4x + 1, f (x) = 2x + 4F (x) = x2 + 4x + 1, f (x) = 2x + 4
467.
F (x) = x2ex, f (x) = ex (x2 + 2x) F (x) = x2ex, f (x) = ex (x2 + 2x)
468.
F (x) = cosx, f (x) = — sinxF (x) = cosx, f (x) = — sinx
469.
F (x) = ex, f (x) = exF (x) = ex, f (x) = ex
Для следующих упражнений найдите первообразную функции.
471.
f (x) = ex − 3×2 + sinxf (x) = ex − 3×2 + sinx
472.
f (x) = ex + 3x − x2f (x) = ex + 3x − x2
473.
f (x) = x − 1 + 4sin (2x) f (x) = x − 1 + 4sin (2x)
Для следующих упражнений найдите первообразную F (x) F (x) каждой функции f (x) .f (x).
478.
f (x) = x1 / 3 + (2x) 1 / 3f (x) = x1 / 3 + (2x) 1/3
479.
f (x) = x1 / 3×2 / 3f (x) = x1 / 3×2 / 3
480.
f (x) = 2sin (x) + sin (2x) f (x) = 2sin (x) + sin (2x)
481.
f (x) = sec2 (x) + 1f (x) = sec2 (x) +1
482.
f (x) = sinxcosxf (x) = sinxcosx
483.
f (x) = sin2 (x) cos (x) f (x) = sin2 (x) cos (x)
485.
f (x) = 12csc2 (x) + 1x2f (x) = 12csc2 (x) + 1×2
486.
f (x) = cscxcotx + 3xf (x) = cscxcotx + 3x
487.
f (x) = 4cscxcotx − secxtanxf (x) = 4cscxcotx − secxtanx
488.
f (x) = 8secx (secx − 4tanx) f (x) = 8secx (secx − 4tanx)
489.
f (x) = 12e − 4x + sinxf (x) = 12e − 4x + sinx
Для следующих упражнений оцените интеграл.
494.
∫ (secxtanx + 4x) dx∫ (secxtanx + 4x) dx
496.
∫ (x − 1/3 − x2 / 3) dx∫ (x − 1/3 − x2 / 3) dx
497.
∫14×3 + 2x + 1x3dx∫14×3 + 2x + 1x3dx
498.
∫ (ex + e − x) dx∫ (ex + e − x) dx
Для следующих упражнений решите задачу начального значения.
499.
f ′ (x) = x − 3, f (1) = 1f ′ (x) = x − 3, f (1) = 1
500.
f ′ (x) = x + x2, f (0) = 2f ′ (x) = x + x2, f (0) = 2
501.
f ′ (x) = cosx + sec2 (x), f (π4) = 2 + 22f ′ (x) = cosx + sec2 (x), f (π4) = 2 + 22
.
502.
f ′ (x) = x3−8×2 + 16x + 1, f (0) = 0f ′ (x) = x3−8×2 + 16x + 1, f (0) = 0
503.
f ′ (x) = 2×2 − x22, f (1) = 0f ′ (x) = 2×2 − x22, f (1) = 0
Для следующих упражнений найдите две возможные функции ff, заданные производными второго или третьего порядка.
505.
f ″ (x) = e − xf ″ (x) = e − x
508.
f (x) = 8e − 2x − sinxf ‴ (x) = 8e − 2x − sinx
509.
Автомобиль движется со скоростью 4040 миль / ч при включенных тормозах. Автомобиль замедляется с постоянной скоростью 1010 фут / сек 2 . Как скоро машина остановится?
510.
В предыдущей задаче вычислите, как далеко проехала машина за время, необходимое для остановки.
511.
Вы выезжаете на автостраду, ускоряясь с постоянной скоростью 1212 фут / сек. 2 .Сколько времени нужно, чтобы достичь скорости слияния 6060 миль в час?
512.
Исходя из предыдущей задачи, как далеко проехал автомобиль, чтобы достичь скорости слияния?
513.
Автомобильная компания хочет, чтобы ее новейшая модель могла остановиться за 88 секунд при движении со скоростью 7575 миль в час. Если мы предполагаем постоянное замедление, найдите значение замедления, при котором это достигается.
514.
Автомобильная компания хочет, чтобы ее новейшая модель могла остановиться на расстоянии менее 450450 футов при движении со скоростью 6060 миль в час.Если мы предполагаем постоянное замедление, найдите значение замедления, при котором это достигается.
Для следующих упражнений найдите первообразную функции, предполагая, что F (0) = 0.F (0) = 0.
516.
[T] f (x) = 4x − xf (x) = 4x − x
517.
[T] f (x) = sinx + 2xf (x) = sinx + 2x
519.
[T] f (x) = 1 (x + 1) 2f (x) = 1 (x + 1) 2
520.
[T] f (x) = e − 2x + 3x2f (x) = e − 2x + 3×2
Для следующих упражнений определите, истинно ли утверждение или нет.Либо докажите, что это правда, либо найдите контрпример, если он неверен.
521.
Если f (x) f (x) — первообразная v (x), v (x), то 2f (x) 2f (x) — первообразная 2v (x) .2v (x).
522.
Если f (x) f (x) — первообразная v (x), v (x), то f (2x) f (2x) — первообразная v (2x) .v (2x).
523.
Если f (x) f (x) — первообразная v (x), v (x), то f (x) + 1f (x) +1 — первообразная v (x) + 1.v (x ) +1.
524.
Если f (x) f (x) является первообразной от v (x), v (x), то (f (x)) 2 (f (x)) 2 является первообразной от (v (x)) 2 .(v (x)) 2.
Исчисление — Основные первообразные — Открытый справочник по математике
Это устройство не может отображать анимацию Java. Вышеупомянутое статическое изображение заменяет
1. Ноль
Первый апплет показывает график слева от постоянной подынтегральной функции, равной 0. Перемещение ползунка x показывает, что никакая область не накапливается. Или используйте поле выбора, чтобы выбрать «Уклон», чтобы изучить этот пример (и другие примеры) с точки зрения уклона. С точки зрения наклона наклон всегда равен нулю, поэтому первообразная должна быть горизонтальной линией.Переместите ползунок C , чтобы увидеть других членов этого семейства. Используя неопределенные интегральные обозначения, мы говорим, что
.2. Постоянная
Выберите второй пример, показывающий постоянную подынтегральную функцию, равную 2. Перемещение ползунка x показывает, что область добавляется линейно. С точки зрения уклона, наклон постоянный, который, как мы знаем, является линией. Так
В более общем смысле:
где k — постоянная. В этом апплете положительная область отображается зеленым, а отрицательная — красным.
3. Линия
Выберите третий пример, показывающий прямую подынтегральную функцию. Переместите ползунок x , чтобы увидеть накопленную площадь. В частности, установите x = 1. Каково значение первообразной? Поскольку это не 1, первообразная не может быть просто x ², а должна быть
Вы можете проверить это, найдя производную от правой части этого уравнения, и вы получите всего x .
4. Парабола
Выберите четвертый пример, показывающий параболу.Снова установите x = 1 и отметьте значение первообразной. Поскольку это не 1, первообразная не может быть просто x ³, а должна быть
Проверьте это, найдя производную от правой части этого уравнения, и вы получите всего x ².
5. Кубик
Выберите пятый пример, показывающий кубик. Вы можете понять, что это за первообразная? Возможно, вы заметили паттерн, который дает нам общую формулу первообразной степенной функции:
Попробуйте найти производную от правой части, чтобы убедиться, что вы действительно получили подынтегральное выражение.
6. Гипербола
Выберите шестой пример, показывающий гиперболу 1/ x (или x -1 ). Правило степенной функции, которое мы только что рассмотрели, не работает в этом случае, потому что тогда знаменатель в правой части будет равен нулю, а деление на ноль даст неопределенный результат. Переместите ползунок x , чтобы увидеть, что наклон построенной на графике первообразной действительно соответствует значению подынтегральной функции (этот пример лучше всего рассматривать с точки зрения наклона).Какая функция имеет производную 1/ x ? Как вы помните, это ln ( x ). Но этот пример немного отличается, потому что 1/ x может принимать как положительные, так и отрицательные значения. Следовательно, правило
где абсолютное значение дает нам правильную кривую на отрицательной стороне.
Если вы посмотрите на вещи с точки зрения площади и переместите ползунок x , вы можете заметить, что область, кажется, начинается и заканчивается на 1 вместо 0. Поскольку подынтегральное выражение не определено как x = 0, мы можем ‘ t используйте функцию накопления от 0 для построения графика первообразной.Вместо этого мы используем функцию накопления с нижним пределом 1 (и программа также по-другому обрабатывает отрицательные x ). Прямо сейчас мы не знаем, как вычислить определенный интеграл на интервале, где подынтегральное выражение стремится к бесконечности; мы вернемся к этой теме позже. Программа использует численные методы для вычисления антипроизводного графа как функции накопления, и у него тоже есть проблемы с бесконечностью.
7. Показательная функция
Выберите седьмой пример, показывающий экспоненциальную функцию.Поскольку мы знаем, что производная e x равна e x , мы можем предположить, что первообразная e x — это e x . Хотя график выглядит правильной формы, он кажется сдвинутым вниз. Это потому, что первообразная изображена как функция накопления:
который равен нулю для x = 0. Таким образом, наша функция накопления дает нам первообразную e x — 1.Поскольку затем мы добавляем к этому результату константу C , а -1 также является константой, мы можем объединить -1 и C только в C , поскольку это произвольная константа. Итак, правило становится:
8. Косинусная функция
Выберите восьмой пример, показывающий косинус. Первообразная выглядит как синус, и, поскольку мы знаем, что производная sin ( x ) равна cos ( x ), правило для первообразной:
9. Функция синуса
Выберите девятый пример, показывающий синус (обратите внимание, что вам, возможно, придется прокрутить окно меню примера, чтобы найти девятый пример).Первообразная выглядит как косинус, но перевернута и сдвинута вверх. Поскольку мы знаем, что производная cos ( x ) равна -sin ( x ), производная -cos ( x ) равна sin ( x ), поэтому можно ожидать, что первообразная sine равна выглядят как -косинус. Сдвиг происходит от графического программного обеспечения с использованием функции накопления.
таким образом, построенная на графике первообразная должна пересекать ось x в начале координат. Как и в примере с экспоненциальной функцией, мы игнорируем этот сдвиг +1, поскольку это просто добавленная константа.Итак, мы пишем правило так:
Исследуйте
Вы можете попробовать ввести свои собственные функции для подынтегрального выражения, особенно те, которые являются производными какой-либо известной функции. Вы можете попробовать сумму двух функций, и вы обнаружите, что определенное интегральное свойство сумм и разностей справедливо и для общих первообразных. Другими словами:
Если вы поиграете с продуктами, факторами и составами функций, вы обнаружите, что, как и производные, нам нужны более сложные правила.Будьте осторожны с функциями с вертикальными асимптотами, такими как sec ( x ) tan ( x ) (где мы знаем, что производная sec ( x ) является этой функцией, поэтому первообразная этой функции должна быть sec ( x ). ) + С .
(Если вы попробуете это, вы получите хороший график, если не пересечете одну из асимптот. Как только график пересечет асимптоту, программное обеспечение для построения графиков запутается, потому что ему трудно оценить функцию накопления, когда эта функция стремится к бесконечности).b f (t) \, dt \), мы можем найти любую первообразную \ (F (t) \) от \ (f (t) \) и вычислить \ (F (b) — F (a) \). Проблема нахождения точного значения определенного интеграла сводится к нахождению некоторой (любой) первообразной \ (F \) подынтегрального выражения и последующему вычислению \ (F (b) — F (a) \). Даже найти одно первообразное может быть сложно, и мы будем придерживаться функций, у которых есть простые первообразные.
Строительные блоки
Антидифференцировка идет в обратном направлении через производный процесс.Таким образом, самые простые производные правила — это просто обратные версии самых простых производных правил. Вспомните из главы 2:
Производные правила: строительные блоки
В дальнейшем \ (f \) и \ (g \) — дифференцируемые функции от \ (x \). 0 \).x \) раньше.
Далее следуют соответствующие правила для первообразных — каждое из правил первообразных просто переписывает правило производных. Все эти первообразные можно проверить путем дифференцирования.
Есть один сюрприз — первообразная \ (\ frac {1} {x} \) на самом деле не просто \ (\ ln (x) \), это \ (\ ln | x | \). Это хорошо — первообразная имеет домен, который соответствует домену \ (\ frac {1} {x} \), который больше, чем домен \ (\ ln (x) \), поэтому мы не Мне не нужно беспокоиться о том, положительны или отрицательны наши \ (x \).Но мы, , должны быть осторожны, чтобы включить эти абсолютные значения в — в противном случае мы можем столкнуться с проблемами домена.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5.
Первоначальные правила: строительные блоки
В дальнейшем \ (f \) и \ (g \) — дифференцируемые функции от \ (x \), а \ (k \), \ (n \) и \ (C \) — константы. 2 \).2 = 147 \]
- Новая популяция = (старая популяция) + (новые бактерии) = 1000 + 147 = 1147 бактерий.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5.
Пример 8
Компания определяет свои предельные издержки производства в долларах на единицу как \ (MC (x) = \ frac {4} {\ sqrt {x}} + 2 \) при производстве \ (x \) тысяч единиц. Найдите стоимость увеличения производства с 4 тыс. Шт. До 5 тыс. Шт.5 \\
= & \ left (8 \ sqrt {5} +2 (5) \ right) — \ left (8 \ sqrt {4} +2 (4) \ right) \\
\ ок & 3,889
\ конец {выравнивание *} \]
Чтобы увеличить производство с 4 до 5 тысяч штук, потребуется 3,889 тысячи долларов. (Окончательный ответ лучше было бы записать как 3889 долларов.)
AC Построение точных графиков первообразных
Раздел 5.1 Построение точных графов первообразных
Мотивирующие вопросы
Учитывая график производной функции, как мы можем построить полностью точный график исходной функции?
Сколько первообразных имеет данная функция? Что общего у всех этих первообразных?
Учитывая функцию \ (f \ text {,} \), как правило \ (A (x) = \ int_0 ^ xf (t) \, dt \) определяет новую функцию \ (A \ text {?} \)
Постоянной темой в нашем обсуждении дифференциального исчисления был вопрос «Учитывая информацию о производной неизвестной функции \ (f \ text {,} \), сколько информации мы можем получить о самом \ (f \)?» В действии 1.8.3, график \ (y = f ‘(x) \) был известен (вместе со значением \ (f \) в одной точке), и мы попытались нарисовать возможный график \ (f \) рядом с известная точка. В примере 3.1.7 мы исследовали, как тест первой производной позволяет нам использовать информацию о \ (f ‘\), чтобы определить, где исходная функция \ (f \) увеличивается и уменьшается, а также где \ (f \) имеет относительные экстремальные значения. Если мы знаем формулу или график \ (f ‘\ text {,} \) путем вычисления \ (f’ ‘\), мы можем найти, где исходная функция \ (f \) вогнута вверх и вогнута вниз.Таким образом, знание \ (f ‘\) и \ (f’ ‘\) позволяет нам понять форму графика \ (f \ text {.} \)
Мы вернулись к этому вопросу еще более подробно в Разделе 4.1. В этой настройке мы знали мгновенную скорость движущегося объекта и работали, чтобы определить как можно больше информации о функции положения объекта. Мы обнаружили связи между чистой подписанной областью под функцией скорости и соответствующим изменением положения функции, и теорема полного изменения дополнительно осветила эти связи между \ (f ‘\) и \ (f \ text {,} \), показывая что полное изменение значения \ (f \) на интервале \ ([a, b] \) определяется чистой подписанной площадью, ограниченной \ (f ‘\) и осью \ (x \) на такой же интервал.
Далее мы исследуем ситуацию, когда у нас есть точный график производной функции вместе с единственным значением функции \ (f \ text {.} \). На основе этой информации мы хотели бы построить график \ (f \), который показывает, где \ (f \) увеличивается, уменьшается, выгибается вверх и вниз, а также предоставляет точное значение функции в любой точке.
Предварительный просмотр деятельности 5.1.1.
Предположим, что следующая информация известна о функции \ (f \ text {:} \) график ее производной, \ (y = f ‘(x) \ text {,} \) приведен на рисунке 5.1.1. Далее, предположим, что \ (f ‘\) кусочно линейно (как показано на рисунке) и что для \ (x \ le 0 \) и \ (x \ ge 6 \ text {,} \) \ (f’ (x) = 0 \ text {.} \) Наконец, указано, что \ (f (0) = 1 \ text {.} \)
Рисунок 5.1.1. Слева график \ (y = f ‘(x) \ text {;} \) справа, оси для построения \ (y = f (x) \ text {.} \)
На каком интервале ( s) является ли \ (f \) возрастающей функцией? На каких интервалах убывает \ (f \)?
На каком интервале (ах) \ (f \) вогнутый вверх? вогнуться вниз?
В какой точке (точках) \ (f \) имеет относительный минимум? относительный максимум?
Напомним, что теорема полного изменения говорит нам, что
\ begin {уравнение *}
е (1) — е (0) = \ int_0 ^ 1 f ‘(x) \, dx \ text {.}
\ end {уравнение *}Каково точное значение \ (f (1) \ text {?} \)
Используйте данную информацию и рассуждения, аналогичные приведенным в (d), чтобы определить точное значение \ (f (2) \ text {,} \) \ (f (3) \ text {,} \) \ (f (4) \ text {,} \) \ (f (5) \ text {,} \) и \ (f (6) \ text {.} \)
Основываясь на ваших ответах на все предыдущие вопросы, нарисуйте полный и точный график \ (y = f (x) \) на представленных осях, обязательно указав поведение \ (f \) для \ ( х \ lt 0 \) и \ (х \ gt 6 \ text {.} \)
Подраздел 5.1.1 Построение графика первообразной
Предварительный просмотр Задание 5.1.1 демонстрирует, что когда мы можем найти точную область под графиком функции на любом заданном интервале, можно построить график первообразной функции. То есть мы можем найти функцию, производная которой задана. Теперь мы можем определить не только общую форму первообразного графа, но и фактическую высоту графа в любой интересующей точке.б е (х) \, дх \ текст {.} \)
Мероприятие 5.1.2.
Предположим, что функция \ (y = f (x) \) задана графиком, показанным на рисунке 5.1.2, и что части \ (f \) являются либо частями линий, либо частями окружностей. Кроме того, пусть \ (F \) является первообразной \ (f \) и скажем, что \ (F (0) = -1 \ text {.} \) Наконец, предположим, что для \ (x \ le 0 \) и \ (x \ ge 7 \ text {,} \) \ (f (x) = 0 \ text {.} \)
Рисунок 5.1.2. Слева график \ (y = f (x) \ text {.} \)
На каком интервале (ах) функция \ (F \) возрастает? На каких интервалах убывает \ (F \)?
На каком интервале (ах) \ (F \) вогнутый вверх? вогнуться вниз? ни один?
В какой точке (точках) \ (F \) имеет относительный минимум? относительный максимум?
Используйте данную информацию, чтобы определить точное значение \ (F (x) \) для \ (x = 1, 2, \ ldots, 7 \ text {.} \) Кроме того, каковы значения \ (F (-1) \) и \ (F (8) \ text {?} \)
Основываясь на ваших ответах на все предыдущие вопросы, нарисуйте полный и точный график \ (y = F (x) \) на представленных осях, обязательно указав поведение \ (F \) для \ ( x \ lt 0 \) и \ (x \ gt 7 \ text {.} \) Четко укажите масштаб на вертикальной и горизонтальной осях вашего графика.
Что произойдет, если мы изменим одну ключевую часть информации: в частности, скажем, что \ (G \) является первообразной от \ (f \) и \ (G (0) = 0 \ text {.} \) Как (если вообще) изменились бы ваши ответы на предыдущие вопросы? Нарисуйте график \ (G \) на тех же осях, что и график \ (F \), который вы построили в (e).
Подраздел 5.1.2 Множественные первообразные одной функции
В последнем вопросе действия 5.1.2 мы столкнулись с очень важной идеей: функция \ (f \) имеет более одного первообразного. Каждая первообразная \ (f \) однозначно определяется своим значением в одной точке. Например, предположим, что \ (f \) — это функция, показанная слева на рисунке 5.1 е (х) \, dx \\
& = 1 + 0,5 \\
& = 1.5 \ текст {.}
\ end {выровнять *}
Аналогично \ (F (2) = 1.5 \ text {,} \) \ (F (3) = -0.5 \ text {,} \) \ (F (4) = -2 \ text {,} \) \ (F (5) = -0,5 \ text {,} \) и \ (F (6) = 1 \ text {.} \) Кроме того, мы можем использовать тот факт, что \ (F ‘= f \) для выяснить, где \ (F \) увеличивается и уменьшается, вогнута вверх и вогнута вниз и имеет относительные экстремумы и точки перегиба. В конечном итоге мы обнаруживаем, что график \ (F \) — это тот, который выделен синим цветом на рис. 5.1.3.
Если нам нужна первообразная \ (G \), для которой \ (G (0) = 3 \ text {,} \), то \ (G \) будет иметь ту же форму, что и \ (F \) (поскольку оба имеют производная \ (f \)), но \ (G \) будет смещена по вертикали от графика \ (F \ text {,} \), как показано красным на рисунке 5.1 f (x) \, dx = 0,5 \ text {,} \) так же, как \ (F (1) — F (0) = 0,5 \ text {,} \), но поскольку \ (G (0) = 3 \ text {,} \) \ (G (1) = G (0) + 0.5 = 3.5 \ text {,} \), тогда как \ (F (1) = 1.5 \ text {.} \) Таким же образом, если мы присвоили первообразной другое начальное значение, скажем \ (H (0) = -1 \ text {,} \), мы получим еще одну первообразную, как показано пурпурным цветом на рисунке 5.1.3.
Этот пример демонстрирует важный факт, который имеет более общее значение:
Если \ (G \) и \ (H \) оба являются первообразными функции \ (f \ text {,} \), тогда функция \ (G — H \) должна быть постоянной.
Чтобы понять, почему этот результат верен, заметьте, что если \ (G \) и \ (H \) оба являются первообразными от \ (f \ text {,} \), то \ (G ‘= f \) и \ (H ‘= f \ text {.} \) Следовательно,
\ begin {уравнение *}
\ frac {d} {dx} [G (x) — H (x)] = G ‘(x) — H’ (x) = f (x) — f (x) = 0 \ text {.}
\ end {уравнение *}
Поскольку функция может иметь нулевую производную только тогда, когда она является постоянной функцией, отсюда следует, что функция \ (G — H \) должна быть постоянной.
Теперь мы видим, что если функция имеет хотя бы одну первообразную, у нее должно быть бесконечно много: мы можем добавить любую константу по нашему выбору к первообразной и получить другую первообразную.3 + \ frac {1} {3} \ text {.} \)
Мероприятие 5.1.3.
Для каждой из следующих функций нарисуйте точный график первообразной, удовлетворяющей заданному начальному условию. Кроме того, нарисуйте график двух дополнительных первообразных данной функции и укажите соответствующие начальные условия, которым удовлетворяет каждое из них. 2, \ amp \ text {if} 1 \ lt x \ lt 2 \\ 0 \ amp \ text {else} \ end {cases} \ text {;} \) начальное условие: \ (P (0) = 1 \ text {;} \) интервал для эскиза: \ ([- 1,3] \)
Подраздел 5.б е (х) \, dx \ текст {.}
\ end {уравнение *}
В нескольких ситуациях мы использовали эту формулу для вычисления \ (F (b) \) для нескольких различных значений \ (b \ text {,} \), а затем построили точки \ ((b, F (b)) \), чтобы помочь нам построить точный график \ (F \ text {.} \). Это говорит о том, что мы можем думать о \ (b \ text {,} \) верхней границе интегрирования как о самой переменной. С этой целью мы вводим идею интегральной функции , функции, формула которой включает определенный интеграл.
Определение 5.x f (t) \, dt \ text {.} \ label {FGz} \ tag {5.1.2}
\ end {уравнение}
Обратите внимание, что поскольку \ (x \) является независимой переменной в функции \ (A \ text {,} \) и определяет конечную точку интервала интегрирования, нам нужно использовать другую переменную в качестве переменной интегрирования. Стандартный выбор — \ (t \ text {,} \), но допустима любая переменная, кроме \ (x \).
Один из способов представить функцию \ (A \) — это функция «чистой подписанной области от \ (a \) до \ (x \)», где мы рассматриваем область, ограниченную \ (y = f (t )\текст{.xf (t) \ dt \ text {.} \)
Функция \ (A \) измеряет чистую знаковую площадь от \ (t = 0 \) до \ (t = x \), ограниченную кривой \ (y = f (t) \ text {;} \) это значение затем сообщается как соответствующая высота на графике \ (y = A (x) \ text {.} \) на http://gvsu.edu/s/ cz, мы находим java-апплет 1 , который оживляет статическое изображение на рис. 5.1.5. Там пользователь может переместить красную точку функции \ (f \) и увидеть, как соответствующая высота изменяется в голубой точке на графике \ (A \ text {.x g (t) \ dt \ text {.} \)
На каком интервале (ах) функция \ (A \) возрастает? На каких интервалах убывает \ (A \)? Почему?
На каком интервале (ах), по вашему мнению, \ (A \) вогнутый вверх? вогнуться вниз? Почему?
В какой точке (точках) \ (A \) имеет относительный минимум? относительный максимум?
Используйте данную информацию, чтобы определить точные значения \ (A (0) \ text {,} \) \ (A (1) \ text {,} \) \ (A (2) \ text {,} \ ) \ (A (3) \ text {,} \) \ (A (4) \ text {,} \) \ (A (5) \ text {,} \) и \ (A (6) \ text { .3 f (x) \, dx \ text {.} \) Когда мы объединяем эту информацию о значениях функций \ (F \) вместе с нашим пониманием того, как поведение \ (F ‘= f \) влияет на общее форму \ (F \ text {,} \) мы можем построить полностью точный граф первообразной \ (F \ text {.} \)
Поскольку производная константы равна нулю, если \ (F \) является первообразной от \ (f \ text {,} \), то \ (G (x) = F (x) + C \) будет также является первообразной функции \ (f \ text {.} \) Более того, любые две первообразные функции \ (f \) отличаются точно на константу.xf (t) \, dt \) определяет новую функцию \ (A \), которая измеряет подписанную сетью область, ограниченную \ (f \) на интервале \ ([a, x] \ text {.} \). вызвать функцию \ (A \) интегральной функцией, соответствующей \ (f \ text {.} \)
Используйте данную информацию для определения \ (s (1) \ text {,} \) \ (s (3) \ text {,} \) \ (s (5) \ text {,} \) и \ (s (6) \ text {.} \)
На каком интервале (ах) увеличивается \ (s \)? На каком интервале (ах) уменьшается \ (s \)?
На каком интервале (ах) \ (ы \) вогнуты вверх? На каком интервале (ах) \ (s \) вогнута вниз?
Нарисуйте точный помеченный график \ (s \) по осям справа на рисунке 5.2 \ text {.} \) Найдите формулу для \ (s \ text {.} \)
Пусть \ (C \) будет первообразной \ (c \ текст {.} \) Что измеряет функция \ (C \)? Что это за единицы?
Предположим, что \ (C (0) = 0 \ text {.} \) Определите точное значение \ (C (t) \) при значениях \ (t = 5, 10, 15, 20, 25, 30 \ text {.} \)
Нарисуйте точный график \ (C \) по осям, представленным справа на рисунке 5.1.8. Обязательно отметьте шкалу на вертикальной оси.{x} f (t) \, dt \ text {.} \)
Для значений \ (x = -1, 0, 1, \ ldots, 6 \ text {,} \) создайте таблицу, в которой перечислены соответствующие значения \ (A (x) \ text {,} \) \ (B (x) \ text {,} \) и \ (C (x) \ text {.} \)
На осях, представленных на рисунке 5.1.9, нарисуйте графики \ (A \ text {,} \) \ (B \ text {,} \) и \ (C \ text {.} \)
Как связаны графики \ (A \ text {,} \) \ (B \ text {,} \) и \ (C \)?
Как бы вы лучше всего описали взаимосвязь между функцией \ (A \) и функцией \ (f \ text {?} \)
Рисунок 5.1.9. Слева, данный график \ (f \ text {.} \) Справа, оси для построения \ (A \ text {,} \) \ (B \ text {,} \) и \ (C \ text { .} \)
AP Calculus Exam Review: Antidifferentiation — Magoosh Blog
Antidifferentiation — важный инструмент для оценки интегралов. Фактически, вы можете сказать, что антидифференциация — это почти то же самое, что найти неопределенный интеграл.
Когда мы антидифференцируем функцию, мы просто находим другую функцию, производная которой равна той, с которой мы начали.
Что такое антидифференцировка?
Антидифференцировка — это обратная дифференциация . Подобно тому, как дифференциация — это процесс поиска производной, дифференциация против является универсальным термином для любой формулы, техники или метода поиска производной против .
Если f — функция, то мы говорим, что F является первообразной для f , если F ‘( x ) = f ( x ).
Сколько первообразных может иметь функция?
Если функция имеет одну первообразную, то она имеет бесконечно первообразных. Это потому, что производная любой константы равна 0. Итак, если F ( x ) является первообразной f ( x ), а C — любая константа, тогда
[ F ( x ) + C ] ‘= F ‘ ( x ) + [C] ‘= f ( x ) + 0 = f ( x ) ).
Следовательно, F ( x ) + C — это , также является первообразной для f . Мы называем C константой интеграции .
Обозначение и связь с интегралом
Неопределенный интеграл функции f по определению является наиболее общей первообразной f . Обозначения для неопределенного интеграла показаны ниже.
Каждый раз, когда мы вычисляем неопределенный интеграл, мы проводим антидифференциацию.
Формулы антидифференцировки
Есть еще много формул и методов антидифференцировки. К счастью, вам нужно знать только основы экзаменов AB и BC.
Экзамен AP Calculus AB охватывает основные формулы антидифференциации и замену переменных.
Экзамен AP Calculus BC включает не только основные формулы и замену, но также интегрирование по частям (IBP) и простые частичные дроби (PF). Этот тест также имеет в целом более сложные задачи.
Обратите внимание, что все эти правила написаны в терминах неопределенных интегралов.
Основные правила
«Основные» правила относятся к тем правилам, которые непосредственно вытекают из правил дифференциации. Некоторые из наиболее распространенных правил включают правило мощности, правило суммы / разности и правило постоянного множественного числа. Также существуют правила для некоторых тригонометрических, экспоненциальных и других элементарных функций.
Правило замещения
Правило замещения или u -замена — это правило, которое «меняет» правило цепочки.
Интеграция по частям
Интеграция по частям (IBP) — мощный метод, который может использоваться, когда в интегрируемом выражении присутствуют определенные виды продуктов. Фактически, вы можете думать о IBP как о способе «перевернуть» правило продукта.
Предположим, что u и v — дифференцируемые функции x . Тогда формула IBP гласит, что:
Частичные дроби
Метод частичных дробей (PF) — это специализированный метод для рациональных функций .Основная идея — разбить дробь на сумму более простых дробей.
К счастью, даже на экзамене BC вам нужно знать только самые простые случаи PF. В простейших случаях знаменатель делится на уникальные линейных множителя.
- Шаг 1. Разложите знаменатель на множители. Каждый из этих факторов станет знаменателем своей дроби.
- Шаг 2. Затем необходимо определить числители констант.Это можно сделать различными алгебраическими способами. Возможно, самый быстрый и простой способ — это метод сокрытия Хевисайда .
Когда есть только линейные факторы, метод сокрытия Хевисайда работает следующим образом:
Для каждого фактора ( x — c ) включите этот фактор в выражение. Затем подставьте корень этого множителя (то есть x = c ) в оставшееся выражение. Результатом является правильное значение постоянной A , соответствующей этому коэффициенту.
- Шаг 3. Наконец, проинтегрируйте каждую более простую дробь. В самых простых случаях это включает простую замену и правило 1/ x . Каждый дробный член следует одному и тому же основному правилу:
Практические задачи
Давайте сделаем антидифференцировку!
Пример 1
Найдите первообразную 4 x 3 — 8 x + 7.
Это задание по основным правилам, включая правило силы.
А теперь давайте проверим нашу работу. Помните, что антидифференцировка — это противоположность дифференциации. Итак, все, что вам нужно сделать, это найти производную своего ответа и убедиться, что она совпадает с исходным подынтегральным выражением.
Пример 2
Это работа для неполных дробей. Во-первых, убедитесь, что числитель имеет меньшую степень, чем знаменатель. (Если бы у него была такая же или большая степень, то вам сначала пришлось бы переписать интеграл, используя полиномиальное деление .Посмотрите это видео, чтобы узнать больше о делении многочленов в столбик.)
Первым делим знаменатель на множители. x 2 — 7 x + 12 = ( x — 3) ( x — 4).
Затем перепишите подынтегральное выражение как сумму дробей с каждым множителем в качестве знаменателя и неизвестной константой в числителе.
Теперь используйте метод сокрытия Хевисайда для каждого фактора.
Наконец, подключите свои константы и выполните интеграцию.
Сводка
Антидифференцировка — это обратное дифференцировке. Это то же самое, что найти первообразную для функции. Неопределенный интеграл — самая общая первообразная. Методы антидифференцировки, необходимые для сдачи экзаменов, включают:
- Основные формулы
- Замена
- Интеграция по частям (только BC)
- Частичные дроби (только BC)
Гарантированно улучшите свой результат SAT или ACT.Начните 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep уже сегодня!
Между прочим, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!
О Шоне Олте
Шон получил докторскую степень по математике в Университете штата Огайо в 2008 году (Go Bucks !!). Он получил степень бакалавра математики и информатику в Оберлинском колледже в 2002 году. Кроме того, Шон получил степень бакалавра наук.Mus. из Консерватории Оберлина в том же году по специальности «музыкальная композиция». Шон по-прежнему любит музыку — почти так же, как математику! — и он (думает, что) может играть на пианино, гитаре и басу. Шон обучал и обучал студентов математике около десяти лет и надеется, что его опыт поможет вам добиться успеха!
.
Упражнения 5.1.5 Упражнения
1. Определенный интеграл от кусочно-линейной функции.
2. Гладкая функция, начинающаяся с 0.
3. Кусочно-постоянная функция.
4. Еще одна кусочно-линейная функция.
5.
Скорость движущейся частицы задается квадратичной функцией \ (v \), показанной на рисунке 5.1.7. Кроме того, указано, что \ (A_1 = \ frac {7} {6} \) и \ (A_2 = \ frac {8} {3} \ text {,} \), а также для соответствующей функции положения \ (s \ text {,} \) \ (s (0) = 0,5 \ text {.} \)
Рисунок 5.1.7. Слева данный график \ (v \ text {.} \) Справа оси для построения \ (s \ text {.} \)
6.
Человек, тренирующийся на беговой дорожке, испытывает разные уровни сопротивления и, таким образом, сжигает калории с разной скоростью, в зависимости от настроек беговой дорожки. На конкретной тренировке скорость, с которой человек сжигает калории, задается кусочно-постоянной функцией \ (c \), показанной на рисунке 5.1.8. Обратите внимание, что единицы на \ (c \) — это «калории в минуту.”
Рисунок 5.1.8. Слева, данный график \ (c \ text {.} \) Справа, оси для построения \ (C \ text {.} \)