Содержание
Кинематика. Формулы
Кинематика. Формулы
| Номер | Название формулы | Запись формулы | Примечание |
| (1) | Закон равноускоренного криволинейного движения | vS0 — модуль начальной скорости; aS — ускорение | |
| (2) | Скорость равномерного прямолинейного движения | ||
| (3) | Скорость | ||
| (4) | Ускорение | ||
| (5) | Касательное ускорение | dv = dl/dt, т.е. путевая скорость вдоль рассматриваемой траектории | |
| (6) | Нормальное ускорение | ||
| (7) | Скорость свободного падения тела | ||
| (8) | Время тела при свободном падении | ||
| (9) | Время при равномерном движении по окружности | ||
| (10) | Скорость равномерного движения по окружности | ||
| (11) | Угловая (мгновенная) скорость равномерного движения по окружности | Единица измерения угловой скорости — радианы в секунду | |
| (12) | Скорость равноускоренного движения по окружности | ||
| (13) | Угловая (мгновенная) скорость равноускоренного движения по окружности |
— версия для печати
- Определение
- Кинематикой называется раздел физики, занимающийся исследованием законов движения идеальных тел
- Пояснение
- Под чертой вверху буквы подразумевается знак вектора.

| Если у вас есть мысли или идеи по поводу данной таблицы или, например, вы считаете, что полезно было бы создать определенную вспомогательную памятку, то мы обязательно рассмотрим ваше предложение, которое можно изложить по ссылке (где вы также можете поделиться с нами любыми мыслями по поводу сайта scolaire.ru). Мы готовы устранить любые неудобства, связанные с использованием данной таблицы, или ей подобных, которые можно найти в разделе «Физика». |
© Школяр. Лингвистика (при поддержке «Ветвистого древа») 2009—2016
Движение по окружности, угловая скорость, частота, период, центростремительное ускорение. Формулы, определения, пояснения
Тестирование онлайн
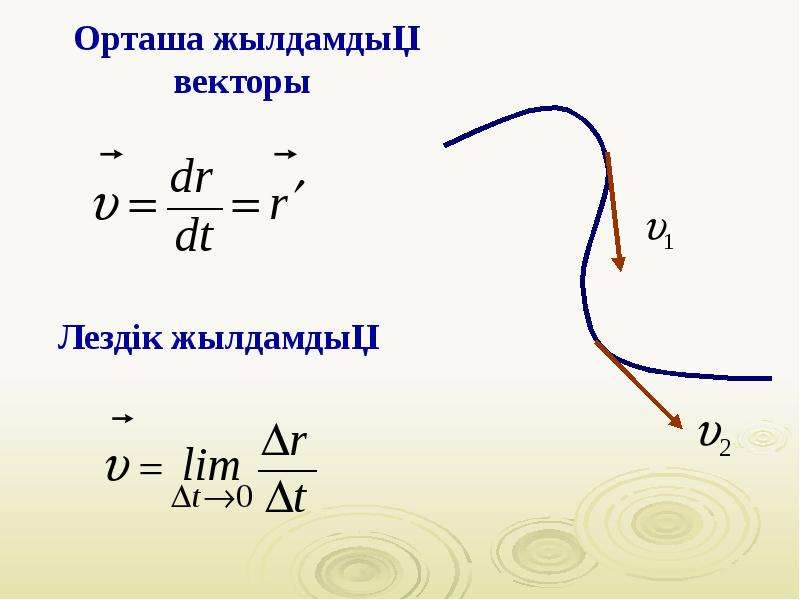
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
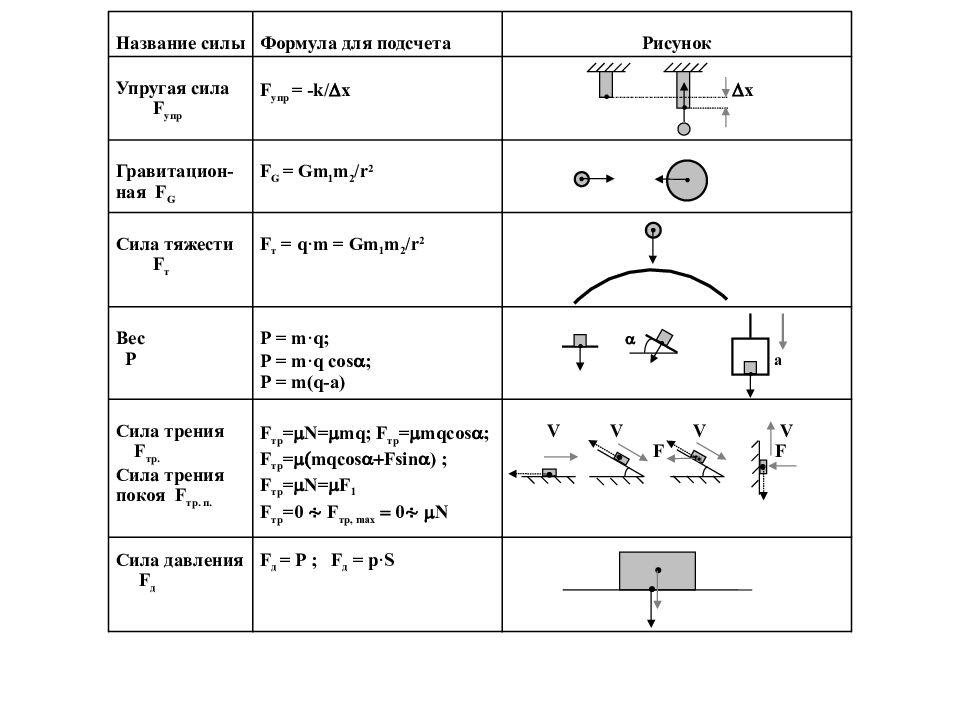
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
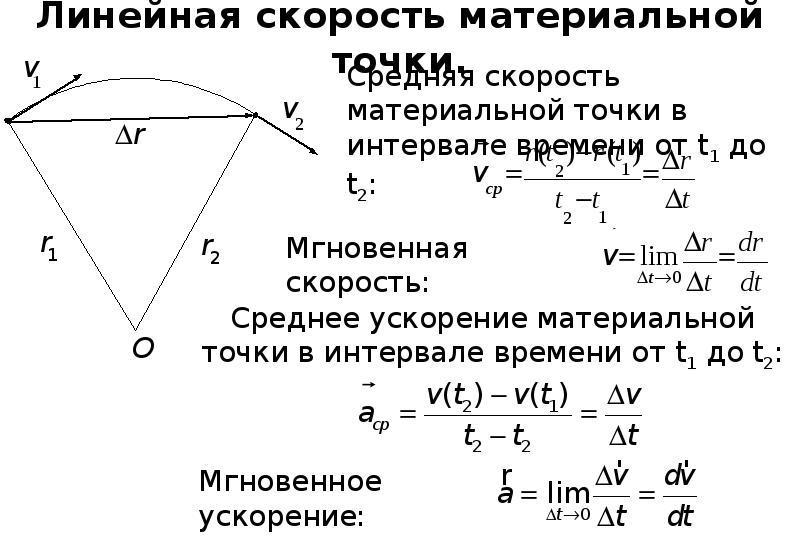
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению.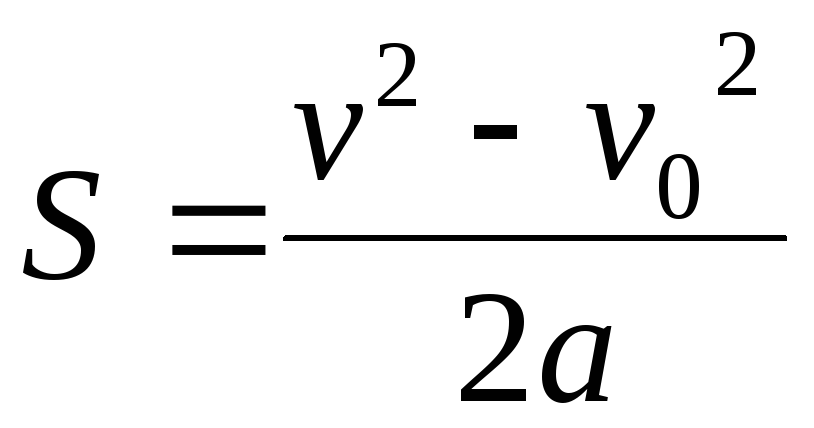 Центростремительное ускорение точки направлено по радиусу к центру окружности.
Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
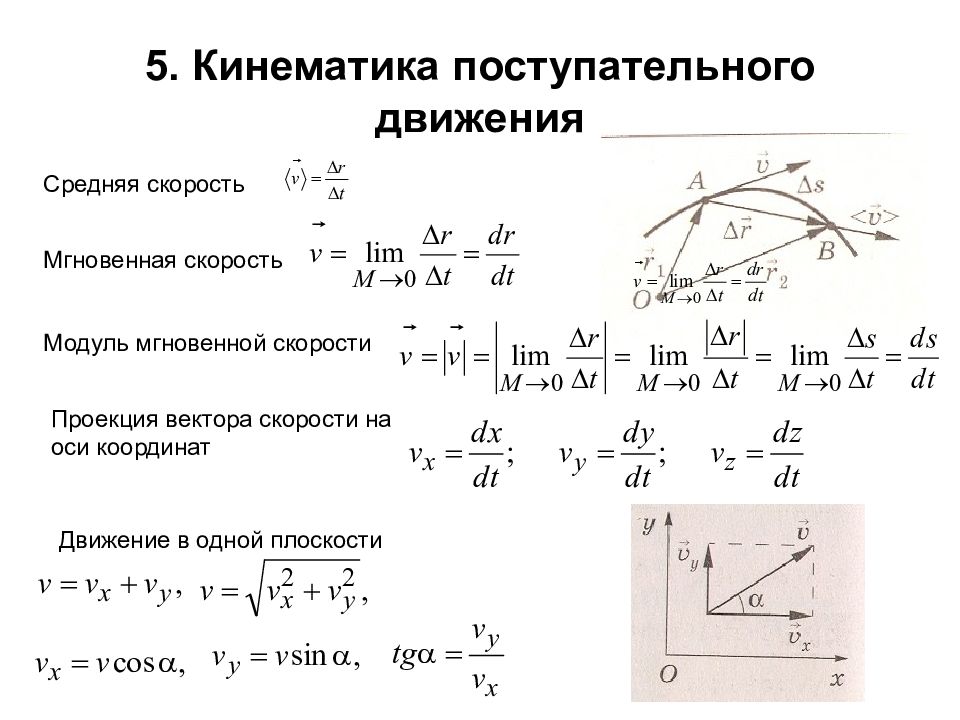
Мгновенная скорость определяется по формуле
Урок 2. равномерное прямолинейное движение материальной точки — Физика — 10 класс
Физика, 10 класс
Урок 2. Равномерное прямолинейное движение материальной точки
Перечень вопросов, рассматриваемых в теме: 1) основная задача механики; 2) относительность механического движения; 3) система отсчёта, материальная точка, перемещение, траектория, скорость; 4) кинематическое уравнение.
Глоссарий по теме:
Раздел механики, в котором изучается движение тел без выяснения причин, вызывающих данное движение, называют кинематикой.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени.
Материальной точкой называют тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь. Тело, относительно которого рассматривается движение, называется телом отсчета. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Траектория — линия, по которой движется точка в пространстве.
Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путем, пройденным за этот промежуток времени.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения.
Скорость равномерного прямолинейного движения точки – величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016.– С.10-30.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.
Открытые электронные ресурсы по теме урока:
http://kvant.mccme.ru/1974/12/byvaet_li_ravnomernoe_dvizheni.htm.
Теоретический материал для самостоятельного изучения
Основная задача классической механики — определить положение тела в пространстве в любой момент времени. По характеру решаемых задач классическую механику делят на кинематику, динамику и статику. В кинематике описывают движение тел без выяснения причин, вызывающих данное движение. Раздел механики, в котором изучаются причины движения, называют динамикой. Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел. Законы сохранения импульса и энергии являются следствиями законов Ньютонов.
Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел. Законы сохранения импульса и энергии являются следствиями законов Ньютонов.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени. Сформулируем закон относительности движения: характер движения тела зависит от того, относительно каких тел мы рассматриваем движение. Нет абсолютно неподвижных тел.
Рассмотрим самое простое движение – прямолинейное равномерное движение. Описать движение тела – это значит, указать способ определения его положения в пространстве в любой момент времени.
Для описания движения нужно ввести некоторые понятия: материальная точка, траектория, путь, перемещение, координата, момент времени, промежуток времени, скорость. Материальной точкой называют тело, размерами которого в условиях рассматриваемой задачи можно пренебречь. Это первая физическая модель реальных тел. Практически всякое тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные её суточным вращением, не влияют на величины, описывающие годовое движение. Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.
Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные её суточным вращением, не влияют на величины, описывающие годовое движение. Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.
Тело, движущееся поступательно, можно принимать за материальную точку даже в том случае, если его размеры соизмеримы с проходимыми им расстояниями. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе.
Что нужно знать для того, чтобы в любой момент времени указать положение тела? Надо, во-первых, знать, где оно было в начальный момент времени; во-вторых, каков вектор перемещения в любой момент времени. Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение рассматривается. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение рассматривается. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Рассмотрим два наиболее часто применяемых способа описания движения тел: координатный и векторный. В координатном способе положение тела в пространстве задается координатами, которые с течением времени меняются.
Рассмотрим движение материальной точки М с координатами (х, y, z) в момент времени t.
Математически это принято записывать в виде:
Количество координат зависит от условия задачи: на прямой – одна, в плоскости – две, в пространстве – три.
В векторном способе используется радиус-вектор. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку. Закон (или уравнение) движения в векторной форме — зависимость радиуса-вектора от времени:
Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку. Закон (или уравнение) движения в векторной форме — зависимость радиуса-вектора от времени:
Итак, для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех трех ее координат от времени, либо зависимость от времени радиус-вектора этой точки.
Три скалярных уравнения или эквивалентное им одно векторное уравнение называются кинематическими уравнениями движения материальной точки.
Двигаясь, материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом она «описывает» в пространстве какую-то линию. Линия, по которой движется точка в пространстве, называется траекторией. По форме траектории все движения делятся на прямолинейные и криволинейные. Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки траектории. Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путём, пройденным за этот промежуток времени, его обозначают буквой S. Путь – скалярная величина.
Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путём, пройденным за этот промежуток времени, его обозначают буквой S. Путь – скалярная величина.
Для описания движения тела нужно указать, как меняется положение точек с течением времени. Если участки криволинейные, то изменение координат тела описывают с помощью такого понятия как перемещение. Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением. Обозначается на чертежах как направленный отрезок, соединяющий начальное и конечное положение тела в пространстве:
Путь и модуль перемещения могут совпадать по значению, только в том случае, если тело движется вдоль одной прямой в одном направлении.
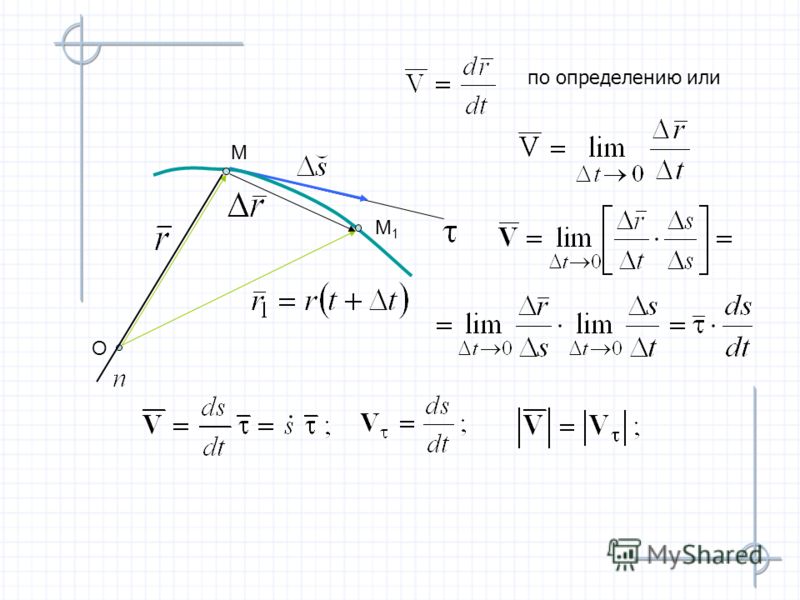
Важной величиной, характеризующей движение тела, является его скорость. Скорость – векторная величина. Она считается заданной, если известен ее модуль и направление. Скорость равномерного прямолинейного движения точки – векторная величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло. Пусть радиус-вектор задает положение точки в начальный момент времени t0, а радиус-вектор- в момент времени t. Тогда промежуток времени:
Пусть радиус-вектор задает положение точки в начальный момент времени t0, а радиус-вектор- в момент времени t. Тогда промежуток времени:
,
и перемещение:
.
Подставляя выражение для скорости, получим:
Если начальный момент времени t0 принять равным нулю, то скорость равна:
Выразим отсюда радиус-вектор :
Это и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:
х=х0+vхt.
Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х0.
Путь S, пройденный точкой при движении вдоль оси ОХ, равен модулю изменения ее координаты:
Его можно найти, зная модуль скорости
Строго говоря, равномерного прямолинейного движения не существует. Но приближенно на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.
Полученные результаты можно изобразить наглядно с помощью графиков. Для прямолинейного равномерного движения график зависимости проекции скорости от времени очень прост. Это прямая, параллельная оси времени.
Как мы уже знаем, зависимость координаты тела от времени описывается формулой х=х0+𝞾хt. График движения представляет собой прямую линию:
Из второго рисунка видим, что углы наклона прямых разные. Угол наклона второй прямой больше угол наклона первой прямой , т. е за одно и тоже время тело, движущееся со скоростью , проходит большее расстояние, чем при движении со скоростью А значит А что же в случае 3, когда угол α < 0? В случае 3 тело движется в сторону, противоположную оси ОХ. Проекция скорости в случае 3 имеет отрицательное значение и график проходит ниже оси ОХ. Проекция скорости определяет угол наклона прямой х(t) к оси t и численно равна тангенсу угла
е за одно и тоже время тело, движущееся со скоростью , проходит большее расстояние, чем при движении со скоростью А значит А что же в случае 3, когда угол α < 0? В случае 3 тело движется в сторону, противоположную оси ОХ. Проекция скорости в случае 3 имеет отрицательное значение и график проходит ниже оси ОХ. Проекция скорости определяет угол наклона прямой х(t) к оси t и численно равна тангенсу угла
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта. В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
Примеры и разбор решения заданий
1. Тело движется равномерно и прямолинейно в положительном направлении оси ОХ. Координата тела в начальный момент времени равна xо = -10м. Найдите координату тела через 5с, если модуль её скорости равен ʋ=2 м/с. Какой путь проделало тело за это время?
Дано: xо = — 10 м, t = 5 c, ʋ = 2 м/с. Найти s, х.
Найти s, х.
Решение: координату точки найдем по формуле:
х = х0 + 𝞾х t
Так как направление вектора скорости совпадает с направлением оси координат, проекция вектора скорости положительна и равна ʋx=ʋ; тогда вычисляем:
х = — 10 + 2· 5 = 0 (м).
Пройденный путь найдем s = ʋ t; s = 2·5 = 10 м.
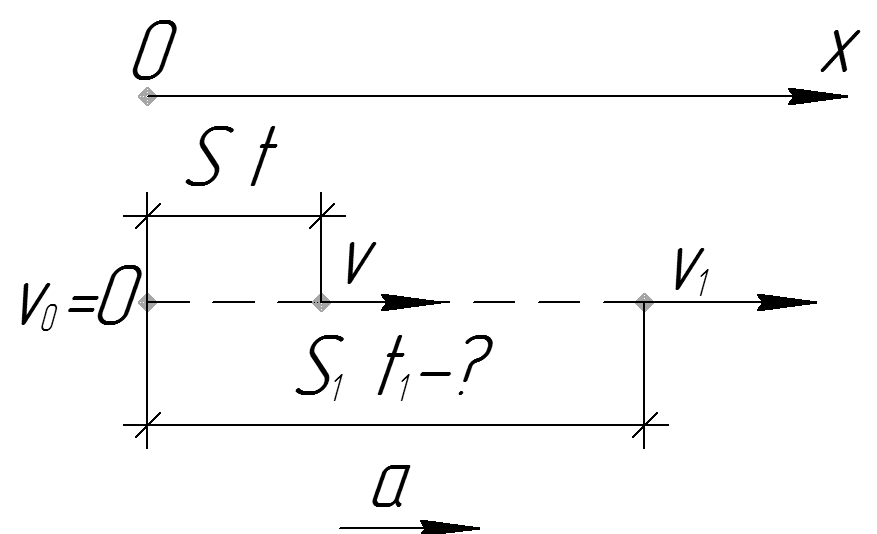
2. Равномерно друг за другом движутся два поезда. Скорость первого равна 72 км/ч, а скорость второго — 54 км/ч. Определите скорость первого поезда относительно второго.
Дано:
Найти .
Решение: Из условия задачи ясно, что векторы скоростей поездов направлены в одну сторону. По закону сложения скоростей запишем:
,
где — искомая величина.
Находим проекцию скоростей на ось ОХ и записываем, чему равен модуль искомой величины
Ответ: .
Глава 7. Вращательное движение. Кинематика и динамика
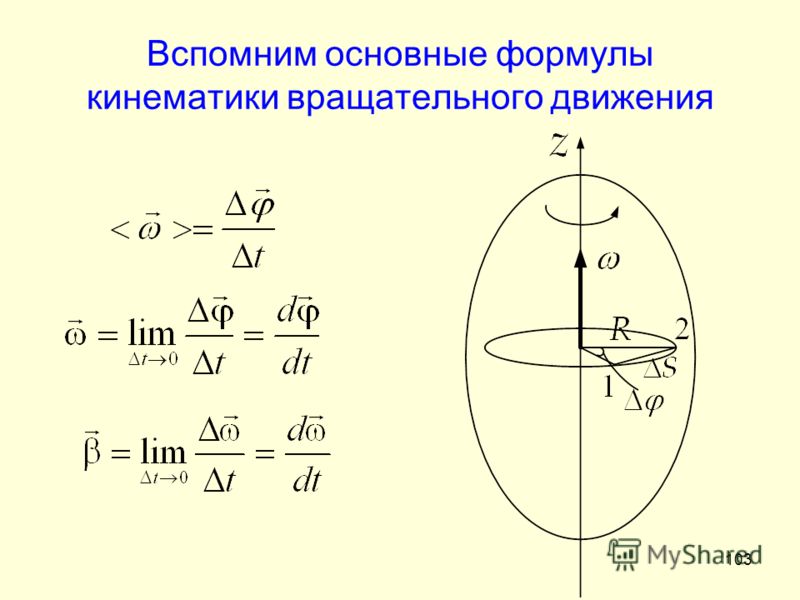
Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
(7.1) |
В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения
(7. |
Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.
Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим
(7.3) |
Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.
Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2. 1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
(7.4) |
Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах
(7.5) |
Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
(7. |
Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.
Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.
Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
Для нахождения линейной скорости конца секундной стрелки часов (задача 7. 1.2) используем связь угловой и линейной скоростей (7.5). Имеем
1.2) используем связь угловой и линейной скоростей (7.5). Имеем
(правильный ответ – 2).
Применяя определение угловой скорости к колесу (задача 7.1.3), получаем
(правильный ответ 1).
Из формулы (7.2) имеем
(задача 7.1.4 – правильный ответ 4).
Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска
А теперь по формуле (7.5) для второй точки получаем
(ответ 2).
Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).
Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно
(ответ 4).
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).
Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).
Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1
(ответ 1).
Для сравнения центростремительных ускорений материальных точек в задаче 7.2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
(ответ 3).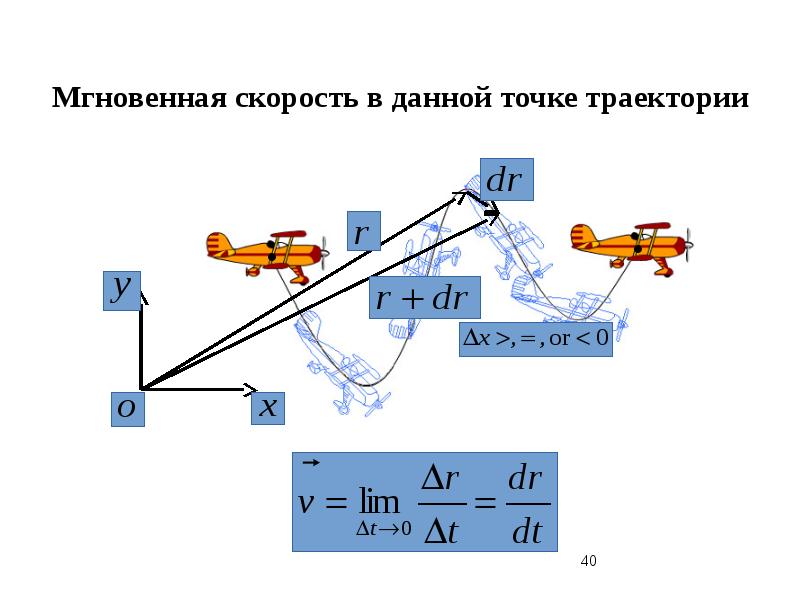
Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим
(7.5) |
Поэтому
(ответ 1).
Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)
где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем
(ответ 2).
Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7. 2.5), центростремительное ускорение сообщается силой трения
2.5), центростремительное ускорение сообщается силой трения
Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
(ответ 4).
В задаче 7.2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
(ответ 3).
В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает
(1) |
На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем
Подставляя в эту формулу силу из формулы (1), находим (ответ 2).
В задаче 7.2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
(ответ 3).
Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):
где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
(задача 7.2.9 – ответ 1).
Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7. 2.10 – ответ 2).
2.10 – ответ 2).
Равноускоренное движение: формулы, примеры
Равноускоренное движение
Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение — частный случай равноускоренного движения с ускорением, равным нулю.
Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.
В любой точке траектории на тело действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону.
Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.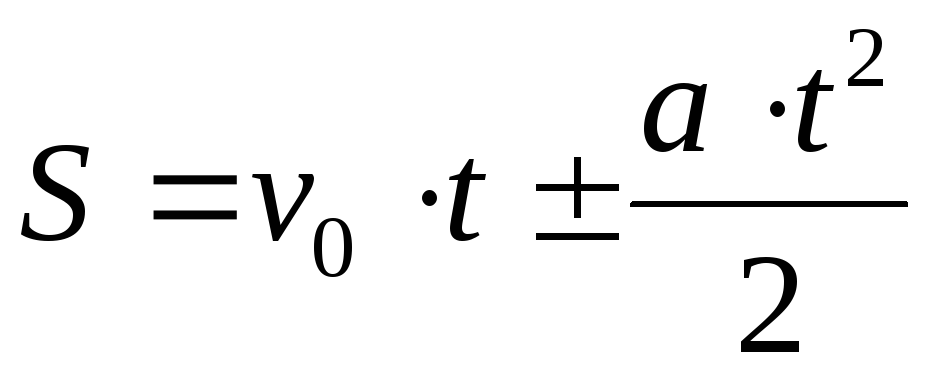
Формулы для равноускоренного движения
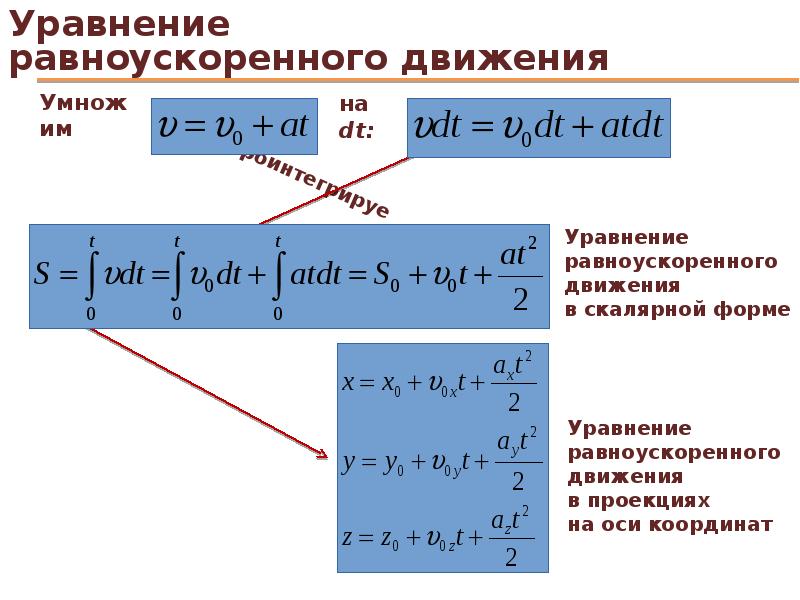
Формула для скорости при равноускоренном движении:
v=v0+at.
Здесь v0 — начальная скорость тела, a=const — ускорение.
Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии.
Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.
a=v-v0t=BCAC
Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.
Для первого графика: v0=-2 мс; a=0,5 мс2.
Для второго графика: v0=3 мс; a=-13 мс2.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
По данному графику можно также вычислить перемещение тела за время t. Как это сделать?
Выделим на графике малый отрезок времени ∆t. Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t. Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.
Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.
Разобьем все время t на бесконечно малые промежутки ∆t. Перемещение s за время t равно площади трапеции ODEF.
s=OD+EF2OF=v0+v2t=2v0+(v-v0)2t.
Мы знаем, что v-v0=at, поэтому окончательная формула для перемещения тела примет вид:
s=v0t+at22
Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.
Закон равноускоренного движения
Закон равноускоренного движения
Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения — нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.
Исключая из записанных выше уравнений t и решая их, получаем:
s=v2-v022a.
По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:
v=v02+2as.
При v0=0 s=v22a и v=2as
Важно!
Величины v, v0, a, y0, s, входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.
формулы, определения, методы решения задач
Кинематика — это специальный раздел теоретической механики. Направление сформировалось несколько позднее, чем статика и динамика: во второй половине XIX столетия. Первые исследования в области кинематики были посвящены огнестрельному оружию. Ученые стремились понять процесс полета снаряда, производили расчет траектории его движения. В дальнейшем кинематика как научное направление получило широкое распространение и существенно повлияло на развитие технического прогресса.
Кинематика — описание
Кинематика является разделом механики, цель которого — изучение механического движения тел с пренебрежением к причинам, вызывающим это движение.
Механика представляет собой научную область физики, которой посвящены исследования механического движения тел. Основной целью данного направления служит определение точного положения тела в пространстве в любой момент времени. Важным понятием этого раздела является материальная точка в виде тела с определенной массой и размерами, которыми можно пренебречь для решения задачи при наличии следующих условий:
- Путь, который преодолевает тело, существенно больше, чем его размеры.
- Расстояние между телами значительно превышает их размеры.
- Объект совершает поступательное движение.
Движение тела рассматривают в системе отсчета, состоящей из системы координат и прибора, измеряющего время. Траекторией называют линию, которую объект описывает, совершая движение. Путь является скалярной величиной, определяемой как длина траектории. Перемещением обозначают вектор, который соединяет начальное и конечное положение тела, преодолеваемое им в течение определенного промежутка времени.
Совершая движение, тело может только увеличивать пройденный путь, при этом перемещение увеличивается или уменьшается. К примеру, уменьшение перемещения наблюдается во время обратного движения тела. Если объект движется прямолинейно в одном направлении, то путь определяется модулем перемещения. В случае криволинейного движения — путь превышает перемещение. При рассмотрении замкнутой траектории перемещение будет равно нулю.
Теория и формулы
Благодаря многолетним исследованиям в области кинематики ученым удалось вывести определенные закономерности движения тела. С помощью справедливых уравнений представляется возможным ответить на многие вопросы о разных характеристиках, которые изменяются либо остаются постоянными во время движения объектов.
Путь, время, скорость
Расстояние представляет собой удаленность одной точки положения тела от другой. Тело преодолевает путь, который представляет собой важную характеристику механического движения. Общепринятым обозначением пути является латинская буква s. Данный параметр измеряют метрами и километрами, если речь идет о больших расстояниях.
Тело преодолевает путь, который представляет собой важную характеристику механического движения. Общепринятым обозначением пути является латинская буква s. Данный параметр измеряют метрами и километрами, если речь идет о больших расстояниях.
Скорость представляет собой путь, который тело преодолело в течение единицы времени. В качестве единицы времени часто используют 1 час, 1 минуту, 1 секунду. Для расчета скорости необходимо определить отношение пути к времени движения. В случае, когда в условиях задачи расстояние измеряется в метрах, а время пути — в секундах, то скорость следует рассчитывать в метрах в секунду (м/с). Для обозначения скорости используют латинскую букву \(v\).
Нередко требуется определить время пути. Данный параметр обозначают с помощью латинской буквы \(t\).
Важно отметить, что скорость, путь и время взаимосвязаны. При известных характеристиках скорости и времени можно определить расстояние, которое преодолело тело. Путь в данном случае равен произведению скорости и времени, рассчитывается по формуле:
\(s=v\times t\)
При известных величинах времени и расстояния достаточно просто определить скорость движения тела, руководствуясь следующим уравнением:
\(v=\frac{s}{t}\)
Равномерное движение
Равномерным движением называют движение тела, которое совершает равные перемещения в течение любых равных промежутков времени.
Источник: goodfon.ru
Скорость при равномерном движении определяется как отношение перемещения ко времени, в течение которого данное перемещение было совершено. Уравнение имеет следующий вид:
\(\vec{v}=\frac{\vec{s}}{t}\)
\(\vec{v}=const\)
Проекция вектора скорости на ось ОХ выглядит таким образом:
\(v_{x}=\frac{s_{x}}{t}\)
\(v_{x}=const\)
Если вектор скорости спроецировать на ось координат, то она будет равна быстроте изменения данной координаты:
\(v_{x}=\frac{x-x_{0}}{t}\)
Прямолинейное равноускоренное движение
Прямолинейным равноускоренным движением называют движение по прямой траектории, для которого характерно постоянное ускорение.
Ускорение для прямолинейного равноускоренного движения обозначают следующим образом:
\(\vec{a}=const\)
При таком движении можно наблюдать увеличение или уменьшение скорости. Чтобы определить скорость, необходимо выполнить следующий расчет:
\(\vec{v}=\vec{v}_{0}+\vec{a}t\)
Если тело разгоняется в проекции оси ОХ, то скорость можно определить по формуле:
\(v_{x}=v_{0x}+a_{x}t\)
a>0, движение является равноускоренным.
Источник: fizi4ka.ru
Во время торможения в проекции на ось ОХ скорость рассчитывают следующим образом:
\(v_{x}=v_{0x}-a_{x}t\)
а<0, движение является равнозамедленным.
Источник: fizi4ka.ru
Графически зависимость ускорения от времени, то есть график ускорения во время равноускоренного движения тела, можно представить в виде:
Источник: fizi4ka.ru
График ускорения, характеризующий равноускоренное движение тела, представляет собой прямую, которая параллельна оси времени:
- график 1 находится над осью t, тело совершает разгон, ах>0;
- график 2 размещен под осью t, тело тормозит, ах<0.
Графически скорость или проекция скорости изображается в виде зависимости скорости от времени:
Источник: fizi4ka.ru
Графически скорость, характерная для равноускоренного движения тела, имеет вид прямой. График 1 направлен вверх, тело будет совершать равноускоренное движение в положительном направлении оси ОХ:
\(v_{0x}>0\)
\(a_x>0\)
\(a_{1x} = tg α \)
График 2 направлен вниз, тело будет двигаться равнозамедленно в положительном направлении оси ОХ:
\(v_{0x}>0\)
\(a_x<0\)
\(a_{2x} = tg α \)
График 3 направлен вниз, тело свершает равноускоренное движение против оси ОХ:
\(v_{0x}<0\)
\(a_x<0\)
Исходя из графика зависимости скорости от времени, определяют перемещение, которое тело преодолело в течение определенного промежутка времени \(t_2-t_1\). {2}}{-2g}\)
{2}}{-2g}\)
В максимальной верхней точке тело, брошенное вверх, будет обладать нулевой скоростью, \(v=0\). Для расчета времени подъема можно воспользоваться формулой:
\(t=\frac{v_{0}}{g}\)
Свободно падающее тело
Свободным падением называют движение тела в условиях безвоздушного пространства под действием силы тяжести.
В условиях свободного падения ускорения тел с разной массой будут равны. Данный параметр называют ускорением свободного падения. Оно всегда направлено к центру нашей планеты, то есть вертикально вниз. Величина обозначается латинской буквой g, а единицами измерения являются м/с2.
Ускорение свободного падения равно 9,8 м/с2. В задачах по физике допускается использовать значение g=10 м/с2.
Движение по окружности с постоянной по модулю скоростью
Движением по окружности при постоянной по модулю скоростью называют простейшим видом криволинейного движения. {-1}\) (Гц).
{-1}\) (Гц).
\(\nu=\frac{N}{t}\)
Период и частота являются взаимно обратными величинами:
\(T=\frac{1}{\nu}\)
\(\nu =\frac{1}{T}\)
Линейная скорость представляет собой скорость движения тела по окружности. Параметр обозначают латинской буквой v, единицами измерения являются м/с. Линейная скорость направлена по касательной к окружности и рассчитывается по формуле:
\(v=\frac{2\pi \times R}{T}\)
\(R\) является радиусом окружности.
Угловой скоростью называют физическую величину, которая определяется как отношение угла поворота и времени, за которое тело совершает этот поворот. Обозначают параметр как ω. Единицами измерения угловой скорости являются рад/с. Угловая скорость определяется по формуле:
\(\omega =\frac{\varphi }{t}\)
\(\varphi\) представляет собой угол поворота.
Источник: fizi4ka.ru
Направление угловой скорости определяют с помощью правила правого винта или буравчика. В случае, когда вращательное движение винта соотносится с направлением движения тела по окружности, то поступательное движение винта и направление угловой скорости совпадают. {2}R\)
{2}R\)
\(\omega = \frac{2\pi }{T}\)
\(\omega = 2\pi v\)
Во время равномерного движения тела по окружности точки, расположенные на радиусе, перемещаются с равной угловой скоростью, так как радиус за одно и то же время поворачивается на одинаковый угол. В это время линейная скорость разных точек радиуса отличается в зависимости от того, насколько близко или далеко от центра они размещены:
\(v_{1}=\omega r\)
\(v_{2}=\omega R\)
\(\frac{v_{1}}{v_{2}}=\frac{r}{R}\)
Источник: fizi4ka.ru
При рассмотрении равномерного движения двух соединенных тел можно наблюдать отсутствие отличий в линейных скоростях, но при этом угловые скорости тел будут различны в зависимости от радиуса тела:
\(\omega _{1}=\frac{v}{R_{1}}\)
\(\omega _{2}=\frac{v}{R_{2}}\)
\(\frac{\omega _{1}}{\omega _{2}}=\frac{R_{1}}{R_{2}}\)
Источник: fizi4ka.ru
Движение тела, брошенного под углом к горизонту
Движение тела, которое бросили под углом к горизонту, можно представить в виде суперпозиции двух движений:
- Равномерного горизонтального перемещения.
 {2}}\)
{2}}\)Дальность полета тела соответствует уравнению:
\(l=v_{0x}t=v_{0x}\sqrt{\frac{2h_{0}}{g}}\)
Вычислить угол между вектором скорости и осью ОХ можно с помощью формулы:
\(\tan \beta =\frac{v_{y}}{v_{x}}=\frac{-gt}{v_{0x}}\)
Задачи по кинематике, их решение
Задача 1
Рассмотрим путь велосипедиста из одного населенного пункта в другой. Половина расстояния была преодолена со скоростью 12 км/ч (\(v_1\)). Далее половину оставшегося времени он ехал со скоростью 6 км/ч (\(v_2\)). Остаток расстояния путник преодолел пешком со скоростью 4км/ч (\(v_3\)). Необходимо рассчитать среднюю скорость на всем пути следования велосипедиста.
Решение
Данный пример относится к теме равномерного прямолинейного движения одного тела. Процесс можно изобразить схематично:
Источник: pandia.ru\(S = S_1 + S_2 + S_3\)
\(t = t_1 + t_2 + t_3\)
На каждый отрезок пути необходимо составить уравнение движения:
\(S_1 = v_1t_1\)
\(S_2 = v_2t_2\)
\(S_3 = v_3t_3\)
Далее можно представить дополнительные условия задачи:
\(S_1 = S_2 + S_3\)
\(t_2 = t_3\)
\(v_{sr}=\frac{S}{t}=\frac{S_{1}+S_{2}+S_{3}}{t_{1}+t_{2}+t_{3}}\)
Следует преобразить формулу и подставить числовые значения:
\(v_{sr}=\frac{2S_{1}}{\frac{S_{1}}{v_{1}}+\frac{2S_{1}}{v_{2}+v_{3}}}=\frac{2v_{1}\left(v_{2}+v_{3} \right)}{2v_{1}+v_{2}+v_{3}}\)
\(v_{sr}=\frac{2\times 12\left(6+4 \right)}{2\times 12+6+4}=7\)
Ответ: средняя скорость составляет \(7\) км/ч.
 {2}}=\frac{9,81}{0,17}=57,7\)
{2}}=\frac{9,81}{0,17}=57,7\)Ответ: камень упал с высоты \(57,7\) м.
Решение задач по кинематике основано на простых формулах. Успешность результата зависит от умения грамотно применять справедливые уравнения в том или ином случае. Бывают ситуации, когда в процессе изучения физики возникают некоторые трудности. Простым решением будет обратиться к порталу Феникс.Хелп.
Формула скорости свободного падения в физике
Задание. Одно тело бросили вертикально вверх с начальной скоростью равной $v_0.$ В этот же момент времени вертикально вниз с начальной скоростью $v_0$ бросили второе тело. Высота, с которой бросили это тело равно высоте максимального подъема первого тела. Какова скорость первого и второго тел в момент встречи этих двух тел? Тела считайте материальными точками, сопротивление воздуха не учитывать.
Решение. Сделаем рисунок.
За основу решения задачи примем уравнение для скорости движения тела в поле тяжести Земли:
\[\overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t\ \left(2.
 2_0}{2g}=v_0+\frac{v_0}{4}=\frac{5}{4}v_0.\]
2_0}{2g}=v_0+\frac{v_0}{4}=\frac{5}{4}v_0.\]Ответ. $v_1=\frac{3}{4}v_0,$ $v_2=\frac{5}{4}v_0$
Уравнения движения — Практика — Физика Гипертекст
Автомобилю с начальной скоростью 60 миль в час нужно 144 фута, чтобы полностью остановиться. Определите тормозной путь этой же машины с начальной скоростью…
- 30 миль / ч
- 20 миль / ч
- 10 миль / ч
Примечание: скорость изменения скорости не зависит от начальной скорости в этой задаче. Быстрые и медленные машины замедляются с одинаковой скоростью.
Первый способ.
Трудный способ решить эту проблему — сделать это так, как многие студенты считают легким: «набираю, отвечаю» или «включай и пей».Этот метод кажется простым, поскольку не требует особых размышлений, но оказывается довольно сложным.
Сначала конвертируем в единицы СИ.
60 миль 1609 кв.м 1 час = 26,8 м / с 1 час 1 миля 3600 с 30 миль 1609 кв. 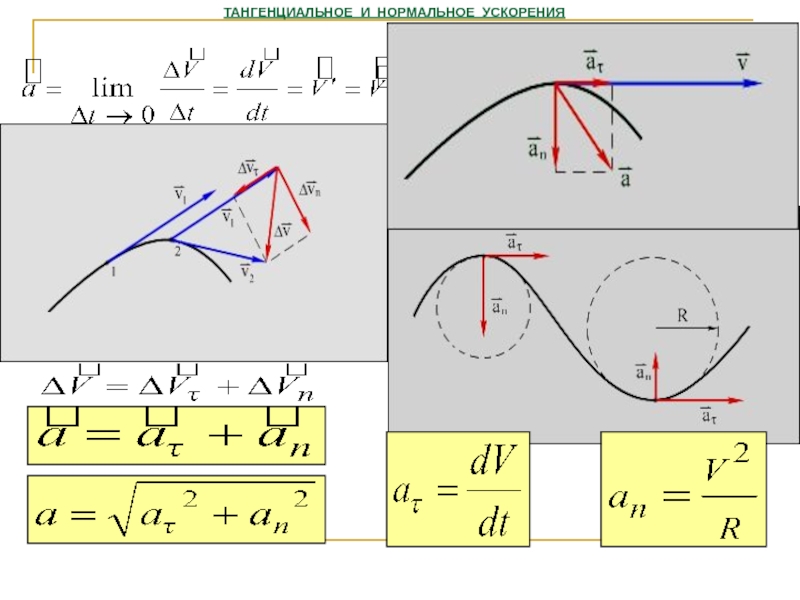 м
м1 час = 13.4 м / с 1 час 1 миля 3600 с 20 миль 1609 кв.м 1 час = 8,94 м / с 1 час 1 миля 3600 с 10 миль 1609 кв.м 1 час = 4,47 м / с 1 час 1 миля 3600 с 144 футов 1 миля 1609 кв.м = 43.9 м 1 5280 футов 1 миля Затем рассчитайте замедление от 60 миль в час.

v 0 = 26,8 м / с v = 0 м / с ∆ с = 43,9 м a = ? v 2 = v 0 2 + 2 a ∆ s a = a = — (26.8 м / с) 2 2 (43,9 м) a = −8,18 м / с 2 Затем используйте это число для расчета расстояний для других скоростей.
v 2 = v 0 2 + 2 a ∆ s
Удалите нулевой член и найдите смещение.
Входные номера. Выходы.
∆ с = — (13,4 м / с) 2 = 11,0 м 2 (−8,18 м / с 2 ) ∆ с = — (8,94 м / с) 2 = 4,89 м 2 (−8,18 м / с 2 ) ∆ с = — (4,47 м / с) 2 = 1.22 м 2 (−8,18 м / с 2 ) И, наконец, конвертируем обратно в английские единицы.
11,0 м 1 миля 5280 футов = 36 футов 1 1609 кв.  м
м1 миля 4,89 м 1 миля 5280 футов = 16 футов 1 1609 кв.м 1 миля 1.22 м 1 миля 5280 футов = 04 фута 1 1609 кв.м 1 миля Второй способ.
Стандартные методы решения проблем работают, но они — огромная трата времени на решение этой проблемы. Любая небольшая ошибка уничтожит ответы и приведет к потере личной умственной энергии, чего мы все хотели бы избежать. Простой способ решить эту проблему не требует каких-либо уловок.Это требует, чтобы вы определили и поняли ключевые концепции, необходимые для решения проблемы. В середине массы уравнений было сделано важное предположение.
 Предполагалось, что тормозное ускорение автомобиля останется постоянным для всех начальных скоростей. Эта проблема состоит в том, чтобы определить взаимосвязь между смещением и скоростью. Уравнение, которое делает это, выглядит так:
Предполагалось, что тормозное ускорение автомобиля останется постоянным для всех начальных скоростей. Эта проблема состоит в том, чтобы определить взаимосвязь между смещением и скоростью. Уравнение, которое делает это, выглядит так:v 2 = v 0 2 + 2 a ∆ s
, который показывает, что смещение пропорционально квадрату скорости (когда ускорение постоянное и либо начальная, либо конечная скорость равна нулю).
∆ с ∝ v 2
В этой задаче мы сравниваем тормозной путь на скорости 30, 20 и 10 миль в час с тормозным путем на скорости 60 миль в час. Квадрат отношения новой скорости к исходной скорости будет отношением нового тормозного пути к исходному тормозному пути.
v 2 ∝ ∆ с ⎛
⎜
⎝30 миль / ч ⎞ 2 ⎠
= ⎛ 90 488 ⎜ 90 488 1 ⎞ 2 ⎠
= 1 = 36 футов 60 миль / ч 2 4 144 футов ⎛
⎜
⎝20 миль / ч ⎞ 2 ⎠
= ⎛ 90 488 ⎜ 90 488 1 ⎞ 2 ⎠
= 1 = 16 футов 60 миль / ч 3 9 144 футов ⎛
⎜
⎝10 миль / ч ⎞ 2 ⎠
= ⎛ 90 488 ⎜ 90 488 1 ⎞ 2 ⎠
= 1 = 04 фута 60 миль / ч 6 36 144 футов Это те же ответы, которые мы получили, используя метод «подключи и давай».
Поезд метро на 10 вагонов сидит на станции. Крейсерская скорость достигается после разгона 0,75 м / с 2 на расстояние, эквивалентное длине станции (184 м). Затем он с постоянной скоростью движется к следующей станции в 18 кварталах (1425 м).
- Определите крейсерскую скорость поезда.
- Определите время, которое потребовалось поезду, чтобы разогнаться от состояния покоя до крейсерской скорости.
- Сколько времени нужно поезду, чтобы проехать 18 кварталов до следующей станции?
Машинист останавливает поезд на второй станции на половине расстояния, которое потребовалось для его запуска на первой станции.
- Какое замедление поезда на второй станции?
Free Fall — The Physics Hypertextbook
Обсуждение
ускорение свободного падения
Хотите, чтобы объект ускорялся?
- Поднимите что-нибудь рукой и уроните. Когда вы отпускаете его из руки, его скорость равна нулю.
 По мере спуска его скорость увеличивается. Чем дольше он падает, тем быстрее движется. Для меня это звучит как ускорение.
По мере спуска его скорость увеличивается. Чем дольше он падает, тем быстрее движется. Для меня это звучит как ускорение. - Но ускорение — это больше, чем просто увеличение скорости.Поднимите тот же предмет и подбросьте его вертикально в воздух. По мере подъема его скорость будет уменьшаться, пока он не остановится и не изменит направление движения. Уменьшение скорости также считается ускорением.
- Но ускорение — это больше, чем просто изменение скорости. Поднимите свой разбитый предмет и запустите его в последний раз. На этот раз бросьте его горизонтально и обратите внимание, как его горизонтальная скорость постепенно становится все более и более вертикальной. Поскольку ускорение — это скорость изменения скорости со временем, а скорость — векторная величина, это изменение направления также считается ускорением.
В каждом из этих примеров ускорение было результатом силы тяжести. Ваш объект ускорялся, потому что гравитация тянула его вниз. Даже подброшенный предмет падает — и он начинает падать в ту же минуту, когда вылетает из вашей руки.
 Если бы это было не так, он бы продолжал удаляться от вас по прямой. Это ускорение под действием силы тяжести .
Если бы это было не так, он бы продолжал удаляться от вас по прямой. Это ускорение под действием силы тяжести .Какие факторы влияют на ускорение свободного падения? Если бы вы спросили об этом обычного человека, он, скорее всего, сказал бы «вес», имея в виду на самом деле «массу» (подробнее об этом позже).То есть тяжелые предметы падают быстро, а легкие — медленно. Хотя это может показаться правдой на первый взгляд, это не отвечает на мой первоначальный вопрос. «Какие факторы влияют на ускорение под действием силы тяжести ?» Масса никак не влияет на ускорение свободного падения. Эти две величины не зависят друг от друга. Легкие объекты ускоряются медленнее, чем тяжелые, только когда действуют силы, отличные от силы тяжести. Когда это происходит, объект может падать, но не в свободном падении. Свободное падение происходит всякий раз, когда на объект действует только сила тяжести.
Попробуйте этот эксперимент.
- Возьмите лист бумаги и карандаш.
 Держите их на одинаковой высоте над ровной поверхностью и одновременно роняйте. Ускорение карандаша заметно больше, чем ускорение листа бумаги, который колеблется и дрейфует на своем пути вниз.
Держите их на одинаковой высоте над ровной поверхностью и одновременно роняйте. Ускорение карандаша заметно больше, чем ускорение листа бумаги, который колеблется и дрейфует на своем пути вниз.
Здесь что-то еще мешает — и это сопротивление воздуха (также известное как аэродинамическое сопротивление).Если бы мы могли как-то уменьшить это сопротивление, у нас был бы настоящий эксперимент. Без проблем.
- Повторите эксперимент, но перед тем, как начать, скатайте лист бумаги как можно более плотным клубком. Теперь, когда бумага и карандаш отпущены, должно быть очевидно, что их ускорения идентичны (или, по крайней мере, более похожи, чем раньше).
Мы приближаемся к сути проблемы. Если бы мы могли вообще как-то устранить сопротивление воздуха. Единственный способ сделать это — бросить предметы в вакуум.Сделать это в классе можно с помощью вакуумного насоса и герметичного столба воздуха. В таких условиях можно показать, что монета и перо ускоряются с одинаковой скоростью.
 (В былые времена в Великобритании использовалась монета, называемая гинеей, и поэтому эту демонстрацию иногда называют «гинеей и пером».) Более драматическая демонстрация была проведена на поверхности Луны, которая максимально приближена к настоящий вакуум, который люди могут испытать в ближайшее время. Астронавт Дэвид Скотт выпустил каменный молот и соколиное перо одновременно во время лунной миссии Аполлона-15 в 1971 году.В соответствии с теорией, которую я собираюсь представить, два объекта приземлились на лунную поверхность одновременно (или почти так). Только объект, находящийся в свободном падении, испытывает чистое ускорение силы тяжести.
(В былые времена в Великобритании использовалась монета, называемая гинеей, и поэтому эту демонстрацию иногда называют «гинеей и пером».) Более драматическая демонстрация была проведена на поверхности Луны, которая максимально приближена к настоящий вакуум, который люди могут испытать в ближайшее время. Астронавт Дэвид Скотт выпустил каменный молот и соколиное перо одновременно во время лунной миссии Аполлона-15 в 1971 году.В соответствии с теорией, которую я собираюсь представить, два объекта приземлились на лунную поверхность одновременно (или почти так). Только объект, находящийся в свободном падении, испытывает чистое ускорение силы тяжести.Пизанская башня
Давайте немного вернемся во времени. В западном мире до XVI века обычно предполагалось, что ускорение падающего тела будет пропорционально его массе, то есть ожидалось, что объект весом 10 кг будет ускоряться в десять раз быстрее, чем объект весом 1 кг.Древнегреческий философ Аристотель из Стагиры (384–322 до н.
 Э.) Включил это правило в, возможно, первую книгу по механике. Это было чрезвычайно популярное произведение среди академиков, и на протяжении веков оно приобрело определенную преданность, граничащую с религиозной. Только когда появился итальянский ученый Галилео Галилей (1564–1642), кто-либо подверг теории Аристотеля проверке. В отличие от всех остальных до этого момента, Галилей на самом деле пытался проверить свои теории путем экспериментов и тщательных наблюдений.Затем он объединил результаты этих экспериментов с математическим анализом в методе, который был совершенно новым в то время, но теперь общепризнан как способ достижения науки. За изобретение этого метода Галилей считается первым ученым в мире.
Э.) Включил это правило в, возможно, первую книгу по механике. Это было чрезвычайно популярное произведение среди академиков, и на протяжении веков оно приобрело определенную преданность, граничащую с религиозной. Только когда появился итальянский ученый Галилео Галилей (1564–1642), кто-либо подверг теории Аристотеля проверке. В отличие от всех остальных до этого момента, Галилей на самом деле пытался проверить свои теории путем экспериментов и тщательных наблюдений.Затем он объединил результаты этих экспериментов с математическим анализом в методе, который был совершенно новым в то время, но теперь общепризнан как способ достижения науки. За изобретение этого метода Галилей считается первым ученым в мире.В сказке, которая может быть апокрифической, Галилей (или его помощник, что более вероятно) уронил два объекта неравной массы с Пизанской башни. Вопреки учению Аристотеля, два объекта ударились о землю одновременно (или почти так).Учитывая скорость, с которой могло бы произойти такое падение, сомнительно, чтобы Галилей мог извлечь много информации из этого эксперимента.
 Большинство его наблюдений за падающими телами на самом деле были круглыми объектами, катящимися по пандусам. Это замедлило процесс до такой степени, что он смог измерить временные интервалы с помощью водяных часов и своего собственного пульса (секундомеры и фотозатворы еще не были изобретены). Он повторил это «целую сотню раз», пока не достиг «такой точности, что отклонение между двумя наблюдениями никогда не превышало одной десятой доли импульса».«
Большинство его наблюдений за падающими телами на самом деле были круглыми объектами, катящимися по пандусам. Это замедлило процесс до такой степени, что он смог измерить временные интервалы с помощью водяных часов и своего собственного пульса (секундомеры и фотозатворы еще не были изобретены). Он повторил это «целую сотню раз», пока не достиг «такой точности, что отклонение между двумя наблюдениями никогда не превышало одной десятой доли импульса».«С такими результатами можно было бы подумать, что университеты Европы удостоили бы Галилея своей высшей награды, но этого не произошло. В то время профессора были потрясены сравнительно вульгарными методами Галилея, доходившими до того, что они отказывались признать то, что каждый мог видеть собственными глазами. В шаге, который теперь любой думающий человек сочтет смешным, метод контролируемого наблюдения Галилея был признан хуже чистого разума. Представь это! Я мог бы сказать, что небо было зеленым, и если бы я представил более веский аргумент, чем кто-либо другой, это будет считаться фактом, противоречащим наблюдениям почти каждого зрячего человека на планете.
Галилей назвал свой метод «новым» и написал книгу под названием Discourses on Two New Sciences , в которой он использовал комбинацию экспериментального наблюдения и математических рассуждений для объяснения таких вещей, как одномерное движение с постоянным ускорением, ускорение свободного падения и т. Д. поведение снарядов, скорость света, природа бесконечности, физика музыки и прочность материалов. Его выводы об ускорении свободного падения были таковы…
: изменение скорости в воздухе между шарами из золота, свинца, меди, порфира и других тяжелых материалов настолько незначительно, что при падении на 100 локтей золотой шар наверняка не обогнал бы медный шар на целых четыре пальца.Наблюдая это, я пришел к выводу, что в среде, полностью лишенной сопротивления, все тела падали бы с одинаковой скоростью.
Ибо я не думаю, что никто не верит, что плавать или летать можно проще или легче, чем те, которые инстинктивно используются рыбами и птицами.
 Поэтому, когда я наблюдаю, как камень, первоначально находящийся в состоянии покоя, падает с возвышенности и постоянно набирает новые приросты скорости, почему я не могу поверить, что такое увеличение происходит чрезвычайно простым и довольно очевидным для всех образом?
Поэтому, когда я наблюдаю, как камень, первоначально находящийся в состоянии покоя, падает с возвышенности и постоянно набирает новые приросты скорости, почему я не могу поверить, что такое увеличение происходит чрезвычайно простым и довольно очевидным для всех образом?Я очень сомневаюсь, что Аристотель когда-либо проверял экспериментальным путем.
Галилео Галилей, 1638
Несмотря на эту последнюю цитату, Галилей не был застрахован от использования разума как средства для подтверждения своей гипотезы. По сути, его аргумент сводился к следующему. Представьте себе два камня, большой и маленький. Поскольку они имеют неравную массу, они будут ускоряться с разной скоростью — большая скала будет ускоряться быстрее, чем маленькая. Теперь поместите маленький камень на вершину большого камня. Что случится? По словам Аристотеля, большая скала оторвется от маленькой.Что, если мы изменим порядок и поместим маленький камень ниже большого камня? Кажется, мы должны рассуждать, что два объекта вместе должны иметь ускорение меньше .
 Маленький камень будет мешать и замедлять большой камень. Но два объекта вместе тяжелее, чем каждый сам по себе, и поэтому мы также должны предположить, что они будут иметь на большее ускорение . Получили противоречие.
Маленький камень будет мешать и замедлять большой камень. Но два объекта вместе тяжелее, чем каждый сам по себе, и поэтому мы также должны предположить, что они будут иметь на большее ускорение . Получили противоречие.Вот еще одна проблема с мыслью. Возьмите два объекта одинаковой массы. Согласно Аристотелю, они должны ускоряться с одинаковой скоростью.Теперь свяжите их вместе легкой веревкой. Вместе они должны иметь вдвое больше первоначального ускорения. Но откуда им это знать? Как неодушевленные предметы узнают, что они связаны? Давайте расширим задачу. Разве каждый тяжелый объект не является просто сборкой более легких частей, склеенных вместе? Как может совокупность легких частей, каждая из которых движется с небольшим ускорением, внезапно быстро ускориться после соединения? Мы загнали Аристотеля в угол. Ускорение свободного падения не зависит от массы.
Галилей провел множество измерений, связанных с ускорением свободного падения, но ни разу не вычислил его значение (а если и делал, то я нигде не видел).
 Вместо этого он изложил свои выводы как набор пропорций и геометрических соотношений — множество из них. Его описание постоянной скорости потребовало одного определения, четырех аксиом и шести теорем. Все эти отношения теперь можно записать в виде единого уравнения в современных обозначениях.
Вместо этого он изложил свои выводы как набор пропорций и геометрических соотношений — множество из них. Его описание постоянной скорости потребовало одного определения, четырех аксиом и шести теорем. Все эти отношения теперь можно записать в виде единого уравнения в современных обозначениях.Алгебраические символы могут содержать столько же информации, сколько несколько предложений текста, поэтому они и используются.Вопреки расхожему мнению, математика облегчает жизнь.
местонахождение, местонахождение, местонахождение
Общепринятое значение ускорения свободного падения на поверхности Земли и вблизи нее составляет…
г = 9,8 м / с 2
или в единицах, не относящихся к системе СИ…
г = 35 км / ч / с = 22 миль / ч / с = 32 фут / с 2
Полезно запомнить это число (как уже знают миллионы людей по всему миру), однако следует также отметить, что это число , а не константа .
 Хотя масса не влияет на ускорение свободного падения, есть три фактора. Это локация, локация, локация.
Хотя масса не влияет на ускорение свободного падения, есть три фактора. Это локация, локация, локация.Каждый, кто читает это, должен быть знаком с изображениями астронавтов, прыгающих по Луне, и должен знать, что гравитация там слабее, чем на Земле — примерно на одну шестую от силы или 1,6 м / с 2 . Вот почему астронавты могли легко прыгать по поверхности, несмотря на вес своих скафандров. Напротив, гравитация на Юпитере сильнее, чем на Земле — примерно в два с половиной раза сильнее, или 25 м / с 2 .Астронавты, путешествуя через верхние слои плотной атмосферы Юпитера, будут изо всех сил пытаться встать внутри своего космического корабля.
На Земле сила тяжести зависит от широты и высоты (будет обсуждаться в следующей главе). Ускорение свободного падения больше на полюсах, чем на экваторе, и больше на уровне моря, чем на вершине Эвереста. Существуют также местные вариации, зависящие от геологии. Значение 9,8 м / с 2 — только с двумя значащими цифрами — верно для всех мест на поверхности Земли и справедливо для высот до +10 км (высота коммерческих реактивных самолетов) и глубин до — 20 км (далеко ниже самых глубоких шахт).

Насколько вы без ума от точности? Для большинства приложений значение 9,8 м / с 2 более чем достаточно. Если вы спешите, или у вас нет доступа к калькулятору, или вам просто не нужно быть настолько точным; Округление г на Земле до 10 м / с 2 часто допустимо. Во время экзамена с несколькими вариантами ответов, когда использование калькуляторов не разрешено, часто бывает так. Если вам нужна более высокая точность, обратитесь к исчерпывающему справочнику, чтобы найти приемлемое значение для вашей широты и высоты.
Если этого недостаточно, приобретите необходимые инструменты и измерьте местное значение с точностью до как можно большего числа значащих цифр. Вы можете узнать что-нибудь интересное о своем местонахождении. Однажды я встретил геолога, который должен был измерить г в части Западной Африки. Когда я спросил его, на кого он работает и почему он это делает, он в основном отказался отвечать, кроме как сказать, что можно вывести внутреннюю структуру Земли по гравиметрической карте , подготовленной на основе его результатов.
 Зная это, можно будет определить структуры, в которых можно найти ценные минералы или нефть.
Зная это, можно будет определить структуры, в которых можно найти ценные минералы или нефть.Как и все профессии, у тех, кто занимается гравиметрией ( гравиметрия, ), есть свой особый жаргон. Единица ускорения в системе СИ — метр в секунду в квадрате [м / с 2 ]. Разделите это на сто частей, и вы получите сантиметр на секунду в квадрате [см / с 2 ], также известный как галлонов [Gal] в честь Галилея. Обратите внимание, что слово для единицы измерения написано строчными буквами, а символ — с большой буквы.Гал — это пример гауссовой единицы.
0001 галлон = 1 см / с 2 = 0,01 м / с 2
100 галлон = 100 см / с 2 = 1 м / с 2 .Разделите галлон на тысячу частей, и вы получите миллигал [мГал].
1 мГал = 0,001 галлона = 10 −5 м / с 2
Поскольку сила тяжести Земли вызывает ускорение поверхности около 10 м / с 2 , миллигал составляет примерно 1 миллионную часть того значения, к которому мы все привыкли.
1 г ≈ 10 м / с 2 = 1000 галлонов = 1000000 мгал
Измерения с такой точностью можно использовать для изучения изменений земной коры, уровня моря, океанских течений, полярных льдов и грунтовых вод. Если продвинуться еще дальше, можно будет даже измерить изменения в распределении массы в атмосфере. Гравитация — важная тема, о которой мы поговорим более подробно позже в этой книге.
Джи, Уолли
Не путайте явление ускорения свободного падения с одноименным устройством.Количество г имеет значение, которое зависит от местоположения и составляет приблизительно …
г = 9,8 м / с 2
практически повсюду на поверхности Земли. Единица г имеет точное значение , равное…
г = 9,80665 м / с 2
по определению.
Они также используют немного другие символы. Определенная единица использует римский или вертикальный g, в то время как естественное явление, которое меняется в зависимости от местоположения, использует курсив или наклонный g .
 Не путайте g с g .
Не путайте g с g .Как упоминалось ранее, значение 9,8 м / с 2 с двумя значащими цифрами действительно для большей части поверхности Земли вплоть до высоты коммерческих реактивных авиалайнеров, поэтому оно используется в этой книге. Значение 9,80665 м / с 2 с шестью значащими цифрами — это так называемое стандартное ускорение свободного падения или стандартное ускорение свободного падения . Это значение подходит для широт около 45 ° и высот не слишком высоко над уровнем моря.Это примерно значение ускорения свободного падения в Париже, Франция — родном городе Международного бюро мер и весов. Первоначальная идея заключалась в том, чтобы установить стандартное значение силы тяжести, чтобы можно было связать единицы массы, веса и давления — набор определений, которые сейчас устарели. Бюро решило использовать это определение для того места, где располагалась их лаборатория. Старые определения единиц измерения вымерли, но значение стандартной гравитации продолжает жить.
 Теперь это просто согласованное значение для сравнений.Это значение, близкое к тому, что мы испытываем в повседневной жизни, но с большой точностью.
Теперь это просто согласованное значение для сравнений.Это значение, близкое к тому, что мы испытываем в повседневной жизни, но с большой точностью.В некоторых книгах рекомендуется компромиссная точность 9,81 м / с 2 с тремя значащими цифрами для расчетов, но в этой книге этого не делается. В моем местонахождении в Нью-Йорке ускорение свободного падения составляет 9,80 м / с 2 . Округление стандартной силы тяжести до 9,81 м / с 2 неверно для моего местоположения. То же самое верно на всем пути на юг до экватора, где сила тяжести равна 9.780 м / с 2 на уровне моря — 9,81 м / с 2 просто слишком велик. Направляйтесь к северу от Нью-Йорка, и сила тяжести становится все ближе и ближе к 9,81 м / с 2 , пока, наконец, не станет. Это отлично подходит для канадцев на юге Квебека, но сила тяжести продолжает увеличиваться по мере того, как вы идете дальше на север. На Северном полюсе (а также на Южном полюсе) сила тяжести составляет колоссальные 9,832 м / с 2 .
 Значение 9,806 м / с 2 находится на полпути между этими двумя крайними значениями, так что можно сказать, что…
Значение 9,806 м / с 2 находится на полпути между этими двумя крайними значениями, так что можно сказать, что…г = 9.806 ± 0,026 м / с 2
Однако это не то же самое, что среднее. Для этого используйте это значение, полученное кем-то другим…
г = 9,798 м / с 2
Вот мои предложения. Используйте значение 9,8 м / с 2 с двумя значащими цифрами для расчетов на поверхности Земли, если не указано иное значение силы тяжести. Это кажется разумным. Используйте значение 9,80665 м / с 2 с шестью значащими цифрами, только если вы хотите преобразовать м / с 2 в g.Это закон.
Единица g часто используется для измерения ускорения системы отсчета. Это технический язык, который будет подробно рассмотрен позже в другом разделе этой книги, но пока я объясню его на примерах. Когда я пишу это, я сижу перед компьютером в домашнем офисе. Гравитация притягивает мое тело к офисному креслу, мои руки к столу, а пальцы к клавиатуре. Это обычный мир весом 1 грамм (одно и то же), к которому мы все привыкли. Я мог взять с собой портативный компьютер в парк развлечений, покататься на американских горках и попытаться там что-нибудь написать.Гравитация работает на американских горках так же, как и дома, но поскольку американские горки ускоряются вверх и вниз (не говоря уже о том, что из стороны в сторону), ощущение нормальной земной гравитации теряется. Бывают моменты, когда я чувствую себя тяжелее, чем обычно, и времена, когда я падаю легче, чем обычно. Они соответствуют периодам более одного g и менее одного g. Я также мог взять с собой ноутбук в путешествие в космос. После короткого периода ускорения в 2 или 3 g (два или три ge) от поверхности Земли большинство космических путешествий проводится в условиях кажущейся невесомости или 0 g (нулевая скорость).Это происходит не потому, что гравитация перестает работать (сила тяжести бесконечна и никогда не бывает отталкивающей), а потому, что космический корабль является ускоряющейся системой отсчета. Как я сказал ранее, эта концепция будет обсуждаться более подробно в следующем разделе этой книги.
Кинематика и движение снаряда | Протокол
Кинематика — это описание движения, которое часто является важным следствием многих физических событий и явлений.
Движение может быть одномерным, двухмерным или трехмерным.Уравнения, которые применяются к движению объекта во всех этих случаях, используют векторные величины положения, то есть смещение относительно начала координат, скорость, которая представляет собой изменение положения во времени, и ускорение, которое представляет собой изменение скорости во времени.
Имея эту информацию, можно рассчитать траектории свободно падающих тел, траектории снарядов и орбиты планет, чтобы привести лишь несколько примеров.
Здесь мы сосредоточимся на кинематических уравнениях, связанных с одномерным подъемом и падением объекта и двумерной дугой объекта, запущенного под углом
Перед описанием движения необходимо иметь систему координат, или система отсчета.Обычно ось x горизонтальна, а ось y вертикальна. Происхождение произвольно, но часто это отправная точка объекта.
Давайте рассмотрим баскетбольный мяч, помещенный в исходную точку и брошенный прямо вверх. Положение мяча — это его расстояние и направление от начала координат в метрах.
Средняя скорость vy — это изменение положения Δy, деленное на изменение во времени Δt, и измеряется в метрах в секунду. Однако, когда Δt приближается к нулю, уравнение средней скорости становится единым для мгновенной скорости.
Практически, думайте о мгновенной скорости как о скорости в этот момент. Таким образом, в начале мгновенная скорость v0 является начальной скоростью, а затем мгновенная скорость непрерывно уменьшается, пока не станет равной нулю на пике.
Уменьшение скорости из-за постоянного ускорения, создаваемого силой тяжести Земли, которая препятствует движению шара и имеет отрицательное значение в этой системе координат.
В условиях такого постоянного ускорения кинематические зависимости приводят к этим уравнениям для величины мгновенной скорости и положения в одном измерении.Используя их, мы можем вычислить движение объекта в любой момент времени.
Давайте применим эти формулы к примеру с баскетболом. Предположим, что скорость запуска баскетбольного мяча v0 составляет 20 метров в секунду. Мы знаем, что конечная мгновенная скорость мяча на пике равна нулю. Ускорение здесь отрицательное g, поскольку оно противодействует движению шара. Таким образом, переписывая это кинематическое уравнение, мы можем получить t — время нарастания, которое составляет примерно две секунды. Теперь, используя кинематическую формулу для положения и говоря, что начальное положение y0 равно нулю, мы можем подставить значения для ускорения скорости запуска из-за силы тяжести и времени подъема, чтобы вычислить максимальное смещение, которое здесь является пиковой высотой, для примерно 20.4 метра. Достигнув пика, мяч падает в течение двух секунд с возрастающей скоростью, пока не упадет на землю в том месте, где он стартовал, в результате чего общее время полета составит примерно 4 секунды.
Для двух измерений вертикальные и горизонтальные движения объекта не зависят друг от друга и могут рассматриваться отдельно, а конечный результат — это векторная сумма. Используя это понимание, вся дуга движения снаряда может быть разложена на два отдельных одномерных движения.
Давайте рассмотрим это на примере: питчер бросает бейсбольный мяч с начальной скоростью 20 метров в секунду под углом в тридцать градусов от земли.Начальная вертикальная составляющая скорости равна этой скорости, умноженной на синус 30 градусов, или 10 метров в секунду. Начальная горизонтальная составляющая — это скорость, умноженная на косинус 30 градусов, или около 17 метров в секунду.
Во время подъема бейсбольного мяча вертикальная скорость увеличивается, а скорость уменьшается под действием силы тяжести. На пике, который является средней точкой, вертикальная скорость на мгновение равна нулю. Затем во время падения он идет вниз с нарастающей скоростью.
Если не учитывать сопротивление воздуха, горизонтальное движение не имеет ускорения и, следовательно, имеет постоянную скорость.
Сложение вектора вертикального и горизонтального положений, а также вертикальной и горизонтальной скоростей дает дугу движения снаряда. Сумма времени нарастания и спада — это общее время полета, которое определяет дальность или горизонтальное расстояние.
Теперь, когда мы увидели, как рассчитать траекторию движущихся объектов, мы проверим кинематические уравнения для шара, брошенного прямо вверх, и шара, брошенного под углом.
В этих экспериментах используются шар, гранатомет с толкателем, два полюса, ведро, два зажима, двухметровая палка и секундомер.Отметим, что начальная скорость гранатомета составляет 6,3 метра в секунду. Для первого эксперимента, демонстрирующего одномерное движение снаряда, прикрепите гранатомет к шесту и поместите двухметровую палку над ним.
Отрегулируйте пусковую установку так, чтобы она была направлена прямо вверх под углом ноль градусов от вертикали. Это соответствует углу запуска в 90 градусов от горизонтали. Обратите внимание на вертикальное положение наконечника пусковой установки, в котором вылетает мяч, и обозначьте его y0.Используйте поршень, чтобы поместить мяч в пусковую установку с максимальным натяжением пружины.
Запуск мяча и запуск секундомера одновременно. Измерьте общее время, за которое мяч вернется в исходную точку в вертикальном положении y0, и запишите результат как время полета. Обратите внимание, что мяч достигает максимальной высоты примерно 2 метра и на мгновение останавливается в этой точке.
Повторите эту процедуру пять раз и используйте среднее общее время для последующих расчетов.
Этот второй эксперимент демонстрирует двумерное движение снаряда.Установите пусковую установку, как в первом эксперименте, и поместите второй столб на расстоянии четырех метров на той же высоте. Прикрепите ковш к этой второй стойке с помощью зажима и отрегулируйте ковш так, чтобы он находился на той же высоте, что и наконечник гранатомета.
Прикрепите двухметровую палку посередине конфигурации и расположите ее так, чтобы высота пусковой установки была не менее одного метра, или y0. Отрегулируйте пусковую установку так, чтобы она находилась под углом 45 градусов к вертикали, то есть под углом запуска 45 градусов к горизонтали.Используйте поршень, чтобы поместить мяч в пусковую установку с максимальным натяжением пружины.
Теперь запустите мяч и одновременно включите секундомер. Измерьте общее время полета, чтобы мяч приземлился в ведре. Отметьте и запишите максимальную высоту, которую достигает мяч. Повторите этот эксперимент пять раз и используйте среднее общее время для последующих расчетов.
Для эксперимента, демонстрирующего движение в одном измерении, начальная скорость шара, выходящего из пускового механизма, составляла 6.3 метра в секунду. Вспомните, когда мяч брошен прямо вверх, его скорость на пике равна 0. Имея эту информацию и кинематическую формулу для скорости, мы можем вычислить теоретическое время подъема мяча, равное 0,64 секунды. Умножив это на 2, мы получим рассчитанное время полета. Затем, используя формулу для определения положения, мы можем вычислить высоту пика, равную 2,02 метра.
Теоретические и измеренные результаты сопоставимы в пределах экспериментальной ошибки, подтверждая кинематические уравнения для одномерного движения.
В эксперименте, демонстрирующем движение в двух измерениях, мяч запускался со скоростью 6.3 метра в секунду под углом 45 градусов. Чтобы вычислить движение снаряда, сначала определите x-компонент начальной скорости-v • cosθ- и y-компонент начальной скорости-v • sinθ. Затем используйте начальную вертикальную скорость и ускорение, чтобы определить время достижения максимальной высоты, которое составляет 0,45 секунды. Следовательно, общее время полета вдвое больше, или 0,9 секунды.
Для расчета максимального вертикального смещения используйте начальную вертикальную скорость, ускорение свободного падения и время подъема.Это дает нам теоретическое максимальное смещение по оси Y в 1 метр. Для расчета максимального горизонтального смещения используйте начальную горизонтальную скорость и общее время полета, что дает теоретическое максимальное смещение по x 4 метра.
Опять же, теория хорошо согласуется с экспериментом, подтверждая кинематические уравнения для двумерного движения.
Использование кинематики и понимание движения снаряда важны и часто незаметны во многих повседневных приложениях.
Автомобильные инженеры часто используют кинематику для расчета различных характеристик автомобиля.
Один из них — это тормозной путь, который является важным параметром безопасности, который может быть вычислен с использованием одномерных кинематических уравнений.
Не зная этого, игрок в гольф выполняет мысленные вычисления с использованием кинематики при каждом взмахе клюшки. Надеясь на лунку, игрок в гольф раскачивается, ударяет по мячу и запускает его с определенной скоростью и углом, чтобы лететь через поле.Идеальная двумерная траектория мяча для гольфа подчиняется уравнениям, определяющим движение снаряда.
Вы только что посмотрели введение JoVE в кинематику и движение снарядов. Теперь вы должны знать, как использовать кинематические уравнения для расчета траектории объекта, движущегося в одном или двух измерениях. Как всегда, спасибо за просмотр!
Кинематические уравнения: список и пример — стенограмма видео и урока
Уравнения кинематики
Есть пять основных кинематических уравнений, о которых вам нужно знать для решения задач.
В этих пяти уравнениях:
- t — время, измеренное в секундах
- vi — начальная скорость, измеренная в метрах в секунду
- vf — конечная скорость, измеренная в метрах в секунду
- a — ускорение, измеренное в метрах в секунду в квадрате
- y (или иногда x ) — смещение, измеряемое в метрах
Также важно отметить, что для падающих объектов ускорение ( a ) — это ускорение свободного падения ( g ), которое всегда отрицательно 9.8 метров на секунду в квадрате.
В каждом из пяти уравнений есть четыре переменные, одна переменная отсутствует. Каждый раз, когда вы решаете задачи кинематики, вам нужно дать три числа и попросить найти четвертое. Итак, все, что вам нужно сделать, это найти уравнение с этими четырьмя величинами в нем, подставить числа и решить.
Пример задачи движения
Давайте рассмотрим пример использования уравнений. Допустим, мяч падает с высоты 6 метров, и он падает, пока не достигнет земли.Сколько времени нужно, чтобы достичь земли?
Падающий мяч — это пример проблемы с движением. Что ж, прежде всего мы должны записать то, что мы знаем. Водоизмещение y составляет -6 метров. Почему отрицательный? Что ж, падает вниз. Обычно в физике мы называем восходящий положительный и нисходящий отрицательный. Однако это довольно произвольно, и пока все ваши признаки совпадают, вы должны получить один и тот же ответ.
Хорошо, теперь у нас есть потенциальная проблема: других номеров в вопросе нет. Но этот вопрос говорит нам о вещах, которые тайком дают нам другие числа, которые мы можем использовать. Во-первых, мяч падает, то есть падает под действием силы тяжести. Таким образом, ускорение, как и для всех падающих предметов, составляет -9,8. Опять же, отрицательный, потому что ускорение направлено вниз.
И вопрос также говорит нам, что мяч упал, а это значит, что начальная скорость равна нулю. Когда вы бросаете мяч, в тот момент, когда вы его отпускаете, он не движется и его скорость равна нулю.И нас просят найти время, t , поэтому t =?.
Итак, мы знаем три числа, и нас просят найти четвертое. Так что эта проблема разрешима.
Нам нужно найти уравнение из пяти, которое содержит y , vi , a и t . И это уравнение таково:
Мы подставляем числа в это уравнение, например:
Первый член равен нулю, поэтому часть исчезает.Затем измените порядок, чтобы сделать t предметом и введите числа в калькулятор. И получаем t = 1,1 секунды. Вот и все; это наш ответ.
Резюме урока
Кинематика — это исследование движения без ссылки на силы, вызывающие движение. В кинематике есть пять важных величин: смещение (изменение положения), начальная скорость, конечная скорость, ускорение и время. Начальная скорость — это скорость движения объекта при t = 0. Конечная скорость — это скорость движения объекта по истечении времени t . Смещение — это то, насколько позиция изменилась за время т . Ускорение — это скорость, с которой скорость изменялась за время t . А время просто … ну, самое время.
Существует пять основных кинематических уравнений, которые необходимо знать для решения задач. В этих пяти уравнениях:
- t — время, измеренное в секундах
- vi — начальная скорость, измеренная в метрах в секунду
- vf — конечная скорость, измеренная в метрах в секунду
- a — ускорение, измеренное в метрах в секунду в квадрате
- y (или иногда x ) — смещение, измеряемое в метрах
Также важно отметить, что для падающих объектов ускорение a — это ускорение свободного падения g , которое всегда отрицательно 9.8 метров на секунду в квадрате. В каждом из пяти уравнений есть четыре переменных, одна переменная отсутствует. Когда вы решаете задачи кинематики, вам нужно дать три числа и попросить найти четвертое. Итак, все, что вам нужно сделать, это найти уравнение с этими четырьмя величинами в нем, подставить числа и решить.
Результаты обучения
После этого урока вы сможете:
- Определить кинематику
- Опишите пять величин в кинематике
- Определите пять основных кинематических уравнений
- Решайте проблемы с помощью этих уравнений
3.2 Представление ускорения с помощью уравнений и графиков
Как кинематические уравнения связаны с ускорением
Мы изучаем концепции, связанные с движением: время, смещение, скорость и особенно ускорение. Нас интересует движение только в одном измерении. Кинематические уравнения применяются к условиям постоянного ускорения и показывают, как эти концепции взаимосвязаны. Постоянное ускорение — это ускорение, которое не меняется со временем. Первое кинематическое уравнение связывает смещение d , среднюю скорость v¯v¯ и время t .
3.4d = d0 + v¯t, начальное смещение d0 часто равно 0, и в этом случае уравнение можно записать как v¯ = dtd = d0 + v¯t, начальное смещение d0 часто равно 0, и в этом случае уравнение можно записать как v¯ = dt
Это уравнение говорит, что средняя скорость — это смещение в единицу времени. Выразим скорость в метрах в секунду. Если мы построим график смещения в зависимости от времени, как на рис. 3.7, наклон будет скоростью. Когда скорость, например скорость, отображается графически, время обычно считается независимой переменной и отображается по оси x .
Рис. 3.7. Наклон смещения в зависимости от времени — это скорость.
Второе кинематическое уравнение, другое выражение для средней скорости v¯, v¯,
это просто начальная скорость плюс конечная скорость, деленная на два.Теперь мы подошли к основной теме этой главы; а именно кинематические уравнения, описывающие движение с постоянным ускорением. В третьем кинематическом уравнении ускорение — это скорость увеличения скорости, поэтому скорость в любой точке равна начальной скорости плюс ускорение, умноженное на время
3.6v = v0 + at Также, если мы начнем с состояния покоя (v0 = 0), мы можем написать a = vtv = v0 + at Также, если мы начнем с состояния покоя (v0 = 0), мы можем написать a = vt
Обратите внимание, что это третье кинематическое уравнение не содержит смещения. Поэтому, если вы не знаете смещение и не пытаетесь найти смещение, это уравнение может быть хорошим вариантом для использования.
Третье кинематическое уравнение также представлено графиком на рисунке 3.8.
Рис. 3.8. График зависимости скорости от времени — это ускорение.
Четвертое кинематическое уравнение показывает, как перемещение связано с ускорением
3.7d = d0 + v0t + 12at2.d = d0 + v0t + 12at2.
При запуске в начале координат d0 = 0d0 = 0, а при запуске из состояния покоя v0 = 0v0 = 0, и в этом случае уравнение может быть записано как
Это уравнение говорит нам, что для постоянного ускорения наклон графика 2 d по сравнению с t 2 является ускорением, как показано на рисунке 3.9.
Рис. 3.9 При постоянном ускорении наклон 2 d по сравнению с t 2 дает ускорение.
Пятое кинематическое уравнение связывает скорость, ускорение и смещение
3.8 v2 = v02 + 2a (d − d0). V2 = v02 + 2a (d − d0).
Это уравнение полезно, когда мы не знаем или нам не нужно знать время.
При запуске из состояния покоя пятое уравнение упрощается до
Согласно этому уравнению, график квадрата скорости в зависимости от удвоенного смещения будет иметь наклон, равный ускорению.
Обратите внимание, что на самом деле известные и неизвестные могут быть разными.Иногда вам может потребоваться изменить кинематическое уравнение так, чтобы известные значения были значениями на осях, а неизвестные значения были наклоном. Иногда точка пересечения не будет в исходной точке (0,0). Это произойдет, когда v 0 или d 0 не равно нулю. Это будет иметь место, когда интересующий объект уже находится в движении или движение начинается в некоторой точке, отличной от начала системы координат.
Virtual Physics
The Moving Man (Part 2)
Посмотрите на симуляцию Moving Man еще раз, и на этот раз воспользуйтесь представлением Charts .Снова измените скорость и ускорение, перемещая красный и зеленый маркеры по шкале. Удержание маркера скорости около нуля сделает эффект ускорения более очевидным. Обратите внимание, как графики положения, скорости и ускорения меняются со временем. Отметьте, какие графики являются линейными, а какие нет.
Проверка захвата
Что представляет собой наклон на графике зависимости скорости от времени?
- Разгон
- Рабочий объем
- Пройденное расстояние
- Мгновенная скорость
Проверка захвата
Что представляет собой наклон на графике положения и времени?
- Разгон
- Рабочий объем
- Пройденное расстояние
- Мгновенная скорость
Кинематические уравнения применимы при постоянном ускорении.
- d = d0 + v¯td = d0 + v¯t, или v¯ = dtv¯ = dt, когда d 0 = 0
- v¯ = v0 + vf2v¯ = v0 + vf2
- v = v0 + atv = v0 + at, или a = vta = vt, когда v 0 = 0
- d = d0 + v0t + 12at2d = d0 + v0t + 12at2, или a = 2dt2a = 2dt2, когда d 0 = 0 и v 0 = 0
- v2 = v02 + 2a (d − d0) v2 = v02 + 2a (d − d0), или a = 2dt2a = 2dt2, когда d 0 = 0 и v 0 = 0
Кинематические уравнения: когда и как использовать каждую формулу (с производными)
Обновлено 28 декабря 2020 г.
Автор GAYLE TOWELL
Уравнения кинематики описывают движение объекта, испытывающего постоянное ускорение.Эти уравнения связывают переменные времени, положения, скорости и ускорения движущегося объекта, позволяя решить любую из этих переменных, если другие известны.
Ниже представлено изображение объекта, совершающего движение с постоянным ускорением в одном измерении. Переменная t предназначена для времени, позиция x, скорость v и ускорение a . Индексы i и f обозначают «начальный» и «конечный» соответственно.2 + 2a (x_f — x_i)
Примечания относительно кинематических уравнений
- Эти уравнения работают только с постоянным ускорением (которое может быть нулевым в случае постоянной скорости).
- В зависимости от того, какой источник вы читаете, окончательные количества могут не иметь нижнего индекса f и / или могут быть представлены в обозначении функций как x (t) — читать « x как функция времени» или « x при времени t » — и v (t) . Обратите внимание, что x (t) НЕ означает x , умноженное на t !
Иногда величина x f — x i записывается как
Δx , что означает «изменение в x », или даже просто как d , что означает смещение.Все равноценны. Положение, скорость и ускорение являются векторными величинами, то есть с ними связано направление. В одном измерении направление обычно указывается знаками — положительные величины находятся в положительном направлении, а отрицательные величины — в отрицательном направлении. Нижние индексы: «0» может использоваться для начального положения и скорости вместо i . Этот «0» означает «при t = 0», а x 0 и v 0 обычно произносятся как «x-ноль» и «v-ноль».»* Только одно из уравнений не включает время. При составлении заданных значений и определении того, какое уравнение использовать, это ключевой момент!
Особый случай: свободное падение
Движение свободного падения — это движение ускоряющегося объекта только за счет силы тяжести при отсутствии сопротивления воздуха. Применяются те же кинематические уравнения; однако значение ускорения у поверхности Земли известно. Величина этого ускорения часто представлена как g , где g = 9.8 м / с 2 . Направление этого ускорения — вниз, к поверхности Земли. (Обратите внимание, что в некоторых источниках значение г может быть приблизительно равно 10 м / с 2 , а в других может использоваться значение с точностью до более чем двух десятичных знаков.)
Стратегия решения проблем кинематики в одном измерении:
Нарисуйте схему ситуации и выберите подходящую систему координат. (Напомним, что x , v и a — все векторные величины, поэтому, задав четкое положительное направление, будет легче отслеживать знаки.)
Напишите список известных величин. (Помните, что иногда известные данные не очевидны. Ищите фразы вроде «начинается с отдыха», что означает, что v i = 0, или «падает на землю», что означает, что x f = 0, и т. д.)
Определите, какое количество вы хотите найти в вопросе. Какое неизвестное вы будете решать?
Выберите соответствующее кинематическое уравнение. Это будет уравнение, которое содержит вашу неизвестную величину вместе с известными величинами.
Решите уравнение для неизвестной величины, затем подставьте известные значения и вычислите окончательный ответ. (Будьте осторожны с единицами измерения! Иногда вам нужно будет преобразовать единицы перед вычислением.)
Примеры одномерной кинематики
Пример 1: В рекламе утверждается, что спортивный автомобиль может разогнаться от 0 до 60 миль в час за 2,7 секунды. Какое ускорение у этой машины в м / с 2 ? Как далеко он проходит за эти 2,7 секунды?
Известные и неизвестные количества:
v_i = 0 \ text {mph} \\ v_f = 60 \ text {mph} \\ t = 2.7 \ text {s} \\ x_i = 0 \\ a = \ text {?} \\ x_f = \ text {?}
Первая часть вопроса требует решения для неизвестного ускорения. Здесь мы можем использовать уравнение № 1:
v_f = v_i + at \ implies a = \ frac {(v_f-v_i)} t
Однако, прежде чем вводить числа, нам нужно преобразовать 60 миль в час в м / с:
60 \ cancel {\ text {mph}} \ Bigg (\ frac {0.477 \ text {m / s}} {\ cancel {\ text {mph}}} \ Bigg) = 26.8 \ text {m / s}
Итак, ускорение будет таким:
a = \ frac {(26.8-0)} {2.2 + 2 (-9,8) (0-1,5)} = \ pm \ sqrt {254.4} \ приблизительно \ pm16 \ text {m / s}
Здесь есть два решения. Какой из них правильный? Из нашей диаграммы мы видим, что конечная скорость должна быть отрицательной. Итак, ответ:
v_f = \ underline {\ bold {-16} \ text {m / s}}
Чтобы найти время, мы можем использовать уравнение №1 или уравнение №2. Поскольку с уравнением № 1 работать проще, мы будем использовать его:
v_f = v_i + at \ implies t = \ frac {(v_f-v_i)} {a} = \ frac {(-16-15)} {-9,8} \ приблизительно \ underline {\ bold {3.2} \ text {s}}
Обратите внимание, что ответ на первую часть этого вопроса был не 0 м / с. Хотя верно, что после того, как мяч приземлится, его скорость будет равна 0, но этот вопрос хочет знать, насколько быстро он летит за долю секунды до удара. Как только мяч касается земли, наши кинематические уравнения больше не применяются, потому что ускорение не будет постоянным.
Кинематические уравнения движения снаряда (два измерения)
Снаряд — это объект, движущийся в двух измерениях под действием силы тяжести Земли.Его путь — парабола, потому что единственное ускорение происходит за счет силы тяжести. Кинематические уравнения движения снаряда немного отличаются от кинематических уравнений, перечисленных выше. Мы используем тот факт, что компоненты движения, которые перпендикулярны друг другу, такие как горизонтальное направление x и вертикальное направление y , являются независимыми.
Стратегия решения проблем для кинематики движения снаряда Задачи:
- Ускорение равно нулю ( a = 0 ), потому что ни величина, ни направление не меняются
- С другой стороны, начальная, средняя и мгновенная скорости всегда имеют одинаковые значения
- x , x 0 : Позиция тела в данный момент времени ( x ) и в начальный момент времени ( x 0 ).Единицей измерения в Международной системе (S.I.) является метр (м)
- v , v 0 : Скорость тела в данный момент времени ( v ) и в начальный момент времени ( v 0 ). Его единица измерения в Международной системе (S.I.) — метр в секунду (м / с)
- a : Разгон кузова. Единицей измерения в Международной системе (S.I.) является метр на секунду в квадрате (м / с 2 )
- Средняя скорость совпадает с мгновенной скоростью
- Нет разгона
Нарисуйте схему ситуации.Как и в случае с одномерным движением, полезно набросать сценарий и указать систему координат. Вместо того, чтобы использовать метки x , v и a для положения, скорости и ускорения, нам нужен способ маркировки движения в каждом измерении отдельно.
Для горизонтального направления чаще всего используется x для позиции и v x для x-компоненты скорости (обратите внимание, что в этом направлении ускорение равно 0, поэтому нам не нужна переменная для Это.) В направлении y чаще всего используется y для позиции и v y для y-компоненты скорости. Ускорение может быть обозначено как a y , или мы можем использовать тот факт, что мы знаем, что ускорение свободного падения составляет g в отрицательном направлении оси y, и просто используем это вместо этого.
Напишите список известных и неизвестных величин, разделив задачу на две части: вертикальное и горизонтальное движение.Используйте тригонометрию, чтобы найти x- и y-компоненты любых векторных величин, которые не лежат вдоль оси. Может быть полезно перечислить это в двух столбцах:
Примечание: если скорость указана как величина вместе с углом, Ѳ , над горизонтом, тогда используйте векторное разложение, v x = vcos (Ѳ ) и v y = vsin (Ѳ) .
Мы можем рассмотреть наши три кинематических уравнения из предыдущих и адаптировать их к направлениям x и y соответственно.2-2g (y_f — y_i)
Обратите внимание, что ускорение в направлении y равно -g, если мы предполагаем, что вверх положительно. Распространенным заблуждением является то, что g = -9,8 м / с 2 , но это неверно; g — это просто величина ускорения: g = 9,8 м / с 2 , поэтому нам нужно указать, что ускорение отрицательное.
Найдите одно неизвестное в одном из этих измерений, а затем вставьте то, что является общим в обоих направлениях. 2 \ подразумевает t = \ sqrt {\ frac {(2 \ times 20)} g} = \ underline {\ bold {2.02} \ text {s}}
Затем, чтобы найти, где он приземляется, x f , мы можем использовать уравнение горизонтального движения:
x_f = x_i + v_xt = 50 \ times2.02 = \ underline {\ полужирный {101} \ text {s}}
Пример 2: Мяч запускается со скоростью 100 м / с от уровня земли под углом 30 градусов к горизонту. Где он приземляется? Когда его скорость наименьшая? Каково его местонахождение в настоящее время?
Известные и неизвестные величины:
Сначала нам нужно разбить вектор скорости на составляющие:
v_x = v_i \ cos (\ theta) = 100 \ cos (30) \ приблизительно 86.6 \ text {m / s} \\ v_ {yi} = v_i \ sin (\ theta) = 100 \ sin (30) = 50 \ text {m / s}
Наша таблица величин:
Сначала нам нужно найти время, в которое мяч находится в полете. Мы можем сделать это с помощью второго вертикального уравнения_. Обратите внимание, что мы используем симметрию параболы, чтобы определить, что конечная скорость _y является отрицательной по отношению к начальной:
Затем мы определяем, как далеко она перемещается в направлении x за это время:
x_f = x_i + v_xt = 86,6 \ умножить на 10. 2 + 2a (x_f — x_i)
Уравнения движения с постоянной скоростью
Движение с постоянной скоростью , также известное как равномерное прямолинейное движение (u.среднеквадратичное значение) , это тот, у которого постоянная скорость , т.е. траектория прямолинейная, а скорость постоянная. В этом разделе мы собираемся объяснить:
Определение движения с постоянной скоростью
Хотя нахождение прямолинейного равномерного движения или постоянного движения с постоянной скоростью в природе встречается довольно редко, его легче всего изучать, и оно будет полезно при изучении других, более сложных движений. Равномерное прямолинейное движение имеет следующие свойства:
Тело имеет движение с постоянной скоростью или равномерное прямолинейное движение , когда его траектория представляет собой прямую линию и его скорость постоянна .Это означает, что он преодолевает равные расстояния за равное время .
Уравнения движения с постоянной скоростью
Прямолинейное и равномерное движение
Равное время тратится на путешествие на равные расстояния. Средняя скорость постоянна и равна величине скорости.
Уравнения движения с постоянной скоростью :
Где:
.
.
Вывести уравнений равномерного прямолинейного движения u.среднеквадратичное значение следует учитывать, что:
С этими ограничениями получаем:
vavg = vvavg = ΔxΔt = x-x0t-t0 = ⏟t0 = 0x-x0t → x-x0 = v⋅t → x = x0 + v⋅t
Пример
Два мраморных игрока смотрят друг на друга со своими шариками в руках. Игра состоит из одновременного бросания шариков по прямой линии так, чтобы они ударялись друг о друга.Игроки расположены в 36 метрах друг от друга, и игрок A запускает шарик со скоростью 2 м / с, а игрок B — со скоростью 4 м / с, в равномерном прямолинейном движении. Вычислите расстояние от игрока B, на котором шарики столкнутся.
.

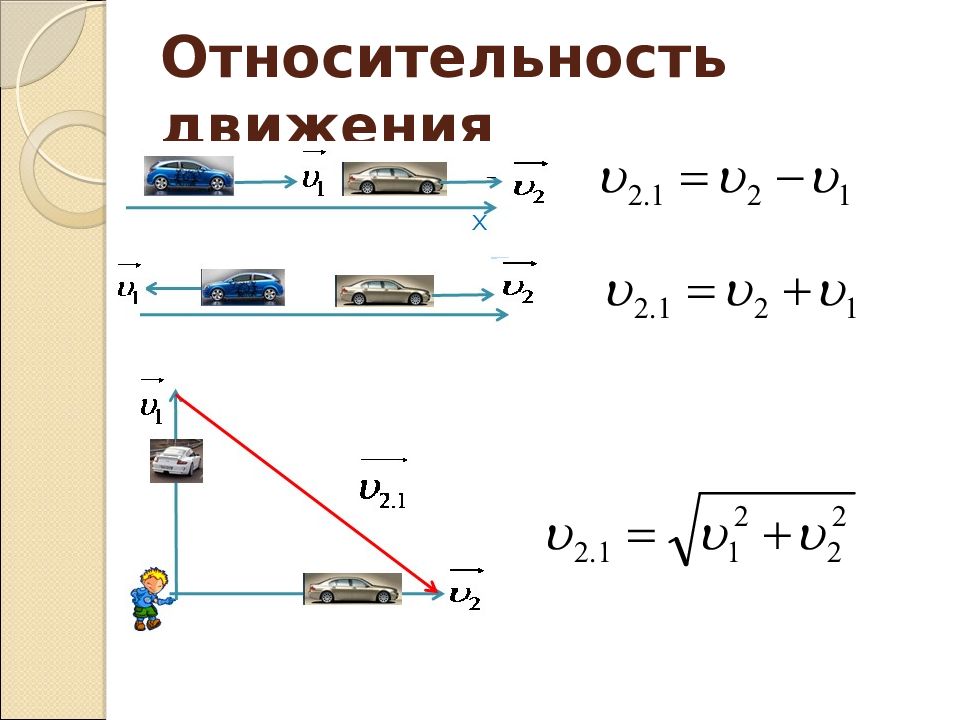 2)
2) 6)
6)