Содержание
Динамика периодического движения. Основные положения
Движение тел по замкнутым орбитам в гравитационном поле Земли является периодическим.
Первая космическая (круговая) скорость — минимальная скорость, которую надо сообщить телу у поверхности Земли для выведения его на круговую орбиту вокруг Земли:
Вторая космическая скорость — минимальная скорость, которую надо сообщить телу у поверхности Земли для того, чтобы оно преодолело гравитационное притяжение Земли.
Форма траектории тела в зависимости от начальной скорости запуска с поверхности Земли:
Колебательное движение в системе может происходить под действием внутренних сил и под действием внешних сил.
Свободные (собственные) колебания — колебания, происходящие под действием внутренних сил в системе, выведенной из положения равновесия и предоставленной самой себе.
Циклическая частота собственных гармонических колебаний пружинного маятника
где k — жесткость пружины, m — масса маятника
Период свободных колебаний пружинного маятника
Амплитуда колебаний — максимальное отклонение колеблющейся величины от положения равновесия. Полная механическая энергия гармонических колебаний пропорциональна квадрату их амплитуды
Полная механическая энергия гармонических колебаний пропорциональна квадрату их амплитуды
Затухающие колебания — колебания, амплитуда которых уменьшается с течением времени. Апериодическое движение в колебательной системе — неповторяющееся (не имеющее периода) движение, возникающее из-за значительных сил трения, противодействующих движению.
Статическое смещение — изменение положения равновесия колебательной системы под действием постоянной силы.
Вынужденные колебания — колебания, происходящие под действием периодической внешней силы. Амплитуда вынужденных колебаний пружинного маятника массой m зависит от частоты со вынуждающей силы.
где ω0 — частота собственных колебаний пружинного маятника, F0 — амплитуда периодической внешней силы F = F0 cos ωt.
Резонанс — явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты внешней силы с частотой собственных колебаний системы. Резонансная кривая — график зависимости амплитуды вынужденных колебаний системы от частоты изменения внешней силы.
Резонансная кривая — график зависимости амплитуды вынужденных колебаний системы от частоты изменения внешней силы.
Этап урока | Деятельность учителя | Деятельность учащихся |
|---|---|---|
1. | I. Самопроверка знаний.
Сегодня у нас необычный урок. Презентация
Перед вами таблица, состоящая из двух частей: в левой части написаны примеры различных видов механического движения, в правой названия видов механического движения.
Ваша задача установить соответствие между видами мех. движения и примерами. На выполнение этого нового для вас, но простого задания — всего 2 минуты. |
|
2. | II. Повторение.
|
|
Что мы рассматриваем? | — Различные виды механического движения. | |
Для выполнения второго задания попрошу выйти к доске двух учащихся. Вам будут предложены вопросы, ваша задача на них ответить, помогая, и исправляя друг друга. Задание классу. Откройте учебник на стр. 79 раздел «Основные положения» найдите и проверьте правильность ответов.
| Два ученика выходят к доске. По очереди отвечают на вопросы. Класс слушает, исправляет и добавляет. | |
1. Что такое механическое движение? | — Механическое движение — изменение пространственного положения тела относительно других тел с течением времени. | |
2. Какой раздел механики занимается изучение механического движения? | — Кинематика изучает механическое движение, не рассматривая причины, которыми это движение вызывается. (Где? Когда? Находилось тело) | |
3. | — Равномерное прямолинейное движение – движение, при котором тело перемещается с постоянной по модулю и направлению скоростью: y = const. | |
4. Баллистическое движение. | — Равноускоренное прямолинейное движение – прямолинейное движение, при котором ускорение параллельно (сонаправлено) скорости и постоянно по модулю. | |
3. | III. Введение в тему: Кинематика периодического движения |
|
Какой из этих видов движения мы с вами еще не изучали? | — Движение по окружности. | |
Правильно. |
| |
Само название периодическоекакими словами вы бы заменили? Как будет происходить движение? | — Периодически — повторять движение — циклически. | |
Существуют ли в природе явления или примеры движения тел, которым присуща повторяемость? | Примеры: повторяющиеся, циклические явления в окружающем нас мире: Смена времен года, смена дня и ночи, солнечные и лунные затмения, перемещение звезд и планет по звездному куполу, колебание маятников и пружин, сердцебиение. | |
Итог: Мы часто в жизни встречаемся с такими примерами и сегодня на уроке мы познакомимся с их физическим объяснением.
Откроем тетрадь и запишем тему урока. |
| |
4 | IV.
| Запись темы урока. |
Может кто-то сможет предложить формулировку
| (Возможные варианты предложений по формулировке ПД) | |
Давайте сравним наши ответы с формулировкой в учебнике.
Повторяющееся |
Учебник: параграф 18 стр. 72. Чтение формулировки.
Запись в тетрадь:
| |
Возвращаемся к примерам: Движение Земли вокруг Солнца, колебания маятника. . . — это примеры ПД. |
| |
5 | IV. Новый материал.Виды периодического движения
Существуют два вида периодического движения:
| Чтение учебника. Запись таблицы. |
Найдем по учебнику и прочитаем: | Вращательное —
| |
Какое к колебательному? | Колебательное —
| |
Итог: |
| |
6. | V. Равномерное движение по окружности.(определение, траектория движения, модуль и вектор скорости). |
|
Запишем подзаголовок:
Демонстрация (Понаблюдаем за движением)
Если размерами тела, движущегося по | Запись подзаголовка:
Наблюдают за демонстрацией движения планет и сравнивают с вращательным движением мяча. — разница размеров тел по сравнению с радиусом. | |
Рассмотрим равномерное движение материальной точки, движущейся по окружности радиусом r, имеющей скорость v.
Начертим в тетради, а один человек на доске — | Один учащийся у доски другие в тетради чертят окружность, показывают:
| |
| При равномерном движении по окружности модуль скорости тела остается постоянным, а направление будет меняться. | Запись определения движения МТ по окружности.
Покажем в произвольных точках вектор скорости (по величине одинаковый, по направлению — разный). | |
| При этом обратим внимание. Что движение наз. Равномерным. Как вы думаете. Что это означает? |
| |
7. | VI.
Кинематика ставит вопросы — Где? Когда? находилось тело в любой момент времени. |
|
Начальный момент времени частица находится в точке А, а ее движение происходит против часовой стрелки (рис. 61).
Вопрос сложный. Пусть нам поможет ответить на него учебник.
Способы определения положения частицы в произвольный момент времени |
Работа с учебником.
| |
Рассмотрим три способа определения положения частицы,
Даю вам на это три минуты. | Нахождение положения частицы в пространстве в произвольный момент времени I можно определит тремя способами: | |
В чем заключается 1-ый способ? Какие математические и физические величины здесь используются? | 1. С помощью пути I,
| |
2-ой — ? | 2. С помощью угла поворота
| |
3-ий — ? | 3. | |
8. | VI. Равномерное движение по окружности.
Для количественного описания движения
|
|
Задание:
Каждый из вас получает табличку, ее
На уроке вы заполняете столбцы: Обозначение, формулы и единицы измерения, дома запишите определения, которые при проверке
Для выполнения откройте страницы
| Заполнение таблицы №1 (Приложение)
| |
9. | VII. Проверка задания.
Проверим, как вы справились с заданием и усвоили сегодняшней материал.
На доске вы видите такую же таблицу как у
| |
К доске один человек, которому
| Ученик дописывает недостающие записи. | |
При проверке обратить внимание на ац. | Проверяют, сравнивают, анализируют выполнение задания у себя по тетради. | |
| VIII. Промежуточное повторение по основным вопросам урока.
Подведение итогов
Задание на дом |
|
Физика: механика | Новый физтех. Университет ИТМО
Содержание курса
Лекция 1 Введение
«Современная картина мира. Микро- и макромир. Задачи современной физики.
Понятия пространства и времени. Классическое представление. Эталоны длины и времени. Способы измерения промежутков времени и длины. Границы применимости классической нерелятивистской механики. Система отсчета. Различные системы координат и связь между ними. «
«
Лекция 2 Нерелятивистская кинематика материальной точки
Основные понятия кинематики материальной точки: радиус-вектор, траектория, перемещение, путь, скорость, ускорение. Выражение скорости и ускорения в различных системах координат. Естественная параметризация движения. Ускорение материальной точки при криволинейном движении, его тангенциальная и нормальная составляющие. Вращательное движение. Циклоида, брахистрона и таутохрона. Баллистическое движение. Кривизная траектории.
Лекция 3 Нерелятивистская динамика материальной точки
Основные понятия динамики материальной точки. Понятие инерции. Первый закон Ньютона. Инерциальные системы отсчета. Импульс. Масса как мера инертности. Сила. Импульс. Второй закон Ньютона. Закон сохранения импульса материальной точки. Третий закон Ньютона. Импульс системы материальных точек. Сохранение импульса замкнутой системы. Центр масс системы материальных точек. Система центра масс. Закон движения центра масс. Приведенная масса. Аддитивность и сохранение массы. Уравнение движения. Закон движения. Начальные условия. Прямая и обратная задача динамики.
Аддитивность и сохранение массы. Уравнение движения. Закон движения. Начальные условия. Прямая и обратная задача динамики.
Лекция 4 Нерелятивистская динамика материальной точки
Интегрирование уравнений движения. Трение. Пример задачи: баллистическое движение с учетом сопротивления воздуха. Движение тел переменной массы. Реактивное движение. Уравнение Мещерского, формула Циолковского. Поворот ракеты.
Лекция 5 Нерелятивистская динамика системы материальных точек
Работа силы. Мощность. Понятие кинетической энергии. Кинетическая энергия системы материальных точек. Преобразование энергии при переходе от одной ИСО к другой и теорема Кенига. Консервативные силы. Потенциальная энергия. Связь потенциальной энергии и силы. Градиент. Закон сохранения полной механической энергии.
Лекция 6 Нерелятивистская динамика
«Эквипотенциальные поверхности и смысл градиента. Примеры потенциалов, встречающихся в физике. Финитное и инфинитное движение.
Столкновения частиц. Упругие столкновения. Векторные диаграммы. Неупругие столкновения. Каналы реакции. Порог реакции.»
Упругие столкновения. Векторные диаграммы. Неупругие столкновения. Каналы реакции. Порог реакции.»
Лекция 7 Нерелятивистская динамика
Момент силы и момент импульса материальной точки и системы материальных точек. Уравнение динамики вращательного движения для материальной точки и системы материальных точек. Закон сохранения момента импульса. Момент импульса относительно оси. Вращение относительно движущегося центра. Рассеяние частиц. Формула Резерфорда. Дифференциальное сечение рассеяния.
Лекция 8 Нерелятивистская динамика
Секториальная скорость. Закон всемирного тяготения. Опыт Кавендиша. Потенциальная и полная энергия гравитационного взаимодействия. Вывод законов Кеплера.
Лекция 9 Гравитационное взаимодействие
«Типы орбит и их связь с полной энергией. Космические скорости. Межпланетные полеты. Приливные силы.
Теорема Гаусса для гравитационного поля, примеры ее применения.»
Лекция 10 Элементы космологии
Элементы космологии. Космологический постулат. Закон Хаббла. Критическая плотность.
Космологический постулат. Закон Хаббла. Критическая плотность.
Лекция 11 Нерелятивистская динамика в неинерциальных системах отсчета
Неинерциальные системы отсчета. Принцип относительности для НИСО. Силы инерции. Закон движения в НИСО. Частные случаи: поступательное движение НИСО и движение с вращением. Ускорение д’Аламбера, Кориолиса, центробежное. Маятник Фуко.
Лекция 12 Нерелятивистская динамика в неинерциальных системах отсчета, введение в СТО
«Динамика движения материальной точки в окрестности поверхности Земли. Отклонение отвеса от направления на центр Земли. Связь инертной и гравитационной масс.
Экспериментальные обоснования СТО»
Лекция 13 Релятивистская кинематика материальной точки
Постулаты специальной теории относительности. Относительность одновременности событий. Способы синхронизации часов. Вывод преобразований Лоренца. Интервал. Причинность. Собственное время. Распад мю-мезонов. Лоренцево сокращение продольных размеров объекта и фотосъемка быстро движущихся объектов.
Лекция 14 Релятивистская кинематика материальной точки
Диаграммы Минковского. Парадокс «пенала». Экспериментальная проверка замедления времени. Релятивистский закон преобразования скоростей. Аберрация света. Продольный и поперечный эффект Доплера для периодической последовательности сигналов. Парадокс близнецов, связь с эффектом Доплера.
Лекция 15 Релятивистская динамика
Релятивистский импульс и релятивистская энергия. Четырехвектор энергии-импульса. Энергия покоя. Преобразование энергии и импульса при переходе между инерциальными системами отсчета. Релятивистский закон сохранения энергии. Связь энергии и массы.
Лекция 16 Релятивистская динамика
Столкновения и распад релятивистских частиц. Порог реакции. Ускорители частиц.
Лекция 17 Кинематика АТТ
«Понятие абсолютно твердого тела (АТТ). Элементы кинематики АТТ. Независимость угловой скорости от начала отчета в ТТ. Сложение вращений. Разложение плоского движения на поступательное и вращательное. Мгновенная ось вращения.
Момент импульса и момент инерции твердого тела. Теорема Гюйгенса-Штайнера. Вычисление моментов инерции. Понятие о тензоре инерции.»
Лекция 18 Динамика АТТ
Динамика вращательного движения АТТ вокруг фиксированной оси. Движение относительно центра масс. Маятник Максвелла. Скатывание тел с наклонной плоскости. Кинетическая энергия вращения. Аналогия между вращательным и поступательным движением.
Лекция 19 Нерелятивистсткая динамика абсолютно твердого тела
Свободный гироскоп. Приближенная теория движения гироскопа под действием внешних сил. Симметричный волчок. Нутация. Тензор и эллипсоид инерции
Лекция 20 Основы теории колебаний
Гармонические колебания материальной точки. Уравнение колебаний. Общее решение и начальные условия. Понятия фазы, частоты, амплитуды. Энергия коллебаний гармонического осциллятора. Метод комплексных амплитуд. Связь колебательного движения с движением по окружности. Сложение колебаний. Фигуры Лиссажу. Фазовое пространство.
Лекция 21 Основы теории колебаний
Затухающие колебания материальной точки при вязком трении, понятие декремента затухания. Вынужденные колебания затухающего осциллятора: различные режимы. Добротность системы. Понятие резонанса. Лоренцева форма резонанса.
Лекция 22 Основы теории колебаний
Установление колебаний. Биения. Связанные осцилляторы. Резонанс Фано. Колебания со многими степенями свободы. Нормальные колебания. Цепочка связанных осцилляторов. Оптические аналогии.
Лекция 23 Основы теории колебаний
Физический маятник. Приведенная длина и центр качания. Адиабатические инварианты. Нелинейные колебания.
Лекция 24 Элементы теории упругости
Деформация простого растяжения. Модуль Юнга. Коэффициент Пуассона. Плотность энергии упругой деформации. Всестороннее гидростатическое сжатие. Деформация сдвига. Модуль сдвига. Деформация кручения. Модуль кручения.
Лекция 25 Элементы механики сплошных сред
Гидростатика несжимаемой жидкости. Закон Архимеда. Стационарное течение жидкости. Идеальная жидкость. Уравнение Бернулли, примеры. Кинематика вязкой жидкости. Вязкость. Внутреннее трение. Ламинарное течение вязкой жидкости по трубке. Формула Пуазейля.
Лекция 26 Элементы механики сплошных сред
Обтекание тел жидкостью и газом. Лобовое сопротивление. Турбулентное движение. Число Рейнольдса. Подъемная сила. Эффект Магнуса. Элементы теории размерности.
Лекция 27 Элементы теории волн
Кинематика волнового движения. Уравнение плоской и сферической волны. Поляризация механических волн. Волновое уравнение, скорость распространения волн. Волны в цепочках связанных осцилляторов.
Лекция 28 Элементы теории волн
Энергия волн в упругой среде. Поток энергии, вектор Умова. Понятие волнового пакета. Групповая скорость, дисперсия. Упругие возмущения. Динамика струны. Звук.
Механические, периодические колебания, характеристики: частота, период, фаза, амплитуда, Виды колебаний, резонанс, примеры
Тестирование онлайн
Колебательное движение
Особый вид неравномерного движения — колебательное. Это движение, которое повторяется с течением времени. Механические колебания — это движения, которые повторяются через определенные промежутки времени. Если промежутки времени одинаковые, то такие колебания называются периодическими.
Колебательная система
Это система взаимодействующих тел (минимум два тела), которые способны совершать колебания. Простейшими колебательными системами являются маятники.
Характеристика колебаний
Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.
Циклическая частота характеризует скорость изменения фазы колебаний.
Начальное состояние колебательной системы характеризует начальная фаза
Амплитуда колебаний A — это наибольшее смещение из положения равновесия
Период T — это промежуток времени, в течение которого точка выполняет одно полное колебание.
Частота колебаний — это число полных колебаний в единицу времени t.
Частота, циклическая частота и период колебаний соотносятся как
Виды колебаний
Колебания, которые происходят в замкнутых системах называются свободными или собственными колебаниями. Колебания, которые происходят под действием внешних сил, называют вынужденными. Встречаются также автоколебания (вынуждаются автоматически).
Если рассматривать колебания согласно изменяющихся характеристик (амплитуда, частота, период и др.), то их можно разделить на гармонические, затухающие, нарастающие (а также пилообразные, прямоугольные, сложные).
При свободных колебаниях в реальных системах всегда происходят потери энергии. Механическая энергия расходуется, например, на совершение работы по преодолению сил сопротивления воздуха. Под влиянием силы трения происходит уменьшение амплитуды колебаний, и через некоторое время колебания прекращаются. Очевидно, что чем больше силы сопротивления движению, тем быстрее прекращаются колебания.
Вынужденные колебания. Резонанс
Вынужденные колебания являются незатухающими. Поэтому необходимо восполнять потери энергии за каждый период колебаний. Для этого необходимо воздействовать на колеблющееся тело периодически изменяющейся силой. Вынужденные колебания совершаются с частотой, равной частоте изменения внешней силы.
Вынужденные колебания
Амплитуда вынужденных механических колебаний достигает наибольшего значения в том случае, если частота вынуждающей силы совпадает с частотой колебательной системы. Это явление называется резонансом.
Например, если периодически дергать шнур в такт его собственным колебаниям, то мы заметим увеличение амплитуды его колебаний.
Если влажный палец двигать по краю бокала, то бокал будет издавать звенящие звуки. Хотя это и незаметно, палец движется прерывисто и передает стеклу энергию короткими порциями, заставляя бокал вибрировать
Стенки бокала также начинают вибрировать, если на него направить звуковую волну с частотой, равной его собственной. Если амплитуда станет очень большой, то бокал может даже разбиться. По причине резонанса при пении Ф.И.Шаляпина дрожали (резонировали) хрустальные подвески люстр. Возникновение резонанса можно проследить и в ванной комнате. Если вы будете негромко пропевать звуки разной частоты, то на одной из частот возникнет резонанс.
В музыкальных инструментах роль резонаторов выполняют части их корпусов. Человек также имеет собственный резонатор — это полость рта, усиливающая издаваемые звуки.
Явление резонанса необходимо учитывать на практике. В одних явлениях он может быть полезен, в других — вреден. Резонансные явления могут вызывать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США.
Явление резонанса используется, когда с помощью небольшой силы необходимо получить большое увеличение амплитуды колебаний. Например, тяжелый язык большого колокола можно раскачать, действуя сравнительно небольшой силой с частотой, равной собственной частоте колебаний колокола.
Кинематика – FIZI4KA
Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
- расстояние, которое проходит тело, много больше его размера;
- расстояние от данного тела до другого тела много больше его размера;
- тело движется поступательно.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
- поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
- вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
- колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;
2. по виду траектории
- прямолинейным — это движение, траектория которого прямая линия;
- криволинейным — это движение, траектория которого кривая линия;
3. по скорости
- равномерным — движение, при котором скорость тела с течением времени не изменяется;
- неравномерным — это движение, при котором скорость тела с течением времени изменяется;
4. по ускорению
- равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
- равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.
Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:
где \( S \) — перемещение тела относительно неподвижной системы отсчета;
\( S_1 \) — перемещение тела относительно подвижной системы отсчета;
\( S_2 \) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:
где \( v \) — скорость тела относительно неподвижной системы отсчета;
\( v_1 \) — скорость тела относительно подвижной системы отсчета;
\( v_2 \) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть \( v_1 \) — скорость первого тела, а \( v_2 \) — скорость второго тела.
Определим скорость первого тела относительно второго \( v_{12} \):
Определим скорость второго тела относительно первого \( v_{21} \):
Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:
Если скорости направлены под углом \( \alpha \) друг к другу, то относительная скорость рассчитывается по теореме косинусов:
Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — \( v \), единицы измерения — м/с (км/ч).
Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:
Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:
Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
Обозначение — \( a \), единица измерения — м/с2.
В векторном виде:
где \( v \) – конечная скорость; \( v_0 \) – начальная скорость;
\( t \) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:
где \( a_n \) – нормальное ускорение, \( a_{\tau} \) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:
Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:
Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если \( a_{\tau} \) ≠ 0, \( a_n \) = 0, то тело движется по прямой;
если \( a_{\tau} \) = 0, \( a_n \) = 0, \( v \) ≠ 0, то тело движется равномерно по прямой;
если \( a_{\tau} \) = 0, \( a_n \) ≠ 0, тело движется равномерно по кривой;
если \( a_{\tau} \) = 0, \( a_n \) = const, то тело движется равномерно по окружности;
если \( a_{\tau} \) ≠ 0, \( a_n \) ≠ 0, то тело движется неравномерно по окружности.
Равномерное движение
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:
Проекция вектора скорости на ось ОХ:
Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:
График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью \( t \), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью \( t \), тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:
Проекция вектора перемещения на ось ОХ:
График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:
График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью \( t \), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью \( t \), тело движется против оси ОХ.
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время \( t \). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Координата тела при равномерном движении рассчитывается по формуле:
График координаты представляет собой зависимость координаты от времени: \( x=x(t) \).
График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:
График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:
Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:
При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:
При разгоне (в проекциях на ось ОХ):
При торможении (в проекциях на ось ОХ):
График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:
График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, \( a_x \) > 0.
График 2 лежит под осью t, тело тормозит, \( a_x \) < 0.
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, \( v_{0x} \) > 0, \( a_x \) > 0.
График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, \( v_{0x} \) > 0, \( a_x \) < 0,
График 3 направлен вниз, тело движется равноускоренно против оси ОХ, \( v_{0x} \) < 0, \( a_x \) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени \( t_2-t_1 \). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:
Перемещение в \( n \)-ую секунду при равноускоренном движении рассчитывается по формуле:
Координата тела при равноускоренном движении рассчитывается по формуле:
Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Обозначение – \( g \), единицы измерения – м/с2.
Важно! \( g \) = 9,8 м/с2, но при решении задач считается, что \( g \) = 10 м/с2.
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:
Если тело падает вниз без начальной скорости, то \( v_0 \) = 0.
Время падения рассчитывается по формуле:
Тело брошено вверх:
Если брошенное вверх тело достигло максимальной высоты, то \( v \) = 0.
Время подъема рассчитывается по формуле:
Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали со скоростью \( v_0=v_{0x} \);
- равноускоренного движения по вертикали с ускорением свободного падения \( g \) и без начальной скорости \( v_{0y}=0 \).
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Дальность полета:
Угол между вектором скорости и осью ОХ:
Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали;
- равноускоренного движения по вертикали с ускорением свободного падения.
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Время подъема на максимальную высоту:
Максимальная высота подъема:
Время полета:
Максимальная дальность полета:
Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость \( v_0 \), с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол \( \alpha \), под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:
Это облегчает решение задач:
Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.
Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – \( a_{цс} \), единицы измерения – м/с2.
Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – \( T \), единицы измерения – с.
где \( N \) – количество оборотов, \( t \) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – \( \nu \), единицы измерения – с–1 (Гц).
Период и частота – взаимно обратные величины:
Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – \( v \), единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:
Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – \( \omega \), единицы измерения – рад/с .
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:
Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:
Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:
Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью \( v_1 \), и все точки обода колеса движутся относительно его центра с такой же линейной скоростью \( v_1 \), то относительно дороги мгновенная скорость разных точек колеса различна.
Мгновенная скорость нижней точки \( (m) \) равна нулю, мгновенная скорость в верхней точке \( (n) \) равна удвоенной скорости \( v_1 \), мгновенная скорость точки \( (p) \), лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке \( (c) \) – по теореме косинусов.
Основные формулы по теме «Кинематика»
Кинематика
2.6 (51.05%) 38 votes
16.3 Простое гармоническое движение: особое периодическое движение — College Physics
Колебания системы, в которой результирующая сила может быть описана законом Гука, имеют особое значение, поскольку они очень распространены. Это также простейшие колебательные системы. Простое гармоническое движение (SHM) — это название, данное колебательному движению для системы, в которой результирующая сила может быть описана законом Гука, и такая система называется простым гармоническим осциллятором. Если результирующая сила может быть описана законом Гука и нет демпфирования (за счет трения или других неконсервативных сил), то простой гармонический осциллятор будет колебаться с равным смещением по обе стороны от положения равновесия, как показано для объекта на пружине на рисунке 16.9. Максимальное смещение от равновесия называется амплитудой XX размером 12 {X} {}. Единицы измерения амплитуды и смещения одинаковы, но зависят от типа колебаний. Для объекта на пружине единицы измерения амплитуды и перемещения — метры; тогда как для звуковых колебаний у них есть единицы давления (а для других типов колебаний есть еще другие единицы). Поскольку амплитуда — это максимальное смещение, она связана с энергией колебаний.
Эксперимент на вынос: SHM и мрамор
Найдите миску или таз, имеющий изнутри форму полусферы.Поместите мрамор внутрь чаши и периодически наклоняйте чашу, чтобы мрамор катился со дна чаши к одинаково высоким точкам по бокам чаши. Почувствуйте силу, необходимую для поддержания этого периодического движения. Что такое восстанавливающая сила и какую роль эта сила играет в простом гармоническом движении (SHM) мрамора?
Рис. 16.9. Предмет, прикрепленный к пружине, скользящей по поверхности без трения, представляет собой несложный простой гармонический осциллятор.При смещении из состояния равновесия объект совершает простое гармоническое движение с амплитудой XX размера 12 {X} {} и периодом TT размером 12 {T} {}. Максимальная скорость объекта достигается при прохождении через равновесие. Чем жестче пружина, тем меньше период TT 12 {T} {}. Чем больше масса объекта, тем больше период TT 12 {T} {}.
Что такого значительного в простом гармоническом движении? Одна особенность заключается в том, что период TT размером 12 {T} {} и частота ff размером 12 {f} {} простого гармонического осциллятора не зависят от амплитуды.Струна гитары, например, будет колебаться с одной и той же частотой, независимо от того, мягко она или сильно нажата. Поскольку период постоянен, в качестве часов можно использовать простой гармонический осциллятор.
Два важных фактора действительно влияют на период простого гармонического осциллятора. Период связан с тем, насколько жесткая система. Очень жесткий объект имеет большую постоянную силы kk size 12 {k} {}, что приводит к тому, что система имеет меньший период. Например, вы можете отрегулировать жесткость трамплина — чем она жестче, тем быстрее она вибрирует и тем короче ее период.Период также зависит от массы колебательной системы. Чем массивнее система, тем больше период. Например, тяжелый человек на трамплине подпрыгивает вверх и вниз медленнее, чем легкий.
Фактически, масса мм, размер 12 {m} {} и силовая постоянная kk, размер 12 {k} {} являются только факторами, которые влияют на период и частоту простого гармонического движения.
Период простого гармонического осциллятора
Период простого гармонического осциллятора определяется как
T = 2πmkT = 2πmk size 12 {T = 2π sqrt {{{m} over {k}}}} {}
16.15
и, поскольку f = 1 / Tf = 1 / T размер 12 {f = 1 / T} {}, частота простого гармонического осциллятора составляет
f = 12πkm.f = 12πkm. размер 12 {f = {{1} больше {2π}} sqrt {{{k} больше {m}}}} {}
16,16
Обратите внимание, что ни размер TT 12 {T} {}, ни размер ff 12 { f} {} имеет любую зависимость от амплитуды.
Домашний эксперимент: колебания массы и линейки
Найдите две одинаковые деревянные или пластиковые линейки. Плотно приклейте один конец каждой линейки к краю стола так, чтобы длина каждой линейки, выступающей из стола, была одинаковой.На свободный конец одной линейки прикрепите тяжелый предмет, например несколько крупных монет. Выщипывайте концы линейок одновременно и наблюдайте, какая из них претерпевает больше циклов за период времени, и измерьте период колебаний каждой из линейок.
Пример 16.4
Расчет частоты и периода колебаний: плохие амортизаторы в автомобиле
Если амортизаторы в автомобиле выходят из строя, то автомобиль будет раскачиваться при малейшей провокации, например, при наезде на неровности дороги и после остановки (см. Рисунок 16.10). Вычислите частоту и период этих колебаний для такого автомобиля , если масса автомобиля (включая его груз) составляет 900 кг, а силовая постоянная ( kk, размер 12 {k} {} ) системы подвески составляет 6,53 × 104 Н / м6,53 × 104 Н / м размер 12 {6 «.» «53» умножить на «10» rSup {размер 8 {4}} «» Н / м «} {}.
Стратегия
Частота колебаний автомобиля будет соответствовать частоте простого гармонического осциллятора, как указано в уравнении f = 12πkmf = 12πkm размер 12 {f = {{1} на {2π}} sqrt {{{k} на {m}} }} {}.Приведены как масса, так и силовая постоянная.
Решение
- Введите известные значения k и m :
f = 12πкм = 12π6,53 × 104 Н / м 900 кг. f = 12πкм = 12π6,53 × 104 Н / м 900 кг. размер 12 {f = {{1} более {2π}} sqrt {{{k} более {m}}} = {{1} более {2π}} sqrt {{{6 «.» «53» умножить на «10» rSup {размер 8 {4}} «Н / м»} больше {«900» «кг»}}}} {}16,17
- Рассчитайте частоту:
12π72,6 / с – 2 = 1,3656 / с – 1≈1,36 / с – 1 = 1.36 Гц. 12π72,6 / с – 2 = 1,3656 / с – 1≈1,36 / с – 1 = 1,36 Гц. размер 12 {{{1} больше {2π}} sqrt {«72» «.» 6 / с rSup {size 8 {2}}} = 1 «.» «36» / с = 1 «.» «36 Гц»} {}16,18
- Вы можете использовать T = 2πmkT = 2πmk size 12 {T = 2π sqrt {{{m} over {k}}} {} для вычисления периода, но проще использовать соотношение T = 1 / fT = 1 / f размер 12 {T = 1 / f} {} и замените только что найденное значение на размер ff 12 {f} {}:
T = 1f = 11,356 Гц = 0,738 с. T = 1f = 11,356 Гц = 0,738 с. размер 12 {T = {{1} больше {f}} = {{1} больше {1 «.»» 36 «» Hz «}} = 0». «» 737 «» s «} {}16,19
Обсуждение
Значения размера TT 12 {T} {} и размера ff 12 {f} {} кажутся подходящими для подпрыгивающего автомобиля. Вы можете наблюдать эти колебания, если сильно надавите на конец автомобиля и отпустите.
Связь между простым гармоническим движением и волнами
Если бы была сделана фотография прыгающего автомобиля с выдержкой времени, когда он проезжал мимо, фара образовала бы волнообразную полосу, как показано на рисунке 16.10. Точно так же на рисунке 16.11 показан объект, подпрыгивающий на пружине, оставляющий волнообразный «след своего положения на движущейся полосе бумаги. Обе волны являются синусоидальными функциями. Все простые гармонические движения тесно связаны с синусоидальными и косинусными волнами.
»
Рисунок 16.10 Подпрыгивающая машина совершает волнообразное движение. Если восстанавливающая сила в системе подвески может быть описана только законом Гука, тогда волна является синусоидальной функцией. (Волна — это след от фары при движении автомобиля вправо.)
Рис. 16.11. Вертикальное положение объекта, подпрыгивающего на пружине, записывается на полоске движущейся бумаги, оставляя синусоидальную волну.
Смещение как функция времени t в любом простом гармоническом движении, то есть таком, в котором результирующая восстанавливающая сила может быть описана законом Гука, задается как
xt = Xcos2πtT, xt = Xcos2πtT, размер 12 { x left (t right) = X «cos» {{2π`t} over {T}}} {}
16.20
где XX размер 12 {X} {} — амплитуда.При t = 0t = 0 размер 12 {t = 0} {} начальное положение равно x0 = Xx0 = X размер 12 {x rSub {size 8 {0}} = X} {}, и смещение колеблется взад и вперед. с периодом TT . (Когда t = Tt = T, мы снова получаем x = Xx = X size 12 {x = X} {}, потому что cos2π = 1cos2π = 1.). Кроме того, из этого выражения для xx размер 12 {x} {} , скорость vv размер 12 {v} {} как функция времени определяется как:
v (t) = — vmaxsin2πtT, v (t ) = — vmaxsin2πtT, размер 12 {v \ (t \) = — v rSub {size 8 {«max»}} «sin» left ({{2π`t} over {T}} right)} {}
16 .21
, где vmax = 2πX / T = Xk / mvmax = 2πX / T = Xk / m размер 12 {v rSub {size 8 {«max»}} = 2πX / T = X sqrt {k / m}} {} . Объект имеет нулевую скорость при максимальном смещении — например, v = 0v = 0 размер 12 {v = 0} {}, когда t = 0t = 0 размер 12 {t = 0} {}, и в это время x = Xx = X размер 12 {x = X} {}. Знак минус в первом уравнении для v (t) v (t) размера 12 {v \ (t \)} {} указывает правильное направление скорости. Например, сразу после начала движения скорость отрицательна, потому что система движется обратно к точке равновесия.Наконец, мы можем получить выражение для ускорения, используя второй закон Ньютона. [Тогда у нас есть x (t), v (t), t, x (t), v (t), t, размер 12 {x \ (t \), v \ (t \), t} {} и a (t) a (t) размер 12 {a \ (t \)} {}, величины, необходимые для кинематики и описания простого гармонического движения.] Согласно второму закону Ньютона, ускорение равно a = F / m = kx / ma = F / m = kx / m размер 12 {a = F / m = ital «kx» / m} {} . Итак, a (t) a (t) size 12 {a \ (t \)} {} также является функцией косинуса:
a (t) = — kXm cos 2πtT.a (t) = — kXm cos 2πtT.size 12 {a \ (t \) = — {{ital «kX»} над {m}} «cos» {{2π t} над {T}}} {}
16.22
Следовательно, a (t) a (t) размер 12 {a \ (t \)} {} прямо пропорционален x (t) x (t) и в противоположном направлении от него.
На рисунке 16.12 показано простое гармоническое движение объекта на пружине и представлены графики x (t), v (t), x (t), v (t), размер 12 {x \ (t \), v \ (t \) `} {} и a (t) a (t) размер 12 {` a \ (t \)} {} в зависимости от времени.
Рисунок 16.12 Графики x (t), v (t), x (t), v (t), размер 12 {x \ (t \), v \ (t \) `} {} и a (t) a (t) размер 12 {`a \ (t \)} {} по сравнению с размером 12 {t} {} для движения объекта на пружине.Общая сила, действующая на объект, может быть описана законом Гука, и поэтому объект совершает простое гармоническое движение. Обратите внимание, что исходное положение имеет вертикальное смещение при максимальном значении XX size 12 {X} {}; vv size 12 {v} {} изначально равен нулю, а затем становится отрицательным по мере движения объекта вниз; и начальное ускорение отрицательное, возвращается к положению равновесия и становится нулевым в этой точке.
Наиболее важным моментом здесь является то, что эти уравнения математически просты и справедливы для всех простых гармонических движений.Они очень полезны при визуализации волн, связанных с простым гармоническим движением, включая визуализацию того, как волны складываются друг с другом.
Проверьте свое понимание
Предположим, вы взяли струну банджо. Вы слышите одну ноту, которая начинается вслух и постепенно затихает. Опишите, что происходит со звуковыми волнами с точки зрения периода, частоты и амплитуды при уменьшении громкости звука.
Решение
Частота и период практически не меняются.При уменьшении громкости уменьшается только амплитуда.
Проверьте свое понимание
Няня толкает ребенка на качелях. В точке, где колебание достигает размера xx 12 {x} {}, где будет находиться соответствующая точка на волне этого движения?
Решение
xx размер 12 {x} {} — максимальная деформация, соответствующая амплитуде волны. Точка на волне будет либо на самом верху, либо на самом низу кривой.
PhET Explorations
Массы и пружины
Реалистичная лаборатория масс и пружин. Подвесьте массы к пружинам и отрегулируйте жесткость и демпфирование пружины. Вы даже можете замедлить время. Перенесите лабораторию на разные планеты. На диаграмме показана кинетическая, потенциальная и тепловая энергия каждой пружины.
Особое периодическое движение — College Physics
Цели обучения
- Опишите простой гармонический осциллятор.
- Объясните связь между простым гармоническим движением и волнами.
Колебания системы, в которой результирующая сила может быть описана законом Гука, имеют особое значение, поскольку они очень распространены. Это также простейшие колебательные системы. Простое гармоническое движение (SHM) — это название, данное колебательному движению для системы, в которой результирующая сила может быть описана законом Гука, и такая система называется простым гармоническим осциллятором. Если результирующая сила может быть описана законом Гука и нет демпфирования (за счет трения или других неконсервативных сил), то простой гармонический осциллятор будет колебаться с равным смещением по обе стороны от положения равновесия, как показано для объект на пружине в (рисунок).Максимальное отклонение от равновесия называется амплитудой. Единицы измерения амплитуды и смещения одинаковы, но зависят от типа колебаний. Для объекта на пружине единицы измерения амплитуды и перемещения — метры; тогда как для звуковых колебаний у них есть единицы давления (а для других типов колебаний есть еще другие единицы). Поскольку амплитуда — это максимальное смещение, она связана с энергией колебаний.
Эксперимент на вынос: SHM и мрамор
Найдите миску или таз, имеющий изнутри форму полусферы.Поместите мрамор внутрь чаши и периодически наклоняйте чашу, чтобы мрамор катился со дна чаши к одинаково высоким точкам по бокам чаши. Почувствуйте силу, необходимую для поддержания этого периодического движения. Что такое восстанавливающая сила и какую роль эта сила играет в простом гармоническом движении (SHM) мрамора?
Что такого значительного в простом гармоническом движении? Одна особенность заключается в том, что период и частота простого гармонического осциллятора не зависят от амплитуды.Струна гитары, например, будет колебаться с одной и той же частотой, независимо от того, мягко она или сильно нажата. Поскольку период постоянен, в качестве часов можно использовать простой гармонический осциллятор.
Два важных фактора действительно влияют на период простого гармонического осциллятора. Период связан с тем, насколько жесткая система. Очень жесткий объект имеет большую постоянную силы, из-за чего система имеет меньший период. Например, вы можете отрегулировать жесткость трамплина — чем она жестче, тем быстрее она вибрирует и тем короче ее период.Период также зависит от массы колебательной системы. Чем массивнее система, тем больше период. Например, тяжелый человек на трамплине подпрыгивает вверх и вниз медленнее, чем легкий.
Фактически, масса и силовая постоянная — это всего лишь факторов, которые влияют на период и частоту простого гармонического движения.
Эксперимент на вынос: колебания массы и линейки
Найдите две одинаковые деревянные или пластиковые линейки. Плотно приклейте один конец каждой линейки к краю стола так, чтобы длина каждой линейки, выступающей из стола, была одинаковой.На свободный конец одной линейки прикрепите тяжелый предмет, например несколько крупных монет. Выщипывайте концы линейок одновременно и наблюдайте, какая из них претерпевает больше циклов за период времени, и измерьте период колебаний каждой из линейок.
Связь между простым гармоническим движением и волнами
Если бы была сделана фотография прыгающего автомобиля с выдержкой времени, когда он проезжал мимо, фара образовала бы волнообразную полосу, как показано на (Рисунок). Точно так же (Рисунок) показывает объект, подпрыгивающий на пружине, оставляющий волнообразный «след своего положения на движущейся полосе бумаги».Обе волны являются синусоидальными функциями. Все простые гармонические движения тесно связаны с синусоидальными и косинусоидальными волнами.
Подпрыгивающая машина совершает волнообразное движение. Если восстанавливающая сила в системе подвески может быть описана только законом Гука, тогда волна является синусоидальной функцией. (Волна — это след от фары при движении автомобиля вправо.)
Вертикальное положение объекта, подпрыгивающего на пружине, записывается на полоске движущейся бумаги, оставляя синусоидальную волну.
Смещение как функция времени t при любом простом гармоническом движении, то есть таком, в котором результирующая восстанавливающая сила может быть описана законом Гука, определяется как
где — амплитуда. В начальное положение равно, и смещение колеблется вперед и назад с периодом . (Когда, мы снова получим, потому что.). Кроме того, из этого выражения для скорость как функция времени определяется как:
где.Объект имеет нулевую скорость при максимальном смещении — например, когда и в это время. Знак минус в первом уравнении для указывает правильное направление скорости. Например, сразу после начала движения скорость отрицательна, потому что система движется обратно к точке равновесия. Наконец, мы можем получить выражение для ускорения, используя второй закон Ньютона. [Тогда у нас есть и, величины, необходимые для кинематики и описания простого гармонического движения.] Согласно второму закону Ньютона, ускорение равно . Итак, это еще и функция косинуса:
Следовательно, прямо пропорционально и в противоположном направлении.
(рисунок) показывает простое гармоническое движение объекта на пружине и представляет графики зависимости от времени.
Наиболее важным моментом здесь является то, что эти уравнения математически просты и справедливы для всех простых гармонических движений. Они очень полезны при визуализации волн, связанных с простым гармоническим движением, включая визуализацию того, как волны складываются друг с другом.
Проверьте свое понимание
Предположим, вы взяли струну банджо. Вы слышите одну ноту, которая начинается вслух и постепенно затихает. Опишите, что происходит со звуковыми волнами с точки зрения периода, частоты и амплитуды при уменьшении громкости звука.
Частота и период практически не изменились. При уменьшении громкости уменьшается только амплитуда.
Проверьте свое понимание
Няня толкает ребенка на качелях. В точке, где достигается качание, где будет находиться соответствующая точка на волне этого движения?
— максимальная деформация, соответствующая амплитуде волны.Точка на волне будет либо на самом верху, либо на самом низу кривой.
Исследования PhET: массы и источники
Реалистичная лаборатория масс и пружин. Подвесьте массы к пружинам и отрегулируйте жесткость и демпфирование пружины. Вы даже можете замедлить время. Перенесите лабораторию на разные планеты. На диаграмме показана кинетическая, потенциальная и тепловая энергия каждой пружины.
Концептуальные вопросы
Какие условия должны быть выполнены для создания простого гармонического движения?
(a) Если частота для некоторого колебания непостоянна, может ли колебание быть простым гармоническим движением?
(b) Вы можете придумать какие-нибудь примеры гармонического движения, в котором частота может зависеть от амплитуды?
Приведите пример простого гармонического осциллятора, особо отметив, что его частота не зависит от амплитуды.
Объясните, почему вы ожидаете, что объект, сделанный из жесткого материала, будет вибрировать с большей частотой, чем аналогичный объект, сделанный из губчатого материала.
Когда вы проезжаете грузовой автомобиль с прицепом по шоссе, вы замечаете, что его прицеп медленно подпрыгивает вверх и вниз. Более вероятно, что прицеп сильно загружен или почти пустой? Поясните свой ответ.
Некоторые люди модифицируют автомобили, чтобы они были намного ближе к земле, чем когда они были изготовлены. Стоит ли устанавливать более жесткие пружины? Поясните свой ответ.
Задачи и упражнения
Тип часов с кукушкой отслеживает время, заставляя массу подпрыгивать на пружине, обычно что-то милое, вроде херувима в кресле. Какая силовая постоянная необходима для получения периода 0,500 с для массы 0,0150 кг?
Если жесткость пружины простого гармонического осциллятора удвоится, на какой коэффициент нужно изменить массу системы, чтобы частота движения оставалась прежней?
А 0.Подвешенный на пружине груз весом 500 кг колеблется с периодом 1,50 с. Какую массу нужно добавить к объекту, чтобы изменить период до 2,00 с?
Насколько проста в выборе массы объекта (как в процентах, так и по массе) в предыдущей задаче, если вы не хотите, чтобы новый период был больше 2,01 с или меньше 1,99 с?
Предположим, вы прикрепляете объект с массой к вертикальной пружине, первоначально находящейся в состоянии покоя, и позволяете ему подпрыгивать вверх и вниз.Вы высвобождаете объект из состояния покоя на исходной длине упора пружины. (а) Покажите, что пружина воздействует на объект с силой, направленной вверх в его самой нижней точке. (b) Если пружина имеет постоянную силы и объект массой 0,25 кг приводится в движение, как описано, найдите амплитуду колебаний. (c) Найдите максимальную скорость.
Дайвер на трамплине совершает простое гармоническое движение. Ее масса 55,0 кг, период движения 0,800 с. Следующий дайвер — мужчина, период простых гармонических колебаний которого равен 1.05 с. Какова его масса, если масса доски ничтожна?
Предположим, что доска для прыжков в воду, на которой никого нет, подпрыгивает вверх и вниз, совершая простое гармоническое движение с частотой 4,00 Гц. Доска имеет полезную массу 10,0 кг. Какова частота простого гармонического движения дайвера весом 75,0 кг на доске?
В этой детской игрушке используются пружины, чтобы развлекать младенцев. (Источник: Humboldthead, Flickr)
Устройство, изображенное на (Рисунок), развлекает младенцев, удерживая их от блужданий.Ребенок подпрыгивает в ремне безопасности, подвешенном к дверной коробке с помощью пружины.
(a) Если пружина тянется на 0,250 м, поддерживая ребенка весом 8,0 кг, какова ее жесткость пружины?
(b) Сколько времени на один полный прыжок этого ребенка? (c) Какова максимальная скорость ребенка, если амплитуда его прыжка составляет 0,200 м?
Парашютист весом 90,0 кг, подвешенный на парашюте, подпрыгивает вверх и вниз с периодом 1,50 с. Что такое новый период колебаний у второго парашютиста, масса которого 60.0 кг, свисает с ног первого, как показано на (Рисунок).
На колебания одного парашютиста вот-вот повлияет второй парашютист. (Источник: армия США, www.army.mil)
Глоссарий
- амплитуда
- максимальное смещение от положения равновесия объекта, колеблющегося вокруг положения равновесия
- простое гармоническое движение
- колебательное движение в системе, где результирующая сила может быть описана законом Гука
- простой генератор гармоник
- устройство, реализующее закон Гука, такое как груз, прикрепленный к пружине, при этом другой конец пружины соединен с жесткой опорой, такой как стена
Кинематика простого гармонического движения — Видео и стенограмма урока
Уравнения
Смещение, скорость и ускорение объекта, совершающего простое гармоническое движение, имеют синусоидальную природу.То есть, если вы построите графики смещения-времени, скорости-времени и ускорения-времени, все их формы будут своего рода синусоидальной кривой. Но эти синусоидальные кривые — это то, что называется не в фазе, что означает, что пик одной кривой не происходит одновременно с пиком других.
Мы можем подумать об этом концептуально, изобразив маятник.
Маятник движется быстрее всего, когда он проходит через самую середину, и на мгновение достигает нулевой скорости на самых краях.Таким образом, график скорость-время будет выглядеть так:
при условии, что мы запускаем секундомер, когда маятник высвобождается с дальней стороны, а не посередине. Это формирует отрицательную или перевернутую синусоидальную кривую. Он отрицательный, потому что на нашей диаграмме скорость указана слева.
Смещение, с другой стороны, начинается положительно, потому что оно начинается с правой стороны.Здесь мы предполагаем, что середина — оригинал. Когда он достигает середины, смещение уменьшается до нуля, а затем становится отрицательным, когда он проходит за начало координат, и так далее. Таким образом, уравнение ускорения представляет собой график с положительным косинусом.
А что с разгоном? Что ж, наибольшее ускорение у левой стороны, а у правой — по краям. Это потому, что именно в этих точках маятник испытывает наибольшую силу, толкая его к центру. Как только он достигает центра, ускорение, по крайней мере на мгновение, равно нулю.Таким образом, ускорение начинается с отрицательного значения, переходит к нулю, становится положительным, возвращается к нулю и так далее. Таким образом, ускорение будет отрицательным косинусоидальным графиком.
Если вы знакомы с математическим расчетом, эти уравнения будут иметь большой смысл:
Если вы дифференцируете уравнение косинуса, вы получите отрицательный синус, а если вы дифференцируете отрицательный синус, вы получите отрицательный косинус. Если вы не знаете математического анализа, не о чем беспокоиться.Важно то, что вы понимаете, что означают формы этих графиков с точки зрения самого маятника. Конечно, эти же уравнения применимы к любому примеру простого гармонического движения. Вместо того, чтобы держать маятник вправо и отпускать его, мы могли бы тянуть груз на пружине вправо; это все равно будет работать.
Эти три уравнения предполагают, что вы отпускаете маятник с правой стороны при t = 0. Если вы начнете с левой стороны, знаки перевернутся, и если вы запустите секундомер, поскольку маятник движется через самое в середине синусы и косинусы поменяются местами.
Для решения проблем вам, в частности, необходимо уметь использовать первое из этих уравнений: уравнение смещения. В этом уравнении A — это амплитуда колебаний (также известная как максимальное смещение — смещение, когда оно находится в крайнем правом или крайнем левом положении), измеренная в метрах, f — это частота колебаний или число полных циклов в секунду, измеряемых в герцах, t — это время в секундах после того, как вы отпустите маятник (крайний правый, как на диаграмме), а x — это, конечно, смещение в метрах.
Резюме урока
Кинематика — это раздел физики, который занимается движением объектов без ссылки на силы, вызывающие это движение. Или, в более практическом смысле, это изучение движения с точки зрения смещения, скорости и ускорения. Кинематика может использоваться не только для изучения линейного движения, но и других движений, включая простое гармоническое движение. Простое гармоническое движение — это любое движение, при котором прикладывается возвращающая сила, пропорциональная смещению, в направлении, противоположном этому смещению.Или, другими словами, чем больше вы его тянете, тем больше он хочет пойти в обратном направлении. Примером может служить блок на пружине или маятник.
Три графика и уравнения описывают смещение, скорость и ускорение объекта, совершающего простое гармоническое движение. Они предполагают, что когда вы запускаете секундомер при t = 0, маятник смещается вправо (с положительным смещением).
Результаты обучения
Повысьте свою способность к достижению этих целей, просмотрев урок:
- Вспомните фокус кинематики
- Перечислите простые гармонические уравнения и их допущения
- Интерпретировать графики, описывающие простые гармонические уравнения
простых гармонических движений | Формула, примеры и факты
Простое гармоническое движение , в физике, повторяющееся движение вперед и назад через равновесное или центральное положение, так что максимальное смещение на одной стороне этого положения равно максимальному смещению на Другая сторона.Временной интервал каждой полной вибрации одинаков. Сила, отвечающая за движение, всегда направлена к положению равновесия и прямо пропорциональна расстоянию от него. То есть F = — kx , где F — сила, x — смещение, а k — постоянная величина. Это соотношение называется законом Гука.
Подробнее по этой теме
механика: простые гармонические колебания
Рассмотрим массу m, удерживаемую пружинами в положении равновесия, как показано на рисунке 2A.Массу можно возмущать, сместив ее до …
Конкретный пример простого гармонического осциллятора — это вибрация груза, прикрепленного к вертикальной пружине, другой конец которой закреплен на потолке. При максимальном перемещении — x, пружина находится под наибольшим напряжением, которое толкает массу вверх. При максимальном смещении + x, пружина достигает максимального сжатия, что заставляет массу снова опускаться. В любом положении максимального смещения сила наибольшая и направлена к положению равновесия, скорость ( v ) массы равна нулю, ее ускорение максимальное, а масса меняет направление.В положении равновесия скорость максимальна, а ускорение ( a ) упало до нуля. Простое гармоническое движение характеризуется этим изменяющимся ускорением, которое всегда направлено к положению равновесия и пропорционально смещению от положения равновесия. Кроме того, интервал времени для каждой полной вибрации постоянен и не зависит от величины максимального смещения. Поэтому в той или иной форме простое гармоническое движение лежит в основе хронометража.
Чтобы выразить, как смещение массы изменяется со временем, можно использовать второй закон Ньютона, F = ma , и установить ma = — kx . Ускорение a — это вторая производная от x по времени t , и можно решить полученное дифференциальное уравнение с x = A cos ω t , где A — максимальное смещение, а ω — угловая частота в радианах в секунду.Время, необходимое массе для перемещения от A до — A и обратно, — это время, необходимое для того, чтобы ω t увеличился на 2π. Следовательно, период T , необходимый для того, чтобы масса сместилась от A к — A и обратно, составляет ω T = 2π или T = 2π / ω. Частота колебаний в циклах в секунду составляет 1/ T или ω / 2π.
Многие физические системы демонстрируют простое гармоническое движение (при условии отсутствия потерь энергии): колеблющийся маятник, электроны в проводе, несущем переменный ток, колеблющиеся частицы среды в звуковой волне и другие совокупности, включающие относительно небольшие колебания относительно положения. устойчивого равновесия.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Движение называется гармоническим, потому что музыкальные инструменты совершают такие колебания, которые, в свою очередь, вызывают соответствующие звуковые волны в воздухе. Музыкальные звуки на самом деле представляют собой комбинацию множества простых гармонических волн, соответствующих множеству способов, которыми вибрирующие части музыкального инструмента колеблются в наборах наложенных простых гармонических движений, частоты которых кратны самой низкой основной частоте.Фактически, любое регулярно повторяющееся движение и любую волну, независимо от того, насколько сложна ее форма, можно рассматривать как сумму ряда простых гармонических движений или волн — открытие, впервые опубликованное в 1822 году французским математиком Жозефом Фурье.
Как рассчитать период движения в физике
Обновлено 28 декабря 2020 г.
Крис Дезил
В естественном мире есть множество примеров периодического движения, от орбит планет вокруг Солнца до электромагнитных колебаний фотонов к нашему собственному сердцебиению.
Все эти колебания связаны с завершением цикла, будь то возвращение движущегося по орбите тела в исходную точку, возврат вибрирующей пружины в точку равновесия или расширение и сжатие сердцебиения. Время, необходимое колебательной системе для завершения цикла, известно как ее период .
Период системы — это мера времени, и в физике он обычно обозначается заглавной буквой T . Период измеряется в единицах времени, подходящих для этой системы, но наиболее распространенными являются секунды.Вторая — это единица времени, первоначально основанная на вращении Земли вокруг своей оси и по ее орбите вокруг Солнца, хотя современное определение основано на колебаниях атома цезия-133, а не на каком-либо астрономическом явлении.
Периоды некоторых систем интуитивно понятны, например, вращение Земли, которое составляет сутки или (по определению) 86 400 секунд. Вы можете рассчитать периоды некоторых других систем, таких как колеблющаяся пружина, используя характеристики системы, такие как масса и жесткость пружины.
Когда дело доходит до колебаний света, все становится немного сложнее, потому что фотоны движутся поперек пространства, пока они колеблются, поэтому длина волны является более полезной величиной, чем период.
Период — величина, обратная частоте
Период — это время, необходимое колебательной системе для завершения цикла, тогда как частота ( f ) — это количество циклов, которое система может завершить за заданный период времени.Например, Земля вращается один раз в день, поэтому период составляет 1 день, а частота также составляет 1 цикл в день. Если вы установите стандарт времени на годы, период составит 1/365 года, а частота — 365 циклов в год. Период и частота являются обратными величинами:
T = \ frac {1} {f}
В расчетах, связанных с атомными и электромагнитными явлениями, частота в физике обычно измеряется в циклах в секунду, также известных как Герцы (Гц), с −1 или 1 / сек. При рассмотрении вращающихся тел в макроскопическом мире число оборотов в минуту (об / мин) также является общепринятой единицей.Период может быть измерен в секундах, минутах или другом подходящем периоде времени.
Период простого гармонического осциллятора
Самый основной тип периодического движения — это движение простого гармонического осциллятора, который определяется как тот, который всегда испытывает ускорение, пропорциональное его расстоянию от положения равновесия и направленное к равновесию. должность. В отсутствие сил трения и маятник, и масса, прикрепленная к пружине, могут быть простыми гармоническими осцилляторами.
Можно сравнить колебания массы на пружине или маятнике с движением тела, вращающегося с равномерным движением по круговой траектории с радиусом r . Если угловая скорость тела, движущегося по окружности, равна ω, его угловое смещение ( θ ) от начальной точки в любой момент времени t составляет θ = ωt , и компоненты x и y его положения равны x = r cos ( ωt ) и y = r sin ( ωt ).
Многие осцилляторы движутся только в одном измерении, и если они движутся горизонтально, они движутся в направлении x . Если амплитуда, наиболее удаленная от положения равновесия, составляет A , то положение в любой момент времени t равно x = A cos ( ωt ). Здесь ω известен как угловая частота, и она связана с частотой колебаний ( f ) уравнением ω = 2π f .Поскольку f = 1/ T , вы можете записать период колебаний следующим образом:
T = \ frac {2π} {ω}
Пружины и маятники: уравнения периода
Согласно Согласно закону Гука, масса на пружине подвергается восстановлению F = — kx , где k — характеристика пружины, известная как жесткость пружины, а x Это смещение. Знак минус означает, что сила всегда направлена против направления смещения.Согласно второму закону Ньютона, эта сила также равна массе тела ( м ), умноженной на его ускорение ( a ), поэтому ma = — kx .
Для объекта, колеблющегося с угловой частотой ω , его ускорение равно — Aω 2 cos ωt или, упрощенно, — ω 2 х . Теперь вы можете написать m (- ω 2 x ) = — kx , исключить x и получить ω = √ ( к / м ).Тогда период колебаний массы на пружине равен:
T = 2π \ sqrt {\ frac {m} {k}}
Вы можете применить аналогичные соображения к простому маятнику, на котором вся масса центрируется на конце строки. Если длина струны составляет L , уравнение периода в физике для малоуглового маятника (т. Е. Такого, в котором максимальное угловое смещение от положения равновесия мало), которое оказывается независимым от массы, имеет вид
T = 2π \ sqrt {\ frac {L} {g}}
, где g — ускорение свободного падения.
Период и длина волны
Как и простой осциллятор, волна имеет точку равновесия и максимальную амплитуду по обе стороны от точки равновесия. Однако, поскольку волна распространяется через среду или пространство, колебания растягиваются вдоль направления движения. Длина волны определяется как поперечное расстояние между любыми двумя идентичными точками в цикле колебаний, обычно точками максимальной амплитуды на одной стороне положения равновесия.
Период волны — это время, за которое одна полная длина волны проходит через контрольную точку, тогда как частота волны — это количество длин волн, которые проходят через контрольную точку за данный период времени. Если период времени равен одной секунде, частота может быть выражена в циклах в секунду (герц), а период выражен в секундах.
Период волны зависит от скорости ее движения и длины волны ( λ ). Волна перемещается на расстояние в одну длину волны за один период времени, поэтому формула скорости волны составляет v = λ / T , где v — скорость.Если преобразовать период в другие величины, получим:
T = \ frac {λ} {v}
Например, если волны на озере разделены 10 футами и движутся со скоростью 5 футов в секунду, период каждой волны 10/5 = 2 секунды.
Использование формулы скорости волны
Все электромагнитное излучение, к одному типу которого относится видимый свет, распространяется с постоянной скоростью, обозначаемой буквой c , через вакуум. Вы можете написать формулу скорости волны, используя это значение, и поступить так, как обычно делают физики, заменив период волны ее частотой.Формула принимает следующий вид:
c = \ frac {λ} {T} = f × λ
Поскольку c является константой, это уравнение позволяет вычислить длину волны света, если вы знаете его частоту и наоборот. наоборот. Частота всегда выражается в герцах, и, поскольку свет имеет чрезвычайно малую длину волны, физики измеряют ее в ангстремах (Å), где один ангстрем равен 10 −10 метров.
Простой калькулятор гармонического движения
Этот простой калькулятор гармонического движения поможет вам определить смещение, скорость и ускорение колеблющейся частицы.Все, что вам нужно сделать, это определить основные свойства периодического движения — например, его частоту и амплитуду — и ввести их в простые уравнения гармонического движения.
Если вас интересует, как гармоническая волна распространяется в пространстве, воспользуйтесь калькулятором уравнения гармонической волны.
Что такое простое гармоническое движение?
Простое гармоническое движение — это разновидность колебательного движения. При таком движении частица всегда движется по одному и тому же пути с ускорением к фиксированной точке.
Прекрасным примером для такого случая может служить простой маятник. Масса, подвешенная на струне, которая перемещается из положения равновесия, будет двигаться вперед и назад, всегда ускоряясь к точке равновесия. Если предположить отсутствие потерь энергии, маятник будет продолжать качаться вечно. В точке равновесия кинетическая энергия максимальна.
Простые уравнения гармонического движения
Если вам известен период колебаний, можно вычислить положение, скорость и ускорение частицы в каждый отдельный момент времени.Все, что вам нужно сделать, это применить следующие простые уравнения гармонического движения:
y = A * sin (ωt)
v = A * ω * cos (ωt)
a = - A * ω² * sin (ωt)
где:
- А — амплитуда колебаний,
- ω — угловая частота колебаний в рад / с. Его можно рассчитать как
ω = 2πf, где f — частота, - t — момент времени, когда вы измеряете смещение частицы,
- y — смещение,
- v — скорость, а
- — это ускорение.
Как рассчитать ускорение колеблющейся частицы?
Давайте проанализируем пример частицы в простом гармоническом движении. Мы хотим узнать, что такое смещение, скорость и ускорение при t = 1,4 с.
- Определите частоту колебаний. Предположим, это равно
f = 1 Гц. - Рассчитайте угловую частоту по формуле
ω = 2πf = 2π * 5 = 6,288 рад / с. - Определите, какова амплитуда колебаний.Возьмем
A = 15 мм. - Подставьте все значения в простые уравнения гармонического движения:
y = 15 * sin (6,28 * 1,4) = 8,82 мм
v = 15 * 6,28 * cos (6,28 * 1,4) - -76,25 мм / с
a = - 15 * 6,28² * sin (6,28 * 1,4) = -348 мм / с²
Конечно, вместо того, чтобы рассчитывать это вручную, вы можете ввести все значения в этот простой калькулятор гармонического движения.
Учебное пособие по физике: Свойства периодического движения
Вибрирующий объект колеблется в фиксированном положении.Как и масса пружины на анимации справа, вибрирующий объект движется по тому же пути с течением времени. Его движение повторяется снова и снова. Если бы не , демпфирующий , колебания продолжались бы вечно (или, по крайней мере, до тех пор, пока кто-нибудь не поймает массу и не остановит ее). Масса на пружине не только повторяет одно и то же движение, но и делает это обычным образом. Время, необходимое для выполнения одного цикла вперед и назад, всегда одинаковое.Если массе требуется 3,2 секунды для завершения первого цикла вперед-назад, то для завершения седьмого цикла вперед-назад потребуется 3,2 секунды. Это как по маслу. Это настолько предсказуемо, что по нему можно настроить часы. В физике регулярное и повторяющееся движение называется периодическим движением. Большинство объектов, которые вибрируют, совершают регулярные и повторяющиеся колебания; их колебания периодические. (Отдельное спасибо Олегу Александрову за анимацию мессы на пружине.Это общественное достояние, приобретенное у WikiMedia Commons. )
Синусоидальная природа вибрации
Предположим, что датчик движения был размещен под вибрирующей массой на пружине, чтобы обнаруживать изменения положения массы с течением времени. И предположим, что данные от детектора движения могут представлять движение массы на графике положения в зависимости от времени. На рисунке ниже изображен такой график. Для обсуждения на графике отмечены несколько точек, которые помогут в последующем обсуждении.
Прежде чем читать дальше, подумайте о типе информации, которая отображается на графике. И найдите время, чтобы подумать о том, какие величины на графике могут быть важны для понимания математического описания массы на пружине. Если вы нашли время, чтобы обдумать эти вопросы, следующее обсуждение, вероятно, будет более содержательным.
Одна очевидная характеристика графика связана с его формой.Многие студенты узнают форму этого графика по опыту на уроках математики. График имеет форму синусоиды. Если y = sine (x) построено на графическом калькуляторе, будет создан график с такой же формой. Вертикальная ось приведенного выше графика представляет положение груза относительно детектора движения. Положение около 0,60 см над детектором соответствует положению покоящегося груза. Таким образом, масса с течением времени колеблется взад и вперед относительно этого фиксированного положения покоя.Есть или синусоидальное колебание массы на пружине. То же самое можно сказать о маятнике, колеблющемся относительно фиксированного положения, или о гитарной струне, или о воздухе внутри духового инструмента. Положение массы является функцией синуса времени.
Второй очевидной характеристикой графа может быть его периодический характер. Движение повторяется регулярно. Время откладывается по горизонтальной оси; поэтому любое измерение, проведенное по этой оси, является мерой времени, когда что-то должно произойти.Полный цикл вибрации можно представить как перемещение груза из положения покоя (A) на максимальную высоту (B), обратно вниз за пределы положения покоя (C) в минимальное положение (D) и затем вернитесь в исходное положение (E). Используя измерения по оси времени, можно определить время для одного полного цикла. Гиря находится в позиции A за 0,0 секунды и завершает свой цикл, когда она находится в позиции E за 2,3 секунды. Требуется 2.3 секунды для завершения первого полного цикла вибрации. Теперь, если движение этой массы является периодическим (то есть регулярным и повторяющимся), то для завершения любого полного цикла вибрации потребуется 2,3 секунды. Те же измерения по оси времени можно провести для шестого полного цикла вибрации. В шестом полном цикле груз перемещается из положения покоя (U) в положение V, обратно вниз через W к X и, наконец, обратно в положение покоя (Y) в интервале времени от 11,6 до 13,9 секунд.Это составляет 2,3 секунды, чтобы завершить шестой полный цикл вибрации. Два времени цикла идентичны. Другие времена цикла указаны в таблице ниже. Осмотрев таблицу, можно с уверенностью заключить, что движение массы на пружине регулярное и повторяющееся; он явно периодический. Небольшое отклонение от 2,3 с в третьем цикле можно объяснить отсутствием точности считывания графика.
Цикл | Письма | раз в начале и | |
1-я | A — E | 0.0 сто 2,3 с | 2,3 |
2-я | E tp I | от 2,3 до 4,6 с | 2,3 |
3-я | от I до M | 4.От 6 до 7,0 с | 2,4 |
4-я | M — Q | от 7,0 до 9,3 с | 2,3 |
5-я | От Q до U | 9.От 3 до 11,6 с | 2,3 |
6-я | U — Y | от 11,6 до 13,9 с | 2,3 |
Студенты, просматривающие приведенный выше график, часто описывают движение массы как «замедление».«Возможно, еще слишком рано говорить подробно о том, что означает замедление . Мы сохраним длительное обсуждение этой темы для страницы позже в этом уроке, посвященной движению массы на пружине. А пока давайте просто говорят, что со временем масса претерпевает изменения в своей скорости синусоидальным образом. То есть скорость массы в любой данный момент времени является функцией синуса времени. Таким образом, масса будет и увеличиваться и замедляться в течение одного цикла.Таким образом, сказать, что масса «замедляется», не совсем точно, так как во время каждого цикла есть два коротких интервала, в течение которых она ускоряется. (Подробнее об этом позже.)
Студенты, которые описывают массу как замедляющуюся (а большинство наблюдательных студентов действительно описывают это таким образом), явно наблюдают что-то на графике, что указывает на «замедление». Прежде чем мы обсудим функцию, которая запускает комментарий «замедление», мы должны повторить вывод из предыдущих параграфов — время завершения одного цикла вибрации НЕ меняется.Для завершения первого цикла потребовалось 2,3 секунды, а для завершения шестого цикла — 2,3 секунды. Что бы ни означало «замедление», мы должны опровергнуть представление о том, что циклы растягиваются по мере продолжения движения. Это мнение явно противоречит имеющимся данным.
Третьей очевидной характеристикой графика является то, что демпфирование происходит с помощью системы масса-пружина. Некоторая энергия со временем рассеивается. Степень перемещения массы выше (B, F, J, N, R и V) или ниже (D, H, L, P, T и X) положения покоя (C, E, G, I и т. Д.)) меняется с течением времени. В показанном первом полном цикле вибрации груз перемещается из своего положения покоя (A) на 0,60 м над детектором движения в высокое положение (B) на 0,99 см над детектором движения. Это полное смещение вверх 0,29 м. В показанном шестом полном цикле вибрации груз перемещается из своего положения покоя (U) на высоте 0,60 м над детектором движения в высокое положение (V) на высоте 0,94 м над детектором движения. Это полное смещение вверх 0,24 м см.В таблице ниже приведены результаты измерений смещения для нескольких других циклов, отображаемых на графике.
Цикл | Письма | Максимум вверх | Максимум вниз |
1-я | A — E | 0.От 60 до 0,99 м | 0,60–0,21 м |
2-я | E до I | 0,60–0,98 м | 0,60–0,22 м |
3-я | от I до M | 0.От 60 м до 0,97 м | 0,60–0,23 м |
6-я | U — Y | 0,60–0,94 м | 0,60–0,26 м |
С течением времени груз продолжает вибрировать, двигаясь от исходного положения покоя и обратно.Однако величина смещения массы на максимальной и минимальной высоте уменьшается от одного цикла к другому. Это показывает, что система масса-пружина теряет энергию. Если дать достаточно времени, вибрация массы в конечном итоге прекратится, поскольку ее энергия рассеивается.
Возможно, это наблюдение рассеяния или потери энергии является наблюдением, которое вызывает комментарий о «замедлении», обсуждавшийся ранее. В физике (или, по крайней мере, в английском языке) «замедление» означает «замедляться» или «терять скорость».Скорость, физический термин, относится к тому, насколько быстро или медленно движется объект. Сказать, что масса на пружине «замедляется» с течением времени, значит сказать, что ее скорость со временем уменьшается. Но, как уже упоминалось (и это будет подробно обсуждаться позже), масса ускоряется в течение двух интервалов каждого цикла. Когда восстанавливающая сила тянет массу обратно в положение покоя (например, от B к C и от D к E), масса ускоряется. По этой причине физик использует другой язык, чтобы передать идею о том, что вибрации «затухают».Мы используем фразу «энергия рассеивается или теряется» вместо того, чтобы говорить «масса замедляется». Когда дело доходит до изучения физики, язык важен. А иногда неправильный язык (в сочетании с поверхностным мышлением) может сбить с толку изучающего физику, искренне пытающегося усвоить новые идеи.
Период и частота
До сих пор в этой части урока мы рассматривали измерения времени и положения груза на пружине.Измерения были основаны на показаниях графика положения-времени. Данные на графике были собраны детектором движения, который фиксировал истории движения с течением времени. Ключевыми измерениями, которые были выполнены, являются:
- время завершения цикла массы, а
- максимальное смещение груза выше (или ниже) положения покоя.
У этих двух измеряемых величин есть имена.Мы называем эти величины периодом и амплитудой.
Периодически движущийся объект — например, гиря на пружине, маятник или кукла-болвана — будет подвергаться возвратно-поступательным колебаниям относительно фиксированного положения регулярным и повторяющимся образом. Тот факт, что периодическое движение является регулярным и повторяющимся, означает, что его можно математически описать величиной, известной как период. Период движения объекта определяется как время, за которое объект выполняет один полный цикл.Поскольку это время, период измеряется в таких единицах, как секунды, миллисекунды, дни или даже годы. Стандартная метрическая единица измерения периода — секунда.
Периодически движущийся объект может иметь длительный или короткий период. Например, маятник, привязанный к веревке длиной 1 метр, имеет период около 2,0 секунд. Для сравнения рассмотрим колебания фортепианной струны, которая воспроизводит среднюю ноту до (ноту до четвертой октавы). Его период примерно равен 0.0038 секунд (3,8 миллисекунды). Сравнивая эти два вибрирующих объекта — маятник длиной 1,0 метр и струну фортепиано, которая воспроизводит среднюю ноту C , — мы бы описали струну фортепиано как вибрирующую относительно часто, а маятник — как колеблющуюся относительно редко. Обратите внимание, что в описании двух объектов используются термины часто и редко . Термины быстро и медленные не используются, поскольку типы физики резервируют слова быстро и медленные для обозначения скорости объекта.Здесь, в этом описании, мы имеем в виду частоту, а не скорость. Объект может находиться в периодическом движении с низкой частотой и высокой скоростью. В качестве примера рассмотрим периодическое движение Луны по орбите вокруг Земли. Луна движется очень быстро; его орбита очень редка. Он движется в космосе со скоростью около 1000 м / с — это быстро. Тем не менее, он совершает полный цикл вокруг Земли каждые 27,3 дня (период около 2,4х10 5 секунд) — это нечасто.
Такие объекты, как фортепианная струна, которые имеют относительно короткий период (т. Е. Низкое значение периода), как говорят, имеют высокую частоту. Частота — еще одна величина, которую можно использовать для количественного описания движения объекта — периодического движения. Частота определяется как количество полных циклов, происходящих за период времени. Поскольку стандартной метрической единицей времени является секунда, частота измеряется в циклах в секунду. Единица циклов в секунду эквивалентна единице Герц (сокращенно Гц).Единица Герца используется в честь Генриха Рудольфа Герца, физика 19 века, который расширил наши представления об электромагнитной теории световых волн.
Понятие и количество частот лучше всего понять, если связать его с повседневным английским значением этого слова. Частота — это слово, которое мы часто используем, чтобы описать, как часто что-то происходит. Вы можете сказать, что часто проверяете свою электронную почту, часто разговариваете с другом или часто моете руки при работе с химическими веществами.Используемый в этом контексте, вы имеете в виду, что выполняете эти действия часто. Сказать, что вы часто проверяете электронную почту, означает, что вы делаете это несколько раз в день — вы делаете это часто. В физике частота используется с тем же значением — она указывает, как часто происходит повторяющееся событие. Периодические высокочастотные события происходят часто с небольшим промежутком времени между ними — например, возвратно-поступательные колебания зубцов камертона. Вибрации настолько часты, что их невозможно увидеть невооруженным глазом.Камертон с частотой 256 Гц имеет зубцы, которые совершают 256 полных возвратно-поступательных колебаний каждую секунду. На этой частоте зубьям требуется всего около 0,00391 секунды для завершения одного цикла. Камертон с частотой 512 Гц имеет еще более высокую частоту. Его колебания происходят чаще; время завершения полного цикла составляет 0,00195 секунды. При сравнении этих двух камертонов очевидно, что камертон с самой высокой частотой имеет самый низкий период. Две величины, частота и период, обратно пропорциональны друг другу.Фактически, они математически противоположны друг другу. Частота является обратной величиной периода, а период — обратной величиной частоты.
Эту взаимную связь легко понять. В конце концов, эти две величины — это концептуальных обратных (фраза, которую я придумал). Рассмотрим их определения, приведенные ниже:
- период = время завершения одного полного цикла; то есть секунд / цикл
- частота = количество циклов, которые выполняются за раз; я.е., циклов / сек
Даже в определениях есть ответное кольцо . Чтобы понять разницу между периодом и частотой, рассмотрим следующее утверждение:
Согласно Википедии (и на момент написания этой статьи) Тим Альстром из Окономовока, штат Висконсин, является рекордсменом по хлопкам в ладоши. Сообщается, что он хлопал в ладоши 793 раза за 60,0 секунды.
Какая частота и каков период, когда мистер Альстрем хлопал в ладоши в эти 60?0-секундный период?
Амплитуда колебаний
Последней измеряемой величиной, описывающей вибрирующий объект, является амплитуда. Амплитуда определяется как максимальное смещение объекта из положения покоя . Положение покоя — это положение, которое принимает объект, когда он не вибрирует. После вибрации объект колеблется в этом фиксированном положении. Если объект представляет собой массу на пружине (например, как обсуждалось ранее на этой странице), то он может быть смещен на максимальное расстояние 35 см ниже положения покоя и 35 см выше положения покоя.В этом случае амплитуда движения составляет 35 см.
С течением времени амплитуда вибрирующего объекта имеет тенденцию становиться все меньше и меньше. Амплитуда движения отражает количество энергии, которой обладает вибрирующий объект. Объект, колеблющийся с относительно большой амплитудой, обладает относительно большим количеством энергии. Со временем часть этой энергии теряется из-за затухания. По мере потери энергии амплитуда уменьшается. Если дать достаточно времени, амплитуда уменьшается до 0, поскольку объект, наконец, перестает вибрировать.На данный момент он потерял всю свою энергию.
Мы хотели бы предложить …
Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных средств Физического класса. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей Mass on Spring Interactive.



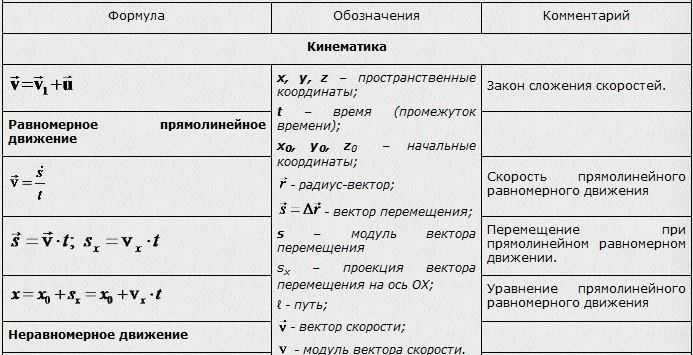 Какие виды механического движения вы знаете?
Какие виды механического движения вы знаете?
 Новый материал. Тема урока:
Новый материал. Тема урока:
 59)
59)
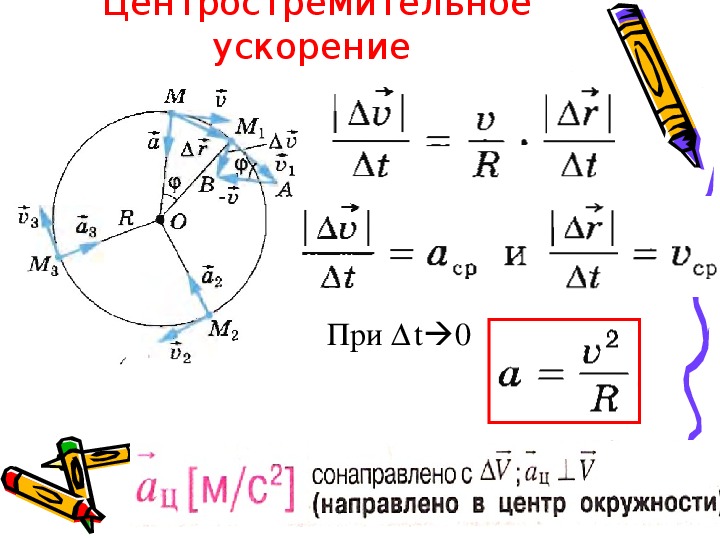
 Равномерное движение по окружности.
Равномерное движение по окружности. 61-63.
61-63. С помощью закона движения
С помощью закона движения
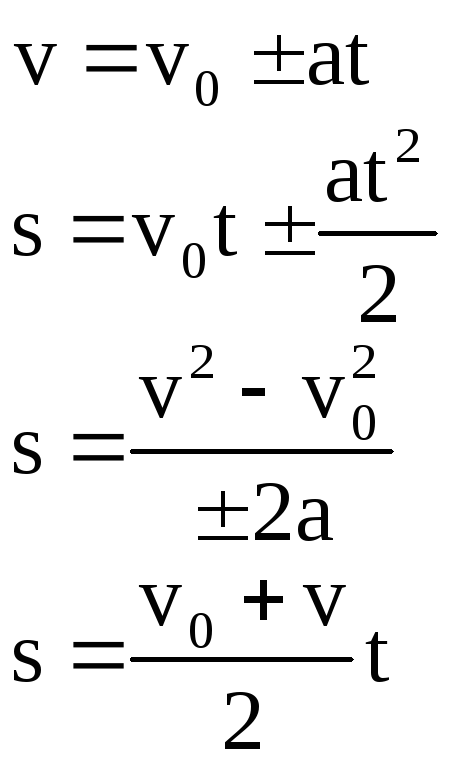
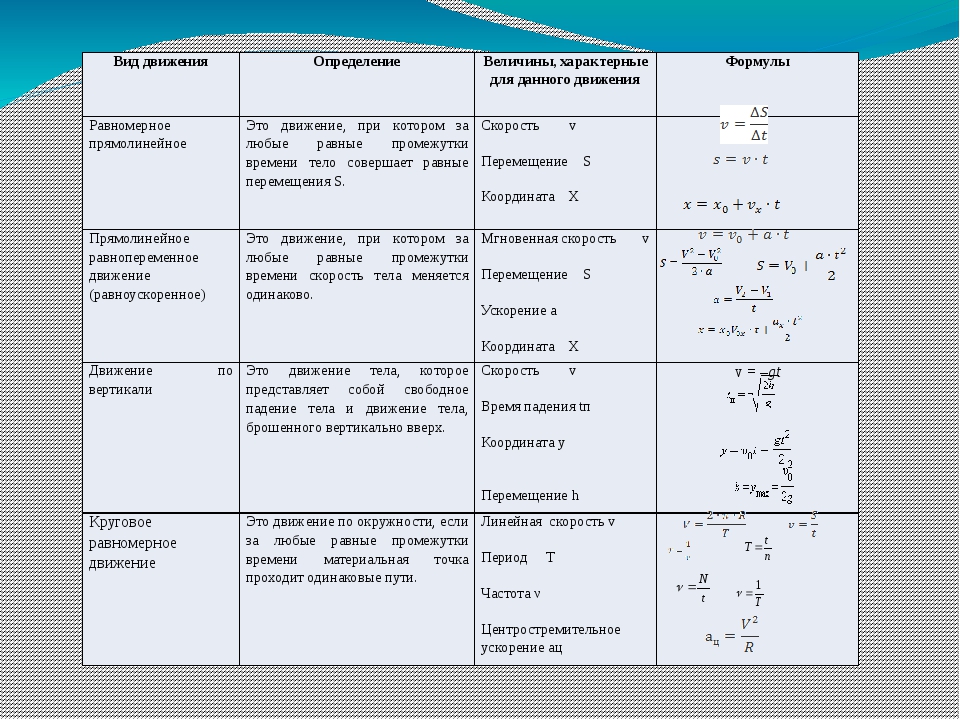 Как зависит ац от скорости и от радиуса?
Как зависит ац от скорости и от радиуса?