|
|
|
|
|
|
|
|
Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне.
| |
|
|
|
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
| |
|
|
|
Площадь треугольника равна корню квадратному из произведения полупериметра этого треугольника и разностей полупериметра и всех его сторон.
| |
|
|
|
Площадь треугольника равна отношению произведения квадрата его стороны на синусы прилежащих углов к удвоенному синусу противолежащего угла.
| |
|
|
|
Площадь треугольника равна отношению произведения квадрата его высоты на синус угла, из вершины которого проведена эта высота, к удвоенному произведению синусов двух других углов.
| |
|
|
|
| |
|
|
|
Площадь прямоугольного треугольника равна половине произведения его катетов.
| |
|
|
|
Площадь равнобедренного треугольника равна половине произведения его основания на корень квадратный из разности квадратов боковой стороны и половины основания.
| |
|
|
|
Площадь равностороннего треугольника равна четверти произведения квадрата стороны этого треугольника и квадратного корня из трёх.
| |
|
|
|
Площадь равностороннего треугольника равна отношению квадрата его высоты к квадратному корню из трёх.
| |
|
|
|
Площадь треугольника равна отношению произведения всех его сторон к четырём радиусам, описанной около него окружности.
| |
|
|
|
Площадь треугольника равна удвоенному произведению квадрата радиуса, описанной около него окружности, и синусов всех его углов.
| |
|
|
|
Площадь треугольника (многоугольника) равна произведению его полупериметра и радиуса окружности, вписанной в этот треугольник (многоугольник).
| |
|
|
|
Площадь треугольника равна произведению квадрата радиуса вписанной окружности на котангенсы половин всех углов треугольника.
| |
|
|
|
Площадь прямоугольника равна произведению двух соседних его сторон.
| |
|
|
|
Площадь квадрата равна квадрату его стороны.
| |
|
|
|
Площадь квадрата равна половине квадрата его диагонали.
| |
|
|
|
Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.
| |
|
|
|
Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними.
| |
|
|
|
Площадь ромба равна произведению квадрата его стороны на синус одного из его углов.
| |
|
|
|
Площадь ромба (как и дельтоида) равна половине произведения его диагоналей.
| |
|
|
|
Площадь трапеции равна произведению полусуммы её оснований на высоту.
| |
|
|
|
Площадь трапеции равна произведению её средней линии на высоту.
| |
|
|
|
Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
| |
|
|
| Площадь четырёхугольника, вписанного в окружность, равна корню квадратному из произведения разностей полупериметра этого четырёхугольника и всех его сторон.
| |
|
|
|
Площадь круга равна произведению числа «пи» на квадрат радиуса.
| |
|
|
|
Площадь круга равна четверти произведения числа «пи» на квадрат диаметра.
| |
|
|
формулы для случаев градусной и радианной мер центральных углов
|
Площадь кругового сектора равна произведению площади единичного сектора (сектор, соответствующий центральному углу с мерой равной единице) на меру центрального угла, соответствующего данному сектору.
| |
|
|
|
Площадь кругового кольца равна произведению числа «пи» на разность квадратов внешнего и внутреннего радиусов.
| |
|
|
|
Площадь кругового кольца равна четверти произведения числа «пи» на разность квадратов внешнего и внутреннего диаметров.
| |
|
|
|
Площадь кругового кольца равна удвоенному произведению числа «пи», среднего радиуса кольца и его ширины.
|
Площади геометрических фигур. 8-й класс
Цели: закреплять навыки в решении задач по
теме “Площади” и готовиться к ОГЭ.
Задачи:
Образовательные:
- обобщить знания и умения учащихся по теме
“Площадь”.
Развивающие:
- формировать умения ясно и четко излагать свои
мысли; - формировать навыки публичного выступления и
умения отстаивать самостоятельное суждение.
Воспитательные:
- создавать условия для реальной самооценки
учащихся, реализации его как личности; - воспитывать познавательный интерес к предмету;
- воспитывать эстетический вкус.
Оборудование: компьютер, проектор, экран,
раздаточный материал.
План урока:
- Организационный. Постановка цели урока.
- Повторение. Устная работа.
- Решение задач.
- Заключительная часть. Подведение итогов урока.
- Домашнее задание.
Ход урока
I. Организационный. Постановка цели урока
Мы заканчиваем изучение темы: “ Площади”.
Сегодня на уроке мы вспомним, как вычисляются
площади различных фигур. Решим задачи, опираясь
на наши знания по этой теме.
II. Устная работа
Перед тем, как начнем решать задачи,
давайте вспомним фигуры, которые мы с вами
изучали и формулы для вычисления их площадей.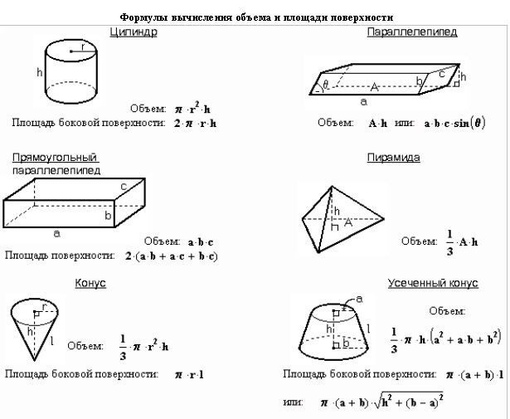
На доске подготовлена таблица.
| № | фигура | формулы |
| 1 | квадрат | |
| 2 | прямоугольник | |
| 3 | параллелограмм | |
| 4 | ромб | |
| 5 | треугольник | |
| 6 | трапеция |
По окончании устно работы таблица имеет такой
вид.
Для проведения устной работы используется
презентация
.
Приложение слайд 1
Задача 1.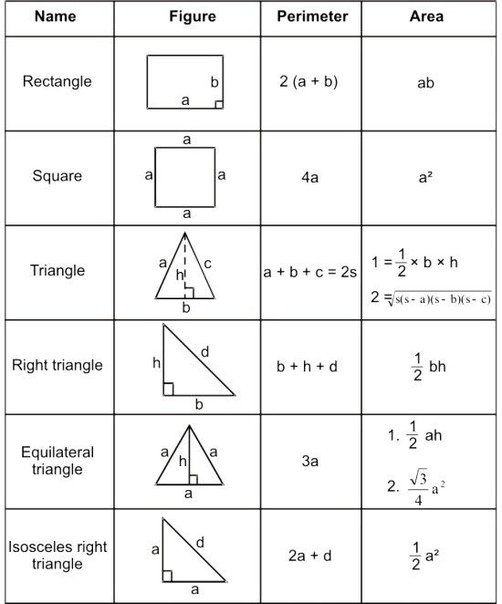 Используя слайды, учащиеся должны
Используя слайды, учащиеся должны
выбрать формулу для вычисления площади
изображенной фигуры и обосновать свой ответ.
Пример.
Фигура ABCD – квадрат, т.к. на чертеже
показано, что у данного четырёхугольника все
стороны равны и все углы по 90°. Значит, для
вычисления площади воспользуемся формулой под
номером.
Слайд 1 включает в себя 4 задачи подобного
типа, решение которых позволяет не только ещё раз
вспомнить формулы, но и
позволяет вспомнить
основные свойства площадей плоских фигур.
III.
Решение задач
Сейчас мы с вами будем решать задачи, которые в
экзаменационных работах стоят в блоке
“Геометрия” № 11. Предлагаю вам разделиться на
группы. На экране будут появляться задачи, та
группа, которая первая найдет решение, отвечает у
доски, остальные помогают. За каждый правильный
полный ответ группа получает 5 баллов. За не
достаточные обоснования снимается 1 балл и
передается той группе, которая сможет дополнить.
Для решения задач используется
презентация.
Приложение слайд 2 – 9
На каждом слайде есть кнопка “Подсказка” с
указанием количества подсказок. Ей имеет смысл
воспользоваться, если возникают затруднения с
решением задач.
IV. Заключительный этап.
Подведение итогов
Домашняя работа
1. Задание 11 № 195. Найдите площадь
параллелограмма, изображённого на рисунке.
2. Задание 11 № 333013. Основания трапеции
равны 1 и 11. Найдите бoльший из отрезков, на
которые делит среднюю линию этой трапеции одна
из её диагоналей.
3. Задание 11 № 323902. Основания
равнобедренной трапеции равны 5 и 17, а ее боковые
стороны равны 10. Найдите площадь трапеции.
Ресурсы Интернет.
- http://100formul.ru
- http://sdamgia.ru/
Калькулятор вычисления периметра и площади геометрических фигур
Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач.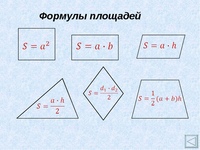 Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.
Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.
Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами. Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.
Круг
Окружность — это множество точек на плоскости, которые равноудалены от центра на некоторое расстояние, называемое радиусом. Многие считают круг и окружность синонимами, однако это не так. Круг — это часть плоскости, ограниченная окружностью. Вы можете отыскать периметр и площадь круга, но у окружности найти можно только длину, так как она представляет собой кривую, не имеющую площади. Длина окружности или периметр круга находятся по простой формуле:
l = 2 pi × R,
где R – радиус фигуры.
Площадь круга рассчитывается согласно следующему выражению:
S = pi R2
Круги часто встречаются в реальной жизни.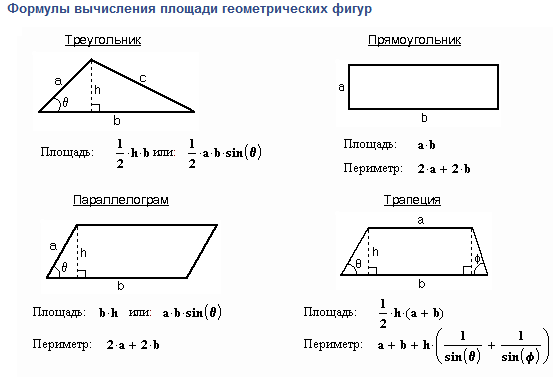 В основном это основания цилиндрических и конических деталей, а также просто круглые поверхности, например, круглые столики, диски, грампластинки или катушки. Вид окружности имеют колеса, обручи или кольца. В трехмерной реальности окружность превращается в сферу, а круг — в шар. Форму этих геометрических тел имеют многие реальные и природные объекты. Благодаря своей эффективности круг охватывает максимальную площадь при минимальном периметре. Именно поэтому форму шара имеют капли, снежные комья, метеориты или планеты.
В основном это основания цилиндрических и конических деталей, а также просто круглые поверхности, например, круглые столики, диски, грампластинки или катушки. Вид окружности имеют колеса, обручи или кольца. В трехмерной реальности окружность превращается в сферу, а круг — в шар. Форму этих геометрических тел имеют многие реальные и природные объекты. Благодаря своей эффективности круг охватывает максимальную площадь при минимальном периметре. Именно поэтому форму шара имеют капли, снежные комья, метеориты или планеты.
Треугольник
Треугольник — первая гармоничная фигура на плоскости, ограниченная тремя отрезками. Свойства треугольника известны людям с античных времен: изучение фигуры стартовало в Древнем Египте и не завершено до сих пор. Огромный вклад в изучение свойств фигуры внесли Евклид, Эйлер и Лобачевский, но даже сегодня продолжается работа над поиском замечательных точек треугольника, которых на данный момент найдено более 6 тысяч. Для определения периметра фигуры достаточно сложить длины всех сторон треугольника по формуле:
P = a + b + c,
где a, b, c – стороны.
Для вычисления площади треугольника используется 5 различных формул плюс нахождение площади через определенный интеграл. Самое простое выражение для вычисления площади:
S = 0,5 a × h,
где a — сторона треугольника, h — его высота.
Наш калькулятор позволяет отыскать площадь или периметр треугольника, зная разные комбинации нескольких параметров, таких как углы, стороны или радиусы связанных окружностей.
Треугольники не слишком распространены в реальной повседневности. В природе они практически не встречаются, за исключением кристаллических решеток некоторых молекул или формы ушей у рыси. А вот в технике, геометрии и прикладных науках треугольник — царь и бог. Наибольшее применение находит следующий тип фигуры.
Прямоугольный треугольник
Прямоугольный треугольник — особая вариация фигуры, у которой две стороны обязательно образуют прямой угол. Эти стороны называются катетами, а противолежащая им сторона — гипотенузой. Соотношение катетов и гипотенузы лежит в основе евклидовой геометрии — эти соотношения определяются теоремой Пифагора. Изучение свойств прямоугольного треугольника положило начало одному из важных разделов математики — тригонометрии, которая используется в самых разных прикладных сферах от компьютерных игр до океанографии.
Изучение свойств прямоугольного треугольника положило начало одному из важных разделов математики — тригонометрии, которая используется в самых разных прикладных сферах от компьютерных игр до океанографии.
Формулы для вычисления периметра и площади прямоугольного треугольника ничем не отличаются от формул для обычных вариаций данной фигуры или вытекают из них.
Трапеция
Трапеция, как и слово трапеза, по-гречески означают «стол». Это плоская фигура, ограниченная четырьмя прямыми, две из которых параллельны, а две — нет. По сути, это выпуклый четырехугольник, поэтому параллелограмм и прямоугольник считаются частными случаями трапеции. В общем случае все стороны трапеции имеют разную длину, и для вычисления периметра используется формула:
P = a + b + c + d,
a, b, c и d – стороны четырехугольника.
Площадь фигуры определяется как:
S = 0,5 (a + b) × h,
где a и b – параллельные стороны трапеции, h – высота.
Трапеция очень часто встречается в рукотворном мире.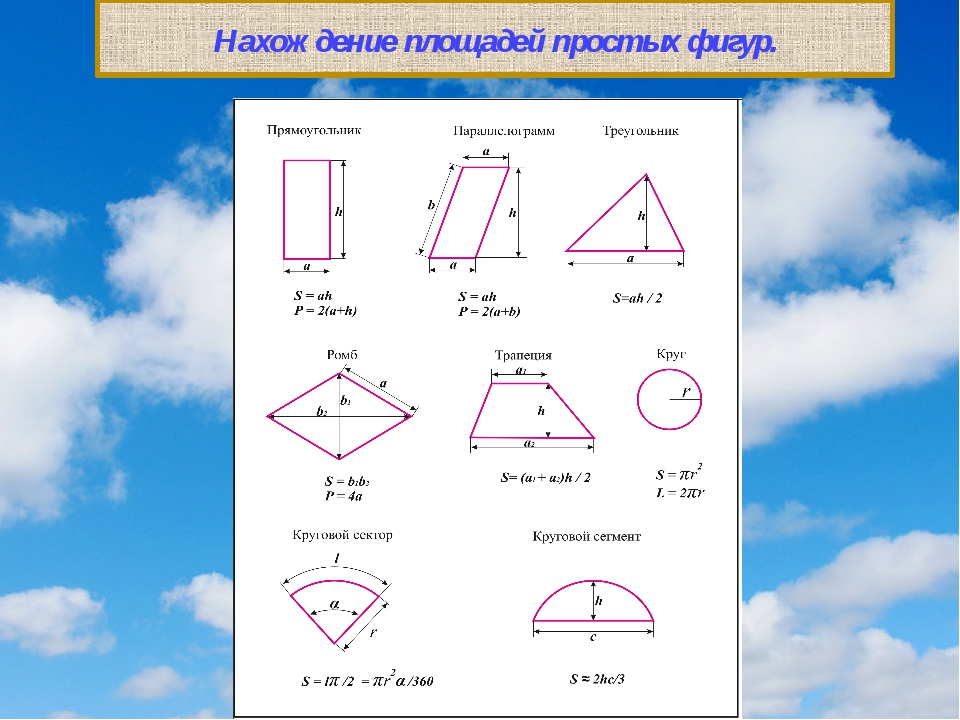 Грани многих предметов имеют вид этого четырехугольника, а буквально трапецеидальную форму имеют такие объекты как автомобильные окна, паруса, скаты крыш или юбки.
Грани многих предметов имеют вид этого четырехугольника, а буквально трапецеидальную форму имеют такие объекты как автомобильные окна, паруса, скаты крыш или юбки.
Параллелограмм
Параллелограмм — это элегантный четырехугольник, пары сторон которого параллельны друг другу. Любой четырехугольник становится параллелограммом, если его противолежащие стороны параллельны, диагонали в точке пересечения разделяются пополам, а противоположные углы равны. Для вычисления периметра параллелограмма используется простая формула, которая иллюстрирует сумму попарно равных сторон:
P = 2 (a + b).
Площадь параллелограмма не зависит от величины его углов, и находится по следующей формуле:
S = a × h.
Параллелограммы часто встречаются в реальной жизни: это грани многих призматических объектов, очертания полей, спортивных площадок или клумб. Форму параллелограммов имеют практически все отделочные материалы: плитка, кафель, гипсокартон, паркет. Такое разнообразие обусловлено тем, что частными случаями параллелограмма являются прямоугольник, ромб и квадрат, формулы для определения периметров и площадей которых аналогичны или выводятся из теоремы Пифагора.
Частные случаи
Ромб — четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.
Прямоугольник — это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.
Квадрат — это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.
Многоугольник
Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы. В зависимости от количества сторон многоугольники имеют собственные названия:
И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников.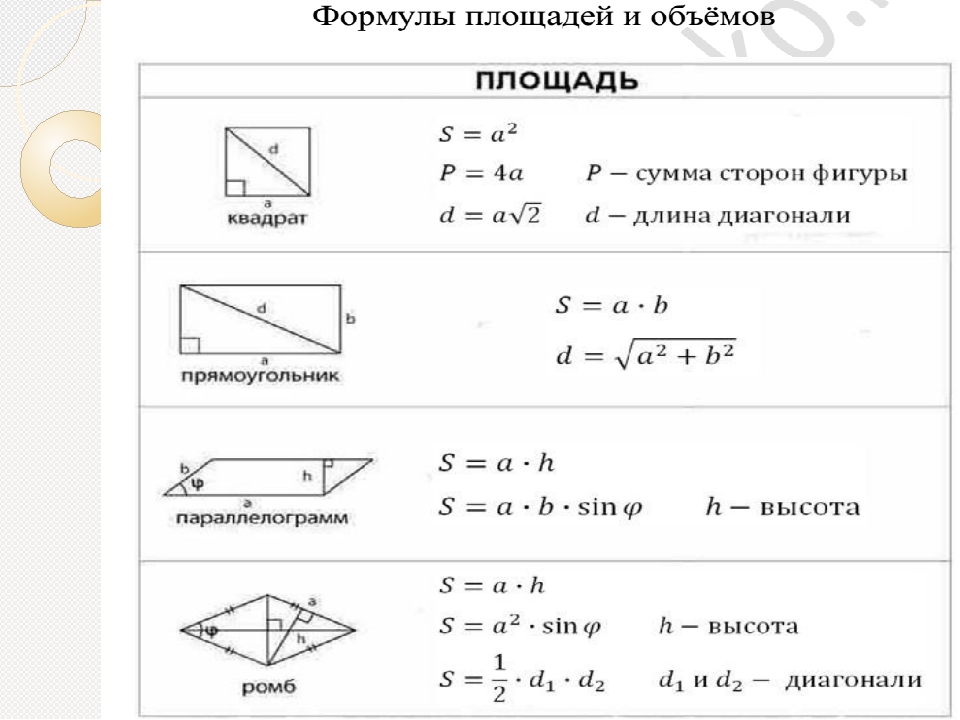 Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:
Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:
P = n × a,
где n – количество сторон многоугольника, a – длина стороны.
Для определения площади используется выражение:
S = n/4 × a2 × ctg(pi/n).
Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.
Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.
Примеры из реальной жизни
Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.
Покраска забора
Покраска поверхностей и расчет краски — это одни из самых очевидных бытовых задач, в которых требуются минимальные математические расчеты.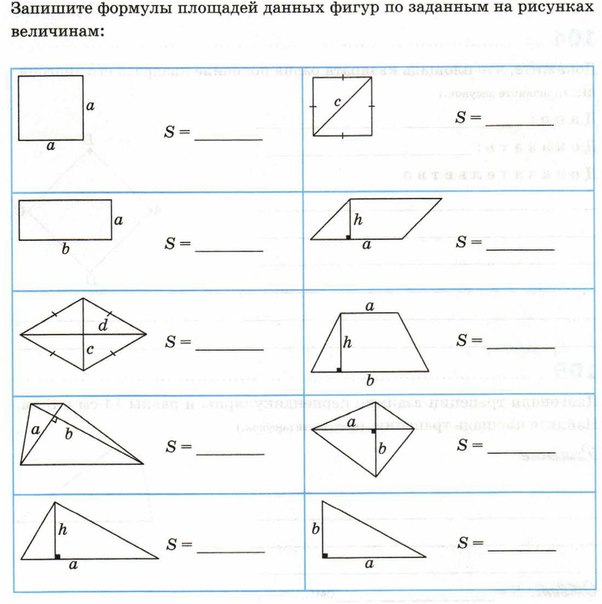 Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр. Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.
Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр. Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.
Отделка бахромой
Пошив одежды — еще одна отрасль, в которой необходимы обширные геометрические познания. Пусть нам надо отделать бахромой платок, который представляет собой равнобедренную трапецию со сторонами 150, 100, 75 и 75 см. Для вычисления расхода бахромы нам потребуется узнать периметр трапеции. В этом нам и пригодится онлайн-калькулятор. Введем эти данные ячейки и получим ответ:
P = 400
Таким образом, нам понадобится 4 м бахромы для отделки платка.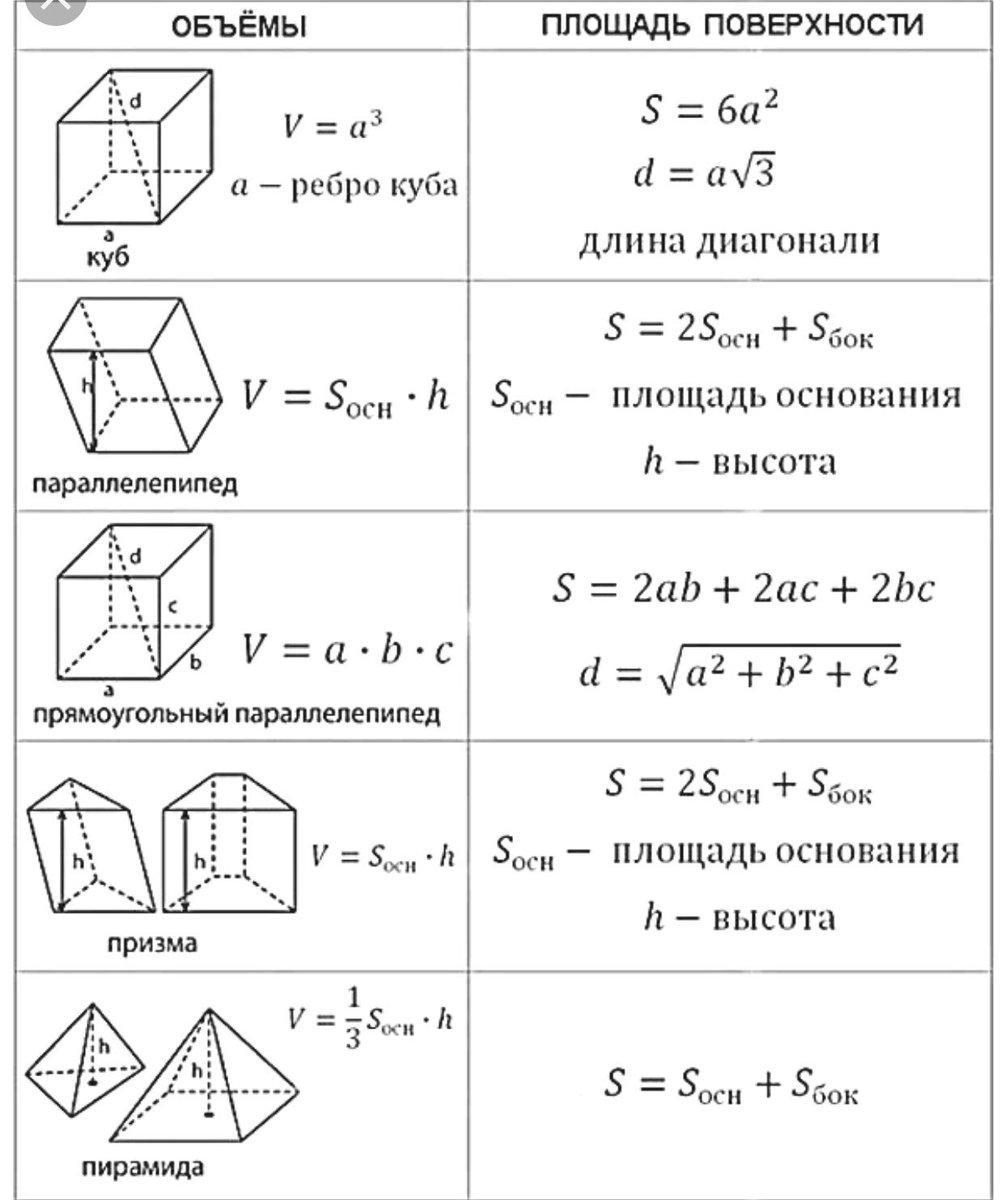
Заключение
Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни. И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.
ВЫЧИСЛЕНИЕ ПЛОЩАДИ ГЕОМЕТРИЧЕСКОЙ ФИГУРЫ, ЗАДАВАЕМОЙ НА КЛЕТЧАТОЙ БУМАГЕ
ВЫЧИСЛЕНИЕ ПЛОЩАДИ ГЕОМЕТРИЧЕСКОЙ ФИГУРЫ, ЗАДАВАЕМОЙ НА КЛЕТЧАТОЙ БУМАГЕ
Зарипова Д.М. 1
1
Кильмаматова З.М. 1
1МБОУ СОШ№1
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Площадь – это величина, характеризующая размер геометрической фигуры. Расположенный на плоскости многоугольник занимает какую-то ее часть. Размер этой части плоскости и будет равен площади многоугольника. Определение площадей геометрических фигур является одной из древнейших задач геометрии, которая и в настоящее время имеет важное практическое значение. Так, например, определение границы земельного участка, и, в конечном итоге вычисление площади земельного участка является одной из основных задач кадастра объектов недвижимости. Картографо-геодезическое обеспечение кадастра направлено на решение указанной задачи. Точность кадастровых работ регламентирована соответствующими нормативными документами. Площадь земельного участка и конечная стоимость земельного участка связаны между собой. Вполне очевидно, что с увеличением стоимости земель должны возрастать требования к точности определения координат точек границы участка. Повышение точности определения координат поворотных точек границ земельных участков может быть достигнуто с использованием современных технологий и средств измерений (спутниковая технология, электронные тахеометры и т.
Расположенный на плоскости многоугольник занимает какую-то ее часть. Размер этой части плоскости и будет равен площади многоугольника. Определение площадей геометрических фигур является одной из древнейших задач геометрии, которая и в настоящее время имеет важное практическое значение. Так, например, определение границы земельного участка, и, в конечном итоге вычисление площади земельного участка является одной из основных задач кадастра объектов недвижимости. Картографо-геодезическое обеспечение кадастра направлено на решение указанной задачи. Точность кадастровых работ регламентирована соответствующими нормативными документами. Площадь земельного участка и конечная стоимость земельного участка связаны между собой. Вполне очевидно, что с увеличением стоимости земель должны возрастать требования к точности определения координат точек границы участка. Повышение точности определения координат поворотных точек границ земельных участков может быть достигнуто с использованием современных технологий и средств измерений (спутниковая технология, электронные тахеометры и т. д.). Таким образом, данная проблема имеет прикладное значение, ее понимание, прежде всего, важно для тех, кто осваивает навыки в области геодезии, картографии и кадастра и других областях, связанных с нахождением площади фигур.
д.). Таким образом, данная проблема имеет прикладное значение, ее понимание, прежде всего, важно для тех, кто осваивает навыки в области геодезии, картографии и кадастра и других областях, связанных с нахождением площади фигур.
Объект исследования – геометрия, предмет исследования – площади геометрических фигур. Цель исследования: овладеть практическими навыками, техническими приёмами, которые потребуются для вычисления площадей геометрических фигур. Задачи исследования:1. Ознакомить с различными формулами вычисления .площадей геометрических фигур.2.Ознакомить с понятием определителей, свойствами определителей, формулой вычисления площади треугольника с помощью определителя.3. Ознакомить с формулой Пика.4.Вычислить площади геометрических фигур, задаваемых на системе координат, различными способами. Выявить слабые и сильные стороны этих способов.
ГЛАВА I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Рассмотрим систему из трех линейных уравнений относительно трех неизвестных
Определение. Определителем третьего порядка, соответствующим матрице системы, назовем число D, равное Для того, чтобы вычислить определитель третьего порядка применяют две вычислительные схемы, позволяющие вычислять определители третьего порядка без особых хлопот. Эти схемы известны как «правило треугольника» (или «правило звездочки») и «правило Саррюса». Правило треугольника: сначала перемножаются и складываются элементы, соединенными на схеме линиями
Определителем третьего порядка, соответствующим матрице системы, назовем число D, равное Для того, чтобы вычислить определитель третьего порядка применяют две вычислительные схемы, позволяющие вычислять определители третьего порядка без особых хлопот. Эти схемы известны как «правило треугольника» (или «правило звездочки») и «правило Саррюса». Правило треугольника: сначала перемножаются и складываются элементы, соединенными на схеме линиями
т.е. получаем сумму произведений: a11a22a33+a12a23a31+a21a13a32. Обратите внимание, что перемножаются элементы, соединенные одной линией, прямой или ломанной, а потом полученные произведения складываются. Затем перемножаются и складываются элементы, соединенные на схеме
т. е. получаем другую сумму произведений a13a22a31+a12a21a33+a11a23a32. И, наконец, чтобы вычислить определитель, из первой суммы вычитают вторую. Тогда окончательно получаем формулу вычисления определителя третьего порядка:
е. получаем другую сумму произведений a13a22a31+a12a21a33+a11a23a32. И, наконец, чтобы вычислить определитель, из первой суммы вычитают вторую. Тогда окончательно получаем формулу вычисления определителя третьего порядка:
D=(a11a22a33+a12a23a31+a21a13a32)-(a13a22a31+a12a21a33+a11a23a32). Правило Саррюса: к определителю справа дописывают два первых столбца, а затем считают сумму произведений элементов определителя в одном направлении и из нее вычитают сумму произведений элементов в другом направлении (Рис. 1):
Правило Саррюса: к определителю справа дописывают два первых столбца, а затем считают сумму произведений элементов определителя в одном направлении и из нее вычитают сумму произведений элементов в другом направлении (Рис. 1):
Рис. 1 Свойства определителей 3 порядкатакже помогают в вычислениях определителей:Свойство 1. Величина определителя не изменяется при замене строк столбцами.Свойство 2. При перестановке двух строк (столбцов) между собой, величина определителя меняет знак.Свойство 3. Определитель с двумя одинаковыми (пропорциональными) строками (столбцами) равен нулю.Свойство 4. Если все элементы некоторой строки (столбца) содержат одинаковый множитель, то этот множитель можно вынести за знак определителя.Свойство 5. Если все элементы некоторой строки (столбца) есть сумма равного числа слагаемых, то определитель будет равен сумме определителей, в которых элементы указанной строки (столбца) записываются отдельными слагаемыми. Свойство 6. Если все элементы некоторой строки (столбца) равны нулю, то весь определитель тоже равен нулю.Свойство 7. Величина определителя не изменится, если к элементам некоторой строки (столбца) добавить соответствующие элементы другой строки (столбца), предварительно умножив их на один и тот же множитель. Миноры и алгебраические дополненияРассмотрим определитель третьего порядка
Свойство 6. Если все элементы некоторой строки (столбца) равны нулю, то весь определитель тоже равен нулю.Свойство 7. Величина определителя не изменится, если к элементам некоторой строки (столбца) добавить соответствующие элементы другой строки (столбца), предварительно умножив их на один и тот же множитель. Миноры и алгебраические дополненияРассмотрим определитель третьего порядка
вычеркнем из определителя одну строку и один столбец, например, первую строку и второй столбец. Из оставшихся элементов составим определитель второго порядка
номер которого (индекс у D) определяется номерами вычеркнутых строки (первой) и столбца (второй). Если из определителя вычеркнуть другие строку и столбец, например, третий и третий, соответственно, то оставшиеся элементы будут также составлять определитель второго порядка, номер которого теперь будет другой –
Определение. Определитель, который получается вычеркиванием одной строки и одного столбца из исходного определителя называется минором основного определителя. Очевидно, что определитель третьего порядка имеет 9 различных миноров второго порядка, т.е. каждый элемент определителя имеет минор.
Очевидно, что определитель третьего порядка имеет 9 различных миноров второго порядка, т.е. каждый элемент определителя имеет минор.
Определение. Назовем алгебраическим дополнением любого элемента определителя D минор этого элемента, взятый со знаком плюс, если сумма номеров элемента четная и минус в противном случае . Теорема 1. Определитель D равен сумме произведений элементов любого столбца или строки на их алгебраические дополнения Очевидно, что для определителя третьего порядка можно записать шесть различных равенств (по трем столбцам и по трем строчкам). Теорема 2. Суммы, произведений элементов для любого столбца (строки) на алгебраические дополнения другого столбца (строки) определителя, равна нулю.Доказательство. Возьмем сумму произведений алгебраических дополнений первой строки на элементы третьей строки. Получим
Разложение определителя по строке или столбцу дает нам правило вычисления любых определителей высоких порядков (четвертого и выше). Определение . Определителем n -го порядка называется число равное алгебраической сумме
Определение . Определителем n -го порядка называется число равное алгебраической сумме
гдеAij=(-1)i+jDij есть алгебраические дополнения элемента aij, а Dij— есть соответствующие миноры, т.е. определители ( n-1 )-го порядка, получающиеся из исходного определителя вычеркиванием первой строки и n -го столбца, на пересечение которых находится элемент aij. Рассмотренные приемы позволяют вычислять определители любых порядков.
При нахождении площадей фигур можно пользоваться следующими приёмами:
1.Площадь треугольника с вершинами в точках вычисляется по формуле:
.
2.Площадь любого треугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника.
3. Любой сложный многоугольник можно представить составленным из более простых многоугольников. В этом случае его площадь равна сумме площадей, входящих многоугольников.
4.Можно воспользоваться формулой Пика Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S – площадь многоугольника, — число клеток, которые целиком лежат внутри многоугольника, и — число клеток, которые имеют с внутренностью. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки многоугольника хоть одну общую точку. Для вычисления площади такого многоугольника можно воспользоваться следующей теоремой: Теорема Пика. Пусть — число целочисленных точек внутри многоугольника, — количество целочисленных точек на его границе, — его площадь. Тогда справедлива формула Пика: .Доказательство теоремы Пика. Сначала заметим, что формула Пика верна для единичного квадрата. Действительно, в этом случае мы имеем . Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны и . Имеем в этом случае и, по формуле Пика, Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами и , рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат целочисленных точек. Тогда для этого случая и получаем, что Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник (Рис. 2 и Рис. 3). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.
Тогда справедлива формула Пика: .Доказательство теоремы Пика. Сначала заметим, что формула Пика верна для единичного квадрата. Действительно, в этом случае мы имеем . Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны и . Имеем в этом случае и, по формуле Пика, Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами и , рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат целочисленных точек. Тогда для этого случая и получаем, что Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник (Рис. 2 и Рис. 3). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.
Рис. 2 Рис. 3
2 Рис. 3
Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно разбить на треугольники (например, диагоналями). Поэтому нужно просто доказать, что при добавлении любого треугольника к произвольному многоугольнику формула Пика остается верной. Пусть многоугольник и треугольник имеют общую сторону. Предположим, что для формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из добавлением . Так как и имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через и получим — число внутренних целочисленных точек нового многоугольника, — число граничных точек нового многоугольника. Из этих равенств получаем Так как мы предположили, что теорема верна для и для по отдельности, то Что и требовалось доказать. Теорема Пика — классический результат комбинаторной геометрии и геометрии чисел.
Теорема Пика — классический результат комбинаторной геометрии и геометрии чисел.
Пример. Для многоугольника на рисунке (Рис. 3) (желтые точки), (синие точки, не забудьте о вершинах!), поэтому квадратных единиц.
Рис. 3
Задание B3. Найдите площади фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (Рис. 4). Ответ дайте в квадратных сантиметрах.
Рис. 4
ГЛАВА II. ПРАКТИЧЕСКАЯ ЧАСТЬ
Задача 1. Вычислить площадь .
1 способ.Решение. Решим задачу с помощью определителя. Введем вспомогательную прямоугольную систему координат (Рис. 5) и определяем координаты вершин данного треугольника: .
Рис. 5
Применим формулу :
Ответ: 8 кв.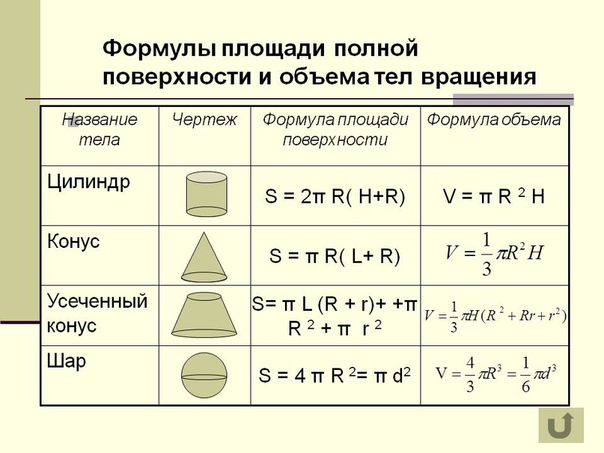 ед.
ед.
2 способ.Решение. Решим задачу с помощью формулы Проведем высоту CD к стороне AB (Рис. 6):
Рис. 6
Ответ: 8 кв.ед.
3 способ.Решение. Решим задачу с помощью способа «вырезания». Достроим прямоугольник (Рис. 7).
Рис. 7
Ответ: 8 кв.ед.
4 способ.Решение. Решим задачу с помощью формула Пика:. Выделим узловые внутренние и граничные точки фигуры (Рис. 8).
Рис. 8
Ответ: 8 кв.ед.
Применить метод «полных» клеток нельзя.
Задача 2. Вычислить площадь трапеции (Рис. 9).
Рис. 9
1 способ.Решение.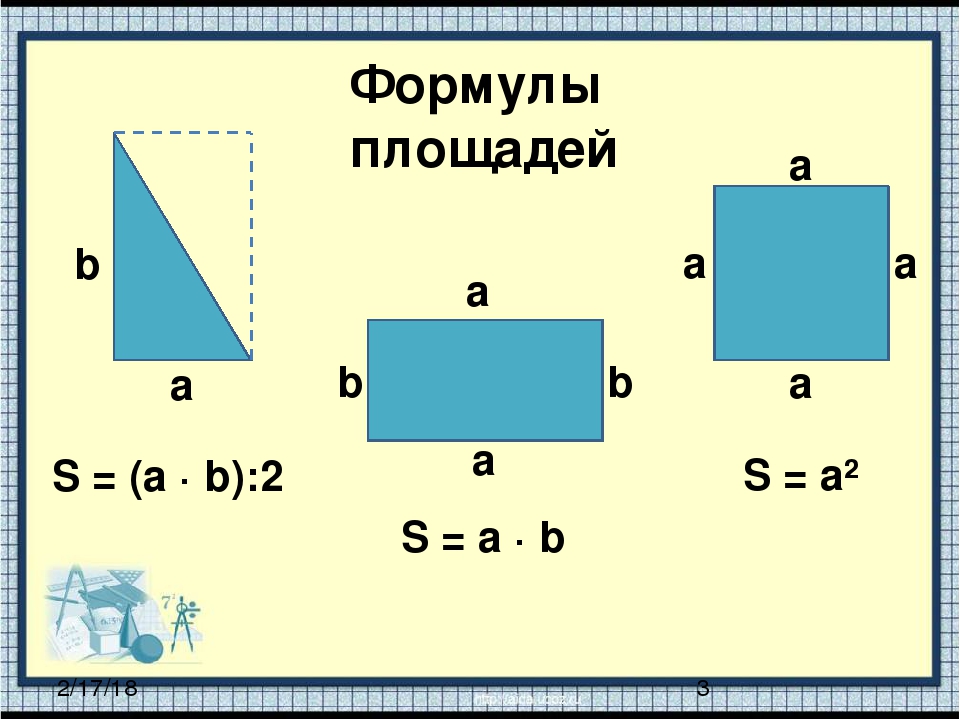 Решим задачу с помощью определителя. Для этого вводим вспомогательную прямоугольную систему координат (Рис. 10), разбиваем трапецию на треугольники, например, , с помощью вспомогательных построений, определяем координаты вершин полученных треугольников: .
Решим задачу с помощью определителя. Для этого вводим вспомогательную прямоугольную систему координат (Рис. 10), разбиваем трапецию на треугольники, например, , с помощью вспомогательных построений, определяем координаты вершин полученных треугольников: .
Рис. 10
Первый определитель вычисляем, замечая, что в первой строке только один элемент не равен нулю, а второй – разложением по второй строке.
Ответ: 10,5 кв.ед.2 способ. Решение. Решим задачу с помощью формулы
Ответ: 10,5 кв.ед.
3 способ.Решение. Решим задачу с помощью способа «вырезания». Достроим прямоугольник (Рис. 11).
Рис. 11
Ответ: 10,5 кв.ед.
4 способ.Решение. Решим задачу с помощью формула Пика:. Выделим узловые внутренние и граничные точки фигуры (Рис.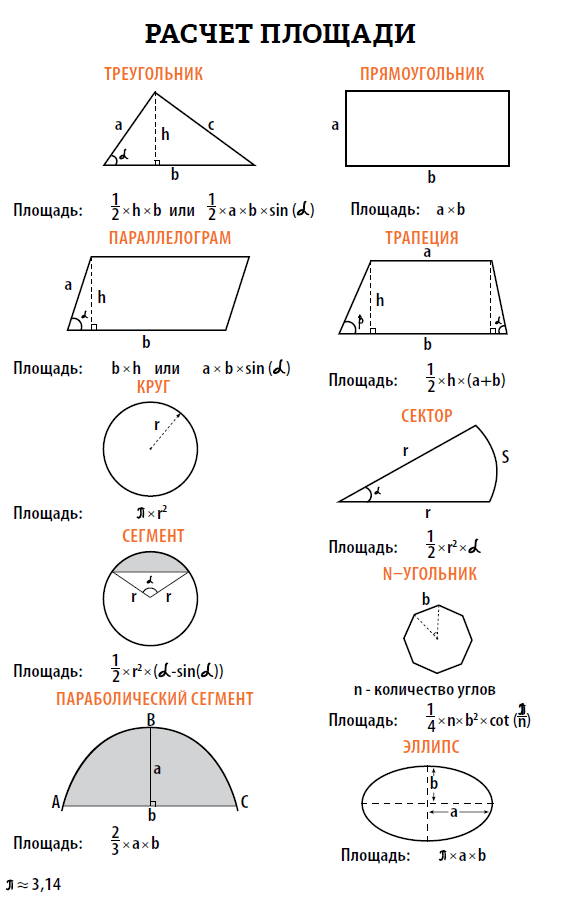 12).
12).
Рис. 12
Ответ: 10,5 кв.ед.
5 способ.Решение. Применим метод «полных» клеток (Рис.13).
Рис. 13
Ответ: 10,5 кв.ед.
Задача 3. Вычислить площадь четырехугольника.
1 способ.Решение. Решим задачу с помощью определителя. Введем вспомогательную прямоугольную систему координат (Рис. 14) и определяем координаты вершин данного четырехугольника: .
Рис. 14
Применим формулу . Первый определитель вычисляем по правилу треугольника, второй – по правилу Саррюса (Рис. 15).
и
Рис. 15
Ответ: 5 кв.ед.
2 способ. Решим задачу с помощью формулы
Решим задачу с помощью формулы
Ответ: 5 кв.ед.
3 способ. Решим задачу с помощью способа «вырезания» (Рис. 16). Достроим прямоугольник
Рис. 16
Ответ: 5 кв.ед.
4 способ.Решение. Решим задачу с помощью формула Пика:. Выделим узловые внутренние и граничные точки фигуры (Рис. 17).
Рис. 17
Ответ: 5 кв.ед.
Применить метод «полных» клеток нельзя.
Задача 4. Вычислить площадь треугольника (Рис. 18).
Рис. 18
1 способ.Решение. Решим задачу с помощью определителя. Введем вспомогательную прямоугольную систему координат (Рис. 19) и определяем координаты вершин данного треугольника: .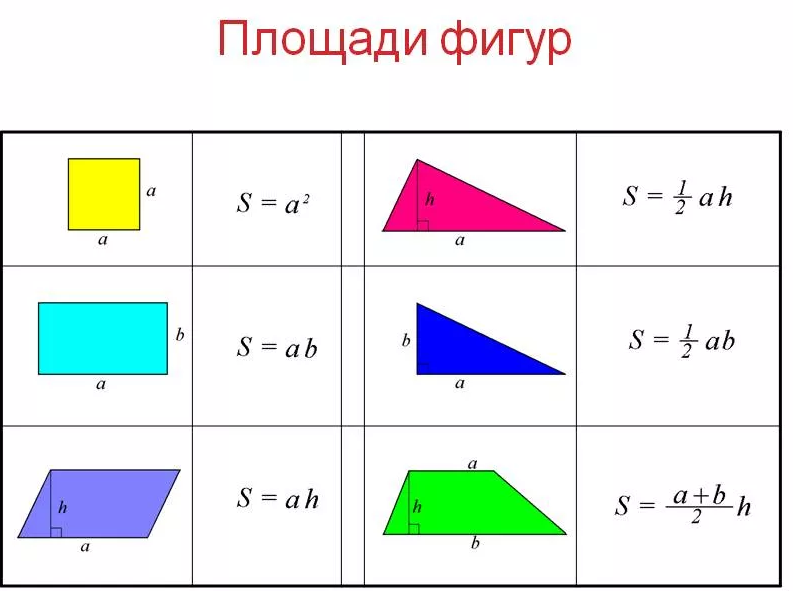
Рис. 19
Применим формулу и приведем определитель к треугольному виду, предварительно переставляя местами первую и последнюю строки:
Ответ: 6 кв.ед.
2 способ.Решение. Решим задачу с помощью формулы Проведем высоту BD к стороне AC (Рис. 20):
Рис.20
Ответ: 6 кв.ед.
3 способ.Решение. Решим задачу с помощью способа «вырезания». Достроим прямоугольник (Рис. 21).
Рис. 21
Ответ: 6 кв.ед.
4 способ.Решение. Решим задачу с помощью формула Пика:. Выделим узловые внутренние и граничные точки фигуры (Рис. 22).
Рис. 22
Ответ: 6 кв.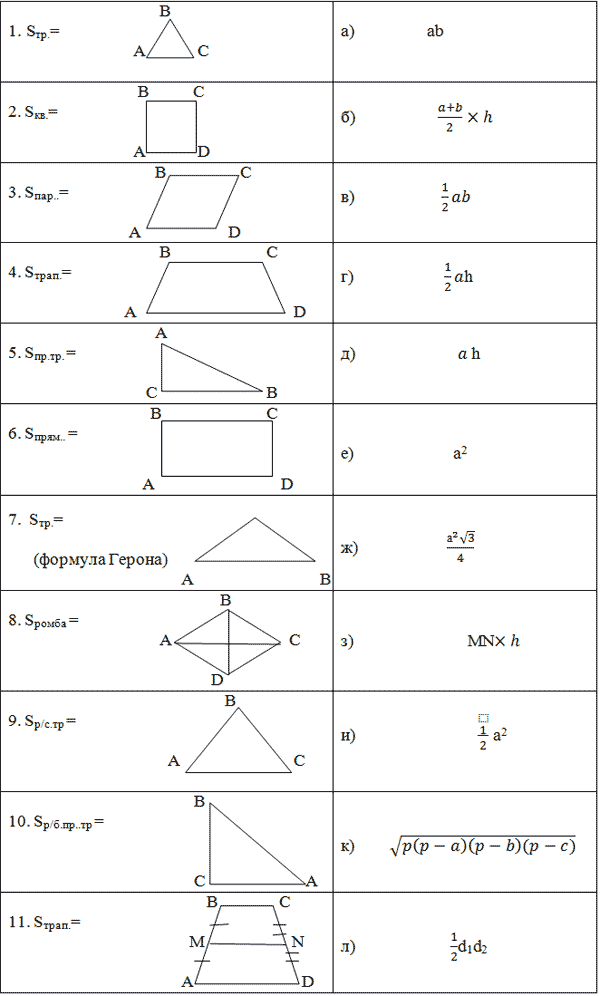 ед.
ед.
Применить метод «полных» клеток нельзя.
Задача 5. Вычислить площадь четырехугольника (Рис. 23).
Рис. 23
1 способ.Решение. Решим задачу с помощью определителя. Введем вспомогательную прямоугольную систему координат (Рис. 24) и определяем координаты вершин данного четырехугольника: .
Рис. 24
Применим формулу :
Ответ: 10 кв.ед.
2 способ.Решение. Так как
Решим задачу с помощью формулы
Ответ: 10 кв.ед.
3 способ.Решение. Решим задачу с помощью способа «вырезания». Достроим прямоугольник (Рис. 25).
Рис. 25
Ответ: 10 кв.ед.
4 способ.Решение. Решим задачу с помощью формула Пика:. Выделим узловые внутренние и граничные точки фигуры (Рис. 26).
Рис. 26
Ответ: 10 кв.ед.
Применить метод «полных» клеток нельзя.
ЗАКЛЮЧЕНИЕ
Результаты исследования предсьавлены в Таблице 1:
|
| |||||||
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
Таблица 1
В процессе исследования была изучена справочная, научно-популярная литература. В результате исследований появилась возможность расширить свои знания о решении задач на клетчатой бумаге, определить классификацию исследуемых задач, убедиться в их многообразии способов вычисления площади многоугольников, нарисованных на клетчатом листке Рассмотренные задачи имеют различный уровень трудности – от простых до олимпиадных. Каждый может найти среди них задачи посильного уровня сложности, отталкиваясь от которых, можно будет переходить к решению более трудных.
В результате исследований появилась возможность расширить свои знания о решении задач на клетчатой бумаге, определить классификацию исследуемых задач, убедиться в их многообразии способов вычисления площади многоугольников, нарисованных на клетчатом листке Рассмотренные задачи имеют различный уровень трудности – от простых до олимпиадных. Каждый может найти среди них задачи посильного уровня сложности, отталкиваясь от которых, можно будет переходить к решению более трудных.
Рассмотренный предмет исследования достаточно многогранен, задачи на клетчатой бумаге многообразны, методы и приёмы их решения также разнообразны. Исследуемые фигуры часто требуют применения векторной геометрии, теоремы Пифагора. К рациональным способам вычисления площади фигуры можно отнести формулу Пика, вычисление площади с помощью определителя. Универсальным способом можно назвать способ вычисления по формулам площадей, значит, возникает необходимость знать всё разнообразие формул.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ
1. НОУ «ИНТУИТ» Лекция Определители – Режим доступа http://www.intuit.ru/ (дата обращения 09.06.2017)
2. Формула Пика. Математические этюды — Режим доступа: http://www.etudes.ru/ru/etudes/pick/ (дата обращения 09.06.2017)
3.Васильев Н. Б. Вокруг формулы Пика // Квант. — 1974. — № 12 стр.39-43
4. Матвеева Н. М.; Валеева А. А. Методическое пособие разработано для проведения практических занятий со студентами 4-го курса, обучающихся по специальности «Почвоведение» — Режим доступа: http://dspace.kpfu.ru/ (дата обращения 09.06.2017)
Просмотров работы: 951
Вычисление площадей фигур, изображенных на клетчатой бумаге
При подготовке к основному государственному экзамену я встретился с заданиями, в которых требуется вычислить площадь фигуры, изображенной на клетчатом листе бумаги. Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой трапецию, параллелограмм или треугольник. Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приемы. Меня заинтересовала данная тема. И естественно возникли вопросы: где в повседневной жизни могут возникнуть задачи на вычисление площадей на клетчатой бумаге? В чем особенность таких задач? Существуют ли другие методы или же универсальная формула для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?
Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой трапецию, параллелограмм или треугольник. Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приемы. Меня заинтересовала данная тема. И естественно возникли вопросы: где в повседневной жизни могут возникнуть задачи на вычисление площадей на клетчатой бумаге? В чем особенность таких задач? Существуют ли другие методы или же универсальная формула для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?
Изучение специальной литературы и интернет источников, показало, что существует универсальная формула, позволяющая вычислить площадь фигуры, изображенной на клетке. Эта формула называется формулой Пика. Однако, в рамках школьной программы данная формула не рассматривается, несмотря на свою простоту в применении и получении результата. Более того, мною проведен опрос друзей и одноклассников (в двух формах: при личной беседе и в социальных сетях), в котором приняли участие 43 учащихся школ города Тобольска. Данный опрос показал, что всего один человек (учащийся 11 класса) знаком с формулой Пика для вычисления площадей.
Более того, мною проведен опрос друзей и одноклассников (в двух формах: при личной беседе и в социальных сетях), в котором приняли участие 43 учащихся школ города Тобольска. Данный опрос показал, что всего один человек (учащийся 11 класса) знаком с формулой Пика для вычисления площадей.
Пусть задана прямоугольная система координат. В этой системе рассмотрим многоугольник, который имеет целочисленные координаты. В учебной литературе точки с целочисленными координатами называются узлами. Причем многоугольник не обязательно должен быть выпуклым. И пусть требуется определить его площадь.
Возможны следующие случаи.
1. Фигура представляет собой треугольник, параллелограмм, трапецию:
1) подсчитывая клеточки нужно найти высоту, диагонали или стороны, которые требуются для вычисления площади;
2) подставить найденные величины в формулу площади.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 1 с размером клетки 1см на 1 см.
Рис. 1. Треугольник
Решение. Подсчитываем клеточки и находим: . По формуле получаем: .
2 Фигура представляет собой многоугольник
Если фигура представляет собой многоугольник то возможно использовать следующие методы.
Метод разбиения:
1) разбить многоугольник на треугольники, прямоугольники;
2) вычислить площади полученных фигур;
3) найти сумму всех площадей полученных фигур.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом разбиения.
Рис. 2. Многоугольник
Решение. Способов разбиения существует множество. Мы разобьем фигуру на прямоугольные треугольники и прямоугольник как показано на рисунке 3.
Рис. 3. Многоугольник. Метод разбиения
Площади треугольников равны: , , , площадь прямоугольника — . Складывая площади всех фигур получим:
Метод дополнительного построения
1) достроить фигуру до прямоугольника
2) найти площади полученных дополнительных фигур и площадь самого прямоугольника
3) из площади прямоугольника вычесть площади всех «лишних» фигур.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом дополнительного построения.
Решение. Достроим нашу фигуру до прямоугольника как показано на рисунке 4.
Рис. 4. Многоугольник. Метод дополнения
Площадь большого прямоугольника равна , прямоугольника, расположенного внутри — , площади «лишних» треугольников — , , тогда площадь искомой фигуры .
При вычислении площадей многоугольников на клетчатой бумаге возможно использовать еще один метод, который носит название формула Пика по фамилии ученого ее открывшего.
Формула Пика
Пусть у многоугольника, изображённого на клетчатой бумаге только целочисленные вершины. Точки у которых обе координаты целые называются узлами решетки. Причем, многоугольник может быть как выпуклым, так и невыпуклым.
Площадь многоугольника с целочисленными вершинами равна , где B — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.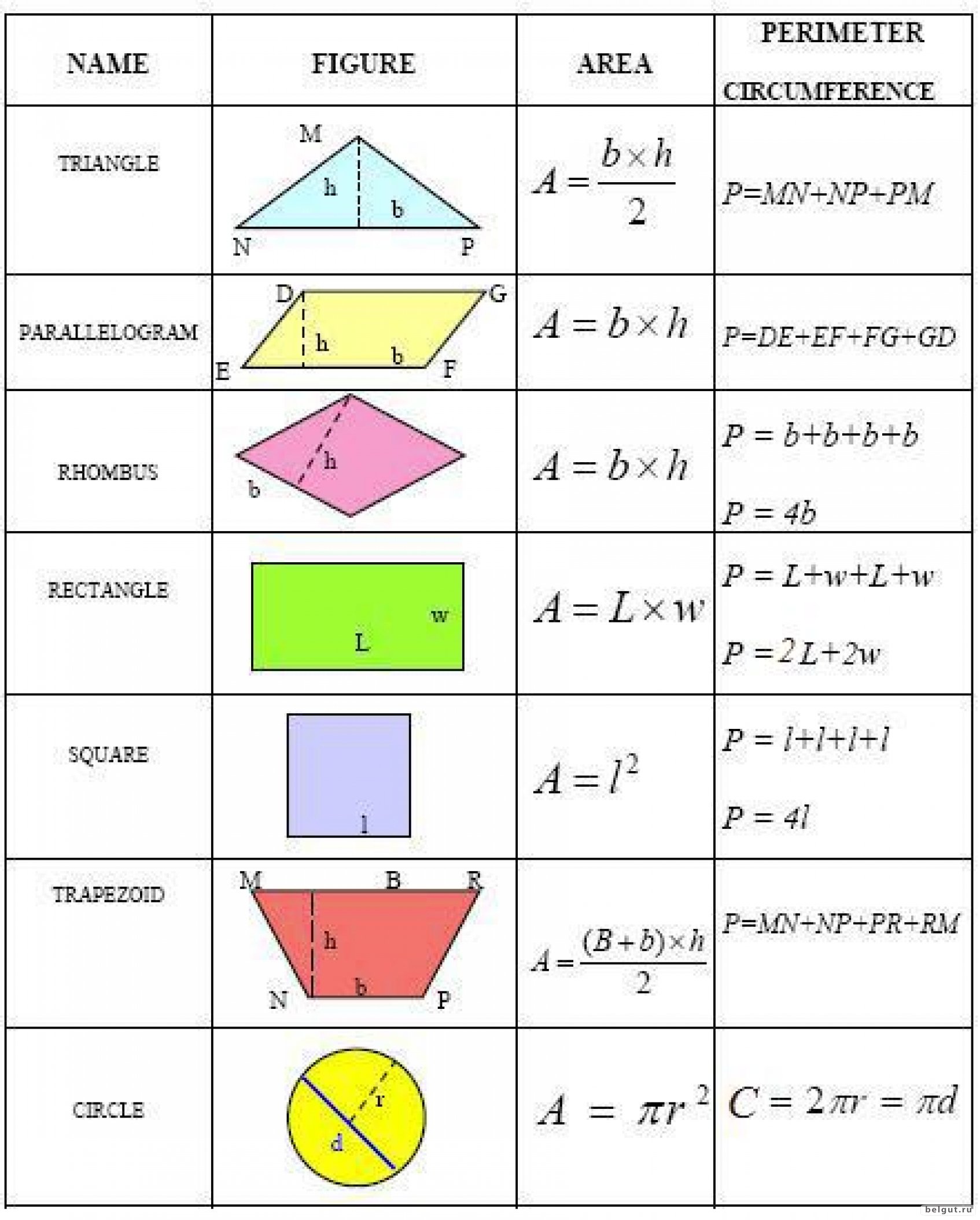
Например, для многоугольника, изображенного на рисунке 5.
Рис. 5. Узлы в формуле Пика
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см по формуле Пика.
Рис. 6. Многоугольник. Формула Пика
Решение. По рисунку 6: В=9, Г=10, тогда по формуле Пика имеем:
Ниже приведены примеры некоторых задач, разработанных автором на вычисление площадей фигур, изображенных на клетчатой бумаге.
1. В детском саду дети сделали аппликации родителям в подарок (рис.7). Найдите площадь аппликации. Размер каждой клетки равен 1см 1см.
Рис. 7. Условие задачи 1
2. Один гектар еловых насаждений может задерживать в год до 32 т пыли, сосновых — до 35 т, вяза — до 43 т, дуба — до 50 т. бука — до 68 т. Посчитайте, сколько тонн пыли задержит ельник за 5 лет. План ельника изображен на рисунке 8 (масштаб 1 см. — 200 м.).
Рис. 8. Условие задачи 2
8. Условие задачи 2
3. В орнаментах хантов и манси, преобладают геометрические мотивы. Часто встречаются стилизованные изображения животных. На рисунке 9 изображен фрагмент мансийского орнамента «Заячьи ушки». Вычислите площадь закрашенной части орнамента.
Рис. 9. Условие задачи 3
4. Требуется покрасить стену заводского здания (рис. 10). Рассчитайте требуемое количество водоэмульсионной краски (в литрах). Расход краски: 1 литр на 7 кв. метров Масштаб 1см — 5м.
Рис. 10. Условие задачи 4
5. Звездчатый многоугольник — плоская геометрическая фигура, составленная из треугольных лучей, исходящих из общего центра, сливающихся в точке схождения. Особого внимания заслуживает пятиконечная звезда — пентаграмма. Пентаграмма — это символ совершенства, ума, мудрости и красоты. Это простейшая форма звезды, которую можно изобразить одним росчерком пера, ни разу не оторвав его от бумаги и при этом ни разу же не пройдя дважды по одной и той же линии.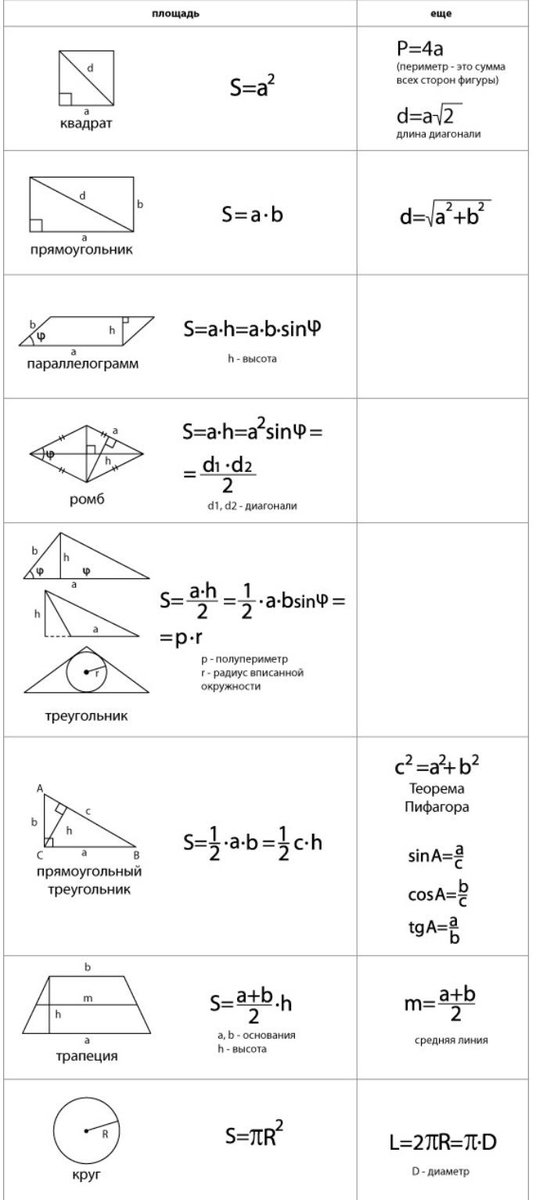 Нарисуйте пятиконечную звездочку не отрывая карандаша от листа клетчатой бумаги, так, чтобы все углы получившегося многоугольника находились в узлах клетки. Вычислите площадь полученной фигуры.
Нарисуйте пятиконечную звездочку не отрывая карандаша от листа клетчатой бумаги, так, чтобы все углы получившегося многоугольника находились в узлах клетки. Вычислите площадь полученной фигуры.
Проанализировав математическую литературу и разобрав большое количество примеров по теме исследования, я пришел к выводу, что выбор метода вычисления площади фигуры на клетчатой бумаге зависит от формы фигуры. Если фигура представляет собой треугольник, прямоугольник, параллелограмм или трапецию, то удобно воспользоваться всем известными формулами для вычисления площадей. Если фигура представляет собой выпуклый многоугольник, то возможно использовать как метод разбиения, так и дополнения (в большинстве случаях удобнее — метод дополнения). Если фигура представляет собой невыпуклый или звездчатый многоугольник, то удобнее применить формулу Пика.
Поскольку формула Пика является универсальной формулой для вычисления площадей (если вершины многоугольника находятся в узлах решетки), то ее можно использовать для любой фигуры.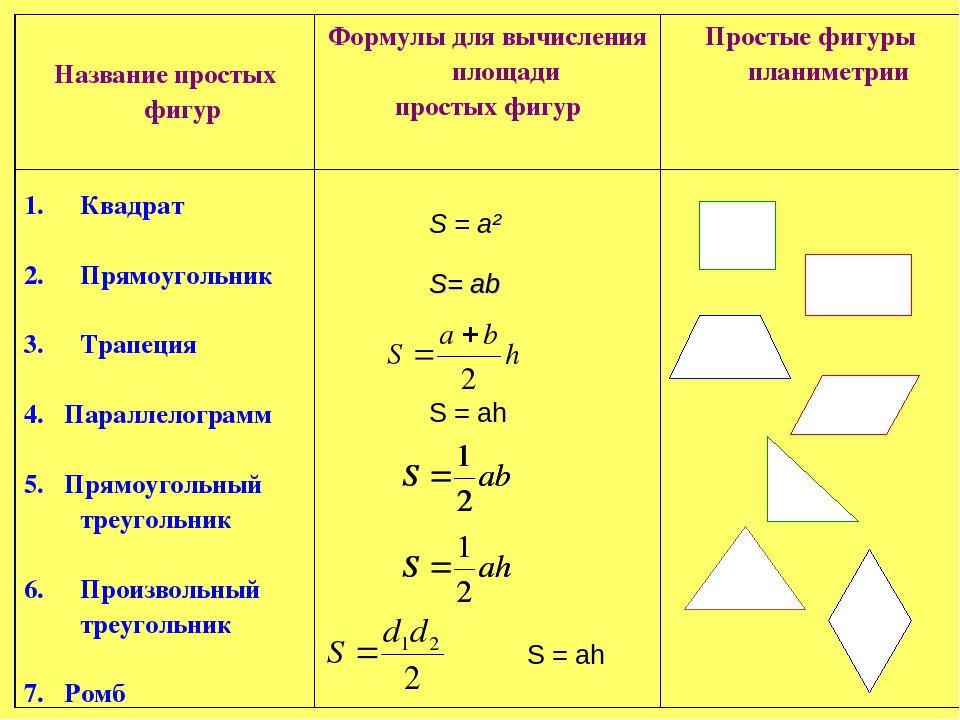 Однако, если многоугольник занимает достаточно большую площадь (или клетки мелкие), то велика вероятность допустить ошибку в подсчетах узлов решетки. Вообще, в ходе исследования, я пришел к выводу, что при решении подобных задач в ОГЭ лучше воспользоваться традиционными методами (разбиения или дополнения), а результат проверить по формуле Пика.
Однако, если многоугольник занимает достаточно большую площадь (или клетки мелкие), то велика вероятность допустить ошибку в подсчетах узлов решетки. Вообще, в ходе исследования, я пришел к выводу, что при решении подобных задач в ОГЭ лучше воспользоваться традиционными методами (разбиения или дополнения), а результат проверить по формуле Пика.
Литература:
- Вавилов В. В., Устинов А. В. Многоугольники на решетках. — М.: МЦНМО, 2006. — 72 с.
- Васильев И. Н. Вокруг формулы Пика// Научно-популярный физико-математический журнал «Квант». — 1974. — № 12. Режим доступа: http://kvant.mccme.ru/1974/12/vokrug_formuly_pika.htm
- Жарковская Н., Рисс Е. Геометрия клетчатой бумаги. Формула Пика. // Первое сентября. Математика. — 2009. -№ 23. — с.24,25.
Основные термины (генерируются автоматически): формула Пика, клетчатая бумага, площадь фигуры, фигура, вычисление площадей, многоугольник, площадь, размер клетки, условие задачи, универсальная формула.
Геометрический способ
Существует три способа определения площади участков: геометрический, аналитический и механический. На местности применяют два первых способа, на картах и планах – все три способа.
Геометрический способ – это вычисление площади геометрических фигур по длинам сторон и углам между ними, значения которых можно получить только из измерений.
Сначала рассмотрим простейшую фигуру – треугольник.
Формулы для вычисления площади треугольника известны:
P = 0.5 * a * h; (6.1)
P = 0.5 * a * b * Sin(C) (6.2)
(6.3)
в этих формулах:
a, b, c – длины сторон треугольника,
A, B, C – углы при вершинах против соответствующих сторон,
h – высота, проведенная из вершины A на сторону a,
p – полупериметр, p=0.5*(a + b + c).
Для решения любого n-угольника нужно знать (2*n – 3) его элементов, причем количество известных углов не должно быть больше (n-1), так как один угол всегда может быть вычислен, если остальные углы известны, на основании формулы:
β = 180 * ( n – 2 ) (6.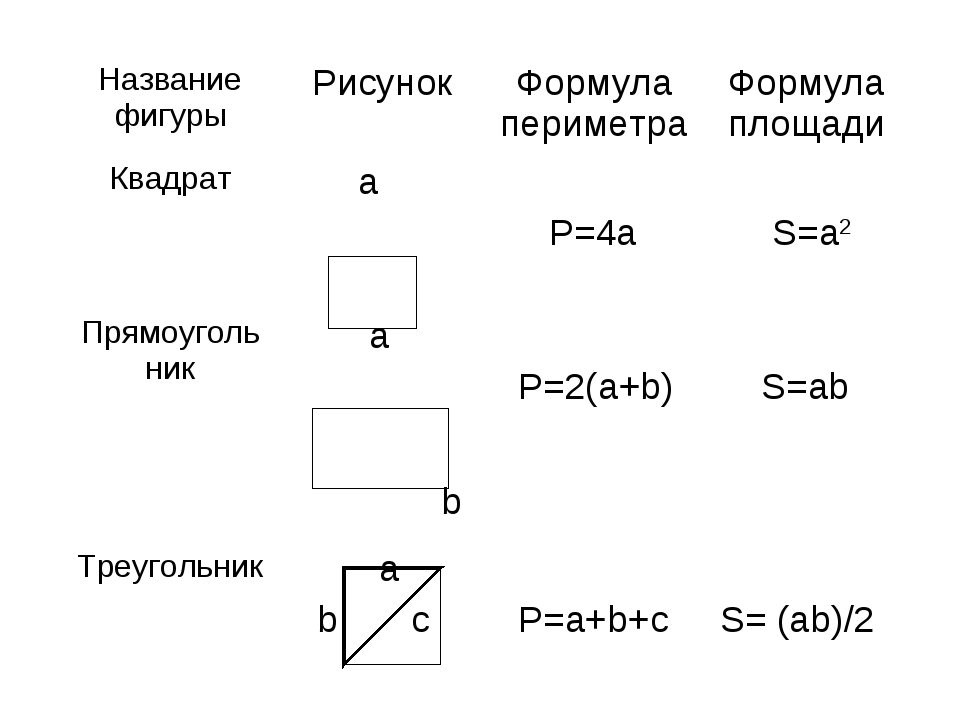 4)
4)
При расчете ошибки определения площади следует учитывать ошибки всех (2n-3) измеряемых элементов.
В треугольнике нужно знать (измерить) три элемента. Формула (6.1) содержит всего два элемента; это значит, что прямой угол между основанием и высотой нужно отдельно обеспечить с необходимой точностью, что равнозначно одному измерению.
Примем относительную ошибку площади mp/P = 1/1000, тогда для применения формулы (6.1) на основании принципа равных влияний необходимо выполнить условия:
и
где ma,mb,β – ср.кв. ошибки сторон a, b и прямого угла между основанием и высотой.
Для формулы (6.2) на основании принципа равных влияний можно написать:
(6.5)
Считая попрежнему mp/P=1/1000, получим:
и mβ= 3.4′ при < C = 60,
mβ= 2.0′ при < C = 45,
mβ= 1.0′ при < C = 26.
Если в треугольнике измерять три стороны с относительной ошибкой mS/S и для вычисления площади применять формулу (6.3), то для равностороннего треугольника получим:
(6. 6)
6)
что при mp/P=1/1000 дает ms/S=1/1500.
Таким образом, вариант с измерением трех сторон треугольника оказывается самым эффективным, так как в нем не требуется измерять углы.
Четырехугольник, как геометрическая фигура, может быть параллелограммом, ромбом, трапецией, прямоугольником, квадратом; но как участок местности его следует считать фигурой произвольной формы, так как обеспечение геометрических свойств той или иной фигуры на местности требует дополнительных измерений.
В четырехугольнике (n=4) нужно измерить пять элементов: три угла и две стороны или два угла и три стороны или один угол и четыре стороны или четыре стороны и одну диагональ. Последний вариант является наиболее предпочтительным, так как, во-первых, в нем не нужно измерять углы, и, во-вторых, согласно формуле:
(6.7)
относительная ошибка площади примерно равна относительной ошибке измерения сторон. Во всех остальных вариантах при оценке точности площади нужно учитывать как ошибки измерения сторон, так и ошибки измерения углов.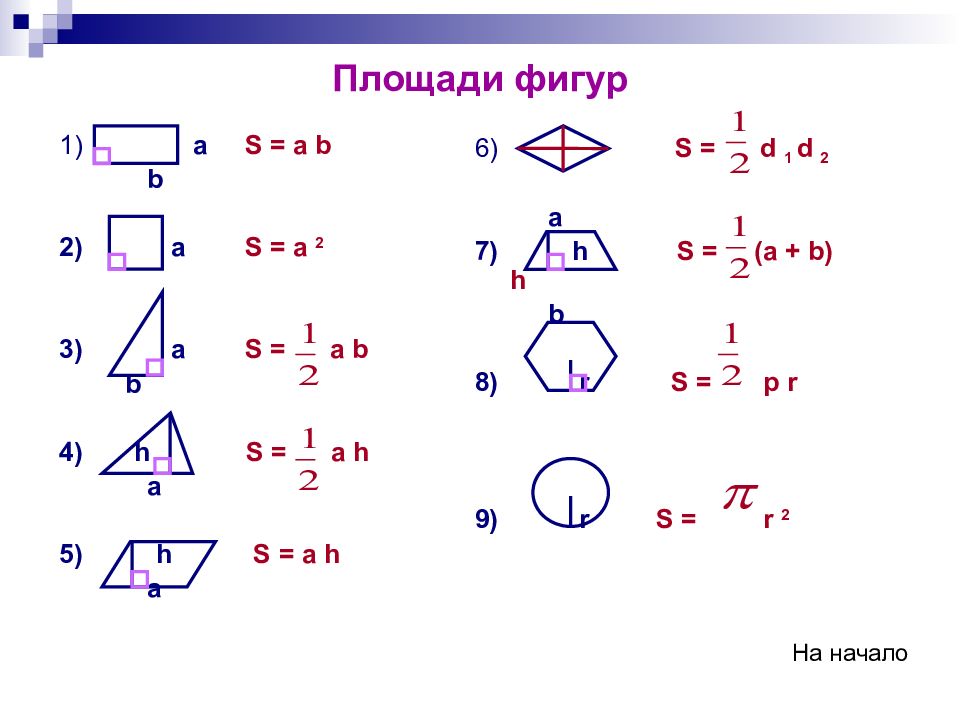
Применение геометрического способа на местности требует разбиения участка на простые геометрические фигуры, что возможно лишь при наличии видимости внутри участка (рис.6.1.)
При определении площади участков на топографических планах и картах стороны и высоты треугольников, стороны и диагонали четырехугольников нужно измерять с помощью поперечного масштаба.
Для определения площади на карте или плане геометрическим способом часто используют палетку – лист прозрачной бумаги, на котором нанесена сетка квадратов или параллельных линий. Палетку с квадратами накладывают на участок и подсчитывают, сколько квадратов содержится в данном участке; неполные квадраты считают отдельно, переводя затем их сумму в полные квадраты. Площадь участка вычисляют по формуле:
P=n*(a*M)2, (6.8)
где a – длина стороны квадрата,
M – знаменатель масштаба карты,
n – количество квадратов на участке.
Рис.6.1
Рекомендовать Google:
Формулы площади поверхности геометрических фигур.

Площадь геометрической фигуры — численная характеристика геометрической фигуры, показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Площадь куба
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.
Формула площади куба
где
S
— площадь куба,
a
— длина грани куба.
Площадь прямоугольного параллелепипеда
Формула площади поверхности прямоугольного параллелепипеда
S = 2(
a · b
+
a · h
+
b · h
)
где
S
— площадь прямоугольного параллелепипеда,
a
— длина,
b
— ширина,
h
— высота.
Площадь цилиндра
Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.
Формула для вычисления площади боковой поверхности цилиндра
Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.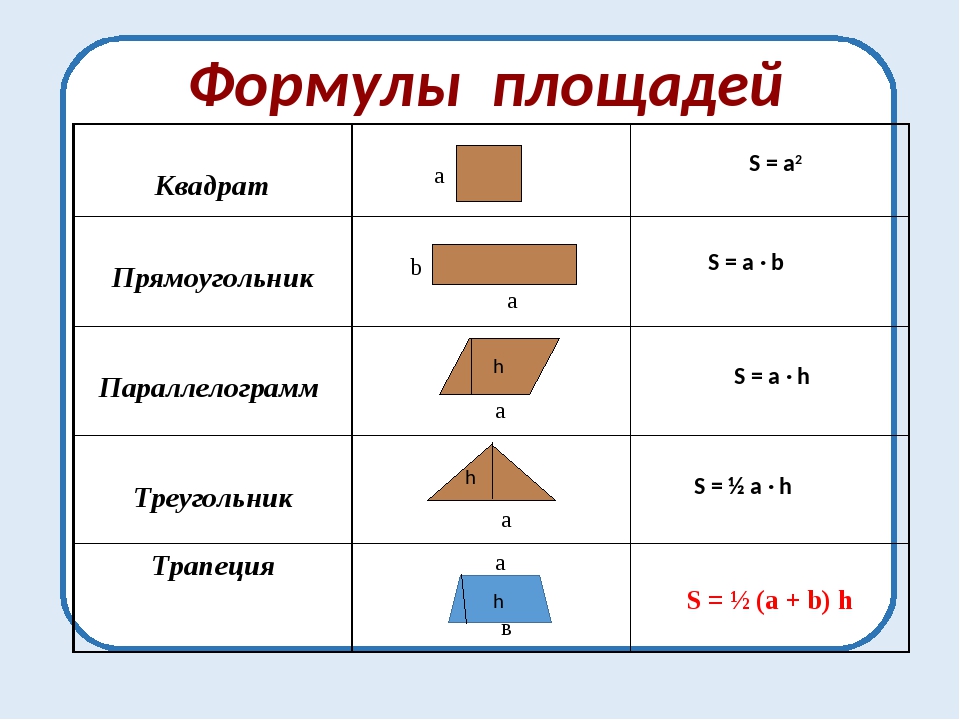
Формула для вычисления площади полной поверхности цилиндра
S = 2
π R h
+ 2
π R
2 = 2
π R
(
R
+
h
)
где
S
— площадь,
R
— радиус цилиндра,
h
— высота цилиндра,
π = 3.141592
.
Площадь конуса
Площадь боковой поверхности конуса равна произведению его радиуса и образующей умноженному на число
π
.
Формула площади боковой поверхности конуса:
Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.
Формула площади полной поверхности конуса:
S =
π R
2 +
π R l
=
π R
(
R
+
l
)
где
S
— площадь,
R
— радиус основания конуса,
l
— образующая конуса,
π = 3.141592
.
Площадь шара
Формулы площади шара
Площадь поверхности шара равна четырем его радиусам в квадрате умноженным на число
π
.

Площадь поверхности шара равна квадрату его диаметра умноженного на число
π
.
где
S
— площадь шара,
R
— радиус шара,
D
— диаметр шара,
π = 3.141592
.
Добавить комментарий
Прямоугольник
(переход к области прямоугольника или периметру прямоугольника)
Прямоугольник — это четырехсторонняя плоская форма, каждый угол которой является прямым (90 °).
| означает «прямой угол» | ||
| равны | ||
| равны | ||
Играть с прямоугольником:
Площадь
прямоугольника
Площадь = a × b |
Пример: прямоугольник шириной 6 м и высотой 3 м, какова его площадь?
Периметр прямоугольника
Периметр — это расстояние по краям.
Периметр 2 раза (a + b) : Периметр = 2 (a + b) |
Пример: прямоугольник имеет длину 12 см и высоту 5 см. Каков его периметр?
Периметр = 2 × (12 см + 5 см)
= 2 × 17 см
= 34 см
Диагонали прямоугольника
Прямоугольник имеет две диагонали, они равны по длине и пересекаются посередине. |
Длина диагонали — это квадратный корень из (a в квадрате + b в квадрате) : Диагональ «d» = √ (a 2 + b 2 ) |
Пример: прямоугольник имеет ширину 12 см и высоту 5 см. Какова длина диагонали?
d = √ (12 2 + 5 2 )
= √ (144 + 25)
= √169
= 13 см
Золотой прямоугольник
Есть также специальный прямоугольник, называемый Золотым прямоугольником:
Калькулятор площади
.
 Найдите область из 16 популярных фигур!
Найдите область из 16 популярных фигур!
Если вам интересно, как рассчитать площадь любой основной формы, вы попали в нужное место — этот калькулятор площади ответит на все ваши вопросы. Воспользуйтесь нашим интуитивно понятным инструментом, чтобы выбрать из шестнадцати различных форм и вычислить их площадь в мгновение ока. Если вы ищете определение площади или, например, формулу ромба, у нас есть все необходимое. Продолжайте прокручивать, чтобы узнать больше, или просто поиграйте с нашим инструментом — вы не будете разочарованы!
Что такое площадь в математике? Определение площади
Проще говоря, площадь — это размер поверхности .Другими словами, его можно определить как пространство, занимаемое плоской формой. Чтобы понять концепцию, обычно полезно думать о площади как о количестве краски, необходимом для покрытия поверхности . Посмотрите на картинку ниже — все фигуры имеют одинаковую площадь, 12 квадратных единиц:
Есть много полезных формул для вычисления площади простых форм. В разделах ниже вы найдете не только хорошо известные формулы для треугольников, прямоугольников и кругов, но и другие формы, такие как параллелограммы, воздушные змеи или кольца.
В разделах ниже вы найдете не только хорошо известные формулы для треугольников, прямоугольников и кругов, но и другие формы, такие как параллелограммы, воздушные змеи или кольца.
Мы надеемся, что после этого объяснения у вас не возникнет проблем с определением области в математике!
Как рассчитать площадь?
Ну конечно это зависит от формы ! Ниже вы найдете формулы для всех шестнадцати форм, представленных в нашем калькуляторе площади. Для ясности мы перечислим только уравнения — их изображения, объяснения и выводы можно найти в отдельных абзацах ниже (а также в инструментах, посвященных каждой конкретной форме).
Вы готовы? Вот наиболее важные и полезные формулы площади для шестнадцати геометрических фигур:
- Квадрат формула площади:
A = a² - Прямоугольник формула площади:
A = a * b - Формулы площади треугольника :
-
A = b * h / 2или -
A = 0,5 * a * b * sin (γ)или -
A = 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))или -
A = a² * sin (β) * sin (γ) / (2 * sin (β + γ))
-
- Круг формула площади:
A = πr² - Сектор круга формула площади:
A = r² * угол / 2 - Эллипс формула площади:
A = a * b * π - Трапеция формула площади:
A = (a + b) * h / 2 - Параллелограмм формулы площади:
-
A = a * hили -
A = a * b * sin (угол)или -
A = e * f * sin (угол)
-
- Ромб формулы площади:
-
A = a * hили -
A = (e * f) / 2или -
A = s² * sin (угол)
-
- Kite формулы площади:
-
A = (e * f) / 2или -
A = a * b * sin (γ)
-
- Пентагон формула площади:
A = a² * √ (25 + 10√5) / 4 - Шестиугольник формула площади:
A = 3/2 * √3 * a² - Восьмиугольник формула площади:
A = 2 * (1 + √2) * a² - Формула площади кольцевого пространства :
A = π (R² - r²) - Четырехугольник формула площади:
A = e * f * sin (угол) - Правильный многоугольник формула площади:
A = n * a² * детская кроватка (π / n) / 4
Если ваша форма неправильная, попробуйте мысленно разделить ее на основные формы, для которых вы можете легко вычислить площадь.
Хотите изменить единицу площади? Просто нажмите на название устройства, и появится раскрывающийся список.
Формула площади
Вы забыли, что такое формула площади? Тогда вы попали в нужное место. Площадь квадрата равна длине его сторон:
-
Площадь квадрата = a * a = a², гдеa— сторона квадрата
Это самая основная и наиболее часто используемая формула, хотя существуют и другие.Например, есть формулы площади, в которых используются диагональ, периметр, радиус описанной окружности или внутренний радиус.
Формула площади прямоугольника
Формула площади прямоугольника тоже несложная задача — это просто умножение сторон прямоугольника:
Расчет площади прямоугольника чрезвычайно полезен в повседневных ситуациях: от строительства здания (оценка необходимой плитки, настила, сайдинга или определение площади крыши) до декорирования вашей квартиры (сколько краски или обоев мне нужно?) До расчета количества людей ваш листовой торт может накормить.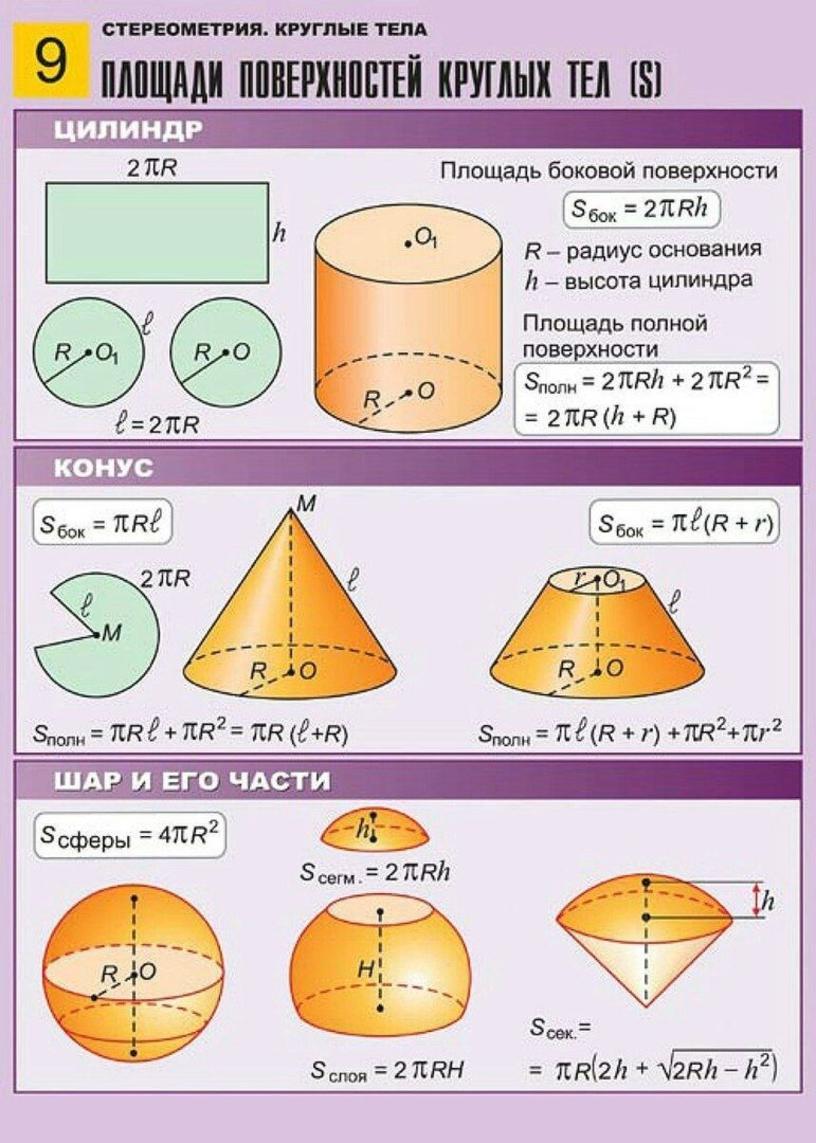
Формула площади треугольника
Существует множество различных формул для вычисления площади треугольника, в зависимости от того, что дано и какие законы или теоремы используются. В этом калькуляторе площади мы реализовали четыре из них:
1. Данные база и высота
-
Площадь треугольника = b * h / 2
2. Даны две стороны и угол между ними (SAS)
-
Площадь треугольника = 0.5 * а * б * sin (γ)
3. Учитывая три стороны (SSS) (Эта формула площади треугольника называется формулой Герона )
-
Площадь треугольника = 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))
4. Даны два угла и сторона между ними (ASA)
-
Площадь треугольника = a² * sin (β) * sin (γ) / (2 * sin (β + γ))
Есть треугольник особого вида, прямоугольный. В этом случае основание и высота — это две стороны, которые образуют прямой угол. Тогда площадь прямоугольного треугольника может быть выражена как:
В этом случае основание и высота — это две стороны, которые образуют прямой угол. Тогда площадь прямоугольного треугольника может быть выражена как:
Площадь прямоугольного треугольника = a * b / 2
Формула площади круга
Формула площади круга — одна из самых известных формул:
-
Площадь круга = πr², гдеr— радиус окружности
В этом калькуляторе мы реализовали только это уравнение, но в нашем круговом калькуляторе вы можете рассчитать площадь по двум разным формулам:
- Диаметр
-
Площадь круга = πr² = π * (d / 2) ²
- Окружность
Кроме того, формула площади круга удобна в повседневной жизни — как серьезная дилемма, какой размер пиццы выбрать.
Формула площади сектора
Формулу площади сектора можно найти, взяв пропорцию круга. Площадь сектора пропорциональна его углу, поэтому, зная формулу площади круга, мы можем записать, что:
α / 360 ° = Площадь сектора / Площадь круга
Преобразование угла говорит нам, что 360 ° = 2π
α / 2π = Площадь сектора / πr²
так:
-
Площадь сектора = r² * α / 2
Формула площади эллипса
Чтобы найти формулу площади эллипса, сначала вспомните формулу площади круга: πr² .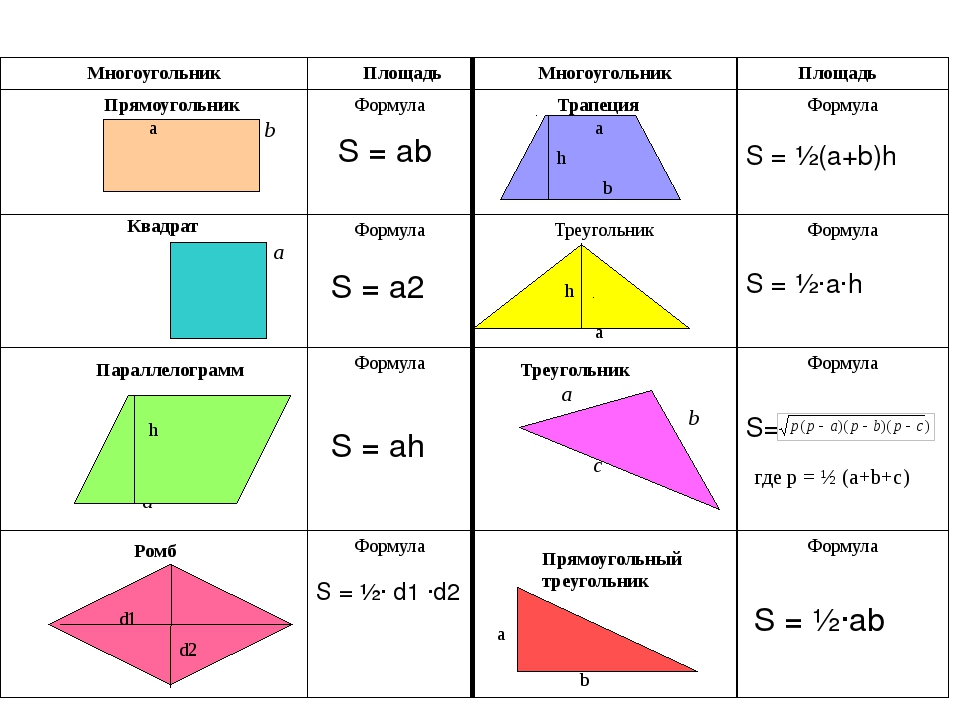 Для эллипса у вас есть не одно значение радиуса, а два разных значения:
Для эллипса у вас есть не одно значение радиуса, а два разных значения: a и b . Единственная разница между формулой площади круга и эллипса заключается в замене r² произведением большой и малой полуосей, a * b :
-
Площадь эллипса = π * a * b
Формула площади трапеции
Площадь трапеции можно найти по следующей формуле:
-
Площадь трапеции = (a + b) * h / 2, гдеaиb— длины параллельных сторон, аh— высота
Также формула площади трапеции может быть выражена как:
Площадь трапеции = м * ч , где м — среднее арифметическое длин двух параллельных сторон
Площадь формулы параллелограмма
Если вы хотите рассчитать площадь с учетом основания и высоты, сторон и угла или диагоналей параллелограмма и угла между ними, вы находитесь в правильном месте.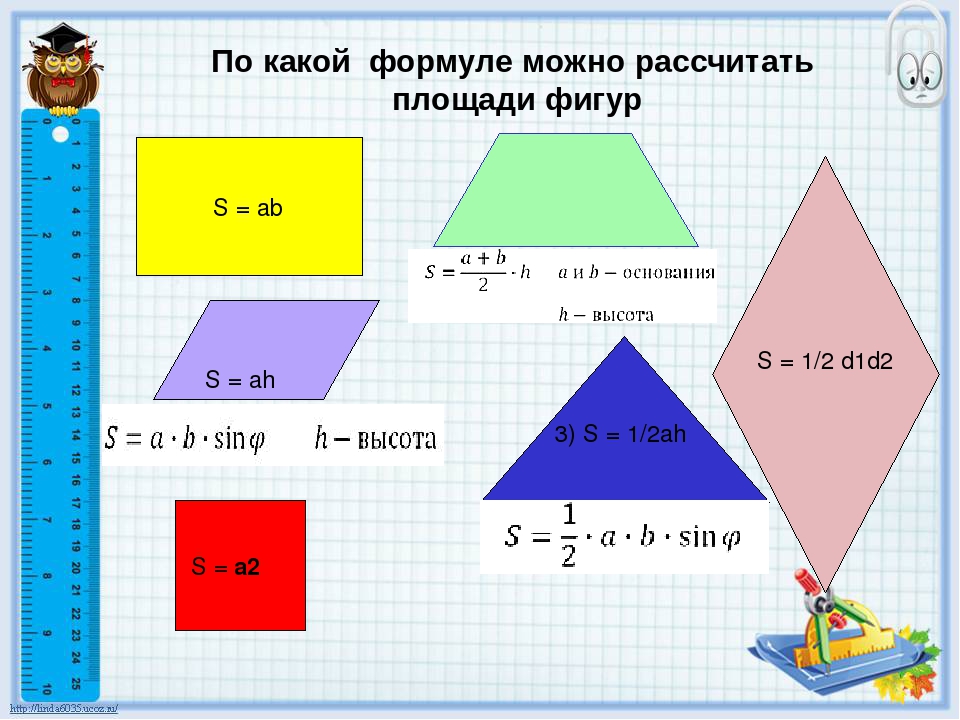 В нашем инструменте вы найдете три формулы площади параллелограмма:
В нашем инструменте вы найдете три формулы площади параллелограмма:
1. Основание и высота
-
Площадь параллелограмма = a * h
2. Стороны и угол между ними
-
Площадь параллелограмма = a * b * sin (α)
3. Диагонали и угол между ними
-
Площадь параллелограмма = e * f * sin (θ)
Площадь формулы ромба
Мы реализовали три полезные формулы для вычисления площади ромба.Вы можете найти этот район, если знаете:
1. Сторона и высота
2. Диагонали
-
Площадь ромба = (e * f) / 2
3. Сторона и любой угол, например, α
-
Площадь ромба = a² * sin (α)
Площадь кайта формулы
Для расчета площади воздушного змея можно использовать два уравнения, в зависимости от того, что известно:
- Площадь формулы воздушного змея с учетом диагоналей змея
- Площадь формулы воздушного змея с учетом двух несовпадающих длин сторон и угла между этими двумя сторонами
-
Площадь змеевика = a * b * sin (α)
Формула площади пятиугольника
Площадь пятиугольника можно рассчитать по формуле:
-
Площадь пятиугольника = a² * √ (25 + 10√5) / 4, где a — сторона правильного пятиугольника
Ознакомьтесь с нашим специальным инструментом пятиугольника, в котором представлены другие важные свойства правильного пятиугольника: сторона, диагональ, высота и периметр, а также радиус описанной и вписанной окружности.
Площадь шестиугольника, формула
Основная формула площади шестиугольника:
-
Площадь шестиугольника = 3/2 * √3 * a², где a — сторона правильного шестиугольника
Так откуда взялась формула? Вы можете представить себе правильный шестиугольник как набор из шести равносторонних равносторонних треугольников. Чтобы найти площадь шестиугольника, все, что нам нужно сделать, это найти площадь одного треугольника и умножить ее на шесть. Формула для площади правильного треугольника равна квадрату стороны, умноженному на квадратный корень из 3, деленный на 4:
.
Площадь равностороннего треугольника = (a² * √3) / 4
Площадь шестиугольника = 6 * Площадь равностороннего треугольника = 6 * (a² * √3) / 4 = 3/2 * √3 * a²
Площадь восьмиугольника по формуле
Чтобы найти площадь восьмиугольника, все, что вам нужно сделать, это знать длину стороны и формулу ниже:
-
Площадь восьмиугольника = 2 * (1 + √2) * a²
Площадь восьмиугольника также можно рассчитать по:
Площадь восьмиугольника = периметр * апофема / 2
Периметр в восьмиугольном корпусе просто 8 * .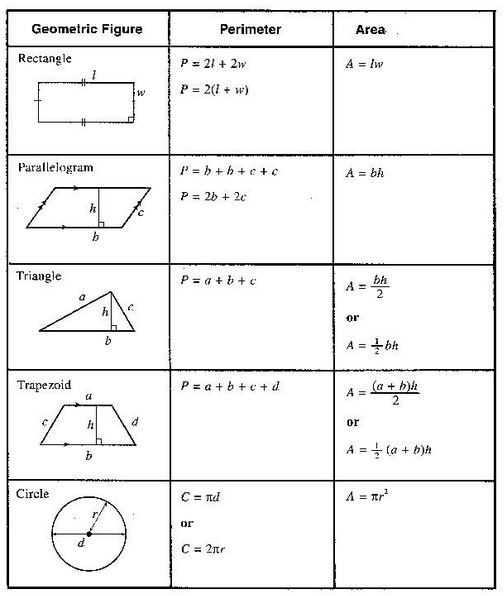 А что такое апофема? Апофема — это расстояние от центра многоугольника до середины стороны. В то же время это высота треугольника, образованного линией от вершин восьмиугольника к его центру. Этот треугольник — один из восьми совпадающих — является равнобедренным треугольником, поэтому его высоту можно рассчитать, например, с помощью теоремы Пифагора по формуле:
А что такое апофема? Апофема — это расстояние от центра многоугольника до середины стороны. В то же время это высота треугольника, образованного линией от вершин восьмиугольника к его центру. Этот треугольник — один из восьми совпадающих — является равнобедренным треугольником, поэтому его высоту можно рассчитать, например, с помощью теоремы Пифагора по формуле:
h = (1 + √2) * a / 4
Итак, наконец, мы получаем первое уравнение:
Площадь восьмиугольника = периметр * апофема / 2 = (8 * a * (1 + √2) * a / 4) / 2 = 2 * (1 + √2) * a²
Формула площади кольцевого пространства
Кольцо — это объект в форме кольца — это область, ограниченная двумя концентрическими окружностями разного радиуса.Найти формулу площади кольца — простая задача, если вы помните формулу площади круга. Вы только посмотрите: площадь кольца — это разница площадей большего круга радиуса R и меньшего радиуса r:
-
Площадь кольца = πR² - πr² = π (R² - r²)
Кстати, вы видели наш конвертер размеров колец?
Площадь четырехугольника формулы
Четырехугольная формула, которую реализует этот калькулятор площади, использует две заданные диагонали и угол между ними.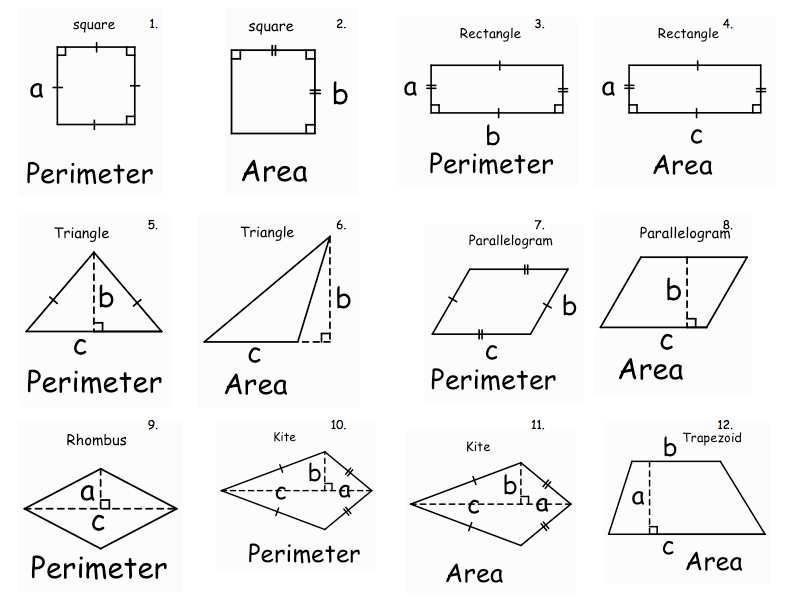
-
Площадь четырехугольника = e * f * sin (α), где e, f — диагонали
Мы можем использовать любой из двух углов, так как мы вычисляем их синус. Зная, что два соседних угла являются дополнительными, мы можем утверждать, что sin (угол) = sin (180 ° - угол) .
Если вы ищете другие формулы для определения площади четырехугольника, воспользуйтесь нашим специальным инструментом для четырехугольника, где вы найдете формулу Бретшнайдера (с учетом четырех сторон и двух противоположных углов) и формулу, в которой используются бимедианы и угол между ними. .
Формула площади правильного многоугольника
Формула для площади правильного многоугольника выглядит следующим образом:
-
Площадь правильного многоугольника = n * a² * детская кроватка (π / n) / 4
где n — количество сторон, а a — длина стороны.
Существуют и другие уравнения, в которых используются, например, такие параметры, как радиус описанной окружности или периметр. Вы можете найти эти формулы в специальном абзаце нашего калькулятора площади многоугольника.
Вы можете найти эти формулы в специальном абзаце нашего калькулятора площади многоугольника.
Если вы имеете дело с неправильным многоугольником, помните, что вы всегда можете разделить фигуру на более простые фигуры.Просто посчитайте площадь каждого из них и в конце просуммируйте их. Разбиение многоугольника на набор треугольников называется триангуляцией многоугольника.
Что такое область 2D-форм?
Что такое площадь 2D-фигур?
Площадь любой 2D-формы — это размер области, заключенной в нее. Есть несколько 2D-форм, таких как квадрат, прямоугольник, круг, ромб и треугольник. Цветная область в каждой форме представляет область соответствующей формы.
Единица площади называется квадратными.У разных форм есть разные формулы для расчета площади.
Площадь квадрата и прямоугольника :
Площадь квадрата и прямоугольника равна произведению двух смежных сторон.
| 2D Форма | Формула площади | Пример |
| Квадрат | Площадь квадрата = Сторона × Сторона Площадь = S × S | Площадь = 4 × 4 = 16 кв. |
| Прямоугольник | Площадь прямоугольника = длина × ширина = длина × ширина | Площадь = 8 × 3 = 24 кв. См |
Площадь треугольника :
Треугольники могут быть разных типов, например равносторонний треугольник, равнобедренный треугольник и прямоугольный треугольник, но формула для площади всех видов треугольников одинакова.
Площадь треугольника определяется по формуле: 1 ⁄ 2 × b × h, где основание (b) — длина любой стороны треугольника, а высота (h) — перпендикулярное расстояние между основанием. и верхняя вершина треугольника.
Пример:
В треугольнике ABC основание составляет 6 единиц, а высота — 4 единицы.
Итак, площадь треугольника ABC = 1 ⁄ 2 × b × h
= 1 ⁄ 2 × 6 × 4
= 12 кв.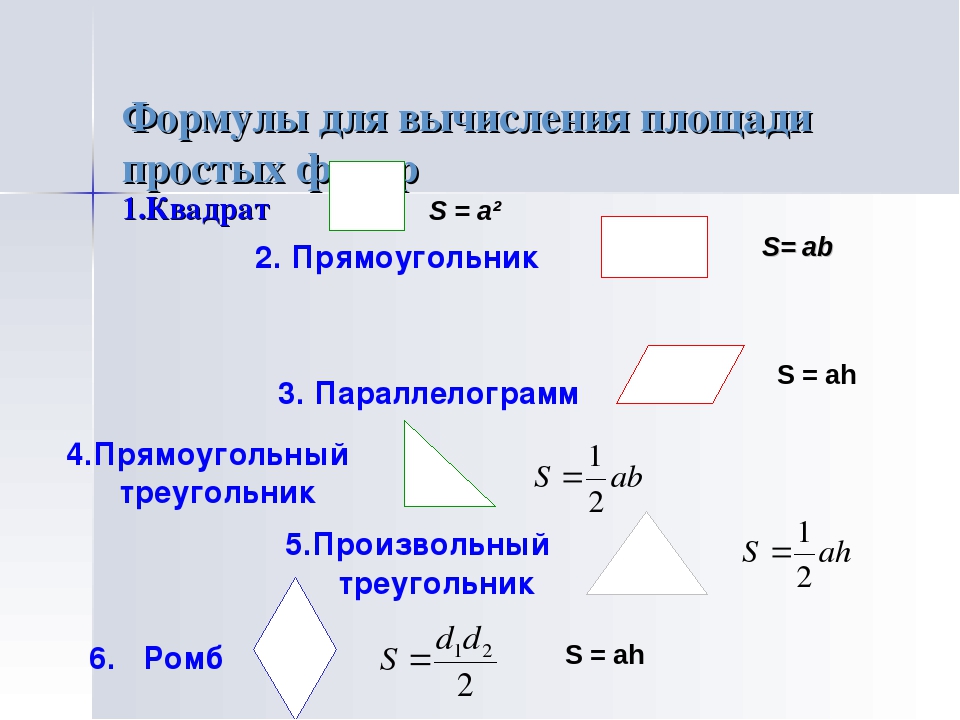 Единиц
Единиц
Круг :
Площадь круга вычисляется по формуле π × r 2 , где r — радиус круга, а π — константа, значение которой равно 227 или 3.14
Пример: Площадь вышеуказанного круга = π × r 2
= 3,14 × 4 2
= 3,14 × 16
= 50,24 кв. См
Ромб :
Формула для определения площади ромба: pq / 2, где p и q — две диагонали ромба.
В ромбе ABCD площадь можно вычислить следующим образом:
Площадь ромба = 1 ⁄ 2 шт.
= 1 ⁄ 2 × 3 × 5
= 7,5 кв. См
Параллелограмм :
Чтобы найти площадь параллелограмма, мы используем формулу b × h, где b обозначает основание, а h обозначает высоту. Высота — это расстояние по вертикали между основанием и верхом.
Пример:
На приведенном выше рисунке площадь параллелограмма равна b × h.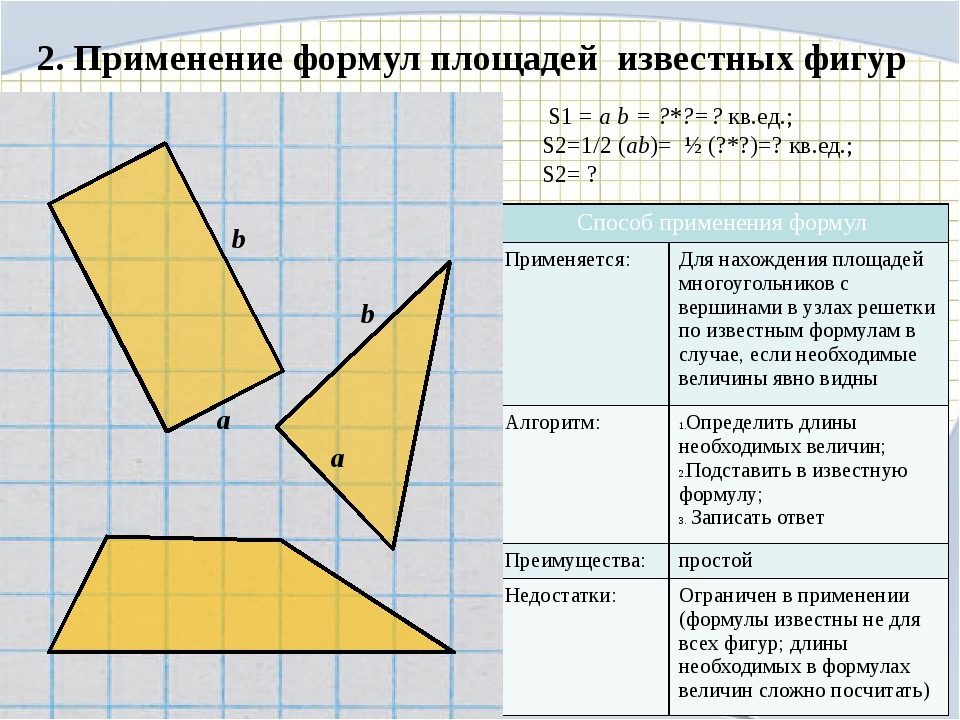 Следовательно, это 6 × 4 = 24 кв. См
Следовательно, это 6 × 4 = 24 кв. См
Интересные факты |
9,5: Площадь и объем геометрических фигур и объектов
- Последнее обновление
- Сохранить как PDF
- Значение и обозначение площади
- Формулы площади
- Поиск областей некоторых общих геометрических фигур
- Значение и обозначение объема
- Формулы объема
- Определение объемов некоторых общих геометрических объектов
- Упражнения
- Упражнения
- Обзор
Цели обучения
- знать значение и обозначения для площади
- знать формулы площади некоторых распространенных геометрических фигур
- уметь найти площади некоторых общих геометрических фигур
- знать значение и обозначения для тома
- знать формулы объема для некоторых обычных геометрических объектов
- уметь находить объем некоторых обычных геометрических объектов
Нередко необходимо умножить одно номинальное число на другое. 2 \), или квадрат длины (квадрат длины), физически можно интерпретировать как площадь поверхности.
2 \), или квадрат длины (квадрат длины), физически можно интерпретировать как площадь поверхности.
Площадь
Площадь поверхности — это количество квадратных единиц длины, содержащихся на поверхности.
Например, 3 кв. Дюйма означает, что 3 квадрата по 1 дюйм с каждой стороны можно точно разместить на некоторой поверхности. (Квадраты, возможно, придется разрезать и переставить так, чтобы они соответствовали форме поверхности.)
Рассмотрим площадь следующих геометрических фигур.
Формулы площади
Мы можем определить площади этих геометрических фигур, используя следующие формулы.
Нахождение областей некоторых общих геометрических фигур
Образец набора A
Найдите площадь треугольника.
Раствор
\ (\ begin {array} {rcl} {A_T} & = & {\ dfrac {1} {2} \ cdot b \ cdot h} \\ {} & = & {\ dfrac {1} {2} \ cdot 20 \ cdot 5 \ text {sq ft}} \\ {} & = & {10 \ cdot 6 \ text {sq ft}} \\ {} & = & {60 \ text {sq ft}} \\ { } & = & {60 \ text {ft} ^ 2} \ end {array} \)
Площадь этого треугольника составляет 60 квадратных футов, что часто записывается как 60 \ (\ text {ft} ^ 2 \).
Образец набора A
Найдите площадь прямоугольника.
Раствор
Давайте сначала преобразуем 4 фута 2 дюйма в дюймы. Поскольку мы хотим преобразовать в дюймы, мы будем использовать дробную единицу \ (\ dfrac {\ text {12 дюймов}} {\ text {1 ft}} \), поскольку у нее есть дюймы в числителе. Затем
\ (\ begin {array} {rcl} {\ text {4 ft}} & = & {\ dfrac {\ text {4 ft}} {1} \ cdot \ dfrac {\ text {12 дюймов}} { \ text {1 ft}}} \\ {} & = & {\ dfrac {4 \ cancel {\ text {ft}}} {1} \ cdot \ dfrac {\ text {12 дюймов.}} {1 \ cancel {\ text {ft}}}} \\ {} & = & {\ text {48 дюймов}} \ end {array} \)
Таким образом, \ (\ text {4 фута 2 дюйма = 48 дюймов + 2 дюйма = 50 дюймов} \)
\ (\ begin {array} {rcl} {A_R} & = & {l \ cdot w} \\ {} & = & {\ text {50 дюймов} \ cdot \ text {8 дюймов}} \\ {} & = & {400 \ text {sq in.}} \ End {array} \)
Площадь этого прямоугольника 400 кв. Дюймов.
Образец набора A
Найдите площадь параллелограмма.
Раствор
\ (\ begin {array} {rcl} {A_P} & = & {b \ cdot h} \\ {} & = & {\ text {10.3 см} \ cdot \ text {6,2 см}} \\ {} & = & {63,86 \ text {sq cm}} \ end {array} \)
Площадь параллелограмма 63,86 см2.
Образец набора A
Найдите площадь трапеции.
Раствор
\ (\ begin {array} {rcl} {A_ {Trap}} & = & {\ dfrac {1} {2} \ cdot (b_1 + b_2) \ cdot h} \\ {} & = & {\ dfrac {1} {2} \ cdot (\ text {14,5 мм + 20,4 мм}) \ cdot (4,1 \ text {мм})} \\ {} & = & {\ dfrac {1} {2} \ cdot (\ текст {34.2} \\ {} & \ приблизительно & {(3.14) \ cdot (\ text {282,24 кв. Фута})} \\ {} & \ приблизительно & {888.23 \ text {sq ft}} \ end {array} \)
Площадь этого круга составляет примерно 886,23 кв. Фута.
Практический набор A
Найдите площадь каждой из следующих геометрических фигур.
- Ответ
36 кв.
 См
См
Практический набор A
- Ответ
37.503 кв. Мм
Практический набор A
- Ответ
13,26 кв. Дюйма
Практический набор A
- Ответ
367.5 кв. Миль
Практический набор A
- Ответ
452,16 кв.футов
Практический набор A
- Ответ
44.3 \), или кубическая единица длины (единица длины у.е.), физически можно интерпретировать как объем трехмерного объекта.
Объем
Объем объекта — это количество кубических единиц длины, содержащихся в объекте.Например, 4 куб.
 Мм означает, что 4 куба, по 1 мм с каждой стороны, точно заполнят какой-нибудь трехмерный объект. (Кубики, возможно, придется разрезать и переставить так, чтобы они соответствовали форме объекта.)
Мм означает, что 4 куба, по 1 мм с каждой стороны, точно заполнят какой-нибудь трехмерный объект. (Кубики, возможно, придется разрезать и переставить так, чтобы они соответствовали форме объекта.)Формулы объема
рисунок Формула объема Заявление Прямоугольный цельный \ (\ begin {array} {rcl} {V_R} & = & {l \ cdot w \ cdot h} \\ {} & = & {\ text {(область основания)} \ cdot \ text {(высота )}} \ end {array} \) Объем прямоугольного твердого тела равен длине, умноженной на ширину, умноженной на высоту.2 \ cdot h} \\ {} & = & {\ text {(область основания)} \ cdot \ text {(высота)}} \ end {array} \) Объем конуса равен \ (\ dfrac {1} {3} \) умноженным на \ (\ pi \) квадрату радиуса, умноженному на высоту. Поиск объемов некоторых общих геометрических объектов
Образец набора B
Найдите объем прямоугольного твердого тела.
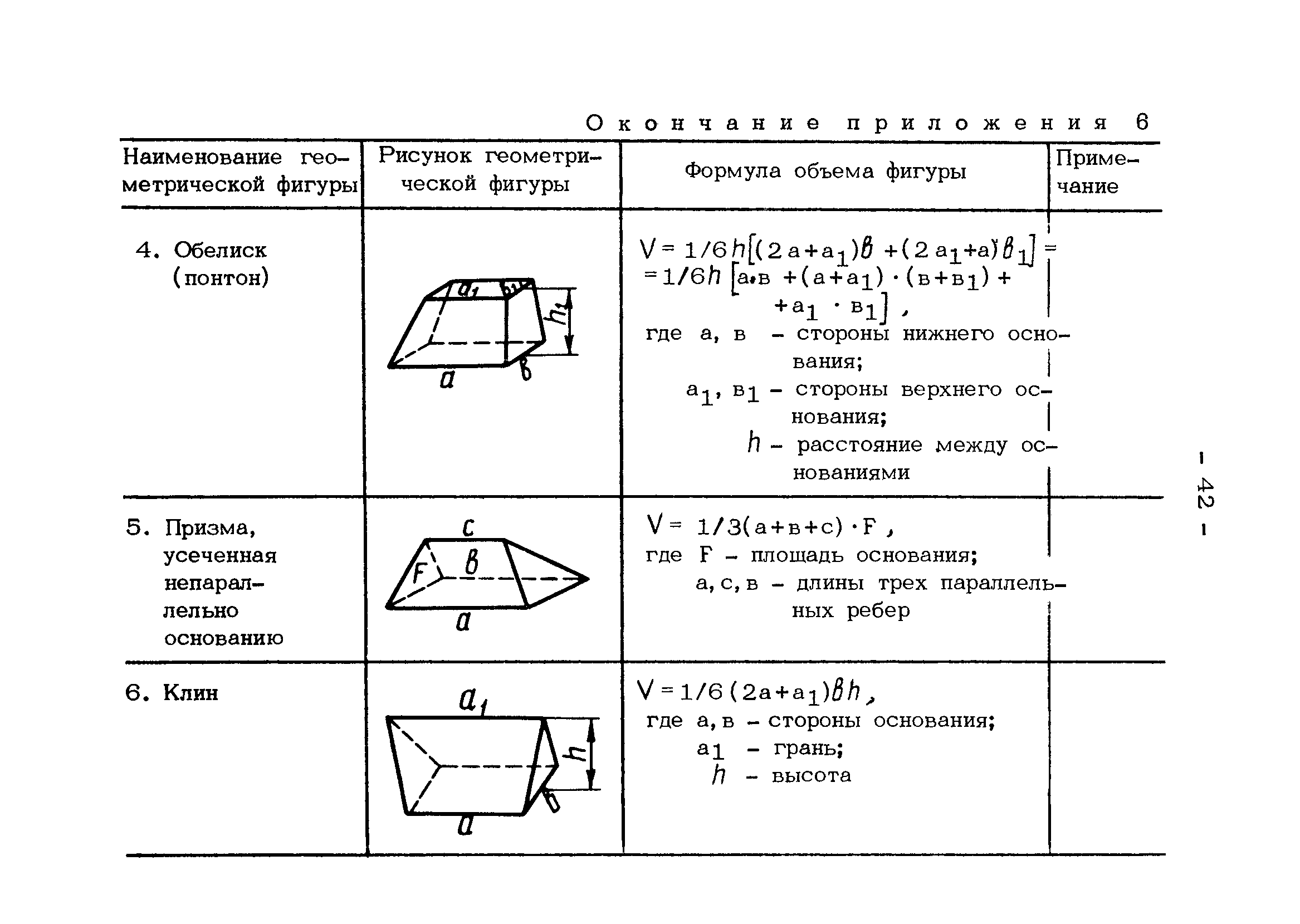 2 \ cdot h} \\ {} & \ приблизительно & {(\ dfrac {1} {3}) \ cdot (3.2 \ cdot \ text {(5 мм)}} \\ {} & \ приблизительно & {(\ dfrac {1} {3}) \ cdot (3.14) \ cdot (\ text {4 кв. Мм}) \ cdot \ текст {(5 мм)}} \\ {} & \ приблизительно & {(\ dfrac {1} {3}) \ cdot (3.14) \ cdot \ text {(20 у.е. мм)}} \\ {} & \ приблизительно & {20.9 \ overline {3} \ text {cu mm}} \\ {} & \ приблизительно & {\ text {20.93 cu mm}} \ end {array} \)
2 \ cdot h} \\ {} & \ приблизительно & {(\ dfrac {1} {3}) \ cdot (3.2 \ cdot \ text {(5 мм)}} \\ {} & \ приблизительно & {(\ dfrac {1} {3}) \ cdot (3.14) \ cdot (\ text {4 кв. Мм}) \ cdot \ текст {(5 мм)}} \\ {} & \ приблизительно & {(\ dfrac {1} {3}) \ cdot (3.14) \ cdot \ text {(20 у.е. мм)}} \\ {} & \ приблизительно & {20.9 \ overline {3} \ text {cu mm}} \\ {} & \ приблизительно & {\ text {20.93 cu mm}} \ end {array} \)Объем этого конуса примерно 20,93 куб. Мм. Объем является приблизительным, потому что мы аппроксимировали \ (\ pi \) с 3,14.
Практический набор B
Найдите объем каждого геометрического объекта.Если требуется \ (\ pi \), округлите его до 3,14 и найдите приблизительный объем.
- Ответ
21 куб. Дюйм
Практический набор B
Сфера
- Ответ
904,32 куб. Футов
Практический набор B
- Ответ
157 куб.
 М
М
Практический набор B
- Ответ
0.00942 у.е. дюйм
Упражнения
Найдите каждое указанное измерение.
Упражнение \ (\ PageIndex {1} \)
Площадь
- Ответ
16 кв.м
Упражнение \ (\ PageIndex {2} \)
Площадь
Упражнение \ (\ PageIndex {3} \)
Площадь
- Ответ
1.21 кв. Мм
Упражнение \ (\ PageIndex {4} \)
Площадь
Упражнение \ (\ PageIndex {5} \)
Площадь
- Ответ
18 кв. Дюймов
Упражнение \ (\ PageIndex {6} \)
Площадь
Упражнение \ (\ PageIndex {7} \)
Точная площадь
- Ответ
\ ((60.
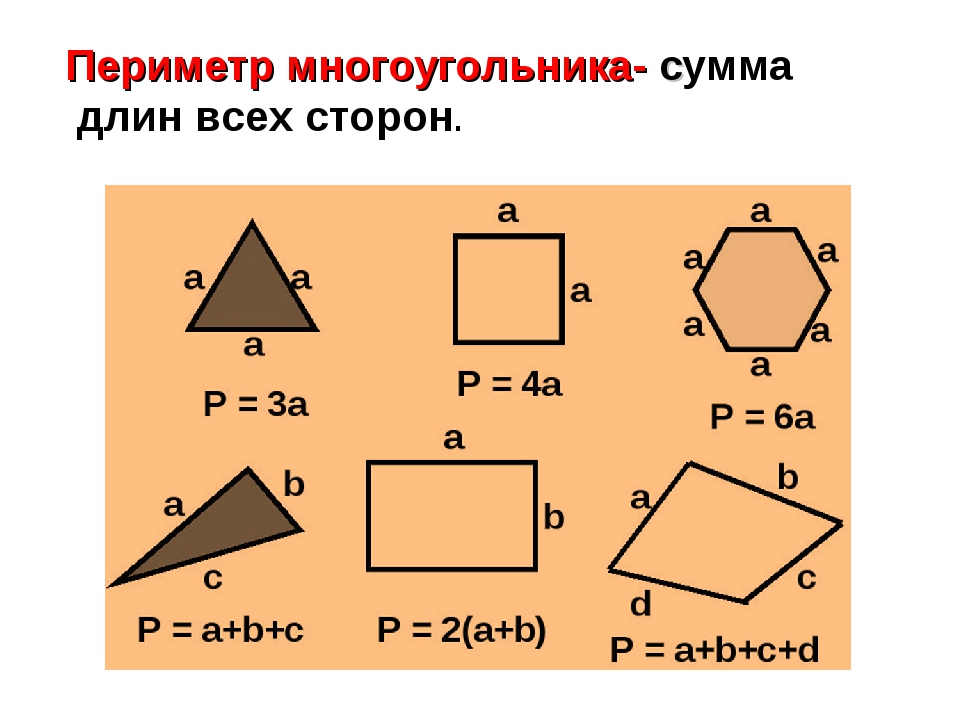 5 \ pi + 132) \ text {sq ft} \)
5 \ pi + 132) \ text {sq ft} \)
Упражнение \ (\ PageIndex {8} \)
Примерная площадь
Упражнение \ (\ PageIndex {9} \)
Площадь
- Ответ
40,8 кв. Дюйма
Упражнение \ (\ PageIndex {10} \)
Площадь
Упражнение \ (\ PageIndex {11} \)
Примерная площадь
- Ответ
31.0132 кв. Дюйм
Упражнение \ (\ PageIndex {12} \)
Точная площадь
Упражнение \ (\ PageIndex {13} \)
Примерная площадь
- Ответ
158,2874 кв. Мм
Упражнение \ (\ PageIndex {14} \)
Точная площадь
Упражнение \ (\ PageIndex {15} \)
Примерная площадь
- Ответ
64.
 2668 кв. Дюймов
2668 кв. Дюймов
Упражнение \ (\ PageIndex {16} \)
Площадь
Упражнение \ (\ PageIndex {17} \)
Примерная площадь
- Ответ
43.96 кв.футов
Упражнение \ (\ PageIndex {18} \)
Объем
Упражнение \ (\ PageIndex {19} \)
Объем
- Ответ
512 куб. См
Упражнение \ (\ PageIndex {20} \)
Точный объем
Упражнение \ (\ PageIndex {21} \)
Примерный объем
- Ответ
11.49 куб.см
Упражнение \ (\ PageIndex {22} \)
Примерный объем
Упражнение \ (\ PageIndex {23} \)
Точный объем
- Ответ
\ (\ dfrac {1024} {3} \ pi \ text {cu ft} \)
Упражнение \ (\ PageIndex {24} \)
Примерный объем
Упражнение \ (\ PageIndex {25} \)
Примерный объем
- Ответ
22.
 08 куб. Дюймов
08 куб. Дюймов
Упражнение \ (\ PageIndex {26} \)
Примерный объем
Упражнения для обзора
Упражнение \ (\ PageIndex {27} \)
Сколько сотен в числе 23 426?
- Ответ
4
Упражнение \ (\ PageIndex {28} \)
Перечислите все множители 32.
Упражнение \ (\ PageIndex {29} \)
Найдите значение \ (4 \ dfrac {3} {4} — 3 \ dfrac {5} {6} + 1 \ dfrac {2} {3} \).
- Ответ
\ (\ dfrac {31} {12} = 2 \ dfrac {7} {12} = 2,58 \)
Упражнение \ (\ PageIndex {30} \)
Найдите значение \ (\ dfrac {5 + \ dfrac {1} {3}} {2 + \ dfrac {2} {15}} \).
Упражнение \ (\ PageIndex {31} \)
Найдите периметр.
- Ответ
27,9 кв.м
Что такое площадь формы?
Площадь фигур
Геометрические фигуры — это фигуры с набором точек, соединенных линиями, в результате чего получается замкнутая фигура.

Например, , треугольник, квадрат, прямоугольник и четырехугольник — это фигуры с 3 и 4 точками, соединенными линиями. Фигуры с ограниченными кривыми не имеют сторон, но имеют окружность.
Зеркала разной формы со сторонами и закруглениями.
Площадь
Площадь фигуры — это «пространство, заключенное внутри периметра или границы» данной фигуры. Рассчитываем площадь для разных форм по математическим формулам.
На следующих рисунках заштрихованная область обозначает область для соответствующих форм.
Имя и форма Недвижимость Площадь Круг
- Длина между центром «o» и точкой на окружности равна радиусу «r»
А = πr2
π = 3.14 (постоянная)
Треугольник
- Один угол — это прямой угол
A = 1 ⁄ 2 × основание × высота Квадрат
- Все стороны равны
- Каждый угол составляет 90 градусов
A = длина стороны 2 Ромб
- Все стороны равны
- Противоположные стороны параллельны
- Противоположные углы равны
А = p × q Прямоугольник
- Противоположные стороны равны и параллельны
- Каждый угол составляет 90 градусов
A = длина × ширина Параллелограмм
- Противоположные стороны равны и параллельны
- Противоположные углы равны
A = основание × высота «Текстурированная» область представляет собой область формы
Единица измерения
Единицей измерения площади всегда является квадрат единицы, в которой даны длины.
 Результирующая единица является произведением единиц данной длины.
Результирующая единица является произведением единиц данной длины.Возьмем для примера площадь квадрата со стороной 8 см:
Площадь = (длина стороны) 2
Площадь = 8 см × 8 см
Площадь = 64 см 2
Заявка
Область применения формулы площади — архитектура, землеустройство и картографирование. Измененная версия области для данного места полезна при разработке инструментов знаний, таких как глобусы и геофизические карты.Расчет площади для двумерной формы — это первый шаг к интерпретации объема трехмерного объекта, такого как конус, цилиндр, шар и куб.
Интересные факты
Вавилонские глиняные таблички с писцами использовались для изучения математики и интерпретации концепции площади с использованием формул в течение 1800-1600 гг. До н.э.
Египтяне построили великие пирамиды, используя свойства на основе площади и соотношение между площадью поверхности сторон и площадью основания для идеально сбалансированной конструкции
Сопутствующая математическая лексика
Формулы площади поверхности
Формулы площади поверхности (Математика | Геометрия
| Формулы площади поверхности)( пи
= = 3.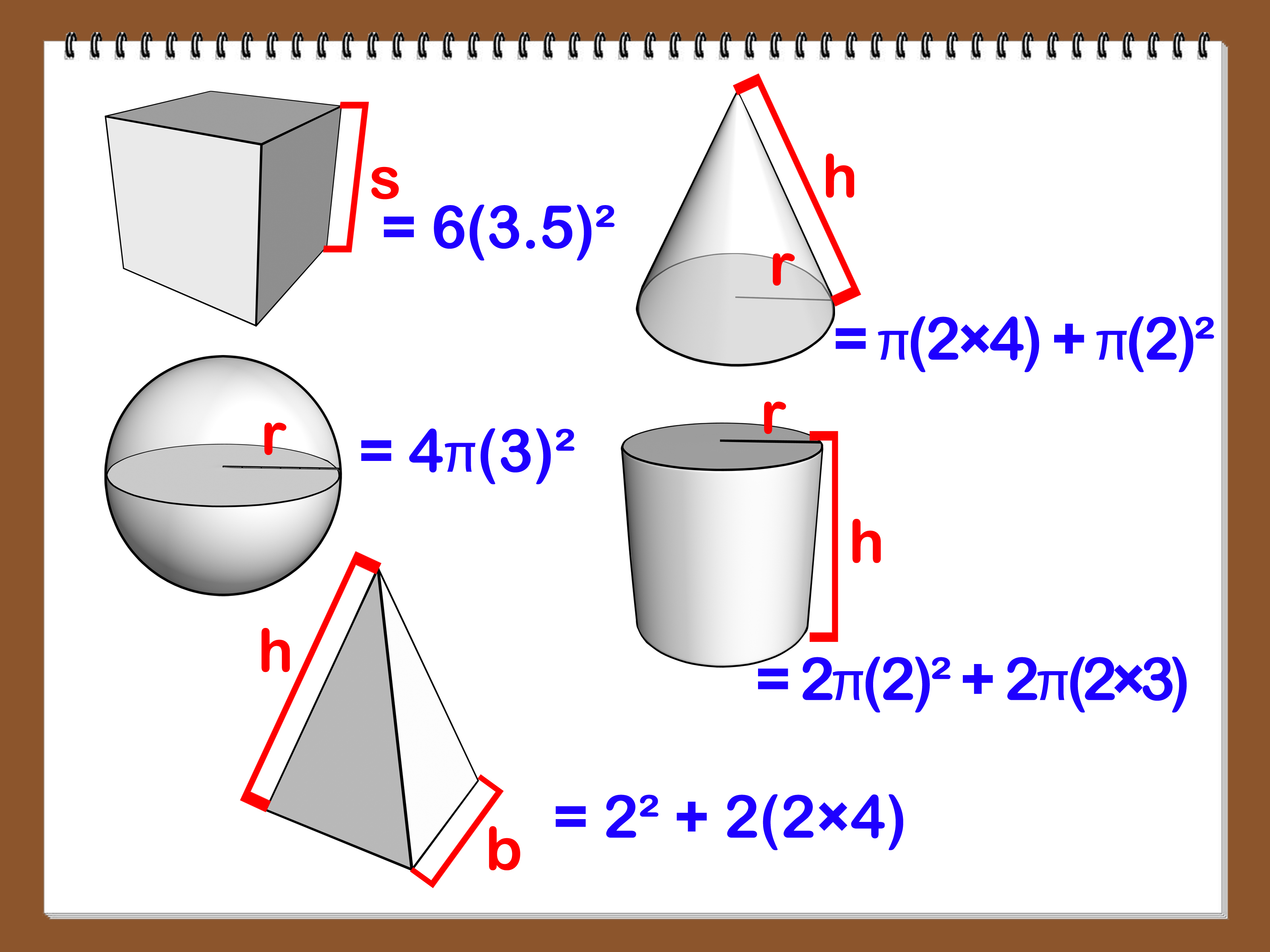 141592 …)
141592 …) Поверхность
Формулы площади
В общем, площадь поверхности является суммой
все области всех форм, которые покрывают поверхность объекта.Куб | Прямоугольный
Призма | Призма | Сфера
| Цилиндр | ЕдиницыПримечание: «ab» означает
«a» умноженное на «b». «а2 » означает
«в квадрате», что то же самое, что «а» умножить на «а».Будьте осторожны !! Количество единиц.Используйте одни и те же единицы для всех измерений. Примеры
Площадь поверхности куба =
6 а 2(а — длина стороны
каждый край куба)Проще говоря, площадь куба — это площадь шести квадратов, которые
накрой это. Площадь одного из них a * a, или 2 . Поскольку эти
Поскольку эти
все одинаковые, вы можете умножить одно из них на шесть, так что поверхность
площадь куба в 6 раз больше квадрата одной из сторон.Площадь поверхности прямоугольника
Призма = 2ab + 2bc + 2ac(a, b и c —
длины трех сторон)Проще говоря, площадь прямоугольной призмы равна площади шести
прямоугольники, которые его покрывают. Но нам не нужно вычислять все шесть, потому что
мы знаем, что верх и низ одинаковы, передняя и задняя — это
то же самое, и левая и правая стороны одинаковы.Площадь верха и низа (длины сторон a и
в) = а * с. Поскольку их два, вы получаете 2ac. Передняя и задняя
имеют длину стороны b и c. Площадь одного из них b * c, а там
их два, поэтому площадь поверхности этих двух равна 2bc. Левая и
правая сторона имеет длину сторон a и b, поэтому площадь поверхности одного из
их это а * б.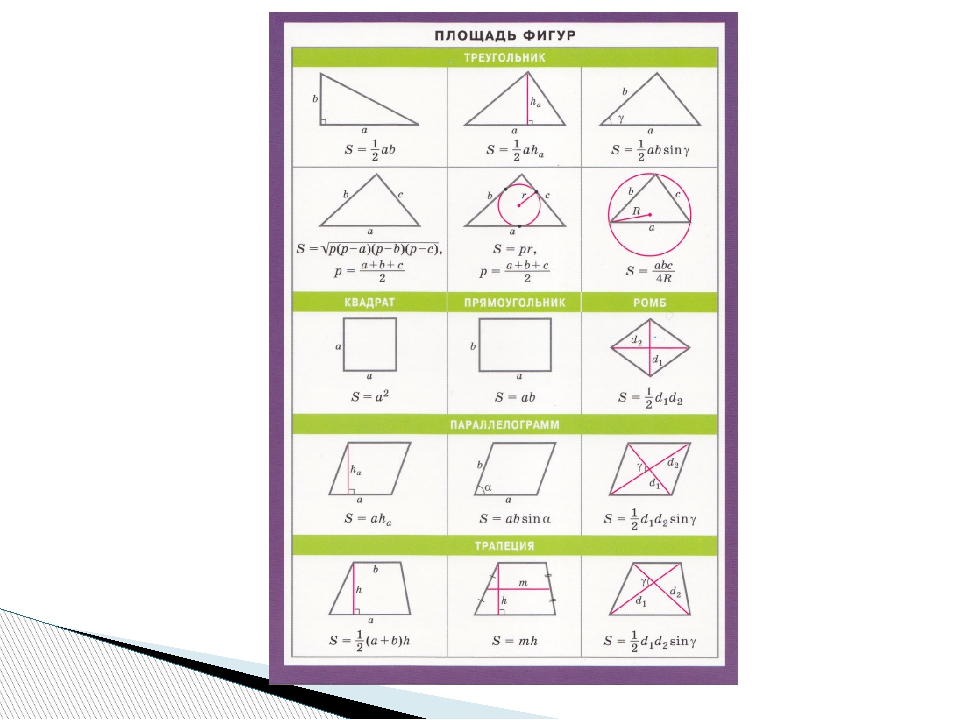 Опять же, их два, поэтому их общая площадь поверхности
Опять же, их два, поэтому их общая площадь поверхности
это 2ab.Площадь любой призмы (б — форма
концов)Площадь поверхности = Боковая площадь + Площадь двух концов
(Боковая площадь) = (периметр формы b ) * L
Площадь поверхности = (периметр формы b ) * L + 2 * (Площадь формы b )
Площадь поверхности сферы
= 4 пи r 2(r — радиус окружности)
Площадь поверхности цилиндра
= 2 pi r 2 + 2 pi r h(h — высота
цилиндра, r — радиус вершины)Площадь поверхности = Области сверху и снизу + Площадь сбоку
Площадь поверхности = 2 (Площадь верха) + (периметр верха) * высота
Площадь поверхности = 2 ( pi r 2 ) + (2 pi r) * h
На словах проще всего представить банку.
 Площадь поверхности — это
Площадь поверхности — это
площади всех частей, необходимых для закрытия банки. Это верх, низ,
и бумажная этикетка, которая оборачивается по центру.Вы можете найти область вверху (или внизу). Это формула
для площади круга ( пи r 2 ). Поскольку есть и верх, и
дно, умноженное на два.Сторона похожа на этикетку банки. Если оторвать и положить
плоский это будет прямоугольник.Площадь прямоугольника — это произведение
с двух сторон. Одна сторона — это высота банки, другая —
периметр круга, так как этикетка один раз оборачивается вокруг банки. Так
площадь прямоугольника (2 pi r) * h.Сложите эти две части вместе, и вы получите формулу поверхности.
площадь цилиндра.Площадь поверхности = 2 ( pi r 2 ) + (2 pi r) * h
Совет! Не забывайте единицы измерения. 
Эти уравнения дадут вам правильные ответы, если вы будете держать единицы прямо.
Например — найти площадь поверхности куба со стороной 5 дюймов,
уравнение:Площадь поверхности = 6 * (5 дюймов) 2
= 6 * (25 квадратных дюймов)
= 150 кв. Дюймов
Геометрические фигуры — площади
Квадрат
Площадь квадрата можно рассчитать как
A = a 2 (1a)
Сторона квадрата может быть рассчитана как
a = A 1/2 (1b)
Диагональ квадрата может быть рассчитана как
d = a 2 1/2 (1c)
Прямоугольник
Площадь прямоугольник можно рассчитать как
A = ab (2a)
Диагональ прямоугольника можно рассчитать как
d = (a 2 + b 2 ) 1/2 (2b )
Параллелограмм
Площадь параллелограмма можно рассчитать как
A = ah
= ab sin α (3a)
Диаметр параллелограмма можно рассчитать как
d 1 = ((a + h cot α ) 2 + h 2 ) 1/2 ( 3b)
d 2 = ((a — h кроватка α ) 2 + h 2 ) 1/2 (3b)
Равносторонний треугольник
Равносторонний треугольник представляет собой треугольник, в котором все три стороны равны.

Площадь равностороннего треугольника можно рассчитать как
A = a 2 /3 3 1/2 (4a)
Площадь равностороннего треугольника можно рассчитать как
h = a / 2 3 1/2 (4b)
Треугольник
Площадь треугольника можно рассчитать как
A = ah / 2
= rs (5a)
r = ah / 2s (5b)
R = bc / 2 h (5c)
s = (a + b + c) / 2 (5d)
x = s — a (5e)
y = s — b (5f)
z = s — c (5g)
9 0071 Трапеция
Площадь трапеции можно рассчитать как
A = 1/2 (a + b) h
= mh (6a)
m = (a + b) / 2 (6b)
Шестигранник
Площадь шестиугольника можно рассчитать как
A = 3/2 a 2 3 1/2 (7a)
d = 2 а
= 2/3 1/2 с
= 1.
 1547005 s (7b)
1547005 s (7b) s = 3 1/2 /2 d
= 0,866025 d (7c)
Круг
Площадь круга может быть рассчитана как
A = π / 4 d 2
= π r 2
= 0,785 .. d 2 (8a)
9000 r3 C = 2
= π d (8b)
где
C = окружность
Сектор и сегмент окружности
Сектор окружности
Сектор окружности
может быть выражено как
A = 1/2 θ r r 2 (9)
900 02 = 1/360 θ d π r 2
где
θ r = угол в радианах
θ d = угол в
Площадь сегмента круга может быть выражена как
A = 1/2 (θ r — sin θ r ) r 2
= 1/2 (π θ d / 180 — sin θ d ) r 2 (10)
Правый круговой цилиндр
Площадь боковой поверхности правильного кругового круга может быть выражена как
A = 2 π rh (11)
, где
h = высота цилиндра (м, фут)
r = радиус основания (м, фут)
Правый круговой конус
Площадь боковой поверхности правого кругового конуса баллона быть выраженным как
A = π rl
= π r (r 2 + h 2 ) 1/2 (12)
, где
h = высота конус (м, фут)
r = радиус основания (м, фут)
l = наклонная длина (м, фут)
Сфера
Площадь боковой поверхности сферы можно выразить как
A = 4 π r 2 (13)
.



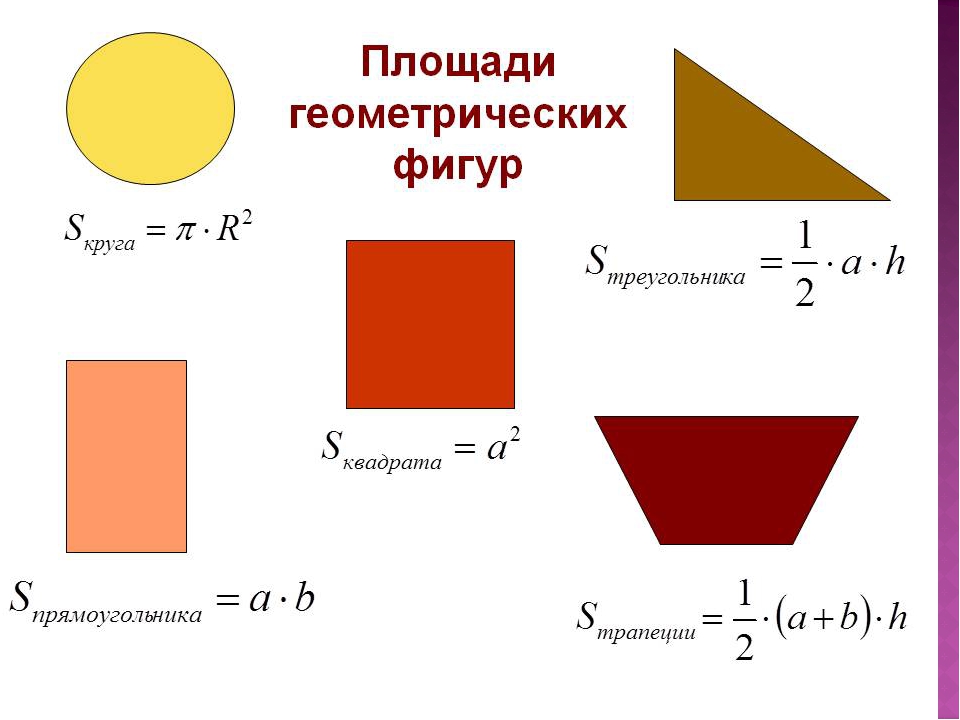
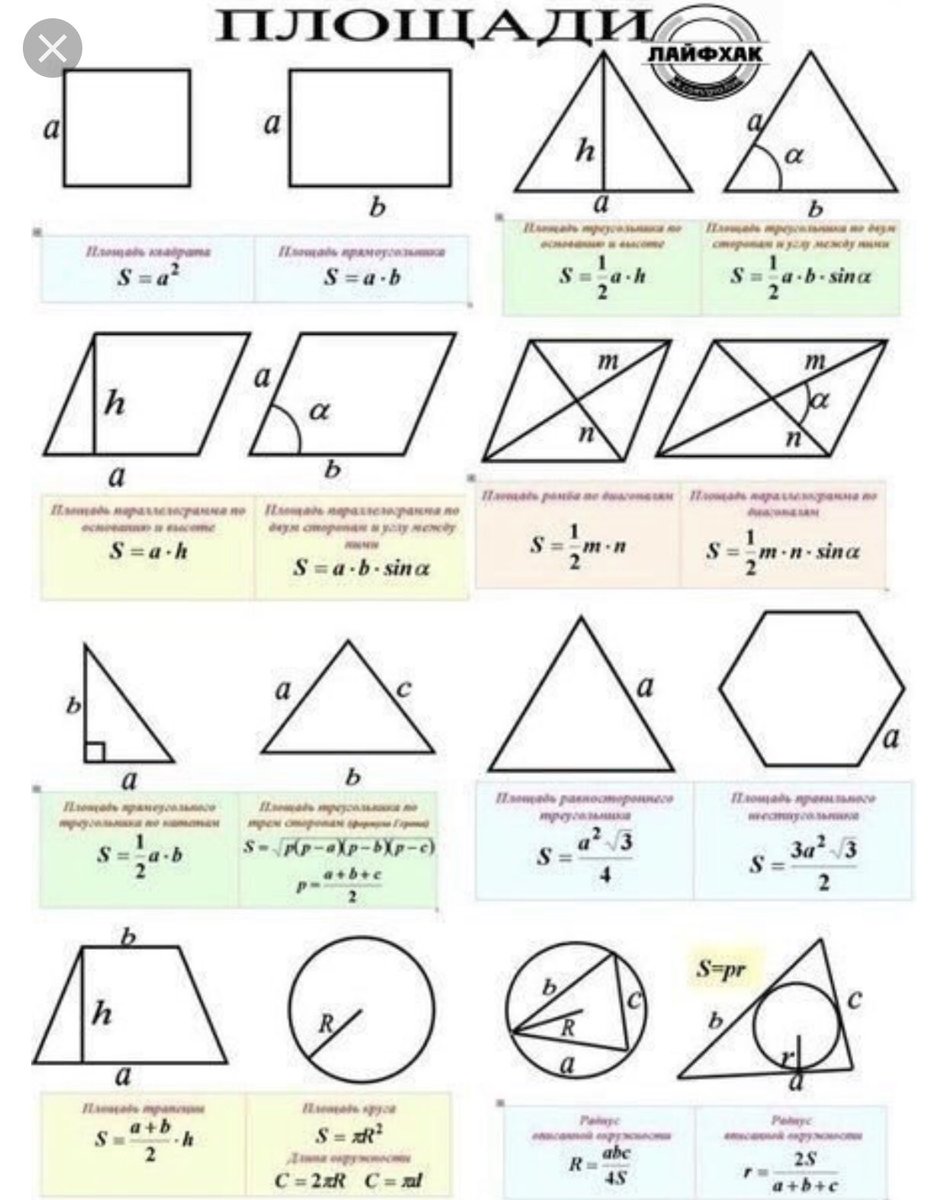
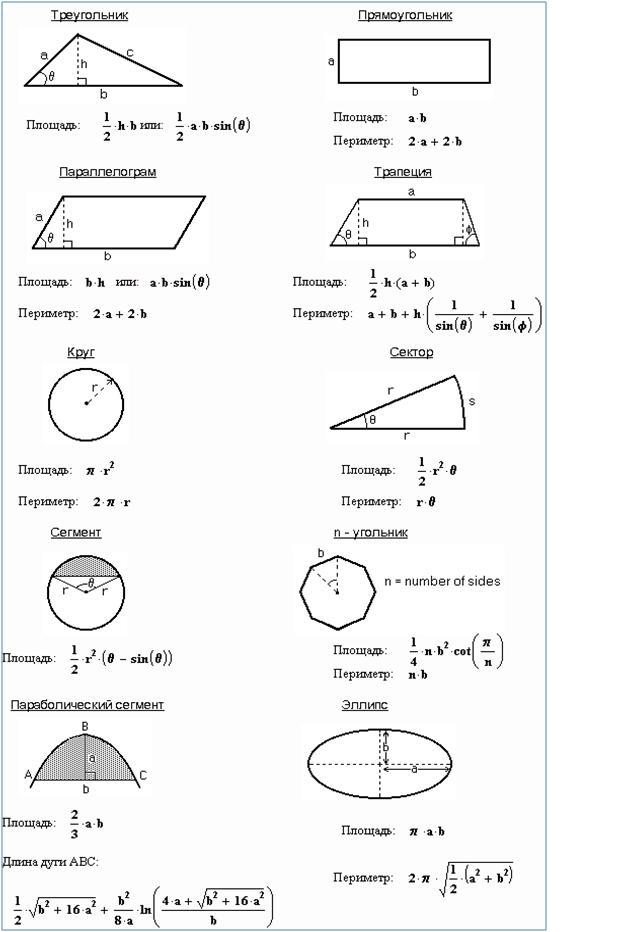
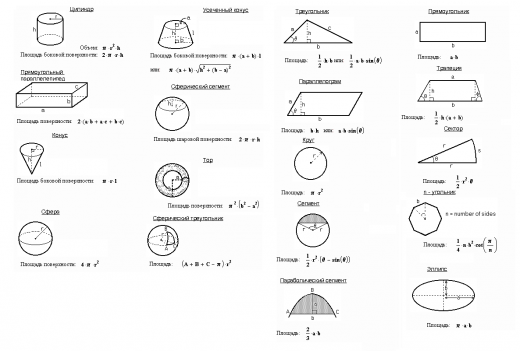
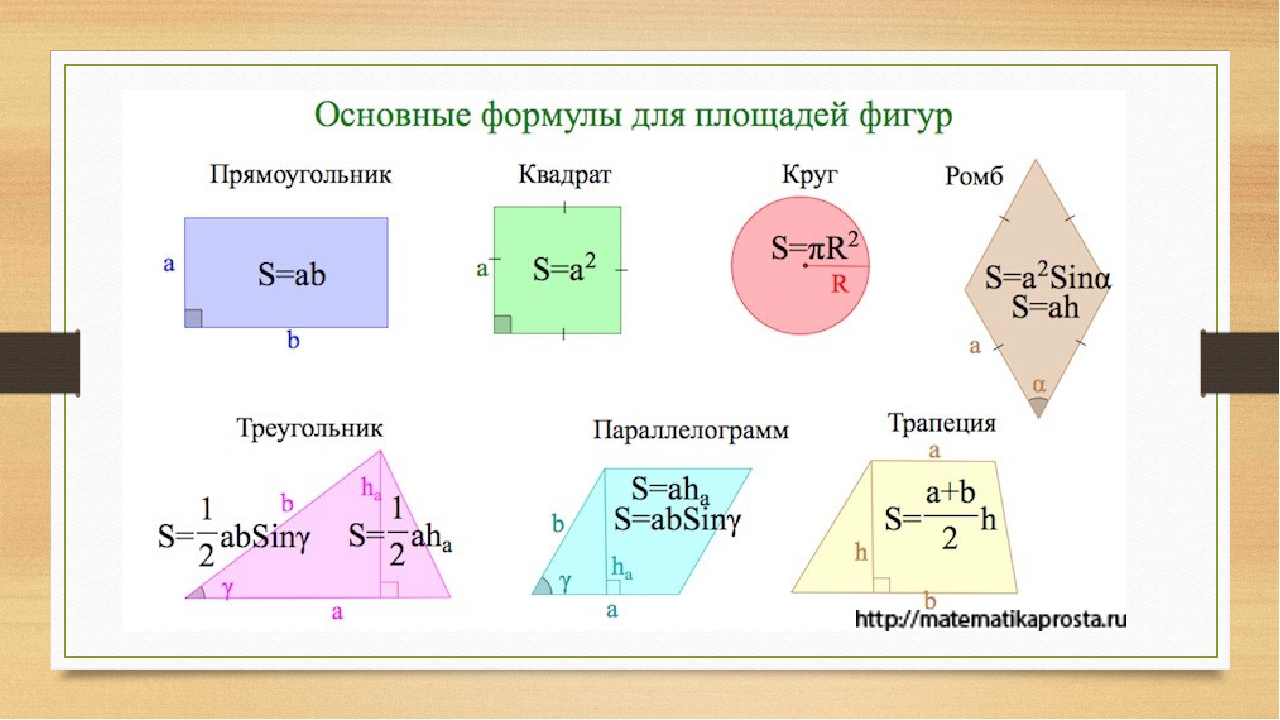
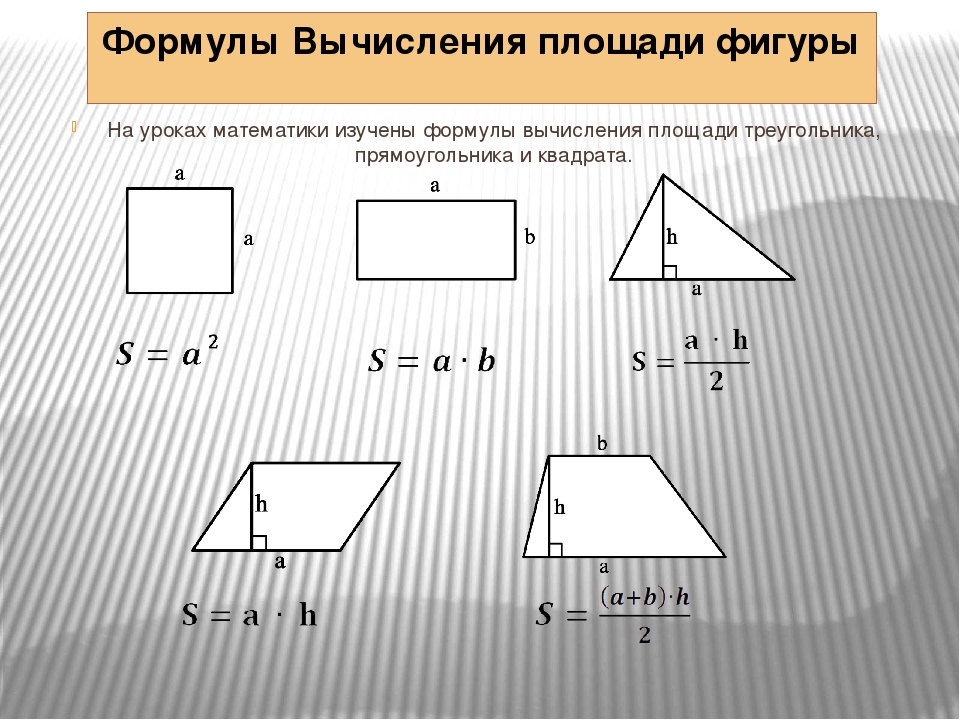

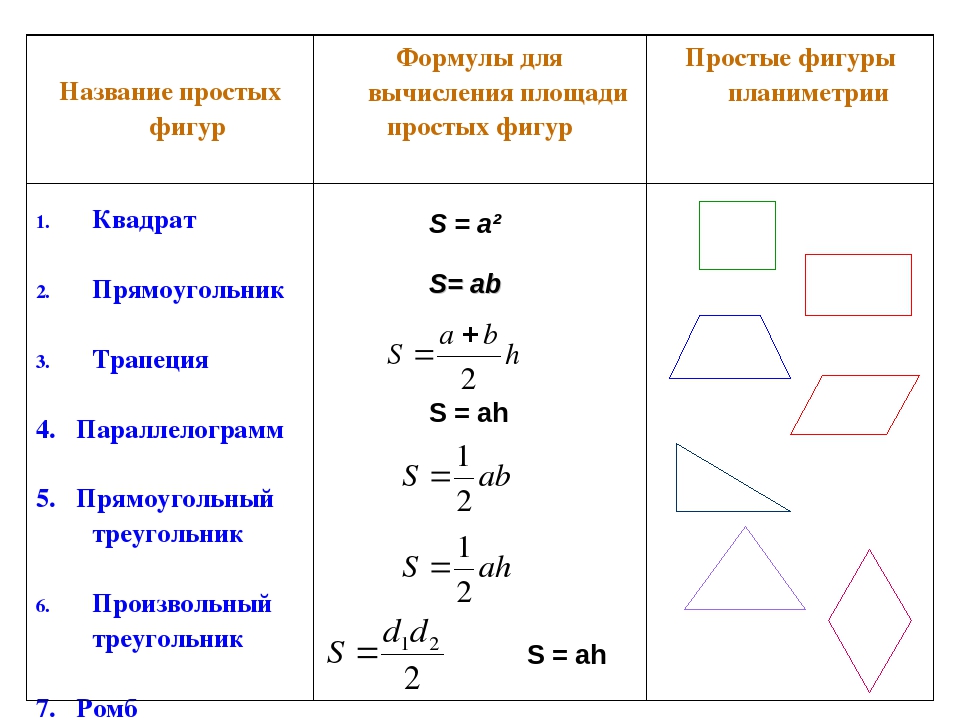
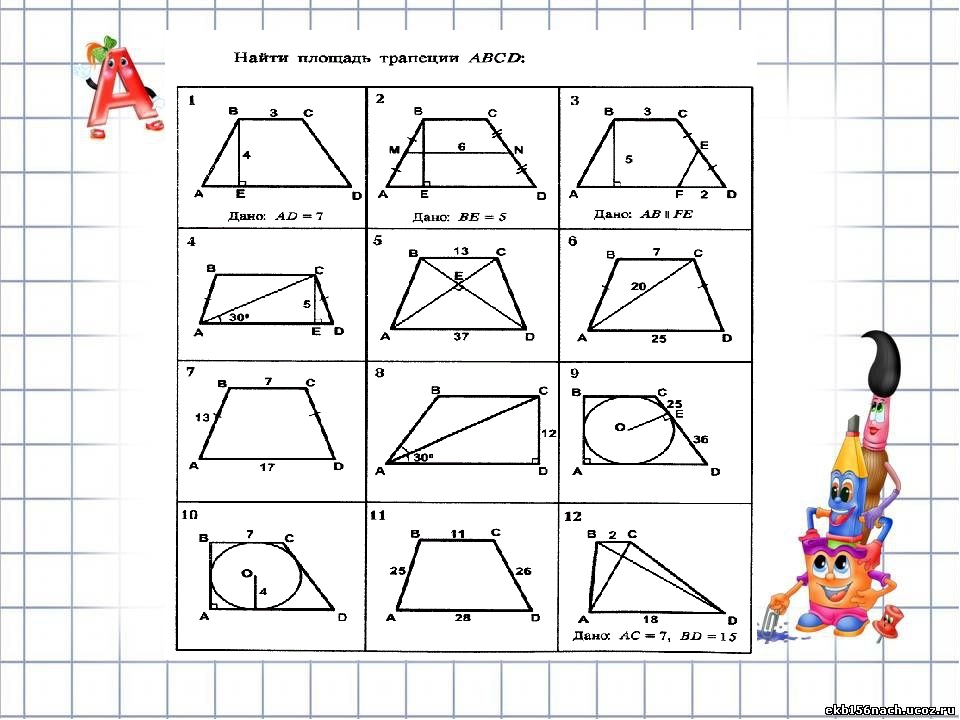 размеры в см
размеры в см