Точка, линия, прямая, луч, отрезок, ломанная

Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать

точка A, точка B, точка C

ABC

точка 1, точка 2, точка 3

123

Можно нарисовать на листке бумаги три точки "А" и предложить ребёнку провести линию через две точки "А". Но как понять через какие?

AAA

Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет

Обозначается строчными (маленькими) латинскими буквами

линия a, линия b, линия c

abc

Линия может быть

1. замкнутой, если её начало и конец находятся в одной точке,
2. разомкнутой, если её начало и конец не соединены

замкнутые линии

разомкнутые линии

Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру.  Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.


Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.


Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.

1. самопересекающейся
2. без самопересечений

самопересекающиеся линии

линии без самопересечений

1. прямой
2. ломанной
3. кривой

прямые линии

ломанные линии

кривые линии

Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны

Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны

Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой

прямая линия a

a

прямая линия AB

BA

Прямые могут быть

1. пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
   • перпендикулярными, если пересекаются под прямым углом (90°).
2. параллельными, если не пересекаются, не имеют общей точки.

параллельные линии

пересекающиеся линии

перпендикулярные линии

Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону

У луча света на картинке начальной точкой является солнце

солнышко

Точка разделяет прямую на две части — два луча
A
A

Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче

луч a

a

луч AB

BA

Лучи совпадают, если

1. расположены на одной и той же прямой,
2. начинаются в одной точке,
3. направлены в одну сторону

лучи AB и AC совпадают

лучи CB и CA совпадают

CBA

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками

Через одну точку можно провести любое число линий, в том числе прямых

Через две точки — неограниченное количество кривых, но только одну прямую

кривые линии, проходящие через две точки

BA

прямая линия AB

BA

От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.
✂
BA✂

Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок

отрезок AB

BA

Задача: где прямая, луч, отрезок, кривая?

Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°

Длинный отрезок «поломали» на несколько коротких

Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.

Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.

Обозначается ломанная перечислением всех её вершин.

ломанная линия ABCDE

вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E

звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE

звено AB и звено BC являются смежными

звено BC и звено CD являются смежными

звено CD и звено DE являются смежными

ABCDE646212752

Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305

Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см.  У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.

Многоугольник — это замкнутая ломанная линия

Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.

Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.

Обозначается многоугольник перечислением всех его вершин.

замкнутая ломанная линия, не имеющая самопересечения, ABCDEF

многоугольник ABCDEF

вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F

вершина A и вершина B являются соседними

вершина B и вершина C являются соседними

вершина C и вершина D являются соседними

вершина D и вершина E являются соседними

вершина E и вершина F являются соседними

вершина F и вершина A являются соседними

сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF

сторона AB и сторона BC являются смежными

сторона BC и сторона CD являются смежными

сторона CD и сторона DE являются смежными

сторона DE и сторона EF являются смежными

сторона EF и сторона FA являются смежными

ABCDEF120605812298141

Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599

Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.

треугольники

четырёхугольники: квадрат, прямоугольник, дельтоид, ромб, параллелограмм, трапеция

пятиугольники

Точка, отрезок, луч, прямая — числовая прямая

Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.

Точка в математике

Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.

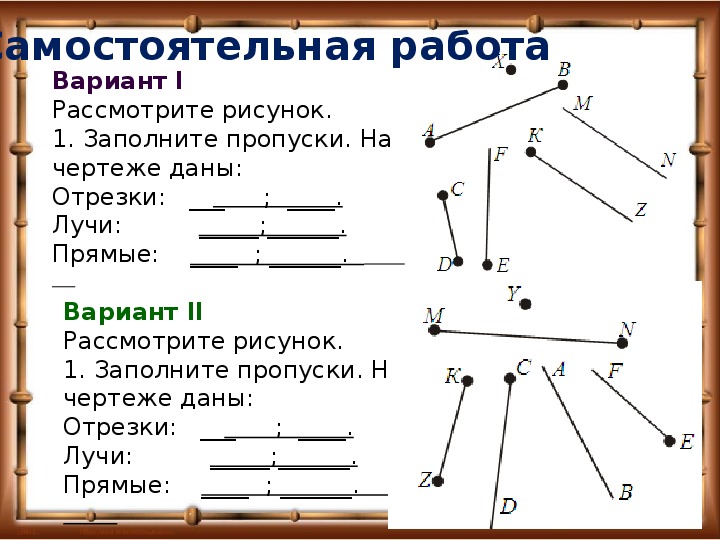
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.

Отрезок в математике

Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.

На рисунке мы видим следующее: отрезки [A;C],[C;D],[D;M],[M;F],[F;E] и [E;T], а также две точки B и S.

Прямая в математике

Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.

На рисунке изображены две прямые: CD и EF.

Луч в математике

Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.

Числовая прямая в математике

Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.

На рисунке изображена числовая прямая, а также луч OD и ED

Нужна помощь в учебе?

Предыдущая тема: Сложение и вычитание дробей с одинаковыми знаменателями: ПРИМЕРЫ
Следующая тема:&nbsp&nbsp&nbspЧтение и запись больших натуральных чисел: разряды, классы + ПРИМЕР

Отрезок, угол, луч — геометрия и искусство

Из истории.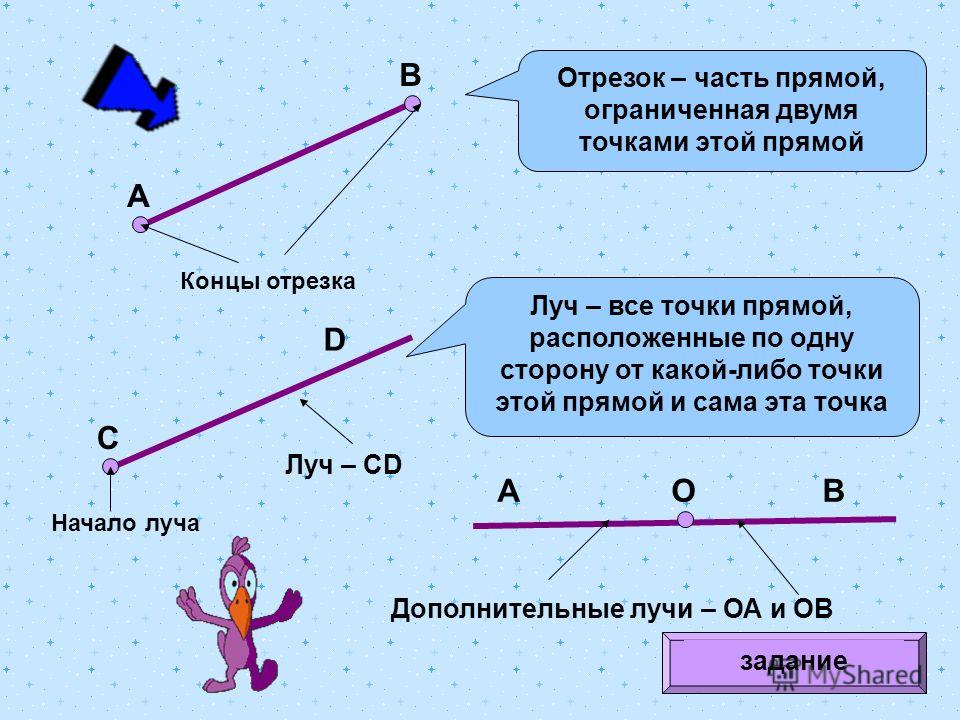 Единицы измерения углов.
Градусное измерение углов возникло в Древнем Вавилоне задолго до новой эры. Жрецы считали, что свой дневной путь Солнце совершает за 180 «шагов», и, значит, один «шаг» равен 1/180 развернутого угла.

В Вавилоне была принята шестидесятиричная система счисления, т. е. фактически числа записывались в виде суммы степеней числа 60, а не 10, как это принято в нашей десятеричной системе. Естественно поэтому, что для введения более мелких единиц измерения углов один «шаг» последовательно делился на 60 частей.

Вавилонская система измерения углов оказалась достаточно удобной, и ее сохранили математики Греции и Рима.

Термины, которыми мы пользуемся для названия угловых величин, имеют латинские корни. Слово «градус» происходит от латинского gradus (шаг, ступень). В переводе с латинского minutus означает «уменьшенный». Наконец, secunda переводится как «вторая». Имеется в виду следующее: деление градуса на 60 частей, т. е. минуты,— это первое деление; деление минуты на 60 секунд — второе деление градуса. Малоупотребительное название 1/60  секунды — терцина, латинское tercina означает «третье» (деление градуса).

Принятая сейчас система обозначения величин углов получила широкое распространение на рубеже XVI и XVII вв.; ею уже пользовались такие известные астрономы, как Н. Коперник и Т. Браге. Но еще К. Птолемей (II в. н. э.) количество градусов обозначал кружком, число минут — штрихом, а секунд — двумя штрихами.

Другая единица измерения углов — радиан — введена совсем недавно. Первое издание (это были экзаменационные билеты), содержащее термин «радиан», появилось в 1873 г. в Англии. Сначала в обозначениях указывалось, что имеется в виду радианная мера , но вскоре инадекс R (или г) стали опускать. Сам термин «радиан» происходит от латинского radius (спица, луч).

Если вспомнить определение угла в один радиан (центральный угол, длина дуги которого равна радиусу окружности), то выбор корня «рад» для названия такого угла представляется совершенно естественным.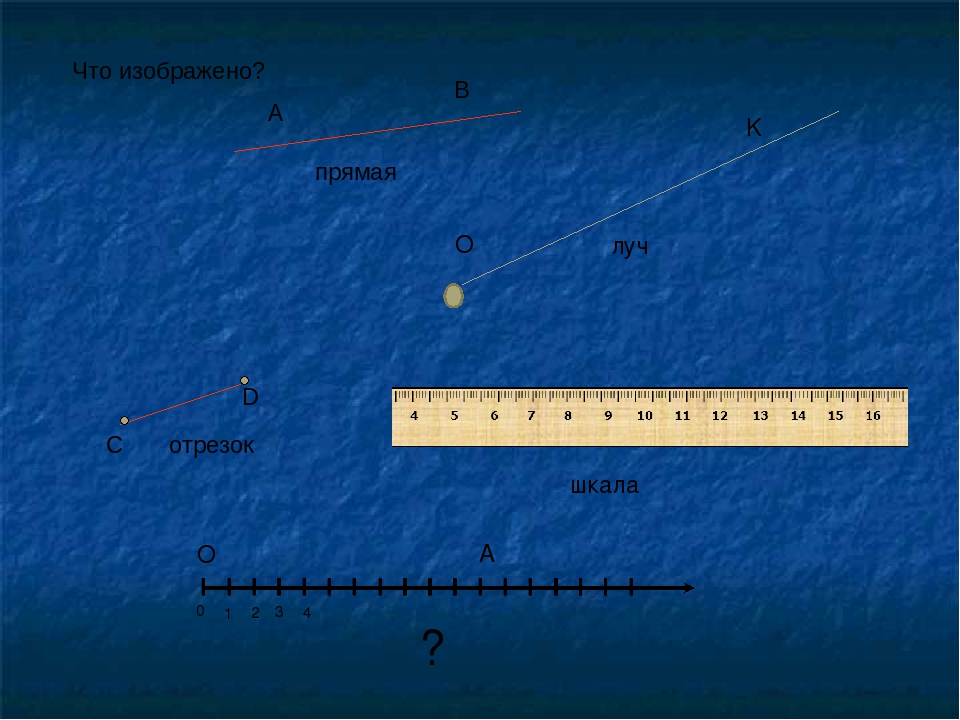

Начальные геометрические сведения. Прямая, отрезок, луч и угол.

1. Базовые сведения о геометрии
2. Прямая и отрезок
3. Луч и угол

Добро пожаловать в удивительный мир геометрии. Сегодня мы познакомимся с очень важными и базовыми понятиями науки математики — прямой, отрезком, лучом и углом.

Базовые сведения о геометрии

Геометрия зародилась очень давно – около двух тысяч лет до нашей эры. Она родилась в связи с практическими нуждами людей в Древнем Египте. Слово «геометрия» — греческое. «Геос» переводится как земля, а «метрео» — измеряю. Геометрия – землемерение. В школах нашей страны изучается евклидова геометрия по имени великого ученого Евклида. Курс школьной геометрии делятся на планиметрию (7-9 класс) и стереометрию (10-11 класс). Планиметрия изучает свойства фигур на плоскости. Стереометрия изучает свойства фигур в пространстве.

Основными фигурами на плоскости точка и прямая. Все фигуры состоят из точек и прямых.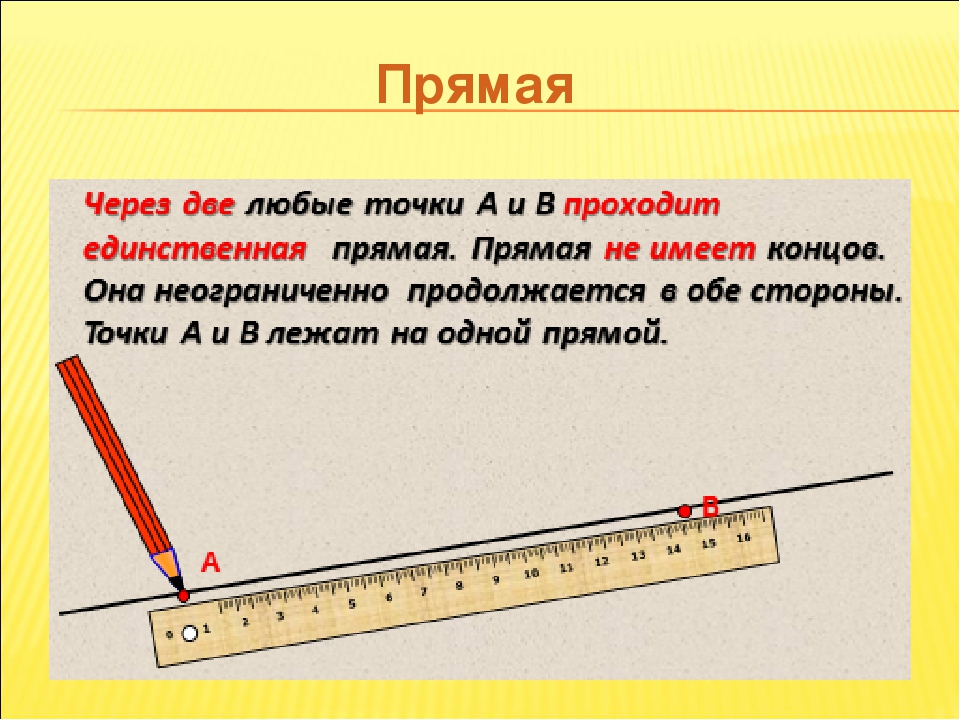 Точки обозначаются большими латинскими буквами. Прямые обозначаются либо двумя большими латинскими буквами, либо одной маленькой. Точка — это мгновенное прикосновение карандаша к бумаге.

Прямая и отрезок

Прямая это фигура не имеет ни начала, ни конца.

Через любые две точки плоскости можно провести прямую и при том только одну. Если прямые имеют одну общую точку, то говорят, что они пересекаются в ней. Если прямые имеют две и более точек, то они совпадают. Если прямые не имеют общих точек, то они параллельны — A параллельна B.

На прямой точки могут лежать, а могут и не лежать. Посмотрите на  рисунок. Вы видите знак принадлежности, непринадлежности. Выражение точка А не принадлежит прямой а записывается короче с использованием этих значков.

Точка B не принадлежит прямой а.
Точка C принадлежит прямой а.
Точка D принадлежит прямой а.
Точка Е принадлежит прямой а
Точка F принадлежит прямой а, потому что прямую а можно продолжить, и тогда она будет проходить через точку F.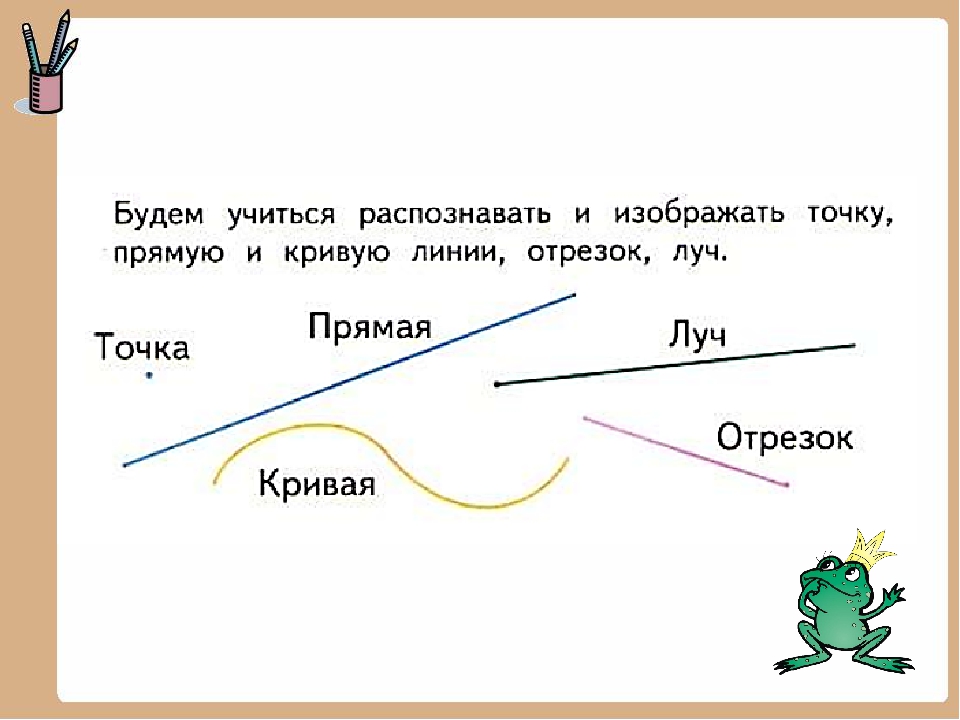 Прямая не имеет ни начала, ни конца.

Если точка О принадлежит прямой а и точка О принадлежит прямой b одновременно, это означает, что прямые a и b пересекаются в точке О.

Часть прямой, ограниченная двумя точками называется отрезком. Отрезок можно обозначить либо AB, либо BA. Точки A и B — концы отрезка. Вообще, отрезок имеет и начало, и конец. Если на отрезке лежит точка О, то существует свойство: если к длине отрезка АО прибавить длину отрезка ОB, то получится весь отрезок AB.

Луч и угол

Если мы нарисуем прямую и далее отметим точку О, то эта точка разбивает прямую на два дополнительных луча — луч ОА и луч ОВ. Точка О — начало этих двух дополнительных лучей. Луч имеет начало, но не имеет конца. Обозначается луч либо двумя большими, либо одной маленькой латинской буквой. Луч — это тоже часть прямой.

Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Точка — это вершина угла, а лучи — это стороны угла. Углы обозначают большими латинскими буквами.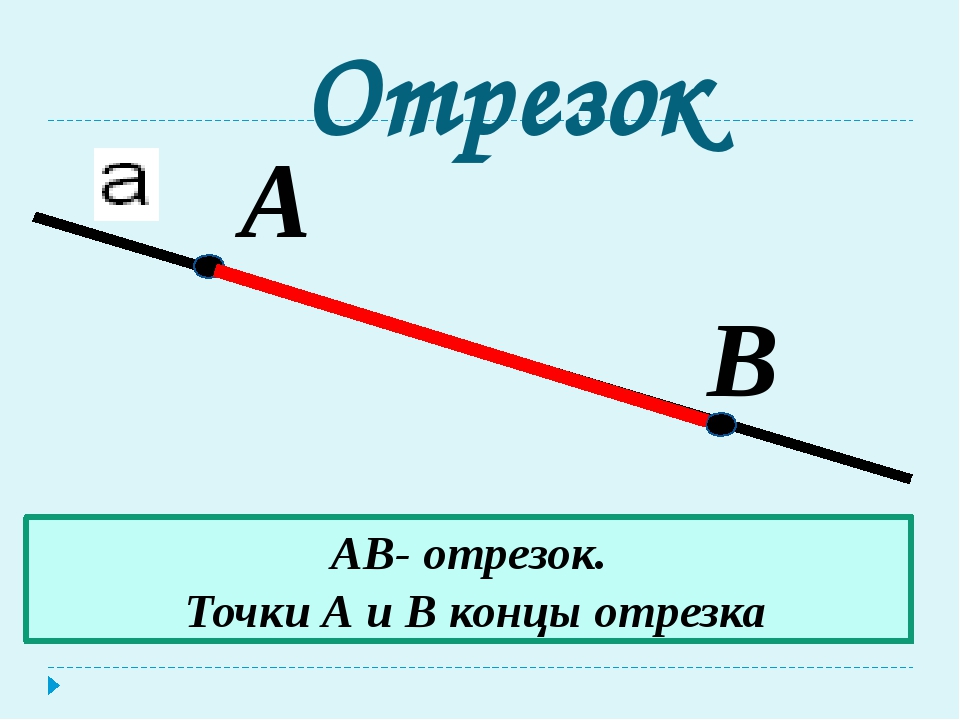 Либо одной большой буквой по вершине угла, либо тремя большими буквами, в этом случае вершина О находится посередине, либо двумя маленькими буквами по названию лучей. Угол делит плоскость на две части – внутреннюю и внешнюю область угла.  Если внутри угла АОС проходит луч ОВ, то существует свойство: если к углу а AОB прибавить угол ВОС, то мы получим угол АОС.

Угол АОВ является частью угла АОС, значит угол АОВ меньше угла АОС. Точно так же угол ВОС – часть большого угла АОС, и значит угол ВОС меньше, чем угол АОС.

Луч, исходящий из вершины угла и делящий его на два равных угла, называют биссектрисой угла. При этом угол АОВ будет равен углу ВОС. ОВ – биссектриса.

Углы измеряются транспортиром. Углы измеряются в градусах, минутах, секундах. Например, угол А равен 60 градусов 51 минута 3 секунды.

1 градус — это 60 минут, 1 минута — это 60 секунд. Значит, в одном градусе 360 секунд. Развёрнутый угол — его градусная мера 180 градусов

Половина развернутого угла — это прямой угол. Мы его обозначаем квадратиком внутри угла, и он равен 90 градусов.

Острый угол находится в диапазоне от 0 до 90 градусов.

Тупой угол находится в диапазоне от 90 градусов до 180 градусов.

Отрезок — что это такое

Обновлено 19 января 2021

1. Отрезок — это…
2. Разница между ним, лучом и прямой
3. Вектор
4. Ломаная линия
5. Отрезок времени

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Одним из понятий геометрии, с которым знакомятся еще в начальной школе, является отрезок. Уйма задач по математике и геометрии строится на понятиях отрезка и прямой.

Понимание, что такое отрезок, поможет решать всевозможные задачи и примеры на уроках математики как в школе, так и в высших учебных заведениях.

Отрезок — это геометрическая фигура

Согласно определению в словаре, отрезком называют часть прямой, ограниченную двумя точками, находящимися на ней. Именно по обозначениям этих точек и дается название отрезка.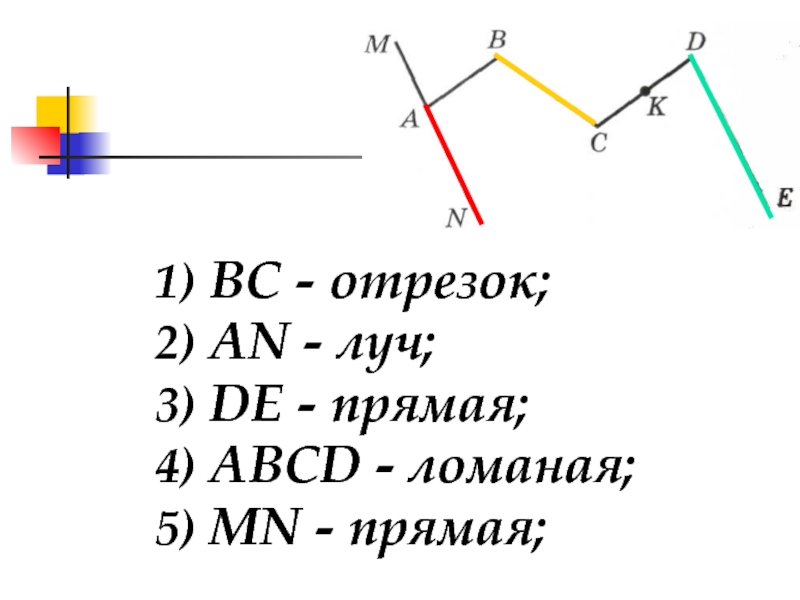

На рисунке, изображенном ниже, показан отрезок AB. Точки A и B являются концами отрезка. Длиной отрезка называют расстояние между его концами.

В математике принято обозначать точки, и соответственно отрезки, большими буквами латинского алфавита. Если нужно нарисовать отрезок, чаще всего его изображают без прямой, а лишь от одного конца до другого.

Также можно сказать, что отрезок — это совокупность всех точек, которые лежат на одной прямой и находятся между двумя заданными точками, которые являются концами данного отрезка.

Если на отрезке между его концами отметить еще одну точку, она разделит данный отрезок на два. Длину отрезка АВ можно посчитать, просуммировав длины отрезков АС и СВ.

Разница между отрезком, лучом и прямой

Школьники иногда путают понятия прямой, луча и отрезка. И вправду, эти понятия очень схожи между собой, однако имеют принципиальное различие:

1. Прямой называется линия, которая не искривляется, а также не имеет начала и конца.
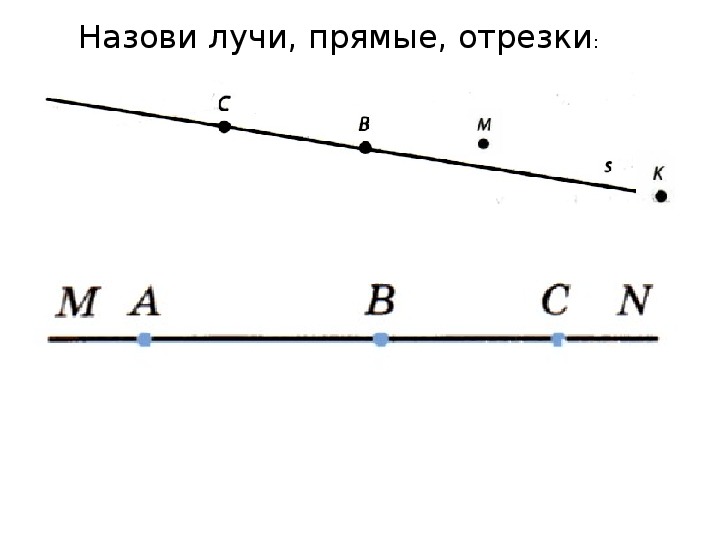
2. Луч — это часть прямой, ограниченная одной точкой. Он имеет начало и не имеет конца.
3. Отрезок ограничивается двумя точками. Он имеет и начало, и конец.

Точка, находящаяся на прямой, делит ее на два луча. Количество же отрезков на одной прямой может быть бесконечным.

Чтобы различать эти фигуры на рисунке, в начале и конце рисуемой линии ставятся или не ставятся точки. Рисуя луч, точка ставится в одном конце, а изображая отрезок — в обоих концах. Прямая не имеет концов, поэтому точки в конце линии не ставятся.

Направленный отрезок — это вектор

Отрезки бывают двух видов:

1. Ненаправленные.
2. Направленные.

Для ненаправленных отрезков, АВ и ВА — одинаковые отрезки, так как направление не имеет значения.

Если же говорить о направленных отрезках, порядок перечисления его концов имеет решающее значение. В таком случае, АВ^➜ и ВА^➜ — разные отрезки, так как они противоположно направленные.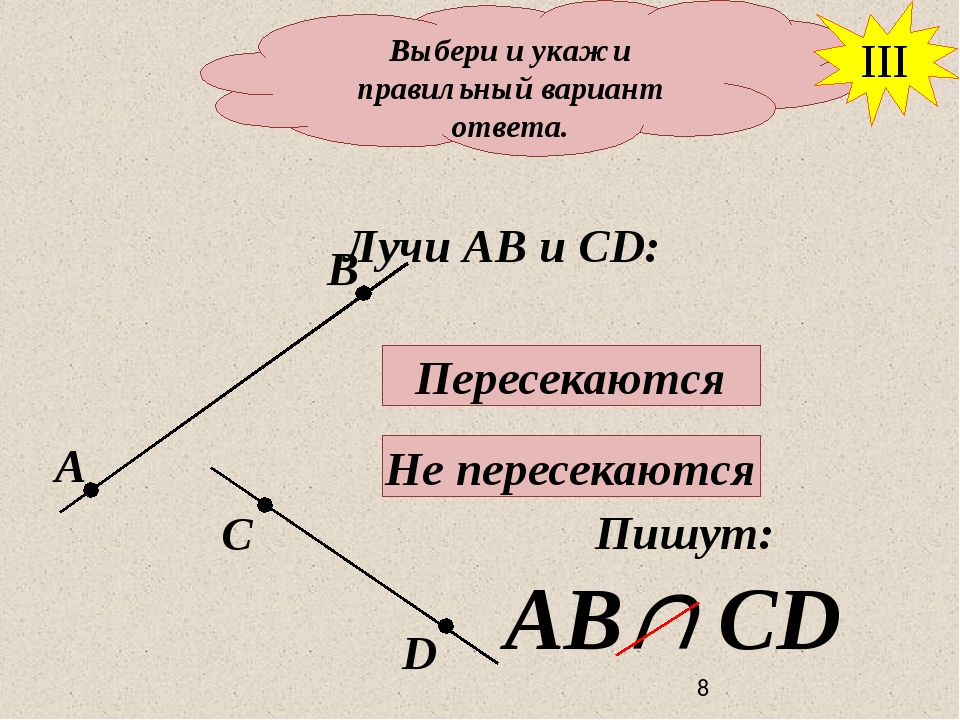

Направленные отрезки называются векторами. Векторы могут обозначаться как двумя заглавными буквами латинского алфавита со стрелочкой над ними, так и одной маленькой буквой со стрелочкой.

Модулем вектора называется длина направленного отрезка. Обозначается как АВ^➜. Модули векторов АВ^➜ и ВА^➜ равны.

Векторы часто рассматривают в системе координат. Модуль вектора равен квадратному корню суммы квадратов координат концов вектора.

Коллинеарными векторами называются те, что лежат на одной или на параллельных прямых.

Ломаная линия — это множество соединенных отрезков

Ломаная линия состоит из множества отрезков, которые называются ее звеньями. Эти отрезки соединены друг с другом своими концами и не расположены под углом 180°.

Вершинами ломаной являются следующие точки:

1. Точка, с которой началась ломаная.
2. Точка, которой ломаная закончилась.
3. Точки, в которых соединяются смежные звенья (отрезки ломаной).

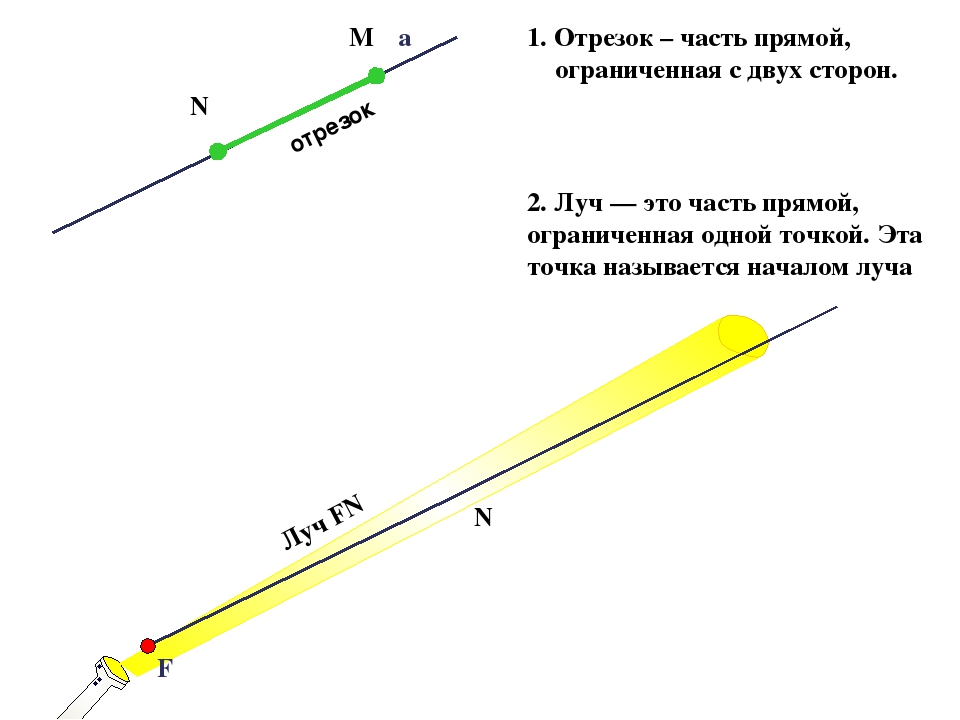
Число вершин ломаной всегда на один больше, чем количество ее звеньев. Обозначается ломаная перечислением всех ее вершин начиная с одного конца и заканчивая другим.

Например, ломаная ABCDEF состоит из отрезков AB, BC, CD, DE и EF и вершин A, B, C, D, E и F. Звенья AB и BC являются смежными, так как имеют общий конец — точку В. Длина ломаной вычисляется как сумма длин всех ее звеньев.

Любая замкнутая ломаная является геометрической фигурой — многоугольником.

Сумма углов многоугольника кратна 180° и вычисляется по следующей формуле 180*(n-2), где n — количество углов или отрезков, составляющих данную фигуру.

Отрезок времени

Интересно, что слово отрезок применимо не только к геометрическим понятиям, но и как временной термин.

Отрезком времени называют период между двумя событиями, датами. Он может измеряться как секундами или минутами, так и годами или даже десятилетиями.

Время в целом в таком случае определяется как временная прямая.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Прямая линия, отрезок, луч — презентация онлайн

81
вычесть 23
?
48
увеличить на19
?
?
уменьшить на 36
40
?
прибавить 7
92

4. 58 67 76 85

58 67 76 85 94 103
Прямые линии – красным цветом,
лучи – синим,
отрезки зеленым.
Найдите точки пересечения этих
дорожек

7. Цель урока: научиться различать прямые линии, отрезки, лучи; научиться их обозначать и находить точки их пересечения.

8. Тема: Прямая, луч, отрезок.

ППрямая
Отрезок
Луч
Прямая линия — она натянутая, ее
можно продлить в оба конца, она
бесконечна.
П
Прямая
Отрезок
Луч
Бесконечна
Можно продлить
в оба конца
А
О
М
В
Отрезок — это часть прямой линии,
ограниченной с двух сторон.
П
Прямая
Отрезок
Луч
Бесконечна
Можно продлить
в оба конца
Ограничен с двух Нельзя продлить
сторон
А
О
М
В
Луч – это часть прямой,
ограниченной с одной стороны.
Прямая
Бесконечна Можно
продлить в оба
конца
Отрезок
Часть
прямой
Часть
прямой
Луч
Ограничен с 2
сторон
Ограничен с
одной стороны,
продлить в 1
сторону

18. Найди прямую, луч, отрезок. Начерти в тетради.

В
X
l
P
М
А
Е
Д
К
R N
Y
C

19. Физкультминутка

20. План.

1.Обозначать лучи.
2.Распознавать луч, прямую и отрезок.
3.Определять, являются ли лучи
пересекающимися

21. Распредели (устно)

Прямая АБ
Отрезок АВ
В
Луч АВ
А
А
А
В
В
Прямая АБ
Отрезок АВ
В
А
Луч АВ
А
А
В
В

23. Начерти в тетради.

• Луч МК пересекает луч АВ
• Луч СЕ пересекает луч ДС

24. Алгоритм

1.Обозначим вершину луча.
2.Построим луч при помощи линейки.
3.Продлим лучи до их пересечения.
4. Проверим, пересекаются ли они.
А
• Д
М
С

26. Домашнее задание

С. 72- №2,№4.
Фото отправь учителю в viber.

27. Молодец!!!!

Точка. Кривая линия. Прямая линия. Отрезок. Луч. Ломаная линия

Однажды дядюшка Филя подарил Любику
интересную книгу.

— Любик, вот тебе книга, которая называется «Геометрия».

— Ого, какое слово незнакомое. Эта книга,
наверное, для взрослых и мне очень тяжело будет её изучать.

— А ты попробуй, даже можешь на помощь
кого-нибудь позвать. А потом мне придёшь и расскажешь, сложно тебе было или
нет.

— Позвал Любик Белочку и Ежика и вместе с ними
стал изучать книгу с загадочным названием «Геометрия».

— Смотрите, вот на первой странице что-то написано
и нарисовано. Белочка, ну-ка прочитай.

— Жил-был карандаш. Однажды карандаш на листе
бумаги решил поставить точку. А точка взяла да и ожила.

Захотела точка узнать, что интересного в мире
творится и говорит карандашу:

— Нарисуй-ка ты мне дорожки, пойду я погуляю.
Нарисовал карандаш прямую и кривую линии. Пошла точка сначала
гулять по кривой линии.

Шла, шла. Тяжело её стало. Решила точка, что по
прямой линии будет легче идти. Перепрыгнула она на прямую линию и пошла дальше.

 Шла долго ли коротко и совсем устала.

— Скоро ли будет конец у этой прямой линии,
пойду-ка я в другую сторону,- думает точка. Только она хотела идти, вдруг
выглянуло солнышко.

— Солнышко, а ты не знаешь, когда закончится эта
прямая линия.

— Вот смешная. Прямая линия бесконечна. У неё нет
ни конца ни края.

— Ой, а что же мне делать? Хотела точка
заплакать, а солнышко погладило точку своими лучами. И точке стало тепло и
хорошо.

— Хорошо тебе солнышко, у твоих лучей есть
начало.

— Зато нет конца. Мои лучи длинные и бесконечные.
И вообще, у любого луча есть начало, но нет конца. Точка, скоро дождь начнётся,
видно и молния будет. Надо тебе куда то спрятаться.

— Вдруг откуда ни возьмись
появились ножницы и обрезали прямую с двух концов, а карандаш на каждом конце
нарисовал маленькие штрихи. Ножницы и карандаш из прямой линии сделали отрезок у
которого есть начало и есть конец.

Обрадовалась точка и решила жить на этом отрезке.
А карандаш нарисовал, в начале отрезка дом, а в конце деревья.

Вот теперь и гуляет точка по этому отрезку, и
очень довольна, что у него есть начало и конец.

А ночью, когда точка заснула, в небе засверкала
молния, прямо как ломаная линия. Только точка этого уже не видела, потому что
крепко спала.

— Ого, какая интересная сказка.

— Подождите, это не все. Здесь еще есть
интересные задания и картинки. Вот первое задание. Нарисуйте-ка на листе в
клеточку, то что я вам сейчас буду говорить:

— Точку и кривую линию.

— Вот.

— А я тоже хочу нарисовать кривую линию. Вот.

— Теперь, Любик, нарисуй прямую  линию.

— А ты Ежик отрезок и луч.

— Вот прямая линия.

— Это отрезок, а чтобы нарисовать луч, я поставлю сначала точку, а потом
от неё нарисую прямую. У нас получился луч,
который имеет начало, но не имеет конца.

— Хорошо. Нарисуйте-ка еще и  ломаные линии.

— Молодцы. Вы внимательно слушали сказку. А
теперь мы рассмотрим картинки и посмотрим, где же эти понятия встречаются в
жизни.

Итак. Прямая
линия идет бесконечно в одну сторону и в другую. Например, в небе летит по
прямой линии самолёт.

Если посмотреть на листья, которые падают с
дерева, то обычно они описывают кривые
линии.

Теперь посмотрим, где же в жизни может
встречаться луч. Луч можно увидеть в
лучах солнца, либо в пламени свечки или в лампочках фонариков.

Как мы уже выяснили, если от
прямой отрезать кусочек, и ограничить его с двух
сторон, то получится отрезок.

Отрезки могут быть разные по длине: короткие и длинные.

— А теперь угадайте-ка, где можно увидеть ломаную
линию.

— Я знаю. Молния на небе очень похожа на ломаную
линию.

— Совершенно верно. Да. Интересную книгу нам дядя
Филя дал. А пойдёмте к нему и расскажем, что мы нового узнали.

— Дядюшка Филя, спасибо. Геометрия оказалась
очень интересная. Спасибо тебе большое.

— Ну раз вы хорошо
потрудились и узнали много нового я вас сейчас чем-то вкусным угощу. Заходите
ко мне в дом.

линий, лучей, отрезков и плоскостей

Наставник: Нарисуйте, пожалуйста,
ось координат на бумаге. Теперь пометьте оси x и y. Теперь пометьте каждую линию на оси x и y знаком
масштаб одного.

Наставник: Вы знали, что координатная ось — это плоскость?

Студент: Нет. Что такое самолет?

Наставник: Плоскость — это плоская поверхность, которая продолжается бесконечно. Лучший способ увидеть, что такое самолет
это как представить себе лист бумаги, который никогда не заканчивается.

Студент: Так же
бесконечность означает бесконечность?

Наставник: Да, это так. Бесконечность представляет собой то, что может продолжаться. Для любой
при заданном значении всегда можно найти большее значение.

Ученик: Итак, самолет простирается до конца вселенной.

Наставник: Да, но более того. Конец вселенной представляет собой конец. Что-то, что может быть
считаться бесконечным не заканчивается.На самом деле ничто из существующего не может быть бесконечным. Это просто
может продолжаться, как наша система счисления или линия. Теперь кто-нибудь может вспомнить, что
линия есть?

Учащийся: линия состоит как минимум из двух точек, находящихся на прямом пути.

Наставник: Да, очень хорошо. Нарисуем один.

Наставник: А теперь у кого-нибудь есть представление о том, что такое луч?

Студент: Луч света, исходящий из лучевой пушки.

Наставник: Хорошая идея. У лучевой пушки есть отправная точка, и она продолжается вечно, если никогда не попадает в цель.
Луч начинается в одной точке и продолжается до бесконечности.

Наставник: Давайте нарисуем луч.

Студент: Итак, в чем разница между линией и лучом?

Наставник: Линия уходит в бесконечность в обоих направлениях, но луч останавливается на одном конце. Если вы разрежете линию
пополам получается два луча.Теперь кто-нибудь может догадаться, что такое отрезок линии?

Студент: Это линия с двумя концами?

Наставник: Совершенно верно. Сегмент линии — это часть линии, имеющей две конечные точки. Нарисуем один на
бумага.

(PDF) Унифицированный анализ алгоритмов на основе FBP при сканировании спирального конического луча, кругового конуса и веерного луча

4350 XPanet al

Предложены алгоритмы для реконструкции изображения в обоих круговых конических лучах

(Feldkamp et al 1984, Hu 1996, Grass et al 2000, Turbell 2001, Yu and Pan 2003) и веером-

луча (Kak and Slaney 1988, Pan 1999, Besson 1999, Pan and Yu 2003).Среди них

алгоритмов на основе фильтрованной обратной проекции (FBP) представляют особый интерес теоретически, а

наиболее широко используются на практике. Общей чертой основанных на FBP алгоритмов является то, что они

реконструируют изображения путем взвешенного обратного проецирования отфильтрованных модифицированных данных. Алгоритм веерного луча

FBP (FFBP) (Как и Слэни, 1988) был разработан для реконструкции изображений

при сканировании с полным и коротким круговым веером. На основе алгоритма FFBP был получен алгоритм FDK

(Feldkamp et al 1984) для приблизительного восстановления изображений при полном сканировании

и короткокруглых конических лучах.За последние несколько лет было предложено

алгоритмов на основе FBP для восстановления точно 2D ROI в уменьшенном круговом сканировании веерным лучом (Noo et al

,

2002) и приблизительно 3D ROI (Kudo et al 2002) в уменьшенном -круглое конусно-лучевое сканирование,

соответственно.

Недавно мы разработали алгоритм на основе 3D FBP для реконструкции изображения на

сегментах линии PI

1

при сканировании спирального конического луча (Zou and Pan 2004). Мы также применили этот алгоритм

для восстановления изображения в 3D ROI на основе данных, полученных с помощью сканирования коническим лучом

с уменьшенной спиралью.В этой работе мы демонстрируем, что наш алгоритм на основе 3D FBP для спирального конусно-лучевого КТ

(Zou and Pan 2004) действительно обеспечивает довольно общую формулировку основанных на FBP-

алгоритмов для восстановления изображений из расходящихся проекций (таких как конусно-лучевые и

веерные проекции). В частности, мы замечаем, что сканирование с круговым коническим лучом и веерным лучом

можно интерпретировать как частные случаи сканирования с спиральным коническим лучом. Поэтому мы выводим

новых (приближенных или точных) алгоритмов из нашего алгоритма на основе 3D FBP для этих особых случаев

.Кроме того, мы демонстрируем, что эти недавно полученные алгоритмы приводят к реконструкциям

, которые математически идентичны реконструкциям, произведенным соответствующими существующими алгоритмами.

Мы также проводим предварительное численное исследование, чтобы проверить наши теоретические результаты в каждом из

случаев.

Мы организовываем статью следующим образом. В разделе 2 мы кратко резюмируем наш основанный на 3D FBP алгоритм

для реконструкции изображений на сегментах линии PI при сканировании спирального конического луча.В разделах 3 и 4

мы выводим новые алгоритмы для реконструкции изображений в круговом конусном луче

и веерном сканировании, соответственно, и показываем, что эти алгоритмы производят изображения, которые

математически идентичны изображениям, реконструированным с большей частью существующие алгоритмы. Результаты

нашего предварительного численного исследования представлены в разделе 5. Наконец, в разделе 6 мы делаем замечания о последствиях и возможном обобщении наших теоретических и численных результатов

.

2. Алгоритм 3D FBP для реконструкции изображения из данных спирального конического луча

В этом разделе мы кратко резюмируем наш алгоритм 3D FBP для реконструкции изображения при сканировании спирального конического луча

(Zou and Pan 2004). Он формирует основу для разработки новых алгоритмов

для восстановления изображений при сканировании с круговым конусом и веерным пучком.

2.1. Сканирование спирального конического луча и линии PI

Как показано на рисунке 1 (a), две системы координат {x, y, z} и {u, v, w} часто используются для

описания геометрии в спиральной сканировать.Они фиксируются на изображаемом объекте и вращающейся точке источника

соответственно и, таким образом, называются фиксированной координатой и координатой вращения

1

При спиральном сканировании рассмотрим прямую линию, которая дважды пересекается со спиральной. траектория. Когда угловая разница

между двумя пересечениями меньше 2π, эта прямая называется PI-линией. Кроме того, мы называем участок

PI-линии внутри спирали сегментом PI-линии.См. Раздел 2.1 для подробных комментариев по сегментам линии PI.

Формирование каустик в свет, инвариантный к распространению

4.

Wang, J., Yang, J.-Y., Fazal, I.M., Ahmed, N. & Yan, Y. et al. Передача данных в терабитном свободном пространстве с использованием мультиплексирования орбитального углового момента. Nat. Фотон. 6 , 488–496 (2012).

ADS
CAS

Google Scholar

11.

Курвуазье Ф., Стоян Р. и Куайрон А. Сверхбыстрая лазерная микро- и нанообработка с недифрагирующими и изогнутыми лучами. Опт. Laser Technol. 80 , 125–137 (2016).

ADS

Google Scholar

23.

Роуз П., Богуславски М. и Денз К. Нелинейные решетчатые структуры на основе семейств сложных недифрагирующих пучков. New J. Phys. 14 , 033018–1–10 (2012).

Google Scholar

Как копирование линейного сегмента аналогично копированию угла_

Углы измеряются целыми числами. Q имеет ровно 1 прямой угол. Если коэффициент масштабирования между P и Q равен $ \ frac15 $, то длина каждой стороны P умножается на $ \ frac15 $, чтобы получить соответствующую длину стороны Q. Если коэффициент масштабирования равен 2, каждый угол в P умножается на 2, чтобы получить соответствующий угол в Q. Строка темы взята прямо из резюме основного текста, что означает, что они будут автоматически выровнены.Главное здесь — выравнивание. Если вы можете поддерживать соответствие между строкой темы, основным текстом и призывом к действию, вы можете попробовать что-то новое и немного отклониться от темы обещания, если хотите.

Повсеместно используется построение в AutoCAD сегмента заданной длины под нужным углом к ​​горизонтальной линии, направленной вправо (по умолчанию), а также других объектов AutoCAD с использованием динамического ввода. Дело в том, что данный способ построения сегментов (объектов) интуитивно понятен из-за наглядности и простоты построения.᭜ 8. Копирование отрезка линии. Шаги 1–4 ниже показывают, как скопировать отрезок линии. Шаг 2 Нарисуйте отрезок прямой, который длиннее отрезка AB. Обозначьте одну из его конечных точек C.

Нарисуйте линейный сегмент и скопируйте его справа от исходного сегмента. Объясните свои шаги и обоснуйте каждый использованный шаг. Разделите исходный отрезок пополам от первого проблемного. Нарисуйте угол и скопируйте его вправо от исходного угла. Объясните свои шаги и обоснуйте каждый использованный шаг. Разделите исходный угол пополам из задачи три.достаточно широкий угол, мы гарантируем, что отношение кратчайшего пути к евклидову расстоянию достаточно мало. Любое фиксированное r> 0 определяет такой «широкий» угол r, который мы называем «большим» углом нашей сети. Интуитивно мы хотели бы, чтобы r было достаточно широким, чтобы пути, которые перемещаются только вокруг этого угла, имели отношение путей меньше или равное r.

Постройте линейный сегмент, длина которого равна сумме длин данных линейных сегментов. 2) Постройте отрезок прямой, длина которого равна разности длин данных отрезков.3) Постройте отрезок прямой, в указанное количество раз длиннее данного отрезка. 4) В 2 раза длиннее. Построить половину отрезка прямой … Он использует решение задач, чтобы найти недостающие длины отрезков и меры углов. Также в урок включены задачи по алгебре. Студенты узнают: Постулат линейки — используется для определения длины сегментов числовой прямой. Постулат сложения сегментов — используется для добавления или вычитания длин сегментов.

3. Соединительная лента Создает биссектрису угла \ ABC.Это следует из конгруэнтности боковых сторон ABE и DBE. Рисунок 1: Угловое деление пополам, шаг 1 Рисунок 2: Угловое деление пополам, шаг 2 Рисунок 3: Угловое деление пополам, шаг 3 Биссектриса перпендикуляра: 1. На отрезке AB нарисуйте две окружности радиуса AB, одну с центром в A и одну с центром в B. 2 Копирование линейного сегмента На этой странице показано, как скопировать линейный сегмент с помощью циркуля и линейки или линейки. Для данного отрезка линии показано, как сделать другой отрезок такой же длины.

Как найти длину линейного сегмента в калькуляторе

Эта формула получена из аппроксимации кривой прямыми линиями, соединяющими последовательные точки на кривой, с использованием теоремы Пифагора для вычисления длины этих сегментов с точки зрения изменения $ x $ и изменение $ y $.СЛОВАРЬ Скопируйте и заполните: Чтобы найти длину} AB с конечными точками A (27, 5) и B (4,26), вы можете использовать? . 2. ПИСЬМО. Объясните, что значит разделить сегмент пополам. Почему нельзя разрезать линию пополам? ПОИСК ДЛИНЫ Линия l делит сегмент пополам.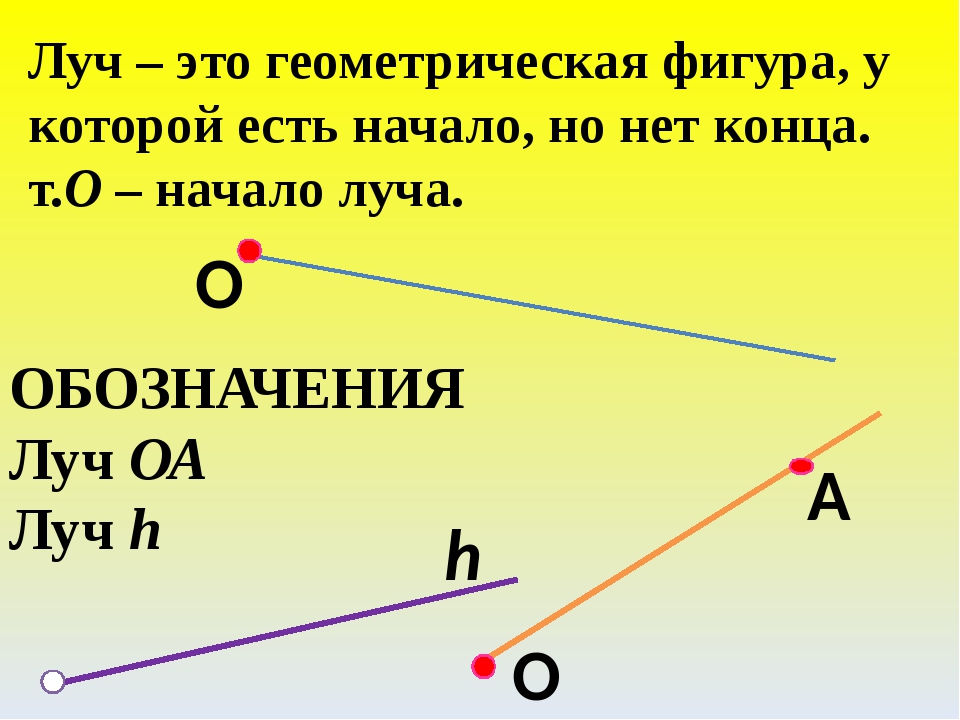 Найдите указанную длину. 3. Найдите RT ifRS 5 5} 1 8 дюймов 4. UW VW 5} 8 5. Найдите EG, если EF 5 13 см. R S … 18 декабря, 2020 · Осмысление 2020 года. 2020 год, наконец, подходит к концу. В этот час мы оглядываемся на моменты, разговоры и важные идеи из прошлых эпизодов, которые помогли нам разобраться в этом странном и беспрецедентном году.Длина линии составляет 6 единиц, а точка на отрезке 1 3 пути от P до Q будет на 2 единицы от P, на 4 единицы от Q и будет в (2, 0). Рассмотрим случай, когда сегмент не является горизонтальной или вертикальной линией. Компоненты направленного сегмента P Q ¯ равны 〈6, 3〉, и нам нужно найти точку, скажем X на … Вычислить расстояние, используя пошаговую формулу расстояния. Математические решения для средней школы — Калькулятор перпендикулярных и параллельных линий. Параллельные линии имеют одинаковый наклон, чтобы найти параллельную линию в заданной точке, вам нужно просто вычислить…Онлайн калькулятор для расчета и отображения расстояния и средней точки для двух точек. Предоставляется пошаговое объяснение. Этот онлайн-калькулятор вычислит и нанесет на карту расстояние и середину отрезка линии. Калькулятор сгенерирует пошаговое объяснение того, как получить результаты. Сферический сегмент * Введите 3 значения в любые допустимые поля … Длина дуги на экваторе (L) Ограничение ввода: градус. θ единица радиан градус; Объем среза: поверхность среза … Дата постулата добавления сегмента _____ Период ____ Найдите указанную длину.1) ВЧ G? 2) RT S? 3) TV U? 4) CE D? 5) Найдите KL IL JK 6) Найдите HJ GJ HI 7) Найдите EC EB DC 8) Найдите IK IL JK Точки A, B и C лежат на одной прямой. Точка B находится между точками A и C. Найдите указанную длину. 9) Найдите AC, если AB = и BC =. 10) Найдите AC, если AB = и BC =. Верните евклидову норму sqrt (xx + yy). Это длина вектора от начала координат до точки (x, y). Вот мое предложение. Это просто синтаксический сахар для конкатенации кортежей. Также кажется, что во фрагменте есть несколько опечаток / ошибок. Самостоятельная линия. args = [Point (* args) for p in args] должно быть скорее self.args … Я извлек линейные сегменты с помощью преобразования Хафа. Я хотел бы сейчас определить длину этих строк, но не знаю, как это сделать. Вы можете найти отрезки линии с помощью. H = получить (gca, ‘дети’). Их координаты должны быть в свойствах xdata и ydata. Длина поиска и середина отрезка линии. Узнайте, как найти наклон между двумя точками. Наклон линии — это крутизна линии. Горизонтальная линия имеет ноль…Калькулятор. Используйте калькулятор ниже, чтобы вычислить площадь сегмента с учетом радиуса и центрального угла сегмента, используя формулу, описанную выше. Помните: в этой версии центральный угол должен быть в градусах. Проверка «Оценить длину полилинии» позволяет вам проверять длину полилиний целиком или только их частей. Используя эту проверку, вы можете указать пороговое значение для длины ломаной линии, части / пути или сегмента, и те, которые соответствуют критериям, возвращаются как результаты проверки. 6 декабря 2010 г. · Ответ (3, -2).Посмотрите на первый пункт и сравните его со вторым. для x, 2-1 = 1. Умножьте на 2, и вы получите 2, прибавьте к исходному, вы получите 3. для y, 1 — 4 = -3 Умножьте снова, и вы получите … 16 мая 2014 г. · Найдите длину сегмента линии — CD с конечной точкой C в (-3, 1) и конечной точкой D в (5, 6). при необходимости округлите ответ до ближайшей десятой. A. 9.4 B. 5.4 C. 3.6] D. 11.7 Найдите середину отрезка FG с точкой F на Калькуляторе наименьшего общего кратного. Найдите НОК набора чисел с помощью этого калькулятора, который также показывает шаги и способы выполнения работы.НОК (a, b) вычисляется путем нахождения факторизации на простые множители как a, так и b. Используйте тот же процесс для НОК для более чем двух чисел. Чтобы найти расстояние, вам нужно знать координаты его конечных точек, заданные как (x1, y1) и (x2, y2), и формулу расстояния. В основном потому, что, если предположить, что это всего лишь один сегмент, средняя точка по определению (середина означает середину) — это точка в точной середине линейного сегмента; тогда как длина . .. Направленный отрезок прямой в пространстве — это отрезок прямой вместе с направлением.Таким образом, направленный отрезок прямой от точки P до точки Q отличается от направленного отрезка от Q до P. отрезок как a … Пусть данный отрезок будет PQ, т.е. известные координаты его концов P x, P y, Q x, Q y. Необходимо построить уравнение прямой в плоскости, проходящей через этот отрезок, т.е. найти коэффициенты A, B, C в уравнении прямой: A x + B y + C = 0.Каковы формулы для ширины и длины микрополосковой подачи строки? См. Главу 14 книги Константина Баланиса «Теория антенн — анализ и проектирование». вы можете найти процедуру.

Когда мы знаем расстояния по горизонтали и вертикали между двумя точками, мы можем вычислить расстояние по прямой следующим образом: distance = √ a 2 + b 2 Представьте, что вы знаете расположение двух точек (A и B), как здесь.

Определение середины и длины отрезка линии В координатной геометрии важно уметь находить средние точки и длину отрезков.а.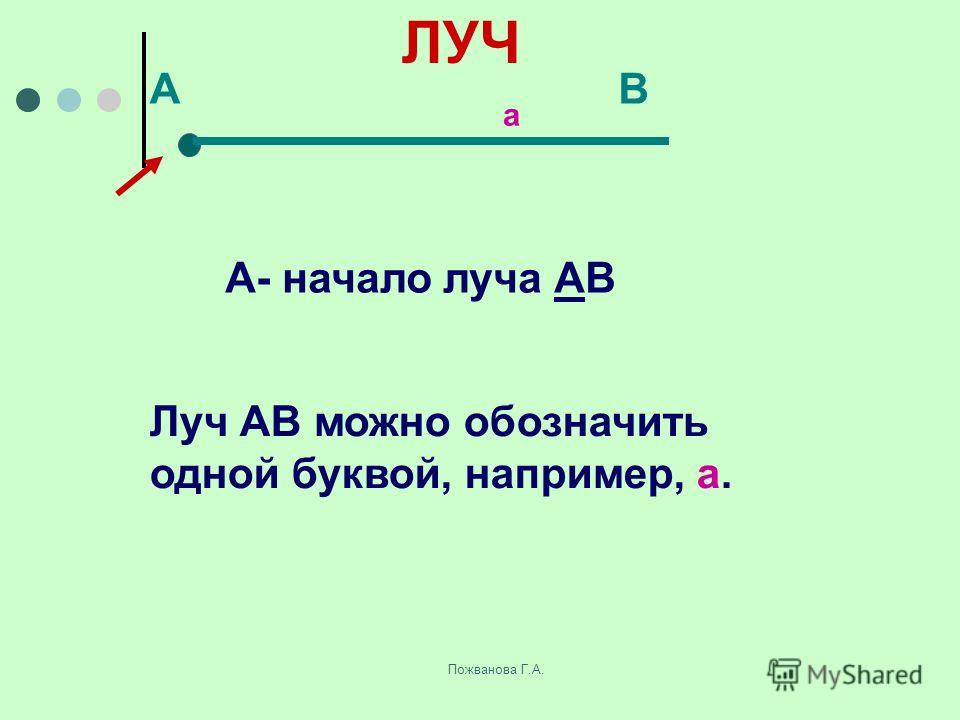 Найдите координаты средних точек TP и AR. б. Сравните длину MN с суммой длин TR и PA. xy 5 10210 25 5 25 A (0, 22) P (26, 1) MNR (12, 0) T (26, 9) 10 15 …

Чтобы найти длину отрезка линии: Определите высоту вертикальной стороны: Определите длину горизонтальной стороны: Используйте теорему Пифагора, чтобы вычислить длину линии A (2, 3) B (12, 10) И снова теорема Пифагора спасает положение!

Сегмент линии — это сегмент или конечная часть бесконечной прямой.Если вам известны координаты конечных точек отрезка прямой, вы можете использовать теорему Пифагора для вычисления длины отрезка.

Проверка «Оценить длину полилинии» позволяет вам проверять длину полилиний целиком или только их частей. Используя эту проверку, вы можете указать пороговое значение для длины ломаной линии, части / пути или сегмента, и те, которые соответствуют критериям, возвращаются как результаты проверки.

Вы можете использовать формулу расстояния, чтобы найти длину такой линии.Эта формула представляет собой теорему Пифагора, которую вы можете увидеть, если представите данный отрезок прямой как гипотенузу прямоугольного треугольника.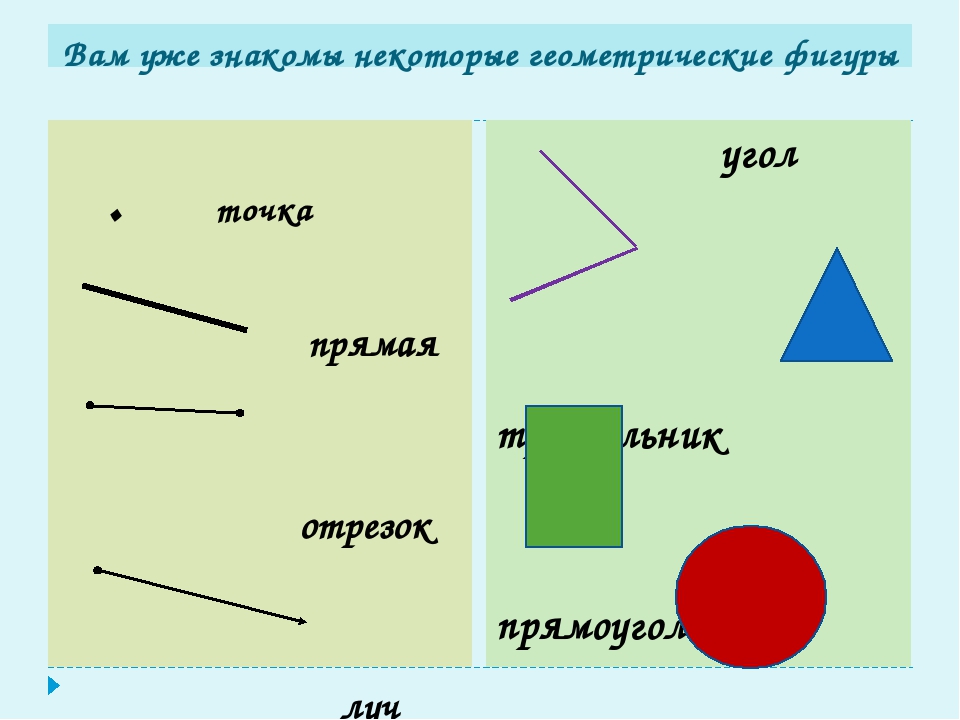 Чтобы использовать формулу расстояния для определения длины линии, начните с определения координат конечных точек линейного сегмента.

Рассчитать значение для? которая является только ЧАСТЬЮ гипотенузы. … Найдите указанную длину сегмента. Предположим, что линии, которые кажутся. касательные являются касательными.

27 августа 2015 г. · Биссектрисы сегмента и угла РАЗДЕЛЯЮТ СЕГМЕНТ НА ​​СЕГМЕНТ Сегмент — это точка, которая делит сегмент, или сегмент на два конгруэнтных сегмента.В этой книге совпадающие красные метки конгруэнтности обозначают совпадающие сегменты на диаграммах. A — это сегмент, луч, линия или плоскость, пересекающая сегмент в его средней точке. M — это середина AB Æ, если CD ¯˘ — это …

Все эти строки разделены, и потребуется вечность, чтобы сделать это вручную на калькуляторе 🙂 Thx! Если вы не знакомы с тем, как использовать lisp, просто скопируйте / вставьте (CTRL + V) ВСЕ текст и символы из приведенной выше ссылки в свою командную строку и нажмите Enter, затем введите TLEN в командную строку и следуйте. ..

Выбрать необходимое количество вычислений Установка длины балки. Рассчитайте реакции на опорах балки. Диаграмма изгибающего момента (BMD) Диаграмма поперечных сил (SFD) Диаграмма осевых сил.

Проверка «Оценить длину полилинии» позволяет вам проверять длину полилиний целиком или только их частей. Используя эту проверку, вы можете указать пороговое значение для длины ломаной линии, части / пути или сегмента, и те, которые соответствуют критериям, возвращаются как результаты проверки.

См. Полный список на сайте onlinemath5all.com

Касательные к окружностям — поиск углов, включающих касательные и окружности, примеры задач определения неизвестных значений с использованием свойств касательной к окружности, примеры и пошаговые решения, Как решить для На следующей диаграмме PA и PB касаются окружности. Найдите значение

Как обычно, мы начинаем с размышлений о том, как аппроксимировать площадь. Мы выбираем несколько точек вдоль интересующей нас части параболы и соединяем соседние точки прямыми линиями; когда точки расположены близко друг к другу, длина каждого отрезка линии будет близка к длине параболы.

Мы узнаем, как вычислить координаты средней точки или средней точки отрезка линии. Формула дана и проиллюстрирована подробным руководством. Мы прорабатываем вопросы типа экзамена, а также предоставляем рабочие листы для скачивания в формате pdf.

Найдите GH. 9,7 мм G и JL 10 Kis между J и L. Сделайте набросок и найдите значение x KL, JK и JL. 2.JK = 6x KL = 3x и JL = 27 3.JK = 2x KL-x + 2, ключевое понятие Между точками Слова Точка Mis между точками P и Q тогда и только тогда, когда P, Q и Mare коллинеарны и PM + PO .Модель Найти длину Найти длину FG. Словарь ON Новая строка словаря …

Объяснение вычисления окружности. Понимание того, что такое длина окружности и как ее вычислить, имеет решающее значение при переходе на более высокий уровень математики. Окружность круга — это расстояние по внешней стороне круга. Он похож на периметр других форм, например квадратов. Вы можете подумать об этом …

Desmos предлагает лучшие в своем классе калькуляторы, цифровые математические задания и учебную программу, чтобы помочь каждому ученику полюбить математику и полюбить ее изучение.

Длина отрезка PQ, соединяющего P (x1; y1) и Q (x2; y2), равна jPQ j = p (x2 x1) 2 + (y2 y1) 2. Иногда длина линейного сегмента выражается как «расстояние между двумя точками», а приведенная выше формула называется «Формула расстояния». Дж. Гарвин | Длина линейного сегмента Слайд 9/15 аналитическая геометрия Длина линейного сегмента Пример

Вы можете найти длину диагональной линии, используя теорему Пифагора. При нахождении длины отрезка в прямоугольном треугольнике вы можете использовать теорему Пифагора: квадрат плюс B…

Найдите длину 4 отрезков по их координатам на графике. Найдите середину отрезка прямой. Найдите периметр замкнутого многоугольника, образованного отрезками прямых. Я прошу учащихся сдать выходной лист, когда он будет заполнен, и я использую его в качестве быстрой формирующей оценки успеваемости каждого учащегося на этом уроке.

Щелкните конечные точки первого сегмента линии. Щелкните конечную точку следующего отрезка линии. Повторите этот процесс, чтобы создать столько сегментов линии, сколько нужно. Обратите внимание, что если на вкладке «Свойства» активирован параметр «Показать значения сегмента», отображается совокупное измерение длины (в дополнение к измерению длины самого сегмента), когда …

находятся длина и середина сегмента линии. Узнайте, как найти наклон между двумя точками. Наклон линии — это крутизна линии. Горизонтальная линия имеет ноль …

Определение середины и длины отрезка линии В координатной геометрии важно уметь находить средние точки и длины отрезков.а. Найдите координаты средних точек TP и AR. б. Сравните длину MN с суммой длин TR и PA. x y 5 10 210 25 5 25 A (0, 22) P (26, 1) M N R (12, 0) T (26, 9) 10 15 …

Смещение определяется с помощью направленного отрезка линии. Он переводит точку в другую точку так, чтобы направленный линейный сегмент от исходной точки до изображения был параллелен данному линейному сегменту и имел ту же длину и направление. На рисунке \ (A ‘\) — это изображение \ (A \) при перемещении, заданном направленным отрезком линии \ (t \).Выберите точку, которая должна быть начальной точкой сегмента. В появившемся окне укажите желаемую длину сегмента. Калькулятор координат точек находит сегменты разделительной линии (соотношения направленных сегментов). Он находит координаты, разбивая линейный сегмент. Координаты точек определяются парой чисел, определяющих положение точки, которая определяет ее точное местоположение на …

Ray Optics Simulation

Веб-приложение с открытым исходным кодом для моделирования отражения и преломления света.
Написано на HTML, CSS и JavaScript.

Запустить приложение
Посмотреть на GitHub
Мобильная версия

Луч

Единственный луч света, определяемый двумя точками.

Балка

Параллельный пучок лучей выходит из отрезка прямой,
с плотностью, контролируемой ползунком «Плотность луча».

Точечный источник

Лучи выходят из единой точки,
с числом, контролируемым ползунком «Плотность луча».

Зеркало

Смоделируйте отражение света на зеркале.

Зеркало (Arc)

Зеркало в форме круга,
который определяется тремя точками.

Идеальное изогнутое зеркало

Идеализированное «изогнутое» зеркало, которое точно подчиняется уравнению зеркала (1 / p + 1 / q = 1 / f).
Фокусное расстояние (в пикселях) можно установить напрямую.

Стекло

Смоделируйте преломление и отражение света на поверхности.
Интенсивности рассчитываются в предположении неполяризованности.

Стекло (Круг)

Стекло круглой формы с центром и точкой на поверхности.

Стекло (прочие формы)

Стекло любой формы, состоящее из отрезков прямых и дуг окружности,
в том числе призмы и «сферические» линзы.

Стекло (идеальный объектив)

Идеальная линза, которая точно подчиняется уравнению тонкой линзы (1 / p + 1 / q = 1 / f).Фокусное расстояние (в пикселях) можно установить напрямую.

Блокиратор

Линейный блокатор света, поглощающий падающие лучи.

Линейка

Линейка из точки в ноль и еще одну точку.
Масштаб в пикселях.

Транспортир

Транспортир, определяемый от центра, и другая точка для нулевого направления.Шкала в градусах.

Сверхвысокий вакуум | LIGO Lab

Предоставлено: Kiwamu Izumi / LIGO.

Оптические компоненты

LIGO спокойно размещаются в колоссальной вакуумной камере объемом 10 000 кубических метров (353 000 кубических футов) с давлением воздуха 10 ^-9 торр или одной триллионной атмосферы.

Создание и поддержание этого вакуума абсолютно необходимо для работы LIGO.Вакуумная среда LIGO предотвращает вибрацию зеркал звуковыми волнами (звук не может проходить через вакуум). Кроме того, работа в вакууме предотвращает возникновение колебаний температуры внутри трубок — изменений, которые могут изменить форму оптики LIGO в достаточной степени, чтобы разрушить качество лазерного луча, который несет в себе секреты источников гравитационных волн. Любые воздушные потоки внутри трубок также могут привести к преломлению лазера, что сделает невозможным обнаружение гравитационных волн.Все эти надоедливые источники шума можно устранить, работая в вакууме.

Потребовалось 1100 часов (40 дней) постоянной откачки, чтобы вакуумировать вакуумные трубки LIGO до идеального рабочего давления. За это время турбонасосные (струйные) вакуумы удаляли основную часть воздуха в трубках, а сами трубки нагревали до 150-170 градусов C в течение 30 дней для удаления остаточных газов и влаги.

Вакуумная система LIGO контролируется и контролируется несколькими уровнями сложных вычислительных систем.На нижнем изображении показаны многочисленные стойки с измерительным оборудованием, которые контролируют здания, в которых находятся вакуумные системы, крионасосы и ионные насосы (среди прочего).

Достичь вакуума — это подвиг. Поддержание этого уровня требует сложных мониторов и средств управления, а также непрерывной работы ионных насосов, которые извлекают молекулы, выделяемые из трубок и других структур и компонентов, находящихся внутри вакуумных систем. Посторонние молекулы воды также удаляются непрерывно работающими крионасосами с жидким азотом; к ним прилипают молекулы воды.

Электронные лампы

LIGO были изготовлены из нержавеющей стали 304L, сваренной по спирали. Благодаря относительно низкому содержанию углерода сталь 304L устойчива к коррозии, особенно на сварных швах. Чтобы сделать трубы такого размера, как LIGO, нужно время, и в процессе их производства в 1990-х годах ржавчина фактически росла на их внутренней части. Это означало, что когда трубки были установлены в LIGO, их внутренности необходимо было тщательно отполировать и очистить, чтобы удалить ржавчину и значительно снизить вероятность того, что чешуйки оксида стали попадут в вакуумную систему и упадут через лазерный луч или попадут на него. зеркала или другие оптические поверхности, последнее может быть губительным для миссии LIGO.

Установка балочной трубы

Руки

LIGO достаточно длинные, чтобы кривизна самой Земли была осложняющим фактором при установке электронных ламп. Инженерам-строителям LIGO было недостаточно сгладить ровный путь и собрать трубы каждого рычага по прямой линии. Чтобы обеспечить идеально ровную траекторию луча, искривлению Земли (более вертикального метра по длине каждого плеча) противодействовали землеройные работы с помощью GPS и высокоточные бетонные работы.Железобетонные перекрытия толщиной 75 см под интерферометрами минимизируют просачивание сейсмических колебаний. Эти этажи отделены от плит, поддерживающих лаборатории и офисы, и от опор, удерживающих вертикальный каркас. Каждый из этих уровней инженерии был разработан для поддержки траектории и стабильности лазерного луча LIGO при его прохождении через интерферометр, а также для сохранения всего прибора как можно более бесшумным.

Сборка сегмента лучевой трубы LIGO.Опорные кольца приварены к спирально-сварной трубе, чтобы значительно повысить структурную целостность стали толщиной 3 мм. (Caltech / MIT / LIGO Lab)

Открытая балочная труба после сборки в LIGO Livingston. (Caltech / MIT / LIGO Lab)

Балочные трубы диаметром 1,2 м были созданы 20-метровыми сегментами. Каждый из них был сделан из непрерывной плоской стальной ленты толщиной всего 3 мм, сваренной в цилиндр, напоминающий трубку от бумажного полотенца.Хотя математически совершенный цилиндр не разрушится, небольшие дефекты в настоящей трубе могут привести к ее деформации под огромным весом атмосферы Земли. Раздавленная вакуумная трубка была бы катастрофой, поэтому трубки LIGO поддерживаются кольцами жесткости, которые обеспечивают значительное сопротивление короблению. Трубы должны выдерживать эти нагрузки не менее 20 лет. Пока что они выдержали испытание временем.

.