Содержание
Теорема Фалеса
Воспользуемся утверждениями пунктов 59 и 60 для доказательства следующей теоремы.
Теорема. Если на одной из сторон угла от его вершины отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие другую сторону угла, то они отсекут на второй стороне равные меду собой отрезки.
Доказательство. Рассмотрим угол с вершиной A, на стороне которого отложены равные друг другу отрезки AA1, A1A2, A2A3, A3A4, …, и через их концы проведены параллельные прямые, пересекающие другую сторону угла в точках B1, B2, B3, B4, … (рис. 75). Докажем, что отрезки AB1, B1B2, B2B3, B3B4, … равны друг другу.
Прямая A1B1 проходит через середину A1 стороны AA2 треугольника AA2B2 параллельно его стороне A2B2, поэтому AB1 = B1B2.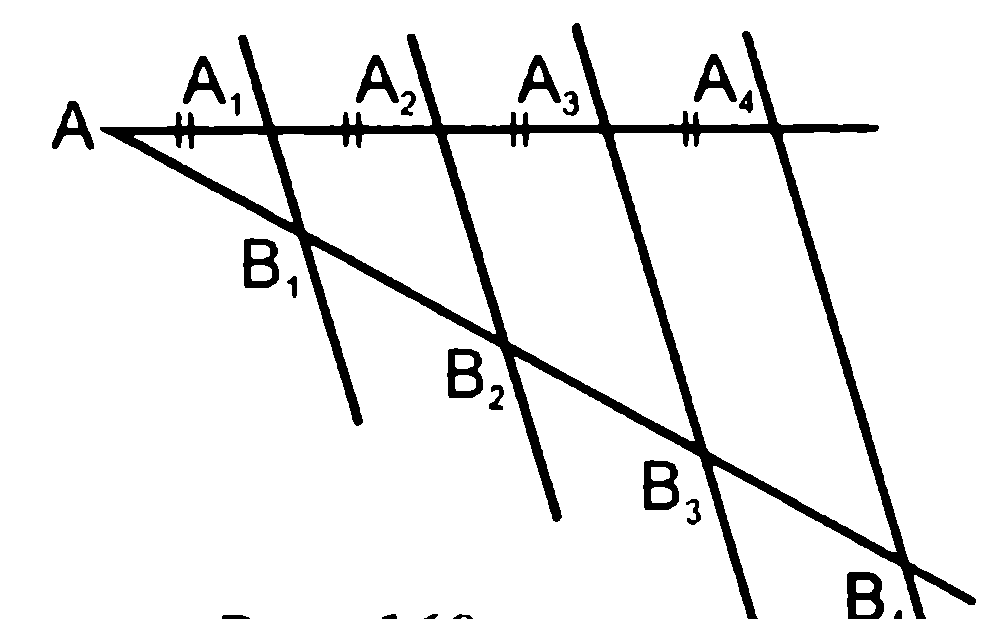 Прямая A2B2 проходит через середину A2 боковой стороны трапеции A1A3B3B1 параллельно ее основаниям, поэтому B1B2 = B2B3. Аналогично доказывается, что B2B3 = B3B4 и т. д. Следовательно, все отрезки AB1, B1B2, B2B3, B3B4, … равны друг другу. Теорема доказана.
Прямая A2B2 проходит через середину A2 боковой стороны трапеции A1A3B3B1 параллельно ее основаниям, поэтому B1B2 = B2B3. Аналогично доказывается, что B2B3 = B3B4 и т. д. Следовательно, все отрезки AB1, B1B2, B2B3, B3B4, … равны друг другу. Теорема доказана.
По мнению некоторых ученых, эту теорему впервые открыл древнегреческий ученый Фалес Милетский (ок. 625-547 до н. э.). Это мнение впервые было высказано много столетий спустя после его смерти. В то время древнегреческие философы и математики, раздумывая о том, как Фалес во время путешествия в Египет смог измерить высоту пирамиды, предположили, что ему для этого могла понадобиться такая теорема. И хотя единого мнения на этот счет нет, ее называют теоремой Фалеса.
Теорема Фалеса позволяет с помощью циркуля и линейки разделить данный отрезок на n равных отрезков. В самом деле, пусть AB — данный отрезок. На произвольном луче с началом A, не лежащем на прямой AB, отложим последовательно n каких-нибудь равных друг другу отрезков AA1, A1A2, …, An-1An (рис. 76). Соединим точки An и B отрезком и проведем через точки A1, A2, …, An-1 прямые, параллельные AnB. По теореме Фалеса эти прямые разделят отрезок AB на n равных отрезков.
В самом деле, пусть AB — данный отрезок. На произвольном луче с началом A, не лежащем на прямой AB, отложим последовательно n каких-нибудь равных друг другу отрезков AA1, A1A2, …, An-1An (рис. 76). Соединим точки An и B отрезком и проведем через точки A1, A2, …, An-1 прямые, параллельные AnB. По теореме Фалеса эти прямые разделят отрезок AB на n равных отрезков.
Обобщённая теорема Фалеса
Основные понятия
Прежде чем сформулировать теорему Фалеса и доказать её, напомним несколько ключевых определений геометрии:
- четырёхугольник;
- параллелограмм;
- трапеция.
Четырёхугольник имеет четыре вершины.
Параллелограмм — это четырёхугольник, противоположные стороны которого попарно параллельны друг другу. В параллелограмме равны противоположные стороны между собой и противоположные углы. {\circ}$. Можно убедиться, что сумма всех углов данной трапеции действительно равна $360$.
{\circ}$. Можно убедиться, что сумма всех углов данной трапеции действительно равна $360$.
Владея ключевыми понятиями, можем перейти к теореме Фалеса и её доказательству.
Теорема Фалеса
Теорема названа в честь древнегреческого ученого Фалеса Милетского. Звучит она следующим образом:
Теорема 1
Если последовательно отложить на прямой несколько равных друг другу отрезков и провести через их концы параллельные прямые, которые пересекают вторую проведённую прямую, то эти параллельные прямые отсекут на ней также равные отрезки.
Доказательство теоремы Фалеса
Докажем эту теорему.
Рассмотрим рисунок:
Рисунок 3. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ
На прямой $a$ отложены следующие отрезки: $A_1 A_2, A_2 A_3, A_3 A_4,…$. Через эти отрезки проведены несколько параллельных прямых, пересекающих прямую $b$ в соответствующих точках $B_1,B_2,B_3,B_4,…$. Докажем, что отрезки $B_1 B_2, B_2 B_3, B_3 B_4,. ..$ равны между собой. Для начала упростим задачу и докажем следующее: $B_1 B_2 = B_2 B_3$.
..$ равны между собой. Для начала упростим задачу и докажем следующее: $B_1 B_2 = B_2 B_3$.
На рисунке прямые $a$ и $b$ параллельны. Следовательно, $A_1 B_1 B_2 A_2$ и $A_2 B_2 B_3 A_3$ — параллелограммы. Это означает, что противоположные стороны параллелограммов равны, следовательно, $A_1 A_2 = B_1 B_2, A_2 A_3 = B_2 B_3$. И из $A_1 A_2=A_2 A_3$ следует, что $B_1 B_2= B_2 B_3$.
Есть и другой случай, когда прямые $a$ и $b$ не параллельны:
Рисунок 4. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ
Проведём такую прямую $c$, которая параллельна $a$:
Рисунок 5. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ
Прямая $c$ пересекает $A_2 B_2$ и $A_3 B_3$ соответственно в т. $C_1, C_2$. Так как $A_1 A_2=A_2 A_3$, то, по аналогии в предыдущем случае, $B_1 C_1 = C_1 C_2$.
Рассмотрим $\triangle C_2 B_1 B_3$. $C_1$ — середина $B_1 C_2$. $B_2 C_1$ параллельна $B_3 C_2$.
Проведём через точку $B_3$ такую прямую, которая параллельна $B_1 C_2$.
Рисунок 6. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ
Точкой $D$ обозначено пересечение $B_2 C_1$ с проведённой прямой. Получаем параллелограмм $C_1 C_2 B_3 D$. Так как $C_1$ — середина $B_1 C_2$, а $C_1 C_2= B_3 D$ (как противоположные стороны параллелограмма), следовательно, $C_1 B_1 = B_3 D$.
Рассмотрим $\triangle C_1 B_1 B_2$ и $\triangle B_2 B_3 D$ Они равны согласно второму признаку равенства треугольников. То есть так как выполняются равенства $C_1 B_1 = B_3 D$, $\angle C_1 B_1 B_2 = \angle B_2 B_3 D$ и $\angle B_1 C_1 B_2=\angle B_2 D B_3$ (как лежащие накрест углы при пересечении параллельных прямых $B_1 C_2$ и $B_3 D$ секущими $B_1 B_3$ и $C_1 D$).
Следовательно, $B_1 B_2= B_2 B_3$.
Аналогично доказывается равенство $B_2 B_3=B_3 B_4$ и другие.
Таким образом, в данной статье мы полностью разобрали теорему Фалеса, произвели подробное её доказательство, фигурируя известными понятиями.
Математика. Основы геометрии: Обобщенная теоремы Фалеса. Пропорции. Масштаб
Главная >
Образование >
Математика >
МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад | Оглавление | Далее >>
Пропорции
Равенство вида
x1 | = | y1 |
x2 | y2 |
называется пропорцией. При этом говорят, что:
x1 относится к x2 как y1 относится к y2,
или
отношение чисел x1 и x2 равно отношению чисел y1 и y2,
или же
числа x1 и x2 соотносятся так же, как числа y1 и y2,
или, наконец,
числа x1 и y1 (!) пропорциональны числам x2 и y2 (то есть числители пропорциональны знаменателям).
Входящие сюда числа x1, x2, y1 и y2 называются членами пропорции. Обычно все они положительны, но это необязательно. Предполагается, однако, что ни одно из них не равно нулю. Особого названия это равенство удостоилось по той причине, что оно часто встречается при решении разных математических задач.
Пропорции можно преобразовывать, перенося члены «с верху» одной части равенства «в низ» другой части равенства и наоборот. Эту процедуру легко обосновать следующим образом. Допустим мы хотим перенести x1 из левой части в правую. Для этого умножим обе части пропорции на 1/x1:
1 |
| x1 | = | 1 |
| y1 | . |
x1 | x2 | x1 | y2 |
В результате получаем
1 | = | y1 | , |
x2 | x1y2 |
то есть переменная x1 у нас переместилась «по диагонали сверху вниз». Перенесем теперь «влево наверх» переменную y2. Это достигается умножением на нее обеих частей данного равенства. В результате имеем
y2 | = | y1 | . |
x2 | x1 |
Мы получили новую пропорцию, которая отличается от исходной перестановкой членов, расположенных «по диагонали». Таким образом, в первоначальном равенстве
x1 | = | y1 |
x2 | y2 |
числители x1 и y1 соотносятся между собой точно так же, как и соответствующие им знаменатели x2 и y2.
Обобщенная теорема Фалеса
Теорема Фалеса, рассмотренная в прошлый раз, допускает следующее обобщение.
Пусть две произвольные прямые x и y пересекаются тремя параллельными прямыми n1, n2 и n3 в точках X1, X2, X3 и Y1, Y2, Y3, как показано на рисунке:
Тогда длины отсекаемых отрезков образуют следующую пропорцию
|Y1Y2| | = | |X1X2| | . |
|Y1Y3| | |X1X3| |
Докажем эту теорему в случае, когда отношение длин
представляет собой рациональное число, то есть может быть выражено в виде несократимой дроби
|X1X2| | = | a | , |
|X1X3| | b |
где a и b — некоторые натуральные числа, a < b. Разобьем отрезок X1X3 на b одинаковых частей. (При этом точка X2 окажется одной из точек деления. ) Проведем через каждую точку деления прямые, параллельные n1, n2 и n3. (Одна из этих прямых совпадет с прямой n2.)
) Проведем через каждую точку деления прямые, параллельные n1, n2 и n3. (Одна из этих прямых совпадет с прямой n2.)
По теореме Фалеса (в ее первоначальном варианте), отрезок Y1Y3 также делится этими прямыми на b равных частей, из которых a частей составляют отрезок Y1Y2. Следовательно,
|Y1Y2| | = | a | = | |X1X2| | , |
|Y1Y3| | b | |X1X3| |
что и требовалось доказать.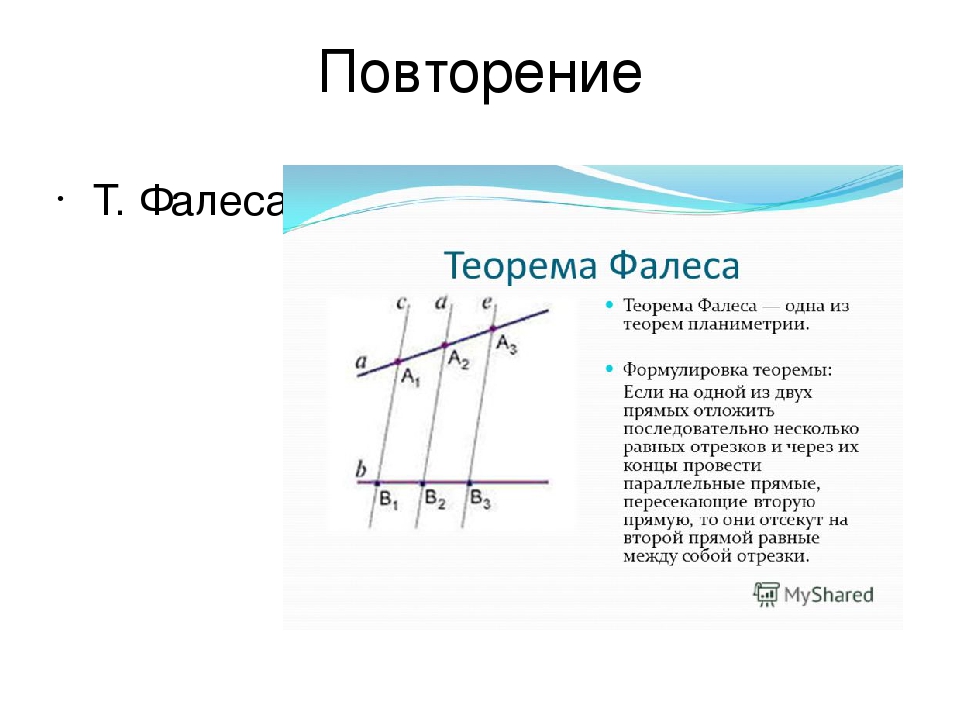 Из нашего построения следует также, что
Из нашего построения следует также, что
|Y2Y3| | = | b − a | = | |X2X3| |
|
|Y1Y3| | b | |X1X3| |
и
|Y2Y3| | = | b − a | = | |X2X3| | . |
|Y1Y2| | a | |X1X2| |
Пользуясь свойствами пропорций, эти равенства можно переписать в виде одной цепочки:
|Y1Y2| | = | |Y2Y3| | = | |Y1Y3| | . |
|X1X2| | |X2X3| | |X1X3| |
Таким образом, отрезки отсекаемые на прямой y пропорциональны соответствующим отрезкам на прямой x.
Теоретически возможна также ситуация, когда отношение длин
не является рациональным числом, поскольку длины отрезков |X1X2| и |X1X3| могут, в принципе, выражаться иррациональными числами. Однако на практике такой случай никогда не встречается. Для определения длин отрезков мы всегда пользуемся каким-либо измерительным прибором (например, школьной линейкой), который выдает лишь округленные результаты в виде конечной десятичной дроби.
Важное следствие
Пусть даны несовпадающие прямые x и y, которые пересекаются в точке O, и еще — две параллельные прямые n1 и n2, которые пересекают прямую x в точках X1 и X2 и прямую y в точках Y1 и Y2, как показано на рисунке.
Введем обозначения:
x1 = |OX1|, x2 = |OX2|;
y1 = |OY1|, y2 = |OY2|;
z1 = |X1Y1|, z2 = |X2Y2|.
Тогда
x1 | = | y1 | = | z1 | . |
x2 | y2 | z2 |
Действительно, оба равенства в этой цепочке непосредственно следует из обобщенной теоремы Фалеса. Для первого равенства это ясно сразу, а для второго это становится очевидным после того, как мы через точку Y1 проведем прямую m, параллельную прямой x.
Верно и обратное утверждение. Пусть дана та же геометрическая конструкция и известно, что
x1 | = | y1 | . |
x2 | y2 |
Тогда прямые n1 и n2 параллельны. В самом деле, проведем через точку X1 вспомогательную прямую, параллельную прямой n2. По обобщенной теореме Фалеса, эта вспомогательная прямая проходит через точку Y1. Следовательно, она совпадает с прямой n1. Таким образом, прямая n1 параллельна прямой n2.
Масштаб
Выйдем на улицу, прихватив с собой лист бумаги и карандаш. Расположим наш лист горизонтально и поставим на нем приблизительно посередине точку O. Из этой точки проведем мысленно лучи в направлении различных примечательных точек на местности, расположенных в радиусе примерно ста метров, — деревьев, столбов, углов зданий и того подобного.
Допустим, у нас есть возможность измерить расстояния до этих примечательных точек. Пусть, например, расстояние до ближайшего дерева равно 10 м. Мысленно отложим от точки O в направлении этого дерева отрезок, длина которого в 1000 раз меньше данного расстояния, и отметим карандашом на бумаге положение второго его конца. Нетрудно рассчитать, что расстояние от точки O до отметки составит 10 м/1000 = 1 см.
Пусть, например, расстояние до ближайшего дерева равно 10 м. Мысленно отложим от точки O в направлении этого дерева отрезок, длина которого в 1000 раз меньше данного расстояния, и отметим карандашом на бумаге положение второго его конца. Нетрудно рассчитать, что расстояние от точки O до отметки составит 10 м/1000 = 1 см.
Подобным же образом, пусть расстояние до какого-то другого примечательного объекта равно x1. Умножим это расстояние на число k, равное 1/1000. Мысленно отложим от точки O отрезок длиной x2 = kx1 вдоль луча, направленного на данный объект. В том месте на бумаге, где находится второй конец отрезка, сделаем отметку карандашом. Проделаем такую процедуру со всеми примечательными точками на местности, используя всё время одно и то же значение параметра k. Если какие-либо из этих точек соединены между собой забором или стеной или же чем-то подобным, то между соответствующими метками на бумаге также проведем линии.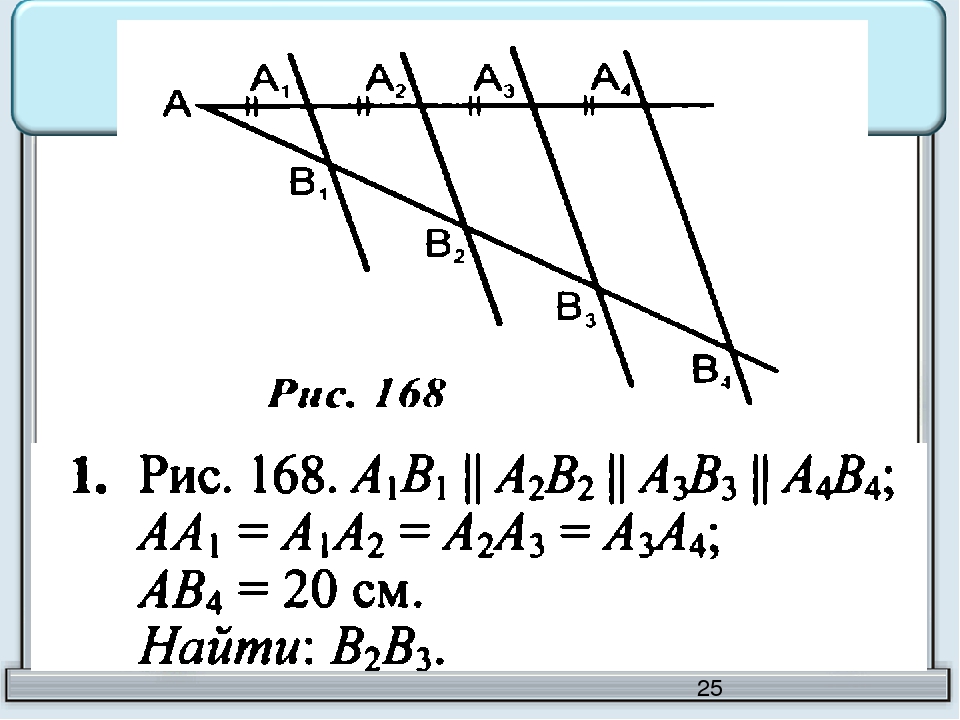
В результате на нашем листе бумаги получится карта местности. В силу теоремы Фалеса и свойств пропорций, все соотношения между расстояниями на бумаге будут в точности такими же, как и в действительности. Более того, все линии на бумаге окажутся параллельны соответствующим линиям на местности. Эта параллельность, конечно, нарушится, когда мы унесем наш лист куда-нибудь в другое место, однако углы между линиями сохранятся.
Параметр k, который мы использовали в нашем построении, называется масштабным коэффициентом или просто масштабом. Разумеется, он необязательно должен быть равен 1/1000. Он может, в принципе, принимать любое значение, важно лишь, чтобы это значение оставалось всё время неизменным в процессе построения карты.
На настоящих географических картах масштаб обязательно указывается в легенде, при этом вместо дробной черты обычно используется двоеточие. Например, масштаб 1:100 000 означает, что один сантиметр на карте соответствует 100000 сантиметрам (то есть одному километру) на местности.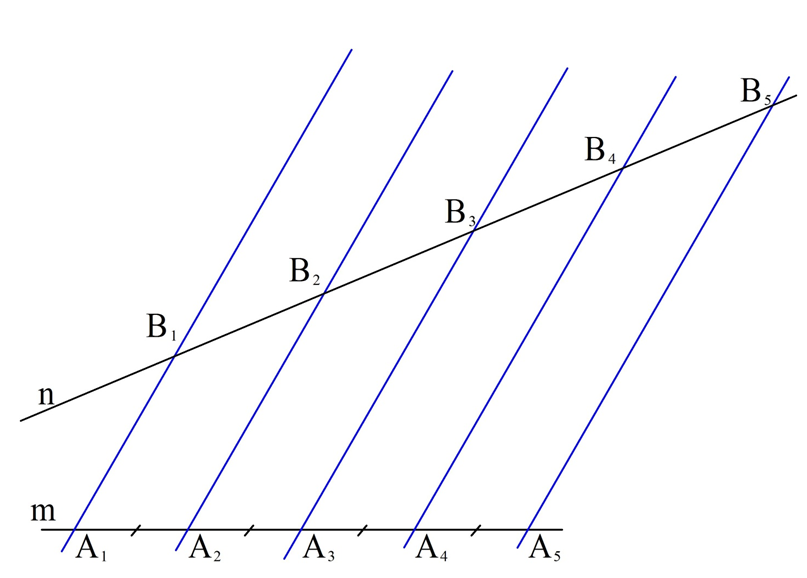
Технические чертежи также всегда выполняются, как говорят, в определенном масштабе. Масштаб 1:1 означает, что деталь начерчена в натуральную величину. А масштаб 10:1 говорит о том, что чертеж выполнен с десятикратным увеличением.
Замечание о параллельных прямых
Мы назвали параллельными такие несовпадающие прямые, угол между которыми равен нулю. Мы отметили, что такие прямые нигде не пересекаются. Докажем теперь, что если прямые лежат в одной плоскости и не параллельны (то есть угол между ними отличен от нуля), то тогда они обязательно где-нибудь пересекутся.
Пусть на плоскости даны две прямые — x и n. Отметим на них произвольные точки — O и Y — и проведем через эти точки третью прямую — y. Если исходить из того, что угол между прямыми x и n не равен нулю, то смежные углы должны оказаться не равны друг другу. Пусть для определенности α1 > α2, как показано на рисунке.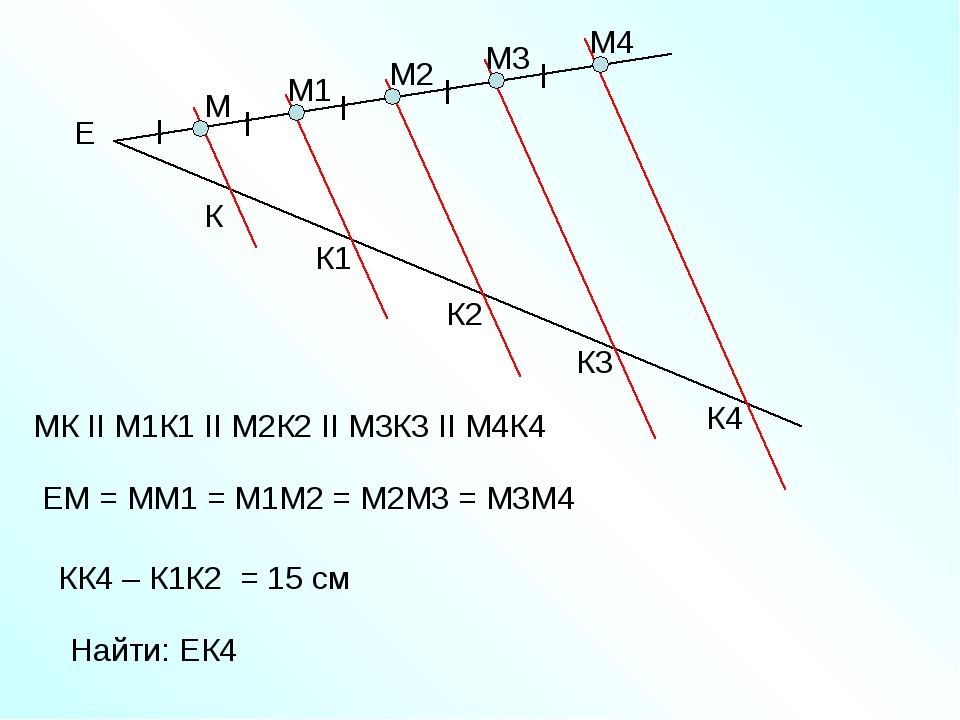
Проведем через точку O прямую n1, параллельную прямой n. Отметим на ней со стороны угла α1 произвольную точку N1 и проведем через эту точку прямую y1, параллельную прямой y. При этом образуется параллелограмм, обозначенный на рисунке серым фоном.
Это значит, что прямая y1 пересекает прямую n в некоторой точке, которую мы обозначим через N. Прямая x, заходя на «территорию» параллелограмма в точке O, обязательно должна где-то оттуда выйти. Она может это сделать либо через отрезок YN, либо через отрезок N1N. В первом случае сразу становится очевидно, что прямая x пересекает прямую n. Рассмотрим второй случай. Обозначим точку пересечения прямой x и отрезка N1N через X1. Проведем через нее прямую n2, параллельную прямой n. Эта прямая разбивает параллелограмм ON1NY на два новых параллелограмма и пересекает прямую y в некоторой точке Y1. Отметим на прямой x такую точку X, для которой выполняется соотношение
Проведем через нее прямую n2, параллельную прямой n. Эта прямая разбивает параллелограмм ON1NY на два новых параллелограмма и пересекает прямую y в некоторой точке Y1. Отметим на прямой x такую точку X, для которой выполняется соотношение
|OY1| | = | |OX1| | . |
|OY| | |OX| |
Проведем через точки X и Y прямую. Согласно рассмотренному выше следствию из теоремы Фалеса, эта прямая параллельна прямой n2, а значит, образует нулевой угол с прямой n. Следовательно, новая прямая совпадает с прямой n, которая, таким образом, пересекает прямую x в точке X.
Мы теперь можем утверждать, что следующие три утверждения о несовпадающих прямых a и b, лежащих в одной плоскости, означают в точности одно и то же:
(1) Угол между прямыми a и b равен нулю.
(2) Прямые a и b нигде не пересекаются.
(3) Прямые a и b параллельны.
В традиционных курсах геометрии определением параллельности прямых служит утверждение 2. Мы выбрали для этих целей утверждение 1. Ведь гораздо проще определить угол между двумя прямыми, чем удостовериться, что они нигде не пересекаются на всём своем бесконечном протяжении.
Конспект
1. Равенство вида x1/x2 = y1/y2 называется пропорцией. Числители пропорциональны знаменателям. Числитель и знаменатель одной дроби соотносятся так же, как числитель и знаменатель другой дроби. Эквивалентное равенство: x1/y1 = x2/y2.
2. Обобщенная теорема Фалеса. Пусть две произвольные прямые a и b пересекаются тремя параллельными прямыми. Тогда отрезки, отсекаемые на прямой a, пропорциональны соответствующим отрезкам, отсекаемым на прямой b.
3. Следствие 1. Пусть стороны угла с вершиной в точке O пересекаются двумя параллельными прямыми n1 и n2. Тогда отрезки, отсекаемые на прямых n1 и n2, соотносятся так же, как отрезки, отложенные на любой из сторон угла от точки O до соответствующих точек пересечения с прямыми n1 и n2.
4. Следствие 2. Пусть на сторонах угла отложены от вершины отрезки таким образом, что отрезки на одной стороне пропорциональны отрезкам на другой. Тогда прямые, проходящие через соответствующие концы этих отрезков, параллельны друг другу.
5. На карте сохраняются все соотношения между расстояниями и все углы. Отношение расстояния между некоторыми двумя точками на карте к расстоянию между соответствующими точками на местности не зависит от выбора точек и называется масштабом.
Отношение расстояния между некоторыми двумя точками на карте к расстоянию между соответствующими точками на местности не зависит от выбора точек и называется масштабом.
6. Если угол между двумя прямыми, лежащими в одной плоскости, не равен нулю, то такие прямые обязательно пересекаются.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Теорема Фалеса. Через произвольные точки
A1, A2, … An–1, An,
лежащие на стороне AO угла AOB (рис.1), проведены параллельные прямые, пересекающие сторону угла OB в точках
B1, B2, … Bn–1, Bn,
соответственно. Тогда справедливы равенства
Рис.1
Доказательство. Докажем сначала следующую лемму.
Докажем сначала следующую лемму.
Лемма. Через произвольную точку C, лежащую на стороне OA треугольника OAB, проведена прямая, параллельная прямой AB и пересекающая сторону OB в точке D (рис.2).
Рис.2
Тогда справедливо равенство
| (1) |
Доказательство леммы. Опустим из точек A и B перпендикуляры AK и BL на прямую CD (рис.3). Заметим, что эти перпендикуляры равны, поскольку AKLB – прямоугольникпрямоугольник.
Рис.3
Из точки D опустим перпендикуляр DF на прямую OA (рис.4).
Рис.4
Из точки C опустим перпендикуляр CG на прямую OB (рис.5).
Рис.5
В соответствии с рисунком 4 площади треугольников OCD и ACD можно вычислить по формулам
Следовательно,
В соответствии с рисунком 5 площади треугольников OCD и BCD можно вычислить по формулам
Следовательно,
Кроме того, заметим, что площади треугольников ACD и BCD равны. Действительно, в соответствии с рисунком 3 справедливы формулы
Действительно, в соответствии с рисунком 3 справедливы формулы
Следовательно,
SΔ ACD = SΔ BCD ,
откуда получаем цепочку равенств
что и завершает доказательство леммы.
Воспользовавшись леммой, заметим (рис.1), что из равенства (1) вытекают равенства
откуда на основе свойств производных пропорций, заключаем, что справедливы равенства
что и завершает доказательство теоремы Фалеса.
Следствие. Если через точки
A1, A2, … An–1, An,
лежащие на стороне AO угла AOB (рис.6) и удовлетворяющие условию
A1A2 = A2A3 = … =
= An–2 An–1 = An–1An ,
проведены параллельные прямые, пересекающие сторону угла OB в точках
B1, B2, … Bn –1, Bn ,
соответственно, то справедливы равенства
B1B2 = B2B3 = … =
= Bn–2Bn–1 = Bn–1Bn ,
Рис.6
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Конспект урока «Теорема Фалеса» — геометрия, уроки
Тема: «Теорема Фалеса»
Тип урока: изучение нового материала
Цели:
Образовательные: способствовать закреплению ранее усвоенного теоретического материала; осуществить взаимоконтроль знаний учащихся; сформулировать и доказать теорему Фалеса.
Воспитательные: содействовать в воспитании навыков учебного труда; формировать ответственность за конечный результат; воспитание интерес к предмету.
Развивающие: создать условия для развития логического мышления; выработки умения систематизировать и обобщать.
Ход урока:
1. Организационный момент
Проверить готовность учащихся к уроку.
2. Проверка домашнего задания
Собрать тетради с домашним заданием.
3. Актуализация знаний
1. Какие отрезки называются равными?
2. Какие прямые называются параллельными?
3. Какие углы называются вертикальными, внутренними накрест лежащими?
4. Сформулируйте теорему о свойстве параллельных прямых, пересечённых третьей прямой.
4. Целемотивационный этап
Сегодня на уроке мы с вами познакомимся с новой теоремой, которая носит название «Теорема Фалеса».
Евклид (300г. до н.э.) счёл эту задачу неразрешимой, при этом ранее Фалес (600г. до н.э.) наоборот решил её как частность в своей теореме.
Фалес – купец, политический деятель, астроном, математик, живший в греческом городе Милете, первый доказал ряд геометрических теорем. Эти положения были частично известны еще вавилонянам и египтянам, но в отличие от вавилонской и египетской геометрии, имевшей преимущественно практический характер, греческая геометрия характеризуется стремлением установить, что геометрические факты справедливы в любом случае.
Как философ, Фалес учил, что явления мира не случайны, мир не хаотичен, а закономерен. Он считал, что вода есть начало всего. Из нее возникло все существующее и в нее, в конце концов, опять превращается.
Фалес сделал ряд открытий в области астрономии: установил время равноденствий и солнцестояний, определил продолжительность года, впервые наблюдал Малую медведицу. Особую славу ему принесло предсказание солнечного затмения, происшедшего в 585 г. до н. э. Вот почему он был причислен к группе “семи мудрецов древности”.
Фалес также входил в число знаменитых семи мудрецов, чьи изречения дошли до наших дней.
4. Изучение нового материала
Сформулировать теорему Фалеса.
Теорема (теорема Фалеса). Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону угла, то на другой стороне угла отложатся равные отрезки.
Дано: АВ = ВС, АА1||ВВ1||СС1
Доказать: A1B1 = B1C1.
Доказательство.
1) Проведем AKA1C1, BMA1C1, тогда AKBM.
2) ABK=BCM по 2-му признаку (AB=BC по условию, ∠BAK=∠CBM и ∠ABK=∠BCM), значит AK=BM.
3) Т.к. AA1B1K и BB1C1M — параллелограммы (их противоположные стороны параллельны), то A1B1 = AK, B1C1 = BM. Значит, A1B1 = B1C1 ЧТД.
Замечания:
1. Отложенных равных отрезков может быть два, три и более.
2. Теорема Фалеса справедлива не только для сторон угла, но и для произвольных прямых.
Сформулировать теорему, обратную теореме Фалеса.
Теорема (обратная теореме Фалеса). Если на сторонах угла от его вершины отложить равные отрезки, то прямые, проходящие через их концы, будут параллельны.
Алгоритм деления отрезка на равные части:
-
Построить отрезок. -
Построить луч, исходящий из одного из концов отрезка. -
С помощью циркуля отложить на луче необходимое количество отрезков равной длины. -
Провести прямую через последнюю точку на луче и другой конец отрезка. -
Провести прямые, проходящие через оставшиеся точки на луче, параллельные прямой, построенной в предыдущем пункте. -
Обозначить точки пересечения прямых с отрезком.
Разделить отрезок на три равные части по данному алгоритму на доске.
5. Первичное закрепление изученного материала
Задача на готовом чертеже:
6. Физкультминутка
Разминка шеи, спины и кистей рук.
7. Решение задач
Решаем задачи из учебника:
Устно: № 95, № 96
Письменно: № 98
8. Домашнее задание: Гл. 1 §7 № 97
9. Подведение итогов. Рефлексия
-
Какова была тема урока? -
Какую задачу ставили? -
Каким способом решали поставленную задачу?
-
Если вы считаете, что поняли тему урока, то разделите отрезок на 9 равных частей. -
Если вы считаете, что не достаточно усвоили материал, то разделите отрезок на 7 равных частей. -
Если вы считаете, что не поняли тему урока, то разделите отрезок на 3 равные части.
Алгоритм деления отрезка на равные части:
-
Построить отрезок. -
Построить луч, исходящий из одного из концов отрезка. -
С помощью циркуля отложить на луче необходимое количество отрезков равной длины. -
Провести прямую через последнюю точку на луче и другой конец отрезка. -
Провести прямые, проходящие через оставшиеся точки на луче, параллельные прямой, построенной в предыдущем пункте.
-
Обозначить точки пересечения прямых с отрезком.
Алгоритм деления отрезка на равные части:
-
Построить отрезок. -
Построить луч, исходящий из одного из концов отрезка. -
С помощью циркуля отложить на луче необходимое количество отрезков равной длины. -
Провести прямую через последнюю точку на луче и другой конец отрезка. -
Провести прямые, проходящие через оставшиеся точки на луче, параллельные прямой, построенной в предыдущем пункте.
-
Обозначить точки пересечения прямых с отрезком.
Алгоритм деления отрезка на равные части:
-
Построить отрезок. -
Построить луч, исходящий из одного из концов отрезка. -
С помощью циркуля отложить на луче необходимое количество отрезков равной длины. -
Провести прямую через последнюю точку на луче и другой конец отрезка. -
Провести прямые, проходящие через оставшиеся точки на луче, параллельные прямой, построенной в предыдущем пункте.
-
Обозначить точки пересечения прямых с отрезком.
Алгоритм деления отрезка на равные части:
-
Построить отрезок. -
Построить луч, исходящий из одного из концов отрезка. -
С помощью циркуля отложить на луче необходимое количество отрезков равной длины. -
Провести прямую через последнюю точку на луче и другой конец отрезка. -
Провести прямые, проходящие через оставшиеся точки на луче, параллельные прямой, построенной в предыдущем пункте.
-
Обозначить точки пересечения прямых с отрезком.
Формулировка теоремы Фалеса по геометрии 8 класса: обобщенная, обратная
В данной публикации мы рассмотрим одну из основных теорем по геометрии 8 класса – теорему Фалеса, которая получила такое название в честь греческого математика и философа Фалеса Милетского. Также разберем пример решения задачи для закрепления изложенного материала.
Формулировка теоремы
Если на одной из двух прямых отмерить равные отрезки и через их концы провести параллельные прямые, то пересекая вторую прямую они отсекут на ней равные между собой отрезки.
- A1A2 = A2A3 …
- B1B2 = B2B3 …
Примечание: Взаимное пересечение секущих не играет роли, т.е. теорема верна и для пересекающихся прямых, и для параллельных. Расположение отрезков на секущих, также, не важно.
Обобщенная формулировка
Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках*: параллельные прямые отсекают на секущих пропорциональные отрезки.
В соответствии с этим для нашего чертежа выше справедливо следующее равенство:
* т.к. равные отрезки, в т.ч., являются пропорциональными с коэффициентом пропорциональности, равным единице.
Обратная теорема Фалеса
1. Для пересекающихся секущих
Если прямые пересекают две другие прямые (параллельные или нет) и отсекают на них равные или пропорциональные отрезки, начиная от вершины, значит эти прямые являются параллельными.
Из обратной теоремы следует:
Обязательное условие: равные отрезки должны начинаться от вершины.
2. Для параллельных секущих
Отрезки на обеих секущих должны быть равны между собой. Только в этом случае теорема применима.
- a || b
- A1A2 = B1B2 = A2A3 = B2B3 …
Пример задачи
Дан отрезок AB на плоскости. Разделите его на 3 равные части.
Решение
Проведем из точки A прямую a и отметим на ней три подряд идущих равных отрезка: AC, CD и DE.
Крайнюю точку E на прямой a соединяем с точкой B на отрезке. После этого через оставшиеся точки C и D параллельно BE проведем две прямые, пересекающие отрезок AB.
Образованные таким образом точки пересечения на отрезке AB делят его на три части, равные между собой (согласно теореме Фалеса).
Математика — 8
Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне конгруэнтные отрезки, то они отсекают конгруэнтные отрезки и на другой его стороне. Если
OA1 ≅ A1A2 ≅ A2A3 тогда OB1 ≅ B1B2 ≅ B2B3.
Запишите в тетради доказательство теоремы, заполнив пропущенные строки.
Доказательство: через точку B2 проведем параллельную прямую к прямой OA3.
|
Предположение |
Обоснование |
|
|
1. Дано. 2. ……………………………. 3.A1 A2 ≅ A2 A3 4. ……………………………. 5. Вертикальные углы 6. Признак УСУ 7. …………………………… |
Если в условии теоремы Фалеса, вместо угла взять две произвольные прямые, то результат не изменится.
Исследование: 1) В треугольнике ∇через точку М — середину стороны АВ, проведите прямую параллельную AC: MN||AC. Какая фигура получилась? Является ли АМNC трапецией? Измерьте и сравните основания полученной трапеции. 2) Измерьте и сравните длины отрезков ВN и NC Можно ли утверждать, что
ВN = NС ?
Определение: Отрезок, соединяющий середины двух сторон треугольника называется средней линией этого треугольника.
Теорема. Средняя линия, соединяющая середины двух сторон треугольника, параллельна третьей стороне и равна ее половине
MN||AC, MN = AC
2
Доказательство. Пусть дан треугольник ∇ABC и его средняя линия МN. Проведём через точку М прямую параллельную стороне АС. По теореме Фалеса, она проходит через середину стороны АВ, т.е. совпадает со средней линией МN Т.е. средняя линия МN параллельна стороне АС. Теперь проведём среднюю линию NК. Т.к. NК||АВ, то четырёхугольник АМNК является параллелограммом. По свойству параллелограмма MN ≅ AK. По теореме Фалеса AK ≅ KC. Тогда MN = AC
2 . Теорема доказана.
Теорема Фалеса — математический путь
Есть несколько теорем, которые приписываются Фалесу Милетскому , мы сосредоточимся особенно на двух из них:
Теорема Фалеса
Теорема Фалеса — это частный случай теоремы о вписанном угле, она относится к прямоугольным треугольникам, вписанным в окружность.
Теорема Фалеса утверждает, что если A , B и C являются разными точками на окружности с центром O ( центр описанной окружности ), где прямая AC является диаметром, то треугольник Δ ABC имеет прямой угол (90) в точке B .Таким образом, Δ ABC — прямоугольный треугольник.
Другими словами, диаметр круга всегда образует прямой угол с любой точкой на окружности.
Доказательство теоремы Фалеса
Если мы соединим центр описанной окружности O с точкой B , мы создадим два треугольника Δ ABO и Δ OBC , которые являются равнобедренными треугольниками, потому что все радиусы r равны ( OA , OB и OC равны).И, согласно теореме о базовом угле, их базовые углы равны. Обозначим базовые углы Δ ABO ‘α’ и Δ ABO ‘β’.
Поскольку это равнобедренные треугольники, каждый из них имеет два равных угла: α и β (см. Рисунок выше).
Как и в любом треугольнике, внутренние углы треугольника Δ ABC в сумме составляют 180 °:
Делим равенство на 2:
Поскольку α + β — это угол Δ ABC в точке B , Теорема Фалеса доказана .
Теорема о перехвате
Теорема о перехвате гласит, что если две пересекающиеся прямые разрезаются параллельными линиями, отрезки отрезков, отрезанные параллельными прямыми от одной из прямых, пропорциональны соответствующим отрезкам отрезка от другой прямой.
Если какие-либо две линии (на изображении: m и n ) разрезаны серией параллельных линий (на изображении: r , s и t ), образующиеся отрезки в одной из них пропорциональны соответствующим отрезкам, образованным в другой линии.
Применяя теорему о перехвате , верно, что:
Где r — отношение.
Теорема о перехвате связана с подобием. Фактически, это эквивалентно понятию подобных треугольников. Применяя теорему о перехвате к треугольникам, мы можем утверждать, что если в данном треугольнике мы проведем линию, параллельную одной из его трех сторон, новый сгенерированный треугольник будет похож на первый. То есть мы создадим два равных треугольника, которые будут в Thales в позиции .
См. Рисунок выше.
В Δ ABC рисуем отрезок линии A’C ’, параллельный стороне AC . Появляется новый Δ A’BC ’, похожий на первый. У них три равных угла, а их стороны пропорциональны.
Согласно теореме о перехвате верно, что:
Это соотношение сохраняется между двумя сторонами одного и того же треугольника, а также между соответствующими сторонами другого:
Знаете ли вы , что Фалес Милетский (родился на Ионическом острове Милет в 7 веке до нашей эры) считался одним из семи мудрецов Греции? Он преуспел в философии, астрономии, геометрии, инженерии и … даже в политике).
Под влиянием египетских и вавилонских знаний было сказано (поддержанное, среди прочего, Плутархом), что на основе своей первой теоремы и путем измерения теней он определил высоту пирамид Гизы.
Теорема Фалеса — объяснение и примеры
После того, как мы изучили теорему о вписанном угле, пришло время изучить другую связанную теорему, которая представляет собой частный случай теоремы о вписанном угле м, , называемый теоремой Фалеса .Как и теорема о вписанном угле, ее определение также основано на диаметре и углах внутри круга.
Из этой статьи вы узнаете:
- Теорема Фалеса,
- Как решить теорему Фалеса; и
- Как решить теорему Фалеса только с одной стороной
Что такое теорема Фалеса?
Теорема Фалеса утверждает, что:
Если три точки A, B и C лежат на окружности круга, при этом прямая AC является диаметром круга, то угол ∠ ABC — прямой угол (90 °).
В качестве альтернативы мы можем сформулировать теорему Фалеса как:
Диаметр круга всегда образует прямой угол с любой точкой на окружности.
Вы заметили, что теорема Фалеса является частным случаем теоремы о вписанном угле (центральный угол = удвоенный вписанный угол).
Теорема Фалеса приписывается Фалесу, греческому математику и философу, который жил в Милете.Фалес первым инициировал и сформулировал теоретическое изучение геометрии, чтобы сделать астрономию более точной наукой.
Есть различных способов доказать теорему Фалеса . Мы можем использовать методы геометрии и алгебры, чтобы доказать эту теорему. Поскольку это тема геометрии, давайте рассмотрим самый простой метод ниже.
Как решить теорему Фалеса?
- Чтобы доказать теорему Фалеса, нарисуйте серединный перпендикуляр к ∠
- Пусть точка M будет средней точкой прямой AC.
- Также пусть ∠ MBA = ∠ BAM = β и ∠ MBC = ∠ BCM = α
- Линия AM = MB = MC = радиус окружности.
- Δ AMB и Δ MCB — равнобедренные треугольники.
По теореме о сумме треугольников
∠ BAC + ∠ ACB + ∠ CBA = 180 °
β + β + α + α = 180 °
Разложите уравнение на множители.
2 β + 2 α = 180 °
2 (β + α) = 180 °
Разделите обе стороны на 2.
β + α = 90 °.
Следовательно, ABC = 90 °, следовательно, доказано
Давайте решим несколько примеров задач, связанных с теоремой Фалеса.
Пример 1
Учитывая, что точка O является центром окружности, показанной ниже, найдите значение x.
Решение
Учитывая, что прямая XY является диаметром окружности, тогда по теореме Фалеса
∠ XYZ = 90 °.
Сумма внутренних углов треугольника = 180 °
90 ° + 50 ° + x = 180 °
Упростить.
140 ° + x = 180 °
Вычтите 140 ° с обеих сторон.
x = 180 ° — 140 °
x = 40 °.
Итак, значение x равно 40 градусам.
Пример 2
Если точка D является центром окружности, показанной ниже, вычислите диаметр окружности.
Решение
По теореме Фалеса треугольник ABC является прямоугольным, где ∠ ACB = 90 °.
Чтобы найти диаметр круга, примените теорему Пифагора.
CB 2 + AC 2 = AB 2
8 2 + 6 2 = AB 2
64 + 36 = AB 2
100 = AB 2 2 2 2 2 2 + 6 2 = AB 2
64 + 36 = AB
AB = 10
Следовательно, диаметр круга равен 10 см.
Пример 3
Найдите величину угла PQR в круге, показанном ниже.Предположим, что точка R является центром круга.
Решение
Треугольник RQS и PQR — равнобедренные треугольники.
∠ RQS = ∠ RSQ = 64 °
По теореме Фалеса ∠ PQS = 90 °
Итак, ∠ PQR = 90 ° — 64 °
= 26 °
Следовательно, величина угла PQR равна 26 °.
Пример 4
Какое из следующих утверждений верно относительно определения теоремы Фалеса?
A. Центральный угол в два раза больше вписанного угла
B. Угол, вписанный в полукруг, будет прямым углом.
C. Диаметр круга — самая длинная хорда.
D. Диаметр окружности в два раза больше радиуса.
Решение
Правильный ответ:
B.Угол, вписанный в полукруг, будет прямым углом.
Пример 5
В круге, показанном ниже, линия AB — это диаметр круга с центром C .
- Найдите размер ∠ до н.э.
- ∠ DCA
- ∠ ACE
- ∠ DCB
Решение
Данный треугольник ACE является равнобедренным треугольником,
5 CE = CA 5 CE =
∠ 33 °
Итак, ∠ ACE = 180 ° — (33 ° + 33 °)
∠ ACE = 114 °
Но углы на прямой = 180 °
Следовательно, ∠ BCE = 180 ° — 114 °
= 66 °
Треугольник ADC — равнобедренный треугольник, поэтому ∠ DAC = 20 °
По теореме суммы треугольников DCA = 180 ° — (20 ° + 20 °)
∠ DCA = 140 °
∠ DCB = 180 ° — 140 °
= 40 °
Пример 6
Какой размер ∠ ABC ?
Решение
Теорема Фалеса утверждает, что BAC = 90 °
И по теореме суммы треугольников
∠ ABC + 40 ° + 90 ° = 180 °
∠ ABC = 180 ° — 130 °
= 50 °
Пример 7
Найдите длину AB в круге, показанном ниже.
Решение
Треугольник ABC — это прямоугольный треугольник.
Примените теорему Пифагора, чтобы найти длину AB .
AB 2 + 12 2 = 18 2
AB 2 + 144 = 324
AB 2 = 324–144
AB = 180
AB = 13,4
Следовательно, длина AB равна 13.4 см.
Приложения теоремы Фалеса
В геометрии ни одна из тем не обходится без реального использования. Следовательно, теорема Фалеса также имеет некоторые приложения:
- Мы можем точно провести касательную к окружности, используя теорему Фалеса. Для этого можно использовать установленный угольник.
- Мы можем точно найти центр круга, используя теорему Фалеса. Инструменты, используемые для этого приложения, представляют собой квадрат и лист бумаги. Во-первых, вы должны разместить угол на окружности — пересечение двух точек с окружностью определяет диаметр.Вы можете повторить это, используя другую пару точек, что даст вам другой диаметр. Пересечение диаметров даст вам центр круга.
Предыдущий урок | Главная страница | Следующий урок
Основная теорема пропорциональности | Теорема Фалеса | Заявление и доказательство
Основная теорема пропорциональности была предложена известным греческим математиком Фалесом, поэтому ее также называют теоремой Фалеса . По словам известного математика, для любых двух равноугольных треугольников отношение любых двух соответствующих сторон данных треугольников всегда одинаково.На основе этой концепции была предложена основная теорема пропорциональности (BPT). Он показывает отношения между сторонами любых двух равносторонних треугольников.
Понятие теоремы Фалеса было введено в подобных треугольниках. Если данные два треугольника похожи друг на друга, то
- Соответствующие углы обоих треугольников равны
- Соответствующие стороны обоих треугольников пропорциональны друг другу
Таким образом, теорема также помогает нам лучше понять концепцию подобных треугольников.Теперь давайте попробуем понять основную теорему пропорциональности.
Формулировка основной теоремы о пропорциональности
Основная теорема пропорциональности, также известная как теорема Фалеса, гласит, что «линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равной пропорции». Например, на данном рисунке линия DE проведена параллельно стороне BC, так что она соединяет две другие стороны, AB и AC.Согласно основной теореме пропорциональности, можно заключить, что AD / DB = AE / EC.
Доказательство основной теоремы о пропорциональности
Давайте теперь попробуем доказать утверждение основной теоремы пропорциональности (BPT).
Заявление: Линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равной пропорции.
Дано: Рассмотрим треугольник ΔABC, как показано на данном рисунке.В этом треугольнике проведем прямую DE, параллельную стороне BC треугольника ABC и пересекающую стороны AB и AC в точках D и E соответственно.
Конструкция: На приведенной выше диаграмме создайте воображаемые линии, где вы можете соединить C с D и B с E. Нарисуйте перпендикуляр DP, перпендикулярный AE, и EQ, перпендикулярный AD.
Проба:
Рассмотрим треугольники ADE и BDE. Оба этих треугольника находятся на одном основании AB и имеют одинаковую высоту EQ.
(Область ADE) / (Область BDE) = (1/2 × AD × EQ) / (1/2 × BD × EQ)
(Площадь ADE) / (Площадь BDE) = AD / BD
Теперь рассмотрим треугольники CDE и ADE. Оба этих треугольника находятся на одном основании AC и имеют одинаковую высоту DP.
(Площадь ADE) / (Площадь CDE) = (1/2 × AE × DP) / (1/2 × CE × DP)
(Площадь ADE) / (Площадь CDE) = AE / CE
Оба треугольника BDE и CDE находятся между одним и тем же набором параллельных прямых.
Площадь треугольника BDE = Площадь треугольника CDE
Применяя это, мы имеем (Площадь треугольника ADE) / (Площадь треугольника BDE) = (Площадь треугольника ADE) / (Площадь треугольника CDE)
AD / BD = AE / CE
Следствие:
Приведенное выше доказательство также полезно для доказательства другой важной теоремы, называемой теоремой о средней точке.Теорема о средней точке утверждает, что отрезок прямой, проведенный параллельно одной стороне треугольника, и половина этой стороны делит две другие стороны в средних точках.
Заключение:
Таким образом, мы доказываем основную теорему о пропорциональности. Следовательно, прямая DE, проведенная параллельно стороне BC треугольника ABC, делит две другие стороны AB, AC в равной пропорции. Также верна обратная теорема о средней точке BPT. В нем говорится, что линия, проведенная через середину стороны треугольника, параллельной другой стороне, делит третью сторону треугольника пополам.
Обращение к основной теореме о пропорциональности
Согласно обратной теореме о пропорциональности, «Если отрезок прямой рассекает две стороны треугольника в равной пропорции, то он параллелен третьей стороне».
Дано:
ABC представляет собой треугольник, и прямая DE разрезает стороны AB и AC в равной пропорции. AD / BD = AE / CE
Проба:
Считайте, что DE не параллельна BC.Поэтому проведем другую линию DF, параллельную BC. Применяя основную теорему о пропорциональности, получаем: AD / BD = AF / CF. Но уже дано, что: AD / BD = AE / CE. Наблюдая равные левые части двух приведенных выше утверждений, мы заключаем следующее утверждение: AE / CE = AF / CF. Добавьте 1 с обеих сторон этого утверждения.
(AE / CE) + 1 = (AF / CF) + 1
(AE + CE) / CE = (AF + CF) / CF
AC / CE = AC / CF
∴ CE = CF
Для приведенного выше утверждения точки E и F — это одни и те же точки, и они совпадают.Следовательно, прямая DE параллельна BC, и это доказывает обратное к основной теореме пропорциональности.
Важные примечания
- Основная теорема о пропорциональности — линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равной пропорции.
- Обратное к основной теореме пропорциональности — линия, проведенная, чтобы разрезать две стороны треугольника в равной пропорции, параллельна третьей стороне.
- Теорема о средней точке. Линия, проведенная параллельно одной стороне треугольника и половине этой стороны, разделяет две другие стороны в его средней точке.
Сложные вопросы
- Диагонали четырехугольника PQRS пересекаются в точке O, так что PO / QO = RO / SO. Докажите, что PQRS — это трапеция.
Часто задаваемые вопросы по основной теореме пропорциональности
Что такое теорема Фалеса?
Теорема Фалеса, которую также называют основной теоремой пропорциональности, утверждает, что линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит эти две стороны в равной пропорции.
Каковы приложения основной теоремы о пропорциональности?
Основная теорема пропорциональности помогает найти длины, на которых две стороны треугольника разделены линией, проведенной параллельно третьей стороне. Кроме того, у него есть приложения для нахождения взаимосвязи между двумя равноугольными треугольниками.
Что такое история теоремы Фалеса?
Теорема Фалеса была предложена Фалесом, греческим математиком и философом около 625 г. до н.э.Теперь это называется основной теоремой пропорциональности, и она помогает найти соотношение между сторонами двух равноугольных треугольников.
Какова формула основной теоремы о пропорциональности?
Базовая формула теоремы пропорциональности для треугольника ABC с точкой D на AB, точкой E на AC и DE // BC выглядит следующим образом:
AD / DB = AE / EC
Что вы имеете в виду под основной теоремой о пропорциональности?
Основная теорема пропорциональности утверждает, что если линия проводится параллельно одной стороне треугольника и пересекает две другие стороны, то она делит две другие стороны в равной пропорции.
Как доказать основную теорему о пропорциональности вырезанием из бумаги?
Чтобы показать основную теорему пропорциональности, вырежьте из цветной бумаги треугольник и отметьте его вершины как ABC. Поместите его на бумагу в линейку так, чтобы одна сторона ВС совпадала с линией на бумаге в линейку. Теперь отметьте точки D на AB и E на AC так, чтобы DE была параллельна стороне BC. Теперь измерьте длины AD, BD, AE и CE и проверьте, пропорциональны ли они.
AD / DB = AE / EC
Как решить теорему Фалеса?
Теорема Фалеса аналогична основной теореме пропорциональности.Чтобы решить эту проблему, мы должны доказать, что линия, проведенная параллельно одной стороне треугольника, делит две другие стороны в равной пропорции.
Основная теорема пропорциональности
Covid-19 привел мир к феноменальному переходу.
За электронным обучением будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Основная теорема пропорциональности (теорема Фалеса): Если линия проводится параллельно одной стороне треугольника, пересекающей две другие стороны, то она делит две стороны в одинаковом соотношении.
| In ∆ABC, если DE || BC и пересекает AB в D и AC в E, затем AD AE —- = —— DB EC |
Доказательство теоремы Фалеса:
Если линия проводится параллельно одной стороне треугольника и пересекает две другие стороны в двух разных точках, то она делит две стороны в одинаковом соотношении.
Дано: In ∆ABC, DE || BC и пересекает AB в D и AC в E.
Докажите, что: AD / DB = AE / EC
Строительство: Присоединитесь к BC, CD и нарисуйте EF ┴ BA и DG ┴ CA.
| Утверждения | Причины |
| 1) EF ┴ BA | 1) Конструкция |
| 2) EF — это высота ∆ADE и ∆DBE Определение | |
| 3) Площадь (∆ADE) = (AD .EF) / 2 | 3) Площадь = (Базовая высота) / 2 |
| 4) Площадь (∆DBE) = (DB.EF) / 2 | 4) Площадь = (Базовая высота) / 2 |
| 5) (Площадь (∆ADE)) / (Площадь (∆DBE)) = AD / DB | 5) Разделить (4) по (5) |
| 6) (Площадь (∆ADE)) / (Площадь (∆DEC)) = AE / EC | 6) То же, что и выше |
| 7) ∆DBE ~ ∆DEC | 7 ) Оба ∆s находятся на одном основании и между одинаковыми || линий. |
| 8) Площадь (∆DBE) = площадь (∆DEC) | 8) Если два треугольника похожи, их площади равны |
| 9) AD / DB = AE / EC | 9) От (5), (6) и (7) |
Некоторые решенные примеры:
1) На данном рисунке PQ || MN.Если КП / ПМ = 4/13 и КН = 20,4 см.
Найдите KQ.
Решение:
In Δ KMN,
PQ || MN
∴ KP / PM = KQ / QN (по теореме BPT)
⇒ KP / PM = KQ / (KN — KQ)
⇒ 4/13 = KQ / (20,4 — KQ)
⇒ 4 (20,4 — KQ) = 13 KQ (перекрестное умножение)
⇒ 81,6 — 4KQ = 13 KQ
⇒ 17KQ = 81,6
⇒ KQ = 81,6 / 17
∴ KQ = 4,8 см.
———————————————— ——————
2) На приведенном ниже рисунке DE || BC.Если AD = x см, DB = x-2 см,
AE = x-1 см, найдите значение x.
Решение:
В треугольнике ABC,
DE || BC
AD / DB = AE / EC (по основной теореме пропорциональности)
⇒ x / (x — 2) = (x + 2) / (x — 1)
⇒ x (x — 1) = (x — 2) (x + 2) (перекрестным умножением)
⇒ x 2 — x = x 2 — 4
⇒ -x = -4
∴ x = 4
Сходство в треугольниках
• Сходство в геометрии
• Свойства подобных треугольников
• Основная теорема пропорциональности (теорема Фалеса)
• Обращение к основной теореме пропорциональности
• Теорема о биссектрисе внутреннего угла
• Теорема о биссектрисе внешнего угла
• Доказательства базовой пропорциональности
• Критерии Сходство треугольников
• Среднее геометрическое количество похожих треугольников
• Области двух похожих треугольников
Домашняя страница
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Теорема Фалеса | Блестящая вики по математике и науке
Есть много способов доказать эту теорему. Одно из самых классических доказательств заключается в следующем:
Мы знаем, что AO = BO = COAO = BO = COAO = BO = CO, поскольку все они являются радиусами круга. Следовательно, ∠OAB = ∠OBA \ angle OAB = \ angle OBA∠OAB = ∠OBA и ∠OBC = ∠OCB \ angle OBC = \ angle OCB∠OBC = ∠OCB, потому что углы, противоположные равным сторонам, равны.\ circ. \ _ \ квадрат
\ end {выровнен} ∠ABC + ∠BCA + ∠CAB∠OAB + (∠OBA + ∠OBC) + ∠OCBα + (α + β) + βα + β∠ABC = 180∘ = 180∘ = 180∘ = 90∘ = 90∘ . □
Есть другой способ доказать это, основанный на другой теореме, называемой теоремой об альтернативном сегменте, которая утверждает, что
Теорема об альтернативном сегменте:
Угол, образованный хордой (или двумя радиусами) в центре круга, в два раза больше угла, образованного им на оставшейся части круга. □ _ \ квадрат □
Попробуем теперь доказать теорему Фалеса с помощью указанной выше теоремы.\ circ 90∘
АБАБАБ — диаметр полукруга.
CCC — точка на окружности.
Что такое угол ACB? ACB? ACB?
Самая длинная хорда в круге — это его диаметр.
Пусть окружность с центром ООО имеет хорду АБАБАБ. Присоединитесь к OAOAOA и OBOBOB, и пусть PPP будет точкой на ABABAB, такой что OP⊥ABOP \ perp ABOP⊥AB.
Мы знаем, что перпендикуляр от центра окружности к хорде делит хорду пополам. Тогда PA = PB = 12ABPA = PB = \ dfrac12 ABPA = PB = 21 AB.Пусть радиус равен rr r, длина хорды ABABAB равна ccc, а расстояние по перпендикуляру между центром и хордой ABABAB равно xxx.
Теперь по теореме Пифагора в △ OPA \ треугольнике OPA △ OPA
OA2 = OP2 + AP2r2 = x2 + (c2) 2⇒c = 2r2 − x2.2} = 2r = 2 \ times \ text {(радиус)} = \ text {(диаметр)}. \ _ \ Squarec = 2r2−02 = 2r2 = 2r = 2 × (радиус) = (диаметр). □
Верно или нет?
Длина наибольшего хорды, возможной в окружности, всегда равна удвоенному радиусу.
Первые доказательства: Фалес и начало геометрии
Podcast: Download
Доказательная геометрия началась с Thales. Приписываемые ему теоремы заключают в себе два способа выполнения математических вычислений, предполагая, что идея доказательства могла исходить из любого из двух источников: внимания к шаблонам и отношениям, возникающим в результате исследовательского конструирования и игры, или осознания того, что «очевидные» вещи могут быть продемонстрировано с использованием формальных определений и доказательства от противного.
Выписка
Как начались доказательства? Это похоже на головоломку с курицей или яйцом. Зачем кому-то садиться и говорить себе: «Я собираюсь доказать некоторые теоремы сегодня», если никто никогда не делал ничего подобного раньше? Как эта идея могла так неожиданно прийти в голову кому-то?
На самом деле, мы вроде как знаем ответ. Греческая традиция говорит нам, у кого был этот момент лампочки: у Фалеса. Примерно в году -600 или около того. За сотни лет до того, как у нас появились какие-либо прямые исторические источники по греческой геометрии.Но мы все еще более или менее знаем, что доказал Фалес. Более поздние источники рассказывают нам о Фалесе. История, возможно, смешана с легендами в подобных отчетах, но ключевые аспекты, вероятно, будут вполне достоверными. Больше фактов, чем выдумок. Давайте проанализируем этот вопрос, вопрос о достоверности, чуть более глубоко позже, но сначала давайте примем истории за чистую монету и посмотрим, как мы можем пережить создание дедуктивной геометрии, как это передано в этих греческих историях.
Итак, начнем: Какая первая теорема была доказана? Что стало той искрой, которая зажгла пожар аксиоматико-дедуктивной математики? Лучшее предположение, основанное на исторических свидетельствах, звучит так.Момент любви с первого взгляда, та теорема, открывшая нам глаза на силу математического доказательства, заключалась в следующем: диаметр разрезает круг пополам.
Довольно обидно, не правда ли? Какая неубедительная теорема. Это вообще даже не теорема. Как можно влюбиться в геометрию, доказывая что-то столь тривиальное и очевидное?
Но не отчаивайтесь. Вообще-то, это приятно. Дело не в теореме, а в доказательстве.
Вот как это доказать. Предположим, что нет. Это будет доказательство от противного.Предположим, диаметр не делит круг на две равные половины. Хорошо, у нас есть линия, проходящая через середину круга, и она разрезана на две части. И мы предполагаем, что эти две части не совпадают. Возьмите один из кусочков и переверните его на другой. Как вы складываете омлет или креп. Мы предположили, что части не равны, поэтому, когда вы кладете одну на другую, они не совпадают. Так что должно быть какое-то место, где одна из двух частей выступает над другой.Теперь нарисуйте радиус в этом направлении от середины круга до места по периметру, где две половины не совпадают. Тогда один радиус длиннее другого. Но это означает, что дело было не в круге с самого начала. Круг — это фигура, одинаково удаленная от средней точки во всех направлениях. Вот что значит быть кругом.
Итак, мы доказали, что две вещи несовместимы друг с другом: нельзя одновременно быть кругом и иметь несовпадающие половинки. Потому что, если у вас есть несовпадающие половинки, у вас также есть «неравные радиусы», а это значит, что вы не круг.
Итак, у круга должны быть равные половины. Бам. Теорема. Скучный результат, но великолепное доказательство. Или убедительное доказательство. Это доказательство, намекающее на новый мир.
Фалес, должно быть, чувствовал себя волшебником, который только что обнаружил, что обладает сверхспособностями. «Ого, ты можешь это сделать ?!» С помощью чистого рассуждения, вычеркивая последствия определения, можно без тени сомнения доказать, что определенные утверждения не могут быть неправильными? Это вещь? Это то, что можно сделать? Ух ты. Давай сделаем это со всем! Верно?
Так вот как Фалес открыл доказательство.Насколько мы можем догадаться.
Несколько других теорем также приписываются Фалесу. Я хочу особо выделить одну, которая, как мне кажется, также является своего рода архетипом того, что из себя представляет математика.
Теорема, которую мы только что рассмотрели, о диаметре, разделяющем окружность пополам, идеально воплощает один из прототипов математических рассуждений. Вы могли бы назвать это парадигмой чистой математики. Логические следствия определений, доказательства от противного. Такие вещи. Доказательство Фалеса действительно поражает своей эстетикой.С тех пор мы делаем одно и то же снова и снова. Например, современный курс теории групп — это просто идея доказательства Фалеса, примененная, по сути, пятьсот раз.
Теперь я хочу взять еще один результат, приписываемый Фалесу, и я хочу утверждать, что он символизирует другой способ математической мысли. Это второй путь к доказательствам. Этот второй способ основан больше на игре, исследовании, открытии, чем на логике и определениях.
Пример, который я хочу использовать, чтобы подчеркнуть эту мысль, действительно часто называют просто «теоремой Фалеса».Который утверждает, что любой треугольник, возвышающийся на диаметре круга, имеет прямой угол. Другими словами, изобразите круг. Разрежьте его пополам диаметром. Теперь поднимите треугольник, используя этот диаметр как одну из его сторон, и третья вершина треугольника находится где-то на окружности. Так что это похоже на палатку, торчащую из диаметра. И это может быть асимметричный шатер, который больше направлен в ту или иную сторону. Независимо от того, как вы устанавливаете эту палатку, до тех пор, пока ее кончик находится в любой точке круга, угол между двумя стенами палатки в этой точке, на вершине, будет прямым углом, 90 градусов. .Это теорема Фалеса.
Как мог Фалес доказать эту теорему? К сожалению, мы не знаем этого, основываясь на исторических данных. Но давайте рассмотрим одну гипотезу, которая имеет смысл с точки зрения контекста.
Мы должны представить, что Фалес каким-то образом наткнулся на доказательство. Мы не пытаемся объяснить, как кто-то может думать о доказательстве этой теоремы как таковой. Это неправильная точка зрения, потому что считается само собой разумеющимся, что в математике кто-то пытается что-то доказать. Нам нужно объяснить, откуда взялось это видение, чтобы доказать все в геометрии.Как мог кто-то случайно натолкнуться на теорему Фалеса и благодаря этой случайности осознать идею дедуктивной геометрии?
Действительно, теорема Фалеса сама по себе не слишком интересна или важна. Если бы у вас было видение систематического доказательства всей геометрии, почему бы вам начать с этой теоремы или сделать ее центральной частью, как якобы сделал Фалес? Ты бы не стал.
Теорема Фалеса интересна не в том, что это был один из первых результатов, к которому математики применили дедуктивное доказательство.Скорее, интересно то, что математики случайно наткнулись на саму идею доказательства.
Есть история о Фалесе, который упал в колодец, потому что он настолько увлекся астрономическими рассуждениями, что забыл о том, что его окружало. У Платона записано: «Когда он изучал звезды и смотрел вверх, он упал в яму. Поскольку ему так хотелось познать вещи в небе, он не мог видеть то, что было перед ним у самых его ног.”
Возможно, это легенда, но открытие теоремы Фалеса, должно быть, было чем-то вроде этого. Обнаружение математического доказательства должно было быть похоже на падение в яму. Вы смотрите в одном направлении и бум! Вы внезапно обнаруживаете, что сначала случайно врезались лицом в эту совершенно не связанную новую вещь, о существовании которой вы даже не подозревали.
Как могла быть теорема Фалеса такой? Что из всех мировых теорем делает теорему Фалеса особенно благоприятной для такого рода случайного открытия доказательства?
Вот моя гипотеза.В этот век невинности, прежде чем кто-либо знал что-либо о доказательствах, людям все еще нравились формы. У них были линейка и компас. Они использовали эти инструменты для измерения полей и прочего, но им также понравилась его эстетика.
Они игрались с линейкой и компасом. Играем с фигурами. После пяти минут игры с компасом вы узнаете, как нарисовать правильный шестиугольник. Помнить? Вы, наверное, делали это в детстве. Нарисуйте круг, а затем, не меняя отверстия компаса, проведите циркулем по окружности.Умещается ровно шесть раз. Очень приятная форма.
Мы точно знаем, что люди делали это до Фалеса. В мозаиках Месопотамии есть шестиугольные мозаичные узоры, датируемые примерно -700 годом.
Додекаэдры — еще одна из таких вещей. Додекаэдр похож на те двенадцатигранные кости, которые вы используете в Dungeons and Dragons и тому подобное. До-дека-эдр, буквально: двухсторонний. Другими словами, так двенадцать сторон. Двенадцать граней, каждое из которых представляет собой правильный пятиугольник.Эти вещи есть в археологических записях. Люди делали их из камня и бронзы. Было обнаружено несколько десятков древних додекаэдров, самые старые из них были найдены еще до Фалеса. Возможно, они использовались для пророческих целей, например, карты Таро или что-то в этом роде. А может, для настольных игр, кто знает?
В любом случае, я хочу сказать, что людей интересовали геометрические узоры для различных целей: художественных, культурных и так далее. Не только для измерения полей в налоговых целях. И они явно работали с такими инструментами, как линейка и компас, чтобы делать эти вещи.
К теореме Фалеса легко прийти, просто играя с линейкой и циркулем, пытаясь нарисовать красивые вещи. Начните с прямоугольника. Нарисуйте его диагонали. Поместите стрелку циркуля в точку пересечения, прямо в середину прямоугольника. Установите перо циркуля в один из углов прямоугольника. Теперь крутите его. У вас получится круг, который идеально и плотно прилегает к прямоугольнику.
Но посмотрите, что получилось. Диагональ прямоугольника становится диаметром круга.А торчащие из него прямоугольники — это именно те треугольники-шатры, о которых говорит Теорема Фалеса. Это внезапно делает теорему очевидной.
Почему теорема Фалеса верна? Почему любая из этих «палаток», поднятых на диаметре круга, имеет прямой угол? Потому что он исходит из прямоугольника. Любая такая палатка представляет собой половину прямоугольника. Это мощный сдвиг в перспективе. Глядя на треугольник таким образом, мы обнаруживаем скрытые отношения, скрытый порядок в природе вещей.Определенные углы всегда должны быть прямыми в силу своего рода метафизической необходимости. Наши глаза были открыты, возможно, впервые, на существование такого рода потребностей, этих видов скрытых отношений, которые существует, чтобы мыслящий человек мог раскрыть.
Итак, ключ к этому сдвигу перспективы, что треугольник «на самом деле» является половиной прямоугольника. Предположим вместо этого, что мы застряли в точке зрения, что мы смотрим на треугольник, вписанный в круг.Тогда те ассоциации и идеи, которые нам напрашиваются, не так полезны для доказательства этой теоремы. С этой точки зрения, если бы вы искали доказательства, что бы вы сделали? Может быть, вы, например, соедините середину круга с концом треугольника. Итак, теперь у вас есть два меньших треугольника. Что ты собираешься с ними делать? Что-нибудь с суммами углов и так далее? Или, может быть, у вас возникнет соблазн опустить перпендикуляр вместо вершины треугольника, а затем вы можете использовать теорему Пифагора о двух маленьких треугольниках, которые вы получите.
Такие вещи не то, что мы хотим. Подобные подходы быстро становятся слишком техническими. Помните, это должно было быть началом геометрии. Вы не должны использовать кучу предыдущих результатов для доказательства. Это должно быть доказательство из первых принципов. Доказательство перед всеми другими доказательствами.
Идея о том, что треугольник «на самом деле» является половиной прямоугольника, отличается. Это меняет то, как мы смотрим на диаграмму. Это меняет акценты. Это меняет то, что мы считаем основным.Теперь прямоугольник идет первым, треугольник — вторым, а круг — последним. С этой точки зрения теорема на самом деле вовсе не касается кругов, так сказать. Круг — это просто вторичный артефакт.
В этом доказательстве мы как художники. Мы отошли от холста, наклонили голову и увидели это прозрение. И прозрение стало возможным благодаря тому, как мы раньше играли с этими идеями. Мы просто играли с линейкой и циркулем, мы исследовали треугольники, прямоугольники и круги с непредубежденной любовью.Из этой пьесы рождаются такие прозрения, как теорема Фалеса. В этом контексте естественно приходит вдохновение.
В отличие от других скучных доказательств, на которые я ссылался, которые были основаны на разрезании треугольника и бросании в него книги: суммы углов, теорема Пифагора, все, что мы можем придумать. Это скучный подход, подход грубой силы. Ему не хватает того эстетического вдохновения, этого прозрения, раскрывающего истинную природу треугольника и его второй половины, с которой ему было суждено воссоединиться.
Геометрия не могла начаться с такого рода практических доказательств, потому что они имеют смысл только после того, как для начала есть книга по геометрии. Но геометрия могла начаться с доказательства типа прозрения. Таким образом, кто-то вроде Фалеса мог прийти к идее доказательства, играя с линейкой и компасом.
Возможно, вы знакомы с «Плачом Локкарта»: отличным эссе о том, что не так с математическим образованием. Иди и прочитай, он доступен в Интернете.Интересно, что Локхарт использует именно этот пример, чтобы доказать свою точку зрения. Он описывает, как его ученики открыли теорему Фалеса, в основном так, как я говорю, что Фалес мог это сделать. Он также красноречиво показывает, насколько это удовлетворяет гораздо больше, чем сухое доказательство, записанное в книге.
Недаром в этом вопросе история и образование идут рука об руку. Доказательство должно было начаться с убедительного эстетического опыта или вау-момента. В то время другого пути не было. Заставить Фалеса запоминать факты для экзамена было некому.Открытие заставило его ценить математику. Если мы хотим развить внутреннюю мотивацию у наших студентов, неплохо было бы в первую очередь подумать, что заставило людей полюбить эти идеи. Первая любовь всегда чистейшая и невинная. Современные учебники похожи на браки по договоренности, навязанные студентам. Но в истории всегда есть настоящая история любви.
Тем не менее, несмотря на все это, вы все равно можете подумать, что теорема Фалеса немного скучна. Что-то всегда есть под прямым углом.Ну и что? Какая разница?
Как я пытался утверждать, Фалеса и его современников, вероятно, впечатлила не сама по себе теорема, а, скорее, идея о том, что теоремы и доказательства вообще существуют. Есть скрытые истины, которые можно раскрыть с помощью рассуждений. Замечательный.
Но на самом деле интересна и сама теорема. Позвольте мне показать вам кое-что интересное, что вы можете сделать с помощью теоремы Фалеса.
Существует древняя легенда о царице Дидоне.Дочь царя Тира, крупного города в древности. Вы все еще можете увидеть руины этого древнего города на территории современного Ливана. В какой-то момент Дидоне пришлось бежать из-за придворных интриг. Убийства и предательства и так далее. Поэтому она берет с прикроватной тумбочки пару диадем, может быть, золотой сундук, который отложила на дождливый день, и торопливо уходит в ночь. С едва ли в мире остался друг.
Ей нужно пройти весь путь до нынешнего Туниса, находящегося за тысячи километров, и попытаться как-то начать все сначала, как приличествует королевской семье.Используя свой сундук с сокровищами, она заключает сделку, чтобы купить землю. Как гласит легенда, столько земли, сколько она может покрыть шкурой быка. Она разрезала бычью шкуру на тонкие полоски и связала их вместе, и что теперь? Итак, теперь у нее есть эта длинная веревка, которую она может использовать как своего рода забор, чтобы изолировать землю, которую она хочет.
Но какой формы сделать? Квадрат, прямоугольник, треугольник? Нет. Дидона знает лучше. Возможно, ее королевское образование включало математику. Сделайте это круглым. Это лучший способ.Круг имеет максимальную площадь среди всех фигур с заданным периметром. Или в данном случае, поскольку она была у океана: полукруг, с другой стороны береговой линией, естественной границей.
Давай докажем это. Что полукруг — лучший выбор. Я собираюсь доказать это с помощью противоречия: предположим, кто-то построил забор на участке, который не является полукругом; затем я могу показать, как это сделать лучше: как переместить забор так, чтобы территория стала еще больше, без добавления забора.
Хорошо, у вас есть береговая линия, это прямая линия. И из одной точки на берегу, идя вглубь, у вас есть этот забор, который затем снова спускается и снова встречается с берегом в какой-то другой точке. Так что вместе с береговой линией он закрывает определенную территорию.
Предположим, эта форма не является полукругом. Если бы это был полукруг, применима теорема Фалеса. И он сказал бы вам, что этот угол, то, что я назвал углом палатки, в любой точке вдоль забора будет прямым углом.Таким образом, если фигура не является полукругом, на заборе должна быть точка, в которой этот угол не является прямым.
Я говорю, что если сделать этот угол прямым, то увеличится площадь покрытия. Вы можете представить это так. Итак, у вас есть форма, окруженная забором: представьте, что у вас есть вырез из картона. А по периметру у вас есть отмеченная точка, где угол палатки не является прямым ангелом. Итак, на вашем картоне нарисован этот треугольник: треугольник, состоящий из прямой береговой линии с одной стороны и двух линий от его концов, идущих вверх, чтобы встретиться в точке палатки по периметру.
Давайте вырежем этот треугольник из картона. Итак, у вас остались две части: любые части, которые торчали из сторон треугольника. Теперь переместите эти две части так, чтобы угол палатки получился прямым. Это означает перемещение конечных точек вдоль береговой линии. Перемещая две точки на береговой линии, вы меняете угол, под которым встречаются две картонные части. Две картонные части встречаются в одной точке, точке палатки, и это похоже на петлю, которая может открываться или закрываться на больший или меньший угол.Таким образом, вы перемещаете эти штуки, пока угол поворота не станет 90 градусов.
Обратите внимание, что вы не меняли периметр таким образом. Вы только что переместили такое же количество забора.
Но вы действительно увеличили огражденную площадь. Потому что, если у вас есть две палки фиксированной длины, и вы хотите сделать из этих палочек самый большой треугольник, лучший способ — сделать угол между ними прямым. Это интуитивно понятно. Вы знаете, что площадь треугольника равна основанию, умноженному на высоту, больше двух.Итак, если одна из ваших палочек является основанием, то для увеличения площади вы хотите максимизировать высоту, то есть перпендикулярную высоту, идущую вверх от основания, что, очевидно, достигается путем направления другой палки прямо вверх под прямым углом.
Итак, это доказывает, что для любого ограждения, не являющегося полукругом, вы можете сделать лучший. Вы можете передвинуть забор и увеличить площадь. Так что полукруг — лучшее решение, а все остальные менее хороши.
Не знаю, сможете ли вы все это представить себе.Но, может быть, позже попытайтесь реконструировать этот аргумент для себя. Это действительно очень интуитивно понятно и красиво.
Так в чем же тогда мораль этой истории? Математически это ответ на вопрос «ну и что?» вопрос относительно теоремы Фалеса. Это могло показаться достаточно скучной теоремой, но здесь мы видим ее в действии красивым и неожиданным образом, как ключевой ингредиент в этом доказательстве о том, как оградить землю. Кто бы мог предвидеть это?
Это говорит о том, что у математики есть своего рода «снежный ком» или аспект самооплодотворения.Теорема Фалеса, в чем дело? Просто скучное наблюдение о треугольнике в круге. Может показаться, что это не так уж и много. Но одно ведет к другому. Когда вам становится понятна теорема Фалеса, вы начинаете видеть ее в других, неожиданных местах. Как эта проблема о районе. Вы бы не подумали, что это связано, но чем больше вы занимаетесь математикой, тем больше связей вы обнаруживаете.
Выберите любую теорему, какой бы скучной она ни была, например, теорема Фалеса, и вы сможете найти эти удивительные вещи, в которых скучная теорема на самом деле является ключевым моментом, открывающим совершенно новые способы осмысления, казалось бы, не связанных между собой проблем.Это для вас математика. Неудивительно, что греки прижились как жук, как только они сдвинулись с мертвой точки. В один момент вы натыкаетесь на какой-то случайный результат, например на теорему Фалеса, а в следующий момент вы знаете, что видите математику везде.
Такова математическая мораль истории. Теперь мы должны вернуться и сказать кое-что об исторической стороне всего этого. Что мы действительно знаем о Фалесе и его теоремах, королеве Дидоне и всем остальном? Сколько истории и сколько легенд?
Если мы начнем с Дидоны, то эта история используется в основном через Вергилия.Энеида, знаменитая эпическая поэма. Это было написано во времена Римской империи, примерно в -20 году. Но это относится к историческим или предположительно историческим событиям, которые произошли еще до Фалеса, может быть, за два столетия до Фалеса, то есть примерно 800-х годов. У нас есть версия Верджила, это то, что до нас дошло, но он просто крадет старую историю. Эти вещи существовали веками в греческой культуре, в различных литературных и исторических пересказах, которые сейчас утеряны.
Совершенно правдоподобно, что действительно существовала такая историческая королева, которая действительно покинула свой королевский дом в Тире и действительно приземлилась на северных берегах Африки, где она основала это новое поселение, которое должно было стать великим городом Карфаген. .Может быть, она даже сделала полукруглыми городские стены, кто знает? Совершенно очевидно, что она могла хотеть минимизировать периметр по какой-либо причине, и что она могла знать, что полукруглая форма была оптимальной для этой цели.
Но в то время не было бы никаких математических доказательств этого, подобных тому, которое я набросал выше. Приведенное мной доказательство принадлежит Якобу Штайнеру в начале 19 века. Со времен Греции у нас есть другое доказательство этого результата.Так что они, конечно, очень хорошо знали результат, что полукруг является оптимальным, если, возможно, не то конкретное доказательство, которое я предложил.
Если история царицы Дидоны говорит что-либо об истории математики, она, вероятно, больше всего не освещает ни время, когда произошли события, около -800, ни время, когда были написаны источники, которые у нас есть, около года 0. Но, может быть, это так. что-то говорит о промежуточных веках, когда история могла бы быть передана и переработана.
История была как бы маринована в греческой культуре.Может быть, именно они придали этому математическую окраску. Подходит для обуви: греки ценили мудрых, аристократических, хорошо образованных правителей, которые разрабатывают рациональную политику для общего блага, основанную на разуме и математике. Может быть, они позволили этим идеалам окрасить то, как они пересказывают историю королевы Дидоны и ее круглого города.
С этой точки зрения мы также можем предположить, что к тому времени, когда Вергилий придет и напишет римскую версию истории, это понимание математики уже не то, чем было раньше.В самом деле, Верджил не раскрывает математический аспект оптимизации истории. Дидона — всего лишь второстепенный персонаж. Его эпос об Энее, который находится в поисках, которые в конечном итоге приведут к основанию Рима.
Эней терпит кораблекрушение и выносится на берег в Карфагене, круглом городе Дидоны. Дидона влюбляется в него, но он не отвечает на ее любовь. Он уплывает, и Дидона убивает себя из-за разбитого сердца. Моррис Клайн завершает рассказ: «Итак, неблагодарный и невосприимчивый человек с жестким умом стал причиной потери потенциального математика.Это был первый удар по математике, нанесенный римлянами ». Конечно, есть еще много всего, откуда это взялось.
Можно рассматривать эту историю как символ этого перехода от мудрых королей-философов (или в данном случае цариц) греческого мира, которые лелеяли математику и использовали ее для улучшения мира. Переход от этого к бессердечному римлянину, который думает только о себе и не заботится о теореме Фалеса. В греческом мире ботаники-математики считались привлекательными, но каким-то образом эти невежественные римляне явно не думали, что королева-геометрист вообще может быть подружкой.
Итак, история о Дидоне и круглом городе, о доказательстве оптимизации и всем остальном очень интересна с точки зрения более широких математических и культурных точек, с которыми она связана, но сама по себе она не является историей как таковой.
С Thales все иначе. Это больше факт, чем легенда. Насколько мы можем определить, Фалес действительно доказал, что диаметр делит окружность пополам, скорее всего, с помощью доказательства, обсужденного выше.
Источники, которые у нас есть, далеки от совершенства.В первую очередь Прокл, писавший примерно в 450 году, то есть через тысячу лет после жизни Фалеса. Такого рода запоздалые источники очень популярны. У них нет авторитета сами по себе. Прокл был никем. Его собственное понимание истории и математики очень плохо. Посредственный мыслитель, посредственный ученый, живущий в посредственном возрасте.
Таковы источники, которые у нас есть. По сути, столь же авторитетный, как факт, который вы читаете на обратной стороне коробки с хлопьями или чего-то еще.
Но есть надежда.Во времена своей славы Греция была просто выдающейся интеллектуальной культурой. И кое-что, например, о Фалесе, можно проследить до тех пор, что делает его весьма достоверным. Ученик Аристотеля Евдем написал историю геометрии. Увы, этого уже нет. Возраст невежества игнорировал это, и теперь его нет. Но что это была бы за работа.
Эти люди знали, что делают. Более поздние люди, подобные Проклу, похожи на некоторых онлайн-рандомов, которые публикуют недоработанные идеи в блоге или плохо информированные комментарии в Facebook.Вот насколько они заслуживают доверия.
Но люди вроде Евдема — совсем другая история. Это больше похоже на первоклассного ученого в исследовательском учреждении со всей инфраструктурой, о которой можно только мечтать: библиотеками, чрезвычайно образованными и умными коллегами с широким спектром знаний, широкой финансовой и культурной поддержкой общественности и политиков и т. . «История геометрии» Евдема была бы настоящей книгой «University Press», прошедшей рецензирование до зубов и с красивой аннотацией Аристотеля в суперобложке.
Такие люди, как Евдем, не занимались распространением случайных сплетен и непроверенных фактоидов, потому что они звучат круто. Они были настоящими учеными и интеллектуалами.
И действительно, многие сведения о Фалесе можно проследить до этого потерянного источника. Когда Прокл говорит, что Фалес был первым, кто доказал, что круг делится пополам по его диаметру, источником этого является Евдем. Следовательно, это очень достоверно. Это случилось с Фалесом на самом деле. На самом деле то, что касается диаметра, разделяющего окружность пополам, более определенно, чем то, что касается теоремы Фалеса.Была ли теорема Фалеса на самом деле теоремой Фалеса? Может быть. Но мы не можем проследить конкретно эту часть до лучших источников. В отличие от диаметра пополам одной и некоторых других деталей. Но с точки зрения контекста это имеет смысл.
Истории Фалеса и происхождения геометрии, очевидно, были хорошо известны не только специализированным ученым, но и широкой афинской публике. Драматург Аристофан несколько раз использует имя Фалеса как символ геометрии в своих пьесах. Так же, как сегодня, можно использовать имя Эйнштейна, например, чтобы вызвать образ ученого.У Аристофана один говорящий в диалоге говорит: «Этот человек — Фалес». Это означает, что человек — геометр. Очевидно, можно было ожидать, что театральная публика в классических Афинах поймет это упоминание. Каждый образованный человек знал бы о Фалесе и истоках геометрии.
На самом деле, общественное уважение к геометрии и ее истории было очевидно настолько велико, что Аристофан даже заставил одного из своих персонажей оплакивать ее как чрезмерную, говоря: «Почему мы продолжаем восхищаться старым Фалесом?» Какое время было бы жить.Когда драматургам приходилось решать такие проблемы, как чрезмерное уважение и интерес к математике среди широкой публики. «Привет, ребята, может быть, нам нужно охладить это тем, насколько мы любим геометрию». Какая проблема с роскошью. Едва ли та, с которой сегодня приходится бороться голливудским блокбастерам.
В любом случае, нам, может быть, не стоит слишком углубляться в эти отдельные цитаты. Но общая интеллектуальная достоверность этого возраста важна. Эти очень умные и серьезные люди записали в научных историях рассказы о Фалесе, основавшем дедуктивную геометрию и доказавшем, что круг делится пополам по своему диаметру.Это всего через двести или триста лет после Фалеса, и в прямой линии от него, вероятно, целые работы Фалеса все еще хранятся в библиотеках и так далее.
Итак, поехали. Истоки доказательства и дедуктивной геометрии. Мы действительно кое-что об этом знаем, и эту историю стоит узнать, если вы спросите меня.
Теорема Фалеса — два случая
Теорема Фалеса — два случая
Теорема Фалеса и рисунок
Ключевой и часто встречающейся фигурой в теории подобных треугольников является
фигура с двумя параллельными линиями и двумя пересекающимися трансверсалиями.В этом
Конечно, мы будем называть эту фигуру фигурой Фалеса в честь раннего
Греческая геометрия, которая якобы измеряет высоту Великой пирамиды с помощью теней.
Теорема Фалеса
Даны две строки AB и CD. Когда AC и BD пересекаются в точке E, а когда
E либо (1) точка, внутренняя по отношению к сегменту AC и сегменту BD, либо (2)
вне обоих сегментов, то треугольники AEB и CED (1) имеют общий угол
AEB = угол CED или (2) эти два угла являются вертикальными углами.Тогда для таких
цифра,
- Линия AB параллельна линии CD тогда и только тогда, когда
- Треугольник AEB похож на треугольник CED тогда и только тогда, когда
- EC / EA = ED / EB
Доказательство: Это задача 4.3 BG (в задании 4), за исключением того, что эта проблема
не совсем правильно, как указано, поскольку неверно, если E является внутренним по отношению к сегменту
AC и внешний по отношению к сегменту BD.
Комментарий: Теорема верна, как указано в BG, если мы допустим ОТРИЦАТЕЛЬНЫЙ
СООТНОШЕНИЯ сегментов, когда ориентированные сегменты указывают в противоположных направлениях.Тогда два отношения положительны в случае (1) и отрицательны в случае (2) и
Теорема верна, как указано в BG, без предположений (1) и (2) выше.
Thales Рисунок
Если любое из этих условий (и, следовательно, все эти условия) верно, то
мы называем фигуру фигурой Фалеса. На этих рисунках показаны случаи (1) и (2). Интерактивный
Рисунки Java Sketchpad, которые показывают соотношение со знаком, находятся на этом
ссылка на сайт.
A и C находятся по одну сторону от E.(и, следовательно, B и D находятся на одной стороне В этом случае EC / EA> 0 и ED / EB> 0. | Пересечение E находится между A и C (и, следовательно, между B и D). Другой В этом случае EC / EA <0 и ED / EB <0. |





