Функции с модулем как строить: Графики функций с модулем — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Построение функций, содержащих модули

Здравствуйте, уважаемые посетители! В этой статье мы попробуем подробно разобраться, как построить график функции, если эта функция содержит модуль. В статье разобраны различные примеры с пошаговым построением и подробным объяснением, как получен тот или иной график.

1. Начнем с построения графика

В “основе” его лежит график функции

и все мы знаем, как он выглядит:

Теперь построим график

Чтобы получить этот график, достаточно всего лишь сдвинуть полученный ранее график на три единицы вправо. Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то мы сдвинули бы график влево:

Теперь необходимо умножить на два все ординаты, чтобы получить график функции

Наконец, сдвигаем график вверх на две единицы:

Последнее, что нам осталось сделать, это построить график данной функции, если она заключена под знак модуля. Для этого отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту часть, что лежит ниже оси х):

2. Теперь построим график функции

Выражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так:

При х>2/3 функция запишется так:

То есть точка х=2/3 делит нашу координатную плоскость на две области, в одной из которых (левее) мы строим функцию

а в другой (правее) – график функции

Строим:

3. Следующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля:

Посмотрим, в каких точках подмодульные выражения меняют знак:

Расставим знаки для подмодульных выражений на координатной прямой:

Раскрываем модули на первом интервале:

На втором интервале:

На третьем интервале:

Таким образом, на интервале (-∞; 1.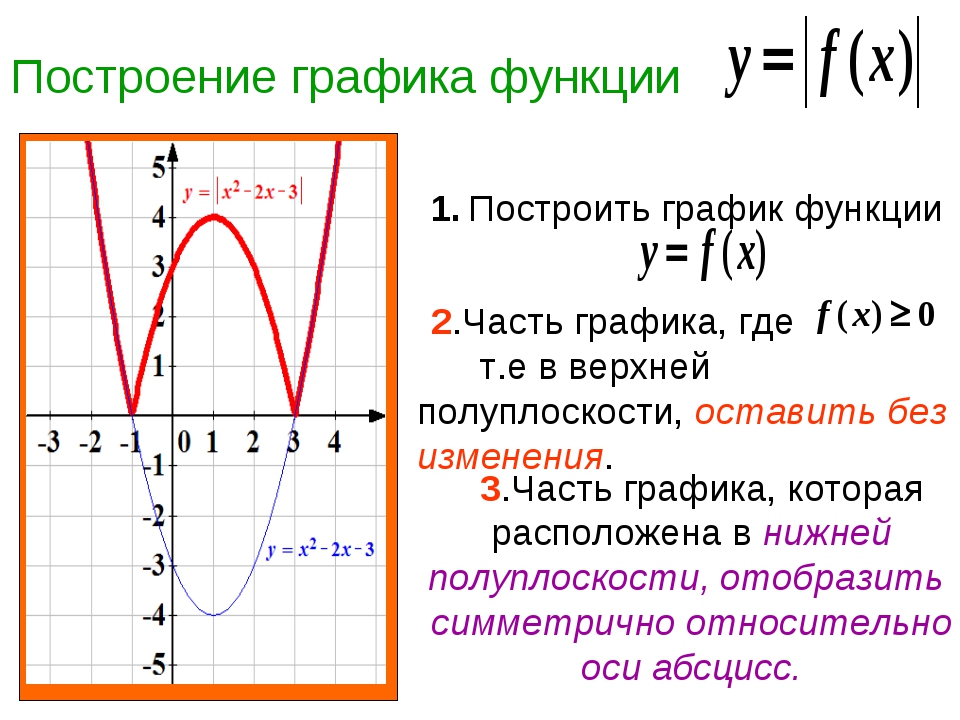 5] имеем график, записанный первым уравнением, на интервале [1.5; 2] – график, записанный вторым уравнением, и на интервале [2;∞) – график по третьему уравнению:

Строим:

4. Теперь можем построить график, похожий на один из предыдущих, и все же отличающийся:

В основе опять знакомый нам график функции

но, если в знаменателе x стоит под знаком модуля,

то график имеет вид:

Теперь произведем сдвиг на три единицы,

при этом сдвинутся обе части: правая – вправо, левая – влево (своеобразное зеркало : отходишь дальше – видно больше)

График этой функции, умноженной на два,

выглядит так:

Теперь можно поднять график по оси у:

и тогда он будет таким:

Наконец, строим окончательный вид графика, отражая все, что ниже оси абсцисс, вверх:

5.Очень интересно выглядит график функции

В точках 2 и (-2) знак подмодульного выражения меняет знак, поэтому функция состоит из трех кусков (точки 2 и (-2) выколоты). На участках (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) – второе:

6. Две следующие функции отличаются знаком, и графики их выглядят по-разному:

7. Еще два похожих графика, вид которых меняется в зависимости от х в показателе степени:

Первый:

Второй:

8.Теперь построим график такой функции:

Здесь точкой перемены знака подмодульного выражения является х=4. Тогда на интервале (-∞; 4] функция выглядит так:

А на интервале [4; ∞) так:

Точка вершины первой параболы (2;-12), она обращена вниз ветвями, точка вершины второй параболы (6, -20), ветви ее обращены вверх. В итоге имеем:

9. Построим график функции, которая, на первый взгляд, выглядит устрашающе:

Однако многочлен в числителе раскладывается на множители:

Точки перемен знака подмодульных выражений – 4 и (-2). Точки эти (они выколоты) разбивают числовую прямую на три интервала, на которых данная функция будет выглядеть:

На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

Строим:

Внесем небольшие изменения, добавив двойку в знаменатель исходной функции:

Тогда точки перемены знака остаются те же, но функция выглядит иначе на разных интервалах:

На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

График изменится:

10. Наконец, последний график мы построим для функции

Начнем построение с “базовой” для этого графика функции

она выглядит так:

Далее добавим знак модуля под корень:

Теперь опустим этот график вниз на 4 единицы по оси у:

“Опрокинем” все, что ниже оси х, вверх,

и не забудем поделить все ординаты на 2:

Методы построения графиков функций содержащих модуль

Цель урока:

повторить построение графиков функций
содержащих знак модуля;

познакомиться с новым методом построения
графика линейно-кусочной функции;

закрепить новый метод при решении задач.

Оборудование:

мультимедиа проектор,

плакаты.

Ход урока

Актуализация знаний

На экране слайд 1 из презентации.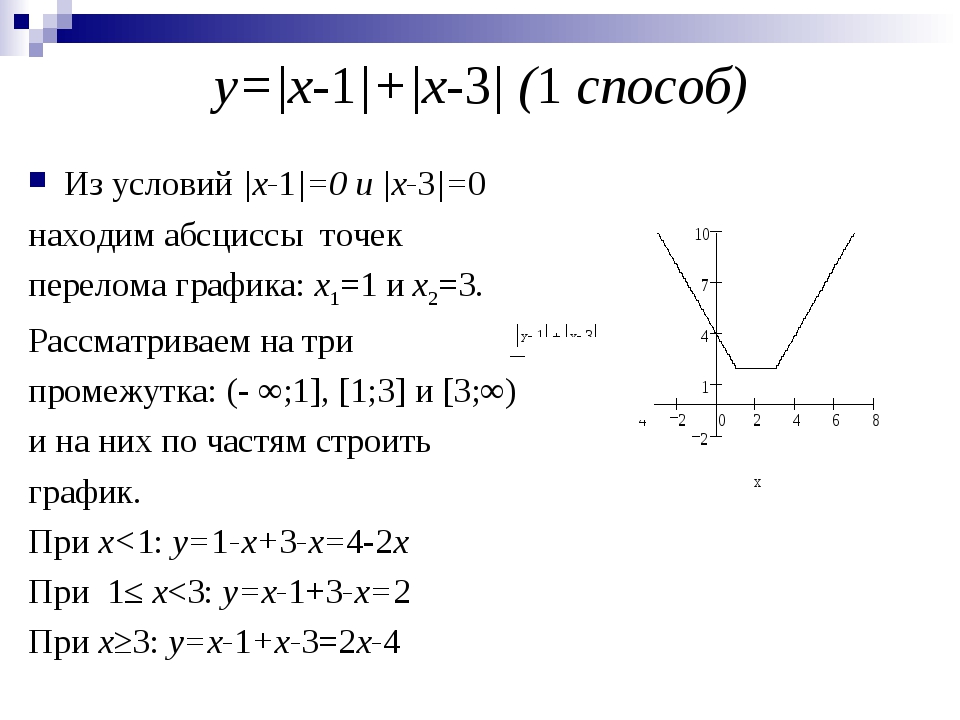

Что является графиком функции y=|x| ? (слайд 2).

(совокупность биссектрис 1 и 2 координатных
углов)

Найдите соответствие между функциями и
графиками, объясните ваш выбор (слайд 3).

Рисунок 1

y=| x+3|

y=| x| +3

y=-2| x| -2

y=6-| x-5|

y=1/3| x-6| -3

Расскажите алгоритм построения графиков
функций вида y=|f(x)| на примере функции y=|x²-2x-3|
(слайд 4)

Ученик: чтобы построить график данной функции
нужно

— построить параболу y=x²-2x-3

— часть графика над ОХ сохранить, а часть
графика расположенную ниже ОХ отобразить
симметрично относительно оси ОХ (слайд 5)

Рисунок 2

Рисунок 3

Расскажите алгоритм построения графиков
функций вида y=f(|x|) на примере функции y=x²-2|x|-3
(слайд 6).

Ученик: Чтобы построить график данной функции
нужно:

— построить параболу.

— часть графика при х 0
сохраняется и отображается симметрии
относительно оси ОУ (слайд 7)

Рисунок 4

Расскажите алгоритм построения графиков
функций вида y=|f(|x|)| на примере функции y=|x²-2|x|-3|
(слайд 8).

Ученик: Чтобы построить график данной функции
нужно:

— нужно построить параболу у=x²-2x-3

— строим у= x²-2|x|-3, часть графика сохраняем
и симметрично отображаем относительно ОУ

— часть над ОХ сохраняем, а нижнюю часть
симметрично отображаем относительно ОХ (слайд 9)

Рисунок 5

Следующее задание выполняем письменно в
тетрадях.

1. Построить график линейно-кусочной
функции у=|х+2|+|х-1|-|х-3|

Ученик на доске с комментарием:

— находим нули подмодульных выражений х₁=-2,
х₂=1, х₃=3

— разбиваем ось на промежутки

— для каждого промежутка запишем функцию

при х < -2, у=-х-4

при -2 х<1, у=х

при 1 х<3, у = 3х-2

при х 3, у = х+4

— строим график линейно-кусочной функции.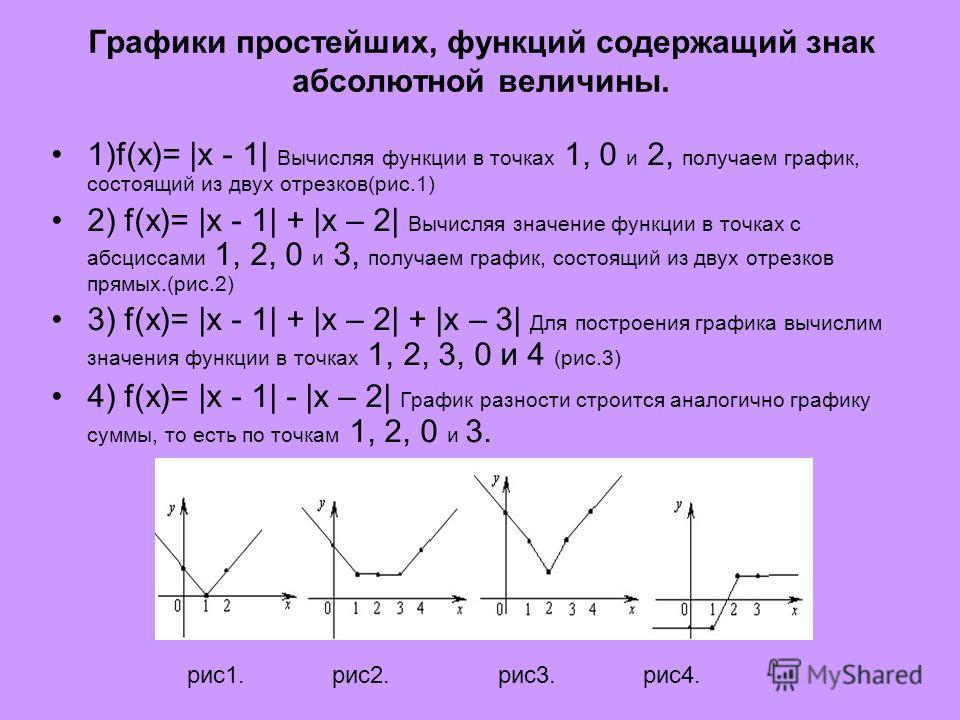

Мы с вами построили график функции используя
определение модуля (слайд 10).

Рисунок 6

Предлагаю вашему вниманию “метод вершин”,
который позволяет строить график
линейно-кусочной функции (слайд 11). Алгоритм
построения дети записывают в тетрадь.

Метод вершин

Алгоритм:

Найдем нули каждого подмодульного выражения

Составим таблицу, в которой кроме нулей запишем
по одному значению аргумента слева и справа

Нанесем точки на координатную плоскость и
соединим последовательно

2. Разберем этот метод на той же функции
у=|х+2|+|х-1|-|х-3|

Учитель на доске, дети в тетрадях.

Метод вершин:

— найдем нули каждого подмодульного выражения;

— составим таблицу, в которой кроме нулей
запишем по одному значению аргумента слева и
справа

х -3 -2 1 3 4

у -1 -2 1 7 8

— нанесем точки на координатную плоскость и
соединим последовательно.

Графиком линейно-кусочной функции является
ломанная с бесконечными крайними звеньями (слайд
12) .

Рисунок 7

Каким же методом график получается быстрее и
легче?

3. Чтобы закрепить данный метод предлагаю
выполнить следующее задание:

При каких значения х функция у=|х-2|-|х+1|
принимает наибольшее значение.

Следуем алгоритму; ученик на доске.

у=|х-2|-|х+1|

х₁=2, х₂=-1

у(-2)=4-1=3

у(-1)=3

у(2)=-3

у(3)=1-4=3, соединяем последовательно точки.

у_наиб= 3

4. Дополнительное задание

При каких значениях а уравнение ||4+x|-|x-2||=a имеет
два корня.

5. Домашняя работа

а) При каких значениях Х функция у =|2x+3|+3|x-1|-|x+2|
принимает наименьшее значение.

б) Построить график функции y=||x-1|-2|-3| .

как построить – сложное простыми словами — ЕГЭ/ОГЭ

График модуля, как построить – очень просто. Особенно, если знать несколько закономерностей. О них расскажу в статье. С помощью них вы поймете как построить график модуля легко и играючи. Без поиска пробных точек.

На самом деле построение графиков функций с модулями – это удовольствие. Раньше они вызывали у вас в лучшем случае пренебрежение? Забудьте – после прочтения статьи вы будете первым по скорости построения графика.

Построение различных видов графиков, содержащих модуль:

Воландеморт среди модулей

Как калькулятор может помочь при построении графика?

Как построить график модуля и одновременно решить уравнение

Война среди модулей

Господа, перед тем, как мы приступим к светской беседе с модулем. (В которой отдадим дань уважения каждому его виду). Я бы хотел обратить ваше внимание, что модуль никогда не бывает отрицательным. Отсюда и все особенности его графика.

Подмечайте фишки каждой функции, но главное – держите в голове его «неотрицательность».

Главный миф о сложности графиков модуля – полный модуль по правой части

Забудьте сказки про сложность модуля – ведь теперь вы скоро узнаете о методе «Зеркало».

Модуль всей правой части y = |f(x)| отражает график относительно оси X. Все, что было под осью Ox зеркально отражается наверх.

Почему так? Обратите внимание, что значение функции (то есть y) является результатом вычисления модуля. Оно не может быть отрицательным. Согласны? Значит, его заменяют на противоположное ему по знаку. А в построении функций эти зеркальные превращения и есть смена знака у функции.

Уже чувствуете себя как Алиса в Зазеркалье? Ничего страшного – объясню на примере:

Пример: y = |X – 3|

Видите, график функции y = |X – 3| состоит из двух ветвей. Первая y = X – 3, а вторая y = – (X – 3) = 3 – X. Все по определению модуля – не придраться. Зеркально отраженная функция и есть противоположная по знаку той, которую отражали.

Можете так себя проверять – сначала просто отзеркальте конец, который улетает в отрицательную бесконечность (под ось Ох). А потом посмотрите, действительно ли он совпадает с минусовой версией подмодульного выражения. Уверяю, если вы были аккуратны – совпадет.

*Читайте понятное определение модуля в статье «Простая инструкция: как решать любые уравнения с модулем». После ее прочтения вы научитесь расправляться со всеми видами уравнений с модулем с помощью всего 1 инструкции!

А теперь перейдем к функции, которая заставляет поежиться от недовольства слишком многих. Если б они знали, что ее настолько просто начертитить…то стали бы решать уравнения с ней только графически.

Воландеморт среди модульных функций — Полный модуль по правой части

Модуль всей левой части |y| = f(x) отражает график относительно оси X. Все, что было над осью Oх зеркально отражается вниз.

Смотрим, что является результатом вычисления подмодульного выражения? Ага, все, что стоит справа. Значит, в данном случае Рубиконом является ось Oy – отзеркаливаем относительно нее.

Пример: |y| = X – 3

Мы разобрали две базы графиков с модулями. Дальше уже идут вариации с дополнительными математическими па: поднимите график, опустите, сузьте – расширьте. Давайте и их разберем!

Как калькулятор может помочь при построении графика? — График содержащий модуль

Это пример сложной функции, такие функции строятся по этапам. Сложной – не потому что она поддается только сильнейшим умам. Просто в ней собрано несколько последовательных действий: модуль и сложение с «потусторонним членом».

С такими функциями работает способ «калькулятор».

Представьте, что вам нужно вычислить выражение: (217 – 327)/72. С чего вы начнете? Вероятно, с возведения в степень, продолжите подсчетом числителя и только потом перейдете к делению.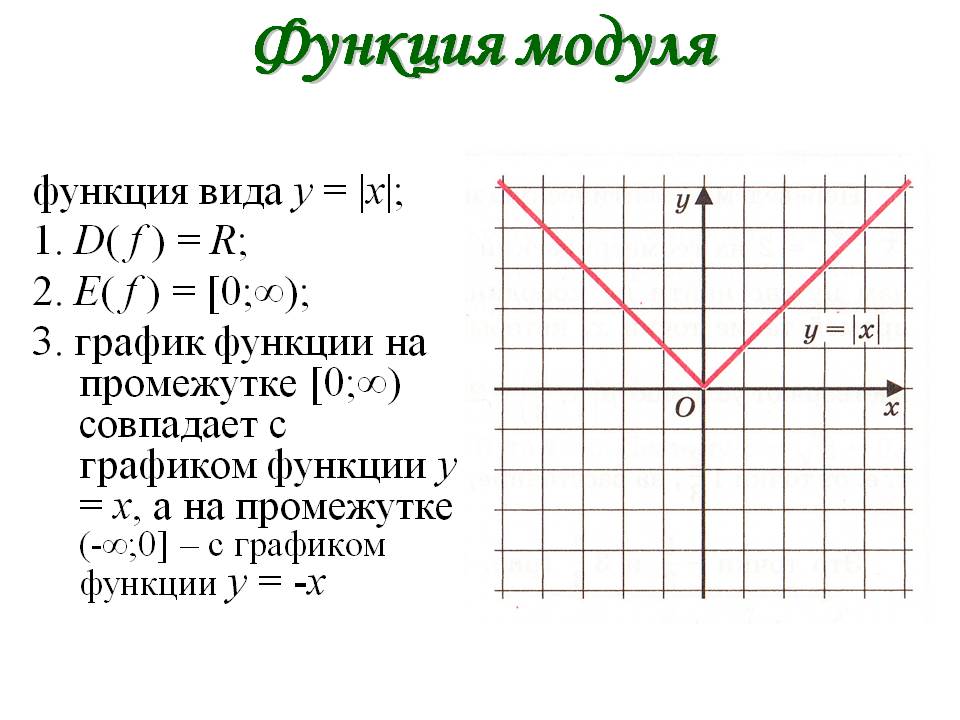 Будете идти от малого к большому.

Тот же метод работает и со сложной функцией. Начните с ядра и продолжайте справляться со всеми остальными прибамбасами вокруг него.

Пример: y = |x–3| + 5 ( ядром является график прямой y=x-3)

1. Y = X – 3 {строим график прямой}

2. Y = |X –3| {отражаем график относительно оси X}

3. Y = |X – 3| + 5 {поднимаем график 2. на +5}.

Вспомните суперспособности графиков – положительное число поднимает график, а отрицательное опускает (вверх/вниз относительно оси Ox). Причем, нет ничего страшного в том, что модульная галка окажется под прямой Ox (в отрицательной области) – это необходимые последующие действия с графиком.

Иногда в качестве «потустороннего члена» выступает переменная. Тут уж хитрить с отражениями и подниманиями – не получится. Придется раскрывать алгебраически модуль для каждого интервала – и уже по вычисленному выражению чертить ветви графика.

О том, как легко раскрыть модуль – написано в статье – Решение уравнений с модулем.

А мы двигаемся навстречу забора из модуля. По правде, такой вид функций очень полезно уметь чертить. Этот скилл способен сэкономить вам время. Ведь частенько по графику намного точнее и проще найти корни уравнения такого вида.

Как построить график модуля и одновременно решить уравнение — Модуль внутри модуля

Пример: y = ||X–2|–3|

{Порядок действий как при работе со сложной функцией – пользуемся методом «Калькулятор»}

1. Y = X – 2

2. Y = |X – 2|

3. Y = |X – 2|–3

4. Y = ||X – 2|–3|

Согласитесь, что раскрывать уравнения такого типа довольно муторно. Да и велик риск просчитаться. Начертить график и по нему оценить корни (иногда точно их посчитать) супер просто.

Поэтому графический метод решения уравнений нужно эксплуатировать на все 100% именно в этом случае.

Теперь нас ждет один из самых непредсказуемых графиков из всего рода модулей. Никогда не знаешь, что именно он приподнесет. Но и с этой неприятной неожиданностью научимся работать)

Война среди модулей — Несколько модулей

Что делать если в бой вступает сразу несколько модулей? – К сожалению, бороться с ними приходится с помощью арифметики и алгебры. Приходится аккуратно раскрывать на разных областях. Так же, как при решении модульных уравнений – алгебраически.

*Подробнее о том, как раскрывать модуль читайте в статье «Простая инструкция: как решать любые уравнения с модулем». В ней на пальцах объяснено, как раскрыть забор из модулей и НЕ запутаться.

Y = |X–2|+|X+2|

I ) X ∈ (–∞;–2] {1 модуль с «–» , 2 модуль с «–»}

Y₁ = – (X – 2) – (X + 2)

Y₁ = – X + 2 – X – 2

Y₁ = –2X

II ) X ∈ (–2;2] {1 модуль с «–» , 2 модуль с «+»}

Y₂ = – (X – 2) + (X + 2)

Y₂ = – X + 2 + X + 2

Y₂ = 4

III) X ∈ (2; +∞) {1 модуль с «+» , 2 модуль с «+»}

Y₃ = (X – 2) + (X + 2)

Y₃ = 2X

Вот такая галочка получилась из трех кусочков различных функций.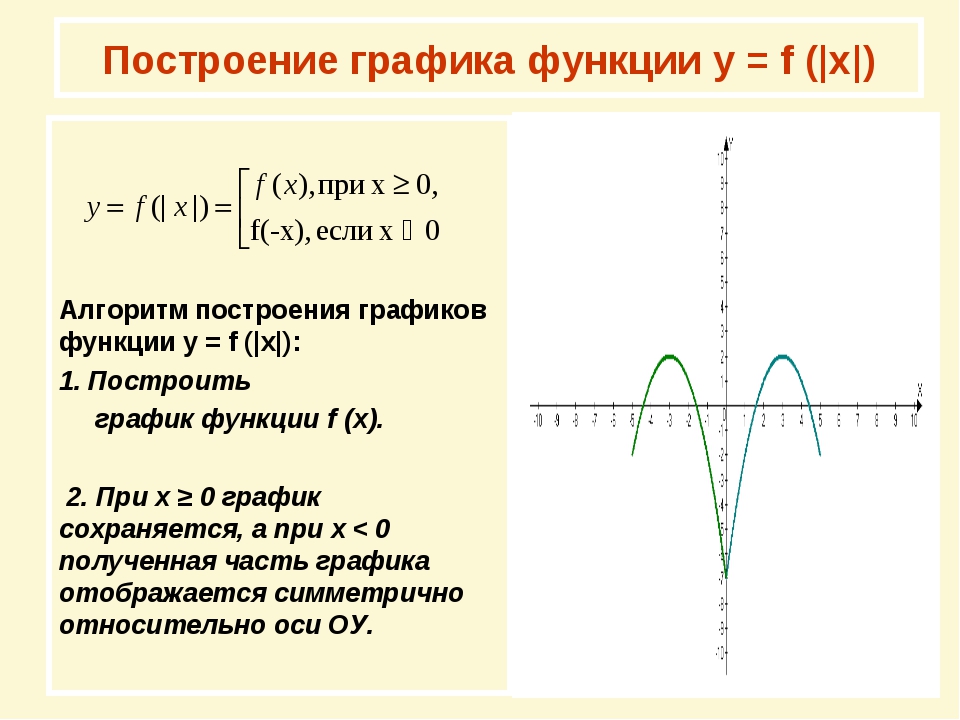

Вы уже заметили, что все модульные функции являются кусочно заданными? Их особенностью является то, что они существуют только на определенных интервалах.

Главное в модулях – понять закономерности. Дальше все пойдет как по маслу. Надеюсь, мне удалось хоть немного прояснить график модуля, как его построить и не надорваться в счете.

Остались вопросы? – обращайтесь! Я с удовольствием проведу первую консультацию бесплатно. Запишитесь на первое бесплатное занятие: напишите мне на почту или в сообщениях ВКонтакте)

До встречи, Ваш Михаил

График функции с модулем и дробью

График функции с модулем и дробью — ещё одна группа заданий номера 23 ОГЭ по математике.

Подобно функциям с переменной в знаменателе, графики таких функций могут содержать выколотую точку. Как и при построении графиков функций с модулем, рассматриваем два варианта раскрытия модуля.

1) Построить график функции

и определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:

Так как x²=|х|², формулу, задающую функцию, перепишем в виде

В знаменателе общий множитель |х| вынесем за скобки

Найдём область определения функции.

|х|(|х|-1)≠0

|х|≠0; |х|-1≠0

x≠0; |х|≠1

x≠0, x≠±1.

D(y):x∈(-∞;-1)∪(-1;0)∪(0;1)∪(1;∞).

Сократив дробь на (|х|-1), получаем

При x>0 |х|=x,

— функция обратной пропорциональности. График — гипербола. Для построения гиперболы возьмём несколько точек (включая выколотую x=1):

При x<0 |х|=-x,

— функция обратной пропорциональности.

Прямая y=kx не имеет с графиком общих точек, если она проходит через выколотые точки либо совпадает с осью Ox, то есть при k=±1 и k=0:

Ответ: -1; 0; 1.

2)Постройте график функции

и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.

Решение:

В числителе вынесем за скобки общий множитель 0,25x:

Ищем область определения функции.

x+2≠0

x≠-2.

D(y):x∈(-∞;-2)∪(-2;∞).

Сокращаем дробь на (x+2):

Получили функцию, содержащую переменную под знаком модуля (при условии x≠-2).
При x=0, y=0,25·0·|0|=0.

При x>0 |х|=x, y=0,25·x·|x|= y=0,25·x·x=0,25x².

y=0,25x² или

— квадратичная функция. График — парабола, полученная из параболы y=x² сжатием к оси Ox в 4 раза.

При x<0 |х|=-x, y=0,25·x·|x|= y=0,25·x·(-x)=-0,25x².

— квадратичная функция. График — парабола, полученная из параболы y=-x² сжатием к оси абсцисс в 4 раза.

Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку, то есть при m=-1:

Ответ: -1.

3) Построить график функции

и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.

Решение:

Найдём область определения функции: x≠0.

D(y):x∈(-∞;0)∪(0;∞).

Если

то есть при x∈[-4;0)∪[4;∞), то

y=x/4 -функция прямой пропорциональности. График — прямая, проходящая через начало координат.

Для построения прямой достаточно взять одну точку, например, при x=4 y=4/4=1. Вторая точка — точка O — на графике выколотая, так как x≠0. Для более точного построения прямой лучше взять ещё одну точку: при x=-4 y=-4/4=-1.

Если

то есть при x∈(-∞;-4)∪(0;4), то

y=4/x — функция обратной пропорциональности. График — гипербола.

Для построения гиперболы возьмём несколько точек из промежутков (-∞;-4)∪(0;4) (-4 и 4 также лучше взять для уточнения построения графика).

Прямая y=m имеет с графиком ровно одну общую точку при m=1 и m=-1:

Ответ: -1; 1.

Графики функций с модулями. 10 класс

1. Графики функций с модулями.

Проект:
Угарина Сергея, ученика
10п класса.

2. Цель работы:

Научится
строить графики функций
с модулями.
Хорошая подготовка к ЕГЭ.

3. 1 ФУНКЦИЯ С МОДУЛЕМ

Y=lXl
Строим график функции у = x
Из-за модуля положительная
часть графика отразится
вдоль оси У.
x 1 2
y 1 2

4. 2 функция с модулем.

У=l10х+4l
Строим график функции
у=10х+4
Подставляем модуль и
функция станет
положительной во всей
области определения.
Положительная часть
первой функции
отразится от х=-0,4
х
у
0
4
-1
-6

5. 3 функция с модулем

У=lx²-4l
Строим график функции у= х²-4
Это квадратичная функция,
графиком является парабола.
Чтобы построить параболу надо
найти как можно больше точек.
Сейчас строим график функции
у=lх²-4l, тогда отрицательная
сторона графика функции
у=х²-4 отразится по оси Х.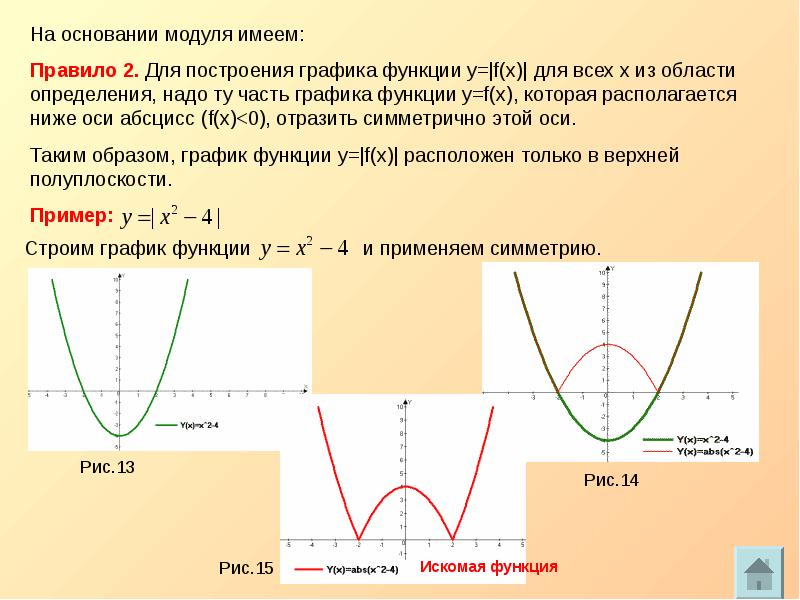
Областью определения будут все
числа, функция будет равняться
нулю в точках х = ±2.
х 1 2 -1 -2
у -4 0 -3 0

6. 4 функция с модулем

У=2х²-5lхl-7
Строим гр.функции
у=2х²-5х-7, приравняем
нулю и получим два
корня х=3,5 и х’=-1
Найдём вершину
функции. В точке х=1,5
у=-10
Строим график функции
у=2х²-5lхl-7.

7. 5 функция с модулем

У=l2х²-5х-7l
Строим график функции
у=2х²-5х-7
Всё также ,как и в
предыдущем слайде.
Потом строим график
функции у=l2х²-5х-7l
Функция станет только
положительным.
Отрицательная сторона
первой функции
отразится по оси Х

8. 6 функция с модулем

У=l2х²-5lхl-7l – сложная
функция. Строим сперва
график функции у=2х²5lхl-7 как в 4-ом слайде.
Потом всю эту функцию
берём под модуль.
Функция у=l2х²-5lхl-7l
будет положительным на
всей области
определения. Функция
будет равняться нулю в
точках х=±3,5

9.

7 функция с модулем

У=lх²+хl
Строим гр.ф у=х²+х
Эта квадратичная функция,
графиком является
парабола. Чтобы построить
параболу надо как можно
больше точек.
Строим гр.ф у=lх²+хl
Отрицательная сторона
отразится в положительную
сторону по оси Х.
х 1 -1 0 -2
у 2 0 0 2

10. 8 функция с модулем

У=lх³+х²-lхl+1l – сложная
функция.
Строи график функции
у=х³+х²-х+1. Это кубическая
функция, графиком является
гипербола. Чтобы построить
гиперболу надо найти как
можно больше точек. Потом
строим гр.ф. у=х³+х²-lхl+1 Изза модуль х, первая функция от
х=0 понижется резко. Потом
строим гр.ф. у=lх³+х²-lхl+1l
х
у
0
1
1
2
-1 2 -2
2 11 -1
Графики
функций с модулями
очень много встречаются на Е.Г.Э.
В средней школе графики функций
с модулями обучают в 10, 11
классах.
Вывод:Графики
функций надо
обязательно уметь строить, чтобы
не было проблем с такими
функциями на экзамене.

Построение графиков содержащих знак модуля построение графика функции содержащей переменную или функцию под знаком модуля согласно определению модуля

Построение графиков, содержащих знак модуля

Построение графика функции, содержащей переменную

или функцию под знаком модуля согласно определению модуля:

x, если х>=0 f(x), если f(x)>=0

|x| = ; |f(x) | =

-x, если x

Пример:

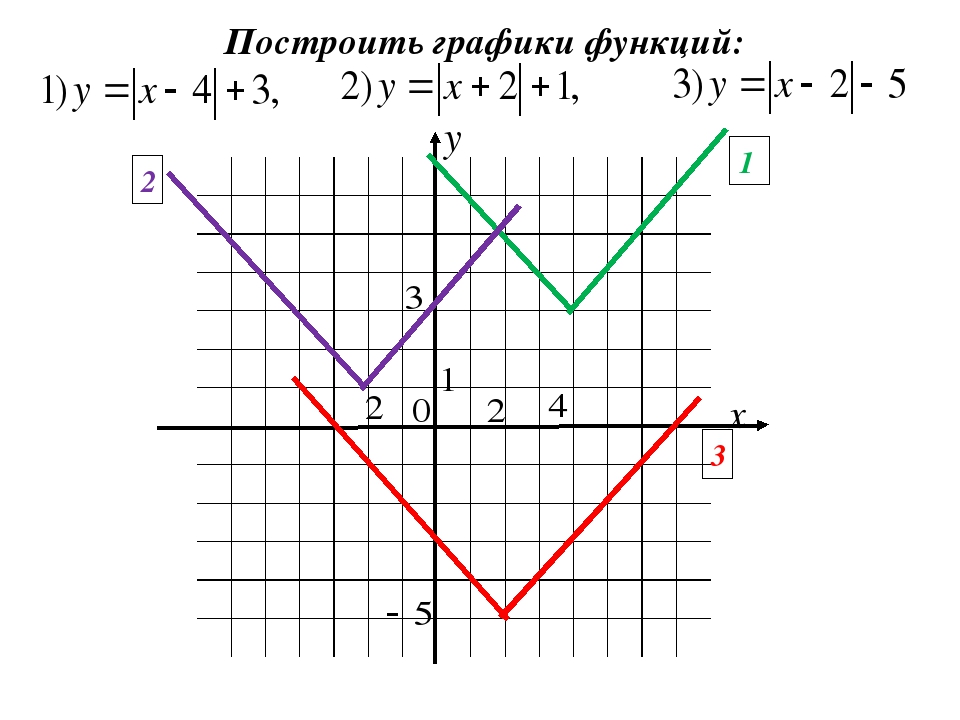
Построить график функции у=|2x-3|-х.

Рассмотрим два случая.

2х-3>=0 2х-3

y=2x-3-x или y=-2x+3-x

x>= xSUB>

y=x-3 y= -3x+3

Таким образом, чтобы построить график функции у=|2x-3|-x, надо построить графики функций, заданными различными выражениями на различных промежутках.

х-3, х>=

у=

— 3х+3, хSUB>

График изображен ниже:

y=|2x-3|-x

Построить график:

Y=|X|+X
Y=|X| · (X-2)
Y=|X+4| · X
Y=
Y=
Y=²–1)
Y=²+4X+3)
Y=
Y=
Y=X — 1 — |X-1|
Y=|3X-4|-X
Y=

13. Y=

Y=
Y=
Y=
Y=X²— 2|X+1|-1
Y=X+
Y=|X²-4X+3|+2X
Y=
Y=|X²-4|+4X
Y=

Элементарные преобразования графика функции у=f(x)

Если формула зависимости имеют вид |y| = f(x):

Надо построить график у = f(x)
Часть графика, расположенную выше оси Ох (и на самой оси) оставить без изменения
Часть графика расположенную ниже оси Ох стереть
Для оставленной части построить симметричную относительно оси Ох

Пример:

Построить график |y| = 2х-1

Построить график:

Y|=5X-4
|Y|=9-X²
|Y|=
|Y|=(X+4)²-5
|Y|=
|Y|=X+2
|Y|=X²-6X+8
|Y|=X²-4X
X|Y|=2
|Y|=
|Y| · (X+1)=1
|Y|=1-
|Y|=|2X-X²|
Y²=-2X
|Y|=8+2X-X²
Y²=0,5X

Элементарные преобразования графика функции у=f(x)

Если формула зависимости у = f(|x|):

Надо построить график функции у = f(x), часть графика расположенную правее оси Оу(и на самой оси) оставить без изменения
Часть графика расположенную левее оси Оу стереть
Построить для оставленной части симметричную относительно оси Оу

Пример:

Построить график у=2|x|-1

Построить график:

Y=5|X|-5
Y=9-|X|²
Y=
Y=
Y=
Y=(|X|+4)²-5
Y=
Y=
Y=|X|-1
Y=
Y=X²-|X|-6
Y=-X²+6|X|-8
Постройте график. 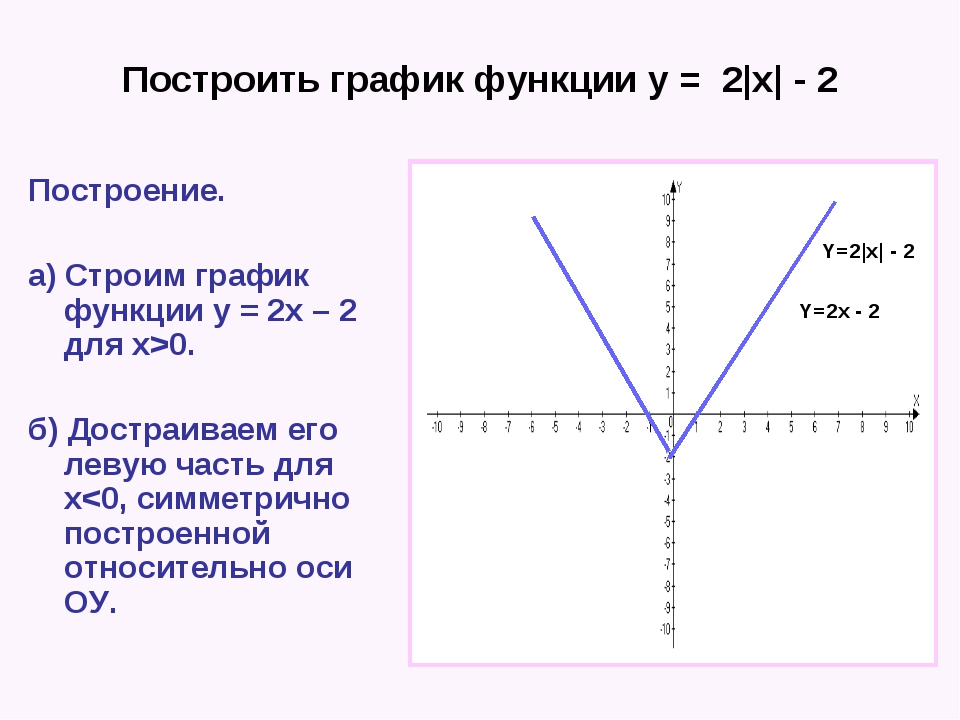С его помощью укажите пути функции, интервалы знакопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции:

2-, если |X|

у= , если |X|>4

Y=X²-|X|-2
Решите уравнение X²+3|X|-18=0 графически.
Y=|X|-X²
Y=

Элементарные преобразования графика функции у=f(x)

Если формула зависимости имеет вид у = |f(x)|,

График функции у = f(x) выше оси Ох (и на самой оси Ох) оставить без изменения
Для части графика расположенной ниже оси Ох строят симметричную относительно

оси Ох

Часть графика расположенная ниже оси Ох стирается.

Пример:

Построить график функции у=|2x-1|

Построить график:

Y=|5X-4|
Y=|9 -X²|
Y=
Y=|(X-4)²-5)|
Y=|X+2|
Y=|X-1|
Y=|X²+2X|
Y=
Y=||
Y=||X²-3|-1|
Y=|X²-1|
Y=|X+1|-2
Y=4+|X-3|
Y=3 ∙ |X-2|
Найдите наибольшее и наименьшее значение функции Y=:

а)на отрезке [-2;2]

б)на луче [0;+ )

в)на луче (- ;3]

г)на отрезке [-5;0]

16. Найдите наименьшее и наибольшее значение функции Y=:

а)на луче (- ;5]

б)на отрезке [4;7]

в)на луче [2;+ )

г)на полуинтервале [-1;6]

17.Решите уравнение графически:

а)|X²-9|=5 б)|X-2|=X² в)|X+1|= -2X²

г)|X²-1|=|X²-X+1| д)|X-3|=X²+1 е)|X+5|=-X-1

ё) -2(X+2)² ж) з)(X+3)²

и)-X

Построение графиков уравнений, содержащих несколько модулей

Пример: построить график функции

1). Найти те значения переменной, при которых выражение, стоящее под знаком модуля, равно нулю. ; ; .

2). Числовую прямую разбивают на промежутки точками, соответствующими найденным значениям переменной

0 1

3). На каждом промежутке определяют знак выражения, стоящего под знаком модуля (берут числа из промежутка и ставят в под модульное выражение).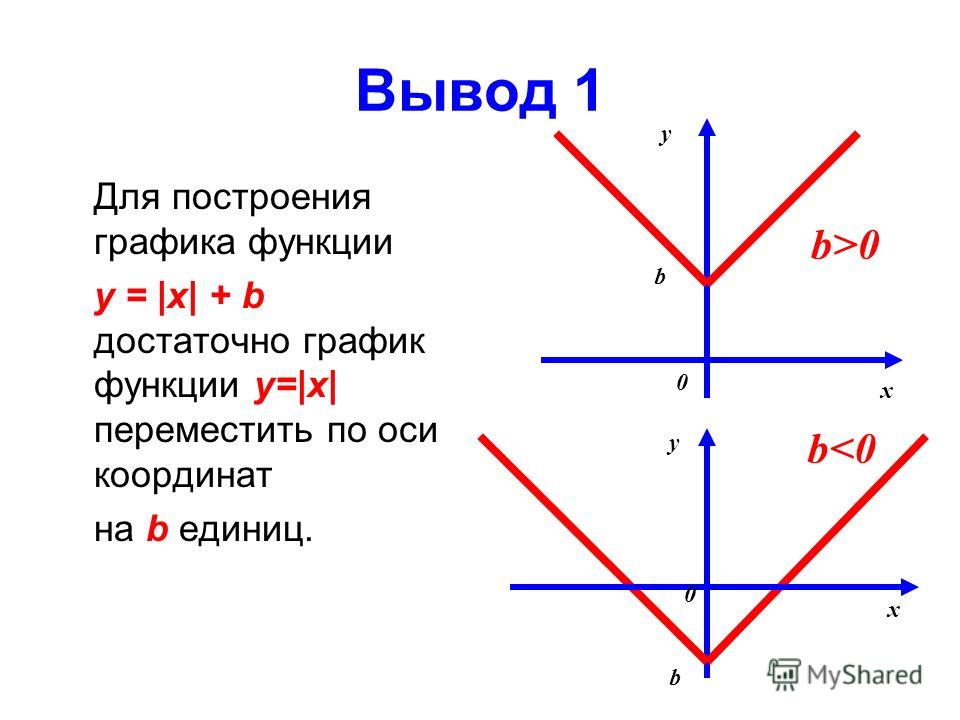 Определяют знак выражения стоящего под знаком модуля

− 0 − 1 +

− + +

4). Берут промежуток, раскрывают модуль (пользуясь определением модуля) на данном промежутке и упрощают

Составляют формулу кусочной функции

Строят график кусочной функции

0 1

1). Найдите промежутки убывания функции и ее наибольшее значение на отрезке . Ответ: , .

2). Найдите множество значений функции и ее наименьшее значение на отрезке . Ответ: , .

3). Найдите множество значений функции и значения, которые функция принимает ровно три раза. Ответ: ; ; .

4). Найдите все значения , при которых значения функции положительны и значения, принимаемые функцией ровно 2 раза. Ответ: ; , .

5). Постройте график функции и для каждого укажите количество общих точек этого графика и прямой .

а). . Ответ: Общих точек нет при ;

При , одна точка;

При и , две точки;

При , бесконечное множество точек.

б). . Ответ: Общих точек нет при ;

При , одна точка;

При и , две точки;

При ,, три точки;

При , четыре точки.

6). Найдите наибольшее и наименьшее значения функции на отрезке . Ответ: ; .

7). Найдите наименьшее значение функции

а). .Ответ: при .

б). .Ответ: при .

9). Докажите, что если , то наименьшее значение функции равно .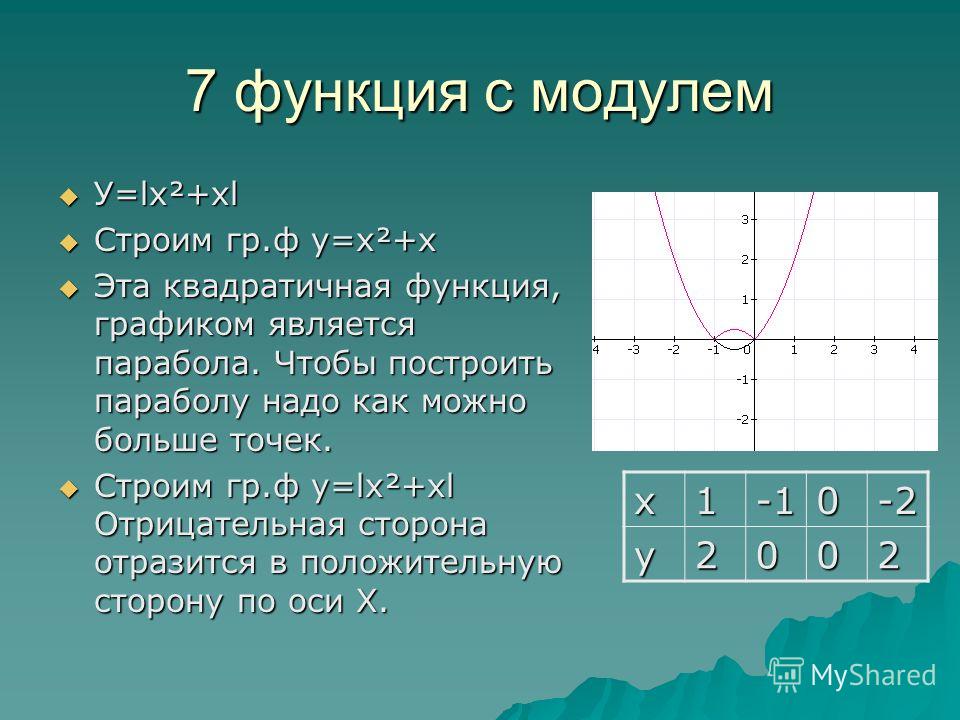

10). Исследуйте функцию на промежутки монотонности

а). . Ответ: На промежутках ; функция убывает. На промежутках возрастает.

б). . Ответ: На промежутках ; функция убывает. На промежутках и возрастает. На промежутках и функция постоянна.

11). Постройте графики функций

1). 2).

3). 4).

Решение неравенств, содержащих знак модуля

Неравенства вида

> , где > 0

Если выражение, стоящее под знаком модуля , обозначить через t (f(x) = t), то данное неравенство примет вид > . Используя геометрический смысл модуля (модуль на числовой прямой представляет собой расстояние от точки, которая изображает данное число, до точки ноль). Изображаем на числовой прямой все точки, расстояние от которых до ноля больше .

———∙——————∙—————∙————►t

—0

t или t >

Решаем совокупность неравенств

Пример:

Решите неравенство > 11

Решение: > 11

Пусть , >11

———∙——————∙—————∙————►t

-11 0 11

; ;

Ответ: ; ;

Неравенство вида > , гдеB>0 верно при всех из области допустимых значений неравенства.

Решите неравенства

1). > 11. Ответ:

2). . Ответ:

3). . Ответ: : .

4). . Ответ: . .

5). . Ответ: .

6). . Ответ: .

7). . Ответ: .

8). . Ответ: .

9). . Ответ: .

10). >2. Ответ: .

Неравенства вида

Учитывая свойство модуля =

и свойство неравенства: если обе части неравенства неотрицательны, то при возведении в квадрат получаем неравенство равносильное данному .

Неравенство > можно заменить равносильным неравенством > это — >0 (—) ∙ (+) >0

Далее решать методом интервалов или заменить совокупностью систем

Аналогично решаются неравенства вида .

Решите неравенства

1). . Ответ: .

2). Найти целочисленные решения неравенства .

Ответ: -8; -7; -6; … -1;0.

3). . Ответ: .

4). . Ответ: .

5). . Ответ: .

6). . Ответ: .

7). . Ответ: .

8). . Ответ: .

9). . Ответ: .

10). . Ответ: .

11). . Ответ: .

12). . Ответ: .

13). . Ответ: .

14). . Ответ: .

15). . Ответ: .

16). . Ответ: .

17). . Ответ: .

18). . Ответ: .

19). . Ответ: .

20). . Ответ: .

21). . Ответ: .

22). . Ответ: .

23). . Ответ: .

Решение неравенств вида

;

Неравенство

Доказательство:

Неравенство

Доказательство:

Решите неравенства

1). . Ответ: .

2). . Ответ: .

3). . Ответ: .

4). . Ответ: .

5). . Ответ: .

6). . Ответ: или .

7). . Ответ: .

8). . Ответ: ; .

9). . Ответ: .

10). . Ответ: .

11). . Ответ: .

12).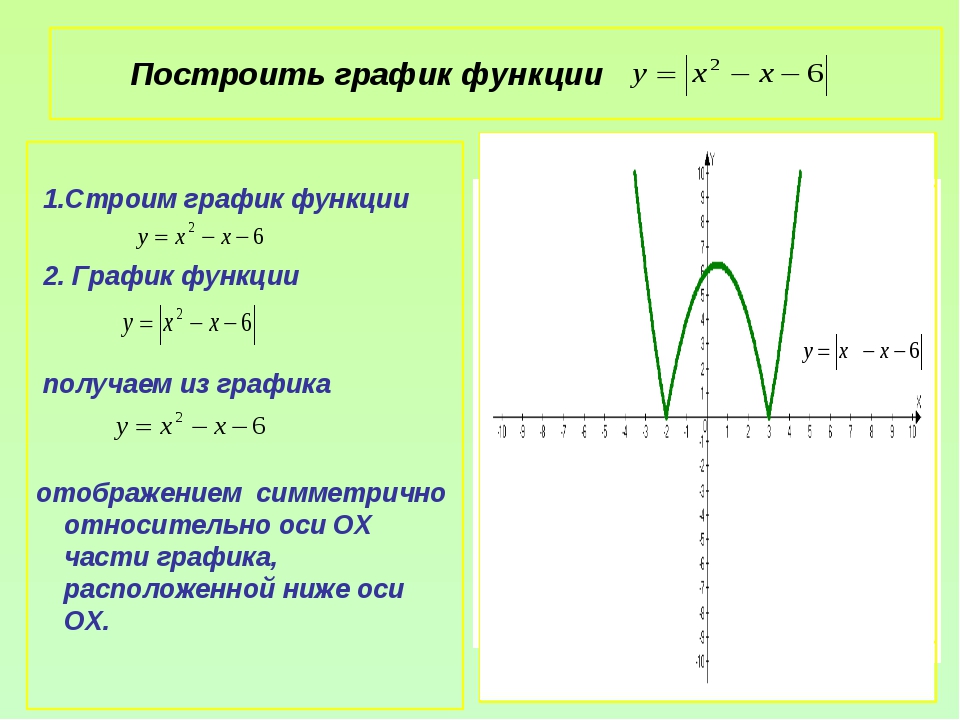 . Ответ: или .

13). . Ответ: ; .

14). . Ответ: или .

15). . Ответ: .

16). . Ответ: .

17). . Ответ: .

18). . Ответ: .

19). . Ответ: .

20). . Ответ: ; .

Решение неравенств, содержащих несколько модулей методом интервалов

Суть метода состоит в следующем:

Пример:

1). Находят те значения переменной при которых выражения, стоящие под знаком модуля равно нулю.

2). Числовую ось разбивают на промежутки точками, соответствующими значениям переменной

3). На каждом промежутке, определяют знак выражения, стоящего под знаком модуля (берут число из промежутка, ставят в подмодульное выражение, определяют знак выражения, стоящего под знаком модуля)

— 0 + 1 +

-1 — — +

4). Берут промежуток, раскрывают каждый модуль, пользуясь определением модуля на данном промежутке, и решают неравенство

5). Проверяют, принадлежат ли найденные решения неравенства рассматриваемому промежутку; если принадлежат, то их включают в ответ

Если нет – отбрасывают. Так поступают с каждым промежутком.

6). Объединяют все решения исходного неравенства, найденные на всех промежутках, и учитывая область допустимых значений первоначального неравенства, выписывают ответ.

Ответ: -2SUB>

Решите неравенство

1). Ответ:

2). Ответ:

3). Ответ:

4). Ответ:

5).Укажите целочисленные решения неравенства Ответ: 3;4

6). Ответ:

7). Ответ:

8). Ответ:

9). Ответ:

10). Ответ:

11). Ответ:

12). Ответ:

13). Ответ:

14). Ответ:

15). Ответ:

16). Ответ:

Решение неравенств, содержащих знак модуля, методом введения новой переменной.

1). Найти область значений переменной, входящей в неравенство.

2). Если в уравнении неоднократно встречается фиксированное выражение, зависящее от неизвестной величины, то имеет смысл обозначить это выражение, какой либо буквой. Когда вводится обозначение желательно сразу отбросить все или некоторые значения при которых уравнение = не имеет решений , т.е. полезно сразу указать область значений функции = .

3). Решить неравенство относительно введенной неизвестной.

4). Решить неравенство относительно исходной переменной.

5). Учитывая область допустимых значений исходного неравенства записать ответ.

Пример:

Учитывая свойство модулей имеем Пусть = , , тогда неравенство примет вид =1; =-3. f

Учитывая, что имеем

Учитывая область допустимых значений исходного неравенства Ответ:

Решите неравенства

1). Ответ:

2). Ответ:

3). Ответ:

4). Ответ:

5). Ответ:

6). Ответ:

7). Ответ:

8). Ответ:

9). Ответ:

10). Ответ:

Изображение на координатной плоскости множества точек, координаты которых удовлетворяют данному неравенству

Чтобы на координатной плоскости изобразить множество точек, координаты которых удовлетворяют неравенству надо:

1). Построить множество точек, координаты которых удовлетворяют уравнению (если неравенство строгое, то линия изображается пунктирной, если не строгое, то сплошной).

2). График или графики уравнений разбивают координатную плоскость на части.

3). Взять координаты точки, принадлежащей каждой части по очереди и поставить в неравенство. Если координаты точки удовлетворяют неравенству, то эту часть координатной плоскости заштриховать.

Пример: Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству .

1). Построим график уравнения .

или

III II I

-1 0 1

Прямые и изображаем сплошными линиями, так как неравенство не строгое. Прямые разбивают координатную плоскость на три области. Неравенству удовлетворяют координаты точек, принадлежащих II части, поэтому заштриховываем II часть.

Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют неравенству.

1). .

2). .

3). .

4). .

5). .

6). .

7). .

8). .

9). .

10). .

11). .

12). .

13). .

14). .

15). .

16). .

17). .

18). .

19).

20). .

21). .

22). .

23. .

24). .

Изобразите на координатной плоскости множество точек, удовлетворяющих условию

а) . б).

в) г)

д) е) .

Системы неравенств с параметрами, содержащие знак модуля

1). Найдите все значения параметра , при которых система неравенств имеет единственное решение.

а). Ответ: При .

б). Ответ: При .

2). При каких значениях параметра система неравенств имеет ровно одно решение?. Для всех таких найдите это решение.

а). Ответ: При , ;

При , .

б). Ответ: При , ;

При , .

3). При каких значениях параметра система не имеет решения.

а). Ответ: При .

б). Ответ: При .

4). Для каждого значения параметра решите систему неравенств.

а). Ответ: При , ;

При , ;

При , .

б). Ответ: При и , ;

При , ;

При , .

Нестандартные уравнения и неравенства, содержащие знак модуля

К нестандартным ,обычно относятся такие уравнения и неравенства, где традиционные алгоритмы решения не проходят. Во многих случаях, решение таких уравнений и неравенств осуществляется на функциональном уровне, т.е с помощью графиков, или за счет сопоставления некоторых свойств функций, содержащихся в левой и правой частях уравнения или неравенства.

Если, например, наименьшее значение одной из функций совпадает с наибольшим значением функции , то уравнение = заменяют равносильной системой , где — наименьшее значение или наибольшее значение .

Решение системы является решением уравнения = .

1). Решите уравнение

Уравнение необходимо решить графически. Ответ:

2). Решите неравенство

. Применить метод оценки. Ответ:

3). Решите уравнение

. Решить уравнение графически. Ответ:

4). Решите уравнение

. Применить свойство: сумма неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю. Ответ:

5). Решите уравнение

.Область допустимых значений (ОДЗ) уравнения состоит из конечного числа значений. Для решения достаточно проверить все эти значения. Ответ:

Применение свойства = для любого

при нахождении значения выражения

Вычислите:

1). Ответ: -6

2). , если t = -10; t = 127. Ответ: -8; 127

3). ∙ . Ответ: 0,125

4). −. Ответ: -6

5). − . Ответ: 2

6). − . Ответ: 8

7). + . Ответ: 2

8). + . Ответ: 6

9). + . Ответ: 2

10). + . Ответ: 10

11). − . Ответ: -3

12). − . Ответ: -6

13). − − 0,5. Ответ: 0

14). + . Ответ:1

15). + Ответ: 1

16). . Ответ: 8

17). Найти и , если = — . Ответ: 28; -2

18). Найти и , если = — . Ответ: 40; -2

19). Сравните значение выражения

с числом . Ответ:

20). Сравните значение выражения

с числом . Ответ:

21). Докажите, что выражение ∙ является корнем уравнения = 1.

22). Докажите, что выражение является корнем уравнения = 1.

23). Удовлетворяет ли число − неравенству 7+58+13>0 .

Ответ: нет

24). Удовлетворяет ли число − неравенству 11+26-730 .

Ответ: да

Л и т е р а т у р а

1). Алгебра: 8; 9; 10 – 11 класс.

Авторы: А.Г.Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.

2). Задания по математике для подготовки к письменному экзамену в 9 классе.

Авторы: Л.И. Звавич, Д.И.Аверьянов, Б.П. Пигарёв, Т.Н. Грушанина.

3). Сборник задач по алгебре 8 – 9 класс.

Авторы: М.Л. Галицкий,А.М. Гольдман, Л.И. Звавич.

4). Сборник для проведения письменного экзамена за курс средней школы 11 класс.

Авторы: Г.В. Дорофеев, Г.К.Муравин, Е.А.Седова.

5). Алгебраический тренажер.

Авторы: А.Г. Мерзляк,В.Б.Полонский, М.С.Якир

6). Материалы ЦТ и ЭГЭ за 2002 – 2005 годы.

7). Математика. Самостоятельные и контрольные работы 8; 9; 10 – 11 классы.

Авторы: А.П. Ершова, В.В. Голобородько.

8). Различные сборники для поступающих в В У З Ы.

Урок по теме «Построение графиков квадратичной функции с модулем»

Урок по теме «Построение графиков квадратичной функции с модулем»

Учебник А.Г.Мордкович, базовый уровень, 4 — й урок темы «Функция y = ax 2 + bx + c, ее свойства и график»

Быкасов Андрей Иванович,

учитель математики НОУ «Нефтеюганская православная гимназия», г.Нефтеюганск, Тюменская область

Тема : «Построение графиков

квадратичной функции с модулем »

Цель: обобщить знание свойств квадратичной функции и научить применять свойства квадратичной функции при построении графиков квадратичной функции с модулем

Задачи:

Выявить степень сформированности у учащихся понятия квадратичной функции, её свойств, особенностей её графика.
Создать условия для формирования умения анализировать, сравнивать, классифицировать графики изученных функций.
Продолжить развитие умения построения графиков квадратичной функции с модулем , используя программу AGrapher .
Формировать умение сотрудничать, работая в группе.

Оборудование: проектор, экран , 4 компьютера, программа AGrapher .

Этапы урока

Организационный
Мотивация к учебной деятельности.
Актуализация знаний и фиксация затруднения в пробном действии (работа с графиками функций).
Выявление места и причины затруднения.
Построение проекта выхода из затруднения.
Реализация построенного проекта.
Самостоятельная работа с самопроверкой по эталону.
Включение в систему знаний и повторение.
Рефлексия учебной деятельности. Оценивание работы на уроке.
Домашнее задание.

1. Организационный

На перемене дети садятся по группам. Группы формируются

на добровольной основе, консультант группы определяется

учителем. Каждой группе выдаются листы контроля

результатов деятельности.

Здравствуйте, ребята! Я рада сегодня вас видеть и очень надеюсь на совместную плодотворную работу. Сегодня мы работаем в группах. В каждой группе мною был назначен консультант, который поможет мне оценить в конце урока каждого из вас. В течение всего урока мы будем накапливать баллы: за каждый правильный, точный и логичный ответ Вы будете получать «+» в таблице, лежащей на вашем столе. Здесь мне будет нужна помощь консультантов. В конце урока мы просуммируем «+» и поставим отметки в зависимости от их количества:

более 8 «+»- «5»

6-7 «+»- «4»

4-5 «+»- «3».

2. Мотивация к учебной деятельности . Задача этапа: Создать условия для возникновения у ученика внутренней потребности включения в учебную деятельность.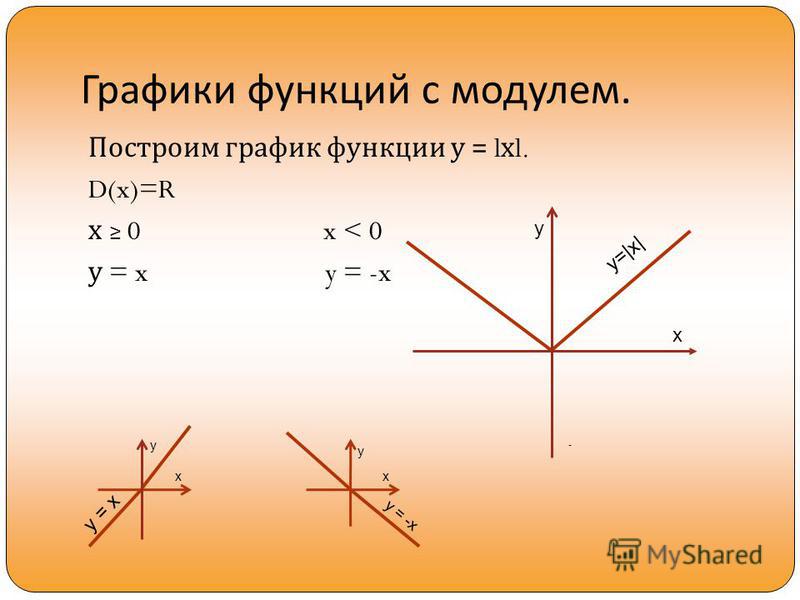

Если вы хотите научиться плавать, то смело

входите в воду, а если хотите научиться

решать задачи, то решайте их!

Дьёрдь Пойя

Сегодня нам предстоит решение многих задач, вы видите, как можно научится их решению по мнению известного венгерского математика Д.Пойя. Согласны ли вы, что такой подход применим и к нашему уроку?( Да )

Для начала предлагаю вспомнить, что мы знаем о функциях.

За каждое выполненное задание, консультант выставляет «+» в лист контроля (максимум 4 балла)

3 . Актуализация знаний и фиксация затруднения в пробном действии.

1 группа

Запишите формулы и названия функций, которые вы видите на графиках. (Каждые 2 правильно записанные формулы оцениваются «+», максимум 4 балла).

Постройте графики функций:

4 группа

2 группа

Постройте графики функций:

№ 1

№ 2

№ 3

№ 4 .

№ 1

№ 2

№ 3

№ 4

3 группа

Постройте графики функций:

№ 1.

№ 2.

№ 3. №4.

2. 1Актуализация знаний и фиксация з1атруднения в пр№1обном действии.

Задание для первой группы

График №1

График №2

График №3

График №5

График №4

Задание для первой группы

График №6

График №7

График №8

Проверка

1группа

№ 1
№ 2
№ 3
№ 4
№ 5
№ 6
№ 7
№ 8

За каждое правильно выполненные 2 задания, консультант выставляет «+» в лист контроля

Проверка

График №1

График № 3

2группа

График №2

График № 4

За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля

Проверка

3 группа

График №2

График №3

График №4

График №1

За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля

Проверка

4 группа

График №1

График №3

График №2

График №4

За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля

3 .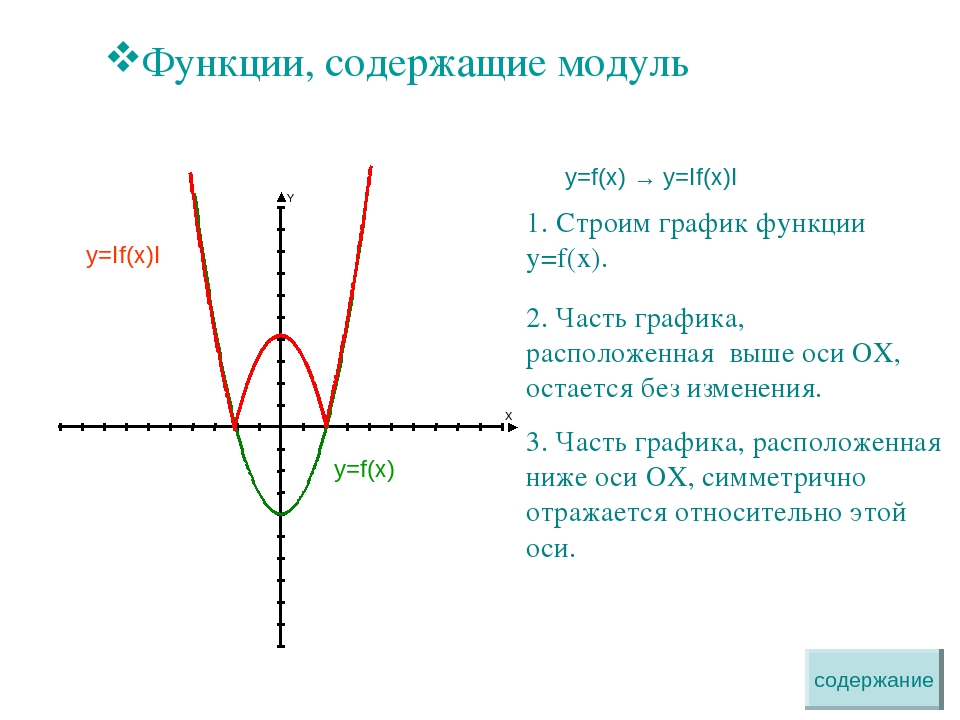 Актуализация знаний и фиксация затруднения в пробном действии.

Повторим определение модуля
Как получаем из функции можно получить функцию ?
Постройте графики функций

За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля

3 . Актуализация знаний и фиксация затруднения

в пробном действии.

1 . Организовать актуализацию изученных способов действий, достаточных для построения нового знания.

2. Зафиксировать актуализированные способы действий в речи.

3. Зафиксировать актуализированные способы действий в знаках (эталонах).

Графики каких функций вам знакомы ?( линейная, прямой и обратной пропорциональности, квадратичная, у = )

Как по графику определить вид функции и её формулу? (уметь пользоваться правилами параллельных переносов вдоль осей Ох,Оу, уметь определять коэффициенты, оси симметрии и асимптоты)

Формулы для каких графиков функций вы не смогли определить? Почему?

(последние формулы видим впервые, поэтому не можем определить вид функции и как строить графики)

Давайте попробуем сформулировать цель нашего урока .

(Научиться строить графики нового вида, научиться узнавать их среди других графиков функций, описывать их свойства.)

А я добавлю к вашей цели еще одну: обобщить знание свойств квадратичной функции и научиться применять свойства квадратичной функции в построении графиков с модулем.

Тема урока

«Построение графиков

квадратичной функции с модулем»

4.Построение проекта выхода из затруднения.

Построим графики квадратичных функций с модулем
Выполнив практическую работу, сделаем вывод о свойствах графика

5. Реализация построенного проекта.

1.Организовать построение нового способа на примере, вызвавшем затруднение. 2.Организовать фиксацию нового способа действия в речи и с помощью эталона.

3. Зафиксировать преодоление возникшего ранее затруднения.

Каждой группе предлагается построить график одной функции в программе AGrapher , описать её свойства по алгоритму:

6 .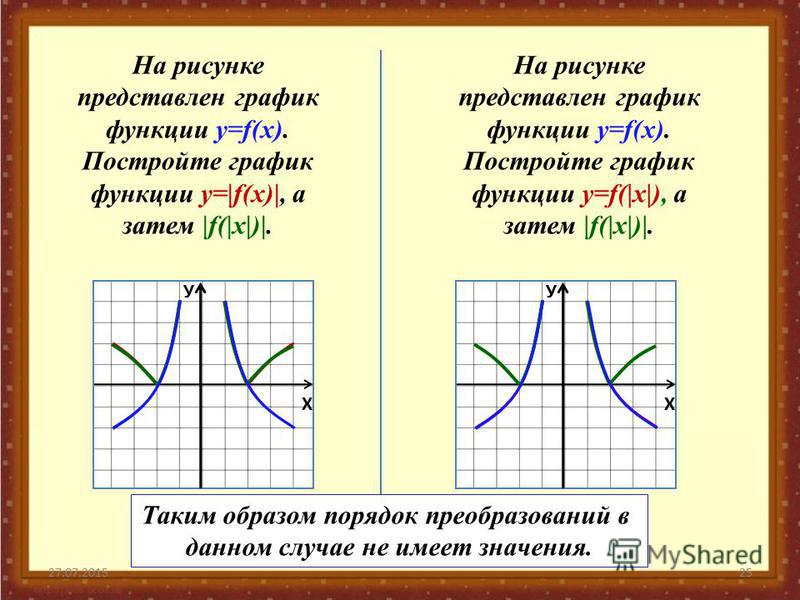 Организовать фиксацию нового способа действия в речи и с помощью эталона.

а) Давайте обобщим способы построения графиков функций, в которых выражение, задающее функцию, находится под знаком модуля, в единый алгоритм (строим график функции без модуля, потом часть графика, находящаяся ниже оси Ох, отображается в верхнюю полуплоскость)

б) Давайте обобщим способы построения графиков функций, в которых аргумент находится под знаком модуля, в единый алгоритм. (строим график функции без модуля, потом часть графика, находящаяся правее оси Оу, отображается в левую полуплоскость)

На основании какого математического понятия мы получаем эти новые способы действия ? (На основании определения модуля выражения)

Сравним полученный нами алгоритм с эталоном .

За каждый правильный ответ, консультант выставляет «+» в лист контроля.

6. Алгоритм построения графика квадратичной функции вида (эталон)

1.Строим график функции у = f (х).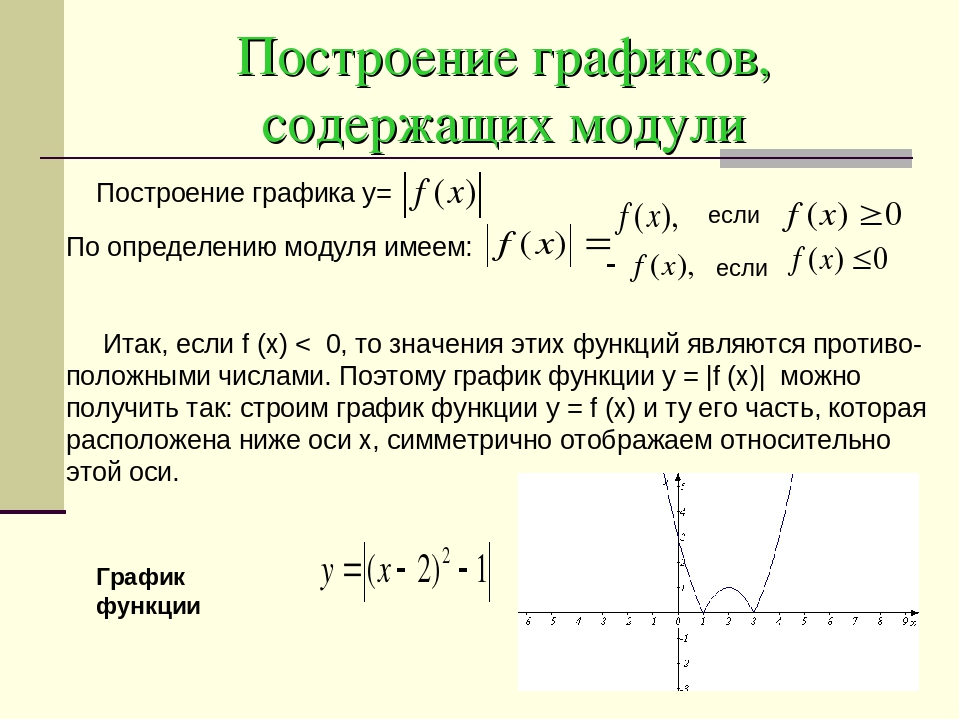

2.Часть графика, для которой, значения функции положительны — оставляем без изменения.

3.Часть графика, для которой, значения функции отрицательны – зеркально отображаем в верхнюю полуплоскость.

Алгоритм построения графика квадратичной функции вида (эталон)

1.Строим график функции у = f (х).

2.Часть графика, для которой, значения аргумента положительны — оставляем без изменения.

3.Часть графика, для которой, значения аргумента положительны – зеркально отображаем в левую полуплоскость.

7 . Самостоятельная работа с самопроверкой по эталону.

Каждой группе выдается задание на построение графиков функций

1 группа

2 группа

3 группа

4 группа

За правильно выполненное задание, консультант выставляет «+» в лист контроля

8. Включение в систему знаний и повторение.

Как построить график квадратичной функции с модулем .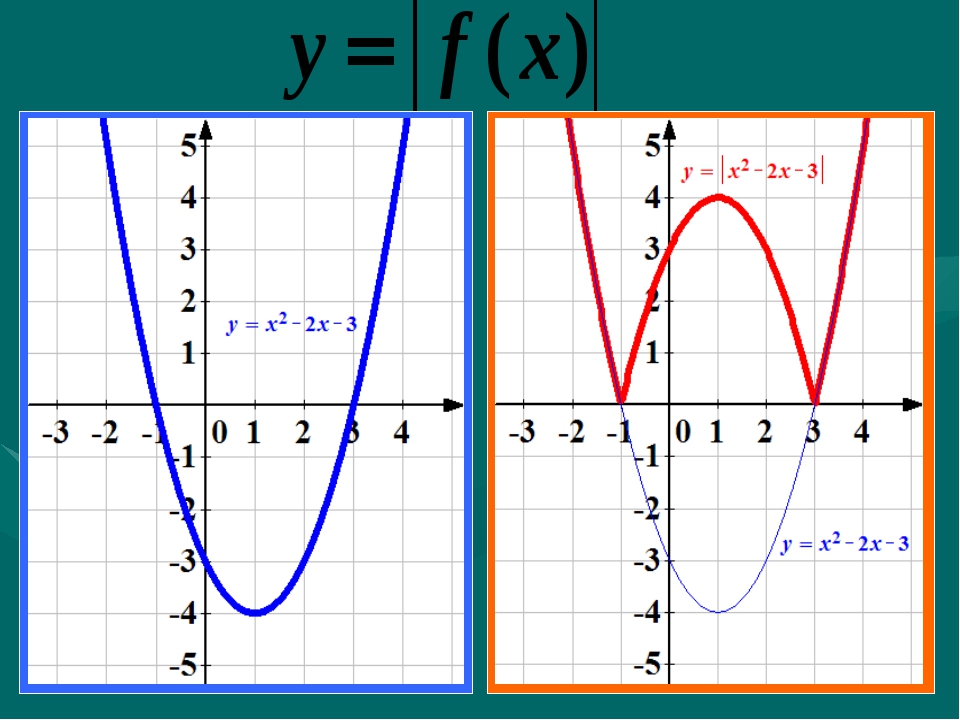 (проговаривают алгоритмы)

Графики каких функций мы можем построить с учетом нового знания, полученного сегодня на уроке? (перечисляют функции)

8. Включение в систему знаний и повторение.

Построить графики функций

8. Включение в систему знаний и повторение. (проверка)

1 . 2. 3.

4. 5.

9. Подведение итогов, рефлексия

Просуммируем «+» и поставим отметки в зависимости от их количества:

более 8 «+» — «5»

6-7 «+» — «4»

4-5 «+» — «3».

В листе контроля укажите, как вы оцениваете свои достижения поставленных целей на этом уроке

1. Затрудняюсь в построении графика без помощи алгоритма

2. Могу построить строить графики функций с модулями

3. Я все понял и могу объяснить другим

10. Домашнее задание

1. Затрудняюсь в построении графика без помощи алгоритма

Выучить определение модуля. Построить графики функций:

2. Могу построить строить графики функций с модулями

3. Я все понял и могу объяснить другим

Самоанализ урока

Тема урока. «Построение графиков квадратичной функции с модулем».

Цель урока: обобщить знание свойств квадратичной функции и научить применять её свойства в п остроении графиков квадратичной функции с модулем.

Урок четвертый в теме «Функция y = ax 2 + bx + c , ее свойства и график».

Цель урока реализовывалась через формирование у учащихся умения анализировать графики функций и делать выводы. Урок построен в деятельностной технологии обучения.

Обучающиеся знают ряд функций (линейная, обратной пропорциональности, квадратичная, ) умеют определять формулу по графику, умеют строить график, зная формулу.

В ходе урока учащиеся углубляют и расширяют знания о функциях. Учатся обобщать полученные знания и применять их в новых ситуациях. Выполняют исследование свойств графиков с модулем на компьютере при помощи программы AGrapher. Задачи урока были выполнены в ходе организации деятельности учащихся через исследование, сравнение, обобщение графиков различных квадратичных функций с модулем. Для решения задач урока использовала различные формы и методы работы, обучающиеся выполняли самостоятельную работу в группах, выступали с выводами, обобщали знания о функциях. На этапах выявления места и причины затруднений и реализации построенного проекта самостоятельная работа способствовала пониманию как строятся графики функций содержащих модуль

Задачи урока соответствуют особенностям учебного материала.

Самоанализ урока

Содержание учебного материала учитывает возрастные особенности обучающихся и

способствует формированию у школьников компетенций:

учебно-познавательных: обучающиеся формулировали цель урока; выбирали основание для сравнения и обобщения , делали выводы; оценивали свою работу.
коммуникативных: приобретали навыки общения, аргументировали свои выводы; выступали с устными комментариями;
информационных: извлекали необходимую информацию, работая с программой для построения графиков функций, работали над созданием алгоритма построения графиков квадратичной функции с модулем;

Ведущими методами на уроке были частично-поисковый, исследовательский методы. Учащиеся были активны на уроке, работоспособны на всех этапах.

Домашняя работа предложена дифференцированно с учетом уровня усвоения материала и самооценки учащегося.

Считаю, что все используемые на уроке методы, формы, приемы, средства способствовали достижению цели урока.

Цель урока реализована: дети научились строить графики квадратичной функции с модулем и описывать её свойства.

6. Модули — документация Python 3.9.4

 >>> import builtins
>>> dir (встроенные)
['ArithmeticError', 'AssertionError', 'AttributeError', 'BaseException',
 BlockingIOError, BrokenPipeError, BufferError, BytesWarning,
 'ChildProcessError', 'ConnectionAbortedError', 'ConnectionError',
 ConnectionRefusedError, ConnectionResetError, DeprecationWarning,
 EOFError, Ellipsis, EnvironmentError, Exception, False,
 FileExistsError, FileNotFoundError, FloatingPointError,
 FutureWarning, GeneratorExit, IOError, ImportError,
 ImportWarning, IndentationError, IndexError, InterruptedError,
 IsADirectoryError, KeyError, KeyboardInterrupt, LookupError,
 MemoryError, NameError, None, NotADirectoryError, NotImplemented,
 NotImplementedError, OSError, OverflowError,
 PendingDeprecationWarning, PermissionError, ProcessLookupError,
 ReferenceError, ResourceWarning, RuntimeError, RuntimeWarning,
 StopIteration, SyntaxError, SyntaxWarning, SystemError,
 SystemExit, TabError, TimeoutError, True, TypeError,
 UnboundLocalError, UnicodeDecodeError, UnicodeEncodeError,
 UnicodeError, UnicodeTranslateError, UnicodeWarning, UserWarning,
 'ValueError', 'Предупреждение', 'ZeroDivisionError', '_', '__build_class__',
 '__debug__', '__doc__', '__import__', '__name__', '__package__', 'abs',
 all, any, ascii, bin, bool, bytearray, bytes, callable,
 chr, classmethod, compile, complex, copyright, credits,
 delattr, dict, dir, divmod, enumerate, eval, exec, exit,
 'filter', 'float', 'format', 'frozenset', 'getattr', 'globals', 'hasattr', 'фильтр', 'с плавающей точкой', 'формат', 'frozenset', 'getattr', 'globals', 'hasattr',
 'hash', 'help', 'hex', 'id', 'input', 'int', 'isinstance', 'issubclass',
 iter, len, лицензия, list, locals, map, max, memoryview,
 min, next, object, oct, open, ord, pow, print, property,
 'quit', 'range', 'repr', 'reverse', 'round', 'set', 'setattr', 'срез',
 'sorted', 'staticmethod', 'str', 'sum', 'super', 'tuple', 'type', 'vars', 'отсортированный', 'статический метод', 'str', 'sum', 'super', 'tuple', 'type', 'vars',
 'zip']

Создание модулей в Python 3

Введение

Python модулей — это .py , которые состоят из кода Python. На любой файл Python можно ссылаться как на модуль.

Некоторые модули доступны через стандартную библиотеку Python и поэтому устанавливаются вместе с вашей установкой Python. Другие могут быть установлены с помощью диспетчера пакетов Python pip . Кроме того, вы можете создавать свои собственные модули Python, поскольку модули состоят из файлов Python .py .

Это руководство поможет вам написать модули Python для использования в других файлах программирования.

Написание и импорт модулей

Написание модуля аналогично написанию любого другого файла Python. Модули могут содержать определения функций, классов и переменных, которые затем можно использовать в других программах Python.

Из нашей локальной среды программирования Python 3 или серверной среды программирования давайте начнем с создания файла hello.py , который мы позже импортируем в другой файл.

Для начала мы создадим функцию, которая печатает Hello, World! :

привет.py

  # Определить функцию
def мир ():
    print ("Привет, мир!")

Если мы запустим программу из командной строки с помощью python hello.py , ничего не произойдет, поскольку мы не указали программе что-либо делать.

Давайте создадим второй файл в том же каталоге с именем main_program.py , чтобы мы могли импортировать только что созданный модуль, а затем вызвать функцию. Этот файл должен находиться в том же каталоге, чтобы Python знал, где найти модуль, поскольку это не встроенный модуль.

main_program.py

  # Импортировать модуль hello
импорт привет


# Вызов функции
Привет мир()

Поскольку мы импортируем модуль, нам нужно вызвать функцию, указав имя модуля в точечной нотации.

Вместо этого мы могли бы импортировать модуль как из hello import world и вызвать функцию напрямую как world () . Вы можете узнать больше об этом методе, прочитав, как использовать из … import при импорте модулей.

Теперь мы можем запустить программу из командной строки:

Когда мы это сделаем, мы получим следующий результат:

   Выход  Привет, мир!

Чтобы увидеть, как мы можем использовать переменные в модуле, давайте добавим определение переменной в наш файл hello.py :

hello.py

  # Определить функцию
def мир ():
    print ("Привет, мир!")

# Определить переменную
акула = "Сэмми"

Затем мы вызовем переменную в функции print () в нашей main_program.py файл:

main_program.py

  # Импортировать модуль hello
импорт привет


# Вызов функции
Привет мир()

# Печатать переменную
печать (hello.shark)

Как только мы снова запустим программу, мы получим следующий результат:

   Выход  Привет, мир!
Сэмми

Наконец, давайте также определим класс в файле hello.py . Мы создадим класс Octopus с атрибутами name и color и функцию, которая будет распечатывать атрибуты при вызове.

hello.py

  # Определить функцию
def мир ():
    print ("Привет, мир!")

# Определить переменную
акула = "Сэмми"


# Определить класс
класс Octopus:
    def __init __ (я, имя, цвет):
        self.color = цвет
        self.name = имя

    def tell_me_about_the_octopus (сам):
        print ("Этот осьминог" + self.color + ".")
        print (self.name + "имя осьминога.")

Теперь мы добавим класс в конец нашего файла main_program.py :

main_program.py

  # Импортировать модуль приветствия
импорт привет


# Вызов функции
Привет мир()

# Печатать переменную
печать (hello.shark)

# Вызов класса
jesse = hello.Octopus («Джесси», «апельсин»)
jesse.tell_me_about_the_octopus ()

После того, как мы вызвали класс Octopus с hello.Octopus () , мы можем получить доступ к функциям и атрибутам класса в пространстве имен файла main_program.py . Это позволяет нам писать jesse.tell_me_about_the_octopus () в последней строке без вызова hello .Мы также могли бы, например, вызвать один из атрибутов класса, например jesse.color , без ссылки на имя модуля hello .

Когда мы запустим программу, мы получим следующий результат:

   Выход  Привет, мир!
Сэмми
Этот осьминог оранжевого цвета.
Джесси - это имя осьминога.

Важно помнить, что хотя модули часто являются определениями, они также могут реализовывать код. Чтобы увидеть, как это работает, давайте перепишем наш hello.py , чтобы он реализовал функцию world () :

hello.py

  # Определить функцию
def мир ():
    print ("Привет, мир!")

# Вызов функции внутри модуля
Мир()

Мы также удалили другие определения в файле.

Теперь в нашем файле main_program.py мы удалим все строки, кроме оператора импорта:

main_program.py

  # Импортировать модуль hello
импорт привет

Когда мы запускаем main_program.py мы получим следующий результат:

   Выход  Привет, мир!

Это связано с тем, что модуль hello реализовал функцию world () , которая затем передается в main_program.py и выполняется при запуске main_program.py .

Модуль — это программный файл Python, состоящий из определений или кода, который вы можете использовать в других программных файлах Python.

`Доступ к модулям из другого каталога`

Модули

могут быть полезны для нескольких программных проектов, и в этом случае не имеет смысла хранить модуль в конкретном каталоге, привязанном к конкретному проекту.

Если вы хотите использовать модуль Python из места, отличного от того же каталога, в котором находится ваша основная программа, у вас есть несколько вариантов.

`Добавление путей`

Один из вариантов — вызвать путь к модулю через файлы программирования, которые используют этот модуль. Это следует рассматривать скорее как временное решение, которое может быть выполнено в процессе разработки, поскольку оно не делает модуль доступным для всей системы.

Чтобы добавить путь модуля к другому файлу программирования, вы начнете с импорта модуля sys вместе с любыми другими модулями, которые вы хотите использовать в основном файле программы.

Модуль sys является частью стандартной библиотеки Python и предоставляет системные параметры и функции, которые вы можете использовать в своей программе для установки пути к модулю, который вы хотите реализовать.

Например, предположим, что мы переместили файл hello.py , и теперь он находится по пути / usr / sammy / , а файл main_program.py находится в другом каталоге.

В нашем файле main_program.py мы все еще можем импортировать модуль hello , импортировав модуль sys , а затем добавив / usr / sammy / к пути, который Python проверяет на наличие файлов.

main_program.py

  import sys
sys.path.append ('/ usr / sammy /')

импорт привет
...

Если вы правильно указали путь для файла hello.py , вы сможете запустить файл main_program.py без каких-либо ошибок и получить тот же результат, что и выше, когда hello.py был в тот же каталог.

`Добавление модуля в путь Python`

Второй вариант, который у вас есть, — добавить модуль в путь, по которому Python проверяет наличие модулей и пакетов.Это более постоянное решение, которое делает модуль доступным для всей среды или всей системы, что делает этот метод более переносимым.

Чтобы узнать, какой путь проверяет Python, запустите интерпретатор Python из среды программирования:

Затем импортируйте модуль sys :

Затем пусть Python распечатает системный путь:

Здесь вы получите какой-то вывод с хотя бы одним системным путем.Если вы работаете в среде программирования, вы можете получить несколько. Вы захотите найти тот, который находится в среде, которую вы используете в настоящее время, но вы также можете добавить модуль в свой основной системный путь Python. То, что вы ищете, будет похоже на это:

   Вывод  '/usr/sammy/my_env/lib/python3.5/site-packages'

Теперь вы можете переместить файл hello.py в этот каталог. После этого вы можете импортировать модуль hello как обычно:

main_program.py

  импорт привет
...

Когда вы запускаете свою программу, она должна завершиться без ошибок.

Изменение пути к вашему модулю может гарантировать, что вы можете получить доступ к модулю независимо от того, в каком каталоге вы находитесь. Это полезно, особенно если у вас есть более одного проекта, ссылающегося на конкретный модуль.

`Заключение`

Написание модуля Python аналогично написанию любого другого файла Python .py . В этом руководстве рассказывается, как писать определения в модуле, использовать эти определения в другом программном файле Python, а также рассмотрены варианты того, где сохранить модуль, чтобы получить к нему доступ.

Вы можете узнать больше об установке и импорте модулей, прочитав Как импортировать модули в Python 3.

`Научитесь создавать и импортировать специальные и встроенные модули`

`Что такое модули в Python?`

Модули

относятся к файлу, содержащему операторы и определения Python.

Файл, содержащий код Python, например: example.py , называется модулем, и его имя модуля будет example .

Мы используем модули для разбиения больших программ на небольшие управляемые и организованные файлы.Кроме того, модули обеспечивают возможность повторного использования кода.

Мы можем определить наши наиболее часто используемые функции в модуле и импортировать его, вместо того, чтобы копировать их определения в разные программы.

Создадим модуль. Введите следующее и сохраните его как example.py .

  # Пример модуля Python

def add (a, b):
   "" "Эта программа добавляет два
   числа и вернуть результат "" "

   результат = a + b
   вернуть результат

Здесь мы определили функцию add () внутри модуля с именем example .Функция принимает два числа и возвращает их сумму.

`Как импортировать модули в Python?`

Мы можем импортировать определения внутри модуля в другой модуль или интерактивный интерпретатор в Python.

Для этого мы используем ключевое слово import . Чтобы импортировать наш ранее определенный модуль , пример , мы вводим следующее в командной строке Python.

  >>> пример импорта

При этом имена функций, определенных в примере , не импортируются непосредственно в текущую таблицу символов.Он только импортирует туда имя модуля , например, .

Используя имя модуля, мы можем получить доступ к функции, используя точку . оператор. Например:

  >>> example.add (4,5.5)
9,5

Python имеет множество стандартных модулей. Вы можете ознакомиться с полным списком стандартных модулей Python и вариантов их использования. Эти файлы находятся в каталоге Lib внутри того места, где вы установили Python.

Стандартные модули можно импортировать так же, как мы импортируем наши пользовательские модули.

Есть разные способы импорта модулей. Они перечислены ниже ..

`Оператор импорта Python`

Мы можем импортировать модуль с помощью оператора import и получить доступ к определениям внутри него с помощью оператора точки, как описано выше. Вот пример.

  # пример инструкции импорта
# для импорта математики стандартного модуля

импортная математика
print ("Значение числа Пи", math.pi)

При запуске программы вывод будет:

  Число Пи равно 3.141592653589793

`Импорт с переименованием`

Мы можем импортировать модуль, переименовав его следующим образом:

  # импортировать модуль, переименовав его

импортировать математику как m
print («Значение пи», m.pi)

Мы переименовали модуль math в m . В некоторых случаях это может сэкономить нам время на набор текста.

Обратите внимание, что имя math не распознается в нашей области. Следовательно, math.pi недействителен, а m.pi — правильная реализация.

`Python from … оператор импорта`

Мы можем импортировать определенные имена из модуля, не импортируя модуль в целом. Вот пример.

  # импортировать только пи из математического модуля

из математического импорта Пи
print («Значение числа Пи равно», Пи)

Здесь мы импортировали только атрибут pi из модуля math .

В таких случаях мы не используем оператор точки. Мы также можем импортировать несколько атрибутов следующим образом:

  >>> из математического импорта pi, e
>>> пи
3.141592653589793
>>> е
2,718281828459045

`Импортировать все имена`

Мы можем импортировать все имена (определения) из модуля, используя следующую конструкцию:

  # импортировать все имена из стандартного модуля math

из математического импорта *
print («Значение числа Пи равно», Пи)

Здесь мы импортировали все определения из математического модуля. Сюда входят все имена, видимые в нашей области видимости, кроме тех, которые начинаются с подчеркивания (частные определения).

Импорт всего, что отмечен символом звездочки (*), не является хорошей практикой программирования. Это может привести к дублированию определений идентификатора. Это также затрудняет читаемость нашего кода.

`Путь поиска модуля Python`

При импорте модуля Python просматривает несколько мест. Интерпретатор сначала ищет встроенный модуль. Затем (если встроенный модуль не найден) Python просматривает список каталогов, определенных в sys.path . Поиск ведется в таком порядке.

Текущий каталог.
PYTHONPATH (переменная среды со списком каталогов).
Зависящий от установки каталог по умолчанию.

>>> import sys
>>> sys.path
['',
'C: \ Python33 \ Lib \ idlelib',
'C: \ Windows \ system32 \ python33.zip',
'C: \ Python33 \ DLLs',
'C: \ Python33 \ lib',
'C: \\ Python33',
'C: \ Python33 \ lib \ site-packages']

Мы можем добавлять и изменять этот список, чтобы добавить наш собственный путь.

`Перезарядка модуля`

Интерпретатор Python импортирует модуль только один раз за сеанс. Это делает вещи более эффективными. Вот пример, показывающий, как это работает.

Предположим, у нас есть следующий код в модуле с именем my_module .

  # Этот модуль показывает эффект
# множественный импорт и перезагрузка

print («Этот код был выполнен»)

Теперь мы видим эффект от множественного импорта.

  >>> импортировать my_module
Этот код был выполнен
>>> импортировать my_module
>>> import my_module

Мы видим, что наш код был выполнен только один раз.Это означает, что наш модуль был импортирован только один раз.

Теперь, если наш модуль изменился во время работы программы, нам пришлось бы его перезагрузить. Один из способов сделать это — перезапустить интерпретатор. Но это мало помогает.

Python предоставляет более эффективный способ сделать это. Мы можем использовать функцию reload () внутри модуля imp для перезагрузки модуля. Сделать это можно следующими способами:

  >>> импортный имп
>>> импортировать my_module
Этот код был выполнен
>>> импортировать my_module
>>> имп.перезагрузить (my_module)
Этот код был выполнен
<модуль 'my_module' из '. \\ my_module.py'>

`Встроенная функция dir ()`

Мы можем использовать функцию dir () , чтобы узнать имена, определенные внутри модуля.

Например, мы определили функцию add () в модуле example , который у нас был в начале.

Мы можем использовать dir в модуле example следующим образом:

  >>> dir (пример)
['__builtins__',
'__cached__',
'__doc__',
'__файл__',
'__initializing__',
'__loader__',
'__название__',
'__упаковка__',
'добавить']

Здесь мы можем увидеть отсортированный список имен (вместе с добавить ).Все остальные имена, начинающиеся с подчеркивания, являются атрибутами Python по умолчанию, связанными с модулем (не определяемыми пользователем).

Например, атрибут __name__ содержит имя модуля.

  >>> пример импорта
>>> пример .__ имя__
'пример'

Все имена, определенные в нашем текущем пространстве имен, можно узнать с помощью функции dir () без каких-либо аргументов.

  >>> а = 1
>>> b = "привет"
>>> импорт математики
>>> dir ()
['__builtins__', '__doc__', '__name__', 'a', 'b', 'math', 'pyscripter']

`Создание и импорт модулей в Python`

`Введение`

В Python модуль — это автономный файл с операторами и определениями Python.Например, file.py можно рассматривать как модуль с именем file . Это отличается от пакета тем, что пакет представляет собой набор модулей в каталогах, которые определяют структуру и иерархию модулей.

Модули

помогают нам разбивать большие программы на небольшие файлы, которыми легче управлять. С модулями возможность повторного использования кода становится реальностью. Предположим, у нас есть функция, которая часто используется в разных программах. Мы можем определить эту функцию в модуле, а затем импортировать ее в различные программы без необходимости каждый раз копировать ее код.

В этой статье мы увидим, как создавать модули Python и как использовать их в коде Python.

`Пишущие модули`

Модуль — это просто файл Python с расширением .py . Имя файла становится именем модуля. Внутри файла у нас могут быть определения и реализации классов, переменных или функций. Затем их можно использовать в других программах Python.

Давайте начнем с создания функции, которая просто печатает «Hello World». Для этого создайте новый файл Python и сохраните его как hello.py . Добавьте в файл следующий код:

  def my_function ():
    print ("Привет, мир")

Если вы запустите приведенный выше код, он ничего не вернет. Это потому, что мы ничего не сказали программе. Это правда, что мы создали в коде функцию с именем my_function () , но мы не вызывали и не вызывали эту функцию. При вызове эта функция должна распечатать текст «Hello World».

Теперь перейдите в тот же каталог, где вы сохранили указанный выше файл, и создайте новый файл с именем main.py . Добавьте в файл следующий код:

  импорт привет

hello.my_function ()

Выход

  Привет, мир

Функция была успешно вызвана. Мы начали с импорта модуля. Имя файла — hello.py , следовательно, имя импортированного модуля — hello .

Также обратите внимание на синтаксис, который мы использовали для вызова функции. Это называется «точечной нотацией», которая позволяет нам вызывать функцию, сначала указывая имя модуля, а затем имя функции.

Однако это всего лишь один из способов импорта модуля и вызова функции. Мы могли сделать это так:

  из hello import my_function

моя_функция ()

Выход

  Привет, мир

В приведенном выше примере первая строка дает команду интерпретатору Python импортировать функцию с именем my_function из модуля с именем hello . В таком случае вам не нужно использовать точечную нотацию для доступа к функции, вы можете просто вызвать ее напрямую.

Однако в случае, когда наш модуль hello имеет несколько функций, оператор из hello import my_function не будет импортировать все функции hello в нашу программу, а только my_function . Если вы попытаетесь получить доступ к любой другой функции, будет сгенерирована ошибка. Вы должны импортировать весь модуль или импортировать каждую отдельную функцию, чтобы использовать их.

Мы можем определить переменную в модуле, которая затем может использоваться другими модулями.Чтобы продемонстрировать это, откройте файл hello.py и добавьте в него следующий код:

  def my_function ():
    print ("Привет, мир")

# Переменная, которая будет использоваться в других модулях
name = "Николай"

Теперь откройте файл main.py и измените его следующим образом:

  импорт привет

hello.my_function ()

печать (привет.имя)

Выход

  Привет, мир
Николай

Мы успешно вызвали и функцию, и переменную, определенные в модуле, поскольку мы импортировали весь модуль, а не только функцию my_function () .

Ранее мы заявляли, что можем определить класс в модуле. Давайте посмотрим, как это сделать в следующем примере. Откройте файл hello.py и измените его следующим образом:

  def my_function ():
    print ("Привет, мир")

# Определение нашей переменной
name = "Николай"

# Определение класса
класс Студент:
    def __init __ (я, имя, курс):
        self.course = курс
        self.name = имя

    def get_student_details (сам):
        print ("Ваше имя" + self.name + ".")
        print ("Вы учитесь" + самокурс)

Здесь мы определили класс с именем Student . В этом классе определены две переменные: имя и курс . В нем также определен метод get_student_details () , который выводит сведения об учащемся на консоль.

Теперь откройте файл main.py и измените его следующим образом:

  импорт привет

hello.my_function ()

печать (привет.название)

nicholas = hello.Student («Николай», «Информатика»)
nicholas.get_student_details ()

Выход

  Привет, мир
Николай
Вас зовут Николас.
Вы изучаете информатику

В приведенном выше сценарии мы снова использовали точечную нотацию для создания объекта класса student из модуля hello . Затем мы использовали функцию get_student_details () , чтобы получить сведения о студенте.

Хотя модули в основном состоят из определений классов (в большинстве случаев), они также могут запускать свой собственный код при импорте.Чтобы продемонстрировать это, давайте изменим файл hello.py , где у нас есть определение функции my_function () вместе с вызовом функции:

  def my_function ():
    print ("Привет, мир")
    
моя_функция ()

Теперь откройте файл main.py и удалите все строки, кроме следующих:

  импорт привет

Выход

  Привет, мир

Приведенный выше вывод показывает, что мы определили , а вызвали функцию в модуле.Когда модуль импортируется, он напрямую возвращает результат из функции без необходимости вызывать функцию. Такое поведение не всегда желательно, но оно полезно для определенных случаев использования, например, для предварительной загрузки данных из кеша при импорте модуля.

`Импорт всех объектов модуля`

Чтобы импортировать все объекты (функции, переменные, классы и т. Д.) Из модуля, мы можем использовать оператор import * . Например, чтобы импортировать все объекты, содержащиеся в модуле hello , мы можем использовать следующий оператор:

  из привет импорта *

После добавления в программу вышеуказанного оператора мы сможем использовать любую функцию, переменную или класс, содержащиеся в модуле hello , без необходимости добавлять к нему префикс hello .

`Доступ к модулю по другому пути`

В Python модули используются более чем в одном проекте. Следовательно, нет смысла хранить свои модули в каталоге одного из проектов, поскольку другие проекты не смогут использовать его так же легко.

У вас есть несколько вариантов, когда вам нужно получить доступ к модулю, который не хранится в том же каталоге, что и ваша программа. Давайте обсудим это в следующих нескольких разделах:

`Добавление путей`

Чтобы импортировать модуль из другого пути, вам сначала нужно импортировать модуль sys , а также любые другие модули Python, которые вы хотели бы использовать в своей программе.

Модуль sys предоставляется стандартной библиотекой Python и предоставляет функции и параметры, зависящие от системы. Функция path.append () из модуля sys может использоваться для добавления пути к модулю в текущий проект.

Чтобы продемонстрировать это, вырежьте файл hello.py из каталога, в котором находится файл main.py . Вставьте его в другой каталог. В моем случае я вставил его в каталог «F: \ Python.«

Теперь откройте файл main.py , импортируйте модуль sys и укажите путь, по которому интерпретатор Python будет искать файлы. Это показано ниже:

  импортная система
sys.path.append ('F: / Python /')

импорт привет

Выход

  Привет, мир

В приведенном выше сценарии строка sys.path.append ('F: / Python /') сообщает интерпретатору Python включить этот путь в список путей, по которым будет производиться поиск при импорте модулей.

`Добавление модуля в путь Python`

Вышеупомянутый метод работает, только если вы импортируете модуль sys . Если вы не импортируете модуль sys и укажете путь к модулю, будет сгенерирована ошибка. Чтобы сделать модуль доступным для всей системы, вы можете добавить его в путь, по которому Python обычно проверяет наличие модулей и пакетов. Таким образом, вам не нужно будет импортировать модуль sys и указывать путь к модулю, как мы сделали в предыдущем разделе.

Прежде чем делать что-либо еще, вы должны сначала определить путь, по которому Python ищет модули и пакеты. Просто откройте командную строку своей операционной системы и выполните команду python . Это приведет вас к терминалу Python.

Импортируйте модуль sys следующим образом:

  импортная система

Затем вы можете запустить следующую команду, чтобы распечатать путь:

  печать (sys.path)

Вывод будет содержать по крайней мере один системный путь.Если вы сделаете это из среды программирования, вы получите несколько путей. В моем случае получилось следующее:

  $ питон
Python 2.7.10 (по умолчанию, 23 октября 2015 г., 19:19:21)
[GCC 4.2.1 совместимый Apple LLVM 7.0.0 (clang-700.0.59.5)] на darwin
Для получения дополнительной информации введите «помощь», «авторские права», «кредиты» или «лицензия».
>>> import sys
>>> печать (sys.path)
['', '/Library/Python/2.7/site-packages/six-1.10.0-py2.7.egg', '/Library/Python/2.7/site-packages/cffi-1.2.1-py2.7 -macosx-10.9-intel.egg ',' /Library/Python/2.7/site-packages/pycparser-2.14-py2.7.egg ',' /Library/Python/2.7/site-packages/virtualenv-13.1.2-py2. 7.egg ',' /System/Library/Frameworks/Python.framework/Versions/2.7/lib/python27.zip ',' /System/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7 ' , '/System/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/plat-darwin', '/System/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/ plat-mac ',' /System/Library/Frameworks/Python.framework/Versions/2.7 / lib / python2.7 / plat-mac / lib-scriptpackages ',' /System/Library/Frameworks/Python.framework/Versions/2.7/Extras/lib/python ',' / System / Library / Frameworks / Python. framework / Versions / 2.7 / lib / python2.7 / lib-tk ',' /System/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/lib-old ',' / System / Library / Frameworks / Python.framework / Versions / 2.7 / lib / python2.7 / lib-dynload ',' /Library/Python/2.7/site-packages ']
>>>

Ваша цель должна заключаться в том, чтобы найти тот, который вы используете в настоящее время.Вы должны искать что-то вроде следующего:

  /Library/Python/2.7/site-packages

Переместите файл hello.py по пути. После этого вы сможете импортировать модуль hello из любого каталога обычным способом, как показано ниже:

  импорт привет

Выход

  Привет, мир

`Заключение`

На этом статья заканчивается. Модуль — это просто файл Python с набором переменных и определений функций.Модуль облегчает повторное использование кода, поскольку вы можете определить функцию в модуле и вызывать ее из разных программ вместо того, чтобы определять функцию в каждой программе. Хотя модуль в основном используется для определений функций и классов, он также может экспортировать переменные и экземпляры классов.

`Создайте свои собственные модули Python — Совет по Linux`

Python — это многоцелевой язык динамического программирования высокого уровня. Он предоставляет множество встроенных модулей и функций для выполнения различных типов задач.Помимо этого, мы также можем создавать наши собственные модули, используя Python. Модуль похож на библиотеку на Java, C, C ++ и C #. Модуль обычно представляет собой файл, содержащий функции и операторы. Функции и операторы модулей обеспечивают определенную функциональность. Модуль Python сохраняется с расширением .py. В этой статье мы научимся создавать собственные модули Python.

Модуль обычно используется для разделения большой функциональности на небольшие управляемые файлы. Мы можем реализовать наши наиболее часто используемые функции в отдельном модуле, а позже мы можем вызывать и использовать его везде.Создание модуля способствует повторному использованию и экономит много времени.

`Создание модулей Python`

Чтобы создать модуль Python, откройте сценарий Python, напишите несколько операторов и функций и сохраните его с расширением .py. Позже мы можем вызывать и использовать эти модули где угодно в нашей программе.

Давайте создадим новый модуль с именем «MathOperations». Этот модуль содержит функции для выполнения сложения, вычитания, умножения и деления.

#creating MathOperation module

# модуль предоставляет функции сложения, вычитания, умножения и деления

# все функции принимают два числа в качестве аргумента

# создание функции сложения

def сложение (num1, num2):

return num1 + num2

# создание функции вычитания

def subtraction (num1, num2):

return num1-num2

# создание функции умножения

def multiplication (num1, num2) num1 * num2

# создание функции деления

def div (num1, num2):

return num1 / num2

Теперь мы можем вызывать этот модуль где угодно, используя команду import, и мы можем использовать эти функции для выполнения связанных задач.Нет необходимости писать код снова и снова для выполнения операций сложения, вычитания, умножения и деления.

`Позвоните на свой модуль`

Давайте вызовем этот модуль в нашем другом скрипте Python с помощью команды import. Прочтите эту статью (https://linuxhint.com/python_import_command/), чтобы узнать больше о команде импорта Python.

import MathOperation

# вызов функции сложения из модуля MathOperation

# функция вызывается с использованием имени модуля

print («Сумма:», MathOperation.сложение (10,4))

# вызов функции вычитания

print («Разница в:», MathOperation.subtraction (100,34))

# вызов функции умножения

print («Умножение is: «, MathOperation.multiplication (4,3))

# вызов функции деления

print (» Результат деления: «, MathOperation.division (200,5))

Выход

`Вызов переменных модуля`

Мы также можем объявлять переменные в наших самостоятельно созданных модулях Python, присваивать значения этим переменным и вызывать их в нашем скрипте Python.Модули также могут содержать словари, списки и т. Д.

# создание переменных

num1 = 10

num2 = 20

# создание списка студентов

student = [‘John’, ‘Mark’, ‘Taylor’, ‘David’]

# создание студенческого словаря

std_dict = {‘name’: ‘Ali’, ‘age’: 12, ’email’: ‘[email protected]’}

Теперь давайте вызовем переменные и объекты в другом скрипте Python.

# импортировать модуль

import MathOperation

# вызов переменной num1

print («Значение num1:», MathOperation.num1)

# вызов переменной num2

print («Значение num1:», MathOperation.num2)

# вызов списка студентов

print («Значение num1:», MathOperation. student)

# вызов элементов списка ученика

print (MathOperation.student [0])

print (MathOperation.student [1])

print (MathOperation.student [2])

print (MathOperation .student [3])

# печать словаря студента

print (MathOperation.std_dict)

# вызов словаря ученика

print (MathOperation.std_dict [‘name’])

print (MathOperation.std_dict [‘age’])

print (MathOperation.std_dict [’email’] )

Выход

Выходные данные показывают, что мы успешно получили доступ к переменным и функциям из модуля «MathOperation».

`Список всех функций и переменных модуля`

Python предоставляет встроенную функцию dir (), которая перечисляет имена всех функций и переменных, присутствующих в конкретном модуле.Давайте воспользуемся функцией dir (), чтобы вывести список имен функций и переменных модуля MathOperation.

Это наши функции и переменные, созданные в нашем модуле «MathOperation».

#creating MathOperation module

# модуль предоставляет функции сложения, вычитания, умножения и деления

# все функции принимают два числа в качестве аргумента

#creating function

def сложение (num1, num2):

return num1 + num2

# создание функции вычитания

def subtraction (num1, num2):

return num1-num2

# создание функции умножения

def multiplication (num1, num2) num1 * num2

# создание функции деления

def div (num1, num2):

return num1 / num2

# создание переменных

num1 = 10

num2 = 20

`08`

ing

список студентов

student = [‘John’, ‘Mark’, ‘Taylor’, ‘David’]

# создание студенческого словаря

std_dict = {‘name’: ‘Ali’, ‘age’: 12, ’email’: ‘[email protected]’}

Теперь давайте вызовем функцию dir () в нашем скрипте Python.

# импорт модуля

import MathOperation

# использование функции dir ()

print (dir (MathOperation))

Выход

`Заключение`

Хотя Python предоставляет множество встроенных модулей и функций для выполнения некоторых конкретных задач, мы также можем создавать наши собственные модули Python. Модуль Python содержит функции и переменные. Модули Python сохраняются с расширением .py. В этой статье объясняется создание ваших собственных модулей Python с помощью простых примеров.

Учебное пособие по

`: создание модуля Go`

Это первая часть учебного пособия, которое знакомит с несколькими фундаментальными особенности языка Go. Если вы только начинаете работать с Go, обязательно взглянуть на Учебное пособие: начало работы с Go, которое знакомит с команда go, , модули Go и очень простой код Go.

В этом уроке вы создадите два модуля. Первая — это библиотека, которая предназначены для импорта другими библиотеками или приложениями.Второй — это вызывающее приложение, которое будет использовать первое.

Последовательность этого руководства включает семь кратких тем, каждая из которых иллюстрирует другая часть языка.

Создать модуль — напишите небольшой модуль с функциями, из которых вы можете вызывать другой модуль.
Вызовите свой код из другого модуля — Импортируйте и используйте свой новый модуль.
Вернуть и обработать ошибку — Добавить простое обработка ошибок.
Возврат случайного приветствия — Обработка данных в срезах (массивы Go с динамическим размером).
Ответные приветствия для нескольких человек — Храните пары ключ / значение на карте.
Добавить тест — использовать встроенное модульное тестирование Go функции для тестирования вашего кода.
Скомпилируйте и установите приложение — Скомпилируйте и установите свой код локально.

Примечание: Другие руководства см. Учебники.

`Предварительные требования`

Некоторый опыт программирования. Код здесь красивый просто, но это помогает кое-что узнать о функциях, циклах и массивах.
Инструмент для редактирования вашего кода. Любой текстовый редактор, который у вас есть, будет работают нормально. Большинство текстовых редакторов хорошо поддерживают Go. Самыми популярными являются VSCode (бесплатно), GoLand (платно) и Vim (бесплатно).
Командный терминал. Go хорошо работает с любым терминалом на Linux и Mac, а также PowerShell или cmd в Windows.

`Запустить модуль, который могут использовать другие`

Начните с создания модуля Go. В модуль, вы собираете один или несколько связанных пакетов для дискретного и полезного набора функций.Например, вы можете создать модуль с пакетами, в которых есть функции для проведения финансового анализа, чтобы другие писали финансовые приложения могут использовать вашу работу. Для получения дополнительной информации о разработке модулей см. Разработка и публикация модулей.

Код Go сгруппирован в пакеты, а пакеты сгруппированы в модули. Ваш модуль определяет зависимости, необходимые для запуска вашего кода, включая Go версия и набор других необходимых модулей.

По мере того, как вы добавляете или улучшаете функциональность в своем модуле, вы публикуете новые версии модуля.Разработчики, пишущие код, вызывающий функции в вашем модуле, могут импортировать обновленные пакеты модуля и протестировать с новой версией перед ввод в производство.

Откройте командную строку и cd в свой домашний каталог. В Linux или Mac: CD В Windows: cd% HOMEPATH%
Создайте каталог greetings для исходного кода модуля Go. Например, из вашего домашнего каталога используйте следующие команды: mkdir привет cd приветствия
Запустите свой модуль, используя go mod init команда. Запустите команду go mod init , указав ей путь к вашему модулю — здесь используйте example.com/greetings . Если вы публикуете модуль, этот должен быть путем, по которому ваш модуль может быть загружен Инструменты Go.Это будет репозиторий вашего кода. $ go mod init example.com/greetings go: создание нового go.mod: module example.com/greetings Команда go mod init создает файл go.mod для отслеживания вашего зависимости кода. Пока что файл включает только имя вашего модуль и версию Go, которую поддерживает ваш код. Но когда вы добавляете зависимости, в файле go.mod будут перечислены версии, от которых зависит ваш код. Это сохраняет строит воспроизводимые и дает вам прямой контроль над тем, какой модуль версии для использования.
В текстовом редакторе создайте файл для написания кода и назовите его привет.
Вставьте следующий код в файл greetings.go и сохраните файл. пакет приветствий импорт "FMT" // Hello возвращает приветствие для указанного человека. func Hello (строка имени) строка { // Возвращаем приветствие, включающее имя в сообщение. message: = fmt.Sprintf ("Привет,% v. Добро пожаловать!", имя) ответное сообщение } Это первый код для вашего модуля.Он возвращает приветствие любому вызывающий абонент, который просит его. Вы напишете код, который вызывает эту функцию в следующий шаг. В этом коде вы: Объявите пакет greetings для сбора связанных функций. Реализуйте функцию Hello , чтобы вернуть приветствие. Эта функция принимает параметр name , тип которого строка .Функция также возвращает строку . В Go функцию, имя которой начинается с заглавной буквы, можно вызывается функцией из другого пакета. В Go это известно как экспортированное имя. Подробнее об экспортированных именах см. Экспортированные имена в Перейти в тур. Объявите сообщение переменной для хранения вашего приветствия. В Go оператор : = — это ярлык для объявления и инициализация переменной в одной строке (Go использует значение справа для определить тип переменной).Пройдя долгий путь, вы могли бы написано это как: строка сообщения var message = fmt.Sprintf ("Привет,% v. Добро пожаловать!", имя) Используйте пакет fmt Sprintf функция для создания приветственного сообщения. В первый аргумент — это строка формата, а Sprintf заменяет имя значение параметра для формата % v глагол. Вставка значения параметра name завершается. текст приветствия. Вернуть отформатированный текст приветствия вызывающему абоненту.

На следующем шаге вы вызовете эту функцию из другого модуля.

Вызовите свой код из другого модуля>

`python 3.x — Как сделать функции из модуля пакета немедленно доступными для корневого приложения в Python3`

Есть ли способ импортировать все модули в пакете из главного приложения корневого уровня и иметь функции в модулях, сразу же доступные в Python 3? Вот пример файлового дерева:

  + приложение
  | - __init__.ру
  | - main.py
  | + пакет
    | - __init__.py
    | - module.py # (содержит функцию1, функцию2 и функцию 3)

Я бы хотел избежать следующего оператора импорта в main.py (он может быть длинным и небрежным для сложных приложений):

  из package.module import function1, function2, function3

Это хорошо, потому что тогда я могу вызвать function1 () из main.py. Импорт функции только из package.module означает, что я должен затем вызвать полный каталог функции, чтобы использовать ее в моем сценарии (или присвоить ей псевдоним в новой функции).Например:

  импорт package.module

package.module.function (param) # не весело ... слишком долго!

# или вот так
def newFunction (параметр):
   '' 'зачем создавать новую функцию для обработки уже существующей?
      Плохая форма и не Pythonic '' '
   возврат package.module.function (параметр)

Если я включу __all__ = ["module1", "module2"] в __init__.py моего пакета, это означает, что я должен сделать следующее:

  из импорта пакета * # тоже говорят, что это дурной тон

модуль.функция (параметр)
# Я просто хочу эту функцию и не хочу также вызывать модуль

Моя цель — импортировать пакет и модуль, а затем полностью использовать все функции в модуле без необходимости явно вызывать пакет и модуль каждый раз, когда я хочу использовать функцию.

Построение функций, содержащих модули

Методы построения графиков функций содержащих модуль

как построить – сложное простыми словами — ЕГЭ/ОГЭ

График функции с модулем и дробью

Графики функций с модулями. 10 класс

1. Графики функций с модулями.

2. Цель работы:

3. 1 ФУНКЦИЯ С МОДУЛЕМ

4. 2 функция с модулем.

5. 3 функция с модулем

6. 4 функция с модулем

7. 5 функция с модулем

8. 6 функция с модулем

9.

10. 8 функция с модулем

Построение графиков содержащих знак модуля построение графика функции содержащей переменную или функцию под знаком модуля согласно определению модуля

Урок по теме «Построение графиков квадратичной функции с модулем»

6. Модули — документация Python 3.9.4

Создание модулей в Python 3

Введение

Написание и импорт модулей

Доступ к модулям из другого каталога

Добавление путей

Добавление модуля в путь Python

Заключение

Научитесь создавать и импортировать специальные и встроенные модули

Что такое модули в Python?

Как импортировать модули в Python?

Оператор импорта Python

Импорт с переименованием

Python from … оператор импорта

Импортировать все имена

Путь поиска модуля Python

Перезарядка модуля

Встроенная функция dir ()

Создание и импорт модулей в Python

Введение

Пишущие модули

Импорт всех объектов модуля

Доступ к модулю по другому пути

Добавление путей

Добавление модуля в путь Python

Заключение

Создайте свои собственные модули Python — Совет по Linux

Создание модулей Python

Позвоните на свой модуль

Вызов переменных модуля

Список всех функций и переменных модуля

08

Заключение

: создание модуля Go

Предварительные требования

Запустить модуль, который могут использовать другие

python 3.x — Как сделать функции из модуля пакета немедленно доступными для корневого приложения в Python3

Добавить комментарий Отменить ответ

`Доступ к модулям из другого каталога`

`Добавление путей`

`Добавление модуля в путь Python`

`Заключение`

`Научитесь создавать и импортировать специальные и встроенные модули`

`Что такое модули в Python?`

`Как импортировать модули в Python?`

`Оператор импорта Python`

`Импорт с переименованием`

`Python from … оператор импорта`

`Импортировать все имена`

`Путь поиска модуля Python`

`Перезарядка модуля`

`Встроенная функция dir ()`

`Создание и импорт модулей в Python`

`Введение`

`Пишущие модули`

`Импорт всех объектов модуля`

`Доступ к модулю по другому пути`

`Добавление путей`

`Добавление модуля в путь Python`

`Заключение`

`Создайте свои собственные модули Python — Совет по Linux`

`Создание модулей Python`

`Позвоните на свой модуль`

`Вызов переменных модуля`

`Список всех функций и переменных модуля`

`08`

`Заключение`

`: создание модуля Go`

`Предварительные требования`

`Запустить модуль, который могут использовать другие`

`python 3.x — Как сделать функции из модуля пакета немедленно доступными для корневого приложения в Python3`

`Добавить комментарий Отменить ответ`