Содержание
Как найти неизвестную сторону равнобедренного треугольника
Треугольник, у которого две стороны равны, называется равнобедренным. Равные стороны в таком треугольнике называются боковыми, третья — основанием. Периметр равнобедренного треугольника (Р) будет равен сумме двух одинаковых боковых сторон (а) и основания (b):
Р = 2а + b
Против равных сторон лежат равные углы. Перпендикуляр, опущенный из вершины треугольника к его основанию, называется высотой равнобедренного треугольника. Проведенные к основанию биссектриса, медиана и высота совпадают между собой, делят треугольник на 2 равных прямоугольных треугольника, гипотенузой которых будет боковая сторона (а), а катетами — высота (h) и половина основания равнобедренного треугольника (b/2). По теореме Пифагора квадрат гипотенузы равен сумме квадратов его катетов, в нашем случае квадрат боковой стороны а (как гипотенузы) равен сумме половины основания (b/2), возведенного в квадрат, и высоте h в квадрате:
а2 = (b/2)2+h2
Отсюда, боковая сторона будет равна корню из суммы половины основания в квадрате и высоты, также возведенной в квадрат:
а = √(b/2)2+h2,
где а — боковая сторона, b/2 — половина основания, h — высота.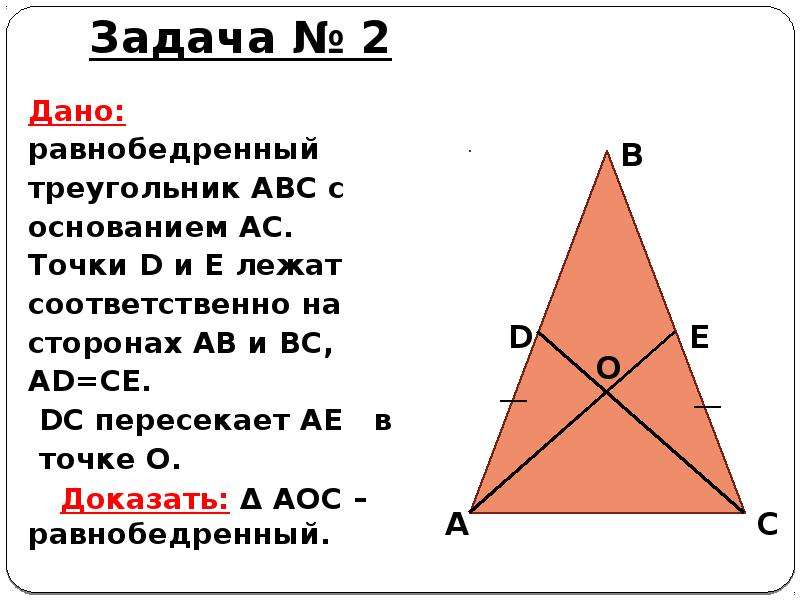
Если в прямоугольном треугольнике известна гипотенуза (в нашем случае это боковая сторона равнобедренного треугольника — а) и один из катетов (высота h), неизвестный катет находим, воспользовавшись теоремой Пифагора. Заметим, что неизвестный катет является половиной основания равнобедренного треугольника (b/2). Тогда, квадрат катета прямоугольного треугольника равен квадрату гипотенузы минус квадрат другого катета:
(b/2)2 = a2 — h2
Половина основания треугольника (b/2) равняется корню квадратному из квадрата гипотенузы минус квадрат другого катета:
b/2 = √а2 — h2,
где b/2 — половина основания, а — боковая сторона, h — высота.
Умножив полученный результат на 2, находим всю длину основания.
Расчет длины стороны равнобедренного треугольника зная сторону и высоту
Математика для блондинок: Сторона равнобедренного треугольника
Вот крик о помощи, в котором просят помочь найти сторону равнобедренного треугольника:
Помогите, пожалуйста! Я не понимаю геометрию(( У меня задача по типу вот
этой, только числа другие.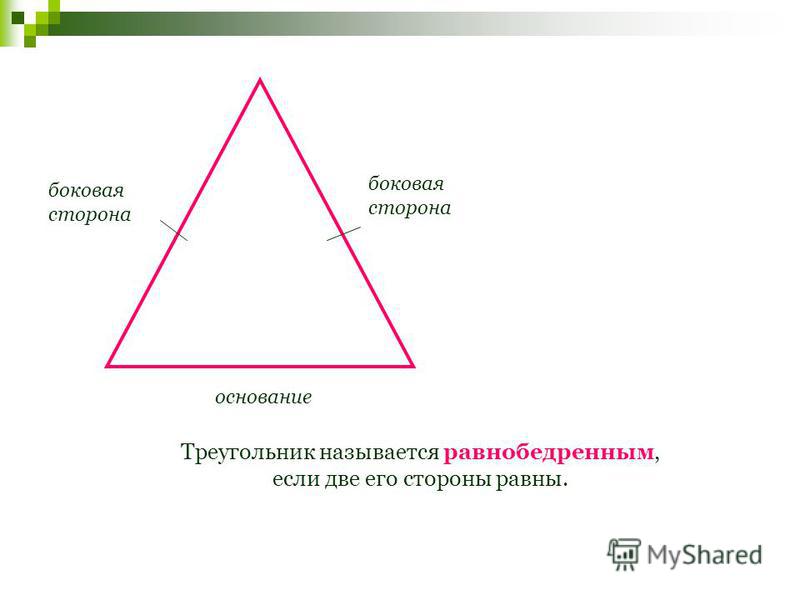 Мне бы сам ход решения.
Мне бы сам ход решения.
ЗАДАЧА: Угол при
вершине, противолежащей основанию равнобедренного треугольника, равен
30°. Найдите боковую сторону треугольника, если его площадь равна 25.
Помочь мне не трудно, но есть одна проблема: я понятия не имею о школьной программе и не представляю, что можно использовать при решении задачи, а что нельзя. Если просто брать математику и использовать её для решения, то задача решается довольно просто.
Начинаем рассуждать. У нас есть площадь равнобедренного треугольника и угол при его вершине. Нужно найти длину боковой стороны. Можно использовать теорему Пифагора, тригонометрические функции и всё то, чему вас учили до этого момента. Используя разные трюки с подстановками, можно в конце концов найти решение этой задачи. Я поступлю гораздо проще.
Для определения площади треугольника существует много разных формул. Вот к ним-то я и предлагаю присмотреться внимательнее.
| Площадь треугольника формулы |
Все эти формулы есть в Википедии, можно их отыскать и в разных математических справочниках. Шестая формула нам подходит как нельзя кстати. Здесь площадь треугольника определяется по боковой стороне и углам. Зная площадь треугольника, можно легко найти сторону. Осталось только с углами разобраться. Углы в основании равнобедренного треугольника равны. На картинке запишем те условия, которые превращают обычный треугольник в равнобедренный.
Шестая формула нам подходит как нельзя кстати. Здесь площадь треугольника определяется по боковой стороне и углам. Зная площадь треугольника, можно легко найти сторону. Осталось только с углами разобраться. Углы в основании равнобедренного треугольника равны. На картинке запишем те условия, которые превращают обычный треугольник в равнобедренный.
| Равнобедренный треугольник |
Как видите, нам даже нет необходимости искать углы в основании равнобедренного треугольника — синусы этих углов равны и сокращаются в дроби. Угол в вершине равен 30 градусов, синус этого угла равен одной второй. Теперь легко можно решить задачу. Выражаем квадрат стороны через площадь и синус угла в вершине, извлекаем квадратный корень и получаем сторону размером в 10 единиц.
Это взрослое решение. Все взрослые пользуются справочниками, не вдаваясь в подробности. Для инквизиторов от математики такое решение может показаться богохульством. Специально для инквизиторов мы сейчас выведем формулу площади равнобедренного треугольника через боковую сторону и синус угла в вершине. Как и предыдущее решение, это будет пример того, как нужно пользоваться математикой.
Специально для инквизиторов мы сейчас выведем формулу площади равнобедренного треугольника через боковую сторону и синус угла в вершине. Как и предыдущее решение, это будет пример того, как нужно пользоваться математикой.
Стоп! Я обещал писать в режиме реального времени. Так вот, всё, что написано до сих пор, писалось в ночь с пятницы на субботу. Сейчас утро воскресенья. Почему я сразу всё не написал? Ну, во-первых, у меня проблемы с картинками тригонометрических формул — программа, в которой я их писал, начала глючить и не переключается на английский язык. Во-вторых, я, наверное, чувствовал, что у этой задачи есть очень простое, детское, решение. Сегодня утром до меня дошло.
Почему-то все самые интересные решения ко мне приходят по утрам. Может, я ночью с инопланетянами общаюсь? Может, это они за меня задачки решают? Есть там у них какой-то канал, типа Ютуба, под названием «Из жизни идиотов». Когда им становится грустно, они включают этот канал и начинают ухохатываться над нашими математиками с их идиотскими определениями и не менее грамотными решениями. Потом появляюсь я со своим; «Не могу решить задачу…». Они долго смеются и один говорит другому: «Покажи этому дурачку картинку, пусть исчезнет с экрана». Формулы можно записывать разными загогулинами и вкладывать в эти загогулины разный смысл. А вот геометрия на всю вселенную одна и у инопланетян равнобедренный треугольник выглядит точно так же, как и у нас. Именно поэтому инопланетяне понимают, что делают наши математики и им становится очень смешно. Мы ведь тоже смеемся, наблюдая за некоторыми проделками животных.
Потом появляюсь я со своим; «Не могу решить задачу…». Они долго смеются и один говорит другому: «Покажи этому дурачку картинку, пусть исчезнет с экрана». Формулы можно записывать разными загогулинами и вкладывать в эти загогулины разный смысл. А вот геометрия на всю вселенную одна и у инопланетян равнобедренный треугольник выглядит точно так же, как и у нас. Именно поэтому инопланетяне понимают, что делают наши математики и им становится очень смешно. Мы ведь тоже смеемся, наблюдая за некоторыми проделками животных.
Это было маленькое лирическое отступление. Теперь перейдем к инквизиторским пыткам и я на время превращусь в математика-садиста, который будет мучить вас тригонометрией. Для начала картинка нашего равнобедренного треугольника с сохранением всех обозначений, принятых для произвольного треугольника. Почему я об этом специально говорю? Из-за тупости отдельных наших математиков. Если в формуле треугольника фигурирует один угол, то математик обозначит его как «альфа» и ему по барабану, этот угол находится в основании или в вершине треугольника. Это уже потом он будет тыкать пальцем в картинку и рассказывать, что именно этот угол он имел в виду, а не какой-нибудь другой. Когда же посторонний человек попробует воспользоваться такой формулой, вот тут и начинаются все проблемы в математике. И так, картинка.
Для начала картинка нашего равнобедренного треугольника с сохранением всех обозначений, принятых для произвольного треугольника. Почему я об этом специально говорю? Из-за тупости отдельных наших математиков. Если в формуле треугольника фигурирует один угол, то математик обозначит его как «альфа» и ему по барабану, этот угол находится в основании или в вершине треугольника. Это уже потом он будет тыкать пальцем в картинку и рассказывать, что именно этот угол он имел в виду, а не какой-нибудь другой. Когда же посторонний человек попробует воспользоваться такой формулой, вот тут и начинаются все проблемы в математике. И так, картинка.
| Равнобедренный треугольник |
Теперь тригонометрические пляски с бубном.
| Вывод формулы площади равнобедренного треугольника |
Краткое пояснение к этой шаманской пляске.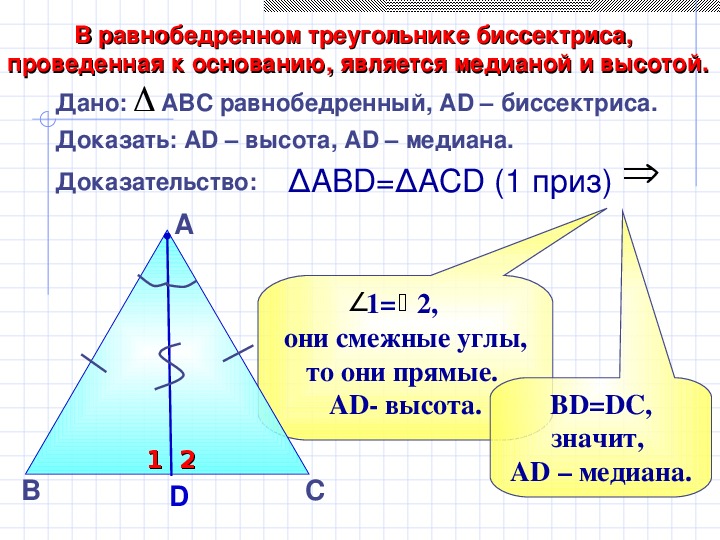 Площадь треугольника равна половине произведения основания на высоту. Высоту и основание выражаем через боковую сторону и тригонометрические функции угла при основании треугольника. Дальше переходим к углу в вершине треугольника, точнее, его половине. На следующем этапе используем тригонометрическую формулу произведения синуса и косинуса, но с учетом того, что у нас одинаковые углы. Потом всё складываем в кучку и получаем искомую формулу площади равнобедренного треугольника.
Площадь треугольника равна половине произведения основания на высоту. Высоту и основание выражаем через боковую сторону и тригонометрические функции угла при основании треугольника. Дальше переходим к углу в вершине треугольника, точнее, его половине. На следующем этапе используем тригонометрическую формулу произведения синуса и косинуса, но с учетом того, что у нас одинаковые углы. Потом всё складываем в кучку и получаем искомую формулу площади равнобедренного треугольника.
Но всё гениальное просто. Давайте разрежем наш равнобедренный треугольник пополам и сложим две половинки в прямоугольник.
| Равнобедренный треугольник и прямоугольник |
А как известно, площадь любого четырехугольника равна половине произведения его диагоналей на синус угла между ними. Наша боковая сторона равнобедренного треугольника превратилась в диагональ прямоугольника, угол в вершине равен углу между диагоналями. Мы получаем ту же формулу площади равнобедренного треугольника.
Мы получаем ту же формулу площади равнобедренного треугольника.
Ну и наконец, само решение задачи.
| Сторона равнобедренного треугольника |
Картинки получились плохими. Но мы это как-нибудь переживем. Главное — их смысл.
Как посчитать стороны равнобедренного треугольника
Чтобы посчитать чему равны стороны равнобедренного треугольника воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить длины сторон равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
для стороны a:
- длину основания (b) и угол α
- длину основания (b) и угол β
- длину основания (b) и высоту (h)
для стороны b:
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и угол β
- длину двух равных сторон (a) и высоту (h)
Введите их в соответствующие поля и получите результат.
Как посчитать сторону a равнобедренного треугольника
Если известна сторона b и угол α
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол α?
Формула
a = b/2⋅cos α
Пример
Если сторона b = 10 см, а ∠α = 30°, то:
a = 10/2⋅cos 30° = 10/(2⋅0.8660) = 5.77см
Если известна сторона b и угол β
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол β?
Формула
a = b/2⋅sin β/2
Пример
Если сторона b = 10 см, а ∠β = 30°, то:
a = 10/2⋅sin 15 = 10/(2⋅0.2588) = 19.31см
Если известна сторона b и высота h
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и высота h?
Формула
a = √1/b2 + h2
Пример
Если сторона b = 10 см, а высота h = 20 см, то:
a = √1/102 + 202 = √0.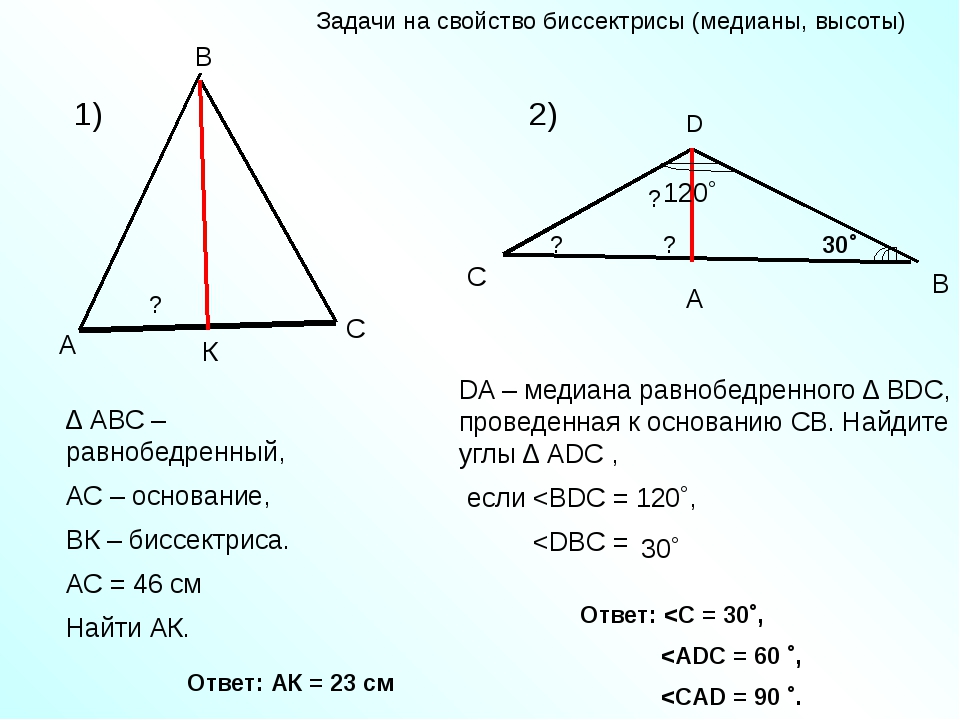 01+400 = 20.61см
01+400 = 20.61см
Как посчитать сторону b (основание) равнобедренного треугольника
Если известна сторона a и угол α
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол α?
Формула
b = 2⋅a⋅cos α
Пример
Если сторона a = 10 см, а ∠α = 30°, то:
b = 2⋅10⋅cos 30° = 2⋅10⋅0.8660 = 17.32см
Если известна сторона a и угол β
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол β?
Формула
b = 2⋅a⋅sin β/2
Пример
Если сторона a = 10 см, а ∠β = 40°, то:
b = 2⋅10⋅sin 40/2 = 2⋅10⋅0.342 = 6.84см
Если известна сторона a и высота h
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и высота h?
Формула
b = 2⋅√a2 — h2 , h
Пример
Если сторона a = 10 см, а высота h = 5 см, то:
b = 2⋅√102 — 52 = 2⋅√75 = 17. 32см
32см
См. также
к основанию, к боковой стороне
В данной публикации мы рассмотрим основные свойства высоты равнобедренного треугольника, а также разберем примеры решения задач по данной теме.
Примечание: треугольник называется равнобедренным, если две его стороны равны (боковые). Третья сторона называется основанием.
Свойства высоты в равнобедренном треугольнике
Свойство 1
В равнобедренном треугольнике две высоты, проведенные к боковым сторонам, равны.
AE = CD
Обратная формулировка: Если в треугольнике две высоты равны, значит он является равнобедренным.
Свойство 2
В равнобедренном треугольнике высота, опущенная на основание, одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.
- BD – высота, проведенная к основанию AC;
- BD – медиана, следовательно, AD = DC;
- BD – биссектриса, следовательно, угол α равен углу β.
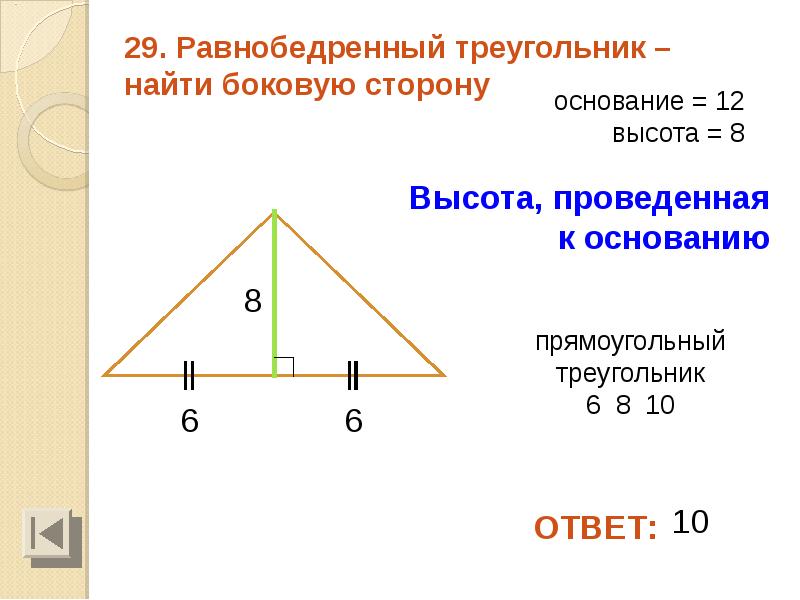
- BD – серединный перпендикуляр к стороне AC.
Свойство 3
Если известны стороны/углы равнобедренного треугольника, то:
1. Длина высоты ha, опущенной на основание a, вычисляется по формуле:
- a – основание;
- b – боковая сторона.
2. Длина высоты hb, проведенной к боковой стороне b, равняется:
p – это полупериметр треугольника, рассчитывается таким образом:
3. Высоту к боковой стороне можно найти через синус угла и длину стороны треугольника:
Примечание: к равнобедренному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.
Пример задачи
Задача 1
Дан равнобедренный треугольник, основание которого равно 15 см, а боковая сторона – 12 см.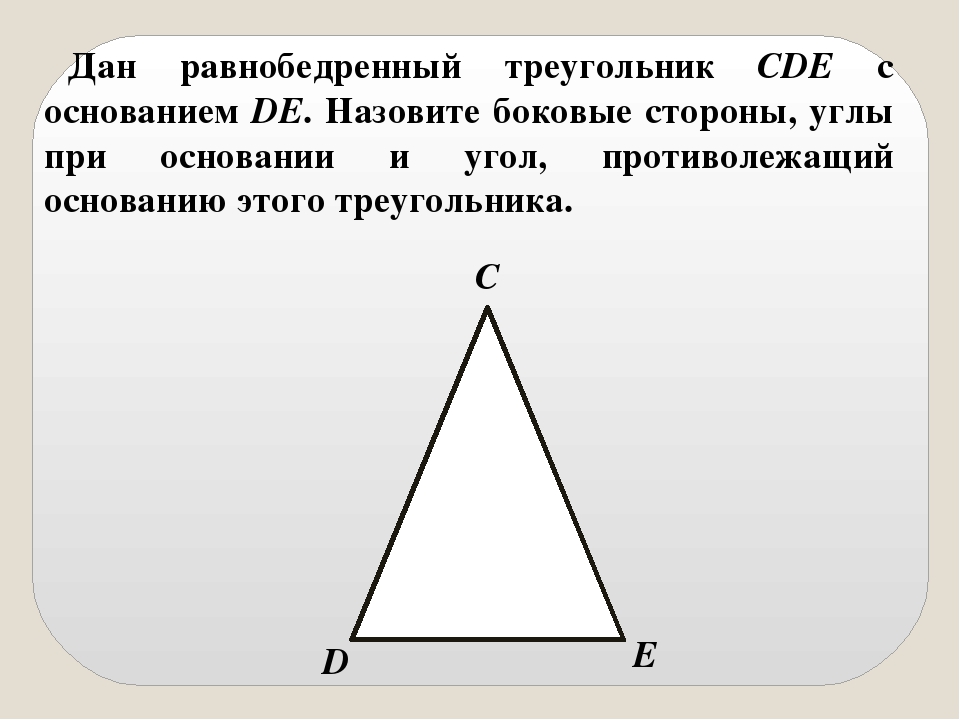 Найдите длину высоты, опущенной к основанию.
Найдите длину высоты, опущенной к основанию.
Решение
Воспользуемся первой формулой, представленной в Свойстве 3:
Задача 2
Найдите высоту, проведенную к боковой стороне равнобедренного треугольника длиной 13 см. Основание фигуры равняется 10 см.
Решение
Для начала вычислим полупериметр треугольника:
Теперь применим соответствующую формулу для нахождения высоты (представлена в Свойстве 3):
Microsoft Word — геометрия-1.doc
%PDF-1.6
%
955 0 obj
>
endobj
952 0 obj
>stream
2009-08-03T12:57:02ZMicrosoft Word — геометрия-1.doc2009-08-12T12:51:21+04:002009-08-12T12:51:21+04:00application/pdf
doPDF Ver 6.1 Build 276 (Windows XP x32)uuid:d60141d8-4b2c-4d57-bdfd-e4ad6bbf2afbuuid:e17ab538-6e84-4259-9962-f18eb34ac9fa
endstream
endobj
956 0 obj
>/Encoding>>>>>
endobj
919 0 obj
>
endobj
920 0 obj
>
endobj
926 0 obj
>
endobj
932 0 obj
>
endobj
938 0 obj
>
endobj
944 0 obj
>
endobj
945 0 obj
>
endobj
946 0 obj
>
endobj
947 0 obj
>
endobj
948 0 obj
>
endobj
949 0 obj
>
endobj
950 0 obj
>
endobj
951 0 obj
>
endobj
706 0 obj
>/ProcSet[/PDF/Text]>>/Type/Page>>
endobj
709 0 obj
>/ProcSet[/PDF/Text]>>/Type/Page>>
endobj
711 0 obj
>/ProcSet[/PDF/Text]>>/Type/Page>>
endobj
713 0 obj
>/ProcSet[/PDF/Text]>>/Type/Page>>
endobj
715 0 obj
>/ProcSet[/PDF/Text]>>/Type/Page>>
endobj
717 0 obj
>/ProcSet[/PDF/Text]>>/Type/Page>>
endobj
719 0 obj
>/ProcSet[/PDF/Text]>>/Type/Page>>
endobj
721 0 obj
>/ProcSet[/PDF/Text]>>/Type/Page>>
endobj
723 0 obj
>/ProcSet[/PDF/Text]>>/Type/Page>>
endobj
725 0 obj
>/ProcSet[/PDF/Text]/ExtGState>>>/QITE_pageid>/Type/Page>>
endobj
1051 0 obj
>stream
HWM
ϯ24z00M
t-hIɲ-{fnǑCo>?/dNhͧNYpG79(NG_iiߦtoIxj
как рассчитать по трем сторонам, формула
Определение
Площадь равнобедренного треугольника — это часть плоскости, заключенной внутри данной геометрической фигуры.
Параметры для расчета
Рассчитать площадь можно с помощью нескольких способов. Для начала приведем обозначения, которые будут использоваться в последующих формулах.
- а — длина одной из двух равных сторон треугольника;
- b — длина основания;
- \(\alpha\) — величина одного из двух равных углов при основании;
- \(\beta\) — величина угла между равными сторонами треугольника и противолежащего его основанию;
- h — длина высоты, опущенная из вершины равнобедренного треугольника на его основание.
Особенности вычислений, зная длину основания и высоту
Рассмотрим треугольник ABC. Если опустить из вершины В высоту, то мы получим два прямоугольных треугольника. Тогда \(S=\frac{h\times AC}2.\)
Задача
Боковая сторона равнобедренного треугольника ABC равна 13 см, а основание равно 10 см.
Найти: площадь равнобедренного треугольника. 2.\)
2.\)
Как посчитать, зная длину двух равных сторон и угол между ними
В таком случае S будет находиться, как половина квадрата боковой стороны, умноженная на синус угла между боковыми сторонами.
Если мысленно опустить высоту на боковую сторону равнобедренного треугольника, заметим, что ее длина будет равна \(\alpha\times\sin\;\beta\). Поскольку длина боковой стороны нам известна, высота, опущенная на нее теперь известна, половина их произведения и будет равна площади данного равнобедренного треугольника.
Примечание
Полное произведение дает площадь прямоугольника, что очевидно. Высота делит этот прямоугольник на два малых прямоугольника, при этом стороны треугольника являются их диагоналями, которые делят их ровно пополам. Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту.
То есть формула будет такая же, как и в первом способе:
\(S=\frac{h\times AC}2\)
Задача
Стороны треугольника равны \(2\sqrt2\) и \(3\), S=3. 2.\)
2.\)
Вписанный и описанный треугольник — материалы для подготовки к ЕГЭ по Математике
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.
Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.
Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
,
где — полупериметр,
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:
Ты нашел то, что искал? Поделись с друзьями!
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен .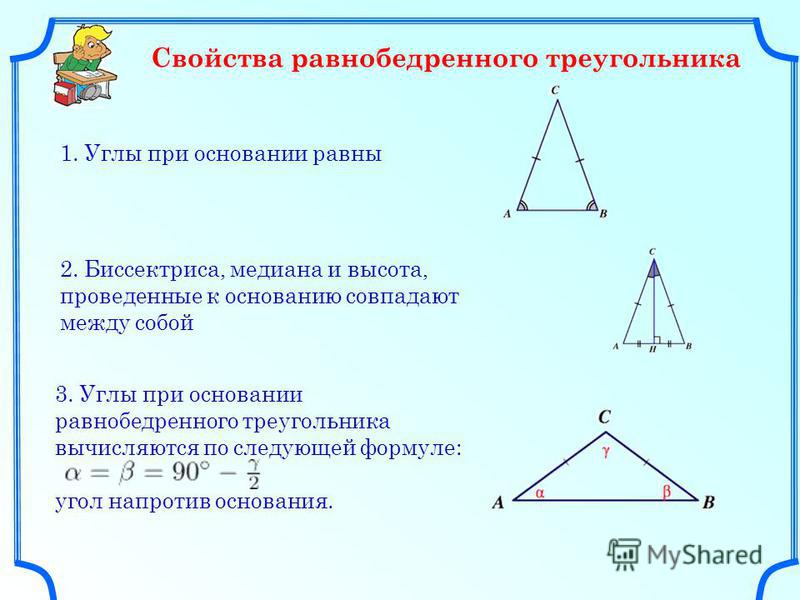 Найдите гипотенузу c этого треугольника. В ответе укажите .
Найдите гипотенузу c этого треугольника. В ответе укажите .
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
Ответ: .
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.
По теореме синусов,
Получаем, что . Угол — тупой. Значит, он равен .
Ответ: .
. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .
По теореме Пифагора найдем . Тогда .
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
Равнобедренный треугольник — математический путь
Равнобедренный треугольник представляет собой многоугольник из трех сторон и двух равных сторон . Другая неравная сторона называется основанием треугольника.
Следовательно, два угла также будут равными (α), а другие — разными (β), т.е. это угол, образованный двумя равными сторонами ( a ).
Двумя частными случаями равнобедренных треугольников являются равносторонний треугольник и равнобедренный прямоугольный треугольник .
Высота равнобедренного треугольника
Высота ( h ) равнобедренного треугольника (или высота ) может быть вычислена по теореме Пифагора.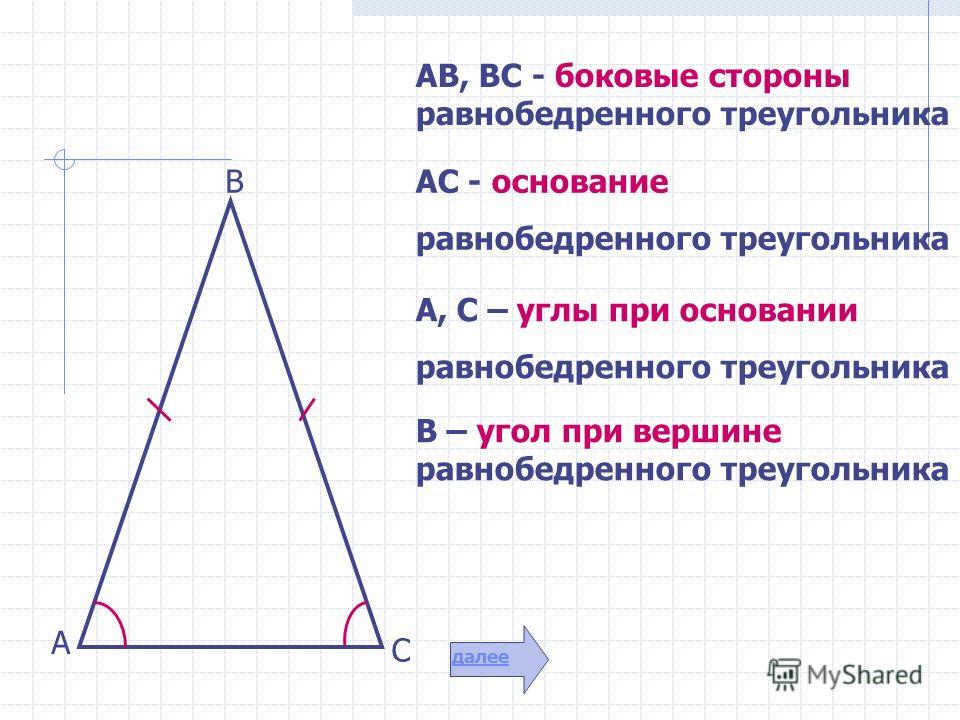 Стороны a , b / 2 и h образуют прямоугольный треугольник. Стороны b / 2 и h являются катетами, а и — гипотенузами.
Стороны a , b / 2 и h образуют прямоугольный треугольник. Стороны b / 2 и h являются катетами, а и — гипотенузами.
По теореме Пифагора:
И получается, что высота h составляет:
В равнобедренном треугольнике высота , соответствующая основанию ( b ), также является биссектрисой угла, серединным перпендикуляром и серединой.
Площадь равнобедренного треугольника вычисляется из основания b (неповторяющаяся сторона) и высоты ( h ) треугольника, соответствующего основанию. Площадь — это произведение базы и высоты, разделенное на два, и его формула следующая:
.
Периметр равнобедренного треугольника получается сложением трех сторон треугольника.Имея две равные стороны, периметр равен удвоенной повторяющейся стороне ( a ) плюс другая сторона ( b ).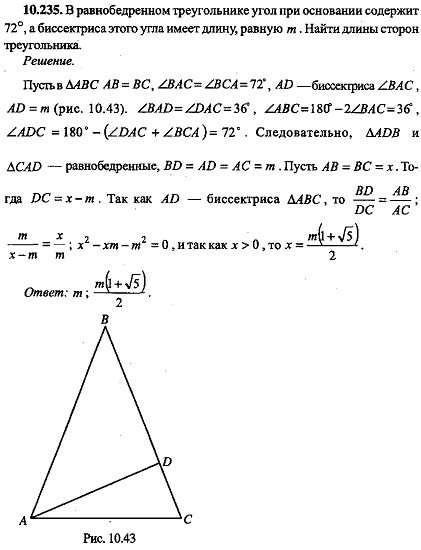
Если повторяющаяся сторона ( a ) и угол двух равных сторон известны, другая сторона ( b ) должна быть найдена по закону косинусов .
Загрузите этот калькулятор , чтобы получить результаты формул на этой странице. Выберите исходные данные и введите их в верхнем левом поле. Для получения результатов нажмите ENTER.
Triangle-total.rar или Triangle-total.exe
Примечание. Предоставлено автором: Хосе Мария Пареха Маркано . Химик. Севилья, испания.
Решенные упражнения
Упражнение в области равнобедренного треугольника
Определите площадь равнобедренного треугольника , зная его две равные стороны ( a = 3 см) и неравную, длина которой составляет 2 см ( b = 2 см).
Какова его площадь ?
Рассчитайте площадь по приведенной выше формуле, умножив основание на высоту:
Площадь равнобедренного треугольника равна 2. 83 см 2 .
83 см 2 .
Упражнение по периметру равнобедренного треугольника
Равнобедренный треугольник с двумя равными сторонами, a = 3 см, а другая сторона b = 2 см.
Каков его периметр ?
Чтобы вычислить периметра , мы добавляем повторяющуюся сторону, умноженную на два, плюс неравную сторону, то есть:
Получается, что периметр равнобедренного треугольника равен 8 см .
Упражнение на высоту равнобедренного треугольника
Найдите стороны и периметр равнобедренного треугольника, высота которого относительно неровной стороны равна h = 6 см, а противоположный угол, также неровный, 40 °.
Найдено по тригонометрическим соотношениям из одного прямоугольного треугольника, на который делится равнобедренный треугольник по высоте h .
Отрезок, противоположный углу β / 2, который является отрезком b /2, мы нашли его через касательную:
Сторона b меры 4. 36 см.
36 см.
Образуется гипотенуза прямоугольного треугольника, то есть сторона и находится по косинусу:
Сторона и имеет размер 6,38 см.
Наконец, периметр треугольника составит:
Получается, что периметр этого равнобедренного треугольника будет составлять 17,12 см.
Равнобедренный прямоугольный треугольник. Темы по тригонометрии
Темы | Дом
5
ПРАВИЛЬНЫЙ ТРЕУГОЛЬНИК ИЗОСЦЕЛЫ — это один из двух особых треугольников.(Другой — треугольник 30 ° -60 ° -90 °.) Студент должен знать соотношение сторон.
(Равнобедренный треугольник имеет две равные стороны. См. Определение 8 в некоторых теоремах плоской геометрии. Там можно найти теоремы, цитируемые ниже.)
Теорема. В равнобедренном прямоугольном треугольнике стороны находятся в соотношении 1: 1 :.
Доказательство . В равнобедренном прямоугольном треугольнике равные стороны составляют прямой угол. У них соотношение равенства 1: 1.
У них соотношение равенства 1: 1.
Чтобы найти отношение числа гипотенузы h , мы имеем, согласно теореме Пифагора,
ч 2 = 1 2 + 1 2 = 2.
Следовательно,
ч =.
(Урок 26 алгебры.) Следовательно, три стороны находятся в соотношении
1: 1:.
Обратите внимание: поскольку прямоугольный треугольник равнобедренный, то углы при основании равны.(Теорема 3.) Следовательно, каждый из этих острых углов равен 45 °.
(Определение углов измерения «градусами» см. В теме 12.)
Пример 1. Оценить sin 45 ° и tan 45 °.
Ответ . По любым вопросам, связанным с углом 45 °, ученику не следует обращаться к Таблице. Лучше нарисуйте треугольник и расставьте числа отношения.
Мы видим:
| sin 45 ° | = | 1 | = ½, |
по рационализации знаменателя.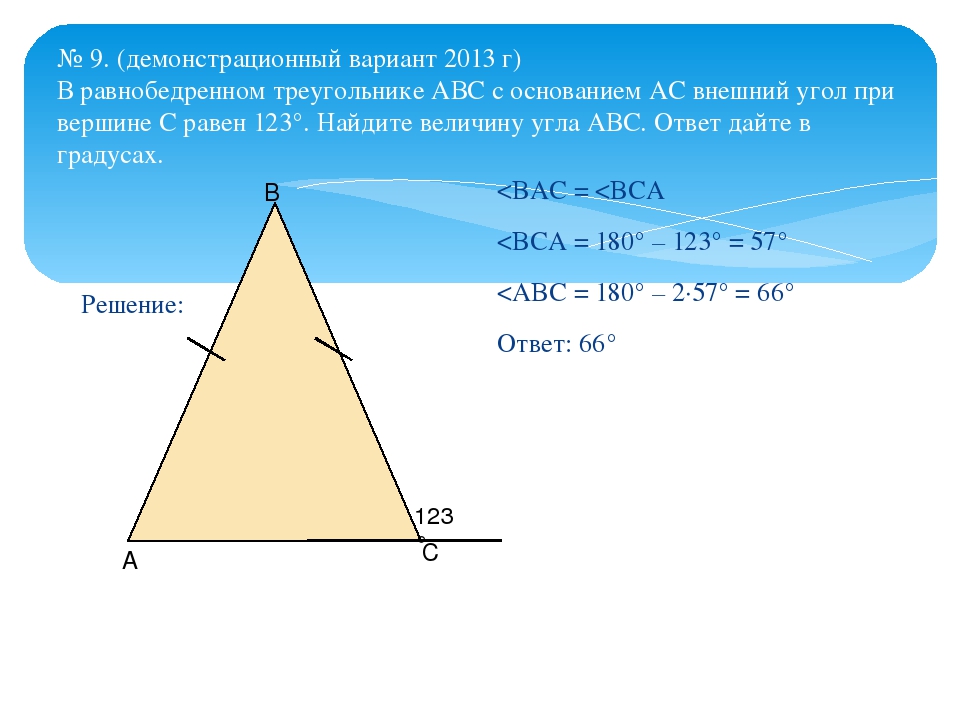 (Урок 26 алгебры.)
(Урок 26 алгебры.)
Проблема. Определите cos 45 ° и csc 45 °.
| cos 45 ° = | 1 | = ½. |
Таким образом, cos 45 ° равен sin 45 °; они дополняют друг друга.
| csc 45 ° = | 1 | =. |
Пример 2.Решите равнобедренный прямоугольный треугольник со стороной 6,5 см.
Ответ . Решить треугольник — значит знать все три стороны и все три угла. Поскольку это равнобедренный прямоугольный треугольник, единственная проблема — найти неизвестную гипотенузу.
Но в каждом равнобедренном прямоугольном треугольнике стороны имеют соотношение 1: 1:, как показано справа. В треугольнике слева сторона, соответствующая 1, умножена на 6,5. Следовательно, каждая сторона будет умножена на 6.5. Гипотенуза.
будет 6.5. (Теорема об одном и том же кратном.)
Всякий раз, когда мы знаем числа отношения, мы используем этот метод подобных фигур для решения треугольника, а не тригонометрическую таблицу.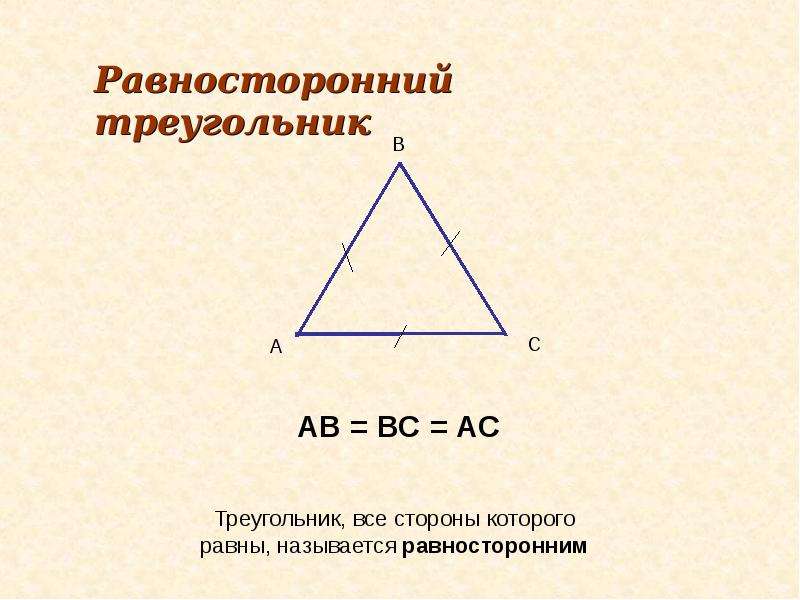
(В теме 6 мы будем решать прямоугольные треугольники, отношения сторон которых нам неизвестны.)
Пример 3. В равнобедренном прямоугольном треугольнике гипотенуза равна дюйму. Какова длина сторон?
Ответ .Ученик должен нарисовать треугольники и указать числа отношения.
Как умножалась сторона, соответствующая?
Согласно правилу умножения радикалов, умножается на. Следовательно, все стороны будут умножены на. И 1 =.
Следующая тема: Решение прямоугольных треугольников
Темы | Дом
Сделайте пожертвование, чтобы TheMathPage оставался в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Калькулятор равнобедренного треугольника
— Решите любой отрезок или угол
Введите любые два известных значения для равнобедренного треугольника, чтобы вычислить длину ребер, высоту, углы, площадь, периметр, внутренний радиус и радиус описанной окружности.
Решение:
α = 33.557 ° | 0,5857 рад
тупой равнобедренный треугольник
Что такое равнобедренный треугольник?
Равнобедренный треугольник — это треугольник, у которого есть два ребра или ножки одинаковой длины.Третий край называется основанием.
Два угла, примыкающие к основанию, называются базовыми углами, а угол, противоположный основанию, называется вершинным углом.
Поскольку ножки имеют одинаковую длину, углы основания также идентичны.
Типы равнобедренных треугольников
Существует четыре типа равнобедренных треугольников: острый , тупой , равносторонний и правый .
Острый равнобедренный треугольник — это треугольник с углом при вершине менее 90 °, но не равным 60 °.
Тупой равнобедренный треугольник — это треугольник с углом при вершине более 90 °.
Равносторонний треугольник и равнобедренный треугольник — это треугольник с углом при вершине, равным 60 °. Равносторонний треугольник — это особый случай, когда все углы равны 60 ° и все три стороны равны по длине. Попробуйте наш калькулятор равностороннего треугольника.
Прямой равнобедренный треугольник и равнобедренный треугольник — это треугольник с углом при вершине, равным 90 °, и углами основания, равными 45 °.У нас есть специальный калькулятор прямоугольного треугольника для вычисления этого типа треугольника.
Как рассчитать длину ребер равнобедренного треугольника
Зная высоту или высоту равнобедренного треугольника и длину одной из ног или основания, можно вычислить длину других сторон.
Определите длину основания
Используйте следующую формулу, чтобы найти длину базовой кромки:
b = 2a² — h²
Базовая длина b равна 2, умноженному на квадратный корень из катета a в квадрате минус высота h в квадрате.
Решите длину ноги
Используйте следующую формулу, чтобы найти длину ног:
a = h² + (b ÷ 2) ²
Длина участка a равна квадратному корню из высоты h в квадрате плюс основание b , разделенное на 2 в квадрате.
Как рассчитать углы равнобедренного треугольника
Учитывая любой угол в равнобедренном треугольнике, можно решить другие углы.
Решите базовый угол
Используйте следующую формулу, чтобы решить базовый угол:
α = 180 ° — β2
Базовый угол α равен 180 ° минус угол при вершине β , деленный на 2.
Решите угол при вершине
Используйте следующую формулу для определения угла при вершине:
β = 180 ° — 2α
Угол при вершине β равен 180 ° минус двукратный угол основания α .
Как рассчитать площадь и периметр
Учитывая стороны равнобедренного треугольника, можно определить периметр и площадь, используя несколько простых формул.
Решить периметр
Решите периметр равнобедренного треугольника по следующей формуле:
р = 2а + Ь
Таким образом, периметр p равен 2-кратному отрезку a плюс основание b .
Полупериметр Solve
Учитывая периметр, вы можете решить полупериметр. Полупериметр s равен половине периметра.
s = p2
Решить область
Чтобы найти площадь, используйте формулу Герона:
Т = s (s — a) (s — a) (s — b)
Формула Херона утверждает, что площадь T равна квадратному корню из полупериметра s , умноженного на полупериметр s минус отрезок a умноженный на полупериметр s минус a умноженный на полупериметр s минус основание b .
Что такое равнобедренный треугольник?
Что такое равнобедренный треугольник?
Определение: Равнобедренный треугольник определяется как треугольник, имеющий две равные стороны или две стороны одинаковой длины.
Равнобедренный треугольник также может быть равносторонним, но это не обязательно.
Определения этих треугольников обычно включают слово «только» или «точно». Эти слова имеют значение при рассмотрении вопроса о том, является ли треугольник равносторонним или равнобедренным треугольником.
Свойства равнобедренного треугольника,
Характеристики и применение
Многие треугольники, встречающиеся в реальном мире, можно считать равнобедренными, включая часть куска пиццы. Часто абстрактные или сложные формы разбиваются на более мелкие, такие как треугольник.
Две стороны одинаковой длины называются ножками, а третья сторона называется основанием. Часто проблема будет использовать этот словарь для передачи информации.
Знание, что у равнобедренного треугольника две стороны равны, приводит нас к первой теореме, связанной с равнобедренными треугольниками.Теперь давайте посмотрим, как найти недостающие стороны равнобедренного треугольника и вычислить их длину.
Теоремы о равнобедренном треугольнике
Теорема № 1 — Если две стороны треугольника равны, углы напротив них равны.
Это означает, что если мы знаем, что в треугольнике две стороны равны, мы знаем, что два угла также совпадают. Чтобы найти противоположный угол, вам нужно посмотреть на угол, частью которого не является сторона.
Одиночные линии на сторонах равнобедренных треугольников — это отметки, указывающие на то, что стороны имеют одинаковую длину или совпадают.Дуги в углах указывают на то, что углы имеют одинаковую меру или конгруэнтны. Обратите внимание, что основание треугольника образовано обоими конгруэнтными углами.
Обратное утверждение этой теоремы выглядит наоборот.
Теорема № 2 (обратное) — Если два угла треугольника совпадают, противоположные стороны равны.
Если мы знаем, что два угла конгруэнтны или имеют одинаковую длину, то мы знаем, что противоположные стороны равны или имеют одинаковую длину.
И снова совпадающие углы образуют основу, а конгруэнтные стороны — ноги.
Эти две теоремы важны для любых доказательств, которые просят вас доказать, что треугольник является равнобедренным треугольником.
Обязательно запомните данное вам определение равнобедренного треугольника. Некоторые определения позволяют доказать, что два угла совпадают, некоторым требуется дополнительный шаг, чтобы показать, что две стороны совпадают.
Решения проблем равнобедренного треугольника
Одна из распространенных проблем, связанных с равнобедренным треугольником, связана с высотой, привязанной к основанию.Высота — это линия, которая проводится от вершины одного угла к противоположной стороне, образуя прямой угол.
Когда высота проводится к основанию равнобедренного треугольника, она образует два равных треугольника. Тип треугольника и место, где нарисована высота, важны. Давайте внимательно рассмотрим эту концепцию.
Когда нам дают равнобедренный треугольник, мы знаем следующие факты.
Равнобедренный треугольник имеет две конгруэнтные стороны (определение равнобедренного треугольника).Это часто будет дано вам по данной маркировке базы. Если YZ — база, то мы знаем, что XY ≅ XZ.
Поскольку мы знаем, какие стороны конгруэнтны, теперь мы знаем, какие углы конгруэнтны. ∠Y ≅ ∠Z (Если две стороны треугольника равны, углы напротив них равны).
Теперь нарисуем высоту под углом X к основанию. Это разделит исходный равнобедренный треугольник на два меньших прямоугольных треугольника.
Поскольку два прямых угла имеют одинаковую величину (90 градусов), мы можем сказать, что прямые углы совпадают.Это дает недостающую часть, чтобы доказать, что по △ XYA ≅ △ XZA by AAS.
Примеры задач равнобедренного треугольника
Задача о равнобедренном треугольнике
Теорема # 1
Как найти сторону равнобедренного треугольника из уравнения x .
Обратите внимание, что два катета треугольника имеют одинаковую длину или совпадают. Это означает, что противоположные углы совпадают. Поскольку один из углов, противоположных ноге, равен 50 градусам, это означает, что недостающее значение также равно 50 градусам.
Задача о равнобедренном треугольнике
Теорема # 2
Давайте рассмотрим пример задачи, в которой это будет использоваться.
Найдите значение y .
Мы видим, что два угла равны 25 градусам. Поскольку это одна и та же мера, мы знаем, что стороны, противоположные углам, также равны по мере. Одна из сторон обозначена как 6 см . Мы знаем, что другая сторона тоже должна быть 6 см .Таким образом, значение y равно 6 см.
Пример:
Дан равнобедренный треугольник ABC с основанием BC. Найдите угол A.
Приведенная информация может помочь нам обозначить диаграмму более подробно. Мы знаем, что треугольник равнобедренный с основанием BC. Это означает, что AB и AC — ноги и конгруэнтны. Это также означает, что противоположные углы совпадают. Поскольку один угол обозначен как 20, мы можем обозначить угол C , угол, противоположный AB, также как 20.
Отсутствует информация о том, что сумма углов треугольника равна 180 °. Обладая этими знаниями, мы можем закончить определение угла A .
Угол A равен 140 °
Теорема о равнобедренном треугольнике (Доказательство, обратное, примеры и видео)
Теорема о равнобедренном треугольнике (доказательство, обратное и примеры)
Равнобедренные треугольники имеют равные ноги (вот что означает слово «равнобедренный»).Ура для них, но что мы знаем об их базовых углах? Откуда знать, что тоже равны? Мы залезаем в набор инструментов нашего геометра и извлекаем теорему о равнобедренном треугольнике. Не нужно подключать его к розетке или заряжать аккумулятор — он прямо у вас в голове!
- Равнобедренный треугольник
Равнобедренный треугольник
Здесь мы видим величественный равнобедренный треугольник △ DUK.Вы можете нарисовать его самостоятельно, взяв за образец △ DUK.
Хеш-метки показывают стороны ∠DU ≅ ∠DK, что указывает на то, что у вас равнобедренный треугольник. Если эти две стороны, называемые ногами , равны, тогда это равнобедренный треугольник. Что еще у тебя есть?
Свойства равнобедренного треугольника
Давайте использовать △ DUK для изучения деталей:
- Как и любой треугольник, △ DUK имеет три внутренних угла: ∠D, ∠U и ∠K
- Все три внутренних угла острые
- Как и любой треугольник, △ DUK имеет три стороны: DU, UK и DK
- ∠DU ≅ ∠DK, поэтому мы называем этих близнецов ногами
- Третья сторона называется основанием (даже если треугольник не находится на этой стороне)
- Два угла, образованные между основанием и ножками, ∠DUK и ∠DKU, или для краткости ∠D и ∠K, называются базовыми углами :
Теорема о равнобедренном треугольнике
Зная части треугольника, вот проблема: как доказать , что углы основания совпадают? Это суть теоремы о равнобедренном треугольнике , которая построена как условное утверждение (если, то) :
Теорема о равнобедренном треугольнике гласит: Если две стороны треугольника совпадают, тогда углов, противоположных этим сторонам, совпадают.
Чтобы математически доказать это, нам нужно ввести срединную линию, линию, построенную от внутреннего угла к средней точке противоположной стороны. Находим точку C на базе UK и строим линейный сегмент DC:
.
Вот! Это просто УТКА! Посмотрите на два треугольника, образованных медианой. Нам дано:
- UC ≅ CK (медиана)
- DC ≅ DC (рефлексивное свойство)
- DU ≅ DK (дано)
Мы только что показали, что три стороны DUC конгруэнтны △ DCK, что означает, что у вас есть Side Side Side Postulate , который дает конгруэнтность.Таким образом, если два треугольника конгруэнтны, то соответствующие части конгруэнтных треугольников конгруэнтны (CPCTC), что означает…
Обращение теоремы о равнобедренном треугольнике
Обратное условное утверждение делается путем замены гипотезы (если…) заключением (тогда…) . Возможно, вам придется повозиться с этим, чтобы убедиться, что это имеет смысл. Итак, вот еще раз теорема о равнобедренном треугольнике:
.
Если две стороны треугольника совпадают, тогда углов, противоположных этим сторонам, совпадают.
Чтобы сделать обратное, мы могли бы точно поменять местами детали, получая что-то вроде мешанины:
Если углов, противоположных этим сторонам, совпадают, , тогда две стороны треугольника совпадают.
Это неудобно, поэтому поправьте формулировку:
Теорема , обратная к равнобедренному треугольнику. Теорема утверждает: Если два угла треугольника совпадают, , тогда сторон, противоположных этим углам, совпадают.
Теперь это имеет смысл, но так ли это? Не все обратные утверждения условного утверждения верны. Если исходный условный оператор ложен, , тогда , обратное также будет ложным. Если предположение истинно, тогда обратное может быть истинным или ложным:
Если увижу медведя, тогда лягу и останусь на месте.
Если лягу и остаюсь неподвижным, тогда увижу медведя.
Для того, чтобы обратное утверждение было правдой, сон в своей постели стал бы странным занятием.
Или вот этот:
Если у меня мед, то медведей привлечу.
Если я привлекаю медведей, то у меня будет мед.
Если медведи не принесут приманки, чтобы поделиться с вами, обратное вряд ли когда-либо произойдет. А медведи очень эгоистичны.
Доказательство обратного утверждения
Чтобы доказать обратное, построим еще один равнобедренный треугольник △ BER.
Учитывая, что ∠BER ≅ ∠BRE, мы должны доказать, что BE ≅ BR.
Добавьте биссектрису угла от ∠EBR вниз к основанию ER. Там, где биссектриса угла пересекает основание ER, обозначьте это точкой A.
Теперь у нас есть два маленьких прямоугольных треугольника вместо одного большого равнобедренного треугольника: △ BEA и △ BAR. Поскольку отрезок BA является биссектрисой, получается EBA ≅ RBA. Поскольку отрезок BA используется в обоих меньших прямоугольных треугольниках, он конгруэнтен сам себе. Что у нас есть?
- ∠BER ≅ ∠BRE (дано)
- ∠EBA ≅ ∠RBA (биссектриса угла)
- BA ≅ BA (рефлексивное свойство)
Посмотрим… это угол, еще один угол и сторона.Это будет Угол Угол Сторона Теорема , AAS:
Теорема AAS гласит: Если два угла и не включенная сторона одного треугольника конгруэнтны соответствующим частям другого треугольника, тогда треугольники конгруэнтны.
Если сами треугольники конгруэнтны, их соответствующие части конгруэнтны (CPCTC), что делает BE ≅ BR. Обратное к теореме о равнобедренном треугольнике верно!
Краткое содержание урока
Выполнив эти упражнения, вы теперь можете распознать и нарисовать равнобедренный треугольник, математически доказать конгруэнтные равнобедренные треугольники с помощью теоремы о равнобедренных треугольниках и математически доказать обратное утверждение теоремы о равнобедренных треугольниках.Теперь вы также должны увидеть связь между теоремой о равнобедренном треугольнике с постулатом «сторона-сторона» и теоремой «угол-сторона».
Следующий урок:
Альтернативные внешние углы
Как найти площадь равнобедренного треугольника?
В этом уроке мы покажем простую стратегию решения следующей задачи: как найти площадь равнобедренного треугольника.
Давайте применим на практике ряд свойств, которые мы доказали до сих пор, в следующей геометрической задаче:
Задача
В равнобедренном треугольнике ΔABC с длиной катета 10 высота до основания равна две трети базы.Найдите площадь треугольника.
Стратегия
Чтобы решить эту проблему, мы будем работать в обратном направлении от того, что нам нужно делать.
Нам нужно найти площадь треугольника, которая, как мы знаем, дается формулой (основание, умноженное на высоту) / 2.
Проблема в том, что мы не знаем ни базовой длины, ни высоты. Но нам дана взаимосвязь между ними, и это подсказка о том, что нам нужно делать. Назовем длину основания BC, x.
Тогда мы знаем, что высота AD равна 2x / 3, как указано в задаче.
Итак, ответ, который мы ищем, будет (базовое умножение на высоту) / 2, или x умноженное на 2x / 3, деленное на два.
Но как нам найти x? В задаче нам были даны две дополнительные вещи, которые мы еще не использовали: длина ноги (10) и тот факт, что это равнобедренный треугольник. Вероятно, нам нужно использовать эти две вещи для решения проблемы.
Давайте рассмотрим свойства равнобедренных треугольников. Одна вещь, которая должна сразу прийти в голову, — это то, что, как мы показали, в равнобедренном треугольнике высота до основания делит основание пополам, поэтому CD = DB = x / 2.
Наконец, AD — это высота, что означает, что угол ∠ADC является прямым углом, и у нас есть прямоугольный треугольник ΔADC, гипотенуза которого мы знаем (10) и можем использовать для поиска катетов с помощью теоремы Пифагора, c 2 = a 2 + b 2,
, где c = 10, a = x / 2 и b = 2x / 3. И мы закончили, остальное просто алгебраическое решение относительно x.
Доказательство
(1) ΔADC — прямоугольный треугольник // заданный, поскольку AD — высота до основания
(2) AC 2 = CD 2 + AD 2 // Теорема Пифагора
( 3) AC = 10 // задано
(4) CB = x
(5) CD = x / 2 // Высота до основания в равнобедренном треугольнике делит основание пополам
(6) AD = 2x / 3 // задано
(7) 10 2 = (x / 2) 2 + (2x / 3) 2 // Заменить в (2)
(8) 100 = x 2 /4 + 4x 2 /9 // упростить
(9) 100 * 36 = 9x 2 + 16x 2 // умножить обе стороны на 36
(10) 100 * 36 = 25x 2 // собрать похожие термины
(11) 4 * 36 = x 2 // разделить на 25
(12) √144 = x // извлечь квадратный корень из обеих сторон
(13) 12 = x = CB
(14) AD = 2x / 3 = 2 * 12/3 = 8
(15) Площадь = 12 * 8/2 = 48
И вот как вы можете легко найти площадь равнобедренного треугольника!
Равнобедренный треугольник
Равнобедренный треугольник — это треугольник, у которого есть как минимум две стороны равной длины.На рисунке ниже приведены два примера.
AB≅AC
Части равнобедренного треугольника
Для равнобедренного треугольника только с двумя конгруэнтными сторонами конгруэнтные стороны называются катетами. Третья сторона называется базой. Угол, противоположный основанию, называется углом при вершине, а углы, противоположные ногам, называются углами основания.
Длины равнобедренного треугольника
Высота равнобедренного треугольника — это отрезок перпендикулярной линии, проведенный от основания треугольника к противоположной вершине.
Используя теорему Пифагора, мы можем найти, что основание, катеты и высота равнобедренного треугольника имеют следующие отношения:
Углы основания равнобедренного треугольника
Углы основания равнобедренного треугольника одинаковы по мере. См. Треугольник ABC ниже.
AB ≅AC, значит, треугольник ABC равнобедренный. ABC можно разделить на два равных треугольника, нарисовав отрезок AD, который также является высотой треугольника ABC.
Используя теорему Пифагора, где l — длина ног,. На основании этого △ ADB≅ △ ADC по теореме Side-Side-Side для конгруэнтных треугольников, поскольку BD ≅CD, AB ≅ AC и AD ≅AD. Итак, ∠B≅∠C, поскольку соответствующие части конгруэнтных треугольников также конгруэнтны.
Симметрия в равнобедренном треугольнике
Высота равнобедренного треугольника также является линией симметрии.
Участок AB отражается на высоте AD в участок AC. Точно так же нога AC отражается в ногу AB.База BC отражается сама на себя, когда отражается на высоте.
45-45-90 треугольников
Когда углы основания равнобедренного треугольника составляют 45 °, треугольник представляет собой специальный треугольник, называемый треугольником 45 ° -45 ° -90 °. Длина основания, называемого гипотенузой треугольника, умножена на длину его катета.
Апофема правильного многоугольника
Апофема правильного многоугольника — это также высота равнобедренного треугольника, образованного центром и стороной многоугольника, как показано на рисунке ниже.
