Луч — Геометрия 8 класс

На этом уроке мы по­го­во­рим о двух
ос­но­во­по­ла­га­ю­щих по­ня­ти­ях гео­мет­рии – луче и угле. Эти слова
вы слы­ша­ли еще в дет­стве: сол­неч­ный луч из­ве­стен каж­до­му,
кто-то мог слы­шать про рент­ге­нов­ские лучи. Угол есть у стола, а
ко­го-то из вас, воз­мож­но, ино­гда ста­ви­ли в угол ком­на­ты.
Раз­бе­рем­ся, что озна­ча­ют эти слова в гео­мет­рии.

На самом деле «гео­мет­ри­че­ский» луч не на­мно­го
от­ли­ча­ет­ся от сол­неч­но­го. Чем ин­те­ре­сен сол­неч­ный луч? У
него есть на­ча­ло – солн­це, а конца нет: его можно огра­ни­чить своей
ла­до­шкой или зем­лей, но если бы пре­пят­ствия не было – он шел бы и
даль­ше. То есть он имеет на­ча­ло, а с дру­гой сто­ро­ны –
бес­ко­не­чен, как пря­мая. (См. Рис. 1.)

Рис. 1. Сол­неч­ный луч

Со­от­вет­ствен­но, опре­де­ле­ние луча:

Лучом на­зы­ва­ет­ся часть пря­мой, огра­ни­чен­ная с одной сто­ро­ны
точ­кой. Эта точка иг­ра­ет роль солн­ца – там «на­чи­на­ет­ся» луч! То
есть луч имеет на­ча­ло, но не имеет конца, в от­ли­чие от от­рез­ка,
ко­то­рый огра­ни­чен с двух сто­рон.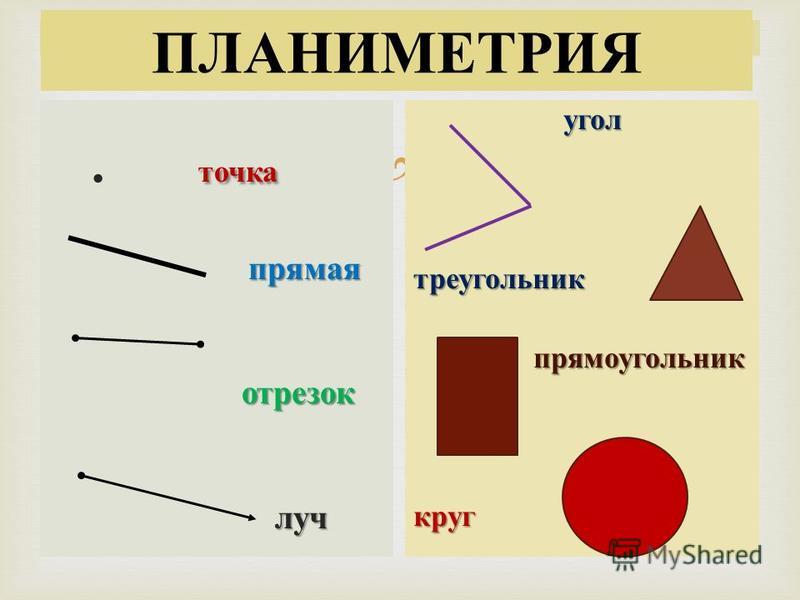 (См. Рис. 2.)

Рис. 2. Раз­ли­чие луча и от­рез­ка

Если рас­смот­реть го­ри­зон­таль­ную пря­мую  и точку  на ней, то точка  раз­би­ва­ет пря­мую на два луча: слева и спра­ва от . (См. Рис. 3.)

Рис. 3. Два луча: слева и спра­ва от

Точка  на­зы­ва­ет­ся вер­ши­ной луча. Чаще всего луч обо­зна­ча­ют двумя точ­ка­ми, на­при­мер . Для этого тре­бу­ет­ся по­ста­вить точку  с нуж­ной сто­ро­ны от . То есть точка  по­ка­зы­ва­ет, в каком на­прав­ле­нии идет луч, но не огра­ни­чи­ва­ет его. (См. Рис. 4.)

Рис. 4. Обо­зна­че­ние луча

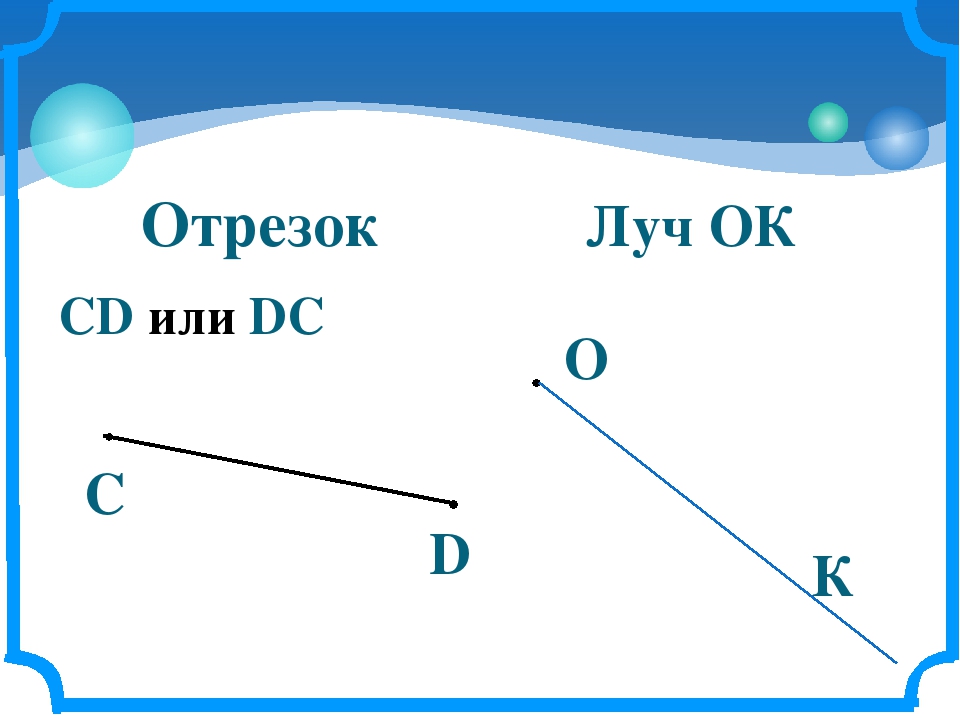
Об­ра­тим вни­ма­ние на раз­ни­цу между лучом , от­рез­ком  и пря­мой . От­ре­зок огра­ни­чен обе­и­ми точ­ка­ми (см. Рис. 5), луч – толь­ко точ­кой  (см. Рис. 6), пря­мая – не огра­ни­че­на (см. Рис. 7).

Рис. 5. От­ре­зок

Рис. 6. Луч

Рис. 7. Пря­мая

Также за­ме­тим, что от­рез­ки  и  – одно и то же, пря­мые  и  – тоже, а вот лучи – раз­ные. (См. Рис. 8.)

Рис. 8. Луч  (оран­же­вый) и луч  (синий)

Реже луч про­сто обо­зна­ча­ют малой бук­вой, но тут за­пу­тать­ся проще, так что ис­поль­зуй­те ис­ход­ные обо­зна­че­ния.

Ино­гда пря­мые, лучи и от­рез­ки обо­зна­ча­ют сле­ду­ю­щим об­ра­зом:  – пря­мая,  – луч,  – от­ре­зок. (См. Рис. 9.)

Рис. 9. От­ре­зок, луч и пря­мая

Вве­дем еще одно опре­де­ле­ние. Если два луча лежат на одной
пря­мой, имеют общую вер­ши­ну, но раз­ные на­прав­ле­ния – то их
на­зы­ва­ют до­пол­ни­тель­ны­ми. (См. Рис. 10.)

Рис. 10. До­пол­ни­тель­ные лучи

Угол – гео­мет­ри­че­ская фи­гу­ра, ко­то­рая со­сто­ит
из точки и двух лучей, ис­хо­дя­щих из этой точки. Лучи на­зы­ва­ют
сто­ро­на­ми угла, а их общее на­ча­ло – вер­ши­на. (См. Рис. 12.)

Рис. 12. Лучи  и  – сто­ро­ны угла, на­ча­ло лучей  – вер­ши­на угла

Обо­зна­ет­ся угол обыч­но тремя бук­ва­ми: одна на одной сто­роне
угла, затем – вер­ши­на, затем – точка на дру­гой сто­роне угла:  или , при­чем . Ино­гда знак «» пи­шет­ся над бук­ва­ми, и по­лу­ча­ет­ся: .

Об­ра­ти­те вни­ма­ние, что в неко­то­рых учеб­ни­ках угол
опре­де­лен иначе – мы дали опре­де­ле­ние по учеб­ни­ку Ата­на­ся­на.

За­ча­стую углы обо­зна­ча­ют и гре­че­ски­ми бук­ва­ми: . (См. Рис. 13.)

Рис. 13. Обо­зна­че­ние угла гре­че­ски­ми бук­ва­ми

На­ко­нец, угол можно обо­зна­чать через лучи, его об­ра­зо­вы­ва­ю­щие, на­при­мер . (См. Рис. 14.) Но в за­да­чах такое обо­зна­че­ние – ред­кость.

Рис. 14. Обо­зна­че­ние угла через на­зва­ния об­ра­зу­ю­щих лучей

Угол на­зы­ва­ет­ся раз­вер­ну­тым, если его сто­ро­ны – до­пол­ни­тель­ные лучи. (См. Рис. 15.)

Рис. 15. Раз­вер­ну­тый угол

За­ме­ча­ние 1. Об­ра­ти­те вни­ма­ние: мно­гие счи­та­ют, что раз­вер­ну­тый угол – .
Это верно, но это не опре­де­ле­ние! Не пу­тай­те, по­жа­луй­ста!
По­ня­тие гра­дус­ной меры нами в курсе гео­мет­рии пока вве­де­но не
было.

За­ме­ча­ние 2. Углом между пря­мы­ми на­зы­ва­ет­ся наи­мень­ший
угол (или один из наи­мень­ших углов), об­ра­зо­ван­ный при их
пе­ре­се­че­нии. (См. Рис. 16.)

Рис. 16. Крас­ным вы­де­лен угол между пря­мы­ми. Угол, вы­де­лен­ный серым цве­том, не счи­та­ет­ся углом между пря­мы­ми.

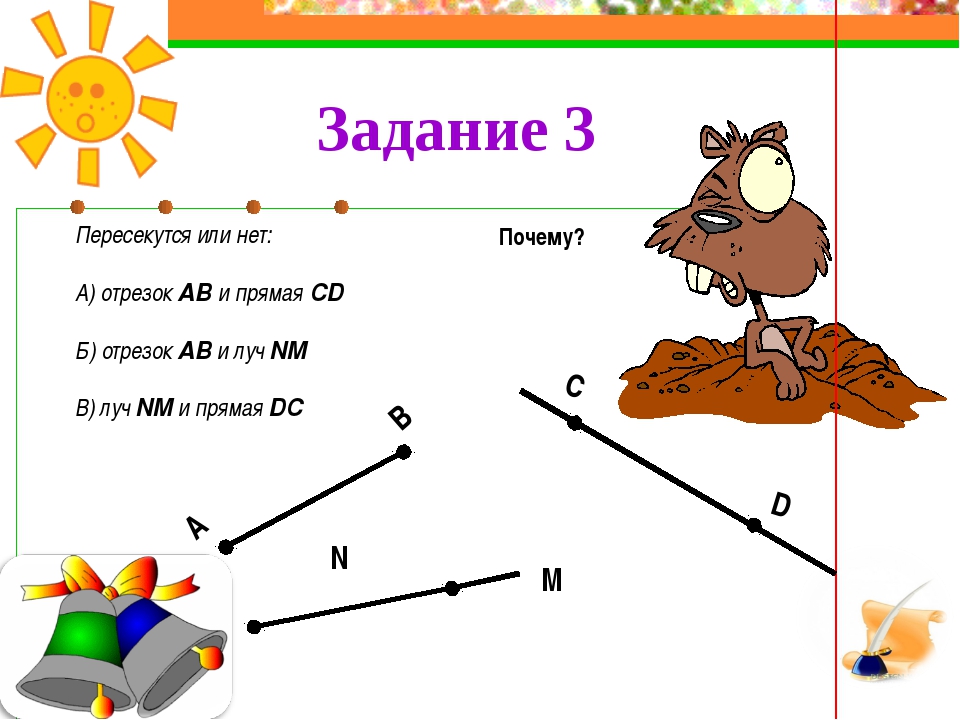
За­да­ча 1. Сколь­ко углов на ри­сун­ке? (См. Рис. 19.)

Рис. 19. Ил­лю­стра­ция к за­да­че 1

Ре­ше­ние: угла: , , . А как же углы , , ? Они сов­па­да­ют уже с упо­мя­ну­ты­ми уг­ла­ми, то есть ,  и .

Ответ:  угла.

За­да­ча 2. Две пря­мые  и  пе­ре­се­ка­ют­ся в точке . Сколь­ко углов с вер­ши­на­ми в дан­ных пяти точ­ках можно на­звать? (См. Рис. 20.)

Рис. 20. Ил­лю­стра­ция к за­да­че 2

Сразу в глаза бро­са­ют­ся , ,  и . Но, кроме этих углов, есть еще и раз­вер­ну­тые углы:  и . Итого,  углов.

Ответ:  углов.

На этом уроке были разо­бра­ны такие ба­зо­вые
по­ня­тия гео­мет­рии, как луч и угол. Луч – часть пря­мой,
огра­ни­чен­ная с одной сто­ро­ны точ­кой. Угол – гео­мет­ри­че­ская
фи­гу­ра, ко­то­рая со­сто­ит из точки и двух лучей, ис­хо­дя­щих из
этой точки.

http://interneturok.ru/geometry/7-klass/nachalnye-geometricheskie-svedeniya/luch-i-ugol

Практическое задание по теме «Луч»

А теперь возьмите в руки карандаш, линейку, отступите от «Классной работы» две клеточки вниз и нарисуйте луч произвольной длины.

(Я рисую на доске).

Обозначим
начало луча буквой О. Теперь отложим на луче 8 отрезков длинною в 1
см., а я на доске буду откладывать отрезки длинною в 1 дм., чтобы вам
было видно. Посмотрите, как я это делаю. Отмечаю на числовом луче
последовательно числа 1, 2, 3, и т.д.

Какая фигура была первоначально?

Теперь мы на луче отметили числа. Как теперь назовем фигуру?

На этом луче можно изобразить любое число в заданном направлении. Какое самое маленькое число можно изобразить на луче?

А можно узнать самое большое число? Почему?

Кто теперь может сформулировать тему нашего урока?

Начальные геометрические сведения.

Прямая, отрезок, луч и угол.

1. Базовые сведения о геометрии
2. Прямая и отрезок
3. Луч и угол

Добро пожаловать в удивительный мир геометрии. Сегодня мы познакомимся с очень важными и базовыми понятиями науки математики — прямой, отрезком, лучом и углом.

Базовые сведения о геометрии

Геометрия зародилась очень давно – около двух тысяч лет до нашей эры. Она родилась в связи с практическими нуждами людей в Древнем Египте. Слово «геометрия» — греческое. «Геос» переводится как земля, а «метрео» — измеряю. Геометрия – землемерение. В школах нашей страны изучается евклидова геометрия по имени великого ученого Евклида. Курс школьной геометрии делятся на планиметрию (7-9 класс) и стереометрию (10-11 класс). Планиметрия изучает свойства фигур на плоскости. Стереометрия изучает свойства фигур в пространстве.

Основными фигурами на плоскости точка и прямая. Все фигуры состоят из точек и прямых. Точки обозначаются большими латинскими буквами. Прямые обозначаются либо двумя большими латинскими буквами, либо одной маленькой. Точка — это мгновенное прикосновение карандаша к бумаге.

Прямая и отрезок

Прямая это фигура не имеет ни начала, ни конца.

Через любые две точки плоскости можно провести прямую и при том только одну. Если прямые имеют одну общую точку, то говорят, что они пересекаются в ней. Если прямые имеют две и более точек, то они совпадают. Если прямые не имеют общих точек, то они параллельны — A параллельна B.

На прямой точки могут лежать, а могут и не лежать. Посмотрите на  рисунок. Вы видите знак принадлежности, непринадлежности. Выражение точка А не принадлежит прямой а записывается короче с использованием этих значков.

Точка B не принадлежит прямой а.
Точка C принадлежит прямой а.
Точка D принадлежит прямой а.
Точка Е принадлежит прямой а
Точка F принадлежит прямой а, потому что прямую а можно продолжить, и тогда она будет проходить через точку F. Прямая не имеет ни начала, ни конца.

Если точка О принадлежит прямой а и точка О принадлежит прямой b одновременно, это означает, что прямые a и b пересекаются в точке О.

Часть прямой, ограниченная двумя точками называется отрезком. Отрезок можно обозначить либо AB, либо BA. Точки A и B — концы отрезка. Вообще, отрезок имеет и начало, и конец. Если на отрезке лежит точка О, то существует свойство: если к длине отрезка АО прибавить длину отрезка ОB, то получится весь отрезок AB.

Луч и угол

Если мы нарисуем прямую и далее отметим точку О, то эта точка разбивает прямую на два дополнительных луча — луч ОА и луч ОВ. Точка О — начало этих двух дополнительных лучей. Луч имеет начало, но не имеет конца. Обозначается луч либо двумя большими, либо одной маленькой латинской буквой. Луч — это тоже часть прямой.

Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Точка — это вершина угла, а лучи — это стороны угла. Углы обозначают большими латинскими буквами. Либо одной большой буквой по вершине угла, либо тремя большими буквами, в этом случае вершина О находится посередине, либо двумя маленькими буквами по названию лучей. Угол делит плоскость на две части – внутреннюю и внешнюю область угла.  Если внутри угла АОС проходит луч ОВ, то существует свойство: если к углу а AОB прибавить угол ВОС, то мы получим угол АОС.

Угол АОВ является частью угла АОС, значит угол АОВ меньше угла АОС. Точно так же угол ВОС – часть большого угла АОС, и значит угол ВОС меньше, чем угол АОС.

Луч, исходящий из вершины угла и делящий его на два равных угла, называют биссектрисой угла. При этом угол АОВ будет равен углу ВОС. ОВ – биссектриса.

Углы измеряются транспортиром. Углы измеряются в градусах, минутах, секундах. Например, угол А равен 60 градусов 51 минута 3 секунды.

1 градус — это 60 минут, 1 минута — это 60 секунд. Значит, в одном градусе 360 секунд. Развёрнутый угол — его градусная мера 180 градусов

Половина развернутого угла — это прямой угол. Мы его обозначаем квадратиком внутри угла, и он равен 90 градусов.

Острый угол находится в диапазоне от 0 до 90 градусов.

Тупой угол находится в диапазоне от 90 градусов до 180 градусов.

Прямая и отрезок. Луч и угол.

Мы
начинаем изучать новый предмет — геометрию.

В
переводе с греческого слово «геометрия» означает «землемерие» (гео — земля, метрео — мерить).
Это одна из самых древних наук.

Зарождение
геометрии было связано с необходимостью определять размеры участков земли, ориентироваться по расположению звёзд на небе,
строить  здания и сооружения. В результате такой деятельности накопилось
много правил, связанных с геометрическими построениями и измерениями, и геометрия
сформировалась как самостоятельная наука, занимающаяся изучением геометрических
фигур.

На
уроках математики вы познакомились с такими геометрическими фигурами как:

Школьный
курс геометрии делится на планиметрию и стереометрию. В планиметрии
рассматриваются свойства уже известных вам фигур на плоскости, таких, как
отрезок, прямоугольник, треугольник:

В
стереометрии изучаются свойства фигур в пространстве. Примерами таких
фигур являются параллелепипед, шар, цилиндр:

Мы
начнём изучение геометрии с планиметрии.

Давайте
поговорим о точках, прямых и отрезках. Точки обозначаются большими латинскими
буквами:

Прямые
обычно обозначаются малыми латинскими буквами. Прямая
не имеет толщины и ширины, простирается неограниченно в обе стороны. Туго
натянутая нить даёт нам представление о прямой:

Часть
прямой а, ограниченная двумя точками А и В (Б),
называется отрезком. Точки А и В,
ограничивающие отрезок, называются концами отрезка. Такой отрезок
обозначается АВ или ВА.

Поговорим
о свойствах прямой. Возьмём некоторую прямую а,
точки А и В, которые лежат на прямой а,
и точки C
и D,
которые не лежат на этой прямой. Другими словами можно сказать, что прямая
проходит через точки А и В, но не проходит через точки
C
и D.
Отметим, что через точки А и В нельзя провести другую
прямую, которая не совпадала бы с прямой а:

Таким
образом, можно сформулировать следующее свойство:

Через
любые две точки можно провести прямую и притом только одну.

Рассмотрим
теперь две прямые. Если прямые а и b
имеют
одну общую точку О, то говорят, что они пересекаются в
этой точке. А вот прямые p и q не
пересекаются:

Любые
две прямые могут иметь не более одной общей точки. Так как иначе, исходя из
сформулированного выше свойства, они будут совпадать. Таким образом, можно
сделать вывод: две прямые либо имеют только одну общую точку, либо не имеют
общих точек.

Поговорим
о луче. Проведём прямую а и отметим на ней точку О. Эта точка
разделяет прямую на две части, каждая из которых называется лучом,
исходящим из точки О. Точка О называется началом каждого из лучей:

Обозначаются
лучи обычно либо малой латинской буквой, например, луч h, либо двумя большими латинскими
буквами, например, луч ОА. Как видите, первая буква О
— начало луча, вторая точка А — произвольная точка на луче:

Угол
— это геометрическая фигура, которая состоит из точки и двух лучей, исходящих
из этой точки. Лучи называются сторонами угла, а их общее начало — вершиной
угла:

Изобразим
угол с вершиной О и сторонами h и
k.
На сторонах отметим точки А и В, тогда данный угол можно
обозначить как угол hk, или угол АОВ, или
просто угол О:

Углы
могут быть развёрнутыми и неразвёрнутыми.
Рассмотрим развёрнутый угол pq с вершиной С:

Обе
стороны такого угла лежат на одной прямой. Можно сказать, что каждая сторона развёрнутого
угла является продолжением второй. Отметим, что угол разбивает плоскость на две
части. У неразвёрнутого угла одна часть называется внутренней областью угла, а
другая — внешней.

А
если же угол развёрнутый, то любую из его частей можно считать внутренней:

Следует
помнить, что фигуру состоящую из угла и его внутренней
области, также называют углом.

В
заключении рассмотрим следующее. Возьмём некоторый неразвёрнутый угол АОВ, проведём
внутри угла из его вершины луч ОС:

Получим
два угла: угол АОС и угол СОВ. Если же взять развёрнутый угол АОВ, то любой луч
ОС, не совпадающий с лучами ОА и ОВ, делит этот угол на два угла АОС и СОВ.

Математика / 6 лет / Луч. Отрезок. Прямая.

Математика для дошкольников: геометрические основы

В возрасте шести лет очень важно уделить время знакомству с основными учебными дисциплинами. Это позволит максимально подготовить ребёнка к поступлению в первый класс общеобразовательной школы. Мозг малыша в этом возрасте переходит к активной фазе, и он способен усваивать большой объём информации. Необходимо не упустить этот момент и использовать его по максимуму. Родителям, при подготовке ребёнка к школе, стоит обратить внимание на различные программы, которые позволят ему изучить основы учебной программы начальных классов.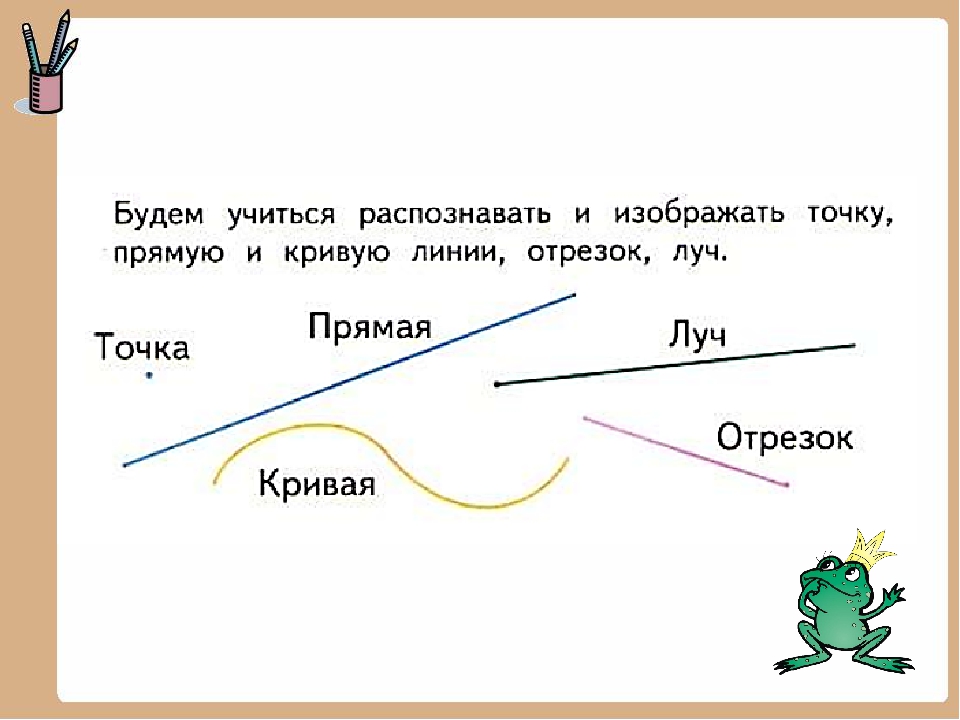  

Наши уникальные онлайн–программы обучения станут отличным помощником для родителей в данном вопросе. Все они разрабатывались командой профессионалов своего дела. Практикующие методисты, детские психологи и учителя младших классов, с большим опытом работы, работали над созданием наших эксклюзивных онлайн–курсов. Они смогли разработать программы, которые полностью соответствуют эмоциональные, возрастным и прочим потребностям современного поколения. 

Основной упор был сделан именно на возрастной особенности. В связи с этим, все наши задания представлены в игровом формате, как и советуют детские психологи. Ведь благодаря такой форме подачи материала, у малыша просыпается интерес к учёбе и получению все новых и новых знаний.

Геометрические основы

Изучая с дошкольником математику, не стоит забывать про основы геометрии, которые необходимо усвоить в возрасте шести лет. Именно в этом возрасте, ребёнок должен понимать, что из себя представляют лучи, отрезки и прямые. Какие из них отмечаются точками с двух сторон, а какие нет. Для того, чтобы помочь малышу в освоении основ геометрии, мы рекомендуем обратиться к нашему уникальному онлайн–курсу «Луч, отрезок, прямая» детям 6 лет. Именно с его помощью, Вы сможете научить своего ребёнка разбираться в этих понятиях легко и быстро. А благодаря игровому формату обучения, даже дошкольник будет увлечён процессом получения новых знаний. 

В данном разделе Вы найдёте:

•Теоретическую часть, с красочными иллюстрациями и основными понятиями геометрии;

•Интерактивные упражнения с картинками и аудиофайлами, которые позволят на практике закрепить полученные знания;

•Статистика успеваемости, с наглядным отражением успехов и сложностей в обучении Вашего ребёнка;

•Система поощрения, которая представлена в виде веселых звёздочек с мотивирующими обращениями.

Пройдя весь онлайн–курс, Вы сможете заметит, что ребёнок начинает лучше ориентироваться в основных геометрических понятиях. Он без труда сможет отличить отрезок от прямой. Эти знания значительно облегчат ему обучение в общеобразовательной школе на будущий год.

Присоединяйтесь к нам сегодня, чтобы уже завтра с гордостью наблюдать за успехами своего ребенка.

Презентация к уроку по геометрии в 7 классе : « Прямая и отрезок» | Презентация к уроку по геометрии (7 класс) по теме:

Слайд 1

Урок геометрии в 7 классе : « Прямая и отрезок» Выполнила учитель математики МКОУ Ясенковская СОШ Клейменова Татьяна Вячеславовна

Слайд 2

Цели урока : Познакомить учащихся с тем , что изучает геометрия, какой раздел геометрии называется планиметрией, какие фигуры в планиметрии называют основными ; систематизировать сведения о взаимном расположении точек и прямых ; рассмотреть свойство прямой : через любые две точки можно провести прямую, и притом только одну; научить обозначать точки и прямые на рисунке ; ввести понятие отрезка; рассказать о практическом проведении (провешивании) прямых на местности.

Слайд 3

Возникновение и развитие геометрии. Геометрия возникла в результате практической деятельности людей : нужно было сооружать жилища, храмы, прокладывать дороги, оросительные каналы, устанавливать границы земельных участков и определять их размеры.

Слайд 4

В переводе с древнегреческого слово «геометрия» означает «земледелие» ( « гео » -земля , а «метро»- мерить). Важную роль играли и эстетические потребности людей : желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений.

Слайд 5

За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания , которые добывались в основном опытным путем , но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построения прямых углов и т. д. Не было еще доказательств этих правил, и их изложение не представляло собой научной теории.

Слайд 6

Первым ,кто начал получать геометрические факты при помощи рас -суждений (доказательств), был древнегреческий ма -тематик Фалес ( VI в.до н.э.), который в своих исследованиях применял перегибание чертежа, поворот части фигуры и так далее, то есть то, что на современном языке называется движением.

Слайд 7

Постепенно геометрия становится наукой, в которой большинство фактов устанавливается путем выводов, рассуждений, доказательств. Попытки греческих ученых привести геометрические факты в систему начинаются уже в V веке до н.э. Наибольшее влияние на всё последующее развитие геометрии оказали труды греческого ученого Евклида , жившего в Александрии в III веке до н.э.

Слайд 8

Сочинение Евклида «Начала» почти 2000 лет служило основной книгой , по которой изучали геометрию . В «Началах» были систематизированы известные к тому времени геометрические сведения, и геометрия впервые предстала как математическая наука. Эта книга была переведена на языки многих народов мира , а сама геометрия, изложенная в ней, стала называться евклидовой геометрией .

Слайд 9

Что изучает геометрия? В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств : массы, цвета и т.д. Отвлекаясь от этих свойств и беря во внимание только форму и размеры предметов, мы приходим к понятию геометрической фигуры.

Слайд 10

Геометрия не только дает представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать , ставить вопросы, анализировать , делать выводы , то есть логически мыслить .

Слайд 11

Школьный курс геометрии делится на : планиметрию стереометрию Планиметрия – это раздел геометрии, изучающий свойства фигур на плоскости ( от латинского слова « платинум » — плоскость и греческого « метрио » — измеряю). Примеры плоских фигур : отрезок , луч , прямая, угол, окружность, круг, треугольник, прямоугольник . Стереометрия – это раздел геометрии, который изучает свойства фигур в пространстве. Примеры объёмных фигур : параллелепипед, шар, цилиндр, пирамида , конус…

Слайд 12

Вам уже знакомы некоторые геометрические фигуры . точка прямая отрезок луч угол треугольник прямоугольник круг

Слайд 13

Примеры объёмных фигур. куб шар конус цилиндр пирамида

Слайд 14

Точки, прямые, отрезки «Точка» в русском языке – конец заточенного гусиного пера. A C B D «Точка есть то, что не имеет частей» Евклид На рисунке изображены точки А , В , С и D .

Слайд 15

Точки, прямые, отрезки 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Прямая – множество точек, построенных с помощью линейки.

Слайд 16

Прямые обозначают так : m прямая m р прямая р А В прямая АВ С D прямая CD

Слайд 17

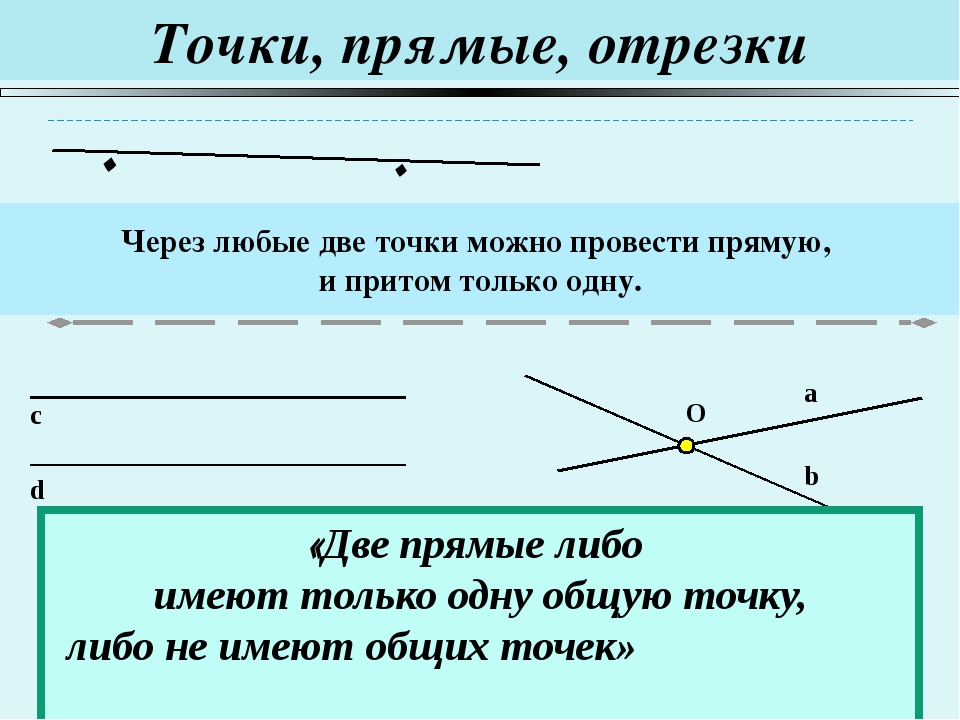
Точки, прямые, отрезки O a b Через любые две точки можно провести прямую, и притом только одну. c Две прямые либо имеют только одну общую точку, либо не имеют общих точек. . . d

Слайд 18

Точки, прямые, отрезки Отрезок – часть прямой, ограниченная двумя точками. Точки A и B – концы отрезка A B Отрезок с концами А и В обозначают АВ или ВА. Он содержит точки А и В и все точки прямой, лежащие между точками А и В.

Слайд 19

Практическое задание. Задания № 1 , 2 , 3 стр. 7

Слайд 20

Ответьте на вопросы: 1. Можно ли через данную точку провести прямую? 2. Сколько прямых можно провести через данную точку? 3. Сколько прямых можно провести через две данные точки? 4. Сколько общих точек могут иметь две прямые?

Слайд 21

Ответьте на вопросы 5. Могут ли прямые ОА и АВ быть различными , если точка О лежит на прямой АВ? 6. Даны две прямые а и в , пересекающиеся в точке С , и точка D , отличная от точки С и лежащая на прямой а. Может ли точка Д лежать на прямой в ?

Слайд 22

Выполните самостоятельно : Задание № 5 стр. 7

Слайд 23

Самостоятельная работа с учебником . 1. Прочитайте п. 2 стр. 6-7. 2. В чём заключается приём «провешивания прямой» и когда он применяется?

Слайд 24

Математический диктант. 1.Начертите прямую и обозначьте её буквой в. а) Отметьте точку М ,лежащую на прямой в. б) Отметьте точку Д , не лежащую на прямой в. в) Используя символы , запишите предложение : «Точка М лежит на прямой в , а точка Д не лежит на ней». 2. Начертите прямые а и в , пересекающиеся в точке К. На прямой а отметьте точку С , отличную от точки К. а) Являются ли прямые КС и а различными прямыми ? Ответ обоснуйте. б) Может ли прямая в проходить через точку С? Ответ обоснуйте.

Слайд 25

Итоги урока. Задайте вопросы своим одноклассникам по содержанию сегодняшнего урока.

Слайд 26

Есть вопросы… Непонятно! Всё понятно! Пункты 1 и2 , ответить на вопросы 1-3 на стр. 25 учебника Задания № 4, 6 , 7.

ПРЯМАЯ И ОТРЕЗОК — НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ

В первой главе рассматриваются простейшие геометрические фигуры — точка, прямая, отрезок, луч, угол, вопрос сравнения и измерения отрезков и углов, вводятся понятия смежных и вертикальных углов, перпендикулярных прямых.

Введение основных понятий опирается на наглядные представления и на тот опыт, который накоплен учащимися при изучении математики в 1-6 классах. Понятие аксиомы в первых двух главах не вводится, и сами аксиомы не формулируются в явном виде. Вместе с тем необходимые исходные положения, на основе которых изучаются свойства геометрических фигур, приведены в описательной форме уже в первой главе.

Изучение первой главы ставит перед учителем сложные методические задачи:

1) начать обучение школьников четким геометрическим формулировкам и рассуждениям;

2) постепенно подводить учащихся к пониманию необходимости доказательства каждого утверждения;

3) начать обучение умению выделить из текста геометрической задачи что дано и что требуется найти (или доказать), отразить ситуацию, данную в условии задачи и возникающую по ходу ее решения, на рисунке, кратко и чётко записать решение задачи. Этому школьники будут обучаться на протяжении всего курса геометрии, но при изучении этой главы закладываются основы будущих умений и навыков.

При решении задач этой главы следует прежде всего опираться на наглядные представления учащихся. Письменные формы работы являются важнейшим видом деятельности, формирующим устойчивые навыки в логических рассуждениях при решении задач.

Форма записи условия задачи, разумные сокращения и обозначения, расположение в тетради вычислений и доказательств дисциплинируют мышление.

Практические приложения геометрического материала, изложенного в этой главе, раскрываются в пунктах «Провешивание прямой на местности», «Единицы измерения. Измерительные инструменты» и «Измерение углов на местности». Соответствующую практическую работу можно выполнить в удобное время учебного года.

Урок 1. ПРЯМАЯ И ОТРЕЗОК (§ 1)

Цели: познакомить учащихся с тем, что изучает геометрия, какой раздел геометрии называется планиметрией, какие фигуры в планиметрии называются основными; систематизировать сведения о взаимном расположении точек и прямых; рассмотреть свойство прямой: через любые две точки можно провести прямую, и притом только одну; научить обозначать точки и прямые на рисунке; ввести понятие отрезка; рассказать о практическом проведении (провешивании) прямых на местности.

Ход урока

I. Вводная беседа о возникновении и развитии геометрии (10-12 мин).

ПЛАН БЕСЕДЫ

1. Зарождение геометрии.

2. От практической геометрии к науке геометрия.

3. Геометрия Евклида.

4. История развития геометрии.

5. Геометрические фигуры.

Геометрия возникла в результате практической деятельности людей: нужно было сооружать жилища, храмы, прокладывать дороги, оросительные каналы, устанавливать границы земельных участков и определять их размеры. В переводе с греческого слово «геометрия» означает «землемерие» («гео» — по-гречески земля, а «метрео» — мерить). Такое название объясняется тем, что зарождение геометрии было связано с различными измерительными работами.

Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений.

За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания, которые добывались в основном опытным путем, но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построения прямых углов и т. д.

Не было еще доказательств этих правил, и их изложение не представляло собой научной теории.

Первым, кто начал получать геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес (VI в. до н. э.), который в своих исследованиях применял перегибание чертежа, поворот части фигуры и так далее, то есть то, что на современном геометрическом языке называется движением.

Постепенно геометрия становится наукой, в которой большинство фактов устанавливается путем выводов, рассуждений, доказательств.

Попытки греческих ученых привести геометрические факты в систему начинаются уже с V в. до н. э. Наибольшее влияние на всё последующее развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в III в. до н. э. Сочинение Евклида «Начала» почти 2000 лет служило основной книгой, по которой изучали геометрию. В «Началах» были систематизированы известные к тому времени геометрические сведения, и геометрия впервые предстала как математическая наука.

Эта книга была переведена на языки многих народов мира, а сама геометрия, изложенная в ней, стала называться евклидовой геометрией.

В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, цвета и т. д. Отвлекаясь от этих свойств и беря во внимание только форму и размеры предметов, мы приходим к понятию геометрической фигуры.

На уроках математики вы познакомились с некоторыми геометрическими фигурами и представляете себе, что такое точка, прямая, отрезок, луч, угол, как они могут быть расположены относительно друг друга. Вы знакомы с такими фигурами, как треугольник, прямоугольник, круг (показать модели этих фигур).

Геометрия не только дает представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, то есть логически мыслить.

Школьный курс геометрии делится на планиметрию и стереометрию. Такие фигуры, как отрезок, луч, прямая, угол, окружность, круг, треугольник, прямоугольник, являются плоскими, то есть целиком укладываются на плоскости. Раздел геометрии, изучающий свойства фигур на плоскости, называется планиметрией (от латинского слова «планум» — плоскость и греческого «метрео» — измеряю).

В стереометрии изучаются свойства фигур в пространстве, таких как параллелепипед, шар, цилиндр, пирамида (показать модели). Мы начнем изучение геометрии с планиметрии.

II. Изучение нового материала.

1. Повторение известного учащимся материала о точках и прямых, их изображении и расположении относительно друг друга.

2. Прямая безгранична, а на рисунке изображается только часть прямой.

3. Обозначение прямых малыми буквами латинского алфавита или двумя большими буквами, соответствующими двум точкам, лежащим на прямой.

(Рисунки выполнять на доске и в тетрадях; рассмотреть по учебнику рисунки 4, 5 и 6 на с. 5.)

4. Выполнение практического задания № 1 (с. 7 учебника). Символы ∈ и ∉.

5. Вопросы к учащимся:

1) Можно ли через данную точку провести прямую?

2) Сколько прямых можно провести через данную точку?

Учащиеся должны сделать вывод: «через данную точку можно провести сколько угодно прямых».

3) Сколько прямых можно провести через две данные точки? (Ответ: только одну.)

Учащиеся проводят прямую через две данные точки и находят в п. 1 учебника утверждение: «через любые две точки можно провести прямую, и притом только одну».

Это утверждение выражает неискривленность прямой, то есть то свойство, которое отличает прямую от других линий (через две данные точки можно провести сколько угодно кривых линий, например окружностей, а прямых — только одну).

6. Рассмотрение различных случаев взаимного расположения двух прямых на плоскости (с помощью рисунков учебника, плакатов, таблиц, транспарантов для графопроектора).

Учащиеся делают вывод: две прямые не могут иметь более одной общей точки.

III. Выполнение практических заданий.

1. Учащиеся выполняют практические задания № 2, 3 на с. 7 учебника.

2. Вопросы к учащимся:

1) Могут ли прямые ОА и АВ быть различными, если точка О лежит на прямой АВ? (Ответ: прямые ОА и АВ не могут быть различными, так как обе они проходят через точки А и О, а через две точки проходит только одна прямая. )

2) Даны две прямые а ив, пересекающиеся в точке С, и точка Д, отличная от точки С и лежащая на прямой а. Может ли точка Д лежать на прямой в? (Ответ: точка Д не может лежать на прямой в, так как две прямые не могут иметь двух общих точек.)

3. Ввести понятие отрезка (использовать рисунок 7 учебника).

4. Самостоятельное выполнение учащимися задания № 5.

5. Изложение материала п. 2. «Провешивание прямой на местности» в виде беседы (по рис. 8 и 9 учебника).

IV. Проверка усвоения изученного материала.

Самостоятельная работа проводится в форме диктанта:

1. Начертите прямую и обозначьте ее буквой в.

1) Отметьте точку М, лежащую на прямой в.

2) Отметьте точку Д, не лежащую на прямой в.

3) Используя символы ∈ и ∉, запишите предложение: «Точка М лежит па прямой в, а точка Д не лежит на ней».

2. Начертите прямые а я в, пересекающиеся в точке К. На прямой а отметьте точку С, отличную от точки К.

1) Являются ли прямые КС и а различными прямыми? Ответ обоснуйте.

2) Может ли прямая в проходить через точку С? Ответ обоснуйте.

3*. Сколько точек пересечения могут иметь три прямые? Рассмотрите все возможные случаи и сделайте соответствующие рисунки.

4*. На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки.

V. Итоги урока.

Учащиеся отвечают на вопросы:

1. Сколько прямых можно провести через две точки?

2. Сколько общих точек могут иметь две прямые?

3. Какая фигура называется отрезком?

4. Как обозначаются точки и прямые на рисунке?

Домашнее задание: пункты 1, 2; ответить на вопросы 1-3 на с. 25 учебника; практические задания № 4, 6 и 7.

На первых уроках, комментируя домашнее задание, следует показать учащимся на примерах вопросов 1-3 повторения, как находить на них ответы в тексте учебника.

Урок в рамках математического кружка «Занимательная геометрия» «Точка, прямая, отрезок, луч»

Цель: Изучить такие математические
понятия как точка, прямая, отрезок, луч в
интерактивной геометрической среде “Geogebra”.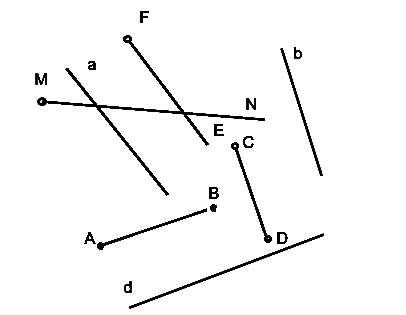

Задачи:

образовательные:

-закрепить понятия точка, прямая,
отрезок, луч;

-закрепить понятие буфер обмена;

-продолжить знакомство учащихся с
основными элементами интерфейса программы
“Geogebra”;

-научить строить простейшие чертежи в
ИГC “Geogebra”;

-научить учащихся решать
разнообразные классы задач из разделов курса
математики (в том числе задач требующих поиска
путей и способов решения, в частности с помощью
информационных ресурсов)

воспитательные:

-воспитание культуры личности через
освоение компьютерной грамотности;

-воспитание отношения к математике как
части общечеловеческой культуры, играющей
особую роль в общественном развитие;

развивающие:

-развивать ясно, грамотно излагать сои
мысли в устной речи, в частности с использованием
компьютерной лексики.

-развивать умения и навыки уверенного
пользователя ПК.

ТСО: ноутбук, мультимедиа-проектор,
экран, ПК(урок проводится в компьютерном классе),
www.geogebra.org
(ИГC “Geogebra”).

План урока

1.Организационный момент.

2.Сообщение цели и темы урока.

3.Повторение опорных знаний и
практического опыта.

4. Закрепление и формирование понятий
точка, отрезок, прямая, луч. Данный материал
отрабатывается включением учащихся в
деятельность актуализации этих понятий (ИГC
“Geogebra”)

5.Выполнение творческого задания.

6.Домашнее задание.

Ход урока

1.Организационный момент.

Здравствуйте, ребята!

2. Сообщение цели и темы урока.

Ребята, тема нашего урока сегодня
“Точка, прямая, отрезок, луч.”.

3.Повторение опорных знаний и
практического опыта.

Из курса математики мы уже знакомились
с понятием точка, прямая, луч. Напомним их еще раз:

Точка — обширное понятие. В русском
языке это знак препинания, в математике –
геометрический объект. Чтобы изобразить точку,
достаточно острием карандаша оставить “след”
на плоскости листа.

Точка (стихотворение)

ТОЧКА

Кто наук не знает точных,

Сказать может так:

«Что такое эта Точка?..

Маленький пустяк!»

Вас, друзья мои, прошу я

Не рубить сплеча.

Ставьте Точку на прямую —

Будет два луча.

Строим мы для разных функций

График-эталон,

Это точек совокупность,

Где един закон.

Не поставив центра точку,

Круг не обведешь.

Не узнав вершину точно,

Угол не найдешь…

Ее роль всегда прекрасна,

Пусть она мала…

Точку ставят не напрасно

Во главу угла!

Далее на доске строятся различные
точки учителем, и обозначаются заглавными
буквами латинского алфавита. После повторения
данного элемента начинается работа на
компьютерах. Учитель задает темп на ПК в ИГC
“Geogebra” демонстрируя при помощи видеопроектора
на экране все операции.

Ребята, в это время параллельно
выполняют это же задание в среде “Geogebra”.

Если точки А и В с помощью линейки
соединить линией, то мы получим объект, который
называется Отрезок (это следующее понятие с
которым мы познакомились)

(Стихотворение про отрезок)

ОТРЕЗКИ

Кто линейку в руки брал,

Тот меня сейчас узнал.

Есть концы — зовусь отрезок,

Убери их — интервал.

Вот две точки пред тобой.

Хочешь видеть облик мой?

Поскорей соедини их

Строгой линией прямой.

Пусть мала моя длина,

Моя помощь всем нужна.

У окружности я — хорда,

У квадрата — сторона.

Мы везде, со всех сторон,

Я совсем не пустозвон:

Там прямее, чем стрела

Тень от столбика легла,

Угол от земли до крыши,

А здесь — краешек стола.

Оцените нас сполна:

Есть особенность одна

У семьи отрезков славной —

Точная величина.

В бесконечность не летим,

Знаем все, чего хотим,

Дайте нам по паре точек,

Мы их вмиг соединим.

Учащиеся на доске строят отрезок,
остальные выполняют это в среде “Geogebra”.
Обозначают начало и конец отрезка. Производят
необходимые измерения.

Начертили отрезок АВ и продолжили его
в обе стороны. Что получим? — Новое понятие-Прямая.

ПРЯМАЯ

Вперед! Назад! А в сторону ни шага —

Вот принцип самый главный у Прямой.

Нужна здесь прямота, нужна отвага,

Чтоб вдруг не изменить себе самой.

Знаком со мною каждый малый школьник

Совсем не зря сложили этот стих,

Ведь состоит любой многоугольник

Из маленьких отрезочков моих.

Вот биссектриса, луч, отрезок, хорда,

Диагонали… всех не перечесть.

Лучи мои, отрезки… Знаю твердо,

Что прямота моя в них точно есть!

А если ты хотя бы на мгновенье,

Меня заставишь сникнуть головой,

Сменить мое захочешь направленье…

Я стану ломаной, но только не кривой!

Оказывается через любые две точки
проходит единственная прямая.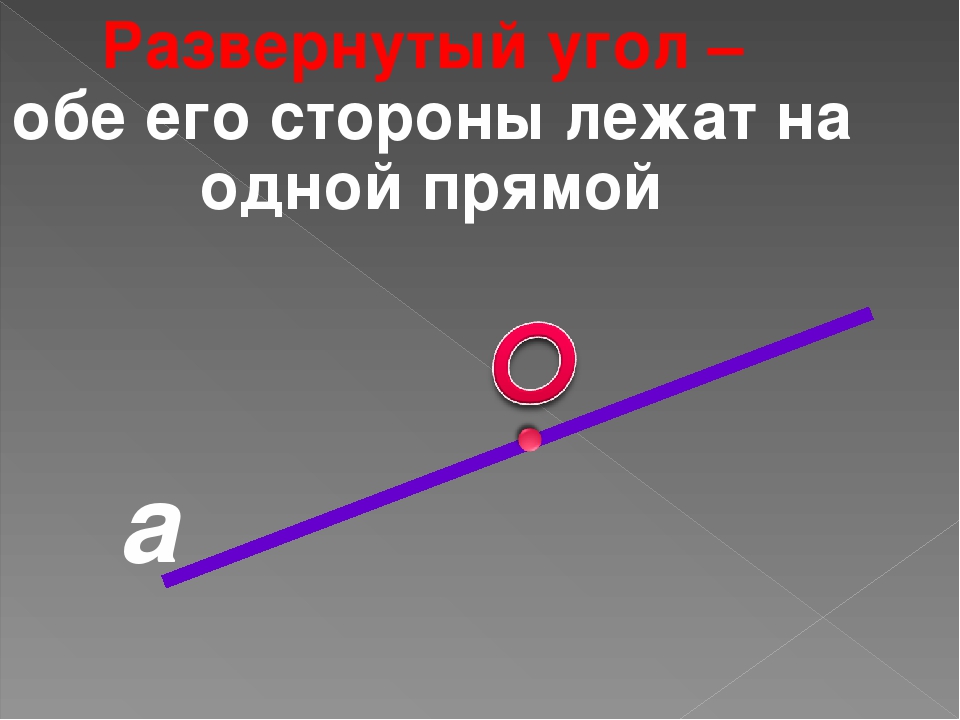 Попробуйте
опровергнуть это утверждение (ребята пробуют это
сделать в графической среде “Geogebra”). На доске
также строятся прямые, с различными
обозначениями. Один из учеников может
демонстрировать свои доказательства на доске,
другой на экране с помощью мультимедийного
проектора.

Если по прямой отметить точку, она
поделит прямую на две части. Каждую из этих
частей называют Лучом. Чертеж луча
демонстрируется на экране.

(Стихотворение про луч)

ЛУЧ

Лучу не свойственна печаль,

И без раздумий, без отсрочки

Он мчится в бесконечность, в даль,

Не помня об исходной точке.

Но коль осудишь, помолчи —

Мы все Земли и Солнца дети,

Известно: Солнышка лучи

Жизнь породили на планете.

Лучи помогут нам везде.

На небе много звёзд сияет,

И мы не знаем о звезде,

Что к нам лучи не посылает.

Но так бывает иногда,

Вот характерная беспечность,

Уже погасла та звезда,

А луч все мчится в бесконечность.

4.Закрепление изученных понятий точка,
отрезок, прямая, луч продолжается с включением
учащихся в деятельность актуализации этих
понятий.

Применение приобретенных знаний
продолжается при построении точки, отрезка,
прямой, луча в “Geogebra”. С этой целью могут быть
предложены творческие задания, которые ученики
могут выполнять на ПК. <Рисунок6>, <Рисунок7>,
<Рисунок8>, < Рисунок9>

5.Выполнение творческого задания.

Выполнившим основные упражнения,
можно открыть доступ к индивидуальному заданию.
Ребята выполняют рисунок в графическом
растровом редакторе Paint при помощи простейших
геометрических фигур. Полученное изображение,
используя буфер обмена, учащиеся переносят в
геометрическую среду “Geogebra”.

6.Домашнее задание.

Изобразить в ИГC “Geogebra” рисунок, где
встречаются геометрические понятия точка,
отрезок, прямая, луч (выполнение задания
возможно преобразовать в более творческом
направление – выполнит рисунок самостоятельно
художественными средствами на бумаге).

Введение в Point, Ray, Line и Line-Segment — MathsTips.com

Point

Point — это основной строительный блок геометрии. Каждая форма создается путем объединения точек.

Маленькая точка, отмеченная карандашом, — это точка. У точки нет ни длины, ни ширины. У него нет толщины. Точка — это знак положения. Точка указывает точное местоположение. Точка обозначена точкой (. ) И названа в алфавитном порядке.

На рисунке выше O — точка, так как на ней есть определенная отметка.Здесь это означает, что эта точка O расположена в центре плоскости. На рисунке ниже есть еще одна точка А. Она находится в правом нижнем углу плана.

Луч

Давайте представим факел. Световые лучи выходят из него и удаляются. Возьмем, к примеру, солнце. Лучи исходят от солнца и расходятся во все стороны, доходя до нас.

Также в геометрии луч начинается из точки и может уходить в бесконечность. У него есть начальная точка, но нет конечной точки. Мы говорим, что луч имеет одну конечную точку и идет без конца в одном направлении.

На приведенном выше рисунке начинается с A, а стрелка означает, что он может уходить в бесконечность.

Его длину невозможно измерить. Неограниченное количество лучей может быть проведено в разные стороны от заданной точки

Лучи, исходящие от факела или солнца, являются примерами лучей.

Это луч, потому что луч имеет одну конечную точку и идет без конца в одном направлении

Строка

Посмотрите на рисунок выше. С двух сторон есть стрелки.Это означает, что он может идти дальше с обеих сторон без конца. Это называется линия.

Линия идет без конца в обоих направлениях. Оба конца линии могут уходить в бесконечность. Линия не имеет конечных точек. Длину линии невозможно измерить. Линия не имеет определенной длины.

Линия называется любыми двумя точками на ней и записывается как линия AB или линия PQ. Можно провести одну и только одну линию, проходящую через две заданные точки A и B. Эта линия называется AB. Его также можно назвать БА. Линия BA совпадает с линией AB.Оба проходят через одни и те же две точки A и B.

Можно провести неограниченное количество линий, проходящих через заданную точку A.

Горизонтальная линия идет прямо влево или вправо. Вертикальная линия идет прямо вверх или вниз.

Диагональная линия может проходить в любом направлении между горизонтальной линией и вертикальной линией.

Линейный сегмент

Теперь посмотрим на рисунок выше. Ни на одном конце стрелки нет. Он начинается с одной точки и заканчивается в другой точке.Это называется отрезком линии. Отрезок линии — это отрезок линии.

Линейный сегмент имеет две конечные точки. Отрезок — это прямая линия, соединяющая две точки. Это кратчайший путь между двумя точками. Отрезок линии имеет определенную длину. Его длину можно измерить.

Отметим карандашом две маленькие точки (.) Как точки A и B. Соединим их, проведя прямую линию. Это образует линейный сегмент. Линейный сегмент называется по двум его конечным точкам и записывается как линейный сегмент AB или линейный сегмент PQ.

На рисунке выше отрезок AB имеет две конечные точки A и B. Он начинается из точки A и заканчивается в точке B. Один и только один отрезок прямой может находиться между двумя заданными точками A и B. называется AB. Его также можно назвать БА. Линия BA совпадает с линией AB. Оба проходят через одни и те же две точки A и B.

Сегмент линии также может быть частью линии, как показано на рисунке ниже.

Линейный сегмент также может быть частью луча.На рисунке ниже отрезок AB имеет две конечные точки A и B. Это часть луча, начинающегося с A.

Параллельные линии

Две линии в одной плоскости либо встречаются, либо не встречаются. Если две прямые на плоскости пересекаются, мы говорим, что две прямые пересекаются, и точка, в которой они встречаются, называется точкой пересечения. Если две линии не могут встретиться ни в одной точке, они называются параллельными линиями. Две точки не могут быть общими для двух параллельных линий.

На рисунке выше две линии не пересекаются.Даже если мы продолжим эти линии дальше, они не будут касаться и встречаться друг с другом. Это параллельные линии.

Пересечение линий

Давайте посмотрим на две линии AB и CD на рисунке выше. Они пересекаются в точке O. Следовательно, они не параллельные прямые.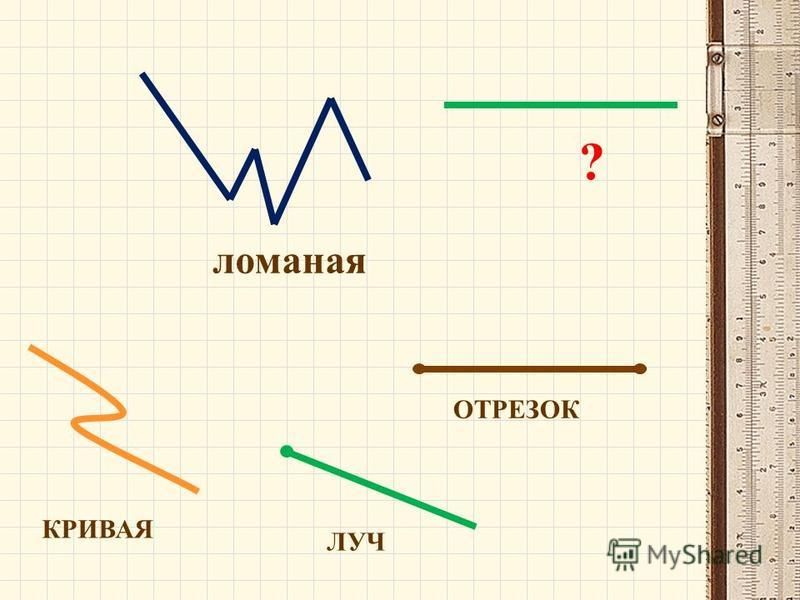 Точка O — это точка их пересечения.

Параллельные линии

Три или более прямых, проходящих через одну и ту же точку на плоскости, называются параллельными линиями. На рисунке ниже три прямые AB, CD и EF пересекаются друг с другом в точке O.

Коллинеарные точки

Три или более точки на плоскости * называются коллинеарными, если все они лежат на одной прямой.

На рисунке выше точки A, B и C находятся на одной линии. Следовательно, эти три точки A, B и C лежат на одной прямой.

* Плоская поверхность в геометрии называется плоскостью. Можно сказать, что листок из нашей тетради — это самолет.

Измерение отрезка

Линейка — геометрический инструмент.Мы используем линейку, чтобы нарисовать отрезок линии. Мы также используем его для измерения длины отрезка линии.

Линейка обычно имеет длину 1 фут (30 см) и называется одноногой линейкой. Иногда это просто называют масштабом. Некоторые линейки имеют длину шесть дюймов (15 см) и называются линейкой на полфута. На одном крае линейки нанесены шкалы в дюймах, а на другом — в сантиметрах.

Размещаем линейку краем вдоль отрезка AB с нулевой отметкой линейки в начальной точке A отрезка.Мы читаем метку на линейке в другой конечной точке B отрезка.

Что следует помнить

1. Маленькая отмеченная точка — это точка.
2. У точки нет длины, ширины или толщины.
3. Точка указывает точное местоположение.
4. Луч начинается из точки и уходит в бесконечность.
5. Линия не имеет конечных точек.
6. Линейный сегмент имеет две конечные точки.
7. Линейный сегмент соединяет обе конечные точки.
8. Если две прямые не могут пересечься ни в одной точке, они называются параллельными линиями.
9. Три или более точки на одной прямой считаются коллинеарными точками
10. Линейка используется для рисования отрезка и измерения его длины.

Вопросы и ответы

Вопрос 1 : Нарисуйте на бумаге две точки A и B и нарисуйте отрезок линии.

Ответ : Мы отмечаем точку A на странице письма, а затем отмечаем другую точку B на той же странице. Соединяем эти две точки линией. Это отрезок линии.

Вопрос 2: Нарисуйте две пересекающиеся линии.

Ответ: Берем линейку и проводим линию АВ. Затем слегка поворачиваем линейку и проводим еще одну линию CD таким образом, чтобы она проходила через любую точку линии AB.

Вопрос 3: Напишите два основных различия между линией и отрезком линии.

Ответ:

1. Линейный сегмент имеет две конечные точки. Линия не имеет конечной точки.
2. Отрезок имеет определенную длину. Но у линии нет определенной длины.

Вопрос 4: Напишите два основных различия между линией и лучом.

Ответ:

1. Линия идет без конца в обоих направлениях, но луч имеет одну конечную точку и идет без конца в одном направлении.
2. Линия AB такая же, как линия BA. Но луч AB отличается от луча BA.

Вопрос 5: Что означают коллинеарные точки?

Ответ: Коллинеарные точки — это точки на одной прямой.Три или более точки на плоскости называются коллинеарными, если все они лежат на одной прямой.

Упражнение

1. Определите рисунок ниже?

1. Луч
2. Строка
3. Линейный сегмент

2. Определить рисунок ниже?

1. Луч
2. Строка
3. Линейный сегмент

3. Обозначить рисунок ниже?

1. Луч
2. Строка
3. Линейный сегмент

4.Что из следующего имеет определенную длину?

1. Луч
2. Строка
3. Линейный сегмент

Верно или неверно

5. Две линии на рисунке ниже — параллельные линии

1. Истинно
2. Ложь

6. Две линии на рисунке ниже — параллельные линии

1. Истинно
2. Ложь

Заполните пропуски

7. ………………… имеет определенную длину

1. Луч
2. Строка
3. Линейный сегмент

8.………………… не имеет конечных точек

1. Луч
2. Строка
3. Линейный сегмент

9. Что из перечисленного является только одной конечной точкой?

1. Луч
2. Строка
3. Линейный сегмент

10. Какое из следующих утверждений НЕ правильно?

1. Через точку можно провести неограниченное количество линий.
2. Две линии всегда встречаются в какой-то момент.
3. Линия длиннее отрезка.

Геометрия — основные положения (предварительная алгебра, введение в геометрию) — Mathplanet

Точка обозначается точкой и представляет конкретное местоположение. У него нет ни шестерки, ни формы.

Линия определяется как линия точек, бесконечно продолжающаяся в двух направлениях, что показано стрелками. Линия определяется двумя точками на линии и имеет только одно измерение.

Сегмент линии — это часть линии, у которой есть две определенные конечные точки.Линейный сегмент представляет собой набор точек внутри конечных точек, и он назван по своим конечным точкам.

Луч — это линия, у которой есть только одна определенная конечная точка и одна сторона, бесконечно идущая от конечной точки. Луч получает имя по его конечной точке и по другой точке на линии.

Угол, образованный двумя лучами с одинаковой конечной точкой, называется вершиной. Вершина измеряется в градусах, проще всего ее измерить с помощью транспортира.

Углы можно измерять с помощью транспортира.

Углы можно классифицировать по их размеру. Прямой угол имеет размер 90 °, тогда как угол между 0 ° и 90 ° называется острым углом. Угол, который составляет от 90 ° до 180 °, называется тупым углом, тогда как прямой угол составляет 180 °.

Плоская поверхность без краев и границ называется плоскостью. Он бесконечно простирается в двух измерениях и назван тремя точками на плоскости, которые не находятся на одной прямой e.грамм. xyz. Примером плоскости может быть координатная плоскость.

Две линии, которые встречаются в точке, называются пересекающимися линиями

Две прямые, которые находятся в одной плоскости и никогда не пересекаются, называются параллельными линиями

Перпендикулярные линии (или лучи) — это линии, пересекающиеся под прямым углом. Обозначение перпендикуляра —

.

Наклонные линии — это линии, которые не находятся в одной плоскости.

Видеоурок

Классифицируйте все углы

Линия, сегмент линии и геометрия лучей

Овладейте семью столпами успеха в школе

Повысьте свои оценки и снизьте уровень стресса

Common Core Standard G. CO.1

Коллинеарность — это когда у вас есть три или более точек на прямой. Точки A, B и C коллинеарны.

Технически линия — это группа точек на прямой. Линейный сегмент отличается от линии, потому что у него есть конечные точки по сравнению с линией, у которой нет конечных точек, и он тянется в обоих направлениях бесконечно. Посмотрите видео слева, чтобы наглядно увидеть линию.

Точка отмечает точное местоположение. В классе геометрии мы обычно отмечаем точку, делая точку карандашом, но на самом деле точка не имеет размера. Точка не имеет размера или размеров, потому что она отмечает место и не является объектом.

Точки обозначаются заглавными буквами.

Вы также можете использовать строчные буквы для наименования строки. Например:

После того, как вы пометили точки, наименование линии упрощается.

Как назвать линию?

В геометрии линия имеет следующие свойства:

• Бесконечно простирается в обоих направлениях

Линия или отрезок можно назвать отрезком чтобы сначала назвать точку. В этом примере у вас будут точки A, B и C.

При названии точки используется заглавная буква.

Шаг 1. Укажите две точки

Шаг 2. Используйте заглавные буквы

Шаг 3. В этой точке вы можете обозначить линию, нарисовав стрелку над прописными буквами, или нарисовать прямую линию для отрезок .

Линия 1 Линия q

Линия 2 Линия м

Что такое луч в геометрии

Луч — это линия с начальной точкой, называемой конечной точкой. Луч движется в одном направлении на бесконечность и может проходить через другие точки на своем пути до бесконечности.

Свойства луча в геометрии

• Имеет начальную точку, называемую конечной точкой

• Продолжается в одном направлении бесконечно

• Иногда называется «полулинией»
  9114 904 Луч в геометрии
  • Используйте стрелку для направления луча
  • Если он проходит через конечную точку, он включается в его имя

  У математики есть свой уникальный язык и метод общения, и вот несколько советов о том, как выражаются линии.

  Quia — Словарь геометрии

  биссектриса

  A	B
  острый угол	угол больше нуля, но меньше 90 градусов.
  смежный угол	два угла рядом друг с другом с общей вершиной
  угол	фигура, образованная двумя лучами с одинаковой конечной точкой
  биссектриса угла	луч, разделяющий угол на два равных угла
  биссектриса отрезка	прямая, отрезок, луч, плоскость или точка, которые пересекают отрезок в его средней точке
  коллинеарные точки	точки на той же прямой
  комплементарные углы	два угла, сумма которых составляет 90 градусов
  копланарных точки	точек в одной плоскости
  равносторонний треугольник	треугольник со всеми углами, равными
  равносторонний треугольник	треугольник со всеми сторонами равно
  геометрия	изучение тех фигур, которые li е на плоской или плоской поверхности.
  пересечение	набор точек на обеих фигурах (две линии
  равнобедренный треугольник	треугольник, по крайней мере, 2 стороны которого равны
  линия	прямое расположение точек, неограниченно продолжающееся на обоих направления
  линейная пара	смежная пара углов, чьи необычные стороны представляют собой пару противоположных лучей.
  средняя точка сегмента	точка, которая делит сегмент на два конгруэнтных сегмента
  некопланарных точек	точки не в одной плоскости
  нелинейные точки	точки не на одной прямой
  тупой угол	угол больше 90 градусов, но меньше 180 градусов
  тупой треугольник	треугольник с одним тупым углом
  противоположные лучи	два луча с общей конечной точкой, образующие линию
  параллельные прямые	Две или более прямых в одной плоскости, которые не пересекаются
  перпендикулярные линии	две прямые, образующие прямые углы
  плоскость	плоская поверхность без толщины, которая простирается во всех направлениях
  точка	не имеет размера, представлена ​​точкой, имя местоположения, названное заглавной буквой
  луч	часть линии который неограниченно идет в одном направлении от конечной точки
  угол отражения	угол больше 180 градусов, но меньше 360 градусов
  прямой угол	угол, равный 90 градусов
  прямоугольный треугольник	треугольник с одним прямым углом
  разносторонний треугольник	треугольник без сторон равен
  сегмент	2 точки на прямой и все точки между ними
  пробел	набор всех точек
  прямой угол	угол, равный 180 градусов
  дополнительные углы	два угла, сумма которых составляет 180 градусов
  вершина	вершина угла является общей конечной точкой лучей, которые составляют угол
  вертикальные углы	Несмежные углы, образованные на пересечении двух линий.
  конгруэнтных сегмента	отрезков одинаковой длины
  3 неопределенных термина	точка, линия и плоскость
  совпадающие углы	два угла с равными размерами
  луч, разделяющий угол на два совпадающих смежных угла
  линии перекоса	2 линии, которые не пересекаются и не копланарны
  параллельные плоскости	2 или более плоскостей, которые не пересекаются

  Как определять точки, отрезки, линии и лучи.

  Привет Эрвин,

  Поскольку в вопросе не уточняется ничего, кроме «как идентифицировать», я не могу точно сказать, что нужно вашей дочери; Если следующего недостаточно, задайте более подробный вопрос. Вкратце, однако:

  Точка — это, по сути, геометрическая фигура, соответствующая тому, что мы называем «точкой» в реальном мире, с ключевым аспектом, заключающимся в том, что геометрическая точка не будет иметь длины, ширины и высоты / глубины, в то время как «точка» «Мы делаем даже очень острым карандашом какой-то размер.Таким образом, геометрическая фигура — это «идеальная» форма, которую нельзя найти в этой точной форме в реальном мире, но которая описывается понятием «точка».

  Точно так же отрезок (иногда называемый отрезком линии в отличие от полной линии, описанной ниже) — это «идеальная» геометрическая фигура, представленная прямым отрезком, который вы могли бы нарисовать карандашом и линейкой. Прямой означает отсутствие «поворота» или изгиба, а «сегмент» означает, что он начинается в одной точке и заканчивается в другой. Идеальная геометрическая фигура имеет длину, но не имеет ширины или глубины, а фигура, которую мы рисуем карандашом, имеет (очень-очень тонкую) ширину, даже если мы используем очень острый карандаш.

  Линия — это то, что вы получаете, когда начинаете с сегмента (или сегмента линии), но позволяете ей продолжаться бесконечно, вечно в каждом из двух противоположных направлений (скажем, одно всегда идет на север, а другое — на Юг), так что есть больше нет конечных точек. Мы не можем рисовать карандашом «вечно», поэтому мы используем «стрелки» на каждой стороне нарисованной линии, чтобы указать «продолжать вечно в этом направлении». Луч похож на линию, за исключением того, что мы начинаем с сегмента линии, сохраняем одну конечную точку из двух и «продолжаем вечно» только в одном направлении.Как конечная точка — это начальная точка для луча, который затем продолжается в прямом направлении (скажем, на север) во веки веков.

  П.С. посмотрите на клавиатуру вашего компьютера. Если он похож на мой, у вас будут «стрелка вверх» и «стрелка вниз», «стрелка влево» и «стрелка вправо». Это изображения четырех лучей! Если у вас есть последующие сообщения, просто спросите здесь. Надеюсь это поможет!

  Дублирование линейного сегмента — проблема 1

  Чтобы продублировать линейный сегмент AB, сначала нарисуйте луч с точкой C с помощью линейки — это будет место, где будет нарисован новый линейный сегмент.Измерьте длину AB с помощью циркуля. Затем, удерживая циркуль на этой длине, с помощью линейки и циркуля нарисуйте копию AB. Переместите циркуль к конечной точке AB, чтобы нарисовать вторую копию AB, удерживая линейку в том же месте. Этот отрезок теперь находится на расстоянии 2AB.

  Как только вы научитесь дублировать отрезок линии, вас попросят применить его разными способами.Один из способов — создать 2AB. Итак, вам дадут отрезок линии и попросят его удвоить. Теперь вы не можете просто нарисовать еще немного этого отрезка и сказать: «Мистер. Макколл, я готов », вам нужно будет быть очень точным, используя два ваших конструктивных инструмента: циркуль и линейку.

  Итак, мы начнем с рисования луча ниже этого отрезка AB. У вас должно быть место, куда можно скопировать новые линейные сегменты. Я возьму линейку и нарисую луч.Итак, я собираюсь продублировать 2AB на этот луч, начиная с точки C.

  Итак, я собираюсь сказать, ну 2AB, это просто AB плюс AB. Итак, если я измерю AB один раз, я могу скопировать его снова и объединить такие же термины AB и AB, как 2AB. Итак, я возьму свой компас и продублирую этот отрезок AB, я поставлю острый конец на одну конечную точку и буду двигать карандашом или маркером, пока он не будет точно на конечная точка. Так что я вообще этого не меняю.

  Я спущусь к точке C и сделаю отметку.Итак, вот это 1AB, поэтому, чтобы сделать 2AB, я собираюсь нанести острый конец этой новой точке и сделать еще одну. Заметьте, что я создал расстояние 2AB. И я собираюсь называть эту конечную точку D.

  Итак, ключевым моментом здесь было осознание того, что 2AB просто дважды повторяет повторяющийся сегмент AB.

  точек, линий и углов — SAS

  Деятельность 1

  Сделайте копии некоторых наконечников стрел и точек ( M-4-5-1_Arrowheads and Points.docx). Они будут раздаваться студентам-волонтерам на протяжении всего мероприятия.

  Нарисуйте на доске точку — сделайте ее большим, чтобы учащиеся могли ее видеть. «Эта точка в геометрии, когда говорят о формах, называется точкой . Многое в геометрии связано с точками. Как выглядит точка? » Студенты, вероятно, заметят, что точка похожа на точку или точку. «Точка, как в конце предложения, — это идеальный способ подумать о точке — очень маленькой точке.”

  Выберите двух добровольцев, которые выйдут впереди класса и держат лист бумаги с острием. «[Имена студентов] на некоторое время будут нашими очками. Итак, представьте, что это маленькие точки. Мы собираемся использовать эти отрезки веревки и наши точки, чтобы показать некоторые вещи, которые мы можем построить, используя точки ». Возьмите каждый конец веревки за концы и попросите их растянуть веревку так, чтобы она была туго натянутой.

  «Представляет линейный сегмент ». Напишите на доске термин , отрезок линии . «Отрезок — это часть прямой линии, как веревка, которая проходит между двумя точками, как наши добровольцы». Нарисуйте линейный сегмент на доске, убедившись, что ясно видны точки с обоих концов. Попросите двух добровольцев сделать один шаг ближе друг к другу.

  «Это отрезок линии?» Обсудите, что это не отрезок прямой, потому что веревка между двумя точками не прямая.

  Спросите учащихся, знает ли кто-нибудь из них слово сегмент .Обсудите, как слово , сегмент означает «часть» или «часть». «Итак, если это отрезок линии, то на самом деле это просто часть линии. Линия прямая, как и наш линейный сегмент, но разница в том, что линия продолжается вечно в обоих направлениях. Это не заканчивается ни на одном из этапов пути «. Дайте каждому из двух добровольцев стрелу и пусть они держат ее над соответствующими концами веревки.

  Нарисуйте линию на доске и обозначьте ее линией , убедившись, что на каждом конце есть стрелки. «Мы рисуем стрелки на конце линии, чтобы показать, что она идет в обоих направлениях».

  «Пока что у нас есть точки и линии, которые продолжаются бесконечно в обоих направлениях, и отрезки линий, которые останавливаются на обоих концах. А как насчет того, что продолжается вечно только в одном направлении? » Попросите одного из добровольцев опустить наконечник стрелы и заменить его острием. «Мы называем это лучом». Напишите на доске слово луч и нарисуйте луч.

  «Что означает слово ray или где вы раньше слышали слово ray ?» Направьте обсуждение в сторону солнечных лучей и укажите, что они начинаются в определенной точке — Солнце — и продолжают вечно проходить через пространство (пока они не натолкнутся ни на что на своем пути). Также обратите внимание на то, что солнечные лучи прямые.

  Передайте конец еще одной веревки ученику, изображающему точку луча.Затем попросите добровольца (желательно более высокого роста) подойти и поднять другой конец выше, чем первый луч, чтобы образовался угол, видимый классу. Второму добровольцу также понадобится наконечник стрелы.

  «Итак, у нас есть два луча. Они оба начинаются с одной и той же точки и образуют V-образную форму на месте встречи. Кто-нибудь знает, как мы это называем, когда у нас есть два луча, начинающиеся в одном месте? » Обсудите, что он называется углом . Напишите это на доске и начертите геометрическую интерпретацию угла. «Вокруг нас углы». Укажите углы в углах комнаты, узоры на рубашках и другие предметы в классе.

  «Уголки бывают разной формы. Те, что в углу комнаты, отличаются от той, которую наши волонтеры сделали из веревки. Под углом, который сделали наши добровольцы, получился довольно узкий; два луча расположены довольно близко друг к другу. Мы называем этот угол острым . Слово с острым углом просто означает, в общем, что это тонкий угол с близкими друг к другу лучами. Напишите на доске слово острый и нарисуйте пример явно острого угла.

  Чтобы изобразить прямой угол, вам, возможно, придется взять конец второго луча, в зависимости от роста третьего добровольца. Возьмите конец и медленно увеличивайте размер угла, а класс продолжит повторять слово с острым углом по мере увеличения размера угла. Когда вы стоите сразу за вершиной двух лучей, пусть класс остановится. «Это уже не острый угол! Теперь это прямой угол.Два луча образуют красивый квадратный угол. В отличие от острых углов, которые могут быть любого размера, прямой угол всегда выглядит точно так же, как красивый квадратный угол ».

  Начните двигаться за вершину, чтобы получился тупой угол. Как только вы выйдете за вершину, скажите классу : «И когда у нас есть угол, который на шире или на больше , чем прямой угол, мы называем его тупым ».

  Верните второй луч добровольцу, напишите и начертите на доске как прямой угол , так и тупой угол .Попросите добровольца продолжать движение, делая все шире и шире тупые углы, пока они не приблизятся к демонстрации прямого угла, после чего они смогут остановиться.

  «Итак, угол — это всего лишь два луча, которые начинаются в одной и той же точке и бывают трех типов: острые, тонкие; правые, которые составляют квадратный угол; и тупые, которые больше прямых углов ».

  Получите четырех новых добровольцев. Прежде чем продолжить, убедитесь, что у первых нескольких добровольцев есть возможность записать любой материал на доске.

  Попросите двух добровольцев сесть на пол или стать на колени, каждый из которых держит один конец веревки (со стрелами), чтобы образовать линию.

  «Как мы это называем, когда он продолжает идти вечно в каждом направлении?» ( линия )

  Попросите двух других добровольцев встать, каждый за одним из первых двух добровольцев, и возьмитесь за вторую веревку (со стрелами), чтобы образовать еще одну линию. Помогите им сделать его параллельным первому, заставив их поднимать или опускать «концы» лески.

  «Теперь у нас есть две линии. Эти две линии пересекают друг друга? » ( № ) Напомните студентам, что две линии продолжают идти в обоих направлениях вечно, в зависимости от того, что указывают стрелки, поэтому они должны использовать свое воображение. Студенты все равно должны сделать вывод, что они не пересекут друг друга. «Эти линии называются параллелью ». Напишите на доске слово параллельно и проведите две параллельные линии. «Любые линии, которые никогда не пересекаются, независимо от их длины, называются параллелью ».

  Теперь направьте двух стоящих студентов. Поставьте одно колено за нижнюю из двух линий, а другое должно держать скакалку прямо вверх. (В зависимости от высоты вам может потребоваться держать веревку прямо вверх.) «Эти линии параллельны?» ( № ) «Почему бы и нет?» ( Потому что они пересекают друг друга .)

  «Когда они пересекаются, какие углы мы получим?» Укажите на два угла, образованных пересечением двух линий. «Есть ли у нас острые, прямые или тупые углы?» ( справа ) «Когда две линии пересекаются и образуют прямые углы, мы называем линии перпендикулярными ». Напишите слово и нарисуйте на доске схему.

  Попросите стоящего ученика «повернуть» верхнюю линию. Он по-прежнему должен пересекать нижнюю линию, но не под прямым углом. «Эти линии параллельны?» ( № ) «Почему бы и нет?» ( Потому что они пересекают друг друга .) «Они перпендикулярны?» ( № ) «Почему бы и нет?» ( Потому что они не образуют прямых углов в местах пересечения .)

  Укажите на один из углов и попросите класс описать его. Затем попросите их описать другой угол.

  В зависимости от вовлеченности класса и времени продолжайте манипулировать двумя линиями для создания различных геометрических фигур и опросить учащихся, что представляет собой каждая модель.

  Деятельность 2

  Раздайте каждому учащемуся по одной копии Контрольного списка (M-4-5-1_Checklist и KEY.docx).

  «В этом упражнении я нарисую на доске фигуру. Ваша задача — решить, какие геометрические атрибуты составляют каждую фигуру. Мы вместе сделаем первую фигуру.

  Нарисуйте на доске две перпендикулярные линии. Сделайте точку на пересечении четкой и убедитесь, что на концах линий есть стрелки. Обозначьте его Рисунок 1 .

  «Посмотрите на строку в контрольном списке для рисунка 1. Первый столбец для каждого рисунка обозначен Point (вверху страницы).Итак, первый квадрат — есть ли точка на рисунке 1. Есть ли точка на рисунке 1? » ( да ) Укажите точку. «Тогда вставьте букву« Y »в рамку« Да ». Есть линия?» ( да ) «Итак, вы поместите букву« Y »в рамку, чтобы заменить« Да ».

  «Есть ли отрезок?» ( Нет, отрезок прямой проходит между двумя точками, а на диаграмме нет двух точек. ) Поговорите о том, почему бы и нет; отрезок линии проходит между двумя точками, а на диаграмме нет двух точек. «Затем введите букву« N »в поле« Нет »»

  Завершите оставшуюся часть ряда. Обратите внимание, что есть луч. Студенты могут сначала не распознать его, но рассматривают часть одной из линий на рисунке от точки пересечения, идущую наружу. (Первая строка должна быть: Y, Y, N, Y, N, Y, N, N, Y .)

  Создайте вторую фигуру, представляющую собой многоугольник. Напишите на доске под фигурой слово , многоугольник . «На рисунке 2 показан пример многоугольника.Многоугольник — это замкнутая фигура. По бокам нет отверстий или пробелов, и все стороны представляют собой отрезки прямых линий. Везде, где пересекаются отрезки прямой, есть точка, которая называется вершиной ». Напишите на доске слово вершина и затем вместе со студентами проработайте контрольный список для рисунка 2.

  На основании результатов, полученных учащимися по первым двум цифрам, предоставьте другие цифры. Рисунки могут включать в себя наборы параллельных линий, параллельных и перпендикулярных линий, треугольников, прямоугольников и других плоских геометрических фигур.Выбор фигур должен производиться в порядке возрастания сложности.

  Деятельность 3

  Предложите учащимся работать в парах. Раздайте каждому студенту копию Контрольного списка студента (M-4-5-1_Student Checklist.docx).

  «Сначала каждый из вас нарисует свой собственный Рисунок 1 на другом листе бумаги, не показывая его своему партнеру. Затем вы заполните строку для рисунка 1 на основе только что нарисованного рисунка. Наконец, вы передадите свой контрольный список своему партнеру.Например, они смогут увидеть, что ваша фигура содержит точку, отрезок линии и, возможно, луч, а затем им нужно будет нарисовать фигуру, в которой есть эти элементы «.

  Укажите учащимся, что им не следует ожидать, что их Рисунок 1 , например, и их партнер Рисунок 1 будут идентичны. (Вы можете позволить ученикам понять это по ходу дела, но многие ученики могут ожидать, что цифры будут идентичными, и предположить, что они сделали ошибку, когда их рисунки не совпадают с рисунками их партнера.Поощряйте учащихся начинать с простых фигур, пока они не получат некоторой практики, а затем переходите к рисункам с большим количеством элементов.

  В зависимости от времени разрешите учащимся проработать до 9 фигур.

  Добавочный номер:

  Используйте следующие стратегии, чтобы адаптировать урок к потребностям учащихся.

  • Программа: В течение года, по мере того как учащиеся продолжают изучать геометрические формы (треугольники, квадраты и т. Д.), Они продолжают использовать правильную терминологию и подчеркивать ее.Например, «Квадрат — это форма, состоящая из четырех точек (вершин), соединенных двумя наборами параллельных отрезков прямых. Есть четыре прямых угла ».

  В течение учебного года, когда позволяет время, учащиеся могут играть в игру на соответствие словаря геометрии на следующем веб-сайте:

  http://www.learninggamesforkids.com/math_games/5th-grade-math/geometry-terms-5th/matchit-geometry-terms-5th.html

  • Малая группа: Учащиеся, которым может пригодиться дополнительная практика, могут быть объединены в небольшие группы.Предложите учащимся в каждой группе поработать вместе, чтобы создать гигантскую фигуру (на куске мясной бумаги и т. Д.), А затем пометьте все геометрические части, которые использовались для создания фигуры. Фигуры могут быть настолько креативными и разнообразными, насколько это нравится ученикам.
  • Расширение: Учащиеся, которые готовы выйти за рамки требований стандарта, могут изучать методы оценки угловых мер, совпадения и сходства, а также выучить названия нескольких геометрических фигур.

  Учащиеся могут попрактиковаться в более продвинутом словарном запасе геометрии с помощью игры на следующем веб-сайте:

  http: // www.aplusmath.com/cgi-bin/games/geopicture

  Учебные материалы и материалы для тестирования доступны для индивидуального изучения студентами на следующем веб-сайте:

  http://www.