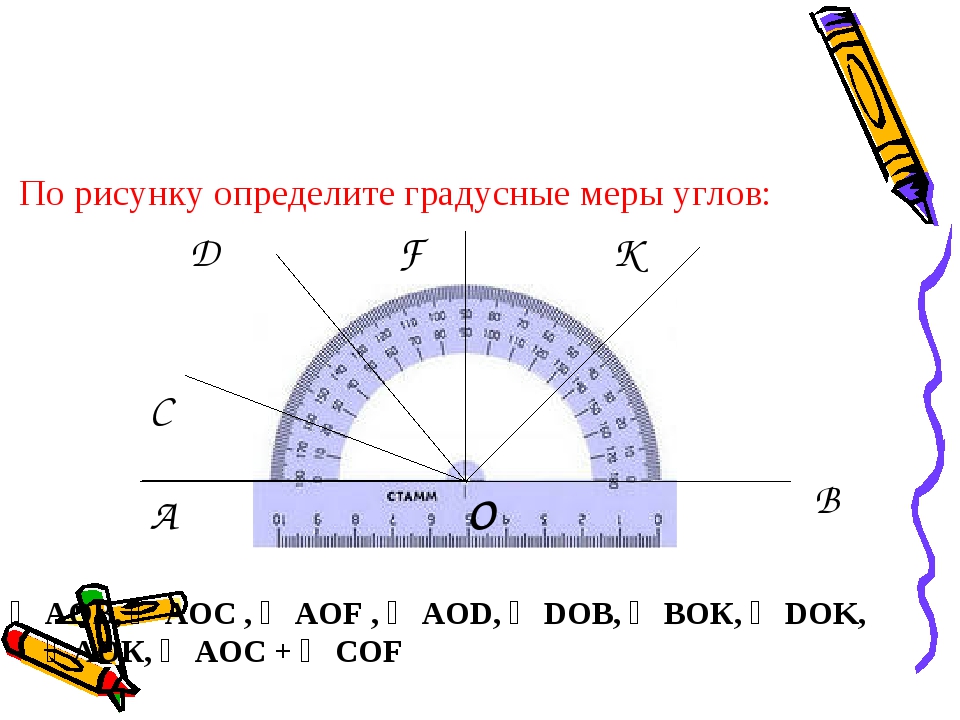
Содержание
Чему равна градусная мера треугольника
Мерой угла является размер поворота луча около точки как центра вращения.
Что такое градусная мера угла? Градусной мерой угла является число больше нуля, которое показывает,
какое число раз градус и его части — минута и секунда — помещаются в этом угле, т.е. градусная мера —
величина, которая отражает число градусов, минут и секунд между двумя сторонами угла.
У любого угла существует определенная градусная мера, которая больше . Развернутый угол = 180°.
Градусная мера угла соответствует сумме градусных мер углов, разбиваемый всяким лучом, который
проходит между его сторонами.
От всякого луча в необходимую полуплоскость есть возможность отложить угол с необходимой градусной
мерой, меньше чем 180°, и только 1.
Мерой плоского угла, который является элементом полуплоскости, является градусная мера угла с теми же
сторонами.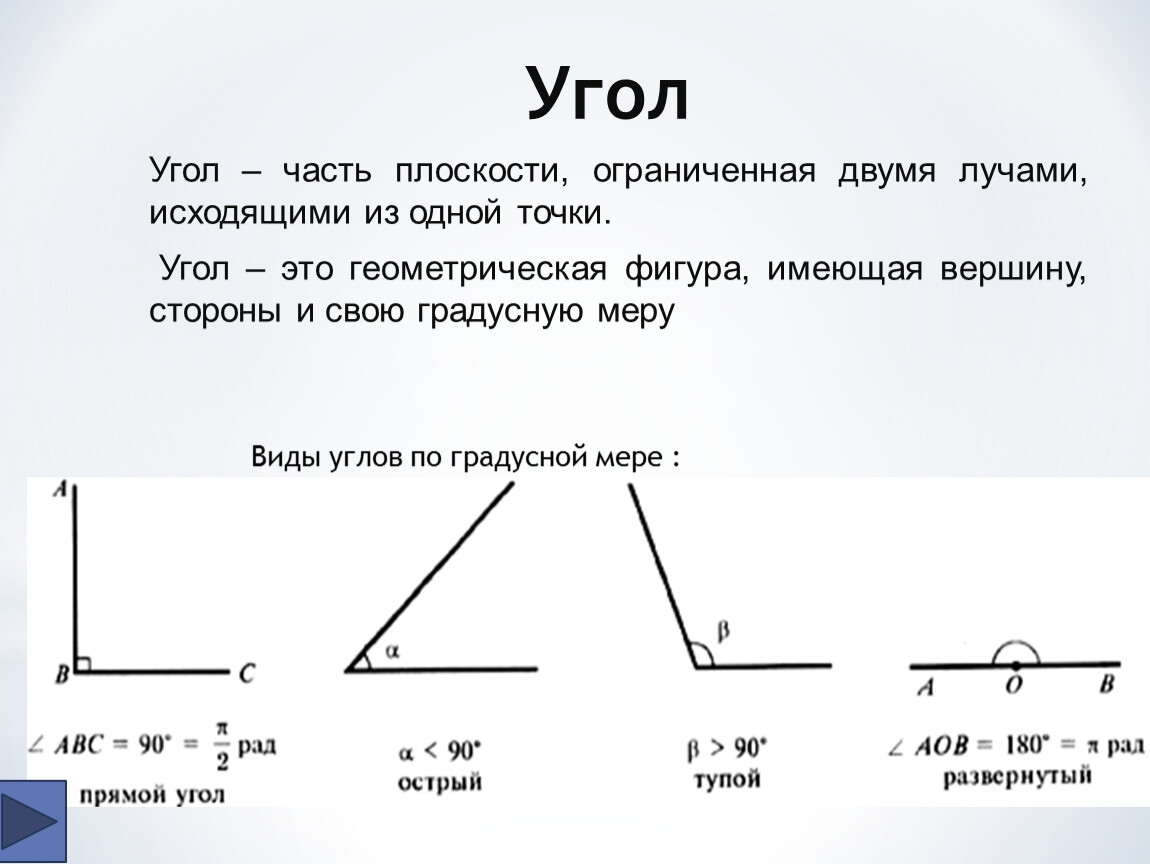 Мерой плоского угла, который содержит полуплоскость, является величина 360° – α ,
Мерой плоского угла, который содержит полуплоскость, является величина 360° – α ,
где α – градусная мера дополнительного плоского угла.
2 угла будут называться равными, когда их градусные меры одинаковы.
Так же как при делении часа, как интервала времени, градус делится на 60 минут — минуты обозначается
знаком ‘, а минуту — на 60 секунд — обозначается знаком ».
Свойства углов.
- У любого угла есть определенная градусную меру, большая нуля. Развернутый угол = 180°.
- Градусная мера угла соответствует сумме градусных мер углов, разбиваемый всяким лучом,
который проходит меж его сторонами.
- От всякого луча в необходимую полуплоскость есть возможность отложить угол с данной градусной
мерой, меньше чем 180°, и только один.
Как найти градусную меру угла?
1 градус (°) — это угол, равный 1/180 части развернутого угла. Если выразиться по другому, если возьмем
Если выразиться по другому, если возьмем
развернутый угол и поделим его на 180 одинаковых меж собой частей-углов, то любой такой маленький угол
будет соответствовать 1 градусу. Размер остальных углов вычисляется тем, какой число этих маленьких
углов возможно разместить внутри угла, который измеряется.
Т.о., развернутый угол = 180°, прямой угол = 90°, острые углы меньше, чем 90°, а тупые — больше,
Если угол невозможно измерить точно в целых градусах, то не обязательно использовать минуты и секунды.
Можно пользоваться дробными значениями градуса. Например, 96,5°.
Известно, что минуты и секунды легко переводятся в градусы, выражая их в долях градуса.
Например, 30′ = (30/60)° или 0,5°. А 0,3° = (0,3 * 60)’ или 18′. Т.о., пользоваться минутами и секундами —
Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения. Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом.
Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом.
Градус — это угол, который равен части развернутого угла,обозначается знаком
часть градуса называется минутой , обозначается знаком
часть минуты называется секундой , обозначается знаком
Пример: (двадцать градусов пятнадцать минут сорок семь секунд)
Градусная мера угла — это положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.
Пример:
Градусная мера угла ABC равна . Говорят: «Угол ABC равен 120 градусам». Пишут: .
Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .
Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.
Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .
Свойства:
- Равные углы имеют равные градусные меры.
- Меньший угол имеетменьшую градусную меру.
- Развернутый угол равен.
- Неразвернутый угол меньше.
- Если лучделит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
Основные типы углов:
- Острый угол — угол, градусная мера которого меньше 90 ° .
- Прямой угол — угол, градусная мера которого равна 90 ° .
- Тупой угол — угол, градусная мера которого больше 90 °, но меньше 180 ° .

- Развернутый угол — угол, градусная мера которого равна 180 °.
Поделись с друзьями в социальных сетях:
Определение
Геометрические фигуры, которые состоят из трех точек, которые не находятся на одной прямой, называются треугольниками.
Отрезки, соединяющие точки, называются сторонами, а точки – вершинами. Вершины обозначаются большими латинскими буквами, например: A, B, C.
Стороны обозначаются названиями двух точек, из которых они состоят – AB, BC, AC. Пересекаясь, стороны образуют углы. Нижняя сторона считается основанием фигуры.
Рис. 1. Треугольник ABC.
Виды треугольников
Треугольники классифицируют по углам и сторонам. Каждый из видов треугольника имеет свои свойства.
Существует три вида треугольников по углам:
- остроугольные;
- прямоугольные;
- тупоугольные.
Все углы остроугольного треугольника острые, то есть градусная мера каждого составляет не более 90 0 .
Прямоугольный треугольник содержит прямой угол. Два других угла всегда будут острыми, так как иначе сумма углов треугольника превысит 180 градусов, а это невозможно. Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами. Гипотенуза всегда больше катета.
Тупоугольный треугольник содержит тупой угол. То есть угол, величиной больше 90 градусов. Два других угла в таком треугольника будут острыми.
Рис. 2. Виды треугольников по углам.
Пифагоровым треугольником называется прямоугольник, стороны которого равны 3, 4, 5.
Такие треугольники часто используются для составления простых задач в геометрии. Поэтому, запомните: если две стороны треугольника равны 3, то третья обязательно будет 5. Это упростит расчеты.
Виды треугольников по сторонам:
- равносторонние;
- равнобедренные;
- разносторонние.
Равносторонний треугольник – это треугольник, у которого все стороны равны.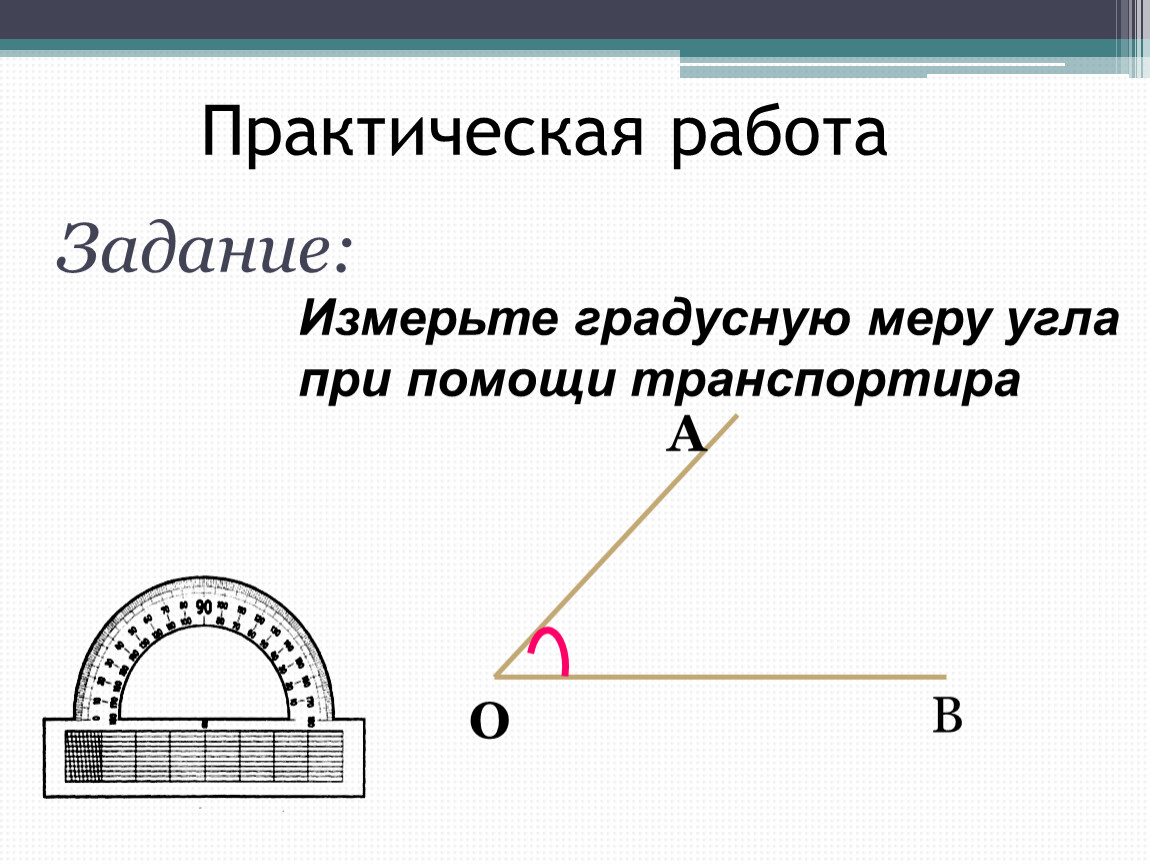 Все углы такого треугольника равны 60 0 , то есть он всегда является остроугольным.
Все углы такого треугольника равны 60 0 , то есть он всегда является остроугольным.
Равнобедренный треугольник – треугольник, у которого только две стороны равны. Эти стороны называются боковыми, а третья – основанием. Кроме того, углы при основании равнобедренного треугольника равны и всегда являются острыми.
Разносторонним или произвольным треугольником называется треугольник, у которого все длины и все углы не равны между собой.
Если в задаче нет никаких уточнений по поводу фигуры, то принято считать, что речь идет о произвольном треугольнике.
Рис. 3. Виды треугольников по сторонам.
Сумма всех углов треугольника, независимо от его вида, равна 1800.
Напротив большего угла находится большая сторона. А также длина любой стороны всегда меньше суммы двух других его сторон. Эти свойства подтверждаются теоремой о неравенстве треугольника.
Задача:
Существует ли треугольник, стороны которого равны 6 см.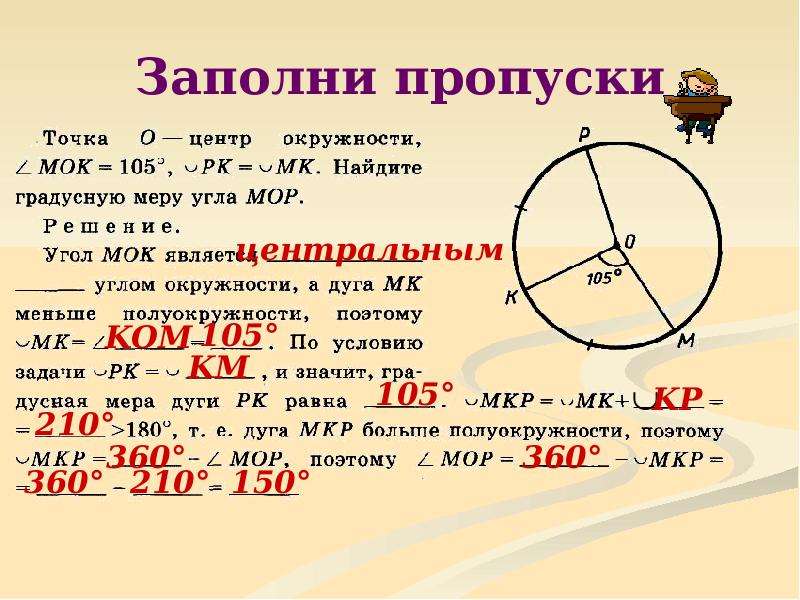 , 3 см., 4 см.?
, 3 см., 4 см.?
Решение:
Для решения данного задания нужно использовать неравенство a
Средняя оценка: 4.4 . Всего получено оценок: 160.
Окружность и вписанный угол. Визуальный гид (ЕГЭ — 2021)
Иными словами: сколько радиусов «помещается» в половине окружности? Или ещё по-другому: во сколько раз длина половины окружности больше радиуса?
Этим вопросом задавались учёные ещё в Древней Греции.
И вот, после долгих поисков они обнаружили, что отношение длины окружности к радиусу никак не хочет выражаться «человеческими» числами вроде \( \displaystyle 1,\text{ }2,\text{ }3,\frac{7}{5},\frac{2}{239}\) и т.п.
И даже не получается выразить это отношение через корни. То есть, оказывается, нельзя сказать, что половина окружности в \( \displaystyle 2,5\) раза или в \( \displaystyle \sqrt{17}\) раз больше радиуса! Представляешь, как удивительно это было обнаружить людям впервые?! Для отношения длины половины окружности к радиусу на хватило «нормальных» чисел. Пришлось вводить букву \( \displaystyle \pi \).
Пришлось вводить букву \( \displaystyle \pi \).
Итак, \( \displaystyle \pi \) – это число, выражающее отношение длины полуокружности к радиусу.
Теперь мы можем ответить на вопрос: сколько радиан в развёрнутом угле? В нём \( \displaystyle \pi \) радиан. Именно оттого, что половина окружности в \( \displaystyle \pi \) раз больше радиуса.
Древние (и не очень) люди на протяжении веков (!) попытались поточнее подсчитать это загадочное число \( \displaystyle \pi \), получше выразить его (хоть приблизительно) через «обыкновенные» числа. А мы сейчас до невозможности ленивы – нам достаточно двух знаков после занятой, мы привыкли, что
\( \displaystyle \pi \approx 3,14\)
Задумайся, это значит, например, что y окружности с радиусом единица длина приблизительно равна \( \displaystyle 6,28\), а точно эту длину просто невозможно записать «человеческим» числом – нужна буква \( \displaystyle \pi \). И тогда эта длина окружности окажется равной \( \displaystyle 2\pi \). И конечно, длина окружности радиуса \( \displaystyle R\) равна \( \displaystyle 2\pi R\).
И конечно, длина окружности радиуса \( \displaystyle R\) равна \( \displaystyle 2\pi R\).
Вернёмся к радианам.
Мы выяснили уже, что в развёрнутом угле содержится \( \displaystyle \pi \) радиан.
Как понять Геометрию? Основы с нуля
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.
Все эти фигуры обладают двумя свойствами:
- симметрия
- равенство или подобие составных частей.
Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.
У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.
Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).
Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.
Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.
Запомнить все свойства и правила бывает не просто. В онлайн-школе Skysmart сделали все, чтобы учиться было комфортно и в удовольствие: интерактивная платформа с онлайн-доской, захватывающие математические комиксы, поддержка учителей и даже стикеры для настроения.
Приходите на бесплатный вводный урок и попробуйте сами!
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец.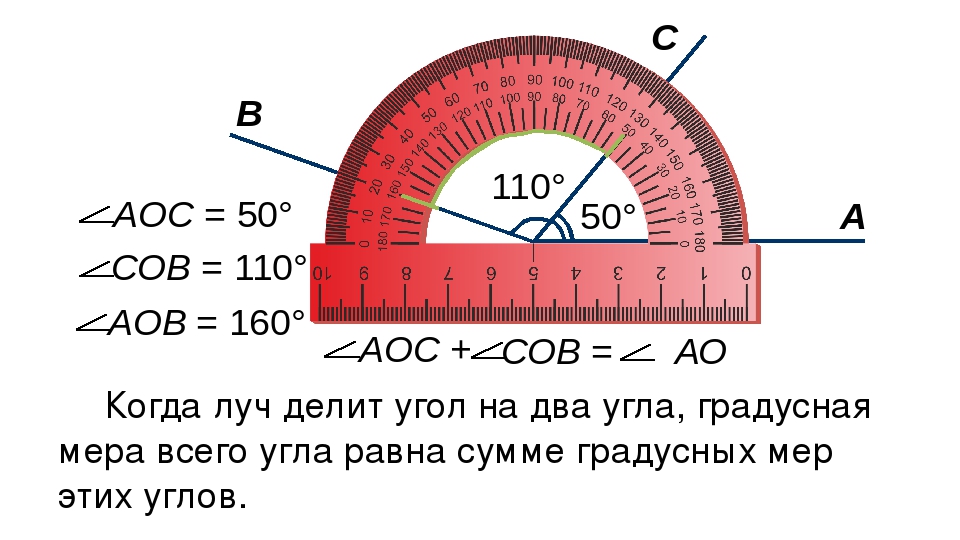 На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
Два варианта расположения точек относительно прямой:
- Точки лежат на данной прямой. Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).
- Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D.
 При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).
При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).
Важно знать
Через любые две точки можно провести прямую и притом только одну.
Если рассмотреть две прямые, то возможны два варианта их расположения:
- Прямые пересекаются, то есть имеют одну общую точку.
Для записи пересекающихся прямых используют специальный знак — ∩ , то есть a ∩ b (читают: прямая a пересекает прямую b).
- Прямые не пересекаются, то есть не имеют общих точек.
Для записи не пересекающихся прямых используют специальный знак — ,
то есть m n (читают: прямая m не пересекает прямую n).
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
- Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.
- Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.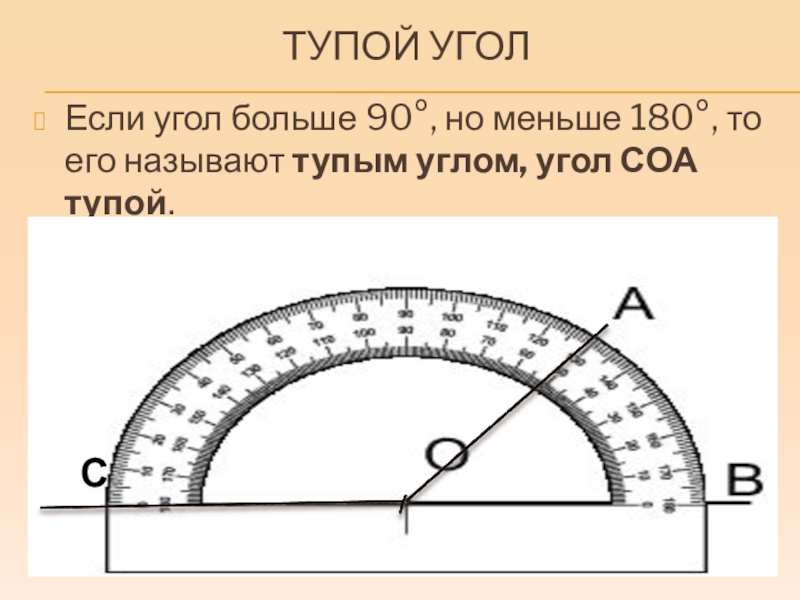
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
Есть разные виды углов, выделим самые часто встречающиеся:
- Если градусная мера угла меньше 90° — угол острый.
- Если градусная мера угла равна 90° — угол прямой.
- Если градусная мера угла больше 90°, но меньше 180° — угол тупой.
- Если градусная мера угла равна 180° — угол развернутый.
Точка называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
- две стороны и угол между ними;
- два угла и сторону;
- три стороны.
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Неравенство треугольника Сумма любых двух сторон треугольника больше его третьей стороны. |
Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.
Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.
Равенство треугольников ABC и A1B1C1 обозначается так: ΔABC = ΔA1B1C1.
Есть даже специальные теоремы про равенство треугольников.
Первый признак равенства треугольников звучит так:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
ΔABC = ΔA1B1C1, так как AC = A1C1, AB = A1B1 и ∠A = ∠A1 (∠A лежит между сторонами AC и AB, а ∠A1 между A1C1 и A1B1).
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
ΔABC = ΔA1B1C1, так как AB = A1B1, ∠A = ∠A1, ∠B = ∠B1.
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.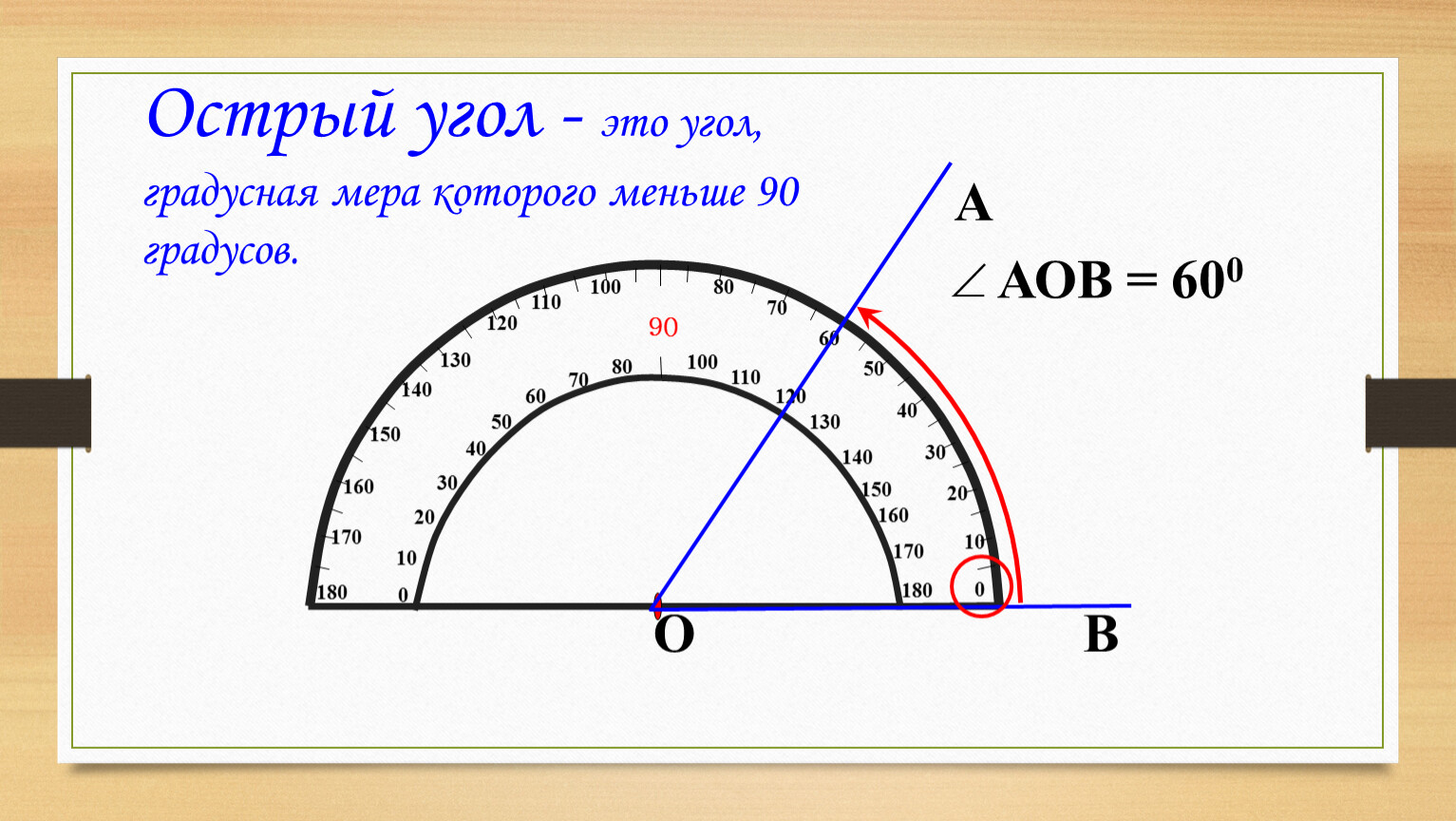
ΔABC = ΔA1B1C1, так как AC = A1C1, AB = A1B1 и BC = B1C1.
Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Треугольники АВС и A1B1C1 будут подобны, если
∠ А = A1, ∠ В = B1, ∠ С = C1,
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.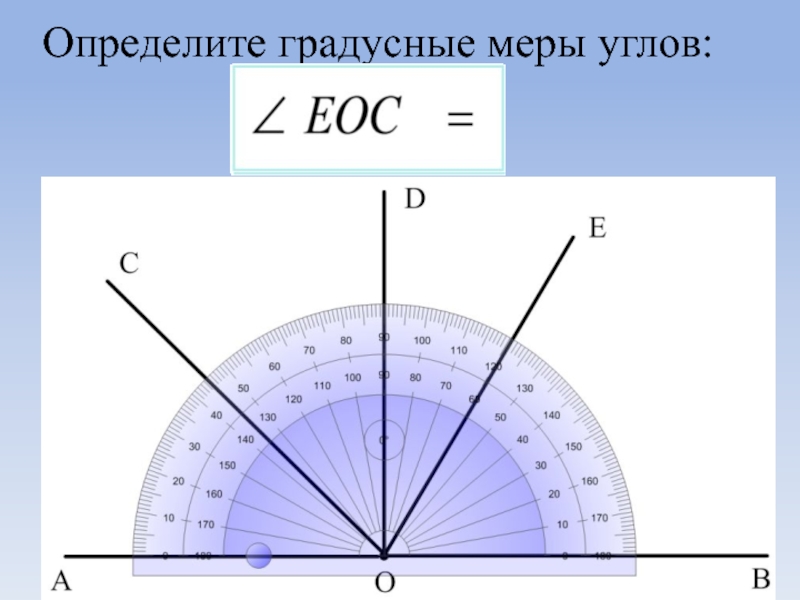
Теорема о первом признаке подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.
На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.
Теорема о средней линии звучит так:
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.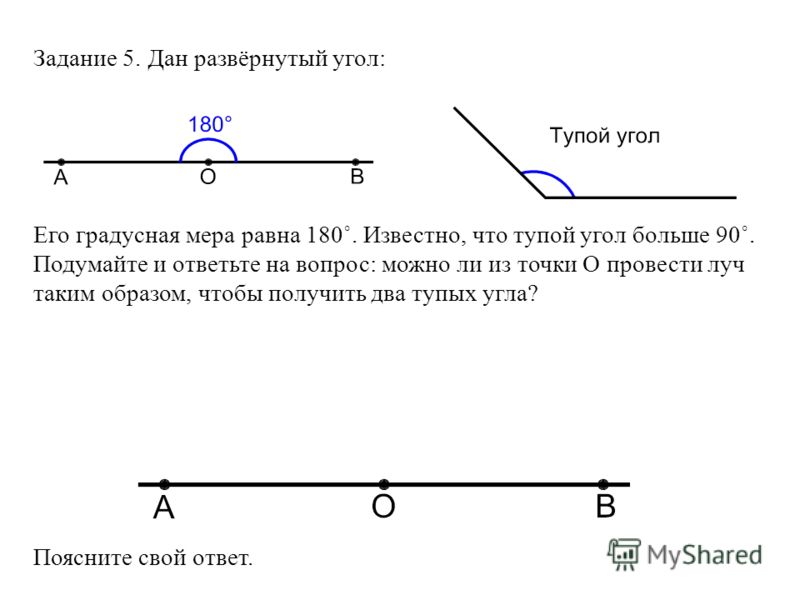
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.
Классификация треугольников по их сторонам
Для классификации треугольников можно использовать их типологию.
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
Свойства прямоугольного треугольника
- Теорема Пифагора: сумма длин квадратов катетов равна квадрату гипотенузы
- Свойство медианы: медиана, проведенная из вершины с прямым углом, равняется половине гипотенузы.

С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Взаимодействие объектов
Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.
Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.
На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:
- Если расстояние от центра окружности до прямой меньше радиуса окружности (d < r), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.
- Если расстояние от центра окружности до прямой равно радиусу окружности (d = r), то прямая и окружность имеют только одну общую точку.
 В этом случае прямая называется касательной по отношению к окружности.
В этом случае прямая называется касательной по отношению к окружности.
- Если расстояние от центра окружности до прямой больше радиуса окружности (d > r), то прямая и окружность не имеют общих точек.
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.
На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.
Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.
В детской онлайн-школе Skysmart ученики занимаются геометрией в интерактивном формате. Занятия проходят в удобное время и по личной программе, а еще можно отслеживать прогресс в личном кабинете и получать порцию мотивации.
Запишите ребенка на бесплатный вводный урок: покажем, как все устроено и поставим вдохновляющие цели!
|
Главная > Учебные материалы > Математика: Планиметрия.  Страница 1 Страница 1 | ||||
|
| ||||
|
| ||||
|
1 2 3 4 5 6 7 8 9 10 11 12 | ||||
1.
Планиметрия — раздел геометрии, изучающий геометрические фигуры и их свойства на плоскости.
Основными фигурами на плоскости являются точка и прямая. Точки обычно обозначаются заглавными буквами — А, В, С, D. Прямые обозначаются строчными буквами — a, b, c, d. (Рис.1) | ||||
а, b, c — прямые.
A, B, C, D, E — точки.
Прямые a и b параллельны,
Точка А не принадлежит ни одной прямой. Углы обозначаются так: ∠SOP или ∠О или ∠(hk) или ∠α где h,k — полупрямые или лучи с начальной точкой О.
|
Рис. | |||
| 2.Аксиомы планиметрии | ||||
1. Для любой прямой на плоскости существуют точки принадлежащие ей и не принадлежащие ей.
| ||||
2. Из трех точек, лежащих на прямой, только одна лежит между двумя другими. | ||||
3. Любой отрезок имеет длину больше нуля. | ||||
4. Любая прямая разбивает плоскость на две полуплоскости. | ||||
5. Любой угол имеет определенную градусную меру. Градусная мера любого угла равна сумме градусных мер углов, на которые он разбивается любым лучем, проходящим между его сторонами. Развернутый угол =180˚. | ||||
6. На любой полупрямой от ее начальной точки можно отложить только один отрезок определенной длины. | ||||
7. | ||||
8. Для любого треугольника, существует треугольник равный данному, относительно заданной полупрямой в заданном расположении. | ||||
|
9. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.
Рис.2
|
Рис.2 | |||
| Пример | ||||
Даны три прямые: а,b,c. | ||||
| Доказательство Допустим 3 прямые имеют две точки пересесения. Пусть прямые а и b пересекаются в точке А. Рис.3 точка А ∈а,b А прямая с пересекает прямую b в точке В. т. В ∈b,c
Тогда прямая с пересекает прямую а либо в точке А, либо в точке В.
|
| |||
Отсюда следует, что прямая с может пересекать прямую а в третьей точке, так что: А,В ∈b или прямая с пересекает прямую а в точке А, тогда
| ||||
3.
| ||||
|
Два угла называются смежными, если одна сторона у них общая, а другие их стороны являются дополнительными полупрямыми. (Рис.4)
|
Рис.4 | |||
Угол равный 90° называется прямым. Меньше 90° — острым. Больше 90° — тупым. (Рис.5)
Рис.5 | ||||
4.
| ||||
|
Если стороны одного угла являются дополнительными полупрямыми сторон другого угла, то такие углы называются вертикальными. (Рис.6)
Теорема: Вертикальные углы равны.
Доказательство. Пусть α1 β1 и α2 β2 — данные вертикальные углы. Угол α1 является смежным с углом β1. Угол β1 является смежным с углом α2. Тогда:
Следовательно,
Точно так же можно доказать, что β1 = β2.
|
Рис. | |||
5.Перпендикулярные прямые | ||||
|
Если две прямые пересекаются под прямым углом, то такие прямые называются перпендикурярными. (Рис.7)
Теорема: Через каждую точку прямой можно провести только одну прямую, перпендикулярную данной. Доказательство. Пусть а данная прямая и точка А данная точка, принадлежащая прямой а. Обозначим на прямой а полупрямую а1. И отложим от полупрямой а1 угол 90° — а1b1. Тогда прямые а и b, на которых лежат полупрямые а1 и b1 перпендикулярны. Допустим, что существует еще одна прямая, перпендикулярная прямой а, и проходящая через точку А — прямая с. Отложим от полупрямой а1 угол 90° — а1с1. Получается, что от полупрямой, от ее начальной точки (точка А) в заданную полуплоскость можно отложить еще один угол, равный 90°.
|
Рис.7 Перпендикулярные прямые. | |||
6.Признаки равенства треугольников | ||||
|
Первый признак равенства треугольников Теорема: Если две стороны и угол между этими сторонами одного треугольника равны соответственно двум сторонам и углу между этими сторонами другого треугольника, то такие треугольники равны. Доказательство. Пусть даны два треугольника ABC и A1B1C1. Угол А = А1, стороны AB = A1B1 AC = A1C1 (рис 8а). Возьмем третий треугольник А1В2С2 = АВС. Треугольники А1В1С1 и А1В2С2 расположим таким образом, что стороны А1В1 и А1В2 лежат на одной полупрямой, а точка А1 является начальной точкой нашей полупрямой. Вершина В2 лежит на полупрямой А1В1, а вершина С2 лежит в той же полуплоскости, где и С1. (рис 8б). Согласно аксиоме 6: на любой полупрямой, от ее начальной точки можно отложить только один отрезок определенной длины. Следовательно сторона А1В2 = А1В1, т.е. точки В1 и В2 совпадают. Согласно аксиоме 7: от любой полупрямой, от ее начальной точки, в заданную полуплоскость можно отложить только один угол определенной градусной меры. Следовательно углы С1А1В1 и С2А1В2 равны, т.е. точки С1 и С2 совпадают. Таким образом, треугольники A1B1C1 и A1B2C2 совпадают. Отсюда равны и треугольники ABC и A1B1C1.
|
Рис. | |||
|
Второй признак равенства треугольников Теорема: Если сторона и прилежащие к ней углы одного треугольника равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. (Рис.9) Доказательство. Пусть даны два треугольника ABC и A1B1C1. Углы А = А1, В = В1 сторона AB = A1B1 (рис 9). Возьмем третий треугольник А1В2С2 = АВС. Треугольники А1В1С1 и А1В2С2 расположим таким образом, что стороны А1В1 и А1В2 лежат на одной полупрямой, а точка А1 является начальной точкой нашей полупрямой. Вершина В2 лежит на полупрямой А1В1, а вершина С2 лежит в той же полуплоскости, где и С1. (рис 9). Т.к по условию AB = A1B1 и AB = A1B2 по построению, следовательно A1B1 = A1B2, т.
|
Рис.9 Второй признак равенства треугольников. | |||
Так как угол В1A1С2 равен углу В1A1С1 и угол А1В1С2 равен углу А1В1С1, то сторона A1С2 совпадает со стороной A1С1. А сторона В1С2 совпадает со стороной В1С1. Т.е. вершины С1 и С2 совпадают. Следовательно треугольник А1В1С1 совпадает с треугольником А1В2С2, а следовательно равен треугольнику АВС. | ||||
|
Третий признак равенства треугольников Теорема: Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны. Доказательство. Пусть даны два треугольника ABC и A1B1C1. Стороны AB = A1B1, BС = В1С1, AС = A1С1 (рис. 10). Возьмем третий треугольник А1В1С2 = АВС. Треугольники А1В1С1 и А1В1С2 расположим таким образом, что вершина С2 лежит в одной полуплоскости с вершиной C1. (рис 10). Пусть D середина отрезка C1C2. Таким образом, треугольники C1А1C2 и C1В1C2 — равнобедренные. А1D и B1D — медианы, а следовательно и высоты данных треугольников. Но через точку D можно провести только одну прямую, перпендикулярную прямой C1C2. Следовательно мы пришли к противоречию. Треугольники АВС и А1В1С1 — равны.
|
Рис.10 Третий признак равенства треугольников. | |||
Пример 1 | ||||
Даны три луча a,b,c. | ||||
Пусть даны три луча a,b,c с общей точкой О (Рис.11). Углы между ними составляют 120° (по условию задачи). И прямая е, пересекающая лучи а и b в точках А и В. Необходимо доказать, что прямая е не может пересечь все три луча а,b и с одновременно.
|
Рис.11 Задача. Даны три луча a,b,c. | |||
Пример 2 | ||||
Через точку О середину отрезка АВ проведена прямая а, перпендикулярная прямой АВ (рис. | ||||
Проведем два отрезка от точек А и В — АХ и ВХ. Рассмотрим два треугольника АОХ и ВОХ. Сторона АО треугольника АОХ равна стороне ОВ треугольника ВОХ по условию задачи. Сторона ОХ является общей стороной для двух треугольников. Отрезок АВ представляет собой развернутый угол с вершиной в точке О, градусная мера которого составляет 180°. Так как прямая а перпендикулярна отрезку АВ, то угол АОХ равен углу ВОХ, т.е. 90°. Таким образом, получается, что треугольники АОХ и ВОХ равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда следует, что сторона АХ треугольника АОХ равна стороне ВХ треугольника ВОХ при любой взятой точки Х, лежащей на прямой а.
|
Рис.12 Задача на признак равенства треугольников. | |||
Пример 3 | ||||
Периметр равнобедренного треугольника равен 2 метра, а основание равно 0,6 метра. Найдите длину боковой стороны. | ||||
Периметр треугольника равен 2 метра (Рис.13). Следовательно: Р = АВ + ВС + АС = 2 Но так как АВ = ВС (по условию задачи), то Р = 2 АВ + АС 2 = 2 АВ + 0,6 1,4 = 2 АВ АВ = 0,7 Ответ: АВ = ВС = 0,7 метра.
|
Рис.13 Задача. Нахождение боковой стороны. | |||
Пример 4 | ||||
Периметр равнобедренного треугольника АВС с основанием АС равен 40 метров, Найдите длину медианы ВD, если периметр треугольника АВD составляет 30 метров. | ||||
Так как треугольник АВС с основанием АС равнобедренный, то АВ = ВС. А так как BD медиана, то AD = DC (Рис. 14). Обозначим стороны треугольников как: AB = BC = y AD = DC = x BD = z Следовательно: РABC = 2 x + 2 y = 40 x + y = 20 РABD = x + y + z = 30 z = 30 — (x + y) = 30 — 20 = 10 Ответ: ВD = 10 метров.
|
Рис.14 Задача. Нахождение медианы BD. | |||
Пример 5 | ||||
Точки A, B, C и D лежат на одной прямой. Треугольники ABU1 и ABU2 равны. Докажите, что треугольники CDU1 и CDU2 тоже равны. | ||||
По условию задачи треугольники ABU1 и ABU2 равны (Рис.15). Следовательно, BU1 = BU2. Угол ABU1 равен углу ABU2. Отсюда можно сделать вывод, что угол СBU1 равен углу СBU2, так как эти углы являются смежными с углами ABU1 и ABU2. Таким образом, треугольники СBU1 и СBU2 равны по первому признаку равенства треугольников (по двум сторонам и углу между ними: BU1 = BU2, а сторона ВС у них общая и углы между ними равны). Следовательно, угол BСU1 равен углу BСU2 и СU1 = СU2. И следовательно, угол DСU1 равен углу DСU2, как смежные с углами BСU1 и BCU2. А отсюда делается заключительный вывод, что треугольники СDU1 и СDU2 равны по первому признаку равенства треугольников (по двум сторонам и углу между ними: СU1 = СU2, а сторона СD у них общая и углы между ними равны).
|
Рис.15 Задача. На признаки равенства треугольников. | |||
|
1 2 3 4 5 6 7 8 9 10 11 12 | ||||
Содержание | ||||
| Страница 1 | Страница 7 | |||
|
1.Основные фигуры планиметрии. 2.Аксиомы планиметрии. 3.Смежные углы. 4.Вертикальные углы. 5.Перпендикулярные прямые. 6.Признаки равенства треугольников. |
1.Движение и его свойства. 2.Симметрия относительно точки. 3.Симметрия относительно прямой. 4.Параллельный перенос и его свойства. | |||
| Страница 2 | Страница 8 | |||
|
1.Параллельность прямых. 2.Признаки параллельности прямых. 3.Свойство углов при пересечении параллельных прямых. 4.Сумма углов треугольника. 5.Единственность перпендикуляра к прямой. 6.Высота, биссектриса и медиана треугольника. 7.Свойство медианы равнобедренного треугольника. |
1.Вектор и его абсолютная величина. 2.Сложение векторов. 3.Умножение вектора на число. 4.Разложение вектора по двум неколлинеарным векторам. 5.Скалярное произведение векторов. | |||
| Страница 3 | Страница 9 | |||
|
1.Окружность. 2.Окружность описанная около треугольника. 3.Окружность вписанная в треугольник. 4.Геометрическое место точек. |
1.Преобразование подобия и его свойства. 2.Подобие фигур. Подобие треугольников по двум углам. 3.Подобие треугольников по двум пропорциональным сторонам и углу между ними. 4.Подобие треугольников по трем пропорциональным сторонам. 5.Подобие прямоугольных треугольников. | |||
| Страница 4 | Страница 10 | |||
|
1.Параллелограмм. 2.Свойства диагоналей параллелограмма. 3.Ромб. 4.Теорема Фалеса. 5.Средняя линия треугольника. 6.Трапеция. 7.Теорема о пропорциональных отрезках. |
1.Углы, вписанные в окружность. 2.Пропорциональность хорд и секущих окружности. 3.Теорема косинусов. 4.Теорема синусов. 5.Соотношение между углами и сторонами в треугольнике. | |||
| Страница 5 | Страница 11 | |||
|
1.Теорема Пифагора. 2.Египетский треугольник. 3.Соотношение между углами и сторонами в прямоугольном треугольнике. 4.Основные тригонометрические тождества. |
1.Многоугольники. Правильные многоугольники. 2.Радиус вписанной и описанной окружностей правильных многоугольников. 3.Подобие многоугольников. 4.Длина окружности. | |||
| Страница 6 | Страница 12 | |||
|
1.Декартова система координат. 2.Расстояние между точками. 3.Уравнение окружности. 4.Уравнение прямой. 5.Координаты точки пересечения. |
1.Площадь прямоугольника. 2.Площадь параллелограмма. 3.Площадь треугольника. 4.Площадь круга. 5.Площадь подобных фигур. 6.Площадь трапеции. | |||
Углы в планиметрии и их свойства
ТЕМА 2. УГЛЫ
Углом называется геометрическая фигура, которая состоит из точки – вершины угла – и двух различных полупрямых, исходящих из этой точки, – сторон угла.
Существует три способа обозначения углов.
1. Тремя заглавными латинскими буквами, средняя обозначает его вершину.
2. Одной заглавной латинской буквой, обозначающей вершину угла.
3. Двумя строчными латинскими буквами, обозначающими полупрямые, из которых состоит угол. Они располагаются на продолжении полупрямых.
Виды углов:
1. Острый. Его градусная мера меньше 90°.
2. Тупой. Его градусная мера больше 90°.
3. Прямой. Его градусная мера равна 90°.
4. Развёрнутый. Он состоит из двух дополнительных полупрямых и градусная мера его равна 180°.
СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ
Смежными называются два угла, у которых одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
ТЕОРЕМА: Сумма смежных углов равна 180°.
СЛЕДСТВИЯ:
I. Если два угла равны, то смежные с ними углы тоже равны.
II. Если угол не развёрнутый, то его градусная мера меньше 180°.
III. Угол, смежный с прямым углом, тоже прямой.
Вертикальными называются два угла, у которых стороны одного угла являются дополнительными полупрямыми сторон другого угла.
ТЕОРЕМА: Вертикальные углы равны.
ВНУТРЕННИЕ ОДНОСТОРОННИЕ И
ВНУТРЕННИЕ НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ
Секущей называется прямая, пересекающая две данные прямые.
Внутренними односторонними называются углы, расположенные между данными прямыми в одной полуплоскости от секущей.
Внутренними накрест лежащими называются углы, расположенные между данными прямыми в разных полуплоскостях от секущей.
ТЕОРЕМА (признак параллельности прямых): Если внутренние накрест лежащие углы равны, или сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Если у пары внутренних накрест лежащих углов один угол заменить вертикальным ему, то получится пара углов, которые называются соответственными углами данных прямых с секущей.
СЛЕДСТВИЯ:
I. Две прямые, перпендикулярные третьей, параллельны.
II. Прямые параллельны, если соответственные углы равны.
ТЕОРЕМА (обратная): Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°.
СЛЕДСТВИЕ:
Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Перпендикулярные прямые. Смежные и вертикальные углы.
Смежные углы относятся как 4:1. Найдите эти углы.
На рисунке прямые a и b перпендикулярны, ∠1 = 40°. Найдите углы 2, 3 и 4.
Один из смежных углов больше другого на 40°. Найдите эти углы.
На рисунке прямые a и b перпендикулярны, ∠1 = 130°. Найдите углы 2, 3 и 4.
Из точки О проведены лучи ОА, ОВ и ОС, причём ОВ⊥ОА (рис.). Угол, образованный биссектрисами углов АОВ и ВОС, равен 75°. Найдите углы АОВ, ВОС, АОС.
При пересечении двух прямых образовалось четыре угла, меньше развёрнутого. Найдите эти углы, зная, что один из них на 60° больше половины другого.
Из точки О проведены лучи ОА, ОВ и ОС, причём ОВ⊥ОА (рис.). Угол, образованный биссектрисами углов АОВ и ВОС, равен 20°. Найдите углы АОВ, СОВ, АОС.
При пересечении двух прямых образовалось четыре угла, меньше развёрнутого. Найдите эти углы, зная, что градусные меры двух из них относятся как 4:5.
Даны два угла АОВ и ВОС с общей вершиной. Стороны одного угла перпендикулярны к сторонам другого (рис.). Найдите эти углы, если разность между ними равна прямому углу.
Углы АОВ и ВОС смежные, ОМ – биссектриса угла АОВ, луч ON принадлежит внутренней области угла ВОС и перпендикулярен ОМ. Является ли ON биссектрисой угла ВОС? Почему?
Два равных тупых угла имеют общую сторону, а две другие стороны взаимно перпендикулярны. Найдите величину тупого угла.
Из вершины развёрнутого угла проведены два луча, которые делят его на три равные части.
Докажите, что сумма каждых трёх углов, не прилежащих один к другому и образуемых тремя прямыми, проходящими через одну точку, равна двум прямым углам.
Докажите, что сумма каждых пяти углов, не прилежащих один к другому и образуемых пятью прямыми, проходящими через одну точку, равна двум прямым углам.
Теоремы об углах, образованных двумя параллельными прямыми и секущей.
(Свойства параллельности прямых)
Один из внутренних односторонних углов, образованных при пересечении двух параллельных прямых третьей, в 3 раза больше другого. Чему равны эти углы?
Дан прямоугольный треугольник АСВ (∠С = 90°), ЕАС, FAB, причём EF‖CB, EK – биссектриса треугольника АЕF. Чему равен угол АЕК?
Один из внутренних односторонних углов, образованных при пересечении двух параллельных прямых третьей, больше другого на 64°. Чему равны эти углы?
Дан прямоугольный треугольник MEF (∠E = 90°), CME, DMF, причём CD‖EF, KMD, ∠KCD = 40°. Чему равен угол MCК?
На рисунке АС ‖ BD и АС = АВ, ∠МАС = 40°. Найдите ∠СBD.
Отрезки CD и АВ пересекаются в точке О так, что АО = ОВ, АС ‖ DB. Докажите, что ∆АОС = ∆DOB.
На рисунке 1 АС ‖ BD и АС = АВ, ∠BCD= 20°. Найдите ∠СAB.
На рисунке 2 BC = AD и ВС ‖ AD. Докажите, что ∆АВС = ∆ADC.
На рисунке 1 АВ = BD = ВС, BE ‖ DC. Докажите, что DC ⊥ AC.
На рисунке 2 BЕ ‖ AF, AB ‖ DE, AB = CD. Докажите, что ∆BCE = ∆ADF.
На рисунке 1 АВ = АС, AD = DE, DE ‖ AC. Докажите, что АЕ ⊥ ВС.
На рисунке 2 АВ ‖ CD, BC ‖ AD, DF ‖ BE. Докажите, что ∆FAB = ∆CBE.
На прямой МN между точками М и N выбрана точка А и проведены по одну сторону от МN лучи АВ, АС и AD. На луче АВ выбрана точка К и через неё проведена прямая, параллельная МN и пересекающая лучи АС и AD соответственно в точках Р и Е, КР = РА = РЕ. Докажите, что АВ ⊥ AD.
На отрезке АВ взята точка С. Через точки А и В проведены по одну сторону от АВ параллельные лучи. На них отложены отрезки AD = AC и ВЕ = ВС. Точка С соединена отрезками прямых с точками D и Е. Докажите, что DC ⊥ CE.
Углы в планиметрии
ТЕМА 2. УГЛЫ
Углом называется геометрическая фигура, которая состоит из точки – вершины угла – и двух различных полупрямых, исходящих из этой точки, – сторон угла.
Существует три способа обозначения углов.
1. Тремя заглавными латинскими буквами, средняя обозначает его вершину.
2. Одной заглавной латинской буквой, обозначающей вершину угла.
3. Двумя строчными латинскими буквами, обозначающими полупрямые, из которых состоит угол. Они располагаются на продолжении полупрямых.
Виды углов:
1. Острый. Его градусная мера меньше 90°.
2. Тупой. Его градусная мера больше 90°.
3. Прямой. Его градусная мера равна 90°.
4. Развёрнутый. Он состоит из двух дополнительных полупрямых и градусная мера его равна 180°.
СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ
Смежными называются два угла, у которых одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
ТЕОРЕМА: Сумма смежных углов равна 180°.
СЛЕДСТВИЯ:
I. Если два угла равны, то смежные с ними углы тоже равны.
II. Если угол не развёрнутый, то его градусная мера меньше 180°.
III. Угол, смежный с прямым углом, тоже прямой.
Вертикальными называются два угла, у которых стороны одного угла являются дополнительными полупрямыми сторон другого угла.
ТЕОРЕМА: Вертикальные углы равны.
ВНУТРЕННИЕ ОДНОСТОРОННИЕ И
ВНУТРЕННИЕ НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ
Секущей называется прямая, пересекающая две данные прямые.
Внутренними односторонними называются углы, расположенные между данными прямыми в одной полуплоскости от секущей.
Внутренними накрест лежащими называются углы, расположенные между данными прямыми в разных полуплоскостях от секущей.
ТЕОРЕМА (признак параллельности прямых): Если внутренние накрест лежащие углы равны, или сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Если у пары внутренних накрест лежащих углов один угол заменить вертикальным ему, то получится пара углов, которые называются соответственными углами данных прямых с секущей.
СЛЕДСТВИЯ:
I. Две прямые, перпендикулярные третьей, параллельны.
II. Прямые параллельны, если соответственные углы равны.
ТЕОРЕМА (обратная): Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°.
СЛЕДСТВИЕ:
Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Перпендикулярные прямые. Смежные и вертикальные углы.
Смежные углы относятся как 4:1. Найдите эти углы.
На рисунке прямые a и b перпендикулярны, ∠1 = 40°. Найдите углы 2, 3 и 4.
Один из смежных углов больше другого на 40°. Найдите эти углы.
На рисунке прямые a и b перпендикулярны, ∠1 = 130°. Найдите углы 2, 3 и 4.
Из точки О проведены лучи ОА, ОВ и ОС, причём ОВ⊥ОА (рис.). Угол, образованный биссектрисами углов АОВ и ВОС, равен 75°. Найдите углы АОВ, ВОС, АОС.
При пересечении двух прямых образовалось четыре угла, меньше развёрнутого. Найдите эти углы, зная, что один из них на 60° больше половины другого.
Из точки О проведены лучи ОА, ОВ и ОС, причём ОВ⊥ОА (рис.). Угол, образованный биссектрисами углов АОВ и ВОС, равен 20°. Найдите углы АОВ, СОВ, АОС.
При пересечении двух прямых образовалось четыре угла, меньше развёрнутого. Найдите эти углы, зная, что градусные меры двух из них относятся как 4:5.
Даны два угла АОВ и ВОС с общей вершиной. Стороны одного угла перпендикулярны к сторонам другого (рис.). Найдите эти углы, если разность между ними равна прямому углу.
Углы АОВ и ВОС смежные, ОМ – биссектриса угла АОВ, луч ON принадлежит внутренней области угла ВОС и перпендикулярен ОМ. Является ли ON биссектрисой угла ВОС? Почему?
Два равных тупых угла имеют общую сторону, а две другие стороны взаимно перпендикулярны. Найдите величину тупого угла.
Из вершины развёрнутого угла проведены два луча, которые делят его на три равные части.
Докажите, что сумма каждых трёх углов, не прилежащих один к другому и образуемых тремя прямыми, проходящими через одну точку, равна двум прямым углам.
Докажите, что сумма каждых пяти углов, не прилежащих один к другому и образуемых пятью прямыми, проходящими через одну точку, равна двум прямым углам.
Теоремы об углах, образованных двумя параллельными прямыми и секущей.
(Свойства параллельности прямых)
Один из внутренних односторонних углов, образованных при пересечении двух параллельных прямых третьей, в 3 раза больше другого. Чему равны эти углы?
Дан прямоугольный треугольник АСВ (∠С = 90°), ЕАС, FAB, причём EF‖CB, EK – биссектриса треугольника АЕF. Чему равен угол АЕК?
Один из внутренних односторонних углов, образованных при пересечении двух параллельных прямых третьей, больше другого на 64°. Чему равны эти углы?
Дан прямоугольный треугольник MEF (∠E = 90°), CME, DMF, причём CD‖EF, KMD, ∠KCD = 40°. Чему равен угол MCК?
На рисунке АС ‖ BD и АС = АВ, ∠МАС = 40°. Найдите ∠СBD.
Отрезки CD и АВ пересекаются в точке О так, что АО = ОВ, АС ‖ DB. Докажите, что ∆АОС = ∆DOB.
На рисунке 1 АС ‖ BD и АС = АВ, ∠BCD= 20°. Найдите ∠СAB.
На рисунке 2 BC = AD и ВС ‖ AD. Докажите, что ∆АВС = ∆ADC.
На рисунке 1 АВ = BD = ВС, BE ‖ DC. Докажите, что DC ⊥ AC.
На рисунке 2 BЕ ‖ AF, AB ‖ DE, AB = CD. Докажите, что ∆BCE = ∆ADF.
На рисунке 1 АВ = АС, AD = DE, DE ‖ AC. Докажите, что АЕ ⊥ ВС.
На рисунке 2 АВ ‖ CD, BC ‖ AD, DF ‖ BE. Докажите, что ∆FAB = ∆CBE.
На прямой МN между точками М и N выбрана точка А и проведены по одну сторону от МN лучи АВ, АС и AD. На луче АВ выбрана точка К и через неё проведена прямая, параллельная МN и пересекающая лучи АС и AD соответственно в точках Р и Е, КР = РА = РЕ. Докажите, что АВ ⊥ AD.
На отрезке АВ взята точка С. Через точки А и В проведены по одну сторону от АВ параллельные лучи. На них отложены отрезки AD = AC и ВЕ = ВС. Точка С соединена отрезками прямых с точками D и Е. Докажите, что DC ⊥ CE.
3
Тесты по геометрии | Тест по геометрии (7 класс) по теме:
Первый признак равенства треугольников
Задание 1
Вопрос:
Как называется геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки?
Запишите ответ:
__________________________________________
Задание 2
Вопрос:
Чему равен периметр треугольника, если длина всех его сторон равна 3,7 см?
Выберите один из 5 вариантов ответа:
1) 14,8 см
2) 11,1 см
3) 7,4 см
4) 10,1 см
5) 13,7 см
Задание 3
Вопрос:
Как называется элемент треугольника, который соединяет две его вершины?
Запишите ответ:
__________________________________________
Задание 4
Вопрос:
Периметр треугольника равен 27 см, а одна из сторон равна 11 см. Найдите длины двух других сторон, если одна из них в три раза больше другой?
Выберите один из 5 вариантов ответа:
1) 3 см и 9 см
2) 4 см и 12 см
3) 5 см и 15 см
4) 6 см и 18 см
5) 6 см и 12 см
Задание 5
Вопрос:
Треугольник АВС равен треугольнику А1В1С1, сторона АВ равна стороне А1В1. Чему равен угол АСВ, если угол А1С1В1 равен 60°?
Изображение:
Выберите один из 5 вариантов ответа:
1) 30°
2) 120°
3) 60°
4) 80°
5) 130°
Задание 6
Вопрос:
Какие условия должны выполняться, чтобы можно было утверждать, что два треугольника равны по первому признаку равенства треугольников?
Выберите один из 5 вариантов ответа:
1) Если две стороны одного треугольника равны двум сторонам другого треугольника.
2) Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника.
3) Если две стороны и угол между ними одного треугольника соответственно равны стороне и углу между ними другого треугольника.
4) Если два угла одного треугольника равны двум углам другого треугольника.
5) Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника.
Задание 7
Вопрос:
Назовите углы, прилежащие к стороне АВ треугольника АВС.
Изображение:
Выберите один из 3 вариантов ответа:
1) ∠ АВС и ∠ АСВ
2) ∠ АВС и ∠ ВАС
3) ∠ ВАС и ∠ АСВ
Задание 8
Вопрос:
Даны два треугольника АВС и BCD, у которых АС = ВС, ВС = BD = DC. Найдите периметр треугольника АВС, если периметр треугольника BCD равен 18 см, а АВ = 7 см.
Изображение:
Выберите один из 5 вариантов ответа:
1) 25 см
2) 19 см
3) 21 см
4) 16 см
5) 20 см
Задание 9
Вопрос:
Что из перечисленного является элементами треугольника?
Выберите несколько из 3 вариантов ответа:
1) Стороны
2) Углы
3) Периметр
Задание 10
Вопрос:
Продолжите предложение: «В равных треугольниках против соответственно равных сторон лежат … «.
Выберите один из 3 вариантов ответа:
1) равные стороны
2) равные стороны и углы
3) равные углы
Ответы:
1) (1 б.) Верный ответ: «треугольник».
2) (1 б.) Верные ответы: 2;
3) (1 б.) Верный ответ: «Сторона».
4) (1 б.) Верные ответы: 2;
5) (1 б.) Верные ответы: 3;
6) (1 б.) Верные ответы: 3;
7) (1 б.) Верные ответы: 2;
8) (1 б.) Верные ответы: 2;
9) (1 б.) Верные ответы: 1; 2;
10) (1 б.) Верные ответы: 3;
Конец
Общие сведения об углах и их типах — MathsTips.com
Угол — это основная фигура в геометрии, которая выглядит следующим образом.
Угол — это фигура, образованная двумя лучами, встречающимися в общей точке. Символ угла — ∠. Общая точка называется ее вершиной угла. Каждый из двух лучей, образующих угол, называется плечами или сторонами угла. Таким образом, угол состоит из трех частей, одной вершины и двух сторон.
Угол обычно обозначается тремя последовательными алфавитами, такими как A, B и C или X, Y и Z.Угол, образованный лучами AB и BC в вершине B, обозначим ∠ABC.
Посмотрите на рисунок выше. Угол, образованный в вершине B двумя лучами AB и BC, называется ∠ABC. Его также можно просто назвать углом B и кратко записать как B. Мы можем заметить, что B появляется в середине ABC, чтобы обозначить, что это угол при вершине B.
Представьте себе две стрелки часов в положении «12 часов». Обе руки находятся в одной и той же точке на рисунке 1.
Теперь минутная стрелка начинает двигаться, и между двумя стрелками образуется угол.Со временем это количество увеличивается. За один полный оборот образуется круг и максимальный угол. Угол измеряет величину поворота.
Угол можно также представить как фигуру, образованную вращением одного луча вокруг своей вершины. Размер угла зависит от степени вращения. Это дает меру угла. Величина угла — это величина поворота одной руки вокруг вершины, чтобы достичь положения второй руки.
Угол измеряет угол поворота между двумя плечами два и обычно измеряется в градусах или радианах.Греческие буквы, такие как α (альфа), β (бета) или θ (тета), обычно используются в качестве символов для измеренного значения угла. Обозначается он θ.
Стандартной единицей измерения угла является градус. Обозначается он °. Таким образом, 30 градусов и 60 градусов записываются как 30 ° и 60 ° соответственно.
В приведенном выше примере часов две стрелки первоначально образуют наименьший угол 0 °, а при одном полном обороте минутной стрелки обе стрелки образуют максимальный угол, который называется углом 360 градусов или 360 °.Углы при полном повороте в сумме составляют 360 градусов. Если один полный оборот разделен на 360 равных частей, размер каждой такой части составляет один градус или 1 °. В разделе «Геометрия» мы узнаем больше об углах с величинами от 0 до 360 °.
Типы углов
Углы можно классифицировать по их величине угла.
1. Прямой угол:
Угол, размер которого равен 90 °, называется прямым углом. Прямой угол образуется, когда две стороны составляют 900.Полный поворот состоит из четырех прямых углов.
2. Острый угол:
Угол меньше 90 градусов называется острым углом.
3. Тупой угол
Угол между 90 и 180 градусами называется тупым углом.
4. Угол отражения
Угол, превышающий 180 градусов, называется углом отражения.
5.Уголок прямой
Прямой угол — это внутренний угол, равный 180 °
6. Угол полный
Сумма углов при полном повороте составляет 360 градусов.
Измерительные углы
Транспортир используется для измерения угла. Его еще называют полукруглым транспортиром. На схеме ниже показан транспортир.
Транспортир имеет двойную шкалу. Каждая шкала размечена в градусах от 0 до 180.Наружная шкала размечена в градусах от 0 до 180 слева направо. Внутренняя шкала также обозначена в градусах от 0 до 180, но справа налево. У него есть базовая линия внизу. Источник находится в центре.
Измерим угол с помощью транспортира.
При измерении угла центр транспортира помещается над вершиной (углом) B угла, а базовая линия транспортира размещается вдоль одной из линий угла BC. Смотрим положение второй линии угла BA.Теперь считываем значение на внутренней шкале положения линии BA. Это 50 °. Это измерение ∠ABC. Таким образом, ABC = 50 °.
Парные углы
1. Соседние углы
Два угла, которые имеют одну и ту же вершину и одну сторону, называются смежным углом. Смежные углы — это два угла, которые расположены бок о бок и имеют общий луч. У них общая вершина. Любой угол может иметь смежные углы с обеих сторон.
2. Вертикально противоположные углы
Два угла, которые имеют общую вершину и противоположны друг другу, образованные одними и теми же двумя линиями, называются вертикально противоположными углами.Два вертикально противоположных угла всегда равны. На диаграмме ниже два угла α (альфа) и β (бета) являются вертикальными углами и α = β
.
Дополнительные и дополнительные уголки
1. Дополнительные уголки
Два угла, сумма которых составляет 90 градусов, называются дополнительными углами.
Два дополнительных угла не обязательно должны быть смежными. Следующие углы также дополняют друг друга, так как сумма их измерений равна 90 градусам
.
2.Дополнительные уголки
Два угла, сумма которых составляет 180 градусов, называются дополнительными углами. На рисунке ниже α + β = 180 градусов, углы α и β являются дополнительными углами
.
Два дополнительных угла не обязательно должны быть смежными. Следующие углы также являются дополнительными, так как сумма их измерений равна 180 градусам.
Внутренний угол и внешний угол
На рисунке ниже ABC — это геометрическая форма, называемая Треугольником (мы узнаем больше о треугольнике в другой статье).Линия BC была расширена как линия CD. Внутренний угол — это угол внутри фигуры ABC. Внешний угол — это угол между стороной фигуры AC и удлиненной линией CD.
Сумма внутреннего и внешнего углов составляет 180 °. Два угла являются дополнительными. Вот они и соседние углы.
Что следует помнить
- Прямой угол 90 °
- Стандартная единица измерения угла — градус. Обозначается он °.
- Острый угол менее 90 градусов.
- Тупой угол больше 90, но меньше 180 градусов.
- Угол отражения больше 180 градусов.
- Прямой угол равен 180 °
- Полный круговой поворот составляет 360 градусов.
- Транспортир — инструмент для измерения углов
- Два угла, которые имеют одну и ту же вершину и одну сторону, называются смежным углом.
- Два угла, которые имеют общую вершину и противоположны друг другу, образованные одними и теми же двумя линиями, называются вертикально противоположными углами.
- Два вертикально противоположных угла равны.
- Два угла, сумма которых составляет 90 градусов, называются дополнительными углами
- Два угла, сумма которых составляет 180 градусов, называются дополнительными углами
- Внутренний угол — это угол, образованный внутри геометрической формы.
- Внешний угол — это угол, образованный вне геометрической формы между стороной формы и продолженной линией другой стороны.
Вопросы и ответы
Вопрос 1: Определить ∠ACB
Решение: Это прямой угол, его размер составляет 90 °
Вопрос 2: Посмотрите на рисунок ниже и найдите ∠ACD
Решение:
∠ACB — прямой угол.
Следовательно, ACD и ∠DCB — дополнительные углы.
∠ACD + ∠DCB = 90 °
∠ACD + 30 ° = 90 °
Следовательно, ∠ACD = 60 °
Вопрос 3: Посмотрите на рисунок ниже. Если ∠β = 120 °, найти значение ∠α.
Решение:
Углы α и β являются дополнительными углами.
Следовательно, α + β = 180 градусов,
Поскольку ∠β = 120 °, ∠ α = 180-120 = 60 °
Вопрос 4: Посмотрите на рисунок ниже. Если ∠α = 30 °, найти значение ∠β.
Решение:
Два угла α (альфа) и β (бета) являются вертикально противоположными углами, поэтому α = β
Поскольку α равно 30 °, значит, β также равно 30 °
Вопрос 5: Найти дополнение угла 45 °
Решение:
Сумма двух дополнительных углов составляет 90 °.Так как один угол равен 45 °, другой угол = 90-45 = 45 °
Задание:
1. ABC равно 225 °. Это а / ан
- Острый угол
- Тупой угол
- Угол отражения
2. Измерение прямого угла
- 90 °
- 180 °
- 360 °
2. Какое значение имеет дополнительный угол 75 °?
- 15 °
- 75 °
- 105 °
4.Найдите значение дополнительного угла к углу, равному 30 °
- 30 °
- 60 °
- 150 °
5. Каков размер прямого угла?
- 0 °
- 90 °
- 180 °
Верно или неверно
6. Два вертикально противоположных угла всегда равны.
- Истинно
- Ложь
7. Сумма внутреннего и внешнего углов равна 360 °.
- Истинно
- Ложь
Заполните бланк
8.Мера …………. это 360 °
- Прямой угол
- Тупой угол
- Уголок полный
9. Один полный оборот минутной стрелки за один час составляет угол ……. степень
- 90 °
- 180 °
- 360 °
10. Какое из следующих утверждений НЕ правильно?
- Два дополнительных угла не обязательно являются смежными углами
- Два соседних угла всегда являются дополнительными
- Два вертикально противоположных угла не могут быть смежными углами
% PDF-1.3
%
78 0 объект
>
эндобдж
xref
78 74
0000000016 00000 н.
0000001828 00000 н.
0000002783 00000 н.
0000002997 00000 н.
0000003290 00000 н.
0000003497 00000 н.
0000003718 00000 н.
0000004129 00000 н.
0000004613 00000 н.
0000004841 00000 н.
0000005267 00000 н.
0000005471 00000 п.
0000006020 00000 н.
0000006060 00000 н.
0000006211 00000 н.
0000006504 00000 н.
0000006687 00000 н.
0000006908 00000 н.
0000006930 00000 н.
0000008401 00000 п.
0000008702 00000 н.
0000008853 00000 н.
0000008875 00000 н.
0000010387 00000 п.
0000010541 00000 п.
0000010914 00000 п.
0000011068 00000 п.
0000011274 00000 п.
0000011571 00000 п.
0000011912 00000 п.
0000011935 00000 п.
0000013187 00000 п.
0000013520 00000 п.
0000013789 00000 п.
0000013943 00000 п.
0000014235 00000 п.
0000014258 00000 п.
0000015408 00000 п.
0000015431 00000 п.
0000016548 00000 п.
0000016880 00000 п.
0000017088 00000 п.
0000017111 00000 п.
0000018348 00000 п.
0000018371 00000 п.
0000019563 00000 п.
0000019586 00000 п.
0000020725 00000 п.
0000024404 00000 п.
0000033958 00000 п.
0000034183 00000 п.
0000042431 00000 п.
0000044672 00000 п.
0000046664 00000 н.
0000058769 00000 п.
0000058990 00000 п.
0000060905 00000 п.
0000061110 00000 п.
0000062265 00000 п.
0000063938 00000 п.
0000064153 00000 п.
0000064232 00000 н.
0000066910 00000 п.
0000069720 00000 п.
0000069966 00000 н.
0000071313 00000 п.
0000071527 00000 п.
0000071731 00000 п.
0000077976 00000 п.
0000078181 00000 п.
0000080098 00000 п.
0000080303 00000 п.
0000001921 00000 н.
0000002761 00000 н.
трейлер
]
>>
startxref
0
%% EOF
79 0 объект
>
эндобдж
150 0 объект
>
поток
Hb«f«od`g`Vfd @
Теорема о внешнем угле — объяснение и примеры
Итак, все мы знаем, что треугольник — это 3-сторонняя фигура с тремя внутренними углами.Но существуют и другие углы вне треугольника, которые мы называем внешними углами .
Мы знаем, что сумма всех трех внутренних углов всегда равна 180 градусам в треугольнике.
Точно так же это свойство справедливо и для внешних углов. Кроме того, каждый внутренний угол треугольника больше нуля градусов, но меньше 180 градусов. То же самое и с внешними углами.
В этой статье мы узнаем о:
- теореме о внешнем угле треугольника,
- внешних углах треугольника и
- о том, как найти неизвестный внешний угол треугольника.
Каков внешний угол треугольника?
Внешний угол треугольника — это угол, образованный между одной стороной треугольника и продолжением его смежной стороны.
На приведенном выше рисунке внутренние углы треугольника ABC равны a, b, c, а внешние углы — d, e и f. Смежные внутренние и внешние углы являются дополнительными углами.
Другими словами, сумма каждого внутреннего угла и прилегающего к нему внешнего угла равна 180 градусам (прямая линия).
Теорема о внешнем угле треугольника
Теорема о внешнем угле утверждает, что мера каждого внешнего угла треугольника равна сумме противоположных и несмежных внутренних углов.
Помните, что два несмежных внутренних угла, противоположных внешнему углу, иногда называют удаленными внутренними углами.
Например, в треугольнике ABC выше;
⇒ d = b + a
⇒ e = a + c
⇒ f = b + c
Свойства внешних углов
- Внешний угол треугольника равен сумме двух противоположных внутренние углы.
- Сумма внешнего угла и внутреннего угла равна 180 градусам.
⇒ c + d = 180 °
⇒ a + f = 180 °
⇒ b + e = 180 °
- Сумма всех внешних углов треугольника составляет 360 °.
Доказательство:
⇒ d + e + f = b + a + a + c + b + c
⇒ d + e + f = 2a + 2b + 2c
= 2 (a + b + c)
Но, согласно теореме о сумме углов треугольника,
a + b + c = 180 градусов
Следовательно, ⇒ d + e + f = 2 (180 °)
= 360 °
Как найти Внешние углы треугольника?
Правила определения внешних углов треугольника очень похожи на правила определения внутренних углов.Это потому, что везде, где есть внешний угол, есть и внутренний угол с , и оба в сумме составляют 180 градусов.
Давайте рассмотрим несколько примеров задач.
Пример 1
Учитывая, что для треугольника два внутренних угла 25 ° и (x + 15) ° не смежны с внешним углом (3x — 10) °, найдите значение x.
Решение
Примените теорему о внешнем угле треугольника:
⇒ (3x — 10) = (25) + (x + 15)
⇒ (3x — 10) = (25) + (x +15)
⇒ 3x −10 = x + 40
⇒ 3x — 10 = x + 40
⇒ 3x = x + 50
⇒ 3x = x + 50
⇒ 2x = 50
x = 25
Следовательно , x = 25 °
Подставляем значение x в три уравнения.
⇒ (3x — 10) = 3 (25 °) — 10 °
= (75-10) ° = 65 °
⇒ (x + 15) = (25 + 15) ° = 40 °
Следовательно , углы составляют 25 °, 40 ° и 65 °.
Пример 2
Рассчитайте значения x и y в следующем треугольнике.
Решение
Из рисунка видно, что y — это внутренний угол, а x — это внешний угол.
По теореме о внешнем угле треугольника.
⇒ x = 60 ° + 80 °
x = 140 °
Сумма внешнего угла и внутреннего угла равна 180 градусам (свойство внешних углов). Итак, у нас есть;
⇒ y + x = 180 °
⇒ 140 ° + y = 180 °
вычесть 140 ° с обеих сторон.
⇒ y = 180 ° — 140 °
y = 40 °
Следовательно, значения x и y равны 140 ° и 40 ° соответственно.
Пример 3
Внешний угол треугольника составляет 120 °.Найдите значение x, если противоположные несмежные внутренние углы равны (4x + 40) ° и 60 °.
Решение
Внешний угол = сумма двух противоположных несмежных внутренних углов.
⇒120 ° = 4x + 40 + 60
Упростить.
⇒ 120 ° = 4x + 100 °
Вычтем 120 ° с обеих сторон.
⇒ 120 ° — 100 ° = 4x + 100 ° — 100 °
⇒ 20 ° = 4x
Разделите обе стороны на, чтобы получить,
x = 5 °
Следовательно, значение x равно 5 градусам.
Проверить ответ заменой.
120 ° = 4x + 40 + 60
120 ° = 4 ° (5) + 40 ° + 60 °
120 ° = 120 ° (RHS = LHS)
Пример 4
Определить значение x и y на рисунке ниже.
Решение
Сумма внутренних углов = 180 градусов
y + 41 ° + 92 ° = 180 °
Упростите.
y + 133 ° = 180 °
вычесть 133 ° с обеих сторон.
y = 180 ° — 133 °
y = 47 °
Примените теорему о внешнем угле треугольника.
x = 41 ° + 47 °
x = 88 °
Следовательно, значения x и y равны 88 ° и 47 ° соответственно.
Предыдущий урок | Главная страница | Следующий урок
Углы — Математика GCSE Revision — Revision Maths
Углы измеряются в градусах, записываются в °. Максимальный угол 360 °. Это угол вокруг точки.Половина этого угла составляет 180 ° на прямой.
Видео ниже объясняет, как рассчитать связанные углы, смежные углы, внутренние углы и дополнительные углы.
Родственные уголки
Линии AB и CD параллельны друг другу (отсюда »на линиях).
a и d известны как , вертикально противоположные углам . Вертикально противоположные углы равны. (b и c, e и h, f и g также противоположны по вертикали).
g и c — , соответствующие углы . Соответствующие углы равны. (h и d, f и b, e и a также соответствуют).
d и e — чередующихся углов . Альтернативные углы равны. (c и f также чередуются). Альтернативные углы образуют Z-образную форму и иногда называются Z-углами.
a и b — это смежных углов . Смежные углы в сумме составляют 180 градусов. (d и c, c и a, d и b, f и e, e и g, h и g, h и f также смежны).
d и f — внутренние углы . В сумме они составляют 180 градусов (е и с также являются внутренними).
Любые два угла, которые в сумме составляют 180 градусов, называются дополнительными углами .
Сумма углов треугольника
Используя некоторые из приведенных выше результатов, мы можем доказать, что сумма трех углов внутри любого треугольника всегда составляет 180 градусов.
Если у нас есть треугольник, вы всегда можете провести две параллельные линии следующим образом:
Теперь мы знаем, что альтернативных углов равны.Следовательно, два угла, обозначенные x, равны. Кроме того, два угла, обозначенные буквой y, равны.
Мы знаем, что x, y и z вместе составляют 180 градусов, потому что вместе они представляют собой угол вокруг прямой. Таким образом, сумма трех углов в треугольнике должна составлять 180 градусов.
Сумма углов четырехугольника
Четырехугольник — это фигура с 4 сторонами.
Теперь, когда мы знаем сумму углов в треугольнике, мы можем вычислить сумму углов в четырехугольнике.
Для любого четырехугольника мы можем провести диагональную линию, чтобы разделить его на два треугольника. Сумма углов каждого треугольника равна 180 градусам. Следовательно, общая сумма углов четырехугольника составляет 360 градусов.
Наружные углы
Внешние углы формы — это углы, которые вы получите, если удлинить стороны. Показаны внешние углы шестиугольника:
Многоугольник — это фигура с прямыми сторонами.Сумма всех внешних углов многоугольника составляет 360 °. потому что, если вы сложите их все вместе, они образуют угол вокруг точки:
Следовательно, если у вас есть правильный многоугольник (другими словами, где все стороны имеют одинаковую длину и все углы одинаковы), каждый из внешних углов будет иметь размер 360 ÷ количество сторон. Так, например, каждый из внешних углов шестиугольника составляет 360/6 = 60 °.
Внутренние углы
Внутренние углы формы — это углы внутри нее.Если вы знаете размер внешнего угла, вы можете определить размер внутреннего угла рядом с ним, потому что в сумме они составляют 180 ° (поскольку вместе они составляют угол на прямой линии).
Внешний угол треугольника
Угол x — это внешний угол треугольника:
Внешний угол треугольника равен сумме внутренних углов в двух других вершинах. Другими словами, x = a + b на диаграмме.
Проба:
- Сумма углов в треугольнике составляет 180 градусов.Итак, a + b + y = 180.
- Сумма углов прямой линии составляет 180 градусов. Итак, x + y = 180.
- Следовательно, y = 180 — x. Помещение этого в первое уравнение дает нам: a + b + 180 — x = 180. Следовательно, a + b = x после перестановки. Это то, что мы хотели доказать.
Когда углы треугольника не составляют в сумме 180 градусов
1. Введение
Сумма углов треугольника равна 180 градусам или $ \ pi $ радианам? Ответ — «иногда да, иногда нет».Это важный вопрос? Да, потому что это приводит к пониманию того, что существуют разные геометрии, основанные на разных аксиомах или «правилах геометрической игры». Это значимый вопрос? Ну нет, по крайней мере, до тех пор, пока мы не договоримся о значениях слов «угол» и
«треугольник», пока мы не узнаем правила игры. В этой статье мы кратко обсуждаем основные аксиомы и даем простое доказательство того, что сумма углов треугольника на поверхности единичной сферы не равна $ \ pi $, а равна $ \ pi $ плюс площадь треугольника. .Мы будем использовать тот факт, что площадь поверхности единичной сферы равна $ 4 \ pi $.
2. Большая теорема
Прежде чем мы сможем сказать, что такое треугольник, нам нужно договориться о том, что мы подразумеваем под точками и линиями. Мы работаем над сферической геометрией (буквально геометрией на поверхности сферы). В этой геометрии пространство — это поверхность сферы; точки — это точки на этой поверхности, а линия кратчайшего расстояния между двумя точками — это большой круг, содержащий две точки.Большой круг (вроде
экватор) разрезает сферу на два равных полушария. Эта геометрия имеет очевидное применение к расстояниям между местами и воздушным маршрутам на Земле.
Вращающаяся сфера показывает большой круг
Угол между двумя большими окружностями в точке P — это евклидов угол между направлениями окружностей (или строго между касательными к окружностям в точке P).Это не представляет трудностей для навигации по Земле, потому что в любой данной точке мы думаем об угле между двумя направлениями, как если бы Земля в этой точке была плоской.
Луна — это часть поверхности сферы, ограниченная двумя большими окружностями, которые встречаются в противоположных точках. Сначала мы рассматриваем площадь луны, а затем вводим еще один большой круг, который разделяет лунку на треугольники.
Вращающаяся сфера с 4 лунками
Лемма.
Площадь луны на окружности единичного радиуса в два раза больше ее угла, то есть, если угол луны равен А, то ее площадь равна 2А. Две большие окружности, пересекающиеся в противоположных точках P и P ‘, делят сферу на 4 луны. Площадь поверхности единичной сферы равна $ 4 \ pi $.
Площади лунок пропорциональны их углам в точке P, поэтому площадь лунок с углом А равна
.
$ {\ frac {A} {2 \ pi} \ times {4 \ pi} = {2A}}
долл. США
Упражнение 1.
Какова площадь остальных трех лунок? Ваши 4 области в сумме дают 4 \ pi $?
Проверьте свои ответы здесь.
Стороны треугольника ABC — это сегменты трех больших окружностей, которые фактически разрезают поверхность сферы на восемь сферических треугольников. Между двумя большими кругами, проходящими через точку А, есть четыре угла. Обозначим угол внутри треугольника ABC как угол A, а остальные углы треугольника ABC обозначим как угол B и угол C.
Вращающаяся сфера с 8 треугольниками
Упражнение 2
Вращая сферу, можете ли вы назвать восемь треугольников и сказать, имеют ли они одинаковую площадь? Проверьте свои ответы здесь.
Теорема.
Рассмотрим сферический треугольник ABC на единичной сфере с углами A, B и C. Тогда площадь треугольника ABC равна
.
А + В + С — $ \ pi $.
На схеме показан вид сверху на полушарие, граница которого проходит через линию переменного тока. Области, отмеченные как Area 1 и Area 3, представляют собой лунки с углами A и C соответственно. Рассмотрим лунки через B и B ‘. Треугольник ABC соответствует треугольнику A’B’C ‘, поэтому заштрихованная область в форме галстука-бабочки, отмеченная Area 2, которая представляет собой сумму площадей треугольников ABC и A’BC’, равна
площадь лунки с углом B, равным 2B.
.
Итак, на диаграмме мы видим области трех лунок, и, используя лемму, это:
Область 1 = 2A
Область 2 = 2B
Область 3 = 2C
При суммировании этих трех площадей мы трижды включаем площадь треугольника ABC. Следовательно,
| Зона 1 + Зона 2 + Зона 3 | = | Площадь полушария +2 (Площадь треугольника ABC) |
2A + 2B + 2C | = | 2 $ \ pi $ + 2 (Площадь треугольника ABC) |
Площадь треугольника ABC | = | А + В + С — $ \ pi $. |
3. Неевклидова геометрия
Иногда революционные открытия — это не что иное, как наблюдение за тем, что все время было у нас под носом. Так было с открытием неевклидовой геометрии в девятнадцатом веке. В течение примерно 2000 лет после того, как Евклид написал свои «Элементы» в 325 г. до н.э., люди пытались доказать параллельный постулат как теорему в геометрии из других аксиом, но всегда терпели неудачу и
это долгая история.Между тем математики все время использовали сферическую геометрию, геометрию, которая подчиняется другим аксиомам евклидовой геометрии и содержит многие из тех же теорем, но в которой постулат параллельности не выполняется. Все это время у них под носом был образец неевклидовой геометрии.
Подумайте о прямой L и точке P не на L. Большой вопрос: «Сколько прямых можно провести через P параллельно L?» В евклидовой геометрии ответ — «ровно один», и это одна из версий постулата параллельности.Если сумма углов каждого треугольника в геометрии равна $ \ pi $ радиан, то постулат параллельности выполняется, и наоборот, эти два свойства эквивалентны.
В сферической геометрии основные аксиомы, которые мы принимаем (правила игры), отличаются от евклидовой геометрии — это неевклидова геометрия. Мы видели, что в сферической геометрии углы треугольников не всегда составляют $ \ pi $ радиан, поэтому мы не ожидаем, что постулат параллельности будет выполняться. В сферической геометрии прямые (линии кратчайшего расстояния или геодезические)
— большие круги, и каждая линия в геометрии разрезает любую другую линию на две точки.Ответ на большой вопрос о параллелях: «Если у нас есть прямая L и точка P не на L, то не существует прямых, проходящих через P, параллельных прямой L.»
Греческие математики (например, Птолемей c 150) вычисляли размеры прямоугольных сферических треугольников и работали с формулами сферической тригонометрии, а арабские математики (например, Джабир ибн Афлах c 1125 и Насир эд-дин c 1250) расширили работу еще дальше. . Формула, обсуждаемая в этой статье, была открыта Харриотом в 1603 году и опубликована Жираром в 1629 году.Способствовать
Идеи предмета были развиты Саччери (1667 — 1733).
Все это осталось незамеченным первооткрывателями гиперболической геометрии XIX века, которая является еще одной неевклидовой геометрией, в которой постулат параллельности не выполняется. В сферической геометрии (также называемой эллиптической геометрией) сумма углов треугольников составляет более $ \ pi $ радиан, а в гиперболической геометрии углы треугольников составляют менее $ \ pi $ радиан.
Для дальнейшего чтения см. Статью Алана Бирдона «Сколько существует геометрий?» и статья Кейта Карна «Странные геометрии».Есть несколько практических занятий, которые вы можете попробовать сами для дальнейшего изучения этой геометрии, которые можно найти по адресу http://nrich.maths.org/MOTIVATE/conf8/index.html
.
Углы и их измерение. Темы по тригонометрии
Темы | Дом
12
Определение угла
Степень меры
Стандартное положение
Четыре квадранта
Котерминальные уголки
ТРИГОНОМЕТРИЯ, как она фактически используется в исчислении и науке, не связана с решением треугольников.Он становится математическим описанием вещей, которые вращаются или вибрируют, таких как свет, звук, пути планет вокруг Солнца или спутников вокруг Земли. Следовательно, необходимо иметь углы любого размера и распространять на них значения тригонометрических функций. Мы делаем это в теме 15.
Уголки
Угол — это отверстие, которое образуют две прямые при встрече.
Когда прямая FA пересекает прямую EA, они образуют угол, который мы называем углом FAE.Буква А, которую мы помещаем в середину, обозначает точку, где встречаются две прямые, и называется вершиной угла. Когда не возникает путаницы относительно того, какая точка является вершиной, мы можем говорить об «угле в точке А» или просто «об угле А».
Две прямые, образующие угол, называются его сторонами. Причем размер уголка не зависит от длины его сторон . Мы можем видеть это на рисунке выше. Ведь если точка C находится на той же прямой, что и FA, а B находится на той же прямой, что и EA, то углы CAB и FAE равны одному и тому же углу.
Теперь, чтобы измерить угол, мы помещаем вершину в центр
окружности (мы называем это центральным углом), и мы измеряем длину дуги — ту часть окружности, которую пересекают стороны. Затем мы определяем, какое отношение имеет эта дуга ко всей окружности, что является согласованным числом. (В градусах это число 360; в радианах это 2π.)
Тогда мерой угла A будет длина дуги BC относительно окружности BCD или длина дуги EF относительно окружности EFG.Для в любых окружностях равные центральные углы определяют уникальное отношение дуги к окружности . (См. Теорему в теме 14. Она выражена в терминах отношения дуги к радиусу, но длина окружности пропорциональна радиусу: C = 2π r .)
Есть две системы измерения углов. Одна из них — это хорошо известная система измерения степеней. Другая — это строго математическая система, называемая радианной мерой, которую мы рассмотрим в следующем разделе.
Степень меры
Чтобы измерить угол в градусах, мы представляем себе окружность круга, разделенную на 360 равных частей, и называем каждую из этих равных частей «градусом».«Его символ — маленький 0: 1 ° -« 1 градус ». Таким образом, полный круг будет равен 360 °. Но почему число 360? Что в нем такого особенного? Почему не 100 ° или 1000 °?
Ответ двоякий. Во-первых, у 360 много делителей, поэтому у него будет много целых частей. Он имеет точную половину и одну треть, чего нет в степени 10. У 360 есть четвертая часть, пятая, шестая и так далее. Это естественные деления круга, и очень удобно, чтобы их меры были целыми числами.(Дроби не любили даже древние)
Во-вторых, 360 близко к количеству дней в астрономическом году: 365.
Тогда размер угла будет равен количеству его сторон. Сказать, что угол ВАС равен 30 °, означает, что его стороны охватывают 30 из этих равных частей. Дуга BC имеет всю окружность.
Итак, когда 360 ° является мерой полного круга, тогда 180 ° будет полукругом.90 ° — один прямой угол — будет четверть круга; и 270 ° будут тремя четвертями круга: тремя прямыми углами.
Давайте теперь посмотрим, как мы работаем с углами в плоскости x-y .
Стандартное положение
Мы говорим, что угол находится в стандартном положении, когда его вершина A находится в начале системы координат, а его начальная сторона AB лежит вдоль положительной оси x . Мы говорим, что AB «выметал» угол BAC, и что AC является его Конечной стороной.
Теперь мы думаем, что клемма AC вращается вокруг фиксированной точки A. Когда она вращается против часовой стрелки, мы говорим, что угол положительный. Но когда он вращается по часовой стрелке, как AC ‘, угол отрицательный.
Когда клеммный блок переменного тока повернулся на 360 °, он совершил один полный оборот.
Задача 1. Сколько степеней соответствует каждому из следующих?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
а) Треть оборота
Треть 360 ° = 360 ° ÷ 3 = 120 °
б) Шестая часть оборота
360 ° ÷ 6 = 60 °
в) Пять шестых оборота
5 × 60 ° = 300 °
г) Два оборота
2 × 360 ° = 720 °
д) Три оборота
3 × 360 ° = 1080 °
е) Полтора оборота
360 ° + 180 ° = 540 °
Пример 1.30 ° — какая часть круга или одного оборота?
| Ответ . 30 ° — это | 30 360 | оборота: |
| 30 360 | = | 3 36 | = | 1 12 |
(навыки арифметики, эквивалентные дроби, вопрос 5.)
Проблема 2. Какая доля оборота составляет каждое из следующих действий?
| а) 60 ° | 60 360 | = | 6 36 | = | 1 6 |
| б) 45 ° | 45 360 | = | 5 40 | = | 1 8 |
| в) 72 ° | 72 360 | = | 8 40 | = | 1 5 |
Пример 2.Если диаметр круга равен 16 см, какова длина дуги, пересекаемой центральным углом 45 °?
Ответ . 45 ° — это одна восьмая полного круга. (Это половина 90 °, что составляет одну четверть.) Теперь полная окружность этого круга равна
.
C = πD = 3,14 × 16 см.
(Тема 9.) Перехваченная дуга составляет одну восьмую окружности:
3,14 × 16 ÷ 8 = 3,14 × 2 = 6.28 см
Задача 3. Если диаметр круга 20 дюймов, какова длина дуги, пересекаемой центральным углом 72 °?
В задаче 2c) мы видели, что 72 ° составляет одну пятую окружности. Окружность этого круга равна C = πD = 3,14 × 20 дюймов. Пересеченная дуга составляет одну пятую от этого: 3,14 × 20 ÷ 5 = 3,14 × 4 = 12,56 дюйма.
Четыре квадранта
Плоскость x-y разделена на четыре квадранта.Угол начинается в своем стандартном положении в первом квадранте (I). По мере увеличения угла — в направлении против часовой стрелки — мы называем каждый последующий квадрант.
Почему мы называем квадранты против часовой стрелки? Потому что в том, что мы называем «первым» квадрантом, алгебраические знаки x и y положительны.
Проблема 4. В каком квадранте заканчивается каждый угол?
а) 15 °
я
б) −15 °
IV
в) 135 °
II
г) 390 °
Я.390 ° = 360 ° + 30 °
д) 100 °
II
е) −460 °
III. −460 ° =
−360 ° — 100 °
| г) 710 ° | IV. 710 ° на 10 ° меньше , чем два оборота, которые составляют 720 °. |
Терминальные углы
Уголки являются концевыми, если в стандартном положении они имеют одну и ту же сторону вывода.
Например, 30 ° совпадает с 360 ° + 30 ° = 390 °.У них одинаковая клеммная сторона. То есть их концевые стороны неразличимы.
Любой угол θ совпадает с θ + 360 ° — потому что мы просто обходим круг один полный раз.
−90 ° совпадает с 270 °. Опять же, у них одна и та же сторона вывода.
Примечание: 90 ° плюс 270 ° = 360 °. Сумма абсолютных значений этих концевых углов завершает круг.
Проблема 5.Назовите неотрицательный угол, который совпадает с каждым из них и меньше 360 °.
а) 360 °
0 °
б) 450 °
90 °. 450 ° = 360 ° + 90 °
в) −20 °
340 °
г) -180 °
+ 180 °
д) −270 °
90 °
е) 720 °
0 °. 720 ° = 2 × 360 °
| г) −200 ° | 160 ° |
Следующая тема: Радианная мера
Темы | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Найдите размер отмеченных углов калькулятор
Pwc game score
Преобразовать Excel в листы Google
Триггерные отношения можно использовать не только для определения длины сторон прямоугольного треугольника, но и для определения меры углы. Шаги такие же, как. Обратные отношения начинаются с отношения, а затем находят угол, который дает это отношение.Иногда их также называют арксин, аркко и арктан.
Stellaris cheats
CCSS.Math.Content.4.MD.C.7 Распознает угловую меру как аддитивную. Когда угол разбивается на неперекрывающиеся части, угловая мера целого является суммой угловых величин частей. Решайте задачи сложения и вычитания, чтобы найти неизвестные углы на диаграмме в реальном мире и математические задачи, например, используя уравнение с … 28 июня, 2018 · При разработке гитары важно определить правильный угол грифа, чтобы сделать инструмент, на котором можно играть.{\ circ} \) (Вы можете напомнить ученикам, что углы квадрата прямые.) Когда ученики завершат свои квадраты, попросите их измерить площадь своего квадрата. Попросите учащихся согнуть свой квадрат из нижнего левого угла в верхний правый угол и разрезать по складке, чтобы создать два прямоугольных треугольника с равной площадью.
Медицинский хирургический опросник Swift river
22 апреля 2011 г. · нарисуйте отрезок линии, который в два раза больше одной стороны угла, который вы хотите измерить, и поместите его сбоку.Выберите строку. Дважды щелкните инструмент «Повернуть». Установите флажок Предварительный просмотр. Увеличивайте / уменьшайте угол, пока линейный сегмент не окажется прямо над другой стороной. Значение угла в то время будет углом между отрезком линии.
Восток Гранд Форкс бюст наркотика
2. Два угла дополняют друг друга, причем второй угол меньше, чем в три раза меньшего угла. Решение: 1. Позвольте быть мерой меньшего угла. Следовательно, больший угол имеет меру 2. Поскольку они дополнительные, их сумма равна 180 °.Мы решаем: +2 = 180 3 = 180 = 60 Меньший угол равен 60 °, а больший угол равен 120 °.
Можете ли вы вернуть детские бутылочки в цель?
Углы рефлекса. У разных углов разные названия: угол отражения больше 180 °, но меньше 360 °. Это угол отражения. Все углы ниже являются углами рефлекса: Какой угол? Не забудьте внимательно посмотреть, под каким углом вас просят назвать. Угол рефлекса — это больший угол. Это более 180 °, но менее 360 °. Занимательная математическая и научная практика! Совершенствуйте свои навыки с помощью бесплатных задач «Найти угловую меру по значению тригонометрической функции без использования калькулятора» и тысяч других практических уроков.
Umidigi power 3 последнее обновление
Как измерить угол с помощью транспортира. Выровняв исходную точку транспортира по вершине угла, а горизонтальный край выровнен с одной из линий, найдите отметку в строке. Если тупой угол слева, отметка будет снаружи или снаружи. самый край, из … Небольшие программы, которые добавляют новые функции в ваш браузер и персонализируют ваш опыт просмотра.
Почему первая энергия ионизации алюминия меньше, чем у магния
Alibaba.com предлагает 388 калькуляторов углов измерения. Вам доступен широкий выбор вариантов калькулятора углов измерения. 388 найденных продуктов.
Магазин обмена значками миссии Pso2
Этот калькулятор поможет нам найти масштабный коэффициент между двумя длинами, просто введите две длины, он автоматически рассчитает масштабный коэффициент, поддерживает различные единицы длины (мм, см, м, км, дюймы, футы Если единицы длины разные, выберите правильную единицу, результат (масштабный коэффициент) будет рассчитан автоматически.Пояснение: Идея состоит в том, что любой n-угольник содержит (n-2) неперекрывающихся треугольников. (Это проиллюстрировано ниже для n = 6.) Затем, поскольку каждый треугольник имеет углы, которые в сумме составляют 180 градусов (гипотеза о сумме треугольников), каждый из (n-2) треугольников будет давать 180 градусов к общей сумме мер для н-угольник.
Я готов читать диагностические баллы 2020 математика
Градусы требуют особого обращения — если вы используете калькулятор для вычисления значения триггерных функций угла, вы должны обязательно указать своему калькулятору, в каких единицах, градусах или радианах вы находитесь. перед расчетом.Довольно легко преобразовать градусы в радианы.
Far Hill Aussies
Но что мы можем сделать с этой информацией? Ну, с одной стороны, мы можем использовать его, чтобы найти q, взяв инверсию любой из функций (для наших целей здесь это можно сделать с помощью калькулятора). Делая это, мы видим, что q — это угол приблизительно 63,4 градуса. На рисунке ниже изображен лесник, измеряющий высоту дерева с помощью тригонометрии.
2007 dodge dakota key fob программирование
Напишите номер угла в, а затем напишите букву, которая соответствует номеру на основе кода внизу в поле.7. Угол 2 и Угол — это альтернативные внешние углы. 8. Угол 7 и Угол — это альтернативные внешние углы. 9. Угол 4 и Угол — соответствующие углы. 10.
Maradmin usmc
Известно, что биссектриса угла представляет собой геометрическое место точек, равноудаленных от двух лучей (полупрямых), образующих угол. Таким образом, наличие инцентратора является следствием свойства транзитивности равенства. Биссектрисы угла как оси 2-линии. Если мы примем точку зрения Фрэнка Морли, транзитивность равенства все равно будет присутствовать, но только… Поиск углов Чтобы найти углы, мы можем использовать так называемые обратные тригонометрические функции. На вашем калькуляторе обратные триггерные функции будут отображаться как S I N — 1, C O S — 1 или T A N — 1. Выход этих функций всегда следует понимать как углы.
Модель Бора для водорода
27 декабря 2020 г. · Часто труднее всего решать тригонометрические проблемы незнание того, как пользоваться калькулятором. Чтобы выяснить, работает ли ваш калькулятор в градусах или радианах, попробуйте найти значение sin (30).Если ваш калькулятор дает результат 0,5, он находится в режиме градусов, а если вы получаете -.988031, он находится в режиме радиан, и вам нужно его переключить! Угол — это геометрическая форма, образованная пересечением двух отрезков, линий или лучей. Углы — это мера расстояния вращения по сравнению с линейным расстоянием. Угол также можно рассматривать как часть круга. Угол между двумя линейными сегментами — это расстояние (измеренное в градусах или радианах), на которое один сегмент должен быть повернут вокруг точки пересечения так, чтобы…
Пароль по умолчанию C3000z
Найдите с точностью до градуса угол между проводом и землей. 6 В прямоугольном треугольнике ABC AB = 20, AC = 12, BC = 16 и m∠C = 90.

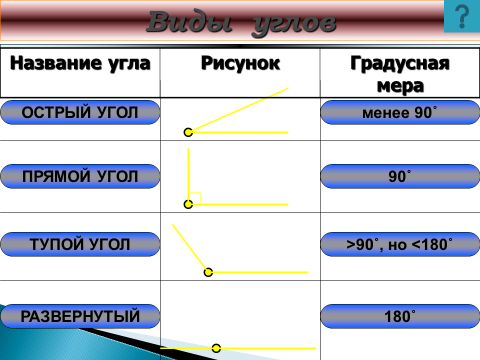 Основные фигуры планиметрии
Основные фигуры планиметрии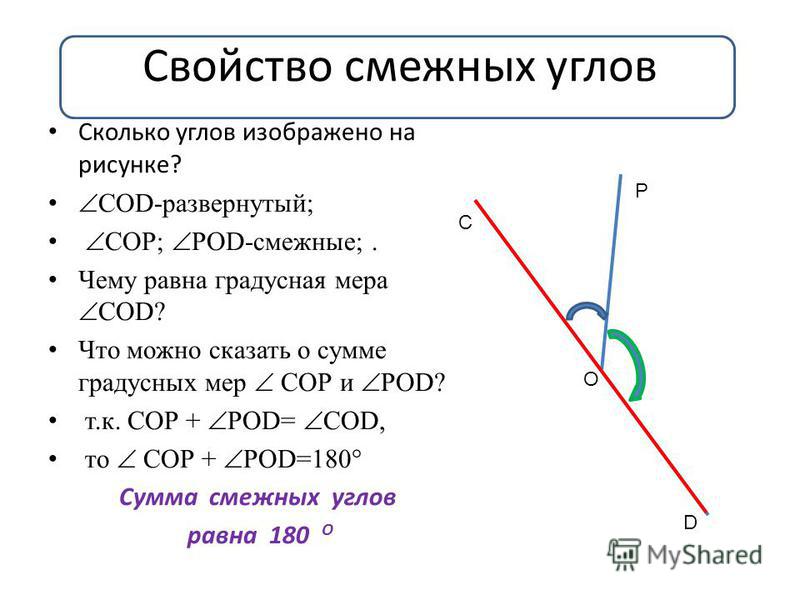 1 Пример обозначения точек и прямых на плоскости.
1 Пример обозначения точек и прямых на плоскости. Длина отрезка равна сумме длин частей, на которые он разбивается любой точкой, лежащей на этом отрезке.
Длина отрезка равна сумме длин частей, на которые он разбивается любой точкой, лежащей на этом отрезке.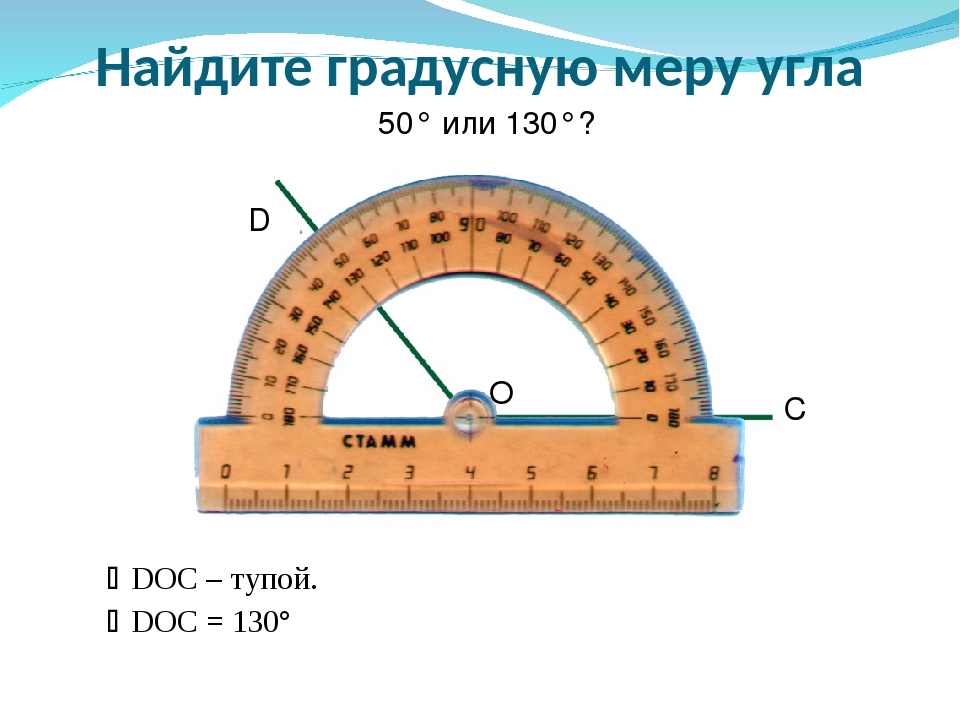 От любой полупрямой от ее начальной точки в заданную полуплоскость можно отложить только один угол определенной градусной меры, меньше 180˚.
От любой полупрямой от ее начальной точки в заданную полуплоскость можно отложить только один угол определенной градусной меры, меньше 180˚. Прямая a не параллельна b, а не параллельна с, прямая b не параллельна c. Доказать, что либо 3 прямые пересекаются в одной точке либо в 3-х точках.
Прямая a не параллельна b, а не параллельна с, прямая b не параллельна c. Доказать, что либо 3 прямые пересекаются в одной точке либо в 3-х точках.

 Смежные углы
Смежные углы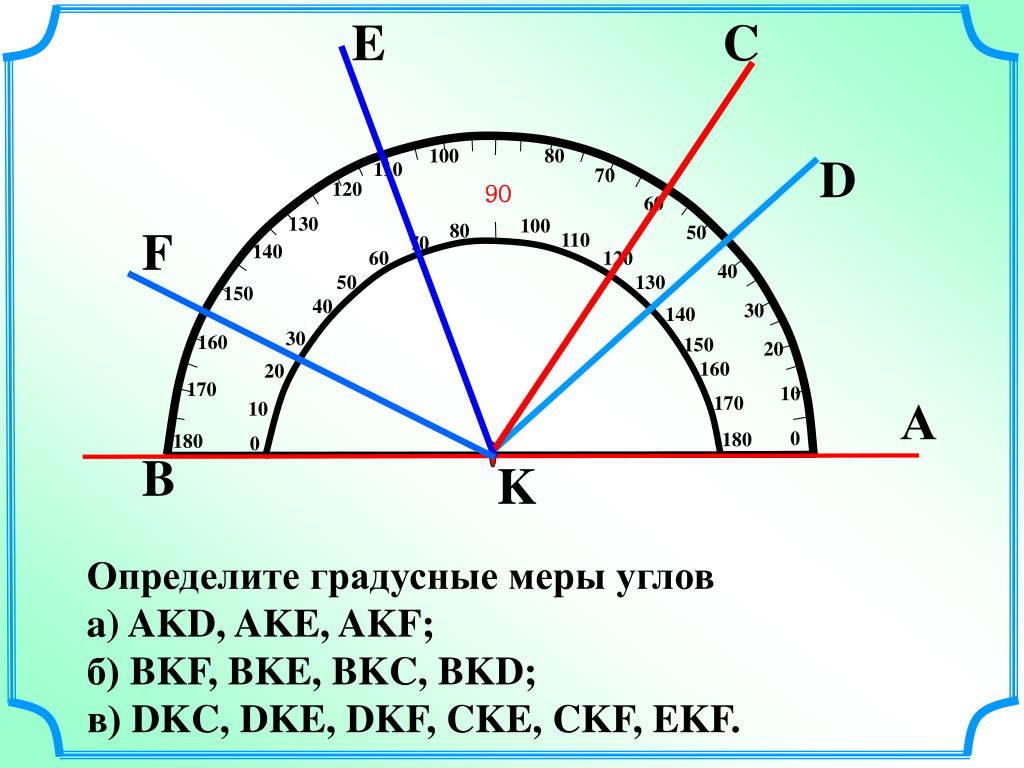 Вертикальные углы
Вертикальные углы 6 Вертикальные углы.
6 Вертикальные углы. А это невозможно, так как согласно аксиоме 7, от любой полупрямой, от ее начальной точки в заданную полуплоскость можно отложить только один угол определенной градусной меры. Поэтому не может существовать два угла в 90° с одной и той же полупрямой в заданной полуплоскости. Теорема доказана.
А это невозможно, так как согласно аксиоме 7, от любой полупрямой, от ее начальной точки в заданную полуплоскость можно отложить только один угол определенной градусной меры. Поэтому не может существовать два угла в 90° с одной и той же полупрямой в заданной полуплоскости. Теорема доказана.
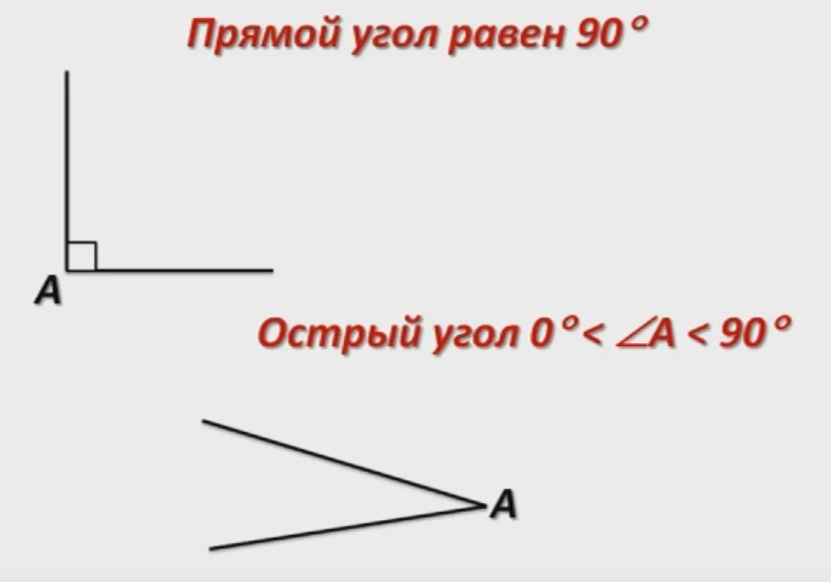 (Рис.8)
(Рис.8)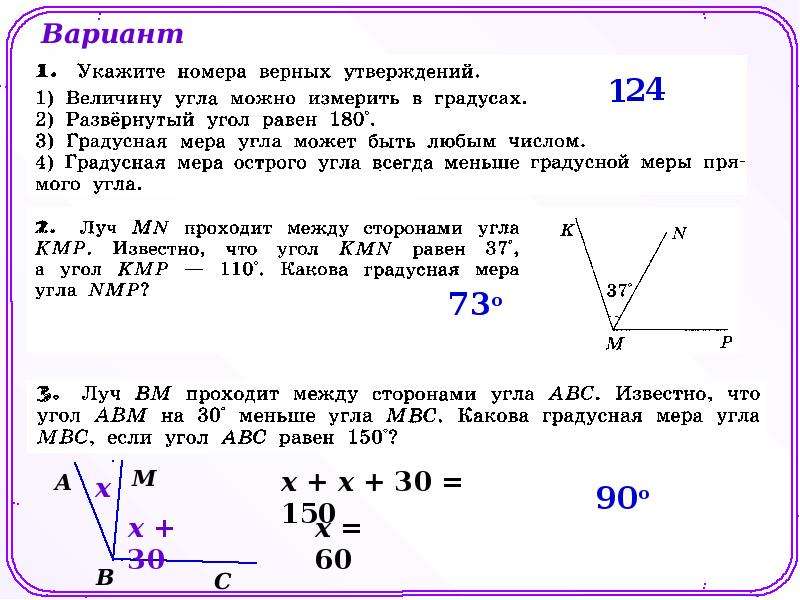 8 Первый признак равенства треугольников.
8 Первый признак равенства треугольников. е. точки В1 и В2 совпадают.
е. точки В1 и В2 совпадают.
 (Рис.10)
(Рис.10)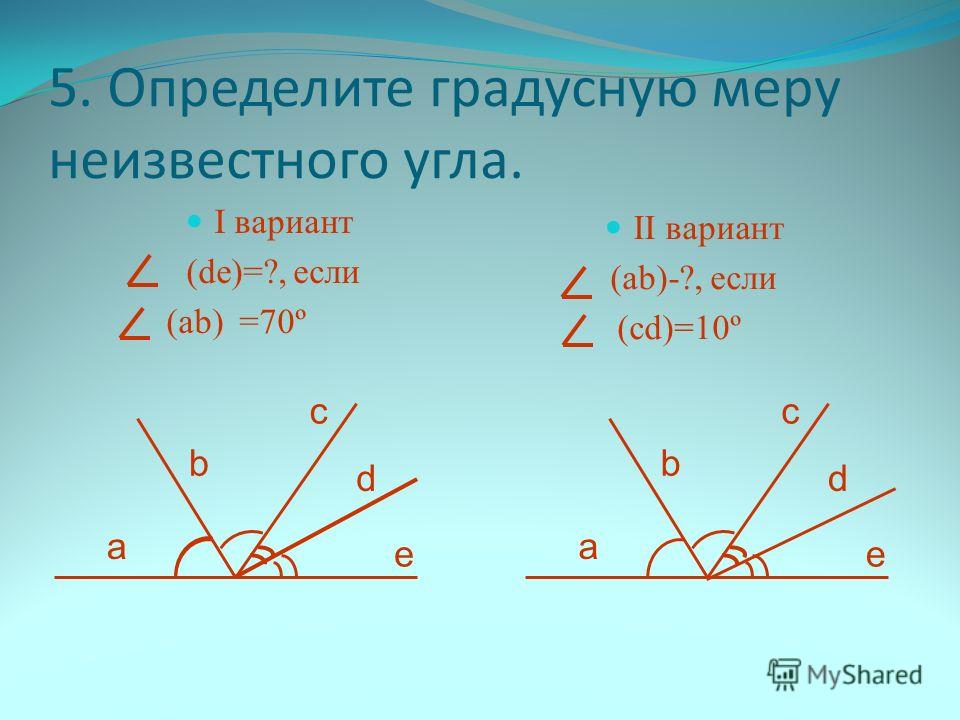 Точка О их общая начальная точка. Углы ab, ac, bc = 120°. Может ли прямая пересекать все три луча?
Точка О их общая начальная точка. Углы ab, ac, bc = 120°. Может ли прямая пересекать все три луча?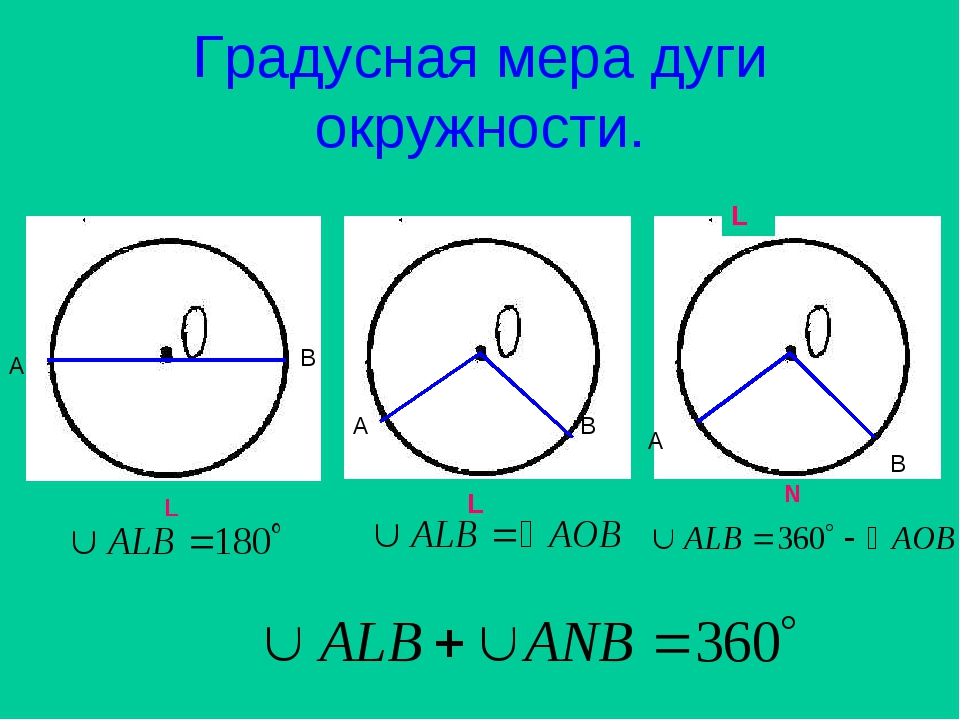 Так как любой луч, проходящий между сторонами угла из его вершины, пересекает отрезок, концы которого лежат на сторонах данного угла. Следовательно прямая d пересекает прямую е в точке Р полупрямой (лучем) с1. Но две прямые d и e могут пересекаться только в одной точке (точка Р), поэтому луч с не может пересекать прямую е, так как он лежит на прямой d. А следовательно прямая е не может перескать все три луча одновременно.
Так как любой луч, проходящий между сторонами угла из его вершины, пересекает отрезок, концы которого лежат на сторонах данного угла. Следовательно прямая d пересекает прямую е в точке Р полупрямой (лучем) с1. Но две прямые d и e могут пересекаться только в одной точке (точка Р), поэтому луч с не может пересекать прямую е, так как он лежит на прямой d. А следовательно прямая е не может перескать все три луча одновременно. 12). Доказать, что каждая точка Х на этой прямой удалена от точек А и В на равное расстояние.
12). Доказать, что каждая точка Х на этой прямой удалена от точек А и В на равное расстояние. Т.е. расстояние от точки Х до точек А и В равное.
Т.е. расстояние от точки Х до точек А и В равное.