График f x 1 x: Mathway | Популярные задачи — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Задание № 7. Производная функции. ЕГЭ . Математика.

БАЗА ЗАДАНИЙ

Задание № 7. Производная функции.

26. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) отрицательна?

27. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены десять точек:

x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. В скольких из этих точек производная функции f(x) положительна?

28. На рисунке изображён график дифференцируемой функции y=f(x) и отмечены девять точек на оси абсцисс:

x1, x2, x3, x4, x5, x6, x7, x8, x9. В скольких из этих точек производная функции f(x) положительна?

29. На рисунке изображён график дифференцируемой функции y=f(x) и отмечены

шесть точек на оси абсцисс:

x1, x2, x3, x4, x5, x6. В скольких из этих точек производная функции f(x) отрицательна?

30. На рисунке изображён график y=f '(x) — производной функции f(x). На оси абсцисс отмечено шесть точек: x1, x2, x3, x4, x5, x6. Сколько из этих точек принадлежит промежуткам возрастания функции f(x)?

31. На рисунке изображён график y=f '(x) — производной функции f(x). На оси абсцисс отмечено семь точек: x1, x2, x3, x4, x5, x6, x7. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?

32. На рисунке изображён график y=f '(x) — производной функции f(x).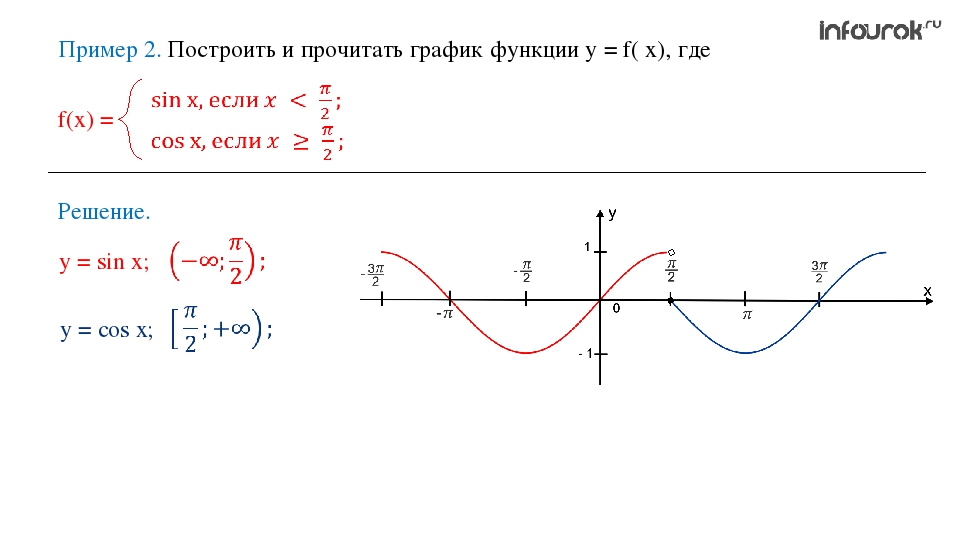 На оси абсцисс отмечено восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек принадлежит промежуткам возрастания функции f(x)?

33. На рисунке изображён график y=f '(x) — производной функции f(x). На оси абсцисс отмечено одиннадцать точек:

x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11. Сколько из

этих точек принадлежит промежуткам убывания функции f(x)?

34. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки − 1, 2, 3, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

35. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки − 2, − 1, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

36.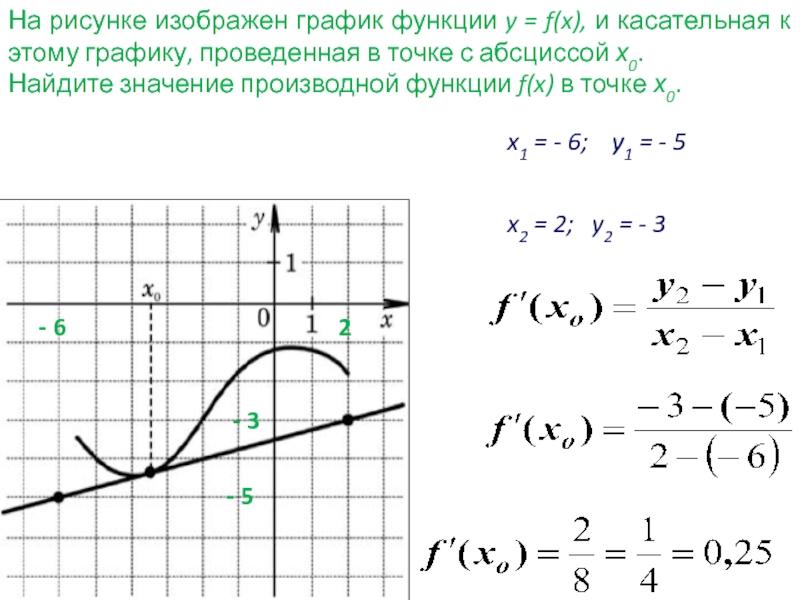 На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

37. На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

38. На рисунке изображён график

y=f '(x) — производной функции f(x), определённой на интервале (− 2; 9). В какой точке отрезка [2; 8] функция f(x) принимает наибольшее значение?

39. На рисунке изображён график

y=f '(x)

—
производной функции f(x), определённой на интервале (− 8; 4). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?

40. На рисунке изображён график

y=f '(x)

—

производной функции f(x), определённой на интервале (− 3; 8). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?

41. На рисунке изображён график

y=f '(x)

—

производной функции f(x), определённой на интервале (− 8; 3). В какой точке отрезка [− 6; −1] функция f(x) принимает наибольшее значение?

42. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].

43.

На рисунке изображён график y=f '(x) — производной функции f(x), определенной на интервале (-11;11). Найдите количество точек экстремума функции f(x) на отрезке [-10;10].

44. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 11; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [− 6; 4].

45. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 3; 19). Найдите количество точек максимума функции f(x), принадлежащих отрезку [− 2; 15].

46.

На рисунке изображён график y=f '(x) — производной функции f(x), определенной на интервале (-11;3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

47.

На рисунке изображён график y=f '(x) — производной функции f(x), определенной на интервале (-2;12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

48. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 2; 11). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней.

49. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 4; 13). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=−2x−10 или совпадает с ней.

50.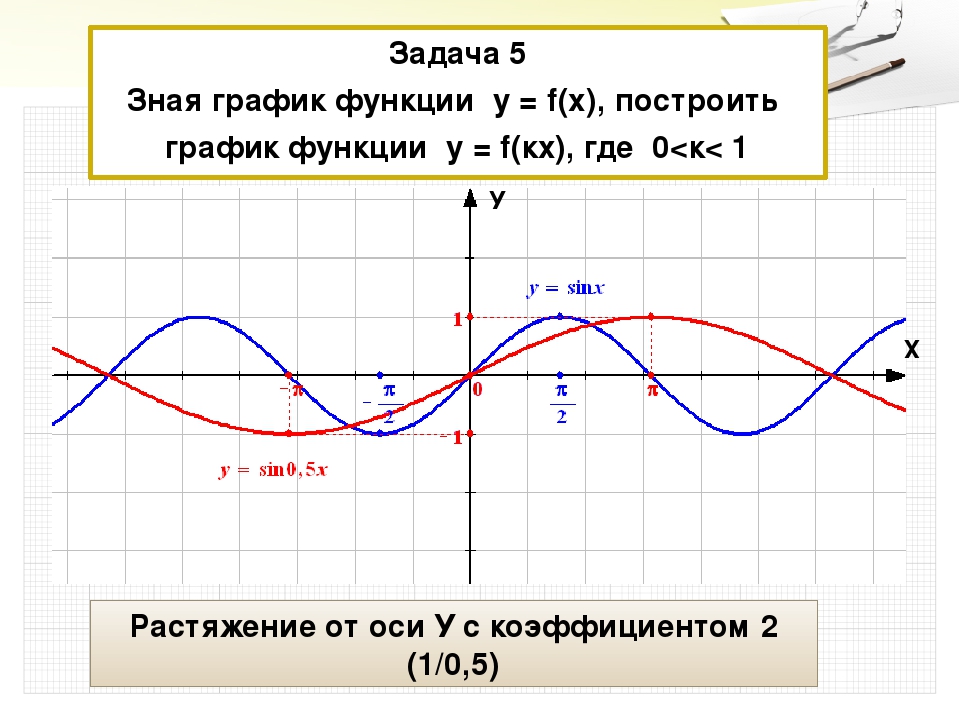 На рисунке изображён график функции y=f(x), определённой на интервале (− 4; 13). Определите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=14.

Калькулятор онлайн — Найти (с решением) производную функции

Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не
просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.

Вы можете посмотреть теорию о производной функции и
правила дифференцирования и таблицу производных, т.е. список формул для нахождения
производных от некоторых элементарных функций.

Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача
Уравнение касательной к графику функции.

Примеры подробного решения >>

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.

Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Определение производной

Определение. Пусть функция $ y = f(x) $ определена в некотором интервале, содержащем внутри себя точку $ x_0 $.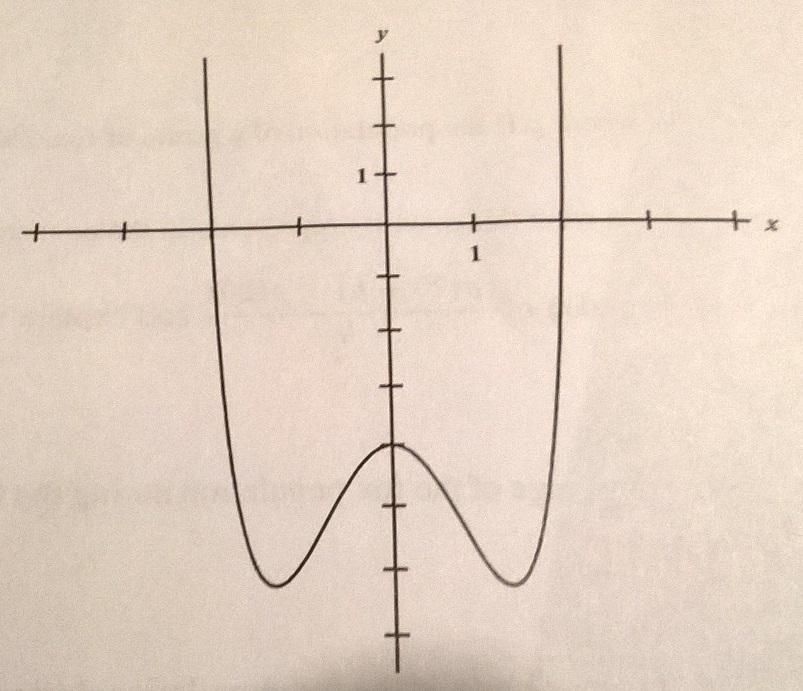
Дадим аргументу приращение $ \Delta x $ такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции
$ \Delta y $ (при переходе от точки $ x_0 $ к точке $ x_0 + \Delta x $ ) и составим отношение
$ \frac{\Delta y}{\Delta x} $. Если существует предел этого отношения при $ \Delta x \rightarrow 0 $, то
указанный предел называют производной функции $ y=f(x) $ в точке $ x_0 $ и обозначают $ f'(x_0) $.

$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f'(x_0) $$

Для обозначения производной часто используют символ $ y’ $.
Отметим, что $ y’ = f(x) $ — это новая функция, но, естественно, связанная с функцией $ y = f(x) $, определенная во всех точках $x$, в которых
существует указанный выше предел. Эту функцию называют так: производная функции $ y = f(x) $.

Геометрический смысл производной состоит в следующем. Если к графику функции $ y = f(x) $ в точке с абсциссой $ x=a $ можно
провести касательную, непараллельную оси $y$, то $ f(a) $ выражает угловой коэффициент касательной:

$ k = f'(a) $

Поскольку $ k = tg(a) $, то верно равенство $ f'(a) = tg(a) $ . 2 \) справедливо приближенное равенство $ \Delta y \approx 2x \cdot \Delta x $.
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.

Сформулируем его.

Как найти производную функции у = f(x) ?

1. Зафиксировать значение $ x $, найти $ f(x) $

2. Дать аргументу $ x $ приращение $ \Delta x $, перейти в новую точку $ x+ \Delta x $, найти $ f(x+ \Delta x) $

3. Найти приращение функции: $ \Delta y = f(x + \Delta x) — f(x) $

4. Составить отношение $ \frac{\Delta y}{\Delta x} $

5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$

Этот предел и есть производная функции в точке $x$.

Если функция $y=f(x)$ имеет производную в точке $x$, то ее называют дифференцируемой в точке $x$. Процедуру нахождения производной
функции $y=f(x)$ называют дифференцированием функции $y=f(x)$.

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция $y=f(x)$ дифференцируема в точке $x$. Тогда к графику функции в точке $ M(x; \; f(x)) $ можно провести касательную,
причем, напомним, угловой коэффициент касательной равен $ f'(x) $. Такой график не может «разрываться» в точке $M$, т. е. функция
обязана быть непрерывной в точке $x$.

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция $y=f(x)$ дифференцируема в точке $x$, то
выполняется приближенное равенство $ \Delta y \approx f'(x) \cdot \Delta x $. Если в этом равенстве $ \Delta x $ устремить к
нулю, то и $ \Delta y $ будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.

Обратное утверждение неверно. Например: функция $ y=|x|$ непрерывна везде, в частности в точке $x=0$, но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.

Еще один пример. Функция $ y=\sqrt[3]{x} $ непрерывна на всей числовой прямой, в том числе в точке $x=0$.
И касательная к графику функции существует в любой точке, в том числе в точке $x=0$. Но в этой точке касательная совпадает с осью $y$,
т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид $x=0$. Углового коэффициента у такой прямой нет, значит, не существует и
$ f'(0) $

Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее
дифференцируемости?

Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси
абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она
перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема. 2} $$

Непрерывность функции в точке и на промежутке. С примерами

На этом уроке будем учиться устанавливать непрерывность функции. Будем делать это
с помощью пределов, причем односторонних — правого и левого, которые совсем не страшны, несмотря на
то что записываются как и
.

Но что такое вообще непрерывность функции? Пока мы не дошли до строгого определения,
проще всего представить себе линию, которую можно начертить, не отрывая карандаш от бумаги. Если такая линия
начерчена, то она непрерывна. Эта линия и является графиком непрерывной функции.

Графически функция непрерывна в точке ,
если её график не «разрывается» в этой точке. График такой непрерывной
функции —
показан на рисунке ниже.

Определение непрерывности функции
через предел. Функция является непрерывной в точке при соблюдении трёх условий:

А могут ли правый и левый пределы хоть когда-нибудь быть не равны, если к значению, к которому
стремится икс, прибавляется или вычитается всего лишь нуль? Могут.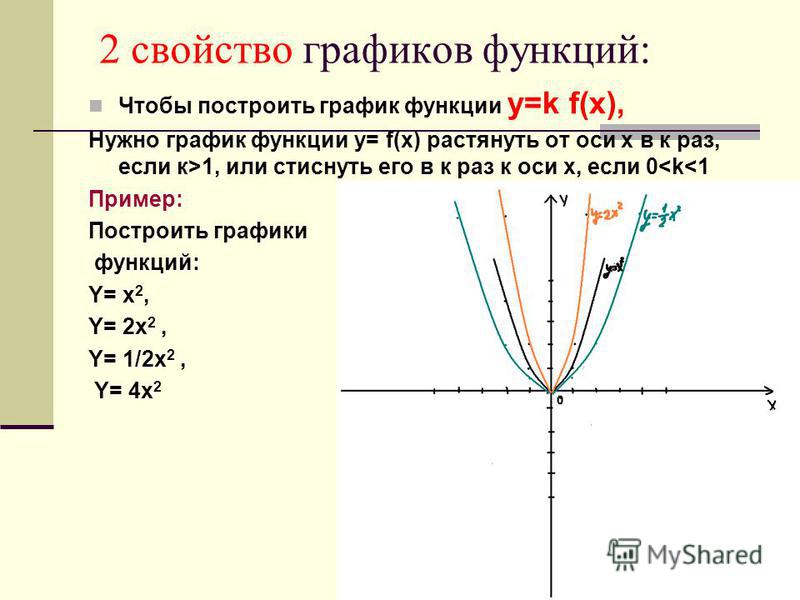 Когда и почему — это объяснено на уроке
о точках разрыва функции и их видах.

Если хотя бы одно из перечисленных условий не соблюдено, функция не является
непрерывной в точке. При этом говорят, что функция терпит разрыв, а точки на
графике, в которых график прерывается, называются точками разрыва функции. График
такой функции , терпящей разрыв в точке x=2 —
на рисунке ниже.

Пример 1. Функция f(x)
определена следующим образом:

Будет ли эта функция непрерывной в каждой из граничных точек её ветвей,
то есть в точках x = 0, x = 1,
x = 3?

Решение. Проверяем все три условия непрерывности функции в каждой
граничной точке. Первое условие соблюдается, так как то, что функция определена в каждой из
граничных точек, следует из определения функции. Осталось проверить остальные два условия.

Точка x = 0. Найдём
левосторонний предел в этой точке:

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 0
должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви.
Находим их:

Как видим, предел функции и значение функции в точке x = 0
равны. Следовательно, функция является непрерывной в точке x = 0.

Точка x = 1. Найдём
левосторонний предел в этой точке:

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 1
должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви.
Находим их:

Предел функции и значение функции в точке x = 1
равны. Следовательно, функция является непрерывной в точке x = 1.

Точка x = 3. Найдём
левосторонний предел в этой точке:

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 3
должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви.
Находим их:

Предел функции и значение функции в точке x = 3
равны. Следовательно, функция является непрерывной в точке x = 3.

Основной вывод: данная функция является непрерывной в каждой граничной точке.

Непрерывное изменение функции
можно определить как изменение постепенное, без скачков, при котором малое изменение
аргумента
влечёт малое изменение функции .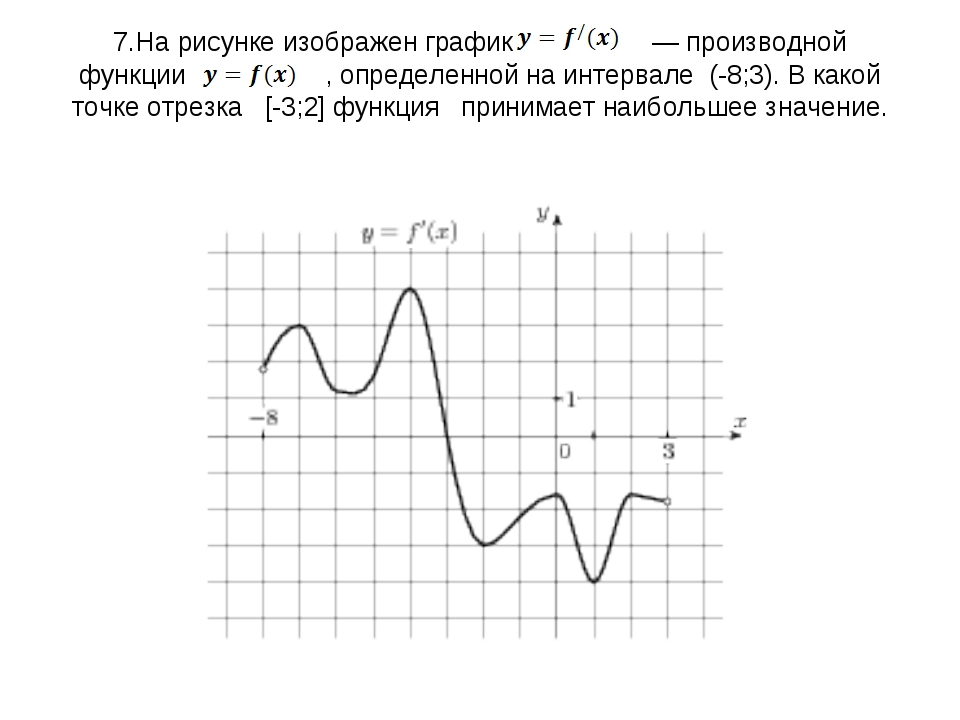

Проиллюстрируем это непрерывное изменение функции на примере.

Пусть над столом висит на нитке груз. Под действием этого груза нитка
растягивается, поэтому расстояние l груза от точки
подвеса нити является функцией массы груза m,
то есть l = f(m),
m≥0.

Непрерывность функции на промежутке

Пусть функция y = f(x)
определена в интервале ]a, b[
и непрерывна в каждой точке этого интервала. Тогда она называется непрерывной в
интервале ]a, b[. Аналогично
определяется понятие непрерывности функции на промежутках вида
]- ∞, b[,
]a, + ∞[,
]- ∞, + ∞[.
Пусть теперь функция y = f(x)
определена на отрезке [a, b].
Разница между интервалом и отрезком: граничные точки интервала не входят в интервал,
а граничные точки отрезка входят в отрезок. Здесь следует упомянуть о так называемой
односторонней непрерывности: в точке a, оставаясь на отрезке [a, b],
мы можем приближаться только справа, а к точке b —
только слева. Функция называется непрерывной на отрезке [a, b],
если она непрерывна во всех внутренних точках этого отрезка, непрерывна справа в точке
a и непрерывна слева в точке b.

Примером непрерывной функции может служить любая из элементарных функций.
Каждая элементарная функция непрерывна на любом отрезке, на котором она определена.
Например, функции и
непрерывны
на любом отрезке [a, b], функция
непрерывна
на отрезке [0, b], функция
непрерывна
на любом отрезке, не содержащем точку a = 2.

Пример 4. Исследовать функцию

на непрерывность.

Решение. Проверяем первое условие. Функция не определена в точках
— 3 и 3. По меньшей мере одно из условий непрерывности функции на всей числовой прямой
не выполняется. Поэтому данная функция является непрерывной на интервалах

Пример 5. Определить, при каком значении
параметра a непрерывна на всей области определения функция

Решение.

Найдём левосторонний предел функции в точке :

Найдём правосторонний предел при :

Очевидно, что значение
в точке x = 2 должно быть
равно ax:

Ответ: функция непрерывна на всей области определения при
a = 1,5.

К понятию непрерывной функции математика пришла, изучая в первую очередь
различные законы движения. Пространство и время бесконечны, и зависимость, например,
пути s от времени
t, выраженная законом s = f(t),
даёт пример непрерывной функции f(t). Непрерывно
изменяется и температура нагреваемой воды, она также является непрерывной функцией от
времени: T = f(t).

В математическом анализе доказаны некоторые свойства, которыми
обладают непрерывные функции. Приведём важнейшие из этих свойств.

1. Если непрерывная на интервале функция принимает на концах
интервала значения разных знаков, то в некоторой точке этого отрезка она принимает
значение, равное нулю. В более формальном изложении это свойство дано в теореме, известной
как первая теорема Больцано-Коши.

2. Функция f(x),
непрерывная на интервале [a, b],
принимает все промежуточные значения между значениями в концевых точках, то есть,
между f(a) и f(b).
В более формальном изложении это свойство дано в теореме, известной как вторая теорема
Больцано-Коши.

3. Если функция непрерывна на интервале, то на этом интервале она
достигает своего наибольшего и своего наименьшего значения: если m —
наименьшее, а M — наибольшее значение функции
на интервале [a, b], то найдутся
на этом отрезке такие точки и
, что
и
. Теорема,
в которой изложено это свойство, называется второй теоремой Вейерштрасса.

Пример 7. Используя первое из приведённых выше свойств непрерывных
функций, доказать, что уравнение

имеет по меньшей мере один вещественный корень в интервале [1; 2].

Решение.

Пусть .

Вычислим значения функции при x = 1 и x = 2.

Получили, что функция на концах интервала принимает значения разных знаков:
и , т. е.

Следовательно, в интервале [1; 2]
существует такое число a, при котором
f(a) = 0. То есть, уравнение
имеет по меньшей мере один вещественный корень в данном интервале.

Установление непрерывности функции может быть как самостоятельной задачей,
так и частью Полного исследования функции и построения графика.

Весь раздел «Исследование функций»

Как plot y=1/x в виде единого графика

Есть ли простой способ plot функции, которая стремится к бесконечности в положительном и отрицательном как единое plot, без plot, соединяющего оба конца положительного и отрицательного?

Например, построение y=1/x с помощью этого кода дает результирующий plot:

import numpy as np
import matplotlib.pyplot as plt

def f(x):
    return 1/x
fx_name = r'$f(x)=\frac{1}{x}$'

x=np.setdiff1d(np.linspace(-10,10,100),[0]) #to remove the zero
y=f(x)
plt. plot(x, y, label=fx_name)
plt.legend(loc='upper left')
plt.show()

Но мне бы хотелось получить такой результат, которого я достигаю, построив две отдельные области:

import numpy as np
import matplotlib.pyplot as plt

def f(x):
    return 1/x
fx_name = r'$f(x)=\frac{1}{x}$'

xfn=np.setdiff1d(np.linspace(-10,0,100),[0])
xfp=np.setdiff1d(np.linspace(0,10,100),[0])
yfn=f(xfn)
yfp=f(xfp)

yf = plt.plot(xfn, yfn, label=fx_name)
plt.plot(xfp, yfp, color=yf[0].get_color())
plt.legend(loc='upper left')
plt.show()

Есть ли здесь короткие пути?
Большое спасибо.

Решение

Включите ноль в массив домена и подавите деление на ноль. Это приводит к тому, что один элемент возвращаемого массива co-domain становится «inf», а «inf» не выводится на график.

import numpy as np
import matplotlib.pyplot as plt

def f(x):
    with np.errstate(divide='ignore', invalid='ignore'):
        return 1/x
fx_name = r'$f(x)=\frac{1}{x}$'

x=np. linspace(-10,10,101)
y=f(x)
plt.plot(x, y, label=fx_name)
plt.legend(loc='upper left')
plt.show()

Я предпочитаю этот метод, так как он позволяет избежать ручного манипулирования массивом и может быть легко повторно использован для других функций, которые разделяют один и тот же домен (например, y=1/(x+2)). спасибо всем за вклад.

python

numpy

matplotlib

plot

Поделиться

Источник

Tim GO

18 мая 2017 в 07:14

3 ответа

Отформатируйте каждую строку в plot(x, y), где x-матрица
Я хочу отформатировать каждую строку в plot, чтобы я мог выбрать заданные цвета для каждой строки. Однако мои значения x находятся в матричном виде, поэтому я не могу использовать формат стиля plot(x,y,’b’,x,y,’r’,…) . Большое спасибо.
как plot x, y, z в matlab?
Я делаю метод Гаусса-Джордана в matlab, и я хочу plot эти уравнения x + y + 4*z = -1 -2*x – y + z= -5 3*x-2*y+3*z=-4 Чтобы увидеть, в какой точке графика они пересекаются, но я не знаю, как plot в matlab

На самом деле вы хотите включить x = 0 , потому что это приводит к y = nan, образуя пробел в plot.

import numpy as np
import matplotlib.pyplot as plt

def f(x):
    return 1/x
fx_name = r'$f(x)=\frac{1}{x}$'

# using 101 steps results in in array including the value 0
x=np.linspace(-10,10,101)
# f(0) = nan -> a nan value creates a gap
y=f(x)
plt.plot(x, y, label=fx_name)
plt.legend(loc='upper left')
plt.show()

Поделиться

Padix Key

18 мая 2017 в 07:35

Не обязательно проще, как ваш обходной путь, но вы можете вставить элемент ‘nan’ в индекс, где знак переворачивается, например:

idx = np.argmax(np.diff(np.sign(y)))+1

x = np.insert(x, idx, np.nan)
y = np.insert(y, idx, np.nan)

‘nan’ заставляет Matplotlib прерывать линию.

Поделиться

Rutger Kassies

18 мая 2017 в 07:27

по материалам Rutger Kassies ides:

n_points = 100
x=np.setdiff1d(np.linspace(-10,10,n_points),[0]) #to remove the zero

y=f(x)
y[n_points//2-1:n_points//2+1] = np.nan

используйте свой оригинальный plot и установите точки от 0 до np.nan. таким образом, слишком много точек будет установлено на None , но это симметрично.

вы также можете настроить свой linspace так, чтобы включить 0 таким образом, чтобы f(x) = np.nan : n_points = 101 . ( этот ответ и 2 комментария заявили об этом прямо перед тем, как я это сделал… пожалуйста, кредит там).

Поделиться

hiro protagonist

18 мая 2017 в 07:38

как plot несколько линий, в то время как значение X и y из файлов в for loop?
У меня есть for loop, в котором для каждого входного файла я читаю x и y из файла и сохраняю их, как я хочу, в отдельных списках, а затем plot в виде графика.2 < 1 в математике? Есть ли какой-нибудь способ сделать это?
base::plot — могу ли я получить соотношение сторон в виде графика?
Я знаю, что могу указать соотношение сторон при построении графика, например plot(x,y,asp=5) . Есть ли какой-нибудь способ получить соотношение сторон после разрешения автомасштабирования (как в…
Отформатируйте каждую строку в plot(x, y), где x-матрица
Я хочу отформатировать каждую строку в plot, чтобы я мог выбрать заданные цвета для каждой строки. Однако мои значения x находятся в матричном виде, поэтому я не могу использовать формат стиля…
как plot x, y, z в matlab?
Я делаю метод Гаусса-Джордана в matlab, и я хочу plot эти уравнения x + y + 4*z = -1 -2*x – y + z= -5 3*x-2*y+3*z=-4 Чтобы увидеть, в какой точке графика они пересекаются, но я не знаю, как plot в…
как plot несколько линий, в то время как значение X и y из файлов в for loop?
У меня есть for loop, в котором для каждого входного файла я читаю x и y из файла и сохраняю их, как я хочу, в отдельных списках, а затем plot в виде графика. Теперь я хочу plot все x-y всех файлов…
Как plot гладкий 2D цвет plot для z = f(x, y)
Я пытаюсь получить полевые данные plot 2D, используя matplotlib. Так что в принципе я хочу что-то похожее на это: В моем случае данные хранятся в файле на жестком диске. Однако для простоты…
Построение графика sin (x)/(x) в Matlab
У меня возникли проблемы с правильным построением графика sin(x)/(x). В частности, когда x = 0, возвращает NaN в Matlab. Однако при применении правила L’hôpital фактическое значение равно y = 1. мой…
Matplotlib : как plot два гистограммных графика с одинаковыми осями x/y, но один начинается поверх другого вдоль оси y
Я пытаюсь plot два графика баров в одной и той же фигуре. В приведенном ниже коде графики расположены один за другим, потому что они лежат вдоль оси y в точке 0. import matplotlib.pyplot as plt…
Как сделать X-Y plot
Я не знаю, как сделать X-Y plot на R. У меня есть набор данных B C. A dataset ID Result 1.1 2 1.2 4 1.3 2.5 1.4 9 B dataset ID Result 1.1 1 1.2 7 1.3 6 1.4 9 C dataset ID Result 1.1 0.5 1.2 8 1.3 9…
График функции y=kf(x) | Алгебра

График функции y=kf(x) (k>1) можно получить из графика функции y=f(x) растяжением от оси Ox в k раз. При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x; ky) графика функции y=kf(x):
(x; y) → (x; ky)
(то есть абсцисса (x) каждой точки начального графика остаётся без изменений, а ордината (y) увеличивается в k раз).
При растяжении от оси Ox точки графика y=f(x), лежащие на оси абсцисс, остаются на месте, так как k∙0=0.
Примеры.
1) График функции y=3x² получен из графика функции y=x² растяжением в 3 раза от оси Ox.
При растяжении графика от оси абсцисс нужно ординату каждой точки увеличить в 3 раза.
Для построения графика отмечаем базовые точки графика y=x². Для каждой точки координату x оставляем неизменной, значение координаты y умножаем на 3. Таким образом, каждая точка нового графика располагается строго над соответствующей точкой графика y=x², в 3 раза дальше от оси Ox.
Вершина параболы y=x², точка O (0; 0), остаётся на месте (так как 3∙0=0).
График y=3x² из y=x²

(1; 1) → (1; 3),
(-1; 1) → (-1; 3),
(2; 4) → (2; 12),
(-2; 4) → (-2; 12)
и т. д.

2) График функции y=2|х| можно получить из графика функции y=|х| растяжением от оси абсцисс в 2 раза.
Точка O (0; 0) остаётся на месте. В I и II координатных четвертях берём по одной точке графика y=|х|, например, (5; 5) и (-5; 5). Их абсциссы оставляем без изменений, а ординаты удваиваем:
График y=2|х| из y=|х|

   (5; 5)→ (5; 10),
   (-5; 5)→ (-5; 10).
Через эти точки из точки O проводим лучи.
Получаем график функции y=2|х|

3) График функции y=4√x можно получить из графика функции y=√x растяжением от оси Ox в 4 раза.
Координату x каждой из базовых точек графика y=√x оставляем без изменений, координату y увеличиваем в 4 раза. Точка O (0; 0) при этом остаётся на месте.
Через полученные точки проводим новый график:
График y=4√x из y=√x

(0; 0) → (0; 0),
(1; 1) → (1; 4),
(4; 2) → (4; 8),
(9; 3) → (9; 12),
и т. д.

Преобразование графиков может быть использовано для построения графиков функций в ходе решения примеров из разных разделов алгебры.
ММО-2020 (01.03.2020)
Олимпиада для 8–11 классов прошла 1 марта 2020 года
(2 день для 11 кл. — 14 марта)
в зданиях МГУ на Воробьевых горах,
а также в школах 58, 444, 625, «Воробьевы горы» и в ЦПМ
(доступна орг. информация).
В ней приняли участие более 5 200 школьников:
8 класс — ок. 2 600 участников,
9 класс — ок. 1 000 участников,

10 класс — ок. 1 000 участников,
11 класс — 599 участников (2 день — 281 участник).
8 класс
Задача 1.
Том написал на заборе из досок слово ММО, а Гек — число 2020. Ширина каждой буквы и цифры 9 см, а ширина доски забора — 5 см. Мог ли Гек испачкать меньше досок, чем Том? (Доски расположены вертикально, а слова и числа пишутся горизонтально. Цифры и буквы пишутся через равные промежутки.)
(Д. Мухин, А. Федулкин, И. Эльман)
Задача 2.
На графике функции $y=1/x$ Миша отмечал подряд все точки с абсциссами 1, 2, 3, … , пока не устал. Потом пришла Маша и закрасила все прямоугольники, одна из вершин которых — это отмеченная точка, еще одна — начало координат, а еще две лежат на осях. Затем учительница попросила ребят посчитать площадь фигуры, состоящей из всех точек, закрашенных ровно один раз. Сколько получилось?
(Д. Мухин)
Задача 3.
Дано натуральное число $N$. Вера делает с ним следующие операции: сначала прибавляет 3 до тех пор, пока получившееся число не станет делиться на 5 (если изначально $N$ делится на 5, то ничего прибавлять не надо). Получившееся число Вера делит на 5. Далее делает эти же операции с новым числом, и так далее. Из каких чисел такими операциями нельзя получить 1?
(А. Шаламова)
Задача 4.
В турнире по гандболу участвуют 20 команд. После того как каждая команда сыграла с каждой по разу, оказалось, что количество очков у всех команд разное. После того как каждая команда сыграла с каждой по второму разу, количество очков у всех команд стало одинаковым. В гандболе за победу команда получает 2 очка, за ничью 1 очко, за поражение — 0 очков. Верно ли, что найдутся две команды, по разу выигравшие друг у друга?
(Б. Френкин, А. Заславский)
Задача 5.
Дана трапеция $ABCD$ с основаниями $AD$ и $BC$. Перпендикуляр, опущенный из точки $A$ на сторону $CD$, проходит через середину диагонали $BD$, а перпендикуляр, опущенный из точки $D$ на сторону $AB$, проходит через середину диагонали $AC$. Докажите, что трапеция равнобокая.
(А. Доледенок)
Задача 6.
У Полины есть колода из 36 карт (4 масти по 9 карт в каждой). Она выбирает из неё половину карт, какие хочет, и отдает Василисе, а вторую половину оставляет себе. Далее каждым ходом игроки по очереди открывают по одной карте по своему выбору (соперник видит масть и достоинство открытой карты), начиная с Полины. Если в ответ на ход Полины Василиса смогла положить карту той же масти или того же достоинства, то Василиса зарабатывает одно очко. Какое наибольшее количество очков Василиса может гарантированно заработать?
(М. Евдокимов)
9 класс
Задача 1.
Существует ли натуральное число, делящееся на $2020$, в котором всех цифр 0, 1, 2, …, 9 поровну?
(М. Евдокимов)
Задача 2.
Из шести палочек попарно различной длины сложены два треугольника (по три палочки в каждом). Всегда ли можно сложить из них один треугольник, стороны которого состоят из одной, двух и трех палочек соответственно?
(В. Новиков)
Задача 3.
Три богатыря сражаются со Змеем Горынычем. Илья Муромец каждым своим ударом отрубает половину всех голов и еще одну, Добрыня Никитич — треть всех голов и еще две, а Алёша Попович — четверть всех голов и еще три.{20}$-головому Змею?
(А. Заславский)
Задача 4.
В остроугольном треугольнике $ABC$ ($AB<BC$) провели высоту $BH$. Точка $P$ симметрична точке $H$ относительно прямой, соединяющей середины сторон $AC$ и $BC$. Докажите, что прямая $BP$ содержит центр описанной окружности треугольника $ABC$.
(А. Соколов)
Задача 5.
К Ивану на день рождения пришли $3n$ гостей. У Ивана есть $3 n$ цилиндров с написанными сверху буквами А, Б и В, по $n$ штук каждого типа. Иван хочет устроить бал: надеть на гостей цилиндры и выстроить их в хороводы (один или больше) так, чтобы длина каждого хоровода делилась на $3$, и при взгляде на любой хоровод сверху читалось бы по часовой стрелке АБВАБВ…АБВ. Докажите, что Иван может устроить бал ровно $(3n)!$ различными способами. (Цилиндры с одинаковыми буквами неразличимы; все гости различны.)
(Г. Погудин)
Задача 6.
Глеб задумал натуральные числа $N$ и $a$, $a<N$. Число $a$ он написал на доске.
Затем он начал выполнять следующую операцию: делить $N$ с остатком на последнее выписанное на доску число, а полученный остаток от деления также записывать на доску.2.
$$
(М. Евдокимов)
Задача 2.
Среди зрителей кинофестиваля было поровну мужчин и женщин. Всем зрителям понравилось одинаковое количество фильмов. Каждый фильм понравился восьми зрителям. Докажите, что не менее 3/7 фильмов обладают следующим свойством: среди зрителей, которым фильм понравился, не менее двух мужчин.
(фольклор)
Задача 3.
Существует ли вписанный в окружность 19-угольник, у которого нет одинаковых по длине сторон, а все углы выражаются целым числом градусов?
(М. Малкин)
Задача 4.
Точка $O$ — центр описанной окружности треугольника $ABC$. Серединный перпендикуляр к $BC$ пересекает $AB$ и $AC$ в точках $X$ и $Y$. Прямая $AO$ пересекает прямую $BC$ в точке $D$, $M$ — середина $BC$. Описанная окружность треугольника $ADM$ пересекает описанную окружность треугольника $ABC$ в точке $E$, отличной от $A$. Докажите, что прямая $OE$ касается описанной окружности треугольника $AXY$.
(А. Соколов)
Задача 5.
На доске написаны 1000 последовательных целых чисел. За ход можно разбить написанные числа на пары произвольным образом и каждую пару чисел заменить на их сумму и разность (не обязательно вычитать из большего меньшее, все замены происходят одновременно). Докажите, что на доске больше никогда не появятся 1000 последовательных целых чисел.
(А. Грибалко)
Задача 6.
Для каких $k$ можно закрасить на белой клетчатой плоскости несколько клеток (конечное число, большее нуля) в черный цвет так, чтобы на любой клетчатой вертикали, горизонтали и диагонали либо было ровно $k$ черных клеток, либо вовсе не было черных клеток?
(А. Динев, К. Гаров, Н. Белухов)
11 класс (1 день)
Задача 1.
Приведите пример числа, делящегося на 2020, в котором каждая из десяти цифр встречается одинаковое количество раз.
(М. Евдокимов)
Задача 2.
Существует ли такая непериодическая функция $f$, определённая на всей числовой прямой, что при любом $x$ выполнено равенство $f(x+1)=f(x+1)f(x)+1?$
(фольклор)
Задача 3.
В остроугольном треугольнике $ABC$ ($AB<BC$) провели высоту $BH$. Точка $P$ симметрична точке $H$ относительно прямой, соединяющей середины сторон $AC$ и $BC$. Докажите, что прямая $BP$ содержит центр описанной окружности треугольника $ABC$.
(А. Соколов)
Задача 4.
Из шахматной доски $8\times8$ вырезали 10 клеток. Известно, что среди вырезанных клеток есть как черные, так и белые. Какое наибольшее количество двухклеточных прямоугольников можно после этого гарантированно вырезать из этой доски?
(А. Кубарев)
Задача 5.
Существует ли тетраэдр, в сечениях которого двумя разными плоскостями получаются квадраты $1\times1$ и $100\times100$?
(М. Евдокимов)
Задача 6.
На доске написаны $2n$ последовательных целых чисел. За ход можно разбить написанные числа на пары произвольным образом и каждую пару чисел заменить на сумму и разность чисел этой пары (не обязательно вычитать из большего числа меньшее, все замены происходят одновременно). Докажите, что на доске больше никогда не появятся $2n$ последовательных чисел.x \right]\right],$$ где $\left[a\right]$ обозначает наибольшее целое число, не превосходящее $a$.
(А. В. Бегунц)
Задача 3.
За круглым вращающимся столом, на котором стоят 8 белых и 7 чёрных чашек, сидят 15 гномов. Они надели 8 белых и 7 чёрных колпачков. Каждый гном берёт себе чашку, цвет которой совпадает с цветом его колпачка и ставит напротив себя, после этого стол поворачивается случайным образом. Какое наибольшее число совпадений цвета чашки и колпачка можно гарантировать после поворота стола (гномы сами выбирают, как сесть, но не знают, как повернётся стол)?
(М. С. Лобанов)
Задача 4.
На стороне $AC$ треугольника $ABC$ взяли такую точку $D$, что угол $BDC$ равен углу $ABC$. Чему равно наименьшее возможное расстояние между центрами окружностей, описанных около треугольников $ABC$ и $ABD$, если $BC = 1$?
(М. А. Евдокимов)
Задача 5.
Кузнечик прыгает по числовой прямой, на которой отмечены точки $-a$ и $b$. Известно, что $a$ и $b$ — положительные числа, а их отношение иррационально.{-6}$.
(П. А. Бородин)
103 Виды и типы графиков на Forex, график баров, японских свечей, тиковый график

Используемые значения
Графики рынка forex обычно составляются в двух координатах — цены (откладывается по вертикальной оси) и времени (откладывается по горизонтальной оси). Иногда по вертикальной оси откладывается также график тикового объема.
Ось времени может иметь различный масштаб, который иногда называется интервалом, торговым периодом или таймфреймом (timeframe).

Традиционно в качестве таймфрейма используются следующие интервалы: год, месяц, неделя, день, 4 часа, 1 час, 30 минут, 15 минут, 5 минут, 1 минута, единичная котировка (тик).
Примечание: единичной котировкой или тиком является изменение цены маркетмейкером рынка переданное через информационные системы одновременно в виде двух новых цен покупки и продажи (Ask и Bid) . Подробнее см. раздел «Как формируются котировки».
Поскольку график forex формируется по цене в определенный период времени, например, час, то в каждом периоде у цены есть 4 значения, которые, как правило, и наносят на график одновременно:

— цена открытия торгового периода (open) — цена на рынке, сложившаяся на начало торгового периода. Поскольку на начало торгового периода всегда существует 2 цены (на покупку и на продажу), то цена открытия обычно рассчитывается как среднее между Ask и Bid т.е. (Ask+Bid)/2. Фактически ценой на начало торгового периода является первая котировка данного периода.

— цена закрытия торгового периода (сlose) — цена на рынке, сложившаяся на конец торгового периода. Поскольку в конце торгового периода всегда существует 2 цены, то цена закрытия также обычно рассчитывается как среднее между Ask и Bid т.е. (Ask+Bid)/2; Фактически ценой на конец торгового периода является последняя котировка данного периода.

— максимальная цена торгового периода (high) — самая высокая цена на рынке Forex, сложившаяся за период (обычно используется Ask, поскольку Ask всегда больше Bid) ;

— минимальная цена торгового периода (low) — самая низкая цена на рынке Forex, сложившаяся за период (обычно используется Bid) ;
Иногда к этим четырем значениям в качестве самостоятельного индикатора на графике отображают тиковый объем.
— тиковый объем (tick volume) — количество тиков (изменений цены маркет-мейкеров) пришедших в информационную систему за данный период времени.
Виды отображения графиков
1. Тиковый график (Tick chart)

Тиковый график имеет самый мелкий масштаб — 1 тик (единичное котирование маркет-мейкером цен покупки и продажи). Это график котировок Bid и Ask, которые выглядят как столбцы на графике цен.
Максимум каждого отдельного столбца в тиковом графике — это котировка Ask, минимум каждого конкретного столбца — это котировка Bid.
Тиковый график как правило не используется для анализа рынка, поскольку его масштаб настолько мал, что не подходит для технического анализа. Однако тиковые графики эффективно используют для точного определения уровней поддержки и сопротивления, а также для того, чтобы повысить эффективность покупок и продаж, делая это на локальных минимумах и максимумах.
2. Линейный график (Line Chart)

Линейный график строится по одной из цен за периоды указанные выше. В большинстве случаев для этого используется цена закрытия (close) , однако также могут быть использованы цены открытия (open), максимальные цены за период (High) , минимальные цены за период (Low) или синтетические варианты: Median Price ([High + Low]/2) или Typical Price ( [High + Low + Close]/3).
Линейный график, по мнению трейдеров, обладает рядом преимуществ и недостатков.

Преимущества:

— удобство при поиске фигур технического анализа (паттернов).

— отсутствие избыточной информации

Недостатки:

— невозможно оценить, что происходило внутри торгового периода, были ли значительные подъемы или падения цен

— невозможно увидеть были ли гэпы (gaps) — ценовые разрывы между закрытием предыдущего и открытием последующего периода.
3. График баров (Bar chart), график интервальных гистограмм
При построении барового графика используются уже все 4 основные значения цены: открытие, максимум, минимум и закрытие (open, high, low, close) .
На графике баров каждый период обозначается вертикальной линией (представляющей собой диапазон колебания цен внутри периода), слева и справа от которой располагается по одной черте.

Каждый период, например час, выглядит следующим образом:
Верхний конец вертикальной черты показывает уровень максимальной цены, которую рынок достигал в данном периоде.

Соответственно, нижний конец вертикальной черты — минимальный уровень цены, который рынок достигал в течение данного периода.

Таким образом, вертикальная черта в целом представляет собой торговый диапазон периода (например, часа) или общие границы колебания цены внутри периода.

Черта слева представляет собой уровень цены, который был в начале периода и именуется ценой открытия (open).

Черта справа указывает уровень цены, который существовал на момент окончания периода (например, определенного часа) и называется ценой закрытия (close) .

Поскольку правая черта означает цену на начало периода (открытие периода), а левая — цену на конец периода (закрытие периода), то если левая черта выше правой, это означает что цена на рынке forex за это период упала. Если наоборот — выросла.

Преимущества:

— Можно примерно оценить, что происходило внутри торгового периода, были ли значительные подъемы или падения цен

— Можно определить наличие гэпов

Недостатки:

— Трудно с первого взгляда оценить, вырос рынок за период или нет.

— Невозможно определить характер движения внутри периода (нужно переходить на более мелкие масштабы).
3. Японские свечи (Japanese candlesticks)
График японских свечей схож по отображению и функциональности с баровым графиком, но более удобен для визуального восприятия.
При построении графика японских свечей также используются все 4 основные значения цены: открытие, максимум, минимум и закрытие (open, high, low, close) . Каждая отдельная свеча также как и на баровом графике означает определенный период времени, например, 1 час.
— Широкая часть свечи (прямоугольник) называется телом (real body или джиттай). Тело — это ценовой диапазон между ценами открытия и закрытия. Заполненное тело свечи означает, что цена закрытия была меньше цены открытия периода, т.е. за период цен в целом упали (черная свеча — «ин-сен»).

— Пустое тело свечи означает, что цена закрытия была больше цены открытия, т.е. цены внутри диапазона росли (белая свеча — «йо-сен»).

— Линия над телом свечи называется верхней тенью (upper shadow или uwakage), а ее верхняя точка указывает максимум, который достигали цены внутри периода.

— Линия под телом свечи называется нижней тенью (lower shadow или shitakage) и ее нижняя точка — это минимум, который достигали цены внутри периода.
Примечание: тело как растущей, так и падающей свечи в различных программах технического анализа могут быть различных цветов. В оригинале красная свеча означает рост, черная — падение. Однако, согласно легенде, первые свечные графики попали в Америку из Японии на ксерокопиях, где падающая свеча осталась черной, а растущая превратилась в белую. Существуют и другие комбинации, например, зеленая растущая, а красная падающая. Обычно действуют следующие правила: заполненная свеча — падающая, а свеча цвета фона — растущая или падающая свеча темнее растущей.
Существуют и другие типы графиков.

— Объемные японские свечи (Candlevolume)

— Эквиобъемные графики (Equivolume).

— Пунктоцифровые графики (Point and Figure, так же называемые XO, или кресты-нули)

— Графики прорыва 3-х линий (Three-Line Break)

— графики Ренко (Renko)

— графики Каги (Kagi)

Примечание:
Будьте внимательны, зачастую на вертикальной оси (цены) используется не арифметическая, а логарифмическая шкала. Она получила распространение при анализе долгосрочных тенденций, когда цена валют на Forex может меняться на десятки процентов. Если на арифметической шкале расстояния между делениями цены на оси одинаковы, то на логарифмической шкале расстояние между делениями отражает одинаковые в процентах изменения цены.
Обратные функции
Обратная функция — наоборот!
Начнем с примера:
Здесь у нас есть функция f (x) = 2x + 3 , записанная в виде блок-схемы:
Обратная функция идет другим путем:
Таким образом, обратное: 2x + 3: (y-3) / 2
Обратное значение обычно отображается путем добавления небольшого «-1» после имени функции, например:
ф ^-1 (у)
Мы говорим « f обратное y»
Итак, обратное к f (x) = 2x + 3 записывается:
f ^-1 (y) = (y-3) / 2
(я также использовал y вместо x , чтобы показать, что мы используем другое значение.)
Вернуться туда, где мы начали
Самое замечательное в обратном преобразовании состоит в том, что он должен вернуть нам исходное значение:
.
Когда функция f превращает яблоко в банан,

Затем обратная функция f ^-1 превращает банан обратно в яблоко
Пример:
Используя приведенные выше формулы, мы можем начать с x = 4:
f (4) = 2 × 4 + 3 = 11
Затем мы можем использовать обратное для 11:
f ^-1 (11) = (11-3) / 2 = 4
И мы волшебным образом снова получаем 4 !
Мы можем написать это одной строкой:
f ^-1 (f (4)) = 4
«f, обратное f 4, равно 4»
Таким образом, применение функции f, а затем ее обратной f ^-1 возвращает нам исходное значение снова:
f ^-1 (f (x)) = x
Мы могли бы также расположить функции в другом порядке, и он все еще работает:
f (f ^-1 (x)) = x
Пример:
Начать с:
f ^-1 (11) = (11-3) / 2 = 4
А потом:
f (4) = 2 × 4 + 3 = 11
Итак, мы можем сказать:
f (f ^-1 (11)) = 11
«f f, обратное 11, равно 11»
Решить с помощью алгебры
Мы можем вычислить обратное, используя алгебру. Положите y вместо f (x) и решите относительно x:
Функция: f (x) = 2x + 3
Положите «y» вместо «f (x)»: y = 2x + 3
Вычтем 3 с обеих сторон: г-3 = 2x
Разделите обе стороны на 2: (у-3) / 2 = x
Поменять местами: х = (у-3) / 2
Решение (вместо «x» подставьте «f ^-1 (y)»): ж ^-1 (г) = (у-3) / 2
Этот метод хорошо подходит для более сложных инверсий.
Фаренгейта в Цельсия
Полезный пример — преобразование между градусами Фаренгейта и Цельсия:
Для преобразования Фаренгейта в Цельсия: f (F) = (F — 32) × 5 9
Обратная функция (Цельсия обратно к Фаренгейту): f ^-1 (C) = (C × 9 5 ) + 32
Для вас: посмотрите, сможете ли вы сделать шаги, чтобы создать инверсию!
Инверсия общих функций
До сих пор это было легко, потому что мы знаем, что обратное к умножению — это деление, а обратное к сложению — вычитание, но как насчет других функций?
Вот список, который вам поможет:
(Примечание: вы можете узнать больше об обратном синусе, косинусе и тангенсе.)
Осторожно!
Вы видели «Осторожно!» столбец выше? Это потому, что некоторые инверсии работают только с определенными значениями .
Пример: квадрат и квадратный корень
Когда мы возводим в квадрат отрицательное число , а затем делаем обратное, происходит следующее:
Квадрат: (- 2) ² = 4
Обратная величина (квадратный корень): √ (4) = 2
Но мы не вернули исходное значение! Мы получили 2 вместо −2 .Наша вина в том, что мы не проявляем осторожности!
Таким образом, квадратная функция (как она есть) не имеет обратной
Но мы можем это исправить!
Ограничить домен (значения, которые могут входить в функцию).
Пример: (продолжение)
Только убедитесь, что мы не используем отрицательные числа.
Другими словами, ограничьте его до x ≥ 0 , и тогда мы сможем получить обратное.
Итак, мы имеем такую ситуацию:
x ² имеет ли не инверсию
но {x ² | x ≥ 0} (в котором говорится, что «x возведен в квадрат так, что x больше или равен нулю» с использованием нотации создателя множеств) имеет обратное значение.
Нет обратного?
Давайте посмотрим наглядно, что здесь происходит:
Чтобы иметь возможность иметь инверсию, нам нужно уникальных значений .
Подумайте … если есть два или более значений x для одного значения y , как мы узнаем, какое из них выбрать, когда вернемся?
Общие функции
Без обратного
Представьте, что мы перешли от x ₁ к определенному значению y, куда мы вернемся? x ₁ или x ₂?
В этом случае у нас не может быть обратного.
Но если мы можем иметь ровно один x для каждого y, мы можем получить обратное.
Это называется «однозначным соответствием» или биективным, как это
Биективная функция
Имеет инверсию
Функция должна быть «биективной», чтобы иметь инверсию.
Таким образом, биективная функция подчиняется более строгим правилам, чем общая функция, что позволяет нам иметь обратную функцию.
Домен
и диапазон
Так что же все эти разговоры о «, ограничивающем домен »?
В простейшей форме область — это все значения, входящие в функцию (а диапазон — это все значения, которые выходят).
В его нынешнем виде функция не имеет обратного значения для функции , потому что некоторые значения y будут иметь более одного значения x.
Но мы могли бы ограничить домен так, чтобы было уникальных x для каждого y …
… и теперь у нас может быть обратное:
Также примечание:
Функция f (x) переходит из области в диапазон,
Обратная функция f ^-1 (y) переходит из диапазона обратно в домен.
Давайте изобразим их оба в терминах x … так что теперь это f ^-1 (x) , а не f ^-1 (y) :
f (x) и f ^-1 (x) похожи на зеркальные изображения

(перевернут по диагонали).
Другими словами:
График f (x) и f ^-1 (x) симметричен по линии y = x
Пример: квадрат и квадратный корень (продолжение)
Первый , мы ограничиваем Домен до x ≥ 0 :
{x ² | x ≥ 0} «x в квадрате, так что x больше или равно нулю»
{√x | x ≥ 0} «квадратный корень из x такой, что x больше или равен нулю»
А вы видите, это «зеркальные отражения»

друг друга по диагонали y = x.
Примечание: когда мы ограничиваем область до x ≤ 0 (меньше или равно 0), обратное значение будет f ^-1 (x) = −√x :
{x ² | х ≤ 0}
{−√x | x ≥ 0}
Которые тоже обратные.
Не всегда разрешимо!
Иногда невозможно найти обратную функцию.
Пример: f (x) = x / 2 + sin (x)
Мы не можем вычислить обратное, потому что мы не можем решить для «x»:
у = х / 2 + грех (х)
г …? = х
Примечания к обозначениям
Даже если мы пишем f ^-1 (x), «-1» — это , а не , показатель степени (или степени):
f ^-1 (x) … отличается от … f (x) ^-1
Функция, обратная f f (x) ^-1 = 1 / f (x)

(Обратный)
Сводка
Значение, обратное f (x), равно f ^-1 (y)
Мы можем найти обратное, перевернув «блок-схему»
Или мы можем найти обратное с помощью алгебры:
Поместите «y» вместо «f (x)» и
Решить относительно x
Нам может потребоваться ограничить домен , чтобы функция имела инверсию
Область и диапазон рациональных функций
В

домен

из
функция
ж
Икс
— это набор всех значений, для которых определена функция, а

диапазон

функции — это набор всех значений, которые
ж
берет.
Рациональная функция — это функция вида
ж
Икс
знак равно
п
Икс
q
Икс
, где
п
Икс
а также
q
Икс
являются многочленами и
q
Икс
≠
0
.
Область определения рациональной функции состоит из всех действительных чисел
Икс
кроме тех, для которых знаменатель
0
. Чтобы найти эти
Икс
значения, которые нужно исключить из области определения рациональной функции, приравнять знаменатель к нулю и решить для
Икс
.
Например, домен
родительская функция
ж
Икс
знак равно
1
Икс
это набор всех действительных чисел, кроме
Икс
знак равно
0
. Или область определения функции
ж
Икс
знак равно
1
Икс
—
4
это набор всех действительных чисел, кроме
Икс
знак равно
4
.
Теперь рассмотрим функцию
ж
Икс
знак равно
Икс
+
1
Икс
—
2
Икс
—
2
.По упрощению, когда
Икс
≠
2
он становится линейной функцией
ж
Икс
знак равно
Икс
+
1
. Но исходная функция не определена в
Икс
знак равно
2
. Это оставляет график с дырой, когда
Икс
знак равно
2
.
Один из способов найти диапазон рациональной функции — найти область определения обратной функции.
Другой способ — нарисовать график и определить диапазон.
Снова рассмотрим родительскую функцию
ж
Икс
знак равно
1
Икс
. Мы знаем, что функция не определена, когда
Икс
знак равно
0
.
В виде
Икс
→
0
по обе стороны от нуля,
ж
Икс
→
∞
. Аналогично, как
Икс
→
±
∞
,
ж
Икс
→
0
.
График приближается
Икс
-ось как
Икс
стремится к положительной или отрицательной бесконечности, но никогда не касается
Икс
-ось.То есть функция может принимать все реальные значения, кроме
0
.
Итак, диапазон функции — это набор действительных чисел, кроме
0
.

Пример 1:

Найдите домен и диапазон функции
у
знак равно
1
Икс
+
3
—
5
.
Чтобы найти исключенное значение в области определения функции, приравняйте знаменатель к нулю и решите для
Икс
.
Икс
+
3
знак равно
0
⇒
Икс
знак равно
—
3
Итак, область определения функции — это действительные числа, кроме
—
3
.
Диапазон функции такой же, как и область определения обратной функции. Итак, чтобы найти диапазон, определите обратную функцию.
Поменять местами
Икс
а также
у
.
Икс
знак равно
1
у
+
3
—
5
Решение для
у
ты получаешь,
Икс
+
5
знак равно
1
у
+
3
⇒
у
+
3
знак равно
1
Икс
+
5
⇒
у
знак равно
1
Икс
+
5
—
3
Итак, обратная функция
ж
—
1
Икс
знак равно
1
Икс
+
5
—
3
.
Исключенное значение в области определения обратной функции можно определить, приравняв знаменатель к нулю и решив для
Икс
.
Икс
+
5
знак равно
0
⇒
Икс
знак равно
—
5
Итак, область определения обратной функции — это набор действительных чисел, кроме
—
5
. То есть диапазон данной функции — это набор действительных чисел, кроме
—
5
.
Следовательно, область определения данной функции равна
{
Икс
∈
ℝ
|
Икс
≠
—
3
}
и диапазон
{
у
∈
ℝ
|
у
≠
—
5
}
.

Пример 2:

Найдите домен и диапазон функции
у
знак равно
Икс
2
—
3
Икс
—
4
Икс
+
1
.
Используйте графический калькулятор, чтобы построить график функции.
Когда вы множите числитель и отменяете ненулевые общие множители, функция сводится к линейной функции, как показано.
у
знак равно
Икс
+
1
Икс
—
4
Икс
+
1
знак равно
Икс
+
1
Икс
—
4
Икс
+
1
знак равно
Икс
—
4
Итак, график линейный с дырой в
Икс
знак равно
—
1
.
Используйте график, чтобы определить домен и диапазон.
Функция не определена для
Икс
знак равно
—
1
. Итак, домен
{
Икс
∈
ℝ
|
Икс
≠
—
1
}
или же
—
∞
,
—
1
∪
—
1
,
∞
.
Диапазон функции:
{
у
∈
ℝ
|
у
≠
k
где
у
—
1
знак равно
k
}
.
Для
Икс
≠
—
1
, функция упрощается до
у
знак равно
Икс
—
4
.Функция не определена в
Икс
знак равно
—
1
или функция не принимает значение
—
1
—
4
знак равно
—
5
. Это,
k
знак равно
—
5
.
Следовательно, диапазон функции равен
{
у
∈
ℝ
|
у
≠
—
5
}
или же
—
∞
,
—
5
∪
—
5
,
∞
.
Асимптоты рациональной функции:

An
асимптота
это линия, к которой график функции приближается, но никогда не касается. В родительской функции
ж
Икс
знак равно
1
Икс
, как
Икс
— а также
у
-оси — это асимптоты. График родительской функции будет приближаться к асимптотам, но никогда не касается их.
Чтобы найти вертикальную асимптоту рациональной функции, приравняйте знаменатель к нулю и решите относительно
Икс
.
Если степень многочлена в числителе меньше степени знаменателя, то горизонтальная асимптота — это
Икс
-ось или
у
знак равно
0
.
Функция
ж
Икс
знак равно
а
Икс
,
а
≠
0
имеет тот же домен, диапазон и асимптоты, что и
ж
Икс
знак равно
1
Икс
.
Теперь график функции
ж
Икс
знак равно
а
Икс
—
б
+
c
,
а
≠
0
гипербола, симметричная относительно точки
б
,
c
.Вертикальная асимптота функции равна
Икс
знак равно
б
а горизонтальная асимптота равна
у
знак равно
c
.
В более общем виде функция
ж
Икс
знак равно
а
Икс
+
б
c
Икс
+
d
имеет вертикальную асимптоту при
Икс
знак равно
—
d
c
и горизонтальная асимптота при
у
знак равно
а
c
.В более общем смысле, если и числитель, и знаменатель имеют одинаковую степень, то горизонтальная асимптота будет иметь вид
у
знак равно
k
где
k
— отношение старшего коэффициента числителя к знаменателю.
Если степень знаменателя на единицу меньше степени числителя, то функция имеет наклонную асимптоту.

Пример 3:

Найдите вертикальную и горизонтальную асимптоты функции
ж
Икс
знак равно
5
Икс
—
1
.
Чтобы найти вертикальную асимптоту, приравняйте знаменатель к нулю и решите относительно
Икс
.
Икс
—
1
знак равно
0
⇒
Икс
знак равно
1
Итак, вертикальная асимптота
Икс
знак равно
1
Поскольку степень многочлена в числителе меньше степени знаменателя, горизонтальная асимптота имеет вид
у
знак равно
0
.
1,7 — Обратные функции
1,7 — Обратные функции
Обозначение
Функция, обратная f, обозначается f ^-1 (если ваш браузер не поддерживает надстрочные символы, это выглядит как f
с показателем -1) и произносится как «f инверсия». Хотя обратная функция выглядит как
вы возводите функцию в степень -1, это не так. Обратная функция не означает
обратная функция.
Обратные
Функция обычно сообщает вам, что такое y, если вы знаете, что такое x.Обратная функция скажет
вы, каким должен быть x, чтобы получить это значение y.
Функция f ^-1 является обратной функцией f, если
для каждого x в области f, f ^-1 [f (x)] = x и
для каждого x в области f ^-1, f [f ^-1 (x)] = x
Область f — это диапазон f ^-1, а диапазон f — это область f ^-1.
График обратной функции
Функция, обратная функции, отличается от функции тем, что все координаты x и y
были переключены.То есть, если (4,6) — точка на графике функции, то (6,4) — точка
на графике обратной функции.
Точки в функции идентичности (y = x) останутся в функции идентичности при переключении. Все
координаты других точек будут изменены, и их местоположение будет перемещено.
График функции и обратный ей график являются зеркальным отображением друг друга. Они размышляют о
функция тождества y = x.
Существование обратной функции
Функция говорит, что для каждого x существует ровно один y.То есть значения y могут дублироваться, но x
значения не могут быть повторены.
Если функция имеет инверсию, которая также является функцией, то для каждого x может быть только один y.
Однозначная функция — это функция, в которой для каждого x существует ровно один y и для каждого y,
есть ровно один x. У однозначной функции есть обратная функция, которая также является функцией.
Есть функции, у которых есть инверсии, которые не являются функциями. Есть и обратные для
связи.По большей части мы не обращаем на них внимания и имеем дело только с функциями, обратными к которым являются
также функции.
Если обратная функция также является функцией, то обратная зависимость должна проходить вертикальную черту.
контрольная работа. Поскольку все координаты x и y переключаются при нахождении обратного, говоря
что обратная функция должна пройти проверку вертикальной линии — это то же самое, что сказать, что исходная функция должна пройти
тест горизонтальной линии.
Если функция проходит как тест вертикальной линии (так что это в первую очередь функция), так и
проверка горизонтальной линии (так что его обратная функция является функцией), тогда функция взаимно однозначна и имеет
обратная функция.
Неформальный поиск инверсий
Инверсия некоторых функций, особенно тех, где есть только одно вхождение
независимая переменная, может быть решена путем отмены операций. Чтобы отменить операции, вы
должен не только изменить порядок, но и использовать обратную операцию.
Пример 1
Функция f (x) = 5x-2
Начать с x: x
Умножить на 5: 5x
Вычесть 2: 5x-2
Обратное f
^-1 (x) = (x + 2) / 5
Начать с x: x
Добавить 2: x + 2
Разделить на 5: (x + 2) / 5
Пример 2
Функция f (x) = 2 (x-3)
²-5, x≥3
Обратите внимание, что на x есть ограничение.
Начать с x: x
Вычесть 3: x-3
Квадрат: (x-3) ²
Умножить на 2: 2 (x-3) ²
Вычесть 5: 2 (x-3) ²-5
Обратное f
^-1 (x) = 3 + sqrt [(x + 5) / 2]
Начать с x: x
Добавить 5: x + 5
Разделить на 2: (x + 5) / 2
Извлеките квадратный корень: ± sqrt [(x + 5) / 2]
Добавить 3: 3 ± sqrt [(x + 5) / 2]
Подождите! Эта инверсия не является функцией, потому что для каждого x есть два значения y.Это из-за ±, которое появилось, когда мы извлекли квадратный корень из обеих частей. Теперь вернемся к исходной области x≥3. Это означает, что для обратного диапазон y≥3. Поскольку y должно быть не меньше 3, нам нужен положительный квадратный корень, а не отрицательный. Без ограничения на x в
исходная функция, у нее не было бы
обратная функция: 3 + sqrt [(x + 5) / 2]
Пример 3
Функция f (x) = x
² — 4x + 6, x≤2
Уххх ????
Что происходит, когда встречается более одного раза
независимая переменная в функции? Ты не
знаю, что вы сделали с x, потому что вы сделали это с двумя
разных x, и вы не сделали одно и то же с обоими
их.
Формальный поиск инверсий
Нельзя сказать, что последний пример не может быть выполнен, но он включает в себя завершение квадрата до
получить f (x) = (x-2) ² +2, а затем инвертировать его, чтобы получить f ^-1 (x) = 2-sqrt (x-2).
Однако есть другой способ, который не слишком полагается на неформальность и будет работать независимо от того,
Вы не можете точно определить, что вы сделали с одним x.
Начать с функции
Заменить f (x) на y, если необходимо
Поменяйте местами x и y.На этом этапе вы имеете дело с инверсией
Решить для y
Замените y на f ^-1 (x), если обратная функция также является функцией, в противном случае оставьте ее как y
Пример 4
Функция f (x) = x
² / (x ² +1), x≥0
Ограничение важно сделать 1-1.
Начните с функции: f (x) = x ² / (x ² +1), x≥0
Заменить f (x) на y: y = x ² / (x ² +1), x≥0
Поменяйте местами x и y: x = y ² / (y ² +1), y ≥0
Решить относительно y:
Умножаем на знаменатель: x (y ² +1) = y ²
Распределить: xy ² + x = y ²
Переместите y в одну сторону, а все остальное в другую: xy ² -y ² = -x
Фактор: y ² (x-1) = — x
Разделить на коэффициент при y ²: y ² = -x / (x-1)
Упростить правую часть: y ² = x / (1-x)
Извлеките квадратный корень: y = ± sqrt [x / (1-x)]
Поскольку y≥0, нам нужен положительный квадратный корень: y = sqrt [x / (1-x)]
Назовите это f ^-1 (x): f ^-1 (x) = sqrt [x / (1-x)]
Для этой последней функции подразумеваемая область обратного преобразования — [0,1).Это означает, что диапазон
исходная функция также должна быть [0,1). Проверьте это на своем калькуляторе, и вы увидите, что это так.
Иногда в инструкциях говорится, что если функция не является взаимно однозначной, то не находите обратную
функция (потому что ее нет). Поэтому всегда проверяйте, прежде чем тратить время на поиск
обратная функция. Теперь, если вы должны найти обратное, независимо от того,
функция или нет, тогда вперед.
Хорошая вещь!
Индивидуальные функции — замечательные вещи.
При решении уравнений вы можете прибавить одно и то же к обеим сторонам, вычесть одно и то же из
обе стороны, умножьте обе стороны на одно и то же ненулевое значение и разделите обе стороны на одно и то же
отличное от нуля, и все равно получите то же решение, не беспокоясь о необходимости проверять свой ответ.
Вы также можете применить взаимно однозначную функцию к обеим сторонам уравнения, не беспокоясь о введении посторонних решений (решений, которые работают после выполнения чего-то, что не работало раньше).Это не обязательно верно для функций, которые не являются взаимно однозначными, как функция возведения в квадрат, где вы всегда должны проверять ответы после возведения в квадрат обеих сторон уравнения. Например, уравнение sqrt (x) = -2 не имеет решения, но если вы возведете в квадрат обе стороны, вы получите x = 4, но оно не проверяется в исходной задаче. Благодаря индивидуальным функциям вы не будете предлагать никаких посторонних решений.
Вау! Говорить о
мощный. Вы не цените этого сейчас, и книга не справится с этим должным образом, пока вы не получите
к главе 4 и имеют дело с логарифмическими и экспоненциальными функциями, и даже тогда они не делают
как бы то ни было.
Хорошо, попробуем сейчас. Поверьте мне на слово, что exp (x) является взаимно однозначной функцией и является
инверсия ln (x).
ln (x) = 3
Решите относительно x.
ехр [ln (x)] = ехр [3]
«Погодите, мистер Джонс» — ваш ответ. Вы никогда не видели такого зверя. Это
хорошо. Возьмите обратную функцию и примените ее к обеим сторонам.
х = ехр (3)
Вернитесь к определению инверсии в верхней части этого документа.x и находится на ключе [2 ^nd] [ln].
Вау — больше сплоченности. Обратную функцию можно найти, взяв функцию [2 ^nd]. Посмотрите
у него для прочего на калькуляторе.
Корень квадратный — это величина, обратная квадрату. Если вы посмотрите на три тригонометрических ключа [sin],
[cos] и [tan], их обратные значения находятся с помощью клавиши [2 ^nd].
Режим мыльницы включен.
Я говорю вам — все сочетается друг с другом.Для тех, кто помнит строчку, которую Ганнибал Смит использовал в
A-Team: «Мне нравится, когда план слагается».
Математика — один из самых совместных предметов. Все дополняет
еще. Я надеюсь, что вы получите от этого курса гораздо больше, чем просто механику
математика, но понимание, понимание и оценка того, как работает система.
Имея такой прочный фундамент, математика может быть менее напряженной и даже приятной. У тебя есть
перестать иметь дело с концепциями как с отдельными вещами, которые не связаны друг с другом и не связаны друг с другом.2 (1-х)?
Ответ:
График функции f — это совокупность всех точек на плоскости вида (x, f (x)). Мы также могли бы определить график f как график уравнения y = f (x). Итак, график функции — это частный случай графика уравнения.
Пример 1.
Пусть f (x) = x2 — 3.
Напомним, что когда мы вводили графики уравнений, мы заметили, что если мы можем решить уравнение относительно y, то легко найти точки, которые находятся на график.Мы просто выбираем число для x, а затем вычисляем соответствующее значение y. Графики функций — это графики уравнений, которые были решены относительно y!
График f (x) в этом примере является графиком y = x2 — 3. На графике легко создавать точки. Выберите значение для первой координаты, затем оцените f для этого числа, чтобы найти вторую координату. В следующей таблице показаны несколько значений x и функции f, вычисленных с этими числами.
x
-2
-1
0
1
2
f (x)
1
-2
-3
-2
1
Каждый столбец чисел в таблице хранятся координаты точки на графике f.2, что мы и хотим!
График f показан ниже.
Упражнение 2:
Постройте график кусочно-определенной функции
Ответ
Мы видели, что некоторые уравнения для x и y не описывают y как функцию от x. Алгебраический способ узнать, определяет ли уравнение y как функцию от x, состоит в решении относительно y. Если нет единственного решения, тогда y не является функцией x.
Предположим, что нам дан график уравнения. Есть простой способ узнать, описывает ли это уравнение y как функцию от x.
Вернуться к содержанию
Тест вертикальной линии
Набор точек на плоскости является графиком функции тогда и только тогда, когда ни одна вертикальная линия не пересекает график более чем в одной точке.
Пример 3.
График уравнения y2 = x + 5 показан ниже.
Согласно тесту вертикальной линии, этот график не является графиком функции, потому что есть много вертикальных линий, которые встречаются с ним более одного раза.
Подумайте о тесте вертикальной линии таким же образом.Точки на графике функции f имеют вид (x, f (x)), поэтому, когда вы знаете первую координату, определяется вторая. Следовательно, на графике функции не может быть двух точек с одинаковой первой координатой.
Все точки на вертикальной линии имеют одинаковую первую координату, поэтому, если вертикальная линия дважды попадает в график, то на графике есть две точки с одинаковой первой координатой. В таком случае график не является графиком функции.
Как нарисовать график функции квадратного корня, (f (x) = √ x)
В этой статье будет показано, как нарисовать графики функции квадратного корня, используя только три различных значения для ‘x’, а затем найти точки через который строится график уравнений / функций, а также будет показано, как график перемещается по вертикали (перемещается вверх или вниз), перемещается по горизонтали (перемещается влево или вправо) и как график одновременно выполняет оба перевода.
Уравнение функции квадратного корня имеет вид … y = f (x) = A√x, где (A) не должно быть равно нулю (0). Если (A) больше нуля ( 0), то есть (A) является положительным числом, тогда форма графика функции квадратного корня аналогична верхней половине буквы «C». Если (A) меньше нуля (0), то есть (A) является отрицательным числом, форма графика аналогична форме нижней половины буквы «C». Пожалуйста, нажмите на изображение для лучшего просмотра.
Чтобы нарисовать график уравнения, … y = f (x) = A√x, мы выбираем три значения для ‘x’, x = (-1), x = (0) и x = (1 ). Мы подставляем каждое значение «x» в уравнение … y = f (x) = A√x и получаем соответствующее соответствующее значение для каждого «y».
Учитывая y = f (x) = A√x, где (A) — вещественное число и (A) не равно нулю (0), и подставив x = (-1) в уравнение, мы получаем y = f (-1) = A√ (-1) = i (мнимое число). Таким образом, первая точка не имеет реальных координат, следовательно, через эту точку нельзя построить никакой график.Теперь подставив x = (0), мы получим y = f (0) = A√ (0) = A (0) = 0. Итак, вторая точка имеет координаты (0,0). Подставив x = (1), мы получим y = f (1) = A√ (1) = A (1) = A. Итак, третья точка имеет координаты (1, A). Поскольку первая точка имела координаты, которые не были реальными, теперь мы ищем четвертую точку и выбираем x = (2). Теперь подставим x = (2) в y = f (2) = A√ (2) = A (1.41) = 1.41A. Итак, четвертая точка имеет координаты (2,1.41A). Теперь мы рисуем кривую через эти три точки. Пожалуйста, нажмите на изображение для лучшего просмотра.
Учитывая уравнение y = f (x) = A√x + B, где B — любое вещественное число, график этого уравнения будет преобразовывать единицы измерения по вертикали (B). Если (B) — положительное число, график будет двигаться вверх (B) единиц, а если (B) — отрицательное число, график будет двигаться вниз (B) единиц. Чтобы нарисовать графики этого уравнения, мы следуем инструкциям и используем те же значения «x» из шага №3. Пожалуйста, нажмите на изображение, чтобы лучше рассмотреть.
Дано уравнение y = f (x) = A√ (x — B), где A и B — любые действительные числа, и (A) не равно нулю (0), и x ≥ B.График этого уравнения будет преобразовывать единицы по горизонтали (B). Если (B) — положительное число, график переместится в правые (B) единицы, а если (B) — отрицательное число, график переместится в левые (B) единицы. Чтобы нарисовать графики этого уравнения, мы сначала устанавливаем выражение «x — B», которое находится под радикальным знаком Больше или равно нулю, и решаем относительно «x». То есть … x — B ≥ 0, тогда x ≥ B.
Теперь мы будем использовать следующие три значения для ‘x’, x = (B), x = (B + 1) и x = (B + 2).Мы подставляем каждое значение «x» в уравнение … y = f (x) = A√ (x — B) и получаем соответствующее соответствующее значение для каждого «y».
Дано y = f (x) = A√ (x — B), где A и B — действительные числа, и (A) не равно нулю (o), где x ≥ B. Подставляя x = (B) в Уравнение получаем y = f (B) = A√ (BB) = A√ (0) = A (0) = 0. Значит, первая точка имеет координаты (B, 0). Теперь подставив x = (B + 1), мы получим y = f (B + 1) = A√ (B + 1 — B) = A√1 = A (1) = A. Итак, вторая точка имеет координаты ( B + 1, A), и подставив x = (B + 2), мы получим y = f (B + 2) = A√ (B + 2-B) = A√ (2) = A (1.41) = 1,41 А. Итак, Третья точка имеет координаты (B + 2,1,41A). Теперь мы рисуем кривую через эти три точки. Пожалуйста, нажмите на изображение для лучшего просмотра.
Дано y = f (x) = A√ (x — B) + C, где A, B, C — действительные числа и (A) не равны нулю (0) и x ≥ B. Пронумеруйте, затем График в ШАГЕ №7 будет преобразовывать единицы измерения по вертикали (C). Если (C) — положительное число, график будет двигаться вверх (C) единиц, а если (C) — отрицательное число, график будет двигаться вниз (C) единиц.Чтобы нарисовать графики этого уравнения, мы следуем инструкциям и используем те же значения «x» из шага №7. Пожалуйста, нажмите на изображение, чтобы лучше рассмотреть.
Асимптоты
Асимптота кривой \ (y = f \ left (x \ right) \), имеющей бесконечную ветвь, называется прямой такой, что расстояние между точкой \ (\ left ({x, f \ left (x \ right)} \ right) \), лежащий на кривой, и прямая стремится к нулю, когда точка движется по ветви на бесконечность.
Асимптоты могут быть вертикальными, наклонными (наклонными) и горизонтальными.Горизонтальную асимптоту часто рассматривают как частный случай наклонной асимптоты.
Вертикальная асимптота
Прямая \ (x = a \) является вертикальной асимптотой графика функции \ (y = f \ left (x \ right) \), если выполняется хотя бы одно из следующих условий:
\ [{\ lim \ limits_ {x \ to a — 0} f \ left (x \ right) = \ pm \ infty, \; \; \;} \ kern-0.3pt {\ lim \ limits_ {x \ в + 0} f \ left (x \ right) = \ pm \ infty.} \]
Другими словами, хотя бы один из односторонних пределов в точке \ (x = a \) должен быть равен бесконечности.
Вертикальная асимптота встречается в рациональных функциях в точках, когда знаменатель равен нулю, а числитель не равен нулю (то есть в точках разрыва второго рода). Например, график функции \ (y = {\ large \ frac {1} {x} \ normalsize} \) имеет вертикальную асимптоту \ (x = 0 \) (рисунок \ (1 \ text {).} \) В этом случае оба односторонних предела (слева и справа) стремятся к бесконечности:
\ [{\ lim \ limits_ {x \ to 0 — 0} \ frac {1} {x} = — \ infty, \; \; \;} \ kern-0.3pt {\ lim \ limits_ {x \ to 0 + 0} \ frac {1} {x} = + \ infty.} \]
Рисунок 1.
Функция, непрерывная на всем множестве действительных чисел, не имеет вертикальных асимптот.
Косая асимптота
Прямая \ (y = kx + b \) называется наклонной (наклонной) асимптотой графика функции \ (y = f \ left (x \ right) \) при \ (x \ to + \ infty \) (Рисунок \ (2 \)), если
\ [{\ lim \ limits_ {x \ to + \ infty} \ left [{f \ left (x \ right) — \ left ({kx + b} \ right)} \ right]} = {0.} \]
Фигура 2.
Аналогично вводятся наклонные асимптоты как \ (x \ to — \ infty. \)
Наклонные асимптоты графика функции \ (y = f \ left (x \ right) \) могут быть разными как \ (x \ to + \ infty \) и \ (x \ to — \ infty. \)
Следовательно, при нахождении наклонных (или горизонтальных) асимптот рекомендуется вычислять их отдельно.
Коэффициенты \ (k \) и \ (b \) наклонной асимптоты \ (y = kx + b \) определяются следующей теоремой:
Прямая \ (y = kx + b \) является асимптотой функции \ (y = f \ left (x \ right) \) при \ (x \ to + \ infty \) тогда и только тогда, когда следующие два предела конечны:
\ [
{\ lim \ limits_ {x \ to + \ infty} \ frac {{f \ left (x \ right)}} {x} = k \; \; \ text {and} \; \; \ ;} \ керн-0.3pt
{\ lim \ limits_ {x \ to + \ infty} \ left [{f \ left (x \ right) — kx} \ right] = b.}
\]
Доказательство.
Необходимость. Пусть прямая \ (y = kx + b \) является асимптотой графика \ (y = f \ left (x \ right) \) при \ (x \ to + \ infty. \). Тогда выполняется следующее условие верно:
\ [\ lim \ limits_ {x \ to + \ infty} \ left [{f \ left (x \ right) — \ left ({kx + b} \ right)} \ right] = 0 \]
или, что эквивалентно,
\ [
{е \ влево (х \ вправо) = кх + Ь + \ альфа \ влево (х \ вправо), \; \; \;} \ керн-0.3pt
{\ text {where} \; \; \ lim \ limits_ {x \ to + \ infty} \ alpha \ left (x \ right) = 0.}
\]
Разделив обе части уравнения на \ (x, \), получим:
\ [
{\ frac {{f \ left (x \ right)}} {x} = \ frac {{kx + b + \ alpha \ left (x \ right)}} {x}, \; \; } \ Rightarrow
{\ frac {{f \ left (x \ right)}} {x} = k + \ frac {b} {x} + \ frac {{\ alpha \ left (x \ right)}} { x}.}
\]
Следовательно, в пределе \ (x \ to + \ infty, \) имеем
\ [
{\ lim \ limits_ {x \ to + \ infty} \ frac {{f \ left (x \ right)}} {x}}
= {\ lim \ limits_ {x \ to + \ infty} \ left [{k + \ frac {b} {x} + \ frac {{\ alpha \ left (x \ right)}} {x}} \ right]} = {k,}
\]
\ [
{\ lim \ limits_ {x \ to + \ infty} \ left [{f \ left (x \ right) — kx} \ right]}
= {\ lim \ limits_ {x \ to + \ infty) } \ left [{b + \ alpha \ left (x \ right)} \ right]} = {b.}
\]
Достаточность. Предположим, что существуют конечные пределы
\ [
{\ lim \ limits_ {x \ to + \ infty} \ frac {{f \ left (x \ right)}} {x} = k \; \; \; \ text {and} \; \ ; \;} \ kern-0.3pt
{\ lim \ limits_ {x \ to + \ infty} \ left [{f \ left (x \ right) — kx} \ right] = b.}
\]
Второй предел можно записать как
.
\ [{\ lim \ limits_ {x \ to + \ infty} \ left [{f \ left (x \ right) — \ left ({kx + b} \ right)} \ right]} = {0,} \]
, отвечающий определению наклонной асимптоты.Таким образом, прямая \ (y = kx + b \) является асимптотой функции \ (y = f \ left (x \ right). \)
Примечание: аналогично мы можем доказать теорему для случая \ (x \ to \ infty. \)
Горизонтальная асимптота
В частности, если \ (k = 0, \), мы получаем горизонтальную асимптоту, которая описывается уравнением \ (y = b. \) Теорема о необходимых и достаточных условиях существования горизонтальной асимптоты формулируется как следует:
Прямая \ (y = b \) является асимптотой функции \ (y = f \ left (x \ right) \) при \ (x \ to + \ infty, \) тогда и только тогда, когда следующий предел конечно:
\ [\ lim \ limits_ {x \ to + \ infty} f \ left (x \ right) = b.\]
Случай \ (x \ to — \ infty \) рассматривается аналогично.
Асимптоты параметрически определенной кривой
Пусть плоская кривая определяется параметрическими уравнениями
\ [{x = \ varphi \ left (t \ right), \; \; \;} \ kern-0.3pt {y = \ psi \ left (t \ right).} \]
Эта кривая имеет вертикальную асимптоту \ (x = a \) при \ (t \ to {t_1} \), если выполняются следующие условия:
\ [
{\ lim \ limits_ {t \ to {t_1}} \ varphi \ left (t \ right) = a \; \; \; \ text {и} \; \; \;} \ kern-0 .3pt
{\ lim \ limits_ {t \ to {t_1}} \ psi \ left (t \ right) = \ pm \ infty.}
\]
Аналогично, параметрически заданная кривая имеет горизонтальную асимптоту \ (y = b \) как \ (t \ to {t_2} \), если
\ [
{\ lim \ limits_ {t \ to {t_2}} \ varphi \ left (t \ right) = \ pm \ infty \; \; \; \ text {and} \; \; \;} \ kern-0.3pt
{\ lim \ limits_ {t \ to {t_2}} \ psi \ left (t \ right) = b.}
\]
Здесь \ (a \) и \ (b \) — конечные величины.
Параметрически заданная кривая имеет наклонную (наклонную) асимптоту \ (y = kx + b \) как \ (t \ to {t_3} \), если при этом значении \ (t, \) оба предела бесконечны:
\ [
{\ lim \ limits_ {t \ to {t_3}} \ varphi \ left (t \ right) = \ pm \ infty, \; \; \;} \ kern-0.3pt
{\ lim \ limits_ {t \ to {t_3}} \ psi \ left (t \ right) = \ pm \ infty,}
\]
, а коэффициенты \ (k \) и \ (b \) имеют конечные значения:
\ [
{k = \ lim \ limits_ {t \ to {t_3}} \ frac {{\ psi \ left (t \ right)}} {{\ varphi \ left (t \ right)}}, \; \; \;} \ kern-0.3pt
{b = \ lim \ limits_ {t \ to {t_3}} \ left [{\ psi \ left (t \ right) — k \ varphi \ left (t \ right) } \ right].}
\]
Асимптота полярной кривой
Рассмотрим кривую, заданную в полярных координатах уравнением
\ [{\ rho = \ rho \ left (\ varphi \ right) \; \; \; \ text {или} \; \; \;} \ kern-0.3pt {F \ left ({\ rho, \ varphi} \ right) = 0.} \]
Его асимптота (если она существует) может быть описана двумя параметрами: расстоянием \ (p \) от центра до асимптоты (отрезок \ (OA \) на рисунке \ (3 \ text {)} \) и угол наклона асимптоты к полярной оси \ (\ alpha \).
Рисунок 3.
Эти параметры \ (\ alpha \) и \ (p \) определяются формулами
\ [
{\ alpha = \ lim \ limits _ {\ rho \ to \ infty} \ varphi, \; \; \;} \ kern-0.3pt
{p = \ lim \ limits _ {\ rho \ to \ infty } \ left [{\ rho \ sin \ left ({\ alpha — \ varphi} \ right)} \ right].}
\]
Примечания:
В последней формуле предельный переход \ (\ rho \ to \ infty \) может быть заменен эквивалентным условием \ (\ varphi \ to \ alpha; \)
Параметр \ (p \) может быть как положительный и отрицательный.
Асимптоты неявной кривой
Неявно заданная алгебраическая кривая описывается уравнением
\ [F \ left ({x, y} \ right) = 0, \]
, где левая часть — многочлен от переменных \ (x \) и \ (y.{n — 1}} + \ ldots} + {{A_ {n — 1}} x + {A_n} = 0,} \]
, где коэффициенты \ ({A_i} \) зависят от параметров асимптоты \ (k \) и \ (b \) (коэффициент \ ({A_0} \) зависит только от \ (k \)). Значения \ (k \) и \ (b \) можно определить из условия:
\ [\ left \ {\ begin {array} {l}
{A_0} \ left (k \ right) = 0 \\
{A_1} \ left ({k, b} \ right) = 0
\ end {array} \ right . {n — 1}} + \ ldots} + {{B_ {n — 1}} y + {B_n} = 0.n} \) в последнем уравнении.
Значение параметра \ (a \) определяется из условия
\ [{B_1} \ left (a \ right) = 0. \]
Приведенные выше формулы для асимптот неявной кривой действительны, если кривая не имеет особых точек на бесконечности.
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Найдите асимптоты функции
\ [f \ left (x \ right) = \ frac {x} {{x + 1}}. \]
Пример 2
Найдите асимптоты функции
\ [f \ left (x \ right) = {\ frac {{2x — 3}} {{x + 1}}}.2} + 1}}}
\]
асимптотически равны друг другу как \ (x \ to + \ infty. \) Оцените погрешность приближенного равенства \ (f \ left ({100} \ right) \ приблизительно g \ left ({100} \ right). \)
Пример 1.
Найдите асимптоты функции
\ [f \ left (x \ right) = \ frac {x} {{x + 1}}. \]
Решение.
При \ (x = -1, \) функция имеет разрыв второго рода. Действительно:
\ [
{\ lim \ limits_ {x \ to — 1 — 0} f \ left (x \ right)}
= {\ lim \ limits_ {x \ to — 1 — 0} \ frac {x} {{ x + 1}}}
= {\ frac {{- 1}} {{\ left ({- 1 — 0} \ right) + 1}}}
= {\ frac {{- 1}} {{- 0}} = + \ infty,}
\]
\ [
{\ lim \ limits_ {x \ to — 1 + 0} f \ left (x \ right)}
= {\ lim \ limits_ {x \ to — 1 + 0} \ frac {x} {{ x + 1}}}
= {\ frac {{- 1}} {{\ left ({- 1 + 0} \ right) + 1}}}
= {\ frac {{- 1}} {{+ 0}} = — \ infty.}
\]
Следовательно, \ (x = -1 \) — уравнение вертикальной асимптоты.
Найдите горизонтальную асимптоту. Вычислите предел:
\ [{\ lim \ limits_ {x \ to \ pm \ infty} \ frac {x} {{x + 1}}} = {\ lim \ limits_ {x \ to \ pm \ infty} \ frac {1} {{1 + \ frac {1} {x}}}} = {1.} \]
Таким образом, для кривой существует горизонтальная асимптота, и ее уравнение имеет вид \ (y = 1. \)
Функция не имеет наклонных асимптот. В этом можно убедиться, вычислив коэффициенты \ (k \) и \ (b: \)
. 2} + x}}}
= {\ lim \ limits_ {x \ to \ pm \ infty} \ frac {{\ frac {1} {x}}} {{1 + \ frac {1} {x }}} = 0,}
\]
\ [
{b = \ lim \ limits_ {x \ to \ pm \ infty} \ left [{y \ left (x \ right) — kx} \ right]}
= {\ lim \ limits_ {x \ to \ pm \ infty} \ left ({\ frac {x} {{x + 1}} — 0} \ right)}
= {\ lim \ limits_ {x \ to \ pm \ infty} \ frac {1} { {1 + \ frac {1} {x}}} = 1.}
\]
Видно, что фактически мы получили горизонтальную асимптоту, которая уже была определена выше.
Итак, график функции имеет вертикальную асимптоту \ (x = -1 \) и горизонтальную асимптоту \ (y = 1 \) (рисунок \ (4 \)).
Рисунок 4.
Пример 2.
Найдите асимптоты функции
\ [f \ left (x \ right) = {\ frac {{2x — 3}} {{x + 1}}}. \]
Решение.
Функция определена для всех \ (x \ ne -1. \). Вычислить односторонние пределы при \ (x = -1: \)
\ [{\ mathop {\ lim} \ limits_ {x \ to — 1 — 0} f \ left (x \ right)} = {\ mathop {\ lim} \ limits_ {x \ to — 1 — 0} \ гидроразрыв {{2x — 3}} {{x + 1}}} = {\ frac {{- 5}} {{- 0}}} = {+ \ infty;} \]
\ [{\ mathop {\ lim} \ limits_ {x \ to — 1 + 0} f \ left (x \ right)} = {\ mathop {\ lim} \ limits_ {x \ to — 1 + 0} \ гидроразрыв {{2x — 3}} {{x + 1}}} = {\ frac {{- 5}} {{+ 0}}} = {- \ infty. 2}}}}} {{1 + \ frac {1} {x}}}} = {\ frac {0} {1}} = {0.2} — 3x + x — 1 + 2}} {{x — 1}}}
= {\ frac {{3x \ cancel {\ left ({x — 1} \ right)}}} {\ cancel {x — 1}} + \ frac {\ cancel {x — 1}} {\ cancel {x — 1}} + \ frac {2} {{x — 1}}}
= {3x + 1 + \ frac {2 } {{x — 1}}} = {3x + 1 + \ alpha \ left (x \ right),}
\]
, где \ (\ alpha \ left (x \ right) \ to 0 \) как \ (x \ to \ pm \ infty. \)
Таким образом, функция имеет наклонную асимптоту \ (y = 3x + 1. \)
Обратите внимание, что рациональная функция может иметь наклонную асимптоту, если степень числителя на единицу больше степени знаменателя.2} — x + x — 1 + 1}} {{x — 1}}} = {\ frac {{x \ left ({x — 1} \ right) + \ left ({x — 1} \ right) + 1}} {{x — 1}}} = {\ frac {{x \ cancel {\ left ({x — 1} \ right)}}} {\ cancel {x — 1}} + \ frac {\ cancel {x — 1}} {\ cancel {x — 1}} + \ frac {1} {{x — 1}}} = {x + 1 + \ frac {1} {{x — 1}}.}.} \]
Как \ (\ mathop {\ lim} \ limits_ {x \ to \ pm \ infty} \ large {\ frac {1} {{x — 1}}} \ normalsize = 0, \) уравнение наклонной асимптоты записывается в виде
\ [y = x + 1. \]
Эта наклонная асимптота существует для \ (x \ to \ pm \ infty.\) Следовательно, функция не имеет горизонтальных асимптот.
Рисунок 9.
Ошибка разрыва связи

Приборная панель
MATH.003.01-WI17

Перейти к содержанию
Приборная панель
Авторизоваться
Панель приборов
Календарь
Входящие
История
Помощь
Закрывать

Функция:	f (x)	=	2x + 3
Положите «y» вместо «f (x)»:	y	=	2x + 3
Вычтем 3 с обеих сторон:	г-3	=	2x
Разделите обе стороны на 2:	(у-3) / 2	=	x
Поменять местами:	х	=	(у-3) / 2

Решение (вместо «x» подставьте «f ^-1 (y)»):	ж ^-1 (г)	=	(у-3) / 2

f ^-1 (x)	… отличается от …	f (x) ^-1
Функция, обратная f		f (x) ^-1 = 1 / f (x) (Обратный)

Задание № 7. Производная функции. ЕГЭ . Математика.

Калькулятор онлайн — Найти (с решением) производную функции

Определение производной

Как найти производную функции у = f(x) ?

Непрерывность функции в точке и на промежутке. С примерами

Непрерывность функции на промежутке

Как plot y=1/x в виде единого графика

Решение

3 ответа

График функции y=kf(x) | Алгебра

ММО-2020 (01.03.2020)

8 класс

9 класс

11 класс (1 день)

103 Виды и типы графиков на Forex, график баров, японских свечей, тиковый график

Обратные функции

Вернуться туда, где мы начали

Пример:

Пример:

Решить с помощью алгебры

Фаренгейта в Цельсия

Инверсия общих функций

Осторожно!

Пример: квадрат и квадратный корень

Но мы можем это исправить!

Пример: (продолжение)

Нет обратного?

и диапазон

Пример: квадрат и квадратный корень (продолжение)

Не всегда разрешимо!

Примечания к обозначениям

Сводка

Область и диапазон рациональных функций

Асимптоты рациональной функции:

1,7 — Обратные функции

Обозначение

Обратные

График обратной функции

Существование обратной функции

Неформальный поиск инверсий

Пример 1

Функция f (x) = 5x-2

Обратное f

Пример 2

Функция f (x) = 2 (x-3)

Обратное f

Пример 3

Функция f (x) = x

Формальный поиск инверсий

Пример 4

Функция f (x) = x

Хорошая вещь!

Как нарисовать график функции квадратного корня, (f (x) = √ x)

Асимптоты

Вертикальная асимптота

Косая асимптота

Доказательство.

Горизонтальная асимптота

Асимптоты параметрически определенной кривой

Асимптота полярной кривой

Примечания:

Асимптоты неявной кривой

Решенные проблемы

Пример 1

Пример 2

Пример 1.

Пример 2.

Ошибка разрыва связи

К сожалению, вы обнаружили неработающую ссылку!

Добавить комментарий Отменить ответ