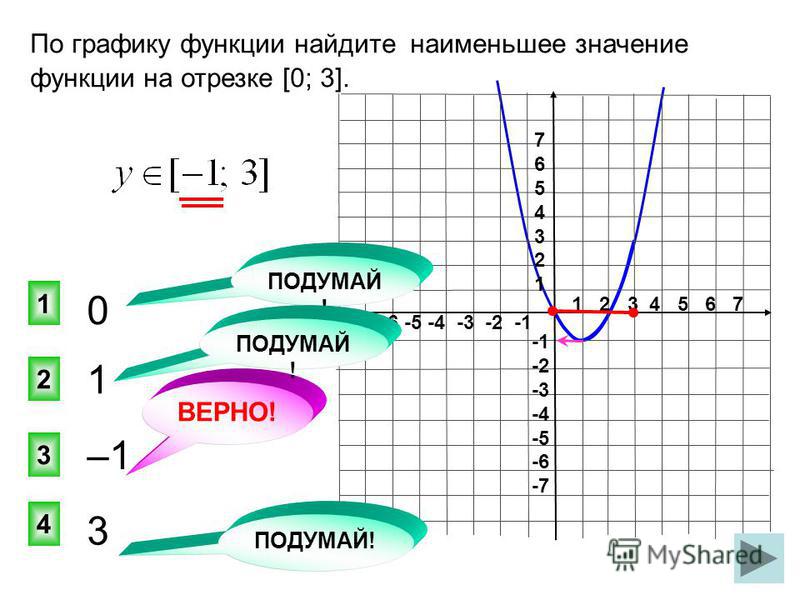
Содержание
Тема 7. Функции — Материалы для подготовки к вступительным экзаменам в СГГА
Тема 7. Функции
1. Понятие функции
Функция y=f(x) – соответствие, при котором каждому числу x из множества D сопоставляется единственное число y из множества E.
x– аргумент функции, y – значение функции; D или D(f) – область определения функции; это совокупность всех значений x, для которых можно вычислить значение функции. E или E(f) – область значений функции; это совокупность всех значений, которые может принимать выражение f(x).
График функции y=f(x) – множество точек (x,y) на координатной плоскости, где x принимает все возможные значения из D(f), а y=f(x).
Четная функция: f(-x)=f(x) для всех ; Нечетная функция: f(-x)=-f(x) для всех ;
График четной функции симметричен относительно оси OY. График нечетной функции симметричен относительно начала координат.
Периодическая функция с периодом T>0: f(x+T)=f(x) для всех .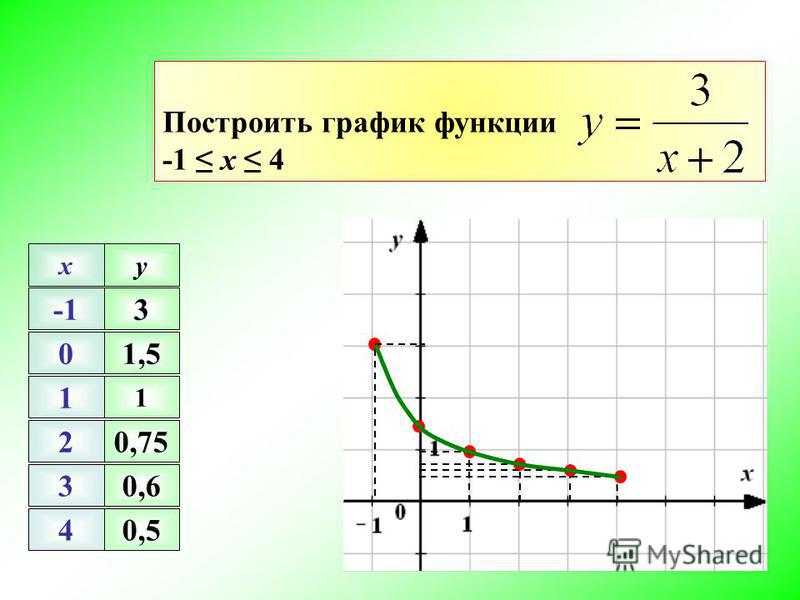
Нули функции – значения x такие, что f(x)=0. Интервалы знакопостоянства – множества значений аргумента, при которых значения функции только положительны или только отрицательны.
На рисунке изображена функция с областью определения [a, e]. Нули функции: x=b, x=c, x=d; интервалы знакопостоянства: y>0 при ; y. Функция возрастает на множестве X, если большему значению аргумента соответствует большее значение функции. То есть для любых , если x12, то f(x1)2). Функция убывает на множестве X, если большему значению аргумента соответствует меньшее значение функции. Т.е. для любых , если x12, то f(x1)>f(x2).
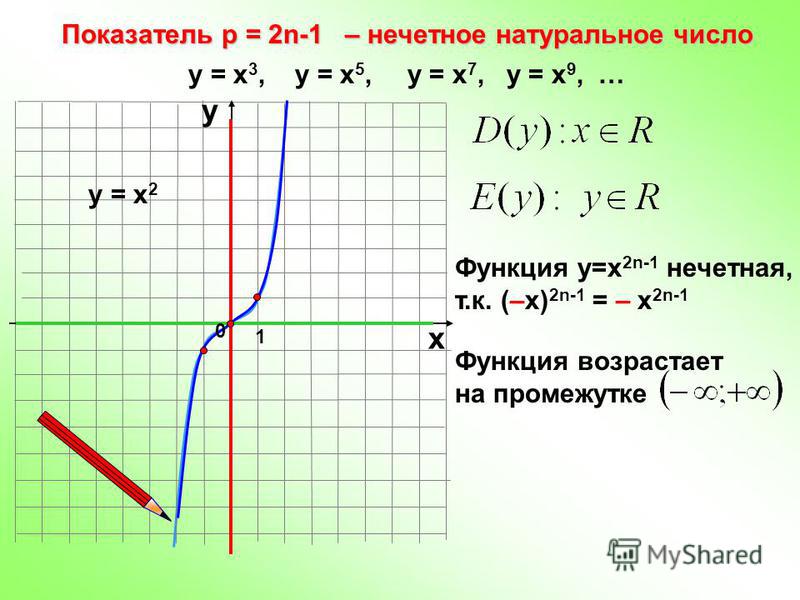
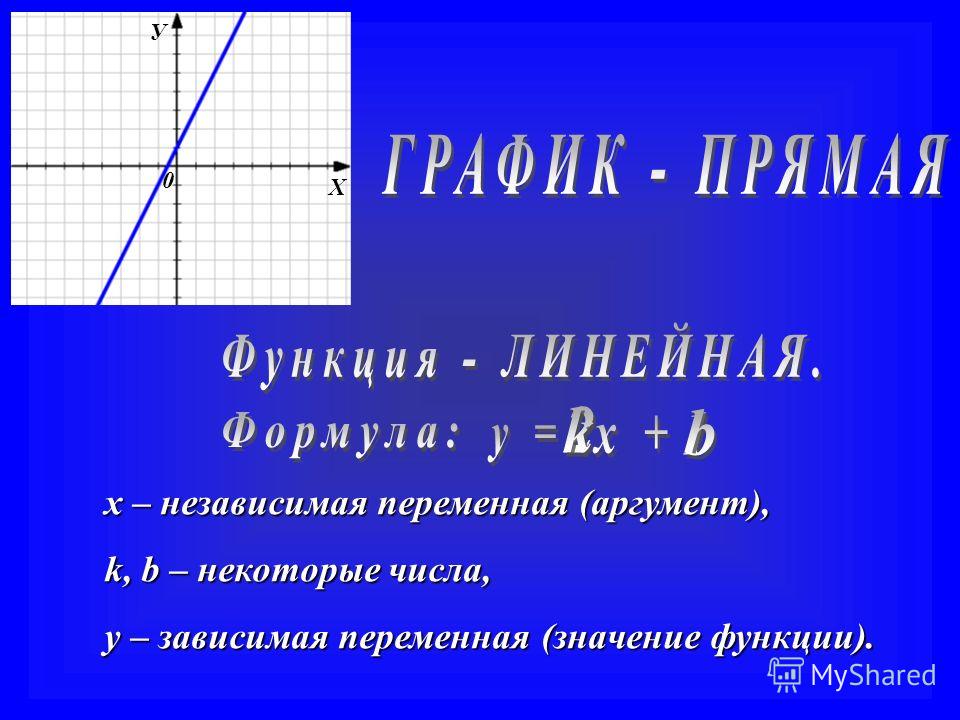
3. Некоторые алгебраические функции
а) линейная . График функции – прямая линия, проходящая через точки (0, b) и .
Функция возрастает при a>0, убывает при a<0.
Частные случаи: y=b – прямая, параллельная оси OX;
y=ax – прямая, проходящая через начало координат.
б) квадратичная . График функции – парабола. Ветви параболы направлены вверх при a>0, вниз при a.
Точки пересечения с осями координат:
с осью OX – (x1, 0) и (x2, 0),
где , D=b2-4ac – корни квадратного трехчлена;
с осью OY – (0, c).
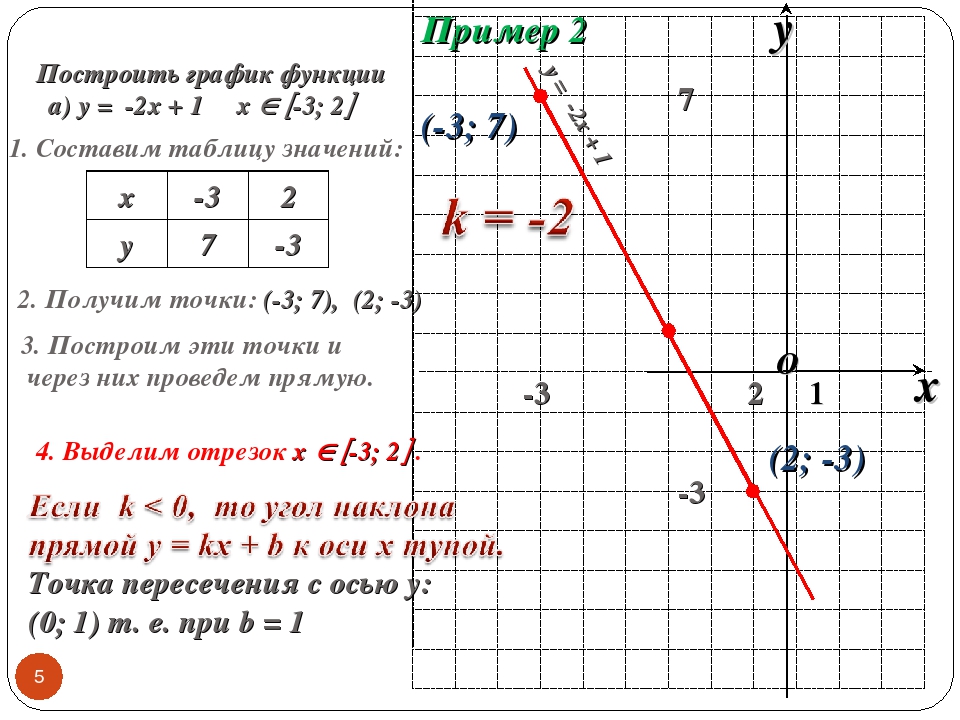
Пример 1. График какой функции является возрастающим:
а) ; б) у = х3 – 27; в) y=2-x?
Решение:
Рассмотрим каждую из функций в отдельности:
а) – степенная функция. Область определения этой функции: . На всей области определения функция монотонна.
Возьмём два значения х1 = 1 и х2 = 4. Им соответствует у1 = – 1, у2 = – 2. Видим, что если х1 < x2 , то у1 > у2. Функция убывающая.
б) у = х3 – 27 – алгебраическая функция. Область определения – множество всех действительных чисел. На всей области определения функция монотонна. Возьмём два значения х1 = 3, х2 = 4. Им соответствует у1 = 0, у2 = 37.
На всей области определения функция монотонна. Возьмём два значения х1 = 3, х2 = 4. Им соответствует у1 = 0, у2 = 37.
Видим, что если х1 < x2 , то и у1 < у2. Функция возрастающая.
в) y=2-x – показательная функция. Областью определения является множество всех действительных чисел. На всей области определения функция монотонна. Пусть х1 = 0, х2 = 1. Им соответствуют у1 = 1, у2 = 0,5.
Видим, что если х1 < x2 , то у1 > у2. Функция убывающая.
Ответ: б) у = х3 – 27.
Пример 2. Парабола у = 2х2 – (а – 3)х + а + 3 проходит через начало координат. Найдите абсциссу вершины параболы.
Решение:
Найдём значение параметра а. Т.к. парабола проходит через начало системы координат, то координаты точки (0; 0) являются корнями уравнения параболы: 0 = 2 ∙ 02 – (а – 3) ∙ 0 + а + 3; а = – 3.
Уравнение параболы примет вид: у = 2х2 + 6х.
Абсцисса вершины параболы находится по формуле: . Получаем .
Ответ: – 1, 5.
Пример 3. В каких точках график функции f(x) = x2 – 3 пересекает прямую у(х) = х – 1?
Решение:
Ответом на данный вопрос является решение системы
х2 – 3 = х – 1; х2 – х – 2 = 0; х1= – 1, или х2 = 2.
Соответственно, у1 = – 2, у2 = 1.
Ответ: (– 1; – 2), (2; 1).
Пример 4. При каких значениях k прямые – kх + 7у = – 13 и 14у – 3х + 5 = 0 параллельны?
Решение:
Две различные прямые у = k1х + b1 и у = k2х + b2 параллельны, если k1 = k2, но при этом b1 ≠ b2.
В обоих уравнениях выразим у через х.
. Следовательно, . При этом .
При этом .
Ответ: при k = – 1,5.
Пример 5. Найти точки пересечения прямой у = 5 + х с осями координат.
Решение:
Когда график функции пресекает ось ОХ, значение у = 0.
Получаем уравнение 5 + х = 0, х = – 5.
Когда график функции пересекает ось OY, значение х = 0, т.е. у = 5.
Ответ: (– 5; 0), (0; 5).
Пример 6. Найти нули функции у = (х + 1)∙(х – 2).
Решение:
Решаем уравнение (х + 1)∙(х – 2) = 0.
х + 1 = 0 или х – 2 = 0; х1 = – 1, х2 = 2.
Ответ: (– 1; 0), (2; 0).
Пример 7. Найти область значений функции .
Решение:
Оцениваем последовательно:
. Ответ: .
Пример 8. Найдите сумму целых значений функции у = 3 – 2 sin x.
Решение:
Оценим значение 3 – 2 sin x.
.
Сумма целых чисел: 1 + 2 + 3 + 4 + 5 = 15.
Ответ: 15.
Пример 12. Графиком квадратичной функции является парабола с вершиной в точке А(0; 2), проходящая через точку В(2; – 6). Задайте эту функцию формулой.
Решение:
Уравнение квадратичной функции у = ах2 + bх + с.
1) точка А является вершиной параболы, следовательно .
Уравнение примет вид: у = ах2 + с.
2) точка А принадлежит графику, следовательно её координаты удовлетворяют уравнению, т.е. 2 = а ∙ 0 + с; с = 2.
Уравнение примет вид: у = ах2 + 2.
3) график проходит через точку В. Её координаты также удовлетворяют уравнению: – 6 = а ∙ 22 + 2, – 8 = 4 ∙ а, а = – 2.
Получили уравнение у = – 2х2 + 2.
Ответ: у = – 2х2 + 2.
Пример 13. Найдите g (x) , если f (x) = 2x – 3, g (f (x)) = x. Вычислите g (1).
Решение:
Так как нужно вычислить g (1), то это значит, что нужно найти x такое, что f (x) = 1.
2x – 3 = 1, х = 2.
Следовательно, g (f (x)) = 2, т.е. g (1) = 2.
Ответ: g (1) = 2.
Пример 14. Написать уравнение прямой, проходящей через точку пересечения кривых y=52x, y=53x-1 и через точку параболы y=(2x-1)2, в которой производная функции, задающей параболу, равна 8.
Решение:
1) найдём точку пересечения кривых:
2) найдём точку параболы, в которой производная равна 8:
3) прямая проходит через две точки (1; 25) и (1,5; 4). Согласно уравнению прямой, проходящей через две точки, имеем:
– 21х + 21 = 0,5у – 12,5; – 42х + 42 = у – 25; у = – 42х + 47.
Ответ: у = – 42х + 47.
Задания для самостоятельного решения
Базовый уровень
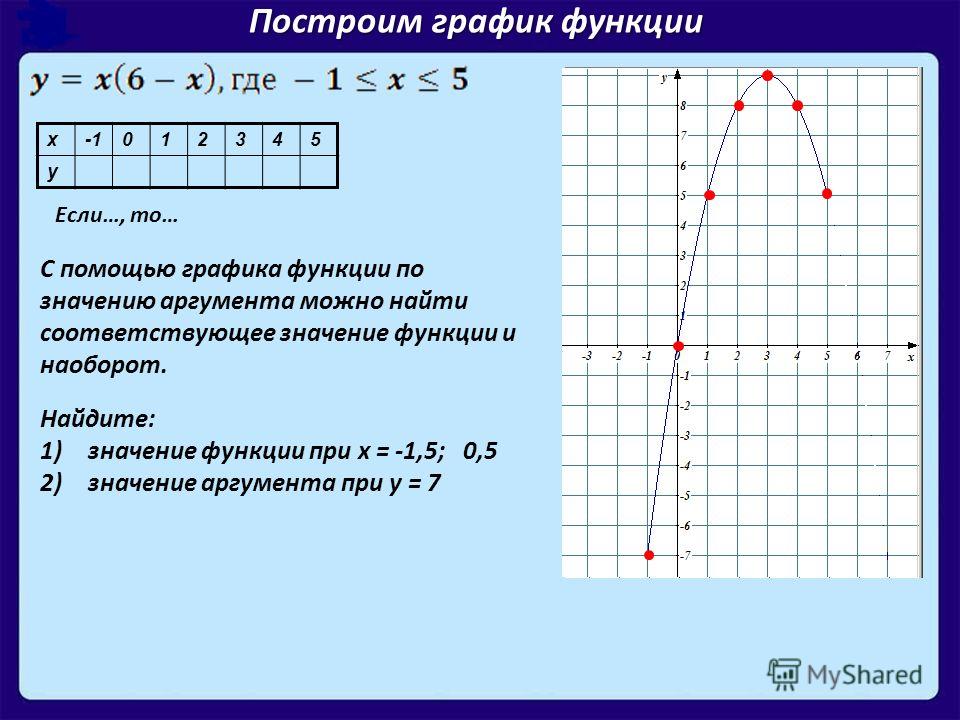
1) Вычислите значение функции в точке х0 = 1. 2) Найдите значение функции при х = 4. 3) Для функции вычислите f(-1)-f(1). 4) Найдите g(f(x)), если Вычислите g(f(2)).
Укажите длину интервала области определения для функций:
24) .
25) y=log4(5x+6-x2)
26) y=log6(x2+3).
Укажите области значения функций:
27) y=-3sinx.
28) y=0,7cos3x.
29) .
Решите задачи:
30) Сколько натуральных значений может принять функция y=log2(4-x2) на всей области определения?
31) Найдите сумму целых значений функции y=3cosx-5.
32) Укажите функцию, областью значений которой является множество . .
33) Укажите график функции, возрастающей на отрезке [-3; 2].
34) Укажите функцию, которая возрастает на всей области определения.
1) y=-x0,5; 2) y=1-e-x; 3) y=ctg2x; 4) y=|-x|.
35) Найдите нули функции . 36) Найдите нули функции
37) Найдите наименьшее значение функции f(x)=32x-1 на промежутке [-3; 1].
38) Вычислите координаты точек пересечения графика функции у = – 2х2 + 4х + 6 с осью OY.
39) Вычислите ординату точки пересечения прямой у = 5 – 2х с осью ОY.
40) Укажите точки пересечения графиков функций у = 2х + 4 и у = – 2х.
41) В каких точках график функции f (x) = 3x2 + 6x пересекает прямую у = 6 – х?
42) Укажите промежутки возрастания функции y=sin3x на интервале . 43) Укажите промежутки убывания функции y=-2cosx на интервале .
Ответы
1) 0; 2) -3/14; 3) – 1; 4) 3; 5) ; 6) ; 7) ;
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.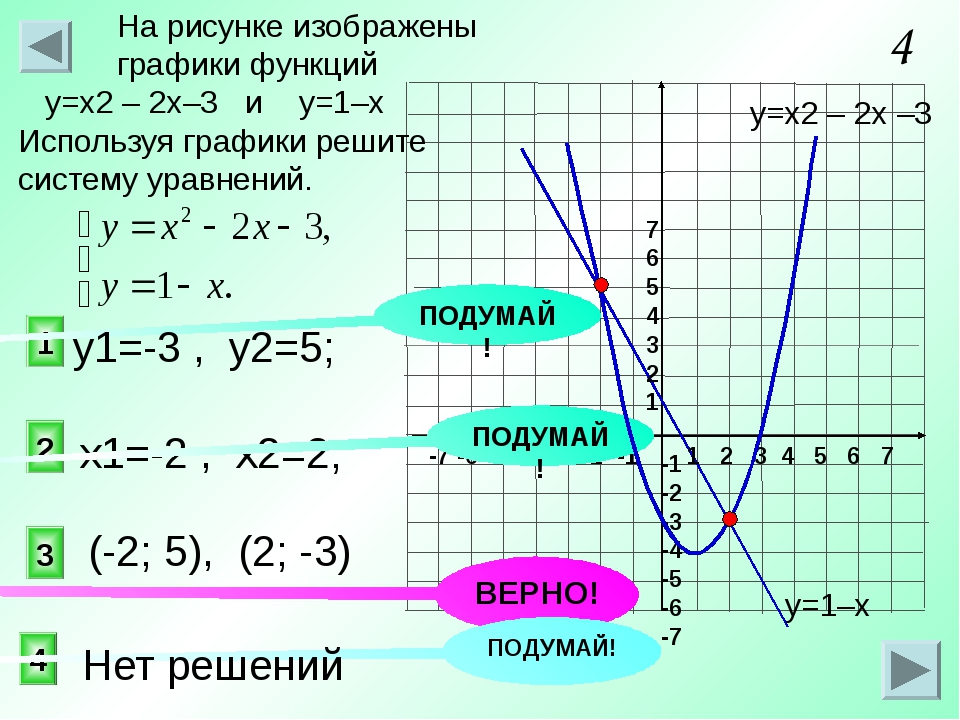
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
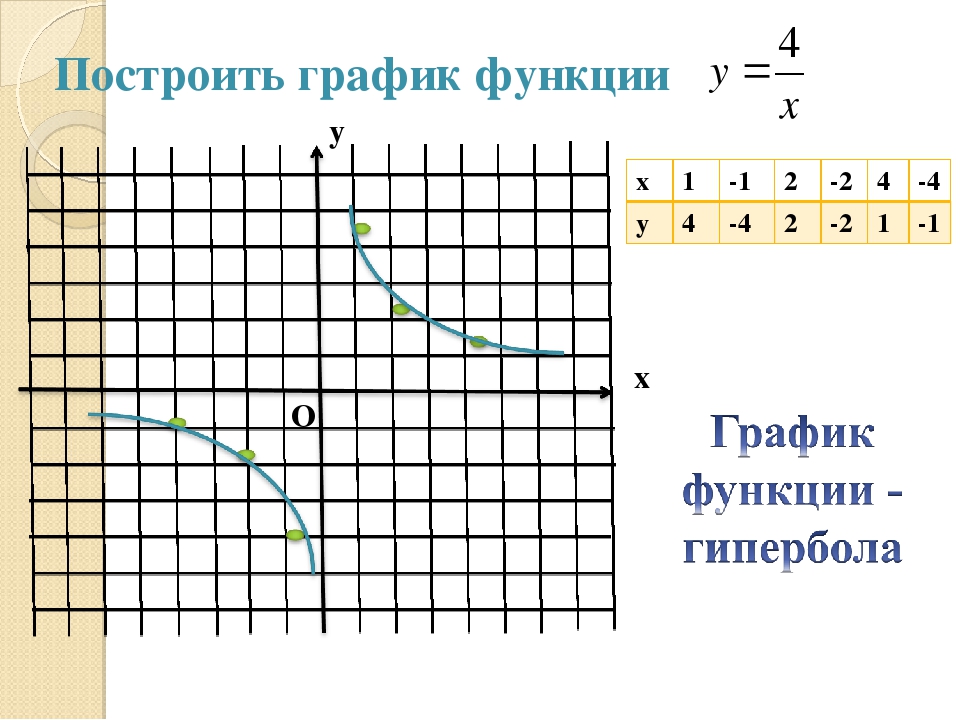
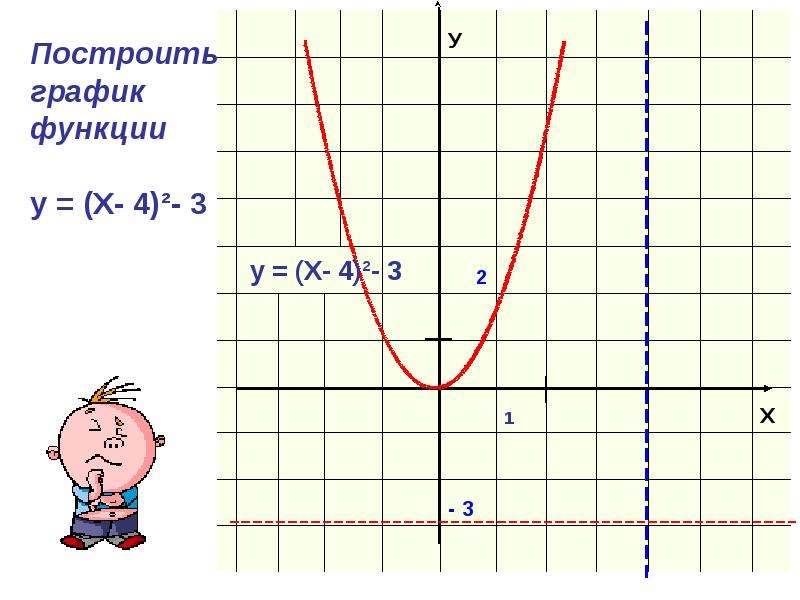
Проверочный тест по алгебре по теме «Функции у = х, у = х2, у = 1/х », (8 класс)
Проверочный тест по теме
«Функции у = х, у = х2, у = » (8 класс)
I вариант:
Обязательная часть.
А1. Выберите вариант ответа, удовлетворяющий условию: точка с координатами (х;у) лежит в III четверти и не принадлежит осям координат.
Варианты ответов:
а) х ≥ 0, у ≤ 0
б) х < 0, у < 0
в) х ≤ 0, у ≤ 0
г) х < 0; у > 0
Ответ: ______
А2.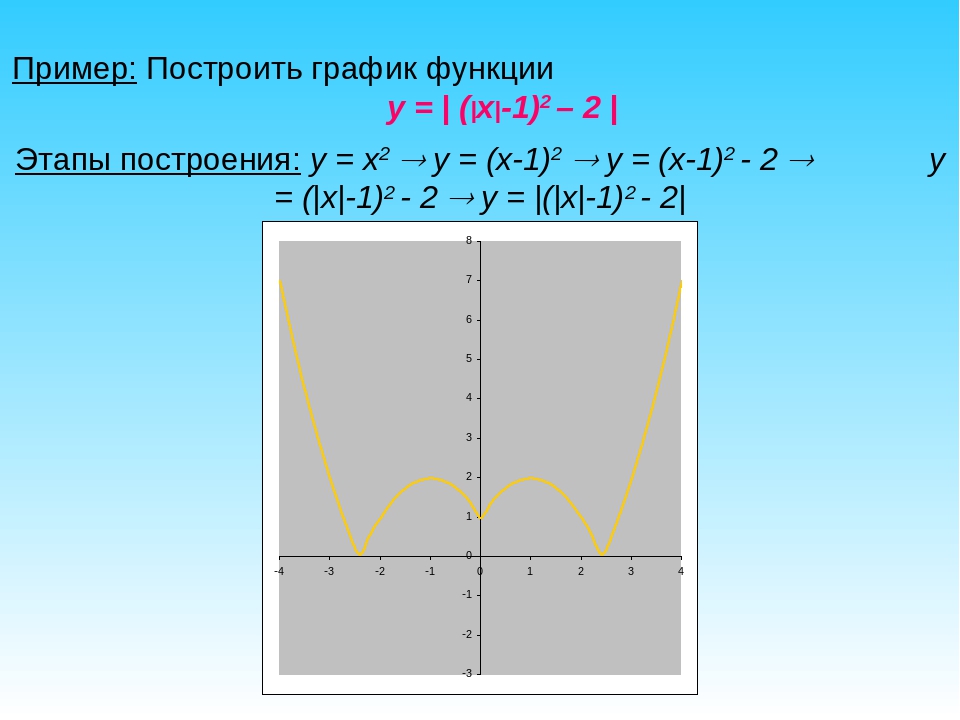 Выберите точку, ордината которой равна 11.
Выберите точку, ордината которой равна 11.
Варианты ответов:
а) А(2; -11)
б) В(11; 2)
в) С(-2; 11)
г) Д(-11;2)
Ответ: _____
А3. Укажите точки, принадлежащие графику функции у = 1 + 2х.
Варианты ответов:
а) А(-1;1)
б) В(0;1)
в) С(1;3)
г) Д(-1;-1)
Ответ: _____
А4. График функции у = называется:
Варианты ответов:
а) парабола
б) гипербола
в) прямая
г) кубическая парабола
Ответ: ____
А5. На указанных множествах выберите убывающие функции.
Варианты ответов:
а) у = х2 на (0; +∞)
б) у = -х на (-∞; +∞)
в) у = на ( -∞; 0)U (0; +∞)
Ответ: ____
А6. Выберите график функции, не проходящий через точки вида (х;у), если область значений функции (-∞;0).
Выберите график функции, не проходящий через точки вида (х;у), если область значений функции (-∞;0).
Варианты ответов:
а) у = х2
б) у = х
в) у =
Ответ: ____
Дополнительная часть.
В1. Заполните таблицу значений для функции у = х2.
Решение:
х | 2 | 7 | ||
у | 9 | 25 |
В2. Запишите промежуток оси ОХ, для всех точек которого ординаты графика функции у = х2 меньше соответствующих ординат графика функции у = х.
Решение: ______________________________________________________________________________________________________________________________________________________
II вариант:
Обязательная часть.
А1. Выберите вариант ответа, удовлетворяющий условию: точка с координатами (х;у) лежит в IV четверти и не принадлежит осям координат.
Варианты ответов:
а) х ≥ 0, у ≤ 0
б) х < 0, у < 0
в) х ≤ 0, у ≤ 0
г) х > 0, у < 0;
Ответ: ______
А2.Выберите точку, абсцисса которой равна -10.
Варианты ответов:
а) А(2; -10)
б) В(10; 2)
в) С(-2; 10)
г) Д(-10;2)
Ответ: _____
А3. Укажите точки, принадлежащие графику функции у = 2х – 1.
Укажите точки, принадлежащие графику функции у = 2х – 1.
Варианты ответов:
а) А(-1;1)
б) В(0;-1)
в) С(1;1)
г) Д(-1;-1)
Ответ: _____
А4. График функции у = х2 называется:
Варианты ответов:
а) парабола
б) гипербола
в) прямая
г) кубическая парабола
Ответ: ____
А5. На указанных множествах выберите возрастающие функции.
Варианты ответов:
а) у = х2 на (0; +∞)
б) у = х на (-∞; +∞)
в) у = на ( -∞; 0)U (0; +∞)
Ответ: ____
А6. Выберите график функции, не проходящий через точки вида (0;у).
Варианты ответов:
а) у = х2
б) у = х
в) у =
Ответ: ____
Дополнительная часть.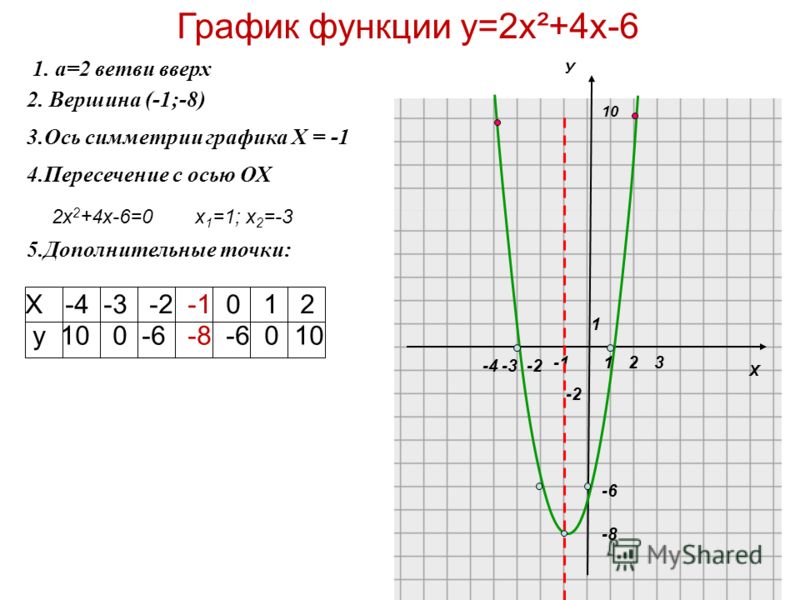
В1. Заполните таблицу значений для функции у =.
Решение:
х | 2 | 0,25 | ||
у | 0,25 | 2 |
В2. Запишите промежутки оси ОХ, для всех точек которых ординаты графика функции у = меньше соответствующих ординат графика функции у = -х.
Решение: ______________________________________________________________________________________________________________________________________________________
Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов. Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».
| ||||
Исследование графика функции. Минимум и максимум
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции
- область значений функции
- нули функции
- промежутки возрастания и убывания
- точки максимума и минимума
- наибольшее и наименьшее значение функции на отрезке.
Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .
Ось ординат — вертикальная ось, или ось .
Аргумент — независимая переменная, от которой зависят значения функции.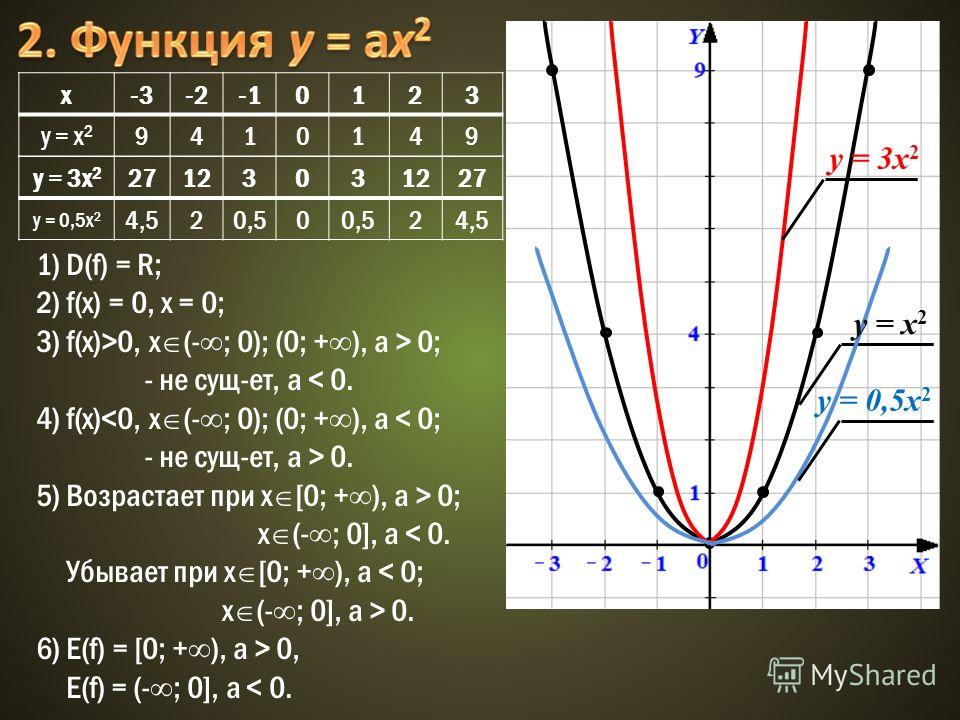 Чаще всего обозначается .
Чаще всего обозначается .
Другими словами, мы сами выбираем , подставляем в формулу функции и получаем .
Область определения функции — множество тех (и только тех) значений аргумента , при которых функция существует.
Обозначается: или .
На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .
Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.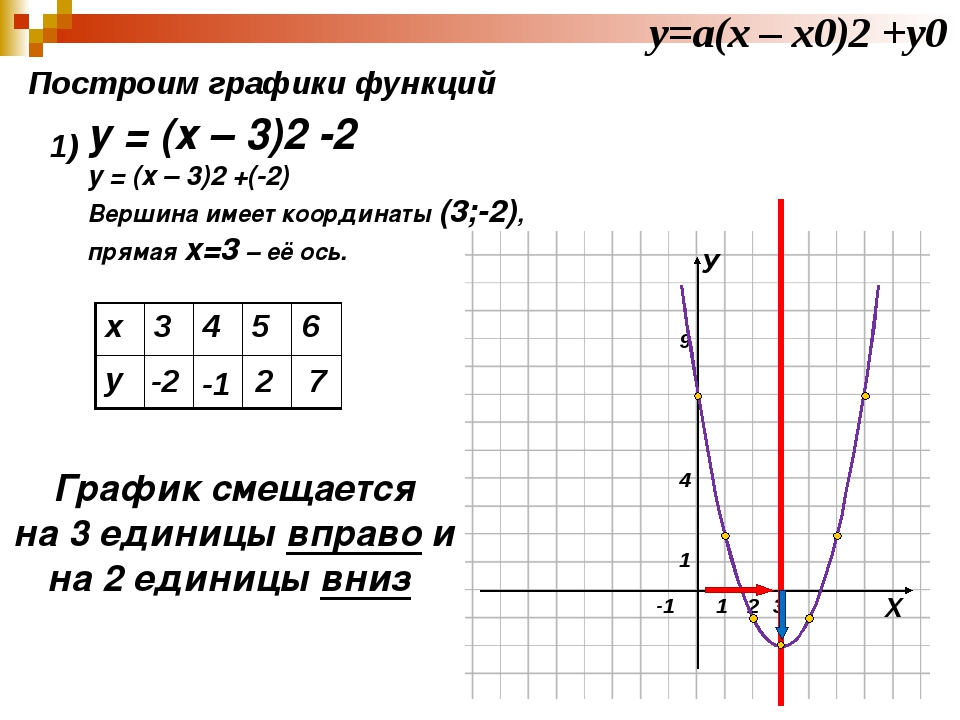
Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.
Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и .
А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке .
Можно сказать, что экстремумы функции равны и .
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.
А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Рациональные функции
Рациональная функция определяется как частное от
многочлены
в которой знаменатель имеет степень не менее
1
. Другими словами, в знаменателе должна быть переменная.
Общий вид рациональной функции:
п
(
Икс
)
q
(
Икс
)
, где
п
(
Икс
)
а также
q
(
Икс
)
являются полиномами и
q
(
Икс
)
≠
0
.
Примеры:
y
знак равно
3
Икс
,
y
знак равно
2
Икс
+
1
Икс
+
5
,
y
знак равно
1
Икс
2
Родительской функцией рациональной функции является
ж
(
Икс
)
знак равно
1
Икс
а график — это
гипербола
.
В
домен и диапазон
это набор всех действительных чисел, кроме
0
.
Домен:
{
Икс
|
Икс
≠
0
}
Диапазон:
{
y
|
y
≠
0
}
Исключенное значение
В рациональной функции исключенное значение — это любое
Икс
-значение, которое делает значение функции
y
неопределенный.Значит, эти значения следует исключить из области определения функции.
Например, исключенное значение функции
y
знак равно
2
Икс
+
3
составляет –3. То есть когда
То есть когда
Икс
знак равно
—
3
, значение
y
не определено.
Итак, область определения этой функции состоит из всех действительных чисел, кроме
—
3
.
Асимптоты
An
асимптота
это линия, к которой график функции приближается, но никогда не касается.В родительской функции
ж
(
Икс
)
знак равно
1
Икс
, как
Икс
— а также
y
-оси — это асимптоты. График родительской функции будет приближаться к асимптотам, но никогда не касается их.
Рациональная функция в виде
y
знак равно
а
Икс
—
б
+
c
имеет вертикальную асимптоту при исключенном значении, или
Икс
знак равно
б
, и горизонтальная асимптота при
y
знак равно
c
.
Смотрите также:
Графическое отображение рациональных функций
Определите вертикальные и горизонтальные асимптоты
Глядя на график рациональной функции, мы можем исследовать ее локальное поведение и легко увидеть, существуют ли асимптоты. Возможно, мы даже сможем приблизительно определить их местонахождение. Однако даже без графика мы все равно можем определить, есть ли у данной рациональной функции какие-либо асимптоты, и вычислить их местоположение.
Вертикальные асимптоты
Вертикальные асимптоты рациональной функции могут быть найдены путем изучения факторов знаменателя, которые не являются общими для множителей в числителе. Вертикальные асимптоты возникают в нулях таких множителей.
Практическое руководство. Для данной рациональной функции определите любые вертикальные асимптоты ее графика.
- Разделите числитель и знаменатель на множители.
- Обратите внимание на любые ограничения в области функции.
- Уменьшите выражение, отбросив общие множители в числителе и знаменателе.{2}} {\ left (2 + x \ right) \ left (1-x \ right)} \ hfill \ end {case} [/ latex]
Чтобы найти вертикальные асимптоты, мы определяем, где эта функция будет неопределенной, установив знаменатель равным нулю:
[латекс] \ begin {case} \ left (2 + x \ right) \ left (1-x \ right) = 0 \ hfill \\ \ text {} x = -2,1 \ hfill \ end {case} [/ латекс]
Ни [latex] x = -2 [/ latex], ни [latex] x = 1 [/ latex] не являются нулями числителя, поэтому два значения указывают на две вертикальные асимптоты. Рисунок 9 подтверждает расположение двух вертикальных асимптот.{2} -2x — 3} [/ latex] можно переписать путем разложения числителя и знаменателя на множители.
[латекс] f \ left (x \ right) = \ frac {\ left (x + 1 \ right) \ left (x — 1 \ right)} {\ left (x + 1 \ right) \ left (x — 3 \ right)} [/ латекс]
Обратите внимание, что [латекс] x + 1 [/ latex] является общим множителем для числителя и знаменателя.
 Нуль этого фактора, [латекс] x = -1 [/ латекс], является местоположением устраняемой несплошности. Также обратите внимание, что [латекс] x — 3 [/ латекс] не является множителем как в числителе, так и в знаменателе. Нуль этого фактора, [латекс] x = 3 [/ latex], является вертикальной асимптотой.
Нуль этого фактора, [латекс] x = -1 [/ латекс], является местоположением устраняемой несплошности. Также обратите внимание, что [латекс] x — 3 [/ латекс] не является множителем как в числителе, так и в знаменателе. Нуль этого фактора, [латекс] x = 3 [/ latex], является вертикальной асимптотой.Рисунок 10
Общее примечание: устраняемые разрывы рациональных функций
Устранимый разрыв появляется на графике рациональной функции при [latex] x = a [/ latex], если a является нулем для множителя в знаменателе, который является общим с множителем в числителе. Мы множим числитель и знаменатель и проверяем общие множители. Если мы что-то находим, мы устанавливаем общий множитель равным 0 и решаем. Это место съемной неоднородности.{2} -4} [/ латекс].
Решение
Разложите на множители числитель и знаменатель.
[латекс] k \ left (x \ right) = \ frac {x — 2} {\ left (x — 2 \ right) \ left (x + 2 \ right)} [/ латекс]
Обратите внимание, что в числителе и знаменателе есть общий множитель, [латекс] x — 2 [/ латекс].
 Нулевое значение для этого фактора — [латекс] x = 2 [/ латекс]. Это место съемной неоднородности.
Нулевое значение для этого фактора — [латекс] x = 2 [/ латекс]. Это место съемной неоднородности.Обратите внимание, что в знаменателе есть множитель, которого нет в числителе, [латекс] x + 2 [/ латекс].{2} + 5x} [/ латекс].
Решение
Горизонтальные асимптоты
В то время как вертикальные асимптоты описывают поведение графика, когда выход становится очень большим или очень маленьким, горизонтальные асимптоты помогают описать поведение графика, когда вход становится очень большим или очень маленьким. Напомним, что поведение конца многочлена будет отражать поведение главного члена. Точно так же поведение конца рациональной функции будет отражать отношение главных членов функций числителя и знаменателя.{2}} = \ frac {4} {x} [/ latex]. Это говорит нам о том, что при неограниченном увеличении или уменьшении входных данных эта функция будет вести себя аналогично функции [latex] g \ left (x \ right) = \ frac {4} {x} [/ latex], а выходы будет приближаться к нулю, что приведет к горизонтальной асимптоте при y = 0.
 Обратите внимание, что этот график пересекает горизонтальную асимптоту.
Обратите внимание, что этот график пересекает горизонтальную асимптоту.Рисунок 12. Горизонтальная асимптота y = 0, когда [латекс] f \ left (x \ right) = \ frac {p \ left (x \ right)} {q \ left (x \ right)}, q \ left (x \ right) \ ne {0} \ text {где степень} p <\ text {степень q} [/ latex].{2}} {x} = 3x [/ латекс]. Это говорит нам о том, что при неограниченном увеличении или уменьшении входных данных эта функция будет вести себя аналогично функции [latex] g \ left (x \ right) = 3x [/ latex]. По мере увеличения входов выходы будут расти, а не выравниваться, поэтому на этом графике нет горизонтальной асимптоты. Однако график [латекс] g \ left (x \ right) = 3x [/ latex] выглядит как диагональная линия, и, поскольку f будет вести себя так же, как g , он приблизится к линии, близкой к [latex ] y = 3x [/ латекс]. Эта линия — наклонная асимптота.{2} -2x + 1} {x — 1} [/ латекс]. Частное составляет [латекс] 3x + 1 [/ latex], а остаток равен 2.
 Наклонная асимптота — это график линии [латекс] g \ left (x \ right) = 3x + 1 [/ latex].
Наклонная асимптота — это график линии [латекс] g \ left (x \ right) = 3x + 1 [/ latex].Рисунок 13. Наклонная асимптота, когда [латекс] f \ left (x \ right) = \ frac {p \ left (x \ right)} {q \ left (x \ right)}, q \ left (x \ справа) \ ne 0 [/ latex], где степень [латекса] p> \ text {степень} q \ text {by} 1 [/ latex].
Случай 3: Если степень знаменателя = степень числителя, существует горизонтальная асимптота в [латексе] y = \ frac {{a} _ {n}} {{b} _ {n}} [ / latex], где [latex] {a} _ {n} [/ latex] и [latex] {b} _ {n} [/ latex] — ведущие коэффициенты [latex] p \ left (x \ right) [/ латекс] и [латекс] q \ left (x \ right) [/ latex] для [латекса] f \ left (x \ right) = \ frac {p \ left (x \ right)} {q \ left ( x \ right)}, q \ left (x \ right) \ ne 0 [/ латекс].{2}} = 3 [/ латекс]. Это говорит нам о том, что по мере увеличения входных данных эта функция будет вести себя как функция [latex] g \ left (x \ right) = 3 [/ latex], которая представляет собой горизонтальную линию.
 Как [latex] x \ to \ pm \ infty, f \ left (x \ right) \ to 3 [/ latex], в результате получается горизонтальная асимптота при y = 3. Обратите внимание, что этот график пересекает горизонтальную асимптоту.
Как [latex] x \ to \ pm \ infty, f \ left (x \ right) \ to 3 [/ latex], в результате получается горизонтальная асимптота при y = 3. Обратите внимание, что этот график пересекает горизонтальную асимптоту.Рисунок 14. Горизонтальная асимптота, когда [латекс] f \ left (x \ right) = \ frac {p \ left (x \ right)} {q \ left (x \ right)}, q \ left (x \ справа) \ ne 0 \ text {где степень} p = \ text {степень} q [/ latex].
Обратите внимание, что, хотя график рациональной функции никогда не пересекает вертикальную асимптоту , график может пересекать или не пересекать горизонтальную или наклонную асимптоту. Кроме того, хотя график рациональной функции может иметь много вертикальных асимптот, график будет иметь не более одной горизонтальной (или наклонной) асимптоты.
Следует отметить, что, если степень числителя больше степени знаменателя более чем на единицу, поведение конца графика будет имитировать поведение фракции уменьшенного поведения конца.
 {4} [/ латекс],
{4} [/ латекс],конечное поведение графика будет похоже на поведение четного многочлена с положительным старшим коэффициентом.
[латекс] от x \ до \ pm \ infty, f \ left (x \ right) \ to \ infty [/ latex]
Общее примечание: горизонтальные асимптоты рациональных функций
Горизонтальная асимптота рациональной функции может быть определена по степеням числителя и знаменателя.
- Степень числителя меньше градусов знаменателя: горизонтальная асимптота при y = 0.{3} -8} [/ latex]: степень [латекса] p = 2 \ text {} <[/ latex] степень [latex] q = 3 [/ latex], поэтому существует горизонтальная асимптота y = 0,
Пример 8: Определение горизонтальных асимптот
В задаче о концентрации сахара ранее мы создали уравнение [латекс] C \ left (t \ right) = \ frac {5 + t} {100 + 10t} [/ latex].
Найдите горизонтальную асимптоту и интерпретируйте ее в контексте задачи.
Решение
И числитель, и знаменатель линейны (степень 1).Поскольку степени равны, будет горизонтальная асимптота в отношении ведущих коэффициентов. В числителе старший член t с коэффициентом 1. В знаменателе старший член 10 t с коэффициентом 10. Горизонтальная асимптота будет при соотношении этих значений:
[латекс] t \ to \ infty, C \ left (t \ right) \ to \ frac {1} {10} [/ latex]
Эта функция будет иметь горизонтальную асимптоту в [latex] y = \ frac {1} {10} [/ latex].
Это говорит нам, что по мере увеличения значений t значения C будут приближаться к [latex] \ frac {1} {10} [/ latex].В контексте это означает, что со временем концентрация сахара в резервуаре будет приближаться к одной десятой фунта сахара на галлон воды или [латекса] \ frac {1} {10} [/ latex] фунтов на галлон.
Пример 9: Определение горизонтальных и вертикальных асимптот
Найдите горизонтальную и вертикальную асимптоты функции
.
[латекс] f \ left (x \ right) = \ frac {\ left (x — 2 \ right) \ left (x + 3 \ right)} {\ left (x — 1 \ right) \ left (x + 2 \ right) \ left (x — 5 \ right)} [/ латекс]
Решение
Во-первых, обратите внимание, что у этой функции нет общих факторов, поэтому нет потенциальных устранимых разрывов.
Функция будет иметь вертикальные асимптоты, когда знаменатель равен нулю, в результате чего функция будет неопределенной. Знаменатель будет равен нулю при [latex] x = 1, -2, \ text {и} 5 [/ latex], что указывает на вертикальные асимптоты при этих значениях.
Числитель имеет степень 2, а знаменатель — степень 3. Поскольку степень знаменателя больше, чем степень числителя, знаменатель будет расти быстрее, чем числитель, в результате чего выходные данные будут стремиться к нулю по мере увеличения входных данных. , и так как [латекс] x \ to \ pm \ infty, f \ left (x \ right) \ to 0 [/ latex].Эта функция будет иметь горизонтальную асимптоту при [latex] y = 0 [/ latex].

Рисунок 15
Попробовать 6
Найдите вертикальную и горизонтальную асимптоты функции:
[латекс] f \ left (x \ right) = \ frac {\ left (2x — 1 \ right) \ left (2x + 1 \ right)} {\ left (x — 2 \ right) \ left (x + 3 \ right)} [/ латекс]
Решение
Общее примечание: перехват рациональных функций
Рациональная функция будет иметь перехват y , когда вход равен нулю, если функция определена на нуле.Рациональная функция не будет иметь перехват y , если функция не определена в нуле.
Аналогично, рациональная функция будет иметь x -перехватов на входах, которые приводят к нулевому выходу. Поскольку дробь равна нулю только тогда, когда числитель равен нулю, x -перехваты могут возникнуть только тогда, когда числитель рациональной функции равен нулю.

Пример 10: Нахождение перехватов рациональной функции
Найдите точки пересечения [латекса] f \ left (x \ right) = \ frac {\ left (x — 2 \ right) \ left (x + 3 \ right)} {\ left (x — 1 \ right) \ left (x + 2 \ right) \ left (x — 5 \ right)} [/ латекс].
Решение
Мы можем найти точку пересечения y , вычислив функцию в нуле
[латекс] \ begin {case} f \ left (0 \ right) = \ frac {\ left (0-2 \ right) \ left (0 + 3 \ right)} {\ left (0-1 \ right) \ left (0 + 2 \ right) \ left (0-5 \ right)} \ hfill \\ \ text {} = \ frac {-6} {10} \ hfill \\ \ text {} = — \ frac { 3} {5} \ hfill \\ \ text {} = — 0,6 \ hfill \ end {case} [/ latex]
Перехват x произойдет, когда функция равна нулю:
[латекс] \ begin {case} 0 = \ frac {\ left (x — 2 \ right) \ left (x + 3 \ right)} {\ left (x — 1 \ right) \ left (x + 2 \ right) \ left (x — 5 \ right)} \ hfill & \ text {Это ноль, когда числитель равен нулю}.
 \ hfill \\ 0 = \ left (x — 2 \ right) \ left (x + 3 \ right) \ hfill & \ hfill \\ x = 2, -3 \ hfill & \ hfill \ end {case} [/ latex ]
\ hfill \\ 0 = \ left (x — 2 \ right) \ left (x + 3 \ right) \ hfill & \ hfill \\ x = 2, -3 \ hfill & \ hfill \ end {case} [/ latex ]Интерпретация y — [латекс] \ left (0, -0.6 \ right) [/ latex], интерцепция x — [латекс] \ left (2,0 \ right) [/ latex] и [латекс] \ влево (-3,0 \ вправо) [/ латекс].
Рисунок 16
Попробовать 7
Учитывая обратную квадратную функцию, которая сдвинута вправо на 3 единицы и на 4 единицы вниз, запишите это как рациональную функцию.Затем найдите точки пересечения x и y , а также горизонтальные и вертикальные асимптоты.
Решение
горизонтальных асимптот | Purplemath
Purplemath
В то время как вертикальные асимптоты — священная почва, горизонтальные асимптоты — просто полезные советы.
В то время как вы никогда не можете коснуться вертикальной асимптоты, вы можете (и часто это делаете) касаться и даже пересекать горизонтальные асимптоты.
В то время как вертикальные асимптоты указывают на очень специфическое поведение (на графике), обычно близко к началу координат, горизонтальные асимптоты указывают на общее поведение, обычно далеко от сторон графика.
Другими словами, горизонтальные асимптоты отличаются от вертикальных асимптот во многих довольно существенных отношениях.
MathHelp.com
Чтобы понять концепцию горизонтальных асимптот, давайте рассмотрим несколько примеров.

Найдите горизонтальную асимптоту следующей функции:
Во-первых, обратите внимание, что знаменатель представляет собой сумму квадратов, поэтому он не множится и не имеет реальных нулей.Другими словами, эта рациональная функция не имеет вертикальных асимптот. Так что с этим у нас все в порядке.
Как упоминалось выше, горизонтальная асимптота функции (при условии, что она есть) примерно сообщает мне, куда пойдет график, когда x станет действительно очень большим. Итак, я посмотрю на очень большие значения для x ; то есть при некоторых значениях x , которые очень далеки от источника:
По сторонам графика, где x сильно отрицательно (например, –1,000) или сильно положительно (например, 10000), «+2» и «+1» в выражении для y действительно не имеет большого значения.
 В итоге я получил действительно большое число, разделенное на действительно большое число в квадрате, которое «упростилось» до очень маленького числа. Значения y в основном взяты из « x » и « x 2 », особенно после того, как x стали очень большими. И поскольку x 2 был «больше», чем x , x 2 перетащил значение всей дроби до y = 0 (то есть до x ось), когда x стали большими.
В итоге я получил действительно большое число, разделенное на действительно большое число в квадрате, которое «упростилось» до очень маленького числа. Значения y в основном взяты из « x » и « x 2 », особенно после того, как x стали очень большими. И поскольку x 2 был «больше», чем x , x 2 перетащил значение всей дроби до y = 0 (то есть до x ось), когда x стали большими.Если задуматься, это имеет смысл. Если у вас есть миллион (плюс два, но кого это волнует?), Разделенный на миллион в квадрате (плюс 1, но кого это волнует?), То, по сути, у вас есть миллион, разделенный на квадрат в миллион. , что упрощается до 1 за миллиард. Что очень и очень мало. Итак, в курсе значение функции становится очень и очень маленьким; а именно, она становится очень, очень близкой к нулю.
Я могу увидеть это поведение на графике, если уменьшу масштаб на оси x :
График показывает, что есть немного интересное поведение в середине, прямо возле начала координат, но остальная часть графика довольно скучна, тянется вдоль оси x .

Если я увеличу масштаб начала координат, я также могу увидеть, что график пересекает горизонтальную асимптоту (у стрелки):
Пересечение горизонтальной асимптоты — обычное дело, и это совершенно нормально.(Это вертикальные асимптоты, которых мне не разрешено касаться.)
Как видно из таблицы значений и графика, горизонтальная асимптота — это ось x .
горизонтальная асимптота: y = 0 (ось x )
В приведенном выше упражнении градус знаменателя (а именно, 2) был больше, чем градус в числителе (а именно, 1), а горизонтальная асимптота была y = 0 (ось x ).Это свойство всегда верно: если градус на x в знаменателе больше, чем градус на x в числителе, то знаменатель, будучи «сильнее», опускает дробь до оси x , когда x становится большим.
 То есть, если полином в знаменателе имеет больший ведущий показатель, чем полином в числителе, то график движется вдоль оси x в крайнем правом и крайнем левом углу графика. Таким образом, каждый раз, когда мощность знаменателя больше, чем мощность числителя, горизонтальная асимптота будет представлять собой ось x , также известную как линия y = 0.
То есть, если полином в знаменателе имеет больший ведущий показатель, чем полином в числителе, то график движется вдоль оси x в крайнем правом и крайнем левом углу графика. Таким образом, каждый раз, когда мощность знаменателя больше, чем мощность числителя, горизонтальная асимптота будет представлять собой ось x , также известную как линия y = 0.Что произойдет, если степени в числителе и знаменателе совпадают? Давайте посмотрим:
Найдите горизонтальную асимптоту следующего числа:
В отличие от предыдущего примера, эта функция имеет полиномы степени 2 сверху и снизу; в частности, степени в числителе и знаменателе совпадают.Поскольку степени одинаковы, числитель и знаменатель «тянут» равномерно; этот график не должен тянуться вниз до оси x и не должен стремиться к бесконечности.
 Но куда это денется?
Но куда это денется?Опять же, мне нужно думать о больших значениях для x . Когда x действительно большой, у меня будет примерно вдвое больше (минус одиннадцать, но кого это волнует?) Разделить на один раз что-то большое (плюс девять, но кого это волнует?).
Как вы могли догадаться из последнего упражнения, «–11» и «+9» не будут иметь большого значения для действительно больших значений x .Вдалеке от графика у меня будет примерно
2 x 2 / x 2 , что сокращается до 2.
Подтверждает ли это таблица значений? Проверим:
Для больших значений x значение функции, как и ожидалось, очень близко к y = 2. И график функции отражает это:
Конечно, вероятно, в середине графика, около начала координат, происходит что-то интересное.
 Но если смотреть по сторонам, график явно придерживается линии y = 2. (В математике вы узнаете, как доказать это сами.)
Но если смотреть по сторонам, график явно придерживается линии y = 2. (В математике вы узнаете, как доказать это сами.)Тогда мой ответ:
горизонтальная асимптота: y = 2
В приведенном выше примере степени в числителе и знаменателе были одинаковыми, а горизонтальная асимптота оказалась горизонтальной линией, значение которой y было равно значению, полученному путем деления ведущих коэффициентов двух полиномов.Это всегда верно: когда степени числителя и знаменателя совпадают, то горизонтальная асимптота находится путем деления главных членов, поэтому асимптота определяется по формуле:
y = (старший коэффициент числителя) / (старший коэффициент знаменателя)
Найдите горизонтальную асимптоту
y = (4 x 3 + 3 x -4) / (5-3 x 3 ).
Теперь, когда я знаю правила о полномочиях, мне не нужно составлять таблицу значений или рисовать график. Я могу просто сравнить показатели.
В этой рациональной функции наибольшая степень в числителе и знаменателе одинакова; а именно куб.
(Эта дробь может показаться немного вводящей в заблуждение, потому что член наивысшей степени в знаменателе не является первым членом.Но это нормально; все, что мне нужно найти, — это тот член, который имеет наибольший показатель степени. Не имеет значения, где в выражении находится этот термин.)
Итак, я знаю, что график этой функции будет иметь горизонтальную асимптоту, которая представляет собой значение деления коэффициентов членов с наивысшими степенями. Эти коэффициенты равны 4 и –3. Тогда мой ответ:
Найдите горизонтальную асимптоту
y = (1- x 2 ) / ( x 5 + 3 x 2 )
Наибольшая степень в числителе равна 2.
 В знаменателе стоит x 2 , но это не имеет значения, потому что наибольшая степень в знаменателе равна 5.
В знаменателе стоит x 2 , но это не имеет значения, потому что наибольшая степень в знаменателе равна 5.Поскольку наибольшая степень внизу больше, чем наибольшая степень сверху, то горизонтальная асимптота будет горизонтальной осью.
URL: https://www.purplemath.com/modules/asymtote2.htm
Поиск горизонтальных асимптот — Бесплатная справка по математике
Что такое горизонтальная асимптота?
Горизонтальная асимптота — это значение y на графике, к которому функция приближается, но фактически не достигает.Вот простой графический пример, в котором изображенная на графике функция приближается, но никогда не достигает, \ (y = 0 \). Фактически, как бы сильно вы ни уменьшили масштаб на этом графике, он все равно не достигнет нуля.
 Однако я должен отметить, что горизонтальные асимптоты могут появляться только в одном направлении и могут пересекаться при малых значениях x. Они будут отображаться для больших значений и покажут тенденцию функции, когда x приближается к положительной или отрицательной бесконечности.
Однако я должен отметить, что горизонтальные асимптоты могут появляться только в одном направлении и могут пересекаться при малых значениях x. Они будут отображаться для больших значений и покажут тенденцию функции, когда x приближается к положительной или отрицательной бесконечности.Чтобы найти горизонтальные асимптоты, мы можем записать функцию в виде «y =».3-8x + 3} \). Они возникают, когда график функции становится все ближе и ближе к определенному значению, даже не достигнув этого значения, поскольку x становится очень положительным или очень отрицательным.
, чтобы найти горизонтальные асимптоты:
1) Поместите уравнение или функцию в форму y =.
2) Умножьте (разверните) любые разложенные на множители многочлены в числителе или знаменателе.
3) Удалите все, кроме членов с наибольшими показателями x в числителе и знаменателе.3-9} $$
Помните, что горизонтальные асимптоты появляются, когда x расширяется до положительной или отрицательной бесконечности, поэтому нам нужно выяснить, к чему приближается эта доля, когда x становится огромным.
 Для этого мы выберем «доминирующие» члены в числителе и знаменателе. Доминирующими являются термины с наибольшими показателями. Поскольку x стремится к бесконечности, другие члены слишком малы, чтобы иметь большое значение.
Для этого мы выберем «доминирующие» члены в числителе и знаменателе. Доминирующими являются термины с наибольшими показателями. Поскольку x стремится к бесконечности, другие члены слишком малы, чтобы иметь большое значение.Наибольшие показатели в этом случае совпадают в числителе и знаменателе (3). Доминирующие члены в каждом имеют показатель степени 3.3} $$
В данном случае 2/3 — это горизонтальная асимптота вышеупомянутой функции. Фактически вы должны выразить это как \ (y = \ frac {2} {3} \). Это значение является асимптотой, потому что, когда мы приближаемся к \ (x = \ infty \), «доминирующие» члены будут затмевать остальные, и функция всегда будет приближаться к \ (y = \ frac {2} {3} \ ). Вот график этой функции в качестве последней иллюстрации, что это правильно:
(Обратите внимание, что в этой функции также присутствует вертикальная асимптота.)
Если показатель степени в знаменателе функции больше показателя степени в числителе, горизонтальная асимптота будет иметь вид y = 0, который является осью x.
 2-4} $$
2-4} $$Горизонтальной асимптоты не будет, потому что в числителе БОЛЬШЕ показателя степени, который равен 3. Видите? Это заставит функцию постоянно увеличиваться, а не приближаться к асимптоте. График этой функции ниже. Обратите внимание, что на графике снова присутствуют вертикальные асимптоты.
Образец B:
Найдите горизонтальные асимптоты: \ (\ frac {(2x-1) (x + 3)} {x (x-2)} \)
В этом примере функция представлена в факторизованной форме. Однако мы должны преобразовать функцию в стандартную форму, как указано в шагах выше перед Образцом A.2 \) в числителе и знаменателе, и у нас останется 2. Наша горизонтальная асимптота для образца B — это горизонтальная линия \ (y = 2 \).
Ссылки на похожие уроки с других сайтов:
Горизонтальные асимптоты (Purplemath.com)
Калькулятор асимптоты
Просто введите свою функцию и выберите «Найти асимптоты» из раскрывающегося списка. Нажмите «Ответ», чтобы увидеть все асимптоты (совершенно бесплатно), или подпишитесь на бесплатную пробную версию, чтобы увидеть полную пошаговую информацию о решении.
7.3: Построение графиков рациональных функций — математика LibreTexts
В этом разделе мы будем использовать нули и асимптоты рациональной функции, чтобы помочь построить график рациональной функции. Мы также исследуем конечное поведение рациональных функций. Начнем с примера.
Пример \ (\ PageIndex {5} \)
Нарисуйте график рациональной функции \ [f (x) = \ frac {x + 2} {x-3} \]
Решение
Во-первых, обратите внимание, что числитель и знаменатель уже разложены на множители.Функция имеет одно ограничение, x = 3. Затем обратите внимание, что x = −2 обнуляет числитель уравнения (9) и не является ограничением. Следовательно, x = −2 — нуль функции. Напомним, что функция равна нулю там, где ее график пересекает горизонтальную ось. Следовательно, график f будет пересекать ось x в точке (−2, 0), как показано на рисунке \ (\ PageIndex {4} \).
Обратите внимание, что рациональная функция (9) уже сведена к младшим членам.
 Следовательно, ограничение на x = 3 поместит вертикальную асимптоту на x = 3, что также показано на рисунке \ (\ PageIndex {4} \).
Следовательно, ограничение на x = 3 поместит вертикальную асимптоту на x = 3, что также показано на рисунке \ (\ PageIndex {4} \).Рисунок \ (\ PageIndex {4} \). Постройте и обозначьте точку пересечения с осью x и вертикальную асимптоту.
На данный момент мы знаем две вещи:
- График пересекает ось x в точке (−2, 0).
- С каждой стороны вертикальной асимптоты при x = 3 может произойти одно из двух. Либо график поднимется до положительной бесконечности, либо график упадет до отрицательной бесконечности.
Чтобы обнаружить поведение вблизи вертикальной асимптоты, давайте построим по одной точке с каждой стороны вертикальной асимптоты, как показано на рисунке \ (\ PageIndex {5} \).
Рисунок \ (\ PageIndex {5} \). Дополнительные точки помогают определить поведение вблизи вертикальной асимптоты.
Рассмотрим правую часть вертикальной асимптоты и отмеченную точку (4, 6), через которую должен пройти наш график. Когда график приближается к вертикальной асимптоте при x = 3, может произойти только одно из двух.
 Либо график возрастает до положительной бесконечности, либо график падает до отрицательной бесконечности. Однако, чтобы последнее произошло, график должен сначала пройти через точку (4, 6), а затем пересечь ось x между x = 3 и x = 4 при спуске до минус бесконечности.Но мы уже знаем, что единственный x-перехват находится в точке (2, 0), поэтому этого не может произойти. Следовательно, справа график должен пройти через точку (4, 6), а затем подняться до положительной бесконечности, как показано на рисунке \ (\ PageIndex {6} \).
Либо график возрастает до положительной бесконечности, либо график падает до отрицательной бесконечности. Однако, чтобы последнее произошло, график должен сначала пройти через точку (4, 6), а затем пересечь ось x между x = 3 и x = 4 при спуске до минус бесконечности.Но мы уже знаем, что единственный x-перехват находится в точке (2, 0), поэтому этого не может произойти. Следовательно, справа график должен пройти через точку (4, 6), а затем подняться до положительной бесконечности, как показано на рисунке \ (\ PageIndex {6} \).Рисунок \ (\ PageIndex {6} \). Поведение вблизи вертикальной асимптоты.
Аналогичное рассуждение справедливо для левой части вертикальной асимптоты при x = 3. График не может пройти через точку (2, −4) и подняться до положительной бесконечности по мере приближения к вертикальной асимптоте, потому что для этого потребуется, чтобы он пересечь ось x между x = 2 и x = 3.Однако для этой цели в этой области нет пересечения по оси x. Следовательно, слева график должен пройти через точку (2, −4) и упасть до отрицательной бесконечности по мере приближения к вертикальной асимптоте при x = 3.
 Это поведение показано на рисунке \ (\ PageIndex {6} \) .
Это поведение показано на рисунке \ (\ PageIndex {6} \) .Наконец, как насчет конечного поведения рациональной функции? Что происходит с графиком рациональной функции при неограниченном увеличении x? Что происходит, когда x неограниченно уменьшается? Один простой способ ответить на эти вопросы — использовать таблицу для численного исследования поведения.Графический калькулятор облегчает эту задачу.
Сначала введите свою функцию, как показано на рисунке \ (\ PageIndex {7} \) (a), затем нажмите 2nd TBLSET, чтобы открыть окно, показанное на рисунке \ (\ PageIndex {7} \) (b). Для того, что мы собираемся сделать, все настройки в этом окне не имеют значения, за исключением одного. Убедитесь, что вы используете клавиши со стрелками, чтобы выделить ASK для Indpnt (независимой) переменной, и нажмите ENTER, чтобы выбрать этот параметр. Наконец, выберите 2nd TABLE, затем введите значения x 10, 100, 1000 и 10000, нажимая ENTER после каждого.
Рисунок \ (\ PageIndex {7} \).
 Использование табличной функции графического калькулятора для исследования конечного поведения при приближении x к положительной бесконечности.
Использование табличной функции графического калькулятора для исследования конечного поведения при приближении x к положительной бесконечности.Обратите внимание на результирующие значения y во втором столбце таблицы (столбец Y1) на рисунке \ (\ PageIndex {7} \) (c). Поскольку x неограниченно возрастает, значения y больше 1, но, похоже, приближаются к числу 1. Поэтому, когда наш график перемещается в крайнее правое положение, он должен приближаться к горизонтальной асимптоте при y = 1, как показано на Рисунок \ (\ PageIndex {9} \).
Аналогичная попытка предсказывает конечное поведение при неограниченном уменьшении x, как показано в последовательности изображений на рисунке \ (\ PageIndex {8} \). Когда x неограниченно уменьшается, значения y становятся меньше 1, но снова приближаются к числу 1, как показано на рисунке \ (\ PageIndex {8} \) (c).
Рисунок \ (\ PageIndex {8} \). Использование табличной функции графического калькулятора для исследования конечного поведения при приближении x к отрицательной бесконечности.
Свидетельство на рисунке \ (\ PageIndex {8} \) (c) показывает, что по мере того, как наш график перемещается в крайнее левое положение, он должен приближаться к горизонтальной асимптоте при y = 1, как показано на рисунке \ (\ PageIndex {9} \).
Рисунок \ (\ PageIndex {9} \). График приближается к горизонтальной асимптоте y = 1 на крайнем правом и левом концах.
Какую работу будет выполнять графический калькулятор с графиком этой рациональной функции? На рисунке \ (\ PageIndex {10} \) (a) мы вводим функцию, настраиваем параметры окна, как показано на рисунке \ (\ PageIndex {10} \) (b), затем нажимаем кнопку GRAPH, чтобы получить результат. на рисунке \ (\ PageIndex {10} \) (c).
Рисунок \ (\ PageIndex {10} \). Построение графика рациональной функции с помощью графического калькулятора.
Как обсуждалось в первом разделе, графический калькулятор очень хорошо управляет графиками «непрерывных» функций, но испытывает трудности с построением графиков с разрывами. В случае данной рациональной функции график «прыгает» с отрицательного значения
.

от бесконечности до положительной бесконечности по вертикальной асимптоте x = 3. Калькулятор знает только одно: построить точку, а затем соединить ее с ранее нанесенной точкой отрезком линии. Следовательно, он делает то, что ему говорят, и «соединяет» бесконечности, когда этого не следует делать.
Однако, если мы заранее подготовили определение нулей и вертикальных асимптот, то мы можем интерпретировать то, что мы видим на экране, показанном на рисунке \ (\ PageIndex {10} \) (c), и использовать эту информацию для построения правильного графика. как показано на рисунке \ (\ PageIndex {9} \). Мы даже можем добавить горизонтальную асимптоту к нашему графику, как показано в последовательности на рисунке \ (\ PageIndex {11} \).
Рисунок \ (\ PageIndex {11} \). Добавление предполагаемой горизонтальной асимптоты.
Это подходящий момент, чтобы сделать паузу и суммировать шаги, необходимые для построения графика рациональной функции.{2} -3 х-4} \]
Решение
Мы будем следовать схеме, представленной в Процедуре построения графиков рациональных функций.
Шаг 1 : Сначала разложите на множители числитель и знаменатель.
\ [f (x) = \ frac {x-2} {(x + 1) (x-4)} \]
Шаг 2 : Таким образом, f имеет два ограничения, x = −1 и x = 4. То есть область определения f равна \ (D_ {f} = \ {s: x \ neq-1,4 \} \).
Шаг 3 : Числитель уравнения (12) равен нулю при x = 2, и это значение не является ограничением.Таким образом, 2 является нулем f, а (2, 0) является пересечением по оси x графика f, как показано на рисунке \ (\ PageIndex {12} \).
Шаг 4 : Обратите внимание, что рациональная функция уже сокращена до наименьших членов (если бы это было не так, мы бы сократили на этом этапе). Обратите внимание, что ограничения x = −1 и x = 4 по-прежнему являются ограничениями сокращенной формы. Следовательно, это положения и уравнения вертикальных асимптот, которые также показаны на рисунке \ (\ PageIndex {12} \).
Рисунок \ (\ PageIndex {12} \).
 Постройте пересечения по оси x и нарисуйте вертикальные асимптоты.
Постройте пересечения по оси x и нарисуйте вертикальные асимптоты.Все ограничения исходной функции остаются ограничениями сокращенной формы. Следовательно, на графике f не будет «дыр».
Шаг 5 : Постройте точки справа и слева от каждой асимптоты, как показано на рисунке \ (\ PageIndex {13} \). Эти дополнительные точки полностью определяют поведение графика около каждой вертикальной асимптоты. Например, рассмотрим точку (5, 1/2) справа от вертикальной асимптоты x = 4 на рисунке \ (\ PageIndex {13} \).Поскольку между x = 4 и x = 5 нет пересечения по оси x, а график уже находится выше оси x в точке (5, 1/2), график вынужден увеличиваться до положительной бесконечности по мере приближения к вертикальная асимптота x = 4. Подобные комментарии необходимы для поведения с каждой стороны каждой вертикальной асимптоты.
Шаг 6 : Используйте табличную утилиту на вашем калькуляторе, чтобы определить конечное поведение рациональной функции при неограниченном уменьшении и / или увеличении x.
 Чтобы определить конечное поведение, когда x стремится к бесконечности (неограниченно возрастает), введите уравнение в свой калькулятор, как показано на рисунке \ (\ PageIndex {14} \) (a).{-4} \), что равно 0,0001). Это означает, что прямая y = 0 (ось x) действует как горизонтальная асимптота.
Чтобы определить конечное поведение, когда x стремится к бесконечности (неограниченно возрастает), введите уравнение в свой калькулятор, как показано на рисунке \ (\ PageIndex {14} \) (a).{-4} \), что равно 0,0001). Это означает, что прямая y = 0 (ось x) действует как горизонтальная асимптота.Вы также можете определить конечное поведение, когда x приближается к отрицательной бесконечности (неограниченно убывает), как показано в последовательности на рисунке \ (\ PageIndex {15} \). Результат на рисунке \ (\ PageIndex {15} \) (c) дает четкое свидетельство того, что значения y стремятся к нулю, когда x стремится к отрицательной бесконечности. Опять же, это делает y = 0 горизонтальной асимптотой.
Рисунок \ (\ PageIndex {15} \). Анализ конечного поведения при приближении x к отрицательной бесконечности
Добавьте горизонтальную асимптоту y = 0 к изображению на рисунке \ (\ PageIndex {13} \).
Шаг 7 : Мы можем использовать всю информацию, собранную на сегодняшний день, чтобы нарисовать изображение, показанное на рисунке \ (\ PageIndex {16} \).

Рисунок \ (\ PageIndex {16} \). Заполненный график сопоставляется с вертикальной и горизонтальной асимптотами и пересекает ось x в нуле функции.
Шаг 8 : Как указано выше, на графике f нет «дыр».
Шаг 9 : Воспользуйтесь графическим калькулятором, чтобы проверить достоверность вашего результата. Обратите внимание, как графический калькулятор обрабатывает график этой рациональной функции в последовательности, показанной на рисунке \ (\ PageIndex {17} \).Изображение на Рисунке \ (\ PageIndex {17} \) (c) далеко не по качеству изображения, которое мы имеем на Рисунке \ (\ PageIndex {16} \), но его достаточно, чтобы интуитивно увидеть фактический график, если вы заранее подготовиться должным образом (нули, вертикальные асимптоты, анализ конечного поведения и т. д.).
Рисунок \ (\ PageIndex {17} \). Пользователь графического калькулятора должен расшифровать изображение на экране просмотра калькулятора.
Использование преобразований в графические функции
Вертикальный и горизонтальный перевод
Когда график функции изменяется по внешнему виду и / или местоположению, мы называем это преобразованием.
 Есть два типа преобразований. Жесткое преобразование — набор операций, которые изменяют положение графика в координатной плоскости, но оставляют неизменными размер и форму. изменяет положение функции в координатной плоскости, но оставляет размер и форму графика неизменными. Нежесткое преобразование — набор операций, которые изменяют размер и / или форму графа в координатной плоскости. изменяет размер и / или форму графика.
Есть два типа преобразований. Жесткое преобразование — набор операций, которые изменяют положение графика в координатной плоскости, но оставляют неизменными размер и форму. изменяет положение функции в координатной плоскости, но оставляет размер и форму графика неизменными. Нежесткое преобразование — набор операций, которые изменяют размер и / или форму графа в координатной плоскости. изменяет размер и / или форму графика.Вертикальный сдвиг — жесткое преобразование, которое сдвигает график вверх или вниз.- жесткое преобразование, которое сдвигает граф вверх или вниз относительно исходного графа. Это происходит, когда к какой-либо функции добавляется константа. Если мы добавим положительную константу к каждой координате y , график сдвинется вверх. Если мы добавим отрицательную константу, график сместится вниз. Например, рассмотрим функции g (x) = x2−3 и h (x) = x2 + 3. Начните с вычисления некоторых значений независимой переменной x .
Теперь постройте точки и сравните графики функций g и h с основным графиком f (x) = x2, который показан ниже с помощью пунктирной серой кривой.

Функция g сдвигает основной график на 3 единицы вниз, а функция h сдвигает основной график на 3 единицы вверх. В общем, это описывает вертикальные переводы; если k — любое положительное действительное число:
Вертикальный сдвиг вверх k единиц:
F (x) = f (x) + k
Вертикальный сдвиг вниз k единиц:
F (x) = f (x) −k
Пример 1
Нарисуйте график функции g (x) = x + 4.
Решение:
Начните с базовой функции, определенной как f (x) = x, и сдвиньте график на 4 единицы вверх.
Ответ:
Горизонтальный сдвиг — жесткое преобразование, которое сдвигает график влево или вправо. — жесткое преобразование, которое сдвигает граф влево или вправо относительно исходного графа. Это происходит, когда мы добавляем или вычитаем константы из координаты x перед применением функции.Например, рассмотрим функции, определенные как g (x) = (x + 3) 2 и h (x) = (x − 3) 2, и создадим следующие таблицы:
Здесь мы складываем и вычитаем координаты x , а затем возводим результат в квадрат. Это производит горизонтальный перевод.
Обратите внимание, что это противоположное тому, что вы могли ожидать. В общем, это описывает горизонтальные переводы; если h — любое положительное вещественное число:
Горизонтальный сдвиг влево ч единиц:
F (x) = f (x + h)
Горизонтальный сдвиг вправо ч единиц:
F (x) = f (x − h)
Пример 2
Нарисуйте график функции g (x) = (x − 4) 3.

Решение:
Начните с базовой функции кубирования, определяемой как f (x) = x3, и сдвиньте график на 4 единицы вправо.
Ответ:
Часто встречаются комбинации переводов.
Пример 3
Нарисуйте график функции g (x) = | x + 3 | −5.
Решение:
Начните с функции абсолютного значения и примените следующие преобразования.
y = | x | Базовая функция y = | x + 3 | Горизонтальный сдвиг влево на 3 единицы y = | x + 3 | −5 Вертикальный сдвиг вниз на 5 единиц
Ответ:
Порядок, в котором мы применяем горизонтальный и вертикальный переводы, не влияет на окончательный график.
Пример 4
Нарисуйте график функции g (x) = 1x − 5 + 3.
Решение:
Начните с обратной функции и определите переводы.
y = 1x Основная функция y = 1x − 5 Горизонтальный сдвиг вправо 5 единиц y = 1x − 5 + 3 Вертикальный сдвиг вверх на 3 единицы
Позаботьтесь о том, чтобы сместить вертикальную асимптоту с оси y на 5 единиц вправо и сместить горизонтальную асимптоту от оси x вверх на 3 единицы.
Ответ:
Попробуй! Нарисуйте график функции g (x) = (x − 2) 2 + 1.
Ответ:
Отражения
Отражение Преобразование, которое создает зеркальное отображение графика вокруг оси. представляет собой преобразование, при котором зеркальное отображение графика создается вокруг оси. В этом разделе мы рассмотрим отражения относительно осей x и y . График функции отражается относительно оси x- , если каждая координата y умножается на -1.
 График функции отражается относительно оси y , если каждая координата x умножается на -1 перед применением функции. Например, рассмотрим g (x) = — x и h (x) = — x.
График функции отражается относительно оси y , если каждая координата x умножается на -1 перед применением функции. Например, рассмотрим g (x) = — x и h (x) = — x.Сравните график g и h с базовой функцией квадратного корня, определяемой f (x) = x, показанной ниже серым пунктиром:
Первая функция g имеет отрицательный множитель, который появляется «внутри» функции; это дает отражение относительно оси y .Вторая функция h имеет отрицательный фактор, который появляется «вне» функции; это дает отражение около оси x . В целом верно то, что:
Отражение относительно оси y :
F (x) = f (−x)
Отражение относительно оси x :
F (x) = — f (x)
При рисовании графиков с отражением сначала рассмотрите отражение, а затем примените вертикальный и / или горизонтальный перенос.

Пример 5
Нарисуйте график функции g (x) = — (x + 5) 2 + 3.
Решение:
Начните с функции возведения в квадрат, а затем определите преобразования, начиная с любых отражений.
y = x2 Основная функция. Y = −x2 Отражение относительно оси x. Y = — (x + 5) 2 Сдвиг по горизонтали влево на 5 единиц. Y = — (x + 5) 2 + 3 Сдвиг по вертикали на 3 единицы.
Используйте эти переводы, чтобы нарисовать график.
Ответ:
Попробуй! Нарисуйте график функции g (x) = — | x | +3.
Ответ:
Расстояния
Горизонтальные и вертикальные смещения, а также отражения называются жесткими преобразованиями, потому что форма основного графа остается неизменной или жесткой.
 Функции, умноженные на действительное число, отличное от 1, в зависимости от действительного числа, кажутся растянутыми по вертикали или по горизонтали. Этот тип нежесткого преобразования называется расширением. Нежесткое преобразование, производимое умножением функций на ненулевое действительное число, которое, кажется, растягивает график либо по вертикали, либо по горизонтали.. Например, мы можем умножить функцию возведения в квадрат f (x) = x2 на 4 и 14, чтобы увидеть, что происходит с графиком.
Функции, умноженные на действительное число, отличное от 1, в зависимости от действительного числа, кажутся растянутыми по вертикали или по горизонтали. Этот тип нежесткого преобразования называется расширением. Нежесткое преобразование, производимое умножением функций на ненулевое действительное число, которое, кажется, растягивает график либо по вертикали, либо по горизонтали.. Например, мы можем умножить функцию возведения в квадрат f (x) = x2 на 4 и 14, чтобы увидеть, что происходит с графиком.Сравните график для g и h с базовой функцией возведения в квадрат, определяемой f (x) = x2, показанной ниже серым пунктиром:
Функция g круче, чем базовая функция возведения в квадрат, и ее график выглядит растянутым по вертикали. Функция h не такая крутая, как базовая функция возведения в квадрат, и, похоже, растянута по горизонтали.
В общем имеем:
Если множитель a представляет собой ненулевую дробь между -1 и 1, он растянет график по горизонтали.
 В противном случае график будет растянут по вертикали. Если коэффициент a отрицателен, то это также приведет к отражению.
В противном случае график будет растянут по вертикали. Если коэффициент a отрицателен, то это также приведет к отражению.Пример 6
Нарисуйте график функции g (x) = — 2 | x − 5 | −3.
Решение:
Здесь мы начинаем с произведения −2 и основной функции абсолютного значения: y = −2 | x |.Это приводит к отражению и расширению.
xyy = −2 | x | ← Расширение и отражение − 1−2y = −2 | −1 | = −2⋅1 = −200y = −2 | 0 | = −2⋅0 = 01−2y = −2 | 1 | = −2⋅1 = −2
Используйте точки {(−1, −2), (0, 0), (1, −2)}, чтобы построить график функции отражения и расширения y = −2 | x |. Затем переместите этот график на 5 единиц вправо и на 3 единицы вниз.
y = −2 | x | Базовый график с растяжением и отражением относительно оси x. Y = −2 | x − 5 | Сдвиг вправо на 5 единиц. Y = −2 | x − 5 | −3 Сдвиг на 3 единицы вниз.
Ответ:
Таким образом, с учетом положительных вещественных чисел h и k :
Вертикальный сдвиг вверх k единиц:
F (x) = f (x) + k
Вертикальный сдвиг вниз k единиц:
F (x) = f (x) −k
Горизонтальный сдвиг влево ч единиц:
F (x) = f (x + h)
Горизонтальный сдвиг вправо ч единиц:
F (x) = f (x − h)
Отражение относительно оси y :
F (x) = f (−x)
Отражение относительно оси x :
F (x) = — f (x)
Ключевые выводы
- Идентификация преобразований позволяет нам быстро рисовать график функций.
 Этот навык будет полезен по мере нашего прогресса в изучении математики. Часто геометрическое понимание проблемы приводит к более элегантному решению.
Этот навык будет полезен по мере нашего прогресса в изучении математики. Часто геометрическое понимание проблемы приводит к более элегантному решению. - Если к функции добавить положительную константу, f (x) + k, график сдвинется вверх. Если из функции f (x) −k вычесть положительную константу, график сдвинется вниз. Основная форма графика останется прежней.
- Если положительная константа добавляется к значению в области до применения функции, f (x + h), график сдвинется влево.Если положительная константа вычтена из значения в области до применения функции, f (x − h), график сдвинется вправо. Основная форма останется прежней.
- Умножение функции на отрицательную константу -f (x) отражает ее график на оси x . Умножение значений в области на -1 перед применением функции f (-x) отражает график относительно оси y .
- При применении нескольких преобразований сначала примените отражения.
- Умножение функции на константу, отличную от 1, a⋅f (x), дает расширение. Если положительное число константы больше 1, график будет казаться растянутым по вертикали. Если положительная константа является дробной частью меньше 1, график будет казаться растянутым по горизонтали.
Ответы
у = х; Сдвинуть вверх на 3 единицы; домен: ℝ; диапазон: ℝ
у = х2; Сдвинуть вверх на 1 единицу; домен: ℝ; диапазон: [1, ∞)
у = х2; Сдвиг вправо на 5 единиц; домен: ℝ; диапазон: [0, ∞)
у = х2; Сдвиг вправо на 5 единиц и на 2 единицы вверх; домен: ℝ; диапазон: [2, ∞)
у = | х |; Сдвиг влево на 4 единицы; домен: ℝ; диапазон: [0, ∞)
у = | х |; Сдвинуть вправо на 1 единицу и вниз на 3 единицы; домен: ℝ; диапазон: [−3, ∞)
у = х; Сдвинуть вниз на 5 единиц; домен: [0, ∞); диапазон: [−5, ∞)
у = х; Сдвиг вправо на 2 единицы и вверх на 1 единицу; домен: [2, ∞); диапазон: [1, ∞)
у = х3; Сдвиг вправо на 2 единицы; домен: ℝ; диапазон: ℝ
у = х3; Сдвинуть вправо на 1 единицу и вниз на 4 единицы; домен: ℝ; диапазон: ℝ
y = 1x; Сдвиг вправо на 2 единицы; область: (−∞, 2) ∪ (2, ∞); диапазон: (−∞, 0) ∪ (0, ∞)
y = 1x; Сдвинуть вверх на 5 единиц; область: (−∞, 0) ∪ (0, ∞); диапазон: (−∞, 1) ∪ (1, ∞)
y = 1x; Сдвинуть влево на 1 единицу и вниз на 2 единицы; область: (−∞, −1) ∪ (−1, ∞); диапазон: (−∞, −2) ∪ (−2, ∞)
Базовый график y = −4; домен: ℝ; диапазон: {−4}
у = х3; Сдвинуть вверх на 6 единиц и вправо на 2 единицы; домен: ℝ; диапазон: ℝ
Как найти горизонтальные асимптоты графика рациональной функции
График рациональной функции во многих случаях имеет одну или несколько горизонтальных линий, то есть, поскольку значения x стремятся к положительной или отрицательной бесконечности, график функции приближается к этим горизонтальным линиям, становясь все ближе и ближе, но никогда не касаясь и даже не пересекая эти линии.
 Эти линии называются горизонтальными асимптотами. В этой статье будет показано, как найти эти горизонтальные линии, на некоторых примерах.
Эти линии называются горизонтальными асимптотами. В этой статье будет показано, как найти эти горизонтальные линии, на некоторых примерах.Учитывая рациональную функцию, f (x) = 1 / (x-2), мы сразу можем увидеть, что при x = 2 у нас есть вертикальная асимптота (Чтобы узнать о вертикальных асимптотах, перейдите к статье » Как найти разницу между вертикальной асимптотой … »того же автора, Z-MATH).
Горизонтальную асимптоту рациональной функции, f (x) = 1 / (x-2), можно найти, выполнив следующие действия: разделите числитель (1) и знаменатель (x-2) на член наивысшей степени в рациональной функции, которым в данном случае является член «x».
Итак, f (x) = (1 / x) / [(x-2) / x]. То есть f (x) = (1 / x) / [(x / x) — (2 / x)], где (x / x) = 1. Теперь мы можем выразить функцию как, f (x) = (1 / x) / [1- (2 / x)]. Когда x приближается к бесконечности, оба члена (1 / x) и (2 / x) стремятся к нулю. , (0). Скажем: «Предел (1 / x) и (2 / x), когда x приближается к бесконечности, равен нулю (0)».
Горизонтальная линия y = f (x) = 0 / (1-0) = 0/1 = 0, то есть y = 0, является уравнением горизонтальной асимптоты. Пожалуйста, нажмите на изображение для лучшего понимания.
Учитывая рациональную функцию, f (x) = x / (x-2), чтобы найти горизонтальную асимптоту, мы делим числитель (x) и знаменатель (x-2) на член с наивысшей степенью в Рациональная функция, которая в данном случае является термином «x».
Итак, f (x) = (x / x) / [(x-2) / x]. То есть f (x) = (x / x) / [(x / x) — (2 / x)], где (x / x) = 1. Теперь мы можем выразить функцию как, f (x) = 1 / [1- (2 / x)]. Когда x приближается к бесконечности, член (2 / x) приближается к нулю, (0). Скажем: «Предел (2 / x), когда x приближается к бесконечности, равен нулю (0)».
Горизонтальная линия y = f (x) = 1 / (1-0) = 1/1 = 1, то есть y = 1, является уравнением горизонтальной асимптоты. Пожалуйста, нажмите на изображение для лучшего понимания.
Таким образом, для рациональной функции f (x) = g (x) / h (x), где h (x) ≠ 0, если степень g (x) меньше степени h (x) , то уравнение горизонтальной асимптоты y = 0.
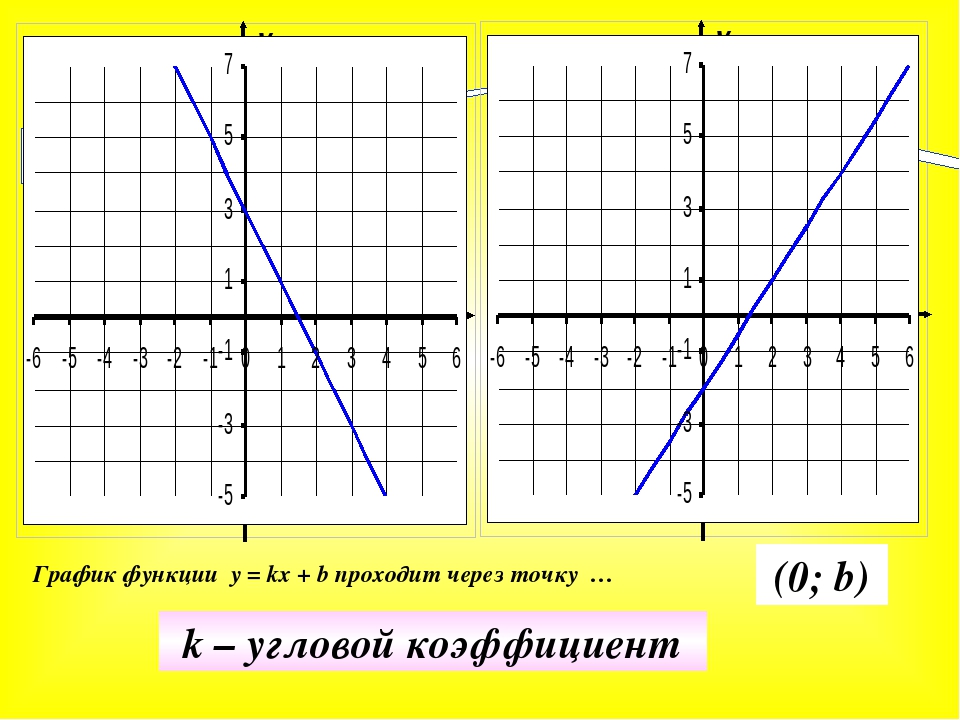
- Степень числителя меньше градусов знаменателя: горизонтальная асимптота при y = 0.{3} -8} [/ latex]: степень [латекса] p = 2 \ text {} <[/ latex] степень [latex] q = 3 [/ latex], поэтому существует горизонтальная асимптота y = 0,

 Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
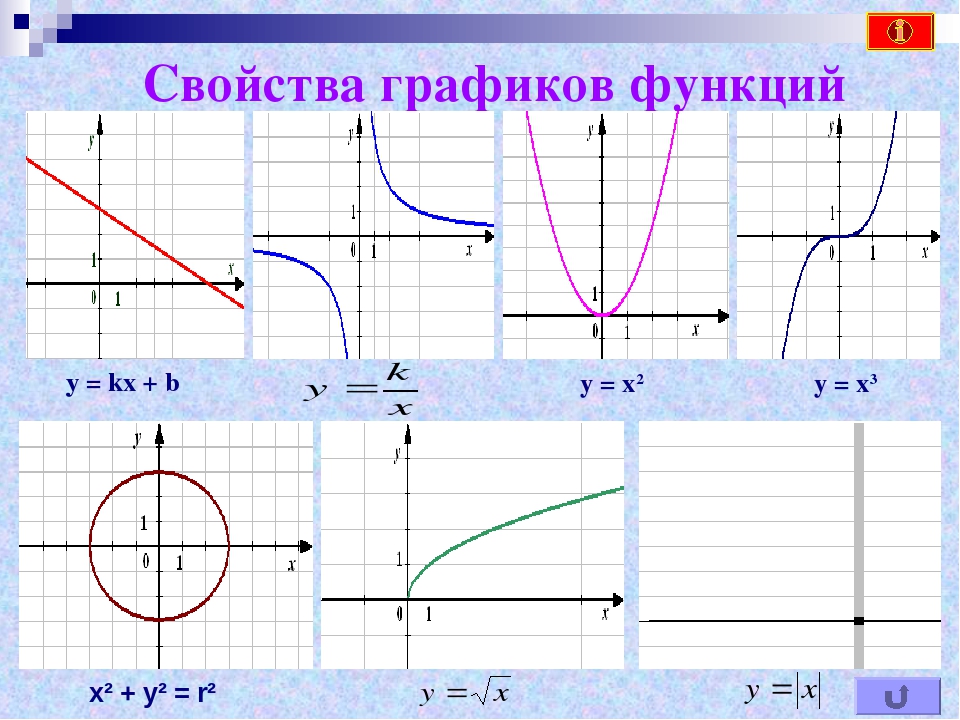
 Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥
Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥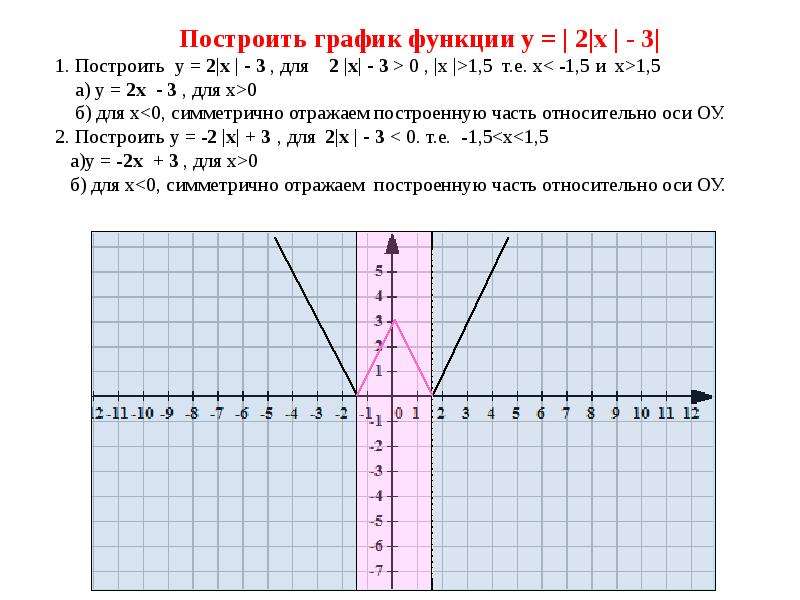 6)
6)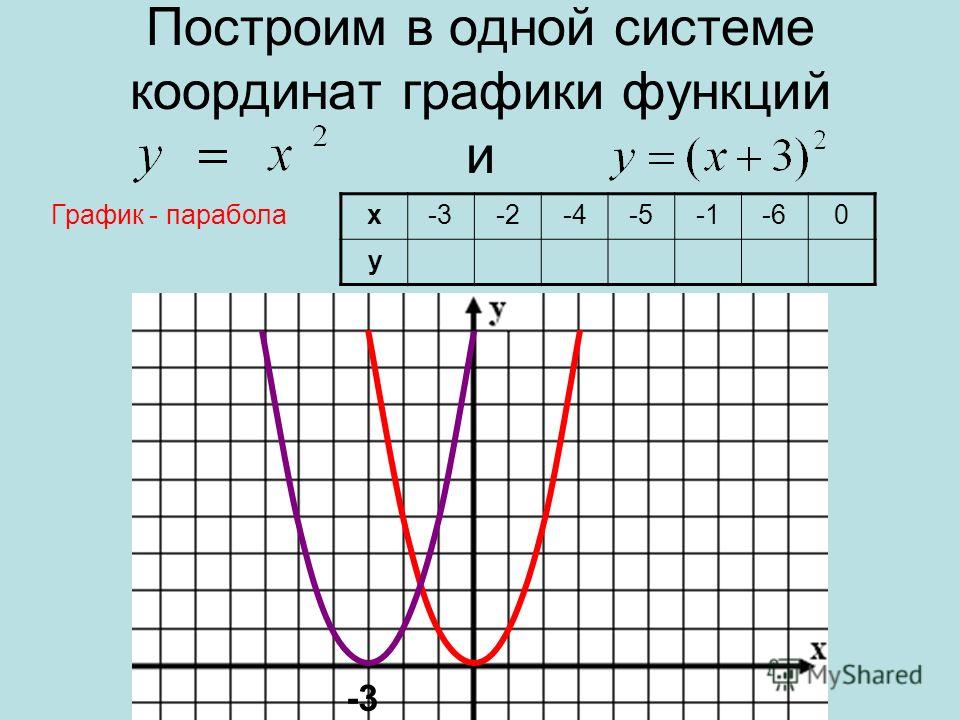

 5, b
5, b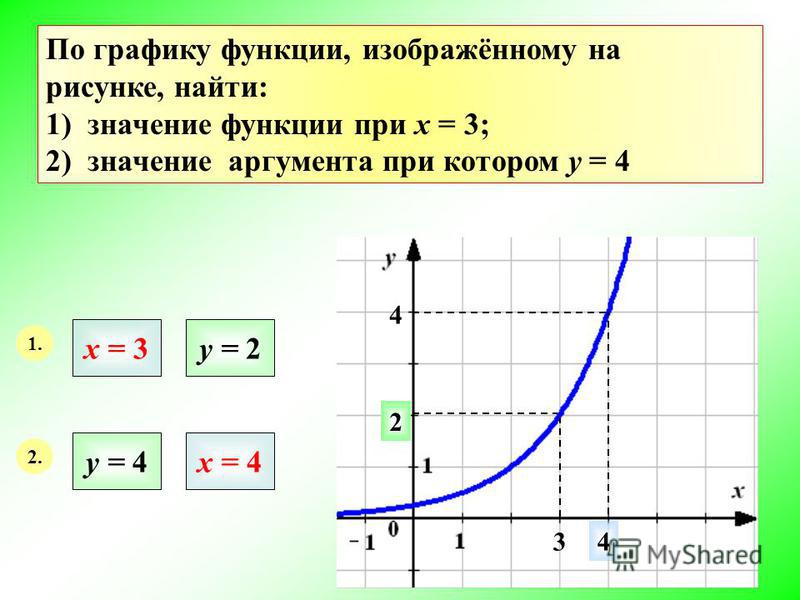
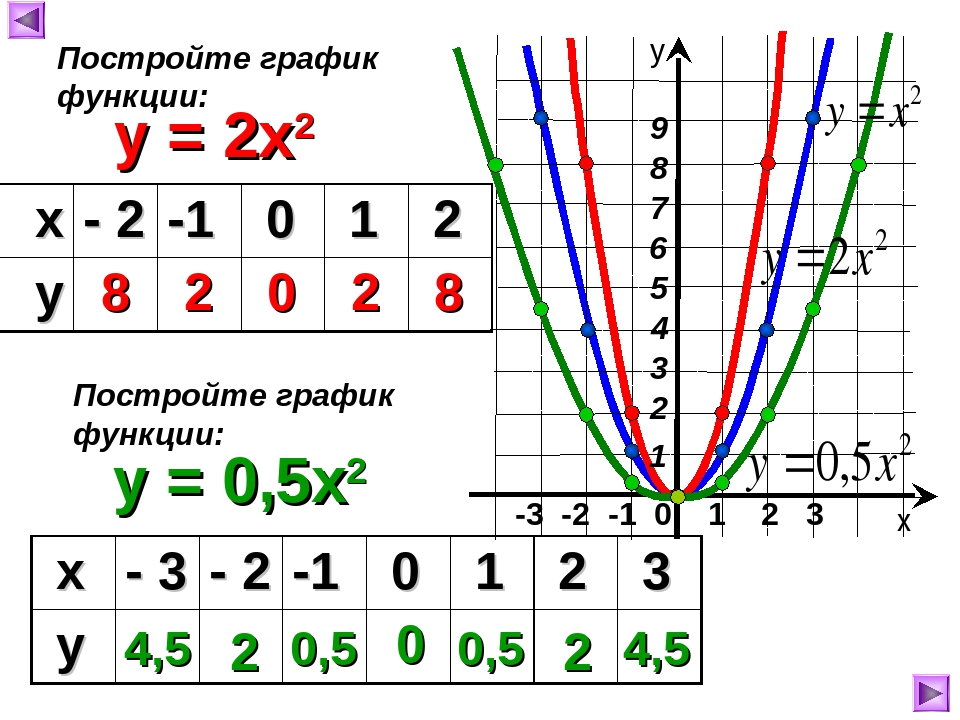 Здесь пример для y = 0,5 x
Здесь пример для y = 0,5 x Случаи с коэффициентами изучаются в разделе «Движение графиков функций».
Случаи с коэффициентами изучаются в разделе «Движение графиков функций». Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?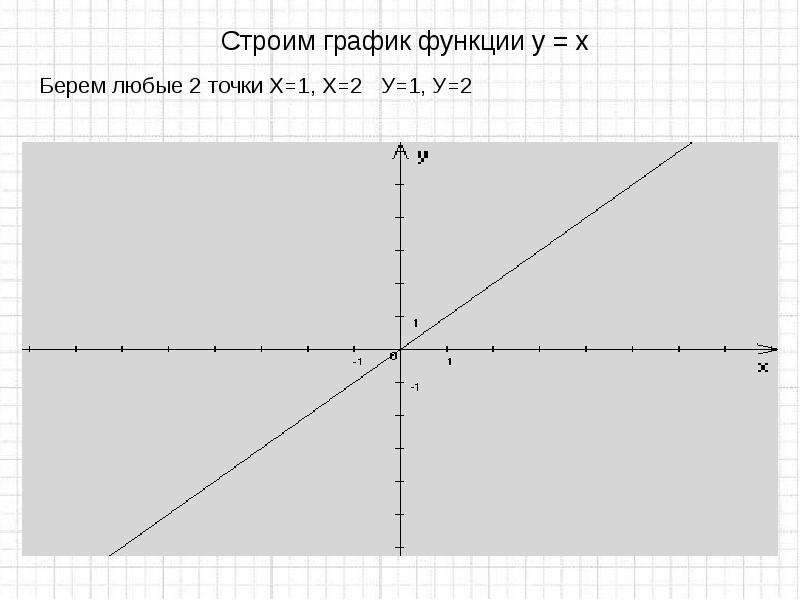 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.