| 1 | Оценить с использованием заданного значения | квадратный корень 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень 1 | |
| 69 | Упростить | квадратный корень 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Аналитическая геометрия в пространстве
Аналитическая геометрия в пространстве
Лабораторная работа №10
Аналитическая геометрия в пространстве
Цель:
- Построение поверхностей второго порядка с помощью системы Mathematica.

Для построения трехмерных поверхностей используется функция:
Plot3D [ f, { x ,xmin, xmax} , {y , ymin, ymax} ]
Чтобы построить график поверхности второго порядка, нужно сначала выразить переменную z из канонического уравнения, например, с помощью функции Solve, которая используется для решения уравнений, указав в качестве переменной только переменную z.
Например, выразим из уравнения эллипсоида x2+y2+z2=1 переменную z:
Solve [ x2 + y2 + z2 = 1, z ]
Получим: { z -> -√(-1-x2-y2), z -> √(-1-x2-y2) }
Это значит, что построение эллипсоида сводится к построению двух поверхностей в одной системе координат:
z = -√(-1-x2-y2) и z = √(-1-x2-y2).
Так как графики нужно построить в одной системе координат, то воспользуемся функцией Show [ z1, z2 ]. При построении графиков с целью улучшения качества графиков используем опцию PlotPoints -> n, которая указывает, сколько точек должно участвовать в построении ( n — натуральное число ). Опция Mesh -> False удаляет линии каркаса поверхности, что способствует большей наглядности в её отображении.
При построении графиков с целью улучшения качества графиков используем опцию PlotPoints -> n, которая указывает, сколько точек должно участвовать в построении ( n — натуральное число ). Опция Mesh -> False удаляет линии каркаса поверхности, что способствует большей наглядности в её отображении.
1. Эллипсоид
Каноническое уравнение: x2 / a2 + y2 / b2 + z2 / c2 = 1.
На рисунке 1 показано построение эллипсоида, заданного уравнением x2 + y2 + z2 = 1.
Задание: Измениет параметры a, b, c и установите, как их увеличение или уменьшение влияет на изображение поверхности.
pис. 1
2. Однополостный гиперболоид
Каноническое уравнение: x2 / a2 + y2 / b2 — z2 / c2 = 1.
На рисунке 2 показано построение однополостного гиперболоида, заданного уравнением x2 / 4 + y2 / 1 — z2 / 4 = 1.
pис. 2
3. Двуполостный гиперболоид
Каноническое уравнение: x2 / a2 — y2 / b2 — z2 / c2 = 1.
На рисунке 3 показано построение двуполостного гиперболоида, заданного уравнением x2 / 4 — y2 / 9 — z2 / 1 = 1.
pис. 3
4. Гиперболический параболоид
Каноническое уравнение: z = x2 / a2 — y2 / b2.
На рисунке 4 показано построение гиперболического параболоида, заданного уравнением z = x2 — y2.
pис. 4
Задание: Постройте эллиптический параболоид. Каноническое уравнение z = x2 / a2 + y2 / b2.
Быстрая навигация: |
|
Лабораторные работы по Mathematica Построение графиков ф-й ч.  I I
Построение графиков ф-й ч.II Решение уравнений Суммы и произведения Пределы Производные Определенные интегралы Трехмерные поверхности Кратные интегралы Разложение функции в ряд Матрицы и операции с ними Дифференциальные уравнения Правильные многогранники Полуправильные многогранники Звездчатые многогранники |
|
ЛИНЕЙНАЯ ФУНКЦИЯ
при k 0 R при k = 0 {b}
если k 0, b 0, то функция ни четная и ни нечетная если k 0, b = 0, то функция нечетная если k = 0, b = 0, то функция четная если k = 0, b = 0, то функция равна нулю
если k 0, то y = 0 при x = -b/k если k = 0, b 0, то нулей нет если k = 0, b = 0, то y = 0 при x R
если k = 0, b > 0, то функция возрастает при x R если k = 0, b x R если k = 0, b = 0, то функция постоянна при x R
|
Documentation Home
О проекте
Здесь представлена документация MATLAB на русском языке. Это обширный ресурс, который служит ускорению инновационного развития технологий в русскоговорящих странах и освоению новых знаний русскоязычными студентами, преподавателями и инженерами.
Перевод осуществляется автоматически с использованием системы ПРОМТ. Инженеры ЦИТМ Экспонента провели первоначальную работу по настройке тысяч тонких параметров алгоритма перевода, словарей, препроцессора и памяти перевода, чтобы системно разрешить огромный объем трудностей машинного перевода.
Этот проект развивается и улучшается с Вашей помощью. Вы можете предлагать лучший вариант перевода, и Ваши исправления станут видны другим пользователям после одобрения модератором. В системе учитывается мнение большого и разнопрофильного профессионального сообщества инженеров и ученых.
Качественные и принятые модератором исправления будут реализованы в словаре и памяти машинного перевода так, чтобы каждый раз в других местах или в следующем релизе документации системно учитывалось Ваше предложение.
∑ Ваш рейтинг в сообществе Экспонента растет с количеством внесенных в память перевода исправлений.
«Документация» это проект сообщества Экспонента. Каждый релиз содержит:
- Более 150 000 страниц локализованной технической документации
- 1.8 Гб текста и 3.5 Гб графических пояснений
- Более 10 000 примеров кода
По вопросам поддержки и коммерческого использования обращайтесь в ЦИТМ Экспонента.
Предыдущие релизы
Вы можете просмотреть документацию предыдущих (архивных) релизов MATLAB. Обратите внимание, что внесение правок в перевод архивных релизов невозможно.
MATLAB R2020b
MATLAB R2020a
MATLAB R2019b
MATLAB R2019a
MATLAB R2018b
УРАВНЕНИЕ ОКРУГА
УРАВНЕНИЕ ОКРУГА
УРАВНЕНИЕ КРУГА.
| Уравнение круга бывает двух видов: | |
| 1) Стандартная форма: (x — h) 2 + (y-k) 2 = Г 2 | |
| 2) Общий вид: x 2 + y 2 + Dx + Ey + F = 0, где D, E, F — постоянные. | |
| Если уравнение круга имеет стандартную форму, мы можем легко идентифицировать центр круга (h, k) и радиус r. 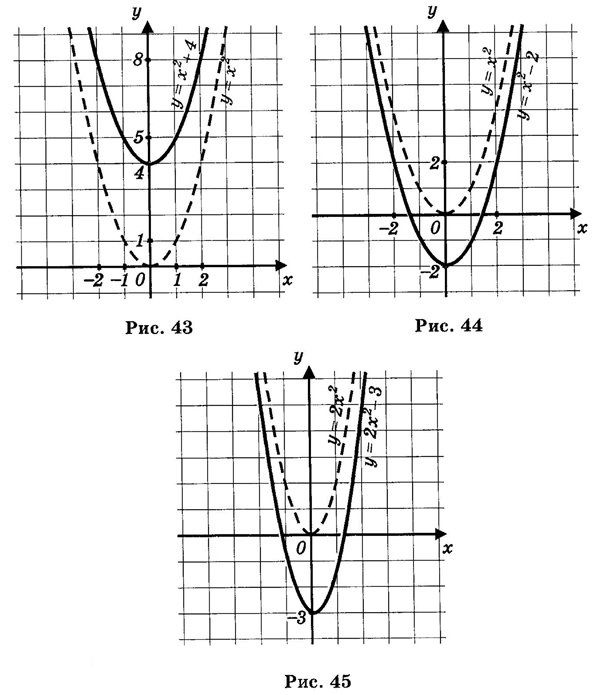 Примечание: радиус, Примечание: радиус,r, всегда положительный. |
| Пример 1: (x-2) 2 + (y-3) 2 = 4. (а) Найдите центр и радиус круг.(б) Изобразите круг. |
| Примечание. Распространенной ошибкой является принятие h = -2 и K = -3. В уравнении если знаки перед h и k, (h, k) отрицательны, тогда h и k положительны. То есть h = 2 и k = 3. 900 · 10 |
| (a) Центр: (h = 2, k = 3) = (2, 3) и радиус r = 2, поскольку r 2 = 4 => г = 4 = 2 900 10 |
(b) График |
Пример 2: (x + 1) 2 + (y-2) 2 = 9. (а) Найдите центр и радиус круг. (б) Изобразите круг. | |
| Примечание: чтобы правильно определить центр круга, мы должны разместить уравнение в стандартной форме: | |
| Стандартная форма: | (х — h) 2 + (y-k) 2 = r 2 |
| (х — (-1)) 2 + (y-2) 2 = (3) 2 .Теперь вы можете определить правильно центрировать. | |
| (a) Центр: (h = -1, k = 2) = (-1, 2) и радиус r = 3, поскольку r 2 = 9> r = 9 = 3 |
| (б) График |
| Пример 3: 2x 2 + 2 года 2 = 8.  (а) Найдите центр и радиус (а) Найдите центр и радиускруга. (б) Изобразите круг. | |
| Примечание: чтобы правильно определить центр круга, мы должны разместить уравнение в стандартной форме. | |
| Сначала разделите уравнение на 2. Новое уравнение: | х 2 + y 2 = 4. |
| Стандартная форма: | (х — в) 2 + (у — к) 2 = Г 2 |
| (х — 0) 2 + (у — 0) 2 = (2) 2 .Теперь вы можете определить правильно центрировать. | |
| (a) Центр: (h = 0, k = 0) = (0, 0) и радиус r = 2, поскольку r 2 = 4 => r = 4 = 2 |
| (б) График |
| Если уравнение в общем виде, мы должны заполнить квадрат и привести уравнение к стандартному виду.  Тогда мы можем идентифицировать центр Тогда мы можем идентифицировать центри радиус правильно. Узнали, как завершить квадрат при работе с квадратными уравнениями (E III). Мы рассмотрим это на примере. |
| Пример 4: x 2 + y 2 — 6x + 4y + 9 = 0. (a) Найдите центр и радиус круг. (б) Изобразите круг. |
| Завершение квадрата: |
|
|
|
Собирая шаги 1-3 вместе, получаем следующее: | |
| (x 2 — 6x +? 1 ) + (Y 2 + 4y +? 2 ) = -9 +? 1 +? 2 | |
| (x 2 — 6x + 9) + (Y 2 + 4y + 4) = -9 + 9 + 4 | |
| (х — 3) 2 + (y + 2) 2 = 4 | |
| (х — 3) 2 + (у — (-2)) 2 = 4 Это уравнение имеет стандартную форму.  | |
(a) Центр: (h = 3, k = -2) = (3, -2) |
(б) График |
| Пример 5: x 2 + y 2 — 6х + 2у + 4 = 0. (а) Найдите центр и радиус круг. (б) Изобразите круг. |
| Завершение квадрата: |
|
|
|
Собирая шаги 1-3 вместе, получаем следующее: | |
| (x 2 — 6x +? 1 ) + (Y 2 + 2y +? 2 ) = -4 +? 1 +? 2 | |
| (x 2 — 6x + 9) + (Y 2 + 2y + 1) = -4 + 9 + 1 | |
| (х — 3) 2 + (y + 1) 2 = 6 | |
| (х — 3 ) 2 + (у — (-1)) 2 = 6 Это уравнение имеет стандартную форму.  | |
(a) Центр: (h = 3, k = -1) = (3, -1) |
(б) График |
| ДОМАШНИЕ ЗАДАНИЯ — Для каждой задачи (а) найдите центр и радиус круга и (b) Постройте график круга. | |||||||||||||||||||||||
| 1. (x-2) 2 + (y + 1) 2 = 4. | |||||||||||||||||||||||
| 2. (х-3) 2 + (г-2) 2 = 9 | |||||||||||||||||||||||
| 3. x 2 + y 2 — 6x — 10y + 30 = 0. | |||||||||||||||||||||||
| 4. x 2 + y 2 — 6x + 4y + 9 = 0. | |||||||||||||||||||||||
| 5.2 = 25 для разных значений k Донна, Дон Дон спросил Они построили график D onna уравнение Дон спросил Модель Отличная работа D onna На том же графике Например, если k = 4 , Определить коническое сечение: Если данное уравнение имеет вид Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0, где B = 0, представленное как A и C.
Если гипербола горизонтальная:.
Если гипербола вертикальная: (y — k) 2 / a 2 — (x — h) 2 / b 2 = 1.
Уравнение: x 2 — y 2 — 4x + 6y — 3 = 0. Сравните приведенное выше уравнение с Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0. A = 1 и C = — 1. Поскольку, A и C имеют противоположные знаки. Данное уравнение представляет собой кривую гиперболу. Напишите уравнение: x 2 — y 2 — 4x + 6y — 3 = 0 в стандартной форме гиперболы:. x 2 — y 2 — 4x + 6y — 3 = 0 x 2 — 4x — 3 = y 2 — 6y. Чтобы преобразовать выражение в полный квадрат , добавьте (половина коэффициента x ) ² и (половина y — коэффициент) ² к каждой стороне выражения. Здесь коэффициент x = — 4, поэтому (половина коэффициента x ) ² = (- 4/2) 2 = 4. Здесь y коэффициент = — 6, поэтому (половина коэффициента x ) ² = (- 6/2) 2 = 9. Добавьте 4 и 9 к каждой стороне уравнения. x 2 — 4x + 4 + 9 — 3 = y 2 — 6y + 9 + 4 (x — 2) 2 + 6 = (y — 3) 2 + 4 (x — 2) 2 — (y — 3) 2 = 4-6 = — 2 — (x — 2) 2 /2 + (y — 3) 2 / 2 = 1 (y — 3) 2 / 2 — (x — 2) 2 /2 = 1 (y — 3) 2 / (√2) 2 — (x — 2) 2 / (√2) 2 = 1. Графики и кривые уровняГрафики и кривые уровня Среда, 25 февраляГрафики и кривые уровня График функции f (x, y) — это набор всех точек Пример 1. f (x, y) = x 2 + y 2 . Пример 2. f (x, y) = x 2 -y 2 . Пример 2. f (x, y) = e -x 2 -y 2 . Пример 3. В примере в понедельник мы рассмотрели функцию стоимости Его график показан ниже. При виде сбоку кажется, что минимальное значение этой функции составляет около 500. Пример 4. f (x, y) = 2e — (x + 1) 2 -y 2 A уровень кривая функции f (x, y) — это набор точек (x, y) Пример 5. Кривые уровня f (x, y) = x 2 + y 2 являются кривыми Можно представить кривую уровня f (x, y) = c как Пример 6. Кривые уровня f (x, y) = x 2 -y 2 Здесь они показаны на соответствующей высоте. Пример 7. Если вы рассмотрите график x 2 — y 2 = 1, это гипербола, и если вы наложите точку (0, 2), вы получите что-то вроде этого: Очевидно, единственная часть графика нам нужно беспокоиться о верхней части (над осью x). x 2 — y 2 = 1 x 2 — 1 = y 2 y = ± √ (x 2 — 1), но, взяв только положительную часть, мы получаем y = √ (x 2 — 1) Формула расстояния d = √ [(x 2 — x 1 ) 2 + (y 2 — y 1 ) 2 ] и пусть (x 2 , y 2 ) будет точкой (0, 2), поэтому формула расстояния станет d = √ [(0 — x 1 ) 2 + (2 — y 1 ) 2 ] Теперь давайте просто отбросим суффикс «1» от x и y, чтобы упростить и упростить получение: d = √ [x 2 + 4 — 4y + y 2 ] где (x, y) находится на графике x 2 — y 2 = 1 Теперь мы знаем, что y = √ (x 2 — 1), поэтому мы можем подставить «√ (x 2 — 1) «в уравнение везде, где мы видим» y «, составляющую уравнение расстояния: d = √ [x 2 + 4 — 4√ (x 9001 5 2 — 1) + (√ (x 2 — 1)) 2 ] Если мы упростим, а затем запишем как функцию от x, мы получим: d (x) = √ (2x 2 — 4√ (x 2 — 1) + 3) или d (x) = [2x 2 — 4 (x 2 — 1) 1/2 + 3] 1/2 Для минимизации возьмите производную и установите ее равной нулю d ‘(x) = 1/2 (2x 2 — 4√ (x 2 -1) + 3) -1/2 • (4x — 2 (x 2 — 1) -1/2 • 2x) Единственный способ, которым это может быть равно нулю, — это если числитель равен нулю, поэтому: 4x — 4x / (x 2 -1) 1/2 = 0 4x (1 — 1 / (x 2 -1) 1/2 ) = 0, поэтому x = 0 или 1 — 1 / (x 2 -1) 1/2 ) = 0 1 = 1 / (x 2 -1) 1/2 (x 2 -1) 1/2 = 1 x 2 — 1 = 1 x 2 = 2 x = ± √ 2 Если x = √2, тогда y = √ ((√2) 2 -1) = √ (2-1) = √1 = 1, поэтому точка равна (√2, 1).
Биоматематика: преобразование графиковЧто такое вертикальное растяжение и усадка? При перемещении точек пересечения x и y базового графа, растягивание и сжатие эффективно вытягивают базовый граф наружу или сжимают базовый граф внутрь, изменяя общие размеры базового графа без изменения его формы.Когда график растягивается или сжимается по вертикали, точки пересечения x действуют как якоря и не изменяются при преобразовании.
Помните, что перехватчики x не перемещаются при вертикальном растяжении и сжатии. Другими словами, если f ( x ) = 0 для некоторого значения x , то k f ( x ) = 0 для того же значения x. Кроме того, вертикальное растяжение / сжатие с коэффициентом k означает, что точка ( x, y ) на графике f ( x ) преобразуется в точку ( x , ky ) на графике г ( x ). Примеры вертикального растяжения и усадки Рассмотрим следующие базовые функции,
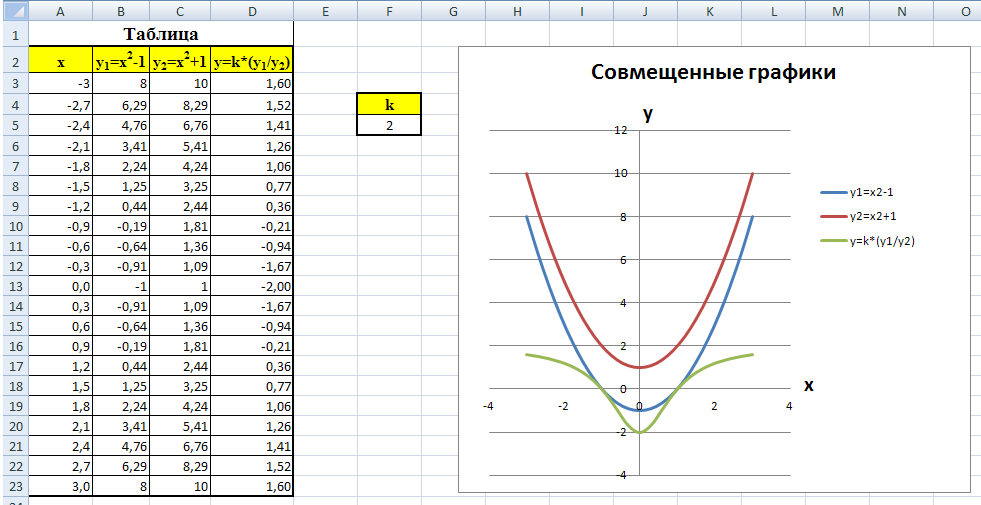
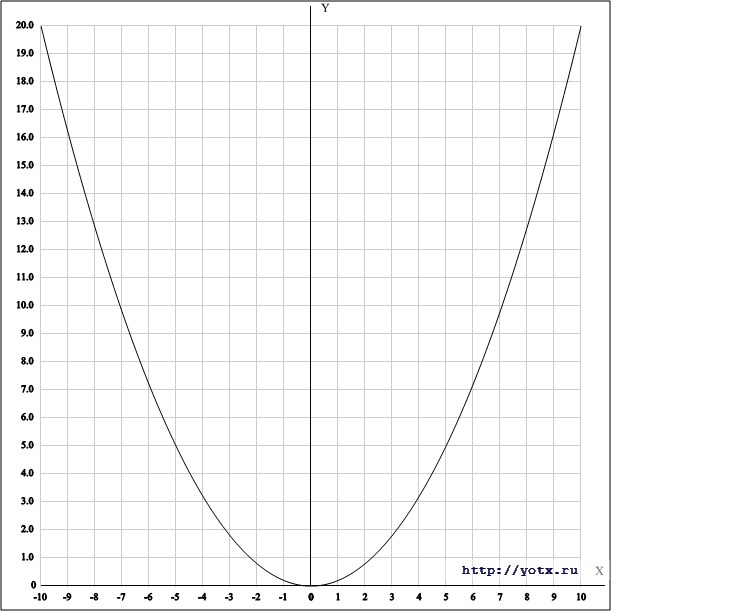
Графическое представление функции (1), f ( x ), представляет собой параболу. y 1 ( x ) = 1/2 f ( x ) как выглядит? Используя определение f ( x ), мы можем записать y 1 ( x ) как, y 1 ( x ) = 1/2 f ( x ) = 1/2 ( x 2 -2) = 1/2 x 2 — 1 . Исходя из определения вертикальной усадки, график y 1 ( x ) должен выглядеть как график f ( x ), уменьшенный по вертикали в 1/2 раза. Взгляните на графики f ( x ) и y 1 ( x ). Обратите внимание, что точки перехвата x не переместились. Функция (2), g ( x ), является синусоидальной функцией. y 2 ( x ) = 6 g ( x ) похож? Используя наши знания о вертикальных растяжках, график y 2 ( x ) должен выглядеть как базовый график g ( x ), растянутый по вертикали в 6 раз. Чтобы проверить это, мы можем написать y 2 ( x ) as, y 2 ( x ) = 6 g ( x ) = 6 sin ( x ), построить таблицу значений и построить график новой функции.Как видите, график y 2 ( x ) на самом деле является базовым графиком g ( x ), растянутым по вертикали с коэффициентом 6. ***** В следующем разделе мы рассмотрим горизонтальное растяжение и сжатие. |

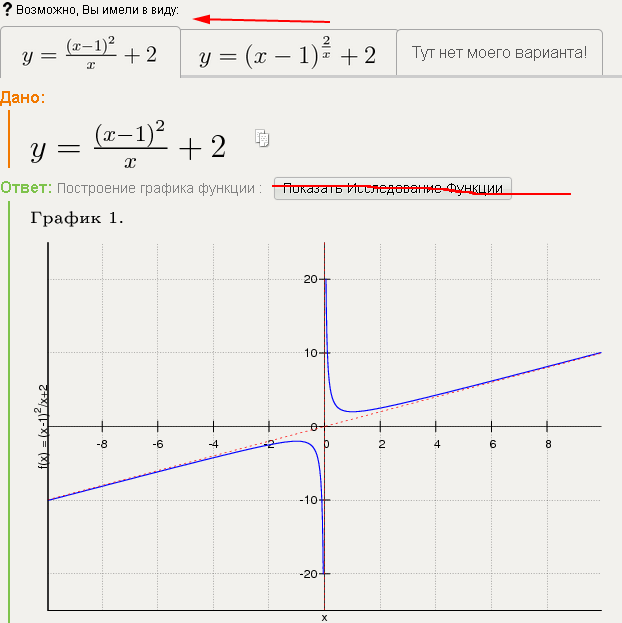
 Построить график функции y = x
Построить график функции y = x Вот почему ты
Вот почему ты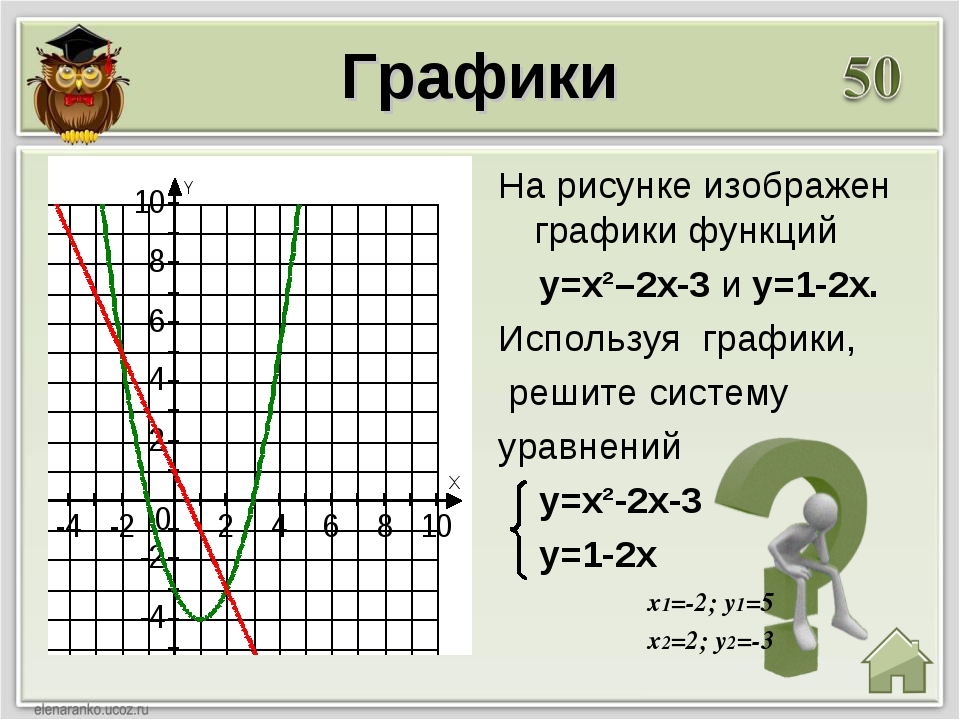 В
В Она
Она Она выбрала
Она выбрала  2 — 4x + 6y — 3 = 0.?
2 — 4x + 6y — 3 = 0.?
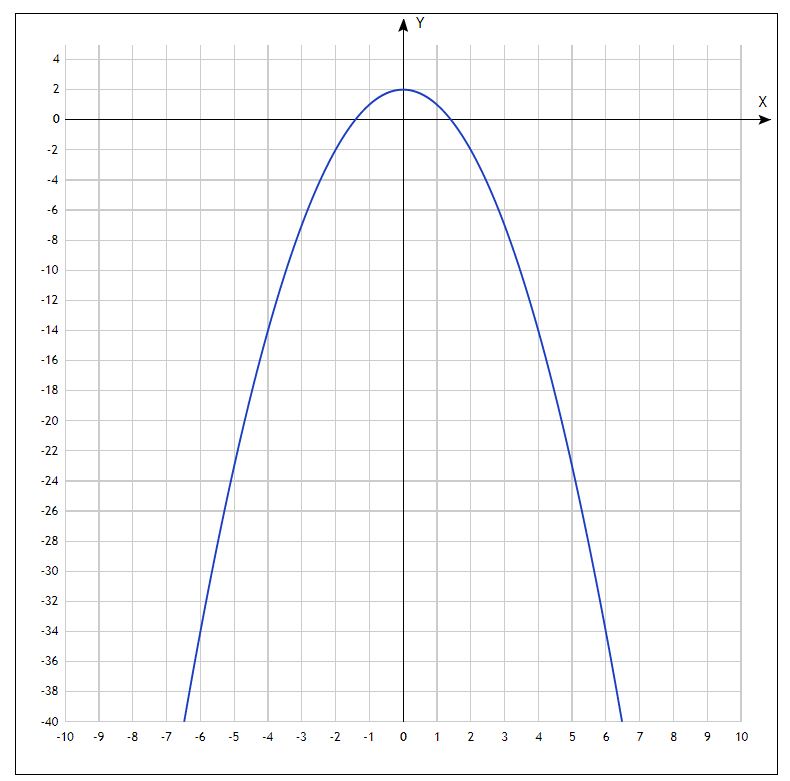
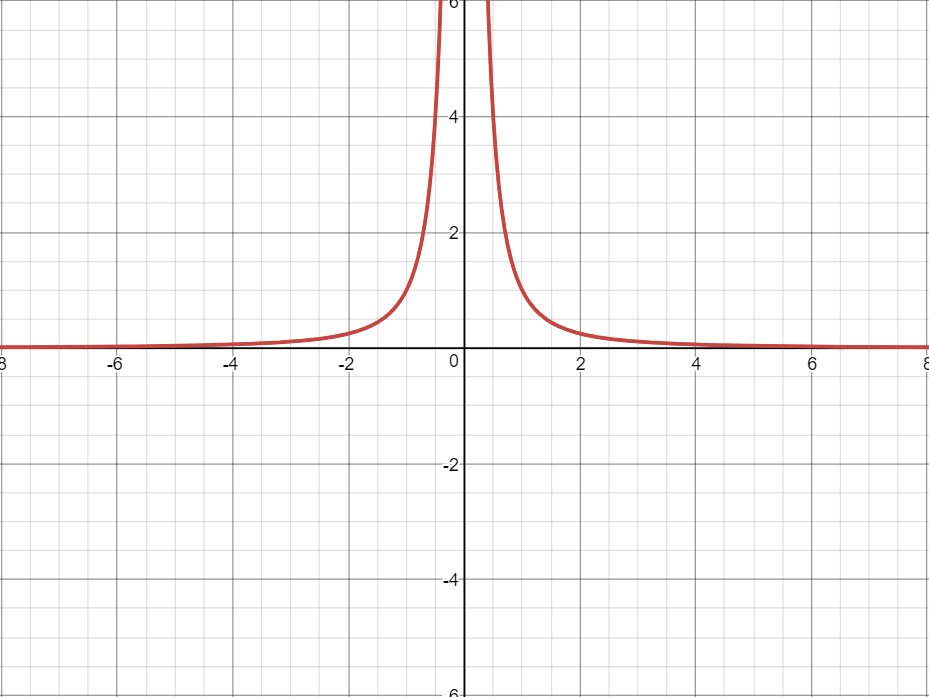
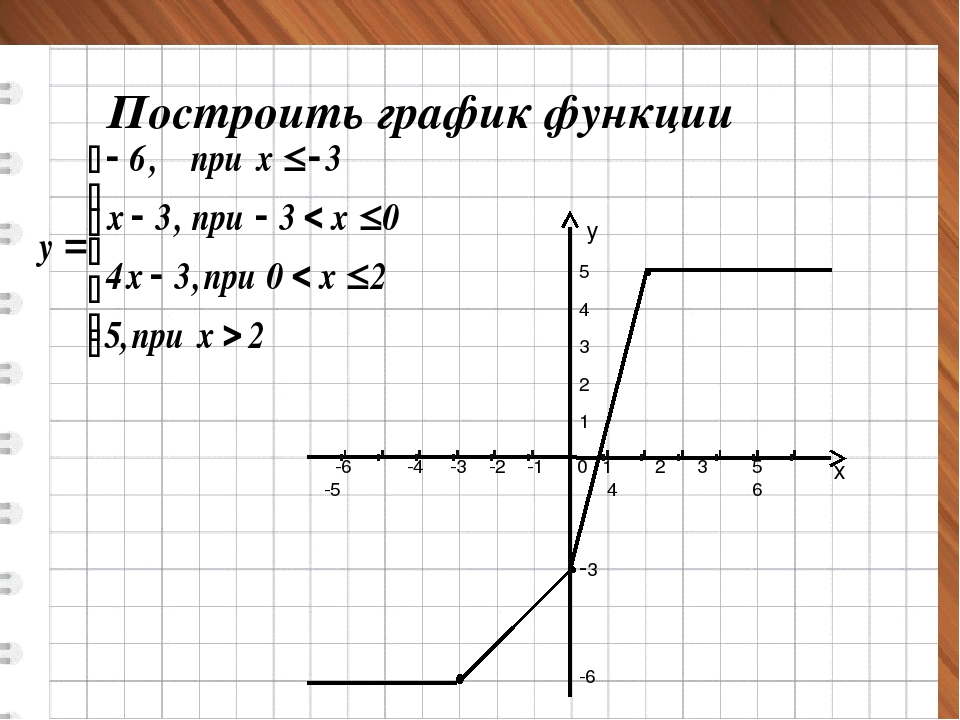

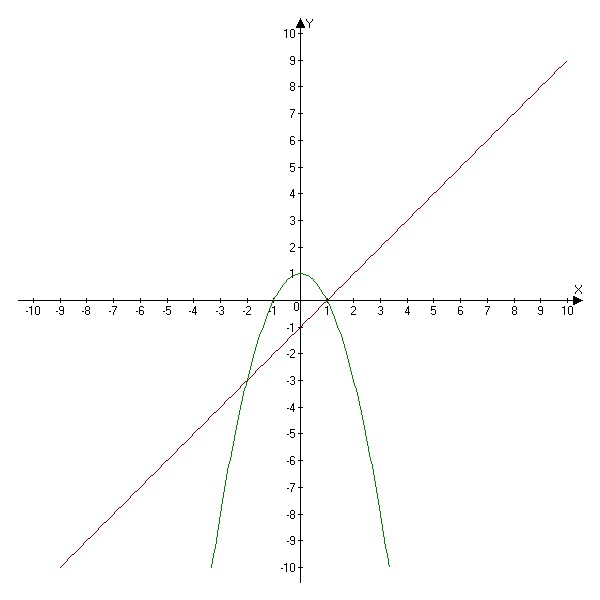
 Эту часть графика можно записать, решив график для y и взяв только положительную часть.
Эту часть графика можно записать, решив график для y и взяв только положительную часть. Соответствующая точка на другой стороне (-√2, 1)
Соответствующая точка на другой стороне (-√2, 1)
 12817, 2.27277).
12817, 2.27277). 
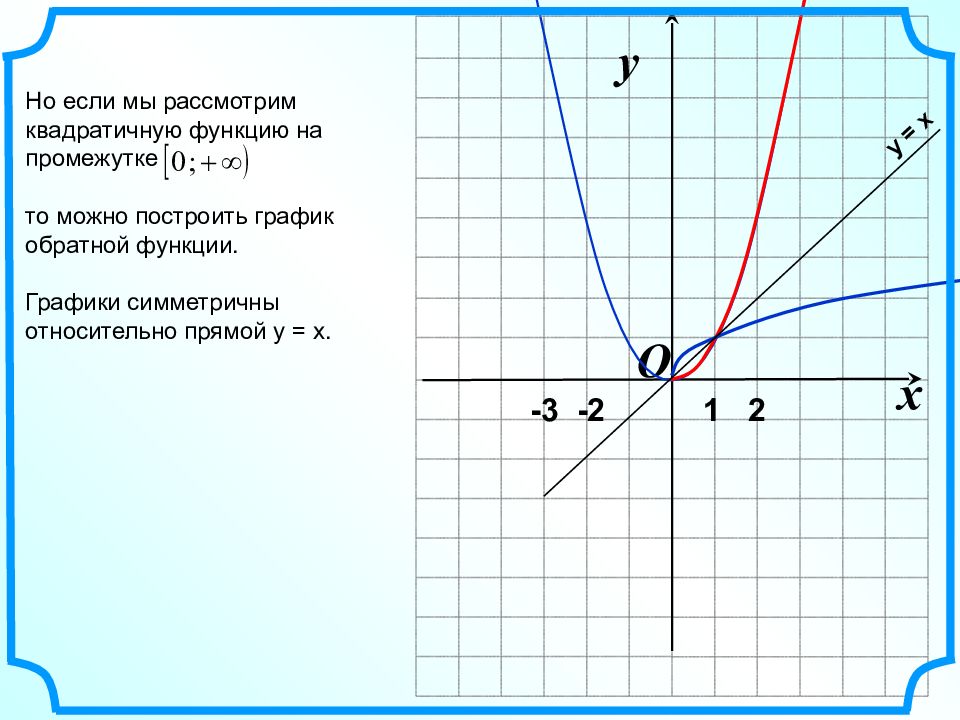 Что вы думаете о графике
Что вы думаете о графике Что бы на графике
Что бы на графике