Метод Крамера . Применение для систем линейных уравнений

Задана система N линейных алгебраических уравнений (СЛАУ) с неизвестными, коэффициентами при которых являются элементы матрицы , а свободными членами — числа

Первый индекс возле коэффициентов указывает в каком уравнении находится коэффициент, а второй — при котором из неизвестным он находится.

Если определитель матрицы не равен нулю

то система линейных алгебраических уравнений имеет единственное решение.

Решением системы линейных алгебраических уравнений называется такая упорядоченная совокупность чисел , которая при превращает каждое из уравнений системы в правильную равенство.

Если правые части всех уравнений системы равны нулю, то систему уравнений называют однородной. В случае, когда некоторые из них отличны от нуля – неоднородной

Если система линейных алгебраических уравнений имеет хоть одно решение, то она называется совместной, в противном случае — несовместимой.

Если решение системы единственное, то система линейных уравнений называется определенной. В случае, когда решение совместной системы не единственный, систему уравнений называют неопределенной.

Две системы линейных уравнений называются эквивалентными (или равносильными), если все решения одной системы является решениями второй, и наоборот. Эквивалентны (или равносильны) системы получаем с помощью эквивалентных преобразований.

Эквивалентные преобразования СЛАУ

1) перестановка местами уравнений;

2) умножение (или деление) уравнений на отличное от нуля число;

3) добавление к некоторого уравнения другого уравнения, умноженного на произвольное, отличное от нуля число.

Решение СЛАУ можно найти разными способами.

МЕТОД КРАМЕРА

ТЕОРЕМА КРАМЕРА. Если определитель системы линейных алгебраических уравнений с неизвестными отличен от нуля то эта система имеет единственное решение, которое находится по формулам Крамера:

— определители, образованные с заменой -го столбца, столбцом из свободных членов.

Если , а хотя бы один из отличен от нуля, то СЛАУ решений не имеет. Если же , то СЛАУ имеет множество решений. Рассмотрим примеры с применением метода Крамера.

—————————————————————

Задача 1.

Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Крамера

Решение.

Найдем определитель матрицы коэффициентов при неизвестных

Так как , то заданная система уравнений совместная и имеет единственное решение. Вычислим определители:

По формулам Крамера находим неизвестные

Итак единственное решение системы.

Задача 2.

Дана система четырех линейных алгебраических уравнений. Решить систему методом Крамера.

Решение.

Найдем определитель матрицы коэффициентов при неизвестных. Для этого разложим его по первой строке.

Найдем составляющие определителя:

Подставим найденные значения в определитель

Детерминант , следовательно система уравнений совместная и имеет единственное решение. Вычислим определители по формулам Крамера:

Разложим каждый из определителей по столбцу в котором есть больше нулей.

По формулам Крамера находим

Решение системы

Данный пример можно решить математическим калькулятором YukhymCALC . Фрагмент программы и результаты вычислений наведены ниже.

——————————

МЕТОД К Р А М Е Р А

|1,1,1,1|

D=|5,-3,2,-8|

|3,5,1,4|

|4,2,3,1|

D=1*(-3*1*1+2*4*2+(-8)*5*3-((-8)*1*2+2*5*1+(-3)*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))+1*(5*5*1+(-3)*4*4+(-8)*3*2-((-8)*5*4+(-3)*3*1+5*4*2))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(-3+16-120+16-10+36)-1*(5+32-72+32-6-60)+1*(25-48-48+160+9-40)-1*(75-12+12-40+27-10)=1*(-65)-1*(-69)+1*58-1*52=-65+69+58-52=10

|0,1,1,1|

Dx1=|1,-3,2,-8|

|0,5,1,4|

|3,2,3,1|

Dx1=-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(1*5*1+(-3)*4*3+(-8)*0*2-((-8)*5*3+(-3)*0*1+1*4*2))-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))= -1*(1+24+0+24+0-12)+1*(5-36+0+120+0-8)-1*(15-9+0-30+0-2)= -1*(37)+1*81-1*(-26)=-37+81+26=70

|1,0,1,1|

Dx2=|5,1,2,-8|

|3,0,1,4|

|4,3,3,1|

Dx2=1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(1+24+0+24+0-12)+1*(0+16-72+0-3-60)-1*(0+4+18+0-9-15)= 1*37+1*(-119)-1*(-2)=37-119+2=-80

|1,1,0,1|

Dx3=|5,-3,1,-8|

|3,5,0,4|

|4,2,3,1|

Dx3=1*(-3*0*1+1*4*2+(-8)*5*3-((-8)*0*2+1*5*1+(-3)*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))= 1*(0+8-120+0-5+36)-1*(0+16-72+0-3-60)-1*(75+0+6-20+27+0)= 1*(-81)-1*(-119)-1*88=-81+119-88=-50

|1,1,1,0|

Dx4=|5,-3,2,1|

|3,5,1,0|

|4,2,3,3|

Dx4=1*(-3*1*3+2*0*2+1*5*3-(1*1*2+2*5*3+(-3)*0*3))-1*(5*1*3+2*0*4+1*3*3-(1*1*4+2*3*3+5*0*3))+1*(5*5*3+(-3)*0*4+1*3*2-(1*5*4+(-3)*3*3+5*0*2))= 1*(-9+0+15-2-30+0)-1*(15+0+9-4-18+0)+1*(75+0+6-20+27+0)= 1*(-26)-1*(2)+1*88=-26-2+88=60

x1=Dx1/D=70,0000/10,0000=7,0000

x2=Dx2/D=-80,0000/10,0000=-8,0000

x3=Dx3/D=-50,0000/10,0000=-5,0000

x4=Dx4/D=60,0000/10,0000=6,0000

Посмотреть материалы:

{jcomments on}

12.

Методы решения определенных слу. (Метод Крамера, матричный метод, метод Гаусса).

13. Решение неопределенных слу.

14. Решение однородных слу.

Однородной
называется СЛУ у которой свободные
члены равны нулю.

Замечание Однородное
СЛУ всегда совместно т.к имеет 0 решение.

Опр1.привиальным
называется решение системы состоящее
из нулей.

Теорема. Для того
что бы СЛУ имело не тривиальное решение,
необходимо и достаточно, что бы ранг
основной м-цы системы был меньше числа
неизвестно, док-во следует из Капелли.

Следствие: Если
число неизвестных n
в однородной СЛУШ больше числа уравнений,
то система имеет не тривиальное решение.

Теорема: для того
, что бы однородный СЛУ, у которого числа
уравнений совпадает с числом неизвестных
имело не тривиальное решение, необходимо
и достаточно что бы определитель
основной м-чной системы равнялся нулю.

15. Собственные числа и вектора матриц.

Опр1. Число лямда
def
собственным числом св. м-цы А, если
АХ=лямда*Х при этом Хdef
………… м-цы А отвечающие этому собственному
числу.

2.Однородноу СЛУ
– это система будет иметь нетривиальное
решение если def(A-лямда
Е)=0. Таким образом , что бы получить
собственные числа м-цы необходимо
решить уравнение.

Опр1.Характеристическим
многочленом P(t)=def(A-tE)=P(t)
многочлен степени.

Замечание:
Собственные числа являются корнями
характеристического многочлена этой
матрицы.

16. Линейные пространства. Основные определения.

Линейными
векторнымпространством называется
множетсво Z₁,Z₂…Z_nесли: Любым
предметом Z₁,Z₂
по
определенному правилу ставится в
соответствии Z3єZ
называемой суммой этих элементов.

2. Каждому элементу
Z1,
ставится по некот. Правилу Z2,
называется по определениям элемента
на число. Где Альфа некоторое число.

Аксиомы операций
сложений + и –

1.Z1+Z2=Z2+Z1

2.Z1+Z2+Z3=Z1+(Z2+Z3)

3.0Єz
для любого ZєZ=>
Z+0=Z

4.ZєZ
cуществует
противополож.

5.для любого ZєZ

Орп2.Элементы
линейного пр-ва будем называть векторами.

Опр3.Арифметическим
называется пространство состоящее из
всех последоватеностей n-вещ-ных
число производится по следущим правилам:

х1+х2=(х11+х21х12+х12…х11+х211)

альфа*х=(альфах11,альфах12….альфах1n)

17. Линейная зависимость векторов.

Опр1.системой
Элементов линейного пространства Z
называется любая не пустая упорядоченное
множество элементов этого пространства.

Опр2.линейно
зависемой системой называется система
элементов линейного пространства Z
если существую такие числа как альфа1
альфа 2 альфаn
є K
среди которых есть одно неравное нулю
и имеет место равенства
альфа1х1+альфа2х2+..+альфаnxn=0

Опр3.Линейно не
зависимой системой элементов называется
система def
{x1}ⁿ,
что равенство альфа1х1+..+альфаnxn=0
возможно тогда и только тогда, когда
все коэфиценты равны нулю.

Теорема. Для того
что бы система элементов {x1}ⁿбыла линейно
зависима , необходимо и достаточно ,,
что бы хотя бы один из элементов являлся
линейной комбинацией .

Теорема.если
некот. Из элементов х1….хnєZ
линейно зависемы , то и вся система этих
элементов линейно зависема.

Свойство линейно
зависемых тел.

1.если среди
элементов х и т.д есть нулевой элемент
, то вся система линейно зависема.

2.если система
векторов системного пространства Z
линейно не зависема , то любая совокупность
векторов выбранных из этой системы так
же линейно не зависема.

3.система если
содержит один вектор то она линейно не
зависема, тогда и только тогда , когда
этот вектор отличен от нуля.

Матричный метод решения системы линейных алгебраических уравнений. Формулы Крамера. Метод Гаусса

Рассмотрим систему, составленную из трех линейных алгебраических уравнений с тремя неизвестными.

(6.1.11.)

Решением (2.1)называется система из трех чисел, удовлетворяющая требованию: если в (2.1) вместо и подставить соответственно и , то получим три верных равенства (три тождества).

(6.1.12)

— основная матрица системы (2.1)

(6.1.13)

— расширенная матрица (2.1)

; ; (6.1.14)

система (2.1) может быть записана в матричном виде так:

AX=D (6. 1.15)

X – неизвестная матрица-столбец. Введем вспомогательные определители:

Предполагая, что матрица A — невырожденная и умножая (2.5) слева и почленно на A^-1, получим

–(6.1.16) матричный способ решения системы.

Используя понятие равенства двух матриц, получим

(6.1.17)

(6.1.18)

(6.1.19)

Элементарными преобразованиями матрицы называются следующие преобразования:

1. Перестановка местами произвольных двух строк (столбцов).
2. Умножение строки (столбца) на отличное от нуля число.
3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число.

Пример 6. 1.2. Найти матрицу, обратную матрице . Проверить результат.

Обратную матрицу находим по формуле .

Вычислим определитель матрицы по правилу треугольника:

Определитель не равен нулю, следовательно, обратная матрица существует. Составляем матрицу из алгебраических дополнений ( ) и транспонируем ее.

;

;

;

;

;

;

;

;

;

.

Выполним проверку:

· =

.

·

Получим: A^-1×A=A×A^-1=E. Следовательно, обратная матрица найдена верно.

Ответ: .

Пример 6.1.3. Решить систему линейных уравнений по формулам Крамера

.

Решение:

Найдем главный определитель системы

Так как число уравнений и число неизвестных системы между собой равны m=n=3 и определитель отличен от нуля, система имеет единственное решение.

Найдем вспомогательные определители:

Неизвестные находим по формулам Крамера:

; .

Ответ: .

Пример 6.1.4.. Решить систему линейных уравнений методом Гаусса

.

Решение.

Метод Гаусса – это метод последовательного исключения неизвестных преобразованием данной системы линейных уравнений к эквивалентной. Преобразования уравнений системы заменяются преобразованием строк расширенной матрицы системы до приведения основной матрицы к треугольной или трапециевидной форме. Обнуление элементов выполняется элементарными преобразованиями матрицы(умножение строк на числа, отличные от нуля с последующим сложением).

.

Ответ: .

Пример 6.1.5. Применить теорему Кронекера – Капели и найти все решения системы методом Гаусса .

Решение.

Однородная матрица всегда имеет тривиальное решение, в данном случае (0;0;0;0), поэтому нас интересуют другие решения системы.

Применяем метод Гаусса:

.

Так как размерности основной и расширенной матриц системы 3×4 и 3×5 соответственно, ранги этих матриц не могут превышать числа 3. Попробуем посмотреть, есть ли для этих матриц минор третьего порядка, отличный от нуля. Составим его из первых двух и четвертого столбца: , так как определитель треугольного вида равен произведению элементов, стоящих на главной диагонали. Следовательно, ранги основной и расширенной матриц равны 3. По теореме Кронекера-Капелли данная система совместна. Так как число уравнений m=3 меньше числа неизвестных n=4, то она имеет бесчисленное множество решений. Закрепленных (базисных) переменных будет 3 (так как r=3), свободных переменных будет (n-r=4-3=1) одна. Минор, который мы составили выше, называется базисным, а переменные, входящие в него, базисными. Следовательно, — базисные переменные, а — свободная, то есть . Выполним обратный ход метода Гаусса:

.

Решением системы будет множество четверок чисел , где .

Например, (0;2;2;0), (0;-1;-1;0), — решения системы.

Ответ: .

Замечание. Обратите внимание, что тривиальное решение тоже задается этим множеством.

Пример 6. 1.6. Даны координаты векторов и в некотором базисе. Показать, что векторы образуют базис и найти координаты вектора в этом базисе.

; ; ; ; .

Решение.

Если векторы образуют базис, то существует разложение вектора в этом базисе , то есть

.

Отсюда вытекает решение задачи: найти координаты вектора в базисе означает решить систему четырех уравнений с четырьмя неизвестными . Эта система будет иметь единственное решение, если ее основной определитель будет отличен от нуля.

Решаем методом Гаусса:

Так как определитель треугольного вида равен произведению элементов, стоящих на главной диагонали , видим, что он отличен от нуля. Следовательно, векторы независимы и образуют базис.

Найдем координаты вектора b в этом базисе

.

Следовательно, или b=(5;0;-1;2) в базисе .

Ответ: .

Узнать еще:

ЗАНЯТИЕ 3 Метод Крамера и матричный метод решения систем линейных уравнений

Аналитическая геометрия. Лекция 1.3

Московский Государственный Технический Университет им. Н.Э. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Аналитическая геометрия Модуль 1. Матричная алгебра. Векторная алгебра Лекция

Подробнее

Линейная алгебра Вариант 4

Линейная алгебра Вариант Задание. Систему уравнений привести к равносильной разрешенной системе, включив в набор разрешенных неизвестных,,. Записать общее решение, найти соответствующее базисное решение:

Подробнее

Тема: Системы линейных уравнений

Линейная алгебра и аналитическая геометрия Тема: Системы линейных уравнений (Метод Гаусса. Системы линейных однородных уравнений) Лектор Рожкова С.В. 0 г. Метод Гаусса (метод исключения неизвестных) Две

Подробнее

1. Требования к знаниям, умениям, навыкам

ПРИЛОЖЕНИЯ Требования к знаниям умениям навыкам Страницы даны по учебнику «Математика в экономике» [] Дополнительные задачи по данному курсу можно найти в учебных пособиях [ 6] Векторы Владеть понятиями:

Подробнее

РАЗДЕЛ 1. Линейная алгебра.

-й семестр. РАЗДЕЛ. Линейная алгебра. Основные определения. Определение. Матрицей размера mn где m- число строк n- число столбцов называется таблица чисел расположенных в определенном порядке. Эти числа

Подробнее

Теорема Кронекера-Капелли

Установить совместность и решить систему линейных уравнений 5xx x xx 5x 0 x4x x 0 а) по формулам Крамера, б) матричным способом, в) методом Гаусса Совместность Совместность системы можно установить: а)

Подробнее

ТЕОРИЯ МАГИЧЕСКИХ МАТРИЦ

Лекции по Математике. Вып. ТММ-1 Ю. В. Чебраков ТЕОРИЯ МАГИЧЕСКИХ МАТРИЦ Санкт-Петербург, 2010 УДК 511+512 ББК 22 Ч45 Р е ц е н з е н т ы: Доктор физико-математических наук, профессор С.-Петерб. техн.

Подробнее

Примеры решений контрольных работ

Примеры решений контрольных работ Л.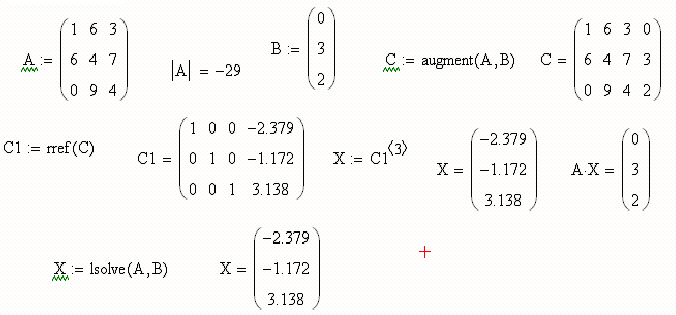 И. Терехина, И.И. Фикс 1 Контрольная работа 1 Линейная алгебра Решить матричное уравнение ( ( 3 1 2 1 X + 2 4 2 3 3 ( 1 0 = 3 2 3 Выполним вначале умножение матриц на

Подробнее

СОДЕРЖАНИЕ. Предисловие… 5

СОДЕРЖАНИЕ Предисловие………………………………………………….. 5 1. Элементы линейной алгебры…………………………………….. 6 ИДЗ 1. Определители……………………………………….

Подробнее

Элементы линейной алгебры

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский государственный университет путей сообщения» Институт экономики и финансов Кафедра «Математика»

Подробнее

Семинар 7. Линейная алгебра

1 Семинар 7. Линейная алгебра Теоретические вопросы для самостоятельного изучения: 1. Определители и их свойства. 2. Матрица. Виды матриц. 3. Действия над матрицами 4. Обратная матрица. Решение матричных

Подробнее

1. Линейная алгебра. a21x1 a12 x2 a13 x3 b2

1. Линейная алгебра 1.1. В 1 представлены задачи на решение линейных алгебраических крамеровских систем с определителем, отличным от нуля, вычисление определителей и действий с матрицами. Линейные алгебраические

Подробнее

Математика (БкПл-100, БкК-100)

Математика (БкПл-100, БкК-100) М.П. Харламов 2009/2010 учебный год, 2-й семестр Лекция 7. Определители, системы линейных уравнений и формулы Крамера 1 Тема 1: Определители 1.1. Понятие определителя Определитель

Подробнее

Решение систем линейных уравнений

Решение систем линейных уравнений Л. В. Калиновская, Ю. Л.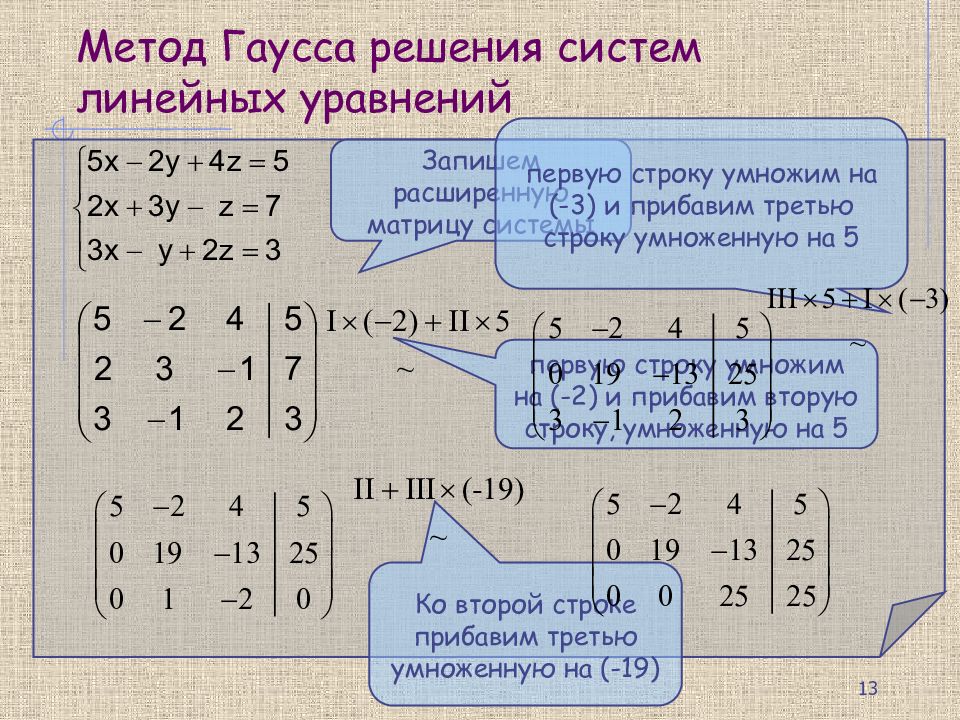 Калиновский Министерство образования Московской области Государственное бюджетное образовательное учреждение высшего образования Московской области

Подробнее

1. Линейные системы и матрицы

1. Линейные системы и матрицы 1. Дать определение умножения матриц. Коммутативна ли эта операция? Ответ пояснить. Произведение C матриц A и B определяется как m p m p A B ij = A ik B kj. Операция не коммутативна.

Подробнее

Практикум по линейной алгебре

Министерство образования и науки РФ Нижегородский государственный университет им. Н.И. Лобачевского В.К. Вильданов Практикум по линейной алгебре Учебно-методическое пособие Нижний Новгород Издательство

Подробнее

Глава 4. Матрицы. Лекция Основные понятия.

Лекция 0. Глава 4. Матрицы. В этой главе мы рассмотрим основные виды матриц, операции над ними, понятие ранга матрицы и их приложения к решению систем линейных алгебраических уравнений. 4.. Основные понятия.

Подробнее

МАТЕМАТИКА ЛИНЕЙНАЯ АЛГЕБРА

ООО «Резольвента», wwwresolventru, resolvent@listru, (95) 509-8-0 Учебный центр «Резольвента» Доктор физико-математических наук, профессор К Л САМАРОВ МАТЕМАТИКА Учебно-методическое пособие по разделу

Подробнее

ПЕРЕСТАНОВКИ. Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,…, n в строчку одно за другим.

ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще

Подробнее

УПРАЖНЕНИЯ ПО ЛИНЕЙНОЙ АЛГЕБРЕ

УПРАЖНЕНИЯ ПО ЛИНЕЙНОЙ АЛГЕБРЕ Как изменится произведение B матриц и B если: а переставить -ю и j -ю строки матрицы? б переставить -й и j -й столбцы матрицы B? в к -й строке матрицы прибавить ее j -ю строку

Подробнее

Ax = y.

A(x 1 x 2 ) = 0, x 1 x 2 Ker(A).

ГЛАВА 10. ЛИНЕЙНЫЕ УРАВНЕНИЯ 1 1. ОБЩЕЕ РЕШЕНИЕ ЛИНЕЙНОГО УРАВНЕНИЯ Одна из основных задач линейной алгебры задача решения линейного уравнения Ax = y. Здесь A : X n Y m есть линейный оператор, y заданный

Подробнее

0.5 setgray0 0.5 setgray1

5 setgray 5 setgray Лекция 5 ТЕОРЕМА О БАЗИСНОМ МИНОРЕ Ранг матрицы Рассмотрим матрицу A K m следующего общего вида: a a a A a 2 a 2 2 a 2 A = = A A 2,A 2,,A =, a m a2 m a m A m где a a a 2 A =,,A a 2

Подробнее

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ. I часть

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский государственный университет путей сообщения» Институт экономики и финансов Кафедра «Математика»

Подробнее

Решение системы линейных уравнений (метод Крамера)

Этот онлайн калькулятор позволит вам очень просто решить систему линейных уравнений (СЛУ) методом Крамера.

Для того чтобы решить систему линейных уравнений методом Крамера, выберите количество неизвестных величин:
2345

Заполните систему линейных уравнений

Для изменения в уравнении знаков с «+» на «-» вводите отрицательные числа. Если в вашем уравнение отсутствует какой-то коэффициент, то на его месте в калькуляторе введите ноль. Вводить можно числа или дроби. Например: 1.5 или 1/7 или -1/4 и т.д.

Решить систему

Воспользуйтесь также:
Решение системы линейных уравнений (метод подстановки)
Решение системы линейных уравнений (метод Гаусса)
Решение системы линейных уравнений (матричный метод)

Решение системы линейных уравнений методом Крамера

Метод Крамера

Метод Крамера — это метод решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (то есть в случае, когда система уравнений имеет единственное решение). Основным математическим действием при решении системы уравнения методом Крамера является вычисление определителей матриц размерностью n (где n — количество уравнений в системе).

На нашем сайте вы можете решать системы уравнений методом Крамера в режиме онлайн. При этом решение вы получаете мгновенно, и оно является полным и подробным. При решении системы уравнений нужно находить определители нескольких разных матриц. Для сокращения решения эта операция упрощена (выдаётся лишь результат). Но вы можете при необходимости получить полное решение нахождения детерминанта матрицы. Соответствующий калькулятор имеется на нашем ресурсе.

Метод Гаусса и Крамера

Матрицы

Метод Гаусса

Формулы Крамера

Матрица Определение

Прямоугольная таблица из m , n чисел, содержащая m – строк и n – столбцов, вида:

называется матрицей размера m  n

Числа, из которых составлена матрица, называются элементами матрицы.

Положение элемента а i j в матрице характеризуются двойным индексом:

первый i – номер строки;

второй j – номер столбца, на пересечении которых стоит элемент.

  Сокращенно матрицы обозначают заглавными буквами: А, В, С…

Коротко можно записывать так:

Иоганн Карл Фридрих Гаусс (30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген)

Метод Гаусса

Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Система т линейных уравнений с п неизвестными имеет вид:

x 1 , x 2 , …, x n – неизвестные.

a i j — коэффициенты при неизвестных.

b i — свободные члены (или правые части)

Типы уравнений

Система линейных уравнений называется совместной , если она имеет решение, и несовместной , если она не имеет решения.

Совместная система называется определенной , если она имеет единственное решение и неопределенной , если она имеет бесчисленное множество решений.

Две совместные системы называются равносильными , если они имеют одно и то же множество решений.

Элементарные преобразования

К элементарным преобразованиям системы отнесем следующее:

• перемена местами двух любых уравнений;
• умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
• прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.

Общий случай

Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:

Дана система:

1-ый шаг метода Гаусса

На первом шаге исключим неизвестное х 1 из всех уравнений системы (1), кроме первого.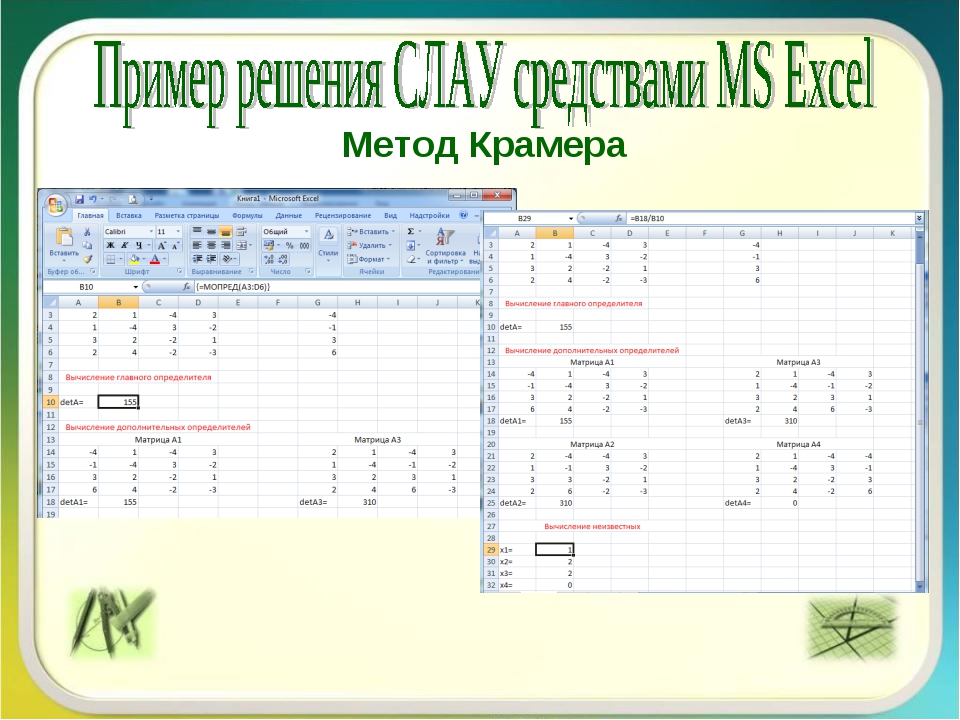 Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а 11 . Получим уравнение:

где

Исключим х 1 из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х 1 (соответственно а 21 и а 31 ).

Система примет вид:

Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.

(1)

(2)

(3)

2-ой шаг метода Гаусса

На втором шаге исключим неизвестное х 2 из третьего уравнения системы (3) . Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3) , получим уравнение:

где

Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:

Предполагая, что находим

(4)

В результате преобразований система приняла вид:

Система вида (5) называется треугольной .

Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2 ) называют прямым ходом метода Гаусса .

Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.

Для этого найденное значение х 3 подставляют во второе уравнение системы (5) и находят х 2 . Затем х 2 и х 3 подставляют в первое уравнение и находят х 1 .

(5)

Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b , где b  0, то это означает, что система несовместна и решений не имеет.

В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.

Треугольная система имеет вид:

Такая система имеет единственное

решение, которое находится в

результате проведения обратного хода метода Гаусса.

Ступенчатая система имеет вид:

Такая система имеет бесчисленное

множество решений.

Рассмотрим на примере

• Покажем последовательность решения системы из трех уравнений методом Гаусса

• Поделим первое уравнение на 2, затем вычтем его из второго (a 21 =1, поэтому домножение не требуется) и из третьего, умножив предварительно на a 31 =3

• Поделим второе уравнение полученной системы на 2, а затем вычтем его из третьего, умножив предварительно на 4,5 (коэффициент при x 2 )

Тогда

x 3 =-42/(-14)=3;

x 2 =8-2×3=2

x 1 =8-0,5×2-2×3=1

Метод Крамера

Метод Крамера—способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы. Создан Габриэлем Крамером в 1751 году.

Габриэль Крамер (31 июля 1704, Женева, Швейцария—4 января 1752, Баньоль-сюр-Сез, Франция)

Рассмотрим систему линейных уравнений с квадратной матрицей A , т. е. такую, у которой число уравнений совпадает с числом неизвестных:

Теорема. Cистема

a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1

a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2

… …

a n1 x 1 +a n2 x 2 +…+a nn x n =b n

• a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1 a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2 … … a n1 x 1 +a n2 x 2 +…+a nn x n =b n
• a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1 a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2 … … a n1 x 1 +a n2 x 2 +…+a nn x n =b n
• a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1 a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2 … … a n1 x 1 +a n2 x 2 +…+a nn x n =b n

Имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля:

a 11 a 12 … a 1n

a 21 a 22 … a 2n

… …

a n1 a n2 … a nn

• a 11 a 12 … a 1n a 21 a 22 … a 2n … … a n1 a n2 … a nn

≠ 0

В этом случае решение можно вычислить по формуле Крамера

Для получения значения x k в числитель ставится определитель, получающийся из det(A) заменой его k- го столбца на столбец правых частей

• Пример. Решить систему уравнений :

Решение.

Найдите оставшиеся компоненты решения.

• Формулы Крамера не представляют практического значения в случае систем с числовыми коэффициентами: вычислять по ним решения конкретных систем линейных уравнений неэффективно, поскольку они требуют вычисления (n+1)-го определителя порядка n , в то время как метод Гаусса фактически эквивалентен вычислению одного определителя порядка n . Тем не менее, теоретическое значение формул Крамера заключается в том, что они дают явное представление решения системы через ее коэффициенты. Например, с их помощью легко может быть доказан результат
• Решение системы линейных уравнений с квадратной матрицей A является непрерывной функцией коэффициентов этой системы при условии, что det A не равно 0 .

Найдите оставшиеся компоненты решения.

• Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра.
• зависящей от параметра , определить предел отношения компонент решения:

Решение.

• В этом примере определитель матрицы системы равен . По теореме Крамера система совместна при . Для случая применением метода Гаусса убеждаемся, что система несовместна. Тем не менее, указанный предел существует. Формулы Крамера дают значения компонент решения в виде

и, хотя при          каждая из них имеет бесконечный предел, их отношение стремится к пределу конечному.

Ответ.

Приведенный пример поясняет также каким образом система линейных уравнений, непрерывно зависящая от параметра, становится несовместной: при стремлении параметра к какому-то критическому значению (обращающему в нуль определитель матрицы системы) хотя бы одна из компонент решения «уходит на бесконечность».

Использованные источники

• В.С. Щипачев, Высшая математика
• Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов.
• Волков Е.А. Численные методы.
• В.Е. Шнейдер и др., Краткий курс высшей математики,том I.

ⓘ Матричный метод решения систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем. Пусть дана система линейных уравнений с n {\disp ..

1. Пример решения неоднородной СЛАУ

{ 3 x + 2 y − z = 4, 2 x − y + 5 z = 23, x + 7 y − z = 5 ; {\displaystyle {\begin{cases}3x+2y-z=4,\\2x-y+5z=23,\\x+7y-z=5;\end{cases}}}

Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.

| 3 2 − 1 2 − 1 5 1 7 − 1 | = 3 − 14 + 10 − 1 − 105 + 4 = − 103 ; {\displaystyle {\begin{vmatrix}3&2&-1\\2&-1&5\\1&7&-1\end{vmatrix}}=3-14+10-1-105+4=-103;}

Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы. {-1}\cdot B;}

X = 34 103 5 103 − 9 103 − 7 103 2 103 17 103 − 15 103 19 103 7 103 ⋅ 4 23 5 = 2 1 4 {\displaystyle X={\begin{pmatrix}{\frac {34}{103}}&{\frac {5}{103}}&-{\frac {9}{103}}\\-{\frac {7}{103}}&{\frac {2}{103}}&{\frac {17}{103}}\\-{\frac {15}{103}}&{\frac {19}{103}}&{\frac {7}{103}}\end{pmatrix}}\cdot {\begin{pmatrix}4\\23\\5\end{pmatrix}}={\begin{pmatrix}2\\1\\4\end{pmatrix}}}

Итак, x = 2; y = 1; z = 4.

9.8: Решение систем с помощью правила Крамера

Мы узнали, как решать системы уравнений с двумя переменными и тремя переменными, а также с помощью нескольких методов: подстановки, сложения, исключения Гаусса, использования обратной матрицы и построения графиков. Некоторые из этих методов применять проще, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.

Вычисление определителя матрицы 2 × 2

Определитель — это действительное число, которое может быть очень полезно в математике, потому что у него есть несколько приложений, таких как вычисление площади, объема и других величин. Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. В наших целях мы ориентируемся на определитель как на показатель обратимости матрицы.Для вычисления определителя матрицы необходимо следовать определенным шаблонам, описанным в этом разделе.

НАЙТИ ОПРЕДЕЛЕНИЕ МАТРИЦЫ 2 × 2

Определитель матрицы 2 × 2, учитывая

\ (A = \ begin {bmatrix} a & b \\ c & d \ end {bmatrix} \)

определяется как

Обратите внимание на изменение обозначений. Есть несколько способов указать определитель, включая \ (\ det (A) \) и замену скобок в матрице прямыми линиями, \ (| A | \).

Пример \ (\ PageIndex {1} \): поиск определителя матрицы \ (2 × 2 \)

Найдите определитель заданной матрицы.

\ (A = \ begin {bmatrix} 5 & 2 \\ — 6 & 3 \ end {bmatrix} \)

Решение

\ [\ begin {align *} \ det (A) & = \ begin {vmatrix} 5 & 2 \\ — 6 & 3 \ end {vmatrix} \\ & = 5 (3) — (- 6) (2) \\ & = 27 \ end {align *} \]

Использование правила Крамера для решения системы двух уравнений с двумя переменными

Теперь мы представим последний метод решения систем уравнений, использующий определители.Этот метод, известный как правило Крамера , восходит к середине 18 века и назван в честь своего новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году в Introduction à l’Analyse des lignes Courbes algébriques . Правило Крамера — это жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, что и неизвестных.

Правило Крамера даст нам единственное решение системы уравнений, если оно существует.Однако, если система не имеет решения или бесконечное число решений, это будет обозначено нулевым определителем. Чтобы выяснить, является ли система непоследовательной или зависимой, необходимо использовать другой метод, например исключение.

Чтобы понять правило Крамера, давайте внимательно рассмотрим, как мы решаем системы линейных уравнений с использованием основных операций со строками. Рассмотрим систему двух уравнений с двумя переменными.

\ [\ begin {align} a_1x + b_1y & = c_1 (1) \ label {eq1} \\ a_2x + b_2y & = c_2 (2) \ label {eq2} \\ \ end {align} \]

Мы исключаем одну переменную, используя операции со строками, и решаем для другой.Скажите, что мы хотим найти \ (x \). Если уравнение \ ref {eq2} умножается на коэффициент, противоположный коэффициенту \ (y \) в уравнении \ ref {eq1}, уравнение \ ref {eq1} умножается на коэффициент при \ (y \) в уравнении \ ref {eq2}, и мы добавляем два уравнения, переменная \ (y \) будет удалена.

\ [\ begin {align *} & b_2a_1x + b_2b_1y = b_2c_1 & \ text {Multiply} R_1 \ text {by} b_2 \\ — & \ underline {b_1a_2x − b_1b_2y = −b_1c_2} & \ text {Multiply} R_2 \ text {by} −b_1 \\ & b_2a_1x − b_1a_2x = b_2c_1 − b_1c_2 \ end {align *} \]

Теперь решите относительно \ (x \).

\ [\ begin {align *} b_2a_1x − b_1a_2x & = b_2c_1 − b_1c_2 \\ x (b_2a_1 − b_1a_2) & = b_2c_1 − b_1c_2 \\ x & = \ dfrac {b_2c_1 − b_1c_2} {b_2a_1 − b_1a_2} = \ dfrac {\ begin {bmatrix} c_1 & b_1 \\ c_2 & b_2 \ end {bmatrix}} {\ begin {bmatrix} a_1 & b_1 \\ a_2 & b_2 \ end {bmatrix}} \ end {align *} \]

Аналогичным образом, чтобы найти \ (y \), мы исключим \ (x \).

\ [\ begin {align *} & a_2a_1x + a_2b_1y = a_2c_1 & \ text {Multiply} R_1 \ text {by} a_2 \\ — & \ underline {a_1a_2x − a_1b_2y = −a_1c_2} & \ text {Multiply} R_2 \ текст {by} −a_1 \\ & a_2b_1y − a_1b_2y = a_2c_1 − a_1c_2 \ end {align *} \]

Решение относительно \ (y \) дает

\ [\ begin {align *} a_2b_1y − a_1b_2y & = a_2c_1 − a_1c_2 \\ y (a_2b_1 − a_1b_2) & = a_2c_1 − a_1c_2 \\ y & = \ dfrac {a_2c_1 − a_1c_2} {a_2b_1 − a_1b_2} = \ dfrac {a_1c_2 − a_2c_1} {a_1b_2 − a_2b_1} = \ dfrac {\ begin {bmatrix} a_1 & c_1 \\ a_2 & c_2 \ end {bmatrix}} {\ begin {bmatrix} a_1 & b_1 \\ a_2 & b_2 \ end {bmatrix}} \ end {align * } \]

Обратите внимание, что знаменатель для \ (x \) и \ (y \) является определителем матрицы коэффициентов.

Мы можем использовать эти формулы для решения относительно \ (x \) и \ (y \), но правило Крамера также вводит новые обозначения:

• \ (D \): определитель матрицы коэффициентов
• \ (D_x \): определитель числителя в решении \ (x \)

  \ [x = \ dfrac {D_x} {D} \]

• \ (D_y \): определитель числителя в решении \ (y \)

  \ [y = \ dfrac {D_y} {D} \]

Ключ к правилу Крамера заключается в замене интересующего столбца переменных столбцом констант и вычислении детерминантов.Тогда мы можем выразить \ (x \) и \ (y \) как частное двух определителей.

ПРАВИЛО КРЕМЕРА ДЛЯ СИСТЕМ \ (2 × 2 \)

Правило Крамера — это метод, использующий детерминанты для решения систем уравнений, которые имеют то же количество уравнений, что и переменные.

Рассмотрим систему двух линейных уравнений с двумя переменными.

\ [\ begin {align *} a_1x + b_1y & = c_1 \\ a_2x + b_2y & = c_2 \ end {align *} \]

Решение, использующее правило Крамера, дается как

\ [\ begin {align} x & = \ dfrac {D_x} {D} = \ dfrac {\ begin {bmatrix} c_1 & b_1 \\ c_2 & b_2 \ end {bmatrix}} {\ begin {bmatrix} a_1 & b_1 \\ a_2 & b_2 \ end { bmatrix}} \; , D \ neq 0 \\ y & = \ dfrac {D_y} {D} = \ dfrac {\ begin {bmatrix} a_1 & c_1 \\ a_2 & c_2 \ end {bmatrix}} {\ begin {bmatrix} a_1 & b_1 \\ a_2 & b_2 \ end {bmatrix }} \; , D \ neq 0 \ end {align} \]

Если мы решаем для \ (x \), столбец \ (x \) заменяется постоянным столбцом. Если мы решаем для \ (y \), столбец \ (y \) заменяется постоянным столбцом.

Пример \ (\ PageIndex {2} \): Использование правила Крамера для решения системы \ (2 × 2 \)

Решите следующую систему \ (2 × 2 \), используя правило Крамера.

\ [\ begin {align *} 12x + 3y & = 15 \\ 2x-3y & = 13 \ end {align *} \]

Решение

Решите относительно \ (x \).

\ [\ begin {align *} x & = \ dfrac {D_x} {D} \\ & = \ dfrac {\ begin {bmatrix} 15 & 3 \\ 13 & -3 \ end {bmatrix}} {\ begin {bmatrix} 12 & 3 \\ 2 & -3 \ end {bmatrix}} \\ & = \ dfrac {-45-39} {- 36-6} \\ & = \ dfrac {-84} {- 42} \\ & = 2 \ end {align *} \]

Решите относительно \ (y \).

\ [\ begin {align *} y & = \ dfrac {D_y} {D} \\ & = \ dfrac {\ begin {bmatrix} 12 & 15 \\ 2 & 13 \ end {bmatrix}} {\ begin {bmatrix} 12 & 3 \\ 2 & -3 \ end {bmatrix}} \\ & = \ dfrac {156-30} {- 36-6} \\ & = — \ dfrac {126} {42} \\ & = -3 \ end {align * } \]

Решение: \ ((2, −3) \).

Упражнение \ (\ PageIndex {1} \)

Используйте правило Крамера для решения системы уравнений \ (2 × 2 \).

\ [\ begin {align *} x + 2y & = -11 \\ -2x + y & = -13 \ end {align *} \]

Ответ

\ ((3, −7) \)

Вычисление определителя матрицы 3 × 3

Найти определитель матрицы 2 × 2 несложно, но найти определитель матрицы 3 × 3 сложнее.Один из способов — увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведения записей на по каждой из трех диагоналей (от нижнего левого угла к верхнему правому). Это легче понять с помощью наглядного пособия и примера.

Найдите определитель матрицы 3 × 3.

\ (A = \ begin {bmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \ end {bmatrix} \)

1. Дополнение \ (A \) с первыми двумя столбцами.

   \ (\ det (A) = \ left | \ begin {array} {ccc | cc} a_1 & b_1 & c_1 & a_1 & b_1 \\ a_2 & b_2 & c_2 & a_2 & b_2 \\ a_3 & b_3 & c_3 & a_3 & b_3 \ end {array} \ right | \)

2. С верхнего левого угла в нижний правый: умножение значений по первой диагонали. Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали.
3. От левого нижнего угла до правого верхнего: вычтите произведение входов вверх по первой диагонали.Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.

Алгебра выглядит следующим образом:

\ (| A | = a_1b_2c_3 + b_1c_2a_3 + c_1a_2b_3 − a_3b_2c_1 − b_3c_2a_1 − c_3a_2b_1 \)

Пример \ (\ PageIndex {3} \): поиск определителя матрицы 3 × 3

Найдите определитель матрицы \ (3 × 3 \) при

\ (A = \ begin {bmatrix} 0 & 2 & 1 \\ 3 & −1 & 1 \\ 4 & 0 & 1 \ end {bmatrix} \)

Решение

Дополните матрицу первыми двумя столбцами, а затем следуйте формуле. Таким образом,

\ [\ begin {align *} | А | & = \ left | \ begin {array} {ccc | cc} 0 & 2 & 1 & 0 & 2 \\ 3 & -1 & 1 & 3 & -1 \\ 4 & 0 & 1 & 4 & 0 \ end {array} \ right | \\ & = 0 (−1) (1) +2 (1) (4) +1 (3) (0) −4 (−1) (1) −0 (1) (0) −1 (3) (2) \\ & = 0 + 8 + 0 + 4−0−6 \\ & = 6 \ end {align *} \]

Упражнение \ (\ PageIndex {2} \)

Найдите определитель матрицы 3 × 3.

\ (\ det (A) = \ begin {vmatrix} 1 & −3 & 7 \\ 1 & 1 & 1 \\ 1 & −2 & 3 \ end {vmatrix} \)

Ответ

\ (- 10 \)

Q&A: Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?

Нет, этот метод работает только для матриц 2 × 2 и 3 × 3.Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.

Использование правила Крамера для решения системы трех уравнений с тремя переменными

Теперь, когда мы можем найти определитель матрицы \ (3 × 3 \), мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными. Правило Крамера простое и соответствует шаблону, соответствующему правилу Крамера для матриц \ (2 × 2 \). Однако по мере увеличения порядка матрицы до \ (3 × 3 \) требуется гораздо больше вычислений.

Когда мы вычисляем, что определитель равен нулю, правило Крамера не дает никаких указаний на то, что у системы нет решения или есть бесконечное количество решений. Чтобы выяснить это, мы должны выполнить устранение в системе.

Рассмотрим систему уравнений \ (3 × 3 \).

\ [\ begin {align} a_1x + b_1y + c_1z & = \ color {blue} d_1 \\ a_2x + b_2y + c_2z & = \ color {blue} d_2 \\ a_3x + b_3y + c_3z & = \ color {blue} d_3 \\ \ end {align} \]

\ (x = \ dfrac {D_x} {D} \), \ (y = \ dfrac {D_y} {D} \), \ (z = \ dfrac {D_z} {D} \), \ (D ≠ 0 \)

где

\ [D = \ begin {vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \ end {vmatrix} \; , \; D_x = \ begin {vmatrix} \ color {blue} d_1 & b_1 & c_1 \\ \ color {blue} d_2 & b_2 & c_2 \\ \ color {blue} d_3 & b_3 & c_3 \ end {vmatrix} \; , \; D_y = \ begin {vmatrix} a_1 & \ color {blue} d_1 & c_1 \\ a_2 & \ color {blue} d_2 & c_2 \\ a_3 & \ color {blue} d_3 & c_3 \ end {vmatrix} \; , \; D_z = \ begin {vmatrix} a_1 & b_1 & \ color {blue} d_1 \\ a_2 & b_2 & \ color {blue} d_2 \\ a_3 & b_3 & \ color {blue} d_3 \ end {vmatrix} \]

Если мы пишем определитель \ (D_x \), мы заменяем столбец \ (x \) постоянным столбцом. Если мы пишем определитель \ (D_y \), мы заменяем столбец y на столбец констант. Если мы пишем определитель \ (D_z \), мы заменяем столбец \ (z \) постоянным столбцом. Всегда проверяйте ответ.

Пример \ (\ PageIndex {4} \): решение системы \ (3 × 3 \) с использованием правила Крамера

Найдите решение данной системы \ (3 × 3 \), используя правило Крамера.

\ [\ begin {align *} x + y-z & = 6 \\ 3x-2y + z & = -5 \\ x + 3y-2z & = 14 \ end {align *} \]

Решение

Используйте правило Крамера.

\ (D = \ begin {vmatrix} 1 & 1 & −1 \\ 3 & −2 & 1 \\ 1 & 3 & −2 \ end {vmatrix} \), \ (D_x = \ begin {vmatrix} 6 & 1 & −1 \\ — 5 & −2 & 1 \ \ 14 & 3 & −2 \ end {vmatrix} \), \ (D_y = \ begin {vmatrix} 1 & 6 & −1 \\ 3 & −5 & 1 \\ 1 & 14 & −2 \ end {vmatrix} \), \ (D_z = \ begin {vmatrix } 1 & 1 & 6 \\ 3 & −2 & −5 \\ ​​1 & 3 & 14 \ end {vmatrix} \)

Затем,

\ [\ begin {align *} x & = \ dfrac {D_x} {D} & = \ dfrac {-3} {- 3} & = 1 \\ y & = \ dfrac {D_y} {D} & = \ dfrac {-9} {- 3} & = 3 \\ z & = \ dfrac {D_z} {D} & = \ dfrac {6} {- 3} & = -2 \\ \ end {align *} \]

Решение: \ ((1,3, −2) \).

Упражнение \ (\ PageIndex {3} \)

Используйте правило Крамера, чтобы решить матрицу \ (3 × 3 \).

\ [\ begin {align *} x-3y + 7z & = 13 \\ x + y + z & = 1 \\ x-2y + 3z & = 4 \ end {align *} \]

Ответ

\ (\ left (−2, \ dfrac {3} {5}, \ dfrac {12} {5} \ right) \)

Пример \ (\ PageIndex {5A} \): использование правила Крамера для решения несовместимой системы

Решите систему уравнений, используя правило Крамера.

\ [\ begin {align} 3x-2y & = 4 \ label {eq3} \\ 6x-4y & = 0 \ label {eq4} \ end {align} \]

Решение

Начнем с нахождения определителей \ (D \), \ (D_x \) и \ (D_y \).

\ (D = \ begin {vmatrix} 3 & −2 \\ 6 & −4 \ end {vmatrix} = 3 (−4) −6 (−2) = 0 \)

Мы знаем, что нулевой определитель означает, что либо система не имеет решения, либо имеет бесконечное количество решений. Чтобы узнать, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.

1. Умножьте уравнение \ ref {eq3} на \ (- 2 \).
2. Добавьте результат в уравнение \ ref {eq4}.

\ [\ begin {align *} & −6x + 4y = −8 \\ & \; \; \; \ underline {6x − 4y = 0} \\ & \; \; \; \; \; \ ; \; \; \; \; 0 = −8 \ end {align *} \]

Получаем уравнение \ (0 = −8 \), которое неверно. Следовательно, у системы нет решения. График системы показывает две параллельные линии. См. Рисунок \ (\ PageIndex {1} \).

Рисунок \ (\ PageIndex {1} \)

Пример \ (\ PageIndex {5B} \): использование правила Крамера для решения зависимой системы

Решите систему с бесконечным количеством решений.

\ [\ begin {align} x-2y + 3z & = 0 \ label {eq5} \\ 3x + y-2z & = 0 \ label {eq6} \\ 2x-4y + 6z & = 0 \ label {eq7} \ end {align} \]

Решение

Давайте сначала найдем определитель. Создайте матрицу, дополненную первыми двумя столбцами.

\ (\ left | \ begin {array} {ccc | cc} 1 & −2 & 3 & 1 & -2 \\ 3 & 1 & −2 & 3 & 1 \\ 2 & −4 & 6 & 2 & -4 \ end {array} \ right | \)

Затем,

\ (1 (1) (6) + (- 2) (- 2) (2) +3 (3) (- 4) −2 (1) (3) — (- 4) (- 2) (1 ) −6 (3) (- 2) = 0 \)

Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное количество решений.Чтобы выяснить это, нам нужно провести отбор.

1. Умножьте уравнение \ ref {eq5} на \ (- 2 \) и добавьте результат к уравнению \ ref {eq7}:

\ [\ begin {align *} & −2x + 4y − 6x = 0 \\ & \; \; \ underline {2x − 4y + 6z = 0} \\ & \; \; \; \; \; \ ; \; \; \; \; \; \; \; \; \; \; 0 = 0 \ end {align *} \]

2. Получение ответа \ (0 = 0 \), утверждение, которое всегда верно, означает, что система имеет бесконечное количество решений. Изобразив систему, мы можем увидеть, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой.См. Рисунок \ (\ PageIndex {2} \).

Рисунок \ (\ PageIndex {2} \)

Понимание свойств детерминантов

Есть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.

СВОЙСТВА ДЕТЕРМИНАНТОВ

1. Если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
2. Когда две строки меняются местами, определитель меняет знак.{−1} \) — величина, обратная определителю матрицы \ (A \).
3. Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.

Пример \ (\ PageIndex {6} \): иллюстрация свойств детерминантов

Проиллюстрируйте каждое из свойств определителей.

Решение

Свойство 1 утверждает, что если матрица имеет верхнюю треугольную форму, определитель является произведением элементов по главной диагонали.

\ (A = \ begin {bmatrix} 1 & 2 & 3 \\ 0 & 2 & 1 \\ 0 & 0 & −1 \ end {bmatrix} \)

Дополните \ (A \) первыми двумя столбцами.

\ (A = \ left [\ begin {array} {ccc | cc} 1 & 2 & 3 & 1 & 2 \\ 0 & 2 & 1 & 0 & 2 \\ 0 & 0 & −1 & 0 & 0 \ end {array} \ right] \)

Затем

\ [\ begin {align *} \ det (A) & = 1 (2) (- 1) +2 (1) (0) +3 (0) (0) -0 (2) (3) -0 (1) (1) +1 (0) (2) \\ & = -2 \ end {align *} \]

Свойство 2 утверждает, что перестановка строк меняет знак.Учитывая

\ [\ begin {align *} B & = \ begin {bmatrix} 4 & -3 \\ — 1 & 5 \ end {bmatrix} \\ \ det (B) & = (4) (5) — (- 1) (- 3) \\ & = 20-3 \\ & = 17 \ end {align *} \]

Свойство 3 утверждает, что если две строки или два столбца идентичны, определитель равен нулю.

\ [\ begin {align *} A & = \ left [\ begin {array} {ccc | cc} 1 & 2 & 2 & 1 & 2 \\ 2 & 2 & 2 & 2 & 2 \\ — 1 & 2 & 2 & -1 & 2 \ end {array} \ right] \\ \ det (A) & = 1 (2) (2) +2 (2) (- 1) +2 (2) (2) +1 (2) (2) -2 (2) (1) -2 (2) (2) \ \ & = 4-4 + 8 + 4-4-8 \\ & = 0 \ end {align *} \]

Свойство 4 утверждает, что если строка или столбец равны нулю, определитель равен нулю.{-1}) & = — 2 \ left (- \ dfrac {1} {2} \ right) — \ dfrac {3} {2} (1) \\ & = — \ dfrac {1} {2} \ конец {выравнивание *} \]

Свойство 6 утверждает, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент. Таким образом,

Пример \ (\ PageIndex {7} \): использование правила Крамера и определяющих свойств для решения системы

Найдите решение данной системы \ (3 × 3 \).

Решение

Используя правило Крамера, имеем

\ (D = \ begin {bmatrix} 2 & 4 & 4 \\ 3 & 7 & 7 \\ 1 & 2 & 2 \ end {bmatrix} \)

Обратите внимание, что второй и третий столбцы идентичны.Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо существует бесконечное число решений. Чтобы выяснить это, нам нужно провести отбор.

1. Умножьте уравнение \ ref {eq10} на \ (- 2 \) и добавьте результат в уравнение \ ref {eq8}.

Получение противоречивого утверждения означает, что система не имеет решения.

Медиа

Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с правилом Крамера.

Страница не найдена | MIT

Перейти к содержанию ↓

• Образование
• Исследовать
• Инновации
• Прием + помощь
• Студенческая жизнь
• Новости
• Выпускников
• О MIT
• Подробнее ↓
  • Прием + помощь
  • Студенческая жизнь
  • Новости
  • Выпускников
  • О MIT

Меню ↓

Поиск

Меню

Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!

Что вы ищете?

Увидеть больше результатов

Предложения или отзывы?

Правило Крамера

Рассмотрим общую линейную систему 2 на 2

Умножение первого уравнения на a ₂₂ , второго на — a ₁₂ и сложение результатов исключает y и позволяет оценить x :

при условии, что a ₁₁ a ₂₂ — a ₁₂ a ₂₁ ≠ 0.Точно так же умножение первого уравнения на — a ₂₁ , второго на a ₁₁ и сложение результатов исключает x и определяет y :

снова предполагая, что a ₁₁ a ₂₂ — a ₁₂ a ₂₁ ≠ 0. Эти выражения для x и y могут быть записаны в терминах определителей как следует:

и

Если исходная система записана в матричной форме,

, то знаменатели в приведенных выше выражениях для неизвестных x и y оба равны определителю матрицы коэффициентов.Кроме того, числитель в выражении для первого неизвестного, x , равен определителю матрицы, которая получается, когда первый столбец матрицы коэффициентов заменяется столбцом констант, а числитель в выражении для второй неизвестный, y , равен определителю матрицы, которая получается, когда второй столбец матрицы коэффициентов заменяется столбцом констант. Это правило Крамера для линейной системы 2 на 2.

Расширение шаблона до линейной системы 3 на 3,

Правило Крамера гласит, что если определитель матрицы коэффициентов отличен от нуля, то выражения для неизвестных x, y и z принимают следующий вид:

Общая форма правила Крамера выглядит следующим образом: Система линейных уравнений n в n неизвестных, записанных в матричной форме A x = b как

будет иметь уникальное решение, если det A ≠ 0, и в этом случае значение неизвестного x _j дается выражением

, где A _j — это матрица, которая получается, когда столбец j матрицы коэффициентов A заменяется матрицей столбцов b .

Два важных теоретических результата о квадратных системах вытекают из правила Крамера:

Теорема F . Система квадратов A x = b будет иметь уникальное решение для каждой матрицы столбцов b тогда и только тогда, когда det A ≠ 0.

Теорема G . Однородная квадратная система A x = 0 будет иметь только тривиальное решение x = 0 тогда и только тогда, когда det A ≠ 0.

Хотя правило Крамера имеет теоретическое значение, поскольку дает формулу для неизвестных, обычно это неэффективный метод решения, особенно для больших систем. Метод исключения Гаусса по-прежнему остается предпочтительным. Однако правило Крамера может быть полезно, когда, например, необходимо значение только одного неизвестного.

Пример 1 : Используйте правило Крамера, чтобы найти значение y , учитывая, что

Поскольку эта линейная система эквивалентна матричному уравнению

Правило Крамера подразумевает, что второе неизвестное, y , дается выражением

при условии, что знаменатель — определитель матрицы коэффициентов — не равен нулю.Сокращение строк с последующим расширением Лапласа по первому столбцу оценивает эти детерминанты:

При этих расчетах (*) означает

Правило Крамера с двумя переменными

Правило Крамера — еще один метод, позволяющий решать системы линейных уравнений с использованием определителей.

В терминах обозначений матрица — это массив чисел, заключенный в квадратные скобки, а определитель — это массив чисел, заключенный в две вертикальные черты.

Обозначения

Формула для определения определителя матрицы 2 x 2 очень проста.

Давайте быстро рассмотрим:

Определитель матрицы 2 x 2

Быстрые примеры того, как найти детерминанты матрицы 2 x 2

Пример 1 : Найдите определитель матрицы A ниже.

Пример 2 : Найдите определитель матрицы B ниже.

Пример 3 : Найдите определитель матрицы C ниже.

Зная, как найти определитель матрицы 2 x 2, теперь вы готовы изучить процедуры или шаги по использованию правила Крамера. Вот так!

Правила Крамера для систем линейных уравнений с двумя переменными

• Присвойте имена каждой матрице

матрица коэффициентов:

X — матрица:

Y — матрица:

От

до найдите переменную x.

От

до найдите переменную y.

Несколько моментов, которые следует учитывать при рассмотрении формулы:

1) Столбцы \ large {x}, \ large {y} и постоянные члены \ large {c} получаются следующим образом:

2) Оба знаменателя при решении \ large {x} и \ large {y} совпадают. Они происходят из столбцов \ large {x} и \ large {y}.

3) Глядя на числитель при решении для \ large {x}, коэффициенты столбца \ large {x} заменяются постоянным столбцом (красным).

4) Таким же образом, чтобы найти \ large {y}, коэффициенты \ large {y} -столбца заменяются постоянным столбцом (красным).

Примеры решения систем линейных уравнений с двумя переменными с использованием правила Крамера

Пример 1 : Решите систему с двумя переменными по правилу Крамера

Начните с извлечения трех соответствующих матриц: коэффициент, \ large {x} и \ large {y}. Затем решите каждый соответствующий определитель.

После того, как все три детерминанта вычислены, пора найти значения \ large {x} и \ large {y}, используя приведенную выше формулу.

Я могу записать окончательный ответ как \ large {\ left ({x, y} \ right) = \ left ({2, — 1} \ right)}.

Пример 2 : Решите систему с двумя переменными по правилу Крамера

Задайте свои коэффициенты, матрицы \ large {x} и \ large {y} из данной системы линейных уравнений. Затем рассчитайте их детерминанты соответственно.

Помните, что мы всегда вычитаем произведений диагональных записей.

• Для матрицы коэффициентов (используйте коэффициенты обеих переменных x и y )

• Для X — матрица (заменить столбец x на постоянный столбец)

• Для Y — матрица (заменить y-столбец на постоянный)

Надеюсь, вам удобно вычислять определитель двумерной матрицы.Чтобы окончательно решить требуемые переменные, я получаю следующие результаты…

Записав окончательный ответ в точечной нотации, я получил \ large {\ left ({x, y} \ right) = \ left ({6, — 5} \ right)}.

Пример 3 : Решите систему с двумя переменными по правилу Крамера

Эту проблему на самом деле довольно легко решить методом исключения. Это связано с тем, что коэффициенты переменной x являются «одинаковыми», но только противоположными по знакам (+1 и -1). Чтобы решить эту проблему с помощью метода исключения, вы добавляете соответствующие столбцы, и переменная x исчезает, оставляя вам одношаговое уравнение в \ large {y}.Я говорю об этом, потому что у каждой техники есть недостатки, и лучше выбрать наиболее эффективную. Всегда уточняйте у своего учителя, можно ли использовать другой подход, если метод не указан для данной проблемы.

В любом случае, поскольку мы учимся решать по правилу Крамера, давайте продолжим и разберемся с этим методом.

Я построю три матрицы (коэффициент, \ large {x} и \ large {y}) и оценю их соответствующие детерминанты.

• Для X — матрица (прописная D с нижним индексом x)

• Для Y — матрица (прописная D с индексом y)

После получения значений трех требуемых определителей я вычислю \ large {x} и \ large {y} следующим образом.

Окончательный ответ в виде баллов: \ large {\ left ({x, y} \ right) = \ left ({- 1,2} \ right)}.

Пример 4 : Решить по правилу Крамера систему с двумя переменными

Поскольку мы уже рассмотрели несколько примеров, я предлагаю вам попробовать решить эту проблему самостоятельно. Затем сравните свои ответы с решением ниже.

Если вы поймете все правильно с первого раза, это означает, что вы становитесь «профи» в отношении правила Крамера. Если вы этого не сделали, попытайтесь выяснить, что пошло не так, и научитесь не совершать ту же ошибку в следующий раз.Так вы станете лучше в математике. Изучите множество проблем и, что более важно, много практикуйтесь самостоятельно.

Вы должны получить ответ ниже…

Пример 5 : Решите систему с двумя переменными по правилу Крамера

В нашем последнем примере я включил ноль в столбец констант. Каждый раз, когда вы видите число ноль в столбце констант, я настоятельно рекомендую использовать правило Крамера для решения системы линейных уравнений.Почему? Потому что вычисление определителей для матриц \ large {x} и \ large {y} стало очень простым. Убедитесь сами!

Окончательное решение этой проблемы —

Практика с рабочими листами

Возможно, вас заинтересует:

Правило Крамера 3 × 3

Правило Крамера | Суперпроф

В мире линейной алгебры правило Крамера играет очень важную роль в поиске определителей, рангов и типов системы.Проще говоря, правило Крамера используется для поиска решения системы линейного уравнения. Кроме того, это также помогает нам определить, будет ли в системе хотя бы одно решение или нет. Это экономит много времени, не говоря уже о том, что этот метод очень точен для прогнозирования решений системы.

Существует еще один метод поиска решения линейной системы, известный как метод исключения Гаусса. На этом этапе у вас может возникнуть вопрос, почему мы должны использовать правило Крамера вместо метода исключения Гаусса? У нас есть ответ.Правило Крамера очень простое в использовании. Вы должны следовать аналогичному шаблону для всей матрицы, с другой стороны, исключение Гаусса требует логических операций со строками. Вам нужно подумать и выбрать операции со строками. Эти операции со строками могут стать трудными при решении системы линейных уравнений. Кроме того, при рассмотрении исключения Гаусса существуют операции, такие как операции поворота строк и столбцов. У них есть свои правила, которые иногда могут расстраивать.

Найдите здесь репетитора по математике.

Как работает правило Крамера?

Чтобы упростить задачу, представьте систему, которая имеет два линейных уравнения:

(1)

(2)

Мы можем исключить одну переменную с помощью операций со строками. Вы можете выбрать любую переменную, но здесь мы решили исключить y, чтобы составить уравнение в терминах x. Для этого нам нужно применить строковую операцию. Если мы умножим уравнение 2 на

и уравнение 1 на, а затем сложим оба уравнения, мы можем легко исключить y из общего уравнения.

отсюда

отсюда

Добавление обоих уравнений:

Принимая x как общее:

Теперь будет применяться тот же метод, но на этот раз мы удалим x и сделаем уравнение через y.

отсюда

отсюда

Складываем оба уравнения:

Принимая y как общее:

Вы что-то заметили? Знаменатели обоих уравнений одинаковы.Этот знаменатель является определителем матрицы коэффициентов. Следовательно, мы можем записать что-то вроде этого:

Где

— определитель матрицы коэффициентов,

— определитель числителя в решении x,

— определитель числителя в y решение.

В приведенном выше примере мы рассматривали систему из двух уравнений, но что, если у вас нет системы из двух уравнений? Тем не менее, вам не о чем беспокоиться, потому что метод точно такой же.Вот иллюстрация, если у вас есть номер системы:

Детерминанты получаются заменой коэффициентов 2-го члена (независимых членов) в 1-м, 2-м, 3-м и n-м столбце соответственно. Однако есть некоторые условия для использования правила Крамера, ниже приведены все условия.

• Количество уравнений равно количеству неизвестных.
• Определитель матрицы коэффициентов отличен от нуля.

Доступны лучшие репетиторы по математике

Первое занятие бесплатно

Примеры

Пример 1

000

000

000

000

Пример 2

0003

0003

0003

0003

0003

Пример 3

0003

0003

0003

Найдите репетитора по математике в Superprof.

Исключение Гаусса — обзор

1.3.7 Исключение Гаусса или Гаусса

Исключение Гаусса (также известное как Исключение Гаусса ) — широко используемый метод для решения систем линейных уравнений в форме [ K ] { u } = { F }. В операциях с матрицами существует три распространенных типа манипуляций, которые служат для создания новой матрицы, обладающей теми же характеристиками, что и исходная:

1.

Поменяйте местами любые два ряда.

2.

Умножьте каждую запись в любой строке на ненулевое постоянное значение.

3.

Добавьте значения из каждой записи одной строки к каждой записи другой строки.

Цель использования исключения Гаусса — создать новую матрицу с теми же свойствами, что и исходная [ K ], но в формате, в котором только верхний треугольник имеет ненулевые элементы. Используя предыдущую матрицу 5 × 5 в качестве примера, верхний треугольник состоит из элементов в правом верхнем треугольнике матрицы и включает элементы в правой диагональной строке в виде

[m11m12m13m14m150m22m23m24m2500m33m34m35000m44m450000m55].

Мы достигаем цели исключения Гаусса, правильно применяя одну из трех вышеупомянутых операций за раз. После того, как верхняя треугольная матрица сформирована, мы используем метод обратной подстановки , чтобы сначала найти последнюю переменную. Причина, по которой этот метод называется «обратной заменой», заключается в том, что последняя строка верхней треугольной матрицы должна быть решена первой. Поскольку в последней строке верхней треугольной матрицы есть только одна ненулевая запись, мы можем найти неизвестную переменную простым арифметическим делением, то есть из

[K] {u2v2u3u4v4} = [m11m12m13m14m150m22m23m24m2500m33m34m35000m44m40000m55u] {u2v2u3f2f2] } → v4 = F4Vm55.

Имея значение v ₄ , мы решаем от второй до последней переменной. Поскольку m ₄₄ u ₄ + m ₄₅ v ₄ = F _{4 H} , мы можем решить для u ₄ как u4 = F4H − m45v4m44. Мы многократно применяем один и тот же набор процедур, пока не будут найдены значения всех переменных.

Мы будем использовать типичный 64-битный компьютер, чтобы проиллюстрировать критическую проблему при использовании исключения Гаусса.Хорошо известно, что такой компьютер хранит действительное (десятичное) число в формате с плавающей запятой, используя 64 бита: 1 бит для представления знака (плюс или минус), 52 бита для представления количества цифр точности (мантисса), и 11 бит для представления экспоненты. При делении числа на другое очень маленькое число имеющихся цифр в мантиссе может быть недостаточно для поддержания необходимой точности, то есть может возникнуть ошибка округления. При исключении Гаусса точка поворота или позиция поворота — это позиция в строке, которая совпадает с правой диагональной линией.Значения в точках поворота используются в качестве знаменателя при формировании верхней треугольной матрицы. Чтобы исключить ошибки округления, возникающие при делении на очень маленькое число, используется первый тип манипуляции для перемещения строки с очень маленьким числом в точке поворота в другую строку. Это достигается простым перестановкой рядов так, чтобы большие числа располагались в точках поворота. Вторую и третью операции мы используем для получения нулей в левой нижней части матрицы, что необходимо для получения верхней треугольной матрицы.

Модифицированной версией метода исключения Гаусса является метод исключения Гаусса – Жордана. Цель исключения Гаусса – Жордана состоит в том, чтобы получить матрицу, которая имеет правую диагональную линию всех единиц (единиц), а все остальные позиции матрицы содержат нули. Это достигается с помощью тех же трех типов манипуляций с матрицами, которые используются в методе исключения Гаусса. Поскольку квадратная матрица состоит только из единичных значений в диагональных элементах, решения для всех неизвестных становятся легко доступными.Один из недостатков метода Гаусса – Жордана заключается в том, что он является более дорогостоящим в вычислительном отношении, чем метод исключения Гаусса. Таким образом, он полезен только для решения проблем путем ручного расчета, когда есть небольшое количество одновременных уравнений. Используя метод исключения Гаусса, а не метод Гаусса – Жордана, мы избегаем многих дополнительных шагов. Поскольку метод FE обычно включает большую систему, чаще используется метод исключения Гаусса.

В следующем разделе мы шаг за шагом продемонстрируем процессы в методе исключения Гаусса.Конечно, вместо ручных вычислений следует написать и использовать компьютерную программу. Используя предыдущий пример в качестве отправной точки, уравнение. (1.68) повторяется ниже.

[K] {u2v2u3u4v4} = 108 [100−50006.6700−6.67−506.44−1.441.9200−1.44400−6.671.92010.67] {u2v2u3u4v4} = {F2HF2VF3HF40003−5002 = {0002002). все, кроме первой записи в первом столбце, равны 0. Мы заметили, что третья строка в этом столбце содержит единственное ненулевое значение. Чтобы управлять третьей строкой, чтобы сделать ведущее число 0, мы должны умножить существующее число (-5) на такое значение, чтобы добавление результата к первой записи в строке один (10) давало 0.Используя правило два, мы умножаем каждую запись в третьей строке на 2:

108 [100-50006,6700-6,67-10012,88-2,883,8400-1,44400-6,671,92010,67] {u2v2u3u4v4} = {00020000-50000}.

Затем мы добавляем строку 1 к строке 3, но мы не затрагиваем строку 1:

108 [100−50006.6700−6.67007.88−2.883.8400−1.44400−6.671.92010.67] {u2v2u3u4v4} = {00020000−50000 }.

Теперь, когда все значения в первом столбце, кроме первого, равны 0, мы применяем аналогичный процесс ко второму столбцу. Мы хотим, чтобы все значения во втором столбце, кроме второго, равнялись 0, а это значит, что мы должны адресовать −6.67 в последнем ряду. Это можно изменить на 0, просто добавив значения из строки 2.

108 [100-50006.6700-6.67007.88-2.883.8400-1.4440001.9204] {u2v2u3u4v4} = {00020000-50000}

Две операции, правила два и три необходимы для преобразования записи в строке четыре, столбце три в 0. Сначала мы умножаем четвертую строку на 7,881,44 (обратите внимание, что эта операция также применяется к вектору силы):

108 [100-50006,6700-6,67007. 88−2.883.8400−7.8821.8

.9204] {u2v2u3u4v4} = {0001.094 × 105−50000},

, а затем добавьте значения из третьей строки к этим результатам, чтобы сформировать новую четвертую строку:

108 [100-50006.6700−6.67007.88−2.883.8400019.013.84001.9204] {u2v2u3u4v4} = {0001.094 × 105−50000}.

Аналогичным образом мы умножаем пятую строку на -7,881,92, а затем складываем значения из третьей строки, чтобы сформировать новую пятую строку:

108 [100-50006,6700-6,67007,88-2,883,8400019,013,84000-2,88-12,58 ] {u2v2u3u4v4} = {0001,094 × 1052,052 × 106}.

К этому моменту должно быть очевидно, что умножение на значение в другой строке с последующим делением на значение в текущей строке дает результат, который можно вычесть из этой другой строки и получить 0.Чтобы еще раз увидеть этот процесс, мы умножаем пятую строку на 19.012.88, затем складываем значения из четвертой строки, чтобы получить новую пятую строку:

108 [100−50006.6700−6.67007.88−2.883.8400019.013.840000−79.20] {u2v2u3u4v4} = {0001,094 × 1051,464 × 106}.

Теперь матрица имеет форму верхней треугольной матрицы, что означает, что все значения ниже и слева от правой диагональной линии являются нулями. На этом этапе мы применяем метод обратной замены для определения узловых смещений.

Начнем с последней строки, которая содержит 108 [0000−79.20], и мы умножаем последовательные значения в этой строке на последовательные значения в векторе узлового смещения:

108 ((0) (u2) + (0) (v2) + (0) (u3) + (0) ( u4) + (- 79.20) (v4)) = 1.464 × 106

Мы можем сделать это проще, признав, что только последнее значение в строке ненулевое, и поэтому v ₄ — это просто последнее значение в вектор силы, деленный на последний элемент в верхней треугольной матрице [ K ]:

v4 = (1,464 × 106) (- 79,2 × 108) = — 1,849 × 10−4

Мы можем использовать v ₄ , чтобы найти u ₄ и т. Д.Ниже приведены расчеты значений узловых смещений в м :

u4 = 1.094 × 105−108 × 3.84 × v419.01 × 108 = 1.804 × 10519.01 × 108 = 0.949 × 10−4,

u3 = 108 × (2,88) × u4−108 × 3,84 × v4108 × 7,88 = 9,837 × 10−47,88 = 1,248 × 10−4,

v2 = 108 × 6,67 × v4108 × 6,67 = −1,849 × 10−4 и

u2 = 108 × 5 × u3108 × 10 = 0,624 × 10−4.

Узловые смещения, рассчитанные с использованием метода MSA или прямого метода жесткости, в точности совпадают с точными решениями проблем, связанных с фермами.Для типов элементов, отличных от фермы или пружины, узловые решения вряд ли будут иметь те же значения, что и точные решения. Простое практическое правило состоит в том, что чем больше элементов используется для представления интересующей структуры, тем точнее результаты будут приближаться к точным решениям. Дополнительные описания других типов элементов приведены в главе 2.

Решение систем линейных уравнений с помощью Python Numpy

Библиотека Numpy может использоваться для выполнения различных математических / научных операций, таких как матричное кросс-произведение и скалярное произведение, поиск значений синуса и косинуса, преобразование Фурье и манипуляции с формой и т. Д.Слово Numpy — это сокращенное обозначение «Числовой Python».

В этой статье вы увидите, как решить систему линейных уравнений с помощью библиотеки Python Numpy.

Что такое система линейных уравнений?

Википедия определяет систему линейных уравнений как:

В математике система линейных уравнений (или линейная система) — это набор двух или более линейных уравнений, включающих один и тот же набор переменных.

Конечная цель решения системы линейных уравнений — найти значения неизвестных переменных.Вот пример системы линейных уравнений с двумя неизвестными переменными, x и y :

Уравнение 1:

  4x + 3y = 20
-5x + 9y = 26
  

Чтобы решить указанную выше систему линейных уравнений, нам нужно найти значения переменных x и y . Есть несколько способов решить такую ​​систему, например, исключение переменных, правило Крамера, метод сокращения строк и матричное решение.В этой статье мы рассмотрим матричное решение.

В матричном решении решаемая система линейных уравнений представлена ​​в виде матрицы AX = B . Например, мы можем представить Уравнение 1 в виде матрицы следующим образом:

  A = [[4 3]
     [-5 9]]

X = [[x]
     [y]]

B = [[20]
     [26]]
  

Чтобы найти значения переменных x и y в уравнении Equation 1 , нам нужно найти значения в матрице X .Для этого мы можем взять скалярное произведение обратной матрицы A и матрицы B , как показано ниже:

  X = инверсный (A) .B
  

Если вы не знакомы с тем, как найти обратную матрицу, взгляните на эту ссылку, чтобы понять, как вручную найти обратную матрицу. Чтобы понять матричное скалярное произведение, ознакомьтесь с этой статьей.

Решение системы линейных уравнений с помощью Numpy

Из предыдущего раздела мы знаем, что для решения системы линейных уравнений нам необходимо выполнить две операции: инверсию матрицы и скалярное произведение матрицы.Библиотека Numpy от Python поддерживает обе операции. Если вы еще не установили библиотеку Numpy, вы можете сделать это с помощью следующей команды pip :

  $ pip install numpy
  

Давайте теперь посмотрим, как решить систему линейных уравнений с помощью библиотеки Numpy.

Использование методов inv () и dot ()

Сначала мы найдем обратную матрицу A , которую мы определили в предыдущем разделе.

Давайте сначала создадим матрицу A на Python.Для создания матрицы можно использовать метод array модуля Numpy. Матрицу можно рассматривать как список списков, где каждый список представляет собой строку.

В следующем скрипте мы создаем список с именем m_list , который дополнительно содержит два списка: [4,3] и [-5,9] . Эти списки представляют собой две строки в матрице A . Чтобы создать матрицу A с помощью Numpy, m_list передается методу массива , как показано ниже:

  импортировать numpy как np

m_list = [[4, 3], [-5, 9]]
А = np.массив (m_list)
  

Чтобы найти обратную матрицу, матрица передается методу linalg.inv () модуля Numpy:

  inv_A = np.linalg.inv (A)

печать (inv_A)
  

Следующий шаг — найти скалярное произведение между обратной матрицей A и матрицей B . Важно отметить, что скалярное произведение матриц возможно только между матрицами , если внутренние размеры матриц равны i.е. количество столбцов левой матрицы должно соответствовать количеству строк в правой матрице.

Чтобы найти скалярное произведение с помощью библиотеки Numpy, используется функция linalg.dot () . Следующий скрипт находит скалярное произведение между обратной матрицей A и матрицей B , которая является решением уравнения 1 .

  B = np.array ([20, 26])
X = np.linalg.inv (A) .dot (B)

печать (X)
  

Выход:

  [2.4.]
  

Здесь 2 и 4 — соответствующие значения для неизвестных x и y в уравнении 1 . Для проверки, если вы вставите 2 вместо неизвестного x и 4 вместо неизвестного y в уравнении 4x + 3y , вы увидите, что результат будет 20.

Давайте теперь решим систему трех линейных уравнений, как показано ниже:

  4x + 3y + 2z = 25
-2x + 2y + 3z = -10
3x -5y + 2z = -4
  

Приведенное выше уравнение можно решить с помощью библиотеки Numpy следующим образом:

Уравнение 2:

  A = np.массив ([[4, 3, 2], [-2, 2, 3], [3, -5, 2]])
B = np.array ([25, -10, -4])
X = np.linalg.inv (A) .dot (B)

печать (X)
  

В приведенном выше сценарии методы linalg.inv () и linalg.dot () объединены в цепочку. Переменная X содержит решение для уравнения 2 и печатается следующим образом:

  [5. 3. -2.]
  

Значения неизвестных x , y и z равны 5, 3 и -2 соответственно.Вы можете подставить эти значения в Equation 2 и проверить их правильность.

Использование метода detect ()

В двух предыдущих примерах мы использовали методы linalg.inv (), и linalg.dot () , чтобы найти решение системы уравнений. Однако библиотека Numpy содержит метод linalg.solve () , который можно использовать для непосредственного поиска решения системы линейных уравнений:

  A = np.array ([[4, 3, 2], [-2, 2, 3], [3, -5, 2]])
B = np.массив ([25, -10, -4])
X2 = np.linalg.solve (A, B)

печать (X2)
  

Выход:

  [5. 3. -2.]
  

Вы можете видеть, что результат такой же, как и раньше.

Пример из реального мира

Давайте посмотрим, как систему линейных уравнений можно использовать для решения реальных задач.

Предположим, продавец фруктов продал 20 манго и 10 апельсинов за один день на общую сумму 350 долларов. На следующий день он продал 17 манго и 22 апельсина за 500 долларов. Если цены на фрукты оставались неизменными в оба дня, какова была цена одного манго и одного апельсина?

Эту задачу легко решить с помощью системы двух линейных уравнений.

Допустим, цена одного манго составляет x , а цена одного апельсина — y . Вышеупомянутую проблему можно преобразовать так:

  20x + 10y = 350
17x + 22y = 500
  

Решение указанной выше системы уравнений показано здесь:

  A = np.array ([[20, 10], [17, 22]])
B = np.array ([350, 500])
X = np.linalg.solve (A, B)

печать (X)
  

А вот результат:

  [10. 15.]
  

Выходные данные показывают, что цена одного манго составляет 10 долларов, а цена одного апельсина — 15 долларов.

Заключение

В статье объясняется, как решить систему линейных уравнений с помощью библиотеки Python Numpy.