2 или y=1/x. А как строить графики со знаком модуля?
Задача 1. Построить графики функций y=|x| y=|x-1|.
Решение. Сравним его с графиком функции y=|x|.При положительных x имеем |x|=x. Значит, для положительных значений аргумента график y=|x| совпадает с графиком y=x, то есть эта часть графика является лучём, выходящим из начала координат под углом 45 градусов к оси абсцисс. При x< 0 имеем |x|= -x; значит, для отрицательных x график y=|x| совпадает с биссектрисой второго координатного угла.
Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y=|x| — чётная, так как |-a|=|a|. Значит, график функции y=|x| симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:
y=|x|
Для построения берём точки (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2).
Теперь график y=|x-1|. Если А — точка графика у=|x| с координатами (a;|a|), то точкой графика y=|x-1| с тем же значением ординаты Y будет точка A1(a+1;|a|).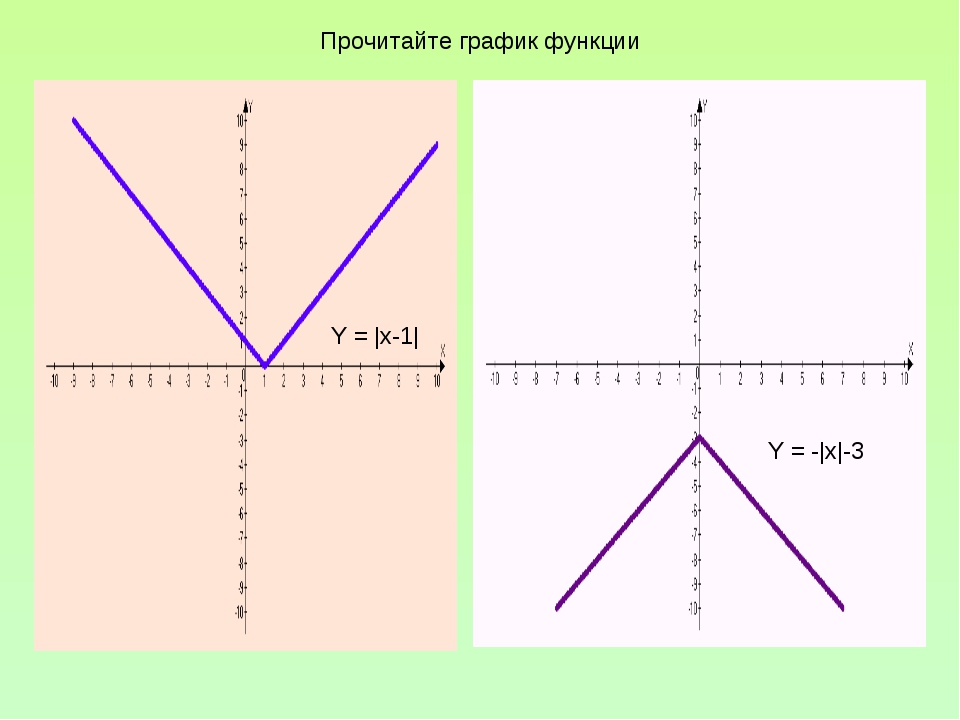 (Почему?) Эту точку второго графика можно получить из точки А(a;|a|) первого графика сдвигом параллельно оси Ox вправо. Значит, и весь график функции y=|x-1|получается из графика функции y=|x| сдвигом параллельно оси Ox вправо на 1.
(Почему?) Эту точку второго графика можно получить из точки А(a;|a|) первого графика сдвигом параллельно оси Ox вправо. Значит, и весь график функции y=|x-1|получается из графика функции y=|x| сдвигом параллельно оси Ox вправо на 1.
Построим графики:
y=|x-1|
Для построения берём точки (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1).
Это была простенькая задачка. Теперь то, что многих приводит в ужас.
Задача 2. Постройте график функции y=3*|x-4| — x + |x+1|.
Решение. Найдем точки, в которых подмодульные выражения обращаются в нуль, т.е. так называемые «критические» точки функции. Такими точками будут х=-1 и х=4. В этих точках подмодульные выражения могут изменить знак.
Пусть x<-1. Тогда х+1<0, |x+1|=-x-1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(-х-1)= -5х+11.
Пусть -1< = x < = 4. Тогда х+1>0, |x+1|=x+1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(х+1)= -3х+13.
Пусть х>4. Тогда х+1>0, |x+1|=x+1, x-4>0; |x-4|=x-4; Следовательно у= 3(х-4)-х+х+1= 3х-11. 2 — |x| — 3|
2 — |x| — 3|
Итак, всем спасибо! Теперь мы получили ту базу знаний, необходимую для построения графиков со знаком модуля! А то его так все боятся.
Вот ссылка, которая поможет вам проверить ваши построения:
Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов.
| ||||
Чему равен модуль х 2. Как решать уравнения с модулем: основные правила
Инструкция
Если модуль представлен в виде непрерывной функции, то значение ее аргумента может быть как положительным, так и отрицательным: |х| = х, х ≥ 0; |х| = — х, х
Модуль нулю, а модуль любого положительного числа – ему . Если аргумент отрицательный, то после раскрытия скобок его знак меняется с минуса на плюс. На основании этого вытекает вывод, что модули противоположных равны: |-х| = |х| = х.
Модуль комплексного числа находится по формуле: |a| = √b ² + c ², а |a + b| ≤ |a| + |b|. Если в аргументе присутствует в виде множителя положительное число, то его можно вынести за знак скобки, например: |4*b| = 4*|b|.
Если аргумент представлен в виде сложного числа, то для удобства вычислений допускается порядка членов выражения, заключенного в прямоугольные скобки: |2-3| = |3-2| = 3-2 = 1, поскольку (2-3) меньше нуля.
Возведенный в степень аргумент одновременно находится под знаком корня того же порядка – он решается при помощи : √a² = |a| = ±a.
Если перед вами задача, в которой не указано условие раскрытия скобок модуля, то избавляться от них не нужно – это и будет конечный результат. А если требуется их раскрыть, то необходимо указать знак ±. Например, нужно найти значение выражения √(2 * (4-b)) ². Его решение выглядит следующим образом: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| >
Модуль нуля равен нулю, а модуль любого положительного числа – ему самому. Если аргумент отрицательный, то после раскрытия скобок его знак меняется с минуса на плюс. На основании этого вытекает вывод, что модули противоположных чисел равны: |-х| = |х| = х.
Модуль комплексного числа находится по формуле: |a| = √b ² + c ², а |a + b| ≤ |a| + |b|. Если в аргументе присутствует в виде множителя целое положительное число, то его можно вынести за знак скобки, например: |4*b| = 4*|b|.
Отрицательным модуль быть не может, поэтому любое отрицательное число преобразуется в положительное: |-x| = x, |-2| = 2, |-1/7| = 1/7, |-2,5| = 2,5.
Если аргумент представлен в виде сложного числа, то для удобства вычислений допускается изменение порядка членов выражения, заключенного в прямоугольные скобки: |2-3| = |3-2| = 3-2 = 1, поскольку (2-3) меньше нуля.
Если перед вами задача, в которой не указано условие раскрытия скобок модуля, то избавляться от них не нужно – это и будет конечный результат. А если требуется их раскрыть, то необходимо указать знак ±. Например, нужно найти значение выражения √(2 * (4-b)) ². Его решение выглядит следующим образом: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| > 0, то в итоге получится 2 * |4-b| = 2 *(4 — b). В качестве неизвестного элемента также может быть задано конкретное число, которое следует принимать во внимание, т. к. оно будет влиять на знак выражения.
к. оно будет влиять на знак выражения.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
А вычисляется в соответствии с такими правилами:
Для краткости записи применяют |а|
. Так, |10| = 10; — 1 / 3 = | 1 / 3 |; | -100| =100 и т. д.
Так, |10| = 10; — 1 / 3 = | 1 / 3 |; | -100| =100 и т. д.
Всякой величине х
соответствует достаточно точная величина |х
|. И значит тождество
у
= |х
| устанавливает у
как некоторую функцию аргумента
х
.
График
этой функции
представлен ниже.
Для x
> 0 |x
| = x
, а для x
x
|= —x
; в связи с этим линия у = |x
| при x
> 0 совмещена с прямой у =х
(биссектриса первого координатного угла), а при х
у = -х
(биссектриса второго координатного угла).
Отдельные уравнения
включают в себя неизвестные под знаком модуля
.
Произвольные примеры таких уравнений — |х
— 1| = 2, |6 — 2х
| =3х
+ 1 и т. д.
Решение уравнений
содержащих неизвестную под знаком модуля базируется на том, что если абсолютная величина неизвестного числа х равняется положительному числу а, то само это число х равняется или а, или -а.
Например
:, если |х
| = 10, то или х
=10, или х
= -10.
Рассмотрим решение отдельных уравнений
.
Проанализируем решение уравнения |х
— 1| = 2.
Раскроем модуль
тогда разность х
— 1 может равняться или + 2, или — 2. Если х — 1 = 2, то х
= 3; если же х
— 1 = — 2, то х
= — 1. Делаем подставновку и получаем, что оба эти значения удовлетворяют уравнению.
Ответ.
Указанное уравнение имеет два корня: x
1 = 3, x
2 = — 1.
Проанализируем решение уравнения
| 6 — 2х
| = 3х
+ 1.
После раскрытия модуля
получаем: или 6 — 2х
= 3х
+ 1, или 6 — 2х
= — (3х
+ 1).
В первом случае х
= 1, а во втором х
= — 7.
Проверка.
При х
= 1 |6 — 2х
| = |4| = 4, 3x
+ 1 = 4; от суда следует, х
= 1 — корен ь
данного уравнения
.
При x
= — 7 |6 — 2x
| = |20| = 20, 3x
+ 1= — 20; так как 20 ≠ -20, то х
= — 7 не является корнем данного уравнения.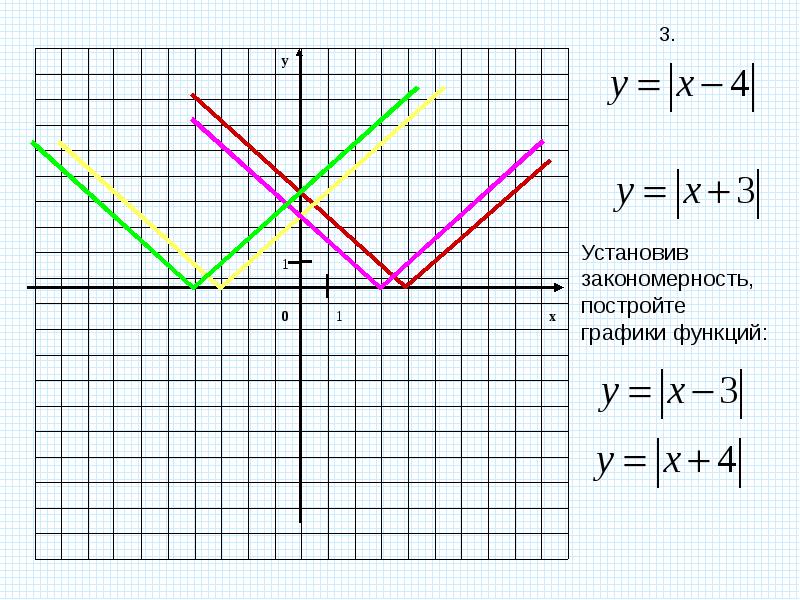
Ответ. У
уравнения единственный корень: х
= 1.
Уравнения такого типа можно решать и графически
.
Так решим, например
, графически уравнение |х-
1| = 2.
Первоначально выполним построение графика функции
у
= |x
— 1|. Первым начертим график функции у
=х-
1:
Ту часть этого графика
, которая расположена выше оси х
менять не будем. Для нее х
— 1 > 0 и потому |х
-1|=х
-1.
Часть графика, которая расположена под осью х
, изобразим симметрично
относительно этой оси. Поскольку для этой части х
— 1 х —
1|= — (х —
1). Образовавшаяся в результате линия
(сплошная линия) и будет графиком функции
у = |х
—1|.
Эта линия пересечется с прямой
у
= 2 в двух точках: M 1 с абсциссой -1 и М 2 с абсциссой 3. И, соответственно, у уравнения |х
— 1| =2 будет два корня: х
1 = — 1, х
2 = 3.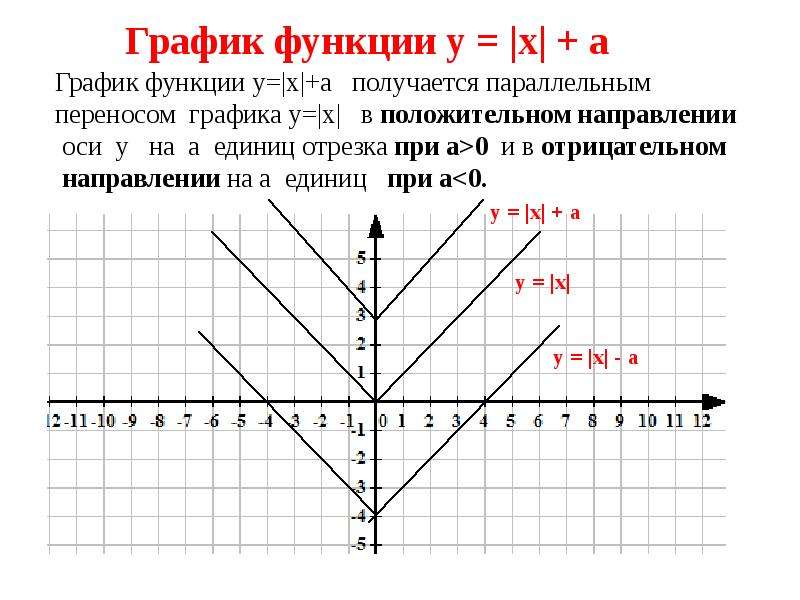
Одна из самых сложных тем для учащихся – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?
На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.
Но для начала вспомним определение модуля
. Итак, модулем числа a
называется само это число, если a
неотрицательно и -a
, если число a
меньше нуля.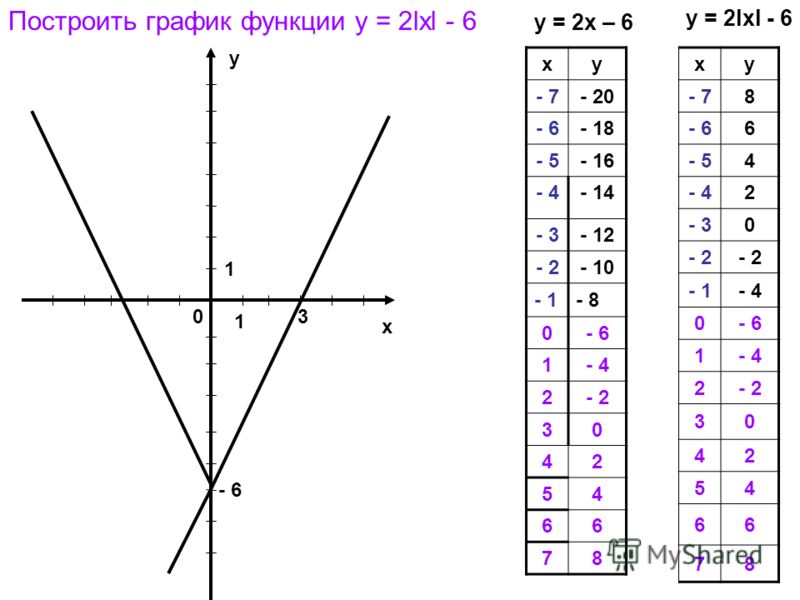 Записать это можно так:
Записать это можно так:
|a| = a, если a ≥ 0 и |a| = -a, если a
Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее координата. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.
Теперь перейдем непосредственно к решению уравнений.
1.
Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.
Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:
{±c, если с > 0
Если |x| = c, то x = {0, если с = 0
{нет корней, если с
1) |x| = 5, т.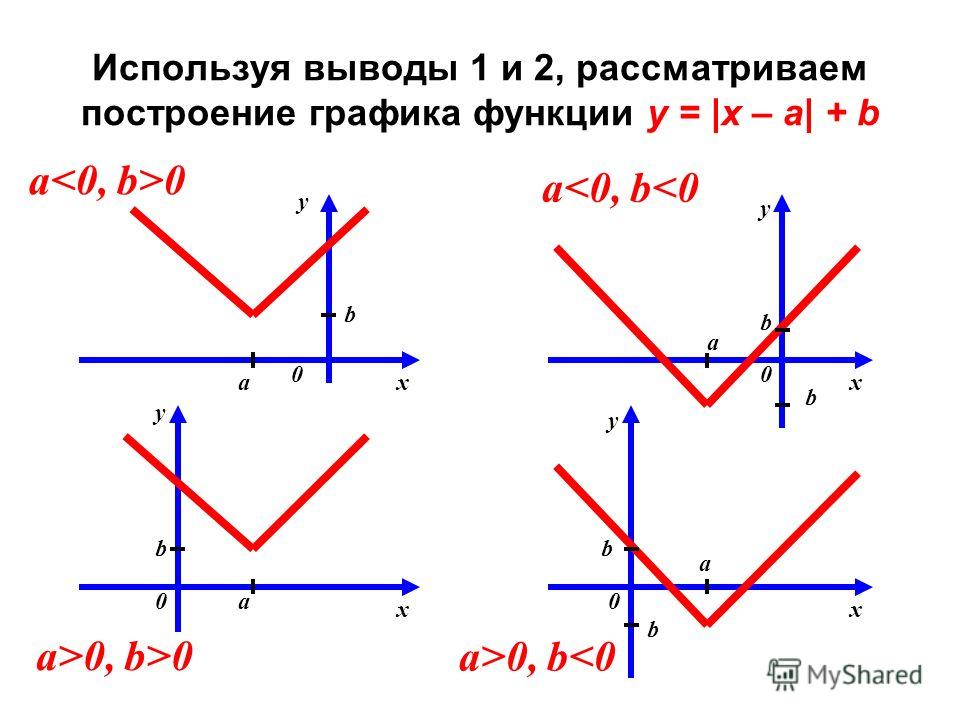 к. 5 > 0, то x = ±5;
к. 5 > 0, то x = ±5;
2) |x| = -5, т.к. -5
3) |x| = 0, то x = 0.
2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b
1) |x + 2| = 4, т.к. 4 > 0, то
x + 2 = 4 или x + 2 = -4
2) |x 2 – 5| = 11, т.к. 11 > 0, то
x 2 – 5 = 11 или x 2 – 5 = -11
x 2 = 16 x 2 = -6
x = ± 4 нет корней
3) |x 2 – 5x| = -8 , т.к. -8
3.
Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:
f(x) = g(x)
или f(x) = -g(x)
.
1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.
1. О.Д.З. 5x – 10 ≥ 0
2. Решение:
2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)
3. Объединяем О.Д.З. и решение, получаем:
Объединяем О.Д.З. и решение, получаем:
Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.
Ответ: x = 3
2) |x – 1| = 1 – x 2 .
1. О.Д.З. 1 – x 2 ≥ 0. Решим методом интервалов данное неравенство:
(1 – x)(1 + x) ≥ 0
2. Решение:
x – 1 = 1 – x 2 или x – 1 = -(1 – x 2)
x 2 + x – 2 = 0 x 2 – x = 0
x = -2 или x = 1 x = 0 или x = 1
3. Объединяем решение и О.Д.З.:
Подходят только корни x = 1 и x = 0.
Ответ: x = 0, x = 1.
4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).
1) |x 2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:
x 2 – 5x + 7 = 2x – 5 или x 2 – 5x +7 = -2x + 5
x 2 – 7x + 12 = 0 x 2 – 3x + 2 = 0
x = 3 или x = 4 x = 2 или x = 1
Ответ: x = 1, x = 2, x = 3, x = 4.
5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:
Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:
x 2 – 6|x| + 5 = 0. По свойству модуля x 2 = |x| 2 , поэтому уравнение можно переписать так:
|x| 2 – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:
t 2 – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:
|x| = 1 или |x| = 5
x = ±1 x = ± 5
Ответ: x = -5, x = -1, x = 1, x = 5.
Рассмотрим еще один пример:
x 2 + |x| – 2 = 0. По свойству модуля x 2 = |x| 2 , поэтому
|x| 2 + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:
t 2 + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:
|x| = -2 или |x| = 1
Нет корней x = ± 1
Ответ: x = -1, x = 1.
6.
Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.
1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:
3 – |x| = 4 или 3 – |x| = -4.
Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.
Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1
Ответ x = -7, x = 7.
2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:
3 + |x + 1| = 5 или 3 + |x + 1| = -5
|x + 1| = 2 |x + 1| = -8
x + 1 = 2 или x + 1 = -2. Нет корней.
Ответ: x = -3, x = 1.
Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.
Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам. Заработай деньги с помощью своих знаний на https://teachs.ru !
Заработай деньги с помощью своих знаний на https://teachs.ru !
Что такое модуль в математике
Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.
Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.
Свойства модуля
Важно помнить о следующих свойствах:
Модуль комплексного числа
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).
Этот направленный отрезок также является вектором, представляющим комплексное число a + bi
, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi
.
Как решать уравнения с модулем
Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения.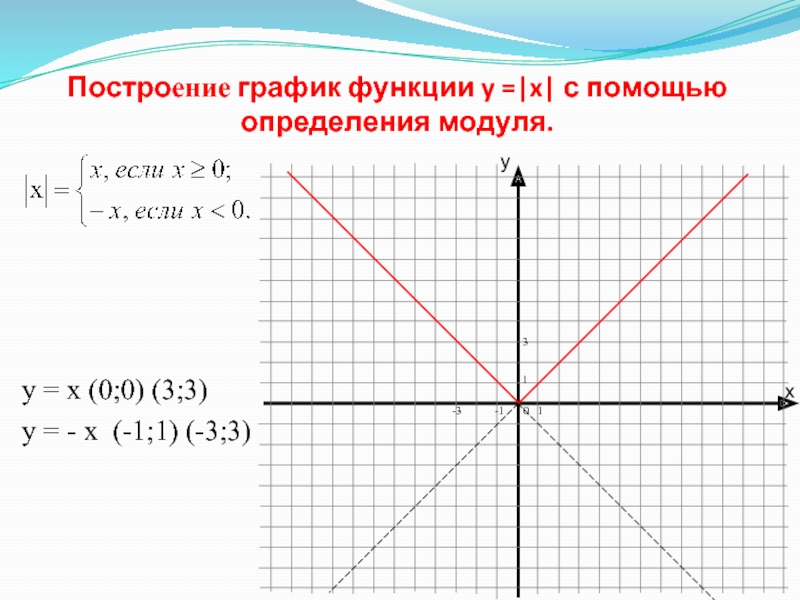 Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.
Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.
Уравнения типа |x| = a
Уравнение |x| = a имеет два ответа x = a и x = –a
, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.
Равенство с абсолютной величиной не имеет решения, если величина отрицательная.
Если |x|
Уравнения типа |x| = |y|
Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.
Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).
Уравнения типа |x| = y
Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.
Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:
Решение неравенств с модулем
Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.
Уравнения вида |x| = a
Пример 1
(алгебра 6 класс). Решить: |x| + 2 = 4.
Решение.
Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.
После перемещения константы вправо получено: |x| = 2
.
Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2
и −2
.
Ответ:
2
и −2
.
Пример 2
(алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.
Решение.
Первое, что нужно сделать, это найти точки, где абсолютное значение изменится.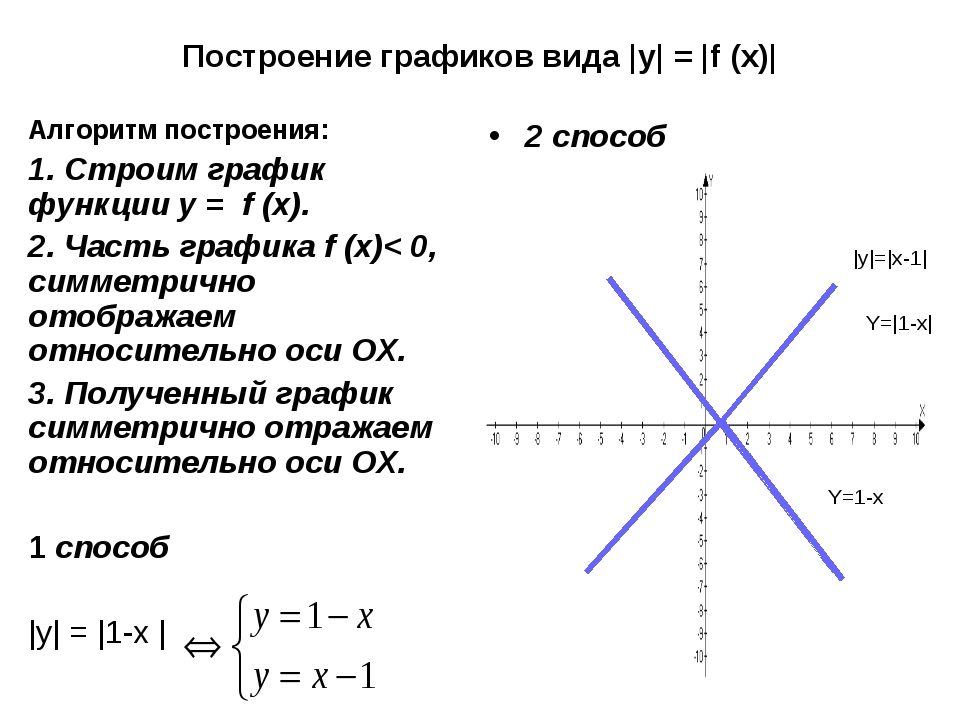 Для этого выражение приравнивается к 0
Для этого выражение приравнивается к 0
. Получено: x = –2
.
Это означает, что –2
– поворотная точка.
Разделим интервал на 2 части:
- для x + 2 ≥ 0
[−1; + ∞).
- для х + 2
Общим ответом для этих двух неравенств является интервал (−∞; –3].
Окончательное решение –
объединение ответов отдельных частей:
x
∈
(–∞; –3]
∪
[–1; + ∞).
Ответ:
x
∈
(–∞; –3]
∪
[–1; + ∞)
.
Уравнения вида |x| = |y|
Пример 1
(алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.
Решение:
Ответ:
x 1 = 3; x 2 = −
1.
Пример 2
(алгебра 8 класс). Решить неравенство:
Решение:
Уравнения вида |x| = y
Пример 1
(алгебра 10 класс). Найти x:
Решение:
Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни.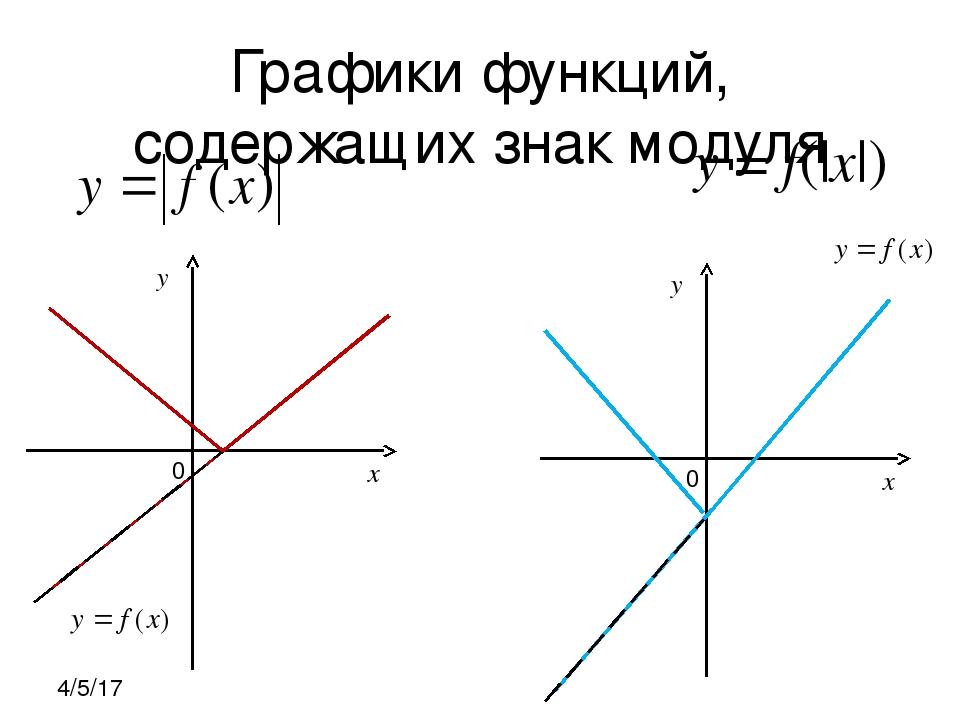 Из системы видно, что не лежит в промежутке.
Из системы видно, что не лежит в промежутке.
Ответ:
x = 0
.
Модуль суммы
Модуль разности
Абсолютная величина разности двух чисел x
и y равна расстоянию между точками с координатами X
и Y
на координатной прямой.
Пример 1.
Пример 2.
Модуль отрицательного числа
Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,
Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.
Модуль нуля
Известно свойство:
Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.
Модуль в квадрате
Модуль в квадрате всегда равен выражению в квадрате:
Примеры графиков с модулем
Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики.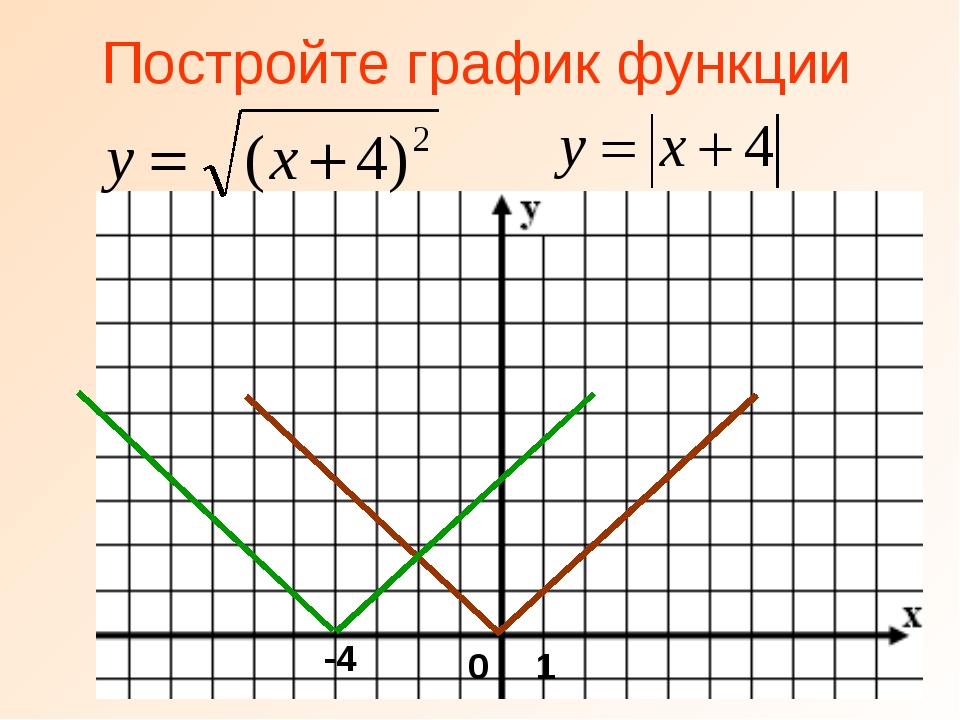 Рассмотрим такие задания.
Рассмотрим такие задания.
Пример 1.
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.
Решение:
Объяснение
: из рисунка видно, что график симметричен относительно оси Y.
Пример 2
. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.
Решение:
Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2
в функции g (x))
.
Координата вершины x
(точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y
– это значение, на которое график сдвигается вверх или вниз.
Строить такие графики можно с помощью онлайн приложений для построения.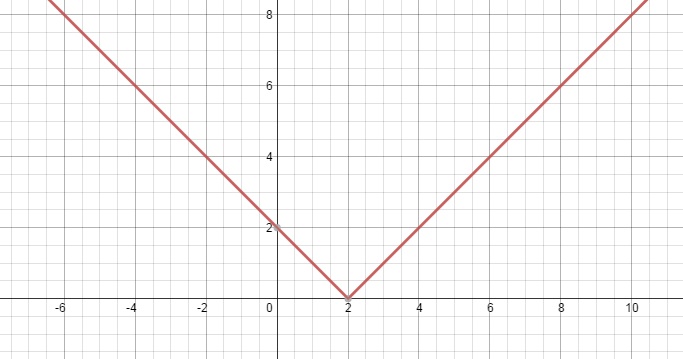 С их помощью можно наглядно посмотреть, как константы влияют на функции.
С их помощью можно наглядно посмотреть, как константы влияют на функции.
Метод интервалов в задачах с модулем
Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.
Для использования метода нужно совершить следующие действия:
- Приравнять каждое выражение к нулю.
- Найти значения переменных.
- Нанести на числовую прямую точки, полученные в пункте 2.
- Определить на промежутках знак выражений (отрицательное или положительное значение) и нарисовать символ – или + соответственно. Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
- Решить неравенства с полученными знаками.
Пример 1
. Решить методом интервалов.
Решение:
Как построить график модуль matplotlib Python
Линейный график
Решил построить несложный график.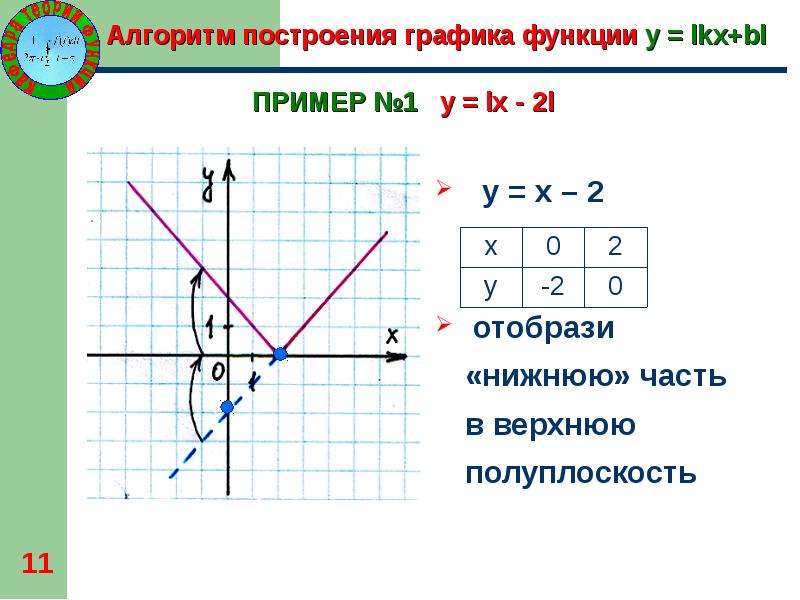 Думал, что будет сложно. Оказалось, что это не сложно составить график. Возможно у меня простое решение. Есть статья: Простой график. Делал все по ней. Описания в ней мало, мне пришлось самому описывать действия функций. Для понимания я переделал описания действий.
Думал, что будет сложно. Оказалось, что это не сложно составить график. Возможно у меня простое решение. Есть статья: Простой график. Делал все по ней. Описания в ней мало, мне пришлось самому описывать действия функций. Для понимания я переделал описания действий.
Для генерации графика используется модуль matplotlib. На вашем компьютере может не быть этой библиотеки. Используйте pip: pip install matplotlib. О том как пользоваться pip смотрите статью: Как загружать библиотеки с pip Python. Предлагаю вам поэкспериментировать с координатами для линий y1…y4. Если вы сгенерируете налету график при помощи функции plt.show(), то появится окно с различными кнопками. В окне есть небольшой блок меню. Вы сможете увеличить векторный график. Можете сжать его по вертикали и горизонтали. Также сможете сохранить его в разных форматах. Показать и сохранить график можно, но выполнение этих действий в одном скрипте приведёт к ошибке. Выберите одно из действий. Для простоты понимания я разукрасил линии в разные цвета и добавил одну черную линию.
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
# от -5 до 2 сделать 100 точек.Чем больше точек, тем точнее график.
x = np.linspace(-5, 2, 100)
# y1...y4 - линии одного графика, для каждой линии свой набор точек.
y1 = x**3 + 5*x**2 + 10
y2 = 3*x**2 + 10*x
y3 = 6*x + 10
y4 = 5*x**2 + 10
# будет 1 график, на нем 4 линии:
fig, ax = plt.subplots()
# функция y1(x), синий, надпись y(x)
ax.plot(x, y1, color="blue", label="голубая линия")
# функция y2(x), красный, надпись y'(x)
ax.plot(x, y2, color="red", label="красная линия")
# функция y3(x), зеленый, надпись y''(x)
ax.plot(x, y3, color="green", label="зелёная линия")
# функция y3(x), зеленый, надпись y''(x)
ax.plot(x, y4, color="black", label="черная линия")
# подпись у горизонтальной оси х
ax.set_xlabel("x")
# подпись у вертикальной оси y
ax.set_ylabel("y")
# показывать условные обозначения
ax.legend()
'''
Тут нужно сделать выбор в пользу одного действия. Либо вы показываете на окне
векторный график, либо записываете график в картинку png
'''
#показать рисунок
plt. show()
# сохранить в файл 1.png
#fig.savefig('1.png')
show()
# сохранить в файл 1.png
#fig.savefig('1.png')
линейный график
Пирог график
Этот график напоминает по виду пирог. Пирог будет поделён на разные части. В списке sizes у меня 4 значения. Из-за этого пирог поделён на 4 части.
Круговая диаграмма. В статье мало описания, поэтому пришлось самому описывать действия.
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
'''
График пирог, блоки будут расположены против часовой стрелки:
labels - названия кусков пирога
'''
labels = 'jQuery', 'PHP', 'Firebird', 'BASH'
sizes = [36,36,11,2]
''
explode - это отступ (разрыв) от основных частей пирога.
если поставите одни нули, то все блоки будут прижаты друг к другу.
''
explode = (0.1, 0.1, 0, 0)
fig1, ax1 = plt.subplots()
'''
sizes - размеры кусков в процентах
explode - отступы
labels - названия кусков
autopct - ?
shadow - тень
startangle - начальный угол, изменяя его, вы поворачиваете все куски.
'''
ax1.pie(sizes, explode=explode, labels=labels, autopct='ų. 1f%%',
shadow=True, startangle=90)
#Равное соотношение сторон гарантирует, что пирог нарисован как круг.
ax1.axis('equal')
# показать график
plt.show()
1f%%',
shadow=True, startangle=90)
#Равное соотношение сторон гарантирует, что пирог нарисован как круг.
ax1.axis('equal')
# показать график
plt.show()
линейный график
просмотры: 13108,
уровень: лёгкий уровень,
рейтинг: 5,
дата: 2017-10-03 22:40:30
Комментарии:
График функции модуля
В этом уроке мы узнаем, как построить графики функций, таких как | x — 4 |, | x + 1 |, | 2x — 1 | и т. Д.
Для их построения мы снова воспользуемся определением, как и для | x |. Начнем с первого.
\ (| x — 4 | = \ left \ {\ begin {matrix}
x, & когда \ x \ ge4 \\
-x, & когда \ x <4
\ end {matrix} \ right. \)
Это означает, что для построения графика y = | x — 4 | мы должны построить график
y = x — 4, когда x ≥ 4
y = 4 — x, когда x <4
То есть, для x ≥ 4 мы нарисуем линию, наклон которой равен 1, а точка пересечения оси y равна –4. Для x <4 мы нарисуем линию с наклоном –1 и пересечением по оси Y 4.
Для x <4 мы нарисуем линию с наклоном –1 и пересечением по оси Y 4.
А вот как бы выглядел график.
Это похоже на график | x |, но «сдвинут» вправо.
Попробуем второй. Вернемся к определению.
\ (| x + 1 | = \ left \ {\ begin {matrix}
x + 1, & когда \ x \ ge-1 \\
-x-1, & когда \ x <-1
\ end {matrix } \ right. \)
Это означает, что для построения графика y = | x + 1 | мы должны построить график
y = x + 1, когда x ≥ –1
y = –x — 1, когда x <–1
А вот как бы выглядел график.
Еще раз аналогично графику | x |, но со смещением влево.
Вы видите закономерность? Можете ли вы построить график | x — 2 | и | x + 3 |?
Вот они.
| x — 2 |
| x + 3 |
Если вы не можете понять, почему графики должны выглядеть так, попробуйте следовать определению, как в первых двух случаях.
Возьмем последний пример, | 2x — 1 |.
\ (| 2x — 1 | = \ left \ {\ begin {matrix}
2x-1, & когда \ x \ ge1 / 2 \\
-2x + 1, & когда \ x <1/2
\ end { матрица} \ right. \)
Это означает, что для построения графика y = | 2x — 1 | мы должны построить график
y = 2x — 1, когда x ≥ 1/2
y = –2x + 1, когда x <1/2
А вот как бы выглядел график.
А вот апплет, который показывает график y = | ax + b |.
Перетащите ползунки, чтобы изменить значения a и b, и посмотрите, как изменится график.На что обратить внимание
- график всегда имеет V-образную форму
- график всегда лежит выше оси X (кроме одной точки)
- крутизна «V» контролируется
- расположение вершины контролируется b (и a)
Вот и все для этого урока. В ближайшее время мы будем использовать эти графики для решения уравнений и неравенств. Это будет весело!
Функция модуля
Функция модуля y = │x│
Абсолютное значение x определяется как
Это всегда дает положительный результат.
Пример
y = 3x 2 + 6x-2 имеет график
В то время как
y = | 3x² + 6x − 2 | имеет график
Обратите внимание, как были отрицательные части
отражается по оси абсцисс.
Пример
y = | 3tanx |
y = | 3x + 2 |
Нечетные и четные функции
Нечетные функции имеют полуоборотную симметрию относительно начала координат,
поэтому f (-x) = — f (x)
Пример
y = x 3
y = x 5 −3x
Пример
Покажите, что x 5 + 3x 3 — нечетная функция.
Четные функции симметричны относительно оси Y
поэтому f (-x) = f (x)
Пример
y = x 4 — 1
Пример
Является ли x 6 + 3x 2 четной функцией?
Асимптоты
Калькулятор асимптот Symbolab
Асимптота кривой — это прямая линия, которая
кривая приближается, но не достигает.
Пример f (x) = 1 / x
График y = 1 / x имеет вертикальную асимптоту x = 0
и горизонтальная асимптота y = 0.
Слева от прямой x = 0 f (x) стремится к — ∞
поскольку x стремится к нулю.
Справа от прямой x = 0 f (x) стремится к ∞
поскольку x стремится к нулю.
Пример f (x) = (x-3) / (x 3 +1)
График y = (x-3) / (x 3 +1) имеет вертикальную асимптоту x = -1
и горизонтальная асимптота y = 0.
Слева от прямой x = -1, f (x) стремится к ∞
поскольку x стремится к -1.
Справа от прямой x = -1, f (x) стремится к -∞
поскольку x стремится к -1.
Пример f (x) = (x + 1) (x − 3) / (x + 3) (x − 4)
График имеет вертикальные асимптоты x = -3 и x = 4
и горизонтальная асимптота y = 1
Нахождение асимптот
Вертикальные асимптоты находятся с учетом
что делает знаменатель нулевым.
Требуется горизонтальная и наклонная асимптоты
немного дальнейших действий.
Используйте алгебраическое деление, чтобы уменьшить функцию.
Частное становится асимптотой.
Пример
Найти асимптоты функции
Альтернативно: —
Можно найти асимптоты, параллельные оси x
приравнивая коэффициент максимальной мощности
x до нуля.Те, которые параллельны оси y, могут быть
найдено приравниванием коэффициента максимальной мощности
y к нулю.
Чтобы найти наклонные асимптоты, подставьте y = mx + c
в уравнение и приравняем коэффициенты
двух старших степеней x к нулю.
Пример
Построение асимптоты
Чтобы набросать функцию, которая имеет асимптоты, выполните следующие действия: —
- Определите любые вертикальные асимптоты
- Определите любые горизонтальные или наклонные асимптоты
- Определите точку пересечения оси y
- Определите точку пересечения по оси x
- Найти стационарные точки
- Определить характер стационарных точек
- Исследуйте, что происходит, когда значения приближаются к бесконечности
- Набросок и аннотирование
Пример
Используя приведенный выше пример, нарисуйте функцию
Вертикальные асимптоты находятся при нулевом знаменателе:
Горизонтальная и наклонная асимптоты находятся делением на дробь:
Перехват по оси y происходит, когда x = 0
Перехват по оси x происходит, когда y = 0
Чтобы найти стационарные точки, установите первую производную
функции до нуля, затем факторизуйте и решите.
Нарисуйте график
Другой пример
набросок функции
Вертикальные асимптоты:
У — перехват:
Х — перехват:
Стационарных точек:
Найдите характер поворотных точек
Эскиз
© Александр Форрест
Абсолютные функции значений
Функция абсолютного значения — это функция, которая содержит алгебраическое выражение в символах абсолютного значения.Напомним, что абсолютное значение числа — это его расстояние от 0 на числовой прямой.
Родительская функция с абсолютным значением, записанная как f (x) = | x |, определяется как
f (x) = {x, если x> 00, если x = 0 — x, если x <0
Чтобы построить график функции абсолютного значения, выберите несколько значений x и найдите несколько упорядоченных пар.
| x | y = | х | |
| −2 | 2 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
Постройте точки на координатной плоскости и соедините их.
Обратите внимание на то, что график имеет V-образную форму.
(1) Вершина графа — (0,0).
(2) Ось симметрии (x = 0 или ось y) — это линия, разделяющая график на две совпадающие половины.
(3) Домен — это набор всех действительных чисел.
(4) Диапазон — это набор всех действительных чисел, больших или равных 0. То есть y≥0.
(5) Оба пересечения по оси x и y равны 0.
Вертикальный сдвиг
Чтобы перевести функцию абсолютного значения f (x) = | х | по вертикали можно использовать функцию
г (х) = е (х) + к.
Когда k> 0, график g (x) переводит k единиц вверх.
Когда k <0, график g (x) переводит k единиц вниз.
Сдвиг по горизонтали
Чтобы перевести функцию абсолютного значения f (x) = | х | по горизонтали можно использовать функцию
г (х) = е (х-ч).
Когда h> 0, график f (x) переводится на h единиц вправо, чтобы получить g (x).
Когда h <0, график f (x) переводится на h единиц влево, чтобы получить g (x).
Растяжение и сжатие
Растяжение или сжатие функции абсолютного значения y = | х | определяется функцией y = a | х | где а — постоянная. График открывается, если a> 0, и открывается вниз, если a <0.
Для уравнений абсолютного значения, умноженных на константу (например, y = a | x |), если 0 1, он растягивается. Кроме того, если a отрицательно, график открывается вниз, а не вверх, как обычно.
Кроме того, если a отрицательно, график открывается вниз, а не вверх, как обычно.
В более общем виде уравнение для функции абсолютного значения имеет вид y = a | х-ч | + к. Также:
- Вершина графа — (h, k).
- Область графа состоит из всех действительных чисел, а диапазон равен y≥k, когда a> 0.
- Область графа состоит из всех действительных чисел, а диапазон равен y≤k, когда a <0.
- Ось симметрии x = h.
- Он открывается, если a> 0, и открывается вниз, если a <0.
- График y = | х |
можно перевести h единиц по горизонтали и k единиц по вертикали, чтобы получить график
у = а | х-ч | + к. - График y = a | х | шире графика y = | х | если | a | <1 и уже, если | a |> 1.
Модуль 02 — Абсолютное значение
Управляйте настройками файлов cookie
Вы можете управлять своими предпочтениями в отношении того, как мы используем файлы cookie для сбора и использования информации, пока вы находитесь на веб-сайтах TI, изменяя статус этих категорий.
| Категория | Описание | Разрешить |
|---|---|---|
| Аналитические и рабочие файлы cookie | Эти файлы cookie, включая файлы cookie из Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI и видеть, как посетители перемещаются по нашим сайтам.Это помогает нам улучшить работу сайтов TI (например, облегчая вам поиск информации на сайте). | |
| Рекламные и маркетинговые файлы cookie | Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах.Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламные объявления в соответствии с вашими интересами, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы. | |
| Функциональные файлы cookie | Эти файлы cookie помогают идентифицировать вас и хранить ваши действия и информацию об учетной записи для обеспечения расширенной функциональности, в том числе более персонализированного и актуального опыта на наших сайтах.Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. | |
| Файлы cookie социальных сетей | Эти файлы cookie позволяют идентифицировать пользователей и контент, подключенный к онлайн-социальным сетям, таким как Facebook, Twitter и другим платформам социальных сетей, и помогают TI улучшить охват социальных сетей. | |
| Строго необходимо | Эти файлы cookie необходимы для работы сайтов TI или для выполнения ваших запросов (например, для отслеживания того, какие товары вы поместили в корзину на сайте TI.com, для доступа к защищенным областям сайта TI или для управления настроенными вами настройки файлов cookie). | Всегда на связи |
Алгебра: необычные графики абсолютных значений
Причудливые графики абсолютных значений
Последнее слово о графическом отображении линейных уравнений, прежде чем я завершу этот раздел.Помните, в разделе «Решение основных уравнений» вы узнали, что уравнения, содержащие x в абсолютных значениях, требуют немного другого метода решения, чем обычные уравнения неабсолютных значений? Чтобы получить ответ, вам пришлось разбить уравнение на две части. Что ж, вам нужно изобразить их немного иначе, чем обычные линейные уравнения. В то время как график нормального линейного уравнения выглядит как линия, график линейного уравнения абсолютного значения выглядит как «V». По сути, это линия с изломом, острая точка (или вершина ), где график меняет направление.
На рис. 5.8 я нарисовал графики y = x — 3 и y = | x — 3 |. Оба графика имеют одинаковые координаты для их значений x больше 3.
Однако, когда x меньше 3, левый график опускается ниже оси x (это означает, что его значения y отрицательны. ). Видите, как правый график делает резкий поворот, чтобы вообще не опускаться ниже оси x ? Это потому, что уравнение, показанное на правом графике, устанавливает y равным абсолютному значению! Помните, что абсолютные значения никогда не могут быть отрицательными, и график отражает это, избегая отрицательных значений y, таких как чума.
Рисунок 5.8 График y = | x — 3 | принимает решительные меры, чтобы избежать отрицательных значений, в отличие от y = x — 3.
Лучший способ построить график линейного абсолютного значения — это точно определить, где находится его вершина, построить ее, а затем построить одну точку вправо и одну точку слева от него, чтобы вы могли нарисовать ветви графика.
Предостережения Келли
Если вы рисуете график абсолютных значений, и он опускается ниже оси x , это не обязательно означает, что вы сделали это неправильно! Некоторые линейные уравнения абсолютных значений будут иметь , но будут иметь отрицательные значения и .Например, если вы подставите x = 2 в уравнение y = | x | — 5, получится y = -3.
Пример 5 : Постройте уравнение y = — 1 2 | x + 4 | — 3.
Решение : Чтобы найти вершину графа, установите только содержимое абсолютных значений равным 0 и решите для x .
Теперь найдите соответствующее значение для y , когда x = — 4, чтобы получить пару координат для вершины.(Вставьте x = — 4 обратно в исходное уравнение.)
- y = 1 2 | (-4) + 4 | — 3
- y = — 1 2 (0) — 3
- y = -3
Рисунок 5.9 График y = — 1 2 | x + 4 | — 3, решение примера 5. Обратите внимание, что эта координатная плоскость смещена, чтобы выделить квадрант III.
У вас проблемы
Задача 5. Постройте уравнение y = | 2 x — 4 | +1.
Вершина графика находится в точке (- 4, -3), поэтому нанесите эту точку на координатную плоскость. Теперь выберите одно значение x слева от вершины и одно справа (другими словами, выберите одно значение x , которое меньше -4, и другое, которое больше), и вставьте их оба в исходное уравнение. Я выбрал x = — 6 и x = -2.
- y = — 1 2 | (-6) + 4 | -3 y = 1 2 | (-2) + 4 | — 3
- y = 1 2 | -2 | — 3 y = 1 2 | 2 | — 3
- y = 1 2 (2) — 3 y = — 1 2 (2) — 3
- y = -1 — 3 y = — 1-3
- y = -4 y = -4
Постройте полученные пары координат, (-6, -4) и (-2, -4), каждый раз рисуя линию, начинающуюся в вершину и проходит через одну из точек, как показано на рисунке 5.9.
Выдержки из Полное руководство для идиотов по алгебре 2004 У. Майкла Келли. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и Barnes & Noble.
Узнайте, как построить график функций абсолютного значения
В этом видео описываются функции абсолютного значения и их графическое представление.После того, как вы закончите этот урок, просмотрите все наши уроки Алгебры 1 и попрактикуйтесь.
Функции абсолютного значения аналогичны обычным линейным функциям, за исключением того, что абсолютное значение элементов в квадратных скобках никогда не может быть отрицательным. Абсолютное значение любого числа является мерой его расстояния от 0, поэтому график функции абсолютного значения будет иметь форму буквы «V».
Сдвиг — это сдвиг функции на координатной плоскости. Функцию абсолютного значения можно смещать по вертикали и горизонтали.
Если константа добавляется / вычитается за пределами столбцов абсолютного значения (например), функция сдвигает вверх или вниз указанное количество единиц («+» = вверх, «-» = вниз)
Если константа добавляется / вычитается в пределах столбцов абсолютного значения (), функция сдвигает влево или вправо на указанное количество единиц. ( *** «+» = сдвиг в сторону ЛЕВО , «-» сдвиг в сторону ВПРАВО *** )
Функция абсолютного значения также может быть расширена или сжата.
Если функция умножается на константу больше единицы (), функция абсолютного значения СЖИМАЕТ (уже).
Если функция умножается на константу, меньшую единицы (), функция абсолютного значения РАСТЯГИВАЕТ (шире).
Построение графиков может быть выполнено путем создания таблицы и ввода значений для поиска координат.
Стенограмма видеоурока
Давайте рассмотрим график функций абсолютного значения.
Итак, фактическая базовая линия —
.
Итак, если тогда,
тогда ,
тогда ,
тогда ,
тогда ,
тогда ,
, а затем.
Теперь давайте изобразим это, используя координаты выше.
Наша линия выглядит как буква «V».
Давайте посложнее.
Например:
Рассмотрим значение и.
Если, то
тогда ,
тогда ,
тогда ,
тогда ,
тогда ,
, а затем.
Если мы построим график, у нас будет еще одна линия, которая выглядит как буква «V».
Но поскольку мы прибавили к абсолютному значению, мы сдвинули всю функцию вверх на точку.
Приведем еще один пример.
Рассмотрим значение и.
Если тогда,
тогда,
тогда,
потом,
потом,
потом,
и потом.
Давайте теперь изобразим это в виде графика.
Выглядит так же, но функциональная строка смещена влево точечно по сравнению с нашим первым примером.
Итак, если мы собираемся добавить число после того, как получим абсолютное значение, мы будем двигаться вверх.
И если мы прибавим число к значению до того, как вы получите абсолютное значение, мы переместимся влево.
Вот более графическое представление:
, затем мы продвигаемся на это число вверх;
, если мы уменьшаемся на это число;
, тогда если мы пойдем налево по этому номеру;
, а если потом переместимся вправо на это число.
Например, у нас есть, тогда мы будем двигаться вправо по пятнам.
Давайте посмотрим на эти два примера:
Давайте нарисуем обычный график абсолютных значений в качестве нашего базового графика.
Чтобы нарисовать примеры, применим приведенные выше правила.
Итак, переместим точки влево и вверх.
Теперь, мы собираемся двигаться в нужные места и вниз по пятнам.
Мы снова начнем с графика абсолютных значений.
Например, у нас
, мы умножим абсолютное значение на постоянное число, большее чем.
Вместо обычного уклона у нас будет уклон на это число круче. В нашем примере это пятна.
Давай
У нас получится линия, по которой наклон идет вверх по точкам.
Давайте посмотрим, что произойдет, если мы умножим абсолютное значение на дробь.
Тогда у нас получится менее крутая линия.
Леска будет шире обычной.
Теперь давайте посмотрим, что произойдет, если перед абсолютным значением будет отрицательное значение.
Здесь наша линия будет перевернута по сравнению с обычной функцией абсолютного значения.
Давай
У нас будет линия, которая идет вниз по точкам.
Приведем еще один пример.
Здесь отрицательное значение, поэтому наша линия будет перевернута, поэтому мы переместимся влево и пройдем вверх.
Стратегии решения проблем для количественного мышления Meas
Иногда вы можете добавить к геометрической фигуре полезные линии, точки или окружности, чтобы облегчить решение проблемы. Вы также можете добавить любую заданную информацию — а также любую новую информацию по мере ее получения — к фигуре, чтобы вам было легче увидеть взаимосвязи внутри фигуры, например, длину отрезка линии или величину угла.
• Эта стратегия используется в следующем примере вопроса.
Это вопрос с несколькими вариантами ответа — выберите один вариант ответа.
На рисунке выше показан график функции f, определенной для всех чисел x. Для какой из следующих функций g, определенных для всех чисел x, график g пересекает график f?
(А)
(В)
(В)
(Г)
(Д)Пояснение
Вы можете видеть, что все пять вариантов являются линейными функциями, графики которых представляют собой линии с различными наклонами и пересечениями по оси Y.График варианта A представляет собой линию с наклоном 1 и точкой пересечения по оси Y, показанной на следующем рисунке.
Ясно, что эта линия не будет пересекать график f слева от оси y. Справа от оси y график f представляет собой линию с наклоном 2, который больше, чем наклон 1. Следовательно, по мере увеличения значения x значение y увеличивается для f быстрее, чем для g, и, следовательно, графики не пересекаются справа от оси y. Вариант B также исключен.Обратите внимание, что если бы точка пересечения по оси Y любой из линий в вариантах A и B была больше или равна 4, а не меньше 4, они пересекали бы график f.
Варианты C и D — это прямые с наклоном 2 и пересечением по оси y меньше 4. Следовательно, они параллельны графику f (справа от оси y) и, следовательно, не будут его пересекать. Любая линия с наклоном больше 2 и точкой пересечения по оси Y меньше 4, например линия в Варианте E, будет пересекать график f (справа от оси Y).Правильный ответ — выбор E,
.


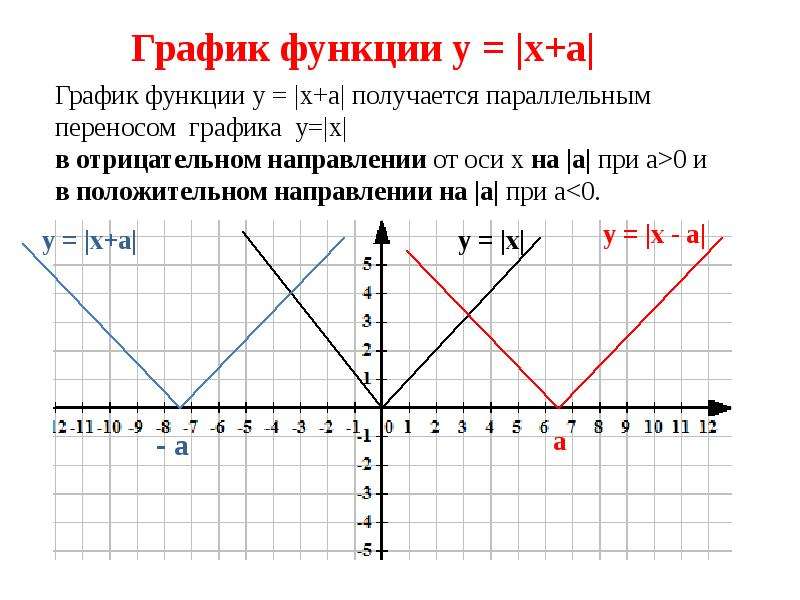
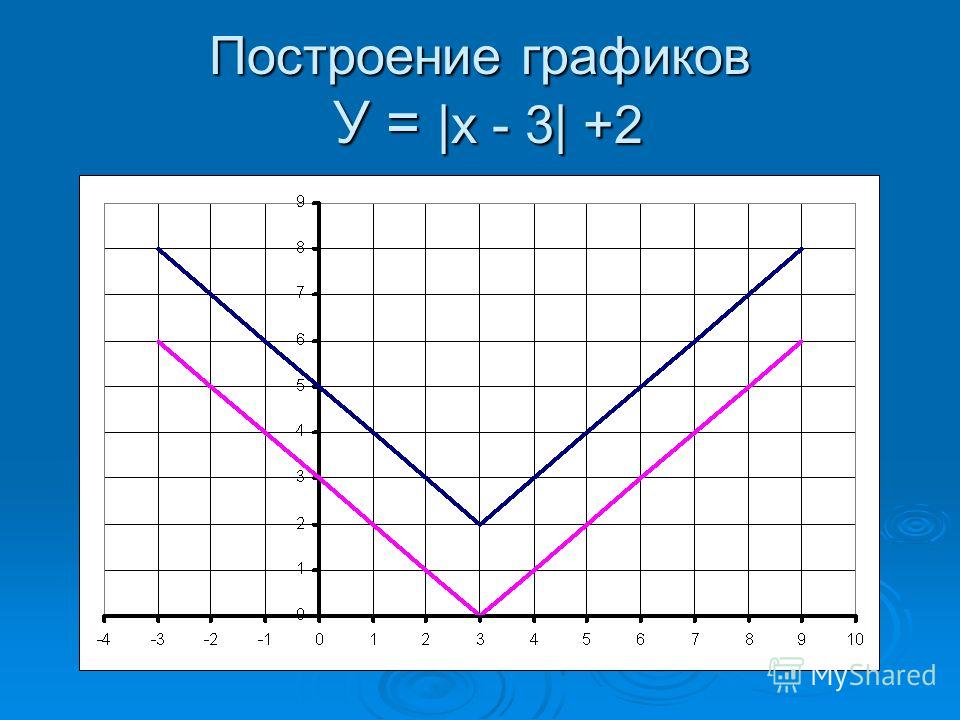 3$.
3$.
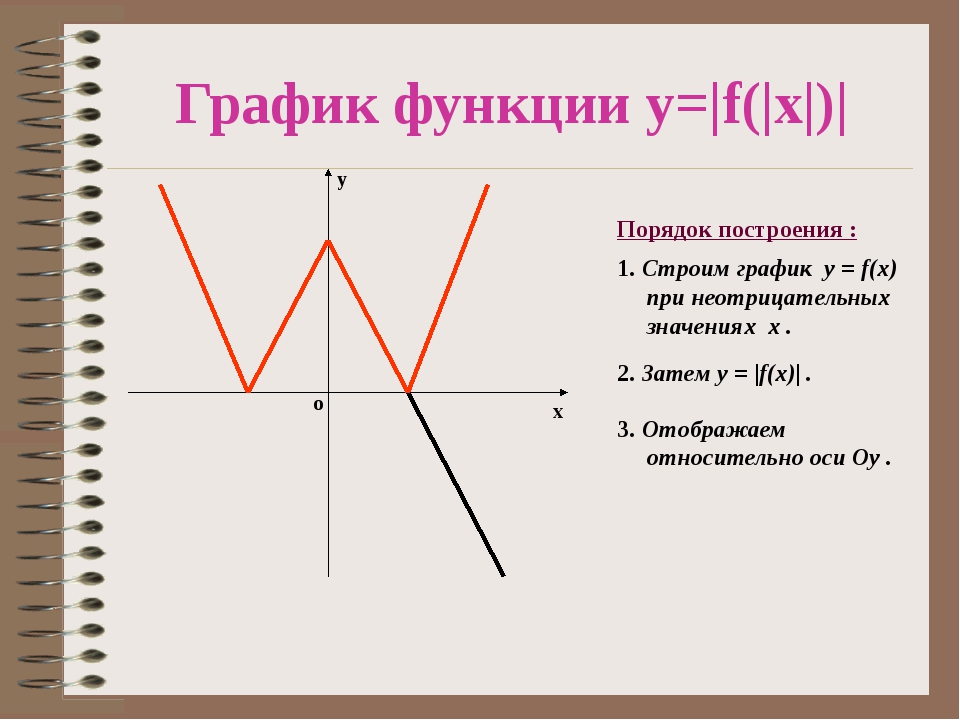 Значит, графики таких функций симметричны относительно оси 0y.
Значит, графики таких функций симметричны относительно оси 0y.
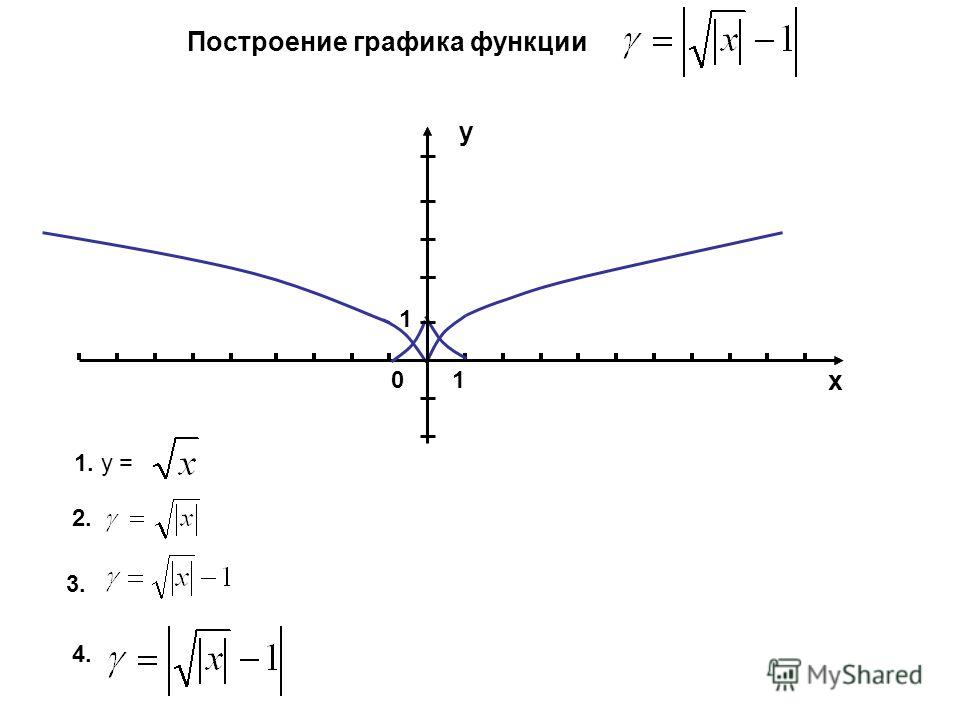 Изобразить график функции y = |-x 2 + 2|x| – 1|.
Изобразить график функции y = |-x 2 + 2|x| – 1|.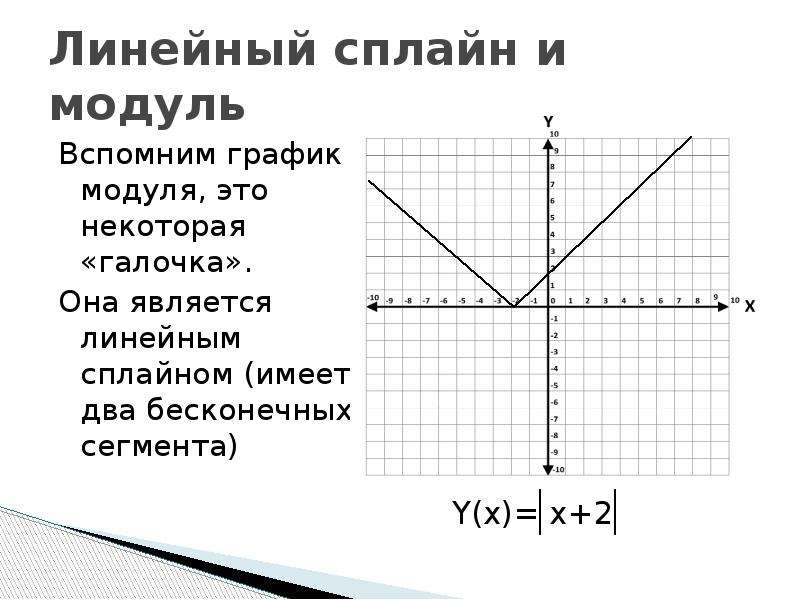 Для этого возвращаемся к алгоритму 2.
Для этого возвращаемся к алгоритму 2.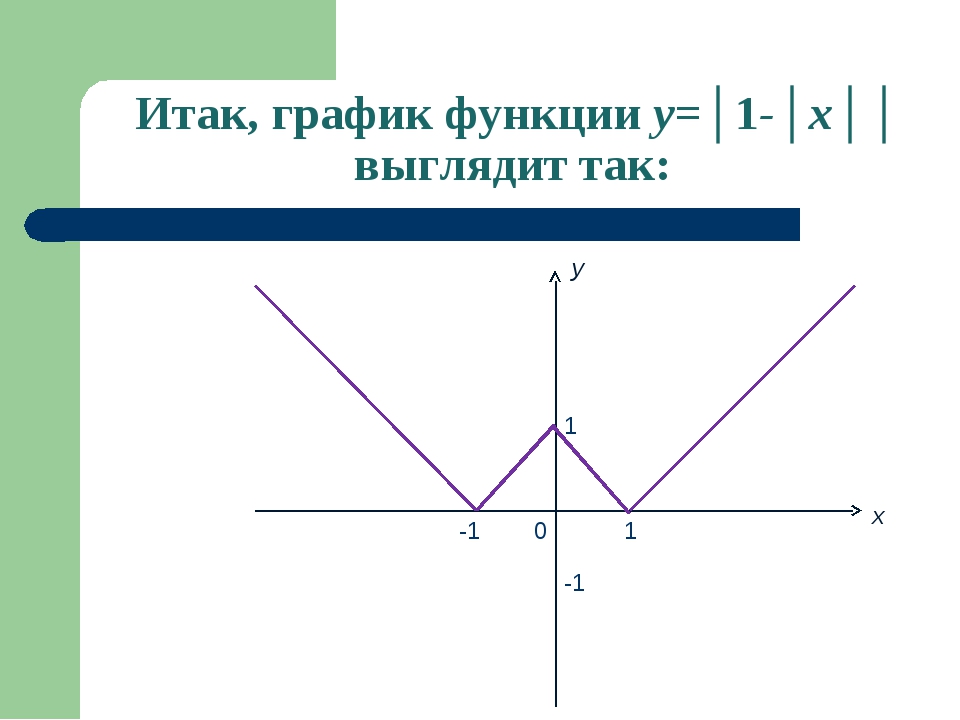 Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».
Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций». На рисунке пример для k
На рисунке пример для k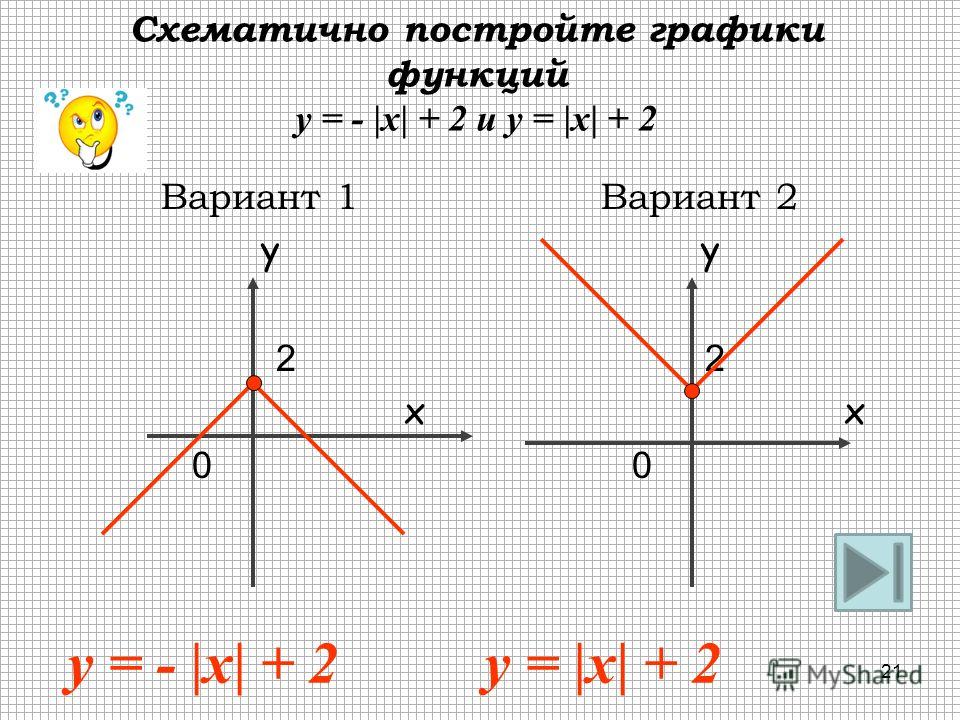 Случаи с коэффициентами изучаются в разделе «Движение графиков функций».
Случаи с коэффициентами изучаются в разделе «Движение графиков функций». Здесь пример для y = 2 x
Здесь пример для y = 2 x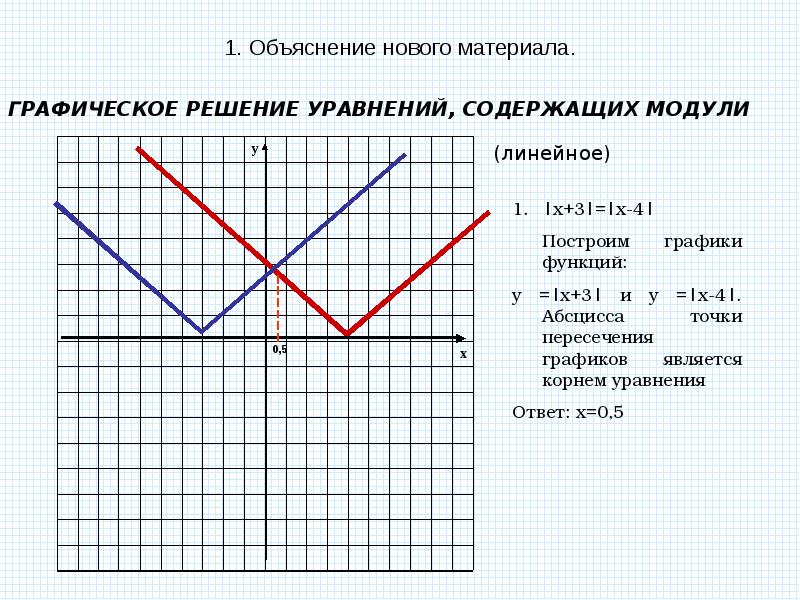 Графики функции существенно зависят от значения параметра a
Графики функции существенно зависят от значения параметра a