x

экспонента от х (e в степени x)

sqrt(x)

квадратный корень из x

sign(x)

функция знака: -1 если x<0, 1 если x>0 и 0 если x=0

Тригонометрические функции

sin(x)

синус х

cos(x)

косинус х

tg(x) или
tan(x)

тангенс х

ctg(x) или
cot(x)

котангенс х

arcsin(x) или
asin(x)

арксинус х

arccos(x) или
acos(x)

арккосинус х

arctg(x) или
atan(x)

арктангенс х

arcctg(x) или
acot(x)

арккотангенс х

sinh(x) или
sh(x)

гиперболический синус х

cosh(x) или
ch(x)

гиперболический косинус х

tanh(x)
th(x)

гиперболический тангенс х

coth(x) или
cth(x)

гиперболический котангенс х

asinh(x)

гиперболический арксинус х

acosh(x)

гиперболический арккосинус х

atanh(x)

гиперболический арктангенс х

acoth(x)

гиперболический арккотангенс х

Построение и решение графиков Функций

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — наглядно.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

• х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Чтобы ребенок разобрался в теории и чувствовал себя увереннее на школьных контрольных, запишите его на современные уроки математики в онлайн-школу Skysmart.

Интерактивные задания, математические комиксы и карта прогресса в личном кабинете — математика еще никогда не была таким увлекательным приключением!

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.

Исследование функции

Важные точки графика функции y = f(x):

• стационарные и критические точки;
• точки экстремума;
• нули функции;
• точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

 

1. Найти область определения функции.
2. Найти область допустимых значений функции.
3. Проверить не является ли функция четной или нечетной.
4. Проверить не является ли функция периодической.
5. Найти нули функции.
6. Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
7. Найти асимптоты графика функции.
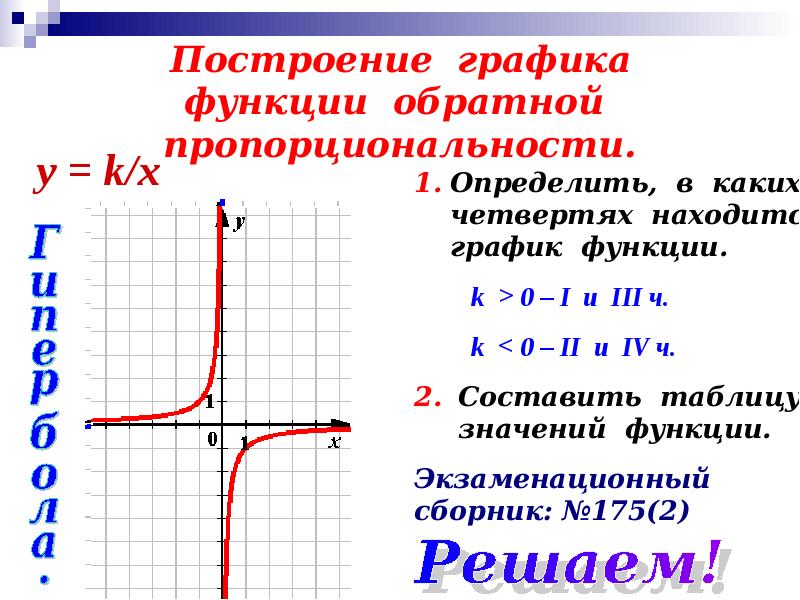
8. Найти производную функции.
9. Найти критические точки в промежутках возрастания и убывания функции.
10. На основании проведенного исследования построить график функции.

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Как решаем:

Упростим формулу функции:

Задача 2. Построим график функции

Как решаем:

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

 

Как решаем:

Вспомним, как параметры a, b и c определяют положение параболы.

 

1. Ветви вниз, следовательно, a < 0.

   Точка пересечения с осью Oy — c = 0.

   Координата вершины

2. Ветви вверх, следовательно, a > 0.

   Точка пересечения с осью Oy — c = 0.

   Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

3. Ветви вниз, следовательно, a < 0.

   Точка пересечения с осью Oy — c > 0.

   Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.

Задача 4. Построить графики функций:

а) y = 3x — 1

б) y = -x + 2

в) y = 2x

г) y = -1

Как решаем:

Воспользуемся методом построения линейных функций «по точкам».

а) y = 3x — 1

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.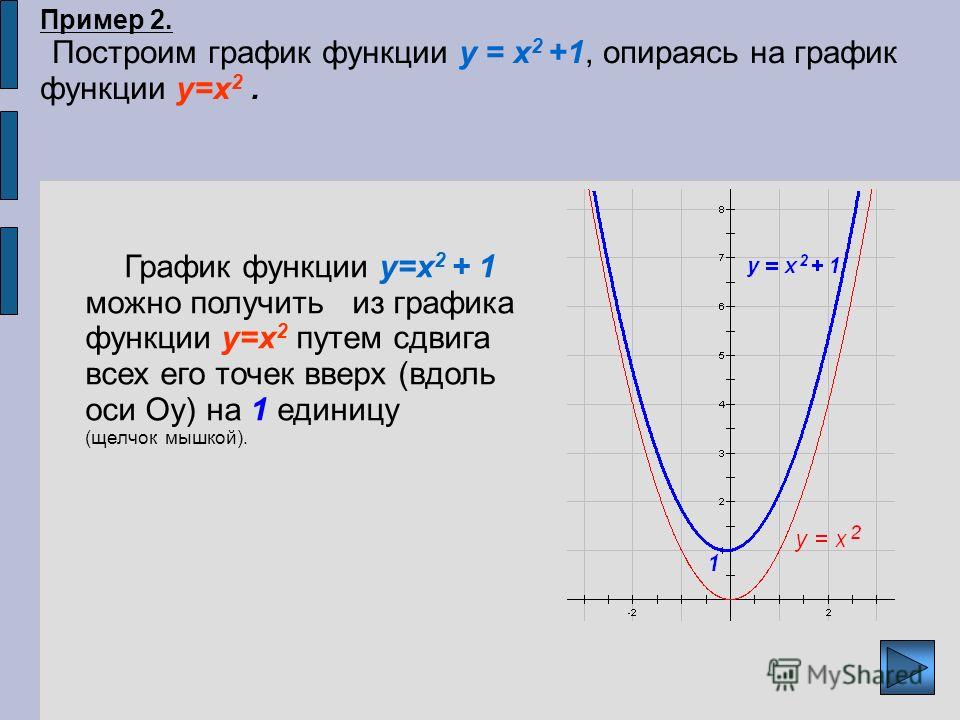

б) y = -x + 2

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

в) y = 2x

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

г) y = -1

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Как решаем:

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

а) y = x² + 1

б)

в) y = (x — 1)² + 2

г)

д)

Как решаем:

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.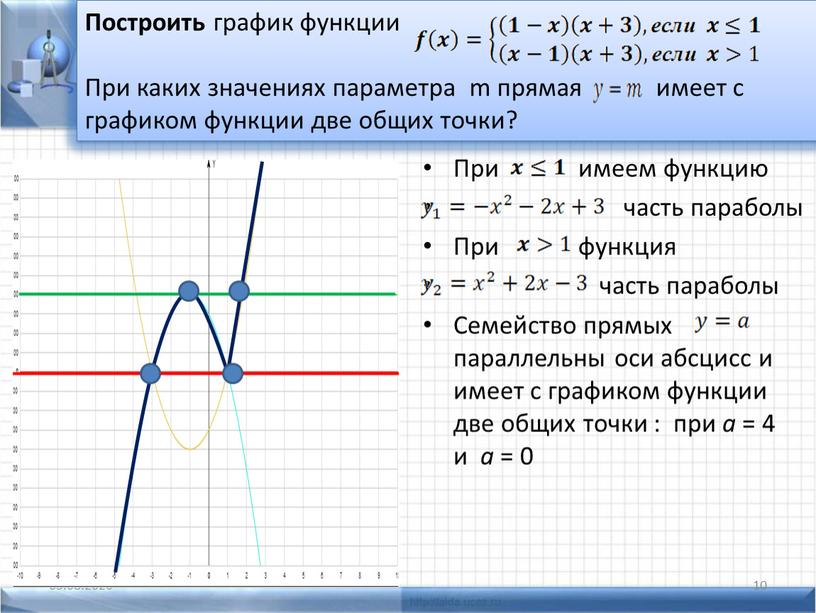

а)

Преобразование в одно действие типа f(x) + a.

y = x²

Сдвигаем график вверх на 1:

y = x² + 1

б)

Преобразование в одно действие типа f(x — a).

y = √x

Сдвигаем график вправо на 1:

y = √x — 1

в) y = (x — 1)² + 2

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

y = x²

Сдвигаем график вправо на 1:

y = (x — 1)²

Сдвигаем график вверх на 2:

y = (x — 1)² + 2

г)

Преобразование в одно действие типа

y = cos(x)

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

В детской школе Skysmart учиники чертят графики на специальной онлайн-доске. Учитель видит, как размышляет ученик и может вовремя его направить в нужную сторону.

Запишитесь на бесплатный вводный урок математики и занимайтесь в современном формате и с поддержкой заботливых учителей.

Построение графиков функций

Функции и их графики — одна из самых увлекательных тем в школьной математике. Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.

Умение строить графики функций необходимо для решения задач с параметрами на ЕГЭ по математике. Это одна из первых тем курса математического анализа в вузе. Это настолько важная тема, что мы в ЕГЭ-Студии проводим по ней специальные интенсивы для старшеклассников и учителей, в Москве и онлайн. И часто участники говорят: «Жаль, что мы не знали этого раньше».

Но это не все. Именно с понятия функции и начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции — это все-таки арифметика. Преобразования выражений — это алгебра. А математика — наука не только о числах, но и о взаимосвязях величин. Язык функций и графиков понятен и физику, и биологу, и экономисту. И, как сказал Галилео Галилей, «Книга природы написана на языке математики».

Точнее, Галилео Галилей сказал так:«Математика есть алфавит, посредством которого Господь начертал Вселенную».

Темы для повторения:

Понятие функции

Типы элементарных функций

Преобразования графиков функций

Производная функции

1. Построим график функции

Знакомая задача! Такие встречались в вариантах ОГЭ по математике. Там они считались сложными. Но сложного ничего здесь нет.

Упростим формулу функции:

при

График функции — прямая с выколотой точкой

2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, применяемый в решении неравенств, построении графиков и оценке целых величин в задачах на числа и их свойства. Он встретится вам также на первом курсе, когда придется брать интегралы.

3. Построим график функции

Он получается из графика функции растяжением в 2 раза, отражением по вертикали и сдвигом на 1 вверх по вертикали

4. Построим график функции

Главное — правильная последовательность действий. Запишем формулу функции в более удобном виде:

Действуем по порядку:

1) График функции y=sinx сдвинем на влево;

2) сожмем в 2 раза по горизонтали,

3) растянем в 3 раза по вертикали,

4) сдвинем на 1 вверх

Сейчас мы построим несколько графиков дробно-рациональных функций. Чтобы лучше понять, как мы это делаем, читайте статью «Поведение функции в бесконечности. Асимптоты».

5. Построим график функции

Область определения функции:

Нули функции: и

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Прямая x = 0 (ось Y) — вертикальная асимптота функции. Асимптота — прямая, к которой бесконечно близко подходит график функции, но не пересекает ее и не сливается с ней (смотри тему «Поведение функции в бесконечности. Асимптоты»)

Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда x стремится к бесконечности.

Раскроем скобки в формуле функции:

Если x стремится к бесконечности, то стремится к нулю. Прямая является наклонной асимптотой к графику функции.

6. Построим график функции

Это дробно-рациональная функция.

Область определения функции

Нули функции: точки — 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты:

Если x стремится к бесконечности, то у стремится к 1. Значит, — горизонтальная асимптота.

Вот эскиз графика:

Еще один интересный прием — сложение графиков.

7. Построим график функции

Если x стремится к бесконечности, то и график функции будет бесконечно близко подходить к наклонной асимптоте

Если x стремится к нулю, то функция ведет себя как Это мы и видим на графике:

Вот мы и построили график суммы функций. Теперь график произведения!

8. Построим график функции

Область определения этой функции — положительные числа, поскольку только для положительных x определен

Значения функции равны нулю при (когда логарифм равен нулю), а также в точках, где то есть при

При значение cos x равно единице. Значение функции в этих точках будет равно при

9. Построим график функции

Функция определена при Она четная, поскольку является произведением двух нечетных функций и График симметричен относительно оси ординат.

Нули функции — в точках, где то есть при при

Если x стремится к бесконечности, стремится к нулю. Но что же будет, если x стремится к нулю? Ведь и x, и sin x будут становиться меньше и меньше. Как же будет вести себя частное ?

Оказывается, что если x стремится к нулю, то стремится к единице. В математике это утверждение носит название «Первого замечательного предела».

А как же производная? Да, наконец-то мы до нее добрались. Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.

10. Построим график функции

Область определения функции — все действительные числа, поскольку

Функция нечетна. Ее график симметричен относительно начала координат.

При x=0 значение функции равно нулю. При значения функции положительны, при отрицательны.

Если x стремится к бесконечности, то стремится к нулю.

Найдем производную функции
По формуле производной частного,

если или

В точке производная меняет знак с «минуса» на «плюс», — точка минимума функции.

В точке производная меняет знак с «плюса» на «минус», — точка максимума функции.

Найдем значения функции при x=2 и при x=-2.

Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?

Общая схема построения графика функции: 

1. Область определения функции

2. Область значений функции

3. Четность — нечетность (если есть)

4. Периодичность (если есть)

5. Нули функции (точки, в которых график пересекает оси координат)

6. Промежутки знакопостоянства функции (то есть промежутки, на которых она строго положительна или строго отрицательна).

7. Асимптоты (если есть).

8. Поведение функции в бесконечности

9. Производная функции

10. Промежутки возрастания и убывания. Точки максимума и минимума и значения в этих точках.

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Схема исследования поведения функций, применяемая для построения графиков функций

      Для построения графика функции   y = f (x)   желательно сначала провести исследование поведения функции   y = f (x)   по следующей схеме.

1. Найти область определения   D ( f ).

2. Выяснить, является ли функция   y = f (x)   четной или нечетной.

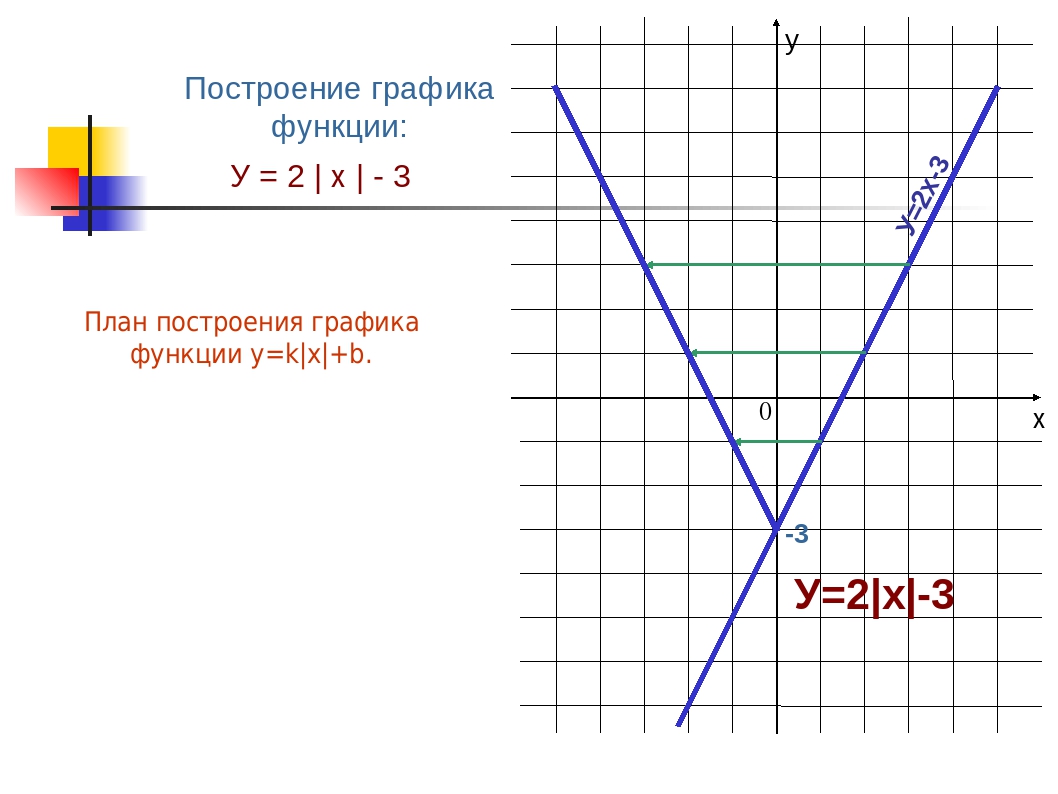
3. Выяснить, является ли функция   y = f (x)  периодической.

4. Найти асимптоты графика функции.

5. Вычислить производную функции   f ‘ (x) .

6. Найти критические точки функции   y = f (x) .

7. Найти интервалы возрастания и убывания функции   y = f (x) .

8. Найти экстремумы функции   y = f (x) .

9. Найти точки пересечения графика функции   y = f (x)   с осями координат.

   Если не удается точно найти нули функции, то есть точки, в которых график функции пересекает ось абсцисс   Ox,   то нужно попытаться найти интервалы, на которых нули функции располагаются. Часто эти интервалы удается найти, зная точки максимума и минимума функции.

10. Вычислить вторую производную функции   f »  (x) .

11. Найти интервалы, на которых функция   y = f (x)   выпукла вверх, а также интервалы, на которых функция   y = f (x)  выпукла вниз.

12. Найти точки перегиба графика функции  y = f (x) .

      Замечание. Желательно рисовать схему поведения функции параллельно с проведением исследования свойств функции по описанному выше плану.

Примеры построения графиков функций

      Пример 1. Построить график функции

y = x3 + 8x2 + 16x + 128

(1)

      Решение. Областью определения функции (1) является вся числовая прямая.

      Функция (1) не является ни четной, ни нечетной.

      Функция (1) не является периодической.

      Вертикальных асимптот у графика функции (1) нет, так как для любого числа   x₀

     Проверим, есть ли у графика функции (1) наклонные асимптоты. Поскольку

то делаем вывод, что наклонных асимптот у графика функции (1) нет.

      Теперь вычислим производную функции (1):

y’ (x) = 3x² + 16x + 16 .

      Поскольку   y’ (x)   существует для всех , то все критические точки функции являются ее стационарными точками, то есть точками, в которых

y’ (x) = 0 .

      Найдем стационарные точки функции (1), интервалы, на которых   y’ (x)   сохраняет знак, а также экстремумы функции. Для этого решим квадратное уравнение

3x² + 16x + 16 = 0.

      Изобразим на рисунке 1 диаграмму знаков производной   y’ (x)

Рис.1

      На интервалах и производная   y’ (x)   положительна, значит, функция (1) возрастает. На интервале производная   y’ (x)   отрицательна, значит, функция (1) убывает. Схематически поведение функции (1) изображено на рисунке 2.

Рис.2

      При переходе через точку   x = – 4   производная функции   y’ (x)   меняет знак с   «+»   на   «–» . Следовательно, точка   x = – 4   является точкой максимума функции (1). При переходе через точку производная функции   y’ (x)   меняет знак с   «–»   на   «+» . Следовательно, точка является точкой минимума функции (1).

      Найдем значения функции (1) в стационарных точках:

y (–4) = 256 ,

     Теперь вычислим вторую производную функции (1):

y» (x) = (y’ (x))‘ = (3x² + 16x + 16)‘ = 6x + 16 .

y» (x) = (y’ (x))‘ =
= (3x² + 16x + 16)‘ =
= 6x + 16 .

     Вторая производная   y» (x)   обращается в нуль при . Изобразим на рисунке 3 диаграмму знаков второй производной   y» (x)

Рис.3

      При переходе через точку вторая производная функции   y» (x)   меняет знак с   «–»   на   «+» . Следовательно, – точка перегиба графика функции (1). При функция (1) выпукла вверх, при функция (1) выпукла вниз.

      Дополним схему поведения функции, представленную на рисунке 2, новыми данными о направлении выпуклости функции (рис. 4).

Рис.4

      Для того, чтобы найти точки пересечения функции (1) с осью   Ox ,   решим уравнение

x³ + 8x² + 16x + 128 = 0 ,

x² (x + 8) + 16 (x + 8) = 0 ,

(x + 8) (x² + 16) = 0 .

      Таким образом, точка   (– 8; 0)   является единственной точкой пересечения графика функции (1) с осью   Ox .   Точкой пересечения графика функции (1) с осью   Oy   будет точка   (0; 128) .

      На схеме поведения функции, представленной на рисунке 4, добавим информацию о знаках функции (1) (рис. 5).

Рис.5

     Принимая во внимание результаты исследования поведения функции (1) (большая часть данных компактно представлена на рисунке 5), мы можем построить график функции (1) (рис. 6):

Рис.6

      Пример 2. Построить график функции

(2)

      Решение. Областью определения функции (2) является вся числовая прямая, за исключением точки   x = 0 ,   то есть .

      Функция (2) не является ни четной, ни нечетной.

      Функция (2) не является периодической.

      Прямая   x = 0   является вертикальной асимптотой графика функции (2), так как

      Для того, чтобы выяснить, имеются ли у графика функции (2) наклонные асимптоты, представим правую часть формулы (2) в другом виде:

(3)

      Из формулы (3) получаем равенство

откуда вытекает, что прямая

y = x + 3

является наклонной асимптотой графика функции (2), как при , так и при .

      Теперь вычислим производную функции (2). Проще всего это сделать, воспользовавшись формулой (3):

(4)

      Для того, чтобы найти стационарные точки функции (2), преобразуем правую часть формулы (4):

      Следовательно,

(5)

и стационарными точками функции (2) являются точки   x = – 1   и   x = 2 .   Поскольку   y’ (x)   не существует при   x = 0 ,   то критическими точками функции (2) являются точки

x = – 1 ,   x = 0,   x = 2 .

      Изобразим на рисунке 7 диаграмму знаков производной   y’ (x)

Рис.7

      На интервалах , и производная   y’ (x)   положительна, значит, функция (2) возрастает на этих интервалах. На интервале   (0, 2)   производная   y’ (x)   отрицательна, значит, функция (2) убывает на этом интервале. Схематически поведение функции (2) изображено на рисунке 8.

Рис.8

      При переходе через точку   x = – 1   производная функции   y’ (x)   знак не меняет, значит, в этой точке экстремума нет. При переходе через точку   x = 2   производная функции   y’ (x)   меняет знак с   «–»   на   «+» .   Следовательно, точка   x = 2   является точкой минимума функции (2).

      Найдем значения функции (1) в стационарных точках:

y (–1) = 0 ,

     Теперь перейдем к вычислению второй производной функции (2). Проще всего это сделать, воспользовавшись формулой (4):

      Вторая производная   y» (x)   обращается в нуль при   x = – 1 .   Изобразим на рисунке 9 диаграмму знаков второй производной   y» (x)

Рис.9

      При переходе через точку   x = – 1   вторая производная функции   y» (x)   меняет знак с   «–»   на   «+» . Следовательно,   x = – 1   – точка перегиба графика функции (2). При   x < – 1   функция (2) выпукла вверх, при   x > – 1   функция (2) выпукла вниз.

      Дополним схему поведения функции, представленную на рисунке 8, данными о направлении выпуклости функции (рис. 10).

Рис.10

      Найдем точки пересечения функции (2) с осями координат: точка   (– 1; 0)   является единственной точкой пересечения графика функции (2) с осью   Ox ,   а точек пересечения графика функции (2) с осью   Oy   нет, поскольку   x = 0   не входит в область определения функции (2).

      На схеме поведения функции, представленной на рисунке 10, добавим информацию о знаках функции (2) (рис. 11).

Рис.11

     Принимая во внимание результаты исследования поведения функции (2) (большая часть данных компактно представлена на схеме рисунка 11), мы можем построить график функции (2) (рис.12):

Рис.12

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Построение графиков функций геометрическими методами / math5school.ru

 

График функции y=f(x)+a

График функции y=f(x–a)

График функции y=kf(x), k>0

График функции y=f(kx), k>0

График функции y=–f(x)

График функции y=f(–x)

График функции y=|f(x)|

График функции y=f(|x|)

 

График функции

y=f(x)+a

Способ построения: параллельный перенос графика функции y=f(x) вдоль оси Oy на а единиц вверх, если a>0, и на |a| единиц вниз, если a<0.

 

       

       

 

 

График функции

y=f(x–a)

Способ построения: параллельный перенос графика функции y=f(x) вдоль оси Ox на а единиц вправо, если a>0, и на |a| единиц влево, если a<0.

 

       

       

 

График функции

y=kf(x), k>0

Способ построения: растяжение графика функции y=f(x) вдоль оси Oy относительно оси Ox в k раз, если k>1, и сжатие в 1/k раз, если 0<k<1.

 

       

       

       

  

 

График функции

y=f(kx), k>0

Способ построения: сжатие графика функции y=f(x) вдоль оси Ox относительно оси Oy в k раз, если k>1, и растяжение в 1/k раз, если 0<k<1.

 

       

       

        

 

 

График функции

y=–f(x)

Способ построения: симметричное отражение графика функции y=f(x) относительно оси Ox.

 

       

       

 

 

График функции

y=f(–x)

Способ построения: симметричное отражение графика функции y=f(x) относительно оси Oy.

 

       

       

 

 

График функции

y=|f(x)|

Способ построения: часть графика функции y=f(x), расположенная ниже оси Ox, симметрично отражается относительно этой оси, остальная его часть остаётся без изменения.

 

       

       

 

 

График функции

y=f(|x|)

Способ построения: часть графика функции y=f(x), расположенная правее оси Oy и на ней, остаётся без изменения, а остальная его часть заменяется симметричным отображением относительно оси Oy части графика, расположенной правее оси Oy.

 

       

       

 

      Смотрите также:

Таблицы чисел

Алгебраические тождества

Степени

Арифметический корень n-й степени

Логарифмы 

Графики элементарных функций

Тригонометрия

Таблицы значений тригонометрических функций

Треугольники

Четырёхугольники

Многоугольники

Окружность 

Площади геометрических фигур

Прямые и плоскости

Многогранники 

Тела вращения 

 

Построение графика квадратичной функций: алгоритм и примеры 9 класс онлайн-подготовка на Ростелеком Лицей

Тема 5.

Построение графика квадратичной функции с помощью преобразований.

Рассмотрим частные случаи

y = ax² + n и y = a(x – m)².

В одной системе координат построим графики функцийy=12×2 и y=12×2+5.

Составим таблицу значений функции: y=12×2

x	-3	-2	-1	0	1	2	3
y	4,5	2	0,5	0	0,5	2	4,5

Чтобы получить таблицу значений для функции y=12×2+5 для тех же значений аргумента, необходимо к найденным значениям функции y=12×2 прибавить 5.

x	-3	-2	-1	0	1	2	3
y	9,5	7	5,5	5	5,5	7	9,5

Получается, что каждую точку второго графика можно получить из некоторой точки первого графика с помощью параллельного переноса на 5 единиц вверх вдоль оси y.

График функции y=12×2+5 – парабола, полученная в результате сдвига вверх графика функции y=12×2.

График функции y = ax² + n – парабола, которую можно получить из графика функции y = ax² с помощью параллельного переноса вдоль оси y на n единиц вверх, если n > 0 или на – n единиц вниз, если n

В одной системе координат построим графики функций y=12×2 и y=12x-52. Составим таблицы значений для этих функций.

y=12×2

x	-3	-2	-1	0	1	2	3
y	4,5	2	0,5	0	0,5	2	4,5

y=12x-52

x	2	3	4	5	6	7	8
y	4,5	2	0,5	0	0,5	2	4,5

Значит, если переместить каждую точку графика y=12×2 вправо на 5 единиц, то получим соответствующую точку графика функции y=12x-52. Иначе говоря, каждую точку второго графика можно получить из соответствующей точки первого графика с помощью параллельного переноса на 5 единиц вправо вдоль оси x.

График функции y=12x-52 – парабола, полученная y=12x-52 в результате сдвига вправо графика функции y=12×2.

График функции y = a(x — m)² – парабола, которую можно получить из графика функции y = ax² с помощью параллельного переноса вдоль оси x на на m единиц вправо, если m > 0 или на – m единиц влево, если m

Полученные выводы позволяют понять, что представляет собой график функции y = a(x — m)². Например, график функции y=12x-52+3 можно получить из графика функции y=12×2 с помощью двух параллельных переносов – сдвига вдоль оси x на 5 единиц вправо и вдоль оси y на 3 единицы вверх.

Таким образом, график функции y = a(x — m)² можно получить из параболы y = ax² с помощью двух параллельных переносов: сдвига вдоль x на m единиц вправо, если m > 0 или на – m единиц влево, если m n единиц вверх, если n > 0 или на – n единиц вниз, если n

Заметим, что данные преобразования можно производить в любом порядке: сначала выполнить параллельный перенос вдоль оси x, а затем вдоль оси y или наоборот.

Преобразования, которые мы рассмотрели применимы для любых функций.

Рассмотрим пример.

Построим график функции y = x² — 4x двумя способами: с помощью преобразований, которые мы сегодня рассмотрели и с помощью таблицы значений функции.

Для того, чтобы построить график функции с помощью преобразований, необходимо его представить в виде y = a(x — m)². Для этого надо выделить полный квадрат. Итак, в нашу функцию y = x² — 4x добавим 4 и вычтем 4. Получим:

y=x2-4x+4-4=x-22-4

График данной функции можно получить из графика функции y = x² с помощью двух параллельных переносов: сдвига вдоль оси x на 2 единицы вправо, и сдвига вдоль оси y на 4 единицы вниз.

Чтобы построить график функции вторым способом, составим таблицу ее значений. Возьми нечетное количество точек, например, пять и семь. В центре поставь координаты вершины параболы.

xв=-b2a=—42∙1=2

yв=22-4∙2=-4

График квадратичной функции симметричен относительно прямой, параллельной оси y, проходящей через вершину параболы. В данном случае прямая x = 2 является осью симметрии.

x	-1	0	1	2	3	4	5
y	5	0	-3	-4	-3	0	5

Построение графиков функций

Документация по синтаксису математических операций,
списку поддерживаемых сервисом функций и констант

Обозначение	Описание
+	Сложение
—	Вычитание
*	Умножение
/	Деление
()	Группирующие символ
x^n	Возведение x в степень n
p(x,n)	Возведение x в степень n
exp(x)	Экспоненциальная функция, т.е. возведение e в степень x
root(x,n)	Корень n-степени из x
sqr(x)	Квадратный корень из x
sqrt(x)	Квадратный корень из x
cbr(x)	Кубический корень из x
cbrt(x)	Кубический корень из x
logn(x,a)	Логарифм x по основанию a
ln(x)	Натуральный логарифм x, т.е. логарифм x по основанию e
lb(x)	Логарифм x по основанию 2
lg(x)	Логарифм x по основанию 10
sin(x)	Синус от x
cos(x)	Косинус от x
tan(x)	Тангенс от x
cotan(x)	Котангенс от x
sec(x)	Секанс от x
csc(x)	Косеканс от x
asin(x)	Арксинус от x
acos(x)	Арккосинус от x
atan(x)	Арктангенс от x
acot(x)	Арккотангенс от x
asec(x)	Арксеканс от x
acsc(x)	Арккосеканс от x
sinh(x)	Гиперболический синус от x
cosh(x)	Гиперболический косинус от x
tanh(x)	Гиперболический тангенс от x
coth(x)	Гиперболический котангенс от x
sech(x)	Гиперболический секанс от x
csch(x)	Гиперболический косеканс от x
asinh(x)	Гиперболический арксинус от x
acosh(x)	Гиперболический арккосинус от x
atanh(x)	Гиперболический арктангенс от x
acoth(x)	Гиперболический арккотангенс от x
asech(x)	Гиперболический арксеканс от x
acsch(x)	Гиперболический арккосеканс от x
gaussd(x,m,n)	Нормальное распределение (распределение Гаусса) со средним значением m и стандартным отклонением n
min(n1,n2)	Возвращает наименьшее из двух значений
max(n1,n2)	Возвращает наибольшее из двух значений
round(x)	Классическое округление x до целого числа
floor(n1,n2)	Округление x вниз до ближайшего целого числа
ceil(n1,n2)	Округление x вверх до ближайшего целого числа
abs(x)	Модуль x
rand	Случайное число от 0 до 1
sgn(x)	Сигнум x. Возвращает 1, если x>0 Возвращает 0, если x=0 Возвращает -1, если x<0
e	Число Эйлера: 2.7182818284…
Phi	Золотое отношение: 1.6180339887…
pi	Число Пи: 3.1415926535…

Выражение графика или функция — MATLAB fplot

Цвет заливки маркера, заданный как 'auto' , триплет RGB, шестнадцатеричный цвет
код, название цвета или короткое название. 'auto' значение использует то же
color как свойство MarkerEdgeColor .

Для пользовательского цвета укажите триплет RGB или шестнадцатеричный цветовой код.

• Триплет RGB — это трехэлементный вектор-строка, элементы которого
  укажите интенсивность красного, зеленого и синего
  компоненты цвета.Интенсивности должны быть в
  диапазон [0,1] ; например, [0,4
0,6 0,7] .

• Шестнадцатеричный цветовой код — это вектор символов или строка.
  скаляр, который начинается с хеш-символа ( # )
  за которыми следуют три или шесть шестнадцатеричных цифр, которые могут варьироваться
  с 0 до F .В
  значения не чувствительны к регистру. Таким образом, цветовые коды
  '# FF8800' ,
  '# ff8800' ,
  '# F80' и
  '# f80' эквивалентны.

Вы также можете указать некоторые общие цвета по имени. В этой таблице перечислены названные цвета
параметры, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.

'w'

Название цвета	Краткое название	Триплет RGB	Шестнадцатеричный код цвета	Внешний вид
'красный'	'r'	[1 0 0]	'# FF0000'
'зеленый'	'g'	[0 1 0]	'# 00FF00'
'синий'	'b'	[0 0 1]	'# 0000FF'
'голубой	'c'	[0 1 1]	'# 00FFFF'
'пурпурный'	'm'	[1 0 1]	'# FF00FF'
'желтый'	'y'	[1 1 0]	'# FFFF0066
'черный'	'k'	[0 0 0]	'# 000000'
'белый66	[1 1 1]	'#FFFFFF'
'none'	Неприменимо	Неприменимо	Неприменимо	N o цвет

Вот триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию, которые MATLAB использует во многих типах графиков.

4940 0,1840 0,5560]

Триплет RGB	Шестнадцатеричный цветовой код	Внешний вид
[0 0,4470 0,7410]	'# 0072BD'	2 0 [0,8500 0,3250 0,0980]	'# D95319'
[0,9290 0,6940 0,1250]	'# EDB120'		'# 7E2F8E'
[0,4660 0,6740 0,1880]	'# 77AC30'	1
'# 4DBEEE'
[0,6350 0,0780 0,1840]	'# A2142F'

Пример: [0.3 0,2 0,1]

Пример: «зеленый»

Пример: '# D2F9A7'

Создание пользовательских функций построения графиков с помощью matplotlib | by Matias Calderini

Краткое руководство, чтобы узнать, как создавать модульные функции, которые включают построение графиков с помощью matplotlib

TL; DR: Определите свои собственные функции, которые включают построение графиков на определенных осях со следующим синтаксисом:

 def custom_plot (x, y, ax = None, ** plt_kwargs): 
, если ax не равно None: 
 ax = plt.gca () 
 ax.plot (x, y, ** plt_kwargs) ## здесь пример графика 
 return (ax) def multiple_custom_plots (x, y, ax = None, plt_kwargs = {}, sct_kwargs = {}): 
 if ax is None: 
 ax = plt.gca () 
 ax.plot (x, y, ** plt_kwargs) #example plot1 
 ax.scatter (x, y, ** sct_kwargs) #example plot2 
 return (ax) 

Вы можете найти исходный репозиторий кода по этой ссылке.

В предыдущем посте я показал вам, как лучше организовать ваши фигуры. Мы увидели, как вы можете аккуратно отображать различные графики с помощью подзаголовков, как добавлять свободно плавающие оси и как легко создать мозаичную организацию ваших осей с помощью GridSpec.

Поскольку в центре внимания этого поста была общая структура и представление общей цифры, сами графики были довольно простыми, поскольку они использовали только одну предопределенную функцию matplotlib, такую ​​как .plot или .hist с параметры по умолчанию. Однако часто в рамках красивой мозаичной структуры, которую вы узнали в предыдущем посте, вам нужно будет нарисовать конкретный собственный график, который объединяет информацию из различных типов основных функций построения графиков вместе с вызовами некоторых других генераторов данных или данных. функция обработки.Например, построение графика распределения случайных выборок с соответствующей теоретической функцией плотности сверху.

Здесь я покажу вам, как создавать свои собственные пользовательские функции построения графиков, которые можно легко использовать, вызывая их на ваших организованных графиках с чем-то вроде следующего:

 fig, axes = plt.subplots (number_of_subplots) 
 for ax in axes: 
 my_custom_plotting_function (ax = ax, function_kwargs) 

Вместе с хорошей организацией подзаголовков это поможет вам максимизировать статические графики на matplotlib (предвещая последующее руководство по динамическим графикам….возможно…) и использовать информацию с разных графиков, чтобы поделиться исчерпывающей историей ваших данных.

Первый шаг к тому, чтобы иметь возможность иметь серию настраиваемых графиков внутри вашей фигуры, — это возможность соединить индивидуальный настраиваемый график с отдельными осями. Первый шаг — передать оси, по которым мы хотим построить график, нашей пользовательской функции. Это можно сделать просто так:

 def custom_plot (x, y, ax = None, ** plt_kwargs): 
 if ax is None: 
 ax = plt.gca () 
 ax.plot (x, y, ** plt_kwargs) ## здесь пример сюжета 
 return (ax) 

Итак, что я там делал? Первой важной частью здесь является аргумент ax . Если вы раньше использовали seaborn , возможно, вы уже знаете, как им пользоваться. По сути, ax будет принимать объект оси, на котором вы хотите построить. Это могут быть оси вспомогательного графика или простые свободно плавающие оси врезки. Идея состоит в том, что организационная часть сюжета будет обрабатываться вне этой функции, возможно, другой функцией.

Почему ax по умолчанию Но нет ? На этот вопрос лучше ответить строками:

, если ax is None: 
 ax = plt.gca () 

, мы видим, что если объект axes не был предоставлен в ax , он по умолчанию None и запускает это , если Состояние . В этом случае, поскольку оси не заданы, по умолчанию функция будет искать последние оси, использованные в текущем рисунке, или создавать их, если их нет в наличии, с помощью функции .gca (что означает получить текущие оси ) и использовать это как оси для построения графика. В конце функции мы также возвращаем этот топор, если мы хотим использовать его для других настроек (не обязательно, но в некоторых случаях практично).

Давайте проверим это, сначала построив график без указания осей, а затем указав конкретные оси:

 # Без указания осей (по умолчанию None -> gca ()) 
 plt.figure (figsize = (10, 5)) 
 custom_plot ([1, 2], [10, 20]) 
 пл.title ('Наш настраиваемый график без осей (по умолчанию .gca ())') 
 plt.xlabel ('x') 
 plt.ylabel ('y') 
 plt.show () 

 # Предоставление осей 
 fig, axes = plt.subplots (2, figsize = (10, 5)) # Построение графика с помощью нашей функции 
 custom_plot ([2, 3], [4, 15], ax = axes [0]) 
 axes [0 ] .set (xlabel = 'x', ylabel = 'y', title = 'Это наш настраиваемый график по указанным осям') # Пример графика для заполнения второго подзаговора (ничего общего с нашей функцией) 
 осей [1 ] .hist (np.random.normal (size = 100)) 
 осей [1].set_title ('Этот график не имеет ничего общего с нашей функцией. Просто гистограмма некоторых случайных чисел') plt.tight_layout () # Это позволяет избежать наложения меток и заголовков на графиках 
 plt.show () 

Пока все хорошо ; мы можем создать функцию для построения данных, и мы можем связать ее с определенными осями нашего графика (она даже позаботится о себе, если оси не были предоставлены). А как насчет ** plt_kwargs ?

Если вы не привыкли работать с ** kwargs (как в аргументах ключевого слова) в своих функциях (фактическое имя аргумента не имеет значения, вы можете назвать его ** kwargs , ** plt_kwargs , ** literally_anything_else , если вы поставите двойную звездочку «**»), это будет легче объяснить, создав и используя сначала новую функцию, в которой нет ** kwargs .

В стороне, однако, если вы действительно не видели этот тип обозначения звездочки раньше, использование одинарных звездочек * и двойных звездочек ** в Python весьма полезно во многих ситуациях, независимо от того, находятся ли они внутри или вне функций, и определенно стоит поискать в Google (возможно, даже написать об этом сообщение в блоге … может быть …). В любом случае, вернемся к нашему примеру custom_plot без ** kwargs :

 def no_kwargs_plot (x, y, ax = None): 
 если ax is None: 
 ax = plt.gca () 
 ax.plot (x, y) ## здесь пример графика 
 return (ax) plt.figure (figsize = (10, 5)) 
 no_kwargs_plot ([1, 2], [10, 20]) 
 plt.show () 

Ни ошибок, ни проблем … А что, если вы хотите сделать линию толще? Обычно в .plot () мы просто устанавливаем для аргумента linewidth более толстое значение. Мы могли бы добавить ширины линии к списку входов в no_kwargs_plot , а затем передать его в .plot () следующим образом:

 def no_kwargs_plot (x, y, ax = None, linewidth = 1): 
 if ax Нет: 
 ax = plt.gca () 
 ax.plot (x, y, linewidth) ## пример графика здесь 

Это решит проблему. Но как насчет всех других возможных аргументов в .plot () . Записывать их все в нашей функции вместе со значениями по умолчанию было бы очень долго и не очень практично:

 def no_kwargs_plot (x, y, ax = None, linewidth = 1, other = 1, ...): 
 if ax is None: 
 ax = plt.gca () 
 ax.plot (x, y, linewidth, other, ....) ## здесь пример графика 

Вот где используется нотация ** ( * * kwargs ) пригодится.При использовании со свободными элементами ключ-значение, такими как бесхозные входы в нашей функции (те, которые не связаны с предопределенными аргументами x, y и ax в нашем случае) ** name будет упаковывать все эти элементы в словарь и сохраните их в переменной name .

Например, если бы мы использовали нашу функцию построения графика как custom_plot (x = xdata, y = ydata, ax = axes [0], linewidth = 2, c = 'g') , в результате получаем словаря plt_kwargs будет {'ширина линии': 2, 'c': 'g'} .Если это все еще не совсем понятно, посмотрите на пример кода ниже, вывод (>>) и схему внизу:

 def print_kwargs_only (x, y, ax = None, ** plt_kwargs): 
 print (plt_kwargs) # чтобы распечатать словарь со всеми сиротами kwargsprint_kwargs_only (x = [1, 2], y = [10, 20], not_xyax = 1, random_orphan_kwarg = 'so lonely', linewidth = 2, c = 'g') >> { 'not_xyax': 1, 'random_orphan_kwarg': 'so lonely', 'linewidth': 2, 'c': 'g'} 

Таким образом, использование ** решает проблему включения всех возможных графических входов в нашу функцию без необходимости их явного предварительного определения и их готовности к использованию внутри словаря.Но как же используется этот словарь дополнительных аргументов ключевых слов?

Ранее я упоминал, что ** ведет себя как функция упаковки при использовании со свободными элементами. Однако, когда вы используете ** в словаре (независимо от того, был ли он упакован ** или нет), ** фактически выполнит противоположное действие, которое он делал раньше: он распакует словарь на разные свободные элементы. В custom_function , когда мы пишем ** plt_kwargs внутри .plot () , т.е. ax.plot (x, y, ** plt_kwargs) , мы фактически просим python взять словарь plt_kwargs и распаковать все его пары ключ-значение отдельно в .plot () работают как отдельные входы.

Таким образом, не зная, сколько и какие настройки графика будут использоваться, мы можем передать их все той части нашей функции, которая будет выполнять построение графика.

Мы можем увидеть это снова, используя нашу оригинальную функцию custom_plot (вы могли заметить, что на этот раз я использовал оси, возвращаемые функцией, чтобы показать вам, как ее можно использовать):

 plt.рисунок (figsize = (10, 5)) 
 out_ax = custom_plot ([1, 2], [10, 20], linewidth = 5, c = 'g') 
 out_ax.set (xlabel = 'xlabel', ylabel = 'ylabel', title = 'Проверка полезности ** kwargs') 
 plt.show () 

Тогда это позаботится об основном синтаксисе. После этого вы уже сможете приступить к созданию более интересных сюжетов.

Однако, прежде чем приступить к работе, нам нужно решить одну потенциальную проблему, с которой вы можете столкнуться при использовании ** kwargs . То есть, что, если бы вы делали несколько графиков внутри функции custom_plot ? Например, что, если вы рисуете две линии, одна из которых должна быть пунктирной, а другая — сплошной.Как ** kwargs узнает, какие аргументы в какой сюжет входят?

Ответ заключается в том, что « ** kwargs упаковочная машина» больше не будет работать и ее нужно будет заменить, но « ** kwargs the unpacking machine» будет работать отлично. Что я имею в виду под Давайте определим новую функцию под названием multiple_custom_plots , чтобы прояснить ее:

 def multiple_custom_plots (x, y, ax = None, plt_kwargs = {}, sct_kwargs = {}): 
 if ax is None: 
 ax = plt.gca () 
 ax.plot (x, y, ** plt_kwargs) 
 ax.scatter (x, y, ** sct_kwargs) 
 return (ax) 

Чем здесь отличается и как его использовать? Сначала посмотрите на список возможных входов. Теперь вместо ** kwargs у нас есть два новых аргумента, по одному для каждого из наших графиков. Также по умолчанию эти аргументы являются пустыми словарями.

Если вы следовали моему объяснению раньше, примерно ** kwargs , надеюсь, это уже достаточно ясно для вас. Идея состоит в том, что, поскольку мы не можем попросить функцию автоматически упаковать все бесхозные входные данные в один словарь (сейчас нам нужны два отдельных словаря), нам вместо этого придется предоставить каждый словарь параметров построения графиков самим, предварительно упакованным.

Использование их позже с двойной звездочкой ничем не отличается от исходного custom_plot , поскольку использование ** в словаре по-прежнему означает, что мы хотим, чтобы его значения были распакованы. Мы используем пустые словари в качестве значений по умолчанию, потому что, если вы не предоставите словарь настроек, мы столкнемся с проблемами при попытке распаковать их (или их отсутствие) с помощью ** . Пустые словари, по сути, предназначены для того, чтобы ничего не распаковывать в функции, если ничего не предусмотрено.

Давайте посмотрим, как мы будем использовать это:

 plot_params = {'linewidth': 2, 'c': 'g', 'linestyle': '-'} 
 scatter_params = {'c': 'red', 'marker': '+', 's': 100} 
 xdata = [1, 2] 
 ydata = [10, 20] plt.figure (figsize = (10, 5)) 
 multiple_custom_plots (xdata, ydata, plt_kwargs = plot_params, sct_kwargs = scatter_params) 
 plt.show () 

Итак, когда дело доходит до создания пользовательских функций, из которых вы можете строить графики, предыдущего раздела должно быть достаточно, чтобы вы могли немного повеселиться со статикой. сюжеты.В этом следующем разделе я просто приведу вам пример сюжета с использованием настраиваемой функции, надеюсь, вдохновит вас на создание собственных сюжетов.

Представьте, что вы хотите увидеть, как размер выборки из заданной случайной величины влияет на оценку лежащего в ее основе распределения вероятностей.

Предположим, что у нас есть непрерывная случайная величина X, которая нормально распределена со средним μ (μ) и стандартным отклонением σ (сигма) (, то есть X ∼N ( μ , σ ²)).Мы хотели бы знать, как на оценку плотности ядра scipy (kde) влияет размер нашей случайной выборки (сколько раз мы выбираем случайным образом из нашего нормального распределения), сравнивая ее с оценкой лежащего в основе истинного распределения плотности вероятности (pdf) .

Мы сделаем это, построив сами образцы, их kde и лежащий в их основе pdf для различных значений N.

 def sample_plot (mu = 0, sigma = 1, N = 100, sct_kwargs = {}, pdf_kwargs = {} , kde_kwargs = {}, ax = None): 
 # сгенерировать образец 
 sample = np.random.normal (loc = mu, scale = sigma, size = N) 
 # генерировать pdf 
 xrange = mu + 5 * sigma * np.linspace (-1, 1, 100) 
 pdf = stats.norm.pdf (xrange , loc = mu, scale = sigma) 
 
 # генерировать kde 
 rating = stats.gaussian_kde (sample) 
 kde = rating (xrange) 
 
 #Plotting 
 if ax is None: 
 ax = plt.gca () 
 ax .scatter (sample, np.zeros_like (sample), ** sct_kwargs) 
 ax.plot (xrange, pdf, ** pdf_kwargs) 
 ax.plot (xrange, kde, ** kde_kwargs) 
 return (xrange) 
 

Давайте разберем функцию пошагово:

Во-первых, входы.Здесь вместо того, чтобы запрашивать массивы данных, мы будем создавать наши собственные данные из генератора случайных чисел Гаусса. Поэтому нам нужно запросить соответствующие статистические параметры μ и σ (среднее и стандартное отклонение соответственно для гауссовых распределений). Нам также нужно спросить количество образцов N. Мы фактически будем перебирать различные значения N позже, чтобы увидеть влияние размера выборки на оценку. Идея состоит в том, чтобы построить образцы как точки разброса, а pdf и kde — как обычные линейные графики.Таким образом, мы предоставим в качестве входных данных словарь для соответствующих параметров построения графика (ширина линии, размер маркера и т. Д.). Наконец, мы спросим оси фигуры, на которой мы хотим построить все три объекта.

Первый раздел функции просто сгенерирует случайную гауссовскую выборку размера N из предоставленных статистических параметров.

Вторая часть кода создаст пары x-y линейного графика, соответствующие pdf нормального распределения, заданного μ и σ.Мы ограничиваем диапазон PDF до ± 5 стандартных отклонений, поскольку все, что находится дальше с обеих сторон, в любом случае будет довольно маленьким.

Третья часть кода сначала вычисляет kde нашего образца, а затем применяет его к тому же диапазону значений на оси x, что и наш pdf.

Наконец, в четвертой части кода мы просто строим в виде диаграммы рассеяния все выбранные значения по оси x (на высоте 0), а pdf и kde — в виде линейных диаграмм. Все три с соответствующими аргументами ключевого слова построения.

 # Параметры выборки 
 sample_sizes = (10, 20, 100, 250, 500, 2_000) 
 mean = 100 
 std = 15 # Параметры графика 
 scatter_params = {'alpha': 0.1, 'c': 'g', 's': 100, 'label': 'samples'} 
 pdf_params = {"linewidth": 2, 'c': 'k', 'label': 'pdf'} 
 kde_params = {"linewidth": 3, 'ls': '-', 'c': 'g', 'label': 'kde'} # Построение графика 
 fig, axes = plt.subplots (6, figsize = (15, 20)) 
 для ax, n в zip (axes, sample_sizes): 
 sample_plot (mu = mean, sigma = std, N = n, ax = ax, 
 sct_kwargs = scatter_params, pdf_kwargs = pdf_params, kde_kwargs = kde_params) 
 ax.set_title (f'N = {n} ') axes [0] .legend () 
 axes [-1] .set_xlabel (' Пример значения ', fontsize = 13) 
 plt.tight_layout () 
 plt.savefig (' finalplot ') 
 plt.show () 

И все! Надеюсь, вы научились добавлять возможности построения графиков к своим функциям, правильно передавая соответствующие оси и аргументы ключевых слов. Это должно помочь вам иметь все более модульный код для быстрого исследования и визуализации ваших данных.

Адаптивное построение функций — Yacas

Здесь мы рассматриваем построение функций \ (y = f (x) \).

С подготовкой графиков функций связаны две задачи:
во-первых, чтобы получить числа, необходимые для сюжета, а во-вторых, чтобы нарисовать
сюжет с топорами, символами, легендой, возможно дополнительными иллюстрациями
и так далее. Здесь мы занимаемся только первой задачей:
подготовки числовых данных для графика. Здесь очень много
программы построения графиков, которые могут читать файл с числами и отображать его в любом
желаемым образом.

Генерация данных для графиков функций обычно не требует
высокоточные расчеты.Однако нам нужен алгоритм, который может
можно настроить для получения данных с разным уровнем точности. В некоторых
особо неблаговидные случаи, точный сюжет будет невозможен
и мы не хотели бы тратить время на создание данных, которые тоже
точно для чего это стоит.

Простым подходом к построению графика было бы разделение интервала на
много равных подинтервалов и вычислить функцию на полученном
сетка. Точность графика можно регулировать, выбрав больший или
меньшее количество баллов.

Однако этот подход не оптимален. Иногда функция меняется
быстро около одной точки, но медленно везде. Например,
\ (f (x) = \ frac {1} {x} \) изменяется очень быстро при малых \ ​​(x \).
Предположим, нам нужно построить эту функцию между \ (0 \) и
\ (100 \). Было бы расточительно использовать одно и то же подразделение
интервал повсюду: более мелкая сетка требуется только на небольшом
часть диапазона построения вблизи \ (x = 0 \).

Адаптивная процедура построения графиков Plot2D'adaptive () использует простую
алгоритм выбора оптимальной сетки для аппроксимации функции одного
аргумент \ (f (x) \).Алгоритм многократно подразделяет сетку
интервалы около точек, где существующая сетка не представляет
функционируют достаточно хорошо. Аналогичный алгоритм для адаптивной сетки
уточнение может быть использовано для численного интегрирования. Идея в том, что
построение графиков и численное интегрирование требуют такого же детального
знание поведения функции.

Алгоритм сначала разбивает интервал на заданный начальный
количество равных подынтервалов, а затем многократно разбивает каждый
подынтервал пополам, пока функция не будет достаточно хорошо аппроксимирована
получившаяся сетка.{depth} \) будут созданы дополнительные точки сетки. В
функция Plot2D'adaptive () должна возвращать список пар точек
{{{x1, y1}, {x2, y2}, ...}} для непосредственного использования для построения графика.

Адаптивный алгоритм построения графика работает следующим образом:

1. Учитывая интервал (\ (a \), \ (c \)), мы разбиваем его пополам,
   \ (b: = (a + c) / 2 \) и сначала вычислите \ (f (x) \) в пяти сетке
   точки \ (a \), \ (a_1: = (a + b) / 2 \), \ (b \),
   \ (b_1: = (b + c) / 2 \), \ (c \).

2. Если в настоящее время \ (глубина <= 0 \), вернуть этот список из пяти точек и значения, потому что мы больше не можем уточнять сетку.

3. В противном случае убедитесь, что функция не колеблется слишком быстро.
   на интервале \ ([a, c] \). Формальным критерием является то, что
   все пять значений конечны и не образуют зигзагообразного узора, такого
   как \ ((1,3,2,3,1) \). Более формально мы используем следующие
   процедура: для каждых трех последовательных значений напишите «1», если
   среднее значение больше, чем два других, или, если оно меньше, чем
   два других, или если один из них не является числом (например, Infinity
   или Не определено} .Если сейчас у нас есть не более двух, то мы
   считают изменение значений «достаточно медленным». В противном случае это
   не «достаточно медленно». В этом случае нам нужно уточнить сетку; перейти к
   шаг 5. В противном случае перейдите к шагу 4.

4. Убедитесь, что значения функции достаточно гладкие через
   интервал. Плавность регулируется параметром
   \ (\ эпсилон \). Значение параметра \ (\ epsilon \):
   (относительная) погрешность численного приближения интеграла
   \ (f (x) \) по сетке.Хорошая эвристическая ценность
   \ (\ epsilon \) равно 1 / (количество пикселей на экране), потому что
   это означает, что в области под
   график. {b_1} g (x) \, \ mathrm {d} x \) с использованием этих пяти
   точки.(Асимметричные квадратуры выбраны, чтобы избежать столкновения с
   случайная симметрия функции; первая квадратура использует
   точки \ (a \), \ (a_1 \), \ (b \), \ (b_1 \) и
   вторая квадратура использует \ (b \), \ (b_1 \), \ (c \).) Если
   абсолютное значение разницы между этими квадратурами меньше
   чем \ (эпсилон \), умноженное на значение второй квадратуры, то мы
   выполнены, и мы возвращаем список этих пяти точек и значений.

5. В противном случае нам нужно уточнить сетку. Мы вычисляем
   Plot2D'adaptive () рекурсивно для двух половин
   интервал, то есть для \ ([a, b] \) и \ ([b, c] \).Мы также
   уменьшите \ (глубину \) на 1 и умножьте \ (\ epsilon \) на 2, потому что мы
   необходимо поддерживать постоянную абсолютную точность , а это означает
   что относительная ошибка для двух подынтервалов может быть вдвое больше
   большой. В результате получаются два списка для двух подынтервалов.
   объединены (исключая двойное значение в точке \ (b \)) и
   вернулся.

Этот алгоритм хорошо работает, если начальное количество точек и
Параметр \ (глубина \) достаточно велик. Эти параметры могут быть
скорректирован для баланса доступного времени вычислений и желаемого уровня
деталей в получившемся сюжете.

Особенности функции обрабатываются на шаге 3. А именно,
изменение в последовательности \ (a \), \ (a_1 \), \ (b \), \ (b_1 \),
\ (c \) всегда считается «слишком быстрым», если один из этих
values ​​не является числом (например, Infinity или Undefined ). Таким образом,
интервал, непосредственно примыкающий к особенности, будет нанесен на
максимально допустимый уровень детализации. При подготовке чертежа
data особые точки просто не печатаются в файле данных, поэтому
что программа построения графиков не вызывает никаких проблем.nc_kf (a_k) \]

где \ (a_k \) — точки сетки, \ (h: = a_1-a_0 \) — сетка
step, а \ (c_k \) — квадратурные коэффициенты. Может показаться
удивительно, но эти коэффициенты \ (c_k \) не зависят от
функция \ (f (x) \) и может быть предварительно вычислена для данного
сетка \ (a_k \). [Квадратурные коэффициенты зависят от
относительные расстояния сетки. Здесь мы предполагаем равномерную сетку с
постоянный шаг \ (h = a_k-a_ {k-1} \). Квадратурные коэффициенты могут
также можно найти для неоднородных сеток.2f (x) \, \ mathrm {d} x \ приблизительно \ frac {5} {12} f (0) + \ frac {2} {3} f (1) — \ frac {1} {12} f ( 2). \]

Эти квадратуры намеренно выбраны асимметричными, чтобы избежать
случайное исключение, когда сама функция \ (f (x) \)
симметричный. (В противном случае оценка ошибки может случайно стать
ровно ноль.)

Здесь мы рассматриваем построение функций \ (z = f (x, y) \).

Задача рисования поверхности — получить изображение
двухмерная поверхность, как если бы это был твердый объект в трех
Габаритные размеры.Графическое изображение поверхности — это сложная
задача. Иногда требуется использовать определенные координаты или
проекции, чтобы раскрасить поверхность, удалить скрытые линии и т. д.
на. Нас будет интересовать только задача получения данных.
для графика от заданной функции двух переменных \ (f (x, y) \).
Специализированные программы могут взять текстовый файл с данными и позволить
Пользователь в интерактивном режиме создает различные графики поверхности.

В настоящее время реализованный алгоритм в функции Plot3DS () :
очень похож на адаптивный алгоритм построения двумерных
сюжеты.Заданная прямоугольная область построения \ (a_1 \ leq x \ leq a_2 \),
\ (b_1 \ leq y \ leq b_2 \) подразделяется, чтобы получить равномерный
прямоугольная сетка точек. Это начальная сетка, которая будет
адаптивно дорабатывается при необходимости. Алгоритм уточнения будет
разделите данный прямоугольник на четыре четверти, если доступная функция
значения указывают на то, что функция не изменяется достаточно плавно на
этот прямоугольник.

Критерий «достаточно плавного» изменения очень похож на критерий
процедура, описанная в предыдущем разделе.Изменение «плавное»
достаточно », если все точки конечны, неособые значения и если
интеграл функции по прямоугольнику достаточно хорошо
аппроксимируется некоторой «кубатурной» формулой младшего порядка. 1 \ mathrm {d} yf (x, y) \ приблизительно \ frac {f (0,0) + f (0,1) + f (1, 0) + f (1,1)} {12} + \ frac {2} {3} f \ left (\ frac {1} {2}, \ frac {1} {2} \ right) \]

Аналогично, 8-точечная кубатура с нулевой суммой используется для оценки
ошибка:

-1/3	2/3	1/6
-1/6	-2/3	-1/2
1/2	0	1/3

Этот набор коэффициентов был намеренно выбран асимметричным по отношению к
избежать возможных точных отмен, когда сама функция
симметричный.

Одна небольшая проблема с адаптивным построением поверхностей заключается в том, что в результате
набор точек может не соответствовать прямоугольной сетке в
пространство параметров \ ((x, y) \). Это потому, что некоторые прямоугольники из
исходную сетку нужно будет делить пополам чаще, чем другие. Так,
если адаптивное уточнение не отключено, функция Plot3DS ()
производит несколько неупорядоченный набор точек. Однако большинство поверхностных
программы построения графиков требуют, чтобы набор точек данных был прямоугольным
сетка в пространстве параметров.Итак, сглаживание и интерполяция
процедура необходима для преобразования не привязанного к сетке набора точек данных
(«Разрозненные» данные) в сетку.

В настоящее время параметрические графики напрямую в Yacas не реализованы.
Однако можно использовать Yacas для получения числовых данных для таких
сюжеты. Затем можно использовать внешние программы для создания реальной графики.

Двумерный параметрический график — это линия на двумерном
пространство, определяемое двумя уравнениями, такими как \ (x = f (t), y = g (t) \).2 \ грех (\ phi) \).

Иногда требуются параметрические графики более высокой размерности. Линия
сюжет в трех измерениях определяется тремя функциями одного
переменной, например \ (x = f (t), y = g (t), z = h (t) \), и диапазон
параметр \ (t \). Трехмерный график поверхности
определяется тремя функциями от двух переменных каждая, например,
\ (x = f (u, v), y = g (u, v), z = h (u, v) \) и прямоугольная область в
\ ((u, v) \) пространство.

Данные для параметрических графиков могут быть сгенерированы отдельно, используя
те же адаптивные алгоритмы построения графиков, что и для графиков обычных функций, как
если все функции, такие как \ (f (t) \) или \ (g (u, v) \), не связаны
функции.В результате получится несколько отдельных наборов данных для
Координаты \ (x, y, \ ldots \). Эти наборы данных затем могут быть
объединены с помощью интерактивной программы построения графиков.

Система компьютерной алгебры абсолютно должна уметь выполнять
вычисления с очень большими целыми числами . Без этого
возможности, многие символьные вычисления (например, точный НОД
полиномы или точное решение полиномиальных уравнений) будет
невозможно.

Другой вопрос заключается в том, действительно ли CAS должна иметь возможность
оценить, скажем, 10 000 цифр значения функции Бесселя некоторого
Комплексный аргумент из 10 000 цифр.Кажется вероятным, что не применяется
проблема естественных наук потребовала бы вычислений с плавающей запятой
специальные функции с такой высокой точностью. Тем не мение,
вычисления произвольной точности, безусловно, полезны в некоторых
математические приложения; например некоторые математические тождества могут быть
впервые догадывается вычислением с плавающей запятой с большим количеством цифр и
потом доказал.

Вычисление специальных функций с очень высокой точностью может быть
пригодится в будущем. Но уже ясно, что расчеты
с умеренно высокой точностью (скажем, 50 или 100 десятичных цифр)
полезно для прикладных задач.2 \). Это число «точное» в том смысле, что оно
состоит из целых чисел и элементарных функций. Но мы не можем сказать a
априори , что это число ненулевое. Проблема «нулевого
определение »(выяснение, равно ли определенное« точное »число нулю)
как известно, алгоритмически неразрешима, если мы допускаем трансцендентные
функции. Единственный практический общий подход, по-видимому, заключается в вычислении
рассматриваемое число, состоящее из многих цифр. Обычно несколько цифр
достаточно, но иногда требуется несколько сотен цифр.

Реализация эффективного алгоритма, который вычисляет 100 цифр
\ (\ sin (\ frac {3} {7}) \) уже связано со многими проблемами, которые также могут
быть актуальным для вычисления 10 000 цифр. Современные алгоритмы позволяют
оценки всех элементарных функций во времени, которое асимптотически
логарифмический по количеству знаков \ (P \) и линейный по стоимости
длинного умножения (обычно обозначается \ (M (P) \)). Почти все
специальные функции могут быть вычислены за время, которое асимптотически
линейные по \ (P \) и \ (M (P) \).(Однако эта асимптотика
стоимость иногда применяется только к очень высокой точности, например,
\ (P> 1000 \), и для
вычисления с меньшей точностью.)

В yacas мы стремимся реализовать все числовые функции до произвольных
точность. Все целочисленные или рациональные функции возвращают точные результаты,
и все функции с плавающей запятой возвращают свое значение с помощью \ (P \)
правильные десятичные цифры (при условии достаточной точности
аргументы). Текущее значение \ (P \) доступно как
Builtin'Precision'Get () и может быть изменен
Набор встроенной точности () .

Реализация вычисления произвольной точности с плавающей запятой
функция \ (f (x) \), например \ (f (x) = \ exp (x) \), обычно требует
следующее:

• Алгоритм, который вычисляет \ (f (x) \) для заданного значения
  \ (x \) до указанной пользователем точности \ (P \) (десятичный)
  цифры. Часто приходится реализовывать несколько алгоритмов для разных
  подобласти пространства (\ (x \) ,: math: P ).

• Оценка вычислительной стоимости алгоритма (ов), как
  функция \ (x \) и \ (P \).Это необходимо для выбора
  лучший алгоритм для данного \ (x, P \).

• Оценка ошибки округления. Это необходимо для выбора
  «Точность обработки», которая обычно несколько выше, чем
  точность конечного результата.

В расчетах с машинной точностью, где количество цифр
исправлено, проблема ошибок округления довольно заметна. Каждый
арифметические операции вызывают небольшую потерю точности; в результате
несколько последних цифр окончательного значения обычно неверны.Но если мы
иметь возможность произвольной точности, мы всегда можем увеличить
точность на несколько цифр во время промежуточных вычислений и
таким образом устраняются все ошибки округления в конечном результате. Мы должны из
Конечно, будьте осторожны, чтобы без надобности не увеличивать точность работы,
потому что любое повышение точности означает более медленные вычисления. Принимая
вдвое больше цифр, чем нужно, и надеясь, что результат будет точным
не лучшее решение.

Выбор алгоритмов для вычислений — самая нетривиальная часть
реализация.Мы хотим добиться сколь угодно высокой точности, поэтому
нам нужно найти либо ряд, либо непрерывную дробь, либо
последовательность, заданная явной формулой, сходящаяся к функции в
контролируемый способ. Недостаточно использовать таблицу предварительно вычисленных
значения или фиксированная формула приближения с ограниченной точностью.

За последние 30 лет интерес к вычислениям произвольной точности
выросло и множество эффективных алгоритмов для элементарных и специальных
функции были опубликованы. Большинство алгоритмов итеративны.Почти
всегда очень важно знать заранее, сколько итераций
необходимо для данного \ (x \), \ (P \). Эти знания позволяют
оценить вычислительные затраты с точки зрения требуемой точности
\ (P \) и стоимости длинного умножения \ (M (P) \), и
выбрать лучший алгоритм.

Обычно все операции относятся к одному из следующих
категорий (по возрастанию стоимости):

• сложение, вычитание: линейно по \ (P \);

• умножение, деление, целая степень, целочисленный корень: линейно по
  \ (M (P) \);

• элементарных функций: \ (\ exp (x) \), \ (\ ln (x) \), \ (\ sin (x) \),
  \ (\ arctan (x) \) и т. д.2) \).

  Некоторым алгоритмам также требуется место для хранения (например, эффективный алгоритм
  для суммирования рядов Тейлора используется временная \ (O (\ ln (P)) \)
  \ (P \) — цифры числа).

  Ниже мы обычно будем обозначать через \ (P \) необходимое количество
  десятичные цифры. Формулы часто содержат заметные факторы
  \ (\ ln (10) \), поэтому будет ясно, как получить аналогичный
  выражения для другой базы. (В большинстве реализаций используется двоичная база
  а не десятичное основание, так как это удобнее для многих
  расчеты.{n + 1}) \]

  , если нам нужно \ (P \) десятичные цифры точности в
  результат. Для конкретности предположим, что \ (| x | <1 \). (Похожий расчет может быть выполнен для любой другой границы \ (x \).)

  Предположим, мы обрезаем ряд после \ (n \) — го члена, а ряд
  сходится «достаточно хорошо» после этого термина. Тогда ошибка будет
  примерно равно первому выпавшему члену. (Это то, что мы
  на самом деле означает «достаточно хорошо сходится», и это обычно
  case во всех приложениях, потому что мы не хотели бы использовать серию
  это не сходится достаточно хорошо.{-P}, \]

  , который нам теперь нужно решить для \ (n \). Левая рука
  сторона убывает с ростом \ (n \). Итак, ясно, что
  неравенство будет выполняться для достаточно больших \ (n \), скажем, для \ (n \ geq n_0 \)
  где \ (n_0 \) — неизвестное (целое) значение. Мы можем взять
  логарифм обеих частей, замените \ (n \) на \ (n_0 \) и получите
  следующее уравнение для \ (n_0 \):

  \ [(n_0 + 2) \ ln ((n_0 + 2) / e) = P * \ ln (10). \]

  Это уравнение не может быть решено точно в терминах
  элементарные функции; это типичная ситуация в таких
  оценки.Однако нам действительно не нужно очень точное решение для
  \ (n_0 \); все, что нам нужно, это оценка его целой части. Это
  тоже типичная ситуация. Это приемлемо, если наша приблизительная стоимость
  of \ (n_0 \) выходит на пару единиц выше необходимого,
  потому что пара лишних терминов из серии Тейлора не поможет
  значительно замедляют алгоритм (но важно, чтобы мы
  не недооценивать \ (n_0 \)). Наконец, нас больше всего интересуют
  имея достаточно хороший ответ для больших значений \ (P \).

  Можно попробовать угадать результат. Самый большой член на LHS растет как
  \ (n_0 \ ln (n_0) \) и он должен быть примерно равен
  \ (P \ ln (10) \); но \ (\ ln (n_0) \) растет очень медленно, так что это дает
  намек на то, что \ (n_0 \) пропорционально \ (P \ ln (10) \). Как
  Сначала мы устанавливаем \ (n_0 = P \ ln (10) -2 \) и сравниваем RHS с
  LHS; мы обнаруживаем, что мы промахнулись на множитель
  \ (\ ln (P) -1+ \ ln (\ ln (10)) \), что не является большим фактором. Теперь мы можем
  компенсировать и разделить \ (n_0 \) на этот коэффициент, поэтому наша вторая попытка —

  \ [n0 = (P \ ln (10)) / (\ ln (P) -1+ \ ln (\ ln (10))) — 2.\]

  (Это приближение
  процедура эквивалентна решению уравнения

  \ [x = (P * \ ln (10)) / (\ ln (x) -1) \]

  прямым повторением, начиная с
  \ (x = P \ ln (10) \).) Если мы заменим нашу вторую попытку на \ (n_0 \)
  в уравнение, мы обнаружим, что мы немного недооценили
  (то есть LHS немного меньше, чем RHS), но наш \ (n_0 \) равен
  теперь меньше, чем должно быть, на величину меньше 1 для
  достаточно большой \ (P \). Поэтому мы должны остановиться на этом и просто
  прибавьте 1 к этому приблизительному ответу.Мы также должны заменить
  \ (\ ln (\ ln (10)) — 1 \) на 0 для простоты (это безопасно, потому что
  немного увеличить \ (n_0 \).)

  Наш окончательный результат — достаточно взять

  \ [n = (P * \ ln (10)) / \ ln (P) -1 \]

  члена ряда Тейлора для вычисления \ (\ exp (x) \) для
  От \ (| x | <1 \) до \ (P \) десятичных цифр. (Конечно, если \ (x \) намного меньше 1, будет достаточно меньшего числа членов.)

  Неизбежные ошибки округления

  По мере роста требуемой точности \ (P \) произвольная точность
  алгоритму потребуется больше итераций или больше членов ряда.Так
  ошибка округления, вносимая каждой операцией с плавающей запятой, будет
  увеличивать. Выполняя вычисления с произвольной точностью, мы всегда можем
  выполнить все расчеты с несколькими цифрами и компенсировать
  ошибка округления. Однако необходимо заранее знать, сколько
  больше цифр нам нужно принять для нашей «рабочей точности». Мы должны
  также учтите это увеличение при оценке общей стоимости
  метод. (В большинстве случаев это увеличение невелико.)

  Вот простая оценка нормальной ошибки округления в
  вычисление \ (n \) членов степенного ряда.{-P} \), то сумма
  накопленная ошибка округления равна \ (3n \ epsilon \). Если родственник
  ошибка \ (3n \ epsilon \), значит наш ответ — что-то
  как \ (a * (1 + 3n \ epsilon) \), где \ (a \) — правильный
  отвечать. Мы видим, что из общего числа \ (P \) цифр этого
  ответ, правильны только первые \ (k \) десятичные цифры, где
  \ (к = — \ ln (3n \ epsilon) / \ ln (10) \). Другими словами, мы потеряли

  \ [P-k = \ ln (3n) / \ ln (10) \]

  цифры из-за накопленного округления
  ошибка. Итак, мы обнаружили, что нам нужно \ (\ ln (3 * n) / \ ln (10) \) дополнительный десятичный
  цифры, чтобы компенсировать эту ошибку округления.

  Эта оценка предполагает несколько вещей о сериале (в основном, что
  сериал «хорошо воспитан»). Эти предположения необходимо проверить в
  каждый конкретный случай. Например, если серия начинается с какого-то
  большие члены, но сходятся к очень малому значению, эта оценка
  неверно (см. следующий подраздел).

  В предыдущем упражнении мы нашли количество членов \ (n \) для
  \ (\ ехр (х) \). Итак, теперь мы знаем, сколько лишних цифр рабочего
  точность, которая нам нужна в данном конкретном случае.М \) является
  необходимое условие, и если \ (P \) велико, находим примерно

  \ [2N + 2 \ приблизительно ((P-M) \ ln (10)) / (\ ln (P-M) -1-M \ ln (10)). \]

  Однако набор сроков еще не гарантирует хорошего результата.
  Члены ряда сначала растут, а затем начинают уменьшаться. В
  сумма этих слагаемых, однако, невелика. Поэтому есть некоторые
  отмены, и нам нужно повысить точность работы, чтобы избежать
  округление. Оценим требуемую точность обработки.

  Нам нужно найти величину наибольшего члена ряда.{\ sqrt {x}} / \ sqrt {x}! \) и поэтому нам нужно около
  \ (M / 2 \ sqrt {x} \) десятичных цифр перед десятичной запятой, чтобы
  представляют этот термин. Но нам также необходимо сохранить не менее \ (P \)
  цифры после десятичной точки, иначе ошибка округления сотрет
  значащие цифры результата. Кроме того, у нас будет
  неизбежная ошибка округления из-за \ (O (P) \) арифметических операций.
  Поэтому мы должны снова увеличить точность на \ (P + \ ln (P) / \ ln (10) \) цифр.
  плюс несколько охранных цифр.

  В качестве примера для вычисления десятичного числа \ (\ sin (10) \) с \ (P = 50 \)
  цифр с помощью этого метода, нам нужна рабочая точность около
  \ (60 \) цифр, а для вычисления \ (\ sin (10000) \) нам нужно работать
  примерно с \ (260 \) цифрами.Это показывает, насколько неэффективно Тейлор
  ряд для \ (\ sin (x) \) становится для больших аргументов \ (x \). А
  простое преобразование \ (x = 2 \ pi n + x ‘\) уменьшило бы \ (x \)
  не более 7, а ненужные вычисления с \ (260 \) цифрами
  можно было бы избежать. Основная причина этой неэффективности заключается в том, что у нас
  складывать и вычитать очень большие числа, чтобы получить относительно небольшие
  результат порядка \ (1 \).

  Мы находим, что метод рядов Тейлора для \ (\ sin (x) \) в целом
  \ (x \) очень неэффективен из-за ошибки округления и должен
  дополняться другими методами.2) \) умножение разрешено до 100-200 десятичных цифр,
  асимптотически самый быстрый метод умножения БПФ хорош на
  точность около 5000 или более десятичных цифр, а Карацуба
  умножение лучше всего в среднем диапазоне.

  Предупреждение: вычисления с использованием внутренней математики yacas с использованием точности
  превышение 10 000 цифр в настоящее время является непрактично медленным.

  В некоторых алгоритмах необходимо вычислять целые части
  такие выражения, как \ (a \ ln (b) / \ ln (10) \) или \ (a \ ln (10) / \ ln (2) \),
  где \ (a \), \ (b \) — короткие целые числа порядка
  \ (O (P) \).Такие выражения часто нужны для оценки
  количество членов в ряду Тейлора или аналогичные параметры
  алгоритмы. В этих случаях важно, чтобы результат не был
  недооценен. Однако было бы расточительно вычислять
  \ (1000 \ ln (10) / \ ln (2) \) с большой точностью только для того, чтобы отбросить большую часть
  эту информацию, взяв целую часть этого числа. это
  более эффективно аппроксимировать такие константы сверху короткими
  рациональные числа, например \ (\ ln (10) / \ ln (2) <28738/8651 \) и \ (\ ln (2) <7050/10171 \).м \). Чтобы найти \ (M \) с \ (P \) (десятичные) цифры, нам понадобится \ (m \) с также не менее \ (P \) цифры. Следовательно, нам действительно нужно оценить \ (\ exp (1000) / \ ln (10) \) с десятичными цифрами \ (434 + P \) до того, как мы может найти \ (P \) цифры мантиссы \ (x \). Мы столкнулись с возможно удивительная ситуация: нужен высокоточный расчет даже найти первую цифру \ (x \), потому что необходимо найти показатель \ (E \) точно как целое число, а \ (E \) - это довольно большое целое число. Обычный числовой расчет с двойной точностью на этом этапе выдаст ошибку переполнения.E \). Мы также можем умножьте или разделите два exp-числа. Но нет смысла умножать ехр-число \ (z \) нормальным числом, потому что мы не можем представить разница между \ (z \) и, скажем, \ (2.52 * z \). По аналогии, добавление \ (z \) к чему-либо еще приведет к полному переполнению, поскольку на самом деле мы не знаем ни одной цифры десятичной дроби представление \ (z \). Итак, если \ (z_1 \) и \ (z_2 \) exp-числа, то \ (z_1 + z_2 \) просто равно либо \ (z1 \) или \ (z2 \) в зависимости от того, какой из них больше.

  Мы находим, что ехр-число \ (z \) действует как эффективная «бесконечность»
  по сравнению с нормальными цифрами. Но exp-числа нельзя использовать как
  устройство для вычисления пределов: неизбежное истощение почти
  безусловно, дают неверные результаты. Например, при попытке проверить

  \ [\ lim_ {x \ to 0} \ frac {\ exp (x) -1} {x} = 1 \]

  заменой \ (x = 1 / z \) на
  некоторое ехр-число \ (z \) дает 0 вместо 1.

  Логарифмирование числа exp возвращает его в область
  нормальные, представимые числа.E) \) с мантиссой с плавающей запятой \ (M \ geq 1 \) и
  целое число \ (E \), удовлетворяющее \ (\ ln (N)

  Логарифм числа exp-small снова делает его нормальным.
  представимое число. Однако, взяв экспоненту от exp-small
  number дает 1 из-за потери значимости. Чтобы получить «дважды
  экспоненциально малое »число, нам нужно взять двойную величину, обратную
  экспоненциально большое число, или возьмите экспоненту экспоненциально большого числа
  большая отрицательная сила.E)) \) 2-ехр-мала.

  Практическое значение exp-номеров довольно ограничено. Мы
  не может получить даже одну значащую цифру числа exp. А
  «Вычисление» с exp-числами — это, по сути, вычисления с плавающей точкой
  вычисление с логарифмами этих exp-чисел. Практическая проблема
  для чего нужны числа такого масштаба, вероятно, можно переформулировать в терминах
  более удобных логарифмов таких чисел. На практике,
  exp-numbers могут быть полезны не как средство для получения числового ответа,
  но как предупреждающий знак о критическом переполнении или недостаточном переполнении.

  Plotting — Sage Tutorial v9.2

  Sage может создавать двухмерные и трехмерные графики.

  Двумерные графики

  В двух измерениях Sage может рисовать круги, линии и многоугольники;
  графики функций в прямоугольных координатах; а также полярные
  графики, контурные графики и графики векторных полей. Мы представляем примеры
  некоторые из них здесь. Для получения дополнительных примеров построения графиков с помощью Sage см.
  Решение дифференциальных уравнений и максимумов, а также
  Конструкции Мудреца
  документация.

  Эта команда создает желтый круг радиуса 1 с центром в
  происхождение:

   мудрец: круг ((0,0), 1, rgbcolor = (1,1,0))
  Графический объект, состоящий из 1 графического примитива
   

  Вы также можете создать закрашенный круг:

   sage: circle ((0,0), 1, rgbcolor = (1,1,0), fill = True)
  Графический объект, состоящий из 1 графического примитива
   

  Вы также можете создать круг, присвоив его переменной; это
  не рисует:

   мудрец: c = круг ((0,0), 1, rgbcolor = (1,1,0))
   

  Для построения используйте c.show () или show (c) , а именно:

  В качестве альтернативы, оценка c.save ('filename.png') сохранит
  сюжет в данный файл.

  Теперь эти «круги» больше похожи на эллипсы, потому что оси
  масштабируется иначе. Вы можете исправить это:

   мудрец: c.show (aspect_ratio = 1)
   

  Команда show (c, aspect_ratio = 1) выполняет то же самое.
  вещь, или вы можете сохранить изображение, используя
  c.save ('filename.png', aspect_ratio = 1) .3), (x, 0,2 * pi), rgbcolor = hue (0,6))
  мудрец: показать (p1 + p2 + p3, axes = false)

  Хороший способ создания форм с заливкой — создание списка
  точек ( L в примере ниже), а затем используйте полигон
  команда для построения фигуры с границей, образованной этими точками. Для
  Например, вот зеленая дельтовидная мышца:

   мудрец: L = [[-1 + cos (pi * i / 100) * (1 + cos (pi * i / 100)),
  ....: 2 * sin (pi * i / 100) * (1-cos (pi * i / 100))] для i в диапазоне (200)]
  мудрец: p = многоугольник (L, rgbcolor = (1 / 8,3 / 4,1 / 2))
  шалфей: p
  Графический объект, состоящий из 1 графического примитива
   

  Введите show (p, axes = false) , чтобы увидеть это без каких-либо осей.

  К сюжету можно добавить текст:

   мудрец: L = [[6 * cos (pi * i / 100) + 5 * cos ((6/2) * pi * i / 100),
  ....: 6 * sin (pi * i / 100) -5 * sin ((6/2) * pi * i / 100)] для i в диапазоне (200)]
  мудрец: p = многоугольник (L, rgbcolor = (1 / 8,1 / 4,1 / 2))
  sage: t = text ("гипотрохоид", (5,4), rgbcolor = (1,0,0))
  шалфей: показать (п + т)
   

  Учителя математического анализа часто рисуют на доске следующий график:
  не одна ветвь arcsin, а несколько из них: т.е.
  график \ (y = \ sin (x) \) для \ (x \) между \ (- 2 \ pi \)
  и \ (2 \ pi \), перевернутый относительно линии под углом 45 градусов.Следующие
  Команды мудреца составляют это:

   sage: v = [(sin (x), x) for x in srange (-2 * float (pi), 2 * float (pi), 0.1)]
  мудрец: линия (v)
  Графический объект, состоящий из 1 графического примитива
   

  Поскольку функция тангенса имеет больший диапазон, чем синус, если вы используете
  тот же трюк, чтобы построить арктангенс, вы должны изменить
  минимальные и максимальные координаты для оси x :

   sage: v = [(tan (x), x) для x в srange (-2 * float (pi), 2 * float (pi), 0,01)]
  sage: show (строка (v), xmin = -20, xmax = 20)
   

  Sage также вычисляет полярные диаграммы, контурные диаграммы и графики векторных полей.
  (для специальных типов функций).Вот пример контура
  участок:

   мудрец: f = лямбда x, y: cos (x * y)
  мудрец: contour_plot (f, (-4, 4), (-4, 4))
  Графический объект, состоящий из 1 графического примитива
   

  Трехмерные участки

  Sage также можно использовать для создания трехмерных сюжетов. 2, (x, -2,2), (y, -2,2))
  Объект Graphics3d

  В качестве альтернативы вы можете использовать paratric_plot3d для построения графика
  параметрическая поверхность, где каждое из \ (x, y, z \) определяется
  функция одной или двух переменных (параметры, обычно
  \ (и \) и \ (v \)).2
  мудрец: параметрический_плот3d ([fx, fy, fz], (u, -1, 1), (v, -1, 1),
  ….: frame = False, color = «yellow»)
  Объект Graphics3d

  Крестовина:

   мудрец: u, v = var ('u, v')
  мудрец: fx = (1 + cos (v)) * cos (u)
  мудрец: fy = (1 + cos (v)) * sin (u)
  мудрец: fz = -tanh ((2/3) * (u-pi)) * sin (v)
  мудрец: параметрический_плот3d ([fx, fy, fz], (u, 0, 2 * pi), (v, 0, 2 * pi),
  ....: frame = False, color = "red")
  Объект Graphics3d
   

  Скрученный тор:

   мудрец: u, v = var ('u, v')
  мудрец: fx = (3 + sin (v) + cos (u)) * cos (2 * v)
  мудрец: fy = (3 + sin (v) + cos (u)) * sin (2 * v)
  мудрец: fz = sin (u) + 2 * cos (v)
  мудрец: параметрический_плот3d ([fx, fy, fz], (u, 0, 2 * pi), (v, 0, 2 * pi),
  .2-1)
  sage: implicit_plot3d (f, (x, -0,5, 0,5), (y, -1, 1), (z, -1, 1))
  Объект Graphics3d
   

  Plotting — документация SymPy 1.8

  Строит трехмерный поверхностный график.

  Использование

  Отдельный участок

  plot3d (expr, range_x, range_y, ** kwargs)

  Если диапазоны не указаны, используется диапазон по умолчанию (-10, 10).

  Множественный график с одинаковым диапазоном.

  plot3d (expr1, expr2, range_x, range_y, ** kwargs)

  Если диапазоны не указаны, используется диапазон по умолчанию (-10, 10).

  Несколько графиков с разными диапазонами.

  plot3d ((выражение1, диапазон_x, диапазон_y), (выражение2, диапазон_x, диапазон_y), ..., ** kwargs)

  Диапазоны должны быть указаны для каждого выражения.

  Диапазон по умолчанию может измениться в будущем, если более расширенный диапазон по умолчанию
  реализован алгоритм обнаружения.

  Аргументы

  expr : Выражение, представляющее функцию вдоль x.

  range_x : (x, 0, 5), кортеж из трех элементов, обозначающий диапазон x
  Переменная.

  range_y : (y, 0, 5), кортеж из трех элементов, обозначающий диапазон переменной y

  .

  Аргументы ключевого слова

  Аргументы для SurfaceOver2DRangeSeries class:

  nb_of_points_x : внутр. Диапазон x выбирается равномерно на
  nb_of_points_x баллов.

  nb_of_points_y : внутр. Диапазон y выбирается равномерно при
  nb_of_points_y баллов.

  Эстетика:

  surface_color : функция, возвращающая число с плавающей запятой. Задает цвет для
  поверхность участка. См. sympy.plotting.Plot для более подробной информации.

  Если имеется несколько графиков, то аргументы одной и той же серии применяются к
  все сюжеты. Если вы хотите установить эти параметры отдельно, вы можете проиндексировать
  вернул объект Plot и установил его.

  Аргументы за Участок класс:

  название : ул.Название сюжета.
  размер : (поплавок, поплавок), опционально
  Кортеж в форме (ширина, высота) в дюймах, чтобы указать размер
  общая цифра. По умолчанию установлено значение Нет , что означает, что размер будет
  быть установленным сервером по умолчанию.

  Примеры

   >>> из символов импорта sympy
  >>> из sympy.plotting import plot3d
  >>> x, y = символы ('x y')
   

  Отдельный участок

   >>> plot3d (x * y, (x, -5, 5), (y, -5, 5))
  Объект участка, содержащий:
  [0]: декартова поверхность: x * y для x больше (-5.0, 5.0) и y больше (-5.0, 5.0)
   

  (png, hires.png, pdf)

  Несколько участков с одинаковым диапазоном

   >>> plot3d (x * y, -x * y, (x, -5, 5), (y, -5, 5))
  Объект участка, содержащий:
  [0]: декартова поверхность: x * y для x больше (-5,0, 5,0) и y больше (-5,0, 5,0)
  [1]: декартова поверхность: -x * y для x больше (-5.0, 5.0) и y больше (-5.0, 5.0)
   

  (png, hires.png, pdf)

  Несколько графиков с разными диапазонами.

   >>> plot3d ((x ** 2 + y ** 2, (x, -5, 5), (y, -5, 5)),
  ... (х * у, (х, -3, 3), (у, -3, 3)))
  Объект участка, содержащий:
  [0]: декартова поверхность: x ** 2 + y ** 2 для x больше (-5,0, 5,0) и y больше (-5,0, 5,0)
  [1]: декартова поверхность: x * y для x больше (-3,0, 3,0) и y больше (-3,0, 3,0)
   

  (png, hires.png, pdf)

  Построение графиков на Python | Set 1

  Эта серия статей познакомит вас с построением графиков на Python с помощью Matplotlib, который, возможно, является самой популярной библиотекой для построения графиков и визуализации данных для Python.

  Установка

  Самый простой способ установить matplotlib — использовать pip. Введите в терминале следующую команду:

   pip install matplotlib 

  ИЛИ вы можете загрузить его отсюда и установить вручную.

  Начало работы (Построение линии)

  import matplotlib.pyplot as plt x 0003 = = 2 , 3 ] y = [ 2 , 4 , 1 000 000 000] 000plot (x, y) plt.xlabel ( 'x - axis' ) plt.ylabel ( 'y - axis' ) plt.title ( 'My first graph!' ) plt.show ()

  Output:

  Были выполнены следующие шаги:

  • Определите ось x и соответствующие значения оси y в виде списков.
  • Изобразите их на холсте с помощью функции .plot () .
  • Дайте имя оси x и оси y с помощью функций .xlabel () и .ylabel () .
  • Дайте название своему сюжету с помощью функции .title () .
  • Наконец, чтобы просмотреть ваш график, мы используем функцию .show () .

  Отображение двух или более линий на одном участке

  import matplotlib.pyplot as plt x1 , 0003 = 2 , 3 ] y1 = [ 2 , 4 , 1 ] ] ]участок (x1, y1, метка = "строка 1" ) x2 = [ 1 , 2, , 2, 2, ] y2 = [ 4 , 1 , 3 ] y2 , этикетка , строка 2 " ) plt.xlabel ( 'x - axis' ) plt.ylabel ( 'y - axis' ) plt.title ( 'Две линии на одном графике!' ! ) plt.legend () plt.show ()

  Выход:
  9000 graph9

  • две линии на одном и том же Мы различаем их, давая им имя ( метка ), которое передается в качестве аргумента.plot () функция.
  • Небольшое прямоугольное поле с информацией о типе линии и ее цвете называется легендой. Мы можем добавить легенду к нашему графику, используя функцию .legend () .

  C Настройка участков

  Здесь мы обсудим некоторые элементарные настройки, применимые практически к любому участку.

  импорт matplotlib.pyplot as plt x = [ 1 , 0003, 4 , 5 , 6 ] y = [ 2 , 4 , 0004 , 2 , 6 ] plt.график (x, y, цвет = 'зеленый' , стиль линий = 'пунктирный' , ширина линии = 3 , маркер 'o' , цвет лица маркера = 'синий' , размер маркера = 12 ) 0003 8 ) плат.xlim ( 1 , 8 ) plt.xlabel ( 'x - ось' ) 'ось ' ) plt.title ( ' Некоторые крутые настройки! ' ) Plt.show: Как видите, мы выполнили несколько настроек, например , установив ширину линии, стиль линии и цвет линии. установка маркера, цвет лица маркера, размер маркера. переопределение диапазона осей x и y. Если переопределение не выполнено, модуль pyplot использует функцию автоматического масштабирования для установки диапазона и масштаба оси. Гистограмма import matplotlib.pyplot as plt слева 0003, 000 000 , 3 , 4 , 5 ] высота = [ 10 0003, 10 0003, , 40 , 5 ] tick_label = [ 'one' '' '' '' , «четыре» , «пять» ] plt.bar (left, height, tick_label = tick_label, width = 0,8 , цвет = [ '' красный ' ' красный ' ]) plt.xlabel ( 'x - axis' ) plt.ylabel ( 'y - axis' t )title ( 'Моя гистограмма!' ) plt.show () Выход: Здесь мы используем plt. для построения гистограммы. Передаются координаты x левой стороны стержней вместе с высотой стержней. вы также можете дать какое-то имя координатам оси x, указав tick_labels Histogram import matplotlib.pyplot as plt возраст = [ 2 , 5 , 70 , 0003 40, 45 , 50 , 45 , 43 , 40 , 44 , 13 , 57 , 18 , 90 , 77 , 32 , 21 0004 40 ] диапазон = ( 0 , 100 ) бункеров = 10 пл.hist (возрасты, ячейки, диапазон , цвет = 'зеленый' , histtype = 'bar' , rwidth = ) plt.xlabel ( 'age' ) plt.ylabel ( 'Кол-во людей' ) «Моя гистограмма» ) plt.show () Вывод: Здесь мы используем функцию plt.hist () для построения гистограммы. частот передаются как список возрастов . Диапазон может быть установлен путем определения кортежа, содержащего минимальное и максимальное значение. Следующим шагом является определение диапазона значений « bin », то есть разделение всего диапазона значений на серию интервалов, а затем подсчет количества значений, попадающих в каждый интервал.Здесь мы определили интервалов = 10. Итак, всего 100/10 = 10 интервалов. Диаграмма рассеяния import matplotlib.pyplot as plt x = 0003 0003 0003 0003 0003 0003 0003 3 , 4 , 5 , 6 , 7 , 8 , 9 , , , , y = [ 2 , 4 , 5 , 7 , 6 , 8, 8, 8, 8, 11 , 12 , 12 ] plt.разброс (x, y, метка = "звездочки" , цвет = "зеленый" , маркер = "*" = 30 ) plt.xlabel ( 'x - axis' ) plt.ylabel ( 9000 axis) PLT.title ( 'My scatter plot!' ) plt.legend () plt.show () 2 Здесь , мы используем функцию plt.scatter () для построения диаграммы рассеяния. Как линия, мы также определяем x и соответствующие значения оси y. маркер аргумент используется для установки символа для использования в качестве маркера.Его размер можно определить с помощью параметра s . Круговая диаграмма import matplotlib.pyplot as plt деятельности = ' , ' работа ' , ' играть ' ] срезы = [ 3 , , , 6 ] цветов = [ 'r' , 'y' , , , 'b' ] plt.круговая диаграмма (срезы, метки = действий, цвета = цветов, startangle = 90 , тень = True ( 0 , 0 , 0,1 , 0 ), радиус = = 2 , autopct = '% 1.1f %%' ) plt.legend () plt.pro Вывод вышеуказанной программы выглядит следующим образом: Здесь мы строим круговую диаграмму, используя метод plt.pie () . Прежде всего, мы определяем меток , используя список под названием activity . Затем можно определить часть каждой метки с помощью другого списка, который называется срезов . Цвет для каждой метки определяется с помощью списка под названием цветов . shadow = True покажет тень под каждой меткой на круговой диаграмме. startangle вращает начало круговой диаграммы на заданные градусы против часовой стрелки от оси x. разнесение используется для задания доли радиуса, на которую мы смещаем каждый клин. autopct используется для форматирования значения каждой метки. Здесь мы установили отображение процентного значения только с точностью до 1 знака после запятой. Графические кривые данного уравнения import matplotlib.pyplot as plt import numpy as np .arange ( 0 , 2 * (нп.pi), 0,1 ) y = np.sin (x) plt.plot (x, y) .show () Результат вышеупомянутой программы выглядит следующим образом: Здесь мы используем NumPy , который является универсальным пакетом обработки массивов на Python. Чтобы установить значения оси x, мы используем np.arange () , в котором первые два аргумента предназначены для диапазона, а третий - для пошагового приращения. Результатом является массив с большим количеством символов. Чтобы получить соответствующие значения оси Y, мы просто используем предопределенный метод np.sin () для массива numpy. Наконец, мы строим точки, передавая массивы x и y функции plt.plot () . Итак, в этой части мы обсудили различные типы графиков, которые мы можем создать в matplotlib. Есть еще участки, которые не были охвачены, но самые важные из них обсуждаются здесь - Эта статья предоставлена ​​ Nikhil Kumar .Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью на сайте deposit.geeksforgeeks.org или отправить свою статью по электронной почте: [email protected]. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам. Пожалуйста, напишите комментарий, если вы обнаружите что-то неправильное, или если вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше. Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы. Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS . Обзор функций построения графиков seaborn - документация seaborn 0.11.1 Большая часть вашего взаимодействия с seaborn будет происходить с помощью набора функций построения графиков. В последующих главах учебника будут рассмотрены конкретные функции, предлагаемые каждой функцией. В этой главе на высоком уровне будут представлены различные виды функций, с которыми вы столкнетесь. Подобные функции для аналогичных задач Пространство имен seaborn плоское; вся функциональность доступна на верхнем уровне. Но сам код имеет иерархическую структуру с модулями функций, которые достигают одинаковых целей визуализации с помощью различных средств. Большинство документов построено вокруг этих модулей: вы встретите такие названия, как «реляционный», «распределительный» и «категориальный». Например, модуль распределения определяет функции, которые специализируются на представлении распределения точек данных.Сюда входят знакомые методы, такие как гистограмма: пингвинов = sns.load_dataset («пингвины») sns.histplot (данные = пингвины, x = "flipper_length_mm", hue = "разновидности", multiple = "стек") Наряду с аналогичными, но, возможно, менее знакомыми параметрами, такими как оценка плотности ядра: sns.kdeplot (данные = пингвины, x = "flipper_length_mm", hue = "разновидности", multiple = "stack") Функции внутри модуля имеют много общего базового кода и предлагают аналогичные функции, которые могут отсутствовать в других компонентах библиотеки (например, multiple = "stack" в приведенных выше примерах).Они предназначены для облегчения переключения между различными визуальными представлениями при исследовании набора данных, поскольку разные представления часто имеют взаимодополняющие сильные и слабые стороны. Функции на уровне фигур в сравнении с функциями на уровне осей В дополнение к различным модулям существует сквозная классификация морских функций на «уровень осей» или «уровень фигур». Приведенные выше примеры являются функциями на уровне осей. Они наносят данные на один объект matplotlib.pyplot.Axes , который является возвращаемым значением функции. Напротив, функции уровня фигуры взаимодействуют с matplotlib через объект морского происхождения, обычно FacetGrid , который управляет фигурой. Каждый модуль имеет одну функцию уровня фигуры, которая предлагает единый интерфейс для различных функций уровня осей. Организация выглядит примерно так: Например, displot () - это функция уровня рисунка для модуля распределений. Его поведение по умолчанию - рисование гистограммы с использованием того же кода, что и histplot () за кулисами: sns.displot (данные = пингвины, x = "flipper_length_mm", hue = "разновидности", multiple = "stack") Чтобы вместо этого нарисовать график плотности ядра, используя тот же код, что и для kdeplot () , выберите его с помощью параметра kind : sns.displot (data = penguins, x = "flipper_length_mm", hue = "views", multiple = "stack", kind = "kde") Вы заметите, что графики на уровне фигур в основном похожи на их аналоги на уровне осей, но есть несколько отличий. Примечательно, что легенда помещена вне сюжета.У них также немного другая форма (подробнее об этом чуть позже). Наиболее полезная особенность, предлагаемая функциями уровня фигур, заключается в том, что они могут легко создавать фигуры с несколькими частями. Например, вместо того, чтобы складывать три распределения для каждого вида пингвинов на одних и тех же осях, мы можем «фасетить» их, нанеся каждое распределение по столбцам рисунка: sns.displot (данные = пингвины, x = "flipper_length_mm", hue = "разновидности", col = "разновидности") Функции уровня фигуры оборачивают свои аналоги на уровне осей и передают аргументы ключевого слова, зависящие от типа (например, размер ячейки для гистограммы), в базовую функцию.Это означает, что они не менее гибки, но есть и обратная сторона: параметры, зависящие от типа, не отображаются в сигнатуре функции или строках документации. Некоторые из их функций могут быть менее заметными, и вам может потребоваться просмотреть две разные страницы документации, прежде чем понять, как достичь конкретной цели. Функции уровня осей образуют автономные графики Функции уровня осей написаны так, чтобы действовать как замена для функций matplotlib. Хотя они автоматически добавляют метки осей и легенды, они не изменяют ничего, кроме осей, в которые они нарисованы.Это означает, что они могут быть составлены в произвольно сложные фигуры matplotlib с предсказуемыми результатами. Функции уровня осей вызывают внутри себя matplotlib.pyplot.gca () , который подключается к интерфейсу конечного автомата matplotlib, чтобы они рисовали свои графики на «текущих активных» осях. Но они дополнительно принимают аргумент ax = , который интегрируется с объектно-ориентированным интерфейсом и позволяет вам точно указать, куда должен идти каждый график: f, axs = plt.подзаголовки (1, 2, figsize = (8, 4), gridspec_kw = dict (width_ratios = [4, 3])) sns.scatterplot (data = penguins, x = "flipper_length_mm", y = "bill_length_mm", hue = "разновидности", ax = axs [0]) sns.histplot (data = penguins, x = "разновидности", hue = "разновидности", shrink = .8, alpha = .8, legend = False, ax = axs [1]) f.tight_layout () Функции уровня фигуры имеют свою фигуру Напротив, функции уровня фигуры не могут (легко) быть скомбинированы с другими графиками. По замыслу, они «владеют» своей собственной фигурой, включая ее инициализацию, поэтому нет никакого понятия об использовании функции уровня фигуры для рисования графика на существующих осях.Это ограничение позволяет функциям уровня фигуры реализовывать такие функции, как размещение легенды за пределами графика. Тем не менее, можно выйти за рамки того, что предлагают функции уровня фигуры, получив доступ к осям matplotlib на объекте, который они возвращают, и добавив таким образом другие элементы к графику: tips = sns.load_dataset ("подсказки") g = sns.relplot (data = tips, x = "total_bill", y = "tip") g.ax.axline (xy1 = (10, 2), slope = .2, color = "b", тире = (5, 2)) Настройка графиков с помощью функции уровня фигуры Функции уровня фигуры возвращают экземпляр FacetGrid , у которого есть несколько методов для настройки атрибутов графика таким образом, чтобы "разумно" организовать подзаголовок.Например, вы можете изменить метки на внешних осях, используя одну строку кода: г = sns.relplot (data = penguins, x = "flipper_length_mm", y = "bill_length_mm", col = "sex") g.set_axis_labels ("Длина флиппера (мм)", "Длина банкноты (мм)") Хотя это удобно, это добавляет немного дополнительной сложности, так как вам нужно помнить, что этот метод не является частью API-интерфейса matplotlib и существует только при использовании функции уровня рисунка. Указание размеров фигур Чтобы увеличить или уменьшить размер графика matplotlib, вы устанавливаете ширину и высоту всей фигуры либо в глобальном параметре rcParams, настраивая график (например,грамм. с параметром figsize из matplotlib.pyplot.subplots () ) или путем вызова метода для объекта figure (например, matplotlib.Figure.set_size_inches () ). При использовании функции уровня осей в seaborn применяются те же правила: размер графика определяется размером фигуры, частью которой он является, и расположением осей на этом рисунке. При использовании функции на уровне цифр есть несколько ключевых отличий. Во-первых, сами функции имеют параметры для управления размером фигуры (хотя на самом деле это параметры лежащей в основе FacetGrid , которая управляет фигурой).Во-вторых, эти параметры, height и aspect , параметризуют размер немного иначе, чем параметры width , height в matplotlib (с использованием параметров seaborn, width = height * apsect ). Наиболее важно то, что параметры соответствуют размеру каждого участка , а не размеру всей фигуры. Чтобы проиллюстрировать разницу между этими подходами, вот вывод по умолчанию matplotlib.pyplot.subplots () с одним подзаголовком: Рисунок с несколькими столбцами будет иметь одинаковый общий размер, но оси будут сжаты по горизонтали, чтобы поместиться в пространстве: f, ax = plt.subplots (1, 2, sharey = True) Напротив, график, созданный функцией уровня фигуры, будет квадратным. Чтобы продемонстрировать это, давайте создадим пустой график, напрямую используя FacetGrid . Это происходит за кулисами в таких функциях, как relplot () , displot () или catplot () : . г = снс.FacetGrid (пингвины) Когда добавляются дополнительные столбцы, сама фигура становится шире, так что его подзаголовки имеют одинаковый размер и форму: г = sns.FacetGrid (пингвины, col = "sex") И вы можете настроить размер и форму каждого подзаголовка без учета общего количества строк и столбцов на рисунке: г = sns.FacetGrid (пингвины, col = "sex", рост = 3,5, аспект = 0,75) В результате вы можете назначать переменные фасетирования, не задумываясь о том, как вам нужно настроить общий размер фигуры.Обратной стороной является то, что, когда вы действительно хотите изменить размер фигуры, вам нужно помнить, что все работает немного иначе, чем в matplotlib. Относительные достоинства функций уровня фигуры Вот краткое изложение плюсов и минусов, которые мы обсудили выше: Преимущества Недостатки Простая фасетка по переменным данных Многие параметры отсутствуют в сигнатуре функции Легенда вне графика по умолчанию Не может быть частью большой фигуры matplotlib Простая настройка на уровне фигур Другой API от matplotlib Параметрирование различных размеров фигур Параметрирование различных размеров фигур В целом, функции на уровне фигур добавляют некоторую дополнительную сложность, которая может запутать новичков, но их отличительные особенности дают им дополнительные возможности.В учебной документации в основном используются функции уровня рисунка, поскольку они создают немного более четкие графики, и мы обычно рекомендуем их использовать для большинства приложений. Единственная ситуация, когда они не являются хорошим выбором, - это когда вам нужно создать сложную автономную фигуру, которая состоит из нескольких различных типов сюжетов. На этом этапе рекомендуется настроить фигуру напрямую с помощью matplotlib и заполнить отдельные компоненты с помощью функций уровня осей. Объединение нескольких представлений данных Две важные функции построения графиков в море не полностью вписываются в схему классификации, описанную выше.Эти функции, Jointplot () и pairplot () , используют несколько видов графиков из разных модулей для представления нескольких аспектов набора данных на одном рисунке. Оба графика являются функциями уровня фигуры и по умолчанию создают фигуры с несколькими частями. Но для управления фигурой они используют разные объекты: JointGrid и PairGrid соответственно. Jointplot () отображает взаимосвязь или совместное распределение двух переменных с добавлением маргинальных осей, которые показывают одномерное распределение каждой из них в отдельности: sns.Jointplot (data = penguins, x = "flipper_length_mm", y = "bill_length_mm", hue = "разновидности") pairplot () похожа - она ​​объединяет совместное и маргинальное представления - но вместо того, чтобы сосредоточиться на одной взаимосвязи, она визуализирует каждую попарную комбинацию переменных одновременно: sns.pairplot (данные = пингвины, оттенок = "виды") За кулисами эти функции используют функции уровня осей, которые вы уже встречали ( scatterplot () и kdeplot () ), и у них также есть параметр kind , который позволяет быстро переключаться в другое представление : sns.Jointplot (data = penguins, x = "flipper_length_mm", y = "bill_length_mm", hue = "разновидности", kind = "hist") . Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт