Как найти корень квадратный из числа: Как вычислить квадратный корень большого числа? — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Что значит корень числа. Как найти квадратный корень числа вручную

Что такое квадратный корень?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Это понятие очень простое. Естественное, я бы сказал. Математики на каждое действие стараются найти противодействие. Есть сложение — есть и вычитание. Есть умножение — есть и деление. Есть возведение в квадрат… Значит есть и извлечение квадратного корня!
Вот и всё. Это действие (извлечение квадратного корня
) в математике обозначается вот таким значком:

Сам значок называется красивым словом «радикал
«.

Как извлечь корень?
Это лучше рассмотреть на примерах
.

Сколько будет квадратный корень из 9? А какое число в квадрате даст нам 9? 3 в квадрате даст нам 9! Т.е:

А вот сколько будет квадратный корень из нуля? Не вопрос! Какое число в квадрате ноль даёт? Да сам же ноль и даёт! Значит:

Уловили, что такое квадратный корень?
Тогда считаем примеры
:

Ответы (в беспорядке): 6; 1; 4; 9; 5.

Решили? Действительно, уж куда проще-то?!

Но… Что делает человек, когда видит какое-нибудь задание с корнями?

Тосковать начинает человек… Не верит он в простоту и лёгкость корней. Хотя, вроде, и знает, что такое квадратный корень
…

Всё потому, что человек проигнорировал несколько важных пунктиков при изучении корней. Потом эти пунктики жестоко мстят на контрольных и экзаменах…

Пунктик первый. Корни надо узнавать в лицо!

Сколько будет корень квадратный из 49? Семь? Верно! А как вы узнали, что семь? Возвели семёрку в квадрат и получили 49? Правильно! Обратите внимание, чтобы извлечь корень
из 49 нам пришлось проделать обратную операцию — возвести 7 в квадрат! И убедиться, что мы не промахнулись. А могли и промахнуться…

В этом и есть сложность извлечения корней
. Возвести в квадрат
можно любое число без особых проблем. Умножить число само на себя столбиком — да и все дела. А вот для извлечения корня
такой простой и безотказной технологии нет. Приходится подбирать
ответ и проверять его на попадание возведением в квадрат.

Этот сложный творческий процесс — подбор ответа — сильно упрощается, если вы помните
квадраты популярных чисел. Как таблицу умножения. Если, скажем, надо умножить 4 на 6 — вы же не складываете четверку 6 раз? Сразу выплывает ответ 24. Хотя, не у всех он выплывает, да…

Для свободной и успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём туда
и обратно.
Т.е. вы должны легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121. Чтобы добиться такого запоминания, есть два пути. Первый — выучить таблицу квадратов. Это здорово поможет решать примеры. Второй — решать побольше примеров. Это здорово поможет запомнить таблицу квадратов.

И никаких калькуляторов! Только для проверки. Иначе на экзамене будете тормозить нещадно…

Итак, что такое квадратный корень
и как извлекать корни
— думаю, понятно. Теперь выясним ИЗ ЧЕГО можно их извлекать.

Пунктик второй. Корень, я тебя не знаю!

Из каких чисел можно извлекать квадратные корни? Да почти из любых. Проще понять, из чего нельзя
их извлекать.

Попробуем вычислить вот такой корень:

Для этого нужно подобрать число, которое в квадрате даст нам -4. Подбираем.

Что, не подбирается? 2 2 даёт +4. (-2) 2 даёт опять +4! Вот-вот… Нет таких чисел, которые при возведении в квадрат дадут нам отрицательное число! Хотя я такие числа знаю. Но вам не скажу). Поступите в институт — сами узнаете.

Такая же история будет с любым отрицательным числом. Отсюда вывод:

Выражение, в котором под знаком квадратного корня стоит отрицательное число — не имеет смысла
! Это запретная операция. Такая же запретная, как и деление на ноль. Запомните этот факт железно!
Или, другими словами:

Квадратные корни из отрицательных чисел извлечь нельзя!

Зато из всех остальных — можно. Например, вполне можно вычислить

На первый взгляд это очень сложно. Подбирать дроби, да в квадрат возводить… Не волнуйтесь. Когда разберёмся со свойствами корней, такие примеры будут сводиться к всё той же таблице квадратов. Жизнь станет проще!

Ну ладно дроби. Но нам ведь ещё попадаются выражения типа:

Ничего страшного. Всё то же самое. Корень квадратный из двух — это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное… Вот оно:

Что интересно, эта дробь не кончается никогда… Такие числа называются иррациональными. В квадратных корнях это — самое обычное дело. Кстати, именно поэтому выражения с корнями называют иррациональными
. Понятно, что писать всё время такую бесконечную дробь неудобно. Поэтому вместо бесконечной дроби так и оставляют:

Если при решении примера у вас получилось что-то неизвлекаемое, типа:

то так и оставляем. Это и будет ответ.

Нужно чётко понимать, что под значками

Конечно, если корень из числа извлекается ровно
, вы обязаны это сделать. Ответ задания в виде, например

вполне себе полноценный ответ.

И, конечно, надо знать на память приблизительные значения:

Это знание здорово помогает оценить ситуацию в сложных заданиях.

Пунктик третий. Самый хитрый.

Основную путаницу в работу с корнями вносит как раз этот пунктик. Именно он придаёт неуверенность в собственных силах… Разберёмся с этим пунктиком как следует!

Для начала опять извлечём квадратный корень их четырёх. Что, уже достал я вас с этим корнем?) Ничего, сейчас интересно будет!

Какое число даст в квадрате 4? Ну два, два — слышу недовольные ответы…

Верно. Два. Но ведь и минус два
даст в квадрате 4… А между тем, ответ

правильный, а ответ

грубейшая ошибка. Вот так.

Так в чём же дело?

Действительно, (-2) 2 = 4. И под определение корня квадратного из четырёх минус два
вполне подходит… Это тоже корень квадратный из четырёх.

Но! В школьном курсе математики принято считать за квадратные корни только неотрицательные числа!
Т. е ноль и все положительные. Даже термин специальный придуман:
из числа а
— это неотрицательное
число, квадрат которого равен а
. Отрицательные результаты при извлечении арифметического квадратного корня попросту отбрасываются. В школе все квадратные корни — арифметические
. Хотя особо об этом не упоминается.

Ну ладно, это понятно. Это даже и лучше — не возиться с отрицательными результатами… Это ещё не путаница.

Путаница начинается при решении квадратных уравнений. Например, надо решить вот такое уравнение.

Уравнение простое, пишем ответ (как учили):

Такой ответ (совершенно правильный, кстати) — это просто сокращённая запись двух
ответов:

Стоп-стоп! Чуть выше я написал, что квадратный корень — число всегда
неотрицательное! А здесь один из ответов — отрицательный
! Непорядок. Это первая (но не последняя) проблемка, которая вызывает недоверие к корням… Решим эту проблемку. Запишем ответы (чисто для понимания!) вот так:

Скобки сути ответа не меняют. Просто я отделил скобками знаки
от корня
. Теперь наглядно видно, что сам корень (в скобках) — число всё равно неотрицательное! А знаки — это результат решения уравнения
. Ведь при решении любого уравнения мы должны записать все
иксы, которые при подстановке в исходное уравнение дадут верный результат. В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.

Вот так. Если вы просто извлекаете квадратный корень
из чего-либо, вы всегда
получаете один неотрицательный
результат. Например:

Потому, что это — арифметический квадратный корень
.

Но если вы решаете какое-нибудь квадратное уравнение, типа:

то всегда
получается два
ответа (с плюсом и минусом):

Потому, что это — решение уравнения.

Надеюсь, что такое квадратный корень
со своими пунктиками вы уяснили. Теперь осталось узнать, что можно делать с корнями, каковы их свойства. И какие там пунктики и подводные кор… извините, камни!)

Всё это — в следующих уроках.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Рациональные числа

Неотрицательный квадратный корень из положительного числа называется арифметическим квадратным корнем
и обозначается с использованием знака радикала .

Комплексные числа

Над полем комплексных чисел решений всегда два, отличающихся только
знаком (за исключением квадратного корня из нуля). Корень из
комплексного числа часто обозначают как , однако использовать это обозначение нужно осторожно. Распространённая ошибка:

Для извлечения квадратного корня из комплексного числа удобно
использовать экспоненциальную форму записи комплексного числа: если

,
,

где корень из модуля понимается в смысле арифметического значения, а k
может принимать значения k=0 и k=1, таким образом в итоге в ответе
получаются два различных результата.

Обобщения

Квадратные корни вводятся как решения уравнений вида и для других объектов: матриц , функций , операторов и т. п. В качестве операции при этом могут использоваться достаточно произвольные мультипликативные операции, например, суперпозиция .

Квадратный корень в информатике

Во многих языках программирования функционального уровня (а также языках разметки типа LaTeX) функция квадратного корня обозначается как sqrt
(от англ. square root

«квадратный корень»).

Алгоритмы нахождения квадратного корня

Нахождение или вычисление квадратного корня заданного числа называется извлечением
(квадратного) корня.

Разложение в ряд Тейлора

при .

Арифметическое извлечение квадратного корня

Для квадратов чисел верны следующие равенства:

То есть, узнать целую часть
квадратного корня числа можно, вычитая из него все нечётные числа по
порядку, пока остаток не станет меньше следующего вычитаемого числа или
равен нулю, и посчитав количество выполненных действий. Например, так:

Выполнено 3 действия, квадратный корень числа 9 равен 3.

Недостатком такого способа является то, что если извлекаемый корень
не является целым числом, то можно узнать только его целую часть, но не
точнее. В то же время такой способ вполне доступен детям, решающим
простейшие математические задачи, требующие извлечения квадратного
корня.

Грубая оценка

Многие алгоритмы вычисления квадратных корней из положительного действительного числа S

требуют некоторого начального значения. Если начальное значение слишком
далеко от настоящего значения корня, вычисления замедляются. Поэтому
полезно иметь грубую оценку, которая может быть очень неточна, но легко
вычисляется. Если S
≥ 1, пусть D
будет числом цифр S
слева от десятичной запятой. Если S
D
будет числом нулей, идущих подряд, справа от десятичной запятой, взятое со знаком минус. Тогда грубая оценка выглядит так:

Если D
нечётно, D
= 2n
+ 1, тогда используем Если D
чётно, D
= 2n
+ 2, тогда используем

Два и шесть используются потому, что и

При работе в двоичной системе (как внутри компьютеров), следует использовать другую оценку (здесь D
это число двоичных цифр).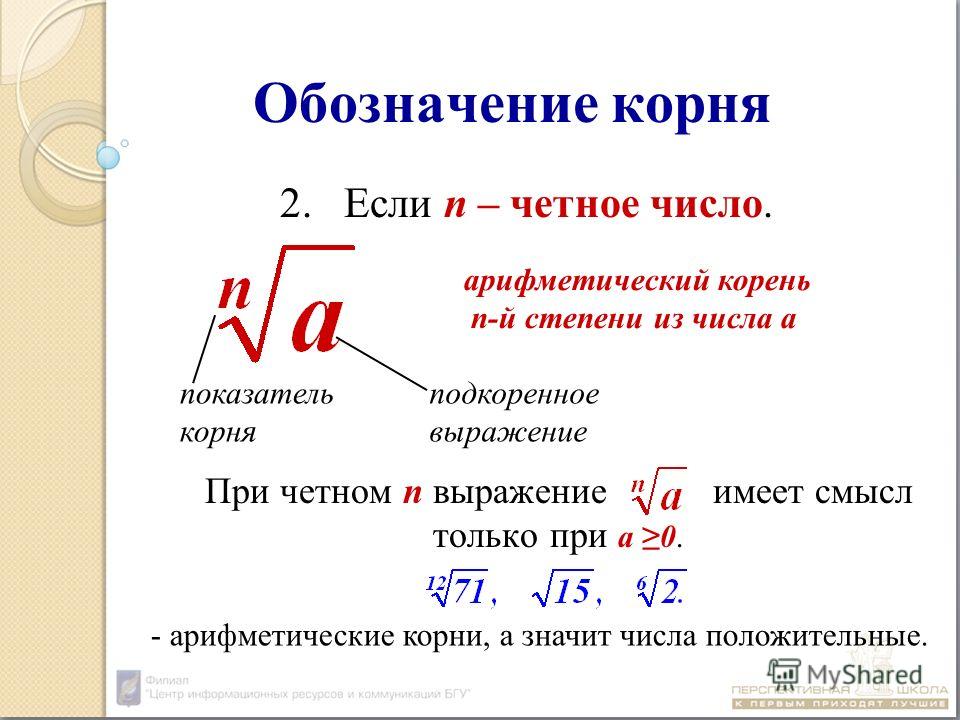

Геометрическое извлечение квадратного корня

Для ручного извлечения корня применяется запись, похожая на деление столбиком .
Выписывается число, корень которого ищем. Справа от него будем
постепенно получать цифры искомого корня. Пусть извлекается корень из
числа
с конечным числом знаков после запятой. Для начала мысленно или метками
разобьём число N на группы по две цифры слева и справа от десятичной
точки. При необходимости, группы дополняются нулями — целая часть
дополняется слева, дробная справа. Так 31234.567 можно представить, как
03 12 34 . 56 70. В отличие от деления снос производится такими группами
по 2 цифры.

Наглядное описание алгоритма:

Математика зародилась тогда, когда человек осознал себя и стал позиционироваться как автономная единица мира. Желание измерить, сравнить, посчитать то, что тебя окружает, — вот что лежало в основе одной из фундаментальных наук наших дней. Сначала это были частички элементарной математики, что позволили связать числа с их физическими выражениями, позже выводы стали излагаться лишь теоретически (в силу своей абстрактности), ну а через некоторое время, как выразился один ученый, «математика достигла потолка сложности, когда из нее исчезли все числа». Понятие «квадратный корень» появилось еще в то время, когда его можно было без проблем подкрепить эмпирическими данными, выходя за плоскость вычислений.

С чего все начиналось

Первое упоминание корня, который на данный момент обозначается как √, было зафиксировано в трудах вавилонских математиков, положивших начало современной арифметике. Конечно, на нынешнюю форму они походили мало — ученые тех лет сначала пользовались громоздкими табличками. Но во втором тысячелетии до н. э. ими была выведена приближенная формула вычислений, которая показывала, как извлечь квадратный корень. На фото ниже изображен камень, на котором вавилонские ученые высекли процесс вывода √2 , причем он оказался настолько верным, что расхождение в ответе нашли лишь в десятом знаке после запятой.

Помимо этого, корень применялся, если нужно было найти сторону треугольника, при условии, что две другие известны. Ну и при решении квадратных уравнений от извлечения корня никуда не деться.

Наравне с вавилонскими работами объект статьи изучался и в китайской работе «Математика в девяти книгах», а древние греки пришли к выводу, что любое число, из которого не извлекается корень без остатка, дает иррациональный результат.

Происхождение данного термина связывают с арабским представлением числа: древние ученые полагали, что квадрат произвольного числа произрастает из корня, подобно растению. На латыни это слово звучит как radix (можно проследить закономерность — все, что имеет под собой «корневую» смысловую нагрузку, созвучно, будь то редис или радикулит).

Ученые последующих поколений подхватили эту мысль, обозначая его как Rx. Например, в XV веке, дабы указать, что извлекается корень квадратный из произвольного числа a, писали R 2 a. Привычная современному взгляду «галочка» √ появилась лишь в XVII веке благодаря Рене Декарту.

Наши дни

С точки зрения математики, квадратный корень из числа y — это такое число z, квадрат которого равен y. Иными словами, z 2 =y равносильно √y=z. Однако данное определение актуально лишь для арифметического корня, так как оно подразумевает неотрицательное значение выражения. Иными словами, √y=z, где z больше либо равно 0.

В общем случае, что действует для определения алгебраического корня, значение выражения может быть как положительным, так и отрицательным. Таким образом, в силу того, что z 2 =y и (-z) 2 =y, имеем: √y=±z или √y=|z|.

Благодаря тому, что любовь к математике с развитием науки лишь возросла, существуют разнообразные проявления привязанности к ней, не выраженные в сухих вычислениях. Например, наравне с такими занятными явлениями, как день числа Пи, отмечаются и праздники корня квадратного. Отмечаются они девять раз в сто лет, и определяются по следующему принципу: числа, которые обозначают по порядку день и месяц, должна быть корнем квадратным из года. Так, в следующий раз предстоит отмечать сей праздник 4 апреля 2016 года.

Свойства квадратного корня на поле R

Практически все математические выражения имеют под собой геометрическую основу, не миновала эта участь и √y, который определяется как сторона квадрата с площадью y.

Как найти корень числа?

Алгоритмов вычисления существует несколько. Наиболее простым, но при этом достаточно громоздким, является обычный арифметический подсчет, который заключается в следующем:

1) из числа, корень которого нам нужен, по очереди вычитаются нечетные числа — до тех пор, пока остаток на выходе не получится меньше вычитаемого или вообще будет равен нулю. Количество ходов и станет в итоге искомым числом. Например, вычисление квадратного корня из 25:

Следующее нечетное число — это 11, остаток у нас следующий: 1

Для таких случаев существует разложение в ряд Тейлора:

√(1+y)=∑((-1) n (2n)!/(1-2n)(n!) 2 (4 n))y n , где n принимает значения от 0 до

+∞, а |y|≤1.

Графическое изображение функции z=√y

Рассмотрим элементарную функцию z=√y на поле вещественных чисел R, где y больше либо равен нулю. График ее выглядит следующим образом:

Кривая растет из начала координат и обязательно пересекает точку (1; 1).

Свойства функции z=√y на поле действительных чисел R

1. Область определения рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль включен).

2. Область значений рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль опять же включен).

3. Минимальное значение (0) функция принимает лишь в точке (0; 0). Максимальное значение отсутствует.

4. Функция z=√y ни четная, ни нечетная.

5. Функция z=√y не является периодической.

6. Точка пересечения графика функции z=√y с осями координат лишь одна: (0; 0).

7. Точка пересечения графика функции z=√y также является и нулем этой функции.

8. Функция z=√y непрерывно растет.

9. Функция z=√y принимает лишь положительные значения, следовательно, график ее занимает первый координатный угол.

Варианты изображения функции z=√y

В математике для облегчения вычислений сложных выражений порой используют степенную форму написания корня квадратного: √y=y 1/2 . Такой вариант удобен, например, в возведении функции в степень: (√y) 4 =(y 1/2) 4 =y 2 . Этот метод является удачным представлением и при дифференцировании с интегрированием, так как благодаря ему корень квадратный представляется обычной степенной функцией.

А в программировании заменой символа √ является комбинация букв sqrt.

Стоит отметить, что в данной области квадратный корень очень востребован, так как входит в состав большинства геометрических формул, необходимых для вычислений. Сам алгоритм подсчета достаточно сложен и строится на рекурсии (функции, что вызывает сама себя).

Корень квадратный в комплексном поле С

По большому счету именно предмет данной статьи стимулировал открытие поля комплексных чисел C, так как математикам не давал покоя вопрос получения корня четной степени из отрицательного числа. Так появилась мнимая единица i, которая характеризуется очень интересным свойством: ее квадратом есть -1. Благодаря этому квадратные уравнения и при отрицательном дискриминанте получили решение. В С для корня квадратного актуальны те же свойства, что и в R, единственное, сняты ограничения с подкоренного выражения.

Площадь квадратного участка земли равна 81 дм². Найти его сторону. Предположим, что длина стороны квадрата равна х
дециметрам. Тогда площадь участка равна х
² квадратным дециметрам. Так как по условию эта площадь равна 81 дм², то х
² = 81. Длина стороны квадрата — положительное число. Положительным числом, квадрат которого равен 81, является число 9. При решении задачи требовалось найти число х, квадрат которого равен 81, т. е. решить уравнение х
² = 81. Это уравнение имеет два корня: x
1 = 9 и x
2 = — 9, так как 9² = 81 и (- 9)² = 81. Оба числа 9 и — 9 называют квадратными корнями из числа 81.

Заметим, что один из квадратных корней х
= 9 является положительным числом. Его называют арифметическим квадратным корнем из числа 81 и обозначают √81, таким образом √81 = 9.

Арифметическим квадратным корнем из числа а
называется неотрицательное число, квадрат которого равен а
.

Например, числа 6 и — 6 являются квадратными корнями из числа 36. При этом число 6 является арифметическим квадратным корнем из 36, так как 6 — неотрицательное число и 6² = 36. Число — 6 не является арифметическим корнем.

Арифметический квадратный корень из числа а
обозначается так: √а.

Знак называется знаком арифметического квадратного корня; а
— называется подкоренным выражением. Выражение √а
читается
так: арифметический квадратный корень из числа а.
Например, √36 = 6, √0 = 0, √0,49 = 0,7. В тех случаях, когда ясно, что речь идет об арифметическом корне, кратко говорят: «корень квадратный из а
«.

Действие нахождения квадратного корня из числа называют извлечением квадратного корня. Это действие является обратным к возведению в квадрат.

Возводить в квадрат можно любые числа, но извлекать квадратные корни можно не из любого числа. Например, нельзя извлечь квадратный корень из числа — 4. Если бы такой корень существовал, то, обозначив его буквой х
, мы получили бы неверное равенство х² = — 4, так как слева стоит неотрицательное число, а справа отрицательное.

Выражение √а
имеет смысл только при а ≥
0. Определение квадратного корня можно кратко записать так: √а ≥
0, (√а
)² = а
. Равенство (√а
)² = а
справедливо при а ≥
0. Таким образом, чтобы убедиться в том, что квадратный корень из неотрицательного числа а
равен b
, т.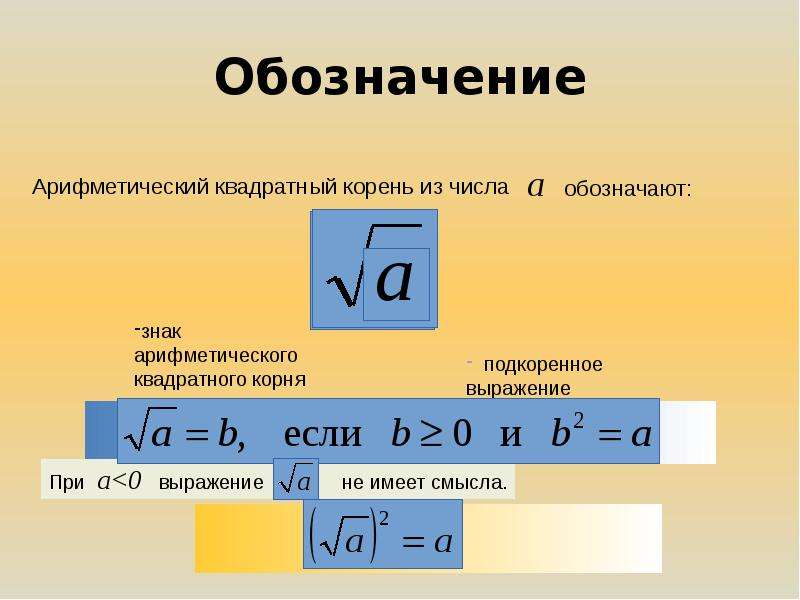 е. в том, что √а
=b
, нужно проверить, что выполняются следующие два условия: b ≥
0, b
² = а.

Квадратный корень из дроби

Вычислим . Заметим, что √25 = 5, √36 = 6, и проверим выполняется ли равенство .

Так как и , то равенство верно. Итак, .

Теорема:
Если а
≥ 0 и b
> 0, то т. е. корень из дроби равен корню из числителя, деленному на корень из знаменателя. Требуется доказать, что: и .

Так как √а
≥0 и √b
> 0, то .

По свойству возведения дроби в степень и определению квадратного корня теорема доказана. Рассмотрим несколько примеров.

Вычислить , по доказанной теореме .

Второй пример: Доказать, что , если а
≤ 0, b
.

Еще примерчик: Вычислить .

Преобразование квадратных корней

Вынесение множителя из-под знака корня. Пусть дано выражение . Если а
≥ 0 и b
≥ 0, то по теореме о корне из произведения можно записать:

Такое преобразование называется вынесение множителя из под знака корня. Рассмотрим пример;

Вычислить при х
= 2. Непосредственная подстановка х
= 2 в подкоренное выражение приводит к сложным вычислениям. Эти вычисления можно упростить, если вначале вынести из-под знака корня множители: . Подставив теперь х = 2, получим:.

Итак, при вынесении множителя из-под знака корня представляют подкоренное выражение в виде произведения, в котором один или несколько множителей являются квадратами неотрицательных чисел. Затем применяют теорему о корне из произведения и извлекают корень из каждого множителя. Рассмотрим пример: Упростить выражение А = √8 + √18 — 4√2 вынося в первых двух слагаемых множители из-под знака корня, получим:. Подчеркнем, что равенство справедливо только при а
≥ 0 и b
≥ 0. если же а

Ученики всегда спрашивают: «Почему нельзя пользоваться калькулятором на экзамене по математике? Как извлечь корень квадратный из числа без калькулятора?» Попробуем ответить на этот вопрос.

Как же извлечь корень квадратный из числа без помощи калькулятора?

Действие извлечения корня квадратного
обратно действию возведения в квадрат.

√81= 9 9 2 =81

Если из положительного числа извлечь корень квадратный и результат возвести в квадрат, получим то же число.

Из небольших чисел, являющихся точными квадратами натуральных чисел, например 1, 4, 9, 16, 25, …,100 квадратные корни можно извлечь устно. Обычно в школе учат таблицу квадратов натуральных чисел до двадцати. Зная эту таблицу легко извлечь корни квадратные из чисел 121,144, 169, 196, 225, 256, 289, 324, 361, 400. Из чисел больших 400 можно извлекать методом подбора используя, некоторые подсказки. Давайте попробуем на примере рассмотреть этот метод.

Пример:
Извлечь корень из числа 676
.

Замечаем, что 20 2 = 400, а 30 2 = 900, значит 20

Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9.
Цифру 6 дают 4 2 и 6 2 .
Значит, если из 676 извлекается корень, то это либо 24, либо 26.

Осталось проверить: 24 2 = 576, 26 2 = 676.

Ответ: √676 = 26
.

Еще пример:
√6889
.

Так как 80 2 = 6400, а 90 2 = 8100, то 80 Цифру 9 дают 3 2 и 7 2 , то √6889 равен либо 83, либо 87.

Проверяем: 83 2 = 6889.

Ответ: √6889 = 83
.

Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители.

Например, найти √893025
.

Разложим число 893025 на множители, вспомните, вы делали это в шестом классе.

Получаем: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945.

Еще пример: √20736
. Разложим число 20736 на множители:

Получаем √20736 = √2 8 ∙3 4 = 2 4 ∙3 2 = 144.

Конечно, разложение на множители требует знания признаков делимости и навыков разложения на множители.

И, наконец, есть же правило извлечение корней квадратных
. Давайте познакомимся с этим правилом на примерах.

Вычислите √279841
.

Чтобы извлечь корень из многоцифрового целого числа, разбиваем его справа налево на грани, содержащие по 2 цифры (в левой крайней грани может оказаться и одна цифра). Записываем так 27’98’41

Чтобы получить первую цифру корня (5), извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани (27).
Потом вычитают из первой грани квадрат первой цифры корня (25) и к разности приписывают (сносят) следующую грань (98).
Слева от полученного числа 298 пишут удвоенную цифру корня (10), делят на нее число всех десятков раннее полученного числа (29/2 ≈ 2), испытывают частное (102 ∙2 = 204 должно быть не больше 298) и записывают (2) после первой цифры корня.
Потом вычитают от 298 полученное частное 204 и к разности (94) приписывают (сносят) следующую грань (41).
Слева от полученного числа 9441 пишут удвоенное произведение цифр корня (52 ∙2 = 104), делят на это произведение число всех десятков числа 9441 (944/104 ≈ 9), испытывают частное (1049 ∙9 = 9441) должно быть 9441 и записывают его (9) после второй цифры корня.

Получили ответ √279841 = 529.

Аналогично извлекают корни из десятичных дробей
. Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями.

Пример
. Найдите значение √0,00956484.

Только надо помнить, что если десятичная дробь имеет нечетное число десятичных знаков, из нее точно квадратный корень не извлекается
.

Итак, теперь вы познакомились с тремя способами извлечения корня. Выбирайте тот, который вам больше подходит и практикуйтесь. Чтобы научиться решать задачи, их надо решать. А если у Вас возникнут вопросы, записывайтесь на мои уроки .

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Арифметический квадратный корень 8 класс онлайн-подготовка на Ростелеком Лицей

Арифметический квадратный корень

Пусть известно, что площадь квадрата равна 64 см². Чему равна длина стороны этого квадрата?

Обозначим длину стороны за х см.

Тогда выражение для площади S = х·х = х²(см²).

Получим уравнение х²= 64.

У этого уравнения два корня – х₁= 8 и х₂= -8.

Но длина стороны квадрата не может быть отрицательным числом, поэтому условию задачи удовлетворяет только х₁.

Квадратным корнем из числа а называют число, квадрат которого равен а.

То есть квадратными корнями из 64 являются числа 8 и -8.

Число 8 – неотрицательный корень из 64, другими словами – арифметический.

Арифметическим квадратным корнем из числа а называется такое неотрицательное число, квадрат которого равен а.

Арифметический квадратный корень из числа а обозначают a. Знак √ называют знаком арифметического квадратного корня или знаком радикала. Выражение, стоящее под знаком корня, называют подкоренным выражением. Запись a читают как «квадратный корень из а», слово «арифметический» при этом опускают.

Приведем примеры нахождения (еще говорят извлечения) арифметических квадратных корней.

4=2, так как 2 – неотрицательное и 2²^{= 4.}

1,21=1,1, так как 1,1 – число неотрицательное и 1,1²= 1,21.

0=0, так как 0 число неотрицательное и 0²^{= 0.}

В общем случае a=b, если выполняются два условия: b≥0 и b2=a.

При а<0 выражение a не имеет смысла.

Арифметический квадратный корень из отрицательных чисел не существует.

Например, -16 не имеет смысла, т. к. нет такого действительного числа a, которое в квадрате равно отрицательному числу: a2=-16.

При любом а, при котором выражение a имеет смысл, верно равенство (a)2=a.

Чтобы найти квадратный корень из числа, необходимо хорошо знать квадраты чисел.

Часто используемые квадраты целых чисел:

1² = 1

100

121

144

169

196

225

256

289

324

361

400

625

Значит, 81=9; 121=11 и т. д.

Обрати внимание!

1=1; 0=0.

Если подкоренное число — десятичная дробь, то необходимо обращать внимание на количество цифр после запятой:

0,09=0,3, так как 0,3²= 0,3·0,3 = 0,09

0,0016=0,04.

Если подкоренное число заканчивается нулями, то необходимо обращать внимание на их количество:

400=20; 121000=1100.

Вычисление целочисленного квадратного корня / Хабр

Возникла нужда проверить, является ли целое число квадратом, и если да, то вычислить корень. Причем хочется сделать это в целочисленной арифметике. Понятно, что можно реализовать метод Ньютона в целых числах, но он требует деления на каждом шаге. А нельзя ли по другому? Найти квадратный корень по модулю степени двойки, и проверить, а не будет ли он обычным квадратным корнем.

Можно ограничиться нечетными числами: для четного числа, если количество нулевых младших разрядов нечетно, то корня нет, а если четно, то можно сдвинуть число вправо, посчитать корень от нечетного, и сдвинуть обратно влево на половину от первоначального количества нулевых бит.

Для нечетного N и 2^k, k > 3, если N ≡ 1 mod 8, то есть 4 разных корня по модулю 2^k, а иначе корней нет. Нам нужен наименьший из этих четырех корней x. При этом другие три корня это 2^k — x, 2^k-1 + x и 2^k — 2^k-1 — x

Хочется что-то подобное вычислению обратного по модулю 2^k — удваивая количество верных бит за итерацию.

Пусть у нас уже есть корень x₀ из N по модулю 2^k: N — x₀² = 2^ka

И мы хотим найти x₁ = x₀ + 2^k-1y, такое чтобы в N — x₁² было больше младших нулевых бит.
N — (x₀ + 2^k-1y)² = 2^ka — 2^kx₀ * y — 2^2k-2y²

Поделим на 2^k: a — x₀ * y — 2^k-2y²

И приравняем к 0 по модулю 2^k-2: y = a * x₀^-1 mod 2^k-2

Получилии x₁ = x₀ + 2^k-1a * (x₀^-1 mod 2^k-2)

И окончательно x₁ = x₀ + (N — x₀²)/2 * (x₀^-1 mod 2^k-2)

Из k бит на следующей итерации получится 2(k-1) бит. Параллельно считаем на каждой итерации обратное к корню.

Тестовый код:

uint8_t sqr16(uint16_t n) {
  if (n % 8 != 1) return 0;
  uint16_t sqr = (n + 1) / 2;  //4 bit
  uint16_t inv = 2 - sqr;

  sqr += inv * (n-sqr*sqr)/2;   //6 bit
  inv *= 2 - sqr * inv;

  sqr += inv * (n-sqr*sqr)/2;  //10 bit
  //inv *= 2 - sqr * inv;

  if (sqr & 256)
    sqr = 0u - sqr;
  sqr = (uint8_t)sqr; // lowest root
  if (n == sqr*sqr) return sqr;
  return 0;
}

Добавив пару итераций, получим корень из uint_64

Сколько квадратный корень из 100

На нашем сайте мы разберемся, сколько получится, если извлечь квадратный корень из цифры 100. Выясним сколько будет квадратный корень из 100, потому как над таким вопросом многие годы ломали головы более 1 тысячи специалистов и многие пришли к такому возможному решению, что невозможно получить квадратный корень из 100. В подобном случае, будет очень важно знать верный вопрос, который касается особенностей получения квадратного корня из 100. Будем максимально точны, тогда мы начнем расчет арифметического корня из 100, потому как в обычном квадратном корне из этой цифры — получится два числа, одними из них являются: 10: -10.

Многие люди задают вопрос, квадратный корень из 100 как высчитать? Чтобы в этом разобраться, потребуется посчитать сумму необходимых нам чисел простым математическим способом при помощи применения вертикальной, стандартной чертой, корни и числа, которые нужно записывать справа вниз. Здесь мы сможем высчитать необходимый квадрат единиц определенного корня, а также умножать 10-ки и вычислять увеличенное на 2, а не утроенное число определенного десятка. Определенные цифры, чтобы ответить на вопрос — корень из 100 чему равен, нам потребуется возвестить в квадрат. У нас в таком случае получится двузначная цифра, когда вышло 10. Следовательно, в таком случае расчет мы выполнили верно.

Необходимо помнить очень важное правило: чтобы узнать сколько будет квадратный корень из 100, первым делом вычисляем извлекаемый любой корень и числа его всех сумм, а также сотен. Когда полученная цифра больше или же равняется 100, теперь требуется найти корень и 100-тен фактических чисел этих 100-тен. После этого из десятков тысяч (то есть фактического значения числа). Это правило будет очень актуально, когда число гораздо превышает 100, после этого нужно будет вычислить квадратный корень из сотен десятков тысяч. То есть, если быть более точными — это будет из миллиона определенного числа. Существует большое количество разнообразных правил, которые непосредственно касаются данного вопроса. Если заниматься прогрессом вычисления, тогда следует обратить повышенное внимание на такой важный факт, что в корне такое же количество цифр, сколько под завершающим количеством граней.

Каким образом вычислить корень определенного числа

Цель нахождения определенного корня состоит в том, что необходимо выполнить обратное действие возведения определенного числа в степень. Следует помнить, что корни могут значительно отличаться: корни II, III, а также IV-степени. Этот момент имеет очень важное значение и его следует понимать. Корень имеет определенный символ: √ – это корень из II-степени. Следует отметить такой момент, что, когда степень по значения выше, чем II-степень, тогда над ним необходимо будет прописать знак степени. Цифра, которая располагается под знаком корня – это называется подкоренное выражение. Выполняя процедуру поиска корня, нам потребуется знать несколько важных правил, которые касаются данного вопроса. Они окажут необходимую помощь и помогут не допустить ошибки выполняя расчеты:

Корень определенной четной степени (когда сама степень 2, 6, 8 и так дальше) из отрицательной цифры не существует. В возможных случаях, когда определенное выражение (подкоренное) является отрицательным, тогда поиск корня необходимо выполнять степени (нечетной) (к примеру: 3, 7 и так дальше). В итоге, результат, мы сможем получить отрицательный. Также, потребуется знать, что корень от 1 всегда будет выглядеть следующим образом: √1 = 1., а также: √0 = 0.

Как рассчитать корень из 100

Когда в поставленной задаче указано, какой степени корень нужно вычислить, тогда считают, что следует найти корень II-степени (то есть квадратный).

Ответим на такой вопрос: √100 = ? Потребуется найти цифру, при выполнении процедуры его возведения в II-степень, у нас будет 100. В таком случае становится понятно, что этим числом будет считаться цифра 10, потому как: 102 = 100. Поэтому, √100 = 10.

Рассчитаем представленное выражение. Чтобы достичь поставленной цели, требуется вынести имеющееся число из под корня. Это будет выглядеть следующим образом.

√100 = 100’1/2 = (10’2)’1/2 = 10′(2 * 1/2) = 10’2/2 = 10’1 = 10.

Также, это выглядит таким образом: √100 = √10’2 = 10.

В итоге у нас получится число 10. Теперь мы знаем, ответ на вопрос: квадратный корень из 100 сколько это будет?

Квадратный корень из 3;2;5 — Квадратный Корень

Квадратный корень из числа 3 — положительное действительное число, которое при умножении само на себя даёт число 3.

Его приблизительным значением с 69 цифрами после запятой является:

Округленное значение 1.732 является правильным с точностью до 0,01 %. Приблизительной правильной дробью является (1,7321 42857…).

Квадратный корень из 3 является иррациональным числом. Также известен как Феодоровская постоянная, названная в честь Феодора Киренского.

Может быть выражен в виде непрерывной дроби [1; 1, 2, 1, 2, 1, 2, …].

Геометрия

Квадратный корень из 3 равен длине между параллельными сторонами правильного шестиугольника со сторонами 1.

Если равносторонний треугольник со сторонами длиной 1 делится на две
равные половины, пересечением внутреннего угла для составления прямого
угла с одной стороной, то получившийся прямоугольный треугольник имеет
гипотенузу со стороной 1 и катеты длиной 1/2 и Поэтому тангенс 60° равен

Так же, это расстояние между параллельными сторонами правильного шестиугольника со сторонами 1.

является длиной диагонали куба со стороной 1.

Использование в других областях

Энергетика

При трехфазной системе токов модуль напряжения между двумя фазами (линейное напряжение) в больше модуля фазного напряжения

Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: Приведём значение корня из 2 с 65 знаками после запятой:

1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99…

Геометрически корень из 2 можно представить как длину диагонали квадрата со стороной 1 (это следует из теоремы Пифагора). Вероятно, это было первое известное в истории математики иррациональное число (то есть число, которое нельзя точно представить в виде дроби).

Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.

Квадратный корень из 2.

Хорошим и часто используемым приближением к является дробь .
Несмотря на то, что числитель и знаменатель дроби лишь двузначные
целые, оно отличается от реального значения меньше, чем на 1/10000.

История

Вавилонская глиняная табличка с примечаниями.

Вавилонская глиняная табличка (ок. 1800—1600 до н. э.) даёт приближённое значение в четырёх шестидесятеричных цифрах, что составляет 8 десятичных цифр:

Другое раннее приближение этого числа в древнеиндийском математическом тексте, Шульба-сутры (ок. 800—200 до н. э.) даётся следующим образом:

Пифагорейцы
обнаружили, что диагональ квадрата несоизмерима с его стороной, или на
современном языке, что квадратный корень из двух является иррациональным.
Мало что известно с определённостью о времени и обстоятельствах этого
выдающегося открытия, но традиционно его авторство приписывается Гиппасу из Метапонта.

Алгоритмы вычисления

Существует множество алгоритмов для вычисления значения квадратного
корня из двух. В результате алгоритма получается приблизительное
значение в виде обыкновенной или десятичной дроби.
Самый популярный алгоритм для этого, который используется во многих
компьютерах и калькуляторах, это вавилонский метод вычисления квадратных
корней.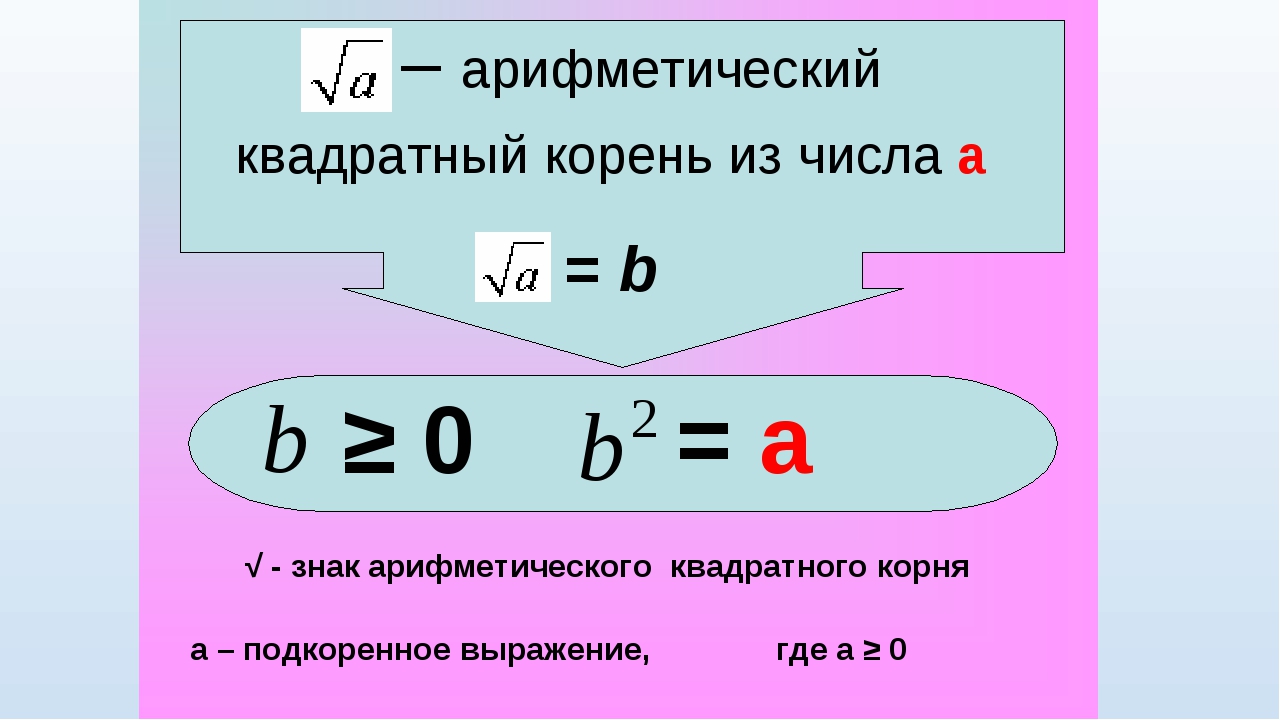 Он состоит в следующем:

Чем больше повторений в алгоритме (то есть, чем больше «n»), тем
лучше приближение квадратного корня из двух. Каждое повторение
приблизительно удваивает количество правильных цифр. Приведём несколько
первых приближений:

3/2 = 1.5
17/12 = 1.416…
577/408 = 1.414215…
665857/470832 = 1.4142135623746…

В 1997 году Ясумаса Канада
вычислил значение √2 до 137,438,953,444 десятичных знаков после
запятой. В феврале 2007 года рекорд был побит: Сигэру Кондо вычислил 200
миллиардов десятичных знаков после запятой в течение 13 дней и 14
часов, используя процессор 3.6 GHz с 16 ГБ ОЗУ. Среди математических констант только было вычислено более точно.

Свойства квадратного корня из двух

Половина √2 приблизительно равна 0.70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора, образующего угол 45° с координатными осями:

Одно из интересных свойств √2 состоит в следующем:

. Потому что

Это является результатом свойства серебряного сечения.

Другое интересное свойство √2:

Квадратный корень из двух может быть выражен в мнимых единицах i используя только квадратные корни и арифметические операции:

Квадратный корень из 2 является единственным числом, отличным от 1, чья бесконечная тетрация равна его квадрату.

Квадратный корень из двух может быть также использован для приближения :

С точки зрения высшей алгебры, является корнем многочлена и поэтому является целым алгебраическим числом. Множество чисел вида , где — рациональные числа, образует алгебраическое поле. Оно обозначается и является подполем поля вещественных чисел.

Доказательство иррациональности

Применим доказательство от противного: допустим, рационален, то есть представляется в виде несократимой дроби , где и — целые числа. Возведём предполагаемое равенство в квадрат:

Отсюда следует, что чётно, значит, чётно и . Пусть , где целое. Тогда

Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.

Непрерывная дробь

Квадратный корень из двух может быть представлен в виде непрерывной дроби:

Подходящие дроби
данной непрерывной дроби дают приближённые значения, быстро сходящиеся к
точному квадратному корню из двух. Способ их вычисления прост: если
обозначить предыдущую подходящую дробь , то последующая имеет вид . Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:

Квадрат последней приведенной дроби равен (округлённо) 2,000000177.

Размер бумаги

Квадратный корень из двух является пропорцией формата бумаги ISO 216.
Соотношение сторон таково, что при разрезании листа пополам параллельно
его короткой стороне получатся два листа той же пропорции.

Квадратный корень из числа 5 — положительное действительное число, которое при умножении само на себя даёт число 5. Это иррациональное и алгебраическое число.^[1]

Его приблизительное значение с 59 цифрами после запятой является:

Округлённое значение 2.236 является правильным с точностью до 0,01 %.
Компьютерная вычисленная точность составляет не менее 1 000 000 знаков.^[2]

Может быть выражено в виде непрерывной дроби [2; 4, 4, 4, 4, 4, 4, …], последовательно это дроби:

Вавилонский метод

Вычисление корня из 5, начиная с r₀ = 2, где r_n+1 = (r_n + 5/r_n) / 2:

Золотое сечение

√5/2 — диагональ половины квадрата, представляет собой геометрическое представление о золотом сечении.

Золотое сечение φ — среднее арифметическое 1 и корня из 5.^[3]

() алгебраически можно выразить так:

Числа Фибоначчи могут быть выражены через корень из 5 так:

Отношение √5 к φ и наоборот дают интересные зависимости непрерывных дробей с числами Фибоначчи и числами Люка:^[4]

Алгебра

Кольцо содержит числа вида , где a и b целые числа и мнимое число . Это кольцо является примером области целостности, не являющейся факториальным кольцом.

Число 6 представляется в данном кольце двумя способами:

Поле — абелево расширение рациональных чисел.

Теорема Кронекера — Вебера утверждает, что корень из 5 можно выразить линейной комбинацией корней из единицы:

Тождества Рамануджана

Корень из 5 появляется во множестве тождеств Рамануджана с непрерывными дробями.^[5]^[6]

Например, случай непрерывных дробей Роджерса-Рамануджана:

Корень из числа: определения, примеры

Квадратный корень, арифметический квадратный корень

Чтобы понять определение корня из числа, и квадратного корня в частности, нужно иметь представление о степени с натуральным показателем. В этом пункте мы часто будем сталкиваться со второй степенью числа — квадратом числа.

Начнем с определения квадратного корня.

Определение

Квадратный корень из числа a — это число, квадрат которого равен a.

Чтобы привести примеры квадратных корней, возьмем несколько чисел, например, 5, −0,3, 0,3, 0, и возведем их в квадрат, получим соответственно числа 25, 0,09, 0,09 и 0 (5²=5·5=25, (−0,3)²=(−0,3)·(−0,3)=0,09, (0,3)²=0,3·0,3=0,09 и 0²=0·0=0). Тогда по данному выше определению число 5 является квадратным корнем из числа 25, числа −0,3 и 0,3 есть квадратные корни из 0,09, а 0 – это квадратный корень из нуля.

Следует отметить, что не для любого числа a существует действительное число, квадрат которого равен a. А именно, для любого отрицательного числа a не существует ни одного действительного числа b, квадрат которого равнялся бы a. В самом деле, равенство a=b² невозможно для любого отрицательного a, так как b² – неотрицательное число при любом b. Таким образом, на множестве действительных чисел не существует квадратного корня из отрицательного числа. Иными словами, на множестве действительных чисел квадратный корень из отрицательного числа не определяется и не имеет смысла.

Отсюда вытекает логичный вопрос: «А для любого ли неотрицательного a существует квадратный корень из a»? Ответ – да. Обоснованием этого факта можно считать конструктивный способ, используемый для нахождения значения квадратного корня.

Тогда встает следующий логичный вопрос: «Каково число всех квадратных корней из данного неотрицательного числа a – один, два, три, или еще больше»? Вот ответ на него: если a равно нулю, то единственным квадратным корнем из нуля является нуль; если же a – некоторое положительное число, то количество квадратных корней из числа a равно двум, причем корни являются противоположными числами. Обоснуем это.

Начнем со случая a=0. Сначала покажем, что нуль действительно является квадратным корнем из нуля.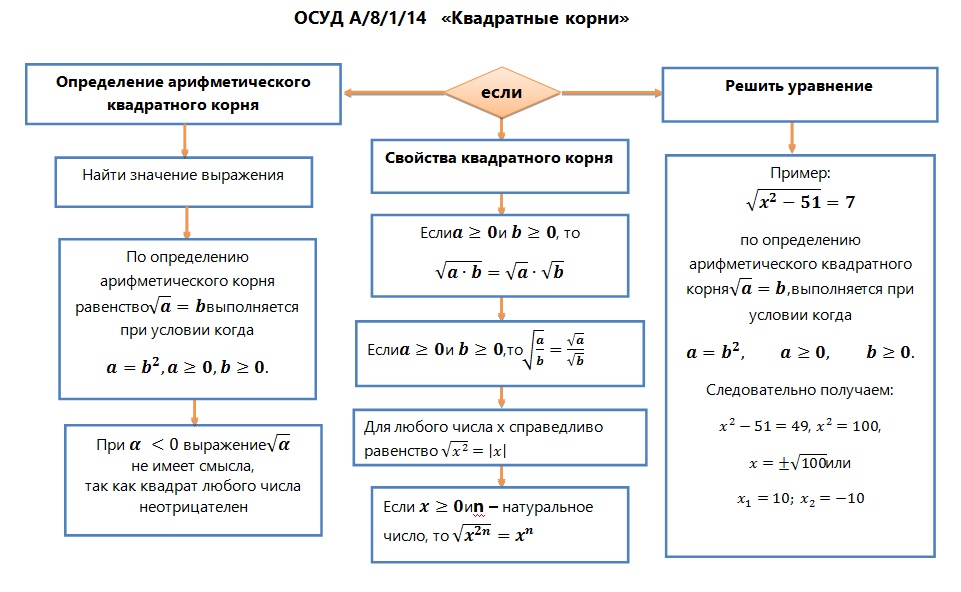 Это следует из очевидного равенства 0²=0·0=0 и определения квадратного корня.

Теперь докажем, что 0 – единственный квадратный корень из нуля. Воспользуемся методом от противного. Предположим, что существует некоторое число b, отличное от нуля, которое является квадратным корнем из нуля. Тогда должно выполняться условие b²=0, что невозможно, так как при любом отличном от нуля b значение выражения b² является положительным. Мы пришли к противоречию. Это доказывает, что 0 – единственный квадратный корень из нуля.

Переходим к случаям, когда a – положительное число. Выше мы сказали, что всегда существует квадратный корень из любого неотрицательного числа, пусть квадратным корнем из a является число b. Допустим, что существует число c, которое тоже является квадратным корнем из a. Тогда по определению квадратного корня справедливы равенства b²=a и c²=a, из них следует, что b²−c²=a−a=0, но так как b²−c²=(b−c)·(b+c), то (b−c)·(b+c)=0. Полученное равенство в силу свойств действий с действительными числами возможно лишь тогда, когда b−c=0 или b+c=0. Таким образом, числа b и c равны или противоположны.

Если же предположить, что существует число d, являющееся еще одним квадратным корнем из числа a, то рассуждениями, аналогичными уже приведенным, доказывается, что d равно числу b или числу c. Итак, число квадратных корней из положительного числа равно двум, причем квадратные корни являются противоположными числами.

Для удобства работы с квадратными корнями отрицательный корень «отделяется» от положительного. С этой целью вводится определение арифметического квадратного корня.

Определение

Арифметический квадратный корень из неотрицательного числа a – это неотрицательное число, квадрат которого равен a.

Для арифметического квадратного корня из числа a принято обозначение . Знак называется знаком арифметического квадратного корня. Его также называют знаком радикала. Поэтому можно часть слышать как «корень», так и «радикал», что означает один и тот же объект.

Число под знаком арифметического квадратного корня называют подкоренным числом, а выражение под знаком корня – подкоренным выражением, при этом термин «подкоренное число» часто заменяют на «подкоренное выражение». Например, в записи число 151 – это подкоренное число, а в записи выражение a является подкоренным выражением.

При чтении слово «арифметический» часто опускается, например, запись читают как «квадратный корень из семи целых двадцати девяти сотых». Слово «арифметический» произносят лишь тогда, когда хотят особо подчеркнуть, что речь идет именно о положительном квадратном корне из числа.

В свете введенного обозначения из определения арифметического квадратного корня следует, что и для любого неотрицательного числа a.

Квадратные корни из положительного числа a с помощью знака арифметического квадратного корня записываются как и . Например, квадратные корни из числа 13 есть и . Арифметический квадратный корень из нуля равен нулю, то есть, . Для отрицательных чисел a записи мы не будем придавать смысла вплоть до изучения комплексных чисел. Например, лишены смысла выражения и .

На базе определения квадратного корня доказываются свойства квадратных корней, которые часто применяются на практике.

Нахождение квадратных корней заслуживает детального изучения, этой теме посвящена отдельная статья извлечение квадратных корней.

В заключение этого пункта заметим, что квадратные корни из числа a являются решениями квадратного уравнения вида x²=a относительно переменной x.

К началу страницы

Самый простой способ найти квадратный корень в Swift?

Я пытался выяснить, как программно найти квадратный корень из числа в Swift. Я ищу самый простой способ сделать это с минимальным количеством необходимого кода. Я сейчас это, наверное, довольно легко сделать, но не могу придумать, как это сделать.

Любой вклад или предложения будут очень признательны.

Заранее спасибо

swift

math

square-root

Поделиться

Источник

Bigfoot11

30 июня 2015 в 19:09

5 ответов

В Swift 3 протокол FloatingPoint , по-видимому, имеет метод squareRoot() . И Float , и Double соответствуют протоколу FloatingPoint . Так:

let x = 4.0
let y = x.squareRoot()

это примерно так же просто, как и получается.

Базовый сгенерированный код должен быть одной машинной инструкцией x86, без перехода к адресу функции и последующего возврата, потому что это переводится в встроенный в промежуточный код LLVM. Таким образом, это должно быть быстрее , чем вызов функции sqrt библиотеки C, которая действительно является функцией, а не просто макросом для кода assembly.

В Swift 3 вам не нужно ничего импортировать,чтобы сделать эту работу.

Поделиться

Paul Buis

01 декабря 2016 в 10:27

Обратите внимание, что sqrt() потребует импорта по крайней мере одного из:

UIKit
Cocoa
Вы можете просто импортировать Darwin вместо полного Cocoa
Основа

Поделиться

Laughing Vergil

30 июня 2015 в 19:18

Первый импорт import UIKit

let result = sqrt(25) // equals to 5

Тогда ваш результат должен быть на переменной «result»

Поделиться

Eddy Ekofo

01 апреля 2018 в 05:19

Квадратный корень переменной типа int32
Я попытался вычислить квадратный корень переменной типа int32 с помощью функции sqrt() , но получил такую ошибку: неопределенная функция ‘sqrt’ для входных аргументов типа ‘int32’. Затем я обнаружил, что существует функция isqrt() , которая вычисляет квадратный корень из целочисленных переменных…
как найти квадратный корень из числа в applescript
У меня есть простой код калькулятора, и я хочу включить в него квадратный корень. Я относительно новичок в applescript и понятия не имею, как это сделать. Может быть, это и Нуби, но все равно спасибо!

функция sqrt, например sqrt(4.0)

Поделиться

Nikita Leonov

30 июня 2015 в 19:12

это должно работать для любого корня,
2 — ∞ , но вам, вероятно, все равно:

func root(input: Double, base: Int = 2) -> Double {
    var output = 0.0
    var add = 0.0
    while add < 16.0 {
        while pow(output, base) <= input {
            output += pow(10. 0, (-1.0 * add))
        }
        output -= pow(10.0, (-1.0 * add))
        add += 1.0
    }
    return output + 0.0
}

Поделиться

Unknown

11 октября 2019 в 13:22

Нахождение квадратного корня и квадратного корня из числа

Что такое квадратный корень?

Чтобы объяснить квадратные корни, давайте сделаем шаг назад и вспомним, что означает возведение числа в квадрат. Возвести в квадрат — это возвести число во вторую степень. Квадратные корни противоположны этому и фактически являются обратной операцией возведения в квадрат. Чтобы извлечь квадратный корень, нужно найти два одинаковых делителя числа.

Как найти квадратный корень из числа

Для чисел, которые представляют собой полные квадраты, вы можете найти целые числа в качестве ответов.Однако для чисел, которые не являются точными квадратами, вам придется использовать метод, включающий оценку (или вы можете использовать таблицу квадратных и квадратных корней).

Нахождение квадратного корня из полного квадратного числа

Давайте сначала рассмотрим этот вопрос здесь:

корень 64

Что такое квадратный корень из 64? Если у вас есть калькулятор, вы всегда можете просто набрать его и получить ответ. Но знаете ли вы, как найти квадратный корень из числа без калькулятора?

Теперь, если вы помните свои точные квадраты чисел, корень из 64 равен восьми.Восемь умножить на восемь даст вам 64. Но допустим, вы не можете свободно вспоминать идеальные числа. Как бы мы сделали это с нуля?

Сначала вам нужно найти все простые множители 64. Итак, давайте продолжим и сделаем это:

простые множители корня 64

Представьте, что вопрос теперь принимает вид 2x2x2x2x2x2 — здесь 2 умножается на 6 раз. Итак, мы только что определили, что 64 — это всего лишь квадратный корень из шести двоек, умноженных вместе.

радикальный знак

Прежде чем мы продолжим, мы должны помнить, что знак корня на самом деле означает «квадратный корень».Символ квадратного корня действительно должен быть записан здесь с крошечными двумя:

квадратный корень

Так как это квадратный корень, вы можете выбрать пару одинаковых чисел для работы и извлечь их из-под корня. В этом случае мы вынимаем 2 из первой пары двоек, еще 2 из второй пары и еще 2 из последней пары. Должно получиться примерно так:

вынимать пары

Теперь, если вы умножите 2 друг на друга, что вы получите? Вы обнаружите, что получите 8, что в точности соответствует тому, что вы запомнили бы, если бы знали свои идеальные квадраты.Однако это правильный способ найти квадратный корень из числа без запоминания.

Нахождение квадратного корня из чисел, не являющихся точными квадратами

Основной метод нахождения квадратного корня из числа, не являющегося полным квадратом, выглядит следующим образом:

Оценка: выберите число, которое при возведении в квадрат близко, но меньше квадратного корня из числа, которое вы пытаетесь найти.
Разделить: разделите число, для которого вы находите квадратный корень, на число, которое вы выбрали на шаге 1
Среднее: возьмите среднее значение числа, полученного на шаге 2, и квадратного корня

Повторите: повторяйте шаги 2 и 3, пока число не будет достаточно точным для вас

Теперь вы научились находить квадратный корень для чисел, которые одновременно являются и не являются точными квадратами.Продолжайте наши уроки, чтобы узнать, как работать с примерами различных радикальных чисел.

Квадратные корни и кубические корни

Чтобы найти кубический корень числа, вы хотите найти какое-то число, которое при двойном умножении на себя дает вам исходное число. Другими словами, чтобы найти кубический корень из 8, вы хотите найти число, которое при двойном умножении на само себя дает 8. Таким образом, кубический корень из 8 равен 2, потому что 2 × 2 × 2 = 8. Обратите внимание, что символ кубического корня — знак корня с маленькой тройкой (так называемый индекс ) вверху и слева.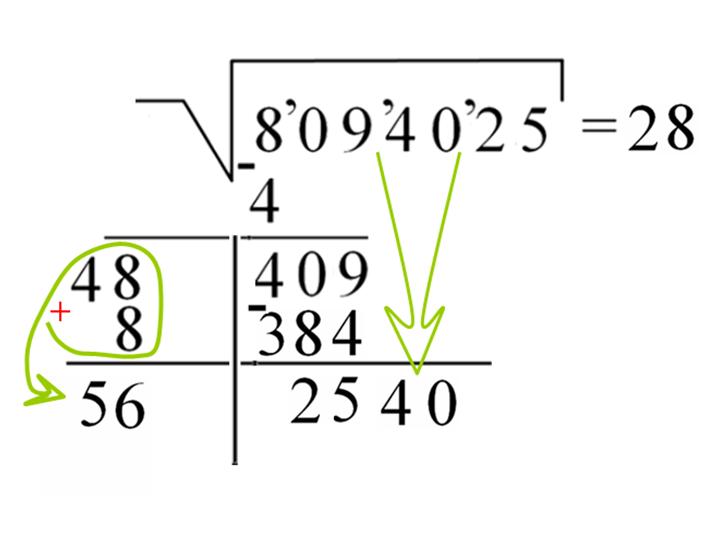 Остальные корни определяются аналогично и идентифицируются указанным индексом. (Под квадратным корнем понимается индекс два, который обычно не записывается.) Ниже приводится список первых одиннадцати совершенных (целое число) кубических корней.

Чтобы найти квадратный корень из числа, которое не является полным квадратом, необходимо будет найти приблизительный ответ , используя процедуру, приведенную в примере

Пример 1

Приблизительно.

Поскольку 6 ² = 36 и 7 ² = 49, то находится между и.

Следовательно, это значение от 6 до 7. Так как 42 находится примерно на полпути между 36 и 49, можно ожидать, что это будет примерно посередине между 6 и 7, или примерно 6,5. Чтобы проверить эту оценку, 6,5 × 6,5 = 42,25, или около 42.

Квадратные корни из несовершенных квадратов можно аппроксимировать, найти в таблицах или найти с помощью калькулятора. Вы можете иметь в виду эти два:

Упрощение квадратных корней

Иногда вам придется упростить квадратных корней или записать их в простейшей форме. В долях может быть уменьшено до. В квадратных корнях можно упростить до.

Существует два основных метода упростить извлечение квадратного корня.

Метод 1: Разложите число под двумя множителями, один из которых является наибольшим возможным полным квадратом. (Совершенные квадраты: 1, 4, 9, 16, 25, 36, 49,…)

Метод 2: Полностью разложите число под множителями на простые множители, а затем упростите, выведя все множители попарно.

Пример 2

Упростить.

В примере

, самый большой идеальный квадрат легко увидеть, и метод 1, вероятно, является более быстрым методом.

Пример 3

Упростить.

В примере

, не так очевидно, что наибольший идеальный квадрат равен 144, поэтому метод 2, вероятно, является более быстрым.

Многие квадратные корни нельзя упростить, потому что они уже представлены в простейшей форме, например, и.

Калькулятор квадратного корня

.

Найдите квадратный корень за один простой шаг.

Наш калькулятор квадратного корня вычисляет квадратный корень любого положительного числа, которое вы хотите. Просто введите выбранный номер и ознакомьтесь с результатами. Все рассчитывается быстро и автоматически ! С помощью этого инструмента вы также можете оценить квадрат желаемого числа (просто введите значение во второе поле), что может оказаться большим подспорьем в поиске точных квадратов по формуле квадратного корня.
Вы боретесь с основными арифметическими операциями: сложение квадратных корней, вычитание квадратных корней, умножение квадратных корней или деление квадратных корней? Уже нет! В следующем тексте вы найдете подробное объяснение о различных свойствах квадратного корня, например.g., как упростить квадратные корни, с множеством различных примеров . Из этой статьи вы раз и навсегда узнаете, как находить квадратные корни!

Вы когда-нибудь задумывались, каково происхождение символа квадратного корня √? Уверяем вас, что эта история не так проста, как вы могли подумать вначале. Происхождение символа корня восходит к древним временам, как происхождение знака процента.

Если вам нужен график квадратного корня или свойства функции квадратного корня, перейдите непосредственно в соответствующий раздел (просто нажмите на ссылки выше!).Здесь мы объясняем, что такое производная квадратного корня, используя определение фундаментального квадратного корня; мы также подробно рассмотрим, как вычислять квадратные корни из экспонент или квадратные корни из дробей. Наконец, если вы будете достаточно настойчивы, вы обнаружите, что квадратный корень из отрицательного числа на самом деле возможен. Таким образом, мы вводим комплексных чисел , которые находят широкое применение в физике и математике.

Символ квадратного корня √

Операция извлечения квадратного корня из числа была известна еще в древности.Самая ранняя глиняная табличка с правильным значением √2 = 1,41421 до 5 знаков после запятой происходит из Вавилонии (1800 г. до н.э. — 1600 г. до н.э.) г. Многие другие документы показывают, что квадратные корни также использовали древние египтяне, индийцы, греки и китайцы. Однако происхождение корневого символа √ все еще остается в значительной степени спекулятивным.

Многие ученые считают, что квадратные корни происходят от буквы «r» — первой буквы латинского слова radix, означающего корень,
другая теория утверждает, что символ квадратного корня был взят из арабской буквы ج , которая была помещена в исходной форме ﺟ в слове جذر — корень (арабский язык пишется справа налево).

Первое использование символа квадратного корня √ не включало горизонтальную «черту» над числами внутри символа квадратного корня (или радикала), √‾. «Бар» на латыни известен как vinculum, что означает облигация . Хотя радикальный символ с винкулумом сейчас используется в повседневной жизни, мы обычно опускаем эту черту во многих текстах, например, в статьях в Интернете. Обозначение высших степеней корня было предложено Альбертом Жираром, который поместил указатель степени в начало знака корня, т.е.г., ³√ или ⁴√.

Последний вопрос: почему операция извлечения квадратного корня называется корнем независимо от ее истинного происхождения? Объяснение станет более очевидным, если мы запишем уравнение x = ⁿ√a в другой форме: xⁿ = a. x называется корнем или радикалом, потому что это скрытое основание a. Таким образом, слово радикальный не означает далеко идущий или крайний , но вместо этого основополагающий, достигающий первопричины .

Определение квадратного корня

В математике традиционными операциями с числами являются сложение, вычитание, умножение и деление.Тем не менее, мы иногда добавляем в этот список некоторые более сложные операции и манипуляции: квадратных корней , возведение в степень, логарифмические функции и даже тригонометрические функции (например, синус и косинус). В этой статье мы сосредоточимся только на определении квадратного корня.

Квадратный корень из заданного числа x — это каждое число y , квадрат которого y² = y * y дает исходное число x . Следовательно, формула квадратного корня может быть выражена как:

√x = y ⟺ x = y² ,

, где ⟺ — математический символ, который означает тогда и только тогда, когда .Каждое положительное действительное число всегда имеет два квадратных корня — первый положительный, а второй отрицательный. Однако для многих практических целей мы обычно используем положительный. Единственное число, имеющее один квадратный корень, — ноль. Это потому, что √0 = 0, а ноль не является ни положительным, ни отрицательным.

Существует также другое распространенное обозначение квадратных корней, которое может быть более удобным во многих сложных вычислениях. Эта альтернативная формула квадратного корня утверждает, что квадратный корень из числа — это число, возведенное в степень дроби, равной половине:

√x = x ^ (1/2) = x ^ (0. 5)

В геометрической интерпретации квадратный корень из данной площади квадрата дает длину его стороны. Вот почему в названии √ есть слово , квадрат . Аналогичная ситуация и с кубическим корнем ∛ . Если вы берете кубический корень из объема куба, вы получаете длину его ребер. В то время как квадратные корни используются при рассмотрении площади поверхности, кубические корни полезны для определения величин, относящихся к объему, например плотности.

Как найти квадратный корень?

Может быть, мы не очень скромны, но мы думаем, что лучший ответ на вопрос, как найти квадратный корень, прост: используйте калькулятор квадратного корня! Вы можете использовать его как на компьютере, так и на смартфоне, чтобы быстро вычислить квадратный корень из заданного числа.К сожалению, бывают ситуации, когда можно рассчитывать только на себя, что тогда? Чтобы подготовиться к этому, вы должны запомнить несколько основных идеальных квадратных корней:

квадратный корень из 1: √1 = 1 , так как 1 * 1 = 1 ;
квадратный корень из 4: √4 = 2 , так как 2 * 2 = 4 ;
квадратный корень из 9: √9 = 3 , так как 3 * 3 = 9 ;
квадратный корень из 16: √16 = 4 , так как 4 * 4 = 16 ;
квадратный корень из 25: √25 = 5 , так как 5 * 5 = 25 ;
квадратный корень из 36: √36 = 6 , так как 6 * 6 = 36 ;
квадратный корень из 49: √49 = 7 , так как 7 * 7 = 49 ;
квадратный корень из 64: √64 = 8 , так как 8 * 8 = 64 ;
квадратный корень из 81: √81 = 9 , так как 9 * 9 = 81 ;
квадратный корень из 100: √100 = 10 , так как 10 * 10 = 100 ;
квадратный корень из 121: √121 = 11 , так как 11 * 11 = 121 ;
квадратный корень из 144: √144 = 12 , так как 12 * 12 = 144 ;

Приведенные выше числа являются простейшими квадратными корнями, потому что каждый раз вы получаете целое число. Попробуй их запомнить! Но что делать, если есть число, у которого нет такого красивого квадратного корня? Есть несколько решений. Прежде всего, можно попробовать предсказать результат методом проб и ошибок . Допустим, вы хотите вычислить квадратный корень из 52 :

Вы знаете, что √49 = 7 и √64 = 8 , поэтому √52 должно быть между 7 и 8 .
Число 52 ближе к 49 (фактически ближе к 7 ), поэтому вы можете попробовать угадать, что √52 — это 7.3 .
Затем возводите в квадрат 7,3 , получая 7,3² = 53,29 (как говорит формула квадратного корня), что больше, чем 52 . Вы должны попробовать с меньшим числом, скажем, 7,2 .
Квадрат 7,2 равен 51,84 . Теперь у вас есть меньшее число, но оно намного ближе к 52 . Если такая точность вас устраивает, можете закончить оценку здесь. В противном случае вы можете повторить процедуру с выбранным числом от 7.2 и 7,3 , например, 7,22 и так далее и так далее.

Другой подход состоит в том, чтобы сначала упростить квадратный корень, а затем использовать приближения квадратных корней простых чисел (обычно с округлением до двух знаков после запятой):

квадратный корень из 2: √2 ≈ 1,41 ,
квадратный корень из 3: √3 ≈ 1,73 ,
квадратный корень из 5: √5 ≈ 2,24 ,
квадратный корень из 7: √7 ≈ 2.65 ,
квадратный корень из 11: √11 ≈ 3,32 ,
квадратный корень из 13: √13 ≈ 3,61 ,
квадратный корень из 17: √17 ≈ 4,12 ,
квадратный корень из 19: √19 ≈ 4,34 и т. Д.

Давайте попробуем снова найти квадратный корень из 52 . Вы можете упростить его до √52 = 2√13 (вы узнаете, как упростить квадратный корень в следующем разделе), а затем замените √13 ≈ 3,61 . Наконец, произведем умножение √52 ≈ 2 * 3.61 = 7,22 . Результат такой же, как и раньше!

Вы можете проверить, является ли число простым или нет, с помощью нашего калькулятора простых чисел. Простое число — это натуральное число (больше единицы), которое не может быть получено как произведение двух меньших натуральных чисел. Например, 7 — простое число, потому что вы можете получить его, только умножив 1 * 7 или 7 * 1 . С другой стороны, число 8 не является простым, потому что вы можете сформировать его, умножив 2 * 4 или 4 * 2 (помимо произведения 1 и самой 8).

Калькулятор квадратного корня

В некоторых ситуациях вам не нужно знать точный результат вычисления квадратного корня. В этом случае наш калькулятор квадратного корня — лучший вариант для оценки значения каждого квадратного корня, который вы хотите . Например, предположим, вы хотите узнать, больше ли 4√5 , чем 9 . Из калькулятора вы знаете, что √5 ≈ 2,23607 , поэтому 4√5 ≈ 4 * 2,23607 = 8,94428 . Он очень близок к 9 , но не больше его! Калькулятор квадратного корня дает окончательное значение с относительно высокой точностью (до пяти цифр в приведенном выше примере).С помощью калькулятора значащих цифр вы можете вычислить этот результат до любого количества значащих цифр.

Помните, что наш калькулятор автоматически пересчитывает числа, введенные в любое из полей. Вы можете найти квадратный корень из определенного числа, заполнив первое окно, или получить квадрат числа, введенного вами во втором окне. Второй вариант удобен в для нахождения идеальных квадратов , которые необходимы во многих аспектах математики и естественных наук.Например, если вы введете 17 во второе поле, вы обнаружите, что 289 — это полный квадрат.

В некоторых приложениях извлечения квадратного корня, особенно относящихся к таким наукам, как химия и физика, предпочтение отдается результатам в научной нотации. Короче говоря, ответ в научном представлении должен иметь десятичную точку между первыми двумя ненулевыми числами и будет представлен как десятичная дробь, умноженная на 10, возведенная в степень. Например, номер 0.00345 записывается как 3,45 * 10⁻³ в экспоненциальном представлении, тогда как 145,67 записывается как 1,4567 * 10² в экспоненциальном представлении. Результаты, полученные с помощью калькулятора квадратного корня, можно преобразовать в экспоненциальную нотацию с помощью калькулятора.

Как упростить извлечение квадратного корня?

Во-первых, давайте спросим себя, какие квадратные корни можно упростить. Чтобы ответить на него, вам нужно взять число, стоящее после символа квадратного корня, и найти его множители.Если какой-либо из его множителей является квадратным числом (4, 9, 16, 25, 36, 49, 64 и т. Д.), То вы можете упростить квадратный корень. Почему эти числа квадратные? Они могут быть соответственно выражены как 2², 3², 4², 5², 6², 7² и так далее. Согласно определению квадратного корня, вы можете назвать их полными квадратами . У нас есть специальный инструмент, называемый калькулятором коэффициентов, который может быть здесь очень кстати. Давайте посмотрим на несколько примеров:

Можете ли вы упростить √27? С помощью упомянутого выше калькулятора вы получаете множители 27: 1, 3, 9, 27.(1/2) ⟺ √ (x * y) = √x * √y ,
Как вы можете использовать эти знания? Аргумент квадратного корня обычно не является точным квадратом, который можно легко вычислить, но он может содержать идеальный квадрат среди своих факторов. Другими словами, вы можете записать это как умножение двух чисел, где одно из чисел представляет собой полный квадрат, например, 45 = 9 * 5 (9 — это полный квадрат). Требование иметь по крайней мере один множитель , который является полным квадратом, необходимо для упрощения квадратного корня.(1/2) = √9 * √5 = 3√5 .
Вы успешно упростили свой первый квадратный корень! Конечно, вам не обязательно записывать все эти расчеты. Если вы помните, что квадратный корень эквивалентен степени половины , вы можете сократить их. Попрактикуемся в упрощении квадратных корней на некоторых других примерах:
Как упростить квадратный корень из 27? √27 = √ (9 * 3) = √9 * √3 = 3√3 ;
Как упростить квадратный корень из 8? √8 = √ (4 * 2) = √4 * √2 = 2√2 ;
Как упростить квадратный корень из 144? √144 = √ (4 * 36) = √4 * √36 = 2 * 6 = 12 .
В последнем примере вам вообще не нужно было упрощать квадратный корень, потому что 144 — это полный квадрат. Вы можете просто вспомнить, что 12 * 12 = 144. Однако мы хотели показать вам, что с помощью процесса упрощения вы также можете легко вычислить квадратные корни из полных квадратов. Это полезно, когда работает с большими числами .
Наконец, вы можете спросить, как упростить корни более высокого порядка, например, кубические корни. Фактически, этот процесс очень похож на квадратные корни, но в случае кубических корней вы должны найти хотя бы один множитель, который является идеальным кубом , а не полным квадратом, т.е.е., 8 = 2³, 27 = 3³, 64 = 4³, 125 = 5³ и так далее. Затем вы делите свое число на две части и кладете под кубический корень. Возьмем следующий пример упрощения ³√192:
∛192 = ∛ (64 * 3) = ∛64 * ∛3 = 4∛3
На первый взгляд это может показаться немного сложным, но после некоторой практики вы сможете упростить корни в своей голове . Доверься нам!
Сложение, вычитание, умножение и деление квадратных корней
Сложение квадратных корней и вычитание квадратных корней
К сожалению, сложение или вычитание квадратных корней не так просто, как сложение / вычитание обычных чисел.Например, если 2 + 3 = 5, это не означает, что √2 + √3 равно √5. Это неправильно! Чтобы понять, почему это так, представьте, что у вас есть два разных типа фигур: треугольники 🔺 и круги 🔵. Что произойдет, если вы добавите один треугольник к одному кругу 🔺 + 🔵? Ничего такого! У вас остались один треугольник и один круг 🔺 + 🔵. С другой стороны, что происходит, когда вы пытаетесь добавить три треугольника к пяти треугольникам: 3 🔺 + 5 🔺? У нас получится восемь треугольников 8 🔺.
Сложение квадратного корня очень похоже на это.Результат сложения √2 + √3 по-прежнему равен √2 + √3. Вы не можете упростить это дальше. Однако это другая ситуация, когда оба квадратных корня имеют одинаковое число под символом корня . Затем мы можем складывать их как обычные числа (или треугольники). Например, 3√2 + 5√2 равно 8√2. То же самое и с вычитанием квадратных корней. Давайте посмотрим на другие примеры, иллюстрирующие это свойство квадратного корня:
Что такое 6√17 + 5√17 ? Ответ: 6√17 + 5√17 = 11√17 ;
Что такое 4√7 - 7√7 ? Ответ: 4√7 - 7√7 = -3√7 ;
Что такое 2√2 + 3√8 ? Ответ: 2√2 + 3√8 = 2√2 + 6√2 = 8√2 , потому что мы упростили √8 = √ (4 * 2) = √4 * √2 = 2√2;
Что такое √45 - √20 ? Ответ: √45 - √20 = 3√5 - 2√5 = √5 , потому что мы упростили √45 = √ (9 * 5) = √9 * √5 = 3√5 и √20 = √ (4 * 5) = √4 * √5 = 2√5;
Что такое 7√13 + 2√22 ? Ответ: 7√13 + 2√22 , мы не можем упростить это дальше;
Что такое √3 - √18 ? Ответ: √3 - √18 = √3 - 3√2 , мы не можем упростить это дальше, чем это, но мы, по крайней мере, упростили √18 = √ (9 * 2) = √9 * √2 = 3√ 2.(1/2) ⟺ √x * √y = √ (x * y) .
В отличие от сложения, вы можете умножить каждые на два квадратных корня. Помните, что умножение имеет коммутативные свойства , это означает, что порядок, в котором умножаются два числа, не имеет значения. Несколько примеров должны прояснить этот вопрос:
Что такое √3 * √2 ? Ответ: √3 * √2 = √6 ;
Что такое 2√5 * 5√3 ? Ответ: 2√5 * 5√3 = 2 * 5 * √5 * √3 = 10√15 , потому что умножение коммутативно;
Что такое 2√6 * 3√3 ? Ответ: 2√6 * 3√3 = 2 * 3 * √6 * √3 = 6√18 = 18√3 , мы упростили √18 = √ (9 * 2) = √9 * √2 = 3√ 2.(1/2) ⟺ √x / √y = √ (x / y) .
Все, что вам нужно сделать, это заменить знак умножения на деление. Однако деление не является коммутативным оператором ! Вы должны отдельно вычислять числа перед квадратными корнями и числа под квадратными корнями. (1/2) .(1/2) ⟺ √x / √y = √ (x / y) ,
, где x / y — дробь. Ниже вы можете найти несколько примеров квадратных корней из дроби:
квадратный корень из 4/9: √ (4/9) = √4 / √9 = 2/3 ,
квадратный корень из 1/100: √ (1/100) = √1 / √100 = 1/10 ,
квадратный корень из 1/5: √ (1/5) = √1 / √5 = 1 / √5 = √5 / 5 .
Оставлять корни в знаменателе — не очень хорошая привычка. Вот почему мы избавились от него в последнем примере.Мы просто умножили числитель и знаменатель на одно и то же число (мы всегда можем сделать это, так как число, которое мы умножаем на 1), в данном случае на √5 .
Функция квадратного корня и график
Функции играют жизненно важную роль не только в математике, но и во многих других областях, таких как физика, статистика или финансы. Функция f (x) — это не что иное, как формула, которая говорит, как значение f (x) изменяется с аргументом x . Чтобы увидеть некоторые примеры, ознакомьтесь с нашими финансовыми инструментами, созданными финансовыми специалистами, например, калькулятор сложных процентов или калькулятор будущей стоимости.Там вы найдете несколько функций, которые можно применить в реальной жизни. Они очень полезны, если вы хотите знать, как рассчитать сложные проценты или оценить будущую стоимость аннуитета.
Ниже вы можете найти график квадратного корня, состоящий из половины параболы . Проверьте это и попробуйте проверить, например, является ли функция квадратного корня x = 9 3 и x = 16 4 (как и должно быть).
Давайте вернемся к функции квадратного корня f (x) = √x и исследуем ее основные свойства .Мы рассматриваем только положительную часть f (x) (как вы можете видеть на графике квадратного корня выше). Итак, функция квадратного корня:
— это непрерывно и увеличивается для всех неотрицательных x ,
является дифференцируемым для всех положительных x (см. Производную квадратного корня для получения дополнительной информации),
приближается к пределу бесконечности , когда x приближается к бесконечности ( lim √x → ∞ , когда x → ∞ ),
— это действительное число для всех неотрицательных x и комплексное число для всех отрицательных x (подробнее об этом мы пишем в разделе квадратного корня из отрицательного числа).
Вы, наверное, уже заметили, что квадратный корень из площади квадрата дает длину его стороны. Эта функция используется в одном из наших строительных калькуляторов — калькуляторе квадратных метров. Если вы планируете что-либо отремонтировать в будущем, эти инструменты могут вам очень помочь. Не забывайте их использовать!
Производная квадратного корня
Производная функции сообщает нам, насколько быстро эта функция изменяется вместе со своим аргументом. Один из простейших примеров в физике — это положение объекта и его скорость (скорость изменения положения).Допустим, функция x (t) описывает, как расстояние движущегося автомобиля от определенной точки изменяется со временем t . Вы знаете, что определяет, насколько быстро меняется пройденное вами расстояние? Ответ — скорость машины! Таким образом, производная положения x (t) равна скорости v (t) (скорость также может зависеть от времени). Для обозначения производной мы обычно используем апостроф v (t) = x '(t) или символ производной v (t) = dx (t) / dt .(-1/2) = 1 / (2√x) .
Так как число в отрицательной степени больше этого числа на единицу, оценка вывода будет включать дроби. У нас есть инструмент, который может оказаться незаменимым при сложении или вычитании дробей с разными знаменателями. Он называется калькулятором НОК и объясняет, как найти наименьшее общее кратное.
Производная квадратного корня необходима для получения коэффициентов в так называемом разложении Тейлора . Мы не хотим вдаваться в подробности слишком глубоко, поэтому, вкратце, серия Тейлора позволяет вам аппроксимировать различные функции с помощью многочленов, которые намного проще вычислить.Например, разложение Тейлора √ (1 + x) относительно точки x = 0 дается следующим образом:
√ (1 + x) = 1 + 1/2 * x - 1/8 * x² + 1/16 * x³ - 5/128 * x⁴ + ... ,
, что действительно для -1 ≤ x ≤ 1 . Хотя в приведенном выше выражении содержится бесконечное количество членов, чтобы получить приблизительное значение, вы можете использовать всего несколько первых членов. Давай попробуем! С x = 0,5 и первыми пятью членами вы получите:
√ (1,5) = 1 + 1/2 * 0.5 - 1/8 * 0,25 + 1/16 * 0,125 - 5/128 * 0,0625 ,
√ (1,5) ≈ 1,2241 ,
, а действительное значение, предоставленное нашим калькулятором, составляет √ (1,5) ≈ 1,2247 . Достаточно близко!
Пока что это было много математики и уравнений. Для тех из вас, кто достаточно настойчив, мы подготовили следующий раздел, в котором объясняется, как вычислить квадратный корень из отрицательного числа.
Корень квадратный из отрицательного числа
В школе вас, вероятно, учили, что квадратного корня из отрицательного числа не существует.Это верно, если рассматривать только действительные числа. Давным-давно для выполнения сложных вычислений математикам пришлось ввести более общий набор чисел — комплексные числа . Их можно выразить в следующей форме:
х = а + Ь * я ,
, где x — комплексное число с действительной частью a и мнимой частью b . Что отличает комплексное число от действительного, так это мнимое число i .Вот несколько примеров комплексных чисел: 2 + 3i , 5i , 1,5 + 4i , 2 . Вы можете быть удивлены, увидев там 2 , что является реальным числом. Да, но это тоже комплексное число с b = 0 . Комплексные числа являются обобщением действительных чисел.
Пока что воображаемое число i , наверное, до сих пор для вас загадка. Что это вообще такое? Что ж, хотя это может показаться странным, это определяется следующим уравнением:
я = √ (-1) ,
, и это все, что вам нужно для вычисления квадратного корня из каждого числа, независимо от того, положительное оно или нет.Давайте посмотрим на несколько примеров:
квадратный корень из -9: √ (-9) = √ (-1 * 9) = √ (-1) √9 = 3i ,
квадратный корень из -13: √ (-13) = √ (-1 * 13) = √ (-1) √13 = i√13 ,
квадратный корень из -49: √ (-49) = √ (-1 * 49) = √ (-1) √49 = 7i .
Разве это не просто? Эта проблема не возникает с кубическим корнем, поскольку отрицательное число можно получить, умножив три одинаковых отрицательных числа (чего нельзя сделать с двумя отрицательными числами).Например:
³√ (-64) = ³√ [(- 4) * (- 4) * (- 4)] = -4 .
Это, вероятно, все, что вам следует знать о квадратных корнях. Мы ценим, что вы остались с нами до этого момента! В качестве награды испеките себе что-нибудь сладкое 🙂 Воспользуйтесь нашим калькулятором идеальных блинов, чтобы узнать, как приготовить идеальный блин, каким бы он вам ни нравился. Вам может понадобиться наш калькулятор граммов в чашки, чтобы помочь вам в этом. Он работает в обоих направлениях, то есть для преобразования граммов в чашки и преобразования чашек в граммы.А если вы спросите себя «Сколько калорий мне нужно съедать в день?», Воспользуйтесь нашим удобным калькулятором калорий!
FAQ
Может ли число иметь более одного квадратного корня?
Да, на самом деле все положительные числа имеют 2 квадратных корня , один положительный, а другой равный первому, но отрицательный. Это потому, что если вы умножите два негатива вместе, негативы аннулируются и результат будет положительным.
Как найти квадратный корень без калькулятора?
Вычислите квадратного корня.Ближайшее квадратное число приемлемо, если вы в затруднении.
Разделите число, из которого вы хотите найти квадратный корень, на оценку.
Добавьте оценку к результату шага 2.
Разделите результат шага 3 на 2. Это ваша новая оценка .
Повторите шаги 2–4 с новой оценкой. Чем больше раз это повторяется, тем точнее будет результат.
Как вычислить квадратные корни?
Найдите ближайшее квадратное число выше и ниже числа, о котором вы думаете.
Квадратный корень будет между квадратными корнями этих чисел.
Близость числа к квадратному корню указывает, насколько близок корень. Например, 26 очень близко к 25, поэтому корень будет очень близок к 5.
Попробуйте несколько раз разобраться .
Является ли квадратный корень из 2 рациональным числом?
Нет, квадратный корень из 2 не является рациональным . Это связано с тем, что когда 2 записывается как дробь, ²/₁, она никогда не может иметь только четные показатели, и поэтому рациональное число не может быть возведено в квадрат для его создания.
Как избавиться от квадратного корня?
В алгебре возведение в квадрат обеих частей уравнения избавит от любых квадратных корней . Результатом этой операции является то, что квадратные корни будут заменены любым числом, из которого они находили квадратный корень.
Являются ли квадратные корни рациональными?
Некоторые квадратные корни являются рациональными , а другие нет. Вы можете определить, является ли квадратный корень рациональным или нет, выяснив, может ли число, которое вы извлекаете квадратным корнем, быть выражено только в терминах четных показателей (например,грамм. 4 = 2 ²/1 ²). Если может, то его корень рациональный .
Является ли квадратный корень из 5 рациональным числом?
Квадратный корень из 5 — это , не рациональное число . Это связано с тем, что 5 не может быть выражено дробью, если числитель и знаменатель имеют четные показатели. Это означает, что рациональное число нельзя возвести в квадрат, чтобы получить 5.
Является ли квадратный корень из 7 рациональным числом?
Результатом квадратного корня 7 является иррациональное число .7 не может быть записано как дробь только с четными показателями, а это означает, что число, возведенное в квадрат для достижения 7, не может быть выражено как дробь целых чисел, и поэтому не является рациональным.
Какая производная квадратного корня из x?
Производная квадратного корня x равна ^{x ^{— ¹/₂}}/₂ или ¹/_{2SQRT (x)}. Это связано с тем, что квадратный корень из x может быть выражен как x ^¹/₂, от которого обычно происходит дифференцирование.
Как найти квадратный корень из десятичной дроби?
Преобразует десятичную дробь в дробь .
Найдите любой квадратный корень из дроби или оцените его. Сделайте дробью, равной квадратному корню, который вы нашли в квадрате.
Отмените квадратный корень и квадрат, оставив дробь.
Запишите дробь как десятичную в качестве окончательного ответа.
Способы нахождения квадратного корня числа — единичные цифры квадратов
Корень числа равен размеру числа.-
Содержание
1. Уловка квадратного корня — единичная цифра квадрата
2. Как найти квадратный корень из четырехзначного числа
Во-первых, нам нужно узнать единицы измерения всех квадратов от 1 до 10.
Квадратные числа 1-10
Как показано в приведенной выше таблице, всякий раз, когда единичная цифра квадратного числа равна 9, единичная цифра квадратного корня этого числа будет определенно 3 или 7.
Кроме того, это правило может применяться к другим номерам с другими цифрами единиц измерения.
Нанять репетиторов по математике онлайн!
Давайте возьмем для этого пример:
Если единичная цифра числа равна 6, то единичная цифра квадратного корня из числа определенно будет 4 или 6.
Как найти квадратный корень из четырехзначного числа — Горячие клавиши
Найти квадратный корень из четырехзначного числа очень просто, если мы проделаем следующие шаги.
Давайте возьмем для этого пример:
Чтобы найти квадратный корень из 4489
Первый шаг -: мы должны сгруппировать последнюю пару цифр и остальные цифры вместе.
Теперь проверьте цифру единицы 4489, которая равна 9. Таким образом, мы можем сказать, что единичная цифра его квадратного корня будет либо 3, либо 9.
Теперь мы берем только первые две цифры, то есть 44. Поскольку 44 находится между квадратами 6 и 7 (6 ² <44 <7 ², , пожалуйста, обратитесь для этого в приведенную выше таблицу), Таким образом, мы можем определенно сказать, что десятичная цифра квадратного корня из 4489 будет 6.
Итак, мы можем сказать, что квадратный корень будет равен 63 или 67.
Теперь, чтобы найти точную цифру единицы, мы рассматриваем цифру десятков, т. Е. 6, и ее последующую цифру, т. Е. 7.
Умножьте эти два члена, и мы получим следующие значения:
Так как 44 больше 42, квадратный корень из 4489 будет больше из двух вариантов, то есть 67.
Итак, квадратный корень из 4489 будет 67.
Это основная тактика нахождения квадратного корня из четырехзначное число.
Давайте рассмотрим другой пример, чтобы лучше понять процедуру:
Пример: — Найдите квадратный корень из 9801.
Продолжим шаг за шагом-:
Первый шаг: — Мы группируем последнюю пару цифр и остальные цифры вместе.
Теперь, поскольку единичная цифра 9801 равна 1. Таким образом, мы можем сказать, что , эта единичная цифра его квадратного корня будет либо 9, либо 1, как на следующей диаграмме.
Теперь посмотрим на первые две цифры i.е. 98. Поскольку 98 находится между квадратами 9 и 10, поэтому мы можем сказать, что десятичные цифры квадратного корня из 9801 будут 9, поэтому мы можем сказать, что квадратный корень будет равен 91 или 99.
Теперь мы найдем точную цифру единицы.
Чтобы найти точную цифру единицы, мы рассматриваем цифру десятков, то есть 9, и следующее число, то есть 10.
Умножение обоих чисел:
Так как 98 больше 90, квадратный корень из 9801 будет больше из двух вариантов i.е 99.
Как рассчитать КВАДРАТНЫЙ КОРЕНЬ в Excel [5 лучших методов] + Добавить символ
Excel похож на швейцарский армейский нож для вычислений. От математических до финансовых — это все, что вам нужно вычислить. Вы можете рассчитывать от простых до самых сложных в Excel.
Возьмем, к примеру, КВАДРАТНЫЙ КОРЕНЬ .
Квадратный корень — довольно распространенное вычисление, которое мы выполняем в нашей повседневной работе, и в Excel вы можете легко вычислить его.
Знаете что?
Я обнаружил, что существует пять различных способов вычисления квадратного корня в Excel. Да, пять разных методов, которые можно использовать в разных ситуациях.
И сегодня в этом посте я хотел бы поделиться с вами этими пятью простыми методами нахождения квадратного корня из числа в Excel.
Итак, давайте узнаем вот что…
Что такое квадратный корень?
Прежде чем мы научимся его вычислять, важно понять, что это на самом деле означает, как мы его обычно вычисляем.
Краткое введение: Вычисление квадратного корня является обратным вычислением для возврата к корню из квадрата.
Итак, когда вы вычисляете квадрат 10, умножая его на себя, получается (10 * 10 = 100).
Тогда квадратный корень означает возврат от 100 к 10.
Вы можете узнать больше об этом из Википедии. Но теперь давайте узнаем, как это можно сделать в Excel.
Лучшие 5 способов вычисления квадратного корня в Excel
Как я уже сказал, мы можем использовать 5 различных способов вычисления квадратного корня в соответствии с потребностями или личными предпочтениями.
Не все методы одинаковы, но полезны.
№1. Используйте функцию КОРЕНЬ, чтобы найти КВАДРАТНЫЙ корень числа
Если вам нужно использовать только один метод для вычисления квадратного корня, это функция КОРЕНЬ. Это особая функция.
Вам просто нужно сослаться на ячейку или указать число.
Синтаксис SQRT:
Где номер — это номер или ссылка на ячейку, которая содержит число, для которого вы хотите найти квадратный корень.
Примеры:
В приведенном ниже примере у нас есть число 625 в ячейке A1. Итак, чтобы вычислить квадратный корень для этого, мы можем вставить приведенную ниже формулу (панель формул) в B1.
Возвращенное значение — 25, что является квадратным корнем из 625.
Как видите, SQRT прост в использовании и удобен в применении.
Но есть одна особенность.
Если у вас отрицательное число, как показано ниже, оно вернет # ЧИСЛО !.
Итак, решение этой проблемы — использовать функцию ABS вместе с SQRT.Вот пример:
Когда мы используем ABS, он преобразует число в абсолютное число. Это означает, что a преобразует отрицательное число в положительное.
2. Вычислить КВАДРАТНЫЙ корень числа с помощью функции СТЕПЕНЬ
Другой способ вычисления квадратного корня — использование функции СТЕПЕНЬ.
Функция POWER имеет большую мощность, чем SQRT, поскольку она возвращает результат возведения числа N-го в заданную степень.
Синтаксис POWER:
Где число — это число или ссылка на ячейку, которая содержит число, для которого вы хотите найти квадратный корень, а power — это показатель степени для увеличения мощности.
Допустим, нам нужно найти квадратный корень из числа из ячейки A1 (то есть 625), тогда мы можем использовать 1/2 в качестве аргумента мощности в этой функции.
И формула будет:
Как вы видите, она возвращает 25 в результате, который является квадратным корнем из 625.
3. Примените формулу экспоненты, чтобы получить КВАДРАТНЫЙ корень числа
Если нам нужно чтобы вставить простую формулу (кроме двух вышеуказанных методов) для вычисления квадратного корня, мы можем использовать простую формулу с использованием оператора экспоненты.
Эта формула похожа на POWER. Единственная разница в том, что вместо функции нам нужно использовать оператор экспоненты.
В приведенной выше формуле, A1 в ячейке, где у нас есть число, для которого нам нужно найти квадратный корень, а затем мы использовали оператор экспоненты, а затем (1/2) для возведения в степень.
Лучшее преимущество этой формулы — ее применение. Помимо квадратного корня, мы можем использовать его для вычисления кубического корня или любого корня n-й степени.
4. Код VBA для отображения КВАДРАТНОГО корня числа
Позвольте мне рассказать вам о другом сценарии, когда нам нужно проверить квадратный корень числа, а не вычислять его в ячейке.
Code-1
Ниже приведен код VBA, который возвращает квадратный корень, когда мы выбираем ячейку и запускаем этот код.
Sub getSquareRoot ()
Dim rng As Range
Dim sqr As Long
Если Application.Selection.Cells.Count> 1 Тогда
MsgBox «Выберите только одну ячейку», vbOKOnly, «Ошибка»
Exit Sub
End If
Set rng = ActiveCell
If IsNumeric (rng) = True Then
sqr = rng ^ (1/2)
MsgBox «Квадратный корень» & rng & «is» & sqr, vbOKOnly, «Квадратный корень»
Else
MsgBox «Выберите числовое значение», vbOKOnly, «Error»
End If
End Sub
Как работает этот код
Когда мы запускаем этот код, он проверяет значение в выбранной ячейке и, если это значение является числом, вычисляет квадратный корень из этого числа и отображает его в окне сообщения. (1/2)
MsgBox «Квадратный корень» & sq & «is» & sqr, vbOKOnly, «Square Root Value»
Else
MsgBox «Пожалуйста, введите число.», vbOKOnly,» Error «
End If
End Sub
Как работает этот код
Когда мы запускаем этот код, он показывает нам поле ввода с запросом числа, для которого нам нужно получить квадратный корень.
И когда мы вводим это число, он вычисляет квадратный корень для этих чисел и показывает окно сообщения с квадратным корнем.
Вы можете использовать любой из приведенных выше кодов, который идеально подходит для вас.
# 5. Power Query для преобразования чисел в квадратные корни
Вот еще один способ, который мы можем использовать, если вам нужно преобразовать несколько чисел в их квадратные корни.
Это Power Query.
Ниже у нас есть таблица, в которой у нас есть несколько чисел, и здесь мы хотим получить квадратный корень из этих чисел за один раз.
Примечание: Использование запроса мощности для квадратного корня — это динамический метод, каждый раз, когда вы вводите новое значение в свою таблицу, он будет возвращать квадратный корень из этого числа.
Теперь выполните следующие простые шаги.
Прежде всего, выберите любую ячейку в таблице и перейдите на вкладку «Данные» ➜ «Получить и преобразовать данные» и нажмите «Из таблицы / диапазона».
Как только вы щелкнете по нему, Excel откроет редактор мощных запросов и добавит в него эту таблицу.
Отсюда нам нужно создать новый столбец со значениями квадратного корня, для этого перейдите на вкладку «Добавить столбец» и нажмите «Пользовательский столбец».
На этом этапе у нас открыто окно Custom Column, и в это окно нам нужно добавить следующее:
Прежде всего, введите имя столбца «Квадратный корень» в поле ввода имени столбца.
После этого введите приведенную ниже формулу в поле ввода формулы настраиваемого столбца и нажмите OK.
Теперь у нас есть новый столбец с квадратными корнями из числа, которое есть в первом столбце.
Отсюда вам нужно удалить первый столбец исходных значений. Итак, щелкните его правой кнопкой мыши и выберите удалить.
После этого перейдите на вкладку «Домашняя страница» и нажмите «Закрыть и загрузить».
Здесь вы видите окно для загрузки данных. Прежде всего, выберите существующий рабочий лист и добавьте диапазон B1.Во-вторых, отметьте галочкой «Добавить в модель данных».
Как я уже сказал, эта таблица динамическая.
Когда вы вводите новое значение в исходную таблицу данных, оно автоматически вычисляет квадратный корень в вашей новой таблице при ее обновлении.
И мы здесь не используем никаких формул.
[Бонусный совет] Как добавить квадратный корень в Excel
После вычисления квадратного корня из числа следующее, что вы можете сделать, это добавить квадратный корень.
И для этого у нас есть два разных способа.
№1. Использование сочетания клавиш
Простым способом добавления символа квадратного корня является сочетание клавиш Alt + 251.
При вводе 251 на цифровой клавиатуре необходимо удерживать нажатой клавишу Alt. и как только вы отпустите клавишу Alt, появится символ.
№ 2. Добавление квадратного корневого символа путем применения пользовательского форматирования
Это наиболее эффективный способ добавления символа.
Все, что вам нужно сделать, это выбрать все ячейки, открыть параметр пользовательского форматирования и добавить форматирование на панель ввода форматирования.
№ 3. VBA для добавления квадратного символа
Вы также можете использовать приведенный ниже код VBA, чтобы применить настраиваемое форматирование ко всем выделенным ячейкам.
Sub Radical ()
Selection.NumberFormat = ChrW (8730) & «General»
End Sub
Примечание: Преимущество использования методов # 2 и # 3 в том, что вам не нужно добавлять символ ко всем ячейкам одну за другой, и когда вы добавляете символ в ячейку, значение в ячейке становится текстом и не может использоваться в дальнейшем как число.
Образец файла
Загрузите этот образец файла отсюда
Заключение
Если вы просто хотите узнать квадратный корень числа, тогда метод VBA является лучшим, выберите ячейку и запустите код.
В противном случае формулы лучше всего подходят, если вам нужно использовать значение квадратного корня в дальнейших вычислениях, и у нас есть три разные формулы в этом списке.
Power Query — это динамический метод, и его необходимо попробовать.
А теперь скажите мне одну вещь.
Какой ваш любимый метод вычисления квадратного корня в Excel?
Поделитесь со мной своим мнением в разделе комментариев, я хотел бы услышать от вас. И не забудьте поделиться этим списком со своими друзьями, я уверен, они это оценят.
Вы должны прочитать это Далее
Рассчитать коэффициент в Excel: Когда дело доходит до Excel, у нас нет какой-либо конкретной единственной функции, которая могла бы помочь нам рассчитать коэффициент. Но вы можете рассчитать его, используя некоторые пользовательские формулы […]
Средневзвешенное значение в Excel: Но я обнаружил, что лучший способ — использовать формулу, комбинируя функции СУММПРОИЗВ и СУММ. Этот метод прост и удобен в применении […]
Сложные проценты в Excel: Сложные проценты — один из наиболее важных финансовых расчетов, которые большинство из нас часто выполняет в своей работе. И необходимо научиться вычислять его в Excel […]
Вставить / ввести символ степени в Excel: если вы используете ноутбук, как я, вы обнаружите, что нет клавиши для ввода символа градуса.Работая с некоторыми данными, я обнаружил, что в Excel вы можете ввести их пятью разными способами […]
Умножение с помощью специальной вставки: Иногда в Excel вам нужно выполнить несколько быстрых вычислений. И вы можете использовать специальную пасту для этих быстрых вычислений вместо формул […]
Расчет возраста в Excel: В Excel, используя DOB человека, вы можете вычислить его / ее возраст с помощью функции РАЗНДАТ […]
Среднее значение ТОП-5 в Excel: чтобы усреднить 5 лучших результатов из списка, вы можете использовать формулу, основанную на комбинации НАИБОЛЬШИХ и СРЕДНИХ […]
Пунит использует Excel еще со времен учебы в колледже. Он помог тысячам людей понять возможности электронных таблиц и изучить Microsoft Excel. Вы можете найти его в Интернете, в Твиттере об Excel, на беговой дорожке или иногда в походе в гору.
Моделирование квадратов и поиск квадратного корня числа
Результаты обучения
Найдите квадратный корень из полного квадрата
Объясните, почему квадратный корень отрицательного числа не является действительным числом
Упростите выражения с помощью квадратного корня
Чтобы начать этот раздел, нам нужно повторить некоторые важные термины и обозначения.{2} = 9 [/ latex]
Число [латекс] 9 [/ latex] называется полным квадратом, потому что это квадрат целого числа.
Выполнение упражнения по манипуляции математикой Квадратные числа помогут вам лучше понять идеальные квадратные числа.
На диаграмме показаны квадраты счетных чисел от [латекс] 1 [/ латекс] до [латекс] 15 [/ латекс]. Вы можете обратиться к нему, чтобы определить идеальные квадраты.
Идеальные квадраты
Полный квадрат — это квадрат целого числа.{2} & = \ left (-8 \ right) \ left (-8 \ right) \\ & = 64 \ hfill \ end {array} [/ latex]
Когда мы умножаем два отрицательных числа, произведение всегда будет положительным . Итак, квадрат отрицательного числа всегда положителен.
На диаграмме показаны квадраты отрицательных целых чисел от [latex] -1 [/ latex] до [latex] -15 [/ latex].
Вы заметили, что эти квадраты такие же, как квадраты положительных чисел?
Квадратные корни
Иногда нам нужно посмотреть на соотношение между числами и их квадратами в обратном порядке.{2} = 100 [/ latex] также, поэтому [latex] -10 [/ latex] также является квадратным корнем из [latex] 100 [/ latex]. Следовательно, и [латекс] 10 [/ латекс], и [латекс] -10 [/ латекс] являются квадратными корнями из [латекса] 100 [/ латекса].
Итак, каждое положительное число имеет два квадратных корня: один положительный и один отрицательный.
Что, если нам нужен только положительный квадратный корень из положительного числа? Знак корня , [латекс] \ sqrt {\ phantom {0}} [/ latex], означает положительный квадратный корень. Положительный квадратный корень также называется главным квадратным корнем.{2} = 121 \ hfill & & & 11 \ hfill \ end {array} [/ latex]
В следующем видео показано еще несколько примеров того, как можно упростить извлечение квадратного корня из полного квадрата.

Каждое положительное число имеет два квадратных корня, а знак корня указывает на положительный. Пишем [латекс] \ sqrt {100} = 10 [/ латекс]. Если мы хотим найти отрицательный квадратный корень из числа, мы помещаем минус перед знаком корня. Например, [латекс] — \ sqrt {100} = — 10 [/ латекс].
пример
Упростить. Ⓐ [латекс] — \ sqrt {9} [/ latex] ⓑ [латекс] — \ sqrt {144.} [/ Латекс]
Показать решение
Решение
ⓐ
[латекс] — \ sqrt {9} [/ латекс]
Отрицательный знак перед радикальным знаком. [латекс] -3 [/ латекс]
ⓑ
[латекс] — \ sqrt {144} [/ латекс]
Негатив перед радикальным знаком.{2} = — 25? [/ Latex]
Ни одно из чисел, с которыми мы имели дело до сих пор, не имеет квадрата [латекс] -25 [/ latex]. Почему? Любое положительное число в квадрате является положительным, и любое отрицательное число в квадрате также положительно. В следующей главе мы увидим, что все числа, с которыми мы работаем, называются действительными числами. Итак, мы говорим, что не существует действительного числа, равного [latex] \ sqrt {-25} [/ latex]. Если нас просят найти квадратный корень из любого отрицательного числа, мы говорим, что решение не является действительным числом.
пример
Упростите: ⓐ [латекс] \ sqrt {-169} [/ latex] ⓑ [латекс] — \ sqrt {121} [/ латекс].
Показать решение
Решение
ⓐ Не существует действительного числа с квадратом [латекс] -169 [/ латекс]. Следовательно, [латекс] \ sqrt {-169} [/ latex] не является действительным числом.
ⓑ Отрицательный знак стоит перед знаком корня, поэтому мы находим противоположность квадратного корня из [латекс] 121 [/ латекс].
[латекс] — \ sqrt {121} [/ латекс]
Негатив перед радикалом. [латекс] -11 [/ латекс]
Как вычислить квадратные корни в вашей голове | by Don Cross
Произведите впечатление на свою семью, друзей и домашних животных с помощью мысленных вычислений
Фото Матеуса Кейроса на Unsplash
В этой статье я покажу вам метод быстрого вычисления квадратного корня из числа без использования калькулятора.Этот метод прост в освоении и, в отличие от традиционных методов ручных вычислений, требует минимум кратковременной памяти. С практикой вы сможете сделать все в своей голове.
Что такое квадратный корень?
Пусть в этой статье Y представляет некоторое положительное число. Цель состоит в том, чтобы найти другое число X , такое, что при умножении X на X вы получите Y . В математической записи мы говорим: X ² = Y .
Например, если я скажу вам, что Y = 144, вы найдете X = 12 в качестве ответа, потому что 12 умноженное на 12 (или 12²) равно 144. Мы говорим, что 12 — это квадратный корень из 144.
Обычно вам не так везет, чтобы начать с числа Y , которое представляет собой идеальный квадрат, например 144 или 25. Более распространенный случай — вам дается число, для которого нет простого целого числа. квадратный корень. Давайте для примера рассмотрим Y = 360. В этом случае квадратный корень X не будет целым числом.Фактически, X будет иррациональным числом , что означает, что оно имеет случайную неповторяющуюся последовательность цифр после десятичной точки. Наша цель — вычислить квадратный корень, то есть нам нужна точность с точностью до двух или трех цифр после десятичной точки.
Выберите ближайшее целое число
Первый шаг — найти целое число, максимально близкое к действительному квадратному корню. Опять же, наш пример: Y = 360. Спросите себя, какое число, умноженное на само себя, близко к 360? Очевидный выбор — 20² = 400.Поскольку это произведение слишком велико, давайте попробуем умножить 19 само на себя.
На этом этапе мысленное возведение в квадрат 19 может утомить вашу краткосрочную память. У меня есть редакторский комментарий. Выполнение арифметики традиционным способом, которым учат в начальной школе, является обратным. Мы учим детей начинать с умножения 9 на 9, и, как взрослые, продолжаем так делать по привычке. Но почему мы начинаем с наименее важной цифры?
У меня есть еще один комментарий: (20–1) ² легче посчитать в голове, чем 19².Мы уже знаем, что 19² должно быть близко к 20² = 400. Почему бы не начать с 400 и не работать дальше? Вот картинка, которая поможет вам возводить числа в квадрат:
Здесь у нас есть большой квадрат размером 20 единиц на 20 единиц, разделенный на 4 цветные области. Площадь всей площади 20² = 400. Мы хотим знать площадь синей области, которая составляет 19 на 19 единиц. Чтобы получить эту область, мы хотим отрезать две полосы, отмеченные желтым, вместе с маленьким красным квадратом.
Давайте посмотрим на размеры деталей, которые мы собираемся удалить.Каждая желтая полоска имеет размер 1×19, а красный квадрат — 1×1. Есть разные способы взглянуть на это, но я рекомендую тот, который поможет вам не усложнять задачу. Если вы думаете об одной желтой полосе плюс красный квадрат, у вас есть область 1×20. Дважды вычтите 1×20. Это заставляет нас дважды вычитать красный квадрат, что неверно. Мы решаем эту проблему, добавляя красный квадрат 1×1 обратно:
19² = 400–40 + 1 = 361
Разве это не более простой способ возвести 19 в квадрат в уме? Самое приятное то, что вы начинаете с самой большой и важной части ответа — 400.Затем вы уточняете его, вычитая следующую наиболее важную часть, 40. Последнее, что вы делаете, это добавляете обратно 1, наименее важную часть.
Кроме того, теперь мы видим, что угадывание X = 19 очень приближает нас к желаемому значению квадратного корня! Это достойная оценка. Как сделать нашу оценку еще лучше?
Уточнить ответ
Хотя 19² = 361 очень близко к 360, это немного больше. Это означает, что 19 очень близко к квадратному корню из 360, но немного выше фактического квадратного корня X .Давайте сделаем диаграмму, подобную той, которую мы использовали выше, чтобы увидеть, какой свет она проливает на ситуацию.
На этой новой диаграмме пусть E представляет величину ошибки между Y и квадратом нашего целочисленного предположения. В нашем примере 19² = 361, что на 1 больше, чем желаемое значение 360. Следовательно, ошибка составляет E = 361–360 = 1. В этом примере ошибка E положительная. В других случаях он будет отрицательным. Когда ошибка положительная, мы хотим уменьшить нашу догадку, чтобы компенсировать ее.Точно так же, когда ошибка отрицательная, мы хотим увеличить предположение для компенсации. Мы корректируем наше предположение, в результате чего получаем гораздо лучшее значение X .
Но насколько мы подстраиваемся? Назовите свое целочисленное предположение G . Затем отрегулируйте на E / (2 G ), чтобы найти уточненное значение квадратного корня. Другими словами, делит ошибку на удвоенное значение предположения и либо прибавляет, либо вычитает его по мере необходимости, приближая предположение к квадратному корню . В этом случае ошибка равна 1, предположение — 19, поэтому мы хотим скорректировать 19, вычитая 1/38.Чтобы сделать это возможным для ментальной арифметики, вычислите приблизительное значение путем вычитания 1/40. Вы знаете, что 1/4 = 0,25, поэтому 1/40 = 0,025. Вычитая, находим X = 19–0,025 = 18,975.
Насколько близка наша оценка? Сначала с помощью калькулятора найдите 18,975². Результат — 360.050625. Это очень хорошо! Кроме того, вы можете использовать научный калькулятор, чтобы найти квадратный корень из 360. Ответ: 18.973665961010276. Это означает, что наш ответ был правильным с точностью до двух знаков после запятой. Не так уж плохо, чтобы делать все это в своей голове!
Почему это работает? На диаграмме выше мы упростим, игнорируя относительно небольшую площадь красного квадрата.Допустим, площадь желтых полосок составляет ошибку E . Следовательно, каждая из двух желтых полосок имеет площадь примерно вдвое меньше, или E /2. Более длинная сторона каждого желтого прямоугольника примерно такая же, как ваше предположение G .
Короткая сторона каждого желтого прямоугольника показывает, насколько мы хотим скорректировать предположение. Следовательно, желаемая, но неизвестная корректировка, умноженная на G , дает нам область E /2. Работая в другом направлении, мы разделим область E /2 на предположение G , чтобы получить E / (2 G ) в качестве требуемой корректировки.
Другой пример
Давайте рассмотрим еще один пример, чтобы убедиться, что метод краткий и понятный. На этот раз давайте найдем квадратный корень из 51. Выполните следующие действия:
Найдите целое число, квадрат которого близок к 51. Давайте выберем 7² = 49.
Определите ошибку. Квадрат нашего предположения меньше цели на 2 единицы: 51–49 = 2.
Поскольку наше предположение слишком мало, нам нужно отрегулировать вверх от целочисленного предположения. Корректировка представляет собой ошибку, деленную на удвоенное предположение: 2 / (2 * 7) = 1/7.Поскольку 1/7 составляет около 0,14, мы складываем, чтобы найти X = 7,14.
Счет с помощью калькулятора: 7,14² = 50,9796. Опять же, это очень хорошо! Также проверьте, взяв квадратный корень из 51. Результат: 7,14142842854285. Еще раз, мысленная оценка верна с точностью до двух знаков после запятой.
Сдвиг десятичной точки по мере необходимости
Вы можете адаптировать этот метод для обработки очень больших или очень малых значений Y , сдвигая десятичные точки. Но нужно быть осторожным. Рассмотрим этот пример: если вы извлечете квадратный корень из 100, вы сразу узнаете, что ответ будет 10, потому что 10 умножить на 10 равно 100.Но что, если вам нужен квадратный корень из 1000? Ответ — не 100, потому что 100 умножить на 100 равно 10 000, что в 10 раз больше, чем 1000.
Обычно, когда вы увеличиваете X в десять раз, X ² становится в 100 раз больше. Каждый раз, когда вы сдвигаете десятичную точку в X влево или вправо на одну цифру, десятичная точка в квадрате сдвигается на две цифры.
Работая в обратном порядке, вы можете вычислить квадратные корни из очень больших или очень маленьких чисел, сдвинув десятичную точку, но вам нужно на сдвинуть десятичную точку данного числа на четное количество цифр .Затем вы должны скорректировать значение оценки квадратного корня, сдвинув вдвое меньшее количество цифр в противоположном направлении.
Пример прояснит это. Выше мы обнаружили, что квадратный корень из 51 составляет примерно 7,14. Что, если вам нужен квадратный корень из 510 000? Вы можете удалить четыре нуля с конца, чтобы получить 51. Тогда вы обнаружите, что приблизительный квадратный корень равен 7,14. Конечно, это слишком мало, чтобы быть квадратным корнем из 510 000. Сдвиньте десятичную точку вправо на две цифры, чтобы получить 714.Вы можете убедиться, что 714² = 509 796.
Если вы действительно хотите выполнить сдвиг на нечетное количество десятичных знаков, просто помните, что квадратный корень из 10 составляет примерно 3,16. Примерно 3 — это неплохо. Итак, если вы знаете, что квадратный корень из 400 равен 20, тогда квадратный корень из 4000 будет примерно в 3 раза больше, или 60. Еще лучшая оценка — 3,16 умножить на 20, или 63,2. Проверить: 63,2² = 3994,24.
Практические советы
Чтобы овладеть этой техникой, полезно использовать карандаш и бумагу и некоторое время практиковаться, пока шаги не станут автоматическими.
Posted in Разное
Навигация по записям
Составь сложные предложения по схемам: Составьте сложные предложения по схемам. 1. *** , и *** . 2. *** , когда *** . 3. *** ,
Системы показательных уравнений примеры решения: Тема 9. «Системы показательных уравнений и неравенств».
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Рубрики
Без рубрики
Дет
Полезн
Разное
Родител
Семья
Успокоит
Уход
2024 © Все права защищены.

ⓐ
	[латекс] — \ sqrt {9} [/ латекс]
Отрицательный знак перед радикальным знаком.	[латекс] -3 [/ латекс]

Что значит корень числа. Как найти квадратный корень числа вручную

Что такое квадратный корень?

Комплексные числа

Обобщения

Квадратный корень в информатике

Алгоритмы нахождения квадратного корня

Разложение в ряд Тейлора

Арифметическое извлечение квадратного корня

Грубая оценка

Геометрическое извлечение квадратного корня

С чего все начиналось

Наши дни

Свойства квадратного корня на поле R

Как найти корень числа?

Графическое изображение функции z=√y

Свойства функции z=√y на поле действительных чисел R

Варианты изображения функции z=√y

Корень квадратный в комплексном поле С

Квадратный корень из дроби

Преобразование квадратных корней

Арифметический квадратный корень 8 класс онлайн-подготовка на Ростелеком Лицей

Вычисление целочисленного квадратного корня / Хабр

Сколько квадратный корень из 100

Каким образом вычислить корень определенного числа

Как рассчитать корень из 100

Квадратный корень из 3;2;5 — Квадратный Корень

Геометрия

Использование в других областях

Энергетика

История

Алгоритмы вычисления

Свойства квадратного корня из двух

Доказательство иррациональности

Непрерывная дробь

Размер бумаги

Вавилонский метод

Золотое сечение

Алгебра

Тождества Рамануджана

Корень из числа: определения, примеры

Квадратный корень, арифметический квадратный корень

Самый простой способ найти квадратный корень в Swift?

5 ответов

Похожие вопросы:

Нахождение квадратного корня и квадратного корня из числа

Что такое квадратный корень?

Как найти квадратный корень из числа

Нахождение квадратного корня из полного квадратного числа

Нахождение квадратного корня из чисел, не являющихся точными квадратами

Квадратные корни и кубические корни

Пример 1

Упрощение квадратных корней

Пример 2

Пример 3

.

Символ квадратного корня √

Определение квадратного корня

Как найти квадратный корень?

Калькулятор квадратного корня

Как упростить извлечение квадратного корня?

Сложение, вычитание, умножение и деление квадратных корней

Функция квадратного корня и график

Производная квадратного корня

Корень квадратный из отрицательного числа

FAQ

Может ли число иметь более одного квадратного корня?

Как найти квадратный корень без калькулятора?

Как вычислить квадратные корни?

Является ли квадратный корень из 2 рациональным числом?

Как избавиться от квадратного корня?

Являются ли квадратные корни рациональными?

Является ли квадратный корень из 5 рациональным числом?

Является ли квадратный корень из 7 рациональным числом?

Какая производная квадратного корня из x?

Как найти квадратный корень из десятичной дроби?

Способы нахождения квадратного корня числа — единичные цифры квадратов

Как рассчитать КВАДРАТНЫЙ КОРЕНЬ в Excel [5 лучших методов] + Добавить символ

Что такое квадратный корень?

Лучшие 5 способов вычисления квадратного корня в Excel

№1. Используйте функцию КОРЕНЬ, чтобы найти КВАДРАТНЫЙ корень числа