Содержание
Трапеция. Свойства, признаки трапеции | Подготовка к ЕГЭ по математике
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Как найти основание трапеции?
Прежде чем начать разговор о том, как найти основание трапеции, важно понимать, что же представляет собой трапеция. Трапеция – это геометрическая фигура, которая является четырёхугольником с двумя параллельными сторонами, которые противолежат друг другу.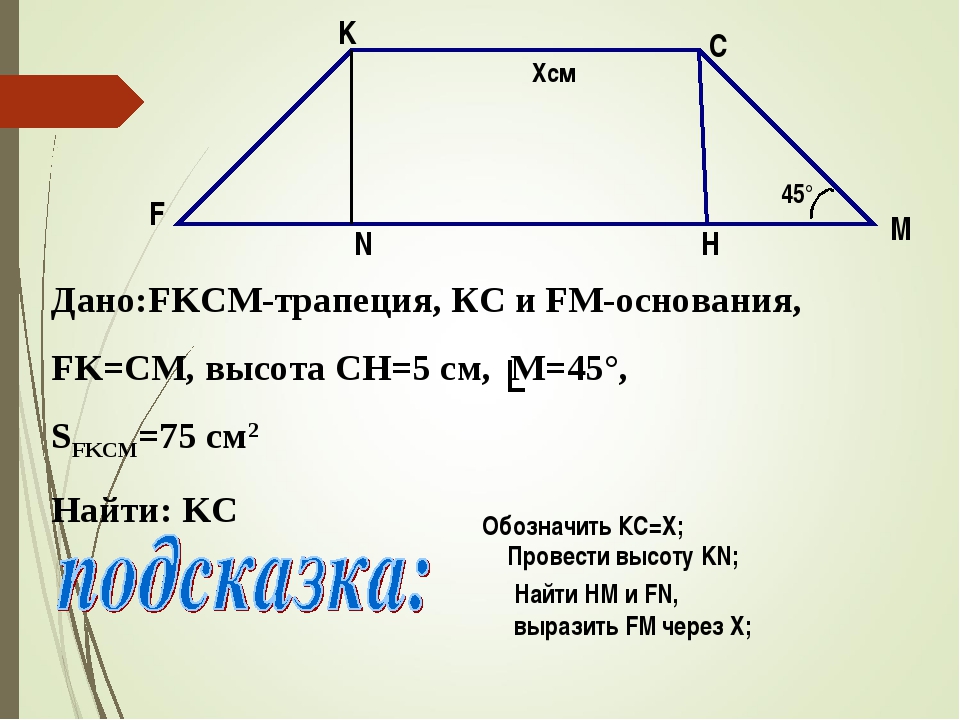 Эти стороны в математике называют основаниями трапеции. Две другие стороны именуются боковыми сторонами. Если соединить между собой центральные точки боковых сторон, мы получим среднюю линию трапеции.Данные свойства этой геометрической фигуры являются основой всех вычислений её характеристик.
Эти стороны в математике называют основаниями трапеции. Две другие стороны именуются боковыми сторонами. Если соединить между собой центральные точки боковых сторон, мы получим среднюю линию трапеции.Данные свойства этой геометрической фигуры являются основой всех вычислений её характеристик.
Для вычисления основания трапеции, как большого, так и малого, используется ряд способов. Выбор способа зависит от количества знаний, которое мы имеем об объекте. Большинство задач располагают условиями, которые содержат в себе данные, заметно упрощающие поиск решения задачи. Зачастую, решение заключается в том, чтобы опустить высоту на основание, применяя теорему Пифагора, в этом случае решить задачу легко.
Как найти основание равнобедренной трапеции
Похожим образом вычисляется основание равнобедренной трапеции. Равнобедренная трапеция – трапеция, которая имеет равные боковые стороны. Фигура имеет симметричный вид относительно центра, это делает пары её углов равными. Таким образом, сведения об одном угле упрощают задачу вычисления всех остальных углов.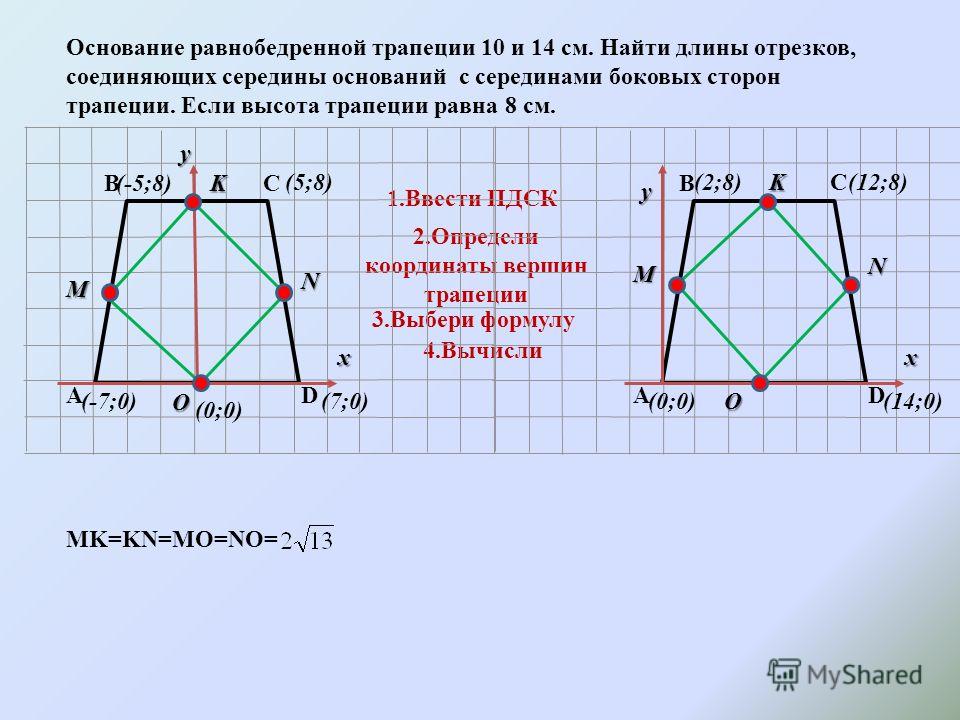
Боковые части трапеции равны друг другу. Например, мы должны найти основание через фрагмент этого основания. Длина второго фрагмента в данном случае будет совпадать с длиной первого фрагмента с абсолютной точностью. Мы можем также получить искомую часть основания через изображение высоты, которая образует треугольник. Параметры углов и одной стороны треугольника помогут нам сделать точные вычисления. В задачах требуется решить вопрос о том, как найти большее основание равнобедренной трапеции или меньшее основание. Рассмотрим пример вычисления величины меньшего основания трапеции.
Как найти меньшее основание равнобедренной трапеции
В случае, когда нам известна величина большего основания, вопрос о том, как найти меньшее основание равнобедренной трапеции перестанет быть острым. Это можно следующим образом:
- На большее основание нужно опустить высоту.
- Записать две теоремы Пифагора, одна из которых отразит параметры треугольника, а другая будет нужна для треугольника, состоящего из гипотенузы.
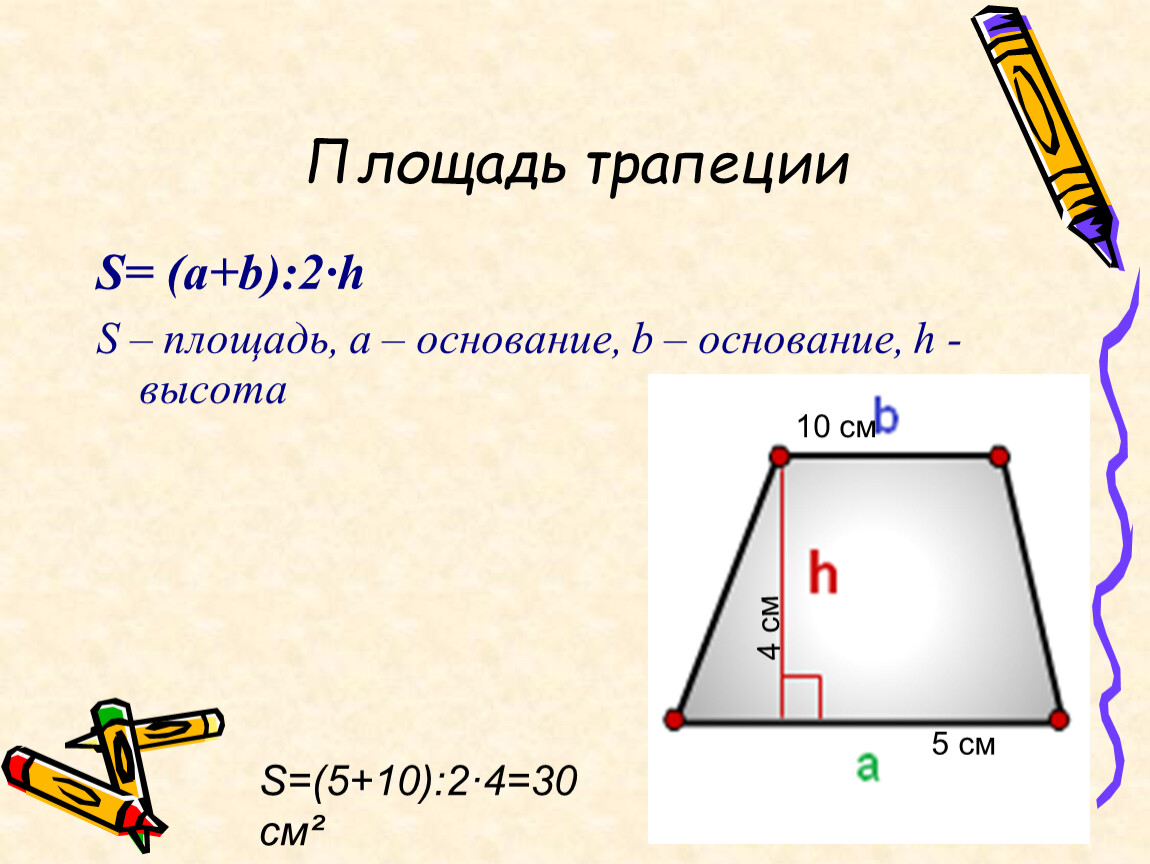 В случае с первой теоремой, в треугольнике роль гипотенузы исполнит диагональ, роль одного катета достанется высоте, а другого – большее основание, не имеющее отрезка. Отрезок будет отсечён высотой. Вторая теорема используется для треугольника, составляющими которого станут гипотенуза – боковая сторона и катет – отрезок большого основания, ограниченный высотой.
В случае с первой теоремой, в треугольнике роль гипотенузы исполнит диагональ, роль одного катета достанется высоте, а другого – большее основание, не имеющее отрезка. Отрезок будет отсечён высотой. Вторая теорема используется для треугольника, составляющими которого станут гипотенуза – боковая сторона и катет – отрезок большого основания, ограниченный высотой. - Составить систему уравнений, которые получили, решить их.
- Найти отрезок, отсечённый высотой от наибольшего расстояния.
- Отнять удвоенные параметры полученного отрезка от параметров наибольшего основания.
- Получить результат – длину наименьшего основания.
Как найти основание прямоугольной трапеции
Прямоугольной трапецией – это вид геометрической трапеции , один из углов которой равен девяноста градусам. Вычислить основание прямоугольной трапеции наиболее легко. Условие задачи, по обыкновению, уже содержит данные о втором основании. От вас потребуется только лишь определить фрагмент основания, образующий угол фигуры вместе с боковой стороной.
По теореме Пифагора, вычисляем эту часть, затем нужно прибавить или отнять эту часть от второго основания. В результате вычислений мы получим искомый параметр. Теперь вы знаете, как найти основание прямоугольной трапеции.
Формулы сторон равнобедренной трапеции
1. Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины основания:
2. Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Площадь трапеции через основания и диагонали
Как найти площадь трапеции через ее основания и диагонали?
Площадь трапеции равна произведению полусуммы оснований на высоту. Поскольку основания известны, задача может быть сведена к нахождению высоты трапеции.
Поскольку основания известны, задача может быть сведена к нахождению высоты трапеции.
На самом деле, зная основания и диагонали, можно найти площадь трапеции и без высоты.
Дано: ABCD — трапеция,
AD || BC, AD=a, BC=b,
AC=d1, BD=d2
Найти:
Решение:
1) Проведём
Через точку C проведем прямую, параллельную диагонали BD. Обозначим точку пересечения этой прямой с прямой, содержащей основание AD трапеции через F:
2) В четырехугольнике BCFD AF || BC (как прямые, содержащие основания трапеции), BD || CF (по построению). Значит, BCFD — параллелограмм (по определению). Следовательно, его противоположные стороны равны: DF=BC=a, CF=BD=d2.
3) Рассмотрим треугольник ACF. AF=AD+DF=a+b.
Площадь треугольника ACF равна
Так как AF=AD+DF,
Все три стороны треугольника ACF известны, поэтому его площадь можно найти по формуле Герона
Вместо a, b и c подставляем a+b, d1 и d2. Получаем:
Получаем:
Таким образом, площадь трапеции через основания и диагонали может быть найдена по формуле
Запоминать её не нужно, достаточно провести аналогичные рассуждения для своей задачи и по формуле Герона вычислить площадь треугольника, стороны которого равны диагоналям трапеции и сумме её оснований.
Задача.
Основания трапеции равны 10 см и 90 см, а диагонали равны 75 см и 35 см. Найти площадь трапеции.
Проводим дополнительные построения и доказываем, что площадь трапеции ABCD равна площади треугольника ACF. Затем находим его площадь по формуле Герона:
Ответ: 1050 см².
В следующий раз рассмотрим, как по основаниям и диагонали найти площадь равнобедренной трапеции.
Площадь трапеции
На данной странице вы можете ознакомиться со всеми формулами для нахождения площади трапеции, как обычной, так и равнобедренной или неправильной. Также здесь есть несколько примеров решения задач по данным формулам, что удобно для нахождения своих ошибок и недочетов. Для экономии времени воспользуйтесь соответствующим онлайн-калькулятором.
Также здесь есть несколько примеров решения задач по данным формулам, что удобно для нахождения своих ошибок и недочетов. Для экономии времени воспользуйтесь соответствующим онлайн-калькулятором.
Площадь трапеции по высоте и двум основаниям
Формула нахождения площади трапеции по высоте и двум основаниям:
$S = \frac{a + b}{2} \cdot h$,
$S$ — площадь трапеции, где
$a$ — малое основание трапеции,
$b$ — большее основание трапеции,
$h$ — высота трапеции.
Площадь трапеции по высоте и средней линии
Формула нахождения площади трапеции по высоте и средней линии:
$S = m \cdot h$, где
$S$ — площадь трапеции,
$m$ — средняя линия,
$h$ — высота трапеции.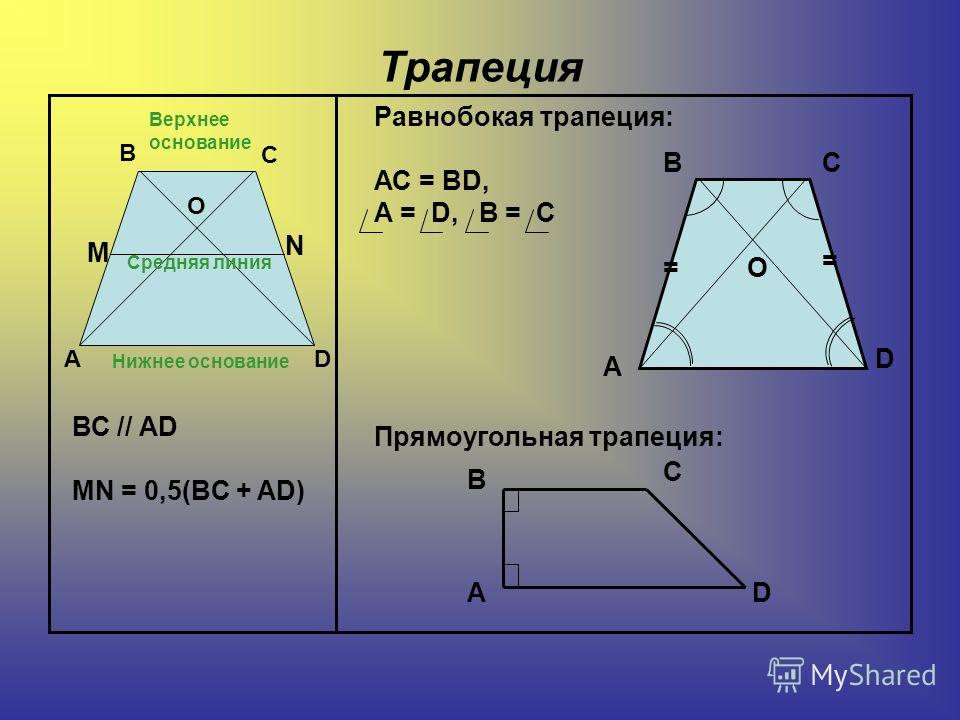 2}$, где
2}$, где
$S$ — площадь трапеции,
$a$ — малое основание,
$b$ — большее основание,
$c, d$ — боковые стороны.
Площадь трапеции по диагонали и углу между диагоналями
Формула нахождения площади трапеции по диагонали и углу между диагоналями:
$S =\frac12 \cdot d1 \cdot d2 \cdot \sin (α)$, где
$S$ — площадь трапеции,
$d1$ — первая диагональ,
$d2$ — вторая диагональ,
$α$ — угол между диагоналями.
Площадь трапеции через ее основание и углы
Формула нахождения площади трапеции через ее основание и углы при основании:
$S = \frac12 \cdot (b^2 — g^2) \cdot \frac{\sin (α) \cdot \sin (γ)}{\sin (α + γ)}$, где
$S$ — площадь трапеции,
$b$ — большее основание,
$g$ — малое основание,
$α$ — первый угол при основании,
$γ$ — второй угол при основании. 2}{4}}$, где
2}{4}}$, где
$S$ — площадь трапеции,
$AB$ — малое основание,
$CD$ — большее основание,
$AC = DB$ — боковая сторона.
Площадь равнобедренной трапеции через малое основание
Формула нахождения площади равнобедренной трапеции через малое основание, боковую сторону и угол при большем основании
$S = c \cdot \sin (α) \cdot (a + c \cdot \cos (α))$, где
$S$ — площадь трапеции,
$a$ — малое основание,
$c$ — боковая сторона
$α$ — угол.
Площадь равнобедренной трапеции через большее основание, боковую сторону и угол
$S = c \cdot \sin (α) \cdot (b — c \cdot \cos (α))$, где
$S$ — площадь трапеции,
$α$ — угол при большем основании,
$c$ — боковая сторона,
$b$ — большее основание. 2 \cdot \sin (α)$, где
2 \cdot \sin (α)$, где
$S$ — площадь трапеции,
$D$ — диагональ трапеции,
$α$ — угол между диагоналями.
Площадь равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
Формула нахождения площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании:
$S = m \cdot c \cdot \sin (α)$, где
$S$ — площадь трапеции,
$m$ — средняя линия трапеции,
$c$ — боковая сторона,
$α$ — угол при основании.
Чтобы проверить правильность своего решения и ответа или найти какие-либо ошибки в действиях необходимо решить пример данной задачи. Для наглядности выполним пример задачи на нахождение равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании. 2}{\sin (α)}$, где
2}{\sin (α)}$, где
$S$ — площадь трапеции,
$R$ — радиус вписанной окружности,
$α$ — угол между сторонами.
Площадь равнобедренной трапеции через два ее основания и радиус вписанной окружности
Формула нахождения площади равнобедренной трапеции через два ее основания и радиус вписанной окружности:
$S = r \cdot (a + b)$, где
$S$ — площадь трапеции,
$r$ — радиус вписанной окружности,
$a$ — малое основание,
$b$ — большее основание
Площадь равнобедренной трапеции через ее основания и угол при большем основании
Формула нахождения площади равнобедренной трапеции через ее основания и угол при большем основании:
$S = \frac {d \cdot b} {\sin (α)}$, где
$S$ — площадь трапеции,
$d$ — малое основание,
$b$ — большее основание,
$α$ — угол при большем основании.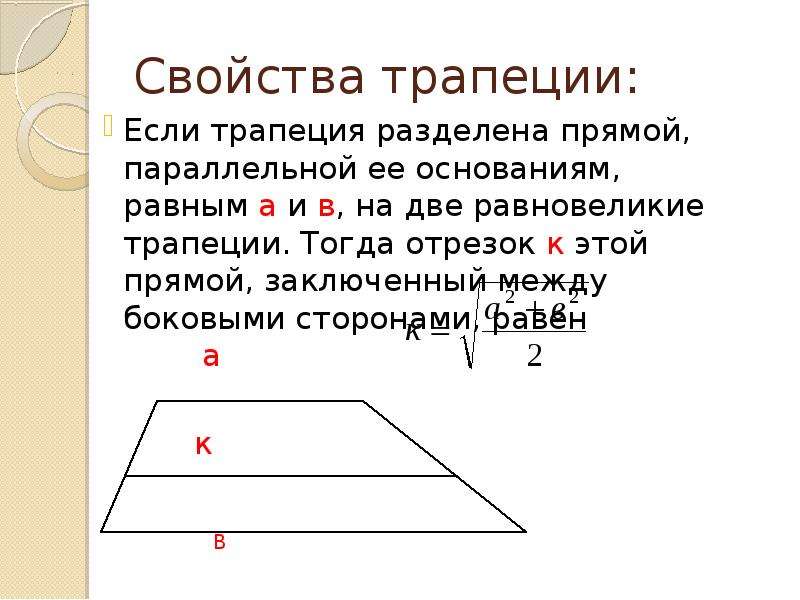
Площадь равнобедренной трапеции через основания и среднюю линию
Формула нахождения площади равнобедренной трапеции через основания и среднюю линию:
$S = m \cdot \sqrt {a \cdot b}$, где
$S$ — площадь трапеции,
$m$ — средняя линия,
$a$ — малое основание,
$b$ — большее основание.
Для того, чтобы сверить свой ответ и решение с онлайн-калькулятором и найти какие-либо свои ошибки, будет полезно рассмотреть пример решения данной задачи на нахождение площади равнобедренной трапеции через заданные основания и среднюю линию.
Пример 3
Дано: малое основание $a = 5$ cм, большее основание $b = 8$ см, $m = 6$ см.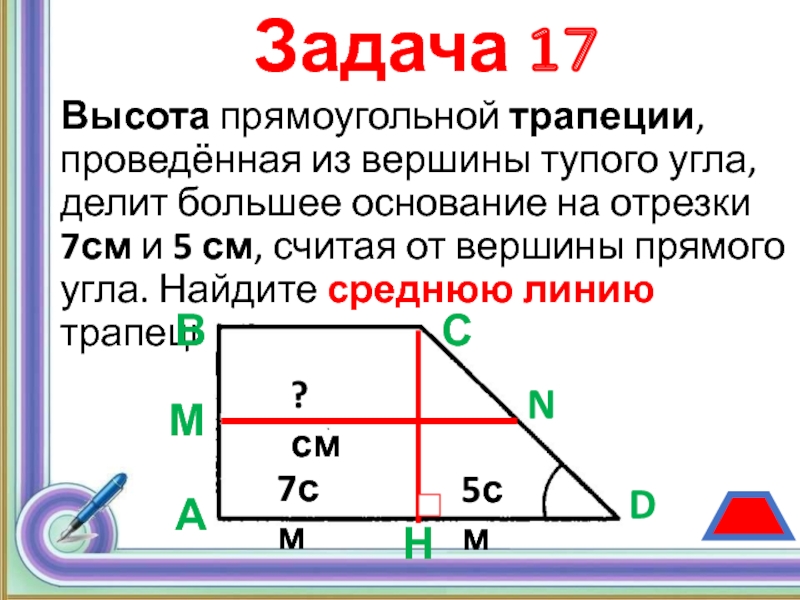 2$
2$
Трапеция [wiki.eduVdom.com]
Трапецией называется четырехугольник, у которого только две противоположные стороны параллельны (Рис.1).
Трапеция
Рис.1
Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.
Отрезок, соединяющий середины ее боковых сторон, называется средней линией трапеции. На рисунке 2 отрезок EF — средняя линия трапеции ABCD.
EF — средняя линия трапеции
Рис.2
Трапеция а) равнобедренная б) прямоугольная
Рис.3
Трапеция, у которой боковые стороны равны, называется равнобокой или равнобедренной (рис.3, а).
Трапеция, один из углов которой прямой, называется прямоугольной (рис.3, б).
С использованием теоремы 1 устанавливается свойство средней линии трапеции.
Теорема 2. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Пример 1. В равнобедренной трапеции перпендикуляр, проведенный из вершины тупого угла, делит большее основание на отрезки 10 см и 20 см. Найти меньшее
основание.
Решение. Пусть условию задачи отвечает рисунок 4, а. Проведем второй перпендикуляр из вершины второго тупого угла (рис.4, б).
Рис.4
Получили два равных прямоугольных треугольника ABE и CDF. Из равенства этих треугольников следует, что FD = 10 см. Значит, EF = 20 — 10 = 10 (см). Четырехугольник EBCF — прямоугольник. Следовательно, BC = EF= 10 см.
Пример 2. Средняя линия трапеции равна 7 м, а одно из оснований больше другого на 4 м. Найти основания трапеции.
EF — средняя линия трапеции
Рис.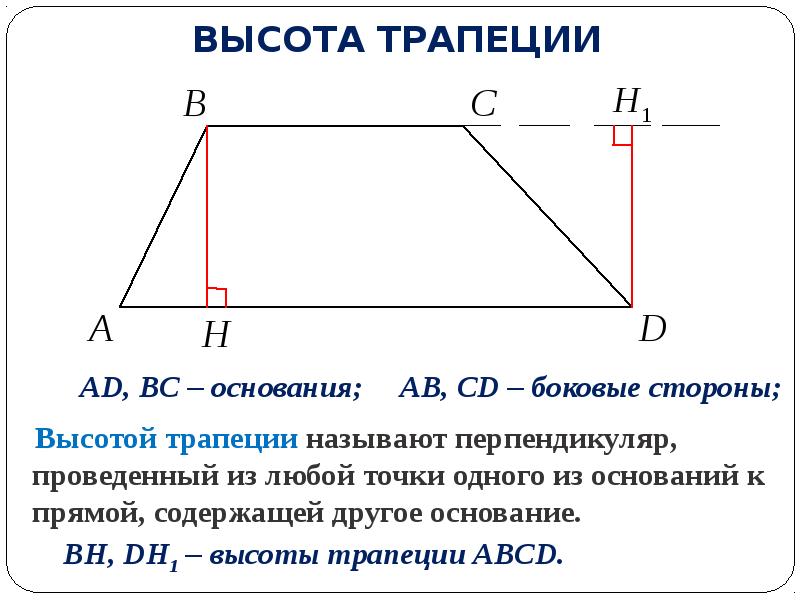 2
2
Решение. Обозначим длину меньшего основания через х. Тогда длина большего основания будет х + 4. Теперь согласно теореме о средней линии трапеции получаем уравнение $$
\frac{x+x+4}{2}=7
$$ , решая которое находим х = 5. Следовательно, основания трапеции 5 м и 9 м.
Формула периметра трапеции
Трапе́ция (от др. -греч. τράπέζιου — «столик» ; τράπεζα — «стол, еда» ) — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.
Иногда трапеция определяется как четырёхугольник, у которого произвольная пара противолежащих сторон параллельна, в этом случае параллелограмм является частным случаем трапеции
Периметр произвольной трапеции
Периметр произвольной трапеции, в которой AB=a, BC=b, CD=c, AD=d, имеет вид:
\[ \LARGE P_{ABCD} = a + b + c + d \]
где:
P — периметр трапеции
a, b, c, d — стороны трапеции
Периметр равнобокой трапеции
Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.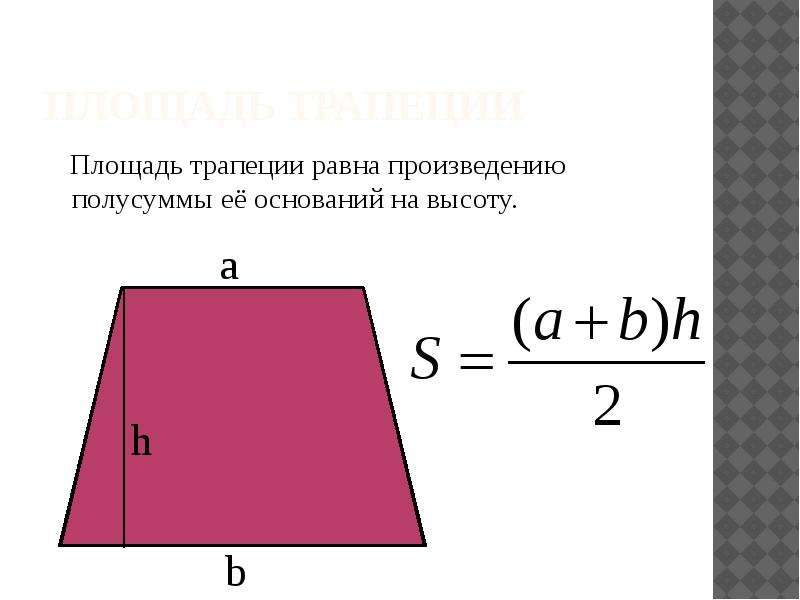
Периметр произвольной трапеции, в которой AB=CD=a, BC=b, AD=c, имеет вид:
\[ \LARGE P_{ABCD} = 2 \cdot a + b + c \]
где:
P — периметр трапеции
a, b, c, d — стороны трапеции
Признаки равнобедренной трапеции
Трапеция будет равнобедренной если выполняется одно из этих условий:
1. Углы при основе равны:
∠ABC = ∠BCD и ∠BAD = ∠ADC
2. Диагонали равны:
AC = BD
3. Одинаковые углы между диагоналями и основаниями:
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
4. Сумма противоположных углов равна 180°:
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
5. Вокруг трапеции можно описати окружность
Также можно найти периметр трапеции, не зная длин оснований, но имея среднюю линию m. Средняя линия по определению представляет собой полусумму оснований трапеции, поэтому умножив ее на два, можно подставить ее вместо оснований в формулу периметра: \( P = 2 \cdot m + c + d \).
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Видео с вопросом: Определение длины основания в трапеции с учетом длины, высоты и площади другого основания
Стенограмма видеозаписи
Трапеция площади 132 и основания 20
имеет высоту 11. Какова длина другого
база?
Было бы разумно начать это
вопрос, нарисовав диаграмму для моделирования информации. В этом вопросе нам сказано, что мы
есть трапеция.Мы можем помнить, что трапеция — это
четырехугольник, то есть четырехугольник с парой параллельных сторон. Высота 11 единиц. Нам сказали, что одна из баз
20, и нам нужно найти длину другого основания. Когда мы говорим о базах в
трапеции, то есть длины параллельных сторон. Мы не знаем, какая база равна 20, но
запишем это как нижнюю базу.
Для расчета длины
другая база, нам понадобится информация о местности.В некоторых странах слово
трапеция используется для обозначения фигуры с одной парой параллельных сторон. Здесь нам говорят, что этот район
132 кв. И мы можем использовать формулу для
площадь трапеции или трапеции, которая говорит нам, что площадь равна половине
ℎ раз 𝑏 суб-один плюс 𝑏 суб-два. ℎ обозначает высоту
трапеция, и 𝑏 sub one и 𝑏 sub two — это две основы. Итак, взяв эту формулу, мы
Можно залить по тому, что площадь 132, высота 11.И мы не знаем ни одной из баз,
так что давайте оставим это как 𝑏 sub one. И затем мы складываем базу 20.
Мы можем преобразовать это уравнение в
найти 𝑏 sub одним несколькими способами. Но давайте начнем с удаления этого
половину, умножив обе части уравнения на два. 132 умноженное на два дает нам
264. А с правой стороны мы
А с правой стороны мы
все еще есть 11 умножить на 𝑏 к югу от единицы плюс 20. Затем мы можем разделить обе части
уравнение на 11.Если разделить 264 на 11, получим 24. И тогда в правой части
у нас будет суб-один плюс 20. Затем мы можем найти 𝑏 суб-один,
вычитая 20 из обеих частей уравнения. Итак, наш ответ таков:
другая база должна была быть длиной в четыре единицы.
Использование свойств трапеций для решения задач
Результаты обучения
- Найдите площадь трапеции по высоте и ширине основания
- Используйте площадь трапеции для ответов на вопросы по применению
Трапеция — это четырехсторонняя фигура, четырехугольник , две стороны которого параллельны, а две — нет.Параллельные стороны называются основаниями. Мы называем длину меньшей основы [латексом] b [/ латексом], а длину большей основы [латексом] B [/ латексом]. Высота [латекс] h [/ латекс] трапеции — это расстояние между двумя основаниями, как показано на изображении ниже.
Высота [латекс] h [/ латекс] трапеции — это расстояние между двумя основаниями, как показано на изображении ниже.
Трапеция имеет большую основу, [латекс] B [/ латекс], и меньшую основу, [латекс] b [/ латекс]. Высота [латекс] ч [/ латекс] — это расстояние между основаниями.
Формула площади трапеции:
[латекс] {\ text {Area}} _ {\ text {trapezoid}} = \ frac {1} {2} h \ left (b + B \ right) [/ latex]
Разделение трапеции на два треугольника может помочь нам понять формулу.Площадь трапеции — это сумма площадей двух треугольников. См. Изображение ниже.
Разделение трапеции на два треугольника может помочь вам понять формулу ее площади.
Высота трапеции — это также высота каждого из двух треугольников. См. Изображение ниже.
Формула площади трапеции
Если раздадим, то получим,
Свойства трапеций
- У трапеции четыре стороны.Видеть .

- Две его стороны параллельны, а две — нет.
- Площадь [латекс] A [/ latex] трапеции составляет [латекс] \ text {A} = \ frac {1} {2} h \ left (b + B \ right) [/ latex].
пример
Найдите площадь трапеции, высота которой составляет [латекс] 6 [/ латекс] дюймов, а основания — [латекс] 14 [/ латекс] и [латекс] 11 [/ латекс] дюймов.
Решение
| Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите , что вы ищете. | площадь трапеции |
| Шаг 3. Имя. Выберите переменную для ее представления. | Пусть [латекс] A = \ text {область} [/ latex] |
| Шаг 4. Перевести. Напишите соответствующую формулу. Запасной. | |
Шаг 5. Решите уравнение. Решите уравнение. | [латекс] A = \ frac {1} {2} \ cdot 6 (25) [/ латекс] [латекс] A = 3 (25) [/ латекс] [латекс] A = 75 [/ латекс] квадратных дюймов |
| Шаг 6. Проверить: Разумный ли этот ответ? |
Если мы нарисуем прямоугольник вокруг трапеции с таким же большим основанием [latex] B [/ latex] и высотой [latex] h [/ latex], его площадь должна быть больше, чем у трапеции.
Если мы нарисуем прямоугольник внутри трапеции с таким же маленьким основанием [латекс] b [/ латекс] и высотой [латекс] h [/ латекс], его площадь должна быть меньше, чем у трапеции.
Площадь большего прямоугольника составляет [латекс] 84 [/ латекс] квадратных дюймов, а площадь меньшего прямоугольника составляет [латекс] 66 [/ латекс] квадратных дюймов.Таким образом, имеет смысл, что площадь трапеции находится между [латексом] 84 [/ латексом] и [латексом] 66 [/ латексом] квадратных дюймов
Шаг 7. Ответьте на вопрос. Площадь трапеции [латекс] 75 [/ латекс] квадратных дюймов.
Ответьте на вопрос. Площадь трапеции [латекс] 75 [/ латекс] квадратных дюймов.
пример
Найдите площадь трапеции, высота которой составляет [латекс] 5 [/ латекс] футов, а основания — [латекс] 10,3 [/ латекс] и [латекс] 13,7 [/ латекс] футов.
Показать решение
Решение
| Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите , что вы ищете. | площадь трапеции |
| Шаг 3. Имя. Выберите переменную для ее представления. | Пусть А = площадь |
| Шаг 4. Перевести. Напишите соответствующую формулу. Запасной. | |
| Шаг 5. Решите уравнение. | [латекс] A = \ frac {1} {2} \ cdot 5 (24) [/ латекс] [латекс] A = 12 (5) [/ латекс] [латекс] A = 60 [/ латекс] квадратных футов |
| Шаг 6. Проверить: Разумный ли этот ответ? Площадь трапеции должна быть меньше площади прямоугольника с основанием [латекс] 13,7 [/ латекс] и высотой [латекс] 5 [/ латекс], но больше площади прямоугольника с основанием [латекс] 10,3 [/ латекс] и высота [латекс] 5 [/ латекс]. | |
| Шаг 7. Ответьте на вопрос. | Площадь трапеции [латекс] 60 [латекс] квадратных футов. |
пример
У Винни есть сад в форме трапеции. Трапеция имеет высоту [латекс] 3,4 [/ латекса] ярда, а основание — [латекс] 8,2 [/ латекс] и [латекс] 5,6 [/ латекс] ярда. Сколько квадратных ярдов будет доступно для посадки?
Показать решение
Решение
| Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите , что вы ищете. | площадь трапеции |
| Шаг 3. Имя. Выберите переменную для ее представления. | Пусть А = площадь |
| Шаг 4. Перевести. Напишите соответствующую формулу. Запасной. | |
| Шаг 5. Решите уравнение. | [латекс] A = \ frac {1} {2} (3,4) (13,8) [/ латекс] [латекс] A = 23,46 [/ латекс] квадратных ярдов. |
| Шаг 6. Проверить: Разумный ли этот ответ? Да. Площадь трапеции меньше площади прямоугольника с основанием [латекс] 8,2 [/ латекс] ярд и высотой [латекс] 3,4 [/ латекс] ярд, но больше площади прямоугольника с основанием [латекс] ] 5.6 [/ латекс] ярд и высота [латекс] 3.4 [/ латекс] ярд. | |
| Шаг 7. Ответьте на вопрос. | У Винни есть [латексные] 23,46 [/ латексные] квадратных ярда, на которых он может сажать растения. |
Геометрия
— Площадь трапеции из двух оснований и диагоналей
Первое решение: Пусть наша трапеция будет $ ABCD $, как на диаграмме, предоставленной pedja. Пусть диагонали пересекаются в точке $ O $.
Обратите внимание, что $ \ треугольник OAB $ и $ \ треугольник OCD $ похожи на . Действительно, мы знаем коэффициент масштабирования.Так как $ AB = 20 $ и $ CD = 7 $, стороны $ \ треугольника OCD $ умножены на $ \ frac {7} {20} $ соответствующих сторон $ \ треугольника OAB $.
Это очень полезно. У нас есть $ AC = 13 = AO + \ frac {7} {20} AO $. Следует, что
$$ AO = \ frac {(20) (13)} {27}, \ quad \ text {и аналогично} \ quad BO = \ frac {(20) (5 \ sqrt {10})} {27}.
$
Если мы хотим использовать обычную формулу для площади трапеции, все, что нам нужно, это высота трапеции. Это на $ 1 + \ frac {7} {20} $, умноженное на высоту $ \ треугольника OAB $.
Высота $ \ треугольника OAB $ может быть найдена разными способами.Например, мы можем использовать формулу Герона, чтобы найти площадь $ \ треугольника OAB $, поскольку нам известны все три стороны. Или мы можем использовать тригонометрию. Закон косинуса можно использовать для вычисления косинуса $ \ angle OAB $. Затем мы можем найти точное (или приблизительное) выражение для синуса этого угла. Отсюда мы можем найти высоту $ \ треугольника OAB $.
Второе решение: Это вариант первого решения, в котором используется несколько больше геометрии. Пусть $ \ alpha $ — площадь $ \ треугольника OAB $.
Сначала мы вычисляем площадь $ \ треугольник COB $. Треугольники $ OAB $ и $ COB $ можно рассматривать как имеющие основания $ OA $ и $ CO $ соответственно, а также и ту же высоту . 2 \ alpha $.2 \ alpha. $$
Милая! Наконец, по аргументу подобия первого решения мы знаем стороны $ \ треугольника OAB $, поэтому мы можем найти $ \ alpha $, используя формулу Герона.
Как определить высоту трапеции — урок математики [видео 2021 года]
Геометрический пример
Давайте посмотрим, как мы можем вычислить высоту трапеции на примере:
Шаг 1:
Мы начнем с рисования линии от вершины наверху трапеции до основания, чтобы создать прямоугольный треугольник или треугольник с углом 90 градусов.
Шаг 2:
Затем мы вычислим основание только что нарисованного треугольника. Этот пример представляет собой равнобедренный треугольник , потому что у него две равные стороны. В этом примере основание трапеции (14 дюймов) равно вершине трапеции (6 дюймов) плюс два основания прямоугольных треугольников ( x ).
В алгебраических терминах 14 = 6 + 2 x .
Шаг 3:
Теперь мы воспользуемся теоремой Пифагора, чтобы вычислить высоту или один катет прямоугольного треугольника.
Шаг 4:
Наконец, мы отформатируем наш ответ в соответствии с исходной задачей. Высота этой трапеции — 3 дюйма.
Подсказка
Важно помнить, что вы можете найти высоту трапеции, только если вы можете точно вычислить основание прямоугольного треугольника, в котором один из катетов является гипотенузой. Это возможно для равнобедренных трапеций и трапеций с прямым углом.Необходимо внимательно рассмотреть неправильные трапеции, чтобы определить, можно ли рассчитать основание прямоугольного треугольника, который будет сформирован.
Пример из реального мира
Прачечная Мэри имеет форму трапеции, показанной на этом изображении.
Она решила повесить бельевую веревку вдоль угловой ножки комнаты, но не знает длины стены. Давайте поможем ей, определив длину наклонной стены.
Шаг 1:
Начнем с рисования прямой линии из правого угла верхней стены, чтобы создать прямоугольный треугольник с наклонной стеной.
Шаг 2:
Чтобы найти основание треугольника, мы вычтем 26–20 = 6. Мы не будем делить на два, потому что в этом примере есть только одна угловая часть.
Шаг 3:
Мы уже знаем высоту в этом примере (10 футов), но мы можем использовать теорему Пифагора, чтобы найти наклонную ногу с имеющейся у нас информацией.
Шаг 4:
Длина наклонной стены составляет 11,66 футов.
Как найти площадь трапеции
Овладейте семью столпами успеха в школе
Повысьте свои оценки и снизьте уровень стресса
Common Core Standard 7.G.6
Площадь трапеции с диагоналями
Видео отвечает на эти вопросы
Зачем использовать формулу 1 / 2h (b1 + b2) для определения площади трапеции?
Какова площадь трапеции с высотой 10 единиц и сторонами 12 и 16 единиц
Какова площадь трапеции со сторонами 4,5 и 9 единиц?
Чтобы решить этот треугольник, вам нужно найти высоту трапеции.
Найдите площадь трапеции ABCD с диагоналями 6 и 8 единиц.
Используйте формулу d1 * d2 / 2
6 * 8/2 = 48/2 = 24 единицы в квадрате
Внимание! Площадь трапеции можно определить по диагоналям, но диагонали должны пересекаться и образуют перпендикулярные линии.
Это создает четыре прямых угла, и вы можете использовать формулу:
Площадь трапеции
Шаг 2. Чтобы найти длину длинной ножки (которая будет равна высоте трапеции), примените правила
для треугольника 30 60 90 , поэтому длинная ножка (высота) равна короткой ножке x √3
- короткое плечо составляет 1/2 гипотенузы
- Гипотенуза всегда противоположна прямому углу, поэтому равняется 4 единицам
- Короткое плечо равно 1/2 x 4 = 2 единицы
- короткая ножка √3,
- Вставьте короткую ножку 2√3 = высота
Найдите площадь трапеции с основаниями 5 и 9 и длина ножки — 4 единицы.Угловая мера составляет 60 °.
Шаг 1 . Пожалуйста, не делайте ошибку, используя длину стороны как свой рост.
Высота этой трапеции образует треугольник 30 60 90. Высота становится длинной ногой треугольника 30 60 90.
Шаг 3. Подставьте высоту в формулу площади трапеции 1 / 2h (b1 + b2)
Шаг 4. ½ * 2√3 (14) = ½ 28√3
Шаг 5. 14√3 = квадрат единиц равняется площади трапеции
Найдите площадь трапеции высотой 10 единиц, основанием 12 единиц и основанием 16 единиц.
Шаг 1 . Вставьте 12 и 16 для b1 и b2 и 10 для высоты.
½ 10 (12 + 16)
Шаг 2. ½ (10 * 28)
Шаг 3. ½ (280) = 140 единиц
Трапеция — это четырехсторонний многоугольник с одна пара параллельных сторон.Площадь — это количество квадратных единиц внутри трапеции. Площадь — это двумерная мера, поэтому она всегда возведена в квадрат. Высота трапеции перпендикулярна двум параллельным основаниям. Одна из распространенных ошибок, которые допускаются при вычислении площади трапеции, — это использование длины стороны в качестве высоты. Опять же, высота измеряется как линия, перпендикулярная двум параллельным основаниям.
Площадь трапеции можно найти по формуле 1 / 2h (b1 + b2)
Формула для площади трапеции равна 1 / 2h (b1 + b2)
h = высота, b1 = основание, b2 = основание
| 1D линия, круговая дуга, парабола, спираль, кривая Коха 2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, девятиугольник, десятиугольник, шестиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: 90 363 Круглые формы: 3D архимедова Solids: Каталонских Сухой остаток: Твердые тела Джонсона: Другие многогранники: 4D | Anzeige Расчеты на трапеции.Трапеция (или трапеция) — это четырехугольник с двумя параллельными сторонами. Введите три длины стороны и один угол между двумя из этих сторон. Выберите количество десятичных знаков и нажмите Рассчитать. Пожалуйста, введите углы в градусах, здесь вы можете конвертировать угловые единицы. Здесь можно рассчитать только те трапеции, где c не перекрывает a (g1, g2 ≥ 0; α, β ≤ 90 °). Форма трапеции: Формулы: Длина стороны, высота, диагонали и периметр указаны в одинаковых единицах измерения (например,грамм. метр), площадь имеет эту единицу в квадрате (например, квадратный метр). Anzeige
Доля: © Jumk.de Веб-проекты Anzeige |
Площадь трапеции
Площадь трапеции определяется как сумма длины ее основания и вершины, умноженная на ее высоту.
| Выражение | Описание |
|---|---|
| Площадь трапеции. | |
| Длина верха трапеции. | |
| Длина основания трапеции. | |
| Высота трапеции |
Площадь трапеции определяется ее высотой, умноженной на сумму ее верхней и нижней частей, разделенных на два.
Этот пример демонстрирует, как найти площадь трапеции с вершиной 3, основанием 5 и высотой 2.
Начните с настройки формулы.
Подставьте значения для верха, основания и высоты в формулу.
Упростите, выполнив умножение и деление или используя другой способ.
Площадь трапеции равна квадрату единиц.
Этот пример демонстрирует, как найти площадь трапеции, вершины 5, основания 8, высоты 4.
Начните с настройки формулы.
Подставьте значения для верха, основания и высоты в формулу.
Упростим числитель и знаменатель.
Площадь трапеции равна квадрату единиц.
Этот пример демонстрирует, как найти площадь трапеции, вершины 4, основания 7, высота 3.
Начните с настройки формулы.
Подставьте значения для верха, основания и высоты в формулу.
