Урок 4. равномерное движение точки по окружности — Физика — 10 класс

Физика, 10 класс

Урок 04.Равномерное движение точки по окружности

Перечень вопросов, рассматриваемых на уроке:

1. Равномерное движение точки по окружности и его характеристики.
2. Центростремительное ускорение.

Глоссарий по теме

Криволинейное движение – это движение по дугам окружностей разных радиусов.

Ускорение – это векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло, при ∆t → 0

Равномерное движение точки по окружности — движение точки с постоянной по модулю скоростью (ν = const) по траектории, представляющей собой окружность.

Ключевые слова

Криволинейное движение; движение по окружности; скорость; радиус кривизны; изменение скорости; центростремительное ускорение.

Основная и дополнительная литература по теме урока:

Мякишев Г. Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56

Марон Е.А., Марон А.Е. Сборник качественных задач по физике. М., Просвещение, 2006

Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22

Открытые электронные ресурсы:

http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm

Теоретический материал для самостоятельного изучения

1. Мы уже знакомы с равноускоренным движением. Как же меняются скорость и ускорение при криволинейном движении? Сегодня рассмотрим равномерное движение по окружности, узнаем, что такое центростремительное ускорение.

Если траектория движения тела прямая линия, то движение прямолинейное; если траектория кривая линия – криволинейное движение. Напомним, что траектория – это линия, вдоль которой двигалось тело.

При изучении равноускоренного движения мы заметили, что в некоторых случаях тело движется по прямой, например свободное падение тел, а в некоторых по кривой – тело, брошенное под углом к горизонту.

Рассмотрим движение тела, брошенного под углом к горизонту. Траекторией является парабола.

Возьмем разные точки на линии и нарисуем векторы скорости . Вектор скорости направлен по касательной, а ускорение свободного падения направлен вниз.

Векторы и не лежат на одной прямой, угол между ними не равен нулю.

Это естественно, так как, если ускорение образует угол со скоростью, то изменение скорости направлено не так, как скорость. Это приводит к изменению направления скорости. Изменение скорости направлено как ускорение. Скорость через некоторый промежуток времени образует некоторый угол с Итак, сформулируем первый вывод: если угол между векторами скорости и ускорения не равен нулю, то движение будет криволинейным.

2.Может ли быть движение одновременно равномерным и криволинейным? Да, например, движение по окружности.

Равномерное движение точки по окружности — это движение точки с постоянной по модулю скоростью (v = const) по траектории, представляющей собой окружность. Но, скорость – это векторная величина, а для векторной величины одинаково важны и модуль, и направление. Т.к. при движении по окружности скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Если есть изменение скорости (точнее её направления), значит, есть ускорение

Сформулируем второй важный вывод: любое криволинейное движение является движением с ускорением, потому что меняется направление вектора скорости.

Решим задачу: найдем ускорение тела, равномерно движущегося по окружности.

Рассмотрим равномерное движение тела по окружности с центром в точке О. В какой-то момент времени, скорость тела в точке А была_.

Модули скоростей равны:

но вектора скоростей не равны.

Поэтому построим вектор для тела, движущегося по окружности. Перенесем вектор в начало вектораи найдем разность векторов.

направлен в сторону.

Вспомним, что векторнаправлен по касательной_, а касательная перпендикулярна радиусу окружности. Проведем радиусы к обеим точкам и обозначим угол между ними через ?.

Что можно сказать об угле между векторами ? Он равен малому углу, как углы с взаимно перпендикулярными сторонами.

Рассмотрим равнобедренный треугольник со сторонами , . Углы у основания равны.

Если угол φ стремится к нулю, то углы у основания совпадут и станут равными 90⁰

Вектор будет перпендикулярен вектору в пределе_, а значит вектор ускорения тоже перпендикулярен т.е направлен по радиусу к центру окружности. Поэтому часто его называют центростремительным ускорением

Теперь следующая задача: как найти модуль вектора ускорения. Давайте рассмотрим два треугольника: треугольник, образованный векторами и треугольник, образованный радиусами и хордой. У этих треугольников углы при вершинах равны, они равнобедренные. Треугольники подобны и, следовательно, выполняются соотношения подобия.

Промежуток времени мал, поэтому очень мал и угол при вершине, в пределе он стремится к нулю. Тогда можно сказать, что длина хорды s равна длине дуги АВ при

Длина дуги АВ это путь, пройденный точкой от А до В,

тогда запишем:

Умножим наи получим:

В левой части мы получили отношение изменения скорости за некоторый промежуток времени к этому промежутку времени т.е. ускорение:

Равномерное движение точки по окружности является движением с переменным ускорением и переменной скоростью. Модули скорости и ускорения остаются постоянными

1. Криволинейное движение — это движение по дугам окружностей разных радиусов.

А если меняется радиус, то меняется и центростремительное ускорение. Чем меньше радиус, тем больше ускорение при одинаковой скорости.

Всегда при равномерном криволинейном движении вектор ускорения перпендикулярен вектору скорости, поэтому центростремительное ускорение иногда называют нормальным ускорением, от слова нормаль, т.е. перпендикуляр.

Основные выводы:

— движение криволинейное, так как траекторией является окружность;

— движение равномерное, так как модуль скорости не меняется;

— вектор скорости направлен по касательной к окружности;

-вектор ускорения направлен к центру окружности;

— модуль центростремительного ускорения равен:

Примеры и разбор решения заданий

1. Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?

При движении по окружности линейная скорость и центростремительное ускорение связаны соотношением

где R = 50 м; υ= км/ч = 10 м/с.

Тогда a_c = (10 м/с)² / 50 м = 2 м/с².

Ответ: 2 м/с²

2. Две материальные точки движутся по окружностям радиусами R₁ = 10 см и R₂ = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?

Дано:

R₁ =10см = 0,10 м

R₂ = 30см = 0,30 м

Найти —

Задано два объекта:

1) материальная точка, которая движется по окружности R₁;

2) материальная точка, которая движется по окружности R₂.

При движении по окружности центростремительное ускорение и линейная скорость связаны соотношением

Для тела 1 уравнение (1) примет вид:

для тела 2:

Тогда

Центростремительное ускорение тела (2) меньше ускорения тела (1) в 3 раза.

Все формулы по физике за 7-9 класс

Определение 1

Физика является естественной наукой, которая изучает общие и фундаментальные закономерности строения и эволюции материального мира.

Важность физики в современном мире огромна. Ее новые идеи и достижения приводят к развитию других наук и новых научных открытий, которые, в свою очередь, используются в технологиях и промышленности. Например, открытия в области термодинамики делают возможным строительство автомобиля, а также развитие радиоэлектроники привело к появлению компьютеров.

Несмотря на невероятное количество накопленных знаний о мире, человеческое понимание процессов и явлений, постоянно меняется и развивается, новые исследования приводят к возникновению новых и нерешенных вопросов, которые требуют новых объяснений и теорий. В этом смысле, физика находится в непрерывном процессе развития и до сих пор далека от возможности объяснить все природные явления и процессы. 3$]

Все формулы за 8 класс

Количество теплоты при нагревании (охлаждении)

$Q=cm(t_2-t_1)$

$Q$ – количество теплоты [Дж], $m$ – масса [кг], $t_1$- начальная температура, $t_2$ — конечная температура, $c$ — удельная теплоемкость

Количество теплоты при сгорании топлива

$Q=q\cdot m$

$Q$ – количество теплоты [Дж], $m$ – масса [кг], $q$ – удельная теплота сгорания топлива [Дж /кг]

Количество теплоты плавления (кристаллизации)

$Q=\lambda \cdot m$

$Q$ – количество теплоты [Дж], $m$ – масса [кг], $\lambda$ – удельная теплота плавления [Дж/кг]

КПД теплового двигателя

$КПД=\frac{A_n\cdot 100%}{Q_1}$

КПД – коэффициент полезного действия [%], $А_n$ – полезная работа [Дж], $Q_1$ – количество теплоты от нагревателя [Дж]

Сила тока

$I=\frac{q}{t}$

$I$ – сила тока [А], $q$ – электрический заряд [Кл], $t$ – время [с]

Электрическое напряжение

$U=\frac{A}{q}$

$U$ – напряжение [В], $A$ – работа [Дж], $q$ – электрический заряд [Кл]

Закон Ома для участка цепи

$I=\frac{U}{R}$

$I$ – сила тока [А], $U$ – напряжение [В], $R$ – сопротивление [Ом]

Последовательное соединение проводников

$I=I_1=I_2$

$U=U_1+U_2$

$R=R_1+R_2$

Параллельное соединение проводников

$U=U_1+U_2$

$I=I_1+I_2$

$\frac{1}{R}=\frac{1}{R_1} +\frac{1}{R_2}$

Мощность электрического тока

$P=U\cdot I$

$P$ – мощность [Вт], $U$ – напряжение [В], $I$ – сила тока [А]

Закон преломления света

$n=sin ⁡α/sin⁡ γ $

Все формулы за 9 класс

Проекция вектора перемещения

$S_x=x-x_0$

$S_y=y-y_0$

Скорость равномерного движения

$^\to_{v}= \frac{^\to_{S}}{t}$

Уравнение движения (зависимость координаты от времени) при равномерном движении

$x=x_0+v_x t$

Движение тела по окружности

$a=\frac{V^2}{R}$

Закон всемирного тяготения

$F=\frac{G (m_1 m_2)}{r^2} $

Импульс тела

$^\to_{p}=mv$

Связь между периодом и частотою колебаний

$T=\frac{1}{V}$

Скорость волны

$v=\frac{\lambda}{T}$

Электрическая ёмкость конденсатора

$C=\frac{q}{U}$

Энергия связи (формула Эйнштейна)

$ΔE=\triangle mc^2$

Физика 10 класс.

Законы, правила, формулы

Свойства паров, жидкостей и твердых тел
• Давление насыщенного пара
  Давление насыщенного пара (p₀) не зависит от объёма, а зависит от температуры (T) и концентрации молекул пара (n)
  ,
  где k – постоянная Больцмана
  СИ: Па
• Относительная влажность воздуха
  Относительной влажностью воздуха (φ) называют отношение парциального давления (р) водяного пара, содержащегося в воздухе при данной температуре, к давлению (р₀) насыщенного пара при той же температуре, выраженной в процентах.
  %
  СИ: %
• Абсолютная влажность воздуха
  Абсолютная влажность воздуха (ρ):
  1) давление, оказываемое водяным паром при данных условиях: ;
  2) это масса (m) водяного пара в единице объёма (V = 1 м³) воздуха: ;
  СИ: Па, кг/м³
• Коэффициент поверхностного натяжения жидкости
  Коэффициент поверхностного натяжения (σ) жидкости равен отношению модуля силы поверхностного натяжения (F) к длине (l) границы поверхности натяжения, на которую действует эта сила.

  СИ: Н/м

• Высота поднятия жидкости в капилляре
  Высота (h) поднятия жидкости в капиллярной трубке (капилляре) прямо пропорциональна коэффициенту поверхностного натяжения (σ) и обратно пропорциональна плотности жидкости (ρ) и радиусу (r) капиллярной трубки.
• Капиллярное давление
  Капиллярное давление (p) жидкости в капилляре пропорционально коэффициенту поверхностного натяжения (σ) и обратно пропорционально радиусу капиллярной трубки (r).

  СИ: Па

• Абсолютная деформация (удлинение — сжатие)
  Абсолютная деформация (Δl) — разность линейных размеров (l₀ и l) твердого тела до и после приложения к нему силы.

  СИ: мм

• Относительная деформация (удлинение — сжатие)
  Относительная деформация (ε) — отношение абсолютной деформации (Δl) к начальной длине твердого тела (l₀).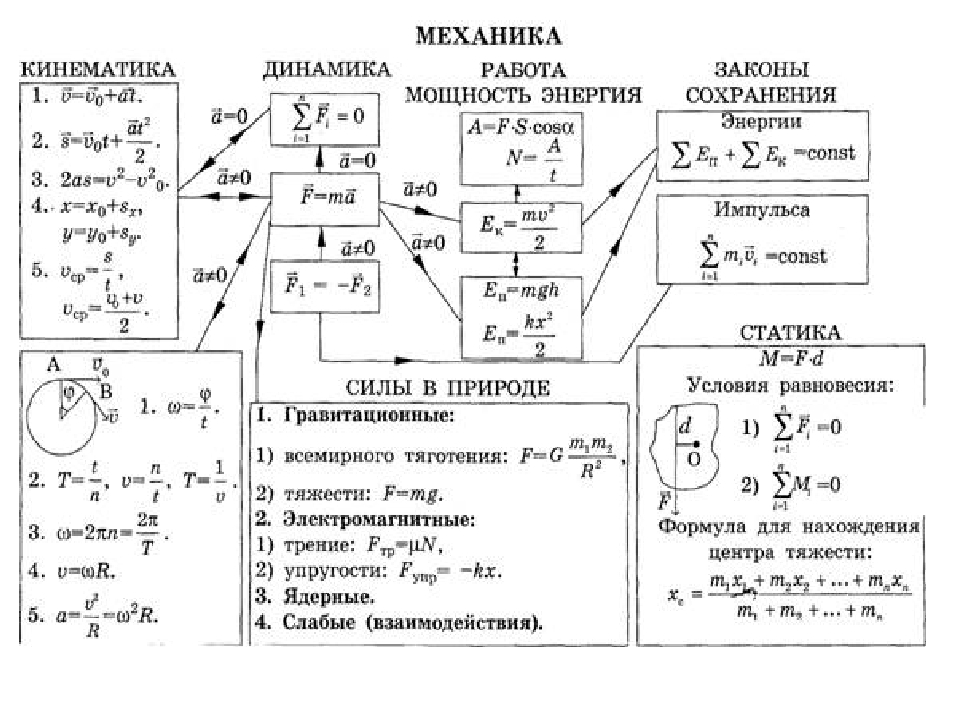
• Механическое напряжение
  Механическое напряжение (σ) — это отношение модуля силы упругости (F) к площади поперечного сечения (S) тела.

  СИ: Па

• Закон Гука для твердого тела
  При малых деформациях напряжение (σ) прямо пропорционально относительному удлинению (ε)

  СИ: Па

• Модуль упругости (модуль Юнга)
  Модуль продольной упругости (Е) — постоянная для данного материала величина, численно равная механическому напряжению (σ), которое необходимо создать в теле, чтобы его относительное удлинение (ε) достигло единицы

  СИ: Па

• Коэффициент запаса прочности
  Коэффициент запаса прочности (n) — это величина, показывающая во сколько раз напряжение (σ_пч), соответствующее пределу прочности, превышает напряжение (σ_доп), допустимое для твердого тела в данных условиях нагружения.
  n=σ_пч/σ_доп

Основы термодинамики
• Внутренняя энергия одноатомного газа
  Внутренняя энергия (U) идеального одноатомного газа прямо пропорциональна количеству вещества (m/М) и его абсолютной температуре (T)

  СИ: Дж

• Внутренняя энергия многоатомного газа
  Внутренняя энергия (U) идеального многоатомного газа прямо пропорциональна его абсолютной температуре (Т) и определяется числом степеней свободы (i) идеального газа.
  ,
  где i=3 – одноатомного;
  i=5 – двухатомных;
  i=6 – трехатомных и более.
  СИ: Дж
• Работа внешних сил над газом
  Работа (А) внешних сил, изменяющих объём газа при изобарном процессе, равна произведению давления (p) на изменение объёма (ΔV) газа.

  СИ: Дж

• Первый закон термодинамики
  1) Изменение внутренней энергии (ΔU) системы при переходе её из одного состояния в другое равно сумме работы внешних сил (А) и количества теплоты (Q), переданного системе: ;
  2) Количество теплоты (Q), переданное системе, идет на изменение её внутренней энергии (ΔU) и на совершение системой работы (А’) над внешними телами: .
  СИ: Дж
• Применение первого закона термодинамики
  1) При изохорном процессе изменение внутренней энергии (ΔU) равно количеству переданной теплоты (Q): , (при V=const)
  2) При изотермическом процессе все переданное газу количество теплоты (Q) идет на совершение работы (А’): , (при T=const)
  3) При изобарном процессе передаваемое газу количество теплоты (Q) идет на изменение его внутренней энергии (ΔU) и на совершение работы (А’): , (при p=const)
  4) При адиабатном процессе изменение внутренней энергии (ΔU) происходит только за счет совершение работы (А): , (при Q=0)
  СИ: Дж
• Работа теплового двигателя
  Работа (А’), совершаемая тепловым двигателем, равна разности количества теплоты (Q₁), полученного от нагревателя, и количества теплоты (Q₂), отданного холодильнику

  СИ: Дж

• КПД теплового двигателя
  Коэффициентом (η) полезного действия (КПД) теплового двигателя называют отношение работы (А’), совершаемой двигателем, к количеству теплоты (Q₁), полученному от нагревателя.
  ;

  СИ: Дж

• КПД идеальной Тепловой машины
  Реальная тепловая машина, работающая с нагревателем, имеющим температуру (T₁), и холодильником с температурой (Т₂), не может иметь КПД, превышающий КПД (7 тах) идеальной тепловой машины.

Электростатика
• Закон сохранения заряда
  В замкнутой системе алгебраическая сумма зарядов (q₁, q₂,…, q_n,) всех частиц остается неизменной.

  СИ: Кл

• Закон Кулона
  Сила взаимодействия (F) двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей заряда (q₁ и q₂) и обратно пропорциональна квадрату расстояния между ними.
  ,
  где k=9×10⁹ (Н×м²)/Кл² — коэффициент пропорциональности.
  СИ: Н
• Заряд электрона
  Заряд электрона (е) — минимальный, механически неделимый, отрицательный заряд, существующий в природе.
  e=1,6×10^-19
  СИ: Кл
• Напряженность электрического поля
  Напряженность электрическою поля () равна отношению силы (), с которой поле действует на точечный заряд, к этому заряду (q).

  СИ: Н/Кл; В/м

• Напряженность поля точечного заряда (в вакууме)
  Модуль напряженности (Е) поля точечного заряда (q₀) на расстоянии (r) от него равен: ,
  где k=9×10⁹ (Н×м²)/Кл² — коэффициент пропорциональности.
  СИ: Н/Кл
• Принцип суперпозиции полей
  Если в данной точке пространства заряженные частицы создают электрические поля, напряженности которых ( ), то результирующая напряженность поля в этой точке равна геометрической (векторной) сумме напряженностей.

  СИ: Н/Кл

• Диэлектрическая проницаемость
  Диэлектрическая проницаемость (ε) — это физическая величина, показывающая, во сколько раз модуль напряженности (Е) электрического поля внутри однородного диэлектрика меньше модуля напряженности (Е₀) поля в вакууме.
• Работа при перемещении заряда в однородном электростатическом поле
  Работа (А) при перемещении заряда (q) в однородном электростатическом поле напряженностью (Е) не зависит от формы траектории движения заряда, а определяется величиной перемещения (Δd=d₂-d₁) заряда вдоль силовых линий поля.

  СИ: Дж

• Потенциальная энергия заряда
  Потенциальная энергия (W_p) заряда в однородном электростатическом поле равна произведению величины заряда (q) на напряженность (Е) поля и расстояние (d) от заряда до источника поля.

  СИ: Дж

• Потенциал электростатического поля
  Потенциал (φ) данной точки электростатического поля численно равен:
  1) потенциальной энергии (W_p) единичного заряда (q) в данной точке: ;
  2) произведению напряженности (Е) поля на расстояние (d) от заряда до источника поля:
  СИ: В
• Напряжение (разность потенциалов)
  Напряжение (U) или разность потенциалов (φ₁-φ₂) между двумя точками равна отношению работы поля (А) при перемещении заряда из начальной точки в конечную к этому заряду (q).

  СИ: В

• Связь между напряженностью и напряжением
  Чем меньше меняется потенциал () на расстоянии (Δd), тем меньше напряженность (Е) электростатического поля.

  СИ: В/м

• Электроёмкость
  Электроёмкость (C) двух проводников — это отношение заряда (q) одного из проводников к разности потенциалов (U) между этим проводников и соседним.

  СИ: Ф

• Электроёмкость конденсатора
  Электроёмкость плоского конденсатора (C) прямо пропорциональна площади пластин (S), диэлектрической проницаемости (ε) размещенного между ними диэлектрика, и обратно пропорциональна расстоянию между пластинами (d).
  ,
  ε₀=8,85×10^-12 Кл²/(Н×м²) – электрическая постоянная
  СИ: Ф
• Энергия заряженного конденсатора
  Энергия (W) заряженного конденсатора равна:
  1) половине произведения заряда (q) конденсатора на разность потенциалов (U) между его обкладками: ;
  2) отношению квадрата заряда (q) конденсатора к удвоенной его ёмкости (С): ;
  3) половине произведения ёмкости конденсатора (C) на квадрат разности потенциалов (U) между его обкладками: .
  СИ: Дж
• Электроёмкость шара
  Электроёмкость шара радиусом R, помещенного в диэлектрическую среду с проницаемостью ε, равна:
  СИ: Ф
• Параллельное соединение конденсаторов
  Общая ёмкость (C_общ) конденсаторов, параллельно соединенных на участке электрической цепи, равна сумме ёмкостей (C₁, C₂, C₃,…) отдельных конденсаторов.
  C_общ=C₁+C₂+C₃+…+ C_n
  СИ: Ф
• Последовательное соединение конденсаторов
  Величина, обратная общей ёмкости (C_общ) конденсаторов, последовательно соединенных на участке электрической цепи, равна сумме величин, обратных ёмкостям (C₁, C₂, C₃,…) отдельных конденсаторов.
  1/C_общ= 1/C₁+1/C₂+1/C₃+…+ 1/C_n
  СИ: Ф

Законы постоянного тока
• Сила тока
  Сила тока (I) равна:
  1) отношению заряда (Δq), переносимого через поперечное сечение проводника за интервал времени (Δt), к этому интервалу времени;
  2) произведению концентрации (n) заряженных частиц в проводнике, заряду каждой частицы (q₀), скорости (v) движения заряженных частиц в проводнике и площади поперечного сечения (S) проводника.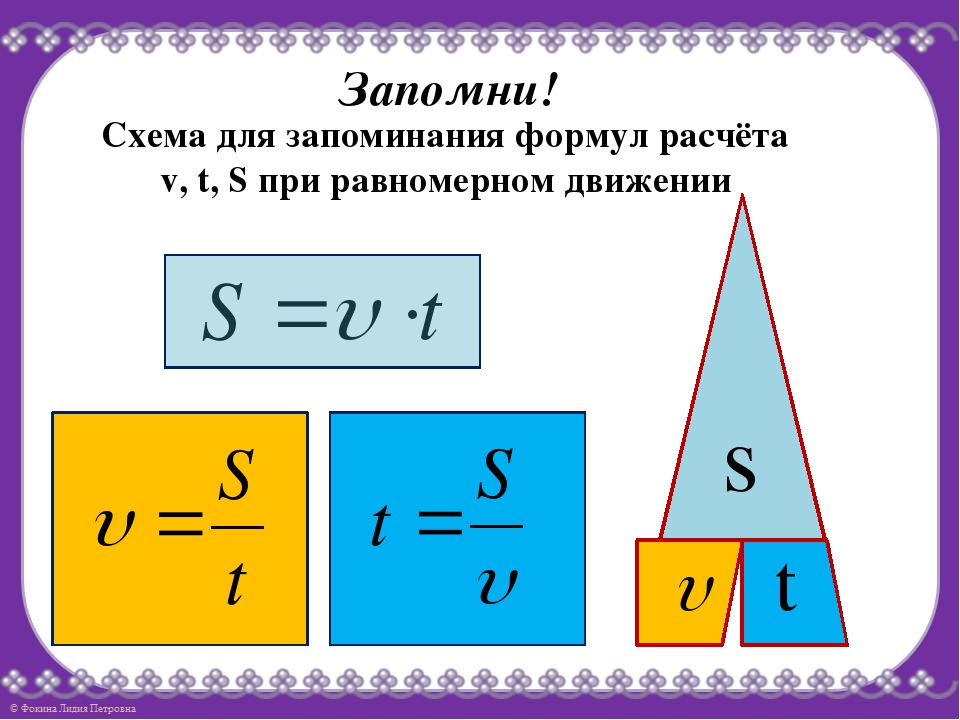
  ,

  СИ: A

• Закон Ома для участка цепи
  Сила тока (I) прямо пропорциональна приложенному напряжению (U) и обратно пропорциональна сопротивлению проводника (R)

  СИ: A

• Сопротивление проводника
  Сопротивление (R) проводника зависит от материала проводника (удельного сопротивления ρ) и его геометрических размеров (длины l и площади поперечного сечения S).

  СИ: Ом

• Удельное сопротивление проводника
  Удельное сопротивление (ρ) проводника — величина, численно равная сопротивлению проводника длиной (l) один метр и площадью поперечного сечения (S) один квадратный метр.

  СИ: Ом×м

• Работа постоянного тока
  Работа (А) постоянного тока на участке цепи:
  1) равна произведению силы тока (I), напряжения (U) и времени (t), в течение которого совершалась работа: ;
  2) равна произведению квадрата силы тока (I), сопротивления участка цепи (R) и времени (t): ;
  3) пропорциональна квадрату напряжения (U), времени (t) и обратно пропорционально сопротивлению (R) участка цепи: .
  СИ: Дж
• Мощность тока
  Мощность (Р) постоянного тока на участке цепи равна:
  1) работе (А) тока, выполняемой за единицу времени (t): ;
  2) произведению напряжения (U) и силы тока (I): ;
  3) произведению квадрата силы тока (I) и сопротивления (R): ;
  4) отношению квадрата напряжения (U) к сопротивлению (R):
  СИ: Вт
• Электродвижущая сила (ЭДС)
  Электродвижущая сила в замкнутом контуре (ξ) представляет собой отношение работы сторонних сил (А_ст) при перемещении заряда внутри источника тока к заряду (q).
  ξ=А_ст/q
  СИ: В
• Закон Ома для полной цепи
  Сила тока (I) в полной цепи равна отношению ЭДС(ξ) цепи к её полному сопротивлению (внутреннему сопротивлению r и внешнему R).

  СИ: A

• Последовательное соединение источников тока
  Если цепь содержит несколько последовательно соединенных элементов с ЭДС (ξ₁, ξ₂, ξ₃,…), то полная ЭДС цепи (ξ) равна алгебраической сумме ЭДС отдельных элементов.
  ξ=ξ₁+ξ₂+ξ₃+…
  СИ: В
• Параллельное соединение источников тока
  Если цепь содержит несколько параллельно соединенных элементов с равными ЭДС (ξ₁=ξ₂=ξ₃=…), то полная ЭДС цепи (ξ) равна ЭДС каждого элемента.
  ξ=ξ₁=ξ₂=ξ₃=…
  СИ: В

Поделитесь с друзьями:

Все формулы по физике за 7-9 класс

Как сдать ОГЭ по физике — Учёба.ру

Чем раньше начнешь готовиться к ЕГЭ,

тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно

Федор Григорьев,

к.х. н., в.н.с. МГУ им. М.В. Ломоносова, доцент НИЯУ МИФИ,

эксперт ОГЭ по физике, учитель физики Предуниверситария НИЯУ МИФИ

По Вашему мнению, насколько хорошо девятиклассники сейчас знают физику? Насколько сложен для них ОГЭ по физике?

Если брать курс физики обычной общеобразовательной школы, то ученики знают предмет в меньшем объеме, чем это требуется для сдачи ОГЭ на отличную оценку. На сегодняшний день типичная проблема школ состоит в том, что физика преподается нерегулярно. С другой стороны, сейчас много подготовительных курсов, которые позволяют восполнить пробелы в знаниях.

ОГЭ — это экзамен за курс средней школы. Это значит, что любой ученик, работающий на уроках, должен его сдать на положительную оценку, поэтому в работе есть простые вопросы, для ответа на которые достаточно регулярных занятий пусть даже в объеме одного часа в неделю. С другой стороны, получить максимально возможный балл довольно сложно, поскольку задания разнообразны и по форме, и по содержанию. Есть вопросы на анализ материала, где надо прочитать предложенный текст и на основе прочитанного сделать вывод. Есть вопросы на различные способы представления информации — табличные, диаграммные, гистограммные. Много вопросов на сопоставление, где необходимо сопоставить информацию из первой и второй колонок таблицы. Хотя сами задания достаточно простые, способы представления информации часто непривычны для неподготовленных учащихся. Поэтому очень важно просмотреть варианты и отработать требуемые форматы вопросов.

Расскажите, пожалуйста, про структуру экзамена и систему начисления баллов.

Всего на экзамене предлагается 26 заданий базового, повышенного и высокого уровня сложности: 22 задания в части 1 и четыре задания в части 2. В первой части большинство вопросов оцениваются в один балл, а за шесть заданий можно получить два балла. Во второй части есть вопросы на два, три и четыре балла. Максимально за работу можно набрать 40 баллов. Тройка ставится за результат от 10 баллов, четверка — от 20 баллов, пятерка — от 31 балла.

Самое «дорогое» задание экзамена (№ 23) оценивается в четыре балла. Оно связано с проведением реального эксперимента: нужно собрать экспериментальную установку и произвести измерения. Это задание вызывает сложности у ребят, поскольку в школах есть проблемы с проведением лабораторных работ. На подготовительных курсах к нему тоже, как правило, готовят только теоретически, потому что учебные центры не располагают комплектами приборов ОГЭ. Если вы претендуете на самый высокий балл за ОГЭ по физике, я бы посоветовал найти возможность поработать с реальными приборами. Сейчас нет проблем с тем, чтобы приобрести, например, амперметр или вольтметр — эти приборы в простом исполнении стоят недорого.

Реально ли получить на ОГЭ по физике максимальный результат?

В моих классах в прошлом году один учащийся сдал экзамен на максимальные 40 баллов. Многие ребята получили пятерку, она ставится за результат от 31 балла. Но следует учесть, что в Предуниверситарии МИФИ (лицей № 1511) на преподавание физики отводится шесть часов в неделю, так что оценка «5» за ОГЭ у нас должна быть нормой.

Важно отметить, что успешная сдача физики на ОГЭ совершенно на гарантирует высокий балл на ЕГЭ, а многих ребят хороший результат после 9 класса расслабляет. Ведь ЕГЭ — это совсем другой экзамен, можно сказать, профессиональный, университетского уровня.

По Вашему опыту преподавания, какие разделы физики самые сложные для школьников? И какие темы самые простые?

Самыми трудными являются вопросы, связанные с магнетизмом и электромагнитным полем, с явлениями индукции и самоиндукции. Это объективно самые сложные темы для учащихся 9 класса. Если честно, я бы исключил их из экзамена. Ведь потом это все ребята проходят в 11 классе. Для того чтобы хорошо объяснить эти темы, нужно вводить довольно сложные для учащихся 9 класса понятия, например, потока магнитного поля. Поэтому задачи на эти темы всегда вызывают определенные сложности у школьников на ОГЭ, а одно-два задания по ним на экзамене всегда присутствует.

Также часто вызывают затруднения у девятиклассников вопросы на геометрическую оптику (линзы, преломление света, глаз как оптический прибор), ядерную физику, строение атома. В условиях обычной школы эти темы находятся на задворках программы, они практически не изучаются. В сумме по всем этим разделам шесть вопросов на экзамене могут быть.

Если говорить о самых простых темах, то это скорость, движение, теплота, вопросы на размерность, например, в чем измеряется сила, давление. Или задания, где требуется определить что-то по графику. У этих вопросов высокий процент выполняемости.

Как подготовиться к ОГЭ по физике наилучшим образом?

Если на подготовку к экзамену в запасе есть год, я бы рекомендовал всю программу физики изучать по темам. Для начала скачайте кодификатор ОГЭ с сайта ФИПИ. Там все вопросы разбиты по темам: механические явления, тепловые явления, кинетические явления и т.д. Потом возьмите «Сборник задач по физике для 7-9 класса» Лукашика и порешайте задачи по темам ОГЭ. После того как этот этап будет пройден, месяца за три до экзамена, начинайте решать варианты ОГЭ за прошлый год (например, на сайте «Решу ОГЭ»), а также диагностические и демонстрационные варианты на сайте ФИПИ.

В оставшиеся до ОГЭ-2018 два месяца надо смотреть варианты, обращая внимание на вторую половину экзамена. В первой половине представлены задачи на механику, кинематику — с этим ребята хорошо справляются. А вот во второй половине сконцентрированы более сложные темы — оптика, квантовые явления, частота, звук, волны, спектры. Обратите внимание на эти вопросы, которым в школе уделяется мало внимания, и решайте по ним задачи.

На что нужно обратить внимание при подготовке к заданиям повышенного и высокого уровня сложности? Какие есть подводные камни у этого типа заданий?

Задание № 7	Это расчетная задача на механические явления. Вопрос повышенного уровня сложности. Оценивается в один балл. Здесь нужно произвести расчет в два действия, а не просто подставить имеющиеся данные в формулу.
Задание № 10	Расчетная задача на тепловые явления. В условии представлен график зависимости температуры t твердого тела от полученного им количества теплоты Q.  Для подготовки к данному типу заданий необходимо тренироваться работать с графиками. Их часто дают в задачах на расчет количества теплоты.
Задание № 16	Расчетная задача на электромагнитные явления. Здесь нужно знать формулу для КПД и формулу для электрической мощности. Обратите внимание на единицы измерения. Например, в демоверсии в этой задаче ответ надо дать в киловаттах, а не в ваттах. Часто школьники считают все правильно, а в ответе пишут не то, что требуется.
Задание № 19	Задача на физические явления и законы, понимание и анализ экспериментальных данных, представленных в виде таблицы, графика или рисунка. Оценивается в два балла. С одной стороны, здесь нужно знать свойства силы трения/скольжения. Она не зависит от скорости и пропорциональна реакции опоры. С другой стороны, необходимо понять, что именно следует из представленного эксперимента. Не должно произойти смешение следствий эксперимента и теории. С этим возникают сложности, поскольку лабораторных работ в школах ребята проводят мало.
Задание № 22	Вопрос на применение информации из текста физического содержания. На него надо потратить немало времени, это единственная сложность. В этом задании девятикласснику предлагается текст, нужно его прочитать, осмыслить и найти ответ на поставленный вопрос. Как правило, в тексте всегда есть ответ на вопрос.
Задание № 23	Экспериментальное задание на механические и электромагнитные явления. Оценивается в четыре балла. Надо собрать экспериментальную установку и выполнить измерения. Здесь нужно продемонстрировать свои умения по теории и умение работать с приборами, то есть показать знания в комплексе. Именно поэтому эта задача оценивается на экзамене выше всех.
Задание № 24	Качественная задача на механические, тепловые или электромагнитные явления. Здесь требуется анализ предлагаемого явления на качественном уровне с упоминанием физических законов и явлений. В рамках одной задачи может встречается несколько тем. Сами формулы, которые нужно применить, простые, но их нужно соединить из разных тем.
Задания № 25, 26	Расчетные задачи на механические, тепловые, электромагнитные явления, каждая из которых оценивается в три балла. Имейте в виду, что правильно записанное условие задачи плюс законы, необходимые для решения, уже дают один балл. Поэтому даже если не знаешь, как решать задачу, есть шанс получить балл за нее.

Серия Практических работ по физике для учащихся 10 класса | Творческая работа учащихся по физике (10 класс) по теме:

Практическая работа из серии «Изучаю себя»

ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА ТЕПЛОТЫ, ОТДАВАЕМОГО  ОРГАНИЗМОМ ЧЕЛОВЕКА В ОКРУЖАЮЩУЮ СРЕДУ.

Приборы и оборудование:  термометр, напольные весы

Суть опыта:

измерив термометром температуру окружающего воздуха и весами – массу своего тела, определить количество теплоты (а также количество вещества), которое отдает ваше тело в окружающее пространство.

Используемый теоретический материал.

Вопросы для учащихся:

1. По какой формуле рассчитывают v — количество вещества?
2. Как еще можно найти данную величину через другие параметры?
3. Что в данной формуле означает величина NA?
4. Чему равна постоянная Авогадро?
5. Как находится количество теплоты, полученное телом при нагревании или отданное при охлаждении?

Ответы:

1. Количество вещества зависит от его массы и определяется формулой: v=m/М

2. Количество вещества можно определить, зная число молекул v = N / NA 

3. NA называется постоянной Авогадро.

4. Постоянная Авогадро NA = 6, 02 ∙ 10 23 1/моль

5. Количество теплоты, полученное телом при нагревании или отданное при охлаждении, определяется формулой: Q = c m ( tтела – t), где c – удельная теплоемкость воды; t  – температура воздуха; t тела — температура вашего тела.

ХОД РАБОТЫ (предлагается классом).

1. Найти массу m собственного тела, используя напольные весы.
2. Повторить измерения массы m не менее 3 раз, не меняя условий опыта, и найти среднее значение массы m ср.
3. Измерить t  – температуру воздуха и t тела — температуру вашего тела.
4. Приняв молярную массу вещества человеческого тела М = 20 г\моль, рассчитать количества вещества по формуле: v = m ср / М
5. По формуле Q = c m ( tтела – t)  найти количество теплоты, отдаваемое вашим организмом в окружающую среду. Удельную теплоемкость человека (так как он состоит на 80% из воды) можно приблизительно считать равной 0,8 с = 0,8 ∙ 4200 Дж\ кг ∙ оС.
6. Оценить погрешность работы.

Дополнительное задание:

Из какого количества молекул состоит ваше тело?

ν = m / M = N / NA          NA = 6, 02 ∙ 10 23 1/моль

Практическая работа из серии «Изучаю себя»

ПРАКТИЧЕСКАЯ РАБОТА.

ТЕМА _______________________________________________________________

_____________________________________________________________________

Цель: ________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

ПРИБОРЫ И МАТЕРИАЛЫ: _______________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

Средняя масса тела:

Количества вещества:

Удельная теплоемкость человека:

Количество теплоты, отдаваемое вашим организмом в окружающую среду, вычисляется по формуле:

Работу выполнил:

Основные формулы по физике за курс 7-8 класса

2 \)

Волны, звук и свет

• \ (v _ {\ text {avg}} = \ dfrac {D} {\ Delta t} \)
• \ (v = f \ лямбда \)
• \ (T = \ dfrac {1} {f} \)
• \ (E = hf \)
• \ (E = h \ dfrac {c} {\ lambda} \)
• \ (n = \ dfrac {c} {v} \)
• \ (n_ {1} \ sin \ theta_ {1} = n_ {2} \ sin \ theta_ {2} \)
• \ (\ theta_ {c} = \ sin ^ {- 1} \ left (\ dfrac {n_ {2}} {n_ {1}} \ right) \)
• \ (f _ {\ text {L}} = \ dfrac {v \ pm v _ {\ text {L}}} {v \ pm v _ {\ text {S}}} f _ {\ text {S}} \)
• \ (\ begin {align} E & = W_0 + E_ \ text {k, max} \\ \ text {where} E & = hf \\ \ text {и} W_0 & = hf_0 \\ \ text {и} E_ \ text {k, max} & = \ dfrac {1} {2} m_ \ text {e} {v_ \ text {max}} ^ 2 \ end {align} \)

Электромагнетизм

• \ (\ phi = BA \ cos \ theta \)
• \ (\ mathcal {E} = -N \ dfrac {\ Delta \ phi} {\ Delta t} \)

Электростатика

• \ (Q = nq _ {\ text {e}} \)
• \ (F = \ dfrac {kQ_1Q_2} {r ^ 2} \)
• \ (\ vec {E} = \ dfrac {\ vec {F}} {q} \)
• \ (E = \ dfrac {kQ} {r ^ 2} \)
• \ (V = \ dfrac {W} {q} \)

Электрические цепи

• \ (I = \ dfrac {Q} {\ Delta t} \)
• \ (R _ {\ text {s}} = R_1 + R_2 + R_3 + \ cdots \) ​​
• \ (\ dfrac {1} {R _ {\ text {p}}} = \ dfrac {1} {R_1} + \ dfrac {1} {R_2} + \ dfrac {1} {R_3} + \ cdots \)
• \ (R = \ dfrac {V} {I} \)
• \ (\ begin {align} P & = VI \\ P & = I ^ 2R \\ P & = \ dfrac {V ^ 2} {R} \ end {align} \)
• \ (E = P \ Delta t \)
• \ (W = Vq \)
• \ (W = VI \ Delta t \)
• \ (W = I ^ 2R \ Delta t \)
• \ (W = \ dfrac {V ^ 2 \ Delta t} {R} \)
• \ (\ mathcal {E} = I (R + r) \)
• \ (P = \ dfrac {W} {\ Delta t} \)

Переменный ток

• \ (I _ {\ text {rms}} = \ dfrac {I _ {\ text {max}}} {\ sqrt {2}} \)
• \ (V _ {\ text {rms}} = \ dfrac {V _ {\ text {max}}} {\ sqrt {2}} \)
• \ (P _ {\ text {avg}} = V _ {\ text {rms}} I _ {\ text {rms}} \)
• \ (P _ {\ text {avg}} = {I _ {\ text {rms}}} ^ {2} R \)
• \ (P _ {\ text {avg}} = \ dfrac {{V _ {\ text {rms}}} ^ {2}} {R} \)

Мощность

Количественная работа связана с силой, вызывающей смещение. Работа не имеет ничего общего с количеством времени, в течение которого эта сила вызывает смещение. Иногда работа выполняется очень быстро, а иногда — довольно медленно. Например, альпинистке требуется необычно много времени, чтобы поднять свое тело на несколько метров вдоль скалы. С другой стороны, турист (который выберет более легкий путь в гору) может поднять свое тело на несколько метров за короткий промежуток времени. Эти два человека могут выполнять одинаковый объем работы, но путешественник выполняет ее значительно быстрее, чем скалолаз.Величина, связанная со скоростью выполнения определенного объема работы, называется мощностью. У туриста номинальная мощность на больше, чем у скалолаза.

Мощность — это скорость выполнения работы. Это соотношение работы / времени. Математически это вычисляется с использованием следующего уравнения.

Мощность = Работа / время

или

P = Вт / т

Стандартная метрическая единица измерения мощности — Вт . Как следует из уравнения мощности, единица мощности эквивалентна единице работы, деленной на единицу времени. Таким образом, ватт эквивалентен джоулям в секунду. По историческим причинам термин лошадиных сил иногда используется для описания мощности, выдаваемой машиной. Одна лошадиная сила эквивалентна примерно 750 Вт.

Большинство машин спроектировано и построено для работы с объектами. Все машины обычно характеризуются номинальной мощностью.Номинальная мощность указывает скорость, с которой эта машина может работать с другими объектами. Таким образом, мощность машины — это соотношение работы / времени для этой конкретной машины. Автомобильный двигатель — это пример машины, которой задана номинальная мощность. Номинальная мощность относится к тому, насколько быстро автомобиль может разгонять автомобиль. Предположим, что двигатель мощностью 40 лошадиных сил может разогнать автомобиль от 0 миль / час до 60 миль / час за 16 секунд. Если бы это было так, то автомобиль с мощностью в четыре раза больше мог бы выполнять такой же объем работы за четверть времени. То есть 160-сильный двигатель мог разогнать тот же автомобиль с 0 миль / час до 60 миль / час за 4 секунды. Дело в том, что при одинаковом объеме работы мощность и время обратно пропорциональны. Уравнение мощности предполагает, что более мощный двигатель может выполнять такой же объем работы за меньшее время.

Человек — это также машина с номинальной мощностью . Некоторые люди более полны власти, чем другие. То есть некоторые люди способны выполнять тот же объем работы за меньшее время или больше за то же время.Обычная физическая лаборатория включает в себя быстрый подъем по лестнице и использование информации о массе, росте и времени для определения личных возможностей ученика. Несмотря на диагональное движение по лестнице, часто предполагается, что горизонтальное движение является постоянным, и вся сила от ступенек используется для подъема ученика вверх с постоянной скоростью. Таким образом, вес ученика равен силе, которая действует на ученика, а высота лестницы — это смещение вверх. Предположим, что Бен Пумпинирон поднимает свое 80-килограммовое тело на 2.0-метровый подъезд за 1,8 секунды. Если бы это было так, то мы могли бы рассчитать номинальную мощность Бена . Можно предположить, что Бен должен приложить к лестнице нисходящую силу 800 Ньютон, чтобы поднять свое тело. Поступая таким образом, лестница толкала тело Бена вверх с достаточной силой, чтобы поднять его тело вверх по лестнице. Также можно предположить, что угол между силой лестницы на Бена и смещением Бена равен 0 градусов. Используя эти два приближения, можно определить номинальную мощность Бена, как показано ниже.

Номинальная мощность Бена — 871 Вт. Он вполне коня .

Другая формула силы

Выражение для мощности — работа / время. А поскольку выражение для работы — это сила * смещение, выражение для мощности можно переписать как (сила * смещение) / время. Поскольку выражение для скорости — это смещение / время, выражение для мощности можно еще раз переписать как «сила * скорость». Это показано ниже.

Это новое уравнение мощности показывает, что мощная машина одновременно сильна (большая сила) и быстра (большая скорость). Мощный автомобильный двигатель — сильный и быстрый. Мощная сельскохозяйственная техника — прочная и быстрая. Сильный тяжелоатлет силен и быстр. Сильный лайнмен в футбольной команде силен и быстр. Машина , достаточно сильная, чтобы приложить большую силу, чтобы вызвать смещение за небольшой промежуток времени (т.е.е., большая скорость) — машина мощная.

Проверьте свое понимание

Используйте свое понимание работы и власти, чтобы ответить на следующие вопросы. По завершении нажмите кнопку, чтобы просмотреть ответы.

1. Два студента-физика, Уилл Н. Эндейбл и Бен Пумпинирон, находятся в зале для тяжелой атлетики. Уилл поднимает 100-фунтовую штангу над головой 10 раз за одну минуту; Бен поднимает 100-фунтовую штангу над головой 10 раз за 10 секунд. Какой студент больше всего работает? ______________ Какой ученик дает больше всего энергии? ______________ Объясните свои ответы.

2. В физической лаборатории Джек и Джилл взбежали на холм. Джек вдвое массивнее Джилл; тем не менее, Джилл преодолевает то же расстояние за половину времени. Кто работал больше всего? ______________ Кто доставил больше всего энергии? ______________ Объясните свои ответы.

3. Уставшая белка (масса около 1 кг) отжимается, прикладывая силу, поднимающую ее центр масс на 5 см, чтобы выполнить работу всего на 0,50 Дж. Если уставшая белка проделает всю эту работу за 2 секунды, то определите ее мощность.

4. При подтягивании студентка-физик поднимает ее 42.0-кг тело на дистанцию ​​0,25 метра за 2 секунды. Какую силу развивают бицепсы ученика?

5. Ежемесячный счет за электроэнергию в вашей семье часто выражается в киловатт-часах. Один киловатт-час — это количество энергии, доставленное потоком 1 киловатт электроэнергии за один час. Используйте коэффициенты преобразования, чтобы показать, сколько джоулей энергии вы получаете, покупая 1 киловатт-час электроэнергии.

6. Эскалатор используется для перемещения 20 пассажиров каждую минуту с первого этажа универмага на второй. Второй этаж расположен на высоте 5,20 метра над первым этажом. Средняя масса пассажира — 54,9 кг. Определите требуемую мощность эскалатора, чтобы переместить это количество пассажиров за это время.

Динамика | Физика для идиотов

Динамика — это название правил движения.Это то, что, как вы могли подумать, должно было быть выяснено в первую очередь, но не было полностью заблокировано до недавнего времени. При этом правила не сильно изменились и довольно предсказуемы, по крайней мере, в больших масштабах. Кто-то однажды сказал мне, что все, что вам нужно знать для экзамена по динамике, это: а все остальное можно извлечь из этого. Я так и не узнал, правы ли они, я узнал и эти на всякий случай:

Если вы уже знакомы с уравнениями, возможно, вы захотите перейти к следующему разделу, иначе я объясню, откуда они пришли и как их использовать.

При работе с измерениями вы можете использовать скалярные или векторные величины.

Скалярные величины:

• Укажите только величину.
• Энергия, Длина, Масса, Скорость, Температура и Время — все это скалярные величины.

Векторные величины:

• Имеют величину и направление
• Смещение, Сила, Скорость, Ускорение и Импульс — все векторные величины.

Иногда может показаться, что скорость и скорость — одно и то же (часто они равны друг другу), но на самом деле они немного отличаются. Скорость — это то, насколько быстро что-то движется, не имеет значения, идет ли он вверх, вниз, влево или вправо, все, что имеет значение, — это то, как далеко он перемещается за установленное время. Вероятно, лучший способ рассматривать скорость — это если вы думаете или обычная ось x, y. Если тело движется горизонтально по прямой со скоростью 10, затем останавливается и движется в совершенно противоположном направлении, при скорости 10, очевидно, произошло изменение, однако скорость этого не отражает. Скорость до разворота такая же, как и после.Однако скорость не та. Если бы мы сказали, что скорость вначале была такой же, как и скорость: 10, тогда, когда тело движется точно в противоположном направлении с той же скоростью, скорость будет -10.

Исаак Ньютон был умным парнем. Мы должны благодарить его за гравитацию (я, вероятно, должен добавить, что он открыл, а не изобрел ее, иначе люди начнут обвинять его каждый раз, когда падают). Больше всего Ньютон известен (помимо случая с яблоком) своими законами движения:

1. Частица останется в покое или продолжит свое движение, если на нее не будет действовать внешняя сила.
2. Сила, действующая на объект, равна его массе, умноженной на его ускорение ().
3. Каждое действие имеет равную и противоположную реакцию.

Все это нормально, но что на самом деле означают эти законы?

1. Частица останется в покое или продолжит свое движение, если на нее не будет действовать внешняя сила.

Это просто означает, что если на частицу не действует внешняя сила, она никоим образом не изменит ее движения. Если бы не было трения или сопротивления воздуха, то частица, движущаяся со скоростью 5, продолжалась бы бесконечно.Очевидно, что в реальной жизни этого не происходит из-за сопротивления воздуха и трения, поэтому практически невозможно иметь внешнюю силу на движущуюся частицу. Однако, если вы думаете о неподвижной частице, это имеет гораздо больший смысл. Если к неподвижной частице не приложить силу, она не начнет двигаться.

2. Сила, действующая на объект, равна его массе, умноженной на его ускорение.

Проще говоря, это, вероятно, одна из самых фундаментальных формул в динамике.Это один из тех, которые часто возникают в Dynamics, и его действительно стоит изучить. Это тоже не так сложно понять. Имеет смысл, что если что-то имеет большую массу, потребуется большая сила, чтобы придать ему такое же ускорение, как и что-то с меньшей массой.

3. Каждое действие имеет равную и противоположную реакцию

Этот закон в основном означает, что если вы толкнетесь о стену, это оттолкнет вас назад, что на самом деле является хорошей работой, потому что в противном случае вы бы прошли прямо!

У них так много разных названий, что иногда трудно угнаться за ними.Возможно, вы слышали, что их называют кинематическими уравнениями, уравнениями движения, уравнениями SUVAT, а может быть, вы вообще о них не слышали. Прежде всего, давайте взглянем на них:

(1)

(2)

(3)

(4)

(5)

Может показаться, что там есть что вспомнить, но поверьте, это не так сложно, как кажется. Как будто эти уравнения невероятно важны в динамике.

SUVAT Equation 1

Как вы, наверное, уже знаете, скорость, разделенная на время, равна ускорению, а скорость, умноженная на время, равна смещению.Это означает, что на графике зависимости скорости от времени уклон линии равен ускорению, а площадь под линией равна смещению.

Если у вас есть начальная скорость и конечная скорость, график будет выглядеть примерно так:

График, показывающий u против t

Как я уже сказал, уклон линии равен ускорению. Так . Переставив это так, чтобы получился объект, мы получаем нашу первую формулу постоянного ускорения:

SUVAT Equation 2

Ладно, один проиграл, осталось четыре!

Мы знаем, что площадь под графиком равна смещению.Итак, мы знаем, что умножение на дает нам нижний прямоугольник площади, а деление на 2 дает нам верхний треугольник. Это дает нам:

Теперь мы уже знаем это, поэтому мы можем переставить это, чтобы получить, а затем подставить это в наше уравнение для смещения. Из этого у нас есть. Если мы просто умножим скобку, которая дает нам нашу вторую формулу:

Для тех из вас, кто любит находить математику там, где это возможно, вам может быть интересно узнать, что это интеграл по отношению к.Если для вас это не имеет смысла, почему бы не заглянуть в замечательный раздел «Интеграция», где все станет ясно!

SUVAT Equation 3

Те из вас, кто увлечен поиском закономерностей, возможно, заметили, что это уравнение очень похоже на предыдущее. Это потому, что он очень похож на предыдущий. Те из вас, кто решил не переходить на страницу интеграции, могут пожалеть об этом сейчас.

Если переставить, чтобы сделать тему, то получится:

Теперь вам просто нужно интегрировать этот результат по времени, чтобы получить наше третье уравнение:

SUVAT Equation 4

Мы уже установили, что площадь под графиком (равная смещению) равна:

Если мы умножим скобку, получим:

, что совпадает с:

Наконец, мы просто разложим это на множители, чтобы получить:

SUVAT Equation 5

Можем переставить, сделать тему:

Затем мы просто подставляем это значение в наше предыдущее уравнение:, что дает нам:

, который можно упростить до,

, а затем

это в конечном итоге дает нам окончательную форму

Вот и все! Эти уравнения определенно стоит изучить, потому что они полезны снова и снова.Есть несколько правил, например, их можно использовать только в тех случаях, когда есть постоянное ускорение. Это означает, что если ускорение составляет примерно 12 мс ^–2 , они в порядке, но если ускорение составляет 12 мс ^–2 , тогда они не будут работать, поскольку ускорение зависит от.

Большая часть динамики достигается за счет игнорирования сопротивления воздуха, и хотя это значительно упрощает работу, всегда стоит знать, какое влияние это окажет.Силу сопротивления любого объекта, движущегося в жидкости, можно рассчитать по формуле:

— это плотность жидкости (998,2071 кг · м для воды при 30 градусах и 1,204 кг · м для воздуха), — скорость объекта, — площадь поперечного сечения объекта и — коэффициент сопротивления. Коэффициент аэродинамического сопротивления — это число, которое относится к аэродинамике объекта: куб имеет, а сфера имеет.

Объект, падающий на Землю, в конечном итоге (если он будет падать достаточно долго) достигнет скорости, при которой сила сопротивления равна силе тяжести, тянущей его вниз.Это называется Конечная скорость , и вы можете получить выражение для этого, приравняв силу сопротивления к, а затем переставив на:

Для человека, падающего в воздухе (сверху), у нас есть 70 кг, площадь 0,5 м и коэффициент сопротивления около 0,8 (приблизительное предположение где-то около углового куба или цилиндра), мы получаем конечную скорость около 53 мс (что оказывается быть довольно хорошей приблизительной оценкой).

Это самый простой экземпляр в динамике.Тело движется по плоской поверхности по прямой. Например:

  1. Преподобный едет на своей машине, как вдруг двигатель перестает работать! Если он едет со скоростью 10 мс  -1 , а его замедление составляет 2 мс  -2 , сколько времени потребуется машине, чтобы остановиться?  

Хорошо, с такого рода проблемами всегда полезно перечислить то, что вы знаете. Нам даны начальная скорость, и ускорение,. Мы также знаем, что если машина собирается финишировать в состоянии покоя, эта конечная скорость должна быть 0 мс ^-1 .Мы хотим узнать время,. Лично я считаю, что лучше всего изложить эту информацию так:

u = 10 мс ^-1
v = 0 мс ^-1
a = -2 мс ^-2
t =? s

Отсюда мы можем увидеть, какое уравнение нам нужно. В этом случае мы видим, что нам нужно уравнение. Мы переставляем это так, чтобы получился предмет, давая нам

Наконец, мы помещаем числа в уравнение:

.

 2. Майкл выходит на дорогу в 30 метрах от места, где двигатель не работает.Очки преподобного упали, и он не видит Майкла. Остановится ли машина вовремя, чтобы не сбить Майкла? 

Еще раз, лучше всего выложить всю имеющуюся у нас информацию:

u = 10 мс ^-1
v = 0 мс ^-1
a = -2 мс ^-2
t = 5 с
s =? м

На этот раз мы хотим найти смещение s, поэтому нам нужно выбрать уравнение с этим in. Я собираюсь использовать. Я мог бы использовать или, однако, поскольку у нас нет времени, а вместо этого мы разработали это самостоятельно, любая ошибка, сделанная в предыдущих расчетах, будет перенесена в эту.
Я снова перегруппирую уравнение, на этот раз сделав его предметом обсуждения. Это хорошая привычка, теперь это может не иметь большого значения, переставляете ли вы уравнение до или после ввода чисел, но с более сложными формулами это может стать действительно беспорядочным, если вы не измените его сначала. Также в экзаменационных ситуациях, если вы допустили ошибку, вы все равно можете получить оценки по методу, если экзаменатор может видеть, что вы сделали.
В любом случае, это дает нам

Подставляя числа в уравнение, получаем:

, значит, Майкл не попадет! (Уф!)

В приведенном выше примере трение полностью проигнорировано.В реальном мире мы не можем этого сделать (очень удачно, потому что мы все время падали, и люди думали, что мы пьяны). А теперь давайте посмотрим на ситуацию с трением. Коэффициент трения обозначается символом μ. Результирующая (нормальная) сила веса уравновешивает вес автомобиля (чтобы он не проезжал по дороге). Сила трения равна μ (или μN).

 3. Автомобиль Преподобного сломался на М1. Ему нужно подтолкнуть его к твердому плечу. Автомобиль весит 5000Н.Rev может выдвинуть около 1800N. Коэффициент трения между автомобилем и дорогой составляет 0,6. Сможет ли Rev подтолкнуть машину к твердой обочине? 

Хорошо, в такой ситуации сначала хорошо нарисовать небольшой набросок того, что происходит.

Диаграмма сил, показывающая, что происходит в примере 3.

Из этого мы знаем, что для того, чтобы машина двигалась, Rev должен толкать с силой не менее μR. Просто умножив коэффициент трения на результирующую силу, мы обнаружим, что сила трения составляет 3000 Н, поэтому Rev не сможет толкнуть автомобиль на обочину дороги.

  4. Бодибилдер случайно проезжает мимо и, пытаясь облегчить заторы на постоянно загруженной трассе M1, решает помочь. Он может толкать с силой 3200Н. Каким будет ускорение машины с учетом того, что бодибилдер и Rev.  

Итак, на самом деле ситуация та же, что и раньше, только на этот раз силы не уравновешиваются и будет ускорение. Мы получили это от очень умного Исаака Ньютона.
Помните, что для определения общей силы необходимо убрать силу трения. Итак, это (3200 + 1800) — 3000. Таким образом, общая сила составляет 2000Н. Опять же, нам нужно изменить формулу, чтобы на этот раз в качестве испытуемого использовалось на . Это дает нам. Подставляя числа, получаем:

a = 3,9 мс ^-2 (2 н.ф.)

Это очень похоже на движение по плоской поверхности, только одна или две другие переменные … о, и мы больше не будем говорить об автомобиле Rev, так как я не уверен, что это поможет ему подняться в гору!

В любом случае, боюсь, я немного сбился с пути.Введение «наклонной плоскости» или «уклона», как ее называют большинство из нас, означает, что вам придется освежить свою тригонометрию. С другой стороны, вы узнаете, почему люди годами пытались вбить это в вас! Если вы знакомы со старым добрым порядком операций, все будет в порядке.

Итак, давайте начнем с простого простого примера.

Пример наклонной плоскости

На рисунке выше показан блок, стоящий на склоне. Хорошее место для начала (вероятно, единственное место, с которого можно начать, если вы хотите получить хоть какой-то шанс получить хоть что-нибудь с вопросом), — это объединить силы.Предполагая, что блок находится в состоянии покоя, мы знаем, что он находится в равновесии, поэтому горизонтальные силы должны быть равны, как и вертикальные силы (если это не один из тех прекрасных левитирующих блоков).

Снаряды ничем не отличаются от Движения по прямой, просто вместо того, чтобы тело двигалось слева направо, оно также движется вверх или вниз. Сначала давайте посмотрим на типичный пример движения снаряда:

 Мяч брошен под углом 30 °. Имеет начальную скорость 20 мс  -1 .Найдите максимальную высоту, которую может достичь мяч. 

Итак, как обычно, рисуем диаграмму:

Пример движения снаряда

Теперь давайте перечислим то, что мы знаем:

• u = 20 sin30 мс ^-1
• v = 0 мс ^-1
• a = -9,81 мс ^-2
• с =? м

Теперь мы выбираем одну из кинематических формул, которая даст нам результат наиболее прямым путем:, и переставляем ее так, чтобы получился объект:

Затем, наконец, введите числа в уравнение:

и выскакивает ответ:

Смотри, не так ли трудно было? Вопросы о снарядах иногда могут показаться довольно сложными, но если вы не забудете просто использовать тригонометрию для поиска компонентов x и y, вы не ошибетесь.

Иногда вы знаете максимальную высоту, но какой-то другой компонент будет отсутствовать. Например, момент, когда мяч находится в воздухе … Опять же, это не проблема, вы просто посмотрите, что вы знаете, , , и воспользуйтесь формулами, чтобы вычислить остальное.

Время, скорость и скорость | Физика

Цели обучения

К концу этого раздела вы сможете:

• Объясните взаимосвязь между мгновенной скоростью, средней скоростью, мгновенной скоростью, средней скоростью, смещением и временем.
• Вычислить скорость и скорость с учетом начального положения, начального времени, конечного положения и конечного времени.
• Постройте график зависимости скорости от времени по графику положения от времени.
• Расскажите о графике зависимости скорости от времени.

Движение — это не только расстояние и перемещение. Такие вопросы, как: «Сколько времени занимает пешая гонка?» и «Какая была скорость бегуна?» невозможно ответить без понимания других концепций. В этом разделе мы добавляем определения времени, скорости и скорости, чтобы расширить наше описание движения.

Как обсуждалось в разделе «Физические величины и единицы», наиболее фундаментальные физические величины определяются тем, как они измеряются. Так обстоит дело со временем. Каждое измерение времени включает в себя измерение изменения некоторой физической величины. Это может быть число на цифровых часах, сердцебиение или положение Солнца на небе. В физике время определяется просто: время, — это изменение, или интервал, в течение которого происходит изменение. Невозможно знать, что время прошло, если что-то не изменится.

Количество времени или изменения калибруется путем сравнения со стандартом. Единицей измерения времени в системе СИ является секунда, сокращенно с. Мы можем, например, наблюдать, что некий маятник совершает полный оборот каждые 0,75 с. Затем мы могли бы использовать маятник для измерения времени, считая его колебания или, конечно, подключая маятник к часовому механизму, который регистрирует время на циферблате. Это позволяет нам не только измерить количество времени, но и определить последовательность событий.

Как время связано с движением? Обычно нас интересует время, затраченное на конкретное движение, например, сколько времени требуется пассажиру самолета, чтобы добраться от своего места до задней части самолета.Чтобы найти истекшее время, мы отмечаем время в начале и в конце движения и вычитаем два. Например, лекция может начаться в 11:00 утра. и закончится в 11:50 утра, чтобы прошедшее время составило 50 минут. Истекшее время Δ t — разница между временем окончания и временем начала,

Δ т = т _f — т ₀ ,

, где Δ t — изменение во времени или прошедшее время, t _f — время в конце движения, а t ₀ — время начала движения.(Как обычно, символ дельты Δ означает изменение следующей за ним величины.)

Жизнь проще, если время начала t ₀ принято равным нулю, как при использовании секундомера. Если бы мы использовали секундомер, он просто показывал бы ноль в начале лекции и 50 минут в конце. Если t ₀ = 0, то Δ t = t _f ≡ t .

В этом тексте для простоты

• движение начинается в момент времени, равный нулю ( t ₀ = 0)
• символ t используется для истекшего времени, если не указано иное (Δ t = t _f ≡ t )

Ваше понятие скорости, вероятно, совпадает с ее научным определением.Вы знаете, что если у вас есть большое смещение за небольшой промежуток времени, у вас есть большая скорость, и эта скорость выражается в единицах расстояния, разделенных на время, например, в милях в час или в километрах в час.

Средняя скорость

Средняя скорость — это смещение (изменение положения), деленное на время перемещения ,

[латекс] \ bar {v} = \ frac {\ Delta x} {\ Delta t} = \ frac {{x} _ {f} — {x} _ {0}} {{t} _ {f} — {t} _ {0}} [/ latex],

, где [latex] \ bar {v} [/ latex] — это средняя скорость, (обозначенная полосой над v ), Δ x — изменение положения (или смещения), а x _f и x ₀ — конечная и начальная позиции временами t _f и t ₀ соответственно.Если время пуска t ₀ принять равным нулю, то средняя скорость будет просто

[латекс] \ bar {v} = \ frac {\ Delta x} {t} [/ latex].

Обратите внимание, что это определение указывает, что скорость является вектором, потому что смещение является вектором . У него есть и величина, и направление. Единица измерения скорости в системе СИ — это метры в секунду или м / с, но широко используются многие другие единицы, такие как км / ч, миль / ч (также обозначаются как мили в час) и см / с. Предположим, например, что пассажиру самолета потребовалось 5 секунд, чтобы переместиться на −4 м (отрицательный знак указывает, что смещение происходит в сторону задней части самолета).Его средняя скорость будет

[латекс] \ bar {v} = \ frac {\ Delta x} {t} = \ frac {-4 \ text {m}} {5 \ text {s}} = — \ text {0,8 м / с. } [/ latex]

Знак минус указывает, что средняя скорость также направлена ​​к задней части самолета.

Однако средняя скорость объекта ничего не говорит нам о том, что с ним происходит между начальной и конечной точкой. Например, по средней скорости мы не можем сказать, останавливается ли пассажир самолета на мгновение или отступает назад, прежде чем он уйдет в заднюю часть самолета.Чтобы получить более подробную информацию, мы должны рассмотреть меньшие сегменты поездки за меньшие промежутки времени.

Чем меньше временные интервалы, учитываемые в движении, тем более подробная информация. Когда мы доводим этот процесс до его логического завершения, у нас остается бесконечно малый интервал. В течение такого интервала средняя скорость становится мгновенной скоростью или скоростью в определенный момент . Например, автомобильный спидометр показывает величину (но не направление) мгновенной скорости автомобиля.(Полиция выдает билеты на основе мгновенной скорости, но при расчете времени, которое потребуется, чтобы добраться из одного места в другое во время поездки, вам необходимо использовать среднюю скорость.) Мгновенная скорость v — это средняя скорость при заданной скорости. конкретный момент времени (или бесконечно малый интервал времени).

Математически, нахождение мгновенной скорости v в точный момент времени t может включать определение предела, операцию вычисления, выходящую за рамки этого текста.Однако во многих случаях мы можем найти точные значения мгновенной скорости без расчетов.

В обиходе большинство людей используют термины «скорость» и «скорость» как синонимы. В физике, однако, они не имеют одинакового значения и представляют собой разные концепции. Одно из основных различий заключается в том, что скорость не имеет направления. Таким образом, скорость является скаляром . Так же, как нам нужно различать мгновенную скорость и среднюю скорость, нам также необходимо различать мгновенную скорость и среднюю скорость.

Мгновенная скорость — величина мгновенной скорости. Например, предположим, что пассажир самолета в один момент времени имел мгновенную скорость -3,0 м / с (минус означает направление к задней части самолета). При этом его мгновенная скорость составляла 3,0 м / с. Или предположим, что однажды во время похода по магазинам ваша мгновенная скорость составляет 40 км / ч на север. Ваша мгновенная скорость в этот момент будет 40 км / ч — такая же величина, но без указания направления.Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, разделенное на затраченное время.

Мы отметили, что пройденное расстояние может быть больше перемещения. Таким образом, средняя скорость может быть больше средней скорости, которая представляет собой смещение, деленное на время. Например, если вы едете в магазин и возвращаетесь домой через полчаса, а одометр вашего автомобиля показывает, что общее пройденное расстояние составляет 6 км, то ваша средняя скорость составляет 12 км / ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение в оба конца равно нулю.(Смещение — это изменение положения и, таким образом, равно нулю для поездки туда и обратно.) Таким образом, средняя скорость равна , а не просто величине средней скорости.

Другой способ визуализировать движение объекта — использовать график. График положения или скорости как функции времени может быть очень полезным. Например, для этой поездки в магазин графики положения, скорости и зависимости скорости от времени показаны на рисунке 4. (Обратите внимание, что на этих графиках изображена очень упрощенная модель поездки.Мы предполагаем, что скорость постоянна во время поездки, что нереально, учитывая, что мы, вероятно, остановимся в магазине. Но для простоты мы смоделируем его без остановок и изменений скорости. Мы также предполагаем, что маршрут между магазином и домом является совершенно прямой линией.)

4 уловки для решения любых физических задач

Физика может быть устрашающей, все эти шкивы, протоны и движение снарядов. Однако, если вы подойдете к этому с правильным мышлением, даже самые сложные проблемы, как правило, будут проще, чем вы думаете.Когда вы сталкиваетесь с трудным вопросом, не паникуйте. Вместо этого начните с этих коротких простых приемов, которые помогут вам справиться с проблемой.

Практически каждый физический вопрос проверяет конкретные знания. Когда вы читаете вопрос, спросите себя, исследует ли это электричество? Крутящий момент? Параболическое движение? Каждая тема связана с определенными уравнениями и подходами, поэтому распознавание предмета направит ваши усилия в правильном направлении. Ищите ключевые слова и фразы, раскрывающие тему.

Этот простой шаг может сэкономить много времени. Прежде чем приступить к решению проблемы, подумайте, как будет выглядеть ответ. Какие бывают единицы; окончательный ответ будет в килограммах или литрах? Также подумайте, какие другие физические величины могут иметь отношение к вашему ответу. Если вы пытаетесь найти скорость, может быть полезно найти ускорение, а затем решить его для скорости. Раннее определение ограничений для ответа также гарантирует, что вы ответите на конкретный вопрос; распространенная ошибка в физике — решение неправильного.

Подумайте, какие детали упоминаются в проблеме. Если вопрос действительно плохой, они, вероятно, предоставили вам именно ту информацию, которая вам нужна для решения проблемы. Не удивляйтесь, если иногда эта информация закодирована на языке; проблема, в которой упоминается пружина с «снятием массы с конца», говорит вам кое-что важное о количестве силы. Запишите каждое количество, известное вам из проблемы, затем переходите к…

Какие уравнения включают величины, которые вам известны, а также те, которые вы ищете? Если у вас есть масса объекта и сила, и вы пытаетесь найти ускорение, начните с F = ma (второй закон Ньютона).Если вы пытаетесь найти электрическое поле, но у вас есть заряд и расстояние, попробуйте E = q / (4πε * r ² ).

Если вы не можете решить, какое уравнение использовать, вернитесь к нашему первому трюку. Какие уравнения связаны с темой? Можете ли вы манипулировать количествами, которые у вас есть, чтобы уместить любое из них?

Этот трюк не всегда работает, но он может дать толчок вашему мозгу. Сначала определите единицы количества, которое вы пытаетесь найти, и количество, которое у вас есть.Используйте только базовые единицы (метры, килограммы, секунды, заряд), а не составные единицы (сила измеряется в ньютонах, а это всего лишь кг * м / с ² ). Умножайте и делите количества до тех пор, пока единицы не совпадут с единицами количества в ответе. Например, если вы пытаетесь найти потенциальную энергию (кг * м ² / с ² ) и у вас есть высота (м), масса (кг) и ускорение свободного падения (м / с ² ), вы можете сопоставить единицы, умножив три величины (м * кг * м / с ² = кг * м ² / с ² ).

Примечание. В отличие от других, этот трюк не всегда работает. Остерегайтесь безразмерных констант. Например, кинетическая энергия равна ½ * масса * скорость ² , а не просто масса * скорость ² , как предполагают единицы измерения. Несмотря на то, что этот трюк не идеален, он все же может быть отличным местом для начала.

Вы заинтересованы в репетиторстве по физике в старших классах, бакалавриате или магистратуре в Кембридже, Нью-Йорке или в Интернете?

Для более релевантного чтения ознакомьтесь с другими сообщениями в блогах, написанными нашими преподавателями физики в Нью-Йорке и Бостоне :

Физическая формула

Часто используемые уравнения в физике.Подходит для учащихся средней школы и выше. В основном на основе алгебры, немного триггера, немного исчисления, немного причудливого исчисления.

Рабочий лист Сиявулы по физическим наукам, охватывающий «Физические формулы».

तरंग के प्रकार. यांत्रिक तरंगे (Механические волны) — वे तरंगें जो पदार्थिक माध्यम (ठोस, द्रव एवं गैस) में संचरित होती है जैसे ध्वनि, पराश्रव्य तरंग (ультразвуковые волны), पराध्वनिक …

Некоторые математические и физические формулы имеют мнемонические устройства, которые были вокруг уже давно.Ваш учитель мог использовать несколько, чтобы научить вас формуле.

1 ноября, 2020 · Technical Physics Letters — это журнал, дополняющий журнал Technical Physics, который предлагает оперативную публикацию разработок в области теоретической и экспериментальной физики с потенциальными технологическими приложениями. В последнее время особое внимание уделяется многим статьям о газовых лазерах и лазерной генерации в полупроводниках, а также многочисленным сообщениям о высокотемпературной сверхпроводимости.

Математическая физика с уравнениями в частных производных предназначена для студентов старших курсов и начинающих аспирантов, изучающих курс математической физики, преподаваемый на математических факультетах.В тексте представлены некоторые из наиболее важных тем и методов математической физики.

Известный американский писатель Билл Брайсон однажды сказал: «На самом деле физика — это не что иное, как поиск предельной простоты, но пока все, что у нас есть, — это своего рода элегантный беспорядок». Физика действительно является наиболее фундаментальной из наук, которая пытается описать всю природу с помощью тысяч математических формул.

Физика — это все, что нужно для формулирования вещей в реальном мире, и она наполнена уравнениями и формулами.Во время домашнего задания неплохо иметь сборник физических формул. Таким образом, мы создали здесь список шпаргалок по физике для быстрого ознакомления в одном месте.

15 февраля 2020 г. · Список формул физики уровня O 15 февраля 2020 г. 14 февраля 2014 г. автор: Mini Physics Этот пост содержит все важные формулы, которые вам нужны для физики уровня GCE O.

Физическая формула

Важные уравнения физики для курса IGCSE Общая физика: 1 Для постоянного движения: R = OP ‘v’ — скорость в м / с, ‘s’ — расстояние или смещение в метрах, а ‘t’ — время в секундах 2 Для ускорения ‘a’ == R− QP u — начальная скорость, v — конечная скорость, а t — время.

2 дня назад · Введение в теоретическую физику от первых принципов до классической механики и общей теории относительности. Теоретическая физика — это раздел физики, который занимается разработкой и развитием теории для объяснения фундаментальной природы Вселенной.

Сайт пересмотра физики — рекомендован учителям в качестве ресурса экзаменационными комиссиями AQA, OCR и Edexcel — также рекомендован BBC Bytesize — победителем IOP Web Awards — 2010 — Cyberphysics — помощником по физике для студентов на KS3 (SATs), KS4 (GCSE) и KS5 (уровень A и AS).

Это несколько обучающих программ, которые я написал, чтобы помочь визуализировать различные концепции в математике, физике и инженерии. Изначально они были написаны на Java, но в основном преобразованы в Javascript, поэтому вы сможете просматривать их без браузера с поддержкой Java.

Physics Formulas — Получите список всех физических формул здесь, на Vedantu.com, подготовленный учителями-предметниками. Также загрузите главу «Важные математические формулы и уравнения», чтобы легко решать проблемы и набирать больше баллов на экзаменах CBSE Board.

Скачать электронную книгу Формулы инженерной физики Начальная школа и инженерная физика Справочник формул ФИЗИЧЕСКИЕ ФОРМУЛЫ 2426 Электрон = -1,602 19 × 10-19 C = 9,11 × 10-31 кг Протон = 1,602 19 × 10-19 C = 1,67 × 10-27 кг Нейтрон = 0 C = 1,67 × 10-27 кг 6,022 × 10 23 атома в одной атомной единице массы e — элементарный заряд: 1,602 19 × 10-19

Формула начальной скорости пули.