2`.
Тіло масою 400 г перебуває на висоті 35 м над поверхнею землі. Обчисліть потенціальну енергію тіла відносно поверхні землі.А 14 Джв 1,4 кДжБ 140 Джг 1
…
4 кДж
Ход работы:
1. Положить под середину линейки карандаш, чтобы линейка находилась в равновесии.
2. Положить на один конец линейки резинку.
3. Уравнов
…
есить рычаг с помощью монет.
4. Учитывая, что масса монет 1 т – 1 г, 5 т – 5 г, 10 т – 10 г. Вычислить массу резинки , m1, кг.
5. Сместить карандаш к одному из концов линейки.
6. Измерить плечи l1 и l2, м.
7. Уравновесить рычаг с помощью монет m2, кг.
8. Определить силы, действующие на концы рычага F1 = m1*g, F2 = m2*g 9. Вычислите момент сил M1 = F1*l1, М2 = F2*l2 10. Заполните таблицу. l1, м l2, м m 1, кг m 2, кг F 1, Н F2, Н М1 , Н *м M 2, Н *м
35 быллов срочно!!!!!!!
Помагите пожалуйста.Мальчик Боря сам собирает радиоуправляемые машинки. Чтобы понять, удачной лиПолучилась машинка, Боря определяет её скорость на тес
…
товой дистанции.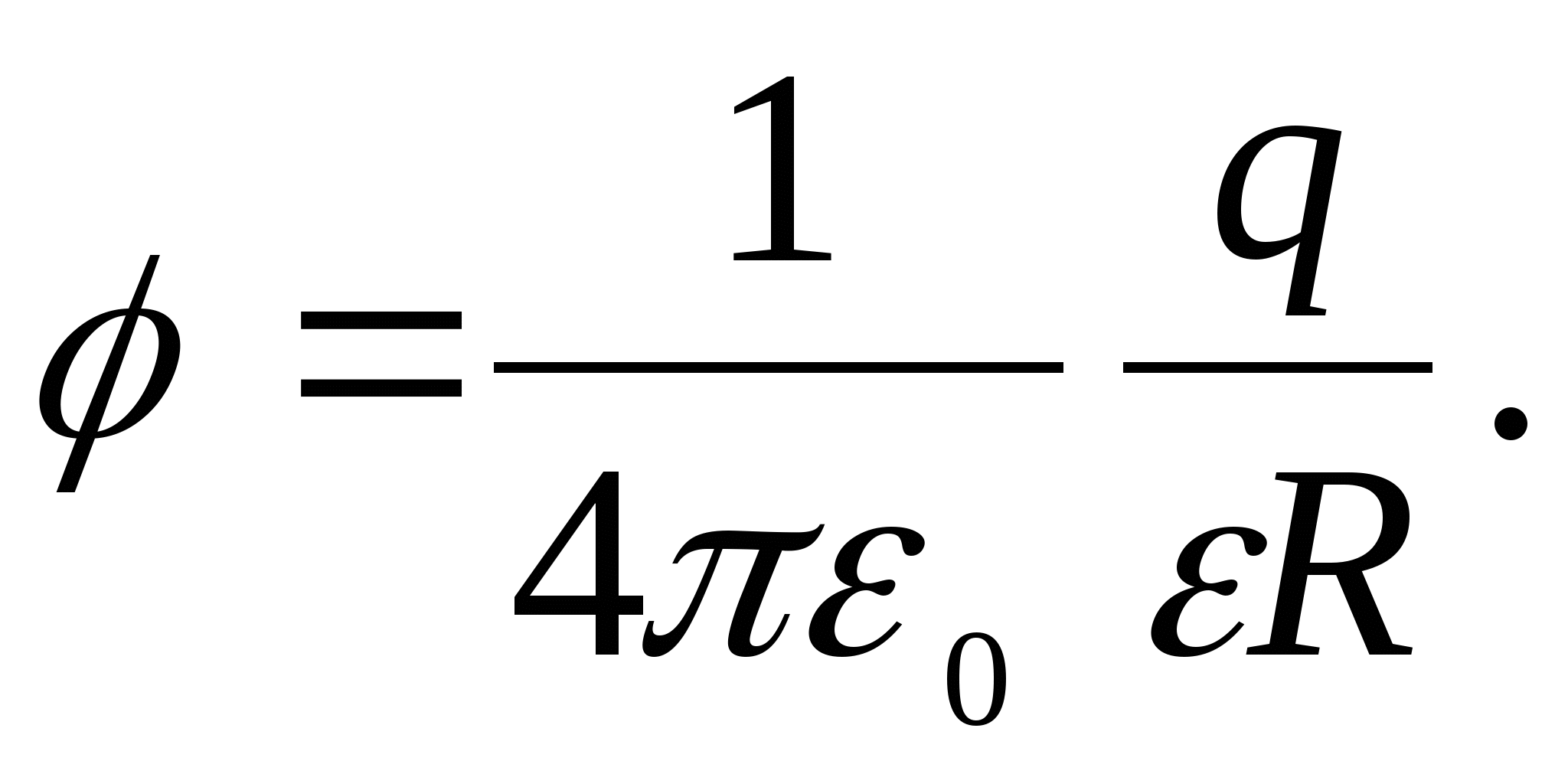 После проверкиодной из машинок Боря потерял листок с расчётами и всё, что у него осталось, это графикзависимости пройденной машинкой дистанции от времени её движения. Помогите Боренайти скорость движения машинки.
После проверкиодной из машинок Боря потерял листок с расчётами и всё, что у него осталось, это графикзависимости пройденной машинкой дистанции от времени её движения. Помогите Боренайти скорость движения машинки.
Помагите плиз. Для приготовлення домашнего майонеза Лизе нужно 270 г оливкового масла. К сожалению,у неё под рукой нет весов, но зато в кухонном шкаф
…
у есть мерный стаканчик для жидкостей.Лиза нашла в учебнике физики таблицу, в которой было указано, что плотность оливковогомасла равна 0,9 г/см. Какой объём масла нужно отмерить Лизе?
Визначити сулу струму та опір електричного кола якщо відомо що R1=R2=R3=25 Oм, R4=R5=R6=31 Oм, R7=R8=R9=40 Oм. U=225В. *
Содержание
Косинус фи — простое объяснение в 3-х словах. Таблицы коэффициента мощности для различных потребителей.
Многие из вас наверняка видели на электроинструментах, двигателях, а также люминесцентных лампах, лампах ДРЛ, ДНАТ и других, такие надписи как косинус фи — cos ϕ.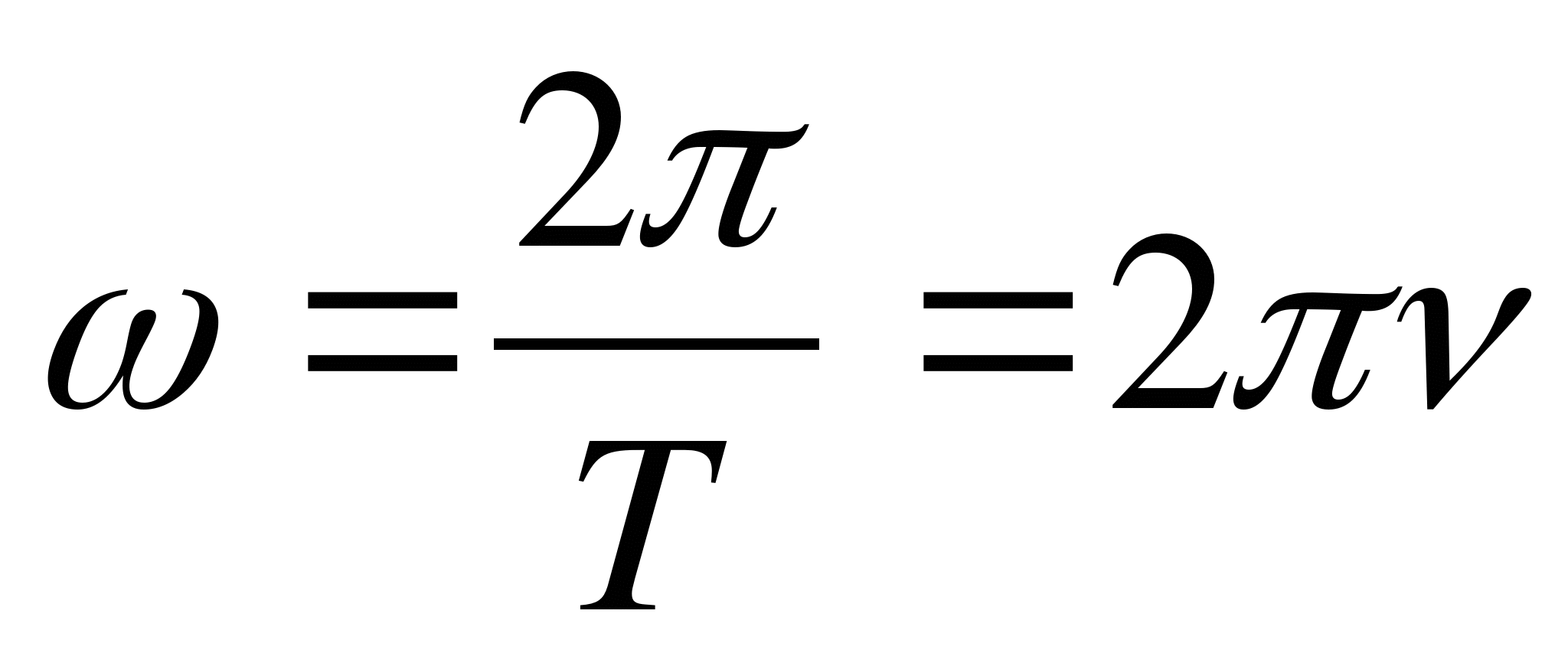
Однако люди далекие от электротехники и позабывшие школьные уроки физики, не совсем понимают, что же означает данный параметр и зачем он вообще нужен.
Давайте рассмотрим и объясним этот косинус, как можно более простыми словами, исключая всякие непонятные научные определения, типа электромагнитная индукция. В двух словах про него конечно не расскажешь, а вот в трех можно попробовать.
Когда ток отстает от напряжения
Предположим перед вами есть 2 проводника. Один из этих проводников имеет потенциал. Не суть важно какой именно — отрицательный (минус) или положительный (плюс).
У другого провода вообще нет никакого потенциала. Соответственно между этими двумя проводниками будет разность потенциалов, т.к. у одного он есть, а у другого его нет.
Эту разность потенциалов как раз таки и принято называть напряжением.
Если вы соедините кончики двух проводов не непосредственно между собой, а через лампочку накаливания, то через ее вольфрамовую нить начнет протекать ток. От одного провода к другому.
От одного провода к другому.
На первый взгляд может показаться, что лампочка загорается моментально. Однако это не так. Ток проходя через нить накала, будет нарастать от своего нулевого значения до номинального, какое-то определенное время.
В какой-то момент он его достигает и держится на этом уровне постоянно. То же самое будет, если подключить не одну, а две, три лампочки и т.д.
А что случится, если вместе с лампой последовательно включить катушку, намотанную из множества витков проволоки?
Изменится ли как-то процесс нарастания тока? Конечно, да.
Данная катушка индуктивности, заметно затормозит время увеличения тока от нуля до максимума. Фактически получится, что максимальное напряжение (разность потенциалов) на лампе уже есть, а вот ток поспевать за ним не будет.
Его нарастание слишком медленное. Из-за чего это происходит и кто виноват? Виноваты витки катушки, которые оказывают влияние друг на друга и тормозят ток.
Если у вас напряжение постоянное, например как в аккумуляторах или в батарейках, ток относительно медленно, но все-таки успеет дорасти до своего номинального значения.
А далее, ток будет вместе с напряжением идти, что называется «нога в ногу».
А вот если взять напряжение из розетки, с переменной синусоидой, то здесь оно не постоянно и будет меняться. Сначала U какое-то время положительная величина, а потом — отрицательная, причем одинаковое по амплитуде. На рисунке это изображается в виде волны.
Эти постоянные колебания не дают нашему току, проходящему сквозь катушку, достигнуть своего установившегося значения и догнать таки напряжение. Только он будет подбираться к этой величине, а напряжение уже начинает падать.
Поэтому в этом случае и говорят, что ток отстает от напряжения.
Причем, чем больше в катушке намотано витков, тем большим будет это самое запаздывание.
Как же это все связано с косинусом фи — cos ϕ?
Что такое коэффициент мощности
А связано это таким образом, что данное отставание тока измеряется углом поворота. Полный цикл синусоиды или волны, который она проходит от нуля до нуля, вместив в себя максимальное и минимальное значение, измеряется в градусах.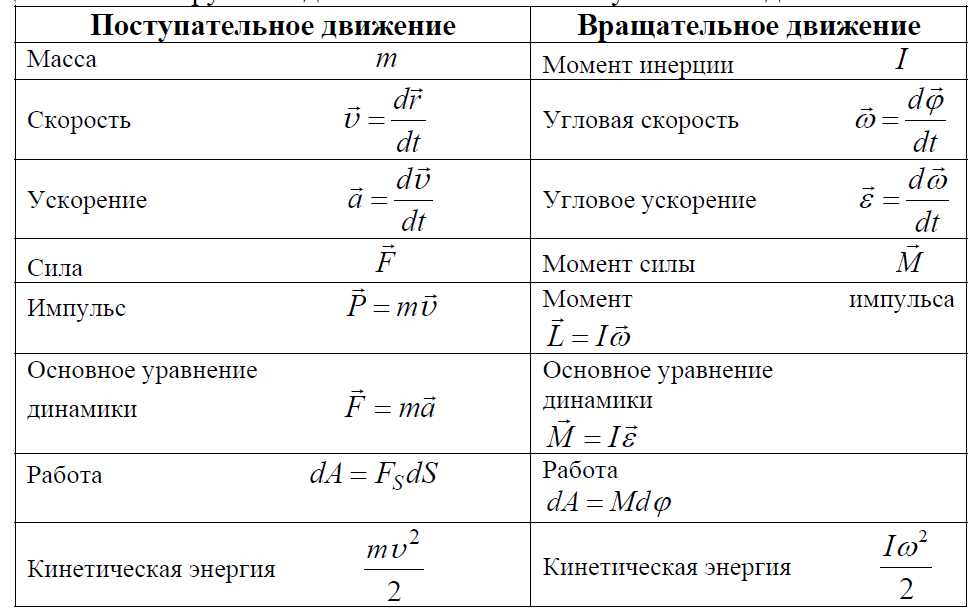 И один такой цикл равен 360 градусов.
И один такой цикл равен 360 градусов.
А вот угол отставания тока от напряжения, как раз таки и обозначается греческой буквой фи. Значение косинуса этого угла опаздывания и есть тот самый cos ϕ.
Таким образом, чем больше ток отстает от напряжения, тем большим будет этот угол. Соответственно косинус фи будет уменьшаться.
По научному, ток сдвинутый от напряжения называется фазовым сдвигом. При этом почему-то многие уверены, что синусоида всегда идеальна. Хотя это далеко не так.
В качестве примера можно взять импульсные блоки питания.
Не идеальность синусоиды выражается коэфф. нелинейных искажений — КНИ. Если сложить две эти величины — cos ϕ и КНИ, то вы получите коэффициент мощности.
Однако, чтобы все не усложнять, чаще всего под понятием коэфф. мощности имеют в виду только лишь один косинус фи.
На практике, данный коэффициент мощности рассчитывают не при помощи угла сдвига фаз, а отношением активной мощности к полной.
Активная и реактивная мощность
Существует такое понятие как треугольник мощностей.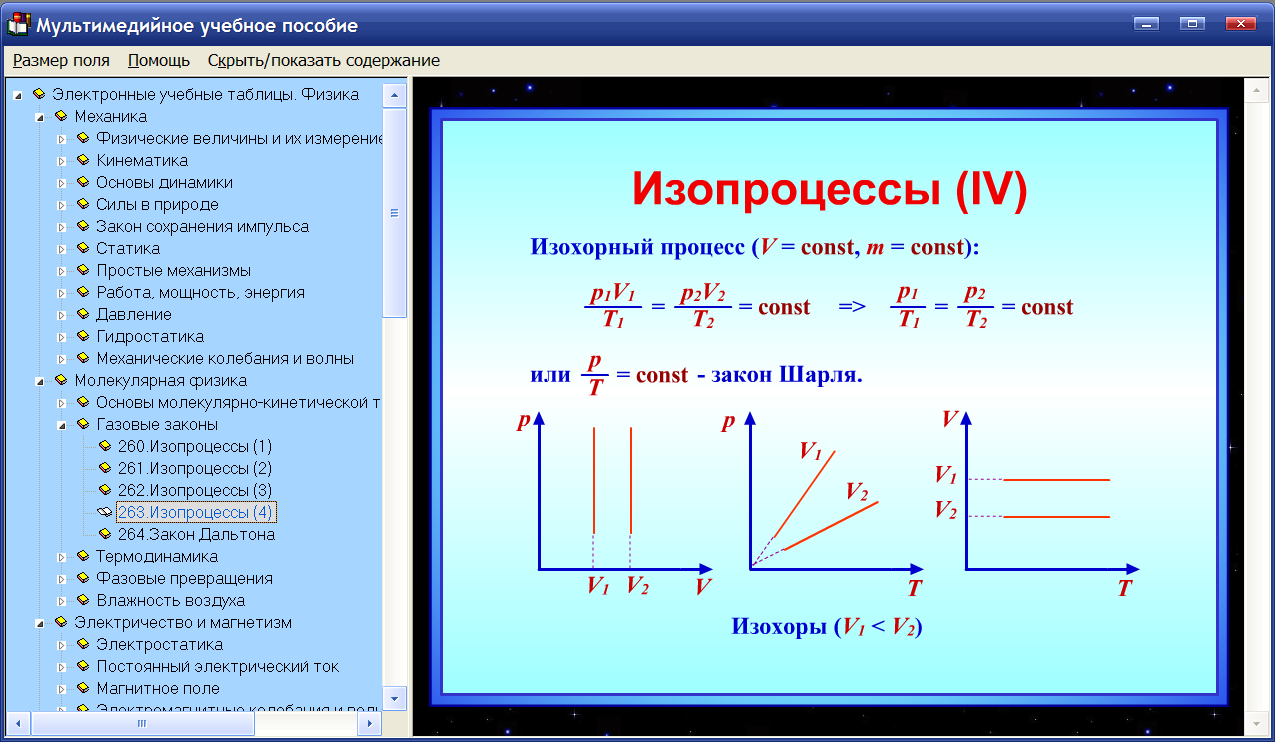 Сам косинус — это тригонометрическая функция, которая и появилась при изучении свойств прямоугольных треугольников.
Сам косинус — это тригонометрическая функция, которая и появилась при изучении свойств прямоугольных треугольников.
Она здорово помогает производить определенные вычисления с ними. Например, наглядно показывает отношение длин прилежащего катета (P-активная мощность) к гипотенузе (S-полная мощность).
То есть, зная угол сдвига, можно узнать, сколько активной мощности содержится в полной. Чем меньше этот угол, тем меньше реактивной составляющей находится в сети, и наоборот.
Только не путайте cos ϕ с КПД. Это разные понятия. Реактивная составляющая не расходуется, а «возвращается» на подстанцию в сеть, т.е. фактически потери ее нет. Только небольшая ее часть может тратиться на нагрев проводов.
В КПД все более четко — полезная мощность используется на нагрев — охлаждение — механическую работу, остальное уходит безвозвратно. Эта разница и показывается в КПД.
Более подробно, с графиками, рисунками и простыми словами, без особых научных формулировок обо всем этом говорится в ролике ниже.
Низкий коэффициент мощности и его последствия
Рассмотренное запаздывание тока относительно напряжения — это не хорошее явление. Как оно может сказаться на ваших лампочках или проводке?
- во-первых, это повышенное потребление электроэнергии
Часть энергии будет просто «болтаться» в катушке, при этом не принося никакой пользы. Правда не пугайтесь, ваш бытовой счетчик реактивную энергию не считает и платить вы за нее не будете.
Например, если вы включите в розетку инструмент или светильник с полной мощностью 100Ва, на блоке питания которого будет указано cos ϕ=0,5. То прибор учета накрутит вам только на половину от этой величины, то есть 50Вт.
Зато по проводам питания будет проходить вся нагрузка, разогревая их бесполезной работой.
- величина тока в проводке увеличится
Вот известное наглядное видео, демонстрирующее последствия этого для проводки.
- для эл.станций и трансформаторов оно вредно перегрузкой
Казалось бы, выбрось катушку и вся проблема исчезнет. Однако делать этого нельзя.
В большинстве светильников, лампы работают не отдельно, а в паре с источниками питания. И в этих самых источниках, как раз таки присутствуют разнообразные катушки.
Катушки просто необходимы как функциональная часть всей схемы и избавиться от них не получится. Например в тех же дроссельных лампах ДРЛ, ДНАТ, люминесцентных и т.п.
Поэтому характеристика коэфф. мощности, здесь больше относится к блоку питания, нежели к самой лампе. Данный cos ϕ может принимать значение от ноля до единицы.
Ноль означает, что полезная работа не совершается. Единица — вся энергия идет на совершение полезной работы.
Чем выше коэффициент мощности, тем ниже потери электроэнергии. Вот таблица косинуса фи для различных потребителей:
Вот таблица косинуса фи для различных потребителей:
Как измерить коэффициент мощности
Если вы не знаете точный коэфф. мощности своего прибора, или его нет на бирке, можно ли измерить косинус фи в домашних условиях, не прибегая к различным формулам и вычислениям? Конечно можно.
Для этого достаточно приобрести широко распространенный инструмент — цифровой ваттметр в розетку.
Подключая любое оборудование через него, можно легко без замеров и сложных вычислений, узнать фактический cos ϕ.
Зачастую, фактические данные могут быть даже точнее, чем написанные на шильдике, которые рассчитаны для идеальных условий.
Если он слишком низкий, что делать, чтобы привести его значение как можно ближе к единице? Можно это дело определенным образом компенсировать. Например, с помощью конденсаторов.
Однако это тема совсем другой статьи.
Наука: Наука и техника: Lenta.
 ru
ru
Ученые рекомендовали показывать фильм «Интерстеллар» на уроках физики в средней школе. Фильм удостоился похвалы за доступное объяснение общей теории относительности, а также за высокую научную точность в изображении кротовых нор. Статьи об образовательной ценности «Интерстеллара» вышли в журналах American Journal of Physics и Classical and Quantum Gravity, сообщает BBC News.
Научным консультантом (а также одним из исполнительных продюсеров) фильма выступил известный физик-теоретик Кип Торн (Kip Thorne) из Калифорнийского технологического института. Вместе с режиссером Кристофером Ноланом (Christopher Nolan) он попытался включить в «Интерстеллар» максимум научных фактов, чтобы вдохновить новое поколение на покорение космоса.
«Все физические явления в фильме были подвергнуты тщательному анализу. Эксперты пришли к единому мнению о научной точности их отображения. Данная статья призвана убедить преподавателей физики показывать «Интерстеллар» на уроках, чтобы объяснять школьникам общую теорию относительности», — отмечают авторы статей.
Хотя кротовые норы играют важную роль в сюжете «Звездного пути» и «Звездных врат», только в «Интерстелларе» этот «туннель» в пространстве изображается так, как его бы видел находящийся рядом человек.
Материалы по теме
08:11 — 29 декабря 2014
09:24 — 20 ноября 2014
При создании компьютерной графики фильма (речь идет о сверхмассивной черной дыре и кротовой норе, соединяющей Солнечную систему с другой галактикой) использовались научные уравнения. Фирма Double Negative, занимающаяся специальными эффектами, разработала новое программное обеспечение, благодаря которому стало возможным рассчитать, как свет проходит сквозь искривленное пространство вокруг черной дыры.
Затем эти программы создали изображения в сверхчетком разрешении, пригодные для голливудского фильма. Обычно в научно-фантастических картинах кротовую нору показывают как гигантскую воронку, куда падают объекты. Однако благодаря ученым авторы спецэффектов представили ее как висящий в космосе хрустальный шар, внутри которого находилось искаженное изображение другой галактики.
В интервью BBC News Нолан отмечает, что научные неточности в современном кино больше недопустимы. «В наше время потребителям легко получить доступ к информации. Когда вы посмотрите фильм о конкретном событии или явлении, вы вернетесь домой и прочитаете об этом в Wikipedia и сразу поймете, насколько правдива была картина», — считает режиссер.
В целом создатели голливудских фильмов стали более внимательны к корректному отражению научных фактов в своем творчестве. Важную роль в этом сыграл проект Национальной академии наук США «Обмен информацией между наукой и индустрией развлечений» (Science and Entertainment Exchange), в рамках которого ученые консультируют режиссеров и продюсеров (как блокбастеров, так и малобюджетных фильмов). Более того, именно голливудские фильмы назвали стимулом роста популярности физики среди молодежи (число студентов-физиков в британских вузах за последние четыре года выросло почти в полтора раза).
Потенциальная энергия: определение, виды, формулы
Определение потенциальной энергии
Энергия, говоря простым языком, это возможность что-либо сделать, возможность совершить работу. То есть, если какое-либо тело может совершить какую-либо работу, то про это тело можно сказать, что оно обладает энергией. По сути, энергия — это мера различных форм движения и взаимодействия материи, а её изменение происходит при совершении некоторой работы. Таким образом, совершённая работа всегда равна изменению какой-либо энергии. А значит, рассматривая вопрос о совершённой телом работе, мы неизбежно приходим к изменению какого-либо вида энергии. Вспомним также и тот факт, что работа совершается только в том случае, когда тело под действием некоторой силы движется, и при этом сама работа определяется как скалярное произведение вектора этой силы и вектора перемещения, то есть А = F*s*cosa, где а — угол между вектором силы и вектором перемещения. Это нам пригодится в дальнейшем для вывода формул различных видов энергии.
То есть, если какое-либо тело может совершить какую-либо работу, то про это тело можно сказать, что оно обладает энергией. По сути, энергия — это мера различных форм движения и взаимодействия материи, а её изменение происходит при совершении некоторой работы. Таким образом, совершённая работа всегда равна изменению какой-либо энергии. А значит, рассматривая вопрос о совершённой телом работе, мы неизбежно приходим к изменению какого-либо вида энергии. Вспомним также и тот факт, что работа совершается только в том случае, когда тело под действием некоторой силы движется, и при этом сама работа определяется как скалярное произведение вектора этой силы и вектора перемещения, то есть А = F*s*cosa, где а — угол между вектором силы и вектором перемещения. Это нам пригодится в дальнейшем для вывода формул различных видов энергии.
Энергию, связанную с взаимодействием тел, называют ПОТЕНЦИАЛЬНОЙ ЭНЕРГИЕЙ. Иначе говоря, если тело за счёт взаимодействия с другим телом может совершить некоторую работу, то оно будет обладать потенциальной энергией, и при совершении работы будет происходить изменение этой энергии. Обозначают механическую потенциальную энергию чаще всего — Еп.
Обозначают механическую потенциальную энергию чаще всего — Еп.
Виды потенциальной энергии
Существуют различные виды потенциальной энергии. К примеру, любое тело на Земле находится в гравитационном взаимодействии с Землёй, а значит обладает потенциальной энергией гравитационного взаимодействия. И ещё пример — витки растянутой или сжатой пружины находятся в упругом взаимодействии друг с другом, а значит сжатая или растянутая пружина будет обладать потенциальной энергией упругого взаимодействия.
Далее мы рассмотрим только виды механической потенциальной энергии и формулы, по которым их можно рассчитать. Но в дальнейшем вы узнаете и о других видах потенциальной энергии — к примеру, о потенциальной энергии электрического взаимодействия заряженных тел, о потенциальной энергии взаимодействия электрона с атомным ядром.
Знакомьтесь: наш мир. Физика всего на свете.
Книга адресована школьникам старших классов, студентам, преподавателям и учителям физики, а также всем тем, кто хочет понять, что происходит в мире вокруг нас, и воспитать в себе научный взгляд на все многообразие явлений природы. Каждый раздел книги представляет собой, по сути, набор физических задач, решая которые читатель укрепит свое понимание физических законов и научится применять их в практически интересных случаях.
Каждый раздел книги представляет собой, по сути, набор физических задач, решая которые читатель укрепит свое понимание физических законов и научится применять их в практически интересных случаях.
Купить
Формулы потенциальной энергии
Перед тем как приступить к выводу формул потенциальной энергии, ещё раз вспомним, что совершённая телом или над телом работа равна изменению его энергии. При этом, если само тело совершает работу, то его энергия уменьшается, а если над телом совершают работу, то его энергия увеличивается. К примеру, если спортсмен поднимает штангу, то он сообщает ей потенциальную энергию гравитационного взаимодействия, а если он отпускает штангу и она падает, то потенциальная энергия гравитационного взаимодействия штанги с Землёй уменьшается. Также, если вы открываете дверь, растягивая пружину, то вы сообщаете пружине потенциальную энергию упругого взаимодействия, но если потом дверь закрывается, благодаря сжатию пружины в начальное состояние, то и энергия упругой деформации пружины уменьшается до нуля.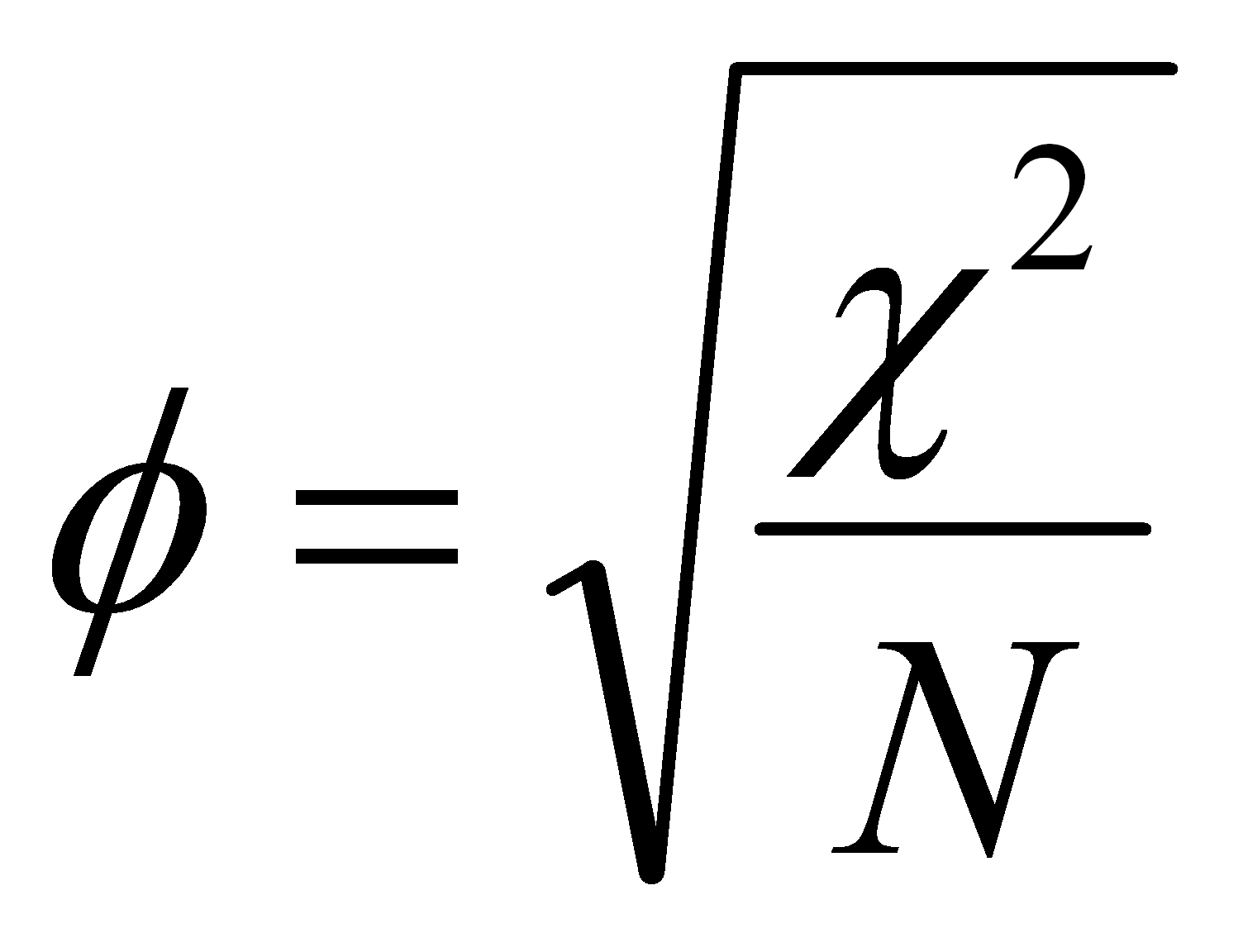
А) Чтобы вывести формулу потенциальной энергии гравитационного взаимодействия, рассмотрим, какую работу совершает тело, двигаясь под действием силы тяжести:
А = F*s = mg*s = mg*(h1
— h2) = mgh1
— mgh2
= Eп1
— Еп2, то есть, мы получили, что потенциальная энергия гравитационного взаимодействия тела с Землёй может быть вычислена по формуле: Еп = mgh.
Здесь важно отметить, что поверхность Земли принимается за начало отсчёта высоты, то есть для тела, находящегося на поверхности Земли Еп = 0, для тела, поднятого над Землёй Еп > 0, а для тела, находящегося в яме глубиной h, Еп < 0.
Отметим также и то, что в формуле работы отсутсвовал cosa. Это не случайно. Ведь если тело движется по сложной траектории, то, какой бы сложной она ни была, её можно разбить на множество вертикальных и горизонтальных участков. Но на горизонтальных участках работа силы тяжести будет равна нулю, так как угол между силой тяжести и перемещением будет прямым, а значит работа будет совершаться только на вертикальных участках траектории, для которых cosa = 1 или cosa = −1.
Тогда можно сделать ещё один важный вывод — работа силы тяжести не зависит от формы траектории, а только от расположения начальной и конечной точки. А это не случайность — это свойство любых сил, сообщающих телам потенциальную энергию. Такие силы называют потенциальными и сила тяжести — одна из них. К потенциальным силам относится и сила упругости.
Б) Чтобы вывести формулу потенциальной энергии упругой деформации, рассмотрим, какую работу нужно совершить, чтобы растянуть пружину, изменив её длину на х (х = l — l0):
А = –Fупр(ср.)*s,
Во-первых, знак минус в формуле стоит потому, что угол между силой упругости и перемещением свободного конца пружины равен 180 градусов и cosa = −1.
Во-вторых, возникающая при растяжении пружины сила упругости является переменной силой, в отличие от силы тяжести, поэтому в формуле работы стоит средняя сила упругости. При этом величина силы упругости, в соответствии с законом Гука, прямо пропорциональна изменению длины пружины, а значит её среднее значение можно определить так:
Fупр(ср. ) = (Fупр(нач.) + Fупр(конеч.))/2
) = (Fупр(нач.) + Fупр(конеч.))/2
И так как Fупр(нач.) = 0, а Fупр(конеч.) = kх, то:
А = —kх*s/2
Но s = x, поэтому: А = —kx2/2 = 0 — kх2/2 = Еп1 — Еп2.
В итоге, мы получили формулу потенциальной энергии упругой деформации: Еп = kx2/2.
Что еще почитать?
Методические советы учителям
1) Обязательно обратите внимание учащихся на связь энергии и работы.
2) Не давайте учащимся формулы потенциальной энергии без вывода.
3) Обратите внимание учащихся на то, что оба вида потенциальной энергии зависят от выбора начальной точки, то есть от системы координат.
4) При выводе формул потенциальной энергии обязательно поясните учащимся почему отсутствует cosa в формуле работы.
5) Отметьте, что и работа силы тяжести, и работа силы упругости не зависят от формы траектории и, следовательно равны нулю на замкнутой траектории — это общее и важное свойство всех потенциальных сил.
#ADVERTISING_INSERT#
Учебные материалы по физике для 7 класса
Преподаватель — Юлия Олеговна Беличенко
Учебные фильмы
В.И. Гервидс. Демонстрации по физике. Фильмы НИЯУ «МИФИ»
«Леннаучфильм», «Empiric School», «Наука и техника», «ФизматФильм»,
«Уроки на Yuotube», «AlexanderEvgrafov», «СЗТУ», «PhysicsField»,
«GetAGlass» «Роман Кунікевич»
Жидкостный и газовый термометры
Теплопроводность. Опыт с гвоздями
Теплопроводность газов. Свечение
Конвекция в воде
Конвекция в жидкости
Тепловое излучение
Теплоемкость металла. Теплота кристализации
Теплота кристализации
Теплопроводность металла и дерева
Инерция тел
Удар тележек. Механика
Перегретая жидкость
Ячейки Бенара
Теплопроводность металлов
Слипание твердых тел
Межмолекулярные силы, плитки Иогансона
Эксперимент «Переохлаждённая жидкость»
Моментальное замерзание воды
Мыльный пузырь замерзает
Теплота кристаллизации
Опыты с жидким азотом. Образование тумана
Возгонка йода. Сублимация
Испарение твердой углекислоты
Найти влажность воздуха по психрометру
Психрометр и гигрометр
Самодельная паровая турбина
Газовый сифон. Тяжелый газ
Тяжелый газ
Плотность вещества
Прибор Анселя
Реактивное движение. Горелка
Принцип действия двигателя внутреннего сгорания
Объем тела
Демонстрация с грузом на пружине
Свободное падение
Электризация трением. Фильм первый
Электризация трением. Фильм второй
Фильм второй
Зависимость упругих свойств от температуры
Закон Гука. Фильм первый
Закон Гука. Фильм второй
Невесомость. Опыт с трубкой Ньютона
Положительное и отрицательное электричество
Изучение электрического поля
Электростатическая защита
Распределение зарядов
Делимость зарядов
Анимация «Строение атома и ядра»
Анимация модели атома
Трение
Сварка трением карданного вала
Дорожка на воздушной подушке
Послушная монета
Статическое электричество
Направление движения электричества
Электрофорная машина
Боржоми. Лампочка горит
Лампочка горит
Положительное и отрицательное электричество
Электричество в технике
Cамодельный моторчик из батарейки
Трение качения. Подшипники
Резка дерева бумажным диском
Давление
Занимательные физические опыты — Физика на воздушных шариках
Живая перчатка
Мы вас приветствуем (Опыт с перчаткой)
Опыт с монетами
Вода в космосе
Учебник по физике.
 Оглавление
Оглавление
Перышкин А.В. Физика. 7 класс. Учебник
Издательство «Дрофа», 2013
Введение
§ 1 Что изучает физика
§ 2 Некоторые физические термины
§ 3 Наблюдения и опыты
§ 4 Физические величины. Измерение физических величин
§ 5 Точность и погрешность измерений
§ 6 Физика и техника
Глава 1.
ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О СТРОЕНИИ ВЕЩЕСТВА
§ 7 Строение вещества
§ 8 Молекулы
§ 9 Броуновское движение
§ 10 Диффузия в газах, жидкостях и твёрдых телах
§ 11 Взаимное притяжение и отталкивание молекул
§ 12 Агрегатные состояния вещества
§ 13 Различие в молекулярном строении твёрдых тел, жидкостей и газов..
Глава 2.
ВЗАИМОДЕЙСТВИЕ ТЕЛ
§ 14 Механическое движение
§ 15 Равномерное и неравномерное движение
§ 16 Скорость. Единицы скорости
§ 17 Расчёт пути и времени движения
§ 18 Инерция
§ 19 Взаимодействие тел
§ 20 Масса тела. Единицы массы
Единицы массы
§ 21 Измерение массы тела на весах
§ 22 Плотность вещества
§ 23 Расчёт массы и объёма тела по его плотности
§ 24 Сила
§ 25 Явление тяготения. Сила тяжести
§ 26 Сила упругости. Закон Гука
§ 27 Вес тела
§ 28 Единицы силы. Связь между силой тяжести и массой тела
§ 29 Сила тяжести на других планетах. Физические характеристики планет
§ 30 Динамометр
§ 31 Сложение двух сил, направленных по одной прямой. Равнодействующая сил
§ 32 Сила трения
§ 33 Трение покоя
§ 34 Трение в природе и технике
Глава 3.
ДАВЛЕНИЕ ТВЁРДЫХ ТЕЛ. ЖИДКОСТЕЙ И ГАЗОВ
§ 35 Давление. Единицы давления
§ 36 Способы уменьшения и увеличения давления
§ 37 Давление газа
§ 38 Передача давления жидкостями и газами. Закон Паскаля
§ 39 Давление в жидкости и газе
§ 40 Расчёт давления жидкости на дно и стенки сосуда
§ 41 Сообщающиеся сосуды
§ 42 Вес воздуха. Атмосферное давление
§ 43 Почему существует воздушная оболочка Земли
§ 44 Измерение атмосферного давления. Опыт Торричелли
Опыт Торричелли
§ 45 Барометр-анероид
§ 46 Атмосферное давление на различных высотах
§ 47 Манометры
§ 48 Поршневой жидкостный насос
§ 49 Гидравлический пресс
§ 50 Действие жидкости и газа на погружённое в них тело
§ 51 Архимедова сила
§ 52 Плавание тел
§ 53 Плавание судов
§ 54 Воздухоплавание
Глава 4.
РАБОТА И МОЩНОСТЬ. ЭНЕРГИЯ
§ 55 Механическая работа. Единицы работы
§ 56 Мощность. Единицы мощности
§ 57 Простые механизмы
§ 58 Рычаг. Равновесие сил на рычаге
§ 59 Момент силы
§ 60 Рычаги в технике, быту и природе
§ 61 Применение закона равновесия рычага к блоку
§ 62 Равенство работ при использовании простых механизмов.
«Золотое правило» механики
§ 63 Центр тяжести тела
§ 64 Условия равновесия тел
§ 65 Коэффициент полезного действия механизма
§ 66 Энергия
§ 67 Потенциальная и кинетическая энергия
§ 68 Превращение одного вида механической энергии в другой
«Бомба» от Тодоровского и Копылова превзошла ожидания Курчатова и Харитона
Рамки остросюжетного сериала, который на четыре вечера прошлой недели приковал внимание зрителей канала «Россия-1», определяются хронологически с точностью до одного дня и даже минуты. И это при том, что фильм создавался и анонсировался как художественный, а не документальный, хотя и с опорой на реальные исторические события, с сохранением подлинных имен и фамилий: Игорь Курчатов, Лаврентий Берия, Юлий Харитон, Борис Ванников, Нильс Бор…
И это при том, что фильм создавался и анонсировался как художественный, а не документальный, хотя и с опорой на реальные исторические события, с сохранением подлинных имен и фамилий: Игорь Курчатов, Лаврентий Берия, Юлий Харитон, Борис Ванников, Нильс Бор…
Завязка — поздний вечер 6 августа 1945 года, когда в Москве по приказу Берии экстренно собрали ученых, чтобы сообщить им пренеприятное известие: американцы сбросили на Хиросиму атомную бомбу.
Финал (у фильма) — 29 августа 1949-го, 7.00 по московскому времени, когда на испытательной башне Семипалатинского полигона привели в действие «изделие РДС-1». Чтобы увидеть ожидаемую картину ядерного взрыва и доложить наверх: есть Реактивный Двигатель Сталина! А уж после этого заявить миру, своим союзникам и антагонистам: Россия Делает Сама.
1473 дня и ночи — больше, чем Великая Отечественная — продолжалась эта неведомая абсолютному большинству, героическая и жертвенная эпопея, давшая начало тому, что полвека спустя назовут Атомным проектом СССР.
Едва ослабли секретные грифы, приоткрылись архивы и сейфы с документами «Особая папка», историки, журналисты, писатели, а вослед им режиссеры и сценаристы документального кино принялись воссоздавать отдельные эпизоды этого прошлого. И уже, надо признать, выстроена довольно полная и подкрепленная документами ретроспектива.
Сказать на этом — документальном — поле что-то принципиально новое уже трудно. А вот средствами художественного кино…
Это будет «Бомба»! — таким заголовком на различных сайтах и медиа-площадках анонсировали телепремьеру одноименного фильма от Валерия Тодоровского (генеральный продюсер) и режиссера-постановщика Игоря Копылова (стал известен недавними фильмами «Ржев» и «Ленинград 46»).
Получилось ли?
Если судить о том, как наглядно, в буквальном смысле на спичках объясняли с экрана неподготовленному зрителю сложнейшие научные и конструкторские задачи, которые пришлось решать героям фильмам — безусловно, да. Тому, как аргументировали и доказывали молодые советские физики преимущества вертикальной компоновки реактора перед горизонтальной, чтобы уже была реализована в США, могут поучиться ведущие научно-популярных и образовательных программ на российском телевидении.
Источник нейтронов и их поглотитель, графит для реактора и йодная яма, плутоний, которого нет в природе, а в бомбе без него никак — разве это материал для остросюжетного кино? Даже в фильме «Девять дней одного года», когда полстраны симпатизировало ученым-физикам, а едва ли не каждый второй мальчишка им завидовал, о таком с экрана не говорили.
А критмасса, имплозия, идеальная симметрия при взрывном сферическом обжатии заряда — как это объяснить телезрителю? И надо ли вообще в художественном фильме? Даже притом, что в Cinema пришла компьютерная графика…
Полосатый астраханский арбуз, попавший в руки физику-экспериментатору Михаилу Рубину (актер Евгений Ткачук) разом отмел сомнения: его простая, как все гениальное, догадка стала прозрением и для зрителя. Захватила, повела вместе с героем дальше и уже не отпустила до самого последнего кадра.
Уверенный в себе и дерзкий, способный нагрубить даже Берии, за что и попал в ГУЛАГ — всю войну лес рубил на Севере — в диалоге с Харитоном он бросает крамольные для того времени слова: «Если б из лагеря меня не вытащили сюда, уже два года был бы на свободе…»
Профессор Харитон, лишь не на много старше, коллегу за такие параллели не осуждает, хотя и не соглашается: «А я не могу перестать здесь работать». И раз за разом, не афишируя, вступается за Михаила Рубина, у которого душа как оголенный нерв, перед Ванниковым и Берией, просит понять и простить его вспыльчивость.
И раз за разом, не афишируя, вступается за Михаила Рубина, у которого душа как оголенный нерв, перед Ванниковым и Берией, просит понять и простить его вспыльчивость.
Историки науки и, в частности, советского Атомного проекта, в образе гениального физика Рубина (на мой взгляд — лучшая актерская работа в фильме) угадывают собирательные черты и факты биографии Якова Зельдовича, Кирилла Щелкина и, конечно, Льва Ландау, хотя имя последнего Михаил сам называет в фильме — словно дистанцируясь и, одновременно, сливаясь с ним.
Рубин — не единственный герой сериала, у которого были и угадываются реальные прототипы.
Самая очевидная аналогия — в позиции и поступках радиолога Анны Галеевой (актриса Евгения Брик) и врача в четвертом поколении, выпускницы Свердловского мединститута Ангелины Гуськовой (1924-2015). Незадолго до ухода из жизни Ангелина Константиновна сама отважится описать свою работу на Урале, связанную с комбинатом «Маяк» и первым реактором, в автобиографической книге «Атомная отрасль глазами врача». Она станет член-корреспондентом Академии медицинских наук СССР, главным научным сотрудником Института биофизики, обладателем высоких и заслуженных наград. Но самым близким человеком в конце жизни будет ей лишь родная сестра — своей семьи Ангелина Гуськова так и не создаст.
Она станет член-корреспондентом Академии медицинских наук СССР, главным научным сотрудником Института биофизики, обладателем высоких и заслуженных наград. Но самым близким человеком в конце жизни будет ей лишь родная сестра — своей семьи Ангелина Гуськова так и не создаст.
Перекличка судеб и времен видна уже в созвучии имен: Ангелина Гуськова — Анна Галеева. И та, и другая добивались организации строгого дозиметрического контроля, чтобы защитить от переоблучения работающих на атомном реакторе и смежных с ним участках радиохимического производства. Сами при этом тоже рисковали — собственным здоровьем, возможностью иметь семью и продолжить род…
И в этом «Бомба» — безусловно, бомба. Но местами сериал для взрослых не по-взрослому метафоричен.
Обручальное кольцо, в сердцах сдернутое с пальца и выброшенное из машины — на ходу, в придорожную грязь, весьма пожую на ту, что месили ногами колонны заключенных, присланные копать котлован для «Аннушки» — первого на Урале промышленного реактора для наработки оружейного плутония.
И первый в своем роде индивидуальный дозиметр — одеваемый, как и кольцо, на палец. Его радиолог Анна Галеева привезла из Москвы, из Института биофизики, и словно в знак примирения успела передать мужу — буквально за мгновение до того, как Игорь Муромцев (актер Виктор Добронравов) и два его товарища-добровольца пойдут, образно говоря, на амбразуру. А в прямом смысле — под жесткий, фактически смертельный поток излучения, чтобы устранить аварийное спекание топлива — так называемый «козел» в одном из каналов действующего реактора.
Следующие за этим сцены — пожалуй, самые метафоричные в фильме: физики в белых комбинезонах с бранспойтами наизготовку, чтобы по первой команде залить взбунтовавшийся реактор — как бронебойщики под Москвой перед надвигающимися танками врага. Тут врага нет, но опасность чудовищная, хотя для глаз невидимая. И что все понимают — рукотворная…
У оператора фильма Сергея Мачильского немало творческих находок, удачных ракурсов и, что хотелось бы особо подчеркнуть, молчаливых сцен. Безмолвных и выразительных. Такие паузы, вопреки мнению отдельных критиков, лично мне не кажутся затянутыми или чересчур театральными. Напряженные «паузы» нужны, чтобы и зритель позволил себе задуматься, а не бежал, глотая попкорн, только за сюжетом…
Безмолвных и выразительных. Такие паузы, вопреки мнению отдельных критиков, лично мне не кажутся затянутыми или чересчур театральными. Напряженные «паузы» нужны, чтобы и зритель позволил себе задуматься, а не бежал, глотая попкорн, только за сюжетом…
Камера оператора не нарочито, но точно акцентирует детали. Очень характерно, например, посверкивали стекла очков у Лаврентия Берии — и в пультовой реактора, и в театральной ложе. Но это, пожалуй, и все, что сближало его кинематографический облик, многократно воссозданный на экране, с тем, который явил в сериале «Бомба» Виталий Коваленко — конечно, не без участия режиссера.
Критиковать «за непохожесть», как и хвалить «за оригинальность», «новое прочтение» не стану. Ведь изначально условились, что речь о кино художественном, и тут нет места категориям «похож — не похож». Но одну ремарку себе позволю.
Лет десять назад вышел из печати и даже был подарен «Российской газете» фолиант на 1180 страниц с провокационным названием «Берия. Лучший менеджер XX века». За псевдонимом Сергей Кремлев не скрывал своего авторства уже знакомый нам по публикациям Сергей Брезкун, в то время сотрудник одного из аналитических подразделений РФЯЦ-ВНИИЭФ — того самого ядерного центра в Сарове, где была сконструирована первая в СССР атомная бомба. Инженер по образованию, а по роду занятий — въедливый историк и публицист-интерпретатор, он издал к этому дню немало резонансных книг, в том числе еще несколько, посвященных Берии, включая его, якобы сохранившиеся дневники. А «гроссбух» в тысячу с лишним страниц стал бестселлером и выдержал шесть переизданий.
Лучший менеджер XX века». За псевдонимом Сергей Кремлев не скрывал своего авторства уже знакомый нам по публикациям Сергей Брезкун, в то время сотрудник одного из аналитических подразделений РФЯЦ-ВНИИЭФ — того самого ядерного центра в Сарове, где была сконструирована первая в СССР атомная бомба. Инженер по образованию, а по роду занятий — въедливый историк и публицист-интерпретатор, он издал к этому дню немало резонансных книг, в том числе еще несколько, посвященных Берии, включая его, якобы сохранившиеся дневники. А «гроссбух» в тысячу с лишним страниц стал бестселлером и выдержал шесть переизданий.
Упоминаю все это, чтобы сказать: образ Лаврентия Берии как руководителя Спецкомитета «по урановой проблеме», созданный в сериале «Бомба», — лучшее, о чем мог бы мечтать автор более чем спорных книг и вольных интерпретаций на болезненные темы из нашего прошлого. Но большинство других историков, думаю, не согласятся принять такую заведомо комплиментарную трактовку.
Если посмотреть все восемь серий «Бомбы» и принять их за чистую монету, невольно подумаешь: «Лучшего руководителя нашим ученым просто и желать нельзя!» Деловой, немногословный, требовательный. Лица и просьбы запоминает — ну просто отец родной! А как слово держит: сказал — сделал.
Лица и просьбы запоминает — ну просто отец родной! А как слово держит: сказал — сделал.
Рядом с «товарищем маршалом» начальник Первого главного управления при ГКО СССР, а до этого, еще в годы войны, нарком боеприпасов Борис Ванников в исполнении Владимира Богданова — просто генерал на побегушках со звездой Героя соцтруда. Да и профессор Курчатов (актер Михаил Хмуров) на том же фоне — что-то усредненное между начальником смены на пульте управления реактором и модератором, как сейчас бы сказали, на коллоквиуме физиков и материаловедов. И пресловутая борода авторитета не добавляет…
А вот товарищ Берия, что самое удивительное, всегда оказывается в нужном месте в самый острый и нужный момент. Будь то спор профессора Курчатова с маститыми академиками, пуск опытного реактора или уже апофеоз — подрыв атомного заряда на полигоне под Семипалатинском.
Лаврентию Павловичу — кому же еще! — предлагает Игорь Курчатов перевести рубильник на пульте подрыва. И актер Виталий Коваленко в образе вездесущего Берии этот «рубильник судьбы» переводит, чего на самом деле не было.
Команда на подрыв, что давно и широко известно, выдавалась запущенной в строго определенный момент автоматикой, она же последовательно включала и синхронизировала всю регистрирующую аппаратуру опытного поля.
…Фильм про физиков и бомбу не стал бы сериалом, не будь построен на любовном треугольнике, где все по классической схеме: любовь, разрыв, арест, разлука, свадьба друга и стараниями друга — нежданное освобождение. А дальше снова споры, сомнения, драка, семейный разлад и каждый — в поисках ответов на вечные вопросы: что делать? с кем быть? где выход?
Мимолетная встреча мятущегося физика с осужденной художницей из Ленинграда (актриса Ольга Смирнова), которая отбывала срок в Сарове, где невольником чувствовал себя и Миша Рубин, стала для обоих знаком судьбы. И соединила их свободные израненные души.
Сначала на земле, но ненадолго. Лишь до поры, пока обозленный таким поворотом начальник женской колонии (а для него — гарема) не отправил Ольгу этапом на Север, где она погибла от крупозного воспаления легких, как и предрекал «гражданин начальник» своей заключенной избраннице и своему обидчику Рубину.
Потом их души соединились навсегда. В тот самый день 29 августа, когда гениальный ученый, физик-экспериментатор и друг, которых поискать, свой в доску Мишка Рубин, получивший накануне радиационной ожог такой степени, когда вся медицина бессильна, не покинул дом-макет рядом с Бомбой. И сгорел, испарился в рукотворном чудовищном шаре, что за мгновение поднялся до самых облаков, на которые еще в саровском храме показывала Ольга.
До облаков, а может быть, и выше.
P.S.
Одновременно с титрами в конце каждой из восьми серий (их показывали по две четыре вечера подряд) зрители могли видеть и слышать мнения ветеранов атомной отрасли, в том числе тех, кто работал рядом и в одно время с академиками Курчатовым, Харитоном, Зельдовичем, кто встречался при жизни с Борисом Ванниковым, помнит и знает не по рассказам то время и обстановку. Их оценки и суждения не касаются самого фильма или каких-то его эпизодов, потому что записывались и монтировались, судя по всему, параллельно или даже независимо от работы над сериалом. И потому в проекции на художественное произведение с большой долей авторского вымысла, сконструированных обстоятельств и собирательных образов выглядят чужеродно, как наспех приклеенные усы.
И потому в проекции на художественное произведение с большой долей авторского вымысла, сконструированных обстоятельств и собирательных образов выглядят чужеродно, как наспех приклеенные усы.
Если б решились показать тем же людям смонтированный фильм, их голоса, уверен, зазвучали бы совсем по-другому.
С какой целью решили соединить вымышленное с документальным? Возможно, лишь для того, чтобы найти компромисс. Между ожиданиями заказчиков и продюсеров фильма (а их под руководством Валерия Тодоровского восемь) и тем, что в итоге получилось у съемочной группы во главе с режиссером-постановщиком Игорем Копыловым.
Как бы там ни было, премьера сериала «Бомба» состоялась и стала событием общественной жизни.
Как найти начальную фазу колебаний
При расчетах, связанных с циклическими явлениями (например, при описании колебаний математического маятника) важно уметь находить состояние системы, с которого начался отсчет процесса — начальную фазу.
Фаза представляет собой угловую координату, описываемую формулой
$\varphi = ω_0 \cdot t$,
где $ω_0$ — угловая скорость, $t$ — прошедшее время.
Выбрав в качестве единицы измерения углов радианы, формулу можно переписать как
$\varphi = 2 \cdot \pi \cdot \frac{t}{T}$,
где $2 \cdot \pi$ — количество радиан в полном цикле, $T$ — период одного колебания. Отношение $\frac{t}{T}$ показывает, сколько колебаний (полных и неполных) выполнила система.
Фазы циклических процессов с одинаковыми угловыми скоростями и длящиеся одинаковое время, могут отличаться в связи с тем, что они в момент начала наблюдений находились в разных состояниях. Такая разница называется сдвигом фаз. Например, углы отклонения от вертикали двух идентичных маятников, колеблющиеся с одинаковой частотой, могут различаться. Это зависит от того, на какой начальный угол каждый из них был отклонен в момент начала отсчета времени. Сдвиг фаз может быть обусловлен тем, что маятники были запущены в разное время (до начала отсчета), или одному из них при меньшем начальном отклонении от вертикали было придано дополнительное угловое ускорение за счет удара и т.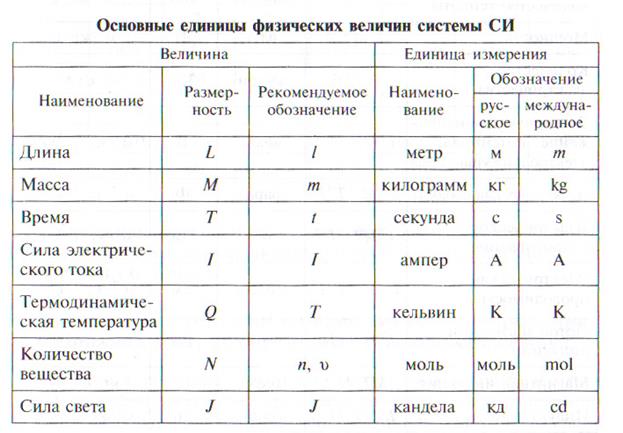 п.
п.
Циклический процесс, в отличие от движения по незамкнутой траектории, характеризуется повторяемостью некоторой характеристики (например, напряжения в сети переменного тока), что можно описать с помощью функций синуса или косинуса:
$x = A \cdot \cos(ω_0 \cdot t + \varphi)$,
$x = A \cdot \sin(ω_0 \cdot t + \varphi)$.
где $A$ — амплитуда (максимальный размах) колебаний, $\varphi$ — начальная фаза.
Функцией синуса удобнее пользоваться, когда угловая координата тела в момент начала наблюдений равна нулю, функцией косинуса — когда имеет место сдвиг фаз. Так, «косинус фи» — устойчивое понятие, применяемое в электротехнике при описании переменного тока.
Пример 1
Найти начальную фазу колебаний с амплитудой $A = 0,2 м$, если в момент начала измерений $t_0$ смещение циклического параметра $x$ составляло $-0,2 м$.
Подставим в уравнение числовые значения:
$x = A \cdot \sin(\omega_0 \cdot t + \varphi)$
$-0,2 = 0,2 \cdot \sin(\omega_0 \cdot 0 + \varphi) \implies -0,2 = 0,2 \cdot \sin(\varphi)$
$\sin(\varphi) = \frac{-0,2}{0,2}$
$\varphi = \arcsin(\frac{-0,2}{0,2}) = \frac{3 \pi}{2}$
Ответ: колебания начались с фазы $1\frac{1}{2} \pi$
Gravity — Что такое гравитационное поле $ \ Phi $ против гравитационного потенциала $ U $
Существует старое соглашение, согласно которому «в скалярах используются греческие буквы, а в векторах — латинские буквы». Это полностью искусственно и даже непоследовательно. Они точно будут обозначать сопротивление как $ R $, а не греческое.
Это полностью искусственно и даже непоследовательно. Они точно будут обозначать сопротивление как $ R $, а не греческое.
Итак, да, потенциал обычно обозначается как $ \ phi $. Это тоже забавно, потому что это не $ \ Phi $ или $ \ varphi $, а $ \ phi $. Они больше не хотят писать $ U $ или $ V $, но я всегда буду использовать это.Фактически, я использую $ V _ {\ vec {g}} $ для гравитационного, что полностью проясняет. Я знаю, что это не было частью вашего вопроса, но, в отличие от общепринятых мыслей, нотация имеет большое значение (по крайней мере, для меня). Конечно, вы можете использовать любой символ, если вы последовательны и четко установите его в начале.
Наконец, нет ничего странного в том, чтобы просить о потенциале. И гравитационное поле, и гравитационный потенциал — ПОЛЯ.
Гравитационное поле — векторное поле.Это функция at «генерирует» вектор в каждой точке пространства. Гравитационное поле задает вектор каждой точке пространства. Этот вектор — $ \ vec {g} $, и он таков, что $ m \ vec {g} $ — действительная сила.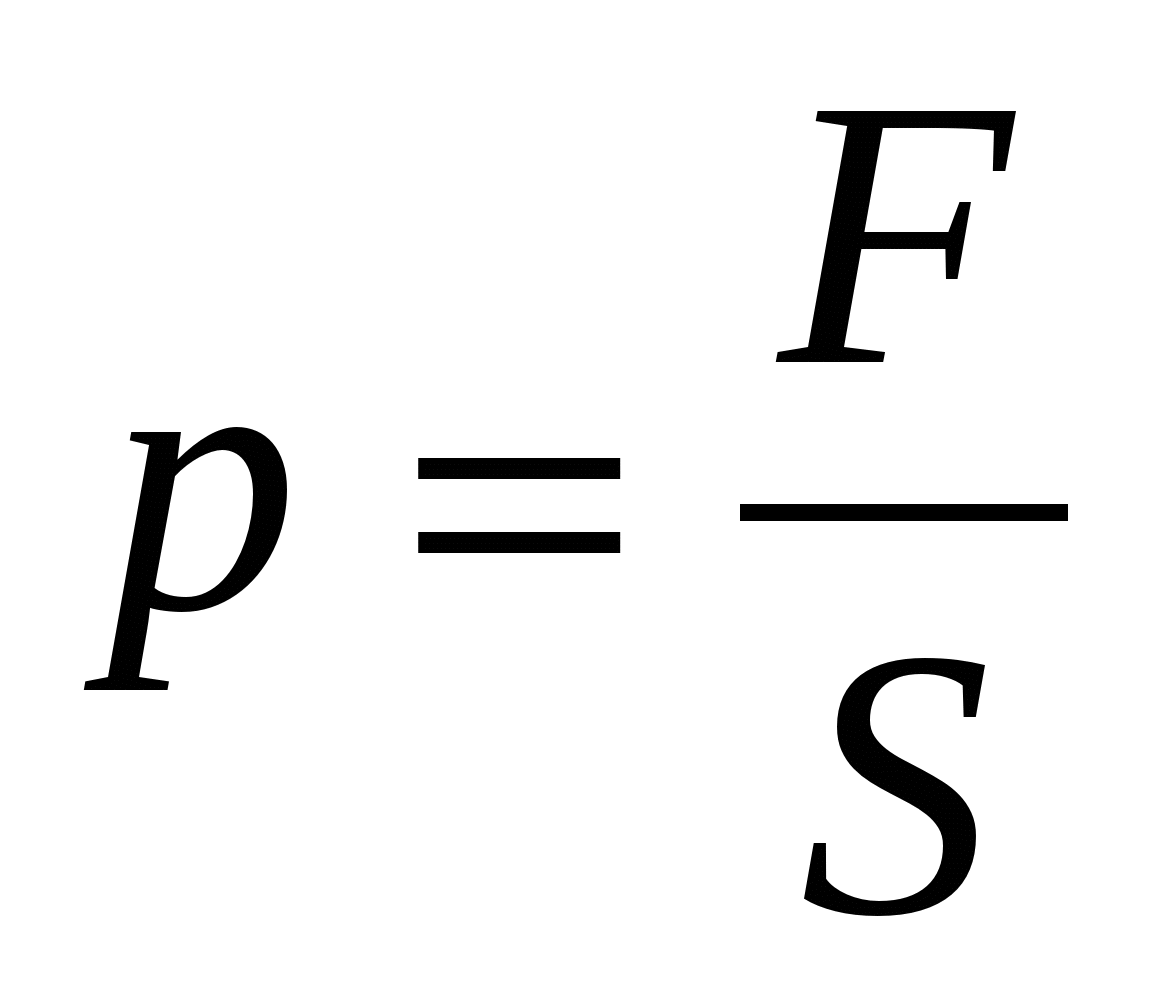
Гравитационный потенциал — это сакаларное поле. Каждой точке пространства присваивается номер $ \ phi_g $ (или $ U $ или что-то еще), так что $ m \ cdot \ phi_g $ является реальной потенциальной энергией.
С пустым пространством ничего нет; но как только вы помещаете в нее массу, каждая точка в пространстве немедленно получает вектор и число ($ \ vec {g}, \ phi_g $).Ничего не произойдет, если вы не поместите вторую массу. Как только вы поместите вторую массу, она получит потенциальную энергию $ E_ {pg} = m \ phi_g $ и столкнется с силой $ \ vec {F} = m \ vec {g} $.
Эти величины действительно меняются от одной точки к другой (в общем), поэтому логично, что проблемы просят вас «найти общую формулу» для этих вещей. Общая формула для $ \ vec {g} $ и $ \ phi_g $, так что вам просто нужно подставить точку $ (x, y, z) $, и вы получите желаемое значение.
квантовая механика — что такое фазовый угол волновой функции $ \ phi \, $?
Чтобы ответить на ваши вопросы 1 и 2: этот график показывает действительную часть $ \ Psi {(\ vec r, t)} = A e ^ {i (\ vec k \ cdot \ vec r- \ omega t)} $ синим цветом, а действительная часть $ \ Psi {(\ vec r, t)} = A e ^ {i (\ phi + \ vec k \ cdot \ vec r- \ omega t)} $ фиолетовым. Очевидно, что $ \ Psi $ является функцией двух переменных, поэтому вы можете рассматривать график либо как постоянный $ \ vec r $ и изменяющий $ t $, либо как постоянный $ t $ и изменяющий $ \ vec r $.
Очевидно, что $ \ Psi $ является функцией двух переменных, поэтому вы можете рассматривать график либо как постоянный $ \ vec r $ и изменяющий $ t $, либо как постоянный $ t $ и изменяющий $ \ vec r $.
Величина $ \ phi $ — это просто разность фаз между двумя волнами, например. расстояние между пиками показано стрелкой на схеме.
Абсолютное значение $ \ phi $ не имеет физического значения, потому что вы можете измерить $ \ phi $ с любой точки отсчета. Однако разница в $ \ phi $ между двумя волновыми функциями имеет очень важный физический смысл, поскольку она определяет, как волны будут интерферировать.
Чтобы ответить на ваш вопрос 3: на самом деле упоминание эксперимента с двойной щелью уместно. Щели разделяют входящий свет (или электроны, или что-то еще) на два источника, назовите их $ \ Psi_a $ и $ \ Psi_b $, и если вы возьмете какую-то точку на экране, эта точка будет получать свет от $ \ Psi_a $ и от $ \ Psi_b $, но фазы двух волн, $ \ phi_a $ и $ \ phi_b $, не будут одинаковыми.
Нет никакого физического смысла в абсолютной фазе $ \ Psi_a $ и $ \ Psi_b $, $ \ phi_a $ и $ \ phi_b $, но если $ \ phi_a — \ phi_b $ является четным кратным $ \ pi $ ($ 2 \ pi $, $ 4 \ pi $ и т. Д.) Волны будут синхронизированы, и вы получите конструктивную интерференцию и яркую область.Если разность фаз кратна $ \ pi $ ($ \ pi $, $ 3 \ pi $ и т. Д.), Волны будут деструктивно интерферировать, и вы получите темное пятно. Именно поэтому вы получаете картину чередования ярких и темных полос в эксперименте с двумя щелями — это потому, что разность фаз, $ \ phi_a — \ phi_b $, изменяется при перемещении по экрану.
Таким образом, ни один эксперимент не может измерить абсолютное значение $ \ phi_a $ или $ \ phi_b $, потому что абсолютное значение не имеет физического значения. Однако эксперимент с двойной щелью может измерить разность фаз $ \ phi_a — \ phi_b $.
Simple Harmonic Oscillator — The Physics Hypertextbook
Обсуждение
Поверьте мне.
 Это просто.
Это просто.
Начните с того, что пружина опирается на горизонтальную (пока что) поверхность без трения. Прикрепите один конец к неподвижному объекту, а другой — к подвижному объекту. Запустите систему в состоянии равновесия — ничего не движется и пружина находится в расслабленном состоянии.
А теперь нарушьте равновесие. Потяните или толкните гирю параллельно оси пружины и отойдите назад.Вы знаете, что будет дальше. Система будет колебаться из стороны в сторону (или назад и вперед) под действием возвращающей силы пружины. (Восстанавливающая сила действует в направлении, противоположном смещению от положения равновесия.) Если пружина подчиняется закону Гука (сила пропорциональна растяжению), то устройство называется простым гармоническим осциллятором (часто сокращенно sho ). и способ его движения называется простым гармоническим движением (часто сокращенно shm ).
Начните анализ со второго закона движения Ньютона.
∑ F = м a
Есть только одна сила — возвращающая сила пружины (которая отрицательна, поскольку действует противоположно смещению массы из положения равновесия). Замените чистую силу законом Гука. Замените ускорение второй производной смещения.
Немного переставить.
| – | к | x = | d 2 x |
| м | дт 2 |
Это линейное дифференциальное уравнение второго порядка.Слева у нас есть функция со знаком минус перед ней (и некоторыми коэффициентами). С правой стороны у нас есть вторая производная от этой функции. Решением этого уравнения является функция, у которой вторая производная стоит со знаком минус. У нас есть две возможные функции, которые удовлетворяют этому требованию — синус и косинус — две функции, которые по сути одинаковы, поскольку каждая является просто версией другой со сдвигом фазы. Когда триггерная функция сдвигается по фазе, ее производная также сдвигается по фазе.Больше ничего не меняется, поэтому мы можем выбрать синус со сдвигом фазы или косинус со сдвигом фазы.
Когда триггерная функция сдвигается по фазе, ее производная также сдвигается по фазе.Больше ничего не меняется, поэтому мы можем выбрать синус со сдвигом фазы или косинус со сдвигом фазы.
| функция | 1-я производная | 2-я производная | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
|
Я думаю, что я воспользуюсь функцией синуса и добавлю произвольный сдвиг фазы или фазовый угол или фаза (φ, «phi»), чтобы наш анализ охватил синус (φ = 0), косинус (φ = π 2 ) и все, что между ними (φ = независимо от ). С физической точки зрения нам нужен фазовый член, чтобы учесть все возможные исходные положения — при движении равновесия в одну сторону (φ = 0), при движении равновесия в другую сторону (φ = π), полностью в одну сторону. (φ = π 2 ), полностью на другую сторону (φ = 3π 2 ) и все, что между ними (φ = независимо от ).
С физической точки зрения нам нужен фазовый член, чтобы учесть все возможные исходные положения — при движении равновесия в одну сторону (φ = 0), при движении равновесия в другую сторону (φ = π), полностью в одну сторону. (φ = π 2 ), полностью на другую сторону (φ = 3π 2 ) и все, что между ними (φ = независимо от ).
| физическое описание | фазовый сдвиг | |
|---|---|---|
| начиная с состояния равновесия, двигаясь вперед | нет (начальная фаза) | 0 радиан |
| полностью в одну сторону, остановился мгновенно | четверть цикл | π 2 радиан |
| возврат к равновесию, движение назад | половина цикла | π радиан |
| полностью на другую сторону, остановился мгновенно | трехчетвертный цикл | 3π 2 радиан |
| возврат к равновесию, движение вперед | полный цикл | 2π радиан |
Нам также нужны коэффициенты для обработки единиц. Решением нашего дифференциального уравнения является алгебраическое уравнение — положение как функция времени ( x ( t )) — которое также является тригонометрическим уравнением. Все триггерные функции являются отношениями, что делает их безразмерными (более точный математический термин) или безразмерными (термин, который я предпочитаю). Единственная единица, которую вы действительно можете поместить в функцию триггера, — это радиан. Согласно математическому определению, угол (φ) — это отношение длины дуги ( s ) к радиусу ( r ).Использование единиц СИ даст нам метры, а не метры, и размерный анализ сводится к нулю. В некотором смысле радиан — это единица измерения ничего.
Решением нашего дифференциального уравнения является алгебраическое уравнение — положение как функция времени ( x ( t )) — которое также является тригонометрическим уравнением. Все триггерные функции являются отношениями, что делает их безразмерными (более точный математический термин) или безразмерными (термин, который я предпочитаю). Единственная единица, которую вы действительно можете поместить в функцию триггера, — это радиан. Согласно математическому определению, угол (φ) — это отношение длины дуги ( s ) к радиусу ( r ).Использование единиц СИ даст нам метры, а не метры, и размерный анализ сводится к нулю. В некотором смысле радиан — это единица измерения ничего.
| φ = | с | ⇒ | ⎡ ⎢ ⎣ | рад = | м | = «без единицы измерения» | ⎤ ⎥ ⎦ |
| r | м |
Способ обойти это — добавить коэффициент, который изменяет нашу входную переменную (время) на то, что может обрабатывать триггерная функция (радианы). Эта вещь называется угловой частотой , которая в данном случае является скоростью изменения фазового угла (φ) во времени ( t ). Его символ — омега в нижнем регистре (ω).
Эта вещь называется угловой частотой , которая в данном случае является скоростью изменения фазового угла (φ) во времени ( t ). Его символ — омега в нижнем регистре (ω).
Единица измерения угловой частоты в системе СИ — радиан в секунду , что сокращается до обратной секунды, поскольку радиан безразмерен.
| ⎡ ⎢ ⎣ | рад | = | 1 | = с −1 | ⎤ ⎥ ⎦ |
| с | с |
Я лично ненавижу это количество.В данном контексте это не имеет физического значения. Угловая частота отлично подходит для систем, которые вращаются (вращаются) или вращаются (перемещаются по кругу), но наша система колеблется (движется вперед и назад). Как одно связано с другим? Поскольку краткий ответ — «абстрактно», разумно вообще избегать ω и использовать коэффициент, основанный на физической реальности.
Периодическая система — это система, в которой время между повторяющимися событиями постоянно. (Система, в которой время между повторяющимися событиями непостоянно, называется апериодической .) Время между повторяющимися событиями в периодической системе называется периодом . Математически это время ( t ) на количество событий ( n ). Обозначение периода — это заглавный курсив T , хотя некоторые профессии предпочитают прописный курсив P .
Единицей измерения периода в системе СИ является секунды , поскольку количество событий безразмерно.
| ⎡ ⎢ ⎣ | с = | с | ⎤ ⎥ ⎦ |
| 1 |
Частота — это скорость, с которой происходит периодическое событие.Математически это количество событий ( n ) за раз ( t ). Обозначение частоты — длинное f , но также подойдет и курсив в нижнем регистре f . (Эти символы часто идентичны в некоторых шрифтах.)
Обозначение частоты — длинное f , но также подойдет и курсив в нижнем регистре f . (Эти символы часто идентичны в некоторых шрифтах.)
Единица измерения частоты в системе СИ — это обратная секунда, которая называется герц и (Гц) в честь Генриха Герца, немецкого физика 19 века, который подтвердил существование радиоволн.
| ⎡ ⎢ ⎣ | Гц = | 1 | = с −1 | ⎤ ⎥ ⎦ |
| с |
Период и частота противоположны друг другу.Конечно, они также обратно пропорциональны, но это упускает суть. Они обратно пропорциональны с коэффициентом пропорциональности, равным единице (без единицы измерения). Следовательно, для уравнивания их обратных величин не требуется никакого коэффициента. Они абсолютно и совершенно взаимны.
| f = | 1 | ⇔ | т = | 1 |
| т | f |
Вернуться к дифференциальному уравнению. Его решение — синус с фазовым сдвигом. Время — это входная переменная в триггерной функции. Триггерные функции не могут принимать числа с единицами измерения. Исправление заключается в использовании угловой частоты (ω). Угловая частота не имеет физической реальности. А вот частота ( f ) есть. Угловая частота определяет количество радианов в секунду. Частота подсчитывает количество событий в секунду. Последовательность событий, которая повторяется, называется циклом. Функция синуса повторяется после того, как она «прошла» через 2π радиан математической абстрактности.Движение простого гармонического осциллятора повторяется после того, как он прошел один полный цикл простого гармонического движения.
| ω = | φ | = | 2π радиан |
| т | 1 период |
| f = | n | = | 1 цикл |
| т | 1 период |
Разделите одно уравнение на другое…
| = | 2π радиан | = | 2π радиан | |
| ω | 1 период | |||
| f | 1 цикл | 1 цикл | ||
| 1 период |
Напомним, что и радианы, и циклы являются безразмерными величинами, что означает…
| ω | = | 2π радиан | = | 2π |
| f | 1 цикл | 1 |
и, следовательно,…
ω = 2π f
Умножение любой части этого уравнения на время исключает единицу измерения из входной части уравнения. А как насчет выходной стороны? Результатом синусоидальной функции является безразмерное число, которое изменяется от +1 до -1. Наше дифференциальное уравнение должно генерировать алгебраическое уравнение, которое выделяет положение между двумя крайними значениями, скажем, + A и — A . Мне нравится символ A , поскольку крайнее значение колебательной системы называется ее амплитудой , а амплитуда начинается с буквы a. Амплитуда использует те же единицы измерения, что и смещение для этой системы — метры [м], сантиметры [см] и т. Д.Умножьте синусоидальную функцию на A , и все готово. Вот решение в общем виде простого гармонического осциллятора (и многих других дифференциальных уравнений второго порядка).
А как насчет выходной стороны? Результатом синусоидальной функции является безразмерное число, которое изменяется от +1 до -1. Наше дифференциальное уравнение должно генерировать алгебраическое уравнение, которое выделяет положение между двумя крайними значениями, скажем, + A и — A . Мне нравится символ A , поскольку крайнее значение колебательной системы называется ее амплитудой , а амплитуда начинается с буквы a. Амплитуда использует те же единицы измерения, что и смещение для этой системы — метры [м], сантиметры [см] и т. Д.Умножьте синусоидальную функцию на A , и все готово. Вот решение в общем виде простого гармонического осциллятора (и многих других дифференциальных уравнений второго порядка).
x = A sin (2π футов + φ)
где…
| x = | позиция [м, см и т. Д.] |
| А = | амплитуда [м, см и т. Д.] |
| f = | частота [Гц] |
| т = | раз [с] |
| φ = | фаза [рад] |
Я сказал, что это алгебраическое уравнение является решением нашего дифференциального уравнения, но я так и не доказал его. Я, наверное, должен это сделать. Это покажет нам кое-что интересное. Начнем с уравнения…
Я, наверное, должен это сделать. Это покажет нам кое-что интересное. Начнем с уравнения…
x = A sin (2π футов + φ)
Найдите его первую производную…
| dx | = 2π фА |
| дт |
, поэтому мы можем найти его вторую производную…
| d 2 x | = −4π 2 f 2 A |
| дт 2 |
Подайте уравнение и его вторую производную обратно в дифференциальное уравнение…
| – | к | x = | d 2 x |
| м | дт 2 |
нравится…
| – | к | A |
| м |
тогда упростите. Обе переменные отменяются (наряду с множеством других вещей), что означает, что мы нашли хорошее решение. Остается это…
Обе переменные отменяются (наряду с множеством других вещей), что означает, что мы нашли хорошее решение. Остается это…
Теперь самое интересное. Решить для частоты…
И пока мы на этом, инвертируем частоту, чтобы получить период…
Простое гармоническое движение со временем развивается как синусоидальная функция с частотой, которая зависит только от жесткости возвращающей силы и массы движущейся массы. Более жесткая пружина колеблется чаще, а большая масса — реже.Вы также можете описать эти выводы в терминах периода простого гармонического движения. Более тяжелая масса колеблется с более длительным периодом, а более жесткая пружина колеблется с более коротким периодом. Амплитуда не влияет на частоту и период. Шо, колеблющееся с большой амплитудой, будет иметь ту же частоту и период, что и идентичный шо, колеблющийся с меньшей амплитудой.
фазовый угол
Положение и время — это некоторые переменные, которые описывают движение (в данном случае shm). Частота и период — это свойства периодических систем (в данном случае ан шо). Амплитуда и фаза — это коэффициенты, которые находятся в уравнениях периодического движения, которые определяются начальными условиями (в данном случае начальным положением и начальной скоростью шо).
Частота и период — это свойства периодических систем (в данном случае ан шо). Амплитуда и фаза — это коэффициенты, которые находятся в уравнениях периодического движения, которые определяются начальными условиями (в данном случае начальным положением и начальной скоростью шо).
Начните с уравнения положения. Подставляем в произвольную начальную позицию x 0 (без нуля), но для удобства назовем начальное время нулем.
| x = A sin (2π футов + φ) x 0 = A sin φ |
Затем сделайте что-то подобное с первой производной положения, более известной как скорость.Заменить любую произвольную начальную скорость v 0 (vee naught)
| v = 2π фА cos (2π ft + φ) v 0 = 2π fA cos φ |
Начальное положение разделить на начальную скорость.
| x 0 | = | A sin φ | = | тангенс угла φ |
| в 0 | 2π фА cos φ | 2π f |
Фазовый угол связан с отношением начального положения к начальной скорости следующим образом…
Напомним, что частота определяется жесткостью пружины и массой.
Фазовый угол тоже можно записать так…
| тангенс угла φ = | x 0 | √ | к |
| в 0 | м |
и даже так…
| тангенс угла φ = √ | kx 0 2 |
| мв 0 2 |
Знакомо? Как насчет того, чтобы я это сделал?
| тангенс угла φ = √ | ½ kx 0 2 |
| ½ мв 0 2 |
Фазовый угол связан с отношением начальной упругой потенциальной энергии к начальной кинетической энергии.
Почти, но не совсем. Когда я переместил начальное положение и начальную скорость под знаком радикала, я возложил их в квадрат. Это не совсем так. Когда я это сделал, я уничтожил информацию о знаке в двух начальных условиях. (Кинетическая и упругая потенциальные энергии всегда положительны.) Эти знаки используются, чтобы определить, в каком квадранте находится фазовый угол.
Это не совсем так. Когда я это сделал, я уничтожил информацию о знаке в двух начальных условиях. (Кинетическая и упругая потенциальные энергии всегда положительны.) Эти знаки используются, чтобы определить, в каком квадранте находится фазовый угол.
| — в 0 | + в 0 | |
|---|---|---|
| + x 0 | 2-й квадрант 090 ° –180 ° | 1-й квадрант 00 ° –90 ° |
| — x 0 | 3-й квадрант 180 ° –270 ° | 4-й квадрант 270 ° –360 ° |
16.3. Математика волн — Physics LibreTexts
Цели обучения
- Смоделируйте волну, движущуюся с постоянной скоростью волны, с помощью математического выражения
- Расчет скорости и ускорения среды
- Показать, чем скорость среды отличается от скорости волны (скорости распространения)
В предыдущем разделе мы описали периодические волны с помощью их характеристик длины волны, периода, амплитуды и скорости волны. Волны также можно описать движением частиц среды, в которой движутся волны. Положение частиц среды можно математически смоделировать как волновую функцию s , которую можно использовать для определения положения, скорости и ускорения частиц среды волны в любое время.
Волны также можно описать движением частиц среды, в которой движутся волны. Положение частиц среды можно математически смоделировать как волновую функцию s , которую можно использовать для определения положения, скорости и ускорения частиц среды волны в любое время.
импульсов
Импульс можно описать как волну, состоящую из одиночного возмущения, которое движется через среду с постоянной амплитудой.Импульс движется в виде шаблона, который сохраняет свою форму, поскольку распространяется с постоянной скоростью волны. Поскольку скорость волны постоянна, расстояние, которое проходит импульс за время Δt, равно Δx = vΔt (рисунок \ (\ PageIndex {1} \)).
Рисунок \ (\ PageIndex {1} \): Импульс в момент времени t = 0 центрируется на x = 0 с амплитудой A . Импульс движется в виде шаблона постоянной формы с постоянным максимальным значением A . Скорость постоянна, и импульс перемещается на расстояние Δx = vΔt за время Δt.Пройденное расстояние измеряется любой удобной точкой на пульсе. На этом рисунке использован герб.
Скорость постоянна, и импульс перемещается на расстояние Δx = vΔt за время Δt.Пройденное расстояние измеряется любой удобной точкой на пульсе. На этом рисунке использован герб.
Моделирование одномерной синусоидальной волны с использованием волновой функции
Рассмотрим струну, имеющую постоянное натяжение \ (F_T \), где один конец закреплен, а свободный конец колеблется между \ (y = + A \) и \ (y = −A \) с помощью механического устройства при постоянной частота. На рисунке \ (\ PageIndex {2} \) показаны снимки волны с интервалом в одну восьмую периода, начиная с одного периода (\ (t = T \)).
Рисунок \ (\ PageIndex {2} \): Снимки поперечной волны, движущейся по струне под натяжением, начиная с момента времени \ (t = T \) и с интервалами \ (\ frac {1} {8} T \ ). Цветные точки используются для выделения точек на строке. Точки, разнесенные на длину волны в направлении x , выделяются одинаковыми цветными точками.
Обратите внимание, что каждая точка выбора на струне (отмеченная цветными точками) колеблется вверх и вниз в простом гармоническом движении между \ (y = + A \) и \ (y = −A \) с периодом \ (T \ ). Волна на струне имеет синусоидальную форму и с течением времени перемещается в положительном направлении оси x.
Волна на струне имеет синусоидальную форму и с течением времени перемещается в положительном направлении оси x.
Здесь полезно вспомнить из вашего изучения алгебры, что если \ (f (x) \) — некоторая функция, то \ (f (x − d) \) — та же функция, переведенная в положительное значение x- направление на расстояние \ (d \). Функция \ (f (x + d) \) — это та же функция, переведенная в отрицательном направлении x на расстояние \ (d \). Мы хотим определить волновую функцию, которая будет давать \ (y \) — положение каждого сегмента строки для каждой позиции x вдоль строки для каждого момента \ (t \).
Глядя на первый снимок на рисунке \ (\ PageIndex {2} \), положение y строки между \ (x = 0 \) и \ (x = λ \) можно смоделировать как синусоидальную функцию. Эта волна распространяется вниз по струне на одну длину волны за один период, как видно на последнем снимке. Следовательно, волна движется с постоянной волновой скоростью \ (v = λ / T \).
Напомним, что синусоидальная функция — это функция угла \ (θ \), колеблющаяся между +1 и -1 и повторяющаяся каждые \ (2π \) радиан (рисунок \ (\ PageIndex {3} \)). Однако положение среды y или волновая функция колеблется между \ (+ A \) и \ (- A \) и повторяет каждую длину волны \ (λ \).
Рисунок \ (\ PageIndex {3} \): функция синуса колеблется между +1 и -1 каждые 2π радиан.
Чтобы построить нашу модель волны с использованием периодической функции, рассмотрим соотношение угла и положения,
\ [\ begin {align *} \ dfrac {\ theta} {x} & = \ frac {2 \ pi} {\ lambda}, \\ [4pt] \ theta & = \ frac {2 \ pi} {\ лямбда} x. \ end {align *} \]
Используя \ (\ theta = \ frac {2 \ pi} {\ lambda} x \) и умножив синусоидальную функцию на амплитуду A , мы теперь можем смоделировать положение строки y как функцию положение x :
\ [y (x) = A \ sin \ left (\ frac {2 \ pi} {\ lambda} x \ right).\ nonumber \]
Волна на струне распространяется в положительном направлении x с постоянной скоростью v и перемещается на расстояние vt за время t . Волновая функция теперь может быть определена с помощью
Волновая функция теперь может быть определена с помощью
.
\ [y (x, t) = A \ sin \ left (\ frac {2 \ pi} {\ lambda} (x-v t) \ right). \ nonumber \]
Часто бывает удобно переписать эту волновую функцию в более компактном виде. Умножение на коэффициент \ (\ frac {2 \ pi} {\ lambda} \) приводит к уравнению
\ [y (x, t) = A \ sin \ left (\ frac {2 \ pi} {\ lambda} x- \ frac {2 \ pi} {\ lambda} v t \ right).\ nonumber \]
Значение \ (\ frac {2 \ pi} {\ lambda} \) определяется как волновое число . Обозначение для волнового числа — k и имеет обратные метры, м −1 :
.
\ [k \ Equiv \ frac {2 \ pi} {\ lambda} \ label {16.2} \]
Напомним из «Колебаний», что угловая частота определяется как \ (\ omega \ Equiv \ frac {2 \ pi} {T} \). Второй член волновой функции принимает вид
.
\ [\ frac {2 \ pi} {\ lambda} vt = \ frac {2 \ pi} {\ lambda} \ left (\ frac {\ lambda} {T} \ right) t = \ frac {2 \ pi } {T} t = \ omega t. \ nonumber \]
\ nonumber \]
Волновая функция простой гармонической волны на струне уменьшается до
.
\ [y (x, t) = A \ sin (k x \ mp \ omega t) \ nonumber \]
, где A — амплитуда, \ (k = \ frac {2 \ pi} {\ lambda} \) — волновое число, \ (\ omega = \ frac {2 \ pi} {T} \) — При угловой частоте знак минус соответствует волнам, движущимся в положительном направлении x , а знак плюс — волнам, движущимся в отрицательном направлении x . Скорость волны равна
.
\ [v = \ frac {\ lambda} {T} = \ frac {\ lambda} {T} \ left (\ frac {2 \ pi} {2 \ pi} \ right) = \ frac {\ omega} { k} \ label {16.3}. \]
Вспомните наше обсуждение массы на пружине, когда положение массы моделировалось как
.
\ [x (t) = A \ cos (ωt + ϕ). \ nonumber \]
Угол \ (ϕ \) — это фазовый сдвиг, добавленный, чтобы учесть тот факт, что масса может иметь начальные условия, отличные от \ (x = + A \) и \ (v = 0 \). По тем же причинам к волновой функции добавляется начальная фаза. Волновая функция, моделирующая синусоидальную волну с учетом начального фазового сдвига \ (ϕ \), равна
\ [y (x, t) = A \ sin (k x \ mp \ omega t + \ phi) \ label {16.4} \]
Значение
\ [(k x \ mp \ omega t + \ phi) \ label {16.5} \]
известен как фаза волны, где \ (\ phi \) — начальная фаза волновой функции. Является ли временной член \ (\ omega t \) отрицательным или положительным, зависит от направления волны. Сначала рассмотрим знак минус для волны с начальной фазой, равной нулю (\ (\ phi \) = 0). Фаза волны будет (\ (kx = \ omega t \)). Рассмотрите возможность отслеживания точки на волне, например гребня.Пик возникает, когда \ (\ sin (kx — \ omega t = 1.00 \), то есть когда \ (k x- \ omega t = n \ pi + \ frac {\ pi} {2} \), для любого интегральное значение n . Например, один конкретный гребень встречается в \ (k x- \ omega t = \ frac {\ pi} {2} \). По мере движения волны время увеличивается, и x также должно увеличиваться чтобы фаза оставалась равной \ (\ frac {\ pi} {2} \). Следовательно, знак минус означает, что волна движется в положительном направлении x . Используя знак плюса, \ (k x + \ omega t = \ frac {\ pi} {2} \). По мере увеличения времени x должно уменьшаться, чтобы фаза оставалась равной \ (\ frac {\ pi} {2} \).Знак плюс используется для волн, движущихся в отрицательном направлении x . Таким образом, \ (y (x, t) = A \ sin (k x- \ omega t + \ phi) \) моделирует волну, движущуюся в положительном направлении x и \ (y (x, t) = A \ sin (k x + \ omega t + \ phi) \) моделирует волну, движущуюся в отрицательном направлении x .
Уравнение \ ref {16.4} известно как простая гармоническая волновая функция. Волновая функция — это любая функция, такая что \ (f (x, t) = f (x-v t) \). Позже в этой главе мы увидим, что это решение линейного волнового уравнения.{\ prime} = \ phi- \ frac {\ pi} {2} \).
Определение характеристик синусоидальной волны
- Чтобы найти амплитуду, длину волны, период и частоту синусоидальной волны, запишите волновую функцию в виде \ (y (x, t) = A \ sin (k x- \ omega t + \ phi) \) .
- Амплитуда может быть определена прямо из уравнения и равна \ (A \).
- Период волны можно определить по угловой частоте \ (\ left (T = \ frac {2 \ pi} {\ omega} \ right) \).
- Частоту можно найти с помощью \ (f = \ frac {1} {T} \)
- Длину волны можно найти с помощью волнового числа \ (\ left (\ lambda = \ frac {2 \ pi} {k} \ right) \).{-1} t \ right) \ end {align *} \]
Найдите амплитуду, длину волны, период и скорость волны.
Стратегия
Все эти характеристики волны можно найти из констант, включенных в уравнение, или из простых комбинаций этих констант.
Решение
1. Амплитуду, волновое число и угловую частоту можно определить непосредственно из волнового уравнения:
\ begin {align *}
y (x, t) = & A \ sin (k x-w t) = 0.{-1}} = 0,25 \: \ mathrm {m} / \ mathrm {s} \ nonumber \]Значение
Все характеристики волны содержатся в волновой функции. Обратите внимание, что скорость волны — это скорость волны в направлении, параллельном движению волны. График высоты среды y в сравнении с положением x для двух значений времени t = 0,00 с и t = 0,80 с может обеспечить графическую визуализацию волны (рисунок \ (\ PageIndex {4} \)).
Рисунок \ (\ PageIndex {4} \): График высоты волны y как функция положения x для моментальных снимков волны с двумя временами.Пунктирная линия представляет волну в момент времени t = 0,00 с, а сплошная линия представляет волну в момент времени t = 0,80 с. Поскольку скорость волны постоянна, расстояние, которое проходит волна, равно скорости волны, умноженной на временной интервал. Черные точки указывают точки, используемые для измерения смещения волны. Среда движется вверх и вниз, а волна движется вправо.
У движения есть вторая скорость. В этом примере волна является поперечной, движущейся горизонтально, когда среда колеблется вверх и вниз перпендикулярно направлению движения.График на рисунке \ (\ PageIndex {5} \) показывает движение среды в точке x = 0,60 м как функцию времени. Обратите внимание, что среда волны колеблется вверх и вниз между y = +0,20 м и y = -0,20 м каждый период 4,0 секунды.
Рисунок \ (\ PageIndex {5} \): График высоты волны y как функция времени t для позиции x = 0,6 м. Среда колеблется между y = +0,20 м и y = -0,20 м каждый период. Представленный период выбирает две удобные точки колебаний для измерения периода.Период может быть измерен между любыми двумя соседними точками с одинаковой амплитудой и одинаковой скоростью, \ ((\ partial y / \ partial t) \). Скорость можно найти, посмотрев на касательную наклон к точке на графике y -versus- t . Обратите внимание, что в моменты времени t = 3,00 с и t = 7,00 с высота и скорости одинаковы, а период колебаний равен 4,00 с.
Упражнение \ (\ PageIndex {1} \)
Волновая функция выше получена с помощью синусоидальной функции.Можно ли вместо этого использовать функцию косинуса?
Скорость и ускорение среды
Как видно из примера \ (\ PageIndex {2} \), скорость волны постоянна и представляет собой скорость волны, когда она распространяется через среду, а не скорость частиц, составляющих среду. Частицы среды колеблются вокруг положения равновесия, когда волна распространяется через среду. В случае поперечной волны, распространяющейся в направлении x, частицы колеблются вверх и вниз в направлении y, перпендикулярном движению волны.Скорость частиц среды непостоянна, что означает ускорение. Скорость среды, которая перпендикулярна скорости волны в поперечной волне, может быть найдена путем взятия частной производной уравнения положения по времени. Для нахождения частной производной берется производная функции и все переменные рассматриваются как константы, за исключением переменной, о которой идет речь. В случае частной производной по времени \ (t \) положение \ (x \) рассматривается как константа.Хотя это может показаться странным, если вы не видели этого раньше, цель этого упражнения — найти поперечную скорость в точке, поэтому в этом смысле положение \ (x \) не меняется. У нас
\ [\ begin {split} y (x, t) & = A \ sin (kx — \ omega t + \ phi) \\ v_ {y} (x, t) & = \ frac {\ partial y (x , t)} {\ partial t} = \ frac {\ partial} {\ partial t} [A \ sin (kx — \ omega t + \ phi)] \\ & = -A \ omega \ cos (kx — \ омега t + \ phi) \\ & = -v_ {y \; max} \ cos (kx — \ omega t + \ phi) \ ldotp \ end {split} \]
Величина максимальной скорости среды равна \ (| v_ {y \, max} | = A \ omega \).{2} \). Частицы среды или элементы массы колеблются в простом гармоническом движении механической волны.
Линейное волновое уравнение
Мы только что определили скорость среды в позиции x, взяв частную производную по времени от позиции y. {2} \ sin (kx — \ omega t + \ phi) \ ldotp \]
Теперь рассмотрим частные производные по другой переменной, позиции x, сохраняющей постоянную времени.{2}} \ ldotp \ label {16.6} \]
Уравнение \ ref {16.6} — это линейное волновое уравнение, которое является одним из самых важных уравнений в физике и технике. Мы вывели его здесь для поперечной волны, но он не менее важен при исследовании продольных волн. Это соотношение также было получено с использованием синусоидальной волны, но оно успешно описывает любую волну или импульс, имеющий форму y (x, t) = f (x ∓ vt). Эти волны возникают из-за линейной возвращающей силы среды — отсюда и название линейного волнового уравнения.Любая волновая функция, удовлетворяющая этому уравнению, является линейной волновой функцией.
Интересный аспект линейного волнового уравнения заключается в том, что если две волновые функции являются индивидуальными решениями линейного волнового уравнения, то сумма двух линейных волновых функций также является решением волнового уравнения. Рассмотрим две поперечные волны, распространяющиеся вдоль оси x в одной и той же среде. Предположим, что отдельные волны можно моделировать с помощью волновых функций y 1 (x, t) = f (x ∓ vt) и y 2 (x, t) = g (x ∓ vt), которые являются решениями линейные волновые уравнения и, следовательно, являются линейными волновыми функциями.{2}} \ right) \ ldotp \ end {split} \]
Это показало, что если две линейные волновые функции сложить алгебраически, результирующая волновая функция также будет линейной. Эта волновая функция моделирует смещение среды результирующей волны в каждом положении по оси x. Если две линейные волны занимают одну и ту же среду, говорят, что они интерферируют. Если эти волны можно моделировать с помощью линейной волновой функции, эти волновые функции складываются, чтобы сформировать волновое уравнение волны, возникающей в результате интерференции отдельных волн.Смещение среды в каждой точке результирующей волны представляет собой алгебраическую сумму смещений, вызванных отдельными волнами.
Продолжая этот анализ, если волновые функции y1 (x, t) = f (x ∓ vt) и y2 (x, t) = g (x ∓ vt) являются решениями линейного волнового уравнения, то Ay 1 (x, t) + By 2 (x, y), где A и B — константы, также является решением линейного волнового уравнения. Это свойство известно как принцип суперпозиции. Интерференция и суперпозиция более подробно описаны в Интерференции волн.
Пример \ (\ PageIndex {2} \): интерференция волн на строке
Рассмотрим очень длинную веревку, натянутую двумя учениками, по одной с каждого конца. Студент A колеблет конец струны, создавая волну, смоделированную с помощью волновой функции y 1 (x, t) = A sin (kx — \ (\ omega \) t), а студент B колеблет струну с удвоенной частотой , двигаясь в обратном направлении. Обе волны движутся с одинаковой скоростью v = \ (\ frac {\ omega} {k} \). Две волны интерферируют, образуя результирующую волну с волновой функцией y R (x, t) = y 1 (x, t) + y 2 (x, t).{2}} \).
Стратегия
Сначала напишите волновую функцию для волны, созданной вторым учеником. Обратите внимание, что угловая частота второй волны в два раза больше частоты первой волны (2 \ (\ omega \)), а поскольку скорости двух волн одинаковы, волновое число второй волны вдвое больше, чем у первая волна (2к). Затем напишите волновое уравнение для полученной волновой функции, которая представляет собой сумму двух отдельных волновых функций. Затем найдите вторую частную производную по положению и вторую частную производную по времени.Используйте линейное волновое уравнение, чтобы найти скорость результирующей волны.
Решение
- Запишите волновую функцию второй волны: y 2 (x, t) = A sin (2kx + 2 \ (\ omega \) t).
- Запишите полученную волновую функцию: $$ y_ {R} (x, t) = y_ {1} (x, t) + y (x, t) = A \ sin (kx — \ omega t) + A \ sin (2kx + 2 \ omega t) \ ldotp $$
- Найдите частные производные: $$ \ begin {split} \ frac {\ partial y_ {R} (x, t)} {\ partial x} & = -Ak \ cos (kx — \ omega t) + 2Ak \ cos (2kx + 2 \ omega t), \\ \ frac {\ partial ^ {2} y_ {R} (x, t)} {\ partial x ^ {2}} & = -Ak ^ {2} \ sin ( kx — \ omega t) — 4Ak ^ {2} \ sin (2kx + 2 \ omega t), \\ \ frac {\ partial y_ {R} (x, t)} {\ partial t} & = -A \ omega \ cos (kx — \ omega t) + 2A \ omega \ cos (2kx + 2 \ omega t), \\ \ frac {\ partial ^ {2} y_ {R} (x, t)} {\ partial t ^ {2}} & = -A \ omega ^ {2} \ sin (kx — \ omega t) — 4A \ omega ^ {2} \ sin (2kx + 2 \ omega t) \ ldotp \ end {split} $ $
- Используйте волновое уравнение, чтобы найти скорость получившейся волны: $$ \ begin {split} \ frac {\ partial ^ {2} y (x, t)} {\ partial x ^ {2}} & = \ frac {1} {v ^ {2}} \ frac {\ partial ^ {2} y (x, t)} {\ partial t ^ {2}}, \\ -Ak ^ {2} \ sin (kx — \ omega t) + 4Ak ^ {2} \ sin (2kx + 2 \ omega t) & = \ frac {1} {v ^ {2}} \ left (-A \ omega ^ {2} \ sin (kx — \ omega t) — 4A \ omega ^ {2} \ sin (2kx + 2 \ omega t) \ right), \\ k ^ {2} \ left (-A \ sin (kx — \ omega t) + 4A \ sin (2kx + 2 \ omega t) \ right) & = \ frac {\ omega ^ {2}} {v ^ {2}} \ left (-A \ sin (kx — \ omega t) — 4A \ sin (2kx + 2 \ omega t) \ right), \\ k ^ {2} & = \ frac {\ omega ^ {2}} {v ^ {2}}, \\ | v | & = \ frac {\ omega} {k} \ ldotp \ end {split} $$
Значение
Скорость образовавшейся волны равна скорости исходных волн \ (\ left (v = \ frac {\ omega} {k} \ right) \).{-1} t + \ frac {\ pi} {10}) \]
— это решение волнового уравнения.
Любое возмущение, которое соответствует волновому уравнению, может распространяться как волна, движущаяся вдоль оси x со скоростью волны v. Это одинаково хорошо работает для волн на струне, звуковых волн и электромагнитных волн. Это уравнение чрезвычайно полезно. Например, с его помощью можно показать, что электромагнитные волны движутся со скоростью света.
Авторы и авторство
Сэмюэл Дж.Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Трудности учащихся с математикой в физике: придание значения символам
Трудности учащихся с математикой в физике: придание значения символам
Продолжайте говорить.
Эдвард Ф.Редиш, Ричард Н. Стейнберг и Джеффри М. Сол
Физический факультет Мэрилендского университета
Колледж-Парк, Мэриленд 20742-4111
Представлено 9 августа 1996 г. на заседании AAPT в Колледж-Парк. Опубликовано
в сети 3 сентября 1996 г.
Абстрактные
Несмотря на то, что проводились исследования понимания студентами природы науки и научного процесса, было мало работ о влиянии понимания студентами символов физики на образовательную практику.Мы видели множество трудностей, связанных с неправильным пониманием учащимися роли математики в физике. Студенты часто могут правильно выполнять математические операции в контексте математической задачи, но не могут выполнять те же операции в контексте физической задачи. Студенты часто не ценят и не понимают богатого смысла символа. Мы видели ряд различных видов неудач этого типа и дадим примеры и предварительную классификацию трудностей учащихся с приданием значения математике в контексте физики.
Изначально доклад был разработан для представления с использованием браузера (Netscape).
Хотя это все один документ, кнопки можно использовать для презентации доклада.
в формате слайда. Чтобы получить нужный размер для слайд-шоу, поместите радужную полосу ниже на
верхнюю часть экрана и настройте
размер вашего окна, чтобы эта полоса проходила полностью, и высоту, чтобы
следующая полоса радуги находится внизу. Если вы используете экран 640×480, должно быть
изменять размер не нужно.Продолжить разговор.
Исследовательская группа по физическому образованию
Мэрилендский университет, Колледж-Парк
Частично поддержано грантом NSF RED-9355849
1
2
Несмотря на то, что проводились исследования понимания студентами природы науки и научного процесса, было мало работ о влиянии понимания студентами символов физики на образовательную практику.
В наших исследованиях ожиданий студентов и эпистемологии мы обнаружили множество трудностей, которые связаны с неправильным пониманием студентами роли математики в физике.
Учащиеся могут совершенно правильно выполнять математические операции в контексте математической задачи, но не понимать те же операции, когда они происходят в физике.
3
Мы наблюдали ряд отказов такого типа.
- неспособность связать символы с измерением
- неспособность отметить связанные вариации
- неспособность проанализировать уравнения
- неспособность понять уравнения как отношения
- неспособность координировать время и пространство
- неспособность трактовать уравнения как представления реальности
3
Отсутствие символов, представляющих
физические измерения, а не числаСтуденты, как правило, хотят сразу же подставлять числа в уравнения, тем самым упрощая структуру поверхности, но разрушая глубинную структуру.Следовательно, они теряют:
- возможность проверки уравнения на непротиворечивость с учетом изменения параметров
- возможность проверки согласованности путем выполнения единичных проверок
- возможность делать несколько дел, тем самым экономя себе труд.
5
Отсутствие соответствующих изменений
Например, многие студенты, рассматривая силу, которую два взаимодействующих объекта действуют друг на друга, будут рассматривать уравнения
F = ma
F = MA
и будет утверждать, что две силы должны быть разными: или , потому что ускорения разные, или массы разные,
игнорируя тот факт, что оба меняются.(Это аналог сохранения количества Пиаже при изучении детей.)6
Неспособность проанализировать уравнения
Уравнения в физике часто имеют большое количество произвольных символов. В курсах математики редко используется такое количество символов — и когда они используются, обычно существует строгий и систематический «кодекс». Приведенное ниже уравнение является типичным физическим примером, содержащим 6 различных символов.
Некоторым учащимся трудно понять, что такое переменные, а что константы в этом выражении.7
Дополнительную трудность вызывает количество различных видов «констант и переменных», используемых в физике.
1. числа 2, e, 5/7 2. универсальные константы c, h, k (Больцмана) 3. экспериментальные параметры m, R, T, k (пружина) 4. начальные условия x0, v0 5. независимые переменные x, y, z, t 6.зависимые переменные x, y, v Обратите внимание на большое количество «омонимов», различающихся по контексту.
8
У нас также есть «гомоглифов» — символы, которые выглядят одинаково, но означают разные вещи.
Представьте, как сложно расшифровать это уравнение для ученика, не замечающего диакритических знаков!В приведенном выше выражении скобки используются для трех различных значений. Также обратите внимание, что строка «(x, y, z)» появляется дважды — с двумя разными контекстно-зависимыми значениями.
9
Неспособность координировать время и пространство
Студенты часто не понимают, как мы используем координаты для количественной оценки времени и пространства. В качестве примера рассмотрим следующую экзаменационную задачу:
Экзаменационный вопрос : Автомобиль движется по овальной колее с постоянной скоростью против часовой стрелки, если смотреть сверху. Когда он окажется в самой северной точке, нарисуйте векторы, определяющие положение, скорость и ускорение автомобиля. 10
Несмотря на значительные усилия на лекции (в том числе рассказывание анекдота о рыбаке и лодке), около 25% студентов в классе инженеров по математике пропустили этот вопрос на экзамене по рисованию.
вектор положения в том же направлении, что и вектор скорости.При опросе они показали, что не понимают координаты как
описание относительно некоторой фиксированной точки отсчета.Многие студенты отметили
Я знаю, где он. Он , здесь (указывает на вершину овала). Но это всего лишь баллов .
Мне нужно направление , чтобы сделать вектор. Единственное направление, которое я могу связать с этим, — это направление, в котором
он идет, поэтому я нарисовал вектор положения в том же направлении, что и вектор скорости11
Неспособность рассматривать уравнения как представления реальности
В физике уравнения — это не просто математические отношения.Иногда физики не интерпретируют уравнения
исключительно по их математическому содержанию, но может интерпретировать математику с использованием физического контекста. Рассмотрим следующий вопрос о
фотоэлектрический эффект.Экзаменационный вопрос: Предположим, вы должны были провести эксперимент с фотоэлектрическим эффектом, используя свет с длиной волны = 250 нм и электрод из никеля (phi = 5,2 эВ). Вы обнаружите, что когда разность потенциалов, измеренная на электродах V, равна нулю вольт, амперметр показывает нулевой ток.Будет ли амперметр показывать нулевой или ненулевой ток, если вы замените никелевый электрод на алюминиевый (phi = 4,2 эВ)? Объясните свои рассуждения. (от Steinberg, Oberem и McDermott)
12
Почти четверть студентов ответили: «Соответствующее уравнение:»
Значит, он будет ненулевым. Если (hf — phi) равно нулю, то изменение phi делает (hf — phi) ненулевым.»
13
Что происходит, так это то, что уравнение действительно имеет вид
но большинству физиков тета-функция не нужна. Поскольку у них есть представление о значениях, они знают, что
Только уравнение имеет смысл, когда кинетическая энергия положительна.Подобного рода «неявные ограничения» часто не видны учителю.
и непонятно для ученика.14
В этом докладе была представлена классификация анекдотических свидетельств трудностей учащихся с использованием математики.
в университетской физике. Дальнейшие подробности и конкретные исследования, включая результаты собеседований и экзаменов.
дается в следующем докладе:Проблемы учащихся с математикой в физике: Почему учащиеся не могут применить то, что они узнали в классе математики?
Джеффри М. Сол, Майкл К. Виттманн, Ричард Стейнберг и Эдвард Ф.КрасноватыйЩелкните заголовок, чтобы прочитать это выступление.
Эту страницу подготовил
Эдвард Ф. Рэдиш
[email protected]Университет Мэриленда
Физический факультет
Колледж-Парк, Мэриленд 20742-4111
(301) 405-6120PHI PHYSICS
PHI PHYSICS
Фи Физика
На пути к единой философии природы
«Моя цель — сначала изучить факты, а потом продемонстрировать, как тела вынуждены действовать.Это метод, которого нужно придерживаться во всех исследованиях природы ». Леонардо да Винчи
ТАЙНА ЗНАНИЙ
Разнообразие форм и энергии, которое нас окружает, поистине поражает. Воздух с его многочисленными аспектами погоды, красота света в бесконечных комбинациях, а также идеи, перспективы и переживания — все это участвует вместе с нами в жизни.
Арена природы обширна и обширна. Знания, которые люди получают в результате переваривания разнообразного опыта, представлений и фактов о природе, в лучшем случае эфемерны, но их можно выразить термином «здравый смысл».«Знания меняются с появлением новых фактов и опыта, однако некоторые теории о законах природы настолько тесно вплетены в ткань опыта, что они выражают динамику или структуру естественного закона существенным образом, который может быть подтвержден многими способами.
Специализированные знания, безусловно, необходимы для глубокого изучения законов природы. Специализированные знания могут стать более применимыми, чем общие знания, отражая тонкие свойства природных эффектов. Хорошим примером того, как специализированное знание становится настолько решительным, что оно разделяется на новые науки, является химия, каждая из ветвей которой становится направлением исследований, биохимия, электрохимия, органическая химия, ядерная химия и т. Д..
По мере того, как знание становится глубже, справедливое и частое синтезирование и перегруппировка базовой философии будет препятствовать передаче знания поколениям, живущим в результате преобразований, которые его породили.
Новые знания — мощный инструмент и воодушевляющая, вдохновляющая сила, особенно для молодых непредубежденных людей. Мысль о том, что факты природы каким-то образом попадают в классы, будучи фактами, ошибочна.
Наука не всегда заботится об образовании публики, только специалисты, входящие в их область, получают высшие учения.
Недостаток ясности в том, что такое наука и чем она занимается, пронизывает средства массовой информации во всех формах. Необходимо приложить усилия, чтобы привнести интерес и любопытство к информации о природе, которая раскрывается перед нами.
Двадцатый век стал свидетелем великолепного роста знаний о мире. В то же время наблюдается более медленный рост ясного представления знаний о природе обычному человеку. Образование современных мужчин и женщин стало специализированным и, вероятно, будет обширным и в основном на новом собственном языке, но это не дает связного синопсиса естественного права в удобоваримой форме.Необходим общий курс естественной философии, который проводится во всех школах.
Междисциплинарные исследования философии природы, охватывающие естественные науки и значение современных исследований и открытий, должны быть доступны каждому. По общему признанию, образование — это нечто большее, чем просто такой вид обучения, но в настоящее время среди ученых ощущается острая нехватка Любителей Мудрости (Философов).
Образовательные стандарты во всех областях и преподавание информации ясным и ИНТЕРЕСНЫМ способом взаимосвязаны.Наибольшая выгода, получаемая получателем образования, находится в пределах возникающих интересов. Если учитель может только передать что-то, возможно, новое знание о высших идеях, возможно, всего лишь один или два вдохновляющих момента, когда возникает внутренний вопрос и на лице молодых людей появляются вспышки озарения.
Изучение натурфилософии должно быть вновь представлено как основа и перспектива, с которой можно легко усвоить три Р и такие рудименты. То, чему учат, важно, но также важно то, как происходит обучение, особенно учение о природе.
Великие идеи обычно рождаются в особых умах. Обмен этими идеями и их изучение можно облегчить с помощью правильных моделей мира природы. Ученые используют новые и интересные модели, чтобы перегруппировать знания, чтобы увидеть новые перспективы или новые основы, образование должно делать то же самое. Следует сконцентрироваться на методе группировки естественнонаучной информации так, чтобы ее можно было четко представить.
Вдохновение и проницательность не будут забыты, если мы сосредоточимся на ПУТИ.
ТРИ СПЕКТРА В ПРИРОДЕ
Три основных наблюдаемых и хорошо известных спектра в природе, которые одушевляют природу и оживляют все сущее, являются величайшей тайной в жизни, хотя в последней части 20 -го века мы начинаем познавать.
ЭЛЕКТРИЧЕСТВО,
ЭЛЕКТРОМАГНИТНЫЙ
ИЗЛУЧЕНИЕ (свет) и ЗВУК (или физическая вибрация) представляют три различных режима вибрации, которым подвержена так называемая «материя».Каким-то образом жизнь проникает сюда, где кажущаяся осязаемой (гравитирующая масса) встречается с невидимым, нематериальным (три спектра в природе).
Электрические явления — это то, что мы видим вокруг себя повсюду. Мы знаем, что электроны, какими бы они ни были, ответственны за производство света вещами, излучающими свет. Лампочки, огонь, химические средства генерации света и т. Д. — все зависит от свойств электронов поглощать и излучать так называемые «фотоны».
Электроны делают свое дело, прыгая в своем танце света, и остальная часть Вселенной почти не знает о том скрытом ядре внутри.Центр внутри атома, ядро тесно связано численно с электронами, населяющими другой домен, в их орбитальных и химических перемещениях.
Число e- и p + -частиц в нейтральном атоме равно. Добавьте еще е и р, и вы получите следующий химический элемент. Нейтроны для каждого атома различны, и у легких атомов их меньше, чем у протонов, в то время как у тяжелых атомов обычно больше нейтронов, чем протонов. По мере приближения к протону электроны оказываются в более плотном электрическом поле, и это поле имеет много интересных аспектов.
Магнитные и электрические силы, кажется, расходятся здесь, там, где протоны и нейтроны встречаются с самим космосом. Они погружены в него глубже, чем электрон.
Итак, похоже, существует верхний предел простой и простой активности ЭМ-фотонов, основанной на электронах. Но не обманывайтесь. Даже великие физики придумали такие странные идеи, как один-единственный электрон, образующий всю вселенную, перемещаясь туда и обратно во времени (Джон Уиллер).
На самом деле есть много возможностей для изучения этих и других идей.Многие идеи соответствуют определенным фактам и могут развиться в теорию, объясняющую принципы, лежащие в основе определенных фактов. У каждого есть множество теорий, которые помогают им заниматься повседневными делами. Немногие точно знают, как работает телевизор, но знают, что определенные функции существуют, и знают, как их использовать.
Это, безусловно, больше изобретение, чем теория, которая определяет эти вещи. Но иногда теория, подобная теории фотоэлектрического эффекта (Альберт Эйнштейн), имеет множество побочных эффектов, которые прекрасно сочетаются с изобретением, и шествие поразительных возможностей для людей Земли продолжается.
Теории, которые делают возможным новое в будущем, являются лучшими. Это может быть только в том случае, если они в чем-то верны в своем подходе. Теории, которые оказались ложными, могут раскрыть правду о некоторых аспектах природы в процессе, поэтому они тоже имеют свои достоинства. Мы можем найти переход от суеверия к мнению, от гипотезы к теории. На самом деле, большинство так называемых теорий — это мнения или гипотезы. Теории эволюционировали немного дальше этого, чтобы наилучшим образом изобразить факты так, как они наблюдаются.Если у них есть образец, который раскрывает что-то вроде принципа природы, закона, который показывает ранее неизвестные отношения, которые можно было бы каким-то образом наблюдать, тогда они могут предсказывать. Последняя форма знания, которая превращается в понимание, — это своего рода способность видеть будущее, способность предсказывать ход вещей. Следовательно, хорошая теория должна что-то предсказывать.
КОСМИЧЕСКАЯ ЭНЕРГИЯ
Если частота достаточно высока и мы внимательно присмотримся (с помощью инструментов), кажется, что нет способа отличить летающие части материи от электромагнитных фотонов.Выше пороговой частоты для образования электронных пар фотоны являются частью временных частиц и частью временных электромагнитных волн. Это затрудняет понимание того, из чего состоят космические лучи. Это атомы разных элементов, частицы и что нет, или это фотоны с ударом. Иногда тысячи или миллионы частиц, таких как электроны, протоны и нейтроны, создаются из-за энергии удара одного космического луча. Что это был за удар? Трудно сказать. Как бы то ни было, это происходило очень, очень быстро, на самом деле кажется, что они движутся со скоростью фотонов, которая является СКОРОСТЬЮ СВЕТА.Все это приводит к тому, что есть предел нашей способности разобраться в организации обширной схемы космических лучей Вселенной на верхнем конце электромагнитного спектра.
Таким образом, атом демонстрирует три спектра;
Кинетическая энергия в форме физической вибрации
Частоты электромагнитной энергии в зависимости от «состояния» атома
Электрические частоты, связанные с движением электрических токов, то есть электронов.
ИЗ КОТОРОГО МЫ ИЗУЧАЕМ Пространство-Время-Энергия-Материя:
Теория измерений и геометрии.
Присущая природе тройственность проявляется во всех областях спектра. В корневой точке находится треугольник, гипотенуза которого равна длине Планка. Это может быть рассчитано с точностью в теории преобразования спиральной энергии.
Каждое измерение смещено в большой вселенной на коэффициент скорости, равный скорости света c. c — универсальная фундаментальная постоянная.
Каждое измерение структурировано числом в форме отношений, которые приблизительно соответствуют идеальному коэффициенту золотого сечения (PHI).Phi-Golden — универсальная и фундаментальная константа. По сути, показательное изучение измерений и света раскрывает АТОМ в его сокровенной структуре и происхождении, а также природу форм, возникающих в области других измерений.
Отношение Пи диаметра к окружности отображается во Вселенной во всех измерениях и является универсальной и фундаментальной константой.
МОДИФИЦИРОВАННАЯ ТЕОРИЯ ПЛАНКА
Квант действия 1 / 2h — это комплексная константа, состоящая из отношения фи, отношения пи и отношения скорости света, которые существуют в совершенном согласии в обмене энергией.Константа, связанная с постоянной Планка, которая показывает истинную структуру материи / энергии, выводится из соотношения Phi, лежащего в основе постоянной Планка, и равна c (в квадрате) x квадратный корень из 1 / 2h. Таким образом, это соотношение является истинной постоянной Планка.
Это PhiX, и это число чрезвычайно важно для универсальной генерации фундаментальных свойств атома.
Из него в сочетании с 2Pi и степенями скорости света могут быть образованы важные фундаментальные константы (путем простой прогрессии).
PHI PHYSICS
Связь золотого сечения с квантовой физикой: Phi Physics.
Соотношение золотого сечения — это идеальное среднее число, имеющее свойство вращения, присущее его идеальному значению.
1,618033988 … инвертированный становится 0,618033988 … [PhiG-1 = 1 / PhiG].
Еще одно число, аналогичным образом отображающее это совершенство, — это число 1. В перевернутом виде оно остается единицей. Однако, когда используется как 10, можно увидеть глубокую симметрию в его обращении к 1/10 или 0.1 = 1/10. Цифры остаются такими же, как и в отношении phi. Более глубокая связь все еще прослеживается в значении корня из 10.
Квадратный корень из единицы равен единице, а квадратный корень из 10 — это число с очень похожими свойствами на PhiG. /10=3.16227766 и обратное значение этого числа — это то же самое число, разделенное на 10. 1 / 3.16227766 = .316227766, все цифры одинаковы, но значение разряда смещено. Именно свойство этих чисел и их инверсии дает возможность проявлению проявиться.Вот почему система base 10 так хорошо работает и ее вполне естественно использовать. С этой точки зрения поток Вселенной проявляется посредством числа в определенных совершенных, гармоничных и симметричных формах. Состояние потока имеет прямое отношение к отношениям Phi, создаваемым совершенными числами. Это верно с математической и философской точек зрения. Проявленное состояние имеет прямое отношение к степени 10 и свойствам его квадратного корня.
Поток и масса [Phi и 10] связаны между собой движением со скоростью света и мощностью этой скорости.
Поток и масса в соотношении и проявлении через число порождают длины силовых линий.
Каббалистический
отрывки текста из «Фонтана мудрости». С комментарием в скобках, показывающим отношение к Phi Physics.
Первый атрибут, длинный, истинный и прямой … (первый принцип — это первое измерение, представление бесконечной линии) Каждый атрибут называется пламенем … (эти атрибуты связаны со светом, теплом и т. Д. От электромагнитного поля). спектр)
Каждое пламя или линия — это тоже глаз.. (глаз получает свет)
Каждый глаз или линия делится на 5 частей … (сравните с Луки 12: 51,52: «Вы думаете, что Я пришел дать мир земле? Нет, говорю вам, но скорее РАЗДЕЛЕНИЕ. : Ибо отныне будет ПЯТЬ в ОДНОМ доме, РАЗДЕЛЕННЫХ, ТРИ ПРОТИВ ДВУХ, И ДВА ПРОТИВ ТРИ.) Из пламени возникает эфир, и эфир сообщает СТРУКТУРУ … (бесконечные линии одного являются корнем всего) эфир, который здесь рассматривается как двумерное поле, и это основа для трехмерных геометрических структур) также эфир сообщает ДЕЙСТВИЮ, ВОССТАНОВЛЕНИЕ, МЕХАНИКУ, ВЫЧИСЛЕНИЕ, РЕЧИ И ГРУППИРОВАНИЕ: все вместе они составляют основу всего сущего.(Семерка)
Святой — первый существующий … нам надлежит понять и созерцать исследование Его реальности и того, как Он начал творение … На каком пути Он появился … Они разделились на части или протяженные сущности … каналы узкие и короткие, пути чрезмерные, дороги широкие, также называемые детьми, матерями и андрогенными .. От пламени нить тянется наружу .. нити утолщаются, становятся скипетрами… Все растворяется и возвращается в эфир который является важным элементом..
До небесного мира, известного как 377 отсеков, существовал эфир, сущность, из которой исходил изначальный свет, очищенный мириадами светил; называется Святой Дух ..
(377 — это 13 -е число Фибоначчи , считая от 1. Число Небес 377 — это число SHaMaYiM = 390 минус 13 атрибутов, таким образом связывая 13 с 377. 13 — это само число Фибоначчи 6 ).
После первого света потянулся еще один фонтан, из которого течет тьма.Эта темнота представляет собой сочетание трех оттенков.
1 ул . зеленый, 2 и . зеленый и голубой, 3 ряд . зеленый, голубой и красный … И это первозданная тьма, возникающая из эфира. (это очень ясно; сначала рассматривается середина солнечного спектра, затем часть в сторону ультрафиолета или синего конца спектра, затем красный в сторону инфракрасного. Зеленый, синий и красный действительно являются тремя основными цветами, называемыми по-разному аддитивные праймериз, праймериз света, праймериз физиков, а также физиологические праймериз.Первичные или субтрактивные пигменты — это красный, желтый и синий. Смысл, который затем подчеркивается в тексте, заключается в том, что эти световые оттенки нельзя увидеть напрямую никакими средствами, что верно, поскольку только поглощение света может обнаружить его, мы видим отраженный и частично поглощенный свет, производящий цвет вокруг нас, а не сам эфирный свет. чего нельзя знать). Поэтому Бог сказал: «Вы увидите Мою спину, но лица Моего не будет видно». «Но с этого момента вы можете знать все». Моисей начал наблюдать первозданный свет, корень всего.. состоящий из двух сущностей, из двух источников, одного света и одного тьмы … Этот поток расширяется и бьет по каналам, и поток снова становится слабым, как поток, и поток снова становится тонким, превращаясь в нить … пока он не станет крошечными капельками … они соединяются, смешиваются, расширяются, и из них выливается сок … Цвета подобны пламени, исходящему из эфира … Два потока на самом деле являются одной материей, исходящей из первобытной тьмы, намекающей на форму. Когда эта форма изменяется, она раскрашивает себя по своим направлениям и оттенкам своих цветов в десять, и каждый отдельный оттенок содержит число десять, что в сумме дает сотню.Сотня снова и снова возвращается к высказываниям, вычислениям и группировке сущностей … пока они не вернутся к сумме единицы, а одна — сущности … (это ясно, что 10 и 10 в квадрате значимы на уровне первые проявления формы, т. е. в основе размерной геометрии).
Тринадцать атрибутов могут быть напрямую связаны с рядами чисел Фибоначчи, 1 2 3 5 8 13 и т. Д., А также могут быть связаны с рядами соотношений, образованных из них, аппроксимирующих фи.1/1 2/1 3/2 5/3 8/5 13/8 21/13 34/21 55/34 89/55 144/89 233/144 377/233 610/377. Эти числа закодированы во всей природе. Неудивительно, что они лежат в основе квантовых событий, а также в самом сердце атома, устанавливая правила, которым следует формирование геометрических объектов, в отличие от того, что изображает современная квантовая физика, которая не имеет геометрической основы.
Эйнштейн всегда верил в геометрию микромира и был прав. От одного исходит вся геометрия фи.
КОНЕЦ ОПРЕДЕЛЯЮТ СРЕДСТВА:
Из бесконечности одномерная линия благодаря соотношению Фи стала длиной, имеющей две крайности. Любая длина будет иметь две крайние точки и, следовательно, также будут иметь средние точки между этими крайними значениями. Три из этих средних точек значимы и естественным образом генерируются потоком чисел. Это АРИФМЕТИЧЕСКИЕ, ГЕОМЕТРИЧЕСКИЕ и ГАРМОНИЧЕСКИЕ средства.
Из этих принципов может быть получена модель АТОМ, основанная на тех же принципах числа, которые наглядно демонстрируют формы жизни.
НОМЕРА И МУЗЫКА
Современная гамма с равномерным темпом для создания музыки — один из многих способов сделать это. Наиболее приятным для уха и голоса может быть C = 512, научная шкала, которая численно превосходит другие, поскольку C также будет равна одному циклу в секунду. A = 440 обычно используется как американский стандарт настройки. Однако нам нужно рассматривать музыку не только как ноты и гаммы, но как аккорды и гармонию, мелодию и ритм. Корень из 2, равный 12 и , является множителем для равномерной темперированной гаммы.Это основано на иррациональных числах.
Продолжается с точностью до пятых. 1/1 3/2 9/4 27/8 81/16.
Базовая пифагорейская настройка выполняется в мажорных третях. Это соотношение составляет 5/4. 4/1 х 5/4 = 5/1. Это = 80/16 = 5.
Конечно, это соответствует числовым корням PhiG, которые происходят от / 5.
КОСМИЧЕСКИЙ СПЕКТР
1. Центр Вселенной.
Есть ли у Вселенной центр? Это звучит как достаточно простой вопрос, но оказывается, что это намного больше.
Пространственно, это вопрос типа Геометрии, который в первую очередь навязывается Вселенной. Геометрии с отрицательной или положительной кривизной и евклидовы геометрии дают разные центральные точки. Пока не известно, является ли Вселенная той или иной, хотя эмпирические данные показывают, что Вселенная в высокой степени евклидова. То, что общая теория относительности точна практически во всех эмпирических методах исследования, показывает, что положительная кривизна действительно дает очень хорошие результаты в математике гравитации.В то время как отрицательная кривизна оказалась геометрическим выражением магнитных сил, как в работе Гаусса. Это интересно и показательно. На первый взгляд может показаться, что потребуются ВСЕ ТРИ формы геометрии, чтобы охватить вселенную, а также будут ТРИ ЦЕНТРАЛЬНЫХ ТОЧКИ в нашей Вселенной. Центр есть? ДЕЙСТВИТЕЛЬНО!
Гравитационный центр, магнитный центр и электромагнитный центр, представляющие три геометрии.
Это можно представить как БУДУЩЕЕ (магнитные, формирующие силы с ОТРИЦАТЕЛЬНОЙ кривизной), прибывающее в НАСТОЯЩЕЕ, становится евклидовым для путей восприятия.Когда наше внимание сосредоточено на микромире атомов и субатомов, вещи кажутся изогнутыми, образуя все более мелкие субструктуры. Эти структуры связаны с ПРОШЛОМ «мировыми линиями».
ПРОШЛОЕ ПОЛОЖИТЕЛЬНО ИЗГИБНАЯ ГЕОМЕТРИЯ
НАСТОЯЩАЯ ГЕОМЕТРИЯ Евклида
БУДУЩАЯ ГЕОМЕТРИЯ ОТРИЦАТЕЛЬНО ИЗогнутой
ПРОШЛОЕ ГРАВИТАЦИОННАЯ МАССА
НАЛИЧИЕ ЭЛЕКТРОМАГНИТНЫХ СИЛ
МАГНИТНЫЕ СИЛЫ БУДУЩЕГО
Центральная точка прошлого — это исходная точка в пространстве-времени, как это выдвигается в Теории Большого взрыва о происхождении Вселенной.Эта теория слишком сильно полагается на положительную в прошлом геометрию гравитации и массы.
Вероятно, по этой причине это неверно.
Центральную точку настоящего нигде не видно, потому что мы можем смотреть только на сигналы, посланные когда-то в прошлом от звезд и галактик. Однако многое можно сказать о расположении центральной точки присутствующего ЭМ в узкой полосе видимого света, а не в каком-то геометрическом сегменте пространства, который мы не можем видеть в его истинном нынешнем состоянии. Это означает именно это; видимый спектр содержит большую часть электромагнитной энергии во всей Вселенной.Инфракрасный, ультрафиолетовый, гамма-лучи, радио и другие диапазоны электромагнитного спектра содержат лишь крошечную часть того, что содержится в спектре видимого света. Причина в том, что большинство звезд сильно излучают видимые цвета, переходя от синего через желтые к красным звездам и т. Д. Во всем ЭМ-спектре видимая часть является очень узкой частью, подобно лазеру, являющемуся сфокусированной узкой полосой видимого света. . Это указывает на центральную точку, которая может пригодиться при исследовании аспектов Вселенной.
В центре будущего будет нечто другое.
3.15. Дельта-функция — документация: справочник по теоретической физике 0.5
Дельта-функция определяется таким образом, что выполняется это соотношение:
(3.15.1)
Такой функции не существует, но можно найти множество последовательностей, «сходящихся» к дельта-функции:
(3.15.2)
точнее:
(3.15.3)
один из примеров такой последовательности:
Ясно, что (3.15.3) выполняется для любой хорошо управляемой функции.
Некоторые математики любят говорить, что неправильно использовать такое обозначение, когда
на самом деле интеграл (3.15.1) не «существует», но мы не будем
их подход, потому что неважно, «существует» что-то или нет,
а, скорее, если ясно, что мы подразумеваем под нашими обозначениями: (3.15.1) — это
сокращение для (3.15.3) и (3.15.2) получает математически строгий
то есть, когда вы объединяете обе стороны и используете (3.15.1), чтобы прийти к
(3.15.3). Таким образом, используются соотношения (3.15.1), (3.15.2),
(3.15.3) для вывода всех свойств дельта-функции.Приведем пример. Позвольте быть единичным вектором в 3D, и мы можем
обозначьте его, используя сферические координаты.
Мы также можем выразить это в декартовых координатах как.(3.15.4)
Выражение как функция от и
у нас(3,15,5)
Выражая (3.15.4) в сферических координатах, получаем
и сравнивая с (3.15.5), окончательно получаем
Точно так же получаем
См. Также (3.17.4.1) для примера, как поступить с большим количеством
сложные выражения, включающие дельта-функцию, например.При интегрировании по конечному интервалу очень полезна эта формула:
другими словами, интеграл равен нулю, если. В лимите и получаем:
Другой интеграл, сходящийся к дельта-функции:
Некоторым математикам нравится использовать распределения и математические обозначения для
то, что, как мне кажется, делает вещи менее ясными, но, тем не менее,
это тоже важно понять, поэтому в этом разделе поясняются обозначения,
но я не рекомендую использовать его — я предлагаю использовать только физические обозначения как
объяснено ниже.Приведенные ниже математические обозначения заключены в кавычки, чтобы
его не путают с физическими обозначениями.Распределение является функциональным, и каждая функция может быть идентифицирована
с распределением, которое он генерирует с использованием этого определения
(
это тестовая функция):кроме этого, можно также определить распределения, которые нельзя отождествить с
регулярные функции, одним из примеров является дельта-распределение (дельта-функция Дирака):Последний интеграл в математике не используется, в физике наоборот
первые выражения () не используются, поэтому всегда означает
что вам нужно интегрировать его, как объяснялось в предыдущем разделе, поэтому он
ведет себя как обычная функция (за исключением того, что такой функции не существует и
точный математический смысл будет только после того, как вы его интегрируете, или через
идентификация выше с дистрибутивами).Затем определяют общие операции, воздействуя на производящую функцию, затем
наблюдает за шаблоном и определяет его для всех распределений. Например
дифференциация:так:
Умножение:
так:
Преобразование Фурье:
так:
Но, как видите, нотация только усложняет задачу, поскольку
Достаточно просто поработать с интегралами и забыть обо всем остальном.Тогда можно
даже опускаем интегралы, понимая, что они неявные.Еще несколько примеров:
Подтверждение:
Подтверждение:
Подтверждение:
Чтобы доказать, что мы делаем
следующий расчет:, где функция ограничена и конечна, поскольку
пробная функция бесконечно дифференцируема. От
По лемме Римана – Лебега интеграл сходится к нулю при
.Вариации и функциональные производные являются обобщением дифференциалов и
частные производные функционалов. Важно освоить этот предмет только
как регулярные дифференциалы / производные в исчислении.3.17.3. Функционалы
Давайте теперь определим функциональные производные и вариации.
Functional присваивает каждой функции номер. Вариация
определяется какМы определяем как
Это также дает формулу для вычисления: мы устанавливаем
и(3.17.3.1)
Иногда функциональная производная определяется с использованием последней формулы, здесь
эта формула просто следует из нашего определения.
Каждую функцию можно рассматривать как функционал (хотя и очень простой):, поэтому мы определяем
таким образом пишем и
имеет два значения — либо
(конечное изменение функции) или вариация
функционала в зависимости от контекста.
Это полностью аналогично.Подведем итоги только необходимых формул
в реальных расчетах — определение вариации (с использованием регулярного
производная):(3.17.3.2)
определение функциональной производной:
и понимание, что означает либо
или вариант. Последнее уравнение — лучший способ
вычислить функциональную производную — применить вариацию, пока не получите
интегрируется в форму, а затем вы читаете
функциональная производная от выражения в скобках.Соответствие между конечномерным и бесконечномерным случаем может быть
резюмировано с помощью функционала, функции непрерывного
параметр (который может быть скаляром или вектором) и его дискретизированный
версия вместе с функцией:Другими словами, основное отличие состоит в том, что непрерывный параметр
заменен дискретным параметром. Тогда функция
становится вектором значений, вариация становится дифференциалом и
функциональная производная становится частной производной.Чтобы минимизировать функционал,
нужно искать нулевую функциональную производную, а в дискретном случае
ищет нулевые частные производные (градиент).Теперь мы расширим обозначение -вариации на любую функцию, которая
содержит изменяемую функцию, вам просто нужно заменить ее на
и применить ко всему, ибо
пример (здесь и):Таким образом, в (3.17.3.2) может быть либо функционал, либо любой
выражение, содержащее функцию.
Эти обозначения позволяют нам очень удобные вычисления, как показано на
следующие примеры.Во-первых, при вычислении вариации некоторого интеграла мы
можно обменять и:В выражении мы должны понимать из контекста, если
мы рассматриваем его как функционал или. В нашем случае это
функционал, так что у нас есть.Второе очень важное замечание касается вариации выражения вроде:
тогда, когда заменяется на, нужно отслеживать
независимая переменная, поэтому заменяется на и заменяется на.Таким образом
две вариации и разные (независимые).
Если есть только одна независимая переменная, можно просто написать как
ясно, что такое независимая переменная. Это аналогично использованию
дифференциалы, например , где нужно отслеживать
независимая переменная, а также для каждого.Еще одна полезная формула — дифференциация функционала
где функция зависит от параметра:, где мы использовали определение вариации и функциональной производной с
:3.17.4. Примеры
Некоторые из этих примеров показывают, как использовать определение дельта-функции
функциональная производная в уравнении (3.17.3.1). Тем не менее
Самый простой способ — сначала вычислить вариацию, а затем считать функционал
производная от результата, как объяснено выше.Следующий пример показывает, что при выборе варианта выражения, содержащего
функция различных независимых переменных, необходимо отслеживать
этих переменных в вариациях:Последнее равенство следует из (любой антисимметричной
часть a не будет способствовать симметричной интеграции).Другой пример — вывод уравнений Эйлера-Лагранжа для
Плотность лагранжиана:Мы также можем записать его, используя функциональную производную как:
Другой пример:
Можно подумать, что приведенный выше расчет неверен, потому что
не определено. В случае
Приведенные выше обозначения автоматически подразумевают работу с некоторыми
последовательность (например) и взятие лимита:(3.17.4.1)
Как видите, мы получили тот же результат, с той же тщательностью, но используя
запутывающая нотация. Вот почему такие очевидные манипуляции с
неявно подразумеваются. Однако лучший способ — сначала
рассчитать вариацию:и сразу считайте функциональную производную:
Другой пример с метрикой как функцией координат
:И пример изменения по метрике:
Другой пример (изменяющийся энергетический функционал):
Другой пример (энергия Хартри):
сначала рассчитываем вариацию:
, поэтому функциональная производная:
Другой пример (функционал с градиентами):
вариант:
, откуда мы считываем функциональную производную:
Нотация Дирака позволяет очень компактно и эффективно писать
уравнения, описывающие разложение функции в базис, как дискретные
(е.грамм. разложение в ряд Фурье) и непрерывное (например, преобразование Фурье)
и подобные вещи. Обозначения составлены таким образом, что их очень легко
помните, и он просто поможет вам написать правильное уравнение.У нас есть функция. Определяем
Следующее уравнение
становится
и, таким образом, мы можем интерпретировать как вектор, как базис и как коэффициенты в разложении базиса:
Вот и все.Возьмите приведенные выше правила как рабочее определение
обозначений Дирака. Это как с дельта-функцией — она написана отдельно.
не имеет никакого значения, но существуют четкие и однозначные правила для
преобразовать любое выражение с помощью в выражение, которое даже математики
понимать (т.е. интегрировать, применять тестовые функции и использовать другие отношения
чтобы избавиться от всех символов в выражении — но результат
обычно намного сложнее, чем исходная формула). То же самое и с
Кет: написанное само по себе, оно не имеет никакого значения, но вы можете
всегда используйте приведенные выше правила, чтобы выражение было понятным для всех.
(я.е. прикрепляя любой бюстгальтер слева и переписывая все скобки
с их эквивалентными выражениями), но это будет сложнее и труднее
помните и, что важно, менее общее.Теперь посмотрим на сферические гармоники:
на единичной сфере, имеем
, таким образом,
и из (3.30.1) получаем
сейчас
из (3.30.3) получаем
, так что у нас
образует ортонормированный базис.Любая функция, заданная на сфере, может быть записана с использованием этого базиса:
где
Если у нас есть функция в 3D, мы можем записать ее как функцию от и и раскрыть только по переменной:
В нотации Дирака мы делаем следующее: разбиваем пространство на угловую и радиальную части
и напишите
где
Давайте посчитаем
т.
Мы должны подчеркнуть, что действует только в пространстве
(не пробел), что означает, чтои оставляет нетронутым.Аналогично
— это единица только в пространстве (т.е. на единичной сфере).
Перепишем уравнение (3.30.4):
Используя соотношение полноты (3.29.1):
, теперь мы можем вывести очень важную формулу, справедливую для каждой функции:
где
или явно написано
(3.18.1)
Функция нескольких переменных есть
однородный степени, еслиПутем дифференцирования по:
и установив так называемое уравнение Эйлера:
в 3D это также можно записать как:
3.19.1. Пример 1
Функция однородна степени 1, потому что:
, а уравнение Эйлера:
или
Что верно.
3.19.2. Пример 2
Функция однородна степени -1, потому что:
, а уравнение Эйлера:
или
Что верно.
Зеленые функции — отличный инструмент для работы с решением для любого ODE или
PDE.В этом тексте мы объясняем, как это работает, а затем показываем, как можно вычислить
их с помощью МКЭ.3.20.2. Граничные условия
Уравнение (3.20.1.3) не определяет функцию Грина однозначно,
потому что к нему можно добавить любое решение однородного уравнения.
Мы можем использовать эту свободу для решения (3.20.1.3) для любого граничного условия.
Итак, зададим граничное условие
и найти функцию Грина (решив (3.20.1.3)), удовлетворяющую условию
граничное условие. Можно показать, что определяется из
(3.20.1.2), то также должно удовлетворять такое же граничное условие.3.20.4. Примеры
Уравнение Пуассона в 1D
Уравнение Пуассона:
Вычисляем функцию Грина с помощью преобразования Фурье:
Чек:
Тогда:
Зеленую функцию также можно записать с помощью и
:Радиальное уравнение Пуассона
Давайте запишем и воспользуемся ступенчатой функцией Хевисайда:
и:
Тогда мы можем различить:
Дано:
(3.20.4.1)
Функция зеленого цвета:
Давайте дифференцируем:
и
Получаем:
Итак, из (3.20.4.1) есть решение радиальной пуассоновской
уравнение:Уравнение Гельмгольца в 1D
с граничными условиями.
Используем преобразование Фурье:Чек:
Общее решение однородного уравнения:
, поэтому общая функция Грина:
Удовлетворение граничным условиям (для всех):
получаем:
и:
и
Чтобы показать, что это действительно работает, возьмем, к примеру.Тогда
Мы можем использовать SymPy для вычисления интегралов:
В [1]: u = -cos (x) * интегрировать (3 * sin (2 * y) * sin (y), (y, 0, x)) - \ sin (x) * интегрировать (3 * sin (2 * y) * cos (y), (y, x, pi / 2)) В [2]: u Из [2]: - (cos (x) * sin (2 * x) - 2 * cos (2 * x) * sin (x)) * cos (x) - (sin (x) * sin (2 * x) + 2 * cos (x) * cos (2 * x)) * sin (x) В [3]: simpleify (u) Из [3]: 2 2 - cos (x) * sin (2 * x) - sin (x) * sin (2 * x) В [4]: trigsimp (_) Out [4]: -sin (2 * x)И получаем
Мы можем легко проверить, что:
>>> u = -sin (2 * x) >>> u.разн (х, 2) + и 3 * грех (2 * х)
, и поскольку мы проверили, что это правильный
решение.Уравнение Пуассона в 2D
Пусть и хотим решить:
Итак имеем:
Решение:
Уравнение Пуассона в 3D
с граничным условием на бесконечности. Тогда:
и
Уравнение Гельмгольца в 3D
с граничным условием на бесконечности.Тогда:
Для целых чисел и биномиальные коэффициенты определяются как:
На самом деле, можно просто использовать вторую формулу как определение:
Пример I:
Пример II:
Биномиальная формула для целого числа:
и для реального, и это можно обобщить до:
Пример: (для)
так:
Другой пример:
, где мы использовали (3.22.2) и
Многочлены Лежандра.
При вычислении двойных сумм можно использовать треугольное суммирование, чтобы переупорядочить их:
(3.22.1)
Также вмещает
(3.22.2)
Неравенство треугольника (условие) означает, что ни одно из трех
количества« больше, чем сумма двух других:(3.23.1)
Это эквивалентно всего одному уравнению:
(3.23.2)
мы можем делать любую перестановку символов, т.е.е. приведенное выше уравнение эквивалентно
на любой из этих:Таким образом, вместо трех неравенств (3.23.1)
удобно просто написать (3.23.2), используя любую перестановку, которая нам нравится.Чтобы показать, что (3.23.1) влечет (3.23.2), перепишем
(3.23.1):т.
и получаем (3.23.2).
Чтобы показать, что (3.23.2) влечет (3.23.1), перепишем
(3.23.2) для первого:так:
перестановка:
, так как положительно, если то еще и получаем
(3.23.1). Наконец, для:так:
перестановка:
, так как положительно, если то еще и получаем
(3.23.1).Гамма-функция определяется следующими свойствами
для:(3.24.1)
(3.24.2)
(3.24.3)
Можно показать, что это однозначно определяет функцию для (это
называется теоремой Бора-Моллерупа), и тогда ее можно аналитически расширить на
вся сложная плоскость.Наиболее распространенная формула удовлетворяет (3.24.1),
(3.24.2) и (3.24.3)
это:(3,24,4)
Он удовлетворяет (3.24.1), потому что:
Он удовлетворяет (3.24.2) интегрированием по частям:
Наконец, он удовлетворяет (3.24.3), проверяя условие выпуклости
напрямую (а):Таким образом, (3.24.4) однозначно определяет гамма-функцию.
Мы можем использовать (3.24.4) для вычисления:Из этого и определения гамма-функции получаем
для целого числа:(3.24,5)
и
(3,24,6)
Верхняя неполная гамма-функция определяется по:
Интегрируя по частям, получаем:
Некоторые специальные значения:
Для целого числа получаем:
и
Нижняя неполная гамма-функция определяется по:
, и поэтому все выражения могут быть легко получены с использованием гаммы и верхнего
неполные гамма-функции.Тогда рекурсивное отношение:Некоторые специальные значения:
Путем повторного применения формулы рекурсии получаем:
(3.25.1)
где мы использовали:
, что доказывается следующим неравенством, использующим тот факт, что
функция является возрастающей функцией для, так как
пока получим:Используя (3.25.1), теперь мы можем писать, используя метод Куммера.
конфлюэнтная гипергеометрическая функция следующим образом:3.25.1. Пример
Рассмотрим класс интегралов:
Запишем их с помощью нижней неполной гамма-функции как:
Мы также можем записать это с помощью конфлюэнтной гипергеометрической функции следующим образом:
Для получения:
Используя соотношение рекурсии, получаем:
Выражая из уравнения, получаем обратное соотношение:
Из (3.25.1) получаем:
Факториал определяется как
Согласно (3.24.5) это может быть записано с использованием гамма-функции как:
Двойной факториал определяется как:
Можно переписать двойной факториал, используя факториал как:
Для нечетного может быть записано с помощью гамма-функции, см. (3.24.6):
3.27.1. Пример
Интеграл Ферми-Дирака (иногда называемый просто интегралом Ферми) определяется
как:Примеры:
Интеграл Ферми-Дирака можно также записать с помощью полилогарифма, см.
