Содержание
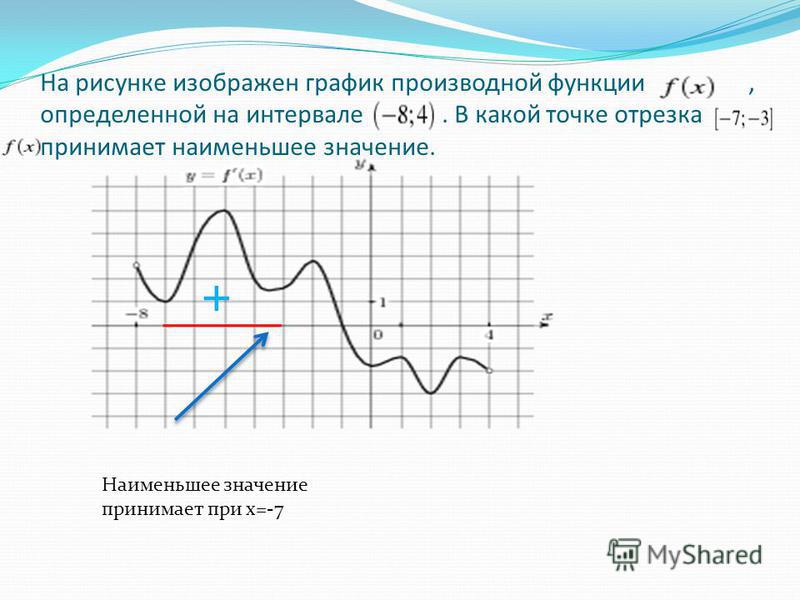
В какой точке значение производной набольшее
Дорогие друзья! В группу заданий связанных с производной входят задачи — в условии дан график функции, несколько точек на этом графике и стоит вопрос:
В какой точке значение производной наибольшее (наименьшее)?
Данные задачи очень просты, не требуется никаких вычислений, решаются устно. Главное что необходимо – это понимать геометрический смысл производной, свойства производной для исследования функций. По представленным ссылкам вы можете повторить (изучить) материал на сайте, также краткая информация есть в справочнике.
Кратко повторим:
Производная в точке равна угловому коэффициенту касательной проходящей через эту точку графика.
Угловой коэффициент касательной в свою очередь равен тангенсу угла наклона этой касательной.
*Имеется ввиду угол между касательной и осью абсцисс.
Далее:
1. На интервалах возрастания функции производная имеет положительное значение.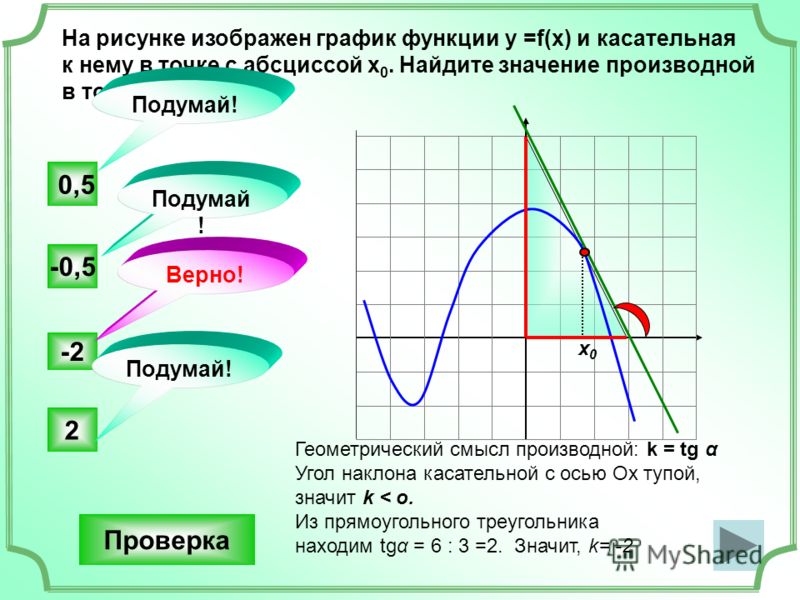
2. На интервалах её убывания производная имеет отрицательное значение.
Рассмотрим следующий эскиз:
В точках 1,2,4 производная функции имеет отрицательное значение, так как данные точки принадлежат интервалам убывания.
В точках 3,5,6 производная функции имеет положительное значение, так как данные точки принадлежат интервалам возрастания.
Как видим, со значением производной всё ясно, то есть определить какой она имеет знак (положительный или отрицательный) в определённой точке графика совсем несложно.
При чём, если мы мысленно построим касательные в этих точках, то увидим, что прямые проходящие через точки 3, 5 и 6 образуют с осью оХ углы лежащие в пределах от 0 до 90о, а прямые проходящие через точки 1, 2 и 4 образуют с осью оХ углы в пределах от 90о до 180о.
*Взаимосвязь понятна: касательные проходящие через точки принадлежащие интервалам возрастания функции образуют с осью оХ острые углы, касательные проходящие через точки принадлежащие интервалам убывания функции образуют с осью оХ тупые углы.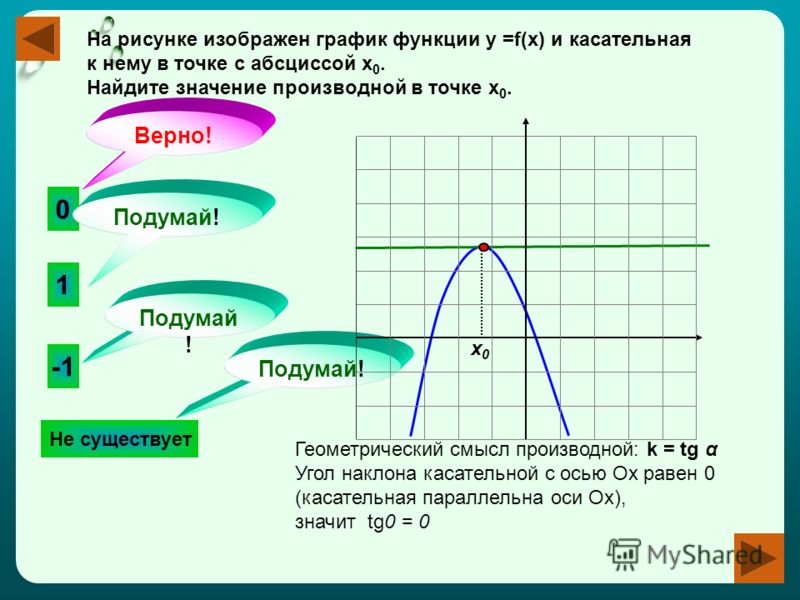
Теперь важный вопрос!
А как изменяется значение производной? Ведь касательная в разных точках графика непрерывной функции образует разные углы, в зависимости от того, через какую точку графика она проходит.
*Или, говоря простым языком, касательная расположена как бы «горизонтальнее» или «вертикальнее». Посмотрите:
Прямые образуют с осью оХ углы в пределах от 0 до 90о
Прямые образуют с осью оХ углы в пределах от 90о до 180о
Поэтому, если будут стоять вопросы:
— в какой из данных точек графика значение производной имеет наименьше значение?
— в какой из данных точек графика значение производной имеет наибольшее значение?
то для ответа необходимо понимать, как изменяется значение тангенса угла касательной в пределах от 0 до 180о.
*Как уже сказано, значение производной функции в точке равно тангенсу угла наклона касательной к оси оХ.
Значение тангенса изменяется следующим образом:
При изменении угла наклона прямой от 0о до 90о значение тангенса, а значит и производной, изменяется соответственно от 0 до +∞;
При изменении угла наклона прямой от 90о до 180о значение тангенса, а значит и производной, изменяется соответственно –∞ до 0.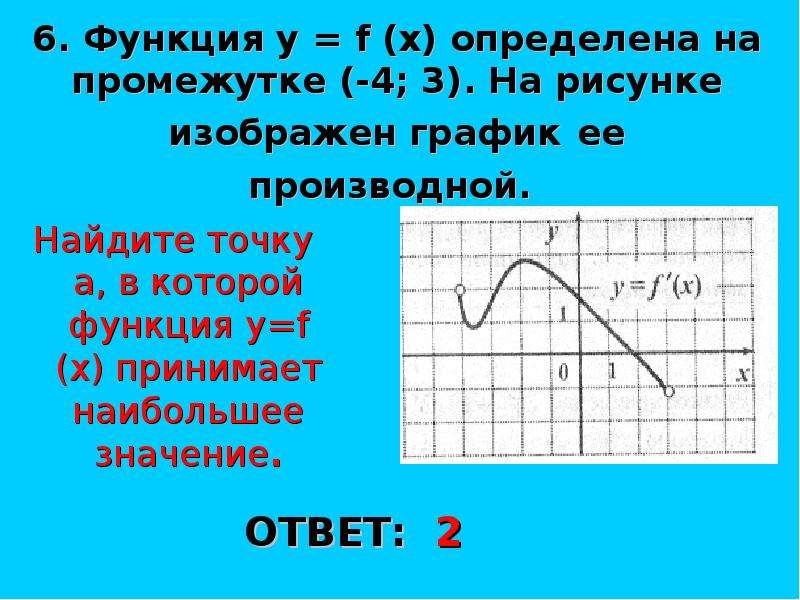
Наглядно это видно по графику функции тангенса:
Говоря простым языком:
При угле наклона касательной от 0о до 90о
Чем он ближе к 0о, тем больше значение производной будет близко к нулю (с положительной стороны).
Чем угол ближе к 90о, тем больше значение производной будет увеличиваться к +∞.
При угле наклона касательной от 90о до 180о
Чем он ближе к 90о, тем больше значение производной будет уменьшаться к –∞.
Чем угол будет ближе к 180о, тем больше значение производной будет близко к нулю (с отрицательной стороны).
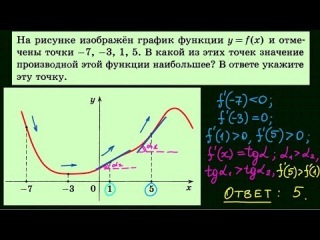
317543. На рисунке изображен график функции y = f(x) и отмечены точки –2, –1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Имеем четыре точки: две из них принадлежат интервалам на которых функция убывает (это точки –1 и 1) и две интервалам на которых функция возрастает (это точки –2 и 2).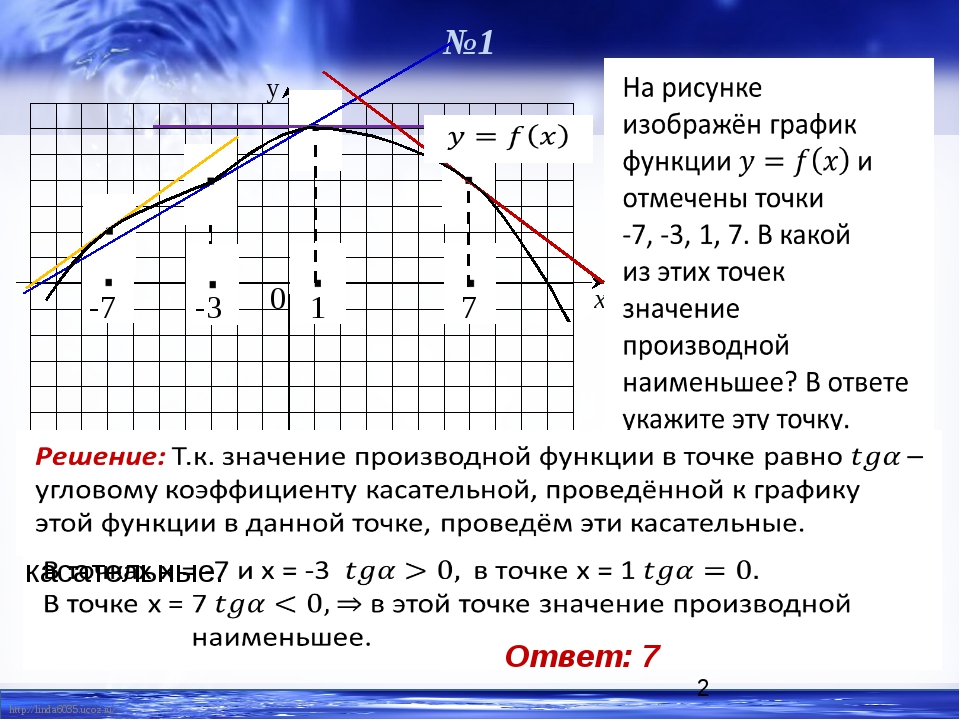
Можем сразу же сделать вывод о том, что в точках –1 и 1 производная имеет отрицательное значение, в точках –2 и 2 она имеет положительное значение. Следовательно в данном случае необходимо проанализировать точки –2 и 2 и определить в какой из них значении будет наибольшим. Построим касательные проходящие через указанные точки:
Значение тангенса угла между прямой a и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке –2 будет наибольшим.
Ответим на следующий вопрос: в какой из точек –2, –1, 1 или 2 значение производной является наибольшим отрицательным? В ответе укажите эту точку.
Производная будет иметь отрицательное значение в точках, принадлежащим интервалам убывания, поэтому рассмотрим точки –2 и 1. Построим касательные проходящие через них:
Видим, что тупой угол между прямой b и осью оХ находится «ближе» к 180о, поэтому его тангенс будет больше тангенса угла, образованного прямой а и осью оХ.
Таким образом, в точке х = 1, значение производной будет наибольшим отрицательным.
317544. На рисунке изображен график функции y = f(x) и отмечены точки –2, –1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Имеем четыре точки: две из них принадлежат интервалам, на которых функция убывает (это точки –1 и 4) и две интервалам, на которых функция возрастает (это точки –2 и 1).
Можем сразу же сделать вывод о том, что в точках –1 и 4 производная имеет отрицательное значение, в точках –2 и 1 она имеет положительное значение. Следовательно, в данном случае, необходимо проанализировать точки –1 и 4 и определить – в какой из них значении будет наименьшим. Построим касательные проходящие через указанные точки:
Значение тангенса угла между прямой a и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке х = 4 будет наименьшим.
Ответ: 4
Надеюсь, что «не перегрузил» вас количеством написанного. На самом деле, всё очень просто, стоит только понять свойства производной, её геометрический смысл и как изменяется значение тангенса угла от 0 до 180о.
Общие рекомендации:
1. Сначала определите знаки производной в данных точках (+ или -) и выберете необходимые точки (в зависимости от поставленного вопроса).
2. Постройте касательные в этих точках.
3. Пользуясь графиком тангесоиды, схематично отметьте углы и отобразите соответствующие им значения.
4. Далее в зависимости от поставленного вопроса в задаче, вы без труда определите точку.
*Если вы понимаете, как изменяется значение тангенса, то можно обойтись без графика.
На этом всё. Успехов Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Как найти наибольшее значение производной в точке. Производная функции
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x 0 ,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x 0 , и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными.
 Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу. - Зная координаты, легко вычислить приращение аргумента Δx = x 2 − x 1 и приращение функции Δy = y 2 − y 1 .
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм.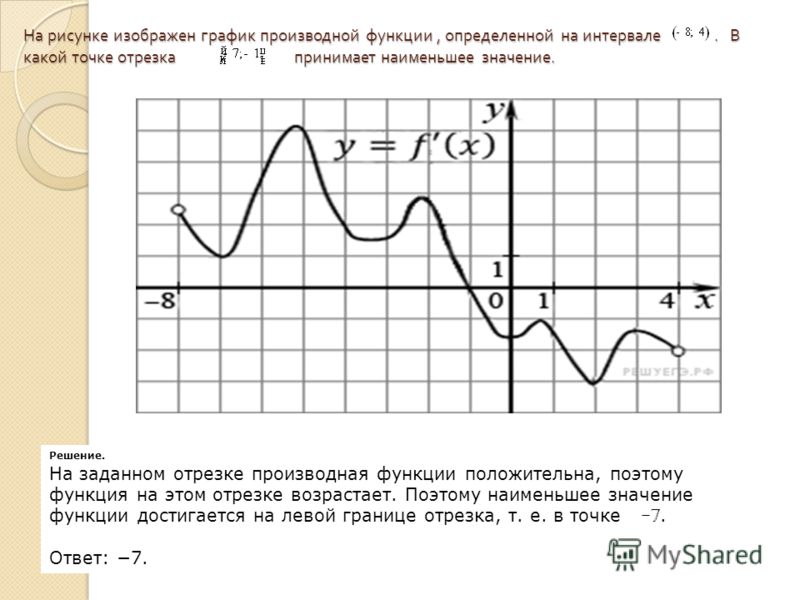 Для начала определимся с терминологией:
Для начала определимся с терминологией:
- Точка x 0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≥ f(x).
- Точка x 0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5.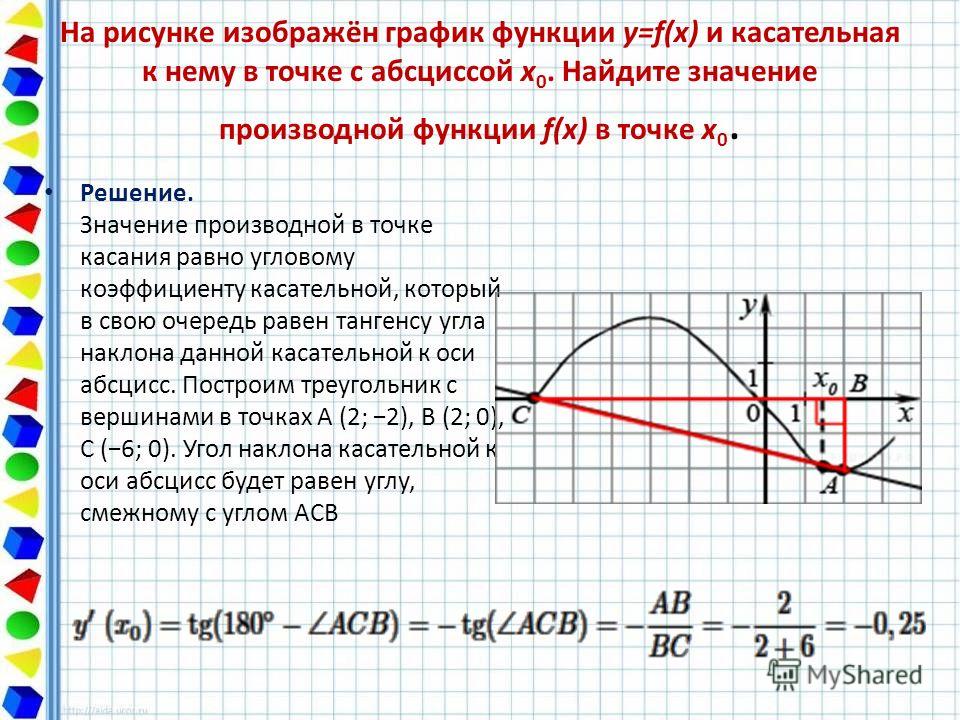 Отметим на полученном графике знаки производной. Имеем:
Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
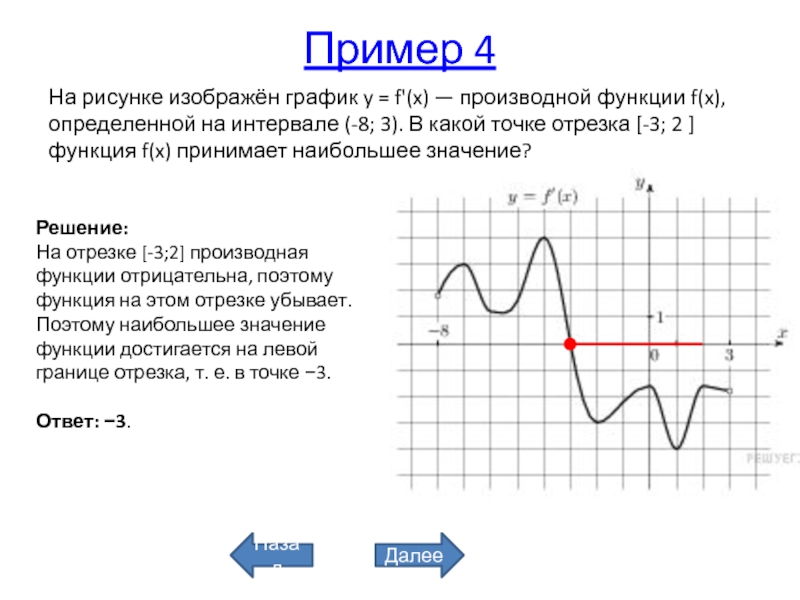
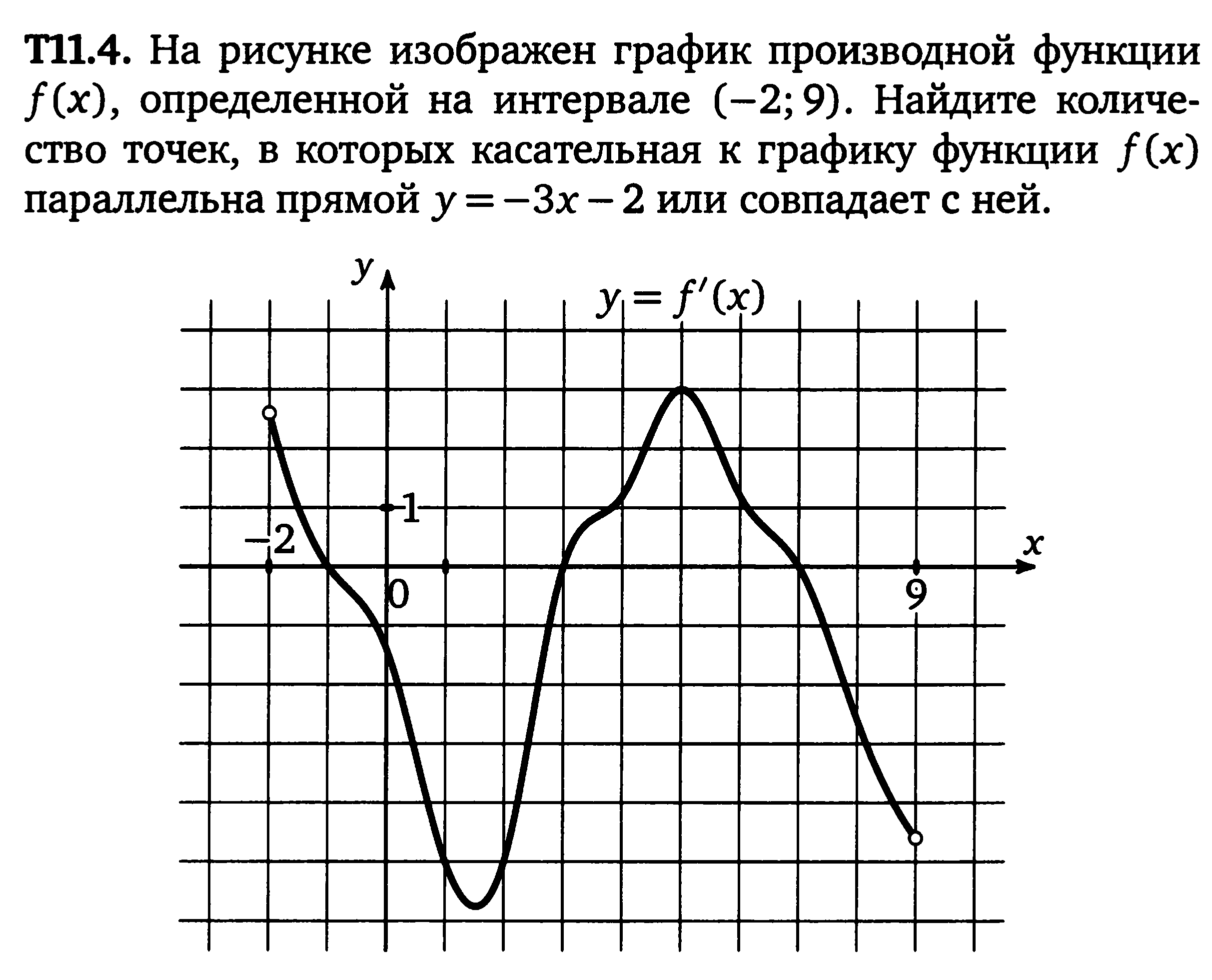
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи.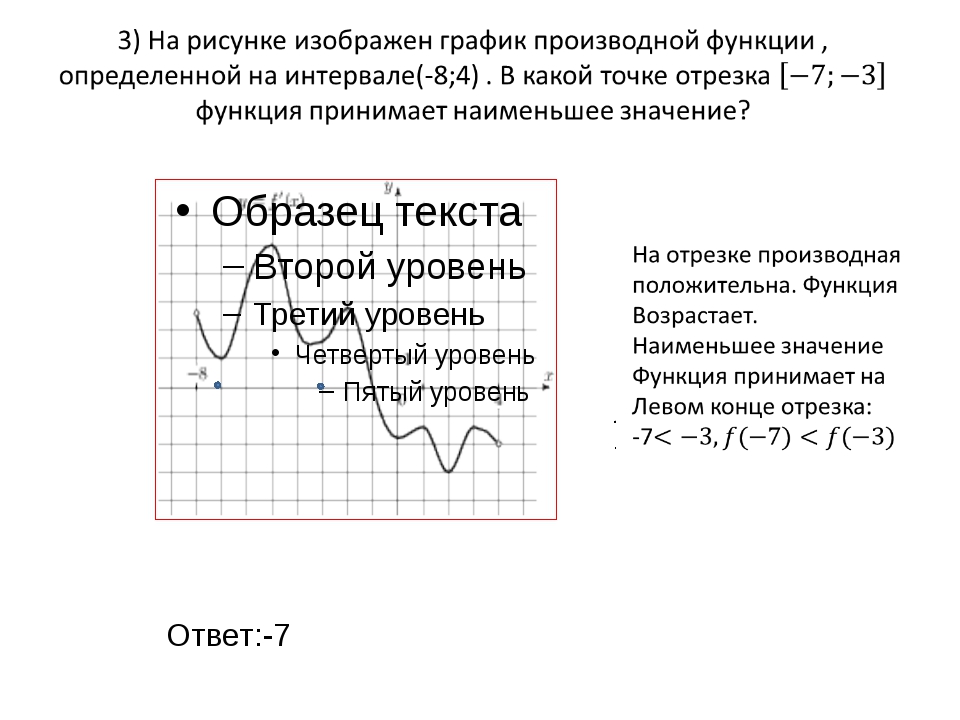 Разумеется, с целочисленными точками такой фокус не пройдет.
Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке , достаточно, чтобы ее производная внутри отрезка была положительна, т.
 е. f’(x) ≥ 0.
е. f’(x) ≥ 0. - Для того чтобы непрерывная функция f(x) убывала на отрезке , достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x).
В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
Вычислим их длины:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l 2 = 5.
Сергей Никифоров
Если производная функции знакопостоянна на интервале, а сама функция непрерывна на его границах, то граничные точки присоединяются как к промежуткам возрастания, так и к промежуткам убывания, что полностью соответствует определению возрастающих и убывающих функций.
Фарит Ямаев
26.10.2016 18:50
Здравствуйте. Как же (на каком основании) можно утверждать, что в точке, где производная равна нулю, функция возрастает. Приведите доводы. Иначе, это просто чей-то каприз. По какой теореме? А также доказательство. Спасибо.
Служба поддержки
Значение производной в точке не имеет прямого отношения к возрастанию функции на промежутке. Рассмотрите, например, функции — все они возрастают на отрезке
Владлен Писарев
02. 11.2016 22:21
11.2016 22:21
Если функция возрастает на интервале (а;b) и определена и непрерывна в точках а и b, то она возрастает на отрезке . Т.е. точка x=2 входит в данный промежуток.
Хотя, как правило возрастание и убывание рассматривается не на отрезке, а на интервале.
Но в самой точке x=2, функция имеет локальный минимум. И как объяснять детям, что когда они ищут точки возрастания (убывания), то точки локального экстремума не считаем, а в промежутки возрастания (убывания) — входят.
Учитывая, что первая часть ЕГЭ для «средней группы детского сада», то наверное такие нюансы- перебор.
Отдельно, большое спасибо за «Решу ЕГЭ» всем сотрудникам- отличное пособие.
Сергей Никифоров
Простое объяснение можно получить, если отталкиваться от определения возрастающей/убывающей функции. Напомню, что звучит оно так: функция называется возрастающей/убывающей на промежутке, если большему аргументу функции соответствует большее/меньшее значение функции. Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.
Ирина Ишмакова
20.11.2017 11:46
Добрый день. Здесь в комментариях я вижу убеждения, что границы включать нужно. Допустим, я с этим соглашусь. Но посмотрите, пожалуйста, ваше решение к задаче 7089. Там при указании промежутков возрастания границы не включаются. И это влияет на ответ. Т.е. решения заданий 6429 и 7089 противоречат друг другу. Проясните, пожалуйста, эту ситуацию.
Александр Иванов
В заданиях 6429 и 7089 совершенно разные вопросы.
В одном про промежутки возрастания, а в другом про промежутки с положительной производной.
Противоречия нет.
Экстремумы входят в промежутки возрастания и убывания, но точки, в которых производная равна нулю, не входят в промежутки, на которых производная положительна.
A Z
28.01.2019 19:09
Коллеги, есть понятие возрастания в точке
(см. Фихтенгольц например)
и ваше понимание возрастания в точке x=2 противочет классическому определению.
Возрастание и убывание это процесс и хотелось бы придерживаться этого принципа.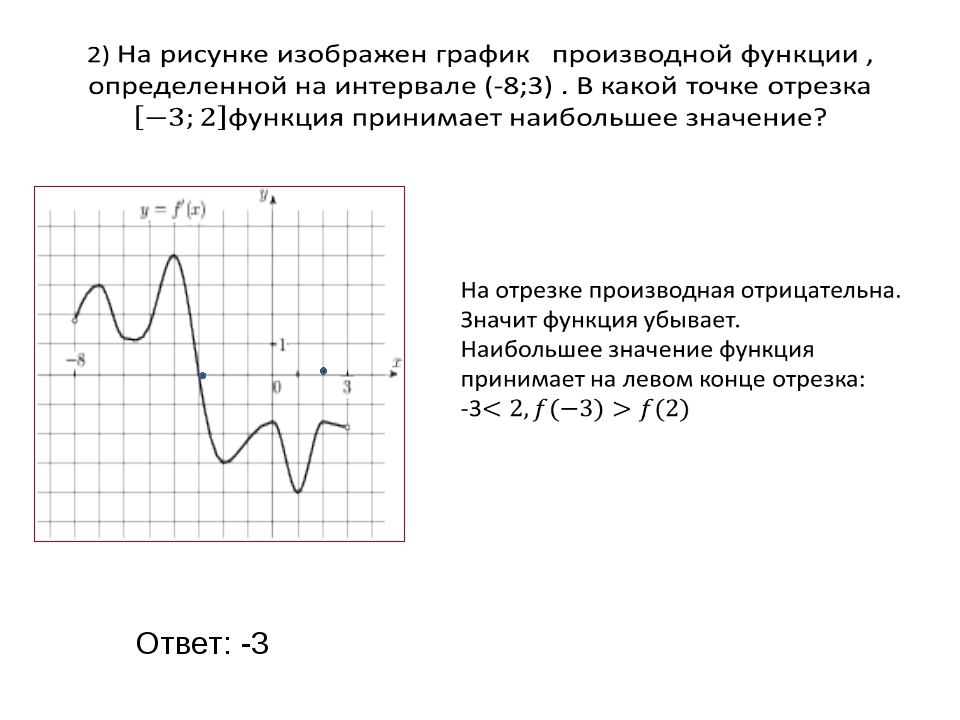
В любом интервале, который содержит точку x=2, функция не является возрастающей. Поэтому включение данный точки x=2 процесс особый.
Обычно, чтобы избежать путаницы о включении концов интервалов говорят отдельно.
Александр Иванов
Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
В точке х=2 функция дифференцируема, а на интервале (2; 6) производная положительна, значит, на промежутке её значения строго положительны, значит функция на этом участке только возрастает, поэтому значение функции в левом конце x
= −3 меньше, чем её значение в правом конце x
= −2.
Ответ: φ
2 (−3) φ
2 (−2)
2) Пользуясь графиком первообразной Φ
2 (x
) (в нашем случае это синий график), определите какое из 2-ух значений функции больше φ
2 (−1) или φ
2 (4)?
По графику первообразной видно, что точка x
= −1 находится на участке возрастания, следовательно значение соответсвующей производной положительно.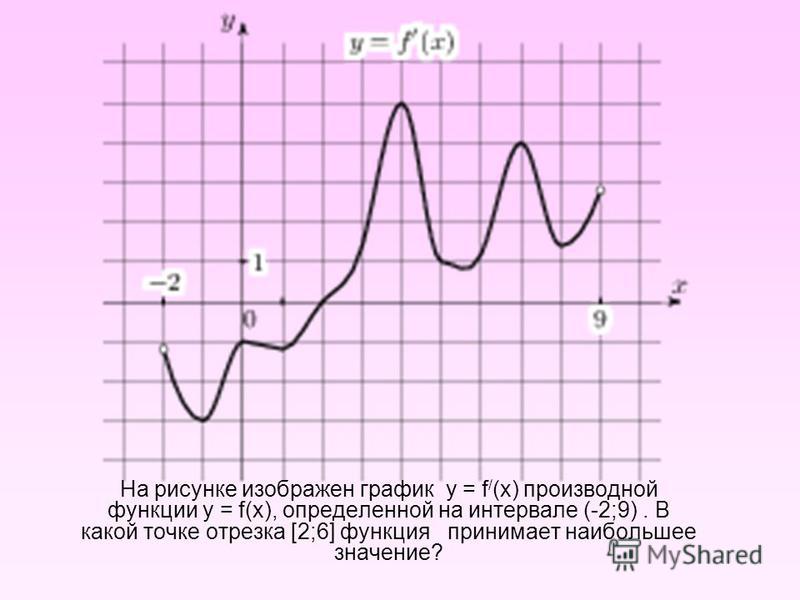 Точка x
Точка x
= 4 находится на участке убывания и значение соответствующей производной отрицательно. Поскольку положительное значение больше отрицательного, делаем вывод — значение неизвестной функции, которая как раз и является производной, в точке 4 меньше, чем в точке −1.
Ответ: φ
2 (−1) > φ
2 (4)
Подобных вопросов по отсутствующему графику можно задать много, что обуславливает большое разноообразие задач с кратким ответом, построенных по такой же схеме. Попробуйте решить некоторые из них.
Задачи на определение характеристик производной по графику функции.
Рисунок 1.
Рисунок 2.
Задача 1
y
= f
(x
), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции положительна.
Производная функции положительна на тех участках, где функция возрастает. По рисунку видно, что это промежутки (−10,5;−7,6), (−1;8,2) и (15,7;19).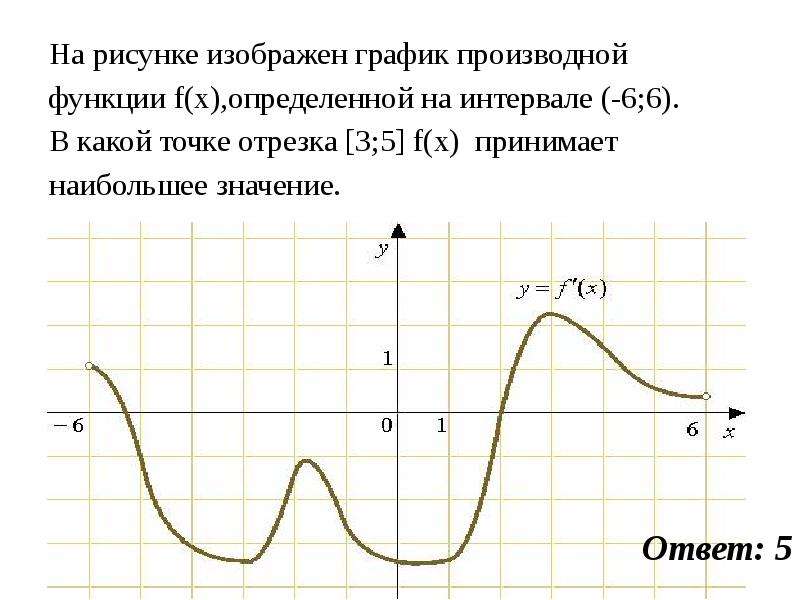 Перечислим целые точки внутри этих интервалов: «−10″,»−9», «−8″,»0», «1»,»2″, «3»,»4″, «5»,»6″, «7»,»8″, «16»,»17″, «18». Всего 15 точек.
Перечислим целые точки внутри этих интервалов: «−10″,»−9», «−8″,»0», «1»,»2″, «3»,»4″, «5»,»6″, «7»,»8″, «16»,»17″, «18». Всего 15 точек.
Ответ: 15
Замечания.
1. Когда в задачах о графиках функций требуют назвать «точки», как правило, имеют в виду только значения аргумента x
, которые являются абсциссами соответствующих точек, расположенных на графике. Ординаты этих точек — значения функции, они являются зависимыми и могут быть легко вычислены при необходимости.
2. При перечислении точек мы не учитывали края интервалов, так как функция в этих точках не возрастает и не убывает, а «разворачивается». Производная в таких точках не положительна и не отрицательна, она равна нулю, поэтому они называются стационарными точками. Кроме того, мы не рассматриваем здесь границы области определения, потому что в условии сказано, что это интервал.
Задача 2
На рисунке 1 изображен график функции y
= f
(x
), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции f »
Определите количество целых точек, в которых производная функции f »
(x
) отрицательна.
Производная функции отрицательна на тех участках, где функция убывает. По рисунку видно, что это промежутки (−7,6;−1) и (8,2;15,7). Целые точки внутри этих интервалов: «−7″,»−6», «−5″,»−4», «−3″,»−2», «9»,»10″, «11»,»12″, «13»,»14″, «15». Всего 13 точек.
Ответ: 13
См. замечания к предыдущей задаче.
Для решения следующих задач нужно вспомнить еще одно определение.
Точки максимума и минимума функции объединяются общим названием — точки экстремума
.
В этих точках производная функции либо равна нулю, либо не существует (необходимое условие экстремума
).
Однако необходимое условие — это признак, но не гарантия существования экстремума функции. Достаточным условием экстремума
является смена знака производной: если производная в точке меняет знак с «+» на «−», то это точка максимума функции; если производная в точке меняет знак с «−» на «+» , то это точка минимума функции; если в точке производная функции равна нулю, либо не существует, но знак производной при переходе через эту точку не меняется на противоположный, то указанная точка не является точкой экстремума функции.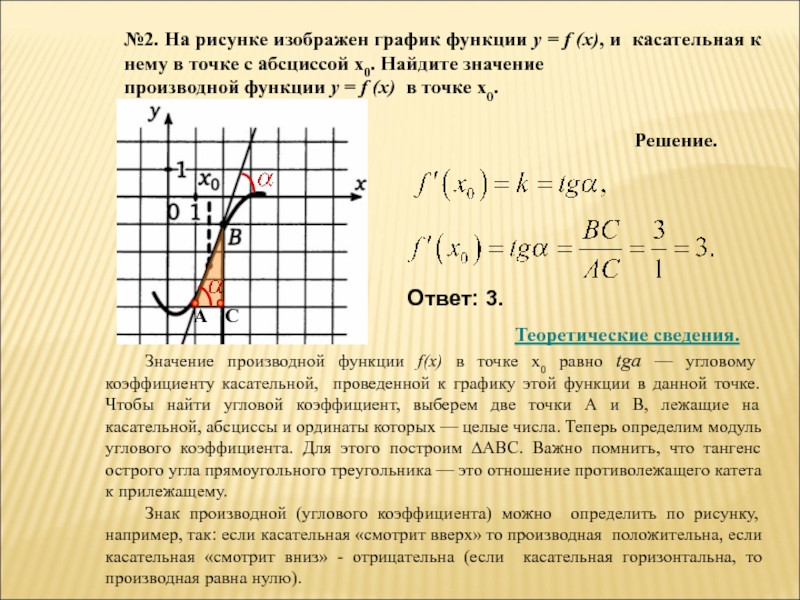 Это может быть точка перегиба, точка разрыва или точка излома графика функции.
Это может быть точка перегиба, точка разрыва или точка излома графика функции.
Задача 3
На рисунке 1 изображен график функции y
= f
(x
), определенной на интервале (−10,5;19). Найдите количество точек, в которых касательная к графику функции параллельна прямой y
= 6 или совпадает с ней.
Вспомним, что уравнение прямой имеет вид y
= kx
+ b
, где k
— коэффициент наклона этой прямой к оси Ox
. В нашем случае k
= 0, т.е. прямая y
= 6 не наклонена, а параллельна оси Ox
. Значит искомые касательные также должны быть параллельны оси Ox
и также должны иметь коэффициент наклона 0. Таким свойством касательные обладают в точках экстремумов функций. Поэтому для ответа на вопрос нужно просто посчитать все точки экстремумов на графике. Здесь их 4 — две точки максимума и две точки минимума.
Ответ: 4
Задача 4
Функции y
= f
(x
), определенной на интервале (−11;23).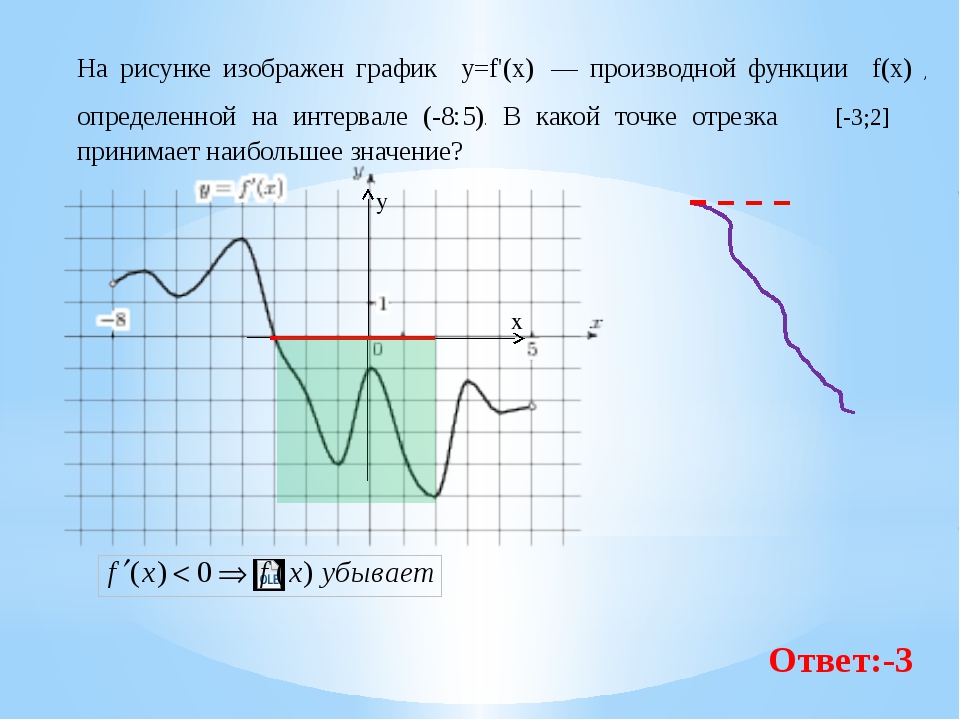 Найдите сумму точек экстремума функции на отрезке .
Найдите сумму точек экстремума функции на отрезке .
На указанном отрезке мы видим 2 точки экстремума. Максимум функции достигается в точке x
1 = 4, минимум в точке x
2 = 8.
x
1 + x
2 = 4 + 8 = 12.
Ответ: 12
Задача 5
На рисунке 1 изображен график функции y
= f
(x
), определенной на интервале (−10,5;19). Найдите количество точек, в которых производная функции f »
(x
) равна 0.
Производная функции равна нулю в точках экстремума, которых на графике видно 4:
2 точки максимума и 2 точки минимума.
Ответ: 4
Задачи на определение характеристик функции по графику её производной.
Рисунок 1.
Рисунок 2.
Задача 6
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23).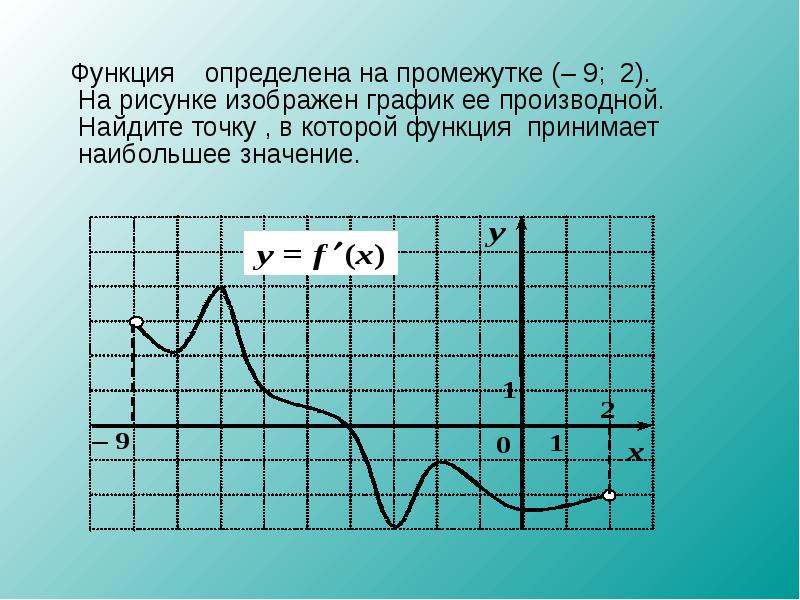 В какой точке отрезка [−6;2] функция f
В какой точке отрезка [−6;2] функция f
(x
) принимает наибольшее значение.
На указанном отрезке производная нигде не была положительной, следовательно функция не возрастала. Она убывала или проходила через стационарные точки. Таким образом, наибольшего значения функция достигала на левой границе отрезка: x
= −6.
Ответ: −6
Замечание:
По графику производной видно, что на отрезке [−6;2] она равна нулю трижды: в точках x
= −6, x
= −2, x
= 2. Но в точке x
= −2 она не меняла знака, значит в этой точке не могло быть экстремума функции. Скорее всего там была точка перегиба графика исходной функции.
Задача 7
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). В какой точке отрезка функция принимает наименьшее значение.
На отрезке производная строго положительна, следовательно функция на этом участке только возрастала. Таким образом, наименьшего значения функция достигала на левой границе отрезка: x
= 3.
Ответ: 3
Задача 8
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). Найдите количество точек максимума функции f
(x
), принадлежащих отрезку [−5;10].
Согласно необходимому условию экстремума максимум функции может быть
в точках, где её производная равна нулю. На заданном отрезке это точки: x
= −2, x
= 2, x
= 6, x
= 10. Но согласно достаточному условию он точно будет
только в тех из них, где знак производной меняется с «+» на «−». На графике производной мы видим, что из перечисленных точек такой является только точка x
= 6.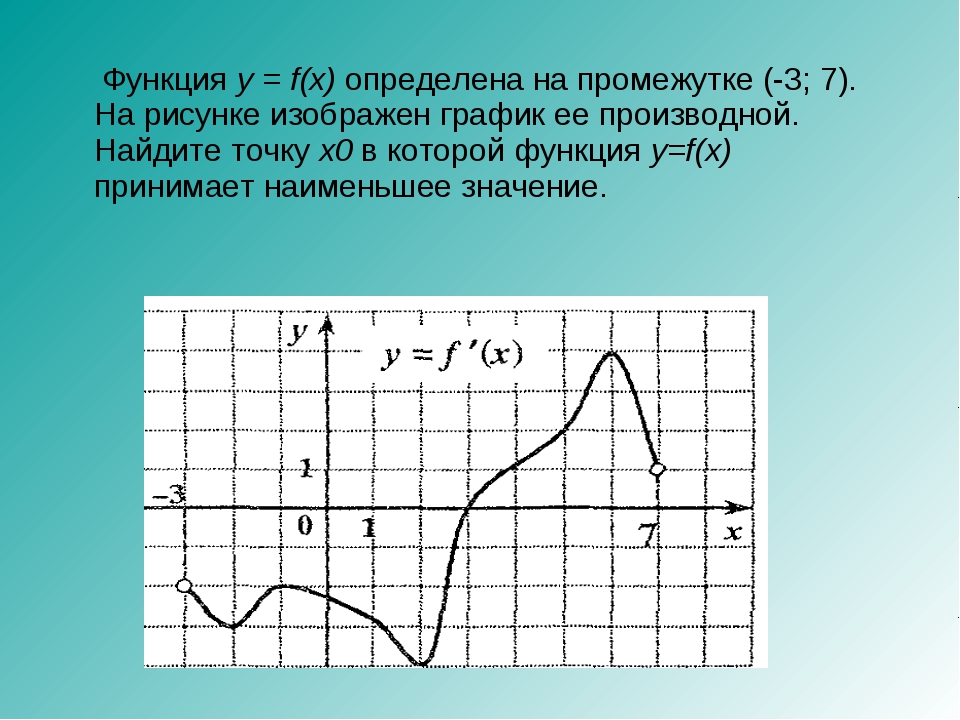
Ответ: 1
Задача 9
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). Найдите количество точек экстремума функции f
(x
), принадлежащих отрезку .
Экстремумы функции могут быть в тех точках, где её производная равна 0. На заданном отрезке графика производной мы видим 5 таких точек: x
= 2, x
= 6, x
= 10, x
= 14, x
= 18. Но в точке x
= 14 производная не поменяла знак, следовательно её надо исключить из рассмотрения. Таким образом, остаются 4 точки.
Ответ: 4
Задача 10
На рисунке 1 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−10,5;19). Найдите промежутки возрастания функции f
(x
). В ответе укажите длину наибольшего из них.
В ответе укажите длину наибольшего из них.
Промежутки возрастания функции совпадают с промежутками положительности производной. На графике мы видим их три — (−9;−7), (4;12), (18;19). Самый длинный из них второй. Его длина l
= 12 − 4 = 8.
Ответ: 8
Задача 11
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). Найдите количество точек, в которых касательная к графику функции f
(x
) параллельна прямой y
= −2x
− 11
или совпадает с ней.
Угловой коэффициент (он же тангенс угла наклона) заданной прямой k = −2. Нас интересуют параллельные или совпадающие касательные, т.е. прямые с таким же наклоном. Исходя из геометрического смысла производной — угловой коэффициент касательной в рассматриваемой точке графика функции, пересчитываем точки, в которых производная равна −2.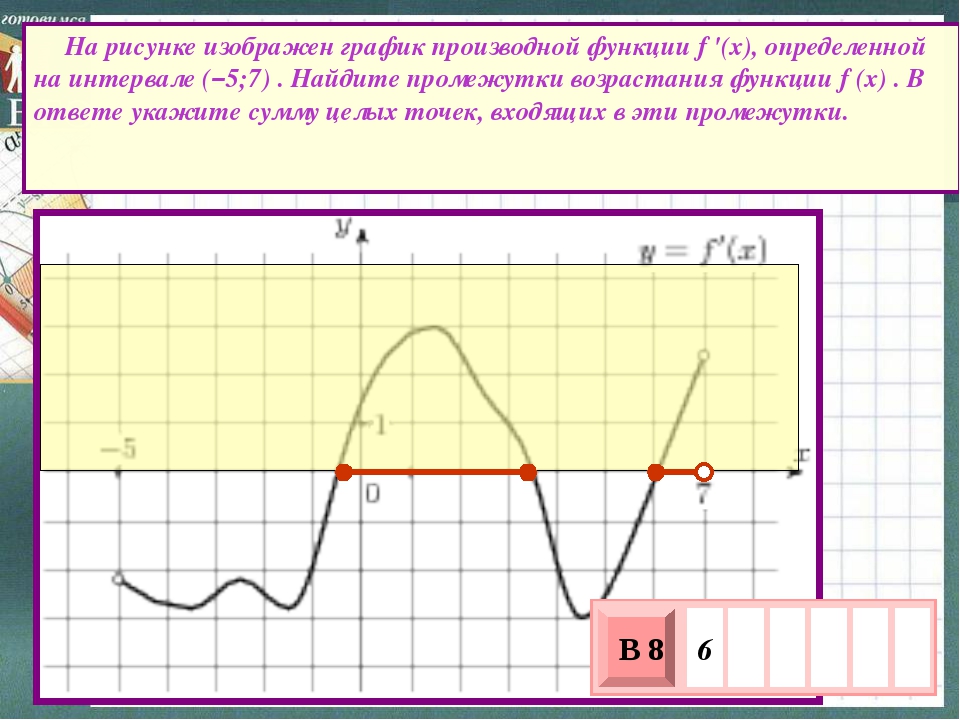 На рисунке 2 таких точек 9. Их удобно считать по пересечениям графика и линии координатной сетки, проходящей через значение −2 на оси Oy
На рисунке 2 таких точек 9. Их удобно считать по пересечениям графика и линии координатной сетки, проходящей через значение −2 на оси Oy
.
Ответ: 9
Как видите, по одному и тому же графику можно задать самые разнообразные вопросы о поведении функции и её производной. Также один тот же вопрос можно отнести к графикам разных функций. Будьте внимательны при решении этой задачи на экзамене, и она покажется Вам очень легкой. Другие виды задач этого задания — на геометрический смысл первообразной — будут рассмотрены в другом разделе.
Подписаться на еженедельную рассылку izhneftyanic.ru
Задание №7. Производная. Поведение функции. Первообразная
Необходимая теория:
Производная функции
Таблица производных
Первообразная функции
Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции.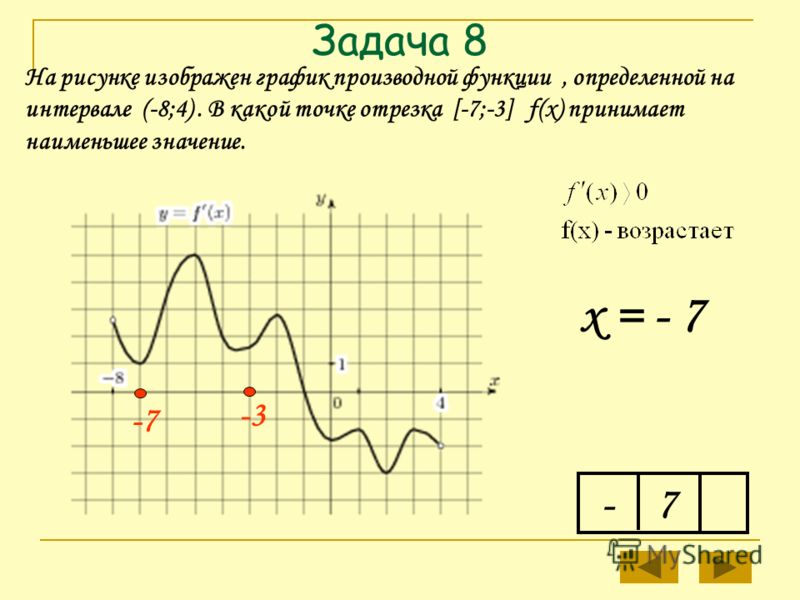 И еще (правда, очень редко) в этих встречаются вопросы о первообразной.
И еще (правда, очень редко) в этих встречаются вопросы о первообразной.
Геометрический смысл производной
Вспомним, что производная — это скорость изменения функции.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.
1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке
Производная функции в точке равна тангенсу угла наклона касательной, проведенной в точке .
Достроив до прямоугольного треугольника АВС, получим:
Ответ: 0,25.
2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке
Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна.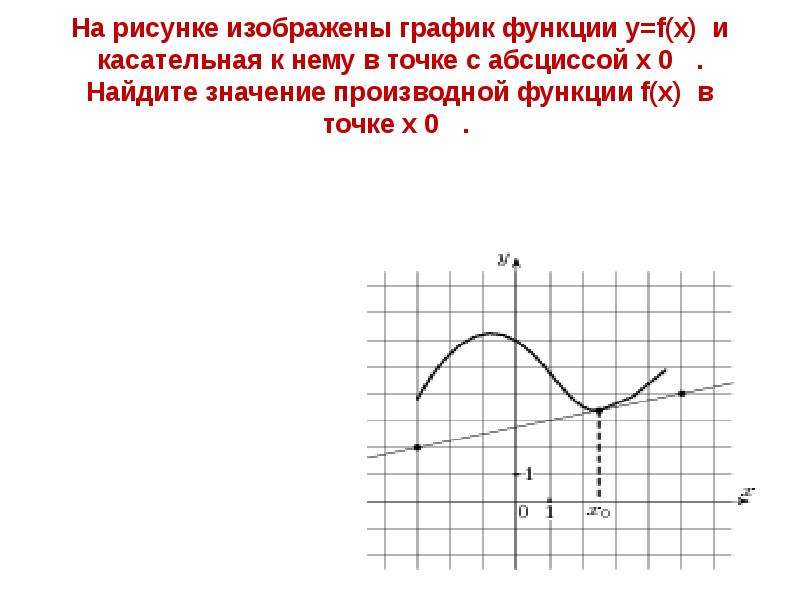 Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .
Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .
Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку , имеем:
Ответ: −0, 25.
Касательная к графику функции
3. Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Запишем условие касания функции и прямой в точке
При значения выражений и равны.
При этом производная функции равна угловому коэффициенту касательной, то есть .
Из второго уравнения находим или Первому уравнению удовлетворяет только .
Физический смысл производной
Мы помним, что производная — это скорость изменения функции.
Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике.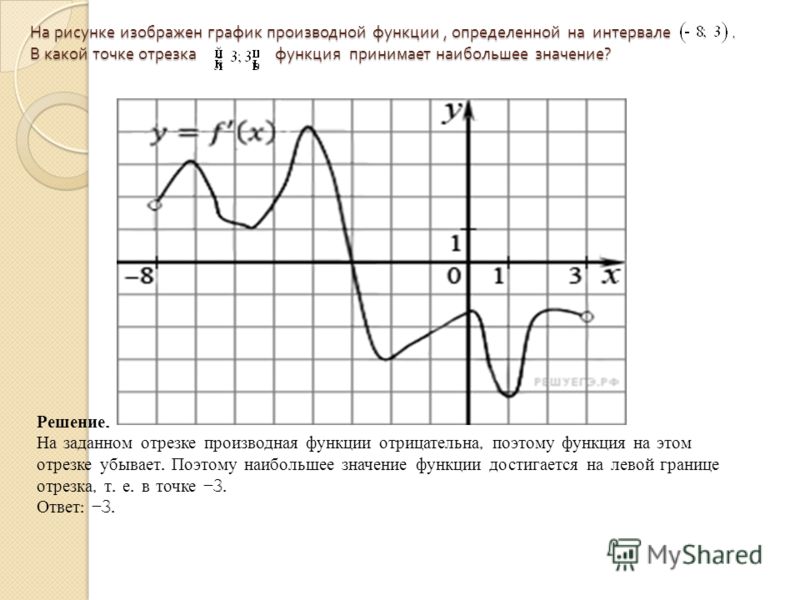 Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.
Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.
Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.
4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени с.
Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:
Найдем скорость материальной точки как производную от координаты по времени:
В момент времени получим:
.
Ответ: 3
Применение производной к исследованию функций
Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.
Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.
Или наоборот. Нарисован график производной — а спрашивают о поведении функции.
И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.
Если , то функция возрастает.
Если , то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
5. На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых производная функции равна 0.
Производная функции в точках максимума и минимума функции Таких точек на графике 5.
Ответ: 5.
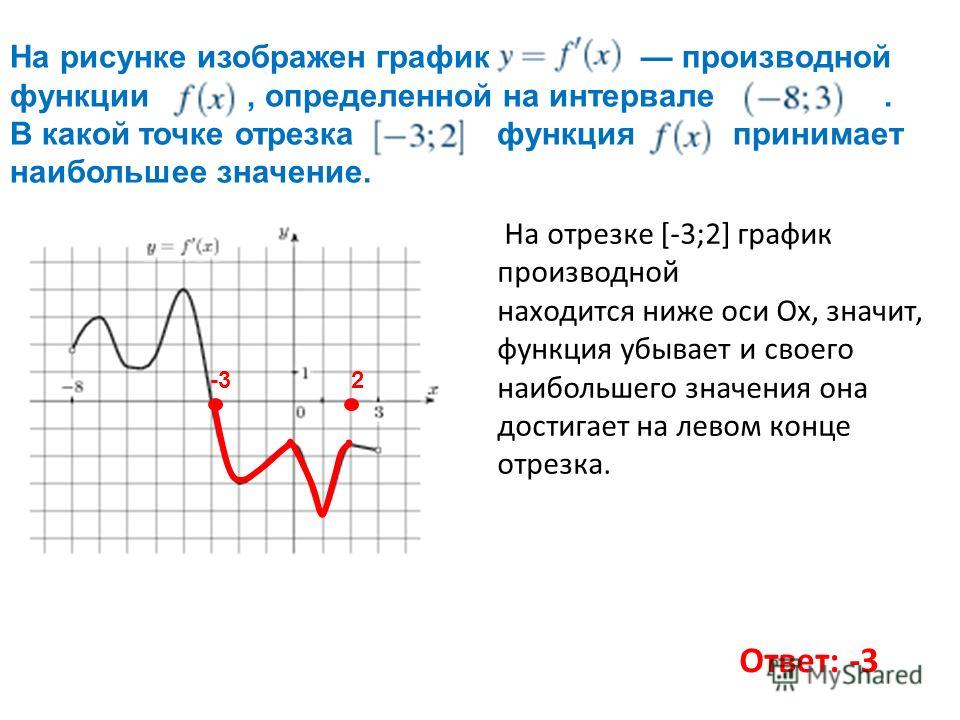
6. На рисунке изображён график — производной функции , определённой на интервале .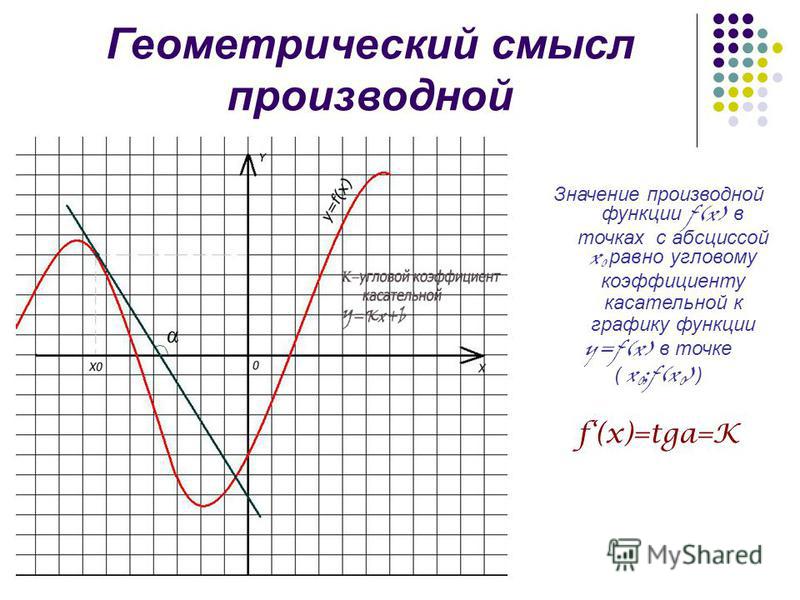 В какой точке отрезка функция принимает наибольшее значение?
В какой точке отрезка функция принимает наибольшее значение?
Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?
Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.
На отрезке производная функции положительна.
Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.
Ответ: 3.
7. На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой
Прямая параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.
Ответ: 7.
8. На рисунке изображен график производной функции , определенной на интервале Найдите количество точек максимума функции на отрезке
Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это
Ответ: 1.
9. На рисунке изображен график производной функции , определенной на интервале Найдите точку экстремума функции на отрезке
Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке В этой точке производная меняет знак с минуса на плюс.
Значит, является точкой экстремума.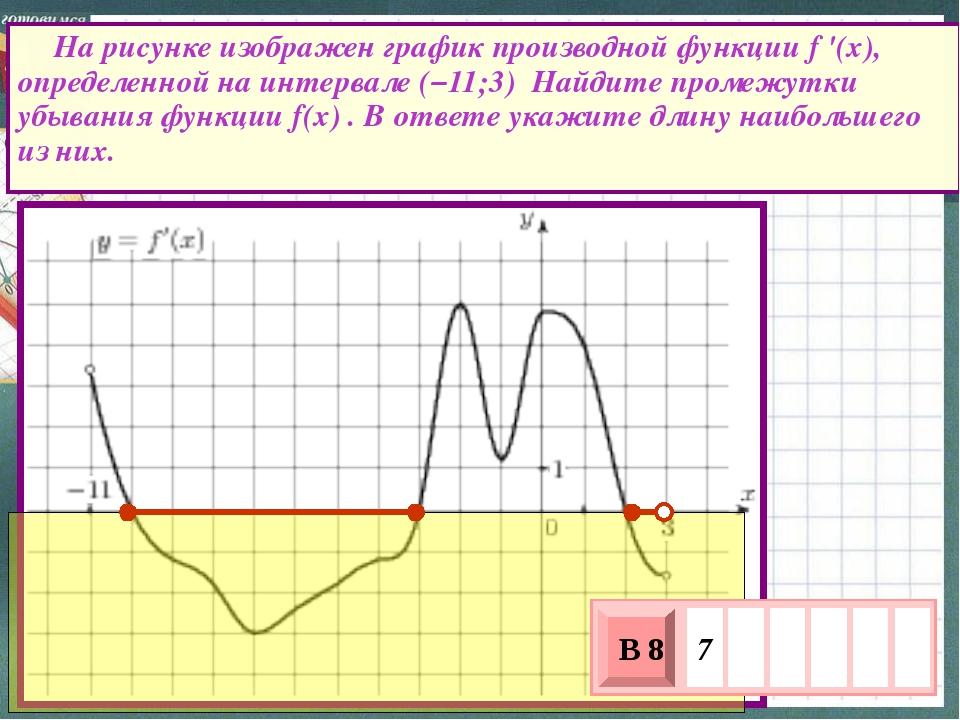
Первообразная и формула Ньютона-Лейбница
Функция , для которой является производной, называется первообразной функции Функции вида образуют множество первообразных функции
10. На рисунке изображён график — одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке
Функция для которой является производной, называется первообразной функции
Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции равна нулю. Это точки максимума и минимума функции На отрезке таких точек 4.
Ответ: 4.
Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье
Первообразная функции. Формула Ньютона-Лейбница.
На рисунке изображен график функции, в какой точке отрезка функция принимает наибольшее значение
Производная
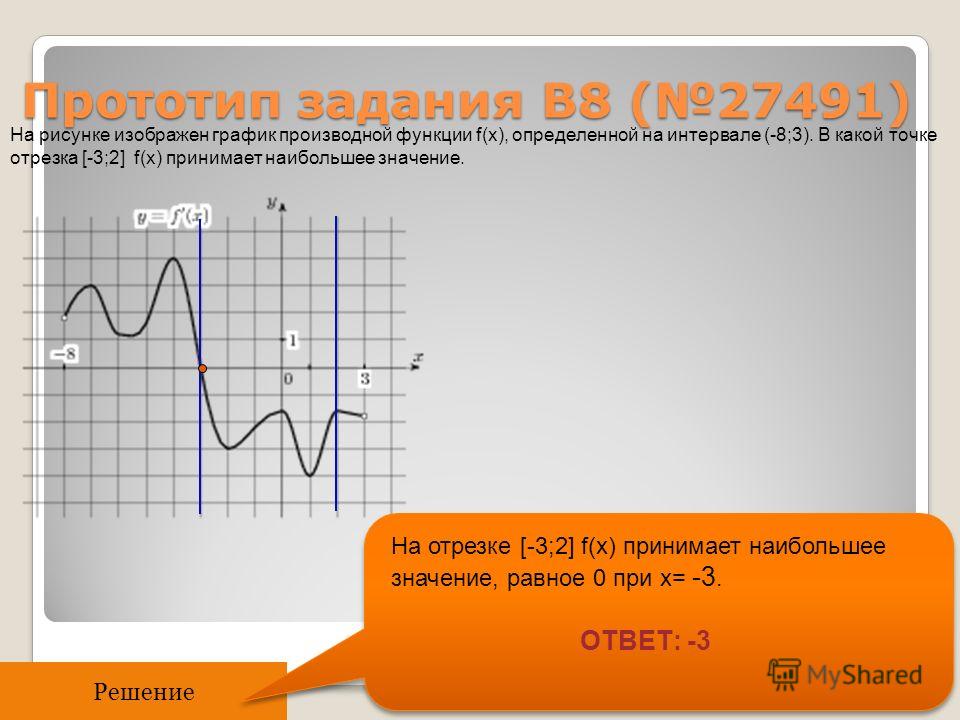
Задание B9 (ЕГЭ 2014)
На рисунке изображен график функции y=f'(x) — производной функции f(x), определенной на интервале от (-6;5).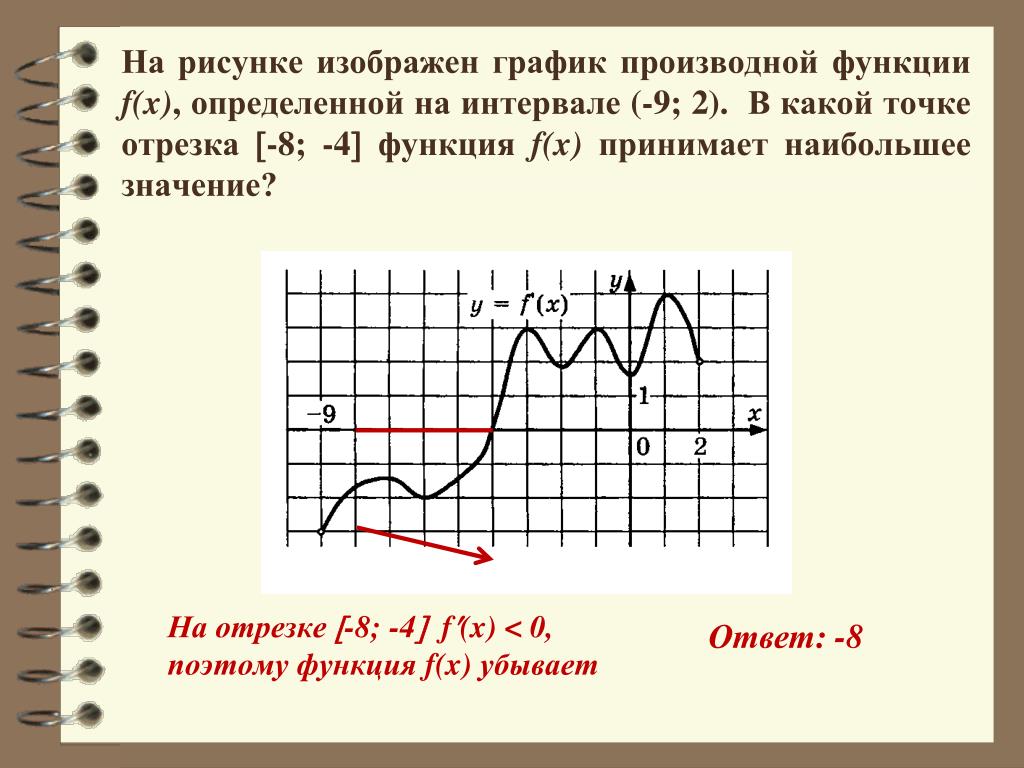 В какой точке отрезка [-5;-1] функция f(x) принимает наибольшее значение?
В какой точке отрезка [-5;-1] функция f(x) принимает наибольшее значение?
Решение
На отрезке [-5;-1] производная f'(x) принимает отрицательные значения, а значит на этом отрезке функция f(x) убывает. Если функция убывает на заданном отрезке, то наибольшее значение она принимает в наименьшей точке отрезка, т.е. в точке -5.
Ответ: -5.
Задание B9 (ЕГЭ 2014)
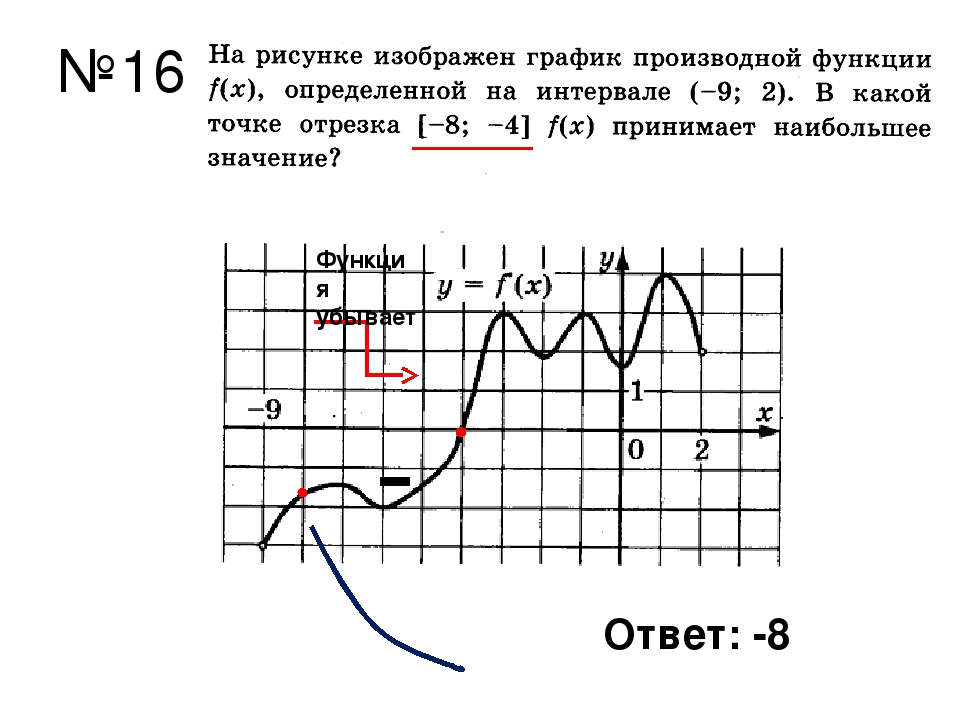
На рисунке изображен график функции y=f'(x) — производной функции f(x), определенной на интервале от (-9;2). В какой точке отрезка [-8;-4] функция f(x) принимает наибольшее значение?
Решение
На отрезке [-8;-4] производная f'(x) принимает положительные значения (так как график производной находится выше оси Ox), а значит на этом отрезке функция f(x) возрастает. Если функция возрастает на заданном отрезке, то наибольшее значение она принимает в наибольшей точке отрезка, т.е. в точке -4.
Если функция возрастает на заданном отрезке, то наибольшее значение она принимает в наибольшей точке отрезка, т.е. в точке -4.
Также можно было сразу отметить, что точка -4 — точка пересечения графика производной с осью Ox, а значит, это точка экстремума. Так как график производной переходит в этой точке с «+» на «-«, то это точка максимума, а значит наибольшее значение на отрезке [-8;-4] функция f(x) принимает именно в этой точке.
Ответ: -4.
Задание B9 (ЕГЭ 2014)
На рисунке изображен график функции y=f'(x) — производной функции f(x), определенной на интервале от (-6;5). В какой точке отрезка [-3;4] функция f(x) принимает наибольшее значение?
Решение
График производной пересекает ось Ox в точке -1. Эта точка принадлежит отрезку [-3;4] и является точкой экстремума функции f(x).
Так как график производной переходит в этой точке с «+» на «-«, то это точка максимума, а значит наибольшее значение на отрезке [-3;4] функция f(x) принимает именно в этой точке.
Ответ: -1.
Задание B9 (ЕГЭ 2014)
На рисунке изображен график функции y=f'(x) — производной функции f(x), определенной на интервале от (-5;6). В какой точке отрезка [-1;3] функция f(x) принимает наибольшее значение?
Решение
В точке -1 график производной пересекает ось Ox, а значит точка -1 — точка экстремума. Но так как график производной переходит в этой точке с «-» на «+», то точка -1 — это точка минимума функции на отрезке [-1;3].
Заметим, что на отрезке [-1;3] график производной положительный, т.к. он находится вышн оси Ox. Это означает, что на данном отрезке функция f(x) монотонно возрастает.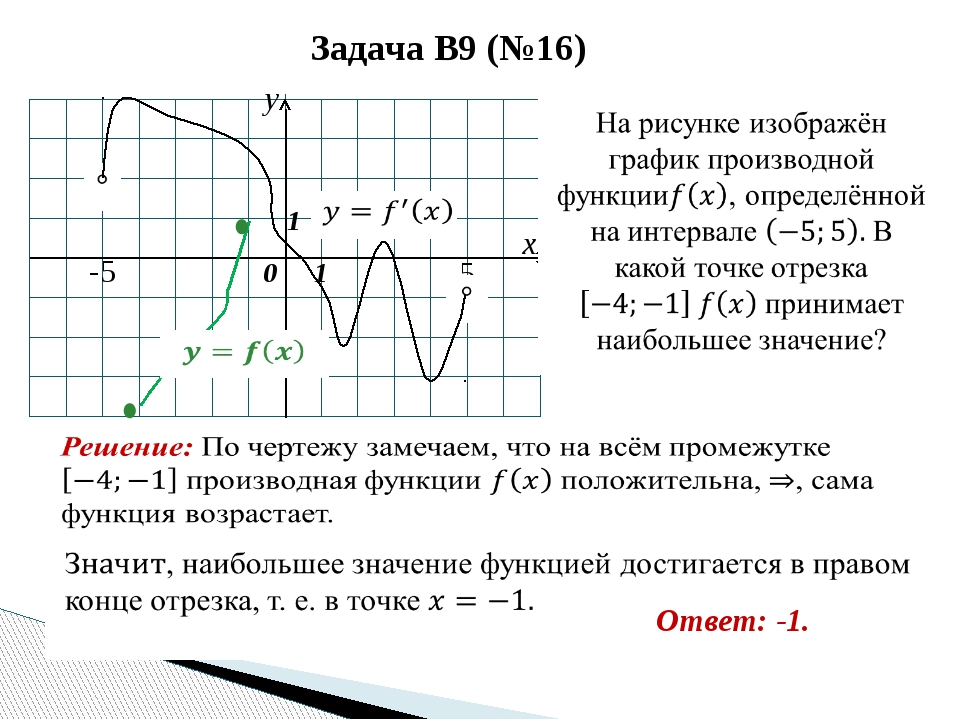 А значит наибольшее значение функция принимает в наибольшей точке отрезка, т.е. в точке 3.
А значит наибольшее значение функция принимает в наибольшей точке отрезка, т.е. в точке 3.
Ответ: 3.
1 2 3 4 5
Наименьшее значение производной. Производная функции
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна
. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.
Запомним определение:
Производная — это скорость изменения функции.
На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?
Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.
Вот другой пример.
Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная
И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная
, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Производная функции обозначается .
Покажем, как найти с помощью графика.
Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной
.
Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.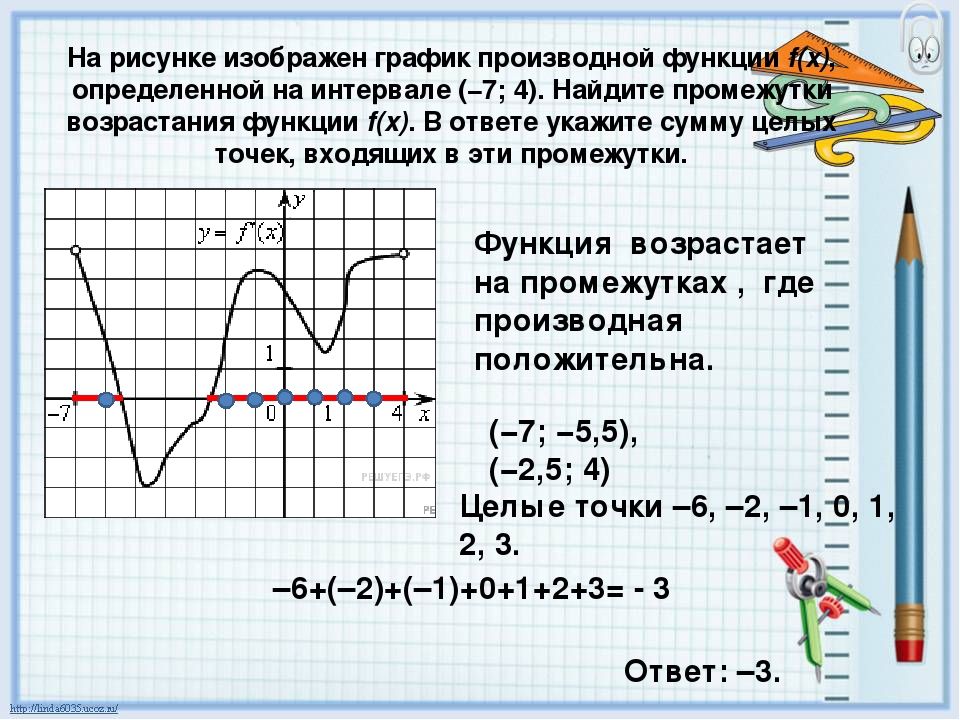
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .
Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.
Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .
Есть и другое важное соотношение. Вспомним, что прямая задается уравнением
Величина в этом уравнении называется угловым коэффициентом прямой
. Она равна тангенсу угла наклона прямой к оси .
.
Мы получаем, что
Запомним эту формулу. Она выражает геометрический смысл производной.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.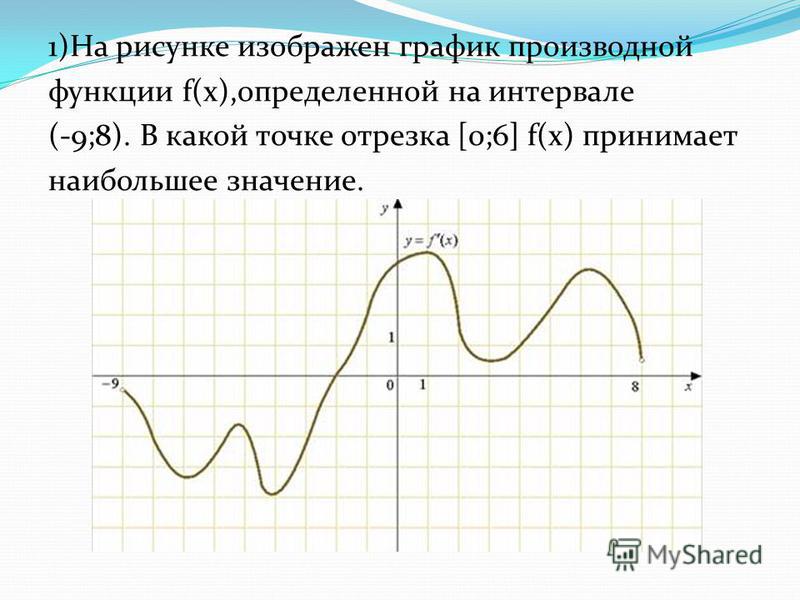
Другими словами, производная равна тангенсу угла наклона касательной.
Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.
Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.
В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол с положительным направлением оси . Значит, в точке производная положительна.
В точке наша функция убывает. Касательная в этой точке образует тупой угол с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.
Вот что получается:
Если функция возрастает, ее производная положительна.
Если убывает, ее производная отрицательна.
А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна.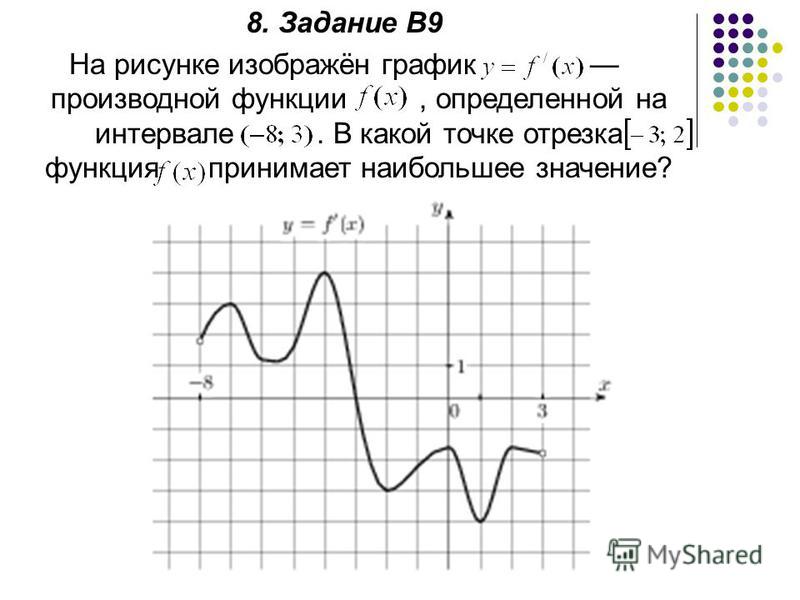 Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».
В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
Если производная положительна, то функция возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | — | 0 | + |
Сделаем два небольших уточнения.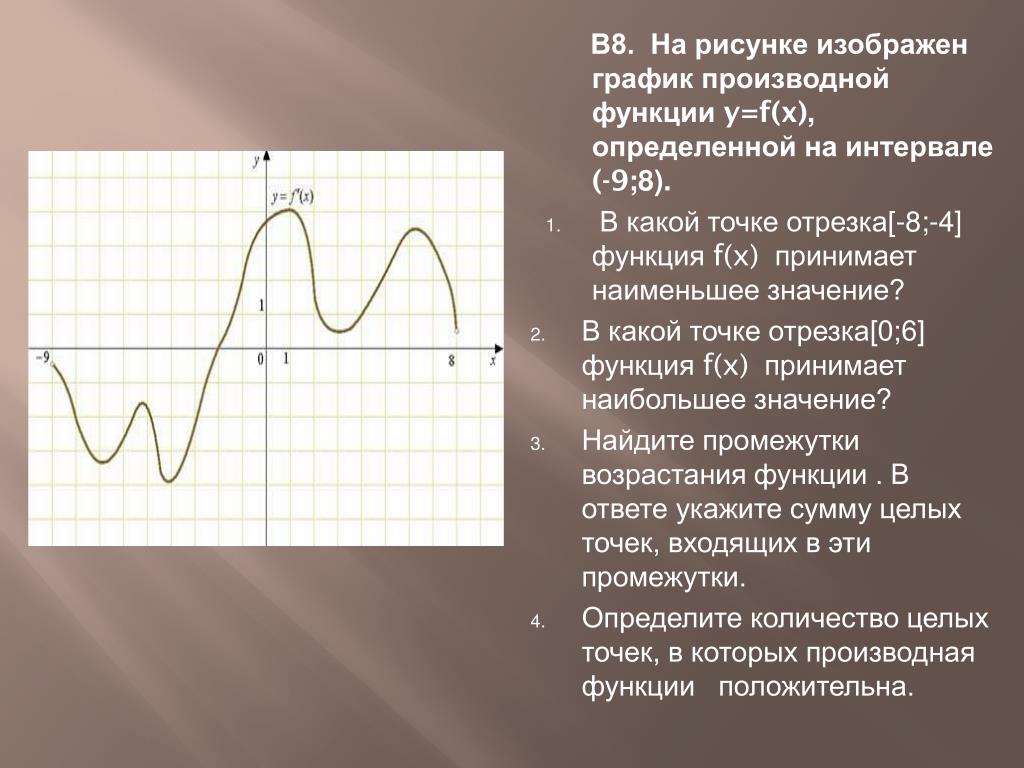 Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.
Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.
Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая :
В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.
Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется
Этот раздел содержит задачи ЕГЭ по математике на темы, связанные с исследованием функций и их производных.
В демонстрационных вариантах ЕГЭ 2020
года они могут встретиться под номером 14
для базового уровня и под номером 7
для профильного уровня.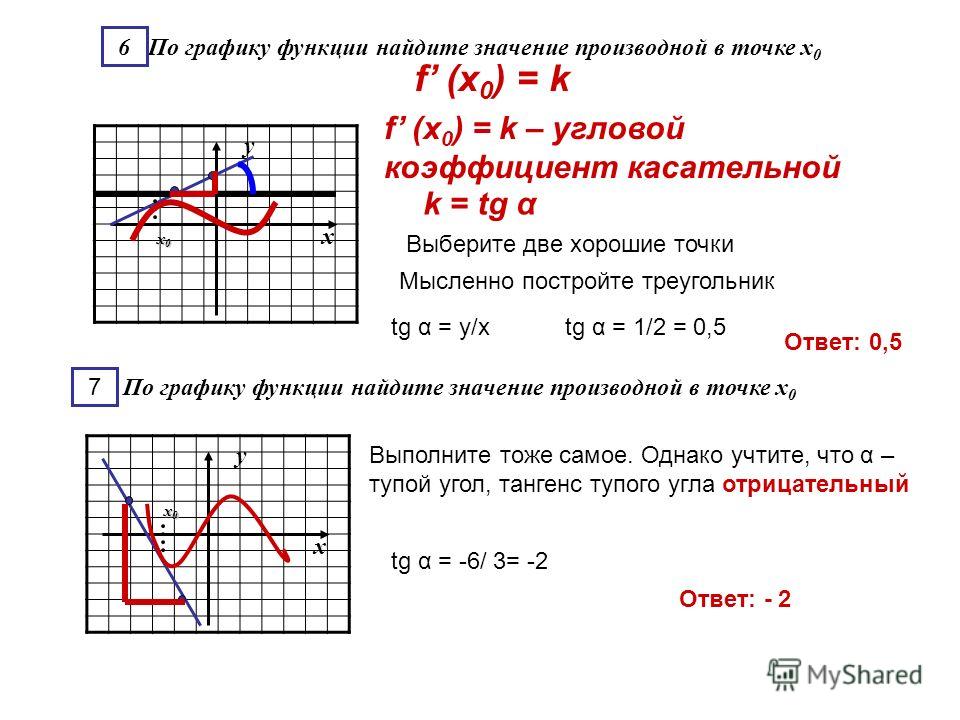
Посмотрите внимательно на эти три графика функций.
Заметили ли вы, что эти функции в некотором смысле «родственники»?
Например, на тех участках, где график зеленой функции расположен выше нуля, красная функция возрастает. На тех участках, где график зеленой функции ниже нуля, красная функция убывает.
Аналогичные замечания можно сделать относительно красного и синего графиков.
Также можно заметить, что нули зеленой функции (точки x
= −1 и x
= 3) совпадают с точками экстремумов красного графика: при x
= −1 на красном графике мы видим локальный максимум, при х
= 3 на красном графике локальный минимум.
Нетрудно заметить, что локальные максимумы и минимумы синего графика достигаются в тех же точках, где красный график проходит через значение y
= 0.
Можно сделать еще несколько выводов об особенностях поведения этих графиков, потому что они действительно связаны между собой. Посмотрите на формулы функций, расположенные под каждым из графиков, и путем вычислений убедитесь, что каждая предыдущая является производной для последующей и, соответственно, каждая следующая является одной из превообразных предыдущей функции.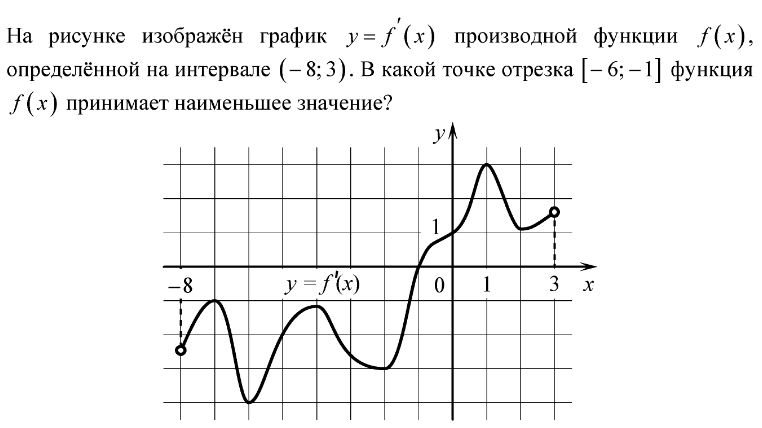
φ
1 (x
) = φ»
2 (x
) φ
2 (x
) = Φ
1 (x
)
φ
2 (x
) = φ»
3 (x
)
φ
3 (x
) = Φ
2 (x
)
Вспомним, что мы знаем о производной:
Производная функции y
= f
(x
) в точке х
выражает скорость изменения функции в точке x
.
Физический смысл производной
заключается в том, что производная выражает скорость протекания процесса, описываемого зависимостью y = f(x).
Геометрический смысл производной
заключается в том, что её значение в рассматриваемой точке равняется угловому коэффициенту касательной, проведенной к графику дифференцируемой функции в этой точке.
А теперь пусть красного графика на рисунке нет. Допустим, что и формулы функций нам неизвестны.
Могу ли я спросить вас о чем то, связанном с поведением функции φ
2 (x
), если известно, что она является производной функции φ
3 (x
) и первообразной функции φ
1 (x
)?
Могу.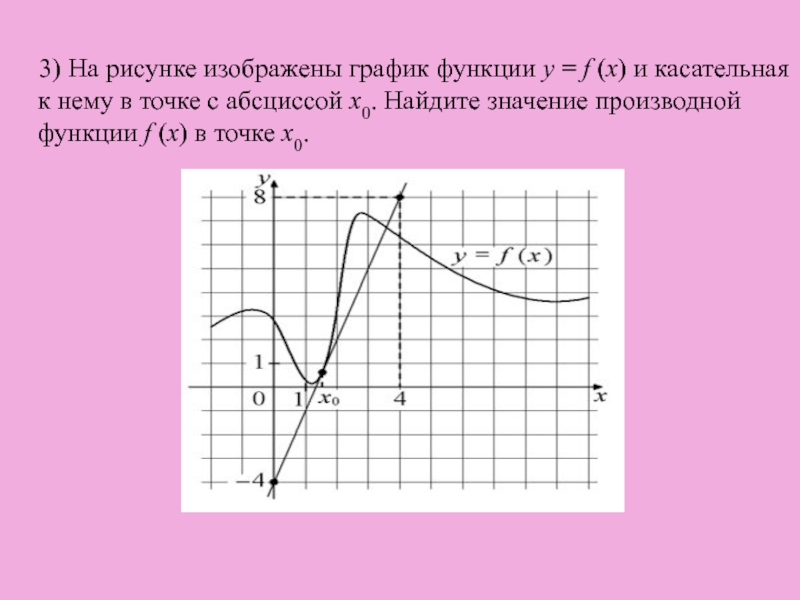 И на многие вопросы можно дать точный ответ, ведь мы знаем, что производная является характеристикой скорости изменения функции, поэтому можем судить о некоторых особенностях поведения одной из этих функций, глядя на график другой.
И на многие вопросы можно дать точный ответ, ведь мы знаем, что производная является характеристикой скорости изменения функции, поэтому можем судить о некоторых особенностях поведения одной из этих функций, глядя на график другой.
Прежде, чем отвечать на следующие вопросы, прокрутите страницу вверх так, чтобы скрылся верхний рисунок, содержащий красный график. Когда ответы будут даны, верните его обратно, чтобы проверить результат. И только после этого смотрите моё решение.
Внимание:
Для усиления обучающего эффекта ответы и решения
загружаются отдельно для каждой задачи последовательным нажатием кнопок на желтом фоне. (Когда задач много, кнопки могут появиться с задержкой. Если кнопок не видно совсем, проверьте, разрешен ли в вашем браузере JavaScript.
)
1) Пользуясь графиком производной φ»
2 (x
) (в нашем случае это зеленый график), определите какое из 2-ух значений функции больше φ
2 (−3) или φ
2 (−2)?
По графику производной видно, что на участке [−3;−2] её значения строго положительны, значит функция на этом участке только возрастает, поэтому значение функции в левом конце x
= −3 меньше, чем её значение в правом конце x
= −2.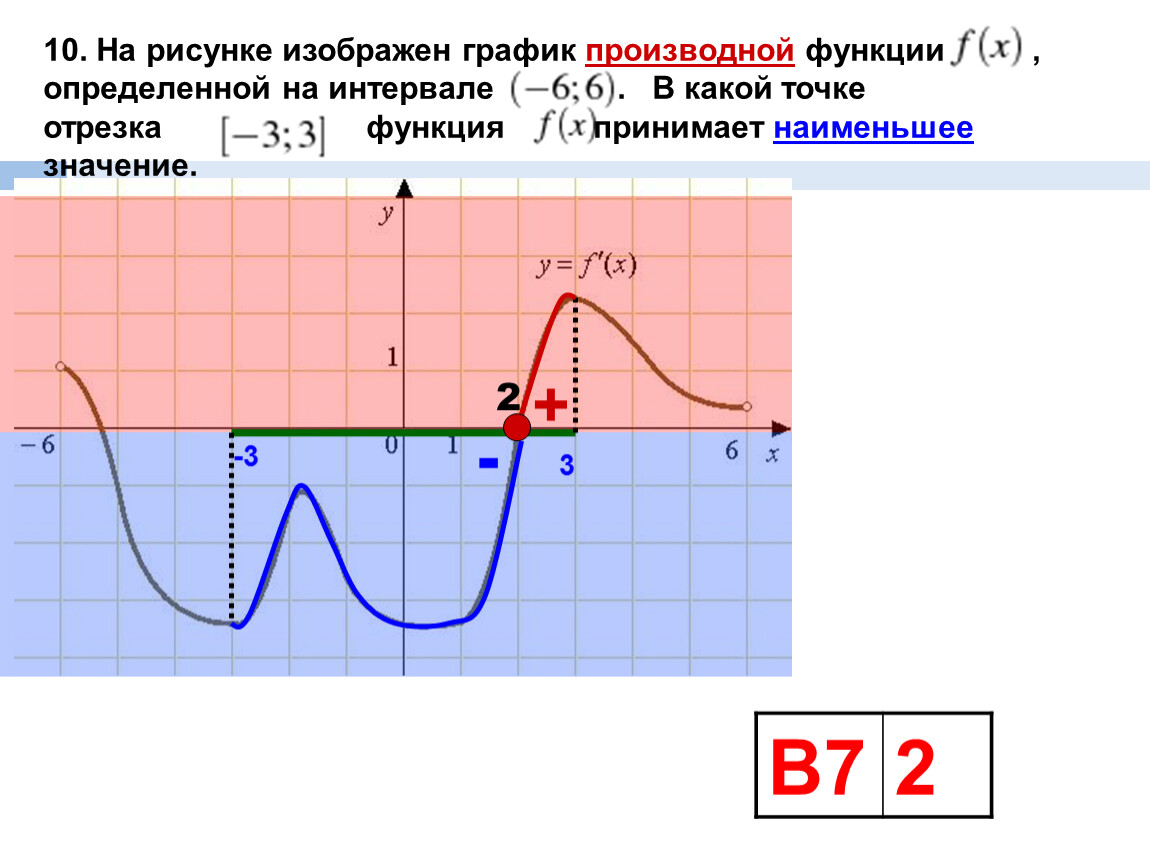
Ответ: φ
2 (−3) φ
2 (−2)
2) Пользуясь графиком первообразной Φ
2 (x
) (в нашем случае это синий график), определите какое из 2-ух значений функции больше φ
2 (−1) или φ
2 (4)?
По графику первообразной видно, что точка x
= −1 находится на участке возрастания, следовательно значение соответсвующей производной положительно. Точка x
= 4 находится на участке убывания и значение соответствующей производной отрицательно. Поскольку положительное значение больше отрицательного, делаем вывод — значение неизвестной функции, которая как раз и является производной, в точке 4 меньше, чем в точке −1.
Ответ: φ
2 (−1) > φ
2 (4)
Подобных вопросов по отсутствующему графику можно задать много, что обуславливает большое разноообразие задач с кратким ответом, построенных по такой же схеме. Попробуйте решить некоторые из них.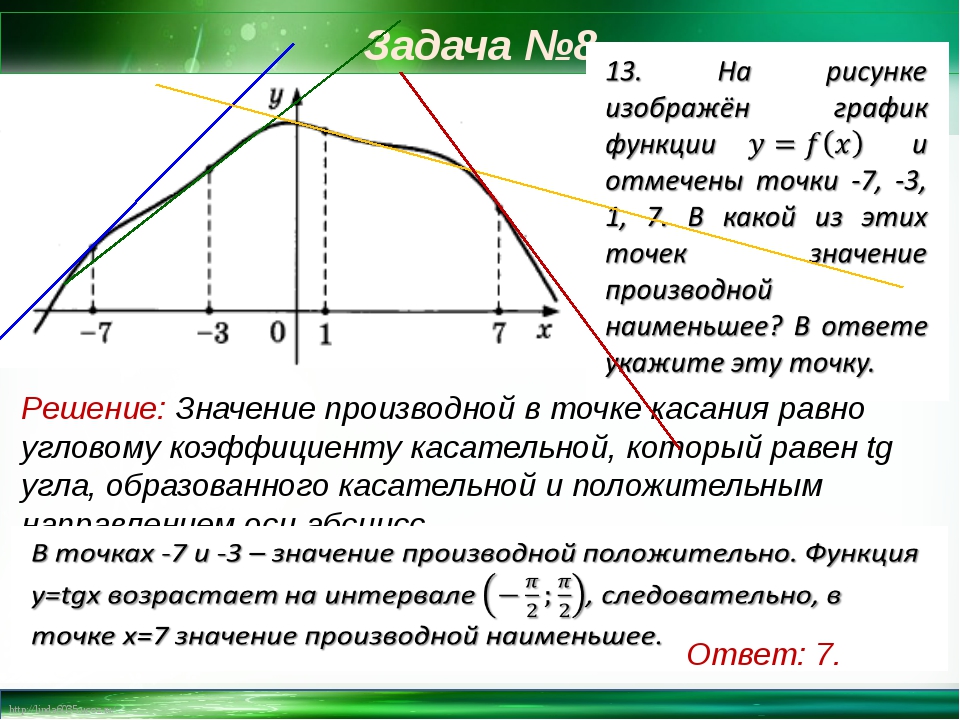
Задачи на определение характеристик производной по графику функции.
Рисунок 1.
Рисунок 2.
Задача 1
y
= f
(x
), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции положительна.
Производная функции положительна на тех участках, где функция возрастает. По рисунку видно, что это промежутки (−10,5;−7,6), (−1;8,2) и (15,7;19). Перечислим целые точки внутри этих интервалов: «−10″,»−9», «−8″,»0», «1»,»2″, «3»,»4″, «5»,»6″, «7»,»8″, «16»,»17″, «18». Всего 15 точек.
Ответ: 15
Замечания.
1. Когда в задачах о графиках функций требуют назвать «точки», как правило, имеют в виду только значения аргумента x
, которые являются абсциссами соответствующих точек, расположенных на графике. Ординаты этих точек — значения функции, они являются зависимыми и могут быть легко вычислены при необходимости.
2. При перечислении точек мы не учитывали края интервалов, так как функция в этих точках не возрастает и не убывает, а «разворачивается». Производная в таких точках не положительна и не отрицательна, она равна нулю, поэтому они называются стационарными точками. Кроме того, мы не рассматриваем здесь границы области определения, потому что в условии сказано, что это интервал.
Задача 2
На рисунке 1 изображен график функции y
= f
(x
), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции f »
(x
) отрицательна.
Производная функции отрицательна на тех участках, где функция убывает. По рисунку видно, что это промежутки (−7,6;−1) и (8,2;15,7). Целые точки внутри этих интервалов: «−7″,»−6», «−5″,»−4», «−3″,»−2», «9»,»10″, «11»,»12″, «13»,»14″, «15». Всего 13 точек.
Ответ: 13
См. замечания к предыдущей задаче.
Для решения следующих задач нужно вспомнить еще одно определение.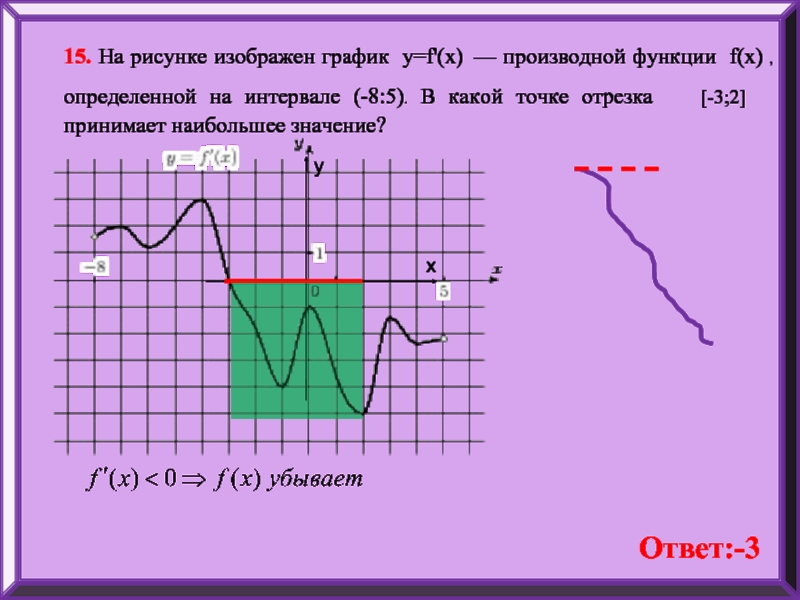
Точки максимума и минимума функции объединяются общим названием — точки экстремума
.
В этих точках производная функции либо равна нулю, либо не существует (необходимое условие экстремума
).
Однако необходимое условие — это признак, но не гарантия существования экстремума функции. Достаточным условием экстремума
является смена знака производной: если производная в точке меняет знак с «+» на «−», то это точка максимума функции; если производная в точке меняет знак с «−» на «+» , то это точка минимума функции; если в точке производная функции равна нулю, либо не существует, но знак производной при переходе через эту точку не меняется на противоположный, то указанная точка не является точкой экстремума функции. Это может быть точка перегиба, точка разрыва или точка излома графика функции.
Задача 3
На рисунке 1 изображен график функции y
= f
(x
), определенной на интервале (−10,5;19).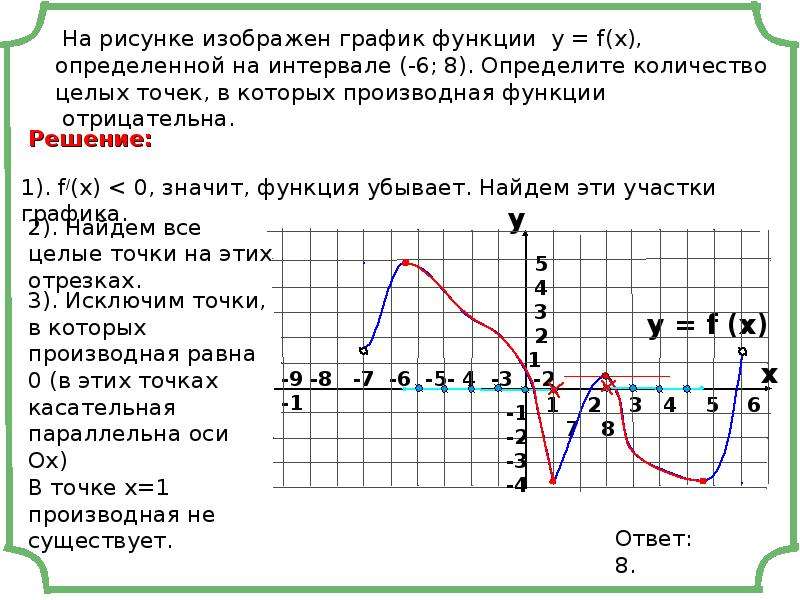 Найдите количество точек, в которых касательная к графику функции параллельна прямой y
Найдите количество точек, в которых касательная к графику функции параллельна прямой y
= 6 или совпадает с ней.
Вспомним, что уравнение прямой имеет вид y
= kx
+ b
, где k
— коэффициент наклона этой прямой к оси Ox
. В нашем случае k
= 0, т.е. прямая y
= 6 не наклонена, а параллельна оси Ox
. Значит искомые касательные также должны быть параллельны оси Ox
и также должны иметь коэффициент наклона 0. Таким свойством касательные обладают в точках экстремумов функций. Поэтому для ответа на вопрос нужно просто посчитать все точки экстремумов на графике. Здесь их 4 — две точки максимума и две точки минимума.
Ответ: 4
Задача 4
Функции y
= f
(x
), определенной на интервале (−11;23). Найдите сумму точек экстремума функции на отрезке .
На указанном отрезке мы видим 2 точки экстремума. Максимум функции достигается в точке x
1 = 4, минимум в точке x
2 = 8.
x
1 + x
2 = 4 + 8 = 12.
Ответ: 12
Задача 5
На рисунке 1 изображен график функции y
= f
(x
), определенной на интервале (−10,5;19). Найдите количество точек, в которых производная функции f »
(x
) равна 0.
Производная функции равна нулю в точках экстремума, которых на графике видно 4:
2 точки максимума и 2 точки минимума.
Ответ: 4
Задачи на определение характеристик функции по графику её производной.
Рисунок 1.
Рисунок 2.
Задача 6
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). В какой точке отрезка [−6;2] функция f
(x
) принимает наибольшее значение.
На указанном отрезке производная нигде не была положительной, следовательно функция не возрастала.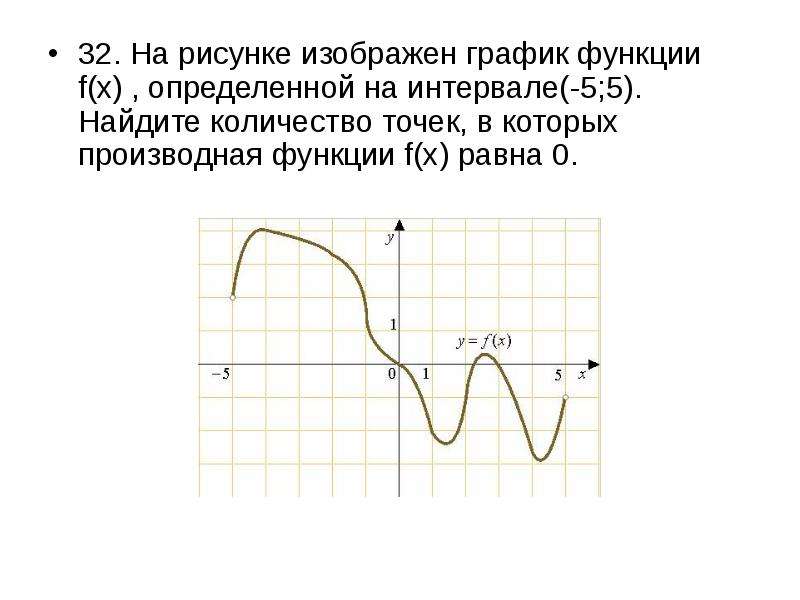 Она убывала или проходила через стационарные точки. Таким образом, наибольшего значения функция достигала на левой границе отрезка: x
Она убывала или проходила через стационарные точки. Таким образом, наибольшего значения функция достигала на левой границе отрезка: x
= −6.
Ответ: −6
Замечание:
По графику производной видно, что на отрезке [−6;2] она равна нулю трижды: в точках x
= −6, x
= −2, x
= 2. Но в точке x
= −2 она не меняла знака, значит в этой точке не могло быть экстремума функции. Скорее всего там была точка перегиба графика исходной функции.
Задача 7
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). В какой точке отрезка функция принимает наименьшее значение.
На отрезке производная строго положительна, следовательно функция на этом участке только возрастала. Таким образом, наименьшего значения функция достигала на левой границе отрезка: x
= 3.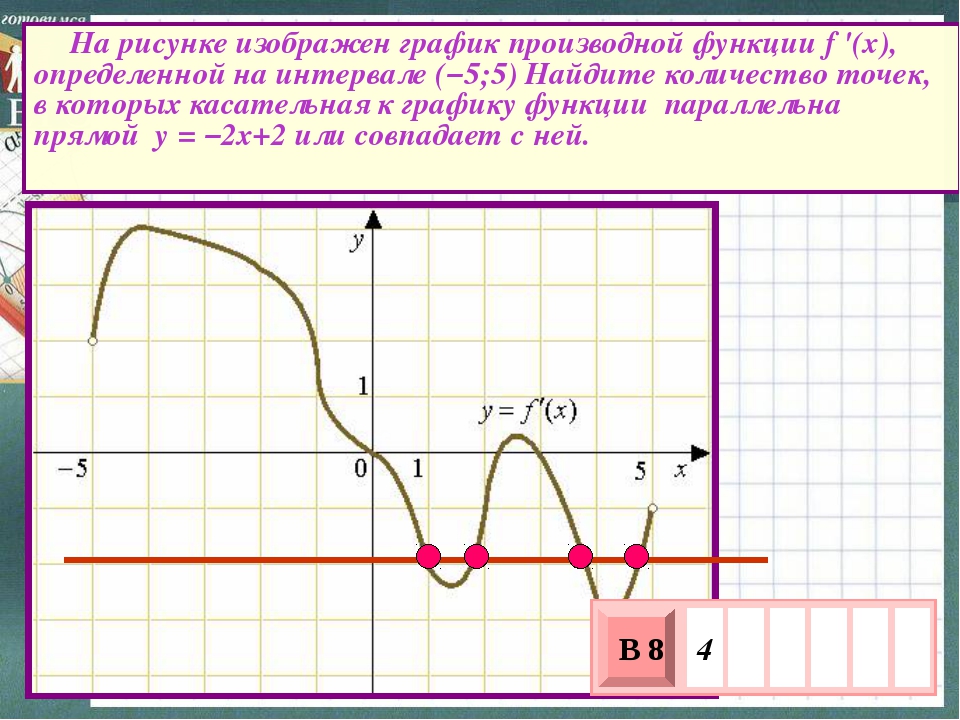
Ответ: 3
Задача 8
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). Найдите количество точек максимума функции f
(x
), принадлежащих отрезку [−5;10].
Согласно необходимому условию экстремума максимум функции может быть
в точках, где её производная равна нулю. На заданном отрезке это точки: x
= −2, x
= 2, x
= 6, x
= 10. Но согласно достаточному условию он точно будет
только в тех из них, где знак производной меняется с «+» на «−». На графике производной мы видим, что из перечисленных точек такой является только точка x
= 6.
Ответ: 1
Задача 9
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). Найдите количество точек экстремума функции f
Найдите количество точек экстремума функции f
(x
), принадлежащих отрезку .
Экстремумы функции могут быть в тех точках, где её производная равна 0. На заданном отрезке графика производной мы видим 5 таких точек: x
= 2, x
= 6, x
= 10, x
= 14, x
= 18. Но в точке x
= 14 производная не поменяла знак, следовательно её надо исключить из рассмотрения. Таким образом, остаются 4 точки.
Ответ: 4
Задача 10
На рисунке 1 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−10,5;19). Найдите промежутки возрастания функции f
(x
). В ответе укажите длину наибольшего из них.
Промежутки возрастания функции совпадают с промежутками положительности производной. На графике мы видим их три — (−9;−7), (4;12), (18;19).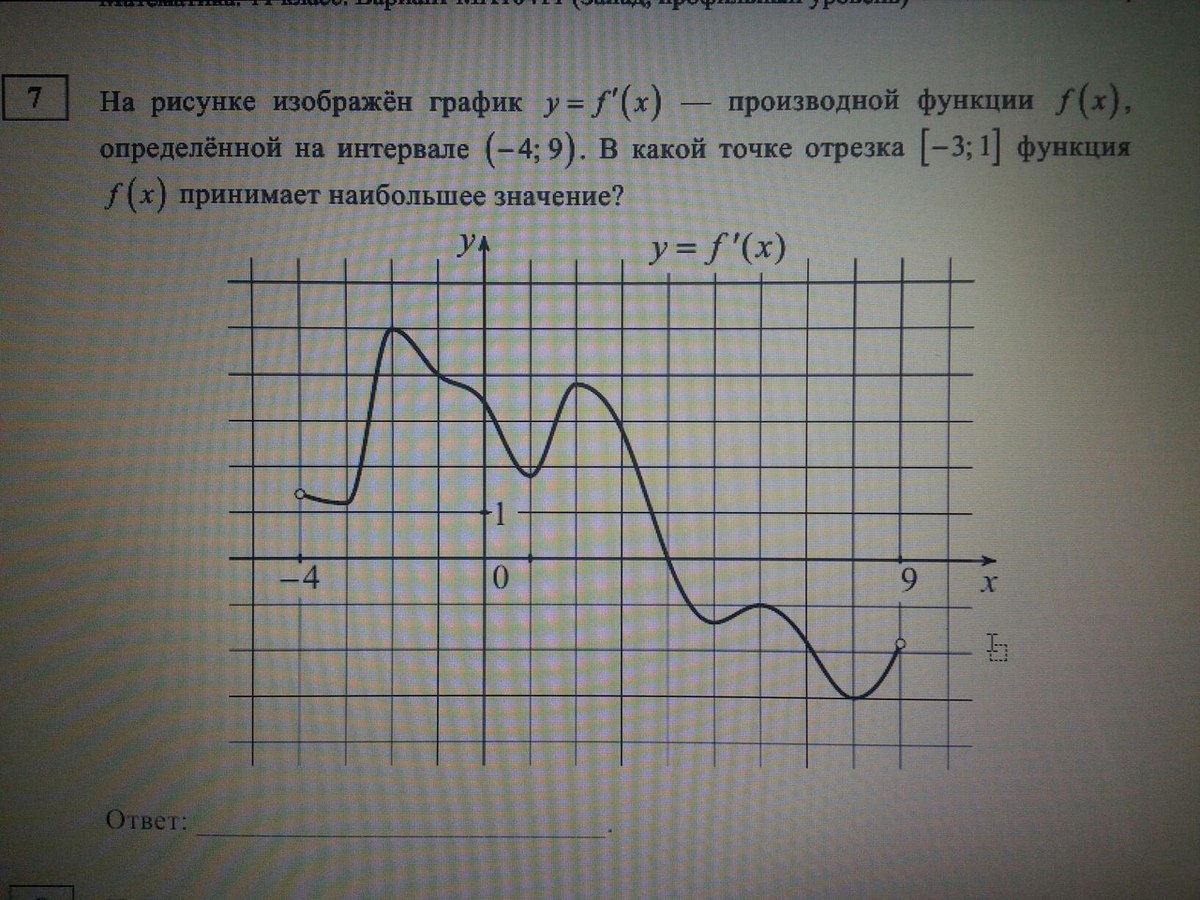 Самый длинный из них второй. Его длина l
Самый длинный из них второй. Его длина l
= 12 − 4 = 8.
Ответ: 8
Задача 11
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). Найдите количество точек, в которых касательная к графику функции f
(x
) параллельна прямой y
= −2x
− 11
или совпадает с ней.
Угловой коэффициент (он же тангенс угла наклона) заданной прямой k = −2. Нас интересуют параллельные или совпадающие касательные, т.е. прямые с таким же наклоном. Исходя из геометрического смысла производной — угловой коэффициент касательной в рассматриваемой точке графика функции, пересчитываем точки, в которых производная равна −2. На рисунке 2 таких точек 9. Их удобно считать по пересечениям графика и линии координатной сетки, проходящей через значение −2 на оси Oy
.
Ответ: 9
Как видите, по одному и тому же графику можно задать самые разнообразные вопросы о поведении функции и её производной. Также один тот же вопрос можно отнести к графикам разных функций. Будьте внимательны при решении этой задачи на экзамене, и она покажется Вам очень легкой. Другие виды задач этого задания — на геометрический смысл первообразной — будут рассмотрены в другом разделе.
Также один тот же вопрос можно отнести к графикам разных функций. Будьте внимательны при решении этой задачи на экзамене, и она покажется Вам очень легкой. Другие виды задач этого задания — на геометрический смысл первообразной — будут рассмотрены в другом разделе.
Сергей Никифоров
Если производная функции знакопостоянна на интервале, а сама функция непрерывна на его границах, то граничные точки присоединяются как к промежуткам возрастания, так и к промежуткам убывания, что полностью соответствует определению возрастающих и убывающих функций.
Фарит Ямаев
26.10.2016 18:50
Здравствуйте. Как же (на каком основании) можно утверждать, что в точке, где производная равна нулю, функция возрастает. Приведите доводы. Иначе, это просто чей-то каприз. По какой теореме? А также доказательство. Спасибо.
Служба поддержки
Значение производной в точке не имеет прямого отношения к возрастанию функции на промежутке. Рассмотрите, например, функции — все они возрастают на отрезке
Рассмотрите, например, функции — все они возрастают на отрезке
Владлен Писарев
02.11.2016 22:21
Если функция возрастает на интервале (а;b) и определена и непрерывна в точках а и b, то она возрастает на отрезке . Т.е. точка x=2 входит в данный промежуток.
Хотя, как правило возрастание и убывание рассматривается не на отрезке, а на интервале.
Но в самой точке x=2, функция имеет локальный минимум. И как объяснять детям, что когда они ищут точки возрастания (убывания), то точки локального экстремума не считаем, а в промежутки возрастания (убывания) — входят.
Учитывая, что первая часть ЕГЭ для «средней группы детского сада», то наверное такие нюансы- перебор.
Отдельно, большое спасибо за «Решу ЕГЭ» всем сотрудникам- отличное пособие.
Сергей Никифоров
Простое объяснение можно получить, если отталкиваться от определения возрастающей/убывающей функции. Напомню, что звучит оно так: функция называется возрастающей/убывающей на промежутке, если большему аргументу функции соответствует большее/меньшее значение функции.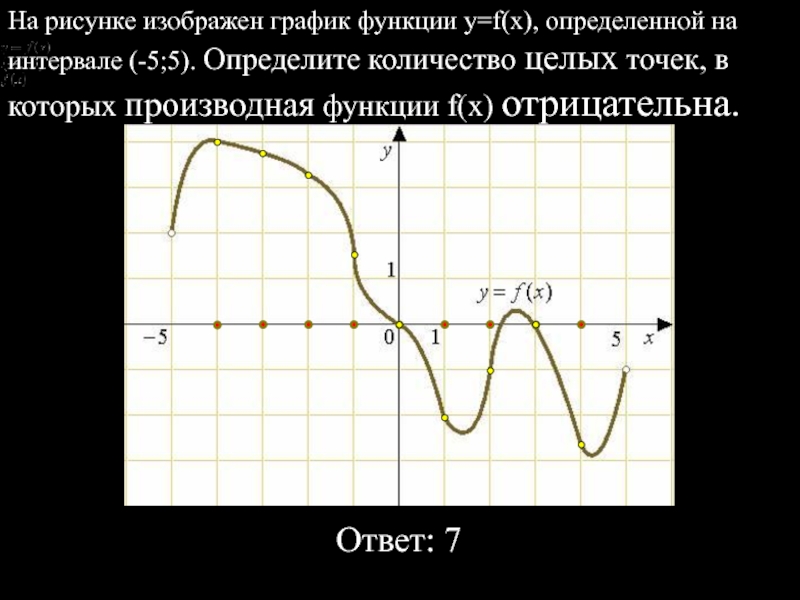 Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.
Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.
Ирина Ишмакова
20.11.2017 11:46
Добрый день. Здесь в комментариях я вижу убеждения, что границы включать нужно. Допустим, я с этим соглашусь. Но посмотрите, пожалуйста, ваше решение к задаче 7089. Там при указании промежутков возрастания границы не включаются. И это влияет на ответ. Т.е. решения заданий 6429 и 7089 противоречат друг другу. Проясните, пожалуйста, эту ситуацию.
Александр Иванов
В заданиях 6429 и 7089 совершенно разные вопросы.
В одном про промежутки возрастания, а в другом про промежутки с положительной производной.
Противоречия нет.
Экстремумы входят в промежутки возрастания и убывания, но точки, в которых производная равна нулю, не входят в промежутки, на которых производная положительна.
A Z
28.01.2019 19:09
Коллеги, есть понятие возрастания в точке
(см.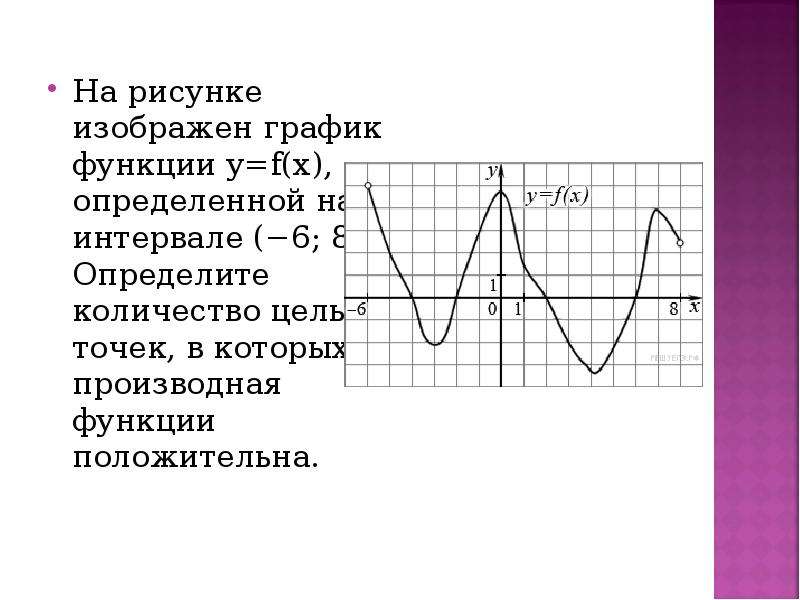 Фихтенгольц например)
Фихтенгольц например)
и ваше понимание возрастания в точке x=2 противочет классическому определению.
Возрастание и убывание это процесс и хотелось бы придерживаться этого принципа.
В любом интервале, который содержит точку x=2, функция не является возрастающей. Поэтому включение данный точки x=2 процесс особый.
Обычно, чтобы избежать путаницы о включении концов интервалов говорят отдельно.
Александр Иванов
Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
В точке х=2 функция дифференцируема, а на интервале (2; 6) производная положительна, значит, на промежутке }
Выработать специфические умения и навыки по работе. Разработка урока на тему «чтение графика функции» Чтение графика производной функции
Тема: Общее повторение курса математики. Подготовка к экзаменам
Урок: Чтение графика функций. Решение задач В2
В нашей жизни графики встречаются довольно часто, взять хотя бы прогноз погоды, который представляется в виде графика изменения каких-либо показателей, например, температуры или силы ветра с течением времени.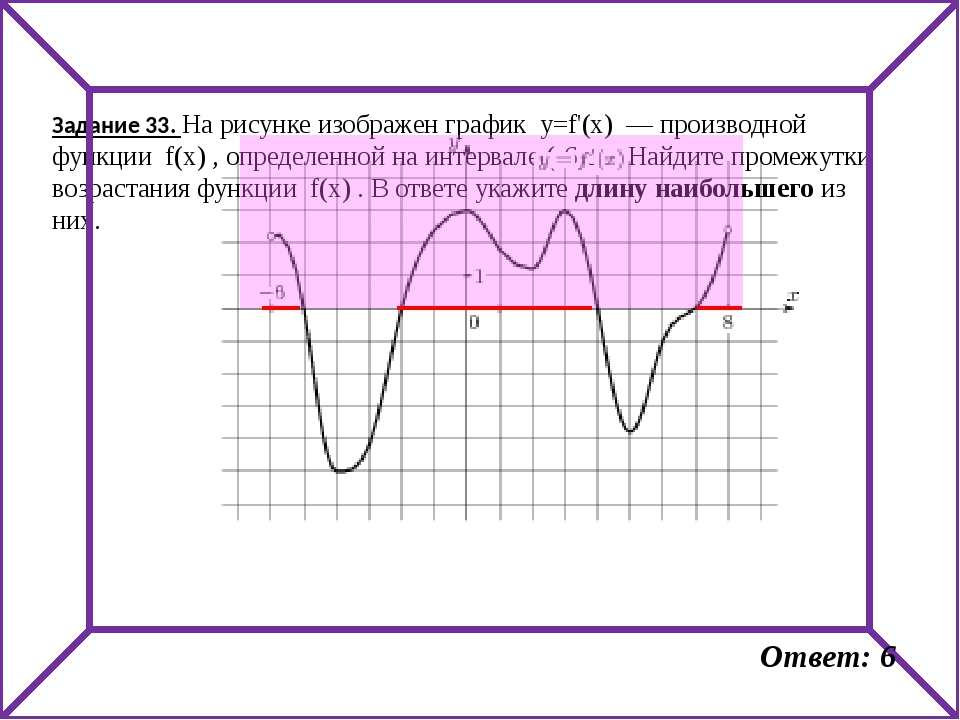 Мы не задумываемся, когда считываем этот график, хотя это, возможно, первое чтение графика в нашей жизни. Также можно привести пример графика изменения курсов валют с течением времени и множество других примеров.
Мы не задумываемся, когда считываем этот график, хотя это, возможно, первое чтение графика в нашей жизни. Также можно привести пример графика изменения курсов валют с течением времени и множество других примеров.
Итак, первый график, который мы рассмотрим.
Рис. 1. Иллюстрация графика 1
Как видно, график имеет 2 оси. Ось, смотрящая вправо (горизонтальная), называется осью . Ось, смотрящая вверх (вертикальная), называется осью .
Для начала разберем ось . На данном графике по этой оси отложены число оборотов в минуту у некоторого автомобильного двигателя. Оно может быть равно и т. д. На этой оси также есть деления, часть из них обозначена цифрами, часть из них является промежуточными и не обозначена. Несложно догадаться, что первое деление от нуля — это , третье — и т. д.
Теперь разберем ось . На данном графике по этой оси отложены числовые значения величины Ньютон на метр (), величины крутящего момента, которые равны и т. д. В данном случае, цена деления равна .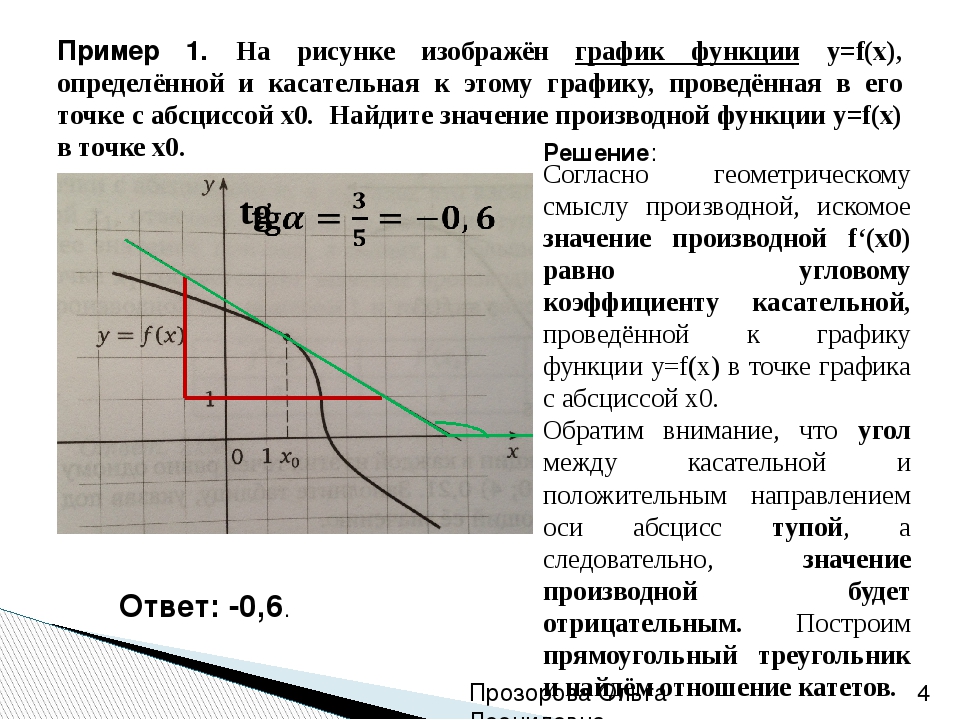
Теперь обратимся к самой функции (к той линии, которая представлена на графике). Как видно, эта линия отражает, сколько Ньютонов на метр, то есть какой крутящий момент, будет при конкретном значении оборотов двигателя в минуту. Если мы возьмем значение 1000 об./мин. и от этой точки на графике пойдем влево, то мы увидим, что линия проходит через точку 20, т. е. значение крутящего момента при 1000 об/мин будет равно (рисунок 2.2).
Если мы возьмем значение 2000 об/мин, то линия пройдет уже в точке (рисунок 2.2).
Рис. 2. Определение крутящего момента по количеству оборотов в минуту
Теперь представим, что наша задача — найти наибольшее значение по этому графику. Ищем самую высокую точку (), соответственно, самым низким значением крутящего момента в этом графике будет считаться 0. Чтобы найти наибольшее значение функции по графику, нужно рассмотреть самое большое значение, которое достигает функция по вертикальной оси. Мы смотрим, какое значение выше всех, и смотрим по вертикальной оси, какое будет самое большое достигающееся число. Если же мы говорим о наименьшем значении, то мы берем, наоборот, самую низкую точку и смотрим её значение по вертикальной оси.
Если же мы говорим о наименьшем значении, то мы берем, наоборот, самую низкую точку и смотрим её значение по вертикальной оси.
Рис. 3. Наибольшее и наименьшее значение функции по графику
Наибольшее значение в данном случае — , а наименьшее значение, соответственно, 0. Важно не перепутать и указать правильно максимальное значение, некоторые указывают максимальное значение 4000 об/мин., это не наибольшее значение, а та точка, в которой принимается наибольшее значение (точка максимума), наибольшее значение — именно .
Также следует обращать внимание на вертикальную ось, ее единицы измерения, то есть, например, если вместо Ньютонов на метр () было бы указано сотни Ньютонов на метр (), значение максимума нужно было бы умножить на сто и т. д.
Наибольшее и наименьшее значение функции очень тесно связаны с производной функции.
Если на рассматриваемом отрезке функция возрастает, то производная функции на этом отрезке положительна либо равна нулю в конечном количестве точек, чаще всего просто положительна. Аналогично, если на рассматриваемом отрезке функция убывает, то производная функции на этом отрезке отрицательна либо равна нулю в конечном количестве точек. Обратное утверждение в обоих случаях верно.
Аналогично, если на рассматриваемом отрезке функция убывает, то производная функции на этом отрезке отрицательна либо равна нулю в конечном количестве точек. Обратное утверждение в обоих случаях верно.
В следующем примере возникают некоторые трудности, связанные с ограничением по горизонтальной оси . Необходимо найти наибольшее и наименьшее значение на указанном отрезке.
На графике изображено изменение температуры с течением времени. По горизонтальной оси мы видим время и дни, а по вертикальной оси — температуру. Необходимо определить наибольшую температуру воздуха на 22 января, т. е. нам нужно рассматривать не весь график, а часть, касающуюся 22 января, т. е. от 00:00 22 января до 00:00 23 января.
Рис. 4. График изменения температуры
Ограничив график, нам становится очевидным, что максимальная температура соответствует точке .
Задан график изменения температуры за трое суток. По оси ox — время дня и числа месяца, по оси oy — значение температуры воздуха в градусах Цельсия.
Нам нужно рассматривать не весь график, а часть, касающуюся 13 июля, т. е. от 00:00 13 июля до 00:00 14 июля.
Рис. 5. Иллюстрация к дополнительному примеру
Если не ввести описанные выше ограничение, можно получить неверный ответ, но на заданном интервале максимальное значение очевидно: , и достигается оно в 12:00 13 июля.
Пример 3: определить, какого числа впервые выпало пять миллиметров осадков:
На графике изображено суточное количество осадков в Казани с 3 по 15 февраля 1909 года. По горизонтали откладываются дни месяца, по вертикали — количество осадков в миллиметрах.
Рис. 6. Суточное выпадение осадков
Начнем по порядку. 3-го числа, мы видим, выпало чуть больше 0, но меньше 1 мм. осадков, 4-го числа выпало 4 мм осадков, и т. д. Впервые цифра 5 появляется на 11-ый день. Для удобства можно было виртуально провести прямую линию напротив пятерки, впервые она пересечет график именно 11 февраля, это и является правильным ответом.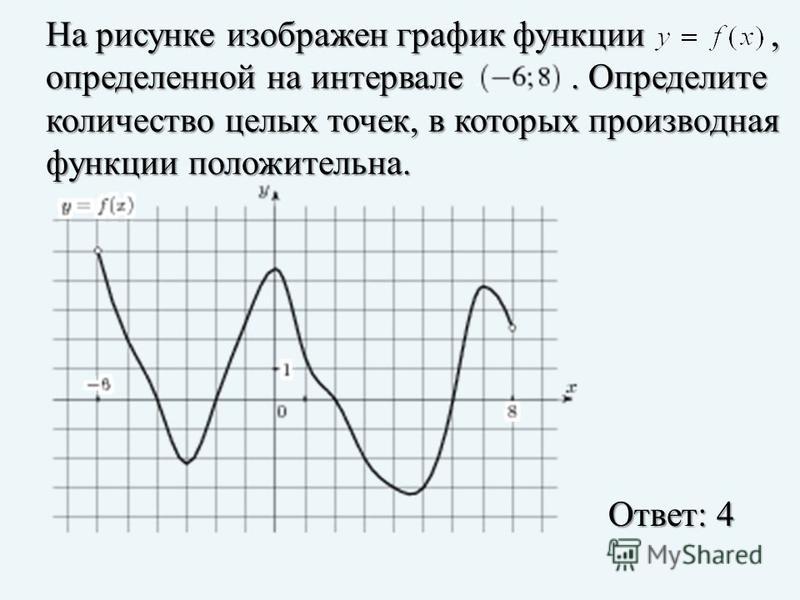
Пример 4: определить, какого числа цена унции золота была наименьшей
На графике показана цена золота на момент закрытия биржевых торгов на каждый день с 5 по 28 марта 1996 года. По горизонтали откладываются дни месяца, по вертикали,
соответственно, цена унции золота в долларах США.
Линии между точками проведены только для наглядности, информацию несут исключительно сами точки.
Рис. 7. График изменения цены золота на бирже
Дополнительный пример: определить, в какой точке отрезка функция принимает наибольшее значение:
На графике задана производная некоторой функции .
Рис. 8. Иллюстрация к дополнительному примеру
Производная определена на отрезке
Как видно, производная функции на заданном отрезке является отрицательной, в левой граничной точке равна нулю. Как мы знаем, если производная функции отрицательная, то функция на рассматриваемом промежутке убывает, следовательно, наша функция убывает на всём рассматриваемом отрезке , в таком случае, наибольшее значение она принимает в самой левой границе.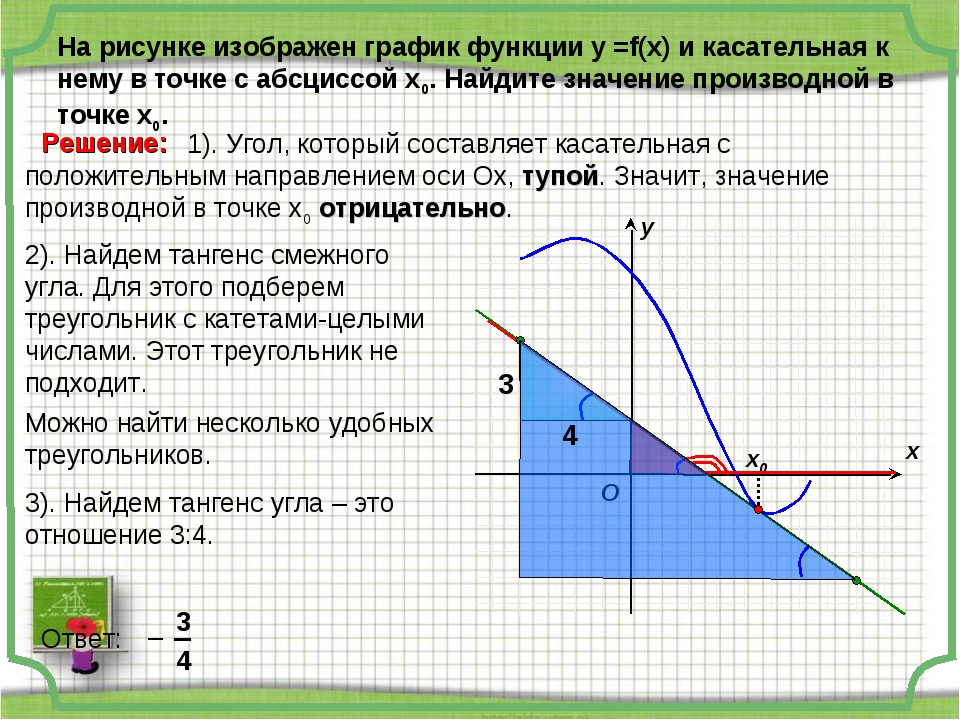 Ответ: точка .
Ответ: точка .
Итак, мы рассмотрели понятие графика функции, изучили, что такое оси на графике, как находить значение функции по графику, как находить наибольшее и наименьшее значение.
- Мордкович А.Г. Алгебра и начала математического анализа. — М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. — М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. — М.: Просвещение.
- ЕГЭ ().
- Фестиваль педагогических идей ().
- Учёба-легко.РФ ().
- На диаграмме (рисунок 9) показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в период с мая по декабрь 1973 года включительно. Ответ дайте в градусах Цельсия.
Рис. 9. График изменения температуры
- По этому же графику (рисунок 9), определите разность между наибольшей и наименьшей среднемесячными температурами в 1973 году.
 Ответ дайте в градусах Цельсия.
Ответ дайте в градусах Цельсия. - На графике (рисунок 10) показан процесс разогрева двигателя внутреннего сгорания при температуре окружающего воздуха 15 градусов. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. К двигателю можно подключить нагрузку, когда температура двигателя достигнет 45 градусов. Какое наименьшее количество минут потребуется выждать, прежде чем подключить нагрузку к двигателю?
Рис. 10. График разогрева двигателя
Слайд 12
Симметрия относительно прямой y=x
Графики данных функций возрастаютприа>1 иубывают при 0
Слайд 13
На одном из рисунков изображен график функции y=2-x.
Укажите этот рисунок.
График показательной функции
График показательной функции проходит через точку (0, 1).Так как основание степени меньше 1,то данная функция должна быть убывающей.
Слайд 14
На одном из рисунков изображен график функции y=log5 (x-4).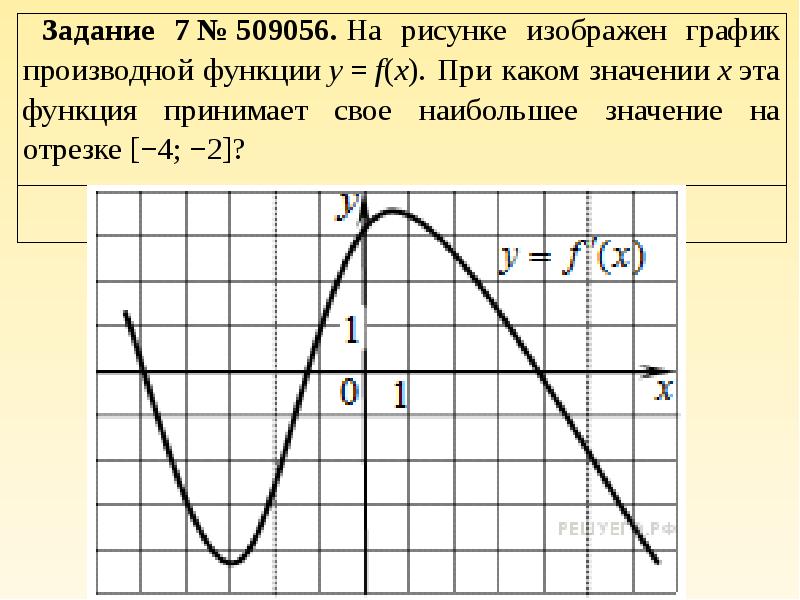
Укажите номер этого графика.
График логарифмической функции y=log5xпроходит через точку (1;0) ,тогда,еслих -4 =1,тоу=0,х=1+4, х=5. (5;0) – точка пересечения графика с осью ОХ Если х -4 = 5, то у=1, х=5+4, х=9,
График логарифмической функции
9
5
1
Слайд 15
Функция y=f(x) определена на промежутке (-6;7). На рисунке изображен график производной этой функции. К графику функции проведены все касательные, параллельныепрямой y=5-2x (или совпадающей с ней). Укажите количество точек графика функции, в которых проведены эти касательные.
K = tga = f’(xo)
По условию k=-2.Следовательно f’(xo)=-2
Проводим прямую у=-2.Она пересекает график в двухточках,значит касательныек функции проведены в двух точках.
Нахождение числа касательных к графику функции по графику ее производной
Слайд 16
Функция y=f(x) определена на промежутке [-7;3]. На рисунке изображен график ее производной. Найдите число точек графика функции y=f(x), в которых касательные к графику параллельны оси абсцисс или совпадают с ней.
Угловой коэффициент прямых, параллельных осиабсцисс или совпадающих с ней равен нулю. Следовательно К=tg a = f `(xo)=0
Ось ОХ пересекает данный график в четырехточках.
Нахождение числа касательных к функции по графику ее производной
Слайд 17
Функция y=f(x)определена на промежутке (-6;6). На рисунке изображен график ее производной. Найдите число точекграфика функции y=f(x), в которых касательные к графику наклонены под углом 135ок положительному направлению оси абсцисс.
K = tg 135o= f’(xo)
tg 135o=tg(180о-45o)=-tg45o=-1Следовательноf`(xo)=-1
Проводим прямую у=-1.Она пересекает график в трех точках,значит касательные к функции проведены в трехточках.
Нахождение числа касательных к функции по графику ее производной
Слайд 18
Функцияy=f(x) определена на промежутке[-2;6]. На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции y=f(x) имеет наименьшийугловой коэффициент
k=tg a=f’(xo)
Наименьшеезначениеу=-3 производная функции принимает в точке х=2.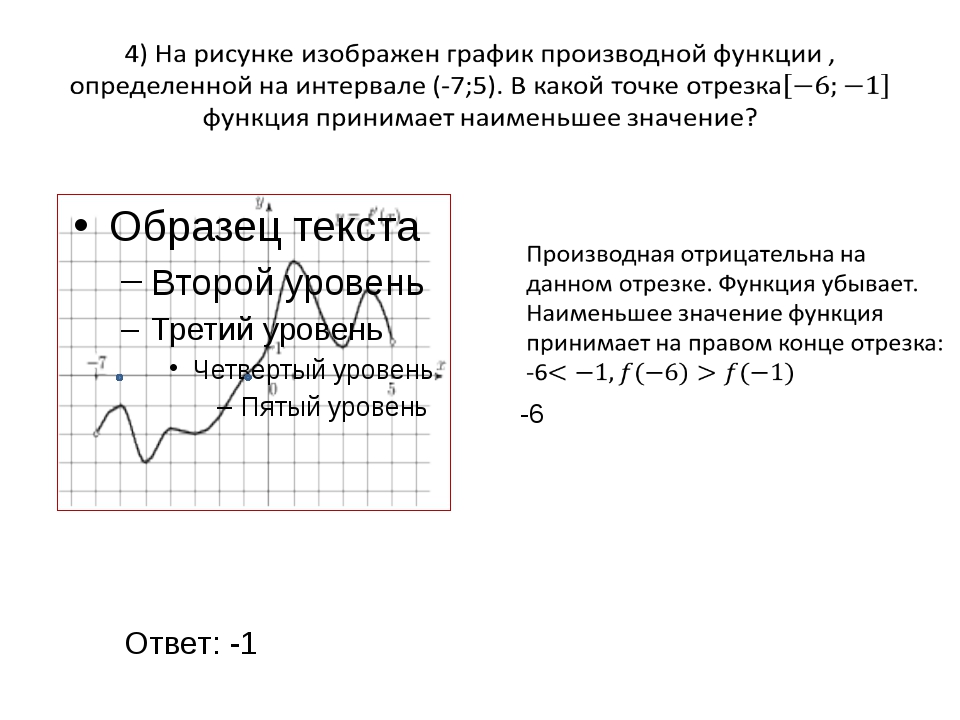 Следовательно, касательная к графику имеет наименьший угловой коэффициент в точке х=2
Следовательно, касательная к графику имеет наименьший угловой коэффициент в точке х=2
Нахождение углового коэффициента касательной
по графику производной функции
-3
2
Слайд 19
Функция y=f(x)определена на промежутке [-7;3]. На рисунке изображен график производной этой функции. Укажите абсциссуточки, в которой касательная к графику функции y=f(x) имеет наибольший угловой коэффициент.
k=tg a=f’(xo)
Наибольшее значение у=3производная функции принимает в точке х=-5.
Следовательно касательная к графику имеетнаибольший угловой коэффициентв точке х=-5
Нахождение углового коэффициента касательной
по графику производной функции
3
-5
Слайд 20
На рисунке изображен график функции y=f(x) и касательная к нему в точке с абсциссой хо. Найдите значение производной f `(x) в точке хо
f ’(xo) =tg a
Так как на рисунке а — тупой угол, то tg a
Слайд 21
Нахождение минимума (максимума) функции по графику ее производной
В точке х=4производная меняет знак с минусанаплюс.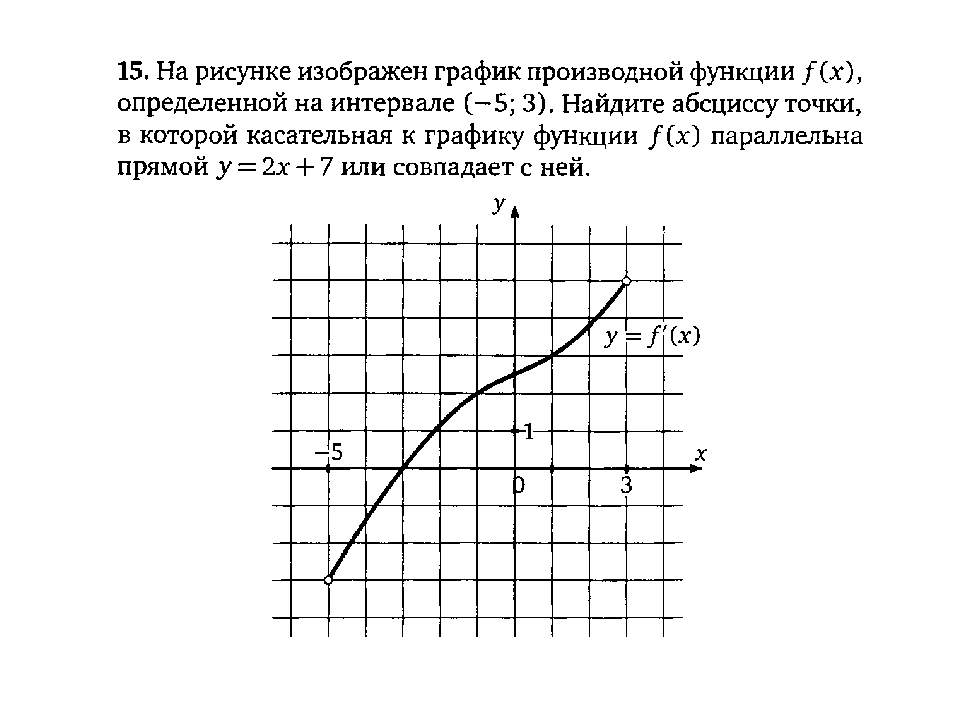 Значитх=4является точкой минимумафункцииy=f(x)
Значитх=4является точкой минимумафункцииy=f(x)
4
В точкех=1производная меняет знак с плюсана. минусЗначитх=1является точкой максимумафункцииy=f(x))
Слайд 22
Самостоятельная работа
Рис.11) Найти область определения функции.
2) Решить неравенствоf(x) ≥ 0
3) Определить промежутки убывания функции.
Рис.2–график производнойфункции y=f(x)
4)Найти точки минимума функции.
5) Укажите абсциссу точки, в которой касательная к графику функции y=f(x) имеет наибольшийугловой коэффициент.
Рис.11) Найти область значений функции.
2) Решить неравенствоf(x)≤ 0
3) Определить промежутки возрастания функции.
Рис.2–график производнойфункции y=f(x)
4)Найти точки максимума функции.
5) Укажите абсциссу точки, в которой касательная к графику функции y=f(x) имеет наименьший угловой коэффициент.
1 Вариант
2 Вариант
ТЕМА «ЧТЕНИЕ ГРАФИКА ПРОИЗВОДНОЙ ФУНКЦИИ»
Цель урока
: формирование умений и навыков по определению свойств производной по графику функции, свойств функции по графику производной, сопоставлению графика функции и графика ее производной.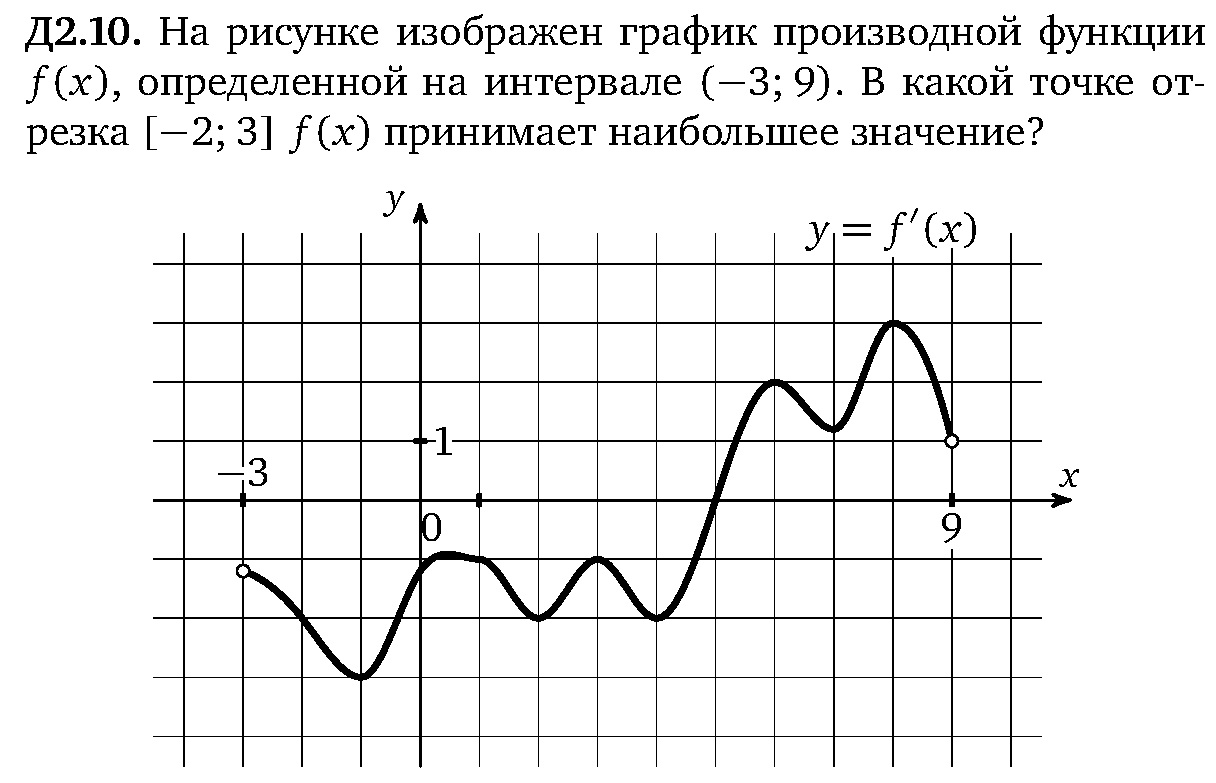
Материалы и оборудование
: компьютерная презентация.
План урока
- Организационный момент.
- Устный счет «Лови ошибку»
- Повторение теоретического материала по теме «Своя опора»
- Отработка умений
- Игра «Компетентность»
- Подведение итогов.
Ход урока.
- Организационный момент. В ходе изучения темы «Исследование функций с помощью производной» были сформированы умения находить критические точки функции, производную, определять с ее помощью свойства функции и строить ее график. Сегодня мы посмотрим на эту тему под иным углом зрения: как через график производной функции определить свойства самой функции. Наша задача: научиться ориентироваться в разнообразии заданий ЕГЭ, связанных с графиками функций и их производных.
- Устный счет
(2х 2) / =2х; (3х-х 3) / =3-3х; х
/ =1
х
- Повторение теоретического материала по теме. (нарисовать человечка в тетради, означающего настроение в начале урока)
Повторим некоторые свойства функции: возрастание и убывание, экстремумы функции.
Достаточный признак возрастания (убывания) функции. Он гласит:
- Если производная функции положительна в каждой точке интервала Х, то функция возрастает на интервале Х.
- Если производная функции отрицательна в каждой точке интервала Х, то функция убывает на интервале Х.
Достаточные условия экстремума:
Пусть функция y=f(x) непрерывна на промежутке Х и имеет внутри промежутка критическую точку х 0 . Тогда если при переходе через точку х 0 производная:
а) меняет знак с « +» на «-» , то х 0 – точка максимума функции,
б) меняет знак с «-» на «+» , то х 0
– точка минимума функции,
в) не меняет знака, то в точке х 0
экстремума нет.
Производная функции сама является функцией. Значит, у нее имеется свой график.
Х
(у нас отрезок [а; b
]) расположен выше оси абсцисс, то функция возрастает на этом интервале.
Если график производной на интервале Х
расположен ниже оси абсцисс, то функция убывает на этом интервале. Причем варианты графиков производной могут быть различны.
Причем варианты графиков производной могут быть различны.
Итак, имея график производной функции, можно сделать вывод о свойствах самой функции.
- Отработка умений. Рассмотрим задачу:
- Игра «Компетентность»
- Подведение итогов. (нарисовать человечка в тетради, означающего настроение в конце урока) Роль «подводящий итоги» (он скажет, какая мысль (вывод, результат…)на уроке была, по его мнению, главной)
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
ЧТЕНИЕ ГРАФИКА ПРОИЗВОДНОЙ ФУНКЦИИ и ли на пути к ЕГЭ
План урока Организационный момент. Устный счет «Лови ошибку» Повторение теоретического материала по теме, конспект «Своя опора» Отработка умений Игра «Компетентность» Подведение итогов.
Устный счет «Найди ошибку» (2х 2) / = х (3х-х 3) / = 3-3 2 4 х 2 — -5
Повторение теоретического материала по теме f(x) f / (x) 5 + – y = f / (x) 1 2 3 4 5 6 7 — 7 — 6 — 5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x + 1 Достаточный признак возрастания (убывания) функции: Если производная функции положительна в каждой точке интервала Х, то функция возрастает на интервале Х. Если производная функции отрицательна в каждой точке интервала Х, то функция убывает на интервале Х. Если график производной на интервале Х расположен выше оси абсцисс, то функция возрастает на этом интервале. Если график производной на интервале Х расположен ниже оси абсцисс, то функция убывает на этом интервале.
f(x) f / (x) 5 + – y = f / (x) 1 2 3 4 5 6 7 — 7 — 6 -5 -4 — 3 -2 — 1 4 3 2 1 -1 -2 -3 -4 -5 y x + 1 « Своя опора» Возрастает Убывает Возрастает
f(x) f / (x) 5 + – y = f / (x) y x + 1 Е сли при переходе через точку х 0 производная: а) меняет знак с « +» на «-» , то х 0 – точка максимума функции, б) меняет знак с «-» на «+» , то х 0 – точка минимума функции, в) не меняет знака, то в точке х 0 экстремума нет. Повторение теоретического материала по теме « Своя опора» Н еобходимое условие существования экстремума: Если функция y=f (x) имеет экстремум в точке х=х 0 , то в этой точке производная либо равна 0, либо не существует. max min
Отработка умений (решение задач из открытого банка ЕГЭ) промежутки возрастания: (-5;-1), (2;8),(11;12) Ответ: 6 1 f(x) f / (x) + + +
Отработка умений промежутки убывания: (-1;0), (9;12) Ответ: 3 2 f(x) f / (x) – – Отработка умений (решение задач из открытого банка ЕГЭ)
Отработка умений Ответ: -3 3 f(x) f / (x) Отработка умений (решение задач из открытого банка ЕГЭ)
Отработка умений Ответ: — 3 4 f(x) f / (x) Отработка умений (решение задач из открытого банка ЕГЭ)
Отработка умений 5 f(x) f / (x) Отработка умений (решение задач из открытого банка ЕГЭ)
Игра «Компетентность » Участники: две команды – фирмы конкуренты Команды придумывают друг для друга по 3 задания по теме урока, обмениваются заданиями, выполняют их и показывают решение на доске. Если соперник не справляется, то задающая вопрос команда сама должна ответить на него. Каждая фирма оценивает работу фирмы-конкурента по 5-бальной системе (каждое задание и каждый ответ) Спонсоры знаний: Петрова Гелена и Семенова Куннэй
Подведение итогов Рисуем человечка Подводим итог: что на уроке было главным? что было интересным? чему научились? Критерии оценок: 28-30 баллов – оценка «5» 20-27 баллов – оценка «4» 10-19 баллов – оценка «3» ниже 10 баллов – рекомендация на кропотливую работу по подготовке к ЕГЭ
Обобщающий урок на тему:
«Применение производной и ее графика для чтения свойств функции»
Тип урока:
обобщающий урок с применением ИКТ в форме презентации.
Цели урока:
Образовательные:
Содействовать усвоению учащимися применению производной в практических заданиях;
Научить учащихся четко использовать свойства функции и производной.
Развивающие:
Развивать умения анализировать вопрос задания и делать выводы;
Развивать умения применять имеющиеся знания в практических заданиях.
Воспитательные:
Воспитание интереса к предмету;
Необходимость данных теоретических и практических умений для продолжения учебы.
Задачи урока:
Выработать специфические умения и навыки по работе с графиком производной функции для их применения при сдаче ЕГЭ;
Подготовиться к контрольной работе.
План урока.
1. Актуализация опорных знаний (АОЗ).
2. Отработка знаний, умений и навыков по теме.
3. Тестирование (В8 из ЕГЭ).
4. Взаимопроверка, выставление оценок «соседу».
5. Подведение уроков урока.
Оборудование: компьютерный класс, доска, маркер, тесты (2 варианта).
Ход урока.
Оргмомент.
Учитель
.
Здравствуйте, садитесь.
В ходе изучения темы «Исследование функций с помощью производной» были сформированы умения находить критические точки функции, производную, определять с ее помощью свойства функции и строить ее график. Сегодня мы посмотрим на эту тему под иным углом зрения: как через график производной функции определить свойства самой функции. Наша задача: научиться ориентироваться в разнообразии заданий, связанных с графиками функций и их производных.
При подготовке к ЕГЭ по математике в КИМах даны задачи на применение графика производной для исследования функций. Поэтому на данном уроке мы должны систематизировать свои знания по этой теме и научиться быстро находить ответы на вопросы заданий В8.
Слайд №1.
Тема:
«Применение производной и ее графика для чтения свойств функций»
Задачи урока:
Отработка ЗУН применения производной, ее геометрического смысла и графика производной для определения свойств функций.
Развитие оперативности выполнения тестов ЕГЭ.
Воспитание таких качеств личности как внимательность, умение работать с текстом, умение работать с графиком производной
2.Актуализация опорных знаний (АОЗ). Слайды с № 4 по № 10.
Сейчас на экране будут появляться вопросы для повторения. Ваша задача: дать четкий и краткий ответ по каждому пункту. Верность вашего ответа можно будет проверить на экране.
(
На экране сначала появляется вопрос, после ответов учащихся для сверки появляется верный ответ.)
Список вопросов для АОЗ.
Определение производной.
Геометрический смысл производной.
Связь между значениями производной, угловым коэффициентом касательной, углом между касательной и положительным направлением оси ОХ.
Применение производной для нахождения промежутков монотонности функции.
Применение производной для определения критических точек, точек экстремума
6
.Необходимые и достаточные условия экстремума
7
. Применение производной для нахождения наибольшего и наименьшего значения функции
(Учащиеся отвечают на каждый пункт, сопровождая свои ответы, записями и чертежами на доске. При ошибочных и неполных ответах, одноклассники исправляют и дополняют их. После ответа учащихся, на экране появляется верный ответ. Таким образом, учащиеся сразу могут определить верность своего ответа.)
3. Отработка знаний, умений и навыков по теме. Слайды № 11 по № 15.
Учащимся предлагаются задания из КИМов ЕГЭ по математике прошлых лет, из сайтов в интернете на применение производной и ее графика для исследования свойств функций. Задания появляются последовательно. Решения учащиеся оформляют на доске, либо устными рассуждениями. Затем на слайде появляется верное решение и сверяется с решением учащихся. Если в решении допущена ошибка, то она анализируется всем классом.
Слайд №16 и №17.
Далее в классе целесообразно рассмотреть ключевую задачу: по приведенному графику производной ученики должны придумать (конечно же, с помощью учителя) различные вопросы, относящиеся к свойствам самой функции. Естественно, что эти вопросы обсуждаются, в случае необходимости корректируются, обобщаются, фиксируются в тетради, после чего наступает этап решения этих заданий. Здесь необходимо добиться того, чтобы ученики не просто давали правильный ответ, а умели его аргументировать (доказывать), с использованием соответствующих определений, свойств, правил.
Тестирование (В8 из ЕГЭ). Слайды с № 18 по № 29. Слайд № 30 – ключи к тесту.
Учитель
:
Итак, мы обобщили ваши знания по данной теме: повторили основные свойства производной, решили задачи, связанные с графиком производной, разобрали сложные и проблемные моменты применения производной и графика производной для исследования свойств функций.
Сейчас проведем тестирование в 2 варианта. Задания будут появляться на экран оба варианта, одновременно. Вы изучаете вопрос, находите ответ, заносите его в бланк для ответов. После завершение теста, меняетесь бланками и проверяете работу соседа по готовым ответам. Выставляете оценку
(до 10 баллов – «2», с 11 до 15 баллов –«3», с 16 до 19 баллов – «4», более 19 баллов – «5».).
Подведение итогов урока
Мы рассмотрели взаимосвязь монотонности функции и знака ее производной, достаточные условия существования экстремума. Рассмотрели различные задания на чтение графика производной функции, которые встречаются в текстах единого государственного экзамена. Все рассмотренные нами задания хороши тем, что на их выполнение не нужно много времени.
Во время единого государственного экзамена это очень важно: быстро и правильно записать ответ.
Бланки с ответами сдайте. Оценка за урок вам уже известна и будет выставлена в журнал.
Считаю, что класс подготовился к контрольной работе.
Домашняя работа будет творческая
.
Слайд № 33
.
Элементы
математического анализа
в ЕГЭ
Малиновская Галина Михайловна
[email protected]
Справочный материал
Таблица производных основных
функций.
Правила дифференцирования
(производная суммы, произведения,
частного двух функций).
Производная сложной функции.
Геометрический смысл производной.
Физический смысл производной.
Справочный материал
Точки экстремума (максимума или
минимума)
функции,
заданной
графически.
Нахождение
наибольшего
(наименьшего) значения функции,
непрерывной на заданном отрезке.
Первообразная функции. Формула
Ньютона-Лейбница.
Нахождение
площади криволинейной трапеции.
Физические приложения
1.1 Материальная точка движется
прямолинейно по закону 𝑥 𝑡 =
−𝑡 4 +6𝑡 3 +5𝑡 + 23 , где x —
расстояние от точки отсчета в метрах,
t — время в секундах, измеренное с
начала движения. Найдите ее скорость
(в метрах в секунду) в момент времени
t= 3с.
1.2
Материальная точка движется
1 3
прямолинейно по закону 𝑥 𝑡 = 𝑡 −
3
3𝑡 2 − 5𝑡 + 3 , где x — расстояние от
точки отсчета в метрах, t — время в
секундах, измеренное с начала
движения. В какой момент времени (в
секундах) ее скорость была равна 2
м/с?
Решение:
Ищем производную х(t) (функции пути по
времени).
В задаче 1.1 подставляем вместо t его
значение и считаем скорость (Ответ: 59).
Во задаче 1.2 приравниваем найденную
производную к данному числу и решаем
уравнение относительно переменной t.
(Ответ: 7).
Геометрические приложения
2.1 Прямая 𝑦
= 7𝑥 −
5 параллельна
касательной к графику
2
функции 𝑦 = 𝑥 + 6𝑥 − 8
. Найдите абсциссу точки
касания.
2.2
Прямая 𝑦 = 3𝑥 + 1
является касательной к
2
графику функции 𝑎𝑥 +
2𝑥 + 3 . Найдите a.
2.3 Прямая
𝑦 = −5𝑥 + 8
является касательной к
2
графику функции 28𝑥 +
𝑏𝑥 + 15 . Найдите b,
учитывая, что абсцисса точки
касания больше 0.
2.4
Прямая
𝑦 = 3𝑥 + 4 является
касательной к графику
2
функции 3𝑥 − 3𝑥 + 𝑐.
Найдите c.
Решение:
В задаче 2.1 ищем производную функции и
приравниваем к угловому коэффициенту
прямой (Ответ: 0,5).
В задачах 2.2-2.4 составляем систему из
двух уравнений. В одном приравниваем
функции, в другом приравниваем их
производные. В системе с двумя
неизвестными (переменной x и параметра)
ищем параметр. (Ответы: 2.2) a=0,125; 2.3)
b=-33; 2.4) c=7).
2.5
На рисунке изображены график
функции y=f(x) и касательная к
нему в точке с абсциссой 𝑥0 .
Найдите значение производной
функции f(x) в точке 𝑥0 .
2.6
На рисунке изображены
график функции y=f(x) и
касательная к нему в точке с
абсциссой 𝑥0 . Найдите значение
производной функции f(x) в точке
𝑥0 .
2.7
На рисунке изображен график
функции y=f(x). Прямая, проходящая
через начало координат, касается
графика этой функции в точке с
абсциссой 10. Найдите значение
производной функции в точке.x=10.
𝑥0 = 0
Решение:
Значение производной функции в точке — это тангенс
угла наклона касательной к графику функции,
проведенной в данной точке.
«Дорисовываем» прямоугольный треугольник и
ищем тангенс соответствующего угла, который
берем положительным, если касательная образует
острый угол с положительным направлением оси Ох
(касательная «растёт») и отрицательным, если угол
тупой (касательная убывает).
В задаче 2.7 необходимо провести касательную
через указанную точку и начало координат.
Ответы: 2.5) 0,25; 2.6) -0,25; 2.7) -0,6.
Чтение графика функции или
графика производной функции
3.1 На рисунке изображен график функции
y=f(x), определенной на интервале (6;8).
Определите количество целых точек, в
которых производная функции
положительна.
3.2 На рисунке изображен график функции
y=f(x), определенной на интервале (-5;5).
Определите количество целых точек, в
которых производная функции
f(x) отрицательна.
Решение:
Знак производной связан с поведением функции.
Если производная положительна, то выделяем ту
часть графика функции, где функция возрастает.
Если производная отрицательна то там, где
функция убывает. Выделяем соответствующий
этой части промежуток на оси Ох.
В
соответствии с вопросом задачи или
пересчитываем количество целых чисел, входящих
в данный промежуток или находим их сумму.
Ответы: 3.1) 4; 3.2) 8.
3.3
На рисунке изображен график
функции y=f(x), определенной на
интервале (-2;12). Найдите сумму
точек экстремума функции f(x).
В первую очередь смотрим, что на рисунке:
график функции или график производной.
Если это график производной, то нас
интересуют только знаки производной и
абсциссы точек пересечения с осью Ох.
Для наглядности можно нарисовать более
привычный
рисунок
со
знаками
производной по полученным промежуткам
и поведением функции.
В соответствии с рисунком ответить на
вопрос задачи. (Ответ: 3.3) 44).
3.4
На рисунке изображен график
′
y=𝑓 (𝑥) — производной функции f(x),
определенной на интервале (-7;14].
Найдите количество точек максимума
функции f(x), принадлежащих отрезку
[-6;9].
3.5 На рисунке изображен график y=𝑓 ′ (𝑥) —
производной функции f(x), определенной на
интервале (-11;11) . Найдите количество
точек экстремума функции f(x),
принадлежащих отрезку [-10;10].
Решение:
Ищем точки пересечения графика производной с
осью Ох, выделяя ту часть оси, которая указана в
задаче.
Определяем знак производной на каждом из
полученных
промежутков
(если
график
производной ниже оси-то «-», если выше-то «+»).
Точками максимума будут те, где знак сменился с
«+» на «-», минимума- с «-» на «+». Точками
экстремума те и другие.
Ответы: 3.4) 1; 3.5) 5.
3.6
На рисунке изображен график
y=𝑓 ′ (𝑥) — производной функции f(x),
определенной на интервале (-8;3). В
какой точке отрезка [-3;2] функция f(x)
принимает наибольшее значение.
3.7 На рисунке изображен график
′
y=𝑓 (𝑥) — производной функции f(x),
определенной на интервале (-8;4). В
какой точке отрезка [-7;-3] функция
f(x) принимает наименьшее значение.
Решение:
Если
производная
меняет
знак
на
рассматриваемом отрезке, то решение
основано на теореме: если непрерывная на
отрезке функция имеет на нем единственную
точку экстремума и это точка максимума
(минимума), то наибольшее (наименьшее)
значение функции на этом отрезке
достигается в данной точке.
Если непрерывная на отрезке функция
монотонна, то она достигает своих
наименьшего и наибольшего значений на
данном отрезке на его концах.
Ответы: 3.6) -3; 3.7) -7.
3.8 На рисунке изображен график функции
y=f(x), определенной на интервале (-5;5).
Найдите количество точек, в которых
касательная к графику функции
параллельна прямой y=6 или совпадает с
ней.
3.9 На рисунке изображён график функции
y=f(x) и восемь точек на оси абсцисс:
𝑥1 ,𝑥2 ,𝑥3 , … , 𝑥12 . В скольких из этих точек
производная функции f(x) положительна?
4.2 На рисунке изображен график
y=𝑓 ′ (𝑥) — производной функции f(x),
определенной на интервале (-5;7). Найдите
промежутки убывания функции f(x). В
ответе укажите сумму целых точек,
входящих в эти промежутки.
4.5 На рисунке изображен
график y=𝑓 ′ (𝑥)- производной функции
f(x), определенной на интервале (-4;8).
Найдите точку экстремума функции f(x),
принадлежащую отрезку [-2;6].
4.6 На рисунке изображен
график y=𝑓 ′ (𝑥)- производной функции
f(x), определенной на интервале (-10;2).
Найдите количество точек, в которых
касательная к графику функции f(x)
параллельна прямой y=-2x-11 или
совпадает с ней.
Решение:
4.6 Так как на рисунке изображен
график производной, а касательная
параллельна данной прямой, то
производная функции в этой точке
равна -2. Ищем точки на графике
производной с ординатой равной -2 и
считаем их количество. Получаем 5.
Ответы: 3.8) 4; 3.9) 5; 4.2) 18; 4.5) 4; 4.6)
5.
4.8 На рисунке изображен
график y=𝑓 ′ (𝑥)- производной функции
f(x). Найдите абсциссу точки, в которой
касательная к графику y=f(x) параллельна
оси абсцисс или совпадает с ней.
Решение:
Если прямая параллельна оси Ох, то её
угловой коэффициент равен нулю.
Угловой коэффициент касательной равен
нулю, значит производная равна нулю.
Ищем абсциссу точки пересечения
графика производной с осью Ох.
Получаем -3.
4.9 На рисунке изображён график функции
y=𝑓 ′ (x) производная функции f(x) и восемь
точек на оси абсцисс: 𝑥1 ,𝑥2 ,𝑥3 , … , 𝑥8 . В
скольких из этих точек производная
функции f(x) возрастает?
Геометрический смысл
определенного интеграла
5.1 На рисунке изображён график
некоторой функции y=f(x) (два луча с
общей начальной точкой). Пользуясь
рисунком, вычислите F(8)-F(2),
где F(x) — одна из первообразных
функции f(x).
Решение:
Площадь
криволинейной
трапеции
вычисляется через определённый интеграл.
Определённый интеграл вычисляется по
формуле Ньютона-Лейбница как приращение
первообразной.
В задаче 5.1 считаем площадь трапеции по
известной формуле курса геометрии (это и
будет приращение первообразной).
В задачах 5.2 и 5.3 уже дана первообразная.
Необходимо вычислить её значения на
концах отрезка и посчитать разность.
5.2 На рисунке изображён график
некоторой функции y=f(x). Функция 𝐹 𝑥 =
15
3
2
𝑥 + 30𝑥 + 302𝑥 − — одна из
8
первообразных функции f(x). Найдите
площадь закрашенной фигуры.
Решение:
Площадь
криволинейной
трапеции
вычисляется
через
определённый
интеграл.
Определённый интеграл вычисляется по
формуле
Ньютона-Лейбница
как
приращение первообразной.
В задаче 5.1 считаем площадь трапеции
по известной формуле курса геометрии
(это
и
будет
приращение
первообразной).
В задаче 5.2 уже дана первообразная.
Необходимо вычислить её значения на
концах отрезка и посчитать разность.
Удачи на
ЕГЭ
по математике
КАК ПО ГРАФИКУ ОПРЕДЕЛИТЬ НАИБОЛЬШЕЕ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ видео онлайн
Видео:
График производной в задаче 7. Функция достигает своего максимума/минимума в тех точках, где производна
Научимся решать задачи на нахождение наименьшего или наибольшего значения функции, если дана производ
Задание №7 (прототип № 27491 профильный уровень) и задача №14 (базовый уровень) ЕГЭ по математике. Поддержа
Объяснение как найти наибольшее и наименьшее значение функции используя график для учеников 8 классов
Также я собрал для тебя самую полезную информацию и по другим предметам Держи ссылочки и получай подар
Показано нахождение наибольшего и наименьшего значений функции на заданном отрезке с помощью производ
Задача 7 по математике (производная, первообразная). Урок 24. Поддержать Проект: ru/r/valeryvolkov …
В данном уроке мы разберём такой тип задания №7 на ЕГЭ по математике профильного уровня, как нахождение
Решение задач на нахождение наибольшего и наименьшего значения функции на отрезке. Применение произво
Решаем задачи(упражнения) на заказ (!). P
Пожалуй, с этого видео и нужно начинать изучение производных в задаче 12. Сегодня мы подробно разберём: ч
Продолжаем разбираться с задачами на производную из ЕГЭ. Сегодня у нас в меню минимумы и максимумы функ
В данном уроке демонстрируется пример решения задачи на использование знаний геометрического смысла .
Мордкович, 10 кл. Как найти наибольшее и наименьшее значение функции на промежутке? Найти производную …
Задача 7 ЕГЭ по математике (производная, первообразная). Поддержать Проект: Мои …
Задание 7 ЕГЭ по математике (производная, первообразная). Поддержать Проект: Мои …
Задачи 7 и 12, математика ЕГЭ профиль, подготовка 2021 года.
Исследование функции по графику.
Максимальные и минимальные значения — подход к исчислению
10
Поворотные точки графика
МЫ ГОВОРИМ, ЧТО ФУНКЦИЯ f ( x ) имеет относительное максимальное значение x = a ,
, если f ( a ) на больше , чем любое предшествующее или последующее значение.
Мы называем это «относительным» максимумом, потому что другие значения функции на самом деле могут быть больше.
Мы говорим, что функция f ( x ) имеет относительное минимальное значение при x = b ,
, если f ( b ) на меньше , чем любое значение, непосредственно предшествующее или последующее.
Опять же, другие значения функции могут быть меньше. С таким пониманием мы откажемся от термина «относительный».
Значение функции, значение y , максимальное или минимальное, называется экстремальным значением.
Теперь, что характеризует график при экстремальном значении?
Касательная к кривой горизонтальна . Мы видим это в точках A и B . Наклон каждой касательной — производная при оценке как a или b — равен 0.
f ‘ ( x ) = 0.
Более того, в точках непосредственно от слева от максимума — в точке C — наклон касательной положительный: f ‘ ( x )> 0.В то время как в точках непосредственно к справа — в точке D — наклон отрицательный: f ‘ ( x )
Другими словами, максимум f ‘ ( x ) меняет знак с + на -.
Как минимум, f ‘ ( x ) меняет знак с — на +. Мы видим, что в точках E и F .
Также можно заметить, что максимум на A график вогнут вниз.(Тема 14 Precalculus.) Хотя как минимум, на B , он вогнутый вверх.
Значение x , при котором функция имеет максимум или минимум, называется критическим значением. На рисунке —
— критические значения: x = a и x = b .
Критические значения определяют точки поворота, в которых касательная параллельна оси x .Критические значения — если таковые имеются — будут решений от до f ‘ ( x ) = 0.
Пример 1. Пусть f ( x ) = x 2 — 6 x + 5.
Есть ли критические значения — какие-то поворотные моменты? Если да, то определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума?
Решение . f ‘ ( x ) = 2 x — 6 = 0 подразумевает x = 3. (Урок 9 алгебры)
x = 3 — единственное критическое значение. Это x — точка поворота. Чтобы определить y -coordinate, оцените f при этом критическом значении — оцените f (3):
| f ( x ) | = | x 2 — 6 x + 5 |
| f (3) | = | 3 2 — 6 · 3 + 5 |
| = | −4. | |
Крайнее значение — 4. Чтобы увидеть, является ли он максимумом или минимумом, в этом случае мы можем просто посмотреть на график.
f ( x ) — парабола, и мы видим, что точка поворота минимальна.
Найдя значение x , где производная равна 0, мы обнаружили, что вершина параболы находится в точке (3, −4).
Но мы не всегда сможем посмотреть на график.Алгебраическим условием минимума является то, что f ‘ ( x ) меняет знак с — на +. Мы видим это в точках E , B , F выше. Величина наклона увеличивается.
Теперь сказать, что наклон увеличивается, значит сказать, что при критическом значении вторая производная (Урок 9), которая представляет собой скорость изменения наклона, равна положительному значению .
Опять же, вот f ( x ):
| f ( x ) | = | x 2 — 6 x + 5. |
| f ‘ ( x ) | = | 2 x — 6. |
| f » ( x ) | = | 2. |
f » оценивается при критическом значении 3 — f » (3) = 2 — положительно. Это алгебраически говорит нам, что критическое значение 3 определяет минимум.
Достаточные условия
Теперь мы можем сформулировать эти достаточные условия для экстремальных значений функции при критическом значении a :
Функция имеет минимальное значение x = a , если f ‘ ( a ) = 0
и f’ ‘ ( a ) = положительное число.
Функция имеет максимальное значение x = a , если f ‘ ( a ) = 0
и f’ ‘ ( a ) = отрицательное число.
В случае максимума наклон тангенса равен , при уменьшении — он изменяется от положительного к отрицательному. Мы видим, что в точках C , A , D .
Пример 2. Пусть f ( x ) = 2 x 3 — 9 x 2 + 12 x — 3.
Есть ли крайние значения? Во-первых, существуют ли какие-либо критические значения — решения для f ‘ ( x ) = 0 — и определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Где поворотные моменты?
| Раствор . f ‘ ( x ) = 6 x 2 — 18 x + 12 | = | 6 ( x 2 — 3 x + 2) |
| = | 6 ( x -1) ( x -2) | |
| = | 0 | |
означает:
x = 1 или x = 2.
(Урок алгебры 37.)
Это критические значения. Каждый определяет максимум или минимум? Чтобы ответить, мы должны оценить вторую производную для каждого значения.
| f ‘ ( x ) | = | 6 x 2 — 18 x + 12. |
| f » ( x ) | = | 12 х — 18. |
| f » (1) | = | 12-18 = −6. |
Вторая производная отрицательна. Таким образом, функция имеет максимум x = 1.
Чтобы найти y -coördinate — экстремальное значение — на этом максимуме мы оцениваем f (1):
| f ( x ) | = | 2 x 3 — 9 x 2 + 12 x -3 |
| f (1) | = | 2–9 + 12–3 |
| = | 2. | |
Максимум приходится на точку (1, 2).
Далее, определяет ли x = 2 максимум или минимум?
| f ‘ ( x ) | = | 12 x — 18. |
| f » (2) | = | 24–18 = 6. |
Вторая производная положительна.Следовательно, функция имеет минимум x = 2.
Чтобы найти y -coördinate — экстремальное значение — при этом минимуме, мы оцениваем f (2):
| f ( x ) | = | 2 x 3 — 9 x 2 + 12 x — 3. |
| f (2) | = | 16–36 + 24–3 |
| = | 1. | |
Минимум находится в точке (2, 1).
Вот собственно график f ( x ):
Решения для f » ( x ) = 0 указывают точку перегиба в этих решениях, а не максимум или минимум. Пример: y = x 3 . y » = 6 x = 0 подразумевает x = 0. Но x = 0 — точка перегиба на графике y = x 3 , а не максимум или минимум .
Другой пример: y = sin x . Решение y » = 0 — это произведение числа π, которое является точками перегиба.
Задача 1. Найти координаты вершины параболы,
y = x 2 — 8 x + 1.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
y ‘ = 2 x — 8 = 0.
Это подразумевает x = 4. Это x -координата вершины. Чтобы найти y -coordinate, оцените y как x = 4:
.
y = 4 2 — 8 · 4 + 1 = −15.
Вершина находится в точке (4, −15).
Задача 2. Проверьте каждую функцию на наличие максимумов и минимумов.
a) y = x 3 — 3 x 2 + 2.
y ‘ = 3 x 2 — 6 x = 3 x ( x -2) = 0 означает
x = 0 или x = 2.
y ‘ ( x ) = 6 x — 6.
у » (0) = −6.
Вторая производная отрицательна. Это означает, что максимальное значение равно x = 0. Это максимальное значение составляет
.
y (0) = 2.
Далее,
y ‘ (2) = 12 — 6 = 6.
Вторая производная положительна. Это означает, что существует минимум x = 2.Это минимальное значение —
.
y (2) = 2 3 — 3 · 2 2 + 2 = 8-12 + 2 = −2.
б) y = −2 x 3 — 3 x 2 + 12 x + 10.
При x = 1 максимум y = 17.
При x = −2 минимум y = −10.
c) y = 2 x 3 + 3 x 2 + 12 x — 4.
Поскольку f ‘ ( x ) = 0 не имеет реальных решений, нет и экстремальных значений.
d) y = 3 x 4 — 4 x 3 — 12 x 2 + 2.
При x = 0 максимальное значение y = 2.
При x = −1 минимум y = −3.
При x = 2 минимум y = −30.
Следующий урок: Применение максимальных и минимальных значений
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Как найти максимальные значения
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Нахождение максимумов и минимумов с использованием производных
Где функция в верхней или нижней точке? Исчисление может помочь!
Максимум — это высшая точка, а минимум — это низкая точка:
В плавно изменяющейся функции максимум или минимум всегда там, где функция выравнивает (за исключением седловой точки ).
Где он расплющивается? Где наклон равен нулю .
Где нулевой наклон? Производная говорит нам!
Давайте сразу рассмотрим пример:
Пример: в воздух подброшен мяч. Его высота в любой момент времени t определяется выражением:
ч = 3 + 14т — 5т 2
Какова его максимальная высота?
Используя производные, мы можем найти наклон этой функции:
d dt h = 0 + 14-5 (2т)
= 14-10т
(См. Ниже этот пример, чтобы узнать, как мы нашли эту производную.)
Теперь найдите, когда наклон равен нулю :
14 — 10 т = 0
10 т = 14
t = 14/10 = 1,4
Наклон равен нулю при t = 1,4 секунды
А высота на тот момент:
h = 3 + 14 × 1,4 — 5 × 1,4 2
ч = 3 + 19,6 — 9,8 = 12,8
А так:
Максимальная высота 12,8 м (при t = 1.4 с)
Краткое руководство по производным инструментам
Производная определяет наклон функции.
В предыдущем примере мы взяли это:
ч = 3 + 14т — 5т 2
и придумал эту производную:
d dt h = 0 + 14-5 (2т)
= 14-10т
, который сообщает нам наклон функции в любое время t
Мы использовали эти производные правила:
- Наклон значения константы (например, 3) равен 0
- Наклон линии , такой как 2x, равен 2, поэтому 14t имеет наклон 14
- Квадрат Функция, такая как t 2 , имеет наклон 2t, поэтому 5t 2 имеет наклон 5 (2t)
- И затем мы сложили их: 0 + 14 — 5 (2t)
Как узнать, что это максимум (или минимум)?
Мы видели это на графике! Но иначе… деривативы снова приходят на помощь.
Возьмем производную от наклона (вторая производная исходной функции):
Производная от 14 до 10t равна −10
Это означает, что наклон постоянно уменьшается (-10): при движении слева направо наклон сначала положительный (функция возрастает), проходит через ноль (плоская точка), а затем наклон становится отрицательным (функция падает). :
Уклон, который становится меньше (и идет через 0), означает максимум.
Это называется тестом второй производной
На графике выше я показал наклон до и после, но на практике мы проводим тест в точке, где наклон равен нулю :
Тест второй производной
Когда наклон функции равен нулю при x , а вторая производная при x равна:
- меньше 0, это локальный максимум
- больше 0, это локальный минимум
- равно 0, тогда тест не пройден (хотя могут быть и другие способы выяснить)
«Вторая производная: меньше 0 — максимум, больше 0 — минимум»
Пример: найти максимумы и минимумы для:
y = 5x 3 + 2x 2 — 3x
Производная (наклон):
d dx y = 15x 2 + 4x — 3
Квадратичная с нулями в:
Могут ли они быть максимальными или минимальными? (Не смотрите пока на график!)
Вторая производная равна y » = 30x + 4
При x = −3/5:
у » = 30 (−3/5) + 4 = −14
меньше 0, поэтому −3/5 — это локальный максимум
При x = +1/3:
г ‘= 30 (+1/3) + 4 = +14
больше 0, поэтому +1/3 — это локальный минимум
(Теперь вы можете посмотреть на график.)
слов
Высшая точка называется максимумом (множественное число максимумов ).
Нижняя точка называется минимумом (множественное число минимумов ).
Общее слово для максимума или минимума — экстремум (множественное число экстремум ).
Мы говорим локальный максимум (или минимум), когда могут быть более высокие (или более низкие) точки в другом месте, но не поблизости.
Еще один пример
Пример: найти максимумы и минимумы для:
y = x 3 — 6x 2 + 12x — 5
Производная:
d dx y = 3x 2 — 12x + 12
Которая квадратична только с одним нулем при x = 2
Это максимум или минимум?
Вторая производная равна y » = 6x — 12
При x = 2:
у » = 6 (2) — 12 = 0
это 0, поэтому тест не пройден
И вот почему:
Это точка перегиба («седловая точка»)… наклон действительно становится нулевым, но он не является ни максимальным, ни минимальным.
Должен быть дифференцируемым
И еще важный технический момент:
Функция должна быть дифференцируемой (производная должна существовать в каждой точке своего домена).
Пример: как насчет функции f (x) = | x | (абсолютная величина) ?
| | x | выглядит так: |
При x = 0 происходит очень резкое изменение!
Фактически, он не дифференцируется там (как показано на дифференцируемой странице).
Итак, мы не можем использовать производный метод для функции абсолютного значения.
Функция также должна быть непрерывной, но любая дифференцируемая функция также является непрерывной, поэтому мы покрыты.
Использование дифференциации для поиска максимальных и минимальных значений — видео и стенограмма урока
Поиск экстремумов
Мы можем использовать это в своих интересах, чтобы найти экстремальные значения.Итак, для некоторой функции y = f (x) первое, что нам нужно сделать, это найти критические точки этой функции. (То есть, когда производная равна нулю.) Итак, мы собираемся найти несколько значений x , где производная равна нулю. Второй шаг — это то, что мы собираемся найти, что такое y в этих критических точках. Мы также собираемся найти y в конечных точках. Таким образом, мы могли бы понять, что Super C достиг вершины своего роста за 1 секунду полета, но теперь мы собираемся выяснить, насколько точно это было — в данном случае это значение y .Третий шаг заключается в том, что мы собираемся сравнить все те значения y , которые мы только что вычислили, и увидим, какое из них является максимальным значением, которое соответствует нашему глобальному максимуму. Мы также увидим, какое из них является нашим минимальным значением, которое будет соответствовать нашему глобальному минимальному значению. Все остальные критические точки могут быть локальными максимумами или минимумами, но не всегда. 2 + 2 (0).Хорошо, это ноль. Итак, эта точка здесь, в конце, равна (0, 0). С правой стороны, при x = 2, f (x) = 0 также. Итак, это точка (2, 0). У меня есть три возможности для глобального и локального максимального и минимального значений. Мой глобальный максимум — это максимум из них. Вот тогда его рост равен 1, значит, в точке (1, 1). Есть два минимальных значения: (0, 0) и (2, 0). В обоих случаях он находится на уровне земли. Именно тогда его подстрелили и когда он упал на землю.2 — 12 (-2) + 1. Это всего лишь 21. Хорошо, у меня есть одно очко — (-2, 21). При x = 1, f (x) = -6. Вот в чем суть (1, -6). При x = 3, f (x) = 46, так что это точка (3, 46). Наконец, при x = -3, f (x) = 10. Вот в чем суть (-3, 10). Я собираюсь взглянуть на них и посмотреть, какой из них будет моим глобальным максимумом, а какой — моим глобальным минимумом.
f (x), y x y x y
Итоги урока
Итак, давайте рассмотрим. Экстремумы — это точки максимума и минимума для некоторого региона. Чтобы найти экстремальные значения, мы сначала хотим найти критические точки, то есть, где производная равна нулю. Затем мы собираемся найти значение нашей функции в этих критических точках, а также в конечных точках. Наконец, мы собираемся сравнить все эти значения, то есть значение нашей функции, в критических и конечных точках, чтобы увидеть, какое из них является глобальным максимумом, а какое — глобальным минимумом.
Максимум функции
Максимум функции
Лори Пирман
EMT 725
Задача: найти максимум f (x) = (1-x) (1 + x) (1 + x).
Один из подходов к этой проблеме — построить график функции на графическом калькуляторе.
или компьютерный инструмент построения графиков, чтобы получить оценку максимума.
Я использовал Algebra Xpresser для построения графика f (x).
Это часть полученного мной графика (показывает интервал от 0 до 1):
Из этого графика я могу оценить, что максимальное значение составляет около 1.18. Это
максимум происходит, когда x составляет около 0,33. Можно продолжать увеличивать «верхнюю часть»
холма »на рисунке, чтобы получить более точные оценки.
Исчисление можно использовать для более точного определения максимума f ‘(x).
Теперь нам нужно установить f ‘(x) = 0, чтобы получить критические значения.
f ‘(x) = (3x-1) (x + 1) = 0
Возможен относительный максимум (или минимум), когда x = 1/3 или x = -1.
Теперь мы можем использовать тест первой или второй производной, чтобы определить, где мы
иметь относительный максимум.
Примечание: -1 не входит в наш интервал от 0 до 1, но я все равно это проверю.
f » (x) = — 6x-2
Я буду использовать второй производный тест.
f » (-1) — положительное значение. Отсюда следует, что при x = -1 график f
(x) вогнута вверх.
Таким образом, f (-1) — относительный минимум.
f » (1/3) — отрицательное значение. Это означает, что при x = 1/3 график
вогнутая вниз.
f (1/3) — относительный максимум.
В интервале от 0 до 1 есть максимум, который равен f (1/3) = 1.185185
Теперь давайте воспользуемся таблицей, чтобы оценить максимум f (x) в
интервал от 0 до 1.
По моему графику Algebra Xpresser я мог сказать, что в интервале [0,1],
максимум имел место где-то между x = 0,2 и x = 0,5. Ниже представлен разворот
таблица листов со значениями x с шагом 0,01, которые находятся в этом интервале.
Если мне нужно еще лучшее приближение, я могу посмотреть на меньший интервал,
например [0,32,0,34].
(Я могу сказать из предыдущей таблицы, что этот интервал содержит
максимум.) Теперь, когда я сузил интервал, содержащий максимум,
легче смотреть на даже меньшие приращения,
таким образом получая более точное приближение к максимальному значению. (Видеть
ниже таблицы.)
Из этой таблицы видно, что максимум происходит примерно при
х = 0,333.
Можно продолжить этот процесс «приближения» по максимуму
значение, используя меньшие интервалы и меньшие приращения для каждой новой таблицы.
Чем больше раз это будет сделано, тем точнее будет максимальное значение.3> или = f (x)
1.185185> or = f (x) с равенством тогда и только тогда, когда (2-2x) = (1 + x).
Максимальное значение f (x) составляет около 1,185, и это происходит, когда x = 1/3.
Вернуться к Лори ЕМТ 725 Страница
Исчисление I — минимальные и максимальные значения
Показать общее уведомление
Показать мобильное уведомление
Показать все заметки Скрыть все заметки
Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST.Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.
Пол
6 мая 2021 г.
Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-3: Минимальные и максимальные значения
Многие из наших приложений в этой главе будут вращаться вокруг минимальных и максимальных значений функции. Хотя мы все можем визуализировать минимальные и максимальные значения функции, мы хотим быть более конкретными в нашей работе.В частности, мы хотим различать два типа минимальных и максимальных значений. Следующее определение дает типы минимальных и / или максимальных значений, которые мы будем рассматривать.
Определение
- Мы говорим, что \ (f \ left (x \ right) \) имеет абсолютный (или глобальный) максимум в \ (x = c \), если \ (f \ left (x \ right) \ le f \ left (c \ right) \) для каждого \ (x \) в области, над которой мы работаем.
- Мы говорим, что \ (f \ left (x \ right) \) имеет относительный (или локальный) максимум в \ (x = c \), если \ (f \ left (x \ right) \ le f \ left (c \ right) \) для каждого \ (x \) в некотором открытом интервале вокруг \ (x = c \).
- Мы говорим, что \ (f \ left (x \ right) \) имеет абсолютный (или глобальный) минимум в \ (x = c \), если \ (f \ left (x \ right) \ ge f \ left (c \ right) \) для каждого \ (x \) в области, над которой мы работаем.
- Мы говорим, что \ (f \ left (x \ right) \) имеет относительный (или локальный) минимум в \ (x = c \), если \ (f \ left (x \ right) \ ge f \ left (c \ right) \) для каждого \ (x \) в некотором открытом интервале вокруг \ (x = c \).
Обратите внимание, что когда мы говорим «открытый интервал вокруг \ (x = c \)», мы имеем в виду, что мы можем найти некоторый интервал \ (\ left ({a, b} \ right) \), не включая концы, такой, что \ (а <с <Ь \).Или, другими словами, \ (c \) будет содержаться где-то внутри интервала и не будет ни одной из конечных точек.
Кроме того, мы будем совместно называть минимальную и максимальную точки функции экстремумами функции. Таким образом, относительные экстремумы будут относиться к относительным минимумам и максимумам, а абсолютные экстремумы относятся к абсолютным минимумам и максимумам.
А теперь давайте немного поговорим о тонкой разнице между абсолютным и относительным в приведенном выше определении.
У нас будет абсолютный максимум (или минимум) в \ (x = c \) при условии, что \ (f \ left (c \ right) \) будет наибольшим (или наименьшим) значением, которое функция когда-либо будет принимать в области, которая мы работаем. Кроме того, когда мы говорим «домен, над которым мы работаем», это просто означает диапазон \ (x \), который мы выбрали для работы с данной проблемой. Могут быть и другие значения \ (x \), которые мы действительно можем подключить к функции, но по какой-то причине исключили их.
Относительный максимум или минимум немного отличается.Все, что требуется для точки, чтобы быть относительным максимумом или минимумом, — это чтобы эта точка была максимумом или минимумом в некотором интервале \ (x \) вокруг \ (x = c \). Могут быть большие или меньшие значения функции в каком-то другом месте, но относительно \ (x = c \) или локально для \ (x = c \), \ (f \ left (c \ right) \) равно больше или меньше, чем все другие значения функции, которые находятся рядом с ним.
Также обратите внимание, что для того, чтобы точка была относительным экстремумом, мы должны иметь возможность смотреть на значения функций по обе стороны от \ (x = c \), чтобы увидеть, действительно ли это максимум или минимум в этой точке.Это означает, что относительные экстремумы не возникают в конечных точках области. Они могут происходить только внутри домена.
По предыдущему пункту на самом деле ведутся споры. Некоторые люди действительно считают, что относительные экстремумы могут возникать в конечных точках области. Однако в этом классе мы будем использовать определение, согласно которому они не могут возникать в конечных точках домена. Это будет обсуждаться более подробно в конце раздела, когда мы позаботимся о соответствующем факте.
Обычно легче понять определения, бегло взглянув на график.
Для функции, показанной на этом графике, мы имеем относительные максимумы в \ (x = b \) и \ (x = d \). Обе эти точки являются относительными максимумами, поскольку они находятся внутри показанной области и являются самой большой точкой на графике в некотором интервале вокруг точки. У нас также есть относительный минимум в точке \ (x = c \), поскольку эта точка находится внутри области и является самой низкой точкой на графике в интервале вокруг нее.Крайняя правая конечная точка \ (x = e \) не будет относительным минимумом, поскольку это конечная точка.
Функция будет иметь абсолютный максимум в точке \ (x = d \) и абсолютный минимум в точке \ (x = a \). Эти две точки являются наибольшим и наименьшим из возможных для функции. Мы также можем заметить, что абсолютные экстремумы для функции будут возникать либо в конечных точках области, либо в относительных экстремумах. Мы будем использовать эту идею в следующих разделах, поэтому она важнее, чем может показаться в настоящее время.2} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{- 1,2} \ right] \]
Показать решение
Так как эту функцию достаточно просто построить график, давайте сделаем это. Однако нам нужен только график на интервале \ (\ left [{- 1,2} \ right] \). Вот график,
Обратите внимание, что мы использовали точки в конце графика, чтобы напомнить нам, что график заканчивается в этих точках.
Теперь мы можем идентифицировать экстремумы на графике.Похоже, у нас есть относительный и абсолютный минимум ноль в точке \ (x = 0 \) и абсолютный максимум четыре в точке \ (x = 2 \). Обратите внимание, что \ (x = — 1 \) не является относительным максимумом, поскольку он находится в конечной точке интервала.
Эта функция не имеет относительных максимумов.
Как мы видели в предыдущем примере, функции не обязательно должны иметь относительные экстремумы. Функция вполне может не иметь относительного максимума и / или относительного минимума.2} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{- 2,2} \ right] \]
Показать решение
Вот график этой функции.
В этом случае у нас все еще есть относительный и абсолютный минимум нуля в \ (x = 0 \). У нас также есть абсолютный максимум — четыре. Однако, в отличие от первого примера, это произойдет в двух точках: \ (x = — 2 \) и \ (x = 2 \).
Опять же, функция не имеет относительных максимумов.2} \]
Показать решение
В данном случае мы не указали домен, поэтому предполагаем, что мы возьмем максимально возможный домен. Для этой функции это означает все действительные числа. Вот график.
В этом случае график не перестает расти ни на одном конце, поэтому для этой функции нет никаких максимумов. Независимо от того, какую точку мы выберем на графике, с обеих сторон будут точки как больше, так и меньше, поэтому у нас не может быть никаких максимумов (любого рода, относительных или абсолютных) на графике.3} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{- 2,2} \ right] \]
Показать решение
Вот график этой функции.
Эта функция имеет абсолютный максимум восемь при \ (x = 2 \) и абсолютный минимум отрицательный восемь при \ (x = — 2 \). У этой функции нет относительных экстремумов.
Итак, функция не обязана иметь относительные экстремумы, как показано в этом примере.
Пример 5 Определите абсолютные и относительные экстремумы для следующей функции.3} \]
Показать решение
Опять же, на этот раз мы не ограничиваем домен, поэтому вот график.
В этом случае функция не имеет ни относительных, ни абсолютных экстремумов.
Как мы видели в предыдущем примере, функции не обязательно должны иметь какие-либо экстремумы, относительные или абсолютные.
Пример 6 Определите абсолютные и относительные экстремумы для следующей функции.\ [е \ влево (х \ вправо) = \ соз \ влево (х \ вправо) \]
Показать решение
Мы не ограничивали домен для этой функции. Вот график.
Косинус имеет экстремумы (относительные и абсолютные), которые встречаются во многих точках. Косинус имеет как относительный, так и абсолютный максимум 1 при
.
\ [x = \ ldots — 4 \ pi, \, — 2 \ pi, \, \, 0, \, \, 2 \ pi, \, \, 4 \ pi, \ ldots \]
Косинус также имеет как относительные, так и абсолютные минимумы -1 на уровне
.
\ [x = \ ldots — 3 \ pi, \, — \ pi, \, \, \ pi, \, \, 3 \ pi, \ ldots \]
Как показал этот пример, на самом деле график может иметь экстремумы, возникающие в большом количестве (в данном случае бесконечном) точек.
Мы проработали довольно много примеров, и мы можем использовать эти примеры, чтобы увидеть хороший факт об абсолютных экстремумах. Прежде всего, заметим, что все перечисленные выше функции были непрерывными. Затем обратите внимание, что каждый раз, когда мы ограничивали домен закрытым интервалом (, т.е. , интервал содержит его конечные точки), мы получали абсолютные максимумы и абсолютные минимумы. Наконец, только в одном из трех примеров, в которых мы не ограничивали область, мы получили как абсолютный максимум, так и абсолютный минимум.
Эти наблюдения приводят нас к следующей теореме.
Теорема об экстремальном значении
Предположим, что \ (f \ left (x \ right) \) непрерывно на интервале \ (\ left [{a, b} \ right] \), тогда есть два числа \ (a \ le c, d \ le b \), так что \ (f \ left (c \ right) \) является абсолютным максимумом для функции, а \ (f \ left (d \ right) \) является абсолютным минимумом для функции.
Итак, если у нас есть непрерывная функция на интервале \ (\ left [{a, b} \ right] \), то мы гарантированно имеем как абсолютный максимум, так и абсолютный минимум для функции где-то в этом интервале.Теорема не говорит нам, где они возникнут или будут ли они встречаться более одного раза, но, по крайней мере, она говорит нам, что они где-то существуют. Иногда все, что нам нужно знать, это то, что они действительно существуют.
Эта теорема ничего не говорит об абсолютных экстремумах, если мы не работаем с интервалом. Выше мы видели примеры функций, у которых были как абсолютные экстремумы, так и один абсолютный экстремум, и не было абсолютных экстремумов, когда мы не ограничивались интервалом. 2}}} \ hspace {0.25 дюймов} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{\ frac {1} {2}, 1} \ right] \]
функция теперь будет иметь оба абсолютных экстремума. Мы можем столкнуться с проблемами только в том случае, если интервал содержит точку разрыва. Если нет, то теорема верна.
Мы также должны указать, что тот факт, что функция не является непрерывной в точке, не означает, что у нее не будет обоих абсолютных экстремумов в интервале, содержащем эту точку. Ниже приведен график функции, которая не является непрерывной в точке данного интервала, но имеет оба абсолютных экстремума.
Этот график не является непрерывным в точке \ (x = c \), но он имеет как абсолютный максимум (\ (x = b \)), так и абсолютный минимум (\ (x = c \)). Также обратите внимание, что в этом случае один из абсолютных экстремумов произошел в точке разрыва, но это не обязательно. Абсолютный минимум мог просто быть в другой конечной точке или в какой-то другой точке внутри региона. Дело в том, что этот график не является непрерывным и все же имеет оба абсолютных экстремума
.
Смысл всего этого в том, что нам нужно быть осторожными и использовать теорему об экстремальном значении только при выполнении условий теоремы и не неправильно интерпретировать результаты, если условия не выполняются.
Чтобы использовать теорему об экстремальном значении, у нас должен быть интервал, который включает в себя его конечные точки, часто называемый закрытым интервалом, и функция должна быть непрерывной на этом интервале. Если у нас нет замкнутого интервала и / или функция не является непрерывной на интервале, тогда функция может иметь или не иметь абсолютных экстремумов.
Нам нужно обсудить одну последнюю тему в этом разделе, прежде чем перейти к первому важному применению производной, которое мы собираемся рассмотреть в этой главе.
Теорема Ферма
Если \ (f \ left (x \ right) \) имеет относительные экстремумы в \ (x = c \) и существует \ (f ‘\ left (c \ right) \), то \ (x = c \) есть критическая точка \ (f \ left (x \ right) \). 3} \ hпространство {0.2} \]
Ясно, что \ (x = 0 \) является критической точкой. Однако мы видели в предыдущем примере, что эта функция не имеет каких-либо относительных экстремумов. Таким образом, критические точки не обязательно должны быть относительными экстремумами.
Также заметьте, что эта теорема ничего не говорит об абсолютных экстремумах. Абсолютные экстремумы могут быть, а могут и не быть критической точкой.
Прежде чем мы покинем этот раздел, нам нужно обсудить пару вопросов.
Во-первых, теорема Ферма работает только для критических точек, в которых \ (f ‘\ left (c \ right) = 0 \).Однако это не означает, что относительных экстремумов не будет в критических точках, где не существует производной. Чтобы убедиться в этом, рассмотрим \ (f \ left (x \ right) = \ left | x \ right | \). Эта функция явно имеет относительный минимум в \ (x = 0 \), и все же в предыдущем разделе мы показали на примере, что \ (f ‘\ left (0 \ right) \) не существует.
Все это означает, что если мы хотим найти относительные экстремумы, все, что нам действительно нужно сделать, это посмотреть на критические точки, поскольку это места, где могут существовать относительные экстремумы.
Наконец, напомним, что в начале раздела мы заявили, что относительных экстремумов не будет в конечных точках рассматриваемого нами интервала. Причина этого в том, что если мы позволим там иметь место относительным экстремумам, это вполне может (и фактически в большинстве случаев) нарушить теорему Ферма. Нет причин ожидать, что конечные точки интервалов будут критическими точками любого рода. Следовательно, мы не допускаем существования относительных экстремумов на концах интервалов.
Бизнес-расчет
В теории и приложениях мы часто хотим максимизировать или минимизировать какое-то количество.Инженер может захотеть максимизировать скорость нового компьютера или минимизировать тепловыделение, производимое устройством. Производитель может захотеть максимизировать прибыль и долю рынка или минимизировать отходы. Учащийся может захотеть максимизировать оценку по математике или свести к минимуму часы обучения, необходимые для получения определенной оценки.
Без исчисления мы знаем только, как найти оптимальные точки на нескольких конкретных примерах (например, мы знаем, как найти вершину параболы). Но что, если нам нужно оптимизировать незнакомую функцию?
Лучший способ без исчисления — это изучить график функции, возможно, используя технологию.Но наш вид зависит от выбранного окна просмотра — мы можем упустить что-то важное. Кроме того, таким образом мы, вероятно, получим только приблизительное значение. (В некоторых случаях этого будет достаточно.)
Calculus предоставляет способы резко сократить количество точек, которые нам нужно исследовать, чтобы найти точное местоположение максимумов и минимумов, и в то же время гарантировать, что мы не пропустили ничего важного.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, который поддерживает видео HTML5
Локальные максимумы и минимумы
Прежде чем мы исследуем, как исчисление может помочь нам найти максимумы и минимумы, нам нужно определить концепции, которые мы будем развивать и использовать.
Определения (локальные максимумы и минимумы)
\ (f (x) \) имеет локальный максимум в \ (x = a \), если \ (f (a) \ geq f (x) \) для всех \ (x \) рядом с \ (a \ ).
\ (f (x) \) имеет локальный минимум в \ (x = a \), если \ (f (a) \ leq f (x) \) для всех \ (x \) рядом с \ (a \ ).
\ (f (x) \) имеет локальный экстремум в \ (x = a \), если \ (f (a) \) является локальным максимумом или минимумом .
Множественное число из них — максимумы и минимумы.Мы часто просто говорим «макс» или «мин»; это экономит много слогов.
В некоторых книгах написано «родственник» вместо «местный».
Процесс поиска максимумов или минимумов называется оптимизацией .
Точка — это локальный максимум (или минимум), если он выше (ниже) всех соседних точек . Эти точки исходят из формы графика.
Определения (глобальные максимумы и минимумы)
\ (f (x) \) имеет глобальный максимум в \ (x = a \), если \ (f (a) \ geq f (x) \) для всех \ (x \) в области \ (е (х) \).
\ (f (x) \) имеет глобальный минимум в \ (x = a \), если \ (f (a) \ leq f (x) \) для всех \ (x \) в области \ (е (х) \).
\ (f (x) \) имеет глобальный экстремум в \ (x = a \), если \ (f (a) \) является глобальным максимумом или минимумом .
В некоторых книгах говорится «абсолютный» вместо «глобальный».
Точка — это глобальный максимум (или минимум), если он выше (ниже) каждой точки на графике. Эти точки исходят из формы графика и окна , через которое мы просматриваем график.
Обозначены локальные и глобальные крайние значения функции на Рисунке 1. Вы должны заметить, что каждая глобальная крайность также является локальной, но есть локальные крайности, которые не являются глобальными крайностями.
Рисунок 1
Если \ (h (x) \) — высота земли над уровнем моря в точке \ (x \), то глобальный максимум \ (h \) равен \ (h \) (вершина горы. Эверест) = 29 028 футов. Локальный максимум \ (h \) для Соединенных Штатов составляет \ (h \) (вершина горы Мак-Кинли) = 20 320 футов.Локальный минимум \ (h \) для Соединенных Штатов составляет \ (h \) (Долина Смерти) = -282 фута.
Пример 1
В таблице показано годовое количество зачисленных в крупный университет. В какие годы была максимальная или минимальная численность учащихся по математике? Каковы были максимальные и минимальные зачисления на математический факультет в мире?
| Год | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Запись | 1257 | 1324 | 1378 | 1336 | 1389 | 1450 | 1523 | 1582 | 1567 | 1545 | 1571 |
В 2002 и 2007 гг. Были локальные максимумы; в 2007 году мировой максимум составлял 1582 студента.В 2003 и 2009 гг. Были локальные минимумы; в 2000 г. глобальный минимум составлял 1257 студентов. Мы предпочитаем не думать о 2000 г. как о локальном минимуме или о 2010 г. как о локальном максимуме; однако некоторые книги будут включать конечные точки. Нам разрешено иметь глобальный максимум или глобальный минимум в конечной точке.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, который поддерживает видео HTML5
Нахождение максимумов и минимумов функции
Как должна выглядеть касательная линия при локальном максимуме или минимуме? Посмотрите на эти два графика еще раз — вы увидите, что во всех крайних точках касательная линия горизонтальна (так что \ (f ‘= 0 \)).На синем графике есть один куспид — там касательная вертикальна (поэтому \ (f ‘\) не определено).
Это дает нам ключ к пониманию того, как находить экстремальные значения.
Определения
Критическое число для функции \ (f \) — это значение \ (x = a \) в области \ (f \), где либо \ (f ‘(a) = 0 \), либо \ (f ‘(a) \) не определено.
Критическая точка для функции f — это точка (a, f (a)), где a — критическое число f.2 — 4x + 3) = 3 (x — 1) (x — 3) \] Итак, \ (f ‘(x) = 0 \) при \ (x = 1 \) и \ (x = 3 \) (и никаких других значений \ (x \)). Нет мест, где \ (f ‘\) не определено.
Критические числа: \ (x = 1 \) и \ (x = 3 \). Итак, критические точки — это (1, 6) и (3, 2).
Это единственные возможные места локальных крайностей \ (f \). Мы еще не обсуждали, как определить, является ли какая-либо из этих точек на самом деле локальной крайностью \ (f \) или какой она может быть. Но мы можем быть уверены, что никакая другая точка не является локальной крайностью.3 \) не имеет локальных крайностей.
Помните этот пример! Недостаточно найти критические точки — мы можем только сказать, что \ (f \) может иметь локальный экстремум в критических точках .
Первые и вторые производные тесты
Эта критическая точка является максимумом или минимумом (или ни тем, ни другим)?
После того, как мы нашли критические точки \ (f \), у нас все еще есть проблема определения, являются ли эти точки максимумом, минимумом или ни одним из них.
Все графики на рисунке ниже имеют критическую точку в (2, 3). Из графиков видно, что точка (2,3) является локальным максимумом в (a) и (d), (2,3) является локальным минимумом в (b) и (e), и (2,3) ) не является локальным экстремумом в (c) и (f).
Критические числа дают только возможных крайних точек, а некоторые критические числа не являются точками крайностей. Критические числа — это кандидатов для положений максимумов и минимумов.
\ (f ‘\) и экстремальные значения \ (f \)
Здесь показаны четыре возможных формы графиков — на каждом графике точка, отмеченная стрелкой, является критической точкой, где \ (f ‘(x) = 0 \). Что происходит с производной вблизи критической точки?
При локальном максимуме, например на графике слева, функция увеличивается слева от локального максимума, а затем уменьшается справа. Производная сначала положительна, затем отрицательна при локальном максимуме. При локальном min функция уменьшается влево и увеличивается вправо, поэтому производная сначала отрицательна, а затем положительна.Когда нет локального экстремума, функция продолжает увеличиваться (или уменьшаться) сразу после критической точки — производная не меняет знак.
Первый производный тест на экстремумы
Найдите критические точки f.
Для каждого критического числа c проверьте знак f ’слева и справа от c. Что происходит со знаком, когда вы двигаетесь слева направо?
- Если \ (f ‘(x) \) изменяется с положительного на отрицательный при \ (x = c \), то \ (f \) имеет локальный максимум при \ ((c, f (c) ) \).
- Если \ (f ‘(x) \) изменяется с отрицательного на положительный при \ (x = c \), то \ (f \) имеет локальный минимум при \ ((c, f (c)) \).
- Если \ (f ‘(x) \) не меняет знак в \ (x = c \), то \ ((c, f (c)) \) не является ни ни локальным максимумом, ни локальным минимумом .
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, который поддерживает видео HTML5
Пример 4
Найдите критические точки \ (f (x) = x ^ 3 — 6x ^ 2 + 9x + 2 \) и классифицируйте их как локальный максимум, локальный минимум или ни то, ни другое.2 — 4x + 3) = 3 (x — 1) (x — 3) \). Здесь проще всего работать с факторизованной формой, так что давайте воспользуемся ею.
В (1, 6) мы могли бы выбрать число немного меньше 1, чтобы подставить его в формулу для \ (f ‘\) — возможно, используйте \ (x = 0 \) или \ (x = 0.9 \). Тогда мы могли бы изучить его знак. Но нас не волнует числовое значение, все, что нас интересует, — это его знак. И для этого нам не нужно ничего подключать:
- Если \ (x \) немного меньше 1, то \ (x-1 \) отрицательно, а \ (x-3 \) отрицательно.Итак, \ (f ‘= 3 (x — 1) (x — 3) \) будет pos (neg) (neg) = положительным.
- Для \ (x \) немного больше 1, мы можем оценить \ (f ‘\) с числом больше 1 (но меньше 3, мы не хотим проходить следующую критическую точку!) — возможно \ (х = 2 \). Или мы можем сделать быстрый аргумент со знаком, как то, что мы сделали выше: для \ (x \) немного больше 1, \ (f ‘= 3 (x — 1) (x — 3) \) будет pos (pos) (neg) = отрицательный.
Итак, \ (f ‘\) изменяется с положительного на отрицательный, что означает, что существует локальный максимум в (1, 6).
В качестве другого подхода мы могли бы провести числовую линию и отметить критические числа:
Мы уже знаем, что производная равна нулю или не определена в критических числах. На каждом интервале между этими значениями производная останется с тем же знаком. Чтобы определить знак, мы могли бы выбрать тестовое значение в каждом интервале и оценить производную в этих точках (или использовать знаковый подход, использованный выше).
At (3, 2) \ (f ‘\) изменяется с отрицательного на положительный, поэтому существует локальный min в (3, 2).Это подтверждает то, что мы видели ранее на графике.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, который поддерживает видео HTML5
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, который поддерживает видео HTML5
\ (f » \) и экстремальные значения \ (f \)
Вогнутость функции также может помочь нам определить, является ли критическая точка максимумом или минимумом или нет.Например, если точка находится внизу функции вогнутого вверх, то точка является минимумом.
Тест второй производной на экстремумы
Найдите все критические точки \ (f \). Для тех критических точек, где \ (f ‘(c) = 0 \), найдите \ (f’ ‘(c) \).
- Если \ (f » (c) \ lt 0 \) (отрицательный), то \ (f \) вогнутая вниз и имеет локальный максимум в точке \ (x = c \).
- Если \ (f » (c) \ gt 0 \) (положительный), то \ (f \) вогнутая вверх и имеет локальный минимум в точке \ (x = c \).2 — 30х + 24 \\
f » (x) = & 12x — 30
\ конец {выравнивание *} \]Затем нам просто нужно вычислить \ (f » \) для каждого критического числа:
\ (x = 1 \): \ (f » (1) = 12 (1) -30 \ lt 0 \), поэтому существует локальный максимум в \ (x = 1 \).
\ (x = 4 \): \ (f » (4) = 12 (4) -30 \ gt 0 \), поэтому существует локальный минимум в \ (x = 4 \).
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, который поддерживает видео HTML5
Многим студентам нравится Второй производный тест.Второй производный тест часто бывает проще использовать, чем первый производный тест. Вам нужно только найти знак одного числа для каждого критического числа, а не двух. И если ваша функция является полиномом, ее вторая производная, вероятно, будет более простой функцией, чем производная.
Однако, если вам нужно правило продукта, правило частного или цепное правило, чтобы найти первую производную, поиск второй производной может потребовать много работы. Кроме того, даже если вторая производная проста, проверка второй производной не всегда дает ответ.Первый производный тест всегда даст вам ответ.
Используйте любой тест, который хотите. Но помните — вы должны провести некоторый тест, чтобы убедиться, что ваша критическая точка на самом деле является локальным максимумом или минимумом.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, который поддерживает видео HTML5
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, который поддерживает видео HTML5
Глобальные максимумы и минимумы
В приложениях мы часто хотим найти глобальную крайность; недостаточно знать, что критическая точка является локальной крайностью.
Например, если мы хотим получить наибольшую прибыль, мы хотим получить наибольшую прибыль из всех. Как мы находим глобальные максимумы и минимумы?
Есть еще несколько вещей, о которых стоит подумать.
Крайние точки конечной точки
Локальные экстремумы функции возникают в критических точках — это точки в функции, которые мы можем найти, подумав о форме (и используя производную, чтобы помочь нам). Но если мы смотрим на функцию на закрытом интервале, конечные точки могут быть крайними.Эти крайние значения конечных точек не связаны с формой функции; они связаны с интервалом, окном, через которое мы просматриваем функцию.
На графике выше видно, что есть три критических точки — одна локальная минимальная, одна локальная максимальная и одна, которая не является ни одной из них. Но глобальный максимум, самая высокая точка из всех, находится в левой конечной точке. Глобальный минимум, самая низкая точка из всех, находится в правой конечной точке.
Как определить, являются ли конечные точки максимальными или минимальными? Это проще, чем вы ожидали — просто подключите конечные точки вместе со всеми критическими числами и сравните \ (y \) — значения.2 — 6x — 9 = 3 (x + 1) (x — 3) \). Нам нужно найти критические точки, и нам нужно проверить конечные точки.
\ (f ‘(x) = 3 (x + 1) (x — 3) = 0 \), когда \ (x = -1 \) и \ (x = 3 \). Конечные точки интервала — \ (x = -2 \) и \ (x = 6 \).
Теперь мы просто сравниваем значения \ (f \) при этих четырех значениях \ (x \):
\ (х \) \ (е (х) \) -2 3 -1 10 3 -22 6 59 Глобальный минимум \ (f \) на \ ([-2, 6] \) равен -22, когда \ (x = 3 \), и глобальный максимум \ (f \) на \ ([ -2, 6] \) равно 59, когда \ (x = 6 \).
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, который поддерживает видео HTML5
Если есть только одна критическая точка
Если функция имеет только одну критическую точку и это локальный максимум (или минимум), тогда это должен быть глобальный максимум (или минимум). Чтобы убедиться в этом, подумайте о геометрии. Посмотрите на график слева — есть локальный максимум, и график идет вниз по обе стороны от критической точки. Допустим, была какая-то другая точка, которая была выше — тогда график должен был бы развернуться.Но этот поворотный момент стал бы еще одним критическим моментом. Если есть только одна критическая точка, график никогда не развернется.
Если сомневаетесь, нарисуйте это и посмотрите.
Если вы пытаетесь найти глобальный максимум или минимум на открытом интервале (или на всей реальной линии), и имеется более одной критической точки, то вам нужно посмотреть на график, чтобы решить, существует ли глобальный максимум или мин. Убедитесь, что все ваши критические точки показаны на вашем графике, и что вы график за ними — это скажет вам то, что вы хотите знать.2 + 9х + 2 \).
Ранее мы обнаружили, что (1, 6) — это локальный максимум, а (3, 2) — локальный минимум. Это не замкнутый интервал, и есть две критические точки, поэтому мы должны обратиться к графику функции, чтобы найти глобальные max и min.
График \ (f \) показывает, что точки слева от \ (x = 4 \) имеют \ (y \) — значения больше 6, поэтому (1, 6) не является глобальным максимумом. Аналогично, если \ (x \) отрицательно, \ (y \) меньше 2, поэтому (3, 2) не является глобальным min. Конечных точек нет, поэтому мы исчерпали все возможности.Эта функция не имеет глобального максимума или минимума.
В поисках глобальных крайностей
Единственные места, где функция может иметь глобальный экстремум, — это критические точки или конечные точки.
- Если функция имеет только одну критическую точку, и это локальный экстремум, то это также глобальный экстремум.
- Если есть конечные точки, найдите глобальные экстремумы, сравнивая \ (y \) — значения во всех критических точках и на конечных точках.
- В случае сомнений нарисуйте функцию, чтобы быть уверенным.(Однако, если проблема явно не говорит вам об обратном, недостаточно, чтобы просто использовать график для получения ответа.