Чем отличается сочетание от размещения

Б. Паскаль  и  Ферма, изучая теорию азартных игр, были основателями нового раздела математики, называемого комбинаторикой. В ней изучается, какое количество комбинаций заданного типа можно составить из предложенных элементов.

Определение

Сочетания — соединения, каждое из которых составлено из  k1 элементов, выбранных из n1 различных элементов, состав которых  отличается  хотя бы на один элемент.

Размещения — cоединения, каждое из которых составлено из  k1 элементов, взятых из n1 различных элементов, у которых состав элементов или их порядок отличают их друг от друга.

к содержанию ↑

Сравнение

Сочетания — соединения, содержащие k1 элементов, выбранных из n1 различных элементов.  Сочетания отличаются друг от друга хотя бы на один элемент. Порядок следования элементов не важен. Число сочетаний равно n1 элементов.

Наборы, которых отличает только порядок следования элементов, но не состав, считаются одинаковыми. Отличие сочетаний друг от друга составом, но не порядком следования элементов.

Пример. Сочетание — нужно выбрать 3 предмета из 6. Есть предметы с номерами от 1 до 6. Выбираем из этого набора предметы в любом порядке с номерами  1, 4 и 6. Это и есть сочетание.

Размещениями называют соединения, каждое из которых содержит k1  элементов, взятых из n1    различных элементов, которых отличает друг от друга порядок или состав элементов. В размещениях не должно быть дубликатов.

Размещения отличают друг от друга состав элементов или их порядок.  Из n1 элементов по к1 (к1 < n1). По-другому, из n1 элементов выбирают к1 элементов и размещают их на А позиций. Число размещений из n1 элементов по к1 обозначают символом Ак1n1 (читается: А из n1 по к1).

При этом две расстановки будут считаться разными, если у них есть отличие друг от друга хотя бы на один элемент. Или они состоят из одних и тех же предметов, но они расположены в разном порядке. Например, есть три элемента, размещаем их в определенном порядке: 15, 11, 12 или 11, 12, 15 или 12, 15,11. Это и есть размещение — различные комбинации с одними и теми же элементами. Число размещений больше числа сочетаний.

к содержанию ↑

Выводы TheDifference.ru

1. Сочетания отличаются от размещений только тем, что они не зависят от порядка следования элементов.

Формулы комбинаторики с примерами. Основные формулы комбинаторики: сочетания, размещения, перестановки

Учитесь решать задачи по комбинаторике? На самом начальном этапе нужно изучить основные формулы комбинаторики: сочетания, размещения, перестановки (смотрите подробнее ниже) и научиться их применять для решения задач.

Как выбрать формулу комбинаторики?

Мы подготовили для вас наглядную схему с примерами решений по каждой формуле комбинаторики:

• алгоритм выбора формулы (сочетания, перестановки, размещения с повторениями и без),
• рекомендации по изучению комбинаторики,
• 6 задач с решениями и комментариями на каждую формулу.

Нужна помощь в решении задач по комбинаторике?

Перестановки

Пусть имеется $n$ различных объектов.
Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

$$P_n=n!=1\cdot 2\cdot 3 \cdot … \cdot (n-1) \cdot n$$

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.

Пример всех перестановок из $n=3$ объектов (различных фигур) — на картинке справа. Согласно формуле, их должно быть ровно $P_3=3!=1\cdot 2\cdot 3 =6$, так и получается.

С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов — уже 3628800 (больше 3 миллионов!). m \cdot P_m.$$

Удобный и бесплатный онлайн калькулятор сочетаний.

Решебник задач по комбинаторике

Изучаем комбинаторику: полезные ссылки

Комбинаторика. Размещения, перестановки, сочетания | Математика, которая мне нравится

В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Рождение комбинаторики как раздела математики связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.

Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну
из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.

Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.

Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.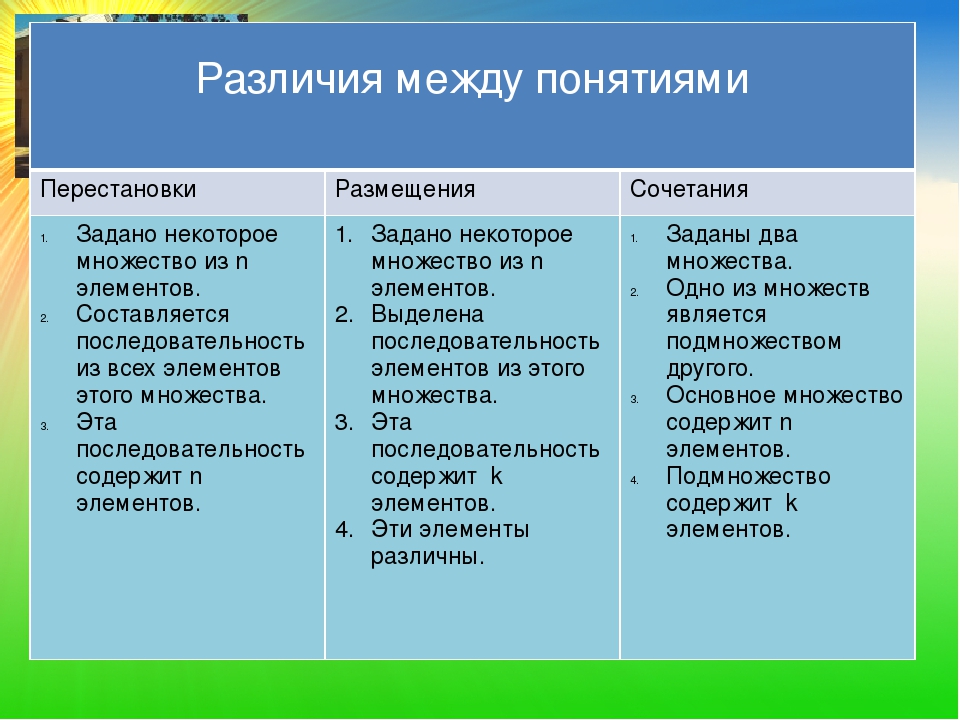

В дальнейшем важную роль будет играть следующая

Лемма. Пусть в множестве элементов, а в множестве — элементов. Тогда число всех различных пар , где будет равно .

Доказательство. Действительно, с одним элементом из множества мы можем составить таких различных пар, а всего в множестве элементов.

Размещения, перестановки, сочетания

Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .

Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по > элементов и отличаются либо самими элементами, либо порядком элементов.

Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .

Теорема. Число размещений множества из элементов по элементов равно

Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:

Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?

Решение. Искомое число трехполосных флагов:

Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.

Так, все различные перестановки множества из трех элементов — это

Очевидно, перестановки можно считать частным случаем размещений при >.

Число всех перестановок из элементов обозначается (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле

Пример. Сколькими способами можно расставить ладей на шахматной доске так, чтобы они не били друг друга?

Решение. Искомое число расстановки ладей

по определению!

Определение. Сочетаниями из различных элементов по элементов называются комбинации, которые составлены из данных элементов по элементов и отличаются хотя бы одним элементом (иначе говоря, -элементные подмножества данного множества из элементов).

Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из элементов по элементов в каждом обозначается (от начальной буквы французского слова “combinasion”, что значит “сочетание”). k

1. .

Действительно, каждому -элементному подмножеству данного -элементного множества соответствует одно и только одно -элементное подмножество того же множества.

2. .

Действительно, мы можем выбирать подмножества из элементов следующим образом: фиксируем один элемент; число -элементных подмножеств, содержащих этот элемент, равно ; число -элементных подмножеств, не содержащих этот элемент, равно .

Треугольник Паскаля

В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа .

.

Теорема.

Доказательство. Рассмотрим множество из элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из элементов данного
множества, в каждой из которых никакой элемент не встречается дважды?

1 способ. Выбираем первый член последовательности, затем второй, третий и т.д. член

2 способ. Выберем сначала элементов из данного множества, а затем расположим их в некотором порядке

Домножим числитель и знаменатель этой дроби на :

Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?

Искомое число способов

Задачи.

1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?
2. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков?
3. Сколько есть шестизначных чисел, делящихся на 5?
4. Сколькими способами можно разложить 7 разных монет в три кармана?
5. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?
6. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
7. Сколько есть пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?
8. На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
9. Сколькими способами можно расставить в ряд числа так, чтобы числа стояли рядом и притом шли в порядке возрастания?
10. Сколько пятизначных чисел можно составить из цифр , если каждую цифру можно использовать только один раз?
11. Из слова РОТ перестановкой букв можно получить еще такие слова: ТОР, ОРТ, ОТР, ТРО, РТО. Их называют анаграммами. Сколько анаграмм можно составить из слова ЛОГАРИФМ?
12. Назовем разбиением натурального числа представление его в виде суммы натуральных чисел. Вот, например, все разбиения числа :

Разбиения считаются разными, если они отличаются либо числами, либо порядком слагаемых.

Сколько существует различных разбиений числа на слагаемых?
13. Сколько существует трехзначных чисел с невозрастающим порядком цифр?
14. Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
15. Сколькими способами можно рассадить в ряд 17 человек, чтобы и оказались рядом?
16. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?
17. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

     При решении задач по комбинаторике используют следующие важные понятия

Размещения

      Рассмотрим следующую задачу.

      Задача.   9   карточек пронумерованы числами   1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 .   Из этих карточек четыре наугад взятых карточки выкладываем в ряд. Сколько при этом можно получить различных четырехзначных чисел?

      Решение.Сначала слева направо пронумеруем места в ряду, куда выкладываем карточки: первое место, второе, третье, четвертое.

      На первое место можно положить одну из   9   карточек. Для этого есть   9   способов. В каждом из этих   9   способов на второе место можно положить одну из оставшихся   8   карточек. Таким образом, существует

способа, чтобы положить карточки на первое и второе места. В каждом из этих   72   способов на третье место можно положить одну из оставшихся   7   карточек. Следовательно, существует

способа, чтобы положить карточки на первое, второе и третье места. В каждом из этих   504   способов на четвертое место можно положить одну из оставшихся   6   карточек. Отсюда вытекает, что существует

различных способа, чтобы выложить в ряд   4   карточки из набора, состоящего из   9   пронумерованных карточек. Таким образом, при выкладывании карточек можно получить   3024   различных четырехзначных числа.

      Ответ:   3024.

      При решении задачи мы провели подсчет числа способов раскладывания карточек, который является частным случаем общего метода подсчета числа размещений и заключается в следующем.

      Определение 1. Рассмотрим множество, содержащее   n   элементов, и все его упорядоченные подмножества, содержащие   k   элементов. Каждое из этих подмножеств называют размещением из   n   элементов по   k   элементов.

      Если обозначить символом  число размещений из   n   элементов по   k   элементов, то будет справедлива формула:

      В соответствии с определением факториала, формулу (1) можно также записать в виде:

      В задаче множеством из   n   элементов является исходный набор из   9   пронумерованных карточек, а упорядоченным подмножеством из   k   элементов –   4   карточки, выложенные в ряд.

      Таким образом, при решении задачи мы на частном примере подсчитали, чему равно число размещений из   9   элементов по   4   элемента, т.е. число

      В соответствии с формулой (1),

что и было получено в задаче.

      Замечание 1.  Введенные в данном разделе размещения также называют размещениями без повторений.

      Замечание 2. Из формул для числа перестановок и числа размещений вытекает формула

смысл которой заключается в следующем.

      Утверждение. Размещение из   n   элементов по   n   элементов является перестановкой из   n   элементов.

Сочетания

      Определение 2. Рассмотрим множество, состоящее из   n   элементов. Каждое его подмножество, содержащее   k   элементов, называют сочетанием из   n   элементов по   k   элементов.

      Число сочетаний из   n   элементов по   k   элементов обозначается символом

      Замечание 3. Важно отметить, что, в отличие от определения размещений, рассмотренные в определении сочетаний подмножества, содержащие   k   элементов, не являются упорядоченными. Поэтому, если в каждом подмножестве, содержащем   k   элементов (из определения 2), совершить всевозможные перестановки, количество которых равно   k ! ,   то мы получим все размещения.

      Таким образом, справедлива формула:

      Следовательно,

откуда вытекает формула

      Теперь рассмотрим несколько примеров подсчета числа сочетаний, которые непосредственно вытекают из формулы (2):

      В заключение приведем часто используемое равенство, также непосредственно вытекающее из формулы (2):

      Замечание 4. С разделом справочника «Сочетания» близко связан раздел «Бином Ньютона», где приведены и доказаны свойства чисел сочетаний.

   С понятиями факториала числа   n   и перестановок из   n   элементов можно познакомиться в разделе «Комбинаторика: факториалы и перестановки» нашего справочника.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Выборки элементов без повторений

Рассмотрим сначала некоторые общие термины.

• Пусть некоторая совокупность содержит n элементов, из которых выбирают k элементов. Каждый такой набор будем называть выборкой объема k из n элементов.
• Будем различать выборки с возвращением и без возвращения. Пусть имеется совокупность n пронумерованных элементов:
  • если отобранный элемент после выбора не возвращается в исходную совокупность и не может повторяться в данной выборке больше одного раза, то такая выборка называется выборкой без возвращения или без повторения;
  • если отобранный элемент после фиксации номера снова возвращается в исходную совокупность и, таким образом, может вновь оказаться в данной выборке, то говорят о выборке с возвращением или с повторением.
• Выборка называется упорядоченной, если порядок следования элементов в ней задан. Если две упорядоченные выборки отличаются только порядком следования элементов, то они считаются разными (например: 12 и 21).
• Выборка называется неупорядоченной, если порядок элементов в ней не имеет значения (т. е. 12 и 21 неразличимы).

Размещения без повторений.

Размещениями без повторений называются упорядоченные выборки, содержащие k различных элементов из данных n элементов.

Обратим внимание на следующие важные положения:

1. Любой элемент может оказаться на любом из k мест, но использоваться может в выборке только один раз.
2. Порядок элементов в выборке важен.

Формула для определения числа размещений без повторений:

Задача. Дана последовательность символов А, Б, С. Сколько вариантов кода, состоящего из двух разных символов, можно составить из заданной последовательности?

Решение.По условию код состоит «из двух разных символов», при этом коды АБ и БА – не одинаковые, поэтому, выборки – размещения без повторений.
Выборка осуществляется из 3 элементов по 2. Значит, n = 3, k = 2.

Действительно, комбинаций, удовлетворяющих условию, всего шесть: {АБ, АС, БА, БС, СА, СБ}

Перестановки без повторений.

Нетрудно заметить, что размещения, в которые входят все n разных элементов заданного множества (т. е. k = n), будут отличаться только порядком следования входящих элементов. Такие размещения называют перестановками.

Перестановками без повторений называются всевозможные упорядоченные выборки, составленные из всех данных n элементов.

Формула для определения числа перестановок без повторений
P_n = n! = n * (n − 1) * (n − 2) *…* 2 * 1

Задача. Сколько вариантов кода длиной 3 символа можно составить из трех букв А, Б, С, если каждая буква входит в последовательность не более одного раза?

Решение. Так как «каждая буква входит в последовательность не более одного раза», то выборки – перестановки без повторений.
P_n = 3! = 3 * 2 * 1 = 6 {АБC, АCБ, БАС, БСА, САБ, СБА}

Сочетания без повторений.

Сочетаниями без повторений называются неупорядоченные выборки, содержащие k различных элементов из данных n элементов.

Отметим, что

1. …«выборки неупорядоченные», т.е. выборки AB и ВА – это одно и тоже сочетание.
2. Любой элемент может оказаться на любом из k мест, но использоваться может в выборке только один раз.

Формула для определения числа сочетаний без повторений:

Задача. Из 4-х кандидатов происходят выборы участников конференции. Сколько существует вариантов выбора делегации?

Решение. Очевидно, один и тот же кандидат в данную выборку может быть избран только один раз. При этом набор А, Б и Б, А – это одни те же участники. Поэтому выборки есть сочетания без повторений.

Воспользуемся формулой для расчета числа различных сочетаний без повторений:

Мастер-класс по теме «Элементы комбинаторики: перестановки, сочетания и размещения»

Элементы комбинаторики: перестановки,
сочетания, размещения.

“Число, положение и комбинация – три

взаимно пересекающиеся, но различные

сферы мысли, к которым можно

отнести все математические идеи”.

Джозеф Сильвестр (1844 г.)

Цели занятия.

Образовательные:

• познакомить студентов с новым разделом
  математики: «Комбинаторика», с его историей,
  основными понятиями и задачами, использованием в
  практических целях и в жизни человека;
• способствовать созданию учебного проекта как
  показатель качественного изучения темы занятия.

Развивающие:

• развивать аналитические способности,
  логическое мышление,
• индивидуальные способности каждого студента,
  создавая комфортную психологическую обстановку
  для каждого студента при обучении и создании
  проекта.

Воспитывающая:

• формировать активность личности студента,
  умение работать в группе, отвечать за свои
  поступки.

Оборудование: компьютеры, проектор, экран,
презентация, электронные и на бумажных носителях
тесты, задачи “Судоку”, кубики Рубика, папки для
ВСР (внеаудиторная самостоятельная работа),
рабочие тетради, чистые ватманы, калькуляторы,
цветная бумага, клей, ножницы, фломастеры.

Ход занятия

I. Организационный момент

Перекличка

Сообщение целей и задач занятия: В связи с тем,
что по дисциплине “Математика” на 2 курсе
специальности “Технология деревообработки” на
тему “Основные понятия комбинаторика:
перестановки, размещения, сочетания” отводится 2
часа, а рассмотреть нужно много материала, решать
задачи, создать проект, вам было выдано задание
на внеаудиторную самостоятельную работу
следующее: в литературе по истории математики, в
энциклопедиях, в учебниках и в интернете найти
материал о разделе математики, имеющем звучное
название “комбинаторика”. Слайды № 1–2. Презентация

В календарно-тематическом плане по дисциплине
“Математика” на 2 курсе специальности
“Технология деревообработки” на тему
“Основные понятия комбинаторика: перестановки,
размещения, сочетания” отводится 2 часа. Изучить
теоретический материал, решить задачи разных
видов за такой временной промежуток невозможно.
Для достижения глубокого изучения материала
было выдано задание на внеаудиторную
самостоятельную работу: в литературе по истории
математики, в энциклопедиях, в учебниках и в
интернете найти материал о разделе математики,
имеющем звучное название “комбинаторика”. Слайды
№ 1–2.

Вопросов для внеаудиторной самостоятельной
работы выделено было три:

1. Определения комбинаторики.
2. Ученые – математики — первооткрыватели этого
   раздела.
3. Применение комбинаторики в современной жизни.

Запись даты, темы урока.

II. Работа над темой занятия

Вступление:

Из глубокой древности до современного
человечества дошли сведения о том, что уже тогда
люди занимались выбором объектов и расположения
их в том или ином порядке и увлекались
составлением различных комбинаций. Так,
например, в Древнем Китае увлекались
составлением квадратов, в которых заданные числа
располагали так, что их сумма по всем
горизонталям, вертикалям и главным диагоналям
была одной и той же (современная игра – задача
“Судоку”). Такие задачи вы могли встречать в
журналах и газетах. В частности, наша Мариинская
газета “Вперед” довольно часто предлагает
читателям такие задачи. В Древней Греции
подобные задачи возникали в связи c такими
играми, как шашки, шахматы, домино, карты и т.д.

Комбинаторика ставится самостоятельным
разделом математики, по сути – самостоятельной
наукой лишь во второй половине XVII века, — в период,
когда возникла теория вероятностей.

Таким образом, — комбинаторика – это
самостоятельный раздел математики, в котором
изучаются вопросы о том, сколько различных
комбинаций, подчинённых тем или условиям, можно
составить из заданных объектов.

Комбинаторика – самостоятельная ветвь
математической науки. Cлайд № 3

Термин “КОМБИНАТОРИКА” происходит от
латинского слова “combina”, что в переводе на
русский означает – “сочетать”, “соединять” — слайд
№ 4.

Как трактует это слово Большой
Энциклопедический Словарь?

Комбинаторика – это раздел математики, в
котором изучаются простейшие “соединения”:
перестановки, размещения, сочетания. Этот раздел
иначе называют “комбинаторный анализ”.

Сегодня мы будем рассматривать перестановки,
размещения, сочетания, как соединения, как
комбинаторные конфигурации.

Разделы комбинаторики: перечислительная,
структурная, вероятностная, топологическая –
слайд № 5.

Давайте вспомним известное вам из детства
сказание о том, как богатырь или другой добрый
молодец, доехав до развилки трех дорог, читает на
камне: “Вперед поедешь – голову сложишь, направо
поедешь – коня потеряешь, налево поедешь – меча
лишишься”. А дальше уже говорится, как он выходит
из того положения, в которое попал в результате
выбора. Но выбирать разные пути или варианты
приходится и современному человеку. Эти пути и
варианты складываются в самые разнообразные
комбинации. И целый раздел математики, именуемый
КОМБИНАТОРИКОЙ, занят поисками ответов на
вопросы: сколько всего есть комбинаций в том или
ином случае, как из всех этих комбинаций выбрать
наилучшую – слайд № 6.

Итак, комбинаторика – раздел математики, в
котором изучается, сколько различных комбинаций,
подчиненных тем или иным условиям, можно
составить из заданных объектов.

Задачей комбинаторики можно считать задачу
размещения объектов по специальным правилам и
нахождение числа способов таких размещений.

Перестановки-соединения, которые можно
составить из n предметов, меняя всеми возможными
способами их порядок; число их

Количество всех перестановок из n элементов
обозначают

Число n при этом называется порядком
перестановки – слайд № 7–10.

Произведение всех натуральных чисел от n до
единицы, обозначают символом n! (Читается “эн -
факториал”). Используя знак факториала, можно,
например, записать:

1! = 1,

2! = 2•1 = 2,

3! = 3 •2 •1 = 6,

4! = 4 •3 •2 •1 = 24,

5! = 5 •4 •3 •2 •1 = 120.

Необходимо знать, что 0!=1

Термин “перестановки” употребил впервые Якоб
Бернулли в книге “Искусство предположений”.

Примеры решения задач:

Задача №1. Сколькими способами 7 книг разных
авторов можно расставить на полке в один ряд?

Перестановками называют комбинации, состоящие
из одних и тех же п различных элементов и
отличающиеся только порядком их расположения.
Число всех возможных перестановок обозначается
Рп и оно равно п!, т.е. Рп = п!, где п!
= 1 * 2 * 3 * … п.

Решение: Р7 = 7!, где 7! = 1 * 2 * 3 * 4 * 5 * 6 * 7 =5040, значит
существует 5040 способов осуществить расстановку
книг.

Ответ: 5040 способов.

Задача № 2 (о квартете)

В знаменитой басне Крылова “Квартет”
“Проказница мартышка, Осел, Козел да косолапый
Мишка” исследовали влияние взаимного
расположения музыкантов на качество исполнения.

Зададим вопрос: Сколько существует способов,
чтобы рассадить четырех музыкантов?

Решение: на слайде

Размещения – соединения, содержащие по m
предметов из числа n данных, различающихся либо
порядком предметов, либо самими предметами;
число их.

Cлайды № 11–13.

В комбинаторике размещением называется
расположение “предметов” на некоторых
“местах” при условии, что каждое место занято в
точности одним предметом и все предметы
различны.

В отличие от сочетаний размещения учитывают
порядок следования предметов. Так, например,
наборы < 2,1,3 > и < 3,2,1 > являются различными,
хотя состоят из одних и тех же элементов {1,2,3} (то
есть, совпадают как сочетания).

Термин “Размещение” употребил впервые Якоб
Бернулли в книге “Искусство предположений”.

Примеры решения задач:

Задача № 1. Сколько можно составить
телефонных номеров из 6 цифр каждый, так чтобы все
цифры были различны? Это пример задачи на
размещение без повторений.

Размещаются здесь десять цифр по 6. Значит,
ответ на выше поставленную задачу будет:

Ответ:151200 способов

Задача № 2. В группе ТД – 21 обучается 24
студентов. Сколькими способами можно составить
график дежурства по техникуму, если группа
дежурных состоит из трех студентов?

Решение: число способов равно числу
размещений из 24 элементов по 3, т. е. равно А₂₄³.
По формуле находим

Ответ: 12144 способа

Сочетания-соединения, содержащие по m предметов
из n, различающиеся друг от друга, по крайней мере,
одним предметом; число их .

Таким образом, количество вариантов при
сочетании будет меньше количества размещений. Cлайды
№ 14–16.

В комбинаторике сочетанием из n по m
называется набор m элементов, выбранных из
данных n элементов. Наборы, отличающиеся
только порядком следования элементов (но не
составом), считаются одинаковыми, этим сочетания
отличаются от размещений.

Термин “сочетание” впервые встречается у
Блеза Паскаля в 1665 году.

Примеры решения задач:

Задача №1. Сколько трехкнопочных комбинаций
существует на кодовом замке (все три кнопки
нажимаются одновременно), если на нем всего 10
цифр?

Решение: Так как кнопки нажимаются
одновременно, то выбор этих кнопок – сочетание.
Отсюда возможно

Ответ: 120 вариантов.

Задача № 2. Сколько экзаменационных комиссий,
состоящих из 3 членов, можно образовать из 10
преподавателей?

Решение: По формуле находим:

комиссий

Ответ: 120 комиссий.

Библиографическая справка – слайд № 17.

Общее у всех этих задач то, что их решением
занимается отдельная область математики,
называемая комбинаторикой. “Особая примета” комбинаторных
задач – вопрос, который всегда можно
сформулировать так, чтобы он начинался словами:
“Сколькими способами…?”. Cлайд № 18.

3. Решение задач: тексты задач с решениями в
приложении 1 – начало на слайде № 19.

4. Исторические сведения о комбинаторике на
слайдах № 20–21 (частично даны сведения при
изучении темы, остальные данные для проекта
студенты возьмут из материалов для ВСР).

5. Связи комбинаторики на слайдах № 22–31 (частично
даны сведения при изучении темы, остальные
данные для проекта студенты возьмут из
материалов для ВСР).

6. Выдвижение гипотезы. Гипотеза – это научное
предположение, выдвигаемое для объяснения
каких-нибудь явлений, вообще – предположение,
требующее подтверждения.

Выдвигается гипотеза: Комбинаторика
интересна и имеет широкий спектр практической
направленности — слайд № 32.

7. Метод проектов: три группы студентов и группа
преподавателей выполняют проект по теме:
“Комбинаторика”, используя знания, полученные
на занятии, а также материалы, подготовленные по
заданию на ВСР: различные определения
комбинаторики, ученые – математики -
первооткрыватели этого раздела, применение
комбинаторики в современной жизни.

8. Защита проектов: при защите проекта сделать
вывод: подтверждает ли проект выдвинутую
гипотезу или опровергает.

9. Тестирование: Часть студентов тестируется на
компьютерах, остальные – на бумажных носителях
по теме занятия. По мере выполнения тестов
студенты решают задачу “Судока” или собирают
кубик Рубика.

10. При выходе из кабинета каждый студент
выбирает прямоугольник по цвету,
соответствующему надписями “всё понятно и
усвоено”, “трудно и не всё понятно”, “не
понятно и не усвоено”, и опускает в
соответствующий конверт.

Информационные ресурсы

1. Фадеев Д.К., Никулин М.С., Соколовский. Элементы
высшей математики для школьников. Москва.
“Наука”, 1987 год.

2. Грэхем Р., Кнут Д.А., Паташник О. Конкретная
математика.. Москва “Мир”, 1998 г.

3. Богомолов Н.В. Практические занятия по
математике: Учеб. Пособие для техникумов, Москва.
“Высшая Школа, 1983.

4. Перельман Я.И. “Занимательная алгебра.
Занимательная геометрия, Москва, АСТ “Астрель”,
2002 год.

5. Савин А.П. “Энциклопедический словарь юного
математика”, Москва “Педагогика”, 1985.

6. Сканави М.И. “Сборник задач по математике для
поступающих в вузы”, Москва, “Высшая школа”, 1998
г.

7. Вентцель Е.С. Теория вероятностей. – 4-е изд. -
М.: Наука, 1969.

8. Элементы теории вероятностей. Математика.
Приложение к газете «Первое сентября»,  №
41, 42.

9. http//portfolio.1sept.ru

10. Лютикас В.С. Факультативный курс по
математике: Теория вероятностей, Москва, “
Просвещение”, 1990.

11. Гнеденко Б.В., Хинчин А.Я. Элементарное
введение в теорию вероятностей. — 6-е изд. — М.:
Наука, 1964.

12. Андреева Е. В. “Комбинаторные задачи”,
Москва, “Чистые пруды”, 2005 г.

Приложение 1

Основы комбинаторики, размещения, перестановки, сочетания

Проказница Мартышка
Осёл,
Козёл,
Да косолапый Мишка
Затеяли играть квартет
…
Стой, братцы стой! –
Кричит Мартышка, — погодите!
Как музыке идти?
Ведь вы не так сидите…
И так, и этак пересаживались –
опять музыка на лад не идет.
Вот пуще прежнего пошли у них
разборы
И споры,
Кому и как сидеть…
знать:
•определения трех важнейших понятий
комбинаторики:
•размещения из n элементов по m;
•сочетания из n элементов по m;
•перестановки из n элементов;
•основные комбинаторные формулы
уметь:
•отличать задачи на «перестановки», «сочетания»,
«размещения» друг от друга;
•применять основные комбинаторные формулы при
решении простейших комбинаторных задач.
множество
Множество характеризуется объединением некоторых
однородных объектов в одно целое.
Объекты, образующие множество, называются
элементами множества.
Множество будем записывать, располагая его
элементы в фигурных скобка {a, b, c, … , e, f}.
Во множестве порядок элементов роли не играет, так
{a, b} = {b, a}.
Множество, не содержащее ни одного элемента,
называется пустым множеством и обозначается
символом ø.
множество
Если каждый элемент множества А является
элементом множества В, то говорят, что множество А
является подмножеством множества В.
Обозначается
В
А
Пример:
Множество {a, b} является
подмножеством множества
{a, b, c, … , e, f}.
Задача
Перечислите возможные варианты подмножества
множества {3, 4, 5, 7, 9}.
Комбинаторикой называется
область
математики,
в
которой изучаются вопросы о
том,
сколько
различных
комбинаций, подчиненных тем
или иным условиям, можно
составить
из
элементов,
принадлежащих
заданному
множеству.
Комбинаторика является
важным разделом математики, который
исследует закономерности расположения,
упорядочения, выбора и распределения
элементов с фиксированного множества.
ПРАВИЛО СУММИРОВАНИЯ
Если два взаимоисключающие действия могут
быть выполнены в соответствии k и m способами,
тогда какое-то одно из этих действий можно
выполнить k + m способами.
Пример №1
Из города А в город В можно добраться 12 поездами, 3
самолетами, 23 автобусами. Сколькими способами можно
добраться из города А в город В?
Решение
N=12+13+23=38
Пример № 2
В ящике имеется n разноцветных шариков.
Произвольным образом вынимаем один шарик.
Сколькими способами это можно сделать?
Решение. Конечно, n способами.
Теперь эти n шариков распределены по двум
ящикам: В первом m шариков, во втором k.
Произвольно из какого-нибудь ящика вынимаем
один шарик. Сколькими разными способами это
можно сделать?
Решение.
Из
первого
ящика
шарик
можно
вытянуть m различными способами, из
второго
k
различными
способами,
всего N = m + k способами.
ПРАВИЛО ПРОИЗВЕДЕНИЯ
Пусть две выполняемые одно за другим
действия могут быть осуществлены в
соответствии k и m способами Тогда обе они
могут быть выполнены k ∙ m способами.
Пример № 3
В турнире принимают участие 8 хоккейных команд. Сколько
существует способов распределить первое, второе и третье места?
Решение
N=8∙7∙6=336
Пример № 4
Сколько можно записать двузначных чисел в
десятичной системе счисления?
Решение. Поскольку число двузначное, то
число десятков (m) может принимать одно
из девяти значений: 1,2,3,4,5,6,7,8,9. Число
единиц (k) может принимать те же значения
и может, кроме того быть равным нулю.
Отсюда следует, что m = 9, а k= 10. Всего
получим двузначных чисел
N = m ·k = 9·10 =90.
Пример № 5
В студенческой группе 14 девушек и 6 юношей.
Сколькими способами можно выбрать, для
выполнения различных заданий, двух студентов
одного пола?
Решение. По правилу умножения двух девушек
можно выбрать 14 ·13 = 182 способами, а двух
юношей 6·5 = 30 способами. Следует выбрать двух
студентов одного пола: двух студентов или
студенток. Согласно правилу сложения таких
способов выбора будет
N =182 + 30 = 212.
ТИПЫ СОЕДИНЕНИЙ
Множества элементов называются соединениями.
Различают три типа соединений:
•перестановки из n элементов;
•размещения из n элементов по m;
•сочетания из n элементов по m (m
ПЕРЕСТАНОВКИ
Определение: Перестановкой из n элементов
называется любое упорядоченное множество из
n элементов.
Иными словами, это такое множество, для
которого указано, какой элемент находится на
первом месте, какой – на втором, какой- на
третьем, …, какой – на n-м месте.
Перестановки – это такие соединения по n элементам из данных
элементов, которые отличаются одно от другого порядком элементов.
Число перестановок из n элементов
обозначают Рn.
Рn = n · (n — 1) · (n – 2) · … · 2 · 1 = n!
ФАКТОРИАЛ
Определение:
Пусть n — натуральное число. Через n! (читается «эн
факториал») обозначается число, равное произведению всех
натуральных чисел 1 от до n:
n! = 1 · 2 · 3 · … · n.
В случае, если n = 0, по определению полагается: 0! = 1.
Пример № 6
Найдем значения следующих выражений:
1!
2!
3!
7!
Пример № 7
Чему равно
а)Р5 ;
б) Р3.
Пример № 8
Упростите
а) 7! · 8
б) 12! · 13 ·14
в) κ! · (κ + 1)
Пример № 9
Сколькими способами можно расставить 8
участниц финального забега на восьми беговых
дорожках?
Решение.
n =8
Р8=8! = 8·7·6·5 · 4 · 3 · 2 ·1 =40320
РАЗМЕЩЕНИЯ
Определение. Размещением из n элементов по
m называется любое упорядоченное множество из
m элементов, состоящее из элементов n
элементного множества.
Число размещений из m элементов по n обозначают:
вычисляют по формуле:
Пример № 9
Учащиеся 11-го класса изучают 9 учебных предметов. В
расписании учебных занятий на один день можно поставить 4
различных предмета. Сколько существует различных способов
составления расписания на один день?
Решение.
Имеем 9-элементное множество, элементы которого учебные
предметы. При составлении расписания мы будем выбирать 4элементное подмножество (уроков) и устанавливать в нем порядок.
Число таких способов равно числу размещений из девяти по четыре
(m=9, n=4) то есть A94:
Пример № 10
Сколькими способами из класса, где учатся 24 ученика, можно
выбрать старосту и помощника старосты?
Решение.
Имеем 24-элементное множество, элементы которого ученики
класса. При выборах старосты и помощника старосты мы будем
выбирать 2-элементное подмножество (ученика) и устанавливать в
нем порядок. Число таких способов равно числу размещений из
девяти по четыре(m=24, n=2), то есть A242:
СОЧЕТАНИЯ
Определение. Сочетанием без повторений из n
элементов
по m -называется любое m
элементное
подмножество
n
-элементного
множества
Число сочетаний из n элементов по m обозначают
и вычисляют по формуле:
Пример № 11
Сколькими способами из класса, где учатся 24 ученика,
можно выбрать два дежурных ?
Решение.
n =24, m=2
Учитывается ли порядок следования
элементов в соединении?
ДА
НЕТ
Все ли элементы входят
в соединение?
ДА
ПЕРЕСТАНОВКИ
Рn = n!
НЕТ
РАЗМЕЩЕНИЯ
СОЧЕТАНИЯ
Определить к какому типу относится соединений относится задача.
1. Сколькими способами можно составить расписание одного
учебного дня из 5 различных уроков?
Учитывается ли порядок следования элементов в соединении?
Все ли элементы входят в соединение?
( да)
( да)
Вывод: перестановка
2. В 9«Б» классе 12 учащихся. Сколькими способами можно
сформировать команду из 4 человек для участия в
математической олимпиаде?
Учитывается ли порядок следования элементов в соединении? (нет)
Все ли элементы входят в соединение?
Вывод: сочетания
(на этот вопрос ответ не нужен)
3.Сколько существует различных двузначных чисел, в
записи которых можно использовать цифры 1, 2, 3, 4, 5,
6, если цифры в числе должны быть различными?
Учитывается ли порядок следования элементов в соединении?
Все ли элементы входят в соединение?
Вывод: размещение
(нет)
( да)
Проказница Мартышка
Осёл,
Козёл,
Да косолапый Мишка
Затеяли играть квартет
…
Стой, братцы стой! –
Кричит Мартышка, — погодите!
Как музыке идти?
Ведь вы не так сидите…
И так, и этак пересаживались – опять
музыка на лад не идет.
Вот пуще прежнего пошли у них
разборы
И споры,
Кому и как сидеть…
Сколько различных вариантов расположения
музыкантов возможно?
Решение.
Учитывается ли порядок следования элементов в соединении?
( да)
Все ли элементы входят в соединение?
(да)
Вывод: перестановка
Рn = n! =n · (n — 1) · (n – 2) · … · 2 · 1
n =4
Р4 = 4! = 4 · 3 · 2 ·1=24
Кто автор высказывания?
«Рано
или
поздно
всякая
правильная
математическая
идея находит применение в том
или ином деле»?
12
5040
А
К
1
Р
9
Е
Ы
В
Н
Е
О
132
720
М
Л
И
Е
56
Ч
Й
С
сочетание
6720
21
120
Результаты решения задач
1
А
8
Н
9
И
2
Л
3
Е
4
К
5
С
10
К
11
О
12
Л
13
А
18
К
19
Р
20
Ы
21
Л
6
Е
14
Е
22
О
7
Й
15
В
23
В
16
И
17
Ч
ДОМАШНЕЕ
ЗАДАНИЕ
Выучить конспект и формулы.
С. 321 № 1062
С. 325 №1074,1075
С. 329 №1081

комбинаций против перестановок. Мы используем термин «комбинация»… | Бретт Берри | Math Hacks

Разница между комбинациями и перестановками — это порядок. При перестановках мы заботимся о порядке элементов, а при комбинациях — нет.

Например, скажем, ваш шкафчик «комбо» — 5432. Если вы введете 4325 в свой шкафчик, он не откроется, потому что это другой порядок (также известный как перестановка).

перестановок из 2, 3, 4, 5:

• 5432, 5423, 5324, 5342, 5234, 5243, 4532, 4523, 4325, 4352, 4253, 4235, 3542, 3524, 3425 , 3452, 3254, 3245, 2543, 2534, 2435, 2453, 2354, 2345

«Комбинация» вашего шкафчика — это конкретная перестановка 2, 3, 4 и 5.Если бы ваш шкафчик работал правильно по комбинации, вы могли бы ввести любую из вышеперечисленных перестановок, и он откроется!

Предположим, вы хотите узнать, сколько существует перестановок чисел 2, 3, 4, 5, не перечисляя их, как я сделал выше. Как бы вы этого добились?

Давайте использовать линейную диаграмму, чтобы помочь нам визуализировать проблему.

Мы хотим найти, сколько возможных 4-значных перестановок можно сделать из четырех различных чисел. Начните с рисования четырех линий, представляющих 4 цифры.

Первая цифра может быть любой из 4 цифр, поэтому поставьте «4» в первый пробел.

Теперь для второго пустого поля осталось 3 варианта, потому что вы уже использовали одно из чисел в первом пустом поле. Поставьте цифру «3» в следующем месте.

Для третьей позиции у вас осталось два числа.

И на последней позиции осталось одно число, поэтому поставьте там «1».

Принцип умножения

Используя принцип умножения комбинаторики, мы знаем, что если есть x способов сделать одно и y способов сделать другое, то общее количество способов сделать и то, и другое равно x • y .Это означает, что нам нужно умножить, чтобы найти общие перестановки.

Это прекрасная возможность использовать сокращенную факторную нотацию (!) :

Есть 24 перестановки, которые соответствуют листингу, который мы сделали в начале этого поста.

Что, если бы я хотел найти общее количество перестановок, включающих числа 2, 3, 4 и 5, но хочу включить такие порядки, как 5555 или 2234, где используются не все числа, а некоторые используются более одного раза ?

Сколько существует этих перестановок?

Это простой расчет.Мы снова составляем 4-значное число, поэтому нарисуйте 4 линии для представления цифр.

В первой позиции у нас есть 4 варианта чисел, поэтому, как и раньше, поместите «4» в первый пробел. Поскольку нам разрешено повторно использовать числа, теперь у нас есть 4 варианта чисел, доступных для второй, третьей и четвертой цифр.

Это то же самое, что:

Допуская повторение чисел, мы получаем 256 перестановок!

Давайте поднимем ставку, решив более сложную задачу:

Сколько разных комбинаций из 5 карт можно собрать из стандартной колоды карт?

В этой задаче порядок не имеет значения, поскольку не имеет значения, в каком порядке мы выбираем карты.

Мы начнем с пяти линий, представляющих нашу руку из 5 карт.

Предполагая, что никто другой не берет карты из колоды, при первом розыгрыше доступно 52 карты, поэтому поместите «52» в первое поле.

После того, как вы выберете карту, в следующем розыгрыше будет на одну карту меньше. Таким образом, у второго бланка будет 51 вариант. При следующем розыгрыше в колоде будет на две карты меньше, поэтому теперь есть 50 вариантов и так далее.

Это 311 875 200 перестановок .

Это перестановки, а не комбинации. Чтобы исправить это, нам нужно разделить на количество рук с разными перестановками, но с одинаковой комбинацией.

Это то же самое, что сказать , сколькими различными способами я могу расположить 5 карточек?

Примечание: это математически аналогично поиску различных перестановок в нашем комбо шкафчика.

Итак, количество комбинаций рук из пяти карт составляет:

Приложив немного изобретательности, мы можем переписать вышеприведенный расчет, используя факториалы.

Мы знаем 52! = 52 • 51 • 50 •… • 3 • 2 • 1, но нам нужны только произведения целых чисел от 52 до 48. Как мы можем выделить только эти целые числа?

Мы хотим разделить все целые числа, кроме от 48 до 52. Для этого разделите на 47! так как это произведение целых чисел от 47 до 1.

Перестановка и комбинация — GeeksforGeeks

Перестановка и комбинация

• Перестановка: это различные расположения заданного количества элементов, взятых один за другим, или некоторые, или все вовремя.Например, если у нас есть два элемента A и B, то есть два возможных варианта: AB и BA.
• Количество перестановок, когда элементы «r» скомпонованы из общего количества элементов «n», составляет ⁿ P _r = n! / (п — г)! . Например, пусть n = 4 (A, B, C и D) и r = 2 (все перестановки размера 2). Ответ — 4! / (4-2)! = 12. Двенадцать перестановок: AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB и DC.
• Комбинация: это различные выборки заданного количества элементов, взятые по одному, или несколько, или все одновременно. Например, если у нас есть два элемента A и B, то есть только один способ выбрать два элемента, мы выбираем оба из них.
• Количество комбинаций при выборе «r» элементов из общего количества «n» элементов составляет ⁿ C _r = n! / [(г!) х (п — г)! ]. Например, пусть n = 4 (A, B, C и D) и r = 2 (все комбинации размера 2). Ответ: 4! / ((4-2)! * 2!) = 6. Шесть комбинаций: AB, AC, AD, BC, BD, CD.
• ⁿ C _r = ⁿ C _{(n — r)}

  ПРИМЕЧАНИЕ: В том же примере у нас есть разные случаи для перестановки и комбинации.Для перестановки AB и BA — это две разные вещи, но для выбора AB и BA одинаковы.

  Примеры задач

  Вопрос 1: Сколько слов можно составить, используя 3 буквы из слова «DELHI»?
  Решение: Слово «ДЕЛИ» состоит из 5 разных слов.
  Следовательно, необходимое количество слов = ⁵ P ₃ = 5! / (5 — 3)!
  => Требуемое количество слов = 5! / 2! = 120/2 = 60

  Вопрос 2: Сколько слов можно составить, используя буквы слова «DRIVER», чтобы все гласные всегда были вместе?
  Решение: В вопросах этого типа мы предполагаем, что все гласные являются одним символом, т. е.е. «IE» — это одиночный символ.
  Итак, теперь у нас есть всего 5 символов в слове, а именно D, R, V, R, IE.
  Но, R встречается 2 раза.
  => Количество возможных расположений = 5! / 2! = 60
  Теперь две гласные можно расположить как 2! = 2 способа.
  => Общее количество возможных слов, при которых гласные всегда вместе = 60 x 2 = 120

  Вопрос 3: Сколько способов мы можем выбрать команду из 4 учеников из заданного выбора из 15?
  Решение: Количество возможных вариантов выбора = ¹⁵ C ₄ = 15! / [(4!) X (11!)]
  => Количество возможных способов выбора = (15 x 14 x 13 x 12) / (4 x 3 x 2 x 1) = 1365

  Вопрос 4: Какими способами можно сформировать группу из 5 человек, выбрав 3 мальчика из 6 и 2 девочки из 5?
  Решение: Количество способов выбрать 3 мальчика из 6 = ⁶ C ₃ = 6! / [(3!) X (3!)] = (6 x 5 x 4) / (3 x 2 x 1) = 20
  Количество способов выбора 2 девушек из 5 = ⁵ C ₂ = 5! / [(2!) X (3!)] = (5 x 4) / (2 x 1) = 10
  Следовательно, общее количество способов формирования группы = 20 x 10 = 200

  Вопрос 5: Сколько слов можно составить из букв слова «ВОДИТЕЛЬ», чтобы все гласные никогда не совпадали?
  Решение: мы предполагаем, что все гласные являются одним символом, т. е.е. «IE» — это одиночный символ.
  Итак, теперь у нас есть всего 5 символов в слове, а именно D, R, V, R, IE.
  Но, R встречается 2 раза.
  => Количество возможных расположений = 5! / 2! = 60
  Теперь две гласные можно расположить как 2! = 2 способа.
  => Общее количество возможных слов, при которых гласные всегда вместе = 60 x 2 = 120
  Кроме того, общее количество возможных слов = 6! / 2! = 720/2 = 360
  Следовательно, общее количество возможных слов, в которых гласные никогда не встречаются вместе = 360 — 120 = 240

  Задачи перестановки и сочетания | Набор-2

  Викторина по перестановке и комбинации
  Практические вопросы по перестановке и комбинации.

  Эту статью предоставил Nishant Arora . Пожалуйста, напишите комментарии, если у вас есть какие-либо сомнения по теме, обсужденной выше, или если вы столкнулись с трудностями в каком-либо вопросе, или если вы хотите обсудить вопрос, отличный от упомянутых выше.

  Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше

  Вниманию читателя! Не прекращайте учиться сейчас. Ознакомьтесь со всеми важными концепциями DSA с помощью курса DSA Self Paced Course по доступной для студентов цене и подготовьтесь к работе в отрасли.

Разница между перестановкой и комбинацией (с примером и сравнительной таблицей)

Последнее обновление: , 26 августа 2017 г. , Surbhi S

В математике вы, возможно, слышали понятия перестановки и комбинации конечного числа раз, но представляли ли вы когда-нибудь, что это два разных понятия? Принципиальное различие между перестановкой и комбинацией — это порядок объектов, в перестановке очень важен порядок объектов, т.е.е. расположение должно быть в установленном порядке количества объектов, взятых только по частям или всем за один раз.

В отличие от этого, в случае комбинации порядок вообще не имеет значения. Не только в математике, но и в практической жизни мы регулярно знакомимся с этими двумя концепциями. Хотя мы этого никогда не замечаем. Итак, внимательно прочтите статью, чтобы понять, чем отличаются эти две концепции.

Содержимое: перестановка против комбинации

1. Сравнительная таблица
2. Определение
3. Ключевые отличия
4. Пример
5. Заключение

Сравнительная таблица

Основа для сравнения	Перестановка	Комбинация
Значение	Перестановка относится к различным способам упорядочивания набора объектов в последовательном порядке.	Комбинация относится к нескольким способам выбора элементов из большого набора объектов, так что их порядок не имеет значения.
Заказ	Соответствует	Неактуально
Обозначения	Расположение	Выбор
Что это?	Заказанные элементы	Неупорядоченные наборы
Ответы	Сколько различных расположений можно создать из данного набора объектов?	Сколько разных групп можно выбрать из большей группы объектов?
Деривация	Множественная перестановка из одной комбинации.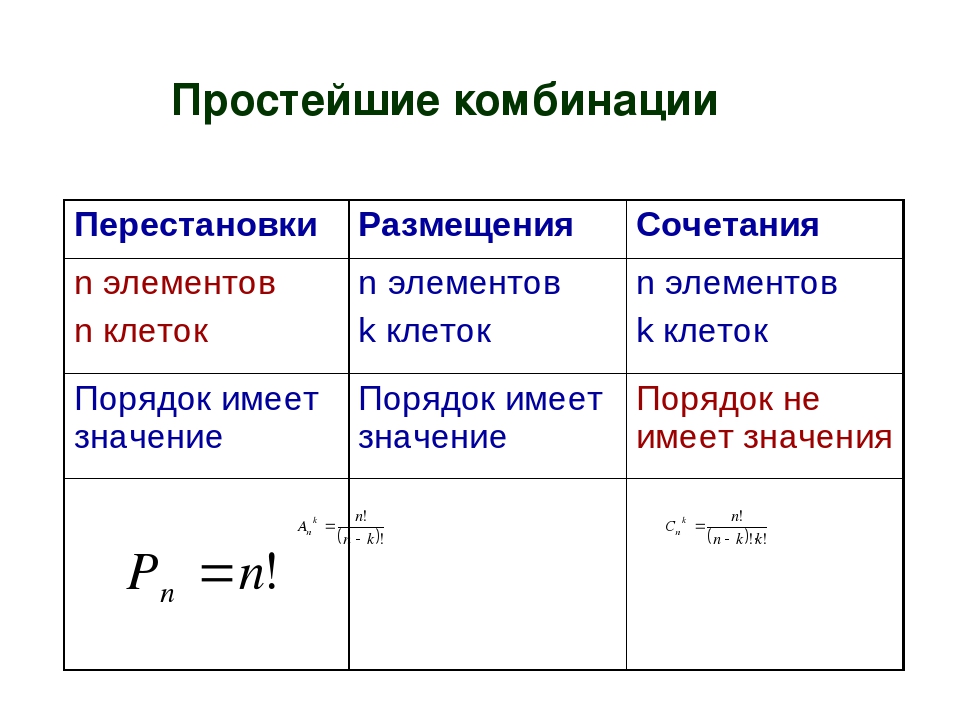	Отдельная комбинация из одной перестановки.

Определение перестановки

Мы определяем перестановку как различные способы упорядочивания некоторых или всех элементов набора в определенном порядке. Он подразумевает все возможные расстановки или перестановки данного набора в различимый порядок.

Например, Все возможные перестановки, созданные буквами x, y, z —

• Принимая все три одновременно: xyz, xzy, yxz, yzx, zxy, zyx.
• Принимая по два за раз: xy, xz, yx, yz, zx, zy.

Общее количество возможных перестановок n вещей, взятых по r за раз, можно рассчитать как:

Определение комбинации

Комбинация определяется как различные способы выбора группы путем взятия некоторых или всех членов набора без следующего порядка.

Например, Все возможные комбинации выбираются буквой m, n, o —

• Когда нужно выбрать три буквы из трех, то единственной комбинацией будет mno
• Если нужно выбрать две буквы из трех, то возможны комбинации mn, no, om.

Общее количество возможных комбинаций из n элементов, взятых по r за раз, можно рассчитать как:

Ключевые различия между перестановкой и комбинацией

Различия между перестановкой и комбинацией четко обозначены по следующим причинам:

1. Термин перестановка относится к нескольким способам упорядочивания набора объектов в последовательном порядке. Комбинация подразумевает несколько способов выбора элементов из большого пула объектов, так что их порядок не имеет значения.
2. Основное различие между этими двумя математическими концепциями — это порядок, размещение и положение, то есть в характеристиках перестановки, упомянутых выше, имеет значение, что не имеет значения в случае комбинации.
3. Перестановка означает несколько способов расположения вещей, людей, цифр, алфавитов, цветов и т. Д. С другой стороны, комбинация указывает на различные способы выбора пунктов меню, еды, одежды, предметов и т. Д.
4. Перестановка — это не что иное, как упорядоченная комбинация, в то время как комбинация подразумевает неупорядоченные наборы или пары значений в рамках определенных критериев.
5. Многие перестановки могут быть получены из одной комбинации. И наоборот, только одна комбинация может быть получена из одной перестановки.
6. Перестановка ответов Сколько различных комбинаций можно создать из данного набора объектов? В отличие от комбинации, которая объясняет, сколько разных групп можно выбрать из большей группы объектов?

Пример

Предположим, есть ситуация, когда вам нужно узнать общее количество возможных выборок двух из трех объектов A, B, C.В этом вопросе, прежде всего, вам нужно понять, связан ли вопрос с перестановкой или комбинацией, и единственный способ узнать это — проверить, важен ли порядок или нет.

Если порядок значительный, то вопрос связан с перестановкой, и возможные выборки будут: AB, BA, BC, CB, AC, CA. Где AB отличается от BA, BC отличается от CB и AC отличается от CA.

Если порядок не имеет значения, тогда вопрос связан с комбинацией, и возможными образцами будут AB, BC и CA.

Заключение

Из приведенного выше обсуждения становится ясно, что перестановка и комбинация — это разные термины, которые используются в математике, статистике, исследованиях и в нашей повседневной жизни. В отношении этих двух концепций следует помнить, что для данного набора объектов перестановка всегда будет выше, чем ее комбинация.

Смешанное размещение на разных платформах: тестирование, когда и где окупается автоматическая оптимизация

Выбрать место для размещения социальной рекламы не так просто, как несколько лет назад.Платформы становятся более надежными, и появляется больше, чем когда-либо, вариантов размещения рекламы. Часто возникает вопрос, лучше ли выбрать несколько мест размещения для рекламной кампании одновременно или оптимизировать рекламную кампанию вручную, разделив отдельные места размещения. Первый вариант, называемый смешанным размещением, основан на алгоритме выбора места показа ваших объявлений. Наши данные показывают, что рекламодатели все чаще выбирают смешанное размещение в Facebook, Twitter и Pinterest — не без оснований.

В Facebook растет использование смешанного размещения

Наши данные показывают, что с 2017 года инвестиции в смешанное размещение на Facebook увеличились по сравнению с прошлым годом, при этом почти две трети расходов идут на автоматически оптимизированные смешанные размещения. Это означает, что рекламодатели размещают рекламу в таких местах размещения, как Messenger, Audience Network, новостные ленты Facebook и Instagram и истории, одновременно в рамках одного набора объявлений, что позволяет алгоритмам Facebook показывать рекламу в том месте, которое она считает наиболее эффективным.

Мы изучили цену за тысячу показов в Facebook с 2017 по 2019 год и обнаружили, что цена за тысячу показов была на 10% эффективнее в кампаниях со смешанными местами размещения по сравнению с одиночными. В 2017 году, когда на смешанное размещение приходилось только 35% кампаний рекламодателей, они обеспечивали гораздо более эффективную цену за тысячу показов (на 22% ниже, чем при одиночном размещении). Теперь, когда почти 70% кампаний проводятся в режиме смешанного размещения, цены за тысячу показов стабилизировались и только на 12% ниже для смешанного размещения по сравнению с одиночным размещением. Несмотря на то, что разрыв в цене за тысячу показов уменьшился, по-прежнему значительно экономичнее проводить кампании со смешанным размещением.

Меняющийся ландшафт размещения в Twitter

Принятие смешанного размещения в Твиттере быстро растет, и сейчас на него приходится 90% всех размещений (по сравнению с 64% в 2017 году). По мере роста объема кампаний со смешанным размещением выросла и цена за тысячу показов. С другой стороны, цена за тысячу показов для одного места размещения снижается, поскольку все меньше рекламодателей выбирают кампании с одним местом размещения.

За последние три года цена за тысячу показов для однократного размещения в среднем была на 10% выше, чем для смешанного размещения.Однако этот баланс быстро меняется, и в первой половине 2019 года цена за тысячу показов для смешанного размещения была на 36% выше, чем для одиночного. Это вызвано, прежде всего, более высокими ценами за тысячу показов для смешанного размещения в целях осведомленности и рассмотрения. Смешанное размещение для целей конверсии по-прежнему намного более рентабельно, чем одинарное размещение для конверсии, которое показывает на 63% более высокие цены за тысячу показов в 2019 году.

Хотя кампании со смешанным размещением не обязательно доступны в Твиттере по более низкой цене, они по-прежнему используются большинством рекламодателей, потому что они обеспечивают больший охват и помогают сделать рекламу более релевантной — гарантируя, что они оптимизированы для размещения в нужном месте. в нужное время для потребителя.

В Pinterest преобладает смешанное размещение

Pinterest продемонстрировал самый сильный рост смешанных размещений среди всех платформ с 2017 по 2019 год, составив 94% от общего числа размещений в первой половине 2019 года, что на 40 пунктов больше, чем в 2017 году. Смешанное размещение также имеет значительно более рентабельные цены за тысячу показов, чем одиночное размещение. на Pinterest, в среднем экономия 33%.

Смешанное размещение на Pinterest особенно просто — оно включает ленту Pinterest и поиск Pinterest. Нет особых причин использовать единое размещение, поскольку смешанное размещение позволяет охватить пользователей, которые настроены на открытие (канал), и тех, кто ищет что-то конкретное (поиск). Эти два места размещения служат разным целям, и, используя смешанное размещение, вы можете охватить клиентов на всех этапах их потребительского пути в Pinterest — при меньших затратах, чем при использовании только отдельных мест размещения.

Лучшие практики для смешанного размещения

Эффективность смешанного размещения варьируется в зависимости от платформы, цели и года, но если смотреть на цифровой ландшафт в целом, затраты на CPM одинаковы независимо от смешанного размещения или использования одного размещения. Без резкой разницы в стоимости стоит использовать смешанное размещение, чтобы увеличить количество потенциальных точек соприкосновения и привлечь больше пользователей в нужное время и в нужном месте с помощью оптимизации на основе алгоритмов.При смешанном размещении также учитываются прогнозные затраты, что означает, что платформа может предсказать, какие варианты вашей кампании будут работать лучше всего по мере ее масштабирования.

Хотя лучше всего использовать автоматическую оптимизацию со смешанными местами размещения, простой выбор всех возможных вариантов размещения для каждой кампании не даст максимальной эффективности. Вместо этого посмотрите на KPI кампании, доступные объявления и общие бизнес-цели, чтобы оценить, какие места размещения имеют наибольший смысл. Например, если у вас есть вертикальная видеореклама с целью повышения узнаваемости бренда, вам следует запустить комбинацию мест размещения в историях, которые обеспечивают высокий охват и узнаваемость и специально разработаны для вашего вертикального креатива.В этом примере вы также можете удалить места размещения на рабочем столе, поскольку вертикальное видео лучше всего подходит для мобильных устройств, если только вы не использовали настройку сегмента сегмента (которая позволяет автоматически оптимизировать креатив для разных мест размещения и форматов рекламы на Facebook).

Существует ряд переменных, которые могут помочь определить, какие места размещения следует выбрать, но данные говорят сами за себя: когда возможно, идеально использовать смешанное размещение и автоматическую оптимизацию для наиболее релевантного охвата при эффективных затратах.

О системе доставки: места размещения

Во многих случаях мы рекомендуем размещать вашу рекламу в семействе приложений и сервисов Facebook. Это дает нашей системе доставки больше гибкости, чтобы вы могли получать больше и лучшие результаты. Мы называем различные места, где мы можем показывать вашу рекламу, «местами размещения». Вы выбираете места размещения в разделе «Места размещения» при создании набора объявлений.

Примечание: В зависимости от типа вашего объявления, содержания и дизайна креатива все места размещения могут быть недоступны.Подробнее о том, какие цели подходят для разных мест размещения.

Есть два подхода к использованию мест размещения: автоматический и ручной.

Автоматические размещения

Автоматические размещения позволяют нам получить наилучшие результаты среди всех мест размещения по умолчанию. Поскольку мы можем выбирать результаты из максимально широкого диапазона, автоматическое размещение, как правило, является наиболее эффективным использованием вашего бюджета и помогает контролировать расходы. Мы рекомендуем его большинству рекламодателей.

Однако вы можете быть сбиты с толку, почему мы рекомендуем это, если вы используете стратегию наименьшей стоимости и проверяете среднюю стоимость за событие оптимизации для каждого места размещения в своих отчетах. Например, если средняя стоимость мероприятия по оптимизации в каналах Facebook значительно ниже, чем в Instagram Stories, вы можете отказаться от размещения своей рекламы в Instagram Stories и разместить больше из них в каналах Facebook.

Мы можем понять, почему вы так считаете, но имейте в виду, что наша система доставки разработана так, чтобы предоставить вам наибольшее количество мероприятий по оптимизации при самой низкой средней стоимости в целом — не самой низкой средней стоимости для каждого места размещения.Это означает, что мы изучаем все доступные возможности для всех мест размещения и выбираем самые дешевые из них, независимо от того, какова будет средняя цена за событие оптимизации для каждого места размещения.

Еще одно преимущество автоматических мест размещения состоит в том, что если вы решите продублировать кампанию, любые новые места размещения автоматически станут доступны для дублированного объявления.

Пример

Вот упрощенный пример, показывающий, как это работает, и почему его легко неверно истолковать:

Допустим, есть 11 возможностей для показа вашей рекламы: 3 в Facebook, 3 в Instagram и 5 в Audience Network.Возможности Facebook стоят 3 доллара за одно мероприятие по оптимизации. Возможности Instagram стоят 5 долларов США за одно мероприятие по оптимизации. Три возможности Audience Network стоят 1 доллар США за событие оптимизации, а две возможности — 7 долларов США за событие оптимизации. Ваш бюджет составляет 27 долларов США.

На графиках ниже:

= возможность получить событие оптимизации в Facebook

= возможность получить событие оптимизации в Instagram

= возможность получить событие оптимизации на Сеть аудитории

Красный кружок вокруг любого из этих значков означает, что реклама была показана в этом месте размещения и получила событие оптимизации.

Если вы выбрали все три из этих мест размещения, в вашем отчете будет показано, что для мест размещения в Facebook средняя цена за событие оптимизации составляет 3 доллара США, для мест размещения в Instagram — средняя стоимость за событие оптимизации 5 долларов США, а для мест размещения в сети аудитории — средняя стоимость за одно событие оптимизации. событие оптимизации стоимостью 1 доллар США. Вы получите девять событий оптимизации за 27 долларов США при средней стоимости 3 доллара США каждое.

Если вы видели эти цифры, у вас может возникнуть соблазн отключить размещение в Instagram, чтобы сосредоточиться на кажущихся более дешевыми размещениях в Facebook и Audience Network.Однако вот что произойдет, если вы отключите его:

мест размещения в Facebook будут иметь среднюю стоимость за событие оптимизации 3 доллара США, не будет места размещения в Instagram, а места размещения в сети аудитории будут иметь среднюю стоимость за событие оптимизации 3,40 доллара США. Вы получите только 8 событий оптимизации за 26 долларов США по 3,25 доллара США каждое в целом. Это менее эффективное расходование вашего бюджета.

Что-то пошло не так

У нас проблемы с воспроизведением этого видео. Чтобы посмотреть видео, обновите свой веб-браузер.

Мы оптимизируем показ ваших объявлений, чтобы снизить общие затраты на оптимизацию. Мы делаем эту оптимизацию в контексте всего спектра имеющихся возможностей. Другими словами, то, что вы не видите в своих отчетах, — это более дорогие результаты, которые вам не приходилось получать из-за дополнительных мест размещения. Важно помнить, что средняя стоимость одного места размещения за событие оптимизации выше, чем у другого, не обязательно означает, что оно неэффективно.

Audience Network автономная

Выбранные рекламодатели теперь могут запускать кампании по установке приложений, используя только Facebook Audience Network.

Хотя выбор автоматических мест размещения по-прежнему является лучшей стратегией для достижения эффективных результатов в большинстве случаев, эта новая функция позволяет вам установить точный бюджет и ставку для ваших кампаний в Audience Network.

Вы можете установить это на уровне набора объявлений в Менеджере рекламы, в разделе Места размещения , за которым следует Изменить места размещения .

Размещение радикалов внутри иероглифов

Введение & raquo Общие радикалы & raquo; Размещение & raquo Использование & raquo; Заключение

Радикальное размещение

Радикалы объединяются вместе с другими радикалами для создания более сложных иероглифов. Давайте посмотрим, как можно соединить радикалы.

Простые комбинации

Это настолько просто, насколько возможно. Два радикала объединяются по вертикали или горизонтали, каждый занимает половину полного квадрата кандзи.Примеры приведены ниже.

Обратите внимание, что большинство модифицированных радикальных форм появляются в крайнем левом месте комбинаций кандзи. Однако случаются исключения, такие как измененная форма 火 (огонь), появляющаяся внизу 黒 (черная).

Сложные комбинации

По мере усложнения кандзи иногда можно встретить три или четыре радикала, составляющие более сложные идеи и значения. Как правило, здесь сводятся правила расстановки простых комбинаций.

Для начала давайте проанализируем 働.

Здесь мы видим три отдельных радикала, сгруппированных вместе. Его конструкция такая же, как и конструкция с двумя половинами выше, за исключением дополнительной половины; иероглифы делятся на трети. Мы вернемся к 働 в следующем уроке, чтобы проанализировать его значение, взглянув на эти радикалы, а пока перейдем к другому.

Здесь вы видите модифицированный радикал в левой половине, как обычно. Правая половина делится на четверти. Обратите внимание, что, хотя комбинируются три радикала разного размера, кандзи в целом остается сбалансированным.Если размышления о компонентах, уравновешивающих друг друга, помогают вам при написании кандзи, примите эту мысль и работайте с ней.

Посмотрите, сможете ли вы определить все радикалы слева в кандзи от слова «любовь». Наведите курсор мыши, чтобы увидеть решение.

Если вы не поняли, не волнуйтесь — это непросто.

Необычные комбинации

Некоторые радикалы сочетаются другим странным образом. Их не нужно запоминать; лучше познакомьтесь с тем, как сочетаются кандзи, чтобы лучше понимать радикалы в действительно сложном персонаже.

Несколько примеров отмечены ниже.

Перейдите к следующему уроку, чтобы узнать, как эффективно использовать эти радикалы.

Размещение сигнализаций | Kidde

Дымовая сигнализация

Дымовые извещатели следует устанавливать в спальнях и жилых помещениях или рядом с ними, на потолке или стене. Потолочный монтаж, как правило, предпочтительнее, так как он позволяет размещать дымовую сигнализацию в более центре комнаты. Если используется настенный монтаж, лучше всего использовать внутреннюю стену, чтобы избежать тепловых потоков воздуха, которые могут возникать вдоль горячих или холодных стен.Наши устройства прошли испытания и будут работать при температуре от 40 до 100 градусов по Фаренгейту.

Сигнализация обнаружения угарного газа и комбинированная сигнализация

Сигнализаторы угарного газа (CO) и комбинированные сигнализаторы следует устанавливать в спальнях и жилых помещениях или рядом с ними, на стене на высоте шести дюймов от потолка до шести дюймов над полом. При установке на потолке убедитесь, что он находится на расстоянии не менее шести дюймов от стены. Поскольку оксид углерода почти такой же плотности, как воздух, он равномерно рассеивается по воздуху в помещении.Наши устройства прошли испытания и будут работать при температуре от 40 до 100 градусов по Фаренгейту.

Если в вашем доме есть система водяного отопления или бойлер, то для наиболее быстрого реагирования рекомендуется установить сигнализацию CO в котельной, а также в комнате над котельной или рядом с ней.

Рекомендуем установить сигнализацию угарного газа или комбинированную сигнализацию на каждом уровне многоэтажного дома. Вы можете использовать количество и расположение дымовых извещателей, установленных в вашем доме, в соответствии с текущими требованиями строительных норм и правил, в качестве ориентира для определения местоположения вашей дымовой сигнализации или комбинированной (-ых) сигнализации (-ов).

Если в доме есть только одна сигнализация угарного газа или комбинированная сигнализация, ее следует установить в главной спальне или в коридоре за пределами спальной зоны.

См. Следующие инструкции по установке одиночного или комбинированного сигнализатора угарного газа:

• Разместите сигнализацию на расстоянии не менее 5-15 футов от приборов для сжигания топлива.

• Убедитесь, что ничто не закрывает и не препятствует устройству.

• Не размещайте блок в мертвых воздушных пространствах, рядом с окном или дверью.

ВНИМАНИЕ: Сигнализация угарного газа будет указывать только на присутствие окиси углерода на датчике. Окись углерода может присутствовать в других частях вашего дома.

Тепловая сигнализация

Тепловые извещатели следует устанавливать либо на потолке, либо на стене. Мы рекомендуем устанавливать тепловую сигнализацию в местах, где могут быть экстремальные температуры; например, на чердаке или в гараже.

ПРИМЕЧАНИЕ. Тревоги с температурой 135 градусов обычно не подходят для использования на чердаке, так как большинство недостроенных чердаков будет превышать рабочую температуру срабатывания сигнализации.Тепловая сигнализация номер модели HD200F подходит для этого использования с релейным модулем SM120X для дыма и реле CO120X для угарного газа.

Размещение всех сигналов тревоги

Мы рекомендуем вам руководствоваться вашими текущими требованиями строительных норм в качестве руководства по размещению ваших сигнализаций.

ВАЖНО: Неправильное расположение может повлиять на чувствительные электронные компоненты при срабатывании сигнализации.

ПРИМЕЧАНИЕ: Для получения дополнительной информации о вашем конкретном будильнике обратитесь к руководству пользователя.

Статьи по теме: Выберите подходящие средства безопасности для вашего дома

.