Содержание
формулы площади, доказательства. Трапеция на занятиях с репетитоом по математике — Колпаков Александр Николаевич
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника.
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению .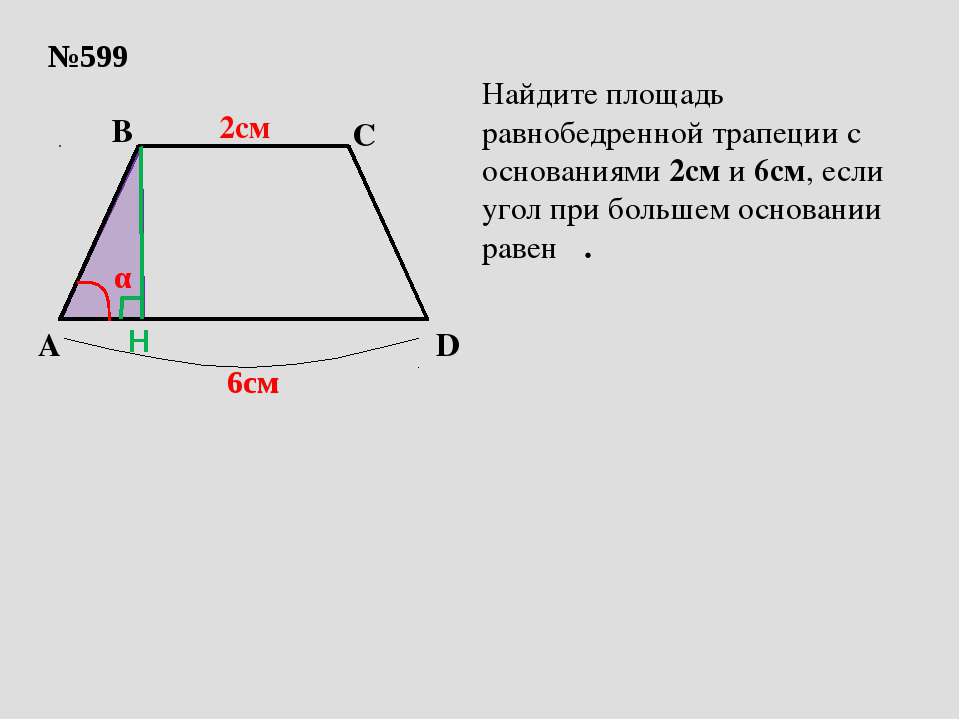 Отсюда
Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции.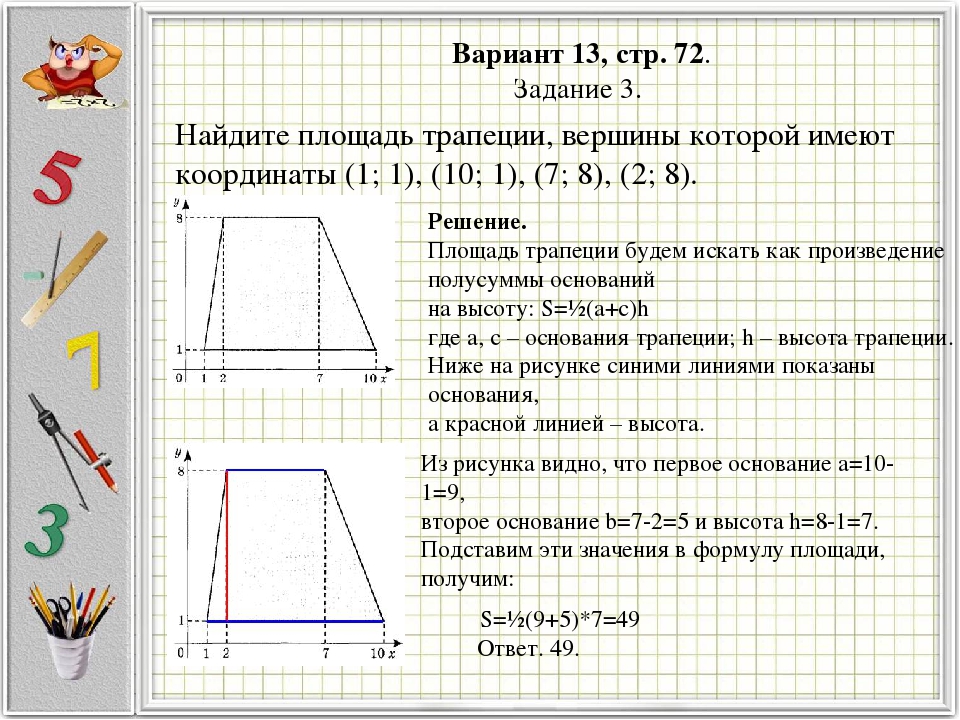 С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы :). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике: Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве, подготовка к ЕГЭ в Строгино.
Площадь трапеции — формулы, примеры расчета,
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a = 3 см, b = 7 см и боковыми сторонами c = 5 см, d = 4 см. найдем площадь фигуры:
найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
Далее рассмотрим еще один пример расчета площади равнобедренной (равнобокой) трапеции. Формула через стороны и прилегающие к основанию углы позволит легко найти площадь фигуры.
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция. Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.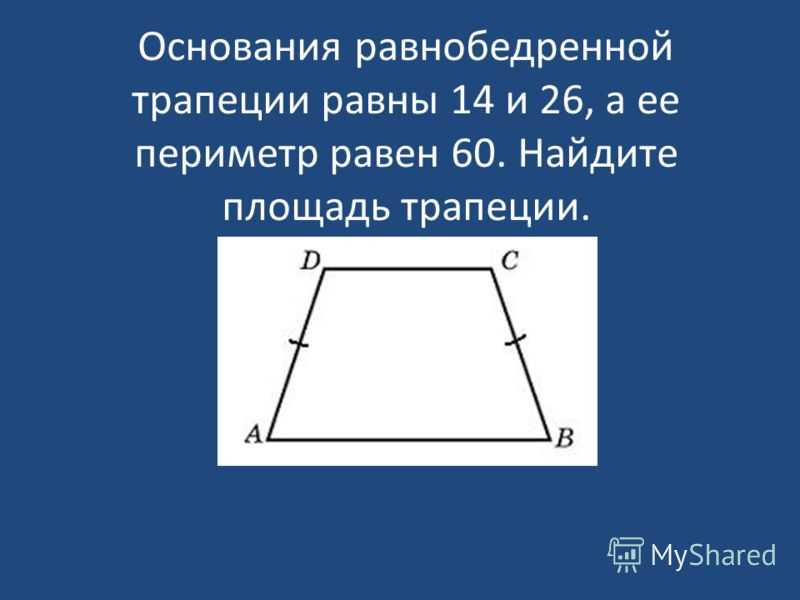
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Площадь трапеции: как вычислить, формула
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту.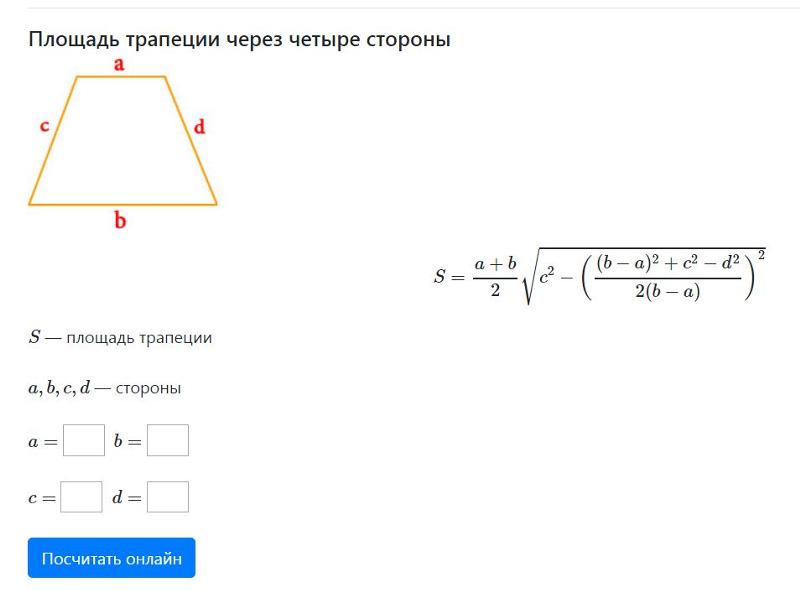 Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Трапеция
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
S = h * m
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон.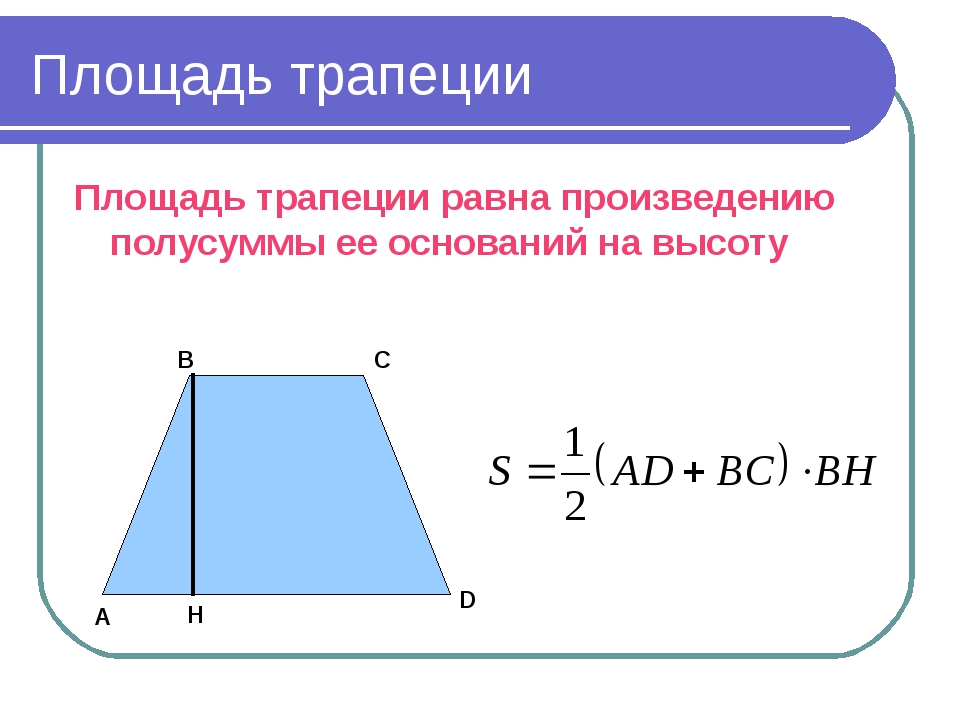 Ее боковые стороны равны.
Ее боковые стороны равны.
Равнобедренная трапеция
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними. В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.

Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Круг в трапеции
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
S = D2 / sin α
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Трапеция в круге
Через основания и радиус окружности площадь ищется так:
S = r * (a + b)
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям.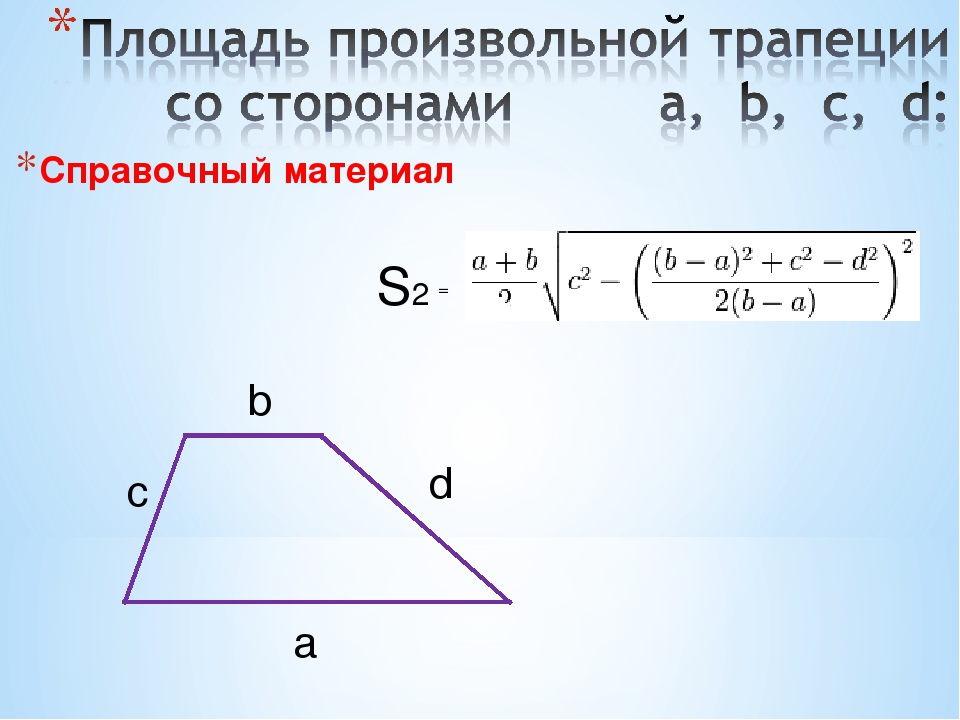 В этом случае боковая сторона по длине совпадает с высотой трапеции.
В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Прямоугольная трапеция
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
S = m * h
или на длину боковой перпендикулярной стороны:
S = m * c
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Прямоугольная трапеция с перпендикулярными диагоналями
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

S = (a + b) * r
Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
S = 2m * r
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке [a;b], осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Криволинейная трапеция
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Как найти площадь трапеции: формулы и примеры
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы.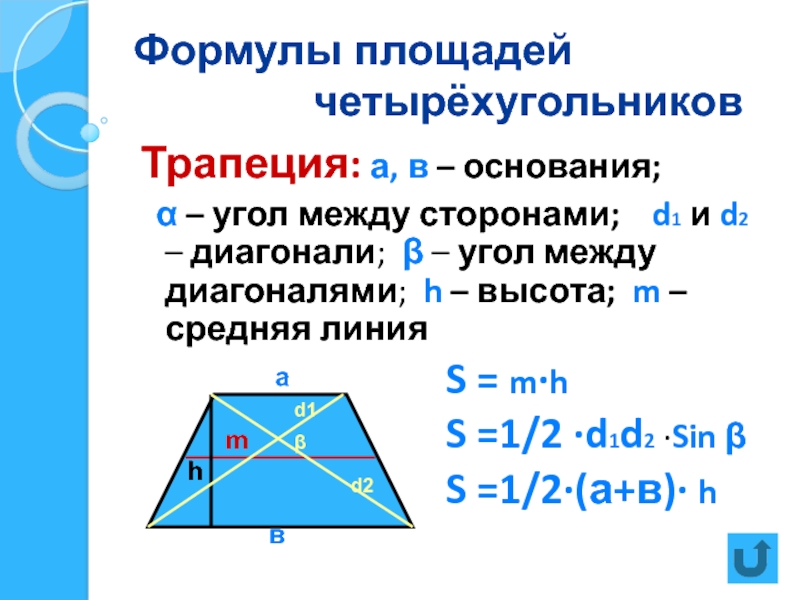 Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h.
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h. Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.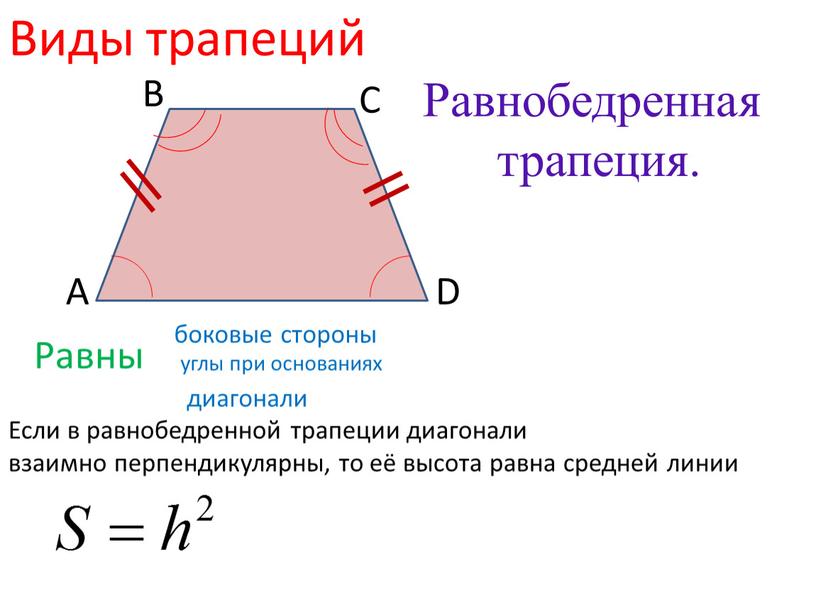
Рассмотрим еще один вариант: в трапеции проведены диагонали d1и d2, которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d1d2 *sinα.
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c2 – ( ( 1/2(b – a)) * ((b – a)2 + c2 – d2) )2.
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной.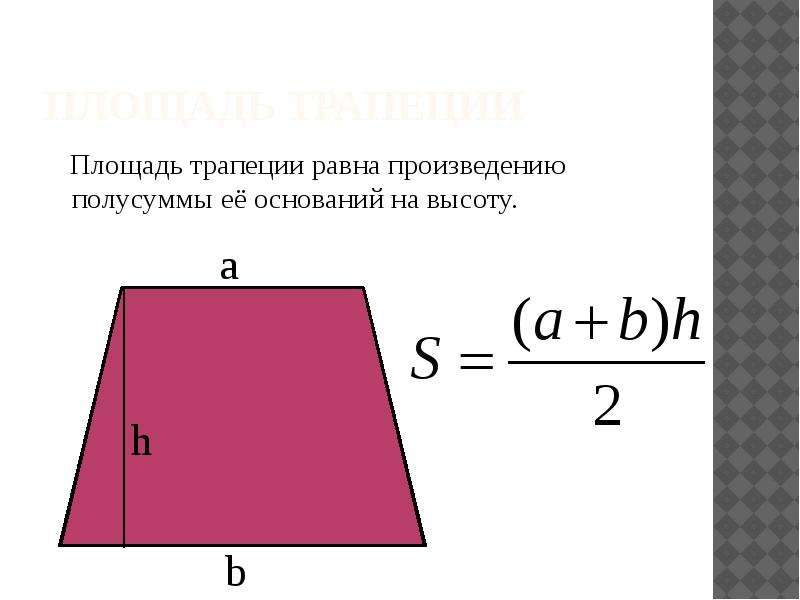 Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r2/sinα. Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 300: S = 8r2.
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d1 и d2, а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h2.
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка [a; b] на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок [a; b]), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫baf(x)dx = F(x)│ba = F(b) – F(a). В этой формуле F – первообразная нашей функции на выбранном отрезке [a; b]. И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ2 = АР2 + РХ2). И высчитать его площадь: SAPX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см2.
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что SAMPC = SAPX = 54 см2.
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h1 для треугольника ТМЕ и высоту h2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а.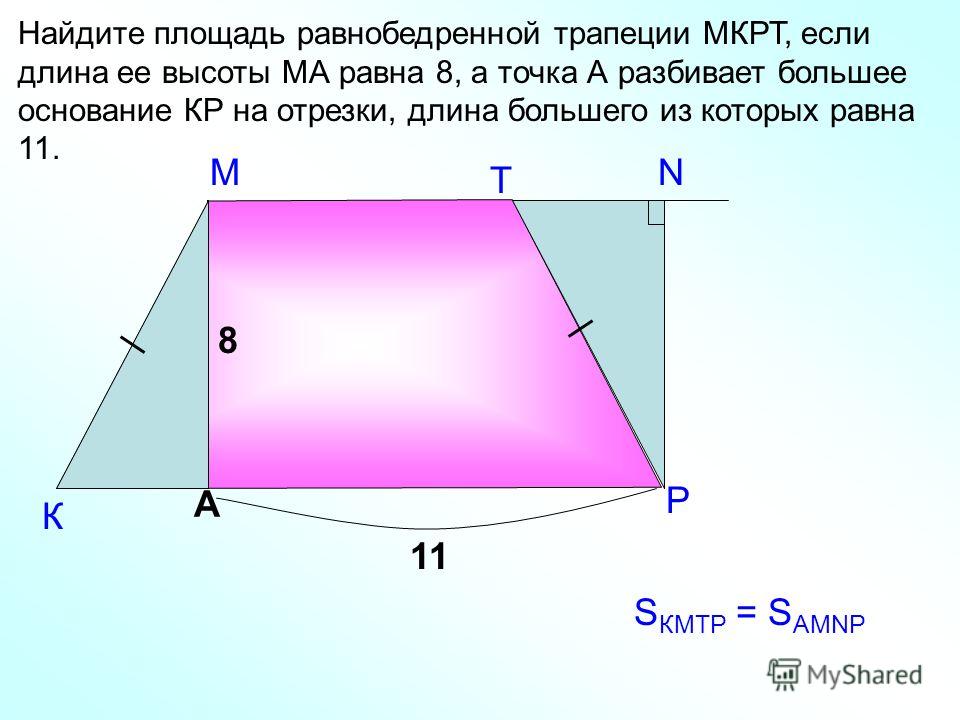 Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h1 = 1/5(b + х) * h2. Преобразуем и получим: h1/ h2 = 1/5 * ((b + х)/(х + а)).
Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h1 = 1/5(b + х) * h2. Преобразуем и получим: h1/ h2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h1/ h2 = (х – а)/( b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х2 – а2) = (b2 – х2) ↔ 6х2 = b2 + 5а2 ↔ х = √(5а2 + b2)/6.
Таким образом, ОЕ = х = √(5а2 + b2)/6.
Также советуем посмотреть вам наше новое видео по теме нахождения площади фигур, в том числе и трапеции:
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
онлайн калькулятор, формула расчета, пример вычисления
Ниже вы узнаете, как выглядят формулы для нахождения площади прямоугольной трапеции, а также сможете воспользоваться онлайн-калькуляторами для её расчёта.
Определение 1
Особенность прямоугольной трапеции в том, что её высота равна стороне, расположенной перпендикулярно двум основаниям.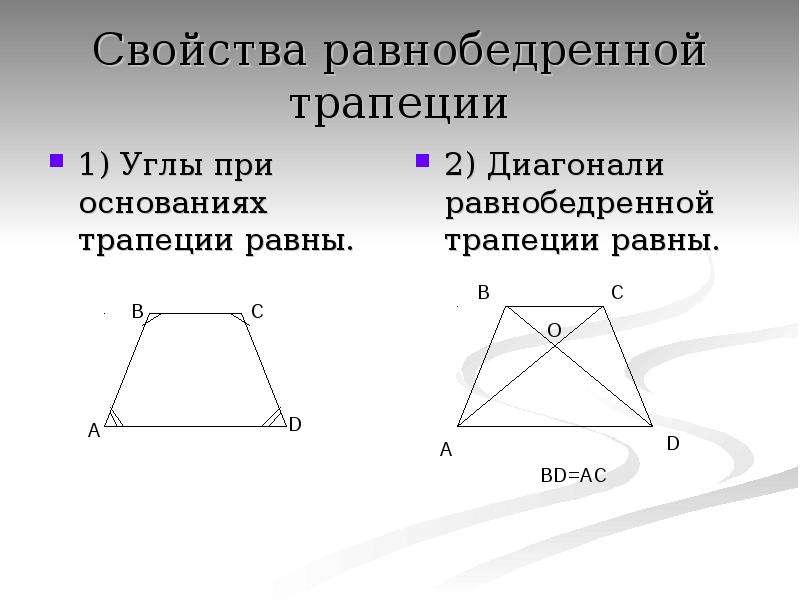
Для того чтобы вычислить площадь прямоугольной трапеции через 3 её стороны, воспользуйтесь нашим онлайн-калькулятором. Для расчёта введите имеющиеся данные в поля для ввода.
Площадь прямоугольной трапеции
Высота прямоугольной трапеции $h$ равна длине стороны $c$, расположенной под прямым углом к двум основаниям трапеции $a$ и $c$.
Следовательно, формула для вычисления площади прямоугольной трапеции имеет вид:
$S = \frac12 \cdot (a + c) \cdot b$, где
$a$ — малое основание;
$с$ — большее основание;
$b$ — перпендикулярная основаниям сторона.
Пример 1
Задача
Дана прямоугольная трапеция, сторона $b$ у которой равна $2.32$ см, сторона $a$ составляет $2. 42$, и сторона $c$ равна $3.94$ см. Чему равна площадь трапеции?
42$, и сторона $c$ равна $3.94$ см. Чему равна площадь трапеции?
Решение:
Воспользуемся приведённой выше формулой:
$S =\frac{(2.42 + 3.93) \cdot 2.32}{2} = 7.37$ кв. см.
Проверим ответ с помощью онлайн-калькулятора. Значения совпадают, а значит, решение найдено верно.
Также площадь прямоугольной трапеции можно рассчитать и по другим формулам, общим для всех видов трапеций, например, через среднюю линию и высоту. Высоту в формуле также можно заменить на сторону, перпендикулярную основаниям.
Площадь трапеции по высоте и средней линии
Формула нахождения площади трапеции по высоте и средней линии:
$S = m \cdot h$, где
$S$ — площадь трапеции,
$m$ — средняя линия,
$h$ — высота трапеции. 2) \cdot \frac{\sin (α) \cdot \sin (γ)}{\sin (α + γ)}$, где
2) \cdot \frac{\sin (α) \cdot \sin (γ)}{\sin (α + γ)}$, где
$S$ — площадь трапеции,
$b$ — большее основание,
$g$ — малое основание,
$α$ — первый угол при основании,
$γ$ — второй угол при основании.
Также площадь прямоугольной трапеции можно найти через диагонали и угол между ними.
Площадь трапеции по диагонали и углу между диагоналями
Формула нахождения площади трапеции по диагонали и углу между диагоналями:
$S =\frac12 \cdot d1 \cdot d2 \cdot \sin (α)$, где
$S$ — площадь трапеции,
$d1$ — первая диагональ,
$d2$ — вторая диагональ,
$α$ — угол между диагоналями.
Рассмотрим пример.
Пример 2
Задача
Дана прямоугольная трапеция с диагоналями $d1$ и $d2$, равными $2.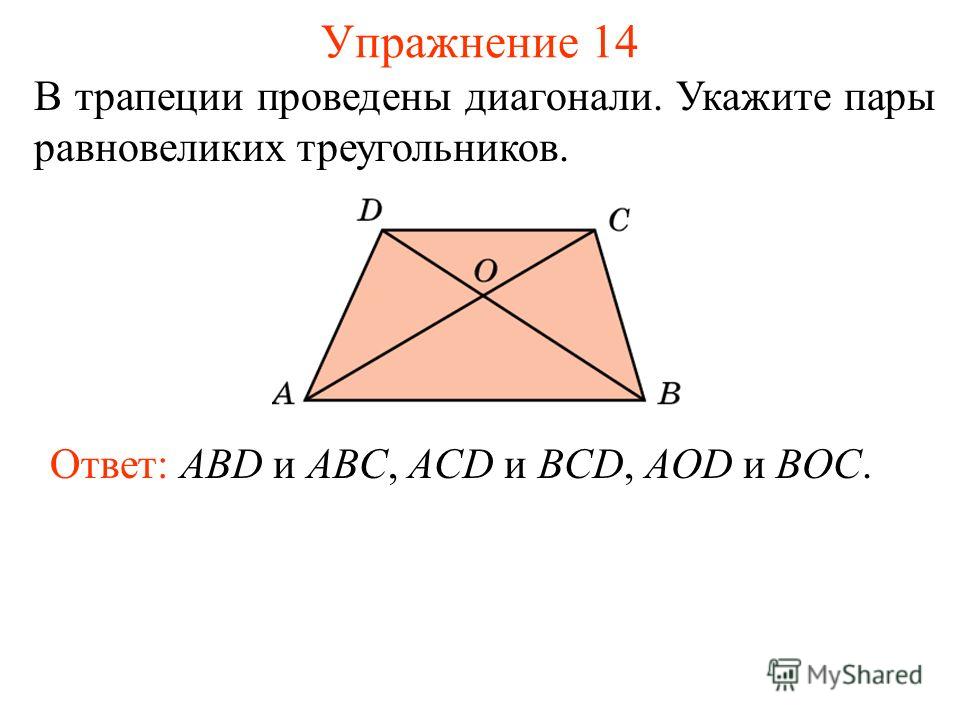 22$ см и $2.64$ см. Угол между диагоналями $α$ равен $56°$. Чему равна площадь прямоугольной трапеции?
22$ см и $2.64$ см. Угол между диагоналями $α$ равен $56°$. Чему равна площадь прямоугольной трапеции?
Решение:
Синус заданного угла $α$ равен $0.83$, найти его можно по специальным таблицам, приведённым на нашем сайте. Теперь подставим все известные значения:
$S = \frac{2.22 \cdot 2.64 \cdot 0.83}{2} = 2.43$ кв. см.
Вычисленный ответ совпадает с ответом онлайн-калькулятора, а значит, решение — верное.
И наконец, рассмотрим случай когда нет данных о том, какие стороны являются основаниями, а какая сторона расположена под прямым углом, но при этом известны все стороны трапеции.
Площадь трапеции по четырём сторонам
Формула нахождения площади трапеции по четырём сторонам выглядит следующим образом:
$S = \frac{a + b}{2} \cdot \sqrt{c^2 — (\frac{(b — a)^2 + c^2 — d^2}{2 \cdot (b — a)})^2}$, где
$S$ — площадь трапеции,
$a$ — малое основание,
$b$ — большее основание,
$c, d$ — боковые стороны.
Площади фигур
Формула площади треугольника
Площадь треугольника (S):
h — высота треугольника;
a — основание.
Площадь прямоугольного треугольника по катетам
Формула площади прямоугольного треугольника, (S):
a, b — катеты треугольника.
Площадь треугольника, формула Герона
Формула (Герона) площади треугольника через полупериметр (S):
a, b, c — стороны треугольника
p — полупериметр, p=(a+b+c)/2
Площадь равнобедренного треугольника
Площадь треугольника с двумя одинаковыми сторонами.
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b, (S):
Формула площади треугольника через, стороны a, b, (S):
Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h — высота
Площадь квадрата через диагональ
Как рассчитать площадь квадрата через диагональ
a — сторона квадрата
c — диагональ
Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
Формула площади ромба
S = a · H
где: H — высота ромба.
a — сторона ромба
Площадь неравнобедренной трапеции :
a — нижнее основание;
b — верхнее основание;
h — высота трапеции.
Формула площади правильного многоугольника
a — сторона многоугольника
n — количество сторон
Записи по теме
Площади кругов и окружностей
Формулы площадей для кругов и окружностей: площадь круга, площадь сегмента круга, площадь кольца, площадь сектора кольца.
Площади поверхностей
Формулы площади поверхностей объёмных фигур. Формулы для расчёта площади поверхности куба, прямоугольного параллелепипеда, правильной и усечённой пирамид, усечённого конуса.
Как найти площадь неравнобедренной трапеции?
Помогите ПЛИЗ
ДАЮ 15 баллов
1. В прямоугольном треугольнике катеты равны 10 см и 15 см. Найдите его площадь.
2. В прямоугольном треугольнике катеты равны 4 см и 13 см. Найдите
…
его площадь.
3. Найдите площадь ромба, если его диагонали равны 8 см и 7 см.
4. Диагонали ромба равны 5 см и 12 см. Найдите площадь ромба.
5. Высота треугольника, равная 6 см, проведена к основанию , равному 18 см. Найдите площадь треугольника.
6. Высота треугольника, равная 8 см, проведена к основанию, равному 17 см. Найдите площадь треугольника.
7. Площадь треугольника равна 25 см2, а основание – 10 см. Найдите высоту, проведенную к данному основанию.
8. Площадь треугольника равна 28 см2, а высота, проведенная к основанию, равна 14 см. Найдите длину основания.
9. Высота параллелограмма равна 8 см, а основание – 34 см. Найдите площадь параллелограмма.
10. Высота параллелограмма равна 7 см, а основание – 23 см. Найдите площадь параллелограмма.
11. Площадь параллелограмма равна 64 см2 , а основание- 16 см. Найдите высоту, проведенную к данному основанию.
12. Площадь параллелограмма равна 45 см2 , а высота- 9 см. Найдите основание параллелограмма, к которому проведена данная высота.
13. Стороны параллелограмма равны 6 см и 10 см, а высота, проведенная к меньшей из них, равна 8 см. Найдите высоту, проведенную к другой стороне.
Найдите высоту, проведенную к другой стороне.
14. Стороны параллелограмма равны 6 см и 10 см, а высота, проведенная к большей из них, равна 5 см. Найдите высоту, проведенную к другой стороне.
15. В параллелограмме две стороны равны 6 и 8 см, а один из углов 1500. Найдите площадь параллелограмма.
16. В параллелограмме одна из сторон равна 10 см, а один из углов 300. Найдите площадь параллелограмма, если его периметр равен 56 см.
17. Две стороны треугольника равны 30 см и 18 см. Высота, опущенная на первую сторону, равна 12 см. Найти длину высоты, опущенной на вторую сторону.
18. Периметр ромба равен 28 дм, а высота- 5 дм. Найти площадь ромба.
19. Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромба равна 27 см2 .
20. Высоты параллелограмма равны 3 см и 6 см, а периметр равен 30 см. Найдите площадь параллелограмма.
Обчисли площу червоного та незафарбованого сегментів, якщо радіус круга дорівнює 4 дм, а менший центральний кут — 90°.
Помогите пожалуйста!
На бумаге в клетку нарисовали прямоугольник. Площадь клетки — 25 условных единиц. Найди размер радиуса
Площадь клетки — 25 условных единиц. Найди размер радиуса
окружности, которую можно
…
описать вокруг такого прямоугольника. Ответ рассчитай в условных единицах, в
поле для ответа вводи только число.
поможіть поможіть поможіть
Помогите пожалуйста! Если кто то не знает то не отвечать)РАСПИСАТЬ ВСЁ ПОДРОБНО А НЕ ТОЛЬКО ОТВЕТЫ
НЕ ПРАВЕЛЬНЫЙ ОТВЕТ, БАН
1. Серед наведених формул
…
укажіть формулу довжини кола, якщо радіус
кола R.
А. Б. В. Г.
2. Закінчіть речення так, щоб утворилося правильне твердження.
«Опуклий многокутник називається правильний, якщо у нього …»
А. всі сторони рівні Б. всі кути рівні
В. всі сторони і кути рівні Г. можна вписати коло
3. Знайдіть площу круга з діаметром 6 см.
А. см 2 Б. см 2 В.см 2 Г. см 2
4. Знайдіть радіус кола, вписаного в квадрат, площа якого дорівнює 100
см 2 .
А. 10 см Б. 5 см В. см Г. см
5. Знайдіть величину кута правильного п’ятикутника.
А. Б. В. Г.
6. Площа кругового сектора становить дві третини площі круга.
Знайдіть центральний кут, який відповідає даному сектору
А. Б. 18 В. Г.
Б. 18 В. Г.
Достатній рівень навчальних досягнень
7. Довжина кола, описаного навколо квадрата, дорівнює 4 см. Знайдіть
площу квадрата.
8. Площа правильного трикутника, описаного навколо даного кола,
дорівнює см 2 . Знайдіть периметр квадрата, вписаного в дане коло.
Високий рівень навчальних досягнень
9. Знайдіть площу квадрата, вписаного в коло, якщо площа правильного
шестикутника, вписаного в це коло, дорівнює см 2 .
Побудуйте рівнобеденний трикутник за медіаною проведеною до до основи і кутом між цієюміж цією медіаною та бічною стороною трикутника
дано м(-3;7), N(-1;1),P(1;3),При паралельному перенесенні середина відрізка MN переходить у точку Р. зробіть малюнок і вкажіть координати точок, у які
…
й переходить М і N.ДАЮ 40 БАЛОВ ПОЖАЛУЙСТА ПОМОГИТЕ ОЧЕНЬ СРОЧНО)
решите пожаааааааалуйста
Якій із координатних площин належить точка N(0;6;-4)
Площадь трапеции
— объяснение и примеры
Напомним, трапеция , также называемая трапецией , , представляет собой четырехугольник с одной парой параллельных сторон и другой парой непараллельных сторон. Подобно квадрату и прямоугольнику, трапеция также плоская. Следовательно, это 2D.
Подобно квадрату и прямоугольнику, трапеция также плоская. Следовательно, это 2D.
В трапеции параллельные стороны называются основаниями, а пара непараллельных сторон — ногами. Расстояние по перпендикуляру между двумя параллельными сторонами трапеции называется высотой трапеции.
Проще говоря, основание и высота трапеции перпендикулярны друг другу.
Трапеции могут быть как правыми трапециями (два угла 90 градусов), так и равнобедренными трапециями (две стороны одинаковой длины). Но иметь один прямой угол невозможно, потому что у него есть пара параллельных сторон, которые ограничивают его, образуя два прямых угла одновременно.
Из этой статьи вы узнаете:
- Как найти площадь трапеции,
- Как получить формулу площади трапеции и,
- Как найти площадь трапеции с помощью трапеции формула площади.
Как найти площадь трапеции?
Площадь трапеции — это область, покрытая трапецией в двухмерной плоскости. Это пространство, заключенное в 2D-геометрии.
Это пространство, заключенное в 2D-геометрии.
На рисунке выше трапеция состоит из двух треугольников и одного прямоугольника. Следовательно, мы можем вычислить площадь трапеции, взяв сумму площадей двух треугольников и одного прямоугольника.
Вывести формулу площади трапеции
Площадь трапеции ADEF = (½ x AB x FB ) + ( BC x FB ) + (½ x CD x EC )
= ( ¹ / ₂ × AB × h ) + ( BC × h ) + (¹ / ₂ × CD × h )
= ¹ / ₂ × h × ( AB + 2 BC + CD )
= ¹ / ₂ × h × ( FE + AD )
Но, FE = b 1 и AB = b 2
Следовательно, Площадь a трапеция ADEF ,
= ¹ / ₂ × h × (b 1 + b 2 ) ……………….(Это формула площади трапеции)
Формула площади трапеции
Согласно формуле площади трапеции, площадь трапеции равна половине произведения высоты и суммы двух оснований.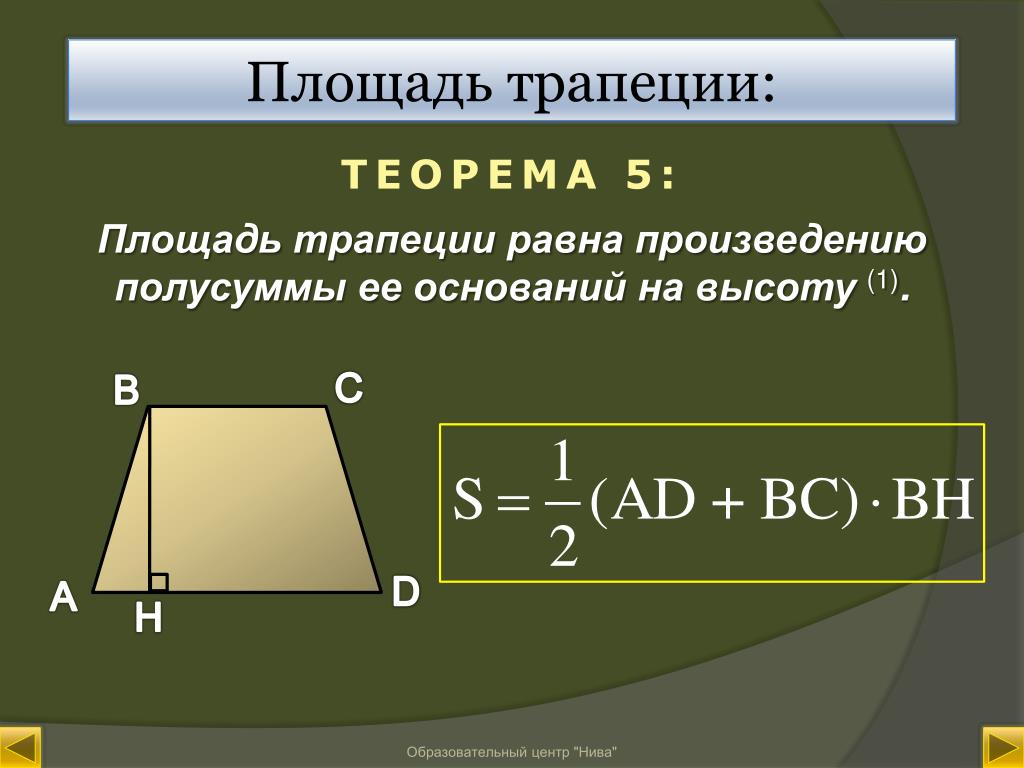
Площадь = ½ x (сумма параллельных сторон) x (расстояние по перпендикуляру между параллельными сторонами).
Площадь = ½ h (b 1 + b 2 )
Где h — высота, а b 1, и b 2 — параллельные стороны трапеции.
Как определить площадь неправильной трапеции?
Неправильная трапеция имеет непараллельные стороны неравной длины. Чтобы найти его площадь, нужно найти сумму оснований и умножить ее на половину высоты.
В вопросе иногда не хватает высоты, что можно найти с помощью теоремы Пифагора.
Как найти периметр трапеции?
Вы знаете, что периметр — это сумма всех длин внешнего края фигуры.Следовательно, периметр трапеции — это сумма длин всех 4 сторон.
Пример 1
Рассчитайте площадь трапеции, высота которой составляет 5 см, а основания — 14 см и 10 см.
Решение
Пусть b 1 = 14 см и b 2 = 10 см
Площадь трапеции = ½ h (b 1 + b 2 ) см 2
= ½ x 5 (14 + 10) см 2
= ½ x 5 x 24 см 2
= 60 см 2
Пример 2
Найдите площадь трапеции с высота 30 мм, а основания 60 мм и 40 мм.
Раствор
Площадь трапеции = ½ h (b 1 + b 2 ) кв. Единиц
= ½ x 30 x (60 + 40) мм 2
= ½ x 30 x 100 мм 2
= 1500 мм 2
Пример 3
Площадь трапеции составляет 322 квадратных дюйма. Если длины двух параллельных сторон трапеции составляют 19 дюймов и 27 дюймов, найдите высоту трапеции.
Раствор
Площадь трапеции = ½ часа (b 1 + b 2 ) кв.единицы измерения.
⇒ 322 квадратных дюйма = ½ x в x (19 + 27) кв. дюймов
⇒ 322 квадратных дюйма = ½ x h x 46 кв. дюймы
⇒ 322 = 23h
Разделите обе стороны на 23.
h = 14
Итак, высота трапеции составляет 14 дюймов.
Пример 4
Учитывая, что высота трапеции составляет 16 м, а длина одного основания — 25 м. Рассчитайте размер другого основания трапеции, если его площадь составляет 352 м 2 .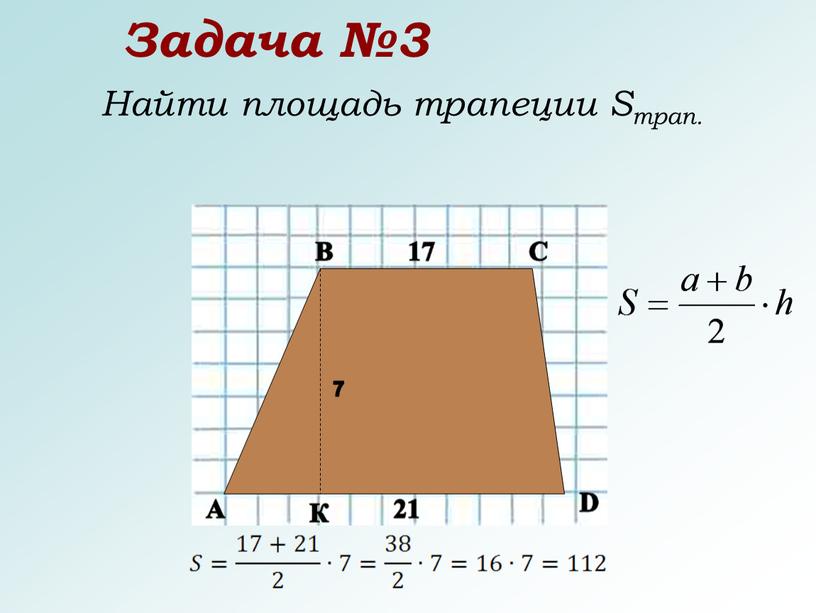
Решение
Пусть b 1 = 25 м
Площадь трапеции = ½ h (b 1 + b 2 ) кв. Единиц
⇒ 352 м 2 = ½ x 16 м x (25 m + b 2 ) кв. Единиц
⇒ 352 = 8 x (25 + b 2 )
⇒ 352 = 200 + 8b 2
Вычтите 200 с обеих сторон.
⇒ 152 = 8b 2
Разделите обе части на 8, чтобы получить;
b 2 = 19
Следовательно, длина другого основания трапеции составляет 19 м.
Пример 5
Рассчитайте площадь трапеции, показанной ниже.
Решение
Поскольку стороны (непараллельные стороны) трапеции равны, высоту трапеции можно рассчитать следующим образом;
Чтобы получить основание двух треугольников, вычтите 15 см из 27 см и разделите на 2.
⇒ (27-15) / 2 см
⇒ 12/2 см = 6 см
12 2 = h 2 + 6 2 По теореме Пифагора высота (h) рассчитывается как;
144 = h 2 + 36.
Вычтем 36 с обеих сторон.
h 2 = 108.
h = 10,39 см.
Следовательно, высота трапеции 10,39 см.
Теперь вычислите площадь трапеции.
Площадь трапеции = ½ ч (b 1 + b 2 ) кв. единицы измерения.
= ½ x 10,39 x (27 + 15) см 2 .
= ½ x 10,39 x 42 см 2 .
= 218,19 см 2 .
Пример 6
Одно основание трапеции на 10 м больше высоты.Если другое основание составляет 18 м, а площадь трапеции равна 480 м 2 , найдите высоту и основание трапеции.
Решение
Пусть высота = x
Другая база равна 10 м, чем высота = x + 10.
Площадь трапеции = ½ h (b 1 + b 2 ) Кв. единицы измерения.
Путем подстановки
480 = ½ * x * (x + 10 + 18)
480 = ½ * x * (x + 28)
Удалите скобки с помощью свойства распределения.
480 = ½x 2 + 14x
Умножьте каждый член на 2.
960 = x 2 + 28x
x 2 + 28x — 960 = 0
Решите квадратное уравнение, чтобы получить;
x = — 48 или x = 20
Подставьте положительное значение x в уравнение высоты и основания.
Высота: x = 20 м.
Другая база = x + 10 = 10 + 20 = 30 м.
Следовательно, другое основание и высота трапеции равны 30 и 20 м соответственно.
Практические задачи
- Найдите площадь трапеции, у которой есть параллельные основания длиной 9 единиц и 12 единиц, а высота равна 15 единицам.
- Для трапециевидной фигуры сумма параллельных оснований составляет 25 м, а высота — 10 м. Определите площадь этой фигуры.
- Рассмотрим трапецию площадью 112b квадратных футов, где b — более короткая базовая длина. Какова высота этой трапеции, если длины двух параллельных оснований таковы, что одно основание в два раза больше, чем другое основание?
Предыдущий урок | Главная страница | Следующий урок
Как рассчитать площадь неправильной трапеции
Обновлено 22 декабря 2020 г.
Эллиот Уолш
Хотя может показаться, что определение площади различных форм и многоугольников ограничивается школьным классом математики, Дело в том, что определение площади полигонов — это то, что применимо практически ко всем сферам жизни.От сельскохозяйственных расчетов до понимания области определенной экосистемы, от биологии до информатики, расчет областей сложной формы является важным навыком, который необходимо освоить.
Обычно проще измерить площадь фигур со всеми равными сторонами и простыми формулами. Однако «неправильные» формы, такие как неправильная трапеция, также известная как неправильная трапеция, обычны и также должны быть рассчитаны. К счастью, существуют калькуляторы площади неправильной трапеции и формула площади трапеции, которая упрощает процесс.
К счастью, существуют калькуляторы площади неправильной трапеции и формула площади трапеции, которая упрощает процесс.
Что такое трапеция?
Трапеция — это четырехсторонний многоугольник, также известный как четырехугольник, который имеет как минимум один набор параллельных сторон . Это отличает трапецию от параллелограмма, поскольку параллелограммы всегда имеют двух наборов параллельных сторон. Вот почему вы можете считать все параллелограммы трапециями, но не все трапеции параллелограммами.
Параллельные стороны трапеции называются основаниями , а непараллельные стороны трапеции называются опорами .Правильная трапеция, также называемая равнобедренной трапецией, представляет собой трапецию, у которой непараллельные стороны (ноги) равны по длине.
Что такое неправильная трапеция?
Неправильная трапеция, также называемая неправильной трапецией, — это трапеция, у которой непараллельные стороны не равны по длине. То есть у них ноги двух разной длины.
То есть у них ноги двух разной длины.
Формула площади трапеции
Чтобы найти площадь трапеции, вы можете использовать следующее уравнение:
\ text {Area} = \ bigg (\ frac {b_1 + b_2} {2} \ bigg) × h
b 1 и b 2 — длины двух оснований трапеции; h равна высоте трапеции, которая представляет собой длину от нижнего основания до верхней базовой линии.
Вы не всегда учитываете высоту трапеции. В таком случае высоту часто можно вычислить с помощью теоремы Пифагора.
Как рассчитать площадь неправильной трапеции: заданные значения
Этот первый пример представляет проблему, когда вы знаете все значения трапеции.
b_1 = 4 \ text {cm} \\ b_2 = 12 \ text {cm} \\ h = 8 \ text {cm}
Просто подставьте числа в формулу площади трапеции и решите.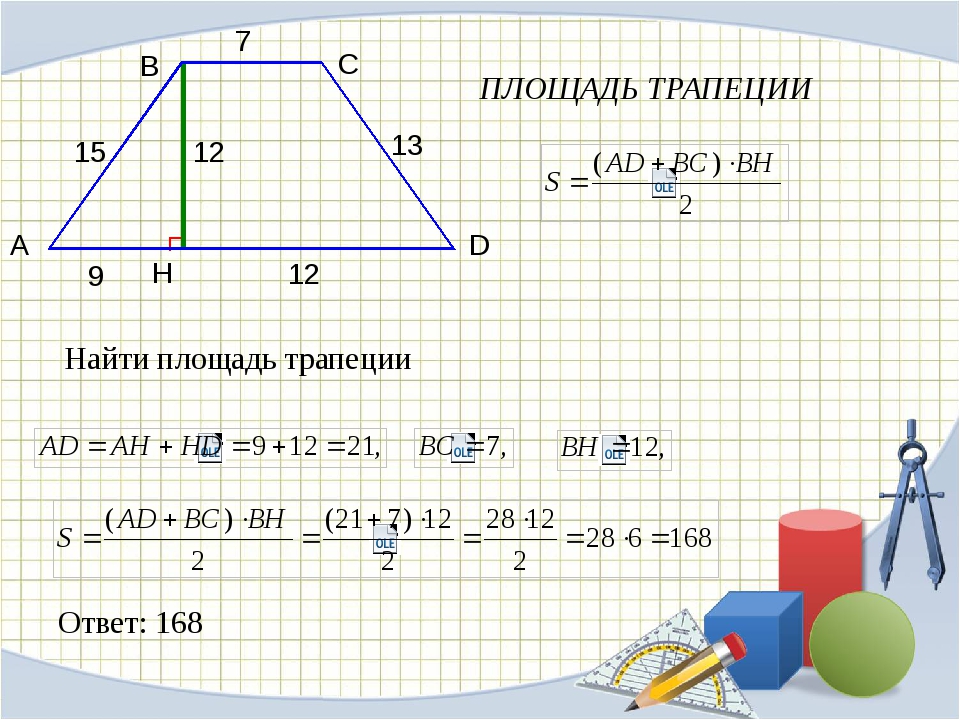 2 \ end {align}
2 \ end {align}
Как рассчитать площадь неправильной трапеции: определение высоты неправильной трапеции
В других проблемах или ситуациях с неправильными трапециями вам часто дают только размеры оснований и опоры трапеции вместе с некоторыми углами трапеции, что позволяет вам рассчитать высоту самостоятельно, прежде чем вы сможете рассчитать площадь.
Затем вы можете использовать длину и углы, чтобы вычислить высоту трапеции, используя общие правила треугольного угла.
Подумайте об этом. . . когда вы рисуете линию высоты на трапеции в конечной точке от меньшей базовой длины до более длинной базовой длины, вы создаете треугольник с этой линией в качестве одной стороны, катетом трапеции в качестве второй стороны и расстоянием от точка, в которой линия высот касается большего основания, до точки, где это основание встречается с ногой в качестве третьей стороны (см. подробное изображение здесь).
подробное изображение здесь).
Допустим, у вас есть следующие значения (см. Изображение на этой странице):
b_1 = 16 \ text {cm} \\ b_2 = 25 \ text {cm} \\ \ text {leg} 2 = 12 \ text { cm} \\ \ text {Угол между} b_2 \ text {и ногой} 2 = 30 \ text {градусы}
Знание углов и одного из значений длины стороны означает, что вы можете затем использовать правила sin и cos, чтобы найти высота.Гипотенуза будет равна катету 2 (12 см), и у нас есть углы для вычисления высоты.
Давайте используем sin, чтобы найти высоту, используя заданный угол 30 градусов, что сделает высоту равной «противоположной» в уравнении sin:
\ sin (\ text {angle}) = \ frac {\ text {height }} {\ text {hypotenuse}} \\ \, \\ \ sin (30) = \ frac {\ text {height}} {12 \ text {cm}} \\ \, \\ \ sin (30) × 12 \ text {cm} = \ text {height} = 6 \ text {cm}
Теперь, когда у вас есть значение высоты, вы можете вычислить площадь, используя формулу площади:
\ begin {align} A & = \ bigg (\ frac {b_1 + b_2} {2} \ bigg) × h \\ & = \ bigg (\ frac {b_1 + b_2} {2} \ bigg) × h \\ & = \ bigg (\ frac {16 \ text {cm} + 25 \ text {cm}} {2} \ bigg) × 6 \ text {cm} \\ & = \ bigg (\ frac {41 \ text {cm}} {2} \ bigg) × 6 \ текст {см} \\ & = 20.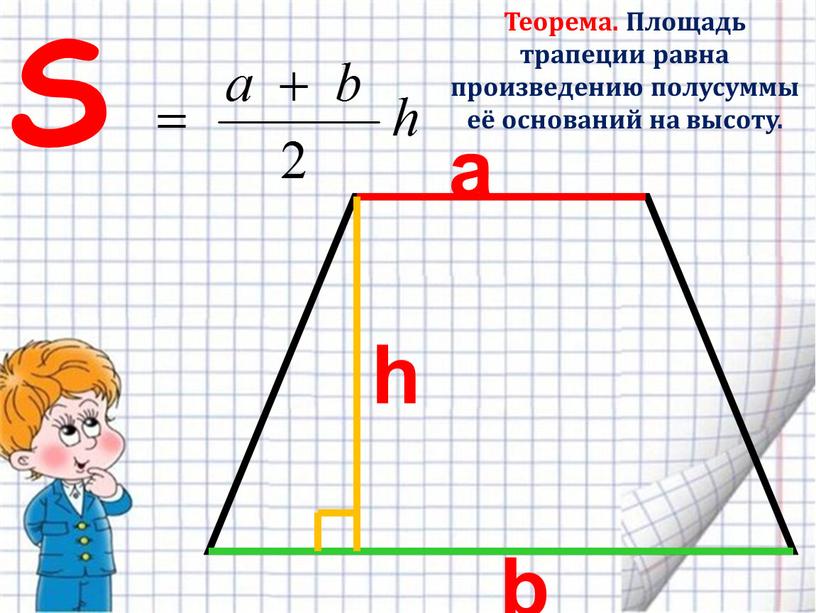 2 \ end {align}
2 \ end {align}
Трапеции: площадь и периметр
А
трапеция
, также называемый
трапеция
в некоторых странах это
четырехугольник
ровно с одной парой
параллельно
стороны.
Параллельные стороны называются
базы
а непараллельные стороны — это
ноги
трапеции.
An
равнобедренная трапеция
представляет собой трапецию, у которой две непараллельные стороны
конгруэнтный
.
В
область
А
трапеции определяется выражением
А
знак равно
б
1
+
б
2
2
час
где
б
1
а также
б
2
— длины двух параллельных сторон, и
час
это высота, как показано на рисунке ниже.
В
периметр
трапеции — это сумма длин ее четырех сторон.Если одна или несколько длин неизвестны, иногда можно использовать
Теорема Пифагора
найти это.
Пример:
Найдите площадь и периметр показанной трапеции.
Чтобы найти площадь, примените формулу.
А
знак равно
б
1
+
б
2
2
час
знак равно
3
+
11
2
(
7
)
знак равно
7
(
7
)
знак равно
49
квадратный
единицы измерения
Чтобы найти периметр, сложите длины всех четырех сторон.
п
знак равно
3
+
10
+
11
+
8
знак равно
32
единицы измерения
Площадь трапеции. Определение, формула и калькулятор
Площадь трапеции. Определение, формула и калькулятор — Открытый справочник по математике
Количество квадратных единиц, необходимое для полного заполнения
трапеция.
Формула: Средняя ширина × высота
Попробуйте это Перетащите оранжевые точки, чтобы переместить трапецию и изменить ее размер. Как размер трапеции
изменяется, производится пересчет площади.
Формула площади
Площадь трапеции равна средней ширине, умноженной на высоту, или по формуле:
где
b1, b2 — длины каждого основания
h — высота (высота)
Напомним, что основания — это две параллельные стороны трапеции.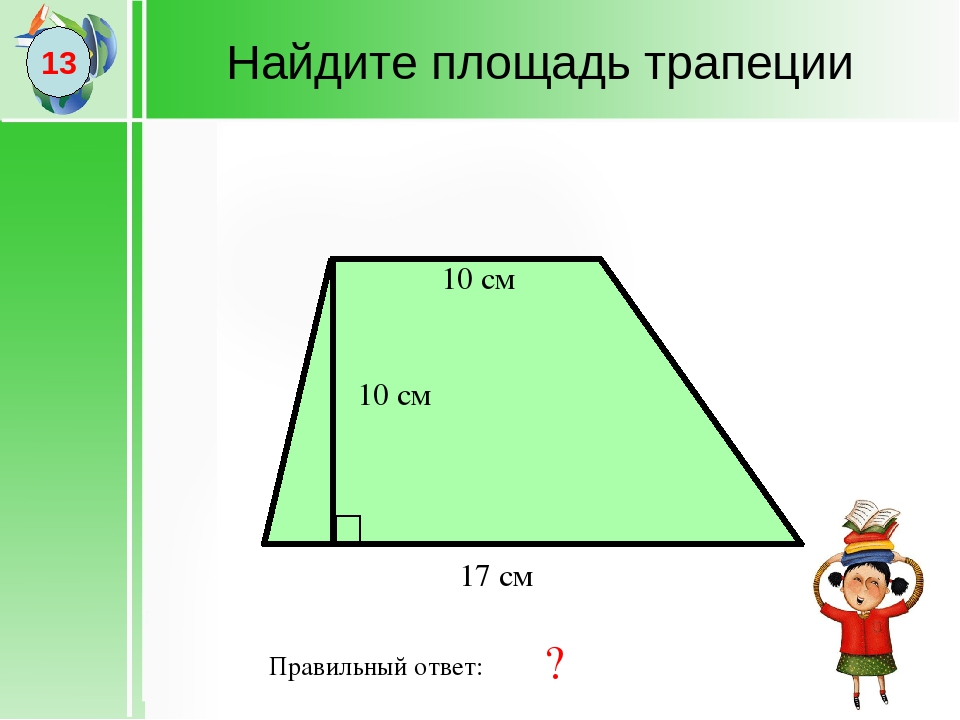
Высота (или высота) трапеции — это
перпендикулярное расстояние
между двумя базами.
В приведенном выше апплете нажмите «заморозить размеры». Когда вы перетаскиваете любую вершину, вы увидите, что трапеция перерисовывается, сохраняя неизменными высоту и основания. Обратите внимание, как область в отображаемой формуле не меняется. Площадь зависит только от высоты и базовой длины, поэтому, как вы можете видеть, существует множество трапеций с заданным набором размеров, которые имеют одинаковую площадь.
Вывод формулы
См. Раздел «Как получить формулу площади трапеции».
Калькулятор
Используйте калькулятор выше, чтобы рассчитать высоту, базовую длину и площадь трапеции.
Введите любые три значения, и будет вычислено недостающее.
Например: введите высоту и две базовые длины и нажмите «Рассчитать». Площадь будет рассчитана.
Точно так же, если вы введете площадь и две длины основания, будет рассчитана высота, необходимая для получения этой площади.
Нахождение высоты по площади
Как найти высоту (высоту) трапеции, задайте две базы и площадь.Приведенная выше основная формула площади имеет четыре переменные (площадь, два основания и высоту). Если мы знаем какие-то три, мы всегда сможем найти четвертый.
Так, например, если мы знаем площадь и две базы, мы можем найти высоту, просто изменив основную формулу:
Где a — это площадь, а b1, b2 — две базы.
Нахождение базы в районе
Как найти основание трапеции, укажите одно из оснований, высоту и площадь.
Приведенная выше основная формула площади имеет четыре переменные (площадь, два основания и высоту).Если мы знаем какие-то три, мы всегда сможем найти четвертый.
Так, например, если мы знаем площадь, одно основание и высоту, мы можем найти недостающее основание, просто изменив основную формулу:
Где a — это площадь, b — известная база, а h — высота (высота).
Если известно медианное значение
Напомним, что
медиана (м) трапеции
это отрезок прямой, соединяющий середины непараллельных сторон.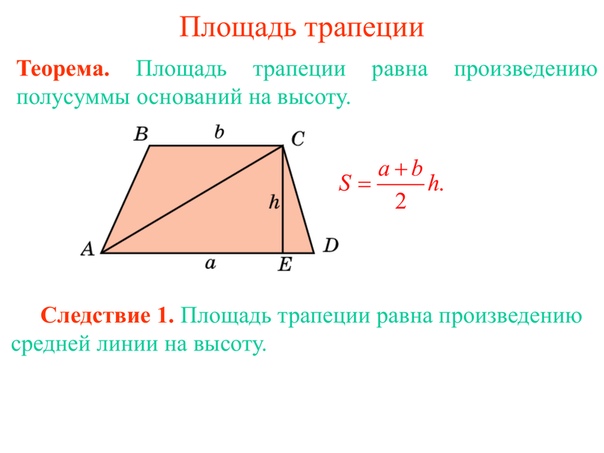 Напомним также, что длина медианы — это среднее значение двух параллельных сторон.См. Медиана трапеции
Напомним также, что длина медианы — это среднее значение двух параллельных сторон.См. Медиана трапеции
Где м — это медиана, а ч — высота (высота).
Площадь сложной формы
Другой способ найти площадь трапеции — рассматривать ее как более простые формы, а затем добавлять или вычитать их площади, чтобы найти результат. Для
Например, трапецию можно рассматривать как меньший прямоугольник плюс два прямоугольных треугольника:
Дополнительные сведения об этой общей технике см. В разделе «Область неправильных многоугольников».
Координатная геометрия
В координатной геометрии, если вы знаете координаты четырех вершин,
вы можете рассчитать различные его свойства, в том числе площадь и периметр.Для получения дополнительной информации см. Площадь и периметр трапеции (Координатная геометрия).
Что попробовать
- На рисунке выше нажмите «скрыть детали»
- Перетащите оранжевые точки на вершинах, чтобы создать трапецию произвольного размера.

- Рассчитайте площадь по формуле
- Теперь попробуйте оценить площадь трапеции, просто глядя на
квадрата внутри нее - Когда вы закончите, нажмите «Показать подробности», чтобы увидеть, насколько близко вы подошли.
Другие темы о многоугольниках
Общие
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные полигоны
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Трапеция
(Перейти к области трапеции или периметру трапеции)
Трапеция — это четырехсторонняя плоская форма с прямыми сторонами, имеющая пару противоположных сторон, параллельных (отмечены стрелками ниже):
| Трапеция | Равнобедренная трапеция |
Трапеция:
| имеет пару параллельных сторон | |
— это равнобедренная трапеция , когда она имеет равных углов от параллельной стороны | |
называется « трапеция » в Великобритании (см.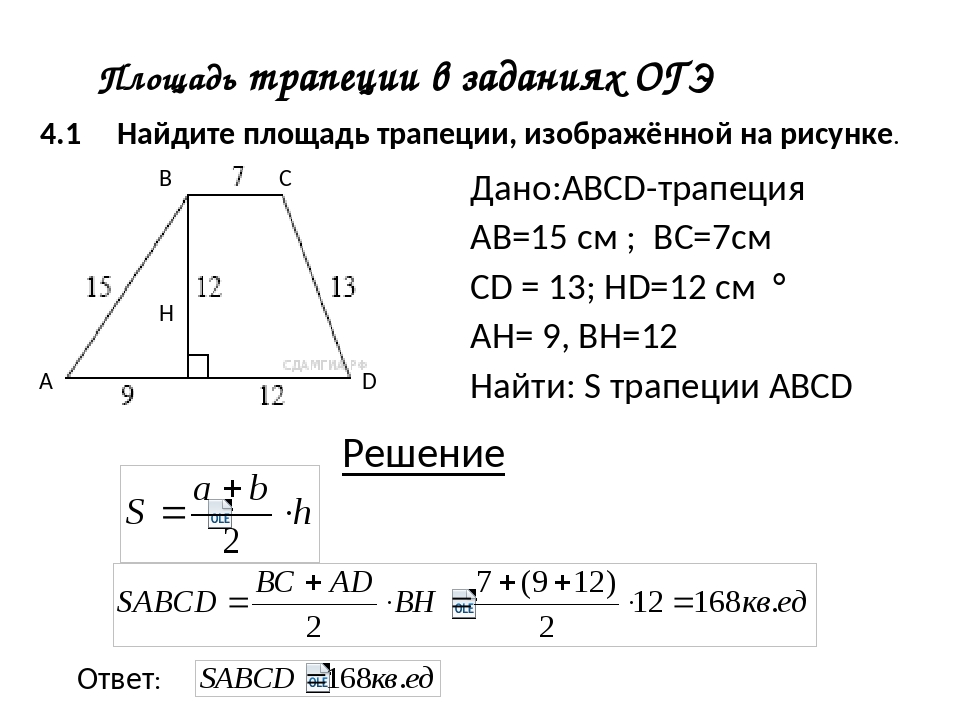 Ниже) Ниже) |
Люфт трапецией:
Параллельные стороны — это «основания»
Две другие стороны — «ножки»
Расстояние (под прямым углом) от одной базы до другой называется «высотой»
Площадь
трапеции
Площадь — это среднее значение для двух базовых длин, умноженное на высоту : Площадь = a + b 2 × h |
Пример: два основания трапеции составляют 6 м и 4 м, а высота — 3 м.Какова его площадь?
Площадь = 6 м + 4 м 2 × 3 м = 5 м × 3 м = 15 м 2
Инструмент «Площадь многоугольника путем рисования» полезен, когда вы можете нарисовать трапецию.
Периметр трапеции
Периметр — это расстояние по краям.
Периметр равен сумме длин всех сторон : Периметр = a + b + c + d |
Пример: Трапеция имеет длину стороны 5 см, 12 см, 4 см и 15 см.
 Каков ее периметр?
Каков ее периметр?
Периметр = 5 см + 12 см + 4 см + 15 см = 36 см
Медиана трапеции
Медиана (также называемая средней линией или срединным сегментом) — это линейный сегмент на полпути между двумя основаниями. Средняя длина — это среднее значение двух базовых длин: м = а + б 2 |
Вы можете вычислить площадь, зная медианное значение, это просто медиана, умноженная на высоту:
Площадь = mh
Трапеция
Трапеция (UK: trapezoid) — четырехугольник без параллельных сторон.
Определения США и Великобритании поменялись местами, например:
| Трапеция | Трапеция | |
| США: | пара параллельных сторон | НЕТ параллельных сторон |
| Великобритания: | НЕТ параллельных сторон | пара параллельных сторон |
3 калькулятора трапеций Прокрутите вниз для получения инструкций и определений. Площадь трапеции = ((сумма оснований) ÷ 2) • высота
|
Что такое трапеция? [Определение, факты и пример]
Что такое трапеция?
Трапеция, также известная как трапеция, представляет собой плоскую замкнутую форму, имеющую 4 прямые стороны с одной парой параллельных сторон.
Параллельные стороны трапеции называются основаниями, а непараллельные стороны — ножками. У трапеции тоже могут быть параллельные ножки. Параллельные стороны могут быть горизонтальными, вертикальными или наклонными.
Расстояние по перпендикуляру между параллельными сторонами называется высотой.
Примеры :
Без примеров :
Типы трапеций
Трапеция бывает трех типов, а именно
1. Правая трапеция : Имеет пару прямых углов.
2. Равнобедренная трапеция : имеет равную длину непараллельных сторон. На изображении стороны AD и BC равны.
3. Трапеция из чешуи : у нее нет равных углов и равных сторон.
Свойства трапеции
Трапеция называется параллелограммом, если обе пары ее противоположных сторон параллельны.
Трапеция — это квадрат, если обе пары его противоположных сторон параллельны; все его стороны равной длины и расположены под прямым углом друг к другу.
Трапеция может быть прямоугольником, если обе пары ее противоположных сторон параллельны; его противоположные стороны равны по длине и расположены под прямым углом друг к другу.
Примеры из реальной жизни
Некоторые из многих примеров трапеции — это лицевая сторона коробки для попкорна, сумочки и мостов.
Интересные факты
|

