Как по диагоналям найти стороны ромба: Сторона ромба | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Как найти сторону ромба?

Ромб представляет собой равносторонний параллелограмм.

Свойства ромба:

диагональ является биссектрисой;
диагонали пересекаются в точке, которая делит их пополам. При этом угол пересечения — 90 градусов;
противоположные стороны параллельны относительно друг друга;
если у ромба прямые углы, то это — квадрат.

Основные формулы:

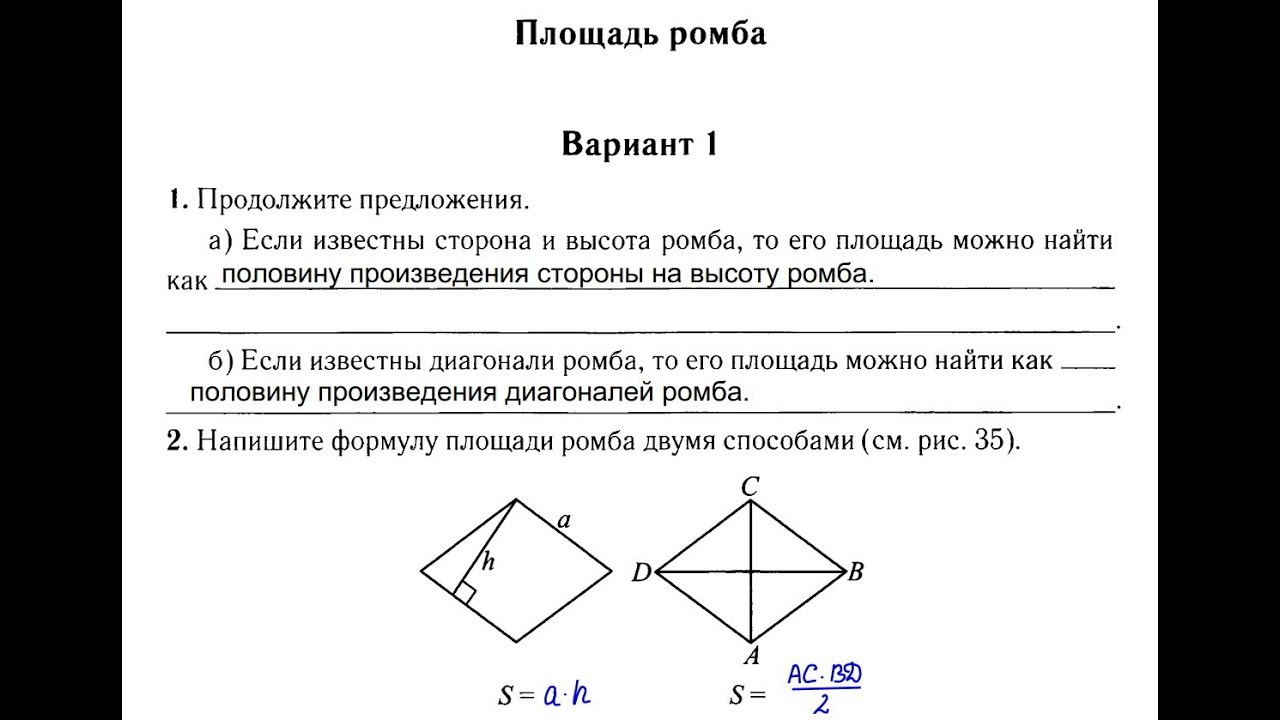
Площадь ромба S можно найти по следующим формулам:

S = ah
S = 2 · r · a, где r – радиус вписанной в ромб окружности, а – сторона ромба.
S = (d1 · d2)/2, где d1 и d2 – диагонали ромба;

где :

a — сторона ромба;
h — высота;
d1 и d2 — диагонали;
r — радиус вписанного круга;

Как найти сторону ромба?

Если нам необходимо найти сторону ромба, то это можно сделать несколькими способами. Рассмотрим на примере. Дан ромб ABCD. Его диагонали — AC и BD:

Рассматриваем неизвестную сторону как гипотенузу прямоугольного треугольника (половины диагоналей ромба — катеты этого треугольника). Вспоминаем теорему Пифагора и находим нужную сторону. А именно, сумма квадратов половины диагоналей ромба будет равняться квадрату искомой стороны.
Если известна площадь ромба и один из его углов, то искать сторону можно с помощью формулы:
- S = a² sinα
- Где: a — сторона ромба;
- α — известный угол между сторонами.
- Из предыдущей формулы выводим, что сторону ромба можно вычислить по формуле: a = √( S/ sinα)

В случае, когда известны только диагонали, сторону можно найти по формуле:

a = (√D²+d²)/2
Где:
D — большая диагональ ромба;

d — меньшая диагональ ромба.

2).

Пусть нам известны площадь ромба (ABCD) и его высота (BH), т.е. длина перпендикуляра, опущенного из вершины (B) на сторону (AD) (или ее продолжение). Как определить сторону ромба (AB) в этом случае?

Как видно из рисунка, ромб состоит из двух треугольников (ABD и DBC) площадь каждого из которых равняется половине произведения высоты на основание. Следовательно площадь ромба будет равна произведению высоты на длину стороны. Отсюда получается простая формула для вычисления длины стороны ромбы: нужно его площадь разделить на длину высоты.

|AB|=S/|BH|

Если известна величина угла ромба и длина одной из диагоналей, то нахождение стороны ромба производится аналогично первому случаю, только вместо теоремы Пифагора необходимо использовать тригонометрические соотношения. При этом следует учесть, что диагонали ромба являются одновременно биссектрисами углов, то есть делят их пополам.

Пусть, например, нам известна величина угла BAD и длина выходящей из него диагонали АС. Исходя из тригонометрических зависимостей в прямоугольном треугольнике ABO, получаем, что длина стороны ромба будет равна частному от половины исходящей диагонали на синус половины угла.

В виде формулы эта зависимость будет выглядеть следующим образом:

|AB|= (|AC|/2)/sin(α/2), где α — величина угла BAD.

Аналогично вычисляется длина стороны ромба в случае, когда заданы другие параметры — длина противоположной углу диагонали, соотношение диагоналей и т.д. Для определения стороны ромба достаточно лишь выбрать подходящую тригонометрическую функцию — косинус, тангенс и т.п.

4, а площадь равна 24 дм 2

РОМБ

Параллелограмм, у которого все стороны равны, называется ромбом.

Свойства ромба:

Диагонали ромба перпендикулярны и являются биссектрисами углов.
Площадь ромба: S=ah, S=(d₁·d₂)/2, где d₁и_{d₂— диагонали ромба, S=2·r·a, где r-радиус вписанной окружности, а-сторона ромба.}

Задача №1

Найти сторону ромба, если его диагонали относятся как 3:4, а площадь равна 24 дм².

Решение: Площадь ромба находится по формуле:

по условию задачи,

, подставив значения, имеем

, значит

BD=8дм, .

.
Ответ: .
Задача №2

Диагонали ромба равны 48 и 14см, Найти его сторону, радиус вписанной окружности.

Решение:

У ромба диагонали точкой пересечения делятся пополам.

AО=AC/2=7 cм

BО=BD/2=24 см

AОB-прямоугольный треугольник, так как диагонали ромба

перпендикулярны.

АВ²=AО²+BО²,

AB²=7²+24²,

AB²=49+576,

АВ² = 625, значит

АВ = 25 см. Так как RМ gif» name=»object18″ align=absmiddle width=17 height=18> АВ, . S =48·14/2=336 (см²) и S=2·r·a, где r-радиус вписанной окружности, а-сторона ромба. 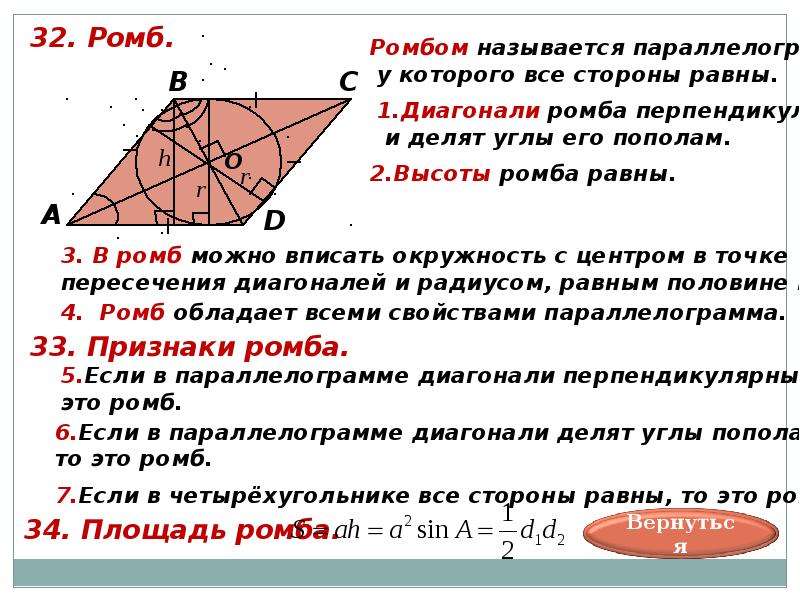r = S/2а, r =336/50=6, 72 (см).

Ответ: 25 см, 6, 72 см.
Задача №3
Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромба равна 27см².

Решение:
1-ый способ:

ВD=1,5·АС

ВО=1,5·АС/2

S_ромба=0, 5·ВD·AC

27=1/2·1,5·АС·АС

27=0,75·АС²

АС²=27:0,75=36 (см²), значит

АС=6 см

ВD=1,5·6=9 (см).
2-ой способ:

S_ромба=1/2·d₁·d_2;S_ABCD=27cм²

Пусть АС= х, ВD=1,5х

1/2х · 1/5х =27 1/2 · 3/2х² =27

3/4х²=27 х²=27·4/3

х²=36, х=6см

1,5·6=9(см)=ВД

Ответ: АС=6см, ВД=9см.

Задача №4
Найдите сторону и площадь ромба, если его диагонали равны 10см и 24см.

Решение:

S=1/2 · АС · ВD =240/2=120 (см²)

АС²+ВD²=2(АВ²+ВС²)

100+576=4 · АВ² => АВ²=169

АВ=13

АВ=ВС=СD=АD=13см

S_ромба=120см²

Ответ:АВ=13см, S=120см².

Задача №5
Диагонали ромба равны 18м и 24м. Найдите периметр ромба и расстояние между параллельными сторонами.

Решение:

АС²+ВD²= 4АВ²

324+576=4·АВ²

АВ²=900/4=225

АВ=15м

Р=15·4=60(м)

ЕF-высота

S=d₁·d₂/2=18·24/2=216(м²)

S=a·h

216=15·h => h=216/15 => h=14, 4м.

Ответ: Р=60м, ЕF=14,4.
Зачёт по теме «Ромб».
Повторите:

свойства ромба;
теорему Пифагора;
нахождение площади ромба по его диагоналям;
вычисление высоты по известной площади;
нахождение радиуса вписанной в ромб окружности.

Индивидуальное задание.

Задание-1.

Дано: а, d_1.

Найти: 1) d₂, 2) S, 3) h, 4) r.

Задание-3.

Дано: а, S.

Найти: 1) h 2) r_, 3), d₂, 4) d₁.

Задание-2.

Дано: d₁, d_2.

Найти: 1)а, 2) S, 3) h, 4) r.

Задание-4.

Дано: S, h_.

Найти: 1)а,2) r , 3) d₁, 4) d_2.

Таблица данных и ответов к индивидуальным заданиям.

Номер варианта	а	d₁	d₂	S	h	r
1	5	8	6	24	4,8	2,4
2	10	16	12	96	9,6	4,8
3	15	24	18	216	14,4	7,2
4	20	32	24	384	19,2	9,6
5	25	40	30	600	24	12
6	30	36	48	864	28,8	14,4
7	25	48	14	336	13,44	6,72
8	35	56	42	1176	33,6	16,8
9	40	64	48	1536	38,4	19,2
10	45	72	54	1944	43,2	21,6
11	50	80	60	2400	48	24
12	55	88	66	2904	52,8	26,4
13	60	96	72	3456	57,6	28,8
14	65	104	78	4056	62,4	31,2
15	70	112	84	4704	67,2	33,6
16	75	120	90	5400	72	36
17	80	128	96	6144	76,8	38,4
18	85	136	102	6936	81,6	40,8
19	90	144	108	7776	86,4	43,2
20	95	152	114	8664	91,2	45,6
21	100	160	120	9600	96	48
22	105	168	126	10584	100,8	50,4
23	110	176	132	11616	105,6	52,8
24	115	184	138	12696	110,4	55,2
25	120	192	144	13824	115,2	57,6

Как найти диагональ ромба?

Параллелепипед — это геометрическая фигура (призма) у которой противоположные грани параллельны и имеют форму параллелограмма и эти грани могут образовывать между собой разные углы.

Попробуем самостоятельно найти объем наклонного параллелепипеда

для этого возьмем произвольный параллелепипед. установим его на горизонтальную поверхность и по высоте опущенной к основанию разрежем его (теоретически) на какое-то число n и например получим высоту этого тоненького параллелепипеда 0,001 мм. Он настолько тонкий, что наклоном можно пренебречь и тогда его объем посчитаем следующим образом

V(тоненького параллелепипеда) = S(параллелограмма (основания параллелепипеда))*0,001

а объем всего параллелепипеда

V(параллелепипеда) = S(основания)*0,001*n = S(основания)*h(высоту)

В случае с прямоугольным параллелепипедом формула наберет вида

V(прямоугольного параллелепипеда) = abc

где a, b, c длина его ребер.

Это химическая формула тестостерона- мужского полового гормона. Вырабатывается в основном половыми железами, главным образом семенниками;надпочечниками, плацентой и печенью. По химической природе является стероидом. Отвечает за формирование первичных и вторичных половых признаков. В медицине применяется для лечения расстройств функций мужских половых желез, а также у женщин при лечении некоторых видов опухолей и климактерических расстройствах.

ГИДРОКСИД АММОНИЯ (10%-35% раствор) — химическая формула:

Nh5OH

Молекулярная масса: 35.1

физические свойства

Температура кипения: (25%) 38°C

Температура плавления: (25%) -58°C

Относительная плотность (вода = 1): (25%) 0.9

Растворимость в воде: смешивается

Давление паров, кПа при 20°C: (25%) 48

Относительная плотность пара (воздух = 1): 0.6-1.2

В предложенной задаче мы получаем произведение числа А и 10 чисел Б.

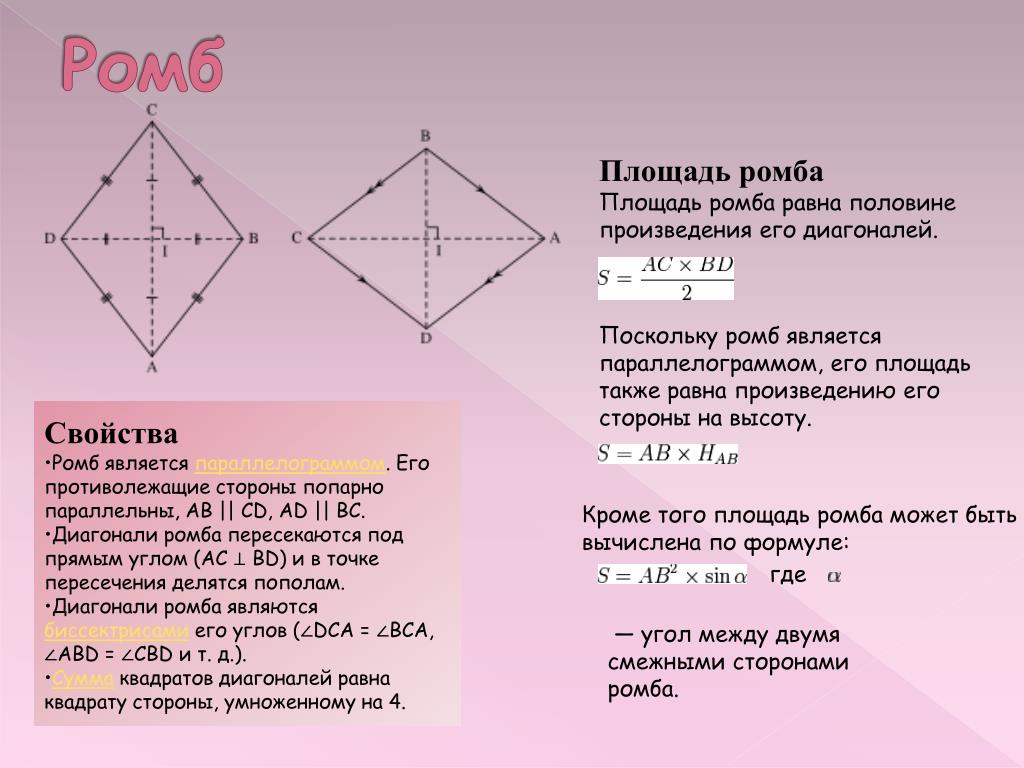
А*Б*Б*Б*Б*Б*Б*Б*Б*Б*Б

Вначале воспользуемся таким свойством умножения как коммутативность. Т.е. от перестановки множителей произведение не меняется.

Б*Б*Б*Б*Б*Б*Б*Б*Б*Б*А

Когда число умножают само на себя, это действие называется возведение в степень. Основание степени Б, показатель степени 10. К сожалению, я не могу здесь написать значками Б в 10-й степени. Поэтому окончательное выражение пишу словами.

А умножить на Б в 10-й степени. Степень относится только к числу Б.

Чтобы посчитать сумму значений ячеек обычно используется функция СУММ, а в качестве аргументов пишутся либо значения, либо диапазоны ячеек либо сами ячейки.

Если требуется вычислить сумму значений ячеек разных диапазонов, то эти диапазоны перечисляются как аргументы функции сумм.

Формула

=СУММ(A3:A8 ; C3:h4)

вычислит сумму чисел, находящихся в ячейках из диапазона A3:A8 и диапазона C3:h4

Если диапазоны чисел находятся на разных листах одной книги, то перед ссылкой на диапазон надо указать наименование листа с восклицательным знаком

=СУММ( A3:A8 ; C3:h4 ; Лист2!A1:A6 )

если диапазоны суммирования находятся в разных книгах, то придется указать и название книги в квадратных скобках пример:

=СУММ(A3:A8 ; C3:h4 ; [Книга3]Лист2!A1:A6 )

всего в функции СУММ можно указывать от 1 до 255 аргументов.

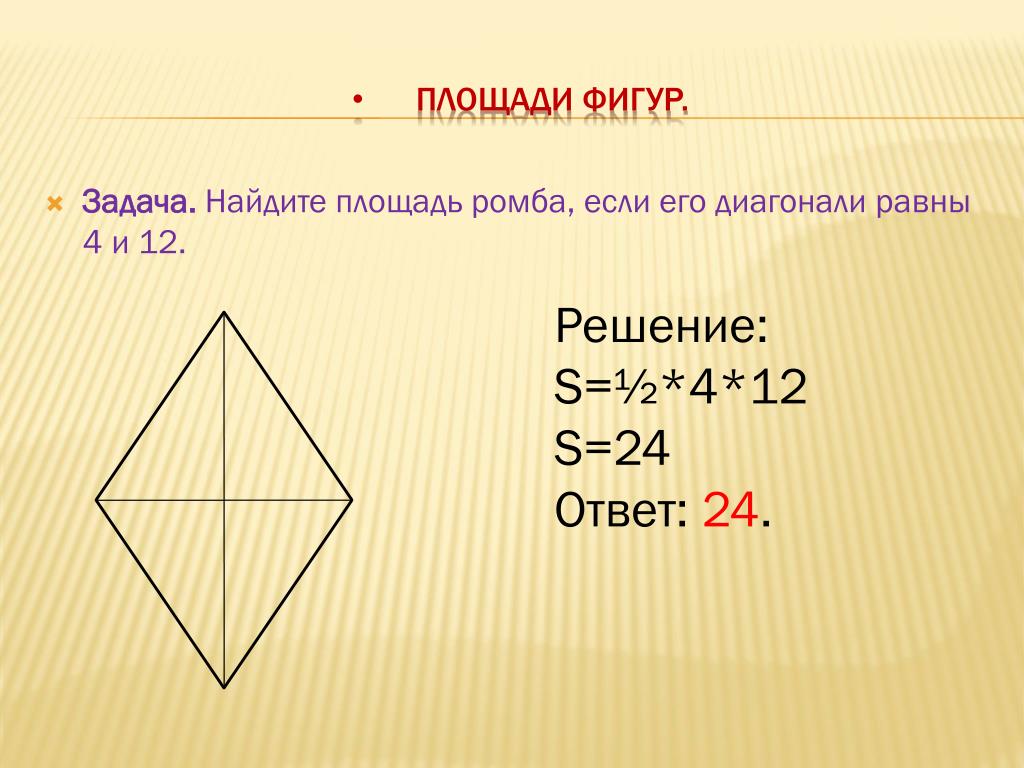
Задачи категории В8. Ромб. Прямоугольник

Продолжаем решать простейшие геометрические задачки, связанные с углами.

Разбираем Задачи №6 ЕГЭ по математике.

Сегодня работаем с ромбом и с прямоугольником.

В категорию «Задания №6» входят также задачи следующих типов + показать

Вы можете пройти автотренинг «Планиметрия»

Ромб

Задача 1.

В ромбе угол равен . Найдите угол . Ответ дайте в градусах.

Решение: + показать

1) По свойству ромба соседние углы в сумме дают .

Значит

2) По свойству ромба диагонали являются биссектрисами углов.

Значит,

Ответ: 72.

Задача 2.

Найдите меньшую диагональ ромба, стороны которого равны 38, а острый угол равен .

Решение: + показать

Задача 3.

Найдите высоту ромба, сторона которого равна , а острый угол равен .

Решение: + показать

Задача 4.

Диагонали ромба равны 12 и 16 см. Найти сторону ромба.

Решение: + показать

По свойству ромба диагонали ромба перпендикулярны и в точке пересечения делятся пополам.

Значит в прямоугольном треугольнике нам известны катеты: .

Тогда по т. Пифагора

Ответ: 10.

Прямоугольник

Задача 1.

Меньшая сторона прямоугольника равна 20, диагонали пересекаются под углом . Найдите диагонали прямоугольника.

Решение: + показать

Задача 2.

В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 41. Найдите диагональ данного прямоугольника.

Решение: + показать

Задача 3.

Диагональ прямоугольника вдвое больше одной из его сторон. Найдите больший из углов, которые образует диагональ со сторонами прямоугольника? Ответ выразите в градусах.

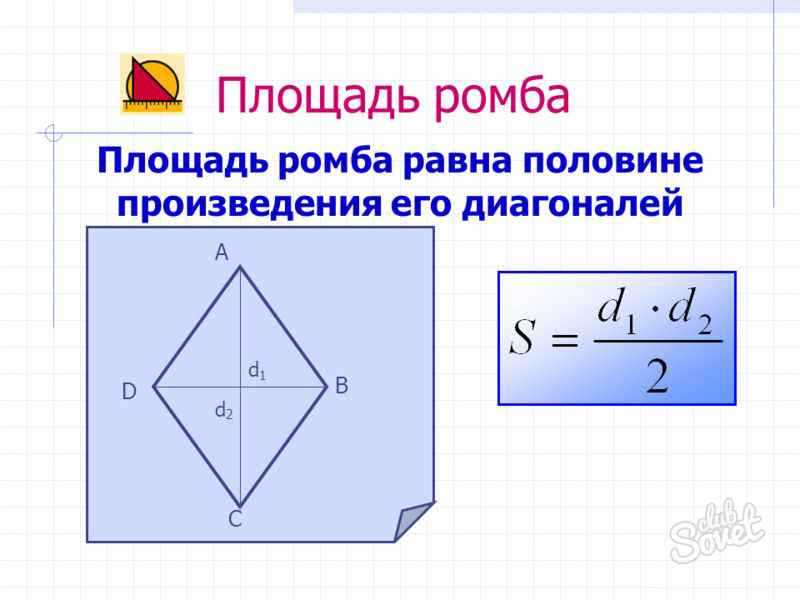
Решение: + показать

Диагональ прямоугольника – гипотенуза прямоугольного треугольника. Так как она вдвое больше одной из сторон прямоугольника (катета прямоугольного треугольника), то угол, лежащий против этой стороны, равен .

Тогда больший угол, который образует диагональ со сторонами прямоугольника, –

Ответ: 60.

Вы можете пройти тест по теме «Ромб. Прямоугольник»

Ромб в основании призмы

Задача.

Основание прямой призмы — ромб с углом 120 градусов. БОльшая диагональ призмы равна 8см и составляет с боковым ребром угол 60 градусов. Найти сторону ромба и меньшую диагональ призмы.

Решение.

Поскольку диагональ AC1 образует с ребром AA1 угол 60 градусов, призма является прямой, то угол C1AC равен 90 — 60 = 30 градусов.

Исходя из этого cos 30 = AC / AC1 = √3 / 2

AC / AC1 = √3 / 2

AC / 8 = √3 / 2

2AC = 8√3

AC = 4√3

Поскольку угол ADC равен 120 градусам, то угол BAD равен 60 градусам. (Сумма углов выпуклого четырехугольника равна 180(n-2) = 360 градусам, углы ромба попарно равны).

Исходя из того, что угол BAD равен 60 градусам, треугольники ABD и BDC- равносторонние. (Так как ABCD — ромб, то они равнобедренные, следовательно углы при основании равны, значит они равны ( 180 — 60 ) / 2 = 60 градусов. Треугольник, у которого все углы равны — равносторонний).

Диагонали параллелограмма в точке пересечения делятся пополам. Таким образом, AO = AC / 2 = 4√3 / 2 = 2√3

Поскольку треугольник ABD правильный, то AO является одновременно высотой и биссектрисой. Учтем, что высота правильного треугольника равна

h = а √3 / 2, тогда

а √3 / 2 = 2√3

а = 4

Зная, что BD = 4 см, DD1 = 4 см, по теореме Пифагора найдем меньшую диагональ:

BD12 = 4 + 4

Таким образом, сторона ромба равна 4 см, а, так как треугольники ABD и BDC- равносторонние, то и меньшая диагональ ромба равна 4 см.

Для того, чтобы найти длину ребра призмы, учтем, что диагональ AC1 = 8 см, а угол C1AC = 30 градусам. Тогда sin 30 = C1C / AC1 = 1/2

C1C / 8 = 1/2

C1C = 4 см

Зная что BD = 4 см (меньшая диагональ ромба), D1D = 4 см (ребро призмы), длину меньшей диагонали призмы найдем по теореме Пифагора:

BD1² = DD1² + BD²

BD1² = 4² + 4²

BD1² = 32

BD1 = 4√2

Ответ: Сторона ромба — 4 см, меньшая диагональ призмы с ромбом в основании равна 4√2 см.

Параллелограмм в основании призмы |

Описание курса

| Пирамида. Решение задач

Ромб — свойства, признаки и формулы нахождения параметров

В геометрии существуют задачи, в которых необходимо находить некоторые параметры ромба. Чтобы применить соотношения, фигуру нужно сначала правильно идентифицировать. Эта операция является очень важной, поскольку от нее зависит правильность дальнейшего решения. После этого шага следует использовать свойства и формулы, ускоряющие процесс нахождения неизвестной величины.

Общие сведения

Ромб является четырехугольником. В геометрии существует несколько видов последних. Для каждой фигуры предусмотрены свои соотношения, теоремы и формулы. Кроме того, математики выделяют специализированные алгоритмы, позволяющие точно и без ошибок определить тип фигуры.

Ученые разработали алгоритм для обучения, позволяющий за короткий промежуток времени перейти к решению сложных математических упражнений без каких-либо финансовых вложений. Он состоит из следующих элементов:

Сведения о ромбе: признаки, свойства и теоремы.
Формулы для нахождения некоторых параметров.

Изучение любой фигуры начинается всегда с ее определения, поскольку на основании этого возникают базовые знания.

Определение и частный случай

Ромбом называется параллелограмм с эквивалентными друг другу сторонами. 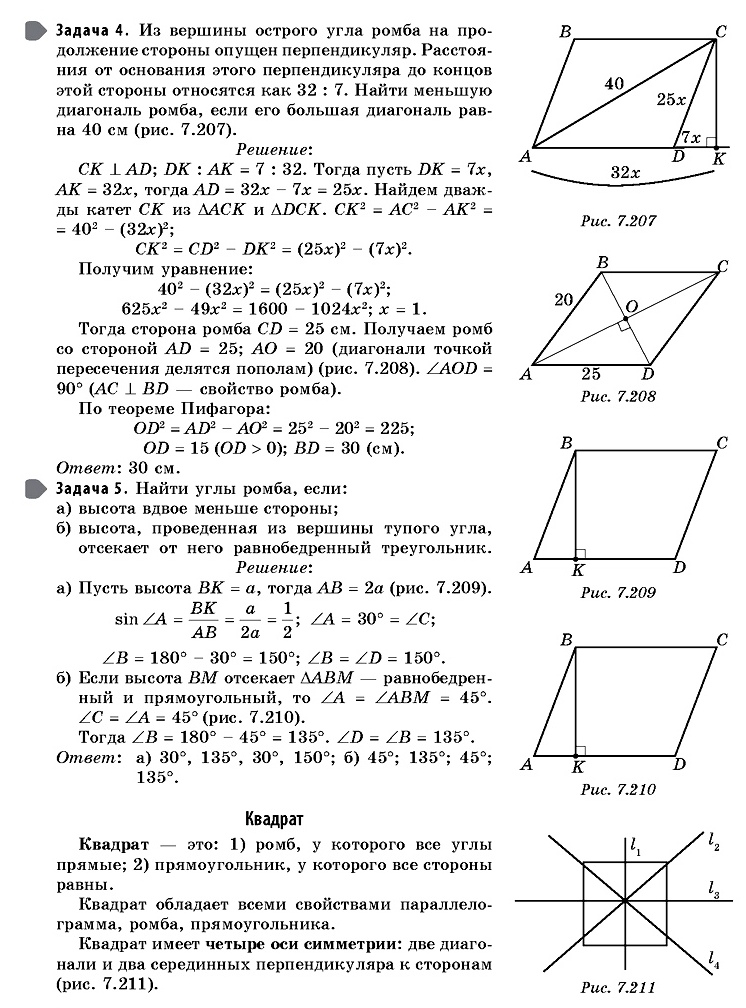О последнем можно сказать, что он относится к правильным четырехугольникам. Термин «правильный» означает равенство сторон одному значению. Следует отметить, что частным случаем ромба является квадрат, поскольку у него также имеются равные стороны. Эти фигуры имеют похожие свойства и формулы, однако некоторые соотношения отличаются.

Следовательно, необходимо правильно идентифицировать фигуру. Такая операция выполняется на основании признаков. Они присущи только конкретной фигуре и позволяют точно определить ее тип. Многие путают два ключевых понятия в геометрии: свойства и признаки. В учебниках существует множество определений, но, к сожалению, не все они понятны для новичков.

Признаками искомой фигуры называются характеристики, которые присущи только ей. Свойства — следствия из определений и доказательств теорем, используемые при доказательстве тождеств, утверждений и решения задач. Следует также обратить внимание на использование очередности. Первыми применяются признаки, а затем свойства.

Основные признаки

Признаки состоят из двух групп. Их формирование связано с количеством фигур, с которыми можно перепутать ромб. Определение последнего раскрывает их не полностью. Следовательно, математики для детального анализа разработали некоторый алгоритм, или первую группу. Различиями между искомой фигурой и параллелограммом являются следующие:

Эквивалентность всех сторон одной величине.
Углы, образованные пересечением диагоналей, являются прямыми.
Стороны, имеющие одну общую точку-вершину, равны между собой.
Биссектрисами внутренних углов ромба (делят угол на две половины) являются диагонали.
Диагонали пересекаются и образуют четыре равных прямоугольных треугольника и 2 группы равнобедренных треугольников, которые равны между собой.
Окружность можно вписать внутрь фигуры.
Высоты, образованные диагоналями при их пересечении, равны между собой.

Семь признаков отсеивают параллелограмм, но не дают провести разделение между ромбом и квадратом (прямоугольником), поскольку два последних также попадают под них. Для этого случая математики также разработали специальный алгоритм, который заключается в следующем:

Произвести идентификацию ромба по одному из признаков отличия от параллелограмма.
Внутренние углы не должны быть прямыми.
Вокруг ромба невозможно описать окружность.

Если у фигуры внутренние углы являются прямыми, то он является квадратом (прямоугольником). Кроме того, вокруг квадрата можно описать окружность. Алгоритмы идентификации являются очень простыми и надежными, поскольку вероятность ошибки эквивалентна нулевому значению. Существуют и другие методики определения типа фигуры, но они считаются сложными. Следовательно, на начальных стадиях обучения не рассматриваются.

Примером одной из них является операция интегрирования, основанная на вычислении размерностей (площадей) и объемов тел вращения, которые получаются в результате вращения ромба вокруг своей оси. Эти характеристики отличаются от характеристик параллелограмма и квадрата.

Свойства фигуры

Ромб является частным случаем параллелограмма и имеет все свойства, которые присущи этой фигуре. Новички не берут их во внимание, что приводит к увеличению объемов вычислений, а также возникновению ошибок. Свойствами параллелограмма являются следующие:

Сумма внутренних углов составляет 360 градусов.
Противолежащие углы эквивалентны одному значению (равны).
Противоположные стороны лежат на параллельных прямых и равны между собой.
Центром симметрии и описанной окружности является точка пересечения диагоналей. Через нее можно провести среднюю линию, которая делит стороны на два равных отрезка.
Треугольники, образованные диагоналями, эквивалентны.
Перпендикулярность биссектрис соседних углов.
Для равнобедренных треугольников, образованных пересечением диагоналей, последние являются биссектрисами, высотами и медианами.
Эквивалентность суммы квадратов диагоналей сумме квадратов всех сторон параллелограмма.
Точка пересечения диагоналей параллелограмма делит пополам.

Следует отметить, что свойства ромба присущи только ему. К ним относятся следующие:

Диагонали пересекаются только под прямым углом и являются взаимоперпендикулярными. Кроме того, они являются биссектрисами его углов, и должны искомой точкой делиться пополам.
Сумма квадратов диагоналей m1 и m2 соответствует квадрату стороны, умноженной на 4.
Только в ромб можно вписать окружность, которая будет касаться точек-середин его сторон.
Пересечение диагоналей обозначается некоторой точкой, которая является центром вписанной окружности и симметрией фигуры.
Описать окружность можно только в том случае, когда диагонали ромба равны, то есть он является квадратом. Во всех остальных случаях этого сделать невозможно.

Все свойства были получены математиками при доказательствах различных теорем. 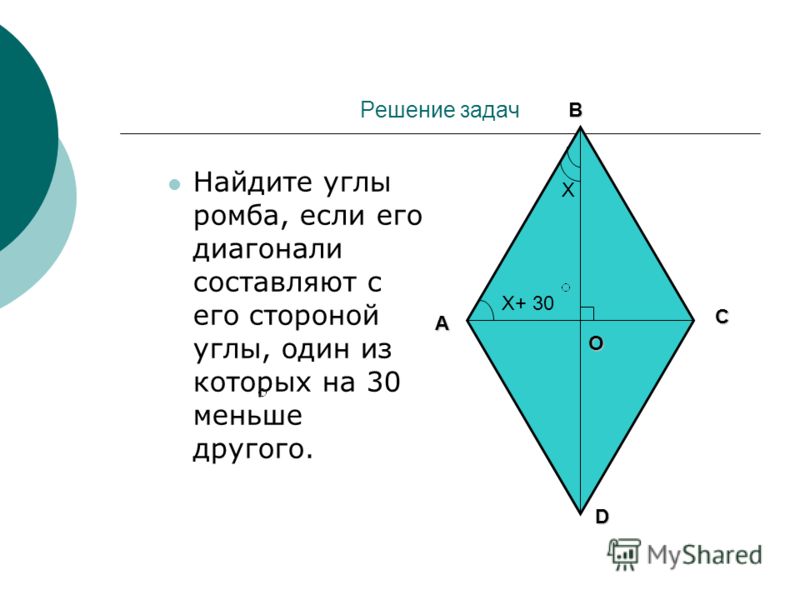Для некоторых также были использованы вспомогательные утверждения. Например, для второго применялась теорема Пифагора.

Теорема о свойствах диагоналей

Математики рекомендуют рассмотреть теорему о свойствах диагоналей ромба, которая гласит, что диагонали искомой фигуры пересекаются в одной точке и взаимоперпендикулярны, а также являются биссектрисами его углов. Для доказательства утверждения следует его разделить на две части: взаимоперпендикулярность диагоналей и последние являются биссектрисами углов фигуры.

Необходимо начертить ромб ABCD со стороной «a», провести диагонали m1 (большую) и m2 (меньшую). Отметить их точку пересечения P. Существует много доказательств этого утверждения. Специалисты рекомендуют всегда выбирать самое простое, поскольку такой прием ценится на экзаменах. Одним из примеров рационального использования знаний является построение прямой в декартовой системе координат.

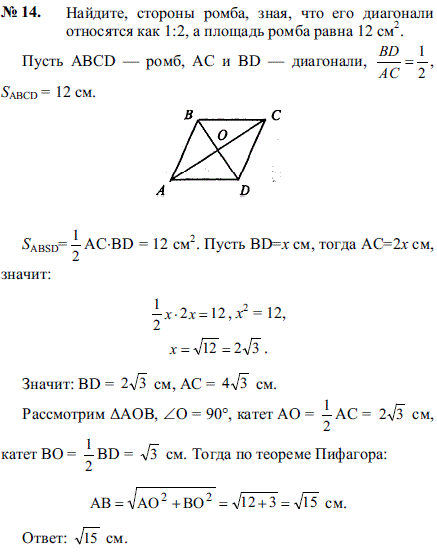
Согласно аксиоме геометрии, чтобы провести прямую, достаточно двух точек. Следовательно, нет смысла использовать 5, 10 и 20 элементов, поскольку все эти действия приведут к одному результату. Методика доказательства упрощенного типа считается самой эффективной. Следует рассмотреть треугольники ABC и ADC, полученные в результате проведения диагонали m1. Для удобства в геометрии слово «треугольник» заменяется символом «Δ», а угол — «∠». Они равны между собой по трем сторонам, то есть боковые стороны равны a (стороны ромба), а общая — эквивалентна значению диагонали m1.

Следует отметить, что они также являются равнобедренными, поскольку их боковые стороны равны между собой, то есть AB = BC = a и AD = CD = a. Далее следует обратить внимание на малую диагональ m1. Она опущена из вершины B и D на сторону AC. Исходя из свойства медианы в равнобедренном Δ, m1 является высотой и биссектрисой, то есть справедливо такое уравнение ∠ABC = ∠ADC = ∠ABP + ∠CPB = ∠APD + ∠CPD. 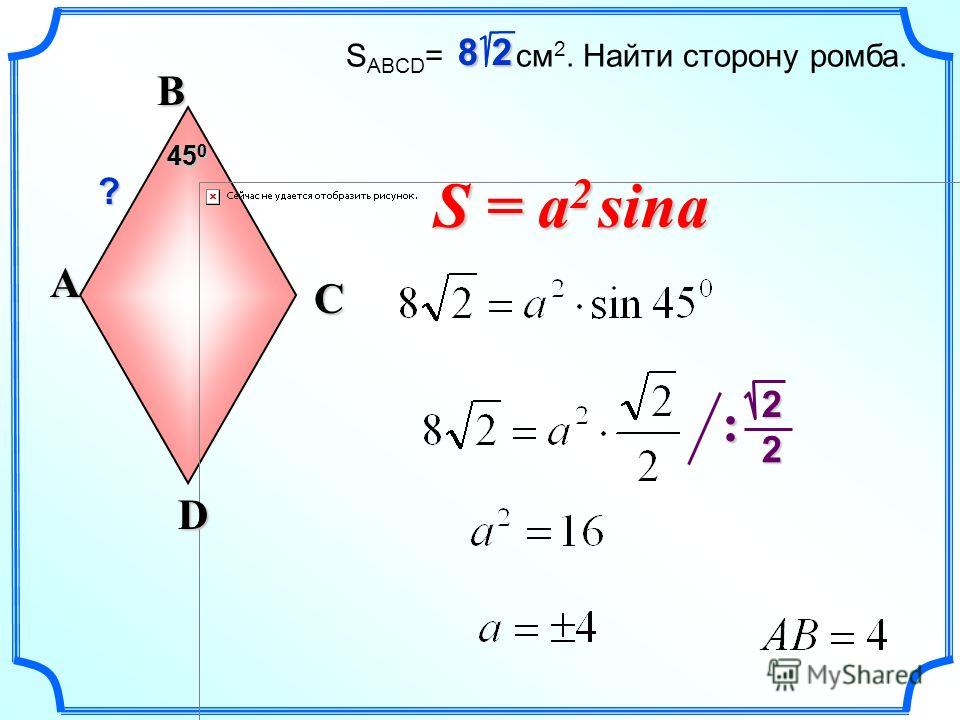Кроме того, высоты BP и DP образуют перпендикуляр со стороной AC.

Утверждение доказывается аналогично для ΔABC и ΔADC. Они равны по трем сторонам (AD = DC и AB = BC, а также по общей стороне BD) и являются равнобедренными, исходя из свойств сторон ромба. Диагональ m1 проходит через эти Δ. Она также является медианой, биссектрисой и высотой. Теорема доказана полностью.

Основные соотношения

Для решения задач применяются формулы. Ромб не является исключением. Соотношения применяются для определения неизвестных параметров фигуры. Однако бывают случаи, когда недостаточно одной формулы, поскольку нужно связать несколько компонентов в единый процесс вычислений. Для корректного использования формул следует ввести класс некоторых обозначений:

Ромб обозначить набором латинских букв ABCD.
Стороны приравнять к некоторому числу, заданному в общей форме: AB = BC = CD = DA = a.
Диагонали: меньшая — m2 и большая = m1. Их точку пересечения следует обозначить литерой P.
Углы: ∠ABC = ∠ADC и ∠BAD = ∠BCD.
Характеристики вписанной окружности: диаметр D и радиус R.
Периметр и площадь (размерность): P и S соответственно.

Периметр и площадь

Периметр ромба — характеристика, которая эквивалентна значению алгебраической суммы всех ее сторон. Площадью называется параметр геометрической фигуры, показывающий ее размерность в определенном геометрическом пространстве. Следует отметить, что величина S существует только у фигуры в двумерном пространстве. В трехмерном нужно рассматривать объем геометрического тела. Кроме того, у объемного тела есть параметр площади поперечного сечения. Эта величина является двумерной.

Периметр вычисляется по следующей формуле: P = 4 * a. Следует отметить, что величину a можно выражать через диагонали, площадь и другие характеристики. Базовая формула площади ромба имеет такой вид: S = a * BP = a * DP = a * AP = a * CP. (½)).

R = m1 * m2 / P = m1 * m2 / 4 * a.

Если нужно найти диаметр, то следует использовать такое соотношение: R = D / 2. Можно также выразить диагонали через стороны. Для этого следует подставить вместо m1 значение со стороной a.

Таким образом, математики предлагают специальный алгоритм, позволяющие без ошибок идентифицировать ромб, а затем применить соответствующие формулы для решения задачи.

Предыдущая

ГеометрияПлощадь пирамиды — определение, свойства и формулы

Следующая

ГеометрияОсновные понятия геометрии — список геометрических определений, терминов и значений

Как найти длину стороны ромба

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

ромбов_masson_buckelew

ромбов_masson_buckelew

EMAT
6690

Статья
# 2

От:

Никки
Массон и Брук Бакелью

Ромбы

Что такое
определение ромба?

Первый,
давайте пройдемся по определению четырехугольника — замкнутого многоугольника
в плоскости, состоящей из четырех отрезков, где отрезки
не пересекайте друг друга.

Ромб — четырехугольник
все стороны которого имеют одинаковую длину.

Отзыв
что определение квадрат — это четырехугольник с четырьмя прямыми углами
все стороны которого имеют одинаковую длину.

Следовательно
квадрат — особый вид ромба. Мы можем использовать наши знания
о квадратах, чтобы строить догадки о ромбах, а затем доказывать
несколько фактов о ромбах.

Примеры:

Деталь
1:
Построение квадрата и ромба с использованием GSP и определения
квадрата и ромба.2.

Нажмите
здесь
чтобы увидеть последний квадрат.

2. Щелкните
здесь
, чтобы открыть эскиз GSP. Вы найдете другой сегмент, который
9,00 см в длину. Постройте ромб в форме «воздушного змея»,
с отрезком AB как одну сторону.

Обзор:
Математическое определение круга — это все точки, которые равны
расстояние от центральной точки. Используйте круги с одинаковым радиусом, чтобы
построить ромб.

Нажмите
здесь
чтобы увидеть последний ромб.

Вопрос:
Объясните, почему четырехугольник ABCD представляет собой ромб.

Путь
построенный нами ромб означает, что все длины равны.
Каждая из сторон ромба — это все радиусы окружностей, которые
были созданы с равными радиусами.

Деталь
2:
Изучение диагоналей ромба.

Разведка
# 1 : Длина
диагонали ромба против квадрата.

1. Щелкните
здесь
открыть квадрат в ГСП и измерить диагонали.

вопросов:
Какую связь вы обнаружили между двумя диагоналями
квадратный?

Ответ:
У них одинаковая длина.

вопросов:
Используйте то, что вы знаете о квадратах, чтобы объяснить, почему диагонали должны
быть равным квадрату?

Ответ:

2. Поскольку
квадрат — это особый вид ромба, если диагонали
ромбов ровняться?

Нажмите
здесь
открыть ромб в ГСП и измерить диагонали.

Вопрос:
Одинаковы ли длины двух диагоналей для ромба?

После
вы измерили длину диагоналей, вы бы обнаружили
что они не равны.

Разведка
# 2 : Середина
диагонали ромба.

1. Теперь,
тем же ромбом отметьте центральную точку E, где диагонали
пересекаются. Теперь исследуем диагонали.

Вопрос:
Есть ли связь между диагоналями? Исследовать точку,
E по каждой диагонали.

Гипотеза:
Пересечение диагоналей в ромбе, это середина
каждой диагонали.

2. Построить
еще один ромб в GSP и проверьте нашу гипотезу.

3. Доказать
наша гипотеза:

4. Должен
эта теорема верна для квадратов, почему или почему нет?

Разведка
# 3 :
Проводить исследования
пересечение диагоналей ромба.

1. Отзыв
что мы только что узнали, что пересечение диагоналей
это середина каждой диагонали. Теперь посмотрим на
четыре угла, которые образуются на пересечении диагоналей.

Нажмите
здесь
раскрыть ромб в
ГСП и измерьте углы, образовавшиеся на пересечении.

2. Гипотеза:
Диагонали ромба перпендикулярны на пересечении.

3. Доказать
наша гипотеза: используйте конгруэнтные треугольники.

Разведка
# 4 : Исследуй углы
в ромб.

1. Открыть
следующий ромб в GSP и измерьте
разные углы. Вы видите какие-нибудь отношения?

2. После
Измеряя разные углы ромба, вы должны
обнаружил, что:

3.Гипотеза:
Диагонали делят пополам каждый из углов ромба.

4. Доказать
наша гипотеза. (Подсказка: используйте предыдущее доказательство, которое мы сделали в исследовании
# 3)

Деталь
3:
Освящение области ромба.

Возврат
на страницу 6690 Никки

Вернуться на страницу Брука 6690

диагоналей параллелограммов, прямоугольников и ромбов [видео]

диагоналей параллелограммов, прямоугольников и ромбов

Привет, и добро пожаловать в это видео о диагоналях! Сегодня мы собираемся исследовать диагонали параллелограммов, прямоугольников, ромбов и квадратов и посмотреть, как эти формы соотносятся друг с другом в целом.Давайте начнем!

Все формы, которые мы рассмотрим сегодня, являются четырехугольниками, то есть все они являются четырехсторонними многоугольниками. Многоугольник — это фигура с несколькими сторонами. Параллелограмм — это четырехугольник, у которого есть два набора параллельных сторон. Синие стрелки обозначают, какие стороны параллельны друг другу. Противоположные стороны параллелограмма, отмеченные зелеными отметками, совпадают, что означает, что они имеют одинаковую меру.

Прямоугольник — это форма, которую мы все хорошо знаем, поскольку она так часто встречается в реальном мире.Но одна вещь, о которой мы обычно не задумываемся, — это то, что прямоугольники — это просто параллелограмм особого вида. Это означает, что противоположные стороны параллельны и конгруэнтны, как и наш первый параллелограмм. Что делает прямоугольник особым параллелограммом , так это то, что его внутренние углы одинаковы. Фактически, они все прямых углов , что означает, что они измеряют 90 градусов.

Другой особый параллелограмм представляет собой ромб .Он обладает всеми свойствами параллелограмма, но все стороны ромба совпадают. Обратите внимание, что все отметки одинаковые, что говорит нам о том, что все стороны имеют одинаковую длину.

Наш последний специальный параллелограмм представляет собой прямоугольник и ромб одновременно, поэтому он имеет прямые углы прямоугольника и равные стороны ромба. Это еще одна форма, которую мы все хорошо знаем… квадрат !

Как видите, противоположные стороны параллельны, все углы прямые, а все стороны равны.

Итак, давайте вспомним наши четырехугольники, прежде чем мы начнем исследовать их диагонали:

Здесь мы расположили наши четырехугольники в виде «дерева», начав с квадрата в качестве ствола. Каждый квадрат представляет собой ромб, а каждый ромб — параллелограмм. Каждый квадрат также является прямоугольником, а каждый прямоугольник — параллелограммом. Вот как это работает, поднимаясь по дереву. Но спуститься не получится. Не каждый параллелограмм — это прямоугольник, и не каждый ромб — квадрат.

Хорошо, теперь давайте исследуем диагонали этих четырех четырехугольников.Диагональ — это отрезок прямой, соединяющий противоположные вершины или углы четырехугольника. Вот наш обычный обычный параллелограмм с показанными диагоналями:

Как видите, диагонали параллелограмма делят друг друга пополам. Другими словами, они разрезают друг друга пополам. Мы могли бы добавить несколько чисел, чтобы лучше проиллюстрировать это …

или мы могли бы использовать отметки, чтобы показать, что диагонали были разделены пополам:

Поскольку все три специальных четырехугольника, о которых мы говорим, являются параллелограммами, все они будут иметь диагонали, разделяющие пополам.

Теперь посмотрим на прямоугольник . Вот прямоугольник с его диагоналями:

Диагонали прямоугольника совпадают, и, опять же, поскольку прямоугольник является параллелограммом, диагонали делят друг друга пополам, делая каждую половину одинаковой длины:

Каждая диагональ прямоугольника также делит прямоугольник на два равных прямоугольных треугольника:

Это означает, что при желании мы могли бы вычислить длину диагонали, используя теорему Пифагора .

Теперь, когда у нас есть прямоугольники, давайте посмотрим, что происходит с другим особым параллелограммом, ромбом :

Еще раз, поскольку каждый ромб является параллелограммом, диагонали делят друг друга пополам. Диагонали НЕ одинакового размера, так что же особенного в этом? Посмотрите на углы пересечения диагоналей. Эти углы выглядят так, как будто все они могут быть одинаковыми, и поскольку их четыре, это должно означать…

Что каждый угол равен 90 градусам! Это означает, что диагонали ромба перпендикулярны друг другу в дополнение к , разделяющим друг друга пополам.

Хорошо, остался только один четырехугольник, квадрат . Помните, что квадрат представляет собой параллелограмм, прямоугольник и ромб, поэтому он должен иметь все свойства этих форм:

Диагонали будут делить друг друга пополам.
Диагонали будут одинаковой длины.
Диагонали будут перпендикулярны друг другу.

Посмотрим, правы ли мы:

Мы были правы! Если мы присмотримся, мы также увидим, что две диагонали разрезают квадрат на четыре равнобедренных прямоугольных треугольника.

Теперь, когда мы рассмотрели наши четыре параллелограмма и их диагонали, давайте закончим обзором, чтобы увидеть, что все вы можете вспомнить.

Какое из следующих утверждений неверно?

Каждый прямоугольник представляет собой параллелограмм.
Каждый ромб — квадрат.
Каждый квадрат представляет собой прямоугольник.
Диагонали параллелограмма делят друг друга пополам.
Диагонали ромба пересекаются под прямым углом.
Диагональ прямоугольника делит его на два равных прямоугольных треугольника.
Диагонали прямоугольника одинаковой длины.
Четырехугольник, диагонали которого пересекаются пополам, пересекаются под прямым углом и совпадают, должен быть квадратом.

Правильный ответ — Б. Помните дерево?

Не каждый ромб — квадрат, но каждый квадрат — ромб.

Спасибо за просмотр и удачной учебы!

проб для ромбов — видео и стенограмма урока

Противоположные углы

Теорема о противоположных углах утверждает, что противоположные углы в ромбе равны.

Чтобы доказать это, давайте рассмотрим ромб ABCD , который имеет AB || CD и BC || CD .

Ромб ABCD

Если мы проведем линию, соединяющую две точки B и D , будут созданы два треугольника: DAB и BCD .

Итак, в этих треугольниках AB = CD , AD = BC , а сторона DB является общей.Следовательно, согласно свойству треугольников сторона сторона сторона сторона, они конгруэнтны.

Следовательно, соответствующие углы будут равны.

То же можно доказать и для двух других углов. Следовательно, у ромба противоположные углы равны.

Диагонали ромба

Диагонали ромба пересекают друг друга пополам и перпендикулярны друг другу.

Рассмотрим тот же ромб ABCD , у которого AB || CD и BC || CD .

Ромб ABCD

Нарисуем две диагонали, AC и BD , пересекающиеся друг с другом в точке O .

Рассмотрим два треугольника, образованных этим: AOD и COB .Линия DB является трансверсальной к параллельным линиям AD и BC . Таким образом, углы ADO и CBO будут равны при использовании теоремы об альтернативных внутренних углах параллельных прямых.

Аналогично, линия AC является трансверсальной параллельным линиям CD и AB . Таким образом, углы DAO и BCO будут равны.

Также стороны AD и BC равны друг другу. Итак, используя свойство треугольников угол-сторона-угол, эти треугольники конгруэнтны.

Следовательно, соответствующие стороны этих треугольников будут равны.

Это доказывает, что O является средней точкой линий AC и BD .Таким образом, диагонали ромба делят друг друга пополам.

Теперь, чтобы доказать, что диагонали перпендикулярны в точке O , рассмотрим треугольники BOC и DOC .

В этих треугольниках мы уже доказали, что BO = OD . Мы знаем, что BC = DC и OC — это общая сторона. Следовательно, с использованием свойства сторона-сторона-сторона треугольники BOC и DOC совпадают.

Теперь соответствующие углы, BOC и DOC , равны.

Кроме того, сумма углов BOC и DOC составляет 180 градусов, потому что они находятся на прямой линии.

Поскольку эти углы равны, каждый из них будет составлять 90 градусов. Следовательно:

Таким образом, доказано, что диагонали перпендикулярны друг другу.

Диагонали и углы при вершинах

Диагонали ромба делят углы при вершинах пополам. Рассмотрим тот же ромб ABCD , у которого AB || CD и BC || CD .

Ромб ABCD

Теперь нарисуем диагональ: DB .

DB действует как трансверсаль для пар параллельных линий: AD и BC , а также AB и CD .Следовательно, углы ADB и CBD равны, как и углы ABD и CDB , из-за свойства чередования внутренних углов параллельных линий.

Мы уже доказали, что противоположные углы ромба равны. Итак:

Это означает, что:

Следовательно:

То же самое можно сказать и о другом наборе углов.Таким образом, доказано, что диагонали делят углы при вершинах пополам.

Итоги урока

Хорошо, давайте рассмотрим. В этом уроке мы определили ромб как четырехугольник, все стороны которого равны, а противоположные стороны параллельны друг другу. Затем мы рассмотрели некоторые важные теоремы, относящиеся к ромбам, а также увидели их доказательства.

Противоположные углы в ромбе равны.
Диагонали ромба пересекают друг друга и перпендикулярны друг другу.
Диагонали ромба делят пополам углы при вершинах.

Параллелограмм, формулы параллелограмма

Четырехугольник с двумя парами параллельных сторон называется параллелограммом .
Все пары противоположных сторон параллелограмма равны.

Чтобы определить, является ли четырехугольник параллелограммом, мы будем использовать следующие критерии:

— если две пары противоположных сторон четырехугольника равны, то этот четырехугольник является параллелограммом;
— если две противоположные стороны в четырехугольнике параллельны и равны, то этот четырехугольник является параллелограммом;
— если в четырехугольнике диагонали делят друг друга пополам, то этот четырехугольник является параллелограммом;

Четырехугольник с четырьмя прямыми углами называется прямоугольником .
Справедливо следующее утверждение: Если параллелограмм является прямоугольником, то его диагонали равны по длине.
Наоборот, если диагонали параллелограмма равны по длине, то этот параллелограмм является прямоугольником.

Параллелограмм, у которого две смежные равные стороны, называется ромбом . Справедливо следующее утверждение о ромбе:
Если параллелограмм является ромбом, то его диагонали перпендикулярны.
И наоборот, если диагонали параллелограмма перпендикулярны, то этот параллелограмм является ромбом.

Квадрат можно рассматривать как прямоугольник с равными смежными сторонами или как ромб с прямым углом.
Следовательно, квадрат обладает всеми свойствами прямоугольника и ромба.

Формулы параллелограмма

∠A + ∠B = 180 ° и ∠A + ∠D = 180 °
∠A = ∠C, ∠B = ∠D

Периметр параллелограмма:

P = 2a + 2b

Площадь параллелограмма (ромба):

$ A = AB \ cdot DE = BC \ cdot DF $
$ A = AB \ cdot AD \ sin \ alpha $
$ A = \ frac12 AC \ cdot BD \ sin \ gamma $

Соотношение сторон и диагоналей параллелограмма (ромба):

p ² + q ² = 2 (a ² + b ²)
или
AC ² + BD ² = 2 (AB ² + BC ²)

Урок КАК решать задачи на сторонах ромба и размеры диагоналей

Как решать задачи на сторонах ромба и размеры диагоналей — Примеры

Задача 1
Найдите периметр ромба, если его сторона равна 7 см.

Решение
Все четыре стороны ромба по определению имеют одинаковую длину.
Следовательно, периметр ромба равен
7 см + 7 см + 7 см + 7 см = 4 * 7 см = 28 см.

Ответ . Периметр ромба 28 см.

Задача 2
Периметр ромба равен 32 см.
Найдите длину стороны ромба.

Решение
Поскольку все четыре стороны ромба имеют одинаковую длину, размер стороны составляет одну четвертую его периметра и равен
32/4 см = 8 см.

Ответ . Сторона ромба 8 см в длину.

Задача 3
Диагонали ромба 12 см и 16 см в длину.
Найдите длину стороны и периметр ромба.

Решение
Диагонали ромба перпендикулярны и делят друг друга пополам
(см. Рисунок ). Итак, диагонали делят ромб на четыре равных
прямоугольных треугольника.Длина катета каждого такого треугольника
равна половине размера соответствующей диагонали ромба.

В нашем случае длина ножек 12/2 см = 6 см и 16/2 см = 8 см.

Теперь легко вычислить длину стороны ромба по
, применив теорему Пифагора к прямоугольному треугольнику. Это равно

= = = 10 см.

Рисунок . Диагонали ромба
делят на четыре равных прямоугольных треугольника

Рассчитав размер стороны, вы легко найдете периметр
ромба.Он равен 4 * 10 см = 40 см.

Ответ . Сторона ромба — 10 см в длину; периметр 40 см.

Задача 4
Периметр ромба 52 см.
Длина одной диагонали ромба 24 см.
Найдите длину второй диагонали ромба.

Решение
Как мы только что отметили при решении предыдущей задачи, диагонали
ромба перпендикулярны и делят друг друга пополам (см. Рисунок ).
Диагонали делят ромб на четыре равных прямоугольных треугольника.
Размер катета каждого такого треугольника равен половине размера
соответствующей диагонали ромба.

Следовательно, используйте следующую стратегию для решения задачи:
— 1) вычислить длину стороны ромба;
— 2) вычислить катет треугольника как половину меры
известной диагонали;
— 3) вычислить другой катет прямоугольного треугольника, применив
теорему Пифагора;
— 4) удвоить найденный размер катета прямоугольного треугольника
, чтобы получить длину второй диагонали ромба.

Рисунок . Диагонали ромба
делят на четыре равных прямоугольных треугольника

Итак, размер ромба сбоку составляет одну четвертую его периметра, то есть 52/4 см = 13 см.
Длина катета прямоугольного треугольника равна половине длины известной диагонали, то есть 24/2 см = 12 см.
Размер другой ноги равен

= = = 5 см

в соответствии с теоремой Пифагора.
Размер другой диагонали ромба равен удвоенной длине катета прямоугольного треугольника, то есть 2 * 5 см = 10 см.

Ответ . Вторая диагональ ромба — 10 см в длину.

Мои другие уроки ромбов на этом сайте

— Диагонали ромба перпендикулярны

— Диагонали ромба делят его углы пополам

— Длина диагоналей ромба

— Круг, вписанный в ромб

— Длина диагоналей ромба

— СВОЙСТВА РОМБИСА

Для навигации по всем темам / урокам онлайн-учебника по геометрии используйте этот файл / ссылку ГЕОМЕТРИЯ — ВАШ ОНЛАЙН-УЧЕБНИК.

Разница между квадратом и ромбом

Что такое квадрат?

Квадрат — это плоская фигура или четырехугольник с четырьмя равными сторонами и углами. Все четыре угла квадрата расположены под прямым углом. Две противоположные стороны квадрата всегда равной длины.

(изображение будет загружено в ближайшее время)

Свойства квадрата

Четыре внутренних угла квадрата равны 90 °.
Четыре стороны квадрата равны и равны друг другу.
Противоположные стороны квадрата равны и параллельны друг другу.
Две диагонали квадрата равны и пересекают друг друга пополам под углом 90 °.
Площадь квадрата равна стороне × стороне.
Две равные диагонали квадрата образуют два одинаковых равнобедренных треугольника.

Что такое ромб?

Ромб также известен как ромб или ромб. Ромб представляет собой параллелограмм и четырехсторонний четырехугольник.В ромбе противоположные углы и стороны равны по длине и параллельны. Диагонали квадрата делят друг друга пополам под углом 90 °. Ромбы или ромбы — форма множественного числа от ромба.

(изображение будет загружено в ближайшее время)

Свойства ромба

Стороны ромба равны
Противоположные стороны ромба параллельны.
Диагонали пересекают друг друга пополам под углом 90 ° в виде ромба
Вокруг ромба нельзя делать описывающие и вписывающие круги.
Диагональ ромба делит его углы пополам.
Два соседних угла ромба равны 180 °.

Различия и сходство ромбов и квадратов

В таблице ниже показаны некоторые точки на разностях ромбов и квадратов.

ромб, также пересекающийся в вершине
противоположные углы которых равны по длине.

Квадрат	Ромб
Квадрат — это четырехсторонняя фигура или параллелограмм с 4 прямыми углами, пересекающимися в вершине
Диагонали квадрата равного размера	Диагонали ромба не равны по размеру
Стороны ромба перпендикулярны друг другу, потому что все четыре угла квадрат равны 90 °	Стороны ромба не перпендикулярны друг другу, потому что противоположные углы ромба равны по длине.

В таблице ниже показаны некоторые точки сходства между ромбом и квадратом.

также считается квадратным параллелограммом четырехсторонняя фигура, все стороны которой равны по длине

Квадрат	Ромб
Квадрат рассматривается как параллелограмм	00 Квадрат

Все четыре стороны ромба также равны по длине
Противоположные стороны квадрата равны друг другу.	Противоположные стороны ромба также равны друг другу.
Две диагонали квадрата перпендикулярны друг другу	Ромб — это параллелограмм, диагонали которого перпендикулярны биссектрисам друг друга.

Квадрат — это ромб?

Квадрат — это ромб, потому что все стороны квадрата равны по длине. Даже диагонали квадрата и ромба перпендикулярны друг другу и делят пополам противоположные углы.Поэтому можно сказать, что квадрат — это ромб.

Приведенная выше таблица, показывающая сходство между ромбом и квадратом, подтверждает предложение «Является ли квадрат ромбом»?

Решенный пример

1. Вычислите площадь ромба с диагоналями, равными 12 см и 8 см.

Решение — Учитывая, что

Диагональ 1 или d₁ = 12 см

Диагональ 2 или d₂ = 8 см

Площадь ромба = (d₁ x d₂)

= (12 x 8) / 2

= 96/2

= 43 см²

2.Пусть вся площадь квадрата равна 8 см. Найдите его площадь, периметр и длину диагонали.

Решение — Сторона квадрата = 8 см

Площадь квадрата = s² = 8² = 64 см²

Периметр квадрата = 4 xa = 4 x 8 см = 32 см

Длина диагонали квадрата = s√2 = 1,414 x 8 = 11,312

Факты

Слово ромб происходит от греческого слова ромб, что означает «Волчок».

Как найти сторону ромба?

Свойства ромба:

Основные формулы:

Как найти сторону ромба?

4, а площадь равна 24 дм 2

Как найти диагональ ромба?

Задачи категории В8. Ромб. Прямоугольник

Ромб

Задача 1.

Задача 2.

Задача 3.

Задача 4.

Прямоугольник

Задача 1.

Задача 2.

Задача 3.

Ромб в основании призмы

Ромб — свойства, признаки и формулы нахождения параметров

Общие сведения

Определение и частный случай

Основные признаки

Свойства фигуры

Теорема о свойствах диагоналей

Основные соотношения

Периметр и площадь

Как найти длину стороны ромба

ромбов_masson_buckelew

диагоналей параллелограммов, прямоугольников и ромбов [видео]

диагоналей параллелограммов, прямоугольников и ромбов

проб для ромбов — видео и стенограмма урока

Противоположные углы

Диагонали ромба

Диагонали и углы при вершинах

Итоги урока

Параллелограмм, формулы параллелограмма

Формулы параллелограмма

Урок КАК решать задачи на сторонах ромба и размеры диагоналей

Как решать задачи на сторонах ромба и размеры диагоналей — Примеры

Разница между квадратом и ромбом

Что такое квадрат?

Свойства квадрата

Что такое ромб?

Различия и сходство ромбов и квадратов

В таблице ниже показаны некоторые точки на разностях ромбов и квадратов.

В таблице ниже показаны некоторые точки сходства между ромбом и квадратом.

Квадрат — это ромб?

Решенный пример

Факты

Добавить комментарий Отменить ответ