Содержание
Задача 7 — геометрический смысл производной
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.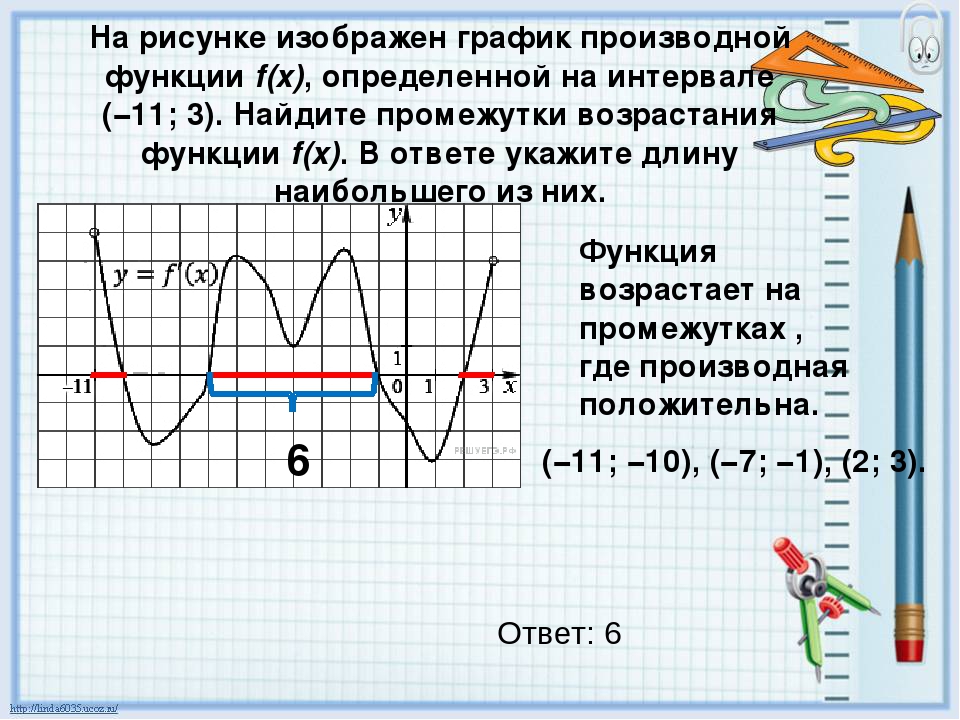
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).

- Точка x0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума.
 И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной.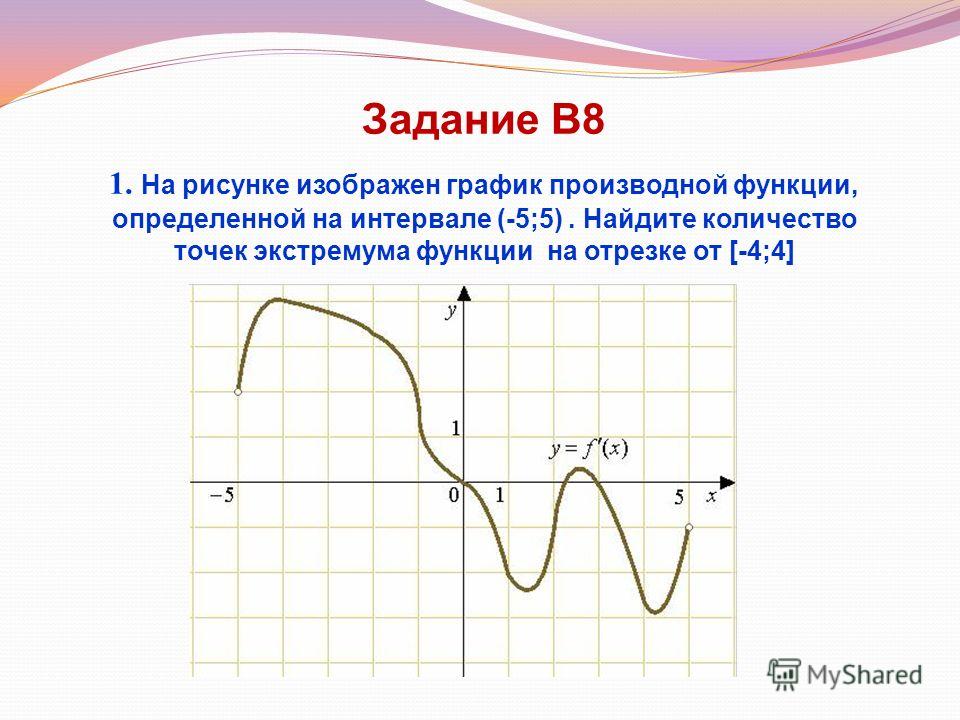 Имеем:
Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.
 е. f’(x) ≥ 0.
е. f’(x) ≥ 0. - Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x).
В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0.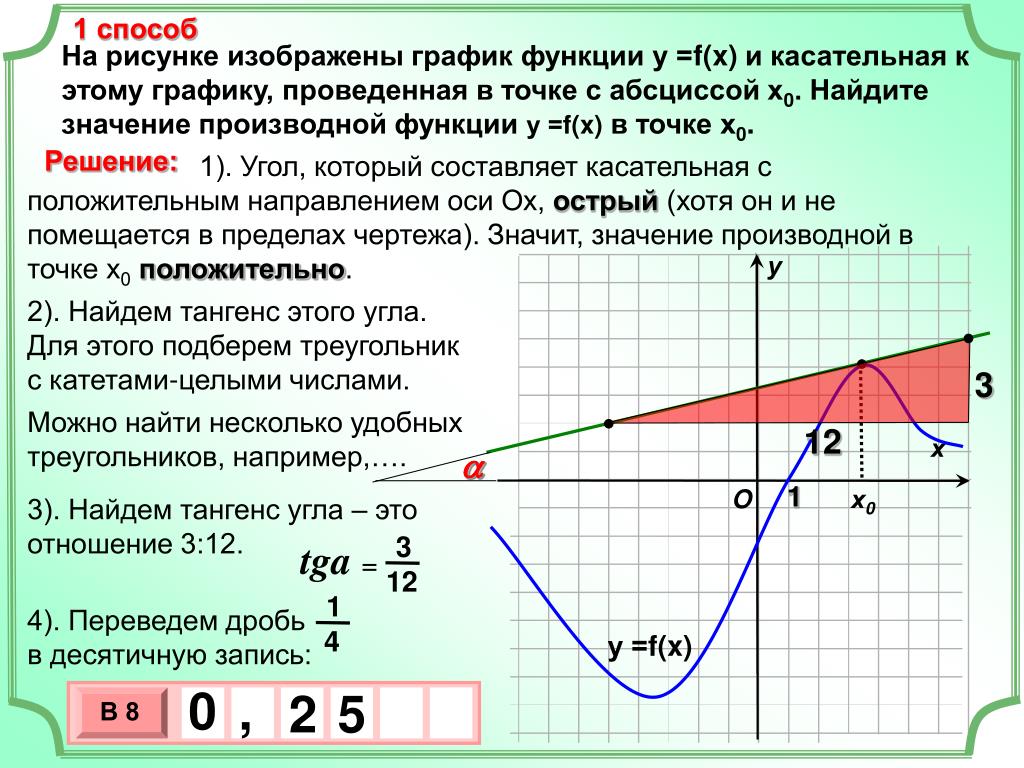 На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
Смотрите также:
- Задача 7: касательная к графику функции
- Задача 7: касательная к графику функции — 2
- Пробный ЕГЭ-2011 по математике, вариант №4
- Пробный ЕГЭ 2012. Вариант 1 (без логарифмов)
- Так сокращать дроби нельзя!
- Быстрое возведение чисел в квадрат без калькулятора
Как определить значение производной по графику. Производная функции. Геометрический смысл производной. Вычисление точек максимума и минимума
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x 0 ,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).

Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x 0 , и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными.
 Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу. - Зная координаты, легко вычислить приращение аргумента Δx = x 2 − x 1 и приращение функции Δy = y 2 − y 1 .
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм.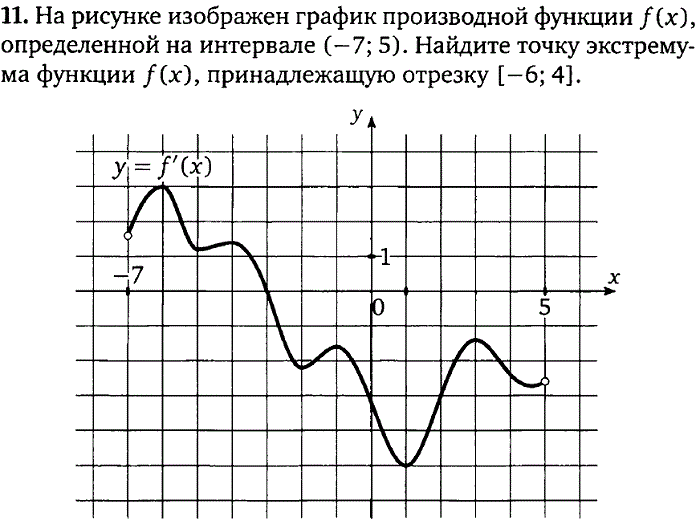 Для начала определимся с терминологией:
Для начала определимся с терминологией:
- Точка x 0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≥ f(x).
- Точка x 0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.

- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5.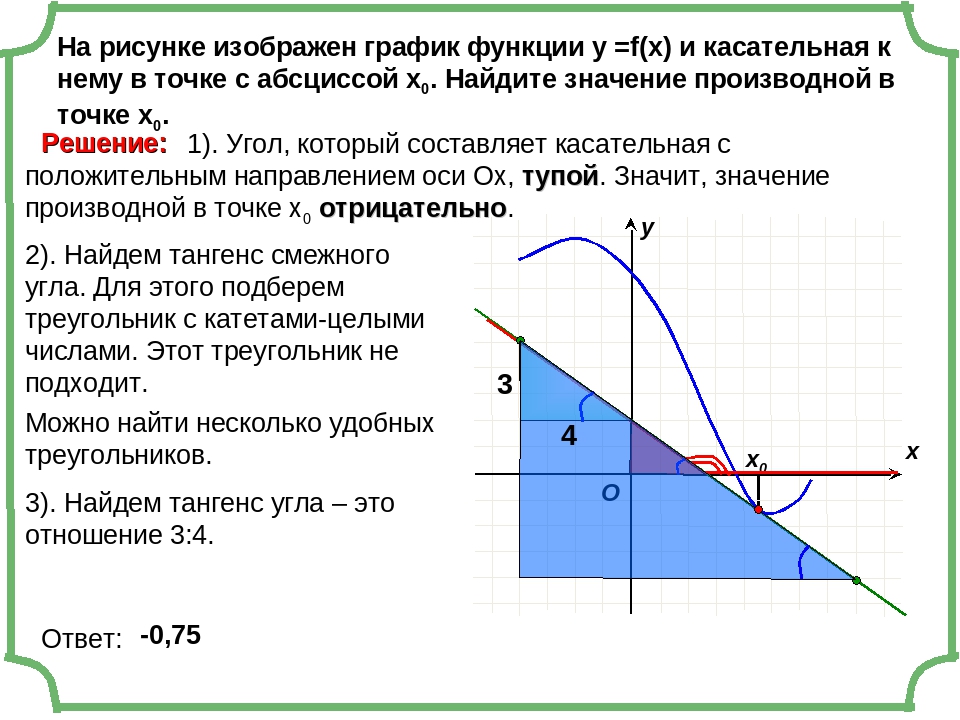 Отметим на полученном графике знаки производной. Имеем:
Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи.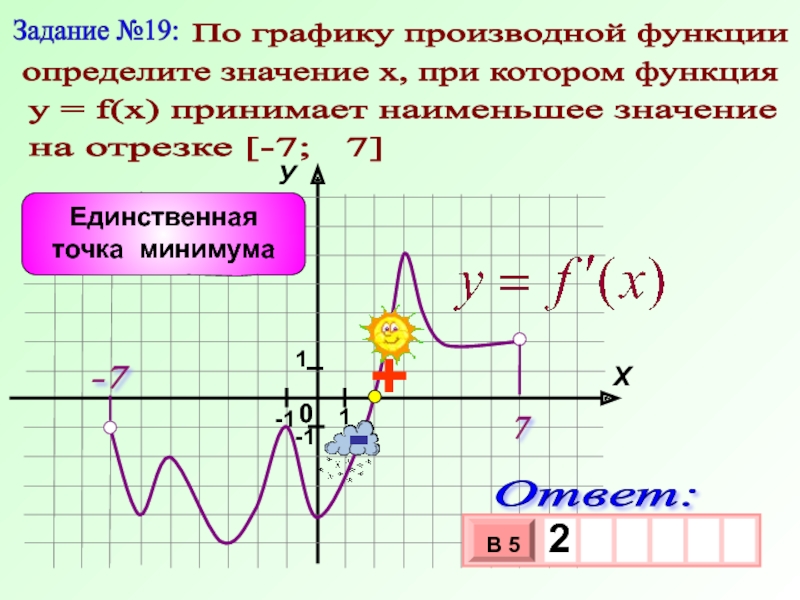 Разумеется, с целочисленными точками такой фокус не пройдет.
Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке , достаточно, чтобы ее производная внутри отрезка была положительна, т.
 е. f’(x) ≥ 0.
е. f’(x) ≥ 0. - Для того чтобы непрерывная функция f(x) убывала на отрезке , достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x).
В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2).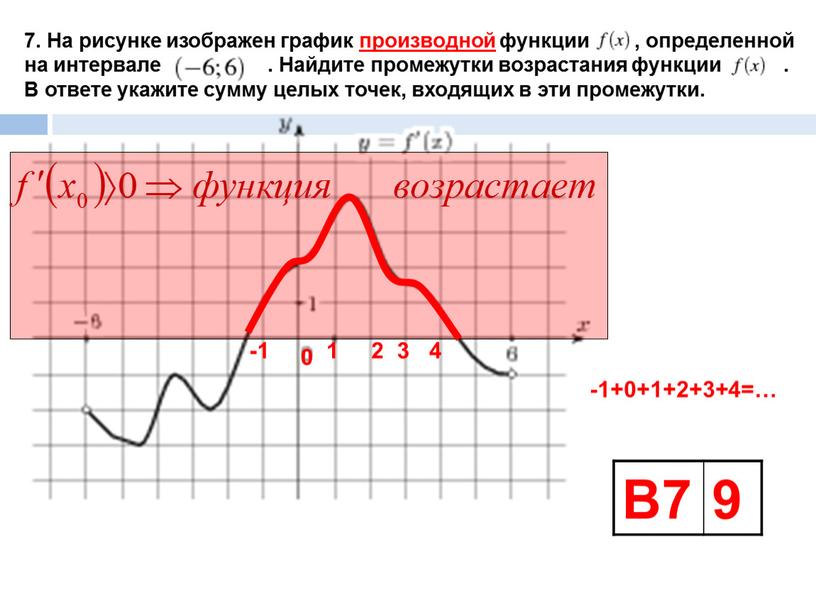 Вычислим их длины:
Вычислим их длины:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l 2 = 5.
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна
. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.
Запомним определение:
Производная — это скорость изменения функции.
На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?
Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.
Вот другой пример.
Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза.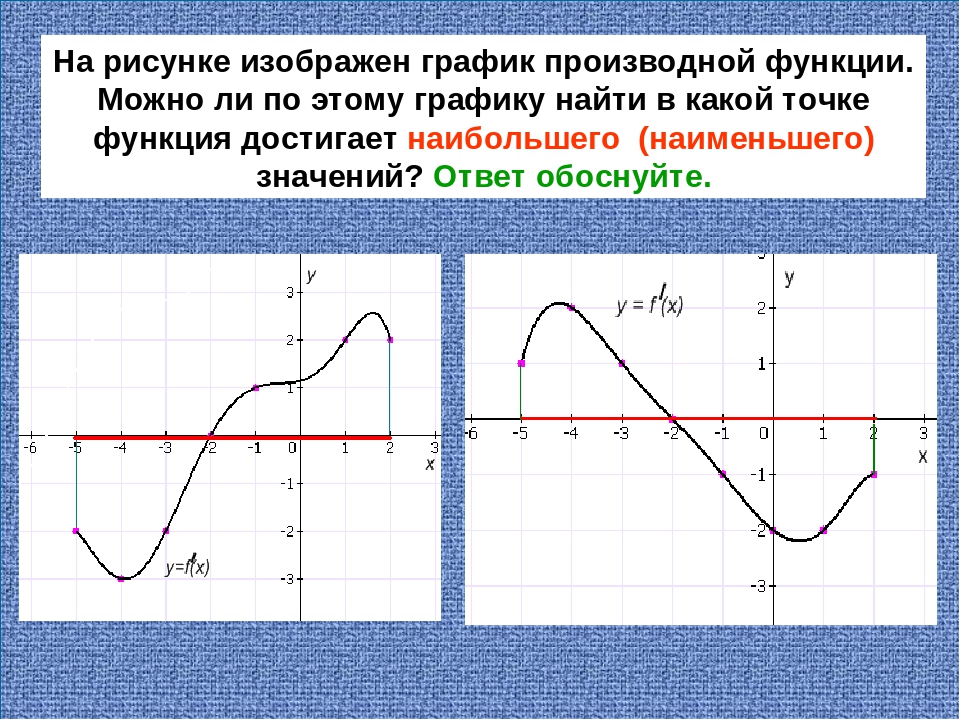 И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная
И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная
, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Производная функции обозначается .
Покажем, как найти с помощью графика.
Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной
.
Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.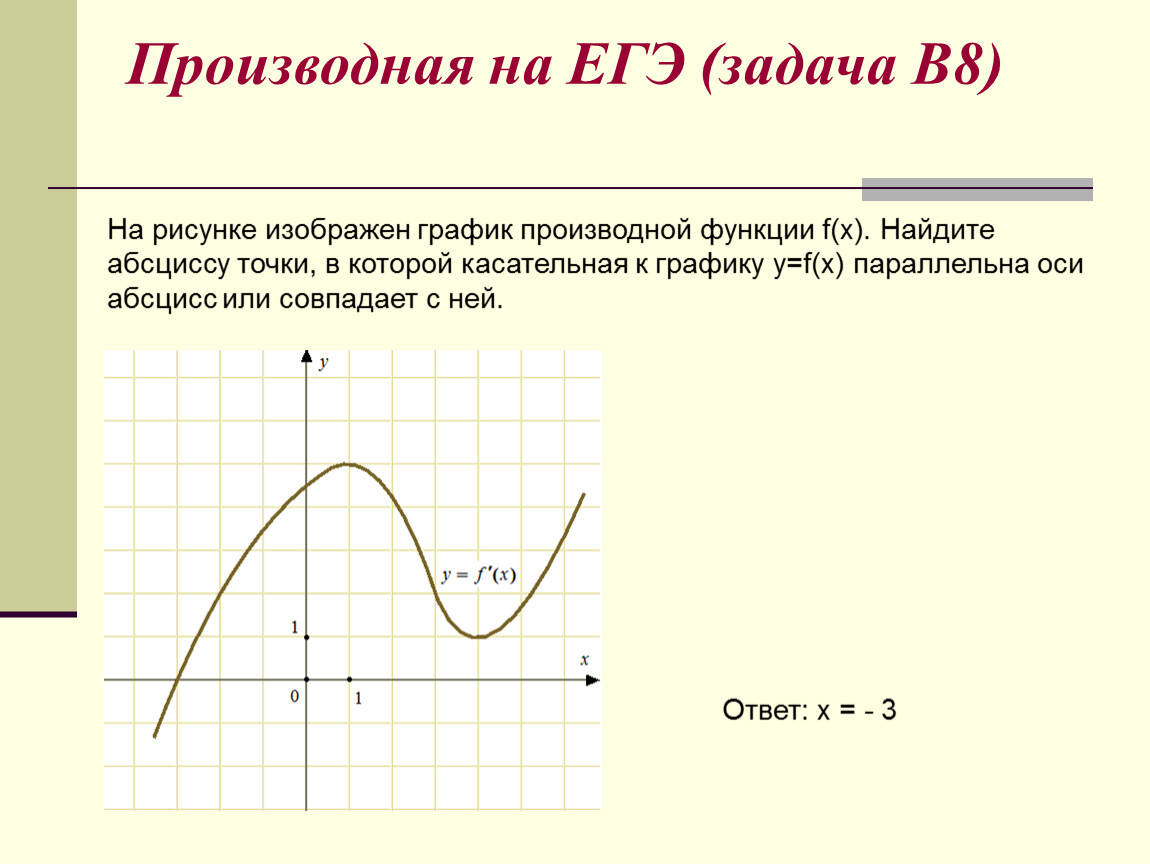
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .
Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.
Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .
Есть и другое важное соотношение. Вспомним, что прямая задается уравнением
Величина в этом уравнении называется угловым коэффициентом прямой
. Она равна тангенсу угла наклона прямой к оси .
.
Мы получаем, что
Запомним эту формулу. Она выражает геометрический смысл производной.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Другими словами, производная равна тангенсу угла наклона касательной.
Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.
Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.
В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол с положительным направлением оси . Значит, в точке производная положительна.
В точке наша функция убывает. Касательная в этой точке образует тупой угол с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.
Вот что получается:
Если функция возрастает, ее производная положительна.
Если убывает, ее производная отрицательна.
А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна.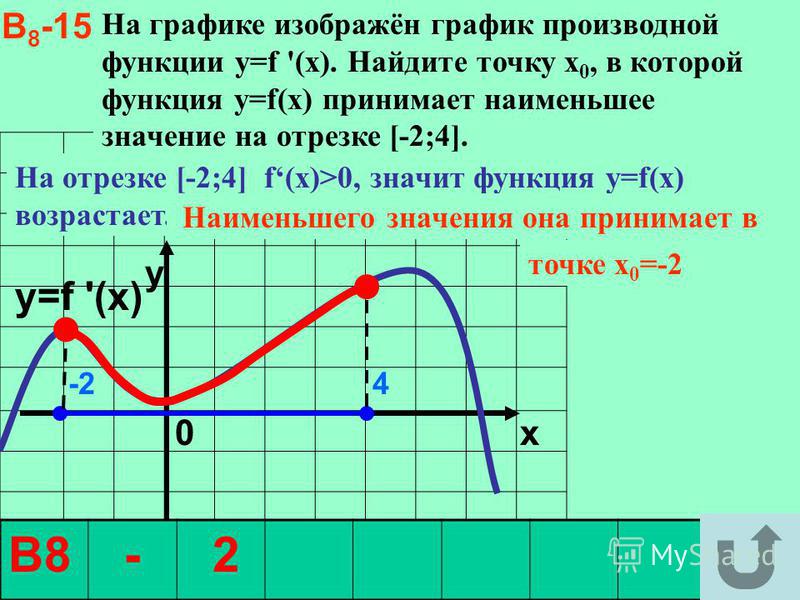 Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».
В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
Если производная положительна, то функция возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | — | 0 | + |
Сделаем два небольших уточнения.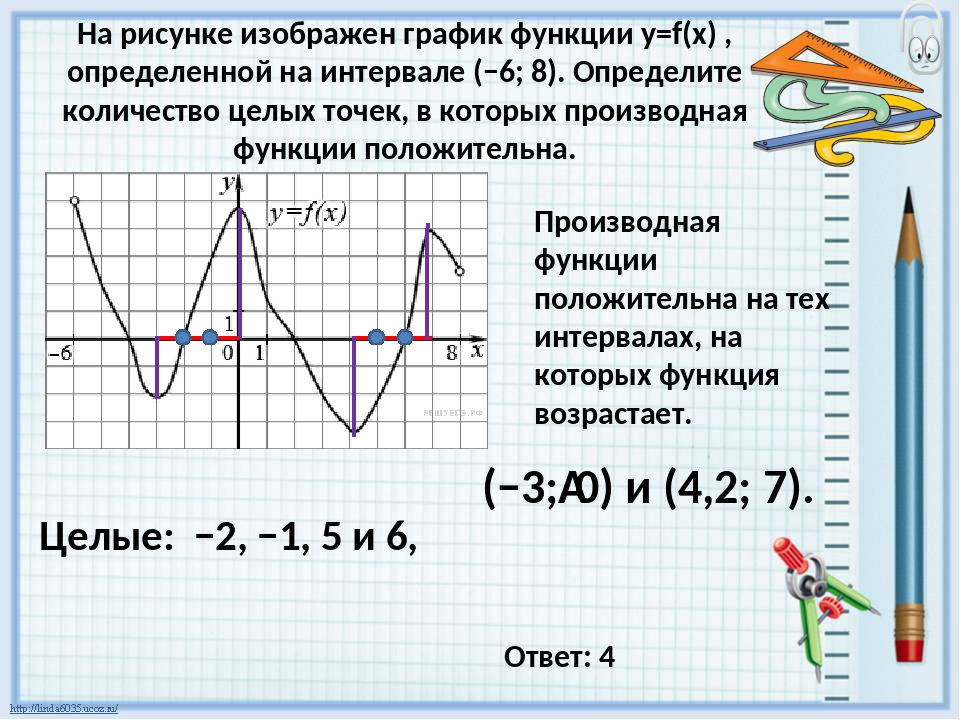 Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.
Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.
Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая :
В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.
Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется
Сергей Никифоров
Если производная функции знакопостоянна на интервале, а сама функция непрерывна на его границах, то граничные точки присоединяются как к промежуткам возрастания, так и к промежуткам убывания, что полностью соответствует определению возрастающих и убывающих функций.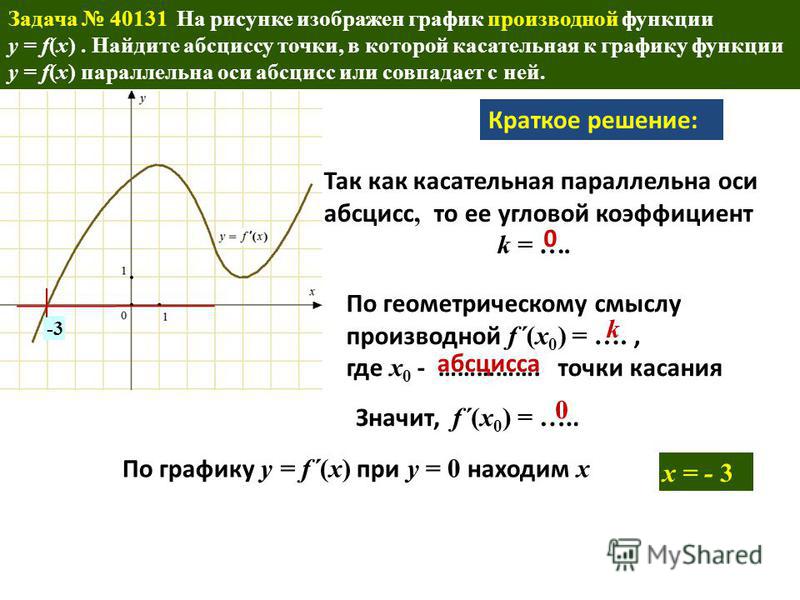
Фарит Ямаев
26.10.2016 18:50
Здравствуйте. Как же (на каком основании) можно утверждать, что в точке, где производная равна нулю, функция возрастает. Приведите доводы. Иначе, это просто чей-то каприз. По какой теореме? А также доказательство. Спасибо.
Служба поддержки
Значение производной в точке не имеет прямого отношения к возрастанию функции на промежутке. Рассмотрите, например, функции — все они возрастают на отрезке
Владлен Писарев
02.11.2016 22:21
Если функция возрастает на интервале (а;b) и определена и непрерывна в точках а и b, то она возрастает на отрезке . Т.е. точка x=2 входит в данный промежуток.
Хотя, как правило возрастание и убывание рассматривается не на отрезке, а на интервале.
Но в самой точке x=2, функция имеет локальный минимум. И как объяснять детям, что когда они ищут точки возрастания (убывания), то точки локального экстремума не считаем, а в промежутки возрастания (убывания) — входят.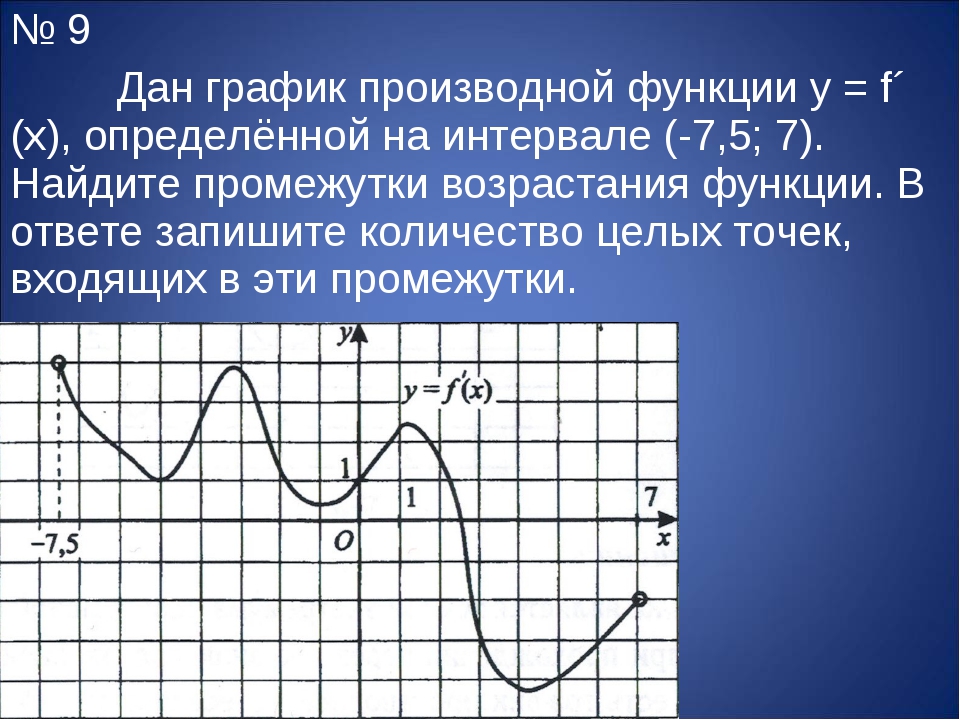
Учитывая, что первая часть ЕГЭ для «средней группы детского сада», то наверное такие нюансы- перебор.
Отдельно, большое спасибо за «Решу ЕГЭ» всем сотрудникам- отличное пособие.
Сергей Никифоров
Простое объяснение можно получить, если отталкиваться от определения возрастающей/убывающей функции. Напомню, что звучит оно так: функция называется возрастающей/убывающей на промежутке, если большему аргументу функции соответствует большее/меньшее значение функции. Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.
Ирина Ишмакова
20.11.2017 11:46
Добрый день. Здесь в комментариях я вижу убеждения, что границы включать нужно. Допустим, я с этим соглашусь. Но посмотрите, пожалуйста, ваше решение к задаче 7089. Там при указании промежутков возрастания границы не включаются. И это влияет на ответ. Т.е. решения заданий 6429 и 7089 противоречат друг другу. Проясните, пожалуйста, эту ситуацию.
Александр Иванов
В заданиях 6429 и 7089 совершенно разные вопросы.
В одном про промежутки возрастания, а в другом про промежутки с положительной производной.
Противоречия нет.
Экстремумы входят в промежутки возрастания и убывания, но точки, в которых производная равна нулю, не входят в промежутки, на которых производная положительна.
A Z
28.01.2019 19:09
Коллеги, есть понятие возрастания в точке
(см. Фихтенгольц например)
и ваше понимание возрастания в точке x=2 противочет классическому определению.
Возрастание и убывание это процесс и хотелось бы придерживаться этого принципа.
В любом интервале, который содержит точку x=2, функция не является возрастающей. Поэтому включение данный точки x=2 процесс особый.
Обычно, чтобы избежать путаницы о включении концов интервалов говорят отдельно.
Александр Иванов
Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
В точке х=2 функция дифференцируема, а на интервале (2; 6) производная положительна, значит, на промежутке её значения строго положительны, значит функция на этом участке только возрастает, поэтому значение функции в левом конце x
= −3 меньше, чем её значение в правом конце x
= −2.
Ответ: φ
2 (−3) φ
2 (−2)
2) Пользуясь графиком первообразной Φ
2 (x
) (в нашем случае это синий график), определите какое из 2-ух значений функции больше φ
2 (−1) или φ
2 (4)?
По графику первообразной видно, что точка x
= −1 находится на участке возрастания, следовательно значение соответсвующей производной положительно. Точка x
= 4 находится на участке убывания и значение соответствующей производной отрицательно. Поскольку положительное значение больше отрицательного, делаем вывод — значение неизвестной функции, которая как раз и является производной, в точке 4 меньше, чем в точке −1.
Ответ: φ
2 (−1) > φ
2 (4)
Подобных вопросов по отсутствующему графику можно задать много, что обуславливает большое разноообразие задач с кратким ответом, построенных по такой же схеме. Попробуйте решить некоторые из них.
Задачи на определение характеристик производной по графику функции.
Рисунок 1.
Рисунок 2.
Задача 1
y
= f
(x
), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции положительна.
Производная функции положительна на тех участках, где функция возрастает. По рисунку видно, что это промежутки (−10,5;−7,6), (−1;8,2) и (15,7;19). Перечислим целые точки внутри этих интервалов: «−10″,»−9», «−8″,»0», «1»,»2″, «3»,»4″, «5»,»6″, «7»,»8″, «16»,»17″, «18». Всего 15 точек.
Ответ: 15
Замечания.
1. Когда в задачах о графиках функций требуют назвать «точки», как правило, имеют в виду только значения аргумента x
, которые являются абсциссами соответствующих точек, расположенных на графике. Ординаты этих точек — значения функции, они являются зависимыми и могут быть легко вычислены при необходимости.
2. При перечислении точек мы не учитывали края интервалов, так как функция в этих точках не возрастает и не убывает, а «разворачивается». Производная в таких точках не положительна и не отрицательна, она равна нулю, поэтому они называются стационарными точками. Кроме того, мы не рассматриваем здесь границы области определения, потому что в условии сказано, что это интервал.
Задача 2
На рисунке 1 изображен график функции y
= f
(x
), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции f »
(x
) отрицательна.
Производная функции отрицательна на тех участках, где функция убывает. По рисунку видно, что это промежутки (−7,6;−1) и (8,2;15,7). Целые точки внутри этих интервалов: «−7″,»−6», «−5″,»−4», «−3″,»−2», «9»,»10″, «11»,»12″, «13»,»14″, «15». Всего 13 точек.
Ответ: 13
См. замечания к предыдущей задаче.
Для решения следующих задач нужно вспомнить еще одно определение.
Точки максимума и минимума функции объединяются общим названием — точки экстремума
.
В этих точках производная функции либо равна нулю, либо не существует (необходимое условие экстремума
).
Однако необходимое условие — это признак, но не гарантия существования экстремума функции. Достаточным условием экстремума
является смена знака производной: если производная в точке меняет знак с «+» на «−», то это точка максимума функции; если производная в точке меняет знак с «−» на «+» , то это точка минимума функции; если в точке производная функции равна нулю, либо не существует, но знак производной при переходе через эту точку не меняется на противоположный, то указанная точка не является точкой экстремума функции. Это может быть точка перегиба, точка разрыва или точка излома графика функции.
Задача 3
На рисунке 1 изображен график функции y
= f
(x
), определенной на интервале (−10,5;19). Найдите количество точек, в которых касательная к графику функции параллельна прямой y
= 6 или совпадает с ней.
Вспомним, что уравнение прямой имеет вид y
= kx
+ b
, где k
— коэффициент наклона этой прямой к оси Ox
. В нашем случае k
= 0, т.е. прямая y
= 6 не наклонена, а параллельна оси Ox
. Значит искомые касательные также должны быть параллельны оси Ox
и также должны иметь коэффициент наклона 0. Таким свойством касательные обладают в точках экстремумов функций. Поэтому для ответа на вопрос нужно просто посчитать все точки экстремумов на графике. Здесь их 4 — две точки максимума и две точки минимума.
Ответ: 4
Задача 4
Функции y
= f
(x
), определенной на интервале (−11;23). Найдите сумму точек экстремума функции на отрезке .
На указанном отрезке мы видим 2 точки экстремума. Максимум функции достигается в точке x
1 = 4, минимум в точке x
2 = 8.
x
1 + x
2 = 4 + 8 = 12.
Ответ: 12
Задача 5
На рисунке 1 изображен график функции y
= f
(x
), определенной на интервале (−10,5;19). Найдите количество точек, в которых производная функции f »
(x
) равна 0.
Производная функции равна нулю в точках экстремума, которых на графике видно 4:
2 точки максимума и 2 точки минимума.
Ответ: 4
Задачи на определение характеристик функции по графику её производной.
Рисунок 1.
Рисунок 2.
Задача 6
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). В какой точке отрезка [−6;2] функция f
(x
) принимает наибольшее значение.
На указанном отрезке производная нигде не была положительной, следовательно функция не возрастала. Она убывала или проходила через стационарные точки. Таким образом, наибольшего значения функция достигала на левой границе отрезка: x
= −6.
Ответ: −6
Замечание:
По графику производной видно, что на отрезке [−6;2] она равна нулю трижды: в точках x
= −6, x
= −2, x
= 2. Но в точке x
= −2 она не меняла знака, значит в этой точке не могло быть экстремума функции. Скорее всего там была точка перегиба графика исходной функции.
Задача 7
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). В какой точке отрезка функция принимает наименьшее значение.
На отрезке производная строго положительна, следовательно функция на этом участке только возрастала. Таким образом, наименьшего значения функция достигала на левой границе отрезка: x
= 3.
Ответ: 3
Задача 8
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). Найдите количество точек максимума функции f
(x
), принадлежащих отрезку [−5;10].
Согласно необходимому условию экстремума максимум функции может быть
в точках, где её производная равна нулю. На заданном отрезке это точки: x
= −2, x
= 2, x
= 6, x
= 10. Но согласно достаточному условию он точно будет
только в тех из них, где знак производной меняется с «+» на «−». На графике производной мы видим, что из перечисленных точек такой является только точка x
= 6.
Ответ: 1
Задача 9
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). Найдите количество точек экстремума функции f
(x
), принадлежащих отрезку .
Экстремумы функции могут быть в тех точках, где её производная равна 0. На заданном отрезке графика производной мы видим 5 таких точек: x
= 2, x
= 6, x
= 10, x
= 14, x
= 18. Но в точке x
= 14 производная не поменяла знак, следовательно её надо исключить из рассмотрения. Таким образом, остаются 4 точки.
Ответ: 4
Задача 10
На рисунке 1 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−10,5;19). Найдите промежутки возрастания функции f
(x
). В ответе укажите длину наибольшего из них.
Промежутки возрастания функции совпадают с промежутками положительности производной. На графике мы видим их три — (−9;−7), (4;12), (18;19). Самый длинный из них второй. Его длина l
= 12 − 4 = 8.
Ответ: 8
Задача 11
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). Найдите количество точек, в которых касательная к графику функции f
(x
) параллельна прямой y
= −2x
− 11
или совпадает с ней.
Угловой коэффициент (он же тангенс угла наклона) заданной прямой k = −2. Нас интересуют параллельные или совпадающие касательные, т.е. прямые с таким же наклоном. Исходя из геометрического смысла производной — угловой коэффициент касательной в рассматриваемой точке графика функции, пересчитываем точки, в которых производная равна −2. На рисунке 2 таких точек 9. Их удобно считать по пересечениям графика и линии координатной сетки, проходящей через значение −2 на оси Oy
.
Ответ: 9
Как видите, по одному и тому же графику можно задать самые разнообразные вопросы о поведении функции и её производной. Также один тот же вопрос можно отнести к графикам разных функций. Будьте внимательны при решении этой задачи на экзамене, и она покажется Вам очень легкой. Другие виды задач этого задания — на геометрический смысл первообразной — будут рассмотрены в другом разделе.
Как найти производную функции в точке x0
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).
- Точка x0 называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
07.06.2019
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (−3; 3), B (5; 5), C (5; 3). Угол наклона касательной к оси абсцисс будет равен углу BAC. Поэтому
Производная функции в точке
Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:
1) Необходимо найти производную.
2) Необходимо вычислить значение производной в заданной точке.
Вычислить производную функции в точке
Справка: Следующие способы обозначения функции эквивалентны: В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».
Сначала находим производную:
Надеюсь, многие уже приноровились находить такие производные устно.
На втором шаге вычислим значение производной в точке :
Небольшой разминочный пример для самостоятельного решения:
Вычислить производную функции в точке
Полное решение и ответ в конце урока.
Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции (следующий параграф), исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др.
Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
Вычислить производную функции в точке . Сначала найдем производную:
Производная, в принципе, найдена, и можно подставлять требуемое значение . Но что-то делать это не сильно хочется. Выражение очень длинное, да и значение «икс» у нас дробное. Поэтому стараемся максимально упростить нашу производную. В данном случае попробуем привести к общему знаменателю три последних слагаемых:
Ну вот, совсем другое дело. Вычислим значение производной в точке :
В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому-что арктангенсов на студенческий век ещё хватит.
Вычислить производную функции в точке .
Это пример для самостоятельного решения.
Уравнение касательной к графику функции
Чтобы закрепить предыдущий параграф, рассмотрим задачу нахождения касательной кграфику функции в данной точке. Это задание встречалось нам в школе, и оно же встречается в курсе высшей математики.
Рассмотрим «демонстрационный» простейший пример.
Составить уравнение касательной к графику функции в точке с абсциссой . Я сразу приведу готовое графическое решение задачи (на практике этого делать в большинстве случаев не надо):
Строгое определение касательной даётся с помощью определения производной функции, но пока мы освоим техническую часть вопроса. Наверняка практически всем интуитивно понятно, что такое касательная. Если объяснять «на пальцах», то касательная к графику функции – это прямая, которая касается графика функции в единственнойточке. При этом все близлежащие точки прямой расположены максимально близко к графику функции.
Применительно к нашему случаю: при касательная (стандартное обозначение) касается графика функции в единственной точке .
И наша задача состоит в том, чтобы найти уравнение прямой .
Производная функции в точке
Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:
1) Необходимо найти производную.
2) Необходимо вычислить значение производной в заданной точке.
Вычислить производную функции в точке
Справка: Следующие способы обозначения функции эквивалентны:
В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».
Сначала находим производную:
Надеюсь, многие уже приноровились находить такие производные устно.
На втором шаге вычислим значение производной в точке :
Небольшой разминочный пример для самостоятельного решения:
Вычислить производную функции в точке
Полное решение и ответ в конце урока.
Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции (следующий параграф), исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др.
Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
Вычислить производную функции в точке .
Сначала найдем производную:
Производная, в принципе, найдена, и можно подставлять требуемое значение . Но что-то делать это не сильно хочется. Выражение очень длинное, да и значение «икс» у нас дробное. Поэтому стараемся максимально упростить нашу производную. В данном случае попробуем привести к общему знаменателю три последних слагаемых:
Ну вот, совсем другое дело. Вычислим значение производной в точке :
В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому-что арктангенсов на студенческий век ещё хватит.
Вычислить производную функции в точке .
Это пример для самостоятельного решения.
Как найти значение производной функции F(x) в точке Хо? Как вообще это решать?
Sfash
Если формула задана, то найти производную и вместо Х подставить Х-нулевое. Посчитать
Если речь идет о б-8 ЕГЭ, график, то надо найти тангенс угла (острый или тупой) , который образует касательная с осью Х (с помощью мысленного построения прямоугольного треугольника и определения тангенса угла)
Тимур адильходжаев
Во-первых, надо определиться со знаком. Если точка х0 находится в нижней части координатной плоскости, то знак в ответе будет минус, а если выше, то +.
Во-вторых, надо знать что такое тангес в прямоугольном прямоугольнике. А это соотношение противолежащей стороны (катета) к прилежащей стороне (тоже катета) . На картине обычно есть несколько черных отметок. Из эти отметок составляешь прямоугольный треугольник и находишь тангес.
Как найти значение производной функции f x в точке x0?
Bk.Ru
В общем случае, что бы найти значение производной какой-либо функции по некоторой переменной в какой-либо точке, нужно продифференцировать заданную функцию по этой переменной. В вашем случае по переменной Х. В полученное выражение вместо Х поставить значение икса в той точке, для которой надо найти значение производной, т.е. в Вашем случае подставить нулевой Х и вычислить полученное выражение.
Ну а ваше стремление разобраться в этом вопросе, на мой взгляд, бесспорно заслуживает +, который ставлю с чистой совестью.
Lady v
Такая постановка задачи на нахождение производной часто ставится для закрепления материала на геометрический смысл производной. Предлагается график некоей функции, совершенно произвольной и не заданной уравнением и требуется найти значение производной (не саму производную заметьте!) в указанной точке Х0. Для этого строится касательная к заданной функции и находится точки ее пересечения с осями координат. Потом составляется уравнение этой касательной в виде y=кx+b.
В этом уравнении коэффициент к и будет являться значением производной. остается лишь найти значение коэффициента b. Для этого находим значение у при х=о, пусть оно равно 3 – это и есть значение коэффициента b. Подставляем в исходное уравнение значения Х0 и У0 и находим к – нашу значение производной в этой точке.
Урок 14. геометрический смысл производной — Алгебра и начала математического анализа — 11 класс
Алгебра и начала анализа, 11 класса.
Урок №14. Геометрический смысл производной.
Перечень вопросов, рассматриваемых в теме
1) Геометрический смысл производной;
2) Алгоритм нахождения касательной к графику функции в точке;
3) Сравнение производных заданной функции по ее графику в различных точках.
Глоссарий по теме
Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Напомним, что графиком линейной функции у=кх + b является прямая.
Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.
Если k>0, то 0<α< π/2, в этом случае функция возрастает
Если k<0, то — π/2<α<0, в этом случае функция убывает
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Рассмотрим график функции y = f ( x ):
Из рисунка видно, что для любых двух точек A и B графика функции: f(x0+Δx)/f(x0)Δx=tgα, где — угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей.
Если зафиксировать точку A и двигать по направлению к ней точку B, то Δx неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.
Отсюда следует:
производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
В этом и состоит геометрический смысл производной.
Уравнение касательной к графику функции y=f(x) в точке x0:
Примеры и разбор решения заданий тренировочного модуля
№1. Составить уравнение касательной к графику функции y=x+e-2x, параллельной прямой y=-x
Решение:
Угловой коэффициент касательной равен значению производной в точке касания x0. Т.к. касательная параллельна прямой y=-x, значит ее угловой коэффициент равен –1. Таким образом, f'(x0) = -1.
Уравнение касательной:
Уравнение касательной: y=1-1(x-0) = 1-x
Ответ: y=1-x.
№2. На параболе у=х2-2х-8 найти точку М, в которой касательная к ней параллельна прямой 4х+у+4=0.
Решение:
Определим угловой коэффициент касательной к параболе у=х2-2х-8:
k =у’=(х2-2х-8)’=2х-2.
Найдем угловой коэффициент прямой 4х+у+4=0:
у=-4х-4, k =-4.
Касательная к параболе и данная прямая по условию параллельны. Следовательно, их угловые коэффициенты равны, т.е.
2х-2=-4;
х=-1 – абсцисса точки касания.
Ординату точки касания М вычислим из уравнения данной параболы у=х2-2х-8, т.е.
у(-1)=(-1)2-2(-1)-8=-5, М(-1;-5).
Ответ: М(-1;-5).
Что такое производная
Производная — главнейшее понятие математического анализа. Она характеризует изменение функции аргумента x в некоторой точке. При этом и сама производная является функцией от аргумента x
Производной функции в точке называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
То есть,
(1)
Наиболее употребительны следующие обозначения производной:
Пример 1. Пользуясь определением производной, найти производную функции
.
Решение. Из определения производной вытекает следующая схема её вычисления.
Дадим аргументу приращение (дельта) и найдём приращение функции:
.
Найдём отношение приращения функции к приращению аргумента:
Вычислим предел этого отношения при условии, что приращение аргумента стремится к нулю,
то есть требуемую в условии задачи производную:
К понятию производной привело изучение Галилео Галилеем закона свободного падения тел, а в
более широком смысле — задачи о мгновенной скорости неравномерного прямолинейного движения точки.
Однако движение свободно падающего тела явно неравномерное. Скорость v падения
постоянно возрастает. И средней скорости уже недостаточно для характеристики быстроты движения на различных участках пути.
Такая характеристика тем точнее, чем меньше промежуток времени .
Поэтому вводится следующее понятие: мгновенной скоростью прямолинейного движения (или скоростью в данный момент времени t)
называется предел средней скорости при :
(при условии, что этот предел существует и конечен).
Так выясняется, что мгновенная скорость есть предел отношения приращения функции s(t)
к приращению аргумента t при
Это и есть производная, которая в общем виде записывается так:.
.
Решение обозначенной задачи представляет собой физический смысл производной. Итак, производной функции y=f(x)
в точке x называется предел (если он существует и конечен) приращения функции к приращению аргумента
при условии, что последнее стремится к нулю.
Пример 2. Найти производную функции
Решение. Из определения производной вытекает следующая схема для её вычисления.
Шаг 1. Дадим аргументу приращение и найдём
Шаг 2. Найдём приращение функции:
Шаг 3. Найдём отношение приращения функции к приращению аргумента:
Шаг 4. Вычислим предел этого отношения при , то есть производную:
Касательной к графику функции в точке М называется предельное положение секущей МР при , или, что то же при .
Из определения следует, что для существования касательной достаточно, чтобы существовал предел
,
причём предел равен углу наклона касательной к оси .
Теперь дадим точное определение касательной.
Из этого определения следует, что производная функции равна угловому коэффициенту касательной к графику этой функции в точке с абсциссой x. В этом состоит геометрический смысл производной:
где — угол наклона касательной к оси абсцисс, т.е. угловой коэффициент касательной.
Пример 3. Найти производную функции и значение этой производной при .
Решение. Воспользуемся схемой, приведённой в примере 1.
Шаг 1.
Шаг 2.
Шаг 3.
Шаг 4.
Выражение под знаком предела не определено при (неопределённость вида 0/0), поэтому преобразуем его, избавившись от иррациональности в числителе и затем сократив дробь:
Найдём значение производной при :
Весь блок «Производная»
Наименьшее значение производной. Производная функции
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна
. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.
Запомним определение:
Производная — это скорость изменения функции.
На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?
Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.
Вот другой пример.
Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная
, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Производная функции обозначается .
Покажем, как найти с помощью графика.
Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной
.
Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .
Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.
Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .
Есть и другое важное соотношение. Вспомним, что прямая задается уравнением
Величина в этом уравнении называется угловым коэффициентом прямой
. Она равна тангенсу угла наклона прямой к оси .
.
Мы получаем, что
Запомним эту формулу. Она выражает геометрический смысл производной.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Другими словами, производная равна тангенсу угла наклона касательной.
Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.
Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.
В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол с положительным направлением оси . Значит, в точке производная положительна.
В точке наша функция убывает. Касательная в этой точке образует тупой угол с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.
Вот что получается:
Если функция возрастает, ее производная положительна.
Если убывает, ее производная отрицательна.
А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».
В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
Если производная положительна, то функция возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | — | 0 | + |
Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.
Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая :
В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.
Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется
Этот раздел содержит задачи ЕГЭ по математике на темы, связанные с исследованием функций и их производных.
В демонстрационных вариантах ЕГЭ 2020
года они могут встретиться под номером 14
для базового уровня и под номером 7
для профильного уровня.
Посмотрите внимательно на эти три графика функций.
Заметили ли вы, что эти функции в некотором смысле «родственники»?
Например, на тех участках, где график зеленой функции расположен выше нуля, красная функция возрастает. На тех участках, где график зеленой функции ниже нуля, красная функция убывает.
Аналогичные замечания можно сделать относительно красного и синего графиков.
Также можно заметить, что нули зеленой функции (точки x
= −1 и x
= 3) совпадают с точками экстремумов красного графика: при x
= −1 на красном графике мы видим локальный максимум, при х
= 3 на красном графике локальный минимум.
Нетрудно заметить, что локальные максимумы и минимумы синего графика достигаются в тех же точках, где красный график проходит через значение y
= 0.
Можно сделать еще несколько выводов об особенностях поведения этих графиков, потому что они действительно связаны между собой. Посмотрите на формулы функций, расположенные под каждым из графиков, и путем вычислений убедитесь, что каждая предыдущая является производной для последующей и, соответственно, каждая следующая является одной из превообразных предыдущей функции.
φ
1 (x
) = φ»
2 (x
) φ
2 (x
) = Φ
1 (x
)
φ
2 (x
) = φ»
3 (x
)
φ
3 (x
) = Φ
2 (x
)
Вспомним, что мы знаем о производной:
Производная функции y
= f
(x
) в точке х
выражает скорость изменения функции в точке x
.
Физический смысл производной
заключается в том, что производная выражает скорость протекания процесса, описываемого зависимостью y = f(x).
Геометрический смысл производной
заключается в том, что её значение в рассматриваемой точке равняется угловому коэффициенту касательной, проведенной к графику дифференцируемой функции в этой точке.
А теперь пусть красного графика на рисунке нет. Допустим, что и формулы функций нам неизвестны.
Могу ли я спросить вас о чем то, связанном с поведением функции φ
2 (x
), если известно, что она является производной функции φ
3 (x
) и первообразной функции φ
1 (x
)?
Могу. И на многие вопросы можно дать точный ответ, ведь мы знаем, что производная является характеристикой скорости изменения функции, поэтому можем судить о некоторых особенностях поведения одной из этих функций, глядя на график другой.
Прежде, чем отвечать на следующие вопросы, прокрутите страницу вверх так, чтобы скрылся верхний рисунок, содержащий красный график. Когда ответы будут даны, верните его обратно, чтобы проверить результат. И только после этого смотрите моё решение.
Внимание:
Для усиления обучающего эффекта ответы и решения
загружаются отдельно для каждой задачи последовательным нажатием кнопок на желтом фоне. (Когда задач много, кнопки могут появиться с задержкой. Если кнопок не видно совсем, проверьте, разрешен ли в вашем браузере JavaScript.
)
1) Пользуясь графиком производной φ»
2 (x
) (в нашем случае это зеленый график), определите какое из 2-ух значений функции больше φ
2 (−3) или φ
2 (−2)?
По графику производной видно, что на участке [−3;−2] её значения строго положительны, значит функция на этом участке только возрастает, поэтому значение функции в левом конце x
= −3 меньше, чем её значение в правом конце x
= −2.
Ответ: φ
2 (−3) φ
2 (−2)
2) Пользуясь графиком первообразной Φ
2 (x
) (в нашем случае это синий график), определите какое из 2-ух значений функции больше φ
2 (−1) или φ
2 (4)?
По графику первообразной видно, что точка x
= −1 находится на участке возрастания, следовательно значение соответсвующей производной положительно. Точка x
= 4 находится на участке убывания и значение соответствующей производной отрицательно. Поскольку положительное значение больше отрицательного, делаем вывод — значение неизвестной функции, которая как раз и является производной, в точке 4 меньше, чем в точке −1.
Ответ: φ
2 (−1) > φ
2 (4)
Подобных вопросов по отсутствующему графику можно задать много, что обуславливает большое разноообразие задач с кратким ответом, построенных по такой же схеме. Попробуйте решить некоторые из них.
Задачи на определение характеристик производной по графику функции.
Рисунок 1.
Рисунок 2.
Задача 1
y
= f
(x
), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции положительна.
Производная функции положительна на тех участках, где функция возрастает. По рисунку видно, что это промежутки (−10,5;−7,6), (−1;8,2) и (15,7;19). Перечислим целые точки внутри этих интервалов: «−10″,»−9», «−8″,»0», «1»,»2″, «3»,»4″, «5»,»6″, «7»,»8″, «16»,»17″, «18». Всего 15 точек.
Ответ: 15
Замечания.
1. Когда в задачах о графиках функций требуют назвать «точки», как правило, имеют в виду только значения аргумента x
, которые являются абсциссами соответствующих точек, расположенных на графике. Ординаты этих точек — значения функции, они являются зависимыми и могут быть легко вычислены при необходимости.
2. При перечислении точек мы не учитывали края интервалов, так как функция в этих точках не возрастает и не убывает, а «разворачивается». Производная в таких точках не положительна и не отрицательна, она равна нулю, поэтому они называются стационарными точками. Кроме того, мы не рассматриваем здесь границы области определения, потому что в условии сказано, что это интервал.
Задача 2
На рисунке 1 изображен график функции y
= f
(x
), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции f »
(x
) отрицательна.
Производная функции отрицательна на тех участках, где функция убывает. По рисунку видно, что это промежутки (−7,6;−1) и (8,2;15,7). Целые точки внутри этих интервалов: «−7″,»−6», «−5″,»−4», «−3″,»−2», «9»,»10″, «11»,»12″, «13»,»14″, «15». Всего 13 точек.
Ответ: 13
См. замечания к предыдущей задаче.
Для решения следующих задач нужно вспомнить еще одно определение.
Точки максимума и минимума функции объединяются общим названием — точки экстремума
.
В этих точках производная функции либо равна нулю, либо не существует (необходимое условие экстремума
).
Однако необходимое условие — это признак, но не гарантия существования экстремума функции. Достаточным условием экстремума
является смена знака производной: если производная в точке меняет знак с «+» на «−», то это точка максимума функции; если производная в точке меняет знак с «−» на «+» , то это точка минимума функции; если в точке производная функции равна нулю, либо не существует, но знак производной при переходе через эту точку не меняется на противоположный, то указанная точка не является точкой экстремума функции. Это может быть точка перегиба, точка разрыва или точка излома графика функции.
Задача 3
На рисунке 1 изображен график функции y
= f
(x
), определенной на интервале (−10,5;19). Найдите количество точек, в которых касательная к графику функции параллельна прямой y
= 6 или совпадает с ней.
Вспомним, что уравнение прямой имеет вид y
= kx
+ b
, где k
— коэффициент наклона этой прямой к оси Ox
. В нашем случае k
= 0, т.е. прямая y
= 6 не наклонена, а параллельна оси Ox
. Значит искомые касательные также должны быть параллельны оси Ox
и также должны иметь коэффициент наклона 0. Таким свойством касательные обладают в точках экстремумов функций. Поэтому для ответа на вопрос нужно просто посчитать все точки экстремумов на графике. Здесь их 4 — две точки максимума и две точки минимума.
Ответ: 4
Задача 4
Функции y
= f
(x
), определенной на интервале (−11;23). Найдите сумму точек экстремума функции на отрезке .
На указанном отрезке мы видим 2 точки экстремума. Максимум функции достигается в точке x
1 = 4, минимум в точке x
2 = 8.
x
1 + x
2 = 4 + 8 = 12.
Ответ: 12
Задача 5
На рисунке 1 изображен график функции y
= f
(x
), определенной на интервале (−10,5;19). Найдите количество точек, в которых производная функции f »
(x
) равна 0.
Производная функции равна нулю в точках экстремума, которых на графике видно 4:
2 точки максимума и 2 точки минимума.
Ответ: 4
Задачи на определение характеристик функции по графику её производной.
Рисунок 1.
Рисунок 2.
Задача 6
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). В какой точке отрезка [−6;2] функция f
(x
) принимает наибольшее значение.
На указанном отрезке производная нигде не была положительной, следовательно функция не возрастала. Она убывала или проходила через стационарные точки. Таким образом, наибольшего значения функция достигала на левой границе отрезка: x
= −6.
Ответ: −6
Замечание:
По графику производной видно, что на отрезке [−6;2] она равна нулю трижды: в точках x
= −6, x
= −2, x
= 2. Но в точке x
= −2 она не меняла знака, значит в этой точке не могло быть экстремума функции. Скорее всего там была точка перегиба графика исходной функции.
Задача 7
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). В какой точке отрезка функция принимает наименьшее значение.
На отрезке производная строго положительна, следовательно функция на этом участке только возрастала. Таким образом, наименьшего значения функция достигала на левой границе отрезка: x
= 3.
Ответ: 3
Задача 8
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). Найдите количество точек максимума функции f
(x
), принадлежащих отрезку [−5;10].
Согласно необходимому условию экстремума максимум функции может быть
в точках, где её производная равна нулю. На заданном отрезке это точки: x
= −2, x
= 2, x
= 6, x
= 10. Но согласно достаточному условию он точно будет
только в тех из них, где знак производной меняется с «+» на «−». На графике производной мы видим, что из перечисленных точек такой является только точка x
= 6.
Ответ: 1
Задача 9
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). Найдите количество точек экстремума функции f
(x
), принадлежащих отрезку .
Экстремумы функции могут быть в тех точках, где её производная равна 0. На заданном отрезке графика производной мы видим 5 таких точек: x
= 2, x
= 6, x
= 10, x
= 14, x
= 18. Но в точке x
= 14 производная не поменяла знак, следовательно её надо исключить из рассмотрения. Таким образом, остаются 4 точки.
Ответ: 4
Задача 10
На рисунке 1 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−10,5;19). Найдите промежутки возрастания функции f
(x
). В ответе укажите длину наибольшего из них.
Промежутки возрастания функции совпадают с промежутками положительности производной. На графике мы видим их три — (−9;−7), (4;12), (18;19). Самый длинный из них второй. Его длина l
= 12 − 4 = 8.
Ответ: 8
Задача 11
На рисунке 2 изображен график f »
(x
) — производной функции f
(x
), определенной на интервале (−11;23). Найдите количество точек, в которых касательная к графику функции f
(x
) параллельна прямой y
= −2x
− 11
или совпадает с ней.
Угловой коэффициент (он же тангенс угла наклона) заданной прямой k = −2. Нас интересуют параллельные или совпадающие касательные, т.е. прямые с таким же наклоном. Исходя из геометрического смысла производной — угловой коэффициент касательной в рассматриваемой точке графика функции, пересчитываем точки, в которых производная равна −2. На рисунке 2 таких точек 9. Их удобно считать по пересечениям графика и линии координатной сетки, проходящей через значение −2 на оси Oy
.
Ответ: 9
Как видите, по одному и тому же графику можно задать самые разнообразные вопросы о поведении функции и её производной. Также один тот же вопрос можно отнести к графикам разных функций. Будьте внимательны при решении этой задачи на экзамене, и она покажется Вам очень легкой. Другие виды задач этого задания — на геометрический смысл первообразной — будут рассмотрены в другом разделе.
Сергей Никифоров
Если производная функции знакопостоянна на интервале, а сама функция непрерывна на его границах, то граничные точки присоединяются как к промежуткам возрастания, так и к промежуткам убывания, что полностью соответствует определению возрастающих и убывающих функций.
Фарит Ямаев
26.10.2016 18:50
Здравствуйте. Как же (на каком основании) можно утверждать, что в точке, где производная равна нулю, функция возрастает. Приведите доводы. Иначе, это просто чей-то каприз. По какой теореме? А также доказательство. Спасибо.
Служба поддержки
Значение производной в точке не имеет прямого отношения к возрастанию функции на промежутке. Рассмотрите, например, функции — все они возрастают на отрезке
Владлен Писарев
02.11.2016 22:21
Если функция возрастает на интервале (а;b) и определена и непрерывна в точках а и b, то она возрастает на отрезке . Т.е. точка x=2 входит в данный промежуток.
Хотя, как правило возрастание и убывание рассматривается не на отрезке, а на интервале.
Но в самой точке x=2, функция имеет локальный минимум. И как объяснять детям, что когда они ищут точки возрастания (убывания), то точки локального экстремума не считаем, а в промежутки возрастания (убывания) — входят.
Учитывая, что первая часть ЕГЭ для «средней группы детского сада», то наверное такие нюансы- перебор.
Отдельно, большое спасибо за «Решу ЕГЭ» всем сотрудникам- отличное пособие.
Сергей Никифоров
Простое объяснение можно получить, если отталкиваться от определения возрастающей/убывающей функции. Напомню, что звучит оно так: функция называется возрастающей/убывающей на промежутке, если большему аргументу функции соответствует большее/меньшее значение функции. Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.
Ирина Ишмакова
20.11.2017 11:46
Добрый день. Здесь в комментариях я вижу убеждения, что границы включать нужно. Допустим, я с этим соглашусь. Но посмотрите, пожалуйста, ваше решение к задаче 7089. Там при указании промежутков возрастания границы не включаются. И это влияет на ответ. Т.е. решения заданий 6429 и 7089 противоречат друг другу. Проясните, пожалуйста, эту ситуацию.
Александр Иванов
В заданиях 6429 и 7089 совершенно разные вопросы.
В одном про промежутки возрастания, а в другом про промежутки с положительной производной.
Противоречия нет.
Экстремумы входят в промежутки возрастания и убывания, но точки, в которых производная равна нулю, не входят в промежутки, на которых производная положительна.
A Z
28.01.2019 19:09
Коллеги, есть понятие возрастания в точке
(см. Фихтенгольц например)
и ваше понимание возрастания в точке x=2 противочет классическому определению.
Возрастание и убывание это процесс и хотелось бы придерживаться этого принципа.
В любом интервале, который содержит точку x=2, функция не является возрастающей. Поэтому включение данный точки x=2 процесс особый.
Обычно, чтобы избежать путаницы о включении концов интервалов говорят отдельно.
Александр Иванов
Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
В точке х=2 функция дифференцируема, а на интервале (2; 6) производная положительна, значит, на промежутке }
вычислить значение производной на каждом из участков графика
Вы искали вычислить значение производной на каждом из участков графика? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить значение производной функции в точке x0, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вычислить значение производной на каждом из участков графика».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычислить значение производной на каждом из участков графика,вычислить значение производной функции в точке x0,геометрический смысл производной примеры решения задач,значение производной в точке,значение производной в точке как найти,значение производной функции f x в точке x,значение производной функции в точке,значение производной функции в точке как найти,как найти значение производной в точке,как найти значение производной в точке х0,как найти значение производной функции,как найти значение производной функции f x в точке x0,как найти значение производной функции f x в точке x0 по графику,как найти значение производной функции в точке,как найти значение производной функции в точке х0 по графику,как найти производную функции в точке x0,как по графику производной найти значение производной в точке,как по графику функции найти значение производной в точке х0,найдите значение производной,найдите значение производной в точке х0,найдите значение производной функции,найдите значение производной функции f x в точке y x0,найдите значение производной функции в точке,найдите значение производной функции в точке x0,найдите значение производной функции в точке х0,найти значение производной в точке x0,найти значение производной функции в точке,найти значение производной функции в точке х0. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычислить значение производной на каждом из участков графика. Просто введите задачу в окошко и нажмите
«решить» здесь (например, геометрический смысл производной примеры решения задач).
Где можно решить любую задачу по математике, а так же вычислить значение производной на каждом из участков графика Онлайн?
Решить задачу вычислить значение производной на каждом из участков графика вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Как оценить производную по графику
Обновлено 8 декабря 2020 г.
Ли Джонсон
Темпы изменений проявляются повсюду в науке, и особенно в физике, через такие величины, как скорость и ускорение. Производные описывают скорость изменения одной величины по отношению к другой математически, но их вычисление иногда может быть сложным, и вам может быть представлен график, а не функция в форме уравнения. Если вам представлен график кривой и вам нужно найти производную от него, возможно, вы не сможете быть столь же точными, как с уравнением, но вы легко сможете сделать твердую оценку.
TL; DR (слишком долго; не читал)
Выберите точку на графике, в которой нужно найти значение производной.
Проведите в этой точке прямую касательную к кривой графика.
Определите наклон этой линии, чтобы найти значение производной в выбранной вами точке на графике.
Что такое производный инструмент?
Если не считать абстрактной установки дифференцирования уравнения, вы можете немного запутаться в том, что на самом деле представляет собой производная.В алгебре производная функции — это уравнение, которое сообщает вам значение «наклона» функции в любой точке. Другими словами, он сообщает вам, насколько одно значение изменяется при небольшом изменении другого. На графике градиент или наклон линии показывают, насколько зависимая переменная (размещенная на оси y ) изменяется с независимой переменной (на оси x ).
Для прямолинейных графиков вы определяете (постоянную) скорость изменения, вычисляя наклон графика.Отношения, описываемые кривыми, не так просты, но принцип, согласно которому производная просто означает наклон (в этой конкретной точке), все еще остается в силе.
Для отношений, описываемых кривыми, производная принимает разные значения в каждой точке кривой. Чтобы оценить производную графика, вам нужно выбрать точку, в которой будет производная. Например, если у вас есть график, показывающий пройденное расстояние в зависимости от времени, на прямолинейном графике наклон будет указывать вам постоянную скорость.Для скоростей, которые меняются со временем, график будет кривой, но прямая линия, которая только касается кривой в одной точке (линия, касательная к кривой), представляет скорость изменения в этой конкретной точке.
Выберите место, где вам нужно знать производную. Используя пример зависимости пройденного расстояния от времени, выберите время, в которое вы хотите узнать скорость движения. Если вам нужно узнать скорость в нескольких разных точках, вы можете выполнить этот процесс для каждой отдельной точки.Если вы хотите узнать скорость через 15 секунд после начала движения, выберите точку на кривой через 15 секунд на оси x .
Нарисуйте линию, касательную к кривой в интересующей вас точке. Не торопитесь, потому что это самая важная и самая сложная часть процесса. Ваша оценка будет лучше, если вы проведете более точную касательную. Поднесите линейку к точке на кривой и отрегулируйте ее ориентацию так, чтобы линия, которую вы рисуете, касалась только кривой в одной интересующей вас точке.
Нарисуйте линию, насколько позволяет график. Убедитесь, что вы можете легко прочитать два значения для координат x и y , одно в начале вашей строки, а другое в конце. Вам не обязательно рисовать длинную линию (технически подходит любая прямая линия), но более длинные линии, как правило, легче измерить.
Найдите два места на вашей линии и запишите их координаты x и y .Например, представьте свою касательную линию в виде двух заметных точек с координатами x = 1, y = 3 и x = 10, y = 30, которые вы можете назвать точкой 1. и Точка 2. Использование символов x 1 и y 1 для представления координат первой точки и x 2 и y 2 для представления координат второй точки уклон м определяется как:
m = \ frac {y_2 — y_1} {x_2 — x_1}
Это показывает производную кривой в точке, где линия касается кривой.В этом примере x 1 = 1, x 2 = 10, y 1 = 3 и y 2 = 30, поэтому:
\ begin {align} m & = \ frac {30-3} {10-1} \\ \, \\ & = \ frac {27} {9} \\ \, \\ & = 9 \ end { выровнено}
В этом примере результатом будет скорость в выбранной точке. Таким образом, если ось x измеряется в секундах, а ось y — в метрах, результат будет означать, что рассматриваемое транспортное средство движется со скоростью 3 метра в секунду.Независимо от конкретной величины, которую вы рассчитываете, процесс оценки производной одинаков.
3.2: Производная как функция
Цели обучения
- Определите производную функцию заданной функции.
- Постройте производную функцию от графика заданной функции.
- Укажите связь между производными и непрерывностью.
- Опишите три условия, когда функция не имеет производной.
- Объясните значение производной высшего порядка.
Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке. Если мы дифференцируем функцию положения в данный момент времени, мы получаем скорость в этот момент. Кажется разумным заключить, что знание производной функции в каждой точке может дать ценную информацию о поведении функции. Однако процесс нахождения производной даже для нескольких значений с использованием методов предыдущего раздела быстро стал бы довольно утомительным.В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
Производные функции
Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная. Мы можем формально определить производную функцию следующим образом.
Определение: производная функция
Пусть \ (f \) — функция. Производная функция , обозначаемая \ (f ‘\), является функцией, область определения которой состоит из таких значений \ (x \), что существует следующий предел:
\ [f ‘(x) = \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h}.\ label {derdef} \]
Функция \ (f (x) \) называется дифференцируемой в точке \ (a \), если существует \ (f ‘(a) \). В более общем смысле, функция называется дифференцируемой на \ (S \), если она дифференцируема в каждой точке открытого множества \ (S \), а дифференцируемая функция — это функция, в которой \ (f ‘( x) \) существует в своем домене.
В следующих нескольких примерах мы используем уравнение \ ref {derdef}, чтобы найти производную функции.
Пример \ (\ PageIndex {1} \): поиск производной функции квадратного корня
Найдите производную от \ (f (x) = \ sqrt {x} \).
Решение
Начните непосредственно с определения производной функции.
Заменить \ (f (x + h) = \ sqrt {x + h} \) и \ (f (x) = \ sqrt {x} \) в \ (f ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \).
| \ (е ‘(х) = \ displaystyle \ lim_ {h → 0} \ frac {\ sqrt {x + h} — \ sqrt {x}} {h} \) | ||
| \ (= \ displaystyle \ lim_ {h → 0} \ frac {\ sqrt {x + h} — \ sqrt {x}} {h} ⋅ \ frac {\ sqrt {x + h} + \ sqrt { x}} {\ sqrt {x + h} + \ sqrt {x}} \) | Умножьте числитель и знаменатель на \ (\ sqrt {x + h} + \ sqrt {x} \) без распределения в знаменателе. 2 \).2−2x \ справа) = 2x − 2 \). Таким образом, для функции \ (y = f (x) \) каждое из следующих обозначений представляет производную от \ (f (x) \): \ (f ‘(x), \ quad \ dfrac {dy} {dx}, \ quad y’, \ quad \ dfrac {d} {dx} \ big (f (x) \ big) \). Вместо \ (f ‘(a) \) мы также можем использовать \ (\ dfrac {dy} {dx} \ Big | _ {x = a} \). Нотация \ (\ dfrac {dy} {dx} \) (называемая нотацией Лейбница) довольно распространена в технике и физике. Чтобы лучше понять это обозначение, напомним, что производная функции в точке — это предел наклона секущих линий, когда секущие линии приближаются к касательной.Наклоны этих секущих часто выражаются в виде \ (\ dfrac {Δy} {Δx} \), где \ (Δy \) — разность значений \ (y \), соответствующая разнице в \ (x \) значения, которые выражаются как \ (Δx \) (Рисунок \ (\ PageIndex {1} \)). Таким образом, производная, которую можно представить как мгновенную скорость изменения \ (y \) по отношению к \ (x \), выражается как \ (\ Displaystyle \ frac {dy} {dx} = \ lim_ {Δx → 0} \ frac {Δy} {Δx} \). Рисунок \ (\ PageIndex {1} \): производная выражается как \ (\ dfrac {dy} {dx} = \ displaystyle \ lim_ {Δx → 0} \ frac {Δy} {Δx} \). График производнойМы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы можем построить график. Учитывая и то, и другое, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку \ (f ‘(x) \) дает скорость изменения функции \ (f (x) \) (или наклон касательной линия к \ (f (x) \)). В примере \ (\ PageIndex {1} \) мы обнаружили, что для \ (f (x) = \ sqrt {x} \), \ (f ‘(x) = \ frac {1} {2 \ sqrt { Икс}}\).Если мы построим график этих функций на тех же осях, как на рисунке \ (\ PageIndex {2} \), мы сможем использовать графики, чтобы понять взаимосвязь между этими двумя функциями. Во-первых, мы замечаем, что \ (f (x) \) увеличивается по всей своей области, а это означает, что наклон его касательных во всех точках положительный. Следовательно, мы ожидаем \ (f ‘(x)> 0 \) для всех значений x в его области определения. Кроме того, по мере увеличения \ (x \) наклон касательных к \ (f (x) \) уменьшается, и мы ожидаем увидеть соответствующее уменьшение \ (f ‘(x) \).2−2x, \; f ‘(x) = 2x − 2 \). Графики этих функций показаны на рисунке \ (\ PageIndex {3} \). Обратите внимание, что \ (f (x) \) убывает при \ (x <1 \). Для тех же значений \ (x \), \ (f '(x) <0 \). Для значений \ (x> 1 \), \ (f (x) \) увеличивается и \ (f ‘(x)> 0 \). Кроме того, \ (f (x) \) имеет горизонтальную касательную в точках \ (x = 1 \) и \ (f ‘(1) = 0 \). Рисунок \ (\ PageIndex {3} \): производная \ (f ‘(x) <0 \), где функция \ (f (x) \) убывает, и \ (f' (x)> 0 \), где \ (f (x) \) возрастает. Производная равна нулю, если функция имеет горизонтальную касательную. Пример \ (\ PageIndex {3} \): эскиз производной с использованием функции Используйте следующий график \ (f (x) \), чтобы нарисовать график \ (f ‘(x) \).2−4 \). На каком интервале находится график \ (f ‘(x) \) над осью \ (x \)?
Деривативы и непрерывностьТеперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков. Во-первых, мы рассматриваем взаимосвязь между дифференцируемостью и непрерывностью.Мы увидим, что если функция дифференцируема в точке, она должна быть там непрерывной; однако функция, непрерывная в какой-то точке, не обязательно должна быть дифференцируемой в этой точке. Фактически, функция может быть непрерывной в точке и не дифференцируемой в этой точке по одной из нескольких причин. Дифференцируемость предполагает непрерывность Пусть \ (f (x) \) — функция и \ (a \) находится в ее области определения. Если \ (f (x) \) дифференцируема в \ (a \), то \ (f \) непрерывна в \ (a \). Проба Если \ (f (x) \) дифференцируемо в \ (a \), то \ (f ‘(a) \) существует и, если мы положим \ (h = x — a \), имеем \ (x = a + h \), и поскольку \ (h = xa \ to 0 \), мы можем видеть, что \ (x \ to a \). Затем \ [f ‘(a) = \ lim_ {h \ to 0} \ frac {f (a + h) -f (a)} {h} \ nonumber \] можно переписать как \ (F ‘(a) = \ displaystyle \ lim_ {x → a} \ frac {f (x) −f (a)} {x − a} \). Мы хотим показать, что \ (f (x) \) непрерывно в \ (a \), показав, что \ (\ displaystyle \ lim_ {x → a} f (x) = f (a). \) Таким образом, \ (\ begin {align *} \ displaystyle \ lim_ {x → a} f (x) & = \ lim_ {x → a} \; \ big (f (x) −f (a) + f (a) \ big) \\ [4pt] Следовательно, поскольку \ (f (a) \) определено и \ (\ displaystyle \ lim_ {x → a} f (x) = f (a) \), мы заключаем, что \ (f \) непрерывно в \ (а \). □ Мы только что доказали, что дифференцируемость предполагает непрерывность, но теперь мы рассмотрим, подразумевает ли непрерывность дифференцируемость. Чтобы определить ответ на этот вопрос, исследуем функцию \ (f (x) = | x | \).2}} = + ∞ \). Таким образом, \ (f ‘(0) \) не существует. Быстрый взгляд на график \ (f (x) = \ sqrt [3] {x} \) проясняет ситуацию. Функция имеет вертикальную касательную в точке \ (0 \) (рисунок \ (\ PageIndex {5} \)). Рисунок \ (\ PageIndex {5} \): функция \ (f (x) = \ sqrt [3] {x} \) имеет вертикальную касательную в точке \ (x = 0 \). Он непрерывен в \ (0 \), но не дифференцируем в \ (0 \). Функция \ (f (x) = \ begin {cases} x \ sin \ left (\ frac {1} {x} \ right), & & \ text {if} x ≠ 0 \\ 0, & & \ text {if} x = 0 \ end {cases} \) также имеет производную, которая демонстрирует интересное поведение в \ (0 \). Мы видим, что \ (е ‘(0) = \ displaystyle \ lim_ {x → 0} \ frac {x \ sin \ left (1 / x \ right) −0} {x − 0} = \ lim_ {x → 0} \ sin \ left (\ frac {1} {x} \ right) \). Этот предел не существует, в основном потому, что наклон секущих линий непрерывно меняет направление по мере приближения к нулю (Рисунок \ (\ PageIndex {6} \)). Рисунок \ (\ PageIndex {6} \): функция \ (f (x) = \ begin {cases} x \ sin \ left (\ frac {1} {x} \ right), & & \ text {if} x ≠ 0 \\ 0, & & \ text {if} x = 0 \ end {ases} \) не дифференцируем в \ (0 \). Итого:
| Упростите числитель. |
| \ (= \ Displaystyle \ lim_ {h → 0} (4x + h − 3) \) | Выносим за скобки \ (h \) в числителе и сокращаем, добавляя \ (h \) в знаменатель. | |
| \ (= 4x − 3 \) | Возьми предел. |
Затем найдите \ (f » (x) \), взяв производную от \ (f ‘(x) = 4x − 3. \)
| \ (f » (x) = \ displaystyle \ lim_ {h → 0} \ frac {f ‘(x + h) −f’ (x)} {h} \) | Используйте \ (f ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \) с \ (f’ (x) \) в место \ (f (x).3 \), найти \ (a (t). \)
Ключевые понятия
Ключевые уравнения\ (е ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \) Глоссарий
Авторы и авторство
Производная функция — задача 3Мы смотрим на производную функцию. Вот еще одна функция. У меня f (x) равно -¼x³ плюс x² плюс ¼x минус 1.Я хочу найти способ приблизительно аппроксимировать производную этой функции f ‘(x). Возможно, вы захотите сделать что-то подобное в случае, когда вы не знаете, как различать функцию. Дифференцировать — значит найти производную. Если вы не знаете, как на самом деле дифференцировать функцию, второй лучший способ — это аппроксимировать производную, и это то, что мы собираемся сделать сегодня. Итак, начнем с определения производной. Теперь это предел, когда h приближается к 0 для f (x + h) минус f (x) по h.Приближение производной означает приближение этого предела. Итак, что я собираюсь сделать, так это аппроксимировать это значение этого коэффициента разности. Теперь я беру предел, когда h приближается к 0. Поэтому имеет смысл приблизить этот предел со значением коэффициента разности, используя достаточно малое h, при очень маленьком h. Так, например, предположим, что h — 1000-е. Таким образом, x плюс точка 001 минус f (x) над точкой 001. Это даст нам разумное приближение к производной. Теперь, в части b, я должен сделать именно это.Он просит меня построить график f и f ‘на TI-84 и найти нули f’ с точностью до сотых. Итак, я собираюсь перейти к TI-84 и приблизительно рассчитать эту производную на своем калькуляторе. Я смотрю на свой ТИ-84. Я уже ввел здесь f (x) как Y1. Итак, я хочу ввести здесь y2 в качестве приближения для производной. В моем калькуляторе это не называется f (x). Он называется Y1. Итак, как мне ввести y1 вместо y2? Ну, если вы зайдете в меню переменных, нажмите кнопку VARS.Затем перейдите к Y-VARS и нажмите Enter. У вас есть список переменных y. Так что я могу снова нажать Enter для y1. Я получаю y1. Итак, я хочу, чтобы Y1 из x плюс точка 001. Затем я должен вычесть Y1 из x. Итак, я снова перехожу в ВАРС вправо. Позвольте мне вернуться назад, VARS, Y-VARS, а затем нажмите Enter. Я хочу Y1. Тогда я хочу X, Y1 (X). Я знаю, что это должно быть разделено на эту точку 001. Так что позвольте мне продолжить. Здесь мне нужно использовать круглые скобки. Во-вторых, вставьте круглые скобки. Я прохожу до последней скобки, разделенной на точку 001. Посмотрим, как это выглядит. График обращений. Теперь потребуется секунда, и затем он будет рисовать это приближение для производной. Тогда вот оно. Это похоже на открывающуюся вниз параболу. Теперь помните, моя задача в части b просит меня найти нули этой производной. Это означает, что производная пересекает ось x. Итак, давайте сначала найдем этот 0. Похоже, что он немного левее 0. Где-то между -1 и 0. Так что ваш калькулятор действительно может сделать это за вас.Вы можете просто нажать на секунду, отследить и попасть в меню РАСЧЕТ. Это вторая запись, номер 2. Вам нужно ввести границу слева и границу справа. Теперь сначала вам нужно убедиться, что вы выбрали правильную функцию. Я не хочу находить нули Y1. Это моя изначальная функция. Я хочу найти нули Y2. Поэтому мне приходится использовать клавишу со стрелкой вверх или вниз для переключения функций. Теперь смотрю на Y2. Для нашей левой границы все, что мне нужно сделать, это курсор немного влево. Итак, теперь я нахожусь слева от своего нуля и нажимаю Enter.Затем я должен навести курсор на правую границу. По сути, он запрашивает у вас интервал для поиска. Теперь вы хотите сделать предположение. Итак, наведите курсор мыши на фактический ноль, это отрицательная точка моего значения 12. Я просто запомню это. Теперь я хочу найти здесь ноль. Правый ноль. Итак, во-вторых, CALC, курсор вниз до 0, нажмите Enter. Теперь я снова ошибаюсь в функции. Я на Y1. Я хочу переключиться на Y2, поэтому я использую стрелки вверх и вниз, и теперь я нахожусь в Y2.Помните, я ищу здесь 0. Похоже, что это между 2 и 3. Я мог бы использовать 2 как левый вниз. Я могу это ввести. 2, введите. Затем в качестве правой границы я мог бы использовать 3. Просто введите 3, введите. Похоже, что 0 составляет около 2,8, поэтому позвольте мне ввести это для предположения. Вот оно 2,79. Итак, это мой второй 0. Теперь, когда у меня оба нуля, позвольте мне вернуться к доске и закончить задачу. Я уже нарисовал f и f ‘. Я хочу найти нули. Итак, f ‘(x) равно 0, когда x был приблизительно отрицательным пунктом 12 или когда x был приблизительно равен 2.79. Это были два места, где парабола пересекала ось здесь и здесь. Вот как вы изобразите производную на своем калькуляторе. Если вы на самом деле не знаете формулу для производной, вы всегда можете использовать коэффициент разности и взять довольно маленькое значение h. Это даст вам довольно хорошее приближение к производной. Помните, что вы в основном делаете именно это. Вы принимаете предел, когда h стремится к 0, поэтому, если вы используете достаточно малое значение h, вы получите хорошее приближение для своей производной. Модуль 10 — Производная функции В модуле 9 вы видели, что скорости соответствуют наклонам на графике положения во времени. Средняя скорость соответствует наклону
секущая линия, соединяющая две точки, а мгновенная скорость соответствует наклону касательной к кривой. Средняя скорость определяется как , который представляет собой наклон секущей линии через точки Мгновенная скорость определяется выражением , который представляет собой наклон касательной к кривой в точке ( a , f ( a )). Наклон касательной к графику функции в точке называется производной функции в этой точке. Формальное определение производной приведено ниже. Производная функции f при x = a равна при условии, что лимит существует. Для функций, имеющих касательную, если точка ( a , f ( a )) на кривой зафиксирована, поскольку h приближается к нулю, вторая точка ( a + h , f ( a + h )) приближается к фиксированной точке, и соответствующие секущие линии сходятся к касательной в этой точке. В описанной ниже процедуре будет найдено значение производной функции f ( x ) = 2 x — x 2 в точке (0,5, 0,75) с использованием метода, аналогичного тому, который вы использовали для найти мгновенные скорости.
На приведенном ниже графике показано f ( x ) = 2 x — x 2 в окне [-1, 3, 1] x [-1, 2, 1] с тремя секущими линиями через фиксированные точка (0,5, 0,75), которая приближается к касательной в точке (0,5, 0,75). Первый шаг в описанной выше процедуре — найти наклон секущих линий, которые будут использоваться для оценки производной.Чтобы найти уклоны, вам нужно ввести функцию f ( x ) = 2 x — x 2 в редакторе Y =. Наклон секущей линии через точки (0,5, f (0,5)) и (0,5 + h , f (0,5 + h )) можно найти, оценив коэффициент разности . Нас интересуют значения h , которые малы, так что две точки находятся близко друг к другу.Результирующая секущая линия будет приближаться к касательной. Вы можете оценить коэффициент разницы для h = 0,1 на TI-83, используя команду, состоящую из двух частей. Первая часть команды сохранит 0,1 в h , а вторая часть команды будет оценивать коэффициент разницы. Две команды будут объединены вместе с символом двоеточия. Наклон секущей линии, содержащей (0.5, f (0,5)) и (0,6, f (0,6)) составляет 0,9. Когда точка (0,5 + h , f (0,5 + h )) приближается к точке (0,5, f (0,5)), h приближается к 0, и секущие линии сходятся к касательной. Чтобы оценить коэффициент разницы для меньших значений h , измените значение H в последнем выражении на главном экране с 0.От 1 до 0,01 и оцените коэффициент разницы. Наклон соответствующей секущей линии равен 0,99.
Наклон секущих линий равен 0,999 и 0,9999 соответственно. 10.1.1 Предскажите производную в (0,5, f (0,5)). Щелкните здесь, чтобы получить ответ. В описанной выше процедуре использовались правые разностные коэффициенты. Коэффициенты левой разности могут быть найдены, если положить h отрицательным числом.
Коэффициенты левой разности Наклон соответствующих секущих линий равен 1,01 и 1,001. С фиксированной точкой (0,5, 0,75) одна секущая линия проходит через (0,49, f (0,49)), а другая через (0,499, f (0,499)). Как указывалось ранее, производная x = 0.5 определяется как предел . Прежде чем этот предел можно будет оценить, выражение должны быть расширены и упрощены. Напомним, что интересующая функция: f ( x ) = 2 x — x 2 . Следовательно, и производная от f ( x ) = 2 x — x 2 при x = 0.5 равно 1. Вы также можете аппроксимировать производную функции в точке с помощью числовой производной команды nDeriv (, которая находится в меню Math. Синтаксис для поиска производной в точке: nDeriv (выражение, переменная, значение ).
Поскольку точка на кривой и производная в этой точке известны, уравнение для касательной можно найти с помощью
точечно-наклонная форма линии. Если наклон касательной в точке (0,5, 0,75) равен 1, то уравнение для касательной линии будет y — 0,75 = 1 ( x — 0,5). График f ( x ) = 2 x — x 2 и его касательная линия в точке (0.5, 0,75).
Линия кажется касательной к кривой при x = 0,5. Математическая сцена — Производные — Урок 2Математическая сцена — Производные — Урок 2 — Дифференцирование многочленов
2 Дифференцирующие многочлены Наклон касательной варьируется в зависимости от Три разных касательных в трех разных Теперь мы собираемся найти общий метод Первый взгляд на константу В данном случае сложно говорить о Правило таково: если f (x) = k Вторая диаграмма показывает y = 2x + 1 имеет градиент 2, поэтому y г г следовательно Все функции первой степени имеют прямую линию Далее мы рассмотрим Мы можем найти Определение производной: Рассчитываем
Пример 1 Дифференцируйте функцию Обратите внимание, что если мы различаем 2x 2 Добавление этих двух результатов Следующее правило, которое
Пример 2 Дифференцируйте функцию . Вместо деления на 2 мы можем думать об этом Отмена для упрощения мы Пример 3 Продифференцируем f (x) = Пример 4 Продифференцируем f (x) = Приведенные выше примеры дают нам f (х) = х 0 f (x) = x 1 имеет производную f (x) = 1x 0 f (x) = x 2 имеет производную f (x) = 2x 1 f (x) = x 3 имеет производную f (x) = 3x 2 f (x) = x 4 имеет производную f (x) = 4x 3 В любом случае результат может Можно показать, что этот результат применим в целом, и мы можем написать следующее
Пример 5 Используйте правила, которые мы нашли f (x) = 5x 4 = 5x 4 Пример 6 Найдите уравнение Начнем с нахождения y f (1) = 1 5 + 4 = 0 Касательная находится в точке (1, Далее мы находим формулу для f (x) = 5x 4 = 5x 4 Мы можем найти градиент f (1) = 5 15 + 4 = 6 Используя формулу для у = 6 (х 1) + 0 г
Попрактикуйтесь в этих методах, а затем шт. Запомните свой контрольный список. Исчисление I — Интерпретация производного инструментаНа первый взгляд это кажется практически невыполнимой задачей. Однако, если у вас есть некоторые базовые знания об интерпретации производной, вы можете получить ее набросок. По большей части это не будет идеальный набросок, но вы сможете уловить большинство основных функций производного скетча. Начнем со следующего наброска функции с парой дополнений. Обратите внимание, что в точках \ (x = — 3 \), \ (x = — 1 \), \ (x = 2 \) и \ (x = 4 \) касательная линия к функции горизонтальна. Это означает, что наклон касательной должен быть нулевым. Теперь мы знаем, что наклон касательной в определенной точке также является значением производной функции в этой точке. Таким образом, теперь мы знаем, что \ [f ‘\ left ({- 3} \ right) = 0 \ hspace {0.5in} f ‘\ left ({- 1} \ right) = 0 \ hspace {0,5in} f’ \ left (2 \ right) = 0 \ hspace {0,5in} f ‘\ left (4 \ right) = 0 \] Это хорошая отправная точка для нас. Это дает нам несколько точек на графике производной. Он также разбивает область определения функции на области, в которых функция увеличивается и уменьшается. Из наших обсуждений выше мы знаем, что если функция возрастает в какой-то точке, тогда производная должна быть положительной в этой точке. Точно так же мы знаем, что если функция убывает в какой-то точке, тогда производная должна быть отрицательной в этой точке. Теперь мы можем дать следующую информацию о производной. \ [\ begin {align *} x & <- 3 & \ hspace {0,5 дюйма} f '\ left (x \ right) & <0 \\ - 3 Помните, что здесь мы указываем знаки производных, и они являются исключительно функцией от того, увеличивается или уменьшается функция.Знак самой функции здесь совершенно несущественен и никоим образом не влияет на знак производной. Может показаться, что у нас недостаточно информации, чтобы получить набросок, но мы можем получить немного больше информации о производной из графика функции. В диапазоне \ (x <- 3 \) мы знаем, что производная должна быть отрицательной, однако мы также можем видеть, что производная должна увеличиваться в этом диапазоне. Здесь она отрицательна, пока мы не достигнем \ (x = - 3 \), и в этой точке производная должна быть равна нулю.Единственный способ, чтобы производная была отрицательной слева от \ (x = - 3 \) и нулем в точке \ (x = - 3 \) означает, что производная увеличивается по мере увеличения \ (x \) в сторону \ (x = - 3 \). Теперь в диапазоне \ (- 3 Далее, для диапазонов \ (- 1 Наконец, в последней области \ (x> 4 \) мы знаем, что производная равна нулю в точке \ (x = 4 \) и положительна справа от \ (x = 4 \). Еще раз, следуя приведенным выше рассуждениям, производная также должна увеличиваться в этом диапазоне. Объединение всего этого материала (и всегда выбор простейших вариантов увеличения и / или уменьшения информации) дает нам следующий набросок производной. Обратите внимание, что это было сделано с фактической производной и поэтому на самом деле является точным.Любой набросок, который вы сделаете, скорее всего, будет выглядеть иначе. «Неровности» в каждой из областей могут быть, например, в разных местах и / или на разной высоте. Также обратите внимание, что мы не использовали вертикальную шкалу, потому что, учитывая информацию, которую мы получили к этому моменту, не было реального способа узнать эту информацию. Однако это не означает, что мы не можем получить некоторые представления о конкретных точках производной, кроме тех, где мы знаем, что производная равна нулю. Чтобы убедиться в этом, давайте посмотрим на следующий график функции (не производной, а функции). В точках \ (x = — 2 \) и \ (x = 3 \) мы нарисовали пару касательных прямых. Мы можем использовать базовую концепцию подъема / наклона для оценки значения производной в этих точках. Начнем с \ (x = 3 \). Здесь на карту поставлено два момента. Мы видим, что каждая из них отходит от линии сетки примерно на четверть расстояния. Итак, принимая во внимание это и тот факт, что мы проходим одну полную сетку, мы можем видеть, что наклон касательной и, следовательно, производной приблизительно равен -1.5. При \ (x = — 2 \) похоже (с некоторой тяжелой оценкой), что вторая точка находится примерно на 6,5 сетки выше первой точки, поэтому здесь наклон касательной линии и, следовательно, производной составляет примерно 6,5. Вот эскиз производной с включенной вертикальной шкалой, и из этого мы видим, что на самом деле наши оценки довольно близки к реальности. Обратите внимание, что эта идея оценки значений производных финансовых инструментов может быть сложным процессом и требует изрядного количества (возможных плохих) приближений, поэтому, хотя ее можно использовать, с ней нужно быть осторожным. Напомним, что определение производной — $$ Отвечать Касательная линия в $$ x = 1 $$ имеет наклон $$ m = 7 $$. Знак производной в определенной точке скажет нам, увеличивается или уменьшается функция вблизи этой точки. Это легко понять, если мы подумаем о производной как о наклоне касательной.Как показано на двух графиках ниже, когда наклон касательной линии положительный, функция будет увеличиваться в этой точке. Точно так же, когда наклон касательной линии отрицательный, функция будет уменьшаться. Мы всегда читаем графики слева направо. Так сказать, функция увеличивается, это означает, что, когда мы смотрим слева направо, значения функции становятся больше — выше по оси $$ y $$ -. Точно так же значения $$ y $$ — убывающей функции становятся меньше, когда мы смотрим слева направо.2 + х — 12) = 6 (х + 4) (х-3) Шаг 2 Нарисуйте быстрый график производной. Шаг 3 Интерпретируйте график. Мы знаем, что когда производная положительна, функция возрастает. График выше показывает, что производная положительна (т.е.е., над осью $$ x $$ -), когда $$ x и $$ x> 3 $$. Мы также можем видеть, что производная отрицательна (ниже оси $$ x $$ -), когда $$ — 4 Отвечать Функция возрастает на интервалах от $$ (- \ infty, -4) \ cup (3, \ infty) $$. Точно так же функция убывает в интервале $$ (- 4,3) $$. График функции показан ниже для справки. Предположим, что $$ D (t) $$ представляет собой расстояние бегуна от стартовой линии. Тогда производная $$ D (t) $$ определяется выражением $$ D ‘(t) = \ lim_ {h \ to 0} \ frac {D (t + h) — D (t)} {(t + h) -t} $$ Без ограничения дробь представляет $$ Когда мы применяем ограничение, прошедшее время приближается к нулю.Таким образом, значение предела — это скорость в конкретный момент времени. Это все еще скорость изменения, но теперь она происходит мгновенно. Предположим, что расстояние бегуна от стартовой линии можно описать функцией $$ D (t) = 10 \ sqrt {t} + 5 $$ для всех значений $$ t \ in (0,16) $$, где $ $ t $$ в секундах, а расстояние в метрах. Какова скорость бегуна при $$ t = 9 $$? Шаг 1 Найдите первую производную.{-1/2} = \ frac 5 {\ sqrt t} Шаг 2 Оцените $$ D ‘(9) $$. $$ Шаг 3 Интерпретируйте числовое значение. Поскольку производная положительна, мы знаем, что функция возрастает.Это означает, что расстояние бегуна от стартовой линии увеличивается, поэтому бегун удаляется от стартовой линии. Значение производной говорит нам, насколько быстро бегун движется. Знак производной говорит нам, в каком направлении движется бегун. Отвечать Через 9 секунд бегун удаляется от линии старта со скоростью $$ \ frac 5 3 \ приблизительно 1.{th} $$ час работы. Что означает уравнение $$ B ‘(4) = 25 $$ с точки зрения продаж и времени? Шаг 1 Определите единицы производной. $$ Единицами производного финансового инструмента являются: книги, проданные за час. Отвечать $$ B ‘(4) = 25 $$ означает, что в течение 4-го рабочего часа книги продавались со скоростью 25 книг в час. Предположим, что $$ f (x) = \ sin x $$.Найдите наклон касательной в точке $$ x = \ frac \ pi 3 $$ Покажи ответ Шаг 1 Найдите первую производную. Шаг 2 Вычислить $$ f ‘\ left (\ frac \ pi 3 \ right) $$. Шаг 2 Ответ $$ Предположим, что $$ f (x) = 5e ^ {3x} $$. 2 — 6x + 3 $$.Найдите интервалы, в течение которых $$ f $$ увеличивается, и интервалы, в течение которых он уменьшается. Покажи ответ Шаг 1 Найдите первую производную. Шаг 1 Ответ $$ Шаг 2 Определите, где $$ f ‘(x)> 0 $$. Шаг 2 Ответ $$ Поскольку производная линейна и положительна, когда $$ x> 12 $$, мы знаем, что производная будет отрицательной, когда $$ x. 2 (4x-5) Шаг 3 Изучите график $$ f ‘(x) $$. Шаг 3 Ответ На графике видно, что производная отрицательна (под осью $$ x $$), когда $$ x. Мы также можем видеть, что производная положительна (над осью $$ x $$ -), когда $$ \ frac 5 4 и $$ x> 2 $$. Отвечать Покажи ответ Функция убывает в интервале $$ (- \ infty, 5/4) $$. 2 $$ представляет собой высоту самолета (в тысячах футов) после $$ t $$ часов полета.Найдите $$ A ‘(3) $$ и интерпретируйте его контекстно. Покажи ответ Шаг 2 Шаг 2 Ответ $$ Шаг 3 Определите единицы производной. Шаг 3 Ответ $$ Шаг 4 Расшифровывает знак производной. Шаг 4 Ответ Поскольку производная отрицательна, мы знаем, что функция (высота) убывает. Значит, самолет должен снижаться. Отвечать Покажи ответ После 3 часов полета самолет снижается со скоростью 4000 футов в час.2 + 13x — 12 $$ представляет собой прибыль, полученную конкретной компанией (в тысячах долларов) от продажи $$ x $$ тонн товаров. Найдите $$ P ‘(15) $$ и интерпретируйте его контекстно. Покажи ответ Шаг 2 Шаг 2 Ответ $$ Шаг 3 Определите единицы производной. Шаг 3 Ответ $$ Шаг 4 Расшифровывает знак производной. Шаг 4 Ответ Поскольку производная отрицательна, функция (прибыль) убывает. Отвечать Покажи ответ При продажах на уровне 15 тонн прибыль уменьшается на 17 тысяч долларов за тонну.То есть, если бы продажи увеличились, можно было бы ожидать, что прибыль упадет с такой скоростью. Примечание: в бизнесе больше продаж не обязательно означает большую прибыль. Если затраты слишком высоки, производство большего количества товаров для продажи может стоить больше, чем деньги, полученные от продажи товаров. Предположим, что $$ B (t) $$ представляет собой количество сахара в кровотоке человека (в миллиграммах сахара на децилитр крови) через $$ t $$ минут после еды.Объясните контекстуально, что означает $$ B ‘(30) = -8 $$. Покажи ответ Шаг 1 Определите единицы производной. Шаг 1 Ответ $$ Шаг 2 Расшифровывает знак производной. Шаг 2 Ответ Поскольку производная отрицательна, функция (уровень сахара в крови) уменьшается. Отвечать Покажи ответ Через 30 минут уровень сахара в крови снижается со скоростью 8 миллиграммов на децилитр в минуту. Предположим, что $$ L (t) $$ представляет собой длину ногтя (в мм) через $$ t $$ дней после того, как он был обрезан.Объясните контекстуально, что означает $$ L ‘(6)> 0,08 $$. Покажи ответ Шаг 1 Укажите единицы производного финансового инструмента. Шаг 1 Ответ $$ Шаг 2 Расшифровывает знак производной. Шаг 2 Ответ Поскольку производная положительна, функция (длина) возрастает. Отвечать Покажи ответ Через шесть дней после стрижки ноготь растет быстрее нуля.08 миллиметров в день. Предположим, что $$ D (t) $$ представляет собой расстояние, на которое конкретный человек находится от своего дома в $$ t $$ минут после 8 утра.Напишите уравнение, которое означает: «В 8:30 этот человек приближался к своему дому со скоростью 400 футов в минуту». Покажи ответ Шаг 1 Определите значение $$ t $$ в измеряемой точке. Шаг 1 Ответ Поскольку в $$ t $$ время измеряется в минутах с 8 утра, интересующее нас время составляет $$ t = 30 $$. Шаг 2 Определите значение производной. Шаг 2 Ответ Поскольку расстояние до человека изменяется со скоростью 400 футов в минуту, значение производной равно 400. Шаг 3 Определите знак производной. Шаг 3 Ответ Поскольку расстояние от дома уменьшается, производная должна быть отрицательной. Отвечать Покажи ответ $$ Предположим, что $$ V (t) $$ представляет собой напряжение в конкретной электрической цепи через $$ t $$ секунд после включения цепи.Напишите неравенство, означающее: «Через шесть секунд после включения цепи напряжение увеличивалось со скоростью 0,04 вольта в секунду». Покажи ответ Шаг 1 Определите значение $$ t $$ в измеряемый момент времени. Шаг 1 Ответ Поскольку мы измеряем напряжение через шесть секунд после включения цепи, $$ t = 6 $$. Шаг 2 Определите значение производной. Шаг 2 Ответ Поскольку напряжение увеличивается со скоростью 0.04 вольта в секунду, значение производной 0,04. Шаг 3 Определите знак производной. Шаг 3 Ответ Поскольку напряжение увеличивается, производная положительна. Ошибка: Нажмите «Не робот», затем повторите попытку. | ||||||||||||||||||||||||||||||||||||||||||||

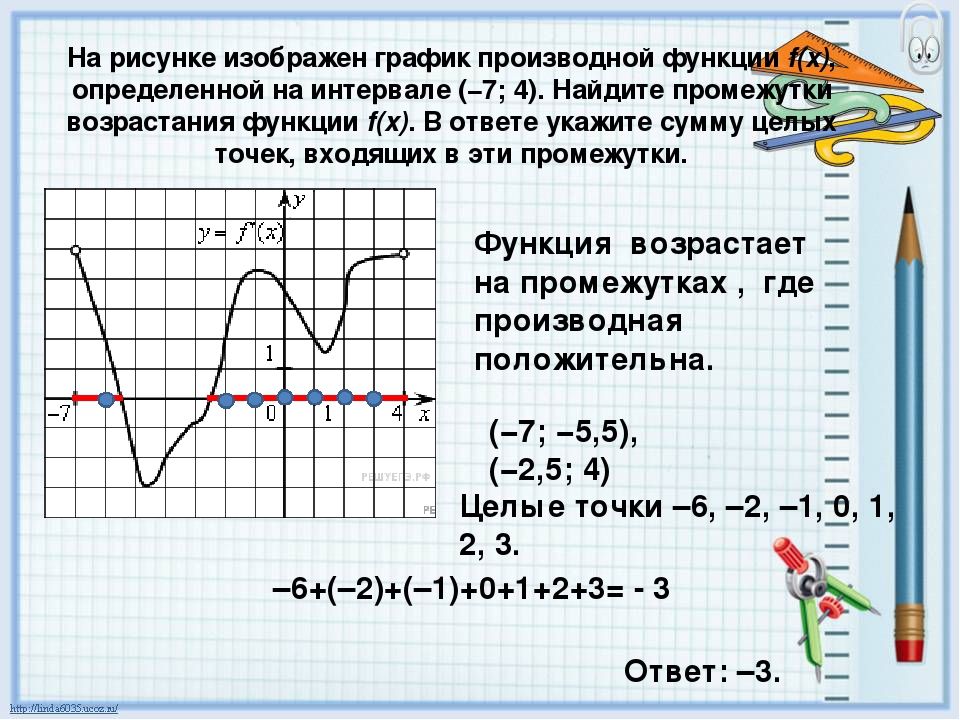
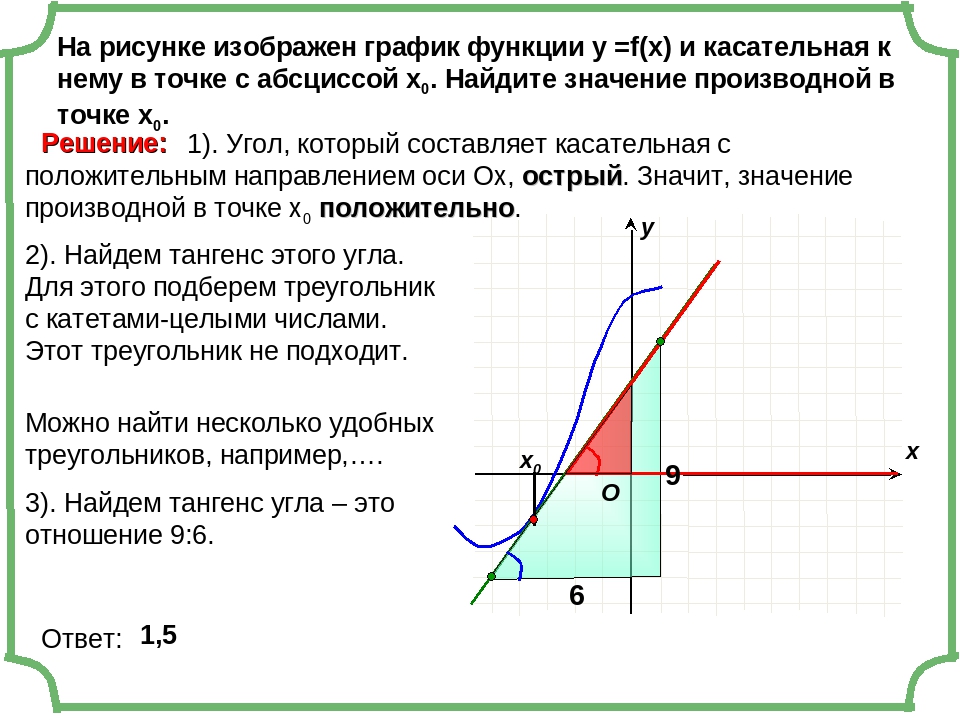
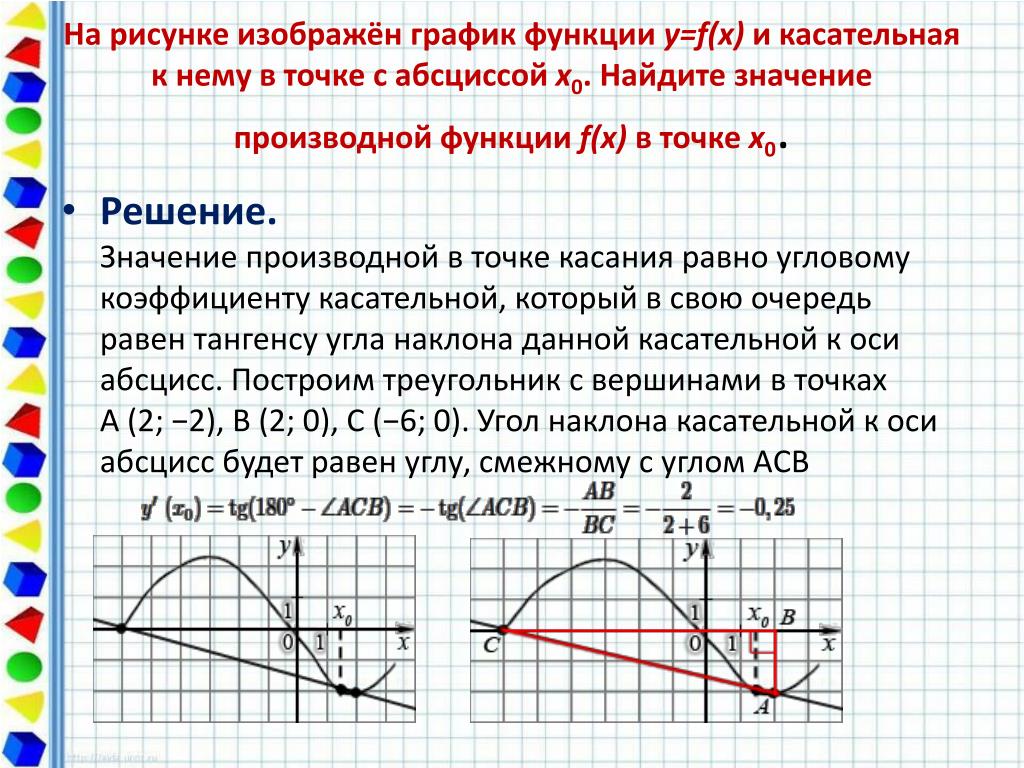 И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.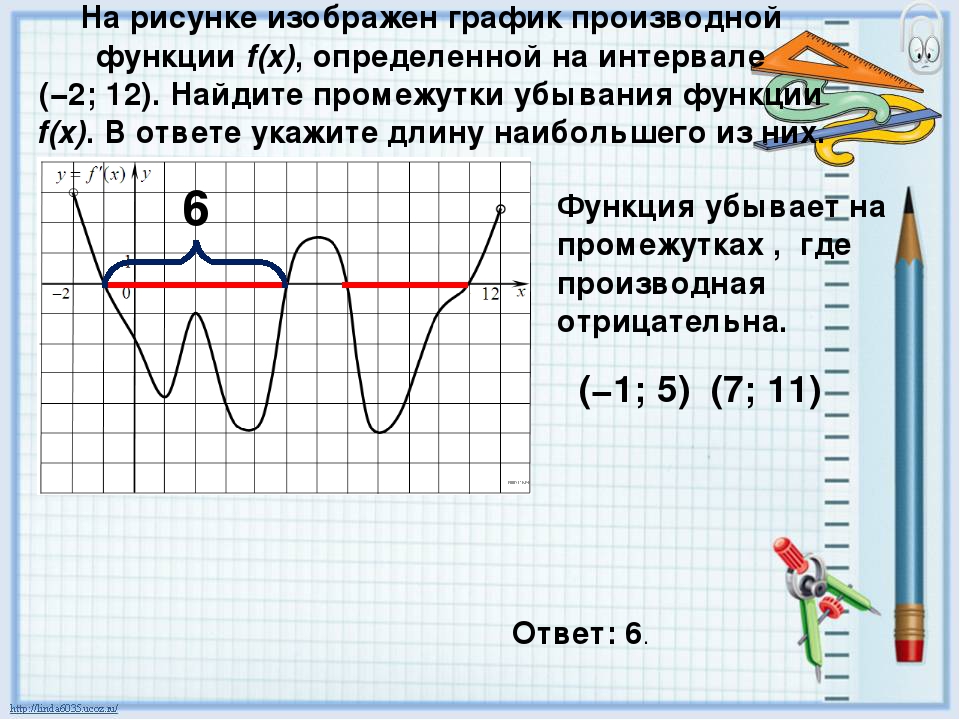 е. f’(x) ≥ 0.
е. f’(x) ≥ 0.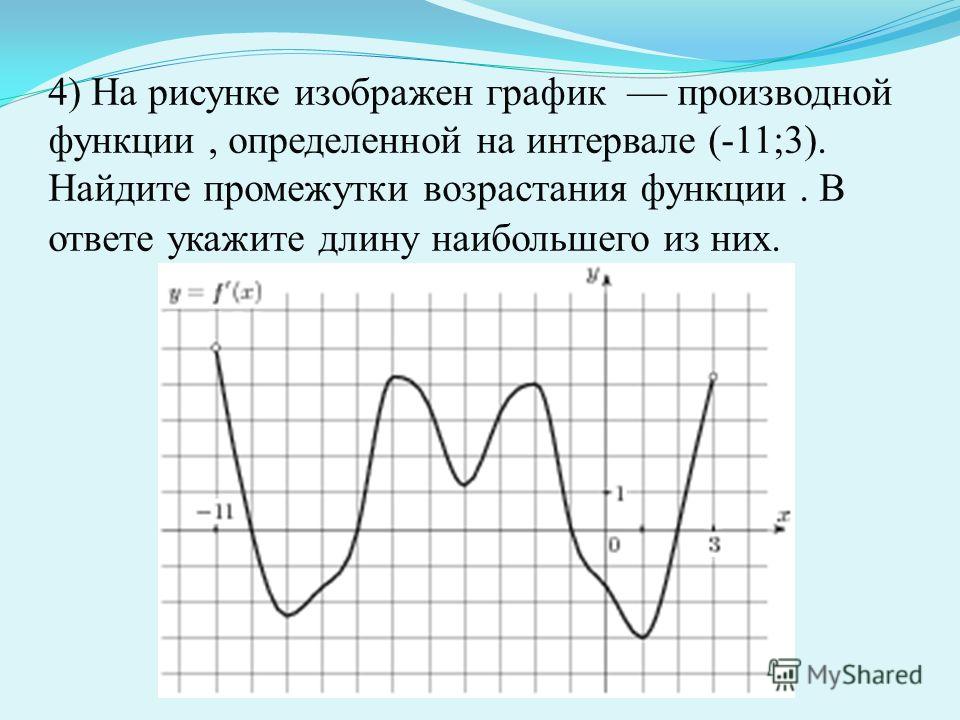 В ответе укажите сумму целых чисел, входящих в эти промежутки.
В ответе укажите сумму целых чисел, входящих в эти промежутки.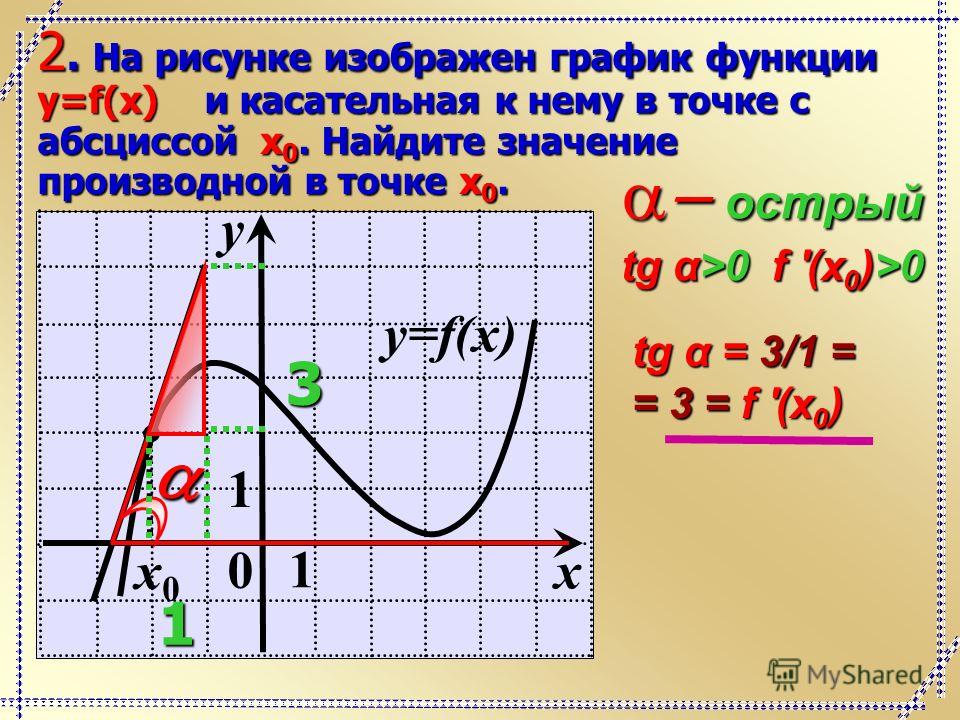
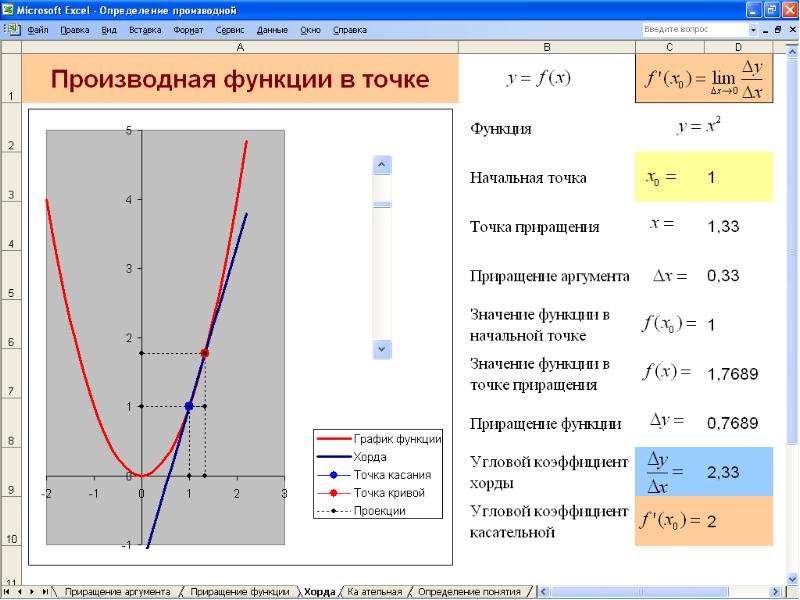 Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.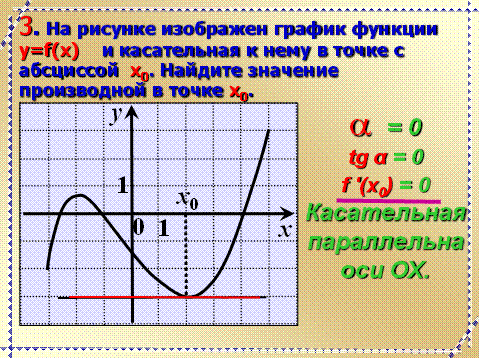

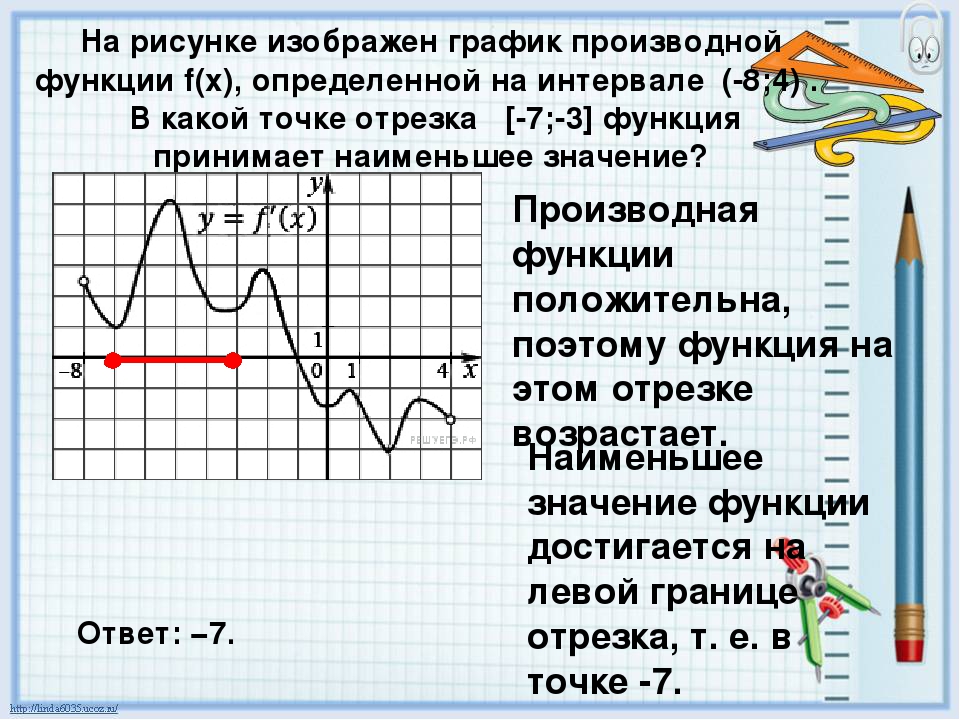 е. f’(x) ≥ 0.
е. f’(x) ≥ 0.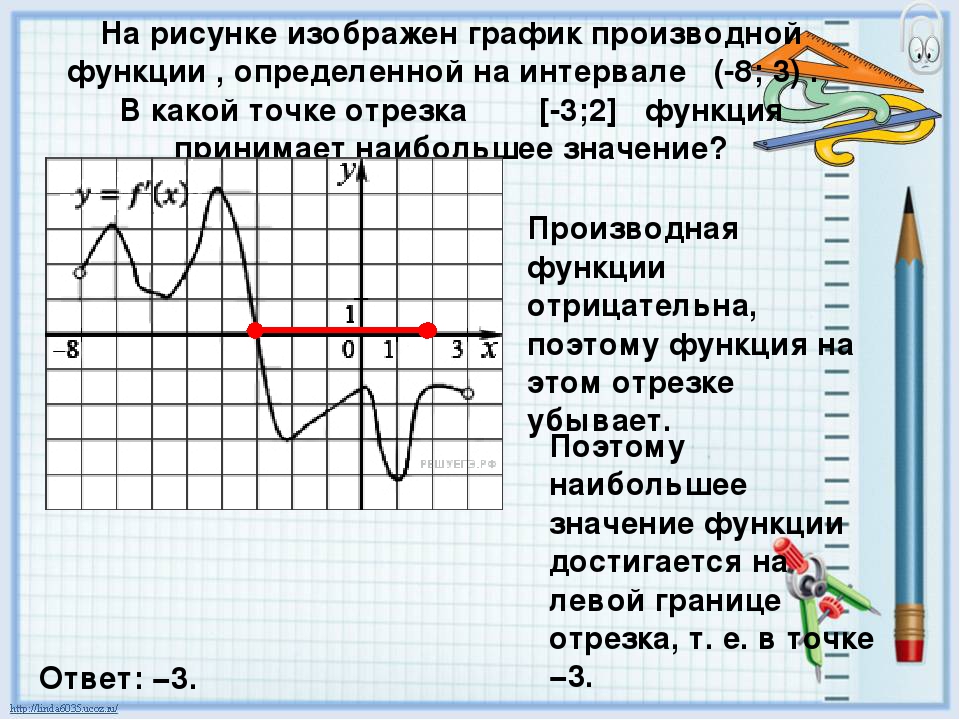 В ответе укажите сумму целых чисел, входящих в эти промежутки.
В ответе укажите сумму целых чисел, входящих в эти промежутки.