Содержание
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Определение 1
Угол наклона прямой y=kx+b называется угол α, который отсчитывается от положительного направления оси ох к прямой y=kx+b в положительном направлении.
На рисунке направление ох обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Определение 2
Угловой коэффициент прямой y=kx+b называют числовым коэффициентом k.
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.
- Угол наклона прямой равняется 0 только при параллельности ох и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0.
 Значит, вид уравнения будет y=b.
Значит, вид уравнения будет y=b. - Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<π2 или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
- Если α=π2, тогда расположение прямой перпендикулярно ох. Равенство задается при помощи равенства x=c со значением с, являющимся действительным числом.
- Если угол наклона прямой y=kx+b тупой, то соответствует условиям π2<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывает.
Определение 3
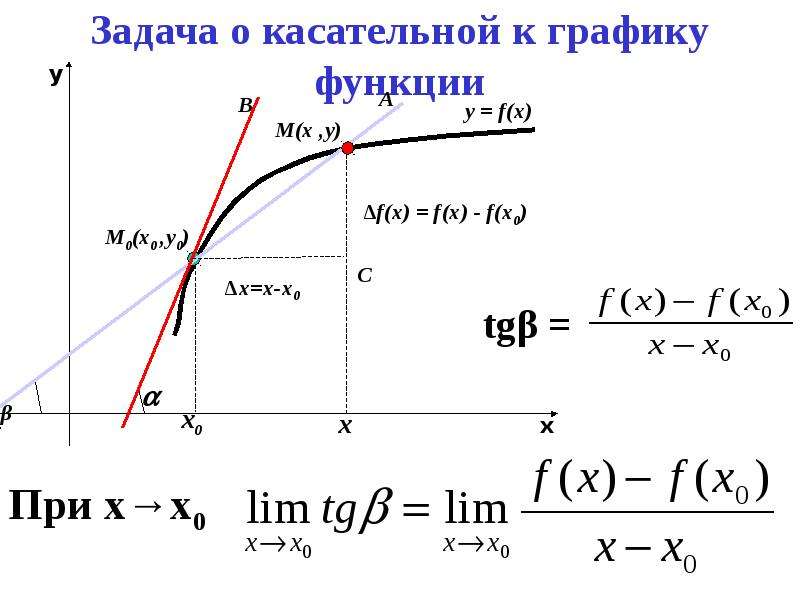
Секущей называют прямую, которая проходит через 2 точки функции f(x). Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что АВ является секущей, а f(x) – черная кривая, α — красная дуга, означающая угол наклона секущей.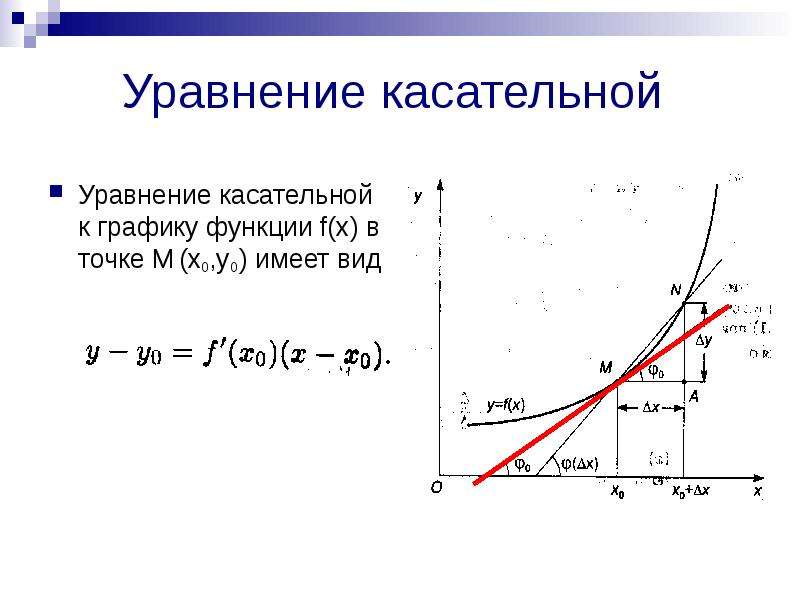
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника АВС можно найти по отношению противолежащего катета к прилежащему.
Определение 4
Получаем формулу для нахождения секущей вида:
k=tg α=BCAC=f(xB)-fxAxB-xA, где абсциссами точек А и В являются значения xA, xB, а f(xA), f(xB) — это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k=f(xB)-f(xA)xB-xA или k=f(xA)-f(xB)xA-xB, причем уравнение необходимо записать как y=f(xB)-f(xA)xB-xA·x-xA+f(xA) или
y=f(xA)-f(xB)xA-xB·x-xB+f(xB).
Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции.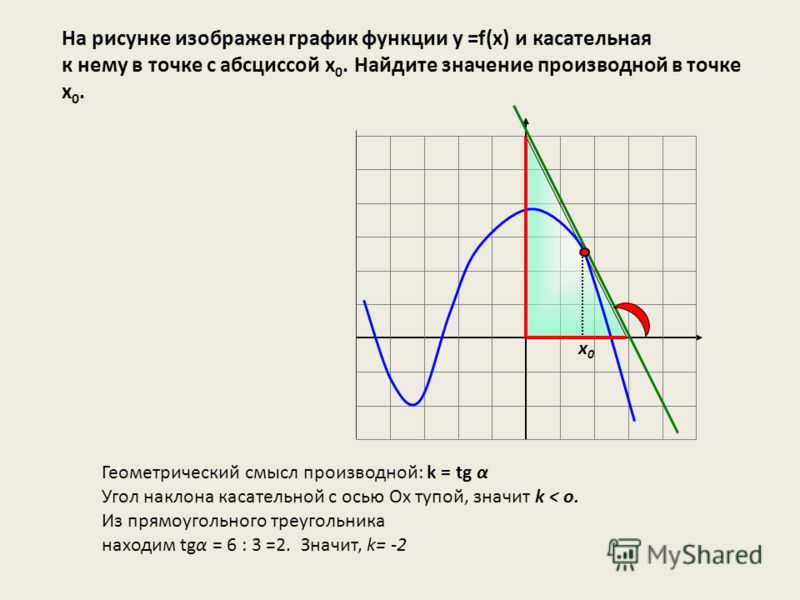 Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Определение 5
Касательная к графику функции f(x) в точке x0; f(x0) называется прямая, проходящая через заданную точку x0; f(x0), с наличием отрезка, который имеет множество значений х, близких к x0.
Пример 1
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y=x+1, считается касательной к y=2x в точке с координатами (1; 2). Для наглядности, необходимо рассмотреть графики с приближенными к (1; 2) значениями. Функция y=2x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y=2x сливается с прямой у=х+1.
Для определения касательной следует рассмотреть поведение касательной АВ при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.
Секущая АВ, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной αx.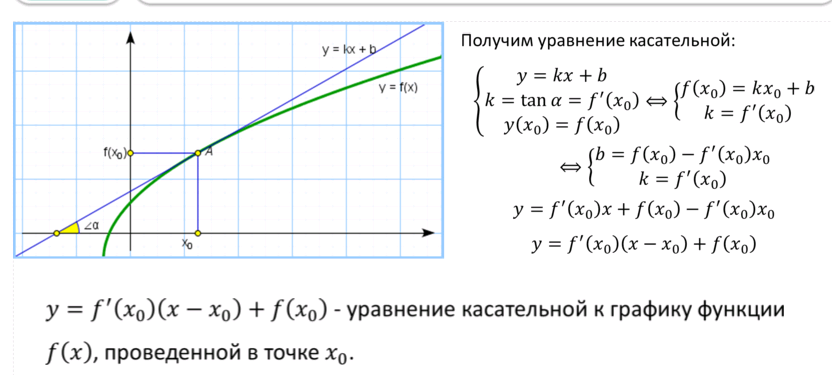
Определение 6
Касательной к графику функции y=f(x) в точке А считается предельное положение секущей АВ при В стремящейся к А, то есть B→A.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
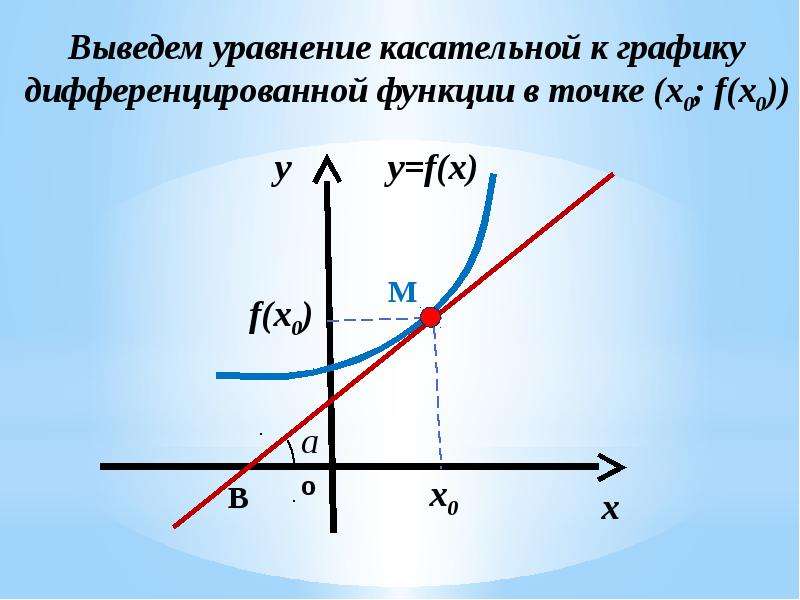
Перейдем к рассмотрению секущей АВ для функции f(x), где А и В с координатами x0, f(x0) и x0+∆x, f(x0+∆x), а ∆x обозначаем как приращение аргумента. Теперь функция примет вид ∆y=∆f(x)=f(x0+∆x)-f(∆x). Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник АВС. Используем определение тангенса для решения, то есть получим отношение ∆y∆x=tg α. Из определения касательной следует, что lim∆x→0∆y∆x=tg αx. По правилу производной в точке имеем, что производную f(x) в точке x0 называют пределом отношений приращения функции к приращению аргумента, где ∆x→0, тогда обозначим как f(x0)=lim∆x→0∆y∆x.
Отсюда следует, что f'(x0)=lim∆x→0∆y∆x=tg αx=kx, где kx обозначают в качестве углового коэффициента касательной.
То есть получаем, что f’(x) может существовать в точке x0 причем как и касательная к заданному графику функции в точке касания равной x0, f0(x0), где значение углового коэффициента касательной в точке равняется производной в точке x0. Тогда получаем, что kx=f'(x0).
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x0 при пересечении.
Уравнение касательной к графику функции y=f(x) в точке x0, f0(x0) принимает вид y=f'(x0)·x-x0+f(x0).
Имеется в виду, что конечным значением производной f'(x0) можно определить положение касательной, то есть вертикально при условии limx→x0+0f'(x)=∞ и limx→x0-0f'(x)=∞ или отсутствие вовсе при условии limx→x0+0f'(x)≠limx→x0-0f'(x).
Расположение касательной зависит от значения ее углового коэффициента kx=f'(x0).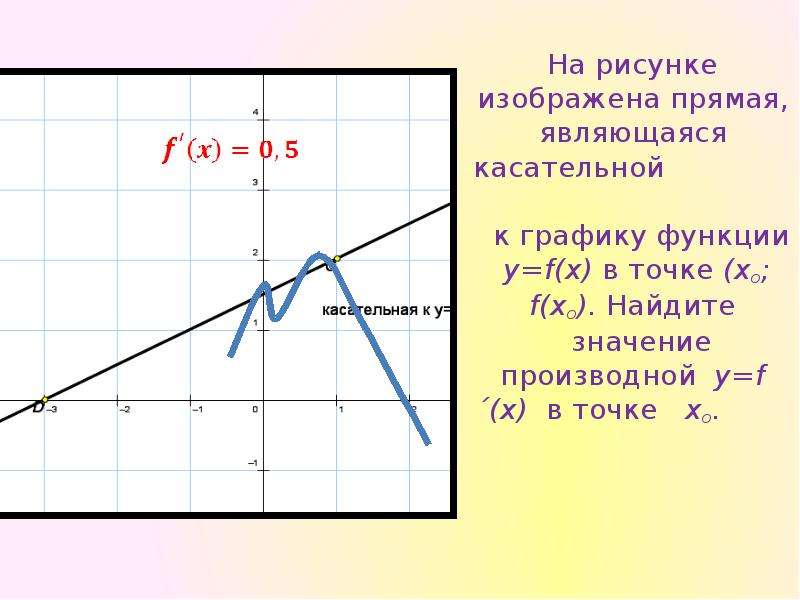 При параллельности к оси ох получаем, что kk=0, при параллельности к оу — kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.
При параллельности к оси ох получаем, что kk=0, при параллельности к оу — kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.
Пример 2
Произвести составление уравнения касательной к графику функции y=ex+1+x33-6-33x-17-33 в точке с координатами (1; 3) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1; 3) является точкой касания, тогда x0=-1, f(x0)=-3.
Необходимо найти производную в точке со значением -1. Получаем, что
y’=ex+1+x33-6-33x-17-33’==ex+1’+x33′-6-33x’-17-33’=ex+1+x2-6-33y'(x0)=y'(-1)=e-1+1+-12-6-33=33
Значение f’(x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда kx=tg αx=y'(x0)=33
Отсюда следует, что αx=arctg33=π6
Ответ: уравнение касательной приобретает вид
y=f'(x0)·x-x0+f(x0)y=33(x+1)-3y=33x-9-33
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Пример 3
Выяснить наличие существования касательной к графику заданной функции
y=3·x-15+1 в точке с координатами (1;1). Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y’=3·x-15+1’=3·15·(x-1)15-1=35·1(x-1)45
Если x0=1, тогда f’(x) не определена, но пределы записываются как limx→1+035·1(x-1)45=35·1(+0)45=35·1+0=+∞ и limx→1-035·1(x-1)45=35·1(-0)45=35·1+0=+∞, что означает существование вертикальной касательной в точке (1;1).
Ответ: уравнение примет вид х=1, где угол наклона будет равен π2.
Для наглядности изобразим графически.
Пример 4
Найти точки графика функции y=115x+23-45×2-165x-265+3x+2, где
- Касательная не существует;
- Касательная располагается параллельно ох;
- Касательная параллельна прямой y=85x+4.
Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x∈-∞; 2 и [-2; +∞). Получаем, что
y=-115×3+18×2+105x+176, x∈-∞; -2115×3-6×2+9x+12, x∈[-2; +∞)
Необходимо продифференцировать функцию. Имеем, что
y’=-115×3+18×2+105x+176′, x∈-∞; -2115×3-6×2+9x+12′, x∈[-2; +∞)⇔y’=-15(x2+12x+35), x∈-∞; -215×2-4x+3, x∈[-2; +∞)
Когда х=-2, тогда производная не существует, потому что односторонние пределы не равны в этой точке:
limx→-2-0y'(x)=limx→-2-0-15(x2+12x+35=-15(-2)2+12(-2)+35=-3limx→-2+0y'(x)=limx→-2+015(x2-4x+3)=15-22-4-2+3=3
Вычисляем значение функции в точке х=-2, где получаем, что
- y(-2)=115-2+23-45(-2)2-165(-2)-265+3-2+2=-2, то есть касательная в точке (-2;-2) не будет существовать.
- Касательная параллельна ох, когда угловой коэффициент равняется нулю.
 Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.
Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.
Когда x∈-∞; -2, тогда -15(x2+12x+35)=0, а при x∈(-2; +∞) получаем 15(x2-4x+3)=0.
Решим:
-15(x2+12x+35)=0D=122-4·35=144-140=4×1=-12+42=-5∈-∞; -2×2=-12-42=-7∈-∞; -2 15(x2-4x+3)=0D=42-4·3=4×3=4-42=1∈-2; +∞x4=4+42=3∈-2; +∞
Вычисляем соответствующие значения функции
y1=y-5=115-5+23-45-52-165-5-265+3-5+2=85y2=y(-7)=115-7+23-45(-7)2-165-7-265+3-7+2=43y3=y(1)=1151+23-45·12-165·1-265+31+2=85y4=y(3)=1153+23-45·32-165·3-265+33+2=43
Отсюда -5; 85, -4; 43, 1; 85, 3; 43 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 .
 Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
-15×2+12x+35=85×2+12x+43=0D=122-4·43=-28<0
Другое уравнение имеет два действительных корня, тогда
15(x2-4x+3)=85×2-4x-5=0D=42-4·(-5)=36×1=4-362=-1∈-2; +∞x2=4+362=5∈-2; +∞
Перейдем к нахождению значений функции. Получаем, что
y1=y(-1)=115-1+23-45(-1)2-165(-1)-265+3-1+2=415y2=y(5)=1155+23-45·52-165·5-265+35+2=83
Точки со значениями -1; 415, 5; 83 являются точками, в которых касательные параллельны прямой y=85x+4.
Ответ: черная линия – график функции, красная линия – график y=85x+4, синяя линия – касательные в точках -1; 415, 5; 83.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Возможно существование бесконечного количества касательных для заданных функций.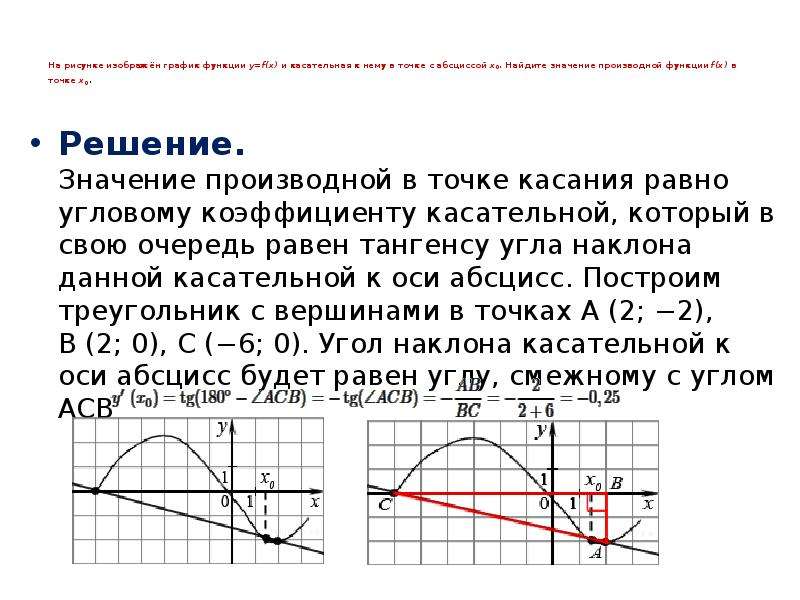
Пример 5
Написать уравнения всех имеющихся касательных функции y=3cos32x-π4-13, которые располагаются перпендикулярно прямой y=-2x+12.
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется -1, то есть записывается как kx·k⊥=-1. Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k⊥=-2, тогда kx=-1k⊥=-1-2=12.
Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x0 получаем, что kx=y'(x0). Из данного равенства найдем значения х для точек касания.
Получаем, что
y'(x0)=3cos32x0-π4-13’=3·-sin32x0-π4·32×0-π4’==-3·sin32x0-π4·32=-92·sin32x0-π4⇒kx=y'(x0)⇔-92·sin32x0-π4=12⇒sin32x0-π4=-19
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.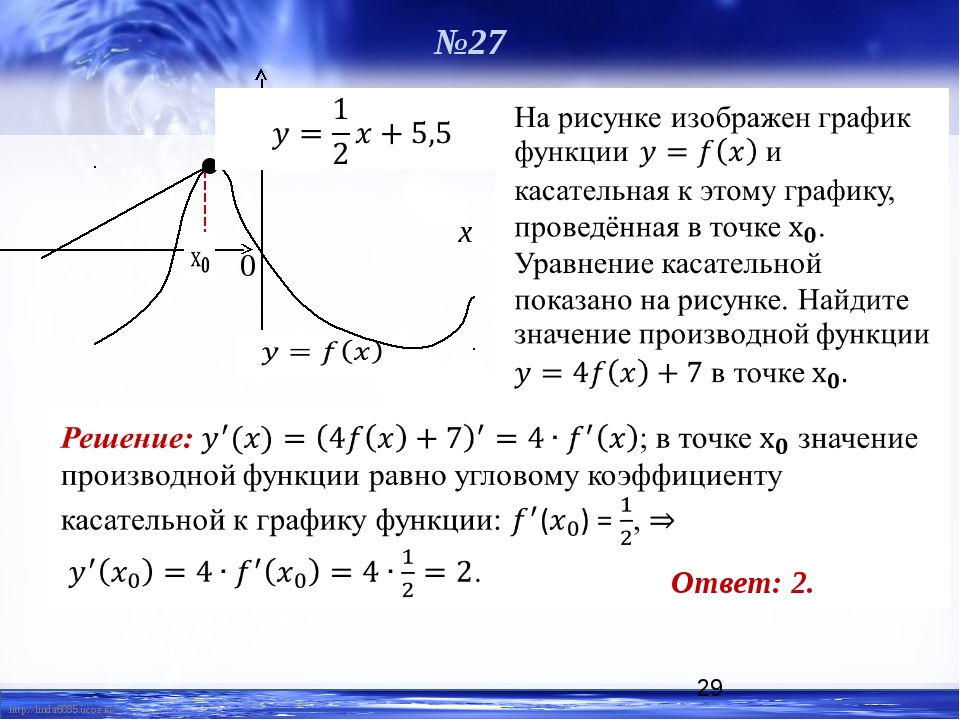
32×0-π4=arcsin-19+2πk или 32×0-π4=π-arcsin-19+2πk
32×0-π4=-arcsin19+2πk или 32×0-π4=π+arcsin19+2πk
x0=23π4-arcsin19+2πk или x0=235π4+arcsin19+2πk, k∈Z
Z- множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у:
y0=3cos32x0-π4-13
y0=3·1-sin232x0-π4-13 или y0=3·-1-sin232x0-π4-13
y0=3·1—192-13 или y0=3·-1—192-13
y0=45-13 или y0=-45+13
Отсюда получаем, что 23π4-arcsin19+2πk; 45-13, 235π4+arcsin19+2πk; -45+13 являются точками касания.
Ответ: необходимы уравнения запишутся как
y=12x-23π4-arcsin19+2πk+45-13,y=12x-235π4+arcsin19+2πk-45+13, k∈Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [-10;10], где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y=-2x+12. Красные точки – это точки касания.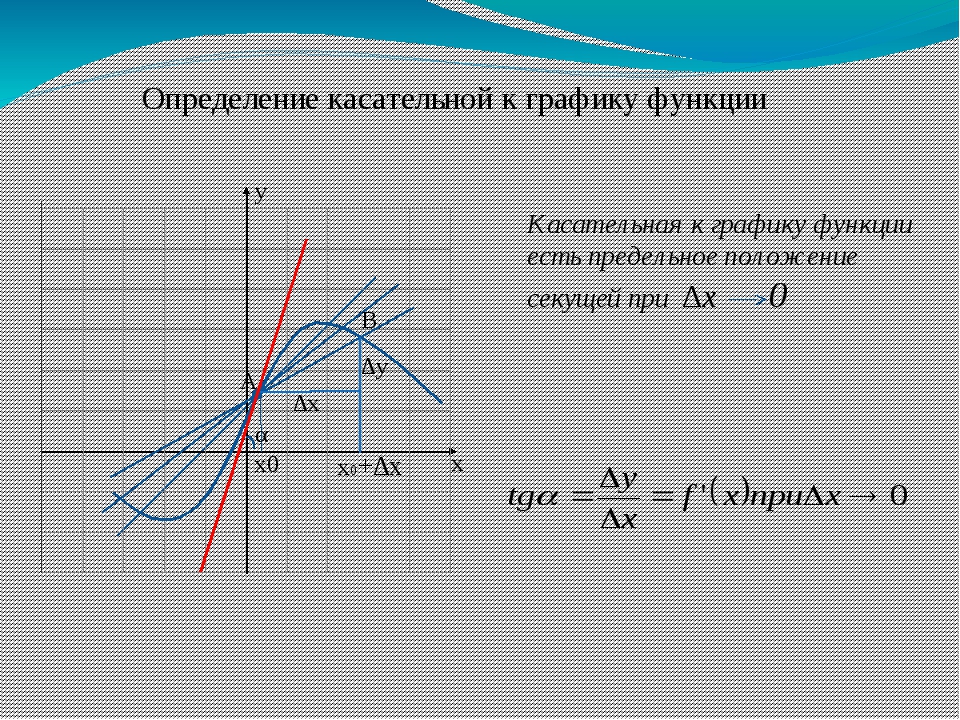
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке xcenter; ycenter и радиусом R применяется формула x-xcenter2+y-ycenter2=R2.
Данное равенство может быть записано как объединение двух функций:
y=R2-x-xcenter2+ycentery=-R2-x-xcenter2+ycenter
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x0; y0, которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y=R2-x-xcenter2+ycenter или y=-R2-x-xcenter2+ycenter в указанной точке.
Когда в точках xcenter; ycenter+R и xcenter; ycenter-R касательные могут быть заданы уравнениями y=ycenter+R и y=ycenter-R, а в точках xcenter+R; ycenter и
xcenter-R; ycenter будут являться параллельными оу, тогда получим уравнения вида x=xcenter+R и x=xcenter-R.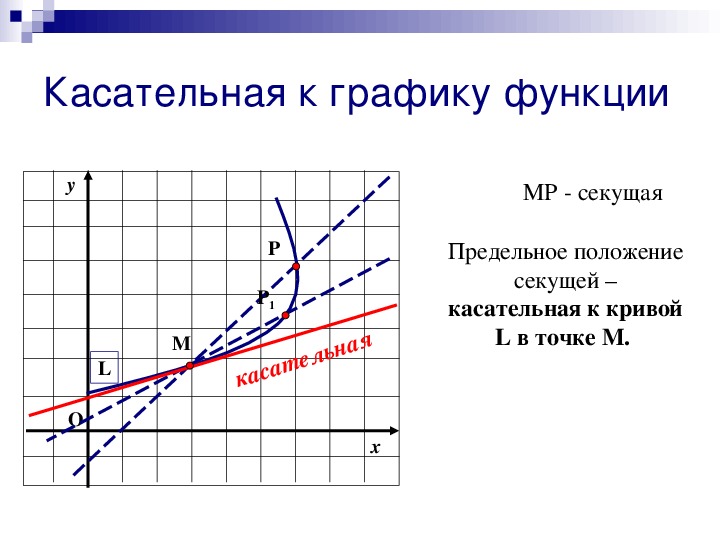
Касательная к эллипсу
Когда эллипс имеет центр в точке xcenter; ycenter с полуосями a и b, тогда он может быть задан при помощи уравнения x-xcenter2a2+y-ycenter2b2=1.
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y=ba·a2-(x-xcenter)2+ycentery=-ba·a2-(x-xcenter)2+ycenter
Если касательные располагаются на вершинах эллипса, тогда они параллельны ох или оу. Ниже для наглядности рассмотрим рисунок.
Пример 6
Написать уравнение касательной к эллипсу x-324+y-5225=1 в точках со значениями x равного х=2.
Решение
Необходимо найти точки касания, которые соответствуют значению х=2. Производим подстановку в имеющееся уравнение эллипса и получаем, что
x-324x=2+y-5225=114+y-5225=1⇒y-52=34·25⇒y=±532+5
Тогда 2; 532+5 и 2; -532+5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y. Получим, что
x-324+y-5225=1y-5225=1-x-324(y-5)2=25·1-x-324y-5=±5·1-x-324y=5±524-x-32
Очевидно, что верхний полуэллипс задается с помощью функции вида y=5+524-x-32, а нижний y=5-524-x-32.
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2; 532+5 будет иметь вид
y’=5+524-x-32’=52·124-(x-3)2·4-(x-3)2’==-52·x-34-(x-3)2⇒y'(x0)=y'(2)=-52·2-34-(2-3)2=523⇒y=y'(x0)·x-x0+y0⇔y=523(x-2)+532+5
Получаем, что уравнение второй касательной со значением в точке
2; -532+5 принимает вид
y’=5-524-(x-3)2’=-52·124-(x-3)2·4-(x-3)2’==52·x-34-(x-3)2⇒y'(x0)=y'(2)=52·2-34-(2-3)2=-523⇒y=y'(x0)·x-x0+y0⇔y=-523(x-2)-532+5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке xcenter; ycenter и вершины xcenter+α; ycenter и xcenter-α; ycenter, имеет место задание неравенства x-xcenter2α2-y-ycenter2b2=1, если с вершинами xcenter; ycenter+b и xcenter; ycenter-b, тогда задается при помощи неравенства x-xcenter2α2-y-ycenter2b2=-1.
Гипербола может быть представлена в виде двух объединенных функций вида
y=ba·(x-xcenter)2-a2+ycentery=-ba·(x-xcenter)2-a2+ycenter или y=ba·(x-xcenter)2+a2+ycentery=-ba·(x-xcenter)2+a2+ycenter
В первом случае имеем, что касательные параллельны оу, а во втором параллельны ох.
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Пример 7
Составить уравнение касательной к гиперболе x-324-y+329=1 в точке 7; -33-3.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x-324-y+329=1⇒y+329=x-324-1⇒y+32=9·x-324-1⇒y+3=32·x-32-4 или y+3=-32·x-32-4⇒y=32·x-32-4-3y=-32·x-32-4-3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7; -33-3.
Очевидно, что для проверки первой функции необходимо y(7)=32·(7-3)2-4-3=33-3≠-33-3, тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y(7)=-32·(7-3)2-4-3=-33-3≠-33-3, значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
Получаем, что
y’=-32·(x-3)2-4-3’=-32·x-3(x-3)2-4⇒kx=y'(x0)=-32·x0-3×0-32-4×0=7=-32·7-37-32-4=-3
Ответ: уравнение касательной можно представить как
y=-3·x-7-33-3=-3·x+43-3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y=ax2+bx+c в точке x0, y(x0), необходимо использовать стандартный алгоритм, тогда уравнение примет вид y=y'(x0)·x-x0+y(x0). Такая касательная в вершине параллельна ох.
Следует задать параболу x=ay2+by+c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что
x=ay2+by+c⇔ay2+by+c-x=0D=b2-4a(c-x)y=-b+b2-4a(c-x)2ay=-b-b2-4a(c-x)2a
Графически изобразим как:
Для выяснения принадлежности точки x0, y(x0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна оу относительно параболы.
Такая касательная будет параллельна оу относительно параболы.
Пример 8
Написать уравнение касательной к графику x-2y2-5y+3, когда имеем угол наклона касательной 150°.
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
-2y2-5y+3-x=0D=(-5)2-4·(-2)·(3-x)=49-8xy=5+49-8x-4y=5-49-8x-4
Значение углового коэффициента равняется значению производной в точке x0 этой функции и равняется тангенсу угла наклона.
Получаем:
kx=y'(x0)=tg αx=tg 150°=-13
Отсюда определим значение х для точек касания.
Первая функция запишется как
y’=5+49-8x-4’=149-8x⇒y'(x0)=149-8×0=-13⇔49-8×0=-3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150° для такой функции не существует.
Вторая функция запишется как
y’=5-49-8x-4’=-149-8x⇒y'(x0)=-149-8×0=-13⇔49-8×0=-3×0=234⇒y(x0)=5-49-8·234-4=-5+34
Имеем, что точки касания — 234; -5+34.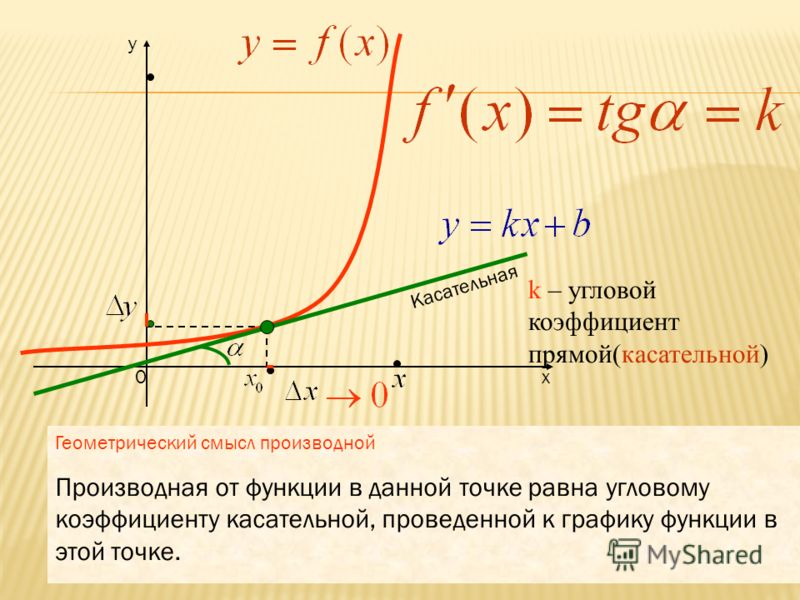
Ответ: уравнение касательной принимает вид
y=-13·x-234+-5+34
Графически изобразим это таким образом:
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Определение 1
Угол наклона прямой y=kx+b называется угол α, который отсчитывается от положительного направления оси ох к прямой y=kx+b в положительном направлении.
На рисунке направление ох обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Определение 2
Угловой коэффициент прямой y=kx+b называют числовым коэффициентом k.
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.
- Угол наклона прямой равняется 0 только при параллельности ох и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0. Значит, вид уравнения будет y=b.
- Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<π2 или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
- Если α=π2, тогда расположение прямой перпендикулярно ох. Равенство задается при помощи равенства x=c со значением с, являющимся действительным числом.
- Если угол наклона прямой y=kx+b тупой, то соответствует условиям π2<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывает.
Определение 3
Секущей называют прямую, которая проходит через 2 точки функции f(x). Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что АВ является секущей, а f(x) – черная кривая, α — красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника АВС можно найти по отношению противолежащего катета к прилежащему.
Определение 4
Получаем формулу для нахождения секущей вида:
k=tg α=BCAC=f(xB)-fxAxB-xA, где абсциссами точек А и В являются значения xA, xB, а f(xA), f(xB) — это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k=f(xB)-f(xA)xB-xA или k=f(xA)-f(xB)xA-xB, причем уравнение необходимо записать как y=f(xB)-f(xA)xB-xA·x-xA+f(xA) или
y=f(xA)-f(xB)xA-xB·x-xB+f(xB).
Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Определение 5
Касательная к графику функции f(x) в точке x0; f(x0) называется прямая, проходящая через заданную точку x0; f(x0), с наличием отрезка, который имеет множество значений х, близких к x0.
Пример 1
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y=x+1, считается касательной к y=2x в точке с координатами (1; 2). Для наглядности, необходимо рассмотреть графики с приближенными к (1; 2) значениями. Функция y=2x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y=2x сливается с прямой у=х+1.
Для определения касательной следует рассмотреть поведение касательной АВ при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.
Для наглядности приведем рисунок.
Секущая АВ, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной αx.
Определение 6
Касательной к графику функции y=f(x) в точке А считается предельное положение секущей АВ при В стремящейся к А, то есть B→A.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей АВ для функции f(x), где А и В с координатами x0, f(x0) и x0+∆x, f(x0+∆x), а ∆x обозначаем как приращение аргумента. Теперь функция примет вид ∆y=∆f(x)=f(x0+∆x)-f(∆x). Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник АВС. Используем определение тангенса для решения, то есть получим отношение ∆y∆x=tg α. Из определения касательной следует, что lim∆x→0∆y∆x=tg αx. По правилу производной в точке имеем, что производную f(x) в точке x0 называют пределом отношений приращения функции к приращению аргумента, где ∆x→0, тогда обозначим как f(x0)=lim∆x→0∆y∆x.
Отсюда следует, что f'(x0)=lim∆x→0∆y∆x=tg αx=kx, где kx обозначают в качестве углового коэффициента касательной.
То есть получаем, что f’(x) может существовать в точке x0 причем как и касательная к заданному графику функции в точке касания равной x0, f0(x0), где значение углового коэффициента касательной в точке равняется производной в точке x0. Тогда получаем, что kx=f'(x0).
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x0 при пересечении.
Уравнение касательной к графику функции y=f(x) в точке x0, f0(x0) принимает вид y=f'(x0)·x-x0+f(x0).
Имеется в виду, что конечным значением производной f'(x0) можно определить положение касательной, то есть вертикально при условии limx→x0+0f'(x)=∞ и limx→x0-0f'(x)=∞ или отсутствие вовсе при условии limx→x0+0f'(x)≠limx→x0-0f'(x).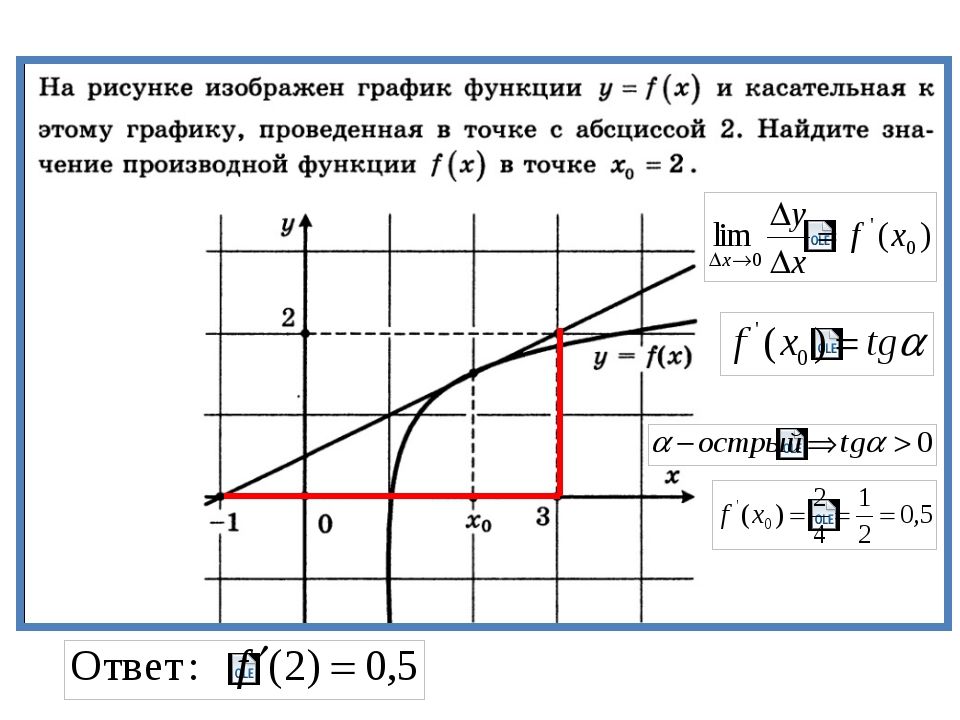
Расположение касательной зависит от значения ее углового коэффициента kx=f'(x0). При параллельности к оси ох получаем, что kk=0, при параллельности к оу — kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.
Пример 2
Произвести составление уравнения касательной к графику функции y=ex+1+x33-6-33x-17-33 в точке с координатами (1; 3) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1; 3) является точкой касания, тогда x0=-1, f(x0)=-3.
Необходимо найти производную в точке со значением -1. Получаем, что
y’=ex+1+x33-6-33x-17-33’==ex+1’+x33′-6-33x’-17-33’=ex+1+x2-6-33y'(x0)=y'(-1)=e-1+1+-12-6-33=33
Значение f’(x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда kx=tg αx=y'(x0)=33
Отсюда следует, что αx=arctg33=π6
Ответ: уравнение касательной приобретает вид
y=f'(x0)·x-x0+f(x0)y=33(x+1)-3y=33x-9-33
Для наглядности приведем пример в графической иллюстрации.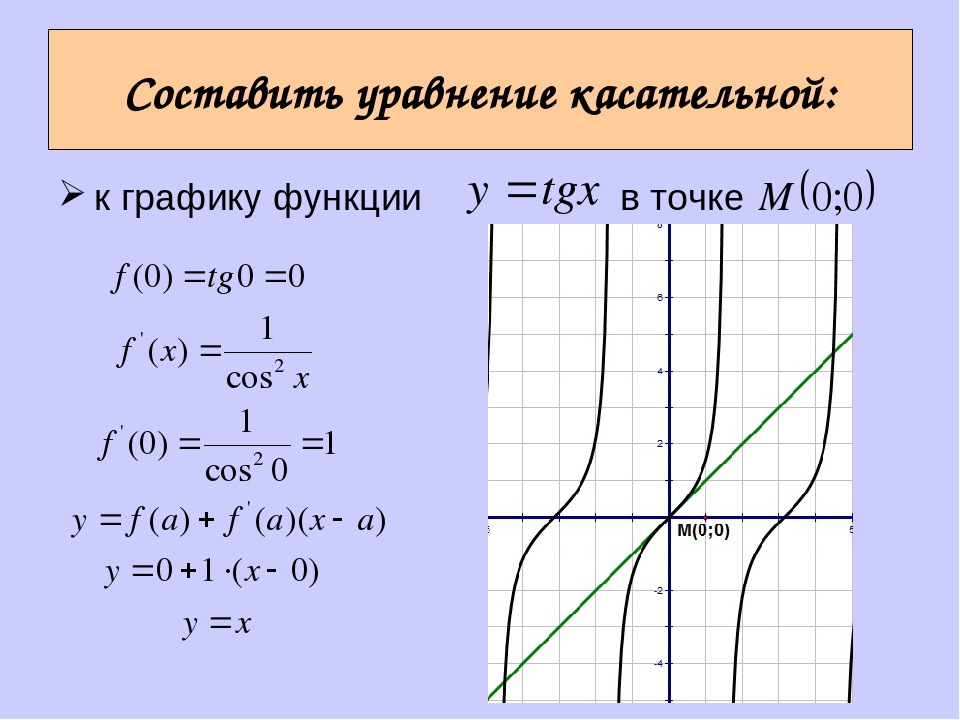
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Пример 3
Выяснить наличие существования касательной к графику заданной функции
y=3·x-15+1 в точке с координатами (1;1). Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y’=3·x-15+1’=3·15·(x-1)15-1=35·1(x-1)45
Если x0=1, тогда f’(x) не определена, но пределы записываются как limx→1+035·1(x-1)45=35·1(+0)45=35·1+0=+∞ и limx→1-035·1(x-1)45=35·1(-0)45=35·1+0=+∞, что означает существование вертикальной касательной в точке (1;1).
Ответ: уравнение примет вид х=1, где угол наклона будет равен π2.
Для наглядности изобразим графически.
Пример 4
Найти точки графика функции y=115x+23-45×2-165x-265+3x+2, где
- Касательная не существует;
- Касательная располагается параллельно ох;
- Касательная параллельна прямой y=85x+4.

Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x∈-∞; 2 и [-2; +∞). Получаем, что
y=-115×3+18×2+105x+176, x∈-∞; -2115×3-6×2+9x+12, x∈[-2; +∞)
Необходимо продифференцировать функцию. Имеем, что
y’=-115×3+18×2+105x+176′, x∈-∞; -2115×3-6×2+9x+12′, x∈[-2; +∞)⇔y’=-15(x2+12x+35), x∈-∞; -215×2-4x+3, x∈[-2; +∞)
Когда х=-2, тогда производная не существует, потому что односторонние пределы не равны в этой точке:
limx→-2-0y'(x)=limx→-2-0-15(x2+12x+35=-15(-2)2+12(-2)+35=-3limx→-2+0y'(x)=limx→-2+015(x2-4x+3)=15-22-4-2+3=3
Вычисляем значение функции в точке х=-2, где получаем, что
- y(-2)=115-2+23-45(-2)2-165(-2)-265+3-2+2=-2, то есть касательная в точке (-2;-2) не будет существовать.
- Касательная параллельна ох, когда угловой коэффициент равняется нулю.
 Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.
Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.
Когда x∈-∞; -2, тогда -15(x2+12x+35)=0, а при x∈(-2; +∞) получаем 15(x2-4x+3)=0.
Решим:
-15(x2+12x+35)=0D=122-4·35=144-140=4×1=-12+42=-5∈-∞; -2×2=-12-42=-7∈-∞; -2 15(x2-4x+3)=0D=42-4·3=4×3=4-42=1∈-2; +∞x4=4+42=3∈-2; +∞
Вычисляем соответствующие значения функции
y1=y-5=115-5+23-45-52-165-5-265+3-5+2=85y2=y(-7)=115-7+23-45(-7)2-165-7-265+3-7+2=43y3=y(1)=1151+23-45·12-165·1-265+31+2=85y4=y(3)=1153+23-45·32-165·3-265+33+2=43
Отсюда -5; 85, -4; 43, 1; 85, 3; 43 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 .
 Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
-15×2+12x+35=85×2+12x+43=0D=122-4·43=-28<0
Другое уравнение имеет два действительных корня, тогда
15(x2-4x+3)=85×2-4x-5=0D=42-4·(-5)=36×1=4-362=-1∈-2; +∞x2=4+362=5∈-2; +∞
Перейдем к нахождению значений функции. Получаем, что
y1=y(-1)=115-1+23-45(-1)2-165(-1)-265+3-1+2=415y2=y(5)=1155+23-45·52-165·5-265+35+2=83
Точки со значениями -1; 415, 5; 83 являются точками, в которых касательные параллельны прямой y=85x+4.
Ответ: черная линия – график функции, красная линия – график y=85x+4, синяя линия – касательные в точках -1; 415, 5; 83.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Возможно существование бесконечного количества касательных для заданных функций.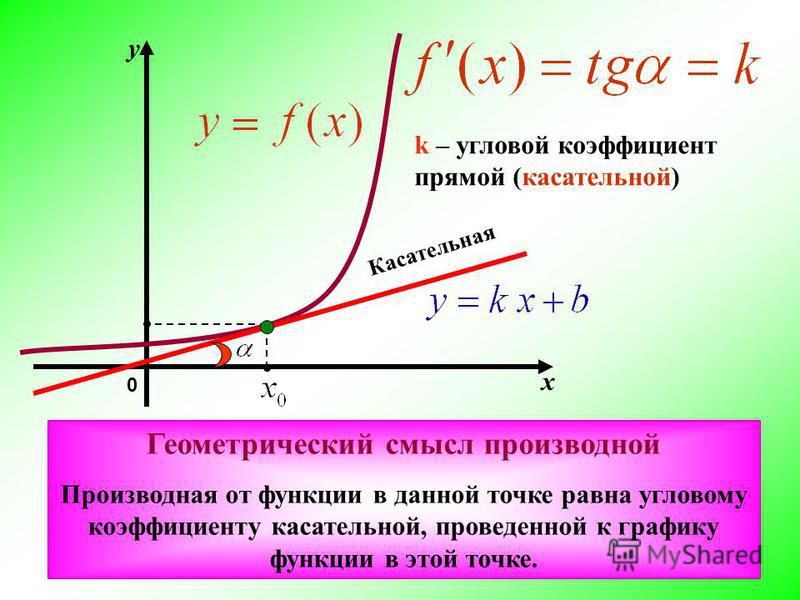
Пример 5
Написать уравнения всех имеющихся касательных функции y=3cos32x-π4-13, которые располагаются перпендикулярно прямой y=-2x+12.
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется -1, то есть записывается как kx·k⊥=-1. Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k⊥=-2, тогда kx=-1k⊥=-1-2=12.
Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x0 получаем, что kx=y'(x0). Из данного равенства найдем значения х для точек касания.
Получаем, что
y'(x0)=3cos32x0-π4-13’=3·-sin32x0-π4·32×0-π4’==-3·sin32x0-π4·32=-92·sin32x0-π4⇒kx=y'(x0)⇔-92·sin32x0-π4=12⇒sin32x0-π4=-19
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.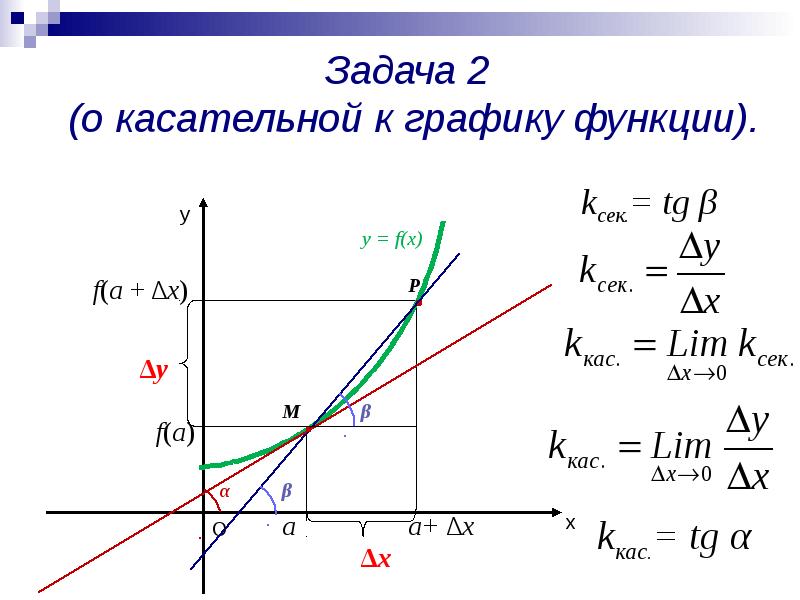
32×0-π4=arcsin-19+2πk или 32×0-π4=π-arcsin-19+2πk
32×0-π4=-arcsin19+2πk или 32×0-π4=π+arcsin19+2πk
x0=23π4-arcsin19+2πk или x0=235π4+arcsin19+2πk, k∈Z
Z- множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у:
y0=3cos32x0-π4-13
y0=3·1-sin232x0-π4-13 или y0=3·-1-sin232x0-π4-13
y0=3·1—192-13 или y0=3·-1—192-13
y0=45-13 или y0=-45+13
Отсюда получаем, что 23π4-arcsin19+2πk; 45-13, 235π4+arcsin19+2πk; -45+13 являются точками касания.
Ответ: необходимы уравнения запишутся как
y=12x-23π4-arcsin19+2πk+45-13,y=12x-235π4+arcsin19+2πk-45+13, k∈Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [-10;10], где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y=-2x+12. Красные точки – это точки касания.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке xcenter; ycenter и радиусом R применяется формула x-xcenter2+y-ycenter2=R2.
Данное равенство может быть записано как объединение двух функций:
y=R2-x-xcenter2+ycentery=-R2-x-xcenter2+ycenter
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x0; y0, которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y=R2-x-xcenter2+ycenter или y=-R2-x-xcenter2+ycenter в указанной точке.
Когда в точках xcenter; ycenter+R и xcenter; ycenter-R касательные могут быть заданы уравнениями y=ycenter+R и y=ycenter-R, а в точках xcenter+R; ycenter и
xcenter-R; ycenter будут являться параллельными оу, тогда получим уравнения вида x=xcenter+R и x=xcenter-R.
Касательная к эллипсу
Когда эллипс имеет центр в точке xcenter; ycenter с полуосями a и b, тогда он может быть задан при помощи уравнения x-xcenter2a2+y-ycenter2b2=1.
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y=ba·a2-(x-xcenter)2+ycentery=-ba·a2-(x-xcenter)2+ycenter
Если касательные располагаются на вершинах эллипса, тогда они параллельны ох или оу. Ниже для наглядности рассмотрим рисунок.
Пример 6
Написать уравнение касательной к эллипсу x-324+y-5225=1 в точках со значениями x равного х=2.
Решение
Необходимо найти точки касания, которые соответствуют значению х=2. Производим подстановку в имеющееся уравнение эллипса и получаем, что
x-324x=2+y-5225=114+y-5225=1⇒y-52=34·25⇒y=±532+5
Тогда 2; 532+5 и 2; -532+5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y. Получим, что
x-324+y-5225=1y-5225=1-x-324(y-5)2=25·1-x-324y-5=±5·1-x-324y=5±524-x-32
Очевидно, что верхний полуэллипс задается с помощью функции вида y=5+524-x-32, а нижний y=5-524-x-32.
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2; 532+5 будет иметь вид
y’=5+524-x-32’=52·124-(x-3)2·4-(x-3)2’==-52·x-34-(x-3)2⇒y'(x0)=y'(2)=-52·2-34-(2-3)2=523⇒y=y'(x0)·x-x0+y0⇔y=523(x-2)+532+5
Получаем, что уравнение второй касательной со значением в точке
2; -532+5 принимает вид
y’=5-524-(x-3)2’=-52·124-(x-3)2·4-(x-3)2’==52·x-34-(x-3)2⇒y'(x0)=y'(2)=52·2-34-(2-3)2=-523⇒y=y'(x0)·x-x0+y0⇔y=-523(x-2)-532+5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке xcenter; ycenter и вершины xcenter+α; ycenter и xcenter-α; ycenter, имеет место задание неравенства x-xcenter2α2-y-ycenter2b2=1, если с вершинами xcenter; ycenter+b и xcenter; ycenter-b, тогда задается при помощи неравенства x-xcenter2α2-y-ycenter2b2=-1.
Гипербола может быть представлена в виде двух объединенных функций вида
y=ba·(x-xcenter)2-a2+ycentery=-ba·(x-xcenter)2-a2+ycenter или y=ba·(x-xcenter)2+a2+ycentery=-ba·(x-xcenter)2+a2+ycenter
В первом случае имеем, что касательные параллельны оу, а во втором параллельны ох.
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Пример 7
Составить уравнение касательной к гиперболе x-324-y+329=1 в точке 7; -33-3.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x-324-y+329=1⇒y+329=x-324-1⇒y+32=9·x-324-1⇒y+3=32·x-32-4 или y+3=-32·x-32-4⇒y=32·x-32-4-3y=-32·x-32-4-3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7; -33-3.
Очевидно, что для проверки первой функции необходимо y(7)=32·(7-3)2-4-3=33-3≠-33-3, тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y(7)=-32·(7-3)2-4-3=-33-3≠-33-3, значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
Получаем, что
y’=-32·(x-3)2-4-3’=-32·x-3(x-3)2-4⇒kx=y'(x0)=-32·x0-3×0-32-4×0=7=-32·7-37-32-4=-3
Ответ: уравнение касательной можно представить как
y=-3·x-7-33-3=-3·x+43-3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y=ax2+bx+c в точке x0, y(x0), необходимо использовать стандартный алгоритм, тогда уравнение примет вид y=y'(x0)·x-x0+y(x0). Такая касательная в вершине параллельна ох.
Следует задать параболу x=ay2+by+c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что
x=ay2+by+c⇔ay2+by+c-x=0D=b2-4a(c-x)y=-b+b2-4a(c-x)2ay=-b-b2-4a(c-x)2a
Графически изобразим как:
Для выяснения принадлежности точки x0, y(x0) функции, нежно действовать по стандартному алгоритму.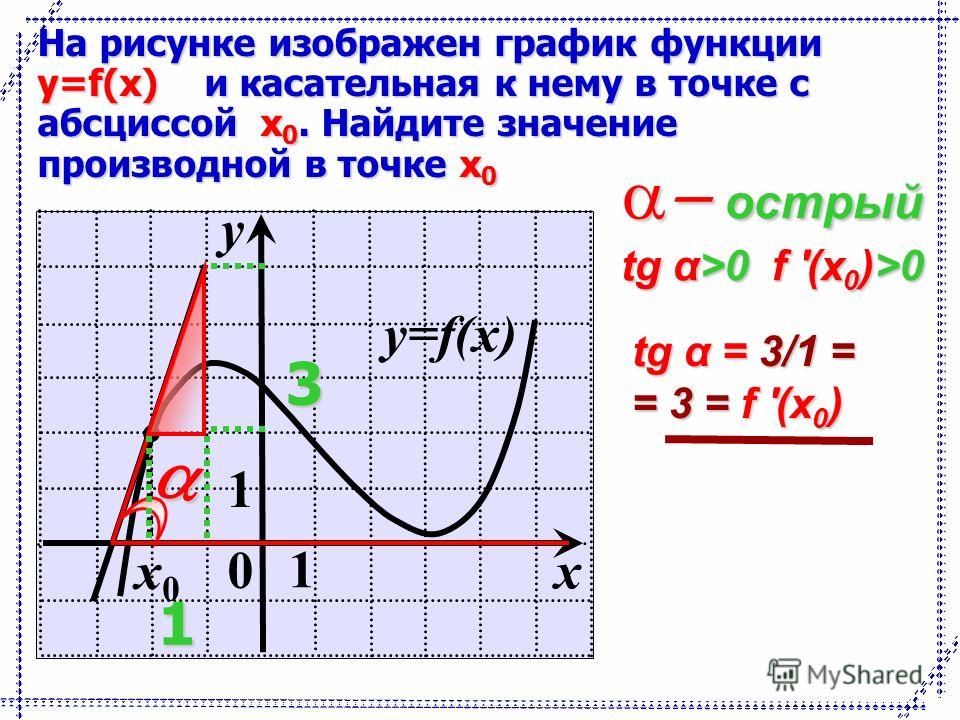 Такая касательная будет параллельна оу относительно параболы.
Такая касательная будет параллельна оу относительно параболы.
Пример 8
Написать уравнение касательной к графику x-2y2-5y+3, когда имеем угол наклона касательной 150°.
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
-2y2-5y+3-x=0D=(-5)2-4·(-2)·(3-x)=49-8xy=5+49-8x-4y=5-49-8x-4
Значение углового коэффициента равняется значению производной в точке x0 этой функции и равняется тангенсу угла наклона.
Получаем:
kx=y'(x0)=tg αx=tg 150°=-13
Отсюда определим значение х для точек касания.
Первая функция запишется как
y’=5+49-8x-4’=149-8x⇒y'(x0)=149-8×0=-13⇔49-8×0=-3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150° для такой функции не существует.
Вторая функция запишется как
y’=5-49-8x-4’=-149-8x⇒y'(x0)=-149-8×0=-13⇔49-8×0=-3×0=234⇒y(x0)=5-49-8·234-4=-5+34
Имеем, что точки касания — 234; -5+34.
Ответ: уравнение касательной принимает вид
y=-13·x-234+-5+34
Графически изобразим это таким образом:
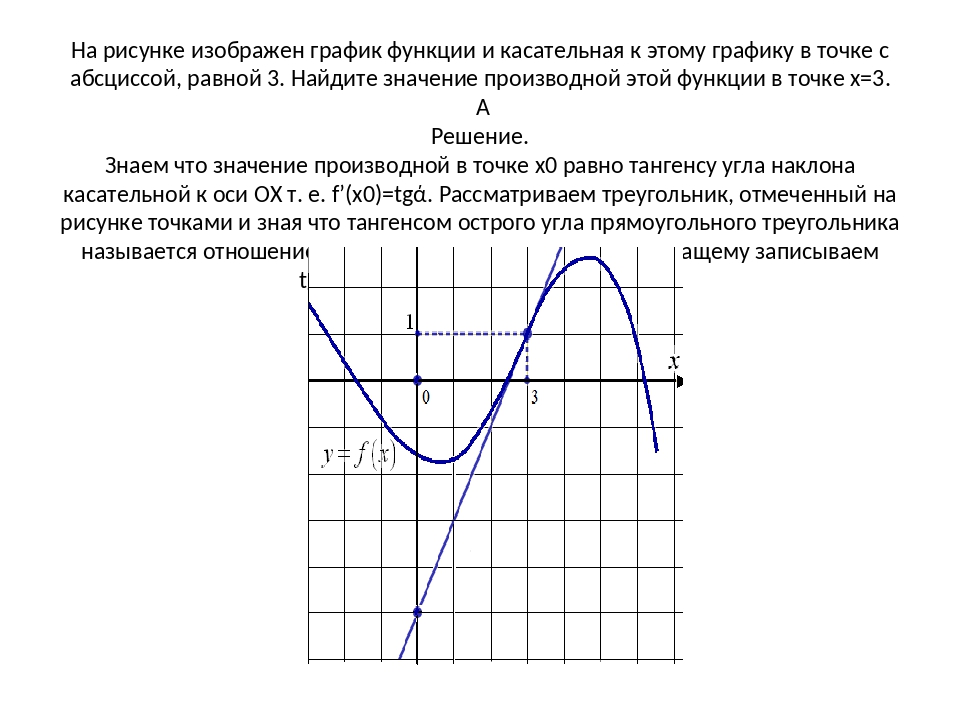
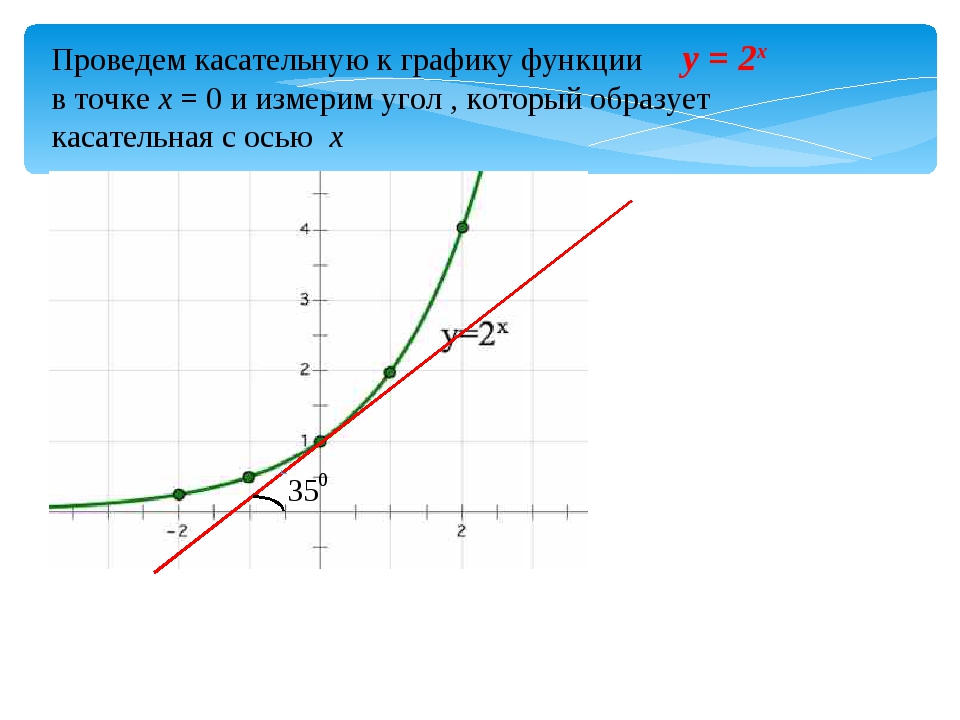
Внеклассный урок — Касательная к графику функции
Касательная к графику функции
Касательная – это прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка (рис.1).
Другое определение: это предельное положение секущей при Δx→0.
Пояснение: Возьмем прямую, пересекающую кривую в двух точках: А и b (см.рисунок). Это секущая. Будем поворачивать ее по часовой стрелке до тех пор, пока она не обретет только одну общую точку с кривой. Так мы получим касательную.
Строгое определение касательной:
Касательная к графику функции f, дифференцируемой в точке xо, — это прямая, проходящая через точку (xо; f(xо)) и имеющая угловой коэффициент f ′(xо).
Угловой коэффициент имеет прямая вида y = kx + b. Коэффициент k и является угловым коэффициентом этой прямой.
Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс:
Здесь угол α – это угол между прямой y = kx + b и положительным (то есть против часовой стрелки) направлением оси абсцисс. Он называется углом наклона прямой (рис.1 и 2).
Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).
Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).
Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис. 3).
3).
Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c, где c – некоторое действительное число (рис.4).
Уравнение касательной к графику функции y = f(x) в точке xо:
|
Алгоритм решения уравнения касательной к графику функции y = f(x):
1. 2. Вычислить производные f ′(x) и f ′(xо). 3. Внести найденные числа xо, f(xо), f ′(xо) в уравнение касательной и решить его. |
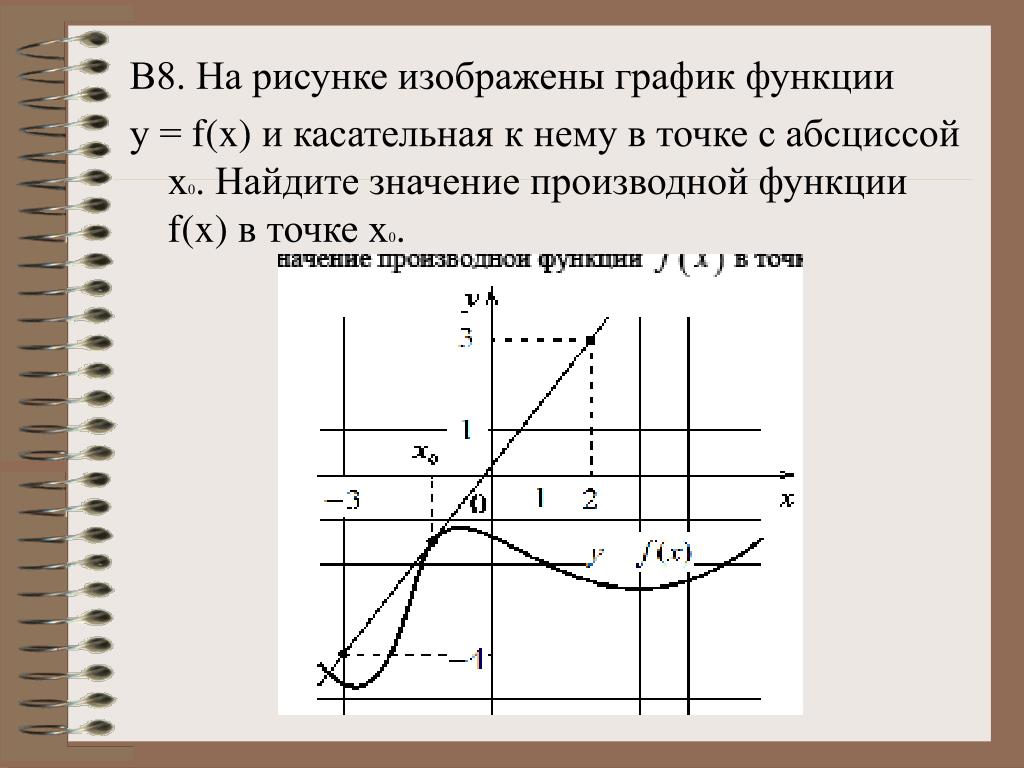
Пример: Найдем уравнение касательной к графику функции f(x) = x3 – 2x2 + 1 в точке с абсциссой 2.
Решение.
Следуем алгоритму.
1) Точка касания xо равна 2. Вычислим f(xо):
f(xо) = f(2) = 23 – 2 ∙ 22 + 1 = 8 – 8 + 1 = 1
2) Находим f ′(x). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х2 = 2х, а х3 = 3х2. Значит:
Значит:
f ′(x) = 3х2 – 2 ∙ 2х = 3х2 – 4х.
Теперь, используя полученное значение f ′(x), вычислим f ′(xо):
f ′(xо) = f ′(2) = 3 ∙ 22 – 4 ∙ 2 = 12 – 8 = 4.
3) Итак, у нас есть все необходимые данные: xо = 2, f(xо) = 1, f ′(xо) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:
у = f(xо) + f ′(xо) (x – xо) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.
Ответ: у = 4х – 7.
Уравнение касательной к графику функции
Пусть дана функция f, которая в некоторой точке x0 имеет конечную производную f (x0). Тогда прямая, проходящая через точку (x0; f (x0)), имеющая угловой коэффициент f ’(x0), называется касательной.
А что будет, если производная в точке x0 не существует? Возможны два варианта:
- Касательная к графику тоже не существует. Классический пример — функция y = |x| в точке (0; 0).
- Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π/2).
Уравнение касательной
Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x0, достаточно знать значение функции и производной в этой точке.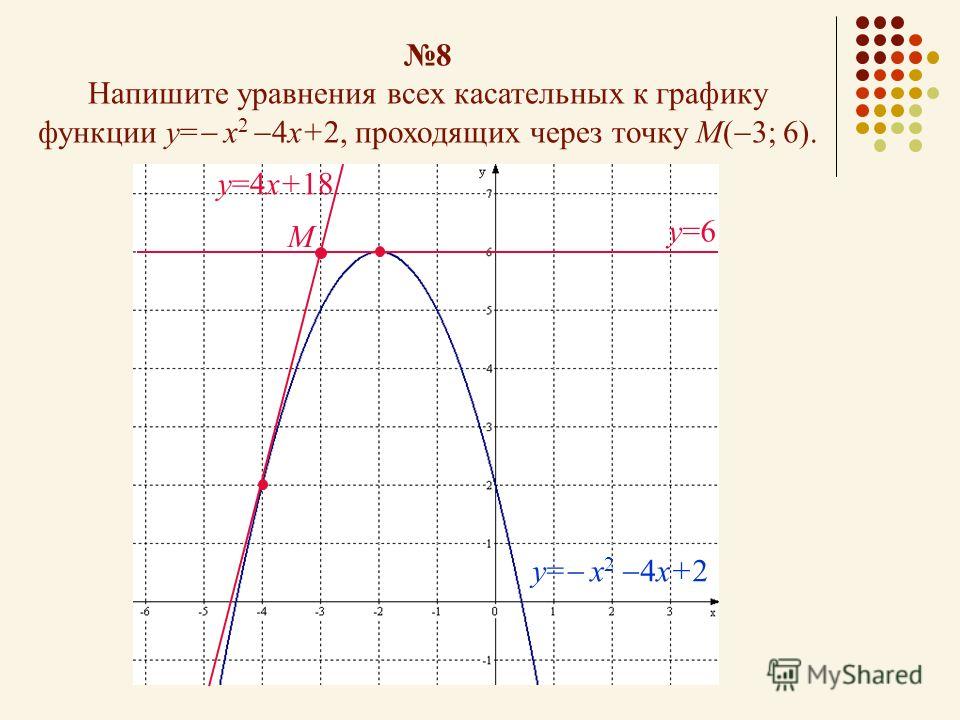
Итак, пусть дана функция y = f (x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x0 ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:
y = f ’(x0) · (x − x0) + f (x0)
Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции.
Задача. Дана функция y = x3. Составить уравнение касательной к графику этой функции в точке x0 = 2.
Уравнение касательной: y = f ’(x0) · (x − x0) + f(x0). Точка x0 = 2 нам дана, а вот значения f (x0) и f ’(x0) придется вычислять.
Для начала найдем значение функции. Тут все легко: f (x0) = f (2) = 23 = 8;
Теперь найдем производную: f ’(x) = (x3)’ = 3x2;
Подставляем в производную x0 = 2: f ’(x0) = f ’(2) = 3 · 22 = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.
Задача. Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке x0 = π/2.
В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:
f (x0) = f (π/2) = 2sin (π/2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f ’(x0) = f ’(π/2) = 2cos (π/2) = 0;
Уравнение касательной:
y = 0 · (x − π/2) + 7 ⇒ y = 7
В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k = 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.
Смотрите также:
- Правила вычисления производных
- Вводный урок по вычислению производных степенной функции
- Пробный ЕГЭ-2011 по математике, вариант №6
- Площадь круга
- Иррациональные неравенства. Часть 1
- Задача B5: вычисление площади методом обводки
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
Секущая графика функции.
 Уравнение секущей графика функции
Уравнение секущей графика функции
Рассмотрим график некоторой функции y = f (x), точки A= (x0; f (x0)) и B = (x1; f (x1)) на графике, прямую, проходящую через точки A и B, и произвольную точку C = (x; y) на этой прямой (рис. 1).
Рис.1
Определение 1. Прямую, проходящую через две произвольные точки графика функции, называют секущей графика функции.
В соответствии с определением 1 прямая, проходящая через точки A и B графика функции y = f (x), является секущей этого графика.
Выведем уравнение секущей графика функции.
Для этого рассмотрим векторы и , координаты которых имеют вид:
Поскольку векторы и лежат на одной прямой, то справедливо равенство
| (1) |
где k – некоторое число.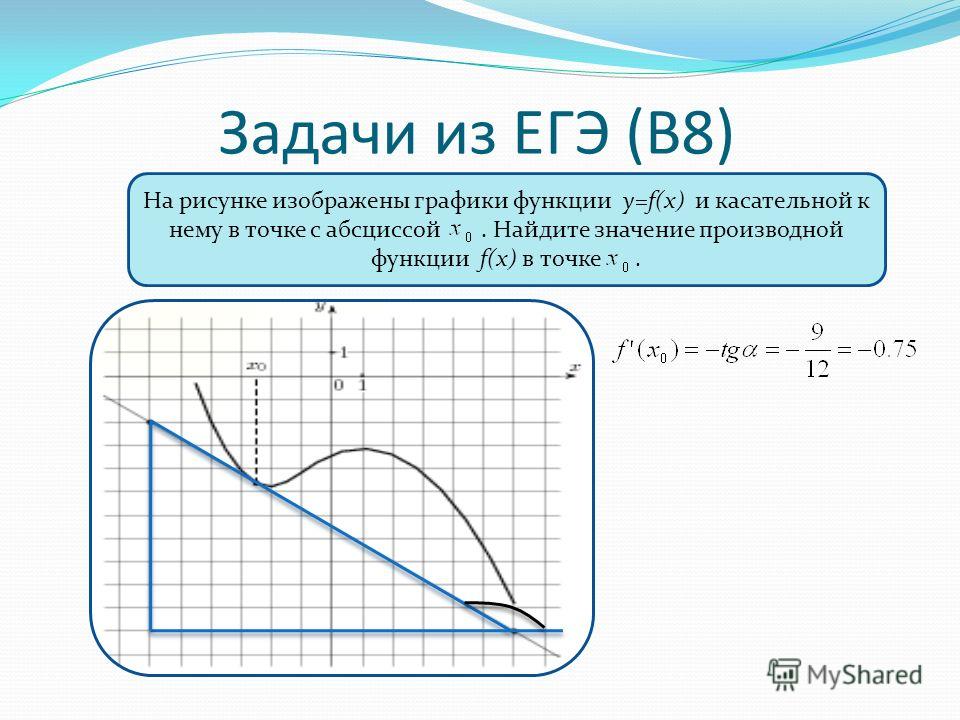
Переписывая равенство (1) в координатах, получим систему (2):
| (2) |
Исключая из системы (2) переменную k , получим систему (3):
| (3) |
второе уравнение которой можно записать в следующем виде
| (4) |
Уравнение (4) и является уравнением секущей графика функции y = f (x), проходящей через точки A = (x0; f (x0)) и B = (x1; f (x1)) этого графика.
Касательная к графику функции
Проведем секущую графика функции y = f (x), проходящую через точки A и B этого графика, и рассмотрим случай, когда точка A неподвижна, а точка B неограниченно приближается к точке A по графику функции y = f (x) (рис. 2).
2).
Рис.2
Неограниченное приближение точки B к точке A принято обозначать
B → A
и произносить «B стремится к A».
Заметим, что, если B → A для точек A = (x0; f (x0)) и B = (x1; f (x1)) графика функции y = f (x), то это означает, что x1 → x0 .
Определение 2. Если при x1 → x0 существует предельное положение секущей графика фукнкции y = f (x), то это предельное положение секущей называют касательной к графику функции y = f (x) в точке A = (x0; f (x0)) (рис. 3) .
Рис.3
Производная функции
Определение 3. Если при x1 → x0 отношение
| (5) |
входящее в формулу (4), стремится к некоторому числу, то это число называют производной функции y = f (x) в точке x0 , обозначают f ′(x0) или и записывают так:
| (6) |
Уравнение касательной к графику функции
Из формул (4) и (6) вытекает следующее
Утверждение. Если у функции y = f (x) существует производная в точке x0 , то к графику функции y = f (x) в точке с координатами (x0; f (x0)) можно провести касательную, а уравнение этой касательной имеет вид:
| y = f′(x0) (x – x0) + f (x0) | (7) |
Геометрический смысл производной
Рассмотрим сначала возрастающую функцию y = f (x) и проведем секущую графика этой функции, проходящую через точки A = (x0; f (x0)) и B = (x1; f (x1)) (рис.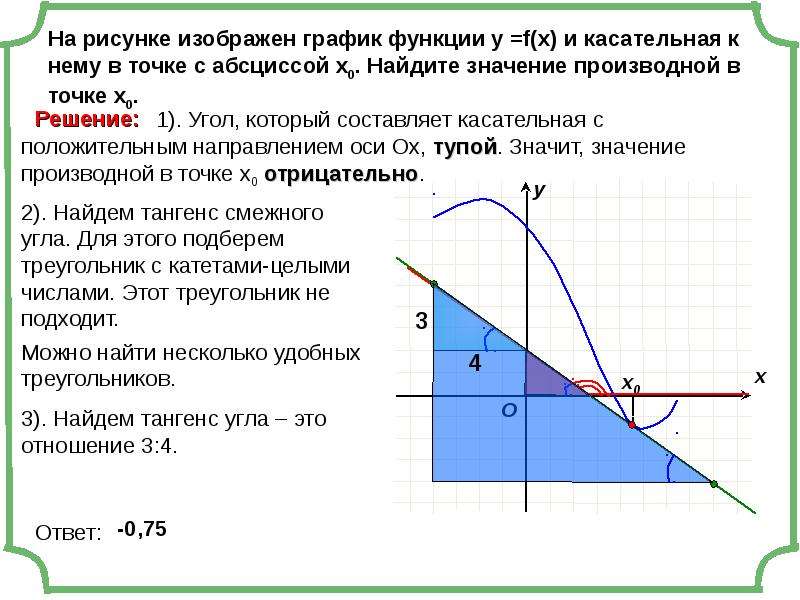 4).
4).
Рис.4
Обозначим буквой φ угол, образованный секущей и положительным направлением оси Ox, отсчитываемый против часовой стрелки. Тогда угол BAD в треугольнике ABD на рисунке 4 равен φ , и по определению тангенса угла получаем равенство
| (8) |
причем по определению углового коэффициента прямой tg φ является угловым коэффициентом секущей графика функции y = f (x), проходящей через точки A = (x0; f (x0)) и B = (x1; f (x1)) этого графика.
Случай, когда функция y = f (x) убывает, изображен на рисунке 5
Рис.5
В этом случае угол φ является тупым, причем
то есть формула (8) справедлива и для случая, когда функция y = f (x) убывает.
Отсюда в соответствии с определением производной функции вытекает соотношение:
где буквой α обозначен угол, образованный касательной к графику функции y = f (x) в точке A = (x0; f (x0)) с положительным направлением оси Ox (рис. 6).
Рис.6
Таким образом, если у функции y = f (x) в точке x0 существует производная, то эта производная равна тангенсу угла наклона касательной к графику функции y = f (x) в точке (x0; f (x0)) :
f′(x0) = tg α ,
где угол наклона α образован касательной и положительным направлением оси Ox и отсчитывается в положительном направлении (то есть против часовой стрелки).
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Касательная к графику ункции: уравнение касательной
Рассмотрим следующий рисунок:
На нем изображена некоторая функция y = f(x), которая дифференцируема в точке a. Отмечена точка М с координатами (а; f(a)). Через произвольную точку Р(a + ∆x; f(a + ∆x)) графика проведена секущая МР.
Если теперь точку Р сдвигать по графику к точке М, то прямая МР будет поворачиваться вокруг точки М. При этом ∆х будет стремиться к нулю. Отсюда можно сформулировать определение касательной к графику функции.
Касательная к графику функции
Касательная к графику функции есть предельное положение секущей при стремлении приращения аргумента к нулю. Следует понимать, что существование производной функции f в точке х0, означает, что в этой точке графика существует касательная к нему.
При этом угловой коэффициент касательной будет равен производной этой функции в этой точке f’(x0). В этом заключается геометрический смысл производной. Касательная к графику дифференцируемой в точке х0 функции f — это некоторая прямая, проходящая через точку (x0;f(x0)) и имеющая угловой коэффициент f’(x0).
Касательная к графику дифференцируемой в точке х0 функции f — это некоторая прямая, проходящая через точку (x0;f(x0)) и имеющая угловой коэффициент f’(x0).
Уравнение касательной
Попытаемся получить уравнение касательной к графику некоторой функции f в точке А(x0; f(x0)). Уравнение прямой с угловым коэффициентом k имеет следующий вид:
y = k*x + b.
Так как у нас угловой коэффициент равен производной f’(x0), то уравнение примет следующий вид: y = f’(x0)*x + b.
Теперь вычислим значение b. Для этого используем тот факт, что функция проходит через точку А.
f(x0) = f’(x0)*x0 + b, отсюда выражаем b и получим b = f(x0) – f’(x0)*x0.
Подставляем полученное значение в уравнение касательной:
y = f’(x0)*x + b = f’(x0)*x + f(x0) – f’(x0)*x0 = f(x0) + f’(x0)*(x — x0).
y = f(x0) + f’(x0)*(x — x0).
Рассмотрим следующий пример: найти уравнение касательной к графику функции f(x) = x3 – 2*x2 + 1 в точке х = 2.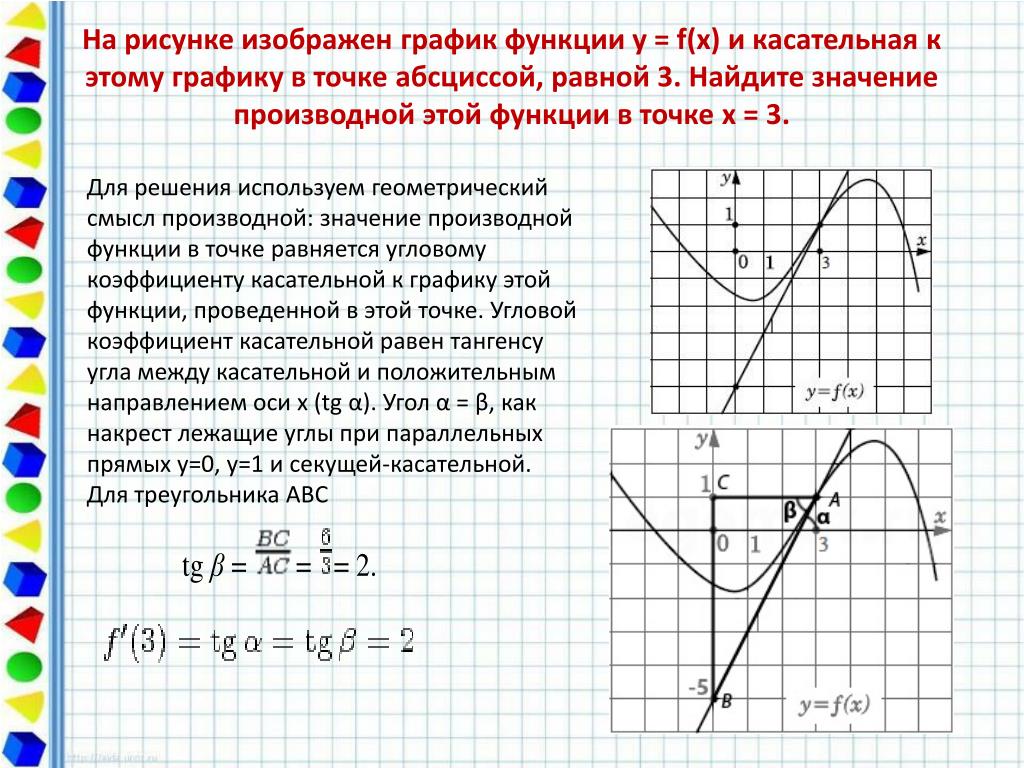
1. х0 = 2.
2. f(x0) = f(2) = 22 — 2*22 + 1 = 1.
3. f’(x) = 3*x2 – 4*x.
4. f’(x0) = f’(2) = 3*22 – 4*2 = 4.
5. Подставим полученные значения в формулу касательной, получим: y = 1 + 4*(x — 2). Раскрыв скобки и приведя подобные слагаемые получим: y = 4*x — 7.
Ответ: y = 4*x — 7.
Общая схема составления уравнения касательной к графику функции y = f(x):
1. Определить х0.
2. Вычислить f(x0).
3. Вычислить f’(x)
4. Вычислить f’(x0)
5. Подставить полученные значения в уравнение касательной y= f(x0) + f’(x0)*(x — x0).
Нужна помощь в учебе?
Предыдущая тема: Применения непрерывности: метод интервалов и примеры
Следующая тема:   Критические точки функции: максимумы и минимумы
Касательная. Задачи на касательную | Статья в журнале «Молодой ученый»
Чтобы
правильно и рационально решать задачи, связанные
с уравнением касательной, нужно четко понимать, что такое
касательная, владеть техникой составления
уравнения касательной к графику функции и
представлять себе, для решения каких задач (в том
числе и задач с параметрами) можно использовать метод касательной.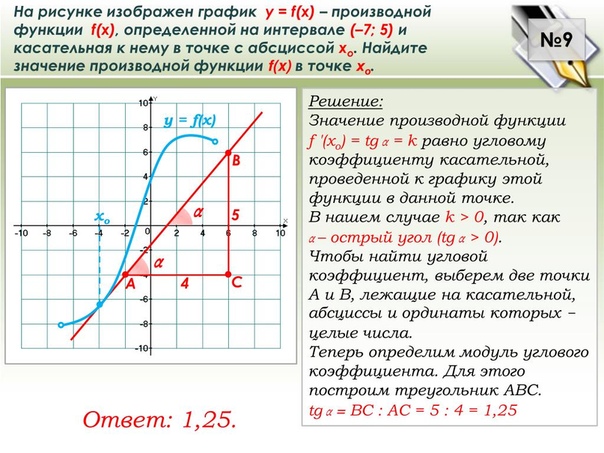
Опр.
1. Касательной к графику функции у
= f(x)
называется
предельное положение секущей MN
при
(рис. 1).
Рис. 1
Касательная к кривой может
иметь с ней несколько общих точек или пересекать ее. Можно дать и
другое определение касательной к кривой.
Опр.
2. Касательной к графику функции у
= f(x) в
точке A0(x0;
f(x0))
называется
прямая, проходящая через точку A0,
угловой
коэффициент которой
равен значению производной функции у
=f(x)
в точке
с абсциссой x0.
Уравнение
касательной
к кривой у =
f(x)
в точке с
абсциссой х0имеет вид:
.
Между
понятием касательной и понятие производной имеется тесная
связь. Геометрический
смысл производной можно выразить так: если функция
у = f(x)
в точке
х0
имеет
производную, то в точке с этой абсциссой определена касательная к
графику функции
,
причем ее
угловой коэффициент
равен
.
Вывод: если в точке х0
есть производная
функции
,
то в точке с
этой абсциссой есть касательная к графику
функции
и наоборот; если
в точке х0
нет производной
функции
,
то в точке с
этой абсциссой нет касательной к графику функции
и наоборот.
Укажем
случаи, когда
функция не имеет в точке касательной, и, следовательно, не
имеет и производной. Таких случаев три: угловая точка, точка
возврата, узловая точка
(рис. 2 а, б, в). Особо
2 а, б, в). Особо
отметим случай, когда в точке функция имеет бесконечную
производную (рис. 2 г).
угловая точка
точка возврата узловая
точка
а) б) в) г)
Рис. 2
Рассмотрим решение
некоторых задач.
Задачи,
связанные с определением того, является ли прямая
у = kx
+ b
касательной к графику функции
у = f(x).
Можно указать два способа решения таких задач.
Находим общие
точки графиков, т. е. решаем уравнение f(x)
= kx
+ b,
а затем для каждого из его решений
вычисляем
.
В тех случаях, когда
= k,
имеет место касание, в других —
пересечение.
Находим корни
уравнения
= k
и для каждого из них проверяем, выполняется ли
равенство f(x)
= kx
+ b.
При его выполнении получаем абсциссы точек
касания.
Обобщая
оба способа, заметим, что для того чтобы прямая у
= kx
+ b
была касательной к графику функции
у = f(x),
необходимо и достаточно существование хотя
бы одного числа х0,
для которого выполняется система
При каких
значениях b
прямая у = 3х +b
является касательной к графику функции у
=?
Решение.
Записав условие касания
получим
Ответ:
.
При каких
значениях а прямая
у=ах+2
является касательной к графику функции
Указание.
Ответ:
а = e-3
При каких
значениях а прямая
является касательной к графику функции
Указание.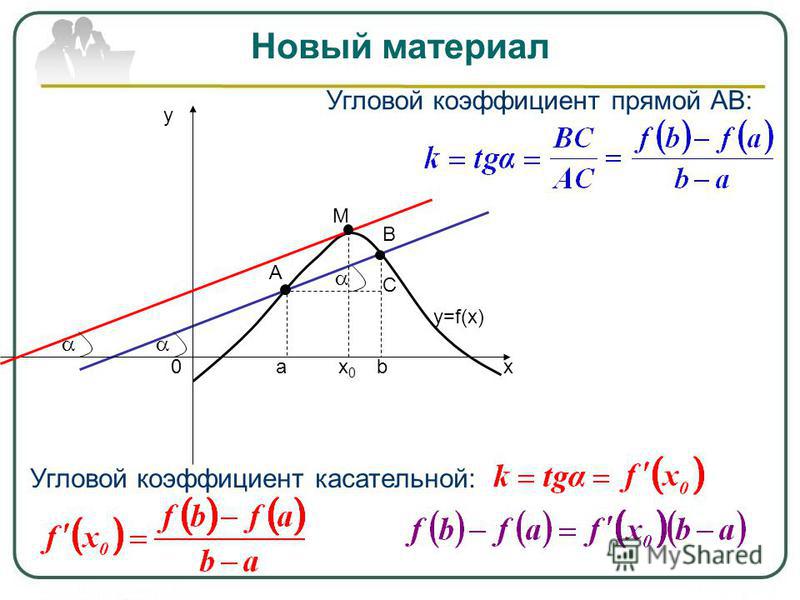
Ответ:
а = 7 или а =
-1.
Является ли
прямая
касательной к графику функции
?
Если является, то найти координаты точки касания.
Решение.
Пусть
.
Из условия следует, что должны выполняться равенство
,
где
-
возможная абсцисса точки касания. Имеем:
Если теперь
составить уравнение касательной к графику заданной функции в каждой
из двух найденных точек, то окажется, что в точке
как раз и получится
.
Значит, точка касания имеет координаты (1;-1).
К графику
функции
проведена
касательная, параллельная прямой
.
Найти ординату точки касания.
Решение.
.
Абсцисса интересующей нас точки касания удовлетворяет уравнению
.
Имеем:
Таким образом,
.
Значит,
-
абсцисса точки касания. Чтобы найти ординату точки касания
Чтобы найти ординату точки касания
преобразуем выражение, задающее функцию:
Ответ: 1.
Написать
уравнение всех касательных к графику функции
,
параллельных прямой
.
Решение.
Так как касательная должна быть параллельна прямой
,
то ее угловой коэффициент, равный у'(х0),
где х0
— абсцисса точки касания, совпадает с
угловым коэффициентом данной прямой, т. е.
.
Отсюда
или
.
Далее составляем уравнение касательной для каждой точки.
Ответ:
,.
Найти все
значения
,
при каждом из которых касательная к графикам функций
и
в
точках с абсциссой
параллельны.
Решение.
Известно, что тангенс угла наклона касательной к графику функций
в точке с абсциссой
равен
.
Следовательно, все искомые значения
будут корнями уравнения
,
откуда
.
Используя формулу разности синусов углов, будем иметь
.
Решая полученное уравнение, получаем
Найти
расстояние между касательными к графику функции
,
расположенными параллельно оси
.
Решение.
Найдем критические точки заданной функции:
Так как,
производная в точках
и
равна нулю, то касательные, проведенные к кривой в точках с этими
абсциссами, параллельны оси
.
Найдем значения функций в этих точках.
Итак,
расстояние d
между касательными, параллельными оси
,
равно
С составлением
уравнения касательной, параллельной данной прямой, связана задача о
нахождении кратчайшего расстояния между графиком
некоторой функции f(x)
и прямой
.
Во многих
случаях удается найти касательную к графику
,
параллельную данной прямой
и делящую плоскость на две части, в одной из
которых расположен график функции, а в другой — заданная
прямая. Тогда кратчайшим расстоянием между графиком функции и прямой
является расстояние от точки М(х0;
у0),
в которой проведена параллельная касательная,
до заданной прямой у =
kx
+ b;
это расстояние можно вычислить по формуле
Найти
кратчайшее расстояние между параболой
и прямой
Решение.
Убедившись, что графики не имеют общих
точек (уравнение
не имеет решений), запишем
уравнение такой касательной к графику функции
,
которая параллельна прямой
Уравнение касательной имеет
вид
касание происходит в точке
Прямая у =
х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной.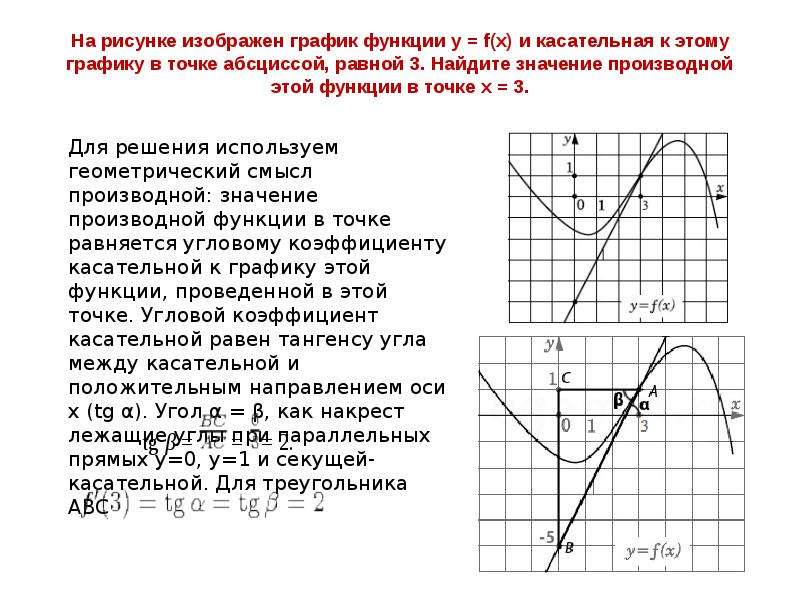 Таким образом, кратчайшее
Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
.
Ответ:
Довольно
сложной является задача составления уравнения всех касательных к
графику функции у = f(x),
проходящих через заданную точку М(х0;
у0),
вообще говоря, не лежащую на графике.
Приведем алгоритм решения этой задачи.
1. Составляем
уравнение касательной к графику функции
у = f(x)
в произвольной
точке графика с абсциссой
t:
2. Решаем
относительно t
уравнение
и для каждого его
решения t
записываем
соответствующую
касательную в виде
.
Написать
уравнение всех касательных к графику функции
,
проходящих через точку
М(2; -2).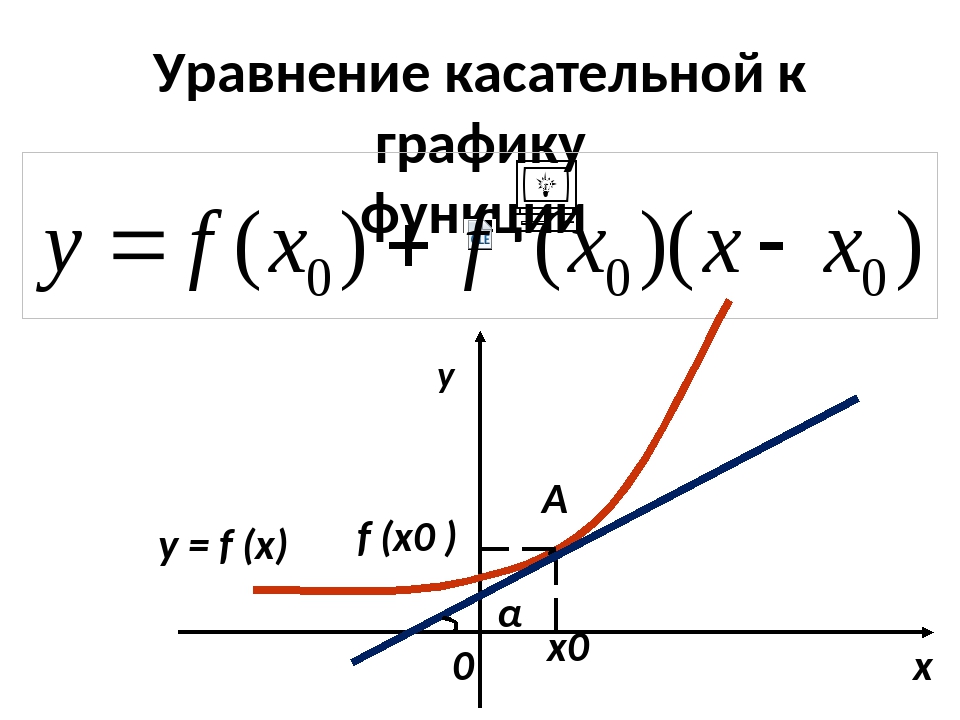
Указание.
Уравнение касательной в точке с абсциссой t
имеет вид
.
Так как эта
касательная проходит через точку
(2; -2), то
,
откуда
.
Ответ:
.
Найти
площадь треугольника, образованного касательными, проведенными
к графику функции
через точку
и секущей,
проходящей через точки касания.
Указание.
Уравнение
дает два
решения: t1
= 1, t2
= 4. Таким
образом, точки K1
(1;1) и
K2(4;2)
являются точками касания.
Ответ:
0,25.
Говорят, что
прямая
является общей касательной графиков функции
и
,
если она касается как одного, так и другого
графиков (но совершенно не обязательно в одной и той же точке).
Например, прямая
является общей касательной графиков функций
(в точке М(2; 5) и
(в точке K(0,5;
-1)). Заметим, что графики функций
и
имеют в точке их пересечения М(х0;
у0)
общую невертикальную касательную тогда и
только тогда, когда
.
Доказать,
что параболы
и
имеют
в их общей точке общую касательную. Найти
уравнение этой общей касательной. Решение.
Уравнение
имеет
единственный корень х=2,
т. е. параболы имеют единственную общую точку
М(2;0). Убедимся, что значения производных для
обеих функций в точке х =
2 равны; действительно,
и
.
Далее составляем уравнение касательной.
Ответ:.
В завершении рассмотрим
решение еще нескольких задач на касательную с параметром.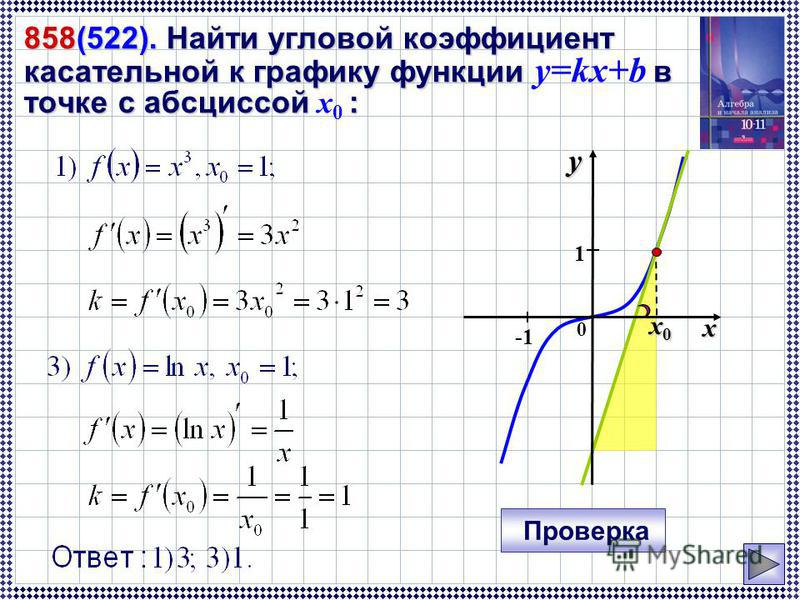
При
каких значениях параметра
касательная
к графику функции
в точке
проходит через точку (2;3)?
Решение.
Составим уравнение касательной к графику заданной функции в точке
:
Так как эта прямая проходит через точку (2;3), то имеет место
равенство
,
откуда находим:
.
Может ли
касательная к кривой
в какой-либо ее точке составлять острый угол с положительным
направлением оси
?
Решение.
Найдем производную функции
.
В любой точке, в которой функция определена, производная
отрицательна. Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.
Ответ: Не
может.
Найти
значение параметра
,
при котором касательная к графику функции
в точке
проходит через точку М(1;7).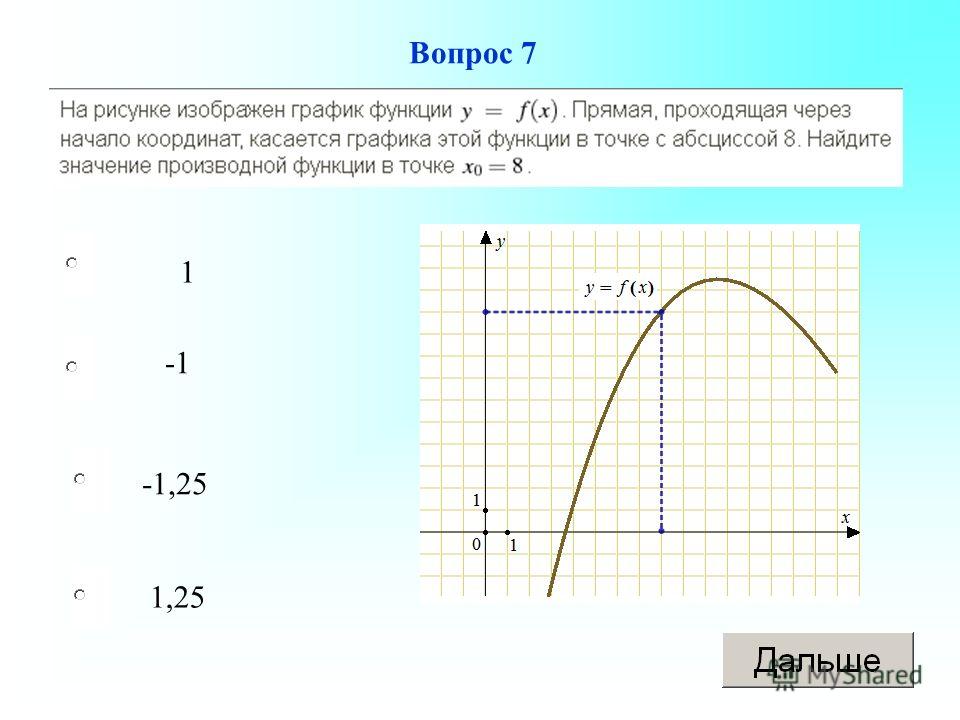
Решение.
Пусть
тогда
.
Составим уравнение касательной:
По условию эта
касательная проходит через точку М(1;7), значит,
,
откуда получаем:
При каких
значениях параметра
прямая
является касательной к графику функции
?
Решение.
Из условия следует, что должно выполнятся равенство
где
абсцисса
точки касания. Значит,
и
связаны между собой равенством
(1). Составим уравнение касательной к графику заданной функции в
точке
Из условия
следует, что должно выполняться равенство
.
Решив это уравнение, получим
.
Тогда из (1) получаем, что
.
При каком
значении
прямая
является касательной у графику
?
Решение.
Так как прямая
является касательной к графику функции
,
то в точке касания угловой коэффициент касательной равен 3.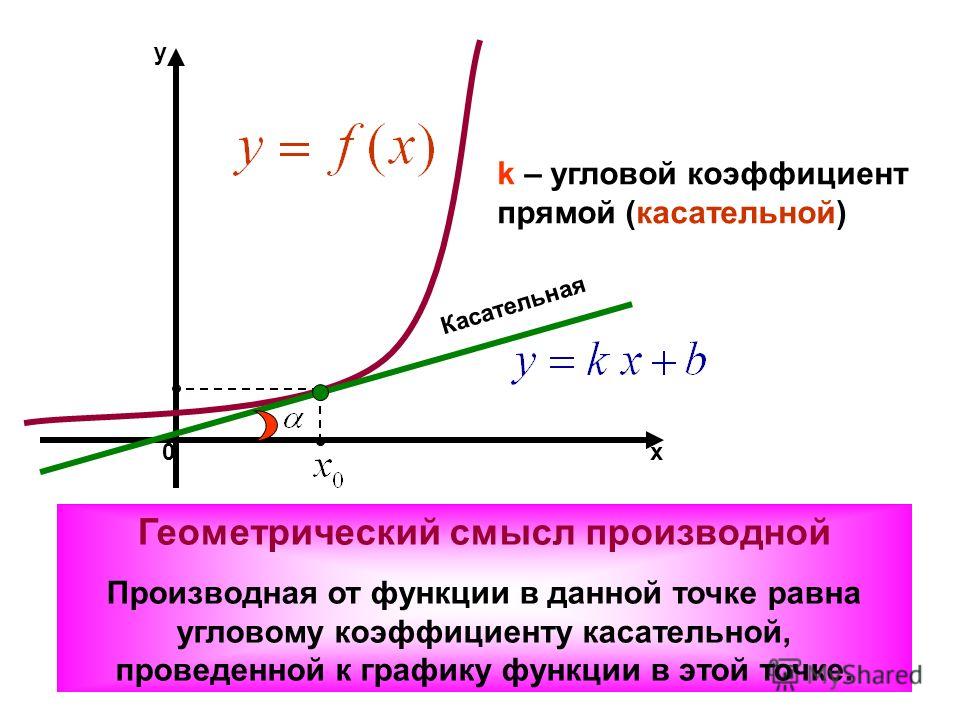 Но
Но
угловой коэффициент касательной равен значению производной функции в
этой точке, то есть
,
откуда
,
следовательно,
-
абсцисса точки касания. Найдем теперь
из
условия равенства значений функций
и
при
.
Имеем
,
откуда
.
При каких
значениях параметра а касательные к графику функции
,
проведенные в точках его пересечения с осью оx,
образуют между собой угол 60о?
Решение.
В этой задаче, как и в предыдущих, речь идет о касательных к графику
функции. Составлять уравнение касательной не надо, достаточно
использовать геометрический смысл производной, то есть угловые
коэффициенты касательных. Графиком данной функции является парабола с
ветвями, направленными вверх, пересекающая ось оx
в двух точках (случай а=0
нас не устраивает):
и
учитываем,
что х2>0
(рис.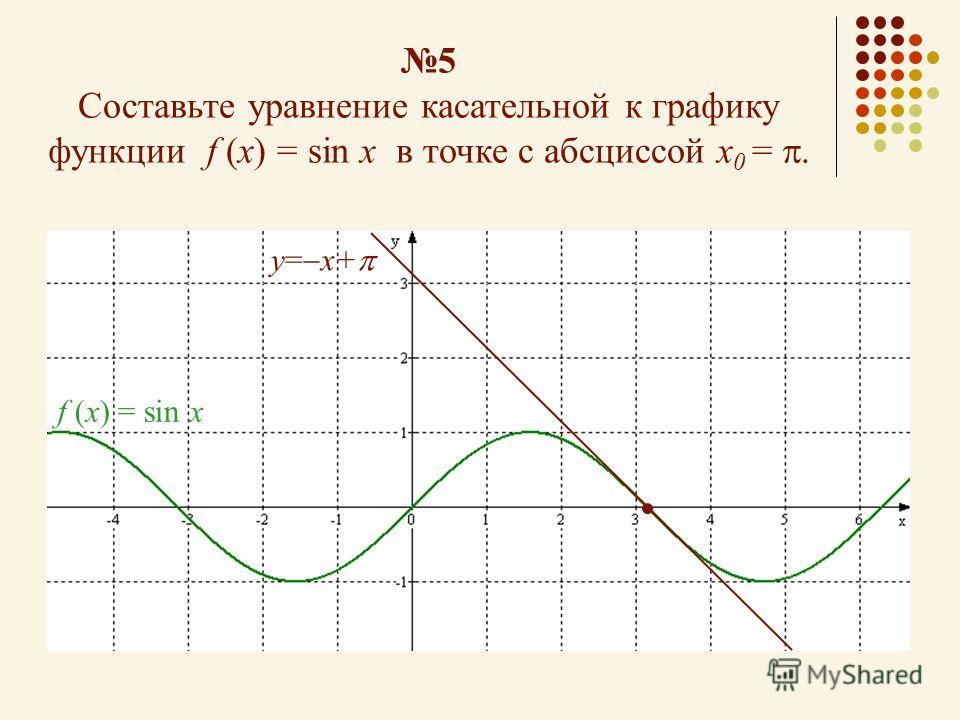 3)
3)
Рис. 3
Касательные АМ
и ВМ пересекаются под углом 60о
в точке М, лежащей на оси параболы, причем возможны два случая: либо
,
либо смежный угол равен 60о.
в первом случае угол между касательной АО и осью х равен 120о,
следовательно, угол коэффициента касательной равен tg120o,
то есть равен
Далее имеем:
.
Таким образом, получаем, что
,
то
.
Во втором случае
,
поэтому угол между касательной АО и остью ох
равен 150о.
Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
.
Таким образом, получаем, что
,
то есть
Ответ:
.
Литература:
Далингер,
В.А. Начала математического анализа в задачах [Текст]: учебное
пособие / В.А. Далингер. – Омск: Изд-во ГОУ ОМГПУ, 2009. –
–
312 с.
Звавич, Л.И. Алгебра и
начала анализа. 8-11 кл. [Текст]: пособие для школ и классов с
углубл. изучением математики / Л. И. Звавич, Л.Я. Шляпочник, М.В.
Чинкина.– М.: Дрофа, 1999. – 352 с.
График функции касательной
В
тригонометрические соотношения
может также рассматриваться как функция переменной, которая является мерой угла. Эту угловую меру можно указать в
градусы
или же
радианы
. Здесь мы будем использовать радианы.
С,
загар
(
Икс
)
знак равно
грех
(
Икс
)
потому что
(
Икс
)
касательная функция не определена, когда
потому что
(
Икс
)
знак равно
0
.Следовательно, касательная функция имеет
вертикальная асимптота
в любое время
потому что
(
Икс
)
знак равно
0
.
Точно так же каждая функция тангенса и синуса имеет нули в целых кратных
π
так как
загар
(
Икс
)
знак равно
0
когда
грех
(
Икс
)
знак равно
0
.
График
касательная
функция
у
знак равно
загар
(
Икс
)
выглядит так:
Свойства касательной функции,
у
знак равно
загар
(
Икс
)
.
Домен
:
Икс
∈
ℝ
,
Икс
≠
π
2
+
п
π
, где
п
целое число.
Диапазон
:
(
—
∞
,
∞
)
у
-перехват
:
(
0
,
0
)
Икс
-перехват
:
п
π
, где
п
целое число.
Период:
π
Симметрия: происхождение (нечетная функция)
Амплитуда и период касательной функции.
У тангенциальной функции нет амплитуды, потому что у нее нет максимального или минимального значения.
Период касательной функции,
у
знак равно
а
загар
(
б
Икс
)
, — расстояние между любыми двумя последовательными вертикальными асимптотами.
Период =
π
|
б
|
Также см
Тригонометрические функции
.
Самый простой способ вычислить тангенс функции — x-engineer.org
Касательная линия к функции в точке — это линия, которая соприкасается с графическим представлением функции только в этой конкретной точке.
Касательная линия касается функции (графика) только в указанной точке.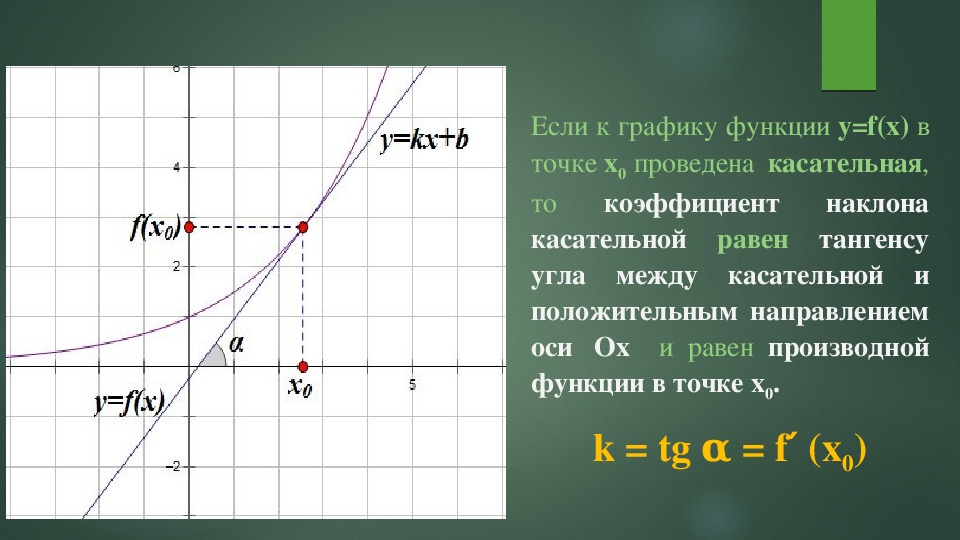 Другими словами, касательная почти не соприкасается с функцией (графиком).
Другими словами, касательная почти не соприкасается с функцией (графиком).
Линия, которая пересекает (пересекает) график функции, называется секущей линией .
Изображение: касательная и секущая к графику функции
В приведенном выше примере красная линия является касательной. Он касается функции f (x) в точке P (x 1 , y 1 ) . Синяя линия является секущей и, как вы можете видеть, пересекает функцию f (x) в двух точках.
Учитывая функцию f (x) и точку P 1 (x 1 , y 1 ) , как вычислить касательную? Нахождение касательной означает нахождение уравнения прямой, касательной к функции f (x) в точке P 1 (x 1 , y 1 ) .
Пример : Найдите тангенс функции f (x) , определенной ниже, в точке x 1 .{3} = 1 \]
Мы знаем, что:
\ [y_ {1} = f (x_ {1}) \]
Это означает, что результат вычисления функции в точке x 1 является y 1 координата. Теперь мы определили точку P 1 (1, 1) . Построим график функции f (x) для x = 0… 2 и точки P 1 с координатами x 1 и y 1 .
Теперь мы определили точку P 1 (1, 1) . Построим график функции f (x) для x = 0… 2 и точки P 1 с координатами x 1 и y 1 .
Изображение: Кубический график функции с точкой касания
Шаг 2 : Определите две точки P 0 и P 2 , слева и справа от P 1 .
Мы выберем точку P 0 при x 0 = 0,6 и P 2 при x 2 = 1,4 . Эти точки должны быть равномерно распределены слева и справа от точки касания P 1 .
Шаг 3 . Вычислите координаты y точки P 0 и P 2 точек
Сначала давайте вычислим координату y точки P 0 .{3} = — 0,744 \\
y_ {2} & = — 0,744
\ end {split} \ end {формула *} \]
Теперь мы определили точку P 2 (1,4, -0,744) .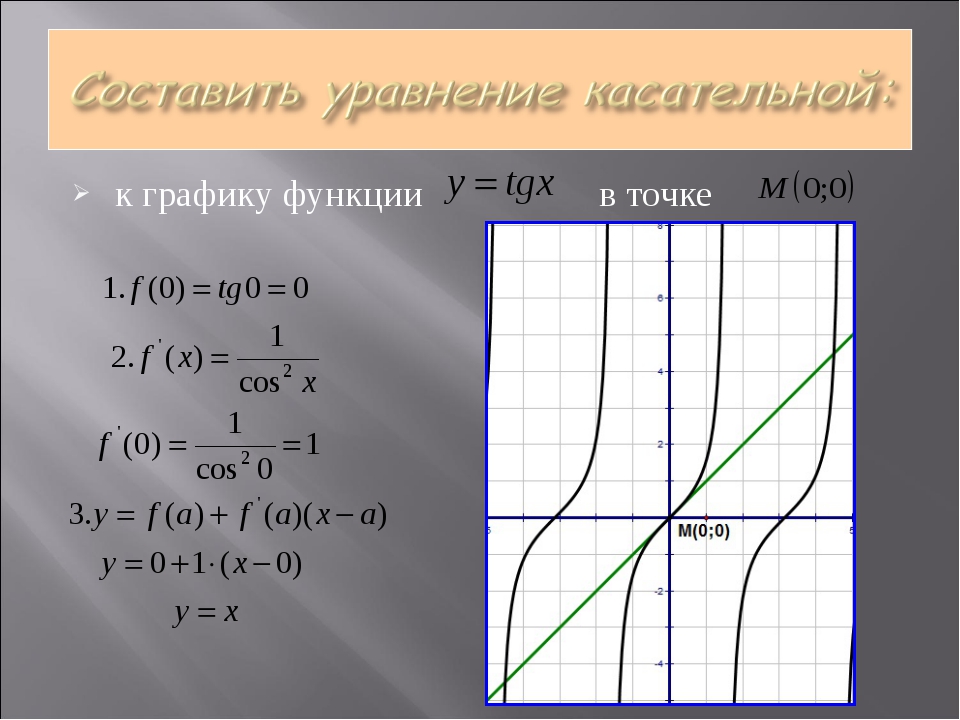
Давайте теперь обновим наш график функции с точками P 0 и P 2 и их координатами.
Изображение: график кубической функции с точкой касания и двумя точками смещения
Шаг 4 . Вычислите наклон линий, определенных между точками P 0 -P 1 и P 1 -P 2
Определив две точки, мы можем легко провести прямую линию между ними.Также с помощью координат двух точек мы можем вычислить наклон линии.
В нашем случае у нас будет две линии, одна между точкой P 0 и P 1 , а вторая между P 1 и P 2 . Для обеих линий мы можем рассчитать их наклон.
Обычно наклон линии обозначается буквой м .
Для первой линии уклон м 0 рассчитывается как:
\ [\ begin {уравнение *} \ begin {split}
m_ {0} & = \ frac {y_ {1} -y_ { 0}} {x_ {1} -x_ {0}} = \ frac {1-1. 784} {1-0.6} = — 1,96 \\
784} {1-0.6} = — 1,96 \\
м_ {0} & = — 1,96
\ end {split} \ end {формула *} \]
Для второй линии уклон м 2 равен рассчитывается как:
\ [\ begin {уравнение *} \ begin {split}
m_ {2} & = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} = \ frac {-0.744-1} {1.4-1} = — 4.36 \\
m_ {2} & = — 4.36
\ end {split} \ end {Equation *} \]
Ниже приведено графическое представление двух линий и функция f (x) . Обе линии секущие нашей функции f (x) .
Изображение: график кубической функции с точкой касания и двумя секущими линиями
Шаг 5 . Вычислить наклон касательной прямой в точке P 1 (1, 1)
Наклон касательной прямой в точке P 1 будет средним арифметическим наклонов двух Секущие линии . Этот метод расчета возможен, потому что мы выбрали точки x 0 и x 2 на равном расстоянии от x 1 .
\ [\ begin {уравнение *} \ begin {split}
m_ {1} & = \ frac {m_ {0} + m_ {2}} {2} = \ frac {-1.96-4.36} {2} = -3,16 \\
m_ {1} & = — 3,16
\ end {split} \ end {формула *} \]
Шаг 6 (последний шаг) . Вычислить уравнение касательной в точке P 1 .
Теперь, когда мы знаем координаты точки касания P1 и значение наклона, мы можем легко вычислить уравнение касательной линии:
\ [\ begin {уравнение *} \ begin {split}
y (x) & = y_ {1} + m_1 \ cdot (x — x_1) \\
y (x) & = 1-3.16 \ cdot (x — 1)
\ end {split} \ end {формула *} \]
Имея уравнение касательной, мы можем построить на том же графике функцию f (x) и касательную y ( х) .
Изображение: график кубической функции с точкой касания и касательной
Как вы можете видеть, касательная линия «касается» функции f (x) в точке P 1 (1, 1) .
Используя тот же метод, мы можем вычислить касательную в точке (1, 1) для следующих функций:
\ [f (x) = x ^ 2 + 2 \ cdot x + 1 \]
Изображение: Квадратичная функция график с точкой касания и касательной
\ [f (x) = 10 \ cdot \ sqrt {2 \ cdot x} + 3 \ cdot x + 2 \]
Изображение: график функции квадратного корня с точкой касания и касательной
Примените тот же метод к своей функции и позвольте нам теперь результат!
Для любых вопросов или замечаний относительно этого руководства, пожалуйста, используйте форму комментариев ниже.
Не забывайте ставить лайки, делиться и подписываться!
Исчисление I — касательные линии и скорости изменения
Показать уведомление для мобильных устройств
Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон).Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от устройства (для их просмотра должна быть возможность прокручивать), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-1: Касательные линии и скорость изменения
В этом разделе мы собираемся взглянуть на две довольно важные проблемы в изучении исчисления.Сейчас есть две причины, чтобы взглянуть на эти проблемы.
Во-первых, обе эти проблемы приведут нас к изучению пределов, что, в конце концов, является темой данной главы. Рассмотрение этих проблем здесь позволит нам начать понимать, что такое ограничение и что он может сказать нам о функции.
Во-вторых, проблема скорости изменений, которую мы собираемся рассмотреть, является одной из наиболее важных концепций, с которыми мы столкнемся во второй главе этого курса.Фактически, это, вероятно, одна из самых важных концепций, с которыми мы столкнемся на протяжении всего курса. Итак, глядя на это сейчас, мы начнем думать об этом с самого начала.
Касательные линии
Первая проблема, которую мы собираемся рассмотреть, — это задача касательной. Прежде чем приступить к этой проблеме, вероятно, лучше всего будет определить касательную линию.
Касательная линия к функции \ (f (x) \) в точке \ (x = a \) — это линия, которая только касается графика функции в рассматриваемой точке и является «параллельной» (некоторым образом ) к графику в этой точке.Взгляните на график ниже.
На этом графике линия представляет собой касательную линию в указанной точке, потому что она просто касается графика в этой точке и также «параллельна» графику в этой точке. Аналогичным образом, во второй показанной точке линия просто касается графика в этой точке, но она не «параллельна» графику в этой точке и, следовательно, не является касательной к графику в этой точке.
Во второй показанной точке (точка, где линия не является касательной) мы иногда будем называть ее секущей линией .
Мы уже пару раз использовали слово «параллель» и, вероятно, нам следует быть с ним немного осторожнее. В общем, мы будем думать о линии и графике как о параллельных в одной точке, если они оба движутся в одном направлении в этой точке. Итак, в первой точке над графиком и линия движутся в одном направлении, и поэтому мы будем говорить, что они параллельны в этой точке. С другой стороны, во второй точке линия и график не движутся в одном направлении, поэтому они не параллельны в этой точке.2} \) при \ (x = 1 \).
Показать решение
Мы знаем из алгебры, что для нахождения уравнения прямой нам нужны либо две точки на прямой, либо одна точка на прямой и наклон прямой. Поскольку мы знаем, что находимся после касательной, у нас есть точка, которая находится на этой прямой. Касательная линия и график функции должны касаться в точке \ (x \) = 1, поэтому точка \ (\ left ({1, f \ left (1 \ right)} \ right) = \ left ({1,13 } \ right) \) должен быть на линии.
Теперь мы подошли к проблеме.Это все, что мы знаем о касательной. Чтобы найти касательную, нам нужна либо вторая точка, либо наклон касательной. Поскольку единственная причина, по которой нам нужна вторая точка, — это позволить нам найти наклон касательной линии, давайте просто сконцентрируемся на том, сможем ли мы определить наклон касательной.
На данный момент все, что мы сможем сделать, это получить оценку наклона касательной линии, но если мы сделаем это правильно, мы сможем получить оценку, которая на самом деле является действительной. наклон касательной.Мы сделаем это, начав с точки, которую мы ищем, назовем ее \ (P = \ left ({1,13} \ right) \). Затем мы выберем другую точку, лежащую на графике функции, назовем эту точку \ (Q = \ left ({x, f \ left (x \ right)} \ right) \).
В качестве аргумента возьмем \ (x = 2 \), поэтому второй точкой будет \ (Q = \ left ({2,7} \ right) \). Ниже приведен график функции, касательной и секущей, соединяющей \ (P \) и \ (Q \).
Из этого графика видно, что секущая и касательная линии в чем-то похожи, поэтому наклон секущей линии должен быть в некоторой степени близок к фактическому наклону касательной.Итак, в качестве оценки наклона касательной мы можем использовать наклон секущей линии, назовем ее \ ({m_ {PQ}} \), то есть
\ [{m_ {PQ}} = \ frac {{f \ left (2 \ right) — f \ left (1 \ right)}} {{2 — 1}} = \ frac {{7 — 13}} { 1} = — 6 \]
Теперь, если бы нас не слишком интересовала точность, мы могли бы сказать, что это достаточно хорошо, и использовать это как оценку наклона касательной. Однако мы хотели бы получить оценку, которая хотя бы в некоторой степени близка к фактической стоимости.Итак, чтобы получить лучшую оценку, мы можем взять \ (x \), который ближе к \ (x = 1 \), и повторить описанную выше работу, чтобы получить новую оценку наклона. Тогда мы могли бы взять третье значение \ (x \) еще ближе и получить еще лучшую оценку.
Другими словами, по мере того, как мы приближаем \ (Q \) к \ (P \), наклон секущей линии, соединяющей \ (Q \) и \ (P \), должен приближаться к наклону касательная линия. Если вы просматриваете это в Интернете, на изображении ниже показан этот процесс.
Как вы можете видеть (если вы читаете это в сети), когда мы приближали \ (Q \) все ближе и ближе к \ (P \), секущие линии начинают все больше и больше походить на касательную, и поэтому приблизительные уклоны (, т.е. наклоны секущих линий) становятся все ближе и ближе к точному уклону. Также не беспокойтесь о том, как я получил точные или приблизительные уклоны. Вскоре мы вычислим приблизительные уклоны, и мы сможем вычислить точный уклон на нескольких участках.
На этом рисунке мы смотрели только на \ (Q \), которые были справа от \ (P \), но мы могли бы так же легко использовать \ (Q \), которые были слева от \ ( P \), и мы получили бы такие же результаты. Фактически, мы всегда должны смотреть на \ (Q \), которые находятся по обе стороны от \ (P \). В этом случае то же самое происходит по обе стороны от \ (P \). Однако со временем мы увидим, что этого не должно происходить. Следовательно, мы всегда должны смотреть на то, что происходит по обе стороны от рассматриваемого вопроса, выполняя такой процесс.
Итак, давайте посмотрим, сможем ли мы получить приблизительные значения наклона, которые мы показали выше, и, следовательно, оценку наклона касательной. Чтобы немного упростить процесс, давайте получим формулу для наклона линии между \ (P \) и \ (Q \), \ ({m_ {PQ}}} \), которая будет работать для любого \ (x \), с которыми мы решили работать. 2}}} {{x — 1}} \]
Теперь давайте выберем некоторые значения \ (x \), приближающиеся к \ (x = 1 \), подключимся и получим несколько уклонов.
| \ (х \) | \ ({m_ {PQ}} \) | \ (х \) | \ ({m_ {PQ}} \) |
|---|---|---|---|
| 2 | -6 | 0 | -2 |
| 1,5 | -5 | 0,5 | -3 |
| 1.1 | -4,2 | 0,9 | -3,8 |
| 1,01 | -4,02 | 0,99 | -3,98 |
| 1,001 | -4,002 | 0,999 | -3,998 |
| 1.0001 | -4,0002 | 0,9999 | -3,9998 |
Итак, если мы возьмем \ (x \) вправо от 1 и переместим их очень близко к 1, то окажется, что наклон секущих линий приближается к -4. Точно так же, если мы возьмем \ (x \) слева от 1 и переместим их очень близко к 1, наклон секущих линий снова будет приближаться к -4.
На основании этого свидетельства кажется, что наклон секущих линий приближается к -4 по мере того, как мы приближаемся к \ (x = 1 \), поэтому мы оценим, что наклон касательной также равен -4.2} \) при \ (x = 1 \) равно
\ [y = 13 — 4 \ left ({x — 1} \ right) = — 4x + 17 \]
Следует отметить несколько важных моментов, касающихся нашей работы выше. Сначала мы посмотрели на точки, которые находились по обе стороны от \ (x = 1 \). В процессе такого рода важно никогда не предполагать, что то, что происходит на одной стороне точки, будет происходить и на другой стороне. Мы всегда должны смотреть на происходящее с обеих сторон. В этом примере мы могли бы набросать график и, исходя из этого, предположить, что то, что происходит на одной стороне, будет происходить и на другой, но обычно у нас не будет графиков перед собой или мы сможем легко их получить.
Затем обратите внимание, что когда мы говорим, что собираемся подойти близко к рассматриваемой точке, мы действительно имеем в виду, что мы собираемся подойти очень близко, и мы также использовали больше, чем просто пару точек. Мы никогда не должны пытаться определить тенденцию на основе пары моментов, которые на самом деле не так уж близки к рассматриваемой.
Следующее, на что следует обратить внимание, — это скорее предупреждение, чем что-либо еще. Значения \ ({m_ {PQ}} \) в этом примере были довольно «хорошими», и после пары вычислений было довольно ясно, к какому значению они приближались.В большинстве случаев это не так. Большинство значений будут гораздо более «беспорядочными», и вам часто потребуется довольно много вычислений, чтобы получить оценку. Вы всегда должны использовать как минимум четыре точки с каждой стороны, чтобы получить оценку. Двух баллов никогда не бывает достаточно, чтобы получить хорошую оценку, и трех баллов также часто бывает недостаточно для получения хорошей оценки. Как правило, вы держите точки все ближе и ближе к точке, на которую смотрите, до тех пор, пока изменение значения между двумя последовательными точками не станет очень небольшим.
Наконец, мы искали кое-что, что происходило в \ (x = 1 \), и мы не могли фактически включить \ (x = 1 \) в нашу формулу для наклона. Несмотря на это ограничение, мы смогли определить некоторую информацию о том, что происходило в \ (x = 1 \), просто взглянув на то, что происходило вокруг \ (x = 1 \). Это более важно, чем вы можете сначала представить, и мы обсудим этот момент подробно в следующих разделах.
Прежде чем двигаться дальше, давайте сделаем быстрый обзор того, что мы сделали в приведенном выше примере.Нам нужна касательная к \ (f \ left (x \ right) \) в точке \ (x = a \). Во-первых, мы знаем, что точка \ (P = \ left ({a, f \ left (a \ right)} \ right) \) будет на касательной. Затем мы возьмем вторую точку на графике функции, назовем ее \ (Q = \ left ({x, f \ left (x \ right)} \ right) \) и вычислим наклон линия, соединяющая \ (P \) и \ (Q \) следующим образом,
\ [{m_ {PQ}} = \ frac {{f \ left (x \ right) — f \ left (a \ right)}} {{x — a}} \]
Затем мы берем значения \ (x \), которые становятся все ближе и ближе к \ (x = a \) (не забудьте посмотреть на \ (x \) по обе стороны от \ (x = a \) и использовать этот список значений для оценки наклона касательной \ (m \).
Тогда касательная линия будет,
\ [y = f \ left (a \ right) + m \ left ({x — a} \ right) \]
Скорость изменения
Следующая проблема, на которую нам нужно обратить внимание, — это проблема скорости изменения. Как упоминалось ранее, это окажется одной из самых важных концепций, которые мы будем рассматривать на протяжении всего курса.
Здесь мы собираемся рассмотреть функцию \ (f \ left (x \ right) \), которая представляет некоторую величину, которая изменяется при изменении \ (x \).Например, возможно, \ (f \ left (x \ right) \) представляет количество воды в резервуаре для хранения через \ (x \) минут. Или, может быть, \ (f \ left (x \ right) \) — это расстояние, которое проехала машина за \ (x \) часов. В обоих этих примерах мы использовали \ (x \) для обозначения времени. Конечно, \ (x \) не обязательно должно представлять время, но это примеры, которые легко визуализировать.
Здесь мы хотим определить, насколько быстро меняется \ (f \ left (x \ right) \) в какой-то момент, скажем, \ (x = a \). Это называется мгновенной скоростью изменения или иногда просто скоростью изменения \ (f \ left (x \ right) \) при \ (x = a \).
Как и в случае с проблемой касательной, все, что мы собираемся сделать на этом этапе, — это оценить скорость изменения. Итак, продолжим с приведенными выше примерами и представим \ (f \ left (x \ right) \) как нечто, что изменяется во времени, а \ (x \) — это измерение времени. Опять же, \ (x \) не обязательно должно представлять время, но это немного упростит объяснение. Хотя на данный момент мы не можем вычислить мгновенную скорость изменения, мы можем найти среднюю скорость изменения.
Для вычисления средней скорости изменения \ (f \ left (x \ right) \) в \ (x = a \) все, что нам нужно сделать, это выбрать другую точку, скажем, \ (x \), а затем средняя скорость изменения составит,
\ [\ begin {align *} A.R.C. & = \ frac {{{\ mbox {change in}} f \ left (x \ right)}} {{{\ mbox {change in}} x}} \\ & = \ frac {{f \ left (x \ right) — f \ left (a \ right)}} {{x — a}} \ end {align *} \]
Затем, чтобы оценить мгновенную скорость изменения в \ (x = a \), все, что нам нужно сделать, это выбрать значения \ (x \), приближающиеся к \ (x = a \) (не забудьте выберите их по обе стороны от \ (x = a \)) и вычислите значения \ (A.2} + 25}} {{t — 5}} \]
Чтобы оценить мгновенную скорость изменения объема в \ (t = 5 \), нам просто нужно выбрать значения \ (t \), которые все ближе и ближе к \ (t = 5 \). Вот таблица значений \ (t \) и средней скорости изменения этих значений.
| \ (т \) | \ (A.R.C. \) | \ (т \) | \ (A.R.C. \) |
|---|---|---|---|
| 6 | 25.0 | 4 | 7,0 |
| 5,5 | 19,75 | 4,5 | 10,75 |
| 5,1 | 15,91 | 4,9 | 14,11 |
| 5,01 | 15.0901 | 4,99 | 14.9101 |
| 5,001 | 15.009001 | 4,999 | 14.9 |
| 5.0001 | 15,000 | 4,9999 | 14.99 1 |
Итак, из этой таблицы похоже, что средняя скорость изменения приближается к 15, и поэтому мы можем оценить, что мгновенная скорость изменения на данный момент составляет 15.
Итак, что это говорит нам об объеме в \ (t = 5 \)? Поставим несколько единиц на ответ сверху. Это может помочь нам увидеть, что происходит с объемом в данный момент. Предположим, что единицы измерения объема были в см 3 . Единицы измерения скорости изменения (как средней, так и мгновенной) равны см 3 / час.
По нашим оценкам, при \ (t = 5 \) объем изменяется со скоростью 15 см 3 / час.Это означает, что при \ (t = 5 \) объем изменяется таким образом, что, если бы скорость была постоянной, то через час в воздушном шаре было бы на 15 см 3 больше воздуха, чем было в \ ( t = 5 \).
Однако здесь нужно быть осторожными. На самом деле, через час в воздушном шаре, вероятно, не останется на 15 см 3 больше воздуха. Скорость изменения громкости обычно непостоянна, поэтому мы не можем реально определить, какой будет объем через час.Мы можем сказать, что объем увеличивается, поскольку мгновенная скорость изменения положительна, и если бы у нас были скорости изменения для других значений \ (t \), мы могли бы сравнить числа и посмотреть, быстрее ли скорость изменения. или медленнее в других точках.
Например, при \ (t = 4 \) мгновенная скорость изменения составляет 0 см 3 / час, а при \ (t = 3 \) мгновенная скорость изменения составляет -9 см 3 / час. Мы предоставим вам возможность проверить скорость изменения.Фактически, это было бы хорошим упражнением, чтобы увидеть, сможете ли вы составить таблицу ценностей, которая поддержит наши утверждения об этих темпах изменений.
Во всяком случае, вернемся к примеру. При \ (t = 4 \) скорость изменения равна нулю, поэтому в этот момент объем вообще не меняется. Это не значит, что он не изменится в будущем. Это просто означает, что ровно при \ (t = 4 \) громкость не меняется. Точно так же при \ (t = 3 \) объем уменьшается, поскольку скорость изменения в этой точке отрицательна.Мы также можем сказать, что, независимо от аспектов увеличения / уменьшения скорости изменения, объем воздушного шара изменяется быстрее при \ (t = 5 \), чем при \ (t = 3 \), поскольку 15 больше. чем 9.
Мы еще поговорим о темпах изменений, когда перейдем к следующей главе.
Проблема скорости
Давайте кратко рассмотрим проблему скорости. Многие книги по математике рассматривают это как отдельную проблему. Однако нам нравится думать об этом как об особом случае проблемы скорости изменения.В задаче о скорости нам дается функция положения объекта \ (f \ left (t \ right) \), которая дает положение объекта в момент времени \ (t \). Затем, чтобы вычислить мгновенную скорость объекта, нам просто нужно вспомнить, что скорость — это не что иное, как скорость, с которой изменяется положение.
Другими словами, чтобы оценить мгновенную скорость, мы сначала вычислим среднюю скорость,
\ [\ begin {align *} A.V. & = \ frac {{{\ mbox {изменение положения}}}} {{{\ mbox {пройденное время}}}} \\ & \\ & = \ frac {{f \ left (t \ right) — f \ left (a \ right)}} {{t — a}} \ end {align *} \]
, а затем возьмите значения \ (t \) все ближе и ближе к \ (t = a \) и используйте эти значения для оценки мгновенной скорости.
Изменение обозначения
Есть еще одна вещь, которую нам нужно сделать в этом разделе, прежде чем мы продолжим. Основная идея этого раздела состояла в том, чтобы познакомить нас с парой ключевых концепций и идей, которые мы увидим в первой части этого курса, а также помочь нам начать движение к пределам.
Прежде чем мы официально перейдем к ограничениям, давайте вернемся и проделаем небольшую работу, которая свяжет обе (или все три, если вы включите скорость как отдельную проблему) проблемы в более общую концепцию.
Во-первых, обратите внимание, что независимо от того, нужна ли нам касательная линия, мгновенная скорость изменения или мгновенная скорость, все они сводятся к использованию одной и той же формулы. А именно
\ begin {уравнение} \ frac {{f \ left (x \ right) — f \ left (a \ right)}} {{x — a}} \ label {eq: eq1} \ end {уравнение}
Это должно означать, что тогда все три проблемы — одна и та же проблема. На самом деле это так, как мы увидим в следующей главе. Мы действительно работаем над одной и той же проблемой в каждом из этих случаев, единственная разница заключается в интерпретации результатов.
При подготовке к следующему разделу, где мы обсудим это более подробно, нам нужно быстро изменить обозначения. Здесь это сделать проще, поскольку мы уже потратили немало времени на решение этих проблем.
Во всех этих задачах мы хотели определить, что происходит в \ (x = a \). Для этого мы выбрали другое значение \ (x \) и подключили его к \ (\ eqref {eq: eq1} \). Для того, что мы здесь делали, это, вероятно, самый интуитивный способ сделать это.Однако, когда мы начнем рассматривать эти проблемы как одну проблему, \ (\ eqref {eq: eq1} \) не будет лучшей формулой для работы.
Вместо этого мы сначала определим, как далеко от \ (x = a \) мы хотим переместиться, а затем определим нашу новую точку на основе этого решения. Итак, если мы хотим переместиться на расстояние \ (h \) от \ (x = a \), новая точка будет \ (x = a + h \). Это показано на рисунке ниже.
Как мы видели в нашей работе выше, важно брать значения \ (x \), которые являются обеими сторонами \ (x = a \).Этот способ выбора нового значения \ (x \) сделает это за нас, как мы можем видеть на скетче выше. Если \ (h> 0 \), мы получим значение \ (x \), которое находится справа от \ (x = a \), а если \ (h <0 \), мы получим значения \ (x \) которые находятся слева от \ (x = a \), и оба заданы как \ (x = a + h \).
Теперь, с этим новым способом получения второго значения \ (x \) \ (\ eqref {eq: eq1} \) станет,
\ [\ frac {{е \ left (x \ right) — f \ left (a \ right)}} {{x — a}} = \ frac {{f \ left ({a + h} \ right) — f \ left (a \ right)}} {{a + h — a}} = \ frac {{f \ left ({a + h} \ right) — f \ left (a \ right)}} {h} \]
Теперь это для определенного значения \ (x \), i.е. \ (x = a \), и мы редко будем смотреть на них при определенных значениях \ (x \). Итак, мы делаем последний шаг в приведенном выше уравнении и заменяем \ (a \) на \ (x \), чтобы получить,
\ [\ frac {{f \ left ({x + h} \ right) — f \ left (x \ right)}} {h} \]
Это дает нам формулу для общего значения \ (x \), и на первый взгляд может показаться, что это будет слишком сложный способ справиться с этим. Однако, как мы увидим, часто будет легче работать с этой формой, чем с исходной формой, \ (\ eqref {eq: eq1} \).
Тригонометрический Разделы: Следующая триггерная функция — касательная, Тангенс будет равен нулю везде, где его числитель. Тангенс будет undefined везде, где Теперь мы можем использовать то, что знаем о синусе, Авторские права © Элизабет Между π / 2 и π, Поскольку синус и косинус периодичны, то
От Теперь мы можем завершить наш график: The Как видите, тангенс имеет период Для построения графиков нарисуйте нули в точках x = 0, π, 2π, Если вы предпочитаете запоминать графики, запомните << Предыдущий Наверх | 1 | 2 | 3 | Возвращаться
|
Графики других тригонометрических функций
Анализ графика y = tan x и его вариаций
Мы начнем с графика функции касательной , нанося точки, как мы делали для функций синуса и косинуса.Напомним, что
[латекс] \ tan x = \ frac {\ sin x} {\ cos x} \\ [/ latex]
Период касательной функции равен π , потому что график повторяется на интервалах kπ , где k — постоянная. Если построить график касательной функции на [latex] — \ frac {\ pi} {2} \\ [/ latex] к [latex] \ frac {\ pi} {2} \\ [/ latex], мы можем увидеть поведение графика на одном полном цикле. Если мы посмотрим на любой больший интервал, мы увидим, что характеристики графика повторяются.
Мы можем определить, является ли тангенс четной или нечетной функцией, используя определение тангенса.
[латекс] \ begin {array} \ tan (−x) = \ frac {\ sin (−x)} {\ cos (−x)} \ hfill & \ text {Определение касательной.} \\ = \ frac { — \ sin x} {\ cos x} \ hfill & \ text {Синус — нечетная функция, косинус — четный.} \\ = — \ frac {\ sin x} {\ cos x} & \ hfill \ text {Частное нечетной и четной функции является нечетной.} \ hfill \\ = — \ tan x \ hfill & \ text {Определение касательной.} \ end {array} \\ [/ latex]
Следовательно, тангенс — нечетная функция.Мы можем дополнительно проанализировать графическое поведение касательной функции, посмотрев значения для некоторых специальных углов, как указано в таблице ниже.
| x | [латекс] — \ frac {\ pi} {2} \\ [/ latex] | [латекс] — \ frac {\ pi} {3} \\ [/ latex] | [латекс] — \ frac {\ pi} {4} \\ [/ latex] | [латекс] — \ frac {\ pi} {6} \\ [/ latex] | 0 | [латекс] \ frac {\ pi} {6} \\ [/ latex] | [латекс] \ frac {\ pi} {4} \\ [/ latex] | [латекс] \ frac {\ pi} {3} \\ [/ latex] | [латекс] \ frac {\ pi} {2} \\ [/ latex] |
| желто-коричневый ( x ) | undefined | [латекс] — \ sqrt {3} \\ [/ латекс] | –1 | [латекс] — \ frac {\ sqrt {3}} {3} \\ [/ латекс] | 0 | [латекс] \ frac {\ sqrt {3}} {3} \\ [/ латекс] | 1 | [латекс] \ sqrt {3} \\ [/ латекс] | undefined |
Эти точки помогут нам нарисовать наш график, но нам нужно определить, как график ведет себя там, где он не определен.Если мы более внимательно рассмотрим значения, когда [latex] \ frac {\ pi} {3}
| x | 1,3 | 1,5 | 1,55 | 1,56 |
| желто-коричневый x | 3.6 | 14,1 | 48,1 | 92,6 |
По мере приближения x к [latex] \ frac {\ pi} {2} \\ [/ latex] выходные данные функции становятся все больше и больше. Поскольку [latex] y = \ tan x \\ [/ latex] является нечетной функцией, мы видим соответствующую таблицу отрицательных значений в таблице ниже.
| x | -1,3 | -1,5 | -1,55 | -1,56 |
| желто-коричневый x | −3.6 | −14,1 | −48,1 | −92,6 |
Мы видим, что по мере приближения x к [latex] — \ frac {\ pi} {2} \\ [/ latex] выходы становятся все меньше и меньше. Помните, что есть некоторые значения x , для которых cos x = 0. Например, [latex] \ cos \ left (\ frac {\ pi} {2} \ right) = 0 \\ [/ latex] и [латекс] \ cos \ left (\ frac {3 \ pi} {2} \ right) = 0 \\ [/ latex]. При этих значениях касательная функция не определена, поэтому график [latex] y = \ tan x [/ latex] имеет разрывы в [latex] x = \ frac {\ pi} {2} \\ [/ latex ] и [латекс] \ frac {3 \ pi} {2} \\ [/ latex].При этих значениях график касательной имеет вертикальные асимптоты. На рисунке 1 представлен график [латекс] y = \ tan x \\ [/ latex]. Касательная положительна от 0 до [latex] \ frac {\ pi} {2} \\ [/ latex] и от π до [latex] \ frac {3 \ pi} {2} \\ [/ latex] , соответствующие квадрантам I и III единичной окружности.
Рисунок 1. График касательной функции
Графические вариации
y = tan x
Как и функции синуса и косинуса, функция тангенса может быть описана общим уравнением.
[латекс] y = A \ tan (Bx) \\ [/ латекс]
Мы можем идентифицировать горизонтальные и вертикальные растяжения и сжатия, используя значения A и B. Горизонтальное растяжение обычно можно определить по периоду графика. В случае касательных графиков часто бывает необходимо определить вертикальное растяжение, используя точку на графике.
Поскольку нет максимальных или минимальных значений тангенциальной функции, термин амплитуда не может быть интерпретирован так же, как для функций синуса и косинуса.Вместо этого мы будем использовать фразу , коэффициент растяжения / сжатия , когда будем ссылаться на константу A .
A Общее примечание: особенности графика
y = A tan ( Bx )
- Коэффициент растяжения | A | .
- Точка [латекс] P = \ frac {\ pi} {| B |} \\ [/ latex].
- Домен состоит из действительных чисел x , где [latex] x \ ne \ frac {\ pi} {2 | B |} + \ frac {\ pi} {| B |} k \\ [/ latex] такой что k — целое число.
- Диапазон составляет (−∞, ∞).
- Асимптоты встречаются в [latex] x = \ frac {\ pi} {2 | B |} + \ frac {\ pi} {| B |} k \\ [/ latex], где k — целое число.
- [latex] y = A \ tan (Bx) \\ [/ latex] — нечетная функция.
Построение графика одного периода растянутой или сжатой касательной функции
Мы можем использовать то, что мы знаем о свойствах функции касательной , чтобы быстро нарисовать график любой растянутой и / или сжатой касательной функции вида [latex] f (x) = A \ tan (Bx) \\ [ /латекс].Мы сосредотачиваемся на одном периоде функции, включая начало координат, потому что свойство периодичности позволяет нам при желании расширить график до остальной области области функции. Тогда наша ограниченная область — это интервал [latex] (- \ frac {P} {2}, \ frac {P} {2}) \\ [/ latex], а график имеет вертикальные асимптоты в [latex] \ pm \ frac {P} {2} \\ [/ latex], где [latex] P = \ frac {\ pi} {B} \\ [/ latex]. На [latex] (- \ frac {\ pi} {2}, \ frac {\ pi} {2}) \\ [/ latex] график выйдет из левой асимптоты в [latex] x = — \ frac {\ pi} {2} \\ [/ latex], пересекает начало координат и продолжает расти по мере приближения к правой асимптоте в [latex] x = \ frac {\ pi} {2} \\ [/ latex ].Чтобы функция приближалась к асимптотам с правильной скоростью, нам также необходимо установить вертикальный масштаб, фактически оценив функцию по крайней мере для одной точки, через которую будет проходить график. Например, мы можем использовать
[латекс] f \ left (\ frac {P} {4} \ right) = A \ tan \ left (B \ frac {P} {4} \ right) = A \ tan \ left (B \ frac {\ pi} {4B} \ right) = A \\ [/ latex]
, потому что [латекс] \ tan \ left (\ frac {\ pi} {4} \ right) = 1 \\ [/ latex].
Как: для функции [latex] f (x) = A \ tan (Bx) \\ [/ latex], построить график с одним периодом.
- Определите коэффициент растяжения | A |.
- Идентифицируйте B и определите период, [латекс] P = \ frac {\ pi} {| B |} \\ [/ latex].
- Нарисуйте вертикальные асимптоты в точках [latex] x = — \ frac {P} {2} \\ [/ latex] и [latex] x = \ frac {P} {2} \\ [/ latex].
- Для A > 0 график приближается к левой асимптоте при отрицательных выходных значениях и к правой асимптоте при положительных выходных значениях (обратная для A <0).
- Постройте контрольные точки в [latex] \ left (\ frac {P} {4} \ text {,} A \ right) \\ [/ latex] (0, 0) и ([latex] — \ frac {P } {4} \\ [/ latex], — A) и проведите график через эти точки.
Пример 1: Построение сжатой касательной
Нарисуйте график одного периода функции [latex] y = 0,5 \ tan (\ frac {\ pi} {2} x) \\ [/ latex].
Решение
Сначала мы идентифицируем A и B .
Рисунок 2
Поскольку [латекс] A = 0,5 [/ латекс] и [латекс] B = \ frac {\ pi} {2} \\ [/ latex], мы можем найти коэффициент растяжения / сжатия и период. Период равен [latex] \ frac {\ pi} {\ frac {\ pi} {2}} = 2 \\ [/ latex], поэтому асимптоты находятся в [latex] x = \ pm 1 [/ latex].За четверть периода от начала координат имеем
[латекс] \ begin {array} f (0,5) = 0,5 \ tan (\ frac {0,5 \ pi} {2}) \ hfill & \\ = 0,5 \ tan (\ frac {\ pi} {4}) \ hfill & \\ = 0,5 \ end {array} \\ [/ latex]
Это означает, что кривая должна проходить через точки (0,5,0,5), (0,0) и (-0,5, -0,5). Единственная точка перегиба находится в начале координат. На рисунке показан график одного периода функции.
Рисунок 3
Попробуй 1
Нарисуйте граф [латекс] f (x) = 3 \ tan \ left (\ frac {\ pi} {6} x \ right) \\ [/ latex].
Решение
Построение одного периода сдвинутой касательной функции
Теперь, когда мы можем построить график касательной функции , которая растягивается или сжимается, мы добавим вертикальный и / или горизонтальный (или фазовый) сдвиг. В этом случае мы добавляем C и D к общей форме касательной функции.
[латекс] f (x) = A \ tan (Bx − C) + D \\ [/ латекс]
График преобразованной касательной функции отличается от базовой тангенциальной функции tan x несколькими способами:
A Общее примечание: особенности графика
y = A tan ( Bx — C ) + D
- Коэффициент растяжения | A |.
- Точка [латекс] \ frac {\ pi} {| B |} \\ [/ latex].
- Домен [latex] x \ ne \ frac {C} {B} + \ frac {\ pi} {| B |} k \\ [/ latex], где k — целое число.
- Диапазон: (−∞, — | A |] ∪ [| A |, ∞).
- Вертикальные асимптоты встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {2 | B |} k \\ [/ latex], где k — нечетное целое число.
- Нет амплитуды.
- [latex] y = A \ tan (Bx) [/ latex] — нечетная функция, потому что это частное от нечетных и четных функций (синус и косинус в перспективе).
Как сделать: для функции [latex] y = A \ tan (Bx − C) + D \\ [/ latex] нарисуйте график одного периода.
- Выразите заданную функцию в виде [латекс] y = A \ tan (Bx-C) + D \\ [/ latex].
- Определите коэффициент растяжения / сжатия , | A |.
- Идентифицируйте B и определите период, [латекс] P = \ frac {\ pi} {| B |} \\ [/ latex].
- Идентифицируйте C и определите фазовый сдвиг, [latex] \ frac {C} {B} \\ [/ latex].
- Нарисуйте график [latex] y = A \ tan (Bx) \\ [/ latex], сдвинутый вправо на [latex] \ frac {C} {B} \\ [/ latex] и вверх на D .
- Нарисуйте вертикальные асимптоты, которые встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {2 | B |} k \\ [/ latex], где k — нечетное целое число.
- Постройте любые три контрольные точки и проведите через эти точки график.
Пример 2: Построение графика одного периода функции смещенного касания
Изобразите один период функции [latex] y = −2 \ tan (\ pi x + \ pi) −1 \\ [/ latex].
Решение
Шаг 1. Функция уже записана в виде [латекс] y = A \ tan (Bx − C) + D \\ [/ latex].
Шаг 2. [латекс] A = -2 [/ латекс], поэтому коэффициент растяжения равен [латекс] | A | = 2 [/ латекс].
Шаг 3. [latex] B = \ pi [/ latex], поэтому период равен [latex] P = \ frac {\ pi} {| B |} = \ frac {\ pi} {\ pi} = 1 \ [/ латекс].
Шаг 4. [latex] C = — \ pi [/ latex], поэтому сдвиг фазы равен [latex] \ frac {C} {B} = \ frac {- \ pi} {\ pi} = — 1 \\[/латекс].
Шаг 5–7. Асимптоты находятся в [latex] x = — \ frac {3} {2} \\ [/ latex] и [latex] x = — \ frac {1} {2} \\ [/ latex] и трех рекомендуемых реперные точки равны (−1.25, 1), (−1, −1) и (−0,75, −3). График показан на рисунке 4.
Рисунок 4
Анализ решения
Обратите внимание, что это убывающая функция, потому что A <0.
Попробуй 2
Как изменился бы график в примере 2, если бы мы сделали A = 2 вместо −2?
Решение
Как: по графику касательной функции определить горизонтальные и вертикальные отрезки.
- Найдите период P на основе расстояния между последовательными вертикальными асимптотами или x -пересечений.
- Запишите [латекс] f (x) = A \ tan (\ frac {\ pi} {P} x) [/ latex].
- Определите удобную точку ( x , f ( x )) на данном графике и используйте ее для определения A .
Пример 3: Определение графика растянутой касательной
Найдите формулу функции, показанной на рисунке 5.
Рисунок 5
Решение
График имеет форму касательной функции.
Шаг 1. Один цикл простирается от –4 до 4, поэтому период составляет [латекс] P = 8 [/ латекс]. Поскольку [latex] P = \ frac {\ pi} {| B |} \\ [/ latex], мы имеем [latex] B = \ frac {\ pi} {P} = \ frac {\ pi} {8} \\[/латекс].
Шаг 2. Уравнение должно иметь вид [latex] \ text {form} f (x) = A \ tan (\ frac {\ pi} {8} x) \\ [/ latex].
Шаг 3. Чтобы найти вертикальный участок A , воспользуемся точкой (2,2).
[латекс] 2 = A \ tan (\ frac {\ pi} {8} \ times2) = A \ tan (\ frac {\ pi} {4}) \\ [/ latex]
Поскольку [латекс] \ tan (\ frac {\ pi} {4}) = 1 \\ [/ latex], A = 2.
Эта функция будет иметь формулу [latex] f (x) = 2 \ tan (\ frac {\ pi} {8} x) \\ [/ latex].
Попробовать 3
Найдите формулу функции на рисунке 6.
Рисунок 6
Решение
Использование графиков тригонометрических функций для решения реальных задач
Многие реальные сценарии представляют периодические функции и могут быть смоделированы тригонометрическими функциями. В качестве примера вернемся к сценарию из начала раздела.Вы когда-нибудь наблюдали луч, образованный вращающимся светом на полицейской машине, и задавались вопросом о движении самого светового луча по стене? Периодическое поведение расстояния, на которое светит свет, как функция времени, очевидно, но как определить расстояние? Мы можем использовать касательную функцию.
Пример 4: Использование тригонометрических функций для решения реальных сценариев
Предположим, что функция [latex] y = 5 \ tan \ left (\ frac {\ pi} {4} t \ right) \\ [/ latex] отмечает расстояние в движении светового луча от верха полицейского автомобиль через стену, где t — время в секундах, а y — расстояние в футах от точки на стене прямо напротив полицейской машины.
- Найдите и интерпретируйте фактор растяжения и период.
- График на интервале [0, 5].
- Вычислите f (1) и обсудите значение функции на этом входе.
Решение
- Мы знаем из общего вида [latex] y = A \ tan (Bt) \\ [/ latex], что | A | — коэффициент растяжения, а π B — период.
Рисунок 7
Мы видим, что коэффициент растяжения равен 5. Это означает, что луч света переместится на 5 футов через половину периода.
Период [латекс] \ frac {\ pi} {\ frac {\ pi} {4}} = \ frac {\ pi} {1} \ times \ frac {4} {\ pi} = 4 \\ [ /латекс]. Это означает, что каждые 4 секунды луч света скользит по стене. Расстояние от места напротив полицейской машины увеличивается по мере приближения полицейской машины.
- Чтобы построить график функции, мы рисуем асимптоту при [latex] t = 2 [/ latex] и используем коэффициент растяжения и период. См. Рисунок 8.
Рисунок 8
- период: [латекс] f (1) = 5 \ tan \ left (\ frac {\ pi} {4} \ left (1 \ right) \ right) = 5 \ left (1 \ right) = 5 \\ [ /латекс]; через 1 секунду луч переместился на 5 футов с места напротив полицейской машины.
Анализ графиков y = sec x и y = cscx и их вариаций
Секущая была определена обратной идентичностью [латекс] \ sec x = \ frac {1} {\ cos x} [/ latex]. Обратите внимание, что функция не определена, когда косинус равен 0, что приводит к вертикальным асимптотам в [latex] \ frac {\ pi} {2} \ text {,} \ frac {3 \ pi} {2} \ text {и т. Д.} [/латекс]. Поскольку косинус никогда не превышает 1 по абсолютной величине, секанс, будучи обратной величиной, никогда не будет меньше 1 по абсолютной величине.
Мы можем построить график [latex] y = \ sec x [/ latex], наблюдая за графиком функции косинуса, потому что эти две функции являются обратными друг другу. См. Рисунок 9. График косинуса показан оранжевой пунктирной волной, поэтому мы можем видеть взаимосвязь. Там, где график функции косинуса уменьшается, график функции секущей увеличивается. Когда график функции косинуса увеличивается, график функции секущей уменьшается. Когда функция косинуса равна нулю, секанс не определен.
Секущий график имеет вертикальные асимптоты при каждом значении x , где косинусный график пересекает ось x ; мы показываем их на приведенном ниже графике пунктирными вертикальными линиями, но не будем показывать явно все асимптоты на всех последующих графиках, включающих секанс и косеканс.
Обратите внимание, что, поскольку косинус является четной функцией, секанс также является четной функцией. То есть [латекс] \ сек (-x) = \ сек x [/ латекс].
Рис. 9. График функции секущей, [латекс] f (x) = \ sec x = \ frac {1} {\ cos x} [/ latex]
Как и для касательной функции, мы снова обратимся к константе | A | как фактор растяжения, а не амплитуда.
A Общее примечание: особенности графика
y = A сек ( Bx )
- Коэффициент растяжения | A |.
- Точка [латекс] \ frac {2 \ pi} {| B |} [/ latex].
- Домен [latex] x \ ne \ frac {\ pi} {2 | B |} k [/ latex], где k — нечетное целое число.
- Диапазон: (−∞, — | A |] ∪ [| A |, ∞).
- Вертикальные асимптоты встречаются при [latex] x = \ frac {\ pi} {2 | B |} k [/ latex], где k — нечетное целое число.
- Нет амплитуды.
- [latex] y = A \ sec (Bx) [/ latex] — четная функция, потому что косинус — четная функция.
Подобно секансу, косеканс определяется обратной идентичностью [латекс] \ csc x = 1 \ sin x [/ latex]. Обратите внимание, что функция не определена, когда синус равен 0, что приводит к вертикальной асимптоте на графике в точках 0, π и т. Д. Поскольку синус никогда не превышает 1 по абсолютной величине, косеканс, будучи обратной величиной, никогда не будет меньше чем 1 по абсолютной величине.
Мы можем построить график [latex] y = \ csc x [/ latex], наблюдая за графиком синусоидальной функции, потому что эти две функции являются обратными друг другу. См. Рисунок 10. График синуса показан оранжевой пунктирной волной, поэтому мы можем видеть взаимосвязь. Когда график синусоидальной функции уменьшается, график функции косеканса увеличивается. Когда график синусоидальной функции увеличивается, график косекансной функции уменьшается.
График косеканса имеет вертикальные асимптоты при каждом значении x , где синусоидальный график пересекает ось x ; мы показываем их на графике ниже вертикальными пунктирными линиями.
Обратите внимание, что, поскольку синус является нечетной функцией, функция косеканса также является нечетной функцией. То есть [латекс] \ csc (−x) = — \ csc x [/ latex].
График косеканса, показанный на рисунке 10, аналогичен графику секанса.
Рис. 10. График функции косеканса, [латекс] f (x) = \ csc x = 1 \ sin x [/ latex]
Общее примечание: особенности графика [латекса] y = A \ csc (Bx)
- Коэффициент растяжения | A |.
- Точка [латекс] \ frac {2 \ pi} {| B |} [/ latex].
- Домен [latex] x \ ne \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- Диапазон равен (−∞, — | A |] ∪ [| A |, ∞).
- Асимптоты встречаются в [latex] x = \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- [latex] y = A \ csc (Bx) [/ latex] — нечетная функция, потому что синус — нечетная функция.
Графические вариации
y = sec x и y = csc x
Для смещенных, сжатых и / или растянутых версий секущих и косекансных функций мы можем использовать методы, аналогичные тем, которые мы использовали для тангенса и котангенса.То есть мы располагаем вертикальные асимптоты, а также оцениваем функции для нескольких точек (в частности, локальных экстремумов). Если мы хотим построить график только для одного периода, мы можем выбрать интервал для периода более чем одним способом. Процедура для секанса очень похожа, потому что идентичность кофункции означает, что граф секанс такой же, как граф косеканса, сдвинутый на полпериода влево. Вертикальный и фазовый сдвиги могут применяться к функции секущей таким же образом, как для секущей и других функций.Уравнения становятся следующими.
[латекс] y = A \ sec (Bx-C) + D [/ латекс]
[латекс] y = A \ csc (Bx-C) + D [/ латекс]
Общее примечание: особенности графика [латекса] y = A \ sec (Bx-C) + D [/ latex]
- Коэффициент растяжения | A |.
- Точка [латекс] \ frac {2 \ pi} {| B |} [/ latex].
- Домен [латекс] x \ ne \ frac {C} {B} + \ frac {\ pi} {2 | B |} k [/ latex], где k — нечетное целое число.
- Диапазон: (−∞, — | A |] ∪ [| A |, ∞).
- Вертикальные асимптоты встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {2 | B |} k [/ latex], где k — нечетное целое число.
- Нет амплитуды.
- [latex] y = A \ sec (Bx) [/ latex] — четная функция, потому что косинус — четная функция.
Общее примечание: особенности графика [латекса] y = A \ csc (Bx-C) + D [/ latex]
- Коэффициент растяжения | A |.
- Точка [латекс] \ frac {2 \ pi} {| B |} [/ latex].
- Домен [латекс] x \ ne \ frac {C} {B} + \ frac {\ pi} {2 | B |} k [/ latex], где k — целое число.
- Диапазон: (−∞, — | A |] ∪ [| A |, ∞).
- Вертикальные асимптоты встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- Нет амплитуды.
- [latex] y = A \ csc (Bx) [/ latex] — нечетная функция, потому что синус — нечетная функция.
Как: для функции вида [latex] y = A \ sec (Bx) [/ latex], построить график с одним периодом.
- Выразите заданную функцию в виде [латекс] y = A \ sec (Bx) [/ latex].
- Укажите коэффициент растяжения / сжатия | A |.
- Идентифицируйте B и определите период, [латекс] P = \ frac {2 \ pi} {| B |} [/ latex].
- Нарисуйте график [латекс] y = A \ cos (Bx) [/ latex].
- Используйте обратную связь между [latex] y = \ cos x [/ latex] и [latex] y = \ sec x [/ latex], чтобы нарисовать график [latex] y = A \ sec (Bx) [/ latex ].
- Изобразите асимптоты.
- Постройте любые две контрольные точки и проведите через эти точки график.
Пример 6: График изменения секущей функции
Изобразите один период [латекса] f (x) = 2,5 \ сек (0,4x) [/ latex].
Решение
Шаг 1. Данная функция уже записана в общем виде [latex] y = A \ sec (Bx) [/ latex].
Шаг 2. [латекс] A = 2,5 [/ латекс], поэтому коэффициент растяжения равен 2,5.
Шаг 3. [латекс] B = 0,4 [/ латекс], поэтому [латекс] P = \ frac {2 \ pi} {0,4} = 5 \ pi [/ латекс]. Период равен 5π единиц.
Шаг 4. Нарисуйте график функции [латекс] g (x) = 2,5 \ cos (0,4x) [/ latex].
Шаг 5. Используйте обратную связь функций косинуса и секанса, чтобы построить функцию косеканса.
Шаги 6–7. Нарисуйте две асимптоты в [latex] x = 1,25 \ pi [/ latex] и [latex] x = 3,75 \ pi [/ latex]. Мы можем использовать две реперные точки: локальный минимум в (0, 2,5) и локальный максимум в (2,5π, −2,5). На рисунке 11 показан график.
Рисунок 11
Попробовать 4
Изобразите один период [латекса] f (x) = — 2.5 \ сек (0.4x) [/ латекс].
Решение
Вопросы и ответы
Влияют ли вертикальное смещение и растяжение / сжатие на диапазон секущей?
Да. Диапазон f (x) = A сек ( Bx — C ) + D равен (−∞, — | A | + D] ∪ [| A | + D, ∞) .
Как сделать: для функции вида [латекс] f (x) = A \ sec (Bx − C) + D [/ latex], построить график с одним периодом.
- Выразите заданную функцию в виде [латекс] y = A \ sec (Bx-C) + D [/ latex].
- Определите коэффициент растяжения / сжатия, | A |.
- Идентифицируйте B и определите период, [latex] \ frac {2 \ pi} {| B |} [/ latex].
- Идентифицируйте C и определите фазовый сдвиг, [латекс] \ frac {C} {B} [/ latex].
- Нарисуйте график [латекс] y = A \ sec (Bx) [/ latex]. но сместите его вправо на [latex] \ frac {C} {B} [/ latex] и вверх на D .
- Нарисуйте вертикальные асимптоты, которые встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {2 | B |} k [/ latex], где k — нечетное целое число.
Пример 7: График изменения секущей функции
Изобразите один период [latex] y = 4 \ sec \ left (\ frac {\ pi} {3} x− \ frac {\ pi} {2} \ right) +1 [/ latex].
Решение
Шаг 1. Выразите заданную функцию в виде [latex] y = 4 \ sec \ left (\ frac {\ pi} {3} x− \ frac {\ pi} {2} \ right) +1 [ /латекс].
Шаг 2. Коэффициент растяжения / сжатия | A | = 4,
Шаг 3. Период
[латекс] \ begin {array} \ frac {2 \ pi} {| B |} = \ frac {2 \ pi} {\ frac {\ pi} {3}} \ hfill & \\ = \ frac {2 \ pi} {1} \ times \ frac {3} {\ pi} \ hfill & \\ = 6 \ end {array} [/ latex]
Шаг 4. Фазовый сдвиг
[латекс] \ begin {array} \ frac {C} {B} = \ frac {\ frac {\ pi} {2}} {\ frac {\ pi} {3}} \ hfill & \\ = \ frac { \ pi} {2} \ times \ frac {3} {\ pi} \ hfill & \\ = 1.5 \ end {array} [/ latex]
Шаг 5. Нарисуйте график [latex] y = A \ sec (Bx) [/ latex], но сдвиньте его вправо на [latex] \ frac {C} {B} = 1,5 [/ latex] и выше на D = 6.
Шаг 6. Нарисуйте вертикальные асимптоты, которые возникают при x = 0, x = 3 и x = 6.Существует локальный минимум в (1.5, 5) и локальный максимум в (4.5, −3). На рисунке 12 показан график.
Рисунок 12
Попробовать 5
Изобразите один период [латекса] f (x) = — 6 \ сек (4x + 2) −8 [/ latex].
Решение
Вопросы и ответы
Домен csc
x был задан как все x , так что [latex] x \ ne k \ pi [/ latex] для любого целого числа k . Будет ли домен [latex] y = A \ csc (Bx − C) + D [/ latex] быть [latex] x \ ne \ frac {C + k \ pi} {B} [/ latex]?
Да.Исключенные точки области следуют вертикальным асимптотам. Их расположение показывает горизонтальный сдвиг и сжатие или расширение, подразумеваемые преобразованием входных данных исходной функции.
Как: для функции вида [latex] y = A \ csc (Bx) [/ latex], построить график с одним периодом.
- Выразите заданную функцию в виде [латекс] y = A \ csc (Bx) [/ latex].
- | A |.
- Идентифицируйте B и определите период, [латекс] P = \ frac {2 \ pi} {| B |} [/ latex].
- Нарисуйте график [латекс] y = A \ sin (Bx) [/ latex].
- Используйте обратную связь между [latex] y = \ sin x [/ latex] и [latex] y = \ csc x [/ latex], чтобы нарисовать график [latex] y = A \ csc (Bx) [/ latex ].
- Изобразите асимптоты.
- Постройте любые две контрольные точки и проведите через эти точки график.
Пример 8: График изменения функции косеканса
Изобразите один период [латекса] f (x) = — 3 \ csc (4x) [/ latex].
Решение
Шаг 1. Данная функция уже записана в общем виде [latex] y = A \ csc (Bx) [/ latex].
Шаг 2. [латекс] | A | = | −3 | = 3 [/ латекс], поэтому коэффициент растяжения равен 3.
Шаг 3. [латекс] B = 4 \ text {, поэтому} P = \ frac {2 \ pi} {4} = \ frac {\ pi} {2} [/ latex]. Точка [латекс ] \ frac {\ pi} {2} [/ latex] единиц.
Шаг 4. Нарисуйте график функции [latex] g (x) = — 3 \ sin (4x) [/ latex].
Шаг 5. Используйте взаимное отношение функций синуса и косеканса, чтобы построить функцию косеканса.
Шаги 6–7. Нарисуйте три асимптоты в [latex] x = 0 \ text {,} x = \ frac {\ pi} {4} \ text {и} x = \ frac {\ pi} {2} [/ latex]. Мы можно использовать две опорные точки: локальный максимум в [latex] \ left (\ frac {\ pi} {8} \ text {,} −3 \ right) [/ latex] и локальный минимум в [latex] \ left ( \ frac {3 \ pi} {8} \ text {,} 3 \ right) [/ latex]. На рисунке 13 показан график.
Рисунок 13
Попробуй 6
Изобразите один период [латекса] f (x) = 0,5 \ csc (2x) [/ latex].
Решение
Как сделать: для функции вида [латекс] f (x) = A \ csc (Bx − C) + D [/ latex], построить график с одним периодом.
- Выразите заданную функцию в виде [латекс] y = A \ csc (Bx-C) + D [/ latex].
- Определите коэффициент растяжения / сжатия, | A |.
- Идентифицируйте B и определите период, [latex] \ frac {2 \ pi} {| B |} [/ latex].
- Идентифицируйте C и определите фазовый сдвиг, [латекс] \ frac {C} {B} [/ latex].
- Нарисуйте график [latex] y = A \ csc (Bx) [/ latex], но сдвиньте его вправо на D вверх и вниз.
- Нарисуйте вертикальные асимптоты, которые встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
Пример 9: Графическое изображение косеканса, растянутого по вертикали, сжатого по горизонтали и смещенного по вертикали
Нарисуйте график [латекс] y = 2 \ csc \ left (\ frac {\ pi} {2} x \ right) +1 [/ latex]. Каковы область и диапазон этой функции?
Решение
Шаг 1. Выразите заданную функцию в виде [латекс] y = 2 \ csc \ left (\ frac {\ pi} {2} x \ right) +1 [/ latex].
Шаг 2. Определите коэффициент растяжения / сжатия, [латекс] | A | = 2 [/ латекс].
Шаг 3. Период [latex] \ frac {2 \ pi} {| B |} = \ frac {2 \ pi} {\ frac {\ pi} {2}} = \ frac {2 \ pi } {1} \ times \ frac {2} {\ pi} = 4 [/ латекс].
Шаг 4. Фазовый сдвиг [latex] \ frac {0} {\ frac {\ pi} {2}} = 0 [/ latex].
Шаг 5. Нарисуйте график [латекс] y = A \ csc (Bx) [/ latex], но сдвиньте его вверх [latex] D = 1 [/ latex].
Шаг 6. Нарисуйте вертикальные асимптоты, которые возникают при x = 0, x = 2, x = 4.
График этой функции показан на рисунке 14.
Рисунок 14
Анализ решения
Вертикальные асимптоты, показанные на графике, отмечают один период функции, а локальные экстремумы в этом интервале показаны точками. Обратите внимание, как график преобразованного косеканса соотносится с графиком [latex] f (x) = 2 \ sin \ left (\ frac {\ pi} {2} x \ right) +1 [/ latex], показанным как оранжевая пунктирная волна.
Попробуйте 7
Учитывая график [латекса] f (x) = 2 \ cos \ left (\ frac {\ pi} {2} x \ right) +1 [/ latex], показанный на рисунке 15, нарисуйте график [латекса] g (x) = 2 \ sec \ left (\ frac {\ pi} {2} x \ right) +1 [/ latex] на тех же осях.
Рисунок 15
Решение
Анализ графика y = cot x и его вариаций
Последняя тригонометрическая функция, которую нам нужно изучить, — это котангенс . Котангенс определяется обратной идентичностью [латекс] \ cot x = \ frac {1} {\ tan x} [/ latex]. Обратите внимание, что функция не определена, когда функция тангенса равна 0, что приводит к вертикальной асимптоте на графике в точках 0, π и т. Д. Поскольку выходные данные функции касательной являются действительными числами, выходные данные функции котангенса также являются все реальные числа.
Мы можем построить график [latex] y = \ cot x [/ latex], наблюдая за графиком касательной функции, потому что эти две функции являются обратными друг другу. См. Рисунок 16. Если график функции тангенса уменьшается, график функции котангенса увеличивается. Если график функции тангенса увеличивается, график функции котангенса уменьшается.
Граф котангенса имеет вертикальные асимптоты при каждом значении x , где [latex] \ tan x = 0 [/ latex]; мы показываем их на графике ниже пунктирными линиями.Поскольку котангенс является обратной величиной касательной, [latex] \ cot x [/ latex] имеет вертикальные асимптоты при всех значениях x , где [latex] \ tan x = 0 [/ latex] и [latex] \ cot x = 0 [/ latex] при всех значениях x, где tan x имеет свои вертикальные асимптоты.
Рисунок 16. Функция котангенса
A Общее примечание: особенности графика
y = A кроватка ( Bx )
- Коэффициент растяжения | A |.
- Точка [латекс] P = \ frac {\ pi} {| B |} [/ latex].
- Домен [latex] x \ ne \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- Диапазон составляет (−∞, ∞).
- Асимптоты встречаются в [latex] x = \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- [latex] y = A \ cot (Bx) [/ latex] — нечетная функция.
Графические вариации
y = детская кроватка x
Мы можем преобразовать график котангенса почти так же, как мы это сделали для тангенса. Уравнение становится следующим.
[латекс] y = A \ cot (Bx − C) + D [/ латекс]
A Общее примечание: Свойства графика
y = A кроватка ( Bx −C) + D
- Коэффициент растяжения | A |.
- Точка [латекс] \ frac {\ pi} {| B |} [/ latex].
- Домен [латекс] x \ ne \ frac {C} {B} + \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- Диапазон: (−∞, — | A |] ∪ [| A |, ∞).
- Вертикальные асимптоты встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- Нет амплитуды.
- [latex] y = A \ cot (Bx) [/ latex] — нечетная функция, потому что это частное четных и нечетных функций (косинус и синус, соответственно)
Как сделать: для данной модифицированной функции котангенса вида [латекс] f (x) = A \ cot (Bx) [/ latex], построить график с одним периодом.
- Выразите функцию в виде [латекс] f (x) = A \ cot (Bx) [/ latex].
- Определите коэффициент растяжения, | A |.
- Укажите период, [латекс] P = \ frac {\ pi} {| B |} [/ latex].
- Нарисуйте график [латекс] y = A \ tan (Bx) [/ latex].
- Постройте любые две опорные точки.
- Используйте взаимное отношение между тангенсом и котангенсом, чтобы нарисовать график [латекс] y = A \ cot (Bx) [/ latex].
- Изобразите асимптоты.
Пример 10: Графики вариаций функции котангенса
Определите коэффициент растяжения, период и фазовый сдвиг [latex] y = 3 \ cot (4x) [/ latex], а затем нарисуйте график.
Решение
Шаг 1. Выражение функции в виде [латекс] f (x) = A \ cot (Bx) [/ latex] дает [latex] f (x) = 3 \ cot (4x) [/ latex].
Шаг 2. Коэффициент растяжения [латекс] | A | = 3 [/ латекс].
Шаг 3. Период [латекс] P = \ frac {\ pi} {4} [/ latex].
Шаг 4. Нарисуйте график [латекс] y = 3 \ tan (4x) [/ latex].
Шаг 5. Постройте две контрольные точки. Две такие точки: [latex] \ left (\ frac {\ pi} {16} \ text {,} 3 \ right) [/ latex] и [latex] \ left (\ frac {3 \ pi} {16} \ текст {,} −3 \ right) [/ latex].
Шаг 6. Используйте взаимное отношение, чтобы нарисовать [латекс] y = 3 \ cot (4x) [/ latex].
Шаг 7. Нарисуйте асимптоты, [latex] x = 0 [/ latex], [latex] x = \ frac {\ pi} {4} [/ latex].
Оранжевый график на Рисунке 17 показывает [латекс] y = 3 \ tan (4x) [/ latex], а синий график показывает [латекс] y = 3 \ cot (4x) [/ latex].
Рисунок 17
Как сделать: для данной модифицированной функции котангенса вида [латекс] f (x) = A \ cot (Bx − C) + D [/ latex], построить график с одним периодом.
- Выразите функцию в виде [латекс] f (x) = A \ cot (Bx-C) + D [/ latex].
- Определите коэффициент растяжения, | A |.
- Укажите период, [латекс] P = \ frac {\ pi} {| B |} [/ latex].
- Определите фазовый сдвиг, [latex] \ frac {C} {B} [/ latex].
- Нарисуйте график [latex] y = A \ tan (Bx) [/ latex], сдвинутый вправо на [latex] \ frac {C} {B} [/ latex] и вверх на D .
- Нарисуйте асимптоты [латекс] x = \ frac {C} {B} + \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- Постройте любые три контрольные точки и проведите через эти точки график.
Пример 11: Построение модифицированного котангенса
Нарисуйте график одного периода функции [latex] f (x) = 4 \ cot (\ frac {\ pi} {8} x− \ frac {\ pi} {2}) — 2 [/ latex].
Решение
Шаг 1. Функция уже записана в общем виде [latex] f (x) = A \ cot (Bx − C) + D [/ latex].
Шаг 2. [латекс] A = 4 [/ латекс], поэтому коэффициент растяжения равен 4.
Шаг 3. [latex] B = \ frac {\ pi} {8} [/ latex], поэтому период равен [latex] P = \ frac {\ pi} {| B |} = \ frac {\ pi} {\ frac {\ pi} {8}} = 8 [/ latex].
Шаг 4. [latex] C = \ frac {\ pi} {2} [/ latex], поэтому сдвиг фазы равен [latex] \ frac {C} {B} = \ frac {\ frac {\ pi } {2}} {\ frac {\ pi} {8}} = 4 [/ латекс].
Шаг 5. Рисуем [латекс] f (x) = 4 \ tan \ left (\ frac {\ pi} {8} x− \ frac {\ pi} {2} \ right) −2 [/ latex ].
Шаг 6-7. Три точки, которые мы можем использовать для построения графика, — это (6,2), (8, −2) и (10, −6).Мы используем взаимное отношение тангенса и котангенса, чтобы нарисовать [латекс] f (x) = 4 \ cot (\ frac {\ pi} {8} x− \ frac {\ pi} {2}) — 2 [/ latex] .
Шаг 8. Вертикальные асимптоты [латекс] x = 4 [/ латекс] и [латекс] x = 12 [/ латекс].
График показан на рисунке 18.
Рисунок 18. Один период модифицированной функции котангенса.
Ключевые уравнения
| Функция касательной со смещением, сжатием и / или растяжением | [латекс] y = A \ tan (Bx-C) + D [/ латекс] |
| Сдвинутая, сжатая и / или растянутая секущая функция | [латекс] y = A \ sec (Bx-C) + D [/ латекс] |
| Сдвинутый, сжатый и / или растянутый косеканс | [латекс] y = A \ csc (Bx-C) + D [/ латекс] |
| Функция котангенса со смещением, сжатием и / или растяжением | [латекс] y = A \ cot (Bx − C) + D [/ латекс] |
Ключевые понятия
- Касательная функция имеет период π.
- [латекс] f (x) = A \ tan (Bx-C) + D [/ latex] — касательная с вертикальным и / или горизонтальным растяжением / сжатием и сдвигом.
- Секанс и косеканс — периодические функции с периодом 2π. [latex] f (x) = A \ sec (Bx-C) + D [/ latex] дает сдвинутый, сжатый и / или растянутый график функции секущей.
- [латекс] f (x) = A \ csc (Bx-C) + D [/ latex] дает сдвинутый, сжатый и / или растянутый график функции косеканса.
- Функция котангенса имеет период π и вертикальные асимптоты в точках 0, ± π, ± 2π,….
- Диапазон котангенса равен (−∞, ∞), и функция убывает в каждой точке своего диапазона.
- Котангенс равен нулю в [latex] \ ne \ frac {\ pi} {2} \ text {,} \ ne \ frac {3 \ pi} {2} [/ latex],….
- [латекс] f (x) = A \ cot (Bx-C) + D [/ latex] — котангенс с вертикальным и / или горизонтальным растяжением / сжатием и сдвигом.
- Реальные сценарии могут быть решены с использованием графиков тригонометрических функций.
Раздел упражнения
1. Объясните, как можно использовать график синусоидальной функции для построения графика [латекс] y = \ csc x [/ latex].
2. Как можно использовать график [latex] y = \ cos x [/ latex] для построения графика [latex] y = \ sec x [/ latex]?
3. Объясните, почему период [latex] \ tan x [/ latex] равен π.
4. Почему на графике [latex] y = \ csc x [/ latex] нет перехватов?
5. Как период [latex] y = \ csc x [/ latex] сравнивается с периодом [latex] y = \ sin x [/ latex]?
Для следующих упражнений сопоставьте каждую тригонометрическую функцию с одним из следующих графиков.
6. [латекс] f (x) = \ tan x [/ латекс]
7. [латекс] f (x) = \ sec x [/ латекс]
8. [латекс] f (x) = \ csc x [/ латекс]
9. [латекс] f (x) = \ cot x [/ латекс]
Для следующих упражнений найдите период и горизонтальный сдвиг каждой функции.
10. [латекс] f (x) = 2 \ tan (4x − 32) [/ латекс]
11. [латекс] h (x) = 2 \ sec \ left (\ frac {\ pi} {4} (x + 1) \ right) [/ latex]
12. [латекс] m (x) = 6 \ csc \ left (\ frac {\ pi} {3} x + \ pi \ right) [/ latex]
13.Если tan x = −1,5, найдите tan (−x).
14. Если sec x = 2, найдите sec (- x ).
15. Если csc x = −5, найдите csc (- x ).
16. Если [латекс] x \ sin x = 2 [/ latex], найдите [латекс] (- x) \ sin (−x) [/ latex].
Для следующих упражнений перепишите каждое выражение так, чтобы аргумент x был положительным.
17. [латекс] \ cot (−x) \ cos (−x) + \ sin (−x) [/ latex]
18. [латекс] \ cos (−x) + \ tan (−x) \ sin (−x) [/ latex]
Для следующих упражнений нарисуйте два периода графика для каждой из следующих функций.Определите коэффициент растяжения, период и асимптоты.
19. [латекс] f (x) = 2 \ tan (4x − 32) [/ латекс]
20. [латекс] h (x) = 2 \ sec \ left (\ frac {\ pi} {4} \ left (x + 1 \ right) \ right) [/ latex]
21. [латекс] m (x) = 6 \ csc \ left (\ frac {\ pi} {3} x + \ pi \ right) [/ latex]
22. [латекс] j (x) = \ tan \ left (\ frac {\ pi} {2} x \ right) [/ latex]
23. [латекс] p (x) = \ tan \ left (x− \ frac {\ pi} {2} \ right) [/ latex]
24. [латекс] f (x) = 4 \ tan (x) [/ латекс]
25. [латекс] f (x) = \ tan \ left (x + \ frac {\ pi} {4} \ right) [/ latex]
26.[латекс] f (x) = \ pi \ tan \ left (\ pi x− \ pi \ right) — \ pi [/ latex]
27. [латекс] f (x) = 2 \ csc (x) [/ латекс]
28. [латекс] f (x) = — \ frac {1} {4} \ csc (x) [/ latex]
29. [латекс] f (x) = 4 \ сек (3x) [/ латекс]
30. [латекс] f (x) = — 3 \ cot (2x) [/ латекс]
31. [латекс] f (x) = 7 \ сек (5x) [/ латекс]
32. [латекс] f (x) = \ frac {9} {10} \ csc (\ pi x) [/ latex]
33. [латекс] f (x) = 2 \ csc \ left (x + \ frac {\ pi} {4} \ right) −1 [/ latex]
34. [латекс] f (x) = — \ sec \ left (x− \ frac {\ pi} {3} \ right) −2 [/ latex]
35.[латекс] f (x) = \ frac {7} {5} \ csc \ left (x− \ frac {\ pi} {4} \ right) [/ latex]
36. [латекс] f (x) = 5 \ left (\ cot \ left (x + \ frac {\ pi} {2} \ right) −3 \ right) [/ latex]
Для следующих упражнений найдите и изобразите два периода периодической функции с заданным коэффициентом растяжения | A |, период и фазовый сдвиг. {2} (x) [/ latex].{2} х [/ латекс]
54. Функция [latex] f (x) = 20 \ tan \ left (\ frac {\ pi} {10} x \ right) [/ latex] отмечает расстояние при движении светового луча от полицейской машины. поперек стены на время x в секундах и расстояние [латекс] f (x) [/ латекс] в футах.
а. График на интервале [0,5].
г. Найдите и интерпретируйте коэффициент растяжения, период и асимптоту.
г. Оцените f (1) и f (2.5) и обсудите значения функции на этих входах.
55. Рыбак стоит на берегу озера и видит вдалеке лодку слева от него.Пусть x , измеренный в радианах, будет углом, образованным линией обзора корабля и линией на север от его местоположения. Предположим, что север равен 0, и x измерены отрицательно слева и положительно справа. (См. Рис. 19.) Лодка движется с запада на восток, и, игнорируя кривизну Земли, расстояние [латекс] d (x) [/ латекс] в километрах от рыбака до лодки определяется выражением функция [латекс] d (x) = 1.5 \ sec (x) [/ latex].
а. Каков разумный домен для [latex] d (x) [/ latex]?
г.График d (x) в этой области.
г. Найдите и обсудите значение любых вертикальных асимптот на графике [latex] d (x) [/ latex].
г. Вычислить и интерпретировать [латекс] d (- \ frac {\ pi} {3}) [/ latex]. Округлить до второго десятичного знака.
e. Вычислить и интерпретировать [латекс] d (\ frac {\ pi} {6}) [/ latex]. Округлить до второго десятичного знака.
ф. Какое минимальное расстояние между рыбаком и лодкой? Когда это происходит?
Рисунок 19
56. Лазерный дальномер зафиксирован на приближающейся к Земле комете.Расстояние [latex] g (x) [/ latex] в километрах от кометы через x дней для x в интервале от 0 до 30 дней определяется как [latex] g (x) = 250,000. \ csc (\ frac {\ pi} {30} x) [/ latex].
а. График [latex] g (x) [/ latex] на интервале [0,35].
г. Оцените [latex] g (5) [/ latex] и интерпретируйте информацию.
г. Какое минимальное расстояние между кометой и Землей? Когда это происходит? Какой константе в уравнении это соответствует?
г. Найдите и обсудите значение любых вертикальных асимптот.
57. Видеокамера сфокусирована на ракете на стартовой площадке в 2 милях от камеры. Угол подъема от земли до ракеты через x секунд составляет [latex] \ frac {\ pi} {120} x [/ latex].
а. Напишите функцию, выражающую высоту [латекс] h (x) [/ latex] в милях над землей после x секунд. Игнорируйте кривизну Земли.
г. График [latex] h (x) [/ latex] на интервале (0,60).
г. Оцените и интерпретируйте значения [латекс] h (0) [/ латекс] и [латекс] h (30) [/ латекс].{2} — 4x + 3 = 0 \\
(х-3) (х-1) = 0 \\
х = 3 \ текст {или} х = 1 \\
\ text {Shape: «frown»} (a Найдите уравнения касательных к \ (f \) в точке:
- \ (y \) — точка пересечения \ (f \).
- поворотный момент \ (f \).
- точка, где \ (x = \ text {4,25} \).
- \ begin {align *}
y _ {\ text {int}}: (0; -3) \\
m _ {\ text {касательная}} = f ‘(x) & = -2x + 4 \\
f ‘(0) & = — 2 (0) + 4 \\
\ поэтому m & = 4 \\
\ text {Касательная} y & = 4x + c \\
\ text {Through} (0; -3) \ поэтому y & = 4x-3
\ end {align *} - \ begin {align *}
\ text {Поворотный момент:} (2; 1) \\
m _ {\ text {касательная}} = f ‘(2) & = -2 (2) + 4 \\
& = 0 \\
\ text {Касательное уравнение} y & = 1
\ end {align *} - \ begin {align *}
\ text {If} x & = \ text {4,25} \\
f (\ text {4,25}) & = — \ text {4,25} ^ {2} +4 (\ text {4,25}) — 3 \\
& = — \ text {4,0625} \\
m _ {\ text {tangent}} \ text {at} x & = \ text {4,25} \\
m & = — 2 (\ text {4,25}) + 4 \\
& = — \ текст {4,5} \\
\ text {Касательная} y & = — \ text {4,5} x + c \\
\ text {Сквозь} (\ text {4,25}; — \ text {4,0625}) \\
— \ text {4,0625} & = — \ text {4,5} (\ text {4,25}) + c \\
\ поэтому c & = \ text {15,0625} \\
y & = — \ text {4,5} x + \ text {15,0625}
\ end {align *}
Нарисуйте три касательных выше на вашем графике \ (f \).
Запишите все наблюдения о трех касательных к \ (f \).
Касательная в точке \ (y _ {\ text {int}} \) (синяя линия): градиент положительный, функция увеличивается в этой точке.
Касательная в точке поворота (зеленая линия): градиент равен нулю, касательная — горизонтальная линия, параллельная оси \ (x \).
Касательная в точке \ (x = \ text {4,25} \) (фиолетовая линия): градиент отрицательный, функция в этой точке убывает.
График функции касания — Тригонометрия
График функции касания — Тригонометрия — Открытый справочник по математике
Тангенс угла откладывается от этой меры угла.
Попробуй это
Перетащите
вершине треугольника и посмотрите, как функция касательной изменяется с углом.
Чтобы построить график функции касательной, мы отмечаем угол по горизонтальной оси x, и для каждого угла мы помещаем тангенс этого угла на вертикальную ось y. В результате, как видно выше, получается довольно неровная кривая, уходящая в положительную бесконечность в одном направлении и в отрицательную бесконечность в другом.
На схеме выше перетащите точку A по круговой траектории, чтобы изменить угол CAB.При этом точка на графике перемещается в соответствии с углом и его касательной. (Если вы отметите поле «прогрессивный режим», кривая будет нарисована по мере перемещения точки A, а не по существующей кривой.)
Область касательной функции имеет дыры
Когда вы перетаскиваете точку A вокруг, обратите внимание, что после полного поворота вокруг точки B форма графика повторяется. Форма касательной кривой одинакова для каждого полного поворота угла, поэтому функция называется «периодической».Период функции равен 360 ° или 2π радиан.
Вы можете вращать точку сколько угодно раз.
Это означает, что вы можете найти тангенс любого угла, независимо от его размера, за одним исключением.
Если вы посмотрите на график выше, вы увидите, что tan90 ° не определен, потому что он требует деления на ноль.
Следовательно, такие углы не входят в область функций tan и дают неопределенный результат. Пытаться
tan90 ° на вашем калькуляторе, и вы получите ошибку, а скажем 89.99 будет работать.
Таким образом, домен функции tan — это набор всех действительных чисел , кроме 90 °, -90 °, 270 °, -270 ° и т. Д. (Или эквивалент в радианах: плюс / минус пи более 2, 3pi более 2 и т. Д. ).
Диапазон
Диапазон функции — это набор значений результата, которые она может создать. Функция касательной имеет диапазон от положительной бесконечности до отрицательной бесконечности.
Чтобы понять, почему это происходит, нажмите «Сброс», затем перетащите точку A против часовой стрелки.По мере приближения к точке 90 ° с почти вертикальным AB, вы можете видеть, что BC становится очень маленьким. Поскольку тангенс угла равен «противоположному по соседнему» (TOA), в результате деления числа на очень маленькое число получается очень большое. В конце концов, сторона BC приближается к нулю, а результат стремится к бесконечности.
То же самое происходит во втором квадранте, за исключением того, что BC тогда отрицательна, и поэтому функция приближается к отрицательной бесконечности.
Бесконечность не является действительным числом, поэтому tan90 ° фактически не определен.Однако, когда угол приближается к 90 °, функция возвращает очень большие числа. Например, загар (89,999 °) превышает 57000.
Функция арктангенса
Что, если бы нас попросили найти арктангенс числа, скажем 4,0? Другими словами, мы ищем угол, загар которого равен 4,0.
Если мы посмотрим на кривую выше, мы увидим четыре угла, тангенс которых равен 4,0 (красные точки). Фактически, поскольку график продолжается бесконечно в обоих направлениях, существует бесконечное количество углов, тангенс которых имеет заданное значение.
Так что же говорит калькулятор?
Если вы попросите калькулятор указать арктангенс (tan -1 или atan) числа, он не сможет вернуть бесконечно длинный список углов, поэтому по соглашению он находит только первый.

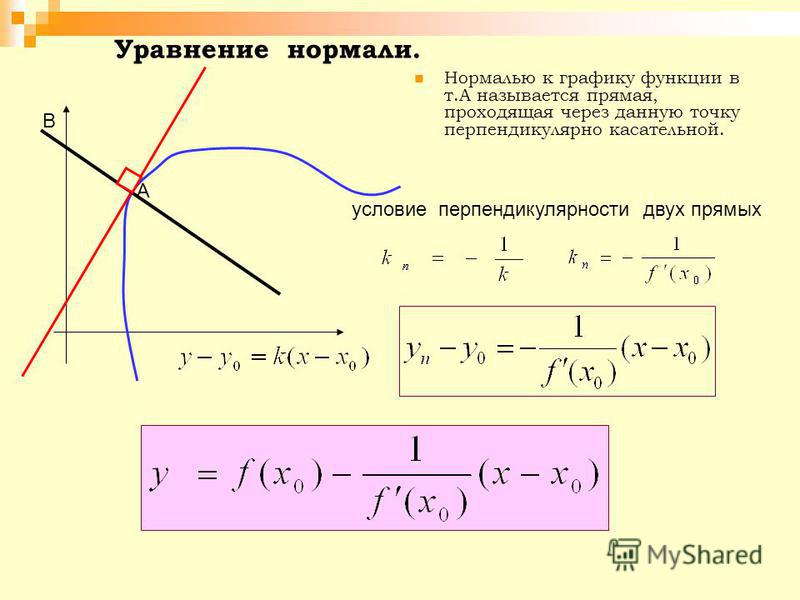 Вычислить f(xо).
Вычислить f(xо).