Как решать уравнения с параметром квадратные: Квадратные уравнения с параметром. Задание 18 в ЕГЭ — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Квадратные уравнения с параметром | О математике понятно

Задачи с параметрами. Простейшие задачи на квадратный трёхчлен.

Сегодня мы рассмотрим задачи на квадратный трёхчлен, про который, в зависимости от параметра, надо будет что-то выяснить. Это «что-то» может быть самым разнообразным, насколько только хватит фантазии у составителей задачи. Это самый простой тип задач с параметрами. И, если на ЕГЭ вам попалась такая — считайте, что вам повезло!

Но, прежде чем приступать к разбору самих задач, ответьте сами себе на такие простые вопросы:

— Что такое квадратное уравнение, как оно выглядит и как решается?

— Что такое дискриминант и куда его пристроить?

— Что такое теорема Виета и где её можно применить?

Если вы верно отвечаете на эти простые вопросы, то 50% успеха в решении параметрических задач на квадратный трёхчлен вам обеспечены! А остальные 50% — это обычная алгебра и арифметика: раскрытие скобок, приведение подобных, решение уравнений, неравенств и систем и т. д.

Итак, приступим!

Для начала рассмотрим совсем безобидную задачку. Для разминки. 🙂

Пример 1

Приступаем к решению. Во-первых, чтобы в будущем не накосячить в коэффициентах, всегда полезно выписать их отдельно. Прямо в столбик. Вот так:

a = 1

b = -(a-1)

c = a-2

Да-да! Часть коэффициентов в уравнении (а именно — b и с) зависит от параметра. В этом как раз и состоит вся фишка таких задач. А теперь снова въедливо перечитываем условие. Ключевой зацепкой в формулировке задания являются слова «единственный корень». И когда же квадратное уравнение имеет единственный корень? Подключаем наши теоретические знания о квадратных уравнениях. Только в одном единственном случае — когда его дискриминант равен нулю.

Так и пишем:

D = 0

Осталось составить выражение для дискриминанта и приравнять его к нулю. Поехали!

Теперь надо приравнять наш дискриминант к нулю:

Можно, конечно, решать это квадратное уравнение через дискриминант, а можно немного схитрить. На что у нас похожа левая часть, если как следует присмотреться? Она у нас похожа на квадрат разности (a-3)²!

Респект внимательным! Верно! Если заменить наше выражение слева на (a-3)², то уравнение будет решаться в уме!

(a — 3)² = 0

a — 3 = 0

a = 3

Вот и всё. Это значит, что единственный корень наше квадратное уравнение с параметром будет иметь только в одном единственном случае — когда значение параметра «а» равно тройке.)

Ответ: 3

Это был разминочный пример. Чтобы общую идею уловить. ) Теперь будет задачка посерьёзнее.

Пример 2

Вот такая задачка. Начинаем распутывать. Первым делом выпишем наше квадратное уравнение:

0,5x² — 2x + 3a + 1,5 = 0

Самым логичным шагом, было бы умножить обе части на 2. Тогда у нас исчезнут дробные коэффициенты и само уравнение станет посимпатичнее. Умножаем:

Выписываем в столбик наши коэффициенты a, b, c:

a = 1

b = -4

c = 6a+3

Видно, что коэффициенты a и b у нас постоянны, а вот свободный член с зависит от параметра «а»! Который может быть каким угодно — положительным, отрицательным, целым, дробным, иррациональным — всяким!

А теперь, чтобы продвинуться дальше, вновь подключаем наши теоретические познания в области квадратных уравнений и начинаем рассуждать. Примерно так:

«Для того чтобы сумма кубов корней была меньше 28, эти самые корни, во-первых, должны существовать. Сами по себе. В принципе. А корни у квадратного уравнения существуют, тогда и только тогда, когда его дискриминант неотрицательный. Кроме того, в задании говорится о двух различных корнях. Эта фраза означает, что наш дискриминант обязан быть не просто неотрицательным, а строго положительным!»

Если вы рассуждаете таким образом, то вы движетесь правильным курсом! Верно.) Составляем условие положительности для дискриминанта:

D = (-4)² — 4·1·(6a+3) = 16-24a-12 = 4-24a

4-24a > 0

-24a > -4

a < 1/6

Полученное условие говорит нам о том, что два различных корня у нашего уравнения будет не при любых значениях параметра «а», а только при тех, которые меньше одной шестой! Это глобальное требование, которое должно выполняться железно. Неважно, меньше 28 наша сумма кубов корней или больше. Значения параметра «а», большие или равные 1/6, нас заведомо не устроят. Гуд.) Соломки подстелили. Движемся дальше.

Теперь приступаем к загадочной сумме кубов корней. По условию она у нас должна быть меньше 28. Так и пишем:

Значит, для того чтобы ответить на вопрос задачи, нам надо совместно рассмотреть два условия:

А дальше начинаем отдельно работать с этой самой суммой кубов. Есть два способа такой работы: первый способ для трудолюбивых и второй способ — для внимательных.

Способ для трудолюбивых заключается в непосредственном нахождении корней уравнения через параметр. Прямо по общей формуле корней. Вот так:

Теперь составляем нужную нам сумму кубов найденных корней и требуем, чтобы она была меньше 28:

А дальше — обычная алгебра: раскрываем сумму кубов по формуле сокращённого умножения, приводим подобные, сокращаем и т. д. Если бы корни нашего уравнения получились покрасивее, без радикалов, то такой «лобовой» способ был бы неплох. Но проблема в том, что наши корни выглядят немного страшновато. И подставлять их в сумму кубов как-то неохота, да. Поэтому, для того чтобы избежать этой громоздкой процедуры, я предлагаю второй способ — для внимательных.

Для этого раскрываем сумму кубов корней по соответствующей формуле сокращенного умножения. Прямо в общем виде:

А дальше проделываем вот такой красивый фокус: во вторых скобках выражаем сумму квадратов корней через сумму корней и их произведение. Вот так:

Итого:

Казалось бы, и что из этого? Сейчас интересно будет! Давайте, посмотрим ещё разок на наше уравнение. Как можно внимательнее:

Чему здесь равен коэффициент при x²? Правильно, единичке! А как такое уравнение называется? Правильно, приведённое! А, раз приведённое, то, стало быть, для него справедлива теорема Виета:

Вот и ещё одна теорема нам пригодилась! Теперь, прямо по теореме Виета, подставляем сумму и произведение корней в наше требование для суммы кубов:

Осталось раскрыть скобки и решить простенькое линейное неравенство:

4·(16-18a-9) < 28

64–72a+36 < 28

-72a < 28-64+36

-72a < 0

a > 0

Вспоминаем, что ещё у нас есть глобальное требование a < 1/6. Значит, наше полученное множество a > 0 необходимо пересечь с условием a < 1/6. Рисуем картинку, пересекаем, и записываем окончательный ответ.

Ответ:

Да. Вот такой маленький интервальчик. От нуля до одной шестой… Видите, насколько знание теоремы Виета, порой, облегчает жизнь!

Вот вам небольшой практический совет: если в задании говорится о таких конструкциях, как сумма, произведение, сумма квадратов, сумма кубов корней, то пробуем применить теорему Виета. В 99% случаев решение значительно упрощается.

Это были довольно простые примеры. Чтобы суть уловить. Теперь будут примеры посолиднее.

Например, такая задачка из реального варианта ЕГЭ:

Пример 3

Что, внушает? Ничего не боимся и действуем по нашему излюбленному принципу: «Не знаешь, что нужно, делай что можно!»

Опять аккуратно выписываем все коэффициенты нашего квадратного уравнения:

a = 1

b = -6

c = a²-4a

А теперь вчитываемся в условие задачи и находим слова «модуль разности корней уравнения». Модуль разности нас пока не волнует, а вот слова «корней уравнения» примем во внимание. Раз говорится о корнях (неважно, двух одинаковых или двух различных), то наш дискриминант обязан быть неотрицательным! Так и пишем:

D ≥ 0

Что ж, аккуратно расписываем наш дискриминант через параметр а:

D = (-6)² — 4·1·(12 + a²-4a) = 36 — 48 — 4а²+ 16а = -4а²+16а-12.

А теперь решаем квадратное неравенство. По стандартной схеме, через соответствующее квадратное уравнение и схематичный рисунок параболы:

Значит, для того чтобы у нашего уравнения в принципе имелись хоть какие-то корни, параметр а должен находиться в отрезке [-1; 3]. Это железное требование. Хорошо. Запомним.)

А теперь приступаем к этому самому модулю разности корней уравнения. От нас хотят, чтобы вот такая штука

принимала бы наибольшее значение. Для этого, ничего не поделать, но теперь нам всё-таки придётся находить сами корни и составлять их разность: x₁ — x₂. Теорема Виета здесь в этот раз бессильна.

Что ж, считаем корни по общей формуле:

Дальше составляем модуль разности этих самых корней:

Теперь вспоминаем, что корень квадратный — величина заведомо неотрицательная. Стало быть, без ущерба для здоровья, модуль можно смело опустить. Итого наш модуль разности корней выглядит так:

И эта функция f(a) должна принимать наибольшее значение. А для поиска наибольшего значения у нас есть такой мощный инструмент, как производная! Вперёд и с песнями!)

Дифференцируем нашу функцию и приравниваем производную к нулю:

Получили единственную критическую точку a = 2. Но это ещё не ответ, так как нам ещё надо проверить, что найденная точка и в самом деле является точкой максимума! Для этого исследуем знаки нашей производной слева и справа от двойки. Это легко делается простой подстановкой (например, а = 1,5 и а = 2,5).

Слева от двойки производная положительна, а справа от двойки — отрицательна. Это значит, что наша точка a = 2 и вправду является точкой максимума. Заштрихованная зона на картинке означает, что нашу функцию мы рассматриваем только на отрезке [1; 3]. Вне этого отрезка нашей функции f(a) попросту не существует. Потому, что в заштрихованной области наш дискриминант отрицательный, и разговоры о каких-либо корнях (и о функции тоже) бессмысленны. Это понятно, думаю.

Всё. Вот теперь наша задача полностью решена.

Ответ: 2.

Здесь было применение производной. А бывают и такие задачи, где приходится решать уравнения либо неравенства с так ненавистными многими учениками модулями и сравнивать некрасивые иррациональные числа с корнями. Главное — не бояться! Разберём похожую злую задачку (тоже из ЕГЭ, кстати).

Пример 4

Итак, приступаем. Первым делом замечаем, что параметр а ни в коем случае не может быть равен нулю. Почему? А вы подставьте в исходное уравнение вместо а нолик. Что получится?

Получили линейное уравнение, имеющее единственный корень x=2. А это уже совсем не наш случай. От нас хотят, чтобы уравнение имело два различных корня, а для этого нам необходимо, чтобы оно, как минимум, было хотя бы квадратным.)

Итак, а ≠ 0.

При всех остальных значениях параметра наше уравнение будет вполне себе квадратным. И, следовательно, чтобы оно имело два различных корня, необходимо (и достаточно), чтобы его дискриминант был положительным. То есть, первое наше требование будет D > 0.

А далее по накатанной колее. Считаем дискриминант:

D = 4(a-1)² — 4a(a-4) = 4a²-8a+4-4a²+16a = 4+8a

Вот так. Значит, наше уравнение имеет два различных корня тогда и только тогда, когда параметр a > -1/2. При прочих «а» у уравнения будет либо один корень, либо вообще ни одного. Берём на заметку это условие и движемся дальше.

Далее в задаче идёт речь о расстоянии между корнями. Расстояние между корнями, в математическом смысле, означает вот такую величину:

Зачем здесь нужен модуль? А затем, что любое расстояние (что в природе, что в математике) — величина неотрицательная. Причём здесь совершенно неважно, какой именно корень будет стоять в этой разности первым, а какой вторым: модуль — функция чётная и сжигает минус. Точно так же, как и квадрат.

Значит, ответом на вопрос задачи является решение вот такой системы:

Теперь, ясен перец, нам надо найти сами корни. Здесь тоже всё очевидно и прозрачно. Аккуратно подставляем все коэффициенты в нашу общую формулу корней и считаем:

Отлично. Корни получены. Теперь начинаем формировать наше расстояние:

Наше расстояние между корнями должно быть больше трёх, поэтому теперь нам надо решить вот такое неравенство:

Неравенство — не подарок: модуль, корень… Но и мы всё-таки уже решаем серьёзную задачу №18 из ЕГЭ! Делаем всё что можно, чтобы максимально упростить внешний вид неравенства. Мне здесь больше всего не нравится дробь. Поэтому первым делом я избавлюсь от знаменателя, умножив обе части неравенства на |a|. Это можно сделать, поскольку мы, во-первых, в самом начале решения примера договорились, что а ≠ 0, а во-вторых, сам модуль — величина неотрицательная.

Итак, смело умножаем обе части неравенства на положительное число |a|. Знак неравенства сохраняется:

Вот так. Теперь в нашем распоряжении имеется иррациональное неравенство с модулем. Ясное дело, для того чтобы решить его, надо избавляться от модуля. Поэтому придётся разбивать решение на два случая — когда параметр а, стоящий под модулем, положителен и когда отрицателен. Другого пути избавиться от модуля у нас, к сожалению, нет.

Итак!

Случай 1 (a>0, |a|=a)

В этом случае наш модуль раскрывается с плюсом, и неравенство (уже без модуля!) принимает следующий вид:

Неравенство имеет структуру: «корень больше функции». Такие иррациональные неравенства решаются по следующей стандартной схеме:

Отдельно рассматривается случай а), когда обе части неравенства возводятся в квадрат и правая часть неотрицательна и отдельно — случай б), когда правая часть всё-таки отрицательна, но зато сам корень при этом извлекается. ) И решения этих двух систем объединяются.

Тогда, в соответствии с этой схемой, наше неравенство распишется вот так:

А теперь можно существенно упростить себе дальнейшую работу. Для этого вспомним, что в случае 1 мы рассматриваем только a>0. С учётом этого требования, вторую систему можно вообще вычеркнуть из рассмотрения, поскольку, второе неравенство в ней (3a<0) эквивалентно неравенству a<0, а условия a>0 и a<0 — это два взаимно исключающих требования.

Упрощаем нашу совокупность с учётом главного условия a>0:

Вот так. А теперь решаем самое обычное квадратное неравенство:

Нас интересует промежуток между корнями. Стало быть,

Отлично. Теперь этот промежуток пересекаем со вторым условием системы a>0:

Есть. Таким образом, первым кусочком ответа к нашему неравенству (а пока не ко всей задаче!) будет вот такой интервал:

Всё. Случай 1 разложен по полочкам. Переходим к случаю 2.

Случай 2 (a<0, |a|=-a)

В этом случае наш модуль раскрывается с минусом, и неравенство принимает следующий вид:

Опять имеем структуру: «корень больше функции». Применяем нашу стандартную схему с двумя системами (см. выше):

С учётом общего требования a<0, мы снова, как и в предыдущем случае, проводим максимальные упрощения: вычёркиваем вторую систему в силу противоречивости двух требований -3а < 0 и нашего общего условия a<0 для всего случая 2.

А дальше снова решаем обычное квадратное неравенство:

И опять сокращаем себе работу. Ибо оно у нас уже решено в процессе разбора случая 1! Решение этого неравенства выглядело вот так:

Осталось лишь пересечь этот интервал с нашим новым условием a<0.

Пересекаем:

Вот и второй кусочек ответа готов:

Кстати сказать, как я узнал, что ноль лежит именно между нашими иррациональными корнями? Легко! Очевидно, что правый корень заведомо положителен. А что касается левого корня, то я просто в уме сравнил иррациональное число

с нулём. Вот так:

А теперь объединяем оба найденных интервала. Ибо мы решаем совокупность (а не систему):

Готово дело. Эти два интервала — это пока ещё только решение неравенства

Кто забыл, данное неравенство отвечает у нас за расстояние между корнями нашего уравнения. Которое должно больше 3. Но! Это ещё не ответ!

Ещё у нас есть условие положительного дискриминанта! Неравенство a>-1/2, помните? Это значит, что данное множество нам ещё надо пересечь с условием a>-1/2. Иными словами, теперь мы должны пересечь два множества:

Но есть одна проблемка. Мы не знаем, как именно расположено на прямой число -1/2 относительно левого (отрицательного) корня. Для этого нам придётся сравнить между собой два числа:

Поэтому сейчас берём черновик и начинаем сравнивать наши числа. Примерно так:

Это значит, что дробь -1/2 на числовой прямой находится левее нашего левого корня.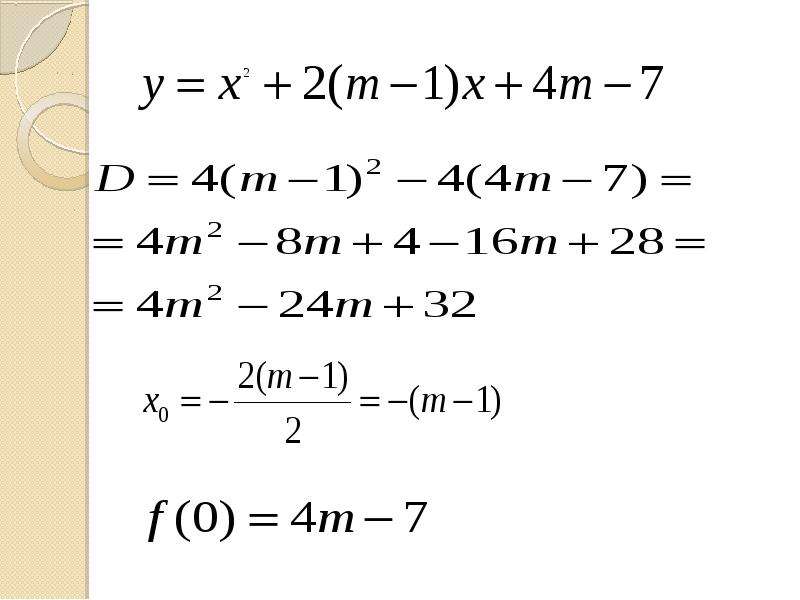 И картинка к окончательному ответу задачи будет какая-то вот такая:

Всё, задача полностью решена и можно записывать окончательный ответ.

Ответ:

Ну как? Уловили суть? Тогда решаем самостоятельно.)

1. Найдите все значения параметра b, при которых уравнение

ax² + 3x +5 = 0

имеет единственный корень.

2. Найдите все значения параметра а, при каждом из которых больший корень уравнения

x² — (14a-9)x + 49a² — 63a + 20 = 0

меньше 9.

3. Найдите все значения параметра а, при каждом из которых сумма квадратов корней уравнения

x² — 4ax + 5a = 0

равна 6.

4. Найдите все значения параметра а, при каждом из которых уравнение

x² + 2(a-2)x + a + 3 = 0

имеет два различных корня, расстояние между которыми больше 3.

Ответы (в беспорядке):

Квадратные уравнения с параметром: определение, пример решения

Понятие уравнения с параметром и его решения

Часто на практике создаётся такая математическая модель, в которой приходится решать не одно, а целое «семейство» похожих уравнений. 2 = 0, $$

один корень $x_0 = -2$

$$ D(a) \gt 0 при -3 \lt a \lt 1 $$

Уравнение имеет два корня:

$$ x_{1,2} = \frac{a-1 \pm \sqrt{-3(a-1)(a+3)}}{2} $$

$$ D(a) \lt 0 при a \lt -3 \cap a \gt 1 $$

Решений нет.

Ответ:

При a = -3 один корень $x_0 = -2$

При a = 1 один корень $x_0 = 0$

При $-3 \lt a \lt 1$ два корня $x_{1,2} = \frac{a-1 \pm \sqrt{-3(a-1)(a+3)}}{2}$

При других a решений нет.

Квадратные уравнения с параметрами

Тема занятия «КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРАМИ»

Цели занятия:

Образовательная: углубить ранее полученные знания об уравнениях с параметрами, закрепить навыки решения уравнений;

Воспитательная: воспитывать навыки учебного труда, умение работать в группах;

Развивающая: развивать логическое мышление, формировать потребность к приобретению знаний.

Опрос:

Вспомним условия расположения корней уравнения,при условии , что оба корня положительные, отрицательные, разных знаков.

Рассмотрим примеры решения квадратных уравнений с параметрами.

ПРИМЕР 1.

Решить уравнение

Решение:

1.Если , то мы имеем линейное уравнение:

2.Если найдём дискриминант D квадратного уравнения :

а)Если , то

б)Если т.е. то

в)Если то действительных корней нет .

Ответ: если

если

решений нет, если

ПРИМЕР 2.

Решить уравнение

Решение:

Уравнение равносильно системе:

Решим уравнение

1.Если т.е. имеем :

Условие выполнено, т.к.

Выясним, при каких значениях Для этого решим уравнения :

Понятно, что при всех отрицательных значениях параметра равенство в первом уравнении невозможно, при возведя в квадрат обе части равенства , мы получим что невозможно.

Второе из рассматриваемых уравнений невозможно при положительных значениях ,а при имеем , как и в первом случае , неверное равенство

Таким образом , если

2. Если то

Т.е. в данном случае уравнение не имеет решений.

3.Если то дискриминант квадратного уравнения отрицательный и, таким образом, нет действительных корней.

Ответ: если

решений нет, если

ПРИМЕР 3.

Определить количество корней уравнения в зависимости от :

Решение:

Обозначим Тогда исходное уравнение имеет вид

или .

Количество корней зависит от знака D₁.

D₁=

1.Если то данное уравнение не имеет корней.

2.При уравнение имеет единственный корень: Итак,

Это уравнение не имеет корней.

3.Если то корни уравнения

Итак ,необходимо выяснить , сколько корней имеет совокупность уравнений:

В первом уравнении дискриминант отсюда следует, что оно не имеет решений при любых значениях параметра

Во втором уравнении

1)Если т.е. то данное уравнение имеет один корень.

2)Если т.е.

Уравнение не имеет действительных корней.

3)Если т.е. уравнение имеет два корня .

Ответ: Два корня , если

один корень, если

действительных корней нет, если

ПРИМЕР 4.

При каких значениях параметра уравнение

имеет единственное решение?

Решение:

Данное уравнение равносильно системе :

Найдём дискриминант квадратного уравнения :

Если , уравнение имеет один корень что удовлетворяет условию

При получим:

Уравнение имеет одно решение , если т. е. при

Ответ: Уравнение имеет один корень, если

ПРИМЕР 5.

При каких значениях параметра уравнение имеет

два разных действительных корня?

Решение:

Данное биквадратное уравнение сводится к совокупности уравнений:

Уравнение имеет два разных корня, если

Ответ: уравнение имеет два разных корня , если

ПРИМЕР 6.

При каких значениях параметра уравнение

имеет единственное решение ?

Решение:

Данное уравнение равносильно системе :

система будет иметь одно решение ,если

т. е. при

Ответ: уравнение имеет единственное решение при

ПРИМЕР 7.

Сколько решений имеет уравнение в зависимости от значения параметра ?

Решение:

Данное уравнение равносильно системе :

При или уравнение имеет два решения, в других случаях – три.

Ответ: два решения , если

три решения, если

ПРИМЕР 8.

При каких значениях параметра уравнение

имеет единственное решение ?

Решение:

Данное уравнение равносильно системе :

Решив квадратное уравнение , имеем :

Система имеет единственное решение, если т.е. или, когда

Ответ: уравнение имеет единственное решение, если

ПРИМЕР 9.

При каких значениях параметра уравнение

имеет единственное решение?

Решение:

1.Если то мы получим линейное уравнение

При

При решений нет .

2.При дискриминант D должен равняться нулю, т.е.

Случай уже рассмотрен .

Ответ:уравнение имеет единственное решение при

ПРИМЕР 10.

При каких значениях параметра сумма корней уравнения

равна 2?

Решение:

Чтобы уравнение имело корни ,

По теореме Виета,

Таким образом, имеем систему:

Ответ: при

ПРИМЕР 11.

При каких значениях параметра уравнение

имеет два разных положительных корня ?

Решение:

Для того, чтобы квадратное уравнение имело два разных действительных корня, необходимо, чтобы дискриминант

По теореме Виета:

Таким образом, имеем систему неравенств :

Ответ: уравнение имеет два разных положительных корня,

если .

ПРИМЕР 12.

При каких значениях параметра один корень уравнения

меньше, чем -2 , три других- больше -1 ?

Решение:

В условии задачи идёт речь о четырёх корнях , т.е. Пусть тогда

данное уравнение примет вид

Чтобы данное уравнение имело четыре действительных корня , которые удовлетворяют условию задачи , необходимо, чтобы корни уравнения относительно t удовлетворяли условиям:

Итак имеем систему неравенств :

где

Ответ: при

ПРИМЕР 13.

При каких значениях параметра уравнение имеет

единственный корень ? Найти его.

Решение:

а) тогда

б) тогда

Ответ: при

ПРИМЕР 14.

Определить количество целых значений параметра из промежутка ,

при которых квадратное уравнение имеет два разных корня.

Решение:

Для того , чтобы квадратное уравнение имело два разных корня, необходимо, чтобы

Ответ: 4.

ПРИМЕР 15.

При каком наименьшем целом значении уравнение

имеет четыре решения ?

Решение :

Построим в одной системе координат графики функций и

Видим, что при эти графики имеют четыре точки пересечения.

Ответ:

ПРИМЕР 16.

Найдите количество целых значений , при которых сумма корней уравнения принадлежит промежутку .

Решение:

Сумма корней уравнения равна

Итак ,

Целые числа, которые удовлетворяют условию 11, 12,13, 14,15.

Ответ: пять.

ПРИМЕР 17.

Найдите количество целых значений , при которых произведение корней уравнения принадлежит промежутку .

Решение:

Произведение корней уравнения равно

Итак,

Целые числа , которые удовлетворяют условию это 23, 24, 25.

Ответ:три.

ПРИМЕР 18.

При каком наименьшем натуральном значении параметра корни уравнения являются рациональными числами?

Решение:

Для того ,чтобы корни уравнения были рациональными числами, необходимо, чтобы выражение было полным квадратом ,т.е.

будет полным квадратом при наименьшем натуральном значении

Ответ: при

ПРИМЕР 19.

При каком значении параметра квадратное уравнение

имеет корни, равные по абсолютной величине и противоположные по значению ?

Решение:

разделим на

Ответ: при

ПРИМЕР 20.

При каком наибольшем целом значении параметра корни уравнения

находятся по разные стороны промежутка ?

Решение:

Запишем левую часть уравнения как функцию

Нарисуем график этой функции ( схематично).

Мы видим, что корни уравнения находятся по разные стороны промежутка

, если выполняются условия:

Ответ:

ПРИМЕР 21.

При каком значении параметра сумма квадратов корней уравнения

равна 12?

Решение:

По теореме Виета: По условию: тогда

Т.е.

Ответ:

ПРИМЕР 22.

При каком значении параметра произведение корней уравнения

будет наибольшим?

Решение:

По теореме Виета произведение корней этого уравнения равняется :

Сумма двух положительных чисел принимает наименьшее значение, если одно из слагаемых равно нулю. Итак ,

Ответ:

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.

1.Решить уравнение:

Ответы:

1) если

корней нет, если если если

2) если

при корней нет при

3) если корней нет, если

2.При каких значениях параметра уравнение

имеет единственное решение ?

Ответ: ни при каких.

3.При каких значениях параметра уравнение

имеет два разных действительных корня?

Ответ: при

4.При каких значениях параметра уравнение

имеет единственное решение ?

Ответ: при

5.Сколько решений имеет уравнение в зависимости от параметра ?

Ответ: два корня, если

три корня, если

6.При каких значениях параметра уравнение

имеет единственное решение?

Ответ: при

7.При каком значении параметра произведение корней уравнения

равно 8?

Ответ: при

8.При каких значениях параметра уравнение имеет

два разных отрицательных корня ?

Ответ: при

9.При каких значениях параметра уравнение имеет

два разных действительных отрицательных корня?

Ответ: при

10.При каких значениях параметра уравнение имеет корни разных знаков ?

Ответ: при

11.При каких значениях параметра уравнение имеет

корни такие, что и ?

Ответ: при

12.Найти все значения , при которых один из корней уравнения

меньше чем 1, а второй – больше 1.

Ответ:

13.Найти все значения , при которых корни уравнения

больше, чем 1.

Ответ:

Квадратные уравнения с параметром.

Презентация на тему:

«Уравнения второй степени с параметром»

Выполнили ученицы 9 В класса:

Возиянова Светлана

Галиева Анастасия

Цели:

Определение количества корней квадратного уравнения в зависимости от параметра;
Решение уравнений с параметром.

Квадратное уравнение

Уравнение вида ах²+bx+с=0, где а, b, с Є R, а ≠ 0 называется квадратным уравнением. D=b²-4ac – дискриминант квадратного уравнения.

Если D0, то уравнение имеет два различных корня:

Если D=0, то уравнение имеет один корень.

Алгоритм решения квадратных уравнений с параметром

1)Если в квадратном уравнении главный коэффициент содержит параметр, то обязательно нужно выяснить, при каких значениях параметра главный коэффициент равен нулю. В этом случае квадратное уравнение превращается в линейное, которое имеет один корень.

2) Если в квадратном уравнении главный коэффициент не содержит параметра, то количество корней зависит только от значения дискриминанта.

Примеры:

Пример 1. При каком значение параметра b уравнение 2х²-bx+18=0 имеет единственный корень?

Решение: Данное уравнение является квадратным. Оно имеет единственный корень, если его дискриминант равен нулю. Имеем:

D=b²-4*2*18 = b²-144;

b²-144=0;

b= -12 или b= 12.

Ответ: b= -12, или b=12

Пример 2. При каком значение параметра b уравнение (b+6)x²-(b-2)x+1=0 имеет единственный корень?

Решение: Считать такое уравнение квадратным является ошибкой. Это уравнение степени не выше второй.

При b= -6 получаем линейное уравнение 8x+1=0, имеющее один корень.

При b ≠ -6 данное уравнение является квадратным; оно имеет единственный корень, если его дискриминант равен нулю:

D=(b-2)²-4(b+6) = b²-4b+4-4b-24 = b²-8b-20

Имеем: b²-8b-20=0, отсюда b= -2 или b=10.

Ответ: b= -2, или b=10, или b= -6

0. Отсюда а-1/3. Однако промежуток (-1/3;+∞) содержит значение а=0, при котором исходное уравнение имеет единственный корень, что не удовлетворяет условию задачи. Ответ: а= -3, или -1/30 «

Пример 3. При каких значениях параметра а уравнение a(a+3)х²+(2a+6)x-3a-9=0 имеет больше одного корня?

Решение: При а=0 получаем линейное уравнение 6х-9=0, имеющее единственный корень.

При а=-3 получаем линейное уравнение 0х=0, имеющее бесконечно много корней.

Если а≠0 и а≠ -3, то, разделив обе части уравнения на а+3, получим квадратное уравнение ах²+2х-3=0. Дискриминант этого уравнения равен 4(1+3а). Для выполнения условия задачи он должен быть положительным, т.е. 4(1+3а)0. Отсюда а-1/3. Однако промежуток (-1/3;+∞) содержит значение а=0, при котором исходное уравнение имеет единственный корень, что не удовлетворяет условию задачи.

Ответ: а= -3, или -1/30

Пример 4. Решить уравнение (a²-b²)х²-2ax+1=0.

Решение: Рассмотрим три случая:

1) a=b=0. Уравнение 0x+1=0 решений не имеет.

2) a²=b²≠0. Уравнение -2ax+1=0 имеет один корень x=1/2a.

3) a²-b²≠0. Корни уравнения: x1= 1/a-b, x2= 1/a+b.

При b=0 D=b²=0, поэтому уравнение имеет один корень x=1/a (a ≠0).

Ответ: x=1/2a при a²=b²≠0; x=1/a при a ≠0, b=0; ∅ при a=0, b=0; x1= 1/a-b, x2= 1/a+b при a ² ≠ b ², b ≠0

Пример 5. Решить уравнение (4a/x²-a²)+ (x-a/x(x+a))=(1/x(x-a))

Решение: При x≠0, x≠a, x≠-a уравнение приведём к равносильному 4ax+x²-2ax+a²-x-a=0.

(x+a)²-(x+a)=0

(x+a)(x+a-1)=0

Так как x≠-a, то уравнение имеет одно решение x=1-a. Условия x≠0, x≠a влекут за собой требования a≠1, a≠1/2. Уравнение 1-a=-a решений не имеет.

Ответ: x=1-a при a≠1/2; a≠1; ∅ при a=1/2, a=1

Пример 6. При каких значениях a уравнение aх²-x+3=0 имеет единственное решение?

Решение: Ошибочно считать данное уравнение квадратным. На самом деле это уравнение степени не выше второй. Исходя из этого соображения, рассмотрим следующие случаи:

1)a=0. При этом уравнение принимает вид -x+3=0, откуда x=3, т.е. решение единственно.

2) a≠0, тогда aх²-x+3=0 – квадратное уравнение, дискриминант D=1-12a. Для того, чтобы уравнение имело единственное решение, нужно, чтобы D=0, откуда a=1/12.

Ответ: a=0 или a=1/12

Пример 7. Один из корней квадратного уравнения х²+2ах+2-3а=0 равен 1. Найдите значение параметра а и второй корень уравнения.

Решение: х1=1 подставим его в уравнение и получим верное равенство: 1²+2а*1+2-3а=0 или 3-а=0, откуда а=3. Подставим это значение параметра а в данное уравнение: х²+2*3*х²+2-3*3=0 или х²+6х-7=0.

Решим это квадратное уравнение: х1=1 и х2= -7.

Получили а=3 и х2= -7

Ответ: а=3; х2= -7

Пример 8. При каких значениях параметра а сумма квадратов корней уравнения x²+ax+a=0 равна 3?

Решение: Пусть x1 и x2 – корни данного уравнения. По условию x1² + x2²=3, т.е. (x1+x2)²-2x1x2 = 3. Применяя теорему Виета, можно записать (-a)²-2a=3; a²-2a-3=0. Отсюда a=-1 или a=3.

Казалось бы, решение завершено. Однако теорема Виета «работает» лишь для тех квадратных уравнений, у которых есть корни. А данное квадратное уравнение имеет корни не при всех значениях параметра a. Существование корней определяется условием D ≥0. Для данного уравнения D=a ²-4a. Следовательно, найденные значения a= -1 и a=3 должны удовлетворять неравенству a²-4a≥0. Легко установить, что подходит только a= -1.

Ответ: а= -1

Пример 9. При каких значениях параметра а уравнение (a+6)х²+2ax+1=0 имеет единственное решение?

Решение: По условию задачи уравнение необязательно является квадратным, поэтому рассмотрим два случая:

1) а+6=0; а=-6

Если а = -6, то -12х+1=0, х = 1/12.

2) Если а ≠ -6, то квадратное уравнение имеет единственное решение, если D =0 D=4a²-4(a+6)=4(a²-a-6) a²-a-6=0 a1=3, a2=-2.

Ответ: при a ∈ {-6, -2, 3}

0. Из неравенства (2a+3)²-4(a²-a+5)0 следует, что 16a-110, откуда a11/16. Наименьшее целое значение a ∈ (11/16; +∞) равно 1. Ответ: a=1. «

Пример 10. Найти наименьшее целое a, при котором уравнение x²+(2a+3)x+a²-a+5=0 имеет два различных корня.

Решение: Уравнение имеет два различных корня, если D0. Из неравенства (2a+3)²-4(a²-a+5)0 следует, что 16a-110, откуда a11/16. Наименьшее целое значение a ∈ (11/16; +∞) равно 1.

Ответ: a=1.

Источники:

1) Алгебра. Углублённый уровень. 8 класс (Мерзляк А. Г., Поляков В. М.)
2) Локоть В.В. Задачи с параметрами. Линейные и квадратные уравнения, неравенства, системы

Урок «Решение квадратных уравнений с параметром»

Министерство образования и науки Самарской области

Государственное автономное образовательное учреждение дополнительного профессионального образования (повышения квалификации) специалистов

САМАРСКИЙ ОБЛАСТНОЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ

И ПЕРЕПОДГОТОВКИ РАБОТНИКОВ ОБРАЗОВАНИЯ

Итоговая работа

На курсах повышения квалификации

«Методические особенности обучения решению задач с параметром в условиях перехода к новым образовательным стандартам».

По ИОЧ ВБ 13.03.2017г-17.03.2017г

по теме:

« Квадратные уравнения с параметрами»

Выполнила:

Тихонова Надежда Викторовна,

Преподаватель математики

БГПОУ Сызранский «политехнический колледж»

Сызрань 2017 г.

. КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРАМИ

Уравнение вида ax2+bx+c=0, где a, b, c – числа, причем а≠0 называется

квадратным уравнением.

а – первый коэффициент, b – второй коэффициент, с – свободный член.

Например:

а) 2х2– 3х + 0,7 = 0

б) -0,9 х2+ 8 – 2 1/6х=0

Найти a, b, c?

Решим уравнение ax2+bx+c=0

а) если а=0, то уравнение имеет вид bx+c=0. Тогда x=-c|b

б) если а≠0, то уравнение имеет:

1) 2 различных корня х1≠х2, если Д>0,

2) 2 равных корня х1=х2, если Д=0

3) не имеет корней, если Д<0.

Рассмотрим примеры.

Пример №1. При каких значениях уравнение имеет 2 корня?

2х2+6х+b=0

Уравнение квадратное.

Найдем Д=36-4*2*b=36-8b. По условию задачи уравнение имеет 2 корня,

значит Д>0.

Решим неравенство 36-8b>0

-8b>-36

b<4,5.

Ответ: при b<4,5.

Пример № 2. При каких значениях имеет один корень?

3х2-6х+2v=0

Уравнение квадратное. Д=36-4*3*2v=36-24v.

Так как уравнение имеет один корень, то Д=0.

36-24v=0

24v=36

V=1,5.

Пример № 3. При каких t уравнение не имеет корней?

2×2-15x+t=0

Уравнение квадратное. Д=225-4*2t=225-8 t По условию Д<0, то

225-8t<0

-8t<-225

t>281/8.

Ответ: при t>281/8/

Пример № 4.

При каких значениях m равно один из корней уравнения равен нулю. х2 – 2х + 2m – 3 = 0

Решение: Если х = 0, то имеем:

02 – 2 .0 + 2m – 3 = 0

2m = 3

m = 1,5

Проверим, не равняется ли второй корень уравнения нулю.

х = 0

х = 2

х2 – 2х = 0

Ответ: m = 1,5

При решении квадратного уравнения с параметрами контрольными будут те значения параметра, при которых коэффициент при х2 обращается в 0. Дело в том, что если этот коэффициент равен нулю, то уравнение превращается в линейное и решается по соответствующему алгоритму; если же этот коэффициент отличен от нуля, то имеем квадратное уравнение, которое решается по иному алгоритму. Дальнейшее решение зависит от дискриминанта.

Пример №.5

Решить уравнение х2 – (2р + 1)х + (р2 + р – 2) = 0

Решение: Здесь коэффициент перед х2 отличен от нуля, значит данное уравнение при любых значениях параметра является квадратным. Найдем дискриминант:

D = (2р + 1)2 – 4∙1(р2 + р – 2) = (4р2 + 4р + 1) – (4р2 + 4р – 8) = 4р2 + 4р + 1 – – 4р2 – 4р + 8 = 9

D > 0, значит квадратное уравнение имеет два решения

х1 = р + 2

х2 = р – 1

Ответ: при любых значениях р х1 = р + 2; х2 = р – 1

Пример № 6.

Решить уравнение рх2 +( 1 – р)х – 1 = 0

Решение: Мы не можем утверждать, что данное уравнение является квадратным. Рассмотрим контрольные (точки) значения р = 0, имеем два случая.

Если р=0, то получается уравнение вида 0∙х2 + х – 1 = 0, которое является линейным и имеет корень х = 1

Если р ≠0, то уравнение является квадратным, можно применять формулы корней квадратного уравнения.

D = (1 – р)2 – 4∙.р .(-1) = 1 – 2р + р2 + 4р = (1+ р)2

х1 = 1

х2 = –

Ответ: при р = 0 х = 1; при р ≠0 х1 = 1 х2 = –

Пример № 7

Решить уравнение: (а – 1)х 2 + 2(2а + 1)х + (4а + 3) = 0

Решение: здесь контрольными будут те значения параметра, при которых коэффициент при х2 обращается в 0.

Если а – 1 = 0, а = 1, уравнение имеет вид 0∙ х2 + 6х + 7 = 0 и является линейным. Корнем этого уравнения является х =

Если а–1 ≠ 0, а ≠ 0, уравнение является квадратным. Найдем его дискриминант.

D = (2∙(2а + 1))2 – 4(а – 1)(4а + 3) = 4(4а2 + 4а + 1) – 4(4а2 – а – 3) = 4(5а + 4)

Дальнейшие рассуждения зависят от значения дискриминанта.

Если D < 0, то квадратное уравнение не имеет корней; если D = 0, то уравнение имеет один корень, если D > 0, то уравнение имеет два корня.

Дискриминант обращается в нуль при а = – (можно сказать, что это – второе контрольное значение параметра; при переходе через него происходит качественное изменение уравнения – меняется число корней уравнения).

Если а < – , то D < 0 и следовательно, квадратное уравнение не имеет корней.

Если а > – , то если D > 0 и, значит квадратное уравнение имеет два корня:

х1 =

х2 =

Если а = – , то D = 0, то уравнение имеет единственное решение

х =

Ответ: при а = 1, х = – ;

при а = –, х = ;

при а < –, корней нет;

при а > –, х1 =

х2 =

Иногда задания сформулированы так, что искать корни нет необходимости.

Пример №8

При каких значениях m ровно один из корней х2+(m+3)х +|m| – 3 = 0

уравнения равен нулю.

Решение. Если нуль является корнем уравнения, квадратный трехчлен х2+(m+3)х +|m| – 3 при х = 0 обращается в нуль. 02+(m+3) .0 +|m| – 3 = 0

|m| – 3 = 0 m1 = 3 m2 = –3

Найдем второй корень при найденных значениях m.

Если m=3, то уравнение принимает вид х2+6х = 0; х1 = 0 х2 = –6

Если m= –3, то уравнение принимает вид х2 = 0, которое имеет два кратных корня, равных нулю.

Ответ: при m = 3

Пример №9

Сколько корней имеет уравнение 3х (х – 1) 2 = kх в зависимости от значения параметра k ?

Решение: 3х (х – 1) 2 = kх

3х (х – 1) 2 – kх = 0

х (3(х – 1) 2 – k) = 0

Один корень есть всегда – х0 = 0

Исследуем 3х 2 – 6х + 3 – k = 0

D = 32 – 3(3 – k) = 3k

а) Если k = 0, существует один корень х = 1;

б) Если k > 0, существуют два корня х1 = х2 = , но необходимо исследовать случай, когда один из корней равен 0.2-ta=t2−t и t≥0t\ge 0t≥0.

Уравнения с параметрами. — Математика

Файл к уроку

Решение уравнений с параметрами.

Не так давно 8 класс познакомился с квадратными уравнениями и алгоритмами их решения. Сегодня мы рассмотрим еще один вид уравнений, который часто встречается на олимпиадах и турнирах, и включен в ЕГЭ по профильной математике – это уравнения с параметром. Что такое параметр? Обычно это число, в зависимости от значения которого уравнение, будь оно линейным или квадратным, может иметь корни, а может их не иметь.

Задачи с параметрами считаются сложными ,однако если разобраться досконально, из каких шагов состоит путь к решению уравнения, то параметр уже не кажется такой злобной величиной.

Линейные уравнения с параметрами.

Уравнение вида

где a, b из R, x — переменная, называется уравнением первой степени (линейным уравнением).

Уравнение равносильно уравнению

ax = – b

откуда следует следующее утверждение.

Если a ≠ 0, то уравнение имеет единственное решение x = – ^b/_a;
Если a = 0, b ≠ 0, то множество решений уравнения пусто;
Если a = 0, b = 0, то любое действительное число является решением уравнения.

Решить уравнение с параметром – значит указать решение при всех значениях параметра, то есть фактически решить бесконечное множество уравнений, объединив их в одно по неким схожим зависимостям от параметра.

Пример 1. Решить уравнение: a²x – 1 = x + a.

Пример 2. Решить уравнение с параметром |6 – x| = a.

Решение.

Легко видеть, что здесь a ≥ 0.

По правилу модуля 6 – x = ±a, выразим х:

x = 6 ± a.

Ответ: х = 6 ± a, где a ≥ 0.

Пример 3. Решить уравнение x/a + 1 = а + х относительно переменной х.

Решение.

Если а = 0, то преобразуем уравнение к виду а + х = а² + ах или (а – 1)х = —а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.

Если а ≠ 1, то последнее уравнение примет вид х = —а.

Данное решение можно проиллюстрировать на координатной прямой (рис. 1)

Ответ: нет решений при а = 0; х – любое число при а = 1; х = —а при а ≠ 0 и а ≠ 1.

Пример 4. При каких значениях параметра b уравнение не имеет корней:

Графический метод

Рассмотрим еще один способ решения уравнений с параметром – графический. Этот метод применяется достаточно часто.

Пример 5. Сколько корней в зависимости от параметра a имеет уравнение ||x| – 2| = a?

Решение. Для решения графическим методом строим графики функций y = ||x| – 2| и y = a (рис. 2).

На чертеже наглядно видны возможные случаи расположения прямой y = a и количество корней в каждом из них.

Ответ: корней у уравнения не будет, если а a 2 и а = 0; три корня уравнение будет иметь в случае а = 2; четыре корня – при 0 a

Пример 6. При каком а уравнение 2|x| + |x – 1| = a имеет единственный корень?

Решение.

Изобразим графики функций y = 2|x| + |x – 1| и y = a. Для y = 2|x| + |x – 1|, раскрыв модули методом промежутков, получим:

{-3x + 1, при x

y = {x + 1, при 0 ≤ x ≤ 1,

{3x – 1, при x 1.

На рисунке 3 хорошо видно, что единственный корень уравнение будет иметь только при а = 1.

Ответ: а = 1.

Пример 7. При каких значениях параметра а неравенство имеет решением все действительные числа:

Системы линейных уравнений с параметрами.

– Система имеет единственное решение.

– Система имеет бесконечное множество решений.

– Система не имеет решений.

Пример 8. Для всех значений параметра а решить систему уравнений

Квадратичные уравнения с параметрами.

Решение уравнений второй степени сводится к исследованию поведения квадратного трехчлена, исследованию знака дискриминанта при различных значениях параметра. Часто при решении нам может помочь теорема Виета, когда вопрос стоит о корнях разных знаков, о корнях одного знака.

Квадратное уравнение может не иметь решений (Da=0 или D=0), два решения (D0) или бесконечное множество решений (когда при каком-то значении параметра получаем 0=0).

Пример 9. Решить уравнение в зависимости от параметра а:

Пример 10. При каких значениях корни уравнения положительны?

Пример 11. Найти значения параметра а, при которых среди корней уравнения имеется ровно один отрицательный:

Пример 12. Найти все значения параметра а, при которых уравнение имеет два различных отрицательных корня:

Пример 13. При каких значениях m корни уравнения 4x² – (3m + 1) x – m – 2 = 0 лежат в промежутке между –1 и 2?

Пример 14: Найти все значения параметра а, при которых меньший корень уравнения x² + (a + 1) x + 3 = 0 лежал в интервале (–1; 3)

Решайте уравнения с квадратными корнями — элементарная алгебра

Цели обучения

К концу этого раздела вы сможете:

Решите радикальные уравнения
Использование квадратного корня в приложениях

Перед тем, как начать, пройдите тест на готовность.

Упростить: ⓐ ⓑ.
Если вы пропустили эту проблему, просмотрите (Рисунок) и (Рисунок).
Решить:.
Если вы пропустили эту проблему, просмотрите (рисунок).
Решить:.
Если вы пропустили эту проблему, просмотрите (рисунок).

Решите радикальные уравнения

В этом разделе мы решим уравнения, в которых переменная находится в подкоренном выражении квадратного корня. Уравнения этого типа называются радикальными уравнениями.

Радикальное уравнение

Уравнение, в котором переменная находится в подкоренном выражении квадратного корня, называется радикальным уравнением.

Как обычно, при решении этих уравнений, то, что мы делаем с одной стороной уравнения, мы должны делать и с другой стороной.Поскольку возведение величины в квадрат и извлечение квадратного корня являются «противоположными» операциями, мы возведем обе стороны в квадрат, чтобы убрать знак корня и найти переменную внутри.

Но помните, что когда мы пишем, мы имеем в виду главный квадратный корень. Так всегда. Когда мы решаем радикальные уравнения, возводя обе части в квадрат, мы можем получить алгебраическое решение, которое будет отрицательным. Это алгебраическое решение не было бы решением исходного радикального уравнения; это постороннее решение. Мы видели посторонние решения и при решении рациональных уравнений.

Для уравнения:

ⓐ Есть решение? Ⓑ Есть решение?

Для уравнения:

ⓐ Есть решение? Ⓑ Есть решение?

ⓐ нет ⓑ

Для уравнения:

ⓐ Есть решение? Ⓑ Есть решение?

ⓐ нет ⓑ

Теперь посмотрим, как решить радикальное уравнение. Наша стратегия основана на соотношении извлечения квадратного корня и возведения в квадрат.

Как решать радикальные уравнения

Решить:.

Решите радикальное уравнение.

Выделите радикал на одной стороне уравнения.
Возведите обе части уравнения в квадрат.
Решите новое уравнение.
Проверьте ответ.

Решить:.

Когда мы используем знак корня, мы имеем в виду главный или положительный корень. Если в уравнении квадратный корень равен отрицательному числу, это уравнение не будет иметь решения.

Решить:.

Решение


Чтобы изолировать радикал, вычтите 1 с обеих сторон.
Упростить.
Поскольку квадратный корень равен отрицательному числу, уравнение не имеет решения.

Решить:.

Если одна сторона уравнения является биномом, мы используем формулу биномиальных квадратов, когда возводим ее в квадрат.

Биномиальные квадраты

Не забывайте про средний семестр!

Решить:.

Когда перед радикалом стоит коэффициент, мы должны возвести его в квадрат.

Решить:.

Решение

Решить:.

Иногда после возведения в квадрат обеих частей уравнения внутри радикала остается переменная.Когда это произойдет, мы повторяем шаги 1 и 2 нашей процедуры. Выделяем радикал и снова возводим обе части уравнения в квадрат.

Решить:.

Решение

Решить:.

Решение

Решить:.

Использование квадратного корня в приложениях

По мере прохождения курсов в колледже вы будете сталкиваться с формулами, включающими квадратные корни во многих дисциплинах.Мы уже использовали формулы для решения геометрических приложений.

Мы будем использовать нашу стратегию решения проблем для геометрических приложений с небольшими изменениями, чтобы дать нам план решения приложений с формулами из любой дисциплины.

Решайте приложения с помощью формул.

Прочтите задачу и убедитесь, что все слова и идеи понятны. При необходимости нарисуйте фигуру и пометьте ее данной информацией.
Определите то, что мы ищем.
Назовите то, что мы ищем, выбрав переменную для его представления.
Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.
Решите уравнение , используя хорошие методы алгебры.
Проверьте ответ в задаче и убедитесь, что он имеет смысл.
Ответьте на вопрос полным предложением.

Мы использовали формулу, чтобы найти площадь прямоугольника длиной L и шириной W .Квадрат — это прямоугольник, у которого длина и ширина равны. Если принять s как длину стороны квадрата, площадь квадрата равна.

Формула дает нам площадь квадрата, если мы знаем длину стороны. Что, если мы хотим найти длину стороны для данной области? Затем нам нужно решить уравнение для s .

Мы можем использовать формулу, чтобы найти длину стороны квадрата для заданной площади.

Площадь квадрата

Мы покажем это в следующем примере.

Кэти хочет посадить квадратный газон перед своим двором. У нее достаточно дерна, чтобы покрыть площадь в 370 квадратных футов. Используйте формулу, чтобы найти длину каждой стороны ее газона. Округлите ответ до ближайшей десятой доли фута.

Серджио хочет сделать квадратную мозаику в качестве инкрустации для стола, который он строит. У него достаточно плитки, чтобы покрыть площадь в 2704 квадратных сантиметра. Используйте формулу, чтобы найти длину каждой стороны его мозаики. Округлите ответ до ближайшей десятой доли фута.

Еще одно применение квадратных корней связано с гравитацией.

Падающие предметы

На Земле, если объект падает с высоты футов, время в секундах, которое потребуется, чтобы достичь земли, определяется по формуле:

Например, если объект падает с высоты 64 фута, мы можем вычислить время, необходимое для достижения земли, подставив его в формулу.



Извлеките квадратный корень из 64.
Упростим дробь.

Чтобы объект, упавший с высоты 64 фута, достиг земли, потребуется 2 секунды.

Кристи уронила свои солнцезащитные очки с моста на высоте 400 футов над рекой. Используйте формулу, чтобы определить, сколько секунд потребовалось солнцезащитным очкам, чтобы добраться до реки.

Вертолет сбросил спасательный пакет с высоты 1296 футов. Используйте формулу, чтобы определить, сколько секунд потребовалось, чтобы пакет достиг земли.

Мойщик окон сбросил ракель с платформы на высоте 196 футов над тротуаром. Используйте формулу, чтобы определить, сколько секунд прошло, чтобы ракель достиг тротуара.

Сотрудники полиции, расследующие автомобильные аварии, измеряют длину следов заноса на тротуаре. Затем они используют квадратные корни для определения скорости в милях в час, которую машина ехала до того, как затормозила.

Следы заноса и скорость автомобиля

Если длина пятен заноса составляет d футов, то скорость автомобиля с до того, как были применены тормоза, можно определить по формуле

После автомобильной аварии следы заноса одной машины достигли 190 футов.Используйте формулу, чтобы найти скорость автомобиля до того, как были задействованы тормоза. Округлите ответ до ближайшей десятой.

Следователь ДТП измерил следы заноса автомобиля. Длина следов заноса составляла 76 футов. Используйте формулу, чтобы найти скорость автомобиля до того, как были задействованы тормоза. Округлите ответ до ближайшей десятой.

Следы заноса автомобиля, попавшего в аварию, были длиной 122 фута. Воспользуйтесь формулой, чтобы найти скорость автомобиля до того, как были задействованы тормоза.Округлите ответ до ближайшей десятой.

Ключевые концепции

Для решения радикального уравнения:
1. Выделите радикал на одной стороне уравнения.
2. Возведите обе части уравнения в квадрат.
3. Решите новое уравнение.
4. Проверьте ответ. Некоторые полученные решения могут не работать в исходном уравнении.
Решение приложений с помощью формул
1. Прочтите задачу и убедитесь, что все слова и идеи понятны.При необходимости нарисуйте фигуру и пометьте ее данной информацией.
2. Определите то, что мы ищем.
3. Назовите то, что мы ищем, выбрав переменную для его представления.
4. Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.
5. Решите уравнение , используя хорошие методы алгебры.
6. Проверьте ответ в задаче и убедитесь, что он имеет смысл.
7. Ответьте на вопрос полным предложением.
Площадь квадрата
Падающие предметы
- На Земле, если объект падает с высоты футов, время в секундах, которое потребуется, чтобы достичь земли, определяется по формуле.
Следы заноса и скорость автомобиля
- Если длина пятен заноса составляет d футов, то скорость автомобиля до того, как были задействованы тормоза, с можно определить по формуле.

Письменные упражнения

Объясните, почему уравнение вида не имеет решения.

ⓐ Решите уравнение.
ⓑ Объясните, почему одно из найденных «решений» на самом деле не было решением уравнения.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.

ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?

Глоссарий

радикальное уравнение: Уравнение, в котором переменная находится в корневом выражении квадратного корня, называется радикальным уравнением

8.3 — Параметрические уравнения

В прошлом мы работали с прямоугольными уравнениями, то есть уравнениями, включающими только x
и y, чтобы их можно было изобразить в декартовой (прямоугольной) системе координат.

У нас также был пример зависимости высоты свободно падающего тела от времени в секундах t.
Эта функция была квадратичной функцией. Если объект не уронили или не бросили прямо в
воздух, также будет горизонтальная составляющая его положения.Горизонтальная составляющая — это
простая функция расстояния (d = rt).

Путь падающего объекта

y (t) = -16t ² — v ₀ t + y ₀

х (т) = г т

v ₀ = начальная вертикальная скорость

y ₀ = начальная высота

r = горизонтальная скорость

t = время в секундах

Обратите внимание, что обе эти функции, вертикальная высота и
горизонтальное расстояние зависит от времени.Итак, чтобы полностью
Чтобы описать путь объекта, нам понадобятся два уравнения. Один
для вертикального компонента и один для горизонтального
составная часть. Обе эти функции являются функциями
третья переменная, т.

Это дает нам параметрические уравнения. Параметр просто
независимая переменная в функции.

Построение плоской кривой

Плоская кривая получается, когда упорядоченные пары (x (t), y (t)) отображаются на графике для всех значений t на некотором
интервал.

Один из способов нарисовать плоскую кривую — составить таблицу значений.Параметр t имеет несколько
значения, перечисленные для него, и соответствующие значения для x (t) и y (t) вычисляются. Затем заказали
пары строятся, а кривая проводится между построенными парами.

Ориентация или направление

При рисовании плоской кривой «направление увеличения t» или «ориентация»
кривой обозначается маленькими стрелками, указывающими, в каком направлении кривая
продвигается, когда стоимость
параметр t увеличивается.

Графический калькулятор

Графический калькулятор прекрасно справляется с графическим отображением параметрических уравнений.Ты должен,
однако сообщите калькулятору, что вы хотите графически отображать параметрические уравнения, а не обычные
функции. Для этого переведите калькулятор в параметрический режим, нажав [РЕЖИМ] и
выбирая опцию [PAR]. Не забудьте сбросить калькулятор обратно на [УДОВОЛЬСТВИЕ] для режима функций.
когда вы закончите с параметрическими уравнениями. Находясь в меню режима, вы можете
установите калькулятор в режим [РАДИАН] вместо режима [ГРАДУСЫ]. Они используются для
тригонометрические функции, которые мы не будем использовать, но они влияют на то, как клавиши масштабирования
Работа.

После настройки калькулятора для параметрического режима, обратите внимание, что когда вы нажимаете клавишу Y =, вы не
больше иметь y ₁ =. Теперь у вас есть пара уравнений, x и y, которые являются функциями t.
Просто введите параметрические уравнения для x и y. Обратите внимание, что ключ, который вы использовали для
X также обозначается T. В параметрическом режиме вместо X автоматически появляется буква T.

Параметры окна

Теперь у вас будет три дополнительных окна, которых у вас не было раньше.Tmin, Tmax и Tstep. Tmin — наименьшее значение параметра, который вы
хотите использовать. Если у вас нет
веская причина не делать этого (например, в домене указано t> = 0), обязательно используйте отрицательные
значения для Tmin. Tmax — это наибольшее значение параметра, который вы хотите
использовать. Если у вас нет веской причины не делать этого,
используйте положительное значение Tmax. Другими словами, убедитесь, что T может взять на себя оба
положительные и отрицательные значения. Tstep — это изменение T, и оно должно быть разумным.
для диапазона значений T
вы указали.

TMin = -5, TMax = 5 и TStep = 0,1 обычно являются хорошими начальными значениями. Если
вы обнаружите, что график не отображается, вы
май
нужно
чтобы изменить эти значения.

Предупреждение! Zoom Standard сбросит настройки
на T. Если вы сделаете стандартное масштабирование, ваш T будет находиться в диапазоне от 0 до 2 пи (в
в радианах) на пи / 24 и от 0 до 360 (в градусном режиме)
на 7,5. Ни один из них не содержит отрицательных значений и может не отображать весь
график.

Направление увеличения t — это направление, в котором калькулятор рисует кривую.
в.Обозначьте это стрелками, направленными вдоль кривой.

Удаление параметра

Другой способ нарисовать плоскую кривую — исключить параметр. Шаги к устранению
параметр прост.

Решите одно из параметрических уравнений относительно t.
Заменить t в другое параметрическое уравнение.

На шаге 1 вы должны решить относительно t в более простом уравнении. Легче решить
не всегда означает меньшую степень.Если у вас есть t ² и t ³,
решить для t в t ³ (если возможно). При выполнении
Таким образом, вы избегаете положительной / отрицательной ситуации, когда извлекаете квадратный корень из t.

Не всегда может быть необходимо полностью решить для t. Это ценно
когда один из членов появляется в других уравнениях.

Пример 1

Удалите параметр из x = 3t ² — 4 и y = 2t.

Функция y определенно является более простой функцией для определения t, и когда вы это сделаете,
вы получите t = y / 2.

Подставьте это в уравнение x для t, и вы получите x = 3 (y / 2) ² —
4. Упростите, чтобы получить x = 3/4 y ² — 4.

Пример 2

Рассмотрим систему уравнений x = e ^t и y = e ^3t.

Если бы вы решили эту проблему, используя шаги, перечисленные выше, вы бы предприняли
x = e ^t уравнение и решите его относительно t, чтобы получить t = ln x. Затем подставьте
это в уравнение y = e ^3t, чтобы получить y = e ^{3ln x}.С использованием
свойства логарифмов, вы бы переместили 3 в степень на x
а затем функции e и ln инвертируют, оставляя вас с y =
х ³.

Теперь подумайте об этом. y = e ^3t = (e ^t) ³.
Поскольку x = e ^t, замените e ^t на x. у = (х) ³
или просто y = x ³. Не было необходимости спускаться полностью до t.

Еще одно замечание об этой проблеме. Поскольку x и y являются экспоненциальными функциями,
диапазон на каждом из них — положительные реалы.Однако это теряется, когда
вы упрощаете до y = x ³. Обязательно наложите ограничение на домен
x, чтобы он был таким же, как оригинал. Это ограничение будет x> 0.

Решение, какой метод использовать при решении квадратных уравнений

Решение, какой метод использовать
при решении квадратных уравнений

При решении квадратного уравнения выполните следующие действия.
(в таком порядке) выбрать метод:

Сначала попробуйте решить уравнение на множители.Быть уверенным
что ваше уравнение имеет стандартную форму (ax ² + bx + c = 0) до того, как вы
начать попытку факторинга. Не тратьте много времени на попытки
фактор вашего уравнения; если вы не можете учесть его менее чем за 60 секунд,
перейти к другому методу.
Затем посмотрите на сторону уравнения, содержащую переменную.
Эта сторона — идеальный квадрат? Если это так, то вы можете решить уравнение
извлекая квадратный корень из обеих частей уравнения.Не забывай
чтобы включить знак ± в уравнение
как только вы извлечете квадратный корень.
Далее, если коэффициент при квадрате члена равен 1 и
коэффициент линейного (среднего) члена четный, завершая квадрат
это хороший метод для использования.
Наконец, квадратичная формула будет работать на любом квадратичном
уравнение. Однако, если использование формулы приводит к слишком большим
числа под знаком радикала, другой метод решения может быть лучше
выбор.

Теперь посмотрим на некоторые уравнения и подумаем о наиболее
подходящий метод их решения.

Пример 1: Решить x ² + 4 = 4x

Во-первых, представьте уравнение в стандартной форме, чтобы мы могли
попробуйте решить это факторингом:

х ² — 4х + 4 = 0

(х — 2) (х — 2) = 0

x — 2 = 0 | х — 2 = 0

x = 2 | х = 2

Итак, решение этого уравнения, найденное путем факторизации,
это x = 2.

Пример 2: Решить (2x — 2) ² = -4

Сторона уравнения, содержащая переменную (
левая сторона) представляет собой идеальный квадрат, поэтому мы извлечем квадратный корень из обеих сторон
для решения уравнения.

(2х — 2) ² = -4

2x — 2 = ± 2i

2x = 2 ± 2i

х = 1 ± я

Обратите внимание, что знак ±
был вставлен в уравнение в точке извлечения квадратного корня.

Пример 3: Решить x ² + 6x — 11 = 0

Это уравнение не факторизуемо, и сторона, содержащая
переменная не является точным квадратом. Но поскольку коэффициент
x ² равен 1, а коэффициент при x четный, завершая
квадрат будет подходящим методом. Чтобы найти номер, который нужно
быть добавленным к обеим частям уравнения, чтобы получить квадрат, возьмите
коэффициент при x, разделите его на 2, а затем возведите это число в квадрат.В
в этой задаче 6 ¸ 2 равно 3, а 3 ²
равно 9, поэтому мы добавим 9 к обеим частям уравнения, как только мы изолировали
переменные условия.

х ² + 6х — 11 = 0

x ² + 6x = 11

x ² + 6x +9 = 11 + 9

(х + 3) ² = 20

Пример 4: Решить 2x ² — x + 5 = 0

Это уравнение не факторизуемо, левая часть не учитывается.
полный квадрат, а коэффициенты при x ² и x членах
не сделает завершение квадрата удобным.Остается квадратичный
формула как лучший метод решения этого уравнения. Мы будем использовать a = 2, b = -1,
и c = 5.

Решение квадратных уравнений

Квадратичное уравнение — это уравнение, которое можно записать как

ось ² + bx + c = 0

, когда a 0.

Существует три основных метода решения квадратных уравнений: разложение на множители, использование формулы квадратов и завершение квадрата.

Факторинг

Чтобы решить квадратное уравнение на множители,

Поместите все члены с одной стороны от знака равенства, оставив ноль с другой стороны.
Коэффициент
.
Установите каждый коэффициент равным нулю.
Решите каждое из этих уравнений.
Проверьте, подставив свой ответ в исходное уравнение.

Пример 1

Решить x ² — 6 x = 16.

Следуя инструкциям,

x ² — 6 x = 16 становится x ² — 6 x — 16 = 0

Коэффициент

( x — 8) ( x + 2) = 0

Установка каждого коэффициента на ноль,

Затем проверить,

Оба значения, 8 и –2, являются решениями исходного уравнения.

Пример 2

Решить y ² = — 6 y — 5.

Устанавливая все члены равными нулю,

y ² + 6 y + 5 = 0

Коэффициент

( y + 5) ( y + 1) = 0

Установка каждого коэффициента на 0,

Для проверки, y ² = –6 y — 5

Квадратичный с отсутствующим членом называется неполным квадратичным элементом (при условии, что член ax ² не пропущен).

Пример 3

Решить x ² — 16 = 0.

Коэффициент

Для проверки, x ² — 16 = 0

Пример 4

Решить x ² + 6 x = 0.

Коэффициент

Для проверки, x ² + 6 x = 0

Пример 5

Решить 2 x ² + 2 x — 1 = x ² + 6 x — 5.

Во-первых, упростите, поместив все термины в одну сторону и комбинируя одинаковые термины.

Теперь фактор.

Для проверки, 2 x ² + 2 x — 1 = x ² + 6 x — 5

Квадратичная формула

Многие квадратные уравнения не могут быть решены факторизацией. Обычно это верно, когда корни или ответы не являются рациональными числами. Второй метод решения квадратных уравнений включает использование следующей формулы:

a, b, и c взяты из квадратного уравнения, записанного в его общем виде

ось ² + bx + c = 0

, где a — это число перед x ², b — это число перед x , а c — это число без переменной рядом с ним (a .k.a., «постоянная»).

При использовании формулы квадратного уравнения вы должны знать о трех возможностях. Эти три возможности различаются частью формулы, называемой дискриминантом. Дискриминант — это значение под знаком корня, b ² — 4 ac . Квадратное уравнение с действительными числами в качестве коэффициентов может иметь следующее:

Два разных действительных корня, если дискриминант b ²-4 ac является положительным числом.
Один действительный корень, если дискриминант b ² — 4 ac равен 0.
Нет действительного корня, если дискриминант b ²-4 ac является отрицательным числом.

Пример 6

Решить относительно x : x ² — 5 x = –6.

Установка всех членов равными 0,

x ²-5 x + 6 = 0

Затем замените 1 (который, как предполагается, стоит перед x ²), –5 и 6 вместо a , b и c, соответственно в формуле корней квадратного уравнения и упростите.

Поскольку дискриминант b ²-4 ac положительный, вы получаете два разных действительных корня.

Пример
производит рациональные корни. В примере
, квадратная формула используется для решения уравнения, корни которого нерациональны.

Пример 7

Решить относительно y : y ² = –2y + 2.

Установка всех членов равными 0,

y ² + 2 y — 2 = 0

Затем замените 1, 2 и –2 на a , b и c, соответственно в формуле корней квадратного уравнения и упростите.

Обратите внимание, что два корня иррациональны.

Пример 8

Решить относительно x : x ² + 2 x + 1 = 0.

Подставляя в формулу корней квадратного уравнения,

Поскольку дискриминант b ²-4 ac равен 0, уравнение имеет один корень.

Квадратичная формула также может использоваться для решения квадратных уравнений, корни которых являются мнимыми числами, то есть они не имеют решения в действительной системе счисления.

Пример 9

Решите относительно x : x ( x + 2) + 2 = 0 или x ² + 2 x + 2 = 0.

Подставляя в формулу корней квадратного уравнения,

Поскольку дискриминант b ² — 4 ac отрицателен, это уравнение не имеет решения в системе действительных чисел.

Но если бы вы выразили решение с помощью мнимых чисел, решения были бы такими.

Завершение квадрата

Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата.

Запишите уравнение в виде ax ² + bx = — c .
Убедитесь, что a = 1 (если a ≠ 1, умножьте уравнение на, прежде чем продолжить).
Используя значение b из этого нового уравнения, добавьте к обеим сторонам уравнения, чтобы получить полный квадрат в левой части уравнения.
Найдите квадратный корень из обеих частей уравнения.
Решите полученное уравнение.

Пример 10

Решить относительно x : x ² — 6 x + 5 = 0.

Оформить в виде

Поскольку a = 1, прибавьте или 9 к обеим сторонам, чтобы завершить квадрат.

Извлеките квадратный корень из обеих частей.

x — 3 = ± 2

Решить.

Пример 11

Решить относительно y : y ² + 2 y — 4 = 0.

Оформить в виде

Поскольку a = 1, прибавьте или 1 к обеим сторонам, чтобы завершить квадрат.

Извлеките квадратный корень из обеих частей.

Решить.

Пример 12

Решите относительно x : 2 x ² + 3 x + 2 = 0.

Оформить в виде

Поскольку a ≠ 1, умножаем уравнение на.

Добавьте или с обеих сторон.

Извлеките квадратный корень из обеих частей.

В действительной системе счисления нет решения. Вам может быть интересно узнать, что завершение квадратного процесса для решения квадратных уравнений использовалось для уравнения ax ² + bx + c = 0 для вывода формулы квадратичного.

Решение буквальных уравнений | Purplemath

Purplemath

Иногда нам дают формулу, например что-то из геометрии, и нам нужно найти какую-то переменную, отличную от «стандартной». Например, формула для периметра P квадрата со сторонами длиной s : P = 4 s .Нам может потребоваться решить это уравнение для s , потому что у нас есть много периметров квадратов, и мы хотим объединить эти значения периметра в одну формулу, и эта формула (возможно, в нашем графическом калькуляторе) выдаст значение длины стороны каждого квадрата. Этот процесс решения формулы для указанной переменной называется «решением буквальных уравнений».

MathHelp.com

Одно из словарных определений «литерала» — это «связанный с буквами или состоящий из букв», а переменные иногда называют литералами. Таким образом, «решение буквальных уравнений» кажется другим способом сказать «взять уравнение с большим количеством букв и решить для одной буквы, в частности.«

На первый взгляд эти упражнения кажутся намного хуже наших обычных решающих упражнений, но на самом деле они не так уж и плохи. Мы в значительной степени делаем то, что делали все это время, для решения линейных уравнений и других типов уравнений; единственное существенное отличие состоит в том, что из-за всех переменных мы не сможем упростить нашу работу по мере продвижения вперед, а также не сможем так сильно, как мы привыкли в конце. Вот как работает решение буквальных уравнений:

Это формула для площади A прямоугольника с основанием b и высотой h .Они просят меня решить эту формулу для основания b .

Если бы они попросили меня решить 3 = 2 b для b , я бы разделил обе стороны на 2, чтобы изолировать (то есть, чтобы получить само по себе или решить для) переменную б . Я бы получил переменную b , равную дробному числу.

В этом случае я не смогу получить простое числовое значение для своего ответа, но я могу поступить таким же образом, используя тот же шаг по той же причине (а именно, что он сам получает b ) .Итак, следуя тем же соображениям для решения этого буквального уравнения, что и для аналогичного линейного уравнения с одной переменной, я делю на « h »:

Единственное различие между решением буквального уравнения выше и решением линейных уравнений, о которых вы впервые узнали, состоит в том, что я разделил на переменную вместо числа (и тогда я не мог упростить, потому что дробь выражалась буквами, а не числами ).Поскольку мы не можем упрощать на ходу (и, вероятно, в конце), может быть очень важно , а не , пытаться сделать слишком много в уме. Запишите все полностью; это поможет вам получить правильные ответы.

Это уравнение представляет собой уравнение «равномерной скорости», «(расстояние) равно (скорость) раз (время)», которое используется в задачах «расстояние», и решение его для указанной переменной работает так же, как решение предыдущего уравнения.

Переменная, которую они хотят, умножена на букву; чтобы изолировать переменную, я должен разделить эту букву. Итак, я решу для указанной переменной r , разделив на t :

Это формула для периметра P прямоугольника длиной L и шириной w .

Если бы они попросили меня решить 3 = 2 + 2 w для w , я бы вычел «свободные» 2 в левую часть, а затем разделил бы на 2, умноженное на переменная. Я могу выполнить те же действия для этого уравнения:

Примечание. Я оставляю свои ответы на том этапе, когда я успешно решил для указанной переменной.Но это означает, что рассматриваемая переменная была в правой части уравнения. Это не «неправильно», но некоторые люди предпочитают помещать решаемую переменную в левую часть уравнения. Если вы предпочитаете это, то ответ выше был бы записан как:

С математической точки зрения подойдет любой формат, поскольку они оба означают одно и то же.

Решите
Q = ^{( c + d )}/₂ для d

Переменная, которую мне нужно выделить, в настоящее время находится внутри дроби.Мне нужно избавиться от знаменателя. Для этого я умножу на знаменатель, равный 2. В левой части я просто произведу простое умножение. С правой стороны, чтобы не усложнять задачу, я конвертирую 2 в дробную форму 2/1.

2 Q = c + d

2 Q — c = c + d — c

2 Q — c = d

Если бы они попросили меня решить 5 = ³/_t для t , я бы умножил на t , а затем разделил бы обе части на 5.Следуя тем же рассуждениям и выполняя те же действия, я получаю:

Это следующее упражнение требует небольшого трюка.

Мне нужно получить переменную и отдельно. В настоящее время это умножается на другие вещи двумя разными способами. Я не могу комбинировать эти термины, потому что они имеют разные переменные части.(У первого члена нет другой переменной, но у второго члена также есть переменная c .) Я хочу разделить то, что умножается на указанную переменную a , но я пока не могу, потому что есть разные вещи умноженный на это в двух разных местах. Но что, если я умножу на ?

«Уловка» заключена во второй строке, где я разложил на спереди с правой стороны.Сделав это, я создал один (большой, неуклюжий) множитель на на , который затем можно было разделить.

Этот метод (разложение для разделения) используется не часто, но он почти гарантированно появится в вашем домашнем задании один или два раза, и почти наверняка на вашем следующем тесте, именно потому, что так много учеников этого не делают. не вижу «хитрости». Так что имейте в виду: если вы не можете выделить желаемую переменную, потому что она является множителем в двух или более членах, соберите эти термины вместе на одной стороне знака «равно», вычтите искомую переменную, а затем разделите на все, что осталось после факторинга.

Решить
A = (½) ah — (½) bh для h

Поскольку каждая из двух дробей в правой части имеет одинаковый знаменатель 2, я начну с умножения на 2, чтобы очистить дроби. Затем я буду работать над выделением переменной h .

В этом примере использовалась та же уловка, что и в предыдущем.В четвертой строке я вычеркнул h. Вы должны знать, как это сделать!

Площадь
A сектора (сектор в форме клина) круга с радиусом r и углом S (в градусах) определяется как Решите это уравнение для S .

Это большое неуклюжее уравнение, но метод решения такой же, как и всегда.На переменную, которую я хочу, на нее умножено и разделено кое-что другое; Я делю и умножаю соответственно, чтобы выделить то, что мне нужно.

URL: https://www.purplemath.com/modules/solvelit.htm

Параметрических уравнений

Прямоугольное уравнение или уравнение в прямоугольной форме — это уравнение, состоящее из таких переменных, как

Икс

а также

который можно изобразить на регулярной декартовой плоскости.Например

знак равно

Икс

— прямоугольное уравнение.

Кривая на плоскости называется параметризованной, если набор координат на кривой

(

Икс

)

, представлены как функции переменной

Икс

знак равно

(

)

знак равно

грамм

(

)

Эти уравнения могут быть изображены на декартовой плоскости, а могут и нет.

Пример 1:

Найдите систему параметрических уравнений для уравнения

знак равно

Икс

Решение:

Присвойте любой из переменных значение

. (сказать

Икс

знак равно

Тогда данное уравнение можно переписать в виде

знак равно

Следовательно, система параметрических уравнений имеет вид

Икс

знак равно

а также

знак равно

Пример 2:

Удалите параметр и найдите соответствующее прямоугольное уравнение.

Икс

знак равно

Решение:

Перепишите уравнение

Икс

знак равно

в виде

с точки зрения

Икс

знак равно

Икс

знак равно

Икс

—

Теперь замените

от (

Икс

—

) в уравнении

знак равно

(

Икс

—

)

Следовательно, соответствующее прямоугольное уравнение имеет вид

знак равно

(

Икс

—

)

Существует еще один тип уравнений, называемых полярными уравнениями, которые необходимо изобразить на графике.

полярная плоскость

параметрических уравнений | Алгебра и тригонометрия

учебных целей

В этом разделе вы:

Параметризация кривой.
Удалите параметр.
Найдите прямоугольное уравнение для параметрической кривой.
Найдите параметрические уравнения для кривых, заданных прямоугольными уравнениями.

Рассмотрим путь, по которому следует Луна, когда она вращается вокруг планеты, которая одновременно вращается вокруг Солнца, как показано на (Рисунок). В любой момент Луна находится в определенном месте относительно планеты. Но как мы можем написать и решить уравнение для положения Луны, когда расстояние от планеты, скорость орбиты Луны вокруг планеты и скорость вращения вокруг Солнца — все это неизвестны? Мы можем решать только одну переменную за раз.

Рисунок 1.

В этом разделе мы рассмотрим системы уравнений, задаваемые [latex] \, x \ left (t \ right) \, [/ latex] и [latex] \, y \ left (t \ right) \, [/ латекс], где [латекс] t [/ латекс] — независимая переменная времени. Мы можем использовать эти параметрические уравнения в ряде приложений, когда мы ищем не только конкретное положение, но и направление движения. Когда мы отслеживаем последовательные значения [latex] \, t, \, [/ latex], ориентация кривой становится ясной. Это одно из основных преимуществ использования параметрических уравнений: мы можем отслеживать движение объекта по траектории в зависимости от времени.Мы начинаем этот раздел с рассмотрения основных компонентов параметрических уравнений и того, что означает параметризация кривой. Затем мы узнаем, как исключить параметр, преобразовать уравнения кривой, определенной параметрически, в прямоугольные уравнения и найти параметрические уравнения для кривых, определяемых прямоугольными уравнениями.

Параметризация кривой

Когда объект движется по кривой или криволинейной траектории в заданном направлении и за заданный промежуток времени, положение объекта в плоскости задается координатой x- и координатой y-.Однако и [латекс] \, x \, [/ latex] и [latex] \, y \, [/ latex]
меняются со временем и, следовательно, являются функциями времени. По этой причине мы добавляем еще одну переменную, параметр, от которого оба [latex] \, x \, [/ latex] и [latex] \, y \, [/ latex] являются зависимыми функциями. В примере в открывателе раздела параметром является время, [latex] \, t. \, [/ Latex] [latex] \, x \, [/ latex] положение луны в момент времени, [latex] \ , t, \, [/ latex] представлен как функция [latex] \, x \ left (t \ right), \, [/ latex] и положение [latex] \, y \, [/ latex] луна в момент времени, [латекс] \, t, \, [/ latex] представлена как функция [латекс] \, y \ left (t \ right).\, [/ latex] Вместе [latex] \, x \ left (t \ right) \, [/ latex] и [latex] \, y \ left (t \ right) \, [/ latex] называются параметрическими уравнения и сгенерировать упорядоченную пару [латекс] \, \ left (x \ left (t \ right), \, y \ left (t \ right) \ right). \, [/ latex] Параметрические уравнения в первую очередь описывают движение и направление.

Когда мы параметризуем кривую, мы переводим одно уравнение с двумя переменными, такими как [latex] \, x \, [/ latex] и [latex] \, y, [/ latex], в эквивалентную пару уравнений в три переменные, [латекс] \, x, y, \, [/ latex] и [латекс] \, t.\, [/ latex] Одна из причин, по которой мы параметризуем кривую, заключается в том, что параметрические уравнения дают больше информации: в частности, направление движения объекта во времени.

При графическом отображении параметрических уравнений мы можем наблюдать индивидуальное поведение [latex] \, x \, [/ latex] и [latex] \, y. \, [/ Latex]. Существует ряд форм, которые не могут быть представлены в виде [латекс] \, y = f \ left (x \ right), \, [/ latex], что означает, что они не являются функциями. {2}.{2}}. \, [/ Latex] Если построить график [latex] \, {y} _ {1} \, [/ latex] и [latex] \, {y} _ {2} \, [/ latex ] вместе, график не пройдет проверку вертикальной линии, как показано на (Рисунок). Таким образом, уравнение графика круга не является функцией.

Рисунок 2.

Однако, если бы мы построили график каждого уравнения отдельно, каждое из них прошло бы проверку вертикальной линии и, следовательно, представило бы функцию. В некоторых случаях концепция разделения уравнения для круга на две функции аналогична концепции создания параметрических уравнений, поскольку мы используем две функции для создания нефункции.Это станет яснее по мере нашего продвижения вперед.

Параметрические уравнения

Предположим, [latex] \, t \, [/ latex] — это число на интервале, [latex] \, I. \, [/ Latex] Множество упорядоченных пар, [latex] \, \ left (x \ left (t \ right), \, \, y \ left (t \ right) \ right), \, [/ latex] где [latex] \, x = f \ left (t \ right) \, [/ latex ] и [латекс] \, y = g \ left (t \ right), [/ latex] образует плоскую кривую на основе параметра [latex] \, t. \, [/ latex] Уравнения [latex] \, x = f \ left (t \ right) \, [/ latex] и [latex] \, y = g \ left (t \ right) \, [/ latex] являются параметрическими уравнениями.{2} -1. [/ Латекс]

Попробуйте

Создайте таблицу значений и постройте параметрические уравнения: [латекс] \, x \ left (t \ right) = t-3, \, \, y \ left (t \ right) = 2t + 4; \, \ , \, — 1 \ le t \ le 2. [/ Латекс]

Показать решение


[латекс] t [/ латекс]	[латекс] х \ левый (т \ правый) [/ латекс]	[латекс] у \ влево (т \ вправо) [/ латекс]
[латекс] -1 [/ латекс]	[латекс] -4 [/ латекс]	[латекс] 2 [/ латекс]
[латекс] 0 [/ латекс]	[латекс] -3 [/ латекс]	[латекс] 4 [/ латекс]
[латекс] 1 [/ латекс]	[латекс] -2 [/ латекс]	[латекс] 6 [/ латекс]
[латекс] 2 [/ латекс]	[латекс] -1 [/ латекс]	[латекс] 8 [/ латекс]

Нахождение пары параметрических уравнений

Найдите пару параметрических уравнений, моделирующих график [latex] \, y = 1- {x} ^ {2}, \, [/ latex], используя параметр [latex] \, x \ left (t \ right ) = t. {3} -2y.{3} -2t \\ y \ left (t \ right) = t \ end {array} [/ latex]

Нахождение параметрических уравнений, моделирующих с учетом критериев

Объект движется с постоянной скоростью по прямому пути [латекс] \, \ left (-5, \, 3 \ right) \, [/ latex] к [latex] \, \ left (3, \, — 1 \ right) \, [/ latex] в одной плоскости за четыре секунды. Координаты измеряются в метрах. Найдите параметрические уравнения для положения объекта.

Показать решение

Параметрические уравнения представляют собой простые линейные выражения, но нам нужно рассматривать эту проблему поэтапно.Значение объекта x начинается с [latex] \, — 5 \, [/ latex] метров и достигает 3 метров. Это означает, что расстояние x изменилось на 8 метров за 4 секунды, что составляет [latex] \, \ frac {\ text {8 m}} {4 \ text {s}}, [/ latex] или [latex] \, 2 \, \ text {m} / \ text {s}. \, [/ latex] Мы можем записать координату x как линейную функцию относительно времени как [latex] \, x \ left (t \ right) = 2t-5. \, [/ latex] В шаблоне линейной функции [latex] \, y = mx + b, 2t = mx \, [/ latex] и [latex] \, — 5 = Б. [/ латекс]

Аналогично, y -значение объекта начинается с 3 и переходит в [latex] \, — 1, \, [/ latex], что представляет собой изменение расстояния y на −4 метра за 4 секунды, который представляет собой коэффициент [латекс] \, \ frac {-4 \ text {m}} {4 \ text {s}}, [/ latex] или [латекс] \, — 1 \ text {m} / \ text {s}.\, [/ latex] Мы также можем записать координату y как линейную функцию [latex] \, y \ left (t \ right) = — t + 3. \, [/ latex] Вместе это параметрические уравнения для положения объекта, где [латекс] \, x \, [/ latex]
и [latex] \, y \, [/ latex]
выражены в метрах, а [latex] \, t \, [/ latex]
представляет время:

[латекс] \ begin {массив} {l} x \ left (t \ right) = 2t-5 \ hfill \\ y \ left (t \ right) = — t + 3 \ hfill \ end {array} [/ латекс]

Используя эти уравнения, мы можем построить таблицу значений для [latex] \, t, x, \, [/ latex] и [latex] \, y [/ latex] (см. (Рисунок)).В этом примере мы ограничили значения [latex] \, t \, [/ latex] неотрицательными числами. Как правило, можно использовать любое значение [latex] \, t \, [/ latex].

[латекс] t [/ латекс]	[латекс] x \ left (t \ right) = 2t-5 [/ латекс]	[латекс] y \ left (t \ right) = — t + 3 [/ латекс]
[латекс] 0 [/ латекс]	[латекс] x = 2 \ слева (0 \ справа) -5 = -5 [/ латекс]	[латекс] y = — \ left (0 \ right) + 3 = 3 [/ латекс]
[латекс] 1 [/ латекс]	[латекс] x = 2 \ слева (1 \ справа) -5 = -3 [/ латекс]	[латекс] y = — \ left (1 \ right) + 3 = 2 [/ latex]
[латекс] 2 [/ латекс]	[латекс] x = 2 \ слева (2 \ справа) -5 = -1 [/ латекс]	[латекс] y = — \ left (2 \ right) + 3 = 1 [/ latex]
[латекс] 3 [/ латекс]	[латекс] x = 2 \ слева (3 \ справа) -5 = 1 [/ латекс]	[латекс] y = — \ left (3 \ right) + 3 = 0 [/ латекс]
[латекс] 4 [/ латекс]	[латекс] x = 2 \ слева (4 \ справа) -5 = 3 [/ латекс]	[латекс] y = — \ left (4 \ right) + 3 = -1 [/ латекс]

Из этой таблицы мы можем создать три графика, как показано на (Рисунок).

Рис. 5. (a) График зависимости [латекса] \, x \, [/ latex] от [latex] \, t, \, [/ latex], представляющий горизонтальное положение во времени. (b) График зависимости [латекса] y [/ латекса] от [латекса] \, t, \, [/ latex], представляющий вертикальное положение во времени. (c) График [латекс] \, y \, [/ latex] по сравнению с [latex] \, x, \, [/ latex], представляющий положение объекта в плоскости в момент времени [latex] \, t . [/ латекс]

Анализ

Опять же, мы видим, что на (Рисунок) (c), когда параметр представляет время, мы можем указать движение объекта по пути с помощью стрелок.

Устранение параметра

Во многих случаях у нас может быть пара параметрических уравнений, но оказывается, что проще нарисовать кривую, если уравнение включает только две переменные, такие как [latex] \, x \, [/ latex] и [latex] \ , y. \, [/ latex] Удаление параметра — это метод, который может упростить построение графиков некоторых кривых. Однако, если нас интересует отображение уравнения по времени, тогда также необходимо указать ориентацию кривой. Существуют различные методы исключения параметра [латекс] \, t \, [/ latex] из набора параметрических уравнений; не каждый метод работает для каждого типа уравнения.Здесь мы рассмотрим методы для наиболее распространенных типов уравнений.

Исключение параметра из полиномиальных, экспоненциальных и логарифмических уравнений

Для полиномиальных, экспоненциальных или логарифмических уравнений, выраженных в виде двух параметрических уравнений, мы выбираем уравнение, которым легче всего манипулировать, и решаем для [латекс] \, t. \, [/ Латекс] Мы подставляем полученное выражение для [латекс] \ , t \, [/ latex]
во второе уравнение. Это дает одно уравнение в [latex] \, x \, [/ latex] и [latex] \, y.{2} +1 \, [/ latex] и [latex] \, y \ left (t \ right) = 2 + t, \, [/ latex] исключают параметр и записывают параметрические уравнения как декартово уравнение.

Показать решение

Мы начнем с уравнения для [latex] \, y \, [/ latex], потому что линейное уравнение для [latex] \, t решить проще. [/ Latex]

[латекс] \ begin {массив} {l} \, \, \, \, \, \, \, \, \, \, y = 2 + t \ hfill \\ y-2 = t \ hfill \ end {array} [/ latex]

Затем замените [латекс] \, y-2 \, [/ latex] на [латекс] \, t \, [/ latex] в [латекс] \, x \ left (t \ right).{2} -4г + 5. [/ Латекс]

Анализ

Это уравнение параболы, в которой в прямоугольных терминах [латекс] \, x \, [/ latex] зависит от [latex] \, y. \, [/ Latex] От вершины кривой в [латексе ] \, \ left (1,2 \ right), \, [/ latex] график выметает вправо. См. (Рисунок). В этом разделе мы рассматриваем системы уравнений, задаваемые функциями [latex] \, x \ left (t \ right) \, [/ latex] и [latex] \, y \ left (t \ right), \, [ / latex], где [latex] \, t \, [/ latex] — независимая переменная времени. Обратите внимание, как [latex] \, x \, [/ latex] и [latex] \, y \, [/ latex] являются функциями времени; так что в целом [латекс] \, y \, [/ latex] не является функцией [latex] \, x.{t} \ hfill \\ y = 3 \ left (\ frac {1} {x} \ right) \ hfill \\ y = \ frac {3} {x} \ hfill \ end {array} [/ latex]

Декартова форма [latex] \, y = \ frac {3} {x}. {2} \, [/ латекс] в [латекс] \, x> 2.{2} \ hfill \\ y \ left (t \ right) = \ mathrm {ln} \, t \, \, \, \, \, \, \, \, t> 0 \ hfill \ end {array} \ end {array} [/ latex]

Показать решение

[латекс] y = \ mathrm {ln} \ sqrt {x} [/ латекс]

Исключение параметра из тригонометрических уравнений

Исключение параметра из тригонометрических уравнений является простой заменой. Мы можем использовать несколько знакомых тригонометрических тождеств и теорему Пифагора.

Во-первых, мы используем идентификаторы:

[латекс] \ begin {array} {l} x \ left (t \ right) = a \ mathrm {cos} \, t \\ y \ left (t \ right) = b \ mathrm {sin} \, t \ end {array} [/ latex]

Решая для [latex] \, \ mathrm {cos} \, t \, [/ latex] и [latex] \, \ mathrm {sin} \, t, \, [/ latex], получаем

[латекс] \ begin {массив} {l} \ frac {x} {a} = \ mathrm {cos} \, t \\ \ frac {y} {b} = \ mathrm {sin} \, t \ end {array} [/ latex]

Затем используйте теорему Пифагора:

[латекс] {\ mathrm {cos}} ^ {2} t + {\ mathrm {sin}} ^ {2} t = 1 [/ latex]

Замена дает

[латекс] {\ mathrm {cos}} ^ {2} t + {\ mathrm {sin}} ^ {2} t = {\ left (\ frac {x} {a} \ right)} ^ {2} + {\ left (\ frac {y} {b} \ right)} ^ {2} = 1 [/ латекс]

Исключение параметра из пары тригонометрических параметрических уравнений

Удалите параметр из данной пары тригонометрических уравнений, где [latex] \, 0 \ le t \ le 2 \ pi \, [/ latex], и нарисуйте график.

[латекс] \ begin {array} {l} x \ left (t \ right) = 4 \ mathrm {cos} \, t \\ y \ left (t \ right) = 3 \ mathrm {sin} \, t \ end {array} [/ latex]

Показать решение

Решая для [latex] \, \ mathrm {cos} \, t \, [/ latex] и [latex] \, \ mathrm {sin} \, t, [/ latex], получаем

[латекс] \ begin {array} {l} \, x = 4 \ mathrm {cos} \, t \ hfill \\ \ frac {x} {4} = \ mathrm {cos} \, t \ hfill \\ \, y = 3 \ mathrm {sin} \, t \ hfill \\ \ frac {y} {3} = \ mathrm {sin} \, t \ hfill \ end {array} [/ latex]

Затем используйте тождество Пифагора и сделайте замены.{2}} {9} = 1 \, [/ latex] в виде эллипса с центром в [latex] \, \ left (0,0 \ right). \, [/ Latex] Обратите внимание, что когда [latex] \, t = 0 \, [/ latex] координаты: [latex] \, \ left (4,0 \ right), \, [/ latex], а когда [latex] \, t = \ frac {\ pi} {2} \, [/ latex] координаты [latex] \, \ left (0,3 \ right). \, [/ latex] Показывает ориентацию кривой с увеличивающимися значениями [latex] \, t. [/ латекс]

Попробуйте

Удалите параметр из данной пары параметрических уравнений и запишите как декартово уравнение: [latex] \, x \ left (t \ right) = 2 \ mathrm {cos} \, t \, [/ latex] и [latex ] \, у \ влево (т \ вправо) = 3 \ mathrm {sin} \, т.{2}} {9} = 1 [/ латекс]

Нахождение декартовых уравнений по параметрически определенным кривым

Когда нам дается набор параметрических уравнений и нам нужно найти эквивалентное декартово уравнение, мы, по сути, «исключаем параметр». Однако есть различные методы, которые мы можем использовать, чтобы переписать набор параметрических уравнений в декартово уравнение. Самый простой способ — установить одно уравнение, равное параметру, например [латекс] \, x \ left (t \ right) = t. \, [/ Latex] В этом случае [latex] \, y \ left ( t \ right) \, [/ latex] может быть любым выражением.{2} -3. [/ Латекс]

Нахождение декартова уравнения альтернативными методами

Используйте два разных метода, чтобы найти декартово уравнение, эквивалентное заданному набору параметрических уравнений.

[латекс] \ begin {массив} {l} \\ \ begin {array} {l} x \ left (t \ right) = 3t-2 \ hfill \\ y \ left (t \ right) = t + 1 \ hfill \ end {array} \ end {array} [/ latex]

Показать решение

Метод 1 . Сначала давайте решим уравнение [latex] \, x \, [/ latex] для [latex] \, t. \, [/ Latex]. Затем мы можем подставить результат в уравнение [latex] y [/ latex].

[латекс] \ begin {array} {l} \ text {} x = 3t-2 \ hfill \\ \ text {} x + 2 = 3t \ hfill \\ \ frac {x + 2} {3} = t \ hfill \ end {array} [/ latex]

Теперь подставьте выражение для [latex] \, t \, [/ latex] в уравнение [latex] \, y \, [/ latex].

[латекс] \ begin {array} {l} y = t + 1 \ hfill \\ y = \ left (\ frac {x + 2} {3} \ right) +1 \ hfill \\ y = \ frac { x} {3} + \ frac {2} {3} +1 \ hfill \\ y = \ frac {1} {3} x + \ frac {5} {3} \ hfill \ end {array} [/ latex]

Метод 2 . Решите уравнение [latex] \, y \, [/ latex] для [latex] \, t \, [/ latex] и подставьте это выражение в уравнение [latex] \, x \, [/ latex].

[латекс] \ begin {массив} {l} \ text {} y = t + 1 \ hfill \\ y-1 = t \ hfill \ end {array} [/ latex]

Сделайте замену и решите [латекс] \, y. [/ Latex]

[латекс] \ begin {array} {l} \ text {} x = 3 \ left (y-1 \ right) -2 \ hfill \\ \ text {} x = 3y-3-2 \ hfill \\ \ текст {} x = 3y-5 \ hfill \\ \, x + 5 = 3y \ hfill \\ \ frac {x + 5} {3} = y \ hfill \\ \ text {} y = \ frac {1} {3} x + \ frac {5} {3} \ hfill \ end {array} [/ latex]

Попробуйте

Запишите данные параметрические уравнения как декартово уравнение: [латекс] \, x \ left (t \ right) = {t} ^ {3} \, [/ latex] и [latex] \, y \ left (t \ справа) = {t} ^ {6}.[/ латекс]

Нахождение параметрических уравнений для кривых, определяемых прямоугольными уравнениями

Хотя мы только что показали, что существует только один способ интерпретировать набор параметрических уравнений как прямоугольное уравнение, существует несколько способов интерпретировать прямоугольное уравнение как набор параметрических уравнений. Любая стратегия, которую мы можем использовать для поиска параметрических уравнений, действительна, если она обеспечивает эквивалентность. Другими словами, если мы выберем выражение для представления [latex] \, x, \, [/ latex], а затем подставим его в уравнение [latex] \, y \, [/ latex], и получится тот же график в той же области, что и прямоугольное уравнение, то система параметрических уравнений справедлива.{2} +1 \ hfill \ end {array} [/ latex]

См. (Рисунок).

Рисунок 6.

Ключевые концепции

Параметризация кривой включает преобразование прямоугольного уравнения с двумя переменными, [latex] \, x \, [/ latex] и [latex] \, y, \, [/ latex] в два уравнения с тремя переменными, x , y и t . Часто больше информации получают из набора параметрических уравнений. См. (Рисунок), (Рисунок) и (Рисунок).
Иногда уравнения проще изобразить, если они записаны в прямоугольной форме.В результате исключения [latex] \, t, \, [/ latex] получается уравнение в [latex] \, x \, [/ latex] и [latex] \, y \, [/ latex].
Чтобы исключить [латекс] \, t, \, [/ latex], решите одно из уравнений для [latex] \, t, \, [/ latex] и подставьте выражение во второе уравнение. См. (Рисунок), (Рисунок), (Рисунок) и (Рисунок).
Нахождение прямоугольного уравнения для параметрической кривой в основном то же самое, что и удаление параметра. Решите относительно [латекс] \, t \, [/ latex] в одном из уравнений и подставьте выражение во второе уравнение.См. (Рисунок).
Существует бесконечное количество способов выбрать набор параметрических уравнений для кривой, определенной как прямоугольное уравнение.
Найдите такое выражение для [latex] \, x \, [/ latex], чтобы область определения набора параметрических уравнений оставалась такой же, как в исходном прямоугольном уравнении. См. (Рисунок).

Упражнения по разделам

Устный

Что такое система параметрических уравнений?

Показать решение

Пара функций, зависящих от внешнего фактора.Две функции записываются с использованием одного и того же параметра. Например, [латекс] \, x = f \ left (t \ right) \, [/ latex] и [latex] \, y = f \ left (t \ right). [/ Latex]

Некоторые примеры третьего параметра: время, длина, скорость и масштаб. Объясните, когда время используется в качестве параметра.

Объясните, как исключить параметр из набора параметрических уравнений.

Показать решение

Выберите одно уравнение, которое нужно решить для [латекс] \, t, \, [/ latex], замените его в другое уравнение и упростите.

В чем преимущество записи системы параметрических уравнений в виде декартова уравнения?

В чем преимущество использования параметрических уравнений?

Показать решение

Некоторые уравнения нельзя записать в виде функций, например круга. Однако, записанные в виде двух параметрических уравнений, по отдельности уравнения являются функциями.

Почему существует множество наборов параметрических уравнений для представления на декартовой функции?

Алгебраические

Для следующих упражнений удалите параметр [latex] \, t \, [/ latex], чтобы переписать параметрическое уравнение как декартово уравнение.{3} -2 [/ латекс]

Для следующих упражнений перепишите параметрическое уравнение как декартово уравнение, построив таблицу [latex] x \ text {-} y [/ latex].

[латекс] \ {\ begin {array} {l} x (t) = 2t-1 \\ y (t) = t + 4 \ end {array} [/ latex]

[латекс] \ {\ begin {array} {l} x (t) = 4-t \\ y (t) = 3t + 2 \ end {array} [/ latex]

[латекс] \ {\ begin {array} {l} x (t) = 2t-1 \\ y (t) = 5t \ end {array} [/ latex]

[латекс] \ {\ begin {array} {l} x (t) = 4t-1 \\ y (t) = 4t + 2 \ end {array} [/ latex]

Для следующих упражнений параметризуйте (напишите параметрические уравнения для) каждое декартово уравнение, задав [latex] x \ left (t \ right) = t [/ latex] или задав [latex] \, y \ left (t \ right ) = t.{2} +3 [/ латекс]

[латекс] y \ left (x \ right) = 2 \ mathrm {sin} \, x + 1 [/ latex]

Показать решение

[латекс] \ {\ begin {array} {l} x (t) = t \ hfill \\ y (t) = 2 \ mathrm {sin} t + 1 \ hfill \ end {array} [/ latex]

[латекс] x \ left (y \ right) = 3 \ mathrm {log} \ left (y \ right) + y [/ latex]

[латекс] x \ влево (y \ вправо) = \ sqrt {y} + 2y [/ латекс]

Показать решение

[латекс] \ {\ begin {array} {l} x (t) = \ sqrt {t} + 2t \ hfill \\ y (t) = t \ hfill \ end {array} [/ latex]

Для следующих упражнений параметризуйте (напишите параметрические уравнения для) каждое декартово уравнение, используя [latex] x \ left (t \ right) = a \ mathrm {cos} \, t [/ latex] и [latex] \, y. \ слева (т \ справа) = Ь \ mathrm {грех} \, т.{2} = 10 [/ латекс]

Показать решение

[латекс] \ {\ begin {array} {l} x (t) = \ sqrt {10} \ mathrm {cos} t \ hfill \\ y (t) = \ sqrt {10} \ mathrm {sin} t \ hfill \ end {array}; \, [/ latex]
Круг

Параметрируйте строку от [latex] \, \ left (3,0 \ right) \, [/ latex] до [latex] \, \ left (-2, -5 \ right) \, [/ latex] так, чтобы линия находится в [latex] \, \ left (3,0 \ right) \, [/ latex] в [latex] \, t = 0, \, [/ latex] и в [latex] \, \ left ( -2, -5 \ right) \, [/ latex] at [latex] \, t = 1. [/ Latex]

Параметризуйте строку от [latex] \, \ left (-1,0 \ right) \, [/ latex] до [latex] \, \ left (3, -2 \ right) \, [/ latex] так, чтобы линия находится в [latex] \, \ left (-1,0 \ right) \, [/ latex] в [latex] \, t = 0, \, [/ latex] и в [latex] \, \ left (3, -2 \ справа) \, [/ латекс] в [латекс] \, t = 1.[/ латекс]

Показать решение

[латекс] \ {\ begin {array} {l} x (t) = — 1 + 4t \ hfill \\ y (t) = — 2t \ hfill \ end {array} [/ latex]

Параметризуйте строку от [latex] \, \ left (-1,5 \ right) \, [/ latex] до [latex] \, \ left (2,3 \ right) [/ latex] так, чтобы линия была в [латекс] \, \ влево (-1,5 \ вправо) \, [/ латекс] в [латекс] \, t = 0, \, [/ латекс] и в [латекс] \, \ влево (2, 3 \ right) \, [/ latex] at [latex] \, t = 1. [/ Latex]

Параметрируйте строку от [latex] \, \ left (4,1 \ right) \, [/ latex] до [latex] \, \ left (6, -2 \ right) \, [/ latex] так, чтобы линия находится в [latex] \, \ left (4,1 \ right) \, [/ latex] в [latex] \, t = 0, \, [/ latex] и в [latex] \, \ left (6 , -2 \ справа) \, [/ латекс] в [латекс] \, t = 1. {2} \ hfill \\ {y} _ {1} (t) = 2t-1 \ hfill \ end {array} \ text {and} \ {\ begin {array} {l} {x} _ {2} (t) = — t + 6 \ hfill \\ {y} _ {2} (t ) = t + 1 \ hfill \ end {array} [/ latex]

Показать решение

да, при [латексе] t = 2 [/ латексе]

В следующих упражнениях воспользуйтесь графическим калькулятором, чтобы заполнить таблицу значений для каждого набора параметрических уравнений.{2} -1 \ hfill \ end {array} [/ latex]


[латекс] t [/ латекс]	[латекс] х [/ латекс]	[латекс] и [/ латекс]
1
2
3

Показать решение


[латекс] t [/ латекс]	[латекс] х [/ латекс]	[латекс] и [/ латекс]
1	-3	1
2	0	7
3	5	17

[латекс] \ {\ begin {array} {l} {x} _ {1} (t) = {t} ^ {4} \ hfill \\ {y} _ {1} (t) = {t} ^ {3} +4 \ hfill \ end {array} [/ latex]

Posted in Разное

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт