Содержание
Возведение алгебраической дроби в степень: правило, примеры
Тема сводится к тому, что нам необходимо производить умножение одинаковых дробей. Данная статья расскажет, какое необходимо использовать правило, чтобы верно возводить алгебраические дроби в натуральную степень.
Правило возведения алгебраической дроби в степень, его доказательство
Перед тем, как начать возводить в степень, необходимо углубить знания при помощи статьи про степень с натуральным показателем, где имеется произведение одинаковых множителей, которые находятся в основании степени, причем их количество определено показателем. К примеру, число 23=2·2·2=8.
При возведении в степень чаще всего используем правило. Для этого в отдельности возводят в степень числитель и отдельно знаменатель. Рассмотрим на примере 232=2232=49. Правило применимо для возведения дроби в натуральную степень.
При возведении алгебраической дроби в натуральную степень получаем новую, где числитель имеет степень исходной дроби, а знаменатель – степень знаменателя. Это все имеет вид abn=anbn , где а и b являются произвольными многочленами, b является ненулевым, а n натуральным числом.
Это все имеет вид abn=anbn , где а и b являются произвольными многочленами, b является ненулевым, а n натуральным числом.
Доказательство данного правила записывается в виде дроби, которую необходимо возвести в степень, основываясь на самом определении с натуральным показателем. Тогда получаем умножение дробей вида abn=ab·ab·…·ab=a·a·…·ab·b·…·b=anbn
Примеры, решения
Правило возведения алгебраической дроби в степень производится последовательно: сначала числитель , потом знаменатель. Когда в числителе и знаменателе имеется многочлен, тогда само задание сведется к возведению заданного многочлена в степень. После чего будет указана новая дробь, которая равна исходной.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 1
Произвести возведение дроби x23·y·z3 в квадрат.
Решение
Необходимо зафиксировать степень x23·y·z32. По правилу возведения алгебраической дроби в степень получаем равенство вида x23·y·z32=x223·y·z32 . Теперь необходимо произвести преобразование полученной дроби к виду алгебраической, выполняя возведение в степень. Тогда получим выражение вида
Теперь необходимо произвести преобразование полученной дроби к виду алгебраической, выполняя возведение в степень. Тогда получим выражение вида
x223·y·z32=x2·232·y2·z32=x49·y2·z6
Все случаи возведения в степень не предполагают подробного разъяснения, поэтому сам решение имеет краткую запись. То есть, получаем, что
x23·y·z32=x223·y·z32=x49·y2·z6
Ответ: x23·y·z32=x49·y2·z6.
Если числитель и знаменатель имеют многочлены, тогда необходимо возводить всю дробь в степень, после чего применять формулы сокращенного умножения для его упрощения.
Пример 2
Возвести дробь 2·x-1×2+3·x·y-y в квадрат.
Решение
Из правила имеем, что
2·x-1×2+3·x·y-y2=2·x-12×2+3·x·y-y2
Чтобы преобразовать выражение, необходимо воспользоваться формулой квадрата суммы трех слагаемых в знаменателе, а в числителе – квадратом разности, что позволит упростить выражение. Получим:
2·x-12×2+3·x·y-y2==2·x2-2·2·x·1+12×22+3·x·y2+-y2+2·x2·3·x·y+2·x2·(-y)+2·3·x·y·-y==4·x2-4·x+1×4+9·x2·y2+y2+6·x3·y-2·x2·y-6·x·y2
Ответ: 2·x-12×2+3·x·y-y2=4·x2-4·x+1×4+9·x2·y2+y2+6·x3·y-2·x2·y-6·x·y2
Заметим, что при возведении в натуральную степень дробь, которую не можем сократить, получаем также несократимую дробь. (1/2)
(1/2)
Если же мы имеем дело с квадратным корнем под которым находится дробь, то мы можем представить эту дробь в числителе которой будет находится квадратный корень 2 – степени ( т.к. квадратный корень)
А в знаменателе также будет находится квадратный корень , т.е. другими словами мы будем видеть отношение двух корней, это может пригодится для решения некоторых задач и примеров.
Если мы возведём дробь, которая находится под квадратным корнем во вторую степень то мы получим ту же самую дробь.
Произведение двух дробей под одной степенью будет равнятся произведению этих двух дробей, каждая в отдельности из которых будет под своей степенью.
Помните: на ноль делить нельзя!
Также не стоит забывать об очень важном замечании для дроби такой как знаменатель не должен равняться нулю. В дальнейшем во многих уравнениях мы будем использовать это ограничение, называемое ОДЗ – область допустимых значений
При сравнении двух дробей с одним и тем же основанием но разными степенями, большее будет являться та дробь у которой степень будет больше, а меньшей та у которой степень меньше, при равенстве не только оснований, но и степеней, дробь считается одинаковой. (1,77+( — 0,75)) = 79,7 – 1,3 = 78,6
(1,77+( — 0,75)) = 79,7 – 1,3 = 78,6
Нужна помощь в учебе?
Предыдущая тема: Умножение и деление дробей: сокращение дробей + полезные советы
Следующая тема:   Преобразование рациональных выражений: способы преобразований и примеры
Возведение дроби в степень правило, как возвести алгебраическую дробь в степень, калькулятор примеров, свойства дробных степеней, как решать примеры со степенью
В алгебре, пожалуй, одной из самых распространённых операций является возведение дроби в степень. Это довольно простое действие, которое похоже на умножение. Обучают ему на уроках математики в восьмом классе. Вычисление ответа заключается в различных нюансах, зависящих от типа дробного выражения. Но при этом существует универсальное правило. Используя его, можно находить как положительную, так и отрицательную степень.
Понятие степени
Представления о степени сложились ещё во времена существования Древнего Египта. Впервые упоминание о её вычислении встречается в знаменитом учебнике по математике Диофанта Александрийского «Арифметика». В своих трудах он описывает понятие как некоторое количество единиц, из которых состоят любые числа, увеличивающиеся до бесконечности. Он выделяет:
Впервые упоминание о её вычислении встречается в знаменитом учебнике по математике Диофанта Александрийского «Арифметика». В своих трудах он описывает понятие как некоторое количество единиц, из которых состоят любые числа, увеличивающиеся до бесконечности. Он выделяет:
- квадраты, образующиеся при произведении чисел или цифр самих на себя;
- кубы, получающиеся при умножении квадрата на сторону;
- биквадраты, произведение квадрата на квадрат;
- квадрато-кубы, возникающие при умножении квадратов на кубы;
- бикубы, произведение кубов на самих себя.
Французский учёный Никола Шюке дополнил этот степенной ряд, введя отрицательный параметр. Современное же обозначение степени предложил Рене Декарт. В «Геометрии» он использовал верхний надстрочный знак для указания величины степени. Что интересно, квадрат математик продолжал обозначать как произведение чисел, то есть в виде n * n. И только потом Лейбниц настоял на универсальной записи для любого возведения в степень.
Под операцией возведения понимается бинарное действие, определяемое в результате умножения числа на себя. То есть справедлива следующая запись: di = d * d* d *… * dk, где k — число, обозначающее количество перемножаемых чисел, равное n. Например, 112 = 11 * 11 = 121. Степень, присущая числу, может быть отрицательной, рациональной, десятичной, вещественной и даже комплексной. Фактически получается, что для того, чтобы посчитать степень числа, его нужно умножить на себя столько раз, сколько указано в степенном показателе.
Но при этом существует нюанс возведения в нулевую степень. Любое число, вне зависимости от вида, в нулевой степени даст единицу. Например, (2/32)0 = 1, -1420 = 1. Выражение же ноль в нулевой степени не имеет смысла, поэтому ответ считается неопределённым.
Правило возведения дроби
В основе правила возведения дроби в степень лежит её определение с дробным показателем. Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6)2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6)2 = 1/4.
Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6)2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6)2 = 1/4.
Доказать это правило можно выполнив элементарные алгебраические действия. Для рассмотренного примера, согласно правилу арифметики, сначала необходимо выполнить деление, а после возведение в степень. Так, три разделить на шесть будет равно: 3/6 = 1/2 = 0,5. Затем полученное число следует возвести в квадрат: 0,52 = 0,5 * 0,5 = 0,25. Найденный ответ можно переписать в виде дроби 1/4, которая при сравнении полностью совпадает с ранее вычисленной.
Утверждение справедливо для любого вида дроби с произвольной степенной функцией. Например, (11 / 14)3. Используя закон, можно записать следующее: (11 / 14)3 = 113 / 143 = (11 * 11 * 11) / (14 * 14 * 14) = 1331 / 2744. Эту дробь сократить, то есть упростить, нельзя. Если нужно получить численное значение, то следует просто разделить числитель на знаменатель: 1331 : 2744 = 0,485.
Эту дробь сократить, то есть упростить, нельзя. Если нужно получить численное значение, то следует просто разделить числитель на знаменатель: 1331 : 2744 = 0,485.
Чтобы убедиться в истинности правила, можно и тут выполнить проверку. Дробь три разделить на пять в степени три можно решить, выполнив сначала деление, а после полученное число возвести в кубическую степень: (11 / 14)3 = (0,78)3 = 0,78 * 0,78 * 0,78 = 0,485. Ответ идентичен предыдущему, что и следовало доказать.
Таким образом, алгоритм возведения будет следующим:
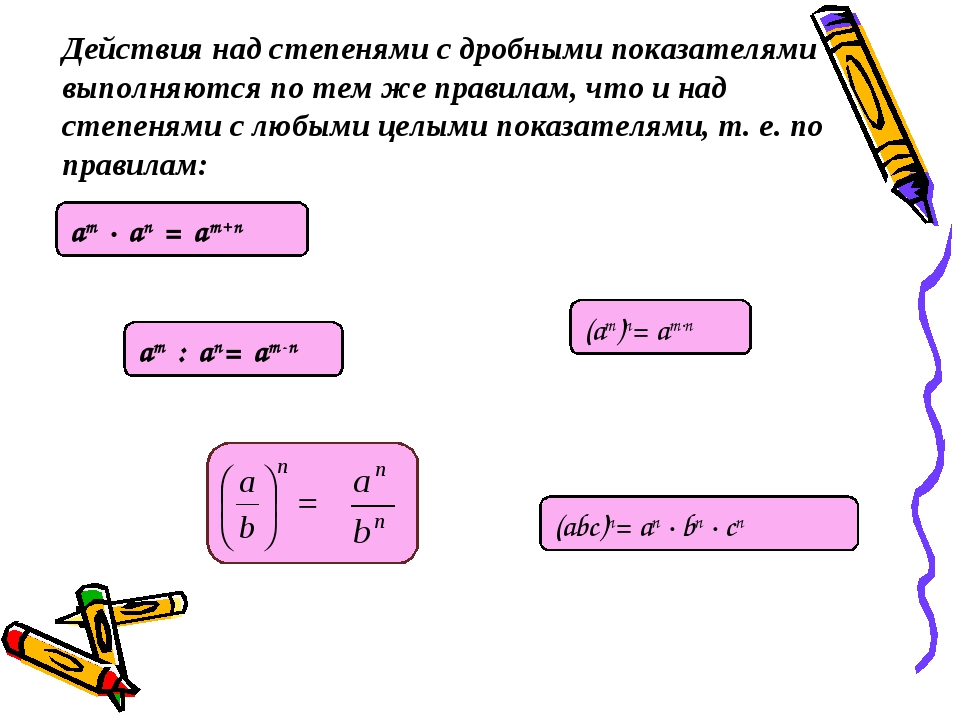
Если показатель степени небольшой, то возведение можно выполнить просто умножив дробь на саму себя необходимое число раз. Например, (2/32)3 = (2/32) * (2/32) *(2/32) = 1/4096. Алгоритм обыкновенного расчёта обычно не вызывает трудности, но часто приходиться иметь дело не только с обыкновенными дробями. При этом степень может быть даже отрицательной.
Но в любом случае нужно помнить, что если верхнюю и нижнюю часть дроби умножить или разделить на одно и то же число, то количественный показатель полученного выражения не изменится. Это важно, так как при возведении приходится часто выполнять преобразования.
Нулевая и отрицательная степень
При вычислении дроби, в показателе которой стоит ноль, исходят из свойств частного степеней с одинаковым основанием.
Так, согласно алгебраическим правилам, для простых чисел a и b, при условии, что a < b, справедливо выражение: ca / cb = ca — b. Тут нужно отметить, что основание не должно быть равным нулю, иначе получится недопустимое деление на ноль. Если a = b, то равенство можно переписать в виде: ca / cb = ca — a = c0. Так как c другой стороны частное ca / сa = 1, то можно утверждать, что с0 = 1.
Тут нужно отметить, что основание не должно быть равным нулю, иначе получится недопустимое деление на ноль. Если a = b, то равенство можно переписать в виде: ca / cb = ca — a = c0. Так как c другой стороны частное ca / сa = 1, то можно утверждать, что с0 = 1.
Для нулевой степени такой подход использовать будет некорректно. При основании, которое равно нулю, применяя предыдущее равенство, можно записать, что ноль в степени a умноженный на ноль в степени ноль, равняется нулю с показателем a. То есть выражение может быт переписано как 0 = 0. Оно будет правильным при любом натуральном показателе, при этом не будет зависеть от того, чему равно выражение 00.
Ответ на 00 может быть любым. Поэтому для избежания путаницы считают, что решение записи 00 не имеет смысла, так же как и деление на ноль. Например, (12 / 34)0 = 120 / 340 = 1 / 1 = 1 или (-3 / 4)0 = 1, а вот для (0 / 23)0 ответ будет не определён.
Чтобы знать, как возвести дробь в отрицательную степень, нужно вспомнить свойство произведения с равными основаниями: ca * cb = ca+ b. Предположив, a = -b, при условии, что основание не равняется нулю, можно записать: c−a * ca = c-a+a = a0 = 1. Несложно сделать вывод о том, что положительный и отрицательный показатель взаимно обратный. Отсюда выходит, что если число нужно возвести в отрицательную степень, то его можно представить в виде дроби: c—a = 1 / ca.
Получается, что для минусового показателя ответ определяется дробью, при условии, что основание отлично от нуля и показатель — натуральное число. Фактически необходимо перевернуть дробь и возвести её по правилу, при этом знак показателя изменить на положительный. Например, (23 / 37)-2 = 1 / (11 / 37)2 = (37 / 22)2 или (1 / 5)-2 = (5 / 1)2 = 52 = 25.
Рациональный показатель
В состав рациональных чисел входят все целые и дробные значения. По сути, ими называют значения, которые можно представить в виде обыкновенной или отрицательной дроби, как цифру ноль. При этом в числителе находится целое число, а в знаменателе – натуральное. Для того чтобы определить степень, нужно выяснить, что же представляет собой число с показателем в дробной форме.
Пусть имеется число n, которое необходимо возвести в степень a / b. Необходимо будет извлечь корень из n. Чтобы выражение соответствовало таблицам степени, должна выполняться формула: n(a / b) * b = na * b / b = na.
Используя полученное выражение, логично предположить, что ca / b = a√cb, но это лишь справедливо, когда показатель степени целый. Можно сделать вывод о том, что если выражение a√cb справедливо, что степенью числа c дробным показателем b / a является корень из c в степени b.
Если принять, что основание больше либо равно нулю, когда b является положительным числом, то буде справедливым равенство: сa / b = a√cb. При этом можно утверждать, что если основание будет равным нулю, то ответом будет тоже ноль: 0a / b = a√0b = 0.
Тут нужно оговориться, что для некоторых одночленов приведённое правило не работает. Например, для 3√ (-12 /3)2 или 4√ -122 оно верное, а для (-1 / 3)-2 / 3 или (-3 / 2)2 / 5 не имеет смысла, так как основание не может быть отрицательным. Поэтому вводится условие, по которому выражение a√ cb имеет смысл, при любых значениях неотрицательного основания.
Что же касается минусовой величины в показателе корней, оно в основании должно отличаться от нуля. Иными словами, если в любом уравнении или равенстве выражение a / b нельзя упростить (сократить), то a * i / b * I = ca — i / b —, причём степень можно заменить на ca / b.
Примеры решения
Для того чтобы понять и усвоить теорию, нужно попрактиковаться. Начинать необходимо с простых заданий, постепенно переходя к более сложным примерам. Возвести дробь в степень можно и на онлайн-калькуляторах, но желательно уметь выполнять это действие самостоятельно. Из наиболее типичных примеров, охватывающих все возможные ситуации, можно выделить следующие:
 Определить ответ в задании вида: (2 11/12)-1 = ((2 * 12 + 11) / 12)-1 = (35 / 12)-1 = (12 / 35 )1 = 12 1 / 351 =12 / 35.
Определить ответ в задании вида: (2 11/12)-1 = ((2 * 12 + 11) / 12)-1 = (35 / 12)-1 = (12 / 35 )1 = 12 1 / 351 =12 / 35. Так как буквой e обозначают экспоненту, то e—3 = 2,718-3 = 0,049. Отсюда можно сделать вывод, что знак в неравенстве неверный: -2,43 < 0,049
Так как буквой e обозначают экспоненту, то e—3 = 2,718-3 = 0,049. Отсюда можно сделать вывод, что знак в неравенстве неверный: -2,43 < 0,049Таким образом, чтобы возвести в степень дробь необходимо знать: правило, свойства степеней, порядок выполнения арифметических операций. А также учитывать знак показателя и вид основания.
Расчёт на онлайн-калькуляторе
В сети существуют сервисы, автоматически выполняющие арифметические операции. Воспользоваться этими сайтами может каждый, имеющий доступ к интернету. Порталы предлагают свои услуги бесплатно. С их помощью можно находить функции, рассчитывать градусы и углы, решать уравнения и неравенства, вычислять дроби и степени.
Для решения дробей со степенями на онлайн-калькуляторах не нужно обладать какими-то особыми знаниями. Всё что требуется от пользователя — вести в предложенную форму задание и нажать кнопку «Рассчитать». Весь процесс вычисления занимает несколько секунд.
Всё что требуется от пользователя — вести в предложенную форму задание и нажать кнопку «Рассчитать». Весь процесс вычисления занимает несколько секунд.
Полезной особенностью таких сайтов является и возможность обучиться правилам расчёта, узнать, как должны обозначаться те или иные операции и действия. Из различных калькуляторов можно выделить три наиболее популярных:
Сайты отличаются удобным и понятным интерфейсом. На их страницах содержится кратко изложенная теория, использующаяся для расчётов и типовые примеры.
Предыдущая
АлгебраФункция y=k/х свойства и график, область определения функции, коэффициент в графике функции, примеры решения задач
Следующая
АлгебраОдночлен 7 класс объяснение понятия, что называют коэффициентом и степенью одночлена стандартного вида, действия над выражением, принцип преобразования, примеры записи и решение типовых задач
Как решать степени с дробями? пример (8/11)степень 2 как это сделать ?
Диограмма бойынша көшбасшысы тандау
Помогите прошу вас❤️
2. Сколько элементов множества С={10, 11,20, 22, 39, 44} являются кратными 11?А) 5 В) 3 C) 4E) 1D) 2
Сколько элементов множества С={10, 11,20, 22, 39, 44} являются кратными 11?А) 5 В) 3 C) 4E) 1D) 2
В таксопарке проходит акция, что на заказ подъедет ближайшая машина. Свободно 20 машин: 2 премиум-класса, 4 комфорт, а остальные эконом. Найди вероятн
…
ость того, что приедет машина премиум-класса.
3. В составе клубники 6 % сахара. Сколько кг сахара в 12 кг клубники.С условием пожалуйста.
Вариант 11. Найти процент от числа: а) 35% от 40; б) 23% от 200,2. Найти число, а) 27% которого равны 81; б) 45 % которого равны 543. В классе 30 учащ
…
ихся писали контрольную работу. На «5» написали – 50% от всего класса,на «4» написали – 40% от всего класса, остальные учащиеся написали на «3». Сколькоучащихся получили оценку «3» ?4. Построить углы: а) 579; б) 125° .5. Построить окружность с центром в точке Он радиусом R=2 см. Проведите в нем хорду ВС идиаметр KM.6. Постройте изображение прямоугольного параллелепипеда. Найдите площадь всех боковыхграней и его объем, если а=5 см, b= 4см, с= 6см. 7. Постройте круговую и столбчатую диаграммы, используя данные таблицы:
7. Постройте круговую и столбчатую диаграммы, используя данные таблицы:
Найди значения выражений:а) 2(6а — 1) + 4(2 – а), если а= -0,625;б) 15b – 3(2b + 5) + 2(-56 + 7), если ь -0.8;в) 2n(n — 4) — n(n — 8), если п= -1,5;г)
…
х(х + y) — y(х — у), если х = -4, y = -5.
1. Найти процент от числа: а) 35001 40; б) 23% от 200.2. Найти число, а) 27% которого равны 81: б) 45 % которого равны 543. В классе 30 учащихся писал
…
и контрольную работу. На «5» написали – 50% от всего класса,Ha «4» Hanica — 40% от всего класса, остальные учащиеся написали на «3». Сколькоучащихся получили оценку «3» ?4. Построить углы: а) 570; б) 1250Построить окружность с центром в точке Он радиусом R=2 см. Проведите в нем хорду ВС идиаметр KM.6. Постройте изображение прямоугольного параллелепипеда. Найдите площадь всех боковыхграней и его объем, если а=5 см, b= 4см, с= 6см7. Постройте круговую и столбчатую диаграммы, используя данные таблицы:
Ne 1. На день рождения мама купила 200 граммов конфет «Мишка на севере», 300граммов конфет «Белочка» и 500 граммов конфет «Коровка». Какую часть от вс
Какую часть от вс
…
ехконфет составляют конфеты «Белочка»?Решение:
На рисунке 199 изображён график изменения температуры воздухана протяжении суток. Пользуясь графиком, установите:1) какой была температура воздуха в 2
…
ч; в 8 ч; в 12 ч; в 16 ч; в 22 ч;2) в котором часу температура воздуха была -3 «С; -6 «C: 0 °C;3) какой была самая низкая температура и в котором часу;4) какой была самая высокая температура и в котором часу;5) на протяжении каких промежутков времени температура воздуха была ниже 0 °C;б) на протяжении каких промежутков времени температура воздухаповышалась; понижалась,
Умножение дробей. Возведение дроби в степень
Для начала давайте
вспомним правило умножения обыкновенных дробей.
Для того чтобы умножить
дробь на дробь, надо числитель
умножить на числитель, а знаменатель на знаменатель
и первое произведение записать в числителе новой дроби,
второе – в знаменателе.
Например
Аналогичным образом происходит
умножение рациональных дробей. Давайте докажем, что это правило
на самом деле действует при умножении рациональных дробей.
Иначе говоря, докажем, что
произведение двух рациональных дробей тождественно
равно дроби, у которой числитель равен произведению
числителей, а знаменатель – произведению знаменателей
перемножаемых дробей при любых допустимых
значениях переменных, кроме b
равное
нулю и d равное нулю.
Получили, что равенство верно при любых
допустимых значениях переменных, т.е. является тождеством.
Правило умножения
рациональных дробей:
Чтобы умножить дробь
на дробь, нужно перемножить их числители и перемножить их знаменатели
и первое произведение записать числителем, а второе – знаменателем
дроби.
В буквенном виде это правило
записывают так:
Это правило выполняется
и когда произведение трёх и более рациональных дробей.
Прежде чем выполнять
умножение рациональных дробей, полезно их числители
и знаменатели разложить на множители. Это облегчит
сокращение той рациональной дроби, которая получится в результате
умножения.
Пример 1: умножить дроби.
Решение:
Пример 2: умножить дроби.
Решение:
Пример 3: Представить произведение дробей в виде
рациональной дроби.
Решение:
Пример 4: выполнить умножение.
Решение:
Теперь рассмотрим, как
выполняется возведение рациональной дроби в степень.
Проверим это равенство
на конкретных примерах.
Правило возведения
рациональной дроби в степень:
Чтобы возвести дробь в
степень, надо возвести в эту степень числитель и знаменатель и
первый результат записать в числителе, а второй в знаменателе дроби.
Пример 5: возвести в третью степень дробь.
Пример 6: возвести во вторую степень дробь.
Пример 7:
Итоги
Чтобы умножить дробь
на дробь, нужно перемножить их числители и перемножить их знаменатели
и первое произведение записать числителем, а второе – знаменателем дроби.
Чтобы возвести дробь
в степень, надо возвести в эту степень числитель и знаменатель
и первый результат записать в числителе, а второй в знаменателе
дроби.
Умножение и деление степеней, алгебра, 7 класс
Дата публикации: . 3=8$.
3=8$.
Сложение дробей
Дробь типа 3 4 говорит, что у нас есть 3 из 4 частей, на которые делится целое.
Чтобы сложить дроби, выполните три простых шага:
- Шаг 1. Убедитесь, что нижние числа (знаменатели) совпадают.
- Шаг 2: сложите верхние числа (числители), поместите полученный ответ над знаменателем
- Шаг 3: Упростите дробь (при необходимости)
Пример:
Шаг 1 .Нижние цифры (знаменатели) уже совпадают. Переходите сразу к шагу 2.
Шаг 2 . Сложите верхние числа и поставьте ответ над тем же знаменателем:
.
1
4
+
1
4
знак равно
1 + 1
4
знак равно
2
4
Шаг 3 . Упростим дробь:
2
4
знак равно
1
2
На картинке это выглядит так:
| 1 4 | + | 1 4 | = | 2 4 | = | 1 2 |
. .. и ты видишь как
.. и ты видишь как
2
4
проще как
1
2
? (см. Эквивалентные дроби.)
Пример:
Шаг 1 : Нижние числа разные. Видите, как ломтики бывают разных размеров?
| 1 3 | + | 1 6 | = | ? | ||
Нам нужно сделать их такими же, прежде чем мы сможем продолжить, потому что не может, добавить их вот так.
Число «6» вдвое больше, чем «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем умножить верхнюю и нижнюю часть первой дроби на 2 , например:
| × 2 |
| × 2 |
Важно: вы умножаете как верхний, так и нижний на одинаковую величину,
, чтобы сохранить значение дроби одинаковым
Теперь дроби имеют одинаковое нижнее число («6»), и наш вопрос выглядит так:
| 2 6 | + | 1 6 | ||||
Нижние числа теперь те же, поэтому мы можем перейти к шагу 2.
Шаг 2 : сложите верхние числа и поместите их над тем же знаменателем:
2
6
+
1
6
знак равно
2 + 1
6
знак равно
3
6
На картинке это выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | ||
Шаг 3 : Упростите дробь:
3
6
знак равно
1
2
На картинке весь ответ выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | = | 1 2 |
С ручкой и бумагой
А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):
Рифма, которая поможет вам вспомнить
♫ «Если ваша цель — сложение или вычитание,
Нижние числа должны быть одинаковыми!
♫» Измените нижнее значение с помощью умножения или деления,
Но то же самое и к верхнему,
♫ » И не забудьте упростить,
Пока не пришло время прощаться «
Пример:
1
3
+
1
5
Опять же, нижние цифры разные (срезы разного размера)!
| 1 3 | + | 1 5 | = | ? | ||
Но давайте попробуем разделить их на меньшие размеры, чтобы каждый был одинаковым :
| 5 15 | + | 3 15 | ||||
Первая дробь: умножив верхнюю и нижнюю части на 5, мы получили
5
15
:
| × 5 |
| × 5 |
Вторая дробь: умножив верхнюю и нижнюю части на 3, мы получили
3
15
:
| × 3 |
| × 3 |
Нижние числа теперь те же, поэтому мы можем продолжить и сложить верхние числа:
| 5 15 | + | 3 15 | = | 8 15 | ||
Результат предельно прост, так что вот ответ:
8
15
1
3
+
1
5
знак равно
8
15
Делаем знаменатели одинаковыми
В предыдущем примере, как мы узнали, что нужно разрезать их на 1 / 15 тысяч, чтобы знаменатели совпадали? Мы просто умножили два знаменателя вместе (3 × 5 = 15).
Прочтите о двух основных способах сделать знаменатели одинаковыми здесь:
Они оба работают, используйте тот, который вам больше нравится!
Пример: кексы
Вы хотите приготовить и продать кексы:
- Друг может предоставить ингредиенты, если вы ему дадите 1 / 3 продаж
- А рыночный прилавок стоит 1 / 4 продаж
Сколько это всего?
Нам нужно добавить 1 / 3 и 1 / 4
Первые делают нижние числа (знаменатели) одинаковыми.
Умножить верхнюю и нижнюю часть 1 / 3 на 4 :
| 1 × 4 | + | 1 | = | ? |
| 3 × 4 | 4 | ? |
И умножьте верхнюю и нижнюю часть 1 / 4 на 3 :
| 1 × 4 | + | 1 × 3 | = | ? |
| 3 × 4 | 4 × 3 | ? |
Сейчас делаю расчеты:
| 4 | + | 3 | = | 4 + 3 | = | 7 |
| 12 | 12 | 12 | 12 |
Ответ:
7
12
продаж идет на ингредиенты и рыночные затраты.
Добавление смешанных фракций
У меня есть специальная (более продвинутая) страница о добавлении смешанных дробей.
Как считать дроби: пошаговое руководство
Что такое дроби?
Дроби — это числовые величины, представляющие значения меньше единицы. Также известные как дробные числа, они обычно используются для измерения частей целого, например:
- Одна половина (1/2)
- Одна пятая (1/5)
- Две трети (2/3)
Дроби состоят из двух чисел, одного над и под разделительной линией.
Нижнее число известно как знаменатель и относится к отдельным частям целого.
Когда мы говорим о знаменателе, мы используем порядковые числа, то есть числа, которые определяют положение, например, «третье» или «четвертое».
Верхнее число дроби называется числителем и указывает, с каким количеством частей целого мы имеем дело.
Самый простой способ определить дробь — представить себе пирог, который поровну разделен на шесть частей.
Пирог — это целое, а отдельные кусочки — это части целого. Поскольку у нас шесть равных частей одного целого, наш знаменатель здесь 6.
Если мы возьмем один кусок пирога, у нас будет одна шестая (1/6). Два среза эквивалентны двум шестым (2/6) и так далее.
Это довольно просто понять. Однако существуют разные типы дробей и разные методы для выполнения каждого типа дробного уравнения.
Ключевые факты о фракциях
Чтобы понять, как вычислить дроби, важно усвоить основы.Во-первых, давайте посмотрим на три различных типа дробей:
Определения и примеры фракций
- Правильная дробь — Правильная дробь — это дробь, в которой числитель имеет меньшее значение, чем знаменатель. 1/2, 10/15 и 85/100 — все примеры правильных дробей. Общее значение правильной дроби всегда меньше единицы.
- Неправильная дробь — В неправильной дроби значение числителя больше, чем знаменателя.6/3, 25/18 и 50/20 — это примеры неправильных дробей.
 Общее значение неправильной дроби всегда больше единицы.
Общее значение неправильной дроби всегда больше единицы. - Смешанные фракции — Смешанные фракции представлены целым числом, за которым следует дробное число, например 2⅔, 6⅘ или 25⅝. Смешанные фракции также известны как смешанные числа.
Ключевые термины
Теперь, когда мы знаем различные типы дробей, давайте посмотрим на некоторые другие ключевые термины и фразы:
- Эквивалентные дроби — Это дроби, которые выглядят разными, но имеют одинаковое значение.Например, 2/3 — это то же самое, что 4/6.
- Упрощенные дроби — Это дроби, приведенные к наименьшей форме. По сути, это более низкий эквивалент более высокой фракции. Итак, используя приведенный выше пример, 2/3 — это упрощенная версия 4/6.
- Reciprocals — здесь дробь меняется на обратную, помещая знаменатель над числителем. Например, величина, обратная 2/3, равна 3/2. Обратные используются при делении и умножении дробей (5 ÷ 1/5 то же самое, что 5 x 5/1 или 5 x 5).
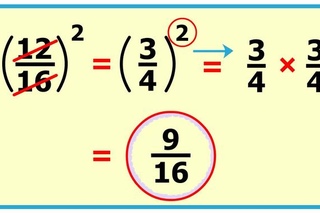
Дроби также могут быть представлены в виде десятичных знаков и процентов . Мы посмотрим, как преобразовать дроби в приведенных ниже примерах уравнений.
10 простых задач на дроби и способы их решения
Ниже приведены десять примеров дробных уравнений и инструкции по их решению. Если вы работаете с дробями на экзамене, обязательно покажите свой метод.
1. Как преобразовать смешанную фракцию в неправильную дробь
Как уже говорилось, смешанная дробь состоит из целого числа, за которым следует дробное число.В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную в цифровом виде как 7⅘.
На запрос преобразовать смешанную дробь в неправильную дробь:
- Сначала умножьте целое число на знаменатель дробной части.
- Возьмите полученное число и прибавьте его к числителю дроби.
- Возьмите эту последнюю цифру в качестве нового числителя и поместите ее над исходным знаменателем.
 Это дает вам неправильную дробь.
Это дает вам неправильную дробь.
Пример:
Используя нашу смешанную дробь 7⅘:
- Целое число, умноженное на дробный знаменатель: 7 x 5 = 35
- Добавьте результат к дробному числителю: 35 + 4 = 39
- Поставим над первоначальным знаменателем: 39/5
Следовательно, правильный ответ: 7⅘ = 39/5
2.Как преобразовать дробь в десятичную
Поскольку оба используются для определения значений меньше единицы, десятичная дробь — это просто другой способ представления дроби.
Метод, используемый для преобразования дроби в десятичную дробь, представляет собой простое деление: вы просто делите числитель на знаменатель.
Пример:
Возьмите дробь 3/10. Разделите числитель на знаменатель, чтобы получить десятичную цифру:
.
3 ÷ 10 = 0,3
Самый простой способ запомнить, как вычислять дроби как десятичные, — это думать о линии, разделяющей числитель и знаменатель, как о символе деления.
3. Как преобразовать дробь в процент
Есть три простых способа преобразовать дробь в проценты. Мы рассмотрим их все, используя одну и ту же долю 7/20.
Метод первый:
Разделите числитель на знаменатель, затем умножьте полученное число на 100, чтобы получить процентное преобразование:
7 ÷ 20 = 0,35
0,35 x 100 = 35%
Метод второй:
Умножьте числитель на 100, затем разделите полученное число на знаменатель:
7 x 100 = 700
700 ÷ 20 = 35%
Метод третий:
Разделите числитель на знаменатель и переместите десятичную запятую в вашем ответе на два разряда вправо:
7 ÷ 20 = 0.35
Перемещение десятичной точки дает конверсию 35%.
При преобразовании дроби в процент всегда не забывайте включать в свой ответ знак%.
4. Как складывать дроби
Процесс сложения дробей прост, если знаменатели совпадают.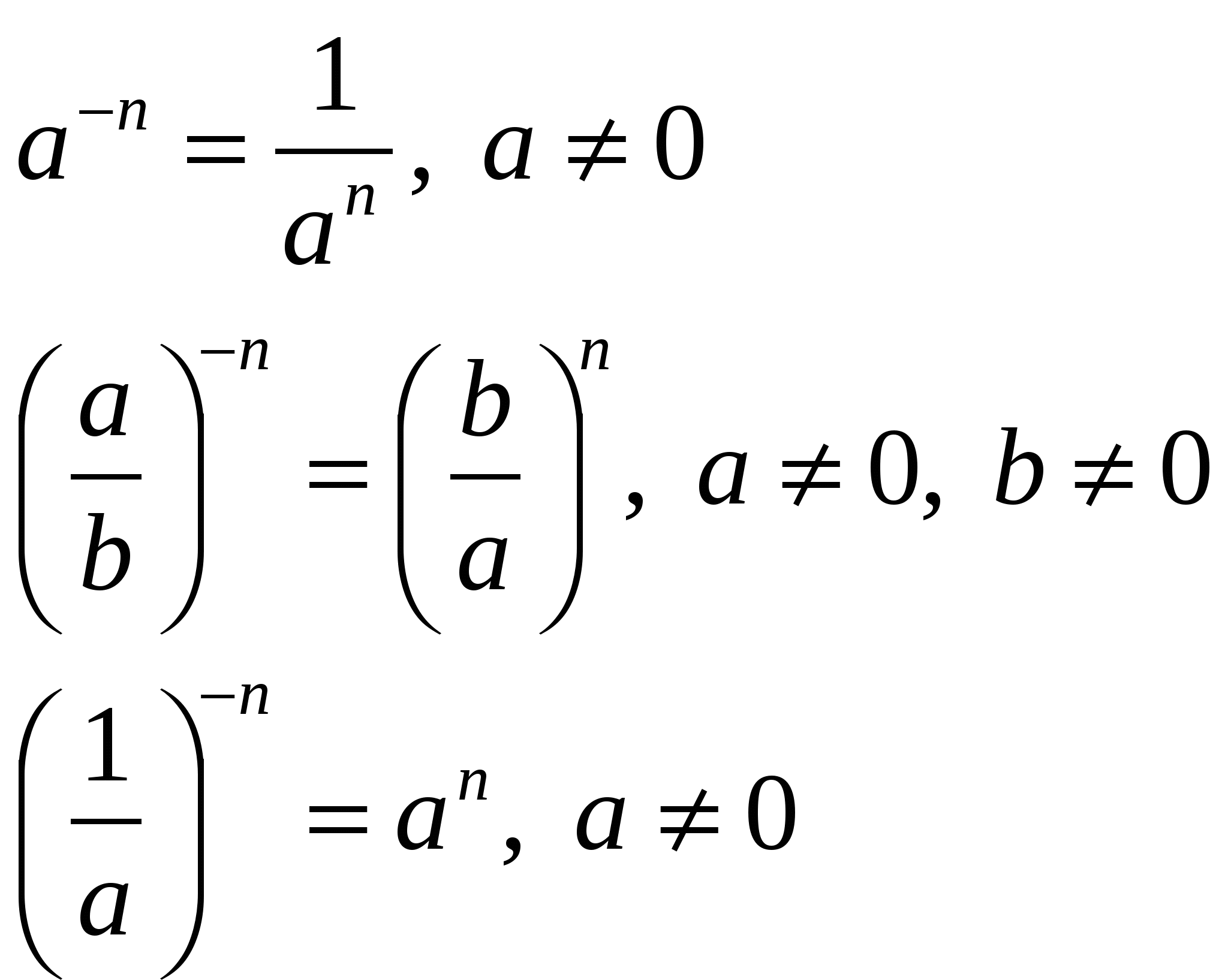
В качестве основного примера возьмем 1/6 + 3/6. В этом случае у вас одинаковые знаменатели, поэтому просто сложите числители обеих дробей, придерживаясь нижней цифры 6:
.
1 + 3 = 4
Итак, 1/6 + 3/6 = 4/6
При сложении дробей, у которых нижние числа не совпадают, вам сначала нужно найти наименьший общий знаменатель .Это наименьшее число, целиком делимое на оба существующих знаменателя.
Пример:
1/4 + 2/3
Наименьшее число, которое делится как на 4, так и на 3, равно 12. Это ваш общий знаменатель.
Теперь вам нужно найти эквивалентные дроби, используя 12 в качестве нижнего числа.
Чтобы превратить 4 в 12, вы умножаете это на 3, поэтому вы также должны умножить числитель на 3, чтобы получить эквивалент дроби:
4 x 3 = 12 и 1 x 3 = 3
Таким образом, ваша доля, эквивалентная 1/4, равна 3/12
Используйте тот же метод для второй дроби :
3 x 4 = 12 и 2 x 4 = 8
Ваша эквивалентная дробь 2/3: 8/12
Теперь просто сложите числители и поместите ответ над 12:
.
3 + 8 = 11
Итак, 3/12 + 8/12 = 11/12
Правильный ответ на уравнение 1/4 + 2/3: 11/12
5.Как вычесть дроби
Как и при сложении, вычитать дроби легко, если знаменатели совпадают. Просто нужно вычесть второй числитель из первого, оставив нижнее число неизменным.
Пример:
Возьмите уравнение 4/7 — 3/7. У вас общий знаменатель, поэтому просто вычтите 3 из 4:
.
4–3 = 1
Итак, 4/7 — 3/7 = 1/7
Теперь давайте посмотрим на вычитание дробей с разными знаменателями .
Пример:
Возьмите уравнение 4/5 — 2/3
Сначала найдите наименьший общий знаменатель; в данном случае 15.
Теперь найдите эквивалентные дроби:
4/5 становится 12/15 (обе части умножаются на 3)
2/3 становится 10/15 (обе части умножаются на 5)
Теперь вы можете вычесть числители:
12–10 = 2
Итак, 12/15 — 10/15 = 2/15
Ответ на уравнение 4/5 — 2/5: 2/15
6.
 Как разделить дроби
Как разделить дроби
Чтобы разделить одну дробь на другую, вам сначала нужно превратить делительную дробь в обратную, поменяв местами знаменатель и числитель.
Пример:
Если взять пример 1/2 ÷ 1/5, последняя дробь как обратная величина равна 5/1.
Теперь умножьте первую дробь на обратную:
.
1/2 х 5/1
Для этого умножьте числители и знаменатели:
1 x 5 = 5 (числители)
2 x 1 = 2 (знаменатели)
Итак, 1/2 x 5/1 = 5/2
Ответ на уравнение 1/2 ÷ 1/5: 5/2 или 2½
7.Как умножать дроби
Процесс вычисления дробей как умножения друг друга прост:
- Умножьте числители
- Умножьте знаменатели
- Напишите новый числитель над новым знаменателем
Пример:
Используя пример уравнения 1/2 x 1/6:
1 x 1 = 1 (числители)
2 x 6 = 12 (знаменатели)
Ответ на 1/2 x 1/6: 1/12
8.
 Как упростить дробь
Как упростить дробь
Упростить дробь — значит привести ее к самой простой форме. По сути, найти наименьшую возможную эквивалентную дробь.
Сначала найдите наибольший общий делитель . Это наибольшее целое число, на которое делятся числитель и знаменатель.
Для этого запишите все множители для обеих частей вашей дроби, как показано ниже на примере 32/48:
.
- Факторы 32: 1, 2, 4, 8, 16, 32
- Факторы 48: 1, 2, 3, 4, 8, 12, 16, 24, 48
Наибольший общий делитель здесь: 16
Теперь разделите числитель и знаменатель на это число, чтобы найти упрощенную дробь:
32 ÷ 16 = 2 (числители)
48 ÷ 16 = 3 (знаменатели)
Следовательно, 32/48 упрощенное: 2/3
Заполняя любую форму дробного уравнения, всегда упрощайте свой ответ до наименьшей возможной формы.
9. Как вычислить доли величин
При представлении количества и просьбе определить дробную часть просто разделите полученное количество на знаменатель дроби, а затем умножьте это число на числитель.
Пример:
У вас 55 конфет, две пятых вы хотите отдать своему соседу, чтобы он забрал домой. Сколько конфет она возьмет?
Разделите полученную сумму на знаменатель дроби: 55 ÷ 5 = 11
Умножьте это число на числитель: 11 x 2 = 22
Следовательно, правильный ответ: 22 конфеты
10.Как определить эквивалентные дроби
Чтобы определить, эквивалентна ли одна дробь другой, умножьте или разделите обе части одной дроби на одно и то же целое число.
Если оба ваших ответа также являются целыми числами, тогда дробь сохраняет свое значение и эквивалентна.
Пример:
Чтобы выяснить, эквивалентно ли 15/12 4/5, разделите 12 и 15 на целое число:
12 ÷ 2 = 6
15 ÷ 2 = 7,5
Так как здесь у вас нет целого числа в качестве ответа, перейдите к следующему основному числу:
12 ÷ 3 = 4
15 ÷ 3 = 5
Это показывает, что 12/15 и 4/5 являются эквивалентными дробями .
Вы также можете сделать это в обратном порядке, умножив обе части младшей дроби:
4 х 3 = 12
5 х 3 = 15
По сути, если одна дробь является упрощенной версией другой, то они эквивалентны.
Как считать дроби: пошаговое руководство
Что такое дроби?
Дроби — это числовые величины, представляющие значения меньше единицы. Также известные как дробные числа, они обычно используются для измерения частей целого, например:
- Одна половина (1/2)
- Одна пятая (1/5)
- Две трети (2/3)
Дроби состоят из двух чисел, одного над и под разделительной линией.
Нижнее число известно как знаменатель и относится к отдельным частям целого.
Когда мы говорим о знаменателе, мы используем порядковые числа, то есть числа, которые определяют положение, например, «третье» или «четвертое».
Верхнее число дроби называется числителем и указывает, с каким количеством частей целого мы имеем дело.
Самый простой способ определить дробь — представить себе пирог, который поровну разделен на шесть частей.
Пирог — это целое, а отдельные кусочки — это части целого. Поскольку у нас шесть равных частей одного целого, наш знаменатель здесь 6.
Если мы возьмем один кусок пирога, у нас будет одна шестая (1/6). Два среза эквивалентны двум шестым (2/6) и так далее.
Это довольно просто понять. Однако существуют разные типы дробей и разные методы для выполнения каждого типа дробного уравнения.
Ключевые факты о фракциях
Чтобы понять, как вычислить дроби, важно усвоить основы.Во-первых, давайте посмотрим на три различных типа дробей:
Определения и примеры фракций
- Правильная дробь — Правильная дробь — это дробь, в которой числитель имеет меньшее значение, чем знаменатель. 1/2, 10/15 и 85/100 — все примеры правильных дробей. Общее значение правильной дроби всегда меньше единицы.
- Неправильная дробь — В неправильной дроби значение числителя больше, чем знаменателя.
 6/3, 25/18 и 50/20 — это примеры неправильных дробей. Общее значение неправильной дроби всегда больше единицы.
6/3, 25/18 и 50/20 — это примеры неправильных дробей. Общее значение неправильной дроби всегда больше единицы. - Смешанные фракции — Смешанные фракции представлены целым числом, за которым следует дробное число, например 2⅔, 6⅘ или 25⅝. Смешанные фракции также известны как смешанные числа.
Ключевые термины
Теперь, когда мы знаем различные типы дробей, давайте посмотрим на некоторые другие ключевые термины и фразы:
- Эквивалентные дроби — Это дроби, которые выглядят разными, но имеют одинаковое значение.Например, 2/3 — это то же самое, что 4/6.
- Упрощенные дроби — Это дроби, приведенные к наименьшей форме. По сути, это более низкий эквивалент более высокой фракции. Итак, используя приведенный выше пример, 2/3 — это упрощенная версия 4/6.
- Reciprocals — здесь дробь меняется на обратную, помещая знаменатель над числителем. Например, величина, обратная 2/3, равна 3/2.
 Обратные используются при делении и умножении дробей (5 ÷ 1/5 то же самое, что 5 x 5/1 или 5 x 5).
Обратные используются при делении и умножении дробей (5 ÷ 1/5 то же самое, что 5 x 5/1 или 5 x 5).
Дроби также могут быть представлены в виде десятичных знаков и процентов . Мы посмотрим, как преобразовать дроби в приведенных ниже примерах уравнений.
10 простых задач на дроби и способы их решения
Ниже приведены десять примеров дробных уравнений и инструкции по их решению. Если вы работаете с дробями на экзамене, обязательно покажите свой метод.
1. Как преобразовать смешанную фракцию в неправильную дробь
Как уже говорилось, смешанная дробь состоит из целого числа, за которым следует дробное число.В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную в цифровом виде как 7⅘.
На запрос преобразовать смешанную дробь в неправильную дробь:
- Сначала умножьте целое число на знаменатель дробной части.
- Возьмите полученное число и прибавьте его к числителю дроби.

- Возьмите эту последнюю цифру в качестве нового числителя и поместите ее над исходным знаменателем. Это дает вам неправильную дробь.
Пример:
Используя нашу смешанную дробь 7⅘:
- Целое число, умноженное на дробный знаменатель: 7 x 5 = 35
- Добавьте результат к дробному числителю: 35 + 4 = 39
- Поставим над первоначальным знаменателем: 39/5
Следовательно, правильный ответ: 7⅘ = 39/5
2.Как преобразовать дробь в десятичную
Поскольку оба используются для определения значений меньше единицы, десятичная дробь — это просто другой способ представления дроби.
Метод, используемый для преобразования дроби в десятичную дробь, представляет собой простое деление: вы просто делите числитель на знаменатель.
Пример:
Возьмите дробь 3/10. Разделите числитель на знаменатель, чтобы получить десятичную цифру:
.
3 ÷ 10 = 0,3
Самый простой способ запомнить, как вычислять дроби как десятичные, — это думать о линии, разделяющей числитель и знаменатель, как о символе деления.
3. Как преобразовать дробь в процент
Есть три простых способа преобразовать дробь в проценты. Мы рассмотрим их все, используя одну и ту же долю 7/20.
Метод первый:
Разделите числитель на знаменатель, затем умножьте полученное число на 100, чтобы получить процентное преобразование:
7 ÷ 20 = 0,35
0,35 x 100 = 35%
Метод второй:
Умножьте числитель на 100, затем разделите полученное число на знаменатель:
7 x 100 = 700
700 ÷ 20 = 35%
Метод третий:
Разделите числитель на знаменатель и переместите десятичную запятую в вашем ответе на два разряда вправо:
7 ÷ 20 = 0.35
Перемещение десятичной точки дает конверсию 35%.
При преобразовании дроби в процент всегда не забывайте включать в свой ответ знак%.
4. Как складывать дроби
Процесс сложения дробей прост, если знаменатели совпадают.
В качестве основного примера возьмем 1/6 + 3/6. В этом случае у вас одинаковые знаменатели, поэтому просто сложите числители обеих дробей, придерживаясь нижней цифры 6:
.
1 + 3 = 4
Итак, 1/6 + 3/6 = 4/6
При сложении дробей, у которых нижние числа не совпадают, вам сначала нужно найти наименьший общий знаменатель .Это наименьшее число, целиком делимое на оба существующих знаменателя.
Пример:
1/4 + 2/3
Наименьшее число, которое делится как на 4, так и на 3, равно 12. Это ваш общий знаменатель.
Теперь вам нужно найти эквивалентные дроби, используя 12 в качестве нижнего числа.
Чтобы превратить 4 в 12, вы умножаете это на 3, поэтому вы также должны умножить числитель на 3, чтобы получить эквивалент дроби:
4 x 3 = 12 и 1 x 3 = 3
Таким образом, ваша доля, эквивалентная 1/4, равна 3/12
Используйте тот же метод для второй дроби :
3 x 4 = 12 и 2 x 4 = 8
Ваша эквивалентная дробь 2/3: 8/12
Теперь просто сложите числители и поместите ответ над 12:
.
3 + 8 = 11
Итак, 3/12 + 8/12 = 11/12
Правильный ответ на уравнение 1/4 + 2/3: 11/12
5.Как вычесть дроби
Как и при сложении, вычитать дроби легко, если знаменатели совпадают. Просто нужно вычесть второй числитель из первого, оставив нижнее число неизменным.
Пример:
Возьмите уравнение 4/7 — 3/7. У вас общий знаменатель, поэтому просто вычтите 3 из 4:
.
4–3 = 1
Итак, 4/7 — 3/7 = 1/7
Теперь давайте посмотрим на вычитание дробей с разными знаменателями .
Пример:
Возьмите уравнение 4/5 — 2/3
Сначала найдите наименьший общий знаменатель; в данном случае 15.
Теперь найдите эквивалентные дроби:
4/5 становится 12/15 (обе части умножаются на 3)
2/3 становится 10/15 (обе части умножаются на 5)
Теперь вы можете вычесть числители:
12–10 = 2
Итак, 12/15 — 10/15 = 2/15
Ответ на уравнение 4/5 — 2/5: 2/15
6.
 Как разделить дроби
Как разделить дроби
Чтобы разделить одну дробь на другую, вам сначала нужно превратить делительную дробь в обратную, поменяв местами знаменатель и числитель.
Пример:
Если взять пример 1/2 ÷ 1/5, последняя дробь как обратная величина равна 5/1.
Теперь умножьте первую дробь на обратную:
.
1/2 х 5/1
Для этого умножьте числители и знаменатели:
1 x 5 = 5 (числители)
2 x 1 = 2 (знаменатели)
Итак, 1/2 x 5/1 = 5/2
Ответ на уравнение 1/2 ÷ 1/5: 5/2 или 2½
7.Как умножать дроби
Процесс вычисления дробей как умножения друг друга прост:
- Умножьте числители
- Умножьте знаменатели
- Напишите новый числитель над новым знаменателем
Пример:
Используя пример уравнения 1/2 x 1/6:
1 x 1 = 1 (числители)
2 x 6 = 12 (знаменатели)
Ответ на 1/2 x 1/6: 1/12
8.
 Как упростить дробь
Как упростить дробь
Упростить дробь — значит привести ее к самой простой форме. По сути, найти наименьшую возможную эквивалентную дробь.
Сначала найдите наибольший общий делитель . Это наибольшее целое число, на которое делятся числитель и знаменатель.
Для этого запишите все множители для обеих частей вашей дроби, как показано ниже на примере 32/48:
.
- Факторы 32: 1, 2, 4, 8, 16, 32
- Факторы 48: 1, 2, 3, 4, 8, 12, 16, 24, 48
Наибольший общий делитель здесь: 16
Теперь разделите числитель и знаменатель на это число, чтобы найти упрощенную дробь:
32 ÷ 16 = 2 (числители)
48 ÷ 16 = 3 (знаменатели)
Следовательно, 32/48 упрощенное: 2/3
Заполняя любую форму дробного уравнения, всегда упрощайте свой ответ до наименьшей возможной формы.
9. Как вычислить доли величин
При представлении количества и просьбе определить дробную часть просто разделите полученное количество на знаменатель дроби, а затем умножьте это число на числитель.
Пример:
У вас 55 конфет, две пятых вы хотите отдать своему соседу, чтобы он забрал домой. Сколько конфет она возьмет?
Разделите полученную сумму на знаменатель дроби: 55 ÷ 5 = 11
Умножьте это число на числитель: 11 x 2 = 22
Следовательно, правильный ответ: 22 конфеты
10.Как определить эквивалентные дроби
Чтобы определить, эквивалентна ли одна дробь другой, умножьте или разделите обе части одной дроби на одно и то же целое число.
Если оба ваших ответа также являются целыми числами, тогда дробь сохраняет свое значение и эквивалентна.
Пример:
Чтобы выяснить, эквивалентно ли 15/12 4/5, разделите 12 и 15 на целое число:
12 ÷ 2 = 6
15 ÷ 2 = 7,5
Так как здесь у вас нет целого числа в качестве ответа, перейдите к следующему основному числу:
12 ÷ 3 = 4
15 ÷ 3 = 5
Это показывает, что 12/15 и 4/5 являются эквивалентными дробями .
Вы также можете сделать это в обратном порядке, умножив обе части младшей дроби:
4 х 3 = 12
5 х 3 = 15
По сути, если одна дробь является упрощенной версией другой, то они эквивалентны.
Как считать дроби: пошаговое руководство
Что такое дроби?
Дроби — это числовые величины, представляющие значения меньше единицы. Также известные как дробные числа, они обычно используются для измерения частей целого, например:
- Одна половина (1/2)
- Одна пятая (1/5)
- Две трети (2/3)
Дроби состоят из двух чисел, одного над и под разделительной линией.
Нижнее число известно как знаменатель и относится к отдельным частям целого.
Когда мы говорим о знаменателе, мы используем порядковые числа, то есть числа, которые определяют положение, например, «третье» или «четвертое».
Верхнее число дроби называется числителем и указывает, с каким количеством частей целого мы имеем дело.
Самый простой способ определить дробь — представить себе пирог, который поровну разделен на шесть частей.
Пирог — это целое, а отдельные кусочки — это части целого. Поскольку у нас шесть равных частей одного целого, наш знаменатель здесь 6.
Если мы возьмем один кусок пирога, у нас будет одна шестая (1/6). Два среза эквивалентны двум шестым (2/6) и так далее.
Это довольно просто понять. Однако существуют разные типы дробей и разные методы для выполнения каждого типа дробного уравнения.
Ключевые факты о фракциях
Чтобы понять, как вычислить дроби, важно усвоить основы.Во-первых, давайте посмотрим на три различных типа дробей:
Определения и примеры фракций
- Правильная дробь — Правильная дробь — это дробь, в которой числитель имеет меньшее значение, чем знаменатель. 1/2, 10/15 и 85/100 — все примеры правильных дробей. Общее значение правильной дроби всегда меньше единицы.
- Неправильная дробь — В неправильной дроби значение числителя больше, чем знаменателя.
 6/3, 25/18 и 50/20 — это примеры неправильных дробей. Общее значение неправильной дроби всегда больше единицы.
6/3, 25/18 и 50/20 — это примеры неправильных дробей. Общее значение неправильной дроби всегда больше единицы. - Смешанные фракции — Смешанные фракции представлены целым числом, за которым следует дробное число, например 2⅔, 6⅘ или 25⅝. Смешанные фракции также известны как смешанные числа.
Ключевые термины
Теперь, когда мы знаем различные типы дробей, давайте посмотрим на некоторые другие ключевые термины и фразы:
- Эквивалентные дроби — Это дроби, которые выглядят разными, но имеют одинаковое значение.Например, 2/3 — это то же самое, что 4/6.
- Упрощенные дроби — Это дроби, приведенные к наименьшей форме. По сути, это более низкий эквивалент более высокой фракции. Итак, используя приведенный выше пример, 2/3 — это упрощенная версия 4/6.
- Reciprocals — здесь дробь меняется на обратную, помещая знаменатель над числителем. Например, величина, обратная 2/3, равна 3/2.
 Обратные используются при делении и умножении дробей (5 ÷ 1/5 то же самое, что 5 x 5/1 или 5 x 5).
Обратные используются при делении и умножении дробей (5 ÷ 1/5 то же самое, что 5 x 5/1 или 5 x 5).
Дроби также могут быть представлены в виде десятичных знаков и процентов . Мы посмотрим, как преобразовать дроби в приведенных ниже примерах уравнений.
10 простых задач на дроби и способы их решения
Ниже приведены десять примеров дробных уравнений и инструкции по их решению. Если вы работаете с дробями на экзамене, обязательно покажите свой метод.
1. Как преобразовать смешанную фракцию в неправильную дробь
Как уже говорилось, смешанная дробь состоит из целого числа, за которым следует дробное число.В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную в цифровом виде как 7⅘.
На запрос преобразовать смешанную дробь в неправильную дробь:
- Сначала умножьте целое число на знаменатель дробной части.
- Возьмите полученное число и прибавьте его к числителю дроби.
- Возьмите эту последнюю цифру в качестве нового числителя и поместите ее над исходным знаменателем. Это дает вам неправильную дробь.
Пример:
Используя нашу смешанную дробь 7⅘:
- Целое число, умноженное на дробный знаменатель: 7 x 5 = 35
- Добавьте результат к дробному числителю: 35 + 4 = 39
- Поставим над первоначальным знаменателем: 39/5
Следовательно, правильный ответ: 7⅘ = 39/5
2.Как преобразовать дробь в десятичную
Поскольку оба используются для определения значений меньше единицы, десятичная дробь — это просто другой способ представления дроби.
Метод, используемый для преобразования дроби в десятичную дробь, представляет собой простое деление: вы просто делите числитель на знаменатель.
Пример:
Возьмите дробь 3/10. Разделите числитель на знаменатель, чтобы получить десятичную цифру:
.
3 ÷ 10 = 0,3
Самый простой способ запомнить, как вычислять дроби как десятичные, — это думать о линии, разделяющей числитель и знаменатель, как о символе деления.
3. Как преобразовать дробь в процент
Есть три простых способа преобразовать дробь в проценты. Мы рассмотрим их все, используя одну и ту же долю 7/20.
Метод первый:
Разделите числитель на знаменатель, затем умножьте полученное число на 100, чтобы получить процентное преобразование:
7 ÷ 20 = 0,35
0,35 x 100 = 35%
Метод второй:
Умножьте числитель на 100, затем разделите полученное число на знаменатель:
7 x 100 = 700
700 ÷ 20 = 35%
Метод третий:
Разделите числитель на знаменатель и переместите десятичную запятую в вашем ответе на два разряда вправо:
7 ÷ 20 = 0.35
Перемещение десятичной точки дает конверсию 35%.
При преобразовании дроби в процент всегда не забывайте включать в свой ответ знак%.
4. Как складывать дроби
Процесс сложения дробей прост, если знаменатели совпадают.
В качестве основного примера возьмем 1/6 + 3/6. В этом случае у вас одинаковые знаменатели, поэтому просто сложите числители обеих дробей, придерживаясь нижней цифры 6:
.
1 + 3 = 4
Итак, 1/6 + 3/6 = 4/6
При сложении дробей, у которых нижние числа не совпадают, вам сначала нужно найти наименьший общий знаменатель .Это наименьшее число, целиком делимое на оба существующих знаменателя.
Пример:
1/4 + 2/3
Наименьшее число, которое делится как на 4, так и на 3, равно 12. Это ваш общий знаменатель.
Теперь вам нужно найти эквивалентные дроби, используя 12 в качестве нижнего числа.
Чтобы превратить 4 в 12, вы умножаете это на 3, поэтому вы также должны умножить числитель на 3, чтобы получить эквивалент дроби:
4 x 3 = 12 и 1 x 3 = 3
Таким образом, ваша доля, эквивалентная 1/4, равна 3/12
Используйте тот же метод для второй дроби :
3 x 4 = 12 и 2 x 4 = 8
Ваша эквивалентная дробь 2/3: 8/12
Теперь просто сложите числители и поместите ответ над 12:
.
3 + 8 = 11
Итак, 3/12 + 8/12 = 11/12
Правильный ответ на уравнение 1/4 + 2/3: 11/12
5.Как вычесть дроби
Как и при сложении, вычитать дроби легко, если знаменатели совпадают. Просто нужно вычесть второй числитель из первого, оставив нижнее число неизменным.
Пример:
Возьмите уравнение 4/7 — 3/7. У вас общий знаменатель, поэтому просто вычтите 3 из 4:
.
4–3 = 1
Итак, 4/7 — 3/7 = 1/7
Теперь давайте посмотрим на вычитание дробей с разными знаменателями .
Пример:
Возьмите уравнение 4/5 — 2/3
Сначала найдите наименьший общий знаменатель; в данном случае 15.
Теперь найдите эквивалентные дроби:
4/5 становится 12/15 (обе части умножаются на 3)
2/3 становится 10/15 (обе части умножаются на 5)
Теперь вы можете вычесть числители:
12–10 = 2
Итак, 12/15 — 10/15 = 2/15
Ответ на уравнение 4/5 — 2/5: 2/15
6.Как разделить дроби
Чтобы разделить одну дробь на другую, вам сначала нужно превратить делительную дробь в обратную, поменяв местами знаменатель и числитель.
Пример:
Если взять пример 1/2 ÷ 1/5, последняя дробь как обратная величина равна 5/1.
Теперь умножьте первую дробь на обратную:
.
1/2 х 5/1
Для этого умножьте числители и знаменатели:
1 x 5 = 5 (числители)
2 x 1 = 2 (знаменатели)
Итак, 1/2 x 5/1 = 5/2
Ответ на уравнение 1/2 ÷ 1/5: 5/2 или 2½
7.Как умножать дроби
Процесс вычисления дробей как умножения друг друга прост:
- Умножьте числители
- Умножьте знаменатели
- Напишите новый числитель над новым знаменателем
Пример:
Используя пример уравнения 1/2 x 1/6:
1 x 1 = 1 (числители)
2 x 6 = 12 (знаменатели)
Ответ на 1/2 x 1/6: 1/12
8.Как упростить дробь
Упростить дробь — значит привести ее к самой простой форме. По сути, найти наименьшую возможную эквивалентную дробь.
Сначала найдите наибольший общий делитель . Это наибольшее целое число, на которое делятся числитель и знаменатель.
Для этого запишите все множители для обеих частей вашей дроби, как показано ниже на примере 32/48:
.
- Факторы 32: 1, 2, 4, 8, 16, 32
- Факторы 48: 1, 2, 3, 4, 8, 12, 16, 24, 48
Наибольший общий делитель здесь: 16
Теперь разделите числитель и знаменатель на это число, чтобы найти упрощенную дробь:
32 ÷ 16 = 2 (числители)
48 ÷ 16 = 3 (знаменатели)
Следовательно, 32/48 упрощенное: 2/3
Заполняя любую форму дробного уравнения, всегда упрощайте свой ответ до наименьшей возможной формы.
9. Как вычислить доли величин
При представлении количества и просьбе определить дробную часть просто разделите полученное количество на знаменатель дроби, а затем умножьте это число на числитель.
Пример:
У вас 55 конфет, две пятых вы хотите отдать своему соседу, чтобы он забрал домой. Сколько конфет она возьмет?
Разделите полученную сумму на знаменатель дроби: 55 ÷ 5 = 11
Умножьте это число на числитель: 11 x 2 = 22
Следовательно, правильный ответ: 22 конфеты
10.Как определить эквивалентные дроби
Чтобы определить, эквивалентна ли одна дробь другой, умножьте или разделите обе части одной дроби на одно и то же целое число.
Если оба ваших ответа также являются целыми числами, тогда дробь сохраняет свое значение и эквивалентна.
Пример:
Чтобы выяснить, эквивалентно ли 15/12 4/5, разделите 12 и 15 на целое число:
12 ÷ 2 = 6
15 ÷ 2 = 7,5
Так как здесь у вас нет целого числа в качестве ответа, перейдите к следующему основному числу:
12 ÷ 3 = 4
15 ÷ 3 = 5
Это показывает, что 12/15 и 4/5 являются эквивалентными дробями .
Вы также можете сделать это в обратном порядке, умножив обе части младшей дроби:
4 х 3 = 12
5 х 3 = 15
По сути, если одна дробь является упрощенной версией другой, то они эквивалентны.
Как считать дроби: пошаговое руководство
Что такое дроби?
Дроби — это числовые величины, представляющие значения меньше единицы. Также известные как дробные числа, они обычно используются для измерения частей целого, например:
- Одна половина (1/2)
- Одна пятая (1/5)
- Две трети (2/3)
Дроби состоят из двух чисел, одного над и под разделительной линией.
Нижнее число известно как знаменатель и относится к отдельным частям целого.
Когда мы говорим о знаменателе, мы используем порядковые числа, то есть числа, которые определяют положение, например, «третье» или «четвертое».
Верхнее число дроби называется числителем и указывает, с каким количеством частей целого мы имеем дело.
Самый простой способ определить дробь — представить себе пирог, который поровну разделен на шесть частей.
Пирог — это целое, а отдельные кусочки — это части целого. Поскольку у нас шесть равных частей одного целого, наш знаменатель здесь 6.
Если мы возьмем один кусок пирога, у нас будет одна шестая (1/6). Два среза эквивалентны двум шестым (2/6) и так далее.
Это довольно просто понять. Однако существуют разные типы дробей и разные методы для выполнения каждого типа дробного уравнения.
Ключевые факты о фракциях
Чтобы понять, как вычислить дроби, важно усвоить основы.Во-первых, давайте посмотрим на три различных типа дробей:
Определения и примеры фракций
- Правильная дробь — Правильная дробь — это дробь, в которой числитель имеет меньшее значение, чем знаменатель. 1/2, 10/15 и 85/100 — все примеры правильных дробей. Общее значение правильной дроби всегда меньше единицы.
- Неправильная дробь — В неправильной дроби значение числителя больше, чем знаменателя.6/3, 25/18 и 50/20 — это примеры неправильных дробей. Общее значение неправильной дроби всегда больше единицы.
- Смешанные фракции — Смешанные фракции представлены целым числом, за которым следует дробное число, например 2⅔, 6⅘ или 25⅝. Смешанные фракции также известны как смешанные числа.
Ключевые термины
Теперь, когда мы знаем различные типы дробей, давайте посмотрим на некоторые другие ключевые термины и фразы:
- Эквивалентные дроби — Это дроби, которые выглядят разными, но имеют одинаковое значение.Например, 2/3 — это то же самое, что 4/6.
- Упрощенные дроби — Это дроби, приведенные к наименьшей форме. По сути, это более низкий эквивалент более высокой фракции. Итак, используя приведенный выше пример, 2/3 — это упрощенная версия 4/6.
- Reciprocals — здесь дробь меняется на обратную, помещая знаменатель над числителем. Например, величина, обратная 2/3, равна 3/2. Обратные используются при делении и умножении дробей (5 ÷ 1/5 то же самое, что 5 x 5/1 или 5 x 5).
Дроби также могут быть представлены в виде десятичных знаков и процентов . Мы посмотрим, как преобразовать дроби в приведенных ниже примерах уравнений.
10 простых задач на дроби и способы их решения
Ниже приведены десять примеров дробных уравнений и инструкции по их решению. Если вы работаете с дробями на экзамене, обязательно покажите свой метод.
1. Как преобразовать смешанную фракцию в неправильную дробь
Как уже говорилось, смешанная дробь состоит из целого числа, за которым следует дробное число.В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную в цифровом виде как 7⅘.
На запрос преобразовать смешанную дробь в неправильную дробь:
- Сначала умножьте целое число на знаменатель дробной части.
- Возьмите полученное число и прибавьте его к числителю дроби.
- Возьмите эту последнюю цифру в качестве нового числителя и поместите ее над исходным знаменателем. Это дает вам неправильную дробь.
Пример:
Используя нашу смешанную дробь 7⅘:
- Целое число, умноженное на дробный знаменатель: 7 x 5 = 35
- Добавьте результат к дробному числителю: 35 + 4 = 39
- Поставим над первоначальным знаменателем: 39/5
Следовательно, правильный ответ: 7⅘ = 39/5
2.Как преобразовать дробь в десятичную
Поскольку оба используются для определения значений меньше единицы, десятичная дробь — это просто другой способ представления дроби.
Метод, используемый для преобразования дроби в десятичную дробь, представляет собой простое деление: вы просто делите числитель на знаменатель.
Пример:
Возьмите дробь 3/10. Разделите числитель на знаменатель, чтобы получить десятичную цифру:
.
3 ÷ 10 = 0,3
Самый простой способ запомнить, как вычислять дроби как десятичные, — это думать о линии, разделяющей числитель и знаменатель, как о символе деления.
3. Как преобразовать дробь в процент
Есть три простых способа преобразовать дробь в проценты. Мы рассмотрим их все, используя одну и ту же долю 7/20.
Метод первый:
Разделите числитель на знаменатель, затем умножьте полученное число на 100, чтобы получить процентное преобразование:
7 ÷ 20 = 0,35
0,35 x 100 = 35%
Метод второй:
Умножьте числитель на 100, затем разделите полученное число на знаменатель:
7 x 100 = 700
700 ÷ 20 = 35%
Метод третий:
Разделите числитель на знаменатель и переместите десятичную запятую в вашем ответе на два разряда вправо:
7 ÷ 20 = 0.35
Перемещение десятичной точки дает конверсию 35%.
При преобразовании дроби в процент всегда не забывайте включать в свой ответ знак%.
4. Как складывать дроби
Процесс сложения дробей прост, если знаменатели совпадают.
В качестве основного примера возьмем 1/6 + 3/6. В этом случае у вас одинаковые знаменатели, поэтому просто сложите числители обеих дробей, придерживаясь нижней цифры 6:
.
1 + 3 = 4
Итак, 1/6 + 3/6 = 4/6
При сложении дробей, у которых нижние числа не совпадают, вам сначала нужно найти наименьший общий знаменатель .Это наименьшее число, целиком делимое на оба существующих знаменателя.
Пример:
1/4 + 2/3
Наименьшее число, которое делится как на 4, так и на 3, равно 12. Это ваш общий знаменатель.
Теперь вам нужно найти эквивалентные дроби, используя 12 в качестве нижнего числа.
Чтобы превратить 4 в 12, вы умножаете это на 3, поэтому вы также должны умножить числитель на 3, чтобы получить эквивалент дроби:
4 x 3 = 12 и 1 x 3 = 3
Таким образом, ваша доля, эквивалентная 1/4, равна 3/12
Используйте тот же метод для второй дроби :
3 x 4 = 12 и 2 x 4 = 8
Ваша эквивалентная дробь 2/3: 8/12
Теперь просто сложите числители и поместите ответ над 12:
.
3 + 8 = 11
Итак, 3/12 + 8/12 = 11/12
Правильный ответ на уравнение 1/4 + 2/3: 11/12
5.Как вычесть дроби
Как и при сложении, вычитать дроби легко, если знаменатели совпадают. Просто нужно вычесть второй числитель из первого, оставив нижнее число неизменным.
Пример:
Возьмите уравнение 4/7 — 3/7. У вас общий знаменатель, поэтому просто вычтите 3 из 4:
.
4–3 = 1
Итак, 4/7 — 3/7 = 1/7
Теперь давайте посмотрим на вычитание дробей с разными знаменателями .
Пример:
Возьмите уравнение 4/5 — 2/3
Сначала найдите наименьший общий знаменатель; в данном случае 15.
Теперь найдите эквивалентные дроби:
4/5 становится 12/15 (обе части умножаются на 3)
2/3 становится 10/15 (обе части умножаются на 5)
Теперь вы можете вычесть числители:
12–10 = 2
Итак, 12/15 — 10/15 = 2/15
Ответ на уравнение 4/5 — 2/5: 2/15
6.Как разделить дроби
Чтобы разделить одну дробь на другую, вам сначала нужно превратить делительную дробь в обратную, поменяв местами знаменатель и числитель.
Пример:
Если взять пример 1/2 ÷ 1/5, последняя дробь как обратная величина равна 5/1.
Теперь умножьте первую дробь на обратную:
.
1/2 х 5/1
Для этого умножьте числители и знаменатели:
1 x 5 = 5 (числители)
2 x 1 = 2 (знаменатели)
Итак, 1/2 x 5/1 = 5/2
Ответ на уравнение 1/2 ÷ 1/5: 5/2 или 2½
7.Как умножать дроби
Процесс вычисления дробей как умножения друг друга прост:
- Умножьте числители
- Умножьте знаменатели
- Напишите новый числитель над новым знаменателем
Пример:
Используя пример уравнения 1/2 x 1/6:
1 x 1 = 1 (числители)
2 x 6 = 12 (знаменатели)
Ответ на 1/2 x 1/6: 1/12
8.Как упростить дробь
Упростить дробь — значит привести ее к самой простой форме. По сути, найти наименьшую возможную эквивалентную дробь.
Сначала найдите наибольший общий делитель . Это наибольшее целое число, на которое делятся числитель и знаменатель.
Для этого запишите все множители для обеих частей вашей дроби, как показано ниже на примере 32/48:
.
- Факторы 32: 1, 2, 4, 8, 16, 32
- Факторы 48: 1, 2, 3, 4, 8, 12, 16, 24, 48
Наибольший общий делитель здесь: 16
Теперь разделите числитель и знаменатель на это число, чтобы найти упрощенную дробь:
32 ÷ 16 = 2 (числители)
48 ÷ 16 = 3 (знаменатели)
Следовательно, 32/48 упрощенное: 2/3
Заполняя любую форму дробного уравнения, всегда упрощайте свой ответ до наименьшей возможной формы.
9. Как вычислить доли величин
При представлении количества и просьбе определить дробную часть просто разделите полученное количество на знаменатель дроби, а затем умножьте это число на числитель.
Пример:
У вас 55 конфет, две пятых вы хотите отдать своему соседу, чтобы он забрал домой. Сколько конфет она возьмет?
Разделите полученную сумму на знаменатель дроби: 55 ÷ 5 = 11
Умножьте это число на числитель: 11 x 2 = 22
Следовательно, правильный ответ: 22 конфеты
10.Как определить эквивалентные дроби
Чтобы определить, эквивалентна ли одна дробь другой, умножьте или разделите обе части одной дроби на одно и то же целое число.
Если оба ваших ответа также являются целыми числами, тогда дробь сохраняет свое значение и эквивалентна.
Пример:
Чтобы выяснить, эквивалентно ли 15/12 4/5, разделите 12 и 15 на целое число:
12 ÷ 2 = 6
15 ÷ 2 = 7,5
Так как здесь у вас нет целого числа в качестве ответа, перейдите к следующему основному числу:
12 ÷ 3 = 4
15 ÷ 3 = 5
Это показывает, что 12/15 и 4/5 являются эквивалентными дробями .
Вы также можете сделать это в обратном порядке, умножив обе части младшей дроби:
4 х 3 = 12
5 х 3 = 15
По сути, если одна дробь является упрощенной версией другой, то они эквивалентны.
Как считать дроби
Что такое дроби?
Дробное число или дробь используется для представления сегмента целого числа.
Дробь состоит из двух чисел, расположенных одно над другим.Первое число, которое находится над строкой, — это числитель . Второе число, расположенное под чертой, — это знаменатель .
Знаменатель указывает общее количество равных частей, на которые что-либо делится. Числитель показывает, сколько из этих равных частей необходимо учитывать.
Самый простой способ запомнить дроби — обозначить линию, разделяющую каждое число, «из». Таким образом, дробь, записанная как 3/5, просто относится к 3 частям из 5 равных частей.
Как можно представить дроби?
Дроби могут быть представлены тремя способами: как правильные дроби, неправильные дроби и смешанные дроби.
- Правильная дробь — это дробь, в которой числитель меньше знаменателя. Например, ⅔ (две трети) или ⅞ (семь восьмых).
- У неправильной дроби числитель больше знаменателя. Например, 8/5 (восемь пятых) или 13/4 (тринадцать четвертей).
- Смешанное число объединяет целое число и дробь.Например, 5¾ (пять и три четверти) или 12⅖ (двенадцать и две пятых).
Упрощение дробей
Процесс упрощения дробей сводит их к простейшей форме. Например, гораздо проще называть что-то ½, а не 4/8.
Есть два способа упростить дробь.
Первый метод — разделить верхнюю и нижнюю части дроби поровну на целые числа больше 1, пока вы не сможете продолжить.В качестве примера возьмем дробь 24/108:
- Разделите каждое число на 2, чтобы получить 12/54
- Разделите на 2 еще раз, чтобы получить 6/27
- Разделите на 3, чтобы получить 2/9
Сложение дробей
Чтобы сложить дроби, вам нужно изменить их так, чтобы знаменатели (нижние числа) были одинаковыми. Затем вы суммируете числители.
Дополнение: Пример 1
Допустим, вы хотите добавить дробь ¼ к ¼.
Знаменатели уже те же, поэтому вы можете перейти ко второму шагу и прибавить 1 к 1.
Вторая половина дроби остается неизменной, поэтому сложение дробей ¼ и ¼ дает 2/4 (или ½).
Дополнение: Пример 2
Допустим, вы хотите сложить дроби ⅓ и ⅙.
Чтобы знаменатели совпали, измените ⅓ на 2/6.
Добавьте 1 к 2, чтобы получить 3, и поместите 6 ниже. Ответ — 3/6. Упростите это до ½.
Вычитание дробей
Вычитание дробей работает аналогично:
- Шаг 1. Убедитесь, что знаменатели совпадают.
- Шаг 2. Вычтите числители
- Шаг 3 — При необходимости упростите дробь
Вычитание: Пример 1
Допустим, вас попросили потренироваться ¾ — ¼
Первый шаг относительно прост, потому что числа совпадают.
Второй шаг включает в себя вычитание первых чисел и затем перенос ответа над тем же знаменателем.
Таким образом, ¾ — be будет обработано как 3-1 = 2
Следовательно, ответ будет 2/4, что составляет ½.
Умножение дробей
Умножение дробей относительно легко; вы просто умножаете верхние числа и нижние числа.
Если, например, вы умножите дроби ½ и ⅓, вы получите. От вас не ждут, что вы найдете общий знаменатель путем умножения.
На дробь
Чтобы разделить дроби, вам нужно перевернуть дробь, которую вы делите, вверх дном. Например, если вы хотите разделить ½ на, вы переписываете уравнение так, чтобы вторая дробь была 3/1. Затем умножьте ½ на 3/1, и вы получите 3/2.
Может потребоваться дальнейшее уменьшение фракции для получения сложной фракции.
Распространенные ошибки и на что следует обращать внимание
При сложении и вычитании дробей может быть легко запутаться.Студенты часто складывают или вычитают знаменатели или числители двух дробей и обычно не замечают связи между знаменателем. Чтобы еще больше усугубить путаницу, к числителям и знаменателям следует подходить в расчетах как к целым числам, например, когда вам необходимо умножить дробь.
Возьмем для примера сложение ¾ и ⅙.
Первое, что нужно сделать, это получить одинаковые знаменатели, поэтому мы умножаем их, чтобы получить 24.
Мы умножили знаменатель 4 на 6, чтобы получить 24, поэтому мы также умножаем числитель на 6, чтобы получить 18/24.
Мы умножили знаменатель 6 на 4, чтобы получить 24, поэтому мы также умножаем числитель на 4, чтобы получить 4/24.
Теперь мы можем просто добавить 18/24 к 4/24, чтобы получить 22/24, что упрощается до 11/12.
Прочие типичных ошибок включают:
- При сложении или вычитании дробей кандидаты могут забыть сначала преобразовать дроби, чтобы у них был общий знаменатель.
- Изменение знаменателя дроби без внесения необходимых изменений в числитель.
- Непонимание вопроса полностью; например, деление вместо вычитания или умножение вместо сложения.
- Знаменатель остается неизменным при ответах на вопросы, относящиеся к умножению или сложению.
Понимание взаимосвязи между смешанными числами и неправильными дробями и того, как переводить одно в другое, имеет решающее значение для работы с дробями.
Пошаговое руководство по вычислению дробей с примерами
Ищете лучший способ похудеть? Если да!! Давайте узнаем, как решать дроби. Звучит странно? Да, вы правильно прочитали! Чтобы эффективно похудеть, вам необходимо знать индекс массы тела (ИМТ) с использованием дробей.
Дамы, ювелир подарит вам украшения 18 или 24 карата? 24 карата считаются чистым золотом, тогда как 18 карат означают 18/24, что составляет 75% золота. Вот как вы можете использовать дроби, чтобы узнать чистоту ювелирных изделий.
Этот блог поможет вам понять, как решать дроби с помощью различных методов. Кроме того, я перечислил несколько полезных советов по использованию дробей.Итак, не создавая путаницы, давайте подробно разберемся с концепцией дробей.
Что нужно знать о дроби !!
Сначала разберитесь, что такое дробь.
Дробь — это числовая величина или значение, которое не является целым числом, например 4/5, 6/7 и т. Д.
| Интересный факт: Есть факт, который поможет вам произвести впечатление на своих учителей и друзей.Это полоса или знак деления в дроби, известной как «ВИНКУЛУМ». |
Следующее, что нужно выучить, — это термины, используемые в нарушениях. Итак, каждая дробь состоит из двух частей.
| Первая часть называется числителем , записанным в верхней части символа деления, и он уравнивает количество частей дроби. Короче говоря, это количество частей, которые у нас есть в долях. | Принимая во внимание, что вторая часть называется знаменателем и написана под символом деления, она в основном равна общему количеству частей в целом, и поэтому обозначает общие части числа в целом. |
Например, в 3/5 дроби, 3 — числитель, а 5 — знаменатель.
Здесь 3 означает, что это третья часть целого числа, а 5 означает, что целое число состоит из 5 частей.
Второе, что нужно узнать о типах дробей.
Мы имеем дело с тремя типами дробей. Давайте проверим каждую из них по очереди.
- Правильная дробь: В этой дроби числитель имеет меньшее значение по сравнению со знаменателем.
| Примечание: Значение правильной дроби всегда меньше 1. | Пример правильной дроби: 3/5, 1/2, 5/7. |
- Неправильная дробь: В этой дроби числитель всегда больше знаменателя.
| Примечание: Значение неправильной дроби всегда больше 1. | Пример неправильной дроби: 6/3, 50/21, 16/25. |
- Смешанная дробь: В этой дроби число представлено как целое число, за которым следуют дробные числа.
| Примечание: Смешанная дробь также называется смешанным числом. | Пример смешанной фракции: 6⅘, 2⅔, 25⅝. |
Как представить дроби в разных формах?
Представляя смешанную дробь целым числом.
Давайте разберемся, как решить смешанные дроби до целого числа на примере.
Измените 7⅘ на целое число.
| Сначала умножьте целое число на знаменатель дроби. То есть 7 * 5 = 35. |
| Теперь прибавьте полученное значение к числителю дроби. То есть 35 + 4 = 39. |
| Возьмите числитель и подставьте исходный знаменатель. То есть 39/5. |
| Конечная целая фракция будет 39/5. |
Представление дроби десятичным числом.
Самый простой способ превратить дробь в десятичную — просто разделить число. Здесь вам нужно разделить числитель со знаменателем.
Преобразует дробь 7/10 в десятичную.
| Вам нужно просто разделить числитель, равный 7, на знаменатель, равный 10.То есть: |
| 7/10 => 0,7 |
Представление дроби в процентах.
Для преобразования дроби в проценты можно использовать три метода. Ниже я привел три разных метода на примере 7/20.
| Разделите числитель на знаменатель и умножьте результат на 100. |
| То есть: 7/20 = 0,350,35 * 100 = 35% |
| Умножьте числитель на 100 , разделите число на знаменатель. |
| 7 * 100 = 700700/20 = 35% |
| Разделите числитель на знаменатель и измените десятичную точку справа от двух знаков. |
| 7/20 = 0,35 Теперь переместите десятичные знаки, чтобы преобразовать их в 35%. |
Пошаговое руководство — Как решать дроби
Давайте сначала научимся складывать две или более дроби на примере.
Предположим, вам нужно добавить 3/4 к 1/4.
Здесь вы можете увидеть, что знаменатели совпадают, поэтому это простейшее сложение дробей.
Итак, первый шаг в том, как решить дроби сложением, — это найти общие знаменатели чисел. В этой задаче оба имеют одинаковый знаменатель, поэтому общее между ними равно 4.
Итак, вы можете записать уравнение следующим образом —
3/4 + 1/4
= (3 + 1) / 4
= 4/4 = 1
Если у вас разные знаменатели, то и вы легко решаете дроби.Давайте узнаем на другом примере —
Предположим, вам нужно сложить 3/4 с 2/5, тогда у вас будет следующее уравнение —
3/4 + 2/5
Затем следующий шаг к решению этой дроби в , как решить дроби , — это найти любой общий знаменатель.
Поскольку у него нет общего знаменателя, мы умножим оба знаменателя и сложим вышеуказанные числа. Посмотрите ниже, чтобы лучше понять.
= (3 + 2) / 4 × 5
= 5/20
= 1/4
А теперь давайте возьмем еще один пример, где мы можем найти общие знаменатели.
Предположим, что нам нужно сложить дроби и ⅝
= 3/4 + 5/8
Теперь мы найдем наименьший общий множитель, который является НОК между двумя знаменателями.
Тогда мы получим 8 как НОК, и, таким образом, уравнение будет следующим —
= (3 × 2 + 5) / 8
Поскольку знаменатель равен 8, а знаменатель первой дроби равен 4, мы умножим первую дробь на 2, чтобы знаменатель дроби был равен 8; таким образом, уравнение будет
= (6 + 5) / 8
= 11/8
Итак, ответ — 11/8.
Теперь давайте узнаем, как вычислять дроби, как вычитать дроби.
Предположим, что уравнение составляет 3/2 — 1/2
Итак, мы будем следовать тому же процессу, и сначала мы выявим общий множитель, поскольку знаменатель в этом уравнении тот же, поэтому такой проблемы нет.
Теперь вы можете напрямую поставить 2 в качестве знаменателя, а затем вычесть 1 из 3. Выполните шаги —
= (3-1) / 2
= 2/2
= 1
Мы получили ответ 1.
Другой пример решения дробей
5/7 — 2/4
Мы не видим общего множителя между знаменателями, поэтому делаем знаменатели одинаковыми, умножая первую дробь на 4, а вторую дробь на 7; тогда мы получим следующее уравнение.
= 5 × 4/7 × 4 — 2 × 7/4 × 7
Мы должны составить общие знаменатели, чтобы решить уравнение, поскольку только тогда мы сможем выполнять в уравнении операции Лютера.Таким образом мы получим следующий ответ —
= (20-14) / 7 × 4
= 6/28
Теперь мы видим, что 2 является общим как для числителя, так и для знаменателя, поэтому мы можем разделить целую дробь на 2 следующим образом —
= 6 \ 2/28 \ 2
= 3/14
Таким образом, ответ — 3/14.
Теперь давайте узнаем, как умножить две дроби. Это также очень важно, чтобы научиться решать дроби.
Возьмем следующий пример —
¾ x
Умножение на дроби очень просто, так как вам просто нужно умножить числители друг на друга, а также знаменатели друг на друга.
Тогда вы получите следующий результат —
= 3 × 1/4 × 5
= 3/20
Таким образом, ответ — 3/20.
Теперь давайте изучим метод деления на дроби, чтобы научиться решать дроби.
Для деления дроби можно взять обратную величину. Чтобы совершить ответный обмен, нужно перевести знаменатель в числитель, а числитель в знаменатель.
Возьмем для примера:
Решите 1/2 ÷ 1/5.
Во-первых, возьмите 1/5 как 5/1.
Возьмите обратную дробь и умножьте ее на другое число (а).
1/2 * 5/1
Чтобы решить эту проблему, умножьте знаменатели и числители:
2 * 1 = 2 (знаменатель)
1 * 5 = 5 (числитель)
То есть: 1/2 * 5/1 = 5/2 = 2,5
Что нужно понимать, чтобы не ошибаться в дробях!
Может быть непросто складывать и вычитать дроби с разными знаменателями.Поэтому разные ученики не решают дроби с разными знаменателями и допускают ошибки.
Во-первых, давайте рассмотрим пример решения дробей с разными знаменателями .
| Решить 3/4 + 1/6. Первое, что вам нужно сделать, это умножить числитель и знаменатель на значение противоположного знаменателя. Это кратно 4 на 6 и 6 на 4. Это даст вам 24 в знаменателе. Аналогичным образом умножьте числитель как 3 * 6 = 18 и 1 * 4 = 4.Теперь сложите 18 + 4 = 22. Это означает, что 3/4 + 1/6 = 22/24 => 11/12 |
Теперь поймите, какие ошибки делают студенты.
- Неправильное понимание требований вопросов, таких как деление вместо умножения и т. Д.
- Когда ученикам нужно сложить или вычесть дробь, они забывают изменить знаменатель дроби. [Как в приведенных выше примерах 4 и 6 меняется на 24].
- Более того, заметно, что числитель также должен измениться, как и знаменатель.[Например, 3 * 6 = 18 и 1 * 4 = 4].
- Наконец, некоторые студенты не могут упростить уравнение. [Например, 22/24 также записывается как 11/12 после деления числа на 2].
| Творческое занятие по обучению ваших детей дробям !! Вы можете научить своих детей дробям, попросив их нарисовать птицу из бумаги. Дайте им инструкции разрезать бумагу в заданной пропорции. Предложите им круг и научите их дробям.Разрежьте круг на 8 частей и научите дроби вроде 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, 8/8. Кроме того, позвольте им упростить дроби как 2/8 => 1/4, 4/8 => 1/2, 6/8 => 3/4 и 8/8 => 1. Наконец, они должны нарисуйте птицу как: |
Заключение
Многие ученики борются с дробями, и дроби на первый взгляд кажутся сложными, но с ними легко работать, когда вы практикуете их ежедневно.
Если вы также ищете , как решать дроби , то мы надеемся, что эта статья помогла вам понять процесс решения дробей.Если вы все еще столкнулись с трудностями при решении дробей, вы можете связаться с нами в любое время. Мы всегда готовы помочь вам. Наши специалисты проконсультируют вас круглосуточно и без выходных. Получите лучшую помощь в домашнем задании по математике от экспертов.
Часто задаваемые вопросы
Какая формула для дробей?
Дробь = выбранное количество частей / общее количество частей
Каждая дробь имеет числитель, который равен выбранному количеству частей, а знаменатель равен общему количеству частей в целом.
Что такое дроби A и B?
Во дроби A и B рассматриваются как A / B. Где число A — числитель, а B — знаменатель.
Что такое 1/3 в виде дроби?
Дробь 1/3 эквивалентна: 2/6, 3/9, 4/12, 5/15, 6/18, 7/21, 8/24, 9/27, 10/30 и т. Д. на.
.

