Содержание
Сложные задачи на проценты | Шевкин.Ru
Задачи этого раздела являются необязательными для всех учащихся, среди них есть действительно сложные задачи, но есть и такие, в которых всем учащимся разобраться полезно. Это задачи на так называемые сложные проценты — проценты начисляемые на процентные деньги. Первая задача этого раздела была дана на олимпиаде Малого мехмата МГУ для семиклассников в 1991 году. Шутливое отражение в ней политических страстей того времени не должно отвлечь учащихся от важного вопроса: что получится, если число сначала увеличить, а потом уменьшить на 50 % (на одно и то же число процентов). Полученный здесь опыт поможет решить и другие олимпиадные задачи.
344.* В начале года винтики, шпунтики и гаечки продавались по одинаковой цене 1 р. за 1 кг. 30 февраля Верховный Совет СССР принял закон о повышении цен на винтики на 50 % и снижению цен на шпунтики на 50 %. 31 февраля Верховный Совет РСФСР принял закон о снижении цен на винтики на 50 % и повышению цен на шпунтики на 50 %. Какой товар будет самым дорогим и какой самым дешевым в марте?
31 февраля Верховный Совет РСФСР принял закон о снижении цен на винтики на 50 % и повышению цен на шпунтики на 50 %. Какой товар будет самым дорогим и какой самым дешевым в марте?
Ошибочное решение задачи 345 нетрудно предвидеть: учащиеся сложат проценты от разных величин.
345.* 1) Число увеличили на 10 %, потом еще на 10 %. На сколько процентов увеличили число за два раза?
2) Число увеличили на 10 %, результат уменьшили на 10 %. Какое получилось число — большее или меньшее первоначального? На сколько процентов?
346.* Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10 % за каждый месяц. На сколько процентов выросли цены за 3 месяца?
347.* Женя за весну похудел на 20 %, потом поправился за лето на 30 %, за осень опять похудел на 20 % и за зиму прибавил в весе 10 %. Остался ли за этот год его вес прежним?
Остался ли за этот год его вес прежним?
Если Женя весил x кг, то после уменьшения веса на 20 % он стал весить 0,8x кг, а после увеличения веса на 30 % – 0,8x·1,3 кг и т. д., в итоге Женя весил 0,8x·1,3·0,8·1,1 или 0,9152x кг, что меньше x кг. Значит, Женя похудел.
348.* Две противоположные стороны прямоугольника увеличили на 10 %. На сколько процентов увеличилась его площадь? Зависит ли результат от того, какую пару сторон увеличили на 10 %?
349.* Все стороны прямоугольника увеличили на 10 %. На сколько процентов увеличилась его площадь?
350.* Каждую сторону квадрата увеличили на 20 %. На сколько процентов увеличилась его площадь?
351.* Две противоположные стороны прямоугольника увеличили на 20 %, две другие — уменьшили на 20 %. Как изменилась площадь прямоугольника?
Как изменилась площадь прямоугольника?
352.* Две противоположные стороны прямоугольника увеличили на 20 %, две другие — уменьшили на 10 %. На сколько процентов увеличилась площадь прямоугольника?
353.* Длину прямоугольника уменьшили на 20 %. На сколько процентов надо увеличить ширину прямоугольника, чтобы его площадь не изменилась?
354.* Магазин продал на прошлой неделе некоторый товар. На этой неделе запланировано продать того же товара на 10 % меньше, но по цене на 10 % больше. Большую или меньшую сумму выручит магазин от продажи товара на этой неделе и на сколько процентов?
355.* На некотором участке пути машинист уменьшил скорость поезда на 25 %. На сколько процентов увеличится время движения на этом участке?
356.* Арбуз массой 20 кг содержал 99 % воды. Когда он немного усох, содержание воды в нем уменьшилось до 98 %. Какова теперь масса арбуза?
Когда он немного усох, содержание воды в нем уменьшилось до 98 %. Какова теперь масса арбуза?
На первый взгляд кажется, что масса арбуза мало изменилась, но это на первый взгляд! Масса «сухого вещества» арбуза составляла 100 – 99 = 1 (%). Это 20·0,01 = 0,2 кг. После усушки его масса составляла уже 100 – 98 = 2 (%). То есть те же самые 0,2 кг составляют 2 % от новой массы арбуза. Найдем эту новую массу: 0,2:0,02 = 10 (кг).
Интересная переформулировка этой известной задачи встретилась недавно на олимпиаде.
357.* Некий леспромхоз решил вырубить сосновый лес, но экологи запротестовали. Тогда директор леспромхоза всех успокоил, сказав: «В нашем лесу 99% сосны. После рубки сосна будет составлять 98% всех деревьев». Какую часть леса может вырубить леспромхоз?
Если бы экологи хорошо знали проценты, то они смогли бы возразить предприимчивому директору леспромхоза, планирующему вырубить как минимум половину леса – это при условии, что вырубать будут только сосны. Если же топор коснется и других деревьев, то от соснового леса можно оставить меньше половины. Ведь удовлетворить условию задачи можно, оставив в лесу 50 деревьев: 49 сосен и 1 березу.
Если же топор коснется и других деревьев, то от соснового леса можно оставить меньше половины. Ведь удовлетворить условию задачи можно, оставив в лесу 50 деревьев: 49 сосен и 1 березу.
358.* а) Яблоки, содержащие 70 % воды, потеряли при сушке 60 % своей массы. Сколько процентов воды содержат сушеные яблоки?
б) Груши, содержащие 65 % воды, потеряли при сушке 50 % своей массы. Сколько процентов воды содержат сушеные груши?
Объясняя решение задачи 358 (а), воспользуемся следующей иллюстрацией.
Вода составляла 70 % массы яблок, 60 из них испарилось, а 10 осталось. Теперь 10 частей воды приходится на 30 частей «сухого вещества» яблок или на 40 частей массы сушеных яблок. Масса воды составляет 10:40 = 0,25, или 25 % массы сушеных яблок?
359.* а) Сколько граммов воды нужно добавить к 600 г раствора, содержащего 15 % соли, чтобы получить 10%-й раствор соли?
б) Сколько граммов воды нужно добавить к 120 г раствора, содержащего 30 % сахара, чтобы получить раствор, содержащий 20 % сахара?
360. * На коробке вермишели написано: «Масса нетто 500 г при влажности 13 %». Какова масса вермишели, если она хранится при влажности 25 %?
* На коробке вермишели написано: «Масса нетто 500 г при влажности 13 %». Какова масса вермишели, если она хранится при влажности 25 %?
361.* Для получения томат-пасты протертую массу томатов выпаривают в специальных машинах. Сколько томат-пасты, содержащей 30 % воды, получится из 28 т протертой массы томатов, содержащей 95 % воды?
362.* Из 40 т руды выплавили 20 т металла, содержащего 6 % примесей. Сколько процентов примесей в руде?
363.* Свежие фрукты содержат 72 % воды, а сухие — 20 %. Сколько сухих фруктов получится из
40 кг свежих?
364.* До сушки влажность зерна составляла 23 %, а после сушки составила 12 %. Сколько процентов массы теряет зерно при сушке?
365.* В драмкружке число мальчиков составляет 80 % от числа девочек. Сколько процентов составляет число девочек от числа мальчиков в этом кружке?
Сколько процентов составляет число девочек от числа мальчиков в этом кружке?
I способ. Число мальчиков составляют 80 % от числа девочек (100 %). Определим, сколько процентовсоставляют 100 % от 80 % :
100/80 = 100×100/80 % = 125 %.
II способ. Число мальчиков (m) составляют 80 % от числа девочек (d), значит, m = 0,8d. Отсюда d = 1,25m, то есть число девочек составляет 125 % от числа мальчиков.
III способ. На 10 девочек приходится 8 мальчиков, число девочек составляет 10/8 или 125 % от числа мальчиков.
366. С 1 октября 1993 г. за хранение денег на срочном депозите в течение года Сбербанк выплачивал доход из расчета 150% от вложенной суммы; в течение полугода — 130% годовых, в течение трех месяцев — 120 % годовых. Каким образом за год на условиях Сбербанка можно было получитьнаибольший доход на 100 000 р.? Каков этот наибольший доход?
Каким образом за год на условиях Сбербанка можно было получитьнаибольший доход на 100 000 р.? Каков этот наибольший доход?
На первый взгляд самое выгодное вложение денег на год — под 150 % годовых (через год сумма обратится в 100·2,5 = 250 тыс. р.). Но это только на первый взгляд! Давайте для сравнения положим деньги на полгода, а через полгода получим их обратно с доходом 130:2 =
= 65 (%) от вложенной суммы. Затем все полученные деньги положим еще на полгода. Таким образом через год мы получим:
100·1,65·1,65 = 272,25 (тыс. р.).
Это несколько больше полученной ранее суммы. Попросите учащихся провести расчеты для третьего случая. Пусть они убедятся, что знание процентов может быть полезным при выборе более выгодного способа вложения денег.
367.* Компания X выплачивает доход по своим акциям ежегодно из расчета 140 % годовых. Компания Y выплачивает доход по акциям 1 раз в полгода из того же расчета. В акции какой компании выгоднее вложить деньги на 1 год?
Компания Y выплачивает доход по акциям 1 раз в полгода из того же расчета. В акции какой компании выгоднее вложить деньги на 1 год?
368.* Производительность труда повысили на 25 %. На сколько процентов уменьшится время выполнения задания.
369.* Если при повышении производительности труда рабочего на 10 % повысить его зарплату на 6,7 %, то это позволит снизить расход на оплату труда в расчете на единицу продукции на 3 %. Проверьте это.
370.* Рабочий повысил производительность труда на 15 %, а его зарплата увеличилась на 10,4 %. На сколько процентов уменьшился расход на оплату труда в расчете на единицу продукции?
371.* Купили конфеты и печенье. За 1 кг конфет заплатили на 50 % больше, чем за 1 кг печенья, но их купили на 50 % меньше, чем печенья. За что заплатили больше?
372. * Кусок сплава весом 700 г, содержащий 80 % олова, сплавили с куском олова весом 300 г. Определите процентное содержание олова в полученном сплаве.
* Кусок сплава весом 700 г, содержащий 80 % олова, сплавили с куском олова весом 300 г. Определите процентное содержание олова в полученном сплаве.
373.* Имеется 500 г 40 %-го раствора кислоты. Сколько воды требуется добавить, чтобы получить 25 %-й раствор кислоты?
374.* В первый день рабочий перевыполнил дневное задание на 2 %, во второй день он перевыполнил дневное задание на 4 %. На сколько процентов рабочий перевыполнил задание двух дней?
375.* В автоинспекции города N подсчитали, что число легковых автомобилей увеличивалось в последние годы на 15 % ежегодно. Во сколько раз увеличится число легковых автомобилей за пять лет, если эта тенденция сохранится?
376.* Деньги, вложенные в акции известной фирмы, приносят ежегодно 20 % дохода. За сколько летвложенная сумма удвоится?
377. * В спортивной секции девочки составляют 60 % числа мальчиков. Сколько процентов числа всех участников секции составляют девочки?
* В спортивной секции девочки составляют 60 % числа мальчиков. Сколько процентов числа всех участников секции составляют девочки?
Если число мальчиков принять за 100 %, то число девочек от него составляет 60 %, а число всех участников секции 160 % от числа мальчиков. 60 % от 160 % составляет 60×100/160 = 37,5 (%). Но понять это решение из-за нагромождения процентов нелегко. Если же число мальчиков обозначитьбуквой x, то те же самые действия легче объяснить и понять. Итак, число девочек равно 0,6x, а число всех участников секции x + 0,6x = 1,6x. Определим, сколько процентов от 1,6х составляет число 0,6х:
0,6x×100/1,6x = 37,5 (%).
- В некотором царстве, в некотором государстве пятиклассники стали изучать математику не 6, а 5 уроков в неделю.
 Кроме того, урок у них стал длиться не 45, а 40 минут. Сколько процентов учебного времени потеряли пятиклассники? Ответ округлите до десятых.
Кроме того, урок у них стал длиться не 45, а 40 минут. Сколько процентов учебного времени потеряли пятиклассники? Ответ округлите до десятых.
Эту задачу могли бы решить учителя математики всего несколько лет назад, чтобы объяснить себе катастрофическую нехватку времени, которая стала ощущаться в связи с указанными в условии задачи нововведениями.
Учебное время теперь составляет 5/6×40/45 = 20/27 от прежнего. Потеря составила 1 – 20/27 =
= 7/27 = 0,2592…, или примерно 25,9 %.
379.* а) Торговец продал книгу со скидкой 5 % от назначенной цены и получил 14 % прибыли. Сколько процентов прибыли планировал получить торговец при продаже книги?
б) Торговец продал товар, имевший небольшой дефект, уступив покупателю 30 % от назначенной цены. При этом он имел 16 % убытка. Какой процент прибыли планировал получить торговец при продаже товара?
Какой процент прибыли планировал получить торговец при продаже товара?
Рассмотрим решение первой задачи. Пусть торговец планировал продать книгу за a р., тогда он продал ее за (1 – 0,05)a = 0,95a р. Эта сумма составила 100 + 14 = 114 (%) цены, по которой торговец сам купил книгу и которая составляла 0,95а/1,14 = 5/6 а р. Подсчитаем доход, который планировал получить торговец (в процентах):
a: 5/6 a ·100 = 120 (%).
Торговец планировал получить 120 – 100 = 20 % дохода.
Текстовые задачи. Задачи на проценты с решениями
Задачи на проценты с решениями
перейти к содержанию курса текстовых задач
- Учитель зарабатывает на 25% меньше, чем профессор.
 На сколько процентов больше, чем учитель, зарабатывает профессор? Решение
На сколько процентов больше, чем учитель, зарабатывает профессор? Решение - Найти число, если известно, что 25% его равны 45% от 640 000. Решение
- После двух последовательных повышений зарплата возросла в раза. На сколько процентов повысилась зарплата в первый раз, если второе повышение было в процентном отношении вдвое больше первого? Решение
- Для офиса решили купить 4 телефона и 3 факса на сумму 1470 долларов. Удалось снизить цену на телефон на 20%, и в результате за ту же покупку уплатили 1326 долларов. Найдите цену факса. Решение
- За первый квартал автозавод выполнил 25% годового плана выпуска машин. Количество машин, выпущенных за второй, третий и четвертый кварталы, оказалось пропорциональным числам 15, 16 и 18. Определить перевыполнение годового плана выпуска в процентах, если во втором квартале автозавод выпустил продукции на 8% больше, чем в первом. Решение
- Рабочий день сократился с 8 ч до 7 ч. На сколько процентов нужны повысить производительность труда, чтобы при тех же расценках заработная плата возросла бы на n % процентов? Решение
- Банк выделил определенную сумму денег на кредиты трем организациям сроком на год.
 Организация A получила кредит в размере 40% от выделенной суммы под 30% годовых, организация B — 40% от оставшейся суммы под 15% годовых. Последнюю часть выделенной суммы получила организация C. Через год, когда кредиты были погашены, оказалось, что банк получил прибыль в размере 21%. Под какие проценты был выдан кредит организации C? Решение
Организация A получила кредит в размере 40% от выделенной суммы под 30% годовых, организация B — 40% от оставшейся суммы под 15% годовых. Последнюю часть выделенной суммы получила организация C. Через год, когда кредиты были погашены, оказалось, что банк получил прибыль в размере 21%. Под какие проценты был выдан кредит организации C? Решение - В результате реконструкции цеха число высвободившихся рабочих заключено в пределах от 1,7 до 2,3 % от общего числа рабочих цеха. Найдите минимальное число рабочих, которое могло быть занято в цехе до реконструкции. Решение
- Объем вещества А составляет половину суммы объемов веществ В и С, а объем вещества В составляет 20% суммы объемов веществ А и С. Найдите отношение объема вещества С к сумме объемов веществ А и В. Решение
- Банк начисляет ежегодно р % от суммы вклада. Через сколько лет внесенная сумма увеличится в 5 раз? Решение
- Предприятие работало три года. Выработка продукции за второй год работы предприятия возросла на р %, а на следующий год прирост был на 10% больше, чем в предыдущий.
 Определите, на сколько процентов увеличилась выработка за второй год, если известно, что за два года она увеличилась в общей сложности на 48,59%. Решение
Определите, на сколько процентов увеличилась выработка за второй год, если известно, что за два года она увеличилась в общей сложности на 48,59%. Решение - В конце года вкладчику на его сбережения сбербанк начислил проценты, что составило 6 долларов. Добавив 44 доллара, вкладчик оставил деньги еще на год. После истечения года вновь были начислены проценты, и теперь вклад вместе с процентами составил 257 долларов 50 центов. Какая сумма первоначально была положена в сбербанк? Решение
- Сухие грибы по массе содержат 12% воды, а свежие — 90%. Сколько получится сухих грибов из 22 кг свежих грибов? Решение
- Число 51,2 трижды увеличивали на одно и то же количество процентов, а затем трижды уменьшали на то же самое количество процентов. В результате получили 21,6. На сколько процентов увеличивали, а затем уменьшали данное число? Решение
Задачи для самостоятельного решения
- В двух мешках вместе находится 140 кг муки. Если из первого мешка переложить во второй 12,5 % муки, находящейся в первом мешке, то в обоих мешках будет одинаковое количество муки.
 Сколько килограммов муки в каждом мешке? Ответ: 80 кг и 60 кг
Сколько килограммов муки в каждом мешке? Ответ: 80 кг и 60 кг - В январе завод выполнил 105% месячного плана, а в феврале дал продукции на 4% больше, чем в январе. На сколько процентов завод перевыполнил двухмесячный план? Ответ: на 7,1 %
- Количество студентов в университете, увеличиваясь на одно и то же число процентов ежегодно, возросло за три года с 5000 до 6655 человек. На сколько процентов увеличивалось число студентов ежегодно? Ответ: на 10%
Вкладчик на свои сбережения через год получил 150 р. процентных денег. Добавив 850 р., он оставил деньги еще на один год. По истечении года вклад вместе с процентами составил 4200 р. Какая сумма была положена первоначально и какие годовые проценты дает банк? Ответ: 3000 р, 5%
Зарплата продавца составляет 3% выручки. Он реализовал товар стоимостью 6000 р. по цене на 5% выше его себестоимости. На сколько повысилась зарплата продавца? Ответ: на 9 р.
Одна сторона прямоугольника в 2,5 раза меньше другой.
 Как и на сколько процентов изменятся его периметр и площадь, если большую сторону уменьшить на 25%, а меньшую увеличить на 80%? Ответ: +5%, +35%
Как и на сколько процентов изменятся его периметр и площадь, если большую сторону уменьшить на 25%, а меньшую увеличить на 80%? Ответ: +5%, +35%- Два брата купили акции одного достоинства на сумму 3640 долларов. Когда цена на эти акции возросла, они продали часть акций на сумму 3927 долларов. Первый брат продал 75% своих акций, а второй — 80% своих. При этом сумма, полученная от продажи акций вторым братом, превышает сумму от продажи акций первым братом на 140%. На сколько процентов возросла цена акции? Ответ: на 37,5%
В начале года вкладчик положил своих денег в один банк, а остальные — в другой. К концу года сумма на этих вкладах выросла до 1340 р., а к концу следующего года — до 1498 р. Было подсчитано, что если бы с самого начала денег вкладчик положил во второй банк, а остальные — в первый, то по итогам первого года сумма на этих вкладах составила бы 1420 р. Определить величину вклада по истечении двух лет, предполагая, что вкладчик положил все деньги в первый банк.
 Ответ: 1452 р.
Ответ: 1452 р.
Метки проценты, текстовые задачи. Смотреть запись.
Как решать задачи на проценты в 6 классе
Предлагаю вашему вниманию легкий способ разобраться, как решать задачи на проценты в 6 классе.
При решении задачи на проценты первым делом нужно определить вид задачи. Задачи на проценты в 6 классе можно подразделить на три вида:
1) Нахождение процентов от числа.
2) Нахождение числа по его процентам.
3) Нахождение процентного отношения двух чисел.
Определить вид задачи на проценты можно по записи ее условия. Если напротив 100% стоит число, то это — задача на нахождение процентов от числа. Если число напротив 100% неизвестно, то это — задача на нахождение числа по его процентам. Если же неизвестное значение стоит в колонке процентов, то это — задача на нахождение процентного отношения двух чисел.
Рассмотрим на примерах, как научиться определять вид задачи на проценты.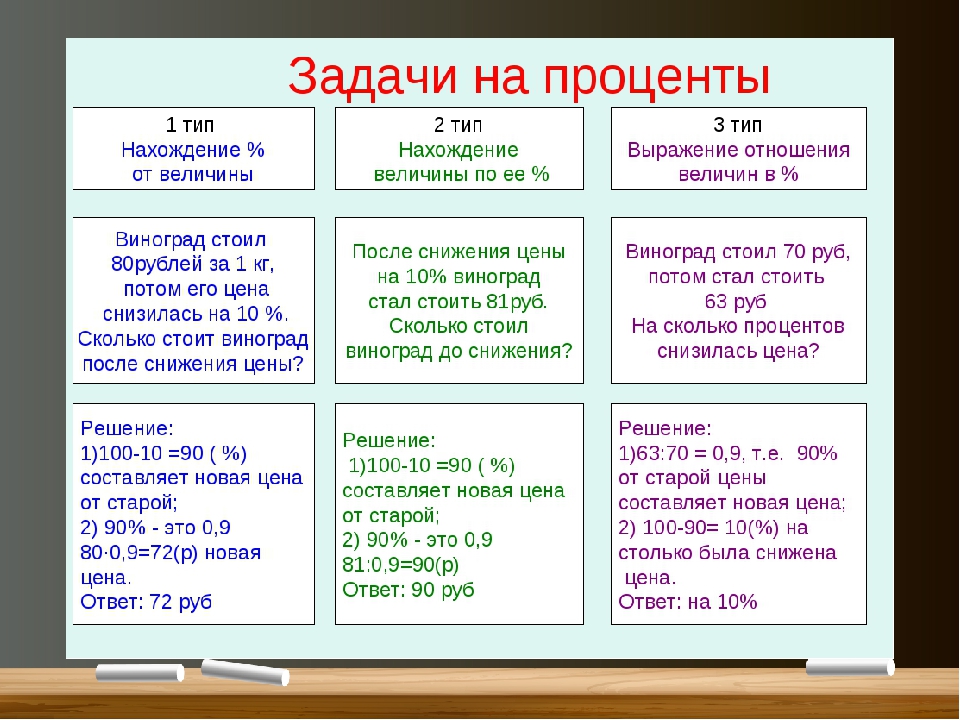
1. Из картофеля выходит 20% крахмала. Сколько крахмала выйдет из 45 т картофеля?
| тонны | % | |
| Картофель | 45т | 100% |
| Крахмал | ? | 20% |
Это задача на нахождение процентов от числа (так как напротив 100% стоит число).
2. Руда содержит 67% железа. Сколько нужно руды для получения 13,4 т железа?
| тонны | % | |
| Руда | ? | 100% |
| Железо | 13,4т | 67% |
Это задача на нахождение числа по его процентам (так как напротив 100% стоит ?)
3. Из 400 зерен пшеницы взошло 360. Определить процент всхожести семян.
Из 400 зерен пшеницы взошло 360. Определить процент всхожести семян.
| Зерна | % | |
| Всего посеяли | 400 | 100% |
| Взошло | 360 | ? |
Это задача на процентное отношение (так как в колонке процентов стоит ?).
Задачи на проценты и десятичные дроби. ВПР по математике для 5 классов | Дневник учителя математики
Во вторник пишут всероссийскую контрольную работу по математике 5 классы. Две пятиклашки у меня, обе почти отличницы, одна из Москвы (по скайпу), учится по учебнику Бунимовича-Дорофеева, другая местная (приходит на дом), учится по Петерсону. Москвичка купила бумажное пособие, местная решает на сайте «Решу ВПР».
Москвичка купила бумажное пособие, местная решает на сайте «Решу ВПР».
Обе попросили помощи по задаче на проценты и по примеру на десятичные дроби, темы еще не проходили по школьной программе. В московской школе велели эти два номера не решать, не проходили, не надо. В моем городе начали лихорадочно изучать десятичные дроби и решать задачи на проценты. Видна на этом примере разница менталитетов: москвичи не дергаются лишний раз, а в моем регионе сказали надо, значит сделаем.
Девочкам проценты объяснила еще две недели назад. Кратко: 1% — это одна сотая часть, 2% — это две сотых, 50% — это 1/2 или половина, потренировались на разных числах. Далее работаем как с частями, задачи на части девочки хорошо решают.
Ученицам понравился способ, который я считаю самым простым и надежным. Читаем внимательно условие, всего (или было) всегда берем за 100%, что надо найти — за х, расставляем данные из условия — числа под числами, проценты под процентами. Чертим крестик, что на одной линии с х, пойдет в знаменатель, что на другой линии, пойдет в виде произведения в числитель. Осталось сократить и посчитать.
Осталось сократить и посчитать.
Десятичные дроби тоже объяснила за 10 минут: после целой части ставится запятая, в знаменателе могут быть только числа, кратные 10, это 10,100,1000, и т.д., сколько нулей у знаменателя, столько значащих цифр должно быть после запятой.
Умножаем столбиком как целые числа, потом считаем, сколько было знаков после запятой всего в обоих числах, столько выделяем с конца в результате.
При делении сначала превращаем десятичные дроби в целые числа, домножаем и числитель и знаменатель на одно и то же число, кратное 10, потом делим целые числа.
Сложение и вычитание выполняем столбиком, записывая в числах запятую под запятой, добавляем нули в конце, если цифр не хватает.
За одно занятие объяснила два раздела математики, обе девочки все поняли с первого раза. Две недели уже решают варианты, проблемы не возникают.
Заниматься с соображающими детьми и с отстающими — это две большие разницы. Некоторые слабые дети в 9 классе эти темы плохо понимают, бывает, и в 10-11 классах задачи на проценты решать не умеют и двигать запятые в десятичных дробях для них — проблема.
Тест Задачи на проценты (6 класс) по математике
Сложность: новичок.1 человек проходит прямо сейчас.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Выразите 4 % в виде десятичной дроби:
- Правильный ответ
- Неправильный ответ
- Вы и еще 81% ответили правильно
- 81% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветить
Вопрос 2 из 10
Выразите дробь 0,3 в процентах:
- Правильный ответ
- Неправильный ответ
- Вы и еще 81% ответили правильно
- 81% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 3 из 10
Вычислите 1 % от 19:
- Правильный ответ
- Неправильный ответ
- Вы и еще 89% ответили правильно
- 89% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 4 из 10
В магазин привезли 62 т картофеля.
 До обеда продали 15 % всего количества. Сколько картофеля осталось еще продать?
До обеда продали 15 % всего количества. Сколько картофеля осталось еще продать?- Правильный ответ
- Неправильный ответ
- Вы и еще 71% ответили правильно
- 71% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 5 из 10
22 ученика класса, что составляет 55 % всего количества, учатся без троек. Сколько человек в классе?
- Правильный ответ
- Неправильный ответ
- Вы и еще 73% ответили правильно
- 73% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 6 из 10
В хоре 15 мальчиков, что составляет 3/5 всего хора. Сколько человек поют в хоре?
- Правильный ответ
- Неправильный ответ
- Вы и еще 83% ответили правильно
- 83% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 7 из 10
Найдите весь путь, если 8 % пути составляет 48 км.

- Правильный ответ
- Неправильный ответ
- Вы и еще 73% ответили правильно
- 73% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 8 из 10
Длина маршрута 36 км. Туристы прошли пешком 25 % пути, а оставшуюся часть пути плыли на плотах. Сколько километров туристы проплыли на плотах?
- Правильный ответ
- Неправильный ответ
- Вы и еще 73% ответили правильно
- 73% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 9 из 10
На сколько процентов увеличится величина от 70 до 77 ?
- Правильный ответ
- Неправильный ответ
- Вы и еще 77% ответили правильно
- 77% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 10 из 10
Приготовили раствор из 45 г соли и 155 г воды.
 Сколько процентов соли он содержит?
Сколько процентов соли он содержит?- Правильный ответ
- Неправильный ответ
- Вы и еще 66% ответили правильно
- 66% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Томирис Бушукова
10/10
Инна Федорова
10/10
Matvey Dzen
9/10
Саша Змеёв
9/10
Милана Пундик
9/10
Ярослав Иванченко
10/10
Руслан Исаков
8/10
Анастасия Арих
10/10
Ольга Линевская
8/10
Вет Громов
9/10
ТОП-3 тестакоторые проходят вместе с этим
Рейтинг теста
Средняя оценка: 4.1. Всего получено оценок: 1534.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Математика и гармония: Задачи на «высушивание»
При решении этих задач следует помнить, что все тела, вещества, продукты содержат в себе воду, которая частично испаряется. Поэтому в решении надо каждый раз разделять данное нам вещество на воду и «сухой остаток». Количество воды может меняться, масса же сухого вещества остаётся неизменной.
Задача 1. Собрали 8 кг свежих цветков ромашки, влажность которых 85%. После того как цветки высушили, их влажность составила 20%. Чему равна масса цветков ромашки после сушки?
Решение. Заполним таблицу по условию задачи:
Масса, в кг | Содержание, в % | ||
воды | Сухого вещества | ||
Свежие цветы | 8 | 85 | 100 — 85 = 15 |
Высушенные | х | 20 | 100 — 20 = 80 |
1) 0,15 · 8 = 1,2 (кг) — масса сухого вещества в 8 кг;
2) 1,2 кг — 80%
x кг — 100%
Отсюда, х = 1,2 · 100 : 80 = 1,5 (кг).
Ответ: 1,5 кг
Задача 2. Из 22 кг свежих грибов получается 2,5 кг сухих грибов, содержащих 12% воды. Каков процент воды в свежих грибах?
Решение. Заполним таблицу по условию задачи:
Масса, в кг | Содержание, в % | ||
воды | Сухого вещества | ||
Свежие грибы | 22 | х | |
Сухие грибы | 2,5 | 12 | 100 — 12 |
Определим процент сухого вещества в высушенных грибах: 100-12 = 88% = 0, 88.
1) 2,5 · 0,88 = 2,2 (кг) — масса сухого вещества;
2) 2,2 кг : 22 · 100 = 10% сухого вещества содержится в свежих грибах;
3) 100 — 10 = 90% воды в свежих грибах.
Ответ: 90%
Задача
3. Свежие
яблоки содержат 80% воды, а сушёные 10%. Сколько надо взять свежих яблок, чтобы
получить 6 кг сушёных?
Решение.
Если
в сушёных яблоках содержится 10% воды,
то сухое вещество составляет 90%.
Найдём
массу сухого вещества в 6 кг сушёных
яблок:
6
·
0,9
= 5,4 9 (кг).
Та
же масса сухого вещества была и в свежих
яблоках, и она составляла 20% от их массы.
Найдём массу свежих яблок:
5,4
: 0,2 = 27 (кг).
Ответ:
27 кг
Задача 4. Только что
добытый каменный уголь содержит 2% воды,
а после двухнедельного пребывания на
воздухе он содержит 12% воды. На сколько
килограммов увеличится масса одной
добытой тонны угля после того, как она
две недели пролежит на воздухе?
Эта задача
обратна предыдущим: здесь влажность
угля увеличивается за счёт поглощения
влаги из воздуха.
Решение.
Заполним таблицу по условию задачи:
Масса, в т | Содержание, в % | ||
воды | Сухого вещества | ||
Было | 1 | 2 | 100 — 2 |
Стало | х | 12 | 100 — 12 |
1) 1000 ·
0,98
= 980
(кг) — масса сухого вещества в
добытом угле;
2)
980
кг — это 88%, 980 : 0,88 ≈ 1114 (кг) — масса угля
после двух недель пребывания на воздухе;
3)
1114
— 1000
= 114
(кг) — увеличение массы одной
добытой
тонны угля.
Ответ:
114
кг
Задача
5. В
свежих грибах 70% влаги, а в сушёных 10%.
Сколько килограммов свежих грибов надо
собрать для того, чтобы получить 30 кг
сушёных?
Решение.
1)
В сушёных грибах сухое вещество составляет
90%.
90%
от 30 кг — это 30 : 100 · 90 = 27 (кг).
2)
27 кг сухого вещества в свежих грибах
составляют 30%.
1%
от 27 кг — это 27 : 30 = 0,9 (кг). Тогда 100%
составляют 0,9 · 100 = 90 (кг).
Ответ:
90 кг
Задачи
для самостоятельного решения.
- Свежие
грибы содержат 90% воды, а сухие — 12% воды.
Сколько получится сухих грибов из 22 кг
свежих грибов? - Трава
при высыхании теряет около 28% своей
массы. Сколько было накошено травы, если
из неё было получено 1,44 т сена? - На
складе хранилась 51 т зерна, влажность
которого была 20%. Перед закладкой зерна
в зернохранилище его просушили, доведя
влажность до 15%. Сколько тонн зерна
засыпали в зернохранилище? - Имеется 0,5 т
целлюлозной массы, содержащей 85% воды.
После выпаривания получили массу,
содержащую 25% целлюлозы. Сколько
килограммов воды было выпарено? - Пчёлы
перерабатывают цветочный нектар в мёд,
освобождая его от воды. Нектар обычно
содержит 84% воды, а полученный из него
мёд — 20%. Сколько килограммов нектара
приходится перерабатывать пчёлам для
получения одного килограмма мёда?
О трудолюбивом
человеке, который практически не сидит
без дела, говорят: «Трудится как пчёлка».
Понять почему так говорят вам помогут
следующие цифры.
Для выработки
100 граммов меда пчела облетает
приблизительно миллион цветов.
Скорость
полета пчелы составляет 65 км/ч, что
приблизительно равно скорости движения
автомобиля по городу.
Пчела за один
полет набирает нектара практически
столько, сколько она весит сама. С полным
медовым желудочком пчела способна
развивать скорость до 30 км/ч.
Чтобы
набрать 1 кг нектара, пчеле придется
совершить до 150 тысяч вылетов из улья.
В среднем за один вылет пчела преодолевает
до 3 километров.
Чтобы произвести
килограмм меда, пчеле необходимо
пролететь в среднем до 450 тысяч километров.
Это значит, что расстояние, которое
пролетает пчела, аналогично расстоянию,
которое необходимо пролететь, чтобы
обогнуть экватор Земли примерно 10 раз.
Процентные расчеты. Формула сложных процентов — АЛГЕБРА — Уроки для 9 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
УРОК № 41
Тема. Процентные расчеты. Формула сложных процентов
Цель урока: добиться усвоения учащимися содержания: определение понятия «сложные проценты»; формулы сложных процентов. Систематизировать знания учащихся о определение понятия «процент от числа»; формулы, выражающие способы решения основных задач на проценты.
Выработать умения: воспроизводить содержание изученных понятий и алгоритмов и применять их для решения упражнений, предполагающих решение основных задач на проценты, а также применение формулы сложных (банковских) процентов.
Тип урока: усвоение знаний, выработка умений.
Наглядность и оборудование: опорный конспект № 24.
Ход урока
I. Организационный этап
Учитель проверяет готовность учащихся к уроку, настраивает их на работу.
II. Проверка домашнего задания
Учитель собирает тетради учащихся на проверку (домашняя работа оценивается как домашняя самостоятельная работа).
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
Учитель напоминает ученикам, что среди прикладных задач, которые могут быть решены методом математического моделирования, значительное место занимают задачи, в которых речь идет о процентах, и приводит примеры таких задач — их можно взять из сборника для ДПА по алгебре в 9 классе (или учитель вместо проведения беседы на этом этапе урока предлагает учащимся решить прикладную задачу на процентные расчеты, и учащиеся приходят к тому же выводу самостоятельно).
В любом случае, учитывая выше сказанное, можно сформулировать цель урока: повторив и систематизировав имеющиеся у учащихся знания и умения по определений процента и способов решения основных задач на проценты, дополнить их знаниями об банковские проценты, а также выработать умение применять формулу сложных процентов при решении задач.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Выполните умножение:
1) 0,5 · 48; 2) 0,2 · 60; 3) 1,5 · 20; 4) 0,1 · 17.
2. Найдите:
1) от 15;
2) 0,3 от 3;
3) число, если от него равна 4,9;
4) какую часть составляет число 5 от числа 25.
3. Найдите значение выражения , если:
1) р = 10; n = 2;
2) р = 50; n = 3.
4. Найдите значение выражения , если:
1) р = 10; n = 2;
2) р = 20; n = 6.
V. Систематизация знаний. Формирование новых знаний
План изучения материала
1. Определение процента от числа. Как записать проценты в виде дроби. Как записать дробь в виде процентов.
2. Формулы решения трех основных задач на проценты.
3. Банковские проценты:
1) формула простых процентов;
2) формула сложных процентов.
Опорный конспект № 24
Процентом (процентом) называется сотая часть целого (принимаемого за единицу). 1 % от числа а равно а Основные задачи на проценты |
1. Нахождение процента от числа. р% от числа а равен а. Пример. 7% от числа 300 равна · 300 = 21. |
2. Нахождение числа по заданной величине его процента. Если р% какого-нибудь числа составляет b, то все число равно . Пример. Число, 30% которого равно 24, — это число х = 24 : = = 80. |
3. Нахождение процентного отношения двух чисел. Число а от числа b составляет · 100%. Пример. Число 26 от числа составляет 65 · 100% = · 100% = 40%. Банковские проценты — процентные деньги по банковским вкладам, начисляются: |
а) ежемесячно (в течение года). — формула простых процентов, где A0, — начальный вклад; г — процентная ежемесячная ставка; n — количество месяцев, за которые начисляется процент; Аn — сумма, которую вкладчик получит через n месяцев; |
б) ежегодно (под определенный процент годовых). — формула сложных процентов, где A0, — начальный вклад; г — ежегодная процентная ставка; n — количество лет; n — наращенный капитал. |
Методический комментарий
Изучение материала урока начинается с повторения и систематизации знаний учащихся, которые они приобрели в предыдущих классах: определение процента от числа, а также способов представления процентов в виде дроби (десятичной и обыкновенной), и наоборот, запись дроби в процентах. Умение выполнять эти преобразования являются основными, которые используются при решении основных задач на проценты. После этого уместно повторить с учащимися известные им виды основных задач на проценты и способы их решения и обобщить эти способы, записав их в виде формул (см. опорный конспект № 24).
Уже повторив и обобщив изученный ранее материал, можно вводить понятие банковских процентов (простых и сложных) и выводить формулы для их вычисления. Следует заметить, что программа по математике не требует от учеников умения доказывать формулы для вычисления банковских процентов, поэтому учитель выводит эти формулы во время беседы на примере решения соответствующих задач.
VI. Формирование умений
Устные упражнения
1. Найдите:
1) 50% от числа 48;
2) 20% от числа 60;
3) 150% от числа 20.
2. Найдите:
1) число, 10% которого равно 17;
2) число, 75% которого равно 150.
3. Найдите процентное отношение чисел:
1) 5 и 25; 2) 45 и 30.
Письменные упражнения
Для реализации дидактической цели урока следует решить упражнения такого содержания:
1) решить различные виды основных задач на проценты;
2) решить задачу на применение формулы простых и сложных процентов;
3) на повторение: прикладная задача на составление математической модели.
Методический комментарий
Для лучшего усвоения учащимися содержания материала урока рекомендуется при выполнении соответствующих упражнений неоднократно повторять определения и формулы.
Важно отработать умение сознательно выполнять решение задачи на проценты, для этого нужно сначала проанализировать ее условие согласно выделенных видов, после чего уже выполнять действия в соответствии с записанных формул.
VII. Итоги урока
Контрольное задание
Пусть начальный взнос равен а грн; годовая процентная ставка Ь%. Сколько денег будет на счете вкладчика через с лет?
1) а; 2) b; 3) а; 4) с.
VIII. Домашнее задание
1. Повторить определение процентов и выучить формулы решения задач на проценты и формулу сложных процентов (см. опорный конспект № 24).
2. Решить задачи на применение изученных формул.
3. Повторить: решение задач на составление и решения математических моделей реальных процессов.
«Инвестиционный» Инвестиционные проблемы обычно Для годовых процентов, Инвестиционные проблемы со словами Во всех случаях этих проблем,
В данном случае P = 1000 долларов, r = 0,06 (потому что мне нужно преобразовать процент в десятичную форму), а время I = (1000) (0.06) (2) Я получу 120 долларов в виде процентов. Другой пример:
Для этого упражнения я Конечно, мне нужно Самое сложное приходит, когда Авторские права
Проблема здесь
Как мне заполнить ЭТА МЕТОДИКА ЯВЛЯЕТСЯ
Теперь я покажу вам, почему
Так как проценты от 0. Тогда y = 50 000 — 31 250 = 18 750. Я должен вложить 31 250 долларов в Фонд X и 18 750 долларов в Фонд Y. Обратите внимание, что ответ сделал Вверх | 1 | 2 | Возвращаться
|
Как решать проблемы, связанные с интересами: шаги и примеры — Урок математики [видео 2021]
Обнаружение интереса
Предположим, что Карен инвестирует свои 500 долларов в счет, приносящий 5% годовых.Ого! Где этот банк? В городе Алгебра вымышленное место с потрясающими процентными ставками! Ой, орехи. В любом случае: сколько процентов она заработает через три года?
Чтобы решить эту проблему, давайте выполним наши действия. Читаем проблему. И мы хотим знать заработанные проценты, которые составляют я . Давайте разберемся, что мы знаем из нашей формулы. Мы знаем, что сумма основного долга составляет 500 долларов. Процентная ставка 5%. И время — три года.
Мы знаем, что сумма основного долга составляет 500 долларов. Процентная ставка 5%. И время — три года.
Следует отметить, что мы используем эту формулу для расчета простых процентов.Этим мы и займемся на протяжении всего урока. Противоположность простому проценту — сложный процент. Сложные проценты немного сложнее. Это то, что происходит, когда заработанные проценты добавляются к основной сумме через определенные интервалы, например, ежемесячно, а затем новые проценты рассчитываются на основе новой основной суммы.
Представьте, что у вас есть 100 долларов, а через месяц вы зарабатываете 5 долларов в виде процентов. Что касается сложных процентов, мы считаем, что основная сумма долга за второй месяц составляет 105 долларов. И основная сумма долга будет расти с каждым периодом.
Но мы просто сосредотачиваемся на более прямом простом проценте, где основная сумма никогда не меняется в течение рассматриваемого периода.
Хорошо, вернемся к Карен и ее 500 долларам. Давайте составим наше уравнение. Помните, что это I = Prt . Мы знаем, что Prt — это 500 * 0,05 * 3. Это сумма основного долга, умноженная на процентную ставку (в виде десятичной дроби), умноженная на время в годах.
Давайте составим наше уравнение. Помните, что это I = Prt . Мы знаем, что Prt — это 500 * 0,05 * 3. Это сумма основного долга, умноженная на процентную ставку (в виде десятичной дроби), умноженная на время в годах.
500 * 0,05 * 3 равно 75. Это означает, что I = 75, и Карен заработала 75 долларов в виде процентов за три года.Это как бесплатные деньги, которые банк заплатил ей только за то, что она позволила им удержать ее 500 долларов.
В поисках времени
В тот же день, когда Карен получает свои 75 долларов процентов, она узнает, что ее родители учредили для нее сберегательный залог, срок выплаты которого наступил. Они вложили 1000 долларов в облигацию с доходностью 4%. Сейчас он стоит 1600 долларов. Как давно они вложили деньги?
На этот раз мы упускаем время. Но мы знаем основную сумму — 1000 долларов и процентную ставку — 4%. Мы также знаем общий интерес.Будьте осторожны, не предполагайте, что это 1600 долларов. Обратите внимание, что это основная сумма и проценты, или общая стоимость после сложения двух сумм. Итак, процент составляет всего 1600 — 1000, или 600.
Итак, процент составляет всего 1600 — 1000, или 600.
Давайте составим наше уравнение. Опять же, это I = Prt . Мы знаем, что 600 = 1000 * 0,04 * t . 1000 * 0,04 равно 40. 600/40 равно 15. Итак, т = 15. Это означает, что инвестиции были сделаны 15 лет назад.
Определение процентной ставки
Итак, 75 долларов в виде процентов, сберегательная облигация на 1600 долларов…все идет, Карен! Позже в тот же прекрасный день Карен ждет еще один сюрприз. Карен не успела оплатить счет четыре года назад за подписку на журнал, которую она купила в Интернете. Видимо, она нажала «выставить счет позже», а потом просто забыла об этом. Подписка изначально стоила 30 долларов, но теперь они утверждают, что она должна 120 долларов. Святая корова! Какая была процентная ставка?
Давайте выясним. Здесь мы знаем, что основная сумма составляет 30 долларов. Срок — 4 года. А как насчет интереса? Если сейчас она должна 120 долларов, то проценты будут 90 долларов, или 120 — 30. Давайте найдем эту скорость.
Давайте найдем эту скорость.
В нашем уравнении I = Prt равно 90 = 30 * r * 4. 30 * 4 равно 120, а 90/120 равно 0,75. Таким образом, процентная ставка составляет 75%. В следующий раз Карен прочтет мелкий шрифт.
Резюме урока
Подводя итог, мы узнали о начислении процентов , или денег, выплачиваемых с течением времени для инвестированных основной суммы . Принципал относится к первоначальным инвестициям.
Мы использовали формулу I = Prt , где I — заработанные проценты, P — основная сумма, r — процентная ставка, а t — время в годах.
Мы можем использовать эту формулу для расчета простых процентов. Мы также можем использовать его, чтобы найти любую из недостающих переменных, например, время или процентную ставку .
Результаты обучения
По завершении этого урока вы сможете:
- Определять проценты и основную сумму
- Различия между простыми и сложными процентами
- Определите формулу для расчета простых процентов
решенных примеров на простой интерес
Covid-19 привел мир к феноменальному переходу.
За электронным обучением будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
В этом разделе я решил примеры по простому интересу. Ссылаясь на них, вы можете решить свои вопросы. Примеры:
1) Ariel берет ссуду в размере 8000 долларов США на покупку бывшего в употреблении грузовика по ставке 9% простых процентов. Рассчитайте годовые проценты, подлежащие уплате на сумму ссуды.
Решение:
Из деталей, приведенных в задаче Принцип = P = 8000 долларов и R = 9% или 0.09 в виде десятичной дроби.
Поскольку годовой процент должен быть рассчитан, период времени T = 1.
Подставляя эти значения в формулу простой процентной ставки,
I = P x T x R
= 8000 x 1 x 0,09
= 720,00
Годовой процент к выплате = 720 долларов США
________________________________________________________________
2) Стив вложил доллары 10 000 на сберегательном счете, который приносил 2% простых процентов. Найдите проценты, заработанные, если сумма хранилась в банке 4 года.
Решение:
Принцип P = 10000 долларов США Период времени T = 4 года и процентная ставка = 2% = 0,02
Подставляя эти значения в формулу простой процентной ставки,
I = PX TXR
= 10 000 X 4 x 0,02
= 800 долларов
Процентные доходы от инвестиций = 800 долларов
________________________________________________________________
3) Райан купил 15000 долларов в банке, чтобы купить автомобиль под 10% простой процентной ставки. Если он заплатил 9000 долларов в качестве процентов при погашении ссуды, найдите время, на которое ссуда была предоставлена.
Если он заплатил 9000 долларов в качестве процентов при погашении ссуды, найдите время, на которое ссуда была предоставлена.
Решение: Принцип = Процентная ставка 15 000 долларов США R = 10% = 0,10, а выплаченный процент = I = 9 000 долларов США. И T нужно найти.
T = I / (PR)
= 9000 / (15000 x 0,10)
= 6 лет.
Заем предоставлен сроком на 6 лет.
________________________________________________________________
Решенные примеры по простому проценту
4) Через сколько времени простой процент на 3500 долларов по ставке 9% в год будет таким же, как простой процент на 4000 долларов по ставке 10. 5% годовых на 4 года? Решение:
5% годовых на 4 года? Решение:
SI на 4000 долларов по ставке 10,5% = 10,5 / 100 = 0,105 на 4 года
SI = (P x R x T) / 100
= 4000 x 0,105 x 4
SI = 1,680 долларов
Процентная ставка в размере 1 680 долларов США такая же, как и процентная ставка по 3 500 долларов США под 9% годовых на предположительно «t» лет.
SI x 100
Время = t = ————
P x R
1680 x 100
Время = t = ————
3500 x 9
168,000
Время = t = ————
31,500
Время = t = 5.33 года.
Простой процент (SI)
• Определение ставки при задании основного долга и времени
• Определение времени при задании основного долга и ставки
• Решенные примеры для простого процента
Из примеров простого процента к бизнес-математике Домашняя страница
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Простые и сложные проценты — математика для нашего мира
Результаты обучения
- Расчет единовременных простых процентов и простых процентов с течением времени
- Определить APY с учетом процентного сценария
- Расчет сложных процентов
Надо работать с деньгами каждый день.В то время как баланс вашей чековой книжки или подсчет ваших ежемесячных расходов на эспрессо требует только арифметики, когда мы начинаем экономить, планируем выход на пенсию или нуждаемся в ссуде, нам нужно больше математики.
Простые проценты
Обсуждение процентов начинается с основной суммы или суммы, с которой начинается ваш счет. Это могут быть стартовые инвестиции или стартовая сумма кредита. Проценты в простейшей форме рассчитываются как процент от основной суммы долга.Например, если вы взяли у друга 100 долларов и согласились выплатить их с 5% -ной процентной ставкой, тогда сумма процентов, которую вы заплатите, будет всего лишь 5% от 100: 100 долларов (0,05) = 5 долларов. Общая сумма, которую вы должны выплатить, составит 105 долларов, включая первоначальную основную сумму плюс проценты.
Это могут быть стартовые инвестиции или стартовая сумма кредита. Проценты в простейшей форме рассчитываются как процент от основной суммы долга.Например, если вы взяли у друга 100 долларов и согласились выплатить их с 5% -ной процентной ставкой, тогда сумма процентов, которую вы заплатите, будет всего лишь 5% от 100: 100 долларов (0,05) = 5 долларов. Общая сумма, которую вы должны выплатить, составит 105 долларов, включая первоначальную основную сумму плюс проценты.
Простые разовые проценты
(1)
Примеры
Друг просит одолжить 300 долларов и соглашается выплатить его в течение 30 дней под 3% годовых. Сколько процентов вы заработаете?
Решение:
(3) = 300 долларов США | основной |
| r = 0.03 | 3% ставка |
| I = 300 долларов (0,03) = 9 долларов. | Вы получите проценты в размере 9 долларов США. |
В следующем видео подробно рассматривается этот пример.
Одноразовые простые проценты обычно используются только для чрезвычайно краткосрочных ссуд. По долгосрочным займам проценты обычно выплачиваются ежедневно, ежемесячно, ежеквартально или ежегодно. В этом случае проценты будут начисляться регулярно.
Например, облигации — это, по сути, ссуды, предоставленные эмитенту облигаций (компании или правительству) вами, держателем облигации. В обмен на ссуду эмитент соглашается выплачивать проценты, часто ежегодно. Облигации имеют дату погашения, когда эмитент выплачивает первоначальную стоимость облигации.
Упражнения
Предположим, ваш город строит новый парк и выпускает облигации, чтобы собрать деньги на его строительство. Вы получаете облигацию на сумму 1000 долларов, по которой выплачивается 5% годовых со сроком погашения 5 лет.Сколько процентов вы заработаете?
Вы получаете облигацию на сумму 1000 долларов, по которой выплачивается 5% годовых со сроком погашения 5 лет.Сколько процентов вы заработаете?
[show-answer q = ”14596 ″] Показать решение [/ show-answer]
[hidden-answer a =” 14596 ″] Каждый год вы будете зарабатывать 5% процентов: 1000 долларов (0,05) = 50 долларов процентов. Таким образом, в течение пяти лет вы заработаете в общей сложности 250 долларов в виде процентов. Когда срок погашения облигации истечет, вы получите обратно 1000 долларов, которые вы изначально заплатили, в результате чего у вас останется 1250 долларов. [/ Hidden-answer]
Дальнейшее объяснение решения этого примера можно увидеть здесь.
Мы можем обобщить эту интересную идею с течением времени.
Простой процент с течением времени
(4)
Единицы измерения времени (годы, месяцы и т. Д.) Должны соответствовать периоду времени для процентной ставки.
Д.) Должны соответствовать периоду времени для процентной ставки.
APR — Годовая процентная ставка
Процентные ставки обычно задаются как годовая процентная ставка (APR) — общая процентная ставка, которая будет выплачиваться в течение года. Если проценты выплачиваются меньшими временными интервалами, годовая процентная ставка будет разделена.
Например, ежемесячная выплата 6% годовых будет разделена на двенадцать 0.5% выплаты.
Ежеквартальная ставка 4%, выплачиваемая ежеквартально, будет разделена на четыре выплаты по 1%.
Пример
Казначейские облигации
(казначейские ноты) — это облигации, выпущенные федеральным правительством для покрытия его расходов. Предположим, вы получаете казначейские облигации на сумму 1000 долларов с годовой ставкой 4%, выплачиваемой раз в полгода, со сроком погашения через 4 года. Сколько процентов вы заработаете?
Решение:
Поскольку проценты выплачиваются раз в полгода (два раза в год), процентная ставка 4% будет разделена на две выплаты по 2%.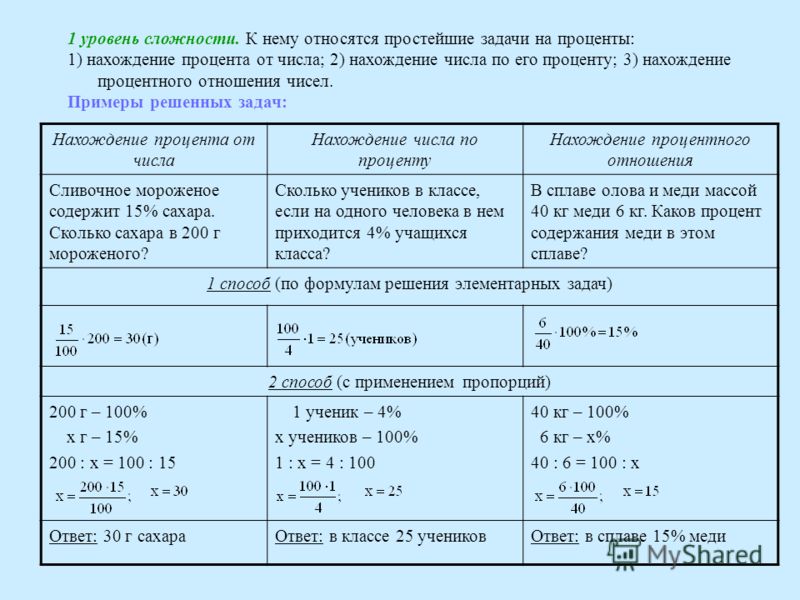
(6) = 1000 долларов США | основной |
| r = 0,02 | Ставка 2% за полгода |
| т = 8 | 4 года = 8 полугодий |
| I = 1000 (0,02) (8) = 160 долларов. | Вы заработаете 160 долларов в течение четырех лет. |
Это видео объясняет решение.
Попробуй
Щелкните здесь, чтобы попробовать решить эту проблему.
Попробуй
Кредитная компания взимает 30 долларов за ссуду на один месяц в размере 500 долларов. Найдите годовую процентную ставку, которую они взимают.
Решение:
I = 30 долларов процентов
= 500 долларов основной суммы
r = неизвестно
t = 1 месяц
Используя, получаем. Решая, получаем r = 0,06, или 6%. Поскольку время было ежемесячным, это ежемесячные проценты.Годовая ставка будет в 12 раз больше: 72% годовых.
Решая, получаем r = 0,06, или 6%. Поскольку время было ежемесячным, это ежемесячные проценты.Годовая ставка будет в 12 раз больше: 72% годовых.
Попробуй
Щелкните здесь, чтобы попробовать решить эту проблему.
Сложные проценты
С простыми процентами мы предположили, что получили проценты, когда получили их. На стандартном банковском счете любые проценты, которые мы зарабатываем, автоматически добавляются к нашему балансу, и мы будем получать проценты с этих процентов в будущие годы. Это реинвестирование процентов называется , составляющим .
Предположим, мы помещаем 1000 долларов на банковский счет с ежемесячной ставкой 3% годовых.Как наши деньги будут расти?
3% годовых — это годовая процентная ставка (APR) — общая сумма процентов, подлежащих выплате в течение года. Поскольку проценты выплачиваются ежемесячно, каждый месяц мы будем зарабатывать 3% ÷ 12 = 0,25% в месяц.
В первый месяц
- P 0 = 1000 долларов США
- r = 0,0025 (0,25%)
- I = 1000 долларов США (0,0025) = 2,50 доллара США
- A = 1000 USD + 2,50 USD = 1002,50 USD
В первый месяц заработаем 2 доллара. 50 процентов, увеличивая баланс нашего счета до 1002,50 долларов США.
50 процентов, увеличивая баланс нашего счета до 1002,50 долларов США.
Во второй месяц
- P 0 = 1002,50 долл. США
- I = 1002,50 USD (0,0025) = 2,51 USD (округлено)
- A = 1002,50 USD + 2,51 USD = 1005,01 USD
Обратите внимание, что во второй месяц мы заработали больше процентов, чем в первый месяц. Это потому, что мы заработали проценты не только на первоначальную 1000 долларов, которые мы вложили, но мы также получили проценты на 2 доллара.50 процентов мы заработали в первый месяц. Это ключевое преимущество, которое дает нам начисления процентов.
Если подсчитать еще несколько месяцев, получим:
| Месяц | Стартовый баланс | Полученные проценты | Конечное сальдо |
| 1 | 1000,00 | 2,50 | 1002,50 |
| 2 | 1002. 50 50 | 2,51 | 1005.01 |
| 3 | 1005.01 | 2,51 | 1007,52 |
| 4 | 1007,52 | 2,52 | 1010,04 |
| 5 | 1010,04 | 2,53 | 1012,57 |
| 6 | 1012,57 | 2,53 | 1015,10 |
| 7 | 1015,10 | 2,54 | 1017.64 |
| 8 | 1017,64 | 2,54 | 1020,18 |
| 9 | 1020,18 | 2,55 | 1022,73 |
| 10 | 1022,73 | 2,56 | 1025.29 |
| 11 | 1025.29 | 2,56 | 1027,85 |
| 12 | 1027,85 | 2,57 | 1030,42 |
Мы хотим упростить процесс расчета сложных процентов, потому что создание таблицы, подобной приведенной выше, занимает много времени. К счастью, математика хороша в том, что дает вам короткие пути. Чтобы найти уравнение для представления этого, если P m представляет сумму денег через m месяцев, то мы могли бы написать рекурсивное уравнение:
К счастью, математика хороша в том, что дает вам короткие пути. Чтобы найти уравнение для представления этого, если P m представляет сумму денег через m месяцев, то мы могли бы написать рекурсивное уравнение:
P 0 = 1000 долларов США
P м = (1 + 0,0025) P м-1
Вы, вероятно, узнаете в этом рекурсивную форму экспоненциального роста. Если нет, мы проделаем шаги, чтобы построить явное уравнение для роста в следующем примере.
Пример
Постройте явное уравнение для роста 1000 долларов, депонированных на банковский счет с 3% -ной процентной ставкой, начисляемой ежемесячно.
Решение:
- P 0 = 1000 долларов США
- P 1 = 1,0025 P 0 = 1,0025 (1000)
- P 2 = 1,0025 P 1 = 1,0025 (1,0025 (1000)) = 1,0025 2 (1000)
- P 3 = 1.
 0025 P 2 = 1,0025 (1,00252 (1000)) = 1,00253 (1000)
0025 P 2 = 1,0025 (1,00252 (1000)) = 1,00253 (1000) - P 4 = 1,0025 P 3 = 1,0025 (1,00253 (1000)) = 1,00254 (1000)
Наблюдая закономерность, можно сделать вывод
Обратите внимание, что 1000 долларов в уравнении были P 0 , начальной суммой. Мы нашли 1,0025, прибавив единицу к скорости роста, разделенной на 12, так как мы увеличивали 12 раз в год.
Обобщая наш результат, мы можем написать
В этой формуле:
- м — количество периодов начисления сложных процентов (в нашем примере месяцев)
- r — годовая процентная ставка
- k — количество соединений в год.
Просмотрите это видео, чтобы ознакомиться с концепцией сложных процентов.
Хотя эта формула работает нормально, чаще используется формула, которая включает количество лет, а не количество периодов начисления сложных процентов. Если N — количество лет, то m = N k . Это изменение дает нам стандартную формулу для сложных процентов.
Если N — количество лет, то m = N k . Это изменение дает нам стандартную формулу для сложных процентов.
Сложные проценты
- P N — остаток на счете после N лет.
- P 0 — начальный баланс счета (также называемый начальным депозитом или основной суммой)
- r — годовая процентная ставка в десятичной форме
- k — количество периодов начисления сложных процентов в году
- Если начисление процентов производится ежегодно (один раз в год), k = 1.
- Если начисление процентов производится ежеквартально, k = 4.
- Если начисление начислений производится ежемесячно, тыс. = 12.
- Если начисление сложных процентов производится ежедневно, k = 365.
Самая важная вещь, которую следует помнить при использовании этой формулы, заключается в том, что она предполагает, что мы помещаем деньги на счет один раз и позволяем им оставаться там, зарабатывая проценты.
В следующем примере мы покажем, как использовать формулу сложных процентов, чтобы найти остаток на депозитном сертификате через 20 лет.
Пример
Депозитный сертификат (CD) — это сберегательный инструмент, который предлагают многие банки.Обычно он дает более высокую процентную ставку, но вы не можете получить доступ к своим инвестициям в течение определенного периода времени. Предположим, вы вкладываете 3000 долларов на компакт-диск с ежемесячной выплатой 6% годовых. Сколько у вас будет на счету через 20 лет?
Решение:
В этом примере
| P 0 = 3000 долл. США | начальный депозит |
| r = 0,06 | 6% годовых |
| к = 12 | 12 месяцев в 1 год |
| N = 20 | , поскольку мы смотрим, сколько у нас будет через 20 лет |
Итак (округлите ответ до ближайшей копейки)
Видео-пошаговое руководство по этому примеру проблемы доступно ниже.
Давайте сравним сумму денег, полученную от начисления сложных процентов, с суммой, которую вы заработали бы от простых процентов
| Годы | Простые проценты (15 долларов в месяц) | 6% начисленных ежемесячно = 0,5% ежемесячно. |
| 5 | $ 3900 | $ 4046,55 |
| 10 | $ 4800 | $ 5458,19 |
| 15 | $ 5700 | $ 7362.28 |
| 20 | 6600 $ | $ 9930,61 |
| 25 | 7500 долл. США | $ 13394.91 |
| 30 | $ 8400 | $ 180 67,73 |
| 35 | $ 9300 | $ 24370,65 |
Как видите, в течение длительного периода времени начисление сложных процентов сильно влияет на баланс счета. Вы можете понять разницу между линейным и экспоненциальным ростом.
Вы можете понять разницу между линейным и экспоненциальным ростом.
Попробуй
Щелкните здесь, чтобы попробовать решить эту проблему.
Пример
Вы знаете, что вам понадобится 40 000 долларов на образование вашего ребенка через 18 лет. Если ваша учетная запись зарабатывает 4% в квартал, сколько вам нужно будет внести сейчас, чтобы достичь своей цели?
Решение:
В этом примере мы ищем P 0 .
| r = 0,04 | 4% |
| к = 4 | 4 квартала за 1 год |
| N = 18 | Поскольку мы знаем баланс за 18 лет |
| P 18 = 40 000 долларов США | Сумма у нас за 18 лет |
В этом случае нам нужно будет составить уравнение и решить для P 0 .
(7)
Итак, вам нужно будет внести 19 539,84 доллара сейчас, чтобы иметь 40 000 долларов через 18 лет.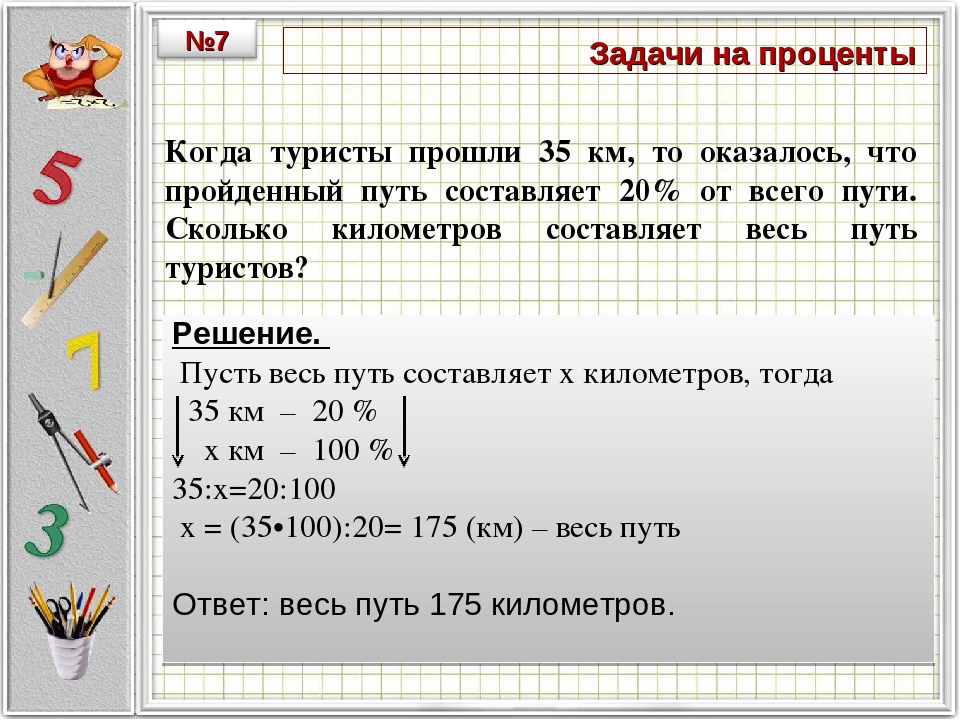
Попробуй
Щелкните здесь, чтобы попробовать решить эту проблему.
Округление
Если вы не вводите всю свою формулу в Desmos и выбираете делать это по частям, важно быть очень осторожным с округлением при вычислении показателей с показателями. В общем, вы хотите использовать как можно больше десятичных знаков во время вычислений. Убедитесь, что содержит не менее 3 значащих цифр (числа после любых ведущих нулей).Округление от 0,00012345 до 0,000123 обычно дает «достаточно близкий» ответ, но всегда лучше оставить больше цифр.
Пример
Чтобы понять, почему так важно не завышать округление, если вы решите не вводить свою формулу сразу в Desmos, предположим, что вы инвестируете 1000 долларов под 5% годовых, начисляемых ежемесячно, в течение 30 лет.
| P 0 = 1000 долларов США | начальный депозит |
| r = 0.05 | 5% |
| к = 12 | 12 месяцев в 1 год |
| N = 30 | , поскольку мы ищем сумму через 30 лет |
Если мы сначала вычислим r / k , мы найдем 0,05 / 12 = 0,00416666666667
Вот результат округления до разных значений:
r / k округлено до: | Возвращает P30 к: | Ошибка |
0. 004 004 | $ 4208,59 | 259,15 $ |
| 0,0042 | $ 4521,45 | $ 53,71 |
| 0,00417 | 4473,09 $ | $ 5,35 |
| 0,004167 | 4468,28 долл. США | 0,54 доллара США |
| 0,0041667 | 4467,80 $ | 0,06 $ |
| без округления | 4467,74 $ |
Если вы работаете в банке, вы, конечно, вообще не станете округлять.Для наших целей ответ, который мы получили путем округления до 0,00417, трех значащих цифр, достаточно близок — 5 долларов от 4500 долларов не так уж и плохо. Конечно, сохранение четвертого десятичного разряда не повредило бы.
Просмотрите следующее для демонстрации этого примера.
Использование калькулятора Desmos
Во многих случаях вы можете полностью избежать округления, введя значения в калькулятор. Например, в приведенном выше примере нам нужно было вычислить
Например, в приведенном выше примере нам нужно было вычислить
Мы можем быстро вычислить это на калькуляторе Desmos, введя формулу сразу:
Чтобы ввести это в калькулятор, введите следующее:
1000 * (1 +.05/12) a b (12 * 30)
Примечание: a b находится в первой строке, втором столбце главного меню выше. Теперь вы можете округлить окончательный ответ до ближайшего цента.
Атрибуции
Эта глава содержит материал, взятый из Math in Society (в OpenTextBookStore) Дэвида Липпмана и используется по лицензии CC Attribution-Share Alike 3.0 United States (CC BY-SA 3.0 US).
Эта глава содержит материал, взятый из книги Math for the Liberal Arts (по Lumen Learning) компании Lumen Learning и используется в соответствии с лицензией CC BY: Attribution .
Задачи Word на Simple Interest
Задача 1:
Найдите простой процент на 2 года на 2000 долларов под 6% в год.
Решение:
Формула для простых процентов:
I = Pnr / 100
Здесь P = 2000, n = 2, r = 6
Подставим эти значения в приведенную выше формулу
I = (2000 ⋅ 2 ⋅ 6) / 100
I = 20 ⋅ 2 ⋅ 6
I = 240
Итак, заработанные проценты составляют 240 долларов.
Задача 2:
В простых процентах денежная сумма удваивается через 10 лет. Найдите количество лет, которое потребуется, чтобы утроиться.
Решение:
Пусть P — это сумма вложенных денег.
Дано: Сумма денег удваивается через 10 лет
Тогда P станет 2P через 10 лет.
Теперь мы можем рассчитать проценты за десять лет, как указано ниже
Из приведенного выше расчета P — это проценты за первые 10 лет.
В случае простых процентов заработанные проценты будут одинаковыми каждый год.
Таким образом, проценты, полученные в следующие 10 лет, также будут равны P.
Это объясняется ниже.
Таким образом, принципалу потребуется 20 лет, чтобы он стал тройным.
Задача 3:
В простых процентах денежная сумма составляет 6200 долларов через 2 года и 7400 долларов через 3 года. Найдите директора.
Решение:
По истечении 2 лет мы получаем 6200 долларов
В конце 3 лет мы получаем 7400 долларов
Из этих двух данных мы можем получить проценты, полученные в 3-м году, как указано ниже.
В простых процентах проценты будут одинаковыми за каждый год.
Исходя из этого, мы можем рассчитать основную сумму, как указано ниже
Итак, основной капитал составляет 3800 долларов.
Задача 4:
Сумма в 46875 долларов была предоставлена под простые проценты, и в конце 1 года 8 месяцев общая сумма составила 50000 долларов. Найдите процентную ставку в год.
Решение:
Исходя из данной информации, мы имеем
P = 46875 и A = 50000
Тогда
Процент = Сумма — Основная сумма
I = 50000 — 46875
I = 3125
значение «n» всегда должно быть в «годах». Но в вопросе это указано как в годах, так и в месяцах.
Но в вопросе это указано как в годах, так и в месяцах.
Чтобы преобразовать месяцы в годы, мы должны разделить данные месяцы на 12.
1 год 8 месяцев = 1 8/12 лет или 1 ⅔ лет
Итак, значение «n» равно 1 ⅔ или 5 / 3.
Формула для простых процентов:
I = Pnr / 100
Здесь P = 46875, n = 5/3
3125 = [46875 ⋅ 5/3 ⋅ r) / 100
312500 = 78125 ⋅ r
312500/78125 = r
4 = r
Итак, годовая процентная ставка составляет 4%.
Задача 5:
Найдите накопленную стоимость депозита в размере 2500 долларов, сделанного в виде простых процентов на 3,5 года под 5% годовых.
Решение:
Сначала давайте найдем заработанные проценты, а затем мы сможем найти накопленную стоимость.
I = Pnr / 100
Здесь P = 2500, n = 3,5, r = 5
I = (2500 ⋅ 3,5 ⋅ 5) / 100
I = 25 ⋅ 3,5 ⋅ 5
I = 437,50
Суммарное значение:
A = P + I
A = 2500 + 437. 50
50
A = 2937,50
Итак, накопленная стоимость составляет 2937,50 долларов США.
Задача 6:
Сколько процентов будет заработано на 3000 долларов под 7% простых процентов в год в течение 9 месяцев?
Решение:
Формула для простых процентов:
I = Pnr / 100
Здесь P = 3000, r = 7%
Значение «n» всегда должно быть в годах. Но в вопросе это указано в месяцах.
Чтобы преобразовать месяцы в годы, мы должны разделить данные месяцы на 12.
9 месяцев = 9/12 лет или 3/4 года
Итак, значение «n» равно 3/4.
Тогда у нас есть
I = [3000 ⋅ 3/4 ⋅ 7] / 100
I = 30 ⋅ 0,75 ⋅ 7
I = 157,50
Итак, заработанные проценты составляют 157,50 долларов США.
Задача 7:
Какая сумма денег принесет 28600 долларов в виде процентов через 3 года и 3 месяца под 2,5% годовых?
Решение:
Формула для простых процентов:
I = Pnr / 100
Здесь I = 28600 долларов, r = 2. 5%
5%
Значение «n» всегда должно быть в «годах». Но в вопросе это указано как в годах, так и в месяцах.
Чтобы преобразовать месяцы в годы, мы должны разделить данные месяцы на 12.
3 года 3 месяца = 3 3/12 года или 3¼ года
Итак, значение «n» равно 3¼ или 13/4.
Пробка I = 28600, r = 2,5 и n = 13/4 в формуле простого интереса.
28600 = [P ⋅ 13/4 ⋅ 2,5] / 100
2860000 = P ⋅ 3,25 ⋅ 2,5
2860000 = P ⋅ 8.125
2860000 / 8,125 = P
352000 = P
Таким образом, необходимая основная сумма составляет 352 000 долларов США.
Задача 8:
Г-н Абрахам инвестировал сумму в 13900 долларов, разделенную на две разные схемы A и B, с простой процентной ставкой 14% годовых. и 11% годовых соответственно. Если общая сумма простых процентов, заработанных за 2 года, составит 3508 долларов, какая сумма была инвестирована в схему B?
Решение:
Пусть «m» будет суммой, инвестированной в схему B.
Тогда сумма, вложенная в схему A = 13900 — млн.
Процент по схеме (A) + Процент по схеме (B) = 3508
(13900 — m) ⋅ 0,14 ⋅ 2 + m ⋅ 0,11 ⋅ 2 = 3508
(13900 — м) ⋅ 0,28 + 0,22 м = 3508
3892 — 0,28 м + 0,22 м = 3508
3892 — 0,06 м = 3508
3892 — 3508 = 0,06 м
384 = 0,06 м
m = 6400
Итак, сумма, вложенная в схему B, составляет 6400 долларов.
Задача 9:
Лили взяла ссуду в размере 1200 долларов с простыми процентами на столько лет, сколько ставка процента. Если она заплатила 432 доллара в качестве процентов в конце периода ссуды, какова была процентная ставка?
Решение:
Пусть «m» будет процентной ставкой.
Дано: Процентная ставка и количество лет одинаковы
Тогда количество лет = m
Формулы для простых процентов равны
I = Pnr / 100
Здесь I = 432 доллара США, P = 1200 долларов США, r = m, n = m
Итак, имеем
432 = (1200 ⋅ м ⋅ м) / 100
432 = 12 м²
36 = м²
6 = m
Итак, процентная ставка 6%.
Задача 10:
A ссудил 5 000 долларов B на 2 года и 3000 долларов C на 4 года под простые проценты по той же ставке процента и получил от них всего 2200 долларов в качестве процентов. Найдите процентную ставку в год.
Решение:
Пусть «m» будет процентной ставкой
Проценты от B + Проценты от C = 2200
(5000 m 2) / 100 + (3000 ⋅ m 4) / 100 = 2200
10000m + 12000m = 220000
22000m = 220000
m = 10
S, процентная ставка 10%.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Алгебра
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словом по цене за единицу
Word задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word по сложным процентам
ngles
Проблемы со словами с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Тригонометрические проблемы со словами
Проблемы с процентным соотношением слов
Проблемы со словами о прибылях и убытках 9006
Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи с уравнениями со словами
Проблемы со словами с линейными неравенствами
Word Ratio и Задачи
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Проблемы со словами по теореме Пифагора
Процент числового слова pr проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибылей и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
Домен и диапазон рациональных функций 9006
Домен и диапазон рациональных функций
функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск квадратного корня с использованием длинного di видение
Л. Метод CM для решения временных и рабочих задач
Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 степени 256 на 17
Остаток при делении 17 степени 23 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
2.1 Практика — Простые и сложные проценты
1) Найдите проценты по кредиту на подержанный автомобиль в размере 5000 долларов по ставке 16% на срок 8 месяцев.
2) Найдите проценты, полученные от вложения 10 000 долларов на счет денежного рынка, на котором выплачивается простая процентная ставка 1,75% в течение 39 недель.
3) Найдите сумму, причитающуюся по инвестициям в размере 10 000 долларов США на счет денежного рынка, на котором выплачивается простая процентная ставка 1,75% в течение 39 недель.
Покажи ответ
А = 10000 + 131.25 = 10 131,25 долл. США
4) Найдите сумму кредита в размере 600 долларов США под 15,75% годовых через 21 месяц.
5) Какова годовая процентная ставка по 33-дневному казначейскому векселю со сроком погашения 1000 долларов, который продается за 996,16 доллара? (Используйте 360 дней в году)
6) Если вы одолжите 3000 долларов под простую процентную ставку 14% на 10 месяцев, сколько вы будете должны через 10 месяцев? Сколько процентов вы заплатите?
Покажи ответ
A = 3350 долларов США, I = 350 долларов США
7) Кредит в 2500 долларов был погашен в конце 39 недель чеком на 2812 долларов. 50. Какая годовая процентная ставка взималась?
50. Какая годовая процентная ставка взималась?
8) Бухгалтер корпорации забыл вовремя уплатить подоходный налог компании в размере 725 896,15 долларов (э-э-э). Правительство взимало штраф в размере 12,7% годовых за 34 дня задержки с выплатой денег. Найдите общую сумму, которую необходимо заплатить.
9) Если инвестор хочет заработать 10,76% годовых по 26-недельному казначейскому векселю со сроком погашения 5000 долларов, сколько инвестор должен заплатить по векселю?
10) Джесси покупает 100 акций по цене 29 долларов.52 за акцию, а затем через 9 месяцев продает акции по 37,85 доллара за акцию. Комиссия за транзакцию составляет 1% от общей суммы транзакции. Какую годовую процентную ставку заработала Джесси?
11) Сколько времени потребуется, чтобы компакт-диск удвоился, если деньги приносят простую процентную ставку 4,8%? Округлите ближайший год.
Покажи ответ
20,8 = 21 год
12) Учитывая r = 12%, начисляется ежемесячно в течение 8 лет; найти n (количество месяцев) и i (ставка за месяц). Запишите i в десятичной форме
Запишите i в десятичной форме
Покажи ответ
n = 96 мес., i = 0,01
13) Учитывая r = 6%, начисляется ежеквартально в течение 50 лет. найти n (количество месяцев) и i (ставка за месяц). Напишите i в десятичной форме.
Покажи ответ
n = 200, i = 0,015
14) Дедушка и бабушка внесли 6000 долларов на счет внука для получения высшего образования. Сколько денег (с точностью до доллара) будет на счете через 17 лет, если счет будет приносить 9% начисленных ежемесячно ?
15) Какую сумму вы должны изначально внести на счет с выплатой 10% начисленных раз в полгода, чтобы иметь 1000000 долларов через 30 лет? б) начисляется ежемесячно? в) ежедневно? г) непрерывное компаундирование
Полугодовой ответ
53 535 долларов.52
Ежемесячный ответ
50 409,83
Непрерывный ответ
49 707,87 долл. США
16) У вас есть 7000 долларов на покупку автомобиля за 10000 долларов. Сколько времени понадобится 7000 долларов, чтобы вырасти до 10000 долларов, если они будут инвестированы с 9% -ным усложнением в квартал? ( Округлите до следующего самого высокого квартала, если не точно. Всегда округлите UP до следующего периода, если только не будет получено точное значение. Причина этого в том, что деньги начисляются только за каждый период.) Убедитесь, что вы решили это с использованием логарифмов.
Всегда округлите UP до следующего периода, если только не будет получено точное значение. Причина этого в том, что деньги начисляются только за каждый период.) Убедитесь, что вы решили это с использованием логарифмов.
Покажи ответ
16,03 —-> 17 кварталов
18) Найдите APY каждого. Какая инвестиция лучше: 9% ежемесячно или 9,1% ежеквартально?
APY, 9,1% ежеквартально
9,42%
Покажи ответ
9,1% с квартальным увеличением
19) Г-н Кан занял у своего друга 5200 долларов на ремонт своего дома. Через 10 месяцев он погасил ссуду с простой процентной ставкой 7%. Затем его друг вложил вырученные деньги в пятилетний компакт-диск, заплатив 6 долларов.3% начисляются ежеквартально. Сколько будет у его друга через 5 лет?
Сумма, возвращенная г-ном Каном
$ 5503,33
20) В Новом Завете Иисус хвалит вдову, которая пожертвовала 2 лепты (примерно 1/4 цента) в храмовую сокровищницу. Предположим, храм инвестировал этих клещей из расчета 4% ежеквартально. Сколько будут стоить эти деньги 2000 лет спустя? (1/4 цента — 0,0025 доллара)
Сколько будут стоить эти деньги 2000 лет спустя? (1/4 цента — 0,0025 доллара)
Покажи ответ
A = 930000000000000000000000000000000000 долларов США (если я насчитал достаточно нулей.)
21) Предположим, вы инвестируете 250 долларов в течение 4 лет. Если деньги начисляются ежемесячно, какую годовую процентную ставку вы должны получать, чтобы иметь 1000 долларов по истечении 4 лет. Какой рут вам пришлось использовать для решения этой проблемы?
Простые проценты | Финансы и рост
9.2 Простые проценты (EMA6M)
- Простые проценты
Простые проценты — это проценты, начисляемые только на первоначальную сумму, которую вы вложили.
В качестве простого примера простого интереса рассмотрим, сколько мы получим, вложив \ (\ text {R} \, \ text {1 000} \) на \ (\ text {1} \) год в банк. который платит \ (\ text {5} \% \) pa простой интерес.
На конец года у нас
\ begin {align *}
\ text {Интерес} & = \ text {R} \, \ text {1 000} \ times \ text {5} \% \\
& = \ text {R} \, \ text {1 000} \ times \ frac {5} {100} \\
& = \ text {R} \, \ text {1 000} \ times \ text {0,05} \\
& = \ текст {R} \, \ текст {50}
\ end {выровнять *}
При начальном сальдо \ (\ text {R} \, \ text {1 000} \) в начале года, итоговое сальдо в конце года будет, следовательно,
\ begin {align *}
\ text {Конечное сальдо} & = \ text {Начальное сальдо} + \ text {Проценты} \\
& = \ text {R} \, \ text {1 000} + \ text {R} \, \ text {50} \\
& = \ текст {R} \, \ текст {1 050}
\ end {выровнять *}
Начальное сальдо в финансовых расчетах часто называют основной суммой, обозначенной в данном примере как \ (P \) (\ (\ text {R} \, \ text {1 000} \)). Процентная ставка обычно обозначается как \ (i \) (\ (\ text {5} \% \) в этом примере, а «годовой год» означает год или год). Сумма процентов помечена \ (I \) (\ (\ text {R} \, \ text {50} \) в примере).
Процентная ставка обычно обозначается как \ (i \) (\ (\ text {5} \% \) в этом примере, а «годовой год» означает год или год). Сумма процентов помечена \ (I \) (\ (\ text {R} \, \ text {50} \) в примере).
Итак, мы видим, что
\ [I = P \ times i \]
и
\ begin {align *}
\ text {Конечное сальдо} & = \ text {Начальное сальдо} + \ text {Проценты} \\
& = P + I \\
& = P + P \ times i \\ & = P \ left (1 + i \ right)
\ end {выровнять *}
Приведенные выше расчеты дают хорошее представление о том, как выглядит простая формула процента.Однако в примере показана инвестиция, срок действия которой составляет всего один год. Если вложение или ссуда рассчитаны на более длительный период, мы должны это учитывать. Мы используем символ \ (n \) для обозначения периода времени, который должен быть указан в годах.
Общая формула расчета простых процентов:
\ begin {align *}
A & = P \ влево (1 + в \ вправо) \\
\ text {Где:} & \\
A & = \ text {накопленная сумма (окончательная)} \\
P & = \ text {основная сумма (начальная)} \\
i & = \ text {проценты в десятичном формате} \\
n & = \ text {количество лет}
\ end {align *}
Рабочий пример 1: Расчет процентов по депозиту
Карин вкладывает \ (\ text {R} \, \ text {1 000} \) на специальный банковский счет, на который выплачивается простая процентная ставка \ (\ text {7} \% \) p. а. на \ (\ text {3} \) лет. Сколько будет на ее счету в конце срока инвестирования?
а. на \ (\ text {3} \) лет. Сколько будет на ее счету в конце срока инвестирования?
Запишите известные значения
\ begin {align *}
P & = \ text {1 000} \\
я & = \ текст {0,07} \\
n & = 3
\ end {align *}
Запишите формулу
\ [A = P \ left (1 + in \ right) \]
Подставить значения
\ begin {align *}
A & = \ text {1 000} \ left (1 + \ text {0,07} \ times 3 \ right) \\
& = \ текст {1 210}
\ end {align *}
Напишите окончательный ответ
По прошествии \ (\ text {3} \) лет у Карин будет \ (\ text {R} \, \ text {1 210} \) на ее банковском счете.
Рабочий пример 2: Расчет процентов по ссуде
Сара занимает \ (\ text {R} \, \ text {5 000} \) у своего соседа по согласованной простой процентной ставке \ (\ text {12,5} \% \) годовых. Она выплатит ссуду единовременно в конце \ (\ text {2} \) лет. Сколько ей придется заплатить соседу?
Она выплатит ссуду единовременно в конце \ (\ text {2} \) лет. Сколько ей придется заплатить соседу?
Запишите известные переменные
\ begin {align *}
P & = \ text {5 000} \\
я & = \ текст {0,125} \\
п & = 2
\ end {align *}
Запишите формулу
\ [A = P \ left (1 + in \ right) \]
Подставить значения
\ begin {align *}
A & = \ text {5 000} \ left (1 + \ text {0,125} \ times 2 \ right) \\
& = \ текст {6 250}
\ end {align *}
Напишите окончательный ответ
По прошествии \ (\ text {2} \) лет Сара заплатит своему соседу \ (\ text {R} \, \ text {6 250} \).
Мы можем использовать простую формулу процента, чтобы найти недостающую информацию. Например, если у нас есть сумма денег, которую мы хотим инвестировать в течение определенного количества времени для достижения целевой суммы, мы можем изменить порядок переменных, чтобы найти требуемую процентную ставку. Те же принципы применимы к определению продолжительности времени, в течение которого нам потребовалось бы инвестировать деньги, если бы мы знали основную сумму, накопленные суммы и процентную ставку.
Те же принципы применимы к определению продолжительности времени, в течение которого нам потребовалось бы инвестировать деньги, если бы мы знали основную сумму, накопленные суммы и процентную ставку.
Важно: Чтобы получить более точный ответ, попробуйте произвести все свои расчеты на калькуляторе за один раз.Это предотвратит влияние ошибок округления на ваш окончательный ответ.
Рабочий пример 3: Определение инвестиционного периода для достижения целевой суммы
Prashant вкладывает \ (\ text {R} \, \ text {30 000} \) на банковский счет с простой процентной ставкой \ (\ text {7,5} \% \) в год. Сколько лет должно он инвестирует для создания \ (\ text {R} \, \ text {45 000} \)?
Запишите известные переменные
\ begin {align *}
A & = \ text {45 000} \\
P & = \ text {30 000} \\
я & = \ текст {0,075}
\ end {align *}
Запишите формулу
\ [A = P \ left (1 + in \ right) \]
Подставляем значения и решаем \ (n \)
\ begin {align *}
\ text {45 000} & = \ text {30 000} \ left (1 + \ text {0,075} \ times n \ right) \\
\ frac {\ text {45 000}} {\ text {30 000}} & = 1 + \ text {0,075} \ times n \\
\ frac {\ text {45 000}} {\ text {30 000}} — 1 & = \ text {0,075} \ times n \\
\ frac {\ left (\ frac {\ text {45 000}} {\ text {30 000}} \ right) -1} {\ text {0,075}} & = n \\
n & = 6 \ frac {2} {3}
\ end {align *}
Напишите окончательный ответ
Потребуются \ (\ text {6} \) лет и \ (\ text {8} \) месяцы, чтобы \ (\ text {R} \, \ text {45 000} \) из \ (\ text { R} \, \ text {30 000} \) по простой процентной ставке \ (\ text {7,5} \% \) p. а.
а.
Рабочий пример 4: Расчет простой процентной ставки для достижения желаемого роста
По какой простой процентной ставке следует инвестировать Фрите, если она хочет вырасти \ (\ text {R} \, \ text {2 500} \) до \ (\ text {R} \, \ text {4 000} \) в \ (\ text {5} \) лет?
Запишите известные переменные
\ begin {align *}
A & = \ text {4 000} \\
P & = \ text {2 500} \\
n & = 5
\ end {align *}
Запишите формулу
\ [A = P \ left (1 + in \ right) \]
Подставляем значения и решаем \ (i \)
\ begin {align *}
\ text {4 000} & = \ text {2 500} \ left (1 + i \ times 5 \ right) \\
\ frac {\ text {4 000}} {\ text {2 500}} & = 1 + i \ times 5 \\
\ frac {\ text {4 000}} {\ text {2 500}} — 1 & = i \ times 5 \\
\ frac {\ left (\ frac {\ text {4 000}} {\ text {2 500}} \ right) — 1} {5} & = i \\
я & = \ текст {0,12}
\ end {align *}
Напишите окончательный ответ
Простая процентная ставка \ (\ text {12} \% \) p. а. потребуется при инвестировании \ (\ text {R} \, \ text {2 500} \) на \ (\ text {5} \) лет, чтобы стать \ (\ text {R} \, \ text {4 000} \).
а. потребуется при инвестировании \ (\ text {R} \, \ text {2 500} \) на \ (\ text {5} \) лет, чтобы стать \ (\ text {R} \, \ text {4 000} \).
Присоединяйтесь к тысячам учеников, улучшающих свои оценки по математике онлайн с помощью Siyavula Practice.
Зарегистрируйтесь здесь
Упражнение 9.1
Сумма \ (\ text {R} \, \ text {3 500} \) инвестируется на сберегательный счет, на который выплачиваются простые проценты по ставке \ (\ text {7,5} \% \) в год. . Рассчитайте остаток, накопленный к концу \ (\ text {2} \) лет.
\ begin {align *}
P & = \ text {3 500} \\
я & = \ текст {0,075} \\
п & = 2 \\
A & =? \\\\
А & = Р (1 + дюйм) \\
A & = \ text {3 500} (1 + (\ text {0,075}) (2)) \\
A & = \ text {3 500} (\ text {1,15}) \\
A & = \ text {R} \, \ text {4 025}
\ end {выровнять *}
Сумма \ (\ text {R} \, \ text {4 090} \) инвестируется на сберегательный счет, на который выплачиваются простые проценты по ставке \ (\ text {8} \% \) в год. Рассчитайте остаток, накопленный к концу \ (\ text {4} \) лет.
Рассчитайте остаток, накопленный к концу \ (\ text {4} \) лет.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & =? \\
P & = \ text {4 090} \\
п & = 4 \\
i & = \ frac {8} {100} = \ text {0,08}
\ end {align *}
\ begin {align *}
А & = Р (1 + дюйм) \\
& = \ text {R} \, \ text {4 090} \ left (\ text {1} + \ left (\ text {0,08} \ right) \ times \ text {4} \ right) \\
& = \ text {R} \, \ text {5 398,80}
\ end {align *}
Сумма \ (\ text {R} \, \ text {1 250} \) инвестируется на сберегательный счет, на который выплачиваются простые проценты по ставке \ (\ text {6} \% \) в год. Рассчитайте остаток, накопленный к концу \ (\ text {6} \) лет.
Рассчитайте остаток, накопленный к концу \ (\ text {6} \) лет.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & =? \\
P & = \ text {1 250} \\
п & = 6 \\
i & = \ frac {6} {100} = \ text {0,06}
\ end {align *}
Формула простого процента:
\ begin {align *}
А & = Р (1 + дюйм) \\
& = \ text {R} \, \ text {1 250} \ left (\ text {1} + \ left (\ text {0,06} \ right) \ times \ text {6} \ right) \\
& = \ text {R} \, \ text {1 700,00}
\ end {align *}
Сумма \ (\ text {R} \, \ text {5 670} \) инвестируется на сберегательный счет, на который выплачиваются простые проценты по ставке \ (\ text {8} \% \) в год. Рассчитайте остаток, накопленный к концу \ (\ text {3} \) лет.
Рассчитайте остаток, накопленный к концу \ (\ text {3} \) лет.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & =? \\
P & = \ text {5 670} \\
п & = 3 \\
i & = \ frac {8} {100} = \ text {0,08}
\ end {align *}
Формула простого процента:
\ begin {align *}
А & = Р (1 + дюйм) \\
& = \ text {R} \, \ text {5 670,00} \ left (\ text {1} + \ left (\ text {0,08} \ right) \ times \ text {3} \ right) \ \
& = \ text {R} \, \ text {7 030,80}
\ end {align *}
Кредит в размере \ (\ text {R} \, \ text {300} \) со ставкой \ (\ text {8} \% \) на \ (\ text {1} \) год.
\ begin {align *}
P & = 300 \\
я & = \ текст {0,08} \\
п & = 1 \\
A & =? \\ \\
А & = Р (1 + дюйм) \\
A & = 300 (1+ (\ text {0,08}) (1)) \\
A & = 300 (\ text {1,08}) \\
A & = \ текст {R} \, \ text {324}
\ end {выровнять *}
Инвестиция в размере \ (\ text {R} \, \ text {2 250} \) по ставке \ (\ text {12,5} \% \) p.а. на \ (\ text {6} \) лет.
\ begin {align *}
P & = \ text {2 250} \\
я & = \ текст {0,125} \\
п & = 6 \\
A & =? \\ \\
А & = Р (1 + дюйм) \\
A & = \ text {2 250} (1+ (\ text {0,125}) (6)) \\
A & = \ text {2 250} (\ text {1,75}) \\
A & = \ text {R} \, \ text {3 937,50}
\ end {выровнять *}
Банк предлагает сберегательный счет, на который выплачиваются простые проценты по ставке \ (\ text {6} \% \) в год. Если вы хотите накопить \ (\ text {R} \, \ text {15 000} \) за \ (\ text {5} \) лет, сколько вам следует инвестировать сейчас?
Если вы хотите накопить \ (\ text {R} \, \ text {15 000} \) за \ (\ text {5} \) лет, сколько вам следует инвестировать сейчас?
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {15 000} \\
P & =? \\
i & = \ frac {6} {100} = \ text {0,06} \\
n & = 5
\ end {align *}
Формула простого процента:
\ begin {align *}
А & = Р (1 + дюйм) \\
\ text {R} \, \ text {15 000} & = P \ left (\ text {1} + \ left (\ text {0,06} \ right) \ times \ text {5} \ right) \\
P & = \ frac {\ text {R} \, \ text {15 000}} {\ text {1,3}} \\
& = \ text {R} \, \ text {11 538,46}
\ end {align *}
Салли хотела подсчитать, сколько лет ей нужно инвестировать в \ (\ text {R} \, \ text {1 000} \), чтобы накопить \ (\ text {R} \, \ text {2 500} \). Ей предложили простую процентную ставку в размере \ (\ text {8,2} \% \) годовых. Через сколько лет деньги вырастут до \ (\ text {R} \, \ text {2 500} \)?
Ей предложили простую процентную ставку в размере \ (\ text {8,2} \% \) годовых. Через сколько лет деньги вырастут до \ (\ text {R} \, \ text {2 500} \)?
\ begin {align *}
A & = \ text {2 500} \\
P & = \ text {1 000} \\
я & = \ текст {0,082} \\
п & =? \\ \\
А & = Р (1 + дюйм) \\
\ text {2 500} & = \ text {1 000} (1+ (\ text {0,082}) (n)) \\
\ frac {\ text {2 500}} {\ text {1 000}} & = 1 + \ text {0,082} n \\
\ frac {\ text {2 500}} {\ text {1 000}} — 1 & = \ text {0,082} n \\
\ left (\ frac {\ text {2 500}} {\ text {1 000}} — 1 \ right) \ div \ text {0,082} & = n \\
п & = \ текст {18,3}
\ end {выровнять *}
Потребуется \ (\ text {19} \) лет, чтобы \ (\ text {R} \, \ text {1 000} \) превратился в \ (\ text {R} \, \ text {2 500} \ ) в \ (\ text {8,2} \% \) p. а.
а.
Джозеф положил \ (\ text {R} \, \ text {5 000} \) на сберегательный счет на пятый день рождения сына. Когда его сыну исполнилось \ (\ text {21} \), остаток на счете вырос до \ (\ text {R} \, \ text {18 000} \). Если использовались простые проценты, рассчитайте ставку, по которой были инвестированы деньги.
\ begin {align *}
A & = \ text {18 000} \\
P & = \ text {5 000} \\
я & =? \\
п & = 21-5 = 16 \\ \\
А & = Р (1 + дюйм) \\
\ text {18 000} = \ text {5 000} (1+ (i) (16)) \\
\ frac {\ text {18 000}} {\ text {5 000}} & = 1 + 16i \\
\ frac {\ text {18 000}} {\ text {5 000}} — 1 & = 16i \\
\ left (\ frac {\ text {18 000}} {\ text {5 000}} — 1 \ right) \ div 16 & = i \\
я & = \ текст {0,1625}
\ end {выровнять *}
Процентная ставка, по которой были инвестированы деньги, составляла \ (\ text {16,25} \% \).
Когда его сын был \ (\ text {6} \)
лет, Метули внес депозит в размере
\ (\ text {R} \, \ text {6 610} \)
в банке. Инвестиции выросли по простой процентной ставке и
когда сын Метули был
\ (\ text {18} \) лет, значение
инвестиции было
\ (\ text {R} \, \ text {11 131,24} \).
По какой ставке были вложены деньги? Дайте правильный ответ с точностью до одного десятичного знака.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {11 131,24} \\
P & = \ text {R} \, \ text {6 610} \\
я & =? \\
n & = 18 — 6 = 12
\ end {align *}
В вопросе говорится, что инвестиции «росли по простой процентной ставке», поэтому мы должны использовать простую формулу процента. Чтобы рассчитать процентную ставку, нам нужно сделать \ (i \)
Чтобы рассчитать процентную ставку, нам нужно сделать \ (i \)
предмет формулы:
\ begin {align *}
А & = Р (1 + дюйм) \\
\ frac {A} {P} & = 1 + в \\
\ frac {A} {P} -1 & = в \\
\ frac {\ frac {A} {P} -1} {n} & = i \\
\ text {Следовательно} i & = \ frac {\ left (\ frac {\ text {} \, \ text {11 131,24}} {\ text {6 610}} \ right) — 1} {\ text { 12}} \\
& = \ текст {0,057} \\
& = \ text {5,7} \% \ text {в год}
\ end {align *}
Когда его сын был \ (\ text {6} \)
лет, Филипп внес депозит в размере
\ (\ text {R} \, \ text {5 040} \)
в банке.Инвестиции выросли по простой процентной ставке и
когда сын Филиппа был
\ (\ text {18} \) лет, значение
инвестиции было
\ (\ text {R} \, \ text {7 338,24} \).
По какой ставке были вложены деньги? Ответьте правильно с точностью до одного десятичного знака.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {7 338,24} \\
P & = \ text {R} \, \ text {5 040} \\
я & =? \\
n & = 18 — 6 = 12
\ end {align *}
В вопросе говорится, что инвестиции «росли по простой процентной ставке», поэтому мы должны использовать простую формулу процента.Чтобы рассчитать процентную ставку, нам нужно сделать \ (i \)
предмет формулы:
\ begin {align *}
А & = Р (1 + дюйм) \\
\ frac {A} {P} & = 1 + в \\
\ frac {A} {P} -1 & = в \\
\ frac {\ frac {A} {P} -1} {n} & = i \\
\ text {Следовательно} i & = \ frac {\ left (\ frac {\ text {} \, \ text {7 338,24}} {\ text {5 040}} \ right) — 1} {\ text { 12}} \\
& = \ текст {0,038} \\
& = \ text {3,8} \% \ text {в год}
\ end {align *}
Когда его сын был \ (\ text {10} \)
лет, Лефу внес депозит в размере
\ (\ text {R} \, \ text {2 580} \)
в банке.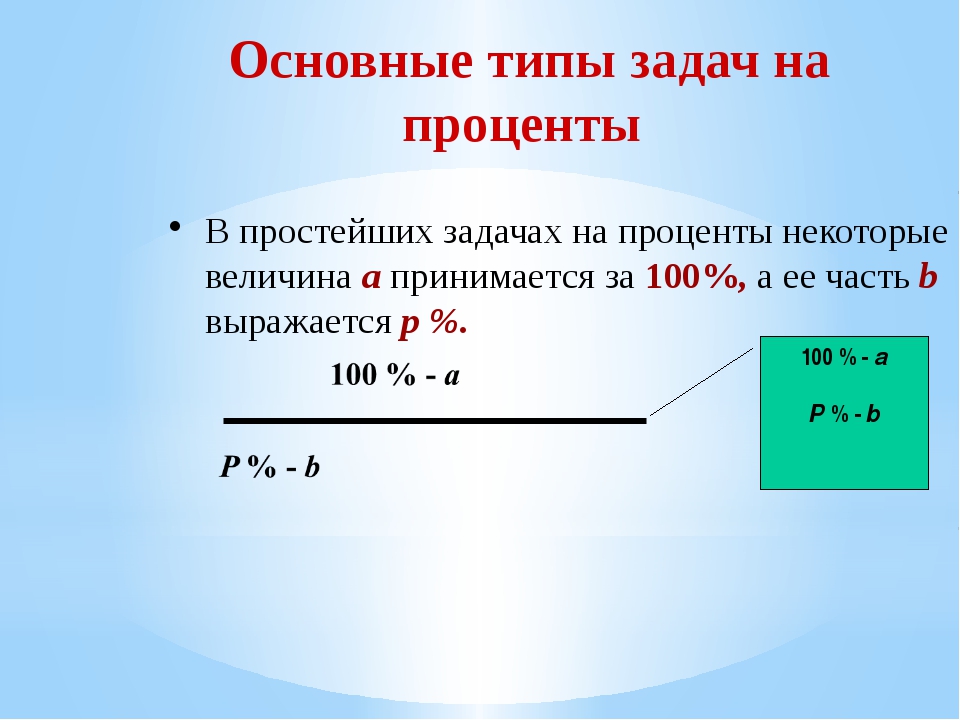 Инвестиции выросли по простой процентной ставке и
Инвестиции выросли по простой процентной ставке и
когда сын Лефу был
\ (\ text {20} \) лет, значение
инвестиции было
\ (\ text {R} \, \ text {3 689,40} \).
По какой ставке были вложены деньги? Ответьте правильно с точностью до одного десятичного знака.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {3 689,40} \\
P & = \ text {R} \, \ text {2 580} \\
я & =? \\
n & = 20 — 10 = 10
\ end {align *}
В вопросе говорится, что инвестиции «росли по простой процентной ставке», поэтому мы должны использовать простую формулу процента.Чтобы рассчитать процентную ставку, нам нужно сделать \ (i \)
предмет формулы:
\ begin {align *}
А & = Р (1 + дюйм) \\
\ frac {A} {P} & = 1 + в \\
\ frac {A} {P} -1 & = в \\
\ frac {\ frac {A} {P} -1} {n} & = i \\
\ text {Следовательно} i & = \ frac {\ left (\ frac {\ text {} \, \ text {3 689,40}} {\ text {2 580}} \ right) — 1} {\ text { 10}} \\
& = \ текст {0,043} \\
& = \ text {4,3} \% \ text {в год}
\ end {align *}
Абдул хочет инвестировать \ (\ text {R} \, \ text {1 080} \) по простой процентной ставке \ (\ text {10,9} \% \) p. а.
а.
Через сколько лет деньги вырастут до \ (\ text {R} \, \ text {3 348} \)? Округлите до , чтобы получить ответ до ближайшего года.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {3 348} \\
P & = \ text {R} \, \ text {1 080} \\
i & = \ frac {\ text {10,9}} {100} = \ text {0,109} \\
п & =?
\ end {align *}
Чтобы вычислить количество лет, нам нужно сделать \ (n \) предметом формулы:
\ begin {align *}
А & = Р (1 + дюйм) \\
\ frac {A} {P} & = 1 + в \\
\ frac {A} {P} -1 & = в \\
\ frac {\ frac {A} {P} -1} {i} & = n \\
\ text {Следовательно} n & = \ frac {\ left (\ frac {\ text {3 348}} {\ text {1 080}} \ right) — \ text {1}} {\ text {0,109}} \ \
& = \ текст {19,3} \\
& = \ text {20} \ text {years} \ quad \ Leftarrow \ text {округлить до ближайшего целого числа}
\ end {align *}
Эндрю хочет инвестировать \ (\ text {R} \, \ text {3 010} \) по простой процентной ставке \ (\ text {11,9} \% \) p.а.
Через сколько лет деньги вырастут до \ (\ text {R} \, \ text {14 448} \)? Округлите до , чтобы получить ответ до ближайшего года.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {14 448} \\
P & = \ text {R} \, \ text {3 010} \\
i & = \ frac {\ text {11,9}} {100} = \ text {0,119} \\
п & =?
\ end {align *}
Чтобы вычислить количество лет, нам нужно сделать \ (n \) предметом формулы:
\ begin {align *}
А & = Р (1 + дюйм) \\
\ frac {A} {P} & = 1 + в \\
\ frac {A} {P} -1 & = в \\
\ frac {\ frac {A} {P} -1} {i} & = n \\
\ text {Следовательно} n & = \ frac {\ left (\ frac {\ text {14 448}} {\ text {3 010}} \ right) — \ text {1}} {\ text {0,119}} \ \
& = \ текст {31,9} \\
& = \ text {32} \ text {years} \ quad \ Leftarrow \ text {округлить до ближайшего целого числа}
\ end {выровнять *}
Округляя до ближайшего года, потребуется \ (\ text {32} \) лет, чтобы достичь цели по экономии \ (\ text {R} \, \ text {14 448} \).






 Вот как с этим справиться:
Вот как с этим справиться: 06
06 Допустим, я поставил « x »
Допустим, я поставил « x »
 Организуя столбцы в соответствии с
Организуя столбцы в соответствии с 06 х
06 х  06 x + 0,14 (50000 — x ) = 4500
06 x + 0,14 (50000 — x ) = 4500  «Проблемы со словом« инвестиции »». Пурпурная математика . Доступна с
«Проблемы со словом« инвестиции »». Пурпурная математика . Доступна с