Содержание
Как найти Время, Скорость и Расстояние
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой S.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути Чтобы найти расстояние, нужно умножить скорость на время движения: S = V * T |
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени.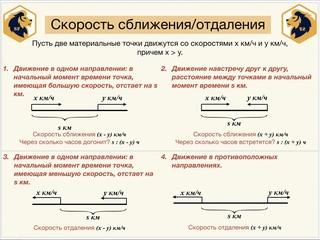 Скорость обозначается латинской буквой v.
Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости Чтобы найти скорость, нужно разделить путь на время: V = S/T |
Показатели скорости чаще всего выражаются в м/сек; км/час.
Скорость сближения — это расстояние, которое прошли два объекта навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, которые движутся в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.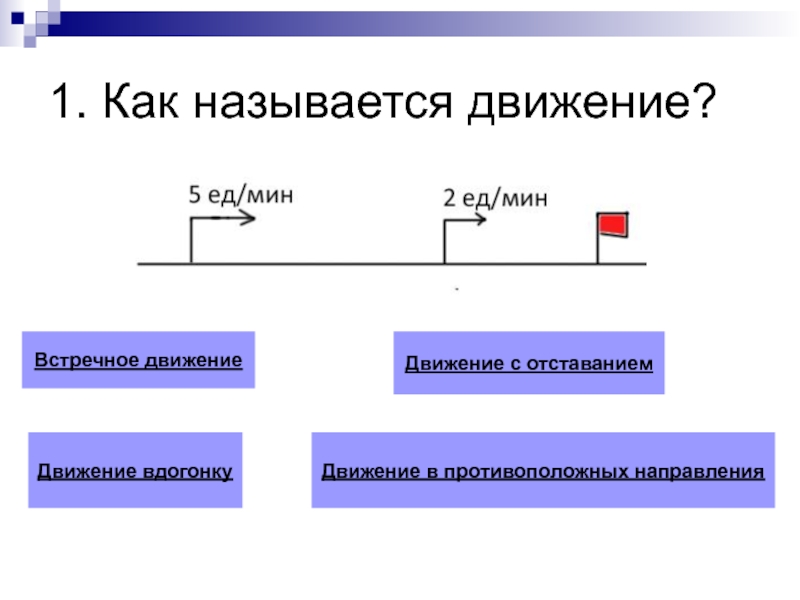
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Единицами времени могут быть секунды, минуты, часы.
Формула времени Чтобы найти время, нужно разделить расстояние на скорость: T = S/V |
Эта формула пригодится, если нужно узнать за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.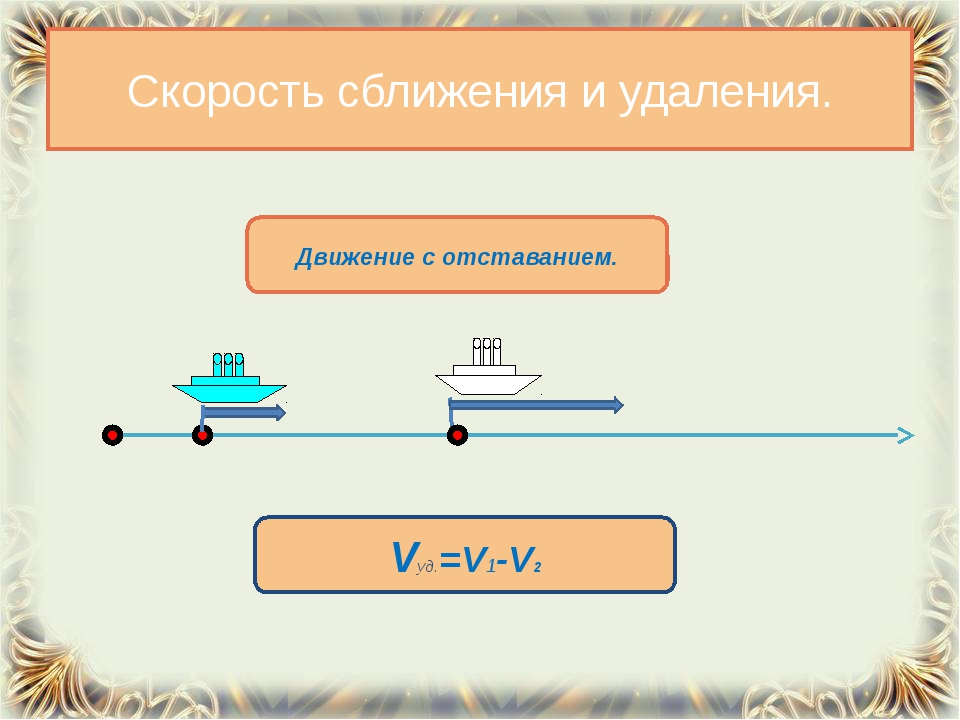
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Как рассуждаем:
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:
v = 50 (м/мин)
t = 15 минут
s = v × t = 50 × 15 = 750
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до магазина с мороженым 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Как рассуждаем:
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше.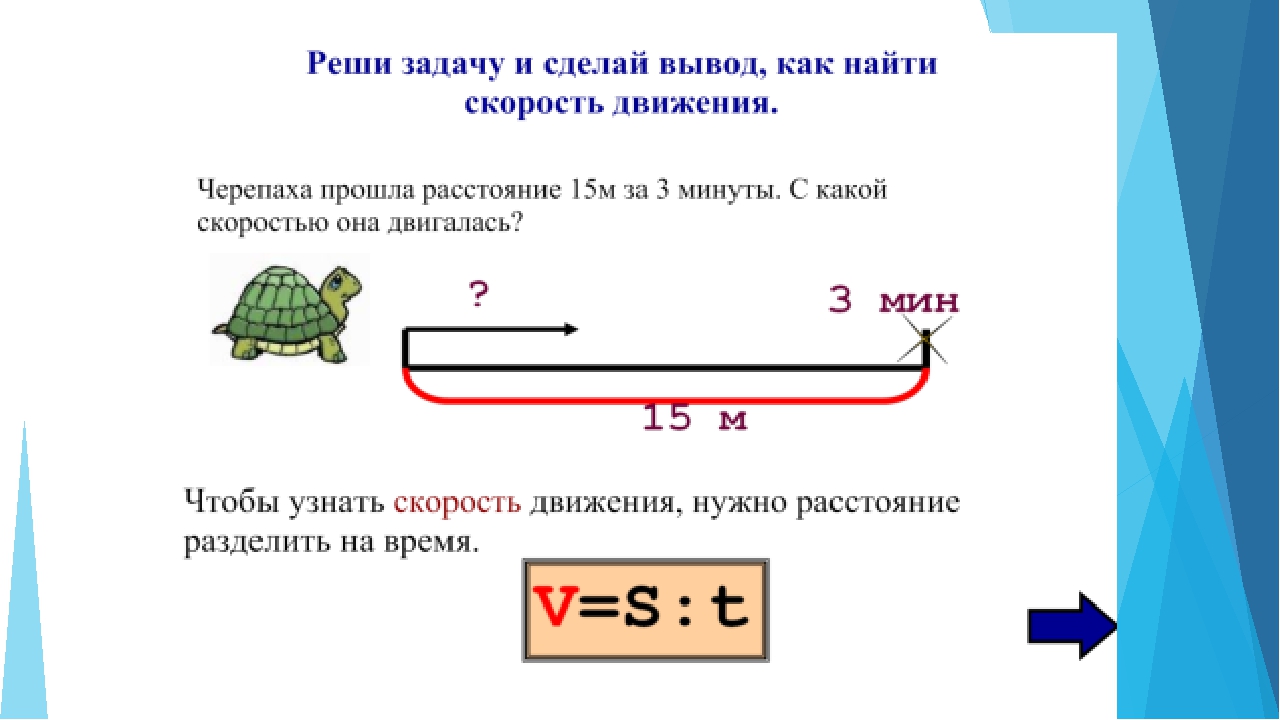 В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.
В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 : 25 = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 : 50 = 2
Значит скорость движения второго школьника составляет 2 метра в секунду.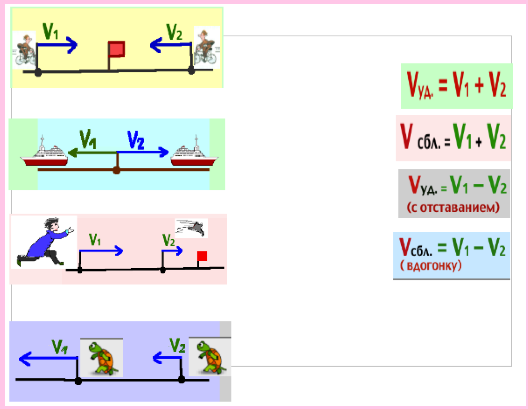
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до магазина с мороженым быстрее.
Ответ: первый школьник добежал быстрее.
Если известна скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Как рассуждаем:
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до стадиона:
s = 500 метров
v = 100 (м/мин)
t = s : v = 500 : 100 = 5
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Еще больше практики — в детской онлайн-школе Skysmart. Ученики решают примеры на интерактивной платформе: в игровом формате и с мгновенной автоматической проверкой. А еще отслеживают прогресс в личном кабинете и вдохновляются на новые свершения.
Запишите ребенка на бесплатный вводный урок математики: покажем, как все устроено и наметим индивидуальную программу, чтобы ребенок лучше учился в школе и не боялся контрольных.
Задачи на скорость сближения и удаления
МКОУ «Основная общеобразовательная школа №12» г. Людиново
Урок математики
6 класс
«Задачи на движение»
Автор: учитель математики Дмитрикова Ольга Викторовна
Тема: «Задачи на движение»
Тип урока: урок-практикум.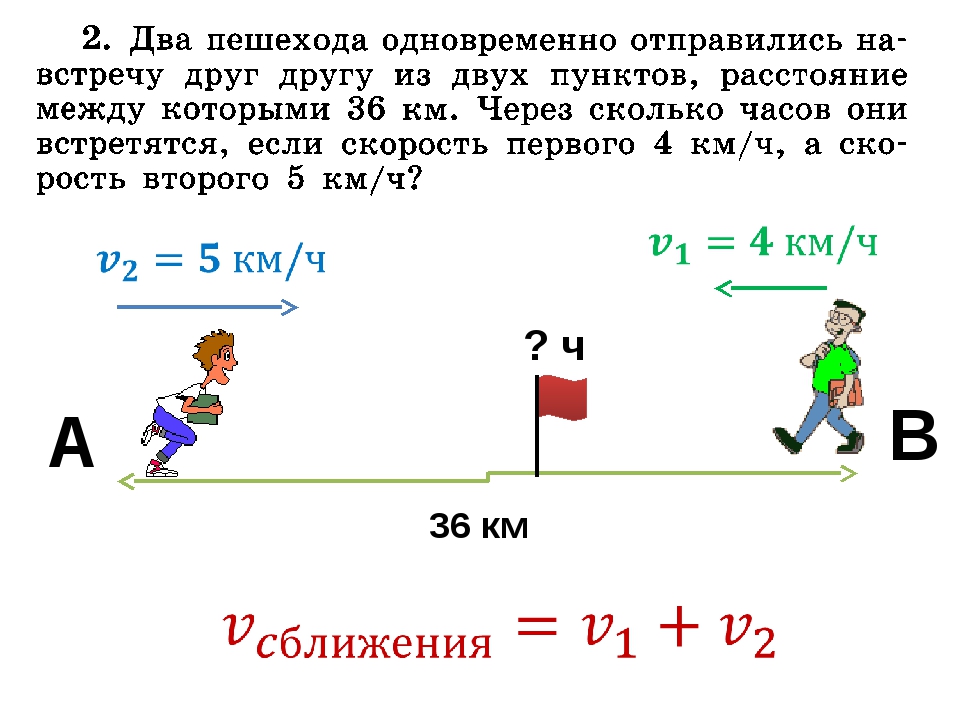
Цель: систематизировать знания учащихся по решению задач на движение.
Задачи:
повторить формулы на движение и закрепить умения их применять при решении задач;
развивать навыки внимания, мышления, самоконтроля, культуры работы в группе;
развивать познавательный интерес;
воспитывать умение организовывать свой труд;
воспитывать аккуратность, умение правильно излагать свои мысли.
Применяемые компетенции: учебно–познавательная, социально-трудовая, коммуникативная, компетенция личного самосовершенствования.
Оборудование: мультимедийный проектор, карточки с задачами
Формы общения: индивидуальная, работа в парах.
Ход урока
Организационный момент.

Учитель приветствует обучающихся, проверяет готовность к уроку. Учитель обращается к учащихся эпиграфом.: «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!» (Д. Пойа)
Целеполагание
Учитель задает обучающимся вопросы как они понимают эпиграф, как он связан с данным уроком.
(Учащиеся делают предположение, что на уроки будут решаться задачи на движение ).
Актуализация опорных знаний и умений
Учитель предлагает учащимся вспомнить как связаны между собой такие величины как Путь, Скорость, Время движения (слайд 2)
Учитель: Скажите пожалуйста какие виды задач на движение мы изучили? (слайд 3)
Работа по готовым чертежам Учащиеся отвечают на вопросы к чертежам
Для каждого случая вычисляют скорость сближения или удаления
(слайд 4-5)
Мотивация учебной деятельности
Учитель объясняет учащимся ещё раз о необходимости умения решать задачи на движения, с которыми мы сталкиваемся ежедневно: идя в школу, поехав в гости, и т. д.
д.
.
Решение задач
Учитель предлагает учащимся самим придумать условие к задаче по заданному чертежу и решать ее. (слайд 6-8)
У доски рассматривают решение задач.
Работа в парах
Учащимся раздаются карточки с задачами. Работают в парах. Затем презентуют решение своих задач у доски.
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч.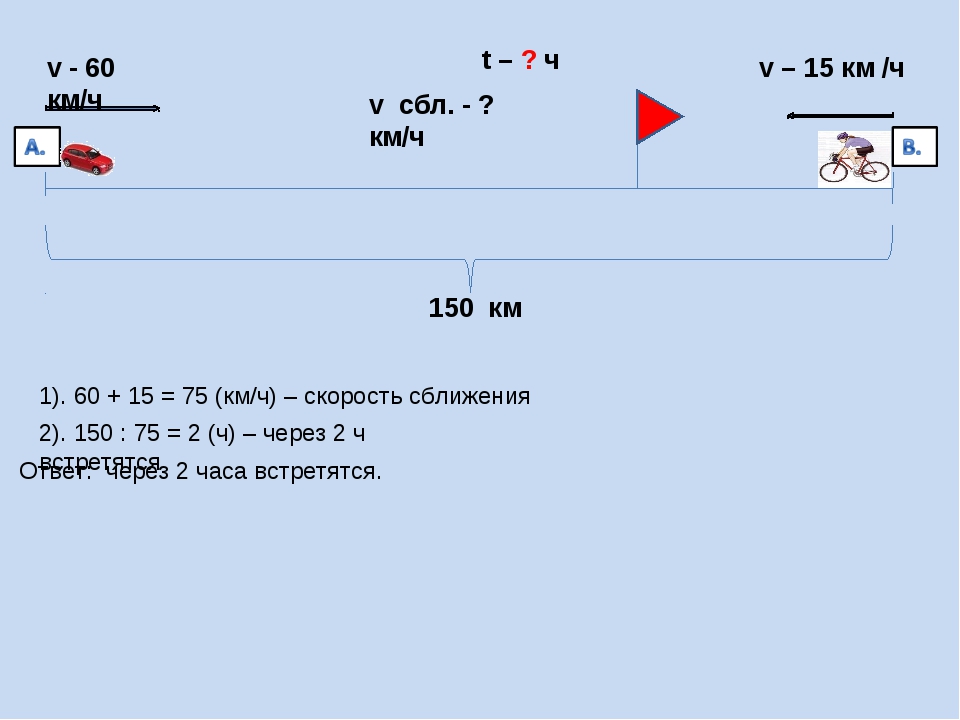 Через сколько часов они встретились?
Через сколько часов они встретились?
Задача 3. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?
Задача 4. Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 2 часа?
5. Подведение итогов
6. Домашнее задание
Сделать коллаж по теме: «Задачи на движение»
7. Рефлексия
Движение навстречу друг другу | Математика
Задачи на движение навстречу друг другу (встречное движение) — один из трех основных видов задач на движение.
Если два объекта движутся навстречу друг другу, то они сближаются:
Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:
Скорость сближения больше, чем скорость каждого из них.
Скорость, время и расстояние связаны между собой формулой пути:
Рассмотрим некоторые задачи на встречное движение.
Задача 1
Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?
Решение:
Условие задач на движение удобно оформлять в виде таблицы:
v, км/ч | t, ч | s, км | |
I велосипедист | 12 | 3 | ? |
II велосипедист | 10 | 3 | ? |
1) 12+10=22 (км/ч) скорость сближения велосипедистов
2) 22∙3=66 (км) было между велосипедистами в начале пути.
Ответ: 66 км.
Задача 2
Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого — 60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?
Решение:
v, км/ч | t, ч | s, км | |
I поезд | 60 | ? | ? |
II поезд | 50 | ? | ? |
1) 60+50=110 (км/ч) скорость сближения поездов
2) 440:110=4 (ч) время, через которое поезда встретятся.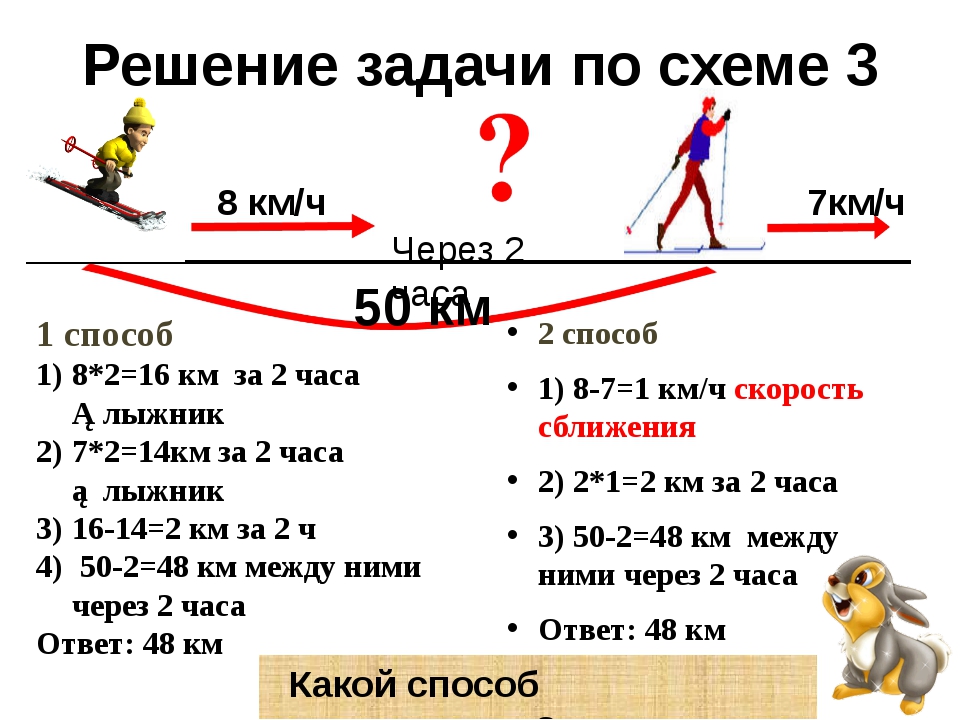
Ответ: через 4 ч.
Задача 3.
Два пешехода находились на расстоянии 20 км друг от друга. Они вышли одновременно навстречу друг другу и встретились через 2 часа. Скорость одного пешехода 6 км/ч. Найти скорость другого пешехода.
v, км/ч | t, ч | s, км | |
I пешеход | 6 | 2 | ? |
II пешеход | ? | 2 | ? |
1) 20:2=10 (км/ч) скорость сближения пешеходов
2) 10-6=4 (км/ч) скорость другого пешехода.
Ответ: 4 км/ч.
Как решать задачи на движение для 4-5 класса
В задачах на движение действие может происходить в разных средах — в воде, на дорогах, в воздухе. Формулы при этом будут использоваться одни и те же.
Традиционные обозначения: s – путь, t – время, v — скорость
1. Путь = скорость∙время. s = v∙t
2. Скорость = путь:время. v = s:t
3. Время в пути = путь:скорость. t =s:v
1. Задачи на сближение при движении по встречным направлениям
При движении по встречным направлениям скорость сближения равна сумме скоростей сближающихся объектов.
Пример
Расстояние между пунктами А и Б равно 400 км. Из пункта А в пункт Б выехал автомобиль
со скоростью 60 км/ч, а из пункта Б в пункт А ему навстречу одновременно с ним другой автомобиль со скоростью 40 км/ч. Через какое время эти автомобили встретятся на дороге?
Как мы видим из схемы, каждый час расстояние между автомобилями
сокращается на 100 км, т. е. скорость сближения действительно
е. скорость сближения действительно
равна сумме скоростей двух сближающихся объектов.
Время сближения = Первоначальное расстояние между объектами : скорость сближения
Скорость сближения = 60 + 40 = 100 км/ч
Время до встречи автомобилей = 400:100 = 4 ч.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
2. Задачи на сближение (догон) при движении в одном направлении
Также эти задачи называются задачами на движение в догонку.
Если более быстрый объект вышел вслед более медленному через какое-то время, то мы говорим о скорости сближения (догона).
Скорость сближения двух объектов, движущихся в одном направлении равна разнице скоростей объектов.
Пример
Из пункта А в пункт Б выехал автобус со скоростью 50 км/ч. Через 2 часа в том же направлении из пункта А выехал автомобиль со скоростью 100 км/ч. Через какое время автомобиль догонит автобус?
3.
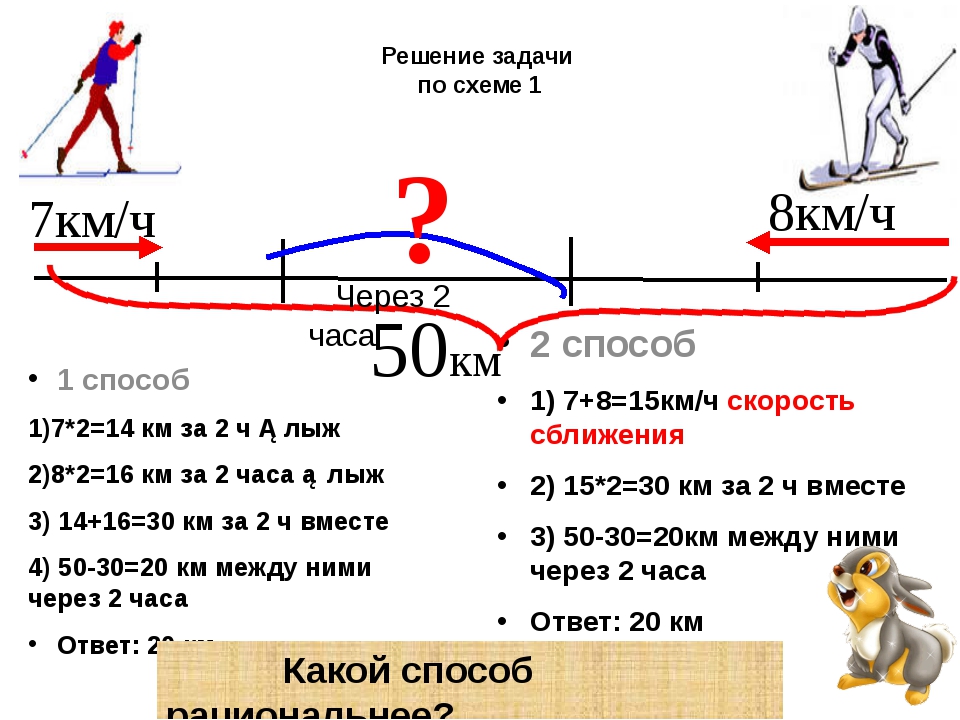 Задачи на удаление. Движение в противоположном направлении
Задачи на удаление. Движение в противоположном направлении
Скорость удаления равна сумме скоростей удаляющихся объектов.
Пример
Расстояние между пунктами А и Б равно 100 км. Посередине между этими пунктами,
на отметке 50 км, велосипедисты начинают ехать в противоположные стороны.
Первый велосипедист движется в сторону пункта А со скоростью 15 км/ч,
а второй велосипедист движется в сторону пункта Б со скоростью 20 км/ч.
На каком расстоянии они будут друг от друга через 2 часа?
Расстояние = Скорость удаления ∙ время
Скорость удаления = 20+15 = 35 км/ч
Расстояние между велосипедистами через 2 часа = 35∙2 = 70 км.
4. Задачи на удаление. Движение в одинаковом направлении
Если два движущихся объекта вышли одновременно из одного пункта и один движется быстрее другого, то мы говорим о скорости удаления.
Скорость удаления равна разнице скоростей удаляющихся объектов.
Пример
Из пункта А в пункт Б одновременно выехали автомобиль со скоростью 100 км/ч
и автобус со скоростью 50 км/ч. На каком расстоянии будет автомобиль от автобуса через 2 часа?
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Расстояние = Скорость удаления ∙ время
Скорость удаления = 100 — 50 = 50 км/ч
Расстояние между автомобилем и автобусом через 2 часа = 50∙2 = 100 км.
5. Задачка на сообразительность
Автобус проехал расстояние 240 км между двумя пунктами за 4 часа. За какое время проедет это расстояние мотоцикл, скорость которого в 2 раза больше?
КАК РЕШАТЬ НЕ НУЖНО
Va = 240:4 = 60 км/ч – скорость автобуса
Vм = 60∙2 = 120 км/ч – скорость мотоцикла
t = 240:120 = 2 ч – время, за которое мотоцикл пройдёт расстояние в 240 км
КАК НУЖНО РЕШАТЬ:
Раз скорость в 2 раза больше, то время, затраченное на преодоление того же пути — в два раза меньше.
t = 4:2 = 2 часа
Вместо трёх действий мы сделали одно действие.
Дата публикации
Супер Логопед | Как научить ребенка не путать скорость сближения и скорость удаления в задачах на движение
Статья:
В 4 классе дети начинают решать задачи на скорость сближения и скорость удаления. Ребята начинают путаться. Часто они не могут определить вид задачи или просто не знают формулы. Однако понять эту тему легко. В этой статье Я расскажу, как учу своих учеников не путаться в задачах данного вида.
Ситуация 1
Представь, что вы с мамой вышли из дома и пошли в разные стороны. Вы будете приближаться друг к другу или удаляться друг от друга? Удаляться. Расстояние между вами будет увеличиваться или уменьшаться? Увеличиваться. Для того, чтобы найти скорость удаления в данной ситуации, нужно две скорости сложить.
Для того, чтобы найти скорость удаления в данной ситуации, нужно две скорости сложить.
Задача
Из города одновременно в разных направлениях выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Какое расстояние будет между автомобилями через 4 часа?
1) 90 + 70 = 160 (км/ч) — скорость удаления.
2) 160 × 4 = 640 (км)
Ответ: 640 км будет расстояние между автомобилями через 4 часа.
Ситуация 2
Представь, что вы с мамой идете навстречу друг другу.
В каждой из обсуждаемых ситуаций я задаю одни и те же вопросы, как в первой ситуации. Поэтому дальше я буду писать только результат наших рассуждений.
Когда мы идем навстречу друг другу, мы приближаемся друг к другу. Поэтому ищем скорость сближения. Расстояние между нами будет становиться меньше. Для того, чтобы найти скорость сближения в данной ситуации, нужно скорости сложить.
Задача
Расстояние между двумя городами 640 км. Из каждой из них одновременно навстречу друг другу выехали два автомобиля. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Через сколько часов автомобили встретятся?
1) 90 + 70 = 160 (км/ч) — скорость сближения
2) 640 : 160 = 4 (ч)
Ответ: автомобили встретятся через 4 часа.
Ситуация 3
Представь, что ты идешь по улице и видишь, что впереди идет мама. Ты решаешь ее догнать. Твоя скорость больше, чем скорость мамы. Ты догонишь маму? Да. Вы будете приближаться к друг другу или удаляться?Расстояние между вами будет увеличиваться или уменьшаться? Уменьшаться. (приближаться, т. к. ребенок сокращает расстояние). В этой ситуации мы находим скорость сближения.
Задача
Из города в посёлок выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч.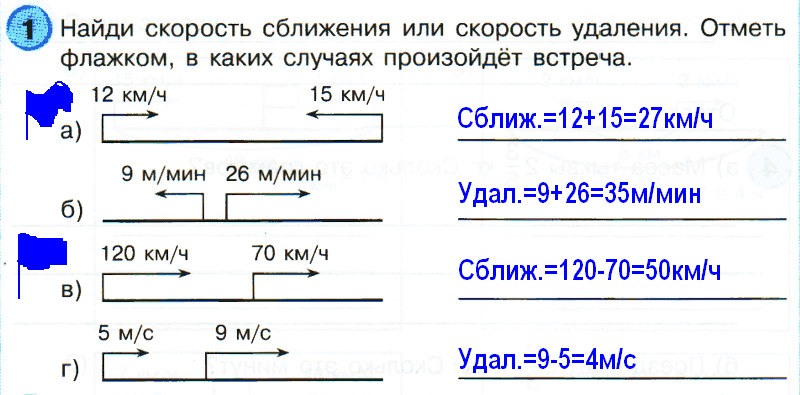 Через сколько часов второй автомобиль догонит первый, если расстояние между ними равно 120 км?
Через сколько часов второй автомобиль догонит первый, если расстояние между ними равно 120 км?
1) 90 — 70 = 20 (км/ч) — скорость сближения
2) 120 : 20 = 6 ( ч)
Ответ: второй автомобиль догонит первый через 6 часов.
Ситуация 4
Представь ту же ситуацию, но теперь скорость больше у мамы. Ты догонишь маму? Нет. Почему? Она будет постоянно удаляться. Находим скорость удаления. Для этого из большей скорости вычитаем меньшую.
Задача
Одновременно из города выехали два автомобиля и поехали в одном направлении. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
1) 90 — 70 = 20 (км/ч) — скорость удаления
2) 20 × 4 = 80 (км)
Ответ: 80 км будет расстояние между автомобилями через 4 часа.
Вся информация взята из открытых источников.
Если вы считаете, что ваши авторские права нарушены, пожалуйста,
напишите в чате на этом сайте, приложив скан документа подтверждающего ваше право.
Мы убедимся в этом и сразу снимем публикацию.
Задачи на движение | Мел
Если пешеход прошёл путь S км за время t ч, то за каждый час он проходил S: t км. Величину v, показывающую, какое расстояние проходит пешеход за 1 час, называют скоростью пешехода:
v = S: t. (1)
Из равенства (1) найдём путь S = v * t и время движения t = S: v.
Остановимся подробнее на задачах с двумя участниками, движущимися в противоположных направлениях или в одном направлении. Их скорости считаем постоянными.
Задача 1. Два пешехода одновременно вышли из села в противоположных направлениях. Их скорости 4 км/ч и 5 км/ч. Какое расстояние будет между ними через 3 часа?
Решение.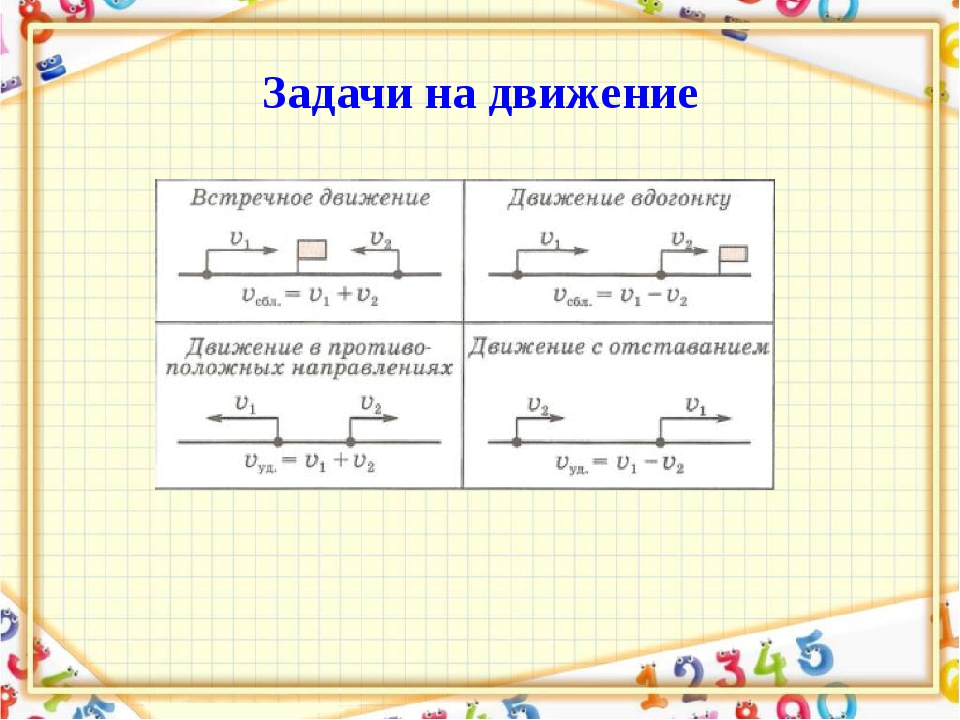 1-й способ.
1-й способ.
1) 4 * 3 = 12 (км) — путь первого пешехода,
2) 5 * 3 = 15 (км) — путь второго пешехода,
3) 12 + 15 = 27 (км) — расстояние между пешеходами через 3 часа.
Составим числовое выражение для решения задачи и вынесем общий множитель за скобки:
4 * 3 + 5 * 3 = (4 + 5) * 3.
Выражение в скобках 4 + 5 показывает, на сколько километров в каждый час удаляются пешеходы.
2-й способ.
1) 4 + 5 = 9 (км/ч) — скорость удаления двух пешеходов,
2) 9 * 3 = 27 (км) — расстояние между пешеходами через 3 часа.
Ответ. 27 км.
Задача 2. Два пешехода одновременно вышли навстречу друг другу из двух сёл, расстояние между которыми 27 км. Их скорости 4 км/ч и 5 км/ч. Через сколько часов они встретились? Через сколько часов расстояние между ними составляло 9 км?
Решение.
1) 4 + 5 = 9 (км/ч) — скорость сближения двух пешеходов,
2) 27: 9 = 3 (ч) — время движения до встречи.
Расстояние между пешеходами составляло 9 км за 1 час до встречи или через 1 ч после встречи, то есть через 3 — 1 = 2 (ч) или через 3 + 1 = 4 (ч) после начала движения.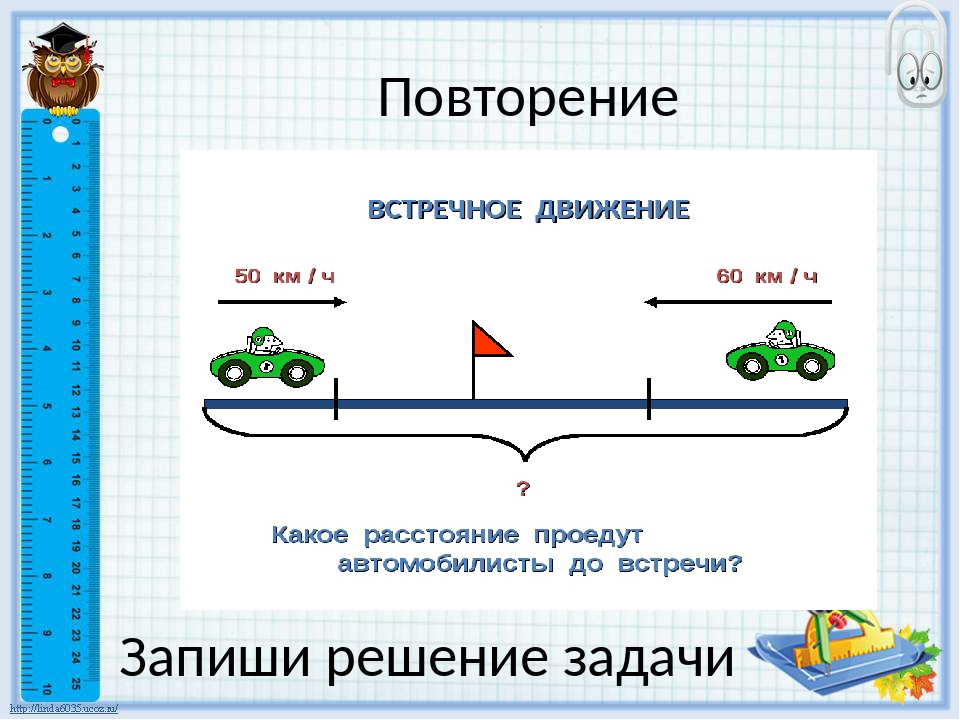
Ответ. Через 3 ч; через 2 ч или через 4 ч.
Заметим, что до встречи пешеходы сближались, а после встречи — удалялись с той же скоростью. В обоих случаях движение происходило в противоположных направлениях, скорости сближения и удаления находили сложением. Теперь рассмотрим движение в одном направлении.
Задача 3. Пешеход и велосипедист одновременно отправились из села в одном направлении. Скорость пешехода 5 км/ч, скорость велосипедиста 12 км/ч. Какое расстояние будет между ними через 3 часа?
Решение. 1-й способ.
1) 12 * 3 = 36 (км) — путь велосипедиста,
2) 5 * 3 = 15 (км) — путь пешехода,
3) 36 — 15 = 21 (км) — расстояние между ними через 3 ч.
Составим числовое выражение для решения задачи и вынесем общий множитель за скобки:
12 * 3 — 5 * 3 = (12 — 5) * 3.
Выражение в скобках 12 — 5 показывает, на сколько километров в каждый час удаляются пешеход и велосипедист друг от друга.
2-й способ.
1) 12 — 5 = 7 (км/ч) — скорость удаления пешехода и велосипедиста,
2) 7 * 3 = 21 (км) — расстояние между ними через 3 ч.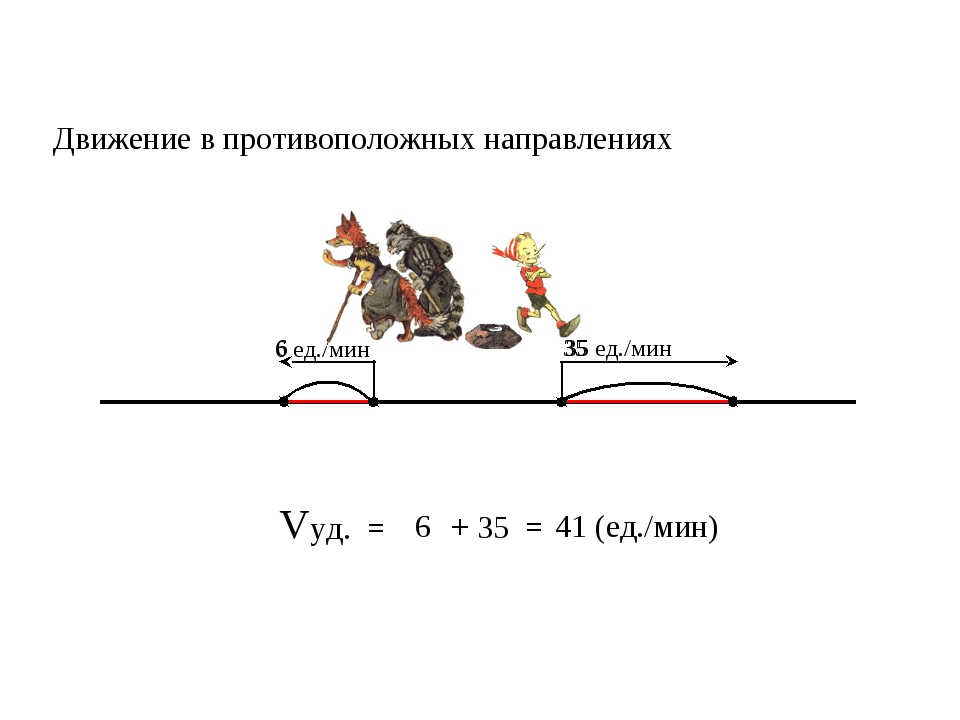
Ответ. 21 км.
Задача 4. Из разных городов, расстояние между которыми равно 54 км, одновременно в одном направлении выехали велосипедист со скоростью 12 км/ч и мотоциклист со скоростью 30 км/ч. Через сколько часов мотоциклист догонит велосипедиста? Через сколько часов расстояние между ними составляло 18 км?
Решение. 1) 30 — 12 = 18 (км/ч) — скорость сближения пешехода и велосипедиста,
2) 54: 18 = 3 (ч) — время, за которое мотоциклист догонит велосипедиста.
Расстояние между пешеходами составляло 18 км за 1 час до встречи или через 1 ч после встречи, то есть через 3 — 1 = 2 часа или через 3 + 1 = 4 часа после начала движения.
Ответ. Через 3 ч; через 2 ч или через 4 ч.
Заметим, что участники движения сначала сближались, а потом удалялись друг от друга со скоростью 18 км/ч. В обоих случаях движение происходило в одном направлении, скорости сближения и удаления находили вычитанием.
В завершение темы рассмотрим задачу про папу и шляпу.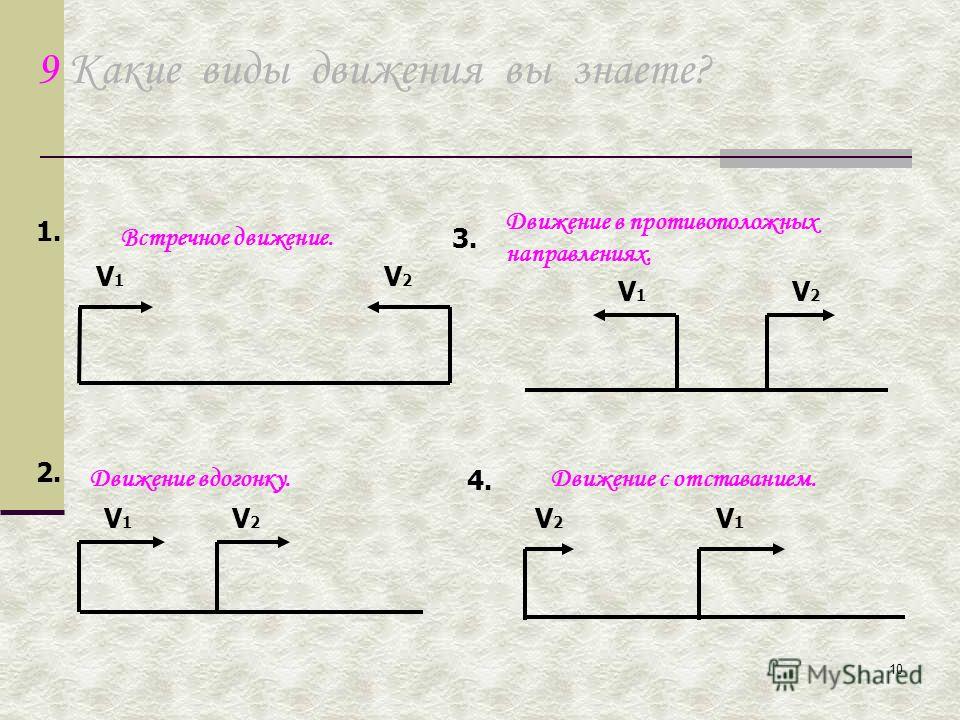
Задача 5*. Папа и сын плывут на лодке против течения. В какой-то момент сын уронил за борт папину шляпу. Только через 15 минут папа заметил пропажу, быстро развернул лодку и они поплыли по течению с той же собственной скоростью. За сколько минут они догонят шляпу?
Скорость удаления лодки и шляпы равна Vпр. т.+ Vт. = Vс.
Скорость сближения лодки и шляпы равна Vпо т.– Vт. = Vс.
Удаление и сближение лодки и шляпы происходило на одно и то же расстояние и с одной и той же скоростью, значит, время движения туда и обратно одинаково. Проверить понимание этого материала можно, предложив учащимся решить ту же задачу, но при условии, что папа и сын сначала плыли по течению, а потом против течения реки.
Как научить ребенка не путать скорость сближения и скорость удаления в задачах на движение. Разбираем с учителем | В помощь родителям младшего школьника
В 4 классе дети начинают решать задачи на скорость сближения и скорость удаления. Ребята начинают путаться. Часто они не могут определить вид задачи или просто не знают формулы. Однако понять эту тему легко. В этой статье Я расскажу, как учу своих учеников не путаться в задачах данного вида.
Ситуация 1
Представь, что вы с мамой вышли из дома и пошли в разные стороны. Вы будете приближаться друг к другу или удаляться друг от друга? Удаляться. Расстояние между вами будет увеличиваться или уменьшаться? Увеличиваться. Для того, чтобы найти скорость удаления в данной ситуации, нужно две скорости сложить.
Задача
Из города одновременно в разных направлениях выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Какое расстояние будет между автомобилями через 4 часа?
1) 90 + 70 = 160 (км/ч) — скорость удаления.
2) 160 × 4 = 640 (км)
Ответ: 640 км будет расстояние между автомобилями через 4 часа.
Ситуация 2
Представь, что вы с мамой идете навстречу друг другу.
В каждой из обсуждаемых ситуаций я задаю одни и те же вопросы, как в первой ситуации. Поэтому дальше я буду писать только результат наших рассуждений.
Когда мы идем навстречу друг другу, мы приближаемся друг к другу. Поэтому ищем скорость сближения. Расстояние между нами будет становиться меньше. Для того, чтобы найти скорость сближения в данной ситуации, нужно скорости сложить.
Задача
Расстояние между двумя городами 640 км. Из каждой из них одновременно навстречу друг другу выехали два автомобиля. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Через сколько часов автомобили встретятся?
1) 90 + 70 = 160 (км/ч) — скорость сближения
2) 640 : 160 = 4 (ч)
Ответ: автомобили встретятся через 4 часа.
Ситуация 3
Представь, что ты идешь по улице и видишь, что впереди идет мама. Ты решаешь ее догнать. Твоя скорость больше, чем скорость мамы. Ты догонишь маму? Да. Вы будете приближаться к друг другу или удаляться?Расстояние между вами будет увеличиваться или уменьшаться? Уменьшаться. (приближаться, т. к. ребенок сокращает расстояние). В этой ситуации мы находим скорость сближения.
Задача
Из города в посёлок выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Через сколько часов второй автомобиль догонит первый, если расстояние между ними равно 120 км?
1) 90 — 70 = 20 (км/ч) — скорость сближения
2) 120 : 20 = 6 ( ч)
Ответ: второй автомобиль догонит первый через 6 часов.
Ситуация 4
Представь ту же ситуацию, но теперь скорость больше у мамы. Ты догонишь маму? Нет. Почему? Она будет постоянно удаляться. Находим скорость удаления. Для этого из большей скорости вычитаем меньшую.
Задача
Одновременно из города выехали два автомобиля и поехали в одном направлении. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
1) 90 — 70 = 20 (км/ч) — скорость удаления
2) 20 × 4 = 80 (км)
Ответ: 80 км будет расстояние между автомобилями через 4 часа.
Делитесь своим мнением в комментариях, подписывайтесь на мой канал
Проблема сходимости
— обзор
5 Модифицированный алгоритм релаксации Лагранжа (предлагаемый подход)
В этом разделе классический алгоритм LR модифицируется для преодоления проблемы сходимости, наблюдаемой в предыдущем разделе. По этой причине теперь рассматривается новая переменная, называемая доступностью промежуточного продукта (AIP). Модификации классического алгоритма LR (см. Раздел 2.1) вводятся следующим образом: на шаге 0 задаются начальные предположения для всех λ и инициализируются переменные AIP как максимальная скорость потока сырья, которая может быть обработана в каждом делении; на шаге 1 ограничения ресурсов добавляются к потоку подачи каждого подразделения, затем все подзадачи решаются независимо.Например, в нашем тематическом исследовании задача оптимизации разбита на три подзадачи, а ограничения ресурсов задаются формулами 5D_2 (v) ≤ AIP 1 (v) для подразделения D_2 и 17D_3 (v) ≤ AIP 2 (v) для деления D_3, где (v) — номер итерации. Ограничение ресурсов не учитывается в D_1, потому что поток F 1 является фиксированным.
(7) D_1MaxP1 * F9 + P2 * F10 − P * F1 + λ1 * 5D_1-OCD_1
(8) D_1s.tОграничения работы в моделях D_1
(9) D_2MaxP3 * F14 − λ1 * 5D_2 + λ2 * 17D_2-OCD_2
(10) D_2s. P5 * F26 − λ217D_2 − OCD_3
(13) D_3s.tModelandoperationalconstraintsD_3
(14) D_317D_3 (v) ≤AIP2 (v)
На шаге 2 множители Лагранжа обновляются методом субградиента, в то время как переменные API принимают переменные значения промежуточного расхода на выходе из предыдущего деления, полученные в результате независимых задач оптимизации.В нашем случае это: AIP1 (v + 1) ← 5D_1 (v) и AIP 2 (v + 1) ← 17D_2 (v) . Это гарантирует, что в следующей итерации скорость подачи каждого деления будет физически доступна. На шаге 3 проверяется критерий сходимости, затем, если разница между λ двух последовательных итераций меньше произвольного допуска (ε), решение было найдено, в противном случае вернитесь к шагу 1.
На рисунке 4 показаны полученные результаты новым подходом.Обратите внимание, что после 9 итераций алгоритм сходится, и теневые цены для промежуточных потоков определяются правильно. Другими словами, теневые цены согласованы с рыночной ценой конечных продуктов (1,85 $ / кг для потоков 5D_1 и 5D_2; 2,8 $ для потоков 17D_2 и 17D_3).
Рисунок 4. Сходимость множителей Лагранжа для предложенного алгоритма
На рисунке 5 показано сравнение нового алгоритма декомпозиции с централизованным подходом. Можно заметить, что расходы промежуточных потоков аналогичны, что означает, что предлагаемый алгоритм оптимизирует всю установку до рабочей точки, близкой к централизованному подходу.
Рисунок 5. Значения расхода, полученные с помощью предложенного алгоритма и централизованного подхода
В таблице 2 представлена некоторая важная информация о проблемах оптимизации каждого подхода, обсуждаемого в настоящей статье. Можно заметить, что распределенные подходы уменьшают сложность проблемы, поскольку уменьшают количество переменных каждой подзадачи. Более того, каждая подзадача, созданная методами декомпозиции, может быть оптимизирована параллельно с использованием разных процессоров для сокращения общего количества времени, затрачиваемого на оптимизацию всего процесса (Darby and White, 1988).
Таблица 2. Соответствующая информация, используемая в каждом подходе
| Структура оптимизации | Централизованная | LR | PISUSA | Предлагаемый подход | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D_1 | D_2 | D_3 | D_1 | D_2 | D_3 | D_1 | D_2 | D_3 | ||||
| # Переменные | 13,640 | 2,393 | 2,746 | 8,510 | 2,393 | 2,746 | 8,510 | 2,39310 | 8,510 | 2,39310 | ||
| # Уравнения | 13,634 | 2391 | 2,743 | 8,507 | 2391 | 2,743 | 8,507 | 2391 | 2,743 | 8,507 | ||
| # Неравенства | 10 | 6 | 10 | 6 | 11 | 11 | ||||||
| GOP (долл. / Ч) | 71622.92 | — | — | 71,754,71 | ||||||||
Распределенный подход получил GOP на 0,184% больше, чем центрированный подход. Это различие связано с нелинейностью исследуемой задачи оптимизации, которая приводит к различным локальным оптимальным решениям.
Улучшение сходимости мультифизических задач
В нашей предыдущей записи блога мы представили алгоритмы Fully Coupled и Segregated , используемые для решения стационарных мультифизических задач в COMSOL.Здесь мы рассмотрим методы ускорения сходимости этих двух методов.
Методы линейного изменения нагрузки и нелинейности
Как мы только что узнали, полностью связанный подход к решению стационарной нелинейной задачи на самом деле использует тот же алгоритм Ньютона-Рафсона с затуханием, который использовался для решения нелинейной задачи одной физики. Хотя этот алгоритм действительно хорошо сходится во многих случаях, он может выйти из строя или сходиться очень медленно, если выбор начальных условий плохой.Поэтому неудивительно, что методы, которые мы уже рассмотрели, такие как линейное изменение нагрузки и линейное изменение нелинейности, также применимы в применении к мультифизической задаче. На самом деле, к этим методикам особо нечего добавить — их можно использовать равнозначно.
Нарастание мультифизических задач
Существует одна новая разновидность техники линейного изменения нелинейности, которая заключается в увеличении взаимосвязи между физикой. Численно на самом деле идентичен уже обсуждавшейся методике линейного нарастания нелинейности, но концептуально это величина взаимосвязей между физикой, которая увеличивается, а не величина нелинейности в одной физике.Единственная трудность — это выбрать и реализовать термин, который следует наращивать. К счастью, большинство мультифизических задач имеют вполне очевидную взаимосвязь между физикой, которую можно найти, просто выписав основные уравнения и граничные условия и изучив, как свойства материала и нагрузки зависят от решаемых переменных.
Наиболее важно помнить, что основной алгоритм, используемый для решения полностью связанной мультифизической задачи, в точности совпадает с алгоритмом, используемым для решения нелинейной однофизической задачи.Помня об этом, вы обнаружите, что полностью связанные задачи мулифизики на самом деле не создают никаких дополнительных концептуальных препятствий, кроме понимания того, как физика в модели взаимодействует друг с другом.
С другой стороны, сегрегированный подход может привести к множеству различных стратегий решения, которые могут значительно ускорить сходимость решения и существенно повлиять на объем памяти, необходимый для решения проблемы. Чтобы понять это, давайте сделаем блок-схему различных методов мультифизического решения.Рассмотрим ту же проблему из нашего предыдущего сообщения в блоге о сборной шине, которая нагревается из-за протекания тока и испытывает термические напряжения.
Полностью связанный подход
Во-первых, полностью связанный решатель начинает с первоначального предположения и применяет итерации Ньютона-Рафсона до тех пор, пока решение не сойдется:
При решении такой задачи вы получите график сходимости, который показывает, что оценка ошибки уменьшается между итерациями Ньютона-Рафсона. В идеале ошибка должна монотонно уменьшаться, если она сходится, а затем приступить к исследованию линейного изменения нагрузок, нелинейностей или мультифизических связей.Этот подход почти всегда требует более интенсивного использования памяти для решения линейной системы уравнений на каждом шаге Ньютона-Рафсона.
Раздельный подход
Теперь сравним полностью связанный подход с раздельным подходом, который решает каждую физику последовательно до сходимости:
Вы получите другой вид графика сходимости для такой задачи, который показывает ошибку, связанную с каждой решаемой вами физикой.Каждый физик может использовать оптимальный решатель, прямой или итерационный метод с меньшим объемом памяти, для решения линейной системы уравнений. Каждый отдельный шаг может быть нелинейной задачей сам по себе и может быть решен с желаемым допуском и с настраиваемым демпфированием в зависимости от конкретной комбинации решаемой физической задачи.
С помощью этого метода решения вы получите по крайней мере два графика сходимости, один для итеративного решателя (-ов), возможно, используемого в отдельном шаге, а второй для общей сходимости сегрегированного подхода:
Приведенный выше график показывает уменьшение ошибки для каждой физики.Хотя для одной и той же проблемы может потребоваться больше итераций, каждый цикл подхода с изолированным решением может быть намного быстрее, чем шаг Ньютона-Рафсона, необходимый для полностью связанного подхода. Вы также можете получить немного больше информации из этого, если только одна или две физики не сходятся, тогда вы сначала захотите проверить их настройку.
Шаг последовательного решения
Одна вещь, которую вы можете вспомнить об этой проблеме, заключается в том, что изменение температуры вызывается резистивным нагревом от тока, а распределение тока зависит от электропроводности, которая зависит от температуры.То есть решения по напряжению и температуре связаны двунаправленно, . С другой стороны, хотя тепловая деформация и модуль Юнга зависят от температуры, решения по напряжению и температуре не зависят от смещений или напряжений. То есть существует однонаправленная связь между тепловой проблемой и структурной проблемой. Сразу видно, что есть еще более эффективный способ решения этой проблемы. Сначала мы можем решить проблему напряжения и температуры, а затем решить проблему смещения:
Итак, мы видим, что существует (по крайней мере) три различных способа решения этой проблемы: полностью связанный, сегрегированный и предполагающий, что связи между всей физикой разделены, или с последовательным шагом решения, чтобы воспользоваться преимуществом однонаправленного связь между температурой и перемещениями.При решении мультифизической задачи COMSOL предполагает взаимосвязь между всей физикой и пытается выбрать оптимальный полностью связанный или сегрегированный подход в зависимости от физики и размера проблемы. Конечно, всегда полезно зайти в настройки решателя, чтобы увидеть, какие настройки выбрало программное обеспечение.
Заключение серии блогов Solver
Эта серия публикаций была разработана, чтобы дать вам понимание алгоритмов, используемых в COMSOL для решения однофизических и мультифизических линейных и нелинейных стационарных задач.Были рассмотрены такие вопросы, как сетка, точность и сходимость. Обладая этой информацией, вы сможете более уверенно подходить к решениям для ваших моделей этого типа.
Итерационных методов для решения Ax = b — Анализ сходимости итерационных методов
На этой и следующей страницах мы пытаемся ответить на два вопроса, касающихся методов Якоби и Гаусса-Зейделя:
- Когда будет работать каждый из этих методов? То есть, при каких условиях они будут производить последовательность приближений x (0) , x (1) , x (2) ,… которая сходится к истинное решение x ?
- Когда они работают, как быстро приближения приблизятся к истинному решению? То есть какова будет скорость сходимости?
В общем, итерационный метод, который находит решение для A x = b , принимает вид
так что
, которое мы можем переписать как
где
B часто называют итерационной матрицей.
Если текущее приближение x ( k ) на самом деле является точным решением x , то итерационный метод обязательно должен произвести следующую итерацию x ( k +1) , это тоже точное решение. То есть должно быть верно, что x = B x +, поэтому
Конечно, поскольку проблема, которую мы пытаемся решить, это A x = b , M и N должны быть выбраны так, чтобы A = M — N .
С другой стороны, выбор A = M — N не обязательно гарантирует, что итерационный метод найдет последовательность векторов x (0) , x ( 1) , x (2) ,… который сходится к истинному решению x . Будет ли работать тот или иной метод, зависит от матрицы итераций B = M -1 N .Фактически, в целом B полностью определяет сходимость (или нет) итерационного метода. В частности, первоначальное предположение обычно не влияет на то, является ли конкретный метод сходимостью или на скорость сходимости. Однако, если первоначальное предположение далеко от истинного решения, потребуется больше итераций для получения приемлемого приближения для истинного решения, чем если бы первоначальное предположение было ближе к истинному решению.
Чтобы понять свойства сходимости итерационного метода
вычтем из уравнения
, что дает нам
То есть, поскольку текущая ошибка — e ( k ) = x — x ( k ) ,
Для ясности, верхний индекс B — это степень B , а верхний индекс вектора e (внутри скобок) — это номер итерации , которому соответствует эта конкретная ошибка.
Полное понимание значимости взаимосвязи e ( k ) = B k e (0) требует некоторого знакомства с нормами матрицы. Так же, как норма вектора, норма матрицы || B || сообщает нам «размер» матрицы (а не ее размеры). Точнее, для любого данного вектора v норма матрицы говорит нам, насколько больше или меньше (в норме) B v будет по сравнению с v .В частности, всегда верно, что || B v || ≤ || B || || v ||.
Следовательно, поскольку || e ( k ) || = || B k e (0) || ≤ || B || к || e (0) ||, затем || e ( k ) || 0 (то же самое, что e ( k ) 0 ), если || B || Как мы покажем на следующей странице, существует определенная матрица итераций B для каждого из методов Якоби и Гаусса-Зейделя.Для каждого метода меньшее || B || есть, чем быстрее ошибка сведется к нулю, то есть тем быстрее приближение приблизится к истинному решению. С другой стороны, если || B || ≥ 1 ошибка просто возрастет, и наши приближения будут уходить от истинного решения, а не к нему.
Мы заканчиваем этот раздел, отмечая, что на практике иногда встречается одно условие, гарантирующее, что || B || заключается в том, что матрица A строго доминирует по диагонали.Это означает, что для каждой строки A абсолютное значение диагонального элемента больше, чем сумма абсолютных значений от -диагональных элементов.
Численный метод и порядок сходимости для дифференциальных уравнений второго порядка с импульсным воздействием | Достижения в разностных уравнениях
Применение метода воспроизводящего ядра в краевых задачах было развито многими исследователями, поскольку этот метод позволяет легко получить точное решение в виде ряда и приближенное решение с более высокой точностью [19, 20] . {3} \) для краткости).{3} [а, б]. $$
От Ref. [20] легко доказать, что \ (\ mathbb {L} \) — ограниченный оператор.
Тогда уравнение. (1) можно преобразовать к следующему виду:
$$ \ textstyle \ begin {case} \ mathbb {L} u = f (x), \ quad x \ in [a, b] \ backslash \ {c \}, \\ u (a) = \ alpha _ {1}, \ quad \ quad u (b) = \ alpha _ {2}, \\ \ Delta u ‘(c) = \ alpha _ {3}, \ quad \ quad \ Delta u (c) = \ альфа _ {4}. \ end {case} $$
(6)
Сходимость линейных стационарных итерационных процессов для решения сингулярных неструктурированных систем линейных уравнений в JSTOR
Abstract
В статье рассматриваются свойства сходимости линейных стационарных итерационных процессов для решения больших неструктурированных систем линейных уравнений.Особое внимание уделяется случаю, когда решаемая система сингулярна и, возможно, противоречива. Обзор начинается с исследования итерации xk + 1 = Hxk + f, k = 0, 1, 2, ⋯, когда система (I — H) x = f несовместна. В этом случае последовательность {xk} всегда расходится. Тем не менее, когда H «сходится», существует вектор q ∈ Null (I — H) такой, что последовательность $ \ hat \ mathbf {x} _k = \ mathbf {x} _k — k \ mathbf {q} $ сходится. Предел этой последовательности $ \ hat \ mathbf {x} $ решает некоторую задачу наименьших квадратов, а последовательность остаточных векторов rk = (I — H) xk — f сходится к $ (I — H) \ hat \ mathbf {x} — \ mathbf {f} $.Кроме того, если H подобна вещественной диагональной матрице, то соответствующие нормы rk и $ \ hat \ mathbf {x} _k — \ hat \ mathbf {x} $ монотонно убывают. Можно сказать больше, когда x0 ∈ Range (I — H). Существует несколько итерационных методов решения симметричной положительно полуопределенной системы линейных уравнений Gx = h, которые имеют вид xk + 1 = Q-1 (Q — G) xk + Q-1h. Здесь итерационная матрица H = Q-1 (Q — G) сходится, если матрица P = Q + QT — G положительно определена. В этом случае мы получаем удивительный результат: последовательность остатков {Gxk — h} сходится, даже когда система Gx = h несовместна.Развитая теория раскрывает интересные свойства «основных» итерационных методов (например, метода Ричардсона, метода Якоби, SOR и SSOR) с минимальными предположениями о структуре G. Например, если H сходится и симметрично, как в методе Ричардсона, то последовательности $ \ {\ | \ hat \ mathbf {x} _k — \ hat \ mathbf {x} \ | \} $ и {| G xk — h |} монотонно убывают, и последовательность {Gxk — h} сходится в $ G \ hat \ mathbf {x} — \ mathbf {h} $, где $ \ hat \ mathbf {x} $ решает задачу наименьших квадратов: минимизировать | Gx — h | 2.Более того, если x0 ∈ Range (G) и система Gx = h разрешима, то последовательность {xk} сходится к решению этой системы с минимальной нормой. Статья заканчивается обсуждением итерационных методов решения общей линейной системы Ax = b, где A большое, разреженное и неструктурированное. Эти методы можно разделить на два класса. Один направлен на решение нормальных уравнений ATAx = ATb (например, столбец SOR или метод Чиммино), а другой нацелен на решение уравнений Бьорка-Эльфвинга x = ATy и AATy = b (например,г., метод Качмарца). Показано, что в обоих случаях теория, развитая для симметричных положительно полуопределенных систем, позволяет охарактеризовать поведение методов и получить упрощенные доказательства сходимости.
Информация о журнале
SIAM Review содержит статьи, написанные для широкого круга читателей.
научная аудитория. Статьи включают пояснительные или обзорные статьи.
сосредоточение внимания на важных достижениях в прикладной или вычислительной математике, или
документы, описывающие математические и вычислительные задачи в
научные или инженерные приложения.Другие функции включают эссе,
обзоры книг, тематические исследования из отрасли, классные заметки и проблемы
и решения.
Информация об издателе
«Общество промышленной и прикладной математики является ведущим
международная ассоциация прикладной математики и ее публикации
мог бы стать ядром адекватного собрания по математике. Один из
Целями этой организации является обеспечение обмена информацией между
университет и промышленность стали более гладкими.Он превосходно выполняет эту задачу
и многие из ведущих академических институтов мира являются ее членами ».
— Журналы для библиотек, восьмое издание, 1995, Р. Р.
Боукер, Нью-Провиденс, Нью-Джерси
Общество промышленной и прикладной математики (SIAM), штаб-квартира
в Филадельфии, была основана в 1951 году для продвижения применения
математики в науку и промышленность, продвигать математические исследования и
предоставлять средства массовой информации для обмена информацией и идеями между
математики, инженеры и ученые.SIAM имеет обширную программу публикаций в прикладных и вычислительных
математика, в том числе 11 престижных исследовательских журналов. Для полного
описание наших журналов и недавно анонсированных SIAM Journals Online,
доступ http://www.siam.org/.
Исчисление II — Схождение / расхождение рядов (практические проблемы)
Показать мобильное уведомление
Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-4: Схождение / расхождение серий
Для задач 1 и 2 вычислить первые 3 члена в последовательности частичных сумм для данного ряда.2}}}} \) Решение
Произошла ошибка при настройке вашего пользовательского файла cookie
Произошла ошибка при настройке вашего пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.
Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie. - Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie.Чтобы исправить это, установите правильное время и дату на своем компьютере. - Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его.
