Как составить пропорцию из отношения: Составить пропорцию — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Составить пропорцию

Составить пропорцию. В этой статье хочу поговорить с вами о пропорции. Понимать, что такое пропорция, уметь составлять её – это очень важно, она действительно спасает. Это вроде бы маленькая и незначительная «буковка» в большом алфавите математики, но без неё математика обречена быть хромой и неполноценной. Для начала напомню, что такое пропорция. Это равенство вида:

что тоже самое (это разная форма записи).

Пример:

Говорят – один относится к двум также, как четыре относится к восьми. То есть это равенство двух отношений (в данном примере отношения числовые).

Основное правило пропорции:

a:b=c:d

произведение крайних членов равно произведению средних

то есть

a∙d=b∙c

*Если какая-либо величина в пропорции неизвестна, ее всегда можно найти.

Если рассматривать форму записи вида:

то можно использовать следующее правило, его называют «правило креста»: записывается равенство произведений элементов (чисел или выражений) стоящих по диагонали

a∙d=b∙c

Как видите результат тот же.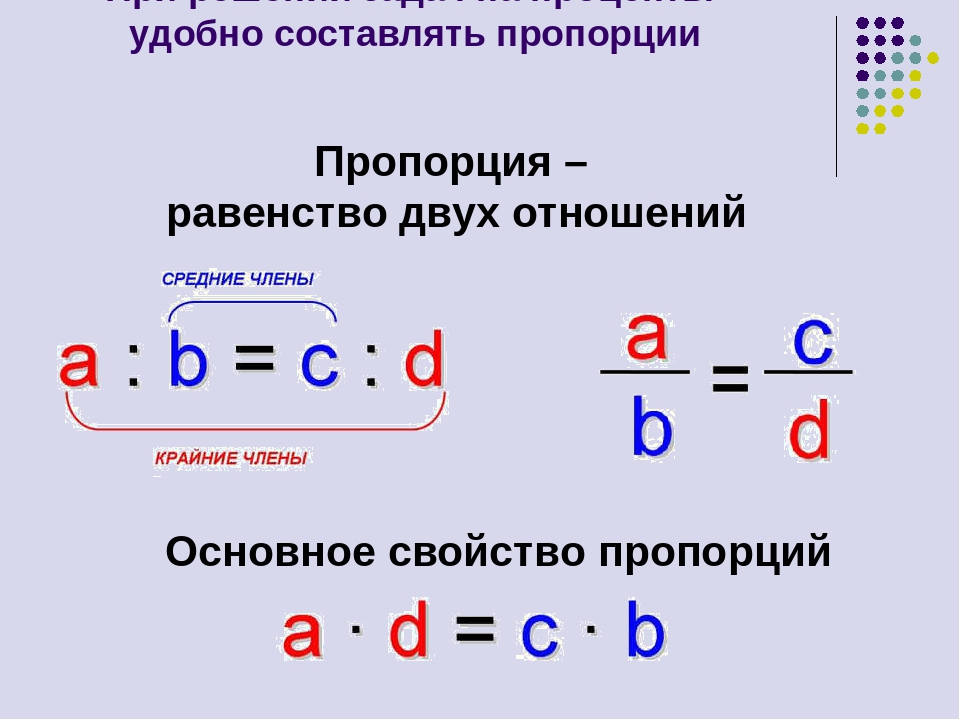

Если три элемента пропорции известны, то мы всегда можем найти четвёртый.

Именно в этом суть пользы и необходимость пропорции при решении задач.

Давайте рассмотрим все варианты, где неизвестная величина х находится в «любом месте» пропорции, где a, b, c – числа:

Величина стоящая по диагонали от х записывается в знаменатель дроби, а известные величины стоящие по диагонали записываются в числитель, как произведение. Его запоминать не обязательно, вы и так всё верно вычислите, если усвоили основное правило пропорции.

Теперь главный вопрос, связанный с названием статьи. Когда пропорция спасает и где используется? Например:

1. Прежде всего это задачи на проценты. Мы рассматривали их в статьях «Задачи на проценты. Часть 1!» и «Задачи на проценты. Часть 2!».

2. Многие формулы заданы в виде пропорций:

> теорема синусов

> отношение элементов в треугольнике

> теорема тангенсов

> теорема Фалеса и другие.

3. В задачах по геометрии в условии часто задаётся отношение сторон (других элементов) или площадей, например 1:2, 2:3 и прочие.

4. Перевод единиц измерения, причём пропорция используется для перевода единиц как в одной мере, так и для перевода из одной меры в другую:

— часы в минуты (и наоборот).

— единицы объёма, площади.

— длины, например мили в километры (и наоборот).

— градусы в радианы (и наоборот).

здесь без составления пропорции не обойтись.

Ключевой момент в том, что нужно правильно установить соответствие, рассмотрим простые примеры:

Необходимо определить число, которое составляет 35% от 700.

В задачах на проценты за 100% принимается та величина, с которой сравниваем. Неизвестное число обозначим как х. Установим соответствие:

Можно сказать, что семисот тридцати пяти соответствует 100 процентов.

Иксу соответствует 35 процентов. Значит,

700 – 100%

х – 35 %

Решаем

Ответ: 245

Переведём 50 минут в часы.

Мы знаем, что одному часу соответствует 60 минут. Обозначим соответсвие — x часов это 50 минут. Значит

1 – 60

х – 50

Решаем:

То есть 50 минут это пять шестых часа.

Ответ: 5/6

Николай Петрович проехал 3 километра. Сколько это будет в милях (учесть, что 1 миля это 1,6 км)?

Известно, что 1 миля это 1,6 километра. Число миль, которые проехал Николай Петрович примем за х. Можем установить соответствие:

Одной миле соответствует 1,6 километра.

Икс миль это три километра.

1 – 1,6

х – 3

Ответ: 1,875 миль

Вы знаете, что для перевода градусов в радианы (и обратно) существуют формулы. Я их не записываю, так как запоминать их считаю излишним, и так вам в памяти приходится держать много информации. Вы всегда сможете перевести градусы в радианы (и обратно), если воспользуетесь пропорцией.

Переведём 65 градусов в радианную меру.

Главное это запомнить, что 180 градусов это Пи радиан.

Обозначим искомую величину как х. Устанавливаем соответствие.

Ста восьмидесяти градусам соответствует Пи радиан.

Шестидесяти пяти градусам соответствует х радиан.

Если записать отношение в общем виде, то получится

То есть, если необходимо перевести градусы в радианы, то подставляете в эту пропорцию градусы и вычисляете радианы; если необходимо перевести радианы в градусы, то подставляете радианы и вычисляете градусы.

Можете изучить статью по этой теме на блоге. Материал в ней изложен несколько по иному, но принцип тот же. На этом закончу. Обязательно будет ещё что-нибудь интересненькое, не пропустите!

Если вспомнить само определение математики, то в нём есть такие слова: математика изучает количественные ОТНОШЕНИЯ (ОТНОШЕНИЯ — здесь ключевое слово). Как видите в самом определении математики заложена пропорция. Вообщем, математика без пропорции это не математика!!!

Всего доброго!

С уважением, Александр

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

составить пропорции из отношений 2) 14:21 8:14 15:10 27:18 18:24 36:54 20:35 6:8

Срочно нужно! Даю 10 баллов у меня дальше не хватит
Не знаю, что такое к/п, но это что то на рисунке (10000%)
1. Отметьте на к/п точки: А (1; 4), В (1
…

; 0), С (1; -4)
2. Найдите координаты точек, показанных на рисунке.
3. Отметьте на координатной площине (переводчик переводит как плоскость, хз) точки: М (-1; 6), N (2; 5), К (3; 0), Е (-2; -3). Проведите отрезки МК і NE, найдите координаты точки — пересечение этих отрезков.
4. Постройте прямоугольник ABCD, если А (-1; -2), В (-1; 1), С (4; 1), D (4; 2). Найдите S і P прямоугольника.

1398.Постройте график уравнения, запиши-те координаты точки пересечения гра-фика с осью ординат:1) 3х + у — 6 = 0;2) -3х + 2y – 4 = 0;3) 2,5х + у — 5
…

= 0;4) 4x + 3y — 12 = 0;5) -3х + 5у – 15 = 0;6) x+2y + 4 = 0.Помогите

Найдите площадь квадрата, если длина стороны квадрата равна ширине прямоугольника, у которого периметр 40 см. — 13

помогите пожалуйста пжпжпжпжпж

Первая задача:Кожний із учнів 6 класу на дистанційному навчанні отримали варіанти із однаковою кількістю завдань. Скільки учнів у класі, якщо було за
…

дано 87 прикладів і 58 задач?Вторая задача:Знайдіть НСК чисел 50 і 30, і ви дізнаєтесь, яку дистанцію у см потрібно тримати один від одного, стоячи в черзіТретья задача:6 клас на дистанційному навчанні пишуть і здають вчителям самостійні роботи з укр.мови кожні 6 днів, з математика кожні 12 днів, а з природознавства кожні 9 днів. Через скільки днів вчителям одночасно прийдуть в один день роботи учнів?

Подскажите пожалуйста не могу понять

очень срочно!!!!!!!!!

как в японии в 11 13 вв складывались новые феодальные отношения

4. Выполните на бумаге в клетку технический рисунок одной из деталей (рис. 101), используя правила построения какой-либо аксонометрической проекции и
…

любого приема оттенения.

очень срочно,буду очень благодарен!!!!

Как составить и рассчитать пропорцию: онлайн калькулятор

Онлайн калькулятор пропорций

Формула пропорций

Пропо́рция — это равенство двух отношений, когда a:b=c:d

средние
		╭	члены	╮
1	:	10	=	7	:	70
╰	крайние члены					╯

0,1			=	0,1

1 10 = 7 70

Основные свойства пропорции

Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d, то a⋅d=b⋅c

1
10 ✕ 7
70

1 ⋅ 70 = 10 ⋅ 7

Обращение пропорции: если a:b=c:d, то b:a=d:c

Перестановка средних членов: если a:b=c:d, то a:c=b:d

Перестановка крайних членов: если a:b=c:d, то d:b=c:a

Решение пропорции с одним неизвестным | Уравнение

1 : 10 = x : 70



1
10 = x
70

Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение

x = 1 ⋅ 70
10 = 7

Как посчитать пропорцию

Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?

Составим пропорцию:
1 таблетка — 10 кг
x таблеток — 70 кг

Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение:
1 таблетка
x таблеток ✕ 10 кг
70 кг

x = 1 ⋅ 70 : 10 = 7

Ответ: 7 таблеток

Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?

Составим пропорцию:
2 статьи — 5 часов 
x статей — 20 часов

x = 2 ⋅ 20 : 5 = 8

Ответ: 8 статей

Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.

Отношения и пропорции в математике

В математике отношением называется то частное, которое получается при делении одного числа на другое. Ранее сам этот термин использовался только в тех случаях, когда было необходимо выражение какой-либо одной величины в долях другой, причем такой, которая однородна первой. К примеру, отношения использовались при выражении площади в долях другой площади, длины в долях другой длины и т.п. Решение этой задачи производилось с помощью деления.

Таким образом, сам смысл термина «отношение» был несколько иной, чем термина «деление»: дело в том, что второй означал разделение определенной именованной величины на любое совершенно отвлеченное абстрактное число. В современной математике понятия «деление» и «отношение» по своему смыслу абсолютно идентичны и являются синонимами. Например, и тот, и другой термин с одинаковым успехом применяют для отношения величин, являющихся неоднородными: массы и объема, расстояния и времени и т.п. При этом многие отношения величин однородных принято выражать в процентах.

Пример

В супермаркете насчитывается четыреста наименований различных товаров. Из них двести произведено на территории Российской Федерации. Определить, каково отношение отечественных товаров к общему числу товаров, продаваемых в супермаркете?

400 – общее число товара

200 – РФ

Ответ: двести разделить на четыреста равняется ноль целых пять десятых, то есть пятьдесят процентов.

200 : 400 = 0,5 или 50%

В математике делимым принято называть предыдущий член отношения, а делителем – последующий член отношения. В приведенном выше примере предыдущим членом являлось число двести, а последующим – число четыреста.

Два равных отношения образуют пропорцию

В современной математике принято считать, что пропорцией является два равным между собой отношения. К примеру, если общее количество наименований товаров, продаваемых в одном супермаркете, – четыреста, а в России из них произведено двести, а те же значения для другого супермаркета составляют шестьсот и триста, то соотношение количества российских товаров к общему их числу, реализовываемых в обеих торговых предприятиях, одинаково:

1. Двести разделить на четыреста равняется ноль целых пять десятых, то есть пятьдесят процентов

200 : 400 = 0,5 или 50%

2.Триста разделить на шестьсот равняется ноль целых пять десятых, то есть пятьдесят процентов

300 : 600 = 0,5 или 50%

В данном случае имеется пропорция, которую можно записать следующим образом:

Если формулировать это выражение так, как это принято делать в математике, то говорится, что двести относится к четыремстам так же, как триста относится к шестистам. При этом двести и шестьсот называются крайними членами пропорции, а четыреста и триста – средними членами пропорции.

Произведение средних членов пропорции

Согласно одному из законов математики, произведение средних членов любой пропорции равняется произведению ее крайних членов. Если возвратиться к приведенным выше примерам, то проиллюстрировать это можно следующим образом:

Двести умноженное на шестьсот равняется сто двадцать тысяч;

200 × 600 = 120 000

Триста умноженное на четыреста равняется сто двадцать тысяч.

300 × 400 = 120 000

Из этого следует, что любой из крайних членов пропорции равен произведению ее средних членов, деленному на другой крайний член. По тому же самому принципу каждый из средних членов пропорции равен крайних ее членов, деленному на другой средний член.

Если вернуться к приведенному выше примеру пропорции, то:

Двести равняется четыреста умноженное на триста и деленное на шестьсот.

Эти свойства широко используются в практических математических вычислениях тогда, когда требуется найти значение неизвестного члена пропорции при известных значениях трех членов остальных.

Урок 8. обобщение и систематизация знаний по теме «отношения и пропорции» — Математика — 6 класс

Математика

6 класс

Урок № 8

Обобщение и систематизация знаний по теме «Отношения и пропорции»

Перечень рассматриваемых вопросов:

Отношение двух величин, масштаб.
Пропорция и основное свойство пропорции.
Прямая и обратная пропорциональность.

Тезаурус

Равенство двух отношений называют пропорцией.

Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.

Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.

Скорость – отношение пройденного пути ко времени движения.

Плотность – отношение массы вещества к его объёму.

Цена – отношение стоимости товара к его массе или количеству единиц товара.

Основная литература

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Дополнительная литература

Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

a, b, c, d – члены пропорции.

a, d – крайние члены пропорции;

b, c – средние члены пропорции.

Масштаб – это отношение длины отрезка на карте к длине соответственного отрезка на местности.

Скорость – отношение пройденного пути ко времени движения.

Плотность – отношение массы вещества к его объёму.

Цена – отношение стоимости товара к его массе или количеству единиц товара.

Урожайность – отношение количества продукции растениеводства к единице посевной площади.

Например, урожайность хороших сортов клубники:

Задача.

Можно ли составить верную пропорцию из отношений:

8 : 5 и 40 : 25;

4 : 7 и 40 : 70;

1 : 9 и 5 : 25;

2 : 5 и 1 : 19?

Решение.

8 : 5 и 40 : 25

Разбор заданий тренировочного модуля

Тип 1. Единичный выбор.

Поезд, скорость которого 55 км/ч, затратил на некоторый путь 6 ч. За сколько часов он пройдёт этот же участок пути, если его скорость будет 33 км/ч?

Варианты ответов: 12; 15; 7; 10.

Для решения задания составим пропорцию. При постоянном пути скорость обратно пропорциональна времени движения. Чтобы найти неизвестный средний член пропорции, надо произведение её крайних членов разделить на известный средний член пропорции.

Тип 2. Множественный выбор.

Выберите верные пропорции.

Решение задания: Нужно воспользоваться основным свойством пропорции.

Найти произведение крайних членов.

Найти произведение средних членов.

Если произведение крайних членов равно произведению средних членов, то пропорция верна.

Пропорции математика. Пропорция – это равенство двух отношений. Соотношение.

Пропорция – это равенство, утверждающее, что два отношения равны. Пропорциональный — значит находящийся в определенном отношении к какой-либо величине. Четыре величины $4, 2, 8 $ и $4$ находятся в отношении, если $\frac{4}{2}=\frac{8}{4}$. Произведение крайних членов пропорции равно произведению средних.

Пропорция всегда включает равные коэффициенты. Когда соотношение остается постоянным, это соотношение называется пропорциональным.

Если $\frac{A}{B} = \frac{C}{D}$, то

Пропорция состоит из двух равных отношений. Однако если $\frac{A}{B}$ не равно $\frac{C}{D}$, то $A, B, C, D $ не называются пропорцией.

Три величины считаются пропорциональными, если отношение первого ко второму равно соотношению второго и третьего.

$A, B , C$ находятся в постоянной пропорции, если $\frac{A}{B} =\frac{C}{D}$

Если $A, B ,C $ находятся в постоянном отношении, то $B$ называется средней в пропорции.

В косвенной пропорции как одно значение увеличивается, так и другое значение уменьшается.

Задача 1. За $5$ дней и $12$ человек построили забор. Сколько дней это займет у $6$ людей?

Решение.

$12$ человек → $5$ дней

$6$ человек → $x$ дней

$\frac{12}{6} = \frac{x}{5}$

умножаем крест на крест члены пропорции и сокращаем на $6$:

$12*5=6x$

$60=6x$

$x=10$

Ответ: $6$ людей будут работать $10$ дней, чтобы закончить работу.

Задача 2. Найдите значение $x$, если $\frac{2}{5}=\frac{x}{15}$

Решение:

$2*15=5x$

$30 =5x$

Делим на 5 обе части равенства: $\frac{30}{5}=x$, откуда находим

Задача 3. Что должно быть добавлено к каждому из четырех чисел 10, 18, 22, 38, чтобы сделать их пропорцией?

Решение:

$(10+x)(18+x)=(22+x)(38+x)$

$380+48x+2x=396+40x+2x$

$8x=16$

$x=2$

Задача 4. Найти четвертый член пропорции $6,10$ и $12$

Решение:

$\frac{6}{10}=\frac{12}{x}$

6×х = 120

x = 120/6

x = 20

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Арифметика

Пропорции, члены пропорции. Основное свойство пропорции

Частное от деления числа a на число b называют отношением числа a к числу b.

Число a называют предыдущим членом отношения, число b – последующим членом отношения.

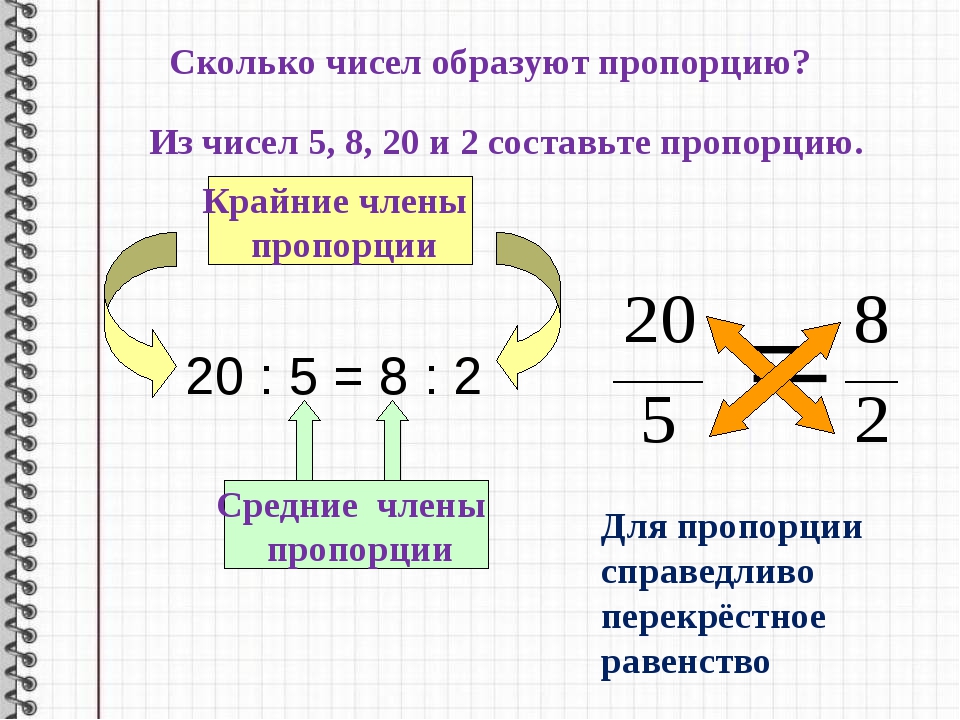
Пропорцией называют равенство двух отношений:

Иногда пропорцию записывают так:

a : b = c : d .

И в одной, и во второй формах записи пропорции числа a и d называют крайними членами пропорции, а числа b и c – средними членами пропорции.

Для любой пропорции справедливо следующее равенство, которое называют основным свойством пропорции:

Словесно это равенство можно сформулировать так: произведение крайних членов пропорции равно произведению средних членов пропорции.

Для того, чтобы доказать основное свойство пропорции, умножим пропорцию на выражение .

В результате получим:

что и требовалось доказать.

Основное свойство пропорции позволяет по трем любым известным членам пропорции найти четвертый неизвестный член пропорции. Покажем это на двух примерах.

Пример 1. Найти неизвестный член пропорции x , если

Решение. Воспользовавшись основным свойством пропорции, получаем:

Ответ: 3,15 .

Пример 2. Найти неизвестный член пропорции x , если

Решение. Воспользовавшись основным свойством пропорции, получаем:

Ответ: .

Из основного свойства пропорции легко вытекают также свойства пропорции, которые называют перестановкой членов пропорции. Эти свойства формулируются так: если

то

Производные пропорции

Справедливы также свойства пропорции, которые называют производными пропорциями. Эти свойства формулируются так: если

то

В качестве примера докажем первое из указанных свойств (остальные свойства доказываются аналогично).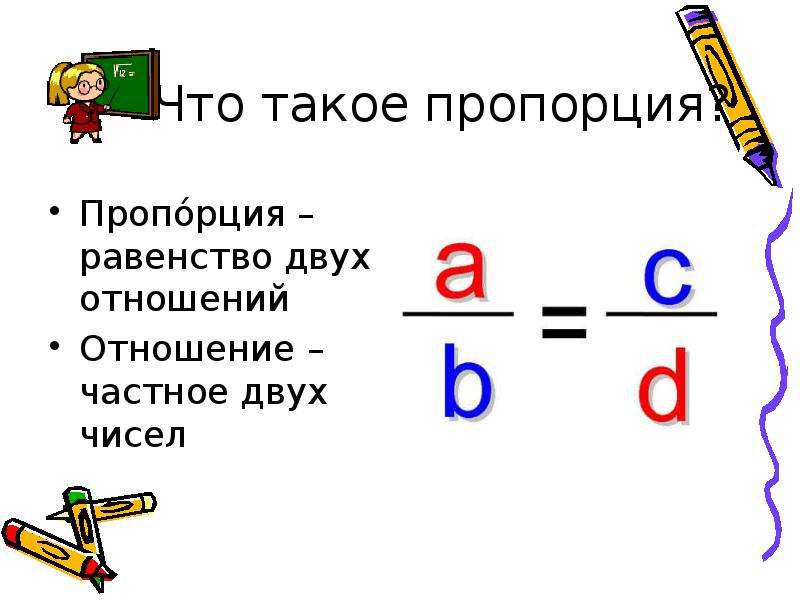 Для этого к обеим частям пропорции

достаточно прибавить 1. В результате получаем,

что и требовалось.

Замечание. Последнее из свойств пропорций является наиболее общим и может быть доказано, например, с помощью основного свойства пропорции.

Свойства равных отношений

Если выполнено соотношение

то выполнено и соотношение

где

k₁, k₂, … k_n

– произвольные числа, которые не могут все одновременно равняться нулю.

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Как вычислять соотношения и пропорции в математике

Обновлено 12 февраля 2020 г.

Кевин Бек

Рецензент: Lana Bandoim, B.S.

Концепция пропорции , вероятно, вам знакома, но вы не сможете дать ей строгое математическое определение. Например, вы можете распознать, что 10-летний ребенок меньше взрослого обычного размера, точно так же, как этот же взрослый меньше профессионального баскетболиста, даже если эти три размера разные.

Точно так же вам, вероятно, знакомо понятие отношения . Например, если вы участвуете в спортивном соревновании и знаете, что соотношение болельщиков-соперников и дружелюбных болельщиков велико, вы можете быть менее демонстративны, когда ваш любимый клуб забивает гол, чем если бы это соотношение было обратным.

В математике и статистике существует множество вопросов о пропорциях, процентах и соотношениях. К счастью, краткого объяснения основных понятий и нескольких примеров должно быть достаточно, чтобы вы пропорционально лучше изучаете математику.

Соотношения и пропорции

Отношение — это, по сути, дробь или два числа, выраженные как частное, например 3/4 или 179/2385. Но это особый вид дроби, которая используется для сравнения связанных величин. Например, если в комнате 11 мальчиков и 13 девочек, соотношение мальчиков и девочек составляет 11 к 13, что может быть записано как 11/13 или 11:13.

Коэффициент — это латинское слово, означающее «разум». Определение рационального числа может быть выражено в виде дроби; некоторые числа, такие как значение π в геометрии, иррациональны и не могут быть выражены таким образом, вместо этого они выражаются как бесконечное десятичное число.Возможно, древние математики сочли такое положение «необоснованным».

Пропорция — это просто выражение, устанавливающее два соотношения, равных друг другу, с использованием различных абсолютных чисел в дробях. Пропорции записываются как соотношения, например, a / b = c / d или a: b = c: d.

Как вычислить соотношения

Для решения большинства простых задач с соотношениями вам не нужна причудливая функция калькулятора соотношений. Например, вы ходите в спортзал 17 раз за 30 дней в месяц.Каково ваше соотношение дней в тренажерном зале к дням без занятий в тренажерном зале в этом месяце?

Ответ — , а не (дни в спортзале / общее количество дней), поэтому не поддавайтесь соблазну думать, что ответ — 17:30. Вместо этого вычтите дни занятий в спортзале из общего количества дней, чтобы получить дни без занятий в спортзале, необходимую вторую часть вашего соотношения. Следовательно, ответ — 17:13 (или 17/13).

Как рассчитать пропорцию

Иногда очевидно, что без выполнения каких-либо вычислений два отношения пропорциональны друг другу. Если вы и ваша собака — единственные два животных в комнате, и вам сказали, что в соседнем спортзале 457 человек и 457 собак, то вы знаете, что соотношение людей к собакам одинаково в обоих помещениях.

Но как насчет соотношений, которые нелегко сравнить с первого взгляда? Например, пропорционально ли 17/52 3/9? Если нет, то что больше?

Один из способов сделать это — вычислить десятичные числа каждой дроби и посмотреть, какая из них больше. Но если вы понимаете пропорции, вы можете вместо этого использовать перекрестное умножение, умножая противоположные знаменатели и числители:

(17/52) =? = (3/9)

(17) (9) = 153; (3) (52) = 156

Таким образом, отношения не совсем равны (3/9 немного больше), и доли не пропорциональны.

Что такое константа пропорциональности?

Константа пропорциональности представляет собой постоянную разницу между отношениями пропорциональности. Если a пропорционально b, то в выражении a = kb , k — константа пропорциональности. Две переменные a и b называются обратно пропорциональными , когда их произведение ab является константой для всех a и b, то есть когда a = C / b и b = C / a.

Пример: Количество поклонников стрельбы из лука пропорционально количеству фанатов бейсбола в данной кофейне.Сначала это 6 любителей стрельбы из лука и 9 любителей бейсбола. Если число фанатов бейсбола увеличится до 24, сколько должно быть поклонников стрельбы из лука?

Решите относительно k, где a = kb, a = 6 и b = 9:
k = 6/9 = 2/3 = 0,667

Теперь решите уравнение a = (0,667) (24), чтобы получить 16 стрельбы из лука. фанаты в теперь более переполненном кафе.

Пропорции — объяснение и примеры

Трудно представить, какой была бы наша жизнь без математических понятий, таких как пропорции. В нашей повседневной жизни мы часто сталкиваемся с пропорциями и соотношениями, когда идем за покупками, готовим еду, путешествуем по профессии и т. Д.

Соотношения и пропорции важны для — эффективной работы. В этой статье мы узнаем, как рассчитать пропорции и применить полученные знания для решения типовых задач, но перед этим давайте начнем с определения соотношений.

Коэффициент — это способ сравнения двух или более величин. Знак, используемый для обозначения отношения, — двоеточие «: » Предположим, что a и b — две разные величины или числа, тогда отношение a к b можно записать как a / b или a: b.Точно так же отношение b к a также может быть представлено как b: a или b / a. Первая величина в соотношении известна как антецедент, а вторая величина — как следствие.

Примеры соотношений: : или 3: 4, 1/5 или 1: 5, 199/389 или 199: 389 и т. Д. Из этого примера очевидно, что соотношение — это просто дробь, в которой антецедент равен числитель и консеквент являются знаменателем.

Знаменитый рисунок Витрувианского человека Леонардо да Винчи был основан на идеальных пропорциях человеческого тела.Каждая часть тела занимает разное соотношение, например, лицо занимает около 1/10 от общей высоты, а голова занимает около 1/8 от общей высоты. Писатели средневековья впервые использовали слово proportio (пропорция). В 1948 году Ле Корбюзье дал систему пропорций

Что такое пропорция?

Пропорция — это выражение, которое говорит нам, что два отношения эквивалентны. Два отношения называются пропорциональными, если они эквивалентны. Пропорции обозначаются знаком «:» или «=».Например, если a, b, c и d — целые числа, тогда пропорция записывается как a: b = c: d или a / b = c / d или b: a = d: c. Например, отношения 3: 5 и 15: 25 пропорциональны и записываются как 3: 5 = 15: 25

Четыре числа a, b, c и d известны как члены пропорции. Первый a и последний член d называются крайними членами, а второй и третий члены в пропорциональном выражении называются средними членами.

Как решить пропорции?

Легко вычислить, пропорциональны ли соотношения.Чтобы проверить, пропорционально ли соотношение a: b и c: d.

Умножьте первый член на последний член: axd
Умножьте второй член на третий член: bxc
Если произведение крайних членов равно произведению средних членов, то отношения пропорциональны: axd = bxc

Непрерывная пропорция

Говорят, что два отношения a: b и b: c находятся в непрерывной пропорции, если a: b = b: c. В этом случае член c называется третьей пропорцией a и b, тогда как b называется средней пропорцией между членами a и c.

Когда члены a, b и c находятся в непрерывной пропорции, получается следующая формула:

a / b = b / c

Перекрестное умножение членов дает; a x c = b x b, Следовательно,

b² = ac

Пример 1

Выясните, пропорциональны ли следующие соотношения: 8:10 и 12:15.

Пояснение

Умножьте первый и четвертый члены соотношений.

8 × 15 = 120

Теперь умножьте второй и третий член.

10 × 12 = 120

Поскольку произведение крайностей равно произведению средних,
Поскольку произведение средних (120) = произведение крайностей (120),
Следовательно, 8 : 10 и 12:15 пропорциональны.

Пример 2

Проверьте, пропорционально ли соотношение 6: 12 :: 12: 24.

Объяснение

Это случай непрерывной пропорции, поэтому примените формулу axc = bxb,
В этом случае a: b: c = 6: 12: 24, поэтому a = 6, b = 12 и c = 24
Умножьте первое и третье слагаемые:

6 × 24 = 144

Квадрат средних членов:

(12) ² = 12 × 12 = 144

Следовательно, соотношение 6:12:24 пропорционально.

Пример 3

Если 12: 18 :: 20: стр. Найдите значение x, чтобы соотношения были пропорциональными?

Объяснение

Дано: 12: 18 :: 20: p

Приравняйте произведение крайностей к произведению средств;
⇒ 12 × p = 20 × 18
⇒ p = (20 × 18) / 12

Решить относительно p;
⇒ p = 30
Следовательно, значение p = 30

Пример 4

Найдите третье, пропорциональное 3 и 6.

Объяснение

Пусть третье пропорционально быть c.
Тогда b² = ac
6 x 6 = 3 xc

C = 36/3

= 12

Таким образом, третье, пропорциональное 3 и 6, равно 12

Пример 5

Вычислить среднее пропорциональное между 3 и 27

Пояснение

Пусть среднее пропорциональное между 3 и 27 будет m.
Применяя формулу b² = ac; ‘

Следовательно, mxm = 27 x 3 = 81

m ² = 81
⇒ m = √81
⇒ m = 9
Следовательно, среднее значение, пропорциональное между 3 и 27, равно 9

Пример 6

Учитывая отношения a: b = 4: 5 и b: c = 6: 7, определите соотношение a: b: c.

Объяснение

Так как b является общим членом между двумя отношениями;
Умножьте каждый член первого отношения на значение b второго отношения;

a: b = 4: 5 = 24:30,

Также умножьте каждый член во втором соотношении на значение b в первом соотношении;

b: c = 6: 7 = 30: 35

Следовательно, соотношение a: b: c = 24:30:35

Золотое сечение

Самым большим применением пропорции является золотое сечение , который очень помог в анализе пропорций различных объектов и искусственных систем, таких как финансовые рынки.Считается, что эти две величины находятся в золотом сечении, если их отношение равно отношению их суммы к большей из двух величин, т.е. (a + b) / a = a / b, где a> b> 0.

Это соотношение обозначается греческой буквой φ. Дальнейшее упрощение этого уравнения дает φ ² — φ — 1 = 0. Решая это с помощью квадратной формулы, мы получаем φ = 1.6180339887…

Евклид и многие математики после него работали над золотым сечением и нашли его в правильном пятиугольнике и золотом прямоугольнике.

Практические вопросы

1. Определите значение пропущенной буквы в каждой из следующих пропорций.

а. 6: 9 = h: 15

б. т: 7 = 12: 21

в. 4: у = 8: 14

д. d: 3 = 0,4: 0,5

д. 1/3 ∶ 1/4 = 1/9:

ф. 9: k = 6: 10

г. 2: 7 = м: 42

ч. 30: 25 = 42: r

i. x: 1,5 = 6,3: 4,5

2. Учитывая первый, второй и четвертый члены в пропорции 9, 21 и 77 соответственно.Вычислите значение третьего члена.

3. Стоимость 4 кг риса 28 долларов США. Найдите стоимость 20 кг риса.

4. Отношение длины цветника к ширине 3/2. Рассчитайте длину цветника, если ширина 36 м.

5. В церковном хоре должны быть сформированы группы из мужчин и женщин. Если каждая группа должна состоять из 6 женщин и 4 мужчин. Сколько мужчин нужно, если в церкви 102 женщины?

Ответы

а. 10

б. 4

г. 7

г. 2.4

e. 1/12

ф. 15

г. 12

ч. 35

и. 2.1

2. 33

3. $ 140

4. 54 м

5. 68

Предыдущий урок | Главная страница | Следующий урок

Соотношение или пропорция?

Вы когда-нибудь задумывались о том, что на самом деле означают эти два слова? Они часто используются вместе как фраза «соотношение и пропорция», но действительно ли это разные термины для одного и того же математического понятия? Если ученик спросит, в чем разница, как вы ответите?

Должен признать, что я сознательно не задумывался о точном значении соотношения или пропорции, пока не начал свою педагогическую подготовку.Я подозреваю, что это не станет особенным сюрпризом, но стоит ли мне беспокоиться об определениях этих терминов? Одна из трудностей, с которыми мы часто сталкиваемся в классе, — это знакомство детей с математическим определением слова, которое также
используется в повседневном языке. Возможно, это в какой-то мере относится к соотношению и пропорции? Где-то в глубине души я, кажется, помню, как мне говорили, что соотношение сравнивает часть с частью, тогда как пропорция сравнивает часть с целым. Но что это на самом деле означает? Это полезно? И это вся история?

Давайте сначала посмотрим на соотношение.На мой взгляд, соотношение — это сравнение двух или более величин. Согласно Оксфордскому словарю английского языка онлайн, соотношение — это «отношение между двумя одинаковыми величинами в отношении количества, определяемое количеством раз, когда одна содержит другую (целиком или дробно)». Например, на бутылке апельсина
сквош можно сказать «разбавьте одну часть концентрата на четыре части воды». Требуемое количество воды выражается в количестве концентрата. Национальная система счета предполагает, что при первом знакомстве с детьми эту идею можно было бы лучше выразить как «на каждую 1 часть концентрата нам нужно 4 части воды».Это соотношение можно проиллюстрировать очень
четко используя простые картинки:

В классе «для каждого» можно смоделировать, на самом деле нарисовав 4 «прямоугольника воды» рядом с каждым «прямоугольником концентрата», чтобы ученики могли решить, сколько частей воды необходимо для определенного количества частей концентрата. Затем на более высоком уровне они смогут подтвердить, действительно ли данное графическое изображение
описывает такое же соотношение. Конечно, оранжевые и белые фишки или кубики были бы другим способом изобразить концентрат и воду.Значит, это не слишком большой прыжок — ввести немного другой словарный запас для одного и того же? «4 на каждую 1» также можно выразить как «4 на каждую 1».

В ходе обсуждения с коллегами мы также поняли, что, когда мы говорим о соотношениях, совершенно уместно игнорировать единицы измерения. Можно сказать, что соотношение яблок к грушам составляет 3: 1, и это идет вразрез с единообразием единиц. Неужели это может только усложнить понимание соотношения?

Математические словари часто включают слово «дробь» в определение соотношения.Например, Математический словарь, опубликованный McGraw-Hill (2003), определяет соотношение двух величин, A и B, как «их частное или дробное A / B». Так как же пропорции соотносятся с этим? Система счисления показывает, что к концу 6-го класса дети должны уметь «относить дроби к
простые пропорции ». Получается, что дроби тоже связаны с пропорцией.

Снова заглянув в Оксфордский словарь английского языка, мы находим пропорцию, определяемую как «часть или часть в ее отношении к целому; сравнительная часть, доля; иногда просто, часть, разделение, часть ».На первый взгляд, это согласуется с моей первоначальной догадкой. Если мы посмотрим на изображение выше, то сможем описать ту же ситуацию с точки зрения пропорции: есть 1 часть концентрата.
через каждые 5 частей. Иными словами, можно сказать, что 1 из каждых 5 частей — это концентрат. На этот раз мы относим количество концентрата (1 часть) к целому (5 частей).

Однако, если мы снова обратимся к математическому словарю, нам скажут, что «пропорция двух величин есть их отношение» (McGraw-Hill, 2003).Математический словарь Коллинза (2002) расширяет эту небольшую схему пропорции как «отношение между четырьмя числами или величинами, в которых отношение первой пары равно отношению второй пары». Я думаю это последнее
математическое определение может включать в себя мое повседневное использование слова «пропорция», и это вовсе не сравнение части с целым.

Что это нам дает? Я с трудом могу сделать какие-либо выводы из вышеизложенного — границы между ними кажутся мне очень размытыми.В лучшем случае я доволен своим пониманием соотношения, но, похоже, слово пропорция используется двумя разными способами. Мне бы очень хотелось услышать ваши собственные мысли по этому поводу, которые я хотел бы добавить в эту статью. Возможно, у вас есть четкие определения в вашем
собственный разум, который может помочь?

Если вы можете пролить свет на «соотношение и пропорции», сообщите нам об этом по электронной почте [email protected]

Артикул:

Borowski, E. J. & Borwein, J. M. eds (2002) Dictionary of Mathematics.Глазго: Издательство Харпер Коллинз.

DfEE (1999) Основы национальной стратегии счета для обучения математике от приема до 6-го класса. Садбери: DfEE.

Геллер, Э. ред (2003) Математический словарь. Нью-Йорк: McGraw-Hill Education.

Обратная связь

Спасибо Филу Уэсту, учителю средней школы MEF в Стамбуле, который прислал нам свои комментарии о соотношении и пропорциях. Щелкните здесь, чтобы прочитать, что сказал Фил.

Вероника Бейтс из Колчестера также прислала нам свои мысли, которые вы можете прочитать здесь.Большое спасибо.

Спасибо также Брюсу Муди из Новой Зеландии, который внес эти идеи.

Дебби Санджая, из Индонезии, написала по электронной почте:

Я просто хочу поделиться своим пониманием. Я думаю, что пропорция — это отношение количества части к целому ». Она предполагает, что пропорция отличается от отношения в том, что« … пропорция не может быть меньше 0: 1 и не может быть больше. чем 1: 1.

Кто-то, кто остался анонимным, написал:
Я бы сказал, отношение — это часть к части, а пропорция — это часть к целому.Они означают разные вещи.

Что такое соотношение 25%? Я бы сказал, что это 1: 3. Остальные утверждают, что это 1: 4. Я не согласен.

Я утверждаю, что соотношение составляет 1 к 3 или 1: 3, а соотношение — 1 к 4. «:» означает, а не входит «.

Марк также отправил нам электронное письмо. Вы можете прочитать то, что он сказал здесь.

Джон Блок написал:

Греки считали, что все величины рациональны (обратите внимание на корень слова «ratio») и могли быть записаны в форме A / B, где A и B — относительно простые целые числа.Это понимание, кажется, указывает на определение соотношения в Математическом словаре как A / B.

Пропорциональная или пропорциональная ситуация возникает, когда две вещи связаны таким образом, что отношения соответствующих частей равны. Тогда может показаться, что Математический словарь Коллинза дает лучшее определение: «… отношение первой пары равно отношению второй пары». Это также, кажется, подчеркивает важность сходства между объектами или ситуациями.

Тем не менее, есть некоторая двусмысленность в использовании слова «пропорция». Например, две ситуации могут быть обратно пропорциональными, тогда A / B не = k, но AB = k. Возможно, это просто неправильное употребление слова «пропорциональный». Тем не менее, «пропорциональный» в описании всегда считается «прямо» пропорциональным, если не присутствует другое слово «обратно». Я думаю соразмерность
а способность математически выражать пропорциональность — основная идея математического образования учащихся.

Еще одна тесно связанная тема — ставка или удельная ставка. Ставка — это соотношение? Не с точки зрения согласованности единиц, а с точки зрения соразмерности ситуаций. Разве 80 км / 1 час не то же самое, что 160 км / 2 часа? Или в задаче 80 км / 1 час = x км / 2 часа? Представление оценок как соотношений, которые вписываются в модель пропорций, помогает учащимся решать задачи, связанные с оценками.

Хелен Лорд написала:
Привет, я прочитала вашу статью с интересом — способ, которым я пришел к соглашению с этими двумя, в моей голове, заключается в том, что соотношение фокусируется на соотношении разделения целого на части, в то время как пропорция показывает ‘разрыв ‘- или’ промежуток между ‘, который необходимо сохранить — почти как если бы он обеспечивает след или параллельные линии, по которым фигуры должны двигаться, чтобы поддерживать свои отношения — я далеко от
отметка?

Рут Кэмпбелл, студентка программы PGCE по математике в Лестерском университете, написала по электронной почте:
Я бы сказал, что отношение — это отношение между двумя величинами. Пропорция — это подмножество этого, поскольку две величины являются частью и целым одного и того же. Концепция пропорциональности расширяет эту идею на любые две величины, которые имеют постоянное мультипликативное отношение. Это, очевидно, ближе к использованию пропорции, чем пропорции, но слово «рациональный» уже было
выделено в другом месте. Таким образом, соотношение теперь является лишь одним из способов представления пропорциональных отношений, другими способами являются дроби, уравнение, график, столбчатая диаграмма и т. Д.

Как научить пропорциям в 7-8 классах по математике

Вы здесь: Главная → Статьи → Соотношения и пропорции обучения

Часто ученики учатся решать пропорции, запоминая шаги, но они также забывают их в мгновение ока после окончания школы.Они могут слабо вспомнить кое-что о крестовом умножении, но это все, что нужно. Как мы, преподаватели, можем помочь им научиться решать пропорции и запоминать их?

Пропорции и пропорции НЕ являются выходом из математики

На самом деле это не так. Мы используем их постоянно, осознаем мы это или нет. Вы когда-нибудь говорили о скорости 55 миль в час? Или посчитайте, сколько времени нужно, чтобы куда-нибудь поехать с такой-то скоростью? Вы видели цены за единицу, такие как 1,22 доллара за фунт, 4 доллара за фут или 2 доллара.50 на галлон. Вы когда-нибудь задумывались, сколько что-то стоит с учетом цены за единицу или какова ваша ежемесячная оплата с учетом почасовой оплаты? Вы использовали соотношения (или ставки) и пропорции.

Какие пропорции?

Следующие две проблемы связаны с пропорцией:

Если 2 галлона бензина стоят 5,40 доллара, сколько будут стоить 5 галлонов?
Если автомобиль преодолевает определенное расстояние за 3 часа, какое расстояние он может проехать за 7 часов?

Общая идея этих задач состоит в том, что у нас есть две величины, которые обе изменяются с одинаковой скоростью .Например, в главной задаче у нас есть (1) бензин, измеренный в галлонах, и (2) деньги, измеренный в долларах. Мы знаем оба количества (и доллары, и галлоны) для в одной ситуации (2 галлона стоят 5,40 доллара), мы знаем ОДНО количество для другой ситуации ( либо долларов, долларов, либо галлон), и нам задают недостающее количество (в данном случае стоимость за 5 галлонов).

Вы можете составить таблицу для систематизации информации. Ниже длинная линия означает «соответствует», а не вычитанию.

Пример 1:

 2 галлона —— 5,40 доллара
5 галлонов —— x долларов

Пример 2:

 110 миль —— 3 часа
 x миль —— 4 часа

В обоих примерах две величины изменяются с одинаковой скоростью. Обе ситуации включают четыре числа, из которых три даны, а одно неизвестно. Как мы можем решить такие проблемы?

Многочисленные способы решения пропорции

На самом деле есть несколько способов найти ответ на вопрос о пропорции — все они включают пропорциональное мышление .

Если два галлона стоят 5,40 доллара и меня спрашивают, сколько стоят 5 галлонов, поскольку количество галлонов увеличилось в 2,5 раза, я также могу просто умножить доллары на 2,5.
Если два галлона стоят 5,40 доллара, я сначала подсчитываю, сколько стоит 1 галлон, а затем умножаю это на пять, чтобы получить стоимость 5 галлонов. Теперь 1 галлон будет стоить 5,40 доллара США ÷ 2 = 2,70 доллара США, а затем 2,70 доллара США × 5 = 13,50 доллара США.
Я могу написать пропорцию и решить ее крестным умножением:
5.40
2 галлона
= x
5 галлонов
После coss-умножения я получаю:
5,40 · 5 = 2 x
x = 5,40 · 5
2
= 13,50 долл. США
Я записываю пропорцию, как указано выше, но вместо перекрестного умножения я просто умножаю обе части уравнения на 5.
Я записываю пропорцию таким образом: (и это все еще работает, потому что вы можете записать два отношения для пропорции несколькими разными способами)
5. 40
x
= 2 галлона
5 галлонов

Я хочу сказать, что для решения задач, подобных приведенному выше, вам не нужно помнить, как написать пропорцию или как ее решить — вы ВСЕГДА можете решить их, просто используя здравый смысл и калькулятор.

Студенты тоже должны это понимать. Дайте им понять основную идею настолько хорошо, чтобы они могли решить проблемы пропорций без использования уравнения, если это необходимо.Тем не менее, я считаю, что вам также следует научить перекрестному умножению, поскольку это очень необходимый «трюк» или сокращение при решении уравнений.

Одна из основных идей, которая всегда работает для решения пропорций, — сначала найти единицу измерения, а затем умножить ее, чтобы получить то, что просят. Например: если автомобиль проезжает 110 миль за 3 часа, сколько он проедет за четыре часа? Сначала вычислите удельную стоимость (сколько машина уезжает за 1 час), затем умножьте это на 4.

Как научить пропорциям

Чтобы познакомить учащихся с пропорциями, дайте им таблиц с эквивалентными коэффициентами для заполнения, например, приведенную ниже.Это поможет им выучить пропорциональных рассуждений .

Мили

905 46 905 905 905 905 905 905 905 905 467 905 905 905 905 905 905 467 905 905 905 905 905 467 905 905 905 905 905 905 467

долларов	3.30
фунты	1		1	2	1

Работайте с этими таблицами (сначала используя простые числа), пока ученики не привыкнут к ним. Вы можете связать некоторые из них с жизненными ситуациями.Например, вы можете взять ситуацию из задачи о пропорциях слов в вашем учебном плане по математике и составить из нее эквивалентную таблицу ставок.

По мере продвижения дайте студентам заполнить таблицы с эквивалентными оценками, где «данность» находится посередине:

долларов

905 905 905 905 905 905 905 905 467 905 905 905 905 905 905 905 467 905 905 905 905 905 905 905 467

905 905 905 905 905 905 905 905 905 47 905 46 905 Часы

905 47

905 43 15. 50

905 905 905

долларов			1	2	3	4	5
Метры	0,10	0,20	0,30	0,40

Конечно, ученики должны заметить, что заполнить таблицу легко, если вы сначала определите ставку за единицу, а затем найдете другие суммы.

Следующий шаг: проблемы пропорций и мышление

Изучив таблицы с эквивалентными оценками, студенты готовы решать словесные задачи. Выбирайте сначала простые, и пусть думают! Они вполне могли бы придумать ответ самостоятельно, составив таблицу или вычислив удельную стоимость. Итак … вам на самом деле не нужно писать фактическую пропорцию, чтобы решить проблему со словом пропорции.

Однако я не хочу записывать уравнения или перекрестное умножение; студентам, изучающим алгебру и предалгебру, все еще необходимо научиться решать пропорции с помощью перекрестного умножения. Просто научиться пользоваться здравым смыслом еще важнее.

Определения

Вы заметили, что я не дал определений терминам соотношение и пропорция? Что ж, не хотелось путать. Иногда вам не нужно заучивать точные определения заранее, но вы можете начать с обучения решению словесных задач — даже проблем из реальной жизни.

СООТНОШЕНИЕ — это две «вещи» (числа или количества) по сравнению друг с другом. Например, «3 доллара за галлон» — это соотношение, а «40 миль в 1 час» — другое.Вот еще несколько: 15 девочек против 14 мальчиков, 569 слов за 2 минуты, 23 зеленых шара против 41 синего шара. В вашем учебнике по математике может быть сказано, что это сравнение двух чисел или количественных величин.

Связанный термин, СТАВКА, определяется как отношение, в котором две величины имеют разные единицы. Некоторые люди различают и говорят, что у двух величин в соотношении должно быть одинаковых единиц ; некоторые люди не делают различий и позволяют также называть «3 доллара за галлон» соотношением.

ПРОПОРЦИЯ — это уравнение, в котором два соотношения равны. Например, «3 доллара за галлон» равняется «6 долларам за два галлона». Или 2 учителя на 20 учеников равны 3 учителям на 30 учеников. Или

3 литра

48 квадратных метров

10 литров

160 квадратных метров

Конечно, чтобы это была проблема , вам нужно сделать одно из этих четырех чисел неизвестным (не дано).

См. Также

Рабочие листы со свободными пропорциями
Бесплатные рабочие листы для простых задач со сложными пропорциями.

Мои варианты колледжа — пропорции, пропорции и вариации

Концепции соотношений, пропорций и вариаций, которые основываются друг на друге, предполагают изменение. Коэффициенты используются для сравнения двух величин. Пропорции — это просто заявления о равенстве, включающие соотношения, а вариации включают задачи, записанные в виде пропорций.

Передаточные числа

Вы можете этого не осознавать, но используете коэффициенты каждый день. Например, когда вы говорите о скорости движения автомобиля 45 миль в час, вы говорите о соотношении пройденного расстояния и времени. Коэффициенты используются для сравнения двух величин. Обычно они записываются одним из двух способов: дробью или двоеточием (:). Соотношение, читаемое как «4 к 10», может быть записано как 4/10 или как 4: 10. Соотношение, выражающее отношение между днем и неделей, может быть записано как 1/7 или 1: 7, потому что в нем 7 дней. неделя.

Имейте в виду, когда вы записываете соотношение в виде дроби, это не дробь в истинном смысле этого слова (то есть часть над целым).

Пропорции

Пропорция — это математическое выражение, приравнивающее два отношения. Два отношения называются равными, если в дробной форме дроби являются эквивалентными дробями. Вы можете сравнивать и решать отношения, используя перекрестное умножение. Если перекрестные произведения равны, отношения равны.

При решении вопроса о пропорциях вы захотите переписать пропорции в дробном формате.Давайте посмотрим на пример:

Обратите внимание, что в приведенном выше примере вы также могли бы решить эту проблему наблюдением, если бы узнали, что 4/12 — это просто 1/3. Одна треть от 6 — 2. Наблюдения, подобные этому, позволят значительно сэкономить время на экзамене, но при решении более сложных задач важно знать основы.

Варианты

Варианты имеют дело с объяснением на математическом языке того, как одна величина изменяется по отношению к одной или нескольким другим величинам.Есть два основных типа вариации: прямая вариация и обратная вариация. Сначала мы рассмотрим их, а затем рассмотрим два расширения этих концепций: совместное изменение и комбинированное изменение.

Прямое изменение

Давайте посмотрим на пример прямого изменения. Количество муки, необходимое для приготовления хлеба, зависит от количества выпекаемых буханок. Для приготовления большего количества буханок потребуется больше муки; для приготовления меньшего количества буханок потребуется меньше муки. В прямом варианте переменные (количество муки и количество буханок в нашем примере) будут двигаться в одном направлении.

Задачи, связанные с прямым изменением, можно решить с помощью пропорций. Давайте посмотрим на это в действии:

Если для покрытия 100 квадратных футов требуется 3 галлона краски, сколько галлонов краски потребуется для покрытия 600 квадратных футов?

Задача дает нам соотношение 3 галлона краски для покрытия 100 квадратных футов. Мы можем использовать эту информацию, чтобы установить нашу пропорцию:

Перемножьте и решите для x:

Когда мы говорим « y прямо пропорционально x », мы также можем написать:

В приведенном выше уравнении k называется постоянной вариации.В примере с краской количество галлонов краски напрямую зависит от площади, которую нужно покрыть. Постоянная вариации 3/100. Тогда у вас будет:

Обратная вариация

Когда две переменные или величины изменяются в противоположных направлениях, происходит обратное изменение. Давайте посмотрим на пример: время, необходимое для покраски дома, зависит от количества людей, выполняющих эту работу.

В этом примере время, необходимое для покраски дома, обратно пропорционально количеству людей, которые рисуют.Это означает, что чем больше людей красит дом, тем меньше времени уйдет на покраску. Когда мы говорим « y изменяется обратно пропорционально x «, мы можем выразить это как:

Еще раз, k — постоянная вариации. Мы можем найти k , переставив формулу как k = xy. Таким образом, k — это просто произведение известных значений двух переменных. Рассмотрим следующий пример:

В конкретном отеле работает обслуживающий персонал из 12 сотрудников, и они обычно могут убрать все гостиничные номера за 6 часов.Если четверо охранников сегодня не на работе, сколько времени потребуется оставшимся охранникам, чтобы убрать все номера в отеле?

В этом примере общее время, необходимое для выполнения задания, обратно пропорционально количеству рабочих. Константа вариации, k , просто равна 6 • 12 = 72. Мы хотим знать, сколько часов потребуется остальным хранителям для выполнения работы. Поскольку 4 отсутствуют, остается 8 рабочих (12 — 4 = 8).

Таким образом, мы можем решить проблему, как описано ниже:

Правильный ответ — 9 часов.

Вариант шарнира

Совместное изменение — это просто продолжение прямого изменения. Когда мы говорим, что « y изменяется вместе с x и z », мы имеем пример вариации сустава. Это можно записать как:

Опять же, k — это постоянная вариации, просто отношение y к x и z ( x умножить на z ) Вот пример:

Переменная y изменяется вместе с x и z .Значение y равно 12, когда x равно 4, и z равно 8. Что такое y , когда x = 6 и z = 10?

Поскольку довольно ясно, что у нас есть проблема вариации сустава, мы решаем для k , подставляя известные переменные ( y = 12, когда x равно 4 и z равно 8) в наше уравнение вариации сустава:

Как только у нас есть значение для, мы вставляем его обратно в уравнение совместной вариации вместе с переменными, которые мы знаем, и решаем для нашего неизвестного:

Комбинированная вариация

Комбинированная вариация включает как прямую, так и обратную вариацию.Например, если мы говорим: « y напрямую изменяется с x и обратно пропорционально z », мы сталкиваемся с комбинированным изменением. Это можно записать так:

Рассмотрим следующий пример:

На раскрашивание 100 футов 6 футов 3 человека требуется 2 часа. ограждение. Если предположить, что каждый человек способен рисовать с одинаковой скоростью, сколько времени потребуется 12 людям, чтобы нарисовать 1 800 футов одного и того же ограждения?

Общее время ( t ), необходимое для покраски секции ограждения, прямо пропорционально длине забора ( l ) и обратно пропорционально количеству людей ( n ), которые красят.(Обратите внимание, мы используем разные буквы для наших переменных, но это не имеет значения!).

Действия такие же, как и в других примерах задач. Сначала мы определяем постоянную вариации, k .

Теперь, когда у нас есть k , мы подставляем его в уравнение и решаем отсутствующую переменную:

Правильный ответ — 9 часов.

Примеры

В классе Тайлера 14 мальчиков и 16 девочек.Какое соотношение лучше всего отражает соотношение между количеством мальчиков и количеством учеников в классе Тайлера?
Если отношение A к B составляет 3: 4, а отношение B к C равно 2: 3, каково значение A, когда C равно 5?

Ответы и пояснения

Правильный ответ — C. Очень важно внимательно прочитать этот вопрос, так как легко допустить ошибку по неосторожности.В вопросе указывается количество мальчиков (14) и количество девочек (16), но при этом запрашивается соотношение между количеством мальчиков (14) и общим количеством учеников (14 + 16 = 30). Подлый. Само соотношение может быть записано в дробном формате (14/30) или 14:30. Однако ни один из этих вариантов не является выбором, поэтому вам нужно уменьшить, чтобы найти ответ, вариант C, который можно было бы так же легко записать как 7: 15. Вы заметите, что варианты также включают варианты соотношения мальчиков и девочек (варианты A и D) и отношения девочек к общему количеству (вариант E).Концептуально это не сложный вопрос, но его легко упустить, если вы не уделяете достаточно внимания!
Правильный ответ — C. Вам даны два отдельных отношения с одной общей переменной (B). Вам нужно будет их объединить. Если отношение A к B составляет 3: 4, а B к C равно 2: 3, общая переменная должна быть одинаковой в обоих отношениях для объединения. Если вы умножите B и C на 2 во втором соотношении, оно на самом деле не изменится — 2: 3 то же самое, что 4: 6, — но теперь вы можете объединить эти два отношения, чтобы получить соотношение A к B и C 3: 4: 6.Удалите B, и вы получите отношение A к C, или 3: 6. Чтобы определить, каким было бы A, если бы C было 5, установите его как пропорцию и умножьте крест-накрест: 32/6 = x /5. Найдите пропущенное значение: 3 • 5 = 6 • x , поэтому 15 = 6 x , и, таким образом, x = 15/6 = 5/2.

Дополнительные ресурсы

Как решить пропорцию — Полный курс арифметики

(Евклид, VII.17.)

Мы уже видели, что соотношение будет сохранено, если мы разделим оба члена на одно и то же число.

Пример 5. Заполните эту пропорцию:

6: 7 =? : 28

Решение . 7 умножили на 4, чтобы получить 28. Следовательно, 6 также нужно умножить на 4:

6: 7 = 24: 28.

Чтобы решить эту пропорцию —

6: 7 =? : 28

— можно сказать:

«7 четыре раза преобразуется в 28. Четыре раза 6 равно 24.«

Все примеры и задачи в этом уроке должны быть простыми мысленными вычислениями.

Пример 6. Решите эту пропорцию:

2: 3 = 12:?

Решение . «2 переходит в 12 шесть раз. Шесть умноженное на 3 равно 18.»

2: 3 = 12: 18

Фактически, рассмотрите эти столбцы, кратные 2 и 3:

2 3

4 6

6 9

8 12

10 15

12 18

14 21

И так далее.

Итак, 2 составляет две трети от 3. (Урок 17.) И каждое кратное 2 составляет две трети от таких же кратных 3:

4 — это две трети от 6.

6 — это две трети от 9.

8 — это две трети от 12.

И так далее. Фактически, это единственные натуральные числа, в которых первое будет составлять две трети второго.

Обратите внимание, что каждая пара имеет общий делитель. И при делении на этот делитель частные в каждом случае равны 2 и 3.Это теорема об общем делителе. 2 и 3 — самые низкие члены. Это наименьшие числа, которые имеют отношение «две трети».

Пример 7. Назовите три пары чисел, первая из которых составляет три пятых второй.

Решение . Элементарная пара — это 3 и 5. Чтобы сгенерировать другие, возьмите одно и то же число, кратное обоим: 6 и 10, 9 и 15, 12 и 20 и так далее.

Пример 8. 27 — это три четверти какого числа?

Решение .Пропорционально:

3: 4 = 27:?

«27 будет девять умножить на 3. Девять умноженное на 4 равно 36».

3: 4 = 27: 36

27 составляет три четверти от 36.

Только , кратное 3 , может быть тремя четвертями другого числа, которое должно быть таким же , что и кратным 4.

Так же, как 3 равно 4, любое количество тройок равно количеству четверок.

Пример 9.Решите эту пропорцию:

9: 45 = 2:?

Решение . Здесь надо смотреть прямо:

9 — пятая часть от 45. И 2 — пятая часть от 10.

9: 45 = 2: 10.

Пример 10. Общий делитель. Заполните эту пропорцию:

12: 200 =? : 100.

Решение . С другой стороны, мы видим, что 200 было разделено на на 2.Следовательно, 12 также необходимо разделить на 2.

12: 200 = 6: 100.

Вместо деления 12 и 200 на 2 мы можем взять половину. Половина 200 — 100. Половина 12 — 6.

Мы видим, что если мы знаем три члена пропорции, то всегда можем решить четвертое. Это называется Правило трех. Мы можем резюмировать это следующим образом.

1-й: 2-й = 3-й: 4-й.

•	Если 4-й член неизвестен, а 3-й член является кратным или частью 1-го (Пример 6), , то 4-й член должен быть таким же кратным или частью 2-го.
	(Аналогично, если 3-й член неизвестен, а 4-й член кратен 2-му; Пример 5)

•	Если 4-й член неизвестен, а 2-й член является кратным или частью 1-го (Пример 9), , то 4-й член должен быть таким же кратным или частью 3-го.

Мы применим это правило, чтобы найти, какой процент одно число от другого.

Что касается теоремы об общем делителе , это то, что мы называем симметричной версией теоремы об одном и том же кратном. Для этой доли

6 равно 100, как 12 равно 200,

, в котором 3-й и 4-й члены появляются как двойники 1-го и 2-го, логически эквивалентно этой пропорции,

12 равно 200 как 6 равно 100,

, в котором 3-й и 4-й члены появляются как половинки 1-го и 2-го.

Пример 11. В классе соотношение девочек и мальчиков составляет 3: 4.

Есть 24 мальчика. Сколько там девушек?

Решение . Пропорционально

Девочки: Мальчики = 3: 4 =? : 24.

Обратите внимание, что 24 соответствует Мальчикам.

Итак, 4 переходит в 24 шесть раз. Таким образом, количество девушек в шесть раз больше 3: 18 .

Это еще один способ приблизиться к Примеру 7 предыдущего урока. И следующий пример — это еще один способ приблизиться к Примеру 8 этого Урока.

Пример 12. Целое равно сумме частей. В классе количество девочек составляет 75% от количества мальчиков. Всего обучается 35 человек. Сколько девочек и мальчиков?

Решение . Сказать, что девочки составляют 75% — три четверти — мальчиков,

означает, что соотношение девочек и мальчиков составляет 3: 4.Но это означает, что 3 из каждых 7 студентов — девочки (3 + 4 = 7), а 4 из каждых 7 — мальчики.

Следовательно, формируем пропорцию:

девочек: общее количество студентов =

3: 7 =? : 35.

Поскольку 35 равно 5 × 7, пропущенный член равен 5 × 3 = 15.

Всего 15 девушек. Итак, есть 20 мальчиков.

На этом этапе, пожалуйста, «переверните» страницу и выполните несколько задач .

или

Введение | Главная | Содержание

Вопросы или комментарии?

Эл. Почта: [email protected]

Справка по пропорциям — WebMath

Быстро! Мне нужна помощь с:
Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DividingFractions, MultiplyingFractions, SubplicationFractions are, SubplicationFractions , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, Equation from slope и y-intLines, The Equation from two pointsLodsottery Практика многочленов Математика, Практика основ , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители с GCF Полиномы, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, РазделениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Методы Правые треугольники, Ветер, рисунок

Составить пропорцию

составить пропорции из отношений 2) 14:21 8:14 15:10 27:18 18:24 36:54 20:35 6:8

Как составить и рассчитать пропорцию: онлайн калькулятор

Онлайн калькулятор пропорций

Формула пропорций

Основные свойства пропорции

Решение пропорции с одним неизвестным | Уравнение

Как посчитать пропорцию

Отношения и пропорции в математике

Два равных отношения образуют пропорцию

Произведение средних членов пропорции

Урок 8. обобщение и систематизация знаний по теме «отношения и пропорции» — Математика — 6 класс

Пропорции математика. Пропорция – это равенство двух отношений. Соотношение.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Арифметика

Пропорции, члены пропорции. Основное свойство пропорции

Производные пропорции

Свойства равных отношений

Как вычислять соотношения и пропорции в математике

Соотношения и пропорции

Как вычислить соотношения

Как рассчитать пропорцию

Что такое константа пропорциональности?

Пропорции — объяснение и примеры

Что такое пропорция?

Как решить пропорции?

Золотое сечение

Соотношение или пропорция?

Артикул:

Как научить пропорциям в 7-8 классах по математике

Пропорции и пропорции НЕ являются выходом из математики

Какие пропорции?

Многочисленные способы решения пропорции

Как научить пропорциям

Следующий шаг: проблемы пропорций и мышление

Определения

См. Также

Мои варианты колледжа — пропорции, пропорции и вариации

Передаточные числа

Пропорции

Варианты

Прямое изменение

Обратная вариация

Вариант шарнира

Комбинированная вариация

Дополнительные ресурсы

Как решить пропорцию — Полный курс арифметики

Справка по пропорциям — WebMath

Добавить комментарий Отменить ответ