Содержание
Простые и Составные Числа
Основные определения
Натуральные числа больше единицы бывают простые и составные.
Простое число — это натуральное число больше 1, у которого есть всего два делителя: единица и само число.
Например:
- 11, 13, 17, 19 — список простых чисел.
- 11 — делится только на 1 и 11.
- 13 — делится на 1 и 13.
- 17 — делится на 1 и 17.
Составное число — похоже на простое. Это точно такое же натуральное число больше единицы, которое делится на единицу, на само себя и еще хотя бы на одно натуральное число.
Например:
- 9, 10, 12, 14 — список составных чисел.
- 9 — делится на 1, на 3 и на 9.
- 10 — делится на 1, на 2, на 5 и на 10.
- 12 — делится на 1, на 2, 3, 4, 6 и на 12.
Число 1 — не является ни простым, ни составным числом, так как у него только один делитель — 1. Число 2 — первое наименьшее простое, единственное четное, простое число. Все остальные — нечетные. Число 4 — первое наименьшее составное число. |
Именно этим оно отличается от всех остальных натуральных чисел.В математике есть первые простые и составные числа, но последних таких чисел не существует.
А еще не существует простых чисел, которые оканчиваются на 4, 6, 8 или 0. В числе простых есть только одно число, которое заканчивается на 2 — и это само число 2. Из оканчивающихся на 5 — число 5. Все остальные оканчиваются на 1, 3, 7 или 9, за исключением 21, 27, 33 и 39.
Таблица простых чисел до 1000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 |
| 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 |
| 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 |
| 257 | 263 | 269 | 271 | 277 | 281 | 283 | 293 | 307 |
| 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 | 419 |
| 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 |
| 647 | 653 | 659 | 661 | 673 | 677 | 683 | 691 | 701 |
| 709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 |
| 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 |
| 887 | 907 | 911 | 919 | 929 | 937 | 941 | 947 | 953 |
| 967 | 971 | 977 | 983 | 991 | 997 |
Урок 41.
простые и составные числа — Математика — 5 класс
Математика
5 класс
Урок №41
Простые и составные числа
Перечень рассматриваемых вопросов:
— простые и составные числа;
— признаки делимости.
Тезаурус
Простым числом называют такое натуральное число, которое больше 1 и делится только на 1 и само на себя.
Составные числа – это непростые натуральные числа больше единицы
Обязательная литература
1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС//С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 кл.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014.
– 95 с.
Теоретический материал для самостоятельного изучения
Посмотрите, на какие числа можно разделить 2 и 10.
Число 2 делится на 1 и 2.
Число 10 делится на 1, 2, 5 и 10.
По тому, на какие числа делятся натуральные числа, их можно классифицировать на простые и составные. Сегодня мы выясним, какими способами можно определить, является данное число простым или составным. Начнём с определения простых и составных чисел.
Простым числом называют такое натуральное число, которое больше 1 и делится только на 1 и само на себя.
Например, это числа 2, 3, 5 и т. д.
Составные числа – это непростые натуральные числа больше 1, Например, числа 4 и 15.
4 делится на 1, 2, 4.
15 делится на 1, 3, 5 и 15.
Важно знать, что 1 – это не простое и не составное число.
Простых и составных чисел очень много. Множество натуральных чисел состоит из простых чисел, составных чисел и единицы.
В ряду простых чисел существует самое первое число – это 2, но самого последнего нет.
Самое первое натуральное составное число – это 4, а самого последнего нет.
Так как простых чисел много, то для удобства составляют таблицу простых чисел. В качестве примера приведём её часть, где представлены все простые числа от 2 до 503.
Ответим с помощью неё на следующий вопрос.
Простым или составным является число 159?
Посмотрим в таблицу простых чисел, этого числа там нет, следовательно, 159 – составное число.
Выполним ещё одно задание.
Разложим составное число 234 на простые множители. Для этого воспользуемся признаками делимости на 2, 3.
Решение:
234 : 2 = 117
117:3 = 39
39: 3 = 13 – простое число.
Следовательно, число 234 можно разложить на простые множители следующим образом:
234 = 2· 3 · 3 ·13
Простые числа учёные пытались найти ещё в Древней Греции. Так, во II веке до н.э. Эратосфен составил алгоритм нахождения простых чисел до некоторого целого числа. Этот алгоритм назвали «решето Эратосфена».
Суть заключается в том, что путём отсеивания составных чисел определяются простые. Опишем этот алгоритм нахождения простых чисел от 1 до 100.
Для начала запишем все числа от 1 до 100.
1 вычеркнем, т. к. это число не простое и не составное. Выделим 2 – это первое простое число – и далее вычеркнем все кратные ему числа до ста (4, 6, 8 и т. д., то есть каждое второе число). Далее отметим следующее простое число – это 3. Вычеркнем все кратные ему числа до ста (6, 9, 12 и т. д., то есть каждое третье число).
Повторяем все шаги пока возможно с остальными простыми числами. В результате получается искомая таблица простых чисел.
Тренировочные задания.
№ 1. Какую из цифр 2,3,1 нужно подставить в число 2_ вместо пропуска, чтобы получить простое число?
Решение. Для решения этой задачи достаточно посмотреть на таблицу простых чисел, из приведённых цифр подходит только 3, т.е. искомое простое число – 23.
Ответ: 3.
№ 2. Подчеркните то число, которое делится одновременно на простые числа 5 и 7.
Варианты ответа: 35; 50; 21.
Решение. Найдём делители каждого из чисел:
35 = 5· 7;
50 = 5· 2 · 5;
21 =7 · 3.
К данному условию подходит только число 35, т.к. только оно имеет делитель и 5, и 7 одновременно.
Ответ: 35.
примеры, таблица простых чисел, решето Эратосфена
В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.
Простые и составные числа – определения и примеры
Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.
Определение 1
Простыми числами называют целые числа, которые больше единицы и имеют два положительных делителя, то есть себя и 1.
Определение 2
Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.
Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.
Определение 3
Простые числа – это натуральные числа, имеющие только два положительных делителя.
Определение 4
Составное число – это натуральное число, имеющее более двух положительных делителей.
Любое число, которое больше 1 является либо простым, либо составным. Из свойства делимости имеем, что 1 и число а всегда будут делителями для любого числа а, то есть оно будет делиться само на себя и на 1. Дадим определение целых чисел.
Определение 5
Натуральные числа, которые не являются простыми, называют составными.
Простые числа: 2, 3, 11, 17, 131, 523. Они делятся только сами на себя и на 1. Составные числа: 6, 63, 121, 6697. То есть число 6 можно разложить на 2 и 3, а 63 на 1, 3, 7,9, 21, 63, а 121 на 11, 11, то есть его делители будут 1, 11, 121. Число 6697 разложится на 37 и 181. Заметим, что понятия простых чисел и взаимно простых чисел – разные понятия.
Таблица простых чисел
Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:
Таблица для всех существующих натуральных чисел нереальна, так как их существует бесконечное множество. Когда числа достигают размеров 10000 или 1000000000, тогда следует задуматься об использовании решета Эратосфена.
Рассмотрим теорему, которая объясняет последнее утверждение.
Теорема 1
Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.
Доказательство 1
Возьмем, что а является натуральным числом, которое больше 1, b является наименьшим отличным от единицы делителем для числа а. Следует доказать, что b является простым числом при помощи метода противного.
Допустим, что b – составное число. Отсюда имеем, что есть делитель для b, который отличен от 1 как и от b. Такой делитель обозначается как b1. Необходимо, чтобы условие 1<b1<b было выполнено.
Из условия видно, что а делится на b, b делится на b1, значит, понятие делимости выражается таким образом: a=b·q и b=b1·q1, откуда a= b1·(q1·q), где q и q1являются целыми числами. По правилу умножения целых чисел имеем, что произведение целых чисел – целое число с равенством вида a=b1·(q1·q). Видно, что b1– это делитель для числа а. Неравенство 1<b1<b не соответствует, потому как получим, что b является наименьшим положительным и отличным от 1 делителем а.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Теорема 2
Простых чисел бесконечно много.
Доказательство 2
Предположительно возьмем конечное количество натуральных чисел n и обозначим как p1, p2, …, pn. Рассмотрим вариант нахождения простого числа, отличного от указанных.
Примем на рассмотрение число р, которое равняется p1, p2, …, pn+1. Оно не равняется каждому из чисел, соответствующих простым числам вида p1, p2, …, pn. Число р является простым. Тогда считается, что теорема доказана. Если оно составное, тогда нужно принять обозначение pn+1и показать несовпадение делителя ни с одним из p1, p2, …, pn.
Если это было бы не так, тогда, исходя из свойства делимости произведения p1, p2, …, pn, получим, что оно делилось бы на pn+1. Заметим, что на выражение pn+1делится число р равняется сумме p1, p2, …, pn+1. Получим, что на выражение pn+1должно делиться второе слагаемое этой суммы, которое равняется 1, но это невозможно.
Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел.
Отсюда следует, что простых чисел бесконечно много.
Так как простых чисел очень много, то таблицы ограничивают числами 100, 1000, 10000 и так далее.
Решето Эратосфена
При составлении таблицы простых чисел следует учитывать то, что для такой задачи необходима последовательная проверка чисел, начиная с 2 до 100. При отсутствии делителя оно фиксируется в таблицу, если оно составное, то в таблицу не заносится.
Рассмотрим пошагово.
Если начать с числа 2, то оно имеет только 2 делителя: 2 и 1, значит, его можно занести в таблицу. Также и с числом 3. Число 4 является составным, следует разложить его еще на 2 и 2. Число 5 является простым, значит, можно зафиксировать в таблице. Так выполнять вплоть до числа 100.
Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.
Способ при помощи решета Эратосфена считают самым удобным.
Рассмотрим на примере таблиц, приведенных ниже. Для начала записываются числа 2, 3, 4, …, 50.
Теперь необходимо зачеркнуть все числа, которые кратны 2. Произвести последовательное зачеркивание. Получим таблицу вида:
Далее вычеркиваем все числа, кратные 3. Получаем таблицу вида:
Переходим к вычеркиванию чисел, кратных 5. Получим:
Вычеркиваем числа, кратные 7, 11. В конечном итоге таблица получает вид
Перейдем к формулировке теоремы.
Теорема 3
Наименьший положительный и отличный от 1 делитель основного числа а не превосходит a, где a является арифметическим корнем заданного числа.
Доказательство 3
Необходимо обозначить b наименьший делитель составного числа а. Существует такое целое число q, где a=b·q, причем имеем, что b≤q. Недопустимо неравенство вида b>q, так как происходит нарушение условия. Обе части неравенства b≤q следует умножить на любое положительное число b, не равное 1. Получаем, что b·b≤b·q, где b2≤a и b≤a.
Из доказанной теоремы видно, что вычеркивание чисел в таблице приводит к тому, что необходимо начинать с числа , которое равняется b2 и удовлетворяет неравенству b2≤a. То есть, если вычеркнуть числа, кратные 2, то процесс начинается с 4, а кратных 3 – с 9 и так далее до 100.
Составление такой таблицы при помощи теоремы Эратосфена говорит о том, что при вычеркивании всех составных чисел, останутся простые, которые не превосходят n. В примере, где n=50, у нас имеется, что n=50. Отсюда и получаем, что решето Эратосфена отсеивает все составные числа, которые по значению не больше значения корня из 50. Поиск чисел производится при помощи вычеркивания.
Данное число простое или составное?
Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.
Пример 1
Доказать что число 898989898989898989 является составным.
Решение
Сумма цифр заданного числа равняется 9·8+9·9=9·17.
Значит, число 9·17 делится на 9, исходя из признака делимости на 9. Отсюда следует, что оно составное.
Такие признаки не способны доказать простоту числа. Если нужна проверка, следует производить другие действия. Самый подходящий способ – это перебор чисел. В течение процесса можно найти простые и составные числа. То есть числа по значению не должны превосходить a. То есть число а необходимо разложить на простые множители. если это будет выполнено, тогда число а можно считать простым.
Пример 2
Определить составное или простое число 11723.
Решение
Теперь необходимо найти все делители для числа 11723. Необходимо оценить 11723.
Отсюда видим, что 11723<200, то 2002=40 000, а 11 723<40 000. Получаем, что делители для 11 723 меньше числа 200.
Для более точной оценки числа 11723 необходимо записать выражение 1082=11 664, а 1092=11 881, то 1082<11 723<1092. Отсюда следует, что 11723<109. Видно, что любое число, которое меньше 109 считается делителем для заданного числа.
При разложении получим, что 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107 – это все простые числа. Весь данный процесс можно изобразить как деление столбиком. То есть разделить 11723 на 19. Число 19 является одним из его множителей, так как получим деление без остатка. Изобразим деление столбиком:
Отсюда следует, что 11723 является составным числом, потому как кроме себя и 1 имеет делитель 19.
Ответ: 11723 является составным числом.
Электронный справочник по математике для школьников арифметика простые и составные числа разложение на множители
Содержание
Простые и составные числа
ОПРЕДЕЛЕНИЕ 1.
Простым числом называется натуральное число, отличное от 1 и такое, которое делится только на 1 и на самого себя.
Поскольку на 1 и на самого себя делится любое натуральное число, то из этого определения вытекает, что у простого числа других делителей нет.
ОПРЕДЕЛЕНИЕ 2. Составным числом называется натуральное число, отличное от 1 и не являющееся простым.
Следовательно, у составного числа существует, по крайней мере, один делитель, отличный от 1 и самого числа.
ОПРЕДЕЛЕНИЕ 3. Делители составного числа, отличные от 1 и самого числа, называют множителями.
Например, числа 2 , 3 , 5 , 7 , 11 , 13 , 17 и т.д. являются простыми. Числа 4 , 6 , 8 , 9 , 10 , 12 и т.д. являются составными.
ЗАДАЧА. Доказать, что полусумма двух последовательных простых чисел, больших 2, является составным числом.
РЕШЕНИЕ. Поскольку все простые числа большие 2 являются нечетными числами, то их сумма будет четным числом, а полусумма — натуральным числом.
Это натуральное число будет больше, чем меньшее из заданных последовательных простых чисел, и меньше, чем большее из них.
Так как заданные простые числа являются последовательными простыми числами, то между ними не может быть других простых чисел, а, значит, их полусумма является составным числом.
ЗАМЕЧАНИЕ. Чтобы выяснить, является ли данное число a простым или составным, достаточно проверить, делится ли это число на простые числа, не превосходящие числа .
Разложение натуральных чисел на множители (каноническое разложение натуральных чисел)
ТЕОРЕМА. Любое натуральное число, отличное от 1 , можно представить в виде произведения множителей, являющихся простыми числами, причем единственным образом.
Иногда эту теорему формулируют так: любое натуральное число, отличное от 1 , можно единственным образом разложить на простые множители.
ПРИМЕР. Разложить на множители число 816 .
РЕШЕНИЕ.
Равенство
и есть единственное разложение числа 816 на простые множители. Простыми множителями в данном примере являются числа 2 , 3 и 17 .
Бесконечность множества простых чисел
ТЕОРЕМА. Множество простых чисел бесконечно.
ДОКАЗАТЕЛЬСТВО. Будем доказывать эту теорему от противного, предположив, что множество простых чисел конечно.
Тогда рассмотрим число, равное произведению всех простых чисел плюс 1 . Это число не делится ни на одно из простых чисел, поэтому его разложение на простые множители с одной стороны должно существовать, а с другой стороны не может содержать ни одного из множителей, являющихся простым числом.
Полученное противоречие доказывает, множество простых чисел должно быть бесконечным.
ЗАМЕЧАНИЕ. В нашем справочнике приведена таблица простых чисел от 1 до 10000 .
Простые непростые числа
А вот для чего. Ещё в древние времена при передаче важного сообщения приходилось считаться с тем, что послание может быть перехвачено противником. Судьба государства часто зависела от умения зашифровывать информацию и расшифровывать «тайнописи» противника.
В современном мире стало ещё сложнее. На каждом шагу люди сталкиваются с проблемой защиты информации, будь то банковские операции, данные персональных компьютеров и т.д. Тут тоже применяется шифрование, в котором и играют главную роль наши простые числа.
Созданием и анализом методов шифрования занимается наука
криптография. Существует огромное количество таких методов. Например, в 1976 году американские математики Уитфилд Диффи и Мартин Хеллман выдвинули концепцию асимметричной криптосистемы, при которой шифрование и дешифрование осуществляются с помощью двух различных ключей — открытого и закрытого (секретного).
Буквально через год американцы Рональд Ривест, Ади Шамир и Леонард Адлеман разрабатывают асимметричную криптосистему RSA, названную по первым буквам фамилий её авторов (Rivest, Shamir, Adleman).
Слева направо: Ади Шамир, Рональд Линн Ривест, Леонард Макс Адлеман
В чём «хитрость» этой криптосистемы? Мы не будем углубляться в детали. Скажем лишь, что в основе ключа расшифровки лежит необходимость разложить очень большое число на два простых множителя.
Чтобы успешно вскрыть шифр, нужно уметь разложить числа на простые множители? Всего-то! Это может любой школьник!
Но хватит ли у вас терпения и времени разложить, например, число 1,409,305,684,859 на два простых множителя? Ответом будут простые числа 705,967 и 1,996,277. Чтобы их найти, придётся перебирать простые числа между числами 1 и 2,000,000, а их в этом списке немало — 148,933. Именно сложность обнаружения простых чисел стала причиной их широкого использования в криптографии.
Пример. Когда авторами криптосистемы RSA был объявлен конкурс на нахождение простых множителей числа, состоящего из 129 цифр, над проблемой работали около 600 математиков и 1600 добровольцев. В конце концов им удалось разложить это число на множители. Однако, чтобы взломать код из 1024 цифр, потребуется время, равное возрасту вселенной — 13,7 миллиарда лет, даже если над этим будут работать одновременно все компьютеры в мире.
Получается, что даже самые мощные компьютеры не в состоянии разложить очень большие числа на два простых множителя за разумное время, в то время как зашифрованная информация устаревает относительно быстро. И то, что сегодня было секретом, через год, а порой и через день, секретом уже не является. Благодаря этому, асимметричная криптосистема RSA получила повсеместное распространение, а потребность в новых простых числах для создания секретных кодов существует постоянно. А теперь давайте разбираться с простыми числами.
Простые и составные числа / Обыкновенные дроби / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Простые и составные числа
Любое натуральное число, за исключением 1, имеет как минимум два делителя (единица имеет единственный делитель — единицу) — это единица и само это число. Пусть — данное натуральное число, действительно, для него мы можем записать, что : 1 = и : = 1.
Некоторые числа имеют только два делителя — единицу и само это число, примером такого число является 11, это число делится только на 1 и на 11. Также только два делителя имеют, например, числа 2, 3, 5, 7, 13, 17. Все такие числа называют простыми числами.
Натуральное число называют простым, если оно имеет только два натуральных делителя: единицу и само это число. |
Наименьшим простым числом является 2, при этом оно единственное чётное простое число, так как все остальные чётные числа делятся не только на себя и единицу, но и на 2, то есть имеют минимум 3 делителя.
Число простых чисел бесконечно, и хотя не известен алгоритм их нахождения.
| Натуральное число называют составным, если оно имеет больше двух натуральных делителей. |
Наименьшим составным числом является 4, оно имеет три делителя: 1, 2, 4.
Число составных чисел бесконечно. При этом любое составное число можно разложить на два множителя, каждый из которых больше 1. Например, рассмотрим число 186:
186 : 6 = 31, значит, 186 = 631.
Говорят, что число 186 на разложено на множители 6 и 31.
Обратите внимание, что 1 не относят ни к составным числам, ни к простым, так как оно имеет только один делитель.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
6 класс
Номер 104,
Мерзляк, Полонский, Якир, Учебник
Номер 122,
Мерзляк, Полонский, Якир, Учебник
Номер 127,
Мерзляк, Полонский, Якир, Учебник
Номер 150,
Мерзляк, Полонский, Якир, Учебник
Номер 170,
Мерзляк, Полонский, Якир, Учебник
Номер 178,
Мерзляк, Полонский, Якир, Учебник
Задание 96,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 128,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 129,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1473,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
© budu5.
com, 2021
Пользовательское соглашение
Copyright
Урок в 5-м классе по теме: «Простые и составные числа»
Тема: Простые и составные числа.
Цели и задачи:
– знакомство с понятием “простые и составные
числа”;
– развитие понятия “число”;
– воспитание математической культуры”.
Ход занятия
1.Орг. момент. Анализ домашней работы.
2. Повторение.
а) устная работа
б) работа у доски
1. Запишите все делители чисел.
22: 1,2,11,22.
17: 1,17.
25: 1,5,25.
19: 1,19.
13: 1,13.
30: 1,2,3,10,15,30.
2. Найдите НОД(15,75).
15: 1,3,5,15.
75: 1,3,5,15,25,75.
3. Запишите три кратных для чисел 9,14,10.
9,18,27,…
14,28,42,…
10,100,1000,…
4.
Найдите НОК(12,48).
12,24, 36,48,…
48, 96,…
в) работа по карточкам.
3. Изучение нового материала.
Сегодня мы познакомимся с новым понятиями
“простые и составные числа”.(Запись темы урока).
Цель урока: Дать ответ на важнейшую задачу
всей арифметики “ Как отличать составные числа
от простых?”
Для решения этой задачи обратимся к заданию 1).
Можно ли эти числа разбить на два вида? По
какому признаку?
Определение:
1.Натуральноет число называется простым числом,
если оно имеет только два делителя; 1 и самого
себя.
2. Натуральное число, имеющие более двух
делителей, называется составным.
Используя эти определения, выполним упражнение
№ 542.
| Число | делители | вывод |
| 11 | 1,11 | простое |
| 26 | 1,2,13,26 | составное |
| 27 | 1,3,9,27 | составное |
| 29 | 1,29 | простое |
| 31 | 1,31 | простое |
| 39 | 1,3,13,39 | составное |
| 43 | 1,43 | простое |
| 51 | 1,3,17,51 | составное |
| 59 | 1,59 | простое |
| 67 | 1,67 | простое |
№ 543.
Способ, выписывания делителей числа, не
единственный. Интересный способ составления
списка простых чисел придумал древнегреческий
математик Эратосфен (III в до н.э.).
Рассмотрим этот метод для нахождения простых
чисел от 1 до 50 (Презентация).
Эратосфен писал на восковых табличках
специальными палочками, а составные числа
выкалывал острым концом, после чего табличка
напоминала решето. С тех пор его способ
называется решето Эратосфена.
Часто бывает сложно определить простое или
составное число. Поэтому с древних времен
математики составили таблицы простых чисел.
Истинным героем в составлении таблиц простых
чисел является профессор чешского университета
в Праге Якуб Кулик. Он составил таблицу делителей
чисел первых ста миллионов и поместил ее в
библиотеке Венской Академии наук.
(Знакомство с таблицей простых чисел). Устная
работа по таблице.
№ 549.
Итог
Д.з. № 547, № 552, № 548.
Простые и составные числа
Определение:
А
простое число
это
целое число
ровно с двумя целыми делителями,
1
и сам.
Номер
1
не является простым числом, так как имеет только один делитель.
Итак, самые маленькие простые числа:
2
,
3
,
5
,
7
,
⋯
Номер
4
не является простым, так как имеет три делителя (
1
,
2
, а также
4
), а также
6
не является простым, так как имеет четыре делителя (
1
,
2
,
3
, а также
6
).
Определение:
А
составное число
целое число с более чем двумя целыми делителями.
Так что все целое
числа (кроме
0
а также
1
) либо простые, либо составные.
Пример:
43 год
простое число, поскольку его единственными делителями являются
1
а также
43 год
.
44 год
составной, поскольку он имеет
1
,
2
,
4
,
11
,
22
а также
44 год
как делители.
Как узнать, что
число простое?
Прежде всего, вот несколько способов узнать, НЕ является ли число простым:
Любое число больше, чем
2
что кратно
2
не является простым числом, так как имеет как минимум три делителя:
1
,
2
, и сам. (Это означает
2
является единственным четным простым числом.)
Любое число больше, чем
3
что кратно
3
не является простым числом, так как имеет
1
,
3
и себя как делители.
(Например,
303
не является простым, так как
303
÷
3
знак равно
101
.)
Любое число, кратное
4
также кратно
2
, поэтому мы можем исключить их.
Любое число больше, чем
5
что кратно
5
не простое. (Итак, единственное простое число, оканчивающееся на
0
или же
5
является
5
сам.)
Любое число, кратное
6
также кратно
2
а также
3
, так что мы можем исключить и их.
Вы можете продолжить так … в основном, вам просто нужно проверить делимость на простые числа!
Первый тест на делимость на
2
.
119
нечетное, поэтому не делится на
2
.
Следующий,
тест на делимость на
3
. Добавьте цифры:
1
+
1
+
9
знак равно
11
. С
11
не является кратным
3
, ни
119
.
(Помните, что этот трюк работает только для проверки делимости на
3
а также
9
.)
С
119
не заканчивается
0
или
5
, не делится на
5
.
Затем проверьте делимость на
7
. Вы обнаружите, что
119
÷
7
знак равно
17
.
Так что ответ НЕТ …
119
не простое.
Первый тест на делимость на
2
.127
нечетное, поэтому не делится на
2
.
Следующий,
тест на делимость на
3
. Добавьте цифры:
1
+
2
+
7
знак равно
10
. С
10
не является кратным
3
, ни
127
.
С
127
не заканчивается
0
или
5
, не делится на
5
.
Затем проверьте делимость на
7
.Вы обнаружите, что
7
не входит равномерно.
Следующее простое число —
11
. Но
11
тоже не входит равномерно.
Вы можете остановиться сейчас … это должно быть просто! Вам не нужно постоянно проверять делимость на следующие простые числа (
13
,
17
,
19
,
23
,
так далее.). Причина в том, что если
13
пошли равномерно, тогда у нас было бы
127
знак равно
13
×
п
для некоторого числа
п
.Но потом
п
должно быть меньше чем
13
… и мы уже знаем, что
127
не делится на любое число меньше, чем
13
.
Так что ответ ДА …
127
простое.
Для более сложных тем и списка первых
400
простые числа, перейдите к
в
Прайм Пейдж
или страницу на
основной
факторизация
.
Факторы, простые числа, композиты и деревья факторов
Факторы, простые числа, композиты и деревья факторов
Вам следует ознакомиться с определениями определенных типов чисел и с тем, как их можно найти.
Факторы
Числа, которые умножаются для получения продукта, называются коэффициентами .
Пример 1
Какие множители 18?
Коэффициент
× коэффициент = 18
1 × 18 = 18
2 × 9 = 18
3 × 6 = 18
Итак, множители 18 равны 1, 2, 3, 6, 9 и 18. Эти числа также называются делителями из 18. Множители числа также называются делителями того же числа.
Простые числа
Простое число — это натуральное число больше 1, которое можно разделить только на себя и 1. Другое определение: простое число — это положительное целое число, которое имеет ровно два разных множителя: само себя и 1.
Пример 2
Является ли 19 простым числом?
Да. Единственные делители 19 — это 1 и 19, поэтому 19 — простое число. То есть 19 делится только на 1 и 19, поэтому оно простое.
Пример 3
Является ли 27 простым числом?
№27 делится на другие числа (3 и 9), поэтому не является простым.
Множители 27 равны 1, 3, 9 и 27, поэтому оно не является простым.
Единственное четное простое число — 2; после этого любое четное число можно разделить на 2. Числа 0 и 1 не являются простыми числами. Простые числа меньше 50 — это 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 и 47.
Составные числа
Составное число — это натуральное число, которое делится не только на 1, но и на само себя. Другое определение: составное число — это положительное целое число, которое имеет более двух различных факторов.Числа 4, 6, 8, 9, 10, 12, 14, 15, 16, 18,… являются составными числами, потому что они «составлены» из других чисел. Цифры 0 и 1 не являются составными числами. (Они не простые и не составные.)
Пример 4
25 — составное число?
Да. 25 делится на 5, поэтому составной. Множители 25: 1, 5 и 25.
Факторные деревья
Каждое составное число может быть выражено как произведение простых множителей.
Вы можете найти простых множителей с помощью факторного дерева.Факторное дерево выглядит так.
Вы также можете сделать дерево, как показано на следующем дереве.
В любом случае, независимо от того, как 18 разлагается на множители, произведение простых чисел одинаково, даже если порядок может быть другим.
Пример 5
Используйте факторное дерево, чтобы выразить 60 как произведение простых множителей.
Таким образом, разложение на простые множители из 60 равно 2 × 2 × 3 × 5, что может быть записано как 2 2 × 3 × 5.Фактические простые множители из 60 равны 2, 3 и 5.
Prime-Composite
Covid-19 привел мир к феноменальному переходу.
За электронным обучением будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Простые составные числа: в этом разделе рассказывается о простых составных числах.
Простые числа : числа, множители которых равны 1, и само число называются простыми числами.
Пример: 2,3,5,7,11,13,…
2 — наименьшее четное простое число, а 3 — наименьшее нечетное простое число.
Простые числа до 100:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97
Составное число : число, которое имеет хотя бы один множитель, кроме 1, и само число.
Пример : 4,6,8,9,12,…
Примечание: 1 не является ни простым, ни составным.
Сочетание простых чисел : два числа, у которых нет общего множителя, кроме 1.
Первые 100 составных чисел:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33,
34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58,
60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85,
86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108,
110, 111, 112, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125,
126, 128, 129.
Пример: 35 и 39
35 = 7 x 5 x 1
39 = 3 x 13 x 1
И 35, и 39 являются составными числами, единственный общий множитель между ними — 1.
∴ 35 и 39 — простые числа.
Еще несколько примеров: : 1) 2,3; 2) 3,4 3) 5,6 4) 8,13 и т. Д.
Простые числа-близнецы : Два простых числа известны как простые числа-близнецы, поскольку между ними есть только одно составное число.
Простые числа-близнецы от 1 до 100 — это
3-5, 5-7, 11-13, 17-19, 29-31, 41-43, 59-61, 71-73
Факторы и кратные
• Простые составные числа
• Правила делимости
• Простое факторизация
• H.C.F или G.C.F
• L.C.M
• Применение в LCM
Простые и составные числа для вычисления множителей и кратных
Система счисления
Домашняя страница
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Простые и составные числа
Простые составные числа
В математике существуют два типа чисел, которые зависят от имеющихся у них множителей.
Эти два типа чисел — простые числа и составные числа. Простое число — это число, которое имеет только два фактора, то есть один и само по себе, тогда как составное число — это число, которое имеет более двух факторов. В этой статье мы изучим, что такое простые числа и составные числа, свойства простых составных чисел и разницу между простыми числами и составными числами
Что такое простые числа и составные числа?
Простые числа считаются числами, в которых сохраняются только два множителя i.е. один и сам. Это означает, что число можно разделить только на 1 и само себя. Все простые числа являются нечетными, кроме 2. Составные числа — это числа, в которых сохраняется более двух множителей. Это означает, что число, кроме одного, может делиться и на другие числа. Каждое непростое число является составным числом.
Список простых чисел от 1 до 100
2 | 3 | 9300007 | 13 | 17 | 19 | 23 |
29 | 31 | 37 9030 | 53 | 59 | 61 | |
67 | 71 | 73 | 97 | |||
Составное число s
Целое число, которое может быть получено путем умножения двух наименьших положительных чисел и включает по крайней мере один делитель, отличный от 1, называется составными числами.
Составные числа не являются ни простым числом, ни единицей.
Например: 4, 6, 8, 9, 10 …… являются составными числами, потому что они имеют более двух факторов.
Типы составных чисел
1. Нечетные составные числа
2. Четные составные числа
Нечетные составные числа
Каждое нечетное целое число, которое не является простым числом, называется нечетным составным числом. Например — 9, 15,21,25,27 и 31 — нечетные составные числа.
Четное составное число
Каждое четное целое, не являющееся простым числом, называется четным составным числом.Например, -4, 6,8,10 и 12 — четные составные числа.
Список составных чисел от 1 до 100
9 | 10 | 12 | 14 | 15 | 16 | 18 | 22 | 24 | 25 | 26 | 27 | 28 | 30 | 30 | 34 | 35 | 36 | 38 | 39 | 40 | 42 | 44 | 45 | 50 | 51 | 52 | 54 | 55 | 56 | 57 | 62 | 63 | 64 | 65 | 66 | 68 | 69 | 9400007 |
74 | 75 | 77 | 78 | 80 | 81 | 82 | 85 87308 | 85 | 88 | 90 | 91 | 92 | 93 | 94 | 94 | 95 | 96409 | 100 | |||||||||||||||
Простые числа
Простое число — это положительное целое число, которое имеет только два множителя i.
е. один и сам. Подразумевается, что число можно разделить только на одно и на себя.
Например — 2, 3, 5, 7, 11…. И т. Д. — некоторые из простых чисел
Простые числа Факты
Число 2 — это только четное простое число. Другие четные числа можно разделить на 2. Таким образом, четные числа, которые можно разделить на 2, не являются простыми числами.
Ноль и 1 не являются простыми числами
Числа o и 1 не считаются ни простым, ни составным числом
Ни одно простое число больше 5 не оканчивается на 5.Поскольку любое число больше 5, оканчивающееся на 5, можно легко разделить на 5. Таким образом, его нельзя рассматривать как простое число.
Решенные примеры
1. Определите, считается ли число 53 простым или нет.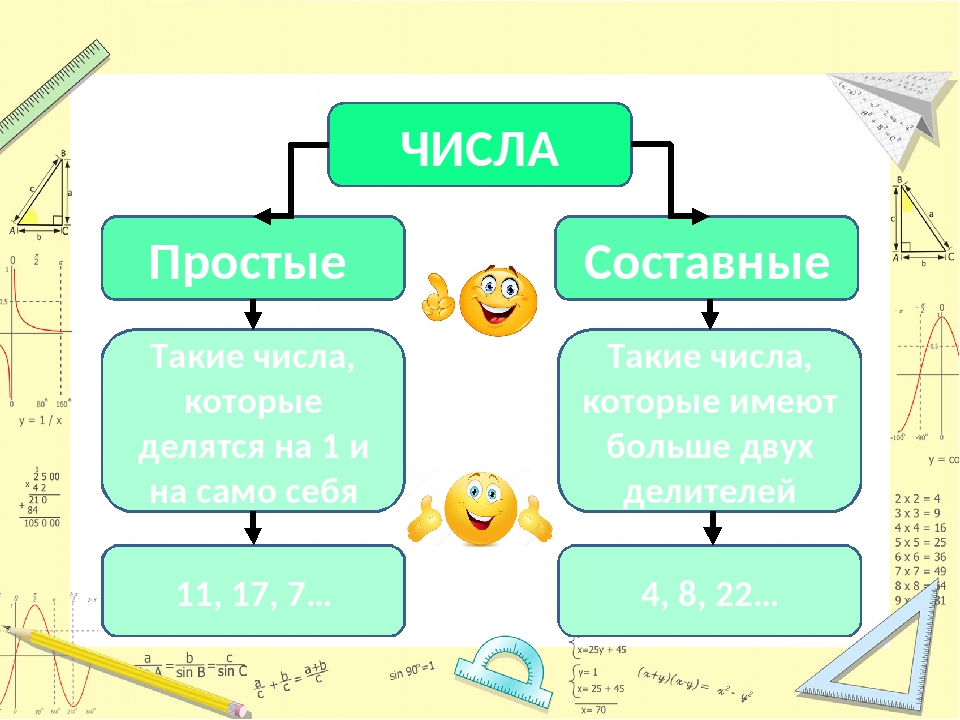
Решение: Множители 53 — 1 и 53.
Число 53 делится только на два числа: 1 и само себя.
Следовательно, 53 — простое число
2. Является ли 6 простым или составным числом?
Решение: делители 6 равны 1,2,3,6
6 можно легко разделить на 1, 2, 3 и 6 собственно
6 — составное число, так как его можно разделить более чем на 2 числа, кроме 1 и сам.
Интересные факты
Число 1 не считается простым или составным числом
Все четные числа, кроме 2, являются составными числами
Единственным четным простым числом является 2. Все остальные простые числа могут делиться на 2
Простые числа иногда используются в криптографии и безопасности для технологий и Интернета.
Самое большое простое число, известное до сих пор, состоит примерно из 13 миллионов цифр.
Греческий математик Евклид исследовал простые числа в 300 году до нашей эры.
Любое целое число больше 1 считается простым или составным числом.
Самая интересная последовательность простых чисел, в которой каждая цифра имеет кружок: 6089, 60899, 608999, 6089999, 60899999, 608999999
Время викторины
1. Сколько составных чисел от 1 до 100?
а. 72
г.74
г. 75
г. 70
2. Число, не являющееся ни простым, ни составным
a. 6
г. 9
г. 1
г. 3
3.
Все числа считаются простыми числами от 50 до 59:
a. 53 и 59
б. 51 и 59
c. 53 и 57
г. Ни одно из этих
простых чисел: что это такое и как их найти
В сегодняшнем посте вы узнаете разницу между простыми и составными числами.Кроме того, мы покажем вам несколько примеров, которые помогут вам лучше их понять.
Что такое простые числа?
Простые числа — это числа, которые делятся только на себя и 1, другими словами, если мы попытаемся разделить их на другое число, результатом будет не целое число. Итак, если вы разделите число на что-либо, кроме единицы или самого себя, вы получите остаток, отличный от нуля.
Простые числа до 100
Мы собираемся создать таблицу со всеми простыми числами, которые существуют до 100.
Начнем с 2. 2 — простое число, но все числа, кратные 2, будут составными числами, поскольку они будут делиться на 2.
Мы вычеркнем все числа, кратные 2, в таблице.
Следующее простое число — 3, поэтому мы можем вычеркнуть все числа, кратные 3, поскольку они будут составными числами.
После 3 стоит следующее простое число 5, поэтому мы вычеркиваем все числа, кратные 5.
Затем у нас есть простое число 7, и мы вычеркиваем все числа, кратные 7.
Следующее простое число — 11, поэтому мы вычеркиваем все числа, кратные 11: 22, 33, 44, 55, 66, 77, 88 и 99. Все эти числа уже были вычеркнуты, поэтому мы закончили. вычеркнув все составные числа в нашей таблице.
Это наш список простых чисел от 1 до 100. Вам не нужно запоминать их, но было бы лучше, если бы вы запомнили меньшие числа, такие как 2, 3, 5, 7, 11, 13.
Сколько существует простых чисел?
Греческий математик Эратосфен (III век до н.э.C) разработал быстрый способ найти все простые числа вплоть до любого заданного числа. Это процесс , называемый Решетом Эратосфена.
Обратите внимание, что от 1 до 100 25 простых чисел. Сколько всего простых чисел? Нам с древних времен известно, что — это бесконечное количество , поэтому перечислить их все невозможно. Поскольку Евклид, который первым показал, что в 4 веке до нашей эры существовало бесконечное количество, не знал концепции бесконечности , он сказал, что «простые числа больше, чем любое их фиксированное множество». означает, если вы вообразите 100 , их больше, и если вы представите миллион, их еще больше.
Простые числа от 100 до 1000
Давайте посмотрим на простые числа от 100 до 1000.
Сожалеем, что мы не можем показать их все, поскольку вы знаете, что их бесконечно много. 😉
Примеры простых чисел
Чтобы помочь вам лучше понять простые числа, мы собираемся объяснить упражнение.
У Сары есть 6 конфет, которыми она хочет поделиться, но она не знает, скольким людям она может их поделиться, чтобы все получили одинаковую сумму и ни одной не осталось.
Сколько способов она может это сделать?
Вот Сара и ее 6 конфет:
Как их разделить?
Первый и самый простой способ — передать их одному человеку, то есть разделить на 1. Таким образом, у этого человека будет 6 конфет.
Следующая возможность — разделить их на 2 человека. Поскольку 6 разделить на 2 равно 3, каждый получит по 3 конфеты!
Мы продолжим со следующим номером, 3.Если мы разделим 6 конфет между 3 людьми, это также будет точное деление, и каждый получит по 2 конфеты:
Давайте продолжим с цифр. У нас нет точных делений на 4 и 5, но есть на 6.
Поскольку 6 разделить на 6 равно 1, мы можем дать 6 детям по 1 конфете.
Мы собираемся собрать некоторую информацию. У нас есть 6 конфет, которые мы можем разделить (с точным разделением) между 1, 2, 3 и 6 людьми .Другими словами, мы можем разделить число 6 и получить 0 в качестве остатка, когда мы разделим его на 1, 2, 3 и 6.
Эти числа известны как делители 6 .
Попробуем другое число, например 7.
Теперь у Сары есть 7 конфет, и она хочет ими поделиться, но не знает, скольким людям она может их поделиться, чтобы все получили одинаковую сумму и ни одной не осталось. Сколько способов она может это сделать?
Генри такой удачливый! Он получил все леденцы!
Есть другие способы сделать это? Мы не можем разделить 7 на 2, 3, 4, 5 или 6,… но 7 возможно!
Сара может разделить леденцы между 7 людьми, давая им по одной штуке :
Итак, 7 можно разделить только на 1 и 7, его единственные делители — 1 и 7. Это типы номеров, которые мы называем простыми числами .
Есть еще простые числа? Конечно! Поищем еще:
- Разве 4? Нет! Поскольку его делители равны 1, 2, и 4.
- 5? Да! Потому что его делители равны 1 и 5.
- Это 8? Нет! Поскольку его делители равны 1, 2, 4, и 8.
Короче говоря, число является простым, если оно имеет только 2 делителя: 1 и само себя.
Теперь вы можете искать множество простых чисел!
Как найти простые числа
Обратите внимание! Мы собираемся дать вам трюк, чтобы узнать, является ли число простым или нет, без необходимости искать его делители, но таким способом, который более интересен и дает нам делители (если они есть).
Давайте выберем случайное число, например 16.
Чтобы проверить, является ли это простым числом, мы собираемся использовать таблицу, которая очень похожа на карты Монтессори для умножения. И мы получим столько шаров, сколько выбрано. В данном случае 16 мячей.
Когда у нас есть стол и шары, мы должны разместить их на столе, начиная с первого места, пытаясь сформировать прямоугольник. Числа, составляющие края прямоугольника, являются делителями этого числа.
В случае, если нам удастся сформировать прямоугольник с тем же числом, которое мы используем, и числом 1, это будет простое число .
Например, в этом случае мы размещаем 8 шаров в первом ряду и еще 8 во втором. Как видите, мы сформировали прямоугольник, и мы можем видеть, что 8, как и 2, являются делителями числа 16. Следовательно, 16 не является простым числом, потому что, как вы знаете, простых чисел — это те, которые являются только делимыми. сами по себе и 1.
Можно попробовать другое число, например 7.
Как мы видим, мы не смогли бы создать полный прямоугольник, мы бы упустили мяч. Поскольку мы не можем сформировать прямоугольник, мы можем сказать, что у числа 7 нет других делителей, кроме самого себя и 1, как мы можем видеть на следующем изображении.
Следовательно, 7 — простое число!
Попробуйте любой другой номер, и вы увидите, как он работает! Вы можете использовать миллиметровую бумагу и искать прямоугольники, используя это количество квадратов.
Почему важны простые числа?
Простые числа являются ключом к арифметике, ниже вы увидите пример, демонстрирующий их важность не только в математике, но и в природе.
Что мы имеем в виду, когда говорим, что простые числа являются ключом к арифметике?
Это потому, что любое число состоит из уникального продукта, состоящего из серии этих чисел.
Считается, что их изучали около 20 000 лет назад, когда наш предок записал ряд простых чисел (11, 13, 17 и 19) на кости Ишанго.Как будто это было совпадением, было подтверждено, что древние египтяне работали с ними 4000 лет назад.
Кроме того, природа очень хорошо их знает, и некоторые виды смогли обнаружить их на протяжении всей своей эволюции и использовать их для выживания.
Я имею в виду несколько видов цикад, таких как Magicicada septendecium , обитающий в Северной Америке . У этого вида цикадов цикл размножения составляет около 13 или 17 лет, а не 12, 14, 15, 16 или 18, а именно 13 или 17 лет.Это позволяет им избегать хищников, у которых также есть периодические репродуктивные циклы; Представьте себе хищника с 4-летним репродуктивным циклом .
Если бы жизненный цикл цикады составлял 12 или 14 лет, он бы совпадал с хищником очень часто, гораздо чаще, чем если бы он составлял 13 или 17 лет. Ровно 2 раза каждые 100 лет, в противном случае они совпали бы в 11 циклах, что поставило бы под угрозу развитие вида.
Безопасность электронного общения также основана на простых числах.Каждое зашифрованное сообщение, отправленное через Интернет (сети сообщений, покупки или электронный банкинг), имеет большое количество связанных с ним, и очень трудно узнать, где оно является основным или нет. У получателя есть один из его делителей, поэтому они могут его расшифровать. Поэтому наличие простых чисел имеет решающее значение для нашей конфиденциальности при электронном общении.
Что такое составные числа?
Составные числа — это числа, которые делятся на 1 и сами себя, а также другие числа.
Мы собираемся рассмотреть пример простого числа и составного числа.
11 может быть записано как умножение 1 x 11, но не может быть записано как любое другое умножение натуральных чисел.
У него есть только делители 1 и 11, поэтому это простое число .
12 можно записать как умножение 1 x 12 и как умножение 3 x 4 и 2 x 6. Поскольку 12 делится на большее количество чисел, чем 1 и само себя, 12 является составным числом .
Является ли 1 простым числом?
Есть люди, которые так считают, потому что говорят, что 1 можно разделить только на 1 и само себя, но в математике число 1 было отброшено как простое число, потому что оно имеет только один делитель. Фактически, критерий «положительное целое число является простым, если оно имеет ровно два положительных делителя» используется для исключения числа один из списка простых чисел. Это не потому, что мы придирчивы к этому, но если бы число один считалось простым, то о многих математических свойствах пришлось бы сказать иначе.
Итак, 1 — составное число?
Что ж, это тоже не составное число, так как оно не может быть представлено как произведение простых чисел.
Число 1 не простое и не составное. И прежде чем вы спросите, ноль тоже не является простым или составным, но это связано со всеми соображениями, которые мы объясняли для положительных чисел, то есть больше нуля.
Делители числа
Делитель числа — это значение, которое делит число на точные части, другими словами, имеет остаток 0.
В качестве примера мы собираемся вычислить делители для 24.
Начнем деление с наименьших чисел, начиная с 1.
- 24/1 = 24. И 1, и 24 являются делителями.
- 24/2 = 12. Значит, 2 и 12 — делители.
- 24/3 = 8. Значит, 3 и 8 — делители.
- 24/4 = 6. Итак, 4 и 6 — делители.
- 24/5 = 4. Это не точное деление, остаток равен 4, поэтому 5 не является делителем.
Следующее число — 6, но поскольку мы уже знаем, что 6 является делителем 24, мы закончили вычисление делителей для 24.
Видео: факторизация и простые числа
Если вы хотите узнать больше о простых и составных числах , посмотрите следующее видео.
Вы также узнаете концепцию факторинга, используя таблицу Монтессори.
Это видео — одно из наших интерактивных учебных пособий, и, хотя оно не является интерактивным, вы все равно можете смотреть его сколько угодно раз и делиться им с друзьями. Если вы хотите получить доступ к нашим интерактивным обучающим материалам, зарегистрируйтесь в Smartick! Онлайн-метод, помогающий детям в возрасте от 4 до 14 лет изучать и практиковать математику.
Если вы хотите продолжить изучение простых чисел и лучшей математики, адаптированной к вашему уровню, зарегистрируйтесь в Smartick и попробуйте бесплатно!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Может ли кто-нибудь помочь мне с простыми и составными числами? Простые числа — это числа
- Вопросы
Может ли кто-нибудь помочь мне с простыми и составными числами?
Простые числа — это подсчитываемые числа, которые можно разделить поровну только на два числа: 1 и самих себя.Простое число также можно описать как счетное число с двумя множителями: 1 и самим собой. Итак, 1, поскольку он имеет только один множитель (сам), не является простым числом. Простое число до 100: 2,3,5,11,13,17,19,23,29,31,37,41,43, 47,53,59,61,67,71,73,79,83,89,97
Составные числа — это все счетные числа, которые не являются простыми числами. Другими словами, составные числа — это числа, которые имеют более двух факторов. Опять же, число 1, поскольку оно имеет только один фактор (сам по себе), не является составным числом.
хорошо, верно, кажется
* Фундаментальная теорема арифметики утверждает, что каждое положительное целое число / число больше 1 является простым или составным, т.
е. может быть выражено как уникальное произведение простых чисел и их показателей только одним способом. .
* Число 1 не считается простым числом, его более традиционно называют единицей.
Аристотель рассматривал единицу не как число, а как элементарную меру всех чисел.
Евклид заявил, что единица — это то свойство каждой вещи во вселенной, которое позволяет называть ее одним, в то время как число может считаться множеством единиц.
* Простое число — это положительное число «p», отличное от 1, которое имеет только два положительных делителя / множителя: 1 и «p».
(Строгая интерпретация этого определения помогает подтвердить утверждение, что число один не является простым числом, поскольку оно буквально имеет только один делитель / множитель, тогда как простое число имеет два множителя.)
Примеры: 2, 3, 5, 7 , 11, 13, 17, 19, 23, 29, 31 и т. Д. Являются простыми числами и делятся без остатка только на 1 и само число.
* Составное число — это число, которое имеет 3 или более делителей / делителей.
2 и т. Д., Где a, b, c и d — простые числа, является составным.
* Любое число больше 1, которое не является простым числом, должно быть составным числом и является результатом умножения простых чисел вместе.
Примеры: 4, 6, 12, 24, 72 и т. Д. Являются составными, каждое из которых делится на меньшие простые числа.
* Каждое число n> 1 делится на некоторое простое число.
* Все простые числа, за исключением числа 2, являются нечетными.
Число 2 — единственное четное простое число, что делает его самым нечетным простым числом.
* Два целых числа, a и b, называются взаимно простыми, если их наибольший общий делитель равен 1. Пример: 7 и 12 взаимно просты как их общий делитель. равно 1.
* Простые числа, различающиеся на 2, называются двойными простыми числами. Примеры: 3-5, 5-7, 17-19, 1,000,000,009,649-1,000,000,009,651.
* Есть только один набор тройных простых чисел — 3, 5 и 7.
Как найти простые числа
Сито Эратосфена
Давайте найдем простые числа от 1 до 100.
Запишите последовательность чисел от 1 до 100.
Зачеркните 1.
Начиная с 2, вычеркните каждое второе число после 2, т. Е. 4, 6, 8, 10 и т. Д.
Начиная с первого оставшееся число, 3, зачеркнуть каждое третье число после 3, т. е. 3, 6, 9, 12 и т. д.
Начиная с первого оставшегося числа, 5, вычеркнуть каждое пятое число после 5, т. е. 5, 10 , 15, 20 и т. Д.
Продолжайте с 7, вычеркивая каждое седьмое число после 7, т. Е. 7, 14, 21, 28 и т. Д.
Продолжайте процесс, пока не дойдете до N или 100.
Оставшиеся числа — простые числа от 1 до 100, а именно 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41 , 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 и 97. По определению, все остальные являются составными числами.
какое наибольшее число нужно будет проверить, чтобы найти простое число 100
Простые числа — элементарная математика
Значение
Неформальный смысл
Номера зданий из меньших строительных блоков: Любое счетное число, кроме 1, может быть построено путем сложения двух или более меньших счетных чисел.
Но только можно составить из счетных чисел, умножив на двух или более меньших счетных чисел.
Простые и составные числа: Мы можем построить 36 из 9 и 4 путем умножения; или мы можем построить его из 6 и 6; или с 18 и 2 лет; или даже умножением 2 × 2 × 3 × 3. Числа типа 10 и 36 и 49, из которых может быть составлено как произведение меньших счетных чисел, называются составными числами .
Некоторые числа не могут быть построены таким образом из более мелких деталей.Например, он может построить 7 только умножением и использованием , только подсчет чисел равен 7 × 1. Чтобы «построить» 7, мы должны использовать 7! Так что на самом деле мы не составляем его из более мелких строительных блоков; нам это нужно для начала. Такие числа называются простыми числами.
Неформально простые числа — это числа, которые нельзя получить путем умножения других чисел. Это хорошо отражает идею, но не является достаточно хорошим определением, потому что в нем слишком много лазеек.
Число 7 может быть составлено как произведение других чисел: например, это 2 × 3. Чтобы уловить идею о том, что «7 не делится на 2», мы должны прояснить, что мы ограничиваем числа, чтобы включать только счетные числа: 1, 2, 3….
Формальное определение
Простое число — это положительное целое число, которое имеет ровно двух различных целочисленных множителя (или делителей), а именно 1 и самого числа.
Разъяснение двух распространенных заблуждений
Две распространенные ошибки:
- Число 1 — это , а не простое число.
- Число 2 — простое. (Это единственное четное простое число.)
Число 1 не простое. Почему бы и нет?
Что ж, определение это исключает. В нем написано «два различных целочисленных множителя », и единственный способ записать 1 как произведение целых чисел — это 1 × 1, в котором множители совпадают, совпадают друг с другом, то есть не различны.
Это исключает даже неформальная идея: его нельзя построить путем умножения других (целых) чисел.
Но зачем это исключать ?! Студенты иногда утверждают, что 1 «ведет себя», как и все другие простые числа: его нельзя «разбить на части». И часть неформального понятия простого числа — мы не можем из составить 1, кроме как с его помощью, поэтому он должен быть строительным блоком — кажется, делает его простым. Почему не включает его в ?
Математика не произвольна. Чтобы понять, почему полезно исключить 1, рассмотрите вопрос «Сколько разных способов 12 можно записать как произведение, используя только простые числа?» Вот несколько способов записать 12 как произведение, но они не ограничиваются простыми числами.
- 3 × 4
- 4 × 3
- 1 × 12
- 1 × 1 x 12
- 2 × 6
- 1 × 1 × 1 × 2 × 6
Использование 4, 6 и 12 явно нарушает ограничение «использовать только простые числа».
Но что насчет этого?
- 3 × 2 × 2
- 2 × 3 × 2
- 1 × 2 × 3 × 2
- 2 × 2 × 3 × 1 × 1 × 1 × 1
Что ж, если мы включим 1, есть бесконечно много способов записать 12 как произведение простых чисел.Фактически, если мы назовем 1 простым числом, то существует бесконечно много способов записать любое число как произведение простых чисел. Включение 1 упрощает вопрос. Без его учета остаются только эти случаи:
- 3 × 2 × 2
- 2 × 3 × 2
- 2 × 2 × 3
Это гораздо более полезный результат , чем выражение любого числа бесконечным числом способов как произведение простых чисел, поэтому мы определяем простое число таким образом, что оно исключает 1.
Число 2 — простое . Почему?
Студенты иногда считают, что все простые числа нечетные. Если кто-то работает только с «шаблонами», это легко сделать, так как 2 — это исключение , только , единственное четное число.
Одно доказательство: поскольку 2 является делителем каждого четного числа, каждое четное число, большее 2, имеет как минимум три различных положительных делителя.
Другой распространенный вопрос: «Все четные числа делятся на 2, поэтому они не простые; 2 — четное, так как оно может быть простым? » Каждое целое число делится само на себя и на 1; все они делятся на или на .Но если число делится только на само на себя и на 1, то оно простое. Итак, поскольку все других четных чисел делятся сами по себе на 1, и 2 , все они составные (так же, как все положительные числа, кратные 3, кроме самого 3, составны).
Математические основы
Уникальная факторизация простых чисел и факторные деревья
Вопрос «Сколько разных способов можно записать число как произведение, используя только простые числа?» (увидеть, почему 1 не является простым) становится даже более интересным, если мы спросим себя, достаточно ли различаются ли 3 × 2 × 2 и 2 × 2 × 3, чтобы рассматривать их « различных способов.
«Если мы рассмотрим только набор используемых чисел — другими словами, если мы проигнорируем то, как эти числа расположены, — мы придем к замечательному и очень полезному факту (доказуемому).
- Каждое целое число больше 1 может быть разложено на уникальный набор простых чисел. Для любого целого числа существует только , один набор простых множителей.
Штрихи и прямоугольники
Можно расположить 12 квадратных плиток в трех различных прямоугольниках.
Семь квадратных плиток можно расположить разными способами, но только одно расположение образует прямоугольник.
Сколько всего простых чисел?
С 1 по 10 четыре простых числа: 2, 3, 5 и 7.
С 11 по 20 снова четыре простых числа: 11, 13, 17 и 19.
С 21 по 30 только 2 простых числа: 23 и 29.
С 31 по 40 снова есть только 2 простых числа: 31 и 37.
От 91 до 100 есть только одно простое число: 97.
Похоже, они редеют.
В этом даже есть смысл; по мере того, как числа становятся больше, появляется все больше маленьких строительных блоков, из которых они могут быть сделаны.
Останавливаются ли когда-нибудь простые числа? Предположим на мгновение, что они в конце концов остановятся. Другими словами, предположим, что было «наибольшим простым числом» — назовем его p . Что ж, если бы мы умножили все известные нам простые числа (все они от 2 до p ), а затем прибавили 1 к этому произведению, мы получили бы новое число — назовем его q — которое не делится ни на одно из уже известных нам простых чисел.(Деление на любое из этих простых чисел приведет к остатку 1.) Итак, либо q само простое число (и определенно больше, чем p ), либо оно делится на некоторое простое число, которое мы еще не перечислили (которое, следовательно, , также должно быть больше p ). В любом случае, предположение, что существует наибольшее простое число — p предположительно было нашим наибольшим простым числом — приводит к противоречию! Таким образом, это предположение должно быть неверным, что — это не «наибольшее простое число»; простые числа никогда не прекращаются.