Содержание
Прямая и обратная пропорциональность. Формулы, обозначение, примеры
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
Виды зависимостей:
- Прямая зависимость. Чем больше одна величина, тем больше вторая. Чем меньше одна величина, тем меньше вторая величина.
- Обратная зависимость. Чем больше одна величина, тем меньше вторая. Чем меньше одна величина, тем больше вторая.
Зависимости также можно классифицировать по формам: функциональная и статистическая.
Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.
В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.
Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.
Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
- Прямая пропорциональность. Это зависимость, при которой увеличение одного числа ведет к увеличению другого во столько же раз.
 А уменьшение одно числа ведет к уменьшению другого во столько же раз.
А уменьшение одно числа ведет к уменьшению другого во столько же раз. - Обратная пропорциональность. Это зависимость, при которой уменьшение одного числа ведет к увеличению другого во столько же раз. А увеличение числа наоборот ведет к уменьшению другого во столько же раз.
Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Чтобы повысить оценки в школе, приходите на уроки математики в онлайн-школу Skysmart. Интерактивный формат, личный учитель, карта прогресса и куча вдохновения — все, чтобы учиться было комфортно.
На бесплатном уроке расскажем, как у нас все устроено и покажем, что математика — совсем не страшная.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
- при постоянной скорости пройденный маршрут прямо-пропорционально зависит от времени;
- периметр квадрата и его сторона — прямо-пропорциональные величины;
- стоимость конфет, купленных по одной цене, прямо-пропорционально зависит от их количества.
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности y = kx, где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности. |
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
y/x = k
Графиком прямо пропорциональной зависимости величин является прямая линия.
Например, при k = 2 график выглядит так:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
Как решаем:
- Вспомним формулу для определения пути через скорость и время: S = V * t.
- Так как оба автомобиля проделали одинаковый путь, можно составить пропорцию из двух выражений: 70 * 2 = V * 7
- Найдем скорость второго автомобиля: V = 70 * 2/7 = 20
Ответ: 20 км/ч.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Как рассуждаем:
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
- х = 1 (блогер) * 30 (раз) : 12/8 (дней).
- х = 1 * 30 : 12/8
- х = 20
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
- время на маршрут и скорость, с которой путь был пройден — обратно пропорциональные величины;
- при одинаковой продуктивности количество школьников, решающих конкретную задачу, обратно пропорционально времени выполнения этой задачи;
- количество конфет, купленных на определенную сумму денег, обратно пропорционально их цене.
Формула обратной пропорциональности y = k/x где y и x — это переменные величины, k — постоянная величина, которую называют коэффициентом обратной пропорциональности. |
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
xy = k.
Графиком обратно пропорциональной зависимости величин является гипербола.
Свойства функции обратной пропорциональности:
- Область определения — множество всех действительных чисел, кроме x = 0.
D(y): (-∞; 0) U (0; +∞).
- Область значений — все действительные числа, кроме y = 0.
Е(у): (-∞; 0) U (0; +∞).
- Не имеет наибольших и наименьших значений.
- Является нечетной, и ее график симметричен относительно начала координат.
- Непериодическая.
- Ее график не пересекает оси координат.
- Не имеет нулей.

- Если k > 0 (аргумент возрастает), функция пропорционально убывает на каждом из своих промежутков. Если k < 0 (аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
- При возрастании аргумента (k > 0) отрицательные значения функции находятся в промежутке (-∞; 0), а положительные — (0; +∞). При убывании аргумента (k < 0) отрицательные значения расположены на промежутке (0; +∞), положительные — (-∞; 0).
Потренируемся
Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
Как рассуждаем:
- В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
- Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.
- Поэтому направим вторую стрелку в противоположную сторону.
 Обратная пропорция выглядит так:
Обратная пропорция выглядит так:
Как решаем:
- Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию: 30 : 24 = 5 : х
- Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член: х = 24 * 5 : 30; х = 4
- Значит, 30 человек раскрутят канал за 4 дня.
Ответ: за 4 дня.
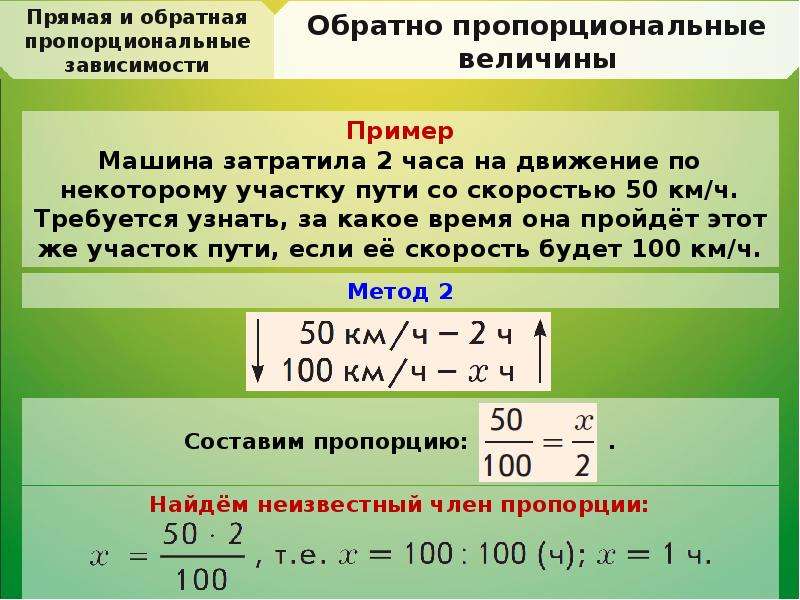
Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Как рассуждаем:
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Обозначим: =
v1 = 75 км/ч
v2 = 52 км/ч
t1 = 13 ч
t2 = х
Как решаем:
- Составим пропорцию: v1/v2 = t2/t1.
Соотношения равны, но перевернуты относительно друг друга.
- Подставим известные значения: 75/52 = t2/13
Ответ: 18 часов 45 минут.
А вот еще одна прямая зависимость: чем больше задачек решаешь — тем проще на экзаменах и контрольных. В онлайн-школе Skysmart собрали тысячи увлекательных примеров в интерактивном формате, чтобы школьники не только прокачивали знания, но и делали это с азартом и огоньком.
Записывайтесь на бесплатный вводный урок математики: покажем, что учиться можно эффективно и в удовольствие.
Урок 7. прямая и обратная пропорциональность. решение задач — Математика — 6 класс
Математика
6 класс
Урок № 7
Прямая и обратная пропорциональность. Решение задач
Перечень рассматриваемых вопросов:
- Понятия прямой и обратной пропорциональной зависимости.
- Краткая запись условия задачи.
- Составление и решение пропорций по условию задачи.
- Решение задач на прямую и обратную пропорциональную зависимость.
Тезаурус
Равенство двух отношений называют пропорцией.
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Основная литература
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Прямая пропорциональность.
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.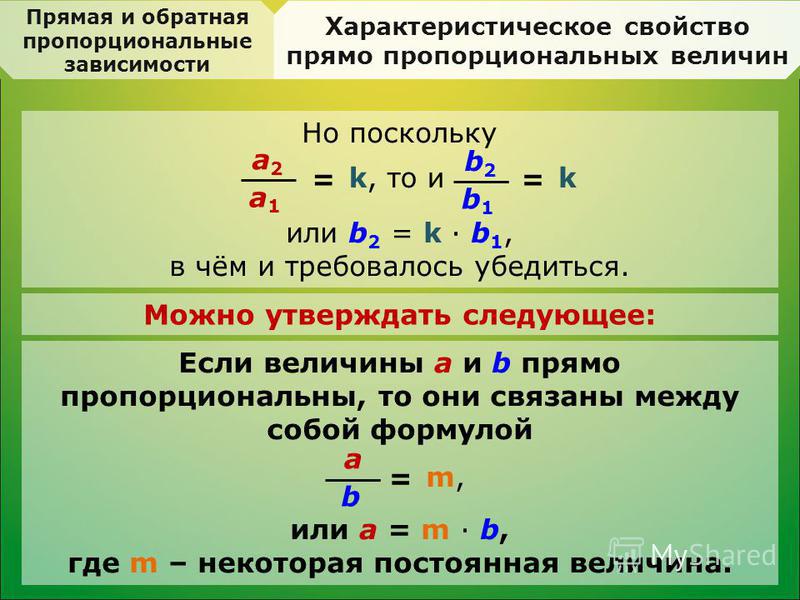
Обратная пропорциональность.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Для решения задач на пропорциональную зависимость, удобно составить таблицу или сделать краткую запись условия.
Столбцы таблицы соответствуют наименованиям зависимых величин.
Строки таблицы соответствуют значениям величин при первом и втором измерении.
Одинаково направленные стрелки показывают прямо пропорциональную зависимость, противоположно направленные – обратно пропорциональную.
Задача.
Поезд, скорость которого 55 км/ч, был в пути 5 часов. За сколько часов пройдёт этот же участок пути товарный поезд, скорость которого 45 км/ч?
Решение.
При постоянном пути скорость и время движения обратно пропорциональны.
Допустим, товарный поезд пройдёт этот же путь со скоростью 45 км/ч за x ч.
Сделаем краткую запись условия.
Задача.
Двигаясь с постоянной скоростью, велогонщик проезжает 40 метров за 3 с. Какой путь проедет велогонщик за 45 с?
Решение.
При постоянной скорости путь прямо пропорционален времени движения.
Пусть х м проедет велогонщик за 45 с.
Сделаем краткую запись условия.
Задача.
Усилие при восхождении на высоту 600 м равно усилию, требуемому для перехода 25 км по равнине. Турист поднялся в горы на 792 м. Какому расстоянию на равнине соответствует этот подъём?
Решение:
Решение.
Задача.
Четыре программиста могут написать игру за 12 месяцев. За сколько месяцев эту работу могут выполнить три программиста?
Решение.
Количество программистов и скорость написания игры – это обратно пропорциональная зависимость.
Разбор заданий тренировочного модуля
№ 1. Подстановка элементов в пропуски в тексте.
Подставьте нужные элементы в пропуски.
Пешеход шёл 3 часа со скоростью 8 км/ч. За сколько часов он пройдёт то же расстояние со скоростью 6 км/ч?
За сколько часов он пройдёт то же расстояние со скоростью 6 км/ч?
Решение:
При фиксированном расстоянии время в пути и скорость – ______ пропорциональны.
Пусть _____ часов – пешеход идёт со скоростью 6 км/ч.
Составим пропорцию:
_________
х=_______
х=_______(ч).
Правильный ответ.
Решение:
При фиксированном расстоянии время в пути и скорость – обратно пропорциональны.
Пусть х часов – пешеход идёт со скоростью 6 км/ч.
№ 2. Подстановка элементов в пропуски в таблице.
Заполните таблицу.
Поезд движется со скоростью 45 км/ч. Какое расстояние он пройдёт, если будет в пути 3 ч; 4 ч; 5 ч; 6 ч.
Варианты ответов:
135 км;
180 км;
225 км;
270 км.
Решение.
При постоянной скорости пройденный путь и время прямо пропорциональны. Скорость движения поезда 45 км/ч означает, что за 1 час поезд преодолевает расстояние в 45 км. Обозначим за x км – расстояние, которое поезд пройдёт за 3, 4, 5 и 6 часов.
Таким же способом находим расстояние, которое пройдёт поезд за 4, 5 и 6 часов, и подставляем соответствующие варианты в таблицу.
Ответ:
6.1.5. Обратно пропорциональные величины.
Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 152 Опубликовано
I. Обратно пропорциональные величины.
Пусть величина у зависит от величины х. Если при увеличении х в несколько раз величина у уменьшается во столько же раз, то такие величины х и у называются обратно пропорциональными.
Примеры.
1. Скорость и время при одинаковой длине пути. Если от А до В 200 км, то при скорости 50 км/ч понадобится 4 часа, а при скорости 40 км/ч понадобится 5 часов, т. е. если скорость уменьшается, то время увеличивается, а если скорость увеличивается, то время уменьшается. Это изобразится так:
е. если скорость уменьшается, то время увеличивается, а если скорость увеличивается, то время уменьшается. Это изобразится так:
2. Количество рабочих и время при определенном объеме работ. Если шести рабочим нужно на выполнение определенной работы 4 часа, то трем рабочим на выполнение той же работы потребуется 8 часов, т.е. чем меньше работников, тем больше нужно времени, чтобы выполнить определенную работу.
Смысл: во сколько раз стало меньше рабочих (в 2 раза), во столько же раз больше (в 2 раза) времени потребуется.
3) Длина и ширина прямоугольника при постоянной площади прямоугольника. Если площадь участка прямоугольной формы с длиной 8 м, равна 48 м², то его ширина будет равна (48:8=6)м. Если же длину взять больше в 2 раза (16 м), то ширина уменьшится тоже в 2 раза (48:16=3)м.
II. Свойство обратной пропорциональности величин.
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Задача 1. Изготавливая по 42 детали в час, рабочий трудился 8 часов. Сколько времени ему понадобилось бы на эту же работу, если бы он делал в час по 48 деталей?
Решение. Составим схему по условию задачи:
42 детали в час ——— 8 часов.
48 деталей в час ——- х часов.
Имеем обратно пропорциональную зависимость: во сколько раз больше деталей в час рабочий будет изготавливать, во столько же раз меньше ему потребуется времени на одну и ту же работу. Используя свойство обратной пропорциональности, запишем:
Ответ: рабочий выполнит ту же работу за 7 часов.
Задача 2. Бассейн можно наполнять через одну из двух труб.Через первую трубу, со скоростью 2 литра в 1 секунду, бассейн наполняется за 45 минут. Какова скорость наполнения бассейна через вторую трубу, если весь бассейн наполняется через вторую трубу за 1 час 15 минут.
Решение.
По условию задачи через первую трубу в бассейн вытекает 2 литра за 1 секунду или 2·60=120 литров за 1 минуту (1 минута=60 секунд), и бассейн наполняется за 45 минут.
Через вторую трубу бассейн наполняется за 1 час 15 минут. Времени требуется больше, значит, скорость наполнения меньше. Имеем обратно пропорциональные величины: скорость наполнения и время наполнения бассейна. Обозначим скорость наполнения бассейна через вторую трубу через х.
120 литров в минуту ——— 45 минут;
х литров в минуту ——— 75 минут. (1 час 15 минут = 60 минут + 15 минут = 75 минут).
(1 час 15 минут = 60 минут + 15 минут = 75 минут).
Во сколько раз скорость наполнения меньше, во столько раз больше потребуется времени для заполнения бассейна.
Мы нашли скорость наполнения бассейна через вторую трубу в литрах в минуту. Итак, через вторую трубу бассейн наполняется со скоростью 72 литра в минуту или 72:60=1,2 литров в секунду.
Ответ: через вторую трубу в бассейн вливается 1,2 литра в 1 секунду.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Арифметика
Две величины y и x , связанные зависимостью
y = kx ,
где k – некоторое число, называются прямо пропорциональными. Число k называется коэффициентом прямой пропорциональности.
Графиком прямо пропорциональной зависимости величин является прямая линия. Например, при k = 2 график прямо пропорциональной зависимости имеет следующий вид
Отношение прямо пропорциональных величин является постоянным числом и равно k :
Две величины y и x , связанные зависимостью
где k – некоторое число, называются обратно пропорциональными. Число k называется коэффициентом обратной пропорциональности.
Число k называется коэффициентом обратной пропорциональности.
Графиком обратно пропорциональной зависимости величин является гипербола. Например, при k = 2 график обратно пропорциональной зависимости имеет следующий вид
Произведение обратно пропорциональных величин является постоянным числом и равно k :
yx = k .
Пример 1. Число 110 разделить на три слагаемых прямо пропорционально числам 1, 3 и 7 .
Решение. Если обозначить слагаемые буквами a , b и c , а коэффициент прямой пропорциональности буквой k и воспользоваться тем, что отношение прямо пропорциональных величин является числом постоянным, то будут выполнены соотношения:
Следовательно,
b = 3a , c = 7a .
Поэтому
Таким образом,
b = 3a = 30, c = 7a = 70.
Итак, первое слагаемое равно 10 , второе слагаемое равно 30 , а третье слагаемое равно 70 . Их сумма равна 110 .
Ответ: 10 , 30 , 70 .
Пример 2. Число 40 разделить на два слагаемых обратно пропорционально числам 1 и .
Решение. Если обозначить слагаемые буквами a и b , а коэффициент обратной пропорциональности буквой k , и воспользоваться тем, что произведение обратно пропорциональных величин является числом постоянным, то будут выполнены соотношения:
Следовательно:
b = 3a , a + b = 40,
a + 3a = 40,
4a = 40,
a = 10, b = 30.
Итак, первое слагаемое равно 10 , а второе слагаемое равно 30 . Их сумма равна 40 .
Ответ: 10 , 30 .
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
какие две величины называют обратно пропорциональными
Точка Tлежит на диагонали АС параллелограмма ABCDи делит её в отношении CT: TA = 2:7. В каком отношениипрямая DT делит сторону ВС?
на двох котушках є 94 м мотузки. після того як з першої котушки використали 12 м мотузки, на ній залишилося на 6 м мотузки більше ніж на другій . скіл
…
ьки метрів мотузки було на кожній котушці спочатку? розвязати за допомогою рівняння
решите пожалуйста 6 класс.
539. Периметр четырёхугольника равен 77 см. Вторая сторона равна пер-вой, третья меньше первой на 20%, а четвёртая меньше третьей на 4 см.Определите д
…
лину четвёртой стороны.
на двох котушках є 94 м мотузки. після того як з першої котушки використали 12 м мотузки, на ній залишилося на 6 м мотузки більше ніж на другій . скіл
…
ьки метрів мотузки було на кожній котушці спочатку? розвязати за допомогою рівняння
написать три дроби равные данные дроби 1/8, 1/4, 3/7, 4/9, 5/8, 7/10.
СРОЧНО!!!!!!!!
Скільки треба змішати розчину солі концентрацію 2% і розчину солі 10% ,щоб одержати 800г розчину,концентрація якого7%
даю 100 баллов
1. В новорічному подарунку льодяників у 2 рази більше, ніж шоколадних
цукерок, а мармеладок на 10 більше, ніж льодяників. Скільки цуке
…
рок
кожного типу містить подарунок, якщо всього в ньому 35 цукерок?
2. У баби Нюри живуть кролі. Білих кролів в неї в 3 рази більше, ніж
сірих, а сірих на 8 менше, ніж білих. Скільки всього кролів живе у баби
Нюри?
3. Знайти сторони трикутника, якщо одна з них в два рази більша за другу
і на 5 см більша за третю, а периметр дорівнює 35 см.
4. На «Чорній Перлині» було втричі більше піратів, ніж на «Барракуді».
Коли 12 піратів перейшли з «Чорної Перлини» на «Барракуду», то
піратів на кораблях стало порівну. Скільки піратів було на «Чорній
Перлині» спочатку?
 В смешанной дроби 5;3/4 Целый частью является;4,5,3,нет целой части
ПОМОГИТЕ! СРОЧНО! (НОМЕР 449)
Обратно пропорциональная зависимость | Математика
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз. Соответственно, при уменьшении одной из них в несколько раз другая увеличивается во столько же раз.
Соответственно, при уменьшении одной из них в несколько раз другая увеличивается во столько же раз.
Зависимость между такими величинами — обратно пропорциональная зависимость. Примеры обратной пропорциональной зависимости:
1) время, затраченное на прохождение определенного пути, и скорость, с которой этот путь был пройден — обратно пропорциональные величины;
2) при одинаковой производительности труда количество рабочих, выполняющих определенную работу, обратно пропорционально времени выполнения этой работы;
3) количество товара, купленного на определенную сумму денег, обратно пропорционально его цене.
Чтобы отличить обратно пропорциональную зависимость от прямой, можно использовать пословицу: «Тише едешь — дальше будешь».
Задачи на обратно пропорциональные величины удобно решать с помощью пропорции.
Рассмотрим примеры задач на обратно пропорциональную зависимость.
1) 24 человека за 5 дней пропололи участок. За сколько дней выполнит ту же работу 30 человек, если будут работать с той же производительностью?
(Рассуждаем так:
1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы. Значит, это — обратно пропорциональная зависимость.
3. Поэтому вторая стрелка имеет противоположное направление).
Решение:
Пусть за х дней могут прополоть участок 30 человек. Составляем пропорцию (в направлении от начала стрелки к ее концу):
Чтобы найти неизвестный крайний член пропорции, надо произведение средних членов разделить на известный крайний член:
24 и 30 сокращаем на 6, 5 и 5 — на 5:
Значит, 30 человек выполнят эту работу за 4 дня.
Ответ: за 4 дня.
2) Для перевозки груза автомашине грузоподъемностью 7,5 тонн пришлось сделать 12 рейсов. Сколько рейсов понадобится сделать автомашине грузоподъемностью 9 тонн для перевозки этого же груза?
(1. В заполненном столбце ставим стрелку в направлении от большего числа к меньшему.
2. Чем больше грузоподъемность машины, тем меньше рейсов ей нужно сделать, чтобы перевезти груз. Значит, это — обратно пропорциональная зависимость.
3. Поэтому вторая стрелка имеет противоположное направление).
Решение:
Пусть х рейсов потребуется машине грузоподъемностью 9 тонн, чтобы перевезти груз. Составляем пропорцию (от начала стрелки к ее концу):
Значит, понадобится 10 рейсов.
Ответ: 10 рейсов.
Прямая и обратная пропорциональная зависимость — Kid-mama
| Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз. |
Проще всего понять прямо пропорциональную зависимость на примере станка, изготавливающего детали с постоянной скоростью. Если за два часа он делает 25 деталей, то за 4 часа он изготовит деталей вдвое больше — 50. Во сколько раз дольше времени он будет работать, во столько же раз больше деталей он изготовит.
Во сколько раз дольше времени он будет работать, во столько же раз больше деталей он изготовит.
Математически это выглядит так:
4 : 2 = 50 : 25 или так: 2 : 4 = 25 : 50
Прямо пропорциональными величинами тут являются время работы станка и число изготовленных деталей.
Говорят: Число деталей прямо пропорционально времени работы станка.
Если две величины прямо пропорциональны, то отношения соответствующих величин равны. (В нашем примере — это отношение времени 1 к времени 2 = отношению количества деталей за время 1 к количеству деталей за время 2)
Обратная пропорциональность
| Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз. |
Обратно пропорциональная зависимость часто встречается в задачах на скорость. Скорость и время являются обратно пропорциональными величинами. Действительно, чем быстрее движется объект, тем меньше времени у него уйдет на путь.
Например:
Если величины обратно пропорциональны, то отношение значений одной величины (скорости в нашем примере) равно обратному отношению другой величины ( времени в нашем примере). ( В нашем примере — отношение первой скорости к второй скорости равно отношению второго времени к первому времени.
Задача 1:
| Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени? |
Решение:
Запишем краткое условие задачи:
Задача 2:
| Для перевозки груза потребовалось 24 машины грузоподъемностью 7,5 тонн. Сколько нужно машин грузоподъемностью 4,5 т, чтобы перевезти тот же груз? |
Решение:
Краткая запись:
обратно пропорционально — определение, формула и примеры
Говорят, что две величины обратно пропорциональны, когда значение одной величины увеличивается по сравнению с уменьшением другой, или наоборот. Это означает, что эти две величины ведут себя противоположно по своей природе. Например, время, необходимое для выполнения задачи, уменьшается с увеличением количества рабочих, выполняющих ее, и увеличивается с уменьшением количества рабочих. Здесь время и количество рабочих обратно пропорциональны друг другу.
Другие термины, которые могут быть использованы здесь для этого типа пропорции, — это обратная пропорция или обратное изменение, или обратное изменение, или обратная пропорция. Две переменные говорят x и y, которые в обратной пропорции представлены как x ∝ 1 / y или x ∝ y -1 . Прямая пропорция и обратная пропорция являются противоположными отношениями по сравнению друг с другом.
Что обратно пропорционально?
В математике и физике мы узнаем о величинах, которые зависят друг от друга, и такие величины называются пропорциональными друг другу.Другими словами, две переменные или величины пропорциональны друг другу, если одна изменяется, то другая также изменяется на фиксированную величину. Это свойство переменных называется пропорциональностью, а символ, используемый для представления пропорциональности, — «∝». Есть два типа пропорциональности переменных. Их:
- Прямо пропорциональный
- Обратно пропорциональный
Когда две величины связаны друг с другом обратно пропорционально, т. Е. Когда увеличение одной величины приводит к уменьшению другой и наоборот, то говорят, что они обратно пропорциональны.В обратной пропорции, если одна переменная уменьшается, другая увеличивается в той же пропорции. Это противоположно прямой пропорции. Или говорят, что две величины обратно пропорциональны , когда одна величина прямо пропорциональна обратной величине других. Например, соотношение скорости и времени. Скорость и время в пути обратно пропорциональны, потому что чем быстрее мы путешествуем, т.е. чем больше скорость, тем короче время.
- По мере увеличения скорости время в пути уменьшается
- И с уменьшением скорости время в пути увеличивается
Общая формула обратно пропорциональной
Символ «∝» обозначает пропорциональную зависимость между двумя величинами.Пусть x и y — две величины. Тогда y обратно пропорционален x — это то же самое, что y прямо пропорционален 1 / x. Тогда говорят, что y обратно пропорционален x, и математически записывается как y ∝ 1 / x
.
Общее уравнение обратной вариации y = k / x, где k — постоянная пропорциональности.
Мы также можем записать это как y × x = k, y × x = Constant
Если x и y находятся в обратной вариации и x имеет два значения x 1 и x 2 , соответствующие y, который также имеет два значения y 1 и y 2 соответственно, то по определению обратной вариации , имеем x 1 y 1 = x 2 y 2 = (k)
В этом случае это становится x 1 / x 2 = y 2 / y 1 = k
Графическое представление обратной пропорциональности
График обратной пропорциональности выглядит следующим образом.
Например, графики уравнений y = 1 / x и y = -1 / x имеют обратно пропорциональные отношения.
Применение обратно пропорционального коэффициента
Концепция обратной пропорциональности широко используется в повседневной жизни, а также при решении многих задач в области науки, статистики и т. Д. В физике существует множество формул, выведенных с использованием концепции обратной пропорциональности. Закон Ома, соотношение скорости и времени, длина волны звука и его частота — это несколько.
Важные примечания по обратно пропорциональной системе
Для обратной пропорциональности необходимо помнить следующие моменты:
- Если одно количество увеличивается, другое уменьшается.
- x ∝ 1 / y или y ∝ 1 / x
- x × y = k, где k называется константой пропорциональности.
Часто задаваемые вопросы об обратно пропорциональной системе
Что такое прямо пропорционально?
Прямо пропорциональные переменные или величины — это переменные, в которых, если одна переменная увеличивается, другая также увеличивается.Это означает, что когда увеличение одного количества приводит к увеличению другого, и наоборот, говорят, что они прямо пропорциональны.
Например, заработок человека прямо пропорционален количеству часов или дней, которые он работает.
Как узнать, пропорционально оно прямо или обратно?
Обратную пропорциональную зависимость между двумя величинами можно понять, как показано ниже,
- Укажите две величины, которые различаются в данной проблеме.
- Если x / y постоянный, то он прямо пропорционален.
- Если x × y постоянно, то обратно пропорционально.
Какова формула обратно пропорционального?
Формула обратной связи помогает математически представить обратно пропорциональную зависимость. Формула обратной вариации: x × y = k или y = k / x
.
Что обратное 1?
Обратное значение любой переменной, например x, можно вычислить как 1 / x.Следовательно, величина, обратная 1, будет 1/1, что равно 1.
.
Что это значит, если две вещи обратно пропорциональны?
Говорят, что две величины обратно пропорциональны, когда значение одной величины увеличивается по сравнению с уменьшением другой, или наоборот. Это означает, что эти две величины ведут себя противоположно по своей природе. Например, соотношение скорости и времени. Скорость и время в пути обратно пропорциональны, потому что чем быстрее мы путешествуем, т.е. чем больше скорость, тем короче время.
Что означает символ обратной пропорциональности?
Для обозначения пропорциональности используется символ «∝». Обратная пропорциональность относится к одному количеству, которое прямо пропорционально обратному значению другого количества. Мы представляем любые две величины в обратной пропорции как, x ∝ 1 / y или x ∝ y -1 .
Что такое пример обратной пропорции?
Обратно пропорциональная зависимость возникает, когда одно значение увеличивается, а другое уменьшается.Например, большее количество рабочих сокращает время, необходимое для выполнения задачи. Таким образом, они обратно пропорциональны.
Обратно пропорционально — объяснение и примеры
Что означает «обратно пропорционально»?
В нашей повседневной жизни мы часто сталкиваемся с ситуациями, когда на изменение значений одной величины влияет изменение значений другой величины.
Например, , сирена приближающейся пожарной машины или машины скорой помощи становится громче по мере приближения автомобиля к вам и тише по мере удаления.Вы заметили, что чем меньше расстояние между вами и автомобилем, тем громче сирена и чем больше расстояние, тем тише становится сирена. Этот тип ситуации называется обратной пропорцией, а иногда и косвенной пропорцией.
Прямая и косвенная пропорция — это два понятия, с которыми мы все знакомы, но, возможно, не на математическом уровне. И прямая, и обратная пропорция используются, чтобы показать, как две величины связаны друг с другом.
В этой статье мы узнаем об обратной и косвенной пропорции и о том, как эти концепции важны в реальных жизненных ситуациях.но прежде чем мы начнем, давайте напомним себе о концепции прямой пропорции.
Прямая пропорция
Две переменные a и b считаются прямо пропорциональными, если увеличение одной переменной вызывает увеличение другой переменной, и наоборот. Это означает, что прямо пропорционально соотношение соответствующих значений переменных остается постоянным. В этом случае, если значения b; b 1 , b 2 соответствует значениям a; a 1 , a 2 соответственно, тогда их соотношение будет постоянным;
a 1/ / b 1 = a 2 / b 2
Прямая пропорция представлена знаком пропорциональности ‘’ как a ∝ b.Формула прямого изменения имеет следующий вид:
a / b = k
, где k называется константой пропорциональности.
Обратная пропорция
В отличие от прямой пропорции, когда одно количество изменяется прямо пропорционально изменениям другого количества, в обратной пропорции, увеличение одной переменной вызывает уменьшение другой переменной, и наоборот. Говорят, что две переменные a и b обратно пропорциональны, если; а∝1 / б. В этом случае увеличение переменной b вызывает уменьшение значения переменной a.Точно так же уменьшение переменной b вызывает увеличение значения переменной a.
Формула косвенной пропорциональности
Если переменная a обратно пропорциональна переменной b, то это может быть представлено в формуле:
a∝1 / b
ab = k; где k — пропорциональная постоянная.
Чтобы создать обратное пропорциональное уравнение, необходимо выполнить следующие шаги:
- Запишите пропорциональное соотношение
- Запишите уравнение, используя константу пропорциональности
- Теперь найдите значение константы, используя заданные значения
- Замените значение константы в уравнении.
Примеры из реальной жизни концепции обратной пропорции
- Время, необходимое определенному количеству рабочих для выполнения части работы, обратно пропорционально количеству рабочих на работе. Это означает, что чем меньше рабочих, тем больше времени требуется для завершения работы, и наоборот.
- Скорость движущегося судна, такого как поезд, транспортное средство или корабль, обратно пропорциональна времени, необходимому для преодоления определенного расстояния. Чем выше скорость, тем меньше времени требуется на преодоление дистанции.
Пример 1
35 рабочих собирают урожай кофе на плантации за 8 дней. Сколько времени потребуется 20 рабочим, чтобы собрать урожай кофе на одной и той же плантации.
Решение
- 35 рабочих собирают кофе за 8 дней
Продолжительность, занятая одним рабочим = (35 × 8) дней
- Теперь вычислите продолжительность, занятую 20 рабочими
= (35 × 8) / 20
= 14 дней
Следовательно, на 20 рабочих потребуется 14 дней.
Пример 2
6 коз или 8 овец пасутся на поле за 28 дней. Сколько времени понадобится 9 козам и 2 овцам, чтобы пасти одно и то же поле.
Решение
6 коз = 8 овец
⇒ 1 коза = 8/6 овец
⇒ 9 коз ≡ (8/6 × 9) овец = 12 овец
⇒ (9 коз + 2 овцы) ≡ (12 овец + 2 овец) = 14 овец
Итак, 8 овец => 28 дней
Одна овца будет пасти (28 × 8) дней
⇒ 14 овец займет (28 × 8) / 14 дней
= 16 дней
Следовательно, 9 коз и 2 овцы будут пасти поле 16 дней.
Пример 3
Девять кранов могут заполнить бак за четыре часа. Сколько времени потребуется двенадцать кранов с одинаковым расходом, чтобы заполнить один и тот же резервуар?
Решение
Пусть отношения;
x 1 / x 2 = y 2/ y 1
⇒ 9 / x = 12/4
x = 3
Таким образом, 12 кранов заполнят бак за 3 часа .
Практические вопросы
- В армейской казарме достаточно еды, чтобы прокормить 80 солдат в течение 60 дней.Подсчитайте, на сколько хватит еды, когда через 15 дней в казарму войдут еще 20 солдат.
- 8 кранов с одинаковым расходом могут заполнить резервуар за 27 минут. Если не открывать два крана, сколько времени потребуется для заполнения бака оставшимися трубами?
- Общая недельная заработная плата для 6 рабочих, работающих по 8 часов в день, составляет 8400 долларов США. Какова будет недельная заработная плата 9 рабочих, работающих по 6 часов в день?
- 1350 литров молока могут выпить 70 студентов за 30 дней. Сколько учеников потребят 1710 литров молока за 28 дней?
- 15 женщин или 12 мужчин могут выполнить определенную задачу за 66 дней.Сколько времени потребуется 3 и 24 женщинам и мужчинам соответственно, чтобы выполнить одну и ту же задачу?
Ответы
- 51 день
- 36 минут
- $ 9450
- 95 студентов
- 30 дней
Предыдущий урок | Главная страница | Следующий урок
Прямо пропорционально и обратно пропорционально
Прямо пропорционально: по мере увеличения одной суммы другая сумма увеличивается с той же скоростью.
| ∝ | Символ «прямо пропорциональный» — ∝ (не путайте его с символом бесконечности ∞) |
Пример: вам платят 20 долларов в час
Ваш заработок составляет , прямо пропорционально тому, сколько часов вы работаете
Работайте больше часов, получайте больше зарплаты; прямо пропорционально.
Это можно было бы написать:
Заработок ∝ Отработанное время
- Если вы работаете 2 часа, вам платят 40 долларов
- Если вы работаете 3 часа, вам платят 60 долларов
- и др…
Константа пропорциональности
«Константа пропорциональности» — это величина, которая связывает две суммы
Пример: вам платят 20 долларов в час (продолжение)
Константа пропорциональности равна 20 , потому что:
Заработок = 20 × Отработанные часы
Это можно записать:
y = kx
Где k — коэффициент пропорциональности
Пример: y прямо пропорционально x, а когда x = 3, тогда y = 15.
Что такое постоянная пропорциональности?
Они прямо пропорциональны, поэтому:
y = kx
Добавьте то, что мы знаем (y = 15 и x = 3):
15 = к × 3
Решить (разделив обе стороны на 3):
15/3 = k × 3/3
5 = к × 1
к = 5
Константа пропорциональности равна 5:
.
y = 5x
Когда мы знаем коэффициент пропорциональности, мы можем ответить на другие вопросы
Пример: (продолжение)
Каково значение y при x = 9?
у = 5 × 9 = 45
Какое значение имеет x, когда y = 2?
2 = 5x
х = 2/5 = 0.4
обратно пропорционально
| Обратно Пропорционально: когда одно значение уменьшается, с той же скоростью, что и другое увеличивается. |
Пример: скорость и время в пути
Скорость и время в пути обратно пропорциональны, потому что чем быстрее мы движемся, тем короче время.
- С увеличением скорости время в пути уменьшается
- И с уменьшением скорости время в пути увеличивается
Это: y обратно пропорционально x
То же, что: y прямо пропорционально 1 / x
Что можно написать:
г =
к x
Пример: 4 человека могут покрасить забор за 3 часа.
Сколько времени займет его покраска 6 человек?
(Предположим, что все работают с одинаковой скоростью)
Это обратная пропорция:
- По мере увеличения количества людей время рисования сокращается.
- По мере того, как количество людей уменьшается, время рисования увеличивается.
Мы можем использовать:
т = к / п
Где:
- t = количество часов
- k = коэффициент пропорциональности
- n = количество человек
«4 человека могут покрасить забор за 3 часа» означает, что t = 3 при n = 4
3 = к / 4
3 × 4 = к × 4/4
12 = к
к = 12
Итак, теперь мы знаем:
т = 12 / п
А при n = 6:
t = 12/6 = 2 часа
Итак, 6 человек покрасят забор за 2 часа.
Сколько человек нужно, чтобы выполнить работу за полчаса?
½ = 12 / п
n = 12 / ½ = 24
Итак, для выполнения работы за полчаса требуется 24 человека.
(При условии, что они не все мешают друг другу!)
Пропорционально …
Также возможно быть пропорциональным квадрату, кубу, экспоненте или другой функции!
Пример: пропорционально x
2
Камень падает с вершины высокой башни.
Расстояние, на которое он падает, составляет , пропорционально квадрату времени падения.
Камень падает 19,6 м через 2 секунды, как далеко он упадет через 3 секунды?
Мы можем использовать:
d = узлы 2
Где:
- d — пройденное расстояние и
- т — время падения
Если d = 19,6, то t = 2
19,6 = к × 2 2
19.6 = 4 тыс.
к = 4,9
Итак, теперь мы знаем:
d = 4,9 т 2
А при t = 3:
d = 4,9 × 3 2
д = 44,1
Значит, он упал на 44,1 м за 3 секунды.
Обратный квадрат
Обратный квадрат : когда одно значение уменьшается на как квадрат на другого значения.
Пример: свет и расстояние
Чем дальше мы от источника света, тем он менее яркий.
На самом деле яркость уменьшается как на квадрат расстояния. Потому что свет распространяется во всех направлениях.
Таким образом, яркость «1» на 1 метре составляет всего «0,25» на 2 метрах (удвоение расстояния приводит к четверти яркости) и так далее.
Обратно пропорционально: определение, формула и примеры — видео и стенограмма урока
Что такое обратно пропорционально?
В математике количество может измениться, когда вы измените другое количество.Когда две величины или переменные связаны, мы говорим, что между ними существует связь. Переменные могут иметь одно из трех соотношений или вариантов: прямое, обратное и совместное .
В этом уроке мы сосредоточимся на понимании определения обратной вариации : если одна величина увеличивается в результате уменьшения другой величины или наоборот, то две величины обратно пропорциональны . Мы можем написать математическое определение обратно пропорциональной зависимости, как показано на рисунке 1.
Допустим, у нас n = 1, тогда определение можно упростить и записать как: y = k / x, где «y» обратно пропорционально «x».
Если x возведено во вторую степень, то мы говорим, что y обратно пропорционально квадрату x или кубу x в третьей степени, и так далее.Значение n также может быть дробью, например, 1/2 степени. Когда у вас есть показатель степени 1/2, он также известен как квадратный корень. В этом случае мы бы сказали, что y обратно пропорционально квадратному корню из x , и мы бы записали его следующим образом:
Давайте лучше поймем, что означает обратно пропорциональная величина, построив график значений x и y для различных значений n :
Взгляните на график, когда y обратно пропорционально x с константой k , равной 50.Обратите внимание, что по мере увеличения значения x значение y уменьшается. 50 делится на увеличивающееся значение x , в результате получаются все меньшие и меньшие значения y . Это происходит потому, что в знаменателе стоит x . Часто вы будете иметь отношение, которое обратно пропорционально, если независимая переменная находится в знаменателе.
Давайте посмотрим, что произойдет, если у вас будет x во второй степени в знаменателе, а не в первой степени.Обратите внимание, что изначально, когда значение x увеличивается, значение y уменьшается очень быстро, но затем снижение происходит медленнее по сравнению с началом графика. Однако тенденция остается той же, что и раньше: по мере увеличения значения x значение y уменьшается.
Если бы вы построили график и как функцию 50, деленную на квадратный корень из x , даже тогда эта тенденция все равно останется прежней.Увеличение значения x приведет к уменьшению значения y или наоборот. Обычно, когда одна переменная движется в одном направлении, другая переменная обычно движется в противоположном направлении. Это причина, по которой этот тип отношений называется обратно пропорциональным.
Теперь, когда мы лучше понимаем эту взаимосвязь, давайте посмотрим, как мы можем применить ее для решения проблем.
обратно пропорционально — определение, пример и методы решения
Прежде чем узнать, что является обратно пропорциональным, разве вы не хотите знать, что означает пропорция? Пропорция — это утверждение, которое показывает, как две величины или переменные связаны друг с другом.Эти переменные могут быть двух типов: прямо пропорциональные и обратно пропорциональные. Когда одно количество увеличивается вместе с другим, это называется прямо пропорциональным, тогда как если одно увеличивается, а другое уменьшается, то оно обратно пропорционально. Например, если на работе больше рабочих, то выполнение работы не займет много времени. Так что же здесь происходит на самом деле? По мере увеличения количества рабочих время, необходимое для выполнения работы, уменьшается. Теперь это то, что мы называем обратно пропорциональным.Вот как может быть представлено обратно пропорциональное значение. Мы скажем, что рабочие и время обратно пропорциональны друг другу. Обратно пропорционально — это, по сути, отношение между двумя переменными, когда их произведение равно постоянному значению. Есть символ, обозначающий обратно пропорциональную величину. Следовательно, обратно пропорциональный символ можно представить как ∝. Обратно пропорциональный символ очень похож на символ бесконечности.
Пример обратной пропорциональности
Пример скорости и времени является основным и подходящим примером обратно пропорциональной зависимости.По мере увеличения скорости время на завершение поездки будет уменьшаться.
Другим обратно пропорциональным примером может быть объем и давление идеального газа. Оба они пропорциональны друг другу (закон Бойля).
Электрический ток обратно пропорционален сопротивлению.
Чем больше расстояние между вами и источником света, тем меньше будет яркость.
Методы решения обратно пропорциональных переменных
Есть два способа решить проблему с обратно пропорциональными переменными.
Метод 1) В обратной пропорции, x1 y1 = x2 y2 = x2 y2 = x2 y2
Следовательно, для решения этой проблемы мы можем использовать уравнение для поиска неизвестных членов, поскольку всегда будет задана одна пара.
Метод 2) Мы также знаем, что в обратной пропорции уравнение x + y = k становится x = k / y. Таким образом, чтобы найти значение k, мы можем использовать известные значения, чтобы найти неизвестные с помощью описанного выше.
Для вычисления сумм также можно использовать обратно пропорциональную формулу.
Создание уравнения
Вы можете настроить уравнение, используя следующие четыре простых шага:
Шаг 1) Сначала запишите пропорциональную зависимость.
Шаг 2) Второй шаг — преобразование в уравнение с использованием константы пропорциональности.
Шаг 3) На третьем шаге используйте данную информацию, чтобы найти константу пропорциональности.
Шаг 4) Последний и последний шаг — подставить константу пропорциональности в уравнение.
Решенные примеры обратной пропорции
Вопрос 1) Время, необходимое (t секунд) для кипячения воды водонагревателем, обратно пропорционально мощности (p ватт), потребляемой водонагревателем. Если p = 2000 Вт, t = 252 с. Найдите время, необходимое для кипячения воды при p = 800 Вт.
Решение 1) t ∝ \ [\ frac {1} {p} \]
t = \ [\ frac {k} {p} \]
252 = \ [\ frac {k} {2000} \ ]
k = 504000
t = \ [\ frac {504000} {p} \]
t = \ [\ frac {504000} {800} \]
t = 630 секунд.
Вопрос 2) Сила (F ньютонов), прилагаемая магнитом к металлическому объекту, обычно обратно пропорциональна квадрату расстояния (d см). Если d = 2 см и F = 50 Н, то выразите:
F через d.
Найдите силу, когда расстояние между металлическим предметом и магнитом равно 10 см.
Найдите расстояние между ними, когда сила равна 8N.
Также объясните, что происходит с F, когда d уменьшается вдвое.{2} \] = 25
Следовательно, d = 5
F, когда d уменьшается вдвое:
d = 10 F = 2
d = 5 F = 8
Следовательно, F становится в четыре раза больше, когда d уменьшается вдвое. {2} \] = 144
Следовательно, A = 12
Вопрос 4) Время (t), необходимое пассажирам для регистрации на рейс, обратно пропорционально квадрату количества работающих сотрудников.{2} \] = 50
с = 7,071
Следовательно, необходимо 8 кадров.
Вопрос 5) Количество дней (d) для завершения исследования обратно пропорционально количеству работающих исследователей. Если исследователям потребуется 125 дней, чтобы завершить работу 16 человек, то сколько человек потребуется для завершения исследования за 40 дней?
Решение 5) D ∝ \ [\ frac {1} {R} \]
D = \ [\ frac {F} {R} \]
125 = \ [\ frac {F} {16} \ ]
2000 = F
D = \ [\ frac {2000} {R} \]
40 = \ [\ frac {2000} {R} \]
40R = 2000
R = 50
Следовательно, для завершения исследования за 40 дней потребуется 50 человек.
Вариант | Люмен Обучающий Колледж Алгебры
Компания по производству подержанных автомобилей только что предложила своему лучшему кандидату, Николь, должность в отделе продаж. Позиция предлагает 16% комиссионных от ее продаж. Ее заработок зависит от объема продаж. Например, если она продаст автомобиль за 4600 долларов, она заработает 736 долларов. Она хочет оценить предложение, но не знает, как это сделать. В этом разделе мы рассмотрим отношения, такие как эта, между доходами, продажами и ставкой комиссии.
Прямое изменение
Компания по производству подержанных автомобилей только что предложила своему лучшему кандидату, Николь, должность в отделе продаж. Позиция предлагает 16% комиссионных от ее продаж. Ее заработок зависит от объема продаж. Например, если она продаст автомобиль за 4600 долларов, она заработает 736 долларов. Она хочет оценить предложение, но не знает, как это сделать. В этом разделе мы рассмотрим отношения, такие как эта, между доходами, продажами и ставкой комиссии.
В приведенном выше примере заработок Николь можно определить, умножив объем продаж на ее комиссионные.Формула e = 0,16 s говорит нам, что ее заработок, e , складывается из произведения 0,16, ее комиссии и продажной цены автомобиля. Если мы создадим таблицу, мы увидим, что по мере увеличения продажной цены увеличивается и прибыль, что должно быть интуитивно понятным.
s , отпускные цены e = 0,16 с Интерпретация 4600 долл. США е = 0.16 (4600) = 736 Продажа автомобиля за 4600 долларов приносит 736 долларов прибыли. 9 200 долл. США e = 0,16 (9 200) = 1 472 Продажа автомобиля за 9 200 долларов приносит прибыль 1472 доллара. 18 400 долл. США e = 0,16 (18 400) = 2 944 Продажа автомобиля за 18 400 долларов приносит прибыль 2944 доллара. Обратите внимание, что прибыль кратна продажам. По мере увеличения продаж прибыль предсказуемо увеличивается.Удвойте продажи автомобиля с 4600 до 9 200 долларов, и мы удвоим прибыль с 736 до 1472 долларов. По мере увеличения входа выход увеличивается как кратное входное. Отношение, в котором одна величина является постоянной, умноженной на другую, называется прямым изменением . Каждая переменная в этом типе отношений напрямую отличается от другой.
На графике ниже представлены данные о потенциальном доходе Николь. Мы говорим, что прибыль напрямую зависит от продажной цены автомобиля.{n}} [/ latex], где k называется константой вариации , которая помогает определить взаимосвязь между переменными.
Как сделать: учитывая описание задачи прямого изменения, решите неизвестное.
- Определите вход, x , и выход, y . {3} [/ latex].{3} \ hfill \\ \ text {} = 675 \ hfill \ end {array} [/ latex]
Анализ решения
График этого уравнения представляет собой простую кубическую форму, как показано ниже.
Вопросы и ответы
Графики всех уравнений прямой вариации похожи на Пример 1?
№. Уравнения прямых вариаций являются степенными функциями — они могут быть линейными, квадратичными, кубическими, квартическими, радикальными и т. Д. Но все графики проходят через (0, 0).
Попробуй
Величина y напрямую зависит от квадрата x .Если y = 24, когда x = 3, найти y , когда x равно 4.
Решение
[латекс] \ frac {128} {3} [/ латекс]
Посмотрите это видео, чтобы получить быстрый урок по прямым вариациям. Вы увидите больше отработанных примеров.
Обратная и совместная вариация
Температура воды в океане изменяется обратно пропорционально глубине воды. На глубине от 250 до 500 футов формула [латекс] T = \ frac {14 000} {d} [/ latex] дает нам температуру в градусах Фаренгейта на глубине в футах ниже поверхности Земли.Рассмотрим Атлантический океан, который покрывает 22% поверхности Земли. В определенном месте, на глубине 500 футов, температура может достигать 28 ° F.
Если мы создадим таблицу, мы увидим, что с увеличением глубины температура воды снижается.
d , глубина [латекс] T = \ frac {\ text {14,000}} {d} [/ латекс] Интерпретация 500 футов [латекс] \ frac {14 000} {500} = 28 [/ латекс] На глубине 500 футов температура воды составляет 28 ° F. 350 футов [латекс] \ frac {14 000} {350} = 40 [/ латекс] На глубине 350 футов температура воды 40 ° F. 250 футов [латекс] \ frac {14 000} {250} = 56 [/ латекс] На глубине 250 футов температура воды 56 ° F. {n}} [/ латекс] , где k — ненулевая константа, тогда мы говорим, что y изменяется обратно пропорционально с n -й степени x .{n} y [/ латекс].
Пример: написание формулы для обратно пропорциональной зависимости
Турист планирует проехать 100 миль. Найдите формулу для времени, которое займет поездка, в зависимости от скорости, которую едет турист.
Решение
Вспомните, что умножение скорости на время дает расстояние. Если мы допустим, что t представляет время вождения в часах, а v представляет скорость (скорость или скорость), с которой едет турист, то vt = расстояние. Поскольку расстояние зафиксировано на 100 милях, vt = 100.{-1} \ hfill \ end {array} [/ latex]
Мы можем видеть, что постоянная вариации равна 100, и, хотя мы можем записать отношение, используя отрицательный показатель степени, чаще всего это выражается в виде дроби.
Как сделать: учитывая описание проблемы косвенного изменения, решите неизвестное. {3}} [/ latex].{3}} \ hfill \\ \ text {} = \ frac {25} {27} \ hfill \ end {array} [/ latex]
Анализ решения
График этого уравнения представляет собой рациональную функцию.
Попробуй
Величина x изменяется обратно пропорционально квадрату x . Если y = 8, когда x = 3, найти y , когда x равно 4.
Решение
[латекс] \ frac {9} {2} [/ латекс]
Следующее видео представляет собой короткий урок по обратной вариации и включает больше отработанных примеров.
Вариант шарнира
Многие ситуации сложнее базовой модели с прямым или обратным изменением. Одна переменная часто зависит от нескольких других переменных. Когда переменная зависит от произведения или частного двух или более переменных, это называется совместным вариантом . Например, стоимость проезда учащихся на автобусе для каждой школьной поездки зависит от количества учащихся и расстояния от школы. Переменная c , стоимость, изменяется вместе с количеством студентов, n , и расстоянием, d .
Общее примечание: вариант соединения
Совместное изменение происходит, когда переменная изменяется прямо или обратно с несколькими переменными.
Например, если x напрямую зависит от y и z , мы имеем x = kyz . Если x напрямую изменяется с y и обратно с z , мы имеем [latex] x = \ frac {ky} {z} [/ latex]. Обратите внимание, что мы используем только одну константу в уравнении совместной вариации.{2}} {\ sqrt [3] {27}} \ hfill \\ \ text {} = 1 \ hfill \ end {array} [/ latex]
Попробуй
x напрямую зависит от квадрата y и обратно пропорционально z . Если x = 40, когда y = 4 и z = 2, найти x , когда y = 10 и z = 25.
Решение
[латекс] x = 20 [/ латекс]
В следующем видео представлен еще один рабочий пример задачи вариации сустава.{n}}, k \ text {ненулевая константа} \\ [/ latex].
- Отношение, в котором одна величина является постоянной, умноженной на другую, называется прямым изменением.
- Две переменные, которые прямо пропорциональны друг другу, будут иметь постоянное соотношение.
- Отношение, в котором одна величина является постоянной, деленной на другую величину, называется обратной вариацией.
- Две переменные, которые обратно пропорциональны друг другу, будут иметь постоянный множитель.
- Во многих задачах переменная изменяется прямо или обратно с несколькими переменными. Мы называем этот тип отношений совместной вариацией.
Глоссарий
- постоянная вариации
- ненулевое значение k , которое помогает определить взаимосвязь между переменными в прямой или обратной вариации
- прямое изменение
- взаимосвязь между двумя переменными, которые являются постоянными кратными друг другу; по мере увеличения одного количества увеличивается и другое
- обратное изменение
- взаимосвязь между двумя переменными, в которой произведение переменных является константой
- обратно пропорционально
- отношение, в котором одна величина является константой, деленной на другую величину; по мере увеличения одной величины другая уменьшается
- вариант шарнира
- взаимосвязь, при которой переменная изменяется прямо или обратно с несколькими переменными
- варьируется напрямую
- соотношение, в котором одна величина является константой, умноженной на другую величину
- изменяется обратно пропорционально
- отношение, в котором одна величина является константой, деленной на другую величину
Обратная пропорциональность: что это такое?
Сегодня мы узнаем об обратной пропорциональности между величинами.
Для начала нам нужно напомнить себе, что величина — это все, что можно измерить.
Если это вас не интересует, просмотрите наш предыдущий пост, в котором мы говорим о прямой пропорциональности и объясняем концепцию величины: Прямая пропорциональность
Многие величины связаны с другими, например:
- Количество игрушек, которые у вас есть, с размером места, которое они занимают.
- Скорость автомобиля и время, необходимое для преодоления расстояния.
- Размер вашей комнаты и время, необходимое для ее уборки.
- Время, в течение которого блюдо находится в горячей духовке, в зависимости от того, насколько оно горячее.
Мы уже видели во введении прямой пропорциональности , что существуют отношения, в которых, как бы сильно ни растет одна величина, растет и другая.
Но когда одна величина растет, а другая пропорционально уменьшается, это называется обратной пропорциональностью.
Две величины обратно пропорциональны, когда одна величина умножается (или делится) на число, а другая величина делится (или умножается) на то же число.
Чем быстрее гоночный автомобиль…
… тем меньше времени потребуется на прохождение круга!
Представим, что для прохождения круга со скоростью 100 миль / час автомобилю требуется 12 минут. В этом примере, зная, что существует обратная пропорциональная зависимость, мы можем сказать, что если мы умножим скорость на 2 (200 миль / час), на финиш круга уйдет половина времени ( 6 минут ).
С другой стороны, если бы скорость была уменьшена вдвое (100 миль / час ÷ 2 = 50 миль / час), время круга было бы удвоено (12 мин x 2 = 24 мин )
Если гоночной машине потребовалось 4 минуты, чтобы финишировать на последнем круге, что бы произошло со скоростью машины на последнем круге?
(12 мин ÷ 4 мин = 3)
Время: , деленное на на 3, поэтому скорость должна быть , умноженной на на 3 (3 x 100 миль / час = 300 миль / час).То есть гоночный автомобиль на последнем круге двигался со скоростью 300 миль / час.
Обратная пропорциональность
На этих примерах мы видим, что этот тип пропорциональности называется INVERSE . Что происходит с одной из величин, так это с ОБРАТНОЙ и другой величины; когда одно увеличивается, другое уменьшается, и наоборот.
Чтобы вычислить пропорциональное рассуждение, нам нужно умножить величины каждой величины друг на друга.
- 100 миль / час x 12 мин = 1200
- 200 миль / час x 6 мин = 1200
- 50 миль / час x 24 мин = 1200
- 300 миль / час x 4 мин = 1200
Глядя на это, мы напоминаем, что пропорциональное рассуждение — это константа ; это всегда одно и то же для каждой пары чисел, представляющих сравниваемые величины. В этом примере пропорциональное рассуждение — 1200 .
Помните, что в Smartick у вас есть множество упражнений и задач с обратной и прямой пропорцией, которые вы можете практиковать.
- Определите вход, x , и выход, y . {3} [/ latex].{3} \ hfill \\ \ text {} = 675 \ hfill \ end {array} [/ latex]

 А уменьшение одно числа ведет к уменьшению другого во столько же раз.
А уменьшение одно числа ведет к уменьшению другого во столько же раз.

 Обратная пропорция выглядит так:
Обратная пропорция выглядит так: