Содержание
Закон Ампера | энергетик
в раздел тоэ
Закон Ампера — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током.
Взаимодействия проводников с током:
(ниже рассмотрим три варианта формул силы взаимодействия токов по Закону Ампера)
Вариант 1
Выражение для силы , с которой магнитное поле действует на элемент объёма проводника с током плотности , находящегося в магнитном поле с индукцией , в Международной системе единиц (СИ) имеет вид:
Если ток течёт по тонкому проводнику, то , где — «элемент длины» проводника — вектор, по модулю равный и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:
Тогда предыдущее равенство можно переписать следующим образом:
Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :
Вариант 2
Сила взаимодействия двух параллельных проводников пропорциональна произведению величин токов в проводниках, пропорциональна длине этих проводников и обратно пропорциональна расстоянию между ними.
F – сила взаимодействия двух параллельных проводников,
I1, I2 – величины токов в проводниках,
∆ℓ − длина проводников,
r – расстояние между проводниками.
Вариант 3
Закон Ампера определяет силу, действующую со стороны магнитного поля на проводник с током. Эта сила называется силой Ампера и равна:
dF= I[dl B]
Направление силы определяется по правилу левой руки:
Рис. 1
1
Если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в ладонь, а вытянутые пальцы указывали направление тока, то отставленный большой палец будет показывать направление силы Ампера.
Рис. 2
Модуль силы Ампера равен: dF = IBdlsin(dl B).
Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два параллельных проводника с токами I1, I2, которые находятся в среде с магнитной проницаемостью m, на расстоянии R (рис.2). Каждый из проводников создаёт магнитное поле, которое действует по закону Ампера на другой проводник с током. Направление вектора В1 определяется по правилу правого винта, а модуль его по формуле:
В1 = .
Направление силы dF1, с которой магнитное поле тока I1 действует на элемент dl тока I2, определяется по правилу левой руки, а модуль силы равен:
dF1 = I2 В1dl = ,
аналогично
dF2 = I1 В2 dl = ,
т. е. dF1 = dF2 = dF.
е. dF1 = dF2 = dF.
Два параллельных элемента тока притягиваются друг к другу с силой dF. Антипараллельные токи отталкиваются.
Вывод:
Открытие этого закона позволило ввести в единицы измерения величину силы тока, которой до того времени не существовало. Так, если исходить из определения силы тока как отношения количества заряда перенесённого через поперечное сечение проводника в единицу времени, то мы получим принципиально не измеряемую величину, а, именно, количество заряда, переносимое через поперечное сечение проводника. На основании этого определения не сможем ввести единицу измерения силы тока. Закон Ампера позволяет установить связь между величинами сил тока в проводниках и величинами, которые можно измерить опытным путём: механической силой и расстоянием. Таким образом, получена возможность ввести в рассмотрение единицу силы тока – 1 А (1 ампер).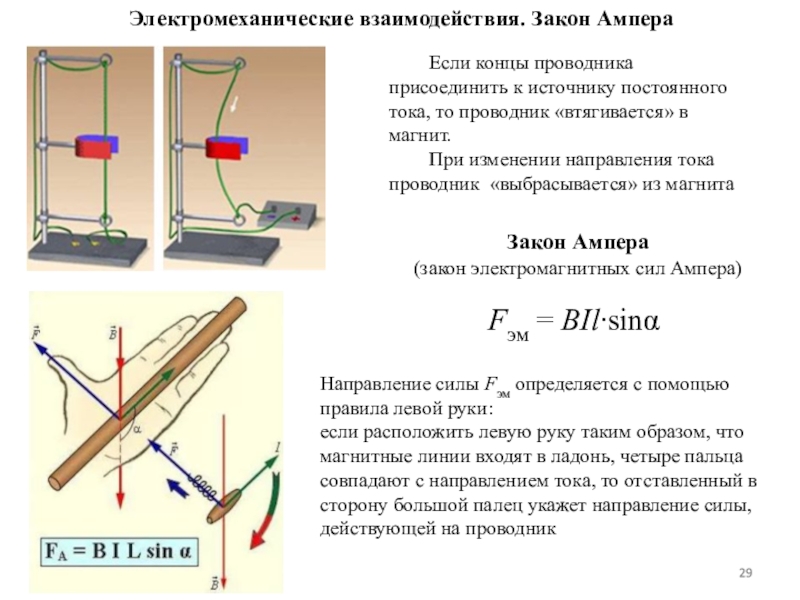
Ток в один ампер – это такой ток, при котором два однородных параллельных проводника, расположенные в вакууме на расстоянии один метр друг от друга взаимодействуют с силой 2∙10-7 Ньютона.
Статья ещё не готова.
в раздел тоэ
Закон Ампера • Джеймс Трефил, энциклопедия «Двести законов мироздания»
Одним из главных направлений развития естественной науки в начале XIX века стало растущее осознание взаимосвязей между, казалось бы, совершенно не связанными между собой феноменами электричества и магнетизма. Ханс Кристиан Эрстед (см. Открытие Эрстеда) экспериментально установил, что провод, по которому течет электрический ток, отклоняет магнитную стрелку компаса. Андре-Мари Ампер так заинтересовался этим явлением, что принялся за углубленное экспериментальное и математическое исследование взаимосвязи между электричеством и магнетизмом. В результате и был сформулирован закон, носящий теперь его имя.
Ключевой эксперимент, проведенный Ампером, достаточно прост. Он положил два прямых провода бок о бок и пропускал по ним электрический ток. Выяснилось, что между проводами действует сила притяжения или отталкивания (в зависимости от направления тока. — Прим. переводчика). Конечно, не надо быть семи пядей во лбу, чтобы прийти к такому выводу. Ведь при достаточно сильном токе провода действительно притягиваются или отталкиваются так, что это видно невооруженным глазом. Но Ампер путем тщательных измерений сумел определить, что сила механического взаимодействия пропорциональна силам токов и падает по мере увеличения расстояния между ними. Исходя из этого Ампер решил, что наблюдаемая сила объясняется возникновением магнитного поля.
Рассуждал Ампер примерно так. Электрический ток в одном проводе производит магнитное поле, конфигурация силовых линий которого представляет собой концентрические круги вокруг сечения провода. Второй провод попадает в область воздействия этого магнитного поля, и в нем возникает сила, действующая на движущиеся электрические заряды. Эта сила передается атомам металла, из которого сделан провод, в результате чего провод и изгибается. Таким образом, эксперимент Ампера демонстрирует нам два взаимодополняющих факта о природе электричества и магнетизма: во-первых, любой электрический ток порождает магнитное поле; во-вторых, магнитные поля оказывают силовое воздействие на движущиеся электрические заряды. Первое из этих утверждений сегодня и называют законом Ампера, и закон этот тесно связан с законом Био—Савара. Именно эти два закона затем легли в основу теории электромагнитного поля (см. Уравнения Максвелла).
Эта сила передается атомам металла, из которого сделан провод, в результате чего провод и изгибается. Таким образом, эксперимент Ампера демонстрирует нам два взаимодополняющих факта о природе электричества и магнетизма: во-первых, любой электрический ток порождает магнитное поле; во-вторых, магнитные поля оказывают силовое воздействие на движущиеся электрические заряды. Первое из этих утверждений сегодня и называют законом Ампера, и закон этот тесно связан с законом Био—Савара. Именно эти два закона затем легли в основу теории электромагнитного поля (см. Уравнения Максвелла).
Если же трактовать закон Ампера чуть шире, то мы поймем, что находящийся в пространстве замкнутый электрический контур формирует вокруг себя магнитное поле, интенсивность которого пропорциональна силе протекающего через контур электрического тока и площади внутри контура. То есть, например, если вокруг отдельного прямолинейного проводника с током формируется магнитное поле, индукция которого равна B на расстоянии r от проводника, то при замыкании такого проводника в круговой контур, путём сложения этих полей внутри контура, образованного замкнутым проводником с током, то есть, выражаясь научным языком, путём интегрирования, мы получим значение интенсивности магнитного поля внутри контура 2рrB, где 2рr — площадь кругового контура. По закону Ампера эта величина и будет пропорциональна силе тока в контуре.
По закону Ампера эта величина и будет пропорциональна силе тока в контуре.
На самом деле вы не раз сталкивались с упоминанием имени Андре-Мари Ампера, возможно сами того не сознавая. Взгляните на любой электроприбор у вас дома — и вы на нем обнаружите его электротехнические характеристики, например: «~220V 50Hz 3,2А». Это значит, что прибор рассчитан на питание от стандартной электросети переменного тока напряжением 220 вольт с частотой 50 герц, а сила потребляемого прибором тока составляет 3,2 ампера. Единица силы тока ампер (сокращенно — А) как раз и названа в честь ученого.
Официальное определение единицы выводится из исходного эксперимента, проделанного Ампером. Это сила тока, протекающего в каждом из двух параллельных прямолинейных проводников, помещенных в вакууме на расстояние одного метра друг от друга, вызывающая между двумя проводниками силу взаимодействия, равную 2×10–7 ньютона на метр длины. (Все научные определения единиц измерения даются в такой строгой формулировке. Причем речь здесь идет о так называемых «идеальных проводниках» бесконечной длины и ничтожно малого поперечного сечения.) Кстати, при силе тока в 1 ампер в любой точке проводника каждую секунду протекает около 6×1023 электронов.
Причем речь здесь идет о так называемых «идеальных проводниках» бесконечной длины и ничтожно малого поперечного сечения.) Кстати, при силе тока в 1 ампер в любой точке проводника каждую секунду протекает около 6×1023 электронов.
См. также:
Закон Ампера — это… Что такое Закон Ампера?
Зако́н Ампе́ра — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы , с которой магнитное поле действует на элемент объёма проводника с током плотности , находящегося в магнитном поле с индукцией , в Международной системе единиц (СИ) имеет вид:
- .
Если ток течёт по тонкому проводнику, то , где — «элемент длины» проводника — вектор, по модулю равный и совпадающий по направлению с током.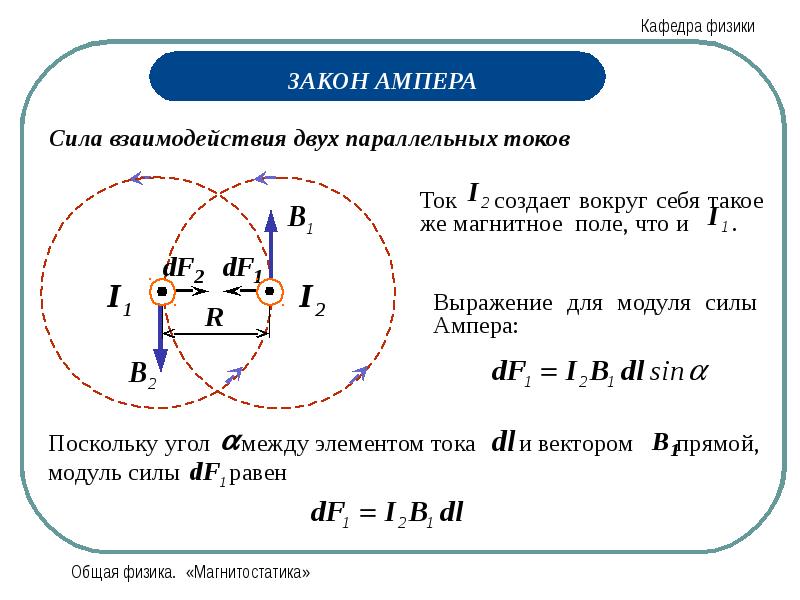 Тогда предыдущее равенство можно переписать следующим образом:
Тогда предыдущее равенство можно переписать следующим образом:
Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.
Модуль силы Ампера можно найти по формуле:
где — угол между векторами магнитной индукции и тока.
Сила максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ():
Два параллельных проводника
Два бесконечных параллельных проводника в вакууме
Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи и . Требуется найти силу, действующую на единицу длины проводника.
В соответствии с законом Био — Савара — Лапласа бесконечный проводник с током в точке на расстоянии создаёт магнитное поле с индукцией
где — магнитная постоянная.
Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:
По правилу буравчика, направлена в сторону первого проводника (аналогично и для , а значит, проводники притягиваются).
Модуль данной силы ( — расстояние между проводниками):
Интегрируем, учитывая только проводник единичной длины (пределы от 0 до 1):
Полученная формула используется в СИ для установления численного значения магнитной постоянной . Действительно, ампер, являющийся одной из основных единиц СИ, определяется в ней как «сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10−7ньютона»[1].
Таким образом, из полученной формулы и определения ампера следует, что магнитная постоянная равна Н/А² или, что то же самое, Гн/ м точно.
Проявления
- Электродинамическая деформация шин (токопроводов) трёхфазного переменного тока на подстанциях при воздействии токов короткого замыкания.
- Раздвигание токопроводов рельсотронов при выстреле.
Применение
Примечания
См. также
Закон Ампера: формула, определение, применение
Закон Закон Ампера — один из важнейших и полезнейших законов в электротехнике, без которого немыслим научно-технический прогресс. Этот закон был впервые сформулирован в 1820 году Андре Мари Ампером. Из него следует, что два расположенные параллельно проводника, по которым проходит электрический ток, притягиваются, если направления токов совпадают, а если ток течёт в противоположных направлениях, то проводники отталкиваются. Взаимодействие здесь происходит посредством магнитного поля, которое перманентно возникает при движении заряженных частиц. Математически закон Ампера в простой форме выглядит так:
F = BILsinα,
где F — это сила Ампера (сила, с которой проводники отталкиваются или притягиваются), где B — магнитная индукция; I — сила тока; L — длина проводника; α — угол между направлением тока и направлением магнитной индукции.
Интересное видео с уроком о силе Ампера:
Любые узлы в электротехнике, где под действием электромагнитного поля происходит движение каких-либо элементов, используют закон Ампера. Самый широко распространённый и используемый чуть-ли не во всех технических конструкциях агрегат, в основе своей работы использующий закон Ампера — это электродвигатель, либо, что конструктивно почти то же самое, генератор.
Именно под действием силы Ампера происходит вращение ротора, поскольку на его обмотку влияет магнитное поле статора, приводя в движение. Любые транспортные средства на электротяге для приведения во вращение валов, на которых находятся колёса, используют силу Ампера (трамваи, электрокары, электропоезда и др). Также магнитное поле приводит в движение механизмы электрозапоров (электродвери, раздвигающиеся ворота, двери лифта). Другими словами, любые устройства, которые работают на электричестве и имеющие вращающиеся узлы основаны на эксплуатации закона Ампера. Также он находит применение во многих других видах электротехники, например, в громкоговорителях.
Также он находит применение во многих других видах электротехники, например, в громкоговорителях.
В громкоговорителе или динамике для возбуждения мембраны, которая формирует звуковые колебания используется постоянный магнит. На него под действием электромагнитного поля, создаваемого расположенным рядом проводником с током, действует сила Ампера, которая изменяется в соответствии с нужной звуковой частотой.
Ещё одно видео о законе Ампера смотрите ниже:
Закон Ампера | mysite
Зако́н Ампе́ра — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.
Формулировка закона: сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником.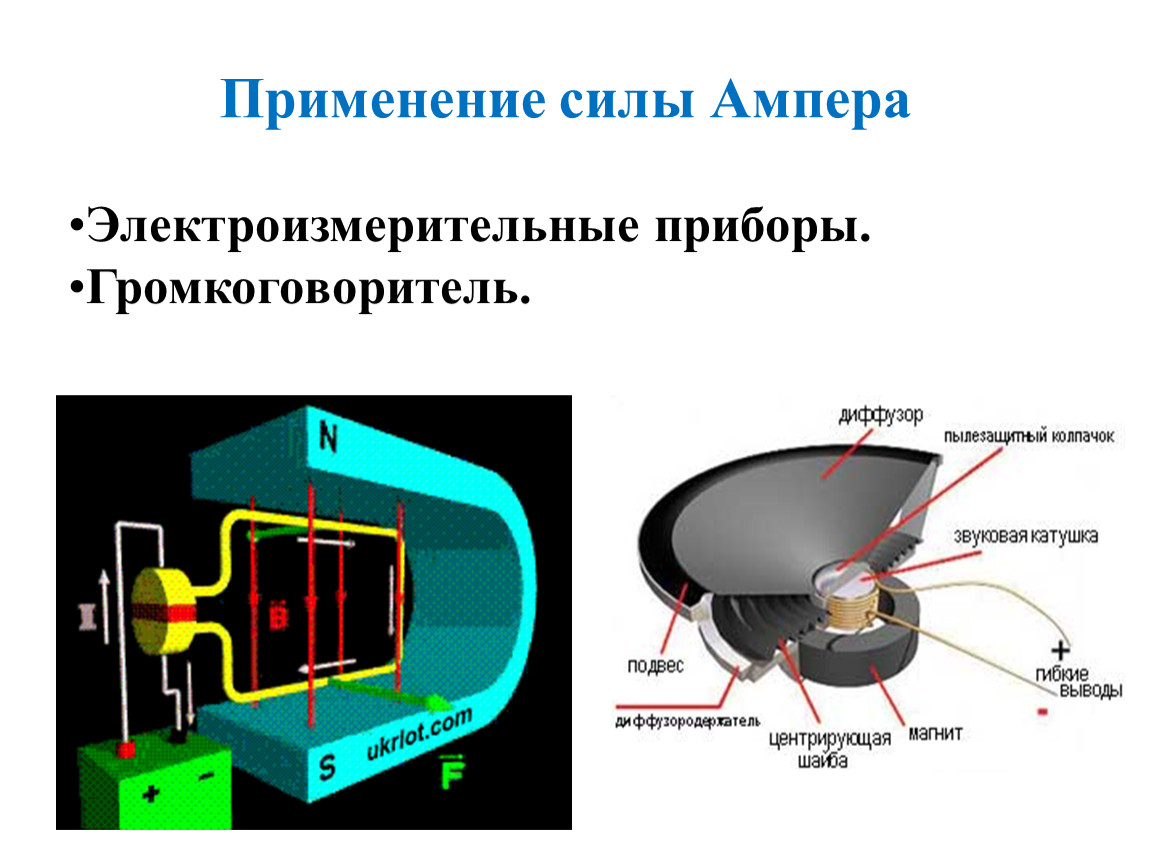
Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом:
Направление силы Ампера определяется по правилу левой руки.
Правило левой руки : если расположить левую руку так, чтобы перпендикулярная составляющая вектора магнитной индукции входила в ладонь, а четыре пальца были вытянуты по направлению тока в проводнике, то отставленный на 90° большой палец, укажет направление силы Ампера.
Яркой иллюстрацией закона Ампера является взаимодействие двух проводников при протекании в них тока. Причем от направления тока в них зависит, будут ли они притягиваться либо же отталкиваться.
При протекании тока в одном направлении проводники притягиваются, а при противоположном отталкиваются. Величина силы взаимодействия между токами определяется по формуле:
Величина силы взаимодействия между токами определяется по формуле:
Где µ0 = 4π*10-7 Гн/м – магнитная постоянная, r – расстояние между проводниками. Если принять длину проводников равной единице, тогда формула примет вид
В международной системе единиц, ампер определяют как силу неизменяющегося тока, которая при протекании через два параллельных проводника бесконечной длины и малой площади поперечного сечения, расстояние между которыми в вакууме 1 м, вызвала бы на каждом участке в 1 м силу взаимодействия равную 2*10-7 Н
37. Магнитное поле. Медицинская физика
37. Магнитное поле
Магнитным полем называют всю материю, посредством которой осуществляется силовое воздействия на движущиеся электрические заряды, помещенные в поле, и другие тела, обладающие магнитным моментом. Для магнитного поля, как и для электростатического, имеется количественная характеристика – магнитный момент (векторная величина).
Магнитная индукция в некоторой точке поля равна отношению максимального вращающего момента, действующего на рамку с током в однородном магнитном поле, к магнитному моменту этой рамки. Единицей магнитного потока является вебер (Вб):
1Вб = 1Тлм2.
Тл – единица магнитной индукции (Тесла). Из формулы видно, что поток может быть как положительным, так и отрицательным.
Закон Ампера. Энергия контура с током в магнитном поле. Одним из главных проявлений магнитного поля является его силовое действие на движущиеся электрические заряды и токи. А. М. Ампером был установлен закон, определяющий это силовое воздействие.
В проводнике, находящемся в магнитном поле, выделим достаточно малый участок dI, который рассматривается как вектор, направленный в сторону тока. Произведение IdI называют элементом тока. Сила, действующая со стороны магнитного поля на элемент тока, равна:
dF = kIB sinb ? dl,
где k – коэффициент пропорциональности; или в векторной форме
dF = ldl ? B.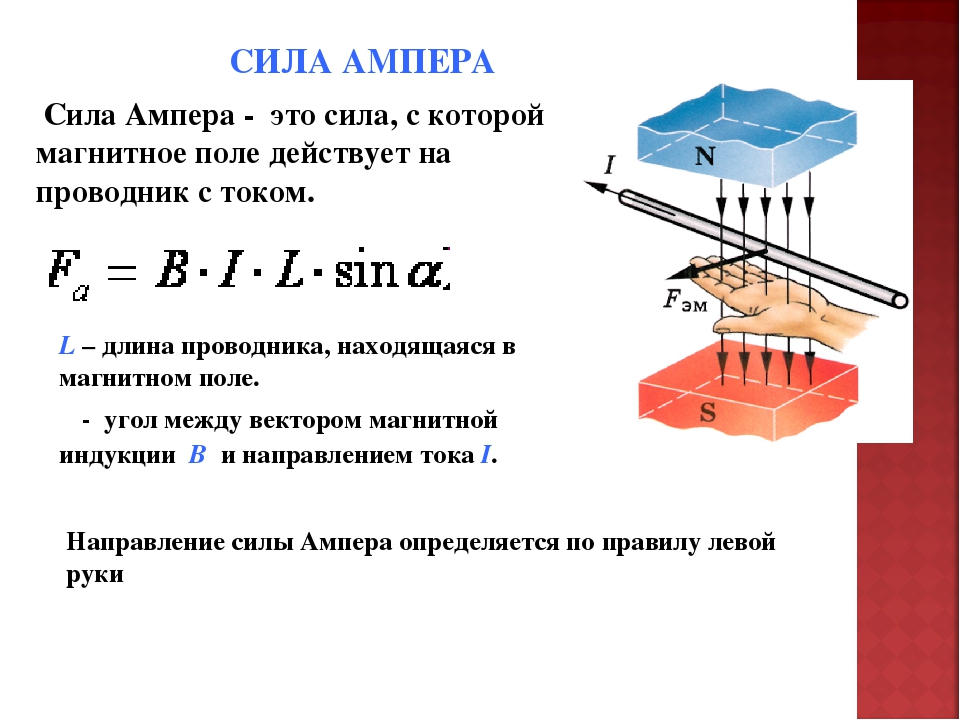
Эти соотношения выражают закон Ампера.
Сила, действующая согласно закону Ампера на проводник с током в магнитном поле, есть результат его воздействия на движущиеся электрические заряды, создающие этот ток. Сила, действующая на отдельный движущийся заряд, определяется отношением силы F, приложенной к проводнику с током, к общему числу N носителей тока в нем:
fЛ = F / N(i)
Сила тока равна:
I = jS,
F = jSBL sinb,
где j – плотность тока. Получаем:
F = jSBL sin b = qnvSBL sinb2,
где n =N/ SI – концентрация частиц.
Подставляя последнее выражение к первому, получаем выражение для силы, действующей со стороны магнитного поля на отдельный движущийся электрический заряд и называемой силой Лоренца:
Направление силы Лоренца можно определить из векторной записи уравнения
fn = qvB.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Закон Ампера — Студопедия
Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.
Формулировка закона: сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником.
Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом:
Направление силы Ампера определяется по правилу левой руки.
Правило левой руки: если расположить левую руку так, чтобы перпендикулярная составляющая вектора магнитной индукции входила в ладонь, а четыре пальца были вытянуты по направлению тока в проводнике, то отставленный на 90°большой палец, укажет направление силы Ампера.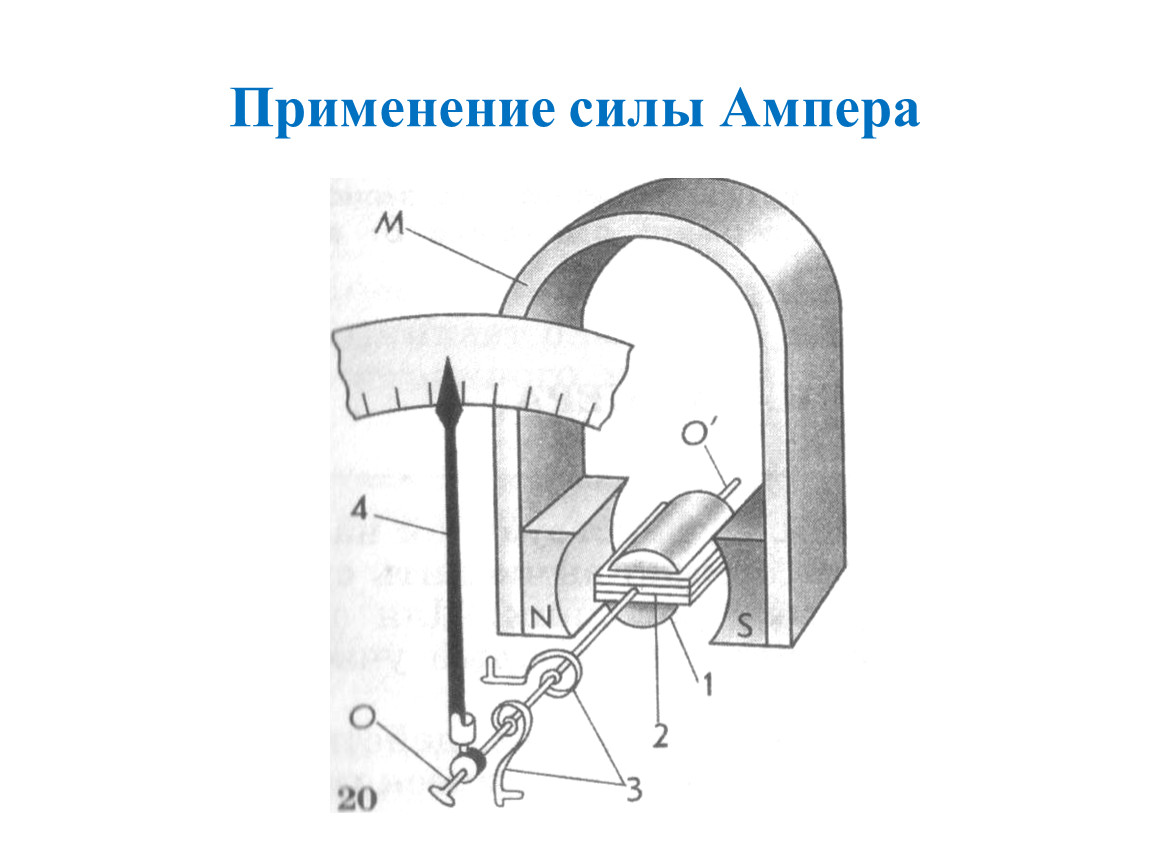
МП движущего заряда. Действие МП на движущийся заряд. Сила Ампера, Лоренца.
Любой проводник с током создает в окружающем пространстве магнитное поле. При этом электрический же ток является упорядоченным движением электрических зарядов. Значит можно считать, что любой движущийся в вакууме или среде заряд порождает вокруг себя магнитное поле. В результате обобщения многочисленных опытных данных был установлен закон, который определяет поле В точечного заряда Q, движущегося с постоянной нерелятивистской скоростью v. Этот закон задается формулой
(1)
где r — радиус-вектор, который проведен от заряда Q к точке наблюдения М (рис. 1). Согласно (1), вектор В направлен перпендикулярно плоскости, в которой находятся векторы v и r: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.
Рис.1
Модуль вектора магнитной индукции (1) находится по формуле
(2)
где α — угол между векторами v и r. Сопоставляя закон Био-Савара-Лапласа и (1), мы видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока: Idl = Qv
Сопоставляя закон Био-Савара-Лапласа и (1), мы видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока: Idl = Qv
Действие МП на движущийся заряд.
Из опыта известно, что магнитное поле оказывает действие не только на проводники с током, но и на отдельные заряды, которые движутся в магнитном поле. Сила, которая действует на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и задается выражением: F = Q где В — индукция магнитного поля, в котором заряд движется.
Чтобы определить направление силы Лоренца используем правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q>0 направления I и v совпадают, для Q На рис. 1 продемонстрирована взаимная ориентация векторов v, В (поле имеет направление на нас, на рисунке показано точками) и F для положительного заряда. Если заряд отрицательный, то сила действует в противоположном направлении.
Модуль силы Лоренца, как уже известно, равен F = QvB sin a; где α — угол между v и В.
МП не оказывает действия на покоящийся электрический заряд. Этим магнитное поле существенно отличается от электрического. Магнитное поле действует только на движущиеся в нем заряды.
Зная действие силы Лоренца на заряд можно найти модуль и направление вектора В, и формула для силы Лоренца может быть применена для нахождения вектора магнитной индукции В.
Поскольку сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, то данная сила может менять только направление этой скорости, не изменяя при этом ее модуля. Значит, сила Лоренца работы не совершает.
В случае, если на движущийся электрический заряд вместе с магнитным полем с индукцией В действует еще и электрическое поле с напряженностью Е, то суммарная результирующая сила F, которая приложена приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца: F = QE + Q[v,B]
Сила Ампера, Лоренца.
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:
F = B.I.l. sin α — закон Ампера.
Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца:
Явление электромагнитной индукции. Закон Фарадея. ЭДС индукции в движущихся проводниках. Самоиндукция.
Фарадей предположил, что если вокруг проводника с током существует магнитное поле, то естественно ожидать, что должно происходить и обратное явление – возникновение электрического тока под действием магнитного поля. И вот в 1831 г. Фарадей публикует статью, где сообщает об открытии нового явления – явления электромагнитной индукции.
Опыты Фарадея были чрезвычайно просты. Он присоединял гальванометр G к концам катушки L и приближал к ней магнит. Стрелка гальванометра отклонялась, фиксируя появление тока в цепи. Ток протекал, пока магнит двигался. При отдалении магнита от катушки гальванометр отмечал появление тока противоположного направления. Аналогичный результат отмечался, если магнит заменяли катушкой с током или замкнутым контуром с током.
Движущиеся магнит или проводник с током создают через катушку L переменное магнитное поле. В случае их неподвижности создаваемое ими поле постоянно. Если вблизи замкнутого контура поместить проводник с переменным током, то в замкнутом контуре также возникнет ток. На основе анализа опытных данных Фарадей установил, что ток в проводящих контурах появляется при изменении магнитного потока через площадь, ограниченную этим контуром.
Этот ток был назван индукционным. Открытие Фарадея было названо явлением электромагнитной индукции и легло в дальнейшем в основу работы электрических двигателей, генераторов, трансформаторов и подобных им приборов.
Итак, если магнитный поток через поверхность, ограниченную некоторым контуром, изменяется, то в контуре возникает электрический ток. Известно, что электрический ток в проводнике может возникнуть только под действием сторонних сил, т.е. при наличии э.д.с.. В случае индукционного тока э.д.с., соответствующая сторонним силам, называется электродвижущей силой электромагнитной индукции εi.
Э.д.с. электромагнитной индукции в контуре пропорциональна скорости изменения магнитного потока Фm сквозь поверхность, ограниченную этим контуром:
где к – коэффициент пропорциональности. Данная э.д.с. не зависит от того, чем вызвано изменение магнитного потока – либо перемещением контура в постоянном магнитном поле, либо изменением самого поля.
Итак, направление индукционного тока определяется правилом Ленца: При всяком изменении магнитного потока сквозь поверхность, ограниченную замкнутым проводящим контуром, в последнем возникает индукционный ток такого направления, что его магнитное поле противодействует изменению магнитного потока.
Обобщением закона Фарадея и правила Ленца является закон Фарадея — Ленца: Электродвижущая сила электромагнитной индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную контуром:
Это выражение представляет собой основной закон электромагнитной индукции.
При скорости изменения магнитного потока 1Вб/с в контуре индуцируется э.д.с. в 1 В.
Пусть контур, в котором индуцируется э.д.с., состоит не из одного, а из N витков, например, представляет собой соленоид. Соленоид – это цилиндрическая катушка с током, состоящая из большого числа витков. Так как витки в соленоиде соединяются последовательно, εi в данном случае будет равна сумме э.д.с., индуцируемых в каждом из витков по отдельности:
Величину Ψ = ΣΦm называют потокосцеплением или полным магнитным потоком. Если поток, пронизывающий каждый из витков, одинаков (т.е. Ψ = NΦm), то в этом случае
Немецкий физик Г. Гельмгольц доказал, что закон Фарадея-Ленца является следствием закона сохранения энергии. Пусть замкнутый проводящий контур находится в неоднородном магнитном поле. Если в контуре течет ток I, то под действием сил Ампера незакрепленный контур придет в движение. Элементарная работа dA, совершаемая при перемещении контура за время dt, будет составлять
dA = IdФm,
где dФm – изменение магнитного потока сквозь площадь контура за время dt. Работа тока за время dt по преодолению электрического сопротивления R цепи равна I2Rdt. Полная работа источника тока за это время равна εIdt. По закону сохранения энергии работа источника тока затрачивается на две названные работы, т.е.
εIdt = IdФm + I2Rdt.
Разделив обе части равенства на Idt, получим
Следовательно, при изменении магнитного потока, сцепленного с контуром, в последнем возникает электродвижущая сила индукции
Электромагнитные колебания. Колебательной контур.
Электромагнитные колебания — это колебания таких величин, индуктивность, как сопротивление, ЭДС, заряд, сила тока.
Колебательный контур — это электрическая цепь, которая состоит из последовательно соединенных конденсатора, катушки и резистора. Изменение электрического заряда на обкладке кон- денсатора с течением времени описывается дифференциальным уравнением:
Электромагнитные волны и их свойства.
В колебательном контуре происходит процесс перехода электрической энергии конденсатора в энергию магнитного поля катушки и наоборот. Если в определенные моменты времени компенсировать потери энергии в контуре на сопротивление за счет внешнего источника, то получим незатухающие электрические колебания, которые через антенну могут быть излучены в окружающее пространство.
Процесс распространения электромагнитных колебаний, периодических изменений напряженностей электрического и магнитных полей, в окружающем пространстве называется электромагнитной волной.
Электромагнитные волны охватывают большой спектр длин волн от 105 до 10 м и по частотам от 104 до 1024 Гц. По названию электромагнитные волны разделяются на радиоволны, инфракрасное, видимое и ультрафиолетовое излучения, рентгеновские лучи и -излучение. В зависимости от длины волны или частоты свойства электромагнитных волн меняются, что является убедительным доказательством диалектико-материалистического закона перехода количества в новое качество.
Электромагнитное поле материальное и обладает энергией, количеством движения, массой, перемещается в пространстве: в вакууме со скоростью С, а в среде со скоростью: V= , где = 8,85 ;
Объемная плотность энергии электромагнитного поля . Практическое использование электромагнитных явлений весьма широкое. Это — системы и средства связи, радиовещания, телевидения, электронно-вычислительная техника, системы управления различного назначения, измерительные и медицинские приборы, бытовая электро- и радиоаппаратура и другие, т.е. то, без чего невозможно представить себе современное общество.
Как действует на здоровье людей мощное электромагнитное излучение, точных научных данных почти нет, есть только неподтвержденные гипотезы и, в общем-то, небезосновательные опасение, что все неестественное действует губительно. Доказано, что ультрафиолетовое, рентгеновское и -излучение большой интенсивности во многих случаях наносят реальный вред всему живому.
Геометрическая оптика. Законы ГО.
Геометрическая (лучевая) оптика использует идеализированное представление о световом луче – бесконечно тонком пучке света, распространяющемся прямолинейно в однородной изотропной среде, а также представления о точечном источнике излучения, равномерно светящем во все стороны. λ – длина световой волны, – характерный размер
предмета, находящегося на пути волны. Геометрическая оптика является предельным случаем волновой оптики и ее принципы выполняются при соблюдении условия:
h/D << 1 т. е. геометрическая оптика, строго говоря, применима лишь к бесконечно коротким волнам.
В основе геометрической оптики лежит так же принцип независимости световых лучей: лучи при перемещении не возмущают друг друга. Поэтому перемещения лучей не мешают каждому из них распространяться независимо друг от друга.
Для многих практических задач оптики можно не учитывать волновые свойства света и считать распространение света прямолинейным. При этом картина сводится к рассмотрению геометрии хода световых лучей.
Основные законы геометрической оптики.
Перечислим основные законы оптики, следующие из опытных данных:
1) Прямолинейное распространение.
2) Закон независимости световых лучей, то есть два луча, пересекаясь, никак не мешают друг другу. Этот закон лучше согласуется с волновой теорией, так как частицы в принципе могли бы сталкиваться друг с другом.
3) Закон отражения. луч падающий, луч отраженный и перпендикуляр к поверхности раздела, восстановленный в точке падения луча, лежат в одной плоскости, называемой плоскостью падения; угол падения равен углу
Отражения.
4) Закон преломления света.
Закон преломления: луч падающий, луч преломленный и перпендикуляр к поверхности раздела, восстановленный из точки падения луча, лежат в одной плоскости – плоскости падения. Отношение синуса угла падения к синусу угла отражения равно отношению скоростей света в обеих средах.
Sin i1/ sin i2 = n2/n1 = n21
где – относительный показатель преломления второй среды относительно первой среды. n21
Если вещество 1 – пустота, вакуум, то n12 → n2 – абсолютный показатель преломления вещества 2. Можно легко показать, что n12 = n2 /n1 , в этом равенстве слева относительный показатель преломления двух веществ (например, 1 – воздух, 2 – стекло), а справа – отношение их абсолютных показателей преломления.
5) Закон обратимости света (его можно вывести из закона 4). Если направить свет в обратном направлении, он пройдёт по тому же пути.
Из закона 4) следует, что если n2 > n1 , то Sin i1 > Sin i2 . Пусть теперь у нас n2 < n1 , то есть свет из стекла, например, выходит в воздух, и мы постепенно увеличиваем угол i1.
Тогда можно понять, что при достижении некоторого значения этого угла (i1)пр окажется, что угол i2 окажется равным π /2 (луч 5). Тогда Sin i2 = 1 и n1 Sin (i1)пр = n2 . Итак Sin
(i1)пр = n2 / n1 .
Закон Ампера
— Видео по физике от Brightstorm
Закон Ампера был открыт в 1819 году Ампером. Закон Ампера гласит, что токи генерируют магнитные поля или, другими словами, когда у вас есть ток, вокруг него циркулирует магнитное поле. Закон Ампера выражается в уравнении магнитное поле x 2 (пи) x радиус = постоянная x ток (проходящий через этот путь) .
Итак, давайте поговорим о законе Ампера.Закон Ампера был обнаружен хорошо, эффект, лежащий в основе закона Ампера, был обнаружен примерно в 1819 году преподавателем физики, который был в середине лекции, и он заметил, что создается магнитное поле, которое перемещается вокруг стрелки компаса, когда он пропускает большой ток через провод, поэтому закон в основном говорит, что токи, если я пропущу ток, он создаст магнитное поле. Есть несколько способов установить этот закон; есть закон [IB], есть закон Эрстеда. Стандартный способ представить это в терминах закона Ампера, который в основном гласит, что всякий раз, когда у вас есть ток, у вас будет магнитное поле, которое циркулирует вокруг этого тока.Теперь, чтобы определить ощущение этой циркуляции, вы используете правую руку и берете за провод большим пальцем, указывающим в направлении тока. Когда вы это сделаете, ваши пальцы покажут вам, в каком смысле циркулирует магнитное поле, поэтому, если у вас есть ток, идущий в этом направлении, магнитное поле будет делать небольшие круги вокруг тока в этом смысле, так что спереди оно будет будет опускаться сзади, он будет подниматься под проводом, который входит в плату, и над проводом он выходит из платы, так что это идея.
Итак, закон Ампера также гласит, что циркуляция магнитного поля, и под этим мы в основном подразумеваем, что магнитное поле, умноженное на длину этой циркуляции, пропорционально тому, какой у нас ток, поэтому мы удваиваем количество тока, тогда мы собирается удвоить размер магнитного поля, хорошо, это также дает нам очень, очень простой способ определить выражение в замкнутой форме для магнитного поля из-за длинного провода, поэтому здесь я получил провод, по которому ток выходит из платы, поэтому вот почему вы не видите провод, потому что ток выходит из платы.Теперь магнитное поле — это синяя линия. Обратите внимание, что я снова хватаю провод большим пальцем, указывающим в направлении тока, и мои пальцы показывают, как магнитное поле циркулирует.
Закон Ампера гласит, что циркуляция магнитного поля, которая является магнитным полем, умножена на длину этой кривой, которая составляет 2 пи r, потому что это наша окружность, пропорциональная, это означает, что она равна константе, умноженной на ток, который выходит из платы. . Что это за константа? Что ж, мы могли бы это измерить, но на самом деле люди используют свободу, которую мы имеем, чтобы определить ампер как единицу измерения, чтобы сделать эту константу ровно 4 пи умножить на 10 до минус 7 в S.I, так что эти единицы равны Тесла, метры на ампер, хорошо, так что 4 пи умножить на 10 до минус 7, что равняется нулю, это называется проницаемостью свободного пространства. Хорошо, поэтому, когда у меня есть это выражение, я собираюсь решить для B, и оно дает мне B равно mue, а не I, более 2 pi r, поэтому это означает, что если вы удвоите расстояние, которое вы находитесь от провода, у вас будет магнитное поле. Если вы утроите расстояние от проволоки, вы разрежете ее на треть.
Хорошо, давайте сделаем пример с этим результатом, поэтому я хочу знать, какое магнитное поле находится в 2 сантиметрах от провода, по которому проходит ток 5 А, хорошо, почему бы мне просто не сделать это напрямую? B равно mue, а не I, более 2 пи р, поэтому я просто подключу 4 пи умножить на 10 к минус 7 умножить на 5 ампер, разделенных на 2 пи, хорошо, что мы знаем, что нам нужно сделать, нам нужно изменить его на S.Я единица также, наше магнитное поле не будет выходить за пределы Теслы, поэтому 2 умножить на 10 с минус 2, хорошо, в этот момент происходят чудесные вещи, посмотрите на эти 4 пи, 4 пи, пи пи, хорошо, так что теперь мы получаем 5 умножить на 10 до эти отрицательные семь плюс 2 — это отрицательные 5 тесла, хорошо или 50 микротесла, хорошо, так что это магнитное поле, это не очень большое магнитное поле, а 5 ампер — довольно большой ток, поэтому, когда мы делаем это только с длинным прямым проводом, обычно мы этого не делаем. в конечном итоге получить огромное магнитное поле. У меня есть другие способы сделать это позже.
Хорошо, предположим, что я хочу определить силу между двумя длинными проводами. Вот идея: два длинных провода, по которым течет ток. Этот длинный провод. Упс. Я использую правило правой руки, и это означает, что здесь есть магнитное поле на плате, здесь, вверх по второму проводу, хорошо, но теперь провод, который проводит ток в магнитном поле, он чувствует силу, что это за сила? Хорошо il крест b, так что сила на самом деле является притягивающей, в этом случае она будет тянуть провод к себе хорошо большая это сила, ну, черт возьми, магнитное поле на расстоянии d от провода с током II 1 является mue, а не I 1 более 2 пи d хорошо.
Сила — это второй ток, умноженный на длину провода, умноженный на магнитное поле, которое я могу так перестроить. Обычно люди делят на длину и получают силу на единицу длины, которую дает эта формула. Обратите внимание, что у нас есть mue, а не произведение двух продуктов, а затем мы делим на 2 pi d. Вот как на самом деле определяется ампер. Усилитель — это ток, который дает силу на единицу длины от 2 умноженных на 10 до минус 7 Ньютонов на метр, когда у вас есть два провода, по которым протекает один и тот же ток, и они находятся на расстоянии 1 метра, это означает, что это 1, это 1 это 1, и мне нужно, чтобы все это было 2 умножить на 10 до минус 7, так что это означает, что это 4 пи умножить на 10 до минус 7, и отсюда происходит определение ампера, и это закон ампера.
ампер: История | NIST
Андре-Мари Ампер
История ампера началась, когда датский физик Ганс Кристиан Эрстед обнаружил, что магнетизм и электричество — это два аспекта одного и того же. В 1820 году он показал, что стрелку компаса можно отклонить с севера, поместив ее рядом с электрическим током. Как обнаружил Эрстед, ток в проводе создает магнитное поле, которое окружает провод и влияет на другие близлежащие поля, такие как поля стержневого магнита.
Французский математик и физик Андре-Мари Ампер был вдохновлен этой демонстрацией, чтобы установить связь между электричеством и магнетизмом. Он обнаружил, что если вы поместите два провода параллельно друг другу и пропустите через них ток, провода будут либо притягиваться друг к другу, либо отталкиваться, в зависимости от того, текут ли токи в одном или противоположных направлениях. Это потому, что каждый провод генерирует магнитное поле. Чем длиннее провода и чем выше токи, проходящие через них, тем больше магнитное отталкивание или притяжение.
До 2019 года определение SI следовало этой схеме. Если бы он был установлен в идеальных условиях с проводами на расстоянии 1 метра друг от друга, сила тока в 1 ампер привела бы к силе между проводами в 2 X 10 -7 ньютонов. Это немного — примерно десятимиллионная веса среднего яблока. Но это есть.
Кредит:
Дж. Ли / NIST
На протяжении столетия люди продолжали разрабатывать правила, регулирующие электромагнетизм (ЭМ).В 1861 году ученые начали предлагать системы единиц для ЭМ. Эти системы включали блоки тока, напряжения и сопротивления. Однако разные ученые использовали разные системы единиц. В какой-то момент одновременно использовалось четыре различных систем ЭМ. Ученые хотели создать систему единиц, доступную для всех.
Выбор ампер
В 1893 году научный комитет под названием Международный электротехнический конгресс (МЭК) собрался в Чикаго и остановился на двух единицах измерения, которые станут основой для других: ом для сопротивления и ампер для тока.Решение Конгресса было официально принято на Международной конференции ученых, собравшейся в Лондоне в 1908 году.
В Национальном бюро стандартов (предшественник NIST) в 1903 году ученый Ф.А.Вольф (справа) работает в масляной ванне, наблюдая за датчиком температуры, чтобы измерить температурный отклик нескольких ячеек Вестона, используемых для калибровки вольтметров. Его коллега слева, похоже, создает ртутные термометры, которые использовались в эксперименте.
Кредит:
NIST
Ом был одним из первых блоков, созданных для электричества. Возможно, это одна из самых простых электрических величин, которую можно представить, поскольку, например, провода разной длины могут иметь разное сопротивление. Но реализация стандарта ома была окольным процессом, начиная с «ртутной единицы Сименса» 1860 года, обозначенной пропусканием электричества через столб чистой ртути длиной 1 метр, до использования различных электрических компонентов, таких как катушки, индукторы и конденсаторы, и, наконец, в 1990-е — явлениям, основанным на квантовой механике.
Этот ампер, называемый «международным ампером», не был тем ампером, который ученые используют сегодня. Вместо этого этот ампер был реализован — преобразованный из определения в практическую реальность — с помощью устройства, называемого серебряным вольтаметром. Это устройство содержало электроды с положительным (анод) и отрицательным (катод) выводами. Анод подвешивали в растворе нитрата серебра. Когда ток проходит через устройство, серебро накапливается на катоде. Затем исследователи определяли массу катода до и после; количество серебра на катоде показало, сколько тока прошло через устройство.
Ампер был определен как ток, который выделяет ровно 0,001118 грамма серебра в секунду из раствора нитрата серебра. Более точные измерения позже показали, что этот ток на самом деле меньше 1 ампера, который, как думали ученые, они измеряли.
Клетки Вестона сфотографированы в музее NIST.
Кредит:
Дж. Ли / NIST
Однако это определение ампера не было абсолютным измерением.Ученым все же пришлось откалибровать серебряный вольтаметр с помощью других инструментов. Одним из них был эталон напряжения, называемый ячейкой Вестона, H-образный стеклянный контейнер, заполненный тщательно уложенными слоями химикатов.
Внутри клетки Вестона.
Кредит:
Дж. Ли / NIST
Элементы
Weston славились своей точностью и надежностью: они могли обеспечивать одинаковое напряжение в течение длительного периода времени.Напряжение, сопротивление и ток взаимосвязаны. Таким образом, исследователи могли использовать элемент Вестона с резистором известного сопротивления, чтобы создать ток, который можно было бы использовать для калибровки серебряного вольтаметра.
После калибровки серебряного вольтаметра его можно использовать в качестве первичного эталона для калибровки другого типа инструмента, обычно используемого для калибровки измерителя тока. Это устройство называлось амперными весами, предшественниками весов Киббла, которые теперь используются в качестве «электронного килограмма» для измерения массы.
Серебряный вольтаметр, сфотографированный в музее NIST.
Кредит:
Дж. Ли / NIST
Идея баланса ампер заключалась в том, что техники пропускали ток через катушки, которые производили физическое движение, которое перемещало индикатор на механической шкале. Положение индикатора на шкале показало им величину тока, протекающего через катушки.
Баланс ампер, сфотографированный в музее NIST.
Кредит:
Дж. Ли / NIST
В поисках лучшего ампера
В 1921 году Генеральная конференция по мерам и весам (CGPM) — международная организация, которая принимает решения по стандартам — официально добавила ампер в качестве единицы электричества, сделав его четвертой единицей СИ. Ампер присоединился к единицам СИ для расстояния, времени и массы, которые были включены со времен Договора о метре 1875 года.Но ученые уже обнаружили, что определение единицы измерения тока на основе серебряного вольтаметра уже не было достаточно точным.
Серебряные вольтаметры, сфотографированные в музее NIST.
Кредит:
Дж. Ли / NIST
Еще раньше ученые жаловались на решение лондонской конференции определить ампер с помощью серебряного вольтаметра. Еще в 1917 году Э. Роза и Г.В. Виналь, два ученых из Национального бюро стандартов (предшественник NIST), написали в Proceedings of the National Academy of Sciences:
Во время этой конференции делегаты из этой страны считали, что вместо ампера следовало выбрать вольт, потому что стандартный элемент был более воспроизводимым, чем серебряный вольтаметр, и использовался тогда, как и сейчас. используется (вместе с омом) для измерения ампер методом падения потенциала.Однако решение конференции было принято как окончательное, и в нескольких разных странах, особенно в этой стране, были предприняты исследования с целью сделать вольтаметр достойным нести ответственность, возложенную на него Лондонской конференцией.
Стандартные ячейки около 1926 г.
Кредит:
NIST
К 1933 году CGPM был полон решимости перейти от этого «международного» ампера, основанного на серебряном вольтаметре, к так называемой абсолютной системе, в которой использовались более фундаментальные единицы измерения — сантиметр, грамм и секунда.
В 1935 году Международный комитет мер и весов (CIPM), который дал рекомендации, которые будут рассмотрены CGPM, единогласно одобрил это предложение.
После перерыва во время Второй мировой войны международное сообщество ученых снова занялось этой проблемой. В 1948 году CIPM официально принял новое определение ампера — силы на единицу длины между двумя длинными проводами. Это восходит к первоначальному эксперименту, проведенному самим Ампера, и включает в себя основные единицы измерения длины, массы и времени.Ученые реализовали этот блок, используя известные резисторы и элементы Вестона, чтобы обеспечить стабильное сопротивление и напряжение.
В 1960 году ампер вместе с шестью другими фундаментальными единицами измерения были интегрированы в систему СИ, которая до сих пор является основой науки об измерениях.
Сотрудник Национального бюро стандартов (предшественник NIST) с электрическими ячейками в 1960-х годах.
Кредит:
NIST
Закон
Ампера: определение и примеры — видео и стенограмма урока
Уравнение
Поле, создаваемое длинным прямым проводом с током, имеет форму концентрических кругов.И по мере того, как вы удаляетесь от проволоки, эти круги отдаляются друг от друга — или, другими словами, поле становится слабее. Мы могли бы создать уравнение для этого, используя закон Ампера и выполнив некоторые вычисления. Но на самом деле мы можем вывести это уравнение вообще без каких-либо исчислений.
Вместо интеграла воспользуемся суммой. Сумма всех элементов магнитного поля, составляющих концентрическую окружность: магнитное поле B, , умноженное на длину элемента delta-L, , равно mu-zero (проницаемость свободного пространства), умноженное на ток в провод I .Это закон Ампера.
Затем поймите, что, суммируя все эти элементы, ваша delta-L становится окружностью концентрической окружности, 2pi r . Переставьте это так, чтобы магнитное поле стало объектом, и вы получите ЭТО окончательное уравнение для поля, создаваемого проводом с током.
Здесь B — магнитное поле в определенной точке пространства, измеренное в теслах.-6. I — ток, протекающий по проводу, измеряется в амперах. А r — это радиальное расстояние от провода, измеренное в метрах. Таким образом, вы можете использовать это уравнение, чтобы вычислить напряженность магнитного поля на расстоянии х от токоведущего провода.
Благодаря уравнению можно рассчитать напряженность поля. Но как насчет направления? Для этого мне нужно, чтобы ты показал мне большой палец правой руки. Нет, серьезно, сделай это прямо сейчас.
Используя эту схему токоведущего провода, укажите большим пальцем в направлении, в котором движется ток, в направлении стрелки, обозначенной I . А теперь представьте, что вы обвиваете пальцами проволоку, хватая ее. Направление, указываемое вашими пальцами, соответствует направлению, в котором указывают линии поля — куда идут стрелки на концентрических кругах. Это называется правилом правой руки, и жизненно важно, чтобы вы случайно не использовали левую руку, потому что вы получите совершенно неправильный ответ.
Примеры
Хорошо, давайте рассмотрим пример. Допустим, у вас есть токоведущий провод, направленный на север. Если по проводу течет ток 0,1 А, каковы величина и направление магнитного поля на расстоянии 0,01 метра над проводом?
Прежде всего, давайте запишем то, что мы знаем. Сила тока I равна 0,1, расстояние от провода r равно 0.-6 тесла. И это наша величина.
В качестве направления вы можете провести ток на листе бумаги, направив его вверх к верхней части страницы, которую вы можете отметить на севере. Теперь поднимите большой палец правой руки, направьте большой палец к верхней части страницы и представьте, как вы сгибаете пальцы вокруг проволоки. Если вы сделаете это правильно, вы увидите, что ваши пальцы будут указывать налево под проводом и направо над проводом. Если вверх по странице север, то вправо будет восток.-6 тесла к востоку.
Краткое содержание урока
Полная версия закона Ампера — одно из уравнений Максвелла, описывающих электромагнитную силу. Закон Ампера , в частности, гласит, что магнитное поле, создаваемое электрическим током, пропорционально величине этого электрического тока с константой пропорциональности, равной проницаемости свободного пространства. Стационарные заряды создают электрические поля, пропорциональные величине заряда. Но движущиеся заряды создают магнитные поля, пропорциональные току (заряд и движение).
Единственная проблема с законом Ампера заключается в том, что это дифференциальное уравнение — другими словами, вам нужно провести некоторое вычисление, чтобы использовать его. Но мы можем избежать этого, посмотрев на результат всех этих вычислений для конкретной ситуации. Если мы изучим магнитное поле, создаваемое длинным прямым проводом с током, мы получим это окончательное уравнение для поля, создаваемого проводом с током.
Здесь B — магнитное поле в определенной точке пространства, измеренное в теслах.-6. I — ток, протекающий по проводу, измеряется в амперах. А r — это радиальное расстояние от провода, измеренное в метрах. Таким образом, вы можете использовать это уравнение, чтобы вычислить напряженность магнитного поля на расстоянии х от токоведущего провода. Чтобы получить направление этого поля, мы должны использовать правило правой руки и указывать большими пальцами в направлении тока.
Результаты обучения
После завершения этого урока вы должны уметь:
- Закон штата Ампера
- Рассчитайте магнитное поле токоведущего провода по закону Ампера
- Вспомните правило правой руки при вычислении текущего направления
Магнитные поля, создаваемые токами: закон Ампера
Цели обучения
К концу этого раздела вы сможете:
- Вычислить ток, создающий магнитное поле.
- Используйте правило правой руки 2, чтобы определить направление тока или направление контуров магнитного поля.
Какая сила тока необходима для создания значительного магнитного поля, возможно, такого же сильного, как поле Земли? Геодезисты скажут вам, что воздушные линии электропередач создают магнитные поля, которые мешают показаниям их компаса. Действительно, когда Эрстед в 1820 году обнаружил, что ток в проводе воздействует на стрелку компаса, он не имел дела с очень большими токами.Как форма проводов, по которым проходит ток, влияет на форму создаваемого магнитного поля? Ранее мы отмечали, что токовая петля создает магнитное поле, подобное магнитному полю, но как насчет прямого провода или тороида (бублика)? Как направление создаваемого током поля связано с направлением тока? Ответы на эти вопросы исследуются в этом разделе вместе с кратким обсуждением закона, регулирующего поля, создаваемые токами.
Магнитное поле, создаваемое длинным прямым проводом с током: Правило правой руки 2
Магнитные поля имеют направление и величину.Как отмечалось ранее, один из способов исследовать направление магнитного поля — это использовать компасы, как показано для длинного прямого токоведущего провода на рисунке 1. Датчики Холла могут определять величину поля. Поле вокруг длинной прямой проволоки находится в виде кольцевых петель. Правило правой руки 2 (RHR-2) возникло в результате этого исследования и справедливо для любого текущего сегмента — направьте большой палец в направлении тока, а пальцы сгибаются в направлении петель магнитного поля , созданных Это.
Рис. 1. (a) Компасы, помещенные рядом с длинным прямым токопроводящим проводом, показывают, что силовые линии образуют круговые петли с центром на проводе. (b) Правило 2 правой руки гласит, что если большой палец правой руки указывает в направлении тока, пальцы сгибаются в направлении поля. Это правило согласуется с полем, отображаемым для длинного прямого провода, и действительно для любого текущего сегмента.
Напряженность (величина) магнитного поля , создаваемая длинным прямым проводом с током , экспериментально определена как
[латекс] B = \ frac {{\ mu} _ {0} I} {2 \ pi r} \ left (\ text {длинная прямая проволока} \ right) \\ [/ latex],
, где I — ток, r — кратчайшее расстояние до провода, а константа [латекс] {\ mu} _ {0} = 4 \ pi \ times 10 ^ {- 7} \ text {T } \ cdot \ text {m / A} \\ [/ latex] — проницаемость свободного пространства .( μ 0 — одна из основных констант в природе. Позже мы увидим, что μ 0 связано со скоростью света.) Поскольку провод очень длинный, величина поля зависит только от на расстоянии от провода r , а не на расстоянии вдоль провода.
Пример 1. Расчет тока, создающего магнитное поле
Найдите ток в длинном прямом проводе, который создаст магнитное поле, вдвое превышающее земное, на расстоянии 5.0 см от проволоки.
Стратегия
Поле Земли составляет около 5,0 × 10 −5 Тл, поэтому здесь B из-за проволоки принимается равным 1,0 × 10 −4 Тл. Уравнение [латекс] B = \ frac {\ mu_ {0} I} {2 \ pi r} \\ [/ latex] можно использовать для поиска I , так как все остальные величины известны.
Решение
Решение I и ввод известных значений дает
[латекс] \ begin {array} {lll} I & = & \ frac {2 \ pi rB} {\ mu _ {0}} = \ frac {2 \ pi \ left (5.{-7} \ text {T} \ cdot \ text {m / A}} \\ & = & 25 \ text {A} \ end {array} \\ [/ latex]
Обсуждение
Итак, умеренно большой ток создает значительное магнитное поле на расстоянии 5,0 см от длинного прямого провода. Обратите внимание, что ответ состоит только из двух цифр, поскольку поле Земли в этом примере указано только из двух цифр.
Закон Ампера и другие
Магнитное поле длинного прямого провода имеет большее значение, чем вы можете сначала подумать. Каждый сегмент тока создает магнитное поле, подобное тому, которое имеет длинный прямой провод, а полное поле тока любой формы является векторной суммой полей, создаваемых каждым сегментом. Формальное определение направления и величины поля, создаваемого каждым сегментом, называется законом Био-Савара . Интегральное исчисление необходимо для суммирования поля для тока произвольной формы. Это приводит к более полному закону, называемому закон Ампера , который связывает магнитное поле и ток в общем виде.Закон Ампера, в свою очередь, является частью уравнений Максвелла , которые дают полную теорию всех электромагнитных явлений. Рассмотрение того, как уравнения Максвелла выглядят для разных наблюдателей, привело к современной теории относительности и к осознанию того, что электрические и магнитные поля являются разными проявлениями одного и того же. Большая часть этого выходит за рамки этого текста как на математическом уровне, требующем вычислений, так и в объеме места, которое может быть отведено под него. Но для заинтересованного студента, и особенно для тех, кто продолжает заниматься физикой, инженерией или подобными занятиями, дальнейшее углубление в эти вопросы откроет описания природы как элегантные, так и глубокие.В этом тексте мы будем иметь в виду общие особенности, такие как RHR-2 и правила для силовых линий магнитного поля, перечисленные в Магнитных полях и линиях магнитного поля, концентрируясь при этом на полях, создаваемых в определенных важных ситуациях.
Установление связей: относительность
Слушая все, что мы делаем об Эйнштейне, у нас иногда складывается впечатление, что он из ничего изобрел теорию относительности. Напротив, одной из мотиваций Эйнштейна было решить трудности, связанные с пониманием того, как разные наблюдатели видят магнитные и электрические поля.
Магнитное поле, создаваемое токонесущей круговой петлей
Магнитное поле около токоведущей петли показано на рисунке 2. Как направление, так и величина магнитного поля, создаваемого токоведущей петлей, являются сложными. RHR-2 можно использовать для определения направления поля около петли, но для получения более подробной информации необходимы картографирование с помощью компасов и правила о силовых линиях, приведенные в разделах «Магнитные поля» и «Магнитные линии поля».Существует простая формула для напряженности магнитного поля в центре круговой петли . Это
[латекс] B = \ frac {\ mu_ {0} I} {2R} \ left (\ text {в центре петли} \ right) \\ [/ latex],
, где R — радиус петли. Это уравнение очень похоже на уравнение для прямого провода, но действительно только в центре круговой петли провода. Сходство уравнений указывает на то, что аналогичная напряженность поля может быть получена в центре петли.Один из способов получить большее поле — это иметь петли N ; тогда поле будет B = Nμ 0 I / (2 R ). Обратите внимание, что чем больше петля, тем меньше поле в ее центре, потому что ток дальше.
Рис. 2. (a) RHR-2 показывает направление магнитного поля внутри и снаружи токоведущей петли. (б) Более подробное картирование с помощью компасов или зонда Холла завершает картину. Поле похоже на поле стержневого магнита.
Магнитное поле, создаваемое токопроводящим соленоидом
Соленоид представляет собой длинную катушку провода (с большим количеством витков или петель, в отличие от плоской петли). Из-за своей формы поле внутри соленоида может быть как очень однородным, так и очень сильным. Поле сразу за катушками почти равно нулю. На рисунке 3 показано, как поле выглядит и как его направление задается RHR-2.
Рис. 3. (a) Из-за своей формы поле внутри соленоида длиной l удивительно однородно по величине и направлению, на что указывают прямые и равномерно разнесенные силовые линии.Поле вне катушек почти равно нулю. (b) Этот разрез показывает магнитное поле, создаваемое током в соленоиде.
Магнитное поле внутри соленоида с током очень однородно по направлению и величине. Только ближе к концам он начинает ослабевать и менять направление. Поле снаружи имеет те же сложности, что и плоские контуры и стержневые магниты, но напряженность магнитного поля внутри соленоида просто равна
[латекс] B = {\ mu} _ {0} nI \ left (\ text {внутри соленоида} \ right) \\ [/ latex],
, где n — количество петель на единицу длины соленоида ( n = N / l , где N — количество петель, а l — длина).Обратите внимание, что B — это напряженность поля в любом месте однородной внутренней части, а не только в центре. Как следует из примера 2, с соленоидами возможны большие однородные поля, распределенные по большому объему.
Пример 2. Расчет напряженности поля внутри соленоида
Что такое поле внутри соленоида длиной 2,00 м, имеющего 2000 петель и пропускающего ток 1600 А?
Стратегия
Чтобы найти напряженность поля внутри соленоида, мы используем [латекс] B = {\ mu} _ {0} nI \\ [/ latex].{-1} \ right) \ left (1600 \ text {A} \ right) \\ & = & 2.01 \ text {T} \ end {array} \\ [/ latex]
Обсуждение
Это большая напряженность поля, которая может быть установлена над соленоидом большого диаметра, например, при использовании в медицине магнитно-резонансной томографии (МРТ). Однако очень большой ток указывает на то, что поля такой силы нелегко получить. Такой большой ток через 1000 петель, сжатых до метра, приведет к значительному нагреву.Более высокие токи могут быть достигнуты с помощью сверхпроводящих проводов, хотя это дорого. Существует верхний предел тока, поскольку сверхпроводящее состояние нарушается очень сильными магнитными полями.
Есть интересные варианты плоской катушки и соленоида. Например, тороидальная катушка, используемая для удержания реактивных частиц в токамаках, очень похожа на соленоид, изогнутый в круг. Поле внутри тороида очень сильное, но круглое. Заряженные частицы движутся по кругу, следуя силовым линиям, и сталкиваются друг с другом, возможно, вызывая синтез.Но заряженные частицы не пересекают силовые линии и не покидают тороид. Целый ряд форм катушек используется для создания всевозможных форм магнитного поля. Добавление ферромагнитных материалов создает большую напряженность поля и может существенно повлиять на форму поля. Ферромагнитные материалы имеют тенденцию улавливать магнитные поля (силовые линии изгибаются в ферромагнитный материал, оставляя более слабые поля за его пределами) и используются в качестве экранов для устройств, на которые неблагоприятно влияют магнитные поля, в том числе магнитное поле Земли. {- 7} \ text {T } \ cdot \ text {m / A} \\ [/ latex] — проницаемость свободного пространства.
[латекс] B = \ frac {\ mu_ {0} I} {2R} \ left (\ text {в центре петли} \ right) \\ [/ latex]
, где R — радиус петли. Это уравнение принимает вид B = μ 0 nI / (2 R ) для плоской катушки из N петель. RHR-2 дает направление поля вокруг петли. Длинная катушка называется соленоидом.
[латекс] B = {\ mu} _ {0} \ text {nI} \ left (\ text {внутри соленоида} \ right) \\ [/ latex]
, где n — количество петель на единицу длины соленоида.Поле внутри очень однородно по величине и направлению.
Концептуальные вопросы
1. Сделайте чертеж и используйте RHR-2, чтобы найти направление магнитного поля токовой петли в двигателе (например, на Рисунке 1 из «Крутящий момент на токовой петле»). Затем покажите, что направление крутящего момента на петле такое же, как и при отталкивании одинаковых полюсов и притяжении разных полюсов.
Глоссарий
- Правое правило 2 (RHR-2):
- правило для определения направления магнитного поля, создаваемого токоведущим проводом: направьте большой палец правой руки в направлении тока, а пальцы согнуты в направлении петель магнитного поля
- Напряженность (величина) магнитного поля, создаваемого длинным прямым проводом с током:
- определяется как [latex] B = \ frac {\ mu_ {0} I} {2 \ pi r} \\ [/ latex], где I — ток, r — кратчайшее расстояние до провода, а мкм 0 — проницаемость свободного пространства
- проницаемость свободного пространства:
- — мера способности материала, в данном случае свободного пространства, поддерживать магнитное поле; константа [латекс] \ mu_ {0} = 4 \ pi \ times 10 ^ {- 7} T \ cdot \ text {m / A} \\ [/ latex]
- Напряженность магнитного поля в центре круговой петли:
- определяется как [латекс] B = \ frac {{\ mu} _ {0} I} {2R} \\ [/ latex], где R — радиус петли
- соленоид:
- Тонкая проволока, намотанная на катушку, которая создает магнитное поле при прохождении через нее электрического тока
- Напряженность магнитного поля внутри соленоида:
- определяется как [латекс] B = {\ mu} _ {0} \ text {nI} \\ [/ latex], где n — количество петель на единицу длины соленоида n = N / l , где N — количество петель и l — длина)
- Закон Био-Савара:
- физический закон, который описывает магнитное поле, создаваемое электрическим током, с помощью специального уравнения
- Закон Ампера:
- физический закон, который гласит, что магнитное поле вокруг электрического тока пропорционально току; каждый сегмент тока создает магнитное поле, подобное тому, которое имеет длинный прямой провод, а общее поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым сегментом
- Уравнения Максвелла:
- Набор из четырех уравнений, описывающих электромагнитные явления
Закон Ампера — Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как закон Ампера связывает магнитное поле, создаваемое током, со значением тока
- Рассчитайте магнитное поле на длинном прямом проводе, тонком или толстом, по закону Ампера.
Основным свойством статического магнитного поля является то, что, в отличие от электростатического, оно не является консервативным.Консервативное поле — это поле, которое выполняет одинаковую работу с частицей, движущейся между двумя разными точками, независимо от выбранного пути. Магнитные поля таким свойством не обладают. Вместо этого существует связь между магнитным полем и его источником, электрическим током. Он выражается в виде линейного интеграла и известен как закон Ампера. Этот закон также может быть выведен непосредственно из закона Био-Савара. Теперь рассмотрим этот вывод для частного случая бесконечной прямой проволоки.
(рисунок) показана произвольная плоскость, перпендикулярная бесконечному прямому проводу, ток которого I направлен за пределы страницы. Силовые линии магнитного поля представляют собой окружности, направленные против часовой стрелки и центрированные на проводе. Для начала рассмотрим закрытые пути M и N . Обратите внимание, что один путь ( M ) охватывает провод, а другой ( N ) — нет. Поскольку силовые линии круглые, это произведение B и проекции dl на проходящую через окружность. Если радиус этого конкретного круга равен r , проекция равна и
Ток I длинного прямого провода направлен за пределы страницы.Интеграл равен и 0 соответственно для путей M и N .
С дано (рисунок),
Для пути M , который проходит по проводу, и
Путь N , с другой стороны, проходит как через положительный (против часовой стрелки), так и через отрицательный (по часовой стрелке) (см. (Рисунок)), и поскольку он закрыт, Таким образом, для пути N ,
Распространение этого результата на общий случай — это закон Ампера.
Закон Ампера
По произвольной замкнутой траектории,
, где I — полный ток, проходящий через любую открытую поверхность S , периметр которой является путем интегрирования. Необходимо учитывать только токи внутри пути интеграции.
Чтобы определить, является ли конкретный ток I положительным или отрицательным, согните пальцы правой руки в направлении пути интегрирования, как показано на (Рисунок). Если I проходит через S в том же направлении, что и ваш вытянутый большой палец, I является положительным; если I проходит через S в направлении, противоположном вашему вытянутому большому пальцу, это отрицательно.
Стратегия решения проблем: закон Ампера
Чтобы рассчитать магнитное поле, создаваемое током в проводе (ах), выполните следующие действия:
- Определите симметрию тока в проводе (ах). Если симметрии нет, используйте закон Био-Савара для определения магнитного поля.
- Определите направление магнитного поля, создаваемого проводом (ами) по правилу правой руки 2.
- Выберите контур, в котором магнитное поле либо постоянное, либо нулевое.
- Рассчитайте ток внутри контура.
- Вычислите линейный интеграл вокруг замкнутого контура.
- Приравнять и решить для
Использование закона Ампера для расчета магнитного поля, обусловленного проводом Используйте закон Ампера для расчета магнитного поля, создаваемого постоянным током I в бесконечно длинном, тонком, прямом проводе, как показано на (Рисунок).
Возможные составляющие магнитного поля B из-за тока I , который направлен за пределы страницы.Радиальная составляющая равна нулю, потому что угол между магнитным полем и траекторией прямой.
Стратегия
Рассмотрим произвольную плоскость, перпендикулярную проводу, с током, направленным за пределы страницы. Возможные компоненты магнитного поля в этой плоскости показаны в произвольных точках на окружности радиуса r с центром на проводе. Поскольку поле цилиндрически симметрично, оно не меняется и не меняется в зависимости от положения на этом круге. Также из-за симметрии радиальные линии, если они существуют, должны быть направлены либо внутрь, либо наружу от провода.Это означает, однако, что чистый магнитный поток должен проходить через произвольный цилиндр, концентричный с проводом. Радиальная составляющая магнитного поля должна быть равна нулю, потому что мы можем применить закон Ампера к круговой траектории, как показано.
Решение По этому пути постоянный и параллельный так
Таким образом, закон Ампера сводится к
Наконец, поскольку это единственный компонент, мы можем опустить нижний индекс и написать
Это согласуется с приведенным выше расчетом Био-Савара.
Значение Закон Ампера хорошо работает, если у вас есть способ интеграции, который дает результаты, которые легко упростить. Для бесконечного провода это легко работает с круговой траекторией вокруг провода, так что магнитное поле не учитывается при интегрировании. Если зависимость от траектории выглядит сложной, вы всегда можете вернуться к закону Био-Савара и использовать его для определения магнитного поля.
Расчет магнитного поля толстого провода по закону Ампера Радиус длинного прямого провода на (рис.) Составляет a , и по проводу проходит ток, который равномерно распределяется по его поперечному сечению.Найдите магнитное поле как внутри, так и снаружи провода.
(а) Модель токоведущего провода с радиусом a и током (b) Поперечное сечение того же провода с радиусом a и петлей Ампера с радиусом x .
Стратегия
Эта задача имеет ту же геометрию, что и (рисунок), но замкнутый ток изменяется, когда мы перемещаем путь интегрирования из-за пределов провода внутрь провода, где он не захватывает весь заключенный ток (см. (Рисунок)).
Решение Для любой круговой траектории радиусом r , центрированной на проводе,
По закону Ампера это равно полному току, проходящему через любую поверхность, ограниченную путем интегрирования.
Рассмотрим сначала круговой путь внутри провода, такой как показанный в части (а) (Рисунок). Нам нужен ток I , проходящий через область, ограниченную дорожкой. Она равна плотности тока в Дж, умноженной на замкнутой площади.Поскольку ток однороден, плотность тока внутри пути равна плотности тока во всем проводе, что составляет Следовательно, ток I , проходящий через область, ограниченную путем, равен
Мы можем учитывать это соотношение, потому что плотность тока Дж постоянна по всей площади провода. Следовательно, плотность тока на части провода равна плотности тока на всей площади. Используя закон Ампера, получаем
, а магнитное поле внутри провода —
За пределами провода ситуация идентична ситуации с бесконечным тонким проводом из предыдущего примера; то есть
Вариант B с r показан на (Рисунок).
Изменение магнитного поля, создаваемое током в длинном прямом проводе радиусом a .
Значение Результаты показывают, что по мере увеличения радиального расстояния внутри толстой проволоки магнитное поле увеличивается от нуля до известного значения магнитного поля тонкой проволоки. Вне провода поле спадает независимо от того, толстый он или тонкий.
Этот результат аналогичен тому, как закон Гаусса для электрических зарядов ведет себя внутри однородного распределения заряда, за исключением того, что закон Гаусса для электрических зарядов имеет однородное объемное распределение заряда, тогда как закон Ампера здесь имеет однородную область распределения тока.Кроме того, падение за пределы толстого провода аналогично тому, как электрическое поле спадает за пределами линейного распределения заряда, поскольку оба случая имеют одинаковую геометрию, и ни один из случаев не зависит от конфигурации зарядов или токов, когда петля выходит за пределы распространение.
Проверьте свое понимание Рассмотрите возможность использования закона Ампера для расчета магнитных полей конечного прямого провода и кольцевой петли провода. Почему это бесполезно для этих расчетов?
В этих случаях интегралы вокруг петли Ампера очень трудны из-за отсутствия симметрии, поэтому этот метод не будет полезен.
Сводка
- Магнитное поле, создаваемое током, идущим по любому пути, является суммой (или интегралом) полей, создаваемых сегментами вдоль пути (величина и направление, как для прямого провода), что приводит к общему соотношению между током и полем, известному как поле Ампера. закон.
- Закон Ампера можно использовать для определения магнитного поля по тонкой или толстой проволоке с помощью геометрически удобного пути интегрирования. Результаты соответствуют закону Био-Савара.
Концептуальные вопросы
Действует ли закон Ампера для всех закрытых дорог? Почему обычно не используется для расчета магнитного поля?
Закон Ампера действителен для всех замкнутых путей, но он бесполезен для расчета полей, когда создаваемое магнитное поле не имеет симметрии, которая может быть использована подходящим выбором пути.
Глоссарий
- Закон Ампера
- физический закон, который гласит, что линейный интеграл магнитного поля вокруг электрического тока пропорционален току
Уравнения Максвелла: Закон Ампера
Четвертое уравнение Максвелла
На этой странице мы объясним значение последнего из уравнений Максвелла,
Закон Ампера , который дан в уравнении [1]:
| [Уравнение 1] |
|---|
Ампер был ученым, экспериментировавшим с силами на проводах, по которым проводился электрический ток.Он проводил эти эксперименты еще в 1820-х годах, примерно в то же время, что и
Фардей работал над законом Фарадея.
Ампер и Фарде не знали, что там работа будет объединена самим Максвеллом,
примерно 4 десятилетия спустя.
Силы на проводах мне не особо интересны, потому что у меня никогда не было
иногда использовать очень сложные уравнения в ходе моей работы
(который включает докторскую степень, некоторые работы в национальной лаборатории, а также
занятость в обеих сторонах защиты
и промышленность бытовой электроники).Итак, я начну с
представляя закон Ампера, который связывает электрический ток, протекающий
и магнитное поле вокруг него:
| [Уравнение 2] |
|---|
Уравнение [2] можно объяснить: Предположим, у вас есть проводник, несущий
ток, I . Тогда этот ток производит
Магнитное поле
который обводит проволоку.
Левая часть уравнения [2] означает: если вы возьмете любое воображаемое
путь, опоясывающий проволоку,
и вы складываете магнитное поле в каждой точке на этом пути, а затем
будет численно равняться количеству тока, окруженного
этот путь (поэтому мы пишем
для замкнутого или замкнутого тока).
Давайте сделаем пример для развлечения. Предположим, у нас есть длинный провод, по которому
постоянный электрический ток, I [Ампер]. Что такое магнитное поле вокруг
провод, на любое расстояние r [метров] от провода?
Давайте посмотрим на схему на рисунке 1. У нас есть длинный провод, по которому течет ток.
I Ампер. Мы хотим знать, что такое магнитное поле на расстоянии
р из проволоки. Итак, мы проводим воображаемый путь вокруг провода, который
синяя пунктирная линия справа на рисунке 1:
Фигура 1.Расчет магнитного поля по закону Ампера.
Закон Ампера [Уравнение 2] гласит, что если мы сложим (интегрируем) Магнитные
Поле вдоль этого синего пути, тогда численно это должно быть равно
вложенный ток I .
Теперь в силу симметрии магнитное поле будет однородным (не меняющимся) при
расстояние р от провода. Длина пути синего пути
на рисунке 1 длина окружности равна радиусу r :
.
Если мы складываем постоянное значение магнитного поля (назовем его
H ), то левая часть уравнения [2] становится простой:
| [Уравнение 3] |
|---|
Таким образом, мы выяснили, какова величина поля H .
А поскольку r было произвольным, мы знаем, что такое H-поле везде.
Уравнение [3] утверждает, что магнитное поле уменьшается по величине при движении.
дальше от провода (из-за члена 1 / r).
Итак, мы использовали закон Ампера (Уравнение [2]), чтобы найти величину
Магнитное поле вокруг провода. Однако поле H является
Векторное поле,
Это означает, что в каждом месте есть как величина, так и направление.
Направление H-поля всюду касательно мнимых петель,
как показано на рисунке 2.
Правило правой руки определяет направление магнитного поля:
Рис. 2. Величина и направление магнитного поля вокруг провода.
Манипулирование математикой закона Ампера
Мы собираемся проделать тот же трюк с теоремой Стокса, который мы сделали.
когда смотришь на
Закон Фарадея.
Мы можем переписать закон Ампера в уравнении [2]:
| [Уравнение 4] |
|---|
В правой части равенства в уравнении [4] мы использовали теорему Стокса
изменить линейный интеграл вокруг замкнутого контура на
завиток
того же поля через поверхность, заключенную в петлю ( S ).
Мы также можем переписать общий ток () как
поверхностный интеграл
Плотность тока ( Дж, ):
| [Уравнение 5] |
|---|
Итак, теперь у нас есть исходный закон Ампера (уравнение [2]), переписанный в терминах
поверхностные интегралы (уравнения [4] и [5]). Следовательно, мы можем заменить их
вместе и получите новую форму закона Ампера:
| [Уравнение 6] |
|---|
Теперь у нас есть новая форма закона Ампера: ротор магнитного поля равен
к
Плотность электрического тока.Если вы проницательный ученик, вы можете заметить, что уравнение [6] не
окончательная форма, которая записана в уравнении [1]. Существует проблема
с уравнением [6], но только в 1860-х годах Джеймс Клерк Максвелл
разобрались в проблеме и объединили электромагнетизм с уравнениями Максвелла.
Плотность тока смещения
Закон Ампера был записан как в Уравнении [6] до Максвелла. Итак, начнем
посмотрите, что с этим не так. Сначала я должен выбросить еще один
векторная идентичность —
расхождение
завиток
любого векторного поля всегда равно нулю:
| [Уравнение 7] |
|---|
Итак, давайте рассмотрим расхождение закона Ампера, записанное в уравнении [6]:
| [Уравнение 8] |
|---|
Таким образом, уравнение [8] следует из уравнений [6] и [7].Но там сказано, что
дивергенция плотности тока Дж, всегда равна нулю. Это правда?
Если расхождение Дж всегда равно нулю, это означает, что электрическая
ток, текущий в любую область, всегда равен электрическому току, текущему
вне региона (без расхождения). Это кажется несколько разумным, поскольку электрический
ток в цепях течет по петле. Но давайте посмотрим, что будет, если мы
поставить в цепь конденсатор:
Рисунок 3. Напряжение, приложенное к конденсатору.
Теперь мы знаем из теории электрических цепей, что если напряжение непостоянно
(например, любая периодическая волна, такая как напряжение 60 Гц, выходящее из вашего
розетки), то через конденсатор будет протекать ток. То есть у нас есть
I не равно нулю на рисунке 3.
Однако конденсатор в основном представляет собой две параллельные проводящие пластины, разделенные
воздуха. Следовательно, нет токопроводящего пути для протекания тока.
Это означает, что электрический ток не может проходить через воздух конденсатора.Это проблема, если мы подумаем об уравнении [8]. Чтобы показать это более ясно,
давайте возьмем объем, который проходит через конденсатор, и посмотрим,
дивергенция Дж равна нулю:
Рис. 4. Дивергенция J не равна нулю.
На рисунке 4 мы нарисовали воображаемый объем красным цветом и хотим проверить
если расходимость плотности тока равна нулю. Выбранный нами объем,
имеет один конец (обозначенный стороной 1), где ток поступает в объем через черный провод.Другой конец нашего объема (обозначенный стороной 2) делит конденсатор пополам.
Мы знаем, что ток течет в петле. Итак, ток поступает через сторону 1
нашего красного тома. Однако на стороне 2 отсутствует электрический ток.
В воздухе конденсатора ток не течет. Это означает, что текущий
входит в объем, но из него ничего не выходит — поэтому расхождение Дж составляет
не ноль. Мы только что нарушили наше уравнение [8],
что означает, что теория не верна.И так было до тех пор, пока
пришел наш друг Максвелл.
Максвелл знал, что электрическое поле (и
Плотность электрического потока ( D )
внутри конденсатора менялся. И он знал, что изменяющееся во времени магнитное поле
возникло соленоидальное электрическое поле (т.е. это закон Фарде —
curl E равен производной по времени B ). Итак, почему это не так
изменяющееся во времени поле D вызовет соленоидальное поле H
(я.е. рождает завиток H ).
Вселенная любит симметрию, так почему бы не ввести этот термин? И другие
Максвелл это сделал, и он назвал этот термин плотностью тока смещения :
| [Уравнение 9] |
|---|
Этот термин «исправит» проблему схемы, показанную на рисунке 4, и сделает
Закон Фарде и Закон Ампера более симметричны. Это был большой вклад Максвелла.
И можно подумать, что это слабый вклад.Но существование этого термина
объединил уравнения и привел к пониманию распространения электромагнитных
волны и доказательство того, что все волны движутся с одинаковой скоростью (скоростью света)!
И именно это объединение уравнений, которое представил Максвелл, привело к
коллективное множество, известное как уравнения Максвелла. Итак, если мы добавим
ток смещения согласно закону Ампера, как записано в уравнении [6], тогда мы
имеют окончательную форму закона Ампера:
| [Уравнение 10] |
|---|
Так появился Закон Ампера!
Интерпретация закона Ампера
Итак, что означает уравнение [10]? Следующие последствия этого закона:
Закон Ампера с участием Максвелла заложил основу для
Электромагнетизм в нашем понимании.Итак, мы знаем, что
изменяющийся во времени D дает начало H поле, но от Фардея
Мы знаем, что изменяющееся поле H порождает поле E ….
и так далее, и так далее, и распространяются электромагнитные волны — и это круто.
Уравнения Максвелла
Эта страница о Законе Ампера для цепей или о том, что защищено авторским правом, в частности
поскольку это относится к уравнениям Максвелла. Авторские права www.maxwells-equations.com,
2012.
Ампера-Максвелла — Электромагнитная геофизика
Уравнение Ампера-Максвелла связывает электрические токи и магнитный поток. Это
описывает магнитные поля, возникающие из-за проводов передатчика или петли в
электромагнитные исследования. Для установившихся токов это ключ к описанию
магнитометрический эксперимент на удельное сопротивление.
Интегральное уравнение
Уравнение Ампера-Максвелла в интегральной форме приведено ниже:
(62) \ [\ int_S \ boldsymbol {\ nabla} \ times \ mathbf {b} \ cdot \ mathbf {da} = \ oint_C \ mathbf {b} \ cdot \ mathbf {dl} = \ mu_0 \ left (I_ { enc} + \ varepsilon_0 \ frac {d} {dt} \ int_S \ mathbf {e} \ cdot \ hat {\ mathbf {n}} ~ \ text {da} \ right), \]
где:
\ (\ mathbf {b} \) — магнитный поток
\ (\ mathbf {e} \) — электрическое поле
\ (I_ {enc} \) — приложенный ток
\ (\ mu_0 \) — магнитная проницаемость свободного пространства
\ (\ varepsilon_0 \) — электрическая проницаемость свободного пространства
\ (\ hat {\ mathbf {n}} \) — нормальная единица, указывающая наружу.
Рис.36 Замкнутый ток.
Первый член правой части уравнения был открыт Ампером. Это показывает отношения
между током \ (I_ {enc} \) и циркуляцией магнитного поля \ (\ mathbf {b} \),
вокруг любой замкнутой контурной линии (см. рис. 36). \ (I_ {enc} \) относится ко всем токам
независимо от их физического происхождения.
Вторая часть уравнения является вкладом Максвелла и показывает, что
циркуляция магнитного поля также вызвана скоростью изменения
электрический поток.Это объясняет, как ток в простой цепи, включающей
батарея и конденсатор могут течь. Этот термин имеет решающее значение для демонстрации того, что
электромагнитная энергия распространяется как волны.
Рис.37 Интеграция через конденсатор
Например, представьте себе интеграцию по поверхности, связанной с замкнутым путем.
например, показанный на рис. 37. Мы можем определить поверхность как
площадь круга, как на рис. 36, или, альтернативно, как
растянутой поверхности, как показано на рис. 37. В первом случае
вложенный ток — это поток зарядов в проводе.Во втором случае
однако зарядов, протекающих через поверхность, нет, но магнитный
поле, определенное на охватывающей кривой \ (C \), должно быть таким же. Это очевидное
несовпадение разрешается, если принять во внимание ток смещения,
который представляет собой скорость изменения электрического поля между двумя
тарелки. Эта интеграция такая же, как если бы мы выполняли интеграцию по квартире.
поверхность с пересекающим ее проводом.
Интегральные формулировки физически проницательны и тесно связаны с
эксперименты, которые их породили.Они также играют формирующую роль в
создание граничных условий для волн, распространяющихся по разным
материалы.
При рассмотрении распространения электромагнитных волн в веществе токи
\ (I_ {enc} \) обычно рассматриваются в терминах плотности тока. В
Таким образом, приведенное выше интегральное уравнение записывается как
(63) \ [\ int_S \ boldsymbol {\ nabla} \ times \ mathbf {b} \ cdot \ mathbf {da} =
\ oint_C \ mathbf {b} \ cdot \ mathbf {dl} =
\ mu_0 \ left (\ int_S \ left (\ mathbf {j_f}
+ \ frac {\ partial \ mathbf {p}} {\ partial t}
+ \ boldsymbol {\ nabla} \ times \ mathbf {m} \ right) \ cdot \ mathbf {da}
+ \ varepsilon_0 \ frac {d} {dt} \ int_S \ mathbf {e} \ cdot \ mathbf {\ hat {n}} ~ \ text {da} \ right), \]
где текущая плотность:
\ (\ mathbf {j_f} \) — свободный ток, вызванный движущимися зарядами
\ (\ mathbf {j_p} = \ frac {\ partial \ mathbf {p}} {\ partial t} \) — это поляризация или связанный ток, где \ (\ mathbf {p} \) — электрическая поляризация, возникающая в результате от связанных зарядов в диэлектриках
\ (\ mathbf {j_m} = \ nabla \ times \ mathbf {m} \) — ток намагничивания, то есть токи, необходимые для создания намагниченности \ (\ mathbf {m} \)
Полная плотность тока представляет собой сумму этих трех вкладов и описывается как
(64) \ [\ mathbf {j} = \ mathbf {j} _f + \ mathbf {j} _p + \ mathbf {j} _m.\]
Примечание
Полный ток, входящий в уравнение Ампера-Максвелла, состоит из свободных
ток и связанный ток, хотя все токи по существу одинаковы от
микроскопическая перспектива. Различный подход к свободному и связанному току
предлагает физическое понимание уравнения Ампера-Максвелла в различных контекстах.
Свободный ток вызывается движущимися зарядами, не связанными с атомами, часто
называется током проводимости. Напротив, связанный ток индуцируется
намагниченность или поляризация в объемных материалах.Когда магнитный материал
помещенный во внешнее магнитное поле, ток намагничивания будет индуцирован
из-за движения электронов в атомах. Точно так же, когда внешний электрический
поле приложено к диэлектрическому материалу, положительные и отрицательные связанные заряды в пределах
диэлектрик может разделиться и вызвать внутреннюю плотность тока поляризации.
Продолжая рассматривать свободный ток и связанный ток отдельно и используя
основные уравнения: \ (\ mathbf {b} = \ mu_0 (\ mathbf {h} + \ mathbf {m}) \) и \ (\ mathbf {d} = \ varepsilon_0 \ mathbf {e} + \ mathbf {p} \) интегральную форму уравнения Ампера-Максвелла можно переформулировать как:
(65) \ [\ int_S \ boldsymbol {\ nabla} \ times \ mathbf {h} \ cdot \ mathbf {da} = \ oint_C \ mathbf {h} \ cdot \ mathbf {dl} = \ int_S \ left (\ mathbf {j} _f + \ frac {\ partial \ mathbf {d}} {\ partial t} \ right) \ cdot \ hat {\ mathbf {n}} ~ \ text {da}.\]
Обратите внимание, что связанный заряд из-за намагничивания интегрирован в магнитную
поле \ (\ mathbf {h} \), тогда как связанный заряд из-за электрической поляризации равен
интегрировано в поле смещения \ (\ mathbf {d} \).
Дифференциальное уравнение во временной области
Есть несколько способов записать уравнение в дифференциальной форме. Каждый
дает собственное понимание. Начнем с рассмотрения дифференциальной формы уравнения (62) в терминах переменных \ (\ mathbf {e, b, p} \) и \ (\ mathbf {m} \):
(66) \ [\ boldsymbol {\ nabla} \ times \ mathbf {b}
— \ varepsilon_0 \ mu_0 \ frac {\ partial \ mathbf {e}} {\ partial t}
= \ mu_0 \ left (\ mathbf {j_f}
+ \ frac {\ partial \ mathbf {p}} {\ partial t}
+ \ boldsymbol {\ nabla} \ times \ mathbf {m} \ right) \]
и аналогично (65), мы можем использовать определяющие отношения \ (\ mathbf {d} = \ varepsilon_0 \ mathbf {e} + \ mathbf {p} \) и \ (\ mathbf {b} = \ mu_0 (\ mathbf {h} + \ mathbf {m}) \), чтобы записать дифференциальное уравнение во временной области в терминах переменных \ (\ mathbf {h, j_f} \) и \ (\ mathbf {d} \):
(67) \ [\ boldsymbol {\ nabla} \ times \ mathbf {h} = \ mathbf {j} _f + \ frac {\ partial \ mathbf {d}} {\ partial t}.{i \ omega t} \) Соглашение о преобразовании Фурье для переноса
наши уравнения из временной области в частотную.
Уравнение становится
(68) \ [\ boldsymbol {\ nabla} \ times \ mathbf {H} — я \ omega \ mathbf {D} = \ mathbf {J} _f. \]
Если мы имеем дело с линейными изотропными средами, то имеем
\ [\ mathbf {D} (\ omega) = \ epsilon \ mathbf {E} (\ omega) \]
(69) \ [\ mathbf {J} _f (\ omega) = \ sigma \ mathbf {E} (\ omega) \]
и уравнения Ампера-Максвелла можно записать как
(70) \ [\ boldsymbol {\ nabla} \ times \ mathbf {H} — \ left (\ sigma + i \ omega \ epsilon \ right) \ mathbf {E} = 0.\]
Открывает закон
Первое наблюдение, которое побудило исследователей искать взаимосвязь
соединение магнитного поля и тока было сделано Гансом Кристианом Эрстедом в 1820 году,
которые заметили, что магнитные иглы отклоняются электрическим током. Этот
привел к параллельному изучению этого явления несколькими европейскими физиками. Пока
Жан-Батист Биот и Феликс Савар экспериментировали с установкой, похожей на
Эрстеда (который в 1820 году привел их к определению отношений, известных сейчас
как закон Био-Савара) эксперимент Андре-Мари Ампера был сосредоточен на
измерение сил, которые два электрических провода действуют друг на друга.Он
сформулировал круговой закон Ампера в 1826 году [Gri99], который
связывает магнитное поле, связанное с замкнутым контуром, с электрическим
ток, проходящий через него. В исходном виде ток заключен в
петля относится только к свободному току, вызванному движущимися зарядами, вызывая несколько
вопросы, касающиеся сохранения электрического заряда и распространения
электромагнитная энергия.
В 1861 году [Max61] Джеймс Клерк Максвелл расширил закон Ампера, введя
ток смещения в член электрического тока, чтобы удовлетворить
уравнение неразрывности электрического заряда.На основе идеи смещения
тока, в 1864 г. [Max65] Максвелл основал теорию электромагнитного
поля, предсказывая распространение волн электромагнитных полей и
эквивалентность распространения света и распространения электромагнитных волн.
Только в конце 1880-х [Her93] Генрих Герц экспериментально доказал существование
электромагнитных волн в соответствии с электромагнитной теорией Максвелла, и
продемонстрировал эквивалентность электромагнитных волн и света.

