Содержание
Определение координат вектора заданного координатами его начальной и конечной точки.
Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Формулы определения координат вектора заданного координатами его начальной и конечной точки
Формула определения координат вектора для плоских задач
В случае плоской задачи вектор AB заданный координатами точек A(Ax ; Ay) и B(Bx ; By) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay}
Формула определения координат вектора для пространственных задач
В случае пространственной задачи вектор AB заданный координатами точек A(Ax ; Ay ; Az) и B(Bx ; By ; Bz) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay ; Bz — Az}
Формула определения координат вектора для n -мерного пространства
В случае n-мерного пространства вектор AB заданный координатами точек A(A1 ; A2 ; .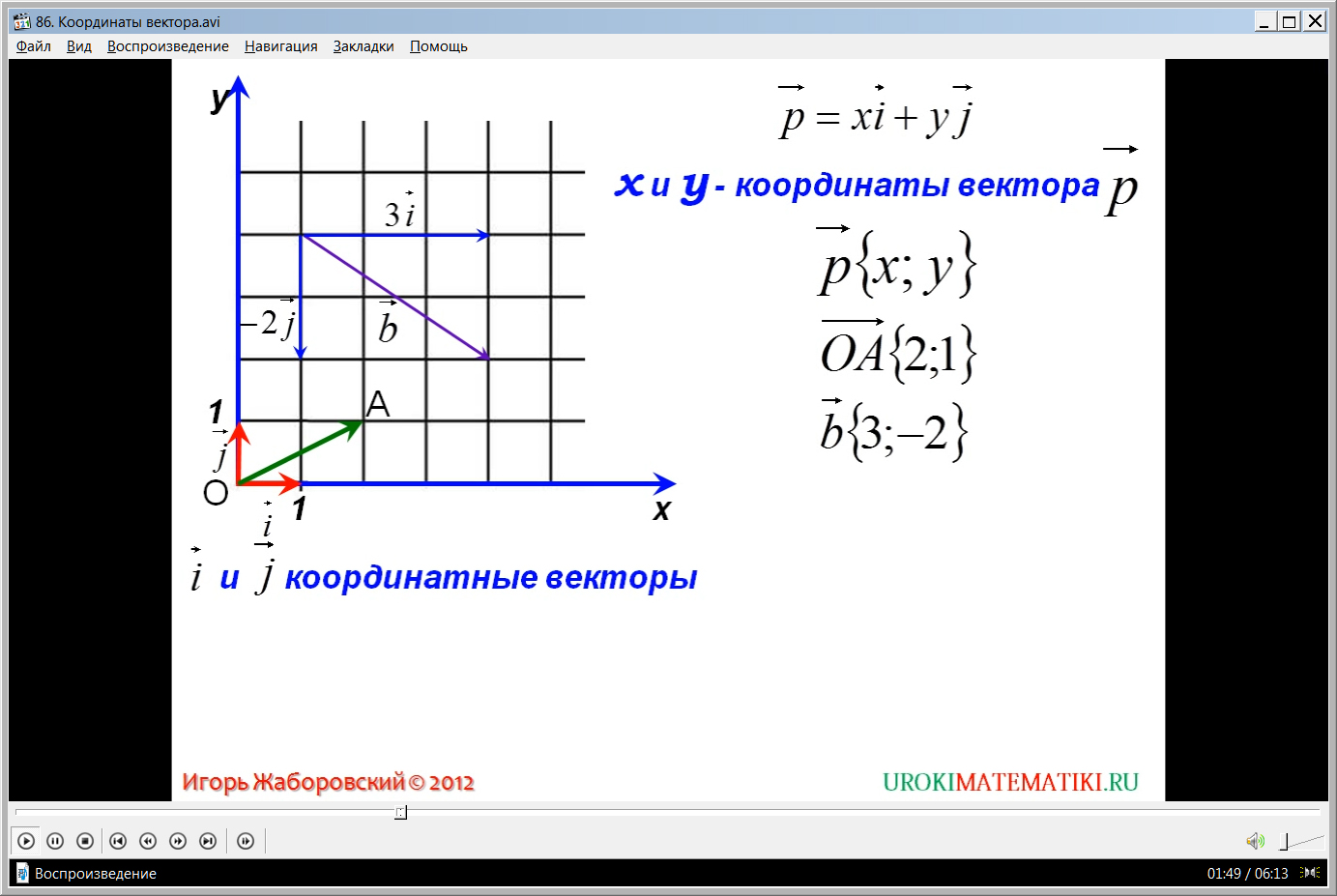 .. ; An) и B(B1 ; B2 ; … ; Bn) можно найти воспользовавшись следующей формулой
.. ; An) и B(B1 ; B2 ; … ; Bn) можно найти воспользовавшись следующей формулой
AB = {B1 — A1 ; B2 — A2 ; … ; Bn — An}
Примеры задач связанных с определением координат вектора по двум точкам
Примеры для плоских задач
Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).
Решение: AB = {3 — 1; 1 — 4} = {2; -3}.
Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).
Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8
ABy = By — Ay => By = ABy + Ay => By = 1 + (-4) = -3
Ответ: B(8; -3).
Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).
Решение:
ABx = Bx — Ax => Ax = Bx — ABx => Ax = 3 — 5 = -2
ABy = By — Ay => Ay = By — ABy => Ay = -4 — 1 = -5
Ответ: A(-2; -5).
Примеры для пространственных задач
Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).
Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.
Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).
Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8
ABy = By — Ay => By = ABy + Ay => By = 1 + (-4) = -3
ABz = Bz — Az => Bz = ABz + Az => Bz = 2 + 3 = 5
Ответ: B(8; -3; 5).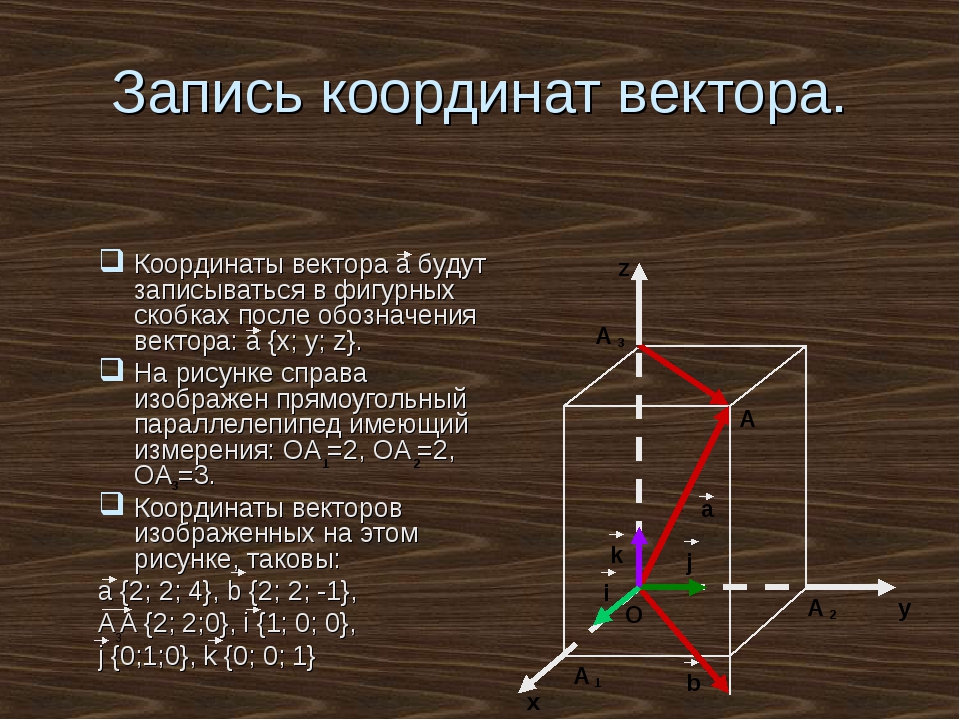
Пример 6. Найти координаты точки A вектора AB = {5; 1; 4}, если координаты точки B(3; -4; 1).
Решение:
ABx = Bx — Ax => Ax = Bx — ABx => Ax = 3 — 5 = -2
ABy = By — Ay => Ay = By — ABy => Ay = -4 — 1 = -5
ABz = Bz — Az => Az = Bz — ABz => Az = 1 — 4 = -3
Ответ: A(-2; -5; -3).
Примеры для n -мерного пространства
Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).
Решение: AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}.
Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).
Решение:
AB1 = B1 — A1 => B1 = AB1 + A1 => B1 = 5 + 3 = 8
AB2 = B2 — A2 => B2 = AB2 + A2 => B2 = 1 + (-4) = -3
AB3 = B3 — A3 => B3 = AB3 + A3 => B3 = 2 + 3 = 5
AB4 = B4 — A4 => B4 = AB4 + A4 => B4 = 1 + 2 = 3
Ответ: B(8; -3; 5; 3).
Пример 9. Найти координаты точки A вектора AB = {5; 1; 4; 5}, если координаты точки B(3; -4; 1; 8).
Решение:
AB1 = B1 — A1 => A1 = B1 — AB1 => A1 = 3 — 5 = -2
AB2 = B2 — A2 => A2 = B2 — AB2 => A2 = -4 — 1 = -5
AB3 = B3 — A3 => A3 = B3 — AB3 => A3 = 1 — 4 = -3
AB4 = B4 — A4 => A4 = B4 — AB4 => A4 = 8 — 5 = 3
Ответ: A(-2; -5; -3; 3).
Координаты вектора
Вспомним, как мы находили координаты вектора на
плоскости.
Пользуясь тем, что любой вектор можно разложить по
двум неколлинеарным векторам, на осях мы задавали единичные векторы.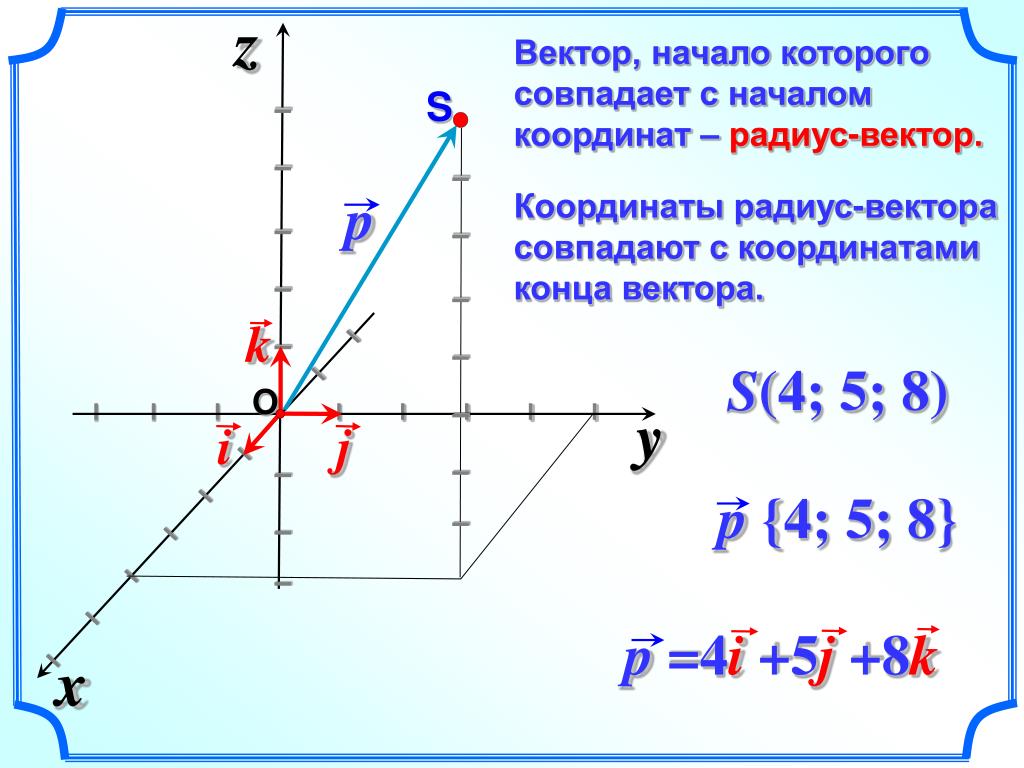 Таким
Таким
образом, любой вектор можно разложить по данным единичным векторам, а
координатами вектора являются коэффициенты этого разложения.
Так же вам уже известно, что любой вектор пространства
можно выразить через 3 некомпланарных вектора, то есть векторы, не лежащие в
одной плоскости.
Изобразим прямоугольную систему координат Охуz.
На каждой из положительных осей от начала координат отложим единичные векторы.
Буквой i
обозначим единичный вектор оси Оx,
буквой j — единичный вектор оси Оy,
буквой k — единичный вектор оси Оz.
Определение:
Векторы i,
j, k
будем называть координатными векторами.
Понятно, что они являются некомпланарными. И
поэтому любой вектор пространства можно разложить по единичным векторам i,
j, k.
Причём коэффициенты разложения х, у и z
определяются единственным образом.
Коэффициенты х, у и z
называют
координатами вектора р в данной системе координат. Координаты
вектора будем записывать в фигурных скобках в последовательности х, у, z.
Задание: Пользуясь
разложениями векторов по координатным векторам, записать их координаты.
Решение:
Задание: пользуясь
координатами векторов, запишем их разложения по координатным векторам i,
j, k.
Решение:
Задача: В
прямоугольном параллелепипеде 𝑂𝐴 =
2, 𝑂𝐵 =
3, а ОО1 = 2. Найти координаты векторов 𝑂𝐴1,
𝑂𝐵1,
𝑂𝑂1,
𝑂𝐶,
𝑂𝐶1,
𝐵𝐶1,
𝐴𝐶1
и 𝑂1 𝐶.
Решение:
После выполнения этого задания можно сделать вывод
о том, что если вектор лежит в некоторой из координатных плоскостей или
параллелен ей, а также лежит или параллелен некоторой из координатных осей, то
его соответствующие координаты равны нулю.
Если вектор лежит в координатной плоскости Оху или
параллелен ей, то его аппликата равна нулю. Если вектор принадлежит или
параллелен координатной плоскости Охz,
то его ордината равна нулю. Если же вектор принадлежит или параллелен
координатной плоскости Оyz,
то его абсцисса равна нулю.
В случае, когда вектор лежит на оси координат Оx
или параллелен ей, то ордината и аппликата равны нулю. Если вектор принадлежит
или параллелен оси Оy, то абсцисса и
аппликата равны нулю. И если вектор принадлежит или параллелен оси Оz,
то абсцисса и ордината равны нулю.
А сейчас поговорим о противоположных векторах. Из
планиметрии известно, что координаты противоположных векторов
противоположны. Это утверждение верно и для векторов в пространстве.
Задание: найти
координаты векторов противоположных данным векторам.
Решение:
Также из курса планиметрии вам известны правила
определения координат вектора суммы, вектора разности и произведения
вектора на число.
Такие же правила действую и для координат векторов в
пространстве.
Задание: 𝑎 ⃗{−1;0;3},
𝑏 ⃗{5;−2;1}
и 𝑐 ⃗{1;7;−2}.
Определить координаты векторов:
1) 𝑎 ⃗+𝑐 ⃗;
2) 𝑏 ⃗−𝑎 ⃗;
3) 2𝑎 ⃗+𝑏 ⃗;
4) 1/2 𝑎 ⃗−2𝑏 ⃗+𝑐 ⃗.
Решение:
Так, используя правила определения координат вектора
суммы, разности и произведения вектора на число, мы определили координаты
данных векторов.
Итоги:
Сегодня мы ввели понятие координатных векторов i,
j, k.
И, пользуясь тем, что любой вектор пространства можно выразить через 3
некомпланарных вектора, записали, что коэффициенты х, у и z
называют координатами вектора p
в данной системе координат.
Мы отметили, что все координаты нулевого вектора равны
нулю. Равные векторы имеют равные координаты, а координаты противоположных
векторов противоположны.
Также мы записали правила, которые позволяют находить
координаты любого вектора, представленного в виде алгебраической суммы данных
векторов, координаты которых известны.
Связь между координатами вектора и координатами его начала и конца 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема 27.
Связь между координатами вектора и координатами его начала и конца.
Ты уже знаком с понятием координат вектора. Ими называют коэффициенты разложения данного вектора по единичным координатным векторам i⃗ и j⃗.
Сегодня мы ответим на вопрос «Как связаны координаты вектора с координатами его начала и конца?».
Но для начала вернёмся к координатам точки в прямоугольной системе координат.
Напомним, что для их определения нужно опустить перпендикуляры из данной точки к осям.
Точки пересечения данных прямых с осями обозначим как M1 и M2.
Абсциссой точки М является число x, которое является длиной отрезка OM1. А ординатой — число y, которое является длиной отрезка OM2.
M(x; y) x = OM1, y = OM2
Мы вспомнили, как определять координаты точек, а теперь вернёмся к общему случаю и, уже рассмотренной, точке M.
Проведём вектор из точки O к точке M. Запомни, вектор OM⃗ называют радиус-вектором точки M.
Сейчас докажем следующее утверждение: координаты точки M равны соответствующим координатам её радиус-вектора.
Доказать: M(x;y)=OM⃗x;y
Понятно, что вектор OM⃗=ОM1⃗+ОM2⃗ по правилу параллелограмма.
Теперь необходимо доказать, что вектор
OM1⃗=xi⃗, а вектор OM2⃗=yj⃗
Тем самым мы докажем, что вектор OM⃗x;y.
Если x > 0, то x = OM1, а векторы OM1⃗ и i⃗ сонаправлены, поэтому
OM1⃗=OM1∙i⃗=xi⃗
Если x x = OM1, а векторы OM1⃗ и i⃗ противоположно направлены. Поэтому OM1⃗=-OM1∙i⃗=xi⃗.
Наконец, если x = 0
OM1⃗=0⃗ и равенство OM1=xi⃗ в этом случае так же справедливо. Таким образом, в любом случае ОM1⃗=xi⃗. Аналогично доказывается, что ОM2⃗=yj⃗.
Следовательно,OM⃗=ОM1⃗+ОM2⃗=xi⃗+yj⃗
Отсюда следует, что координаты радиус-вектора OM равны (x; y), то есть равны соответствующим координатам точки M.
Пользуясь доказанным утверждением, выразим координаты вектора AB⃗ через координаты его начала A и конца B. Пусть точка A имеет координаты x1;y1, а точка B – координаты x2;y2.
Вектор AB⃗ равен разности векторов OB⃗ и OA⃗, поэтому его координаты равны разностям соответствующих координат векторов OB⃗ и OA⃗. Но OB⃗ и OA⃗ – радиус-векторы точек B и A, и, значит, OB⃗ имеет координаты x2;y2, а OA⃗ имеет координаты x1;y1. Следовательно, вектор AB⃗ имеет координаты x2-x1;y2-y1.
Но OB⃗ и OA⃗ – радиус-векторы точек B и A, и, значит, OB⃗ имеет координаты x2;y2, а OA⃗ имеет координаты x1;y1. Следовательно, вектор AB⃗ имеет координаты x2-x1;y2-y1.
Таким образом, каждая координата вектора равна разности соответствующих координат его конца и начала.
Введение системы координат дает возможность изучать геометрические фигуры и их свойства с помощью уравнений и неравенств и, таким образом, использовать в геометрии методы алгебры. Такой подход к изучению свойств геометрических фигур называется методом координат.
Рассмотрим три вспомогательные задачи:
-
Как найти координаты середины отрезка.
Пусть в системе координат Oxy точка A имеет координаты x1;y1, а точка B – координаты x2;y2. Выразим координаты x;y середины C отрезка AB через координаты его концов. Так как точка C – середина отрезка AB, то
OC⃗=12OA⃗+OB⃗.
x=x1+x22; y=y1+y22
Таким образом, каждая координата середины отрезка равна полусумме соответствующих координат его концов. -
Вычисление длины вектора по его координатам.
Пусть вектор a⃗x;y, тогда длина вектора вычисляется по формуле:
a⃗=x2+y2 -
Вычисление расстояния между двумя точками. Пусть точка M1 имеет координаты (x1; y1), точка M2 – координаты (x2; y2). Выразим расстояние d между точками M1 и M2 через их координаты.
Рассмотрим вектор M1M2⃗. Его координаты равны x2-x1;y2-y1. Следовательно, длина этого вектора может быть найдена по формуле:
M1M2⃗=x2-x12+y2-y12
Пример:
-
Найти длину вектора a⃗-3;4
a⃗=x2+y2=-32+42=25=5
Ответ: 5 -
Найти расстояние между точкой A(2; 7) и точкой B(-2; 7)
d=-2-22+7-72=16=4
Ответ: 4
|
Зафиксируем в пространстве некоторую точку О и три взаимно перпендикулярных вектора единичной длины I, J И K. Рис. 7 Совокупность точки О и векторов I, J, K называется Декартовой прямоугольной системой координат. Прямые, проходящие через точку О параллельно векторам I, J И K, называются Координатными осями и носят названия осей Абсцисс (Ох), Ординат (Оу) и Аппликат (Oz) соответственно. Пусть задан вектор А. Совместим его начальную точку с началом координат О, а через его конечную точку А проведем плоскости, перпендикулярные координатным осям. Пусть эти плоскости пересекают оси Ox, Oy, Oz в точках L, M, N соответственно. Рис. 8 Нетрудно убедиться, что Поскольку вектора коллинеарны векторам I, J, K соответственно, то найдутся числа X1, Y1, Z1 такие, что Следовательно, любой вектор А может быть представлен в виде Представление (1) единственно. Действительно, если предположить, что наряду с (1) существует другое представление A = X′1I + Y′1J + Z′1K, То, вычитая это равенство из (7.1), получим 0 = (X1 – X′1)I + (Y1 – Y′1)J + (Z1 – Z′1)K. Если Х1 ≠ Х′1, то Что невозможно, т. к. вектор в правой части лежит в плоскости, параллельной осям Оу и Oz, а вектор I перпендикулярен этой плоскости. Х1 = Х′1. Аналогично доказывается, что Y1 = Y′1 и Z1 = Z′1. Числа X1, Y1, Z1 в представлении (1) называются Координатами вектора А. Вместе с равенством (1) будет использоваться также запись вида Радиусом-вектором точки А называется вектор, начало которого совпадает с началом координат О, а конец – с точкой А. Координатами точки А называются координаты радиус-вектора точки А. При этом, если = (X1, Y1, Z1), будем писать
|
Координаты точки и координаты вектора. Как найти координаты вектора
Прямоугольная система координат
Чтобы определить понятие координат точек, нам необходимо ввести систему координат, в которой мы и будем определять ее координаты.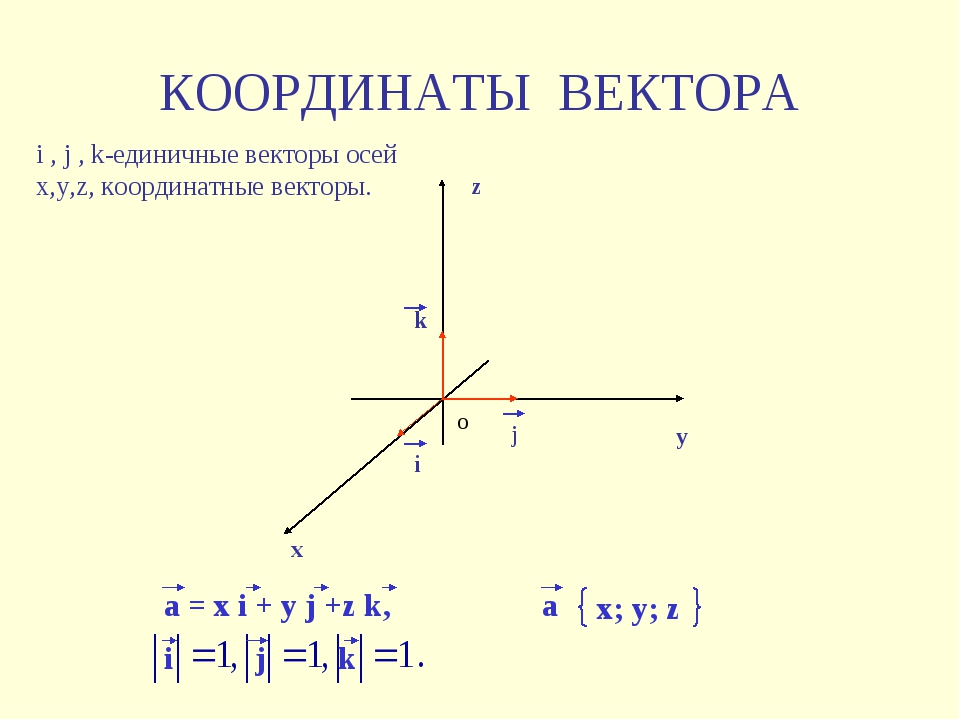 Одна и та же точка в разных системах координат может иметь различные координаты. Здесь мы будем рассматривать прямоугольную систему координат в пространстве.
Одна и та же точка в разных системах координат может иметь различные координаты. Здесь мы будем рассматривать прямоугольную систему координат в пространстве.
Возьмем в пространстве точку $O$ и введем для нее координаты $(0,0,0)$. Назовем ее началом системы координат. Проведем через нее три взаимно перпендикулярные оси $Ox$, $Oy$ и $Oz$, как на рисунке 1. Эти оси будут называться осями абсцисс, ординат и аппликат, соответственно. Осталось только ввести масштаб на осях (единичный отрезок) – прямоугольная система координат в пространстве готова (рис. 1)
Рисунок 1. Прямоугольная система координат в пространстве. Автор24 — интернет-биржа студенческих работ
Координаты точки
Теперь разберем, как определяют в такой системе координаты любой точки. Возьмем произвольную точку $M$ (рис. 2).
Рисунок 2. Произвольная точка. Автор24 — интернет-биржа студенческих работ
Построим на координатных осях прямоугольный параллелепипед, так, что точки $O$ и $M$ противоположные его вершины (рис.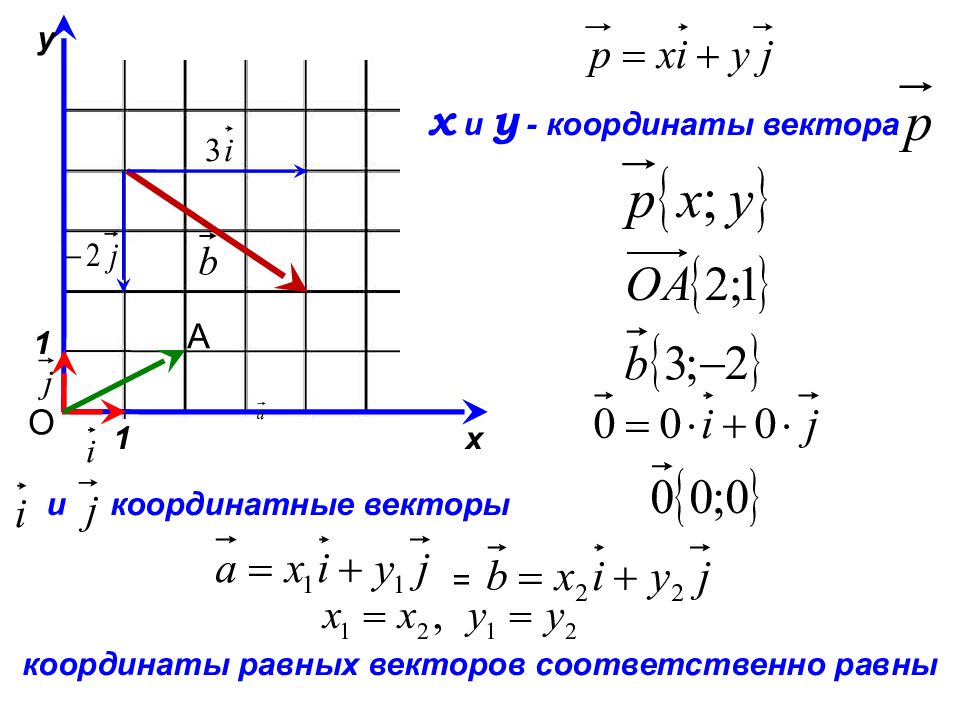 3).
3).
Рисунок 3. Построение прямоугольного параллелепипеда. Автор24 — интернет-биржа студенческих работ
Тогда точка $M$ будет иметь координаты $(X,Y,Z)$, где $X$ – значение на числовой оси $Ox$, $Y$ – значение на числовой оси $Oy$, а $Z$ – значение на числовой оси $Oz$.
Пример 1
Необходимо найти решение следующей задачи: написать координаты вершин параллелепипеда, изображенного на рисунке 4.
Рисунок 4. Параллелепипед. Автор24 — интернет-биржа студенческих работ
Решение.
Точка $O$ начало координат, следовательно, $O=(0,0,0)$.
Точки $Q$, $N$ и $R$ лежат на осях $Ox$, $Oz$ и $Oy$, соответственно, значит
$Q=(2,0,0)$, $N=(0,0,1.5)$, $R=(0,2.5,0)$
Точки $S$, $L$ и $M$ лежат в плоскостях $Oxz$, $Oxy$ и $Oyz$, соответственно, значит
$S=(2,0,1.5)$, $L=(2,2.5,0)$, $R=(0,2.5,1.5)$
Точка $P$ имеет координаты $P=(2,2.5,1.5)$
Координаты вектора по двум точкам и формула нахождения
Чтобы узнать, как найти вектор по координатам двух точек, необходимо рассмотреть введенную нами ранее систему координат.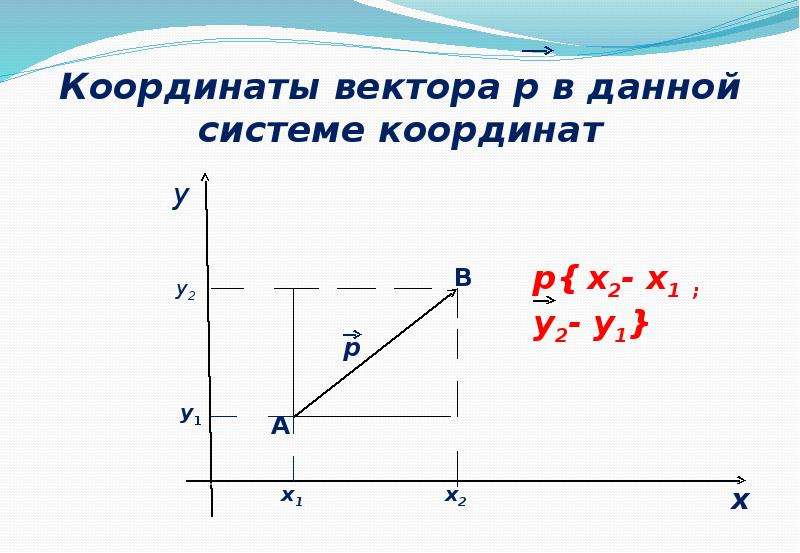 В ней от точки $O$ по направлению оси $Ox$ отложим единичный вектор $\overline{i}$, по направлению оси $Oy$ — единичный вектор $\overline{j}$, а единичный вектор $\overline{k}$ нужно направлять по оси $Oz$.
В ней от точки $O$ по направлению оси $Ox$ отложим единичный вектор $\overline{i}$, по направлению оси $Oy$ — единичный вектор $\overline{j}$, а единичный вектор $\overline{k}$ нужно направлять по оси $Oz$.
Для того чтобы ввести понятие координат вектора, введем следующую теорему (здесь ее доказательство мы рассматривать не будем).
Теорема 1
Произвольный вектор в пространстве может быть разложен по трем любым векторам, которые не лежат в одной плоскости, причем коэффициенты в таком разложении будут единственным образом определены.
Математически это выглядит следующим образом:
$\overline{δ}=m\overline{α}+n\overline{β}+l\overline{γ}$
Так как векторы $\overline{i}$, $\overline{j}$ и $\overline{k}$ построены на координатных осях прямоугольной системы координат, то они, очевидно, не будут принадлежать одной плоскости. Значит любой вектор $\overline{δ}$ в этой системе координат, по теореме 1, может принимать следующий вид
$\overline{δ}=m\overline{i}+n\overline{j}+l\overline{k}$ (1)
где $n,m,l∈R$.
Определение 1
Три вектора $\overline{i}$, $\overline{j}$ и $\overline{k}$ будут называться координатными векторами.
Определение 2
Коэффициенты перед векторами $\overline{i}$, $\overline{j}$ и $\overline{k}$ в разложении (1) будут называться координатами этого вектора в заданной нами системе координат, то есть
$\overline{δ}=(m,n,l)$
Линейные операции над векторами
Теорема 2
Теорема о сумме: Координаты суммы любого числа векторов определяются суммой их соответствующих координат.
Доказательство.
Будем доказывать эту теорему для 2-х векторов. Для 3-х и более векторов доказательство строится аналогичным образом. Пусть $\overline{α}=(α_1,α_2,α_3)$, $\overline{β}=(β_1,β_2 ,β_3)$.
Эти вектора можно записать следующим образом
$\overline{α}=α_1\overline{i}+ α_2\overline{j}+α_3\overline{k}$, $\overline{β}=β_1\overline{i}+ β_2\overline{j}+β_3\overline{k}$
$\overline{α}+\overline{β}=α_1\overline{i}+α_2\overline{j}+α_3\overline{k}+β_1\overline{i}+ β_2\overline{j}+β_3\overline{k}=(α_1+β_1 )\overline{i}+(α_2+β_2 )\overline{j}+(α_3+β_3)\overline{k}$
Следовательно
$\overline{α}+\overline{β}=(α_1+β_1,α_2+β_2,α_3+β_3)$
Теорема доказана.
Замечание 1
Замечание: Аналогично, находится решение разности нескольких векторов.
Теорема 3
Теорема о произведении на число: Координаты произведения произвольного вектора на действительное число определяется произведением координат на это число.
Доказательство.
Возьмем $\overline{α}=(α_1,α_2,α_3)$, тогда $\overline{α}=α_1\overline{i}+α_2\overline{j}+α_3\overline{k}$, а
$l\overline{α}=l(α_1\overline{i}+ α_2\overline{j}+α_3\overline{k})=lα_1\overline{i}+ lα_2\overline{j}+lα_3\overline{k}$
Значит
$k\overline{α}=(lα_1,lα_2,lα_3)$
Теорема доказана.
Пример 2
Пусть $\overline{α}=(3,0,4)$, $\overline{β}=(2,-1,1)$. Найти $\overline{α}+\overline{β}$, $\overline{α}-\overline{β}$ и $3\overline{α}$.
Решение.
$\overline{α}+\overline{β}=(3+2,0+(-1),4+1)=(5,-1,5)$
$\overline{α}-\overline{β}=(3-2,0-(-1),4-1)=(1,1,3)$
$3\overline{α}=(3\cdot 3,3\cdot 0,3\cdot 4)=(9,0,12)$
3.
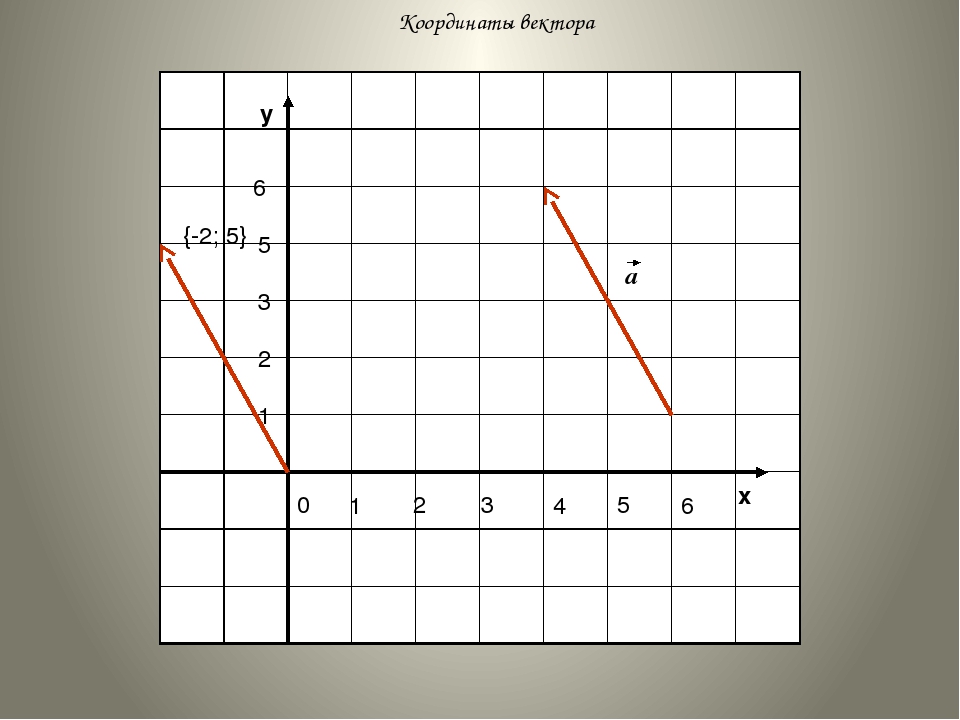 На практике координаты векторов удобно представлять в виде матриц-столбцов (или матриц-строк), которые называются координатными столбцами (координатными строками).
На практике координаты векторов удобно представлять в виде матриц-столбцов (или матриц-строк), которые называются координатными столбцами (координатными строками).
Понятие
вектор
Векторы
занимают особое место среди объектов,
рассматриваемых в высшей математике,
поскольку каждый вектор имеет не только
числовое значение — длину, но и физическое
и геометрическое — направленность.
Вектор, представленный направленным
отрезком, идущим от точки A к точке B,
обозначается так: .
Вектор — это вид представления точки,
до которой требуется добраться из
некоторой начальной точки. Например,
трёхмерный вектор, как правило,
записывается в виде (х, y, z). Говоря совсем
просто, эти числа означают, как далеко
требуется пройти в трёх различных
направлениях, чтобы добраться до точки.
Пусть дан
вектор. При этом x = 3 (правая рука указывает
направо), y = 1 (левая рука указывает
вперёд), z = 5 (под точкой стоит лестница,
ведущая вверх). По этим данным вы найдёте
По этим данным вы найдёте
точку, проходя 3 метра в направлении,
указываемом правой рукой, затем 1 метр
в направлении, указываемом левой рукой,
а далее Вас ждёт лестница и, поднимаясь
на 5 метров, Вы, наконец, окажетесь в
искомой точке.
Все остальные
термины — это уточнения представленного
выше объяснения, необходимые для
различных операций над векторами, то
есть, решения практических задач.
Пройдёмся по этим более строгим
определениям, останавливаясь на типичных
задачах на векторы.
Физическими
примерами векторных величин могут
служить смещение материальной точки,
двигающейся в пространстве, скорость
и ускорение этой точки, а также действующая
на неё сила.
Координаты
вектора на плоскости и в пространстве
Первым
пунктом рассмотрим векторы на плоскости.
Изобразим декартову прямоугольную
систему координат и от начала координат
отложим единичные векторы и :
Векторы и ортогональны. Ортогональны
= Перпендикулярны. Рекомендую потихоньку
привыкать к терминам: вместо параллельности
и перпендикулярности используем
соответственно слова коллинеарность
и ортогональность.
Обозначение:
ортогональность векторов записывают
привычным значком перпендикулярности,
например: .
Рассматриваемые
векторы называют координатными векторами
или ортами. Данные векторы образуют
базис на плоскости. Что такое базис,
думаю, интуитивно многим понятно, более
подробную информацию можно найти в
статье Линейная (не) зависимость векторов.
Базис векторов. Простыми словами, базис
и начало координат задают всю систему
– это своеобразный фундамент, на котором
кипит полная и насыщенная геометрическая
жизнь.
Иногда
построенный базис называют ортонормированным
базисом плоскости: «орто» – потому что
координатные векторы ортогональны,
прилагательное «нормированный» означает
единичный, т.е. длины векторов базиса
равны единице.
Обозначение:
базис обычно записывают в круглых
скобках, внутри которых в строгой
последовательности перечисляются
базисные векторы, например: . Координатные
векторы нельзя переставлять местами.
Любой вектор
плоскости единственным образом
выражается в виде:
, где –
числа, которые называются координатами
вектора в данном базисе.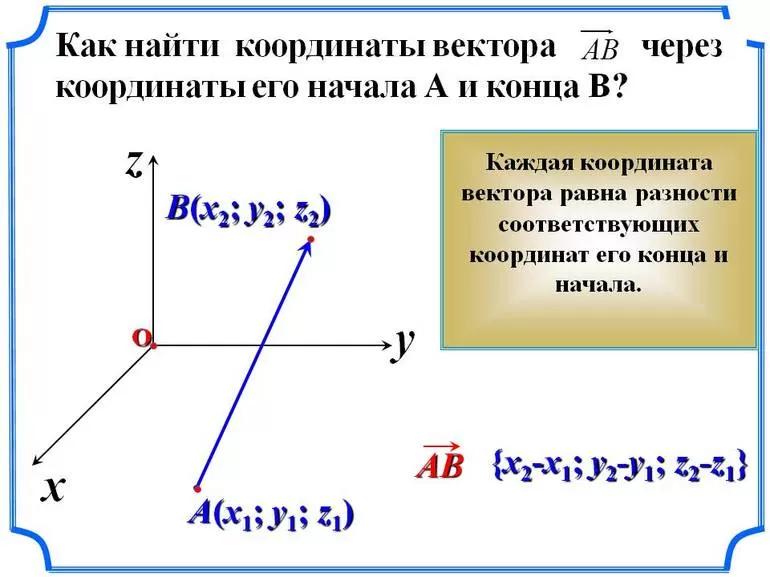 А само выражение
А само выражение
называется разложением вектора по
базису .
Теперь рассмотрим векторы в трехмерном
пространстве, здесь практически всё
так же! Только добавится ещё одна
координата. Трехмерные чертежи выполнять
тяжко, поэтому ограничусь одним вектором,
который для простоты отложу от начала
координат:Перед вами ортонормированный базис
трехмерного пространства и прямоугольная
система координат, единичные векторы
данного базиса попарно ортогональны:
и . Ось наклонена под углом 45 градусов
только для того, чтобы складывалось
визуальное впечатление пространства.
О том, как правильно выполнять плоские
и трехмерные чертежи на клетчатой
бумаге, читайте в самом начале методички
Графики и свойства функций.
Любой вектор
трехмерного пространства можно
единственным способом разложить по
ортонормированному базису :
, где –
координаты вектора (числа) в данном
базисе.
Пример с
картинки: . Давайте посмотрим, как здесь
работают правила действий с векторами.
Во-первых, умножение вектора на число:
(красная стрелка), (зеленая стрелка) и
(малиновая стрелка).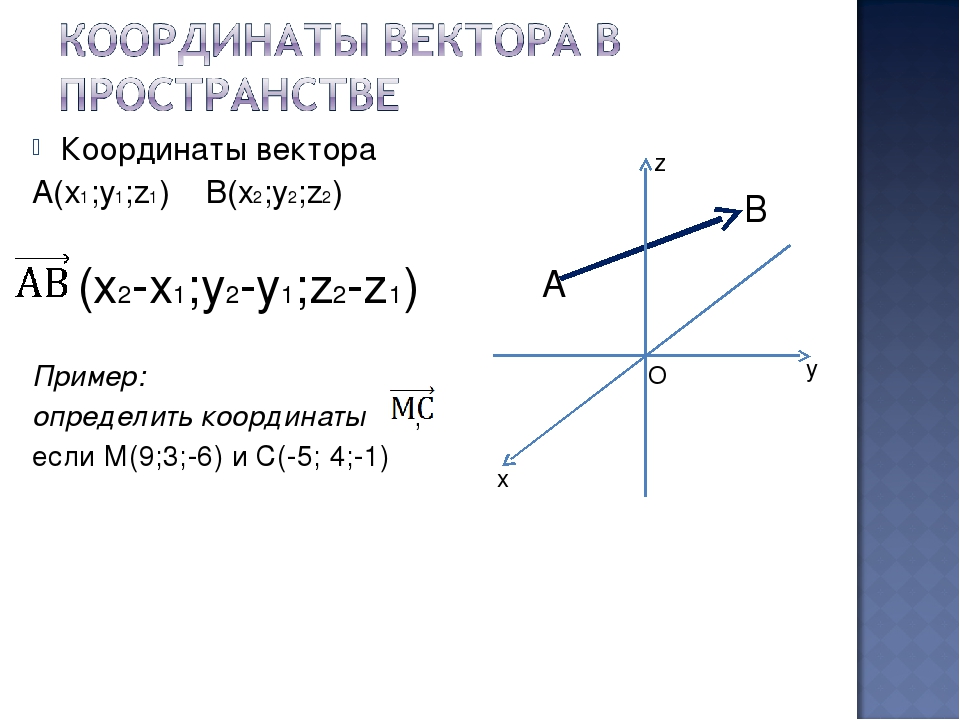 Во-вторых, перед
Во-вторых, перед
вами пример сложения нескольких, в
данном случае трёх, векторов: . Вектор
суммы начинается в исходной точке
отправления (начало вектора ) и утыкается
в итоговую точку прибытия (конец вектора
).
Все векторы
трехмерного пространства, естественно,
тоже свободны, попробуйте мысленно
отложить вектор от любой другой точки,
и вы поймёте, что его разложение
«останется при нём».
Аналогично
плоскому случаю, помимо записи широко
используются версии со скобками: либо
.
Если в
разложении отсутствует один (или два)
координатных вектора, то вместо них
ставятся нули. Примеры:
вектор
(дотошно ) – запишем ;
вектор
(дотошно ) – запишем ;
вектор
(дотошно ) – запишем .
Базисные
векторы записываются следующим образом:
Линейные операции
над векторами в координатной форме
Равенство
векторов и линейные операции (сложение
векторов и умножение вектора на число)
удобно представлять в координатной
форме. При этом справедливы следующие
свойства.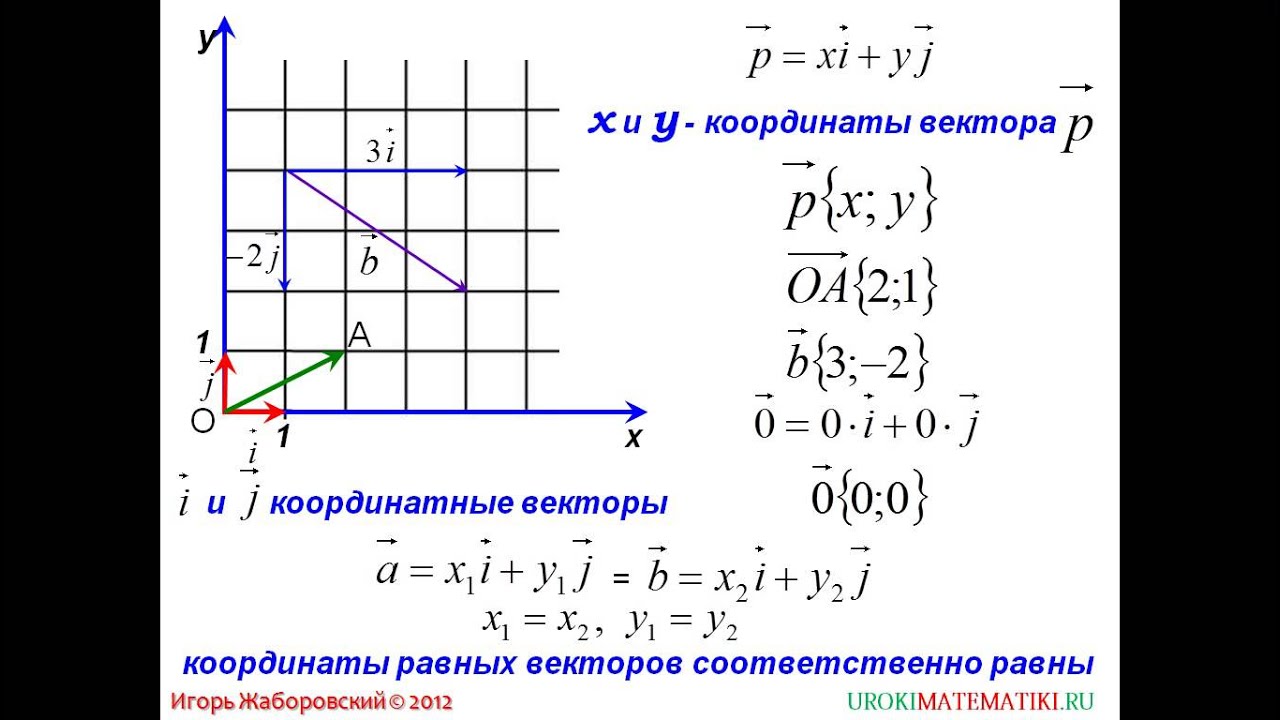
1. Равные
векторы имеют равные координаты (в одном
и том же базисе).
2. Каждая
координата суммы векторов равна сумме
соответствующих координат слагаемых.
3. Каждая
координата произведения вектора на
число равна произведению этого числа
на соответствующую координату вектора.
4. Каждая
координата линейной комбинации векторов
равна линейной комбинации соответствующих
координат векторов.
Докажем,
например, последнее свойство. Проекция
линейной комбинации векторов на прямую,
содержащую базисный вектор \vec{e}_1, равна
линейной комбинации проекций векторов
(составляющих линейную комбинацию) на
эту прямую. Поэтому абсцисса линейной
комбинации векторов равна линейной
комбинации абсцисс этих векторов.
Аналогичное рассуждение справедливо
для ординат и аппликат.. Основные
теоремы 1.3-1.5 о разложении вектора по
базису устанавливают взаимно однозначное
соответствие между множеством векторов
пространства и множеством их координат
в данном базисе. А именно, между векторами
на прямой и действительными числами,
между векторами на плоскости и
упорядоченными парами чисел, между
векторами пространства и упорядоченными
тройками чисел.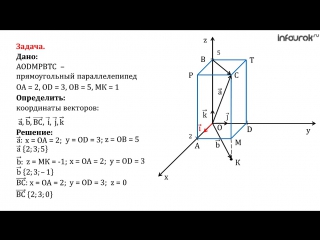 Например, при фиксированном
Например, при фиксированном
базисевекторуоднозначно соответствует упорядоченная
тройка чисел, и наоборот, каждой упорядоченной тройке
чиселсоответствует векторт.еВ частности, если векторв базисеимеет разложението этому вектору соответствует тройка
чисели наоборот. Нулевому вектору в любом
базисе в пространстве соответствует
нулевая тройка (0;0;0).
(вектор его координаты)
сохраняет
линейные операции: сумме векторов
соответствует сумма их одноименных
координат, произведению вектора на
число соответствует произведение его
координат на это число. Такое взаимно
однозначное соответствие называется
изоморфизмом.
В
базисе
вектору соответствует
координатный столбец .Обозначение
базиса можно
не указывать, если не может возникнуть
неоднозначности. Линейным операциям
над векторами соответствуют линейные
операции над их координатными столбцами.
Например, если в одном и том же
базисе векторам и соответствуют
координатные столбцы и ,
то их линейной комбинации соответствует
координатный столбец ,
т.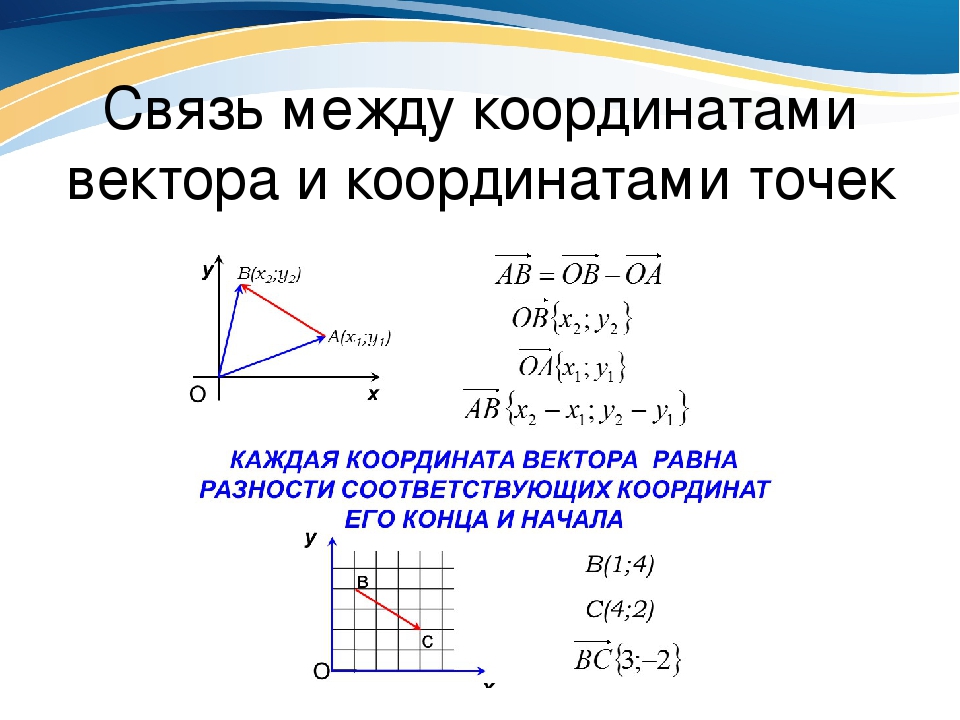 е.координатный
е.координатный
столбец линейной комбинации векторов
равен линейной
Координаты точки, радиус- вектор точки, произвольные вектора. Длина вектора.
Проекция т. М на αЧтобы
найти проекцию точки на прямую, нужно
через точку провести плоскость
перпендикулярно этой прямой.Опр. Вектор, соединяющий начало координат
т. О с произвольной точкой пространства
называется радиус- вектор этой точки.
Радиус- вектор т. М – ОМ.
Найдем
координаты радиус- вектора ОМ
ОА= xi
ОВ= yj
ОС= zk
OM= OP+ PM= OA+ OB+
OC= xi+ yj+ zk= (x, y, z)
Вывод: координаты
радиус- вектора точки совпадает с
координатами самой точки ОМ= (x, y, z)
Вектор
ОМ является диагональю параллелепипеда,
по свойству диагоналей d2=
a2+
b2+
c2 отсюда
следует, что │ОМ│2= x2+
y2+
z2.
Извлекая, квадратный корень получаем
длину
Возьмем
две произвольные точки. т. А(x1,
y1,
z1)
и т. В (x2,
В (x2,
y2,
z2).
Соединим АВ.
Вспомогательные векторы
ОА=
(x1,
y1,
z1)
ОВ=
(x2,
y2,
z2)
АВ=
ОВ- ОА= (x2,
y2,
z2)-
(x1,
y1,
z1)=
(x2—
x1,
, y2—
y1,
z2—
z1)
Вывод: чтобы
найти координаты вектора нужно их
координат конца вектора вычесть
соответствующие координаты начала
вектора.
АВ=
(x2—
x1,
, y2—
y1,
z2—
z1)
Пр. Даны
3 точки. т. А(2,-1,3), т. В(4,0,1), т. С(-1,2,1). Найти
АВ и его длину │АВ│, m= AB- 2BC.
Деление
отрезка в данном отношении
Если
точка М(x;
y)
лежит на прямой, проходящей через две
данные точки (,)
и (,),
и дано отношение ,
в котором точка М делит отрезок,
то координаты точки М определяются по
формулам
, . j;
j;
2) |k|=1, но | i x
j| = |i| • |J| • sin(90°)=1;
3) векторы i
, j и k образуют правую тройку (см. рис.
16).
7.2. Свойства
векторного произведения
1. При
перестановке сомножителей векторное
произведение меняет знак, т.е. а хb =(b хa
) (см. рис. 19).
Векторы ахb
и b ха коллинеарны, имеют одинаковые
модули (площадь параллелограмма остается
неизменной), но противоположно направлены
(тройки а , b , а хb и a , b , bxa противоположной
ориентации). Стало быть axb = -(bxa ).
2. Векторное
произведение обладает сочетательным
свойством относительно скалярного
множителя, т. е. l(а хb ) = (lа ) х b = а х (lb ).
Пусть l>0. Вектор l(ахb ) перпендикулярен
векторам а и b . Вектор ( lа)хb также
перпендикулярен векторам а и b (векторы
а, lа лежат в одной плоскости). Значит,
векторы l(ахb ) и ( lа)хb коллинеарны.
Очевидно, что и направления их совпадают.
Имеют одинаковую длину:Поэтому l(a хb )= lахb . Аналогично доказывается
при l<0.
3. Два ненулевых
вектора а и b коллинеарны тогда и только
тогда, когда их векторное произведение
равно нулевому вектору, т. е. а||b <=>ахb
е. а||b <=>ахb
=0.
4. Векторное произведение
обладает распределительным свойством:
(a+b) хс= ахс+b хс.
Примем без
доказательства.
Геометрия данных 2. Определение ди- и би-координат / Хабр
В
первой статье
определен метрический базис на элементах, — набор вершин симплекса или графа с известными значениями скалярных произведений (грамиан) или связей (лапласиан) между ними. Здесь рассмотрим, как на таком базисе определить координаты элементов.
Дистанционные координаты
Дистанционные координаты представляют собой значения
скалярных произведений элемента и реперов
— вершин базиса. Будем именовать их
ди-координатами
.
Количество компонент ди-координат на единицу больше количества базовых вершин
и на две единицы больше мерности пространства базиса
. Примером ди-координат может служить строка (или колонка) дистанционного метрического тензора (ДМТ).
Дистанционные координаты элемента будем обозначать как , в тензорной форме — нижним индексом, указывающем на базис: . Если надо будет указать, к какому именно элементу относятся координаты, то используем скобки: .
Полный базис включает в себя нормаль пространства (является мажорным), — соответственно в ди-координатах можно выделить скалярную единицу (произведение элемента и нормали) и набор скалярных произведений элемента и вершин базиса :
.
Набор скалярных произведений будем называть также минорными компонентами.
Приведем примеры значений дистанционных координат. Допустим, рядом с нашим базовым треугольником есть еще три точки с известными дистанциями до вершин треугольника — P, Q и R (см. рисунок). Для расчета дистанций используем декартовы координаты точек на плоскости (XY), которые приводим для контроля и сверки:
Матрица декартовых координат точек:
\begin{array}{c | c c c c c c}
XY & A & B & C & P & Q & R \\
\hline
X & 0 & 3 & 0 & 1 & 3 & 5 \\
Y & 0 & 0 & 4 &-1 & 2 & 0 \\
\end{array}
Кортеж дистанций от точки
P
до точек
A
,
B
,
С
здесь такой:
. Соответственно ди-координаты точки будут такими:
Соответственно ди-координаты точки будут такими:
. У всех точек пространства значение скалярной компоненты ди-координат одно и то же (в рамках данной серии статей).
Ди-координаты точек Q и R:
Элементы и векторы
Разность элементов задает
вектор
. У ди-координат вектора скалярная компонента равна нулю — по этому признаку вектор
можно отличить от элемента.
Геометрия, в которой описание координат точек и векторов отличается, называется аффинной. В такой геометрии вектор можно прибавить к какому-либо элементу (точке) и получить новый элемент. Для векторов определены операции сложения и вычитания (значение скалярной компоненты при этом остается нулевым). Но обычно нет смысла в операции сложения элементов.
Термин <вектор> перегружен.
В мире (линейной) алгебры обычно под векторным пространством понимают некое линейное пространство, в котором элементы характеризуются набором чисел, и определены операции сложения и вычитания.
В таком пространстве нет различия между элементами и векторами — «все вектор».
В нашем пространстве это не так.
Дистанция между элементами
Несложно показать, что метрическим тензором для дистанционных координат является лапласиан (ЛМТ). Для определения квадрата расстояния (дистанции) между элементами
P
и
Q
надо найти вектор разности элементов
и рассчитать его
норму
. Норма вектора определяется через
билинейную форму
— умножение координат вектора слева и справа и на метрический тензор. Для дистанционных координат это записывается так:
где — ди-координаты вектора, — лапласовский метрический тензор.
Проверяем. Координаты искомого вектора: . Данные координаты умножаем с двух сторон на лапласовский метрический тензор (ЛМТ) и получаем ответ: . Можно свериться с расчетом расстояния через дистанции в декартовых координатах: . Ответы совпали, метрика работает.
Для проверки расчетов приводим значение ЛМТ нашего базиса из предыдущей статьи
\begin{array}{c | c c c c}
Lm(A,B,C) & * & A & B & C \\
\hline
* & 6. 25 & 0 & 0.5 & 0.5 \\
25 & 0 & 0.5 & 0.5 \\
A & 0 & 25/144 & -16/144 & -9/144 \\
B & 0.5 & -16/144 & 16/144 & 0 \\
C & 0.5 & -9/144 & 0 & 9/144 \\
\end{array}
Элемент и его проекция на базовое пространство
Симплекс из
вершин определяет
-мерное пространство
. Базисный треугольник определяет базовую плоскость
. Количество дистанционных компонент в ди-координатах элемента на единицу больше мерности пространства. Это означает, что ди-координаты позволяют задавать элементы, выходящие за пределы базового пространства и принадлежащие
. В нашем примере элементы могут лежать не только в плоскости базового треугольника, но и на (под) ним.
Координаты элемента не позволяют определить, с какой стороны базового пространства находится элемент (если он находится вне). В примере с треугольником элементы, расположенные над и под плоскостью треугольника, будут иметь одни и те же координаты.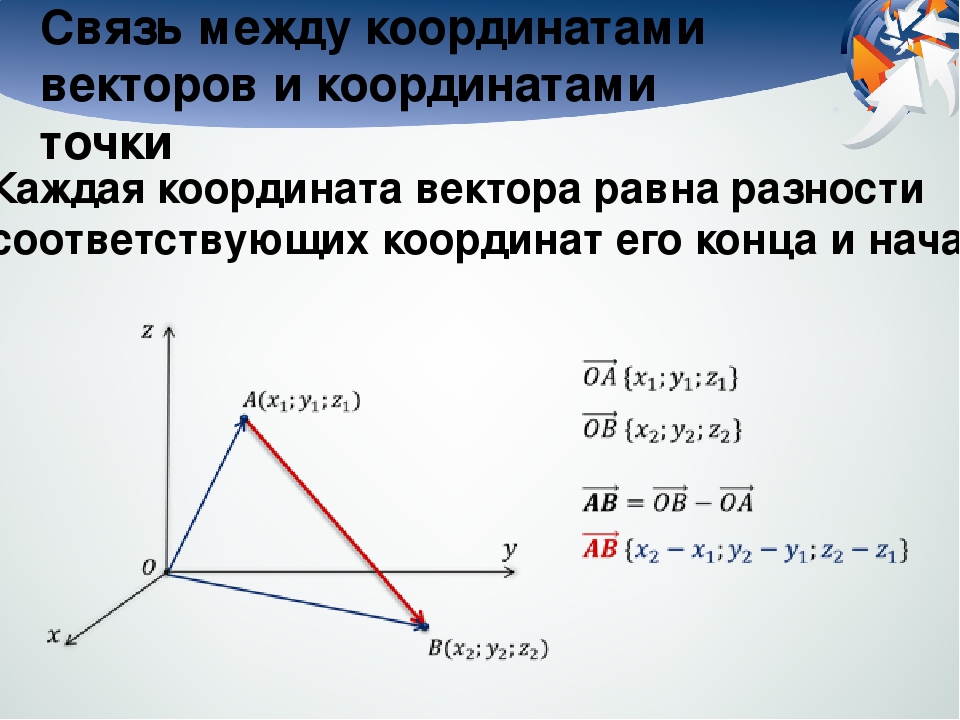
Если элемент не принадлежит базовому пространству, то следует различать положение элемента и его проекции на пространство . Формула дистанции между элементами (2.1) работает только в базовом пространстве (поэтому в ней дистанция помечена штрихом), то есть определяет квадрат расстояния между проекциями элементов (а не между самими элементами):
Здесь через индекс обозначен базис, на пространство которого проецируется дистанция между элементами. В декартовых (и подобных им) координатах нет способа задания координат элементов, выходящих за него. Поэтому в декартовой системе координат таких нюансов нет.
Норма элемента и дистанция до базового пространства
Раскрывая скобки в формуле (2.1), получаем «теорему косинусов для элементов». По форме она похожа на
обычную
, только здесь у нас координаты элементов (а не векторов). Поэтому нет ни углов, ни косинусов. Зато получаем определения норм элементов относительно базиса:
Скаляр будем называть нормой элемента, а скаляр — скалярным произведением элементов. Здесь скалярное произведение выражено через билинейную форму.
Здесь скалярное произведение выражено через билинейную форму.
Рассчитаем норму элемента , изображенного на рисунке. Умножая дважды ди-координаты элемента на метрический тензор ЛМТ, получаем ноль: . Что это значит?
Норма элемента характеризует его положение относительно базового пространства,- равна отрицательной дистанции от элемента до пространства:
.
Значение нормы позволяет определить, принадлежит элемент пространству базиса или нет, и если нет, то насколько он от него удален.
Элементы с нулевой нормой удобно называть точками пространства — это локальные элементы. Элементы с ненулевой нормой — нелокальны относительно пространства базиса.
Скалярное произведение элементов
Геометрический смысл скалярного произведения векторов хорошо известен — отражает косинус угла между их направлениями.
Для интерпретации скалярного произведения элементов обратимся к формуле (2.2), (см. также рисунок проекций). Перегруппировав слагаемые, получим с учетом (2.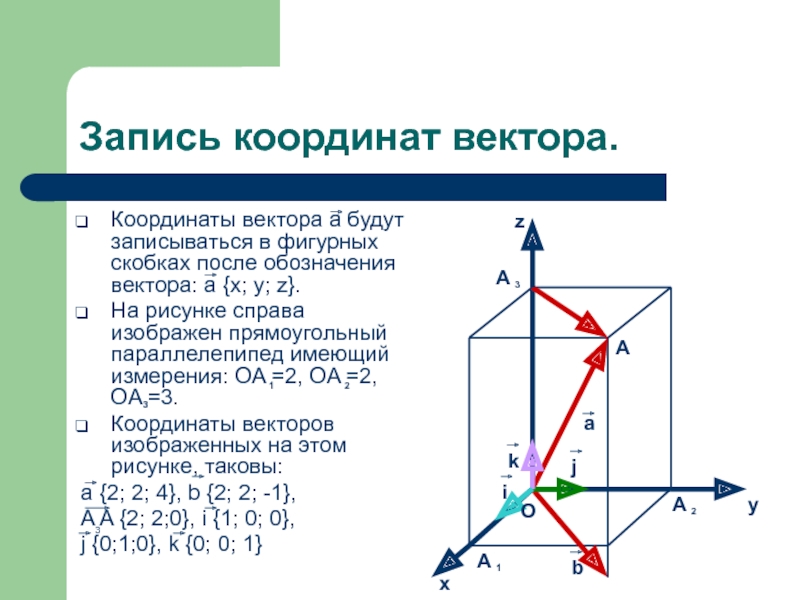 4.1):
4.1):
Видим, что удвоенное скалярное произведение представляет собой сумму дистанций от элементов до базового пространства и дистанции между проекциями элементов в базовом пространстве.
Обозначим через следующую комбинацию дистанций:
Данное выражение представляет собой скалярное произведение упорядоченных пар и нормалей элементов к пространству. Теперь можно выразить произведение элементов через дистанцию между ними и произведение нормалей:
Данная формула позволяет определять дистанции до элементов вне пространства базиса.
Если скалярное произведение нормалей равно нулю (например, один из элементов принадлежит пространству базиса), то дистанция между элементами определяется их скалярным произведением:
Формула (2.6.1) раскрывает смысл скалярного произведения элементов — оно отражает квадрат расстояния между элементами с коэффициентом (-1/2).
Дистанция между элементами вне базисного пространства
Если элементы находятся вне базового пространства, то для определения точной дистанции между ними помимо координат требуется дополнительная информация — а именно значение скалярного произведения нормалей на пространство
. Данное скалярное произведение можно вычислить при условии, что элементы принадлежат одному и тому же надпространству. В этом случае скалярное произведение между нормалями элементов — это просто произведение их длин. Тогда «магическая» формула вычисления дистанции между нелокальными элементами будет такой:
Данное скалярное произведение можно вычислить при условии, что элементы принадлежат одному и тому же надпространству. В этом случае скалярное произведение между нормалями элементов — это просто произведение их длин. Тогда «магическая» формула вычисления дистанции между нелокальными элементами будет такой:
Значение скаляра равно 1, если элементы расположены с одной стороны пространства и -1, если с разных. Данная формула — просто частный (но важный) случай тождества (2.6). Во многих прикладных задачах расположение элементов всегда одностороннее, поэтому формула (2.7) может быть использована для определения дистанции между объектами (находящимися, например, в воздухе) если известны их ди-координаты относительно реперов (радаров на земле).
Непросто представить, что, например, у 3-мерного пространства тоже есть сторона, но математика говорит, что есть. В декартовых координатах сторона, которой принадлежит элемент, определяется знаком значения n-ой компоненты, которая не входит в базовые. Если тетраэдр задан в декартовых координатах x, y, z, и при этом еще существует одна компонента (например, t — время), то можно считать, что плоскость t=0 делит базовое пространство на две стороны. Элементы, у которых компонента t > 0, лежат с одной стороны базового пространства, а у которых t < 0 — с другой.
Если тетраэдр задан в декартовых координатах x, y, z, и при этом еще существует одна компонента (например, t — время), то можно считать, что плоскость t=0 делит базовое пространство на две стороны. Элементы, у которых компонента t > 0, лежат с одной стороны базового пространства, а у которых t < 0 — с другой.
Би-координаты
Взаимными по отношению к дистанционным координатам являются
би-координаты
элемента. Термин связан с тем, что би-координаты фактически представляют собой расширение
барицентрических
координат. Метрическим тензором для би-координат является дистанционный тензор.
Би-координаты элемента обозначаются в тензорной форме верхним индексом . Переход от ди-координат к би-координатам (и обратно) выполняется умножением на соответствующий метрический тензор базиса:
Рассчитаем би-координаты элемента P относительно вершин нашего треугольника. Выполняя умножение ЛМТ на ди-координаты элемента, получаем:
Особенность барицентрических координат в том, что сумма их компонент равна 1 (в нашем примере 11/12 + 1/3 — 1/4 = 1).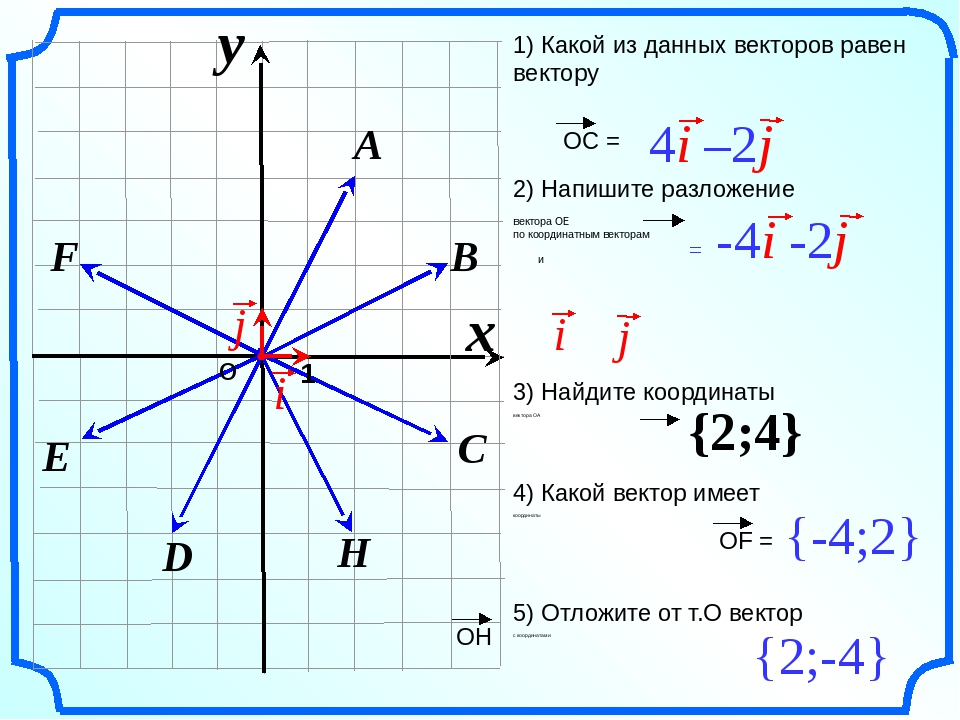 Каждая барицентрическая компонента — это вклад (вес) вершины базиса в координату элемента. Чем больше значение компоненты — тем ближе находится элемент к базовой вершине.
Каждая барицентрическая компонента — это вклад (вес) вершины базиса в координату элемента. Чем больше значение компоненты — тем ближе находится элемент к базовой вершине.
Орбиталь элемента
Структура би-координат может быть записана как:
.
Здесь
— барицентрические координаты, а
—
орбиталь
элемента. Орбиталь отражает скалярное произведение элемента и ортоцентра базиса
:
В геометрии есть понятие степени точки — положение точки относительно заданной сферы. Задается как разность между дистанцией от точки до центра сферы и радиусом сферы :
На рисунке квадрат длины катета треугольника (от точки до касания сферы) равен значению степени точки P. Точки M и N на рисунке демонстрируют полезное свойство степени, а именно, что ее значение равно произведению длин отрезков и .
Орбиталь элемента может быть выражена через степень элемента относительно ортоцентра:
.
Если орбиталь больше нуля — элемент лежит внутри ортоцентра (сферы) базиса, если меньше — снаружи.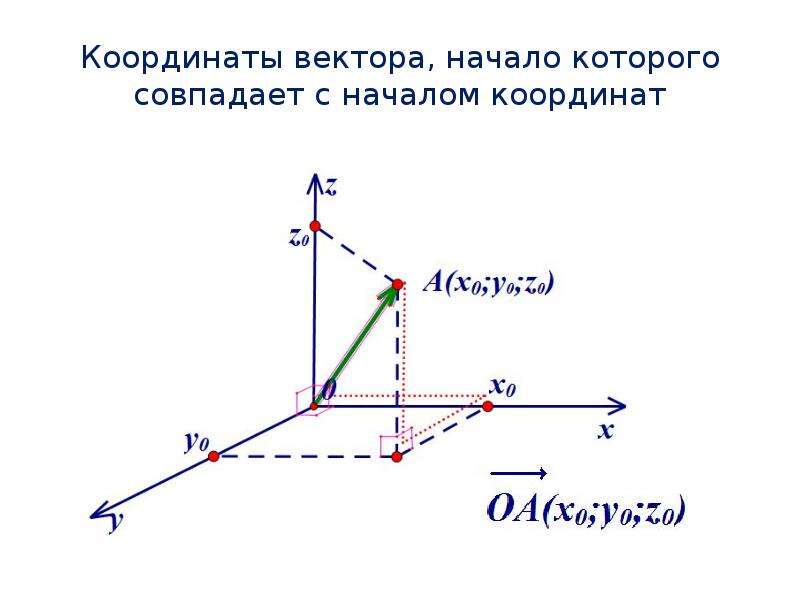 Барицентрические координаты характеризуют положение проекции элемента в пространстве базового симплекса, а скалярная компонента — задает пространственное положение относительно ортоцентра.
Барицентрические координаты характеризуют положение проекции элемента в пространстве базового симплекса, а скалярная компонента — задает пространственное положение относительно ортоцентра.
Орбиталь вершин базиса равна нулю (поскольку элементы базиса принадлежат поверхности базисной сферы). Би-координаты вершин базиса представляют собой единичные координаты (с единицей в своей базисной компоненте и нулем в остальных — обычно обозначаются как ). Например, би-координаты вершины A треугольника будут равны [0; 1, 0, 0].
Если элемент не принадлежит пространству базиса, то его дистанция до ортоцентра равна сумме дистанций от элемента до его проекции и дистанции от проекции до центра . Первая равна норме элемента с обратным знаком. Тогда можно выразить орбиталь элемента через орбиталь его проекции и норму :
В свою очередь орбиталь проекции можно определить через би-линейную форму барицентрических координат элемента и минорного грамиана базиса :
В 5-й части покажем, что понятие орбитали элемента относительно ортоцентра можно обобщить до определения взаимной орбитали элементов.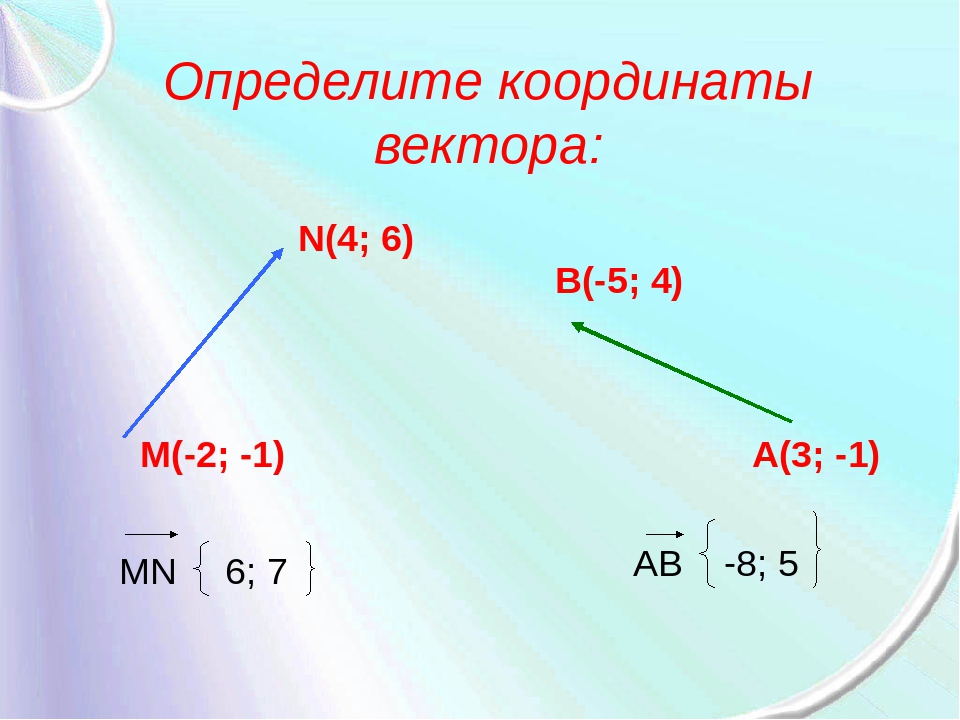 Которое в свою очередь связано с понятием скалярного произведения векторов.
Которое в свою очередь связано с понятием скалярного произведения векторов.
Би-координаты элементов и векторов
Как и в случае ди-координат следует отличать би-координаты элемента от би-координат вектора разности элементов (аффинная геометрия). Однако критерий отличия двух типов координат в данной системе иной. Сумма барицентрических компонент элемента равна 1, а сумма компонент вектора будет равна 0 (поскольку разность) —
балансовые векторы
. (Балансовые векторы используются в проводках бухгалтерского учета). Остальное аналогично. Би-векторы можно складывать и вычитать — при этом результат остается в пространстве векторов.
Орбиталь (скалярная компонента би-координат) вектора отражает величину проекции ортоцентра базиса на вектор. Не зависит от нормы ортоцентра (квадрата радиуса сферы).
Би-координаты ортоцентра образуют окаймление лапласовского метрического тензора. Вспоминая, что сумма компонент лапласиана равна нулю, можно заключить, что строки (колонки) лапласиана базиса отражают би-координаты неких векторов. Это векторы дуального базиса, здесь на них подробно не останавливаемся.
Это векторы дуального базиса, здесь на них подробно не останавливаемся.
Дистанция и нормы в би-координатах
Скалярная компонента добавляет метрику к барицентрическим координатам. При наличии известного метрического тензора (ДМТ) можно вычислять дистанции между элементами, принадлежащими базовому пространству. Все стандартно — через билинейную форму умножения разности координат на метрический тензор. Формулы аналогичны выражениям в ди-координатах с заменой метрического тензора
на
и ди-координат
на би-координаты
. Обозначив би-координаты вектора разности элементов как
, получаем:
Дистанция между проекциями:
Норма элемента:
Скалярное произведение:
Знание би-координат элементов и их положения относительно базового пространства также позволяет вычислять дистанцию между элементами вне базового пространства по формуле (2.6). И это круто. Обычно считается, что барицентрические координаты задают лишь относительное положение элементов. Оказывается, что если добавить к ним скалярную компоненту в виде орбитали, то можно определять пространственное положение не только самого элемента, но и дистанции между элементами вне базового пространства.
Оказывается, что если добавить к ним скалярную компоненту в виде орбитали, то можно определять пространственное положение не только самого элемента, но и дистанции между элементами вне базового пространства.
Объединяем ди- и би-координаты
Нормаль к пространству — особый вектор
Как уже отмечалось, в полный (мажорный) набор элементов базиса входит вектор нормали пространства
. Ди-координаты нормали имеют вид: [0; 1, 1,…]. Соответственно, би-координаты нормали взаимно обратны: [1; 0, 0,…]. Ди-координаты вектора нормали входят в структуру дистанционного метрического тензора.
О том, что нормаль это вектор, говорит значение нуля в скалярной компоненте ди-координат и равенство нулю суммы барицентрических координат.
Норма нормали (свертка ди- и би-координат) всегда равна нулю, поскольку проекция нормали на любое пространство всегда будет точкой.
Как следствие, — нормаль пространства можно прибавлять к элементам. Такая операция изменяет норму элемента, но не его положение в пространстве. Зная координаты проекции элемента и норму , всегда можно определить координаты самого элемента . Для этого вектор нормали умножаем на полунорму элемента и прибавляем полученный вектор к координатам проекции.
Зная координаты проекции элемента и норму , всегда можно определить координаты самого элемента . Для этого вектор нормали умножаем на полунорму элемента и прибавляем полученный вектор к координатам проекции.
Связь параметров базиса с координатами элементов
Если в формуле связи ди- и би-координат (2.8) раскрыть структуру умножаемых матриц и векторов, то можно получить полезные тождества для скалярной и минорной компонент координат. Для би-координат имеем:
Здесь — минорные ди- и би-координаты элементов. Таким образом:
Выражение (2.12.1) демонстрирует, что результат действия лапласиана на вектор можно интерпретировать как вектор разности элемента и ортоцентра.
Тождество (2.12.2) (при выводе использовано также (2.9) и (2.10)) показывает, как зная минорную составляющую ди-координат, получить ее степень и дистанцию до ортоцентра.
Перейдем к структуре ди-координат:
Откуда:
Первое тождество показывает, что сумма барицентрических компонент равна 1, это и так знали (но тут видно почему — потому что используем единичный вектор в качестве окаймления дистанционной матрицы).
Второе показывает роль орбитали в дистанционных координатах. Дистанционный вектор складывается из весовой суммы дистанционных векторов вершин базиса и вектора нормали к базовому пространству, величина которого задается орбиталью элемента.
Нормы — это свертка координат разных типов
Используя скалярное произведение координат обоих типов (би- и ди-), можно избавиться в формулах от метрических тензоров.
Дистанция между проекциями:
Норма элемента:
Скалярное произведение:
Собираем все вместе
Кратко перечислим основные определения.
— ди-координаты элемента, набор скалярных произведений элемента и реперов базиса,
— би-координаты элемента, коэффициенты линейного разложения элемента по реперам базиса,
Изменение типа координат (от ди- к би- и обратно) («жонглирование индексами») выполняется умножением на соответствующий метрический тензор:
Скалярное произведение элементов:
— вектор, разность элементов,
Норма вектора разности — дистанция между проекциями элементов на пространство базиса:
___
В следующей статье рассмотрим скалярное произведение упорядоченных пар.
2.4: Системы координат и компоненты вектора (Часть 1)
Цели обучения
- Опишите векторы в двух и трех измерениях с точки зрения их компонентов, используя единичные векторы вдоль осей.
- Различайте векторные компоненты вектора и скалярные компоненты вектора.
- Объясните, как величина вектора определяется в терминах компонентов вектора.
- Определяет угол направления вектора на плоскости.
- Объясните связь между полярными координатами и декартовыми координатами на плоскости.
Векторы обычно описываются в терминах их компонентов в системе координат. Даже в повседневной жизни мы естественно обращаемся к концепции ортогональных проекций в прямоугольной системе координат. Например, если вы спросите кого-нибудь, как проехать к определенному месту, вам, скорее всего, предложат пойти на 40 км на восток и 30 км на север, чем на 50 км в направлении 37 ° к северу от востока.
В прямоугольной (декартовой) системе координат xy на плоскости точка на плоскости описывается парой координат (x, y). Аналогичным образом вектор \ (\ vec {A} \) на плоскости описывается парой своих векторных координат. Координата x вектора \ (\ vec {A} \) называется его x-компонентой, а координата y вектора \ (\ vec {A} \) называется его y-компонентой. X-компонента вектора — это вектор, обозначаемый \ (\ vec {A} _ {x} \). Y-компонента вектора — это вектор, обозначаемый \ (\ vec {A} _ {y} \).В декартовой системе компоненты вектора x и y вектора являются ортогональными проекциями этого вектора на оси \ (x \) и \ (y \) соответственно. Таким образом, следуя правилу параллелограмма для сложения векторов, каждый вектор на декартовой плоскости может быть выражен как векторная сумма его векторных компонентов:
Аналогичным образом вектор \ (\ vec {A} \) на плоскости описывается парой своих векторных координат. Координата x вектора \ (\ vec {A} \) называется его x-компонентой, а координата y вектора \ (\ vec {A} \) называется его y-компонентой. X-компонента вектора — это вектор, обозначаемый \ (\ vec {A} _ {x} \). Y-компонента вектора — это вектор, обозначаемый \ (\ vec {A} _ {y} \).В декартовой системе компоненты вектора x и y вектора являются ортогональными проекциями этого вектора на оси \ (x \) и \ (y \) соответственно. Таким образом, следуя правилу параллелограмма для сложения векторов, каждый вектор на декартовой плоскости может быть выражен как векторная сумма его векторных компонентов:
\ [\ vec {A} = \ vec {A} _ {x} + \ vec {A} _ {y} \ ldotp \ label {2.10} \]
Как показано на рисунке \ (\ PageIndex {1} \), вектор \ (\ vec {A} \) — это диагональ прямоугольника, в котором компонент x \ (\ vec {A} _ {x} \) равен сторона, параллельная оси x, и компонента y \ (\ vec {A} _ {y} \) — сторона, параллельная оси y. Компонента вектора \ (\ vec {A} _ {x} \) ортогональна компоненту вектора \ (\ vec {A} _ {y} \).
Компонента вектора \ (\ vec {A} _ {x} \) ортогональна компоненту вектора \ (\ vec {A} _ {y} \).
Рисунок \ (\ PageIndex {1} \): Вектор \ (\ vec {A} \) на плоскости в декартовой системе координат — это векторная сумма его векторных x- и y-компонент. Компонента вектора x \ (\ vec {A} _ {x} \) — это ортогональная проекция вектора \ (\ vec {A} \) на ось x. Компонента вектора y \ (\ vec {A} _ {y} \) — это ортогональная проекция вектора \ (\ vec {A} \) на ось y. Числа A x и A y , которые умножают единичные векторы, являются скалярными компонентами вектора.
Обычно положительное направление на оси x обозначается единичным вектором \ (\ hat {i} \), а положительное направление на оси y — единичным вектором \ (\ hat {j} \). Единичные векторы осей \ (\ hat {i} \) и \ (\ hat {j} \) определяют два ортогональных направления в плоскости. Как показано на рисунке \ (\ PageIndex {1} \), компоненты x и y вектора теперь могут быть записаны в терминах единичных векторов осей:
\ [\ begin {cases} \ vec {A} _ {x} = A_ {x} \ hat {i} \\ \ vec {A} _ {y} = A_ {y} \ hat {j} \ end {case} \ label {2. 11} \]
11} \]
Векторы \ (\ vec {A} _ {x} \) и \ (\ vec {A} _ {y} \), определенные уравнением 2.11, являются векторными компонентами вектора \ (\ vec {A} \). Числа A x и A y , которые определяют компоненты вектора в уравнении \ ref {2.11}, являются скалярными компонентами вектора \ (\ vec {A} \). Комбинируя уравнение \ ref {2.10} с уравнением \ ref {2.11}, мы получаем компонентную форму вектора :
\ [\ vec {A} = A_ {x} \ hat {i} + A_ {y} \ hat {j} \ ldotp \ label {2.12} \]
Если нам известны координаты \ (b (x_b, y_b) \) начальной точки вектора (где b означает «начало») и координаты e (x e , y e ) конца точки вектора (где e означает «конец»), мы можем получить скалярные компоненты вектора, просто вычитая координаты исходной точки из координат конечной точки:
\ [\ begin {cases} A_ {x} = x_ {e} — x_ {b} \\ A_ {y} = y_ {e} — y_ {b} \ ldotp \ end {cases} \ label {2.13} \]
Пример \ (\ PageIndex {1} \): смещение указателя мыши
Указатель мыши на мониторе компьютера в исходном положении находится в точке (6,0 см, 1,6 см) по отношению к нижнему левому углу. Если вы переместите указатель на значок, расположенный в точке (2,0 см, 4,5 см), каков вектор смещения указателя?
Если вы переместите указатель на значок, расположенный в точке (2,0 см, 4,5 см), каков вектор смещения указателя?
Стратегия
Начало системы координат xy — левый нижний угол монитора компьютера.Следовательно, единичный вектор \ (\ hat {i} \) на оси x указывает горизонтально вправо, а единичный вектор \ (\ hat {j} \) на оси y указывает вертикально вверх. Начало вектора смещения находится в точке b (6.0, 1.6), а конец вектора смещения расположен в точке e (2.0, 4.5). Подставьте координаты этих точек в уравнение \ ref {2.13}, чтобы найти скалярные компоненты D x и D y вектора смещения \ (\ vec {D} \). Наконец, подставьте координаты в уравнение \ ref {2.12}, чтобы записать вектор смещения в виде компонента вектора.
Решение
Мы идентифицируем x b = 6,0, x e = 2,0, y b = 1,6 и y e = 4,5, где физическая единица равна 1 см. Скалярные x- и y-компоненты вектора смещения равны
.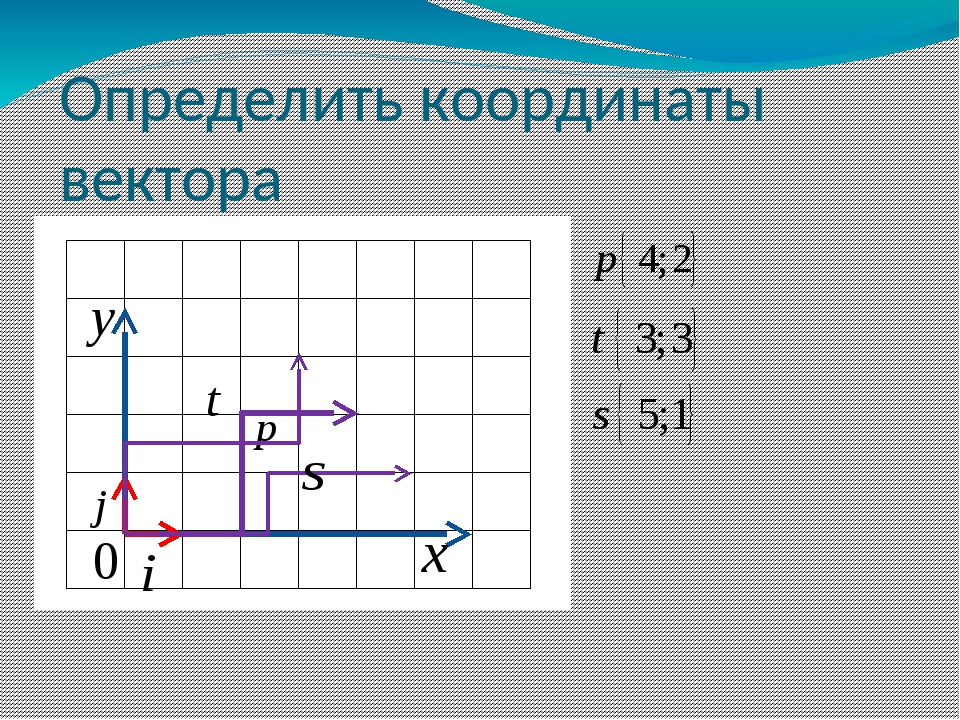
\ [D_ {x} = x_ {e} — x_ {b} = (2.0 — 6.0) \; см = -4,0 \; см, \]
\ [D_ {y} = y_ {e} — y_ {b} = (4.5 — 1.6) \; см = + 2,9 \; см \ ldotp \]
Компонентная форма вектора смещения равна
.
\ [\ vec {D} = D_ {x} \; \ hat {i} + D_ {y} \; \ hat {j} = (-4.0 \; см)\; \ hat {i} + (2,9 \; см) \; \ hat {j} = (-4,0 \; \ hat {i} + 2,9 \; \ hat {j}) \; см \ ldotp \ label {2.14} \]
Это решение показано на рисунке \ (\ PageIndex {2} \).
Рисунок \ (\ PageIndex {2} \): график вектора смещения. Вектор указывает от начальной точки в \ (b \) до конечной точки в \ (e \).
Значение
Обратите внимание, что физическая единица — здесь 1 см — может быть размещена либо с каждым компонентом непосредственно перед единичным вектором, либо глобально для обоих компонентов, как в уравнении \ ref {2.14}. Часто второй способ удобнее, потому что он проще.
Компонента x вектора \ (\ vec {D} _ {x} \) = −4.0 \ (\ hat {i} \) = 4.0 (\ (- \ hat {i} \)) вектора смещения имеет величина | \ (\ vec {D} _ {x} \) | = | — 4.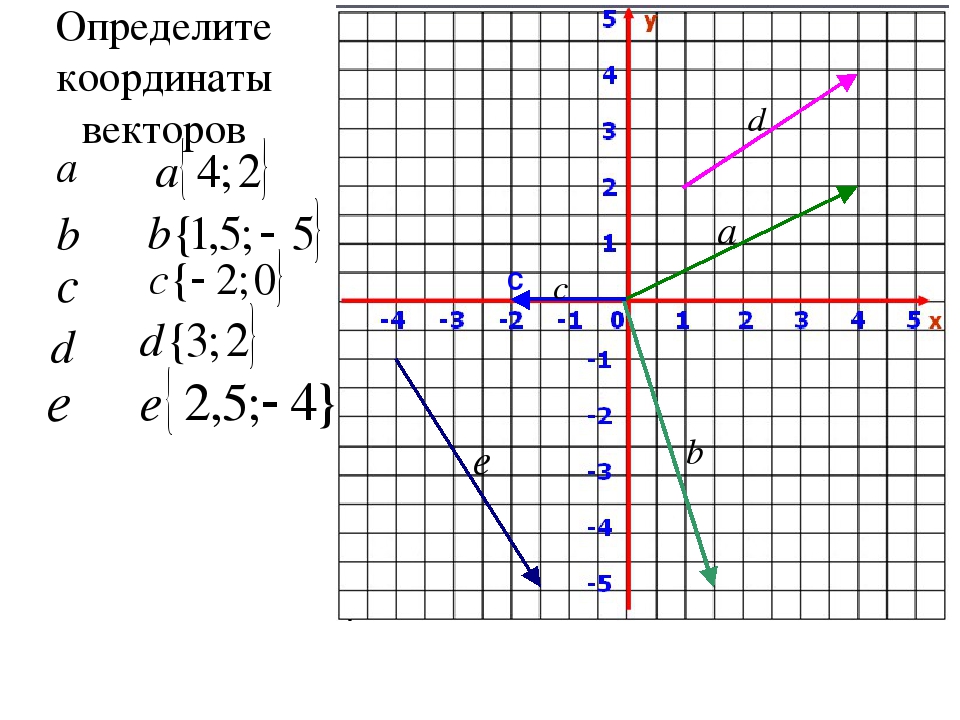 0 || \ (\ hat {i} \) | = 4.0, поскольку величина единичного вектора равна | \ (\ hat {i} \) | = 1. Также обратите внимание, что направление x-компоненты равно \ (- \ hat {i} \), что антипараллельно направлению оси + x; следовательно, вектор x-компоненты \ (\ vec {D} _ {x} \) указывает налево, как показано на рисунке \ (\ PageIndex {2} \).Скалярная x-компонента вектора \ (\ vec {D} \) равна D x = −4,0. Аналогично, y-компонента вектора \ (\ vec {D} _ {y} \) = \ (+ 2.9 \ hat {j} \) вектора смещения имеет величину | \ (\ vec {D} _ {y} \) | = | 2.9 || \ (\ hat {j} \) | = 2,9, поскольку величина единичного вектора равна | \ (\ hat {j} \) | = 1. Направление y-компоненты равно \ (+ \ hat {j} \), которое параллельно направлению оси + y. Следовательно, вектор y-компоненты \ (\ vec {D} _ {y} \) указывает вверх, как показано на рисунке \ (\ PageIndex {2} \). Скалярная y-компонента вектора \ (\ vec {D} \) равна D y = + 2.9. Вектор смещения \ (\ vec {D} \) является равнодействующей двух его компонент вектора.
0 || \ (\ hat {i} \) | = 4.0, поскольку величина единичного вектора равна | \ (\ hat {i} \) | = 1. Также обратите внимание, что направление x-компоненты равно \ (- \ hat {i} \), что антипараллельно направлению оси + x; следовательно, вектор x-компоненты \ (\ vec {D} _ {x} \) указывает налево, как показано на рисунке \ (\ PageIndex {2} \).Скалярная x-компонента вектора \ (\ vec {D} \) равна D x = −4,0. Аналогично, y-компонента вектора \ (\ vec {D} _ {y} \) = \ (+ 2.9 \ hat {j} \) вектора смещения имеет величину | \ (\ vec {D} _ {y} \) | = | 2.9 || \ (\ hat {j} \) | = 2,9, поскольку величина единичного вектора равна | \ (\ hat {j} \) | = 1. Направление y-компоненты равно \ (+ \ hat {j} \), которое параллельно направлению оси + y. Следовательно, вектор y-компоненты \ (\ vec {D} _ {y} \) указывает вверх, как показано на рисунке \ (\ PageIndex {2} \). Скалярная y-компонента вектора \ (\ vec {D} \) равна D y = + 2.9. Вектор смещения \ (\ vec {D} \) является равнодействующей двух его компонент вектора.
Форма векторной составляющей вектора смещения Уравнение \ ref {2.14} говорит нам, что указатель мыши был перемещен на мониторе на 4,0 см влево и 2,9 см вверх от своего исходного положения.
Упражнение 2.4
Синяя муха приземляется на миллиметровую бумагу в точке, расположенной на 10,0 см правее ее левого края и на 8,0 см выше ее нижнего края, и медленно идет к точке, расположенной на 5.0 см от левого края и 5,0 см от нижнего края. Выберите прямоугольную систему координат с началом в левом нижнем углу листа и найдите вектор смещения мухи. Проиллюстрируйте свое решение графиком.
Когда мы знаем скалярные компоненты A x и A y вектора \ (\ vec {A} \), мы можем найти его величину A и угол направления \ (\ theta_ {A} \). Угол направления — или, для краткости, направление — это угол, который вектор образует с положительным направлением на оси x.{-1} \ left (\ dfrac {A_ {y}} {A_ {x}} \ right) \ ldotp \ label {2. 16} \]
16} \]
Рисунок \ (\ PageIndex {3} \): для вектора \ (\ vec {A} \) его величина A и его угол направления \ (\ theta_ {A} \) связаны с величинами его скалярных компонентов, поскольку A , A x и A y образуют прямоугольный треугольник.
Когда вектор лежит либо в первом квадранте, либо в четвертом квадранте, где компонент A x положителен (рисунок \ (\ PageIndex {4} \)), угол \ (\ theta \) в уравнении \ ref { 2.16}) совпадает с направлением угла \ (\ theta_ {A} \).Для векторов в четвертом квадранте угол \ (\ theta \) отрицательный, что означает, что для этих векторов угол направления \ (\ theta_ {A} \) измеряется по часовой стрелке от положительной оси x. Точно так же для векторов во втором квадранте угол \ (\ theta \) отрицательный. Когда вектор лежит во втором или третьем квадранте, где компонент A x отрицателен, угол направления равен \ (\ theta_ {A} \) = \ (\ theta \) + 180 ° (Рисунок \ (\ PageIndex {4} \)).
Рисунок \ (\ PageIndex {4} \): Скалярные компоненты вектора могут быть положительными или отрицательными. Векторы в первом квадранте (I) имеют обе скалярные компоненты положительные, а векторы в третьем квадранте имеют обе скалярные компоненты отрицательные. Для векторов в квадрантах II и III угол направления вектора равен \ (\ theta_ {A} \) = \ (\ theta \) + 180 °.
Векторы в первом квадранте (I) имеют обе скалярные компоненты положительные, а векторы в третьем квадранте имеют обе скалярные компоненты отрицательные. Для векторов в квадрантах II и III угол направления вектора равен \ (\ theta_ {A} \) = \ (\ theta \) + 180 °.
Пример \ (\ PageIndex {2} \): величина и направление вектора смещения
Вы перемещаете указатель мыши на мониторе из его исходного положения в точке (6,0 см, 1,6 см) к значку, расположенному в точке (2,0 см, 4,5 см). Какова величина и направление вектора смещения указателя?
Стратегия
В примере \ (\ PageIndex {1} \) мы нашли вектор смещения \ (\ vec {D} \) указателя мыши (см. Уравнение \ ref {2.{o} \ ldotp \]
Упражнение 2.5
Если вектор смещения синей мухи, идущей по листу миллиметровой бумаги, равен \ (\ vec {D} = (−5.00 \; \ hat {i} — 3.00 \; \ hat {j}) \) см, найдите его величина и направление.
Во многих приложениях величины и направления векторных величин известны, и нам нужно найти равнодействующую многих векторов. Например, представьте 400 автомобилей, движущихся по мосту Золотые Ворота в Сан-Франциско под сильным ветром. Каждая машина толкает мост в разных направлениях, и мы хотели бы знать, насколько большим может быть результирующий толчок.У нас уже есть некоторый опыт геометрического построения векторных сумм, поэтому мы знаем, что задача нахождения результирующей путем рисования векторов и измерения их длины и углов может довольно быстро стать неразрешимой, что приведет к огромным ошибкам. Подобные опасения не возникают, когда мы используем аналитические методы. Самый первый шаг в аналитическом подходе — найти компоненты вектора, когда известны направление и величина вектора.
Например, представьте 400 автомобилей, движущихся по мосту Золотые Ворота в Сан-Франциско под сильным ветром. Каждая машина толкает мост в разных направлениях, и мы хотели бы знать, насколько большим может быть результирующий толчок.У нас уже есть некоторый опыт геометрического построения векторных сумм, поэтому мы знаем, что задача нахождения результирующей путем рисования векторов и измерения их длины и углов может довольно быстро стать неразрешимой, что приведет к огромным ошибкам. Подобные опасения не возникают, когда мы используем аналитические методы. Самый первый шаг в аналитическом подходе — найти компоненты вектора, когда известны направление и величина вектора.
Вернемся к правому треугольнику на рисунке \ (\ PageIndex {3} \).Отношение смежной стороны A x к гипотенузе A является функцией косинуса угла направления \ (\ theta_ {A} \), A x / A = cos \ (\ theta_ {A} \) и отношение противоположной стороны A y к гипотенузе A является синусоидальной функцией \ (\ theta_ {A} \), A y / A = sin \ (\ theta_ {A} \).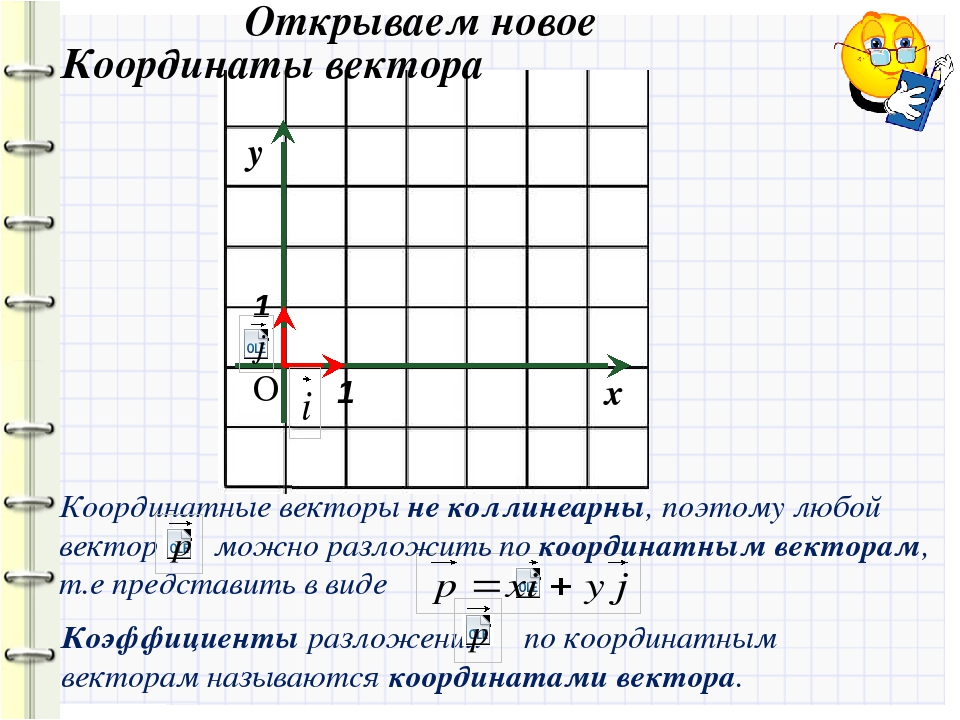 Когда величина A и направление \ (\ theta_ {A} \) известны, мы можем решить эти соотношения для скалярных компонентов:
Когда величина A и направление \ (\ theta_ {A} \) известны, мы можем решить эти соотношения для скалярных компонентов:
\ [\ begin {cases} A_ {x} = A \ cos \ theta_ {A} \\ A_ {y} = A \ sin \ theta_ {A} \ ldotp \ end {cases} \ label {2.17} \]
При вычислении компонентов вектора с помощью уравнения \ ref {2.17} необходимо соблюдать осторожность с углом. Направляющий угол \ (\ theta \) A вектора — это угол, измеренный против часовой стрелки от положительного направления по оси x к вектору. Измерение по часовой стрелке дает отрицательный угол.
Пример \ (\ PageIndex {3} \): компоненты векторов смещения
Группа спасения пропавшего ребенка следует за поисковой собакой по имени Десантник. Солдат много блуждает и делает много пробных обнюхиваний разными путями.Солдат в конце концов находит ребенка, и у истории счастливый конец, но его перемещения на разных ногах кажутся действительно запутанными. На одной из ног он идет 200,0 м на юго-восток, затем бежит на север примерно на 300,0 м. На третьей ноге он внимательно исследует запахи на 50,0 м в направлении 30 ° к западу от севера. На четвертом этапе Trooper идет прямо на юг на 80,0 м, улавливает свежий запах и поворачивает на 23 ° к западу от юга на 150,0 м. Найдите скалярные компоненты векторов смещения солдата и его векторы смещения в форме векторных компонентов для каждой ноги.
На третьей ноге он внимательно исследует запахи на 50,0 м в направлении 30 ° к западу от севера. На четвертом этапе Trooper идет прямо на юг на 80,0 м, улавливает свежий запах и поворачивает на 23 ° к западу от юга на 150,0 м. Найдите скалярные компоненты векторов смещения солдата и его векторы смещения в форме векторных компонентов для каждой ноги.
Стратегия
Давайте возьмем прямоугольную систему координат с положительной осью X в направлении географического востока и положительным направлением Y в направлении на географический север. Явно единичный вектор \ (\ hat {i} \) оси x указывает на восток, а единичный вектор \ (\ hat {j} \) оси y указывает на север. Десантник имеет пять ног, значит, есть пять векторов смещения. Мы начинаем с определения их величин и углов направления, затем используем уравнение \ ref {2.17}, чтобы найти скалярные компоненты смещений, и уравнение \ ref {2.12} для векторов смещений.
Решение
На первом отрезке величина смещения L 1 = 200,0 м, направление — юго-восток.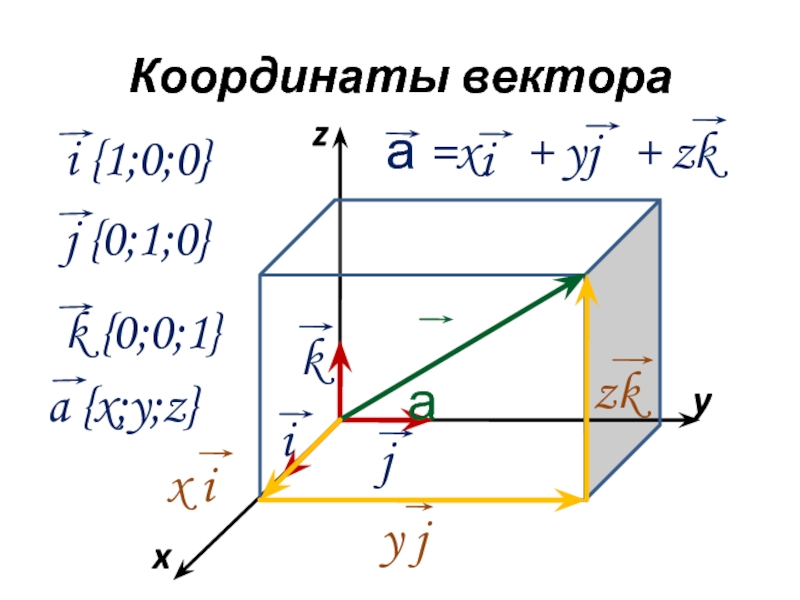 В качестве угла направления \ (\ theta_ {1} \) мы можем взять либо 45 °, измеренное по часовой стрелке с восточного направления, либо 45 ° + 270 °, измеренное против часовой стрелки с восточного направления. При первом выборе \ (\ theta_ {1} \) = -45 °. При втором выборе \ (\ theta_ {1} \) = + 315 °.{o} = -138,1 \; м, \]
В качестве угла направления \ (\ theta_ {1} \) мы можем взять либо 45 °, измеренное по часовой стрелке с восточного направления, либо 45 ° + 270 °, измеренное против часовой стрелки с восточного направления. При первом выборе \ (\ theta_ {1} \) = -45 °. При втором выборе \ (\ theta_ {1} \) = + 315 °.{o} = -138,1 \; м, \]
\ [\ vec {L} _ {5} = L_ {5x} \; \ hat {i} + L_ {5y} \; \ hat {j} = (-58,6 \; \ hat {i} — 138,1 \; \ hat {j}) \; м \ ldotp \]
Упражнение 2.6
Если Десантник бежит на 20 м на запад перед тем, как отдохнуть, каков его вектор перемещения?
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (by 4.0).
линейная алгебра — В чем разница между компонентами вектора и его координатами?
Это чрезвычайно распространенная путаница, и, по моему опыту, люди, как известно, плохо объясняют эту концепцию.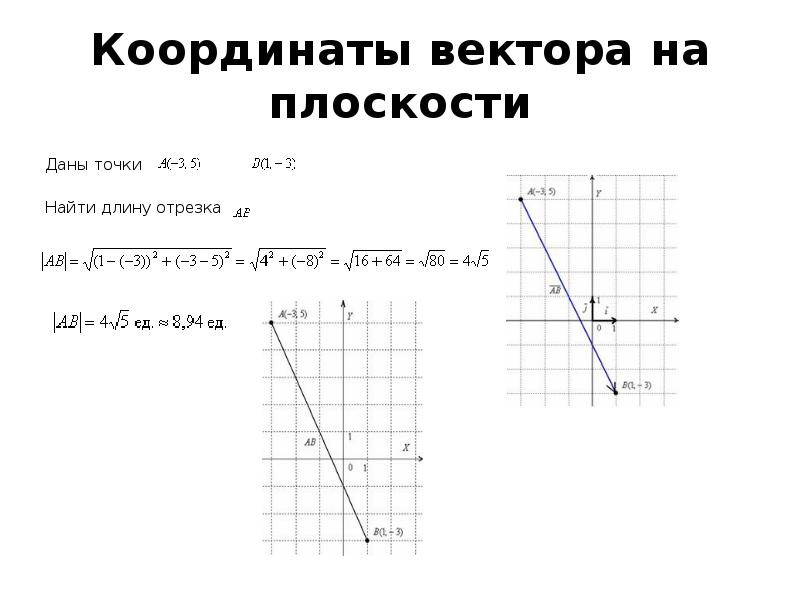 n $, но тогда это просто наложение, потому что любое другое биективное линейное преобразование выберет другое потенциальные «компоненты».n $ из-за фактического характера задействованных объектов. Таким образом, вам не нужна основа, вы можете просто посмотреть на произвольный объект $ (a, b, \ dots, n) $ и найти любой из его компонентов, потому что они встроены в объект. Это может сбивать с толку, потому что мы также записываем векторы координат таким образом, и когда базис является стандартным, нет разницы между компонентами и координатами. Однако на любой другой основе будет разница.
n $, но тогда это просто наложение, потому что любое другое биективное линейное преобразование выберет другое потенциальные «компоненты».n $ из-за фактического характера задействованных объектов. Таким образом, вам не нужна основа, вы можете просто посмотреть на произвольный объект $ (a, b, \ dots, n) $ и найти любой из его компонентов, потому что они встроены в объект. Это может сбивать с толку, потому что мы также записываем векторы координат таким образом, и когда базис является стандартным, нет разницы между компонентами и координатами. Однако на любой другой основе будет разница.
( Edit: Val сделал важное замечание в комментариях).2 $. Это определенно коллекция, и объекты в ней определенно являются векторами, но это не векторное пространство.
Я предполагаю, что вы имели в виду под «коллекцией» то, что мы могли бы назвать «осмысленно структурированной коллекцией», а значимая структура описывается именно как абелева группа, элементы которой могут масштабироваться объектами в поле. В этом смысле ваше мнение верно, хотя и менее прозрачно.
В этом смысле ваше мнение верно, хотя и менее прозрачно.
векторов и 2D движение
Точка может быть расположена в системе координат x, y по ее
координаты x и y.
Координата x описывает, как далеко по оси x точка
расположена, а координата y описывает, как далеко по
По оси ординат расположена точка.
Координаты x и y могут быть положительными или отрицательными, как
видно в примерах выше.
Мы будем использовать жирный шрифт для обозначения вектора, например
р . При написании вектора от руки укажем, что
something является вектором, нарисовав над ним стрелку как.Некоторые такие отличительные обозначения важны. Не писать
вектор без какой-либо отличительной характеристики или
обозначение.
Мы можем описать точку (x, y) как точку, расположенную на
вектор r , который имеет компоненты x и y.
Мы можем назвать эту x-компоненту вектором вдоль x-направления
length x и укажите, что это вектор размером x или
.
Точно так же мы можем назвать эту y-компоненту вектором вдоль
y-направление длины y, и указать, что это вектор,
y или.Тогда мы можем написать
г = х + у
или
=
+
Обратите внимание, что _ не _ верно написать r = x +
у.
r — длина вектора или величина вектора.
Угол
(тета) дает направление вектора. Как r, x, y и
связанные с?
Обратите внимание, что r, x и y образуют стороны правой стороны .
треугольник .Правые треугольники особенные, потому что
связь с функциями тригонометрии.
Если мы знаем r, x и y, мы можем найти триггерные функции для
угол .
Скорее всего, это ситуация, когда мы знаем x и y и хотим
найти r и.
Или мы можем знать r и и
хотите найти x и y. Все эти ситуации можно разрешить с помощью
триггерные функции.
Обычно угол измеряют от
положительная ось абсцисс и для ее измерения положительная для
против часовой стрелки направление.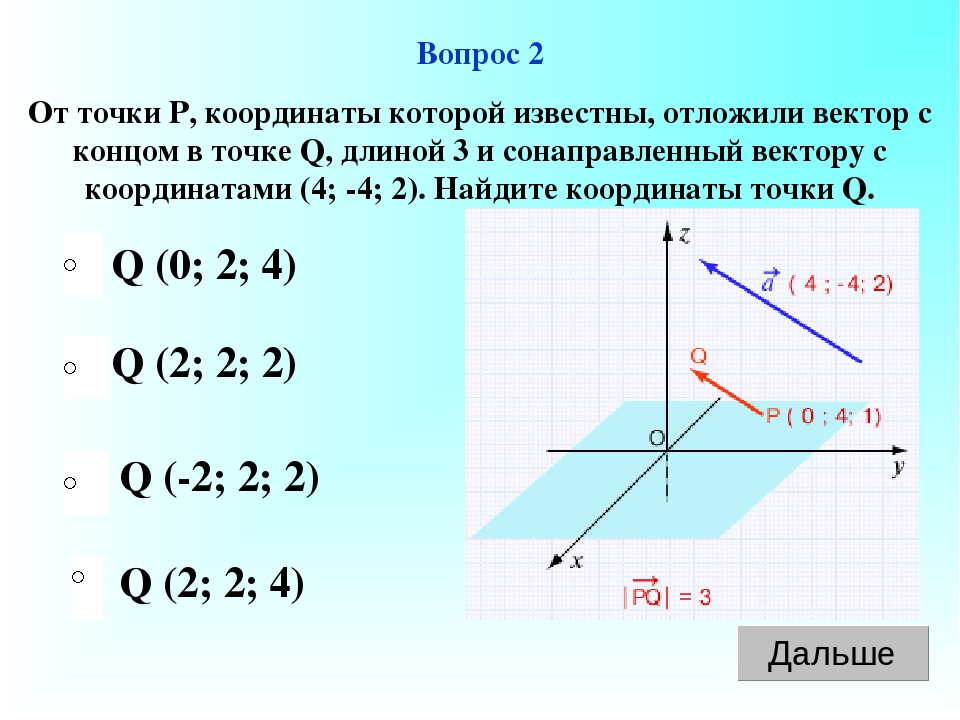 Пример, показанный ниже, может
Пример, показанный ниже, может
быть для угла =
53 или . Тогда при r = 10 компонент будет
х = г cos =
(10) (0,6) = 6
г = г грех
= (10) (0,8) = 8
Пожалуйста, , а не , запомни эти уравнения. Помните
более базовые определения триггерных функций,
грех
= opp / hyp
cos
= adj / hyp
загар
= opp / adj
Затем , для данного конкретного случая измерения угла
из
по оси абсцисс, имеем
r = hyp
x = прил.
y = opp
и , что означает, что
грех =
г / г
cos
= х / г
загар
= у / х
или
x = r cos
y = r sin
Конечно, угол
не нужно ограничивать первым квадрантом.Ниже может быть
диаграмма для
= 150 o . Опять же, пусть r = 10 для этого числового примера.
В этом случае
х = г cos =
(10) (cos 150 o ) = (10) (- 0,866) = — 8,66
у = г грех =
(10) (sin 150 o ) = (10) (0,500) = 5,00
Обратите внимание на знаки и сравните их со схемой.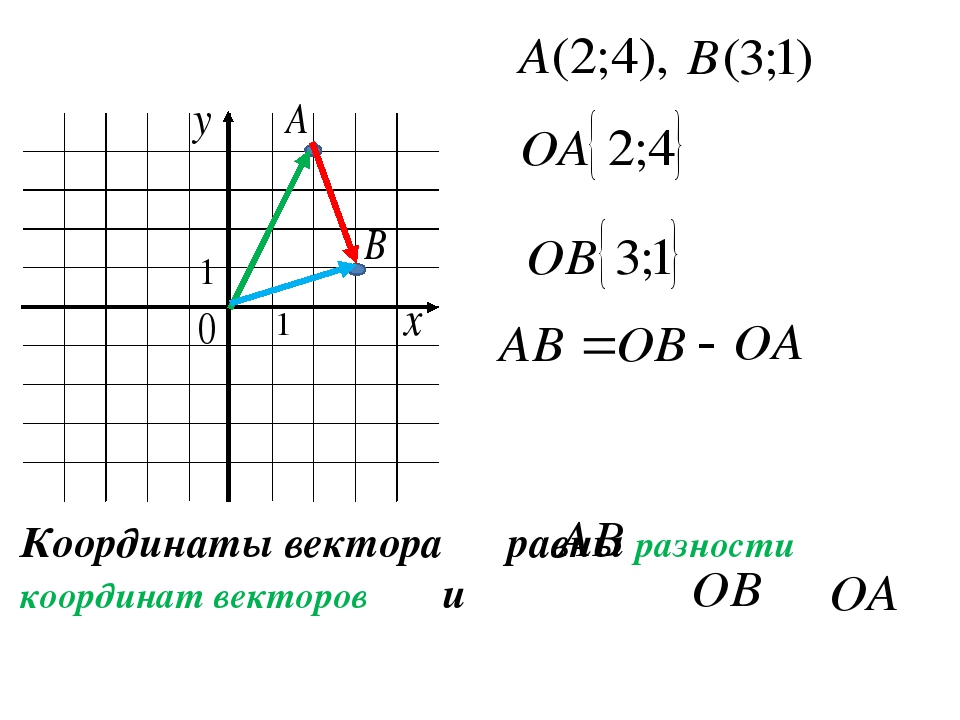 х = — 8,66
х = — 8,66
находится от слева от , а y = + 5.00 находится от до .
Всегда составляйте схему! А затем сравните свои результаты — ваш
ответы — с вашей диаграммой.Знаки жизненно важны, и это тоже
их легко сбросить и просто использовать величины.
Диаграмма ниже может быть для r = 10 и =
210 или . Для этих значений мы можем найти компоненты
по
х = г cos =
(10) (cos 210 o ) = (10) (- 0,866) = — 8,66
у = г грех =
(10) (sin 210 o ) = (10) (- 0,500) = —
5,00
Снова обратите внимание на знаки и сравните их со схемой. х =
— 8.66 находится слева от и y = — 5.00
вниз . Всегда составляйте схему! А затем сравните свой
результаты — ваши ответы — с вашей диаграммой. Знаки жизненно важны, и это
слишком легко отбросить их и просто использовать величины.
Мы можем описать этот вектор как r = 10, =
210 o , как указано выше. Или мы можем измерить угол
Или мы можем измерить угол
по часовой стрелке
как показано ниже, и описываем этот вектор как r = 10, =
— 150 или .Любое описание ничем не хуже другого.
Это два способа описания одного и того же вектора или одного и того же
точка.
Хотя это обычный для измерения углов от оси x и
измерить их как положительных , если они
против часовой стрелки , это _ не _ делать это необходимо.
Пилоты самолетов обычно измеряют углы или направления от
North (y) и измерьте их как положительный для
по часовой стрелке углов.Ниже может быть местоположение или вектор
r = 10 км, =
53 или . В данном случае у нас
х = г грех =
(10 км) (sin 53 o ) = (10 км) (0,8) = 8 км
y = r cos =
(10 км) (cos 53 o ) = (10 км) (0,6) = 6 км
Обратите внимание, что для этого расположения x теперь соответствует , противоположному
сторона (сторона прямоугольного треугольника, противоположная углу
) а также
y теперь смежная сторона (сторона прямоугольного треугольника
рядом с углом).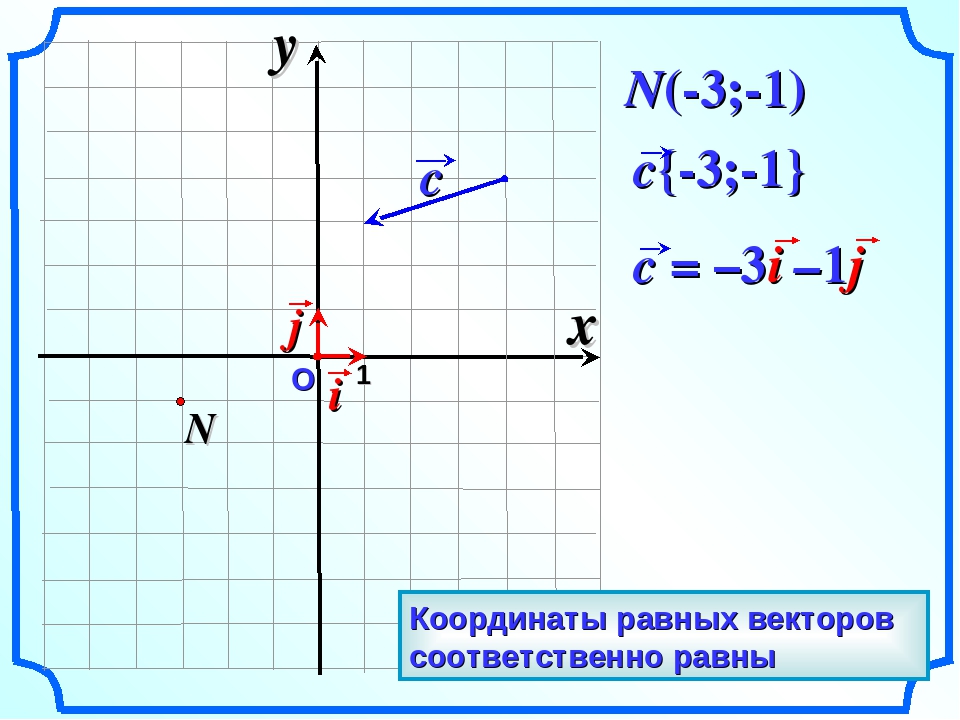 Если вы всегда начинаете с с основных определений синуса и
Если вы всегда начинаете с с основных определений синуса и
косинус, у тебя не будет проблем.
Задание местоположения или вектора через координаты (x,
y) означает, что мы используем декартову систему координат (или
опорный кадр).
Задание местоположения или вектора через координаты (r,
)
означает, что мы используем полярную систему координат (или опорную
Рамка).
c) 2002 год, Дуг Дэвис; все права защищены
Ортогональные системы координат — декартова, цилиндрическая и сферическая — Fosco Connect
Базовые векторы
В трехмерном пространстве точка может быть расположена как пересечение трех поверхностей.Эти три поверхности описываются номером
.
u 1 = постоянная
u 2 = постоянная
u 3 = постоянная
u 1 , u 2 и u 3 не обязательно должны иметь длину, как показано в таблице ниже.
| u 1 | u 2 | u 3 | |
| Декартова система координат | x | y | z |
| Цилиндрическая система координат | р | φ | z |
| Сферическая система координат | р | θ | φ |
Если эти три поверхности (на самом деле, их векторы нормалей) взаимно перпендикулярны друг к другу, мы называем их ортогональной системой координат .
Декартова система координат:
В декартовой системе координат точка находится на пересечении следующих трех поверхностей:
- Плоскость, параллельная плоскости y-z ( x = постоянная, нормальная к оси x , единичный вектор)
- Плоскость, параллельная плоскости x-z ( y = постоянная, нормальная к оси y , единичный вектор)
- Плоскость, параллельная плоскости x-y ( z = постоянная, нормальная к оси z , единичный вектор)
Это показано на рисунке ниже.
Базовые векторы:
, и — единичные векторы в трех координатных направлениях. Они называются базовыми векторами .
Базовые векторы удовлетворяют следующим соотношениям:
Цилиндрическая система координат:
В цилиндрических системах координат точка P (r 1 , θ 1 , z 1 ) является пересечением следующих трех поверхностей, как показано на следующем рисунке.
- Круглая цилиндрическая поверхность r = r 1
- Полуплоскость, содержащая ось z и составляющая угол φ = φ 1 с плоскостью xz
- Плоскость, параллельная плоскости xy в точке z = z 1 .
Базовые векторы:
- Базовый вектор в точке P перпендикулярен цилиндрической поверхности постоянной r 1 .
- Базовый вектор в точке P перпендикулярен полуплоскостной поверхности постоянной φ 1 и касательной к цилиндрической поверхности постоянной r 1 .
- Базовый вектор перпендикулярен плоскости константы z 1 .

Базовые векторы удовлетворяют следующим соотношениям:
Сферическая система координат:
Точка P (R 1 , θ 1 , φ 1 ) в сферических координатах расположена на пересечении следующих трех поверхностей:
- Сферическая поверхность с центром в начале координат с радиусом R = R 1 (сфера постоянной R )
- Прямой круговой конус с вершиной в начале координат, ось которой совпадает с осью + z и имеет половину угла θ = θ 1 (конус постоянной θ )
- Полуплоскость, содержащая ось z и составляющая угол φ = φ 1 с плоскостью xz (плоскость постоянной φ )
Это показано ниже.
Базовые векторы:
- Базовый вектор в точке P радиален от начала координат и перпендикулярен сфере постоянной R = R 1
- Базовый вектор в точке P перпендикулярен конусу постоянной θ = θ 1
- Базовый вектор в точке P перпендикулярен плоскости константы φ = φ 1
Базовые векторы удовлетворяют следующим соотношениям:
Метрические коэффициенты
В векторном исчислении и электромагнетизме нам часто требуется выполнять линейный, поверхностный и объемный интегралы.В этих случаях нам нужно найти изменение дифференциальной длины ( dl ) , изменение дифференциальной площади ( ds ) и изменение дифференциального объема ( dv ) в выбранной системе координат.
Линейный интегральный
Поверхностный интегральный
Интегральный объем
Декартова система координат основана на длине, так как dx , dy , dz — это все длины.Однако в других криволинейных системах координат, таких как цилиндрическая и сферическая системы координат, некоторые дифференциальные изменения не зависят от длины, например, d θ, dφ .
Таким образом, нам нужен коэффициент преобразования для преобразования (отображения) разностного изменения, не зависящего от длины ( d θ , dφ , и т. Д.) В изменение длины dl , как показано ниже.
dl i = h i du i
, где i = (1, 2 или 3), h i называется метрическим коэффициентом и может быть функцией от u 1 , u 2 , и 3 .
u 1 , u 2 , u 3 — оси координат в выбранной системе, соответствующие x , y , z в декартовой координате, r , φ , z в цилиндрической координате и R , θ , φ в сферической координате система.
Примеры:
В двумерных полярных координатах ( u 1 , u 2 ) = ( r , φ ), изменение дифференциала dφ (= du 2 ) соответствует дифференциальному изменению длины dl 2 = r dφ ( h 2 = r = u 1 ).
В декартовых системах координат, так как dx , dy , dz уже основаны на длине, h 1 = h 2 = h 3 = 1.
Дифференциальная длина
Из приведенного выше обсуждения мы можем видеть изменения дифференциальной длины dl 1 , dl 2 , dl 3 составляют:
дл 1 = h 1 du 1
дл 2 = ч 2 ду 2
дл 3 = h 3 du 3
где h 1 , h 2 , h 3 могут быть функциями u 1 , u 2 , и u 3 .
Направленное дифференциальное изменение длины dl в произвольном направлении может быть записано как векторная сумма изменений длины компонента:
или
, где a u1 , a u2 , a u3 — базовые векторы.
Дифференциальная зона
В общих ортогональных криволинейных координатах дифференциальная область ds 1 ( dA , как показано на рисунке выше), нормальная к единичному вектору a u1 составляет:
ds 1 = дл 2 дл 3
, таким образом,
ds 1 = h 2 h 3 du 2 du 3
Аналогично, дифференциальные площади, нормальные к единичным векторам a u2 , a u3 , составляют:
ds 2 = h 1 h 3 du 1 du 3
ds 3 = h 1 h 2 du 1 du 2
Например, в декартовой системе координат:
ds x = dy dz
ds y = dz dx
ds z = dx dy
, где h 1 = h 2 = h 3 = 1.
Объем дифференциала
Дифференциальный объем dv , образованный дифференциальными изменениями координат du 1 , du 2 и du 3 в направлениях a u1 , a u2 и a u3 , соответственно, составляет (dl 1 dl 2 dl 3 ) :
dv = dl 1 dl 2 dl 3 = h 1 h 2 h 3 du 1 ду 2 ду 3
Декартовы координаты
Цилиндрические координаты
Сферические координаты
Для удобства базовые векторы, метрические коэффициенты, разностные длины, разностные площади и разностный объем перечислены в следующей таблице.
Amazon.com: Декартовы координаты: Введение в векторы и основные векторные функции (Новая математика для миллионов, книга 20), электронная книга: Брускевич, Патрик: Kindle Store
Измерения, которые проводятся в физических науках, включают различные типы величин. Некоторые из них просто измерения величины, вещи, которые называются скалярами. Некоторые измерения включают как величину, так и направление, вещи, которые называются векторами, а некоторые еще более сложные измерения включают вещи более высокого порядка, называемые тензорами.
Эта книга представляет собой введение в векторы, написанное для учащихся средней школы или первого курса университета. Книги написаны для студентов, которые никогда раньше не работали с векторами, а также подходят для студентов, которые хотят повторить или улучшить свое понимание векторов.
Есть также тридцать два проработанных примера, а также вопросы из книг, призванные помочь вам узнать о векторах.
Первые два типа измерений — измерения звездных величин и измерения как величины, так и направления — являются предметом этой книги.Тензоры не будут затронуты в этой книге, но станут темой для другой книги «Новая математика для миллионов».
Одно из старейших открытий, открытие, которое восходит к древним временам, заключается в том, что все природные явления можно охарактеризовать с помощью измерений их физических характеристик.
Фактически пифагорейцы верили в то, что порядок во вселенной можно охарактеризовать с помощью чисел. Последние двадцать веков добавили смысла в поиски научных знаний.Современная наука и математика, а также наша вера в измерение как основу для установления причинно-следственных связей — того, что мы называем феноменами — делают нас современными пифагорейцами.
Измерение простых величин, измерения с использованием скаляров преподаются в средней школе. Когда старшеклассники впервые сталкиваются с векторами — измерениями, включающими как величину, так и направление, — они чаще всего начинают беспокоиться. Иногда такое случается, когда они сталкиваются с исчислением.
Хотя «Исчисление — это просто прикладная алгебра с добавлением нескольких новых идей», векторы менее сложны, чем даже алгебра, которой нас учат в средней школе. Если вы освоили алгебру, то освоите и математику, и векторы. Для тех из вас, кто заинтересован, в серии «Новая математика для миллионов» есть несколько книг, в которых затрагиваются различные аспекты исчисления.
Если это ваше первое знакомство с векторами, не волнуйтесь. Если это напоминание или вы работаете над освоением векторов, могу ли я перефразировать то, что однажды сказал физик, лауреат Нобелевской премии Ричард Фейнман, когда его спросили, как он узнал свою физику:
«Если бы я что-то не понял с первого раза» , Я бы прочитал это во второй раз.Если я не понял во второй раз, я прочитал в третий раз. Если я не понимал этого в третий раз, я отбрасывал вещь и переходил к чему-то другому ».
На что журналист пошутил: «Вы, должно быть, шутите над доктором Фейнманом». Ричард Фейнман только покачал головой.
вывод единичных векторов в криволинейных координатах
Пусть (u, v, w) — любая не декартова система координат такая, что
| x = x (u, v, w), y = y (u, v, w), z = z (u, v, w) | (1) |
Мы можем объединить три приведенных выше уравнения в одно векторное уравнение, которое дает вектор положения r → любой точки P = (x, y, z) в пространстве как функцию координат u, v, w:
| r → = x (u, v, w) i ^ + y (u, v, w) j ^ + z (u, v, w) k ^ |
Если бы мы зафиксировали u.т. u = u0, тогда вектор положения становится параметрическим уравнением поверхности (называемой координатной поверхностью) u = u0, где v, w играют роль параметров. Кроме того, если мы фиксировали u и v, st u = u0 и v = v0, то вектор положения становится параметрическим уравнением кривой (называемой координатной кривой), образованной пересечением поверхностей u = u0 и v = v0. , в котором w действует как параметр вдоль кривой.
Теперь, как нам найти касательные векторы ? Ну а что означает касательный вектор? Касательный вектор — это вектор, который является касательным к координатной кривой, образованной пересечением двух координатных поверхностей.Другими словами, это вектор, который указывает направление, в котором одна из координат, скажем u, увеличивается, в то время как две другие координаты (то есть v и w) остаются фиксированными. Звучит знакомо? Да конечно частные производные ! Частная производная по u возьмет производную вектора положения r → вдоль координатной кривой, образованной пересечением поверхностей v = v0 и w = w0, и, следовательно, вернет вам касательный вектор вдоль этой кривой! Следовательно, взяв частную производную r → одну за другой по всем трем координатам, мы получили бы все три касательных вектора, которые касаются своих соответствующих координатных кривых.| = (∂x∂u) 2+ (∂y∂u) 2+ (∂z∂u) 2
и аналогично hv = | e → v |, hw = | e → w | где hu, hv, hw известны как масштабные коэффициенты (или метрические коэффициенты).
Векторная алгебра:
ВЕКТОРНЫЕ МЕТОДЫ
Приоритетные направления:
- Векторы и
векторное сложение - Единичные векторы
- базовых векторов
и компоненты вектора - прямоугольный
координаты в 2-D - прямоугольный
координаты в 3-D - Вектор
соединение двух точек - Точечный продукт
- Перекрестное произведение
- Трехместный
товар - Трехместный
векторный продукт
Векторы и
векторное сложение:
Скаляр — это величина, такая как масса или температура, которая имеет только величину.» на полужирном символе (т.е.,). Следовательно,
Любой вектор можно превратить в единичный вектор, разделив его на длину.
Любой вектор можно полностью представить, указав его величину и единицу.
вектор по его направлению.
Базовые векторы и
компоненты вектора:
Базовые векторы — это набор векторов, выбранных в качестве базовых для представления всех остальных
векторы.Идея состоит в том, чтобы построить каждый вектор из сложения векторов
по базовым направлениям. Например, вектор на рисунке можно записать
как сумма трех векторов u 1 , u 2 и
u 3 , каждый по направлению одного из базовых векторов e 1 ,
e 2 и e 3 , так что
Каждый из векторов u 1 , u 2 и u 3
параллельна одному из базовых векторов и может быть записана как скалярное кратное
эта база.Пусть u 1 , u 2 и u 3
обозначим эти скалярные множители так, чтобы получилось
Оригинальный вектор u банка
теперь записывается как
Скалярные множители u 1 , u 2 и u 3
известны как компоненты и в базе, описанной базой
векторы e 1 , e 2 и e 3 .Если базовые векторы являются единичными векторами, то компоненты представляют собой
длины трех векторов соответственно u 1 , u 2 ,
и u 3 . Если базовые векторы являются единичными векторами и взаимно
ортогонально, то основание называется ортонормированным, евклидовым или декартовым
база.
Вектор может быть разрешен по любым двум направлениям в плоскости, содержащей его.
На рисунке показано, как правило параллелограмма используется для построения векторов a .
и b , что в сумме дает c .
В трех измерениях вектор может быть разрешен вдоль любых трех некомпланарных
линий. На рисунке показано, как можно разрешить вектор по трем направлениям.
сначала найдя вектор в плоскости двух направлений, а затем
разрешение этого нового вектора по двум направлениям на плоскости.
Когда векторы представлены в терминах базовых векторов и компонентов,
сложение двух векторов приводит к сложению компонентов
векторы.Следовательно, если два вектора A, и B представлены как
тогда,
прямоугольный
компоненты в 2-D:
Базовые векторы прямоугольной системы координат x-y задаются формулой
единичные векторы и вдоль x и y
направления соответственно.
Используя базовые векторы, можно представить любой вектор F как
В силу ортогональности базисов имеют место следующие соотношения.
прямоугольный
координаты в 3-D:
Базовые векторы прямоугольной системы координат задаются набором
три взаимно ортогональных единичных вектора, обозначенных,, и что
расположены вдоль координатных направлений x , y и z ,
соответственно, как показано на рисунке.
Показанная система является системой для правой руки, поскольку большой палец правой руки
указывает в направлении z , если пальцы таковы, что представляют
вращение вокруг оси z от x до y . Эта система может
можно превратить в левостороннюю систему, изменив направление любого из
координатные линии и связанный с ними базовый вектор.
В прямоугольной системе координат компонентами вектора являются
проекции вектора на x , y и z
направления. Например, на рисунке проекции вектора A
по x, y, и z направлениям задаются A x , A y ,
и A z соответственно.
В результате теоремы Пифагора и ортогональности базы
векторов, величина вектора в прямоугольной системе координат может быть
рассчитано по
Направляющий косинус:
Направляющие косинусы определены как
где углы, и —
углы показаны на рисунке.Как показано на рисунке, направляющие косинусы
представляют собой косинусы углов между вектором и тремя
координаты направления.
Направляющие косинусы могут быть вычислены из
компоненты вектора и его величина через соотношения
Три направляющих косинуса не являются независимыми
и должно удовлетворять соотношению
Эти результаты формируют тот факт, что
Единичный вектор может быть построен вдоль вектора
используя направляющие косинусы в качестве компонентов вдоль x , y и
z направлений.Например, единичный вектор вдоль вектора A
получается из
Следовательно,
Вектор
соединение двух точек:
Вектор, соединяющий точку A с точкой B
дается
Единичный вектор вдоль линии A-B может быть получен из
Вектор F по линии A-B и величиной F может
таким образом получается из соотношения
Точечный продукт:
Скалярное произведение обозначается «» между двумя векторами.В
скалярное произведение векторов A и B приводит к скаляру, заданному
отношение
где — угол между двумя векторами. Порядок не важен в
скалярное произведение, как видно из определения скалярных произведений. В результате один
получает
Скалярное произведение имеет следующие свойства.
Поскольку косинус 90 o равен нулю, скалярное произведение двух
ортогональные векторы приведут к нулю.
Поскольку угол между вектором и самим собой равен нулю, а косинус нуля
единица, величина вектора может быть записана в терминах скалярного произведения
используя правило
Прямоугольные координаты:
При работе с векторами, представленными в
прямоугольная система координат по компонентам
, то скалярное произведение может быть оценено из
отношение
Это можно проверить прямым умножением
векторы и отмечая, что из-за ортогональности базовых векторов
прямоугольная система
Проекция вектора на линию:
Ортогональная проекция вектора вдоль прямой
получается перемещением одного конца вектора на линию и опусканием
перпендикулярно линии от другого конца вектора.Результирующий
отрезок на прямой — это ортогональная проекция вектора или просто его
проекция.
Скалярная проекция вектора A вдоль направления
единичный вектор — длина ортогональной проекции A
вдоль линии, параллельной, и может быть оценен с помощью скалярного произведения. В
отношение для проекции
Векторная проекция A вдоль агрегата.
вектор просто умножает скалярную проекцию на единичный вектор, чтобы
получить вектор вместе.Это дает соотношение
Крест
товар:
Перекрестное произведение векторов a и b — это вектор, перпендикулярный
к обоим a и b и имеет величину, равную площади
параллелограмм, полученный из a и b . Направление креста
продукт определяется правилом правой руки.Перекрестное произведение обозначается
«» между векторами
Порядок важен в перекрестном произведении. Если порядок операций изменится
в перекрестном произведении направление результирующего вектора меняется на противоположное. То есть
Перекрестное произведение имеет следующие свойства.
Прямоугольные координаты:
При работе в прямоугольных системах координат,
перекрестное произведение векторов a и b , заданных
можно оценить с помощью правила
Можно также использовать прямое умножение основания
векторов с использованием соотношений
Тройной
товар:
Тройное произведение векторов a , b и c равно
Стоимость тройного произведения равна объему параллелепипеда.
построенный из векторов.Это видно из рисунка с
Тройной продукт имеет следующие свойства
Прямоугольные координаты:
Рассмотрим векторы, описанные в прямоугольнике.
система координат как
Тройное произведение можно оценить с помощью
отношение
Тройной вектор
товар:
Произведение тройного вектора имеет свойства
.

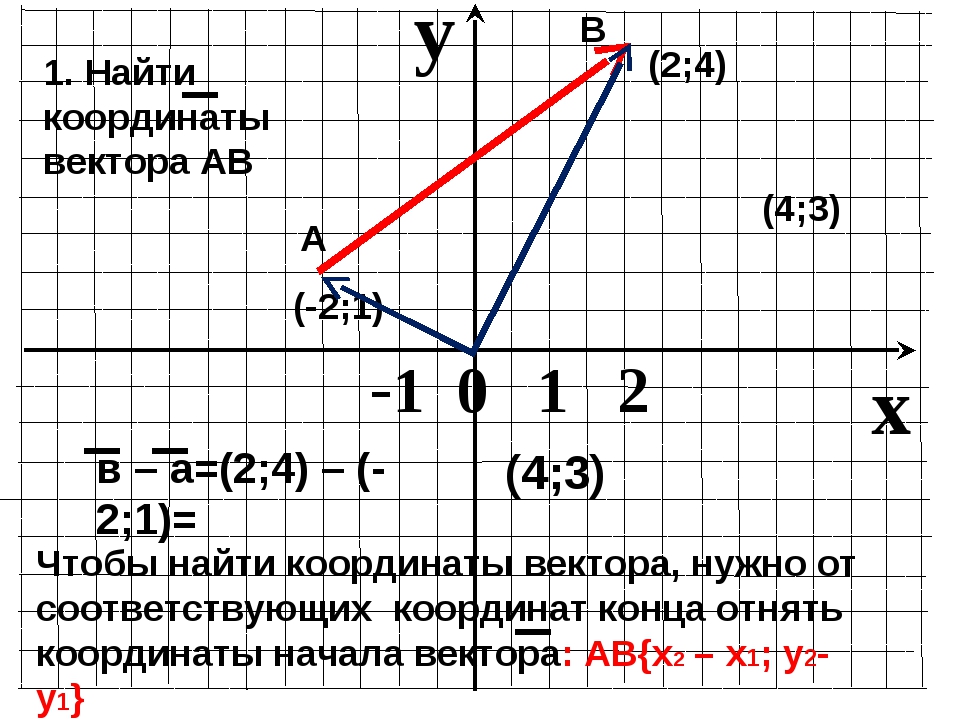 1.3. Координаты вектора и точки
1.3. Координаты вектора и точки
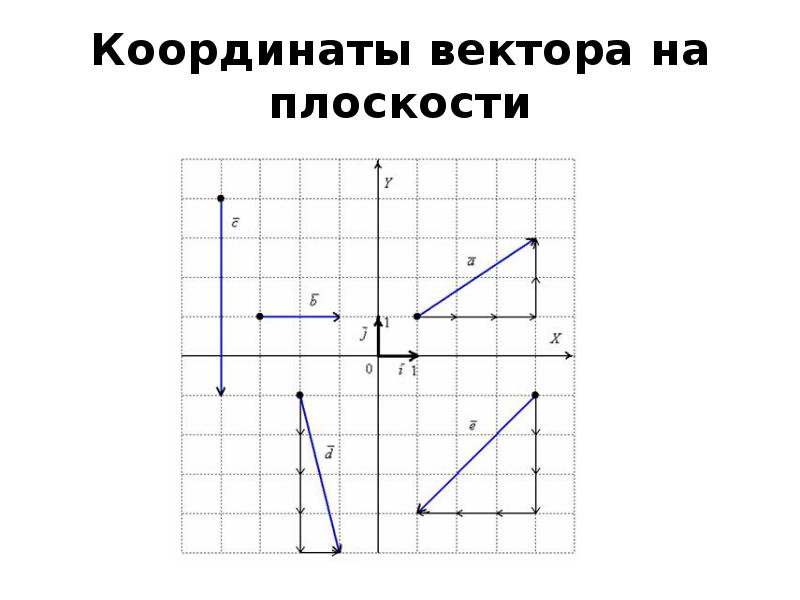 Следовательно,
Следовательно,