Корень 2 степени: Онлайн калькулятор: Корень и степень — ошкольное образовательное учреждение № 4 «Алёнушка»

{n}=\underbrace{b*b*b*…*b}_{n \; раз}=a. $$

Число $n$ при этом называют показателем корня.

Если $n=2$, то перед вами корень 2-й степени или обычный квадратный корень.

Если $n=3$, то корень 3-й степени и т.д.

Операция извлечения корня n-й степени является обратной к операции возведения в n-ю степень.

Пример 1
$$ \sqrt[3]{27}=3 $$

Кубический корень из числа 27 равняется 3. Действительно, если число 3 возвести в 3-ю степень, то мы получим 27.

Пример 2
$$ \sqrt[4]{16}=2 $$

Корень 4-й степени из 16-и равен 2. Двойка в 4-й степени равна 16.

Пример 3
$$ \sqrt[3]{0}=0 $$

Если извлечь корень n-й степени из 0, всегда будет 0.

Пример 4
$$ \sqrt[3]{19}= ? $$

Мы не можем в уме подобрать такое число, которое при возведении в 3-ю степень даст 19. Если посчитать на калькуляторе, то получим $2,668…$ – иррациональное число с бесконечным количеством знаков после запятой.

Обычно, в математике, когда у вас получается иррациональное число, корень не считают и оставляют так как есть $\sqrt[3]{19}$.

Что же делать, если под рукой нет калькулятора, а нужно оценить, чему равен такой корень. В этом случае нужно подобрать справа и слева такие ближайшие числа, корень из которых посчитать можно:

$$ \sqrt[3]{8} \le \sqrt[3]{19} \le \sqrt[3]{27} $$
$$ 2 \le \sqrt[3]{19} \le 3 $$

Получается, что наш корень лежит между числами 2 и 3.

Содержание

Корень четной и нечетной степени

Надо четко различать правила работы четными и нечетными степенями. Дело в том, что корень четной степени можно взять только из положительного числа. Из отрицательных чисел корень четной степени не существует.

Корень нечетной степени можно посчитать из любых действительных чисел. Иногда в школьной программе встречаются задания, в которых требуется определить имеет ли смысл выражение:

Пример 5
$$ \sqrt[3]{-27}=-3 $$

Данное выражение имеет смысл, так как корень нечетной степени можно посчитать из любого числа, даже отрицательного.

Пример 6
$$ \sqrt[4]{-27} $$

Так как корень четной степени, а под корнем стоит отрицательное число, то выражение не имеет смысла. k} $$

Квадратный корень в Python 3 — Извлечение кубических и n-ой степени

Под извлечением корня из какого-либо числа чаще всего подразумевают нахождение решение уравнения x в степени n = value, соответственно для квадратного корня, число n — это два, для кубического — 3. Чаще всего под результатом и числом подразумеваются вещественные числа.

В программировании нахождение корней используется очень часто. Разберемся, как и какими методами можно эффективно извлекать корни из числа. Вначале рассмотрим, какие способы есть в Python, и определим самый эффективный. Потом более подробно разберём, как можно найти не только квадратный корень из числа, но и кубический, и потом корень n степени.

Способы извлечения корня

В языке программирования Python 3 существует три способа извлечения корней:

Использование функции sqrt из стандартной математической библиотеки math.
Операция возведения в степень **
Применение функции pow(x, n)

Чтобы воспользоваться первым способом, необходимо вначале импортировать sqrt из модуля math. Это делается с помощью ключевого слова import: from math import sqrt. При помощи этой функции можно извлекать только квадратный корень из числа. Приведем пример:

from math import sqrt
x = sqrt(4)
print(x)

2.0

Если же нам нужно вычислить в Python корень квадратный из суммы квадратов, то можно воспользоваться функцией hypot из модуля math. Берется сумма квадратов аргументов функции, из нее получается корень. Аргументов у функции два.

from math import hypot
x = hypot(4,3)
print(x)

5.0

Еще одним, чуть более универсальным методом, будет использование возведения в степень. Известно, что для того, чтобы взять корень n из числа, необходимо возвести его в степень 1/n. Соответственно, извлечение квадратного корня из числа 4 будет выглядеть так:

n = 2
x = 4**(1./n)
print(x)

2.0

Обратите внимание, что в Python 2 необходимо ставить точку после единицы, иначе произойдет целочисленное деление, и 1/n == 0, а не нужной нам дроби. В Python 3 можно не ставить точку.

Последний метод использует функцию pow(value, n). Эта функция в качестве аргумента value возьмет число, которое необходимо возвести в степень, а второй аргумент будет отвечать за степень числа. Как и в предыдущем методе, необходимо использовать дробь, для того, чтобы получить корень числа.

x = pow(4, 0.5)
print(x)

2.0

Какой метод быстрее?

Для того, чтобы определить какой же метод предпочтительнее использовать, напишем программу. Замерять время выполнения будем с помощью метода monotonic библиотеки time.

from time import monotonic
from math import sqrt
iterations = 1000000
start = monotonic()
for a in range(iterations):
    x = sqrt(4)
print("sqrt time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
    x = 4 ** 0.5
print("** time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
    x = pow(4, 0. 5)
print("pow time: {:>.3f}".format(monotonic() - start) + " seconds")

sqrt time: 0.266 seconds
** time: 0.109 seconds
pow time: 0.453 seconds

Как видно, самое быстрое решение — использовать **. На втором месте метод sqrt, а pow — самый медленный. Правда, метод sqrt наиболее нагляден при вычислении в Python квадратных корней.

Таким образом, если критична скорость, то используем **. Если скорость не критична, а важна читаемость кода, то следует использовать sqrt.

Квадратный корень

Для извлечения квадратного корня самым наглядным способом, правда не самым быстрым, будет использование sqrt из модуля math.

from math import sqrt
x = sqrt (value)

Но можно использовать и трюки с возведением в степень 1/2, что тоже будет приводить к нужному результату.

x = value ** (0.5) или x = pow(value, 0.5).

Кубический корень

Для извлечения кубического корня в Python 3 метод sqrt не подойдет, поэтому воспользуйтесь возведением в степень 1/3:

x = value ** (1. /3) или x=pow(value, 1/3).

Корень n-степени

Корень n-степени из числа в Python извлекается можно получить двумя способами с помощью возведения в степень 1.0/n:

С помощью оператора **.
Используя функцию pow.

Как было проверено выше, оператор ** быстрее. Поэтому его использовать более целесообразно. Приведем пример вычисления кубических корней в Python 3 с помощью этих двух методов:

n = 4.
x = 16.0 ** (1./n)
print(x)
x = pow(16.0, 1./n)
print(x)

2.0
2.0

Корень отрицательного числа

Рассмотрим, как поведут себя функции, если будем брать корень из отрицательного числа.

from math import sqrt
x = sqrt(-4)

File "main.py", line 2, in 
    x = sqrt(-4)
ValueError: math domain error

Как видим, функция sqrt выдаёт исключение.

Теперь посмотрим, что будет при использовании других методов.

x = -4 ** 0. 5
print(x)
x = pow(-4, 0.5)
print(x)

-2.0
(1.2246467991473532e-16+2j)

Как видно из результата, оператор ** не выдает исключения и возвращает некорректный результат. Функция pow работает корректно. В результате получаем комплексное число 2j, что является верным.

Вывод

В Python существуют два универсальных способа для извлечения корня из числа. Это возведение в необходимую степень 1/n. Кроме того, можно воспользоваться функцией из математического модуля языка, если необходимо извлечь квадратный корень числа.

Все эти методы имеют свои преимущества и недостатки. Самый наглядный это sqrt, но подходит только для квадратный корней из числа. Остальные методы не такие элегантные, но легко могут извлечь корень нужной степени из числа. Кроме того оператор ** оказался наиболее быстрым при тестировании.

Необходимо также помнить про целочисленное деление, неправильное использование которого может приводить к ошибке в вычислении.

Определение корня n-ой степени.

Свойства арифметического корня n-ой степени 9 класс онлайн-подготовка на Ростелеком

Тема 15.

Определение корня n-ой степени. Свойства арифметического корня n-ой степени.

Давай вспомним, что квадратным корнем из числа а называется такое число, квадрат которого равен а. Аналогично определяется корень любой натуральной степени n.

Итак, корнем n-ой степени из числа а называется такое число, n-ая степень которого равна а.

Например, корнем пятой степени из 32 является число 2, так как 2⁵=32, корнем четвертой степени из 81 является каждое из чисел 3 и -3, так и 3⁴=81 и (-3)⁴=81. Корень второй степени принято называть квадратным корнем, а корень третьей степени – кубическим корнем.

Если n — нечетное число, то выражение an имеет смысл при любом a; если n — четное число, то выражение an имеет смысл при a≥0.

Из определения корня n-ой степени следует, что при всех значениях а, при которых выражение anимеет смысл, верно равенствоann=a.

Определение: Арифметическим корнем n-ой степени из неотрицательного числа а называется неотрицательное число, n-ая степень которого равна а.

Корень нечетной степени из отрицательного числа можно выразить через арифметический корень. Например,

-83=-83=-2

Значит, при любом положительном a и нечетном n верно равенство:

-an=-an

Решим уравнение: x⁶ = 7. Корнями уравнения служат числа, шестая степень которых равна 7. И таких чисел два: 76 и -76.

Решим уравнение x³ = 27. Уравнение имеет единственный корень, это число, третья степень которого равна 27, то есть 273=3.

Рассмотрим свойства арифметического корня n-ой степени.

Если a≥0 и b≥0, то abn=anbn

Корень из неотрицательных множителей равен произведению корней из этих множителей.

Например, найдем значение выражения 16∙814=164∙814=2∙3=6

Если a≥0 и b>0, то abn=anbn

Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.

Например, найдем значение выражения 210273=64273=643273=43=113.

Если n и k – натуральные числа и a≥0, то akn=ank

Если n,k и m – натуральные числа и a≥0, то amknk=amn

Если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.

Рассмотрим некоторые примеры.

Вычислим значение выражения:

1353∙253=135∙253=27∙5∙253=27∙1253=3∙5=15

5106212∙526=510∙212∙526=512∙2126=10126=102=100

8-373∙8+373=8-378+373=64-373=273=3

%d0%ba%d0%be%d1%80%d0%b5%d0%bd%d1%8c%20n-%d0%b9%20%d1%81%d1%82%d0%b5%d0%bf%d0%b5%d0%bd%d0%b8 — со всех языков на все языки

1
delatorius
dēlātōrius, a, um (delator), zum Angeber gehörig, eines Angebers, curiositas, Ulp. dig. 22, 6, 6: libelli, Denunziationschriften, Cod. Theod. 10, 10, 7: calices perlucidi sine delatoria nota, Fronto de fer. Als. 3. p. 224, 20N.
lateinisch-deutsches > delatorius
2
delatorius
dēlātōrius, a, um (delator), zum Angeber gehörig, eines Angebers, curiositas, Ulp. dig. 22, 6, 6: libelli, Denunziationschriften, Cod. Theod. 10, 10, 7: calices perlucidi sine delatoria nota, Fronto de fer. Als. 3. p. 224, 20N.
Ausführliches Lateinisch-deutsches Handwörterbuch > delatorius

См. также в других словарях:

20N — may refer to : * New York State Route 20N * 20 N, an abbreviation for two well known dates in Spanish historyee also* N20 … Wikipedia
20N — Este artículo trata sobre la conmemoración del aniversario de los fallecimientos de Francisco Franco y José Antonio Primo de Rivera. Para otros acontecimientos relacionados con la fecha, véase 20 de noviembre. Para las elecciones previstas para… … Wikipedia Español
New York State Route 20N — NYS Route 20N Map of the Syracuse area with NY 20N highlighted in red Route information … Wikipedia
List of highways numbered 20N — The following highways are numbered 20N:* (Former) … Wikipedia
New York State Route 20SY — NYS Route 20SY Map of the Syracuse area with NY 20SY highlighted in red Route information … Wikipedia
List of numbered roads in Durham Region — The numbered roads in the Regional Municipality of Durham account for about 832 kilometres (517 mi) of the county road system in the Canadian province of Ontario. The Durham Region Works Department owns and maintains the regional roads and… … Wikipedia
New York State Route 92 — NYS Route 92 Map of the Syracuse area with NY 92 highlighted in red Route information … Wikipedia
New York State Route 173 — NYS Route 173 Map of the Syracuse area with NY 173 highlighted in red Route information … Wikipedia
Doomsday argument — World population from 10,000 BC to AD 2000 The Doomsday argument (DA) is a probabilistic argument that claims to predict the number of future members of the human species given only an estimate of the total number of humans born so far. Simply… … Wikipedia
New York State Route 174 — NYS Route 174 Map of the Syracuse area with NY … Wikipedia
New York State Route 175 — NYS Route 175 Map of the Syracuse area with NY 175 highlighted in red … Wikipedia

Корень степени N

15 января 2017

Поздравляю: сегодня мы будем разбирать корни — одну из самых мозговыносящих тем 8-го класса.:)

У вас тоже так? Читайте дальше — и всё поймёте

Многие путаются в корнях не потому, что они сложные (чего там сложного-то — пара определений и ещё пара свойств), а потому что в большинстве школьных учебников корни определяются через такие дебри, что разобраться в этой писанине могут разве что сами авторы учебников. Да и то лишь с бутылкой хорошего виски.:)

Поэтому сейчас я дам самое правильное и самое грамотное определение корня — единственное, которое вам действительно следует запомнить. {2}}=1$.

Кубические корни тоже часто встречаются — не надо их бояться:

\[\begin{align} & \sqrt[3]{27}=3; \\ & \sqrt[3]{-64}=-4; \\ & \sqrt[3]{343}=7. \\ \end{align}\]

Ну, и парочка «экзотических примеров»:

\[\begin{align} & \sqrt[4]{81}=3; \\ & \sqrt[5]{-32}=-2. \\ \end{align}\]

Если вы не поняли, в чём разница между чётной и нечётной степенью — перечитайте определение ещё раз. Это очень важно!

А мы тем временем рассмотрим одну неприятную особенность корней, из-за которой нам и потребовалось вводить раздельное определение для чётных и нечётных показателей.

Зачем вообще нужны корни?

Прочитав определение, многие ученики спросят: «Что курили математики, когда это придумывали?» И вправду: зачем вообще нужны все эти корни?

Чтобы ответить на этот вопрос, вернёмся на минутку в начальные классы. Вспомните: в те далёкие времена, когда деревья были зеленее, а пельмени вкуснее, основная наша забота была в том, чтобы правильно умножать числа. {n}}=a\]

Не спорю: зачастую эти корни легко считаются — мы видели несколько таких примеров выше. Но всё-таки в большинстве случаев, если вы загадаете произвольное число, а затем попробуете извлечь из него корень произвольной степени, вас ждёт жестокий облом.

Да что там! Даже самый простой и всем знакомый $\sqrt{2}$ нельзя представить в привычном нам виде — как целое число или дробушка. А если вы вобьёте это число в калькулятор, то увидите вот это:

\[\sqrt{2}=1,414213562…\]

Как видите, после запятой идёт бесконечная последовательность цифр, которые не подчиняются никакой логике. Можно, конечно, округлить это число, чтобы быстро сравнить с другими числами. Например:

\[\sqrt{2}=1,4142…\approx 1,4 \lt 1,5\]

Или вот ещё пример:

\[\sqrt{3}=1,73205…\approx 1,7 \gt 1,5\]

Но все эти округления, во-первых, довольно грубые; а во-вторых, работать с примерными значениями тоже надо уметь, иначе можно словить кучу неочевидных ошибок (кстати, навык сравнения и округления в обязательном порядке проверяют на профильном ЕГЭ).

Поэтому в серьёзной математике без корней не обойтись — они являются такими же равноправными представителями множества всех действительных чисел $\mathbb{R}$, как и давно знакомые нам дроби и целые числа.

Невозможность представить корень в виде дроби вида $\frac{p}{q}$ означает, что данный корень не является рациональным числом. Такие числа называются иррациональными, и их нельзя точно представить иначе как с помощью радикала, либо других специально предназначенных для этого конструкций (логарифмов, степеней, пределов и т.д.). Но об этом — в другой раз.

Рассмотрим несколько примеров, где после всех вычислений иррациональные числа всё же останутся в ответе.

Пример.
\[\begin{align} & \sqrt{2+\sqrt[3]{27}}=\sqrt{2+3}=\sqrt{5}\approx 2,236… \\ & \sqrt[3]{\sqrt[5]{-32}}=\sqrt[3]{-2}\approx -1,2599… \\ \end{align}\]

Естественно, по внешнему виду корня практически невозможно догадаться о том, какие числа будут идти после запятой. {2}}=4\]

С первым числом всё понятно — оно положительное, поэтому оно и есть корень:

\[\sqrt{4}=2\]

Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$\sqrt{4}=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)

В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y, т.е. не принимает отрицательных значений.

Подобная проблема возникает у всех корней с чётным показателем:

Строго говоря, корней с чётным показателем $n$ у каждого положительного числа будет сразу две штуки;
Из отрицательных чисел корень с чётным $n$ вообще не извлекается. {3}}$:
Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа
Из этого графика можно сделать два вывода:
Ветви кубической параболы, в отличие от обычной, уходят на бесконечность в обе стороны — и вверх, и вниз. Поэтому на какой бы высоте мы ни проводили горизонтальную прямую, эта прямая обязательно пересечётся с нашим графиком. Следовательно, кубический корень можно извлечь всегда, абсолютно из любого числа;
Кроме того, такое пересечение всегда будет единственным, поэтому не нужно думать, какое число считать «правильным» корнем, а на какое — забить. Именно поэтому определение корней для нечётной степени проще, чем для чётной (отсутствует требование неотрицательности).
Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.
Да, я не спорю: что такое арифметический корень — тоже надо знать. И я подробно расскажу об этом в отдельном уроке. Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.
Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.
А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:
Корень чётной степени существует лишь из неотрицательного числа и сам всегда является неотрицательным числом. Для отрицательных чисел такой корень неопределён.
А вот корень нечётной степени существует из любого числа и сам может быть любым числом: для положительных чисел он положителен, а для отрицательных — как намекает кэп, отрицательный.
Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.
Основные свойства и ограничения
У корней много странных свойств и ограничений — об этом будет отдельный урок. {2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.

Таким образом, ни в коем случае нельзя бездумно сокращать корни и степени, тем самым якобы «упрощая» исходное выражение. Потому что если под корнем стоит отрицательное число, а его показатель является чётным, мы получим кучу проблем.

Впрочем, все эти проблемы актуальны лишь для чётных показателей.

Вынесение минуса из-под знака корня

Естественно, у корней с нечётными показателями тоже есть своя фишка, которой в принципе не бывает у чётных. А именно:

\[\sqrt[2n+1]{-a}=-\sqrt[2n+1]{a}\]

Короче говоря, можно выносить минус из-под знака корней нечётной степени. Это очень полезное свойство, которое позволяет «вышвырнуть» все минусы наружу:

\[\begin{align} & \sqrt[3]{-8}=-\sqrt[3]{8}=-2; \\ & \sqrt[3]{-27}\cdot \sqrt[5]{-32}=-\sqrt[3]{27}\cdot \left( -\sqrt[5]{32} \right)= \\ & =\sqrt[3]{27}\cdot \sqrt[5]{32}= \\ & =3\cdot 2=6. \end{align}\]

Это простое свойство значительно упрощает многие вычисления. Теперь не нужно переживать: вдруг под корнем затесалось отрицательное выражение, а степень у корня оказалась чётной? Достаточно лишь «вышвырнуть» все минусы за пределы корней, после чего их можно будет умножать друг на друга, делить и вообще делать многие подозрительные вещи, которые в случае с «классическими» корнями гарантированно приведут нас к ошибке.

И вот тут на сцену выходит ещё одно определение — то самое, с которого в большинстве школ и начинают изучение иррациональных выражений. И без которого наши рассуждения были бы неполными. Встречайте!

Арифметический корень

Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?

А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них. {n}}=a$.

Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.

Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:

Область поиска арифметического корня — неотрицательные числа

Как видите, отныне нас интересуют лишь те куски графиков, которые расположены в первой координатной четверти — там, где координаты $x$ и $y$ положительны (или хотя бы ноль). Больше не нужно смотреть на показатель, чтобы понять: имеем мы право ставить под корень отрицательное число или нет. Потому что отрицательные числа больше в принципе не рассматриваются.

Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»

Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным. {2}}}=\sqrt[6]{4} \gt 0. \\ \end{align}$

Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.

WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.

Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.

Алгебраический корень: для тех, кто хочет знать больше

Долго думал: выносить эту тему в отдельный параграф или нет. В итоге решил оставить здесь. Данный материал предназначен для тех, кто хочет понять корни ещё лучше — уже не на среднем «школьном» уровне, а на приближенном к олимпиадному. {n}}=a \right. \right\}\]

Принципиальное отличие от стандартного определения, приведённого в начале урока, состоит в том, что алгебраический корень — это не конкретное число, а множество. А поскольку мы работаем с действительными числами, это множество бывает лишь трёх типов:

Пустое множество. Возникает в случае, когда требуется найти алгебраический корень чётной степени из отрицательного числа;
Множество, состоящее из одного-единственного элемента. Все корни нечётных степеней, а также корни чётных степеней из нуля попадают в эту категорию;
Наконец, множество может включать два числа — те самые ${{x}_{1}}$ и ${{x}_{2}}=-{{x}_{1}}$, которое мы видели на графике квадратичной функции. Соответственно, такой расклад возможен лишь при извлечении корня чётной степени из положительного числа.

Последний случай заслуживает более подробного рассмотрения. Посчитаем парочку примеров, чтобы понять разницу.

Пример. Вычислите выражения:
\[\overline{\sqrt{4}};\quad \overline{\sqrt[3]{-27}};\quad \overline{\sqrt[4]{-16}}. \]
Решение. С первым выражением всё просто:
\[\overline{\sqrt{4}}=\left\{ 2;-2 \right\}\]
Именно два числа входят в состав множества. Потому что каждое из них в квадрате даёт четвёрку.
\[\overline{\sqrt[3]{-27}}=\left\{ -3 \right\}\]
Тут мы видим множество, состоящее лишь из одного числа. Это вполне логично, поскольку показатель корня — нечётный.
Наконец, последнее выражение:
\[\overline{\sqrt[4]{-16}}=\varnothing \]

Получили пустое множество. Потому что нет ни одного действительного числа, которое при возведении в четвёртую (т.е. чётную!) степень даст нам отрицательное число −16.

Финальное замечание. Обратите внимание: я не случайно везде отмечал, что мы работаем с действительными числами. Потому что есть ещё комплексные числа — там вполне можно посчитать и $\sqrt[4]{-16}$, и многие другие странные вещи.
Однако в современном школьном курсе математики комплексные числа почти не встречаются. Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».

На этом всё. В следующем уроке мы рассмотрим все ключевые свойства корней и научимся, наконец, упрощать иррациональные выражения.:)

Смотрите также:

Умножение корней n-й степени
Свойства арифметического квадратного корня
Тест к уроку «Округление с избытком и недостатком» (1 вариант)
Пробный ЕГЭ 2012 от 7 декабря. Вариант 5 (без производной)
Задача B4: случай с неизвестным количеством товара
Задача B2 про комиссию в терминале

Корень n-ной степени из действительного числа /qualihelpy

Если показатель корня четное число, то подкоренное выражение не может быть отрицательным числом, так как четная степень и положительного и отрицательного числа есть число положительное.

Если показатель корня нечетное число, то подкоренное выражение может быть положительным числом, отрицательным числом и числом .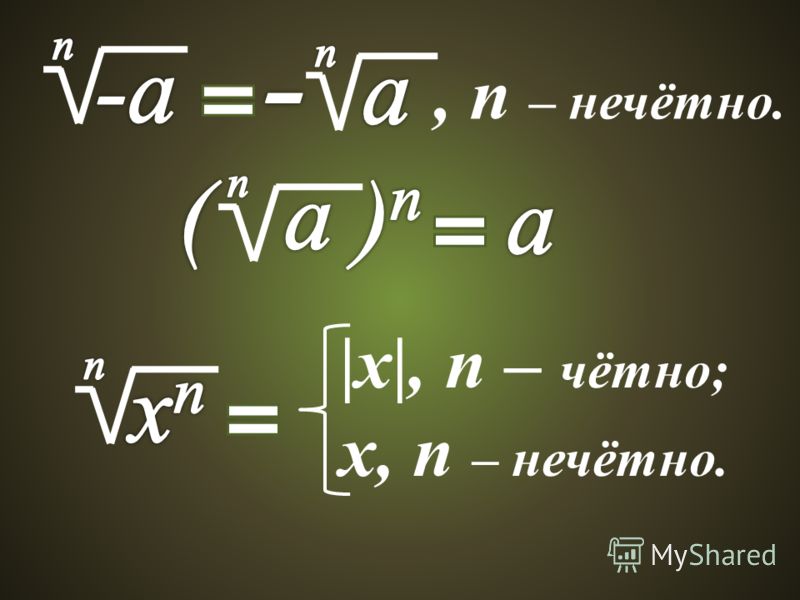

Свойства корней:

; (1.16) ; (1.17) ; (1.18)
; (1.19) . (1.20)

Внесение множителя под знак корня

Если показатель корня нечетное число, то для любого числа и натурального числа справедливо равенство: . (1.21)Если , то . Например, .

Вынесение множителя из-под знака корня

Если показатель корня нечетное число, то справедливо равенство:

. (1.22)

Если показатель корня четное число, то справедливо равенство:

. (1.23)Например: ; .

Сравнение выражений, содержащих корни

1. Если , то . Например, .2. Если и , то . Например, .3. Если и , то . Например, .4. Чтобы сравнить числа и , необходимо представить их в виде корня одной и той же степени.

Степень с действительным показателем

Степени с действительным показателем обладают всеми свойствами степеней с целым показателем. При этом следует помнить, что:

а) степень числа с натуральным показателем имеет смысл для любого основания, так как эта степень определяется с помощью операции умножения;

б) степень с целым отрицательным показателем имеет смысл для любого основания, кроме основания , так как эта степень определяется с помощью операций умножения и деления;

в) степень с рациональным показателем определяется с помощью операции извлечения корня, которая всегда выполнима, если основание степени положительное число и не всегда выполнима, если основание степени отрицательное число;

г) степень с любым действительным показателем всегда определена, если ее основание – положительное число.

Среднее арифметическое и среднее геометрическое

Чтобы найти среднее арифметическое нескольких чисел необходимо сумму этих чисел разделить на их количество.

Например, среднее арифметическое чисел , и равно .

Корень квадратный из числа

Мы с вами уже уяснили себе, что каждому математическому действию соответствует аналогичное, но обратное по направлению действие.

Для сложения таким обратным действием является вычитание, для умножения — деление. Теперь попробуем выяснить, какое действие является обратным для возведения в степень. Поскольку возведение в степень — это многократное умножение, то, очевидно, обратным действием будет многократное деление.

Например, 32 можно разделить на 2 и получить 16, затем 16 разделить на 2 и получить 8; затем 8 разделить на 2 и получить 4; затем 4 разделить на 2 и получить 2; наконец, затем 2 разделить на 2 и получить 1. В краткой форме эти действия можно записать как 32:2:2:2:2:2=1. (Наша задача заключалась в том, чтобы добраться до 1.) Поскольку мы произвели деление 5 раз и добрались до 1, то можно сказать, что 2 — это корень пятой степени из 32.

Если мы рассмотрим число 81, то увидим, что 81:3:3:3:3=1, таким образом, 3 является корнем четвертой степени из 81. (Почему, собственно, корнем? Откуда взялось это слово? Это можно объяснить таким образом: число 32 растет из основания 2, а 81 — из основания 3 так же, как растение произрастает из корней.)

Такая математическая операция обозначается как $\sqrt{}$. На разнообразие корней указывает число в верхней левой части корня. Так, корень пятой степени из 32 можно записать как $\sqrt[5]{32}$, корень четвертой степени из 81 можно записать как $\sqrt[4]{81}$. Значок $\sqrt{ }$ называется знаком радикала, а числа, содержащие корни, называются радикалами. Слово «радикал» пришло к нам из латыни, где оно означает просто «корень».

Мы редко встречаемся с корнями высоких степеней, чаще всего приходится иметь дело с операциями, обратными возведению во вторую степень, то есть в квадрат. 5=32$, это означает, что если 32 пять раз разделить на 2, то результатом будет 1. (Если мы возвели число в какую-то степень, нетрудно пойти в обратном порядке.)

На практике арифметический метод определения корней заключается в серии обратных действий. Попробуем извлечь квадратный корень из 625. Схема вычислений будет следующей:

Первую цифру ответа, 2, мы получаем подбором. Мы знаем, что 2×2=4, это ближайшее возможное число, меньшее 6, поскольку 3×3=9, что больше 6. Затем проводим вычитание и выносим две цифры вместо одной, как это принято при обычном делении в столбик. (Если бы мы извлекали кубический корень, мы выносили бы три цифры, в случае корня четвертой степени — четыре цифры и так далее.) Чтобы получить следующую цифру, надо разделить 225 на 45. Цифру 45 вы получаете, удваивая первую цифру ответа, что дает вам 4. Вторая цифра должна быть равна второй цифре вашего ответа, таким образом, ее тоже можно найти подбором, так, чтобы получить число, ближайшее к 225. 2$ — это $1\frac{24}{25}$, а нам нужно получить число $1\frac{25}{25}$, то есть 2.

Но можно получить и более точный ответ. Если помножить дробное число $1\frac{41}{100}$ на себя самое, мы получим $1\frac{9881}{10000}$, что гораздо ближе к 2. Может показаться, что, если делать более точные вычисления, мы рано или поздно найдем точное значение дробного числа, которое является корнем квадратным из 2, хотя, возможно, это будет очень сложное число.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

2 + f q — 2) z + (1 — f q) $ с $ f, q \ in \ mathbb R $. Следующее покажет, что если $ f \ ne 0 $ и $ | f + q | \ lt 2 $, то $ P (z) = 0 $ имеет два комплексных корня, и для каждого такого корня:

$$
| z — 1 | = | f | \\
\ cos \ varphi = — sgn (f) \ frac {f + q} {2} \, \, \, \, \ text {where} \, \, \ varphi = \ arg (z — 1) \, \ , \ text {and} \, \, sgn \, \, \ text {- функция signum}

В комплексной плоскости это означает:

для $ f = const $ геометрическое место корней $ z $ из $ P (z) $ представляет собой окружность с центром в точке $ (1, 0) $;
для $ f + q = const $ геометрическое место $ z $ представляет собой пару прямых, проходящих через точку $ (1, 0) $. 2 $, что доказывает первое.
Тогда два корня равны $ z, \ bar z = | f | (\ cos \ varphi \ pm i \ sin \ varphi) $ и их сумма равна $ z + \ bar z = 2 | f | \ cos \ varphi = -f (f + q) $ снова по формулам Виета. В итоге отсюда следует, что:
$$
\ cos \ varphi = — \ frac {f} {| f |} \ frac {f + q} {2} = — sgn (f) \ frac {f + q} {2}
$
[РЕДАКТИРОВАТЬ] Это продолжение вопроса о , геометрическая интерпретация q , заданного в исходном сообщении и снова в комментарии. Короткий ответ заключается в том, что, похоже, не существует прямой «красивой» геометрической интерпретации $ q $, и вот почему.
Ответ выше был сосредоточен на корнях $ Q (z) $, а геометрические интерпретации для $ f $ и $ f + q $ следовали как следствия, почти как случайно. Однако к проблеме можно подойти и с другой стороны. Предположим, кто-то хочет напрямую определить, как параметры влияют на корни, в частности, каково геометрическое место корней $ z, \ bar z $, если параметр остается постоянным. Ниже приведен ответ для $ f $, поскольку это более простой из двух вычислений, а также объясняется, почему не существует сравнительно простой геометрической интерпретации для $ q $.2 = 0 $. Это то же соотношение, полученное в исходном ответе, и имеет красивую прямую геометрическую интерпретацию. Это означает, что $ | f | $ — это абсолютное значение $ z $, поэтому корни для $ f = const $ лежат на окружности с центром в начале координат.
Конечно, технически возможно провести такой же анализ для $ q $. Но поскольку уравнения квадратичны по $ f $, исключить их между ними труднее, и конечным результатом будет кривая четвертой степени, параметризованная в $ f $. Каждый $ q = const $ дает различную кривую четвертой степени, но кроме этого нет очевидной (для меня) геометрической интерпретации для $ q $.
второй степени, с нулями — 6-6 и 2, 2, и идет t o — ∞ t o — ∞ при x — ∞ x — ∞
Привет,
В вопросе отсутствует информация, а точнее точка (x, y), которая лежит на кривой многочлена второй степени.
С учетом сказанного, многочлен второй степени представляет собой квадратичную функцию, когда он представлен как функция в «Факторизованной форме» как:
y = a (x — r ₁ ) (x — r ₂ ), , где «a» — ведущий коэффициент, а «r ₁ » и «r ₂ » — нули / корни / x -перехватывания на графике.
Во-вторых, они могут быть записаны как нечетные или четные кратности, повторяющиеся множители и нечетное или четное количество раз. Напомним, что корни / факторы, которые имеют нечетную кратность, пересекают ось x от положительного квадранта значений «y» в квадрант отрицательных значений «y», т.е. положительных, отрицательных или отрицательных, положительных.
Четные множественности касаются корня / точки пересечения по оси x и возвращаются в область диапазона, откуда она возникла. Таким образом, если кривая многочлена находится в квадрантах, где значения «y» положительны, кривая после касания точки пересечения с x будет возвращаться в положительную область или положительную, положительную.Если значение «y» отрицательное, то оно будет отрицательным, отрицательным.
Возвращаясь к вашему первоначальному вопросу, нам говорят, что у нас есть многочлен второй степени с двумя корнями -6 и +2, таким образом, это двойные корни, также известные как «кратности событий». Мы преобразуем эти корни обратно в их факторизованную форму следующим образом:
Шаг 1): Установите -6 и +2 равными x следующим образом:
x = — 6 & x = +2
Шаг 2) Используйте алгебру для манипулировать приведенными выше выражениями, равными нулю, чтобы вернуть их в факторизованную форму
x + 6 = 0 & x — 2 = 0 → Помещая круглые скобки, мы получаем (x + 6) и (x — 2)
*** ПРИМЕЧАНИЕ *** Из вашего первоначального вопроса неясно, должен ли это быть многочлен второй степени, поскольку, если решения удваиваются или дублируются, вместо этого будет четвертая степень ***
Шаг 3) Поскольку оба корня являются четными кратностями исходя из первоначального вопроса, мы помещаем степень двойки, чтобы указать множественность двух, поскольку эти факторы дублируют друг друга дважды.
(x + 6) ² и (x — 2) ²
Шаг 4): Создайте полином степени, используя приведенный выше шаблон разложенной формы следующим образом:
Возможное решение 1:
y = a (x + 6) ² (x — 2) ², таким образом, это будет многочлен четвертой степени с корнями -6 и 2, оба имеют кратность два, потому что они встречаются / повторяются дважды. Мы можем найти значение a , если нам дана точка (x, y), которая лежит на кривой этой функции
Возможное решение 2:
y = a (x + 6) (x — 2 ) , если нам нужно вывести из вашего первоначального вопроса, что -6 и 2 повторяются один раз, а не дважды, они будут иметь нечетные кратности или степени 1, в которых 1 понимается, а не обозначается понимаемым.Таким образом, это решение создает полином второй степени, но снова нам нужна точка, которая лежит на кривой, чтобы найти истинный ведущий коэффициент a , чтобы представить фактический полином.
Ким Поттер обвинен в Манслаугтере 2-й степени
Протестующие маршируют от полицейского управления Бруклинского центра к ближайшему офису ФБР 13 апреля 2021 года в Бруклинском центре, Миннесота. Демонстрации стали обычным явлением с тех пор, как в воскресенье 20-летняя Даунт Райт была застрелена полицейским Бруклинского центра Кимберли Поттер.Фото: Стивен Мэрилн (Getty Images)
Ким Поттер, ныне бывший Бруклинский центр, Миннесота, полицейский, застреливший Даунте Райт во время остановки движения в воскресенье, был обвинен в непредумышленном убийстве второй степени. Для активистов и членов сообщества, которые требовали справедливости в отношении Райта со дня стрельбы — и, вероятно, уже находятся в напряжении из-за суда над Дереком Човеном по делу о смерти Джорджа Флойда — обвинение легко не будет соответствовать истинной ответственности, даже если она признан виновным.
Из CNN:
В Миннесоте непредумышленное убийство второй степени применяется, когда власти утверждают, что кто-то стал причиной чьей-то смерти из-за «виновной халатности, когда человек создает необоснованный риск и сознательно рискует причинить смерть или серьезные телесные повреждения другому человеку. . »
Лицо, признанное виновным по данному обвинению, будет приговорено к лишению свободы сроком до 10 лет и / или штрафу в размере до 20 000 долларов.
За исключением энтузиастов «спиной к голубым», которые хотя бы сделают вид, будто верят, что 26-летний ветеран полиции принял свое служебное оружие за электрошокер, никого не устроит, что Поттеру грозит максимум десять лет. в тюрьме и / или небольшой пятизначный штраф.
Бюро уголовного преследования Миннесоты объявило в среду, что Поттер был взят под стражу около 11:30 утра и что она будет помещена в тюрьму округа Хеннепин.
G / O Media может получить комиссию
BCA также отметило, что «это остается активным и продолжающимся расследованием», и что «BCA было и будет продолжать работать с прокуратурой округа Вашингтон по мере продвижения дела. . »
Как ранее сообщал The Root , Поттер вместе с начальником полиции Бруклинского центра Тимом Гэнноном ушли в отставку во вторник из-за возмущения по поводу стрельбы, но полицейские утверждают, что смерть Райта произошла в результате несчастного случая.
Итак, мы смотрим на еще одну тяжелую битву с надеждой, что результатом будет некое подобие справедливости. Конечно, в то время как в настоящее время мы являемся свидетелями съезда газлайтинга и обвинения жертв, то есть судебного процесса над Шовеном, те из нас, кто устал от внесудебных казней чернокожих от рук полиции, столкнутся с Трудно найти в себе силы выдержать еще один судебный процесс, который может закончиться обвинительным приговором, а может и не закончиться.
Люди уже истощены, и если история Райта чему-то нас научила, так это тому, что все протесты в мире, похоже, не удерживают полицейских от чрезмерных действий с подозреваемыми черными.
Алгебра — нули / корни многочленов
Показать уведомление для мобильных устройств
Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана (, т. е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 5-2: Нули / корни многочленов
Мы начнем этот раздел с определения, что такое корень или ноль многочлена.Мы говорим, что \ (x = r \) является корнем или нулем многочлена \ (P \ left (x \ right) \), если \ (P \ left (r \ right) = 0 \). Другими словами, \ (x = r \) является корнем или нулем многочлена, если он является решением уравнения \ (P \ left (x \ right) = 0 \).
В следующих двух разделах нам нужно будет найти все нули для данного многочлена. Итак, прежде чем мы перейдем к этому, нам нужно получить некоторые идеи относительно нулей многочленов, которые помогут нам в этом процессе.
Процесс нахождения нулей \ (P \ left (x \ right) \) на самом деле сводится к не более чем решению уравнения \ (P \ left (x \ right) = 0 \), и мы уже знаем, как это сделать. что для полиномов второй степени (квадратичных).2} = 0 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \, \, \, \, \, \, \, \, \, x = 7 \]
Итак, этот многочлен второй степени имеет единственный ноль или корень. Также вспомните, что когда мы впервые посмотрели на них, мы назвали такой корень двойным корнем .
Мы решили каждую из них, сначала разложив многочлен на множители, а затем применив свойство нулевого множителя в факторизованной форме. Когда мы впервые посмотрели на свойство нулевого фактора, мы увидели, что оно гласит, что если произведение двух членов равняется нулю, то один из членов должен быть равен нулю для начала. 2} \ left ({x + 5} \ right) \ left ({x + 4} \ right) \) Показать решение
С этим полиномом у нас есть четыре члена и нули здесь,
\ [x = — 5, \, \, \, x = — 1, \, \, \, x = 1, \, \, \, {\ mbox {and}} \, \, \, x = — 4 \]
Теперь у нас есть некоторая терминология, чтобы не мешать.2} \ left ({x + 5} \ right) \ left ({x + 4} \ right) \)

Показать решение

Мы уже определили нули каждого из них в предыдущей работе или примерах в этом разделе, поэтому не будем переделывать эту работу. В каждом случае мы просто запишем ранее найденные нули, а затем вернемся к факторизованной форме многочлена, посмотрим на показатель степени каждого члена и дадим кратность.

a В этом случае у нас есть два простых нуля: \ (x = — 5, \, \, x = 3 \).

b Здесь \ (x = 7 \) — ноль кратности 2.

c У этого многочлена два нуля: \ (x = — 1 \) с кратностью 2 и \ (x = 2 \) с кратностью 3.

d В данном случае у нас три нуля. : \ (x = — 5 \) простой, \ (x = 0 \) с кратностью 4 и \ (x = 3 \) с кратностью 3.

e В последнем случае у нас четыре нуля. \ (x = — 5 \), который является простым, \ (x = — 1 \) с кратностью 3, \ (x = 1 \) с кратностью 2 и \ (x = — 4 \), который является простым.

Этот пример приводит нас к нескольким интересным фактам о многочленах. Вот первое и, наверное, самое важное.

Основная теорема алгебры

Если \ (P \ left (x \ right) \) — многочлен степени n , то \ (P \ left (x \ right) \) будет иметь ровно \ (n \) нулей, некоторые из которых могут повторяться .

Этот факт говорит о том, что если вы перечислите все нули и перечислите каждый \ (k \) раз, где \ (k \) — его кратность, у вас будет ровно \ (n \) чисел в списке.Другой способ сказать этот факт состоит в том, что кратность всех нулей должна складываться со степенью многочлена.

Мы можем вернуться к предыдущему примеру и проверить, что это верно для полиномов, перечисленных там.

Это будет приятный факт в нескольких разделах, когда мы подробно рассмотрим нахождение всех нулей многочлена. Если мы знаем верхнюю границу количества нулей для многочлена, тогда мы будем знать, когда мы все их найдем, и поэтому можем перестать искать.

Также обратите внимание, что некоторые нули могут быть сложными. В этом разделе мы работали с многочленами, у которых есть только действительные нули, но это не позволяет вам прийти к выводу, что эта теорема применима только к действительным нулям. Вполне возможно, что комплексные нули появятся в списке нулей.

Иногда бывает очень полезен и следующий факт.

Факторная теорема

Для многочлена \ (P \ left (x \ right) \),

Если \ (r \) является нулем \ (P \ left (x \ right) \), то \ (x — r \) будет множителем \ (P \ left (x \ right) \).
Если \ (x — r \) является множителем \ (P \ left (x \ right) \), то \ (r \) будет нулем \ (P \ left (x \ right) \).

Опять же, если мы вернемся к предыдущему примеру, мы увидим, что это подтверждается полиномами, перечисленными там.

Фактор-теорема приводит к следующему факту.

Факт 1

Если \ (P \ left (x \ right) \) является многочленом степени \ (n \) и \ (r \) является нулем \ (P \ left (x \ right) \), то \ (P \ left (x \ right) \) можно записать в следующем виде.

\ [P \ left (x \ right) = \ left ({x — r} \ right) Q \ left (x \ right) \]

, где \ (Q \ left (x \ right) \) — многочлен степени \ (n — 1 \). \ (Q \ left (x \ right) \) можно найти, разделив \ (P \ left (x \ right) \) на \ (x — r \).

Есть еще один факт, который нам нужно убрать с дороги.

Факт 2

Если \ (P \ left (x \ right) = \ left ({x — r} \ right) Q \ left (x \ right) \) и \ (x = t \) является нулем \ (Q \ left (x \ right) \), то \ (x = t \) также будет нулем \ (P \ left (x \ right) \).

Этот факт достаточно легко проверить напрямую. Во-первых, если \ (x = t \) является нулем \ (Q \ left (x \ right) \), то мы знаем, что

\ [Q \ left (t \ right) = 0 \]

, так как это значит быть нулем. Итак, если \ (x = t \) должен быть нулем \ (P \ left (x \ right) \), то все, что нам нужно сделать, это показать, что \ (P \ left (t \ right) = 0 \ ) и это на самом деле довольно просто. Вот она,

\ [P \ left (t \ right) = \ left ({t — r} \ right) Q \ left (t \ right) = \ left ({t — r} \ right) \ left (0 \ right) = 0 \]

, и поэтому \ (x = t \) является нулем \ (P \ left (x \ right) \).2} — 5x — 6 \) Факт 1 говорит нам, что мы можем записать \ (P \ left (x \ right) \) как,

\ [P \ left (x \ right) = \ left ({x — 2} \ right) Q \ left (x \ right) \]

и \ (Q \ left (x \ right) \) будет квадратичным многочленом. Затем мы можем найти нули \ (Q \ left (x \ right) \) любым из методов, которые мы рассмотрели до этого момента, и по факту 2 мы знаем, что два нуля, которые мы получаем из \ (Q \ left (x \ right) \) будет также нулями \ (P \ left (x \ right) \). На этом этапе у нас будет 3 нуля, и на этом все готово.

Итак, давайте найдем \ (Q \ left (x \ right) \). Для этого все, что нам нужно сделать, — это быстрое синтетическое разделение, как показано ниже.

\ [\ begin {align *} \ left. {\ underline {\, 2 \,}} \! \ право | & \, \, \, \ begin {array} {* {20} {l}} 1 & {\, \, 2} & {- 5} & {- 6} \ end {array} \\ & \, \ , \, \, \, \, \ underline {\, \, \ begin {array} {* {20} {l}} {} & 2 & {\, \, \, \, 8} & {\, \, \, \, \, 6} \ end {array}} \\ & \, \, \, \, \, \ begin {array} {* {20} {l}} {\, 1} & {4} & {\, \, 3} & {\, \, \, \, \, 0} \ end {array} \ end {align *} \]

Перед записью \ (Q \ left (x \ right) \) вспомните, что последнее число в третьей строке — это остаток, и что мы знаем, что \ (P \ left (2 \ right) \) должно быть равно этому номер.Итак, в этом случае мы имеем \ (P \ left (2 \ right) = 0 \). Если задуматься, мы уже должны знать, что это правда. В постановке задачи нам указывалось, что \ (x = 2 \) является нулем \ (P \ left (x \ right) \), а это означает, что мы должны иметь \ (P \ left (2 \ right) = 0 \).

Итак, зачем об этом говорить? Это отличная проверка нашего синтетического подразделения. Поскольку мы знаем, что \ (x = 2 \) является нулем \ (P \ left (x \ right) \), и мы получаем любое другое число, кроме нуля в этой последней записи, мы будем знать, что мы сделали что-то не так, и мы можем вернуться и найти ошибку.2} — 5х — 6 \). Подставляя факторизованную форму \ (Q \ left (x \ right) \) в \ (P \ left (x \ right) \), получаем

\ [P \ left (x \ right) = \ left ({x — 2} \ right) \ left ({x + 3} \ right) \ left ({x + 1} \ right) \]

Кстати, так факторизовались многочлены в первом наборе примеров. Для этого потребуется немного больше работы, но это можно сделать таким же образом.

Как найти область определения, диапазон и корни многочленов и рациональных функций

Полином
градусов
Линейная функция
Уклон у -перехват
x -перехват
Корень
Ноль (функции) Квадратичная функция
Квадратичная формула
Рациональная функция

Цели

Определить многочлены и их основные характеристики
Определить рациональные функции
Найдите область определения, диапазон и корни простых многочленов и рациональных функций.

Введение в многочлены

Полиномы — это тип функций, которые вы будете регулярно видеть при изучении математики.Полином — это серия членов, каждый из которых является произведением постоянного коэффициента и целой степени независимой переменной. Общая полиномиальная функция f в терминах переменной x выражена ниже.

Здесь коэффициенты c _i постоянны, а n — это градусов полинома ( n должно быть целым числом, где 0 ≤ n <∞).Обратите внимание, что линия, имеющая форму (или, что более привычно, y = mx + b ), является многочленом первой степени или многочленом первой степени. Квадратичная функция является многочленом второй степени.

Линейные функции

Линейные функции (помимо функций постоянной или нулевой степени) являются простейшими полиномами. Учитывая форму , наклон линии равен c ₁, а точка пересечения y- равна c ₀.Здесь наклон определяется как изменение значения f (или Δ f ), деленное на соответствующее изменение в x (или Δ x ), а интервал y — это значение of f при x = 0. Эти характеристики проиллюстрированы графически ниже для функции .

В общем, многие функции имеют y -перехват — опять же, для функции f ( x ) это просто f (0).(Не , но все функции имеют перехват y , поскольку не все определены при x = 0. Например, функция не определена при x = 0, поэтому у нее нет y -перехват.) Поскольку функция должна пройти проверку вертикальной линии, как мы отметили ранее, функция может иметь не более одного -перехвата .

Некоторые функции могут также иметь точки пересечения x- : для функции g ( x ), это значения x , для которых g ( x ) = 0.Другими словами, перехват x является решением уравнения g ( x ) = 0. Значения x , которые удовлетворяют этому уравнению, также называются корнями или нулями функции . Функция может иметь несколько корней, один или не иметь корней. В приведенном выше линейном примере функция имеет корень , поскольку

Корень этой функции показан графически ниже.

Квадратичные функции

Вы также можете быть знакомы с квадратичными функциями (многочлены второй степени), которые имеют вид . Квадратичные функции, как и все многочлены, имеют точку пересечения y c ₀. У них не может быть ни одного, одного или двух корней, которые можно определить с помощью квадратной формулы , , которая выражена ниже.

Обратите внимание, что многочлен первой степени (линейная функция) может иметь не более одного корня. Шаблон верен для всех многочленов: многочлен с корнем n может иметь максимум n корня.

Практическая задача: Найдите корни функции , если они существуют.

Решение: Вы можете использовать несколько различных методов решения.Один из них — вычислить квадратную формулу:

т = 1, 4

В качестве альтернативы, вы можете разложить на множители, чтобы найти значения x , которые делают функцию h равной нулю.

т = 1, 4

Вы также можете построить график функции, чтобы найти расположение корней, но не забудьте проверить свои ответы в уравнении, поскольку графики обычно не являются точными методами решения. График для h ( t ) показан ниже с корнями, отмеченными точками.

Найти корни многочленов более высокой степени — более сложная задача.

Введение в рациональные функции

Рациональные функции — это дроби, содержащие многочлены. Рациональная функция f ( x ) имеет общий вид, показанный ниже, где p ( x ) и q ( x ) являются полиномами любой степени (с оговоркой, что q ( x ) ≠ 0, так как это приведет к функции # ff0000).

Обратите внимание, что все многочлены являются рациональными функциями (многочлен — это рациональная функция, для которой q ( x ) = 1), но не все рациональные функции являются многочленами. Пример рациональной функции следующий.

Предупреждение: хотя приведенное выше выражение можно упростить, результат может не совпадать с исходной функцией.Чтобы проиллюстрировать этот момент, давайте разложим числитель g ( r ).

Естественно, есть соблазн отменить один множитель r — 1 как из числителя, так и из знаменателя, оставив выражение ниже:

Таким образом, мы видим, что g ( r ) линейно. И если мы построим график первого выражения (со знаменателем полинома), результатом будет линия r — 1 , за исключением , которое r не может равняться 1, поскольку r = 1 не находится в области g. ( r ).На графике этот странный результат выглядит как «дыра», как показано ниже с помощью белого кружка при r = 1. Таким образом, мы должны осторожно относиться к рациональным функциям в отношении изменения выражения.

Практическая задача: Найдите домен и диапазон функции и построите график функции.

Решение: Область многочлена — это весь набор действительных чисел.Ограничивающим фактором области определения рациональной функции является знаменатель, который не может быть равен нулю. Значения, не входящие в область значений t ( x ), являются корнями многочлена в знаменателе. Разложим на множители числитель и знаменатель.

Из этого факторинга видно, что область значений t ( x ) — это все действительные числа, кроме x = –1. То есть область включает интервалы (-∞, -1) и (-1, ∞).Чтобы найти диапазон, построим график функции. Для этого мы можем упростить его, исключив подобные факторы:

Поскольку ограничение, заключающееся в том, что x не может быть –1, остается после упрощения, мы можем построить упрощенную функцию, не беспокоясь о пропуске дыр на графике.

Обратите внимание, что x никогда не может быть –1, потому что функция стремится к бесконечности (или отрицательной бесконечности) по мере приближения к этому значению.Также обратите внимание, что диапазон функции включает все действительные значения, кроме t = 1. Он очень близок к t = 1, но никогда не достигает этого значения (числитель никогда не равен знаменателю!).

нулей полиномиальных функций | Безграничная алгебра

Основная теорема алгебры

Основная теорема утверждает, что каждый непостоянный многочлен от одной переменной с комплексными коэффициентами имеет по крайней мере один комплексный корень.

Цели обучения

Обсудить основную теорему алгебры

Основные выводы

Ключевые моменты

Основная теорема алгебры утверждает, что каждый непостоянный многочлен от одной переменной с комплексными коэффициентами имеет по крайней мере один комплексный корень. Сюда входят полиномы с действительными коэффициентами, поскольку каждое действительное число является комплексным числом с нулем в качестве коэффициента.
Фундаментальная теорема также формулируется следующим образом: каждый ненулевой многочлен с одной переменной степени [latex] n [/ latex] с комплексными коэффициентами имеет, если считать с кратностью, ровно [latex] n [/ latex] корней.{n-1} + \ ldots c_0 [/ латекс]
, где [latex] n> 0 [/ latex] и [latex] c_n \ not = 0 [/ latex], имеет по крайней мере один комплексный корень.
Есть много доказательств основной теоремы алгебры. Однако, несмотря на свое название, чисто алгебраического доказательства не существует, поскольку каждое доказательство использует тот факт, что [latex] \ mathbb {C} [/ latex] является полным.
В частности, поскольку каждое действительное число также является комплексным числом, каждый многочлен с действительными коэффициентами допускает комплексный корень.3 (x + \ pi) [/ латекс]
допускает один комплексный корень кратности [latex] 4 [/ latex], а именно [latex] x_0 = 0 [/ latex], один комплексный корень кратности [latex] 3 [/ latex], а именно [latex] x_1 = i [ / latex] и один комплексный корень из кратности [latex] 1 [/ latex], а именно [latex] x_2 = — \ pi [/ latex]. Сумма кратностей корней равна степени многочлена, [латекс] 8 [/ латекс]. Для ненулевых комплексных многочленов это оказывается верным в общем случае и непосредственно следует из основной теоремы алгебры.
Действительно, многочлен степени [latex] 0 [/ latex] принимает форму [latex] c_0 [/ latex], где [latex] c_0 \ not = 0 [/ latex], и, следовательно, не имеет нулей.
Для общего многочлена [latex] f (x) [/ latex] степени [latex] n [/ latex] основная теорема алгебры гласит, что мы можем найти один корень [latex] x_0 [/ latex] из [latex] ] f (x) [/ латекс]. Таким образом, мы можем разложить [латекс] f (x) [/ latex] на
[латекс] f (x) = (x-x_0) f_1 (x) [/ латекс]
, где [латекс] f_1 (x) [/ latex] — ненулевой многочлен степени [латекс] n-1.[/ latex] Итак, если кратности корней [латекса] f_1 (x) [/ latex] добавить к [latex] n-1 [/ latex], кратность корней [latex] f [/ latex] добавить в [латекс] н [/ латекс].
Итак, поскольку свойство верно для всех многочленов степени [latex] 0 [/ latex], оно также верно для всех многочленов степени [latex] 1 [/ latex]. И поскольку это верно для всех многочленов степени [latex] 1 [/ latex], это также верно для всех многочленов степени [latex] 2 [/ latex]. В общем, для любого [латекса] n \ in \ mathbb {N} [/ latex] мы сможем сделать вывод, что свойство верно для всех многочленов степени [латекс] n.[/ latex] Таким образом, свойство верно для всех многочленов.
И наоборот, если кратности корней многочлена складываются с его степенью, и если его степень не меньше [latex] 1 [/ latex] (т.е. она не постоянна), то из этого следует, что он имеет хотя бы один ноль. .
Таким образом, альтернативная формулировка фундаментальной теоремы алгебры:
Кратности комплексных корней ненулевого многочлена с комплексными коэффициентами добавляют к степени указанного многочлена.2 [/ latex], мы получаем еще один действительный многочлен, для которого снова применима теорема о комплексном сопряженном корне. Таким образом, мы видим, что общая кратность невещественных комплексных корней многочлена с действительными коэффициентами всегда должна быть четной .
Это последнее замечание, вместе с альтернативным утверждением основной теоремы алгебры, говорит нам, что четность действительных корней (с учетом кратности) многочлена с действительными коэффициентами должна быть такой же, как четность степени указанного многочлена. .Следовательно, многочлен четной степени допускает четное число действительных корней, а многочлен нечетной степени допускает нечетное число действительных корней (считая с кратностью). В частности, каждый многочлен нечетной степени с действительными коэффициентами допускает хотя бы один действительный корень. [латекс] [/ латекс]
Нахождение многочленов с заданными нулями
Чтобы построить многочлен из заданных нулей, установите [latex] x [/ latex] равным каждому нулю, переместите все в одну сторону, затем умножьте каждое полученное уравнение.3 [/ латекс].
Каждый заданный ноль в конечном итоге будет одним членом факторизованного полинома. Найдя все разложенные на множители члены, просто перемножьте их вместе, чтобы получить полином целиком.
Поскольку многочлен и многочлен, умноженный на константу, имеют одинаковые корни, каждый раз, когда многочлен строится из заданных нулей, общее решение включает константу, обозначенную здесь как [latex] c [/ latex]. 0 [/ латекс].Важно отметить, что поскольку все показатели положительные, невозможно разделить на [латекс] х [/ латекс].
ноль : Также известный как корень, ноль — это значение [latex] x [/ latex], при котором функция [latex] x [/ latex] равна [latex] 0 [/ latex].

Задача одного типа — построить полином из заданных нулей. Это можно решить, используя свойство, что если [latex] x_0 [/ latex] является нулем многочлена, то [latex] (x-x_0) [/ latex] является делителем этого многочлена, и наоборот.

Мы предполагаем, что постановка задачи следующая: нам даны нули. Если не указано, какова кратность нулей, мы хотим, чтобы нули имели кратность один. Других нулей нет, т.е. если число не упомянуто в постановке задачи, оно не может быть нулем найденного нами многочлена.

Степень полинома

Помните, что степень полинома, наивысший показатель степени, определяет максимальное количество корней, которое он может иметь. Таким образом, степень многочлена с заданным числом корней равна или больше числа заданных корней.Если в этом числе мы уже посчитали кратность, то степень равна количеству корней. Например, если нам даны два нуля, то нужно построить многочлен второй степени.

Решение и константы

Если [latex] x_1, x_2, \ ldots x_n [/ latex] — это нули [latex] f (x) [/ latex], а ведущий коэффициент [latex] f (x) [/ latex]] равен [latex] ] 1 [/ latex], тогда [latex] f (x) [/ latex] разлагается на

[латекс] f (x) = (x-x_1) (x-x_2) \ cdots (x-x_n) [/ латекс]

Это уже дает нам решение нашей проблемы: ответ на наш вопрос — это просто произведение всех факторов [латекс] (x-x_i) [/ latex], где [latex] x_i [/ latex] — это заданные нули. ! Однако мы видим, что этот многочлен не единственный:

Для любой ненулевой константы [latex] a [/ latex], мы имеем, что [latex] (af) (x) = af (x) [/ latex] разлагается как

[латекс] af (x) = a (x-x_1) (x-x_2) \ cdots (x-x_n) [/ латекс]

Таким образом, если мы найдем решение [latex] g (x) [/ latex] для нашей проблемы, мы фактически найдем бесконечно много решений [latex] cg (x) [/ latex], по одному для каждого ненулевого числа [latex ] c [/ латекс].2 + 2cx [/ латекс]

На рисунке ниже синий график представляет решение для [latex] c [/ latex], равное [latex] 1 [/ latex]. Красный график представляет решение для [latex] c [/ latex], равное [latex] -1/2 [/ latex].

Пример: Два многочлена с одинаковыми нулями: Оба [latex] f (x) [/ latex] и [latex] g (x) [/ latex] имеют нули [latex] 0, 1 [/ latex] и [ латекс] 2 [/ латекс]. Они равны с точностью до константы. Изменение значения и знака константы не меняет нулей, так как ноль, умноженный на любую константу, по-прежнему равен нулю.

Нахождение нулей факторизованных многочленов

Факторизованная форма многочлена показывает его нули, которые определяются как точки, в которых функция касается оси [latex] x [/ latex].

Цели обучения

Используйте факторизованную форму многочлена, чтобы найти его нули

Основные выводы

Ключевые моменты

Полиномиальная функция может иметь ноль, один или несколько нулей.
Все полиномиальные функции положительного нечетного порядка имеют по крайней мере один нуль, в то время как полиномиальные функции положительного четного порядка могут не иметь нуля.
Независимо от четности или нечетности, любой многочлен положительного порядка может иметь максимальное количество нулей, равное его порядку.

Ключевые термины

ноль : Также известный как корень, ноль — это значение [latex] x [/ latex], при котором функция [latex] x [/ latex] равна [latex] 0 [/ latex].

Факторизованная форма многочлена может показать, где функция пересекает ось [latex] x [/ latex]. Значение [latex] x [/ latex], при котором это происходит, называется «нулем» или «корнем».

Число нулей полинома

Рассмотрим факторизованную функцию:

[латекс] f (x) = (x-a_1) (x-a_2)… (x-a_n) [/ latex]

Каждое значение [латекс] a_1, a_2 [/ latex] и т. Д. Равно нулю.

Полиномиальная функция может иметь много нулей, один или не иметь нулей. 2 — 5x — 6 = (x + 3) (x + 1) (x-2).[/ latex] Мы видим, что его корни равны отрицательным вторым коэффициентам его первой степени факторов

Факторинг и нули

В общем, мы знаем из теоремы об остатке, что [latex] a [/ latex] является нулем [latex] f (x) [/ latex] тогда и только тогда, когда [latex] xa [/ latex] делит [латекс] f (x). [/ latex] Таким образом, если мы можем разложить [latex] f (x) [/ latex] на многочлены настолько малой степени, насколько это возможно, мы узнаем его нули, посмотрев на все линейные члены в факторизации. Вот почему факторизация так важна: возможность быстро распознавать нули многочлена.

Из основной теоремы алгебры и факта, называемого теоремой о комплексном сопряженном корне, следует, что каждый многочлен с действительными коэффициентами может быть разложен на линейные многочлены и квадратичные многочлены без действительных корней. Таким образом, если вы нашли такую факторизацию данной функции, вы можете быть полностью уверены, каковы нули этой функции.

Целочисленные коэффициенты и теорема о рациональных нулях

Каждое решение многочлена, выраженного как [latex] x = \ frac {p} {q} [/ latex], должно удовлетворять тому, что [latex] p [/ latex] и [latex] q [/ latex] являются целочисленными множителями. of [latex] a_0 [/ latex] и [latex] a_n [/ latex] соответственно.{n-1} +… + a_0 = 0 [/ latex] с целыми коэффициентами.

Если [latex] a_0 [/ latex] и [latex] a_n [/ latex] не равны нулю, то каждое рациональное решение [latex] x [/ latex], записанное в виде дроби [латекс] x = \ frac { p} {q} [/ latex] в наименьших терминах (т.е. наибольший общий делитель [latex] p [/ latex] и [latex] q [/ latex] равен [latex] 1 [/ latex]), удовлетворяет следующее: [латекс] 1 [/ латекс]) [латекс] p [/ латекс] является целочисленным множителем постоянного члена [латекс] a_0 [/ латекс] и [латекс] 2 [/ латекс]) [латекс] q [/ latex] — это целочисленный коэффициент ведущего коэффициента [latex] a_n [/ latex].

Ключевые термины

Лемма Евклида : Одно из фундаментальных свойств простых чисел. Утверждает, что если простое число делит произведение двух чисел, оно должно делить хотя бы один из множителей. Например, поскольку 133 × 143 = 19019 делится на 19, одно или оба числа 133 или 143 также должны делиться. Фактически, 19 × 7 = 133. Оно используется при доказательстве основной теоремы арифметики.

coprime : Отсутствие положительных целых множителей, кроме [latex] 1 [/ latex], общих с одним или несколькими заданными другими положительными целыми числами.{n-1} +… + a_0 = 0 [/ latex]
С целыми коэффициентами [латекс] a_n, a_ {n-1}, \ ldots, a_0. [/ Latex]
Если [latex] a_0 [/ latex] и [latex] a_n [/ latex] не равны нулю, то каждое рациональное решение [latex] x = \ frac {p} {q} [/ latex], где [latex] p [ / latex] и [latex] q [/ latex] являются взаимно простыми целыми числами (т.е. их наибольший общий делитель равен [latex] 1 [/ latex]), удовлетворяет:
[латекс] п [/ латекс] является делителем постоянного члена [латекс] а_0 [/ латекс] _.
[latex] q [/ latex] — делитель ведущего коэффициента [latex] a_n [/ latex].
Итак, [latex] a_0 [/ latex] должен быть кратным [latex] p [/ latex], а [latex] a_n [/ latex] должен быть кратным [latex] q [/ latex].
Поскольку у любого целого числа есть только конечное число делителей, теорема о рациональном корне дает нам конечное число кандидатов на место рациональных корней. Получив многочлен с целыми коэффициентами, мы можем подключить всех этих кандидатов и посмотреть, являются ли они нулем данного многочлена. Как только мы нашли все рациональные нули (и посчитали их кратность, например, делением с использованием длинного деления), мы узнаем количество иррациональных и комплексных корней.2 + 5x-2 [/ latex] имеет один реальный корень между [latex] 0 [/ latex] и [latex] 1 [/ latex]. Мы можем использовать Rational Root Test, чтобы проверить, является ли этот корень рациональным.
то есть его числитель должен делить [латекс] 2 [/ латекс], а его знаменатель должен делить [латекс] 3 [/ латекс]. Это дает список возможных ответов
[латекс] 1, -1,2, -2, \ frac 13, — \ frac 13, \ frac 23, — \ frac 23 [/ латекс]
Эти корневые кандидаты можно проверить, подключив их напрямую или разделив и проверив, есть ли остаток, например, с помощью деления в столбик.Преимущество этого состоит в том, что как только мы нашли корень, мы сразу же нашли полином меньшей степени, для которого мы снова хотим найти корни, и теорема о рациональном корне предоставит нам еще меньше кандидатов на этот корень. Более того, как только мы установили корень, мы все равно должны использовать деление, чтобы проверить, является ли он множественным корнем.
Минус в том, что приходится чаще использовать длинное деление. Когда есть много нулевых кандидатов для полинома малой степени, мы можем просто включить кандидатов и использовать деление только тогда, когда мы нашли корень.k [/ latex] для всех положительных целых чисел [latex] k [/ latex], мы можем заменить [latex] x [/ latex] на [latex] t + x_0 [/ latex], чтобы найти многочлен с тем же старшим коэффициентом, что и наш исходный многочлен и постоянный член, равный значению многочлена в [latex] x_0 [/ latex]. В этом случае мы заменяем [latex] x [/ latex] на [latex] t + 1 [/ latex] и получаем многочлен от [latex] t [/ latex] с ведущим коэффициентом [latex] 3 [/ latex] и константой термин [латекс] 1 [/ латекс]. Таким образом, кандидатами на нули в этом многочлене от [latex] t [/ latex] являются
[латекс] t = \ pm \ frac 1 {1,3} [/ латекс]
Таким образом, кандидаты в корни многочлена в [latex] x [/ latex] должны быть на единицу больше, чем один из этих кандидатов:
[латекс] x = 1 + t = 2,0, \ frac 43, \ frac 23 [/ латекс]
Корневые кандидаты, которых нет в обоих списках, исключаются.Таким образом, список рациональных корневых кандидатов сократился до [latex] x = 2 [/ latex] и [latex] x = 2/3 [/ latex]. После проверки этих кандидатов мы видим, что единственный рациональный корень (с кратностью [latex] 1) [/ latex] — это [latex] 2/3 [/ latex], что также можно увидеть на графике выше.
Правило знаков
Правило знаков дает верхнюю границу количества положительных или отрицательных корней многочлена.
Цели обучения
Используйте правило знаков, чтобы определить максимальное количество положительных и отрицательных корней многочлена
Основные выводы
Ключевые моменты
Правило знаков дает нам верхнюю границу положительных или отрицательных корней многочлена.Это не полный критерий, то есть он не указывает точное количество положительных или отрицательных корней.
Правило гласит, что если члены многочлена с действительными коэффициентами упорядочены по убывающей переменной экспоненты, то количество положительных корней многочлена либо равно количеству разницы знаков между последовательными ненулевыми коэффициентами, либо меньше на несколько из 2.
Как следствие правила, количество отрицательных корней — это количество изменений знака после умножения коэффициентов членов с нечетной степенью на [латекс] -1 [/ латекс] или меньше на кратное 2.
Ключевые термины
знак : положительная или отрицательная полярность. 4 [/ латекс]).Как только вы их найдете, умножьте каждый на [latex] -1 [/ latex]. Затем процедура такая же; подсчитать количество изменений знака между последовательными ненулевыми коэффициентами. Это число или любое число, кратное 2, может быть вашим числом отрицательных корней. Снова важно отметить, что несколько корней одного и того же значения следует подсчитывать отдельно.
Это также можно сделать, взяв функцию [latex] f (x) [/ latex] и заменив [latex] x [/ latex] на [latex] -x [/ latex], чтобы получить функция [латекс] f (-x) [/ латекс].2-х-1 [/ латекс]
Эта функция имеет одно изменение знака между вторым и третьим членами. Следовательно, он имеет ровно один положительный корень. Не забывайте, что у первого члена есть знак, который в данном случае положительный.
Далее мы переходим к поиску отрицательных корней. Измените экспоненты коэффициентов с нечетной степенью, не забывая менять знак первого члена. Как только вы это сделали, вы получили второй многочлен и готовы найти количество отрицательных корней.2 + x-1 [/ латекс]
Знак этого многочлена меняется дважды после первого и третьего слагаемых. Следовательно, мы знаем, что он имеет не более двух отрицательных корней. Мы знаем, что количество корней любого знака равно количеству смен знака или кратному на два меньше этого числа. Итак, этот многочлен имеет отрицательные корни [latex] 2 [/ latex] или [latex] 0 [/ latex]. Мы можем проверить это алгебраически, как показано ниже.
Сначала разложите многочлен на множители:
[латекс] f (x) = (x + 1) (x + 1) (x-1) [/ латекс].2 + б [/ латекс]
Чтобы найти положительные корни, мы подсчитываем смену знака. В этом примере мы предположим, что [latex] b> 0 [/ latex]. Поскольку нет смены знака, нет положительных корней [латекс] (p = 0) [/ latex]. Теперь ищем отрицательные корни. Поскольку нечетные коэффициенты мощности отсутствуют, перед поиском изменений знака не нужно вносить никаких изменений; следовательно, нет отрицательных корней [латекс] (q = 0) [/ латекс]. Теперь применим уравнение комплексного корня: [латекс] n — (p + q) = 2 — (0 + 0) = 2 [/ latex].Есть 2 сложных корня.
Как решать полиномиальные уравнения
Как решать полиномиальные уравнения
Авторские права © 20022020 Стэн Браун
Резюме:
В алгебре вы тратите много времени на решение многочлена
уравнения или факторизации многочленов (что одно и то же).
Было бы легко потеряться во всех техниках, но эта статья
связывает их все вместе в единое целое.
Генеральный план
Убедитесь, что вас не смущает терминология.Все это
то же:
Решение полиномиального уравнения p ( x ) = 0
Нахождение корней полиномиального уравнения p ( x ) = 0
Нахождение нулей полиномиальной функции p ( x )
Факторизация полиномиальной функции p ( x )
Есть коэффициент для каждого корня, и наоборот.
( x — r ) является фактором тогда и только тогда, когда r является корнем.Это
Теорема о факторах : поиск корней или факторов
по сути то же самое. (Основное различие заключается в том, как вы относитесь к
постоянный коэффициент.)
Точное или Приблизительное?
Чаще всего, когда мы говорим о решении уравнения или факторизации
под полиномом подразумевается точное (или аналитическое) решение . В
другой тип, приблизительное (или числовое) решение ,
всегда возможно, а иногда и единственная возможность.
Когда найдешь, точное решение лучше .Вы всегда можете найти численное приближение к точному решению,
но пойти другим путем гораздо труднее. Эта страница тратит больше всего
своего времени на методы точных решений, но также расскажет, что нужно
делать, когда аналитические методы терпят неудачу.
Шаг за шагом
Как найти множители или нули многочлена (или корни
полиномиального уравнения)? По сути, вам сточить . Каждый раз
вы вычеркиваете множитель или корень из многочлена, у вас остается
полином на одну степень проще.Используйте этот новый уменьшенный
полином, чтобы найти оставшиеся факторы или корни.
На любом этапе процедуры, если вы попадете в
кубическое или четвертое уравнение (степень 3 или 4), у вас есть выбор
продолжения факторинга или использования
кубические или четвертичные формулы. Этих формул много
работы, поэтому большинство людей предпочитают продолжать факторинг.
Следуйте этой процедуре шаг за шагом:
При решении уравнения запишите его в стандартную форму с 0
с одной стороны и упрощают .[ подробности ]
Знайте , сколько корней ожидать.
[ подробности ]
Если у вас есть линейное или квадратное уравнение
(степень 1 или 2), решите осмотром или по формуле корней квадратного уравнения.
[ подробности ]

Затем переходите к шагу 7.
Найдите один рациональный фактор или корень. Это самая сложная часть,
но есть много методов, которые могут вам помочь.
[ подробности ]

Если вы можете найти фактор или корень, перейдите к шагу 5 ниже; если
не можете, переходите к шагу 6.
Разделите на множитель . Это оставляет вас с новым
приведенный многочлен , степень которого на 1 меньше.
[ подробности ]

Для остальной части задачи вы будете работать с сокращенным
многочлен, а не оригинал. Продолжайте с шага 3.
Если вы не можете найти множитель или корень , обратитесь к
численные методы.
[ подробности ]

Затем переходите к шагу 7.
Если нужно было решить это уравнение, запишите корни .
Если это был многочлен для разложения на множители, запишите его в факторизованной форме ,
включая любые постоянные факторы, которые вы вывели на шаге 1.
Это пример алгоритма , набор шагов
что приведет к желаемому результату за конечное количество операций.
Это итеративная стратегия , потому что средние шаги
повторять столько, сколько необходимо.
Кубические и четвертые формулы
Приведенные здесь методы находят рациональный корень и
использовать синтетическое деление проще всего.
Но если вы не можете найти рациональный корень, есть специальные методы для
кубические уравнения (степень 3) и
уравнения четвертой степени (степень 4), оба в Mathworld.Альтернативный подход предоставляется
Дик Никаллс в PDF для
кубический
а также
четвертичная
уравнения.
Шаг 1. Стандартная форма и упрощение
К сожалению, это легко не заметить.
Если у вас есть полиномиальное уравнение , отложите все члены в одну сторону
и 0 с другой.
И будь то проблема факторизации или уравнение, которое нужно решить, положите
ваш многочлен в стандартной форме от до наименьшей степени .
Например, вы не можете решить это уравнение в такой форме:
x + 6 x + 12 x = −8
Вы должны изменить его на эту форму:
x + 6 x + 12 x + 8 = 0
Также убедитесь, что вы упростили, исключив любые
общие факторы .Это может включать в себя вычитание −1
так что наивысшая степень имеет положительный коэффициент. Пример: коэффициент
7-6 x -15 x —
2 х
начнем с его стандартной формы:
−2 x -15 x -6 x + 7
, а затем вычтите −1
— (2 x + 15 x + 6 x -7)
или же
(−1) (2 x + 15 x + 6 x -7)
Если вы решаете уравнение, вы можете выбросить любой
общий постоянный множитель.Но если вы факторизуете многочлен, вы должны
сохранить общий множитель .
Пример: решить
8 x + 16 x + 8 = 0, вы можете
разделите левую и правую на общий множитель 8. Уравнение
х + 2 х + 1 = 0
имеет те же корни, что и исходное уравнение .
Пример: Фактор
8 x + 16 x + 8, вы узнаете
общий множитель 8 и перепишем многочлен в виде
8 ( x + 2 x + 1), что является
идентичен исходному многочлену .(Хотя это правда, что вы
сосредоточит ваши дальнейшие усилия по факторингу на
x + 2 x + 1, это будет ошибкой
написать, что исходный многочлен равен
х + 2 х + 1.)
Ваш общий фактор может быть
дробь, потому что вы должны вычесть любые дроби, чтобы
многочлен имеет целочисленных коэффициентов .
Пример: решить
(1/3) x + (3/4) x — (1/2) x + 5/6 = 0,
вы узнаете общий множитель 1/12 и разделите обе стороны на 1/12.Это точно так же, как распознавание и умножение на
наименьший общий знаменатель из 12. В любом случае вы получите
4 x + 9 x — 6 x + 10 = 0,
которое имеет те же корни, что и исходное уравнение .
Пример: Фактор
(1/3) x + (3/4) x — (1/2) x + 5/6,
вы узнаете общий множитель 1/12 (или наименьший общий
знаменатель 12) и вычитаем 1/12. Ты получаешь
(1/12) (4 x + 9 x -6 x + 10),
что идентично исходному многочлену .
Шаг 2. Сколько корней?
Многочлен степени n будет иметь n корня, некоторые из которых могут быть
множественные корни.
Как узнать, что это правда? В
Фундаментальная теорема алгебры говорит вам, что многочлен
имеет хотя бы один корень. Теорема о множителях говорит вам, что если r
является корнем, тогда ( x — r ) является множителем. Но если разделить многочлен
степени n на множитель ( x — r ), степень которого равна 1, вы получите
многочлен степени n −1.Неоднократно применяя Фундаментальный
Теорема и теорема о множителях дают вам n корней и n факторов.
Правило знаков Декарта
Правило знаков Декарта может сказать вам , сколько положительных значений и
сколько отрицательных действительных нулей многочлен. Это
большое трудосберегающее устройство, особенно когда вы решаете, какой
возможные рациональные корни, которые нужно искать.
Чтобы применить Правило знаков Декарта, вам необходимо понимать термин
изменение знака .Когда многочлен расположен в
стандартная форма, вариант
знак возникает, когда знак коэффициента отличается от знака
предыдущего коэффициента. (Нулевой коэффициент игнорируется.) Для
пример,
p ( x ) = x ⁵ —
2 x ³ + 2 x ² — 3 x + 12
имеет четыре варианта знака.
Правило знаков Декарта:
Число положительных корней из p ( x ) = 0 либо равно
количество вариаций знака p ( x ), или меньше, чем на четное
номер.
Число отрицательных корней из p ( x ) = 0 либо равно
количество вариаций знака p (- x ), или меньше, чем на четное
номер.
Пример: рассмотрим p ( x ) выше. Поскольку у него четыре варианта
в знаке должно быть либо четыре положительных корня, либо два положительных корня,
или нет положительных корней.
Теперь сформируйте p (- x ), заменив x на (- x ) в
выше:
p (- x ) = (- x ) ⁵ — 2 (- x ) ³ + 2 (- x ) ² — 3 (- x ) + 12
p (- x ) = — x ⁵ + 2 x ³ + 2 x ² + 3 x + 12
p (- x ) имеет один вариант знака, поэтому
исходный p ( x ) имеет один минус
корень.Поскольку вы знаете, что p ( x ) должен иметь отрицательный корень, но он может
или может не иметь положительных корней, сначала ищите отрицательные
корнеплоды.
p ( x ) — полином пятой степени, поэтому он должен иметь пять нулей.
Поскольку x не является множителем, вы знаете, что x = 0 не является
нуль полинома. (Для полинома с действительными коэффициентами, например
в этом случае комплексные корни встречаются парами.)
Следовательно, есть три возможности:
количество нулей
, которые являются
положительными отрицательными сложными
не реальными
первой возможностью 4 1 2 1 2
третий вариант 0 1 4
Сложные корни
Если полином имеет действительных коэффициентов , то либо все
корни настоящие или есть
четное число не действительных комплексных корней в сопряженных парах .
Например, если 5 + 2i является нулем многочлена с вещественными
коэффициентов, то 5−2i также должен быть нулем этого многочлена.
Также верно и то, что если ( x −5−2i) множитель, то
( x −5 + 2i) также является фактором.
Почему это правда? Потому что, когда у вас есть фактор с воображаемым
часть и умножьте ее на комплексное сопряжение, вы получите реальную
результат:
( x −5−2i) ( x −5 + 2i) =
x −10 x + 25−4i =
х −10 х +29
Если ( x −5−2i) было фактором, но
( x −5 + 2i) не было, тогда многочлен будет иметь
воображение в его коэффициентах, независимо от других факторов
возможно.Если многочлен имеет только действительные
коэффициентов, то любые комплексные корни должны входить в сопряженные пары.
Иррациональные корни
По аналогичным причинам, если многочлен имеет
рациональных коэффициентов то иррациональные корни, включающие
квадратный
корни встречаются (если вообще встречаются) в сопряженных парах.
Если ( x −2 + √3) является множителем многочлена с рациональными
коэффициентов, то ( x −2 − √3) также должно быть
фактор. Чтобы понять почему, вспомните, как вы рационализируете бином.
знаменатель; или просто проверьте, что происходит, когда вы умножаете эти два
факторы.(1/3) и два
сложные корни.
Интересная проблема, есть ли иррациональность
с четными корнями порядка ≥4 также должны встречаться в сопряженных
пары. У меня нет немедленного ответа. Я работаю над
пруф, как я успеваю.
Множественные корни
Когда данный множитель ( x — r ) встречается m раз в полиноме, r равно
называется кратным корнем или корнем кратности м .
Если кратность m — четное число, график касается
Ось x при x = r , но не пересекает ее.
Если кратность m — нечетное число, график пересекает
Ось x при x = r . Если кратность 3, 5, 7 и т. Д., График
горизонтально в точке пересечения оси.
Примеры: сравните эти два многочлена и их графики:
f ( x ) =
( x −1) ( x −4) ² =
x ³ — 9 x ² +
24 х -16
г ( x ) =
( x −1) ³ ( x −4) ² =
x ⁵-11 x ⁴ + 43 x ³
— 73 x ² + 56 x — 16
Эти многочлены имеют одинаковые нули, но корень 1 встречается
с разной кратностью.Посмотрите на графики:
Оба полинома имеют нули только в точках 1 и 4. f ( x ) имеет степень 3,
что означает три корня. Вы видите из факторов, что 1 является корнем
кратность 1 и 4 является корнем из кратности 2. Следовательно, граф
пересекает ось в точке x = 1 (но не горизонтально там) и касается в точке
x = 4 без пересечения.
Напротив, g ( x ) имеет степень 5. ( g ( x ) = f ( x ) раз
( x −1) ².) Из пяти корней 1 встречается с
кратность 3: график пересекает ось при x = 1 и является горизонтальным
там; 4 встречается с кратностью 2, и график касается
ось при x = 4 без пересечения.
Шаг 3. Квадратичные множители
Когда у вас есть квадратичные множители (Ax + Bx + C), он может или не может
можно будет их дополнительно проанализировать.
Иногда вы можете просто увидеть факторы, как в случае с
x — x −6 = ( x +2) ( x −3).В других случаях не так очевидно,
квадратичный можно разложить на множители. Вот тогда квадратная формула
(показан справа) ваш друг.
Например, предположим, что у вас есть коэффициент
12 x — x −35. Можно ли это еще раз проанализировать? Судом и
ошибка вам придется перепробовать много комбинаций! Вместо этого используйте факт
что коэффициенты соответствуют корням , и примените формулу к
найти корни из 12 x — x −35 = 0, например:
x = [- (- 1) √1 — 4 (12) (- 35)] / 2 (12)
x = [1 √1681] / 24
√1681 = 41, следовательно,
x = [1 41] / 24
x = 42/24 или -40/24
x = 7/4 или -5/3
Если 7/4 и −5/3 — корни, то ( x −7/4) и ( x +5/3)
факторы.Следовательно,
12 x — x −35 =
(4 x −7) (3 x +5)
А как насчет x −5 x +7? Этот выглядит как лучший,
но как ты можешь быть уверен? Снова примените формулу:
x = [- (- 5) √25 — 4 (1) (7)] / 2 (1)
x = [5 √ − 3] / 2
Что с этим делать, зависит от исходной проблемы. Если это
должен был разложить на множители реалы, тогда x −5 x +7 простое число.Но если
этот фактор был частью уравнения, и вы должны были найти все
сложные корни, у вас их два:
x = 5/2 + (√3 / 2) i, x = 5/2 — (√3 / 2) i
Поскольку исходное уравнение имело действительные коэффициенты, эти
сложные корни встречаются в сопряженной паре.
Шаг 4. Найдите один фактор или корень
Этот шаг является сердцем факторизации многочлена или решения
полиномиальное уравнение. Есть много методов, которые могут вам помочь
найти фактор.
Иногда можно найти факторы путем осмотра (см. Первые два
следующие разделы). Это отличный способ быстрого доступа, поэтому проверьте
легкие факторы, прежде чем начинать более напряженные
методы.
Мономиальные множители
Всегда начинайте с поиска любых мономиальных множителей, которые вы видите. Например,
если ваша функция
f ( x ) = 4 x ⁶ + 12 x ⁵ + 12 x ⁴ + 4 x ³
, вы должны немедленно разложить его на
f ( x ) = 4 x ³ ( x ³ + 3 x ² + 3 x + 1)
Получение числа 4 упрощает оставшиеся числа,
x ³ дает вам корень x = 0 (с кратностью
3), и теперь у вас есть только кубический многочлен (степени 3) вместо
sextic (степень 6).Фактически, теперь вы должны распознать эту кубику как
особый продукт, идеальный куб
( x +1) ³.
Когда вы вычитаете множитель общей переменной, убедитесь, что вы
помните об этом в конце, когда перечисляете фактор или корни.
x +3 x +3 x +1 = 0 имеет определенные корни, но
x ( x +3 x +3 x +1) = 0 имеет те же корни и
также корень при x = 0 (с кратностью 3).
Особые продукты
Будьте внимательны к применению специальных продуктов .Если вы сможете применить их, ваша задача станет намного проще. Специальный
Продукты:
полный квадрат (2 формы): A 2 A B + B = ( A B )
сумма квадратов: A + B не может быть разложена на множители на действительные числа, как правило (для исключительных случаев см. Как разложить на множители сумму квадратов)
разность квадратов: A — B = ( A + B ) ( A — B )
идеальный куб (2 формы): A 3 A B + 3 A B B = ( A B )
сумма кубов: A + B = ( A + B ) ( A — A B + B )
разность кубов: A — B = ( A — B ) ( A + A B + B )
Выражения для суммы или разности двух кубов имеют вид
хотя они должны учитывать дополнительные факторы, но они этого не делают. A A B + B является простым над реалами.
Рассмотрим
p ( x ) = 27 x — 64
Вы должны узнать это как
p ( x ) = (3 x ) — 4
Вы умеете множить разницу двух кубов:
p ( x ) = (3 x −4) (9 x +12 x +16)
Бинго! Как только вы дойдете до квадратичной, вы можете применить
Квадратичная формула, и все готово.
Вот другой пример:
q ( x ) = x ⁶ + 16 x ³ + 64
Это просто полный квадрат трехчлена, но вместо этого в x ³
из x . Вы учитываете это точно так же:
q ( x ) = ( x ³) ² + 2 (8) ( x ³) + 8 ²
q ( x ) = ( x ³ + 8) ²
И вы можете легко разложить ( x ³ +8) ² как
( x +2) ² ( x ² −2 x +4) ².
Рациональные корни
Предполагая, что вы уже учли легкое
мономиальные факторы и
специальные продукты, что вы будете делать, если
у вас все еще есть многочлен степени 3 или выше?
Ответ — Rational Root Test .
Он может показать вам некоторые корни кандидатов
когда вы не видите, как разложить полином на множители, как показано ниже.
Рассмотрим многочлен стандартной формы, записанный с высшей степени
до самого низкого и всего с целыми коэффициентами :
f ( x ) = a _n x ⁿ +… + a _o
Теорема о рациональном корне говорит вам, что , если
многочлен имеет рациональный нуль
, затем , это должна быть дробь p / q ,
где p — коэффициент конечной константы a _o и
q — множитель старшего коэффициента a _n.
Пример:
p ( x ) = 2 x ⁴ — 11 x ³ — 6 x ² + 64 x + 32
Коэффициенты старшего коэффициента (2) равны 2 и 1.В
коэффициенты постоянного члена (32) равны 1, 2, 4, 8, 16 и 32.
Следовательно, возможные рациональные нули: 1, 2, 4, 8, 16 или
32 разделить на 2 или 1:
любой из 1/2, 1/1, 2/2, 2/1, 4/2, 4/1, 8/2, 8/1, 16/2, 16/1, 32/2, 32/1
уменьшено: любое из, 1, 2, 4, 8, 16, 32
Что мы имеем в виду, когда говорим, что это список всех
возможных рациональных корней ? Мы имеем в виду, что никакое другое рациональное число,
как или 32/7, может быть нулем этого конкретного многочлена.
Внимание : Не делайте Rational Root Test
больше, чем есть.Это не означает, что рациональные числа являются корнями , просто
что никакие другие рациональные числа не могут быть корнями. И это не говорит
вы что-нибудь о том, какие иррациональные или даже сложные корни
существовать. Rational Root Test — это только отправная точка.
Предположим, у вас есть многочлен с нецелыми коэффициентами.
Вы застряли? Нет, вы можете исключить наименее распространенные
знаменатель (LCD) и получите многочлен с целыми коэффициентами, которые
способ. Пример:
(1/2) x — (3/2) x + (2/3) x — 1/2
ЖК-дисплей 1/6.Вынося за скобки 1/6 получаем многочлен
.
(1/6) (3 x — 9 x + 4 x — 3)
Эти две формы эквивалентны, и поэтому имеют одинаковые
корнеплоды. Но вы не можете применить Rational Root Test к первой форме,
только ко второму. Тест говорит вам, что единственно возможное рациональное
корни — любые из 1/3, 1, 3.
После того, как вы определили возможных рациональных нулей, как
вы можете их проверить? Метод грубой силы заключался бы в том, чтобы взять каждый
возможное значение и замените его на x в полиноме: если
результат равен нулю, тогда это число является корнем.Но есть лучше
способ.
Используйте Synthetic Division, чтобы узнать,
кандидат делает полином равным нулю. Это лучше на троих
причины. Во-первых, это проще в вычислительном отношении, потому что вам не нужно
вычислить высшие степени чисел. Во-вторых, в то же время он сообщает
независимо от того, является ли данное число корнем, он производит
сокращенный многочлен , который вы будете использовать, чтобы найти оставшийся
корнеплоды. Наконец, результаты синтетического деления могут дать вам
верхняя или нижняя граница, даже если число
тестирование оказывается не рутом.
Иногда правило знаков Декарта может
поможет вам в дальнейшем выявить возможные рациональные корни. Например,
Rational Root Test сообщает, что если
q ( x ) = 2 x ⁴ + 13 x ³ + 20 x ² + 28 x + 8
имеет какие-либо рациональные корни, они должны происходить из списка
любой из, 1, 2, 4, 8. Но не начинайте с замены или
синтетическое разделение. Поскольку нет изменений знака, нет
положительные корни.Есть ли отрицательные корни?
q (- x ) = 2 x ⁴-13 x ³ + 20 x ²-28 x + 8
имеет четыре смены знака. Следовательно, может быть целых четыре
отрицательные корни. (Также может быть два отрицательных корня или ни одного.)
Нет гарантии, что какой-либо из корней является рациональным, но любой корень
рациональное должно происходить из списка -, −1,
−2, −4, −8.
(Если у вас есть
графического калькулятора, вы можете предварительно просмотреть рациональные корни, построив график
полином и увидеть, где он, кажется, пересекает ось x .Но ты
по-прежнему необходимо проверить корень алгебраически, чтобы увидеть, что f ( x ) равно
ровно 0, а не почти 0.)
Помните, что Rational Root Test гарантирует нахождение всех
рациональных корня. Но он полностью упустит настоящие корни, которых нет.
рациональные, как корни x −2 = 0, которые
√2, или корни из x + 4 = 0, которые равны
2i.
Наконец, помните, что Rational Root Test работает, только если все
коэффициенты — целые числа.Посмотрите еще раз на эту функцию, которая
на графике справа:
p ( x ) = 2 x ⁴ — 11 x ³ — 6 x ² + 64 x + 32
Теорема о рациональном корне говорит вам, что единственно возможный рациональный
нули равны 1, 2, 4, 8, 16, 32. Но предположим, что вы
вычтите 2 (как я когда-то сделал в классе), написав эквивалент
функция
p ( x ) = 2 ( x ⁴ — (11/2) x ³ — 3 x ² + 32 x + 16)
Эта функция аналогична предыдущей, но вы не можете
дольше применять Rational Root Test, потому что коэффициенты не
целые числа.По сути — это ноль р ( х ), но это не так.
появляются, когда я (незаконно) применил Rational Root Test к
вторая форма. Моя ошибка заключалась в том, что я забыл, что применима теорема о рациональном корне.
только когда все коэффициенты многочлена равны
целые числа.
Графические подсказки
Построение графика функции вручную или с помощью графика
Вы можете понять, где находятся корни,
примерно, и сколько существует настоящих корней.
Пример: Если Rational Root Test
говорит вам, что 2 возможных рациональных корня, вы можете посмотреть на
график, чтобы увидеть, пересекает ли он (или касается) оси x в точках 2 или
−2.Если да, используйте синтетическое деление, чтобы
убедитесь, что предполагаемый корень на самом деле является корнем. Да ты всегда
нужно проверить по графику, вы никогда не можете быть уверены
является ли точка пересечения на ваш возможный рациональный корень или
просто рядом с это.
Границы корней
Некоторые методы не сообщают вам конкретное значение корня, но
скорее, что корень существует между двумя значениями или что все корни
меньше определенного числа больше определенного числа. Этот
помогает сузить область поиска.
Теорема о промежуточном значении
Эта теорема говорит вам, что если график многочлена находится выше
ось x для одного значения x и ниже ось x для
другое значение x , оно должно пересекать ось x где-то посередине.
(Если вы можете построить график функции, пересечения
обычно будет очевидным.)
Пример:
p ( x ) = 3 x + 4 x — 20 x −32
Рациональные корни
(если есть) должны быть из списка
любой из 1/3, 2/3, 1, 4/3, 2, 8/3, 4, 16/3, 8, 32/3, 16, 32.Естественно, сначала вы посмотрите на целые числа, потому что арифметика
Полегче. Пробуя синтетическое деление, вы
найти p (1) = −45, p (2) = −22 и
p (4) = 144. Поскольку p (2) и p (4) имеют противоположные знаки, вы
знайте, что график пересекает ось между x = 2 и x = 4, поэтому
хотя бы один корень между этими числами. Другими словами, либо 8/3 — это
корень или корень от 2 до 4 иррациональны. (По факту,
синтетическое деление показывает, что 8/3 — это корень.)
Теорема о промежуточном значении может сказать вам, где находится
root, но он не может сказать вам, где нет root. Например,
считать
q ( x ) = 4 x — 16 x + 15
q (1) и q (3) оба положительные, но это вам не говорит
может ли график касаться или пересекать ось между ними. (Это на самом деле
дважды пересекает ось, при x = 3/2 и
х = 5/2.)
Верхняя и нижняя границы
Одним из побочных эффектов синтетического деления является
что даже если число, которое вы тестируете, окажется не корневым, оно может
сказать вам, что все корни меньше или больше этого
номер:
Если вы выполните синтетическое деление на положительное число a , и каждые
число в нижнем ряду положительное или нулевое, тогда — это
верхняя граница для корней, что означает, что все настоящие корни
≤ — .
Если вы делаете синтетическое деление на
отрицательное число b , а числа в нижнем ряду чередуются
знак, тогда b — это нижняя граница для корней, что означает, что все
действительные корни ≥ b .
Что делать, если нижняя строка содержит нули? Более полный
Утверждение состоит в том, что чередуются неотрицательные и неположительные знаки ,
после синтетического деления на отрицательное число показать нижнюю границу
корень. Следующие два примера поясняют это.
(Кстати, правило для нижних оценок следует
из правила для верхних оценок.
Нижние пределы корней p ( x ) равны верхним пределам
корни p (- x ), и деление на (- x + r ) аналогично
деление на — ( x — r ).)
Пример:
q ( x ) = x ³ + 2 x ² — 3 x — 4
Использование Rational Root
Тест, вы определяете единственные возможные рациональные корни как
4, 2 и 1.Вы решаете попробовать −2 как
возможный корень, и вы тестируете его с синтетическим делением:
-2 | 1 2 -3-4 | -2 0 6 | ------------------ 1 0–3 2
−2 не является корнем уравнения f ( x ) = 0.
В третьей строке чередуются знаки, и вы делили на
отрицательное число; однако этот ноль все портит.
Напомним, что у вас есть нижняя граница, только если знаки в нижнем ряду
чередовать неположительный и неотрицательный.1 положительный
(неотрицательный), и 0 может считаться неположительным, но
−3 не считается неотрицательным. Чередование
битая, а ты не знаешь есть ли корни
меньше -2. (Фактически, графический или
численные методы покажут корень около -2,5.)
Следовательно, вам нужно попробовать наименьший возможный рациональный корень, −4:
.
-4 | 1 2 -3-4 | -4 8-20 | ------------------ 1–2 5–24
Здесь знаки чередуются; поэтому вы знаете, что нет
корни ниже −4.(Остаток −24 показывает, что
−4 сам по себе не является корнем.)
Вот другой пример:
r ( x ) = x + 3 x — 3
Rational Root Test сообщает вам
что возможные рациональные корни — 1 и 3. С синтетическим
деление на −3:
-3 | 1 3 0-3 | -3 0 0 | ------------------ 1 0 0-3
−3 не является корнем, но знаки здесь чередуются, так как
первый 0 считается неположительным, а второй — неотрицательным.Следовательно, −3 — это нижняя граница корней, а это означает, что
уравнение не имеет вещественных корней ниже −3.
Коэффициенты и корни
Существует интересная взаимосвязь между коэффициентами
многочлен и его нули. Я упоминаю об этом в последнюю очередь, потому что это больше подходит
для формирования многочлена, который имеет нули с желаемыми свойствами,
вместо нахождения нулей существующего многочлена. Однако если вы
знать все корни многочлена, кроме одного или двух, вы можете легко использовать это
техника, чтобы найти оставшийся корень.
Рассмотрим многочлен
f ( x ) =
a _n x ⁿ +
а _{n -1} x ^{n -1} +
a _{n −2} x ^{n −2} + … +
а ₂ x ² +
а ₁ x +
а _или
Существуют следующие отношения:
— a _{n −1} a _n = сумма всех корней
+ a _{n − 2} a _n = сумма произведений корней
взято по два за раз
— a _{n −3} a _n = сумма произведений корней
взято по три за раз
и так далее, пока
(-1) ⁿ a ₀ a _n = произведение всех корней
Пример: f ( x ) = x ³ — 6 x ² —
7 x — 8 имеет степень 3 и, следовательно, не более трех действительных нулей.Если
записываем действительные нули как r ₁, r ₂,
r ₃, тогда сумма корней равна
r ₁ + r ₂ + r ₃ = — (- 6) = 6; в
сумма произведений корней, взятых по два за раз, равна
r ₁ r ₂ + r ₁ r ₃ + r ₂ r ₃ =
−7, а произведение корней равно
r ₁ r ₂ r ₃ =
(-1) ³ (-8) = 8.
Пример: Учитывая, что многочлен
г ( x ) = x ⁵-11 x ⁴ + 43 x ³-73 x ² + 56 x -16
имеет тройной корень при x = 1, найдите два других корня.
Решение: Пусть два других корня будут c и d .
Тогда вы знаете, что сумма всех корней равна 1 + 1 + 1 + c + d =
— (- 11) = 11, или c + d = 8.Ты
также знайте, что продукт всех корней
111 c d =
(−1) ⁵ (−16) = 16, или
c d = 16. c + d = 8,
c d = 16; поэтому c = d =
4, поэтому оставшиеся корни представляют собой двойной корень с размером x = 4.
Дополнительные коэффициенты и корни
Есть еще несколько теорем о соотношении
между коэффициентами и корнями.
Статья в Википедии
Свойства корней полиномов
дает хорошее, хотя и несколько краткое резюме.
Шаг 5. Разделите на множитель
Помните, что r является корнем тогда и только тогда, когда x — r является множителем;
это факторная теорема. Так что если ты хочешь
чтобы проверить, является ли r корнем, вы можете разделить многочлен на
x — r и посмотрите, выйдет ли оно четным (остаток от 0).
Элизабет Стапель имеет хороший
пример деления многочленов делением в столбик.
Но делать синтетическое деление проще и быстрее.Если твой
синтетическое деление немного заржавело, вы можете взглянуть на Dr.
Математика короткая
Учебник по синтетическому дивизиону;
если вам нужен более длинный учебник, Элизабет Стапельс
Синтетический дивизион отличный.
(У доктора Мата также есть страница о
почему работает Synthetic Division.)
Синтетическое подразделение также имеет некоторые побочные преимущества. Если вы подозреваете
корень на самом деле является корнем, синтетическое деление дает вам
приведенный многочлен . А иногда и тебе везет, и
синтетическое деление показывает вам верхнюю или нижнюю
связаны на корнях.
Вы можете использовать синтетическое деление при делении на
бином вида x — r для константы r . Если вы делите на
x −3, вы проверяете, является ли 3 корнем, и вы синтетическое деление
на 3 (не на −3). Если вы делите на x +11, вы тестируете
является ли −11 корнем, и вы синтетически делите на −11 (не
11).
Пример:
p ( x ) = 4 x ⁴ — 35 x ² — 9
Вы подозреваете, что x −3 может быть фактором, и проверяете это с помощью
синтетическое деление, например:
3 | 4 0-35 0-9 | 12 36 3 9 | -------------------- 4 12 1 3 0
Поскольку остаток равен 0, вы знаете, что 3 является корнем
p ( x ) = 0, а x −3 является множителем p ( x ).Но ты знаешь
более. Поскольку 3 положительно и нижняя строка синтетического деления
все положительные или нулевые, вы знаете, что все корни
p ( x ) = 0 должно быть ≤ 3. И вы также знаете
что
p ( x ) = ( x −3) (4 x ³ + 12 x ² + x + 3)
4 x ³ + 12 x ² + x + 3
— это приведенный многочлен .Все его факторы также
коэффициентов исходного p ( x ), но его степень на единицу ниже , поэтому его
с ним легче работать.
Шаг 6. Численные методы
Когда у вашего уравнения больше нет рациональных корней (или
многочлен не имеет более рациональных множителей) можно перейти к числовым
методы нахождения приблизительного значения иррациональных корней:
Статья в Википедии
Алгоритм поиска корней
имеет достойное резюме с указателями на конкретные методы.
Многие графические калькуляторы имеют
Команда Root или Zero, которая поможет вам найти
приблизительные корни. Например, на ТИ-83 или ТИ-84 вы
график
функцию, а затем выберите [2nd] [Calc] [zero].
Полный пример
Решить для всех сложных корней:
4 x + 15 x — 36 = 0
Шаг 1. Уравнение уже в стандартной форме, с
только ноль с одной стороны и степень x от наибольшей к наименьшей.Там
нет общих факторов.
Шаг 2. Так как уравнение имеет степень 3, будет 3
корнеплоды. Есть одна вариация знака, а от
Правило знаков Декарта, которое, как вы знаете, должно
быть одним положительным корнем. Изучите многочлен с заменой — x
x :
−4 x -15 x -36
Знаков нет, значит, нет
отрицательные корни. Следовательно, два других корня должны быть сложными,
и конъюгаты друг друга.
Шаги 3 и 4. Возможные рациональные корни
к сожалению, довольно много: любые из 1, 2, 3, 4, 6, 9, 12, 18, 36
делится на любое из 4, 2, 1. (перечислены только положительные корни, потому что вы
уже определили, что для этого нет отрицательных корней
уравнение.) Вы решаете сначала попробовать 1:
1 | 4 0 15 -36 | 4 4 19 | ----------------- 4 4 19-17
1 не является корнем, поэтому вы проверяете 2:
2 | 4 0 15 -36 | 8 16 62 | ----------------- 4 8 31 26
Увы, 2 тоже не рут.Но обратите внимание, что
f (1) = −17 и f (2) = 26. У них противоположные
знаки, что означает, что график пересекает ось x между x = 1
и x = 2, а корень находится между 1 и 2. (В данном случае это единственный
root, поскольку вы определили, что существует один положительный корень и
нет отрицательных корней.)
Единственный возможный рациональный корень между 1 и 2 — 3/2, и
поэтому либо 3/2 является корнем, либо корень иррационален. Вы пытаетесь 3/2
по синтетическому отделению:
3/2 | 4 0 15 -36 | 6 9 36 | ----------------- 4 6 24 0
Ура! 3/2 — это корень.Приведенный полином равен
4 x + 6 x + 24. Другими словами,
(4 x + 15 x — 36)
( х −3/2) =
4 х + 6 х + 24
Приведенный многочлен имеет степень 2,
так что нет необходимости в большем
методом проб и ошибок, и вы переходите к шагу 5.
Шаг 5. Теперь вы должны решить
4 x + 6 x + 24 = 0
Сначала разделите общий множитель 2:
2 x + 3 x + 12 = 0
Нет смысла пытаться множить этот квадратичный коэффициент, потому что
вы определили, используя Правило знаков Декарта, что больше нет
настоящие корни.Итак, вы используете квадратичный
формула:
x = [−3 √9 — 4 (2) (12)] / 2 (2)
x = [−3 √ − 87] / 4
x = −3/4 (√87 / 4) i
Шаг 6. Помните, что вы нашли корень в
более ранний шаг! Полный список корней —
3/2, −3/4 + (√87 / 4) я,
−3/4 — (√87 / 4) я
Что нового
19 окт.

	положительными	отрицательными	сложными не реальными
	количество нулей , которые являются
первой возможностью	4	1		2	1	2
третий вариант	0	1	4

Корень четной и нечетной степени

Квадратный корень в Python 3 — Извлечение кубических и n-ой степени

Способы извлечения корня

Какой метод быстрее?

Квадратный корень

Кубический корень

Корень n-степени

Корень отрицательного числа

Вывод

Определение корня n-ой степени.

%d0%ba%d0%be%d1%80%d0%b5%d0%bd%d1%8c%20n-%d0%b9%20%d1%81%d1%82%d0%b5%d0%bf%d0%b5%d0%bd%d0%b8 — со всех языков на все языки

См. также в других словарях:

Корень степени N

Зачем вообще нужны корни?

Основные свойства и ограничения

Вынесение минуса из-под знака корня

Арифметический корень

Алгебраический корень: для тех, кто хочет знать больше

Корень n-ной степени из действительного числа /qualihelpy

Корень квадратный из числа

второй степени, с нулями — 6-6 и 2, 2, и идет t o — ∞ t o — ∞ при x — ∞ x — ∞

Ким Поттер обвинен в Манслаугтере 2-й степени

Алгебра — нули / корни многочленов

Раздел 5-2: Нули / корни многочленов

Основная теорема алгебры

Факторная теорема

Факт 1

Факт 2

Как найти область определения, диапазон и корни многочленов и рациональных функций

нулей полиномиальных функций | Безграничная алгебра

Основная теорема алгебры

Цели обучения

Основные выводы

Ключевые моменты

Нахождение многочленов с заданными нулями

Степень полинома

Решение и константы

Нахождение нулей факторизованных многочленов

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Число нулей полинома

Факторинг и нули

Целочисленные коэффициенты и теорема о рациональных нулях

Ключевые термины

Правило знаков

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Как решать полиномиальные уравнения

Генеральный план

Точное или Приблизительное?

Шаг за шагом

Кубические и четвертые формулы

Шаг 1. Стандартная форма и упрощение

Шаг 2. Сколько корней?

Правило знаков Декарта

Сложные корни

Иррациональные корни

Множественные корни

Шаг 3. Квадратичные множители

Шаг 4. Найдите один фактор или корень

Мономиальные множители

Особые продукты

Рациональные корни

Графические подсказки

Границы корней

Теорема о промежуточном значении

Верхняя и нижняя границы

Коэффициенты и корни

Дополнительные коэффициенты и корни

Шаг 5. Разделите на множитель

Шаг 6. Численные методы

Полный пример

Что нового

Добавить комментарий Отменить ответ