Содержание
Степень уравнения | Математика
Кроме разделения уравнений по количеству неизвестных, уравнения также разделяются по степеням неизвестных: уравнения первой степени, уравнения второй степени и так далее.
Чтобы определить степень уравнения, в нём нужно предварительно сделать следующие преобразования:
- раскрыть скобки,
- освободить уравнение от дробных членов,
- перенести все неизвестные члены в одну из частей уравнения,
- сделать приведение подобных членов.
После выполнения всех этих преобразований, степень уравнения определяется по следующим правилам:
Степенью уравнения с одним неизвестным называется показатель при неизвестном в том члене уравнения, в котором этот показатель наибольший.
Примеры:
10 — x = 2 — уравнение первой степени с одним неизвестным;
x2 + 7x = 16 — уравнение второй степени с одним неизвестным;
x3 = 8 — уравнение третьей степени с одним неизвестным.
Степенью уравнения с несколькими неизвестными называется сумма показателей при неизвестных в том члене уравнения, в котором эта сумма наибольшая.
Для примера возьмём уравнение
3x2y + xy + 25 = 0.
Для наглядности расставим показатели первой степени (которые обычно не ставят):
3x2y1 + x1y1 + 251 = 0.
Теперь посчитаем суммы показателей для тех членов уравнения, в которых присутствуют неизвестные:
3x2y1 — сумма показателей равна 2 + 1 = 3;
x1y1 — сумма показателей равна 1 + 1 = 2.
Сумма показателей у первого члена уравнения больше, чем у второго, значит, при определении степени уравнения будем ориентироваться на сумму показателей первого члена. Это значит, что про данное уравнение можно сказать, что это уравнение третьей степени с двумя неизвестными.
Примеры:
2xy — x = 25 — уравнение второй степени с двумя неизвестным,
xy2 — 2xy + 8y = 0 — уравнение третьей степени с двумя неизвестными.
Примеры решения показательных уравнений
Примеры решения показательных уравнений
Примеры решения показательных уравнений
Пример №1
1000x=100
Представим левую и правую часть уравнения в виде степени, имеющую одинаковые основания:
103x=102
Теперь, когда основания одинаковые, нужно приравнять показатели степеней.
3x=2
x=2/3
Ответ: x=2/3 .
Главное в показательных уравнениях — свести левую и правую часть уравнения к общему основанию:
Пример №2
(2/5)x=(5/2)4
Представим (2/5)x как (5/2)-x:
(5/2)-x=(5/2)4
Основания одинаковые, следовательно, приравниваем показатели:
-x=4
x=-4
Ответ: x=-4
Пример №3
√3х=9
√3х распишем как 3x/2, а 9 — как 32:
3х/2=32
Приравниваем показатели:
х/2=2
х=4
Ответ: x=4
Пример №4
3х2-х-2=81
Заметим, что 81=34
3х2-х-2=34
Приравниваем показатели:
х2-х-2=4
х2-х-6=0
Получили квадратное уравнение:
D=1+24=25, D>0, следовательно, уравнение имеет два действительных корня
х1=(1+5)/2=3
х2=(1-5)/2=-2
Ответ: х=3 и х=-2
Пример №5
4х+1+4х=320
В таких случаях выносится основание с наименьшим показателем. В данном уравнении наименьшим показателем является х. Вынесем 4х за скобки:
В данном уравнении наименьшим показателем является х. Вынесем 4х за скобки:
4х(4+1)=320
4х*5=320
Представим 320 в виде 5*43, тогда:
4х*5=5*43
Поделим левую и правую часть уравнения на 5:
4х=43
Приравняем показатели:
х=3
Ответ: х=3
Пример №6
7х+2+4*7х-1=347
Степенью с наименьшим показателем в этом уравнении является х-1, следовательно, за скобки выносим 7x-1. Получаем:
7х-1*(73+4)=347
7х-1*347=347
Поделим левую и правую часть уравнения на 347:
7х-1=1
Заметим, что любое число в нулевой степени равно 1. Следовательно, распишем 1 как 70:
7х-1=70
Приравняв показатели, получим:
х-1=0
х=1
Ответ: х=1
Пример №7
4х-5*2х+4=0
Представим 4х как 22х, получим:
22х-5*2х+4=0
Введем подстановку: 2х обозначим переменной t. Cледовательно: 22х=t2. Получим:
Cледовательно: 22х=t2. Получим:
t2-5t+4=0
Найдем корни уравнения по теореме Виета:
t1=1
t2=4
Заменим t на 2х:
2х=1
Заметим, что 20=1
2х=20
Приравняем показатели:
х=0
2х=4
Заметим, что 4=22
2х=22
Приравняем показатели:
х=2
Уравнение имеет два действительных корня 0 и 2.
Ответ: х=0 и х=2
Пример №8
(√2+√3)х + (√2-√3)х=4
Введем подстановку: (√2+√3)х обозначим переменной t. А (√2-√3)х домножим на сопряженные и получим:
((√2+√3)х*(√2-√3)х) / (√2+√3)х = (√4-3)х/(√2+√3)х = 1 x/(2+√3)x = 1/(2+√3)x
Следовательно, 1/(√2+√3)х=1/t.
Получаем:
t+1/t=4
Отметим, что t=0, т.к. деление на 0 не определено. Домножим левую и правую часть на t:
t2+1=4t
t2-4t+1=0
Решим квадратное уравнение:
D=16-4=12, D>0, следовательно, уравнение имеет два действительных корня
t1=(4-2√3)/2=2-√3
t2=(4+2√3)/2=2+√3
Заменим t на (√2+√3)х:
(√2-√3)х=2+√3
Домножим 2+√3 на сопряженные и получим:
1/(2-√3)=2+√3
Cледовательно:
(√2-√3)х=1/2-√3
Заметим, что 1/2-√3=(√2-√3)-2
(√2+√3)х=(√2-√3)-2
Приравняв показатели, получим:
х=-2
Заменим t на 2+√3
(√2+√3)х=2+√3
Заметим, что 2+√3=(√2+√3)2
Приравняв показатели, получим:
х=2
Ответ: х=-2 и х=2
Пример №9
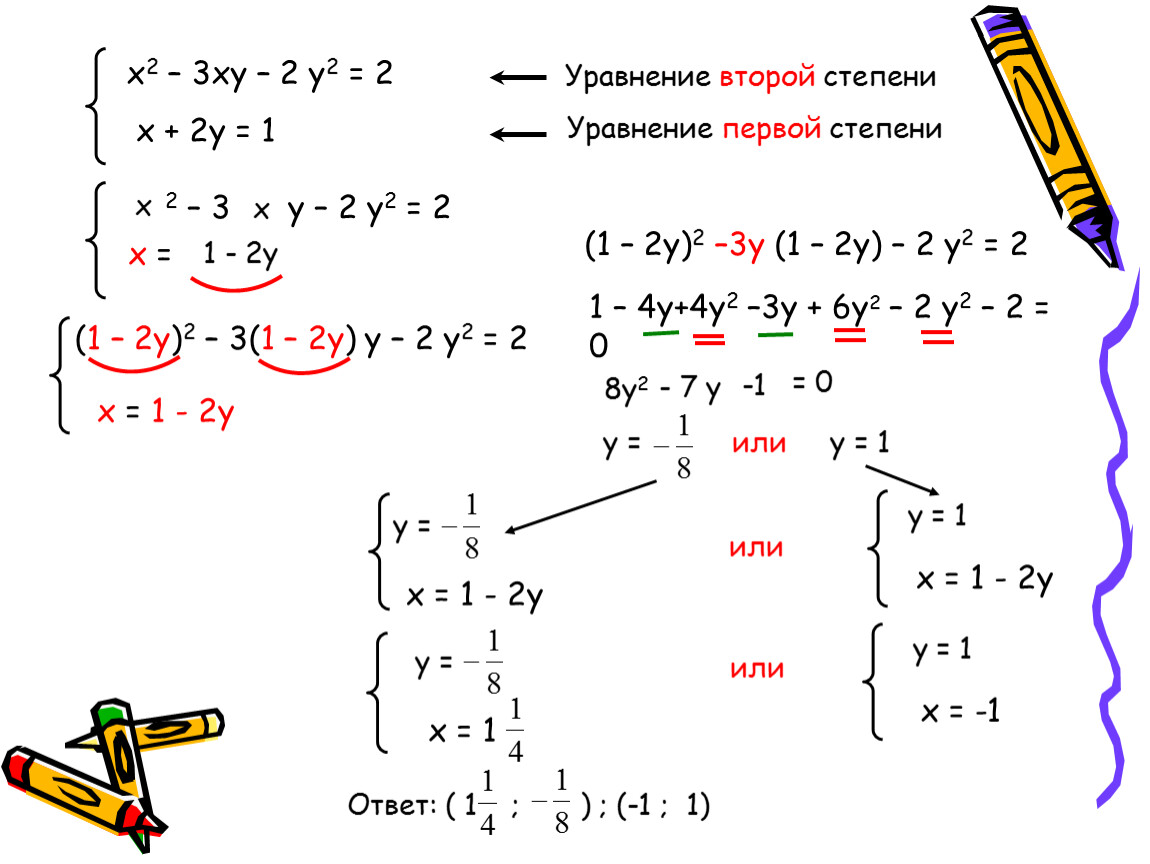
x+y=6
xy2+7y+12=1
Выразим x:
x=6-y
xy2+7y+12=1
Заметим, что x0=1:
x=6-y
xy2+7y+12=x0
Приравним показатели:
x=6-y
y2+7y+12=0
Решим отдельно квадратное уравнение:
y2+7y+12=0
D=49-48=1, D>0, следовательно, уравнение имеет два действительных корня
y1=(-7+1)=-3
y2=(-7-1)=-4
y=-3
x=6-(-3)=9
y=-4
x=6-(-4)=10
Ответ: x=9; y=-3 и x=10; y=-4
<< Назад ] [ Начало ] [ Вперед >>
Калькулятор онлайн — Решение показательных уравнений
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать. n} \)
n} \)
6) an > 0
7) an > 1, если a > 1, n > 0
8) anm, если a > 1, n
9) an > am, если 0
В практике часто используются функции вида y = ax, где a — заданное положительное число, x — переменная.
Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является
показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = ax, где а — заданное число, a > 0, \( a \neq 1\)
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень ax где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение ax = b, где а > 0, \( a \neq 1\), не имеет корней,
если \( b \leqslant 0\), и имеет корень при любом b > 0.
3) Показательная функция у = ax является возрастающей на множестве всех действительных чисел, если a > 1, и
убывающей, если 0
Это следует из свойств степени (8) и (9)
Построим графики показательных функций у = ax при a > 0 и при 0 Использовав рассмотренные свойства отметим, что график функции у = ax при a > 0 проходит через точку (0; 1) и
расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = ax при 0
Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является
горизонтальной асимптотой графика.
Если х
Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т. е. уравнений, в которых неизвестное содержится в показателе степени.
е. уравнений, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения ax = ab где а > 0, \( a \neq 1\),
х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны
тогда и только тогда, когда равны их показатели.
Решить уравнение 23x • 3x = 576
Так как 23x = (23)x = 8x, 576 = 242, то уравнение можно записать в виде
8x • 3x = 242, или в виде 24x = 242, откуда х = 2.
Ответ х = 2
Решить уравнение 3х + 1 — 2 • 3x — 2 = 25
Вынося в левой части за скобки общий множитель 3х — 2, получаем 3х — 2(33 — 2) = 25,
3х — 2 • 25 = 25,
откуда 3х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2
Решить уравнение 3х = 7х
Так как \( 7^x \neq 0 \) , то уравнение можно записать в виде \( \frac{3^x}{7^x} = 1 \), откуда \( \left( \frac{3}{7} \right) ^x = 1 \), х = 0
Ответ х = 0
Решить уравнение 9х — 4 • 3х — 45 = 0
Заменой 3х = t данное уравнение сводится к квадратному уравнению t2 — 4t — 45 = 0. {x-2} = 1 \)
{x-2} = 1 \)
x — 2 = 0
Ответ х = 2
Решить уравнение 3|х — 1| = 3|х + 3|
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1)2 = (х + 3)2, откуда
х2 — 2х + 1 = х2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1
Определите степень уравнения — математика, прочее
Степень уравнения — это максимальный или наибольший показатель степени переменной, присутствующей в уравнении. Чтобы ее определить, достаточно обратить внимание на значение степеней имеющихся переменных. Максимальная величина и определяет степень уравнения.
Просмотр содержимого документа
«Определите степень уравнения»
Как определить степень уравнения
Уравнение представляет собой математическое соотношение, которое отражает равенство двух алгебраических выражений. Чтобы определить его степень, необходимо внимательно посмотреть на все присутствующие в нем переменные.
Чтобы определить его степень, необходимо внимательно посмотреть на все присутствующие в нем переменные.
Инструкция
1
Решение любого уравнения сводится к нахождению таких значений переменной х, которые после подстановки в исходное уравнение дают верное тождество — выражение, не вызывающее никаких сомнений.
2
Степень уравнения — это максимальный или наибольший показатель степени переменной, присутствующей в уравнении. Чтобы ее определить, достаточно обратить внимание на значение степеней имеющихся переменных. Максимальная величина и определяет степень уравнения.
3
Уравнения бывают разных степеней. К примеру, линейные уравнения вида ax+b=0 имеют первую степень. В них присутствуют только неизвестные в названной степени и числа. Важно отметить отсутствие дробей с неизвестной величиной в знаменателе. 2+bx+c=0, дальнейшее решение довольно простое и предполагает не более двух корней. В 1591 году Франсуа Виет вывел формулы для нахождения корней квадратных уравнений. А Евклид и Диофант Александрийский, Аль-Хорезми и Омар Хайям использовали геометрические способы нахождения их решений.
2+bx+c=0, дальнейшее решение довольно простое и предполагает не более двух корней. В 1591 году Франсуа Виет вывел формулы для нахождения корней квадратных уравнений. А Евклид и Диофант Александрийский, Аль-Хорезми и Омар Хайям использовали геометрические способы нахождения их решений.
5
Существует также и третья группа уравнений, которая называется дробными рациональными уравнениями. Если в исследуемом уравнении присутствуют дроби с переменной в знаменателе, то это уравнение — дробное рациональное или же просто дробное. Чтобы найти решения таких уравнений, надо всего лишь уметь с помощью упрощений и преобразований сводить их к рассмотренным двум известным типам.
6
Все остальные уравнения составляют четвертую группу. Их больше всего. Сюда входят и кубические, и логарифмические, и показательные, и тригонометрические их разновидности.
7
Решение кубических уравнений состоит также в упрощении выражений и нахождении не более 3 корней. Уравнения, имеющие более высокую степень, решаются разными способами, в том числе и графическим, когда на основе известных данных рассматриваются построенные графики функций и отыскиваются точки пересечений линий графиков, координаты которых и являются их решениями.
Уравнения, имеющие более высокую степень, решаются разными способами, в том числе и графическим, когда на основе известных данных рассматриваются построенные графики функций и отыскиваются точки пересечений линий графиков, координаты которых и являются их решениями.
11.3.4. Решение показательных уравнений, приводящихся к квадратным уравнениям.
Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 319 Опубликовано
Многие показательные уравнения заменой переменной сводятся к квадратному уравнению вида: ax2+bx+c=0.
Примеры.
Решить уравнение:
1) 4x+2x+1-3=0. Представим 4x в виде степени с основанием 2.
(22)x+2x∙21-3=0; при возведении степени в степень основание оставляют, а показатели перемножают: 2·х=х·2, поэтому:
(2x)2+2∙2x-3=0;
вводим новую переменную: пусть 2x=y;
y2+2y-3=0.
Дискриминант для четного второго коэффициента: D1=12-1∙(-3)=1+3=4=22 – полный квадрат, поэтому применим теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
y1+y2=-2, y1∙y2=-3. Подбираем корни: y1=-3, y2=1.
Возвращаемся к переменной х:
1) 2x=-3, нет решений, так как значения показательной функции: Е(у)=(0; +∞). (только положительные числа).
2) 2x=1. Число 1 можно представлять в виде нулевой степени по любому основанию.
2x=20;
x=0.
Ответ: 0.
2) 0,252x-5∙0,52x+4=0. Решаем аналогично. Представляем 0,252x— в виде степени с основанием 0,5.
(0,52)2x-5∙0,52x+4=0;
(0,52x)2-5∙0,52x+4=0.
0,52x=y; ввели новую переменную у и получили приведенное квадратное уравнение:
y2—5y+4=0;
Дискриминант D=b2-4ac=52-4∙1∙4=25-16=9=32 — полный квадрат, применяем теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
y1+y2=5, y1+y2=4. Корни приведенного квадратного уравнения находим подбором: y1=1, y2=4 и возвращаемся к переменной х:
1) 0,52x=1; число 1 можно представлять в виде нулевой степени по любому основанию.
0,52x=0,50;
2x=0;
x=0.
2) 0,52x=4; приведем степень 0,52x к основанию 2, применив формулу: (1/a)x =а-х
(1/2)2x=22;
2-2x=22; приравниваем показатели:
— 2x=2 |:(-2)
x=-1.
Ответ: -1; 0.
Представим левую и правую части в виде степеней с основанием 4, используя формулы: а-х=1/ax и ax∙ay=ax+y .
Если равны две степени с одинаковыми основаниями, то основания можно опустить и приравнять показатели степеней. Переносим дробь из правой части равенства в левую и упрощаем левую часть.
Находим дискриминант приведенного квадратного уравнения. Дискриминант является квадратом целого числа, поэтому, подбираем корни, пользуясь теоремой Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Дискриминант является квадратом целого числа, поэтому, подбираем корни, пользуясь теоремой Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Степенные или показательные уравнения.
Приветствую вас дорогие учащиеся!
Рекомендуем подписаться на канал на youtube нашего сайта TutoMath.ru, чтобы быть в курсе всех новых видео уроков.
Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a•a•…•a=an
1. a0 = 1 (a ≠ 0)
2. a1 = a
3. an • am = an + m
4. (an)m = anm
5. anbn = (ab)n
6. a-n= 1/an
a-n= 1/an
7. an/am= an — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
6x=36
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2x*5=10
16x — 4x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
2х = 23
Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:
2х = 23
х = 3
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
2х+2 = 24
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
33х — 9х+8 = 0
Для начала переносим девятку в правую сторону, получаем:
33х = 9х+8
Теперь нужно сделать одинаковые основания. Мы знаем что 9=32 . Воспользуемся формулой степеней (an)m = anm.
33х = (32)х+8
Получим 9х+8 =(32)х+8 =3 2х+16
33х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
22х+4 — 10•4х = 24
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (an)m = anm.
4х = (22)х = 22х
И еще используем одну формулу an • am = an + m:
22х+4 = 22х•24
Добавляем в уравнение:
22х•24 — 10•22х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 22х ,вот и ответ — 22х мы можем вынести за скобки:
Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 22х ,вот и ответ — 22х мы можем вынести за скобки:
22х(24 — 10) = 24
Посчитаем выражение в скобках:
24 — 10 = 16 — 10 = 6
6•22х = 24
Все уравнение делим на 6:
22х = 4
Представим 4=22:
22х = 22 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.
Решим уравнение:
9х – 12*3х +27= 0
Преобразуем:
9х = (32)х = 32х
Получаем уравнение:
32х — 12•3х +27 = 0
Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:
В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:
3х = t
Тогда 32х = (3х)2 = t2
Заменяем в уравнении все степени с иксами на t:
t2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t1 = 9
t2 = 3
Возвращаемся к переменной x.
Берем t1:
t1 = 9 = 3х
Стало быть,
3х = 9
3х = 32
х1 = 2
Один корень нашли. Ищем второй, из t2:
t2 = 3 = 3х
3х = 31
х2 = 1
Ответ: х1 = 2; х2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
Вступайте в группу ВКОНТАКТЕ
Показательные уравнения.
 Решения
Решения
Решение множества показательных уравнений не обходится без замен, квадратных уравнений и сложных преобразований. Приведенные ниже примеры помогут Вам в этом быстро разобраться и научат решать самые сложные из них. Также Вы сможете выучить некоторые свойства логарифмов без которых показательные уравнения в простой способ не решить. Начнем с самых азов — теоретического материала об уравнениях.
Показательными называют уравнения в которых неизвестная величина содержится в показателе степени, при этом основа степени не содержит неизвестной величины. Самое простое показательных уравнения ax=b решают логарифмированием x=log[a](b).
При решении показательных уравнений используют свойство показателей: если в уравнение степени с одной и той же основой то равные показатели степени или основание равно единице.
Из равенства следует или .
Некоторые уравнения требуют замены переменной и сводится к решению степенного уравнения. Например уравнения
легко сводится к квадратному если сделать замену
При этом исходное уравнение примет вид
После его решения нужно вернуться к замене и решить полученное уравнение.
Если показательной уравнение содержит две различные показательные функции ( основы не сводятся к одной) , то выполняют деления уравнения на одну из основ в соответствующей степени и переход до показательного уравнения которое содержит функцию с дробной основой.
Находя решения показательных уравнений следует помнить что показательная функция принимает только положительные значения. Отрицательные значения или нули замененной переменной не принимаются к рассмотрению.
На этом необходимый теоретический материал заканчивается и переходим к рассмотрению распространенных примеров.
Пример 1.Решить показательное уравнение
Решение. Перепишем уравнение к следующему виду
Второе слагаемое распишем как произведение
и сделаем замену в уравнении
Исходное уравнение преобразуем к следующему
Областью допустимых значений будет действительная ось за исключением точки y=0.
Умножим его на y и переносим все в левую сторону
Получили квадратное уравнение корни которого находим по теореме Виета. Нетрудно убедиться что они принимают значения
Нетрудно убедиться что они принимают значения
Возвращаемся к замене и находим решения
Выполняем проверку
Итак оба решения удовлетворяют уравнению.
Пример 2. Решить показательное уравнение
Решение. Используя одну из свойств логарифма записываем правую сторону уравнения в виде
Приравнивая показатели находим
Пример 3. Решить уравнение
Решение. Такого сорта примеры решают логарифмированием обеих сторон что приводит к сведению показательного уравнения к простому виду.
Полученное уравнение относительно переменной решаем через дискриминант
Корни уравнения приобретут значения
Другого метода позволяющего аналитически получить решения Вы не найдете ни в интернете, ни на форумах.
Пример 4. Решить уравнение
Решение. Выполним некоторые преобразования с показателями чтобы упростить уравнение
Эквивалентные значения подставим в уравнение, в результате получим
Выполняем замену
Уравнение превратится к квадратному
Вычисляем дискриминант
Найденное значение подставляем в формулу корней
Возвращаемся к замене и находим
Задача решена.
Пример 5.Решить уравнение
Решение. Такого типа уравнения решают с постоянной основой . За основу классически берут 10 , однако , если взять другую (для данного примера 5 или 9 ) то решение примет компактный вид
Рассмотрим оба метода.
1. Прологарифмируем обе части равенства
Раскрываем скобки и группируем слагаемые при неизвестных
Такой интересный результат.
2. Прологарифмируем обе части равенства по основанию 9
Группируя слагаемые содержащие переменную получим
Оба метода достаточно быстрые и эффективные, для себя выбирайте который Вам больше подходит.
Пример 6.Решить уравнение
Решение.Такого рода задачи решают по следующей схеме. Показательное уравнения превращают к виду
Все слагаемые разделяем на величину чтобы свести к дробному виду
После этого выполняем замену
Уравнение переписываем в виде
Умножаем на переменную и решаем квадратное уравнение
Дискриминант принимает нулевое значение, при етом корни уравнения совпадают
Возвращаемся к замене и решаем
Итак x=2 — единственное решение.
Используйте приведенную схему в подобных задач и гарантированно получите верный результат.
Пример 7. Решить уравнение
Решение. На первый взгляд уравнения достаточно сложное и неизвестно как его упрощать, однако схема решения данного примера и подобных довольно проста и интересна. Выполним над уравнением преобразования
Нужно это уравнение преобразовать к квадратному
Выполним замену
и перепишем уравнение в виде следуещого
Вычисляем дискриминант
и корни уравнения
Возвращаемся к совершенной замене
Такое уравнение сводим к квадратному, выполнив замену
В результате получим
Решаем через дискриминант
Возвращаемся к замене и определяем переменную x
Второе значение рассматривать не будем, поскольку оно отрицательное, а показательная функция всюду положительная.
Решаем вторую половину задачи
Используя предыдущую замену получим
Дискриминант примет значение
Находим корни уравнения
Первый корень имеет место бить, второй — отрицательный и не подходит.
Получили два решения показательного уравнения
Хорошо разберитесь с приведенными методами решения показательных уравнений, возможно некоторые из них пригодятся при прохождении ВНО, экзамене или контрольной работе. Будьте внимательны при упрощении, первое время используйте подстановку для проверки результатов.
Похожие материалы:
Мощность
Количественная работа связана с силой, вызывающей смещение. Работа не имеет ничего общего с количеством времени, в течение которого эта сила вызывает смещение. Иногда работа выполняется очень быстро, а иногда — довольно медленно. Например, скалолазу требуется ненормально много времени, чтобы поднять свое тело на несколько метров вдоль скалы. С другой стороны, турист (который выберет более легкий путь в гору) может поднять свое тело на несколько метров за короткий промежуток времени.Эти два человека могут выполнять одинаковый объем работы, но путешественник выполняет ее значительно быстрее, чем скалолаз. Величина, связанная со скоростью выполнения определенного объема работы, называется мощностью. У туриста номинальная мощность выше, чем у скалолаза.
Величина, связанная со скоростью выполнения определенного объема работы, называется мощностью. У туриста номинальная мощность выше, чем у скалолаза.
Мощность — это скорость выполнения работы. Это соотношение работы / времени. Математически это вычисляется с использованием следующего уравнения.
Мощность = Работа / время
или
P = Вт / т
Стандартная метрическая единица измерения мощности — Вт .Как следует из уравнения мощности, единица мощности эквивалентна единице работы, деленной на единицу времени. Таким образом, ватт эквивалентен джоулям в секунду. По историческим причинам, лошадиных сил иногда используется для описания мощности, выдаваемой машиной. Одна лошадиная сила эквивалентна примерно 750 Вт.
Большинство машин спроектировано и построено для работы с объектами. Все машины обычно характеризуются номинальной мощностью.Номинальная мощность указывает скорость, с которой эта машина может работать с другими объектами. Таким образом, мощность машины — это соотношение работы / времени для этой конкретной машины. Автомобильный двигатель — это пример машины, которой задана номинальная мощность. Номинальная мощность относится к тому, насколько быстро автомобиль может разгонять автомобиль. Предположим, что двигатель мощностью 40 лошадиных сил может разогнать автомобиль от 0 миль / час до 60 миль / час за 16 секунд. Если бы это было так, то автомобиль с четырехкратной мощностью в лошадиных силах мог бы выполнять такой же объем работы за четверть времени.То есть 160-сильный двигатель мог разогнать тот же автомобиль с 0 миль / час до 60 миль / час за 4 секунды. Дело в том, что при одинаковом объеме работы мощность и время обратно пропорциональны. Уравнение мощности предполагает, что более мощный двигатель может выполнять такой же объем работы за меньшее время.
Таким образом, мощность машины — это соотношение работы / времени для этой конкретной машины. Автомобильный двигатель — это пример машины, которой задана номинальная мощность. Номинальная мощность относится к тому, насколько быстро автомобиль может разгонять автомобиль. Предположим, что двигатель мощностью 40 лошадиных сил может разогнать автомобиль от 0 миль / час до 60 миль / час за 16 секунд. Если бы это было так, то автомобиль с четырехкратной мощностью в лошадиных силах мог бы выполнять такой же объем работы за четверть времени.То есть 160-сильный двигатель мог разогнать тот же автомобиль с 0 миль / час до 60 миль / час за 4 секунды. Дело в том, что при одинаковом объеме работы мощность и время обратно пропорциональны. Уравнение мощности предполагает, что более мощный двигатель может выполнять такой же объем работы за меньшее время.
Человек — это также машина с номинальной мощностью . Некоторые люди более властны, чем другие. То есть некоторые люди способны выполнять тот же объем работы за меньшее время или больше за то же время. Обычная физическая лаборатория включает в себя быстрый подъем по лестнице и использование информации о массе, росте и времени для определения личных возможностей ученика. Несмотря на диагональное движение по лестнице, часто предполагается, что горизонтальное движение является постоянным, и вся сила от ступенек используется для подъема ученика вверх с постоянной скоростью. Таким образом, вес ученика равен силе, которая воздействует на ученика, а высота лестницы — это смещение вверх. Предположим, что Бен Пумпинирон поднимает свое 80-килограммовое тело на 2.0-метровый подъезд за 1,8 секунды. Если бы это было так, то мы могли бы рассчитать номинальную мощность Бена . Можно предположить, что Бен должен приложить к лестнице нисходящую силу 800 Ньютон, чтобы поднять свое тело. Поступая таким образом, лестница толкала тело Бена вверх с достаточной силой, чтобы поднять его тело вверх по лестнице. Также можно предположить, что угол между силой лестницы на Бена и смещением Бена равен 0 градусов.
Обычная физическая лаборатория включает в себя быстрый подъем по лестнице и использование информации о массе, росте и времени для определения личных возможностей ученика. Несмотря на диагональное движение по лестнице, часто предполагается, что горизонтальное движение является постоянным, и вся сила от ступенек используется для подъема ученика вверх с постоянной скоростью. Таким образом, вес ученика равен силе, которая воздействует на ученика, а высота лестницы — это смещение вверх. Предположим, что Бен Пумпинирон поднимает свое 80-килограммовое тело на 2.0-метровый подъезд за 1,8 секунды. Если бы это было так, то мы могли бы рассчитать номинальную мощность Бена . Можно предположить, что Бен должен приложить к лестнице нисходящую силу 800 Ньютон, чтобы поднять свое тело. Поступая таким образом, лестница толкала тело Бена вверх с достаточной силой, чтобы поднять его тело вверх по лестнице. Также можно предположить, что угол между силой лестницы на Бена и смещением Бена равен 0 градусов. Используя эти два приближения, можно определить номинальную мощность Бена, как показано ниже.
Используя эти два приближения, можно определить номинальную мощность Бена, как показано ниже.
Номинальная мощность Бена — 871 Вт. Он вполне лошади .
Другая формула мощности
Выражение для мощности — работа / время. А поскольку выражение для работы — это сила * смещение, выражение для мощности можно переписать как (сила * смещение) / время. Поскольку выражение для скорости — это смещение / время, выражение для мощности можно еще раз переписать как «сила * скорость».Это показано ниже.
Это новое уравнение мощности показывает, что мощная машина одновременно сильна (большая сила) и быстра (большая скорость). Мощный автомобильный двигатель — сильный и быстрый. Мощная сельскохозяйственная техника — прочная и быстрая. Сильный тяжелоатлет силен и быстр. Сильный лайнсмен футбольной команды силен и быстр. Машина , достаточно сильная, чтобы приложить большую силу, чтобы вызвать смещение за небольшой промежуток времени (т. е., большая скорость) — машина мощная.
е., большая скорость) — машина мощная.
Проверьте свое понимание
Используйте свое понимание работы и власти, чтобы ответить на следующие вопросы. По завершении нажмите кнопку, чтобы просмотреть ответы.
1. Два студента-физика, Уилл Н. Эндейбл и Бен Пумпинирон, в зале для тяжелой атлетики. Уилл поднимает 100-фунтовую штангу над головой 10 раз за одну минуту; Бен поднимает 100-фунтовую штангу над головой 10 раз за 10 секунд.Какой студент больше всего работает? ______________ Какой ученик дает больше всего энергии? ______________ Объясните свои ответы.
2. В физической лаборатории Джек и Джилл взбежали на холм. Джек вдвое массивнее Джилл; тем не менее, Джилл преодолевает то же расстояние за половину времени. Кто работал больше всего? ______________ Кто доставил больше всего энергии? ______________ Объясните свои ответы.
3. Уставшая белка (масса около 1 кг) отжимается, прикладывая силу, поднимающую ее центр масс на 5 см, чтобы выполнить работу всего на 0,50 Дж. Если уставшая белка проделает всю эту работу за 2 секунды, то определите ее мощность.
4. При выполнении подтягивания студентка-физик поднимает ее 42.0-кг тело на дистанцию 0,25 метра за 2 секунды. Какую силу развивают бицепсы ученика?
5. Ежемесячный счет за электроэнергию в вашей семье часто выражается в киловатт-часах. Один киловатт-час — это количество энергии, доставленное потоком 1 киловатт электроэнергии за один час. Используйте коэффициенты преобразования, чтобы показать, сколько джоулей энергии вы получаете, покупая 1 киловатт-час электроэнергии.
6. Эскалатор используется для перемещения 20 пассажиров каждую минуту с первого этажа универмага на второй. Второй этаж находится на высоте 5,20 метра от первого этажа. Средняя масса пассажира — 54,9 кг. Определите требуемую мощность эскалатора, чтобы переместить это количество пассажиров за это время.
Второй этаж находится на высоте 5,20 метра от первого этажа. Средняя масса пассажира — 54,9 кг. Определите требуемую мощность эскалатора, чтобы переместить это количество пассажиров за это время.
Решение экспоненциальных уравнений с логарифмами
Purplemath
Большинство экспоненциальных уравнений не решаются точно; не будет возможности преобразовать основания в одинаковые, например преобразование 4 и 8 в степени 2.При решении этих более сложных уравнений вам придется использовать логарифмы.
Логарифмирование позволит нам воспользоваться правилом журнала, которое гласит, что мощности внутри журнала могут быть перенесены вперед как множители. Взяв журнал экспоненты, мы можем затем переместить переменную (находящуюся в экспоненте, которая теперь находится внутри журнала) вперед, как множитель в журнале. Другими словами, правило журнала позволит нам переместить переменную обратно на землю, где мы сможем ее получить.
Другими словами, правило журнала позволит нам переместить переменную обратно на землю, где мы сможем ее получить.
Например:
MathHelp.com
Если бы это уравнение попросило меня «Решить 2 x = 32», то найти решение было бы легко, потому что я мог бы преобразовать 32 в 2 5 , установить равные показатели и решить для « x = 5».Но, в отличие от 32, 30 — это не степень двойки, поэтому я не могу установить степени, равные друг другу. Мне нужен другой метод получения x , потому что я не могу решить уравнение с переменной, плавающей там выше 2; Мне нужно, чтобы он снова опустился на землю, где ему и место, где я смогу добраться до него. И мне придется использовать логарифмы, чтобы уменьшить эту переменную.
И мне придется использовать логарифмы, чтобы уменьшить эту переменную.
Имея дело с уравнениями, я могу делать с уравнением все, что захочу, при условии, что я делаю одно и то же с обеими сторонами.И, чтобы решить уравнение, я должен получить переменную отдельно от знака «равно»; чтобы изолировать переменную, я должен «отменить» все, что было сделано с переменной.
В этом случае переменная x помещена в показатель степени. Обратные (технически «обратные») экспоненты — это логарифмы, поэтому мне нужно отменить экспоненту, взяв логарифм обеих частей уравнения. Это полезно для меня из-за правила журнала, которое гласит, что показатели внутри журнала можно превратить в множители перед журналом:
Когда я беру логарифм обеих сторон уравнения, я могу использовать любой журнал, который мне нравится (логарифм по основанию 10, логарифм по основанию 2, натуральный логарифм и т. Д.), Но некоторые из них иногда более полезны, чем другие.Поскольку основание в уравнении «2 x = 30» равно «2», я мог бы попробовать использовать журнал с основанием 2:
Д.), Но некоторые из них иногда более полезны, чем другие.Поскольку основание в уравнении «2 x = 30» равно «2», я мог бы попробовать использовать журнал с основанием 2:
Любой журнал базы журнала возвращает значение 1, поэтому журнал 2 (2) = 1. Тогда:
x · лог 2 (2) = лог 2 (30)
x (1) = лог 2 (30)
x = журнал 2 (30)
Если вас просят «найти решение», то приведенный выше ответ должен быть приемлемым.Однако это значение, хотя и является «точным», не будет очень полезным для задач со словами (или в «реальной жизни»), если вам нужно числовое приближение.
Но мы не можем вычислить это выражение в наших калькуляторах в его нынешнем виде. Во-первых, нам нужно применить формулу смены базы, чтобы преобразовать выражение во что-то в основе, понятное нашим калькуляторам; а именно, натуральный журнал или обычный журнал. Это преобразование выглядит так:
Во-первых, нам нужно применить формулу смены базы, чтобы преобразовать выражение во что-то в основе, понятное нашим калькуляторам; а именно, натуральный журнал или обычный журнал. Это преобразование выглядит так:
Напоминание: «ln» — это сокращение от «logarithmus naturalis», латинской версии того, что в английском языке стало «натуральным логарифмом».Аббревиатура произносится как «ell-enn» и пишется со строчной буквы «L», за которой следует строчная буква «N». В названии функции нет «я» («глаз»)!
Что бы произошло, если бы я просто использовал натуральный логарифм вместо логарифма с основанием два? Процесс был бы точно таким же, и конечный ответ был бы эквивалентным.
2 х = 30
ln (2 x ) = ln (30)
x · ln (2) = ln (30)
x = ln (30) / ln (2)
В любом случае, я получаю тот же ответ, но использование естественного журнала было проще и короче.
Примечание: я мог бы использовать общий журнал (base-10) вместо естественного (то есть base- e ), и все равно получить то же значение (при оценке в калькуляторе).
Поскольку наука очень часто использует натуральный логарифм и поскольку это один из двух логарифмов, которые могут вычислять калькуляторы, я предпочитаю использовать натуральный логарифм обеих сторон при решении экспоненциальных уравнений. Это (как правило) не требуется, но часто более полезно, чем другие варианты.
Решите 5
x = 212. Дайте ответ в точной форме и в виде десятичного приближения с точностью до трех знаков.
Поскольку 212 не является степенью 5, мне придется использовать журналы для решения этого уравнения. Я мог бы взять логарифм по основанию 5 для каждой стороны, решить, а затем применить формулу изменения базы, но я думаю, что лучше просто использовать естественный логарифм в первую очередь:
5 х = 212
ln (5 x ) = ln (212)
x · ln (5) = ln (212)
x = ln (212) / ln (5)
. ..или около 3,328 с округлением до трех десятичных знаков.
..или около 3,328 с округлением до трех десятичных знаков.
Поскольку 52 — это не степень 10, мне придется использовать журналы, чтобы решить эту проблему. В данном конкретном случае, поскольку база равна 10 и поскольку на калькуляторе можно вести журналы по основанию 10, я буду использовать общий журнал вместо натурального журнала для решения этого конкретного уравнения:
10 2 x = 52
журнал (10 2 x ) = журнал (52)
2 x · журнал (10) = журнал (52)
2 x (1) = журнал (52)
2 x = журнал (52)
x = журнал (52) / 2
…или около 0,858 с округлением до трех десятичных знаков.
Прежде чем я смогу начать смотреть на экспоненту, мне сначала нужно избавиться от 3, поэтому я разделю это, чтобы получить:
Поскольку
350 / 3 не является степенью двойки, мне придется использовать журналы. В этом случае я буду использовать естественный журнал:
В этом случае я буду использовать естественный журнал:
…или около 2,866 с округлением до трех десятичных знаков.
Примечание: вы также можете решить вышеуказанную проблему, используя правила экспоненты, чтобы разделить мощность на 2:
2 x +4 = (2 x ) (2 4 ) = (2 x ) (16)
Затем разделите на 16 и упростите, чтобы получить:
(2 x ) (16) = 350/3
2 x = 350 / (3 · 16) = 175/24
Затем бревно с каждой стороны.Вы получите ответ в виде:
Когда вы оцените это, вы получите тот же десятичный эквивалент 2,866 в своем калькуляторе. Не стесняйтесь проявлять гибкость!
Не стесняйтесь проявлять гибкость!
URL: https://www.purplemath.com/modules/simpexpo2.htm
Мощность и энергия | Клуб электроники
Энергетика и энергетика | Клуб электроники
Мощность | Рассчитать |
Перегрев | Энергия
Следующая страница: AC, DC и электрические сигналы
См. Также: напряжение и ток
Что такое мощность?
Мощность — это скорость использования или поставки энергии:
Мощность измеряется в ваттах (Вт)
Энергия измеряется в джоулях (Дж)
Время измеряется в секундах (с)
Электроника в основном связана с малым количеством энергии, поэтому мощность часто
измеряется в милливаттах (мВт), 1 мВт = 0.001W. Например, светодиод потребляет около 40 мВт.
а бипер потребляет около 100 мВт, даже лампа, такая как фонарик, потребляет всего около 1 Вт.
Типичная мощность, используемая в электрических цепях сети, намного больше, поэтому эта мощность может быть
измеряется в киловаттах (кВт), 1 кВт = 1000 Вт. Например, в обычной сетевой лампе используется
60 Вт, а чайник потребляет около 3 кВт.
Расчет мощности по току и напряжению
Уравнения
| Мощность = Ток × Напряжение |
Есть три способа написать уравнение для мощности, тока и напряжения:
где:
P = мощность в ваттах (Вт)
V = напряжение в вольтах (В)
I = ток в амперах (A)
или:
P = мощность в милливаттах (мВт)
V = напряжение в вольтах (В)
I = ток в миллиамперах (мА)
Треугольник PIV
Вы можете использовать треугольник PIV, чтобы запомнить эти три уравнения.Используйте его так же, как треугольник закона Ома:
- Чтобы вычислить мощность , P : поместите палец на P,
это оставляет I V, поэтому уравнение P = I × V - Чтобы рассчитать ток , I : положите палец на I,
это оставляет P над V, поэтому уравнение I = P / V - Для расчета напряжения, В : поместите палец над V,
это оставляет P над I, поэтому уравнение V = P / I
Усилитель довольно большой для электроники, поэтому мы часто измеряем ток в миллиамперах (мА), а мощность в милливаттах (мВт).
1 мА = 0,001 А и 1 мВт = 0,001 Вт.
Расчет мощности с использованием сопротивления
Уравнения
Используя закон Ома V = I × R
мы можем преобразовать P = I × V в:
где:
P = мощность в ваттах (Вт)
I = ток в амперах (A)
R = сопротивление в Ом ()
В = напряжение в вольтах (В)
Треугольники
Вы также можете использовать треугольники, чтобы помочь с этими уравнениями:
Потраченная впустую мощность и перегрев
Обычно используется электроэнергия, например, зажигание лампы или двигателя.Однако электрическая энергия преобразуется в тепло всякий раз, когда ток проходит через
сопротивление, и это может быть проблемой, если оно вызывает перегрев устройства или провода. В
электроники эффект обычно незначителен, но если сопротивление низкое (провод или
резистора номинального значения, например) ток может быть достаточно большим, чтобы вызвать проблему.
Из уравнения P = I² × R видно, что для данного
сопротивление мощность зависит от тока в квадрате , поэтому удвоение тока даст в 4 раза большую мощность.
Резисторы рассчитаны на максимальную мощность, которую они могут развить в них без повреждений,
но номинальная мощность редко указывается в списках деталей, потому что подходят стандартные значения 0,25 Вт или 0,5 Вт.
для большинства схем. Дополнительная информация доступна на странице резисторов.
Провода и кабели рассчитаны на максимальный ток, который они могут пропускать без перегрева.
У них очень низкое сопротивление, поэтому максимальный ток относительно велик. Для получения дополнительной информации о
текущий рейтинг см. на странице кабелей.
Энергия
Количество потребляемой (или подаваемой) энергии зависит от мощности и времени, в течение которого она используется:
Устройство малой мощности, работающее в течение длительного времени, может потреблять больше энергии, чем устройство высокой мощности
работает непродолжительное время.
Например:
- Лампа мощностью 60 Вт, включенная на 8 часов, потребляет 60 Вт × 8 × 3600 с = 1728 кДж.
- Чайник мощностью 3 кВт, включенный на 5 минут, потребляет 3000 Вт × 5 × 60 с = 900 кДж.
Стандартной единицей измерения энергии является джоуль (Дж), но 1Дж — очень небольшое количество энергии для электросети.
поэтому в научной работе иногда используются килоджоуль (кДж) или мегаджоуль (МДж).
Дома мы измеряем электрическую энергию в киловатт-часах (кВтч), которые часто называют просто «единицей».
электричества, когда контекст ясен. 1 кВт · ч — это энергия, потребляемая электроприбором мощностью 1 кВт при включении на 1 час:
Например:
- Лампа мощностью 60 Вт, включенная на 8 часов, потребляет 0,06 кВт × 8 = 0,48 кВт · ч.
- Чайник мощностью 3 кВт, включенный на 5 минут, потребляет 3 кВт × 5 / 60 = 0,25 кВтч.
Возможно, вам потребуется преобразовать бытовую единицу кВтч в научную единицу энергии, джоуль (Дж):
1 кВтч = 1 кВт × 1 час = 1000 Вт × 3600 с = 3. 6MJ
6MJ
Следующая страница: Сигналы постоянного и переменного тока | Исследование
Политика конфиденциальности и файлы cookie
Этот сайт не собирает личную информацию.
Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет
используется только для ответа на ваше сообщение, оно не будет передано никому.
На этом веб-сайте отображается реклама, если вы нажмете на
рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден.
Рекламодателям не передается никакая личная информация.Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации.
Этот веб-сайт использует службу Google AdSense, которая использует файлы cookie для показа рекламы на основе использования вами веб-сайтов.
(включая этот), как объяснил Google.
Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста,
посетите AboutCookies. org.
org.
electronicsclub.info © Джон Хьюс 2021 г.
Решение уравнений с показателями — Подготовка к оценке TSI
Решение уравнений с показателями.
Рассмотрим эти два уравнения:
Уравнение 1: x 2 = 4 и Уравнение 2: x 3 = 27
Уравнение 1 имеет два решения : 2 и -2, поскольку 2 2 = 4 и (-2) 2 = 4.
Уравнение 2 имеет только , одно решение : x = 3.
Всякий раз, когда уравнение содержит все четные показатели, вы должны рассматривать как положительные, так и отрицательные решения. Если показатель степени является нечетной степенью, есть только одно решение.
Решение уравнений с показателями: x m = k
Если m четное: x = ± m √ k
Если m нечетное: x = m √ k
Для уравнений, которые включают корни, отличные от квадратного корня, вы хотите удалить корни путем (1) выделения корневого члена на одной стороне уравнения и (2) возведения обеих сторон уравнения в соответствующую степень.
Пример 1. Решить ( x ² + 6 x ) 1/4 = 2
Решение
Напомним, что дробная экспонента на самом деле является корнем: a m / n = ( n √ a) m
Удалите корень 4-й степени, возведя каждую часть уравнения в 4-ю степень.
[( x ² + 6 x ) 1/4 ] 4 = 2 4
Упростите каждую часть уравнения.
x ² + 6 x = 16
Установите уравнение равным нулю.
x ² + 6 x — 16 = 0
Разложите на множители левую часть уравнения.
( x + 8) ( x — 2) = 0
Установите коэффициенты равными нулю и решите.
0 = x + 8 или 0 = x — 2
x = — 8 или x = 2
Наши возможные решения: x = — 8 и x = 2. Оба этих решения необходимо проверить, используя исходное уравнение.
Оба этих решения необходимо проверить, используя исходное уравнение.
Чек x = — 8:
[(- 8) ² + 6 (- 8)] 1/4 = 2
[64–48] 1/4 = 2
[16] 1/4 = 2
4√16 = 2
2 = 2 — истинное утверждение. Следовательно, x = — 8 — это решение.
Чек x = 2:
[(2) ² + 6 (2)] 1/4 = 2
[4 + 12] 1/4 = 2
[16] 1/4 = 2
4√16 = 2
2 = 2 — истинное утверждение.Следовательно, x = 2 — это решение.
Решения уравнения ( x ² + 6 x ) 1/4 = 2, равны x = — 8 и x = 2.
Пример 2 : Решить относительно w: 5 w 2/3 + 3 = 23
Решение.
Выделите член w в левой части уравнения. Вычтите 3 из каждой части уравнения.
5 w 2/3 = 23 — 3
5 w 2/3 = 20
Разделите каждую часть уравнения на 5.
w 2/3 = 20 ÷ 5
w 2/3 = 4
Изолируйте w , возведя обе части уравнения в степень 3/2. Поскольку числитель экспоненты четный, будет два ответа.
w = ± 4 3/2 = ± (√ 4) 3
w = ± 2 3 = ± 8
Два ответа на уравнение 5 w 2/3 + 3 = 23, это 8 и -8.x} = 9 \) Показать решение
Итак, мы сказали выше, что если бы у нас был логарифм перед левой частью, мы могли бы получить \ (x \) из экспоненты. Сделать это достаточно просто. Мы просто поставим логарифм перед левой частью. Однако, если мы поместим туда логарифм, мы также должны поставить логарифм перед правой частью. Это обычно обозначается как , где логарифм обеих сторон равен .
Мы можем использовать любой логарифм, поэтому давайте попробуем натуральный логарифм.x} & = \ ln 9 \\ x \ ln 7 & = \ ln 9 \ end {align *} \]
Теперь нам нужно найти \ (x \). Это проще, чем кажется. Если бы у нас было \ (7x = 9 \), то мы все могли бы решить для \ (x \), просто разделив обе части на 7. Здесь это работает точно так же. И ln7, и ln9 — просто числа. По общему признанию, потребуется калькулятор, чтобы определить, что это за числа, но это числа, и поэтому мы можем сделать то же самое здесь.
\ [\ begin {align *} \ frac {{x \ ln 7}} {{\ ln 7}} & = \ frac {{\ ln 9}} {{\ ln 7}} \\ x & = \ frac {{\ ln 9}} {{\ ln 7}} \ end {align *} \]
Это технически точный ответ.Однако в этом случае обычно лучше получить десятичный ответ, так что давайте сделаем еще один шаг.
\ [x = \ frac {{\ ln 9}} {{\ ln 7}} = \ frac {{2.19722458}} {{1.945
7 \]
Обратите внимание, что ответы на эти вопросы чаще всего являются десятичными.
Также будьте осторожны, чтобы не допустить следующей ошибки.
\ [1.12
7 = \ frac {{\ ln 9}} {{\ ln 7}} \ ne \ ln \ left ({\ frac {9} {7}} \ right) = 0.y} = 0 \) Показать решение
В этом случае мы не можем просто поставить логарифм перед обеими сторонами. На это есть две причины. Сначала в правой части у нас есть ноль, и мы знаем из предыдущего раздела, что не можем логарифмировать ноль. Затем, чтобы сместить показатель вниз, он должен быть на всем члене внутри логарифма, и этого не будет с этим уравнением в его нынешнем виде.
Итак, первым делом переместим члены на другую сторону от знака равенства, затем мы возьмем логарифм обеих сторон, используя натуральный логарифм.y} \\ \ left ({4y + 1} \ right) \ ln 2 & = y \ ln 3 \ end {align *} \]
Хорошо, это выглядит неаккуратно, но опять же, это действительно не так уж и плохо. Давайте сначала посмотрим на следующее уравнение.
\ [\ begin {align *} 2 \ left ({4y + 1} \ right) & = 3y \\ 8y + 2 & = 3y \\ 5y & = — 2 \\ y & = — \ frac {2} { 5} \ end {align *} \]
Мы все можем решить это уравнение, а это значит, что мы можем решить то, что у нас есть. Опять же, ln2 и ln3 — это просто числа, поэтому процесс точно такой же.Ответ будет сложнее, чем это уравнение, но процесс идентичен. Вот работа для этого.
\ [\ begin {align *} \ left ({4y + 1} \ right) \ ln 2 & = y \ ln 3 \\ 4y \ ln 2 + \ ln 2 & = y \ ln 3 \\ 4y \ ln 2 — y \ ln 3 & = — \ ln 2 \\ y \ left ({4 \ ln 2 — \ ln 3} \ right) & = — \ ln 2 \\ y & = — \ frac {{\ ln 2} } {{4 \ ln 2 — \ ln 3}} \ end {align *} \]
Итак, мы получили все члены с \ (y \) в них с одной стороны и всеми другими членами с другой стороны.{е \ влево (х \ вправо)}} = е \ влево (х \ вправо) \]
Мы видели это в предыдущем разделе (в более общем виде), и, используя это здесь, мы значительно упростим нашу жизнь. Использование этого свойства дает
\ [\ begin {align *} t + 6 & = \ ln 2 \\ t & = \ ln \ left (2 \ right) — 6 = 0,69314718 — 6 = — 5,30685202 \ end {align *} \]
Обратите внимание на скобки вокруг 2 в логарифме на этот раз. Они нужны для того, чтобы мы не допустили следующей ошибки.{2z + 4}} & = \ ln \ left ({\ frac {8} {5}} \ right) \\ 2z + 4 & = \ ln \ left ({\ frac {8} {5}} \ right ) \\ 2z & = \ ln \ left ({\ frac {8} {5}} \ right) — 4 \\ z & = \ frac {1} {2} \ left ({\ ln \ left ({\ frac {8} {5}} \ right) — 4} \ right) = \ frac {1} {2} \ left ({0,470003629 — 4} \ right) = — 1,76499819 \ end {align *} \]
Power — Мощность и эффективность — Edexcel — GCSE Physics (Single Science) Revision — Edexcel
Когда работа выполняется с объектом, происходит передача энергии. Скорость, с которой эта энергия передается, называется мощностью.Таким образом, чем мощнее устройство, тем больше энергии оно передает каждую секунду.
Расчетная мощность
Уравнение, используемое для расчета мощности:
\ [power = \ frac {work \\ done} {time \ made} \]
\ [P = \ frac {E} {t } \]
Это когда:
- мощность ( P ) измеряется в ваттах (Вт)
- выполненная работа ( E ) измеряется в джоулях (Дж)
- время ( t ) равно измеряется в секундах (с)
Один ватт равен одному джоулю в секунду (Дж / с).Это означает, что на каждый дополнительный джоуль, передаваемый в секунду, мощность увеличивается на один ватт.
Пример
Два электродвигателя используются для подъема груза 2 Н на высоту 10 м по вертикали.
Первый мотор делает это за 5 секунд.
Второй двигатель делает это за 10 секунд.
Для обоих двигателей переданная энергия — проделанная работа — составляет 20 Дж.
\ [E = F \ times d = 2 \ times 10 = 20 \\ Дж \]
Для одного двигателя:
\ [ P = \ frac {E} {t} = \ frac {20} {5} = 4 \\ W \]
Для второго двигателя:
\ [P = \ frac {E} {t} = \ frac { 20} {10} = 2 \\ W \]
Поскольку один двигатель передает вдвое больше энергии в секунду, можно сказать, что первый двигатель в два раза мощнее, чем второй.
- Вопрос
Фен передает 48 000 Дж энергии за одну минуту. Какая мощность у фена?
- Показать ответ
\ [P = \ frac {E} {t} \]
\ [P = \ frac {48,000} {60} \]
\ [P = 800 \\ W \]
Мощность — это количество энергии, передаваемое за секунду.
Функция мощности — свойства, графики и приложения
Вы когда-нибудь работали с функцией, содержащей один термин? Скорее всего, вы работали с степенной функцией.Этот тип функции настолько разнообразен, что если вы изучаете функции, мы на 100% уверены, что вы уже встречались с типом степенной функции, даже не зная, что это так.
Почему бы нам не начать с определения степенных функций?
Степенная функция — это функция, состоящая из одного члена, которая содержит переменную в основе и константу в качестве экспоненты.
Это означает, что существует множество родительских функций, которые также являются степенными функциями.В этой статье мы узнаем:
- Концепция силовых функций.
- Особые свойства, которые может проявлять степенная функция.
- Примените эти свойства при построении графиков и определении степенных функций.
Обязательно имейте под рукой блокнот, так как здесь подробно обсуждаются функции управления питанием. Мы даже научимся применять степенные функции в текстовых задачах.
Почему бы нам не начать с его определения и некоторых примеров степенных функций?
Что такое степенная функция?
Прежде чем мы углубимся в важные свойства степенной функции, мы должны понять фундаментальное определение степенных функций.Вот общий вид степенных функций:
Давайте продолжим и разберем эту общую форму и найдем примеры степенных функций, использующих это определение.
Обязательно ознакомьтесь с этой формой, поскольку мы будем использовать ее неоднократно на протяжении всей статьи.
Определение и примеры силовых функций
Как показано в предыдущем разделе, степенные функции — это функции в форме f (x) = kx a или y = kx a , где k — ненулевой коэффициент, а — действительное число.
Вот несколько примеров степенных функций:
- y = -5x 2
- y = 2 √x
- f (x) = 3 / x 2
- г (x) = 2x 3
Обратите внимание, что каждая функция содержит только один термин для каждого примера — важный идентификатор степенных функций. Показатели степенных функций также должны быть действительными числами, поэтому давайте проверим каждый показатель из примеров, чтобы подтвердить это.
- Функция y = -5x 2 и g (x) = 2x 3 — это функции с целыми числами в качестве экспонентов, поэтому они являются степенными функциями.
- Функция квадратного корня y = 2 √x может быть переписана как y = 2x 1/2 , поэтому ее показатель степени является действительным числом, поэтому это также степенная функция.
- Мы применяем тот же процесс с f (x) = 3 / x 2 и получаем f (x) = 3x -2 , подтверждая, что это степенная функция, поскольку -2 — действительное число.
Ниже приведены лишь некоторые родительские функции, и давайте посмотрим, почему все они также считаются степенными функциями.
| Родительская функция | Функциональная форма |
| Постоянная функция | y = |
| Линейная функция | у = х |
| Квадратичная функция | у = х 2 |
| Кубическая функция | у = х 3 |
| Реципрокная функция | у = 1 / х, у = 1 / х 2 |
| Квадратный корень Функция | y = √x |
Поскольку эти родительские функции содержат по одному члену и действительные числа для их показателей, все они являются степенными функциями.
Как построить график степенных функций?
При построении графиков степенных функций мы должны помнить об этих двух важных свойствах степенных функций: их симметрии и конечном поведении .
Вот краткое руководство по построению графиков функций мощности, чтобы показать вам, почему эти два показателя могут помочь вам сэкономить время:
- Определите, является ли степенная функция нечетной или четной.
- Применяйте преобразования всякий раз, когда можете.
- Найдите точки, которые помогут построить график половины степенной функции.
- Примените свойство симметрии данной степенной функции.
- Еще раз проверьте их конечное поведение.
Почему бы нам не обновить свои знания о нечетных и четных функциях и не посмотреть, как они влияют на график степенной функции?
Симметрия и поведение концов четных степенных функций
Степенные функции либо четные, либо нечетные, поэтому они также либо симметричны относительно оси y и начала координат .Мы также можем предсказать конечное поведение степенных функций на основе их коэффициента и мощности .
Давайте посмотрим на график этих четных степенных функций: y = 2x 2 и y = -4x 4 . Чтобы построить график каждой функции, нарисуйте несколько точек справа и отразите эту кривую по оси ординат.
Для обоих графиков, поскольку показатели четные, функции также четные, и, следовательно, их графики симметричны по оси y.
Начнем с четных степенных функций, где коэффициент положительный, например y = 2x 2 .
- Поскольку коэффициент 2 положительный, график открывается вверх на .
- Мы можем видеть, что когда x <0, функция убывает, а когда x> 0, функция убывает.
- Следовательно, и левая, и правая стороны кривой будут расти (↑) .
Теперь давайте рассмотрим четных степенных функций с отрицательным коэффициентом , например y = -4x 4 .
- Поскольку коэффициент -4 отрицательный, график открывается вниз .
- Здесь мы можем видеть, что когда x <0, функция увеличивается, а когда x> 0, функция убывает.
- Это означает, что для с обеих сторон мы ожидаем, что кривая пойдет вниз (↓).
Симметрия и поведение конца нечетных степенных функций
Как насчет нечетных степенных функций? Давайте продолжим и рассмотрим эти две функции: y = 3x 3 и y = -x 5 .
Чтобы построить график этих двух функций, мы можем нанести некоторые значения либо на левую, либо на правую сторону координатной плоскости. Отразите график над началом координат.
Из определения нечетных функций мы видим, что обе степенные функции симметричны относительно начала координат .
Вот некоторые вещи, которые мы можем наблюдать на графике y = 3x 3 , где коэффициент положителен :
- Мы видим, что когда x <0, функция увеличивается, , а когда x> 0, функция увеличивается на .
- Следовательно, левая сторона идет вниз (↓) , а правая сторона идет вверх (↑) .
Теперь рассмотрим поведение нечетных функций при отрицательном коэффициенте .
- Мы видим, что когда x <0 и x> 0, функция убывает
- Следовательно, левая сторона поднимается (↑) , а правая сторона опускается (↓) .
Понимание эффекта экспоненты, a
Мы подробно обсудили влияние на график степенной функции на основе ее четности и значения k.Теперь давайте попробуем увидеть разницу, когда a — это дробь, а когда a — целое число.
Случай 1. Когда a = 0 и a = 1 , мы ожидаем, что график сведется к постоянной функции и линейной функции соответственно.
Графики y = 2 и y = 2x могут подтвердить это. Такое же поведение применяется ко всем значениям k.
Доменом для этого случая будут все действительные числа или в интервальной записи, то есть (-∞, ∞).
Случай 2: Когда a <0 .Давайте посмотрим на графики y = x -1 и y = x -2 :
.
Когда a отрицательно и степенная функция возвращает рациональное выражение, мы можем видеть, что графиков приближаются, но никогда не равны 0 . Это означает, что областью значений этих степенных функций будет любое действительное число, кроме 0, , поэтому область значений будет (-∞, 0) U (0, ∞) .
Два графика — , также вогнутые вверх с обеих сторон .
Случай 3: Когда 1 .Давайте посмотрим на графики y = x 1/2 и y = x 1/3 :
Когда a является дробью, а степенная функция возвращает радикальное выражение. Мы видим, что домен будет зависеть от того, четный или нечетный знаменатель:
- Если знаменатель четный, только положительные значения x будут частью области или [0, ∞).
- Если знаменатель нечетный, все его области могут быть действительными числами или (-∞, ∞).
Два графика также вогнуты вниз с обеих сторон .
Случай 4. Когда a> 1 , давайте рассмотрим графики y = x 5 и y = x 6 .
Когда показатель степени положительный, , мы ожидаем, что графики будут вогнутыми вверх . Доменом для этого типа степенной функции будут все действительные числа или интервальные обозначения , (-∞, ∞) .
Как найти степенную функцию?
Иногда нам дается график степенной функции или несколько точек, проходящих через его график.Мы все еще можем найти выражение, представляющее степенную функцию, используя две точки.
- Подставьте эти две точки в общую форму степенных функций: y = kx a .
- Найдите способ сохранить либо k , либо a в одном из уравнений.
- Определите значения для k и a и подставьте их обратно в общую форму степенных функций.
Допустим, мы хотим найти степенную функцию, проходящую через (2, 16) и (3, 54). Подставьте эти значения в общую форму:
| (2, 16) | 16 = к (2) а 16/2 a = k |
| (3, 54) | 54 = к (3) а 54/3 a = k |
Приравняем оба выражения в правой части и получим:
16/2 a = 54/3 a
8/2 a = 27/3 a
2 3 /2 a = 3 3 /3 a
2 3 — а = 3 3 — а
Это уравнение будет истинным, только если обе стороны равны 1.Это означает, что 3 — a должно быть равно 0. Следовательно, a = 3.
Замените это обратно на любое из выражений k:
к = 16/2 3
= 16/8
= 2
Теперь, когда у нас есть a = 3 и k = 2, мы можем записать выражение степенной функции: y = 2x 3 .
Что, если мы хотим найти выражение степенной функции на основе ее графика? Просто обратите внимание на две точки, через которые проходит график функции, а затем примените тот же процесс.
Прежде чем мы попробуем еще несколько вопросов, связанных со степенными функциями, почему бы нам не подытожить все, что мы знаем о степенных функциях?
Резюме формул степенной функции и их свойств
Вот несколько полезных напоминаний при работе с функциями питания и их приложениями:
- При определении того, является ли функция степенной функцией, убедитесь, что выражение является одним членом , k — константой , а a — действительным числом .
- будут зависеть от значений k и a.
- Применяйте свойства четных и нечетных функций, когда это применимо.
- При нахождении выражения для степенной функции всегда используйте общую форму: y = kx a .
- Используйте приведенную ниже таблицу, чтобы спрогнозировать конечное поведение степенных функций.
Графики функций мощности
| Состояние k | Функции четной мощности | Функции нечетной мощности |
| Когда k> 0 | Функция уменьшается при x <0: При x → — ∞, y → ∞ Функция увеличивается, когда x> 0: При x → ∞, y → ∞ | Функция возрастает в интервале x: При x → — ∞, y → -∞ При x → ∞, y → ∞ |
| Когда k <0 | Функция увеличивается при x <0: При x → — ∞, y → — ∞ Функция уменьшается, когда x> 0: При x → ∞, y → — ∞ | Функция убывает в интервале x: При x → — ∞, y → ∞ При x → ∞, y → — ∞ |
Убедитесь, что вы понимаете концепцию силовых функций и знакомы с различными конечными поведениями.Когда будете готовы, давайте попробуем решить некоторые задачи!
Пример 1
Какие из следующих функций считаются степенными?
а. f (x) = -2x 2 · 3x
б. г (х) = 2√х + 5
г. h (x) = 0,5x π
d. м (х) = — (х + 1) 2
д. п (х) = 1 / х 3
Решение
Проверьте каждую из указанных функций и по возможности упростите выражения.
а. Функцию все еще можно упростить до f (x) = -6x 3 . Мы видим, что он содержит только один член и имеет действительное число для его коэффициента и показателя степени, поэтому f (x) является степенной функцией .
Следующие два элемента (b и d) содержат более одного члена и не могут быть упрощены, поэтому функции g (x) и m (x) не считаются степенными функциями .
г. Мы всегда возвращаемся к фундаментальному определению степенных функций: они содержат один член, а коэффициент и показатели являются действительными.И 0,5, и π являются действительными числами, поэтому h (x) также является степенной функцией .
e. Поскольку 1 / x 3 = 1 · x -3 , мы можем видеть путем осмотра, что он удовлетворяет условиям степенных функций, поэтому n (x) также является степенной функцией .
Следовательно, функций в a, c и e являются степенными функциями .
Пример 2
Заполните пропуски всегда , иногда и никогда , чтобы следующие утверждения были верными.
а. Кубические функции — это ______________ степенные функции.
г. Постоянные функции — это _____________ степенные функции.
г. У степенных функций ___________ будут отрицательные показатели.
Решение
Давайте продолжим и проверим каждую выписку:
а. Некоторые примеры кубических функций: 2x 3 и x 3 — x 2 + x — 1. Мы видим, что первый пример является степенной функцией, а второй — нет. Это означает, что кубические функции могут быть , иногда степенными функциями.
г. Общий вид постоянных функций — y = c, где c — любая ненулевая константа. Из общей формы видно, что независимо от значения c, постоянные функции всегда будут иметь один член с действительными числами для их коэффициента и экспоненты. Следовательно, постоянные функции будут всегда степенными функциями.
г. Пока функция содержит один член и экспоненту действительного числа, она будет считаться степенной функцией. Это означает, что степенная функция может иметь положительные и отрицательные показатели.Таким образом, они могут иметь , иногда иметь отрицательные показатели.
Пример 3
Определите конечное поведение следующих функций мощности:
а. f (х) = х 3
г. г (х) = -4x 4
г. ч (х) = (-3х) 3
Решение
При прогнозировании конечного поведения степенной функции проверьте знак коэффициента и значение показателя степени. Используйте таблицу, которую мы предоставили, чтобы помочь вам предсказать конечное поведение.
а. Функция f (x) = x 3 имеет коэффициент 1 и положительный показатель степени 3. Поскольку степень нечетная, ожидается, что функция будет увеличиваться во всей области определения.
Это означает, что левая сторона кривой идет вниз, а правая — вверх: (↓ ↑).
г. Для второй функции g (x) = -4x 4 , имеет отрицательный коэффициент и четный положительный показатель степени. Это означает, что график должен открываться вниз.Функция также будет увеличиваться, когда x <0, и уменьшаться, когда x> 0.
Это означает, что как левая, так и правая стороны кривой, как ожидается, будут идти вниз: (↓↓).
г. Давайте сначала упростим выражение для h (x): h (x) = -27x 3 . Мы видим, что h (x) имеет отрицательный коэффициент и нечетную экспоненту. Когда это происходит, функция уменьшается во всем своем домене.
Кривая графика: вверх с левой стороны и спуск с правой стороны: (↑ ↓).
Пример 4
Покажите, что произведение двух степенных функций всегда также возвращает степенную функцию.
Решение
Пусть две степенные функции равны f (x) = mx p и g (x) = nx q , где m и n — действительные числовые коэффициенты. Показатели p и q также являются действительными числами.
Умножение двух функций даст:
f (x) · g (x) = (mx p ) · (nx q )
= мн х р + д
Пусть mn = k и p + q = a, следовательно, f (x) · g (x) = kx a .
Поскольку mn и p + q — действительные числа, k и a также будут действительными числами. Продукт по-прежнему возвращает степенную функцию, поэтому мы только что подтвердили, что произведение двух степенных функций также будет степенной функцией.
Пример 5
Изобразите степенную функцию f (x) = -3x 5 и ответьте на следующие вопросы.
а. Каков домен и диапазон функции?
г. Если график сдвинуть на 6 единиц вверх, будет ли полученная функция по-прежнему степенной?
Решение
Поскольку f (x) — нечетная функция, мы ожидаем, что график будет симметричным относительно начала координат.
Мы можем нанести эти точки на половину кривой и отразить ее по началу координат.
а. Поскольку показатель степени положительный и нечетный, область определения и диапазон f (x) будут все действительными числами или (-∞, ∞) . Это также можно подтвердить, просмотрев график.
г. Когда мы переводим f (x) на 6 единиц, мы добавляем 6 к выражению. Следовательно, выражение новой функции теперь будет -3x 5 + 6. Это выражение будет содержать два члена, и, таким образом, новая функция больше не будет степенной функцией .
Пример 6
Используйте приведенный ниже график, чтобы найти выражение для h (x).
Решение
Поскольку график h (x) проходит через (-1, -2), (1, -2) и (1/2, -8), мы можем использовать любую из этих трех точек в общем виде степенная функция: y = kx a .
Обратите внимание на график? Кривые приближаются, но никогда не могут быть равны 0, поэтому мы ожидаем, что показатель степени будет дробным.
Давайте сначала подставим (1, -2) в общий вид степенной функции. (Это будет лучший вариант, поскольку k1 a уменьшится до k.)
-2 = к (1) а
-2 = к
Примените тот же процесс для (1/2, -8), но на этот раз давайте также использовать k = -2.
-8 = (-2) (- 1/2) a
4 = (-1/2) а
(-1/2) -2 = (-1/2) a
Чтобы это было правдой, a должно быть равно -2.Следовательно, мы имеем h (x) = -2x -2 .
Пример 7
Степенная функция g (x) проходит через точки (4, -6) и (9, -9).
а. Каково выражение для g (x)?
г. Постройте график функции g (x).
г. Найдите его домен и диапазон, затем опишите его конечное поведение.
Решение
Подставим каждую пару значений в общий вид степенных функций: y = kx a и упростим полученное уравнение.
| (4, -6) | -6 = к (4) а -6 = k4 a -6/4 a = k |
| (9, -9) | -9 = k (9) a -9 = k9 a -9/9 a = k |
Теперь, когда у нас есть k в правой части уравнений, приравняем выражения в левой части. Решите относительно a из полученного уравнения.
-6/4 a = -9/9 a
-2/4 a = -3/9 a
-2 1 /2 2a = -3 1 /3 2a
-2 1-2a = -3 1-2a
Это уравнение будет истинным, только если обе стороны равны 1, поэтому показатель степени должен быть равен 0.
1-2a = 0
1 = 2a
а = ½
Подставьте значение a в одно из выражений для k.
к = -6/4 а
= -6 / 4 1/2
= -6 / 2
= -3
Подставьте эти два значения обратно в общую форму степенных функций, чтобы найти выражение для g (x).
г (x) = kx a
= -3x 1/2
= -3√x
а. Следовательно, мы имеем g (x) = -3√x .
Давайте используем две заданные точки, чтобы соединить кривую. Вспомните форму родительской функции функции извлечения квадратного корня, чтобы знать, чего ожидать от графика g (x).
г.
Мы можем найти домен и диапазон g (x), проверив график. Поскольку g (x) имеет рациональную экспоненту с четным знаменателем, мы ожидаем, что для x будут только положительные значения. График также может это подтвердить.
Поскольку график g (x) никогда не поднимается выше отрицательной оси y, мы ожидаем, что его диапазон будет состоять только из отрицательных чисел.
г. Следовательно, область для g (x) равна [0, ∞) , а диапазон составляет (-∞, 0] . График показывает, что она непрерывно уменьшается, а кривая последовательно идет вниз на .
Пример 8
Площадь круга прямо пропорциональна квадрату его радиуса r. Площадь круга с радиусом 10 единиц составляет 314 единиц 2, и круга с радиусом 20 единиц составляет 1256 единиц 2 .
а. Найдите степенную функцию A (r), представляющую площадь круга через r. Что представляет собой коэффициент при A (r)?
г. Без учета ограничений на r, будет ли A (r) четным или нечетным?
г.Каково конечное поведение A (r)?
г. Если мы примем во внимание тот факт, что r представляет радиус круга, изменится ли домен?
Решение
Поскольку площадь прямо пропорциональна r 2 , мы можем выразить A (r) как kr 2 , где k — ненулевая константа.
Давайте используем любую из двух заданных пар значений, чтобы найти k.
A (год) = 2
шведских крон
314 = к (10) 2
314 = 100 тыс.
к = 3.14
а. Подставляем обратно k в выражение, и получаем A (r) = 3,14r 2 . Напомним, что 3,14 — это приблизительное значение π, , поэтому коэффициент A (r) представляет π .
г. Поскольку A (r) — квадратичное выражение; это четная функция .
г. Коэффициент при A (r) положительный, а его показатель четный, поэтому мы ожидаем, что график будет уменьшаться, когда x <0, и увеличиваться, когда x> 0. Следовательно, ожидается, что оба конца кривой будут идти. вверх .
г. Первоначально, поскольку A (r) представляет собой квадратичное выражение, мы ожидаем, что оно будет иметь область определения (-∞, ∞). Но с учетом того факта, что измерения должны быть больше 0, область теперь становится (0, ∞).
Практические вопросы
1. Какие из следующих функций считаются степенными?
а. f (x) = -3x 2 · 2x + 2x · x
б. г (х) = 12√x
г. h (x) = πx √3
г.м (х) = х 2 — 3х + 4
e. п (х) = 1 / 2х
2. Заполняйте пропуски всегда , иногда и никогда не делают следующие утверждения верными.
а. Взаимные функции — это ______________ степенные функции.
г. Радикальные функции — это _____________ степенные функции.
г. Степенные функции будут ___________ иметь область (-∞, ∞).
3. Определите конечное поведение следующих степенных функций:
а.f (x) = -2x 5
г. г (х) = 3х 6
г. ч (х) = (-2х) 4
4. Верно или неверно? Сумма двух степенных функций также всегда будет возвращать степенную функцию. Обосновать ответ.
5. Степенная функция g (x) проходит через точки (1,4) и (2, 2).
а. Каково выражение для g (x)?
г. Постройте график функции g (x).
г. Найдите его домен и диапазон, затем опишите его конечное поведение.
6. Изобразите степенную функцию y = 2x 4 и ответьте на следующие вопросы.
а. Каков домен и диапазон функции?
г. Если график сдвинуть на 2 единицы вверх, будет ли полученная функция по-прежнему степенной?
7. Объем конуса прямо пропорционален кубу его радиуса r. Объем конуса с радиусом 10 единиц равен 100π / 3 единиц 3, и круга с радиусом 20 единиц составляет 400π / 3 единиц 3 .
а. Найдите степенную функцию V (r), представляющую объем конуса через r.
г. Без учета ограничений на r, будет ли V (r) четным или нечетным?
г. Каково конечное поведение V (r)?
г. Если мы примем во внимание тот факт, что r представляет радиус круга, изменится ли домен?
8. Мощность P (в ваттах), производимая гидроэлектростанцией, прямо пропорциональна квадрату скорости относительно воды v (в милях в час).
